线面平行与垂直的证明题

平行、垂直问题的证明-高考数学大题精做之解答题题型全覆盖高端精品

高考数学大题精做之解答题题型全覆盖高端精品第三篇立体几何专题01平行、垂直问题的证明类型对应典例证明线线平行典例1证明线面平行典例2证明面面平行典例3证明线线垂直典例4证明线面垂直典例5证明面面垂直典例6【典例1】如图，在四棱锥P ABCD -中，平面PAB ⊥平面ABCD ，四边形ABCD 为正方形，△PAB 为等边三角形，E 是PB 中点，平面AED 与棱PC 交于点F .（Ⅰ）求证：//AD EF ；（Ⅱ）求证：PB ⊥平面AEFD ；（III ）记四棱锥P AEFD -的体积为1V ，四棱锥P ABCD -的体积为2V ，直接写出12V V 的值.【典例2】在如图所示的几何体中，四边形ABCD 是菱形，ADNM 是矩形，平面ADNM ⊥平面ABCD ，60DAB ∠= ，2AD =，1AM =，E 为AB 的中点．（1）求证：AN ∥平面MEC ；（2）在线段AM 上是否存在点P ，使二面角P EC D --的大小为3π？若存在，求出AP 的长；若不存在，请说明理由．【典例3】如图，在长方体1111ABCD A B C D -中，1,2,,AB AD E F ==分别为1,AD AA 的中点，Q 是BC 上一个动点，且(0)BQ QC λλ=>.（1）当1λ=时，求证：平面BEF P 平面1A DQ ；（2）是否存在λ，使得BD FQ ⊥？若存在，请求出λ的值；若不存在，请说明理由.【典例4】如图，菱形ABCD 中，2AB =，60DAB ∠= ，M 是AD 的中点，以BM 为折痕，将ABM ∆折起，使点A 到达点1A 的位置，且平面1A BM ⊥平面BCDM ，（1）求证：1A M BD ⊥；（2）若K 为1AC 的中点，求四面体1M A BK -的体积．【典例5】如图，在四棱锥P ABCD -中，四边形ABCD 为正方形，PA ⊥平面ABCD ，PA AB =，M 是PC 上一点，且BM PC ⊥.（1）求证：PC ⊥平面MBD ；（2）求直线PB 与平面MBD 所成角的正弦值.【典例6】已知四棱锥中P ABCD -，底面ABCD 为菱形，60ABC ∠=︒，PA ⊥平面ABCD ，E 、M 分别是BC 、PD 上的中点，直线EM 与平面PAD 所成角的正弦值为155，点F 在PC 上移动.（Ⅰ）证明：无论点F 在PC 上如何移动，都有平面AEF ⊥平面PAD ；（Ⅱ）求点F 恰为PC 的中点时，二面角C AF E --的余弦值.1.在如图所示的五面体ABCDEF 中,四边形ABCD 为菱形,且60,22,//,DAB EA ED AB EF EF AB M ∠=︒====为BC 中点.(1)求证:FM ∕∕平面BDE ;(2)若平面ADE ⊥平面ABCD ,求F 到平面BDE 的距离.2.已知空间几何体ABCDE 中，△BCD 与△CDE 均是边长为2的等边三角形，△ABC 是腰长为3的等腰三角形，平面CDE ⊥平面BCD ，平面ABC ⊥平面BCD .(1)试在平面BCD 内作一条直线，使得直线上任意一点F 与E 的连线EF 均与平面ABC 平行，并给出证明；(2)求三棱锥E －ABC 的体积.3.已知三棱锥P ABC -中，AB AC ⊥，AB AP ⊥.若平面α分别与棱PA PB BC AC 、、、相交于点,,,E F G H 且PC P 平面α.求证:（1）∥EH FG ；（2）AB FG ⊥.4.如图，在四边形'A BCD 中，'E 是'A D 的中点，'A BD ∆为正三角形，2DB =，1DC =，BC =.将'A BD ∆沿直线BD 折起，使'A 到达A 处，'E 到达E 处，此时平面ABD ⊥平面BCD .（1）求证：DC BE ⊥；（2）求点D 到平面BCE 的距离.5.如图，直三棱柱111ABC A B C -中，090BAC ∠=，AB AC =，,D E 分别为1AA 、1B C 的中点.（1）证明：DE ⊥平面11BCC B ；（2）已知1B C 与平面BCD 所成的角为030，求二面角1D BC B --的余弦值.6.在四棱锥P ABCD -中，底面ABCD 为正方形，PB PD =.（1）证明：面PAC ⊥面ABCD ；（2）若PA 与底面ABCD 所成的角为30 ，PA PC ⊥，求二面角B PC D --的余弦值．参考答案【典例1】解：（I ）证明：因为正方形ABCD ，所以//AD BC .因为AD ⊄平面PBC ，BC ⊂平面PBC ，所以//AD 平面PBC .因为AD ⊂平面AEFD ，平面AEFD ⋂平面PBC EF =，所以//AD EF .（II ）证明：因为正方形ABCD ，所以AD AB ⊥.因为平面PAB ⊥平面ABCD ，平面PAB ⋂平面ABCD AB =，AD ⊂平面ABCD ，所以AD ⊥平面PAB .因为PB ⊂平面PAB ，所以AD PB ⊥.因为PAB ∆为等边三角形，E 是PB 中点，所以PB AE ⊥.因为AE ⊂平面AEFD ，AD ⊂平面AEFD ，AE AD A ⋂=，所以PB ⊥平面AEFD .（III ）解：由（Ⅰ）知，122133C AEFDE ABCF ADC C AEFD V V V V V V ，＝，----===513BC AEFD V V -∴＝，则1158133P ABCD V V V V -+＝＝，1238V V ∴．【典例2】解：()I CM 与BN 交于F ，连接EF ．由已知可得四边形BCNM 是平行四边形，所以F 是BN 的中点．因为E 是AB 的中点，所以//AN EF ．又EF ⊂平面MEC ，AN ⊂平面MEC ，所以//AN 平面MEC ．()II 由于四边形ABCD 是菱形，60DAB ∠=，E 是AB 的中点，可得DE AB ⊥．又四边形ADNM 是矩形，面ADNM ⊥面ABCD ，DN ∴⊥面ABCD ，如图建立空间直角坐标系D xyz -，则(0D ，0，0)，E 0，0)，(0C ，2，0)，P 1-，)h，CE = ，2-，0)，(0EP =，1-，)h ，设平面PEC 的法向量为1(n x =，y ，)z ．则11·0·0CE n EP n ⎧=⎪⎨=⎪⎩ ，∴200y y hz -=-+=⎪⎩，令y =，∴1(2n h =，又平面ADE 的法向量2(0n =，0，1)，1cos n ∴<，12212·12n n n n n >===，解得377h =， 3717>，∴在线段AM 上不存在点P ，使二面角P EC D --的大小为3π．【典例3】解：（1）当1λ=时，Q 为BC 中点，因为E 是AD 的中点，所以,ED BQ ED BQ = ，则四边形BEDQ 是平行四边形，所以BE QD .又BE ⊄平面1,A DQ DQ ⊂平面1A DQ ，所以BE 平面1A DQ .因为,E F 分别是1,AD A A 中点，所以1EF A D ，因为EF ⊄平面11,A DQ A D ⊂平面1A DQ ，所以EF 平面1A DQ .因为,BE EF E EF ⋂=⊂平面,BEF BE ⊂平面BEF ，所以平面BEF 平面1A DQ .（2）如图，连接,AQ BD 与FQ ，因为1A A ⊥平面,ABCD BD ⊂平面ABCD ，所以1A A BD ⊥.若,BD FQ ⊥又1,A A FQ ⊂平面1A AQ ，且1A A FQ F ⋂=，所以BD ⊥平面1A AQ .因为AQ ⊂平面1A AQ ，所以AQ BD ⊥.在矩形ABCD 中，由AQ BD ⊥，得AQB DBA ∽，所以2AB AD BQ =⋅.又1,2AB AD ==，所以13,22BQ QC ==，则13BQ QC =，即13λ=.【典例4】解：（1）证明：在左图中，∵四边形ABCD 是菱形，60DAB ∠= ，M 是AD 的中点，∴AD BM ⊥，故在右图中，1A M BM ⊥，∵平面1A BM ⊥平面BCDM ，平面1A BM 平面BCDM BM =，∴1A M ⊥平面BCDM ，又BD ⊂平面BCDM ，所以1A M BD ⊥.（2）解：在左图中，∵四边形ABCD 是菱形，AD BM ⊥，AD BC ∥，∴BC BM ⊥，且3BM =，在右图中，连接CM ，则1111132313323A BCM BCM V S A M -∆=∙=⨯⨯=，∵K 为1AC 的中点，∴1111113226M A BK K MA B C MA B A BCM V V V V ----====．【典例5】解：（1）连接AC ，由PA ⊥平面ABCD ，BD Ø平面ABCD 得BD PA ⊥，又BD AC ⊥，PA AC A ⋂=，∴BD ⊥平面PAC ，得PC BD ⊥，又PC BM ⊥，BD BC B ⋂=，∴PC ⊥平面MBD .（2）法1：由（1）知PC ⊥平面MBD ，即PBM ∠是直线PB 与平面MBD 所成角，易证PB BC ⊥，而BM PC ⊥，不妨设1PA =，则1BC =，PC =，PB =，在Rt PBC ∆中，由射影定理得22::2:1PM MC PB BC ==，可得22333PM PC ==，所以63PM sin PBM PB ∠==，故直线PB 与平面MBD所成角的正弦值为3.法2：取A 为原点，直线MB ，MD ，MP 分别为x ，y ，z 轴，建立坐标系A xyz -，不妨设1PA AB ==，则0,0,1)P（，()1,0,0B ，()1,1,0C ，由（1）知平面MBD 得法向量()1,1,1PC =- ，而()1,0,1PB =-，∴1,0,11,1,1,cos PB PC -⋅-= 63=.故直线PB 与平面MBD 所成角的正弦值为63.【典例6】解：（Ⅰ）连接AC∵底面ABCD 为菱形，60ABC ∠=︒，∴ABC ∆是正三角形，∵E 是BC 中点，∴AE BC ⊥又AD BC ，∴AE AD⊥∵PA ⊥平面ABCD ，AE ⊂平面ABCD ，∴PA AE ⊥，又PA AE A ⋂=∴AE ⊥平面PAD ，又AE ⊂平面AEF ∴平面AEF ⊥平面PAD .（Ⅱ）由（Ⅰ）得，AE ，AD ，AP 两两垂直，以AE ，AD ，AP 所在直线分别为x 轴，y 轴，z 轴建立如图所示的空间直角坐标系，∵AE ⊥平面PAD ，∴AME ∠就是EM 与平面PAD 所成的角，在Rt AME ∆中，15sin 5AME ∠=，即62AE AM =，设2AB a =，则AE =，得AM =，又2AD AB a ==，设2PA b =，则()0,,M a b ，所以AM ==，从而b a =，∴2PA AD a ==，则()0,0,0A，),,0Ba -，),,0Ca ，()0,2,0D a ，()0,0,2P a，),0,0E，3,,22a F a ⎛⎫⎪ ⎪⎝⎭，所以),0,0AE =，3,,22a AF a ⎛⎫= ⎪ ⎪⎝⎭，(),3,0BD a=，设(),,n x y z是平面AEF 一个法向量，则n AE n AF ⎧⋅=⇒⎨⋅=⎩3022ayaz ⎧=++=⎪⎩取z a =，得()0,2,n a a =- 又BD ⊥平面ACF，∴(),3,0BD a=是平面ACF 的一个法向量，∴cos ,n BD n BD n BD⋅==⋅2155=-∴二面角C AF E --的余弦值为155.1.【思路引导】(1)取BD 中点O ,连接,OM OE ,因为,O M 分别为,BD BC 的中点,所以//OMCD ,且12OM CD =,因为四边形ABCD 为菱形,所以//,CD AB CD ⊄又平面,ABFE AB ⊂平面ABFE ,所以//CD 平面ABFE .因为平面ABFE 平面,CDEF EF CD =⊂平面CDEF ,所以CD EF ∕∕.又2AB CD ==,所以12EF CD =.所以四边形OMFE 为平行四边形，所以//MF OE .又OE ⊂平面BDE ，且MF ⊄平面BDE ,所以//MF 平面BDE .(2)由(1)得//FM 平面BDE ,所以F 到平面BDE 的距离等于M 到平面BDE 的距离.取AD 的中点H ,连接,EH BH ,因为四边形ABCD 为菱形,且60,2DAB EA ED AB EF ∠==== ,所以,EH AD BH AD ⊥⊥,因为平面ADE ⊥平面ABCD ,平面ADE 平面ABCD AD =,所以EH ⊥平面,ABCD EH BH ⊥,因为3EH BH ==,所以6BE =所以22161562222BDES ⎛⎫=-= ⎪ ⎪⎝⎭,设F 到平面BDE 的距离为h ,又因为113342242BDM BCD S S ==⨯⨯=,所以由E BDM M BDE V V --=,得1311533232h =⨯⨯,解得155h =.即F 到平面BDE 的距离为155．2.【思路引导】（1）取DC 的中点N ，取BD 的中点M ，连接MN ，则MN 即为所求，证明EN ∥AH ，MN ∥BC 可得平面EMN ∥平面ABC 即可（2）因为点E 到平面ABC 的距离与点N 到平面ABC 的距离相等，求三棱锥E －ABC 的体积可转化为求三棱锥N －ABC 的体积，根据体积公式计算即可.解：(1)如图所示，取DC 的中点N ，取BD 的中点M ，连接MN ，则MN 即为所求.证明：连接EM，EN，取BC的中点H，连接AH，∵△ABC是腰长为3的等腰三角形，H为BC的中点，∴AH⊥BC，又平面ABC⊥平面BCD，平面ABC∩平面BCD＝BC，AH⊂平面ABC，∴AH⊥平面BCD，同理可证EN⊥平面BCD，∴EN∥AH，∵EN⊄平面ABC，AH⊂平面ABC，∴EN∥平面ABC.又M，N分别为BD，DC的中点，∴MN∥BC，∵MN⊄平面ABC，BC⊂平面ABC，∴MN∥平面ABC.又MN∩EN＝N，MN⊂平面EMN，EN⊂平面EMN，∴平面EMN∥平面ABC，又EF⊂平面EMN，∴EF∥平面ABC，即直线MN上任意一点F与E的连线EF均与平面ABC平行.(2)连接DH，取CH的中点G，连接NG，则NG∥DH，由(1)可知EN∥平面ABC，∴点E到平面ABC的距离与点N到平面ABC的距离相等，又△BCD是边长为2的等边三角形，∴DH⊥BC，又平面ABC⊥平面BCD，平面ABC∩平面BCD＝BC，DH⊂平面BCD，∴DH⊥平面ABC，∴NG⊥平面ABC，易知DH NG ＝32，又S △ABC ＝12·BC ·AH ＝12，∴V E －ABC ＝13·S △ABC ·NG ＝3.3.解：证明（1）因为PC P 平面α，平面α 平面PAC EH =,PC ⊂平面PAC ，所以有PC EH ,同理可证出PC FG ,根据平行公理，可得∥EH FG ；（2）因为AB AC ⊥，AB AP ⊥，AP AC A ⋂=,,AP AC ⊂平面PAC ，所以AB ⊥平面PAC ,而PC ⊂平面PAC ,所以AB PC ⊥,由（1）可知PC FG EH ,所以AB FG ⊥.4.【思路引导】（1）先由题证明BD DC ⊥，再证明DC ⊥平面ABD 则可得DC BE ⊥；（2）用等体积转化法D BCE E BCD V V --=，求点D 到平面BCE 的距离．解：（1）由2DB =，1DC =，BC =，可知222DB DC BC +=，∴BD DC ⊥，又∵平面ABD ⊥平面BCD ，且平面ABD ⋂平面BCD BD =.∴DC ⊥平面ABD ，又BE ⊂平面ABD ，∴DC BE ⊥.（2）取BD 的中点F ，连接AF .∵'A BD ∆为正三角形，∴ABD ∆也为正三角形，∴AF BD ⊥.由2BD =，知AF =.∵平面ABD ⊥平面BCD ，平面ABD ⋂平面BCD BD =，∴AF ⊥平面BCD ，又∵E 为'E 对应的点，∴E 为AD 的中点，∴点E 到底面BCD 的距离为32，BE =，1ED =，又CD AD ⊥，1CD =，∴CE =，又BC =，∴222BE CE BC +=，∴BE CE ⊥，∴116222BCE S BE CE ∆=⨯==，1121122BCD S BD DC ∆=⨯=⨯⨯=.设D 点到平面BCE 的距离为h .∵D BCE E BCD V V --=，∴11133222BCE BCD S h S h ∆∆⋅=⨯⇒=⨯，解得22h =，∴点D 到平面BCE 的距离为22.5.【思路引导】解法1：（1）建立空间直角坐标系，利用直线的向量和平面法向量平行证明线面垂直；（2）设AD a =，利用1B C 与平面BCD 所成的角为030得到a 的值，再求出两个面的法向量之间的夹角余弦值，得到二面角的余弦值.解法2：（1）取BC 中点F ，连接AF 、EF ，易证AF ⊥平面11BCC B ，再证明DE AF ,可得DE ⊥平面11BCC B（2）设AD a =，利用1B C 与平面BCD 所成的角为030得到a 的值，再求出两个面的法向量之间的夹角余弦值，得到二面角的余弦值.解法3：（1）同解法2（2）设12AA a =，利用三棱锥1B BDC -等体积转化，得到1B 到面BCD 的距离，利用1B C 与平面BCD 所成的角为30︒得到1B C 与d 的关系，解出a ，在两个平面分别找出,DF EF 垂直于交线，得到二面角，求出其余弦值.【详解】解法1：（1）以A 为坐标原点，射线AB 为x 轴的正半轴，建立如图所示的直角坐标系A xyz -．设1AB =，AD a =，则()1,0,0B ，()0,1,0C ，()11,0,2B a ，()0,0,D a ，()11,0,2B a ，11,,22E a ⎛⎫⎪⎝⎭，11,,022DE ⎛⎫= ⎪⎝⎭，()1,1,0BC =- ，()11,1,2B C a =--．因为0DE BC ⋅=，10DE B C ⋅= ，所以DE BC ⊥，1DE B C ⊥，BC ⊂面11BCC B ，1B C ⊂面11BCC B ，1BC B C B ⋂=于是DE ⊥平面11BCC B ．（2）设平面BCD 的法向量()000,,n x y z =，则0n BC ⋅= ，0n BD ⋅=，又()1,1,0BC =- ，()1,0,BD a =-，故000000x y x az -+=⎧⎨-+=⎩，取01x =，得11,1,n a ⎛⎫= ⎪⎝⎭．因为1B C 与平面BCD 所成的角为30︒，()11,1,2B C a =--，所以1cos ,sin30n B C =︒ ，11n B C n B C⋅∴=⋅12=，解得22a =，(n= ．由（1）知平面1BCB 的法向量11,,022AF ⎛⎫= ⎪⎝⎭ ，11222cos ,2n AF n AF n AF+⋅==⋅，所以二面角1D BC B --的余弦值为22．解法2：（1）取BC 中点F ，连接AF 、EF ,AB AC = ∴AF BC ⊥，1BB ⊥平面ABC ，AF ⊂平面ABC ∴1BB AF ⊥，而BC ⊂平面11BCC B ,1B B ⊂平面11BCC B ,1BC B B B⋂=∴AF ⊥平面11BCC B ．E 为1B C 中点，∴1EF BB ，112EF BB =，∴EF DA ，EF DA ＝，∴四边形ADEF 为平行四边形，∴AF DE ．∴DE ⊥平面11BCC B ．（2）以A 为坐标原点，射线AB 为x 轴的正半轴，建立如图所示的直角坐标系A xyz -．设()1,0,0B ，()0,1,0C ，()11,0,2B a ，则()0,0,D a ，()11,0,2B a ，11,,022F ⎛⎫ ⎪⎝⎭．设平面BCD 的法向量()000,,n x y z =，则0n BC ⋅= ，0n BD ⋅=，又()1,1,0BC =- ，()1,0,BD a =-，故000000x y x az -+=⎧⎨-+=⎩，取01x =，得11,1,n a ⎛⎫= ⎪⎝⎭．因为1B C 与平面BCD 所成的角为30︒，()11,1,2B C a =--，所以1|cos ,)|sin30n B C <>=︒ ，11n B C n B C⋅∴=⋅12=，解得22a =，(n= ．由（1）知平面1BCB 的法向量11,,022AF ⎛⎫= ⎪⎝⎭，1122cos ,2n AF n AF n AF +⋅==⋅所以二面角1D BC B --的余弦值为2．解法3：（1）同解法2．（2）设1AB AC ==，12AA a =，则BC =22AF =,BD DC==DF ∴==122BDC SBC DF ∴=⋅= ，1112BCB S BB BC =⋅= ，D 到平面1BCB 距离22DE =，设1B 到面BCD 距离为d ，由11B BDCD BCB V V --=得11133BCB BDC SDE S d ⋅=⋅，即113232d⋅=⋅⋅d =因为1B C 与平面BCD 所成的角为30︒，所以12sin30d B C d ===︒，而在直角三角形1B BC 中1BC ==2=，解得22a =．因为AF ⊥平面11BCC B ，BC ⊂平面11BCC B ,所以AF BC ⊥，EF ⊥平面11BCC B ，BC ⊂平面11BCC B 所以EF BC ⊥，所以BC ⊥平面DEFA ，DF ⊂ 平面DBC ,EF ⊂平面1B BC所以EFD ∠为二面角1D BC B --的平面角，而22DA AF ==,可得四边形DAFE 是正方形，所以45EFD ∠=︒，所以二面角1D BC B --的余弦值为22．6.【思路引导】（1）要证面面垂直，一般先证线面垂直，设AC 与BD 交点为O ，则PO ⊥BD ，而正方形中AC ⊥BD ，于是可证得结论．（2）由线面角的定义可得030PAC ∠=，以A 为坐标原点，,AB AD为x,y 轴的正方向建立空间直角坐标系，然后写出各点坐标，求出面BPC 和面DPC 的法向量，再由法向量的夹角的余弦值得二面角的余弦．解：（1）证明：连接AC,BD 交点为O ，∵四边形ABCD 为正方形，∴AC BD⊥∵PB PD =，OB OD =,∴BD OP ⊥,又∵OP AC O ⋂=,∴BD PAC ⊥面又BD PAC ⊂面,∴PAC ABCD ⊥面面.（2）∵PAC ABCD ⊥面面，过点P 做PE AC ⊥,垂足为E∴ABCD PE ⊥面∵PA 与底面ABCD 所成的角为030，∴030PAC ∠=,又PA PC ⊥，设2PC =,则3,4,AP PE AE AC AD =====如图所示，以A 为坐标原点，,AB AD 为x,y 轴的正方向建立空间直角坐标系A xyz -()()()()32320,0,0,,,0,,,22A B C D P ⎛ ⎝设面PBC 法向量为()1,,n x y z =，()220,,,22BC CP ⎛==--⎝1100n BC n CP ⎧⋅=⎪⎨⋅=⎪⎩,∴022022x y ⎧=+-=⎪⎩，1,0,z y x ===令则)1n = 同理PCD 面的法向量()2n = ，1212121cos ,7n n n n n n ⋅==∴求二面角B PC D --的余弦值17-。

空间中的平行与垂直例题和知识点总结

空间中的平行与垂直例题和知识点总结在立体几何的学习中，空间中的平行与垂直关系是非常重要的内容。

理解和掌握这些关系，对于解决相关的几何问题具有关键作用。

下面我们通过一些例题来深入探讨，并对相关知识点进行总结。

一、平行关系（一）线线平行1、定义：如果两条直线在同一平面内没有公共点，则这两条直线平行。

2、判定定理：如果平面外一条直线与此平面内的一条直线平行，那么该直线与此平面平行。

例 1：在正方体 ABCD A₁B₁C₁D₁中，E，F 分别是 AB，BC 的中点，求证：EF∥A₁C₁。

证明：连接 AC，因为 E，F 分别是 AB，BC 的中点，所以 EF∥AC。

又因为正方体中，AC∥A₁C₁，所以 EF∥A₁C₁。

（二）线面平行1、定义：如果一条直线与一个平面没有公共点，则称这条直线与这个平面平行。

2、判定定理：平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行。

例 2：已知四棱锥 P ABCD 的底面是平行四边形，M 是 PC 的中点，求证：PA∥平面 MBD。

证明：连接 AC 交 BD 于 O，连接 MO。

因为四边形 ABCD 是平行四边形，所以 O 是 AC 的中点。

又因为 M 是 PC 的中点，所以MO∥PA。

因为 MO⊂平面 MBD，PA⊄平面 MBD，所以 PA∥平面MBD。

（三）面面平行1、定义：如果两个平面没有公共点，则称这两个平面平行。

2、判定定理：一个平面内的两条相交直线与另一个平面平行，则这两个平面平行。

例 3：在正方体 ABCD A₁B₁C₁D₁中，求证：平面 A₁BD∥平面 B₁D₁C。

证明：因为 A₁B∥D₁C，A₁D∥B₁C，且 A₁B 和 A₁D 是平面A₁BD 内的两条相交直线，D₁C 和 B₁C 是平面 B₁D₁C 内的两条相交直线，所以平面 A₁BD∥平面 B₁D₁C。

二、垂直关系（一）线线垂直1、定义：如果两条直线所成的角为 90°，则这两条直线垂直。

线面垂直平行证明解答基础

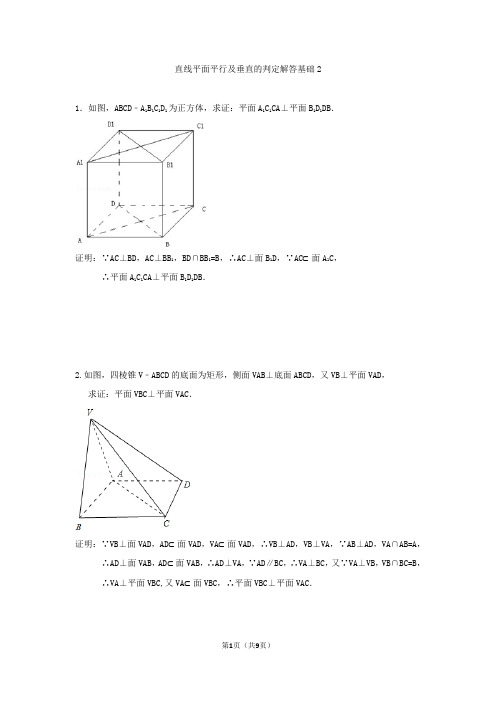
直线平面平行及垂直的判定解答基础21．如图，ABCD﹣A1B1C1D1为正方体，求证：平面A1C1CA⊥平面B1D1DB．证明：∵AC⊥BD，AC⊥BB1，BD∩BB1=B，∴AC⊥面B1D，∵AC⊂面A1C，∴平面A1C1CA⊥平面B1D1DB．2.如图，四棱锥V﹣ABCD的底面为矩形，侧面VAB⊥底面ABCD，又VB⊥平面VAD，求证：平面VBC⊥平面VAC．证明：∵VB⊥面VAD，AD⊂面VAD，VA⊂面VAD，∴VB⊥AD，VB⊥VA，∵AB⊥AD，VA∩AB=A，∴AD⊥面VAB，AD⊂面VAB，∴AD⊥VA，∵AD∥BC，∴VA⊥BC，又∵VA⊥VB，VB∩BC=B，∴VA⊥平面VBC,又VA⊂面VBC，∴平面VBC⊥平面VAC．3．如图，三棱柱ABC﹣A1B1C1中，AA1⊥面ABC，D是AB中点，AC⊥BC．（1）求证：BC1∥面A1DC．（2）求证：面A1BC⊥面A1AC．解：（1）证明：取AC1的中点M，∵D是AB中点，∴MD是三角形ABC1的中位线，∴MD∥BC1．而MD在平面A1DC中，BC1不在平面A1DC中，∴BC1∥面A1DC．（2）∵AA1⊥面ABC，∴AA1⊥BC，又 AC⊥BC，AC∩AA1=A，∴BC⊥面A1AC．∵BC⊂面A1BC，∴面A1BC⊥面A1AC．5．如图为正方体ABCD﹣A1B!C!D1切去一个三棱锥B1﹣A!BC1后得到的几何体．（1）画出该几何体的正视图；（2）若点O为底面ABCD的中心，求证：直线D1O∥平面A1BC1；（3）求证：平面A1BC1⊥平面BDD1．解：（1）几何体的正视图为：（2）将其补成正方体ABCD﹣A1B1C1D1，设B1D1和A1C1交于点O1，连接O1B，依题意可知，D1O1∥OB，且D1O1=OB，∴四边形D1OBO1为平行四边形，∴D1O∥O1B，∵BO1⊂平面BA1C1，D1O⊄平面BA1C1，∴直线D1O∥平面A1BC1．（3）在正方体ABCD﹣A1B1C1D1中，DD1⊥平面A1B1C1D1，则DD1⊥A1C1，又∵B1D1⊥A1C1且DD1∩B1D1，∴A1C1⊥平面BD1D，又∵A1C1⊂平面A1BC1，∴平面A1BC1⊥平面BD1D．6．如图，在三棱锥S﹣ABC中，OA=OB，O为BC中点，SO⊥平面ABC，E为SC中点，F为AB 中点．（1）求证：OE∥平面SAB；（2）求证：平面SOF⊥平面SAB．证明：（1）取AC的中点G，连接OG，EG，∵OG∥AB，EG∥AS，EG∩OG=G，SA∩AB=A，∴平面EGO∥平面SAB，OE⊂平面OEG∴OE∥平面SAB．（2）∵SO⊥平面ABC，∴SO⊥OB，SO⊥OA，又∵OA=OB，SA2=SO2+OA2，SB2=SO2+OB2，∴SA=SB，又F为AB中点，∴SF⊥AB，又SO⊥AB，SF∩SO=S，∴AB⊥平面SOF，∵AB⊂平面SAB，∴平面SOF⊥平面SAB．7．如图，在三棱锥A﹣BCD中，BC=AC，AD=BD，作BE⊥CD，E为垂足，作AH⊥BE于H．求证：AH⊥平面BCD．解：如图，取AB中点F，连接CF，DF,∵BC=AC，AD=BD，∴AB⊥CF，AB⊥DF，CF∩DF=F；∴AB⊥平面CDF，CD⊂平面CDF,∴CD⊥AB，CD⊥BE，BE∩AB=B；∴CD⊥平面ABE，AH⊂平面ABE,∴CD⊥AH，即AH⊥CD，又AH⊥BE，BE∩CD=E；∴AH⊥平面BCD．8．如图，棱锥V﹣ABC中，VO⊥平面ABC，O∈CD，VA=VB，AD=BD．求证：（1）AB⊥平面VDC （2）AB⊥CD．证明：（1）连接VD，从而∵VA=VB，AD=BD,∴VD⊥AB,∵VO⊥平面ABC，∴VO⊥AB∴AB⊥平面VDO，∵C在直线DO上，∴AB⊥平面VDC；（2）由（1）得AB⊥平面VDC,∵CD⊂平面VDC∴AB⊥CD．13．如图，在底面为直角梯形的四棱锥P﹣ABCD中，AD∥BC，∠ABC=90°，PA⊥平面ABCD， AC∩BD=E，AD=2，AB=2，BC=6，求证：平面PBD⊥平面PAC．证明：在Rt△ABC中，tan∠BAC===，∴∠BAC=60°；又∵AD∥BC，∴∠BAD=90°；在Rt△BAD，tan∠ABD===，∴∠ABD=30°；∴∠AEB=90°，∴BD⊥AC；∵PA⊥平面ABCD，∴PA⊥BD；又PA∩AC=A，∴BD⊥平面PAC；∵BD⊂平面PBD，∴平面PBD⊥平面PAC．14．如图所示，在四面体P﹣ABC中，已知PA=BC=6，PC=AB=10，AC=8，PB=2求证：BC⊥平面PAC，PA⊥平面ABC．证明：∵PA2+AC2=36+64=100=PC2，∴PA⊥AC∵PA2+AB2=36+100=136=PB2，∴PA⊥AB∵AB∩AC=A∴PA⊥平面ABC∵PC2+BC2=100+36=136=PB2，∴PC⊥BC∵BC2+AC2=36+64=100=AB2，∴BC⊥AC∵PC∩AC=C∴BC⊥平面PAC．17．如图，四棱锥P﹣ABCD的底面是正方形，PA⊥底面ABCD，∠PDA=45°，点E为棱AB的中点，求证：平面PCE⊥平面PCD．证明：∵PA⊥底面ABCD∴PA⊥AD，PA⊥CD，又AD⊥CD，PA∩AD=A∴CD⊥平面ADP，∵AF⊂平面ADP，∴CD⊥AF．直角三角形PAD中，∠PDA=45°∴△PAD为等腰直角三角形，∴PA=AD．∵F是PD的中点，∴AF⊥PD，又CD∩PD=D．∴AF⊥平面PCD．∵AF∥EG，∴EG⊥平面PCD，又EG⊂平面PCE，∴平面PCE⊥平面PCD．18．如图所示，四边形ABCD是平行四边形，直线SC⊥平面ABCD，E是SA的中点求证：平面BDE⊥平面ABCD．证明：如图，连接AC，交BD于O点，连接OE．∵四边形ABCD是平行四边形，E是SA的中点，∴AO=OC，AE=ES，∴OE∥SC∵直线SC⊥平面ABCD，∴OE⊥平面ABCD，∵OE⊂平面BDE∴平面BDE⊥平面ABCD．19．已知如图底面ABC为直角三角形，∠C=90°，PA⊥平面ABC，求证：平面PBC⊥平面PAC．证明：∵PA⊥平面ABC，BC⊂平面ABC，∴PA⊥BC，又BC⊥AC，PA⊂平面PAC，AC⊂平面PAC，PA∩AC=A，∴BC⊥平面PAC，∵BC⊂平面PBC，∴平面PBC⊥平面PAC．。

线面平行、垂直经典练习题汇编

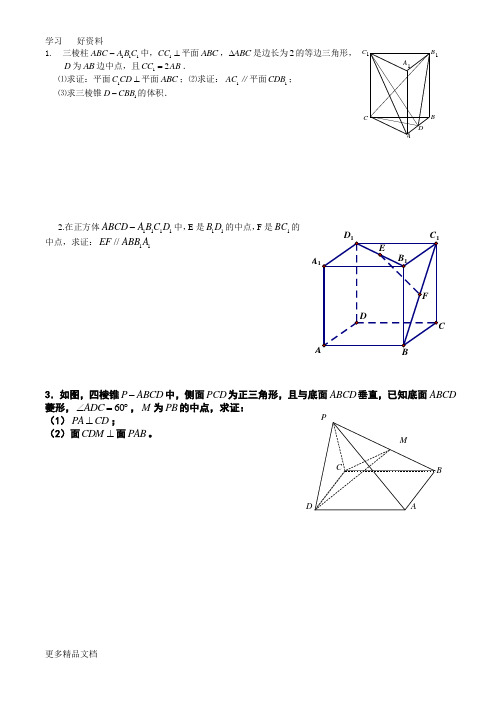
1. 三棱柱111ABC A B C -中，1CC ⊥平面ABC ，ABC ∆是边长为2的等边三角形，D 为AB 边中点，且12CC AB =．⑴求证：平面1C CD ⊥平面ABC ；⑵求证：1AC ∥平面1CDB ； ⑶求三棱锥1D CBB -的体积．2.在正方体1111ABCD A B C D -中，E 是11B D 的中点，F 是1BC 的中点，求证：11//EF ABB A3．如图，四棱锥P ABCD -中，侧面PCD 为正三角形，且与底面ABCD 垂直，已知底面ABCD 菱形，60ADC ∠=︒，M 为PB 的中点，求证：（1）PA CD ⊥；（2）面CDM ⊥面PAB 。

C 1B 1A 1D CBAA B4．（07天津理19，本小题满分12分）如图，在四棱锥P ABCD -中，PA ⊥底面ABCD ，60AB AD AC CD ABC ⊥⊥∠=，，°，PA AB BC ==，E 是PC 的中点．（Ⅰ）证明CD AE ⊥；（Ⅱ）证明PD ⊥平面ABE ；5、如图，P 为ABC ∆所在平面外一点，PA ┴面BAC ，<90,ABC ∠=oAE ┴PB 于E ，AF ┴PC 于F ，求证：（1）BC ┴面PAB ，（2）AE ┴面PBC ，（3）PC ┴面AEF 。

6．（2010年高考山东卷文科20）（本小题满分12分）在如图所示的几何体中，四边形ABCD 是正方形， MA ⊥平面ABCD ，//PD MA ，E 、G 、F 分别为MB 、PB 、PC 的中点，且2AD PD MA ==.（I ）求证：平面EFG ⊥平面PDC ；（II ）求三棱锥P MAB -与四棱锥P ABCD -的体积之比.A CBPEFABCDPPEB2. 如图，棱长为1的正方体ABCD-A 1B 1C 1D 1中，(1) 求证：AC ⊥平面B 1D 1DB; (2) 求证：BD 1⊥平面ACB 1 (3) 求三棱锥B-ACB 1体积．3.如图，ABCD 是正方形，O 是正方形的中心，PO ⊥底面 ABCD ，E 是PC 的中点。

专题06五种直线、平面平行与垂直的判定与性质解题方法(解析版)

专题06五种直线、平面平行与垂直的判定与性质解题方法题型一：求异面直线所成角题型二：证明线线、线面平行的方法题型三：证明面面平行的方法题型四：证明线线、线面垂直的方法题型五：证明面面垂直的方法题型一：求异面直线所成角一、单选题1．（2019·江苏苏州·高一期末）正方体1111ABCD A B C D -中，异面直线1AA 与BC 所成角的大小为（） A ．30B ．45︒C ．60︒D ．90︒【答案】D【分析】利用异面直线1AA 与BC 所成角的的定义，平移直线BC ，即可得答案．【详解】在正方体1111ABCD A B C D -中，易得190A AD ∠=︒．//AD BC ∴异面直线1AA 与BC 垂直，即所成的角为90︒.故选：D ．【点睛】本题考查异面直线所成角的定义，考查对基本概念的理解，属于基础题.2．（2020·宁夏银川·高一期末）下图的正方体ABCD A B C D ''''-中，异面直线AA '与BC '所成的角是（）A ．30B ．45C ．60D ．90【答案】B 【解析】只需将异面直线AA '与BC '平移至同一个平面内，转化为两条相交直线，即可求出它们所成的角．【详解】在正方体ABCD A B C D ''''-中，因为//AA BB ''，所以B BC ''∠即为异面直线AA '与BC '所成的角，因为45B BC ''∠=，所以异面直线AA '与BC '所成的角为45.故选：B.【点睛】本题主要考查异面直线所成角的求法．求两条异面直线所成角的大小，一般方法是通过平行移动直线，把异面问题转化为共面问题来解决，根据空间等角定理及推论可知，异面直线所成角的大小与顶点位置无关，往往可以选在其中一条直线上（线面的端点或中点）利用三角形求解．3．（2021·陕西·西安市远东一中高一期末）如图，在正三棱锥D ABC -中，AD DC ⊥，点F 为棱AC 的中点，则异面直线DF 与AB 所成角的大小为（）A ．30°B ．45°C ．60°D ．90°【答案】C 【分析】取BC 的中点E ，∠DFE 即为所求，结合条件即求.【详解】如图取BC 的中点E ，连接EF ，DE ，则EF ∠AB ，∠DFE 即为所求，设DF a =，在正三棱锥D ABC -中，AD DC ⊥，故2,AB AC BC a DA DB DC ======，∠EF DE DF a ===，∠60DFE ∠=，即异面直线DF 与AB 所成角的大小为60.故选：C.4．（2021·湖北孝感·高一期末）在正方体1111ABCD A B C D -中，M 为11A C 和11B D 的交点，则异面直线BM 与1AD 所成的角为（）A ．6πB ．4πC ．3πD ．2π 【答案】A 【分析】平移直线1AD 至1BC ，将直线PB 与1AD 所成的角转化为PB 与1BC 所成的角，解三角形即得结果.【详解】如图，连接1,BC MB ，因为1AD ∠1BC ，所以MBC 1∠或其补角为直线MB 与1AD 所成的角，因为1BB ⊥平面1111D C B A ，所以11BB MC ⊥，又111MC B D ⊥，1111BB B D B ⋂=，111,BB B D ⊂平面1MBB ，所以MC 1⊥平面1MBB ，所以1MC PB ⊥，设正方体棱长为2，则111112BC MC AC ===1111sin 2MC MBC BC ∠===，而直角三角形中MBC 1∠是锐角，所以16MBC π∠=，即异面直线BM 与1AD 所成的角是6π. 故选：A. 5．（2021·贵州毕节·高一期末）在空间四边形ABCD 中，AB CD =，E ，F 分别为BC ，AD 的中点，若AB 与CD 所成的角为40°，则EF 与AB 所成角的大小为（）A ．20°B ．70°C ．20°或70°D ．40°或140°【答案】C【分析】根据异面直线所成角的定义转化为相交直线所成角，利用几何图形求EF 与AB 所成角的大小.【详解】取AC 的中点M ，BD 的中点N ，连接,,,,ME EN NF FM EF ，,,,M E N F 分别是,,,AC BC BD AD 的中点，//,//ME AB NF AB ∴，∴//ME NF ，同理//EN MF ，∴四边形MENF 是平行四边形，又AB CD =，∴=ME EN ，四边形MENF 是菱形，AB 与CD 所成的角为40，40MEN ∴∠=或140，∴EF 与AB 所成角是1202MEF MEN ∠=∠=或70. 故选：C二、多选题6．（2021·江苏常州·高一期末）下图是一个正方体的平面展开图，则在该正方体中（）A ．//BF CDB ．DG BH ⊥C ．CH 与BG 成60°角D ．BE 与平面ABCD 所成角为45°【答案】BCD 【分析】由正方体的平面展开图还原原正方体，再由正方体的结构特征结合空间角的概念逐个分析判断即可【详解】由正方体的平面展开图还原原正方体如图所示，由正方体的结构特征可知，BF 与CD 异面垂直，所以A 错误，DG CH ⊥，而CH 为BH 在平面DCGH 上的射影，所以DG BH ⊥，所以B 正确，连接AH ，由AB ∠GH ，AB GH =，可得四边形ABGH 为平行四边形，则AH ∠BG ，所以AHC ∠或其补角为异面直线CH 与BG 所成的角，连接AC ，可得AHC 为等边三角形，得CH 与BG 成60°角，所以C 正确，因为AE ⊥平面ABCD ，所以EBA ∠为BE 与平面ABCD 所成角为45︒，所以D 正确，故选：BCD三、填空题7．（2020·天津市红桥区教师发展中心高一期末）正方体1111ABCD A B C D -中，异面直线1A B 与1B C 所成角的大小为_________. 【答案】3π 【分析】连接1A D 、BD ，证明11//A D B C ，可得1DA B ∠即为异面直线1A B 与1B C 所成角，在1DA B △求1DA B ∠即可求解.【详解】如图，连接1A D 、BD ，因为11A B DC ，所以四边形11A B CD 是平行四边形，所以11//A D B C ，所以1DA B ∠即为异面直线1A B 与1B C 所成角，设正方体1111ABCD A B C D -的棱长为a ，在1DA B △中，11DA A B BD ===，所以1DA B △是等边三角形，所以13DA B π∠=，即异面直线1A B 与1B C 所成角为3π，故答案为：3π 【点睛】思路点睛：平移线段法是求异面直线所成角的常用方法，具体步骤如下（1）平移：平移异面直线中的一条或两条，作出异面直线所成的角；（2）认定：证明作出的角就是所求异面直线所成的角；（3）计算：求该角的值，常利用解三角形；（4）取舍：由异面直线所成的角的取值范围是0,2π⎛⎤ ⎥⎝⎦，当所作的角为钝角时，应取它的补角作为两条异面直线所成的角．8．（2022·陕西西安·高一期末）在正方体1111ABCD A B C D -中，则异面直线1AB 与1BC 的夹角为_________．【答案】3π 【解析】先证明11//AD BC ，可得11D AB ∠或其补角即为异面直线1AB 与1BC 所成的角，连接11D B ，在11AB D 中求11D AB ∠即可.【详解】在正方体1111ABCD A B C D -中，//,AB DC AB CD =， 1111//,,D C DC D C DC =所以1111//,AB D C AB D C =，所以四边形11ABC D 是平行四边形，所以11//AD BC ，所以11D AB ∠或其补角即为异面直线1AB 与1BC 所成的角，连接11D B ，由1111ABCD A B C D -为正方体可得11AB D 是等边三角形，所以113D AB π∠=.故答案为：3π 【点睛】思路点睛：平移线段法是求异面直线所成角的常用方法，其基本思路是通过平移直线，把异面直线的问题化归为共面直线问题来解决，具体步骤如下：（1）平移：平移异面直线中的一条或两条，作出异面直线所成的角；（2）认定：证明作出的角就是所求异面直线所成的角；（3）计算：求该角的值，常利用解三角形；（4）取舍：由异面直线所成的角的取值范围是0,2π⎛⎤ ⎥⎝⎦，当所作的角为钝角时，应取它的补角作为两条异面直线所成的角．9．（2020·湖北湖北·高一期末）已知M 是长方体1111ABCD A B C D -的棱1BB 的中点，底面ABCD 为正方形且12AA AB =，则AM 与11B D 所成角的大小用弧度制可以表示为______. 【答案】3π 【分析】取1AA 中点N ，连接11,B N D N ，可判断11D B N 即为AM 与11B D 所成角，求出即可.【详解】如图，取1AA 中点N ，连接11,B N D N ，设12=2AA AB =，,M N 是中点，可知1//AN B M 且1AN B M ，∴四边形1AMB N 是平行四边形，1//AM B N ∴,则11D B N 即为AM 与11B D 所成角，可知11112,2,2B N B D D N ，113D B N，即AM 与11B D 所成角为3π. 故答案为：3π. 【点睛】本题考查异面直线所成角的求解，属于基础题.10．（2021·吉林·长春市第二十中学高一期末）如图，在正方体ABCD ﹣A 1B 1C 1D 1中，E ，F 依次是A 1D 1和B 1C 1的中点，则异面直线AE 与CF 所成角的余弦值为_____.【答案】35【解析】先推导出BF ∠AE ，从而∠BFC 是异面直线AE 与CF 所成角（或所成角的补角），由此能求出异面直线AE 与CF 所成角的余弦值.【详解】解：在正方体ABCD ﹣A 1B 1C 1D 1中，∠E ，F 依次是A 1D 1和B 1C 1的中点，∠BF ∠AE ，∠∠BFC 是异面直线AE 与CF 所成角（或所成角的补角），设正方体ABCD ﹣A 1B 1C 1D 1中棱长为2，则BF ＝CF ==∠cos ∠BFC 35==. ∠异面直线AE 与CF 所成角的余弦值为35. 故答案为：35.【点睛】本题考查异面直线所成角的余弦值的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查运算求解能力，是中档题.11．（2021·山西吕梁·高一期末）已知正三棱柱中111ABC A B C -中，2AB =，14BB =，D ，E 分别是棱11A C ，1BB 的中点，则异面直线1B D 与AE 所成角的正切值为______.【分析】作出辅助线，证得1DB F ∠或其补角为异面直线1B D 与AE 所成角，然后求出相关线段的长度，进而在1B DF 中，利用余弦定理求出余弦值，进而可以求出结果.【详解】取1A A 的中点F ，连接1,B F DF ,因为E 分别是棱1BB 的中点，所以1AF B E =且1//AF B E ，所以四边形1AFB E 为平行四边形，故1//FB EA ，所以1DB F ∠或其补角为异面直线1B D 与AE 所成角，因为111A B C △为等边三角形，D 分别是棱11A C 的中点，所以111B DA C ，所以1B D ，在1Rt A DF 中，DF在Rt ABE △中，AE =1B F =在1B DF 中，2221cos DB F +-∠==0,2π⎛⎫ ⎪⎝⎭，故1DB F ∠为异面直线1B D 与AE 所成角，而1tan DB F ∠=题型二：证明线线、线面平行的方法一、单选题1．（2020·湖南师大附中高一期末）设a 是直线，α是平面，则能推出//a α的条件是（）A ．存在一条直线b ，//a b ，b α⊂B ．存在一条直线b ，a b ⊥，b α⊥C ．存在一个平面β，a β⊂，//αβD ．存在一个平面β，a β⊥，αβ⊥【答案】C【分析】利用a α⊂可得到ABD 的反例，利用面面平行性质知C 正确.【详解】对于A ，若a α⊂，可满足//a b ，b α⊂，但无法得到//a α，A 错误；对于B ，若a α⊂，可满足a b ⊥，b α⊥，但无法得到//a α，B 错误；对于C ，由面面平行的性质知：若//αβ，a β⊂，则//a α，C 正确；对于D ，若a α⊂，可满足a β⊥，αβ⊥，但无法得到//a α，D 错误.故选：C.2．（2019·天津市红桥区教师发展中心高一期末）下列正方体中，A ，B 为正方体的两个顶点， M ，N ，P 分别为其所在棱的中点，能得出直线AB ∠平面MNP 的图形的序号是（）A．①③B．①②C．①④D．②③【答案】A【分析】运用线面平行的判定、面面平行及线面相交、面面平行的性质，并结合图形即可判断结论在各图中是否正确NC PC，得平面MCPN【详解】图①，如图，作MC//NP，连接,AB NC，NC⊂平面MCPN∠AB//平面MCPN//即AB//平面MNP，故①项正确；AC AD CD图②，如图，连结,,由已知可得平面MNP//平面ACD；∠AB和平面ACD相交，∠AB不平行于平面MNP，故②项错误；图③，如图，连接CD由已知可得AB//CD，而MP//CD，可得AB//MP，∠平面AB⊄/平面MNP，又∠MP⊂平面MNP∠AB //平面MNP ，故③项正确；③④项，如图，由DB //MN ，MN ⊂平面MNP ，若AB //平面MNP ，又ABDB B = 则平面ACBD //平面MNP而由图可知，平面ACBD 不可能平行平面MNP∠AB 不平行于平面MNP ，故④项错误.综上，①③符合题意.故选：A二、填空题3．（2021·天津河东·高一期末）如图，CD αβ=，EF αγ=，AB βγ=，AB//α，则CD 与EF 的位置关系为___________．【答案】//CD EF【分析】由线面平行的性质有//AB CD ，根据线面平行的判定可得//CD γ，最后再由线面平行的性质即可得//CD EF .【详解】∠AB//α，AB β⊂，CD αβ=，∠//AB CD ，又AB γ⊂，CD γ⊄，∠//CD γ，又CD α⊂，EF αγ=， ∠//CD EF .故答案为：//CD EF4．（2021·浙江·高一期末）空间四边形ABCD 中，,E F 分别在边,AD CD 上，且满足DE DF EA FC =，则直线EF 与平面ABC 的位置关系是_________．【答案】平行【分析】由已知得//EF AC ，由此能证明//EF 平面ABC ．【详解】空间四边形ABCD 中，E ，F 分别是AD ，CD 上的点，且DE DF EA FC= //EF AC ∴，EF ⊄平面ABC ，AC ⊂平面ABC ，//EF ∴平面ABC ．故答案为：平行．5．（2022·陕西·宝鸡市金台区教育体育局教研室高一期末）如图，平面////αβγ，直线,l m 分别与α、β、γ相交于点A 、B 、C 和点D 、E 、F ，若13AB BC =，20DF =，则EF =_______.【答案】15【分析】分两种情况：（1）直线l 和m 在同一平面内（2）直线l 和m 不在同一平面内，即l 和m 异面然后利用面面平行的性质定理得到线线平行，进一步利用平行线分线段成比例定理得到结果．【详解】分两种情况：（1）直线l 和m 在同一平面内，设该平面为τ，连结,,AD BE CF因为平面////αβγ，==,=,AD BE CF αβγτττ，所以////AD BE CF ，所以13AB DE BC EF ==，又20DF = ，所以15EF = ；（2）直线l 和m 不在同一平面内，即l 和m 异面，过D 作//DH AC ，平面////αβγ，∠,AB DG BC GH ==，设直线DH 与AC 所确定的平面为ξ，又,GE HF ξβξγ==，又//βγ，所以//GE HF ，利用平行线分线段成比例，可得13AB DG DE BC GH EF ===，又20DF =，所以15EF =. 综上，15EF =.故答案为：15．三、解答题6．（2021·新疆·伊宁市第四中学高一期末）已知E F G H 、、、为空间四边形ABCD 的边AB BC CD DA 、、、上的中点，求证：//EH FG .【分析】根据中位线定理与平行公理证明即可.【详解】证明：∠ 在ABD △中，E H 、为边AB DA 、的中点，∠ //EH BD ，∠在BCD △中，F G 、为边BC CD 、上的中点，∠//FG BD ，∠//EH FG .7．（2022·陕西·铜川阳光中学高一期末）如图，在正方体1111ABCD A B C D -中，点,E F 分别是棱11,BB DD 的中点．求证：(1)//BD 平面AEF ；(2)EF ⊥平面11ACC A ．【分析】（1）易证得四边形BDFE 为平行四边形，可知//BD EF ，由线面平行的判定可得结论；（2）由正方形性质和线面垂直性质可证得BD AC ⊥，1AA BD ⊥，由线面垂直的判定可得BD ⊥平面11ACC A ，由//EF BD 可得结论.(1),E F 分别为11,BB DD 的中点，11BB DD =，11//BB DD ，//BE DF ∴且BE DF =，∴四边形BDFE 为平行四边形，//BD EF ∴，又EF ⊂平面AEF ，BD ⊄平面AEF ，//BD ∴平面AEF .(2)四边形ABCD 为正方形，//BD AC EF BD BD EF ∴⊥∴⊥；1AA ⊥平面ABCD ，BD ⊂平面ABCD ，11//AA BDEF BD AA EF ∴⊥∴⊥，又1AC AA A =∩，1,AC AA ⊂平面11ACC A ，11EF ACC A ∴⊥平面8．（2021·陕西·西安市远东一中高一期末）如图，正方体1111ABCD A B C D -中，点E ，F 分别为棱1DD ，BC 的中点.(1)证明：1A D ⊥平面11ABC D ；(2)证明：//EF 平面11ABC D .【分析】（1）利用线面垂直的判定定理即证；（2）设11A D AD G ⋂=，由题可得EF ∠GB ，再利用线面平行的判定定理可证.(1)由正方体1111ABCD A B C D -的性质，可得11A D AD ⊥，AB ⊥平面11ADD A ，∴1AB A D ⊥，又1AD AB A ⋂=，∠1A D ⊥平面11ABC D ；(2)设11A D AD G ⋂=，连接,EG BG ，则11//,,//,,22EG AD EG AD BF AD BF AD == ∠//,EG BF EG BF =，∠四边形BFEG 为平行四边形，∠EF ∠GB ，又EF ⊄平面11ABC D ，GB ⊂平面11ABC D ，∠//EF 平面11ABC D9．（2022·陕西渭南·高一期末）如图，在正方体1111ABCD A B C D -中，E 、F 分别为1DD 、1CC 的中点，AC 与BD 交于点O .求证：(1)1//CE FD ；(2)平面//AEC 平面1BFD .【分析】（1）证明出四边形1CED F 为平行四边形，可证得结论成立；（2）证明出//OE 平面1BFD ，//CE 平面1BFD ，利用面面平行的判定定理可证得结论成立.(1)证明：在正方体1111ABCD A B C D -中，11//CC DD 且11CC DD =，因为E 、F 分别为1DD 、1CC 的中点，则1//CF D E 且1CF D E =，所以，四边形1CED F 为平行四边形，则1//CE FD .(2)证明：因为四边形ABCD 为正方形，ACBD O =，则O 为BD 的中点，因为E 为1DD 的中点，则1//OE BD ， OE ⊄平面1BFD ，1BD ⊂平面1BFD ，所以，//OE 平面1BFD ，因为1//CE FD ，CE ⊄平面1BFD ，1FD ⊂平面1BFD ，所以，//CE 平面1BFD ，因为OE CE E ⋂=，因此，平面//ACE 平面1BFD .题型三：证明面面平行的方法一、单选题1．（2021·贵州铜仁·高一期末）已知a ，b ，c 表示直线，α表示平面，给出下列命题：①若//a α，//b α，那么//a b ；②若b α⊂，//a α，那么//a b ；③若a c ⊥，b c ⊥，则a b ⊥；④若a α⊥，b α⊥，那么//a b ．其中正确的命题个数是（）A ．0B ．1C ．2D ．3【答案】B 【分析】对于①②③可以判断出直线a b 、可能平行，可能相交，也可能异面；对于②直线a b 、可能平行，也可能异面；对于④利用线面垂直的性质定理直接证明即可.【详解】对于①若//a α，//b α，那么直线a b 、可能平行，可能相交，也可能异面；故①错误；对于②若b α⊂，//a α，那么直线a b 、可能平行，也可能异面；故②错误；对于③若a c ⊥，b c ⊥，那么直线a b 、可能平行，可能相交，也可能异面；故③错误；对于④若a α⊥，b α⊥，按照线面垂直的性质定理可得: //a b .故④正确.故选:B2．（2021·贵州·黔西南州同源中学高一期末）已知两条不重合的直线m n ，和两个不重合的平面αβ，，有下列命题：①若m α⊂，n β⊥，//αβ，则//m n ；②若m α⊥，n β⊥，//m n ，则//αβ；③若m n ⊥，m α⊥，则//n α；④若//m α，//n α，则//m n ．其中正确命题的个数是（）A ．1B ．2C ．3D ．4【答案】A【分析】利用空间线面、线线，面面的位置关系一一判定各选项即可.【详解】①当m α⊂，n β⊥，//αβ，则m n ⊥，所以①错误；②因为m α⊥，//m n n α⇒⊥，又n β⊥则//αβ，所以②正确；③若m n ⊥，m α⊥，则//n α或n a ⊂，所以③错误；④若//m α，//n α，则//m n 或,m n 相交或,m n 异面，所以④错误.故选：A.二、多选题3．（2021·江苏·金陵中学高一期末）已知,m n 是两条不同的直线，,αβ是两个不重合的平面，则下列结论正确的是（）A ．若,//m n n α⊥，则m α⊥B ．若,,m n αβαβ⊥⊥⊥，则m n ⊥C ．若,,,m n m αβαβ⊥⋂=⊥则n β⊥D ．若,m n αα⊂⊂，且m 与n 不平行，//,//,m n ββ则//αβ【答案】BD【解析】结合空间线面位置关系及平行垂直的判定与性质定理对选项进行分别判断.【详解】A ：若,//m n n α⊥，则m 与α平行或相交或m α⊂，A 选项错误；B ：因为,ααβ⊥⊥m ，所以//m β或m β⊂，又n β⊥，所以m n ⊥，B 选项正确；C ：若,,,m n m αβαβ⊥⋂=⊥则n 与β相交或平行或n β⊂，C 选项错误；D ：若一个平面内两条相交直线都平行与另一个平面，则这两个平面平行，D 选项正确；故选：BD.三、填空题4．（2019·湖南·临澧县第一中学高一期末）平面几何中我们有“垂直于同一条直线的两条直线平行”，试将该命题中的直线（部分或全部）换成平面，写出一个在空间中成立的命题：_________.【答案】“垂直于同一直线的两个平面平行”或“垂直于同一平面的两直线平行”【分析】从直线到平面，从平面到空间进行类比得解.【详解】从直线到平面，从平面到空间进行类比得到一个在空间中成立的命题：“垂直于同一直线的两个平面平行”或“垂直于同一平面的两直线平行”.故答案为：“垂直于同一直线的两个平面平行”或“垂直于同一平面的两直线平行”【点睛】本题主要考查空间位置关系，考查类比推理，意在考查学生对这些知识的理解掌握水平.四、解答题5．（2021·贵州黔东南·高一期末）如图，在四棱锥P ABCD -中，ABCD 是正方形，PD ⊥平面ABCD ，PD AB =， ,,E F G 分别是,,PC PD BC 的中点．(1)求证：PC AD ⊥；(2)求证：平面//PAB 平面EFG ．【分析】（1）由PD ⊥平面ABCD ，得AD PD ⊥，再根据线面垂直的判定定理和性质定理得证（2）由//EF AB 证明//EF 平面PAB ，由//EG PB 证明//EG 平面PAB ，再由面面平行的判定定理证明即可.(1)由PD ⊥平面ABCD ，得AD PD ⊥，又AD CD ⊥(ABCD 是正方形)，PD CD D ⋂=，所以AD ⊥平面PDC ，所以AD PC ⊥.(2)由,E F 分别是线段,PC PD 的中点，所以//EF CD ，又ABCD 为正方形，//AB CD ，所以//EF AB ，又EF ⊄平面PAB ，所以//EF 平面PAB .因为,E G 分别是线段,PC BC 的中点，所以//EG PB ，又EG ⊄平面PAB ，所以//EG 平面PAB .因为,,EF EG E EF EG =⊂平面EFG ，所以平面//EFG 平面PAB . 6．（2021·广东江门·高一期末）如图，AB 是圆O 的直径，PA 垂直圆O 所在的平面，C 是圆O 上的点.（1）求证：BC ⊥平面PAC ；（2）设Q 为PA 的中点，G 为AOC △的重心，求证：面//OQG 平面PBC .【分析】（1）根据圆直径的性质，得BC AC ⊥，由PA ⊥平面ABC 得BC PA ⊥，利用线面垂直的判定定理，可证BC ⊥平面PAC ；（2）延长OG ，交AC 于M ，连结GM 、QM ，证出QM 是PAC △的中位线，得//QM PC .利用线面平行的判定定理证出//QM 平面PBC ，同理可得//QO 平面PBC ，根据面面平行的判定定理，可得平面//OQG 平面PBC .【详解】解：（1）∠AB 是圆O 的直径，∠BC AC ⊥，又∠PA ⊥平面ABC ，BC ⊂平面ABC ，∠BC PA ⊥.∠PA AC A =，∠BC ⊥平面PAC ；（2）延长OG ，交AC 于M ，连结GM 、QM ，∠G 为AOC △的重心，∠OM 是AOC △的中线，∠Q 为PA 的中点，M 为AC 的中点，∠//QM PC ，∠QM ⊄平面PBC ，PC ⊂平面PBC ，∠//QM 平面PBC ，同理可得//QO 平面PBC ，∠QM 、QO 是平面OQG 内的相交直线，∠平面//OQG 平面PBC .7．（2021·贵州毕节·高一期末）如图甲，已知在四棱锥P ABCD -中，底面ABCD 为平行四边形，点M ，N ，Q 分别在PA ，BD ，PD 上（1）若:::PM MA BN ND PQ QD ==，求证：平面//MNQ 平面PBC ；（2）如图乙所示，若Q 满足:2PQ QD =，PM tPA =，当t 为何值时，//BM 平面AQC ．【答案】（1）证胆见解析，（2）12t = 【分析】（1）由已知比例式结合平行线截线段成比例证明线线平行，进一步得到线面平行，再由面面平行的判定定理可证得结论；（2）连接AC 交BD 于O ，连接OQ ，取PQ 的中点G ，连接BG ，则可得BG ∠OQ ，可得BG ∠平面AQC ，取PA 的中点M ,连接GM ，则GM ∠AQ ，可得GM ∠平面AQC ，则平面BGM ∠平面AQC ，则BM ∠平面AQC ，可得M 为PA 的中点.【详解】（1）证明：因为::PM MA PQ QD =，所以QM ∠AD ，因为AD ∠BC ，所以QM ∠BC ，因为QM ⊄平面PBC ，BC ⊂平面PBC ，所以QM ∠平面PBC ，因为::BN ND PQ QD =，所以QN ∠PB ，因为QN ⊄平面PBC ，PB ⊂平面PBC ，，所以QN ∠平面PBC ，因为QM QN Q =,QM ⊂平面MNQ ,QN ⊂平面MNQ ，所以平面//MNQ 平面PBC ；（2）连接AC 交BD 于O ，连接OQ ，取PQ 的中点G ，连接BG ，则BG ∠OQ ，因为QO ⊂平面AQC ,BG ⊄平面AQC ，所以BG ∠平面AQC ，取PA 的中点M ,连接GM ，则GM ∠AQ ，因为AQ ⊂平面AQC ，GM ⊄平面AQC ，，所以GM ∠平面AQC ，因为BG GM G ⋂=，所以平面BGM ∠平面AQC ，因为BM ⊂平面BGM ，所以BM ∠平面AQC ，此时M 为PA 的中点，所以12PM PA =，因为PM tPA =，所以12t =题型四：证明线线、线面垂直的方法一、单选题1．（2021·辽宁·辽河油田第一高级中学高一期末）设α，β，γ为不同的平面，m ，n ，l 为不同的直线，则下列条件一定能得到m β⊥的是（） A ．m αγ=，αγ⊥，βγ⊥ B ．αβ⊥，l αβ=，m l ⊥C ．n α⊥，n β⊥，m α⊥D ．αγ⊥，βγ⊥，m α⊥【答案】C【解析】根据排除法，结合线面垂直的判定，可得结果. 【详解】在A 中，因为m αγ=，所以,m m αγ⊂⊂，而,m βγ⊥并不垂直于β内的所有直线，所以β和m 可能不垂直，故A 错误；在B 中，m 只垂直β内的一条直线，所以不能推出m β⊥，故B 错误；在C 中，因为,n n αβ⊥⊥，所以α//β，又m α⊥，所以m β⊥，故C 正确；在D 中，由,αγβγ⊥⊥，不能推出α//β，所以由m α⊥不能推出m β⊥，故D 错误. 故选：C【点睛】本题主要是线面垂直的判定，属基础题.2．（2021·陕西·西安市远东一中高一期末）已知α，β，γ是三个不同的平面，l 是一条直线，则下列说法正确的是（） A ．若αβ⊥，αγ⊥，l βγ=，则l α⊥B ．若αβ⊥，l α⊂，则l β⊥C ．若αβ⊥，βγ⊥，则αγ⊥D ．若αβ⊥，l αβ=，l γ∥，则βγ⊥【答案】A【分析】利用面面垂直的性质，线面的位置关系，面面的位置关系，结合几何模型即可判断.【详解】对于A ，在平面α内取一点P ，在平面α内过P 分别作平面α与β，α与γ的交线的垂线a ,b ，则由面面垂直的性质定理可得,a b βγ⊥⊥，又l βγ=，∠,l a l b ⊥⊥，由线面垂直的判定定理可得l α⊥，故A 正确；对于B ，若αβ⊥，l α⊂，则l 与β位置关系不确定，可能l 与β平行、相交或l 在β内，故B 错误；对于C ，若αβ⊥，βγ⊥，则α与γ相交或平行，故C 错误；对于D ，如图平面,αβγ，且αβ⊥，l αβ=，l γ∥，显然β与γ不垂直，故D 错误. 故选：A.3．（2022·陕西·宝鸡市渭滨区教研室高一期末）在空间中，如果一个角的两边和另一个角的两边分别垂直，则这两个角的大小关系为（） A ．相等 B ．互补 C ．相等或互补 D ．不确定【答案】D【分析】EDF ∠的边DE 垂直平面EOF ，所以DE OE ⊥ ，作EF OF ⊥ 则DF OF ⊥.【详解】如下图所示，EOF ∠确定一个平面，EDF ∠的边DE 垂直平面EOF ，所以DE OE ⊥ ，作EF OF ⊥，因为DE ⊥平面EOF ，而OF ⊂平面EOF ，故DE OF ⊥，而EF DE E ⋂=，故OF ⊥平面EDF ，又DF ⊂平面EDF 中，则DF OF ⊥，对于给定的EOF ∠，当D 变化时，EDF ∠的取值范围为0,2π⎛⎫ ⎪⎝⎭，故EOF ∠的大小跟EDF ∠无关.故选：D 二、填空题4．（2022·宁夏·银川唐徕回民中学高一期末）如图，在直四棱柱1111ABCD A B C D -中，当底面ABCD 满足条件___________时，有111AC B D ⊥.（只需填写一种正确条件即可）【答案】AC BD ⊥(答案不唯一)【分析】直四棱柱1111ABCD A B C D -，11A C 是1A C 在上底面1111D C B A 的投影，当1111AC B D ⊥时，可得111AC B D ⊥，当然底面ABCD 满足的条件也就能写出来了. 【详解】根据直四棱柱1111ABCD A B C D -可得：1BB ∠1DD ，且11BB DD =，所以四边形11BB D D 是矩形，所以BD ∠11B D ，同理可证：AC ∠11A C ，当AC BD ⊥时，可得：1111AC B D ⊥，且1CC ⊥底面1111D C B A ，而11B D ⊂底面1111D C B A ，所以111CC B D ⊥，而1111AC CC C =，从而11B D ⊥平面11A CC ，因为1AC ⊂平面11A CC ，所以111AC B D ⊥，所以当AC BD ⊥满足题意. 故答案为：AC BD ⊥. 三、解答题5．（2021·江苏·南京市第二十九中学高一期末）已知直线//m 平面α，直线l ⊥平面α.求证：l m ⊥. 【分析】过m 作平面β交平面α于直线m '，根据线面平行的性质易知//m m '，再由线面垂直的性质有l ⊥m '，由平行线的性质即可证结论.【详解】证明：如下图，过m 作平面β交平面α于直线m '， ∠//m α，m βα'⋂=， ∠//m m '，∠l ⊥α，而m α'⊂， ∠l ⊥m '，综上，l m ⊥，得证.6．（2021·陕西·西安市远东一中高一期末）如图，在四棱锥P ABCD -中，底面ABCD 为平行四边形，90ADB PDC ∠=∠=︒，平面PAD ⊥底面ABCD ，M 是棱PC 上的点.(1)证明：PD ⊥底面ABCD ；(2)若三棱锥A BDM -的体积是四棱锥P ABCD -体积的14，设PM tMC =，试确定t 的值.【答案】(1)详见解析；(2)1t =.【分析】（1）利用面面垂直的性质定理，可得BD ⊥平面PAD ，然后利用线面垂直的判定定理即证；（2）由题可得14A BDM M ABD P ABCD V V V ---==，进而可得12MC PC =，即得.(1)∠90ADB ∠=︒，平面PAD ⊥底面ABCD ，∠AD BD ⊥，平面PAD 底面ABCD =AD ，BD ⊂底面ABCD ， ∠BD ⊥平面PAD ，PD ⊂平面PAD ， ∠BD ⊥PD ，又90PDC ∠=︒， ∠PD DC ⊥，BD DC D =， ∠PD ⊥底面ABCD ；(2)设PD h =，M 到底面ABCD 的距离为h '，∠三棱锥A BDM -的体积是四棱锥P ABCD -体积的14，∠14A BDM M ABD P ABCD V V V ---==，又11,33M ABD ABDP ABCD ABCDV Sh V Sh --'=⋅=⋅，12ABDABCDSS =，∠12h h '=，故12MC PC =，又PM tMC =，所以1t =.题型五：证明面面垂直的方法一、多选题1．（2021·浙江嘉兴·高一期末）已知,a b 是两条不重合的直线，αβ，是两个不重合的平面，则下列命题为真命题的是（）A ．若//αβ，a 与α所成的角和b 与β所成的角相等，则//a bB ．若a α⊥，a β⊥，则//αβC ．若//a b ，a α⊥，//b β，则αβ⊥D ．若//a α，//αβ，则//a β 【答案】BC【分析】判断命题真假可以直接对各选项逐个判断.对于A 可通过直观想象判断其存在平行或异面或相交几种情况；对于B 可通过直线与平面垂直的性质得到；对于C 通过直线与平面垂直性质和平面与平面垂直的判定定理判断；对于D 可直观想象知存在//a β或a β⊂两种情况.【详解】对于A ，若//αβ，a 与α所成的角和b 与β所成的角相等，则//a b 或a 与b 相交或a 与b 异面，故A 错误；对于B ，若a α⊥，a β⊥，由线面垂直的性质可知//αβ，故B 正确；对于C ，若//a b ，a α⊥，则b α⊥，又因为//b β，则αβ⊥，故C 正确；对于D ，若//a α，//αβ，则//a β或a β⊂，故D 错误. 故选:BC 二、解答题2．（2021·江苏南通·高一期末）如图，在四棱锥P ABCD -中，底面ABCD 是矩形，点E 、F 分别是棱PC 和PD 的中点．（1）求证：//EF 平面P AB（2）若AP AD =，平面PAD ⊥平面ABCD ，证明：平面PAD ⊥平面PCD【分析】（1）根据三角形中位线定理，结合矩形的性质、线面平行的判定定理进行证明即可；（2）根据面面垂直的性质定理、线面垂直的判定定理，结合面面垂直的判定定理进行证明即可. 【详解】（1）证明：因为点E 、F 分别是棱PC 和PD 的中点，所以//EF CD 又在矩形ABCD 中，//AB CD ，所以//EF AB 又AB平面P AB ，EF ⊄平面P AB所以//EF 平面.PAB（2）证明：在矩形ABCD 中，AD CD ⊥，又平面PAD ⊥平面ABCD ，平面PAD 平面ABCD AD =，CD ⊂平面ABCD所以CD ⊥平面P AD ，又AF ⊂平面P AD所以.CD AF ⊥①因为PA AD =且F 是PD 的中点，所以AF PD ⊥，②由①②及PD ⊂平面PCD ，CD ⊂平面PCD ，PD CD D ⋂=所以AF ⊥平面PCD ．又AF ⊂平面P AD ，所以平面PAD ⊥平面PCD ．3．（2021·广东·封开县渔涝中学高一期末）如图，在四棱锥P ﹣ABCD 中，底面ABCD 是边长为3的正方形，AP =PD =APD ∠平面ABCD ，E 为AP 的中点，F 为CD 的中点．（1）求证：EF ∠平面PBC ；（2）求证：平面APB ∠平面PCD ．【分析】（1）根据三角形中位线定理，结合平行四边形的判定定理和性质、线面平行的判定定理进行证明即可；（2）根据勾股定理的逆定理，结合线面垂直的判定定理、面面垂直的判定定理进行证明即可. 【详解】（1）设PB 的中点为G ，连接,EG FG ，因为E 为AP 的中点，所以//EG AB 且12EG AB =，因为F 为CD 的中点，底面ABCD 是正方形，所以//FC AB 且12FC AB =，因此//FC EG 且FC EG =，所以四边形EGCF 是平行四边形，因此//EF GC ，因为EF ⊄平面PBC ，GC ⊂平面PBC ，所以EF ∠平面PBC ；（2）因为底面ABCD 是边长为3的正方形，所以3AD =，因为AP =PD = 所以有222AD PA PD =+，因此PD PA ⊥，因为底面ABCD 是正方形，所以BA DA ⊥，因为平面APD ∠平面ABCD ，平面APD平面ABCD AD =，所以AB ⊥平面APD ，因为PD ⊂平面APD ，所以AB PD ⊥，因为AB PA A ⋂=，,AB PA ⊂平面APB ，所以PD ⊥平面APB ，因为PD ⊂平面APD ，所以平面APB ∠平面PCD .4．（2021·江苏扬州·高一期末）正方体1111ABCD A B C D -中，E 为棱1DD 中点.（1）求证：1//BD 平面AEC ；（2）求证：平面1⊥B AC 平面11B BDD .【分析】（1）由线面平行的判定定理可证得结果；（2）证得AC ⊥平面11BDD B ，进而由面面垂直的判定定理可证得结果.【详解】（1）设AC 与BD 交于点O ，连结OE .因为1111ABCD A B C D -是正方体，所以ABCD 为正方形，O 为BD 中点.又因为E 为1DD 中点，所以1//OE BD .又因为OE ⊂平面1,AEC BD ⊄平面AEC ，所以1//BD 平面AEC .（2）因为1111ABCD A B C D -是正方体，1BB ⊥平面ABCD .又AC ⊂平面ABCD ，所以1AC BB ⊥.又ABCD 为正方形，所以AC BD ⊥.因为11,,AC BD AC BB BB ⊥⊥⊂平面11,BDD B BD ⊂平面111,BDD B BB BD B ⋂=，所以AC ⊥平面11BDD B .又因为AC ⊂平面1B AC ，所以平面1⊥B AC 平面11B BDD .5．（2021·山东枣庄·高一期末）如图，AB 是圆O 的直径，点C 是圆O 上异于A ，B 的点，直线PC ⊥平面ABC ，E ，F 分别是线段PA ，PC 的中点．（1）证明：平面BEF ⊥平面PBC ；（2）记平面BEF 与平面ABC 的交线为l ，试判断直线EF 与直线l 的位置关系，并说明理由．【答案】（1）证明见解析；（2）//EF l ，理由见解析.【分析】（1）推导出AC PC ⊥，AC BC ⊥，AC ⊥平面PBC ，从而//EF AC ，进而EF ⊥平面PBC ，由此能证明平面BEF ⊥平面PBC ．（2）推导出//EF AC ，//EF 平面ABC ，根据线面平行的性质，即能证明//EF l ．【详解】解：（1）因为PC ⊥平面ABC ，AC ⊂平面ABC ，所以AC PC ⊥.因为C 是以AB 为直径的圆O 上的点，所以AC BC ⊥．又PC BC C ⋂=，所以AC ⊥平面PBC ．因为E ，F 分别是PA ，PC 的中点，所以//EF AC ．所以EF ⊥平面PBC ．又EF ⊂平面BEF ，故平面BEF ⊥平面PBC ．。

直线、平面平行与垂直地判定及其性质(证明题详解)

直线、平面平行与垂直的判定及其性质7. 在四棱锥P－ABCD中，四边形ABCD是梯形，AD∥BC，∠ABC=90°，平面PAB⊥平面ABCD，平面PAD⊥平面ABCD.（1）求证：PA⊥平面ABCD；（2）若平面PAB平面PCD l，问：直线l能否与平面ABCD平行？请说明理由.【解析】（1）因为∠ABC=90°，AD∥BC，所以AD⊥AB.而平面PAB⊥平面ABCD，且平面PAB平面ABCD=AB,所以AD⊥平面PAB, 所以AD⊥PA.同理可得AB⊥PA.由于AB、AD平面ABCD，且AB AD=A,所以PA⊥平面ABCD.（2）（方法一）不平行.证明：假定直线l∥平面ABCD,由于l平面PCD，且平面PCD平面ABCD=CD, 所以l∥CD.同理可得l∥AB, 所以AB∥CD.这与AB和CD是直角梯形ABCD的两腰不平行相矛盾,故假设错误，所以直线l与平面ABCD不平行.（方法二）因为梯形ABCD中AD∥BC,所以直线AB与直线CD相交，设AB CD=T.由T CD，CD平面PCD得T平面PCD.同理T平面PAB.即T为平面PCD与平面PAB的公共点，于是PT为平面PCD与平面PAB的交线.所以直线l与平面ABCD不平行.DCPAB（第16题）8. 如图，在三棱柱111ABC A B C 中，11,,AB BC BC BC AB BC ，,,E F G 分别为线段1111,,AC AC BB 的中点，求证：（1）平面ABC平面1ABC ;（2）//EF 面11BCC B ；（3）GF平面11ABC 【解析】(1)BCAB11BC BC ABBC BBC 平面1ABC BC平面ABC平面ABC 平面1ABC (2)111,AEEC A F FC ,1//EF AA 11//BB AA 1//EF BB 11EFBCC B 面//EF 面11BCC B ；(3)连接EB ，则四边形EFGB 为平行四边形11111111111111BE FG A C EB AC FG AC BC ABC B C ABC B C B C B C C 面面,GF平面11AB C 。

专题20立体几何中的平行与垂直问题(解析版)

专题20 立体几何中的平行与垂直问题一、题型选讲题型一、线面平行与垂直知识点拨：证明直线与平面的平行与垂直问题，一定要熟练记忆直线与平面的平行与垂直判定定理和性质定理，切记不可缺条件。

直线与平面的平行有两种方法：一是在面内找线；二是通过面面平行转化。

直线与平面垂直关键是找两条相交直线例1、（2019南通、泰州、扬州一调）如图，在四棱锥PABCD中，M, N分别为棱PA, PD的中点.已知侧面PAD丄底面ABCD,底面ABCD是矩形，DA=DP.求证：（1）MN〃平面PBC；MD丄平面PAB.【证明】（1）在四棱锥P-ABCD中，M, N分别为棱PA, PD的中点，所以MN〃AD.（2分）又底面ABCD是矩形，所以BC〃AD.所以MN〃BC.（4分）又BC U平面PBC，MN Q平面PBC，所以MN〃平面PBC. （6分）（2）因为底面ABCD是矩形，所以AB丄AD.又侧面PAD丄底面ABCD，侧面PAD n底面ABCD=AD, AB U底面ABCD，所以AB丄侧面PAD.（8分）又MD U侧面PAD，所以AB丄MD.（10分）因为DA=DP,又M为AP的中点，从而MD丄PA. （12分）又PA，AB在平面PAB内，PA n AB=A，所以MD丄平面PAB.（14分）例2、（2019扬州期末）如图所示，在三棱柱ABCA1B1C1中，四边形AA1B1B为矩形，平面AA1B1B丄平面ABC,点E，F分别是侧面AA1B1B，BB1C1C对角线的交点.（1）求证：EF〃平面ABC；（2）求证：BB］丄AC.规范解答（1）在三棱柱ABCA1B1C1中，四边形AA1B1B,四边形BB1C1C均为平行四边形，E, F分别是侧面AA1B1B, BB1C1C对角线的交点，所以E, F分别是AB1，CB1的中点，所以EF〃AC.（4分）因为EF Q平面ABC, AC U平面ABC，所以EF〃平面ABC.（8分）（2）因为四边形AA1B1B为矩形，所以BB1丄AB.因为平面AA1B1B丄平面ABC,且平面AA1B1B n平面ABC=AB, BB1U平面AA1B1B, 所以BB1丄平面ABC.（12分）因为AC U平面ABC，所以BB1丄AC.（14分）例3、（2019南京、盐城二模）如图，在三棱柱ABCA1B1C1中，AB=AC, A1C丄BC］, AB］丄BC1，D, E 分别是AB1和BC的中点.求证：（1）DE〃平面ACC1A1；（2）AE丄平面BCC1B1.A _________ c,规范解答⑴连结A1B，在三棱柱ABCA1B1C1中，AA1#BB1且AA1=BB1，所以四边形AA1B1B是平行四边形．又因为D是AB1的中点，所以D也是BA1的中点.（2分）在厶BA1C中，D和E分别是BA1和BC的中点，所以DE〃A］C.又因为DE G平面ACC1A1，A1C U平面ACC1A1，所以DE〃平面ACC1A1.（6分）（2）由（1）知DE〃A］C，因为A1C丄BC” 所以BC］丄DE.（8 分）又因为BC］丄AB1，AB1H DE=D，AB1，DE U平面ADE，所以BC1丄平面ADE.又因为AE U平在ADE,所以AE丄BC1.（10分）在厶ABC中，AB=AC，E是BC的中点，所以AE丄BC.（12分）因为AE丄BC1，AE丄BC，BC1H BC=B，BC1，BC U平面BCC1B1，所以AE丄平面BCC1B1. （14 分）例4、（2019苏锡常镇调研）如图，三棱锥DABC中，已知AC丄BC，AC丄DC，BC=DC，E，F 分别为BD，CD 的中点．求证：（1）EF〃平面ABC；（2）BD丄平面ACE.所以EF 〃平面ABC.（6分）（2）因为AC丄BC，AC丄DC，BC H DC = C，BC，DC U平面BCD所以AC丄平面BCD，（8分）因为BD U平面BCD，所以AC丄BD，（10分）因为DC=BC，E为BD的中点，所以CE丄BD，（12分）因为AC n CE = C, AC，CE U平面ACE，所以BD丄平面ACE.（14分）例5、（2019苏州三市、苏北四市二调）如图，在直三棱柱ABCA1B1C1中，侧面BCC1B1为正方形，A1B1 丄B1C1•设A1C与AC1交于点D, B1C与BC1交于点E.求证：（1） DE〃平面ABB1A1；（2） BC］丄平面A1B1C.规范解答（1）因为三棱柱ABCA1B1C1为直三棱柱，所以侧面ACC1A1为平行四边形．又A1C 与AC1 交于点D,所以D为AC]的中点，同理，E为BC]的中点•所以DE〃AB.（3分）又AB U平面ABB]A], DE G平面ABB]A], 所以DE〃平面ABB]A].（6分）（2）因为三棱柱ABCA]B]C]为直三棱柱，所以BB]丄平面A]B]C]. 又因为A]B]U平面A]B]C],所以BB]丄A]B i.（8分）又A]B]丄B]C], BB], B]C] U 平面BCC]B], BB]n B]C1=B1，所以A]B]丄平面BCC]B].（10 分）又因为BC]U平面BCC]B1，所以A]B丄BC].（12分）又因为侧面BCC]B1为正方形，所以BC]丄BQ.又A1B1n B1C=B1，A1B1，B1C U平面A1B1C, 所以BC1丄平面A1B1C.（14分）例6、（2017苏北四市一模）如图，在正三棱柱ABCA1B1C1中，已知D, E分别为BC, B1C1的中点，点F 在棱CC1上，且EF丄CD.求证：（1）直线A1E〃平面ADC1；⑴证法1连结ED,因为D, E分别为BC, B1C1的中点，所以B&/BD且B1E=BD, 所以四边形BBDE是平行四边形，（2分）所以BB/DE且BB1=DE. 又BB]〃AA]且BB]=AA], 所以AA/DE且AA1=DE, 所以四边形AA]ED是平行四边形，所以A]E〃AD.（4分）又因为AE G平面ADC, AD U平面ADC，所以直线AE〃平面ADC.（7分）1 1 1畀 ------ 1B证法2连结ED,连结A1C, EC分别交AC” DC1于点M, N,连结MM,则因为D, E分别为BC,B1C1的中点，所以C1E^CD且C、E=CD,所以四边形C1EDC是平行四边形，所以N是CE的中点.（2分）因为A1ACC1为平行四边形，所以M是A1C的中点，（4分）所以MN//A\E.又因为A]E G平面ADC，MN U平面ADC，，所以直线Af〃平面ADC、.（7分）（2）在正三棱柱ABCA1B1C1中，BB]丄平面ABC.又AD U平面ABC，所以AD丄BB、.又A ABC是正三角形，且D为BC的中点，所以AD丄BC.（9分）又BB，，BC U 平面BBCC，，BB1A BC=B，所以AD丄平面B,BCC,，又EF U平面BBCC，所以AD丄EF.（11分）又EF丄CD，CD，AD U平面ADC,，C,D A AD=D，所以直线EF丄平面ADC,.（14分）题型二、线面与面面平行与垂直证明平面与平面的平行与垂直问题，一定要熟练记忆平面与平面的平行与垂直判定定理和性质定理，切记不可缺条件。

专题06五种直线、平面平行与垂直的判定与性质解题方法(解析版)

专题06五种直线、平面平行与垂直的判定与性质解题方法题型一：求异面直线所成角题型二：证明线线、线面平行的方法题型三：证明面面平行的方法题型四：证明线线、线面垂直的方法题型五：证明面面垂直的方法题型一：求异面直线所成角一、单选题1．（2019·江苏苏州·高一期末）正方体1111ABCD A B C D -中，异面直线1AA 与BC 所成角的大小为（） A ．30B ．45︒C ．60︒D ．90︒【答案】D【分析】利用异面直线1AA 与BC 所成角的的定义，平移直线BC ，即可得答案．【详解】在正方体1111ABCD A B C D -中，易得190A AD ∠=︒．//AD BC ∴异面直线1AA 与BC 垂直，即所成的角为90︒.故选：D ．【点睛】本题考查异面直线所成角的定义，考查对基本概念的理解，属于基础题.2．（2020·宁夏银川·高一期末）下图的正方体ABCD A B C D ''''-中，异面直线AA '与BC '所成的角是（）A ．30B ．45C ．60D ．90【答案】B 【解析】只需将异面直线AA '与BC '平移至同一个平面内，转化为两条相交直线，即可求出它们所成的角．【详解】在正方体ABCD A B C D ''''-中，因为//AA BB ''，所以B BC ''∠即为异面直线AA '与BC '所成的角，因为45B BC ''∠=，所以异面直线AA '与BC '所成的角为45.故选：B.【点睛】本题主要考查异面直线所成角的求法．求两条异面直线所成角的大小，一般方法是通过平行移动直线，把异面问题转化为共面问题来解决，根据空间等角定理及推论可知，异面直线所成角的大小与顶点位置无关，往往可以选在其中一条直线上（线面的端点或中点）利用三角形求解．3．（2021·陕西·西安市远东一中高一期末）如图，在正三棱锥D ABC -中，AD DC ⊥，点F 为棱AC 的中点，则异面直线DF 与AB 所成角的大小为（）A ．30°B ．45°C ．60°D ．90°【答案】C 【分析】取BC 的中点E ，∠DFE 即为所求，结合条件即求.【详解】如图取BC 的中点E ，连接EF ，DE ，则EF ∠AB ，∠DFE 即为所求，设DF a =，在正三棱锥D ABC -中，AD DC ⊥，故2,AB AC BC a DA DB DC ======，∠EF DE DF a ===，∠60DFE ∠=，即异面直线DF 与AB 所成角的大小为60.故选：C.4．（2021·湖北孝感·高一期末）在正方体1111ABCD A B C D -中，M 为11A C 和11B D 的交点，则异面直线BM 与1AD 所成的角为（）A ．6πB ．4πC ．3πD ．2π 【答案】A 【分析】平移直线1AD 至1BC ，将直线PB 与1AD 所成的角转化为PB 与1BC 所成的角，解三角形即得结果.【详解】如图，连接1,BC MB ，因为1AD ∠1BC ，所以MBC 1∠或其补角为直线MB 与1AD 所成的角，因为1BB ⊥平面1111D C B A ，所以11BB MC ⊥，又111MC B D ⊥，1111BB B D B ⋂=，111,BB B D ⊂平面1MBB ，所以MC 1⊥平面1MBB ，所以1MC PB ⊥，设正方体棱长为2，则111112BC MC AC ===1111sin 2MC MBC BC ∠===，而直角三角形中MBC 1∠是锐角，所以16MBC π∠=，即异面直线BM 与1AD 所成的角是6π. 故选：A. 5．（2021·贵州毕节·高一期末）在空间四边形ABCD 中，AB CD =，E ，F 分别为BC ，AD 的中点，若AB 与CD 所成的角为40°，则EF 与AB 所成角的大小为（）A ．20°B ．70°C ．20°或70°D ．40°或140°【答案】C【分析】根据异面直线所成角的定义转化为相交直线所成角，利用几何图形求EF 与AB 所成角的大小.【详解】取AC 的中点M ，BD 的中点N ，连接,,,,ME EN NF FM EF ，,,,M E N F 分别是,,,AC BC BD AD 的中点，//,//ME AB NF AB ∴，∴//ME NF ，同理//EN MF ，∴四边形MENF 是平行四边形，又AB CD =，∴=ME EN ，四边形MENF 是菱形，AB 与CD 所成的角为40，40MEN ∴∠=或140，∴EF 与AB 所成角是1202MEF MEN ∠=∠=或70. 故选：C二、多选题6．（2021·江苏常州·高一期末）下图是一个正方体的平面展开图，则在该正方体中（）A ．//BF CDB ．DG BH ⊥C ．CH 与BG 成60°角D ．BE 与平面ABCD 所成角为45°【答案】BCD 【分析】由正方体的平面展开图还原原正方体，再由正方体的结构特征结合空间角的概念逐个分析判断即可【详解】由正方体的平面展开图还原原正方体如图所示，由正方体的结构特征可知，BF 与CD 异面垂直，所以A 错误，DG CH ⊥，而CH 为BH 在平面DCGH 上的射影，所以DG BH ⊥，所以B 正确，连接AH ，由AB ∠GH ，AB GH =，可得四边形ABGH 为平行四边形，则AH ∠BG ，所以AHC ∠或其补角为异面直线CH 与BG 所成的角，连接AC ，可得AHC 为等边三角形，得CH 与BG 成60°角，所以C 正确，因为AE ⊥平面ABCD ，所以EBA ∠为BE 与平面ABCD 所成角为45︒，所以D 正确，故选：BCD三、填空题7．（2020·天津市红桥区教师发展中心高一期末）正方体1111ABCD A B C D -中，异面直线1A B 与1B C 所成角的大小为_________. 【答案】3π 【分析】连接1A D 、BD ，证明11//A D B C ，可得1DA B ∠即为异面直线1A B 与1B C 所成角，在1DA B △求1DA B ∠即可求解.【详解】如图，连接1A D 、BD ，因为11A B DC ，所以四边形11A B CD 是平行四边形，所以11//A D B C ，所以1DA B ∠即为异面直线1A B 与1B C 所成角，设正方体1111ABCD A B C D -的棱长为a ，在1DA B △中，11DA A B BD ===，所以1DA B △是等边三角形，所以13DA B π∠=，即异面直线1A B 与1B C 所成角为3π，故答案为：3π 【点睛】思路点睛：平移线段法是求异面直线所成角的常用方法，具体步骤如下（1）平移：平移异面直线中的一条或两条，作出异面直线所成的角；（2）认定：证明作出的角就是所求异面直线所成的角；（3）计算：求该角的值，常利用解三角形；（4）取舍：由异面直线所成的角的取值范围是0,2π⎛⎤ ⎥⎝⎦，当所作的角为钝角时，应取它的补角作为两条异面直线所成的角．8．（2022·陕西西安·高一期末）在正方体1111ABCD A B C D -中，则异面直线1AB 与1BC 的夹角为_________．【答案】3π 【解析】先证明11//AD BC ，可得11D AB ∠或其补角即为异面直线1AB 与1BC 所成的角，连接11D B ，在11AB D 中求11D AB ∠即可.【详解】在正方体1111ABCD A B C D -中，//,AB DC AB CD =， 1111//,,D C DC D C DC =所以1111//,AB D C AB D C =，所以四边形11ABC D 是平行四边形，所以11//AD BC ，所以11D AB ∠或其补角即为异面直线1AB 与1BC 所成的角，连接11D B ，由1111ABCD A B C D -为正方体可得11AB D 是等边三角形，所以113D AB π∠=.故答案为：3π 【点睛】思路点睛：平移线段法是求异面直线所成角的常用方法，其基本思路是通过平移直线，把异面直线的问题化归为共面直线问题来解决，具体步骤如下：（1）平移：平移异面直线中的一条或两条，作出异面直线所成的角；（2）认定：证明作出的角就是所求异面直线所成的角；（3）计算：求该角的值，常利用解三角形；（4）取舍：由异面直线所成的角的取值范围是0,2π⎛⎤ ⎥⎝⎦，当所作的角为钝角时，应取它的补角作为两条异面直线所成的角．9．（2020·湖北湖北·高一期末）已知M 是长方体1111ABCD A B C D -的棱1BB 的中点，底面ABCD 为正方形且12AA AB =，则AM 与11B D 所成角的大小用弧度制可以表示为______. 【答案】3π 【分析】取1AA 中点N ，连接11,B N D N ，可判断11D B N 即为AM 与11B D 所成角，求出即可.【详解】如图，取1AA 中点N ，连接11,B N D N ，设12=2AA AB =，,M N 是中点，可知1//AN B M 且1AN B M ，∴四边形1AMB N 是平行四边形，1//AM B N ∴,则11D B N 即为AM 与11B D 所成角，可知11112,2,2B N B D D N ，113D B N，即AM 与11B D 所成角为3π. 故答案为：3π. 【点睛】本题考查异面直线所成角的求解，属于基础题.10．（2021·吉林·长春市第二十中学高一期末）如图，在正方体ABCD ﹣A 1B 1C 1D 1中，E ，F 依次是A 1D 1和B 1C 1的中点，则异面直线AE 与CF 所成角的余弦值为_____.【答案】35【解析】先推导出BF ∠AE ，从而∠BFC 是异面直线AE 与CF 所成角（或所成角的补角），由此能求出异面直线AE 与CF 所成角的余弦值.【详解】解：在正方体ABCD ﹣A 1B 1C 1D 1中，∠E ，F 依次是A 1D 1和B 1C 1的中点，∠BF ∠AE ，∠∠BFC 是异面直线AE 与CF 所成角（或所成角的补角），设正方体ABCD ﹣A 1B 1C 1D 1中棱长为2，则BF ＝CF ==∠cos ∠BFC 35==. ∠异面直线AE 与CF 所成角的余弦值为35. 故答案为：35.【点睛】本题考查异面直线所成角的余弦值的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查运算求解能力，是中档题.11．（2021·山西吕梁·高一期末）已知正三棱柱中111ABC A B C -中，2AB =，14BB =，D ，E 分别是棱11A C ，1BB 的中点，则异面直线1B D 与AE 所成角的正切值为______.【分析】作出辅助线，证得1DB F ∠或其补角为异面直线1B D 与AE 所成角，然后求出相关线段的长度，进而在1B DF 中，利用余弦定理求出余弦值，进而可以求出结果.【详解】取1A A 的中点F ，连接1,B F DF ,因为E 分别是棱1BB 的中点，所以1AF B E =且1//AF B E ，所以四边形1AFB E 为平行四边形，故1//FB EA ，所以1DB F ∠或其补角为异面直线1B D 与AE 所成角，因为111A B C △为等边三角形，D 分别是棱11A C 的中点，所以111B DA C ，所以1B D ，在1Rt A DF 中，DF在Rt ABE △中，AE =1B F =在1B DF 中，2221cos DB F +-∠==0,2π⎛⎫ ⎪⎝⎭，故1DB F ∠为异面直线1B D 与AE 所成角，而1tan DB F ∠=题型二：证明线线、线面平行的方法一、单选题1．（2020·湖南师大附中高一期末）设a 是直线，α是平面，则能推出//a α的条件是（）A ．存在一条直线b ，//a b ，b α⊂B ．存在一条直线b ，a b ⊥，b α⊥C ．存在一个平面β，a β⊂，//αβD ．存在一个平面β，a β⊥，αβ⊥【答案】C【分析】利用a α⊂可得到ABD 的反例，利用面面平行性质知C 正确.【详解】对于A ，若a α⊂，可满足//a b ，b α⊂，但无法得到//a α，A 错误；对于B ，若a α⊂，可满足a b ⊥，b α⊥，但无法得到//a α，B 错误；对于C ，由面面平行的性质知：若//αβ，a β⊂，则//a α，C 正确；对于D ，若a α⊂，可满足a β⊥，αβ⊥，但无法得到//a α，D 错误.故选：C.2．（2019·天津市红桥区教师发展中心高一期末）下列正方体中，A ，B 为正方体的两个顶点， M ，N ，P 分别为其所在棱的中点，能得出直线AB ∠平面MNP 的图形的序号是（）A．①③B．①②C．①④D．②③【答案】A【分析】运用线面平行的判定、面面平行及线面相交、面面平行的性质，并结合图形即可判断结论在各图中是否正确NC PC，得平面MCPN【详解】图①，如图，作MC//NP，连接,AB NC，NC⊂平面MCPN∠AB//平面MCPN//即AB//平面MNP，故①项正确；AC AD CD图②，如图，连结,,由已知可得平面MNP//平面ACD；∠AB和平面ACD相交，∠AB不平行于平面MNP，故②项错误；图③，如图，连接CD由已知可得AB//CD，而MP//CD，可得AB//MP，∠平面AB⊄/平面MNP，又∠MP⊂平面MNP∠AB //平面MNP ，故③项正确；③④项，如图，由DB //MN ，MN ⊂平面MNP ，若AB //平面MNP ，又ABDB B = 则平面ACBD //平面MNP而由图可知，平面ACBD 不可能平行平面MNP∠AB 不平行于平面MNP ，故④项错误.综上，①③符合题意.故选：A二、填空题3．（2021·天津河东·高一期末）如图，CD αβ=，EF αγ=，AB βγ=，AB//α，则CD 与EF 的位置关系为___________．【答案】//CD EF【分析】由线面平行的性质有//AB CD ，根据线面平行的判定可得//CD γ，最后再由线面平行的性质即可得//CD EF .【详解】∠AB//α，AB β⊂，CD αβ=，∠//AB CD ，又AB γ⊂，CD γ⊄，∠//CD γ，又CD α⊂，EF αγ=， ∠//CD EF .故答案为：//CD EF4．（2021·浙江·高一期末）空间四边形ABCD 中，,E F 分别在边,AD CD 上，且满足DE DF EA FC =，则直线EF 与平面ABC 的位置关系是_________．【答案】平行【分析】由已知得//EF AC ，由此能证明//EF 平面ABC ．【详解】空间四边形ABCD 中，E ，F 分别是AD ，CD 上的点，且DE DF EA FC= //EF AC ∴，EF ⊄平面ABC ，AC ⊂平面ABC ，//EF ∴平面ABC ．故答案为：平行．5．（2022·陕西·宝鸡市金台区教育体育局教研室高一期末）如图，平面////αβγ，直线,l m 分别与α、β、γ相交于点A 、B 、C 和点D 、E 、F ，若13AB BC =，20DF =，则EF =_______.【答案】15【分析】分两种情况：（1）直线l 和m 在同一平面内（2）直线l 和m 不在同一平面内，即l 和m 异面然后利用面面平行的性质定理得到线线平行，进一步利用平行线分线段成比例定理得到结果．【详解】分两种情况：（1）直线l 和m 在同一平面内，设该平面为τ，连结,,AD BE CF因为平面////αβγ，==,=,AD BE CF αβγτττ，所以////AD BE CF ，所以13AB DE BC EF ==，又20DF = ，所以15EF = ；（2）直线l 和m 不在同一平面内，即l 和m 异面，过D 作//DH AC ，平面////αβγ，∠,AB DG BC GH ==，设直线DH 与AC 所确定的平面为ξ，又,GE HF ξβξγ==，又//βγ，所以//GE HF ，利用平行线分线段成比例，可得13AB DG DE BC GH EF ===，又20DF =，所以15EF =. 综上，15EF =.故答案为：15．三、解答题6．（2021·新疆·伊宁市第四中学高一期末）已知E F G H 、、、为空间四边形ABCD 的边AB BC CD DA 、、、上的中点，求证：//EH FG .【分析】根据中位线定理与平行公理证明即可.【详解】证明：∠ 在ABD △中，E H 、为边AB DA 、的中点，∠ //EH BD ，∠在BCD △中，F G 、为边BC CD 、上的中点，∠//FG BD ，∠//EH FG .7．（2022·陕西·铜川阳光中学高一期末）如图，在正方体1111ABCD A B C D -中，点,E F 分别是棱11,BB DD 的中点．求证：(1)//BD 平面AEF ；(2)EF ⊥平面11ACC A ．【分析】（1）易证得四边形BDFE 为平行四边形，可知//BD EF ，由线面平行的判定可得结论；（2）由正方形性质和线面垂直性质可证得BD AC ⊥，1AA BD ⊥，由线面垂直的判定可得BD ⊥平面11ACC A ，由//EF BD 可得结论.(1),E F 分别为11,BB DD 的中点，11BB DD =，11//BB DD ，//BE DF ∴且BE DF =，∴四边形BDFE 为平行四边形，//BD EF ∴，又EF ⊂平面AEF ，BD ⊄平面AEF ，//BD ∴平面AEF .(2)四边形ABCD 为正方形，//BD AC EF BD BD EF ∴⊥∴⊥；1AA ⊥平面ABCD ，BD ⊂平面ABCD ，11//AA BDEF BD AA EF ∴⊥∴⊥，又1AC AA A =∩，1,AC AA ⊂平面11ACC A ，11EF ACC A ∴⊥平面8．（2021·陕西·西安市远东一中高一期末）如图，正方体1111ABCD A B C D -中，点E ，F 分别为棱1DD ，BC 的中点.(1)证明：1A D ⊥平面11ABC D ；(2)证明：//EF 平面11ABC D .【分析】（1）利用线面垂直的判定定理即证；（2）设11A D AD G ⋂=，由题可得EF ∠GB ，再利用线面平行的判定定理可证.(1)由正方体1111ABCD A B C D -的性质，可得11A D AD ⊥，AB ⊥平面11ADD A ，∴1AB A D ⊥，又1AD AB A ⋂=，∠1A D ⊥平面11ABC D ；(2)设11A D AD G ⋂=，连接,EG BG ，则11//,,//,,22EG AD EG AD BF AD BF AD == ∠//,EG BF EG BF =，∠四边形BFEG 为平行四边形，∠EF ∠GB ，又EF ⊄平面11ABC D ，GB ⊂平面11ABC D ，∠//EF 平面11ABC D9．（2022·陕西渭南·高一期末）如图，在正方体1111ABCD A B C D -中，E 、F 分别为1DD 、1CC 的中点，AC 与BD 交于点O .求证：(1)1//CE FD ；(2)平面//AEC 平面1BFD .【分析】（1）证明出四边形1CED F 为平行四边形，可证得结论成立；（2）证明出//OE 平面1BFD ，//CE 平面1BFD ，利用面面平行的判定定理可证得结论成立.(1)证明：在正方体1111ABCD A B C D -中，11//CC DD 且11CC DD =，因为E 、F 分别为1DD 、1CC 的中点，则1//CF D E 且1CF D E =，所以，四边形1CED F 为平行四边形，则1//CE FD .(2)证明：因为四边形ABCD 为正方形，ACBD O =，则O 为BD 的中点，因为E 为1DD 的中点，则1//OE BD ， OE ⊄平面1BFD ，1BD ⊂平面1BFD ，所以，//OE 平面1BFD ，因为1//CE FD ，CE ⊄平面1BFD ，1FD ⊂平面1BFD ，所以，//CE 平面1BFD ，因为OE CE E ⋂=，因此，平面//ACE 平面1BFD .题型三：证明面面平行的方法一、单选题1．（2021·贵州铜仁·高一期末）已知a ，b ，c 表示直线，α表示平面，给出下列命题：①若//a α，//b α，那么//a b ；②若b α⊂，//a α，那么//a b ；③若a c ⊥，b c ⊥，则a b ⊥；④若a α⊥，b α⊥，那么//a b ．其中正确的命题个数是（）A ．0B ．1C ．2D ．3【答案】B 【分析】对于①②③可以判断出直线a b 、可能平行，可能相交，也可能异面；对于②直线a b 、可能平行，也可能异面；对于④利用线面垂直的性质定理直接证明即可.【详解】对于①若//a α，//b α，那么直线a b 、可能平行，可能相交，也可能异面；故①错误；对于②若b α⊂，//a α，那么直线a b 、可能平行，也可能异面；故②错误；对于③若a c ⊥，b c ⊥，那么直线a b 、可能平行，可能相交，也可能异面；故③错误；对于④若a α⊥，b α⊥，按照线面垂直的性质定理可得: //a b .故④正确.故选:B2．（2021·贵州·黔西南州同源中学高一期末）已知两条不重合的直线m n ，和两个不重合的平面αβ，，有下列命题：①若m α⊂，n β⊥，//αβ，则//m n ；②若m α⊥，n β⊥，//m n ，则//αβ；③若m n ⊥，m α⊥，则//n α；④若//m α，//n α，则//m n ．其中正确命题的个数是（）A ．1B ．2C ．3D ．4【答案】A【分析】利用空间线面、线线，面面的位置关系一一判定各选项即可.【详解】①当m α⊂，n β⊥，//αβ，则m n ⊥，所以①错误；②因为m α⊥，//m n n α⇒⊥，又n β⊥则//αβ，所以②正确；③若m n ⊥，m α⊥，则//n α或n a ⊂，所以③错误；④若//m α，//n α，则//m n 或,m n 相交或,m n 异面，所以④错误.故选：A.二、多选题3．（2021·江苏·金陵中学高一期末）已知,m n 是两条不同的直线，,αβ是两个不重合的平面，则下列结论正确的是（）A ．若,//m n n α⊥，则m α⊥B ．若,,m n αβαβ⊥⊥⊥，则m n ⊥C ．若,,,m n m αβαβ⊥⋂=⊥则n β⊥D ．若,m n αα⊂⊂，且m 与n 不平行，//,//,m n ββ则//αβ【答案】BD【解析】结合空间线面位置关系及平行垂直的判定与性质定理对选项进行分别判断.【详解】A ：若,//m n n α⊥，则m 与α平行或相交或m α⊂，A 选项错误；B ：因为,ααβ⊥⊥m ，所以//m β或m β⊂，又n β⊥，所以m n ⊥，B 选项正确；C ：若,,,m n m αβαβ⊥⋂=⊥则n 与β相交或平行或n β⊂，C 选项错误；D ：若一个平面内两条相交直线都平行与另一个平面，则这两个平面平行，D 选项正确；故选：BD.三、填空题4．（2019·湖南·临澧县第一中学高一期末）平面几何中我们有“垂直于同一条直线的两条直线平行”，试将该命题中的直线（部分或全部）换成平面，写出一个在空间中成立的命题：_________.【答案】“垂直于同一直线的两个平面平行”或“垂直于同一平面的两直线平行”【分析】从直线到平面，从平面到空间进行类比得解.【详解】从直线到平面，从平面到空间进行类比得到一个在空间中成立的命题：“垂直于同一直线的两个平面平行”或“垂直于同一平面的两直线平行”.故答案为：“垂直于同一直线的两个平面平行”或“垂直于同一平面的两直线平行”【点睛】本题主要考查空间位置关系，考查类比推理，意在考查学生对这些知识的理解掌握水平.四、解答题5．（2021·贵州黔东南·高一期末）如图，在四棱锥P ABCD -中，ABCD 是正方形，PD ⊥平面ABCD ，PD AB =， ,,E F G 分别是,,PC PD BC 的中点．(1)求证：PC AD ⊥；(2)求证：平面//PAB 平面EFG ．【分析】（1）由PD ⊥平面ABCD ，得AD PD ⊥，再根据线面垂直的判定定理和性质定理得证（2）由//EF AB 证明//EF 平面PAB ，由//EG PB 证明//EG 平面PAB ，再由面面平行的判定定理证明即可.(1)由PD ⊥平面ABCD ，得AD PD ⊥，又AD CD ⊥(ABCD 是正方形)，PD CD D ⋂=，所以AD ⊥平面PDC ，所以AD PC ⊥.(2)由,E F 分别是线段,PC PD 的中点，所以//EF CD ，又ABCD 为正方形，//AB CD ，所以//EF AB ，又EF ⊄平面PAB ，所以//EF 平面PAB .因为,E G 分别是线段,PC BC 的中点，所以//EG PB ，又EG ⊄平面PAB ，所以//EG 平面PAB .因为,,EF EG E EF EG =⊂平面EFG ，所以平面//EFG 平面PAB . 6．（2021·广东江门·高一期末）如图，AB 是圆O 的直径，PA 垂直圆O 所在的平面，C 是圆O 上的点.（1）求证：BC ⊥平面PAC ；（2）设Q 为PA 的中点，G 为AOC △的重心，求证：面//OQG 平面PBC .【分析】（1）根据圆直径的性质，得BC AC ⊥，由PA ⊥平面ABC 得BC PA ⊥，利用线面垂直的判定定理，可证BC ⊥平面PAC ；（2）延长OG ，交AC 于M ，连结GM 、QM ，证出QM 是PAC △的中位线，得//QM PC .利用线面平行的判定定理证出//QM 平面PBC ，同理可得//QO 平面PBC ，根据面面平行的判定定理，可得平面//OQG 平面PBC .【详解】解：（1）∠AB 是圆O 的直径，∠BC AC ⊥，又∠PA ⊥平面ABC ，BC ⊂平面ABC ，∠BC PA ⊥.∠PA AC A =，∠BC ⊥平面PAC ；（2）延长OG ，交AC 于M ，连结GM 、QM ，∠G 为AOC △的重心，∠OM 是AOC △的中线，∠Q 为PA 的中点，M 为AC 的中点，∠//QM PC ，∠QM ⊄平面PBC ，PC ⊂平面PBC ，∠//QM 平面PBC ，同理可得//QO 平面PBC ，∠QM 、QO 是平面OQG 内的相交直线，∠平面//OQG 平面PBC .7．（2021·贵州毕节·高一期末）如图甲，已知在四棱锥P ABCD -中，底面ABCD 为平行四边形，点M ，N ，Q 分别在PA ，BD ，PD 上（1）若:::PM MA BN ND PQ QD ==，求证：平面//MNQ 平面PBC ；（2）如图乙所示，若Q 满足:2PQ QD =，PM tPA =，当t 为何值时，//BM 平面AQC ．【答案】（1）证胆见解析，（2）12t = 【分析】（1）由已知比例式结合平行线截线段成比例证明线线平行，进一步得到线面平行，再由面面平行的判定定理可证得结论；（2）连接AC 交BD 于O ，连接OQ ，取PQ 的中点G ，连接BG ，则可得BG ∠OQ ，可得BG ∠平面AQC ，取PA 的中点M ,连接GM ，则GM ∠AQ ，可得GM ∠平面AQC ，则平面BGM ∠平面AQC ，则BM ∠平面AQC ，可得M 为PA 的中点.【详解】（1）证明：因为::PM MA PQ QD =，所以QM ∠AD ，因为AD ∠BC ，所以QM ∠BC ，因为QM ⊄平面PBC ，BC ⊂平面PBC ，所以QM ∠平面PBC ，因为::BN ND PQ QD =，所以QN ∠PB ，因为QN ⊄平面PBC ，PB ⊂平面PBC ，，所以QN ∠平面PBC ，因为QM QN Q =,QM ⊂平面MNQ ,QN ⊂平面MNQ ，所以平面//MNQ 平面PBC ；（2）连接AC 交BD 于O ，连接OQ ，取PQ 的中点G ，连接BG ，则BG ∠OQ ，因为QO ⊂平面AQC ,BG ⊄平面AQC ，所以BG ∠平面AQC ，取PA 的中点M ,连接GM ，则GM ∠AQ ，因为AQ ⊂平面AQC ，GM ⊄平面AQC ，，所以GM ∠平面AQC ，因为BG GM G ⋂=，所以平面BGM ∠平面AQC ，因为BM ⊂平面BGM ，所以BM ∠平面AQC ，此时M 为PA 的中点，所以12PM PA =，因为PM tPA =，所以12t =题型四：证明线线、线面垂直的方法一、单选题1．（2021·辽宁·辽河油田第一高级中学高一期末）设α，β，γ为不同的平面，m ，n ，l 为不同的直线，则下列条件一定能得到m β⊥的是（） A ．m αγ=，αγ⊥，βγ⊥ B ．αβ⊥，l αβ=，m l ⊥C ．n α⊥，n β⊥，m α⊥D ．αγ⊥，βγ⊥，m α⊥【答案】C【解析】根据排除法，结合线面垂直的判定，可得结果. 【详解】在A 中，因为m αγ=，所以,m m αγ⊂⊂，而,m βγ⊥并不垂直于β内的所有直线，所以β和m 可能不垂直，故A 错误；在B 中，m 只垂直β内的一条直线，所以不能推出m β⊥，故B 错误；在C 中，因为,n n αβ⊥⊥，所以α//β，又m α⊥，所以m β⊥，故C 正确；在D 中，由,αγβγ⊥⊥，不能推出α//β，所以由m α⊥不能推出m β⊥，故D 错误. 故选：C【点睛】本题主要是线面垂直的判定，属基础题.2．（2021·陕西·西安市远东一中高一期末）已知α，β，γ是三个不同的平面，l 是一条直线，则下列说法正确的是（） A ．若αβ⊥，αγ⊥，l βγ=，则l α⊥B ．若αβ⊥，l α⊂，则l β⊥C ．若αβ⊥，βγ⊥，则αγ⊥D ．若αβ⊥，l αβ=，l γ∥，则βγ⊥【答案】A【分析】利用面面垂直的性质，线面的位置关系，面面的位置关系，结合几何模型即可判断.【详解】对于A ，在平面α内取一点P ，在平面α内过P 分别作平面α与β，α与γ的交线的垂线a ,b ，则由面面垂直的性质定理可得,a b βγ⊥⊥，又l βγ=，∠,l a l b ⊥⊥，由线面垂直的判定定理可得l α⊥，故A 正确；对于B ，若αβ⊥，l α⊂，则l 与β位置关系不确定，可能l 与β平行、相交或l 在β内，故B 错误；对于C ，若αβ⊥，βγ⊥，则α与γ相交或平行，故C 错误；对于D ，如图平面,αβγ，且αβ⊥，l αβ=，l γ∥，显然β与γ不垂直，故D 错误. 故选：A.3．（2022·陕西·宝鸡市渭滨区教研室高一期末）在空间中，如果一个角的两边和另一个角的两边分别垂直，则这两个角的大小关系为（） A ．相等 B ．互补 C ．相等或互补 D ．不确定【答案】D【分析】EDF ∠的边DE 垂直平面EOF ，所以DE OE ⊥ ，作EF OF ⊥ 则DF OF ⊥.【详解】如下图所示，EOF ∠确定一个平面，EDF ∠的边DE 垂直平面EOF ，所以DE OE ⊥ ，作EF OF ⊥，因为DE ⊥平面EOF ，而OF ⊂平面EOF ，故DE OF ⊥，而EF DE E ⋂=，故OF ⊥平面EDF ，又DF ⊂平面EDF 中，则DF OF ⊥，对于给定的EOF ∠，当D 变化时，EDF ∠的取值范围为0,2π⎛⎫ ⎪⎝⎭，故EOF ∠的大小跟EDF ∠无关.故选：D 二、填空题4．（2022·宁夏·银川唐徕回民中学高一期末）如图，在直四棱柱1111ABCD A B C D -中，当底面ABCD 满足条件___________时，有111AC B D ⊥.（只需填写一种正确条件即可）【答案】AC BD ⊥(答案不唯一)【分析】直四棱柱1111ABCD A B C D -，11A C 是1A C 在上底面1111D C B A 的投影，当1111AC B D ⊥时，可得111AC B D ⊥，当然底面ABCD 满足的条件也就能写出来了. 【详解】根据直四棱柱1111ABCD A B C D -可得：1BB ∠1DD ，且11BB DD =，所以四边形11BB D D 是矩形，所以BD ∠11B D ，同理可证：AC ∠11A C ，当AC BD ⊥时，可得：1111AC B D ⊥，且1CC ⊥底面1111D C B A ，而11B D ⊂底面1111D C B A ，所以111CC B D ⊥，而1111AC CC C =，从而11B D ⊥平面11A CC ，因为1AC ⊂平面11A CC ，所以111AC B D ⊥，所以当AC BD ⊥满足题意. 故答案为：AC BD ⊥. 三、解答题5．（2021·江苏·南京市第二十九中学高一期末）已知直线//m 平面α，直线l ⊥平面α.求证：l m ⊥. 【分析】过m 作平面β交平面α于直线m '，根据线面平行的性质易知//m m '，再由线面垂直的性质有l ⊥m '，由平行线的性质即可证结论.【详解】证明：如下图，过m 作平面β交平面α于直线m '， ∠//m α，m βα'⋂=， ∠//m m '，∠l ⊥α，而m α'⊂， ∠l ⊥m '，综上，l m ⊥，得证.6．（2021·陕西·西安市远东一中高一期末）如图，在四棱锥P ABCD -中，底面ABCD 为平行四边形，90ADB PDC ∠=∠=︒，平面PAD ⊥底面ABCD ，M 是棱PC 上的点.(1)证明：PD ⊥底面ABCD ；(2)若三棱锥A BDM -的体积是四棱锥P ABCD -体积的14，设PM tMC =，试确定t 的值.【答案】(1)详见解析；(2)1t =.【分析】（1）利用面面垂直的性质定理，可得BD ⊥平面PAD ，然后利用线面垂直的判定定理即证；（2）由题可得14A BDM M ABD P ABCD V V V ---==，进而可得12MC PC =，即得.(1)∠90ADB ∠=︒，平面PAD ⊥底面ABCD ，∠AD BD ⊥，平面PAD 底面ABCD =AD ，BD ⊂底面ABCD ， ∠BD ⊥平面PAD ，PD ⊂平面PAD ， ∠BD ⊥PD ，又90PDC ∠=︒， ∠PD DC ⊥，BD DC D =， ∠PD ⊥底面ABCD ；(2)设PD h =，M 到底面ABCD 的距离为h '，∠三棱锥A BDM -的体积是四棱锥P ABCD -体积的14，∠14A BDM M ABD P ABCD V V V ---==，又11,33M ABD ABDP ABCD ABCDV Sh V Sh --'=⋅=⋅，12ABDABCDSS =，∠12h h '=，故12MC PC =，又PM tMC =，所以1t =.题型五：证明面面垂直的方法一、多选题1．（2021·浙江嘉兴·高一期末）已知,a b 是两条不重合的直线，αβ，是两个不重合的平面，则下列命题为真命题的是（）A ．若//αβ，a 与α所成的角和b 与β所成的角相等，则//a bB ．若a α⊥，a β⊥，则//αβC ．若//a b ，a α⊥，//b β，则αβ⊥D ．若//a α，//αβ，则//a β 【答案】BC【分析】判断命题真假可以直接对各选项逐个判断.对于A 可通过直观想象判断其存在平行或异面或相交几种情况；对于B 可通过直线与平面垂直的性质得到；对于C 通过直线与平面垂直性质和平面与平面垂直的判定定理判断；对于D 可直观想象知存在//a β或a β⊂两种情况.【详解】对于A ，若//αβ，a 与α所成的角和b 与β所成的角相等，则//a b 或a 与b 相交或a 与b 异面，故A 错误；对于B ，若a α⊥，a β⊥，由线面垂直的性质可知//αβ，故B 正确；对于C ，若//a b ，a α⊥，则b α⊥，又因为//b β，则αβ⊥，故C 正确；对于D ，若//a α，//αβ，则//a β或a β⊂，故D 错误. 故选:BC 二、解答题2．（2021·江苏南通·高一期末）如图，在四棱锥P ABCD -中，底面ABCD 是矩形，点E 、F 分别是棱PC 和PD 的中点．（1）求证：//EF 平面P AB（2）若AP AD =，平面PAD ⊥平面ABCD ，证明：平面PAD ⊥平面PCD【分析】（1）根据三角形中位线定理，结合矩形的性质、线面平行的判定定理进行证明即可；（2）根据面面垂直的性质定理、线面垂直的判定定理，结合面面垂直的判定定理进行证明即可. 【详解】（1）证明：因为点E 、F 分别是棱PC 和PD 的中点，所以//EF CD 又在矩形ABCD 中，//AB CD ，所以//EF AB 又AB平面P AB ，EF ⊄平面P AB所以//EF 平面.PAB（2）证明：在矩形ABCD 中，AD CD ⊥，又平面PAD ⊥平面ABCD ，平面PAD 平面ABCD AD =，CD ⊂平面ABCD所以CD ⊥平面P AD ，又AF ⊂平面P AD所以.CD AF ⊥①因为PA AD =且F 是PD 的中点，所以AF PD ⊥，②由①②及PD ⊂平面PCD ，CD ⊂平面PCD ，PD CD D ⋂=所以AF ⊥平面PCD ．又AF ⊂平面P AD ，所以平面PAD ⊥平面PCD ．3．（2021·广东·封开县渔涝中学高一期末）如图，在四棱锥P ﹣ABCD 中，底面ABCD 是边长为3的正方形，AP =PD =APD ∠平面ABCD ，E 为AP 的中点，F 为CD 的中点．（1）求证：EF ∠平面PBC ；（2）求证：平面APB ∠平面PCD ．【分析】（1）根据三角形中位线定理，结合平行四边形的判定定理和性质、线面平行的判定定理进行证明即可；（2）根据勾股定理的逆定理，结合线面垂直的判定定理、面面垂直的判定定理进行证明即可. 【详解】（1）设PB 的中点为G ，连接,EG FG ，因为E 为AP 的中点，所以//EG AB 且12EG AB =，因为F 为CD 的中点，底面ABCD 是正方形，所以//FC AB 且12FC AB =，因此//FC EG 且FC EG =，所以四边形EGCF 是平行四边形，因此//EF GC ，因为EF ⊄平面PBC ，GC ⊂平面PBC ，所以EF ∠平面PBC ；（2）因为底面ABCD 是边长为3的正方形，所以3AD =，因为AP =PD = 所以有222AD PA PD =+，因此PD PA ⊥，因为底面ABCD 是正方形，所以BA DA ⊥，因为平面APD ∠平面ABCD ，平面APD平面ABCD AD =，所以AB ⊥平面APD ，因为PD ⊂平面APD ，所以AB PD ⊥，因为AB PA A ⋂=，,AB PA ⊂平面APB ，所以PD ⊥平面APB ，因为PD ⊂平面APD ，所以平面APB ∠平面PCD .4．（2021·江苏扬州·高一期末）正方体1111ABCD A B C D -中，E 为棱1DD 中点.（1）求证：1//BD 平面AEC ；（2）求证：平面1⊥B AC 平面11B BDD .【分析】（1）由线面平行的判定定理可证得结果；（2）证得AC ⊥平面11BDD B ，进而由面面垂直的判定定理可证得结果.【详解】（1）设AC 与BD 交于点O ，连结OE .因为1111ABCD A B C D -是正方体，所以ABCD 为正方形，O 为BD 中点.又因为E 为1DD 中点，所以1//OE BD .又因为OE ⊂平面1,AEC BD ⊄平面AEC ，所以1//BD 平面AEC .（2）因为1111ABCD A B C D -是正方体，1BB ⊥平面ABCD .又AC ⊂平面ABCD ，所以1AC BB ⊥.又ABCD 为正方形，所以AC BD ⊥.因为11,,AC BD AC BB BB ⊥⊥⊂平面11,BDD B BD ⊂平面111,BDD B BB BD B ⋂=，所以AC ⊥平面11BDD B .又因为AC ⊂平面1B AC ，所以平面1⊥B AC 平面11B BDD .5．（2021·山东枣庄·高一期末）如图，AB 是圆O 的直径，点C 是圆O 上异于A ，B 的点，直线PC ⊥平面ABC ，E ，F 分别是线段PA ，PC 的中点．（1）证明：平面BEF ⊥平面PBC ；（2）记平面BEF 与平面ABC 的交线为l ，试判断直线EF 与直线l 的位置关系，并说明理由．【答案】（1）证明见解析；（2）//EF l ，理由见解析.【分析】（1）推导出AC PC ⊥，AC BC ⊥，AC ⊥平面PBC ，从而//EF AC ，进而EF ⊥平面PBC ，由此能证明平面BEF ⊥平面PBC ．（2）推导出//EF AC ，//EF 平面ABC ，根据线面平行的性质，即能证明//EF l ．【详解】解：（1）因为PC ⊥平面ABC ，AC ⊂平面ABC ，所以AC PC ⊥.因为C 是以AB 为直径的圆O 上的点，所以AC BC ⊥．又PC BC C ⋂=，所以AC ⊥平面PBC ．因为E ，F 分别是PA ，PC 的中点，所以//EF AC ．所以EF ⊥平面PBC ．又EF ⊂平面BEF ，故平面BEF ⊥平面PBC ．。

必修2-2.2线面平行面面平行的经典7道证明题

D CA 1A For personal use only in study and research; not for commercial use必修2 —2.2线面平行、面面平行的证明经典练习1.直三棱柱111C B A ABC -中，D 是AB 的中点，证明：1BC //平面1ACD 2.如图，在四棱锥ABCD P -中，平面PAD ⊥平面ABCD ，AB=AD ，∠BAD=60°，E 、F 分别是AP 、AD 的中点。

求证：直线EF ∥平面PCD ；3.4.5.如图，在四棱锥P —ABCD中，底面ABCD 是正方形，侧棱PD⊥底面ABCD ，PD=DC ，E 是PC 的中点，作EF ⊥PB 交PB 于点F 。

证明PA//平面EDB ；6.正三棱柱111C B A ABC -的底面边长是2，侧棱长是3，D 是AC 的中点。

求证：//1C B 平面BD A 1；7.两个边长均为3的正方形ABCD 和ABEF 所在平面垂直相交于AB ，,AC M∈FB N ∈,且FN AM =.（1）证明：//MN 平面BCE ；仅供个人用于学习、研究；不得用于商业用途。

For personal use only in study and research; not for commercial use.Nur für den persönlichen für Studien, Forschung, zu kommerziellen Zwecken verwendet werden.Pour l 'étude et la recherche uniquement à des fins personnelles; pas à des fins commerciales.толькодля людей, которые используются для обучения, исследований и не должны использоваться в коммерческих целях.以下无正文。

空间垂直平行证明练习题

空间垂直平行证明练习题一、线线垂直证明1. 在空间直角坐标系中，已知直线l通过点A(1,2,3)且方向向量是向量a=(2,0,1)，直线m通过点B(0,1,4)且方向向量是向量b=(1,2,1)。

证明直线l与直线m垂直。

2. 已知平面α上的两条相交直线AB和CD，且AB垂直于CD。

若直线EF平行于AB，证明EF垂直于CD。

3. 在正方体ABCDA1B1C1D1中，证明对角线AC1垂直于面对角线BD。

二、线面垂直证明1. 已知平面α的法向量是向量n=(3,4,5)，直线l通过点P(1,2,3)且方向向量是向量m=(2,3,1)。

证明直线l垂直于平面α。

2. 在空间直角坐标系中，直线l的方程为x=2，y=3，z=4。

平面α的方程为3x4y+5z=6。

证明直线l垂直于平面α。

3. 已知四棱锥PABCD，底面ABCD为矩形，且PA垂直于底面ABCD。

证明侧面PBC垂直于底面ABCD。

三、面面垂直证明1. 已知平面α的法向量是向量n1=(1,2,3)，平面β的法向量是向量n2=(2,1,4)。

证明平面α与平面β垂直。

2. 在正方体ABCDA1B1C1D1中，证明平面ABB1A1垂直于平面BCC1B1。

3. 已知三棱锥PABC，底面ABC为等边三角形，且PA垂直于底面ABC。

证明侧面PAB垂直于侧面PBC。

四、线线平行证明1. 在空间直角坐标系中，直线l的方程为x=2t，y=3t，z=4t，直线m的方程为x=2t+1，y=3t2，z=4t+3。

证明直线l与直线m平行。

2. 已知平面α上的两条直线AB和CD，且AB平行于CD。

若直线EF平行于AB，证明EF平行于CD。

3. 在长方体ABCDA1B1C1D1中，证明对角线AC平行于对角线A1D1。

五、线面平行证明1. 已知平面α的方程为2x3y+4z=5，直线l的方程为x=2t+1，y=3t2，z=4t+3。

证明直线l平行于平面α。

2. 在空间直角坐标系中，直线l通过点A(1,2,3)且方向向量是向量a=(2,4,6)，平面α的方程为2x4y+6z=8。

线面平行证明经典练习题

线面平行证明经典练习题1、在底面为平行四边形的四棱锥P-ABCD中，点E是PD的中点。

证明：连接AE和PC，由于底面ABCD为平行四边形，所以AE和PC平行。

又因为PE=ED，所以三角形PED 为等腰三角形，所以PE和CD平行。

因此，PB//平面AEC成立。

2、在四棱锥P-ABCD中，底面ABCD是矩形，M、N分别是AB、PC的中点。

证明：连接PN和AD，由于底面ABCD为矩形，所以PN和AD平行。

又因为MN=NA=ND，所以三角形MND为等腰三角形，所以MN和PD平行。

因此，MN//平面PAD成立。

3、在三棱柱ABC-A1B1C1中，D是AC的中点。

证明：连接DB1和BC，由于三棱柱ABC-A1B1C1的底面为等边三角形ABC，所以AB1和BC平行。

又因为D是AC的中点，所以DB1和BC平行。

因此，AB1//平面DBC1成立。

4、在正方体ABCD-A1B1C1D1中，O是底面ABCD对角线的交点。

证明：连接C1O和AD1，由于O为对角线的交点，所以C1O和AD1平行。

又因为底面ABCD为正方形，所以AC1和BD1平行。

因此，C1O//平面AD1B1成立。

5、已知棱柱ABC-A1B1C1的底面为正三角形，D是AC的中点。

证明：连接A1B1和DC，由于底面为正三角形，所以AB1和DC平行。

又因为D是AC的中点，所以AB1和A1C1平行。

因此，AB1//平面DBC1成立。

6、正四棱锥S-ABCD中，E是侧棱SC的中点。

证明：连接SE和BD，由于E是侧棱SC的中点，所以SE和BD平行。

又因为三角形SBD和SCE共顶点S，所以它们在S处的角相等。

因此，直线SA//平面BDE成立。

7、已知四棱锥P-ABCD中，底面ABCD是矩形，E、F分别是AB、PD的中点。

证明：连接AF和PC，由于底面ABCD是矩形，所以AF和PC平行。

又因为PE=ED，所以三角形PED为等腰三角形，所以PE和CD平行。

因此，AF//平面PEC成立。

直线与平面的平行垂直判定经典例题

一、教学目标1. 巩固直线与平面的平行、垂直判定二、上课内容1、回顾上节课内容2、直线与平面的平行、垂直判定知识点回顾3、经典例题讲解4、课堂练习三、课后作业见课后练习一、上节课知识点回顾1．平面的基本性质公理1：如果一条直线上的两点在一个平面内.那么这条直线在此平面内． 2．直线与直线的位置关系(1)位置关系的分类⎩⎪⎨⎪⎧共面直线⎩⎪⎨⎪⎧平行相交异面直线：不同在任何一个平面内3．直线与平面平行的判定与性质4.二、直线与平面平行、垂直的判定知识点回顾1．直线与平面垂直(1)判定直线和平面垂直的方法①定义法．②利用判定定理：一条直线和一个平面内的两条相交直线都垂直.则该直线和此平面垂直．③推论：如果在两条平行直线中.有一条垂直于一个平面.那么另一条直线也垂直这个平面．(2)直线和平面垂直的性质①直线垂直于平面.则垂直于平面内任意直线．②垂直于同一个平面的两条直线平行．③垂直于同一条直线的两平面平行．2．斜线和平面所成的角斜线和它在平面内的射影所成的锐角.叫斜线和平面所成的角．3．平面与平面垂直(1)平面与平面垂直的判定方法①定义法．②利用判定定理：一个平面过另一个平面的垂线.则这两个平面垂直．(2)平面与平面垂直的性质两平面垂直.则一个平面内垂直于交线的直线垂直于另一个平面．4．二面角的有关概念(1)二面角：从一条直线出发的两个半平面所组成的图形叫做二面角．(2)二面角的平面角：二面角棱上的一点.在两个半平面内分别作与棱垂直的射线.则两射线所成的角叫做二面角的平面角．[难点正本疑点清源]1．两个平面垂直的性质定理两个平面垂直的性质定理.即如果两个平面垂直.那么在一个平面内垂直于它们交线的直线垂直于另一个平面是作点到平面距离的依据.要过平面外一点P作平面的垂线.通常是先作(找)一个过点P并且和α垂直的平面β.设β∩α＝l.在β内作直线a⊥l.则a⊥α.2．两平面垂直的判定(1)两个平面所成的二面角是直角；(2)一个平面经过另一平面的垂线．方法与技巧1．证明线面垂直的方法(1)线面垂直的定义：a 与α内任何直线都垂直⇒a ⊥α； (2)判定定理1：⎭⎪⎬⎪⎫m 、n ⊂α，m ∩n ＝A l ⊥m ，l ⊥n⇒l ⊥α；(3)判定定理2：a ∥b .a ⊥α⇒b ⊥α； (4)面面平行的性质：α∥β.a ⊥α⇒a ⊥β；(5)面面垂直的性质：α⊥β.α∩β＝l .a ⊂α.a ⊥l ⇒a ⊥β. 2．证明线线垂直的方法(1)定义：两条直线所成的角为90°； (2)平面几何中证明线线垂直的方法； (3)线面垂直的性质：a ⊥α.b ⊂α⇒a ⊥b ； (4)线面垂直的性质：a ⊥α.b ∥α⇒a ⊥b . 3．证明面面垂直的方法(1)利用定义：两个平面相交.所成的二面角是直二面角； (2)判定定理：a ⊂α.a ⊥β⇒α⊥β. 4．转化思想：垂直关系的转化在证明两平面垂直时一般先从现有的直线中寻找平面的垂线.若这样的直线图中不存在.则可通过作辅助线来解决．失误与防范1．在解决直线与平面垂直的问题过程中.要注意直线与平面垂直定义、判定定理和性质定理的联合交替使用.即注意线线垂直和线面垂直的互相转化．2．面面垂直的性质定理是作辅助线的一个重要依据．我们要作一个平面的一条垂线.通常是先找这个平面的一个垂面.在这个垂面中.作交线的垂线即可．三、经典例题讲解（一）直线与平面垂直的判定与性质例1：如图所示.在四棱锥P—ABCD中.PA⊥底面ABCD.AB⊥AD.AC⊥CD.∠ABC＝60°.PA＝AB＝BC.E是PC的中点．证明：(1)CD⊥AE；(2)PD⊥平面ABE.（二）平面与平面垂直的判定与性质例2：如图.在直三棱柱ABC－A1B1C1中.A1B1＝A1C1.D.E分别是棱1上的点(点D不同于点C).且AD⊥DE.F为B1C1的中点．求证：(1)平面ADE⊥平面BCC1B1；(2)直线A1F∥平面ADE.（三）线面、面面垂直的综合应用例3：如图所示.在四棱锥P—ABCD中.平面PAD⊥平面ABCD.AB∥DC.△PAD是等边三角形.已知BD＝2AD＝8.AB＝2DC＝4 5.(1)设M是PC上的一点.求证：平面MBD⊥平面PAD；(2)求四棱锥P—ABCD的体积．（四）线面角、二面角的求法例4：如图.在四棱锥P—ABCD中.PA⊥底面ABCD.AB⊥AD.AC⊥CD.∠ABC＝60°.PA＝AB＝BC.E是PC的中点．(1)求PB和平面PAD所成的角的大小；(2)证明AE⊥平面PCD；(3)求二面角A—PD—C的正弦值．四、课堂练习选择题：1、如图.四棱锥S －ABCD 的底面为正方形.SD ⊥底面ABCD .则下列结论中不正．．确的是 ( )A ．AC ⊥SB B ．AB ∥平面SCDC ．SA 与平面SBD 所成的角等于SC 与平面SBD 所成的角 D ．AB 与SC 所成的角等于DC 与SA 所成的角2、正方体ABCD －A 1B 1C 1D 1中.BB 1与平面ACD 1所成角的余弦值为 ( )A.23B.33C.23D.633、已知l .m 是不同的两条直线.α.β是不重合的两个平面.则下列命题中为真命题的是( )A ．若l ⊥α.α⊥β.则l ∥βB ．若l ∥α.α⊥β.则l ∥βC ．若l ⊥m .α∥β.m ⊂β.则l ⊥αD ．若l ⊥α.α∥β.m ⊂β.则l ⊥m4、已知矩形ABCD .AB ＝1.BC ＝ 2.将△ABD 沿矩形的对角线BD 所在的直线进行翻折.在翻折过程中 ( )A ．存在某个位置.使得直线AC 与直线BD 垂直B ．存在某个位置.使得直线AB 与直线CD 垂直C ．存在某个位置.使得直线AD 与直线BC 垂直D．对任意位置.三对直线“AC与BD”.“AB与CD”.“AD与BC”均不垂直填空题：1．在正四棱锥P—ABCD中.PA＝32AB.M是BC的中点.G是△PAD的重心.则在平面PAD中经过G点且与直线PM垂直的直线有________条．2．已知a、b、l表示三条不同的直线.α、β、γ表示三个不同的平面.有下列四个命题：①若α∩β＝a.β∩γ＝b.且a∥b.则α∥γ；②若a、b相交.且都在α、β外.a∥α.a∥β.b∥α.b∥β.则α∥β；③若α⊥β.α∩β＝a.b⊂β.a⊥b.则b⊥α；④若a⊂α.b⊂α.l⊥a.l⊥b.l⊄α.则l⊥α.其中正确命题的序号是________．解答题：1、(1)如图所示.证明命题“a是平面π内的一条直线.b是π外的一条直线(b不垂直于π).c是直线b在π上的投影.若a⊥b.则a⊥c”为真；(2)写出上述命题的逆命题.并判断其真假(不需证明)．2、如图所示.已知长方体ABCD —A 1B 1C 1D 1的底面ABCD 为正方形.E 为线段AD 1的中点.F 为线段BD 1的中点. (1)求证：EF ∥平面ABCD ；(2)设M 为线段C 1C 的中点.当D 1DAD 的比值为多少时.DF ⊥平面D 1MB ？并说明理由．3、如图.在三棱柱ABC —A 1B 1C 1中.AA 1⊥BC .∠A 1AC ＝60°.A 1A ＝AC ＝BC ＝1.A 1B ＝ 2.(1)求证：平面A 1BC ⊥平面ACC 1A 1； (2)如果D 为AB 中点.求证：BC 1∥平面A 1CD .五、课后练习1、已知三棱锥S－ABC中.底面ABC为边长等于2的等边三角形.SA垂直于底面ABC.SA＝3.那么直线AB与平面SBC所成角的正弦值为( )A.34B.54C.74D.342、已知P为△ABC所在平面外一点.且PA、PB、PC两两垂直.则下列命题：①PA⊥BC；②PB⊥AC；③PC⊥AB；④AB⊥BC.其中正确的个数是________．3、如图.在四棱锥P－ABCD中.平面PAD⊥平面ABCD.AB＝AD.∠BAD ＝60°.E.F分别是AP.AD的中点．求证：(1)直线EF∥平面PCD；(2)平面BEF⊥平面PAD. . .。

线面垂直判定经典证明题

线面垂直判定经典证明题第一篇：线面垂直判定经典证明题线面垂直判定1、已知：如图，PA⊥AB，PA⊥AC。

求证：PA⊥平面ABC。

2、已知：如图，PA⊥AB，BC⊥平面PAC。

求证：PA⊥BC。

3、如图，在三棱锥V-ABC中，VA=VC，AB=BC。

求证：VB⊥AC4、在正方体ABCD-EFGH中，O为底面ABCD中心。

求证：BD⊥平面AEGC5、如图，AB是圆O的直径，PA⊥AC, PA⊥AB,求证：BC⊥平面PAC6、如图，AD⊥BD, AD⊥DC,AD=BD=CD,∠BAC=60°求证：BD⊥平面ADC7、.如图所示，PA⊥矩形ABCD所在平面，M、N分别是AB、PC的中点.(1)求证：MN∥平面PAD.(2)求证：MN⊥CD.(3)若∠PDA＝45°，求证：MN⊥平面PCD.8、已知：如图，P是棱形ABCD所在平面外一点，且PA=PC 求证：AC⊥平面PBD __C9、已知四面体ABCD中，AB=AC,BD=CD,平面ABC⊥平面BCD,E为棱BC的中点。

（1）求证：AE⊥平面BCD;（2）求证：AD⊥BC;BECD10、三棱锥A-BCD中，AB=1，AD=2，求证：AB⊥平面BCD11、在四棱锥S-ABCD中，SD⊥平面ABCD，底面ABCD是正方形求证：AC⊥平面SBD12、如图，正方形ABCD所在平面与三角形CDE所在平面相交于CD，AE⊥平面CDE，求证：AB⊥平面ADE；AED13、三棱锥P-ABC中，三条侧棱PA，PB，PC两两垂直，H是△ABC的垂心求证:PH 底面ABC14、正方体ABCD-A1B1C1D1中，求证：A1C⊥平面BC1D._A_115、S是△ABC所在平面外一点，SA⊥平面ABC,平面SAB⊥平面SBC,求证AB⊥BCSCAB16、如图，直三棱柱ABC—A1B1C1 中，AC ＝BC ＝1，∠ACB ＝90°，AA1 ＝2，D 是A1B1 中点．求证C1D ⊥平面A1B ；第二篇：线面垂直的判定漯河高中2013—2014高一数学必修二导学案2.3.3直线与平面垂直的性质2.3.4平面与平面垂直的性质编制人：魏艳丽方玉辉审核人：高一数学组时间：2013.12.03【课前预习】一、预习导学1、直线与平面垂直的性质定理：_________________________________________.2、垂直于同一条直线的两个平面____________.3、平面与平面垂直的性质定理：_________________________________________.4、如果两个平面互相垂直，那么经过第一个平面内的一点垂直于第二个平面的直线在___________.二、预习检测教材P71、P73【课内探究】［例1］如果两个相交平面都垂直于第三个平面，那么它们的交线垂直于第三个平面.［例2］如图，已知矩形ABCD，过A作SA⊥平面AC，再过A作AE⊥SB交SB于E，过E作EF⊥SC交SC于F.（1）求证：AF⊥SC；（2）若平面AEF交SD于G，求证：AG⊥SD.我主动，我参与，我体验，我成功第1页（共4页）［例3］10、在三棱锥P—ABC中，△PAB是等边三角形，∠PAC=∠PBC=90º.（1）证明：AB⊥PC；（2）若PC=4，且平面PAC⊥平面PBC，求三棱锥P—ABC的体积.［例4］如图所示，在斜三棱柱A1B1C1—ABC中，底面是等腰三角形，AB=AC，侧面BB1C1C⊥底面ABC.（1）若D是BC的中点，求证：AD⊥CC1；（2）过侧面BB1C1C的对角线BC1的平面交侧棱于M，若AM=MA1，求证：截面MBC1⊥侧面BB1C1C；（3）若截面MBC1⊥平面BB1C1C，则AM=MA1吗？请叙述你的判断理由.我主动，我参与，我体验，我成功第2页（共4页）【巩固训练】1．已知两个平面互相垂直，那么下列说法中正确的个数是()①一个平面内的直线必垂直于另一个平面内的无数条直线；②一个平面内垂直于这两个平面交线的直线必垂直于另一个平面内的任意一条直线；③过一个平面内一点垂直于另一个平面的直线，垂足必落在交线上；④过一个平面内的任意一点作交线的垂线，则此直线必垂直于另一个平面． A．4B．3C．2D．1()()2．在圆柱的一个底面上任取一点(该点不在底面圆周上)，过该点作另一底面的垂线，则这条垂线与圆柱的母线所在直线的位置关系是A．相交B．平行C．异面D．相交或平行3．若m、n表示直线，α表示平面，则下列命题中，正确命题的个数为m∥n⎫m⊥α⎫⎪⎪⎬⎬⇒m∥n；①⇒n⊥α；②⎪⎪m⊥α⎭n⊥α⎭m⊥α⎫m∥α⎫⎪⎪⎬⎬⇒n⊥α.③⇒m⊥n;④⎪⎪n∥α⎭m⊥n⎭A．4B．3C．2D．1D．重心oo4．在△ABC所在的平面α外有一点P，且PA＝PB＝PC，则P在α内的射影是△ABC的()A．垂心B．外心C．内心5.如图所示，平面α⊥平面β，A∈α，B∈β，AB与两平面α、β所成的角分别为45和30.过A、B分别作两平面交线的垂线，垂足分别为A′、B′，则AB∶A′B′等于()A．3∶1B．2∶1C．3∶2D．4∶36．设α－l－β是直二面角，直线a⊂α，直线b⊂β，a，b与l都不垂直，那么()A．a与b可能垂直，但不可能平行B．a与b不可能垂直，但可能平行 C．a与b可能垂直，也可能平行 D．a与b不可能垂直，也不可能平行7．若α⊥β，α∩β＝AB，a∥α，a⊥AB，则a与β的关系为________．8．直线a和b在正方体ABCD－A1B1C1D1的两个不同平面内，使a∥b成立的条件是________．①a和b垂直于正方体的同一个面；②a和b在正方体两个相对的面内，且共面；③a和b平行于同一条棱；④a和b在正方体的两个面内，且与正方体的同一条棱垂直．9.如图，在三棱锥P－ABC中，PA⊥平面ABC，平面PAB⊥平面PBC.我主动，我参与，我体验，我成功第3页（共4页）求证：BC⊥AB.10.如图所示，在正方体ABCD—A1B1C1D1中，M是AB上一点，N是A1C的中点，MN⊥平面A1DC.求证：(1)MN∥AD1；(2)M是AB的中点．11．如图所示，在多面体P—ABCD中，平面PAD⊥平面ABCD，AB∥DC，△PAD是等边三角形，已知BD＝2AD＝8，AB＝2DC＝4(1)设M是PC上的一点，求证：平面M BD⊥平面PAD；(2)求四棱锥P—ABCD的体积．※12．如图，直三棱柱ABC－A1B1C1中，AC＝BC＝1，D是棱AA12的中点，DC1⊥BD.(1)证明：DC1⊥BC；(2)求二面角A1－BD－C1的大小．我主动，我参与，我体验，我成功第4页（共4页）第三篇：线面垂直的判定1（模版）深圳市第二课堂文化教育徐老师***直线与平面垂直的判定1．一条直线和三角形的两边同时垂直，则这条直线和三角形的第三边的位置关系是（）A．平行B．垂直C．相交不垂直D．不确定2．直线a与b垂直，b⊥平面α，则a与平面α的位置关系是()A．a∥αB．a⊥αC．a⊂αD．a⊂α或a∥α3．已知m，n为两条不同的直线，α，β为两个不同的平面，则下列命题中正确的是（）A ．m⊂α,n⊂α,m//β,n//β⇒α//βB．α//β,m⊂α,n⊂β⇒m//nC．m⊥α,m⊥n⇒n//αD． m//n,n⊥α⇒m⊥α4．已知两条直线m,n，两个平面α,β，给出下面四个命题：①m//n,m⊥α⇒n⊥α②α//β,m⊂α,n⊂β⇒m//n③m//n,m//α⇒n//α④α//β,m//n,m⊥α⇒n⊥β其中正确命题的序号是（）A．①③B．②④C．①④D．②③5．已知正三棱柱ABC－A1B1C1的侧棱长与底面边长相等，则AB1与侧面ACC1A1所成角的正弦等于（）A．BC．D26．如图，已知正三棱柱ABC-A1B1C1的所有棱长都相等，D是A1C1的中点，则直线AD 与平面B1DC所成角的正弦值为.7．如图，在正三棱柱ABC-A1B1C1中，侧棱长为2，底面三角形的边长为1，则BC1与侧面ACC1A1所成的角是．（第6题图）（第7题图）8．已知∆ABC所在平面外一点P到∆ABC三顶点的距离都相等，则点P在平面ABC内的射影是∆ABC的。

第二章线面平行与垂直判定证明习题

• 高考重在考查数学中普遍运用的常规方法，侧重通性通法，适当淡化技巧；不要为解题而解题，要学会举一反三；由一题带动多题，要从不同角度思考问题，当不满足已有的解法时，从其他角度考虑，这种做法对解决难题尤其有好处．解题时，弄清各概念之间的包含关系，理清定理的来龙去脉，从条件、结论和使用范围上去比较容易混淆的各个定理，从内涵和外延上比较容易混淆的各个概念，注重化归、转化思想，掌握常见的化归转化方法，如：立几问题向平面问题转化，符号语言、文字语言、图形语言的相互转化等；注重模型化方法和整体考虑问题、处理问题的方法，如有时把形体纳入不同的几何背景之中，从而宏观上把握形体，巧妙地解决问题．要把握常见图形及常见题型，关注新题型的考查，比如：存在性问题、与代数结合的最值问题等等．对于一些特殊的技巧要能理解并灵活运用，比如求线面角时，可能转化为斜线段外端点到平面的距离与斜线段的长度的比得线面角的正弦值；距离问题可以用等体积法转化，用这种方法能简化作图、证明与计算的过程．
•
• • • •
• •
点到面的距离可直接向面作垂线，但要考虑垂足的位置，如果垂足的位置不可确定，往往采取由点向面上某一条线作垂线，再证明此垂足即为面的垂足。
1.在正方体中，与正方体的一条对角线垂直的各面的对角线的条数是。
• 2.如图，ABCD为正方形，SA垂直ABCD所在的平面，过A
且垂直SC的平面分别交SB，SC，SD于E，F，G。求证：
中，AB=AD=1，
• 7.S是△ABC所在平面外一点，SA⊥平面ABC, 平面SAB⊥平面SBC,求证AB⊥BC.
S
A
C B
• 8.如图，在四棱锥P－ABCD中，平面PAD⊥平面ABCD，AB＝AD， ∠BAD＝60°，E、F分别是AP、AD的中点．求证：(1)直线EF∥平面 PCD；(2)平面BEF⊥平面PAD. •

线面、面面平行、垂直例题

¤学习目旳：以立体几何旳定义、公理和定理为出发点,通过直观感知、操作确认、思辨论证,结识和理解空间中线面平行旳鉴定,掌握直线与平面平行鉴定定理,掌握转化思想“线线平行⇒线面平行”. ¤知识要点:1. 定义:直线和平面没有公共点,则直线和平面平行.2. 鉴定定理:平面外旳一条直线与此平面内旳一条直线平行,则该直线与此平面平行. 符号表达为：,,////a b a b a ααα⊄⊂⇒．图形如右图所示. ¤例题精讲：【例1】已知P 是平行四边形ABCD 所在平面外一点,Ｅ、F 分别为AB 、PD 旳中点,求证:AF ∥平面PEC【例2】在正方体ＡB ＣD -A 1B 1Ｃ１D 1中,E 、Ｆ分别为棱BC 、C 1D １旳中点．求证:EF ∥平面ＢＢ１Ｄ１D.【例３】如图，已知P 是平行四边形ABCD 所在平面外一点,M 、N 分别是AB 、PC 旳中点（1)求证:ＭN //平面PA Ｄ；(２）若4MN BC ==，43PA =,求异面直线PA 与MN 所成旳角旳大小．．¤学习目旳：以立体几何旳定义、公理和定理为出发点,通过直观感知、操作确认、思辨论证,结识和理解空间中面面平行旳鉴定,掌握两个平面平行旳鉴定定理与应用及转化旳思想.¤知识要点:面面平行鉴定定理：如果一种平面内有两条相交直线都平行于另一种平面，那么这两个平面平行.用符号表达为：,,////,//a b ab P a b βββααα⊂⊂=⎫⇒⎬⎭. ¤例题精讲:【例1】如右图，在正方体A ＢC Ｄ—A 1B 1Ｃ1D １中,Ｍ、N 、Ｐ分别是C 1C 、B １Ｃ1、C １Ｄ1旳中点,求证:平面ＭＮP ∥平面A 1B Ｄ.．【例２】已知四棱锥P －A ＢCD 中，底面ABCD 为平行四边形. 点M 、N 、Q 分别在ＰA 、BD 、P Ｄ上，且PM ：ＭＡ=BN ：ND ＝PQ ：ＱD .求证：平面MNQ ∥平面P ＢC .第14讲 §2.２.3 直线与平面平行旳性质¤学习目旳:通过直观感知、操作确认、思辨论证,结识和理解空间中线面平行旳性质,掌握直线和平面平行旳性质定理，灵活运用线面平行旳鉴定定理和性质定理，掌握“线线”“线面”平行旳转化.NM P DCQB A¤知识要点:线面平行旳性质：如果一条直线和一种平面平行，通过这条直线旳平面和这个平面相交，那么这条直线和交线平行. 即：////a a a b b αβαβ⎫⎪⊂⇒⎬⎪=⎭. ¤例题精讲:【例１】通过正方体ABCD -Ａ1B 1C 1D 1旳棱ＢB 1作一平面交平面AA １D 1D 于E 1E ，求证：E 1E ∥Ｂ1B【例2】如右图，平行四边形EFG Ｈ旳分别在空间四边形AB ＣD 各边上,求证:BD ／/平面ＥＦG Ｈ.第１5讲 §2.2.4 平面与平面平行旳性质¤学习目旳：通过直观感知、操作确认、思辨论证，结识和理解空间中面面平行旳性质，掌握面面平行旳性质定理,灵活运用面面平行旳鉴定定理和性质定理,掌握“线线”“线面”“面面”平行旳转化. ¤知识要点:1. 面面平行旳性质:如果两个平行平面同步与第三个平面相交，那么它们旳交线平行. 用符号语言表达为：//,,//a b a b αβγαγβ==⇒.2．其他性质:①//,//l l αβαβ⊂⇒； ②//,l l αβαβ⊥⇒⊥；βaαb③夹在平行平面间旳平行线段相等. ¤例题精讲:【例1】如图，设平面α∥平面β，A Ｂ、C Ｄ是两异面直线，M 、N 分别是AB 、CD 旳中点，且A 、Ｃ∈α，B 、D ∈β. 求证：MN ∥α.【例4】如图,已知正方体1111ABCD A B C D -中,面对角线1AB ，1BC 上分别有两点Ｅ、F ，且11B E C F =. 求证：ＥF ∥平面ＡＢCD ．第16讲 §2.３.1 直线与平面垂直旳鉴定¤学习目旳:以立体几何旳定义、公理和定理为出发点，通过直观感知、操作确认、思辨论证,结识和理解空间中线面垂直旳鉴定,掌握直线与平面垂直旳定义，理解直线与平面垂直旳鉴定定理,并会用定义和鉴定定理证明直线与平面垂直旳关系. 掌握线面角旳定义及求解． ¤知识要点:1. 定义:如果直线l 与平面α内旳任意一条直线都垂直，则直线l 与平面α互相垂直,记作l α⊥. l －平面α旳垂线,α－直线l 旳垂面,它们旳唯一公共点P 叫做垂足．（线线垂直→线面垂直）２. 鉴定定理:一条直线与一种平面内旳两条相交直线都垂直,则这条直线与该平面GNMFEEC DBAD 1C 1B 1A 1βαEN MDBCA垂直. 符号语言表达为：若l ⊥m ,l ⊥n ,m ∩n =B ，m α,nα，则l ⊥α３. 斜线和平面所成旳角，简称“线面角”，它是平面旳斜线和它在平面内旳射影旳夹角. 求直线和平面所成旳角,几何法一般先定斜足，再作垂线找射影,然后通过解直角三角形求解，可以简述为“作（作出线面角）→证(证所作为所求)→求（解直角三角形）”. 一般，通过斜线上某个特殊点作出平面旳垂线段,垂足和斜足旳连线是产生线面角旳核心． ¤例题精讲：【例1】四周体ABCD 中，,,AC BD E F =分别为,AD BC 旳中点,且22EF AC =,90BDC ∠=,求证:BD ⊥平面ACD ．【例２】已知ABCD 是矩形，PA ⊥平面ABCD ,2AB =，4PA AD ==，E 为BC 旳中点．（1）求证：DE ⊥平面PAE ；(2）求直线DP 与平面PAE 所成旳角．【例3】三棱锥P ABC -中，PA BC PB AC ⊥⊥，,PO ⊥平面AB Ｃ,垂足为O ,求证：O 为底面△ＡBC 旳垂心.第１7讲 §２．3.2 平面与平面垂直旳鉴定¤学习目旳：通过直观感知、操作确认、思辨论证,结识和理解空间中面面垂直旳鉴BD CAE FG定,掌握二面角和两个平面垂直旳定义，理解平面与平面垂直旳鉴定定理并会用鉴定定理证明平面与平面垂直旳关系，会用所学知识求两平面所成旳二面角旳平面角旳大小.¤知识要点:１. 定义:从一条直线出发旳两个半平面所构成旳图形叫二面角(dihedral a ｎgl ｅ）. 这条直线叫做二面角旳棱,这两个半平面叫做二面角旳面．记作二面角AB αβ－－． (简记P AB Q －－）2. 二面角旳平面角：在二面角l αβ－－旳棱l 上任取一点O ,以点O 为垂足,在半平面,αβ内分别作垂直于棱l 旳射线OA 和OB ,则射线OA 和OB 构成旳AOB ∠叫做二面角旳平面角．范畴：0180θ︒<<︒.3. 定义:两个平面相交,如果它们所成旳二面角是直二面角,就说这两个平面互相垂直. 记作αβ⊥.4. 鉴定:一种平面过另一种平面旳垂线,则这两个平面垂直. (线面垂直→面面垂直) ¤例题精讲:【例1】已知正方形ABC Ｄ旳边长为1，分别取边ＢC 、CD 旳中点E 、F ，连结AE 、ＥＦ、A Ｆ,以A Ｅ、EF 、ＦＡ为折痕，折叠使点B 、C 、D 重叠于一点P ．（1）求证：A Ｐ⊥EF ；(2)求证:平面ＡPE ⊥平面APF .【例2】如图, 在空间四边形A ＢCD 中,,,AB BC CD DA ==,,E F G分别是,,CD DA AC 旳中点，求证:平面BEF ⊥平面BGD .【例３】如图，在正方体1111ABCD A B C D -中，E 是1CC 旳中点，求证：1A BD BED ⊥平面平面．第18讲 §2.３.3 线面、面面垂直旳性质¤学习目旳:通过直观感知、操作确认、思辨论证,结识和理解空间中线面、面面垂直旳有关性质,掌握两个性质定理及定理旳应用. ¤知识要点:１. 线面垂直性质定理:垂直于同一种平面旳两条直线平行． (线面垂直→线线平行) ２．面面垂直性质定理：两个平面垂直，则一种平面内垂直于交线旳直线与另一种平面垂直. 用符号语言表达为:若αβ⊥,l αβ=，a α⊂，a l ⊥,则a β⊥．（面面垂直→线面垂直) ¤例题精讲：【例1】如图，在四棱锥P ABCD -中,底面ABCD 是060DAB ∠=且边长为a 旳菱形，侧面PAD 是等边三角形，且平面PAD 垂直于底面ABCD ． (1）若G 为AD 旳中点,求证：BG ⊥平面PAD ； (2)求证:AD PB ⊥；(３)求二面角A BC P --旳大小．【例２】如图，已知空间四边形ABCD 中,,BC AC AD BD ==，E 是AB 旳中点。

线面平行与垂直的证明题

线面平行与垂直的证明1：如图，在棱长为1的正方体ABCD-A 1B 1C 1D 1中. （1）求证：AC ⊥平面B 1BDD 1；（2）求三棱锥B-ACB 1体积．2：如图，ABCD 是正方形，O 是正方形的中心， PO ⊥底面ABCD ，E 是PC 的中点．求证：（1）PA∥平面BDE ；（2）平面PAC ⊥平面BDE ．3：如图：在底面是直角梯形的四棱锥S —ABCD 中， ∠ABC = 90°，SA ⊥面ABCD ，SA = AB = BC = 1，21=AD ．（Ⅰ）求四棱锥S —ABCD 的体积；（Ⅱ）证明：平面SBC ⊥平面SCD .4：已知多面体ABCDFE 中，四边形ABCD 为矩形，AB ∥EF ，AF ⊥BF ，平面ABEF ⊥平面ABCD ， O 、M 分别为AB 、FC 的中点，且AB = 2，AD = EF = 1. （Ⅰ）求证：AF ⊥平面FBC ；（Ⅱ）求证：OM ∥平面DAF .5：．如图，在四棱锥P-ABCD 中，底面ABCD 是正方形，侧棱PD ⊥底面ABCD ，PD =DC ，E 是P C 的中点，作EF ⊥PB 交PB 于点F ．（1）证明 P A //平面EDB ；（2）证明PB ⊥平面EFD ；D 1C 1B 1A 1CDBA6：已知正方形ABCD 和正方形ABEF 所在的平面相交于AB ，点M ，N 分别在AC 和BF 上，且AM=FN. 求证：MN ‖平面BCE.7：如图，正方体1111D C B A ABCD -中，棱长为a （1）求证：直线//1B A 平面1ACD （2）求证：平面1ACD ⊥平面D BD 1；8：如图，已知△ABC 是正三角形，EA 、CD 都垂直于平面ABC ，且EA=AB=2a,DC=a,F 是BE 的中点，求证：(1) FD ∥平面ABC (2) AF ⊥平面EDB.9：如图，在正方体ABCD-A 1B 1C 1D 1中，E 、F 、G 分别是CB 、CD 、CC 1的中点，（1）求证：平面A B 1D 1∥平面EFG; （2）求证：平面AA 1C ⊥面EFG.10：如图，PC AB N M ABCD PA 、分别是、所在的平面，矩形⊥的中点. （1）求证：PAD MN 平面//；（2）求证：CD MN ⊥；CNMPDCBAP11：如图，棱长为1的正方体ABCD-A 1B 1C 1D 1中，求证：⑴ AC ⊥平面B 1D 1DB;⑵ 求证：BD 1⊥平面ACB 1 ⑶ 求三棱锥B-ACB1体积．12: 四棱锥ABCD 中，底面ABCD 是正方形，O 是正方形ABCD 的中心，PO ⊥底面ABCD ，E 是PC 的中点．求证：（Ⅰ）PA ∥平面BDE ；（Ⅱ）平面PAC ⊥平面BDE .13：在三棱锥S ABC -中，已知点D 、E 、F 分别为棱AC 、SA 、SC 的中点. ①求证：EF ∥平面ABC .②若SA SC =，BA BC =，求证：平面SBD ⊥平面ABC .14：如图, 已知正三角形PAD , 正方形ABCD ,平面PAD ⊥平面ABCD , E 为PD 的中点.（Ⅰ）求证：CD AE ⊥; （Ⅱ）求证：AE ⊥平面PCD .15：四棱锥P ABCD -中，底面ABCD 是矩形，PA ⊥平面ABCD ，M N 、分别是AB PC 、的中点，PA AO a ==．（1）求证：//MN 平面PAD ；（2）求证：平面PMC ⊥平面PCD ．（自己画图）D 1C 11 CDBAB16：如图，在三棱锥P ABC -中，PC ⊥底面ABC ，AB BC ⊥， D 、E 分别是AB 、PB 的中点.（1）求证：DE ∥平面PAC ；（2）求证：AB ⊥PB ；17：如图，在直三棱柱ABC －A 1B 1C 1中，AC ＝BC ＝CC 1＝2，AC ⊥BC ，D 为AB 的中点.(1)求证：AC 1∥平面B 1CD ； (2)求二面角B －B 1C －D 的正弦值.18：已知直角梯形ABCD 中，AB ∥CD ，AB ⊥BC ，AB ＝1，BC ＝2，CD ＝1＋3，过A 作AE ⊥CD ，垂足为E ，G 、F 分别为AD 、CE 的中点，现将△ADE 沿AE 折叠，使DE ⊥EC .(1)求证：BC ⊥平面CDE ； (2)求证：FG ∥平面BCD ； (3)求四棱锥D －ABCE 的体积.ACPB DE。

高考中线线,线面,面面的平行与垂直关系专题

高考中线线,线面,面面的平行与垂直关系专题
直线与直线平行 (1)平行直线与平面平行平面与平面平行直线与直线垂直 (2)垂直直线与平面垂直平面与平面垂直
考向三平行与垂直关系的综合应用【例3】►如图，在四面体ABCD中，CB＝CD，AD⊥BD，点 E、F分别是AB、BD的中点．求证： (1)直线EF∥平面ACD； (2)平面EFC⊥平面BCD. [审题视点] EFC. 第(1)问需证明EF∥AD；第或b⊂α，故A错误；由面面平行的判定定理知，B错误；若α∥β，b∥α，则b∥β或b⊂β，故C 错误．答案 D
4．(2012· 温州模拟)已知m、n为两条不同的直线，α、β为两个不同的平面，则下列命题中正确的是( A．m∥n，m⊥α⇒n⊥α B．α∥β，m⊂α，n⊂β⇒m∥n C．m⊥α，m⊥n⇒n∥α D．m⊂α，n⊂α，m∥β，n∥β⇒α∥β )．
A．l1⊥l2，l2⊥l3⇒l1∥l3 B．l1⊥l2，l2∥l3⇒l1⊥l3 C．l1∥l2∥l3⇒l1，l2，l3共面 D．l1，l2，l3共点⇒l1，l2，l3共面错因实录受平面几何知识限制，未能全面考虑空间中的情况．甲同学：A 乙同学：C 丙同学：D.
3．(2012· 银川质检)在空间中，下列命题正确的是( A．若a∥α，b∥a，则b∥α B．若a∥α，b∥α，a⊂β，b⊂β，则β∥α C．若α∥β，b∥α，则b∥β D．若α∥β，a⊂α，则a∥β
考向三利用向量求二面角【例3】►(2011· 全国新课标)如图，四棱锥PABCD中，底面 ABCD为平行四边形，∠DAB＝60° ，AB＝2AD，PD⊥底面 ABCD. (1)证明：PA⊥BD； (2)若PD＝AD，求二面角APBC的余弦值． [审题视点] 会判断法向量的方向，找准向量夹角与二面角是

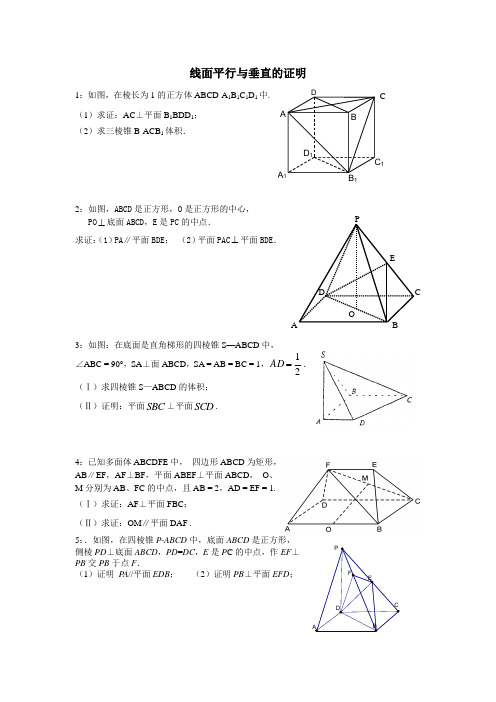
线面平行与垂直的证明题

平行、垂直问题的证明-高考数学大题精做之解答题题型全覆盖高端精品

空间中的平行与垂直例题和知识点总结

线面垂直平行证明解答基础

线面平行、垂直经典练习题汇编

专题06五种直线、平面平行与垂直的判定与性质解题方法(解析版)

直线、平面平行与垂直地判定及其性质(证明题详解)

专题20立体几何中的平行与垂直问题(解析版)

专题06五种直线、平面平行与垂直的判定与性质解题方法(解析版)

必修2-2.2线面平行面面平行的经典7道证明题

空间垂直平行证明练习题

线面平行证明经典练习题

直线与平面的平行垂直判定经典例题

线面垂直判定经典证明题

第二章 线面平行与垂直判定证明 习题

线面、面面平行、垂直例题

线面平行与垂直的证明题

高考中线线,线面,面面的平行与垂直关系专题

第二章线面平行与垂直判定证明习题