初二全等三角形所有知识点总结和常考题提高难题压轴题练习(含答案解析)
八年级数学上册第十二章全等三角形知识点总结归纳(带答案)

八年级数学上册第十二章全等三角形知识点总结归纳单选题1、如图,OD平分∠AOB,DE⊥AO于点E,DE=5,点F是射线OB上的任意一点,则DF的长度不可能是()A.4B.5C.6D.7答案:A分析:根据角平分线的性质,可知点D到OB和OA的距离相等,并且点到直线的线段中,垂线段最短,最短距离为5,即可判断.∵OD平分∠AOB,DE⊥AO于点E,DE=5,∴D到OB的距离等于5,∴DF≥5故DF的长度不可能为4,故选A.小提示:本题考查了角平分线的性质,点到直线的线段中,垂线段最短,熟练掌握性质是本题的关键.2、下列说法正确的是()A.两个面积相等的图形一定是全等图形B.两个全等图形形状一定相同C.两个周长相等的图形一定是全等图形D.两个正三角形一定是全等图形答案:B分析:根据全等图形的定义进行判断即可.解:A:两个面积相等的图形不一定是全等图形,故A错误,不符合题意;B:两个全等图形形状一定相同,故B正确,符合题意;C:两个周长相等的图形不一定是全等图形,故C错误,不符合题意;D:两个正三角形不一定是全等图形,故D错误,不符合题意;故选:B.小提示:本题考查了全等图形,熟练运用“能够完全重合的两个图形叫做全等形”是本题的关键.3、如图,在△ABC中,AD是BC边上的高,∠BAF=∠CAG=90°,AB=AF,AC=AG,连接FG,交DA的延长线于点E,连接BG,CF,则下列结论:①BG=CF;②BG⊥CF;③∠EAF=∠ABC;④EF=EG,其中正确的有()A.①②③B.①②④C.①③④D.①②③④答案:D分析:证得△CAF≌△GAB(SAS),从而推得①正确;利用△CAF≌△GAB及三角形内角和与对顶角,可判断②正确;证明△AFM≌△BAD(AAS),得出FM=AD,∠FAM=∠ABD,则③正确,同理△ANG≌△CDA,得出NG=AD,则FM=NG,证明△FME≌△GNE(AAS).可得出结论④正确.解:∵∠BAF=∠CAG=90°,∴∠BAF+∠BAC=∠CAG+∠BAC,即∠CAF=∠GAB,又∵AB=AF=AC=AG,∴△CAF≌△GAB(SAS),∴BG=CF,故①正确;∵△FAC≌△BAG,∴∠FCA=∠BGA,又∵BC与AG所交的对顶角相等,∴BG与FC所交角等于∠GAC,即等于90°,∴BG⊥CF,故②正确;过点F作FM⊥AE于点M,过点G作GN⊥AE交AE的延长线于点N,∵∠FMA=∠FAB=∠ADB=90°,∴∠FAM+∠BAD=90°,∠FAM+∠AFM=90°,∴∠BAD=∠AFM,又∵AF=AB,∴△AFM≌△BAD(AAS),∴FM=AD,∠FAM=∠ABD,故③正确,同理△ANG≌△CDA,∴NG=AD,∴FM=NG,∵FM⊥AE,NG⊥AE,∴∠FME=∠ENG=90°,∵∠AEF=∠NEG,∴△FME≌△GNE(AAS).∴EF=EG.故④正确.故选:D.小提示:本题综合考查了全等三角形的判定与性质及等腰三角形的三线合一性质与互余、对顶角,三角形内角和等几何基础知识.熟练掌握全等三角形的判定与性质是解题的关键.4、如图,BD是△ABC的角平分线,AE⊥BD,垂足为F,若∠ABC=35°,∠C=50°,则∠CDE的度数为()A .35°B .40°C .45°D .50°答案:C分析:根据角平分线的定义和垂直的定义得到∠ABD =∠EBD =12∠ABC =35°2,∠AFB =∠EFB =90°,推出AB =BE ,根据等腰三角形的性质得到AF =EF ,求得AD =ED ,得到∠DAF =∠DEF ,根据三角形的外角的性质即可得到结论. 解:∵BD 是△ABC 的角平分线,AE ⊥BD ,∴∠ABD =∠EBD =12∠ABC =35°2,∠AFB =∠EFB =90°,∴∠BAF =∠BEF ,∴AB =BE ,AE ⊥BD ,∴BD 是AE 的垂直平分线,∴AD =ED ,∴∠DAF =∠DEF ,∵∠BAC =180°-∠ABC -∠C =95°,∴∠BED =∠BAD =95°,∴∠CDE =95°-50°=45°,故选C .小提示:本题考查了三角形的内角和,全等三角形的判定和性质,三角形的外角的性质,熟练掌握全等三角形的判定和性质是解题的关键.5、如图,△ABC ≌△DEF ,若∠A =80°,∠F =30°,则∠B 的度数是( )A.80°B.70°C.65°D.60°答案:B分析:由△ABC≌△DEF根据全等三角形的性质可得∠C=∠F=30°,再利用三角形内角和进行求解即可.∵△ABC≌△DEF,∴∠C=∠F,∵∠F=30°,∴∠C=30°,∵∠A=80°,∠A+∠B+∠C=180°,∴∠B=180°−∠A−∠C=70°,故选:B.小提示:本题考查了全等三角形的性质及三角形的内角和定理,熟练掌握知识点是解题的关键.6、小明同学只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”他这样做的依据是()A.在角的内部,到角的两边距离相等的点在角的平分线上B.角平分线上的点到这个角两边的距离相等C.三角形的三条高交于一点D.三角形三边的垂直平分线交于一点答案:A分析:过两把直尺的交点P作PF⊥BO与点F,由题意得PE⊥AO,因为是两把完全相同的长方形直尺,可得PE=PF,再根据角的内部到角的两边的距离相等的点在这个角的平分线上可得OP平分∠AOB如图所示:过两把直尺的交点P作PF⊥BO与点F,由题意得PE⊥AO,∵两把完全相同的长方形直尺,∴PE=PF,∴OP平分∠AOB(角的内部到角的两边的距离相等的点在这个角的平分线上),故选A.小提示:本题主要考查了基本作图,关键是掌握角的内部到角的两边的距离相等的点在这个角的平分线上这一判定定理.7、如图,在Rt△ABC中,∠C=90°,∠BAC的平分线交BC于点D,DE//AB,交AC于点E,DF⊥AB于点F,DE=5,DF=3,则下列结论错误的是()A.BF=1B.DC=3C.AE=5D.AC=9答案:A分析:根据角平分线的性质得到CD=DF=3,故B正确;根据平行线的性质及角平分线得到AE=DE=5,故C正确;由此判断D正确;再证明△BDF≌△DEC,求出BF=CD=3,故A错误.解:在Rt△ABC中,∠C=90°,∠BAC的平分线交BC于点D,DF⊥AB,∴CD=DF=3,故B正确;∵DE=5,∴CE=4,∵DE//AB,∴∠ADE=∠DAF,∵∠CAD=∠BAD,∴∠CAD=∠ADE,∴AE=DE=5,故C正确;∴AC=AE+CE=9,故D正确;∵∠B=∠CDE,∠BFD=∠C=90°,CD=DF,∴△BDF≌△DEC,∴BF=CD=3,故A错误;故选:A.小提示:此题考查了角平分线的性质定理,平行线的性质,等边对等角证明角相等,全等三角形的判定及性质,熟记各知识点并综合应用是解题的关键.8、已知图中的两个三角形全等,则∠α等于()A.72∘B.60∘C.58∘D.50∘答案:D分析:根据全等三角形的性质:全等三角形对应角相等,即可得到结论.∵图中的两个三角形全等,∠α为a和c的夹角又∵第一个三角形中a和c的夹角为50°∴∠α=50°故选:D.小提示:本题考查了全等三角形的性质,准确找到对应角是解题的关键.9、下列四个图形中,有两个全等的图形,它们是()A.①和②B.①和③C.②和④D.③和④答案:B分析:根据全等形的概念:能够完全重合的两个图形叫做全等形可得答案.解:①和③可以完全重合,因此全等的图形是①和③.故选:B.小提示:此题主要考查了全等图形,关键是掌握全等图形的概念.AD,BD平分∠ABC,则点D到AB的距离等于( ) 10、如图,在ΔABC中,∠C=90°,AC=8,DC=13A.4B.3C.2D.1答案:C分析:如图,过点D作DE⊥AB于E,根据已知求出CD的长,再根据角平分线的性质进行求解即可.如图,过点D作DE⊥AB于E,∵AC=8,DC=1AD,3∴CD=8×1=2,1+3∵∠C=90°,BD平分∠ABC,∴DE=CD=2,即点D到AB的距离为2,故选C.小提示:本题考查了角平分线的性质,熟练掌握角平分线上的点到角两边的距离相等是解题的关键.填空题11、如图,四边形ABCD中,∠B+∠D=180°,AC平分∠DAB,CM⊥AB于点M,若AM=4cm,BC=2.5cm,则四边形ABCD的周长为_____cm.答案:13分析:过C作CE⊥AD的延长线于点E,由条件可证△AEC≌△AMC,得到AE=AM.证明△ECD≌△MBC,由全等的性质可得DE=MB,BC=CD,则问题可得解.解:如图,过C作CE⊥AD的延长线于点E,∵AC平分∠BAD,∴∠EAC=∠MAC,∵CE⊥AD,CM⊥AB,∴∠AEC=∠AMC=90°,CE=CM,在Rt△AEC和Rt△AMC中,AC=AC,CE=CM,∴Rt△AEC≌Rt△AMC(HL),∴AE=AM=4cm,∵∠ADC+∠B=180°,∠ADC+∠EDC=180°,∴∠EDC=∠MBC,在△EDC和△MBC中,{∠DEC=∠CMB∠EDC=∠MBCCE=CM,∴△EDC≌△MBC(AAS),∴ED=BM,BC=CD=2.5cm,∴四边形ABCD的周长为AB+AD+BC+CD=AM+BM+AE﹣DE+2BC=2AM+2BC=8+5=13(cm),所以答案是:13.小提示:本题考查全等三角形的判定与性质,掌握常用的判定方法是解题的关键.12、把两个全等的三角形重合到一起,重合的顶点叫做_________,重合的边叫做_________,重合的角叫做_________.记两个三角形全等时,通常把表示_________的字母写在对应位置上.答案:对应顶点对应边对应角对应顶点分析:根据能够完全重合的两个图形叫做全等形,以及对应顶点、对应边、对应角的概念填空.解:把两个全等的三角形重合到一起,重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角.记两个三角形全等时,通常把表示对应顶点的字母写在对应位置上.所以答案是:对应顶点;对应边;对应角;对应顶点.小提示:此题主要考查了全等形及相关概念,属于基本概念题,是需要识记的内容.13、如图,在Rt△ABC中,∠C=90°,AC=12cm,BC=6cm,一条线段PQ=AB,P,Q两点分别在AC和过点A且垂直于AC的射线AX上运动,要使△ABC和△QPA全等,则AP=_____.答案:12cm或6cm##6cm或12cm分析:当AP=12cm或6cm时,△ABC和△PQA全等,根据HL定理推出即可.解:∵∠C=90°,AO⊥AC,∴∠C=∠QAP=90°,①当AP=6cm=BC时,在Rt△ACB和Rt△QAP中∵{AB=PQ,BC=AP∴Rt△ACB≌Rt△QAP(HL),②当AP=12cm=AC时,在Rt△ACB和Rt△PAQ中{AB=PQ,AC=AP∴Rt△ACB≌Rt△PAQ(HL),所以答案是:12cm或6cm.小提示:本题考查了全等三角形的判定定理的应用,注意:判定两直角三角形全等的方法有ASA,AAS,SAS,SSS,HL.14、如图,在△ACB中,∠ACB=90°,AC=BC,点C的坐标为(﹣2,0),点B的坐标为(1,5),则A点的坐标是_____.答案:(-7,3)分析:先作辅助线AD ⊥OC 、BE ⊥OC ,通过导角证明∠CAD =∠BCE ,再证明△ADC ≌△CEB , 得到AD 的长度(A 的纵坐标长度)、DC 长度(加上OC 得到A 横坐标长度),根据A 点所在象限的符号,确定A 点坐标. 如图,过点A 作AD ⊥OC 于点D ,过点B 作BE ⊥OC 于点E∵ 点C 的坐标为(-2,0),点B 的坐标为(1,5)∴ OC =2,OE =1,BE =5∵∠ACB =90°∴∠ACD +∠CAD =90°,∠ACD +∠BCE =90°∴∠CAD =∠BCE在△ADC 和△CEB 中,{∠ADC =∠BEC =90°∠CAD =∠BCE AC =BC∴△ADC ≌△CEB(AAS)∴DC =BE =5,AD =CE =1+2=3∴OD =2+5=7∴ A 点的坐标是(-7,3) .小提示:本题考查了全等三角形的证明(在两个三角形中,如果有两组对应角,和其中一组对应角的对边分别相等,那么这两个三角形全等) .15、如图是由九个边长为1的小正方形拼成的大正方形,图中∠1+∠2+∠3+∠4+∠5的度数为______.答案:225°分析:首先判定△ABC≌△AEF,△ABD≌△AEH,可得∠5=∠BCA,∠4=∠BDA,然后可得∠1+∠5=∠1+∠BCA=90°,∠2+∠4=∠2+∠BDA=90°,即可求得∠1+∠2+∠3+∠4+∠5的值.解:如图所示:在△ABC和△AEF中,{AB=AE∠B=∠E=90°BC=EF∴△ABC≌△AEF(SAS),∴∠5=∠BCA,∴∠1+∠5=∠1+∠BCA=90°,在Rt△ABD和Rt△AEH中,{AB=AEAD=AH∴Rt△ABD≌Rt△AEH(HL),∴∠4=∠BDA,∴∠2+∠4=∠2+∠BDA=90°,∵∠3=45°,∴∠1+∠2+∠3+∠4+∠5=90°+90°+45°=225°.所以答案是:225°.小提示:此题主要考查了全等三角形的判定和性质,关键是掌握全等三角形的性质:全等三角形对应角相等即可求解.解答题16、(1)如图,在正方形ABCD中,E、F分别是BC,CD上的点,且∠EAF=45°.直接写出BE、DF、EF之间的数量关系;(2)如图,在四边形ABCD中,AB=AD,∠B=∠D=90°,E、F分别是BC,CD上的点,且∠EAF=1∠BAD,求证:EF=BE+DF;2(3)如图,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,延长BC到点E,延长CD到点F,使得∠BAD,则结论EF=BE+DF是否仍然成立?若成立,请证明;不成立,请写出它们的数量关系并∠EAF=12证明.答案:(1)EF=BE+DF,理由见详解;(2)见详解;(3)结论EF=BE+FD不成立,应当是EF=BE−FD.理由见详解.分析:(1)在CD的延长线上截取DM=BE,连接AM,证出△ABE≌△ADM,根据全等三角形的性质得出BE=DM,再证明△AEF≌△AMF,得EF=FM,进而即可得出答案;(2)在CD的延长线上截取DG=BE,连接AG,证出△ABE≌△ADG,根据全等三角形的性质得出BE=DG,再证明△AEF≌△AGF,得EF=FG,即可得出答案;(3)按照(2)的思路,我们应该通过全等三角形来实现相等线段的转换.就应该在BE上截取BG,使BG=DF,连接AG.根据(2)的证法,我们可得出DF=BG,GE=EF,那么EF=GE=BE−BG=BE−DF.所以(1)的结论在(3)的条件下是不成立的.(1)解:EF=BE+DF,理由如下:延长CD,使DM=BE,连接AM,∵在正方形ABCD中,AB=AD,∠B=∠ADM=90°,∴△ABE≌△ADM,∴∠BAE=∠DAM,AE=AM,∵∠EAF=45°,∴∠BAE+∠DAF=∠DAM+∠DAF =90°-45°=45°,∴∠EAF=∠MAF=45°,又∵AF=AF,AE=AM,∴△AEF≌△AMF,∴EF=MF=MD+DF=BE+DF;(2)在CD的延长线上截取DG=BE,连接AG,如图,∵∠ADF=90°,∠ADF+∠ADG=180°,∴∠ADG=90°,∵∠B=90°,∴∠B=∠ADG=90°,∵BE=DG,AB=AD,∴△ABE≌△ADG(SAS),∴∠BAE=∠DAG,AG=AE,∴∠EAG=∠EAD+∠DAG=∠EAD+∠ABE=∠BAD,∵∠EAF=1∠BAD,2∴∠EAF=1∠EAG,2∴∠EAF=∠FAG,又∵AF=AF,AE=AG,∴△AEF≌△AGF(SAS),∴EF=FG=DF+DG=EB+DF;(3)结论EF=BE+FD不成立,应当是EF=BE−FD.理由如下:如图,在BE上截取BG,使BG=DF,连接AG.∵∠B +∠ADC =180°,∠ADF +∠ADC =180°,∴∠B =∠ADF .∵在△ABG 与△ADF 中,{AB =AD∠ABG =∠ADF BG =DF,∴△ABG ≌△ADF (SAS ).∴∠BAG =∠DAF ,AG =AF .∴∠BAG +∠EAD =∠DAF +∠EAD =∠EAF =12∠BAD =12∠GAF . ∴∠GAE =12∠BAD =∠EAF .∵AE =AE ,AG =AF .∴△AEG ≌△AEF .∴EG =EF ,∵EG =BE −BG∴EF =BE −FD .小提示:本题考查了三角形综合题,三角形全等的判定和性质等知识,解题的关键是学会利用旋转变换的思想添加辅助线,构造全等三角形解决问题,解题时注意一些题目虽然图形发生变化,但是证明思路和方法是类似的,属于中考压轴题.17、(1)如图1,已知△ABC 中,∠BAC =90°,AB =AC ,直线m 经过点A,BD ⊥直线m ,CE ⊥直线m ,垂足分别为点D,E .求证:DE =BD +CE .(2)如图2,将(1)中的条件改为:在△ABC 中,AB =AC,D,A,E 三点都在直线m 上,并且有∠BDA =∠AEC=∠BAC.请写出DE,BD,CE三条线段的数量关系,并说明理由.答案:(1)证明见解析;(2)DE=BD+CE,证明见解析分析:(1)利用已知得出∠CAE=∠ABD,进而利用AAS得出则△ABD≌△CAE,即可得出DE=BD+CE;(2)根据∠BDA=∠AEC=∠BAC,得出∠CAE=∠ABD,在△ADB和△CEA中,根据AAS证出△ADB≌△CEA,从而得出AE=BD,AD=CE,即可证出DE=BD+CE;(1)DE=BD+CE.理由如下:∵BD⊥m,CE⊥m,∴∠BDA=∠AEC=90°又∵∠BAC=90°,∴∠BAD+∠CAE=90°,∠BAD+∠ABD=90°,∴∠CAE=∠ABD在△ABD和△CAE中,{∠ABD=∠CAE∠ADB=∠CEA=90°AB=AC,∴△ABD≌△CAE(AAS)∴BD=AE,AD=CE,∵DE=AD+AE,∴DE=CE+BD;(2)DE=BD+CE,理由如下:∵∠BDA=∠AEC=∠BAC,∴∠DBA +∠BAD =∠BAD +∠CAE ,∴∠CAE =∠ABD ,在△ADB 和△CEA 中,{∠ABD =∠CAE∠ADB =∠CEA AB =AC,∴△ADB ≌△CEA (AAS ),∴AE =BD ,AD =CE ,∴BD +CE =AE +AD =DE ;小提示:本题考查了全等三角形的判定与性质综合中的“一线三等角”模型:判定三角形全等的方法有“SSS ”、“SAS ”、“ASA ”、“AAS ”;全等三角形的对应边相等.也考查了等边三角形的判定与性质.18、如图,在五边形ABCDE 中,AB =CD ,∠ABC =∠BCD ,BE ,CE 分别是∠ABC ,∠BCD 的角平分线.(1)求证:△ABE ≌△DCE ;(2)当∠A =80°,∠ABC =140°,时,∠AED =_________度(直接填空).答案:(1)见解析;(2)100分析:(1)根据∠ABC =∠BCD ,BE ,CE 分别是∠ABC ,∠BCD 的角平分线,可得∠ABE =∠DCE ,∠CBE =∠BCE ,推出BE =CE ,由此利用SAS 证明△ABE ≌△DCE ;(2)根据三角形全等的性质求出∠D 的度数,利用公式求出五边形的内角和,即可得到答案.(1)证明:∵∠ABC =∠BCD ,BE ,CE 分别是∠ABC ,∠BCD 的角平分线,∴∠ABE =∠CBE =12∠ABC ,∠BCE =∠DCE =12∠BCD ,∴∠ABE =∠DCE ,∠CBE =∠BCE ,∴BE=CE,又∵AB=CD,∴△ABE≌△DCE(SAS);(2)∵△ABE≌△DCE,∴∠D=∠A=80°,∵五边形ABCDE的内角和为(5−2)×180°=540°,∴∠AED=540°−80°×2−140°×2=100°,所以答案是:100.小提示:此题考查了全等三角形的判定及性质,多边形内角和计算,正确掌握全等三角形的判定及性质定理是解题的关键.。
(文末带解析)八年级数学全等三角形常考必考知识点总结

(文末带解析)八年级数学全等三角形常考必考知识点总结单选题1、工人师傅常常利用角尺构造全等三角形的方法来平分一个角.如图,在∠AOB的两边OA、OB上分别在取OC=OD,移动角尺,使角尺两边相同的刻度分别与点C、D重合,这时过角尺顶点M的射线OM就是∠AOB的平分线.这里构造全等三角形的依据是()A.SAS B.ASA C.AAS D.SSS2、小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、3、4的四块),你认为将其中的哪一些块带去,就能配一块与原来一样大小的三角形?应该带()A.第1块B.第2块 C.第3块D.第4块3、如图,△ABC和△EDF中,∠B=∠D=90°,∠A=∠E,点B,F,C,D在同一条直线上,再增加一个条件,不能判定△ABC≌△EDF的是( )A.AB=EDB.AC=EFC.AC∥EFD.BF=DC4、如图,AB//DC,AB=DC,要使∠A=∠C,直接利用三角形全等的判定方法是()A.AASB.SASC.ASAD.SSS∠AOB,则OC是∠AOB的平分线③a>b,则5、下列说法:①若AC=BC,则C为AB的中点②若∠AOC=12a2>b2④若a=b,则|a|=|b|,其中正确的有()A.1个B.2个C.3个D.4个6、如图是作ΔABC的作图痕迹,则此作图的已知条件是()A.已知两边及夹角B.已知三边C.已知两角及夹边D.已知两边及一边对角7、作∠AOB平分线的作图过程如下:作法:(1)在OA和OB上分别截取OD、OE,使OD=OE.DE的长为半径作弧,两弧交于点C.(2)分别以D,E为圆心,大于12(3)作射线OC,则OC就是∠AOB的平分线.用下面的三角形全等的判定解释作图原理,最为恰当的是()A.SSS B.SAS C.ASA D.AAS8、如图,△ABC≌△AEF,AB=AE,∠B=∠E,则对于结论:①AC=AF;②∠FAB=∠EAB;③EF=BC;④∠EAB=∠FAC,其中正确结论的个数是()A.1个B.2个C.3个D.4个填空题9、如图,已知AD=AE,请你添加一个条件,使得△ADC≌△AEB,你添加的条件是_____.(不添加任何字母和辅助线)10、如图,在Rt△ABC与Rt△DEF中,∠B=∠E=90°,AC=DF,AB=DE,若∠A=50°,则∠DFE的度数为________.11、如图,△ABC≌△DEF,BE=5,BF=1,则CF=_____.12、如图,AB=12,CA⊥AB于A,DB⊥AB于B,且AC=4m,P点从B向A运动,每分钟走1m,Q点从B向D运动,每分钟走2m,P、Q两点同时出发,运动______分钟后△CAP与△PQB全等.13、如图,在△ABC中,点E在AB上,D为AC的中点,过点C作CF∥AB交ED的延长线于点F.若AB=15cm,CF=10cm,则BE=_____cm.解答题14、如图(1),AB=4cm,AC⊥AB,BD⊥AB,AC=BD=3cm.点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.它们运动的时间为t(s).(1)若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,并判断此时线段PC和线段PQ的位置关系,请分别说明理由;(2)如图(2),将图(1)中的“AC⊥AB,BD⊥AB”为改“∠CAB=∠DBA=60°”,其他条件不变.设点Q的运动速度为xcm/s,是否存在实数x,使得△ACP与△BPQ全等?若存在,求出相应的x、t的值;若不存在,请说明理由.15、如图,在△ABC中,AB=AC,∠BAC=90°,∠1=∠2,CE⊥BD交BD的延长线于点E.求证:BD=2CE.(文末带解析)八年级数学全等三角形_009参考答案1、答案:D解析:根据全等三角形的判定条件判断即可.解:由题意可知OC=OD,MC=MD在△OCM和△ODM中{OC=OD OM=OM MC=MD∴△OCM≅△ODM(SSS)∴∠COM=∠DOM∴OM就是∠AOB的平分线故选:D小提示:本题考查全等三角形的判定及性质、角平分线的判定、熟练掌握全等三角形的判定是关键.2、答案:B解析:本题应先假定选择哪块,再对应三角形全等判定的条件进行验证.解:1、3、4块玻璃不同时具备包括一完整边在内的三个证明全等的要素,所以不能带它们去,只有第2块有完整的两角及夹边,符合ASA,满足题目要求的条件,是符合题意的.故选:B.小提示:本题主要考查三角形全等的判定,看这4块玻璃中哪个包含的条件符合某个判定.判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.3、答案:C解析:根据全等三角形的判定方法即可判断.A. AB=ED,可用ASA判定△ABC≌△EDF;B. AC=EF,可用AAS判定△ABC≌△EDF;C. AC∥EF,不能用AAA判定△ABC≌△EDF,故错误;D. BF=DC,可用AAS判定△ABC≌△EDF;故选C.小提示:此题主要考查全等三角形的判定,解题的关键是熟知全等三角形的判定方法.4、答案:B解析:根据平行线性质得出∠ABD=∠CDB,再加上AB=DC,BD=DB,根据全等三角形的判定定理SAS即可推出△ABD≌△CDB,从而推出∠A=∠C,即可得出答案.∵AB//DC,∴∠ABD=∠CDB,在△ABD和△CDB中,{AB=CD∠ABD=∠CDBBD=BD,∴△ABD≌△CDB(SAS),∴∠A=∠C,故选B.小提示:本题考查了平行线性质、全等三角形的判定与性质的应用,熟练掌握全等三角形的判定与性质定理是解题的关键.5、答案:A解析:根据直线中点、角平分线、有理数大小比较以及绝对值的性质,逐一判定即可.当三点不在同一直线上的时候,点C不是AB的中点,故错误;当OC位于∠AOB的内部时候,此结论成立,故错误;当a、b为负数时,a2<b2,故错误;若a=b,则|a|=|b|,故正确;故选:A.小提示:此题主要考查直线中点、角平分线、有理数大小比较以及绝对值的性质,熟练掌握,即可解题.6、答案:C解析:观察ΔABC的作图痕迹,可得此作图的条件.解:观察ΔABC的作图痕迹,可得此作图的已知条件为:∠α,∠β,及线段AB,故已知条件为:两角及夹边,故选C.小提示:本题主要考查三角形作图及三角形全等的相关知识.7、答案:A解析:根据作图过程可得OD=OE,CE=CD,根据OC为公共边,利用SSS即可证明△OCE≌△OCD,即可得答案.∵分别以D,E为圆心,大于12DE的长为半径作弧,两弧交于点C;∴CE=CD,在△OCE和△OCD中,{OE=OD CD=CE OC=OC,∴△OCE≌△OCD(SSS),故选:A.小提示:本题考查全等三角形的判定,正确找出相等的线段并熟练掌握全等三角形的判定定理是解题关键.8、答案:C解析:根据全等三角形对应边相等,对应角相等,结合图象逐个分析即可.解:∵△ABC≌△AEF,∴AC=AF,EF=BC,∠EAF=∠BAC,故①③正确;∵∠EAF=∠EAB+∠BAF,∠BAC=∠FAC+∠BAF,∴∠EAB=∠FAC,故④正确;条件不足,无法证明∠FAB=∠EAB,故②错误;综上所述,结论正确的是①③④共3个.故选:C.小提示:本题考查了全等三角形的性质,熟记性质并准确识图,准确确定出对应边和对应角是解题的关键.9、答案:AB=AC或∠ADC=∠AEB或∠ABE=∠ACD.解析:根据图形可知证明△ADC≌△AEB已经具备了一个公共角和一对相等边,因此可以利用ASA、SAS、AAS证明两三角形全等.∵∠A=∠A,AD=AE,∴可以添加AB=AC,此时满足SAS;添加条件∠ADC=∠AEB,此时满足ASA;添加条件∠ABE=∠ACD,此时满足AAS,故答案为AB=AC或∠ADC=∠AEB或∠ABE=∠ACD;小提示:本题考查了全等三角形的判定,是一道开放题,解题的关键是牢记全等三角形的判定方法.10、答案:40°解析:先利用HL定理证明Rt△ABC≌Rt△DEF,得出∠D的度数,再根据直角三角形两锐角互余即可得出∠DFE的度数.解:在Rt△ABC与Rt△DEF中,∵∠B=∠E=90°,AC=DF,AB=DE,∴Rt△ABC≌Rt△DEF(HL)∴∠D=∠A=50°,∴∠DFE=90°-∠D=90°-50°=40°.所以答案是:40°.小提示:此题主要考查直角三角形全等的HL定理.理解斜边和一组直角边对应相等的两个直角三角形全等是解题关键.11、答案:3解析:先利用线段和差求EF=BE﹣BF=4,根据全等三角形的性质BC=EF,再结合线段和差求出FC 可得答案.解:∵BE=5,BF=1,∴EF=BE﹣BF=4,∵△ABC≌△DEF,∴BC=EF=4,∴CF=BC﹣BF=4-1=3,所以答案是:3.小提示:本题考查全等三角形的性质,线段和差,解题的关键是根据全等三角形的性质得出BC=EF.12、答案:4解析:分当△CPA≌△PQB时和当△CPA≌△PQB时,两种情况进行讨论,求得BQ和BP的长,分别求得P和Q运动的时间,若时间相同即可,满足全等,若不等,则不能成立.当△CPA≌△PQB时,BP=AC=4(米),则BQ=AP=AB-BP=12-4=8(米),P的运动时间是:4÷1=4(分钟),Q的运动时间是:8÷2=4(分钟),则当t=4分钟时,两个三角形全等;当△CPA≌△QPB时,BQ=AC=4(米),AB=6(米),AP=BP=12则P运动的时间是:6÷1=6(分钟),Q运动的时间是:4÷2=2(分钟),故不能成立.综上,运动4分钟后,△CPA与△PQB全等,所以答案是:4.小提示:本题考查了全等三角形的判定,注意分△CPA≌△PQB和△CPA≌△QPB两种情况讨论是关键.13、答案:5解析:由D为AC的中点可得AD=CD,由CF∥AB可得∠AED=∠F,∠A=∠FCD,根据全等三角形的判定定理AAS证得结论即可.解:∵D为AC的中点∴AD=CD∵CF∥AB∴∠AED=∠F,∠A=∠FCD在△AED和△CFD中{AD=CD∠AED=∠F∠A=∠FCD∴△AED≌△CFD(AAS)∴AE=CF∵AB=15cm,CF=10cm,BE=AB-AE=AB-CF=15-10=5cm所以答案是:5小提示:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL根据具体情况选择恰当的判定方法是解题关键14、答案:(1)全等,理由见详解;PC⊥PQ,理由见解析;(2)存在,{t=1x=1或{t=2x=32.解析:(1)利用SAS 证得△ACP ≌△BPQ ,得出∠ACP=∠BPQ ,进一步得出∠APC+∠BPQ=∠APC+∠ACP=90°得出结论即可;(2)由△ACP ≌△BPQ ,分两种情况:①AC=BP ,AP=BQ ,②AC=BQ ,AP=BP ,建立方程组求得答案即可. 解:(1)当t =1时,AP =BQ =1,BP =AC =3,又∵∠A =∠B =90°,在ΔACP 和ΔBPQ 中,{AP =BQ ∠A =∠B AC =BP∴ΔACP ≅ΔBPQ (SAS ).∴∠ACP =∠BPQ ,∴∠APC +∠BPQ =∠APC +∠ACP =90°.∴∠CPQ =90°,即线段PC 与线段PQ 垂直.(2)①若ΔACP ≅ΔBPC ,则AC =BP ,AP =BQ ,则{3=4−t t =xt, 解得:{t =1x =1; ②若ΔACP ≅ΔBQP ,则AC =BQ ,AP =BP ,则{3=xt t =4−t, 解得:{t =2x =32 ;综上所述,存在{t =1x =1 或{t =2x =32使得ΔACP 与ΔBPQ 全等. 小提示:本题主要考查了全等三角形的判定与性质,两边及其夹角分别对应相等的两个三角形全等.在解题时注意分类讨论思想的运用.15、答案:证明见解析.解析:延长CE 、BA 交于F ,根据角边角定理,证明△BEF ≌△BEC ,进而得到CF=2CE 的关系.再证明∠ACF=∠1,根据角边角定理证明△ACF ≌△ABD ,得到BD=CF ,至此问题得解.证明:分别延长BA ,CE 交于点F.∵BE ⊥CE ,∴∠BEF =∠BEC =90°.又∵∠1=∠2,BE =BE ,∴△BEF ≌△BEC(ASA),∴CE =FE =12CF. ∵∠1+∠F =90°,∠ACF +∠F =90°,∴∠1=∠ACF.又∵AB =AC ,∠BAD =∠CAF =90°,∴△ABD ≌△ACF(ASA),∴BD=CF,∴BD=2CE小提示:本题考查了全等三角形的判定与性质.解题的关键是恰当添加辅助线,构造全等三角形,将所求问题转化为全等三角形内边间的关系来解决.。
专题03 全等三角形的六种模型全梳理(解析版)-2024年常考压轴题攻略(8年级上册人教版)

专题03全等三角形的六种模型全梳理几何探究类问题一直属于考试压轴题范围,在三角形这一章,压轴题主要考查是证明三角形各种模型,或证明线段数量关系等,接来下我们针对其做出详细分析与梳理。
类型一、倍长中线模型目的:①构造出一组全等三角形;②构造出一组平行线。
将分散的条件集中到一个三角形中。
如图1,ABC 中,若86AB AC ==,,求BC 边上的中线小明在组内经过合作交流,得到了如下的解决方法:如图连接BE .请根据小明的方法思考:(1)如图2,由已知和作图能得到ADC EDB ≌△△A .SSS B .SAS C .AAS D .ASA(2)如图2,AD 长的取值范围是.(2)根据全等三角形的性质得到6AC BE ==,由三角形三边关系得到AB BE AE AB BE -<<+,即可求出17AD <<;(3)延长AD 到点M ,使AD DM =,连接BM ,证明ADC MDB △△≌,得到BM AC CAD M =∠=∠,,由AE EF =得到CAD AFE ∠=∠,进而推出BF BM =,即可证明AC BF =.【详解】解:(1)如图2,延长AD 到点E ,使DE AD =,连接BE .∵AD 为BC 的中线,∴BD CD =,又∵AD DE ADC BDE =∠=∠,,∴()SAS ADC EDB ≌△△,故答案为:B ;(2)解:∵ADC EDB ≌△△,∴6AC BE ==,在ABE 中,AB BE AE AB BE -<<+,∴86286AD -<<+,∴17AD <<,故答案为:C ;(3)证明:延长AD 到点M ,使AD DM =,连接BM ,∵AD 是ABC 中线,∴CD BD =,∵在ADC △和MDB △中,DC DB ADC MDB AD HD =⎧⎪∠=∠⎨⎪=⎩,∴()SAS ADC MDB ≌△△,∴BM AC CAD M =∠=∠,,∵AE EF =,(1)如图1,求证:12BF AD =;(2)将DCE △绕C 点旋转到如图2所示的位置,连接,AE BD ,过C 点作CM ⊥①探究AE 和BD 的关系,并说明理由;②连接FC ,求证:F ,C ,M 三点共线.【答案】(1)见解析(2)①,AE BD AE BD =⊥,理由见解析②见解析【分析】(1)证明≌ACD BCE V V ,得到AD BE =,再根据点F 为BE 中点,即可得证;则:AGB CBD BHG ∠=∠+∠=∠∵CBD EAC ∠=∠,∴90BHG ACB ∠=∠=︒,∴AE BD ⊥,综上:,AE BD AE BD =⊥;②延长CF 至点P ,使PF CF =∵F 为BE 中点,∴BF FE =,∴()SAS BFP EFC ≌,∴,BP CE BPF ECF =∠=∠,∴CE BP ,∴180CBP BCE ∠+∠=︒,∵360180BCE ACD ACB DCE ∠+∠=︒-∠-∠=︒,∴CBP ACD ∠=∠,又,CE CD BP AC BC ===,∴()SAS PBC DCA ≌,∴BCP CAD ∠=∠,延长FC 交AD 于点N ,则:18090BCP ACN ACB ∠+∠=︒-∠=︒,∴90CAD ACN ∠+∠=︒,∴90ANC ∠=︒,∴CN AD ⊥,∵CM AD ⊥,∴点,M N 重合,即:F ,C ,M 三点共线.【点睛】本题考查全等三角形的判定和性质,等腰三角形判定和性质.熟练掌握手拉手全等模型,倍长中线法构造全等三角形,是解题的关键.【变式训练1】如图,ABC 中,BD DC AC ==,E 是DC 的中点,求证:2AB AE =.【答案】见解析【分析】利用中线加倍证DEF CEA △≌△(SAS ),可得DF AC BD ==,FDE C ∠=∠,由DC AC =,可得ADC CAD ∠=∠进而可证ADF ADB ∠=∠.,再证ADB ADF △≌△(SAS )即可.【详解】证明:延长AE 到F ,使EF AE =,连结DF ,∵E 是DC 中点,∴DE CE =,∴在DEF 和CEA 中,DE CE DEF CEA EF EA =⎧⎪∠=∠⎨⎪=⎩,∴DEF CEA △≌△(SAS ),∴DF AC BD ==,FDE C ∠=∠,∵DC AC =,∴ADC CAD ∠=∠,又∵ADB C CAD ∠=∠+∠,ADF FDE ADC ∠=∠+∠,∴ADF ADB ∠=∠,在ADB 和ADF △中,AD AD ADB ADF DB DF =⎧⎪∠=∠⎨⎪=⎩,∴ADB ADF △≌△(SAS ),∴2AB AF AE ==.【点睛】本题考查中线加倍构图,三角形全等判定与性质,等腰三角形性质,掌握中线加倍构图,三角形全等判定与性质,等腰三角形性质是解题关键.【变式训练2】(1)如图1,已知ABC 中,AD 是中线,求证:2AB AC AD +>;(2)如图2,在ABC 中,D ,E 是BC 的三等分点,求证:AB AC AD AE +>+;(3)如图3,在ABC 中,D ,E 在边BC 上,且BD CE =.求证:AB AC AD AE +>+.【答案】(1)见解析;(2)见解析;(3)见解析【分析】(1)利用“倍长中线”法,延长AD ,然后通过全等以及三角形的三边关系证明即可;(2)取DE 中点H ,连接AH 并延长至Q 点,使得AH =QH ,连接QE 和QC ,通过“倍长中线”思想全等证明,进而得到AB =CQ ,AD =EQ ,然后结合三角形的三边关系建立不等式证明即可得出结论;(3)同(2)处理方式一样,取DE 中点M ,连接AM 并延长至N 点,使得AM =NM ,连接NE ,CE ,结合“倍长中线”思想证明全等后,结合三角形的三边关系建立不等式证明即可得出结论.【详解】证:(1)如图所示,延长AD 至P 点,使得AD =PD ,连接CP ,∵AD 是△ABC 的中线,∴D 为BC 的中点,BD =CD ,在△ABD 与△PCD 中,BD CD ADB PDC AD PD =⎧⎪∠=∠⎨⎪=⎩∴△ABD ≌△PCD (SAS ),∴AB =CP ,在△APC 中,由三边关系可得AC +PC >AP ,∴2AB AC AD +>;(2)如图所示,取DE 中点H ,连接AH 并延长至Q 点,使得AH =QH ,连接QE 和QC ,∵H 为DE 中点,D 、E 为BC 三等分点,∴DH =EH ,BD =DE =CE ,∴DH =CH ,在△ABH 和△QCH 中,BH CH BHA CHQ AH QH =⎧⎪∠=∠⎨⎪=⎩,∴△ABH ≌△QCH (SAS ),同理可得:△ADH ≌△QEH ,∴AB =CQ ,AD =EQ ,此时,延长AE ,交CQ 于K 点,∵AC +CQ =AC +CK +QK ,AC +CK >AK ,∴AC +CQ >AK +QK ,又∵AK +QK =AE +EK +QK ,EK +QK >QE ,∴AK +QK >AE +QE ,∴AC +CQ >AK +QK >AE +QE ,∵AB =CQ ,AD =EQ ,∴AB AC AD AE +>+;(3)如图所示,取DE 中点M ,连接AM 并延长至N 点,使得AM =NM ,连接NE ,CE ,∵M 为DE 中点,∴DM =EM ,∵BD =CE ,∴BM =CM ,在△ABM 和△NCM 中,BM CM BMA CMN AM NM =⎧⎪∠=∠⎨⎪=⎩∴△ABM ≌△NCM (SAS ),同理可证△ADM ≌△NEM ,∴AB =NC ,AD =NE ,此时,延长AE ,交CN 于T 点,∵AC +CN =AC +CT +NT ,AC +CT >AT ,∴AC +CN >AT +NT ,又∵AT +NT =AE +ET +NT ,ET +NT >NE ,∴AT +NT >AE +NE ,∴AC +CN >AT +NT >AE +NE ,∵AB =NC ,AD =NE ,∴AB AC AD AE +>+.【点睛】本题考查全等三角形证明问题中辅助线的添加,掌握“倍长中线”的基本思想,以及熟练运用三角形的三边关系是解题关键.【答案】(1)1.5 6.5AE <<;(2)见解析;(3)BE DF EF +=,理由见解析【分析】(1)如图①:将ACD △绕着点D 逆时针旋转180 得到EBD △可得BDE ≅ 得出5BE AC ==,然后根据三角形的三边关系求出AE 的取值范围,进而求得AD 范围;(2)如图②:FDC △绕着点D 旋转180︒得到NDB 可得BND CFD ≅ ,得出BN∴1.5 6.5AD <<;故答案为1.5 6.5AD <<;(2)证明:如图②:FDC △绕着点D 旋转180︒得到NDB∴BND CFD ≅ (SAS ),∴BN CF =,DN DF=∵DE DF⊥∴EN EF =,在BNE 中,由三角形的三边关系得:BE BN EN +>,∴BE CF EF +>;(3)BE DF EF +=,理由如下:如图③,将DCF 绕着点C 按逆时针方向旋转100︒∴△DCF ≌△BCH ,∴100CH CF DCB FCH ∠∠=︒=,=∴HBC D DF BH∠∠==,∵180ABC D ∠+∠︒=∴180HBC ABC ∠+∠︒=,∴点A 、B 、H 三点共线∵100FCH ∠=︒,50FCE ∠=︒,∴50ECH ∠=︒∴FCE ECH ∠∠=,在HCE 和FCE △中,===CF CH ECF ECH CE CE ∠∠⎧⎪⎨⎪⎩,∴HCE FCE ≌ (SAS )∴EH EF =,∵BE BH EH DF BH+==,∴BE DF EF +=.【点睛】本题属于三角形综合题,主要考查对全等三角形的性质和判定、三角形的三边关系定理、旋转的性质等知识点,通过旋转得到构造全等三角形是解答本题的关键.类型二、截长补短模型截长补短法使用范围:线段和差的证明(往往需证2次全等)(1)求证:CD BC DE=+;(2)若75B∠=︒,求E∠的度数.【答案】(1)见解析(2)105︒【分析】(1)在CD上截取CF∵CA平分BCD∠,∴BCA FCA∠=∠.在BCAV和FCA△中,⎧⎪∠⎨⎪⎩,∠=︒BAC60【答案】(1)5.8;(2)4.3【分析】(1)由已知条件和辅助线的作法,证得△ACD≌△ECD,得到由于∠A=2∠B,推出∠DEC=2∠B,等量代换得到∠B=∠EDB形,得出AC =CE =3.6,DE =BE =2.2,相加可得BC 的长;(2)在BA 边上取点E ,使BE =BC =2,连接DE ,得到△DEB ≌△DBC (SAS ),在DA 边上取点F ,使DF =DB ,连接FE ,得到△BDE ≌△FDE ,即可推出结论.【详解】解:(1)如图2,在BC 边上取点E ,使EC =AC ,连接DE .在△ACD 与△ECD 中,AC CE ACD ECD CD CD =⎧⎪∠=∠⎨⎪=⎩,∴△ACD ≌△ECD (SAS ),∴AD =DE ,∠A =∠DEC ,∵∠A =2∠B ,∴∠DEC =2∠B ,∴∠B =∠EDB ,∴△BDE 是等腰三角形;∴BE =DE =AD =2.2,AC =EC =3.6,∴BC 的长为5.8;(2)∵△ABC 中,AB =AC ,∠A =20°,∴∠ABC =∠C =80°,∵BD 平分∠B ,∴∠1=∠2=40°,∠BDC =60°,在BA 边上取点E ,使BE =BC =2,连接DE ,在△DEB 和△DBC 中,12BE BC BD BD =⎧⎪∠=∠⎨⎪=⎩,∴△DEB ≌△DBC (SAS ),∴∠BED =∠C =80°,∴∠4=60°,∴∠3=60°,在DA 边上取点F ,使DF =DB ,连接FE ,同理可得△BDE ≌△FDE ,∴∠5=∠1=40°,BE =EF =2,∵∠A =20°,∴∠6=20°,∴AF =EF =2,∵BD =DF =2.3,∴AD =BD +BC =4.3.【点睛】本题考查了全等三角形的性质与判定,等腰三角形的性质,熟悉这些定理是解决本题的关键.类型三、一线三等角模型应用:①通过证明全等实现边角关系的转化,便于解决对应的几何问题;②与函数综合应用中有利于点的坐标的求解。
八年级数学全等三角形综合(含知识点、练习题、答案、作业)

∴ Rt△ ABF ≌ Rt△CDE ( HL ), ∴ BF=DE .
BFG 在△ BFG 和△ DEG 中 BGF
DEG DGE ,
BF DE
∴△ BFG ≌△ DGE( AAS ). ∴ EG=FG . ( 2)( 1)中结论依然成立. 理由如下:∵ AE=CF , ∴ AE ﹣EF=CF ﹣ EF. ∴ AF=CE . ∵ DE ⊥AC , BF⊥ AC , ∴∠ DEG= ∠BFE=90°.
ACG B 45
BGH 与 CGK 均为旋转角,
BGH CGK
B KCG
在 BGH 与 CGK 中, BG CG
BGH
CGK
BGH≌ CGK ASA
BH CK , S BGH S CGK
S四边形 CHGK
S CHG
S CGK
S CHG S BGH
1 S ABC
2
11 44 4
22
( 2) AC
BC 4 , BH x , CH
( 1)在上述旋转过程中, BH 与 CK 有怎样的数量关系,四边形 CHGK的面积有何变化?证明你发现
的结论;
( 2)连接 HK,在上述旋转过程中,设 BH=X, GKH 的面积为 y,求 y 与 x 之间的函数关系式,并
写出自变量 x 的取值范围;
( 3)在( 2)的前提下,是否存在某一位置,使 求出此时 x 的值;若不存在,说明理由.
例 1.1.6 已知:等边 ABC 中,点 O 是边 AC , BC 的垂直平分线的交点, M , N 分别在直线 AC ,
BC 上,且 MON 60 . ( 1)如图 1 ,当 CM CN 时, M , N 分别在边 AC , BC 上时,请写出 AM 、 CN 、 MN 三者之 间的数量关系; ( 2)如图 2,当 CM CN 时, M , N 分别在边 AC , BC 上时,( 1)中的结论是否仍然成 立?若成立,请你加以证明;若不成立,请说明理由;
初二数学 全等三角形压轴几何题知识点总结及答案

初二数学 全等三角形压轴几何题知识点总结及答案一、全等三角形旋转模型1.ABC △和ADE 都是等腰直角三角形,CE 与BD 相交于点,M BD 交AC 于点,N CE 交AD 于点H .试确定线段BD CE 、的关系.并说明理由.解析:BD CE ⊥且BD CE =【分析】由已知条件可证明BAD CAE ≅△△,再根据全等三角形的性质,得到BD CE ∴= ADB AEC ∠=∠,在AEH △中90AEC AHE ∠+∠=︒,又AHE MHD ∠=∠,可得:90HMD ∠=︒,即可证明BD CE ⊥且BD CE =.【详解】解: ABC 和ADE 是直角三角形BAC DAE ∴∠=∠AB AC =AD AE =则BAC CAD DAE CAD ∠+∠=∠+∠即BAD CAE ∠=∠在BAD 与CAE 中AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩S )AS BAD CAE ∴≅(△△BD CE ∴= ADB AEC ∠=∠在AEH △中90AEC AHE ∠+∠=︒又AHE MHD ∠=∠90ADB MHD ∴∠+∠=︒则MHD 中90HMD ∠=︒,即,BD CE ⊥,综上所述,BD CE ⊥且BD CE =.【点睛】本题主要考查三角形全等的判定方法和性质定理和等腰直角三角形的性质,从复杂的图形中找到全等三角形和“8”字形三角形是解题的关键.2.探究问题:(1)方法感悟:如图①,在正方形ABCD中,点E,F分别为DC,BC边上的点,且满足∠BAF=45°,连接EF,求证DE+BF=EF.感悟解题方法,并完成下列填空:将△ADE绕点A顺时针旋转90°得到△ABG,此时AB与AD重合,由旋转可得:AB=AD,BG=DE,∠1=∠2,∠ABG=∠D=90°,∴∠ABG+∠ABF=90°+90°=180°,因此,点G,B,F在同一条直线上.∵∠EAF=45°∴∠2+∠3=∠BAD-∠EAF=90°-45°=45°.∵∠1=∠2,∠1+∠3=45°.即∠GAF=∠________.又AG=AE,AF=AE∴△GAF≌△________.∴ _________=EF,故DE+BF=EF.(2)方法迁移:如图②,将Rt△ABC沿斜边翻折得到△ADC,点E,F分别为DC,BC边上的点,且∠EAF =∠DAB.试猜想DE,BF,EF之间有何数量关系,并证明你的猜想.答案:E解析:(1)EAF、△EAF、GF;(2)DE+BF=EF.【解析】【分析】(1)利用角之间的等量代换得出∠GAF=∠FAE,再利用SAS得出△GAF≌△EAF,得出答案;(2)将△ADE顺时针旋转90°得到△ABG,再证明△AGF≌△AEF,即可得出答案;【详解】解:(1)如图①所示;根据等量代换得出∠GAF=∠FAE,利用SAS得出△GAF≌△EAF,∴GF=EF,故答案为:FAE;△EAF;GF;(2)DE+BF=EF,理由如下:假设∠BAD的度数为m,将△ADE绕点A顺时针旋转,m°得到△ABG,如图,此时AB与AD重合,由旋转可得:AB=AD,BG=DE,∠1=∠2,∠ABG=∠D=90°,∴∠ABG+∠ABF=90°+90°=180°,因此,点G,B,F在同一条直线上.∵,∴.∵∠1=∠2,∴∠1+∠3=.即∠GAF=∠EAF.∵在△AGF和△AEF中,,∴△GAF≌△EAF(SAS).∴GF=EF.又∵GF=BG+BF=DE+BF,∴DE+BF=EF.【点睛】此题主要考查了全等三角形的判定和性质、以及折叠的性质和旋转变换性质等知识,证得△GAF≌△EAF是解题的关键.3.如图,△ABC中,O是△ABC内一点,AO平分∠BAC,连OB,OC.(1)如图1,若∠ACB=2∠ABC,BO平分∠ABC,AC=5,OC=3,则AB=;(2)如图2,若∠CBO+∠ACO=∠BAC=60°,求证:BO平分∠ABC;(3)如图3,在(2)的条件下,若BC=3B绕点O逆时针旋转60°得点D,直接写出CD的最小值为.答案:A解析:(1)8;(2)见解析;(3)33【分析】(1)先补充证明角平分线的性质定理:如图,△ABC中,AD是角平分线,则:BD DC=AB AC .如图1中,延长CO交AB于E,由OA平分∠EAC,推出AEAC=OEOC,推出AEEO=AC OC =53,设AE=5k,OE=3k,利用相似三角形的性质构建方程求出k即可解决问题.(2)如图2中,过点O作EF⊥OA交AB于E,交AC于F,作CG∥EF交AB于G,连接OG.证明△AGO≌△ACO(SAS),推出OG=OC,推出∠OGC=∠OCG,证明O,G,B,C 四点共圆,可得结论.(3)如图3中,以BC为边向上作等边△BCH,连接OH,作HM⊥BC于M.证明△HBO≌△CBD(SAS),推出OH=CD,由(2)可知∠BOC=120°,推出当点O落在HM 上时,OH的值最小.【详解】解:(1)先补充证明角平分线的性质定理:如图,△ABC中,AD是角平分线,则:BD DC=AB AC.理由:过C作CE∥DA,交BA的延长线于E,∵CE∥DA,∴∠1=∠E,∠2=∠3,∠1=∠2,∴∠E=∠3,∴AE=AC,∵BDDC =BAAE,∴BDDC =ABAC.如图1中,延长CO交AB于E,∵OA平分∠EAC,∴AEAC=OEOC,∴AEEO =ACOC=53,设AE=5k,OE=3k,∵OB平分∠ABC,∴OC平分∠ACB,∵∠ACB=2∠ABC,∴∠BCE=12∠ACB=∠EBC,∴EB=EC=3k+3,∵∠ACE=∠ABC,∠CAE=∠BAC,∴△ACE∽△ABC,∴ACAB =AEAC,∴5533k k =55k,解得k=58或﹣1(舍弃),∴AB=8k+3=8.故答案为:8.(2)如图2中,过点O作EF⊥OA交AB于E,交AC于F,作CG∥EF交AB于G,连接OG.∵AO平分∠AEF,∴∠OAE=∠OAF,∵AO=AO,∠AOE=∠AOF=90°,∴△AOE≌△AOF(ASA),∴AE=AF,∵∠EAF=60°,∴△AEF是等边三角形,∴∠AEF=∠AFE=60°=∠FOC+∠FCO,∵∠OBC+∠FCO=60°,∴∠FOC=∠OBC,∵EF∥CG,∴∠AGC=∠AEF=60°,∠ACG=∠AFE=60°,∴∠AGC=∠ACG,∴AG=AC,∵∠GAO=∠CAO,AO=AO,∴△AGO≌△ACO(SAS),∴OG=OC,∴∠OGC=∠OCG,∵∠FOC=∠OCG,∴∠OBC=∠OGC,∴O,G,B,C四点共圆,∴∠ABO=∠OCG,∴∠ABO=∠OBC,∴OB平分ABC.(3)如图3中,以BC为边向上作等边△BCH,连接OH,作HM⊥BC于M.∵△OBD,△BCH都是等边三角形,∴∠HBC=∠OBD=60°,BH=BC,BO=BD,∴∠HBO=∠CBD,∴△HBO≌△CBD(SAS),∴OH=CD,由(2)可知∠BOC=120°,∴当点O落在HM上时,OH的值最小,此时OH=HM﹣OM=33∴CD的最小值为33.故答案为:33【点睛】本题主要考查角平分线、三角形相似的判定和性质、三角形全等的判定和性质、等边三角形等相关知识点,解题关键在于作出辅助线构造相应图形.4.定义:按螺旋式分别延长n边形的n条边至一点,若顺次连接这些点所得的图形与原多边形相似,则称它为原图形的螺旋相似图形.例如:如图1,分别延长多边形A1A2…A n 的边得A1′,A2′,…,A n′,若多边形A1′A2′…A n′与多边形A1A2…An相似,则多边形A1′A2′…A n′就是A1A2…A n的螺旋相似图形.(1)如图2,已知△ABC是等边三角形,作出△ABC的一个螺旋相似图形,简述作法,并给以证明.(2)如图3,已知矩形ABCD,请探索矩形ABCD是否存在螺旋相似图形,若存在,求出此时AB与BC的比值;若不存在,说明理由.(3)如图4,△ABC是等腰直角三角形,AC=BC=2,分别延长CA,AB,BC至A′,B′,C′,使△A′B′C′是△ABC的螺旋相似三角形.若AA′=kAC,请直接写出BB′,CC′的长(用含k的代数式表示)答案:A解析:(1)见解析;(2)AB:BC=1;(3)BB′=2k,CC′=k.【分析】(1)如图2中,延长AB到E,延长BC到F,延长CA到D,使得BE=CF=AD,连接EF,DF,DE.则△DEF是△ABC的一个螺旋相似图形,证明△DEF是等边三角形即可解决问题.(2)如图3中,假设存在.四边形EFGH是矩形ABCD的螺旋相似图形,设AB=CD=a,BC=AD=b,BE=DG=x,CF=AH=y.分两种情形,利用相似三角形的性质以及相似矩形的性质,构建关系式证明a=b即可解决问题.(3)如图4中,作B′T⊥CB交CB的延长线于T.设TB=TB′=m,证明△A′CC′≌△A′TB′(ASA),推出A′C=TC′,CC′=TB′=BT,构建关系式推出m=k即可解决问题.【详解】解:(1)如图2中,延长AB到E,延长BC到F,延长CA到D,使得BE=CF=AD,连接EF,DF,DE.则△DEF是△ABC的一个螺旋相似图形.理由:∵△ABC是等边三角形,∴AB=BC=AC,∠CAB=∠ABC=∠ACB,∴∠DAE=∠FCD=∠EBF=120°,∵BE=CF=AD,∴CD=AE=BF,∴△FCD≌△DAE≌△EBF(SAS),∴DF =DE =EF ,∴△DEF 是等边三角形,∴△DEF ∽△ABC ,∴△DEF 是△ABC 的一个螺旋相似图形.(2)如图3中,假设存在.四边形EFGH 是矩形ABCD 的螺旋相似图形,设AB =CD =a ,BC =AD =b ,BE =DG =x ,CF =AH =y .由题意:△BEF ∽△AHE , ∴EF EH =BE AH =BF AE, ∴x y =b y a x++, 当EF HE =BC AB =b a 时,b a =x y =b y a x++, ∴x =b a•y ,ax +x 2=by +y 2, ∴by +22b a•y 2=by +y 2, ∴a 2=b 2,∴a =b ,即AB :BC =1. 当EF EH =AB BC =a b 时.a b =x y =b y a x ++, ∴x =a b•y ,ax +x 2=by +y 2, ∴2a b •y +22a b•y 2=by +y 2, ∴22a b b -•y (1+y b)=0, ∵y ≠0,1+y b≠0,∴a2=b2,∴a=b,即AB:BC=1,综上所述,AB:BC=1.(3)如图4中,作B′T⊥CB交CB的延长线于T.∵AC=BC=2,∠ACB=90°,∴∠ABC=∠CAB=45°,∴∠TBB′=∠ABC=45°,∴∠TB′B=∠TBB′=45°,∴TB=TB′,设TB=TB′=m,∵△A′B′C′是△ABC的螺旋相似三角形,∴A′C′=B′C′,∠A′C′B′=90°,∵∠A′C′C+∠B′C′=90°,∠A′CC+∠C′A′C=90°,∴∠C′A′C=∠B′C′T,∵∠A′CC′=∠T=90°,∴△A′CC′≌△A′TB′(ASA),∴A′C=TC′,CC′=TB′=BT,∴2+2k=2+2m,∴m=k,∴BB′2k,CC′=k.【点睛】本题属于相似形综合题,考查了等边三角形的性质,矩形的性质,等腰直角三角形的判定和性质等知识,解题的关键是理解题意,学会利用参数解决问题,学会用分类讨论的思想思考问题,属于中考压轴题.5.△CDE和△AOB是两个等腰直角三角形,∠CDE=∠AOB=90°,DC=DE=1,OA=OB=a(a>1).(1)将△CDE的顶点D与点O重合,连接AE,BC,取线段BC的中点M,连接OM.①如图1,若CD,DE分别与OA,OB边重合,则线段OM与AE有怎样的数量关系?请直接写出你的结果;②如图2,若CD在△AOB内部,请你在图2中画出完整图形,判断OM与AE之间的数量关系是否有变化?写出你的猜想,并加以证明;③将△CDE绕点O任意转动,写出OM的取值范围(用含a式子表示);(2)是否存在边长最大的△AOB,使△CDE的三个顶点分别在△AOB的三条边上(都不与顶点重合)?如果存在,请你画出此时的图形,并求出边长a的值;如果不存在,请说明理由.答案:A解析:(1)①OM =12AE ;②OM =12AE ,证明详见解析;③12a -≤OM ≤12a +;(2)5【分析】(1)①利用△CDE ≌△AOB 得出BC =AE ,再由直角三角形斜边的中线等于斜边的一半求解.②作辅助线,利用△COF ≌△EOA 及三角形中位线得出OM =12AE . ③分两种情况,当OC 与OB 重合时OM 最大,当OC 在BO 的延长线上时OM 最小,据此求出OM 的取值范围.(2)分两种情况:当顶点D 在斜边AB 上时,设点C ,点E 分别在OB ,OA 上.由DM +OM ≥OF 求出直角边a 的最大值;当顶点D 在直角边AO 上时,点C ,点E 分别在OB ,AB 上时,利用△EHD ≌△DOC ,得出OD =EH ,在Rt △DHE 中,运用勾股定理ED 2=DH 2+EH 2,得出方程,由△判定出a 的最大值.【详解】解:(1)①∵△CDE 和△AOB 是两个等腰直角三角形,∴CD =ED ,AO =B 0,∠CDE =∠AOB ,在△CDE 和△AOB 中,CD ED CDE AOB AO BO =⎧⎪∠=∠⎨⎪=⎩∴△CDE ≌△AOB (SAS ),∴BC =AE∵M 为BC 中点,∴OM =12BC ,∴OM =12AE . ②猜想:OM =12AE . 证明:如图2,延长BO 到F ,使OF =OB ,连接CF ,∵M 为BC 中点,∴OM =12CF , ∵△CDE 和△AOB 是两个等腰直角三角形,∴CD =ED ,AO =BO =OF ,∠CDE =∠AOB ,∵∠AOC +∠COB =∠BOE +∠COB =90°,∴∠AOC =∠BOE ,∠FOC =∠AOE ,在△COF 和△EOA 中,CD ED FOC AOE OF AO =⎧⎪∠=∠⎨⎪=⎩∴△COF ≌△EOA ,∴CF =AE ,∴OM =12AE . ③Ⅰ、如图3,当OC 与OB 重合时,OM 最大,OM=11122 a a-++=Ⅱ、如图4,当OC在BO的延长线上时,OM最小,OM=12a+﹣1=12a-,所以12a-≤OM≤12a+,(2)解:根据△CDE的对称性,只需分两种情况:①如图5,当顶点D在斜边AB上时,设点C,点E分别在OB,OA上.作OF⊥AB于点F,取CE的中点M,连接OD,MD,OM.∵△AOB和△CDE是等腰直角三角形,∠AOB=∠CDE=90°,OA=OB=a(a>1),DC=DE=1,∴AB =2a ,OF =12AB =22a , ∴CE =2,DM =12CE =22, 在RT △COE 中,OM =12CE =22, 在RT △DOM 中,DM +OM ≥OD ,又∵OD ≥OF , ∵DM +OM ≥OF ,即22+22≥22a , ∴a ≤2,∴直角边a 的最大值为2.②如图6,当顶点D 在直角边AO 上时,点C ,点E 分别在OB ,AB 上,作EH ⊥AO 于点H . ∵∠AOB =∠CDE =∠DHE =90°,∵∠HED +∠EDH =∠CDO +∠EDH =90°,∴∠HED =∠CDO ,∵DC =DE ,在△EHD 和△DOC 中,EHD COD HED CDO DE DC ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△EHD ≌△DOC (AAS )设OD =x ,∴OD =EH =AH =x ,DH =a ﹣2x ,在Rt △DHE 中,ED 2=DH 2+EH 2,∴1=x 2+(a ﹣2x )2,整理得,5x 2﹣4ax +a 2﹣1=0,∵x 是实数,∴△=(4a )2﹣4×5×(a 2﹣1)=20﹣4a 2≥0,∴a 2≤5,∴a 2的最大值为5,∴a的最大值为5.综上所述,a的最大值为5.【点睛】本题主要考查了几何变换综合题及三角形全等的判定和性质,解题的关键是在取最大值时,对三角形的位置进行讨论分别求值.6.已知:在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B、C重合).以AD为边作正方形ADEF,连接CF.(1)如图1,当点D在线段BC上时,请直接写出线段BD与CF的数量关系:;(2)如图2,当点D在线段BC的延长线上时,其它条件不变,若AC=2,CD=1,则CF= ;(3)如图3,当点D在线段BC的反向延长线上时,且点A、F分别在直线BC的两侧,其它条件不变:①请直接写出CF、BC、CD三条线段之间的关系:;②若连接正方形对角线AE、DF,交点为O,连接OC,探究△AOC的形状,并说明理由.答案:B解析:(1)BD=CF;(2)221;(3)①CD=CF+BC,②等腰三角形,见解析【分析】(1)△ABC是等腰直角三角形,利用SAS即可证明△BAD≌△CAF;(2)同(1)相同,利用SAS即可证得△BAD≌△CAF,从而证得BD=CF,即可得到CF=CD+BC,然后求出答案;(3)中的①与(1)相同,可证明BD=CF,又点D、B、C共线,故:CD=BC+CF;②由(1)猜想并证明BD⊥CF,从而可知△FCD为直角三角形,再由正方形的对角线的性质判定△AOC三边的特点,再进一步判定其形状.【详解】解:(1)证明:∵∠BAC=90°,AB=AC,∴∠ABC=∠ACB=45°,∵四边形ADEF是正方形,∴AD=AF,∠DAF=90°,∵∠BAC=∠BAD+∠DAC=90°,∠DAF=∠CAF+∠DAC=90°,∴∠BAD=∠CAF,在△BAD和△CAF中,AB AC BAD CAF AD AF =⎧⎪∠=∠⎨⎪=⎩,∴△BAD ≌△CAF (SAS ),∴BD=CF ,(2)与(1)同理,证△BAD ≌△CAF ;∴BD=CF ,∴CF=BC+CD ,∵AC=AB=2,CD=1,∴BC ==∴CF=1;(3)①BC 、CD 与CF 的关系:CD=BC+CF理由:与(1)同法可证△BAD ≌△CAF ,从而可得:BD=CF ,即:CD=BC+CF②△AOC 是等腰三角形理由:与(1)同法可证△BAD ≌△CAF ,可得:∠DBA=∠FCA ,又∵∠BAC=90°,AB=AC ,∴∠ABC=∠ACB=45°,则∠ABD=180°-45°=135°,∴∠ABD=∠FCA=135°∴∠DCF=135°-45°=90°∴△FCD 为直角三角形.又∵四边形ADEF 是正方形,对角线AE 与DF 相交于点O ,∴OC=12DF , ∴OC=OA ∴△AOC 是等腰三角形.【点睛】本题考查了等腰三角形、正方形的性质及全等三角形的判定与性质等知识点,一般情况下,要证明两条线段相等,就得证明这两条线段所在的两个三角形全等,关键是掌握图形特点挖掘题目所隐含的条件.7.问题提出(1)如图①,在ABC 中,AD 是BC 边上的高,若∠BAD =45°,∠DAC =30°,则ABD ACD S S = .问题探究(2)如图②,在正方形ABCD 中,边长为8,点E 是AB 的中点,作∠EDF =45°,交BC 于点F ,求DEF 的面积.问题解决(3)如图③,某市为迎接城市运动会,打造融体育、文化、饮食、旅游为一体的综合商业品牌,规划了如图所示的矩形ABCD 观光区,如图,在矩形ABCD 中,AB =16km ,AD =12km ,要求在边AB 上确定一点E 为观光区的南门,在边BC 上确定一点F 为观光区的东门,且∠EDF =30°,同时为了方便市民游览,还要修建一条观光通道FG ,使FG ∥AB ,交DE 于点G (观光带的宽度不计),为了节约成本,要使FG 的长度最小,那么是否存在符合条件的修建方案?若存在,请求出FG 的最小值;若不存在,请说明理由.答案:B解析:3(2)803,(3) 323. 【分析】(1)根据∠BAD =45°,∠DAC =30°,求出BD 、AD 、DC 的关系即可;(2)将△DCF 绕点D 顺时针旋转90°得到△DAG ,可证△DEF ≌△DEG ,得到EF =CF +AE ,求出CF 长即可;(3) 作DM ⊥DF ,交BA 延长线于点M ,作EN ⊥DF 于N ,EH ⊥DM 于H ,作△DME 的外接圆⊙O ,连接OD 、OE 、OM ,作OQ ⊥ME 于Q ,求出△DEF 的面积最小值,再用面积求FG 最小值.【详解】解:(1)∵AD 是BC 边上的高,若∠BAD =45°,∠DAC =30°,∴AD =BD ,AD = tan 603DC DC ︒=,12312ABD ACD BD AD SS CD AD ⋅==⋅ (2) 将△DCF 绕点D 顺时针旋转90°得到△DAG ,∵∠DAG =∠C =90°,∠DAE =90°,∴G 、A 、E 三点共线,由旋转可知,∠FDG =∠CDA =90°,DF =DG ,∴∠GDE =∠FDE =45°,DE =DE ,∴△GDE ≌△FDE ,∴GE =EF ,∴EF =AE +CF ,设EF 为x ,则CF =x -4,BF =12-x ,2224(12)x x +-=,解得,x =203, DEF 的面积=DEG 的面积=120808233⨯⨯=;(3)作DM ⊥DF ,交BA 延长线于点M ,作EN ⊥DF 于N ,EH ⊥DM 于H ,作△DME 的外接圆⊙O ,连接OD 、OE 、OM ,作OQ ⊥ME 于Q ,∵∠FDM =∠CDA =90°, ∴∠ADM =∠CDF ,∵∠C =∠DAM =90°,∴△ADM ∽△CDF ,∴34MD AD DF DC ==, ∵∠FDE =30°,∴∠EDM =60°, ∵1sin 302EN DE DE =︒=,3sin 60EH DE DE =︒=, ∴3EH EN =,1432192DEFDME DF EN S S DM EH ⋅==⋅, 设⊙O 的半径为R ,∵∠MDE =60°,∴∠MOE =120°, ∠MOQ =60°,3sin 602R MQ OM =︒=,ME 3R ,OQ =12R , OD +OQ ≥AD , 1122R R +≥,解得,8R ≥,138122DME S ≥⨯⨯⨯,即483DME S ≥,DME S △的最小值为483,DEF S △的最小值为43483649⨯=, 1()62DEF DGF EGF S S S FG CF BF FG =+=+=, FG 的最小值为643263=.【点睛】本题考查了全等三角形的判定与性质,相似三角形的判定与性质,三角形的外接圆,解直角三角形等,解题关键是充分理解题意,恰当的构建全等三角形、相似三角形和外接圆. 8.如图1,在等腰Rt △ABC 中,∠ABC =90°,AB =BC =6,过点B 作BD ⊥AC 交AC 于点D ,点E 、F 分别是线段AB 、BC 上两点,且BE =BF ,连接AF 交BD 于点Q ,过点E 作EH ⊥AF 交AF 于点P ,交AC 于点H .(1)若BF =4,求△ADQ 的面积;(2)求证:CH =2BQ ;(3)如图2,BE =3,连接EF ,将△EBF 绕点B 在平面内任意旋转,取EF 的中点M ,连接AM ,CM ,将线段AM 绕点A 逆时针旋转90°得线段AN ,连接MN 、CN ,过点N 作NR ⊥AC 交AC 于点R .当线段NR 的长最小时,直接写出△CMN 的周长.答案:A解析:(1)1.8;(2)证明见解析;(3)2+. 【分析】 (1)利用等腰直角三角形的性质求出12BD AD CD AC ====积相等和勾股定理分别求出AQ 和QD ,最后利用三角形面积公式即可求解;(2)如图,先作辅助线构造()AEH CFG ASA ∆∆≌,得到AH CG =,再通过转化得到2AH DQ =,最后利用AC ,得到一个相等关系,即()2AH HC BQ QD +=+,利用等式性质即可得到所求;(3)如图,通过做辅助线构造全等三角形确定出当HN ⊥AC ,且N 点位于H 、R 之间时,此时NR 的长最小,接着利用勾股定理和等腰直角三角形的性质,分别求出CM 、MN 、CN 的长,相加即可.【详解】解:6AB BC ==,°90ABC =∠,AC ==∴又∵AC BD ⊥∴BD 平分AC ,且BD 是∠ABC 的角平分线∴12BD AD CD AC ====Q 点到BA 和BC 边的距离相等; ∵4BF =, ∴6342ABQ BFQ S S ∆∆==, ∴32AQ FQ =,∵AF ===∴355AQ AF ==,∴5QD ===,∴1 1.82ADQ S ∆==, ∴△ADQ 的面积为1.8.(2)如图,作CG ⊥AC ,垂足为C ,交AF 的延长线于点G ,∴°90ACG =∠∵°45ACB CAB ==∠∠,∴°45GCB CAB ==∠∠,∵EH ⊥AF ,∴°90EAP AEP +=∠∠,又∵°90EAP AFB +=∠∠∴AEP AFB =∠∠,∴AEP CFG =∠∠∵BE BF =,BA BC =∴AE CF =,在AEH ∆和CFG ∆中,AEH CFG AE CFEAH FCG ∠=∠⎧⎪=⎨⎪∠=∠⎩∴()AEH CFG ASA ∆∆≌∴AH CG =;∵BD ⊥AC ,CG ⊥AC ,∴BD ∥CG ,∵D 点是AC 的中点,且BD ∥CG ,∴DQ 是ACG ∆的中位线, ∴12DQ CG =, ∴2DQ CG AH ==; ∵AC =2BD ,∴()2AH HC BQ QD +=+,∵2AH DQ =,∴CH =2BQ .(3)如图①,作AH ⊥AB ,且AH =AB ,∴∠NAH +∠HAM =∠HAM +∠BAM =90°,∴∠BAM =∠NAH ,∵AB =AH ,AM =AN ,∴()ABM AHN SAS ∆∆≌,∴HN =BM ,∵BE =BF =3,∠EBF =90°, ∴EF ==∴由M 点是EF 的中点,可得122BM EF ==,∴2NH =,∴N 点在以H 点为圆心,2为半径的圆上, 如图②,当HN ⊥AC ,且N 点位于H 、R 之间时,此时NR 的长最小,为2NR HR HN HR =-=-, ∵∠BAC =45°,∴∠HAC =45°,∴∠AHN =45°,HR =AR ,∵222HR AR AH +=,∴HR AR ===,∴22NR HR =-=, ∵AC == ∴CR AC AR =-=∴CN AN === ∵∠MAN =90°,AM =AN ,∴MN ==∴∠ABM =45°,∴∠EBM =45°,∴F 点在BA 上,E 点在CB 延长线上,如图,作MP ⊥EC ,垂足为P ,∴1322BP MP EB ===, ∴315622PC PB BC =+=+=,∴2MC ==∴3263351022MC MN CN ++=++, ∴△CMN 的周长为3263351022++.【点睛】本题综合考查了等腰直角三角形的性质、全等三角形的判定与性质、旋转的性质、勾股定理、圆等知识,要求学生熟练掌握相关概念并能灵活应用它们,本题的综合性较强,难点在于作辅助线构造全等三角形以及线段之间的关系转化等,考查了学生综合分析和推理论证以及计算的能力,本题属于压轴题,蕴含了数形结合和转化的思想方法等.9.在ABC 中,,AB AC BAC α=∠=,点P 为线段CA 延长线上一动点,连接PB ,将线段PB 绕点P 逆时针旋转,旋转角为α,得到线段PD ,连接,DB DC .(1)如图1,当60α=︒时,请直接写出线段PA 与线段CD 的数量关系是__________,DCP ∠为______度;(2)如图2,当120α=︒时,写出线段PA 和线段DC 的数量关系,并说明理由; (3)如图2,在(2)的条件下,当23AB =13BP PC +的最小值.答案:A解析:(1)PA =DC ,60;(2)CD =3PA .理由见详解;(2)3+22【分析】(1)先证明△ABC ,△PBD 是等边三角形,再证明△PBA ≌△DBC ,进而线段PA 与线段CD 的数量关系,利用全等三角形的性质以及三角形内角和等于180°,解决问题即可;(2)证明△CBD ∽△ABP ,可得3CD BC PA AB==,解决问题; (3)过点C 作射线CM ,使得sin ∠ACM =13,过点P 作PN ⊥CM 于点N ,则PN =13PC , 过点B 作BG ⊥BA 于点G ,当点B 、P 、N 共线时,BP +PN 最小,即13BP PC +最小,由BGP CNP ∽,得13GP NP BP CP ==,结合勾股定理求出GP ,从而得CP ,进而即可求解. 【详解】(1)①证明: ∵将线段PB 绕点P 逆时针旋转,旋转角为α,得到线段PD , ∴PB =PD ,∵AB =AC ,PB =PD ,∠BAC =∠BPD =60°,∴△ABC ,△PBD 是等边三角形,∴∠ABC =∠PBD =60°,∴∠PBA =∠DBC ,∵BP =BD ,BA =BC ,∴△PBA ≌△DBC (SAS ),∴PA =DC .设BD 交PC 于点O ,如图1,∵△PBA ≌△DBC ,∴∠BPA =∠BDC ,∵∠BOP =∠COD ,∴∠OBP =∠OCD =60°,即∠DCP =60°.故答案是:PA =DC ,60;(2)解:结论:CD 3.理由如下:∵AB =AC ,PB =PD ,∠BAC =∠BPD =120°,∴BC =2•AB •cos30°,BD ═2BP •cos30°, ∴BC BDBA BP= ∵∠ABC =∠PBD =30°,∴∠ABP =∠CBD ,∴△CBD ∽△ABP ,∴CD BC PA AB== ∴CD; (3) 过点C 作射线CM ,使得sin ∠ACM =13,过点P 作PN ⊥CM 于点N ,则PN =13PC ,过点B 作BG CA ⊥于点G ,则BG =AB ×sin ∠BAG =3,AG = AB ×cos ∠BAG 当点B 、P 、N 共线时,BP +PN 最小,即13BP PC +最小, ∵∠BGP =∠CNP =90°,∠BPG =∠CPN , ∴BGP CNP ∽, ∴13GP NP BP CP ==,设GP =x ,则AP -x ,BP =3x ,∴()22233x x +=,解得:x∴BPAP∴CP =AC +AP∴13BP PC +最小值13+【点睛】本题属于几何变换综合题,考查了全等三角形的判定和性质,相似三角形的判定和性质,解直角三角形等知识,第(1)(2)题解题的关键是正确寻找全等三角形或相似三角形解决问题,第(3)题的关键是过点C 作射线CM ,使得sin ∠ACM =13,过点P 作PN ⊥CM 于点N .10.如图1,在正方形ABCD 中,点,E F 分别在边,AB AD 上,且AE AF =,延长FD 到点G ,使得DG DF =,连接,,EF GE CE .(特例感知)(1)图1中GE 与CE 的数量关系是______________.(结论探索)(2)图2,将图1中的AEF 绕着点A 逆时针旋转()090αα︒<<︒,连接FD 并延长到点G ,使得DC DF =,连接,,GE CE BE ,此时GE 与CE 还存在(1)中的数量关系吗?判断并说明理由.(拓展应用) (3)在(2)的条件下,若5,32AB AE ==EFG 是以EF 为直角边的直角三角形时,请直接写出GE 的长.答案:G解析:(1) GE 2CE ,(2)存在,证明见解析,(3)25810或16或4.【分析】(1)连接GC,证△CDG≌△CBE,得出△GCE为等腰直角三角形即可;(2)类似(1)的方法,先证△AFD≌△AEB,再证△CDG≌△CBE,得出△GCE为等腰直角三角形即可;(3)根据E、F是直角顶点分类讨论,结合(2)中结论,利用勾股定理求解即可.【详解】解:(1)连接GC,∵AE=AF,AD=AB,∴DF=BE,,∵DG DF∴DG = BE,∵∠GDC=∠B=90°,DC=BC,∴△CDG≌△CBE,∴CE=CG,∠GCD=∠ECB,∵∠ECB+∠DCE=90°,∴∠GCE=∠GCD+∠DCE=90°,∴GE=2CE;故答案为:GE=2CE;(2) 存在,连接GC,∵AE=AF,AD=AB,∠FAE=∠DAB=90°,∴∠FAD=∠EAB,∴△FAD≌△EAB,∴FD=EB=GD,∠FDA=∠EBA,∵∠GDC+∠FDA=90°,∠EBC+∠EBA=90°,∴∠GDC=∠EBC,∵DC=BD,∴△CDG≌△CBE,与(1)同理,GE=2CE;(3)当∠FEG=90°时,如图1,因为∠FEA=∠GEC=45°,所以,A、E、C在一条直线上,∵AB=5,∴AC=52,CE=52-32=22,GE=2EC=4;如图2,E在CA延长线上,同理可得,EC2,GE2EC=16;当∠EFG =90°时,如图3,∠AFD =∠EFG +∠AFE =135°,由(2)得,∠AFD =∠AEB =135°,DF =BE ,所以,B 、E 、F 在一条直线上,作AM ⊥EF ,垂足为M , ∵5,32AB AE ==,∴EF =6,AM =ME =MF =3,224BM AB AM =-=,BE =DF =1,FG =2,22210GE FG EF =+=;如图4,同图3,BE =DF =7,FG =14,EF =6,22258GE FG EF =+=,综上,GE 的长为258或210或16或4.【点睛】本题考查了旋转的性质、全等三角形的判定与性质、勾股定理和等腰直角三角形的性质,解题关键是恰当的连接辅助线,构造全等三角形;会分类讨论,结合题目前后联系,解决问题.11.回答下列问题:(1)(发现)如图1,点A 为线段BC 外一动点,且4BC =,2AB =.填空:线段AC 的最大值为 .图1(2)(应用)点A 为线段BC 外一动点,且3BC =,2AB =,如图2所示,分别以AB ,AC 为边,作等腰直角ABD △和等腰直角ACE ,连接CD ,BE .图2①证明:BE DC =.②求线段BE 的最大值.(3)(拓展)如图3,在平面直角坐标系中,直线l ;4y x =+与坐标轴交于点A 、B 两点,点C 为线段AB 外一动点,且2CB =,以AC 为边作等边ACD △,连接BD ,求线段BD 长的最大值并直接写出此时点C 的横坐标.图3答案:A解析:(1)6(2)①证明见解析. ②322+(3)42226-26+ 【分析】(1)根据点A 位于CB 的延长线上时,线段AC 的长取得最大值,即可得到结论;(2) ①由“SAS” 可证△DAC ≌△BAE ,可得BE=DC ;②由于线段长BE 的最大值=线段DC 的最大值,根据(1)中的结论即可得到结果,(3)以BC 为边作等边三角形BCE ,可以证明△ACE ≌△DCB(SAS) ,从而得到BD=AE ,BE=BC ,由AE≤AB+BE ,当且仅当A 、B 、E 三点共线时,AE 取得最大值,即BD 取得最大值,当BD 取得最大值时,①当C 在直线AB 的上方时,过C 作CH ⊥y 轴于H ,作BC 的垂直平分线交BH 于N ,求出CH 的长度,即可求出点C 的横坐标,②当C 在直线AB 的下方时,按同①的方法也可以求出点C 的横坐标.【详解】(1)当A 在选段BC 的延长线上时, max 6AC AB BC =+=.(2)①∵等腰直角AEC 与等腰直角三角形ABD ,∴AD AB =,AE AC =,90DAB EAC ∠=∠=︒,∴DAB BAC EAC BAC ∠+∠=∠+∠,∴DAC EAB ∠=∠,在DAC △和BAE 中,DA BA DAC BAE AB AE =⎧⎪∠=∠⎨⎪=⎩,∴()SAS DAC BAE ≌△△, ∴BE CD =.②由①可知,BE DC =,∵线段BE 的最大值即线段DC 的最大值.在等腰直角ABD △中,222BD AB ==,∵CD BC BD ≤+,∴当点D 在CB 的延长线上时, CD 取得最大值为322+.∴线段BE 的最大值为322+.(3)如图,以BC 为边作等边三角形BCE ,则BC CE =,60BCE ∠=︒.∵60ACD ∠=︒,∴ACD ECD BCE ECD ∠-∠=∠-∠,∴ACE DCB ∠=∠.在ACE 与DCB 中,AC DC ACE DCB CE CB =⎧⎪∠=∠⎨⎪=⎩,∴()SAS ACE DCB ≌△△, ∴BD AE =.对于一次函数4y x =+,令0x =,则4y =,∴()0,4B ,令0y =,则4x =-,∴()4,0A -.∴224442AB =+=又∵2BE BC ==,∴AE AB BE ≤+,∴当且仅当A 、B 、E 三点共线时,AE 取得最大值,即BD 取得最大值为422+;当BD 取得最大值时,①当C 在直线AB 的上方时过C 作CH y ⊥轴于H ,∵45ABO HBE ∠=∠=︒,60CBE ∠=︒,∴15CBH CBE HBE ∠=∠-∠=︒,作BC 的垂直平分线交BH 于N ,∴CN BN =,15NCB NBC ∠=∠=︒,∴30CNB ∠=︒,在Rt CHN △中,设CH x =.则3HN x =,2CN x =,∴2BN x =,∴)32BH HN BN x =+=, 在Rt BHC △中,22222HC BH BC +==,∴)222322x x ⎡⎤+=⎣⎦, 整理得(227434x x ++=, 223x =,)12312x =,)22312x =-(舍), ∴62CH -=2②当C 在直线AB 的下方时,过C 作CL ⊥y 轴于L ,∵∠ABO=45°,∠CBE=60°,∴∠CBL=180°-∠CBE−∠ABO=75°,∴∠BCL=15°,作BC 的垂直平分线交BL 于M ,∴CM=BM ,∠MCB=∠MBC=15°,∴∠LMB=30°,在Rt △CLB 中,设BL=y .则3,BM=2y ,∴CM=2y ,∴3+2)y ,在Rt △BLC 中,BL 2+CL 2=BC 2=22,∴)222322y y ⎡⎤+=⎣⎦, 整理得(227434y y ++=, 223y = )1231y =,)2231y =(舍去), 622BL =∴CL=)32BL 26+2综合以上可得点C 的横坐标为:262-或 262+ 【点睛】 本题是三角形综合题,考查了全等三角形的判.定和性质,等腰直角三角形的性质,最大值问题,旋转的性质正确的作出辅助线构造全等三角形是解题的关键.12.已知等腰三角形底边中点,可以考虑与顶点连接用“三线合一”.请利用上面信息解决以下问题:已知Rt ABC 中,AC BC =,90C ∠=︒,D 为AB 边的中点,90EDF ∠=︒,EDF ∠绕D 点旋转,它的两边分别交AC 、CB (或它们的延长线)于E 、F .(1)当EDF ∠绕D 点旋转到DE AC ⊥于E 时(如图①),求证:12DEF CEF ABC S S S +=△△△; (2)当EDF ∠绕D 点旋转到DE 和AC 不垂直时,在图②和图③这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立,DEF S △、CEF S △、ABCS又有怎样的数量关系?请写出你的猜想,不需要证明.答案:D解析:(1)见解析;(2)图2成立,图3不成立:12DEF CEF ABC S S S -=△△△ 【分析】(1)根据等腰直角三角形和正方形的性质得到AED 、DFB △、EDF 、ECF △为全等的等腰直角三角形,据此即可证明;(2)对于图2:过点D 作DM AC ⊥,DN BC ⊥,根据中位线的性质和等量代换证得MD ND =和MDE NDF ∠=∠,结合90DME DNF ∠=∠=︒,证得DME DNF ∆≅∆,根据全等三角形的性质即可求证;对于图3:根据ASA 证明DME DNF ∆≅∆,根据全等三角形的性质即可求证.【详解】(1)证明:连接CD∵D 为AB 边的中点,AC BC =∴AD=CD=BD∴45DAC DCA DCB DBC ∠=∠=∠=∠=︒又∵DE AC ⊥,90EDF ∠=︒,90C ∠=︒,∴四边形ECFD 为矩形∴∠CFD=90°又∵∠DCF=45°∴CF=DF∴四边形ECFD 是正方形∴DE=DF∴DEF CEF DEC DFC S S S S +=+△△△△又∵12DCF DBF ABC S S S +=△△△,且DCF DBF S S =△△ ∴12DEF CEF ABC S S S +=△△△ (2)图2成立,图3不成立对于图2:过点D 作DM AC ⊥,DN BC ⊥,如图2,则90DME DNF MDN ∠=∠=∠=︒又∵90C ∠=︒∴DM BC ,DN AC∵D 为AB 边的中点 ∴根据中位线定理得到:12DN AC =,12MD BC = ∵AC=BC∴MD=ND∵90EDF ∠=︒∴90MDE EDN ∠+∠=︒,90NDF EDN ∠+∠=︒∴MDE NDF ∠=∠在DME ∆与DNF ∆中DME DNF MD NDMDE NDF ∠=∠⎧⎪=⎨⎪∠=∠⎩∴DME DNF ∆≅∆∴DME DNF S S ∆∆=∴DEF CEF DMCN DECF S S S S ∆∆==+四边形四边形 ∴12DMCN ABC S S =△ ∴12DEF CEF ABC S S S +=△△△ 对于图3:连接DC ,在DEC ∆与DBF ∆中135DCE DBF DC DBCDE BDF ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩∴DEC DBF ∆≅∆∴12DEF CFE DBC CFE ABC DBFEC S S S S S S ∆∆∆∆∆==+=+五边形 ∴12DEF CEF ABC S S S ∆∆∆-=. 【点睛】本题考查了全等三角形的判定和性质,中位线的性质,等腰直角三角形的性质,题目较为综合,利用作出的辅助线将不规则的三角形转化为直角三角形进行解决.13.矩形ABCD 中,6,8AB BC ==,点,M N 分别在边,BC AD 上,且3,2BM DN ==,连接MN 并延长,交CD 的延长线于点E ,点Q 为射线MN 上一动点,过点Q 作AQ 的垂线,交CD 于点P .(1)特例发现,如图,若点P 恰好与点D 重合,填空:①DE =________;②QA 与QP 的等量关系为_________.(2)拓展探究如图,若点Q 在MN 的延长线上,QA 与QP 能否相等?若能,求出DP 的长;若不能,请说明理由.(3)思维延伸如图,点G 是线段CD 上异于点D 一点,连接AG ,过点G 作直线GI AG ⊥,交直线MN 于点I ,是否存在点G ,使,AG GI 相等?若存在,请直接写出DG 的长;若不存在,请说明理由.答案:E解析:(1)①4; ②QA QP =;(2)QA 与QP 能够相等,理由详见解析;(3)(3),AG GI 能够相等,43DG =【分析】(1)①根据END EMC ,利用对应边成比例列式求出ED 长;②过点Q 作//HG BC ,交AB 于点H ,交DC 于点G ,设QG x =,利用AHQ QGD ,对应边成比例列式求出x ,得到这两个三角形其实是全等的,所以QA QP =;(2)过点Q 作QF AB ⊥,交BA 的延长线于点F ,延长FQ 交CE 于点G ,构造“k”字型全等三角形,设AF x =,再利用相似三角形的性质列式求解;(3)过点G 作GK AB ⊥于点K ,过点I 作IS KG ⊥,交KG 的延长线于点S ,延长AD 交IS 于点T ,同(2)构造“k”字型全等三角形,DG y =,再利用相似三角形的性质列式求解.【详解】(1)①∵//ND MC ,∴END EMC ,∴ED ND EC MC=,835MC BC BM =-=-=,6DC =, 265ED ED =+,解得4ED =, 故答案是:4;②如图,过点Q 作//HG BC ,交AB 于点H ,交DC 于点G ,可得HG AB ⊥,HG DC ⊥,∴90AHQ QGD ∠=∠=︒,∵AQ QD ⊥,∴90AQH DQG ∠+∠=︒,∵90QAH AQH ∠+∠=︒,∴QAH DQG ∠=∠,∴AHQ QGD ,∴AH HQ QG GD=, 设QG x =,8HQ x =-, ∵//QG MC ,∴EQG EMC , ∴QG EG MC EC =,4510x DG +=,得24DG x =-, ∴24AH x =-,根据AH HQ QG GD =,得24824x x x x --=-,解得4x =, ∴4AH HQ QG GD ====,∴AHQ QGD ≅,∴AQ QD QP ==,故答案是:QA QP =;(2)QA 与QP 能够相等,163PD =, 如图,过点Q 作QF AB ⊥,交BA 的延长线于点F ,延长FQ 交CE 于点G , 90,90,AQF PQG GPQ PQG AQF GPQ ∠+∠=︒∠+∠=︒∴∠=∠,又90,,,,AFQ PGQ AQ PQ FAQ GDP AF QG FQ PG ∠=∠=︒=∆≅∆∴==, 设AF x =,则,,4QG x DG x EG x ===-,42,2EG ED x QG ND x -==∴=,解得43x =, 经检验,43x =是该分式方程的根,42020204168,,333333FQ PG PD ∴=-=∴==-=;(3),AG GI 能够相等,43DG =, 如图,过点G 作GK AB ⊥于点K ,过点I 作IS KG ⊥,交KG 的延长线于点S ,延长AD 交IS 于点T ,根据“k ”字型全等得,,8AKG GSI AK GS IS KG ∆≅∆∴===, 设DG y =,则,8,2AK TS GS DT y IT y NT y ====∴=-=+,84tan ,22IT ED y INT NT ND y -∠==∴=+,解得43y =,故DG 的长为43.【点睛】本题考查“k ”字型全等三角形,相似三角形的性质和判定,解题的关键是作辅助线构造“k ”字型全等,再利用相似三角形对应边成比例列式求解.14.如图,在四边形ABCD 中,AB AC =,AD 是对角线,60BAC ∠=︒,4B C ADB BAC ∠+∠+∠=∠,(1)求ADC ∠的度数;(2)若AD BD CD =+,求证:AD 平分BDC ∠;(3)在(2)的条件下,E 、F 分别在AC 、AB 上,连接BE 、CF ,交于点P ,使得BPC BDC ∠=∠,若7BD EF ==,15AD =,求EFP ∆的面积答案:A解析:(1)=60∠︒ADC ;(2)证明见详解;(3)4003129. 【分析】(1)先由四边形内角和得到++300B C BDC ∠∠∠=︒,再由4B C ADB BAC ∠+∠+∠=∠可得答案;(2)把ABD △绕点A 逆时针旋转60︒得到ACE △,由(1)及题意易得D 、C 、E 三点共线,从而得到ADE 是等边三角形,由等边三角形的性质及旋转的性质易得60ADB E ∠=∠=︒,故得证;(3)过点B 、点F 分别作BG ⊥CD ,FH ⊥AC ,分别交CD 的延长线于点G 、AC 于点H ,连接BC ,由(2)及题意易得DC=8,由BPC BDC ∠=∠易得EBC FCA ∠=∠,进而得到AFC CEB △≌△,设AF=CE=x ,根据勾股定理得到AF 、CE 、BC 的长,最后根据BFE BPC 、的面积比等于FP 与PC 的比,进而求解即可.【详解】(1)解:=60BAC ∠︒,∴++36060300B C BDC ∠∠∠=︒-︒=︒,又BDC ADB ADC ∠=∠+∠,4B C ADB BAC ∠+∠+∠=∠,∴30024060ADC ∠=︒-︒=︒;(2)证明:把ABD △绕点A 逆时针旋转60︒得到ACE △,由(1)得:∴AD=AE ,BD=CE ,=ADC=60DAE ∠∠︒AD BD CD =+,DE=DC+CE ,∴D 、C 、E 三点共线,。
《常考题》初中八年级数学上册第十二章《全等三角形》知识点总结(含答案解析)

一、选择题1.如图,△ABC ≌△ADE ,AB =AD ,AC =AE ,∠B =28︒,∠E =95︒,∠EAB =20︒,则∠BAD 等于( )A .75︒B .57︒C .55︒D .77︒2.如图,已知16AB AC +=,点O 为ABC ∠与ACB ∠的平分线的交点,且OD BC 于D .若4OD =,则四边形ABOC 的面积是( )A .36B .32C .30D .643.如图O 是ABC 内的一点,且O 到三边AB 、BC 、CA 的距离==OF OD OE .若70A ∠=︒,则BOC ∠( ).A .125°B .135°C .105°D .100° 4.如图,,,AB AD CB CD AC BD ==、相交于点O ,则下列说法中正确的个数是( ) ①OD OB =;②点O 到CB CD 、的距离相等;③BDA BDC ∠=∠;④BD AC ⊥A .4B .3C .2D .15.MAB ∠为锐角,AB a ,点C 在射线AM 上,点B 到射线AM 的距离为d ,BC x =,若△ABC 的形状、大小是唯一确定的,则x 的取值范围是( )A .x d =或x a ≥B .x a ≥C .x d =D .x d =或x a > 6.如图,,AD BC ⊥垂足为,D BF AC ⊥,垂足为,F AD 与BF 交于点,5,2E AD BD DC ===,则AE 的长为( )A .2B .5C .3D .77.下列四个命题中,真命题是( )A .如果 ab =0,那么a =0B .面积相等的三角形是全等三角形C .直角三角形的两个锐角互余D .不是对顶角的两个角不相等8.用三角尺画角平分线:如图,先在AOB ∠的两边分别取OM ON =,再分别过点M ,N 作OA ,OB 的垂线,交点为P .得到OP 平分AOB ∠的依据是( )A .HLB .SSSC .SASD .ASA9.如图,在Rt△ABC中,∠ACB=90°,BC=5cm,在AC上取一点E,使EC=BC,过点E 作EF⊥AC,连接CF,使CF=AB,若EF=12cm,则下列结论不正确的是()A.∠F=∠BCF B.AE=7cm C.EF平分AB D.AB⊥CF10.如图,AB与CD相交于点E,AD=CB,要使△ADE≌△CBE,需添加一个条件,则添加的条件以及相应的判定定理正确的是()A.AE=CE;SAS B.DE=BE;SASC.∠D=∠B;AAS D.∠A=∠C;ASA11.如图,OB平分∠MON,A为OB的中点,AE⊥ON,EA=3,D为OM上的一个动点,C 是DA延长线与BC的交点,BC//OM,则CD的最小值是()A.6 B.8 C.10 D.1212.下列命题,真命题是()A.全等三角形的面积相等B.面积相等的两个三角形全等C.两个角对应相等的两个三角形全等D.两边和其中一边的对角对应相等的两个三角形全等13.如图,C是∠AOB的平分线上一点,添加下列条件不能判定△AOC≌△BOC的是()A .OA =OB B .AC =BC C .∠A =∠BD .∠1=∠2 14.如图,已知AE 平分∠BAC ,BE ⊥AE 于E ,ED ∥AC ,∠BAE =34°,那么∠BED =( )A .134°B .124°C .114°D .104° 15.已知,如图,OC 是∠AOB 内部的一条射线,P 是射线OC 上任意点,PD ⊥OA ,PE ⊥OB ,下列条件中:①∠AOC =∠BOC ,②PD =PE ,③OD =OE ,④∠DPO =∠EPO ,能判定OC 是∠AOB 的角平分线的有( )A .1个B .2个C .3个D .4个二、填空题16.如图,△ABC 中,∠ACB =90°,点D 在边AC 上,DE ⊥AB 于点E ,DC =DE ,∠A =32°,则∠BDC 的度数为________.17.如图,已知在ABC ∆和ADC ∆中,,ACB ACD ∠=∠请你添加一个条件:_________,使ABC ADC ∆≅∆(只添一个即可).18.如图,AOP BOP ∠=∠,PD OA ⊥,C 是OB 上的动点,连接PC ,若4PD =,则PC 的最小值为_________.19.如图,在Rt ABC △中,90C ∠=︒,AD 平分BAC ∠交BC 于点D .若3BC =,且:5:4BD DC =,5AB =,则ABD △的面积是______.20.如图,点D 、E 分别在线段AB 、AC 上,BE 与CD 相交于点O .若AB AC =,AD AE =,60A ∠=︒,80ADC ∠=︒,则B 的度数为______.21.如图所示,在ABC 中,D 是BC 的中点,点A 、F 、D 、E 在同一直线上.请添加一个条件,使BDE CDF ≌(不再添其他线段,不再标注或使用其他字母),并给出证明.你添加的条件是______22.如图,AC AE =,AD AB =,90ACB DAB ∠=∠=︒,33BAE ∠=︒,//CB AE ,AC 与DE 相交于点F .(1)DAC ∠=______.(2)当1AF =时,BC 的长为______.23.如图,BD 平分ABC ∠交AC 于点D ,DE BC ⊥于点E ,若2DE =,7BC =,12ABC S =△,则AB 的长为______.24.如图所示,ABC ≅△AB C '',20CAC ∠'=︒,BAB ∠'=___度.25.如图,AB ⊥BC ,DC ⊥BC ,垂足分别为B 、C ,垂足为B 、C ,AC 与BD 相交于点E ,AC=BD 且∠A=50°,则∠BEA=___________.26.如图,ABC ∆的两条高AD 、CE 交于点H ,已知6EH EB ==,8AE =,则ACH ∆的面积为______.三、解答题27.如图,在△ABC 中,AC =BC ,∠ACB =90°,点D 在边BC 上(不与点B ,C 重合),过点C 作CE ⊥AD ,垂足为点E ,交AB 于点F ,连接DF .(1)请直接写出∠CAD 与∠BCF 的数量关系;(2)若点D 是BC 中点,在图2中画出图形,猜想线段AD ,CF ,FD 之间的数量关系,并证明你的猜想.28.如图,已知A ABC ∠=∠,D CBD ∠=∠,ABD CBD ∠=∠,点E 在BC 的延长线上.求证:CD 平分ACE ∠.29.如图,在△ABC 中,∠BAC 的平分线AD 交BC 于点D ,过点D 作DE ⊥AB ,DF ⊥AC ,垂足分别是E ,F ,连接EF .写出两个结论(∠BAD =∠CAD 和DE =DF 除外),并选择一个结论进行证明.(1)____________;(2)____________.30.在Rt ABC △中,90C ∠=︒,8cm AC =,6cm BC =,点D 在AC 上,且6cm AD =,过点A 作射线AE AC ⊥(AE 与BC 在AC 同侧),若点P 从点A 出发,沿射线AE 匀速运动,运动速度为1cm/s ,设点P 运动时间为t 秒.连结PD 、BD .(1)如图①,当PD BD ⊥时,求证:PDA DBC △≌△; (2)如图②,当PD AB ⊥于点F 时,求此时t 的值.。
三角形全等的判定(6种题型)-2023年新八年级数学核心知识点与常见题型(浙教版)(解析版)
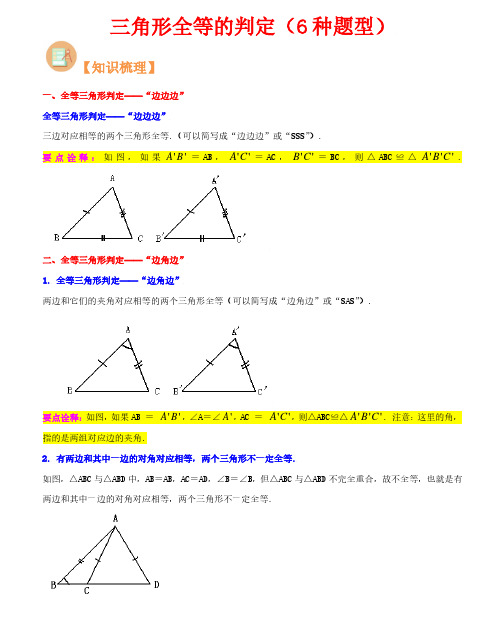
三角形全等的判定(6种题型)【知识梳理】一、全等三角形判定——“边边边”全等三角形判定——“边边边”三边对应相等的两个三角形全等.(可以简写成“边边边”或“SSS ”).要点诠释:如图,如果''A B =AB ,''A C =AC ,''B C =BC ,则△ABC ≌△'''A B C .二、全等三角形判定——“边角边”1. 全等三角形判定——“边角边”两边和它们的夹角对应相等的两个三角形全等(可以简写成“边角边”或“SAS ”).要点诠释:如图,如果AB = ''A B ,∠A =∠'A ,AC = ''A C ,则△ABC ≌△'''A B C . 注意:这里的角,指的是两组对应边的夹角.2. 有两边和其中一边的对角对应相等,两个三角形不一定全等.如图,△ABC 与△ABD 中,AB =AB ,AC =AD ,∠B =∠B ,但△ABC 与△ABD 不完全重合,故不全等,也就是有两边和其中一边的对角对应相等,两个三角形不一定全等.三、垂直平分线:1.定义:垂直于一条线段,并且平分这条线段的直线叫做这条线段的垂直平分线,简称中垂线.2.性质定理:线段垂直平分线上的点到线段两端的距离相等四、全等三角形判定——“角边角”全等三角形判定——“角边角”两角和它们的夹边对应相等的两个三角形全等(可以简写成“角边角”或“ASA ”).要点诠释:如图,如果∠A =∠'A ,AB =''A B ,∠B =∠'B ,则△ABC ≌△'''A B C .五、全等三角形判定——“角角边” 1.全等三角形判定——“角角边”两个角和其中一个角的对边对应相等的两个三角形全等(可以简写成“角角边”或“AAS ”)要点诠释:由三角形的内角和等于180°可得两个三角形的第三对角对应相等.这样就可由“角边角”判定两个三角形全等,也就是说,用角边角条件可以证明角角边条件,后者是前者的推论.2.三个角对应相等的两个三角形不一定全等.如图,在△ABC 和△ADE 中,如果BC ,那么∠ADE =∠B ,∠AED =∠C ,又∠A =∠A ,但△ABC 和△ADE 不全等.这说明,三个角对应相等的两个三角形不一定全等.六、角平分线的性质定理:角平分线上的点到角两边的距离相等.【考点剖析】题型一、全等三角形的判定——“边边边”例1、已知:如图,△RPQ 中,RP =RQ ,M 为PQ 的中点.求证:RM 平分∠PRQ .【思路点拨】由中点的定义得PM =QM ,RM 为公共边,则可由SSS 定理证明全等.【答案与解析】证明:∵M 为PQ 的中点(已知),∴PM =QM在△RPM 和△RQM 中,()(),,RP RQ PM QM RM RM ⎧=⎪=⎨⎪=⎩已知公共边 ∴△RPM ≌△RQM (SSS ).∴ ∠PRM =∠QRM (全等三角形对应角相等).即RM 平分∠PRQ.【总结升华】在寻找三角形全等的条件时有的可以从图中直接找到,如:公共边、公共角、对顶角等条件隐含在题目或图形之中. 用全等三角形的性质和判定.【变式】已知:如图,AD =BC ,AC =BD.试证明:∠CAD =∠DBC.【答案】证明:连接DC ,在△ACD 与△BDC 中()AD BC AC BDCD DC ⎧=⎪=⎨⎪=⎩公共边 ∴△ACD≌△BDC(SSS )∴∠CAD =∠DBC (全等三角形对应角相等)【变式2】、如图,在△ABC 和△ADE 中,AB =AC ,AD =AE ,BD =CE ,求证:∠BAD =∠CAE.【答案与解析】证明:在△ABD 和△ACE 中,AB AC AD AE BD CE =⎧⎪=⎨⎪=⎩∴△ABD ≌△ACE (SSS )∴∠BAD =∠CAE (全等三角形对应角相等).【总结升华】把证明一对角或线段相等的问题,转化为证明它们所在的两个三角形全等,综合应用全等三角形的判定和性质. 要证∠BAD =∠CAE ,先找出这两个角所在的三角形分别是△BDA 和△CAE ,然后证这两个三角形全等.题型二、全等三角形的判定——“边角边”例2、已知:如图,AB =AD ,AC =AE ,∠1=∠2.求证:BC =DE .【思路点拨】由条件AB =AD ,AC =AE ,需要找夹角∠BAC 与∠DAE ,夹角可由等量代换证得相等.【答案与解析】证明: ∵∠1=∠2∴∠1+∠CAD =∠2+∠CAD ,即∠BAC =∠DAE在△ABC 和△ADE 中AB AD BAC DAE AC AE =⎧⎪∠=∠⎨⎪=⎩∴△ABC ≌△ADE (SAS )∴BC =DE (全等三角形对应边相等)【总结升华】证明角等的方法之一:利用等式的性质,等量加等量,还是等量.【变式】如图,将两个一大、一小的等腰直角三角尺拼接 (A 、B 、D 三点共线,AB =CB ,EB =DB ,∠ABC =∠EBD =90°),连接AE 、CD ,试确定AE 与CD 的位置与数量关系,并证明你的结论.【答案】AE =CD ,并且AE ⊥CD证明:延长AE 交CD 于F ,∵△ABC 和△DBE 是等腰直角三角形∴AB =BC ,BD =BE在△ABE 和△CBD 中90AB BC ABE CBD BE BD =⎧⎪∠=∠=︒⎨⎪=⎩∴△ABE ≌△CBD (SAS )∴AE =CD ,∠1=∠2又∵∠1+∠3=90°,∠3=∠4(对顶角相等)∴∠2+∠4=90°,即∠AFC =90°∴AE ⊥CD例3、如图,AD 是△ABC 的中线,求证:AB +AC >2AD .【思路点拨】延长AD 到点E ,使AD =DE ,连接CE .通过证全等将AB 转化到△CEA 中,同时也构造出了2AD .利用三角形两边之和大于第三边解决问题.【答案与解析】证明:如图,延长AD 到点E ,使AD =DE ,连接CE .在△ABD 和△ECD 中,AD DE ADB EDC BD CD ⎧⎪∠∠⎨⎪⎩===.∴△ABD ≌△ECD (SAS ).∴AB =CE .∵AC +CE >AE ,∴AC +AB >AE =2AD .即AC +AB >.【总结升华】证明边的大小关系主要有两个思路:(1)两点之间线段最短;(2)三角形的两边之和大于第三边.要证明AB +AC >2AD ,如果归到一个三角形中,边的大小关系就是显然的,因此需要转移线段,构造全等三角形是转化线段的重要手段.可利用旋转变换,把△ABD 绕点D 逆时针旋转180°得到△CED ,也就把AB 转化到△CEA 中,同时也构造出了2AD .若题目中有中线,倍长中线,利用旋转变换构造全等三角形是一种重要方法.例4、已知,如图:在△ABC 中,∠B =2∠C ,AD ⊥BC ,求证:AB =CD -BD .【思路点拨】在DC 上取一点E ,使BD =DE ,则△ABD ≌△AED ,所以AB =AE ,只要再证出EC =AE 即可.【答案与解析】证明:在DC 上取一点E ,使BD =DE∵ AD ⊥BC ,∴∠ADB =∠ADE在△ABD 和△AED 中,BD DE ADB=ADE AD AD ⎧⎪⎨⎪⎩=∠∠=∴△ABD ≌△AED (SAS ).∴AB =AE ,∠B =∠AED .又∵∠B =2∠C =∠AED =∠C +∠EAC .∴∠C =∠EAC .∴AE =EC .∴AB =AE =EC =CD —DE =CD —BD .【总结升华】此题采用截长或补短方法.上升到解题思想,就是利用翻折变换,构造的全等三角形,把条件集中在基本图形里面,从而使问题加以解决.如图,要证明AB =CD -BD ,把CD -BD 转化为一条线段,可利用翻折变换,把△ABD 沿AD 翻折,使线段BD 运动到DC 上,从而构造出CD -BD ,并且也把∠B 转化为∠AEB ,从而拉近了与∠C 的关系.【变式】已知,如图,在四边形ABCD 中,AC 平分∠BAD ,CE ⊥AB 于E ,并且AE =12(AB +AD ), 求证:∠B +∠D =180°. AE D CB【答案】证明:在线段AE 上,截取EF =EB ,连接FC ,∵CE ⊥AB ,∴∠CEB =∠CEF =90°在△CBE 和△CFE 中,CEB CEF EC =EC EB EF =⎧⎪∠=∠⎨⎪⎩∴△CBE 和△CFE (SAS )∴∠B =∠CFE∵AE =12(AB +AD ),∴2AE = AB +AD ∴AD =2AE -AB∵AE =AF +EF ,∴AD =2(AF +EF )-AB =2AF +2EF -AB =AF +AF +EF +EB -AB =AF +AB -AB ,即AD =AF在△AFC 和△ADC 中(AF AD FAC DAC AC AC =⎧⎪∠=∠⎨⎪=⎩角平分线定义)∴△AFC ≌△ADC (SAS )∴∠AFC =∠D∵∠AFC +∠CFE =180°,∠B =∠CFE.∴∠AFC +∠B =180°,∠B +∠D =180°.题型三、全等三角形的判定——“角边角”例5、已知:如图,E ,F 在AC 上,AD ∥CB 且AD =CB ,∠D =∠B .求证:AE =CF .【答案与解析】证明:∵AD ∥CB∴∠A =∠C在△ADF 与△CBE 中A C AD CB D B ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ADF ≌△CBE (ASA )∴AF =CE ,AF +EF =CE +EF故得:AE =CF【总结升华】利用全等三角形证明线段(角)相等的一般方法和步骤如下:(1)找到以待证角(线段)为内角(边)的两个三角形;(2)证明这两个三角形全等;(3)由全等三角形的性质得出所要证的角(线段)相等.【变式】(2022•长安区一模)已知:点B 、E 、C 、F 在一条直线上,AB ∥DE ,AC ∥DF ,BE =CF .求证:△ABC ≌△DEF .【分析】先利用平行线的性质得到∠B=∠DEF,∠ACB=∠F,再证明BC=EF,然后根据“ASA”可判断△ABC≌△DEF.【解答】证明:∵AB∥DE,∴∠B=∠DEF,∵AC∥DF,∴∠ACB=∠F,∵BE=CF,∴BE+EC=CF+EC,即BC=EF,在△ABC和△DEF中,{∠B=∠DEF BC=EF∠ACB=∠F,∴△ABC≌△DEF(ASA).5种判定方法是解决问题的关键.选用哪一种判定方法,取决于题目中的已知条件.例6、如图,G是线段AB上一点,AC和DG相交于点E.请先作出∠ABC的平分线BF,交AC于点F;然后证明:当AD∥BC,AD=BC,∠ABC=2∠ADG时,DE=BF.【思路点拨】通过已知条件证明∠DAC=∠C,∠CBF=∠ADG,则可证△DAE≌△BCF【答案与解析】证明:∵AD∥BC,∴∠DAC=∠C∵BF平分∠ABC∴∠ABC=2∠CBF∵∠ABC=2∠ADG∴∠CBF=∠ADG在△DAE 与△BCF 中⎪⎩⎪⎨⎧∠=∠=∠=∠C DAC BCAD CBF ADG ∴△DAE≌△BCF(ASA )∴DE=BF【总结升华】利用全等三角形证明线段(角)相等的一般方法和步骤如下:(1)找到以待证角(线段)为内角(边)的两个三角形;(2)证明这两个三角形全等;(3)由全等三角形的性质得出所要证的角(线段)相等.【变式】已知:如图,在△MPN 中,H 是高MQ 和NR 的交点,且MQ =NQ .求证:HN =PM.【答案】证明:∵MQ 和NR 是△MPN 的高,∴∠MQN =∠MRN =90°,又∵∠1+∠3=∠2+∠4=90°,∠3=∠4∴∠1=∠2在△MPQ 和△NHQ 中,12MQ NQ MQP NQH ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△MPQ ≌△NHQ (ASA )∴PM =HN题型四、全等三角形的判定——“角角边”例7.(2021秋•苏州期末)如图,在四边形ABCD 中,E 是对角线AC 上一点,AD ∥BC ,∠ADC =∠ACD ,∠CED +∠B =180°.求证:△ADE ≌△CAB .【分析】由等角对等边可得AC=AD,再由平行线的性质可得∠DAE=∠ACB,由∠CED+∠B=180°,∠CED+∠AED=180°,得∠AED=∠B,从而利用AAS可判定△ADE≌△CAB.【解答】证明:∵∠ADC=∠ACD,∴AD=AC,∵AD∥BC,∴∠DAE=∠ACB,∵∠CED+∠B=180°,∠CED+∠AED=180°,∴∠AED=∠B,在△ADE与△CAB中,{∠DAE=∠ACB ∠AED=∠BAD=AC,∴△ADE≌△CAB(AAS).【点评】本题主要考查全等三角形的判定,解答的关键是由已知条件得出相应的角或边的关系.例8、已知:如图,AB⊥AE,AD⊥,∠E=∠B,DE=CB.求证:AD=AC.【思路点拨】要证AC=AD,就是证含有这两个线段的三角形△BAC≌△EAD.【答案与解析】证明:∵AB⊥AE,AD⊥AC,∴∠CAD=∠BAE=90°∴∠CAD+∠DAB=∠BAE+∠DAB ,即∠BAC=∠EAD在△BAC和△EAD中BAC EAD B E CB=DE ∠=∠⎧⎪∠=∠⎨⎪⎩∴△BAC ≌△EAD (AAS )∴AC =AD【总结升华】我们要善于把证明一对角或线段相等的问题,转化为证明它们所在的两个三角形全等. 题型五:线段的垂直平分线 例9.(2023秋·浙江杭州·八年级校考开学考试)如图所示,在ABC 中,8AC =,5BC =,AB 的垂直平分线DE 交AB 于点D ,交AC 于点E ,则BCE 的周长为( )A .13B .18C .10.5D .21【答案】A 【分析】根据线段垂直平分线的性质得到AE BE =,再将BCE 的周长转化为AC BC +的长,即可求解.【详解】解:DE 是AB 的垂直平分线,∴AE BE =,∴BCE 的周长为BE EC BC AE EC BC AC BC ++=++=+,8AC =,5BC =,∴BCE 的周长为8513AC BC +=+=,故选:A .【点睛】本题主要考查的是线段垂直平分线的性质,掌握线段垂直平分线的性质是解题的关键.【变式1】(2022秋·浙江温州·八年级校考期中)如图,点D 是ABC 边AC 的中点,过点D 作AC 的垂线交BC 于点E ,已知6AC =,ABC 的周长为14,则ABE 的周长是( )A .6B .14C .8D .20【答案】C 【分析】由题意可知:ED 垂直平分AC ,故EA EC =,结合6AC =,ABC 的周长为14,即可得出答案.【详解】解:∵点D 是ABC 边AC 的中点, ED AC ⊥,∴ED 垂直平分AC ,∴EA EC =,∵6AC =,ABC 的周长为14,∴1468AB BC +=−=,∴8AB BC AB BE EC AB BE AE +=++=++=,∴ABE 的周长是8.故选:C .【点睛】此题考查了垂直平分线的性质和判定,掌握垂直平分线的性质和判定是解题的关键.【答案】C 【分析】根据垂直平分线的性质可知,到A ,B ,C 表示三个居民小区距离相等的点,是AC ,BC 两边垂直平分线的交点,由此即可求解.【详解】解:如图所示,分别作AC ,BC 两边垂直平分线MN ,PQ 交于点O ,连接OA,OB,OC,∵MN,PQ是AC,BC两边垂直平分线,==,∴OA OB OC∴点O是到三个小区的距离相等的点,即点O是AC,BC两边垂直平分线的交点,故选:C.【点睛】本题主要考查垂直平分线的性质,掌握垂直平分线的性质是解题的关键.八年级专题练习)如图,在ABC中,是ABC外的一点,且【分析】根据到线段两端距离相等的点在线段的垂直平分线上,即可证明A、D都在BC的垂直平分线上,由此即可证明结论.AB AC,【详解】证明:∵=∴点A在BC的垂直平分线上,BD CD,∵=∴点D在BC的垂直平分线上,∴A、D都在BC的垂直平分线上,∴AD垂直平分BC.【点睛】本题主要考查了线段垂直平分线的判定,熟知线段垂直平分线的判定条件是解题的关键.【变式】.(2022秋·浙江·八年级专题练习)如图,点E是△ABC的边AB的延长线上一点,∠BCE=∠A+∠ACB,求证:点E在BC的垂直平分线上.【分析】由三角形的外角性质得到∠EBC=∠A+∠ACB,结合已知推出∠BCE=∠EBC,得到BE=CE,即可得到结论.【详解】证明:∵∠BCE=∠A+∠ACB,∠EBC=∠A+∠ACB,∴∠BCE=∠EBC,∴BE=CE,∴点E在BC的垂直平分线上.【点睛】本题考查了三角形的外角性质,线段垂直平分线的判定,用到的知识点:到线段两端点的距离相等的点在线段的垂直平分线上.题型六:角平分线【答案】A【分析】根据角平分线上的点到两边的距离相等即可解答.【详解】根据题意要使集贸市场到三条公路的距离相等即集贸市场应建在三个角的角平分线的交点.故本题选A .【点睛】本题考查了角平分线的性质,熟记角平分线的性质是解答本题的关键. 的中点,ABC ,则BED 的面积为( 【答案】C【分析】作DF AC ⊥于F ,DM AB ⊥于点M ,根据角平分线的性质求出DM ,根据三角形的面积公式计算即可.【详解】解:作DF AC ⊥于F ,DM AB ⊥于点MAD 是ABC 的角平分线DF AC ⊥于F ,DM AB ⊥,112122AC DF AB DM ∴⋅+⋅=,112122AC DM AB DM ⋅+⋅=∴即:3421DM DM +=得3DM =8AB =, E 是AB 的中点,142BE AB ∴== 1143622BEDS BE DM ∴=⋅=⨯⨯= 故选:C .【点睛】本题考查了角平分线上的点到角的两边距离相等的性质,三角形的面积,熟记性质并利用三角形的面积列出方程是解题的关键. 例12.(2022秋·浙江·八年级专题练习)已知:如图,90B C ∠=∠=,M 是BC 的中点,DM 平分ADC ∠.(1)若连接AM ,则AM 是否平分BAD ∠?请你证明你的结论;(2)线段DM 与AM 有怎样的位置关系?请说明理由.【答案】(1)AM 平分BAD ∠,证明见解析(2)DM AM ⊥,理由见解析【分析】(1)过点M 作ME AD ⊥,垂足为E ,证明ME MC MB ==即可得证.(2)利用两直线平行,同旁内角互补,证明1390∠+∠=.【详解】(1)AM 平分BAD ∠,理由为:证明:过点M 作ME AD ⊥,垂足为E ,∵DM 平分ADC ∠,∴12∠=∠,∵ME AD ⊥,MC CD ⊥∴MC ME =(角平分线上的点到角两边的距离相等),又∵MC MB =,∴ME MB =,∵MB AB ⊥,ME AD ⊥,∴AM 平分BAD ∠(到角的两边距离相等的点在这个角的平分线上).(2)DM AM ⊥,理由如下:∵90B C ∠=∠=,∴,DC CB AB CB ⊥⊥,∴DC AB ∥(垂直于同一条直线的两条直线平行),∴180DAB CDA ∠+∠=(两直线平行,同旁内角互补)又∵111,322CDA DAB ∠=∠∠=∠(角平分线定义) ∴2123180∠+∠=,∴1390∠+∠=,∴90AMD ∠=.即DM AM ⊥.【点睛】本题考查了角平分线的性质定理和判定定理,平行线的性质,熟练掌握以上的知识是解题的关键. 【变式1】(2023秋·浙江台州·八年级统考期末)如图 90B C ∠=∠=︒,E 为BC 上一点,AE 平分BAD ∠,DE 平分CDA ∠.(1)求AED ∠的度数;(2)求证:E 是BC 的中点.【答案】(1)90︒(2)见解析.【分析】(1)利用已知条件可以得到180BAD CDA ∠+∠=︒,想要求AED ∠的度数,只需要根据三角形内角和定理和角平分线的性质即可得到结论.(2)过点E 做EF AD ⊥,根据角平分线上的点到角的两边距离相等即可得结论.【详解】(1)解:∵90B C ∠=∠=︒,∴DC AB ∥,∴180BAD CDA ∠+∠=︒,∵AE 平分BAD ∠,DE 平分CDA ∠, ∴12EAD BAD ∠=∠,12EDA CDA ∠=∠, ∴1()902EAD EDA BAD CDA ∠+∠=∠+∠=︒,∴180()90AED EAD EDA ∠=︒−∠+∠=︒;(2)证明:过点E 作EF AD ⊥于点F ,∵AE 平分BAD ∠,90B Ð=°,EF AD ⊥,∴EF EB =.∵DE 平分CDA ∠,90C ∠=︒,EF AD ⊥,∴EF EC =.∴EB EC =,即E 是BC 的中点.【点睛】本题考查了平行线的判定与性质,以及角平分线上的点到角两边距离相等的性质,熟记性质和定理并做出辅助线是解题的关键.【变式2】.(2022秋·浙江杭州·八年级校考期中)如图,在ABC 外作两个大小不同的等腰直角三角形,其中90DAB CAE ∠=∠=︒,AB AD =,AC AE =.连接DC 、BE 交于F 点.(1)求证:DAC BAE ≌△△; (2)直线DC 、BE 是否互相垂直,试说明理由;(3)求证:AF 平分DFE ∠.【答案】(1)见解析(2)DC BE ⊥,理由见解析(3)见解析【分析】(1)由题意可得AD AB =,AC AE =,由90DAB CAE ∠=∠=︒,可得到DAC BAE ∠=∠,从而可证DAC BAE ≌△△;(2)由(1)可得ACD AEB ∠=∠,再利用直角三角形的性质及等量代换即可得到结论;(3)作AM DC ⊥于M ,AN BE ⊥于N ,利用全等三角形的面积相等及角平分线的判定即可证得结论.【详解】(1)证明:∵90DAB CAE ∠=∠=︒,∴DAB BAC CAE BAC ∠+∠=∠+∠,即DAC BAE ∠=∠,又∵AD AB =,AC AE =,∴()SAS DAC BAE ≌△△;(2)解:DC BE ⊥,理由如下;∵DAC BAE ≌△△, ∴ACD AEB ∠=∠,∵90AEB AOE ∠+∠= ,AOE FOC ∠=∠,∴90FOC ACD ∠+∠=,∴90EFC ∠=,∴DC BE ⊥;(3)证明:作AM DC ⊥于M ,AN BE ⊥于N ,∵DAC BAE ≌△△, ∴DAC BAE S S ∆∆=,DC BE =, ∴1122DC AM BE AN ⋅=⋅,∴AM AN =,∴AF 平分DFE ∠.【点睛】本题主要考查全等三角形的判定和性质,及直角三角形的性质,角平分线的判定,熟练掌握判定和性质是解决本题的关键.【变式3】(2023春·浙江金华·八年级浙江省义乌市后宅中学校考阶段练习)已知:OP 平分MON ∠,点A ,B 分别在边OM ,ON 上,且180OAP OBP ∠∠+=︒.(1)如图1,当90OAP ∠=︒时,求证:OA OB =;(2)如图2,当90OAP ∠<︒时,作PC OM ⊥于点C .求证:①PA PB =;②请直接写出OA ,OB ,AC 之间的数量关系 .【答案】(1)见解析(2)①见解析;②2OA OB AC −=【分析】(1)证明()AAS OPA OPB ≌,即可得证;(2)①作PD ON ⊥于点D ,证明()AAS PAC PBD ≌,即可得证; ②证明()AAS OCP ODP ≌,得出OD =,根据AC BD =,即可得证.【详解】(1)证明:180OAP OBP ∠∠+=︒,且90OAP ∠=︒,90OAP OBP ∠∠∴==︒,OP 平分MON ∠,POA POB ∠∠∴=,OP OP =,()AAS OPA OPB ∴≌,OA OB ∴=;(2)证明:①如图2,作PD ON ⊥于点D ,PC OM ⊥于点C ,PC PD ∴=,90PCA PDB OCP ∠∠∠===︒,180OAP OBP ∠∠+=︒,180DBP OBP ∠∠+=︒,OAP DBP ∠∠∴=,在PAC 和PBD 中,CAP DBP PCA PDBPC PD ∠=∠⎧⎪∠=∠⎨⎪=⎩, ()AAS PAC PBD ∴≌, PA PB ∴=;②结论:2OA OB AC −=.理由:在OCP 和ODP 中,OCP ODP COP DOP OP OP ∠=∠⎧⎪∠=∠⎨⎪=⎩,()AAS OCP ODP ∴≌,OC OD ∴=,OA AC OB BD ∴−=+,AC BD =,2OA OB AC BD AC ∴−=+=.故答案为:2OA OB AC −=.【点睛】本题考查了角平分线的性质,全等三角形的性质与判定,掌握全等三角形的性质与判定是解题的关键.【过关检测】一、单选题 1.(2022秋·浙江·八年级专题练习)如图,在ABC 中,90A ∠=︒,点D 是边AC 上一点,3DA =,若点D 到BC 的距离为3,则下列关于点D 的位置描述正确的是( )A .点D 是AC 的中点B .点D 是B ∠平分线与AC 的交点 C .点D 是BC 垂直平分线与AC 的交点D .点D 与点B 的距离为5【答案】B 【分析】作DE BC ⊥于E ,连接BD ,利用角平分线的判定定理可证明BD 是ABC ∠的角平分线,即可作答.【详解】解:如图所示:作DE BC ⊥于E ,连接BD ,∵3DA =,点D 到BC 的距离为3,∴=AD DE ,∵90A ∠=︒,∴DA BA ⊥,∵DE BC ⊥,∴BD 是ABC ∠的角平分线,即点D 是ABC ∠的角平分线与AC 的交点,故B 项正确;其余选项,利用现有条件均无法得出,故选:B .【点睛】本题主要考查了角平分线的判定定理,作出辅助线,证明BD 是ABC ∠的角平分线,是解答本题的关键. 2.(2023·浙江·九年级专题练习)如图,已知BF DE =,AB ∥DC ,要使ABF CDE ≅△△,添加的条件可以是( )A.BE DF =B .AF CE =C .AB CD = D .B D ∠=∠【答案】C 【分析】根据AB ∥DC ,可得B D ∠=∠,又BF DE =,所以添加AB CD =,根据SAS 可证ABF CDE ≅△△.【详解】解:应添加AB DC =,理由如下:AB ∥DC ,B D ∴∠=∠.在ABF △和CDE 中,AB CD B DBF DE =⎧⎪∠=∠⎨⎪=⎩,(SAS)ABF CDE ∴≅,故选:C .【点睛】本题主要考查了平行线的性质以及全等三角形的判定,熟练掌握全等三角形的判定是解题的关键.3.(2023·浙江金华·统考二模)如图,ABC 和DEF 中,AB DE ∥,A D ∠=∠,点B ,E ,C ,F 共线,添加一个条件,不能判断ABC DEF ≌△△的是( )A .AB DE =B .ACB F ∠=∠C .BE CF =D .AC DF =【答案】B 【分析】根据AB DE ∥可得B DEF ∠=∠,加上A D ∠=∠,可知ABC 和DEF 中两组对角相等,因此一组对边相等时,即可判断ABC DEF ≌△△. 【详解】解:AB DE ∥,∴B DEF ∠=∠, 又A D ∠=∠,∴ABC 和DEF 中两组对角相等,当AB DE =时,根据ASA 可证ABC DEF ≌△△,故A 选项不合题意; 当ACB F ∠=∠时,ABC 和DEF 中,三组对角相等,不能判断ABC DEF ≌△△,故B 选项符合题意; 当BE CF =时,BC EF =,根据AAS 可证ABC DEF ≌△△,故C 选项不合题意; 当AC DF =时,根据AAS 可证ABC DEF ≌△△,故D 选项不合题意; 故选B .【点睛】本题考查添加条件使三角形全等,解题的关键是熟练掌握全等三角形的各种判定方法..ABC 的三条中线的交点.ABC 三边的垂直平分线的交点.ABC 三条角平分线的交点.ABC 三条高所在直线的交点【答案】C【分析】角平分线上的点到角的两边的距离相等,由此可解.【详解】解:要使凉亭到草坪三条边的距离相等,∴凉亭应在ABC 三条角平分线的交点处.故选C .【点睛】本题考查了角平分线的性质,解题的关键是注意区分三角形中线的交点、高的交点、垂直平分线的交点以及角平分线的交点之间的区别. 5.(2020秋·浙江·八年级期末)如图,AD 是ABC 中BAC ∠的平分线,DE AB ⊥交AB 于点E ,DF AC ⊥交AC 于点F ,若7ABC S =△,2DE =,4AB =,则AC 的长为( )A .3B .4C .5D .6【答案】A 【分析】先根据角平分线的性质得到2DF DE ==,再利用三角形面积公式得到11242722AC ⨯⨯+⨯⨯=,然后解关于AC 的方程即可.【详解】解:∵AD 是BAC ∠的平分线,DE AB ⊥,DF AC ⊥,2DE =,∴2DF DE ==,∵7ABC S =△,4AB =,又∵ABD ACD ABC S S S +=△△△,∴111124272222AB DE DF AC AC ⋅+⋅=⨯⨯+⨯⨯=,∴3AC =.故选:A .【点睛】本题考查角平分线的性质:角的平分线上的点到角的两边的距离相等.理解和掌握角平分线的性质是解题的关键.本题也考查了三角形的面积及等积变换.6.(2022秋·浙江·八年级专题练习)如图,用B C ∠=∠,12∠=∠,直接判定ABD ACD ≌△△的理由是( )A .AASB .SSSC .ASAD .SAS【答案】A 【分析】根据三角形全等的判定方法判定即可.【详解】解:在ABD △和ACD 中,12B CAD AD ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴()AAS ABD ACD ≌,故A 正确. 故选:A .【点睛】本题主要考查三角形全等的判定,解题的关键是掌握证明全等三角形的几种证明方法:AAS 、ASA 、SSS 、SAS 、HL .A .2B .【答案】C 【分析】由FC AB ∥,得F ADE ∠=∠,FCE A ∠=∠,即可根据全等三角形的判定定理“AAS”证明CFE ADE ≅,则4CF AD AB BD ==−=.【详解】解:FC AB ∥,F ADE ∴∠=∠,FCE A ∠=∠,在CFE 和ADE V 中,F ADE FCE AFE DE ∠=∠⎧⎪∠=∠⎨⎪=⎩,()AAS CFE ADE ∴≅, CF AD ∴=,5AB =,1BD =,514AD AB BD ∴=−=−=,4CF ∴=,CF ∴的长度为4.故选:C .【点睛】此题重点考查平行线的性质、全等三角形的判定与性质等知识,正确地找到全等三角形的对应边和对应角并且证明CFE ADE ≅是解题的关键.A .SSS【答案】B 【分析】根据已知条件两边,及两边的夹角是对顶角解答.【详解】解:在AOB 和COD △中,OA OC AOB COD OB OD =⎧⎪∠=∠⎨⎪=⎩,()AOB COD SAS ∴≌. 故选:B .【点睛】本题考查了全等三角形的应用,准确识图判断出两组对应边的夹角是对顶角是解题的关键. 9.(2022秋·浙江嘉兴·九年级校考期中)在联欢会上,有A 、B 、C 三名选手站在一个三角形的三个顶点位置上,他们在玩“抢凳子”游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则凳子应放在ABC 的( )A .三边垂直平分线的交点B .三杂中线的交点C .三条角平分线的交点D .三条高所在直线的交点【答案】A【分析】根据题意可知,当木凳所在位置到A 、B 、C 三个顶点的距离相等时,游戏公平,再由线段垂直平分线的性质即可求解.【详解】解:由题意可得:当木凳所在位置到A 、B 、C 三个顶点的距离相等时,游戏公平,∵线段垂直平分线上的点到线段两端的距离相等,∴木凳应放的最适当的位置是在ABC 的三边垂直平分线的交点,故选:A .【点睛】本题考查线段垂直平分线的性质的应用,掌握线段垂直平分线的性质是解题的关键. )可说明ABC 与△ 【答案】A 【分析】先根据垂直的定义可得90ACB ADB ∠=∠=︒,再根据角平分线的定义可得CAB DAB ∠=∠,然后根据AAS 定理即可得.【详解】解:,BC AC BD AD ⊥⊥,90ACB ADB ∴∠=∠=︒,AB 平分CAD ∠,CAB DAB ∴∠=∠,在ABC 和ABD △中,90ACB ADB CAB DABAB AB ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩,()AAS ABC ABD ∴≌,故选:A . 【点睛】本题主要考查了三角形全等的判定,熟练掌握三角形全等的判定方法是解题关键.二、填空题【答案】CA FD =,B E ∠=∠,A D ∠=∠,AB DE ∥等【分析】可选择CA FD =添加条件后,能用SAS 进行全等的判;也可选择B E ∠=∠添加条件后,能用ASA 进行全等的判定;也可选择A D ∠=∠添加条件后,能用AAS 进行全等的判定;也可选择AB DE ∥添加条件后,能用ASA 进行全等的判定即可;【详解】解:添加CA FD =,∵12∠=∠,BC EF =,∴()SAS ABC DEF ≌△△,故答案为:CA FD =;或者添加B E ∠=∠,∵BC EF =,12∠=∠,∴()ASA ABC DEF ≌△△,故答案为:B E ∠=∠;或者添加A D ∠=∠,∵12∠=∠,BC EF =,∴()AAS ABC DEF ≌△△,故答案为:A D ∠=∠;或者添加AB DE ∥,∵AB DE ∥,∴B E ∠=∠,∵12∠=∠,BC EF =,∴()AAS ABC DEF ≌△△,故答案为:AB DE ∥.【点睛】本题考查了全等三角形的判定,解答本题关键是掌握全等三角形的判定定理,本题答案不唯一.【答案】AB DC =【分析】添加条件AB DC =,利用SAS 证明ABC DCB △≌△即可.【详解】解:添加条件AB DC =,理由如下:在ABC 和DCB △中,AB DC ABC DCBBC CB =⎧⎪∠=∠⎨⎪=⎩, ∴()SAS ABC DCB △≌△, 故答案为:AB DC =.【点睛】本题主要考查了全等三角形的判定,熟知全等三角形的判定定理是解题的关键,全等三角形的判定定理有SSS SAS AAS ASA HL ,,,,. 13.(2023秋·浙江湖州·八年级统考期末)如图,已知AC DB =,要使得ABC DCB ≅,根据“SSS”的判定方法,需要再添加的一个条件是_______.【答案】ABDC =【分析】要使ABC DCB ≅,由于BC 是公共边,若补充一组边相等,则可用SSS 判定其全等.【详解】解:添加AB DC =.在ABC 和DCB △中AB DC BC CB AC BD =⎧⎪=⎨⎪=⎩, ∴()ABC DCB SSS ≅△△, 故答案为:AB DC =.【点睛】本题考查三角形全等的判定方法;判定两个三角形全等的一般方法有:SSS 、SAS 、ASA 、AAS 、HL .添加时注意:AAA 、SSA 不能判定两个三角形全等,不能添加,根据已知结合图形及判定方法选择添加的条件是正确解答本题的关键.14.(2022秋·浙江丽水·八年级统考期末)如图,在ABC 中,CD 是边AB 上的高,BE 平分ABC ∠,交CD 于点E ,6BC =,若BCE 的面积为9,则DE 的长为______.【答案】3【分析】过E 作EF BC ⊥于F ,根据角平分线性质求出EF DE =,根据三角形面积公式求出即可.【详解】解:过E 作EF BC ⊥于F ,CD 是AB 边上的高,BE 平分ABC ∠,交CD 于点E ,DE EF ∴=,192BCE S BC EF =⋅=,1692EF ∴⨯⨯=,3EF DE ∴==,故答案为:3.【点睛】本题考查了角平分线性质的应用,能根据角平分线性质求出3EF DE ==是解此题的关键,注意:在角的内部,角平分线上的点到角的两边的距离相等. 八年级期末)如图,在ABC 中, 【答案】4【分析】根据线段垂直平分线的性质得到2AD BD ==,则4CD AC AD =−=.【详解】解:∵AB 的垂直平分线交AB 于点E ,交AC 于点D ,∴2AD BD ==,∵6AC =,∴4CD AC AD =−=,故答案为:4.【点睛】本题主要考查了线段垂直平分线的性质,熟知线段垂直平分线上的点到线段两端的距离相等是解题的关键. 16.(2022秋·浙江温州·八年级校联考期中)如图,在ABC 中,DE 是AC 的中垂线,分别交AC ,AB 于点D ,E .已知BCE 的周长为9,4BC =,则AB 的长为______.【答案】5【分析】先利用三角形周长得到5CE BE +=,再根据线段垂直平分线的性质得到EC EA =,然后利用等线段代换得到AB 的长.【详解】解:∵BCE 的周长为9,9CE BE BC ∴++=,又4BC =,5CE BE ∴+=,又DE 是AC 的中垂线,EC EA ∴=,5AB AE BE CE BE ∴=+=+=;故答案为:5.【点睛】本题考查了垂直平分线的性质:垂直平分线上任意一点,到线段两端点的距离相等.17.(2023秋·浙江杭州·八年级校考开学考试)如图,已知12∠=∠,要说明ABC BAD ≌,(1)若以“SAS ”为依据,则需添加一个条件是__________;(2)若以“ASA ”为依据,则需添加一个条件是__________.【答案】 BC AD = BAC ABD ∠=∠【分析】(1)根据SAS 可添加一组角相等,故可判定全等;(2)根据ASA 可添加一组角相等,故可判定全等;【详解】解:(1)已知一组角相等和一个公共边,以“SAS ”为依据,则需添加一组角,即BC AD =故答案为:BC AD =;(2)已知一组角相等,和一个公共边,以“ASA ”为依据,则需添加一组角,即BAC ABD ∠=∠. 故答案为:BAC ABD ∠=∠.【点睛】本题主要考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS SAS ASA AAS HL 、、、、.添加时注意:AAA SSA 、不能判定两个三角形全等. 18.(2019秋·浙江嘉兴·八年级校考阶段练习)如图,点B 、E 、C 、F 在一条直线上,AB ∥DE ,AB=DE ,BE=CF ,AC=6,则DF=________【答案】6.【分析】根据题中条件由SAS 可得△ABC ≌△DEF ,根据全等三角形的性质可得AC=DF=6.【详解】∵AB ∥DE ,∴∠B=∠DEF∵BE=CF ,∴BC=EF ,在△ABC 和△DEF 中,AB DE B DEFBC EF =⎧⎪∠=∠⎨⎪=⎩,∴△ABC ≌△DEF (SAS ),∴AC=DF=6.考点:全等三角形的判定与性质.。
初二全等三角形压轴题 附答案

全等三角形压轴题1.如图,已知BD⊥DE,CE⊥DE,垂足分别是D、E,AB=AC,∠BAC=90°,试探索DE、BD、CE长度之间的关系,并说明你的结论的正确性.2.已知四边形ABCD中,AB=AD,AB⊥AD,连接AC,过点A作AE⊥AC,且使AE=AC,连接BE,过A作AH⊥CD于H交BE于F.如图1,当E在CD的延长线上时,求证:①△ABC≌△ADE;②BF=EF;3.如图,已知∠ABC=90°,D是直线AB上的点,AD=BC.(1)如图1,过点A作AF⊥AB,并截取AF=BD,连接DC、DF、CF,判断△CDF的形状并证明;(2)如图2,E是直线BC上一点,且CE=BD,直线AE、CD相交于点P,∠APD的度数是一个固定的值吗?若是,请求出它的度数;若不是,请说明理由.4.已知:△ABC中,BD、CE分别是AC、AB边上的高,BQ=AC,点F在CE 的延长线上,CF=AB,求证:AF⊥AQ.5.阅读下题及证明过程:已知:如图,D是△ABC中BC边上一点,E是AD上一点,EB=EC,∠ABE=∠ACE,求证:∠BAE=∠CAE.证明:在△AEB和△AEC中,∵EB=EC,∠ABE=∠ACE,AE=AE,∴△AEB≌△AEC…第一步∴∠BAE=∠CAE…第二步问上面证明过程是否正确?若正确,请写出每一步推理的依据;若不正确,请指出错在哪一步,并写出你认为正确的证明过程.6.如图1,在△ABC中,∠ACB为锐角,点D为射线BC上一点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.(1)如果AB=AC,∠BAC=90°,①当点D在线段BC上时(与点B不重合),如图2,线段CF、BD所在直线的位置关系为____,线段CF、BD的数量关系为____;②当点D在线段BC的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;7.一节数学课后,老师布置了一道课后练习题:如图,已知在Rt△ABC中,AB=BC,∠ABC=90°,BO⊥AC于点O,点P、D分别在AO和BC上,PB=PD,DE⊥AC于点E,求证:△BPO≌△PDE.(1)理清思路,完成解答(2)本题证明的思路可用下列框图表示:根据上述思路,请你完整地书写本题的证明过程.(2)特殊位置,证明结论若PB平分∠ABO,其余条件不变.求证:AP=CD.(3)知识迁移,探索新知若点P是一个动点,点P运动到OC的中点P′时,满足题中条件的点D也随之在直线BC上运动到点D′,请直接写出CD′与AP′的数量关系.(不必写解答过程)8.探究问题1 已知:如图1,三角形ABC中,点D是AB边的中点,AE⊥BC,BF⊥AC,垂足分别为点E,F,AE,BF交于点M,连接DE,DF.若DE=kDF,则k的值为_____.拓展问题2 已知:如图2,三角形ABC中,CB=CA,点D是AB边的中点,点M 在三角形ABC的内部,且∠MAC=∠MBC,过点M分别作ME⊥BC,MF⊥AC,垂足分别为点E,F,连接DE,DF.求证:DE=DF.9.已知:直线a∥b,点A、B在直线a上,点C、D在直线b上,如图(1)若S△CBD=6cm2,则S△ADCcm2(2)若S△AOB=S△COD,那么△ACD≌△DBA吗?说明你的理由.10.(1)如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE =90°.①当点D在AC上时,如图1,线段BD、CE有怎样的数量关系和位置关系?直接写出你猜想的结论;②将图1中的△ADE绕点A顺时针旋转α角(0°<α<90°),如图2,线段BD、CE有怎样的数量关系和位置关系?请说明理由.(2)当△ABC和△ADE满足下面甲、乙、丙中的哪个条件时,使线段BD、CE 在(1)中的位置关系仍然成立?不必说明理由.甲:AB:AC=AD:AE=1,∠BAC=∠DAE≠90°;乙:AB:AC=AD:AE≠1,∠BAC=∠DAE=90°;丙:AB:AC=AD:AE≠1,∠BAC=∠DAE≠90°.11.(1)如图,在四边形ABCD中,AB=AD,∠B=∠D=90°,E、F分别是边1∠BAD.BC、CD上的点,且∠EAF=2求证:EF=BE+FD;(2)如图,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是边BC、1∠BAD,(1)中的结论是否仍然成立?CD上的点,且∠EAF=2(3)如图,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E、F分别是边1∠BAD,(1)中的结论是否仍然成立?BC、CD延长线上的点,且∠EAF=2若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.12.【问题提出】学习了三角形全等的判定方法(即“SAS”、“ASA”、“AAS”、“SSS”)和直角三角形全等的判定方法(即“HL”)后,我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究.【初步思考】我们不妨将问题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,然后,对∠B进行分类,可分为“∠B是直角、钝角、锐角”三种情况进行探究.【深入探究】第一种情况:当∠B是直角时,△ABC≌△DEF.(1)如图①,在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E=90°,根据 _____,可以知道Rt△ABC≌Rt△DEF.第二种情况:当∠B是钝角时,△ABC≌△DEF.(2)如图②,在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E,且∠B、∠E都是钝角,求证:△ABC≌△DEF.第三种情况:当∠B是锐角时,△ABC和△DEF不一定全等.(3)在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E,且∠B、∠E都是锐角,请你用尺规在图③中作出△DEF,使△DEF和△ABC不全等.(不写作法,保留作图痕迹)(4)∠B还要满足什么条件,就可以使△ABC≌△DEF?请直接写出结论:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,且∠B、∠E都是锐角,若________,则△ABC≌△DEF.13.问题背景:如图1:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E,F分别是BC,CD上的点.且∠EAF=60°.探究图中线段BE,EF,FD之间的数量关系.小王同学探究此问题的方法是,延长FD到点G.使DG=BE.连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是______;探索延伸:如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E,F分别是BC,1∠BAD,上述结论是否仍然成立,并说明理由;CD上的点,且∠EAF=2实际应用:如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里/小时的速度前进.1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离.14.将两个全等的直角三角形ABC和DBE按图①方式摆放,其中∠ACB=∠DEB=90°,∠A=∠D=30°,点E落在AB上,DE所在直线交AC所在直线于点F.(1)求证:AF+EF=DE;(2)若将图①中的△DBE绕点B按顺时针方向旋转角α,且0°<α<60°,其它条件不变,请在图②中画出变换后的图形,并直接写出你在(1)中猜想的结论是否仍然成立;(3)若将图①中的△DBE绕点B按顺时针方向旋转角β,且60°<β<180°,其它条件不变,如图③.你认为(1)中猜想的结论还成立吗?若成立,写出证明过程;若不成立,请写出AF、EF与DE之间的关系,并说明理由.15.已知:如图所示,直线MA∥NB,∠MAB与∠NBA的平分线交于点C,过点C作一条直线l与两条直线MA、NB分别相交于点D、E.(1)如图1所示,当直线l与直线MA垂直时,猜想线段AD、BE、AB之间的数量关系,请直接写出结论,不用证明;(2)如图2所示,当直线l与直线MA不垂直且交点D、E都在AB的同侧时,(1)中的结论是否成立?如果成立,请证明;如果不成立,请说明理由;(3)当直线l与直线MA不垂直且交点D、E在AB的异侧时,(1)中的结论是否仍然成立?如果成立,请说明理由;如果不成立,那么线段AD、BE、AB 之间还存在某种数量关系吗?如果存在,请直接写出它们之间的数量关系.16.在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.(1)当直线MN绕点C旋转到图1的位置时,求证:①△ADC≌△CEB;②DE=AD+BE;(2)当直线MN绕点C旋转到图2的位置时,求证:DE=AD-BE;(3)当直线MN绕点C旋转到图3的位置时,试问DE、AD、BE具有怎样的等量关系?请写出这个等量关系,并加以证明.。
初二全等三角形所有知识点总结和常考题提高难题压轴题练习(含答案解析)

初二全等三角形所有知识点总结和常考题1.基本定义:⑴全等形:能够完全重合的两个图形叫做全等形 .⑵全等三角形:能够完全重合的两个三角形叫做全等三角形.⑶对应顶点:全等三角形中互相重合的顶点叫做对应顶点.⑷对应边:全等三角形中互相重合的边叫做对应边 .⑸对应角:全等三角形中互相重合的角叫做对应角 .2.基本性质:⑴三角形的稳定性:三角形三边的长度确定了,这个三角形的形状、大小就全确定,这个性质叫做三角形的稳定性.⑵全等三角形的性质:全等三角形的对应边相等,对应角相等.3.全等三角形的判定定理:⑴边边边(SSS):三边对应相等的两个三角形全等.⑵边角边(SAS):两边和它们的夹角对应相等的两个三角形全等.⑶角边角(ASA):两角和它们的夹边对应相等的两个三角形全等.⑷角角边(AAS):两角和其中一个角的对边对应相等的两个三角形全等⑸斜边、直角边(HL ):斜边和一条直角边对应相等的两个直角三角形全等.4.角平分线:⑴画法:⑵性质定理:角平分线上的点到角的两边的距离相等 .⑶性质定理的逆定理:角的内部到角的两边距离相等的点在角的平分线上5.证明的基本方法:⑴明确命题中的已知和求证.(包括隐含条件,如公共边、公共角、对顶角、角平分线、中线、高、等腰三角形等所隐含的边角关系)⑵根据题意,画出图形,并用数字符号表示已知和求证.⑶经过分析,找出由已知推出求证的途径,写出证明过程 .一.选择题(共14小题)1.使两个直角三角形全等的条件是()A. 一个锐角又t应相等B.两个锐角对应相等C. 一条边对应相等D.两条边对应相等2.如图,已知AE=CF /AFD=/ CEB那么添加下列一个条件后,仍无法判定△AD陷4CBE的是()A. /A=/ CB. AD=CBC. BE=DFD. AD // BC3.如图所示,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是()A. SSSB. SASC. AASD. ASA4.到三角形三条边的距离都相等的点是这个三角形的(A.三条中线的交点B.三条高的交点C.三条边的垂直平分线的交点D.三条角平分线的交点5.如图,△ AC阴NA CB'/BCB =30°则/ ACA的度数为(A. 20°B. 300C. 350D. 40°6.如图,直线11、12、13表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则供选择的地址有()A. 1处B. 2处C. 3处D. 4处7.如图,AD是4ABC中/ BAC的角平分线,D已AB于点E, S AABC=7, DE=ZAB=4,则AC长是()8.如图,在△ ABC和4DEC中,已知AB=DE还需添加两个条件才能使△ ABCDEC不能添加的一组条件是()A. BC=EC /B=/ EB. BC=EC AC=DCC. BC=DC /A=/DD. / B=/ E,/ A=/ D9.如图,已知在△ ABC中,CD是AB边上的高线,BE平分/ ABC,交CD于点E, BC=5 DE=2,贝BCE的面积等于()A. 10B. 7C. 5D. 410.要测量河两岸相对的两点A, B的距离,先在AB的垂线BF上取两点C, D, 使CD=BC再定出BF的垂线DE,使A, C, E在一条直线上(如图所示),可以说明△ED8 AABC,彳3ED=AB因此测得ED的长就是AB的长,判定△ ED8 △ ABC最恰当的理由是()A.边角边B.角边角C.边边边D.边边角11.如图,4ABC的三边AB, BC, CA长分别是20, 30, 40,其三条角平分线将△ ABC分为三个三角形,则S A ABO):S A BCO:S A CAO等于()BC AA. 1:1:1B. 1: 2: 3C. 2: 3: 4D. 3: 4: 512.尺规作图作/ AOB的平分线方法如下:以O为圆心,任意长为半径画弧交OA, OB于C, D,再分别以点C, D为圆心,以大于tCD长为半径画弧,两弧交于点P,作射线OP由作法得^ OC国4ODP的根据是()A.有两边和其中一边的对角对应相等的两个三角形全等B.有两边对应相等,且有一角为 30°的两个等腰三角形全等C.有一角和一边对应相等的两个直角三角形全等D.有两角和一边对应相等的两个三角形全等14.如图,已知/ 1=/2, AC=AD,增加下列条件:① AB=AE ②BC=ED ③C C= /D;④/ B=/ E.其中能使△ AB ®ZXAED 的条件有( )A. 4个B. 3个C. 2个D. 1个二.填空题(共11小题)15 .如图,在△ ABC 中,/C=90°, AD 平分/CAB BC=8cm, BD=5cm,那么点 D 到线段AB 的距离是 cm.16 .如图,△ ABC 中,/ C=90°, AD 平分/BAC AB=5, CD=2,则△ ABD 的面积17 .如图为6个边长等的正方形的组合图形,则/ 1+/ 2+/3=19 .如图所示,某同学把一块三角形的玻璃打碎成了三块, 现在要到玻璃店去配 一块完全一样的玻璃,那么最省事的办法是带 去玻璃店.18.如图,△AB ®ADEF5请根据图中提供的信息,写出* F x= ______是 _______20.如图,已知AB// CF, E为DF的中点,若AB=9cm, CF=5cm 贝U BD=cm.B C21.在数学活动课上,小明提出这样一个问题:/ B=Z C=90°, E是BC的中点, DE 平分/ADC, /CED=35,如图,则/ EAB是多少度?大家一起热烈地讨论交流,小英第一个得出正确答案,是度.D C22.如图,/XABeAADEE, / B=100°, / BAC=30,那么/ AED=度.23.如图所示,将两根钢条AA', BB'的中点。
八年级数学上册第十二章全等三角形重难点归纳(带答案)

八年级数学上册第十二章全等三角形重难点归纳单选题1、如图,若△ABC≌△ADE则下列结论中不成立...的是()A.∠BAD=∠CAEB.∠BAD=∠CDEC.DA平分∠BDED.AC=DE答案:D分析:根据全等三角形的性质得出∠B=∠ADE,∠BAC=∠DAE,AB=AD,∠E=∠C,再逐个判断即可.解:A.∵△ABC≌△ADE,∴∠BAC=∠DAE,∴∠BAC−∠DAC=∠DAE−∠DAC,∴∠BAD=∠CAE,故本选项不符合题意;B.如图,∵△ABC≌△ADE,∴∠C=∠E,∵∠AOE=∠DOC,∠E+∠CAE+∠AOE=180°,∠C+∠COD+∠CDE=180°,∴∠CAE=∠CDE,∵∠BAD=∠CAE,∴∠BAD=∠CDE,故本选项不符合题意;C.∵△ABC≌△ADE,∴∠B=∠ADE,AB=AD,∴∠B=∠BDA,∴∠BDA=∠ADE,∴AD平分∠BDE,故本选项不符合题意;D.∵△ABC≌△ADE,∴BC=DE,故本选项符合题意;故选:D.小提示:本题考查了全等三角形的性质,等腰三角形的性质和三角形内角和定理,能熟记全等三角形的性质是解此题的关键,注意:全等三角形的对应角相等,对应边相等.2、下列说法不正确的是()A.有两条边和它们的夹角对应相等的两个三角形全等B.有三个角对应相等的两个三角形全等C.有两个角及其中一角的对边对应相等的两个三角形全等D.有三条边对应相等的两个三角形全等答案:B分析:根据全等三角形的判定定理逐一判断即可得答案.A.符合判定SAS,故该选项说法正确,不符合题意,B.全等三角形的判定必须有边的参与,AAA不能判定两个三角形全等,故该选项说法不正确,符合题意,C.正确,符合判定AAS,故该选项说法正确,不符合题意,D.正确,符合判定SSS,故该选项说法正确,不符合题意,故选:B.小提示:本题考查全等三角形的判定,全等三角形常用的判定方法有:SSS、SAS、AAS、ASA、HL,注意:AAS、AAA不能判定两个三角形全等,当利用SAS判定两个三角形全等时,角必须是两边的夹角;熟练掌握全等三角形的判定定理是解题关键.3、小明同学只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”他这样做的依据是()A.在角的内部,到角的两边距离相等的点在角的平分线上B.角平分线上的点到这个角两边的距离相等C.三角形的三条高交于一点D.三角形三边的垂直平分线交于一点答案:A分析:过两把直尺的交点P作PF⊥BO与点F,由题意得PE⊥AO,因为是两把完全相同的长方形直尺,可得PE=PF,再根据角的内部到角的两边的距离相等的点在这个角的平分线上可得OP平分∠AOB如图所示:过两把直尺的交点P作PF⊥BO与点F,由题意得PE⊥AO,∵两把完全相同的长方形直尺,∴PE=PF,∴OP平分∠AOB(角的内部到角的两边的距离相等的点在这个角的平分线上),故选A.小提示:本题主要考查了基本作图,关键是掌握角的内部到角的两边的距离相等的点在这个角的平分线上这一判定定理.4、如图,在Rt△ABC中,∠C=90°,∠BAC的平分线交BC于点D,DE//AB,交AC于点E,DF⊥AB于点F,DE=5,DF=3,则下列结论错误的是()A.BF=1B.DC=3C.AE=5D.AC=9答案:A分析:根据角平分线的性质得到CD=DF=3,故B正确;根据平行线的性质及角平分线得到AE=DE=5,故C正确;由此判断D正确;再证明△BDF≌△DEC,求出BF=CD=3,故A错误.解:在Rt△ABC中,∠C=90°,∠BAC的平分线交BC于点D,DF⊥AB,∴CD=DF=3,故B正确;∵DE=5,∴CE=4,∵DE//AB,∴∠ADE=∠DAF,∵∠CAD=∠BAD,∴∠CAD=∠ADE,∴AE=DE=5,故C正确;∴AC=AE+CE=9,故D正确;∵∠B=∠CDE,∠BFD=∠C=90°,CD=DF,∴△BDF≌△DEC,∴BF=CD=3,故A错误;故选:A.小提示:此题考查了角平分线的性质定理,平行线的性质,等边对等角证明角相等,全等三角形的判定及性质,熟记各知识点并综合应用是解题的关键.5、如图,锐角△ABC的两条高BD、CE相交于点O,且CE=BD,若∠CBD=20°,则∠A的度数为()A.20°B.40°C.60°D.70°答案:B分析:由BD、CE是高,可得∠BDC=∠CEB=90°,可求∠BCD=70°,可证Rt△BEC≌Rt△CDB(HL),得出∠BCD =∠CBE=70°即可.解:∵BD、CE是高,∠CBD=20°,∴∠BDC=∠CEB=90°,∴∠BCD=180°﹣90°﹣20°=70°,在Rt△BEC和Rt△CDB中,,{CE=BDBC=CB∴Rt△BEC≌Rt△CDB(HL),∴∠BCD=∠CBE=70°,∴∠A=180°﹣70°﹣70°=40°.故选:B.小提示:本题考查三角形高的定义,三角形全等判定与性质,三角形内角和公式,掌握三角形高的定义,三角形全等判定与性质,三角形内角和公式是解题关键.6、如图,为测量桃李湖两端AB的距离,南开中学某地理课外实践小组在桃李湖旁的开阔地上选了一点C,测得∠ACB的度数,在AC的另一侧测得∠ACD=∠ACB,CD=CB,再测得AD的长,就是AB的长.那么判定△ABC≌△ADC的理由是()A.SASB.SSSC.ASAD.AAS答案:A分析:已知条件是∠ACD=∠ACB,CD=CB,AC=AC,据此作出选择.解:在△ADC与△ABC中,{CD=CB∠ACD=∠ACBAC=AC.∴△ADC≌△ABC(SAS).故选:A.小提示:此题考查了全等三角形的应用,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS,做题时注意选择.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.7、如图,已知△ABC和△ADE都是等腰三角形,∠BAC=∠DAE=90°,BD,CE交于点F,连接AF,下列结论:①BD=CE;②BF⊥CF;③AF平分∠CAD;④∠AFE=45°.其中正确结论的个数有()A.1个B.2个C.3个D.4个答案:C分析:①证明△BAD≌△CAE,再利用全等三角形的性质即可判断;②由△BAD≌△CAE可得∠ABF=∠ACF,再由∠ABF+∠BGA=90°、∠BGA=∠CGF证得∠BFC=90°即可判定;③分别过A作AM⊥BD、AN⊥CE,根据全等三角形面积相等和BD=CE,证得AM=AN,即AF平分∠BFE,即可判定;④由AF平分∠BFE结合BF⊥CF即可判定.解:∵∠BAC=∠EAD∴∠BAC+∠CAD=∠EAD+∠CAD,即∠BAD=∠CAE在△BAD和△CAE中AB=AC, ∠BAD=∠CAE,AD=AE∴△BAD≌△CAE∴BD=CE故①正确;∵△BAD≌△CAE∴∠ABF=∠ACF∵∠ABF+∠BGA=90°、∠BGA=∠CGF∴∠ACF+∠BGA=90°,∴∠BFC=90°故②正确;分别过A作AM⊥BD、AN⊥CE垂足分别为M、N ∵△BAD≌△CAE∴S△BAD=S△CAE,∴12BD⋅AM=12CE⋅AN∵BD=CE∴AM=AN∴AF平分∠BFE,无法证明AF平分∠CAD.故③错误;∵AF平分∠BFE,BF⊥CF∴∠AFE=45°故④正确.故答案为C.小提示:本题考查了全等三角形的判定与性质、角平分线的判定与性质以及角的和差等知识,其中正确应用角平分线定理是解答本题的关键.8、如图,若△ABC≌△ADE,则下列结论中一定成立的是()A.AC=DE B.∠BAD=∠CAE C.AB=AE D.∠ABC=∠AED答案:B分析:根据全等三角形的性质即可得到结论.解:∵△ABC≌△ADE,∴AC=AE,AB=AD,∠ABC=∠ADE,∠BAC=∠DAE,∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,即∠BAD=∠CAE.故A,C,D选项错误,B选项正确,故选:B.小提示:本题考查了全等三角形的性质,熟练掌握全等三角形的性质是解题的关键.9、如图,在△ABC中,∠C=90°,以点B为圆心,任意长为半径画弧,分别交AB、BC于点M、N.分别以点M、MN的长度为半径画弧,两弧相交于点P,过点P作线段BD,交AC于点D,过点D作N为圆心,以大于12∠ABC;③BC=BE;④AE=BE中,一定正确的是()DE⊥AB于点E,则下列结论①CD=ED;②∠ABD=12A.①②③B.①②③④C.②④D.②③④答案:A分析:由作法可知BD是∠ABC的角平分线,故②正确,根据角平分线上的点到角两边的距离相等可得①正确,由HL可得Rt△BDC≌Rt△BDE,故BC=BE,③正确,解:由作法可知BD是∠ABC的角平分线,故②正确,∵∠C=90°,∴DC⊥BC,又DE⊥AB,BD是∠ABC的角平分线,∴CD=ED,故①正确,在Rt△BCD和Rt△BED中,,{DE=DCBD=BD∴△BCD≌△BED,∴BC=BE,故③正确.故选A.小提示:本题考查了角平分线的画法及角平分线的性质,熟练掌握相关知识是解题关键.10、判断两个直角三角形全等的方法不正确...的有()A.两条直角边对应相等B.斜边和一锐角对应相等C.斜边和一条直角边对应相等D.两个锐角对应相等答案:D分析:根据直角三角形全等的判定条件逐一判断即可.解:A、两条直角边对应相等,可以利用SAS证明两个直角三角形全等,说法正确,不符合题意;B、斜边和一锐角对应相等,可以利用AAS证明两个直角三角形全等,说法正确,不符合题意;C、斜边和一条直角边对应相等,可以利用HL证明两个直角三角形全等,说法正确,不符合题意;D、两个锐角对应相等,不可以利用AAA证明两个直角三角形全等,说法错误,符合题意;故选D.小提示:本题主要考查了全等三角形的判定,熟知全等三角形的判定条件是解题的关键.填空题11、如图,AC平分∠BAD,∠B+∠D=180°,CE⊥AD于点E,AD=18cm,AB=11cm,那么DE的长度为_____________________cm.答案:3.5分析:过C点作CF⊥AB于F,如图,根据角平分线的性质得到CF=CE,再证明Rt△ACE≌Rt△ACF得到AF=AE,证明△CBF≌△CDE得到BF=DE,然后利用等线段代换,利用AF=AE得到11+DE=18-DE,从而可求出DE的长.解:过C点作CF⊥AB于F,如图,∵AC平分∠BAD,CE⊥AD,CF⊥AB,∴CF=CE,在Rt△ACE和Rt△ACF中,,{AC=ACCF=CE∴Rt△ACE≌Rt△ACF(HL),∴AF=AE,∵∠ABC+∠D=180°,∠ABC+∠CBF=180°,∴∠CBF=∠D,在△CBF和△CDE中,{∠CBF=∠D∠CFB=∠CEDCF=CE,∴△CBF≌△CDE(AAS),∴BF=DE,∵AF=AE,∴AB+BF=AD-DE,即11+DE=18-DE,∴DE=3.5cm.所以答案是:3.5.小提示:本题考查了角平分线的性质:角的平分线上的点到角的两边的距离相等.也考查了全等三角形的判定与性质.12、如图,四边形ABCD中,∠BAC=∠DAC,请补充一个条件____,使△ABC≌△ADC.答案:∠D=∠B(答案不唯一)分析:本题是一道开放型的题目,答案不唯一,只要符合全等三角形的判定定理即可.解:添加的条件为∠D=∠B,理由是:在△ABC和△ADC中,{∠BAC =∠DAC∠D =∠B AC =AC,∴△ABC ≌△ADC (AAS ),所以答案是:∠D =∠B .小提示:本题主要考查全等三角形的判定定理,能熟记全等三角形的判定定理是解决本题的关键,注意:全等三角形的判定定理有SAS ,ASA ,AAS ,SSS ,两直角三角形全等还有HL .13、如图,OP 平分∠MON,PE ⊥OM 于点E ,PF ⊥ON 于点F ,PE =PF,OA =OB ,则图中有__________对全等三角形.答案:3分析:根据角平分线的性质得到PE =PF ,根据全等三角形的判定定理判断即可.解:如图,OP 平分∠MON,PE ⊥OM 于点E ,PF ⊥ON 于点F ,PE =PF ,∴∠1=∠2,在△AOP 和△BOP 中,{OA =OB ,∠1=∠2,OP =OP ,∴△AOP ≌△BOP (SAS ),∴AP =BP ,在Rt △EOP 和Rt △FOP 中,{PE =PF ,OP =OP,∴Rt △EOP ≌Rt △FOP (HL ),在Rt △AEP 和Rt △BFP 中,{PA =PB,PE =PF,∴Rt △AEP ≌Rt △BFP (HL ),∴图中有3对全等三角形.所以答案是:3.小提示:本题考查的是角平分线的性质、全等三角形的判定,掌握角的平分线上的点到角的两边的距离相等是解题的关键.14、如图,在△ABC 中,∠C =90°,AD 平分∠BAC ,AB =5,CD =2,则△ABD 的面积是________.答案:5分析:过D 作DE ⊥AB 于E ,由△DAE ≌△DAC 得到DE 的长,进而解答;解:如图,过D 作DE ⊥AB 于E ,△DAE 和△DAC 中,AD 平分∠BAC ,则∠DAE =∠DAC ,∠DEA =∠DCA =90°,DA =DA ,∴△DAE ≌△DAC (AAS ),∴DE =DC =2,∴△ABD 的面积=12×AB ×DE =12×5×2=5,所以答案是:5;小提示:本题考查了角平分线的概念,全等三角形的判定(AAS )和性质;熟练掌握全等三角形的判定和性质是解题的关键.15、如图,在等腰Rt △ABC 中,AC =BC ,D 为△ABC 内一点,且∠BCD =∠CAD ,若CD =4,则△BCD 的面积为________.答案:8分析:由线段CD 的长求ΔBCD 的面积,故过B 作CD 的垂线,则由三角形面积公式可知:S ΔBCD =12×CD ×BE ,再由题中的∠BCD =∠CAD 和等腰直角三角形ABC ,即可求证ΔACD ≌ΔCBE ,最后由CD =BE =4即可求解. 解:过点B 作CD 的垂线,交CD 的延长线于点E∵∠ACB =90°∴∠BCD +∠ACD =90°∵∠BCD =∠CAD∴∠ACD +∠CAD =90°∴∠ADC =90°∵BE ⊥CD∴∠E =90°∴∠BCD +∠CBE =90°∴∠ACD =∠CBE∵AC =CB∴ΔACD ≌ΔCBE∴CD =BE =4∴SΔBCD=12×CD×BE=12×4×4=8故答案是:8.小提示:本题主要考察全等三角形的证明、辅助线的画法、等腰三角形的性质和三角形面积公式,属于中档难度的几何证明题.解题的关键是由三角形面积公式画出合适的辅助线.解答题16、已知:等腰Rt△ABC和等腰Rt△ADE中,AB=AC,AE=AD,∠BAC=∠EAD=90°.(1)如图1,延长DE交BC于点F,若∠BAE=68°,则∠DFC的度数为;(2)如图2,连接EC、BD,延长EA交BD于点M,若∠AEC=90°,求证:点M为BD中点;(3)如图3,连接EC、BD,点G是CE的中点,连接AG,交BD于点H,AG=9,HG=5,直接写出△AEC的面积.答案:(1)68°;(2)见解析;(3)36分析:(1)由已知条件可得∠D=∠C=45°,对顶角∠AQD=∠CQF,则∠DAC=∠DFC,根据∠DAE=∠CAB即可的∠DFC=∠BAE;(2)过点B作ME的垂线交EM的延长线于N,证明△AEC≌△BNA,得AE=BN,进而可得AD=NB,再证明△DAM≌△BNM即可得证点M为BD中点;(3)延长AG至K,使得GK=AG=9,连接CK,设AE交BC于点P,先证明△ABE≌△ACD,进而证明△AEG≌△KCG,根据角度的计算以及三角形内角和定理求得∠BAD=∠KCA,进而证明△ABD≌△CAK,再根据∠CAG=∠ABD,∠BAC=90°,证明AH⊥BD,根据已知条件求得S△ABD最后证明S△AEC=S△ABD即可.(1)设DF交AC于Q,如图1,∵△ABC是等腰Rt△ABC和△ADE是等腰Rt△ADE∴∠D=∠C=45°∵∠AQD=∠CQF∵∠DAQ=180−∠D−∠AQD,∠QFC=180−∠C−∠CQF∴∠DAQ=∠QFC∵∠BAC=∠EAD=90°即∠BAE+∠EAQ=∠EAQ+∠QAD∴∠BAE=∠QAD∴∠DFC=∠BAE∵∠BAE=68°∴∠DFC=68°故答案为68°(2)如图2,过点B作ME的垂线交EM的延长线于N,∴∠N=90°∵∠AEC=90°∴∠N=∠AEC∵∠BAC=90°∴∠EAC+∠NAB=90°∵∠NAC+∠ACE=90°∴∠NAB=∠ECA∵△ABC是等腰Rt△ABC和△ADE是等腰Rt△ADE∴AB=AC,AD=AE 又∵AC=AB∴△AEC≌△BNA∴NB=AE∵AE=AD∴AD=NB∵∠DAE=90°∴∠DAM=90°∴∠DAM=∠N又∵∠DMA=∠BMN∴△DAM≌△BNM∴DM=BM即M是BD的中点(3)延长AG至K,使得GK=AG=9,连接CK,设AE交BC于点P,如图∵∠BAC=∠EAD=90°即∠BAE+∠EAC=∠EAC+∠CAD∴∠BAE=∠CAD∵△ABC是等腰Rt△ABC和△ADE是等腰Rt△ADE∴AB=AC,AE=AD在△ABE与△ACD中,{AE=AD∠BAE=∠CAD AB=AC∴△ABE≌△ACD(SAS)∴S△ABE=S△ABD,BE=CD∵G点是EC的中点∴EG=GC∵∠AGE=∠KGC,AG=GK∴△AGE≌△KGC(SAS)∴AE=CK,∠AEG=∠KCG∴AE=KC=AD,∠ACK=∠ACB+∠BCE+∠KCG=45°+∠AEC+∠BCE=45°+∠ABC+∠BAP=90°+∠BAE=∠BAD∴△AKC≌△ABD(SAS)∴BD=AK=18,∠CAK=∠ABD∵∠BAG+∠CAG=90°∴∠ABD+∠BAG=90°即∠AHB=90°∵AG=9,HG=5∴AH=AG−HG=9−5=4∴S△ABD=12BD⋅AH=12×18×4=36∵S△AEC=S△AEG+S△AGC=S△GCK+S△AGC=S△ACK=S△ABD=36∴S△AEC=36小提示:本题考查了三角形全等的性质与判定,等腰直角三角形的性质,三角形内角和定理,三角形外角性质,构造辅助线是解题的关键.17、如图,在四边形ABCD中,点E为对角线BD上一点,∠A=∠BEC,∠ABD=∠BCE,且AD=BE.(1)证明:①△ABD≅△ECB;②AD≌BC;(2)若BC=15,AD=6,请求出DE的长度.答案:(1)①证明见解析;②证明见解析(2)9分析:(1)①由ASA证明全等即可,②由①可证明;(2)由△ABD≌△ECB可证DE=BD-BE=15-6=9.(1)解:证明:①在△ABD和△ECB中,{∠A=∠BEC∠ABD=∠BCEAD=BE,∴△ABD≌△ECB(ASA),②由①得:△ABD≌△ECB∴∠ADB=∠EBC,∴AD∥BC;(2)∵△ABD≌△ECB,BC=15,AD=6,∴BD=BC=15,BE=AD=6,∴DE=BD-BE=15-6=9.小提示:本题考查了全等三角形的判定与性质、平行线的判定等知识,证明△ABD≌△ECB是解题的关键.18、如图1,已知ΔABC中,∠ACB=90°,AC=BC,BE、AD分别与过点C的直线垂直,且垂足分别为E,D.(1)猜想线段AD、DE、BE三者之间的数量关系,并给予证明.(2)如图2,当过点C的直线绕点C旋转到ΔABC的内部,其他条件不变,如图2所示,①线段AD、DE、BE三者之间的数量关系是否发生改变?若改变,请直接写出三者之间的数量关系,若不改变,请说明理由;②若AD=2.8,DE=1.5时,求BE的长.答案:(1)DE=AD+BE,证明见解析(2)①发生改变,DE=AD−BE;②1.3分析:(1)证明ΔACD≅ΔCBE,可得AD=CE,CD=BE,即可求解;(2)①证明ΔACD ≅ΔCBE ,可得AD =CE ,CD =BE , 即可求解;②由①可得DE =AD −BE ,从而得到BE =AD −DE ,即可求解.(1)解:DE =AD +BE , 理由如下:∵BE 、AD 分别与过点C 的直线垂直,∴∠BEC =∠ADC =90°,∴∠ACD +∠CAD =90°,∵∠ACB =90°,∴∠ACD +∠BCE =90°,∴∠CAD =∠BCE ,在ΔACD 和ΔCBE 中,{∠ADC =∠BEC∠CAD =∠BCE AC =BC,∴ΔACD ≅ΔCBE (AAS ),∴AD =CE ,CD =BE ,∵ DE =EC +CD ,∴DE =AD +BE ;(2)解:①发生改变.∵BE 、AD 分别与过点C 的直线垂直,∴∠BEC =∠ADC =90°,∴∠ACD +∠CAD =90°,∵∠ACB =90°,∴∠ACD +∠BCE =90°,∴∠CAD =∠BCE ,在ΔACD 和ΔCBE 中,{∠ADC =∠BEC∠CAD =∠BCE AC =BC,∴ΔACD≅ΔCBE(AAS),∴AD=CE,CD=BE,∵DE=CE-CD,∴DE=AD−BE;②由①知:DE=AD−BE,∴BE=AD−DE=2.8−1.5=1.3,∴BE的长为1.3.小提示:本题主要考查了全等三角形的判定和性质、等角的余角相等,熟练掌握全等三角形的判定和性质是解题的关键.。
初二数学全等三角形压轴几何题(讲义及答案)含答案

初二数学全等三角形压轴几何题(讲义及答案)含答案一、全等三角形旋转模型1.问题背景:如图1,在四边形ABCD 中,90BAD ∠=︒,90BCD ∠=︒,BA BC =,120ABC ∠=︒,60MBN ∠=︒,MBN ∠绕B 点旋转,它的两边分别交AD 、DC 于E 、F .探究图中线段AE ,CF ,EF 之间的数量关系.小李同学探究此问题的方法是:延长FC 到G ,使CG AE =,连接BG ,先证明BCG BAE △≌△,再证明BFC BFE △≌△,可得出结论,他的结论就是_______________;探究延伸1:如图2,在四边形ABCD 中,90BAD ∠=︒,90BCD ∠=︒,BA BC =,2ABC MBN ∠=∠,MBN ∠绕B 点旋转,它的两边分别交AD 、DC 于E 、F .上述结论是否仍然成立?请直接写出结论(直接写出“成立”或者“不成立”),不要说明理由. 探究延伸2:如图3,在四边形ABCD 中,BA BC =,180BAD BCD ∠+∠=︒,2ABC MBN ∠=∠,MBN ∠绕B 点旋转,它的两边分别交AD 、DC 于E 、F .上述结论是否仍然成立?并说明理由.实际应用:如图4,在某次军事演习中,舰艇甲在指挥中心(O 处)北偏西30的A 处舰艇乙在指挥中心南偏东70︒的B 处,并且两舰艇到指挥中心的距离相等接到行动指令后,舰艇甲向正东方向以75海里/小时的速度前进,同时舰艇乙沿北偏东50︒的方向以100海里/小时的速度前进,1.2小时后,指挥中心观测到甲、乙两舰艇分别到达E 、F 处,且指挥中心观测两舰艇视线之间的夹角为70︒,试求此时两舰艇之间的距离.答案:E解析:EF=AE+CF .探究延伸1:结论EF=AE+CF 成立.探究延伸2:结论EF=AE+CF 仍然成立.实际应用:210海里.【分析】延长FC 到G ,使CG AE =,连接BG ,先证明BCG BAE △≌△,可得BG=BE ,∠CBG=∠ABE ,再证明BGF BEF ≌,可得GF=EF ,即可解题;探究延伸1:延长FC 到G ,使CG AE =,连接BG ,先证明BCG BAE △≌△,可得BG=BE ,∠CBG=∠ABE ,再证明BGF BEF ≌,可得GF=EF ,即可解题;探究延伸2:延长FC 到G ,使CG AE =,连接BG ,先证明BCG BAE △≌△,可得BG=BE ,∠CBG=∠ABE ,再证明BGF BEF ≌,可得GF=EF ,即可解题;实际应用:连接EF ,延长AE ,BF 相交于点C ,然后与探究延伸2同理可得EF=AE+CF ,将AE 和CF 的长代入即可.【详解】解:EF=AE+CF理由:延长FC 到G ,使CG AE =,连接BG ,在△BCG 和△BAE 中,90BC BA BCG BAE CG AE =⎧⎪∠=∠=︒⎨⎪=⎩,∴BCG BAE △≌△(SAS ),∴BG=BE ,∠CBG=∠ABE ,∵∠ABC=120°,∠MBN=60°,∴∠ABE+∠CBF=60°,∴∠CBG+∠CBF=60°,即∠GBF=60°,在△BGF 和△BEF 中,BG BE GBF EBF BF BF =⎧⎪∠=∠⎨⎪=⎩,∴△BGF ≌△BEF (SAS ),∴GF=EF ,∵GF=CG+CF=AE+CF ,∴EF=AE+CF .探究延伸1:结论EF=AE+CF 成立.理由:延长FC 到G ,使CG AE =,连接BG ,在△BCG 和△BAE 中,90BC BA BCG BAE CG AE =⎧⎪∠=∠=︒⎨⎪=⎩,∴BCG BAE △≌△(SAS ),∴BG=BE ,∠CBG=∠ABE ,∵∠ABC=2∠MBN ,∴∠ABE+∠CBF=12∠ABC , ∴∠CBG+∠CBF=12∠ABC , 即∠GBF=12∠ABC , 在△BGF 和△BEF 中,BG BE GBF EBF BF BF =⎧⎪∠=∠⎨⎪=⎩,∴△BGF ≌△BEF (SAS ),∴GF=EF ,∵GF=CG+CF=AE+CF ,∴EF=AE+CF .探究延伸2:结论EF=AE+CF 仍然成立.理由:延长FC 到G ,使CG AE =,连接BG ,∵180BAD BCD ∠+∠=︒,∠BCG+∠BCD=180°,∴∠BCG=∠BAD在△BCG 和△BAE 中,BC BA BCG BAE CG AE =⎧⎪∠=∠⎨⎪=⎩,∴BCG BAE △≌△(SAS ),∴BG=BE ,∠CBG=∠ABE ,∵∠ABC=2∠MBN ,∴∠ABE+∠CBF=12∠ABC , ∴∠CBG+∠CBF=12∠ABC , 即∠GBF=12∠ABC , 在△BGF 和△BEF 中,BG BE GBF EBF BF BF =⎧⎪∠=∠⎨⎪=⎩,∴△BGF ≌△BEF (SAS ),∴GF=EF ,∵GF=CG+CF=AE+CF ,∴EF=AE+CF .实际应用:连接EF ,延长AE ,BF 相交于点C ,∵∠AOB=30°+90°+(90°-70°)=140°,∠EOF=70°,∴∠EOF=12∠AOB ∵OA=OB ,∠OAC+∠OBC=(90°-30°)+(70°+50°)=180°,∴符合探索延伸中的条件∴结论EF= AE+CF 仍然成立即EF=75×1.2+100×1.2=210(海里)答:此时两舰艇之间的距离为210海里.【点睛】本题考查了全等三角形的判定与性质.作辅助线构造全等三角形是解题的关键. 2.一位同学拿了两块45︒三角尺MNK ∆,ACB ∆做了一个探究活动:将MNK ∆的直角顶点M 放在ACB ∆的斜边AB 的中点处,设4AC BC ==.(1)如图1所示,两三角尺的重叠部分为ACM ∆,则重叠部分的面积为______,周长为______.(2)将如图1所示中的MNK ∆绕顶点M 逆时针旋转45︒,得到如图2所示,此时重叠部分的面积为______,周长为______.(3)如果将MNK ∆绕M 旋转到不同于如图1所示和如图2所示的图形,如图3所示,请你猜想此时重叠部分的面积为______.(4)在如图3所示情况下,若1AD =,求出重叠部分图形的周长.答案:A解析:(1)4,4+;(2)4,8;(3)4;(4)4+【分析】()1根据4AC BC ==,90ACB ∠=,得出AB 的值,再根据M 是AB 的中点,得出AM MC =,求出重叠部分的面积,再根据AM ,MC ,AC 的值即可求出周长;()2易得重叠部分是正方形,边长为12AC ,面积为214AC ,周长为2.AC ()3过点M 分别作AC 、BC 的垂线MH 、ME ,垂足为H 、.E 求得Rt MHD ≌Rt MEG ,则阴影部分的面积等于正方形CEMH 的面积. ()4先过点M 作ME BC ⊥于点E ,MH AC ⊥于点H ,根据DMH EMH ∠∠=,MH ME =,得出Rt DHM ≌Rt EMG ,从而得出HD GE =,CE AD =,最后根据AD 和DF 的值,算出DM =.【详解】解:()14AC BC ==,90ACB ∠=,AB ∴== M 是AB 的中点,AM ∴=45ACM ∠=,AM MC ∴=,∴重叠部分的面积是42=, ∴周长为:44AM MC AC ++==+故答案为4,4+;()2重叠部分是正方形,∴边长为1422⨯=,面积为14444⨯⨯=, 周长为248⨯=.故答案为4,8.()3过点M 分别作AC 、BC 的垂线MH 、ME ,垂足为H 、E , M 是ABC 斜边AB 的中点,4AC BC ==, 12MH BC ∴=, 12ME AC =, MH ME ∴=,又90NMK HME ∠∠==,90NMH HMK ∠∠∴+=,90EMG HMK ∠∠+=, HMD EMG ∠∠∴=,在MHD 和MEG 中,HMD GME MH MEDHM MEG ∠=∠⎧⎪=⎨⎪∠=∠⎩, MHD ∴≌()MEG ASA ,∴阴影部分的面积等于正方形CEMH 的面积, 正方形CEMH 的面积是1144422ME MH ⋅=⨯⨯⨯=; ∴阴影部分的面积是4;故答案为4.()4如图所示, 过点M 作ME BC ⊥于点E ,MH AC ⊥于点H ,∴四边形MECH 是矩形,MH CE ∴=,45A ∠=,45AMH ∠∴=,AH MH ∴=,AH CE ∴=,在Rt DHM 和Rt GEM 中,DMH EMG MH MEDHM GEM ∠=∠⎧⎪=⎨⎪∠=∠⎩, Rt DHM ∴≌.Rt GEMGE DH ∴=,AH DH CE GE ∴-=-,CG AD ∴=,1AD =,1.DH ∴= 145DM ∴=+= .∴四边形DMGC 的周长为:CE CD DM ME +++2AD CD DM =++425=+.【点睛】此题考查了等腰直角三角形,利用等腰直角三角形的性质,等腰直角三角形的面积公式,正方形的面积公式,全等三角形的判定和性质求解.3.如图1,在Rt △ABC 中,∠A =90°,AB =AC ,点D ,E 分别在边AB ,AC 上,AD =AE ,连接DC ,点M ,P ,N 分别为DE ,DC ,BC 的中点.(1)观察猜想:图1中,线段PM 与PN 的数量关系是 ,位置关系是 ;(2)探究证明:把△ADE 绕点A 逆时针方向旋转到图2的位置,连接MN ,BD ,CE ,判断△PMN 的形状,并说明理由;(3)拓展延伸:把△ADE 绕点A 在平面内自由旋转,若AD =4,AB =10,请直接写出△PMN 面积的最大值.解析:(1)PM =PN ,PM ⊥PN ;(2)△PMN 是等腰直角三角形.理由见解析;(3)S △PMN 最大=492. 【分析】(1)由已知易得BD CE =,利用三角形的中位线得出12PM CE =,12PN BD =,即可得出数量关系,再利用三角形的中位线得出//PM CE 得出DPM DCA ∠=∠,最后用互余即可得出位置关系;(2)先判断出ABD ACE ∆≅∆,得出BD CE =,同(1)的方法得出12PM BD =,12PN BD =,即可得出PM PN =,同(1)的方法由MPN DCE DCB DBC ACB ABC ∠=∠+∠+∠=∠+∠,即可得出结论;(3)方法1:先判断出MN 最大时,PMN ∆的面积最大,进而求出AN ,AM ,即可得出MN 最大AM AN =+,最后用面积公式即可得出结论.方法2:先判断出BD 最大时,PMN ∆的面积最大,而BD 最大是14AB AD +=,即可得出结论.【详解】解:(1)点P ,N 是BC ,CD 的中点,//PN BD ∴,12PN BD =, 点P ,M 是CD ,DE 的中点, //PM CE ∴,12PM CE =, AB AC =,AD AE =,BD CE ∴=,PM PN ∴=,//PN BD ,DPN ADC ∴∠=∠,//PM CE ,DPM DCA ∴∠=∠,90BAC ∠=︒,90ADC ACD ∴∠+∠=︒,90MPN DPM DPN DCA ADC ∴∠=∠+∠=∠+∠=︒,PM PN ∴⊥,故答案为:PM PN =,PM PN ⊥;(2)PMN ∆是等腰直角三角形.由旋转知,BAD CAE ∠=∠,AB AC =,AD AE =,()ABD ACE SAS ∴∆≅∆,ABD ACE ∴∠=∠,BD CE =, 利用三角形的中位线得,12PN BD =,12PM CE =, PM PN ∴=,PMN ∴∆是等腰三角形,同(1)的方法得,//PM CE ,DPM DCE ∴∠=∠,同(1)的方法得,//PN BD ,PNC DBC ∴∠=∠,DPN DCB PNC DCB DBC ∠=∠+∠=∠+∠,MPN DPM DPN DCE DCB DBC ∴∠=∠+∠=∠+∠+∠BCE DBC ACB ACE DBC =∠+∠=∠+∠+∠ACB ABD DBC ACB ABC =∠+∠+∠=∠+∠,90BAC ∠=︒,90ACB ABC ∴∠+∠=︒,90MPN ∴∠=︒,PMN ∴∆是等腰直角三角形;(3)方法1:如图2,同(2)的方法得,PMN ∆是等腰直角三角形,MN ∴最大时,PMN ∆的面积最大,//DE BC ∴且DE 在顶点A 上面,MN ∴最大AM AN =+,连接AM ,AN ,在ADE ∆中,4AD AE ==,90DAE ∠=︒,22AM ∴=在Rt ABC ∆中,10AB AC ==,52AN =22522MN ∴=最大,222111149(72)22242PMN S PM MN ∆∴==⨯=⨯=最大. 方法2:由(2)知,PMN ∆是等腰直角三角形,12PM PN BD ==, PM ∴最大时,PMN ∆面积最大,∴点D 在BA 的延长线上,14BD AB AD ∴=+=,7PM ∴=,2211497222PMN S PM ∆∴==⨯=最大. 【点睛】此题属于几何变换综合题,主要考查了三角形的中位线定理,等腰直角三角形的判定和性质,全等三角形的判断和性质,直角三角形的性质的综合运用;解(1)的关键是判断出12PM CE =,12PN BD =,解(2)的关键是判断出ABD ACE ∆≅∆,解(3)的关键是判断出MN 最大时,PMN ∆的面积最大.4.如图,△ABC 中,O 是△ABC 内一点,AO 平分∠BAC ,连OB ,OC .(1)如图1,若∠ACB =2∠ABC ,BO 平分∠ABC ,AC =5,OC =3,则AB = ; (2)如图2,若∠CBO +∠ACO =∠BAC =60°,求证:BO 平分∠ABC ;(3)如图3,在(2)的条件下,若BC =3B 绕点O 逆时针旋转60°得点D ,直接写出CD 的最小值为 .答案:A解析:(1)8;(2)见解析;(3)33【分析】(1)先补充证明角平分线的性质定理:如图,△ABC 中,AD 是角平分线,则:BD DC=AB AC .如图1中,延长CO 交AB 于E ,由OA 平分∠EAC ,推出AE AC =OE OC,推出AE EO =AC OC =53,设AE =5k ,OE =3k ,利用相似三角形的性质构建方程求出k 即可解决问题. (2)如图2中,过点O 作EF ⊥OA 交AB 于E ,交AC 于F ,作CG ∥EF 交AB 于G ,连接OG .证明△AGO ≌△ACO (SAS ),推出OG =OC ,推出∠OGC =∠OCG ,证明O ,G ,B ,C 四点共圆,可得结论.(3)如图3中,以BC 为边向上作等边△BCH ,连接OH ,作HM ⊥BC 于M .证明△HBO ≌△CBD (SAS ),推出OH =CD ,由(2)可知∠BOC =120°,推出当点O 落在HM 上时,OH 的值最小.【详解】解:(1)先补充证明角平分线的性质定理:如图,△ABC 中,AD 是角平分线,则:BD DC =AB AC. 理由:过C 作CE ∥DA ,交BA 的延长线于E ,∵CE∥DA,∴∠1=∠E,∠2=∠3,∠1=∠2,∴∠E=∠3,∴AE=AC,∵BDDC =BAAE,∴BDDC =ABAC.如图1中,延长CO交AB于E,∵OA平分∠EAC,∴AEAC=OEOC,∴AEEO =ACOC=53,设AE=5k,OE=3k,∵OB平分∠ABC,∴OC平分∠ACB,∵∠ACB=2∠ABC,∴∠BCE=12∠ACB=∠EBC,∴EB=EC=3k+3,∵∠ACE=∠ABC,∠CAE=∠BAC,∴△ACE∽△ABC,∴ACAB =AEAC,∴5533k k =55k,解得k=58或﹣1(舍弃),∴AB=8k+3=8.故答案为:8.(2)如图2中,过点O作EF⊥OA交AB于E,交AC于F,作CG∥EF交AB于G,连接OG.∵AO平分∠AEF,∴∠OAE=∠OAF,∵AO=AO,∠AOE=∠AOF=90°,∴△AOE≌△AOF(ASA),∴AE=AF,∵∠EAF=60°,∴△AEF是等边三角形,∴∠AEF=∠AFE=60°=∠FOC+∠FCO,∵∠OBC+∠FCO=60°,∴∠FOC=∠OBC,∵EF∥CG,∴∠AGC=∠AEF=60°,∠ACG=∠AFE=60°,∴∠AGC=∠ACG,∴AG=AC,∵∠GAO=∠CAO,AO=AO,∴△AGO≌△ACO(SAS),∴OG=OC,∴∠OGC=∠OCG,∵∠FOC=∠OCG,∴∠OBC=∠OGC,∴O,G,B,C四点共圆,∴∠ABO=∠OCG,∴∠ABO=∠OBC,∴OB平分ABC.(3)如图3中,以BC为边向上作等边△BCH,连接OH,作HM⊥BC于M.∵△OBD,△BCH都是等边三角形,∴∠HBC=∠OBD=60°,BH=BC,BO=BD,∴∠HBO=∠CBD,∴△HBO≌△CBD(SAS),∴OH=CD,由(2)可知∠BOC=120°,∴当点O落在HM上时,OH的值最小,此时OH=HM﹣OM=3﹣3,∴CD的最小值为3﹣3.故答案为:3﹣3.【点睛】本题主要考查角平分线、三角形相似的判定和性质、三角形全等的判定和性质、等边三角形等相关知识点,解题关键在于作出辅助线构造相应图形.5.已知:在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B、C重合).以AD为边作正方形ADEF,连接CF.(1)如图1,当点D在线段BC上时,请直接写出线段BD与CF的数量关系:;(2)如图2,当点D在线段BC的延长线上时,其它条件不变,若AC=2,CD=1,则CF= ;(3)如图3,当点D在线段BC的反向延长线上时,且点A、F分别在直线BC的两侧,其它条件不变:①请直接写出CF、BC、CD三条线段之间的关系:;②若连接正方形对角线AE、DF,交点为O,连接OC,探究△AOC的形状,并说明理由.答案:B解析:(1)BD=CF;(2)221;(3)①CD=CF+BC,②等腰三角形,见解析【分析】(1)△ABC 是等腰直角三角形,利用SAS 即可证明△BAD ≌△CAF ;(2)同(1)相同,利用SAS 即可证得△BAD ≌△CAF ,从而证得BD=CF ,即可得到CF=CD+BC ,然后求出答案;(3)中的①与(1)相同,可证明BD=CF ,又点D 、B 、C 共线,故:CD=BC+CF ; ②由(1)猜想并证明BD ⊥CF ,从而可知△FCD 为直角三角形,再由正方形的对角线的性质判定△AOC 三边的特点,再进一步判定其形状. 【详解】解:(1)证明:∵∠BAC=90°,AB=AC , ∴∠ABC=∠ACB=45°, ∵四边形ADEF 是正方形, ∴AD=AF ,∠DAF=90°,∵∠BAC=∠BAD+∠DAC=90°,∠DAF=∠CAF+∠DAC=90°, ∴∠BAD=∠CAF , 在△BAD 和△CAF 中,AB AC BAD CAF AD AF =⎧⎪∠=∠⎨⎪=⎩, ∴△BAD ≌△CAF (SAS ), ∴BD=CF ,(2)与(1)同理,证△BAD ≌△CAF ; ∴BD=CF , ∴CF=BC+CD , ∵AC=AB=2,CD=1,∴BC ==∴CF=1;(3)①BC 、CD 与CF 的关系:CD=BC+CF理由:与(1)同法可证△BAD ≌△CAF ,从而可得: BD=CF , 即:CD=BC+CF②△AOC 是等腰三角形理由:与(1)同法可证△BAD ≌△CAF ,可得:∠DBA=∠FCA , 又∵∠BAC=90°,AB=AC , ∴∠ABC=∠ACB=45°, 则∠ABD=180°-45°=135°, ∴∠ABD=∠FCA=135° ∴∠DCF=135°-45°=90° ∴△FCD 为直角三角形.又∵四边形ADEF是正方形,对角线AE与DF相交于点O,∴OC=12DF,∴OC=OA∴△AOC是等腰三角形.【点睛】本题考查了等腰三角形、正方形的性质及全等三角形的判定与性质等知识点,一般情况下,要证明两条线段相等,就得证明这两条线段所在的两个三角形全等,关键是掌握图形特点挖掘题目所隐含的条件.6.综合与探究问题情境在Rt△ABC中,∠BAC=90°,AB=AC,点D是射线BC上一动点,连接AD,将线段AD绕点A逆时针旋转90°至AE,连接DE,CE.探究发现(1)如图1,BD=CE,BD⊥CE,请证明;探究猜想;(2)如图2,当BD=2DC时,猜想AD与BC之间的数量关系,并说明理由;探究拓广(3)当点D在BC的延长线上时,探究并直接写出线段BD,DC,AD之间的数量关系.答案:B解析:(1)证明见解析;(2)10AD BC=,理由见解析;(3)2222BD CD AD+=.【分析】(1)根据题意计算得∠BAD=∠CAE;再根据旋转的性质,通过证明△BAD≌△CAE,从而完成求解;(2)结合(1)的结论,通过△BAD≌△CAE,得CE;通过勾股定理,得2DE=;再通过勾股定理计算,记得得到答案;(3)过点A作AM BC⊥交BC于点M;根据等腰三角形三线合一的性质,得BM CM=,再根据直角三角形斜边中线的性质,得12AM BM CM BC===;根据勾股定理的性质,通过计算,即可得到线段BD,DC,AD之间的数量关系.【详解】(1)由题意得,∠BAC =∠DAE =90° ∵∠BAD +∠CAD =∠CAE +∠CAD ∴∠BAD =∠CAE∵线段AD 绕点A 逆时针旋转90°至AE ∴AD=AE 又∵AB=AC , ∴△BAD ≌△CAE ∴BD=CE ,∠B =∠ACE =45° ∴∠ECD =90°,BD ⊥CE . (2)由(1)得:△BAD ≌△CAE ∴BD=CE ,∠B =∠ACE =45° ∵13CD BC =,BD =2DC ,即23BD BC =, ∴23BD CE BC ==, ∵AD=AE ∴222DE AD AE AD =+=∴∠B =∠ACB =45° ∴∠BCE =∠ACB+∠ACE =90°∴CD 2+CE 2=DE 2,即22212()()233BC BC AD +=, ∴106AD BC =; (3)如图,过点A 作AM BC ⊥交BC 于点M∵∠BAC =90°,AB =AC ∴12BM CM BC ==∴12AM BM CM BC ===∴()1122AM BC BD CD ==-,()1122DM CM CD BC CD BD CD =+=+=+ ∵222AM DM AD +=∴()()2221122BD CD BD CD AD ⎡⎤⎡⎤-++=⎢⎥⎢⎥⎣⎦⎣⎦∴2222BD CD AD +=. 【点睛】本题考查了旋转、等腰直角三角形、勾股定理、直角三角形斜边中线的知识;解题的关键是熟练掌握旋转、等腰三角形三线合一、勾股定理、直角三角形斜边中线的性质,从而完成求解.7.如图1所示,在Rt ABC △中90BAC ∠=︒,AB AC =,2BC =,以BC 所在直线为x 轴,边BC 的垂直平分线为y 轴建立平面直角坐标系,将ABC 绕P 点0,1顺时针旋转.(1)填空:当点B 旋转到y 轴正半轴时,则旋转后点A 坐标为______;(2)如图2所示,若边AB 与y 轴交点为E ,边AC 与直线1y x =-的交点为F ,求证:AEF 的周长为定值;(3)在(2)的条件下,求AEF 内切圆半径的最大值.解析:(1)2,21;(2)见解析;(3)324【分析】(1)作出图形,'''A B C 是ABC 绕 P 点0,1顺时针旋转,点B 旋转到y 轴正半轴时得到的图形,连接 BP ,CP ,根据2BC =,y 轴垂直平分BC , AB AC =,()0,1P -可证得四边形ABPC 是正方形,则有 '''2BP B PAB A B ,'0'21B B PPO,可得点 A 坐标;(2)作BPQ CPF ∠=∠,交AB 延长线于Q 点,根据四边形ABPC 是正方形,得到90QBP FCP ∠=∠=︒,BP CP =,可证BPQ CPF ASA ≌△△,得BQ CF =,QP FP =,利用ASA 再可证得QPE FPE ≌△△,得QE FE =则AEF 的周长22AB AC =+=(3)设EF m =,AE n =,Rt AEF 的内切圆半径为r ,由(2)可得22AF m n =--则2AE AF EF r +-=222n m n m+---=2m =-,当m 最小时,r 最大.得到22222n m nm 整理得:2224220nm n m,关于n的一元二次方程有解,即22244220m m化简得24280m m +-≥,利用二次函数图像可得422m ≥-或422m ≤--(不合题意,舍去)可得m 的最小值为422-,即r 的最大值为2422324,则有AEF 内切圆半径的最大值为324-.【详解】解:(1)如图示,'''A B C 是ABC 绕 P 点0,1顺时针旋转,点B 旋转到y 轴正半轴时得到的图形,连接 BP ,CP ,∵2BC =,y 轴垂直平分BC ∴1BO CO ==又∵Rt ABC △中,AB AC = ∴1AO =,2AB AC ==∵()0,1P - ∴1PO =∴AO BO CO PO === ∴四边形ABPC 是正方形 ∴'''2BP B P AB A B∴'0'21B B PPO∴点A 坐标为2,21(2)如图2所示,作BPQ CPF ∠=∠,交AB 延长线于Q 点 ∵四边形ABPC 是正方形∴90QBP FCP ∠=∠=︒, BP CP = ∴BPQ CPF ASA ≌△△∴ BQ CF =,QP FP =∵点F 在直线1y x =-∴45FPE ∠=︒∴ 45BPE FPC ∠+∠=︒ ∴45BPE BPQ ∠+∠=︒∴45QPE FPE ∠=∠=︒ ∵EP EP =∴QPE FPE ASA ≌△△∴ QE FE =∴AEF 的周长AE EF AF AE QE AF =++=++ AE BE BQ AF AE BE FC AF =+++=+++22AB AC =+=(3)设EF m =,AE n =,Rt AEF 的内切圆半径为 r , 由(2)可得22AF m n =-则2AE AF EFr +-=22n m n m+---=2m =∴当m 最小时,r 最大.∵在Rt AEF 中,222AE AF EF +=∴22222n m nm 整理得: 2224220nm nm ∵关于n 的一元二次方程有解∴22244220m m∴24280m m +-≥利用二次函数图像可得422m ≥-422m ≤--(不合题意,舍去) ∴m 的最小值为422-r 2422324即AEF 内切圆半径的最大值为324. 【点睛】本题主要考查了一次函数的综合应用以及根的判别式、全等三角形的判定与性质、旋转、三角形内切圆等知识,能熟练应用相关性质是解题关键. 8.问题解决一节数学课上,老师提出了这样一个问题:如图①,点P 是等边ABC 内的一点,6PA =,8PB = ,10PC =.你能求出APB ∠的度数和等边ABC 的面积吗?小明通过观察、分析、思考,形成了如下思路:如图①将BPC △绕点B 逆时针旋转60°,得到BPA △,连接PP ',可得BPP '是等边三角形,根据勾股定理逆定理可得AP P '是直角三角形,从而使问题得到解决. (1)结合小明的思路完成填空:PP '=_____________,APP '∠=_______________,APB ∠=_____________ ,ABCS= ______________.(2)类比探究Ⅰ如图②,若点P 是正方形ABCD 内一点,1PA = ,2PB =,3PC =,求APB ∠的度数和正方形的面积.Ⅱ如图③,若点P 是正方形ABCD 外一点,3PA = ,1PB =, 11PC =,求APB ∠的度数和正方形的面积.答案:B解析:(1)8,90˚,150˚,25336;(2)Ⅰ135APB ∠=︒, 722ABCD S =+正方形;Ⅱ45APB ∠=︒, 1032ABCD S =-正方形【分析】(1)根据小明的思路,然后利用等腰三角形和直角三角形性质计算即可;(2)Ⅰ将△BPC 绕点B 逆时针旋转90°,得到△BP′A ,连接PP′,求出∠APB 的度数;先利用旋转求出∠PBP'=90°,BP'=BP=2,AP'=CP=3,利用勾股定理求出PP',进而判断出△APP'是直角三角形,得出∠APP'=90°,即可得出结论;过B 作BE ⊥AP 于点E ,然后利用勾股定理求出AB 的长度即可求出正方形面积;Ⅱ将△BPC 绕点B 逆时针旋转90°,得到△BP′A ,连接PP′,求出∠APB 的度数;先利用旋转求出∠PBP'=90°,BP'=BP=2,AP'=CP=3,利用勾股定理求出PP',进而判断出△APP'是直角三角形,得出∠APP'=90°,即可得出结论;过B 作BF ⊥AP 于点F ,然后利用勾股定理求出AB 的长度即可求出正方形面积; 【详解】解:(1)由题易有P BP '∆是等边三角形,AP P '∆是直角三角形 ∴PP '=BP=8,90?APP '=∠,60?P PB '=∠,∴APB ∠=APP '∠+=P PB '∠150˚, 如图1,过B 作BD ⊥AP 于点D∵APB ∠=150°∴30?BPD =∠在Rt △BPD 中,30?BPD =∠,BP=8∴BD=4,PD=43 ∴AD=6+43∴AB 2=AD 2+BD 2=100+483∴ABC S =234AB =25336+ (2)Ⅰ.如图2,将△BPC 绕点B 逆时针旋转90°,得到△BP′A ,连接PP′,∴△ABP'≌△CBP ,∴∠PBP'=90°,BP'=BP=2,AP'=CP=3,在Rt △PBP'中,BP=BP'=2,∴∠BPP'=45°,根据勾股定理得,PP'=2BP=22,∵AP=1,∴AP 2+PP'2=1+8=9,∵AP'2=32=9,∴AP 2+PP'2=AP'2,∴△APP'是直角三角形,且∠APP'=90°,∴∠APB=∠APP'+∠BPP'=90°+45°=135°;过B 作BE ⊥AP 于点E ,∵∠APB=135°∴∠BPE=45°∴△BPE 是等腰直角三角形∴BE=BP=22BP =2 ∴AE=1+2∴AB 2=AE 2+BE 2=7+22 ∴2722ABCD S AB ==+正方形Ⅱ.如图3,将△BPC 绕点B 逆时针旋转90°,得到△BP′A ,连接PP′,∴△ABP'≌△CBP ,∴∠PBP'=90°,BP'=BP=1,AP'=CP=11,在Rt △PBP'中,BP=BP'=1,∴∠BPP'=45°,根据勾股定理得,PP'=2BP=2,∵AP=3,∴AP 2+PP'2=9+2=11,∵AP'2=(11)2=11,∴AP 2+PP'2=AP'2,∴△APP'是直角三角形,且∠APP'=90°,∴∠APB=∠APP'-∠BPP'=90°-45°=45°.过B 作BF ⊥AP 于点F∵∠APB=45°∴△BPF 为等腰直角三角形∴PF=BF=22BP =22 ∴2 ∴AB 2=AF 2+BF 2=1032-∴21032ABCD S AB ==-正方形【点睛】此题是四边形综合题,主要考查了正方形的性质,旋转的性质,直角三角形的性质和判定,勾股定理,正确作出辅助线是解本题的关键.9.如图1,在△ABC 和△ADE 中,∠DAE=∠BAC ,AD=AE ,AB=AC .(1)求证:△ABD ≌△ACE ;(2)如图2,在△ABC 和△ADE 中,∠DAE=∠BAC ,AD=AE ,AB=AC ,∠ADB=90°,点E 在△ABC 内,延长DE 交BC 于点F ,求证:点F 是BC 中点;(3)△ABC 为等腰三角形,∠BAC=120°,AB=AC ,点P 为△ABC 所在平面内一点,∠APB=120°,AP=2,BP=4,请直接写出 CP 的长.答案:D解析:(1)证明见详解;(2)证明见详解;(3)2713【分析】(1)因为∠DAE=∠BAC ,可以得到∠DAB=∠EAC ,因为AD=AE ,AB=AC ,即可得到△ABD ≌△ACE ;(2)连接CE ,延长EF 至点H ,取CF=CH ,连接CH ,由(1)可得△ABD ≌△ACE ,所以∠AEC=90°和CE=BD ,可以推出∠BDF=∠CEF ,再证明△DBF ≌△ECH ,所以BF=CH ,等量代换即可得到BF=FC ,即可解决;(3)点P 在△ABC 内部,将△ABP 逆时针旋转120°,得到ACP ∆',连接PP '和PC ,可以得到△PP C '是直角三角形,利用勾股定理即可求出PC 的值;当点P 在△ABC 外部,将△APB 绕点A 逆时针旋转120︒得到PDC ∆,连接PP '和PC ,过点P 作PD ⊥'CP 于点D ,连接PD 可以得到△PP D ',△PP D '是直角三角形和,利用勾股定理即可求出'DP 及PC 的值.【详解】解:(1)证明:∵∠DAE=∠BAC∴∠DAB=∠EAC∵AD=AE ,AB=AC∴△ABD ≌△ACE(2)证明:连接CE ,延长EF 至点H ,取CF=CH ,连接CH ,如图所示:∵△ADB≌△AEC∴BD=EC,∠ADB=∠AEC=90°∵AD=AE∴∠ADE=∠AED∵∠ADE+∠EDB=∠AED+∠CEH=90°∴∠EDB=∠CEH∵CF=CH∴∠CFH=∠CHF∴∠DFB=∠H∵CE=BD∴△DBF≌△ECH∴BF=CH∴BF=CF∴点F是BC的中点∆',连接(3)当点P在△ABC内部,如图所示,将△ABP逆时针旋转120°,得到ACPPP'和PC∆'∵将△ABP旋转120°得到ACP∴∠PAP'=120°,AP='AP=2,BP=CP'=4∴PP'3∵∠AP C'=120°,∠AP P'=30°,∴∠PP C'=90°,∴()2223427+=.当点P在△ABC外部,如图所示,将△APB 绕点A 逆时针旋转120︒到△'AP C ,过点P 作PD ⊥'CP 于点D ,连接PD , ∵将△ABP 旋转120°得到ACP ∆'∴∠PAP '=120°,AP='AP =2,BP=CP '=4,∴PP '=23, ∵∠AP C '=120°,∠AP P '=30°,∴∠PP C '=150°,∴∠PP D '=30°,在Rt 'PDP 中,1'32PD PP ==, 22''3DP PP PD ∴=-=,''347DC DP P C ∴=+=+=,()222237213PC PD DC ∴=+=+= . 综上所述,27213PC =或【点睛】本题主要考查了全等三角形以及旋转,合理的作出辅助线以及熟练旋转的性质是解决本题的关键.10.如图,直线y =﹣x +c 与x 轴交于点B (3,0),与y 轴交于点C ,过点B ,C 的抛物线y =﹣x 2+bx +c 与x 轴的另一个交点为A .(1)求抛物线的解析式和点A 的坐标;(2)P 是直线BC 上方抛物线上一动点,PA 交BC 于 D .设t =PD AD,请求出t 的最大值和此时点P 的坐标;(3)M 是x 轴上一动点,连接MC ,将MC 绕点M 逆时针旋转90°得线段ME ,若点E 恰好落在抛物线上,请直接写出此时点M 的坐标. 答案:A解析:(1)y=﹣x2+2x+3,A(﹣1,0);(2)t的最大值为916,此时P (32,154);(3)M(9332-,0)或(9332+,0).【分析】(1)利用待定系数法解决问题即可;(2)连接AC,PC,PB,过点A作AE⊥BC于E,过等P作PF⊥BC于F.设P(m,﹣m2+2m+3).利用相似三角形的性质构建二次函数解决问题即可;(3)过点E作EH⊥x轴于H.设M(m,0),利用全等三角形的性质求出点E的坐标(用m表示),再利用待定系数法解决问题即可.【详解】解:(1)∵直线y=﹣x+c与x轴交于点B(3,0),与y轴交于点C,∴0=﹣3+c,解得c=3,∴C(0,3),∵抛物线经过B,C,∴9303b cc-++=⎧⎨=⎩,解得23bc=⎧⎨=⎩,∴抛物线的解析式为y=﹣x2+2x+3,令y=0,得到﹣x2+2x+3=0,解得x=﹣1或3,∴A(﹣1,0);(2)如图,连接AC,PC,PB,过点A作AE⊥BC于E,过点P作PF⊥BC于F.设P(m,﹣m2+2m+3).∵AE∥PF,∴△PFD∽△AED,∴PDAD =PFAE,∵S△PBC=12•BC•PF,S△ACB=12•BC•AE,∴PDAD =PBCABCSS∆∆,∵S △ABC =12•AB •OC =12×4×3=6, ∴t =PD AD =6PBC S ∆=211133(23)332226m m m ⨯⨯+⨯⨯-++-⨯⨯=﹣14m 2+34m =﹣14(m ﹣32)2+916, ∵﹣14<0, ∴m =32时,t 有最大值,最大值为916,此时P (32,154); (3)如图,过点E 作EH ⊥x 轴于H ,∵∠COM =∠EHM =∠CME =90°,∴∠EMH +∠CMH =90°,∠EMH +∠MEH =90°,∴∠MEH =∠CMO ,∵MC =ME ,∴△COM ≌△MHE (AAS ),∴OC =MH =3,OM =EH ,设M (m ,0),则E (m ﹣3,﹣m ),把E (m ﹣3,﹣m )代入y =﹣x 2+2x +3,可得﹣(m ﹣3)2+2(m ﹣3)+3=﹣m , 整理得,m 2﹣9m +12=0,解得m 933-933+, ∴M 933-,0933+0). 【点睛】本题考查的是二次函数综合题,涉及全等三角形的性质和判定,相似三角形的性质和判定,解题的关键是利用数形结合的思想,在二次函数图象上构造全等三角形或相似三角形,利用几何的性质进行点坐标的求解.11.综合与实践实践操作:①如图1,ABC ∆是等边三角形,D 为BC 边上一个动点,将ACD ∆绕点A 逆时针旋转60︒得到AEF ∆,连接CE .②如图2,在ABC ∆中,AD BC ⊥于点D ,将ABD ∆绕点A 逆时针旋转90︒得到AEF ∆,延长FE 与BC 交于点G .③如图3,将图2中得到AEF ∆沿AE 再一次折叠得到AME ∆,连接MB .问题解决:(1)小明在探索图1时发现四边形ABCE 是菱形.小明是这样想的:请根据小明的探索直接写出图1中线段CD ,CF ,AC 之间的数量关系为 : (2)猜想图2中四边形ADGF 的形状,并说明理由;问题再探:(3)在图3中,若AD=6,BD=2,则MB 的长为 .答案:C解析:(1)CD+CF=AC ;(2)四边形ADGF 为正方形;理由见解析;(3)13【分析】(1)先证明C 、F 、E 在同一直线上,再证明△BAD ≌△CAF (SAS ),则∠ADB=∠AFC ,BD=CF ,可得AC=CF+CD ;(2)先根据∠ADC=∠DAF=∠F=90°,证明得四边形ADGF 是矩形,由邻边相等可得四边形ADGF 是正方形;(3)证明△BAM ≌△EAD (SAS ),根据BM=DE 及勾股定理可得结论.【详解】解:(1)如图:由旋转得:∠DAF=60°=∠BAC,AD=AF,∴∠BAD=∠CAF,∵△ABC是等边三角形,∴AB=AC,∴△BAD≌△CAF(SAS),∴∠ADB=∠AFC,BD=CF,∵∠ADC+∠ADB=∠AFC+∠AFE=180°,∴C、F、E在同一直线上,∴AC=BC=BD+CD=CF+CD,+=;故答案为:CD CF AC(2)四边形ADGF是正方形,理由如下:如图:∵Rt△ABD绕点A逆时针旋转90°得到△AEF,∴AF=AD,∠DAF=90°,∵AD⊥BC,∴∠ADC=∠DAF=∠F=90°,∴四边形ADGF是矩形,∵AF=AD,∴四边形ADGF是正方形;(3)如图3,连接DE,∵四边形ADGF是正方形,DG=FG=AD=AF=6,∵△ABD绕点A逆时针旋转90°,得到△AEF,∴∠BAD=∠EAF,BD=EF=2,∴EG=FG-EF=6-2=4,∵将△AFE沿AE折叠得到△AME,∴∠MAE=∠FAE,AF=AM,∴∠BAD=∠EAM,∴∠BAD+∠DAM=∠EAM+∠DAM,即∠BAM=∠DAE,∵AF=AD,∴AM=AD,在△BAM和△EAD中,∵AM ADBAM DAEAB AE=⎧⎪∠=∠⎨⎪=⎩,∴△BAM≌△EAD(SAS),∴BM=DE=22EG DG+=2246213+=.故答案为:213.【点睛】本题属于四边形综合题,主要考查了旋转的性质、全等三角形的判定与性质、等边三角形的判定与性质、正方形的性质以及勾股定理的综合应用,解决问题的关键是熟练掌握等边三角形和全等三角形的性质,依据图形的性质进行计算求解.12.如图,BC⊥CA,BC=CA,DC⊥CE,DC=CE,直线BD与AE交于点F,交AC于点G,连接CF.(1)求证:△ACE≌△BCD;(2)求证:BF⊥AE;(3)请判断∠CFE与∠CAB的大小关系并说明理由.答案:C解析:(1)见解析;(2)见解析;(3)∠CFE=∠CAB,见解析【分析】(1)根据垂直的定义得到∠ACB =∠DCE =90°,由角的和差得到∠BCD =∠ACE ,即可得到结论;(2)根据全等三角形的性质得到∠CBD =∠CAE ,根据对顶角的性质得到∠BGC =∠AGE ,由三角形的内角和即可得到结论;(3)过C 作CH ⊥AE 于H ,CI ⊥BF 于I ,根据全等三角形的性质得到AE =BD ,S △ACE =S △BCD ,根据三角形的面积公式得到CH =CI ,于是得到CF 平分∠BFH ,推出△ABC 是等腰直角三角形,即可得到结论.【详解】(1)证明:∵BC ⊥CA ,DC ⊥CE ,∴∠ACB =∠DCE =90°,∴∠BCD =∠ACE ,在△BCD 与△ACE 中,BC CA ACD ACE CD CE =⎧⎪∠=∠⎨⎪=⎩,∴△ACE ≌△BCD ;(2)∵△BCD ≌△ACE ,∴∠CBD =∠CAE ,∵∠BGC =∠AGE ,∴∠AFB =∠ACB =90°,∴BF ⊥AE ;(3)∠CFE =∠CAB ,过C 作CH ⊥AE 于H ,CI ⊥BF 于I ,∵△BCD ≌△ACE ,∴ACE BCD AE BD,S S ∆∆==,∴CH =CI ,∴CF 平分∠BFH ,∵BF ⊥AE ,∴∠BFH =90°,∠CFE =45°,∵BC ⊥CA ,BC =CA ,∴△ABC 是等腰直角三角形,∴∠CAB =45°,∴∠CFE =∠CAB .【点睛】角的和差、对顶角的性质这些知识点在证明全等和垂直过程中经常会遇到,需要掌握。
专题 全等三角形压轴题(30题)(解析版)

八年级上册数学《第十二章全等三角形》专题全等三角形压轴题训练(30题)1.(2022秋•忠县期末)在△ABC中,点D、E分别在AB、AC边上,设BE与CD相交于点F.(1)如图①,设∠A=60°,BE、CD分别平分∠ABC、∠ACB,证明:DF=EF.(2)如图②,设BE⊥AC,CD⊥AB,点G在CD的延长线上,连接AG、AF;若∠G=∠6,BD=CD,证明:GD=DF.【分析】(1)在BC上截取BM=BD,连接FM,证明△BFD≌△BFM,△ECF≌△MCF,进而可以解决问题;(2)根据已知条件证明△BDF≌△CDA,进而可以解决问题.【解答】证明:(1)如图,在BC上截取BM=BD,连接FM,∵∠A=60,∴∠BFC=90°+60°÷2=120°,∴∠BFD=60°,∵BE平分∠ABC,∴∠1=∠2,在△BFD和△BFM中,BD=BM∠1=∠2,BF=BF∴△BFD≌△BFM(SAS),∴∠BFM=∠BFD=60°,DF=MF,∴∠CFM=120°﹣60°=60°,∵∠CFE=∠BFD=60°,∴∠CFM=∠CFE,∵CD平分∠ACB,∴∠3=∠4,又CF=CF,在△ECF和△MCF中,∠CFE=∠CFMFC=FC,∠3=∠4∴△ECF≌△MCF(ASA),∴EF=MF,∴DF=EF;(2)∵BE⊥AC,CD⊥AB,∴∠BDF=∠CDA=90°,∴∠1+∠BFD=90°,∠3+∠CFE=90°,∠BFD=∠CFE,∴∠1=∠3,∵BD=CD,在△BDF和△CDA中,∠BDF=∠CDABD=CD,∠1=∠3∴△BDF≌△CDA(ASA),∴DF=DA,∵∠ADF=90°,∴∠6=45°,∵∠G=∠6,∴∠5=45°∴∠G=∠5,∴GD=DA,∴GD=DF.【点评】本题属于三角形的综合题,考查了全等三角形的判定与性质,角平分线的性质,解决本题的关键是掌握全等三角形的判定与性质.2.如图,△ABC中,AB=AC,D为AC边上一点,E为AB延长线上一点,且CD=BE,DE与BC相交于点F.(1)求证:DF=EF.=5,求EG的长.(2)过点F作FG⊥DE,交线段CE于点G,若CE⊥AC,CD=4,S△EFG【分析】(1)过点D作DH∥AB交BC于点H,根据等腰三角形的性质及平行线的性质得到∠BEF=∠HDF,∠DHC=∠DCH,则DH=CD,结合∠BFE=∠HFD,即可利用AAS判定△BEF≌△HDF,根据全等三角形的性质即可得解;(2)根据三角形的面积公式求解即可.【解答】(1)过点D作DH∥AB交BC于点H,∵AB=AC,∴∠ABC=∠ACB,∵DH∥AB,∴∠DHC=∠ABC,∴∠DHC=∠ACB=∠DCH,∴DH=CD,∵CD=BE,∴DH=BE,∵DH∥AB,∴∠BEF=∠HDF,在△BEF和△HDF中,∠BFE=∠HFD∠BEF=∠HDFBE=DH,∴△BEF≌△HDF(AAS),∴DF=EF;(2)连接DG,∵DF=EF,FG⊥DE,∴S△DFG =S△EFG=5,∴S△DEG=10,∵CE⊥AC,CD=4,∴S△DEG =12EG•CD=12EG×4,∴12EG×4=10,∴EG=5.【点评】此题考查了全等三角形的判定与性质,利用AAS判定△BEF≌△HDF是解题的关键.3.如图1,在等腰直角三角形ABC中,AB=AC,∠BAC=90°,点P为BC边上的一个动点,连接AP,以AP为直角边,A为直角顶点,在AP右侧作等腰直角三角形PAD,连接CD.(1)当点P在线段BC上时(不与点B重合),求证:△BAP≌△CAD;(2)当点P在线段BC的延长线上时(如图2),试猜想线段BP和CD的数量关系与位置关系分别是什么?请给予证明.【分析】(1)证得∠BAP=∠CAD,根据SAS可证明△BAP≌△CAD;(2)可得∠BAP=∠CAD,由SAS可证明△BAP≌△CAD,可得BP=CD,∠B=∠ACD,则结论得证.【解答】(1)证明:∵∠BAC=∠PAD=90°,∴∠BAC﹣∠PAC=∠PAD﹣∠PAC,即:∠BAP=∠CAD,在△BAP和△CAD中AB=AC∠BAP=∠CAD,PA=DA∴△BAP≌△CAD(SAS);(2)猜想:BP=CD,BP⊥CD.证明:∵∠BAC=∠PAD=90°,∴∠BAC+∠PAC=∠PAD+∠PAC,即:∠BAP=∠CAD,在△BAP和△CAD中AB=AC∠BAP=∠CAD,PA=DA∴△BAP≌△CAD(SAS),∴BP=CD(全等三角形的对应边相等),∠B=∠ACD(全等三角形的对应角相等),∵∠B+∠ACB=90°,∴∠ACD+∠ACB=90°,即:BP⊥CD.【点评】本题考查了全等三角形的判定与性质,等腰直角三角形的性质,根据同角的余角相等求出两边的夹角相等是证明三角形全等的关键.4.在△ABC中,∠ABC=90°.点G在直线BC上,点E在直线AB上,且AG与CE相交于点F,过点A 作边AB的垂线AD,且CD∥AG,EB=AD,AE=BC.(1)如图①,当点E在△ABC的边AB上时,求∠DCE的度数;(2)如图②,当点E在线段BA的延长线上时,求证:AB=BG.【分析】(1)如图①,连接ED,根据已知条件得到△ADE≌△BEC(SAS),根据全等三角形的性质得到∠AED=∠BCE,ED=CE,于是得到结论;(2)如图②,连接DE,根据已知条件得到△ADE≌△BEC(SAS),根据全等三角形的性质得到∠AED =∠BCE,ED=CE,根据等腰三角形的性质得到∠EDC=∠ECD,推出AF平分∠DAE,于是得到结论.【解答】解:(1)如图①连接ED,∵AD⊥AB,∴∠DAE=90°,∵∠ABC=90°,∵AD=EB,AE=BC,∴△ADE≌△BEC(SAS),∴∠AED=∠BCE,ED=CE,∴∠AED+∠BEC=∠BCE+∠BEC;∴∠AED+∠CEB=90°,∴∠DEC=90°,∴∠DCE=45°;(2)如图②,连接DE,∵AD⊥AB,∴∠DAE=90°,∵∠ABC=90°,∴∠DAE=∠ABC,∵AD=EB,AE=BC,∴△ADE≌△BEC(SAS),∴∠ADE=∠BEC,ED=CE,∵ED=CE,∴∠EDC=∠ECD,即∠ADE+∠ADC=∠ECD,∴∠BEC+∠DAF=∠AFC,∵∠BEC+∠EAF=∠AFC,∴∠DAF=∠EAF,∴AF平分∠DAE,∵∠DAE=90°,∴∠EAF=45°,∵∠EAF=∠BAG,∴∠BAG=45°,∵∠ABC=90°,∴∠ABG=90°,∴∠BGA=∠BAG,∴AB=BG.【点评】本题考查了平行线的性质,全等三角形的判定和性质,角平分线的定义,等腰直角三角形的判定和性质,正确的识别图形是解题的关键.5.在Rt△ABC中,∠ABC=90°,点D是CB延长线上一点,点E是线段AB上一点,连接DE.AC=DE,BC=BE.(1)求证:AB=BD;(2)BF平分∠ABC交AC于点F,点G是线段FB延长线上一点,连接DG,点H是线段DG上一点,连接AH交BD于点K,连接KG.当KB平分∠AKG时,求证:AK=DG+KG.【分析】(1)证明Rt△ACB≌Rt△DEB即可解决问题;(2)作BM平分∠ABD交AK于点M,证明△BMK≌△BGK,△ABM≌△DBG,即可解决问题.【解答】证明:(1)在Rt△ACB和Rt△DEB中,AC=DEBC=BE,∴Rt△ACB≌Rt△DEB(HL),∴AB=BD,(2)如图:作BM平分∠ABD交AK于点M,∵BM平分∠ABD,KB平分∠AKG,∴∠ABM=∠MBD=45°,∠AKB=∠BKG,∵∠ABF=∠DBG=45°∴∠MBD=∠GBD,在△BMK和△BGK中,∠MBD=∠GBDBK=BK,∠AKB=∠BKG∴△BMK≌△BGK(ASA),∴BM=BG,MK=KG,在△ABM和△DBG中,AB=BD∠ABM=∠DBG,BM=BG∴△ABM≌△DBG(SAS),∴AM=DG,∵AK=AM+MK,∴AK=DG+KG.【点评】本题考查了全等三角形的判定与性质,解决本题的关键是得到△BMK≌△BGK.6.(2023春•市南区期末)如图,在△ABC中,AB=AC,AD⊥BC于点D,E为AC边上一点,连接BE与AD交于点F,G为△ABC外一点,满足∠ACG=∠ABE,∠FAG=∠BAC,连接EG.(1)求证:△ABF≌△ACG;(2)求证:BE=CG+EG.【分析】(1)根据已知条件可得∠BAD=∠CAG,然后利用ASA即可证明△ABF≌△ACG;(2)结合(1)的结论,再证明△AEF≌△AEG,即可解决问题.【解答】(1)证明:∵∠BAC=∠FAG,∴∠BAC﹣∠CAD=∠FAG﹣∠CAD,∴∠BAD=∠CAG,在△ABF和△ACG中,∠BAD=∠CAGAB=AC,∠ABF=∠ACG∴△ABF≌△ACG(ASA);(2)证明:∵△ABF≌△ACG,∴AF=AG,BF=CG,∵AB=AC,AD⊥BC,∴∠BAD=∠CAD,∵∠BAD=∠CAG,∴∠CAD=∠CAG,在△AEF和△AEG中,AF=AG∠FAE=∠GAE,AE=AE∴△AEF≌△AEG(SAS).∴EF=EG,∴BE=BF+FE=CG+EG.【点评】本题考查了全等三角形的判定与性质,解决本题的关键是得到△AEF≌△AEG.7.(2022秋•新市区校级期中)已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足.求证:(1)AD=AE=EC.(2)BA+BC=2BF.【分析】(1)由△BCD和△BEA为等腰三角形,∠ABD=∠EBC,得出∠BCD=∠BEA,由△ABD≌△EBC可得∠BCE=∠BDA,由∠BCE=∠BCD+∠DCE,∠BDA=∠DAE+∠BEA得出∠BCD+∠DCE=∠DAE+∠BEA,进而得出∠DCE=∠DAE,即可证明AE=EC;(2)过点E作EG⊥BC交BC的延长线于点G,由“HL”得出Rt△BFE≌Rt△BGE和Rt△BFE≌Rt△BGE,从而得出BF=BG,FA=CG,再通过等量代换即可得出结论.【解答】(1)证明:∵BD为△ABC的角平分线,∴∠ABD=∠EBC,在△ABD与△EBC中,AB=EB∠ABD=∠EBD,BD=BC∴△ABD≌△EBC(SAS),∴∠BCE=∠BDA,∵∠BCE=∠BCD+∠DCE,∠BDA=∠DAE+∠BEA,∴∠BCD+∠DCE=∠DAE+∠BEA,∵BD=BC,BE=BA,∴△BCD和△BEA为等腰三角形,∵∠ABD=∠EBC,∴∠BCD=∠BEA,∴∠DCE=∠DAE,∴AE=EC,∵△ABD≌△EBC,∴AD=EC,∴AD=EC=AE;(2)证明:如图,过点E作EG⊥BC交BC的延长线于点G,∵BE平分∠ABC,EF⊥AB,EG⊥BG,∴EF=EG,在Rt△BFE与Rt△BGE中,EF=EGBE=BE,∴Rt△BFE≌Rt△BGE(HL),∴BF=BG,在Rt△AFE与Rt△CGE中,EF=EGEA=EC,∴Rt△AFE≌Rt△CGE(HL),∴FA=CG,∴BA+BC=BF+FA+BG﹣CG=BF+BG=2BF.【点评】本题考查了全等三角形的判定与性质,掌握三角形全等的判定方法是解决问题的关键.8.(2023春•余江区期末)如图,大小不同的两块三角板△ABC和△DEC直角顶点重合在点C处,AC=BC,DC=EC,连接AE、BD,点A恰好在线段BD上.(1)找出图中的全等三角形,并说明理由;(2)当AD=AB=4cm,则AE的长度为 cm.(3)猜想AE与BD的位置关系,并说明理由.【分析】(1)根据SAS证明△CBD≌△CAE即可;(2)根据全等三角形的性质解答即可;(3)根据全等三角形的性质和垂直的定义解答即可.【解答】解:(1)△CBD≌△CAE,理由如下:∵∠ACB=∠DCE=90°,∴∠ACB+∠ACD=∠DCE+∠ACD,即∠BCD=∠ACE,在△CBD与△CAE中,BC=AC∠BCD=∠ACE,DC=EC∴△CBD≌△CAE(SAS);(2)∵△CBD≌△CAE,∴BD=AE=AD+AB=4+4=8(cm),故答案为:8;(3)AE⊥BD,理由如下:AE与CD相交于点O,在△AOD与△COE中,∵△CBD≌△CAE,∴∠ADO=∠CEO,∵∠AOD=∠COE,∴∠OAD=∠OCE=90°,∴AE⊥BD.【点评】此题考查全等三角形的判定和性质,关键是根据SAS得出△CBD与△CAE全等解答.9.已知,△ABC中,∠ACB=90°,AC=BC,点E是BC上一点,连接AE(1)如图1,当AE平分∠BAC时,EH⊥AB于H,△EHB的周长为10m,求AB的长;(2)如图2,延长BC至D,使DC=BC,将线段AE绕点A顺时针旋转90°得线段AF,连接DF,过点B作BG⊥BC,交FC的延长线于点G,求证:BG=BE.【分析】(1)根据等腰三角形的性质得到∠B=45°,根据角平分线的性质得到CE=EH=BH,根据全等三角形的性质得到AH=AC,于是得到结论;(2)先连接AD,依据AAS判定△ADF≌△ABE,得到DF=BE,再判定△BCG≌△DCF,得出DF=BG,进而得到BG=BE.【解答】解:(1)∵∠ACB=90°,AC=BC,∴∠B=45°,∵AE平分∠BAC时,EH⊥AB于H,∴CE=EH=BH,在Rt△ACE与Rt△AHE中,CE=EH AE=AE,∴Rt△ACE与Rt△AHE(HL),∴AH=AC,∴AH=BC,∵△EHB的周长为10m,∴AB=AH+BH=BC+BH=10m;(2)如图所示,连接AD,线段AE绕点A顺时针旋转90°得线段AF,则AE=AF,∠EAF=90°,∵AC⊥BD,DC=BC,∴AD=AB,∠ABE=∠ADC=45°,∴∠BAD=90°=∠EAF,∴∠BAE=∠DAF,∴△ABE≌△ADF(SAS),∴DF=BE,∠ADF=∠ABE=45°,∴∠FDC=90°,∵BG⊥BC,∴∠CBG=∠CDF=90°,又∵BC=DC,∠BCG=∠DCF,∴△BCG≌△DCF(ASA),∴DF=BG,∴BG=BE.【点评】本题主要考查了旋转的性质,等腰直角三角形的性质以及全等三角形的判定与性质的综合运用,解决问题的关键是作辅助线构造全等三角形,依据全等三角形的对应边相等得出结论.10.在△ABC中,∠ABC=45°,AM⊥MB,垂足为M,点C是BM延长线上一点,连接AC.(1)如图①,点D在线段AM上,且DM=CM.求证:△BDM≌△ACM;(2)如图②,在(1)的条件下,点E是△ABC外一点,且满足EC=AC,连接ED并延长交BC于点F,且F为线段BC的中点,求证:∠BDF=∠CEF.【分析】(1)利用SAS即可证明△BMD≌△AMC.(2)延长EF到点G,使得FG=EF,证△BMD≌△AMC得AC=BD,再证△BFG≌△CFE可得BG=CE,∠G=∠E,从而得BD=BG=CE,即可得∠BDG=∠G=∠CEF.【解答】(1)证明:∵∠ABM=45°,AM⊥BM,在△BMD和△AMC中,DM=CM∠BMD=∠AMC BM=AM,∴△BMD≌△AMC(SAS);(2)证明:延长EF到点G,使得FG=EF,连接BG.如图所示:∵△BMD≌△AMC∴BD=AC,又∵CE=AC,∴BD=CE,在△BFG和△CFE中,BF=FC∠BFG=∠EFC FG=FE,∴△BFG≌△CFE(SAS),∴BG=CE,∠G=∠CEF,∴BD=CE=BG,∴∠BDF=∠G=∠CEF.∴∠BDF=∠CEF.【点评】本题主要考查全等三角形的判定与性质,等腰直角三角形的性质等知识点,熟练掌握全等三角形的判定与性质是解题的关键.11.如图1,在△ABC中,∠A=120°,∠C=20°,BD平分∠ABC,交AC于点D.(1)求证:BD=CD.(2)如图2,若∠BAC的角平分线AE交BC于点E,求证:AB+BE=AC.(3)如图3,若∠BAC的外角平分线AE交CB的延长线于点E,则(2)中的结论是否成立?若成立,给出证明,若不成立,写出正确的结论.【分析】(1)根据∠A=120°,∠C=20°,可得∠ABC的度数,再根据BD平分∠ABC,可得∠DBC=∠C=20°,进而可得结论;(2)如图2,过点E作EF∥BD交AC于点F,证明△ABE≌△AFE,可得BE=EF=FC,进而可得AB+BE =AC;(3)如图3,过点A作AF∥BD交BE于点F,结合(1)和AE是∠BAC的外角平分线,可得FE=AF=AC,进而可得结论BE﹣AB=AC.【解答】(1)证明:∵∠A=120°,∠C=20°,∴∠ABC=180°﹣120°﹣20°=40°,∵BD平分∠ABC,∴∠ABD=∠DBC=12∠ABC=20°,∴∠DBC=∠C=20°,∴BD=CD;(2)证明:如图2,过点E作EF∥BD交AC于点F,∴∠FEC=∠DBC=20°,∴∠FEC=∠C=20°,∴∠AFE=40°,FE=FC,∴∠AFE=∠ABC,∵AE是∠BAC的平分线,∴∠BAE=∠FAE,在△ABE和△AFE中,∠BAE=∠FAE∠ABE=∠AFE,AE=AE∴△ABE≌△AFE(AAS),∴BE=EF,∴BE=EF=FC,∴AB+BE=AF+FC=AC;(3)(2)中的结论不成立,正确的结论是BE﹣AB=AC.理由如下:如图3,过点A作AF∥BD交BE于点F,∴∠AFC=∠DBC=20°,∴∠AFC=∠C=20°,∴AF=AC,∵AE是∠BAC的外角平分线,∴∠EAB=12(180°﹣∠ABC)=30°,∵∠ABC=40°,∴∠E=∠ABC﹣∠EAB=10°,∴∠E=∠FAE=10°,∴FE=AF,∴FE=AF=AC,∴BE﹣AB=BE﹣BF=EF=AC.【点评】本题考查了全等三角形的判定与性质,解决本题的关键是掌握全等三角形的判定与性质.12.(2022秋•渝北区校级期末)已在等腰Rt△ABC中,∠ABC=90°,AB=CB,D为直线AB上一点,连接CD,过点C作CE⊥CD,且CE=CD,连接DE,交AC于点F.(1)如图1,当点D在线段AB上,且∠DCB=30°时,请探究DF,EF,CF之间的数量关系,并说明理由;(2)如图2,在(1)的条件下,在FC上任取一点G,连接DG,作射线GP使∠DGP=60°,交∠DFG 的平分线于点Q,求证:FD+FG=FQ.【分析】(1)在EF上找到G点使得FG=CF,易证△CFG是等边三角形,可得CG=CF=GF,即可求得∠ECG=∠ACD,即可证明△ECG≌△CDF,可得DF=EG,即可解题;(2)在FP上找到H点,使得FH=FG,易证△FGH是等边三角形,可得∠GHF=∠FGH=60°,GH =FG=FH,即可求得∠FGD=∠QGH,即可证明△DFG≌△QHG,可得DF=QH,即可解题.【解答】(1)解:EF=DF+CF;在EF上找到G点使得FG=CF,如图2,∵∠BCD=30°,∠ACB=45°,∴∠ACD=15°,∴∠CFG=∠CDE+∠ACD=60°,∵FG=CF,∴△CFG是等边三角形,∴CG=CF=GF,∠FCG=60°,∴∠GCE=90°﹣15°﹣60°=15°,在△ECG和△CDF中,CG=CF∠ECG=∠ACD,CE=CD∴△ECG≌△CDF,(SAS)∴DF=EG,∵EF=EG+GF,∴EF=DF+CF;(2)证明:在FQ上找到H点,使得FH=FG,如图3,∵FQ平分∠DFG,∴∠QFG=60°,∵FG=FH,∴△FGH是等边三角形,∴∠GHF=∠FGH=60°,GH=FG=FH,∵∠AFD=∠CDE+∠ACD=60°,∴∠GHQ=∠DFG=120°,∵∠FGD+∠DGH=60°,∠DGH+∠QGH=60°,∠QGH=∠DGF,∴∠FGD=∠QGH,在△DFG和△QHG中,∠DFG=∠QHG=120°FG=HG,∠FGD=∠QGH∴△DFG≌△QHG,(ASA)∴DF=QH,∵FQ=FH+QH,∴FQ=FG+FD.【点评】本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△ECG≌△CDF和△DFG≌△QHG是解题的关键.13.(2022春•运城期末)综合与探究如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,CE的延长线交BD于点F.(1)求证:△ACE≌△ABD.(2)若∠BAC=∠DAE=50°,请直接写出∠BFC的度数.(3)过点A作AH⊥BD于点H,求证:EF+DH=HF.【分析】(1)可利用SAS证明结论;(2)由全等三角形的性质可得∠AEC=∠ADB,结合平角的定义可得∠DAE+∠DFE=180°,根据∠BFC+∠DFE=180°,可求得∠BFC=∠DAE,即可求解;(3)连接AF,过点A作AJ⊥CF于点J.结合全等三角形的性质利用HL证明Rt△AFJ≌Rt△AFH,Rt△AJE≌Rt△AHD可得FJ=FH,EJ=DH,进而可证明结论.【解答】(1)证明:∵∠BAC=∠DAE.∴∠CAE=∠BAD.在△ACE和△ABD中,AC=AB∠CAE=∠BAD,AE=AD∴△ACE ≌△ABD (SAS );(2)解:∵△ACE ≌△ABD ,∴∠AEC =∠ADB ,∴∠AEF +∠AEC =∠AEF +∠ADB =180°.∴∠DAE +∠DFE =180°,∵∠BFC +∠DFE =180°,∴∠BFC =∠DAE =∠BAC =50°;(3)证明:如图,连接AF ,过点A 作AJ ⊥CF 于点J .∵△ACE ≌△ABD ,∴S △ACE =S △ABD ,CE =BD ,∵AJ ⊥CE ,AH ⊥BD .∴12CE ⋅AJ =12BD ⋅AH ,∴AJ =AH .在Rt △AFJ 和Rt △AFH 中,AF =AF AJ =AH ,∴Rt △AFJ ≌Rt △AFH (HL ),∴FJ =FH .在Rt △AJE 和Rt △AHD 中,AE =AD AJ =AH ,∴Rt △AJE ≌Rt △AHD (HL ),∴EJ =DH ,∴EF +DH =EF +EJ =FJ =FH .【点评】本题主要考查全等三角形的判定与性质,掌握全等三角形的判定条件是解题的关键.14.(2022春•沙坪坝区校级期中)如图,在△ABC 中,∠ABC 、∠ACB 的平分线交于点D ,延长BD 交AC 于E ,G 、F 分别在BD 、BC 上,连接DF 、GF ,其中∠A =2∠BDF ,GD =DE .(1)当∠A =80°时,求∠EDC 的度数;(2)求证:CF =FG +CE .【分析】(1)方法一:先求∠ABC 和∠ACB 的和为100°,再根据角平分线求∠DBC +∠DCB =50°,再根据外角即可解决问题;方法二:在BC 上取点M ,使CM =CE ,证明△CDE ≌△CDM (SAS ),可得DE =DM ,∠DEC =∠DMC ,∠EDC =∠MDC ,证明∠BDM =180°−12∠ABC ﹣∠DMB =180°−12∠ABC ﹣∠AEB =∠A =80°,进而可以解决问题.(2)结合(1)然后证明△DGF ≌△DMF (SAS ),可得GF =MF ,进而可以解决问题.【解答】(1)解:方法一:∵∠A =80°,∴∠ABC +∠ACB =100°,∵BE 平分∠ABC 、CD 平分∠ACB ,∴∠DBC +∠DCB =50°,∴∠EDC =∠DBC +∠DCB =50°;方法二:如图,在BC 上取点M ,使CM =CE ,∵CD 平分∠ACB ,∴∠ACD=∠BCD,在△CDE和△CDM中,CE=CM∠ECD=∠MCDCD=CD,∴△CDE≌△CDM(SAS),∴DE=DM,∠DEC=∠DMC,∠EDC=∠MDC,∵GD=DE,∴GD=MD,∵∠DEC+∠AEB=180°,∠DMC+∠DMF=180°,∴∠AEB=∠DMF,∵BE平分∠ABC,∴∠ABE=∠CBE=12∠ABC,∴∠BDM=180°−12∠ABC﹣∠DMB=180°−12∠ABC﹣∠AEB=∠A=80°,∴∠EDM=100°,∴∠EDC=50°;(2)证明:∵∠A=2∠BDF,∴∠BDM=2∠BDF,∴∠FDM=∠BDF,在△DGF和△DMF中,DG=DM∠GDF=∠MDFDF=DF,∴△DGF≌△DMF(SAS),∴GF=MF,∴CF=CM+FM=CE+GF.∴CF=FG+CE.【点评】本题考查了全等三角形的判定与性质,角平分线的定义,解决本题的关键是根据题意准确作出辅助线得到△DGF≌△DMF.15.如图,在△ABC中,∠C=90°,AD是∠BAC的角平分线交BC于点D,过D作DE⊥BA于点E,点F在AC上,且BD=DF.(1)求证:AC=AE;(2)求证:∠BAC+∠FDB=180°;(3)若AB=9.5,AF=1.5,求线段BE的长.【分析】(1)证△ACD≌△AED(AAS),即可得出结论;(2)设∠DAC=∠DAE=α,在AB上截取AM=AF,连接MD,证△FAD≌△MAD(SAS),得FD=MD,∠ADF=∠ADM,再证Rt△MDE≌Rt△BDE(HL),得∠DME=∠B,然后证∠FDB=90°+90°﹣2α=180°﹣2α,即可得出结论;(3)求出MB=AB﹣AM=8,由全等三角形的性质得ME=BE,即可求解.【解答】(1)证明:∵AD平分∠BAC,∴∠DAC=∠DAE,∵DE⊥BA,∴∠DEA=∠DEB=90°,∵∠C=90°,∴∠C=∠DEA=90°,在△ACD和△AED中,∠C=∠DEA∠DAC=∠DAE,AD=AD∴△ACD≌△AED(AAS),∴AC=AE;(2)证明:设∠DAC=∠DAE=α,∵∠C=∠DEA=90°,∴∠ADC=90°﹣α,∠ADE=90°﹣α,则∠FDB=∠FCD+∠DFC=90°+∠DFC,在AB上截取AM=AF,连接MD,如图所示:在△FAD和△MAD中,AF=AM∠DAF=∠DAM,AD=AD∴△FAD≌△MAD(SAS),∴FD=MD,∠ADF=∠ADM,∵BD=DF,∴BD=MD,在Rt△MDE和Rt△BDE中,MD=BDDE=DE∴Rt△MDE≌Rt△BDE(HL),∴∠DME=∠B,∵∠DAC=∠DAE=α,∴∠DAC+∠ADF=∠ADM+∠ADM,在△FAD中,∠DAC+∠ADF=∠DFC,在△AMD中,∠DAE+∠ADM=∠DME,∴∠DFC=∠DME,∴∠DFC=∠B,∵∠C=90°,在△ABC中,∠B=90°﹣2α,∴∠DFC=90°﹣2α,∴∠FDB=90°+90°﹣2α=180°﹣2α,∵∠BAC=∠DAC+∠DAE=2α,∴∠FDB+∠BAC=180°﹣2α+2α=180°;(3)解:∵AF=AM,且AF=1.5,∴AM=1.5,∵AB=9.5,∴MB=AB﹣AM=9.5﹣1.5=8,由(2)得:Rt△MDE≌Rt△BDE,∴ME=BE,∴BE=12BM=4,即BM的长为4.【点评】本题考查了全等三角形的判定与性质、角平分线定义、直角三角形的性质、三角形的外角性质等知识;证明△FAD≌△MAD和Rt△MDE≌Rt△BDE是解题的关键.16.在△ABC中,AB=AC,D是直线BC上一点,以AD为一条边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC,连接DE,CE.(1)如图,当点D在BC延长线上移动时,求证:BD=CE.(2)设∠BAC=α,∠DCE=β.①当点D在线段BC的延长线上移动时,α与β之间有什么数量关系?请说明理由.②当点D分别在线段BC上、线段BC的反向延长线上移动时,α与β之间有什么数量关系?请说明理由.【分析】(1)根据SAS证△BAD≌△CAE,可得结论;(2)①由△BAD≌△CAE,推出∠B=∠ACE,根据三角形外角性质求出即可;②α+β=180°或α=β,根据三角形外角性质求出即可.【解答】(1)证明:∵∠DAE=∠BAC,∴∠DAE+∠CAD=∠BAC+∠CAD,∴∠BAD=∠CAE,在△BAD和△CAE中,AB=AC∠BAD=∠CAE,AD=AE∴△BAD≌△CAE(SAS),(2)解:①当点D在线段BC的延长线上移动时,α与β之间的数量关系是α=β,理由是:由(1)知△BAD≌△CAE,∴∠B=∠ACE,∵∠ACD=∠B+∠BAC=∠ACE+∠DCE,∴∠BAC=∠DCE,∵∠BAC=α,∠DCE=β,∴α=β;②分三种情况:i)当D在线段BC上时,如图2,α+β=180°,理由是:同理可证明:△ABD≌△ACE(SAS),∴∠ADB=∠AEC,∠ABC=∠ACE,∵∠ADC+∠ADB=180°,∴∠ADC+∠AEC=180°,∴∠DAE+∠DCE=180°,∵∠BAC=∠DAE=α,∠DCE=β,∴α+β=180°,ii)当点D在线段BC反向延长线上时,如图3,α=β.如图3,同理可证明:△ABD≌△ACE(SAS),∴∠ABD=∠ACE,∵∠ACE=∠ACD+∠DCE,∠ABD=∠ACD+∠BAC,∴∠ACD+∠DCE=∠ACD+∠BAC,∴∠BAC=∠DCE,∵∠BAC=α,∠DCE=β,∴α=β;ii)当点D在线段BC的延长线上时,如图1,α=β.综上,当点D在BC上移动时,α=β或α+β=180°.【点评】本题是三角形的综合题,考查了全等三角形的性质和判定,三角形的外角性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.17.(2022春•南海区校级月考)如图,在△ABC中,∠ACB为锐角,点D为射线BC上一动点,连接AD.以AD为直角边且在AD的上方作等腰直角三角形ADF.(1)若AB=AC,∠BAC=90°.①当点D在线段BC上时(与点B不重合),试探讨CF与BD的数量关系和位置关系;②当点D在线段BC的延长线上时,①中的结论是否仍然成立,请在图②中画出相应的图形并说明理由;(2)如图③,若AB≠AC,∠BAC≠90°,∠BCA=45°,点D在线段BC上运动,试探究CF与BD 的位置关系.【分析】(1)①根据同角的余角相等求出∠CAF=∠BAD,然后利用“边角边”证明△ACF和△ABD全等,根据全等三角形的性质及等腰直角三角形的性质求解即可;②先求出∠CAF=∠BAD,然后与①的思路相同求解即可;(2)过点A作AE⊥AC交BC于E,可得△ACE是等腰直角三角形,根据等腰直角三角形的性质可得AC=AE,∠AED=45°,再根据同角的余角相等求出∠CAF=∠EAD,然后利用“边角边”证明△ACF 和△AED全等,根据全等三角形对应角相等可得∠ACF=∠AED,然后求出∠BCF=90°,从而得到CF ⊥BD.【解答】解:(1)①CF=BD,CF⊥BD,理由如下:∵∠BAC=90°,△ADF是等腰直角三角形,AB=AC,∴∠CAF+∠CAD=90°,∠BAD+∠CAD=90°,∠B=∠ACB=45°,∴∠CAF=∠BAD,在△ACF和△ABD中,AC=AB∠CAF=∠BAD,AF=AD∴△ACF≌△ABD(SAS),∴CF=BD,∠ACF=∠B=45°,∵∠ACB=45°,∴∠FCB=45°+45°=90°,∴CF⊥BD;②①中的结论成立,理由如下:如图②:∵∠BAC=90°,△ADF是等腰直角三角形,AB=AC,∴∠BAC=∠DAF=90°,∠B=∠ACB=45°,∴∠BAC+∠CAD=∠DAF+∠CAD,即∠CAF=∠BAD,在△ACF和△ABD中,AC=AB∠CAF=∠BAD,AF=AD∴△ACF≌△ABD(SAS),∴CF=BD,∠ACF=∠B,∴∠BCF=∠ACF+∠ACB=45°+45°=90°,∴CF⊥BD;(3)如图③,过点A作AE⊥AC交BC于E,∵∠BCA=45°,∴△ACE是等腰直角三角形,∴AC=AE,∠AED=45°,∵∠CAF+∠CAD=90°,∠EAD+∠CAD=90°,∴∠CAF=∠EAD,在△ACF和△AED中,AC=AE∠CAF=∠EAD,AF=AD∴△ACF≌△AED(SAS),∴∠ACF=∠AED=45°,∴∠BCF=∠ACF+∠BCA=45°+45°=90°,∴CF⊥BC.【点评】此题是三角形综合题,主要考查了全等三角形的判定与性质,等腰直角三角形的性质,作出合理的辅助线根据同角的余角相等求出两边的夹角相等是证明三角形全等的关键.18.如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CB,垂足为F.(1)△ABC≌△ADE吗?为什么?(2)求∠FAE的度数;(3)延长BF到G,使得FG=FB,试说明CD=2BF+DE.【分析】(1)由“SAS”可证△ABC≌△ADE;(2)由等腰直角三角形的性质可得∠AEC=∠ACE=45°,由全等三角形的性质可得∠ACB=∠AED=45°,即可求解;(3)由全等三角形的性质可得∠ABC=∠ADE,BC=DE,由线段垂直平分线的性质和等腰三角形的性质可得AB=AG=AD,∠ABG=∠AGB=∠ADC,由“AAS”可证△ACD≌△ACG,可得CD=CG,可得结论.【解答】证明:(1)△ABC≌△ADE,理由如下:∵∠BAD=∠CAE=90°,∴∠EAD=∠CAB,在△ABC和△ADE中,AB=AD∠BAC=∠DAE,AC=AE∴△ABC≌△ADE(SAS);(2)∵∠CAE=90°,AC=AE,∴∠AEC=∠ACE=45°,∵△ABC≌△ADE,∴∠ACB=∠AED=45°,∵AF⊥CB,∴∠FAC=45°,∴∠FAE=135°;(3)∵△ABC≌△ADE,∴∠ABC=∠ADE,BC=DE,∴∠ADC=∠ABG,∵AF⊥BF,BF=FG,∴AB=AG,∴AG=AD,∠ABG=∠AGB=∠ADC,又∵∠ACG=∠ACD=45°,∴△ACD≌△ACG(AAS),∴CD=CG,∴CD=BG+CB=2BF+DE.【点评】本题是三角形综合题,考查了全等三角形的判定和性质,等腰三角形的判定和性质,线段垂直平分线的性质等知识,证明△ACD≌△ACG是解题的关键.19.Rt△ABC中,∠C=90°,点D在直线AC上,点E在直线AB上,∠ADE=∠ABC.(1)如图1,当点D、E分别在边AC、AB上时,求证:DE⊥AB;(2)如图2,当点D在CA延长线上,点E在BA延长线上时,DE、BC延长线交于点F,作∠EAC的角平分线AG交DF于点G,求证:∠D+2∠DGA=90°;(3)如图3,在(2)的条件下,连接BG交CD于点H,若∠DGH=∠DHG,∠AGB=3∠CBH,求∠DGA的度数.【分析】(1)根据直角三角形的两锐角互余得到∠ABC+∠A=90°,等量代换得出∠ADE+∠A=90°,进而得出∠AED=90°,根据垂直的定义即可得解;(2)过点G作GN∥FB交CD于点N,根据平行线的性质及垂直的定义推出∠AEG=∠ANG=90°,根据角平分线定义得出∠EAG=∠NAG,利用AAS证明△EAG≌△NAG,根据全等三角形的性质及直角三角形的性质即可得解;(3)根据直角三角形的性质及对顶角相等得出∠DGH=90°−13∠AGB,根据等腰三角形的性质推出∠DGH=90°−12∠D,则90°−13∠AGB=90°−12∠D,进而推出∠AGB=32∠D,则∠DGA+32∠D=90°−12∠D,结合(2)求解即可.【解答】(1)证明:∵∠C=90°,∴∠ABC+∠A=90°,∵∠ADE=∠ABC,∴∠ADE+∠A=90°,∴∠AED=90°,∴DE⊥AB;(2)证明:如图2,过点G作GN∥FB交CD于点N,则∠GNC=∠ACB=90°,∴GN⊥CD,∵∠ACB=90°,∴∠ABC+∠BAC=90°,∵∠ADE=∠ABC,∠BAC=∠DAE,∴∠ADE+∠DAE=90°,∴∠DEA=90°,∴BE⊥DF,∴∠AEG=∠ANG=90°,∵AG平分∠EAC,∴∠EAG=∠NAG,在△EAG和△NAG中,∠AEG=∠ANG∠EAG=∠NAGAG=AG,∴△EAG≌△NAG(AAS),∴∠DGA=∠NGA,∴∠DGN=2∠DGA,∵∠D+∠DGN=90°,∴∠D+2∠DGA=90°;(3)解:∵∠AGB=3∠CBH,∴∠CBH=13∠AGB,∵∠DHG=∠CHB=90°﹣∠CBH,∴∠DGH=90°−13∠AGB,∵∠DGH=∠DHG,∴∠DGH=12(180°﹣∠D)=90°−12∠D,∴90°−13∠AGB=90°−12∠D,∴∠AGB=32∠D,∵∠DGH=∠DGA+∠AGB,∴∠DGA+∠AGB=90°−12∠D,∴∠DGA+32∠D=90°−12∠D,∴2∠D+∠DGA=90°,由(2)知,∠D+2∠DGA=90°,∴∠D=∠DGA,∴3∠DGA=90°,∴∠DGA=30°.【点评】此题是三角形综合题,考查了直角三角形的判定与性质、全等三角形的判定与性质、等腰三角形的性质、平行线的性质等知识,熟练掌握直角三角形的判定与性质、全等三角形的判定与性质、等腰三角形的性质并作出合理的辅助线是解题的关键.20.(2023春•新市区期末)在△ABC中,∠ACB=90°,AC=BC,D是直线AB上一点(点D不与点A、B重合),连接DC并延长到E,使得CE=CD,过点E作EF⊥直线BC,交直线BC于点F.(1)如图1,当点D为线段AB上的任意一点时,用等式表示线段EF、CF、AC的数量关系,并证明;(2)如图2,当点D为线段BA的延长线上一点时,依题意补全图2,猜想线段EF、CF、AC的数量关系是否发生改变,并证明;(3)如图3,当点D在线段AB的延长线上时,直接写出线段EF、CF、AC之间的数量关系.【分析】(1)过D作DH⊥CB于H,由“AAS”可证△FEC≌△HDC,可得CH=FC,DH=EF,可得结论;(2)过D作DH⊥CB于H,由“AAS”可证△FEC≌△HDC,可得CH=FC,DH=EF,可得结论.(3)过D作DH⊥CB交CB的延长线于H,由“AAS”可证△FEC≌△HDC,可得CH=FC,DH=EF,可得结论.【解答】解:(1)结论:AC=EF+FC.理由如下:过D作DH⊥CB于H,∴∠DHC=∠DHB=90°,∵EF⊥CF,∴∠EFC=∠DHC=90°,在△FEC和△HDC中,∠EFC=∠DHC=90°∠FCE=∠DCH,EC=DC∴△FEC≌△HDC(AAS),∴CH=FC,DH=EF,∵∠ACB=90°,AC=BC,∴∠B=45°,∵∠DHB=90°,∴∠B=∠HDB=45°,∴DH=HB=EF,∵BC=CB+HB,∴AC=FC+EF;(2)依题意补全图形,结论:AC=EF﹣CF,理由如下:过D作DH⊥CB交BC的延长线于H,∵EF⊥CF,∴∠EFC=∠DHC=90°,在△FEC和△HDC中,∠FCE=∠DCH∠EFC=∠DHC=90°,EC=DC∴△FEC≌△HDC(AAS),∴CH=FC,DH=EF,∵∠DHB=90°,∴∠B=∠HDB=45°,∴DH=HB=EF,∵BC=HB﹣CH,∴AC=EF﹣CF;(3)AC=CF﹣EF.如图3,过D作DH⊥CB交CB的延长线于H,同理可证△FEC≌△HDC(AAS),∴CH=FC,DH=EF,∵∠DHB=90°,∴∠B=∠HDB=45°,∴DH=HB=EF,∵BC=CH﹣BH,∴AC=CF﹣EF.【点评】本题是三角形综合题,考查了全等三角形的判定和性质,添加恰当辅助线构造全等三角形是本题的关键.21.如图1,在△ABC中,∠ACB为锐角,点D为射线BC上一点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.(1)如果AB=AC,∠BAC=90°,①当点D在线段BC上时(与点B不重合),如图2,线段CF、BD所在直线的位置关系为 ,线段CF、BD的数量关系为 ;②当点D在线段BC的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;(2)如果AB≠AC,∠BAC是锐角,点D在线段BC上,当∠ACB满足什么条件时,CF⊥BC(点C、F 不重合),并说明理由.【分析】(1)当点D在BC的延长线上时①的结论仍成立.由正方形ADEF的性质可推出△DAB≌△FAC,所以CF=BD,∠ACF=∠ABD.结合∠BAC=90°,AB=AC,得到∠BCF=∠ACB+∠ACF=90°.即CF⊥BD.(2)当∠ACB=45°时,过点A作AG⊥AC交CB的延长线于点G,则∠GAC=90°,可推出∠ACB=∠AGC,所以AC=AG,由(1)①可知CF⊥BD.【解答】证明:(1)①正方形ADEF中,AD=AF,∵∠BAC=∠DAF=90°,∴∠BAD=∠CAF,又∵AB=AC,∴△DAB≌△FAC,∴CF=BD,∠B=∠ACF,∴∠ACB+∠ACF=90°,即CF⊥BD.②当点D在BC的延长线上时①的结论仍成立.由正方形ADEF得AD=AF,∠DAF=90度.∵∠BAC=90°,∴∠DAF=∠BAC,∴∠DAB=∠FAC,又∵AB=AC,∴△DAB≌△FAC,∴CF=BD,∠ACF=∠ABD.∵∠BAC=90°,AB=AC,∴∠ABC=45°,∴∠ACF=45°,∴∠BCF=∠ACB+∠ACF=90度.即CF⊥BD.(2)当∠ACB=45°时,CF⊥BD(如图).理由:过点A作AG⊥AC交CB的延长线于点G,则∠GAC=90°,∵∠ACB=45°,∠AGC=90°﹣∠ACB,∴∠AGC=90°﹣45°=45°,∴∠ACB=∠AGC=45°,∴AC=AG,∵∠DAG=∠FAC(同角的余角相等),AD=AF,∴△GAD≌△CAF,∴∠ACF=∠AGC=45°,∠BCF=∠ACB+∠ACF=45°+45°=90°,即CF⊥BC.【点评】本题考查三角形全等的判定和直角三角形的判定,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.22.(1)如图1,∠B=∠D=90°,E是BD的中点,AE平分∠BAC,求证:CE平分∠ACD.(2)如图2,AM∥CN,∠BAC和∠ACD的平分线并于点E,过点E作BD⊥AM,分别交AM、CN于B、D,请猜想AB、CD、AC三者之间的数量关系,请直接写出结论,不要求证明.(3)如图3,AM∥CN,∠BAC和∠ACD的平分线交于点E,过点E作不垂直于AM的线段BD,分别交AM、CN于B、D点,且B、D两点都在AC的同侧,(2)中的结论还成立吗?若成立,请加以证明;若不成立,请说明理由.【分析】(1)过点E作EF⊥AC于F,根据角平分线上的点到角的两边的距离相等可得OB=OE,从而求出OE=OD,然后根据到角的两边距离相等的点在角的平分线上证明;(2)如图2,过E作EF⊥AC于F,根据平行线的性质得到BD⊥CD,由角平分线的性质得到BE=EF,证得Rt△AEF≌Rt△ABE,根据全等三角形到现在得到AF=AB,同理CF=CD,等量代换得到结论;(3)成立,如图3,在AC上截取AF=AB,根据角平分线的定义得到∠BAE=∠FAE,推出△ABE≌△AFE,根据全等三角形的性质得到∠AFE=∠ABE,根据角平行线的性质得到∠ABE+∠CDE=180°,求得∠CFE=∠CDE,证得△CEF≌△CDE,根据全等三角形的性质即可得到结论.【解答】解:(1)如图1,过E作EF⊥AC于F,∵∠B=90°,AE平分∠BAC,∴EF=BE,∵E是BD的中点,∴BE=DE,∴EF=DE,∵∠D=90°,∴CE平分∠ACD;(2)如图2,过E作EF⊥AC于F,∵AM∥CN,BD⊥AM,∴BD⊥CD,∵AE平分∠BAC,∴BE=EF,在Rt△AEF与Rt△ABE中,BE=EF AE=AE,∴Rt△AEF≌Rt△ABE,∴AF=AB,同理CF=CD,∵AC=AF+CF,∴AC=AB+CD;(3)成立,如图3,在AC上截取AF=AB,∵AE平分∠BAC,∴∠BAE=∠FAE,在△ABE与△AFE中,AB=AF∠BAE=∠FAEAE=AE,∴△ABE≌△AFE,∴∠AFE=∠ABE,∵AM∥CN,∴∠ABE+∠CDE=180°,∵∠AFE+∠EFC=180°,∴∠CFE=∠CDE,∵CE平分∠ACD,∴∠FCE=∠DCE,在△CEF与△CDE中,∠CFE=∠CDE ∠FCE=∠DCE CE=CE,∴△CEF≌△CDE,∴CF=CD,∵AC=AF+CF,∴AC=AB+CD.【点评】本题考查了全等三角形的判定和性质,角平分线的性质,角平分线的定义,平行线的性质,正确的作出辅助线构造全等三角形是解题的关键.23.将两个全等的直角三角形ABC和DBE按图①方式摆放,其中∠ACB=∠DEB=90°,∠A=∠D=30°,点E落在AB上,DE所在直线交AC所在直线于点F.(1)求证:AF+EF=DE;(2)若将图①中的△DBE绕点B按顺时针方向旋转角α,且0°<α<60°,其它条件不变,请在图②中画出变换后的图形,并直接写出你在(1)中猜想的结论是否仍然成立;(3)若将图①中的△DBE绕点B按顺时针方向旋转角β,且60°<β<180°,其它条件不变,如图③.你认为(1)中猜想的结论还成立吗?若成立,写出证明过程;若不成立,请写出AF、EF与DE之间的关系,并说明理由.【分析】(1)我们已知了三角形BED和CAB全等,那么DE=AF+CF,因此只要求出EF=CF就能得出本题所求的结论,可通过全等三角形来实现,连接BF,那么证明三角形BEF和BCF全等就是解题的关键,这两三角形中已知的条件有BE=BC,一条公共边,根据斜边直角边定理,这两个直角三角形就全等了,也就得出EF=CF,也就能证得本题的结论了;(2)解题思路和辅助线的作法与(1)完全一样;(3)结论不成立.结论:AF=DE+EF.同(1)得CF=EF,由△ABC≌△DBE,可得AC=DE,AF=AC+FC=DE+EF.【解答】(1)证明:连接BF(如图①),∵△ABC≌△DBE(已知),∴BC=BE,AC=DE.∵∠ACB=∠DEB=90°,∴∠BCF=∠BEF=90°.在Rt△BFC和Rt△BFE中,BF=BFBC=BE∴Rt△BFC≌Rt△BFE(HL).∴CF=EF.又∵AF+CF=AC,∴AF+EF=DE.(2)解:画出正确图形如图②∴(1)中的结论AF+EF=DE仍然成立;(3)不成立.结论:AF=DE+EF.。
初二全等三角形所有的知识点地总结和常考的题目提高难的题目压轴的题目练习题目(详解解析汇报)

初二全等三角形所有知识点总结和常考题知识点:1. 基本定义:⑴全等形:能够完全重合的两个图形叫做全等形.⑵全等三角形:能够完全重合的两个三角形叫做全等三角形•⑶对应顶点:全等三角形中互相重合的顶点叫做对应顶点.⑷对应边:全等三角形中互相重合的边叫做对应边.⑸对应角:全等三角形中互相重合的角叫做对应角.2. 基本性质:⑴三角形的稳定性:三角形三边的长度确定了,这个三角形的形状、大小就全确定,这个性质叫做三角形的稳定性.⑵全等三角形的性质:全等三角形的对应边相等,对应角相等.3. 全等三角形的判定定理:⑴边边边(SSS):三边对应相等的两个三角形全等.⑵边角边(SAS):两边和它们的夹角对应相等的两个三角形全等. ⑶角边角(ASA):两角和它们的夹边对应相等的两个三角形全等.⑷角角边(AAS):两角和其中一个角的对边对应相等的两个三角形全等⑸斜边、直角边(HL):斜边和一条直角边对应相等的两个直角三角形全等.4. 角平分线:⑴画法:⑵性质定理:角平分线上的点到角的两边的距离相等.⑶性质定理的逆定理:角的内部到角的两边距离相等的点在角的平分线上5. 证明的基本方法:⑴明确命题中的已知和求证.(包括隐含条件,如公共边、公共角、对顶角、角平分线、中线、高、等腰三角形等所隐含的边角关系)⑵根据题意,画出图形,并用数字符号表示已知和求证.⑶经过分析,找出由已知推出求证的途径,写出证明过程.常考题:一•选择题(共14小题)1 •使两个直角三角形全等的条件是()A. —个锐角对应相等B.两个锐角对应相等C•一条边对应相等D.两条边对应相等2.如图,已知AE=CF Z AFD W CEB那么添加下列一个条件后,仍无法判定△A. Z A=Z CB. AD=CBC. BE=DFD. AD// BC3•如图所示,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是()A. SSSB. SAS C AAS D. ASA4. 到三角形三条边的距离都相等的点是这个三角形的()A.三条中线的交点B.三条高的交点C.三条边的垂直平分线的交点D .三条角平分线的交点5. 如图,△ ACB^A A CB,/ BCB =30。
全等三角形压轴训练(多解、动点、新定义型压轴)(解析版)—24-25学年八年级数学上册单元(人教版)

全等三角形压轴训练(多解、动点、新定义型压轴)目录题型一 利用三角形全等求时间或线段长的多解问题...........................................................................................1题型二 与全等三角形有关的多结论问题 (7)题型三 全等三角形中的动点综合问题 (13)题型四 全等三角形中的新定义型综合问题 (27)题型一 利用三角形全等求时间或线段长的多解问题【答案】4【分析】本题主要考查了全等三角形的性质和判定,解一元一次方程,先设运动全等;分两种情况:12x x -=,得出x =01 压轴总结02 压轴题型∴CAP V ≌PBQ V ;②若BP AP =,则12x x -=,解得:6x =,可知12(cm)BQ AC =¹,此时CAP V 与PQB △不全等.综上所述:运动4s 后CAP V 与PQB △全等.故答案为:4.巩固训练1.(23-24七年级下·陕西西安·期末)如图,ABC V 中,90ACB Ð=°,6cm AC =,8cm BC =,直线l 经过点C 且与边AB 相交.动点P 从点A 出发沿A C B ®®路径向终点B 运动;动点Q 从点B 出发沿B C A ®®路径向终点A 运动.点P 和点Q 的速度分别为1cm /s 和2cm /s ,两点同时出发并开始计时,当点P 到达终点B 时计时结束.在某时刻分别过点P 和点Q 作PE l ^于点E ,QF l ^于点F ,设运动时间为t 秒,则当t 为( )秒时,PEC V 与QFC V 全等.A .12或43B .2或45或10C .1或43D .2或143或12由题意得,,AP t BQ ==∵6cm,8cm AC BC ==,由题意得,,2AP t BQ ==∵6cm,8cm AC BC ==,∴6,28CP t CQ t =-=-,当PEC QFC △≌△,则PC CQ =,由题意得,AP t =,∵6cm AC =,∴6,6CP t CQ =-=,2.(23-24八年级上·重庆·阶段练习)如图,在长方形ABCD 中,4,6AB AD ==,延长BC 到点E ,使2CE =,连接DE ,动点P 从点B 出发,以每秒2个单位的速度沿BC CD DA →→向终点A 运动,设点P 的运动时间为t 秒,当t 的值为 秒时,ABP V 与DCE △全等.3.(23-24八年级上·山东日照·阶段练习)如图,CA AB ^,垂足为点A ,12AB =米,6AC =米,射线BM AB ^,垂足为点B ,动点E 从A 点出发以2米/秒沿射线AN 运动,点D 为射线BM 上一动点,随着E 点运动而运动,且始终保持ED CB =,当点E 经过 秒时(不包括0秒),由点D E B 、、组成的三角形与BCA V 全等.【答案】3秒或9秒或12【分析】本题考查了三角形全等的判定与性质,分四种情况:当点E 在线段AB 上,AC BE =时,ACB BED V V ≌;当E 在BN 上,AC BE =时,ACB BED V V ≌;当E 在线段AB 上,AB EB =时;当E 在BN 上,AB EB =时,ACB BDE V V ≌;分别利用三角形全等的性质进行求解即可,熟练掌握三角形全等的判定与性质是解此题的关键.【详解】解:当点E 在线段AB 上,AC BE =时,ACB BED V V ≌,6AC =Q ,6BE \=,1266AE AB BE \=-=-=,\点E 的运动时间为623¸=(秒);当E 在BN 上,AC BE =时,ACB BED V V ≌,6AC =Q ,6BE \=,12618AE AB BE \=+=+=,\点E 的运动时间为1829¸=(秒);当E 在线段AB 上,AB EB =时,此时E 在A 点未动,时间为0秒,不符合题意;当E 在BN 上,AB EB =时,ACB BDE V V ≌,12AB =Q ,12BE \=,121224AE AB BE \=+=+=,\点E 的运动时间为24212¸=(秒);综上所述,当点E 经过3秒或9秒或12秒时(不包括0秒),由点D E B 、、组成的三角形与BCA V 全等,故答案为:3秒或9秒或12.4.如图,ABC V 中,90ACB Ð=°,12AC =,16BC =,点P 从A 点出发沿A C B ®®路径向终点运动,终点为B 点;点Q 从B 点出发沿B C A ®®路径向终点运动,终点为A 点.点P 和Q 分别以2和6的运动速【答案】1或72或12【分析】根据题意分为五种情况,根据全等三角形的性质得出可.【详解】解:设点运动t秒时,以Q PE l^,QF l^,\90PEC QFCÐ=Ð=°,Q90ACBÐ=°,\90EPC PCEÐ+Ð=°,Q 由①知:PC CQ =,\212616t t -=-,=1t \;因为此时60t -<,所以此种情况不符合题意;122616PC t t =-=-,7=2t ;④当Q 到A 点停止,P 在BC ⑤因为P 的速度是每秒2,Q 题型二 与全等三角形有关的多结论问题例题:(23-24七年级下·江西吉安·期末)如图,在Rt AEB V 和Rt AFC △中,BE 与AC 相交于点M ,与CF 相交于点D ,AB 与CF 相交于点N ,90E F ÐÐ==°,EAC FAB ÐÐ=,AE AF =.给出下列结论:①B C Ð=Ð;②CD DN =;③BE CF =;④ACN ABM @V V .其中正确的结论是( )A .①③④B .①②③④C .①②③D .①②④【答案】A 【分析】本题考查了两个全等三角形的判定及性质,根据已知条件判定两个三角形全等,可得到对应边及对应角相等,据此可判断①③,再结合条件证明两个三角形全等,可得到④,即可求得结果,灵活运用两个全等三角形的条件及性质是解题的关键.【详解】解:∵EAC FAB Ð=Ð,∴EAB FAC Ð=Ð,在EAB V 和FAC V 中,90E F AE AFEAB FAC Ð=Ð=°ìï=íïÐ=Ðî,∴()ASA EAB FAC V V ≌,∴,,B C BE CF AB AC Ð=Ð==,∴①③都正确,在ACN ABM △和△中,B C AB AC CAN BAM Ð=Ðìï=íïÐ=Ðî,∴()ASA ACN ABM V V ≌,故④正确,根据已知条件无法证明②是否正确,故①③④正确,故选:A .巩固训练1.(23-24七年级下·四川巴中·期末)如图,在Rt ABC △中,点M ,N 分别是边AB BC ,上的点,且M ,N 两点满足AM CN =,BP AN ^交AC 于点P ,过点P 作PQ MC ^交AN 延长线于点Q ,交BC 于点F ,AN 与CM 交于点E ,若AB BC =,则下列结论:①连接BE ,则BE 平分ABC Ð;②AME CNE △≌△;③CFQ AME Ð=Ð;④AQ CE PQ =+.成立的是( ).A .①②③B .①②④C .②③④D .①②③④【答案】D 【分析】本题主要考查了等腰直角三角形的性质、全等三角形的判定等知识点,灵活运用全等三角形的判定与性质成为解题的关键.先证明()SAS AMC CNA V V ≌可得MCA NAC Ð=Ð,再证明()AAS AME CNE V V ≌可得ME NE =,进而证明()SSS BME BNE V V ≌得到MBE NBE Ð=Ð即可判定①;由()SAS AMC CNA V V ≌可得MCA NAC Ð=Ð,然后证明()AAS AEM CEN V V ≌即可判定②;由全等三角形的性质可得AME ENC Ð=Ð,再结合三角形外角的性质即可判定③;先证明()ASA BHE CHP ÐÐV V ≌可得EH HP =,再证明()AAS EGH PDH V V ≌可得HG HD =,然后证明()HL QGH QHD V V ≌可得QE QP =,再说明AE CE =,最后根据线段的和差及等量代换即可证明结论.【详解】解:∵AB BC =,∴BAC BCA Ð=Ð,∵AM CN =,∴()SAS AMC CNA V V ≌,∴MCA NAC Ð=Ð.∵AM CN =,AEM NEC Ð=Ð,∴()AAS AME CNE V V ≌,即②正确;∴ME NE =,∵AB BC =,AM CN =,∴MB BN =,∵BE BE =,∴()SSS BME BNE V V ≌,∴MBE NBE Ð=Ð,即BE 平分ABC Ð,故①正确;∵()AAS AEM CEN V V ≌,∴AME ENC Ð=Ð,BCM BAE Ð=Ð,∵90ENC BAE ABC BAN Ð=Ð+Ð=Ð+°,90CFQ BCM CDF BCM Ð=Ð+Ð=Ð+°,∴ENC CFQ Ð=Ð,即③正确;∴BNQ CFQ Ð=Ð∴90,90BNQ CBP BGN CBP QFC BCH QDC BCH Ð=Ð+Ð=Ð+°Ð=Ð+Ð=Ð+°,∴CBP BCM Ð=Ð,∴BH CH =,∵45MBE NBE Ð=Ð=°,45BCA Ð=°,∴EBN CBP BCA BCM Ð-Ð=Ð-Ð,即EBP ECP Ð=Ð,∵BHE CHP Ð=Ð,∴()ASA BHE CHP V V ≌,∴EH HP =,∵90EGH HDP Ð=Ð=°,EHG PHD Ð=Ð,∴()AAS EGH PDH V V ≌,∴HG HD =,如图:连接HQ ∵90QGH QDH Ð=Ð=°,HQ HQ =,∴()HL QGH QHD V V ≌,∴QE QP =,∵AEM CEN V V ≌,∴AE CE =,∴AQ AE EQ CE PQ =+=+,即④正确.故选D .2.(23-24八年级下·黑龙江哈尔滨·开学考试)如图所示,在ABC V 中,90BAC Ð=°,AD BC ^于D ,BE 平分ABC Ð交AD 于E ,F 在BC 上,并且BF AB =,则下列四个结论:①EF AC ∥,②EFB BAD Ð=Ð,③AE EF =,④ABE FBE △≌△,其中正确的结论有( )A .①③B .②④C .②③④D .①②③④【答案】D【分析】本题主要考查了全等三角形的判定与性质、角平分线的定义;根据SAS 证明ABE FBE △≌△,再利用三角形全等的性质证明EFB BAD Ð=Ð,AE EF =,进而得出EF AC ∥,熟练掌握全等三角形的判定和性质是解此题的关键.【详解】解:Q BE 平分ABC Ð交AD 于E ,ABE FBE \Ð=Ð,在ABE V 和FBE V 中,AB BF ABE FBE BE BE =ìïÐ=Ðíï=î,()SAS ABE FBE \V V ≌,故④正确;EFB BAD AE EF \Ð=Ð=,,故②③正确;90BAC Ð=°Q ,AD BC ^于D ,90BAE ABD \Ð+Ð=°,90C ABD Ð+Ð=°,C BAE EFB \Ð=Ð=Ð,EF AC ∥∴,故①正确;综上所述,正确的有①②③④,故选:D .3.(22-23七年级下·江苏南通·期末)如图,在ABC V 中,90BAC Ð=°,高AD 与角平分线BE 相交于点F ,DAC Ð的平分线AG 分别交BC ,BE 于点G ,O ,连接FG ,下列结论:①C EBG Ð=Ð;②AEF AFE Ð=Ð;③AG EF ^;④ACD ABG S S =△△,其中所有正确结论的序号是( )A .①②④B .②③C .③④D .②③④题型三 全等三角形中的动点综合问题例题:(23-24七年级下·上海闵行·期末)如图,已知在 ABC V 中, (060)AB BC ABC a a =Ð=<<°,,,射线AM AB ^,点P 为射线AM 上的动点(点P 不与点A 重合),连接BP ,将线段BP 绕点B 顺时针旋转角度α后, 得到线段BQ , 连接PQ 、QC .(1)试说明 PAB QCB V V ≌的理由;(2)延长QC 交射线AM 于点D ,在点P 的移动过程中, QDM Ð的大小是否发生变化?若改变请说明理由,若不改变,请求出 QDM Ð的大小(用含α的代数式表示);(3)当BQ AC ∥时, AB m AP n ==,, 过点Q 作QE 垂直射线AB , 垂足为E ,那么 AEQ S =V (用m 、 n 的代数式表示) .【答案】(1)理由见解析(2)不改变,QDM aÐ=(3)mn【分析】(1)先证明PBA QBC Ð=Ð,再根据两条边相等,即可证得两个三角形全等;(2)先证明()SAS DAB DCB V V ≌,得到DA DC =,DBA DBC Ð=Ð,再计算出DBA Ð的值,再证明DAC DBA Ð=Ð,最后根据三角形外角定理即可求得QDM Ð的大小;(3)证明QB 是ABE Ð的角平分线,根据角平分线定理得到BC BE =,QE QC =,再根据BC AB m ==,QC PA n ==,即可得到BE 和QE ,根据三角形面积公式进行计算即可.【详解】(1)证明:根据旋转的性质得到PN QB =,PBQ a Ð=,∴PBQ ABC Ð=Ð,∴PBA QBC Ð=Ð,∵PB QB PBA QBC AB BC =ìïÐ=Ðíï=î,∴()SAS PAB QCB V V ≌;(2)解:如下图所示,连接BD ,∵()SAS PAB QCB V V ≌,∴90QCB PAB Ð=Ð=°,∵BQ AC ∥,∴ACB CBQ CAB Ð=ÐÐ,∵ACB CAB Ð=Ð,∴QBE CBQ Ð=Ð,∴QB 是ABE Ð的角平分线,1.(23-24八年级上·湖南株洲·期末)如图,等腰Rt ACB △中,90ACB Ð=°,AC BC =,E 点为射线CB 上一动点,连接AE ,作AF AE ^且AF AE =.(1)如图1,过F 点作FG AC ^交AC 于G 点,求证:V V ≌AGF ECA ;(2)如图2,连接BF 交AC 于D 点,若3AD CD =,求证:E 点为BC 中点;(3)如图3,当E 点在CB 的延长线上时,连接BF 与AC 的延长线交于D 点,若43BC BE =,则AD CD = .AGF ECA QV V ≌,FG AC BC \==,在FGD V 和BCD △中,由(1)(2)知:V AGF CD DG \=,AG CE =\47AC AG =,\4AC =,2.(23-24八年级上·江西赣州·阶段练习)如图(1),在Rt ABC △中,90C Ð=°,8cm AC =,6cm BC =,10cm AB =,现有一动点P ,从点A 出发,沿着三角形的边AC CB BA ®®运动,回到点A 停止,速度为2cm /s ,设运动时间为s t .(1)如图(1),当t =________时,APC △的面积等于ABC V 面积的一半:(2)如图(2),在DEF V 中,90E Ð=°,4cmDE =,5cm DF =,D A Ð=Ð.在ABC V 的边上,若另外有一个动点Q ,与点P 同时从点A 出发,沿着边AB BC CA ®®运动,回到点A 停止.在两点运动过程中的某一时刻,恰好APQ △全等于DEF V ,求点Q 的运动速度.∴13cm 2CP BC ==∴()8311s 22t +==当P 在AB 上时,如图,∴12AP BP AB ===∴(6851922t ++==综上所述,当t 为(2)解:设点Q∴425x ¸=¸,解得52x =;②当点P 在AC 上,点Q 在∴5cm AP DF AQ DE ====,∴524x ¸=¸,解得85x =;③当点P 在AB 上,点Q 在∴5cm AP DF AQ DE ====,∴点P 的路程为68105++-∴19220x ¸=¸,解得4019x =;④当点P 在AB 上,点Q 在∴4cm AP DE AQ DF ===,∴点P 的路程为68104++-∴20219x ¸=¸,解得1910x =;∴Q 运动的速度为5cm/s 2或853.如图,在等腰ABC V 中,BA BC =,100ABC Ð=°,AB 平分WAC Ð.在线段AC 上有一动点D ,连接BD ,E 为直线AW 上异于A 的一点,连接BE 、DE .(1)如图1,当点E 在射线AW 上时,若DE AE DC +=,直接写出:EBD Ð=______;(2)如图2,当点E 在射线AW 的反向延长线上时,①若(1)中的结论仍成立,则DE 、AE 、DC 应满足怎样的数量关系,请证明;②若6BCD ABDE S S -=V 四边形,且25DE AE =,94AD AE =,求ABC S V 的值.4.(23-24八年级上·浙江嘉兴·期末)如图,在直角坐标系xOy 中,点()0,4A ,点B 为x 轴正半轴上一个动点,以AB 为边作ABC V ,使BC AB =,90ABC Ð=°,且点C 在第一象限内.(1)如图1,若()2,0B ,求点C 的坐标.(2)如图2,过点B 向x 轴上方作BD OB ^,且BD BO =,在点B 的运动过程中,探究点C ,D 之间的距离是否为定值.若为定值,求出该定值,若不是,请说明理由.(3)如图3,过点B 向x 轴下方作BD OB ^,且BD BO =,连结CD 交x 轴于点E ,当ABD △的面积是BEC V 的面积的2倍时,求OE 的长.【答案】(1)点C 的坐标为(6,2)(2)点C ,D 之间的距离是为定值,定值为4,理由见解析(3)6OE =【分析】本题考查坐标与图形,全等三角形的判定及性质,添加辅助线,构造全等三角形是解决问题的关键.90Q,Ð=°ABC\Ð+Ð=°,90ABO CBDÐ+Ð=°Q,OAB ABO90\Ð=Ð,OAB CBDAOBÐìï90OBA ABD Ð+Ð=°Q ,DBC ÐOBA DBC \Ð=Ð,在OAB V 和DCB △中,OB OBA AB =ìïÐíï=î()SAS OAB DCB \V V ≌.CF BO \=,BD BO =Q ,CF BD \=,4BF OA ==.CEF DEB Ð=ÐQ ,CFE Ð=()AAS CFE DBE \V V ≌,题型四 全等三角形中的新定义型综合问题例题:(23-24七年级下·辽宁本溪·期末)新定义:如果两个三角形不全等但面积相等,那么这两个三角形叫做积等三角形.【初步尝试】(1)如图1,在ABC V 中,4AB AC BC >=,,P 为边BC 上一点,若ABP V 与ACP V 是积等三角形,求BP 的长;【理解运用】(2)如图2,ABD V 与ACD V 为积等三角形,若24AB AC ==,,且线段AD 的长度为正整数,求AD 的长.【综合应用】(3)如图3,在Rt ABC △中90,BAC AB AC Ð=°=,过点C 作MN AC ^,点D 是射线CM 上一点,以AD 为边作Rt ,90,ADE DAE AD AE Ð=°=V ,连接BE .请判断BAE V 与ACD V 是否为积等三角形,并说明理由.【答案】(1)2;(2)2;(3)是积等三角形,证明见解析【分析】本题考查了等腰直角三角形的性质,三角形的中线的性质,三角形的三边关系等知识,解题的关键是正确寻找全等三角形解决问题.(1)利用三角形的中线的性质即可解决问题;(2)证明ADB NDC V V ≌,推出2AB NC ==,利用三角形的三边关系即可解决问题;(3)过过点E 作EH AB ^于点H ,先证明HAE CAD V V ≌, 则,AC AH EH CD ==,然后再依据积等三角形(2)解:如图2,延长V为积等三角形,QV与ACDABD\=BD CD(3)是积等三角形证明:如图3,过点E作^QMN AC\Ð=Ð=°ACD AHE90巩固训练1.(2024八年级下·全国·专题练习)定义:顶角相等且顶点重合的两个等腰三角形叫做“同源三角形”,我们称这两个顶角为“同源角”.如图,ABC V 和CDE V 为“同源三角形”,AC BC =,CD CE =,ACB Ð与DCE Ð为“同源角”.(1)如图1,ABC V 和CDE V 为“同源三角形”,试判断AD 与BE 的数量关系,并说明理由.(2)如图2,若“同源三角形”ABC V 和CDE V 上的点B ,C ,D 在同一条直线上,且90ACE Ð=°,则Ð=EMD ______°.(3)如图3,ABC V 和CDE V 为“同源三角形”,且“同源角”的度数为90°时,分别取AD ,BE 的中点Q ,P ,连接CP ,CQ ,PQ ,试说明PCQ △是等腰直角三角形.【答案】(1)AD BE =,详见解析(2)45(3)见解析【分析】本题考查了新定义,全等三角形的判定与性质,等腰直角三角形的判定,三角形内角和定理等知识,(1)由“同源三角形”的定义可证ACD BCE Ð=Ð,然后根据SAS 证明≌ACD BCE V V 即可;(2)由“同源三角形”的定义和90ACE Ð=°可求出45DCE ACB Ð==°,由(1)可知≌ACD BCE V V ,得ADC BEC ÐÐ=,然后根据“8”字形图形即可求出EMD Ð的度数;(3)由(1)可知≌ACD BCE V V ,可得CAQ CBP BE AD ÐÐ=,=,根据SAS 证明ACQ BCP △≌△,可得CQ CP ACQ BCP =Ð=Ð,,进而可证结论成立;熟练掌握全等三角形的判定与性质是解答本题的关键.【详解】(1)AD BE =.理由:∵ABC V 和CDE V 是“同源三角形”,∴ACB DCE Ð=Ð,∴ACD BCE Ð=Ð.在ACD V 和BCE V 中,ACBC ACD BCE CD CE =ìïÐ=Ðíï=î,∴()SAS ACD BCE V V ≌,∴AD BE =.(2)∵ABC V 和CDE V 是“同源三角形”,∴ACB DCE Ð=Ð.∵90ACE Ð=°,∴45DCE ACB Ð=Ð=°.由(1)可知≌ACD BCE V V ,∴ADC BEC ÐÐ=.∵MOE COD Ð=Ð,∴45EMD DCE Ð=Ð=°.故答案为:45;(3)由(1)可知≌ACD BCE V V ,∴CAQ CBP Ð=Ð,BE AD =.AD ,BE 的中点分别为,Q P ,∴AQ BP =.在ACQ V 和BCP V 中,CA CB CAQ CBP AQ BP =ìïÐ=íï=î,∴()SAS ACQ BCP V V ≌,∴CQ CP =,ACQ BCP Ð=Ð.∵90BCP PCA °Ð+Ð=,∴90ACQ PCA °Ð+Ð=,∴90PCQ Ð=°,∴PCQ △是等腰直角三角形.2.(23-24七年级下·陕西宝鸡·期末)【阅读理解】定义:在同一平面内,点A ,B 分别在射线PM ,PN 上,过点A 垂直PM 的直线与过点B 垂直PN 的直线交于点Q ,则我们把AQB Ð称为APB Ð的“边垂角”.【迁移运用】(1)如图1,CD ,BE 分别是ABC V 的两条高,两条高交于点F ,根据定义,我们知道DBE Ð是DCE Ð的“边垂角”或DCE Ð是DBE Ð的“边垂角”,DAE Ð的“边垂角”是______;(2)若AQB Ð是APB Ð的“边垂角”,则AQB Ð与APB Ð的数量关系是______;(3)若ACD Ð是ABD Ð的“边垂角”,且AB AC =.如图2,BD 交AC 于点E ,点C 关于直线BD 对称点为点F ,连接AF ,EF ,且45CAF Ð=°,求证:BE CF CE =+.【答案】(1)DFEÐ(2)AQB APB Ð=Ð或180AQB APB Ð+Ð=°(3)见解析【分析】本题主要考查了全等三角形的性质与判定,四边形内角和定理:(1)根据“边垂角”的定义即可得到答案;(2)分两种情况画出图形,根据四边形的内角和定理以及等角的余角相等即可得出结论;(3)延长,BA CD 交于点G ,先证明(ASA)ABE ACG V V ≌,再证明(SAS)AGF AEF V V ≌,依据题意得出GF EC =,即可得到结论.【详解】(1)解:根据“边垂角”的定义,DAE Ð的“边垂角”是DFE Ð;(2)解:若AQB Ð是APB Ð的“边垂角”,分两种情况①如图,Q AQB Ð是APB Ð的“边垂角”,,AQ PA BQ PB \^^,190,290AQB APB \Ð+Ð=°Ð+Ð=°,12Ð=ÐQ ,AQB APB \Ð=Ð,②如图,Q AQB Ð是APB Ð的“边垂角”,,AQ PA BQ PB \^^,90,90PAQ PBQ \Ð=°Ð=°,360PAQ AQB APB PBQ Ð+Ð+Ð+Ð=°Q ,\180AQB APB Ð+Ð=°,综上所述,AQB Ð与APB Ð的数量关系是AQB APB Ð=Ð或180AQB APB Ð+Ð=°;(3)解:延长,BA CD 交于点G ,Q ACD Ð是ABD Ð的“边垂角”,∴CG BD BG AC ⊥,⊥,90,90ABE AEB ACD DEC \Ð+Ð=°Ð+Ð=°,AEB DEC Ð=ÐQ ,ABE ACF \Ð=Ð,90BAE CAG \Ð=Ð=°,AB AC =Q ,\(ASA)ABE ACG V V ≌,,AG AE BE CG \==,45FAC Ð=°Q ,9045GAF FAC \Ð=°-Ð=°,AF AF =Q ,\(SAS)AGF AEF V V ≌,GF EF \=,Q 点C 关于直线BE 对称点为点F ,EF EC \=,BE CG CF FG CF EF CF CE \==+=+=+,BE CF CE \=+;3.(23-24七年级下·辽宁沈阳·阶段练习)【阅读理解】定义:在同一平面内,点A ,B 分别在射线PM ,PN 上,过点A 垂直PM 的直线与过点B 垂直PN 的直线交于点Q ,则我们把AQB Ð称为APB Ð的“边垂角”.【迁移运用】(1)如图1,CD ,BE 分别是ABC V 的两条高,两条高交于点 F ,根据定义,我们知道DBE Ð是DCE Ð的“边垂角”或DCE Ð是DBE Ð的“边垂角”,DAE Ð的“边垂角”是 ;(2)若AQB Ð是APB Ð的“边垂角”,则AQB Ð与APB Ð的数量关系是 ;(3)若ACD Ð是ABD Ð的“边垂角”,且AB AC =.①如图2,已知B C Ð=Ð,BD 交AC 于点E ,点C 关于直线BD 对称点为点F ,连接AF ,EF ,且 45CAF Ð=°,90BAC Ð=°,求证:BE CF CE =+;对于上述问题,小明有这样的想法:在BD 上截取BH CF =,连接AH ,如图3.你明白小明的做法吗?接下来请你求证BE CF CE =+.②如图4,若92CD BD +=,直接写出四边形ABDC 的面积.【答案】(1)DFE Ð②如图,Q AQB Ð是APB Ð的“边垂角”,,AQ PA BQ PB \^^,90,90PAQ PBQ \Ð=°Ð=°,综上所述,AQB Ð与APB Ð的数量关系是AQB APB Ð=Ð或180AQB APB Ð+Ð=°;(3)解:①延长,BA CD 交于点G ,Q ACD Ð是ABD Ð的“边垂角”,90,90ABE AEB ACD DEC \Ð+Ð=°Ð+Ð=°,AEB DEC Ð=ÐQ ,ABE ACF \Ð=Ð,90BAE CAG \Ð=Ð=°,AB AC =Q ,\(ASA)ABE ACG V V ≌,,AG AE BE CG \==,45FAC Ð=°Q ,9045GAF FAC \Ð=°-Ð=°,AF AF =Q ,\(SAS)AGF AEF V V ≌,GF EF \=,Q 点C 关于直线BE 对称点为点F ,EF EC \=,BE CG CF FG CF EF CF CE \==+=+=+,BE CF CE \=+;②连接AD ,过点A 作AE AD ^与DB 延长交于点E ,Q ACD Ð是ABD Ð的“边垂角”,180ACD ABD \Ð+Ð=°,180ABE ABD Ð+Ð=°Q ,ABE ACD \Ð=Ð,90DAC BAD BAD EAB Ð+Ð=Ð+Ð=°Q ,【点睛】本题主要考查新定义,四边形的内角和定理,直角三角形的性质,全等三角形的判定与性质,熟练理解“边垂角”的定义是解题的关键.4.(22-23七年级下·江苏淮安α(0180a °<<°)得到AB ¢,把AC 绕点A 逆时针旋转β得到AC ¢,连接B C ¢¢.当180a b +=°时,我们称AB C ¢¢△是ABC V 的“旋补三角形”,AB C ¢¢△边B C ¢¢上的中线AD 叫做ABC V 的“旋补中线”,点A 叫做“旋补中心”.(1)【探索一】如图1,AB C ¢¢△是ABC V 的“旋补三角形”,AD 是ABC V 的“旋补中线”,探索AD 与BC 的数量关系.在探索这个问题之前,请先阅读材料:【材料】如图2在ABC V 中,若10AB =,8BC =.求AC 边上的中线BD 的取值范围.是这样思考的:延长BD 至E ,使DE BD =,连结CE .利用全等将边AB 转化到CE ,在BCE V 中利用三角形三边关系即可求出中线BD 的取值范围.中线BD 的取值范围是 .请仿照上面材料中的方法,猜想图1中AD 与BC 的数量关系,并给予证明.(2)【探索二】如图3,当90a b ==°时,AB C ¢¢△是ABC V 的“旋补三角形”,AE BC ^,垂足为点E ,AE 的反向延长线交B C ¢¢于点D ,探索AD 是否是ABC V 的“旋补中线”,如果是,请给出证明,如果不是,请说明理由.【答案】(1)19BD <<;2BC AD =,证明见解析;(2)AD 是ABC V 的“旋补中线”, 证明见解析【分析】(1)材料:三角形三边关系可得CE BC BE CE BC -<<+,进而可得中线BD 的取值范围;探索一:延长AD 至点E 使AD DE =,连接C E ¢,证明()SAS B DA CDE ¢≌V V ,可得AB CE ¢=,B AD E ¢Ð=Ð,求出BAC AC E ¢Ð=Ð,再证()SAS ABC C EA ¢≌V V ,根据全等三角形的性质可得结论;(2)作C H AD ¢^于H ,作B F AD ¢^交AD 延长线于F ,求出B B AF ¢Ð=Ð,证明()AAS ABE B AF ¢≌V V ,可得=B F AE ¢,同理证明()AAS ACE C AH ¢≌V V ,可得=AE C H ¢,求出=B F C H ¢¢,可证()AAS B DF C DH ¢¢≌V V ,根据全等三角形的性质可得B D C D ¢=¢,然后可得AD 是ABC V 的“旋补中线”.【详解】(1)解:材料:由题意得:10AB CE ==,8BC =,2BE BD =,由三角形三边关系可得:CE BC BE CE BC -<<+,即218BD <2<,∴19BD <<,故答案为:19BD <<;探索一:2BC AD =;证明:如图1,延长AD 至点E 使AD DE =,连接C E ¢,∵AD 是ABC V 的“旋补中线”,∴AD 是AB C ¢¢△的中线,即B D CD ¢=,又∵B DA C DE ¢¢Ð=Ð,∴()SAS B DA C DE ¢¢V V ≌,∴AB C E ¢¢=,B AD E ¢Ð=Ð,∵AB AB ¢=,∴AB C E ¢=,∵AD 是ABC V 的“旋补中线”,∴180BAC B AC BAC B AD EAC ¢¢¢Ð+Ð=Ð+Ð+Ð=°,∵180AC E E EAC ¢Ð+Ð+Ð=°,B AD E ¢Ð=Ð,∴BAC AC E ¢Ð=Ð,∵AC AC ¢=,BAC AC E ¢Ð=Ð,AB C E¢=∴()SAS ABC C EA ¢≌V V ,∴2BC AE AD ==.(2)AD 是ABC V 的“旋补中线”;证明:如图,作C H AD ¢^于H ,作B F AD ¢^交AD 延长线于F ,∵AE BC ^,∴90F BEA Ð=Ð=°,∴90BAE B Ð+Ð=°,∵90a b ==°,即90BAB CAC ¢¢Ð=Ð=°,∴90BAE B AF ¢Ð+Ð=°,∴B B AF ¢Ð=Ð,又∵¢=BA AB ,∴()AAS ABE B AF ¢≌V V ,∴=B F AE ¢,又∵90AEC C HA ¢Ð=Ð=°,90CAC ¢Ð=°,∴90CAE C Ð+Ð=°,90CAE C AH ¢Ð+Ð=°,∴C C AH ¢Ð=Ð,∵CA AC ¢=,∴()AAS ACE C AH ¢≌V V ,∴=AE C H ¢,∴=B F C H ¢¢,∵90F C HD ¢Ð=Ð=°,B DF C DH ¢¢Ð=Ð,∴()AAS B DF C DH ¢¢≌V V ,∴B D C D ¢=¢,∴AD 是AB C ¢¢△的中线,∴AD 是ABC V 的“旋补中线”.【点睛】本题主要考查了全等三角形的判定和性质、同角的余角相等,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,构造全等三角形解决问题.。
初二三角形所有知识点总结和常考题提高难题压轴题练习(含答案解析)

初二三角形所有知识点总结和常考题知识点:1.三角形:由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形.2.三边关系:三角形任意两边的和大于第三边,任意两边的差小于第三边.3.高:从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足间的线段叫做三角形的高。
4。
中线:在三角形中,连接一个顶点和它对边中点的线段叫做三角形的中线。
5。
角平分线:三角形的一个内角的平分线与这个角的对边相交,这个角的顶点和交点之间的线段叫做三角形的角平分线。
6。
三角形的稳定性:三角形的形状是固定的,三角形的这个性质叫三角形的稳定性.7。
多边形:在平面内,由一些线段首尾顺次相接组成的图形叫做多边形。
8。
多边形的内角:多边形相邻两边组成的角叫做它的内角.9。
多边形的外角:多边形的一边与它的邻边的延长线组成的角叫做多边形的外角。
10.多边形的对角线:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.11.正多边形:在平面内,各个角都相等,各条边都相等的多边形叫正多边形。
12。
平面镶嵌:用一些不重叠摆放的多边形把平面的一部分完全覆盖,叫做用多边形覆盖平面,13。
公式与性质:⑴三角形的内角和:三角形的内角和为180°⑵三角形外角的性质:性质1:三角形的一个外角等于和它不相邻的两个内角的和。
性质2:三角形的一个外角大于任何一个和它不相邻的内角。
⑶多边形内角和公式:边形的内角和等于·180°⑷多边形的外角和:多边形的外角和为360°.⑸多边形对角线的条数:①从边形的一个顶点出发可以引条对角线,把多边形分成个三角形。
②边形共有条对角线。
常考题:一.选择题(共13小题)1.已知三角形的两边长分别为4cm和9cm,则下列长度的四条线段中能作为第三边的是()A.13cm B.6cm C.5cm D.4cm2.一个正方形和两个等边三角形的位置如图所示,若∠3=50°,则∠1+∠2=()A.90°B.100°C.130° D.180°3.已知如图,△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于()A.315°B.270° C.180° D.135°4.如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是()A. B. C. D.5.如图,在四边形ABCD中,∠A+∠D=α,∠ABC的平分线与∠BCD的平分线交于点P,则∠P=()A.90°﹣αB.90°+αC. D.360°﹣α6.如图,Rt△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上A′处,折痕为CD,则∠A′DB=()A.40°B.30°C.20°D.10°7.如图,在锐角△ABC中,CD,BE分别是AB,AC边上的高,且CD,BE相交于一点P,若∠A=50°,则∠BPC=()A.150°B.130°C.120° D.100°8.如图,为估计池塘岸边A、B的距离,小方在池塘的一侧选取一点O,测得OA=15米,OB=10米,A、B间的距离不可能是()A.20米B.15米C.10米D.5米9.将一个n边形变成n+1边形,内角和将()A.减少180°B.增加90°C.增加180°D.增加360°10.一个多边形除一个内角外其余内角的和为1510°,则这个多边形对角线的条数是()A.27 B.35 C.44 D.5411.一个多边形的边数每增加一条,这个多边形的()A.内角和增加360°B.外角和增加360°C.对角线增加一条 D.内角和增加180°12.一个三角形三个内角的度数之比为2:3:7,这个三角形一定是() A.等腰三角形B.直角三角形C.锐角三角形D.钝角三角形13.如图,一个多边形纸片按图示的剪法剪去一个内角后,得到一个内角和为2340°的新多边形,则原多边形的边数为()A.13 B.14 C.15 D.16二.填空题(共13小题)14.若一个多边形的内角和是其外角和的3倍,则这个多边形的边数是.15.如图,小亮从A点出发,沿直线前进10米后向左转30°,再沿直线前进10米,又向左转30°,…,照这样走下去,他第一次回到出发地A点时,一共走了米.16.将一副直角三角板如图放置,使含30°角的三角板的短直角边和含45°角的三角板的一条直角边重合,则∠1的度数为度.17.当三角形中一个内角α是另一个内角β的两倍时,我们称此三角形为“特征三角形",其中α称为“特征角”.如果一个“特征三角形”的“特征角”为100°,那么这个“特征三角形”的最小内角的度数为.18.若一个多边形内角和等于1260°,则该多边形边数是.19.如图是由射线AB,BC,CD,DE,EA组成的平面图形,则∠1+∠2+∠3+∠4+∠5=.20.一个多边形的内角和比外角和的3倍多180°,则它的边数是.21.若正多边形的一个内角等于140°,则这个正多边形的边数是.22.在△ABC中,三个内角∠A、∠B、∠C满足∠B﹣∠A=∠C﹣∠B,则∠B=度.23.如图,在△ABC中,∠A=m°,∠ABC和∠ACD的平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;…∠A2012BC和∠A2012CD的平分线交于点A2013,则∠A2013=度.24.如图,△ABC中,∠A=40°,∠B=72°,CE平分∠ACB,CD⊥AB于D,DF⊥CE,则∠CDF=度.25.用一条宽相等的足够长的纸条,打一个结,如图(1)所示,然后轻轻拉紧、压平就可以得到如图(2)所示的正五边形ABCDE,其中∠BAC=度.26.平面上,将边长相等的正三角形、正方形、正五边形、正六边形的一边重合并叠在一起,如图,则∠3+∠1﹣∠2=.三.解答题(共14小题)27.如图,直线DE交△ABC的边AB、AC于D、E,交BC延长线于F,若∠B=67°,∠ACB=74°,∠AED=48°,求∠BDF的度数.28.如图,已知D为△ABC边BC延长线上一点,DF⊥AB于F交AC于E,∠A=35°,∠D=42°,求∠ACD的度数.29.已知△ABC中,∠ACB=90°,CD为AB边上的高,BE平分∠ABC,分别交CD、AC 于点F、E,求证:∠CFE=∠CEF.30.如图,AD为△ABC的中线,BE为△ABD的中线,(1)若∠ABE=25°,∠BAD=50°,则∠BED的度数是度.(2)在△ADC中过点C作AD边上的高CH.(3)若△ABC的面积为60,BD=5,求点E到BC边的距离.31.如图,在△ABC中,AD平分∠BAC,P为线段AD上的一个动点,PE⊥AD交直线BC于点E.(1)若∠B=35°,∠ACB=85°,求∠E的度数;(2)当P点在线段AD上运动时,猜想∠E与∠B、∠ACB的数量关系,写出结论无需证明.32.如图所示,在△ABC中,∠B=∠C,FD⊥BC,DE⊥AB,垂足分别为D,E,∠AFD=158°,求∠EDF的度数.33.如图,AD平分∠BAC,∠EAD=∠EDA.(1)∠EAC与∠B相等吗?为什么?(2)若∠B=50°,∠CAD:∠E=1:3,求∠E的度数.34.(1)如图1,有一块直角三角板XYZ放置在△ABC上,恰好三角板XYZ的两条直角边XY、XZ分别经过点B、C.△ABC中,∠A=30°,则∠ABC+∠ACB=,∠XBC+∠XCB=.(2)如图2,改变直角三角板XYZ的位置,使三角板XYZ的两条直角边XY、XZ 仍然分别经过B、C,那么∠ABX+∠ACX的大小是否变化?若变化,请举例说明;若不变化,请求出∠ABX+∠ACX的大小.35.已知:∠MON=40°,OE平分∠MON,点A、B、C分别是射线OM、OE、ON 上的动点(A、B、C不与点O 重合),连接AC交射线OE于点D.设∠OAC=x°.(1)如图1,若AB∥ON,则①∠ABO的度数是;②当∠BAD=∠ABD时,x=;当∠BAD=∠BDA时,x=.(2)如图2,若AB⊥OM,则是否存在这样的x的值,使得△ADB中有两个相等的角?若存在,求出x的值;若不存在,说明理由.36.平面内的两条直线有相交和平行两种位置关系(1)如图a,若AB∥CD,点P在AB、CD外部,则有∠B=∠BOD,又因∠BOD是△POD的外角,故∠BOD=∠BPD+∠D,得∠BPD=∠B﹣∠D.将点P移到AB、CD 内部,如图b,以上结论是否成立?若成立,说明理由;若不成立,则∠BPD、∠B、∠D之间有何数量关系?请证明你的结论;(2)在图b中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图c,则∠BPD﹑∠B﹑∠D﹑∠BQD之间有何数量关系?(不需证明)(3)根据(2)的结论求图d中∠A+∠B+∠C+∠D+∠E+∠F的度数.37.如下几个图形是五角星和它的变形.(1)图(1)中是一个五角星,求∠A+∠B+∠C+∠D+∠E.(2)图(2)中的点A向下移到BE上时,五个角的和(即∠CAD+∠B+∠C+∠D+∠E)有无变化说明你的结论的正确性.(3)把图(2)中的点C向上移到BD上时(1)如图(3)所示,五个角的和(即∠CAD+∠B+∠ACE+∠D+∠E)有无变化说明你的结论的正确性.38.Rt△ABC中,∠C=90°,点D、E分别是△ABC边AC、BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.(1)若点P在线段AB上,如图(1)所示,且∠α=50°,则∠1+∠2=°;(2)若点P在边AB上运动,如图(2)所示,则∠α、∠1、∠2之间的关系为:;(3)若点P运动到边AB的延长线上,如图(3)所示,则∠α、∠1、∠2之间有何关系?猜想并说明理由.(4)若点P运动到△ABC形外,如图(4)所示,则∠α、∠1、∠2之间的关系为:.39.如图所示,求∠A+∠B+∠C+∠D+∠E+∠F的度数.40.将纸片△ABC沿DE折叠使点A落在A′处的位置.(1)如果A′落在四边形BCDE的内部(如图1),∠A′与∠1+∠2之间存在怎样的数量关系?并说明理由.(2)如果A′落在四边形BCDE的BE边上,这时图1中的∠1变为0°角,则∠A′与∠2之间的关系是.(3)如果A′落在四边形BCDE的外部(如图2),这时∠A′与∠1、∠2之间又存在怎样的数量关系?并说明理由.初二三角形所有知识点总结和常考题提高难题压轴题练习(含答案解析)参考答案与试题解析一.选择题(共13小题)1.(2008•福州)已知三角形的两边长分别为4cm和9cm,则下列长度的四条线段中能作为第三边的是()A.13cm B.6cm C.5cm D.4cm【分析】此题首先根据三角形的三边关系,求得第三边的取值范围,再进一步找到符合条件的数值.【解答】解:根据三角形的三边关系,得:第三边应大于两边之差,且小于两边之和,即9﹣4=5,9+4=13.∴第三边取值范围应该为:5<第三边长度<13,故只有B选项符合条件.故选:B.【点评】本题考查了三角形三边关系,一定要注意构成三角形的条件:两边之和>第三边,两边之差<第三边.2.(2013•河北)一个正方形和两个等边三角形的位置如图所示,若∠3=50°,则∠1+∠2=()A.90°B.100°C.130° D.180°【分析】设围成的小三角形为△ABC,分别用∠1、∠2、∠3表示出△ABC的三个内角,再利用三角形的内角和等于180°列式整理即可得解.【解答】解:如图,∠BAC=180°﹣90°﹣∠1=90°﹣∠1,∠ABC=180°﹣60°﹣∠3=120°﹣∠3,∠ACB=180°﹣60°﹣∠2=120°﹣∠2,在△ABC中,∠BAC+∠ABC+∠ACB=180°,∴90°﹣∠1+120°﹣∠3+120°﹣∠2=180°,∴∠1+∠2=150°﹣∠3,∵∠3=50°,∴∠1+∠2=150°﹣50°=100°.故选:B.【点评】本题考查了三角形的内角和定理,用∠1、∠2、∠3表示出△ABC的三个内角是解题的关键,也是本题的难点.3.(2010•西藏)已知如图,△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于()A.315°B.270° C.180° D.135°【分析】利用三角形内角与外角的关系:三角形的任一外角等于和它不相邻的两个内角之和解答.【解答】解:∵∠1、∠2是△CDE的外角,∴∠1=∠4+∠C,∠2=∠3+∠C,即∠1+∠2=2∠C+(∠3+∠4),∵∠3+∠4=180°﹣∠C=90°,∴∠1+∠2=2×90°+90°=270°.故选:B.【点评】此题主要考查了三角形内角与外角的关系:三角形的任一外角等于和它不相邻的两个内角之和.4.(2015•长沙)如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是() A. B. C. D.【分析】根据三角形高线的定义:过三角形的顶点向对边引垂线,顶点和垂足之间的线段叫做三角形的高线解答.【解答】解:为△ABC中BC边上的高的是A选项.故选A.【点评】本题考查了三角形的角平分线、中线、高线,熟记高线的定义是解题的关键.5.(2014•达州)如图,在四边形ABCD中,∠A+∠D=α,∠ABC的平分线与∠BCD 的平分线交于点P,则∠P=()A.90°﹣αB.90°+αC. D.360°﹣α【分析】先求出∠ABC+∠BCD的度数,然后根据角平分线的性质以及三角形的内角和定理求解∠P的度数.【解答】解:∵四边形ABCD中,∠ABC+∠BCD=360°﹣(∠A+∠D)=360°﹣α,∵PB和PC分别为∠ABC、∠BCD的平分线,∴∠PBC+∠PCB=(∠ABC+∠BCD)=(360°﹣α)=180°﹣α,则∠P=180°﹣(∠PBC+∠PCB)=180°﹣(180°﹣α)=α.故选:C.【点评】本题考查了多边形的内角和外角以及三角形的内角和定理,属于基础题.6.(2009•荆门)如图,Rt△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A 落在边CB上A′处,折痕为CD,则∠A′DB=()A.40°B.30°C.20°D.10°【分析】由三角形的一个外角等于与它不相邻的两个内角的和,得∠A′DB=∠CA'D ﹣∠B,又折叠前后图形的形状和大小不变,∠CA’D=∠A=50°,易求∠B=90°﹣∠A=40°,从而求出∠A′DB的度数.【解答】解:∵Rt△ABC中,∠ACB=90°,∠A=50°,∴∠B=90°﹣50°=40°,∵将其折叠,使点A落在边CB上A′处,折痕为CD,则∠CA'D=∠A,∵∠CA'D是△A’BD的外角,∴∠A′DB=∠CA'D﹣∠B=50°﹣40°=10°.故选:D.【点评】本题考查图形的折叠变化及三角形的外角性质.关键是要理解折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,只是位置变化.解答此题的关键是要明白图形折叠后与折叠前所对应的角相等.7.(2004•陕西)如图,在锐角△ABC中,CD,BE分别是AB,AC边上的高,且CD,BE相交于一点P,若∠A=50°,则∠BPC=()A.150°B.130°C.120° D.100°【分析】根据垂直的定义和四边形的内角和是360°求得.【解答】解:∵BE⊥AC,CD⊥AB,∴∠ADC=∠AEB=90°,∴∠BPC=∠DPE=180°﹣50°=130°.故选B.【点评】主要考查了垂直的定义以及四边形内角和是360度.注意∠BPC与∠DPE 互为对顶角.8.(2009•黑河)如图,为估计池塘岸边A、B的距离,小方在池塘的一侧选取一点O,测得OA=15米,OB=10米,A、B间的距离不可能是()A.20米B.15米C.10米D.5米【分析】根据三角形的三边关系,第三边的长一定大于已知的两边的差,而小于两边的和,求得相应范围,看哪个数值不在范围即可.【解答】解:∵15﹣10<AB<10+15,∴5<AB<25.∴所以不可能是5米.故选:D.【点评】已知三角形的两边,则第三边的范围是:>已知的两边的差,而<两边的和.9.(2014•临沂)将一个n边形变成n+1边形,内角和将()A.减少180°B.增加90°C.增加180°D.增加360°【分析】利用多边形的内角和公式即可求出答案.【解答】解:n边形的内角和是(n﹣2)•180°,n+1边形的内角和是(n﹣1)•180°,因而(n+1)边形的内角和比n边形的内角和大(n﹣1)•180°﹣(n﹣2)•180=180°.故选:C.【点评】本题主要考查了多边形的内角和公式,是需要识记的内容.10.(2015•莱芜)一个多边形除一个内角外其余内角的和为1510°,则这个多边形对角线的条数是()A.27 B.35 C.44 D.54【分析】设出题中所给的两个未知数,利用内角和公式列出相应等式,根据边数为整数求解即可,再进一步代入多边形的对角线计算方法,即可解答.【解答】解:设这个内角度数为x°,边数为n,∴(n﹣2)×180﹣x=1510,180n=1870+x=1800+(70+x),∵n为正整数,∴n=11,∴=44,故选:C.【点评】此题考查多边形的内角和计算公式以及多边形的对角线条数的计算方法,属于需要识记的知识.11.(2011春•滨城区期末)一个多边形的边数每增加一条,这个多边形的()A.内角和增加360°B.外角和增加360°C.对角线增加一条 D.内角和增加180°【分析】利用多边形的内角和定理和外角和特征即可解决问题.【解答】解:因为n边形的内角和是(n﹣2)•180°,当边数增加一条就变成n+1,则内角和是(n﹣1)•180°,内角和增加:(n﹣1)•180°﹣(n﹣2)•180°=180°;根据多边形的外角和特征,边数变化外角和不变.故选:D.【点评】本题主要考查了多边形的内角和定理与外角和特征.先设这是一个n 边形是解题的关键.12.(2012•滨州)一个三角形三个内角的度数之比为2:3:7,这个三角形一定是()A.等腰三角形B.直角三角形C.锐角三角形D.钝角三角形【分析】已知三角形三个内角的度数之比,根据三角形内角和定理,可求得三角的度数,由此判断三角形的类型.【解答】解:三角形的三个角依次为180°×=30°,180°×=45°,180°×=105°,所以这个三角形是钝角三角形.故选:D.【点评】本题考查三角形的分类,这个三角形最大角为180°×>90°.本题也可以利用方程思想来解答,即2x+3x+7x=180,解得x=15,所以最大角为7×15°=105°.13.(2014•毕节市)如图,一个多边形纸片按图示的剪法剪去一个内角后,得到一个内角和为2340°的新多边形,则原多边形的边数为()A.13 B.14 C.15 D.16【分析】根据多边形内角和公式,可得新多边形的边数,根据新多边形比原多边形多1条边,可得答案.【解答】解:设新多边形是n边形,由多边形内角和公式得(n﹣2)180°=2340°,解得n=15,原多边形是15﹣1=14,故选:B.【点评】本题考查了多边形内角与外角,多边形的内角和公式是解题关键.二.填空题(共13小题)14.(2015•资阳)若一个多边形的内角和是其外角和的3倍,则这个多边形的边数是8.【分析】任何多边形的外角和是360°,即这个多边形的内角和是3×360°.n边形的内角和是(n﹣2)•180°,如果已知多边形的边数,就可以得到一个关于边数的方程,解方程就可以求出多边形的边数.【解答】解:设多边形的边数为n,根据题意,得(n﹣2)•180=3×360,解得n=8.则这个多边形的边数是8.【点评】已知多边形的内角和求边数,可以转化为方程的问题来解决.15.(2006•镇江)如图,小亮从A点出发,沿直线前进10米后向左转30°,再沿直线前进10米,又向左转30°,…,照这样走下去,他第一次回到出发地A点时,一共走了120米.【分析】由题意可知小亮所走的路线为一个正多边形,根据多边形的外角和即可求出答案.【解答】解:∵360÷30=12,∴他需要走12次才会回到原来的起点,即一共走了12×10=120米.故答案为:120.【点评】本题主要考查了多边形的外角和定理.任何一个多边形的外角和都是360°.16.(2014•随州)将一副直角三角板如图放置,使含30°角的三角板的短直角边和含45°角的三角板的一条直角边重合,则∠1的度数为75度.【分析】根据三角形三内角之和等于180°求解.【解答】解:如图.∵∠3=60°,∠4=45°,∴∠1=∠5=180°﹣∠3﹣∠4=75°.故答案为:75.【点评】考查三角形内角之和等于180°.17.(2013•上海)当三角形中一个内角α是另一个内角β的两倍时,我们称此三角形为“特征三角形”,其中α称为“特征角”.如果一个“特征三角形"的“特征角”为100°,那么这个“特征三角形”的最小内角的度数为30°.【分析】根据已知一个内角α是另一个内角β的两倍得出β的度数,进而求出最小内角即可.【解答】解:由题意得:α=2β,α=100°,则β=50°,180°﹣100°﹣50°=30°,故答案为:30°.【点评】此题主要考查了新定义以及三角形的内角和定理,根据已知得出β的度数是解题关键.18.(2013•遂宁)若一个多边形内角和等于1260°,则该多边形边数是9.【分析】根据多边形内角和定理及其公式,即可解答;【解答】解:∵一个多边形内角和等于1260°,∴(n﹣2)×180°=1260°,解得,n=9.故答案为9.【点评】本题考查了多边形的内角定理及其公式,关键是记住多边形内角和的计算公式.19.(2015•北京)如图是由射线AB,BC,CD,DE,EA组成的平面图形,则∠1+∠2+∠3+∠4+∠5=360°.【分析】首先根据图示,可得∠1=180°﹣∠BAE,∠2=180°﹣∠ABC,∠3=180°﹣∠BCD,∠4=180°﹣∠CDE,∠5=180°﹣∠DEA,然后根据三角形的内角和定理,求出五边形ABCDE的内角和是多少,再用180°×5减去五边形ABCDE的内角和,求出∠1+∠2+∠3+∠4+∠5等于多少即可.【解答】解:∠1+∠2+∠3+∠4+∠5=(180°﹣∠BAE)+(180°﹣∠ABC)+(180°﹣∠BCD)+(180°﹣∠CDE)+(180°﹣∠DEA)=180°×5﹣(∠BAE+∠ABC+∠BCD+∠CDE+∠DEA)=900°﹣(5﹣2)×180°=900°﹣540°=360°.故答案为:360°.【点评】此题主要考查了多边形内角和定理,要熟练掌握,解答此题的关键是要明确:(1)n边形的内角和=(n﹣2)•180 (n≥3)且n为整数).(2)多边形的外角和指每个顶点处取一个外角,则n边形取n个外角,无论边数是几,其外角和永远为360°.20.(2014•自贡)一个多边形的内角和比外角和的3倍多180°,则它的边数是9.【分析】多边形的内角和比外角和的3倍多180°,而多边形的外角和是360°,则内角和是3×360°+180°.n边形的内角和可以表示成(n﹣2)•180°,设这个多边形的边数是n,得到方程,从而求出边数.【解答】解:根据题意,得(n﹣2)•180°=3×360°+180°,解得:n=9.则这个多边形的边数是9.故答案为:9.【点评】考查了多边形内角与外角,此题只要结合多边形的内角和公式寻求等量关系,构建方程即可求解.21.(2015•徐州)若正多边形的一个内角等于140°,则这个正多边形的边数是9.【分析】首先根据求出外角度数,再利用外角和定理求出边数.【解答】解:∵正多边形的一个内角是140°,∴它的外角是:180°﹣140°=40°,360°÷40°=9.故答案为:9.【点评】此题主要考查了多边形的外角与内角,做此类题目,首先求出正多边形的外角度数,再利用外角和定理求出求边数.22.(2013•黔东南州)在△ABC中,三个内角∠A、∠B、∠C满足∠B﹣∠A=∠C ﹣∠B,则∠B=60度.【分析】先整理得到∠A+∠C=2∠B,再利用三角形的内角和等于180°列出方程求解即可.【解答】解:∵∠B﹣∠A=∠C﹣∠B,∴∠A+∠C=2∠B,又∵∠A+∠C+∠B=180°,∴3∠B=180°,∴∠B=60°.故答案为:60.【点评】本题考查了三角形的内角和定理,是基础题,求出∠A+∠C=2∠B是解题的关键.23.(2013•达州)如图,在△ABC中,∠A=m°,∠ABC和∠ACD的平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;…∠A2012BC和∠A2012CD 的平分线交于点A2013,则∠A2013=度.【分析】利用角平分线的性质、三角形外角性质,易证∠A1=∠A,进而可求∠A1,由于∠A1=∠A,∠A2=∠A1=∠A,…,以此类推可知∠A2013=∠A=°.【解答】解:∵A1B平分∠ABC,A1C平分∠ACD,∴∠A1BC=∠ABC,∠A1CA=∠ACD,∵∠A1CD=∠A1+∠A1BC,即∠ACD=∠A1+∠ABC,∴∠A1=(∠ACD﹣∠ABC),∵∠A+∠ABC=∠ACD,∴∠A=∠ACD﹣∠ABC,∴∠A1=∠A,∴∠A1=m°,∵∠A1=∠A,∠A2=∠A1=∠A,…以此类推∠A2013=∠A=°.故答案为:.【点评】本题考查了角平分线性质、三角形外角性质,解题的关键是推导出∠A1=∠A,并能找出规律.24.(2012春•金台区期末)如图,△ABC中,∠A=40°,∠B=72°,CE平分∠ACB,CD ⊥AB于D,DF⊥CE,则∠CDF=74度.【分析】利用三角形的内角和外角之间的关系计算.【解答】解:∵∠A=40°,∠B=72°,∴∠ACB=68°,∵CE平分∠ACB,CD⊥AB于D,∴∠BCE=34°,∠BCD=90﹣72=18°,∵DF⊥CE,∴∠CDF=90°﹣(34°﹣18°)=74°.故答案为:74.【点评】主要考查了三角形的内角和外角之间的关系.(1)三角形的外角等于与它不相邻的两个内角和;(2)三角形的内角和是180度,求角的度数常常要用到“三角形的内角和是180°”这一隐含的条件;(3)三角形的一个外角>任何一个和它不相邻的内角.注意:垂直和直角总是联系在一起.25.(2006•临安市)用一条宽相等的足够长的纸条,打一个结,如图(1)所示,然后轻轻拉紧、压平就可以得到如图(2)所示的正五边形ABCDE,其中∠BAC=36度.【分析】利用多边形的内角和定理和等腰三角形的性质即可解决问题.【解答】解:∵∠ABC==108°,△ABC是等腰三角形,∴∠BAC=∠BCA=36度.【点评】本题主要考查了多边形的内角和定理和等腰三角形的性质.n边形的内角和为:180°(n﹣2).26.(2015•河北)平面上,将边长相等的正三角形、正方形、正五边形、正六边形的一边重合并叠在一起,如图,则∠3+∠1﹣∠2=24°.【分析】首先根据多边形内角和定理,分别求出正三角形、正方形、正五边形、正六边形的每个内角的度数是多少,然后分别求出∠3、∠1、∠2的度数是多少,进而求出∠3+∠1﹣∠2的度数即可.【解答】解:正三角形的每个内角是:180°÷3=60°,正方形的每个内角是:360°÷4=90°,正五边形的每个内角是:(5﹣2)×180°÷5=3×180°÷5=540°÷5=108°,正六边形的每个内角是:(6﹣2)×180°÷6=4×180°÷6=720°÷6=120°,则∠3+∠1﹣∠2=(90°﹣60°)+(120°﹣108°)﹣(108°﹣90°)=30°+12°﹣18°=24°.故答案为:24°.【点评】此题主要考查了多边形内角和定理,要熟练掌握,解答此题的关键是要明确:(1)n边形的内角和=(n﹣2)•180 (n≥3)且n为整数).(2)多边形的外角和指每个顶点处取一个外角,则n边形取n个外角,无论边数是几,其外角和永远为360°.三.解答题(共14小题)27.(2013春•临清市期末)如图,直线DE交△ABC的边AB、AC于D、E,交BC 延长线于F,若∠B=67°,∠ACB=74°,∠AED=48°,求∠BDF的度数.【分析】先根据三角形的内角和定理求出∠A的度数,再根据三角形外角的性质求出∠BDF的度数.【解答】解:因为∠A+∠B+∠ACB=180°,所以∠A=180°﹣67°﹣74°=39°,所以∠BDF=∠A+∠AED=39°+48°=87°.【点评】本题考查三角形外角的性质及三角形的内角和定理,解答的关键是外角和内角的关系.28.(2013•湖州校级模拟)如图,已知D为△ABC边BC延长线上一点,DF⊥AB 于F交AC于E,∠A=35°,∠D=42°,求∠ACD的度数.【分析】根据三角形外角与内角的关系及三角形内角和定理解答.【解答】解:∵∠AFE=90°,∴∠AEF=90°﹣∠A=90°﹣35°=55°,∴∠CED=∠AEF=55°,∴∠ACD=180°﹣∠CED﹣∠D=180°﹣55°﹣42°=83°.答:∠ACD的度数为83°.【点评】三角形外角与内角的关系:三角形的一个外角等于和它不相邻的两个内角的和.三角形内角和定理:三角形的三个内角和为180°.29.(2015秋•全椒县期中)已知△ABC中,∠ACB=90°,CD为AB边上的高,BE平分∠ABC,分别交CD、AC于点F、E,求证:∠CFE=∠CEF.【分析】题目中有两对直角,可得两对角互余,由角平分线及对顶角可得两对角相等,然后利用等量代换可得答案.【解答】证明:∵∠ACB=90°,∴∠1+∠3=90°,∵CD⊥AB,∴∠2+∠4=90°,又∵BE平分∠ABC,∴∠1=∠2,∴∠3=∠4,∵∠4=∠5,∴∠3=∠5,即∠CFE=∠CEF.【点评】本题考查了三角形角平分线、中线和高的有关知识;正确利用角的等量代换是解答本题的关键.30.(2010春•横峰县校级期末)如图,AD为△ABC的中线,BE为△ABD的中线,(1)若∠ABE=25°,∠BAD=50°,则∠BED的度数是度.(2)在△ADC中过点C作AD边上的高CH.(3)若△ABC的面积为60,BD=5,求点E到BC边的距离.【分析】(1)根据三角形的一个外角等于与它不相邻的两个内角和,∠BED=∠ABE+∠BAE=75°;(2)三角形高的基本作法:用圆规以一边两端点为圆心,任意长为半径作两段弧,交于角的两边,再以交点为圆心,用交轨法作两段弧,找到两段弧的交点,连接两个交点,并过另一端点作所成直线的平行线,叫该边所在直线一点,连接该点和另一端点,则为高线;(3)我们通过证明不难得出三角形中线将三角形分成面积相等的两个三角形,那么可依据D 是BC 中点,E 是AD 中点,求出三角形BED 的面积.三角形BDE 中,E 到BD 的距离就是BD 边上的高,有了三角形BDE 的面积,BD 的长也容易求得.那么高就求出来了.【解答】解:(1)∠BED=∠ABE +∠BAE=75°;(2)CH 为所求的高.(3)解:如图,过点E 作EF ⊥BD 于点F,∵AD 是BC 的中线∴BD=CD∴S △ABD =S △ACD ==×60=30同理S △BED =S △ABE ==×30=15又∵S △BED =BD•EF=×5EF=15∴EF=6即点E 到BC 边的距离为6.【点评】本题主要考查了基本作图中,三角形高的作法,三角形的内角和外角等知识点.31.(2015春•单县期末)如图,在△ABC 中,AD 平分∠BAC ,P 为线段AD 上的一个动点,PE ⊥AD 交直线BC 于点E .(1)若∠B=35°,∠ACB=85°,求∠E 的度数;(2)当P 点在线段AD 上运动时,猜想∠E 与∠B 、∠ACB 的数量关系,写出结论无需证明.【分析】(1)中,首先根据三角形的内角和定理求得∠BAC 的度数,再根据角平分线的定义求得∠DAC 的度数,从而根据三角形的内角和定理即可求出∠ADC 的度数,进一步求得∠E 的度数;(2)中,根据第(1)小题的思路即可推导这些角之间的关系.【解答】解:(1)∵∠B=35°,∠ACB=85°,∴∠BAC=60°,∵AD 平分∠BAC ,∴∠DAC=30°,∴∠ADC=65°,∴∠E=25°;(2).设∠B=n°,∠ACB=m°,∵AD 平分∠BAC ,∴∠1=∠2=∠BAC ,∵∠B +∠ACB +∠BAC=180°,∵∠B=n°,∠ACB=m°,∴∠CAB=(180﹣n ﹣m)°,∴∠BAD=(180﹣n ﹣m )°,∴∠3=∠B+∠1=n°+(180﹣n﹣m)°=90°+n°﹣m°,∵PE⊥AD,∴∠DPE=90°,∴∠E=90°﹣(90°+n°﹣m°)=(m﹣n)°=(∠ACB﹣∠B).【点评】运用了三角形的内角和定理以及角平分线的定义.特别注意第(2)小题,由于∠B和∠ACB的大小不确定,故表达式应写为两种情况.32.(2010春•朝阳区期末)如图所示,在△ABC中,∠B=∠C,FD⊥BC,DE⊥AB,垂足分别为D,E,∠AFD=158°,求∠EDF的度数.【分析】要求∠EDF的度数,只需求出∠BDE和∠FDC的度数即可,由FD⊥BC,得∠FDC=90°;而∠BDE在Rt△BDE中,故只需求出∠B的度数.因∠B=∠C,只需求出∠C的度数即可.因∠AFD是△CDF的外角,∠AFD=158°∴∠C=∠AFD﹣∠FDC=158°﹣90°=68°.【解答】解:∵FD⊥BC,所以∠FDC=90°,∵∠AFD=∠C+∠FDC,∴∠C=∠AFD﹣∠FDC=158°﹣90°=68°,∴∠B=∠C=68°.∵DE⊥AB,∵∠DEB=90°,∴∠BDE=90°﹣∠B=22°.又∵∠BDE+∠EDF+∠FDC=180°,∴∠EDF=180°﹣∠BDE﹣∠FDC=180°﹣22°﹣90°=68°.【点评】考查三角形内角和定理,外角性质,垂直定义等知识.33.(2014春•岱岳区期末)如图,AD平分∠BAC,∠EAD=∠EDA.(1)∠EAC与∠B相等吗?为什么?(2)若∠B=50°,∠CAD:∠E=1:3,求∠E的度数.【分析】(1)由于AD平分∠BAC,根据角平分线的概念可得∠BAD=∠CAD,再根据三角形的一个外角等于和它不相邻的两个内角和,结合已知条件可得∠EAC与∠B相等;(2)若设∠CAD=x°,则∠E=3x°.根据(1)中的结论以及三角形的内角和定理及其推论列方程进行求解即可.【解答】解:(1)相等.理由如下:∵AD平分∠BAC,∴∠BAD=∠CAD.又∠EAD=∠EDA,∴∠EAC=∠EAD﹣∠CAD=∠EDA﹣∠BAD=∠B;(2)设∠CAD=x°,则∠E=3x°,由(1)知:∠EAC=∠B=50°,∴∠EAD=∠EDA=(x+50)°在△EAD中,∵∠E+∠EAD+∠EDA=180°,∴3x+2(x+50)=180,解得:x=16.∴∠E=48°.。
八年级上册数学《全等三角形》知识归纳与题型突破含解析

第十二章 全等三角形知识归纳与题型突破(题型清单)一、全等图形形状、大小相同的图形放在一起能够完全重合.能够完全重合的两个图形叫做全等形.要点诠释:一个图形经过平移、翻折、旋转后,位置变化了,但形状、大小都没有改变,即平移、翻折、旋转前后的图形全等.两个全等形的周长相等,面积相等.二、全等三角形能够完全重合的两个三角形叫全等三角形.三、全等三角形的性质全等三角形的对应边相等;全等三角形的对应角相等.要点诠释:全等三角形对应边上的高相等,对应边上的中线相等,周长相等,面积相等.全等三角形的性质是今后研究其它全等图形的重要工具.四、全等三角形的判定01 思维导图02 知识速记五、全等三角形的证明思路SAS HLSSS AAS SAS ASAAAS ASA AAS→ → → →→ → → → → → 找夹角已知两边找直角找另一边边为角的对边找任一角找夹角的另一边已知一边一角边为角的邻边找夹边的另一角找边的对角找夹边已知两角找任一边六、全等三角形证明方法全等三角形是平面几何内容的基础,这是因为全等三角形是研究特殊三角形、四边形、相似图形、圆等图形性质的有力工具,是解决与线段、角相关问题的一个出发点.运用全等三角形,可以证明线段相等、线段的和差倍分关系、角相等、两直线位置关系等常见的几何问题.可以适当总结证明方法.1.证明线段相等的方法:(1) 证明两条线段所在的两个三角形全等.(2) 利用角平分线的性质证明角平分线上的点到角两边的距离相等.(3) 等式性质.2.证明角相等的方法:(1) 利用平行线的性质进行证明.(2) 证明两个角所在的两个三角形全等.(3) 利用角平分线的判定进行证明.(4) 同角(等角)的余角(补角)相等.(5) 对顶角相等.3.证明两条线段的位置关系(平行、垂直)的方法;可通过证明两个三角形全等,得到对应角相等,再利用平行线的判定或垂直定义证明.4.辅助线的添加:(1)作公共边可构造全等三角形;(2)倍长中线法;(3)作以角平分线为对称轴的翻折变换全等三角形;(4)利用截长(或补短)法作旋转变换的全等三角形.5. 证明三角形全等的思维方法:(1)直接利用全等三角形判定和证明两条线段或两个角相等,需要我们敏捷、快速地发现两条线段和两个角所在的两个三角形及它们全等的条件.(2)如果要证明相等的两条线段或两个角所在的三角形全等的条件不充分时,则应根据图形的其它性质或先证明其他的两个三角形全等以补足条件.(3)如果现有图形中的任何两个三角形之间不存在全等关系,此时应添置辅助线,使之出现全等三角形,通过构造出全等三角形来研究平面图形的性质.七、 角平分线概念:从一个角的顶点引出一条射线,把这个角分成完全相同的角,这条射线叫做这个角的角平分线。
八年级数学上册第十二章全等三角形知识点汇总(带答案)

八年级数学上册第十二章全等三角形知识点汇总单选题1、如图,已知点A、D、C、F在同一条直线上,∠B=∠E =90°,AB=DE,若添加一个条件后,能用“HL”的方法判定Rt△ABC≌Rt△DEF,添加的条件可以是()A.BC=EF B.∠BCA=∠F C.AB∥DE D.AD=CF答案:D分析:根据题目给的条件可知道直角边和直角,因为需用“HL”的方法判定Rt△ABC≌Rt△DEF,故只能添上斜边这一条件,即可解答.解:∵∠B=∠E=90°,AB=DE,∴添加条件AC=DF,根据“HL”即可判定Rt△ABC≌Rt△DEF;或添加条件AD=CF,也可得出AC=DF,根据“HL”即可判定Rt△ABC≌Rt△DEF,故D正确.故选:D.小提示:本题主要考查了利用“HL”判定三角形全等,掌握三角形全等的判定是解题的关键.2、如图,锐角△ABC的两条高BD、CE相交于点O,且CE=BD,若∠CBD=20°,则∠A的度数为()A.20°B.40°C.60°D.70°答案:B分析:由BD、CE是高,可得∠BDC=∠CEB=90°,可求∠BCD=70°,可证Rt△BEC≌Rt△CDB(HL),得出∠BCD =∠CBE=70°即可.解:∵BD、CE是高,∠CBD=20°,∴∠BDC=∠CEB=90°,∴∠BCD=180°﹣90°﹣20°=70°,在Rt△BEC和Rt△CDB中,{CE=BDBC=CB,∴Rt△BEC≌Rt△CDB(HL),∴∠BCD=∠CBE=70°,∴∠A=180°﹣70°﹣70°=40°.故选:B.小提示:本题考查三角形高的定义,三角形全等判定与性质,三角形内角和公式,掌握三角形高的定义,三角形全等判定与性质,三角形内角和公式是解题关键.3、如图,为测量桃李湖两端AB的距离,南开中学某地理课外实践小组在桃李湖旁的开阔地上选了一点C,测得∠ACB的度数,在AC的另一侧测得∠ACD=∠ACB,CD=CB,再测得AD的长,就是AB的长.那么判定△ABC≌△ADC的理由是()A.SASB.SSSC.ASAD.AAS答案:A分析:已知条件是∠ACD=∠ACB,CD=CB,AC=AC,据此作出选择.解:在△ADC与△ABC中,{CD=CB∠ACD=∠ACBAC=AC.∴△ADC≌△ABC(SAS).故选:A.小提示:此题考查了全等三角形的应用,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS,做题时注意选择.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.4、为了测量工件的内径,设计了如图所示的工具,点O为卡钳两柄的交点,且有OA=OB=OC=OD,只要量得CD之间的距离,就可知工件的内径AB.其数学原理是利用△AOB≌△COD,判断的依据是()A.SSSB.SASC.ASAD.AAS答案:B分析:利用“边角边”证明△ABO和△CDO全等,根据全等三角形对应边相等解答.解:在△ABO和△CDO中{OA=OC ∠AOB=COD OB=OD∴△ABO≌△CDO(SAS)故选B小提示:本题考查了全等三角形的应用,熟练掌握三角形全等的判定方法是解题的关键.5、观察下列作图痕迹,所作线段CD为△ABC的角平分线的是()A.B.C .D .答案:C 分析:根据角平分线画法逐一进行判断即可.A :所作线段为AB 边上的高,选项错误;B :做图痕迹为AB 边上的中垂线,CD 为AB 边上的中线,选项错误;C :CD 为∠ACB 的角平分线,满足题意。
整理八年级数学上册第十二章全等三角形带答案总结(重点)超详细

(名师选题)整理八年级数学上册第十二章全等三角形带答案总结(重点)超详细单选题1、如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC的面积是30cm2,AB=13cm,AC=7cm,则DE的长()A.3cmB.4cmC.5cmD.6cm2、如图,在△ABC中,点D是BC边上一点,已知∠DAC=α,∠DAB=90°−α2,CE平分∠ACB交AB于点E,连接DE,则∠DEC的度数为()A.α2B.α3C.30°−α2D.45°−α3、如图,已知AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连接BF,CE.下列说法正确的是()①BD=CD;②∠BAD=∠CAD;③△BDF≌△CDE;④BF∥CE;⑤CE=AEA.①②B.③⑤C.①③④D.①④⑤4、如图,已知△ABC≌△DBE,AB=5,BE=12,则CD的长为()A.5B.6C.7D.85、观察下列作图痕迹,所作线段CD为△ABC的角平分线的是()A.B.C.D.6、如图,在平面直角坐标系中,已知点A(0,4),B(2,0),在平面内有一点C(不与点B重合),使得△AOC与△AOB全等,这样的点C有()A.1个B.2个C.3个D.4个7、如图,四边形ABCD中,AC、BD为对角线,且AC=AB,∠ACD=∠ABD,AE⊥BD于点E,若BD=6,CD=4.则DE的长度为()A.2B.1C.1.4D.1.68、一个三角形的两边长分别为5和9,设第三边上的中线长为x,则x的取值范围是()A.x>5B.x<7C.4<x<14D.2<x<79、如图,△ABC≌△DEF,若∠A=80°,∠F=30°,则∠B的度数是()A.80°B.70°C.65°D.60°10、如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边三角形ABC和等边三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ.以下结论错误的是()A.∠AOB=60°B.AP=BQC.PQ∥AE D.DE=DP解答题11、(1)模型:如图1,在△ABC中,AD平分∠BAC,DE⊥AB,DF⊥AC,求证:S△ADB:S△ADC=AB:AC.(2)模型应用:如图2,AD平分∠EAC交BC的延长线于点D,求证:AB:AC=BD:CD.(3)类比应用:如图3,AB平分∠DAE,AE=AD,∠D+∠E=180°,求证:BE:CD=AB:AC.12、如图,AC平分∠BAD,CB⊥AB,CD⊥AD,垂足分别为B,D.(1)求证:△ABC≌△ADC;(2)若AB=4,CD=3,求四边形ABCD的面积.13、如图,△ACB中,AC=BC,∠ACB=90°,D为边BC上一点(不与点C重合),CD<BD,点E在AD的延长线上,且ED=AD,连接BE,过点B作BE的垂线,交边AC于点F.(1)依题意补全图形;(2)求证:BE=BF;(3)用等式表示线段AF与CD的数量关系,并证明.整理八年级数学上册第十二章全等三角形带答案(二十一)参考答案1、答案:A分析:根据角平分线的性质求出DE =DF ,根据三角形的面积公式列式计算即可. 解:∵AD 是∠BAC 的平分线,DE ⊥AB 于点E ,DF ⊥AC 于点F , ∴DE =DF ,∴12×AB ×DE +12AC ×DF =S △ABC =30, 即12×13DE +12×7DE =30,解得DE =3.故选:A .小提示:本题主要考查了角平分线的性质以及三角形的面积,灵活运用角平分线的性质成为解答本题的关键. 2、答案:A分析:过点E 作EM ⊥AC 于M ,EN ⊥AD 于N ,EH ⊥BC 于H ,先计算出∠EAM ,则AE 平分∠MAD ,根据角平分线的性质得EM =EN ,再由CE 平分∠ACB 得到EM =EH ,则EN =EH ,于是根据角平分线定理的逆定理可判断DE 平分∠ADB ,再根据三角形外角性质解答即可.解:过点E 作EM ⊥AC 于M ,EN ⊥AD 于N ,EH ⊥BC 于H ,如图:∵∠DAC =α,∠DAB =90°−α2, ∴∠EAM =90°−α2, ∴AE 平分∠MAD , ∴EM =EN , ∵CE 平分∠ACB ,∴EM =EH ,∠2=12∠ACB∴EN=EH∴DE平分∠ADB,∴∠1=12∠ADB,∵由三角形外角可得:∠1=∠DEC+∠2,∵∠2=12∠ACB,∴∠1=∠DEC+12∠ACB,而∠ADB=∠DAC+∠ACB,∴∠DEC=12∠DAC=12α,故选:A.小提示:本题考查了角平分线的性质和判定定理,三角形的外角性质定理,解决本题的关键是运用角平分线定理的逆定理证明DE平分∠ADB.3、答案:C分析:①根据三角形的中线直接进行判断即可;②一般三角形一条边上的中线不一定是这条边所对的角的平分线;③根据“SAS”直接进行判断即可;④根据三角形全等的性质直接判定∠F=∠DEC,根据平行线的判定方法得出结果;⑤根据全等三角形的性质可以判定CE=BF,不能判定CE=AE.解:①∵AD是△ABC的中线,∴BD=CD,故①正确;②∵AD为△ABC的中线,∴BD=CD,∠BAD和∠CAD不一定相等,故②错误;③在△BDF和△CDE中{BD=CD∠BDF=∠CDEDF=DE,∴△BDF≌△CDE(SAS),故③正确;④∵△BDF≌△CDE,∴∠F=∠DEC,∴BF∥CE,故④正确;⑤∵△BDF≌△CDE,∴CE=BF,故⑤错误;综上分析可知,①③④正确,故C正确.故选:C.小提示:本题考查了全等三角形的判定与性质,三角形中线的定义,熟练掌握三角形全等的判定方法并准确识图,是解题的关键.4、答案:C分析:根据全等三角形的性质,可得BC=BE=12,AB=BD=5,即可求解.解:∵△ABC≌△DBE,AB=5,BE=12,∴BC=BE=12,AB=BD=5,∴CD=BC−BD=12−5=7,故选:C.小提示:本题主要考查了全等三角形的性质,熟练掌握全等三角形的对应角相等,对应边相等是解题的关键.5、答案:C分析:根据角平分线画法逐一进行判断即可.A:所作线段为AB边上的高,选项错误;B:做图痕迹为AB边上的中垂线,CD为AB边上的中线,选项错误;C:CD为∠ACB的角平分线,满足题意。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初二全等三角形所有知识点总结和常考题知识点:1.基本定义:⑴全等形:能够完全重合的两个图形叫做全等形.⑵全等三角形:能够完全重合的两个三角形叫做全等三角形.⑶对应顶点:全等三角形中互相重合的顶点叫做对应顶点.⑷对应边:全等三角形中互相重合的边叫做对应边.⑸对应角:全等三角形中互相重合的角叫做对应角.2.基本性质:⑴三角形的稳定性:三角形三边的长度确定了,这个三角形的形状、大小就全确定,这个性质叫做三角形的稳定性.⑵全等三角形的性质:全等三角形的对应边相等,对应角相等.3.全等三角形的判定定理:⑴边边边(SSS):三边对应相等的两个三角形全等.⑵边角边(SAS):两边和它们的夹角对应相等的两个三角形全等.⑶角边角(ASA):两角和它们的夹边对应相等的两个三角形全等.⑷角角边(AAS):两角和其中一个角的对边对应相等的两个三角形全等.⑸斜边、直角边(HL):斜边和一条直角边对应相等的两个直角三角形全等.4.角平分线:⑴画法:⑵性质定理:角平分线上的点到角的两边的距离相等.⑶性质定理的逆定理:角的部到角的两边距离相等的点在角的平分线上.5.证明的基本方法:⑴明确命题中的已知和求证.(包括隐含条件,如公共边、公共角、对顶角、角平分线、中线、高、等腰三角形等所隐含的边角关系)⑵根据题意,画出图形,并用数字符号表示已知和求证.⑶经过分析,找出由已知推出求证的途径,写出证明过程.常考题:一.选择题(共14小题)1.使两个直角三角形全等的条件是()A.一个锐角对应相等B.两个锐角对应相等C.一条边对应相等D.两条边对应相等2.如图,已知AE=CF,∠AFD=∠CEB,那么添加下列一个条件后,仍无法判定△ADF≌△CBE的是()A.∠A=∠C B.AD=CB C.BE=DF D.AD∥BC3.如图所示,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是()A.SSS B.SAS C.AAS D.ASA4.到三角形三条边的距离都相等的点是这个三角形的()A.三条中线的交点B.三条高的交点C.三条边的垂直平分线的交点 D.三条角平分线的交点5.如图,△ACB≌△A′CB′,∠BCB′=30°,则∠ACA′的度数为()A.20°B.30°C.35°D.40°6.如图,直线l1、l2、l3表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则供选择的地址有()A.1处B.2处C.3处D.4处7.如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=7,DE=2,AB=4,则AC长是()A.3 B.4 C.6 D.58.如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是()A.BC=EC,∠B=∠E B.BC=EC,AC=DC C.BC=DC,∠A=∠D D.∠B=∠E,∠A=∠D9.如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于()A.10 B.7 C.5 D.410.要测量河两岸相对的两点A,B的距离,先在AB的垂线BF上取两点C,D,使CD=BC,再定出BF的垂线DE,使A,C,E在一条直线上(如图所示),可以说明△EDC≌△ABC,得ED=AB,因此测得ED的长就是AB的长,判定△EDC≌△ABC 最恰当的理由是()A.边角边B.角边角C.边边边D.边边角11.如图,△ABC的三边AB,BC,CA长分别是20,30,40,其三条角平分线将△ABC分为三个三角形,则S△ABO :S△BCO:S△CAO等于()A.1:1:1 B.1:2:3 C.2:3:4 D.3:4:512.尺规作图作∠AOB的平分线方法如下:以O为圆心,任意长为半径画弧交OA,OB于C,D,再分别以点C,D为圆心,以大于CD长为半径画弧,两弧交于点P,作射线OP由作法得△OCP≌△ODP的根据是()A.SAS B.ASA C.AAS D.SSS13.下列判断正确的是()A.有两边和其中一边的对角对应相等的两个三角形全等B.有两边对应相等,且有一角为30°的两个等腰三角形全等C.有一角和一边对应相等的两个直角三角形全等D.有两角和一边对应相等的两个三角形全等14.如图,已知∠1=∠2,AC=AD,增加下列条件:①AB=AE;②BC=ED;③∠C=∠D;④∠B=∠E.其中能使△ABC≌△AED的条件有()A.4个B.3个C.2个D.1个二.填空题(共11小题)15.如图,在△ABC中,∠C=90°,AD平分∠CAB,BC=8cm,BD=5cm,那么点D 到线段AB的距离是cm.16.如图,△ABC中,∠C=90°,AD平分∠BAC,AB=5,CD=2,则△ABD的面积是.17.如图为6个边长等的正方形的组合图形,则∠1+∠2+∠3= °.18.如图,△ABC≌△DEF,请根据图中提供的信息,写出x= .19.如图所示,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是带去玻璃店.20.如图,已知AB∥CF,E为DF的中点,若AB=9cm,CF=5cm,则BD= cm.21.在数学活动课上,小明提出这样一个问题:∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CED=35°,如图,则∠EAB是多少度?大家一起热烈地讨论交流,小英第一个得出正确答案,是度.22.如图,△ABC≌△ADE,∠B=100°,∠BAC=30°,那么∠AED= 度.23.如图所示,将两根钢条AA′,BB′的中点O连在一起,使A A′,BB′可以绕着点O自由转动,就做成了一个测量工具,则A′B′的长等于槽宽AB,那么判定△OAB≌△OA′B′的理由是.24.如图,在四边形ABCD中,∠A=90°,AD=4,连接BD,BD⊥CD,∠ADB=∠C.若P是BC边上一动点,则DP长的最小值为.25.如图,△ABC中,∠C=90°,CA=CB,点M在线段AB上,∠GMB=∠A,BG ⊥MG,垂足为G,MG与BC相交于点H.若MH=8cm,则BG= cm.三.解答题(共15小题)26.已知:如图,C为BE上一点,点A,D分别在BE两侧,AB∥ED,AB=CE,BC=ED.求证:AC=CD.27.已知:如图,OP是∠AOC和∠BOD的平分线,OA=OC,OB=OD.求证:AB=CD.28.已知,如图所示,AB=AC,BD=CD,DE⊥AB于点E,DF⊥AC于点F,求证:DE=DF.29.如图,C是AB的中点,AD=BE,CD=CE.求证:∠A=∠B.30.已知:如图,在梯形ABCD中,AD∥BC,BC=DC,CF平分∠BCD,DF∥AB,BF 的延长线交DC于点E.求证:(1)△BFC≌△DFC;(2)AD=DE.31.如图,已知,EC=AC,∠BCE=∠DCA,∠A=∠E;求证:BC=DC.32.如图,把一个直角三角形ACB(∠ACB=90°)绕着顶点B顺时针旋转60°,使得点C旋转到AB边上的一点D,点A旋转到点E的位置.F,G分别是BD,BE 上的点,BF=BG,延长CF与DG交于点H.(1)求证:CF=DG;(2)求出∠FHG的度数.33.已知,如图,△ABC和△ECD都是等腰直角三角形,∠ACB=∠DCE=90°,D 为AB边上一点.求证:BD=AE.34.如图,点M、N分别是正五边形ABCDE的边BC、CD上的点,且BM=CN,AM 交BN于点P.(1)求证:△ABM≌△BCN;(2)求∠APN的度数.35.如图,四边形ABCD中,E点在AD上,其中∠BAE=∠BCE=∠ACD=90°,且BC=CE,求证:△ABC与△DEC全等.36.如图,△ABC和△ADE都是等腰三角形,且∠BAC=90°,∠DAE=90°,B,C,D在同一条直线上.求证:BD=CE.37.我们把两组邻边相等的四边形叫做“筝形”.如图,四边形ABCD是一个筝形,其中AB=CB,AD=CD.对角线AC,BD相交于点O,OE⊥AB,OF⊥CB,垂足分别是E,F.求证OE=OF.38.如图,在△ABC中,∠ACB=90°,CE⊥AB于点E,AD=AC,AF平分∠CAB交CE于点F,DF的延长线交AC于点G.求证:(1)DF∥BC;(2)FG=FE.39.如图:在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AD、AG.(1)求证:AD=AG;(2)AD与AG的位置关系如何,请说明理由.40.如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.(1)如果点P在线段BC上以3cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.①若点Q的运动速度与点P的运动速度相等,经过1s后,△BPD与△CQP是否全等,请说明理由;②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,求经过多长时间点P与点Q第一次在△ABC 的哪条边上相遇?初二全等三角形所有知识点总结和常考题提高难题压轴题练习(含答案解析)参考答案与试题解析一.选择题(共14小题)1.(2013•)使两个直角三角形全等的条件是()A.一个锐角对应相等B.两个锐角对应相等C.一条边对应相等D.两条边对应相等【分析】利用全等三角形的判定来确定.做题时,要结合已知条件与三角形全等的判定方法逐个验证.【解答】解:A、一个锐角对应相等,利用已知的直角相等,可得出另一组锐角相等,但不能证明两三角形全等,故A选项错误;B、两个锐角相等,那么也就是三个对应角相等,但不能证明两三角形全等,故B选项错误;C、一条边对应相等,再加一组直角相等,不能得出两三角形全等,故C选项错误;D、两条边对应相等,若是两条直角边相等,可利用SAS证全等;若一直角边对应相等,一斜边对应相等,也可证全等,故D选项正确.故选:D.【点评】本题考查了直角三角形全等的判定方法;三角形全等的判定有ASA、SAS、AAS、SSS、HL,可以发现至少得有一组对应边相等,才有可能全等.2.(2013•)如图,已知AE=CF,∠AFD=∠CEB,那么添加下列一个条件后,仍无法判定△ADF≌△CBE的是()A.∠A=∠C B.AD=CB C.BE=DF D.AD∥BC【分析】求出AF=CE,再根据全等三角形的判定定理判断即可.【解答】解:∵AE=CF,∴AE+EF=CF+EF,∴AF=CE,A、∵在△ADF和△CBE中∴△ADF≌△CBE(ASA),正确,故本选项错误;B、根据AD=CB,AF=CE,∠AFD=∠CEB不能推出△ADF≌△CBE,错误,故本选项C、∵在△ADF和△CBE中∴△ADF≌△CBE(SAS),正确,故本选项错误;D、∵AD∥BC,∴∠A=∠C,∵在△ADF和△CBE中∴△ADF≌△CBE(ASA),正确,故本选项错误;故选B.【点评】本题考查了平行线性质,全等三角形的判定的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS.3.(2014秋•江津区期末)如图所示,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是()A.SSS B.SAS C.AAS D.ASA【分析】根据图象,三角形有两角和它们的夹边是完整的,所以可以根据“角边角”画出.【解答】解:根据题意,三角形的两角和它们的夹边是完整的,所以可以利用“角边角”定理作出完全一样的三角形.故选D.【点评】本题考查了三角形全等的判定的实际运用,熟练掌握判定定理并灵活运用是解题的关键.4.(2007•)到三角形三条边的距离都相等的点是这个三角形的()A.三条中线的交点B.三条高的交点C.三条边的垂直平分线的交点 D.三条角平分线的交点【分析】因为角的平分线上的点到角的两边的距离相等,所以到三角形的三边的距离相等的点是三条角平分线的交点.【解答】解:∵角的平分线上的点到角的两边的距离相等,∴到三角形的三边的距离相等的点是三条角平分线的交点.故选:D.【点评】该题考查的是角平分线的性质,因为角的平分线上的点到角的两边的距离相等,所以到三角形的三边的距离相等的点是三条角平分线的交点,易错选项5.(2011•呼伦贝尔)如图,△ACB≌△A′CB′,∠BCB′=30°,则∠ACA′的度数为()A.20°B.30°C.35°D.40°【分析】本题根据全等三角形的性质并找清全等三角形的对应角即可.【解答】解:∵△ACB≌△A′CB′,∴∠ACB=∠A′CB′,即∠ACA′+∠A′CB=∠B′CB+∠A′CB,∴∠ACA′=∠B′CB,又∠B′CB=30°∴∠ACA′=30°.故选:B.【点评】本题考查了全等三角形的判定及全等三角形性质的应用,利用全等三角形的性质求解.6.(2000•)如图,直线l1、l2、l3表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则供选择的地址有()A.1处B.2处C.3处D.4处【分析】到三条相互交叉的公路距离相等的地点应是三条角平分线的交点.把三条公路的中心部位看作三角形,那么这个三角形两个角平分线的交点以及三个外角两两平分线的交点都满足要求.【解答】解:满足条件的有:(1)三角形两个角平分线的交点,共一处;(2)三个外角两两平分线的交点,共三处.故选:D.【点评】本题考查了角平分线的性质;这是一道生活联系实际的问题,解答此类题目时最直接的判断就是三角形的角平分线,很容易漏掉外角平分线,解答时一定要注意,不要漏解.7.(2014•)如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=7,DE=2,AB=4,则AC长是()A.3 B.4 C.6 D.5【分析】过点D作DF⊥AC于F,根据角平分线上的点到角的两边距离相等可得DE=DF,再根据S△ABC =S△ABD+S△ACD列出方程求解即可.【解答】解:如图,过点D作DF⊥AC于F,∵AD是△ABC中∠BAC的角平分线,DE⊥AB,∴DE=DF,由图可知,S△ABC =S△ABD+S△ACD,∴×4×2+×AC×2=7,解得AC=3.故选:A.【点评】本题考查了角平分线上的点到角的两边距离相等的性质,熟记性质是解题的关键.8.(2013•)如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是()A.BC=EC,∠B=∠E B.BC=EC,AC=DC C.BC=DC,∠A=∠D D.∠B=∠E,∠A=∠D【分析】根据全等三角形的判定方法分别进行判定即可.【解答】解:A、已知AB=DE,再加上条件BC=EC,∠B=∠E可利用SAS证明△ABC ≌△DEC,故此选项不合题意;B、已知AB=DE,再加上条件BC=EC,AC=DC可利用SSS证明△ABC≌△DEC,故此选项不合题意;C、已知AB=DE,再加上条件BC=DC,∠A=∠D不能证明△ABC≌△DEC,故此选项符合题意;D、已知AB=DE,再加上条件∠B=∠E,∠A=∠D可利用ASA证明△ABC≌△DEC,故此选项不合题意;故选:C.【点评】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.9.(2015•)如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于()A.10 B.7 C.5 D.4【分析】作EF⊥BC于F,根据角平分线的性质求得EF=DE=2,然后根据三角形面积公式求得即可.【解答】解:作EF⊥BC于F,∵BE平分∠ABC,ED⊥AB,EF⊥BC,∴EF=DE=2,=BC•EF=×5×2=5,∴S△BCE故选C.【点评】本题考查了角的平分线的性质以及三角形的面积,作出辅助线求得三角形的高是解题的关键.10.(1998•)要测量河两岸相对的两点A,B的距离,先在AB的垂线BF上取两点C,D,使CD=BC,再定出BF的垂线DE,使A,C,E在一条直线上(如图所示),可以说明△EDC≌△ABC,得ED=AB,因此测得ED的长就是AB的长,判定△EDC≌△ABC最恰当的理由是()A.边角边B.角边角C.边边边D.边边角【分析】由已知可以得到∠ABC=∠BDE,又CD=BC,∠ACB=∠DCE,由此根据角边角即可判定△EDC≌△ABC.【解答】解:∵BF⊥AB,DE⊥BD∴∠ABC=∠BDE又∵CD=BC,∠ACB=∠DCE∴△EDC≌△ABC(ASA)故选B.【点评】本题考查了全等三角形的判定方法;需注意根据垂直定义得到的条件,以及隐含的对顶角相等,观察图形,找着隐含条件是十分重要的.11.(2017•模拟)如图,△ABC的三边AB,BC,CA长分别是20,30,40,其三条角平分线将△ABC分为三个三角形,则S△ABO :S△BCO:S△CAO等于()A.1:1:1 B.1:2:3 C.2:3:4 D.3:4:5【分析】利用角平分线上的一点到角两边的距离相等的性质,可知三个三角形高相等,底分别是20,30,40,所以面积之比就是2:3:4.【解答】解:利用同高不同底的三角形的面积之比就是底之比可知选C.故选C.【点评】本题主要考查了角平分线上的一点到两边的距离相等的性质及三角形的面积公式.做题时应用了三个三角形的高时相等的,这点式非常重要的.12.(2009•鸡西)尺规作图作∠AOB的平分线方法如下:以O为圆心,任意长为半径画弧交OA,OB于C,D,再分别以点C,D为圆心,以大于CD长为半径画弧,两弧交于点P,作射线OP由作法得△OCP≌△ODP的根据是()A.SAS B.ASA C.AAS D.SSS【分析】认真阅读作法,从角平分线的作法得出△OCP与△ODP的两边分别相等,加上公共边相等,于是两个三角形符合SSS判定方法要求的条件,答案可得.【解答】解:以O为圆心,任意长为半径画弧交OA,OB于C,D,即OC=OD;以点C,D为圆心,以大于CD长为半径画弧,两弧交于点P,即CP=DP;∴在△OCP和△ODP中,∴△OCP≌△ODP(SSS).故选:D.【点评】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.13.(2002•)下列判断正确的是()A.有两边和其中一边的对角对应相等的两个三角形全等B.有两边对应相等,且有一角为30°的两个等腰三角形全等C.有一角和一边对应相等的两个直角三角形全等D.有两角和一边对应相等的两个三角形全等【分析】判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL,对比选项进行分析.【解答】解:A、只有两个三角形同为锐角三角形或者钝角三角形或者直角三角形时,才能成立;B、30°角没有对应关系,不能成立;C、如果这个角是直角,此时就不成立了;D、符合全等三角形的判断方法:AAS或者ASA.故选D.【点评】本题要求对全等三角形的几种判断方法熟练运用,会对特殊三角形全等进行分析判断.14.(2006•)如图,已知∠1=∠2,AC=AD,增加下列条件:①AB=AE;②BC=ED;③∠C=∠D;④∠B=∠E.其中能使△ABC≌△AED的条件有()A.4个B.3个C.2个D.1个【分析】∠1=∠2,∠BAC=∠EAD,AC=AD,根据三角形全等的判定方法,可加一角或已知角的另一边.【解答】解:已知∠1=∠2,AC=AD,由∠1=∠2可知∠BAC=∠EAD,加①AB=AE,就可以用SAS判定△ABC≌△AED;加③∠C=∠D,就可以用ASA判定△ABC≌△AED;加④∠B=∠E,就可以用AAS判定△ABC≌△AED;加②BC=ED只是具备SSA,不能判定三角形全等.其中能使△ABC≌△AED的条件有:①③④故选:B.【点评】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、SSA、HL.做题时要根据已知条件在图形上的位置,结合判定方法,进行添加.二.填空题(共11小题)15.(2006•)如图,在△ABC中,∠C=90°,AD平分∠CAB,BC=8cm,BD=5cm,那么点D到线段AB的距离是 3 cm.【分析】求D点到线段AB的距离,由于D在∠BAC的平分线上,只要求出D到AC的距离CD即可,由已知可用BC减去BD可得答案.【解答】解:CD=BC﹣BD,=8cm﹣5cm=3cm,∵∠C=90°,∴D到AC的距离为CD=3cm,∵AD平分∠CAB,∴D点到线段AB的距离为3cm.故答案为:3.【点评】本题考查了角平分线的性质;知道并利用CD是D点到线段AB的距离是正确解答本题的关键.16.(2013•邵东县模拟)如图,△ABC中,∠C=90°,AD平分∠BAC,AB=5,CD=2,则△ABD的面积是 5 .【分析】要求△ABD的面积,有AB=5,可为三角形的底,只求出底边上的高即可,利用角的平分线上的点到角的两边的距离相等可知△ABD的高就是CD的长度,所以高是2,则可求得面积.【解答】解:∵∠C=90°,AD平分∠BAC,∴点D到AB的距离=CD=2,∴△ABD的面积是5×2÷2=5.故答案为:5.【点评】本题主要考查了角平分线上的一点到两边的距离相等的性质.注意分析思路,培养自己的分析能力.17.(2016秋•宁城县期末)如图为6个边长等的正方形的组合图形,则∠1+∠2+∠3= 135 °.【分析】观察图形可知∠1与∠3互余,∠2是直角的一半,利用这些关系可解此题.【解答】解:观察图形可知:△ABC≌△BDE,∴∠1=∠DBE,又∵∠DBE+∠3=90°,∴∠1+∠3=90°.∵∠2=45°,∴∠1+∠2+∠3=∠1+∠3+∠2=90°+45°=135°.故填135.【点评】此题综合考查角平分线,余角,要注意∠1与∠3互余,∠2是直角的一半,特别是观察图形的能力.18.(2013•)如图,△ABC≌△DEF,请根据图中提供的信息,写出x= 20 .【分析】先利用三角形的角和定理求出∠A=70°,然后根据全等三角形对应边相等解答.【解答】解:如图,∠A=180°﹣50°﹣60°=70°,∵△ABC≌△DEF,∴EF=BC=20,即x=20.故答案为:20.【点评】本题考查了全等三角形的性质,根据角度确定出全等三角形的对应边是解题的关键.19.(2009•浦区二模)如图所示,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是带③去玻璃店.【分析】本题就是已知三角形破损部分的边角,得到原来三角形的边角,根据三角形全等的判定方法,即可求解.【解答】解:第一块和第二块只保留了原三角形的一个角和部分边,根据这两块中的任一块均不能配一块与原来完全一样的;第三块不仅保留了原来三角形的两个角还保留了一边,则可以根据ASA来配一块一样的玻璃.应带③去.故答案为:③.【点评】这是一道考查全等三角形的判定方法的开放性的题,要求学生将所学的知识运用于实际生活中,要认真观察图形,根据已知选择方法.20.(2015秋•西区期末)如图,已知AB∥CF,E为DF的中点,若AB=9cm,CF=5cm,则BD= 4 cm.【分析】先根据平行线的性质求出∠ADE=∠EFC,再由ASA可求出△ADE≌△CFE,根据全等三角形的性质即可求出AD的长,再由AB=9cm即可求出BD的长.【解答】解:∵AB∥CF,∴∠ADE=∠EFC,∵∠AED=∠FEC,E为DF的中点,∴△ADE≌△CFE,∴AD=CF=5cm,∵AB=9cm,∴BD=9﹣5=4cm.故填4.【点评】本题考查的是平行线的性质、全等三角形的判定定理及性质,比较简单.21.(2009秋•期末)在数学活动课上,小明提出这样一个问题:∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CED=35°,如图,则∠EAB是多少度?大家一起热烈地讨论交流,小英第一个得出正确答案,是35 度.【分析】过点E作EF⊥AD,证明△ABE≌△AFE,再求得∠CDE=90°﹣35°=55°,即可求得∠EAB的度数.【解答】解:过点E作EF⊥AD,∵DE平分∠ADC,且E是BC的中点,∴CE=EB=EF,又∠B=90°,且AE=AE,∴△ABE≌△AFE,∴∠EAB=∠EAF.又∵∠CED=35°,∠C=90°,∴∠CDE=90°﹣35°=55°,即∠CDA=110°,∠DAB=70°,∴∠EAB=35°.【点评】三角形全等的判定是中考的热点,一般以考查三角形全等的方法为主,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.22.(2012秋•期末)如图,△ABC≌△ADE,∠B=100°,∠BAC=30°,那么∠AED= 50 度.【分析】先运用三角形角和定理求出∠C,再运用全等三角形的对应角相等来求∠AED.【解答】解:∵在△ABC中,∠C=180﹣∠B﹣∠BAC=50°,又∵△ABC≌△ADE,∴∠AED=∠C=50°,∴∠AED=50度.故填50【点评】本题考查的是全等三角形的性质,全等三角形的对应边相等,对应角相等.是需要识记的容.23.(2015秋•蒙城县期末)如图所示,将两根钢条AA′,BB′的中点O连在一起,使A A′,BB′可以绕着点O自由转动,就做成了一个测量工具,则A′B′的长等于槽宽AB,那么判定△OAB≌△OA′B′的理由是SAS .【分析】已知二边和夹角相等,利用SAS可证两个三角形全等.【解答】解:∵OA=OA′,OB=OB′,∠AOB=∠A′OB′,∴△OAB≌△OA′B′(SAS)所以理由是SAS.【点评】本题考查了三角形全等的应用;根据题目给出的条件,要观察图中有哪些相等的边和角,然后判断所选方法,题目不难.24.(2011•)如图,在四边形ABCD中,∠A=90°,AD=4,连接BD,BD⊥CD,∠ADB=∠C.若P是BC边上一动点,则DP长的最小值为 4 .【分析】根据垂线段最短,当DP垂直于BC的时候,DP的长度最小,则结合已知条件,利用三角形的角和定理推出∠ABD=∠CBD,由角平分线性质即可得AD=DP,由AD的长可得DP的长.【解答】解:根据垂线段最短,当DP⊥BC的时候,DP的长度最小,∵BD⊥CD,即∠BDC=90°,又∠A=90°,∴∠A=∠BDC,又∠ADB=∠C,∴∠ABD=∠CBD,又DA⊥BA,BD⊥DC,∴AD=DP,又AD=4,∴DP=4.故答案为:4.【点评】本题主要考查了直线外一点到直线的距离垂线段最短、角平分线的性质,解题的关键在于确定好DP垂直于BC.25.(2015•鄂尔多斯)如图,△ABC中,∠C=90°,CA=CB,点M在线段AB上,∠GMB=∠A,BG⊥MG,垂足为G,MG与BC相交于点H.若MH=8cm,则BG= 4 cm.【分析】如图,作MD⊥BC于D,延长DE交BG的延长线于E,构建等腰△BDM、全等三角形△BED和△MHD,利用等腰三角形的性质和全等三角形的对应边相等得到:BE=MH,所以BG=MH=4.【解答】解:如图,作MD⊥BC于D,延长MD交BG的延长线于E,∵△ABC中,∠C=90°,CA=CB,∴∠ABC=∠A=45°,∵∠GMB=∠A,∴∠GMB=∠A=22.5°,∵BG⊥MG,∴∠BGM=90°,∴∠GBM=90°﹣22.5°=67.5°,∴∠GBH=∠EBM﹣∠ABC=22.5°.∵MD∥AC,∴∠BMD=∠A=45°,∴△BDM为等腰直角三角形∴BD=DM,而∠GBH=22.5°,∴GM平分∠BMD,而BG⊥MG,∴BG=EG,即BG=BE,∵∠MHD+∠HMD=∠E+∠HMD=90°,∴∠MHD=∠E,∵∠GBD=90°﹣∠E,∠HMD=90°﹣∠E,∴∠GBD=∠HMD,∴在△BED和△MHD中,,∴△BED≌△MHD(AAS),∴BE=MH,∴BG=MH=4.故答案是:4.【点评】本题考查了全等三角形的判定与性质:判定三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”;全等三角形的对应边相等.也考查了等腰直角三角形的性质.三.解答题(共15小题)26.(2008•)已知:如图,C为BE上一点,点A,D分别在BE两侧,AB∥ED,AB=CE,BC=ED.求证:AC=CD.【分析】根据AB∥ED推出∠B=∠E,再利用SAS判定△ABC≌△CED从而得出AC=CD.【解答】证明:∵AB∥ED,∴∠B=∠E.在△ABC和△CED中,,∴△ABC≌△CED.∴AC=CD.【点评】本题是一道很简单的全等证明,纵观近几年市中考数学试卷,每一年都有一道比较简单的几何证明题:只需证一次全等,无需添加辅助线,且全等的条件都很明显.27.(2007•)已知:如图,OP是∠AOC和∠BOD的平分线,OA=OC,OB=OD.求证:AB=CD.【分析】根据角平分线的性质得出∠AOP=∠COP,∠BOP=∠DOP,从而推出∠AOB=∠COD,再利用SAS判定其全等从而得到AB=CD.【解答】证明:∵OP是∠AOC和∠BOD的平分线,∴∠AOP=∠COP,∠BOP=∠DOP.∴∠AOB=∠COD.在△AOB和△COD中,.∴△AOB≌△COD.∴AB=CD.【点评】本题考查三角形全等的判定方法,以及全等三角形的性质.判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.本题比较简单,读已知时就能想到要用全等来证明线段相等.28.(2014•黄冈)已知,如图所示,AB=AC,BD=CD,DE⊥AB于点E,DF⊥AC于点F,求证:DE=DF.【分析】连接AD,利用SSS得到三角形ABD与三角形ACD全等,利用全等三角形对应角相等得到∠EAD=∠FAD,即AD为角平分线,再由DE⊥AB,DF⊥AC,利用角平分线定理即可得证.【解答】证明:连接AD,在△ACD和△ABD中,,∴△ACD≌△ABD(SSS),∴∠EAD=∠FAD,即AD平分∠EAF,∵DE⊥AE,DF⊥AF,∴DE=DF.【点评】此题考查了全等三角形的判定与性质,以及角平分线定理,熟练掌握全等三角形的判定与性质是解本题的关键.29.(2013•)如图,C是AB的中点,AD=BE,CD=CE.求证:∠A=∠B.【分析】根据中点定义求出AC=BC,然后利用“SSS”证明△ACD和△BCE全等,再根据全等三角形对应角相等证明即可.【解答】证明:∵C是AB的中点,∴AC=BC,在△ACD和△BCE中,,∴△ACD≌△BCE(SSS),∴∠A=∠B.【点评】本题考查了全等三角形的判定与性质,比较简单,主要利用了三边对应相等,两三角形全等,以及全等三角形对应角相等的性质.30.(2008•)已知:如图,在梯形ABCD中,AD∥BC,BC=DC,CF平分∠BCD,DF∥AB,BF的延长线交DC于点E.求证:(1)△BFC≌△DFC;(2)AD=DE.【分析】(1)由CF平分∠BCD可知∠BCF=∠DCF,然后通过SAS就能证出△BFC ≌△DFC.(2)要证明AD=DE,连接BD,证明△BAD≌△BED则可.AB∥DF⇒∠ABD=∠BDF,又BF=DF⇒∠DBF=∠BDF,∴∠ABD=∠EBD,BD=BD,再证明∠BDA=∠BDC则可,容易推理∠BDA=∠DBC=∠BDC.。
