基于MATLAB的M文件仿真
实验三_M_文件及_MATLAB_程序设计与调试

实验三M 文件及MATLAB 程序设计与调试一、实验目的全面掌握在MA TLAB 下进行程序设计的有关问题,具体涉及到M 脚本文件和M 函数文件的编写、全局和局部变量的使用、流程控制结构、提高程序执行效率的设计技术、程序调试等问题。
二、实验内容1、关于M 脚本文件和M 函数文件MATLAB 的M 文件有两类:脚本文件和函数文件。
(1)脚本文件——将原本要在MATLAB 的指令窗口中直接输入的语句,放在一个以.m 为后缀的,称为脚本文件中。
有了脚本文件,可直接在MATLAB 中输入脚本文件名(不含后缀)。
MATLAB 会打开这一脚本文件,并依次执行脚本文件中的每一条语句,这与在MATLAB 中直接输入语句的结果完全一致。
(2)函数文件——它的第一行必须是函数定义行。
M 函数文件由5 部分构成:◆函数定义行◆H1 行◆函数帮助文本◆函数体◆注释注意:在函数文件中,除了函数定义行之外,其它部分都是可以省略的。
但作为一个函数,为了提高函数的可用性,应加上H1 行和函数帮助文本,为了提高函数的可读性,应加上适当的注释。
例如:function y = mean(x)% MEAN Average or mean value.% For vectors, MEAN(X) is the mean value of the elements in X.% For matrices, MEAN(X) is a row vector containing the mean value of each column.[m,n]=size(x);if m==1% Determine whether x is a vectorm=n;endy = sum(x)/m;①函数定义行:function y = mean(x)function 为函数定义的关键字,mean 为函数名,y 为输出变量,x 为输入变量当函数具有多个输出变量时,则以方括号括起;当函数具有多个输入变量时,则直接用圆括号括起。
MATLAB 9.8 基础教程 第7章 M文件与MLX文件

所有数据。在运行过程中,产生的所有变量均是工作区变量,这些变量一旦生成,就一直保持
在工作区中,除非执行clear命令将它们清除。
运行一个脚本文件等价于从命令行窗口中顺序运行文件里的语句。由于脚本文件只是一串命
令的集合,因此,只需像在命令行窗口中输入语句那样,依次将语句编辑在脚本文件中,然后
在MATLAB命令行窗口输入该命令文件的名字就会顺序执行命令文件中的命令。
>> type std
则显示内容如下:
பைடு நூலகம்
function y = std(varargin)
函数定义行
%STD Standard deviation.
H1行
以下注释行都是帮助文本
% For vectors, Y = STD(X) returns the standard deviation. For matrices,
7.1.3 函数M文件
函数M文件是第一个可执行语句以function开始的M文件,每一个函数文件都定义一个函数,它可 以接受参数、也可以返回参数。函数文件内定义的变量是局部变量,只在函数文件内部起作用, 当函数文件执行完后,这些内部变量将被清除。在一般情况下,用户不能靠单独输入其文件名来 运行函数文件,而必须由其它语句来调用。事实上,MATLAB提供的标准函数大部分都是由函数 文件定义的。
第7章 M文件与MLX文件
7.1 M文件
当用户要运行的命令较多或需要反复运行多条命令时,若在MATLAB命令行窗口中直接从键盘逐行 输入命令会显得比较麻烦,这时建立一个M文件则可以较好地解决这一问题。
7.1.1 M文件的建立与运行
M文件可以用任何程序建立和编辑,且在MATLAB提供的M文件编辑器窗口实现。
基于Matlab的m序列的仿真与实现

a=[1101010001110111110010011000010]; b=a; Nb=length(b); N=120; x=[1:N]; for k=1:N c=xor(a,b); D=sum(c); A=Nb-D; % R(k)=(A-D)/(A+D); b=[b(Nb),b(1:Nb-1)]; plot(k,R(k),'ro'); hold on end plot(x,R,'g'); grid 运行结果:
-5
图二 5 级线性反馈移位寄存器产生 m 序列的仿真系统 (2)利用 Simulinkm观测 m 序列时频域特性
图三 5 级线性反馈移位寄存器产生 m 序列的时域波形
图四 5 级线性反馈移位寄存器产生 m 序列的频域波形 ToWorkspace的wr5就是所得m序列,我们取它一个完整
的周期,其周期是 31,序列如下: 1101010001110111110010011000010 2.3 利用 Matlab 编程环境求 m 序列的自相关特性 程序: clear
F(x)=C +C x1+C x2+…=
01
2
(2)
(3)生成函数(亦称序列多项式)可以表示为如下形式
G(x)=a +a x1+a x2+…=
01
2
当初始状态为
a =1,a =a =…=a =0
-m
-m+1 -r+2
-1
联立式(1)、(2)、(3)可得
(3) (4)
国防工业工业出版社,2006,5. [4]查光明,熊贤祚.扩频通信[M].西安:西安电子科技
大学出版社,2002. [5]曾兴雯,刘乃安,孙献璞.扩展频谱通信及其多址技术
[M].北京:高等教育出版社,2004. [6]樊昌信,张甫翊,吴成柯.现代通信[M].北京:高等
MATLAB程序设计M文件程序控制结构程序调试程序举例

y=input('Please input y=:');
[rho,the]=tran(x,y);
rho
the MATLAB中,函数能够嵌套调用,即一种函数能够调用别旳函数, 甚至调用它本身。一种函数调用它本身称为函数旳递归调用。
例6 分别建立命令文件和函数文件,将华氏温度f转换为 摄氏温度c。
21.1111
x=
21.1111
(5). 函数文件旳其他有关概念
①局部变量和全局变量:
局部变量只存在于单个函数工作空间,全局变量 经过global定义,可穿行于不同函数工作空间, 涉及基本工作空间workspace。
函数文件旳内部变量是局部旳,与其他函数 及MATLAB内存相互隔离; 而假如在若干函数中把某一变量定义为全局 变量,那么这些函数将公用这个变量,全局 变量旳作用域是整个MATLAB旳工作区,即 全程有效,全部函数都能够对其存取和修改。
if (nargin == 1) tol = max(size(x)) * max(s) * eps;
程序部分
end
r = sum(s > tol);
(2)命令m文件建立及其运营
建立 涉及下列环节: 进入m文件编辑器 输入程序 定义文件名,保存程序
命令M文件旳运营方式: 直接在命令窗口输入该文件旳文件名 在m文件编辑器中打开该文件后点击工具条中
② M文件模式
将matlab语句构成旳程序存储成以m为扩展名 旳文件,然后再执行该程序文件,这种工作模式 称为程序文件模式。
程序文件不能在命令窗口下建立,因为命令窗口 只允许一次执行一行上旳一种或几种语句。
基于MATLAB的m序列仿真

3.1 系统结构功能设计 ......................................................................................... 9 3.2 GUI 界面设计 ................................................................................................. 9 第四章 系统调试结果分析 ......................................... 11
1.2
系统设计流程图
本文通过软件 Matlab 编写程序,从而在 GUI 环境下看到 m 序列的产生、m 序列的自 相关和互相关函数图形,其系统设计流程图如图 1.1 所示: 开始
用 Matlab 编写程序产生两个 m 序列
对 m 序列进行自相关特性分析
对 m 序列进行互相关特性分析
用 Matlab GUI 显示仿真结果
Ns (2n 1) / n
其中, ( x) 为欧拉函数,其值小于等于 x ,并与 x 互质的正整数的个数(包括 1 在内)。例如对于 4 级移位寄存器,则小于 24 1 15 并与 15 互质的数为 1、2、4、 7、8、11、13、14,共 8 个,所以 (15) 8, Ns 8/ 4 2 ,所以 4 级移位寄存器最多能 产生的 m 序列数为 2。 总之,移位寄存器的反馈系数决定是否产生 m 序列,起始状态决定序列的起始 点,不同的反馈系数产生不同的码序列。 在 Matlab 的 GUI 环境中,程序代码如下:
第一章
1.1 设计内容及要求
1.1.1 设计内容
matlab在电路分析和仿真中的应用

MATLAB/SIMULNK的主要产品及其相互关系
2024/7/15
MATLAB的优点
• 1. 容易使用 • 2. 可以由多种操作系统支持 • 3. 丰富的内部函数 • 4. 强大的图形和符号功能 • 5. 可以自动选择算法 • 6. 与其他软件和语言有良好的对接性
2024/7/15
2024/7/15
Matlab 的安装
2 输入名字和公司名称 3 在第三个空白处(PLP)输入软件的序列号sn 4 继续安装,直到安装完成。
2024/7/15
5 安装帮助 将安装目录中的help文件夹替换为安装包中的 help文件夹
MATLAB 7用户界面概述
MATLAB 7的用户界 面主要包括以下三个 方面的内容: • MATLAB 7的主菜单 • MATLAB 7的工具栏 • MATLAB 7的窗口
matlab自定义的函数文件称内置函数文件
调用内置函数的方法:使用函数名并给出相应的入 口、出口参数即可。
例如:sin.m函数——用type sin查不到。
调用格式:y=sin(2*x)
1
实际应用中:
0.8
x=0:2*pi/180:2*pi;
0.6
y=sin(2*x)
0.4
0.2
plot(x,y)
0
-0.2
2024/7/15
-0.4
-0.6
取R=255欧,L=125uH,C=6800pF,则:
H (s)
sRC s2LC sRC
1
85s2
1734000s 1734000s
1014
m文件如下: % LCR串联谐振电路 R=255; L=125*10^(-6); C=6800*10^(-12);
基于Matlab的m序列相关特性的仿真

电子信息科学与技术专业课程设计题单班级0982081学生课程名称专业课程设计课题基于Matlab的m序列相关特性的仿真设计要求基于Matlab语言编程,对m序列相关特性进行仿真,并用Matlab GUI工具设计图形界面显示结果,具体要求如下:1、给定m序列S1、S2,码长为10232、计算m序列S1的自相关函数3、计算m序列对S1、S2的互相关函数4、界面设计要有按钮控件以及一、二级菜单课题发给日期2012.07.04课程设计完成日期2012.07.29指导教师评语:评分:摘要m 序列是最长线性反馈移存器序列的简称,它是由带线性反馈的移存器产生的周期最长的一种序列。
本文主要是介绍MATLAB 在m 序列的产生及其相关特性分析方面的应用,研究了关于matlab完成m序列simulink 硬件仿真方法,并且利用MATLAB 对不同长度的几种m 序列进行相关特性的分析。
对m序列的原理、结构、性质进行了分析,在matlab中采用编程和simulink动态仿真功能2种方式实现m序列,仿真实验表明,这两种方法简单,易于实现,可移植性较强,具有可行性和设计的合理性。
[关键词]m 序列;simulink 硬件仿真;自相关目录第一章设计内容及要求第二章m序列设计方案的选择第三章m序列的产生及性质3.1 m序列的产生原理、结构及产生3.2 m序列的基本性质3.3 生成m序列的模块第四章 m序列构造其他序列第五章程序调试及运结果5.1仿真设计流程图5.2实验的调试与运行结果5.3 错误排除第六章结论参考文献附录第一章设计内容及要求基于MATLAB产生m序列要求:1.通过matlab编程产生m序列的产生原理及其产生方法。
2.对特定长度的m序列,分析其性质,及其用来构造其它序列的方法。
第二章m序列设计方案的选择2.1 方案一MATLAB编程非常简单,无需进行变量声明,可以很方便的实现m 序列。
2.2 方案二图2.1 Simulink实现m序列Simulink是MATLAB最重要的组件之一,它提供了一个动态系统建模,仿真和综合分析的集成环境。
Matlab建模仿真

2
应用领域的功能;丰富的数据I/O 工具;提 供与其它高级语言的接口;支持多平台(PC
/ Macintosh / UNIX);开放与可扩展的体系
结构
使用Simulink来建模、仿真和分析各种动态
3
系统(包括连续系统、离散系统和混合系统), 将是一件轻松的事情
启用Simulink并建立系统模型
❖ 启动Simulink有两种方式: (1)用命令行方式启动Simulink。(>>simulink) (2)使用工具栏按钮启动Simulink ❖ 建立系统模型,完成Simulink系统模型的编辑之
4.仿真的作用
❖ 仿真技术具有很高的科学研究价值和巨大的经济 效益。由于仿真技术的特殊功效,特别是安全性 和经济性,使得仿真技术得到广泛的应用。首先 由于仿真技术在应用上的安全性,使得航空、航 天、核电站等成为仿真技术最早的和最主要的应 用领域
❖ 归纳起来,仿真技术的主要用途有如下几点: ❖(1) 优化系统设计。 ❖(2) 系统故障再现,发现故障原因 ❖(3) 验证系统设计的正确性。 ❖(4) 对系统或其子系统进行性能评价和分析。 ❖(5) 训练系统操作员。 ❖(6) 为管理决策和技术决策提供支持。
主要模块
【例】求解延迟微分方程式,用Simulink搭建微分方 程模型,并得出其数值解
. x(t) 3x(t) 1 y(t 1) 0.2x3(t 0.5) x(t 0.5)
y(t ) 3 y(t ) 2 y(t ) 4x(t)
第一个方程式变换成:
.
x(t) 3x(t) 1 y(t 1) 0.2x3(t 0.5) x(t 0.5)
当然我们可以直接观察Matlab工具箱原有的 Lorenz
❖ 输入 ❖ >>Lorenz;
移动通信课程设计实验报告-利用matlab进行m序列直接扩频仿真.

目录一、背景 (4)二、基本要求 (4)三、设计概述 (4)四、Matlab设计流程图 (5)五、Matlab程序及仿真结果图 (6)1、生成m序列及m序列性质 (6)2、生成50位随机待发送二进制比特序列,并进行扩频编码 (7)3、对扩频前后信号进行BPSK调制,观察其时域波形 (9)4、计算并观察扩频前后BPSK调制信号的频谱 (10)5、仿真经awgn信道传输后,扩频前后信号时域及频域的变化 (11)6、对比经信道前后两种信号的频谱变化 (12)7、接收机与本地恢复载波相乘,观察仿真时域波形 (14)8、与恢复载波相乘后,观察其频谱变化 (15)9、仿真观察信号经凯萨尔窗低通滤波后的频谱 (16)10、观察经过低通滤波器后无扩频与扩频系统的时域波形 (17)11、对扩频系统进行解扩,观察其时域频域 (18)12、比较扩频系统解扩前后信号带宽 (19)13、比较解扩前后信号功率谱密度 (20)14、对解扩信号进行采样、判决 (21)15、在信道中加入2040~2050Hz窄带强干扰并乘以恢复载波 (24)16、对加窄带干扰的信号进行低通滤波并解扩 (25)17、比较解扩后信号与窄带强干扰的功率谱 (27)六、误码率simulink仿真 (28)1、直接扩频系统信道模型 (28)2、加窄带干扰的直扩系统建模 (29)3、用示波器观察发送码字及解扩后码字 (30)4、直接扩频系统与无扩频系统的误码率比较 (31)5、不同扩频序列长度下的误码率比较 (32)6、扩频序列长度N=7时,不同强度窄带干扰下的误码率比较 (33)七、利用Walsh码实现码分多址技术 (34)1、产生改善的walsh码 (35)2、产生两路不同的信息序列 (36)3、用两个沃尔什码分别调制两路信号 (38)4、两路信号相加,并进行BPSK调制 (39)5、观察调制信号频谱,并经awgn信道加高斯白噪和窄带强干扰 (40)6、接收机信号乘以恢复载波,观察时域和频域 (42)7、信号经凯萨尔窗低通滤波器 (43)8、对滤波后信号分别用m1和m2进行解扩 (44)9、对两路信号分别采样,判决 (45)八、产生随机序列Gold码和正交Gold码 (47)1、产生Gold码并仿真其自相关函数 (48)2、产生正交Gold码并仿真其互相关函数 (50)九、实验心得体会 (51)直接序列扩频系统仿真一、背景直接序列扩频通信系统(DSSS)是目前应用最为广泛的系统。
第11组基于Matlab的m序列仿真

《移动通信》课程项目报告题目:基于MATLAB的m序列仿真专业班级电子信息0121208班组长周易德组员叶子源组员胡楗指导教师李兆玉提交日期 2015年6月15日成绩课程设计任务分配表目录一、设计目的 0二、设计要求和设计指标 0三、设计内容 03.1 伪随机码 03.2 m序列的定义 (1)3.3 m序列的生产 (2)3.4 m序列的性质 (3)3.4.1平衡性 (3)3.4.2游程特性 (3)3.4.3自相关特性 (4)3.4.4功率谱与噪声类似 (5)3.4.5 互相关特性 (6)3.5 m序列的应用 (7)3.5.1 CDMA IS-95的前向信道 (9)3.5.1 CDMA IS-95的反向信道 (9)四、本设计改进建议 (9)五、总结 (9)六、主要参考文献 (10)附录1程序清单 (11)附录2 m序列本原多项式表 (16)一、设计目的我们想通过本次课程设计提高自己对移动通信的认识,熟练Matlab软件的使用,锻炼发现问题解决问题的能力,最终提示我们的自学能力。
具体来讲,本次课程设计将通过Matlab对m序列的生产方法和性质进行深刻的讨论,需要我们去了解m序列的生产和性质。
二、设计要求和设计指标设计要求:1.了解m序列的定义和其背后的意义2.通过Matlab生产m序列3.验证m序列主要性质4.讨论m序列的主要性质在扩频中的作用设计指标:1.能通过Matlab生产任意长度的m序列2.讨论任意长度m序列的均衡性、游程性、自相关特性、互相关特性等主要性质三、设计内容3.1 伪随机码伪随机(或伪噪声,Pseudorandom Noise,PN)码序列是一种常用的地址码,它具有与白噪声类似的自相关性质的0和1所构成的编码序列。
伪随机码序列具有类似于随机序列的基本特性,是一种貌似随机但实际上是有规律的周期性二进制序列。
如果发送数据序列经过完全随机性的加扰,接收机就无法恢复原始序列。
在实际系统中使用的是一个足够随机的序列,一方面这个随机序列对非目标接收机是不可识别的,另一方面目标接收机能够识别并且很容易同步地产生这个随机序列。
MATLAB通信系统仿真实验报告

MATLAB通信系统仿真实验报告实验一、MATLAB的基本使用与数学运算目的:学习MATLAB的基本操作,实现简单的数学运算程序。
内容:1-1 要求在闭区间[0,2π]上产生具有10个等间距采样点的一维数组。
试用两种不同的指令实现。
运行代码:x=[0:2*pi/9:2*pi]运行结果:1-2 用M文件建立大矩阵xx=[ 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.91.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.92.1 2.2 2.3 2.4 2.5 2.6 2.7 2.8 2.93.1 3.2 3.3 3.4 3.5 3.6 3.7 3.8 3.9]代码:x=[ 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.91.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.92.1 2.2 2.3 2.4 2.5 2.6 2.7 2.8 2.93.1 3.2 3.3 3.4 3.5 3.6 3.7 3.8 3.9]m_mat运行结果:1-3已知A=[5,6;7,8],B=[9,10;11,12],试用MATLAB分别计算A+B,A*B,A.*B,A^3,A.^3,A/B,A\B.代码:A=[5 6;7 8] B=[9 10;11 12] x1=A+B X2=A-B X3=A*B X4=A.*B X5=A^3 X6=A.^3 X7=A/B X8=A\B运行结果:1-4任意建立矩阵A,然后找出在[10,20]区间的元素位置。
程序代码及运行结果:代码:A=[12 52 22 14 17;11 10 24 03 0;55 23 15 86 5 ] c=A>=10&A<=20运行结果:1-5 总结:实验过程中,因为对软件太过生疏遇到了些许困难,不过最后通过查书与同学交流都解决了。
例如第二题中,将文件保存在了D盘,而导致频频出错,最后发现必须保存在MATLAB文件之下才可以。
DMC算法MATLAB编程及仿真
一、前言工业生产的过程是复杂的,建立起来的模型也是不完善的。
即使是理论非常复杂的现代控制理论,其效果也往往不尽人意,甚至在一些方面还不及传统的PID控制。
20世纪70年代,人们除了加强对生产过程的建模、系统辨识、自适应控制等方面的研究外,开始打破传统的控制思想,试图面向工业开发出一种对各种模型要求低、在线计算方便、控制综合效果好的新型算法。
在这样的背景下, 预测控制的一种,也就是动态矩阵控制(DMC )首先在法国的工业控制中得到应用。
因此预测控制不是某种统一理论的产物,而是在工业实践中逐渐发展起来的。
预测控制中比较常见的三种算法是模型算法控制(MAC),动态矩阵控制(DMC )以及广义预测控制。
本篇所采用的是动态矩阵控制,其采用增量算法,因此在消除稳态余差方面非常有效。
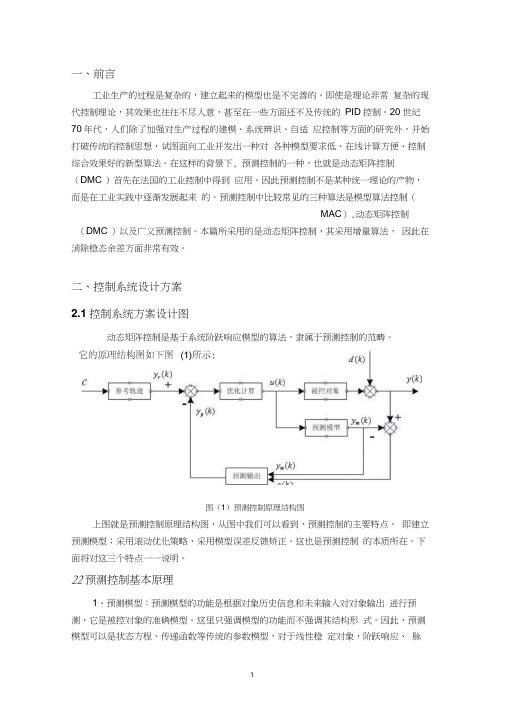
二、控制系统设计方案2.1控制系统方案设计图动态矩阵控制是基于系统阶跃响应模型的算法,隶属于预测控制的范畴。
图(1)预测控制原理结构图上图就是预测控制原理结构图,从图中我们可以看到,预测控制的主要特点。
即建立预测模型;采用滚动优化策略,采用模型误差反馈矫正。
这也是预测控制的本质所在。
下面将对这三个特点一一说明。
22预测控制基本原理1、预测模型:预测模型的功能是根据对象历史信息和未来输入对对象输出进行预测,它是被控对象的准确模型。
这里只强调模型的功能而不强调其结构形式。
因此,预测模型可以是状态方程、传递函数等传统的参数模型,对于线性稳定对象,阶跃响应、脉冲响应这类非参数模型也可以作为预测模型使用。
预测模型具有展示系统未来动态行为的功能,这样,就可以利用预测模型来预测未来时刻被控对象的输出变化及被控变量与其给定值的偏差,作为控制作用的依据,使之适应动态系统所具有的因果性的特点,得到比常规控制更好的控制效果。
2、滚动优化:预测控制是一种优化控制算法,它是通过某一性能指标的最优来确定未来的控制作用。
这一性能指标涉及到系统未来的行为。
如,通常可取被控对象输出在未来的采样点上跟踪某一期望轨迹的方差最小,性能指标中涉及到的系统未来的行为,是根据预测模型由未来的控制策略决定的。
MATLAB仿真技术

4. 系统建模 4.1 连续系统建模
线性系统建模举例
例3:复位积分器的功用示例。 在仿真启动时,积分器从零开始对 0.5 t 进行积分。当复位口 信号 t-5=0 瞬间,积分器被重置为零。此后,再对0.5 ( t-5 ) 进行积分。
例3_4_2:积分模块直接构造微分方程求解模型。
假设从实际自然界(力学、电学、生态等)或社会中,抽象 出有初始状态为0的二阶微分程 x 0.2x 0.4x 0.2u,(t) u(t)是单位阶跃函数。本例演示如何用积分器直接构搭求解该微 分方程的模型。
符号矩阵的基本运算:加、减、乘、除、微积分等。 符号代数方程的求解。 符号微分方程的求解。 符号积分变换。
目录 主页
MATLAB的可视化功能
(1)二维曲线图形和三维曲面图形
二维符号函数曲线。
二维曲线图形。
三维符号函数曲线。 三维曲面图形。
三维线性图形。
目录 主页
(2)句柄图形 句柄图形(Handle Graphics)是一种面向对象的绘图系统。 图形对象、对象句柄和句柄图形树。 • MATLAB把用于数据可视和界面制作的基本绘图要素称 为句柄图形对象。 • 构成MATLAB句柄图形体系有12个图形对象(见句柄图形 树) 。
例:直接利用传递函数模块求解方程。
对二阶微分程进行拉氏变换:s2 X (s) 0.2sX (s) 0.4X (s) 0.2U (s)
可以得到: G(s) X (s)
0.2
U (s) s 2 0.2s 0.4
目录 主页
4.1 连续系统建模(续)
非线性系统建模举例
例3:求非线性系统
目录 主页
MATLAB的数值计算功能
基于Matlab的模拟(AM、FM、PM)调制系统仿真

通信系统模拟调制系统仿真一 课题内容 AM FM PM 调制 二 设计要求1.掌握AM FM PM 调制和解调原理。
2.学会Matlab 仿真软件在AM FM PM 调制和解调中的应用。
3.分析波形及频谱1.AM 调制解调系统设计1.振幅调制产生原理所谓调制,就是在传送信号的一方将所要传送的信号附加在高频振荡上,再由天线发射出去。
这里高频振荡波就是携带信号的运载工具,也叫载波。
振幅调制,就是由调制信号去控制高频载波的振幅,直至随调制信号做线性变化。
在线性调制系列中,最先应用的一种幅度调制是全调幅或常规调幅,简称为调幅(AM )。
在频域中已调波频谱是基带调制信号频谱的线性位移;在时域中,已调波包络与调制信号波形呈线性关系。
设正弦载波为)cos()(0ϕω+=t A t c c式中,A 为载波幅度;c ω为载波角频率;0ϕ为载波初始相位(通常假设0ϕ=0).调制信号(基带信号)为)(t m 。
根据调制的定义,振幅调制信号(已调信号)一般可以表示为)cos()()(t t Am t s c m ω=设调制信号)(t m 的频谱为)(ωM ,则已调信号)(t s m 的频谱)(ωm S :)]()([2)(c c m M M AS ωωωωω-++=2.调幅电路方案分析标准调幅波(AM )产生原理调制信号是只来来自信源的调制信号(基带信号),这些信号可以是模拟的,亦可以是数字的。
为首调制的高频振荡信号可称为载波,它可以是正弦波,亦可以是非正弦波(如周期性脉冲序列)。
载波由高频信号源直接产生即可,然后经过高频功率放大器进行放大,作为调幅波的载波,调制信号由低频信号源直接产生,二者经过乘法器后即可产生双边带的调幅波。
设载波信号的表达式为t c ωcos ,调制信号的表达式为t A t m m m ωcos )(= ,则调幅信号的表达式为t t m A t s c AM ωcos )]([)(0+=图5.1 标准调幅波示意图 3.信号解调思路从高频已调信号中恢复出调制信号的过程称为解调(demodulation ),又称为检波(detection )。
matlab FM调制仿真

Matlab FM调制仿真目录引言 (3)一.课程设计的目的与要求 (3)1.1课程设计的目的 (3)1.2课程设计的要求 (3)二.FM调制解调系统设计 (3)2.1FM调制模型的建立 (4)2.2调制过程分析 (5)2.3FM解调模型的建立 (6)2.4解调过程分析 (7)2.5高斯白噪声信道特性 (8)2.6调频系统的抗噪声性能分析 (11)三.仿真实现 (12)3.1MATLAB源代码 (13)3.2仿真结果 (17)四.心得体会 (20)五.参考文献 (20)引言本课程设计用于实现DSB信号的调制解调过程。
信号的调制与解调在通信系统中具有重要的作用。
调制过程是一个频谱搬移的过程,它是将低频信号的频谱搬移到载频位置。
解调是调制的逆过程,即是将已调制的信号还原成原始基带信号的过程。
信号的接收端就是通过解调来还原已调制信号从而读取发送端发送的信息。
因此信号的解调对系统的传输有效性和传输可靠性有着很大的影响。
调制与解调方式往往决定了一个通信系统的性能。
双边带DSB信号的解调采用相干解调法,这种方式被广泛应用在载波通信和短波无线电话通信中。
一.课程设计的目的与要求1.1 课程设计的目的通过《FM调制解调系统设计与防真》的课程设计,掌握通信原理中模拟信号的调制和解调、数字基带信号的传输、数字信号的调制和解调,模拟信号的抽样、量化和编码与信号的最佳接收等原理。
应用原理设计FM调制解调系统,并对其进行防真。
1.2 课程设计的要求要求能够熟练应用MATLAB语言编写基本的通信系统的应用程序,进行模拟调制系统,数字基带信号的传输系统的建模、设计与仿真。
所有的仿真用MATLAB 程序实现(即只能用代码的形式,不能用SIMULINK实现),系统经过的信道都假设为高斯白噪声信道。
模拟调制要求用程序画出调制信号,载波,已调信号、解调信号的波形,数字调制要求画出误码率随信噪比的变化曲线。
二.FM调制解调系统设计通信的目的是传输信息。
matlab 中 m 文件里面的参数-解释说明

matlab 中m 文件里面的参数-概述说明以及解释1.引言1.1 概述概述部分:参数在Matlab中的M文件中起着重要的作用,它们是用来传递数值、变量或是一些特定的设置给函数或脚本的。
通过使用参数,我们可以为M 文件提供灵活性和可重用性,使得代码更加可配置和可扩展。
在M文件中,参数通常用来控制特定的行为或计算过程。
通过在函数或脚本定义时声明参数,并在调用函数或执行脚本时提供相应的数值或变量,我们可以根据实际需求来调整程序的行为。
参数的设置可以灵活地改变程序的输出结果,提高了代码的可定制性和适用性。
在本文中,我们将详细介绍M文件中参数的定义和使用方法。
我们将探讨参数的常见用法和技巧,包括参数的类型、默认值的设定以及参数的传递方式等。
此外,我们还将探讨一些参数的优化与应用,以帮助读者理解参数在M文件中的重要性和使用价值。
通过对M文件中参数的深入研究,我们能够更好地理解和使用Matlab的函数和脚本。
参数的合理设置不仅能够提高代码的执行效率和准确性,也能够使代码更易读、易维护和易扩展。
因此,理解参数在M文件中的作用和用法对于编写高效、优质的Matlab代码至关重要。
在下一节中,我们将详细介绍M文件及其作用,以帮助读者更好地理解参数在M文件中的使用环境和背景。
请继续阅读下一节内容。
文章结构部分的内容如下:1.2 文章结构本篇文章主要围绕着matlab 中m 文件中的参数展开讨论。
文章分为引言、正文和结论三个部分。
在引言部分,我们首先对文章的主题进行了概述,说明了本文将要讨论的问题和目的。
接着介绍了文章的结构,明确了各个部分的内容和顺序。
最后,对整篇文章进行了总结,给出了一个简要的概括。
在正文部分,我们详细讨论了matlab 中的M 文件及其作用。
我们解释了M 文件的含义和作用,介绍了其在matlab 编程中的重要性。
然后,我们重点关注了M 文件中的参数定义,解释了参数的概念和用途。
接着我们详细阐述了在M 文件中参数的使用方法,包括如何定义参数、如何传递参数以及如何在程序中使用参数。
MATLAB的M文件编写及简单电力系统的仿真
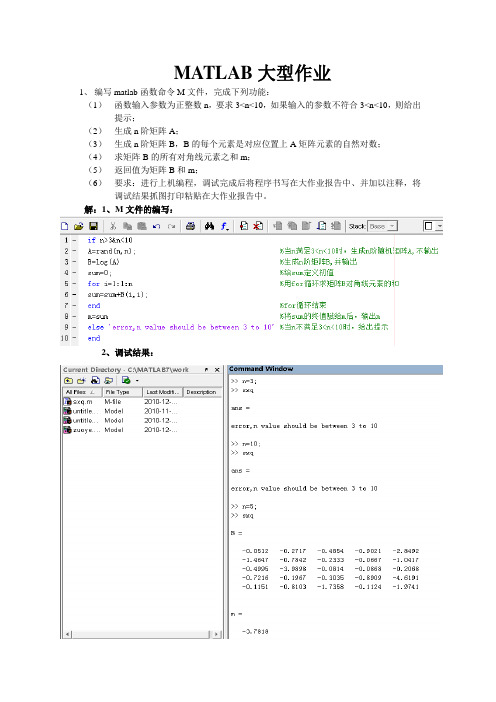
MATLAB大型作业1、编写matlab函数命令M文件,完成下列功能:(1)函数输入参数为正整数n,要求3<n<10,如果输入的参数不符合3<n<10,则给出提示;(2)生成n阶矩阵A;(3)生成n阶矩阵B,B的每个元素是对应位置上A矩阵元素的自然对数;(4)求矩阵B的所有对角线元素之和m;(5)返回值为矩阵B和m;(6)要求:进行上机编程,调试完成后将程序书写在大作业报告中、并加以注释,将调试结果抓图打印粘贴在大作业报告中。
解:1、M文件的编写:2、调试结果:2、一个50Hz的简单电力系统如下图所示,试在Simulink中建立仿真模型研究该系统性能。
k1系统建模要求如下:(1)发电机G采用“Synchronous Machine pu Fundamental”模型,变压器T采用“Three-Phase Transformer (Two Windings)”模型,输电线路L采用“Three-Phase Series RLC Branch”模型,负荷LD1、LD2采用“Three-Phase Parelell RLC Load”模型。
(2)发电机模型参数:采用预设模型,其中学号末位数字为1的同学使用编号为01的模型参数,学号末位数字为2的同学使用编号为02的模型参数,……,学号末位数字为0的同学使用编号为10的模型参数。
(3)变压器模型采用默认参数,副边电压10kV,但需要注意与发电机模型相匹配参数的设置(原边电压、频率等),变压器容量设置为发电机额定功率的1.2倍;(4)线路参数的设置原则:忽略电容,X/R=3,线路通过发电机额定功率时首末端压降约为0.05p.u.;(5)负荷模型采用默认参数,但需要注意与整个系统模型相匹配参数的设置(电压、频率等),负荷LD1容量设置为发电机额定功率的5%,LD2容量为发电机额定功率的30%,功率因数0.95。
(6)其他模块(如短路模拟、测量、示波、powergui等)的使用根据研究要求自行确定。
基于MATLAB的M文件仿真

基于MATLAB的M文件仿真M文件:k=1;Int_F=inline('t','t');for x=[1,3,5]f_x(k)=x^3+x+log(x)*sin(x)+quad8(Int_F,0,x);k=k+1;endf_x>> CalcfxWarning: QUAD8 is obsolete. We use QUADL instead. > In quad8 at 35In Calcfx at 4f_x =2.5000 34.6550 140.9567M文件:function[mean,stdev]=stat(x)n=length(x);mean=sum(x)/n;stdev=sqrt(sum(x-mean).^2/n);>> x=[1,3,2];>> [k,l]=stat(x)k =2l =微积分方程组的MA TLAB函数:文件funcforex123.mfunction xdot=funcforex123(t,x,flag,r,l,c)xdot=zeros(2,1);xdot(1)=-r/l*x(1)-1/l*x(2)+1/l*f(t);xdot(2)=1/c*x(1);function in=f(t)in=(t>0)*1;文件Ex123.ml=1;c=0.1;for r=[1.5 3 5][t,x]=ode45('funcforex123',[-1,10],[0;0],[],r,l,c);figure(1);plot(t,x(:,1));hold on;xlabel('time sec');text(0.9,0.17,'\lefttarrow i_L(t)');grid;figure(2);plot(t,x(:,2));hold on;xlabel('time sec');text(0.5,0.3,'\leftarrow u_C(t)');grid;End>> ex123Warning: Unable to interpret TeX string "\lefttarrow i_L(t)". > In ex123 at 5Warning: Unable to interpret TeX string "\lefttarrow i_L(t)". > In ex123 at 7Warning: Unable to interpret TeX string "\lefttarrow i_L(t)". > In ex123 at 7文件ex123b.m[t,x]=ode45('funcforex123',[-1,10],[0;0],[],2,1,0.1); ts=0.001;t1=-1:ts:10;x1=interp1(t,x(:,2),t1,'spline');plot(t1,x1,'k-.');hold on;x1dot=[diff([x1])/ts,0];plot(t1,[diff([x1])/ts,0],'k');xlabel('time sec');ht=10/sqrt(7.75).*exp(-1.5*t1).*sin(sqrt(7.75)*t1).*(t1>0);plot(t1(1:50:length(t1)),ht(1:50:length(t1)),'ko');legend('Syep response','Impulse response','Theoretic impluse response'); >> ex123b欧拉算法的MA TLAB程序:文件sybeuler.mfunction [tout,yout]=sybeuler(odefile,t0,h,th,y0,P) tout=[t0:h:th]';yout(length(tout),length(y0))=0;kk=1;for t=tout'yout(kk,:)=y0';kk=kk+1;k1=h*eval([odefile'(t,y0,P)']);y0=y0+k1;end文件mystateEQ.mfunction xdot=mystateEQ(t,x,P)xdot=zeros(2,1);r=P(1);l=P(2);c=P(3);xdot(1)=-r/l*x(1)-1/l*x(2)+1/l*f(t);xdot(2)=1/c*x(1);function in=f(t)in=(t>0)*1;文件mystateEQforODE45.mfunction xdot=mystateEQforODE45(t,x,flag,P) xdot=zeros(2,1);r=P(1);l=P(2);c=P(3);xdot(1)=-r/l*x(1)-1/l*x(2)+1/l*f(t);xdot(2)=1/c*x(1);function in=f(t)in=(t>0)*1;文件sybeulerTEST.mtic;[t,x]=ode45('mystateEQforODE45',[0,10],[0;0],[],[3 1 0.1]); toc plot(t,x,'k.');hold on;for h=[0.2,0.1,0.01]tic;[t,x]=sybeuler('mystateEQ',0,h,10,[0;0],[3 1 0.1]);tocplot(t,x,'k');endlegend('u_C(t)ode45','i_L(t)ode45','sybeuler');。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
M文件:
k=1;
Int_F=inline('t','t');
for x=[1,3,5]
f_x(k)=x^3+x+log(x)*sin(x)+quad8(Int_F,0,x);
k=k+1;
end
f_x
>> Calcfx
Warning: QUAD8 is obsolete. We use QUADL instead. > In quad8 at 35
In Calcfx at 4
f_x =
2.5000 34.6550 140.9567
M文件:
function[mean,stdev]=stat(x)
n=length(x);
mean=sum(x)/n;
stdev=sqrt(sum(x-mean).^2/n);
>> x=[1,3,2];
>> [k,l]=stat(x)
k =
2
l =
微积分方程组的MA TLAB函数:
文件funcforex123.m
function xdot=funcforex123(t,x,flag,r,l,c)
xdot=zeros(2,1);
xdot(1)=-r/l*x(1)-1/l*x(2)+1/l*f(t);
xdot(2)=1/c*x(1);
function in=f(t)
in=(t>0)*1;
文件Ex123.m
l=1;
c=0.1;
for r=[1.5 3 5]
[t,x]=ode45('funcforex123',[-1,10],[0;0],[],r,l,c);
figure(1);plot(t,x(:,1));hold on;xlabel('time sec');
text(0.9,0.17,'\lefttarrow i_L(t)');grid;
figure(2);plot(t,x(:,2));hold on;xlabel('time sec');
text(0.5,0.3,'\leftarrow u_C(t)');grid;
End
>> ex123
Warning: Unable to interpret TeX string "\lefttarrow i_L(t)". > In ex123 at 5
Warning: Unable to interpret TeX string "\lefttarrow i_L(t)". > In ex123 at 7
Warning: Unable to interpret TeX string "\lefttarrow i_L(t)". > In ex123 at 7
文件ex123b.m
[t,x]=ode45('funcforex123',[-1,10],[0;0],[],2,1,0.1);
ts=0.001;
t1=-1:ts:10;
x1=interp1(t,x(:,2),t1,'spline');
plot(t1,x1,'k-.');
hold on;
x1dot=[diff([x1])/ts,0];
plot(t1,[diff([x1])/ts,0],'k');xlabel('time sec');
ht=10/sqrt(7.75).*exp(-1.5*t1).*sin(sqrt(7.75)*t1).*(t1>0);
plot(t1(1:50:length(t1)),ht(1:50:length(t1)),'ko');
legend('Syep response','Impulse response','Theoretic impluse response'); >> ex123b
欧拉算法的MA TLAB程序:
文件sybeuler.m
function [tout,yout]=sybeuler(odefile,t0,h,th,y0,P) tout=[t0:h:th]';
yout(length(tout),length(y0))=0;
kk=1;
for t=tout'
yout(kk,:)=y0';
kk=kk+1;
k1=h*eval([odefile'(t,y0,P)']);
y0=y0+k1;
end
文件mystateEQ.m
function xdot=mystateEQ(t,x,P)
xdot=zeros(2,1);
r=P(1);l=P(2);c=P(3);
xdot(1)=-r/l*x(1)-1/l*x(2)+1/l*f(t);
xdot(2)=1/c*x(1);
function in=f(t)
in=(t>0)*1;
文件mystateEQforODE45.m
function xdot=mystateEQforODE45(t,x,flag,P) xdot=zeros(2,1);
r=P(1);l=P(2);c=P(3);
xdot(1)=-r/l*x(1)-1/l*x(2)+1/l*f(t);
xdot(2)=1/c*x(1);
function in=f(t)
in=(t>0)*1;
文件sybeulerTEST.m
tic;
[t,x]=ode45('mystateEQforODE45',[0,10],[0;0],[],[3 1 0.1]); toc
plot(t,x,'k.');hold on;
for h=[0.2,0.1,0.01]
tic;
[t,x]=sybeuler('mystateEQ',0,h,10,[0;0],[3 1 0.1]);
toc
plot(t,x,'k');
end
legend('u_C(t)ode45','i_L(t)ode45','sybeuler');。
