关于使用matlab绘制眼图
基带信眼图实验m精编b仿真

基带信眼图实验m精编b仿真文件排版存档编号:[UYTR-OUPT28-KBNTL98-UYNN208]数字基带信号的眼图实验——m a t l a b 仿真一、实验目的1、掌握无码间干扰传输的基本条件和原理,掌握基带升余弦滚降系统的实现方法;2、通过观察眼图来分析码间干扰对系统性能的影响,并观察在输入相同码率的NRZ 基带信号下,不同滤波器带宽对输出信号码间干扰大小的影响程度;3、熟悉MATLAB 语言编程。
二、实验预习要求1、复习《数字通信原理》第七章节——奈奎斯特第一准则内容;2、复习《数字通信原理》第七章节——数字基带信号码型内容;3、认真阅读本实验内容,熟悉实验步骤。
三、实验原理和电路说明 1、基带传输特性基带系统的分析模型如图3-1所示,要获得良好的基带传输系统,就应该图3-1 基带系统的分析模型抑制码间干扰。
设输入的基带信号为()n s na t nT δ-∑,s T 为基带信号的码元周期,则经过基带传输系统后的输出码元为()n s na h t nT -∑。
其中1()()2j th t H ed ωωωπ+∞-∞=⎰(3-1)理论上要达到无码间干扰,依照奈奎斯特第一准则,基带传输系统在时域应满足:10()0,s k h kT k =⎧=⎨⎩,为其他整数 (3-2)频域应满足:()0,ss T T H πωωω⎧≤⎪=⎨⎪⎩,其他 (3-3)图3-2 理想基带传输特性此时频带利用率为2/Baud Hz ,这是在抽样值无失真条件下,所能达到的最高频率利用率。
由于理想的低通滤波器不容易实现,而且时域波形的拖尾衰减太慢,因此在得不到严格定时时,码间干扰就可能较大。
在一般情况下,只要满足:222(),s i s s s si H H H H T T T T T ππππωωωωω⎛⎫⎛⎫⎛⎫+=-+++=≤⎪ ⎪⎪⎝⎭⎝⎭⎝⎭∑ (3-4)基带信号就可实现无码间干扰传输。
这种滤波器克服了拖尾太慢的问题。
使用matlab绘制眼图

使用matlab 绘制数字基带信号的眼图实验一、实验目的1、掌握无码间干扰传输的基本条件和原理,掌握基带升余弦滚降系统的实现方法;2、通过观察眼图来分析码间干扰对系统性能的影响,并观察在输入相同码率的NRZ 基带信号下,不同滤波器带宽对输出信号码间干扰大小的影响程度;3、熟悉MATLAB 语言编程。
二、实验原理和电路说明1、基带传输特性基带系统的分析模型如图3-1所示,要获得良好的基带传输系统,就应该图3-1基带系统的分析模型抑制码间干扰。
设输入的基带信号为()nsna t nT δ-∑,sT 为基带信号的码元周期,则经过基带传输系统后的输出码元为()nsna h t nT -∑。
其中1()()2j t h t H e d ωωωπ+∞-∞=⎰(3-1)理论上要达到无码间干扰,依照奈奎斯特第一准则,基带传输系统在时域应满足:10()0,s k h kT k =⎧=⎨⎩,为其他整数(3-2)频域应满足:()0,ss T T H πωωω⎧≤⎪=⎨⎪⎩,其他 (3-3)图3-2理想基带传输特性此时频带利用率为2/Baud Hz ,这是在抽样值无失真条件下,所能达到的最高频率利用率。
由于理想的低通滤波器不容易实现,而且时域波形的拖尾衰减太慢,因此在得不到严格定时时,码间干扰就可能较大。
在一般情况下,只要满足:222(),s i s s s si H H H H T T T T T ππππωωωωω⎛⎫⎛⎫⎛⎫+=-+++=≤⎪ ⎪⎪⎝⎭⎝⎭⎝⎭∑ (3-4)基带信号就可实现无码间干扰传输。
这种滤波器克服了拖尾太慢的问题。
从实际的滤波器的实现来考虑,采用具有升余弦频谱特性()H ω时是适宜的。
(1)(1)1sin (),2(1)()1,0(1)0,s s s s s s T T T T H T T ππαπαωωαπαωωπαω⎧⎡⎤-+--≤≤⎪⎢⎥⎣⎦⎪⎪-⎪=≤≤⎨⎪⎪+>⎪⎪⎩(3-5)这里α称为滚降系数,01α≤≤。
手写 matlab的rectifystereoimages代码-概述说明以及解释

手写matlab的rectifystereoimages代码-概述说明以及解释1.引言引言部分是文章的开头,应该对整篇文章进行简要介绍和概述。
下面是关于1.1 概述部分的内容:概述部分旨在介绍本文的主题和内容。
本文将讨论手写Matlab 的rectifystereoimages 代码,这是一个在立体视觉处理中常用的函数。
我们将分析rectifystereoimages 函数的作用和功能,并探讨为什么有必要自己手写这个函数的代码。
在立体视觉中,常常需要对立体图像进行校正,以消除镜头畸变并使两幅图像在水平线上对齐。
这样做能够提高图像处理和计算机视觉算法的准确性和性能。
Matlab 提供了rectifystereoimages 函数,它可用于对立体图像进行校正。
然而,有时候我们需要理解函数的内部工作原理,或者需要根据特定需求进行修改和优化函数。
因此,学习如何手写rectifystereoimages 的代码是非常有意义的。
本文将首先对Matlab 中的rectifystereoimages 函数进行介绍,包括它的输入和输出以及常见的参数选项。
然后,我们将详细说明手写rectifystereoimages 代码的必要性。
通过手动实现该函数,我们可以更好地理解校正图像的原理和算法,同时可以灵活地根据特定任务的需求进行修改和优化。
此外,手写代码还有助于加深对立体视觉算法的理解和应用。
本文的结论部分将总结手写rectifystereoimages 代码的优势,并讨论对学习和理解算法的影响。
通过自己手写代码,我们可以更好地掌握rectifystereoimages 函数的内部机制,并在实际应用中灵活运用。
本文的目标是帮助读者理解和掌握rectifystereoimages 函数,以及手写算法的重要性和价值。
接下来,我们将详细介绍Matlab 中的rectifystereoimages 函数,并探讨手写代码的必要性。
(完整word版)使用matlab绘制眼图.docx

使用 matlab 绘制数字基带信号的眼图实验一、实验目的1、掌握无码间干扰传输的基本条件和原理,掌握基带升余弦滚降系统的实现方法;2、通过观察眼图来分析码间干扰对系统性能的影响,并观察在输入相同码率的NRZ 基带信号下,不同滤波器带宽对输出信号码间干扰大小的影响程度;3、熟悉 MATLAB语言编程。
二、实验原理和电路说明1、基带传输特性基带系统的分析模型如图3-1 所示,要获得良好的基带传输系统,就应该a n t nT s基带传输a n h t nT sn n抽样判决H ( )图 3-1基带系统的分析模型抑制码间干扰。
设输入的基带信号为a n t nT s, T s为基带信号的码元周期,则经过n基带传输系统后的输出码元为a n h t nT s。
其中nh(t )1H ()e j t d(3-1 )2理论上要达到无码间干扰,依照奈奎斯特第一准则,基带传输系统在时域应满足:,k 0h( kT s)(3-2)0,k为其他整数频域应满足:T s,T s(3-3)H ( )0,其他H ( )T sT sT s图 3-2 理想基带传输特性此时频带利用率为2Baud / Hz , 这是在抽样值无失真条件下,所能达到的最高频率利用率。
由于理想的低通滤波器不容易实现,而且时域波形的拖尾衰减太慢,因此在得不到严格定时时,码间干扰就可能较大。
在一般情况下,只要满足:2 i H2 2 ,(3-4)HH ( ) HT s iT sT sT sT s基带信号就可实现无码间干扰传输。
这种滤波器克服了拖尾太慢的问题。
从实际的滤波器的实现来考虑,采用具有升余弦频谱特性H ( ) 时是适宜的。
1 sinT s ( ) , (1 ) (1 )2T sT sT sH ( )1, (1 ) 0(3-5)T s0,(1 )T s这里称为滚降系数,1。
所对应的其冲激响应为:sin tcos( t T s )h(t )T s (3-6)t 1 4 2t 2 T s 2T s此时频带利用率降为 2 / (1 ) Baud/ Hz ,这同样是在抽样值无失真条件下,所能达到的最高频率利用率。
眼图实验(含总结)

实验报告20 年度春季学期数字通信原理课程名称实验二眼图实验名称实验名称:眼图实验目的:理解升余弦滚降系统的特性;理解眼图的含义。
实验要求:1.绘制滚降系数分别为0,0.5,1的升余弦系统的时域波形和频谱,并分析之。
2.画出滚降系数为1的升余弦系统的眼图。
实验过程:1.打开MATLAB新建一个文件,然后按照老师所给的PPT的实验教程指南打上以下的程序:Ts=1;N=17;dt=Ts/N;df=1.0/(20.0*Ts);t=-10*Ts:dt:10*Ts;f=-2/Ts:df:2/Ts;a=[0,0.5,1];for n=1:length(a)for k=1:length(f)if abs(f(k))>0.5*(1+a(n))/TsXf(n,k)=0;elseif abs(f(k))<0.5*(1-a(n))/TsXf(n,k)=Ts;elseXf(n,k)=0.5*Ts*(1+cos(pi*Ts/(a(n)+eps)*(abs(f(k))-0.5*(1-a(n))/Ts)));end;end;xt(n,:)=sinc(t/Ts).*(cos(a(n)*pi*t/Ts))./(1-4*a(n)^2*t.^2/Ts^2+eps);endsubplot(211);plot(f,Xf);axis([-1 1 0 1.2]);xlabel('f/Ts');ylabel('升余弦滚降频谱');subplot(212);plot(t,xt);axis([-10 10 -0.5 1.1]);xlabel('t');ylabel('升余弦滚降波形');图1 升余弦滚降函数代码2.之后点击运行,然后能看见结果:图2 升余弦滚降3.然后在按照老师所给的实验操作指南,打上眼图的源代码,如下:图3眼图源代码(1)图4 眼图源代码(4)4.之后自己编写一段sigexpand函数,然后运行它之后在运行眼图代码,得到结果如下:图5 眼图运行结果实验小结:通过本次对眼图与升余弦滚降系统的特性分析让我对于其的结构理解、更加的深刻,我不断地翻阅书籍和网上的相关知识得到了滚降系数α:在无码间串扰条件下所需带宽W 和码元传输速率Rs 的比值(即奈奎斯特频率),将本来很模糊的概念到最后的融会贯通。
MATLAB技术图像去红眼处理

MATLAB技术图像去红眼处理近年来,随着数码相机的普及与发展,我们可以随时随地用相机记录生活中的美好瞬间。
然而,有时候我们会发现在照片中的人物眼睛中出现了令人不太愉快的红眼现象。
红眼通常在低光照环境下发生,当闪光灯照射到被拍摄者的眼睛时,光线会反射回镜头,从而导致眼睛出现红色。
为了解决这个问题,科学家们提出了各种各样的算法和技术。
其中,MATLAB 作为一种功能强大的计算机软件,拥有丰富的图像处理工具箱,可以帮助我们进行图像去红眼处理。
首先,我们需要了解红眼现象的原理。
当闪光灯照射到被拍摄者的眼睛时,光线会穿过瞳孔进入眼底,然后被血红素吸收。
这些被吸收的光线在经过相机镜头时会反射回来,形成红色的反光,从而导致红眼现象的产生。
在MATLAB中,我们可以利用图像处理工具箱中的函数和算法来消除红眼。
首先,我们需要将原始图像加载到MATLAB的工作环境中。
接下来,我们可以使用MATLAB内置的红眼消除算法来处理图像。
该算法主要基于两个步骤:红眼检测和红眼修复。
红眼检测是指通过对图像进行分析,找到图片中的红眼区域。
在MATLAB中,我们可以使用颜色分量检测技术来实现红眼检测。
该技术主要利用了红眼区域和其他区域在颜色空间上的差异。
通过对图像进行颜色分量转换,提取出红色通道,我们可以将红眼区域与其他区域进行区分和识别。
红眼修复是指对检测到的红眼区域进行处理,将其转换为自然色彩。
在MATLAB中,我们可以使用图像增强和灰度调整的技术来实现红眼修复。
图像增强技术主要通过调整图像的对比度、亮度和饱和度等参数来改善图像的视觉效果。
而灰度调整技术则通过调整图像的色调和亮度来实现对红眼区域的处理。
在对图像进行红眼修复后,我们可以将处理后的图像保存,并进行进一步的后期处理。
例如,我们可以使用MATLAB中的图像滤波和降噪技术来提高图像的质量和清晰度。
同时,我们还可以应用其他图像处理技术,如锐化、旋转和裁剪等,对图像进行进一步的优化和调整。
使用matlab绘制眼图

使用matlab 绘制数字基带信号的眼图实验一、实验目的1、掌握无码间干扰传输的基本条件和原理,掌握基带升余弦滚降系统的实现方法;2、通过观察眼图来分析码间干扰对系统性能的影响,并观察在输入相同码率的NRZ 基带信号下,不同滤波器带宽对输出信号码间干扰大小的影响程度;3、熟悉MATLAB 语言编程。
二、实验原理和电路说明1、基带传输特性基带系统的分析模型如图3-1所示,要获得良好的基带传输系统,就应该图3-1基带系统的分析模型抑制码间干扰。
设输入的基带信号为()nsna t nT δ-∑,sT 为基带信号的码元周期,则经过基带传输系统后的输出码元为()nsna h t nT -∑。
其中1()()2j th t H ed ωωωπ+∞-∞=⎰(3-1)理论上要达到无码间干扰,依照奈奎斯特第一准则,基带传输系统在时域应满足:10()0,s k h kT k =⎧=⎨⎩,为其他整数 (3-2)频域应满足:()0,ss T T H πωωω⎧≤⎪=⎨⎪⎩,其他 (3-3)图3-2 理想基带传输特性此时频带利用率为2/Baud Hz ,这是在抽样值无失真条件下,所能达到的最高频率利用率。
由于理想的低通滤波器不容易实现,而且时域波形的拖尾衰减太慢,因此在得不到严格定时时,码间干扰就可能较大。
在一般情况下,只要满足:222(),s i s s s si H H H H T T T T T ππππωωωωω⎛⎫⎛⎫⎛⎫+=-+++=≤⎪ ⎪⎪⎝⎭⎝⎭⎝⎭∑ (3-4)基带信号就可实现无码间干扰传输。
这种滤波器克服了拖尾太慢的问题。
从实际的滤波器的实现来考虑,采用具有升余弦频谱特性()H ω时是适宜的。
(1)(1)1sin (),2(1)()1,0(1)0,s s s s s s T T T T H T T ππαπαωωαπαωωπαω⎧⎡⎤-+--≤≤⎪⎢⎥⎣⎦⎪⎪-⎪=≤≤⎨⎪⎪+>⎪⎪⎩(3-5)这里α称为滚降系数,01α≤≤。
matlab中eyes函数

matlab中eyes函数Matlab中的eyes函数是一个非常有趣和实用的函数,它可以用来创建一个具有指定形状和颜色的眼睛图像。
这个函数的语法非常简单,只需要指定眼睛的形状和颜色即可。
在本文中,我们将深入探讨eyes函数的用法和一些实际应用。
让我们来看一下eyes函数的基本语法。
在Matlab中,我们可以使用如下的命令来调用eyes函数:```Matlabeyes(shape, color)```其中,shape表示眼睛的形状,可以是'circle'、'square'或'ellipse';color表示眼睛的颜色,可以是'blue'、'green'、'red'、'yellow'等等。
例如,如果我们想创建一个蓝色的圆形眼睛,可以使用以下命令:```Matlabeyes('circle', 'blue')```接下来,让我们来看一些具体的示例。
首先我们使用以下命令创建一个蓝色的圆形眼睛:eyes('circle', 'blue')```然后,我们可以使用以下命令创建一个绿色的方形眼睛:```Matlabeyes('square', 'green')```除了基本的形状和颜色之外,eyes函数还可以接受一些其他的参数来定制眼睛的细节。
例如,我们可以使用以下命令来创建一个具有指定半径和线宽的圆形眼睛:```Matlabeyes('circle', 'blue', 'radius', 50, 'linewidth', 2)```这个命令将创建一个半径为50像素,线宽为2像素的蓝色圆形眼睛。
除了创建眼睛图像之外,eyes函数还可以用于一些实际的应用。
基于MATLAB的眼图仿真《通信原理》

基于MATLAB的眼图仿真——及其与通信实验箱之结果的比较摘要通信实验往往可以从硬件和软件两方面着手设计,并加以横向比较,从而达到更深刻地理解和领会通信理论原理的目的。
本设计选取眼图为研究对象。
可靠性是通信系统的重要指标之一,而眼图是定性衡量传输系统可靠性能——码间串扰大小及受信道噪声的影响等——的方法,简单直观;除了用通信实验箱实现眼图的观察外,软件仿真具有前者所不具备的优点,本设计以MATLAB为主要工具实现了眼图的仿真模拟。
硬件方面使用北京掌宇金仪科教仪器设备有限公司生产的TIMS-301 F系列实验系统,只需较少的模块就能完成眼图的实现,缺点是灵活性不够;MATLAB由初始的矩阵实验室发展成一款具有广泛用途的科学实验软件,在通信系统仿真方面是有效而便捷的。
MATLAB本身内置功能强大的函数库和讲解详细的帮助文档,前者使得眼图的仿真更加高效。
眼图仿真考虑了以下几方面因素的影响:调制数字信号的方式、传输系统(滤波)、信道噪声及其大小等等;给出了MATLAB语言编程和Simulink动态建模两种眼图的实现方式,通过仿真有效的验证了眼图判断噪声大小、系统性能的有效性,并尝试了通过眼图调整通信系统的抗干扰能力。
关键字:通信系统,眼图,仿真,MATLABSimulation of Eye Diagram Based on Matlab——& Comparison with the rusult of TIMSAbstractExperiment in communication system can often be coducted on hardware as well as by sofeware, and by drawing comparison with each other, the principles of the theories in communication system could be understood more deeply and properly . The Eye Diagram was chosed to be studied in this design. The reliability is one of the most important indexes in evaluating the performance of a communication system. Eye Diagram is such a tool to observe the performance of communication systems. By using an Eye Diagram, the magnitude of the noise and the Intersymbole Interference (ISI) could be diagnosed by and large.Two methods were employed to achieve the Eye Diagram. One was the TIMS-301F teaching & experimental system, which is simple but inflexible; the other was using the language of MATLAB which contains programming by matlab and establishing drammic models of communication system in Simulink. Comparison was drawn between the two.Many factors were considered in the simulation of Eye Diagram, such as the way which a digital signal was modulated before transmiting, the transmit system, noise of the channel, the filter and so on. Some phenomenons can be observed and some principles be tested, beside, it also tries to improve/adjust the communication system with the help of the Eye Diagram.Key Words: Communication System, Eye Diagram, Simulation, MATLAB目录1 绪论 (4)1.1引言 (4)1.2通信系统及其性能指标 (5)1.3码间干扰及无失真传输 (7)1.4眼图及其模型 (8)2 眼图的硬件实现 (10)2.1TIMS系统简介 (10)2.2眼图的观察及结果 (11)3 眼图的MATLAB仿真 (15)3.1MATLAB简介 (15)3.2眼图的仿真及结果 (17)4 两种结果的比较及结论 (35)5 附录 (36)致谢 (38)参考文献 (39)1 绪论1.1引言21世纪将是一个信息高速膨胀的信息社会,社会生产力水平的大力发展要求社会成员间的合作更加紧密和高效,通信系统的设计与优化因此显得越来越重要;通常,通信系统的性能指标涉及有效性、可靠性、适应性、标准性等等,但从研究消息传输角度考虑,通信的可靠性和有效性是主要的矛盾所在,可靠性主要指消息的“质量“问题(;对于数字通信系统,具体来说,就是传输速率和差错率,差错率就是从可靠性的角度具体化的一个概念。
基于MATLAB的QAM 眼图和星座图

南昌大学信息工程学院《随机信号分析》课程作业题目:QAM调制信号的眼图及星座图仿真指导老师:虞贵财作者:毕圣昭日期:2011-12-05QAM调制信号的眼图及星座图仿真1. 眼图眼图是在数字通信的工程实践中测试数字传输信道质量的一种应用广泛、简单易行的方法。
实际上它的一个扫描周期是数据码元宽度1~2倍并且与之同步的示波器。
对于二进制码元,显然1和0的差别越大,接受判别时错判的可能性就越小。
由于传输过程中受到频带限制,噪声的叠加使得1和0的差别变小。
在接收机的判决点,将“1”和“0”的差别用眼图上“眼睛”张开的大小来表示,十分形象、直观和实用。
MATLAB工具箱中有显示眼图和星座图的仪器,下面通过具体的例子说明它们的应用。
图1-1所示是MATLAB Toolbox\Commblks中的部分内容,展示了四进制随机数据通过基带QPSK调制、升余弦滤波(插补)及加性高斯白噪声传输环境后信号的眼图。
图1-1 通过QPSK基带调制升余弦滤波及噪声环境后观察眼图的仿真实验系统图1-2所示是仿真运行后的两幅眼图,上图是I(同相)信号,下图是Q(正交)信号。
图1-2 通过QPSK基带调制及噪声传输环境后观察到的眼图2. 星座图星座图是多元调制技术应用中的一种重要的测量方法。
它可以在信号空间展示信号所在的位置,为系统的传输特性分析提供直观的、具体的显示结果。
为了是系统的功率利用率、频带利用率得到充分的利用,在特定的调制方式下,在信号空间中如何排列与分布信号?在传输过程中叠加上噪声以后,信号之间的最小距离是否能保证既定的误码率的要求这些问题的研究用星座图仪十分直观方便。
多元调制都可以分解为In-phase(同相)分量及Quadrature(正交)分量。
将同相分量用我们习惯的二维空间的X轴表示,正交分量用Y轴表示。
信号在X-Y平面(同相-正交平面)的位置就是星座图。
MATLAB通信系统的工具箱里有着使用方便、界面美观的星座图仪。
04 码间串扰——眼图(补充)
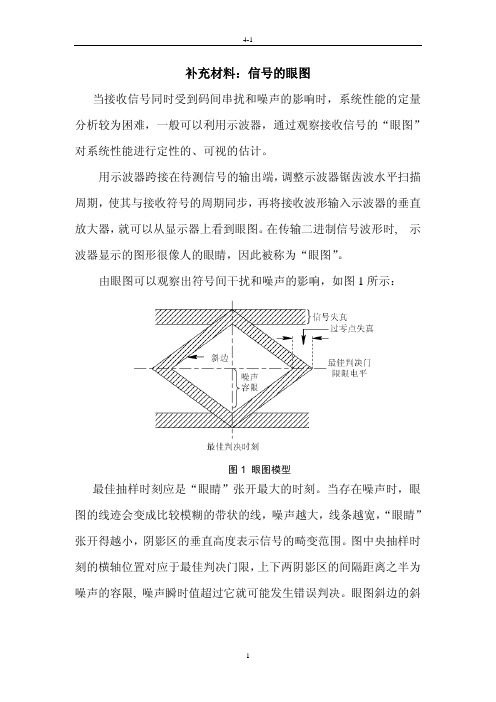
补充材料:信号的眼图当接收信号同时受到码间串扰和噪声的影响时,系统性能的定量分析较为困难,一般可以利用示波器,通过观察接收信号的“眼图”对系统性能进行定性的、可视的估计。
用示波器跨接在待测信号的输出端,调整示波器锯齿波水平扫描周期,使其与接收符号的周期同步,再将接收波形输入示波器的垂直放大器,就可以从显示器上看到眼图。
在传输二进制信号波形时, 示波器显示的图形很像人的眼睛,因此被称为“眼图”。
由眼图可以观察出符号间干扰和噪声的影响,如图1所示:图1 眼图模型最佳抽样时刻应是“眼睛”张开最大的时刻。
当存在噪声时,眼图的线迹会变成比较模糊的带状的线,噪声越大,线条越宽,“眼睛”张开得越小,阴影区的垂直高度表示信号的畸变范围。
图中央抽样时刻的横轴位置对应于最佳判决门限,上下两阴影区的间隔距离之半为噪声的容限, 噪声瞬时值超过它就可能发生错误判决。
眼图斜边的斜率决定了系统对抽样定时误差的灵敏程度:斜率越大,对定时误差越灵敏。
下面以三个BPSK码元为例,给出用Matlab生成的眼图,其中发射端采用sinc成型滤波器。
三个码元的可能组合为8种形式,即[-1 -1 -1 ; -1 -1 1; -1 1 -1 ; -1 1 1; 1 -1 -1; 1 -1 1; 1 1 -1; 1 1 1]。
将8种可能的信号组合形成的时域波形逐一画到同一张图上,即可得到三个符号时的眼图,当信道存在噪声时,接收信号的眼图中也将叠加噪声。
无噪声和有噪声干扰下的眼图如下所示:(a) 无噪声(b)有噪声图2 三个符号时的眼图同理,考虑五个码元周期时,眼图形状如下:(a)无噪声(b)有噪声图3 五个符号时的眼图实际系统中,符号序列的长度是无限的,因此其眼图实际上是更多待定信号波形的叠加。
不同的传输信号幅度将产生不同的眼图,同时眼图还与发端滤波器的时域波形有关。
下图给出了多进制信号的眼图:图4 多进制信号的眼图。
matlab中的eyediagram语法

一、简介eyediagram是Matlab中用来绘制眼图的函数。
眼图是用来观察数字信号在接收端的信号质量以及其中包含的噪声和失真情况的重要工具。
眼图通过将数字信号分成若干窗口进行显示,可以直观地观察到信号的抖动和时钟偏移情况,对于分析和诊断信号的传输质量非常有帮助。
二、语法在Matlab中使用eyediagram函数可以按照以下语法进行调用:eyediagram(x,n)其中,x代表输入的数字信号序列,n代表每个窗口中包含的采样点数。
三、参数说明在使用eyediagram函数时,可以根据实际需求调整参数以获得最佳的眼图效果。
1. x:输入的数字信号序列,可以是一维数组或矩阵。
对于多通道的数字信号,可以将各通道的信号分别传入eyediagram函数进行绘制。
2. n:每个窗口中包含的采样点数。
这个参数决定了眼图中水平方向的分辨率,可以根据信号的速率和时钟频率进行调整。
四、示例下面是一个使用eyediagram函数绘制眼图的简单示例:```matlab% 定义输入信号fs = 1000; % 采样频率t = 0:1/fs:1-1/fs; % 时间序列x = cos(2*pi*100*t) + 0.5*sin(2*pi*200*t) + 0.2*randn(size(t));% 绘制眼图eyediagram(x, 64); % 显示64个采样点```五、注意事项在使用eyediagram函数时,需要注意以下几点:1. 确保输入的数字信号序列长度足够长,以便获得准确的眼图显示。
2. 根据实际情况调整每个窗口中的采样点数,以获得清晰的眼图效果。
3. 结合其他工具和方法,对眼图结果进行更深入的分析和诊断,以获取更多有关数字信号传输质量的信息。
六、总结eyediagram函数是Matlab中用于绘制眼图的重要工具,通过对数字信号进行分窗显示,提供直观的信号质量分析方法。
在工程实践中,眼图是分析和诊断数字通信系统的重要手段,通过对信号抖动、时钟偏移等现象的观察,可以帮助工程师及时发现和解决问题,提高系统的性能和稳定性。
eye_pattern

MATLAB演示升余弦
眼图的CLK
• 采样示波器的CLK通常可能是用户提供的时钟,恢复时钟,或者与数据 信号本身同步的码同步信号. • 实时示波器通过一次触发完成所有数据的采样,不需附加的同步信号和 触发信号.通常通过软件PLL方法恢复时钟.Tektronix RT-Eye软件即使 用此方法.
TDS8200 ET Scope (20GHz 80E03)
眼图
定义:
眼图是一系列数字信号在示波器上累积而显示的图形。
意义:
码间串扰&噪声
眼图体现了数字信号整体的特征,从而估计系统优劣程度,因而 眼图分析是高速互连系统信号完整整,以减小码间 串扰,改善系统的传输性能。
眼图的形成原理
示波器眼图的形成原理
TDS6154C RT w. DSP
眼图与CLK-时钟速率提高,眼图质量下降
125M CLK
250M CLK
500M CLK
眼图与误码率
基于MATLAB的人眼检测

目录摘要 (I)ABSTRACT........................................................... I I 1 绪论.. (1)1.1 研究背景及意义 (1)1.2 国内外疲劳驾驶研究现状 (2)1.3本文的主要研究内容及组织结构 (3)2 人脸检测与定位技术 (4)2.1人脸检测与定位技术概述 (4)2.1.1基于图像的人脸检测方法 (4)2.1.2基于特征的人脸检测方法 (5)2.2 Adaboost算法介绍 (6)2.2.1 AdaBoost 算法描述 (7)2.3 AdaBoost算法分类器 (10)2.3.1 分类器级联策略 (10)2.3.2 级联分类器误差分析 (11)3 人眼定位技术 (12)3.1 常见的几种人眼检测方法 (12)3.2 矩形特征及积分图 (14)3.2.1 矩形特征 (14)3.2.2 积分图 (15)3.3 AdaBoost算法的改进 (16)3.4 构建双层AdaBoost分类器进行人眼检测 (18)3.4.1 人脸定位与人眼定位的差异 (18)3.4.2 人眼定位预处理 (19)3.4.3 人眼定位双层分类器的构建 (20)3.5 人眼定位算法的设计与实现 (20)4 人眼状态识别 (21)4.1 基于椭圆拟合的人眼状态分析 (21)5 基于PERCLOS标准的疲劳状态分析 (23)5.1 PERCLOS方法介绍 (23)6 总结 (25)参考文献 (26)附录A (28)摘要随着汽车工业的不断发展,随之而来的社会问题也愈加严重。
交通事故给人们造成巨大伤害的同时,也给社会带来沉重的负担和影响。
由于疲劳驾驶是引起交通事故的一个主要原因。
因此,研究一种合理有效、实时准确检测驾驶员疲劳驾驶的非接触式车载装置对于减少交通事故,道路安全有重大意义。
本文研究的主要内容包括:人脸检测、人眼定位、眼睛特征提取和状态识别、疲劳程度的计算等算法的原理及实现。
(完整)基于MATLAB下的16QAM仿真

1。
课程设计目的随着现代通信技术的发展,特别是移动通信技术高速发展,频带利用率问题越来越被人们关注.在频谱资源非常有限的今天,传统通信系统的容量已经不能满足当前用户的要求.正交幅度调制QAM(Quadrature Amplitude Modulation)以其高频谱利用率、高功率谱密度等优势,成为宽带无线接入和无线视频通信的重要技术方案.首先介绍了QAM调制解调原理,提出了一种基于MATLAB的16QAM系统调制解调方案,包括串并转换,2—4电平转换,抽样判决,4—2电平转换和并串转换子系统的设计,对16QAM的星座图和调制解调进行了仿真,并对系统性能进行了分析,进而证明16QAM调制技术的优越性。
2.课程设计要求(1)设计一个16QAM调制与解调系统。
(2)设计程序时必须使得程序尽可能的简单。
(3)利用MATLAB进行程序编写并对系统进行仿真分析。
3。
相关知识随着现代通信技术的发展,特别是移动通信技术高速发展,新的需求层出不穷,促使新的业务不断产生,因而导致频率资源越来越紧张.在有限的带宽里要传输大量的多媒体数据,频谱利用率成为当前至关重要的课题,由于具有高频谱利用率、高功率谱密度等优势,16QAM技术被广泛应用于高速数据传输系统.在很多宽带应用领域,比如数字电视广播,Internet宽带接入,QAM 系统都得到了广泛的应用。
QAM也可用于数字调制。
数字QAM有4QAM、8QAM、16QAM、32QAM等调制方式。
其中,16QAM和32QAM广泛用于数字有线电视系统。
当今国际市场上出现了采用16QAM 调制技术的卫通调制解调器,如美国COMTECH EF DATA公司新推出的CDM—600。
该卫通调制解调器支持速率高达20Mbps[1]。
无线通信技术的迅猛发展对数据传输速率、传输效率和频带利用率提出了更高的要求.选择高效可行调制解调手段,对提高信号的有效性和可靠性起着至关重要的作用。
由于QAM已经成为宽带无线接入和无线视频通信的重要技术方案。
Matlab中的成像方法和算法

Matlab中的成像方法和算法近年来,成像技术在各个领域中得到了广泛的应用。
尤其是在医学、天文学和工业检测等领域,成像方法的发展使我们能够更清晰地观察和理解复杂的现象。
Matlab作为一种功能强大的科学计算软件,提供了丰富的成像方法和算法,可以帮助研究人员进行各种复杂的成像问题的解决。
本文将介绍在Matlab中常用的成像方法和算法,探讨它们的原理和应用。
一、计算机断层成像(CT)首先我们来介绍计算机断层成像(CT)这一常见的成像方法。
CT通过扫描目标物体并获取不同角度上的投影图像,然后利用逆过程重构出目标物体的三维结构。
在Matlab中,CT的主要算法是基于Radon变换和滤波反投影算法。
Radon变换可以将二维图像转换为投影角度的函数,而滤波反投影算法则是根据投影图像的数据进行反投影和滤波操作,重建出三维结构。
二、磁共振成像(MRI)磁共振成像(MRI)是一种利用核磁共振原理进行成像的方法。
它通过在静态磁场和梯度磁场的作用下,对被测物体进行激励和检测,得到图像信息。
在Matlab中,MRI的主要算法包括傅里叶变换、梯度下降等。
傅里叶变换可用于将信号从时间域转换为频率域,并对数据进行滤波和重建。
而梯度下降法则可以优化MRI图像的重建过程,提高图像质量。
三、光学相干层析成像(OCT)光学相干层析成像(OCT)是一种非侵入性的高分辨率显微成像技术,广泛应用于医学和生物领域。
它利用光学干涉原理,通过分析样品处不同深度处的反射光信号,得到高分辨率的断层图像。
在Matlab中,OCT的主要算法包括傅里叶变换、谱域相位解调等。
傅里叶变换可用于将光信号从时域转换为频域,而谱域相位解调则可提取出样品的光学路径长度信息,从而实现图像重建。
四、数字全息成像数字全息成像是一种利用光学全息原理进行三维图像重建的技术,它不仅可以记录物体的振幅信息,还可以保留物体的相位信息。
在Matlab中,数字全息成像的主要算法包括菲涅尔全息和Fresnel-Kirchhoff全息。
matlab绘图知识点总结

matlab绘图知识点总结一、Matlab基本绘图函数1. plot函数plot函数是Matlab中最基本的绘图函数之一,用于绘制二维图表。
其基本语法为:plot(x, y)。
其中x是横轴坐标数据,y是纵轴坐标数据。
通过plot函数可以绘制折线图、散点图等。
2. bar函数bar函数用于绘制条形图,其基本语法为:bar(x, y)。
其中x是条形的横轴坐标位置,y是条形的高度。
3. pie函数pie函数用于绘制饼图,其基本语法为:pie(x, labels)。
其中x是用来指定各个扇形区域的大小的矩阵,labels则是用来指定每个扇形区域的标签。
4. hist函数hist函数用于绘制直方图,其基本语法为:hist(x, bins)。
其中x是待绘制的数据,bins则是用来指定直方图的条形数目。
5. scatter函数scatter函数用于绘制散点图,其基本语法为:scatter(x, y)。
其中x和y分别是散点的横轴和纵轴坐标数据。
6. contour函数contour函数用于绘制等高线图,其基本语法为:contour(x, y, z)。
其中x和y分别是网格的横轴和纵轴坐标,z则是用来指定等高线的数值。
二、自定义图形1. 设置标题、标签和图例在Matlab中,可以使用title、xlabel、ylabel和legend等函数分别设置图表的标题、横轴和纵轴标签以及图例。
2. 设置图表样式可以使用line属性、marker属性以及color属性等来设置折线图、散点图等的样式。
3. 修改图表坐标轴可以使用xlim、ylim函数来设置图表的横轴和纵轴范围,并使用xticks和yticks函数来设置坐标刻度。
4. 绘制多个数据集可以使用hold on函数来绘制多个数据集,并使用hold off函数来结束绘制多个图表。
5. 设置图表背景可以使用grid、box、axis equal等函数来设置图表的背景。
三、子图表绘制1. subplot函数subplot函数用于在一个图形窗口中绘制多个子图表,其基本语法为:subplot(m,n,p)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
使用matlab 绘制数字基带信号的眼图实验一、实验目的1、掌握无码间干扰传输的基本条件和原理,掌握基带升余弦滚降系统的实现方法;2、通过观察眼图来分析码间干扰对系统性能的影响,并观察在输入相同码率的NRZ 基带信号下,不同滤波器带宽对输出信号码间干扰大小的影响程度;3、熟悉MATLAB 语言编程。
二、实验原理和电路说明1、基带传输特性基带系统的分析模型如图3-1所示,要获得良好的基带传输系统,就应该图3-1基带系统的分析模型抑制码间干扰。
设输入的基带信号为()nsna t nT δ-∑,sT 为基带信号的码元周期,则经过基带传输系统后的输出码元为()nsna h t nT -∑。
其中1()()2j th t H ed ωωωπ+∞-∞=⎰(3-1)理论上要达到无码间干扰,依照奈奎斯特第一准则,基带传输系统在时域应满足:10()0,s k h kT k =⎧=⎨⎩,为其他整数 (3-2)频域应满足:()0,ss T T H πωωω⎧≤⎪=⎨⎪⎩,其他 (3-3)图3-2 理想基带传输特性此时频带利用率为2/Baud Hz ,这是在抽样值无失真条件下,所能达到的最高频率利用率。
由于理想的低通滤波器不容易实现,而且时域波形的拖尾衰减太慢,因此在得不到严格定时时,码间干扰就可能较大。
在一般情况下,只要满足:222(),s i s s s si H H H H T T T T T ππππωωωωω⎛⎫⎛⎫⎛⎫+=-+++=≤⎪ ⎪⎪⎝⎭⎝⎭⎝⎭∑ (3-4)基带信号就可实现无码间干扰传输。
这种滤波器克服了拖尾太慢的问题。
从实际的滤波器的实现来考虑,采用具有升余弦频谱特性()H ω时是适宜的。
(1)(1)1sin (),2(1)()1,0(1)0,s s s s s s T T T T H T T ππαπαωωαπαωωπαω⎧⎡⎤-+--≤≤⎪⎢⎥⎣⎦⎪⎪-⎪=≤≤⎨⎪⎪+>⎪⎪⎩(3-5)这里α称为滚降系数,01α≤≤。
所对应的其冲激响应为:()222sin cos()()14s s s stT t T h t t t T T παππα=-(3-6)此时频带利用率降为2/(1)Baud/Hz α+,这同样是在抽样值无失真条件下,所能达到的最高频率利用率。
换言之,若输入码元速率'1/s s R T >,则该基带传输系统输出码元会产生码间干扰。
2、眼图所谓眼图就是将接收滤波器输出的,未经再生的信号,用位定时以及倍数作为同步信号在示波器上重复扫描所显示的波形(因传输二进制信号时,类似人的眼睛)。
干扰和失真所产生的畸变可以很清楚的从眼图中看出。
眼图反映了系统的最佳抽样时间,定时的灵敏度,噪音容限,信号幅度的畸变范围以及判决门限电平,因此通常用眼图来观察基带传输系统的好坏。
图3-3 眼图示意图三、仿真程序设计1、程序框架双极性NRZ码元序列产生升余弦滚降系统NRZ码元序列抽样画眼图NRZ(n)图3-4 程序框架首先,产生M进制双极性NRZ码元序列,并根据系统设置的抽样频率对该NRZ码元序列进行抽样,再将抽样序列送到升余弦滚降系统,最后画出输出码元序列眼图。
2、参数设置该仿真程序应具备一定的通用性,即要求能调整相应参数以仿真不同的基带传输系统,并观察输出眼图情况。
因此,对于NRZ码元进制M、码元序列长度Num、码元速率Rs,采样频率Fs、升余弦滚降滤波器参考码元周期Ts、滚降系数alpha、在同一个图像窗口内希望观测到的眼图个数Eye_num等均应可以进行合理设置。
3、实验内容根据现场实验题目内容,设置仿真程序参数,编写仿真程序,仿真波形,并进行分析给出结论。
不同进制的码元序列经过不同带宽的升余弦滚降系统后的眼图通用程序(1)Rs=50 Ts=10 M=2 a=0.2close all;alpha=0.2;Ts=1e-2;Fs=1e3;Rs=50;M=2;Num=100;Samp_rate=Fs/Rs;Eye_num=2;NRZ=2*randint(1,Num,M)-M+1;figure(1);stem(NRZ);title('双极性NRZ码元序列');Samp_data=zeros(1,Samp_rate*Num);for r=1:Num*Samp_rateif rem(r,Samp_rate)==0Samp_data(r)=NRZ(r/Samp_rate);endend[ht,a]=rcosine(1/Ts,Fs,'fir',alpha);figure(2);subplot(2,1,1);plot(ht);ylabel('冲激响应');title('升余弦滚降系统冲激响应');st=conv(Samp_data,ht)/(Fs*Ts);subplot(2,1,2);plot(st);ylabel('信号幅度');title('经过升余弦滚降系统后的码元');figure(3);for k=10:floor(length(st)/Samp_rate)-10ss=st(k*Samp_rate+1:(k+Eye_num)*Samp_rate);plot(ss);hold on;endylabel('信号幅度');title('基带信号眼图');而升余弦滚降滤波器和FIR滤波器的等效带宽B=60Hz(Ts=10ms),Rs<2B,满足了奈奎斯特第一准则的条件。
(2) Rs=50 Ts=10 M=4 a=0.2close all;alpha=0.2;Ts=1e-2;Fs=1e3;Rs=50;M=4;Num=100;Samp_rate=Fs/Rs;Eye_num=4;NRZ=2*randint(1,Num,M)-M+1;figure(1);stem(NRZ);title('双极性NRZ码元序列');Samp_data=zeros(1,Samp_rate*Num);for r=1:Num*Samp_rateif rem(r,Samp_rate)==0Samp_data(r)=NRZ(r/Samp_rate);endend[ht,a]=rcosine(1/Ts,Fs,'fir',alpha);figure(2);subplot(2,1,1);plot(ht);ylabel('冲激响应');title('升余弦滚降系统冲激响应');st=conv(Samp_data,ht)/(Fs*Ts);subplot(2,1,2);plot(st);ylabel('信号幅度');title('经过升余弦滚降系统后的码元');figure(3);for k=10:floor(length(st)/Samp_rate)-10ss=st(k*Samp_rate+1:(k+Eye_num)*Samp_rate);plot(ss);hold on;endylabel('信号幅度');从眼图张开程度可以得出没有发生码间干扰,这是因为基带信号的码元速率Rs为50Baud,而升余弦滚降滤波器和FIR滤波器的等效带宽B=60Hz(Ts=10ms),Rs<2B,满足了奈奎斯特第一准则的条件。
眼图是由各段码元波形叠加而成的,M=4,所以能看到3只眼睛。
(3) Rs=50 Ts=20 M=2 a=0.2close all;alpha=0.2;Ts=2*1e-2;Fs=1e3;Rs=50;M=2;Num=100;Samp_rate=Fs/Rs;Eye_num=2;NRZ=2*randint(1,Num,M)-M+1;figure(1);stem(NRZ);title('双极性NRZ码元序列');Samp_data=zeros(1,Samp_rate*Num);for r=1:Num*Samp_rateif rem(r,Samp_rate)==0Samp_data(r)=NRZ(r/Samp_rate);endend[ht,a]=rcosine(1/Ts,Fs,'fir',alpha);figure(2);subplot(2,1,1);plot(ht);ylabel('冲激响应');title('升余弦滚降系统冲激响应');st=conv(Samp_data,ht)/(Fs*Ts);subplot(2,1,2);plot(st);ylabel('信号幅度');title('经过升余弦滚降系统后的码元');figure(3);for k=10:floor(length(st)/Samp_rate)-10ss=st(k*Samp_rate+1:(k+Eye_num)*Samp_rate);plot(ss);hold on;endylabel('信号幅度');title('基带信号眼图');而升余弦滚降滤波器和FIR滤波器的等效带宽B=30Hz(Ts=10ms),Rs=2B,满足了奈奎斯特第一准则的条件。
能看到一只清晰的眼睛。
(4)Rs=50 Ts=50 M=2 a=0.2close all;alpha=0.2;Ts=5*1e-2;Fs=1e3;Rs=50;M=2;Num=100;Samp_rate=Fs/Rs;Eye_num=2;NRZ=2*randint(1,Num,M)-M+1;figure(1);stem(NRZ);title('双极性NRZ码元序列');Samp_data=zeros(1,Samp_rate*Num);for r=1:Num*Samp_rateif rem(r,Samp_rate)==0Samp_data(r)=NRZ(r/Samp_rate);endend[ht,a]=rcosine(1/Ts,Fs,'fir',alpha);figure(2);subplot(2,1,1);plot(ht);ylabel('冲激响应');title('升余弦滚降系统冲激响应');st=conv(Samp_data,ht)/(Fs*Ts);subplot(2,1,2);plot(st);ylabel('信号幅度');title('经过升余弦滚降系统后的码元');figure(3);for k=10:floor(length(st)/Samp_rate)-10ss=st(k*Samp_rate+1:(k+Eye_num)*Samp_rate);plot(ss);hold on;endylabel('信号幅度');眼图基本闭合,存在较为严重的码间干扰,这是因为码元速率Rs虽然仍为50Baud,但滤波器等效带宽已经变为12Hz(Ts=50ms),Rs>2B不再满足奈奎斯特第一准则。
