吉林大学历届高数考题及答案
吉林大学经管类高等数学CII资料

2.设可导函数 f ( x) 满足
f ( x) cos x 2 f (t )sin tdt x 1
0 x
求 f ( x) .
(共 6 页
第 3 页 )
3.设平面区域 D ( x, y) x 2 y 2 1, x 0 ,计算二重积分
D
1 xy dxdy . 1 x2 y 2
0
4 − r 2 dr
(共 6 页
(D)
∫
2π
0
dθ ∫
2
0
4 − r 2 dr
第 1 页 )
5. 设空间区域 Ω = {( x, y, z ) x 2 + y 2 + z 2 ≤ 2, z ≥ x 2 + y 2 } , f ( x, y, z ) 为连续函 数,则三重积分
∫∫∫ f ( x, y, z)dV = (
.
6. 微分方程 y 3 y 2 y 0 的通解为
(共 6 页
第 2 页 )
得 分
三、按要求解答下列各题(共 4 道小题,每小题 8 分,满分 32 分). 1.设 f 为 C (2) 类函数,且 z f ( x y, x y) ,求 d z 和
2 z . xy
即 f ′( x) = − f ( x) tan x + sec x ……………3 分 解得
f ( x) = C cos x + sin x ……………6 分
由 f (0) = 1 得 C = 1
f ( x) = cos x + sin x ……………8 分
3.设平面区域 D = ( x, y ) x 2 + y 2 ≤ 1, x ≥ 0 ,计算二重积分 ∫∫
高等数学I试题解答 吉大大一

高等数学I 试题解答一、1.解:cos ()()0y yy y x e xe y x ''⋅++=y xe e x y yycos )(+-=',1)0(-='y2.解: ⎰+dx x x )cos (sin5dxx xdx ⎰⎰+=cos sin 53.解:⎰⎰+-+=+6 2 624111421412dxx x dx x x4.解:3sin sin sin 2 22 2=-==⎰⎰⎰dx x dx x dx x S ππππππ二、1.解:2)ln(limnx m be a x x +++∞→n nx be a nx m be x x x 1)()(lim 2=++=+∞→2.解:因1)1(-=y ,得2-=++c b a 。
b ax x x y ++='23)(2,a x x y 26)(+=''。
由0)1(=''y 得3-=a ,由0)0(='y 得0=b ,所以1=c 。
由)2(363)(2-=-='x x x x x y ,易得2=x 是)(x y 的极小值点,3)2(-=y 。
3.解:t t dxdy -+-=11,323222)1(2121)11(y t tt t dx y d -=--=+'-+-=,即02223=+dx y d y 。
三、解:令()2sin [0,]f x x x k C =--∈+∞所以)(x f 在)3,0(+k 有一正根,即方程k x x =-sin 2至少有一正根。
x四、解:如图,设切点为00(,)M x y (026x <<),01)(x x y =',切线方程:0ln 1x x xy +-=00ln 16)6(x x y +-=,所以所求图形的面积为)14(4)(020x x x S +-=',令0)(0='x S ,得唯一驻点40=x 。
吉林大学考试复习试题高等数学

高等数学(一)机考复习题一.单项选择题(在每小题列出的四个选项中只有一个选项是符合题目要求的,请将正确选项前的字母填在题干后的括号内.)1.函数y=x 1-+arccos21x +的定义域是(B) A.x<1B.-3≤x ≤1 C.(-3,1)D.{x|x<1}∩{x|-3≤x ≤1} 2.下列函数中为奇函数的是(D )A.y=cos 3xB.y=x 2+sinxC.y=ln(x 2+x 4)D.y=1e 1e x x+-3.设f(x+2)=x 2-2x+3,则f[f(2)]=(D) A.3B.0 C.1D.24.y=的反函数是xx 323+(C)A.y=233xx +-- B.y=xx 332+ C.y=log 3x 1x 2- D.y=log 3x2x1-5.设n n u ∞→lim =a,则当n →∞时,u n 与a 的差是(A )A .无穷小量B.任意小的正数C .常量D.给定的正数6.设f(x)=⎪⎪⎩⎪⎪⎨⎧<>0x ,x 1sin x 0x ,x1sin ,则)x (f lim 0x +→=(D )A .-1B.0 C.1D.不存在 7.当0x →时,x cos x sin 21是x 的(A)A.同阶无穷小量B.高阶无穷小量C.低阶无穷小量D.较低阶的无穷小量8.x21sinx 3lim x •∞→=(D) A.∞B.0 C.23D.329.设函数⎩⎨⎧≤<-≤<-=3x 1,x 21x 0,1x )x (f 在x=1处间断是因为(D)A.f(x)在x=1处无定义B.)x (f lim 1x -→不存在C.)x (f lim 1x +→不存在D.)x (f lim 1x →不存在10.设f(x)=⎩⎨⎧≥+<0x )x 1ln(0x ,x ,则f(x)在x=0处(B)A.可导B.连续,但不可导C.不连续D.无定义 11.设y=2cosx ,则y '=(C)A.2cosx ln2B.-2cosx sinxC.2cosx (ln2)sinxD.-2cosx-1sinx12.设f(x 2)=)x (f ),0x (x11'≥+则=(C) A.-2)x 1(1+ B.2x 11+ C.-2)x 1(x 21+ D.2)x 1(x 21+13.曲线y=1x x132=在处切线方程是(D)A.3y-2x=5B.-3y+2x=5C.3y+2x=5D.3y+2x=-514.设y=f(x),x=e t,则22dt y d =(D)A.)x (f x 2''B.)x (f x 2''+)x (f x 'C.)x (f x ''D.)x (f x ''+xf(x)15.设y=lntg x ,则dy=(D)A.xtg dx B.xtg x d C.dx xtg x sec 2 D.xtg )x tg (d16.下列函数中,微分等于xln x dx的是(B) A.xlnx+cB.21ln 2x+cC.ln(lnx)+cD.xxln +c 17.下列函数在给定区间满足拉格朗日中值定理条件的是(B)A.y=|x|,[-1,1]B.y=x1,[1,2]C.y=32x ,[-1,1]D.y=2x 1x -,[-2,2]18.函数y=sinx-x 在区间[0,π]上的最大值是(A)A.22B.0C.-πD.π 19.下列曲线有水平渐近线的是(B ) A.y=e x B.y=x 3 C.y=x 2D.y=lnx20.⎰-2x x dee =(A)A.-c e 21x 2+ B.-c e 2x+C-c e 212x +- D.c e 412x+-21.⎰=dx 2x3(A)A.c 2ln 231x 3+ B.31(ln2)23x+cC.3123x +cD.c 2ln 2x3+ 22.⎰+πdx )14(sin=(D) A.-cos4π+x+cB.-c x 4cos 4++ππ C.c 14sin x ++πD.c x 4sin x ++π 23.⎰-)x cos 1(d =(C)A.1-cosxB.x-sinx+cC.-cosx+cD.sinx+c24.⎰-aax 〔f(x)+f(-x)〕dx=(C)A.4⎰axf(x)dxB.2⎰ax 〔f(x)+f(-x)〕dxC.0D.以上都不正确25.设F(x)=⎰-x adt )t (f a x x,其中f(t)是连续函数,则)x (F lim a x +→=(C)A.0B.aC.af(a)D.不存在26.下列积分中不能直接使用牛顿—莱布尼兹公式的是(D)A.⎰+10xe 1dx B.⎰π40tgxdx C.dx x 1x 12⎰+ D.⎰π40ctgxdx27.设f(x)=⎩⎨⎧≤≤<≤-1x 0,20x 1,1,则⎰-11dx )x (f 21=(B)A.3B.23C.1D.228.当x>2π时,⎰π'x2dt )ttsin (=(C) A.x x sin B.x x sin +cC x x sin -π2D.xx sin -π2+c29.下列积分中不是广义积分的是(A)A.⎰-2122)x 1(dx B.⎰e1xln x dxC.⎰-113xdx D.⎰+∞-0x dx e30.下列广义积分中收敛的是(D)A.⎰+∞xdx sin B.⎰-11xdx C.⎰--012x 1dx D.⎰∞--0x dx e31.下列级数中发散的是(D)A.∑∞=--1n 1n n 1)1( B.∑∞=-++-1n 1n )n 11n 1()1( C.∑∞=-1n nn1)1( D.∑∞=-1n )n1(32.下列级数中绝对收敛的是(A)A.∑∞=--1n 1n nn )1( B.∑∞=--1n 1n n1)1(C.∑∞=-3n n n ln )1( D.∑∞=--1n 321n n )1(33.设+∞=∞→n n u lim ,则级数)u 1u 1(1n 1n n ∑∞=+-(A) A.必收敛于1u 1B.敛散性不能判定C.必收敛于0D.一定发散 34.设幂级数∑∞=-0n n n )2x (a 在x=-2处绝对收敛,则此幂级数在x=5处(C)A.一定发散B.一定条件收敛C.一定绝对收敛D.敛散性不能判定35.设函数z=f(x,y)的定义域为D={(x,y)|0≤x ≤1,0≤y ≤1},则函数f(x 2,y 3)的定义域为(B)A.{(x,y)|0≤x ≤1,0≤y ≤1}B.{(x,y)|-1≤x ≤1,0≤y ≤1}C.{(x,y)|0≤x ≤1,-1≤y ≤1}D.{(x,y)|-1≤x ≤1,-1≤y ≤1}36.设z=(2x+y)y,则=∂∂)1,0(xz (B)A.1B.2C.3D.037.设z=xy+yx,则dz=(A)A.(y+dy )yx x (dx )y12-+ B.dy )y 1y (dx )yxx (2++- C.(y+dy )yx x (dx )y12++ D.dy )y 1y (dx )y xx (2+++38.过点(1,-3,2)且与xoz 平面平行的平面方程为(C)A.x-3y+2z=0B.x=1C.y=-3D.z=239.⎰⎰≤≤-≤≤1y 11x 0dxdy=(C)A.1B.-1C.2D.-240.微分方程y x 10y +='的通解是(D)A.c 10ln 1010ln 10y x =--B.c 10ln 1010ln 10y x =- C.10x +10y =cD.10x +10-y =c 41.设函数f )x1x (+=x 2+2x 1,则f(x)=(B )A .x 2B .x 2-2C .x 2+2D .24x 1x +42.在实数范围内,下列函数中为有界函数的是(B ) A .e x B .1+sinxC .lnx D .tanx43.=++++∞→2x 1x x limx (C )A .1B .2C .21D .∞44.函数f(x)=⎪⎩⎪⎨⎧=≠0x ,00x ,x1sin x ,在点x=0处(D ) A .极限不存在 B .极限存在但不连续C .可导D .连续但不可导45.设f(x)为可导函数,且1x2)x (f )x x (f lim000x =∆-∆+→∆,则=')x (f 0(C ) A .1 B .0 C .2 D .2146.设F(x)=f(x)+f(-x),且)x (f '存在,则)x (F '是(A )A .奇函数B .偶函数C .非奇非偶的函数D .不能判定其奇偶性的函数47.设y=xxln ,则dy=(C ) A .2x x ln 1- B .dx x x ln 12-C .2x 1x ln - D .dx x 1x ln 2-48.函数y=2|x |-1在x=0处(D)A.无定义B.不连续C.可导D.连续但不可导49.下列四个函数中,在[-1,1]上满足罗尔定理条件的是(B )A .y=|x|+1B .y=4x 2+1 C .y=2x 1D .y=|sinx|50.函数y=3x3x ln2-+的水平渐近线方程是(C ) A .y=2 B .y=1 C .y=-3 D .y=051.若)x (F '=f(x),则⎰'dx )x (F =(C ) A .F(x)B .f(x)C .F(x)+CD .f(x)+C52.设f(x)的一个原函数是x ,则⎰xdx cos )x (f =(A )A .sinx+CB .-sinx+CC .xsinx+cosx+CD .xsinx -cosx+C53.设F(x)=dt te 1xt 2⎰-,则)x (F '=(D )A .2x xeB .2x xe -C .2x xe -D .2x xe --54.设广义积分⎰+∞α1x1发散,则α满足条件(A )A .α≤1B .α<2C .α>1D .α≥155.设z=cos(3y -x),则xz∂∂=(A ) A .sin(3y -x) B .-sin(3y -x)C .3sin(3y -x)D .-3sin(3y -x)56.函数z=x 2-y 2+2y+7在驻点(0,1)处(C )A .取极大值B .取极小值C .无极值D .无法判断是否取极值57.设D={(x,y)|x ≥0,y ≥0,x+y ≤1},⎰⎰⎰⎰βα+=+=D2D1dxdy )y x (I ,dxdy )y x (I ,0<α<β,则(A )A .I 1>I 2B .I 1<I 2C .I 1=I 2D .I 1,I 2之间不能比较大小58.级数5n 7n)1(1n 1n --∑∞=-的收敛性结论是(A )A .发散B .条件收敛C .绝对收敛D .无法判定59.幂级数n1n n x 3n 3∑∞=+的收敛半径R=(C )A .41B .4C .31D .360.微分方程y ln y y x ='的通解是(C )A .e x +CB .e -x +CC .e CxD .e -x+C61.下列集合中为空集的是( D )A.{x|e x =1}B.{0}C.{(x,y)|x 2+y 2=0}D.{x|x 2+1=0,x ∈R}62.函数f(x)=2x 与g(x)=x 表示同一函数,则它们的定义域是( B )A.(]0,∞-B.[)+∞,0C.()+∞∞-,D.()+∞,063.函数f(x)==π-⎩⎨⎧≥<)4(f ,1|x |,01|x ||,x sin |则( C )A.0B.1C.22D.-22 64.设函数f(x)在[-a,a](a>0)上是偶函数,则f(-x)在[-a,a]上是( B )A.奇函数B.偶函数C.非奇非偶函数D.可能是奇函数,也可能是偶函数65.=+→)2x (x x2sin lim0x ( A ) A.1 B.0 C.∞ D.266.设2x10x e )mx 1(lim =-→,则m=( B )A.21 B.2 C.-2D.21-67.设f(x)=⎩⎨⎧=≠2x ,12x ,x 2,则=→)x (f lim 2x ( D )A.2B.∞C.1D.468.设x1e y -=是无穷大量,则x 的变化过程是( B )A.x →0+B.x →0-C.x →+∞D.x →-∞69.函数在一点附近有界是函数在该点有极限的( A )A.必要条件B.充分条件C.充分必要条件D.无关条件70.定义域为[-1,1],值域为(-∞,+∞)的连续函数( B )A.存在B.不存在C.存在但不唯一D.在一定条件下存在71.下列函数中在x=0处不连续的是( B )A.f(x)=⎪⎩⎪⎨⎧=≠0x ,10x ,|x |xsinB.f(x)=⎪⎩⎪⎨⎧=≠0x ,00x ,x1sin x C.f(x)=⎩⎨⎧=≠0x ,10x ,e xD.f(x)=⎪⎩⎪⎨⎧=≠0x ,00x ,x1cos x 72.设f(x)=e 2+x,则当△x →0时,f(x+△x)-f(x)→( D )A.△xB.e 2+△xC.e 2D.0 73.设函数f(x)=⎪⎩⎪⎨⎧<-≥0x ,1x 0x ,e 2x ,则=---→0x )0(f )x (f lim 0x ( C ) A.-1 B.-∞C.+∞ D.174.设总收益函数R(Q)=40Q-Q 2,则当Q=15时的边际收益是( B )A.0B.10C.25D.37575.设函数f(x)=x(x-1)(x-3),则f '(0)=( C )A.0B.1C.3D.3!76.设y=sin 33x,则y '=( D )A.3x sin 32B.3x sin 2C.3xcos 3x sin 32D.3xcos 3x sin 277.设y=lnx,则y (n)=( C )A.(-1)n n!x -nB.(-1)n (n-1)!x -2nC.(-1)n-1(n-1)!x -nD.(-1)n-1n!x -n+178.=)x (d )x (sin d 2( D ) A.cosx B.-sinxC.2xcos D.x2xcos 79.f '(x)<0,x ∈(a,b),是函数f(x)在(a,b)内单调减少的( C )A.充分条件B.必要条件C.充分必要条件D.无关条件80.函数y=|x-1|+2的极小值点是( B )A.0B.1C.2D.381.函数y=2ln3x3x -+的水平渐近线方程为( C ) A.y=2 B.y=1 C.y=-3 D.y=082.设f(x)在[a,b](a<b)上连续且单调减少,则f(x)在[a,b]上的最大值是( A )A.f(a)B.f(b)C.)2ba (f + D.)3a2b (f + 83.=-⎰2)3y 2(dy( D ) A.C )3y 2(613+--B.C )3y 2(613+- C.C 3y 21+- D.C )3y 2(21+--84.设f(x)在(-∞,+∞)上有连续的导数,则下面等式成立的是( B )A.⎰+='C )x (f dx )x (f x 22B.⎰+='C )x (f 21dx )x (f x 22 C.⎰=')x (f 21)dx )x (xf (22D.⎰=)x (f dx )x (xf 2285.⎰=)tgx (xd sin ln ( A ) A.tgxlnsinx-x+CB.tgxlnsinx+x+CC.tgxlnsinx-⎰xcos dxD.tgxlnsinx+⎰xcos dx86.=+⎰--21dx 3x x( B )A.-1-3ln2B.-1+3ln2C.1-3ln2D.1+3ln2 87.⎰=π210dx )x 2(tg ( C ) A.2ln 21- B.2ln 21 C.2ln 1πD.2ln 1π-88.经过变换x t =,⎰=-94dx 1x x ( D )A.⎰-94dt 1t tB.⎰-942dt 1t t2 C.⎰-32dt 1t tD.⎰-322dt 1t t 2 89.⎰∞+-=1x dx e x1( A )A.e2B.-e2C.2eD.-2e90.⎰=-211x dx ( A )A.2B.1C.∞D.3291.级数∑∞=-1n nn25)1(的和等于( B )A.35B.-35C.5 D.-592.下列级数中,条件收敛的是( C )A.∑∞=--1n n 1n )32()1(B.∑∞=-+-1n 21n 2n n )1(C.∑∞=--1n 31n n1)1(D.∑∞=--1n 31n n51)1(93.幂级数∑∞=---1n n1n n)1x ()1(的收敛区间是( A ) A.(]2,0 B.(]1,1- C.[]0,2-D.()+∞-∞,94.点(-1,-1,1)在下面哪一张曲面上( D )A.z y x 22=+B.z y x 22=-C.1y x 22=+D.z xy = 95.设f(u,v)=(u+v)2,则)yx ,xy (f =( B )A.22)x1x (y + B.22)y1y (x + C.2)y1y (x + D.2)x1x (y +96.设)x2y x ln()y ,x (f +=,则=')0,1(f y ( A ) A.21 B.1 C.2 D.097.设22y xy 3x 2z -+=,则=∂∂∂yx z2( B )A.6B.3C.-2D.298.下列函数中为微分方程0y y =+'的解的是( C )A.x eB.-x eC.x e -D.x e +x e -99.下列微分方程中可分离变量的是( B )A.2x x ydx dy += B.y xydx dy += C.)0k (1)b y )(a x (k dxdy≠+++=, D.x y sin dxdy=- 100.设D :0≤x ≤1,0≤y ≤2,则⎰⎰+Ddxdy x1y=( D )A.ln2B.2+ln2C.2D.2ln2101.设函数f(x)=x x x kx +-≠=⎧⎨⎪⎩⎪4200,,在点x=0处连续,则k 等于(B) A.0B.14C.12D.2102.设F(x)是f(x)的一个原函数,则∫e -x f(e -x )dx 等于(B)A.F(e -x)+cB.-F(e -x)+cC.F(e x )+cD.-F(e x )+c103.下列函数中在区间[-1,1]上满足罗尔中值定理条件的是(C)A.y=1xB.y=|x|C.y=1-x 2D.y=x -1104.设f t dt x()0⎰=a 2x -a 2,f(x)为连续函数,则f(x)等于(D)A.2a2xB.a 2x lnaC.2xa2x -1D.2a 2xlna105.下列式子中正确的是(B)A.e dx e dx x x 0112⎰⎰≤B.e dx e dx x x 01012⎰⎰≥C.e dx e dx x x 01012⎰⎰=D.以上都不对106.下列广义积分收敛的是(D)A.cos 1+∞⎰xdx B.sin 1+∞⎰xdx C.ln xdx 1+∞⎰ D.121xdx +∞⎰107.设f(x)=e x --21,g(x)=x 2,当x →0时(C)A.f(x)是g(x)的高阶无穷小B.f(x)是g(x)的低阶无穷小C.f(x)是g(x)的同阶但非等价无穷小D.f(x)与g(x)是等价无穷小108.交换二次积分dy f x y dx yy(,)⎰⎰01的积分次序,它等于(B)A.dx f x y dy xx(,)⎰⎰01B.dx f x y dy xx(,)201⎰⎰C.dx f x y dy xx(,)⎰⎰01D.dx f x y dy xx (,)21⎰⎰109.若级数n n u =∞∑1收敛,记S n =i ni u ∑∞=,则(B)A.lim n n S →∞=0B.lim n n S S →∞=存在C.lim n n S →∞可能不存在D.{S n }为单调数列110.对于微分方程y ″+3y ′+2y=e -x ,利用待定系数法求其特解y *时,下面特解设法正确的是(D)A.y *=ae-xB.y *=(ax+b)e -xC.y *=axe -xD.y *=ax 2e -x二.判断题(正确的在括弧里用R 表示,错误的在括弧里用F 表示。
吉林大学高数b下作业答案

第一次作业学院 班级 姓名 学号一、单项选择题 1.22003limx y xyx y →→=+( D ). (A )32; (B )0; (C )65; (D )不存在.2.二元函数⎪⎩⎪⎨⎧=≠+=)0,0(),(,0)0,0(),(,),(22y x y x y x xyy x f 在)0,0(处( C ).(A )连续,偏导数存在; (B )连续,偏导数不存在; (C )不连续,偏导数存在;(D )不连续,偏导数不存在.3.设22(,)(1)(2)f x y y x x y =-+-,在下列求(1,2)x f 的方法中,不正确的一种是( B ).(A )因2(,2)2(1),(,2)4(1)x f x x f x x =-=-,故1(1,2)4(1)|0x x f x ==-=; (B )因(1,2)0f =,故(1,2)00x f '==;(C )因2(,)2(1)(2)x f x y y x y =-+-,故12(1,2)(,)0x x x y f f x y ====;(D )211(,2)(1,2)2(1)0(1,2)lim lim 011x x x f x f x f x x →→---===--.4.若(,)f x y 的点00(,)x y 处的两个偏导数都存在,则( C ). (A )(,)f x y 在点00(,)x y 的某个邻域内有界; (B )(,)f x y 在点00(,)x y 的某个邻域内连续;(C )0(,)f x y 在点0x 处连续,0(,)f x y 在点0y 处连续; (D )(,)f x y 在点00(,)x y 处连续.5.设22(,),2zz f x y y∂==∂,且(,0)1,(,0)y f x f x x ==,则(,)f x y 为( B ).(A )21xy x -+; (B )21xy y ++; (C )221x y y -+; (D )221x y y ++. 二、填空题1.z =的定义域为2224,01y x x y ≤<+<. 2.00x y →→= 1/2 .3.设22),(y x y x y x f +-+=,则=')4,3(x f 2/5,=')4,3(y f 1/5 . 4.设ln(32)u x y z =-+,则d u =3232dx dy dzx y z-+-+.5.设yz x =,则2z x y∂=∂∂()11ln y x y x -+. 三、计算题1.已知2)z f =,且当1y =时z x =,求()f t 及z 的表达式.将1,y z x ==代入,)12x f =+有)21fx =-解一:)))222423f=-+ ∴()243f t t t =-+解二:令2t =,则()22x t =-∴()()221f t t =--∴)22211z x =--=-2.讨论函数2222222,0,(,)0,0x xyx y f x y x y x y ⎧++≠⎪=+⎨⎪+=⎩的连续性..解一:当(),p x y 沿y 轴(x=0)趋于0(0,0)时,222200limlim0x y y x xyx y y →→→+==+ 当(),p x y 沿y x =,趋于0(0,0)时,222220002lim lim 12x x y x x xy x x y x →→=→+==+ ∴()00lim,x y f x y →→不存在 ∴不连续解二:当(),p x y 沿y kx =趋于0(0,0)时,()()222222200011lim lim 11x x y kx k x x xy k x y k k x →→=→+++==+++ 与k 有关,∴不连续 3.设(1)y z xy =+,求d z .()()11211y y z y xy y y xy x--∂=⋅+⋅=+∂ 解一:取对数()ln ln 1z y xy =+()1ln 11z x xy y z y xy ∂⋅=++⋅∂+,∴()()1ln 11y z xy xy xy y xy ⎡⎤∂=+++⎢⎥∂+⎣⎦解二:()()()()ln 1ln 1e ,e ln 111y y xy y xy z x xy y xy y xy ++⎡⎤∂∂==⋅++⋅=+⎢⎥∂+⎣⎦∴()()()12d 1d 1ln 1+xy d 1y y x z y xy x xy y xy -⎡⎤=++++⎢⎥+⎣⎦4.求2e d yzt xz u t =⎰的偏导数.t220e e xzyzt u dt dt =-+⎰⎰22x z e u z x ∂=-⋅∂ 22y e z u z y∂=⋅∂ 2222x y e e z z u x y z∂=-⋅+⋅∂5.设r =0r ≠时,有2222222r r r x y z r∂∂∂++=∂∂∂.r x x r ∂==∂ 222223xr x rr x r xr r -⋅∂-==∂,同理:2222222323,r r y r r z y r z r ∂-∂-==∂∂∴()2222222222233322r x y x r r r r x y z r r r-++∂∂∂++===∂∂∂6.证明函数(,)f x y =(0, 0)处:(1)连续;(2)偏导数存在;(3)不可微.(1)0ε∀>0=≤0ε-<ε<取δ=,则当0δ<<0ε<,∴()()000lim ,lim00,0x x y y f x y f →→→→===(或:()00lim00,0x y f →→==),(),f x y =(2)()(),00,0,0x f x f =;()()0,0,0,00y f y f == (3)()(),0,00,0x y z x y z f x f y x y =⋅-⋅-=⋅考察:()()()(22200limlimxx y y x yx yx x y →→→→⋅⋅=++当(),p x y 沿直线y kx =趋于0(0,0)有00limlim1x x y k x k→→=⋅→=+与k 有关∴上式不存在,不可微第二次作业学院 班级 姓名 学号一、单项选择题 1.设22()y z f x y =-,其中()f u 为可导函数,则zx∂∂=( B ). (A )2222()xyf x y --;(B )222222()()xyf x y f x y '---;(C )22222()()yf x y f x y '---;(D )2222222()()()f x y yf x y f x y '-----.2.设方程(,,)0F x y y z z x ---=确定z 是x ,y 的函数,F 是可微函数,则z x∂∂=( D ).(A )13F F '-'; (B )13F F ''; (C )x zy zF F F F --;(D )1323F F F F ''-''-.3.设(,),(,),(,)x x y z y y z x z z x y ===都由方程(,,)0F x y z =所确定的隐函数,则下列等式中,不正确的一个是( C ).(A )1x yy x∂∂=∂∂; (B )1x zz x∂∂=∂∂; (C )1x y zy z x∂∂∂=∂∂∂;(D )1x y zy z x∂∂∂=-∂∂∂.4.设(,),(,)u u x y v v x y ==都是可微函数,C 为常数,则在下列梯度运算式中,有错误的是( A ).(A )0C ∇=;(B )()Cu C u ∇=∇; (C )()u v u v ∇+=∇+∇;(D )()uv v u u v ∇=∇+∇.5.()u f r =,而r =,且函数()f r 具有二阶连续导数,则22ux∂+∂2222u uy z ∂∂+=∂∂( B ). (A )1()()f r f r r '''+;(B )2()()f r f r r '''+; (C )211()()f r f r r r'''+;(D )212()()f r f r r r '''+.二、填空题1.已知(1,2)4,d (1,2)16d 4d ,d (1,4)64d 8d f f x y f x y ==+=+,则(,(,))z f x f x y =在点(1, 2)处对x 的偏导数为 192 .2.由方程e z xy yz zx -+=所确定的隐函数(,)z z x y =在点(1, 1)处的全微分为 d dy x +.3.r 在点(0, 0)处沿x 轴正向的方向导数为 1 . 4.函数2222u x y z xy yz =++-+在点(1,2,3)--三、计算与解答题 1.设f 是C (2)类函数,22(e ,)xyz f x y =-,求2zx y∂∂∂.''''[1212e 2e 2xy xy zf y f x y f xf x∂=⋅⋅+⋅=+∂ ()()2''"''''''1111122122e e e e 22e 2xy xy xy xy xy z f y xf y f x f y x f x f y x y∂⎡⎤⎡⎤=+⋅⋅+⋅+⋅-+⋅⋅+⋅-⎣⎦⎣⎦∂∂ ()()'2"22""11112221e e 2e 4xy xy xy xy f xy f x y f xyf =+++-- 2.设32(32)x y z x y -=-,求d z .解一:()()()()()()()d ln d 32ln 32,1d d 3x-2y ln 3232d ln 32z x y x y z x y x y x y z=-⋅-=⋅-+-⋅- ()()()32d 32ln 3213d 2dy x yz x y x y x -=--+-⎡⎤⎣⎦解二:,32,32vz u u x y v x y ==-=- ()()3213332ln 321x yv x u x v x z z u z v v ux y x y --=⋅+⋅=⋅⋅=-⋅-+⎡⎤⎣⎦()()()321y 2232ln 321x yv u y v y z z u z v v u x y x y --=⋅+⋅=⋅⋅-=--⋅-+⎡⎤⎣⎦∴()()()32d 32ln 3213d 2dy x yz x y x y x -=--+-⎡⎤⎣⎦3.设f ,ϕ是C (2)类函数,x y z yf x y x ϕ⎛⎫⎛⎫=+ ⎪ ⎪⎝⎭⎝⎭,证明:(1)2220z z x y x x y ∂∂+=∂∂∂; (2)2222220z z x y x y ∂∂-=∂∂. 证21z y y yf x f x y x x ϕϕϕϕ∂⎛⎫''''=⋅++⋅⋅-=+- ⎪∂⎝⎭222222311z y y y y y f f x y x x x x yx ϕϕϕϕ∂⎛⎫⎛⎫''''''''''=⋅+⋅-+-⋅-=+ ⎪ ⎪∂⎝⎭⎝⎭2222111z x y x yf f x y y x x x x y x ϕϕϕϕ⎛⎫∂''''''''''=⋅-+⋅--=-- ⎪∂∂⎝⎭21z x xf y f x f f y y x y ϕϕ⎛⎫∂''''=+⋅-+⋅=-+ ⎪∂⎝⎭222222311z x x x x x f f f f y y y y y x y x ϕϕ⎛⎫⎛⎫∂'''''''''=⋅-+-⋅⋅-+⋅=+ ⎪ ⎪∂⎝⎭⎝⎭4.设arctan yx,求22d d y x .()''2222221122ln arctan ,221y x yyx y y x x y xx y y x -+⋅+=⋅=+⎛⎫+ ⎪⎝⎭''2222x yy y x yx y x y+-=++∴ ()(),x yy x y x y y x y+''-=-+=- ()()()()()()()()()()'''22"222321122x y x y y x y x y y x y y x y x y y x y x y x y x y ⎛⎫+⋅- ⎪+--+-⋅-+-⎝⎭====---- 一阶:()()22222222112,ln arctan ,221x yy x x y x F x y x y F x x y x y y x -+=+-=⋅-=++⎛⎫+ ⎪⎝⎭22222211221y y y x x F y x y x y x-=⋅-=+++∴d d y Fx x y x y x Fy y x x y ++=-=-=-- 二阶:()()()()222'2'""''"11/1,y x y x y yy y y x y y y x y x y+++-++⋅=+-==--()()()()()2222332x y x y x y x y x y +-++==--5.设e sin ,e cos ,uux u v y u v ⎧=+⎪⎨=-⎪⎩求,u v x y ∂∂∂∂. ()1d cos e sin cos e sin cos 1,sin d cos d d sin e cos sin u uu x u v v u v D u v v D u v x u v y y u v v u v+⎡⎤==-+==-⎣⎦- ∴()()1sin cos d d d sin cos 1sin cos 1u D v vu x y D e v v eu v v ==--+-+ ∴()sin e sin cos 1u u v x v v ∂=∂-+ ()2e sin d e sin d e cos d e -cos d u u u u v x D v y v x v y+==+--∴()()()2u cos e d e sin d d e sin -cos 1u uv x v y D v D u v v -++==⎡⎤+⎣⎦∴()e sin e sin cos 1u u v vy u v v ∂+=∂-+ 6.设2(,,),(,e ,)0,sin y u f x y z x z y x ϕ===,其中求f ,ϕ是C (1)类函数,求d d ux. ()()22''''223,,,e ,2,e ,y z F x y z x xz Fx x Fy F ϕϕϕϕ==⋅== ∴''12''332e ,y x z Fx z Fyx Fz y Fz ϕϕϕϕ∂∂=-=--=-=--∂∂ '''''12123''332e d cos cos d y x u f f x f x x ϕϕϕϕ⎛⎫=+⋅+--⋅ ⎪⎝⎭()''''sin '12312cos 2e cos x f f x f x x ϕϕ=+⋅++解二:全微分'''123'''123d d d d 2d e d d 0d cos d y u f x f y f zx x y z y x xϕϕϕ⎧=⋅++⎪⋅+⋅⋅+=⎨⎪=⎩即'''231'''231d d d d e d d 2d d cos d y u f y f z f x y z x x y x x ϕϕϕ⎧--=⎪+=-⎨⎪=⎩代入消元解得:'sin ''''12123'32cos d cos d x x e x u f f x f x ϕϕϕ⎛⎫+=+- ⎪⎝⎭∴…… 7.求函数ln()z x y =+的点(1, 2)处沿着抛物线24y x =的该点切线方向的方向导数.()()111,,1,21,23zx zy zx zy x y x y ====++()''1,221tan 1y y y α=====121233,,,4444ππααπββπ====11cos cos cos4παβ===223cos cos cos4παβ=== ∴()()()111,21111,2cos 1,2cos 32323zzx zy αβ∂=⋅+=+⋅=∂()()()221,22111,2cos 1,2cos 33zzx zy αβ⎛⎛∂=⋅+=⋅+= ∂⎝⎭⎝⎭第三次作业学院 班级 姓名 学号一、单项选择题1.在曲线23,,x t y t z t ==-=的所有切线中,与平面24x y z ++=平行的切线( B ). (A )只有一条;(B )只有两条;(C )至少有三条; (D )不存在.2.设函数(,)f x y 在点(0, 0)附近有定义,且(0,0)3,(0,0)1x y f f ==,则( C ). (A )d (0,0)3d d z x y =+;(B )曲面(,)z f x y =在点(0,0,(0,0))f 的法向量为{3,1,1}; (C )曲线(,),0z f x y y =⎧⎨=⎩在点(0,0,(0,0))f 的切向量为{1,0,3};(D )曲线(,),z f x y y =⎧⎨=⎩在点(0,0,(0,0))f 的切向量为{3,0,1}.3.曲面()z x f y z =+-的任一点处的切平面 ( D ). (A )垂直于一定直线;(B )平等于一定平面; (C )与一定坐标面成定角;(D )平行于一定直线.4.设(,)u x y 在平面有界闭区域D 上是C (2)类函数,且满足20ux y∂≠∂∂及22220u ux y ∂∂+=∂∂,则(,)u x y 的 ( B ). (A )最大值点和最小值点必定都在D 的内部; (B )最大值点和最小值点必定都在D 的边界上; (C )最大值点在D 的内部,最小值点在D 的边界上; (D )最小值点在D 的内部,最得到值点在D 的边界上. 二、填空题1.如果曲面6xyz =在点M 处的切平面平行于平面63210x y z -++=,则切点M 的坐标是 (-1,2,-3) .2.曲线2224914,1x y z x y z ⎧++=⎨++=⎩在点(1,1,1)-处的法平面方程是 13x -10y -3z -6=0 .3.22z x y =+在条件1x y +=下的极小值是12.4.函数u 在点(1,1,1)M 处沿曲面222z x y =+在该点的外法线方向的方向导数是13.三、计算题1.求曲线222226,x y z z x y ⎧++=⎪⎨=+⎪⎩在点(1,1,2)处的切线方程. 解一:22222yy zz x yy z x ''⎧+=-⎪⎨''-+=⎪⎩①② ①+②:0z '=代入(),1,1,21xy y y''=-=- ∴()1,1,0s =-切成:112110x y z ---==,即112x y z -=-⎧⎨=⎩ 解二:()()2221,,6,2,2,2,2,2,4F x y z x y z Fx x Fy y Fz z n =++-====取()1121,1,2,n s n n ==⨯()()222,,.2.2 1.2,2,1G x y z x y z Gx x Gy y n =+-===-=-1s 切平面:()()()1111220260x y z x y z ⋅-+⋅-+-=+-=即+2s 切平面:()()()21212020x y z x y z -+---=--=即:2+2∴2602220x y z x y z ++-=⎧⎨+--=⎩ 2.过直线102227,x y z x y z +-=⎧⎨+-=⎩作曲面222327x y z +-=的切平面,求其方程.解:设切点为0000(,,)M x y z ,切平面方程为:0003270x x y y z z +--=……① 过已知直线的平面束方程为()1022270x y z x y z λ+--++-= 即:()(10)2(2)270x y z λλλ++++---=……②当①②为同一平面时有:000103,2,2x y z λλλ+=+=--=-且222000327x y z +-=解得00000033117117x x y y z z ==-⎧⎧⎪⎪==-⎨⎨⎪⎪==-⎩⎩或对应的切平面方程为:927091717270x y z x y z +--=+-+=3.证明曲面2/32/32/32/3(0)x y z a a ++=>上任意点处的切平面在各个坐标轴上的截距平方和等于2a ..设000M x 0(,y ,z )为曲面上任一点 切平面方程为:()()111333000000222()0333x x x y y y z z z ----+-+-=即:11123333000x x y y z z a --++= 令0y z ==得x 轴截距1233x n a = 同理121233332,Y z a Z z a ==∴222422223333()X Y Z x y z a a ++=++=4.求函数22(,)(2)ln f x y x y y y =++的极值..①令222(2)02ln 10x yf x y f x y y '⎧=+=⎪⎨'=++=⎪⎩ ②得驻点10,e M ⎛⎫ ⎪⎝⎭③2212(2),4,2xx xy f y f xy fyy x y =+==+④M 处: AC-B 2>0,A>0,∴极小值110,f e e⎛⎫=-⎪⎝⎭5.求函数22(,)1216f x y x y x y =+-+在区域22{(,)|25}D x y x y =+≤上的最大值和最小值.2120621608fx x x fy y y =-==⎧⎧⎨⎨=+==-⎩⎩ 不在D 内,∴D 内无极值点 在边界2225x y +=上,(),251216f x y x y =-+()()22,25121625L x y x y x y λ=-+++-12201620Lx x Ly y λλ=-+=⎧⎨=+=⎩ 解得3344x x y y ==-⎧⎧⎨⎨=-=⎩⎩2225x y +=()3,475f -=- 最小()3,4125f -= 最大61的一个切平面,使其在三个坐标轴上的截距之积为最大. 设切点为()()0000,,,,,1M x y z F x y zFn Fy ==)))0000x x y y z z -+--=1=令0y z ==,得x轴截距X = 0x z ==,得y轴截距Y = 0x y ==,得z轴截距Z =XYZ ()),,1f x y z xyz λ=+令000113fx yz yzx x fy xz xzy y fz xy xyz z ⎧=+==⎪⎪⎪=+==⎪⎪⎨⎪=+==⎪==== 19x y z === 即切点为111,,999⎛⎫ ⎪⎝⎭切平面为:13x y z ++=第四次作业学院 班级 姓名 学号一、单项选择题1.设(,)f x y 连续,且(,)(,)d d Df x y xy f x y x y =+⎰⎰,其中D 是由0y =,2y x =,1x =所围区域,则(,)f x y 等于( C ).(A )xy ;(B )2xy ;(C )18xy +; (D )1xy +.2.设D 是xOy 平面上以(1, 1), (-1, 1)和(-1, -1)为顶点的三角形区域,D 1是D 的第一象限部分,则(cos sin )d d Dxy x y x y +⎰⎰等于( A ).(A )12cos sin d d D x y x y ⎰⎰;(B )12d d D xy x y ⎰⎰;(C );14cos sin )d d D xy x y x y +⎰⎰( (D )0.3.设平面区域22:14,(,)D x y f x y ≤+≤是在区域D 上的连续函数,则d d Df x y ⎰⎰等于 ( A ).(A )212()d rf r r π⎰;(B )21002()d ()d rf r r rf r r π⎡⎤+⎣⎦⎰⎰;(C )2212()d rf r r π⎰; (D )2122002()d ()d rf r r rf r r π⎡⎤+⎣⎦⎰⎰.4.设有空间区域22221:,0x y z R z Ω++≤≥及22222:x y z R Ω++≤,0x ≥,0y ≥,0z ≥,则( C ).(A )12d 4d x V x V ΩΩ=⎰⎰⎰⎰⎰⎰; (B )12d 4d y V y V ΩΩ=⎰⎰⎰⎰⎰⎰;(C )12d 4d z V z V ΩΩ=⎰⎰⎰⎰⎰⎰;(D )12d 4d xyz V xyz V ΩΩ=⎰⎰⎰⎰⎰⎰.二、填空题1.积分2220d e d y x x y -=⎰⎰()-411e 2-. 2.交换积分次序:14012d (,)d d (,)d x x f x y y x f x y y -+=⎰⎰⎰⎰()2221d ,d y yy f x y x +-⎰⎰.3.设区域D 为||||1x y +≤,则(||||)d d Dx y x y +=⎰⎰43. 4.设区域D 为222x y R +≤,则2222d d Dx y x y a b ⎛⎫+= ⎪⎝⎭⎰⎰422114R a b π⎛⎫+ ⎪⎝⎭.5.直角坐标中三次积分22110d (,,)d x y I x y f x y z z +-=⎰⎰⎰在柱面坐标中先z 再r 后θ顺序的三次积分是()221d d cos ,sin ,d r r f r r z r z πθθθ⎰⎰⎰三、计算题1.计算|cos()|d d Dx y x y +⎰⎰,其中D 是由直线,0,2y x y x π===所围成的三角形区域.原式()()12cos d d cos d d D D x y x y x y x y =+-+⎰⎰⎰⎰()()42204d cos d d cos d yxyxx y x y x x x y y πππππ--=+-+⎰⎰⎰⎰()()422024sin d sin yxyx x y y x y πππππ--=+-+⎡⎤⎡⎤⎣⎦⎣⎦⎰⎰4204sin sin 2d sin 2sin d 22y y x x πππππ⎛⎫⎛⎫=--- ⎪ ⎪⎝⎭⎝⎭⎰⎰=[][]240411cos 2cos 2122242y x ππππππ+++=- 2.计算sin d d Dx yx y y⎰⎰,其中D 是由2y x =和y x =所围成的区域. ①图交点,先x,②:01y x D y ⎧≤≤⎪⎨≤≤⎪⎩③21100sin sin d d d 22y y y y F f x y y y ⎛⎫==⋅- ⎪⎝⎭⎰⎰110011sin d sin d 22y y y y y =-⎰⎰()()111cos1cos1sin 22x =-+-()11sin12=-3.计算22()d d Dx y x y +⎰⎰,其中{(,)|02,D x y x y =≤≤≤.①图,极坐标,方程②2cos 2:02r D θπθ≤≤⎧⎪⎨≤≤⎪⎩ ③22202cos d d I r r r πθθ=⋅⎰⎰()24422002cos d =41cos d 4r ππθθθθ⎡⎤=-⎢⎥⎣⎦⎰⎰3135442242244πππππ=⋅-⋅⋅⋅=-=4.计算23d xy z V Ω⎰⎰⎰,其中Ω是由曲面z xy =与平面,1y x x ==和0z =所围成的闭或区域.①图,投影域Dxy②0:001z xy y y x ≤≤⎧⎪Ω≤≤⎨⎪≤≤⎩③1230d d d x xyI x y sy z z =⎰⎰⎰7115120001d d 728xy x x x x ⎡⎤==⎢⎥⎣⎦⎰⎰1112813364=⨯= 5.计算d I xyz V Ω=⎰⎰⎰,其中222{(,,)|1,0,0,0}x y z x y z x y z Ω=++≤≥≥≥.①图,已求坐标r=1②01:0202r πϕπθ⎧⎪≤≤⎪⎪Ω≤≤⎨⎪⎪≤≤⎪⎩③12220d d sin cos sin sin cos sin d I x r r r r r ππϕϕθϕθϕϕ=⋅⋅⋅⋅⋅⋅⎰⎰⎰135220sin cos d sin cos d d r r ππθθθϕϕϕ=⋅⋅⋅⋅⎰⎰⎰3220011111sin dsin sin d sin 662448ππθθϕϕ=⋅⋅⋅⋅=⋅⋅=⎰⎰6.设()d F t fV Ω=⎰⎰⎰,其中2222:,()x y z t f t Ω++≤在0t =可导,且(0)0f =,求4()lim t F t tπ+→. ()()2t20d d sin d F t f r r r ππθϕϕ=⋅⎰⎰⎰()2t20d sin d d f r r r ππθϕϕ=⋅⋅⋅⎰⎰⎰()204d tf r r r π=⋅⋅⎰()()2'4F t f t t π=⋅⋅∴()()()()()()02043000040lim lim lim lim '040t t t t F t f t t f t f t f f t t t t πππ→→→→⋅-+====- 四、证明题设函数)(x f 在闭区间],[b a 上连续且恒大于零,证明2d ()d ()()bbaaxf x x b a f x ≥-⎰⎰. 证明:设:a x bD a y b≤≤⎧⎨≤≤⎩∵2d d 0D x y ≥⎰⎰ 即:()()()()d d 2d d D Df x f y x y x y f y f x ⎡⎤+≥⎢⎥⎣⎦⎰⎰⎰⎰ ∴()()()()()211d d d d 2b bb b aaa a f x x y f y y xb a f y f x +⋅≥-⎰⎰⎰⎰∴()()()212d d 2bbaaf x x x b a f x ⋅≥-⎰⎰∴()()()21d d bbaaf x x x b a f x ⋅≥-⎰⎰第五次作业学院 班级 姓名 学号一、单项选择题1.设L 是圆周222x y a +=,则22()d n L x y s +=⎰(D ) . (A )2n a π;(B )12n a π+;(C )22n a π;(D )212n a π+.2.设L 是由(0, 0), (2, 0), (1, 1)三点连成的三角形边界曲线,则d L y s =⎰( A ).(A(B )2+(C )(D )2+3.设∑是锥面222x y z +=在01z ≤≤的部分,则22()d x y S ∑+=⎰⎰( D ). (A )1300d d r r πθ⎰⎰; (B )21300d d r r πθ⎰⎰;(C 1300d d r r πθ⎰;(D 21300d d r r πθ⎰.4.设∑为2222(0)x y z a z ++=≥,1∑是∑在第一卦限中的部分,则有(C ). (A )1d 4d x S x S ∑∑=⎰⎰⎰⎰;(B )1d 4d y S x S ∑∑=⎰⎰⎰⎰;(C )1d 4d z S x S ∑∑=⎰⎰⎰⎰;(D )1d 4d xyz S xyz S ∑∑=⎰⎰⎰⎰.二、填空题1.设曲线L 为下半圆y =22()d L x y s +=⎰1d π1LS =⋅⎰.2.设L 为曲线||y x =-上从1x =-到1x =的一段,则d L y s =⎰.3.设Γ表示曲线弧,,,(02)2t x t y t z t π==≤≤,则222()d x y z s Γ++=⎰332ππ23+. 4.设∑是柱面222(0)x y a a +=>在0z h ≤≤之间的部分,则2d x S ∑=⎰⎰3a h π.5.设∑是上半椭球面2221(0)94x y z z ++=≥,已知∑的面积为A ,则222(4936)d x y z xyz S ∑+++=⎰⎰36A .三、计算题 1.计算22ed x y L s +⎰,其中L 为圆周222x y a +=,直线y x =及x 轴在第一象限内所围成的扇形的整个边界.解:123222123:0,0::,02L L L L L y x a L x y a a L y x x =++=≤≤+==≤≤1e d e 1ax a L s x==-⎰⎰224a aL L as e ds e π==⎰⎰4aπ3e 1a L s x ==-⎰所以:原式=2(1-ae )+4aπa e2.2d z s Γ⎰,其中2222,:0.x y z a x y z ⎧++=Γ⎨++=⎩.(222d d d rrrx s y s z s ==⎰⎰⎰)2Γ222223d 1()d 31d 322π.33r r z sx y z s a s a a a π=++==⋅=⎰⎰⎰ 3.计算曲面积分()d xy yz zx S ∑++⎰⎰,其中曲面:z ∑=被柱面222x y x +=所截得部分。
吉林大学《高等数学》2021-2022学年第一学期期末试卷B

姓名:吉林大学2021-2022学年第一学期期末试卷学号:课程名称: 高等数学试卷: B 试卷共6 页院系:级 班一.填空题(每小题4分,共24分)1.若⎩⎪−>⎨=⎪≤⎧b x x f x e x ax(1),0(),02处处可导, 则a =, b =。
2. 若⎝⎭− ⎪=⎛⎫+→∞x a x a x xlim 4, 则a =。
3.已知f x )(可导,=df x arcsin ___________)(。
4. 若=f x x '(cos )sin 22,且=f (0)0,则f x ()=。
5.11342cos 32sin 2x x x x dx −⎰−+=。
6. 已知πf x dx ⎰=02(sin )1, 则π2(cos )f x dx ⎰=。
二.单项选择题(每小题4分,共24分)1.设当x f x x x e x x 211()11,1,01,−=−−≠=⎧⎨⎪⎩⎪ 则x =1是f (x )的( )A. 连续点B. 第一类间断点(跳跃间断点)C. 可去间断点D. 第二类间断点2.若a x x x f ax =+→])(3ln[lim20(其中a >0的常数),则必有( )A. )(lim 0x f x +→存在且不为0B. a x xx f )(lim 0+→存在且不为0 C. 20)(lim x x f x +→存在且不为0 D. a x x x f +→+20)(lim 存在且不为0 3.曲线32116132y x x x =+++在点(0,1)处的切线与x 轴交点的坐标为( )A. (-1,0)B. (0,61−)C. (1,0)D. (0,61)4.设f (x )是在点x 0=0的某个领域(0,)(0)δδ>内的连续函数,⎰=xdt t f x 0)()(φ,(0,)x δ∈,且0)(lim3>=→A x x f x (A 为常数),则( ) A. )0(φ是)(x φ的极小值; B. )0(φ是)(x φ的极大值C. )0(φ一定不是)(x φ的极值D. 不能断定)0(φ是不是)(x φ的极值5. 积分=⎰−dx e x ( )A. c ex+−B. ⎪⎩⎪⎨⎧<+≥+−−0,,x c e x c e x xC. ⎪⎩⎪⎨⎧<−+≥+−−0,20,x c e x c e x xD. ⎪⎩⎪⎨⎧<+−≥+−0,,x c e x c e x x6.方程20cos 0t x e dt −+=⎰⎰在[0,]2π区间中根的个数( )A. 0B. 1C. 2D. 3三.计算下列各题(每小题5分,共30分)1. 2)1(21limx x x x +−+→2. xx xdt e xt x −−⎰−→sin lim23.求函数(ln x y e =+的导数。
吉大高数作业及答案

1:1.32.3.44.2:1.单调增加2.单调减少3.无最大值4.无最小值3:1.2.3.4.4:1.可去间断点2.跳跃间断点3.无穷间断点4.非无穷型的第二类间断点5:1.2.3.4.6:1.2.3.4.7:1.2.3.4.8:下列函数中是隐函数的为()1.2.3.4.9:1.2.3.4.10:1.2.f(x)的间断点3.4.以上都不对窗体顶端1:正确错误2:正确错误3:正确错误4:正确错误5:正确错误6:正确错误7:正确错误8:正确错误9:正确错误10:正确错误窗体顶端1:下列各种计算中,不正确的是()1.2.3.4.2:1.12.03.1/24.23:1.2.3.4.4:1.2.3.4.5:幂函数的原函数一定是()。
1.幂函数2.指数函数3.对数函数4.幂函数或对数函数6:1.02.13.4.27:1.2.3.4.8:1.12.03.34.9:1.2.3.4. 10:1.-12.13.04.窗体顶端1:正确错误2:正确错误3:正确错误4:正确错误5:初等函数可导。
( )正确错误6:正确错误7:正确错误8:正确错误9:正确错误10:正确错误窗体顶端1:1.2.3.4.2:1.2.3.3:1.2.3.4.4:1.2.3.4.05:下列各式中正确的是()1.2.3.4.6:1.02.13.27:1.2.3.4.8:1.单调增加的2.先减后增3.先增后减4.单调减少的9:1.12.e3.4.10:1.02.13.-14.窗体顶端1:正确错误2:两个无穷大之和还是无穷大()正确错误3:正确错误4:正确错误5:正确错误6:正确错误7:正确错误8:正确错误9:正确错误10:正确错误窗体顶端1:1.充要条件2.充分条件3.必要条件4.无关的条件2:1.02.13.24.33:1.2.3.4.4:1.2.3.4.5:1.2.3.4.6:1.2.3.4.7:1.无间断点2.3.4.8:1.2.3.4.9:1.奇函数2.偶函数3.非奇非偶函数4.既是奇函数又是偶函数10:下列各种计算中,不正确的是()1.2.3.4.:正确错误2:正确错误3:正确错误4:常数与无穷大量的乘积仍为无穷大。
吉林大学考试复习试题高中起点数学复习题

高中起点数学复习题 一.多选题1. 已知},)14(|{},,)12(|{Z k k y y Y Z n n x x X ∈±==∈+==ππ,那么下列各式中不正确的是(ACD ). A .Y X ⊂B .Y X =C .Y X ⊃D .∅=Y X2.若函数1)1()1()(22+-+-=x m x m x f 是偶函数,则在区间]0,(-∞上)(x f 是(BC )A .不可能是增函数,也不可能是常函数B .增函数C .常函数D .减函数3.已知}3|),{(},311|),{(+===+-=kx y y x B x yy x A ,并且∅≠B A ,则k 的值是( BD )A .K ≠2B .K =2C .K ≠3 D.K =34.设集合},,{},,,,,{e a c Y e d c b a X ==,则这两个集合不满足的关系是( ABD )。
A.X Y X =⋂; B.Y Y X =⋃; C.X Y X =⋃; D.Y Y X X =⋂⋃)( 6.原点到直线2+=kx y 的距离2是,则k 等于 ( BD ) A.K ≠1 B.K =1 C.K ≠-1 D.K =-17.函数3519222+-=x x y 的定义域是 ( AD )A .25≠x B.25=x C.7=x D.7≠x 8.原点到直线2+=kx y 的距离2是,则k 等于( AB ) A. K = -1 B.K = 1 C.K ≠-1 D.K ≠1 9.已知13log <a ,则a 的取值范围是( BC ).A.-1<a<0B.0<a<1C.a>3D.a<310.已知}3{},4{2<=>=x x N x x M ,下列结论中不正确的是( BCD )A.R N M =⋃; B.}4{2>=⋃x x N M ;C.}32{<<=⋂x x N M ; D.}2{-<=⋂x x N M11. 函数)(x f y =在(0, 2)上是增函数,函数)2(+=x f y 是偶函数,则下列结论中不正确的是( B ).A .)27()25()1(f f f <<B .)25()1()27(f f f <<C .)1()25()27(f f f <<D .)27()1()25(f f f <<12.两直线542,0322=+=++y x y x k 没有公共交点,则K 值是( AB ) A .K=1 B .K=–1 C.K=2 D.K=–213.两平行线分别过)0,1(A ,)5,0(B 且距离为5,则它们的方程是( AD ) A.y=0 B.y=1 C.y=2 D.y=514.已知0},,{},2,,{2≠=++=a aq aq a N d a d a a M ,且N M =,则q 的值( A ) A .1=q B 。
2006—2013年吉林大学数学分析、高等代数考研试题与答案

大学2006年攻读硕士学位研究生入学考试试题数学分析卷一、(共 30 分)判断题1、若函数)(x f 在()b a ,上Riemann 可积,则 []2)(x f 在()b a ,上Riemann 也可积;2、若级数∑∞=1n n a 收敛,则级数∑∞=1n n a 也收敛;3、任何单调数列必有极限;4、数列(){}n1-的上、下极限都存在;5、区间 ()b a , 上的连续函数必能达到最小值;6、x sin 在整个实轴上是一致连续的;7、若函数()y x f ,沿着任何过原点的直线连续,则()y x f ,在()0,0连续; 8、若函数()x f 在点0x 取极小值,则()0x f '=0; 9、若()0x f '=0,()00<''x f ,则()x f 再点0x 取最大值; 10、向量场()222222,,x z z y y x ---是无源场。
二、(共 20 分)填空题1、设))(sin(z y x y x u +++=,则gradu =( );2、设),,(x z z y y x F +++=,则F div =();3、设),,-(xy z zx y yz x F --=,则F rot =( );4、设s 表示单位球面1222=++z y x ,则第一型曲边梯形ds x s⎰⎰2=();5、数列()⎭⎬⎫⎩⎨⎧+2211-n n n 的下极限为( );三、(共 20 分)计算下列极限1、n nk n k 1120061lim ⎪⎭⎫ ⎝⎛∑=∞→;2、()x x xx 31211lim30+-+→;3、()112007120061lim ++++∞→++n n n n n ;4、dx x x x n ⎰++∞→10221lim ; 四、(共 20 分)判断下列级数的敛散性1、∑∞=-1200520072006n n n n; 2、∑∞=1n n u ,其中0>n u ,()2211+≤-n n u u nn ,⋅⋅⋅=2,1n ; 五、(10 分)设函数)(x f 在[]1,0两次连续可微,满足0)1()0(==f f 且()01=⎰dx x f 。
吉林大学 2008-2009高数BII试题答案

吉林大学2008~2009学年第二学期《高等数学B Ⅱ》试卷参考答案(注:可根据实际情况对评分标准进行调整)一、单项选择题:1. 2.d x y . 3.1a <. 4.32. 5.8π. 6.12. 三、按要求解答下列各题1.求椭球面222239x y z ++=的平行于平面23210x y z -++=的切平面方程.解:设222239F x y z =++-,则4,6,2x y z F x F y F z '''=== ………2分于是椭球面222239x y z ++=上过点(,,)x y z 的切平面的法线向量{}2,3,n k x y z =平面23210x y z -++=的法向量{}12,3,2n =- ,且1//n n所以112,,x y z k k k==-= …………….4分 又点(,,)x y z 在椭球面上,代入得切点为(1,1,2),(1,1,2)---……………6分 从而所求切平面方程为2329x y z -+=± …………………………………8分2.设函数2(,)x z y f x y =+,其中f 具有二阶连续偏导数,求zx ∂∂和2z x y∂∂∂.解:121z f f x y∂''=+∂ ………………………………………………………4分 2212222231z x xf f f x y y y y∂'''''=---∂∂ ………………………………………8分 3.计算二重积分2222I [sin()e ]d d ,yDx x y x x y -=++⎰⎰其中D 是以(0,0),(1,1),(1,1)-为顶点的三角形闭区域.解:222222I sin()d d e d d 0e d d y yDDDx x y x y x x y x x y --=++=+⎰⎰⎰⎰⎰⎰ …4分 22122012I e d d d e d 13e y y y y Dx x y y x x ---⎛⎫===- ⎪⎝⎭⎰⎰⎰⎰ ……………………….8分4.将d e 1,0d ()1,02x x x x f x x ⎧⎛⎫-≠⎪ ⎪⎪⎝⎭=⎨⎪=⎪⎩展开成x 的幂级数,并求数项级数1(1)!n nn ∞=+∑的和.解:22111e 1112!12!3!xx x x x xx +++--==+++ ……………..4分所以d e 1d x x x ⎛⎫- ⎪⎝⎭=2123,(,)2!3!4!x x x +++∈-∞+∞ ………………..6分 1121d e 1e e 11(1)!d x x x x x n n x n x x x ∞===⎛-⎫-+=== ⎪+⎝⎭∑ ……………..……….8分5.计算曲面积分()333I c o s c o s c o s d xy z S αβγ∑=++⎰⎰ ,其中∑是球面2221x y z ++=,,,αβγ是∑在点(,,)x y z 处的外向法线的方向角.解法1:直接利用高斯公式222I 3()d x y z v Ω=++⎰⎰⎰ ………………………………………4分2403d d sin d ar r ππθϕϕ=⎰⎰⎰ ………………………….………6分512.5a π=…………………………………………8分 解法2:利用对面积的曲面积分的计算球面上任一点(,,)x y z 的外法线通过原点,故有{},,n x y z =….2分{}cos ,cos ,cos ,,n x y z a a a n αβγ⎧⎫==⎨⎬⎩⎭………………………..4分4441I ()d x y z S a ∑=++⎰⎰ 512.5a π= ……………………………8分 6. 求幂级数(21)nn n x∞=+∑的收敛域,并求其和函数.解:1lim1nn n a R a →∞+==,当1x =±时,发散,收敛域为(1,1)- ………..4分 和函数()0(21)2nnn n n n S x n xnx x ∞∞∞====+=+∑∑∑21,(1,1)(1)xx x +=∈-- …………………………………….8分 7. 求微分方程2e xy y y x '''++=的通解.解:特征方程为2210r r ++=,121r r ==- …………………………..2分对应的齐次方程的通解为12()e xy C C x -=+ ……………………………4分 因为1不是特征根,设特解的形式为*()e xy ax b =+ 代入原方程得*111,,(1)e 444x a b y x ==-=- ………………….6分 所求通解为121()e (1)e 4xx y C C x x -=++- ……………………8分 8. (1)确定函数()f x ,使曲线积分()(),0,0e (1)()d ()d 1x y x nn x f x y x f x y x ⎡⎤+++⎢⎥+⎣⎦⎰与路径无关;(2)如果(0)0f =,计算此曲线积分.解:(1)(1)()()1x n P Q ne xf x f x y x n ∂∂'=⇒++=∂∂+ ………………………..2分 解此一阶线性非齐次方程得()(1)(e )nxf x x C =++ ………………………4分 (2)(0)0f =⇒()(1)(e 1)nxf x x =+- ………………………………………6分 所求曲线积分(1)(e 1)nxx y =+- ………………………………….8分。
吉大高等数学试题及答案

吉大高等数学试题及答案一、选择题(每题4分,共20分)1. 下列函数中,哪一个是奇函数?A. \( f(x) = x^2 \)B. \( f(x) = x^3 \)C. \( f(x) = \sin(x) \)D. \( f(x) = \cos(x) \)答案:B2. 计算不定积分 \(\int \frac{1}{x} dx\) 的结果是?A. \( x \)B. \( \ln|x| + C \)C. \( e^x \)D. \( \ln(x) \)答案:B3. 以下哪个极限不存在?A. \(\lim_{x \to 0} \frac{\sin(x)}{x}\)B. \(\lim_{x \to \infty} \frac{1}{x}\)C. \(\lim_{x \to 0} \frac{1 - \cos(x)}{x^2}\)D. \(\lim_{x \to 0} \frac{1}{x}\)答案:D4. 微分方程 \( y' + 2y = 0 \) 的通解是?A. \( y = Ce^{-2x} \)B. \( y = Ce^{2x} \)C. \( y = C\sin(2x) \)D. \( y = C\cos(2x) \)答案:A5. 以下哪个级数是发散的?A. \(\sum_{n=1}^{\infty} \frac{1}{n^2}\)B. \(\sum_{n=1}^{\infty} \frac{1}{n}\)C. \(\sum_{n=1}^{\infty} \frac{1}{2^n}\)D. \(\sum_{n=1}^{\infty} \frac{(-1)^n}{n}\)答案:B二、填空题(每题5分,共20分)1. 函数 \( f(x) = x^2 - 4x + 4 \) 的最小值是 _______。
答案:02. 函数 \( y = \ln(x) \) 的导数是 _______。
答案:\( \frac{1}{x} \)3. 函数 \( y = e^x \) 的二阶导数是 _______。
吉林大学高数bii作业答案.-2013-2(一)复习课程

吉林大学高数B I I作业答案.2012-2013-2(一)高等数学作业答案BⅡ吉林大学公共数学教学与研究中心2013年3月收集于网络,如有侵权请联系管理员删除收集于网络,如有侵权请联系管理员删除第一次作业学院 班级 姓名 学号一、单项选择题 1.223limx y xyx y →→=+( D ). (A )32; (B )0; (C )65;(D )不存在.2.二元函数⎪⎩⎪⎨⎧=≠+=)0,0(),(,0)0,0(),(,),(22y x y x y x xyy x f 在)0,0(处( C ). (A )连续,偏导数存在; (B )连续,偏导数不存在; (C )不连续,偏导数存在;(D )不连续,偏导数不存在.3.设22(,)(1)(2)f x y y x x y =-+-,在下列求(1,2)x f 的方法中,不正确的一种是( B ).(A )因2(,2)2(1),(,2)4(1)x f x x f x x =-=-,故1(1,2)4(1)|0x x f x ==-=; (B )因(1,2)0f =,故(1,2)00x f '==;(C )因2(,)2(1)(2)x f x y y x y =-+-,故12(1,2)(,)0x x x y f f x y ====;(D )211(,2)(1,2)2(1)0(1,2)lim lim 011x x x f x f x f x x →→---===--. 4.若(,)f x y 的点00(,)x y 处的两个偏导数都存在,则( C ). (A )(,)f x y 在点00(,)x y 的某个邻域内有界; (B )(,)f x y 在点00(,)x y 的某个邻域内连续;收集于网络,如有侵权请联系管理员删除(C )0(,)f x y 在点0x 处连续,0(,)f x y 在点0y 处连续; (D )(,)f x y 在点00(,)x y 处连续.5.设22(,),2zz f x y y∂==∂,且(,0)1,(,0)y f x f x x ==,则(,)f x y 为( B ).(A )21xy x -+; (B )21xy y ++; (C )221x y y -+; (D )221x y y ++.二、填空题1.z =的定义域为2224,01y x x y ≤<+<. 2.0x y →→= 1/2 . 3.设22),(y x y x y x f +-+=,则=')4,3(x f 2/5,=')4,3(y f 1/5 . 4.设ln(32)u x y z =-+,则d u =3232dx dy dzx y z-+-+.5.设yz x =,则2z x y∂=∂∂()11ln y x y x -+. 三、计算题1.已知2)z f =,且当1y =时z x =,求()f t 及z 的表达式.将1,y z x ==代入,)12x f=+有)21fx =-解一:)))222423f =-+ ∴()243f t t t =-+解二:令2t =,则()22x t =- ∴()()221f t t =--∴)22211z x =--=-收集于网络,如有侵权请联系管理员删除2.讨论函数2222222,0,(,)0,0x xyx y f x y x y x y ⎧++≠⎪=+⎨⎪+=⎩的连续性..解一:当(),p x y 沿y 轴(x=0)趋于0(0,0)时, 2222limlim0x y y x xyx y y →→→+==+ 当(),p x y 沿y x =,趋于0(0,0)时,222220002lim lim 12x x y x x xy x x y x→→=→+==+ ∴()00lim,x y f x y →→不存在 ∴不连续解二:当(),p x y 沿y kx =趋于0(0,0)时,()()222222200011lim lim 11x x y kx k x x xy k x y k k x →→=→+++==+++ 与k 有关,∴不连续 3.设(1)y z xy =+,求d z .()()11211y y z y xy y y xy x--∂=⋅+⋅=+∂ 解一:取对数()ln ln 1z y xy =+()1ln 11z x xy y z y xy ∂⋅=++⋅∂+,∴()()1ln 11y z xy xy xy y xy ⎡⎤∂=+++⎢⎥∂+⎣⎦ 解二:()()()()ln 1ln 1e ,e ln 111y y xy y xy z x xy y xy y xy ++⎡⎤∂∂==⋅++⋅=+⎢⎥∂+⎣⎦ ∴()()()12d 1d 1ln 1+xy d 1y y x z y xy x xy y xy -⎡⎤=++++⎢⎥+⎣⎦4.求2e d yzt xz u t =⎰的偏导数.t220e e xz yzt u dt dt =-+⎰⎰22x z e uz x ∂=-⋅∂ 22y e z uz y∂=⋅∂收集于网络,如有侵权请联系管理员删除2222x y e e z z ux y z∂=-⋅+⋅∂5.设r =0r ≠时,有2222222r r r x y z r∂∂∂++=∂∂∂.r xx r ∂==∂ 222223xr x rr x r x r r -⋅∂-==∂,同理:2222222323,r r y r r z y r z r ∂-∂-==∂∂∴()2222222222233322r x y x r r r r x y z r r r-++∂∂∂++===∂∂∂6.证明函数(,)f x y =(0, 0)处:(1)连续;(2)偏导数存在;(3)不可微. (1)0ε∀>0=≤0ε<ε<<取δ=,则当0δ<<0ε<,∴()()000lim ,lim00,0x x y y f x y f →→→→===(或:()00lim00,0x y f →→==),(),f x y =(2)()(),00,0,0x f x f =;()()0,0,0,00y f y f == (3)()()0,00,0x y z z f x f y =-⋅-=V V V V 考察:000limlimx x y y →→→→=V V V V 当(),p x y 沿直线y kx =趋于0(0,0)有00lim limx x y k x →→=⋅→=V V V V 与k 有关∴上式不存在,不可微收集于网络,如有侵权请联系管理员删除收集于网络,如有侵权请联系管理员删除第二次作业学院 班级 姓名 学号一、单项选择题 1.设22()y z f x y =-,其中()f u 为可导函数,则zx∂∂=( B ). (A )2222()xyf x y --;(B )222222()()xyf x y f x y '---;(C )22222()()yf x y f x y '---;(D )2222222()()()f x y yf x y f x y '-----. 2.设方程(,,)0F x y y z z x ---=确定z 是x ,y 的函数,F 是可微函数,则zx∂∂=( D ). (A )13F F '-'; (B )13F F ''; (C )x zy zF F F F --;(D )1323F F F F ''-''-. 3.设(,),(,),(,)x x y z y y z x z z x y ===都由方程(,,)0F x y z =所确定的隐函数,则下列等式中,不正确的一个是( C ).(A )1x yy x∂∂=∂∂; (B )1x zz x∂∂=∂∂; (C )1x y zy z x ∂∂∂=∂∂∂;(D )1x y zy z x∂∂∂=-∂∂∂.4.设(,),(,)u u x y v v x y ==都是可微函数,C 为常数,则在下列梯度运算式中,有错误的是( A ).收集于网络,如有侵权请联系管理员删除(A )0C ∇=; (B )()Cu C u ∇=∇;(C )()u v u v ∇+=∇+∇;(D )()uv v u u v ∇=∇+∇.5.()u f r =,而r ()f r 具有二阶连续导数,则22ux∂+∂2222u uy z ∂∂+=∂∂( B ). (A )1()()f r f r r'''+; (B )2()()f r f r r '''+; (C )211()()f r f r r r'''+;(D )212()()f r f r r r'''+.二、填空题1.已知(1,2)4,d (1,2)16d 4d ,d (1,4)64d 8d f f x y f x y ==+=+,则(,(,))z f x f x y =在点(1, 2)处对x 的偏导数为 192 .2.由方程e z xy yz zx -+=所确定的隐函数(,)z z x y =在点(1, 1)处的全微分为 d dy x +.3.r 在点(0, 0)处沿x 轴正向的方向导数为 1 . 4.函数2222u x y z xy yz =++-+在点(1,2,3)--处的方向导数的最大值等于三、计算与解答题 1.设f 是C (2)类函数,22(e ,)xyzf x y =-,求2zx y∂∂∂.''''[1212e 2e 2xy xy zf y f x y f xf x∂=⋅⋅+⋅=+∂ ()()2''"''''''1111122122e e e e 22e 2xy xy xy xy xy z f y xf y f x f y x f x f y x y∂⎡⎤⎡⎤=+⋅⋅+⋅+⋅-+⋅⋅+⋅-⎣⎦⎣⎦∂∂ ()()'2"22""11112221e e 2e 4xy xy xy xy f xy f x y f xyf =+++-- 2.设32(32)x y z x y -=-,求d z .收集于网络,如有侵权请联系管理员删除解一:()()()()()()()d ln d 32ln 32,1d d 3x-2y ln 3232d ln 32z x y x y z x y x y x y z=-⋅-=⋅-+-⋅- ()()()32d 32ln 3213d 2dy x yz x y x y x -=--+-⎡⎤⎣⎦解二:,32,32v z u u x y v x y ==-=- ()()3213332ln 321x yv x u x v x z z u z v v u x y x y --=⋅+⋅=⋅⋅=-⋅-+⎡⎤⎣⎦()()()321y 2232ln 321x yv u y v y z z u z v v u x y x y --=⋅+⋅=⋅⋅-=--⋅-+⎡⎤⎣⎦∴()()()32d 32ln 3213d 2dy x yz x y x y x -=--+-⎡⎤⎣⎦3.设f ,ϕ是C (2)类函数,x y z yf x y x ϕ⎛⎫⎛⎫=+ ⎪ ⎪⎝⎭⎝⎭,证明:(1)2220z z x y x x y ∂∂+=∂∂∂; (2)2222220z z x y x y ∂∂-=∂∂. 证21z y y yf x f x y x x ϕϕϕϕ∂⎛⎫''''=⋅++⋅⋅-=+- ⎪∂⎝⎭222222311z y y y y y f f x y x x x x yx ϕϕϕϕ∂⎛⎫⎛⎫''''''''''=⋅+⋅-+-⋅-=+ ⎪ ⎪∂⎝⎭⎝⎭2222111z x y x y f f x y y x x x x y x ϕϕϕϕ⎛⎫∂''''''''''=⋅-+⋅--=-- ⎪∂∂⎝⎭21z x xf y f x f f y y x y ϕϕ⎛⎫∂''''=+⋅-+⋅=-+ ⎪∂⎝⎭222222311z x x x x x f f f f y y y y y x y x ϕϕ⎛⎫⎛⎫∂'''''''''=⋅-+-⋅⋅-+⋅=+ ⎪ ⎪∂⎝⎭⎝⎭4.设arctan yx,求22d d y x .()''2222221122ln arctan ,221y x yyx y y x x y xx y y x -+⋅+=⋅=+⎛⎫+ ⎪⎝⎭''2222x yy y x yx y x y+-=++∴ ()(),x yy x y x y y x y+''-=-+=-()()()()()()()()()()'''22"222321122x y x y y x y x y y x y y x y x y y x y x y x y x y ⎛⎫+⋅- ⎪+--+-⋅-+-⎝⎭====---- 一阶:()()22222222112,ln arctan ,221x yy x x y x F x y x y F x x y x y y x -+=+-=⋅-=++⎛⎫+ ⎪⎝⎭22222211221y y y x x F y x y x y x -=⋅-=+++∴d d y Fx x y x y x Fy y x x y ++=-=-=-- 二阶:()()()()222'2'""''"11/1,y x y x y yy y y x y y y x y x y+++-++⋅=+-==--()()()()()2222332x y x y x y x y x y +-++==--5.设e sin ,e cos ,uux u v y u v ⎧=+⎪⎨=-⎪⎩求,u v x y ∂∂∂∂. ()1d cos e sin cos e sin cos 1,sin d cos d d sin e cos sin u u u x u v v u v D u v v D u v x u v y y u v v u v+⎡⎤==-+==-⎣⎦-∴()()1sin cos d d d sin cos 1sin cos 1u D v vu x y D e v v eu v v ==--+-+ ∴()sin e sin cos 1u u v x v v ∂=∂-+ ()2e sin d e sin d e cos d e -cos d u u u u v x D v y v x v y+==+--∴()()()2u cos e d e sin d d e sin -cos 1u uv x v y D v D u v v -++==⎡⎤+⎣⎦∴()e sin e sin cos 1u u v vy u v v ∂+=∂-+6.设2(,,),(,e ,)0,sin y u f x y z x z y x ϕ===,其中求f ,ϕ是C (1)类函数,求d d u x. ()()22''''223,,,e ,2,e ,y z F x y z x xz Fx x Fy F ϕϕϕϕ==⋅== ∴''12''332e ,y x z Fx z Fyx Fz y Fz ϕϕϕϕ∂∂=-=--=-=--∂∂ '''''12123''332e d cos cos d y x u f f x f x x ϕϕϕϕ⎛⎫=+⋅+--⋅ ⎪⎝⎭()''''sin '12312cos 2e cos x f f x f x x ϕϕ=+⋅++解二:全微分'''123'''123d d d d 2d e d d 0d cos d y u f x f y f zx x y z y x x ϕϕϕ⎧=⋅++⎪⋅+⋅⋅+=⎨⎪=⎩ 即'''231'''231d d d d e d d 2d d cos d yu f y f z f x y z x x y x x ϕϕϕ⎧--=⎪+=-⎨⎪=⎩代入消元解得:'sin ''''12123'32cos d cos d x x e x u f f x f x ϕϕϕ⎛⎫+=+- ⎪⎝⎭∴…… 7.求函数ln()z x y =+的点(1, 2)处沿着抛物线24y x =的该点切线方向的方向导数.()()111,,1,21,23zx zy zx zy x y x y ====++()''1,221tan 1y y y α=====121233,,,4444ππααπββπ====11cos cos cos42παβ===223cos cos cos 4παβ===∴()()()111,21111,2cos 1,2cos 33zzx zy αβ∂=⋅+==∂l()()()221,22111,2cos 1,2cos 32323z zx zy αβ⎛⎛∂=⋅+=⋅-+-=- ∂⎝⎭⎝⎭l第三次作业学院 班级 姓名 学号一、单项选择题1.在曲线23,,x t y t z t ==-=的所有切线中,与平面24x y z ++=平行的切线( B ). (A )只有一条;(B )只有两条;(C )至少有三条;(D )不存在.2.设函数(,)f x y 在点(0, 0)附近有定义,且(0,0)3,(0,0)1x y f f ==,则( C ).(A )d (0,0)3d d z x y =+;(B )曲面(,)z f x y =在点(0,0,(0,0))f 的法向量为{3,1,1}; (C )曲线(,),0z f x y y =⎧⎨=⎩在点(0,0,(0,0))f 的切向量为{1,0,3};(D )曲线(,),0z f x y y =⎧⎨=⎩在点(0,0,(0,0))f 的切向量为{3,0,1}.3.曲面()z x f y z =+-的任一点处的切平面 ( D ). (A )垂直于一定直线;(B )平等于一定平面; (C )与一定坐标面成定角;(D )平行于一定直线.4.设(,)u x y 在平面有界闭区域D 上是C (2)类函数,且满足20ux y∂≠∂∂及22220u ux y ∂∂+=∂∂,则(,)u x y 的 ( B ). (A )最大值点和最小值点必定都在D 的内部; (B )最大值点和最小值点必定都在D 的边界上; (C )最大值点在D 的内部,最小值点在D 的边界上; (D )最小值点在D 的内部,最得到值点在D 的边界上. 二、填空题1.如果曲面6xyz =在点M 处的切平面平行于平面63210x y z -++=,则切点M 的坐标是 (-1,2,-3) .2.曲线2224914,1x y z x y z ⎧++=⎨++=⎩在点(1,1,1)-处的法平面方程是 13x -10y -3z -6=0.3.22z x y =+在条件1x y +=下的极小值是12.4.函数u =在点(1,1,1)M 处沿曲面222z x y =+在该点的外法线方向的方向导数是13.三、计算题1.求曲线222226,x y z z x y ⎧++=⎪⎨=+⎪⎩在点(1,1,2)处的切线方程. 解一:22222yy zz x yy z x ''⎧+=-⎪⎨''-+=⎪⎩①②①+②:0z '=代入(),1,1,21xy y y''=-=- ∴()1,1,0s =-v切成:112110x y z ---==,即112x y z -=-⎧⎨=⎩解二:()()2221,,6,2,2,2,2,2,4F x y z x y z Fx x Fy y Fz z n =++-====u u v取()1121,1,2,n s n n ==⨯u v v u v u u v()()222,,.2.2 1.2,2,1G x y z x y z Gx x Gy y n =+-===-=-u u v1s 切平面:()()()1111220260x y z x y z ⋅-+⋅-+-=+-=即+2s 切平面:()()()21212020x y z x y z -+---=--=即:2+2∴2602220x y z x y z ++-=⎧⎨+--=⎩ 2.过直线102227,x y z x y z +-=⎧⎨+-=⎩作曲面222327x y z +-=的切平面,求其方程.解:设切点为0000(,,)M x y z ,切平面方程为:0003270x x y y z z +--=……① 过已知直线的平面束方程为()1022270x y z x y z λ+--++-= 即:()(10)2(2)270x y z λλλ++++---=……②当①②为同一平面时有:000103,2,2x y z λλλ+=+=--=-且222000327x y z +-= 解得00000033117117x x y y z z ==-⎧⎧⎪⎪==-⎨⎨⎪⎪==-⎩⎩或对应的切平面方程为:927091717270x y z x y z +--=+-+=3.证明曲面2/32/32/32/3(0)x y z a a ++=>上任意点处的切平面在各个坐标轴上的截距平方和等于2a . .设000M x 0(,y ,z )为曲面上任一点 切平面方程为:()()111333000000222()0333x x x y y y z z z ----+-+-=即:11123333000x x y y z z a --++= 令0y z ==得x 轴截距1233x n a = 同理121233332,Y z a Z z a ==∴222422223333()X Y Z x y z a a ++=++=4.求函数22(,)(2)ln f x y x y y y =++的极值..①令222(2)02ln 10x yf x y f x y y '⎧=+=⎪⎨'=++=⎪⎩ ②得驻点10,e M ⎛⎫⎪⎝⎭③2212(2),4,2xx xy f y f xy fyy x y=+==+④M 处: AC-B 2>0,A>0,∴极小值110,f e e ⎛⎫=- ⎪⎝⎭5.求函数22(,)1216f x y x y x y =+-+在区域22{(,)|25}D x y x y =+≤上的最大值和最小值.2120621608fx x x fy y y =-==⎧⎧⎨⎨=+==-⎩⎩ 不在D 内,∴D 内无极值点 在边界2225x y +=上,(),251216f x y x y =-+()()22,25121625L x y x y x y λ=-+++-12201620Lx x Ly y λλ=-+=⎧⎨=+=⎩ 解得3344x x y y ==-⎧⎧⎨⎨=-=⎩⎩2225x y +=()3,475f -=- 最小()3,4125f -= 最大6.求曲面1=的一个切平面,使其在三个坐标轴上的截距之积为最大.设切点为()()0000,,,,,1M x y z F x y zFn Fy ==切平面:)))0000x x y y z z ---=即:1+=令0y z ==,得x轴截距X = 0x z ==,得y轴截距Y = 0x y ==,得z轴截距Z =XYZ =()),,1f x y z xyz λ=+令000113fx yz yzx x fy xz xzy y fz xy xyz z ⎧===⎪⎪⎪=+==⎪⎪⎨⎪=+==⎪==== 19x y z ===即切点为111,,999⎛⎫⎪⎝⎭切平面为:13x y z ++=第四次作业学院 班级 姓名 学号一、单项选择题1.设(,)f x y 连续,且(,)(,)d d Df x y xy f x y x y =+⎰⎰,其中D 是由0y =,2y x =,1x =所围区域,则(,)f x y 等于( C ).(A )xy ; (B )2xy ; (C )18xy +;(D )1xy +.2.设D 是xOy 平面上以(1, 1), (-1, 1)和(-1, -1)为顶点的三角形区域,D 1是D 的第一象限部分,则(cos sin )d d Dxy x y x y +⎰⎰等于( A ).(A )12cos sin d d D x y x y ⎰⎰;(B )12d d D xy x y ⎰⎰;(C );14cos sin )d d D xy x y x y +⎰⎰((D )0.3.设平面区域22:14,(,)D x y f x y ≤+≤是在区域D 上的连续函数,则d d Df x y ⎰⎰等于 ( A ).(A )212()d rf r r π⎰;(B )21002()d ()d rf r r rf r r π⎡⎤+⎣⎦⎰⎰; (C )2212()d rf r r π⎰;(D )2122002()d ()d rf r r rf r r π⎡⎤+⎣⎦⎰⎰. 4.设有空间区域22221:,0x y z R z Ω++≤≥及22222:x y z R Ω++≤,0x ≥,0y ≥,0z ≥,则( C ).(A )12d 4d x V x V ΩΩ=⎰⎰⎰⎰⎰⎰;(B )12d 4d y V y V ΩΩ=⎰⎰⎰⎰⎰⎰;(C )12d 4d z V z V ΩΩ=⎰⎰⎰⎰⎰⎰;(D )12d 4d xyz V xyz V ΩΩ=⎰⎰⎰⎰⎰⎰.二、填空题 1.积分2220d e d y x x y -=⎰⎰()-411e 2-.2.交换积分次序:14012d (,)d d (,)d x x f x y y x f x y y -+=⎰⎰⎰⎰()2221d ,d y yy f x y x +-⎰⎰.3.设区域D 为||||1x y +≤,则(||||)d d Dx y x y +=⎰⎰43. 4.设区域D 为222x y R +≤,则2222d d Dx y x y a b ⎛⎫+= ⎪⎝⎭⎰⎰422114R a b π⎛⎫+ ⎪⎝⎭. 5.直角坐标中三次积分22110d (,,)d x y I x y f x y z z +-=⎰⎰⎰在柱面坐标中先z再r 后θ顺序的三次积分是()221d d cos ,sin ,d r r f r r z r z πθθθ⎰⎰⎰三、计算题1.计算|cos()|d d Dx y x y +⎰⎰,其中D 是由直线,0,2y x y x π===所围成的三角形区域.原式()()12cos d d cos d d D D x y x y x y x y =+-+⎰⎰⎰⎰()()42204d cos d d cos d yxyxx y x y x x x y y πππππ--=+-+⎰⎰⎰⎰()()422024sin d sin yxyx x y y x y πππππ--=+-+⎡⎤⎡⎤⎣⎦⎣⎦⎰⎰4204sin sin 2d sin 2sin d 22y y x x πππππ⎛⎫⎛⎫=--- ⎪ ⎪⎝⎭⎝⎭⎰⎰ =[][]240411cos 2cos 2122242y x ππππππ+++=- 2.计算sin d d Dx yx y y⎰⎰,其中D 是由2y x =和y x =所围成的区域. ①图交点,先x,②:01y x D y ⎧≤≤⎪⎨≤≤⎪⎩③21100sin sin d d d 22y y y y F f x y y y ⎛⎫==⋅- ⎪⎝⎭⎰⎰110011sin d sin d 22y y y y y =-⎰⎰ ()()111cos1cos1sin 22x =-+- ()11sin12=-3.计算22()d d Dx y x y +⎰⎰,其中{(,)|02,D x y x y =≤≤≤.①图,极坐标,方程②2cos 2:02r D θπθ≤≤⎧⎪⎨≤≤⎪⎩ ③22202cos d d I r r r πθθ=⋅⎰⎰()24422002cos d =41cos d 4r ππθθθθ⎡⎤=-⎢⎥⎣⎦⎰⎰3135442242244πππππ=⋅-⋅⋅⋅=-=4.计算23d xy z V Ω⎰⎰⎰,其中Ω是由曲面z xy =与平面,1y x x ==和0z =所围成的闭或区域. ①图,投影域Dxy②0:001z xy y y x ≤≤⎧⎪Ω≤≤⎨⎪≤≤⎩③1230d d d x xyI x y sy z z =⎰⎰⎰7115120001d d 728xy x x x x ⎡⎤==⎢⎥⎣⎦⎰⎰1112813364=⨯= 5.计算d I xyz V Ω=⎰⎰⎰,其中222{(,,)|1,0,0,0}x y z x y z x y z Ω=++≤≥≥≥.①图,已求坐标r=1②01:0202r πϕπθ⎧⎪≤≤⎪⎪Ω≤≤⎨⎪⎪≤≤⎪⎩③12220d d sin cos sin sin cos sin d I x r r r r r ππϕϕθϕθϕϕ=⋅⋅⋅⋅⋅⋅⎰⎰⎰135220sin cos d sin cos d d r r ππθθθϕϕϕ=⋅⋅⋅⋅⎰⎰⎰3220011111sin dsin sin d sin 662448ππθθϕϕ=⋅⋅⋅⋅=⋅⋅=⎰⎰6.设()d F t f V Ω=⎰⎰⎰,其中2222:,()x y z t f t Ω++≤在0t =可导,且(0)0f =,求40()limt F t tπ+→. ()()2t 20d d sin d F t f r r r ππθϕϕ=⋅⎰⎰⎰()2t20d sin d d f r r r ππθϕϕ=⋅⋅⋅⎰⎰⎰()204d tf r r r π=⋅⋅⎰()()2'4F t f t t π=⋅⋅∴()()()()()()02043000040lim lim lim lim '040t t t t F t f t t f t f t f f t t t t πππ→→→→⋅-+====- 四、证明题设函数)(x f 在闭区间],[b a 上连续且恒大于零,证明2d ()d ()()bbaaxf x x b a f x ≥-⎰⎰. 证明:设:a x bD a y b≤≤⎧⎨≤≤⎩∵2d d 0D x y ≥⎰⎰ 即:()()()()d d 2d d D Df x f y x y x y f y f x ⎡⎤+≥⎢⎥⎣⎦⎰⎰⎰⎰∴()()()()()211d d d d 2b bb b aaa a f x x y f y y xb a f y f x +⋅≥-⎰⎰⎰⎰∴()()()212d d 2b baaf x x x b a f x ⋅≥-⎰⎰∴()()()21d d b baaf x x x b a f x ⋅≥-⎰⎰第五次作业学院 班级 姓名 学号一、单项选择题1.设L 是圆周222x y a +=,则22()d nL x y s +=⎰Ñ(D ) .(A )2n a π; (B )12n a π+; (C )22n a π;(D )212n a π+.2.设L 是由(0, 0), (2, 0), (1, 1)三点连成的三角形边界曲线,则d L y s =⎰Ñ( A ).(A )(B )2(C )(D )2+.3.设∑是锥面222x y z +=在01z ≤≤的部分,则22()d x y S ∑+=⎰⎰( D ).(A )1300d d r r πθ⎰⎰; (B )21300d d r r πθ⎰⎰;(C 1300d d r r πθ⎰;(D 21300d d r r πθ⎰.4.设∑为2222(0)x y z a z ++=≥,1∑是∑在第一卦限中的部分,则有(C ).(A )1d 4d x S x S ∑∑=⎰⎰⎰⎰;(B )1d 4d y S x S ∑∑=⎰⎰⎰⎰;(C )1d 4d z S x S ∑∑=⎰⎰⎰⎰;(D )1d 4d xyz S xyz S ∑∑=⎰⎰⎰⎰.二、填空题1.设曲线L 为下半圆y =22()d L x y s +=⎰1d π1LS =⋅⎰.2.设L 为曲线||y x =-上从1x =-到1x =的一段,则d L y s =⎰.3.设Γ表示曲线弧,,,(02)2t x t y t z t π==≤≤,则222()d x y z s Γ++=⎰332ππ23+.4.设∑是柱面222(0)x y a a +=>在0z h ≤≤之间的部分,则2d x S ∑=⎰⎰3a h π.5.设∑是上半椭球面2221(0)94x y z z ++=≥,已知∑的面积为A ,则222(4936)d x y z xyz S ∑+++=⎰⎰36A .三、计算题 1.计算L s ⎰Ñ,其中L 为圆周222x y a +=,直线y x =及x 轴在第一象限内所围成的扇形的整个边界.解:123222123:0,0::,02L L L L L y x a L x y a aL y x x =++=≤≤+==≤≤1e d e 1ax a L s x ==-⎰⎰224a aL L as e ds e π==⎰⎰4aπ3e 1a L s x ==-⎰所以:原式=2(1-a e )+4aπa e2.2d z s Γ⎰Ñ,其中2222,:0.x y z a x y z ⎧++=Γ⎨++=⎩.(222d d d r rrx s y s z s ==⎰⎰⎰Q蜒?)2Γ222223d 1()d 31d 322π.33r r z s x y z s a s a a a π=++==⋅=⎰⎰⎰ÑÑÑ 3.计算曲面积分()d xy yz zx S ∑++⎰⎰,其中曲面:z ∑=被柱面222x y x +=所截得部分。
吉大《高等数学(理专)》作业考核试题满分答案

答案:C
1
函数y=sinx没有拐点存在。()
A错误
B正确
答案:A
2
一元函数可导的充要条件是左右导数都存在且相等。
A错误
B正确
答案:B
3
函数y=sinx没有拐点存在。()
A错误
B正确
答案:A
4
复合函数对自变量的导数,等于函数对中间变量的导数乘以中间变量对
3
下列函数中()是奇函数
A xsinx
B x+cosx
C x+sinx
D |x|+cosx
答案:C
设f(x)=x(x-1)(x-2)(x-3),则f’(0)=( )
A -6
B -2
C 3
D -3
答案:A
5
已知函数y= 2cos3x-5e2x,则x=0时的微分dy=()
A 10
B 10dx
C -10
答案:A
13
已知f(x)的一个原函数是e^(-x),则∫xf'(x)dx等于()
A xe^(-x)+e^(-x)+C
B xe^(-x)-e^(-x)+C
C -xe^(-x)-e^(-x)+C
D -xe^(-x)+e^(-x)+C
答案:C
14
集合B是由能被3除尽的全部整数组成的,则B可表示成
A {3,6,…,3n}
D -10dx
答案:D
6
集合A={±2,±3,±4,±5,±6}表示
A A是由绝对值小于等于6的全体整数组成的集合
B A是由绝对值大于等于2,小于等于6的全体整数组成的集合
吉林大学---高数-A3作业

吉林大学---高数-A3作业高等数学作业AⅢ吉林大学公共数学教学与研究中心2013年9月1第一次作业学院 班级 姓名 学号一、单项选择题1.设L 是圆周222x y a +=,则22()d n L x y s +=⎰( ) .(A )2n a π; (B )12n a π+; (C )22n a π;(D )212n a π+.2.设L 是由(0, 0), (2, 0), (1, 1)三点连成的三角形边界曲线,则d L y s =⎰( ).(A(B)2 (C) (D)2+3.设∑是锥面222x y z +=在01z ≤≤的部分,则22()d x y S ∑+=⎰⎰( ). (A )1300d d r rπθ⎰⎰; (B )21300d d r r πθ⎰⎰; (C1300d d r r πθ⎰; (D21300d d r r πθ⎰. 4.设∑为2222(0)x y z a z ++=≥,1∑是∑在第一卦限中的部分,则有( ).(A )1d 4d x S x S ∑∑=⎰⎰⎰⎰; (B )1d 4d y S x S ∑∑=⎰⎰⎰⎰;(C )1d 4d z S x S ∑∑=⎰⎰⎰⎰; (D )1d 4d xyz S xyz S ∑∑=⎰⎰⎰⎰.3.计算曲面积分()d xy yz zx S ∑++⎰⎰,其中曲面:z ∑=222x y x +=所截得部分。
14.求222d Sx y z ∑++⎰⎰,其中∑是介于0z =与4z =之间的柱面224x y +=.2四、应用题1.求底圆半径相等的两个直交圆柱面222x y R +=及222x z R +=所围立体的表面积.2.求面密度1ρ=的均匀半球壳2222(0)++=≥x y z a z 关于z轴的转动惯量.34第二次作业学院 班级 姓名 学号一、单项选择题1.设L 是圆周222(0)xy a a +=>负向一周,则曲线积分3223()d ()d L x x y x xy y y -+-=⎰ ( ) .(A )0; (B )42a π-; (C )4a π-; (D )4a π.2.设L 是椭圆2248xy x +=沿逆时针方向,则曲线积分 2e d d y L x x y +=⎰ ( ).(A )2π; (B )π; (C )1;(D )0.3. 设曲线积分2d ()d L xy x y x y ϕ+⎰与路径无关,其中()x ϕ具有连续的导数,且(0)0ϕ=,则(1,1)2(0,0)d ()d xy x y x y ϕ+⎰等于( )(A )38 (B )12 (C )34 (D )14.已知2()d d ()x ay y y xx y +-+为某函数的全微分,则a = ( )正确.(A )1-; (B )0; (C )2 (D )1.二、填空题1.设L 为22(1)4x y +-=正向一周,则22d d (1)Lx y y xx y -=+-⎰ . 2.设L 为封闭折线||||1x x y ++=正向一周,则22d cos()d Lx y x x y y -+=⎰ .3.设L 为0tan d xy t t =⎰从x=0到4x π=一段弧,将(,)d (,)d L P x y x Q x y y+⎰化为第一型曲线积分为 .4.设L 为封闭折线||||1x y +=沿顺时针方向,则22dd Lxy x x yx y+=+⎰ . 三、计算题1.计算2d d Ly x x y -⎰,其中L 是抛物线2y x =上从点(1,1)A 到(1,1)B -,再沿直线到(0,2)C 的曲线.2.计算2()d (sin )d Lxy x x y y--+⎰,其中L 是圆周y 上从(2,0)A 到(0,0)O 的一段弧.3.设()f x 在(,)-∞+∞内具有一阶连续导数,L 是半平面(0)y >内的有向分段光滑曲线,其起点为(,)a b ,终点为(,)c d .证明2221[1()]d [()1]d L xI y f xy x y f xy yy y=++-⎰(1)证明曲线积分I 与路径L 无关 (2)当ab cd =时,求I 的值4.设力2y x y -+=i j F ,证明力F 在上半平面内所作的功与路径无关,并求从点(1,2)A 到点(2,1)B 力F 所作的功.5.计算[][]()cos d ()sin d AMBI y x y x y x y ϕπϕπ'=-+-⎰,其中AMB 在连结点(,2)A π与(3,4)B π的线段之下方的任意路线,且该路线与AB 所围成的面积为2,()y ϕ具有连续的导数。
吉林大学历届高数考题及答案

2021~2021学年第一学期?高等数学B Ⅰ?试卷2009年1月12日一、填空题〔共7道小题,每题3分,总分值21分〕1.2lim 1nn n n →∞-⎛⎫= ⎪+⎝⎭.2.设2log y =d y = .3.假设00()()f x x f x +∆-与sin2x ∆为0x ∆→时的等价无穷小,那么0()f x '= .4.设函数)(x y y =由方程331,x t y t t⎧=-⎪⎨=-⎪⎩所确定,那么1d d t y x == .5.曲线2610y x x =-+在点(3,1)处的曲率为 .6.设()d cos f x x x C =+⎰,那么()()d n f x x ⎰= .7.31211d 1x x x -+=+⎰ .二、单项选择题〔共7道小题,每题3分,总分值21分〕1.以下表达正确的选项是〔A 〕有界数列一定有极限. 〔B 〕无界数列一定是无穷大量. 〔C 〕无穷大量数列必为无界数列. 〔D 〕无界数列未必发散. [ ]2.设数列(){}0,1,2,n n a a n >=满足1lim 0n n n a a +→∞=,那么 〔A 〕lim 0n n a →∞=.〔B 〕lim 0n n a C →∞=>.〔C 〕lim n n a →∞不存在.〔D 〕{}n a 的收敛性不能确定.[ ]3.设()f x ,()g x 在区间[,]a b 上可导,且()()f x g x ''>,那么在[,]a b 上有 〔A 〕()()0f x g x ->.〔B 〕()()0f x g x -≥.〔C 〕()()()()f x g x f b g b ->-.〔D 〕()()()()f x g x f a g a ->-. [ ]4.设()f x 有三阶连续导数,且满足000()()0,()0f x f x f x ''''''==<,那么以下结论正确的选项是〔A 〕()f x '的极小值为0. 〔B 〕0()f x 是()f x 的极大值.〔C 〕0()f x 是()f x 的极小值. 〔D 〕点00(,())x f x 是曲线()y f x =的拐点.[ ]5.||e d 1k x x +∞-∞=⎰,那么k =〔A 〕0.〔B 〕-2.〔C 〕-1.〔D 〕-0.5. [ ]6.摆线(sin )(1cos )x a t t y a t =-⎧⎨=-⎩的一拱与x 轴所围的平面图形绕x 轴旋转所得旋转体的体积x V =〔A 〕2220(1cos )d[(sin )]aa t a t t ππ--⎰. 〔B 〕2220(1cos )d a t t ππ-⎰. 〔C 〕2220(1cos )d aa t t ππ-⎰.〔D 〕2220(1cos )d[(sin )]a t a t t ππ--⎰. [ ]7.设向量,a b 满足||||-=+a b a b ,那么必有〔A 〕-=a b 0. 〔B 〕+=a b 0. 〔C 〕0⋅=a b . 〔D 〕⨯=a b 0. [ ]三、计算题〔共5道小题,每题8分,总分值40分〕1.设21cos ,0,()0,0,x x f x xx ⎧≠⎪=⎨⎪=⎩ 求()f x '.2.求极限 0lim →x 222010cos d x x t tx-⎰.3.设()f x 的一个原函数为sin x ,求 2()d x f x x ''⎰.4.计算 12x ⎰.5.假设点M 与(2,5,0)N 关于直线4120:2230x y z l x y z --+=⎧⎨+-+=⎩对称,求点M 的坐标.四、应用题〔总分值8分〕设曲线2=->.过点(2,0)(4)(0)y a x a-及(2,0)作曲线的两条法线,求a的值,使得曲线与这两条法线所围成的平面图形面积最小.五、证明题〔共2道小题,每题5分,总分值10分〕1.设()f x 在[0,1]上连续,在()0,1内可导,且(1)0f =.证明在()0,1内至少存在一点ξ,使得 ()()f f ξξξ'=-.2. 设130d 1sin n n tx t t=+⎰,12n n u x x x =+++,证明数列{}n u 收敛.2021~2021学年第一学期?高等数学B Ⅰ?试卷 答案 2009年1月12日一、填空题〔共7道小题,每题3分,总分值21分〕1.2lim 1nn n n →∞-⎛⎫= ⎪+⎝⎭3e - .. 2.设2log y =,那么dy =223(1)ln 2xdx x -- .. 3.假设00()()f x x f x +∆-与sin2x ∆为0x ∆→时的等价无穷小,那么0()f x '= 2 .4.设函数)(x y y =由方程331,x t y t t⎧=-⎪⎨=-⎪⎩所确定,那么1t dy dx == 23 .5.曲线2610y x x =-+在点(3,1)处的曲率为 2 .6.设()d cos f x x x c =+⎰,那么()()d n f x x ⎰=cos 2n C x π⎛⎫++⎪⎝⎭.7.31211d 1x x x -+=+⎰ 2. 二、单项选择题〔共7道小题,每题3分,总分值21分〕1.以下表达正确的选项是 〔A 〕有界数列一定有极限; 〔B 〕无界数列一定是无穷大量; 〔C 〕无穷大量数列必为无界数列;〔D 〕无界数列未必发散。
吉林大学历届高数考题及答案
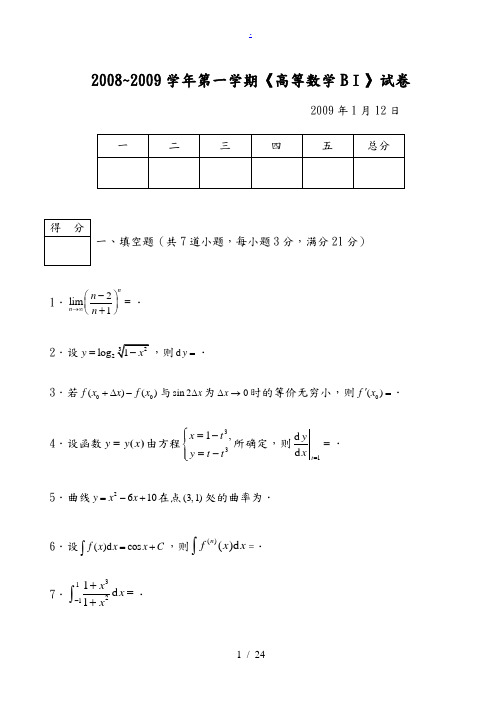
2008~2009学年第一学期《高等数学B Ⅰ》试卷2009年1月12日一、填空题(共7道小题,每小题3分,满分21分)1.2lim 1nn n n →∞-⎛⎫= ⎪+⎝⎭.2.设2log y =d y =.3.若00()()f x x f x +∆-与sin 2x ∆为0x ∆→时的等价无穷小,则0()f x '=.4.设函数)(x y y =由方程331,x t y t t⎧=-⎪⎨=-⎪⎩所确定,则1d d t y x ==.5.曲线2610y x x =-+在点(3,1)处的曲率为.6.设()d cos f x x x C =+⎰,则()()d n f x x ⎰=.7.31211d 1x x x -+=+⎰.二、单选题(共7道小题,每小题3分,满分21分)1.下列叙述正确的是(A )有界数列一定有极限. (B )无界数列一定是无穷大量. (C )无穷大量数列必为无界数列. (D )无界数列未必发散. [ ]2.设数列(){}0,1,2,n na a n >=满足1lim 0n n n a a +→∞=,则 (A )lim 0n n a →∞=.(B )lim 0n n a C →∞=>.(C )lim n n a →∞不存在.(D ){}n a 的收敛性不能确定.[ ]3.设()f x ,()g x 在区间[,]a b 上可导,且()()f x g x ''>,则在[,]a b 上有 (A )()()0f x g x ->.(B )()()0f x g x -≥.(C )()()()()f x g x f b g b ->-.(D )()()()()f x g x f a g a ->-. [ ]4.设()f x 有三阶连续导数,且满足000()()0,()0f x f x f x ''''''==<,则下列结论正确的是(A )()f x '的极小值为0. (B )0()f x 是()f x 的极大值.(C )0()f x 是()f x 的极小值. (D )点00(,())x f x 是曲线()y f x =的拐点.[ ]5.已知||ed 1k x x +∞-∞=⎰,则k =(A )0. (B )-2.(C )-1.(D )-0.5. [ ]6.摆线(sin )(1cos )x a t t y a t =-⎧⎨=-⎩的一拱与x 轴所围的平面图形绕x 轴旋转所得旋转体的体积x V =(A )2220(1cos )d[(sin )]aa t a t t ππ--⎰. (B )2220(1cos )d a t t ππ-⎰. (C )2220(1cos )d aa t t ππ-⎰.(D )2220(1cos )d[(sin )]a t a t t ππ--⎰. [ ]7.设向量,a b 满足||||-=+a b a b ,则必有(A )-=a b 0. (B )+=a b 0. (C )0⋅=a b . (D )⨯=a b 0. [ ]三、计算题(共5道小题,每小题8分,满分40分)1.设21cos ,0,()0,0,x x f x xx ⎧≠⎪=⎨⎪=⎩ 求()f x '.2.求极限 0lim→x 222010cos d x x t tx -⎰.3.设()f x 的一个原函数为sin x ,求 2()d x f x x ''⎰.4.计算 12x ⎰.5.若点M 与(2,5,0)N 关于直线4120:2230x y z l x y z --+=⎧⎨+-+=⎩对称,求点M 的坐标.四、应用题(满分8分)设曲线2=->.过点(2,0)(4)(0)y a x a-及(2,0)作曲线的两条法线,求a的值,使得曲线与这两条法线所围成的平面图形面积最小.五、证明题(共2道小题,每小题5分,满分10分)1.设()f x 在[0,1]上连续,在()0,1可导,且(1)0f =.证明在()0,1至少存在一点ξ,使得 ()()f f ξξξ'=-.2. 设130d 1sin n n tx t t=+⎰,12n n u x x x =+++,证明数列{}n u 收敛.2008~2009学年第一学期《高等数学B Ⅰ》试卷 答案 2009年1月12日一、填空题(共7道小题,每小题3分,满分21分)1.2lim 1nn n n →∞-⎛⎫= ⎪+⎝⎭3e -.. 2.设2log y =dy =223(1)ln 2xdx x --..3.若00()()f x x f x +∆-与sin 2x ∆为0x ∆→时的等价无穷小,则0()f x '= 2 .4.设函数)(x y y =由方程331,x t y t t⎧=-⎪⎨=-⎪⎩所确定,则1t dy dx ==23. 5.曲线2610y x x =-+在点(3,1)处的曲率为 2 .6.设()d cos f x x x c =+⎰,则()()d nf x x ⎰=cos 2n C x π⎛⎫++ ⎪⎝⎭.7.31211d 1x x x -+=+⎰2π. 二、单选题(共7道小题,每小题3分,满分21分)1.下列叙述正确的是 (A )有界数列一定有极限;(B )无界数列一定是无穷大量; (C )无穷大量数列必为无界数列;(D )无界数列未必发散。
大学高等数学期末考试试题与答案

大学高等数学期末考试试题与答案下列哪个公式不是牛顿-莱布尼茨公式的应用?B) (4x3 + 5x2 + 6x + 7)′D) (e2x + 3y)′答案:D) (e2x + 3y)′填空题(每题3分,共18分)略解答题(每题10分,共60分)略综合题(每题15分,共30分)略当谈论数学时,大家可能会想到那些复杂的公式和令人头疼的问题。
然而,数学在我们的日常生活中无处不在,它不仅是一门学科,更是一种思维方式。
在吉林大学,高等数学课程一直受到高度重视。
本文将通过学生们的期末试题来展示数学的魅力和应用。
试题是数学学习的重要组成部分。
通过做题,学生不仅可以巩固所学知识,还可以培养解决问题的能力和举一反三的思维方式。
以下是一道吉林大学高等数学的期末试题:求函数 y=x^3-3x^2+2在区间 [0,4]上的最大值和最小值。
这道题目的答案是:最大值为28,最小值为-16。
要解决这个问题,我们需要对函数进行求导,并确定函数的极值点。
然后,我们可以在给定的区间内找到函数的最大值和最小值。
除了在高等数学中学习数学基础知识,我们还可以将这些知识应用到实际生活中。
例如,在经济学的课程中,学生们可以使用数学模型来分析股票市场的波动;在工程学中,可以使用数学方法来设计桥梁和建筑的结构等。
数学是人类文化的重要组成部分,它为我们的日常生活提供了很多帮助。
通过学习高等数学,我们可以更好地理解数学的应用价值,提高我们的思维能力和解决问题的能力。
在未来的学习和工作中,这些能力将是我们不可或缺的竞争优势。
吉林大学高等数学期末试题不仅考察了学生的数学知识,还体现了数学在生活中的应用价值。
通过学习数学,我们可以培养举一反三的思维方式,提高解决问题的能力和竞争力。
让我们一起感受数学的魅力吧!下列哪个选项是高等数学中“极限”的概念? ( )下列哪个选项是高等数学中“导数”的概念?( )下列哪个选项是高等数学中“积分”的概念?( )积分在高等数学中是一个非常广泛的概念,它涉及到面积、体积、平均值等多个方面,但不能简单地说积分就是求面积或体积或平均值。
[吉林大学]20年4月《高等数学(理专)》作业考核试题-复习资料答案
![[吉林大学]20年4月《高等数学(理专)》作业考核试题-复习资料答案](https://img.taocdn.com/s3/m/56ca0101b9d528ea80c77902.png)
【奥鹏】-吉大20年4月《高等数学(理专)》作业考核试题提示:请认真核对题目后,确定是您需要的科目以及试题复习资料在下载!!!
一、单选题 (共 15 道试题,共 60 分)
【题目序号】数y=e^(cx)+1是微分方程yy"=(y')^2+y"的()
A.通解
B.特解
C.是解,但既不是通解,也不是特解
D.不是解
提示:本题为必答题,请认真阅读题目后再作答
--本题参考答案:C
【题目序号】数y=|sinx|在x=0处( )
A.连续
B.有定义,但不连续
C.无定义,但连续
D.无定义
提示:本题为必答题,请认真阅读题目后再作答
--本题参考答案:A
【题目序号】列函数中()是奇函数
A.|x|+cosx
B.xsinx
C.x+sinx
D.x+cosx
提示:本题为必答题,请认真阅读题目后再作答
--本题参考答案:C
【题目序号】f(x)=x(x-1)(x-2)(x-3),则f’(0)=( )
A.3
B.-6
C.-3
D.-2
提示:本题为必答题,请认真阅读题目后再作答
--本题参考答案:B
【题目序号】知函数y= 2cos3x-5e2x, 则x=0时的微分dy=()
A.10dx。
2006—2013年吉林大学《数学分析、高等代数》考研试题及答案

吉林大学2006年攻读硕士学位研究生入学考试试题数学分析卷一、(共 30 分)判断题1、若函数)(x f 在()b a ,上Riemann 可积,则 []2)(x f 在()b a ,上Riemann 也可积;2、若级数∑∞=1n n a 收敛,则级数∑∞=1n n a 也收敛;3、任何单调数列必有极限;4、数列(){}n1-的上、下极限都存在;5、区间 ()b a , 上的连续函数必能达到最小值;6、x sin 在整个实轴上是一致连续的;7、若函数()y x f ,沿着任何过原点的直线连续,则()y x f ,在()0,0连续; 8、若函数()x f 在点0x 取极小值,则()0x f '=0; 9、若()0x f '=0,()00<''x f ,则()x f 再点0x 取最大值; 10、向量场()222222,,x z z y y x ---是无源场。
二、(共 20 分)填空题1、设))(sin(z y x y x u +++=,则gradu =( );2、设),,(x z z y y x F +++=,则F div =();3、设),,-(xy z zx y yz x F --=,则F rot =( );4、设s 表示单位球面1222=++z y x ,则第一型曲边梯形ds x s⎰⎰2=();5、数列()⎭⎬⎫⎩⎨⎧+2211-n n n 的下极限为( );三、(共 20 分)计算下列极限1、nn k n k 1120061lim ⎪⎭⎫ ⎝⎛∑=∞→;2、()x x xx 31211lim30+-+→;3、()112007120061lim ++++∞→++n n n n n ;4、dx x x x n ⎰++∞→10221lim ; 四、(共 20 分)判断下列级数的敛散性1、∑∞=-1200520072006n n nn; 2、∑∞=1n n u ,其中0>n u ,()2211+≤-n n u u n n ,⋅⋅⋅=2,1n ; 五、(10 分)设函数)(x f 在[]1,0两次连续可微,满足0)1()0(==f f 且()01=⎰dx x f 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
吉林大学历届高数考题及答案(共 30 页 第 2 页)2008~2009学年第一学期《高等数学B Ⅰ》试卷2009年1月12日一 二 三 四 五 总分得 分一、填空题(共7道小题,每小题3分,满分21分)1.2lim 1nn n n →∞-⎛⎫= ⎪+⎝⎭.2.设322log 1y x =-,则d y = .3.若00()()f x x f x +∆-与sin2x ∆为0x ∆→时的等价无穷小,则0()f x '= .4.设函数)(x y y =由方程331,x t y t t⎧=-⎪⎨=-⎪⎩所确定,则1d d t y x == .5.曲线2610y x x =-+在点(3,1)处的曲率为 .6.设()d cos f x x x C =+⎰,则()()d n f x x ⎰= .7.31211d 1x x x -+=+⎰ .(共 30 页 第 3 页)得 分二、单选题(共7道小题,每小题3分,满分21分)1.下列叙述正确的是(A )有界数列一定有极限. (B )无界数列一定是无穷大量. (C )无穷大量数列必为无界数列. (D )无界数列未必发散. [ ]2.设数列(){}0,1,2,n n a a n >=满足1lim 0n n n a a +→∞=,则 (A )lim 0n n a →∞=.(B )lim 0n n a C →∞=>.(C )lim n n a →∞不存在.(D ){}n a 的收敛性不能确定.[ ]3.设()f x ,()g x 在区间[,]a b 上可导,且()()f x g x ''>,则在[,]a b 上有 (A )()()0f x g x ->.(B )()()0f x g x -≥.(C )()()()()f x g x f b g b ->-.(D )()()()()f x g x f a g a ->-. [ ]4.设()f x 有三阶连续导数,且满足000()()0,()0f x f x f x ''''''==<,则下列结论正确的是(A )()f x '的极小值为0. (B )0()f x 是()f x 的极大值.(C )0()f x 是()f x 的极小值. (D )点00(,())x f x 是曲线()y f x =的拐点.[ ]5.已知||e d 1k x x +∞-∞=⎰,则k = (A )0. (B )-2. (C )-1.(D )-0.5. [ ]6.摆线(sin )(1cos )x a t t y a t =-⎧⎨=-⎩的一拱与x 轴所围的平面图形绕x 轴旋转所得旋转体的体积x V =(A )2220(1cos )d[(sin )]aa t a t t ππ--⎰. (B )2220(1cos )d a t t ππ-⎰.(共 30 页 第 4 页)(C )2220(1cos )d aa t t ππ-⎰.(D )2220(1cos )d[(sin )]a t a t t ππ--⎰. [ ]7.设向量,a b 满足||||-=+a b a b ,则必有(A )-=a b 0. (B )+=a b 0. (C )0⋅=a b . (D )⨯=a b 0. [ ] 得 分三、计算题(共5道小题,每小题8分,满分40分)1.设21cos ,0,()0,0,x x f x xx ⎧≠⎪=⎨⎪=⎩ 求()f x '.2.求极限 0lim →x 222010cos d x x t tx-⎰.(共 30 页 第 5 页)3.设()f x 的一个原函数为sin x ,求 2()d x f x x ''⎰.4.计算 1221x x-⎰.5.若点M 与(2,5,0)N 关于直线4120:2230x y z l x y z --+=⎧⎨+-+=⎩对称,求点M 的坐标.得分四、应用题(满分8分)设曲线2=->.过点(2,0)y a x a(4)(0)-及(2,0)作曲线的两条法线,求a的值,使得曲线与这两条法线所围成的平面图形面积最小.(共 30 页第 6 页)(共 30 页 第 7 页)得 分五、证明题(共2道小题,每小题5分,满分10分)1.设()f x 在[0,1]上连续,在()0,1内可导,且(1)0f =.证明在()0,1内至少存在一点ξ,使得 ()()f f ξξξ'=-.2. 设13d 1sin n n tx t t=+⎰,12n n u x x x =+++,证明数列{}n u 收敛.2008~2009学年第一学期《高等数学B Ⅰ》试卷(共 30 页 第 8 页)答案 2009年1月12日一 二 三 四 五 总分得分一、填空题(共7道小题,每小题3分,满分21分) 1.2lim 1nn n n →∞-⎛⎫= ⎪+⎝⎭3e - ..2.设322log1y x =-,则dy =223(1)ln 2xdx x -- ..3.若0()()f x x f x +∆-与sin2x ∆为0x ∆→时的等价无穷小,则0()f x '= 2 .4.设函数)(x y y =由方程331,x t y t t⎧=-⎪⎨=-⎪⎩所确定,则1t dydx==23. 5.曲线2610y x x =-+在点(3,1)处的曲率为(共 30 页 第 9 页)2 .6.设()d cos f x x x c =+⎰,则()()d n fx x⎰=cos 2n C x π⎛⎫++ ⎪⎝⎭. 7.31211d 1x x x -+=+⎰ 2π .得分二、单选题(共7道小题,每小题3分,满分21分) 1.下列叙述正确的是(A )有界数列一定有极限; (B )无界数列一定是无穷大量;(C )无穷大量数列必为无界数列; (D )无界数列未必发散。
答:C2.设数列(){}0,1,2,n n a a n >=满足1limn n na a +→∞=,则(A )lim 0nn a→∞= (B )lim 0nn aC →∞=>(共 30 页 第 10 页)(C )lim nn a →∞不存在 (D ){}na 的收敛性不能确定 答:A3.设()f x ,()g x 在区间[,]a b 上可导,且()()f x g x ''>,则在[,]a b 上有(A )()()0f x g x -> (B )()()0f x g x -≥ (C )()()()()f x g x f b g b ->- (D )()()()()f x g x f a g a ->- 答:D 4.设()f x 具有三阶连续导数,且000()()0,()0f x f x f x ''''''==<,则下列结论正确的是(A )()f x '的极小值为0 (B )0()f x 是()f x 的极大值(C )0()f x 是()f x 的极小值 (D )点0(,())x f x 是曲线()y f x =的拐点 答:D5.已知||e d 1k x x +∞-∞=⎰,则k = (A )0. (B )-2. (C )-1. (D )-0.5. 答:B6.摆线(sin )(1cos )x a t t y a t =-⎧⎨=-⎩的一拱与x 轴所围的平面图形绕x 轴旋转所得的旋转体的体积V = (A )2220(1cos )d[(sin )]a a t a t t ππ--⎰ (B )2220(1cos )d a t tππ-⎰(C )2220(1cos )d a a t tππ-⎰(D )2220(1cos )d[(sin )]a t a t t ππ--⎰答:D7.设向量,a b 满足||||-=+a b a b ,则必有 (A )-=a b 0 (B )+=a b 0 (C )⋅=a b 0 (D )⨯=a b 0 答:C得分三、计算题(共5道小题,每小题8分,满分40分) 1.设21cos ,0,()0,0,x x f x xx ⎧≠⎪=⎨⎪=⎩ 求()f x '.x ≠时11()2cos sinf x x x x'=+…………(4分)x =时2001cos ()(0)(0)limlim 0x x x f x f x f xx →→-'===…………(8分)112cos sin ,0,()0,0x x f x x xx ⎧+≠⎪'=⎨⎪=⎩2.求极限lim→x 222010cos x x t dtx-⎰解222010490480880cos lim22cos lim (2)101cos lim (4)52lim (6)51.(8)10x x x x x x t dtx x x x x x x x x →→→→--=-===⎰分分分分3. 设()f x 的一个原函数为sin x ,求2()d x f x x ''⎰.22222()d ()2()d (2)()2()()d (4)()2()2sin (6)(sin )2cos 2sin xf x x x f x x f x xx f x xf x f x x x f x xf x x C x x x x x C''''=-⋅⎡⎤'=--⎣⎦'=-++=⋅--++⎰⎰⎰分分分=2sin 2cos 2sin x x x x x C--++. …………(8分) 4.计算121xx-⎰.解:()1212201312arcsin (4)333.(8)6xxx x π-=--=-⎰分分5.若点M 与(2,5,0)N 关于直线4120:2230x y z l x y z --+=⎧⎨+-+=⎩对称,求M 的坐标.解:l 的方向向量为3(2,2,1)114212==----i j kS…………(2分) L 的参数方程为5272x t y t z t =-+⎧⎪=-⎨⎪=⎩过N 垂直l 的平面为π:2260x y z -++=, …………(5分)l ,π交点为(1,3,2)-,即为MN 中心设0(,,)M x y z ,则0251,3,2222x y z ++=-==解得M 为(4,1,4)-.…………(8分) 得 分四、应用题(满分8分)设曲线2(4)(0)y a x a =->.过点(2,0)-及(2,0)作曲线的两条法线,求a 的值使曲线与这两条法线所围成的平面图形面积最小. 解:2,(2)4y ax y a''=-=-,法线:1(2)4y x a=-. …………(2分)2(4)y a x =-是偶函数.22012d (4)(2)4S xa x x a ⎡⎤∴=---⎢⎥⎣⎦⎰22023202212d 44224382321.3321()336()0,,32x x ax a a a x x x a ax a a a aS a a S a a a ⎛⎫=--++ ⎪⎝⎭⎛⎫=--++ ⎪⎝⎭=+'=-'===⎰…………(5分)32()0S a a ''=>,当6a =时,S为最小.…………(8分)得分五、证明题(共2道小题,每小题5分,满分10分)1.设()f x 在[0,1]上连续,在()0,1内可导,(1)0f =.证明在()0,1内至少存在一点ξ, 使得()()f f ξξξ'=-.证明:设()()F x x f x =,在[0,1]上连续,在()0,1内可导,()()010,F F ==(3分)在()0,1内至少存在一点ξ,使得()0F ξ'=。
