分数的互化

合集下载

分数和小数的互化方法

13 65 13 0.65= 100 = 20 20
3
75
3
1.075=1 1000 = 1 40
40
A
11
三、分数化小数
7 10
=
331 100
=
4231 1000
=
分母是10、100、1000…的分数化小数，可以直接去掉分母，看分母中 1 后面有几个零，就在分子中从最后一位起向左数出几位，点上小数点。
31 25
=
31÷25=1.24
A
4
既有分数又有小数时的比较大小
统一方法（也是最简单、方便的方法）：
只将分数化成小数进行比较。
比如：比较下列各数的大小： 0.35 2 8 0.4 0.35
5 25
2 5
= 0.4
8 25
=
0.32
8 25
<
0.35
<
0.35 < A
0.4
=
2 5
5
A
6
0.72×50
2
3
1
20 0.12 9 0.375 5 3.025 3 8
A
20
变式训练
• 1.把0.9999……化成分数。 • 2.把7.383838……化成分数。 • 方法：纯循环小数化成分数，分子是一个循
环的小数所组成的数，分母的各位数字都是 9，9的各数同循环节的位数相同。
• 字母表示： 0.abab……= ab 99
=
0.28
分母不是10、100、1000… …的分数化小数，要用分子去除以分母；
11 = 11÷45≈0.24 (保留两位小数) 45
除不尽的，可以根据需要按四舍五入法保留几位小数。

分数和小数的互化方法

5、比较下面每组数的大小
5 2 8 和 2.769 1 和 0.365 3
6、把下面各数按从小到大的顺序排列起来
3 20
0.15 3
2 9
0.222
3.025
3 5
0.6
1 38
3.125
0.12
0.375
20
‹ 0.12 ‹
2
9
‹
0.375
‹
3
5
‹ 3.025 ‹ 3 8
1
变式训练
• 1.把0.9999……化成分数。 • 2.把7.383838……化成分数。 • 方法：纯循环小数化成分数，分子是一个循环的小数所组成的数，分母的各位数字都是 9，9的各数同循环节的位数相同。 • 字母表示： 0.abab……= ab
139 7 21 =0.139 =0.7 =0.21 1000 10 100 13 3 13 =1.3 =0.03 =0.013 10 100 1000 331 4231 =3.31 =4.231 100 1000 765431 3249 =76.5431 =32.49 10000 100
7 = 7÷25 = 0.28 25
常用分数与小数的互化（要牢牢记住）：
1 =0.5 2 1 =0.25 4 3 =0.75 4 1 =0.2 5
2 =0.4 5 3 =0.6 5 4 =0.8 5 1 =0.125 8
1 =0.05 20
1 =0.04 25
小数化分数
★ 常用的小数化分数，直接写结果
2
比如：0.4
=
2 5
不要再写作 0.4 = 4
56÷0.04
0.9×0.21
45×0.7
21×0.4

分数、小数、百分数的互化

=
：10=(
)小数（2010 年）
【目标范例】例 4. 在 0．738231693450 的小数部分添上表示循环节的两点，使其变成循环小数，已知小数点后第 100 位上的数字是 3，那么这个循环小数是多少？【思路点拨】 0.738231693450 的小数部分中有 3 个数字 3，要使第 100 位上的数字是 3，是哪一个数字 3?假若循环节正好是由这 12 个数字组成，那么 100÷ 12=8 „4，这 12 个数字组成的循环节第四个数字不是 3，因此不合题意；假若循环节是从百分位上的 3 开始的，(100-1)÷11=9，那么第 100 个数字正好是循环节最后的数字 0,不是数字 3，不合题意；假若是从千分位上的数字 8 开始，那么（100 -2） ÷10 =9 „8，这样第 100 个数字是循环节的第 8 个数字 4，不是 3，
9 10 6
) （2010 年） C．甲>丙>乙 D.
B．丙>乙>甲
）.（ 2012 年） C.
19 26
B .
20 25
D.
21 24
【实战演练】一、填空题
1.分数化成小数后，小数点后的第 2011 位上的数字是________。
7
4
2．分母是 8 的所有最简真分数的和是__________。 3．甲数是乙数的1 4，那么乙数是甲数的______% 4．一个百分数 87.5%化成小数是_________，化成分数是_________. 5．一个数的倒数与它相等，这个数是______，它比 2 少________%。 6．小数的小数部分最大的计数单位是_______，它是 80%的________。 7．3.807807„小数部分的第 807 位上的数字是，3. 80707„小数部分的第 708 位上的数字是_________。 8．分数10 8化成百分数是_______，写成小数是 9．如果最简真分数二、选择题: 1．一堆煤，用了的是这堆煤的( A．40%千克

分数和小数的互化知识点总结

分数和小数的互化知识点总结在数学中，分数和小数是常见的数的表示形式。

它们可以表示同一个数值，但采用不同的分数形式或小数形式。

本文将总结分数和小数的互化知识点，包括互化的基本方法和实例应用。

一、分数转换为小数的方法1. 直接除法法：将分子除以分母，所得结果即为分数的小数形式。

例如：将2/3转换为小数，计算2 ÷ 3 = 0.6666...（以6无限循环表示）。

2. 除法的整数部分加上小数部分法：将分子除以分母，将得到的商的整数部分作为小数的整数部分，再将得到的商的小数部分写成小数形式。

例如：将5/4转换为小数，计算5 ÷ 4 = 1.25。

3. 小数点移位法：将分子乘以10的n次方（n为正整数），然后除以分母，得到的商就是所需的小数形式。

例如：将3/5转换为小数，计算3 × 10 ÷ 5 = 6。

二、小数转换为分数的方法1. 小数转换为有限小数的分数：将小数的数位作为分子，分母为10的数位数次方；然后将分数化简至最简形式。

例如：将0.6转换为分数，分子为6，分母为10，化简得到3/5。

2. 小数转换为无限循环小数的分数：设小数部分重复的数字位数为n，将小数的数位减去非循环位数后作为分子，分母为9乘以非循环位数为n的0.9倍的10的n次方，然后将分数化简至最简形式。

例如：将0.444...转换为分数，分子为4，分母为9乘以0.9的10的1次方，化简得到4/9。

三、实例应用实例1：将1/4转换为小数。

解法：1 ÷ 4 = 0.25。

因此，1/4转换为小数为0.25。

实例2：将0.6转换为分数。

解法：6/10化简为3/5。

因此，0.6转换为分数为3/5。

实例3：将0.363636...转换为分数。

解法：将0.363636...的非循环位数减去，得到36-3=33作为分子，分母为99=9×11。

化简得到33/99，可以继续化简为1/3。

因此，0.363636...转换为分数为1/3。

分数小数的互化方法

分数小数的互化方法分数和小数是数学中常见的数值表示方法，它们之间的互化是数学学习中的基本内容之一。

下面详细介绍分数和小数的互化方法。

一、分数转换为小数的方法：要将分数转换为小数，可使用除法的运算方法，具体步骤如下：1. 将分数的分子除以分母；2. 若商是有限的小数，则该小数即为分数的小数表示；3. 若商是无限循环小数，则可以通过长除法或使用计算器等工具计算到一定精度进行近似表示。

例如，我们将分数2/3转换为小数：2 ÷3 = 0.666666...可见，商为无限循环小数，接下来是具体的计算过程：0.666666...= 0.666 ×10/10 + 0.666 ×1/10 + 0.666 ×1/100 + ...= 6/10 + 6/100 + 6/1000 + ...= 6 ×1/10 + 6 ×1/100 + 6 ×1/1000 + ...= 0.6 + 0.06 + 0.006 + ...= 6/10 + 6/100 + 6/1000 + ...= 600/1000 + 60/1000 + 6/1000 + ...= (600 + 60 + 6) / 1000= 666/1000所以，2/3转换为小数表示为0.666。

二、小数转换为分数的方法：要将小数转换为分数，可根据小数的性质进行科学化简，具体步骤如下：1. 找到小数部分的数位，并确定要转换为分数的部分；2. 分子是小数部分数位除以10的位数；3. 分母是10的位数。

例如，我们将小数0.25转换为分数：0.25的小数部分是0.25，有两个小数位数。

根据分数的定义，我们可以得到以下转换：0.25 = 25/100所以，0.25转换为分数表示为25/100。

再例如，我们将小数0.555...转换为分数：0.555...的小数部分是0.555...，由于小数部分是无限循环的，我们可以用一个未知数x表示，并进行如下计算：x = 0.555...10x = 5.555...因为10x与x的小数部分相同，所以我们可以得到以下等式：10x - x = 5.555... - 0.555...9x = 5x = 5/9所以，0.555...转换为分数表示为5/9。

分数小数的互化(全面)

分数与小数的互化同学们已经知道，任何一个分数通过除法运算（分数的分子除以分母）都可以化成小数。

一个分数可以化成有限小数或无限循环小数（无限不循环小数不属于分数的范围，到中学以后再研究）。

由于“任何一个整数都能分解成若干个质数的积的形式”，我们把分数化为小数，可在分母的质因子分解上分类讨论。

结论1：一个最简分数，如果分母中除了2和5以外，不含有其他质因子，则按这个分数必化为有限小数且在这个有限小数中，小数部分的位数等于分母中含2，5因子个数的最大数。

结论2：一个最简分数，如果分母中只能分解出2和5以外的质因子，则这个分数必化成纯循环小数，这个纯循环小数的循环节的最少位数等于能被分母整除的，由9构成的数中最小数的9的个数。

结论3：一个最简分数的分母中，如果既有2，5这样的因子，又含有2，5以外的这个质因子，则这个分数必能化成混循环小数，它的不循环部分的数字个数等于分母因子中2，5个数较多一个的个数，循环节的最小位数等于分母中除2，5以外的因子积能整除的由9构成的数中最小数的9的个数。

例题求解例1 将1337,,,28254050这些分数化成小数。

例2 将分数6815,,,12733377化成小数。

例3 将分数75441,,,12412505120化成小数。

例4 将0.27∙∙和1.081∙∙化成分数。

（纯循环小数化成分数）结论4：从上面例题可知，一个纯循环小数的小数部分可以化成分数，这个分数的分子是一个循环节表示的数，分母的各位数都是9，9的个数与循环节的个数相同。

最后能约分再约分。

按上述方法很容易把纯循环小数化成分数，如：0.2∙16∙=216999=837， 1.0∙53∙=1+0.0∙53∙=1+53531999999=。

例5 将0.28∙和0.136∙∙化成分数。

（混循环小数化成分数）结论5：由以上例题可以看出，一个混循环小数的小数部分可以化成分数，这个分数的分子是第二个循环节以前的小数部分组成的数与小数部分中不循环部分组成的数的差，分母的头几位数是9，末几位数是0，9的个数与循环节中的位数相同，0的个数与不循环部分的位数相同。

带分数与假分数的互化

带分数与假分数的互化在数学中，分数是表示一个数被分为若干等分的形式，通常由一个分子和一个分母组成。

常见的分数包括带分数和假分数。

带分数由一个整数和一个真分数组成，而假分数则是分子大于分母的分数。

在解决数学问题时，我们经常需要将带分数和假分数进行互相转化。

本文将介绍带分数与假分数的互化方法。

一、带分数转化为假分数假设我们有一个带分数，例如3个整数和4分之3。

要将其转化为假分数，可以按照以下步骤进行：步骤一：将整数与分母相乘，再加上分子，得到新的分子。

在这个例子中，我们将3乘以3，得到9。

步骤二：将新的分子除以原来的分母，得到新的分子和新的分母。

在这个例子中，我们将9除以4，得到2和1，即新的分子是2，新的分母是4。

最后，我们得到的假分数是2分之1。

二、假分数转化为带分数现在假设我们有一个假分数，例如5分之7。

要将其转化为带分数，可以按照以下步骤进行：步骤一：将分子除以分母，得到整数部分。

在这个例子中，我们将5除以7，得到0余5。

步骤二：将余数作为新的分子，分母保持不变，得到新的带分数。

在这个例子中，我们得到的带分数是0个整数和5分之7。

通过以上两种方法，我们可以很方便地在带分数和假分数之间进行转化。

这对于解决数学问题和简化计算过程有很大的帮助。

带分数和假分数的互化在实际生活中也有很多应用。

例如，在烹饪中，我们常常会遇到需要将食材的比例转化为带分数或假分数的情况。

这可以帮助我们更好地掌握食材的用量，确保烹饪的准确性和美味度。

总结起来，带分数和假分数的互化是数学中重要的一部分。

带分数可以通过乘法和加法得到假分数，而假分数则可以通过除法和取余数得到带分数。

熟练掌握带分数和假分数的互化方法，可以帮助我们更好地理解和解决数学问题。

同时，在实际生活中的应用也能体现出分数的实用性和重要性。

带分数与假分数的互化是数学中的基础操作之一，理解和掌握这一概念对于学习和应用数学都具有重要意义。

通过本文的介绍和示例，相信读者对于带分数和假分数的互化方法有了更深入的了解，能够更加熟练地运用于实际问题。

常见分数小数互化必背表

常见分数小数互化必背表一、常见分数转小数1/2 = 0.51/3 = 0.333...2/3 = 0.666...1/4 = 0.253/4 = 0.751/5 = 0.22/5 = 0.43/5 = 0.64/5 = 0.81/6 = 0.166...5/6 = 0.833...1/8 = 0.1253/8 = 0.3755/8 = 0.6257/8 = 0.8751/10 = 0.13/10 = 0.37/10 = 0.79/10 = 0.9二、常见小数转分数0.1 = 1/100.2 = 1/50.25 = 1/40.3 = 3/100.4 = 2/50.5 = 1/20.6 = 3/50.625 = 5/80.666... = 2/30.7 = 7/100.75 = 3/40.8 = 4/50.833... = 5/60.875 = 7/80.9 = 9/10三、人类视角下的分数小数互化当我们在日常生活中进行计算或者遇到一些实际问题时，常常需要将分数转化为小数，或者将小数转化为分数。

这样可以方便我们进行计算，也更加符合我们对实际问题的理解。

举个例子，假设我们要计算一件商品打折后的价格，原价是100元，折扣是四分之一。

我们可以将四分之一转化为小数，即0.25，然后用原价乘以0.25，就可以得到打折后的价格25元。

又比如，我们要计算一个圆的面积，半径是1/2米。

这时，我们可以将1/2转化为小数，即0.5，然后利用圆的面积公式πr²，就可以计算出圆的面积为π × (0.5)² = 0.7854 平方米。

在实际生活中，分数和小数的互化经常出现在各种计算和测量中。

掌握常见的分数小数互化必背表，可以提高我们解决问题的效率和准确性，让我们更好地应对各种实际情况。

总结：分数和小数的互化在日常生活中非常常见，我们需要熟练掌握常见的分数小数互化必背表。

通过将分数转化为小数或将小数转化为分数，我们能够更加方便地进行计算和解决实际问题。

小学数学分数和小数互化知识点归纳大全

小学数学分数和小数互化知识点归纳大全1.小数化成分数：原来有几位小数，就在1的后面写几个零作分母，把原来的小数去掉小数点作分子，能约分的要约分。

2.分数化成小数：用分母去除分子。

能除尽的就化成有限小数，有的不能除尽，不能化成有限小数的，一般保留三位小数。

3.一个最简分数，如果分母中除了2和5以外，不含有其他的质因数，这个分数就能化成有限小数;如果分母中含有2和5以外的质因数，这个分数就不能化成有限小数。

4.小数化成百分数：只要把小数点向右移动两位，同时在后面添上百分号。

5.百分数化成小数：把百分数化成小数，只要把百分号去掉，同时把小数点向左移动两位。

6.分数化成百分数：通常先把分数化成小数(除不尽时，通常保留三位小数)，再把小数化成百分数。

7.百分数化成小数：先把百分数改写成分数，能约分的要约成最简分数。

1.分数的意义把单位1平均分成若干份，表示这样的一份或者几份的数叫做分数。

在分数里，中间的横线叫做分数线;分数线下面的数，叫做分母，表示把单位1平均分成多少份;分数线下面的数叫做分子，表示有这样的多少份。

把单位1平均分成若干份，表示其中的一份的数，叫做分数单位。

2.分数的分类真分数：分子比分母小的分数叫做真分数。

真分数小于1假分数：分子比分母大或者分子和分母相等的分数，叫做假分数。

假分数大于或等于1带分数：假分数可以写成整数与真分数合成的数，通常叫做带分数。

3.约分和通分把一个分数化成同它相等但是分子、分母都比较小的分数，叫做约分。

分子分母是互质数的分数，叫做最简分数。

把异分母分数分别化成和原来分数相等的同分母分数，叫做通分。

4.百分数表示一个数是另一个数的百分之几的数叫做百分数,也叫做百分率或百分比。

百分数通常用%来表示。

百分号是表示百分数的符号。

基本方法：①通分分子法：使所有分数的分子相同，根据同分子分数大小和分母的关系比较。

②通分分母法：使所有分数的分母相同，根据同分母分数大小和分子的关系比较。

小学数学常用分数、小数互化

小学数学常用分数、小数互化常用分数和小数的互换：1/2 = 0.5 = 50%1/3 = 0.333… ≈ 0.3332/3 = 0.666… ≈ 0.6671/4 = 0.25 = 25%3/4 = 0.75 = 75%1/5 = 0.2 = 20%2/5 = 0.4 = 40%3/5 = 0.6 = 60%4/5 = 0.8 = 80%1/8 = 0.125 = 12.5%3/8 = 0.375 = 37.5%5/8 = 0.625 = 62.5%7/8 = 0.875 = 87.5%1/20 = 0.053/20 = 0.157/20 = 0.359/20 = 0.4511/20 = 0.5513/20 = 0.6517/20 = 0.8519/20 = 0.951/16 = 0.06251/32 = 0.1/64 = 0.1/128 = 0.xxxxxxx1/256 = 0.xxxxxxxx1/512 = 0.xxxxxxxx51/1024 = 0.xxxxxxxx251/7 = 0.xxxxxxxxxxxxxxxxxx… ≈ 0.143 2/7 = 0.xxxxxxxxxxxxxxxx14… ≈ 0.286 3/7 = 0.xxxxxxxxxxxxxxxx71… ≈ 0.429 4/7 = 0.xxxxxxxxxxxxxxxx28… ≈ 0.571 5/7 = 0.xxxxxxxxxxxxxxxx85… ≈ 0.714 6/7 = 0.xxxxxxxxxxxxxxxx42… ≈ 0.857常用圆周率的计算：π×1 = 3.14π×3 = 9.42π×5 = 15.70π×7 = 21.98π×9 = 28.26π×16 = 50.24π×20 = 62.80π×32 = 100.48π×49 = 153.86π×81 = 254.34常用的平方数：1² = 12² = 43² = 94² = 165² = 256² = 367² = 498² = 64常用倍数的计算：2 = 6.284 = 12.566 = 18.848 = 25.1212 = 37.6818乘以56.52，25乘以78.50，36乘以113.04，64乘以200.96，121乘以379.94，39除以81，10乘以100，11的平方是121，12的平方是144，13的平方是169，14的平方是196，15的平方是225，16的平方是256.172的平方是289，182的平方是324，192的平方是361，202的平方是400.常用的立方数有13等于1，23等于8，33等于27，43等于64，53等于125，63等于216，73等于343，83等于512，93等于729，103等于1000，113等于1331，123等于1728，133等于2197，143等于2744，153等于3375，163等于4096，173等于4913，183等于5832，193等于6859，203等于8000.约分时常用的乘法算式有11乘以2等于22，12乘以2等于24，12乘以4等于48，12乘以5等于60，12乘以7等于84，12乘以8等于96，13乘以3等于39，13乘以4等于52，13乘以6等于78，13乘以7等于91，14乘以3等于42，14乘以4等于56，14乘以6等于84，14乘以7等于98.3的3次方等于27，3的6次方等于216，3的7次方等于729，3的8次方等于1728，3的9次方等于3375，3的10次方等于5832，2乘以3的平方等于36，5乘以3的平方等于45，15乘以4等于60，15乘以5等于75，15乘以6等于90，16乘以2等于32，16乘以3等于48，16乘以4等于64，16乘以5等于80，16乘以6等于96，17乘以2等于34，17乘以3等于51，17乘以4等于68，17乘以5等于85，18乘以2等于36，18乘以3等于54，18乘以4等于72，19乘以3等于57，21乘以2等于42，21乘以5等于105，22乘以2等于44，22乘以5等于110，23乘以4等于92，24乘以3等于72，25乘以2等于50.25×5=12526×3=7828×2=5628×5=14031×2=62 32×3=96 35×2=70 37×2=74 5=904=763=636=126 3=662=465=115 4=963=756=150 2=543=842=583=932=863=1052=76长度单位换算：1千米=1000米1米=10分米1分米=10厘米1米=100厘米1厘米=10毫米1米=100厘米1千米=厘米面积单位换算：1平方千米=100公顷1公顷=平方米1平方米=100平方分米1平方分米=100平方厘米1平方千米=xxxxxxx平方米体积单位换算：1立方米=1000立方分米1立方分米=1000立方厘米1立方分米=1升1立方厘米=1毫升1立方米=1000升1升=1000立方厘米1立方分米=1000毫升质量单位换算：1吨=1000千克1千克=1000克人民币单位换算：1元=10角1角=10分1元=100分时间单位换算：无明显错误。

常用分数小数的互化

×49=
×64=
×81=
×121=
三、常用的完全平方数
12=1
22=4
32=9
42=16
52=25
62=36
72=49
82=64
92=81
102=100
112=121
122=144
132=169
142=196
152=225
162=256
172=289
182=324
192=361
202=400
四、常用的立方数
小月(30天)的有:4、6、9、11月
平年2月28天,
闰年2月29天
平年全年3654小时
1时=60分
1分=60秒
1时=3600秒
13=1
23=8
33=27
43=64
53=125
63=216
73=343
83=512
93=729
103=1000
113=1331
123=1728
133=2197
143=2744
153=3375
163=4096
173=4913
183=5832
193=6859
203=8000
五、常用单位换算
长度单位换算
7/20==35%
9/20==45%
11/20==55%
13/20==65%
17/20==85%
19/20==95%
1/16==%
1/32==%
1/64==%
二、常用圆周率的计算
×1=
×2=
×3=
×4=
×5=
×6=
×7=
×8=
×9=
×10=

百分数与分数的互化

百分数、分数的互化百分数、
把百分数化成小数，把百分数化成小数，小数化成百分数 0.32= 32% 1.59%= 0.0159 1= 100% 200%= 2 28%= 0.28 0.01%= 0.0001 5%= 0.05 5= 500% 59.8%= 0.598 1.41= 141% 2.1%= 0.021 81.2= 8120%
填表。填表。
百分数 32% 小数分数 0.32 8 25
33.3% 150% 37.5% 0.333 1 3 1.5 1 1 2 0.375 3 8
百分数与分数的互化百分数与分数的互化
3、按由小到大的顺序排列下列各数。排列下列各数。
0.58 0.85 7 =0.875 8 85.1% =0.851
百分
ห้องสมุดไป่ตู้
百分分 , 分分百分
分
100 分 . 分数
分别用百分数、小数、分数表示图中的涂色部分百分数： 37.5% 小数：0.375 数：0.375 3 分数： — 8
分别用小数、分数、分别用小数、分数、百分数表示直线上的各点
百分数小数分数 0.05 1 20 0.18 9 50 0.28 7 25 0.39 39 100 5% 18% 28% 39%
5 ≈0.833 6
﹤
﹤
﹤
﹤
百分
百分分 , 分
分
100 分 . 分数
把百分数化成分数：把百分数化成分数： 7 14 14%= = 100 50 0.5 = 5 = 1 0.5%= 100 1000 200 21 21%= 100 125 = 5 125%= 100 4
百分分百分
分数

常用分数、小数、百分数之间的互化

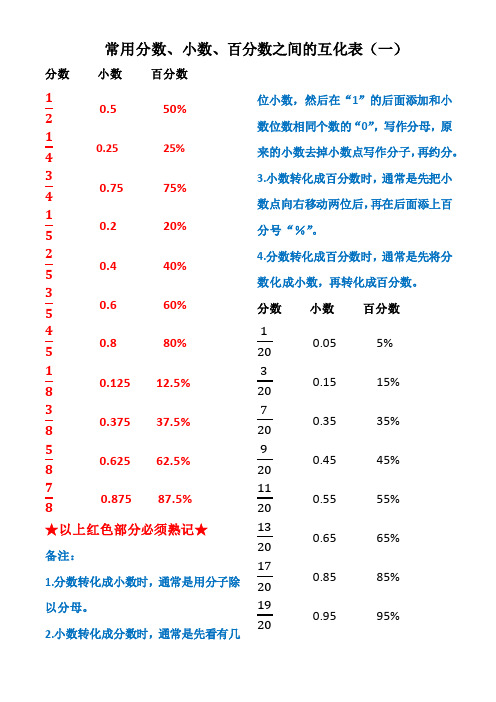
分数小数百分数120.5 50%140.25 25%340.75 75%150.2 20%250.4 40%350.6 60%450.8 80%180.125 12.5%380.375 37.5%580.625 62.5%780.875 87.5%★以上红色部分必须熟记★备注：1.分数转化成小数时，通常是用分子除以分母。

2.小数转化成分数时，通常是先看有几位小数，然后在“1”的后面添加和小数位数相同个数的“0”，写作分母，原来的小数去掉小数点写作分子，再约分。

3.小数转化成百分数时，通常是先把小数点向右移动两位后，再在后面添上百分号“％”。

4.分数转化成百分数时，通常是先将分数化成小数，再转化成百分数。

分数小数百分数1200.05 5%3200.15 15%7200.35 35%9200.45 45%11200.55 55%13200.65 65%17200.85 85%19200.95 95%分数小数百分数分数小数百分数1250.04 4%2250.08 8%3250.12 12%4250.16 16%6250.24 24%7250.28 28%8250.32 32%9250.36 36%11250.44 44%12 250.48 48%13250.52 52%14250.56 56%16250.64 64%17250.68 68%18250.72 72%19250.76 76%21250.84 84%22250.88 88%23250.92 92%24250.96 96%备注：1. 分母为20的分数转化成小数，先用分子乘以“5”，再把所得的积的小数点向左移动两位即可。

2. 分母为25的分数转化成小数，先用分子乘以“4”，再把所得的积的小数点向左移动两位即可。

分数的互化的方法

分数的互化的方法
互化分数是将一个分数转换为另一个等价的分数，但分子和分母的值发生了改变。

常见的互化方法有以下几种：
1. 通分：当两个分数的分母不相等时，可以通过找到它们的公共倍数来使它们的分母相等。

分别将分子乘以对应的倍数，然后分别得到的分数就具有相同的分母了。

例如：将1/2和1/3互化为相同的分母，可以将1/2乘以3得到3/6，将1/3
乘以2得到2/6，得到两个分数的分母都是6，所以可以将它们进行比较。

2. 化简：当一个分数的分子和分母可以同时被一个数整除时，可以将这个数约去，从而得到一个更简化的分数。

这个过程也被称为分数化简。

例如：分数10/20可以同时被2整除，所以可以将分子和分母都除以2，得到最简分数5/10。

3. 互倒：将一个分数的分子与分母对调，得到的分数为原分数的倒数。

例如：分数3/4的倒数为4/3。

通过以上的互化方法，可以将分数转换为等价的形式，便于进行比较、计算和运
算。

百分数和分数小数的互化

百分数、分数和小数可以互相转换。

下面是它们之间的具体转换方法：
1. 百分数转化为分数或小数：将百分号去掉，除以100，即可得到分数或小数。

例如，75%可以表示为75/100，也可以表示为0.75。

2. 分数转化为百分数或小数：将分子除以分母，得到小数后乘以100，即可得到百分数或小数。

例如，3/4可以表示为0.75或75%。

3. 小数转化为百分数或分数：将小数乘以100，然后将结果写成分数形式，即可得到百分数或分数。

例如，0.6可以表示为60%或3/5。

需要注意的是，在进行转换时，应尽量保留准确的数字，避免四舍五入等误差。

另外，在学习数学的过程中，应当掌握这些转换方法，并且能够熟练地应用于各种数学问题中。

常用分数、小数互化表五年级

For personal use only in study andresearch; not for commercial use 不得用于商业用途不得用于商业用途常见分数、小数互化表1、熟练的掌握常见分数和小数的互化，对于提高运算速度，增强数感，有着很好的帮助。

2、记忆方法：（1）可以用一张卡片盖住左边的分数，看着小数说出与相等的分数，再交换。

（2）C列分数化小数的记法：分子乘5，小数点向左移动两位。

（3）D、E两列分数化小数的记法：分子乘4，小数点向左移动两位。

1 2 =0.5=50%、14=0.25=25%、34=0.75=75%、15=0.2=20%、25=0.4=40%、35=0.6=60%、1 8 =0.125=12.5%、38=0.375=37.5%、58=0.625=62.5%、78=0.875=87.5%、120=0.05=5%、125=0.04=4%3.14×2=6.28 3.14×3=9.42 3.14×4=12.563.14×5=15.70 3.14×6=18.84 3.14×7=21.98 3.14×8=25.12 3.14×9=28.26 3.14×16=50.243.14×25=78.5不得用于商业用途仅供个人参考仅供个人用于学习、研究；不得用于商业用途。

For personal use only in study and research; not for commercial use.Nur für den persönlichen für Studien, Forschung, zu kommerziellen Zwecken verwendet werden.Pour l 'étude et la recherche uniquement à des fins personnelles; pas à des fins commerciales.толькодля людей, которые используются для обучения, исследований и не должны использоваться в коммерческих целях.以下无正文不得用于商业用途。

百分数分数互化

学习目标1
1、掌握百分数化分数的方法。 2、能熟练运用方法进行百分数和分数的互化
学习指导
认真看课本81页例3，思考： 1、理解百分数化成分数的过程。 2、百分数化成分数的步骤是怎样的？
检
测
完成81页做一做
百分数和分数的互化
把27%、50% 、12.5%化成分数、化成分数 27% = 27 100 50% = 50 ＝ 1 100 2 12.5 125 1 ＝＝ 12.5% = 100 1000 8
分数、小数、分数、小数、百分数的互化
城关镇中心小学
王成华
复习
把下面的分数化成小数。把下面的分数化成小数。 1
2 5= 1.44 Nhomakorabea5= 4÷25= 0.16
21 100
=21÷100=0.21
小结：小结：分数化小数用分子除以分母就可以完成。就可以完成。
小数
化成分母是10、的分数，化成分母是、100、1000的分数，再约分。、的分数再约分。
分数
分子除以分母。
百分数和小数的互化
把小数化成百分数，只要把小数点向右移动两位，把小数化成百分数，只要把小数点向右移动两位，同时在后面添上百分号；把百分数化成小数，同时在后面添上百分号；把百分数化成小数，只要把百分号去掉，同时把小数点向左移动两位。把百分号去掉，同时把小数点向左移动两位。
2 ≈ 1.286= 128.6％ 1 7
百分数和分数的互化
把分数化成百分数，通常先把分数化成小数（把分数化成百分数，通常先把分数化成小数（除不尽时，通常保留三位小数），再把小数化成百分数；把百通常保留三位小数），再把小数化成百分数；），再把小数化成百分数分数化成分数，先把百分数改写成分数，分数化成分数，先把百分数改写成分数，能约分的要约成最简分数。成最简分数。