语音中提取基音频率matlab程序
自相关函数法基音周期提取(matlab版)

function nmax=find_maxn(r)%maxn,为峰值最大的nzer=find(r==0); %找第一个零点如果存在jiaocha=0; %找第一近零点ii=1;while (jiaocha<=0)if(r(ii)>0 && r(ii+1)<0 && (ii+1)<length(r))jiaocha=ii;endii=ii+1;if ii==length(r) %没有找到符合要求的点jiaocha=1;endendif length(zer)>0 %检查是否存在零点if zer(1)<jiaocha %存在,则和jiaocha比较大小,用于祛除前点的对基音周期的查找带来的影响jiaocha=zer(1);endendr(1:jiaocha)=0; %祛除影响maxn=max(r); %找最大值temp=find(r==maxn);%返回第一个最大值nmax=temp(1);function jiyinzhouqi(filename,shift)%短时自相关分析%filename语音文件*.wav%zhouqi基音周期shift=10;[signal,fs]=wavread('f:/mywork/1.wav');shift=round(fs*shift); %帧移n1=fix(fs*0.97)+1; %分析起点970ms,帧长30msn2=fix(fs*1)+1;ii=1;for ii=1:(length(signal)-n1)/shift %分析次数if n2<length(signal)data=signal(n1:n2);N=n2-n1+1;R=zeros(1,N); %基音周期(n)多次分析数组for k=1:N-1for jj=1:N-kR(k)=R(k)+data(jj)*data(jj+k);endendvalue(ii)=find_maxn(R); %调用基音周期(n)分析函数n1=n1+shift; %移动帧n2=n2+shift;endend%figure(3)%plot(R);%axis([0,1000 -300 300])figure(1)stem(value);axis([0 length(value) 0 1000])len =length(value); %基音周期(n)多次分析数组长度aver=mean(value);index=find(abs((value-aver))>aver/5);value(index)=0; %去除大野点的影响len=len-length(index);for jj=1:3:len/3 %中值平滑,滑动窗口宽度3,精度为中值1/4(剔除野点)average=(value(jj)+value(jj+1)+value(jj+2))/3;for kk=1:3if abs((value(jj-1+kk))-average)>average/4value(jj-1+kk)=0; %将野点置零,同时数组长度减一len=len-1;endendendfigure(2)stem(value);axis([0 length(value) 0 max(value)])Tp=sum(value)/len/fs %求基音周期(Tp)。
基音周期提取1-原理说明
基⾳周期提取1-原理说明Matlab 基⾳周期提取1-原理说明
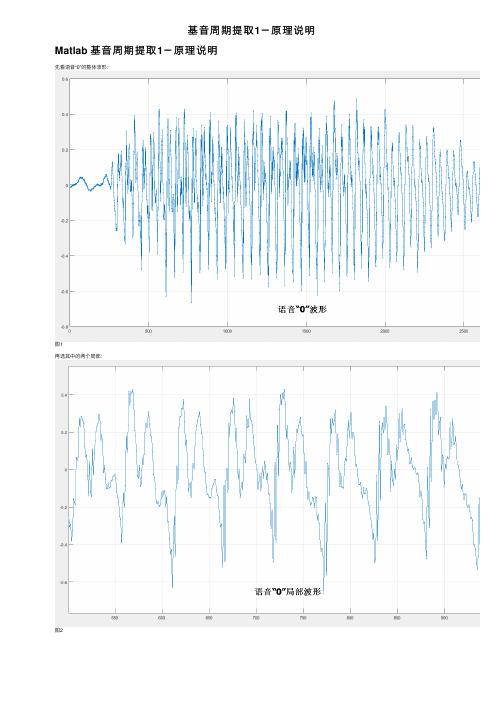
先看语⾳“0”的整体波形:
图1
再选其中的两个局部:
图2
图3
以上三幅图为语⾳“0”以8KHz采样的波形。
可以看出,汉语语⾳具有⾮常明显的**准周期特性**。
相邻的两个周期的波形基本⼀致,随时间推移,波形规律性的**逐渐**改变。
基⾳周期提取的常⽤⽅法参数有:**短时⾃相关**、短时平均幅度差、线性预测倒谱、⼩波⾃相关函数、三电平削波的互相关函数等[2]。
这⾥对便于理解的短时⾃相关法说明如下,直接引⽤参考⽂献内容。
图4(参考⽂献[3])
公式通俗理解:
式3.13中,R(k)等于原序列x中,由负⽆穷到正⽆穷,所有间隔为k的两个样点,相乘后求和。
式3.14中,R(k)等于原序列x中,由负⽆穷到正⽆穷,所有间隔为k的两个样点,相乘后求和,再除以求和的项数,即相隔为k的样点乘积的平均值。
图5(参考⽂献[3])
参考⽂献:
1、《实⽤语⾳识别基础》王炳锡屈丹彭煊等,国防⼯业出版社 2005
2、《MATLAB在语⾳信号分析和合成中的应⽤》宋知⽤,北京航空航天⼤学出版社 2013
3、《数字语⾳处理及MATLAB仿真》张雪英,电⼦⼯业出版社 2010
4、⽹络资源。
基于MATLAB的语音信号的采集与分析

基于MATLAB的语音信号的采集与分析摘要:我们通过学习使用MA TLAB仿真软件实现语音信号分析,加深对信号与系统这门课程所学习内容的理解,锻炼自学能力和动手能力。
我们通过电脑的声卡采集声音信号,借助已有的知识和MATLAB对采集的声音信号进行时域波形和频域频谱的显示,研究男女声信号的差别,通过查找资料提取声音信号的基音频率,并通过大量测试确定门限值来自动判别男女声信号,最后对信号进行降采样处理并播放,重新绘制频谱图分析,验证抽样定理。
关键词:MA TLAB仿真、频谱分析、基音频率、降采样、抽样定理。
1.音频信号的采集我们所要分析的语音信号需要自行采集,所以信号分析的第一步就是采集音频信号。
实现音频信号的采集最简单的办法就是通过电脑的声卡直接进行采集,这样采集到的音频信号虽然已经被转化成了数字量存储在电脑中,但通过查询我们了解到电脑录音所使用的采样频率是为44100Hz,完全保证了人类耳朵能听到所有声音频率分量的无失真采集,如果通过MA TLAB软件采集还能够调节采样频率,所以能够完全满足我们实验的要求。
1.1使用MATLAB采集语音信号通过上网查询,我们了解到MATLAB有自带的音频信号采集函数audiorecord(),通过它可以在程序运行时即时采集音频信号进行存储并处理,并且可以通过改变输入参数来改变采样频率,可以直接模拟降采样的过程,直观地验证抽样定理。
但鉴于我们需要重复进行试验和演示,即时采集信号显得繁琐且不必要,而且会增加我们非界面化编程的难度,所以我们放弃了这种方法。
1.2使用电脑录音机采集语音信号通过电脑自带的录音机软件可以实现更简单的音频信号采集操作,虽然采样频率不可调节,但其固有的采样频率完全满足了我们对所采集信号的要求,可以通过MATLAB的降采样处理的到较低采样频率的信号。
这样采集的音频信号会直接以文件的形式存储在电脑中,方便我们随时进行调用,方便分析与演示,所以我们决定采用这种方式实现语音信号的采集。
基于MATLAB的语音信号的基音周期检测

基于MATLAB的语音信号的基音周期检测摘要:MATLAB是一种科学计算软件,专门以矩阵的形式处理数据。
MATLAB将要性能的数值计算和可视化集成在一起,并提供了大量的内置函数,从而被广泛的应用于科学计算、控制系统和信息处理等领域的分析、仿真和设计工作。
MATLAB在信号与系统中的应用主要包括符号运算和数值计算仿真分析。
由于信号与系统课程的许多内容都是基于公式演算,而MATLAB 借助符号数学工具箱提供的符号运算功能,基本满足设计需要。
例如:解微分方程、傅里叶正反变换、拉普拉斯正反变换和Z正反变换等。
MATLAB在信号与系统中的另一主要应用是数值计算与仿真分析,主要包括函数波形绘制、函数运算、冲击响应仿真分析、信号的时域分析、信号的频谱分析、系统的S域分析和零极点图绘制等内容。
本次课程设计为语音信号的基音周期检测,采集语音信号,对语音信号进行处理,区分清音浊音,并通过对采样值进行滤波、分帧、求短时自相关函数,得到浊音的基音周期。
关键字:清音、浊音、基音周期、基音检测、自相关函数目录1 概述 (1)2 AMDF算法原理及实现 (1)2.1 AMDF算法源程序 (2)3 ACF算法原理及实现 (4)3.1 用短时平均能量进行清/浊音的判断 (4)3.2 自相关函数基音检测的原理 (6)3.3 算法实现及相关程序 (6)3.3.1 带通滤波 (7)3.3.2 取样与分帧 (7)3.3.3 短时能量分析 (8)3.3.4 自相关函数分析 (11)4 总结与心得体会 (13)参考文献 (13)1 概述基音周期检测也称为基频检测(Pitch Detection) ,它的目标是找出和声带振动频率完全一致的基音周期变化轨迹曲线,或者是尽量相吻合的轨迹曲线。
基音周期检测在语音信号的各个处理领域中,如语音分析与合成、有调语音的辨意、低速率语音压缩编码、说话人识别等都是至关重要的,它的准确性及实时性对系统起着非常关键的作用,影响着整个系统的性能。
语音信号基音周期检测的matlab程序

function nmax=find_maxn(r)%寻找峰值最大的n值及基音周期%r,自相关序列%maxn,为峰值最大的nzer=find(r==0); %找第一个零点如果存在jiaocha=0; %找第一近零点ii=1;while (jiaocha<=0)if(r(ii)>0 && r(ii+1)<0 && (ii+1)<length(r))jiaocha=ii;endii=ii+1;if ii==length(r) %没有找到符合要求的点jiaocha=1;endendif length(zer)>0 %检查是否存在零点if zer(1)<jiaocha %存在,则和jiaocha比较大小,用于祛除前点的对基音周期的查找带来的影响jiaocha=zer(1);endendr(1:jiaocha)=0; %祛除影响maxn=max(r); %找最大值temp=find(r==maxn);%返回第一个最大值nmax=temp(1);function jiyinzhouqi(filename,shift)%短时自相关分析%filename语音文件*.wav%zhouqi基音周期shift=10;[signal,fs]=wavread('f:/mywork/1.wav');shift=round(fs*shift); %帧移n1=fix(fs*0.97)+1; %分析起点970ms,帧长30msn2=fix(fs*1)+1;ii=1;for ii=1:(length(signal)-n1)/shift %分析次数if n2<length(signal) %防止溢出data=signal(n1:n2);N=n2-n1+1;R=zeros(1,N); %基音周期(n)多次分析数组for k=1:N-1 %求自相关序列for jj=1:N-kR(k)=R(k)+data(jj)*data(jj+k);endendvalue(ii)=find_maxn(R); %调用基音周期(n)分析函数n1=n1+shift; %移动帧n2=n2+shift;endend%figure(3)%plot(R);%axis([0,1000 -300 300])figure(1)stem(value);axis([0 length(value) 0 1000])len =length(value); %基音周期(n)多次分析数组长度aver=mean(value);index=find(abs((value-aver))>aver/5);value(index)=0; %去除大野点的影响len=len-length(index);for jj=1:3:len/3 %中值平滑,滑动窗口宽度3,精度为中值1/4(剔除野点)average=(value(jj)+value(jj+1)+value(jj+2))/3;for kk=1:3if abs((value(jj-1+kk))-average)>average/4value(jj-1+kk)=0; %将野点置零,同时数组长度减一len=len-1;endendendfigure(2)stem(value);axis([0 length(value) 0 max(value)])Tp=sum(value)/len/fs %求基音周期(Tp)。
matlab语音信号基频参数提取

[b,a]=ellip(4,0.1,20,wp); % 构造椭圆滤波器
data=filter(b,a,data2);
%plot(data);% 求加窗处理后的数据经过滤波器的响应
[xmax,index]=max(data1);
%画基频图
plot(yy);
[ymax,maxindex] = max(yy);
fmax=fs/(maxindex+30);
%fmaxce2;
fmaxce2=fmax;
%fmax=roundn(fmax,-3);
fmax21=roundn((fmax-5),3);
fmax22=roundn((fmax+5),3);
run(cc,'runtohalt')
%ddatV=read(cc,address(cc,'fIn'),'single',256)
%idattV=read(cc,address(cc,'fOut'),'single',1000)
%plot(abs(idattV))
timewin=floor(0.015*fs);
xwin=data1(index-timewin:index+timewin);
[y,lags]=xcov(xwin);
ylen=length(y);
halflen=(ylen+1)/2 +30;
yy=y(halflen: ylen);
blocksize =length(data1); % 计算窗函数长度
window = hanning(blocksize); % 计算汉宁窗函数(此函数为MATLAB自带)
Matlab基于倒谱和EMD的语音基音周期的提取

---------------------------------------------------------------范文最新推荐------------------------------------------------------ Matlab基于倒谱和EMD的语音基音周期的提取在语音信号处理中,常用的语音特性是基于Mel频率的倒谱系数(MFCC)以及一些语音信号的固有特征,如基音周期等。
倒谱法可以较好地将语音信号中的激励信号和声道响应分离,并只需要用一些倒谱系数就能较好地描述语言信号的声道响应,在语音信号处理中占有很重要的位臵。
而倒谱解卷积法受加性噪声影响比较大,抗噪声性能不是很好。
针对这一存在问题,利用EMD 方法在理论上可以应用于任何类型的信号的分解,在处理非平稳及非线性数据上, 具有非常明显的优势这一优点。
本文中提出一种基于倒谱和EMD的语音基音周期提取的改进算法。
并在Matlab 中予以实现。
关键字:基音周期倒谱法EMD8664TitlePitch Period Extraction of Speech Signals based1 / 8on Cepstrum and EMDAbstractIn voice signal processing, MFCC and some inherent characteristics of voice signals, such as the frequency of pitch. Cepstrum can be used to separate the excitation signal and channel response, and can represent channel response with only a dozen cepstral coefficients. As a result, it has been a very important role in voice signal processing. While cepstrum deconvolution method is largely influenced by additive noise,and anti-noise performance is not very good.The EMD method can be applied to decompose any type of signals,and thus,having a very distinct advantage in handing non-stationary and non-linear data.For this problem,in this paper,an improved algorithm of pitch period extraction of speech signals based on cepstrum and EMD is proposed. Its implementation in MATLAB are described in detail.Key words:pitch periodCepstrumEMD---------------------------------------------------------------范文最新推荐------------------------------------------------------ 目次1 引言11 引言1.1 背景由于语言是人们在日常生活中的主要交流手段,因此语音信号处理在现代信息社会中占用重要地位。
使用Matlab进行声音信号处理的基本技巧

使用Matlab进行声音信号处理的基本技巧声音信号处理是一门重要的领域,它涵盖了音频合成、语音识别、音频修复等多个应用方向。
Matlab是一款功能强大的数学软件,也可以用于声音信号处理。
本文将介绍使用Matlab进行声音信号处理的基本技巧,包括声音读取、时域分析、频域分析、滤波和音频合成等内容。
1. 声音读取首先,我们需要将声音文件读取到Matlab中进行处理。
Matlab提供了`audioread`函数用于读取声音文件。
例如,我们可以使用以下代码读取一个wav格式的声音文件:```matlab[y, Fs] = audioread('sound.wav');```其中,`y`是声音信号的向量,每个元素代表一个采样点的数值;`Fs`是采样率,即每秒采样的次数。
通过这个函数,我们可以将声音文件以数字信号的形式加载到Matlab中进行后续处理。
2. 时域分析在声音信号处理中,常常需要对声音信号在时域上进行分析。
我们可以使用Matlab的绘图函数来展示声音信号的波形。
例如,以下代码可以绘制声音信号的波形图:```matlabt = (0:length(y)-1)/Fs;plot(t, y);xlabel('Time(s)');ylabel('Amplitude');title('Sound waveform');```这段代码中,`t`是时间轴,通过除以采样率,我们可以得到每个采样点对应的时间。
`plot`函数用于绘制声音信号的波形图,横轴表示时间,纵轴表示振幅。
通过这种方式,我们可以直观地观察声音信号的时域特征。
3. 频域分析除了时域分析,频域分析也是声音信号处理中常用的方法。
通过对声音信号进行傅里叶变换,我们可以得到声音信号在频域上的表示。
Matlab提供了`fft`函数用于进行傅里叶变换。
以下代码可以绘制声音信号的频谱图:```matlabN = length(y);f = (-N/2:N/2-1)/N*Fs;Y = fftshift(fft(y));plot(f, abs(Y));xlabel('Frequency (Hz)');ylabel('Magnitude');title('Sound spectrum');```在这段代码中,`N`是声音信号的长度,`f`是频率轴,通过调整`f`的取值范围可以实现将零频移动到中心位置。
实验二语音信号的基音周期提取最终报告

实验二语音信号的基音周期提取一、实验目的1、熟练运用MATLAB软件的运用,学习通过MATLAB软件编程来进行语音信号的基因周期提取。
2、掌握语音信号的基音周期提取的方法,实现其中一种基频提取方法。
3、学会用自相关法进行语音信号的基因检测.二、实验仪器设备及软件HP D538、MATLAB三、实验原理浊音信号的自相关函数在基因周期的整数倍位置上出现峰值,而清音的自相关函数没有明显的峰值出现。
因此检测自相关函数是否有峰值就可以判断是清音还是浊音,而峰-峰值之间对应的就是基音周期。
影响从自相关函数中正确提取基音周期的最主要原因是声道响应。
当基音的周期性和共振峰的周期性混在一起时,被检测出来的峰值可能会偏离原来峰值的真实位置。
另外,在某些浊音中,第一共振频率可能会等于或低于基音频率.此时,如果其幅度很高,它就可能在自相关函数中产生一个峰值,而该峰值又可以同基音频率的峰值相比拟。
1、自相关函数对于离散的语音信号x(n),它的自相关函数定义为:R(k)=Σx(n)x(n-k),如果信号x(n))具有周期性,那么它的自相关函数也具有周期性,而且周期与信号x(n)的周期性相同。
自相关函数提供了一种获取周期信号周期的方法。
在周期信号周期的整数倍上,它的自相关函数可以达到最大值,因此可以不考虑起始时间,而从自相关函数的第一个最大值的位置估计出信号的基音周期,这使自相关函数成为信号基音周期估计的一种工具.2、短时自相关函数语音信号是非平稳的信号,所以对信号的处理都使用短时自相关函数。
短时自相关函数是在信号的第N 个样本点附近用短时窗截取一段信号,做自相关计算所得的结果Rm(k)=Σx(n)x(n-k)式中,n表示窗函数是从第n点开始加入。
3、算法通过对自相关基音检测原理的分析,考虑到检测准确度和检测速率2方面的因素,提出了算法实现方案,并对算法进行了Matlab编程实现。
算法包含6个功能模块:带通滤波、取样、分帧、短时能量分析、相关运算、基音检测。
如何使用Matlab进行语音信号处理

如何使用Matlab进行语音信号处理引言:语音信号处理是一个重要的领域,在各种应用中都有广泛的应用,如语音识别、语音合成、音频编码等。
而Matlab是一个功能强大的工具,提供了许多用于语音信号处理的函数和工具箱,使得处理语音信号变得更加简单和高效。
本文将介绍如何使用Matlab进行语音信号处理的基本流程和一些常用的处理方法。
一、语音信号处理基础知识1.1 语音信号的特点语音信号是一种时变信号,具有时间和频率的特性。
它由一系列的声音波形组成,通过声音传感器(如麦克风)捕获并转换为电信号。
语音信号具有频谱的特征,包括基频、共振峰等。
了解语音信号的基本特点是进行语音信号处理的前提。
1.2 语音信号处理的基本流程语音信号处理的基本流程包括预处理、特征提取、模型建立、参数估计和应用等步骤。
预处理包括去噪、降采样等操作,特征提取包括MFCC(Mel频率倒谱系数)等方法,模型建立包括隐藏马尔可夫模型(HMM)等,参数估计通过最大似然估计等方法进行参数估计,应用包括语音识别、语音合成等。
二、使用Matlab进行语音信号处理的基本方法2.1 读取和保存语音文件Matlab提供了许多函数用于读取和保存语音文件。
可使用"audioread"函数读取.wav格式的语音文件,并得到语音信号的时域波形,可以使用"audiowrite"函数保存处理后的语音文件。
2.2 语音信号的时域和频域分析Matlab提供了许多函数用于对语音信号进行时域和频域分析。
可以使用"waveform"函数绘制语音信号的波形,使用"spectrogram"函数绘制语音信号的频谱图。
2.3 语音信号的预处理在语音信号处理之前,通常需要对语音信号进行预处理,如去除噪声、降低采样率等。
Matlab提供了丰富的函数和工具箱用于语音信号的预处理,如"noisegate"函数用于去除噪声,"resample"函数用于降低采样率。
Matlab在基音周期检测教学中的应用研究

Matlab在基音周期检测教学中的应用研究我们需要了解一些基本的概念和原理。
基音周期指的是连续说话过程中声带振动的周期性,它对应于声道系统的特征,可以通过周期估计来获取。
常见的基音周期估计方法有自相关法、互相关法和短时傅立叶变换法等。
这些方法在Matlab中都可以很方便地实现。
对于自相关法,Matlab提供了xcorr函数来计算信号的自相关函数,然后可以通过寻找自相关函数的峰值来估计基音周期。
我们可以使用如下的代码来实现基音周期的自相关估计:```matlab[x, Fs] = audioread('音频文件名.wav');x = x(:,1); % 取一个声道R = xcorr(x); % 计算自相关函数[~,I] = max(R);T = I / Fs; % 基音周期```对于短时傅立叶变换法,Matlab提供了stft函数来计算短时傅立叶变换,然后可以通过寻找频谱的峰值来估计基音周期。
下面是一个使用短时傅立叶变换法进行基音周期估计的示例代码:使用这些基音周期估计方法,可以对语音信号进行周期性分析,进一步研究和应用各种语音处理算法。
我们可以通过基音周期检测来识别说话人的特征,从而实现说话人识别系统;我们也可以根据基音周期检测结果来实现语音转换,实现男声转女声、音乐转唱等效果。
Matlab在基音周期检测教学中具有重要的应用研究价值。
通过Matlab提供的强大的科学计算功能,我们可以方便地实现基音周期估计算法,并进行相关的研究和分析。
基音周期检测的研究不仅对语音信号处理具有重要意义,同时也可以为语音合成、说话人识别、语音转换等应用领域提供支持和指导。
matlab 基频提取

matlab 基频提取Matlab是一种强大的数学软件,被广泛应用于科学计算、数据分析等领域。
在信号处理领域,基频提取是一个重要的任务,它可以帮助我们分析音频信号中的基本频率成分。
本文将介绍基频提取在Matlab中的应用方法。
我们需要明确什么是基频。
在音频信号中,基频即为最低频率的成分,也是声音的主要音高。
基频提取的目标就是从音频信号中准确地找到基频值。
在Matlab中,有多种方法可以实现基频提取。
其中,最常用的方法是基于自相关函数的算法。
自相关函数可以描述信号与其自身延迟后的版本之间的相关性。
基于自相关函数的基频提取算法主要包括自相关法、差值自相关法和短时自相关法。
我们来介绍自相关法。
该方法的基本思想是计算音频信号与其自身延迟后的版本之间的相似度。
具体步骤如下:1. 首先,将音频信号进行分帧处理,将长时间的信号拆分成多个短时段的小片段。
2. 对每个小片段进行自相关计算,得到自相关函数。
3. 在自相关函数中,寻找第一个极大值点,其对应的延迟就是基频周期。
4. 计算基频值,即音频信号的采样率除以基频周期。
另一种常用的方法是差值自相关法。
该方法的基本思想是计算音频信号与其自身延迟后的版本之间的差异度。
具体步骤如下:1. 同样地,对音频信号进行分帧处理,得到多个小片段。
2. 对每个小片段进行差值自相关计算,得到差值自相关函数。
3. 在差值自相关函数中,寻找第一个零交叉点,其对应的延迟就是基频周期。
4. 计算基频值,即音频信号的采样率除以基频周期。
我们来介绍短时自相关法。
该方法的基本思想是将音频信号分成多个短时段,分别计算每个短时段的基频值,然后通过插值等方法得到整个音频信号的基频值。
具体步骤如下:1. 将音频信号进行分帧处理,得到多个小片段。
2. 对每个小片段进行自相关计算,得到短时自相关函数。
3. 在短时自相关函数中,寻找第一个极大值点,其对应的延迟就是该短时段的基频周期。
4. 根据短时段的基频周期,通过插值等方法得到整个音频信号的基频值。
使用Matlab进行语音信号处理的基本步骤

使用Matlab进行语音信号处理的基本步骤引言:语音信号处理是一门涉及声音的数字信号处理领域。
它涉及到一系列的算法,用于提取、分析、合成和改变人类语音的特征。
在计算机科学和工程学中,Matlab 是最常用的工具之一,它可以有效地用于语音信号处理。
本文将介绍使用Matlab 进行语音信号处理的基本步骤。
一、导入音频文件和预处理在开始语音信号处理之前,需要导入音频文件并进行预处理。
首先,使用Matlab的音频读取函数将音频文件导入到工作环境中。
常用的音频读取函数有audioread()和wavread()等。
导入音频文件后,可以使用滤波器对音频信号进行去除噪声等预处理操作。
Matlab提供了丰富的滤波器函数,如fir1()和filter()等,可以在预处理阶段使用。
二、时域分析在对音频信号进行时域分析时,常用的技术包括时域增益和自相关函数。
时域增益可以帮助我们调整音频信号的音量。
Matlab提供了amp2db()函数,可以将线性增益转换为分贝增益。
自相关函数可以帮助我们识别音频信号中的周期性特点。
利用Matlab的xcorr()函数可以计算音频信号的自相关函数,并通过绘图工具(如plot()函数)来可视化结果。
三、频域分析频域分析是语音信号处理中的关键步骤之一。
在频域分析中,常用的技术包括傅里叶变换和功率谱密度估计。
Matlab提供了fft()函数用于计算音频信号的傅里叶变换,并通过频率域绘图工具(如plot()函数)来可视化结果。
功率谱密度估计是计算音频信号功率谱的一种技术。
Matlab提供了pwelch()函数来估计音频信号的功率谱密度,并通过plot()函数来可视化结果。
四、频率特征提取在语音信号处理中,频率特征提取是非常重要的一步。
常用的频率特征包括基频、共振峰和频率包络等。
基频代表语音信号的基本频率,可以通过自相关函数或基频提取算法来计算。
共振峰表示语音信号的共振峰位置,可通过线性预测分析或峰值检测算法来提取。
Matlab在基音周期检测教学中的应用研究

Matlab在基音周期检测教学中的应用研究
一、基音周期检测原理
影响人声音高的因素有很多,如声带长度、张力、共振等。
其中,声带振动是人声音
高的主要形成原因,而声带的振动周期即为基音周期。
基音周期检测就是在语音信号中准
确地确定基音周期的位置和长度。
基音周期检测是语音信号分析和合成的基础,对于语音
识别、说话人识别和语音合成等领域有着重要的实际意义。
二、Matlab的应用
1. 语音波形的绘制和分析
Matlab提供了丰富的绘图函数,可以方便快捷地绘制语音波形图、频谱图等。
在开始基音周期检测实验之前,首先需要加载一个语音信号样本,利用Matlab内置的绘图函数,对语音波形进行绘制,并对其进行分析。
2. 基音周期提取算法的实现
目前,基音周期提取算法主要分为时域法和频域法两种。
其中,时域法包括自相关函
数法、跳数法和动态规划法等;频域法包括基谐比值法和平均期差法等。
这里选择自相关
函数法来实现基音周期提取算法。
3. 基音周期检测实验
利用Matlab实现基音周期检测的实验,可以通过手动调节算法的参数、绘制波形和
频谱图等方式,直观感受基音周期检测的原理和应用。
三、教学应用
基音周期检测的实验可以有效地培养学生的实际操作能力,并且可以将课堂理论与实
际应用结合起来,让学生更好地理解和掌握基音周期检测算法的原理和应用。
总之,Matlab在基音周期检测教学中的应用具有较大的实际意义和教学价值。
通过Matlab进行实验操作,可以更好地实现基音周期检测的算法研究和应用,并且可以提高学生的实践能力和创新意识。
MATLAB的语音信号频谱分析

MATLAB的语音信号频谱分析MATLAB是一个功能强大的数学软件环境,它可以用于语音信号的频谱分析。
频谱分析是通过计算信号在不同频率上的能量分布来了解信号的频域特性。
在语音信号处理中,频谱分析可以用于声音的特征提取、语音识别、音频信号处理等各个方面。
要进行语音信号的频谱分析,我们需要首先将语音信号加载到MATLAB环境中。
这可以通过读取音频文件或者录制声音来实现。
然后,我们可以使用MATLAB中的信号处理工具箱中的函数来进行频谱分析。
下面是进行语音信号频谱分析的主要步骤:1.加载语音信号首先,我们需要将语音信号加载到MATLAB环境中。
可以使用`audioread`函数读取音频文件,或者使用`audiorecorder`函数录制声音。
```matlab[x, fs] = audioread('speech.wav');%或者recorder = audiorecorder(fs, 16, 1);recordblocking(recorder, 5); % 录制5秒声音x = getaudiodata(recorder);```2.预处理语音信号在进行频谱分析之前,通常需要对语音信号进行预处理。
这包括去除静音段、去除噪声等操作。
常用的预处理方法有均衡增强、滤波、语音端点检测等。
3.计算幅度谱幅度谱是频谱分析的最基本形式,它描述了信号在不同频率上的幅度分布。
可以使用`fft`函数对语音信号进行傅里叶变换,然后取幅度谱的绝对值。
```matlabX = abs(fft(x));```4.计算功率谱密度功率谱密度是幅度谱的平方值,它表示了信号在不同频率上的功率分布。
可以通过幅度谱的平方值来计算功率谱密度。
```matlabP=X.^2;```5.均衡化谱图为了更好地可视化频谱分析结果,可以对频谱图进行均衡化处理。
可以使用`db`函数将功率谱密度转换为分贝尺度。
```matlabdB = 10 * log10(P);```6.绘制谱图最后,可以使用`plot`函数绘制频谱图。
实现基于共振峰和基音的语音合成 matlab代码

实现基于共振峰和基音的语音合成 matlab代码要实现基于共振峰和基音的语音合成,可以使用MATLAB来进行编程。
以下是一个简单的示例代码,演示如何使用MATLAB生成基于共振峰和基音的合成语音:matlab设置基本参数fs = 44100; 采样率(Hz)T = 1; 合成语音的时长(秒)f0 = 100; 基音频率(Hz)vowel = 'a'; 要合成的元音声音计算共振峰参数f1 = 730; 第一个共振峰频率(Hz)f2 = 1090; 第二个共振峰频率(Hz)b1 = 100; 第一个共振峰带宽(Hz)b2 = 50; 第二个共振峰带宽(Hz)计算基音周期和长度period = round(fs/f0);n = round(fs*T);生成基音信号x = zeros(n, 1);for i = 1:period:nx(i:i+period-1) = ones(period, 1);end生成共振峰滤波器[b, a] = resonator([f1 f2], [b1 b2], fs);对基音信号进行共振峰滤波y = filter(b, a, x);播放合成的语音soundsc(y, fs);在这个示例中,首先设置了一些基本的参数,如采样率、合成语音时长、基音频率和要合成的元音声音。
然后,根据提供的共振峰参数计算滤波器系数。
接下来,生成基音信号,以及应用共振峰滤波器生成合成的语音信号。
最后,使用`soundsc`函数播放合成的语音。
请注意,这只是一个简单的示例,涵盖了基本的合成过程。
实际的语音合成可能需要更多的复杂处理和算法,以便更准确地模拟人类语音的特征。
实验三 语音信号的基频提取

实验三语音信号的基频提取一、实验目的1.掌握语音信号基频的概念,加深对基频刻画声调特征作用的理解。
2.掌握语音信号基频特征的典型求解方法二、仪器设备HP计算机、Matlab软件三、实验原理浊音信号的自相关函数在基因周期的整数倍位置上出现峰值,而清音的自相关函数没有明显的峰值出现。
因此检测自相关函数是否有峰值就可以判断是清音还是浊音,而峰-峰值之间对应的就是基音周期四、实验内容实验程序:function pitchx=wavread('w1.wav');figure(1);stem(x,'.');n=180;for m=1:length(x)/n;for k=1:n;Rm(k)=0;for i=(k+1):n;Rm(k)=Rm(k)+x(i+(m-1)*n)*x(i-k+(m-1)*n);endendp=Rm(10:n);[Rmax,N(m)]=max(p);endN=N+10;T=N/8;figure(2);stem(T,'.');axis([0 length(T) 0 10]);xlabel('帧数(n)');ylabel('周期(ms)');title('各帧基音周期');T1= medfilt1(T,5);figure(3);stem(T1,'.');axis([0 length(T1) 0 10]);xlabel('帧数(n)');ylabel('周期(ms)');title('各帧基音周期');五、实验结果结果分析:图二正常就可以提取出基音周期了,但是还需要有滤波处理使其变得平滑一些,所以才会有图三。
图三则是最后的基音周期的图。
基音周期提取2-基于线性相关系数的Matlab实现

基⾳周期提取2-基于线性相关系数的Matlab实现基⾳周期提取2-基于线性相关系数的Matlab实现基⾳周期提取结果图1 基⾳提取结果算法说明线性相关系数也称“⽪尔逊积矩相关系数”(Pearson product-moment correlation coefficient)通常⽤γ或ρ表⽰,是⽤来度量两个变量之间的相互关系(线性相关),取值范围在[-1,+1]之间。
γ>0为正相关,γ<0为负相关,γ=0表⽰不相关。
γ的绝对值越⼤,相关程度越⾼。
r=1时为完全正相关;如两者呈负相关则r为负值,⽽r=-1时为完全负相关。
通常|r|⼤于0.75时,认为两个变量有很强的线性相关性。
图2 线性相关系数计算公式式中x,y为两个向量,这⾥理解为两帧语⾳的采样序列。
当x,y为相邻的两帧数据,且帧长等于基⾳周期时,其相关系数为最⼤值(最接近1)。
Matlab应⽤编程Matlab中可⽤corrcoef(x,y)函数计算相关系数。
%inx: 输⼊的语⾳采样数据%Pos: 查找Pos点处的基⾳周期%minpth: 基⾳周期最⼩值对应的采样点数%maxpth: 基⾳周期最⼤值对应的采样点数%plotfig: 为1时绘制计算过程曲线图%%out: 以不同样点数作为期⾳周期的相似系数,其最⼤值点就对应基⾳周期function [out] = findPitchCorrcoef(inx,Pos,minpth,maxpth,plotfig)[line,row] = size(inx);out = 0;if(line<Pos+ceil(maxpth))return;endif(Pos<ceil(maxpth))return;endout=zeros(ceil(maxpth),1);for i=floor(minpth):ceil(maxpth)xa = inx(Pos-i:Pos); %以i为帧长,Pos点为分界,取其前后两帧数据xb = inx(Pos+1:Pos+1+i);if(max(abs(xa))<0.05) %为减⼩计算量,幅度⼩于0.05时认为是噪⾳,不作计算continue;endif(max(abs(xb))<0.05)continue;endcorrcoefxab = corrcoef(xa,xb);out(i)=corrcoefxab(2,1);endif(plotfig == 1) %绘计算过程曲线figure;subplot(2,1,1);plot(inx,'.-');grid on;subplot(2,1,2);plot(out,'*-');grid on;end图3 基⾳计算过程曲线由图3可以看出,在帧长为42点时(8K采样,对应190.5Hz),相邻两帧语⾳具有最⼤相似系数0.9359。
Matlab在基音周期检测教学中的应用研究

Matlab在基音周期检测教学中的应用研究
基音周期检测是语音信号处理中的一个重要任务,它用于测量和分析语音信号的基频,也被称为基音周期或基频周期。
在不同的语音处理应用中都需要对语音信号进行基音周期
检测,例如语音合成、声音识别以及语音增强等。
首先是基于自相关函数的方法。
自相关函数是指语音信号自身与自身经过不同时间延
迟的信号之间的相关性。
通过计算自相关函数的峰值位置和间隔,可以获得语音信号的基
音周期。
在Matlab中,可以使用xcorr函数计算自相关函数,然后通过寻找峰值来确定基音周期。
另外还有一些更高级的基音周期检测算法,例如利用神经网络、隐马尔可夫模型等方
法进行基音周期检测。
在Matlab中,可以使用Neural Network Toolbox和Hidden Markov Model Toolbox等工具箱来实现这些算法。
除了基音周期检测算法,Matlab还提供了许多其他的语音信号处理工具,例如滤波器设计、频谱分析、语音合成等,这些功能都可以与基音周期检测结合使用,以实现更复杂
的语音处理任务。
Matlab在基音周期检测教学中的应用研究非常广泛。
通过使用Matlab提供的工具箱
和函数,可以方便地实现不同的基音周期检测算法,并应用于语音处理的各个领域。
