绳端速度分解模型
小船过河问题的总结

曲线运动习题课一、船过河模型1、处理方法:小船在有一定流速的水中过河时,实际上参与了两个方向的分运动,即随水流的运动(水冲船的运动)和船相对水的运动,即在静水中的船的运动(就是船头指向的方向),船的实际运动是合运动。
2、若小船要垂直于河岸过河,过河路径最短,应将船头偏向上游,如图甲所示,此时过河时间:3、若使小船过河的时间最短,应使船头正对河岸行驶,如图乙所示,此时过河时间(d为河宽)。
因为在垂直于河岸方向上,位移是一定的,船头按这样的方向,在垂直于河岸方向上的速度最大。
二、绳端问题(绳子末端速度分解)绳子末端运动速度的分解,按运动的实际效果进行可以方便我们的研究。
例如在右图中,用绳子通过定滑轮拉物体船,当以速度v匀速拉绳子时,求船的速度。
解析:船的运动(即绳的末端的运动)可看作两个分运动的合成:a)沿绳的方向被牵引,绳长缩短,绳长缩短的速度等于左端绳子伸长的速度。
即为v;b)垂直于绳以定滑轮为圆心的摆动,它不改变绳长。
这样就可以求得船的速度为, 当船向左移动,α将逐渐变大,船速逐渐变大。
虽然匀速拉绳子,但物体A却在做变速运动。
绳子末端速度的分解问题,是本章的一个难点,同学们在分解时,往往搞不清哪一个是合速度,哪一个是分速度。
以至解题失败。
下面结合例题讨论一下。
例1、如图1所示,在河岸上利用定滑轮拉绳索使小船靠岸,拉绳速度大小为v1,当船头的绳索与水平面夹角为θ时,船的速度多大解析我们所研究的运动合成问题,都是同一物体同时参与的两个分运动的合成问题,而物体相对于给定参照物(一般为地面)的实际运动是合运动,实际运动的方向就是合运动的方向。
本例中,船的实际运动是水平运动,它产生的实际效果可以A点为例说明:一是A点沿绳的收缩方向的运动,二是A点绕O点沿顺时针方向的转动,所以,船的实际速度v可分解为船沿绳方向的速度v1和垂直于绳的速度v2,如图1所示。
由图可知:v=v1/cosθ点评不论是力的分解还是速度的分解,都要按照它的实际效果进行。
速度分解模型常见的几种应用

速度分解模型常见的几种应用
秦付平
【期刊名称】《数理化解题研究:高中版》
【年(卷),期】2011(000)007
【摘要】一、利用模型判断物体运动情况例1如图1所示,在不计滑轮摩擦和绳质量的条件下,当小车匀速向右运动时,物体A的受力情况是()A.绳的拉力大于A 的重力B.绳的拉力等于A的重力C.绳的拉力小于A的重力D.拉力先大于A的重力,后小于重力解析把小车的速度为合速度进行分解,即根据运动效果向沿绳的方向(径向)和与绳垂直的方向(切向)进行正交分解,分别是v2、v1.如图所示,
【总页数】3页(P40-42)
【作者】秦付平
【作者单位】合浦廉州中学物理组,广西536100
【正文语种】中文
【中图分类】G633.6
【相关文献】
1.虚拟现实技术在风景园林规划与设计中的应用研究——几种常见虚拟现实技术的应用评价分析 [J], 李国松;杨柳青
2.几种速度分析方法的对比分析与应用 [J], 高妍
3.关联速度问题——绳端、杆端或接触面速度分解模型 [J], 王若冰
4.用好速度分解模型,防止解题陷阱例析 [J], 张云山
5.关于Z算子的几种常见迭代序列收敛速度的比较 [J], 范瑞琴;薛志群
因版权原因,仅展示原文概要,查看原文内容请购买。
“绳端模型”中两物体加速度的关系剖析

轻 绳 两 端 各 连 接 一 个 物 体 ,当 一 个 物 体 运 动 时 , 会 引 起 另 一 个 物 体 运 动 ,通 常 把 这 类 模 型 称 作 “绳端 模 型 ”。判 断 该 模 型 中 两 物 体 的 速 度 关 系 和 加 速 度 关 系 是 高 中 物 理 的 常 考 问 题 ,研 究 两 物 体 的 速 度 关 系 时 ,只 需 要 将 绳 端 两 物 体 的 速 度 均 沿 绳 和 垂 直 绳 进 行 正 交 分 解 (速 度 方 向 与 绳 共 线 的 不 用 分 解 ),抓住绳两 端物体沿绳方向的速度大小相等这一隐含条件列出 方 程 即 可 解 决 ,大 多 数 学 生 都 能 熟 练 掌 握 。但 是 ,在 讨 论 绳 两 端 物 体 加 速 度 的 关 系 时 ,学 生 普 遍 感 到 困 难 ,下 面 从 动 力 学 的 角 度 ,深 刻 剖 析 该 问 题 ,旨在探索
Vol.5() No.6
Jun.2021
+ £ ’糾 ?教 学 参 考
习题研究
“绳 端 模 型 ”中 两 物 体 加 速 度 的 关 系 剖 析
易俊平 ( 湖 北 省 襄 阳 市 第 一 中 学 湖 北 襄 阳 441000)
文 章 编 号 :l〇〇2-218X (2021)06-0055-02
中 图 分 类 号 :G 632. 479
w2 ( s i n ~h
d2 )3
,方 向 指 向 圆 心 ,由 于 小 车 在 沿 绳 方 向 上
的 分 加 速 度 为 零 ,根 据 同 一 直 线 上 矢 量 合 成 的 规 律 可 以 得 出 ,小 车 在 沿 绳 方 向 一 定 有 一 个 远 离 圆 心 的 加 速
度 ,其 大 小 〜 等 于 ^ 。因 为 细 绳 不 能 伸 长 ,故 物 体 P 的加速度^2;> 的 方 向 沿 斜 面 向 上 ,其 大 小 为 a P = a 2 =
(完整版)高中物理二级结论模型归纳

先想前提,后记结论力学 一.静力学:1.几个力平衡,则一个力是与其它力合力 平衡的力。
2.两个力的合力:F +F ≥F ≥F -F 。
三个大小相等的力平衡,力之间的夹大小合大小角为120度。
3.物体沿斜面匀速下滑,则μ=tanα。
4.两个一起运动的物体“刚好脱离”时:貌合神离,弹力为零。
此时速度 加速度相等,此后不等。
二.运动学:1.在描述运动时,在纯运动学问题中,可以任意选取参照物;在处理动力学问题时,只能以地为参照物。
2.匀变速直线运动:用平均速度思考匀变速直线运动问题,总是带来方便:=V ==-V 2/t 221V V +TS S 221+3.匀变速直线运动:当时间等分时:S n -Sn-1=aT .2位移中点的即时速度:V s/2= ,V s/2>V t/222221V V +纸带点迹求速度加速度:V t/2=, a=, a=T S S 212+212TSS -21)1(T n S S n--4.自由落体:V t (m/s): 10 20 30 40 50 = gtH 总(m ):5 20 45 80 125 = gt 2/2H 分(m):5 15 25 35 45 = gt 22/2 – gt 12 /2g=10m/s 25.上抛运动:对称性:t 上= t 下 V 上= -V下6.相对运动:相同的分速度不产生相对位移。
7.“刹车陷阱”:给出的时间大于滑行时间,则不能用公式算。
先求滑行时间,确定了滑行时间小于给出的时间时,用V 2=2aS 求滑行距离。
8."S=3t+2t 2”:a=4m/s 2,V 0=3m/s 。
(s = v 0t+ at 2/2)9.绳端物体速度分解:对地速度是合速度,分解为沿绳的分速度合垂直绳的分速度。
三.运动定律:1.水平面上滑行:a=-µg2.系统法:动力-阻力=m总g绳牵连系统3.沿光滑斜面下滑:a=gSinα时间相等: 450时时间最短: 无极值:4.一起加速运动的物体:N=F,(N为物体间相互作用力),与有无摩212mmm+擦(μ相同)无关,平面斜面竖直都一样。
曲线运动运动的合成与分解知识要点归纳总结

曲线运动运动的合成与分解要点归纳一、曲线运动1.曲线运动:运动轨迹是曲线的运动。
2.曲线运动速度:1)方向:沿轨迹上各点的切线方向。
2)大小:可以变化,也可以不变化。
3.运动的性质:变速运动(加速度一定不为零)4.做曲线运动的条件:⑴运动学角度说:a的方向与v的方向不在同一条直线上。
⑵从动力学角度说:F合的方向与v的方向不在同一条直线上。
①F合(a)与v的夹角0°<θ<90°时:物体做加速曲线运动;②F合(a)与v的夹角θ=90°时:物体做匀速率曲线运动;③ F合(a)与v的夹角90°<θ<180°时:物体做减速曲线运动。
5.物体做曲线运动时的受力特点:F合(a)总是指向轨迹弯曲的内(凹)侧。
二.运动的合成与分解1.合运动与分运动1)合运动:物体对地的实际运动。
2)分运动:除合运动外,物体同时参与的其它运动。
3)合运动与分运动之间:①等效性②等时性分运动与分运动之间:③独立性2.运动的合成与分解1)运动的合成:已知分运动求合运动。
即已知分运动的位移、速度、和加速度等求合运动的位移、速度、和加速度等,遵从平行四边形定则。
2)运动的分解:已知合运动求分运动。
它是运动合成的逆运算。
处理曲线问题往往是把曲线运动按实效分解成两个方向上的分运动。
3.合运动的性质和轨迹1)合运动的性质由a决定:①a=0(F合=0)时:静止或匀速直线运动;②a≠0(F合≠0)且恒定时:匀变速运动⎩⎨⎧曲线运动不共线时物体做匀变速与线运动共线时物体做匀变速直与vava③a≠0(F合≠0)且变化时:非匀变速运动⎩⎨⎧减)速曲线运动不共线时物体做变加(与)速直线运动共线时物体做变加(减与vava2)合运动的轨迹由a与v的方向决定:①两个分运动均是匀速直线运动,其合运动是匀速直线运动;②一个分运动是匀速直线运动,另一个分运动是匀变速直线运动,当它们共线时,其合运动是匀变速直线运动,当它们互成一定夹角时,它们的合运动是匀变速曲线运动;③两个互成夹角的匀变速直线运动的合运动是匀变速运动,若a与v共线其合运动是匀变速直线运动,若a与v不共线其合运动是匀变速曲线运动。
高中物理 曲线运动 典型例题(含答案)【经典】

第四章 曲线运动第一讲:曲线运动条件和运动特点、运动的合成与分解考点一:运动的合成与分解 1、(多选)质量为m =2 kg 的物体在光滑的水平面上运动,在水平面上建立xOy 坐标系,t =0时物体位于坐标系的原点O.物体在x 轴和y 轴方向的分速度vx 、vy 随时间t 变化的图线如图甲、乙所示.则( ). A .t =0时,物体速度的大小为3 m/s 答案 ADB .t =8 s 时,物体速度的大小为4 m/sC .t =8 s 时,物体速度的方向与x 轴正向夹角为37°D .t =8 s 时,物体的位置坐标为(24 m,16 m)2.(多选)在一光滑水平面内建立平面直角坐标系,一物体从t =0时刻起,由坐标原点O(0,0)开始运动,其沿x 轴和y 轴方向运动的速度—时间图象如图甲、乙所示,下列说法中正确的是( ).答案 AD A .前2 s 内物体沿x 轴做匀加速直线运动B .后2 s 内物体继续做匀加速直线运动,但加速度沿y 轴方向C .4 s 末物体坐标为(4 m,4 m)D .4 s 末物体坐标为(6 m,2 m) 3.(单选)如图,从广州飞往上海的波音737航班上午10点到达上海浦东机场,若飞机在降落过程中的水平分速度为60 m/s ,竖直分速度为6 m/s ,已知飞机在水平方向做加速度大小等于2 m/s2的匀减速直线运动,在竖直方向做加速度大小等于0.2 m/s2的匀减速直线运动,则飞机落地之前( ).答案 D A .飞机的运动轨迹为曲线B .经20 s 飞机水平方向的分速度与竖直方向的分速度大小相等C .在第20 s 内,飞机在水平方向的分位移与竖直方向的分位移大小相等D .飞机在第20 s 内,水平方向的平均速度为21 m/s4、(多选)质量为0.2 kg 的物体在水平面上运动,它的两个正交分速度图线分别如图甲、乙所示,由图可知( )A .最初4 s 内物体的位移为8 2 m 答案 ACB .从开始至6 s 末物体都做曲线运动C .最初4 s 内物体做曲线运动,接下来的2 s 内物体做直线运动D .最初4 s 内物体做直线运动,接下来的2 s 内物体做曲线运动 5、(单选)各种大型的货运站中少不了旋臂式起重机,如图所示,该起重机的旋臂保持不动,可沿旋臂“行走”的天车有两个功能,一是吊着货物沿竖直方向运动,二是吊着货物沿旋臂水平运动.现天车吊着货物正在沿水平方向向右匀速行驶,同时又启动天车上的起吊电动机,使货物沿竖直方向做匀减速运动.此时,我们站在地面上观察到货物运动的轨迹可能是下图中的( ). 答案 D6.汽车静止时,车内的人从矩形车窗ABCD 看到窗外雨滴的运动方向如图图线①所示.在汽车从静止开始匀加速启动阶段的t 1、t 2两个时刻,看到雨滴的运动方向分别如图线②③所示.E 是AB 的中点.则( ) A .t2=2t 1 B .t 2=2t 1 C .t 2=5t 1D .t 2=3t 1 答案 A解析 静止时,雨滴相对于地面做的是竖直向下的直线运动,设雨滴的速度为v0,汽车匀加速运动后,在t1时刻,看到的雨滴的运动方向如图线②,设这时汽车的速度为v1,这时雨滴水平方向相对于汽车的速度大小为v1,方向向左,在t2时刻,设汽车的速度为v2,则雨滴的运动方向如图线③,雨滴水平方向相对于汽车速度大小为v2,方向水平向左,根据几何关系,v1OA =v0AB ,v2OA =v012AB ,得v2=2v1,汽车做匀加速运动,则由v =at 可知,t2=2t1,A 项正确.7.一物体在光滑水平面上运动,它在x 方向和y 方向上的两个分运动的速度—时间图象如图所示. (1)判断物体的运动性质;(2)计算物体的初速度大小;(3)计算物体在前3 s 内和前6 s 内的位移大小.答案 (1)匀变速曲线运动 (2)50 m/s (3)3013m 180 m8.如图所示,为一次洪灾中,德国联邦国防军的直升机在小城洛伊宝根运送砂袋.该直升机A 用长度足够长的悬索(重力可忽略不计)系住一质量m =50 kg 的砂袋B ,直升机A 和砂袋B 以v0=10 m/s 的速度一起沿水平方向匀速运动,某时刻开始将砂袋放下,在5 s 时间内,B 在竖直方向上移动的距离以y =t2(单位:m)的规律变化,取g =10 m/s2.求在5 s 末砂袋B 的速度大小及位移大小.答案 10 2 m/s 25 5 m9、如图所示,在竖直平面内的xOy 坐标系中,Oy 竖直向上,Ox 水平向右.设平面内存在沿x 轴正方向的恒定风力.一小球从坐标原点沿Oy 方向竖直向上抛出,初速度为v0=4 m/s ,不计空气阻力,到达最高点的位置如图中M 点所示(坐标格为正方形,g =10 m/s2)求:(1)小球在M 点的速度v1;(2)在图中定性画出小球的运动轨迹并标出小球落回x 轴时的位置N ; (3)小球到达N 点的速度v2的大小.答案 (1)6 m/s (2)见解析图 (3)410 m/s解析 (1)设正方形的边长为x0. 竖直方向做竖直上抛运动,有v0=gt1,2x0=v02t1水平方向做匀加速直线运动,有3x0=v12t1. 解得v1=6 m/s.(2)由竖直方向的对称性可知,小球再经过t1到x 轴,水平方向做初速度为零的匀加速直线运动,所以回到x 轴时落到x =12处,位置N 的坐标为(12,0).(3)到N 点时竖直分速度大小为v0=4 m/s 水平分速度vx =a 水平tN =2v1=12 m/s , 故v2=v 20+v 2x =410 m/s.考点二:绳(杆)端速度分解模型(结合受力和机械能守恒)1、如图所示,人用绳子通过定滑轮以不变的速度0v 拉水平面上的物体A ,当绳与水平方向成θ角时,求物体A 的速度。
高三复习考点强化:小船渡河模型及绳(杆)端速度分解模型 课件

其二:与绳(杆)垂直的速度v⊥
方法:v∥与v⊥的合成遵循平行四边形定则。 3.解题原则: 根据沿绳(杆)方向的分速度大小相等求解。 常见实例如下:
课堂互动 【例 3】 (2019·宝鸡模拟)如图所示,水平光滑长杆上套有一物块 Q,跨过悬挂于 O
点的轻小光滑圆环的轻绳一端连接 Q,另一端悬挂一物块 P。设轻绳的左边部分与水平方向 的夹角为 θ,初始时 θ 很小。现将 P、Q 由静止同时释放,关于 P、 Q 以后的运动下列说法正确的是( )
多维训练
1.(多选)一只小船渡河,水流速度各处相同且恒定不变,方向平行于岸边。小船相 对于水分别做匀加速、匀减速、匀速直线运动,运动轨迹如图12所示。船相对于水的 初速度大小均相同,方向垂直于岸边,且船在渡河过程中船头方向始终不变。由此可 以确定( )
A.沿AD轨迹运动时,船相对于水做匀减速直线运动 B.沿三条不同路径渡河的时间相同 C.沿AC轨迹渡河所用的时间最短 D.沿AC轨迹到达对岸的速度最小
A.小船渡河的轨迹为直线 B.小船在河水中的最大速度是 5 m/s C.小船在距南岸 200 m 处的速度小于在距北岸 200 m 处的速度 D.小船渡河的时间是 160 s
转到解析
备选训练
3. 如图所示,AB杆以恒定角速度绕A点转动,并带动套在光滑水平杆OC上的质量 为M的小环运动,运动开始时,AB杆在竖直位置,则小环M的速度将( )
多维训练
2.如图所示,不计所有接触面之间的摩擦,斜面固定,物块和滑块质量分别为 m1 和 m2,且 m1<m2。若将滑块从位置 A 由静止释放,当沿杆落到位置 B 时,滑块的速度 为 v2,且与滑块牵连的绳子与竖直方向的夹角为 θ,则此时物块的速度大小 v1 等于( )
绳船模型中的速度和加速度关系深度分析

绳船模型中的速度和加速度关系深度分析摘要:速度合成和分解中,绳子两端绳上的点的速度沿绳子方向的分量才相等,而不是绳子两端的物体的速度沿绳子方向的分量相等。
同时,绳子两端的点的加速度沿绳子方向的分量也不是单纯意义上的相等,本文通过绳船模型定量给出速度及加速度的关系。
关键词:速度加速度分解相等绳杆端速度分解模型中,在绳子不松弛的情况下,在同一时刻必须具有相同的沿杆绳方向的分速度[1]。
这里的速度分量指,绳子两端点的速度沿绳子方向分量,而不是绳子两端物体的速度分量。
绳子两端点的速度与绳子两端物体的速度有很大的区别,如图1所示,数值方向的动滑轮模型,绳子端点C的速度是绳子两端物体(滑轮)速度的两倍。
本文将通过绳船模型详细说明速度关系。
图1在教学过程中,学生从速度关系直接类比加速度关系,绳子两端的点的加速度沿绳方向分量相等,这样的理解显然是不对的。
如图2所示,物体绕圆心o作匀速圆周运动,半径为r,速率为v,分析绳子两端的点的加速度沿绳方向分量的关系?绳子一端物体的加速度,这个加速度为物体的合加速度,此加速度沿半径方向的分量为,绳子一端圆心的加速度0,此加速度沿半径方向的分量为0,显然绳子两端的点的加速度沿绳方向的分量不相等。
本文将通过绳船模型详细说明加速度关系。
1、单绳船模型中速度关系如图3所示,人用轻质细绳通过定滑轮牵引小船靠岸,如果收绳的速度为,则在绳与水平方向夹角为的时刻,船头到滑轮的距离为,船的速度有多大[2]?分析:船在水面在直线运动,实际发生的运动就是合运动,这个合运动有两个运动效果,一是使小船沿绳拉力方向以速度运动,二是使小船随绳的一端绕滑轮做顺时针方向的圆周运动。
靠近船头绳上的速度和船的速度一样,由于绳子不松软,所以沿绳方向速度分量相等:①由①式变形得船的速度:②2、单绳船模型中加速度关系如图3所示,如果人拉绳子以恒定的加速度向前奔跑,则在绳与水平方向夹角为的时刻,船头到滑轮的距离为,船的速度有多大?错误的理解,由于绳子不松软,所以沿绳方向加速度分量相等。
曲线运动 运动的合成与分解

第1讲 曲线运动 运动的合成与分解一、曲线运动1.速度的方向:质点在某一点的速度方向,沿曲线在这一点的切线方向.2.运动的性质:做曲线运动的物体,速度的方向时刻在改变,所以曲线运动一定是变速运动.3.运动的条件:物体所受合力的方向跟它的速度方向不在同一条直线上或它的加速度方向与速度方向不在同一条直线上.4.合外力方向与轨迹的关系:物体做曲线运动的轨迹一定夹在合外力方向与速度方向之间,速度方向与轨迹相切,合外力方向指向轨迹的“凹”侧.判断正误 (1)做曲线运动的物体加速度方向一定变化.( ) (2)物体在恒力作用下不可能做曲线运动.( ) (3)物体在变力作用下可以保持速率不变.( ) 二、运动的合成与分解1.遵循的法则:位移、速度、加速度都是矢量,故它们的合成与分解都遵循平行四边形定则. 2.合运动与分运动的关系(1)等时性:合运动和分运动经历的时间相等,即同时开始、同时进行、同时停止. (2)独立性:一个物体同时参与几个分运动,各分运动独立进行,不受其他运动的影响. (3)等效性:各分运动的规律叠加起来与合运动的规律有完全相同的效果. 3.运动性质的判断⎩⎨⎧加速度(或合外力)⎩⎪⎨⎪⎧ 变化:非匀变速运动不变:匀变速运动加速度(或合外力)方向与速度方向⎩⎪⎨⎪⎧共线:直线运动不共线:曲线运动4.两个直线运动的合运动性质的判断标准:看合初速度方向与合加速度方向是否共线.自测(2019·广东深圳市4月第二次调研)2018珠海航展,我国五代战机“歼20”再次闪亮登场.表演中,战机先水平向右,再沿曲线ab向上(如图1),最后沿陡斜线直入云霄.设飞行路径在同一竖直面内,飞行速率不变.则沿ab段曲线飞行时,战机()A.所受合外力大小为零B.所受合外力方向竖直向上C.竖直方向的分速度逐渐增大D.水平方向的分速度不变1.条件物体受到的合外力方向与速度方向始终不共线.2.特征(1)运动学特征:做曲线运动的物体的速度方向时刻发生变化,即曲线运动一定为变速运动.(2)动力学特征:由于做曲线运动的物体所受合外力一定不为零且和速度方向始终不在同一条直线上(做曲线运动的条件).合外力在垂直于速度方向上的分力改变物体速度的方向,合外力在沿速度方向上的分力改变物体速度的大小.(3)轨迹特征:曲线运动的轨迹始终夹在合外力的方向与速度的方向之间,而且向合外力的一侧弯曲.(4)能量特征:如果物体所受的合外力始终和物体的速度垂直,则合外力对物体不做功,物体的动能不变;若合外力不与物体的速度方向垂直,则合外力对物体做功,物体的动能发生变化.例1(2020·江西上饶市重点中学六校第一次联考)下列关于运动和力的叙述中,正确的是()A.做曲线运动的物体,其加速度方向一定是变化的B.物体做圆周运动,所受的合力一定是向心力C.物体所受合力恒定,该物体速率随时间一定均匀变化D.物体运动的速率在增加,所受合力一定做正功变式1(2019·河南新乡市模拟)图2是质点做匀变速曲线运动轨迹的示意图.已知质点在B点的加速度方向与速度方向垂直,则下列说法中正确的是()A.A点的速率小于B点的速率B.A点的加速度比C点的加速度大C.C点的速率大于B点的速率D.从A点到C点加速度与速度的夹角先增大后减小,速率先减小后增大1.基本思路:分析运动的合成与分解问题时,一般情况下按运动效果进行分解.2.解题关键:两个方向上的分运动具有等时性,这常是处理运动分解问题的关键点.3.注意问题:要注意分析物体在两个方向上的受力及运动规律,分别在两个方向上列式求解.例2(2019·江西宜春市第一学期期末)如图3所示是物体在相互垂直的x方向和y方向运动的v-t图象.以下判断正确的是()A.在0~1 s内,物体做匀速直线运动B.在0~1 s内,物体做匀变速直线运动C.在1~2 s内,物体做匀变速直线运动D.在1~2 s内,物体做匀变速曲线运动变式2(2020·福建厦门市期末调研)如图4所示,帆板在海面上以速度v朝正西方向运动,帆船以速度v朝正北方向航行,以帆板为参照物()A.帆船朝正东方向航行,速度大小为vB.帆船朝正西方向航行,速度大小为vC.帆船朝南偏东45°方向航行,速度大小为2vD.帆船朝北偏东45°方向航行,速度大小为2v1.船的实际运动:是水流的运动和船相对静水的运动的合运动.2.三种速度:船在静水中的速度v船、水的流速v水、船的实际速度v.3.两类问题、三种情景渡河时间最短当船头方向垂直河岸时,渡河时间最短,最短时间t min=dv船渡河位移最短如果v船>v水,当船头方向与上游河岸夹角θ满足v船cos θ=v水时,合速度垂直河岸,渡河位移最短,等于河宽d如果v船<v水,当船头方向(即v船方向)与合速度方向垂直时,渡河位移最短,等于d v水v船4.例3(多选)甲、乙两船在同一河流中同时开始渡河,河水流速为v0,船在静水中的速率均为v,甲、乙两船船头均与河岸成θ角,如图5所示,已知甲船恰能垂直到达河正对岸的A点,乙船到达河对岸的B点,A、B之间的距离为L,则下列判断正确的是()A.乙船先到达对岸B.若仅是河水流速v0增大,则两船的渡河时间都不变C.不论河水流速v0如何改变,只要适当改变θ角,甲船总能到达正对岸的A点D.若仅是河水流速v0增大,则两船到达对岸时,两船之间的距离仍然为L变式3一只小船渡过两岸平行的河流,河中水流速度各处相同且恒定不变,方向平行于河岸.小船的初速度均相同,且船头方向始终垂直于河岸,小船相对于静水分别做匀加速、匀减速和匀速直线运动,其运动轨迹如图6所示.下列说法错误..的是()A.沿AC和AD轨迹小船都是做匀变速运动B.AD是匀减速运动的轨迹C.沿AC轨迹渡河所用时间最短D.小船沿AD轨迹渡河,船靠岸时速度最大1.模型特点沿绳(杆)方向的速度分量大小相等.2.思路方法合速度→绳(杆)拉物体的实际运动速度v分速度→⎩⎪⎨⎪⎧其一:沿绳(杆)的速度v1其二:与绳(杆)垂直的速度v2方法:v 1与v 2的合成遵循平行四边形定则. 3.解题原则把物体的实际速度分解为垂直于绳(杆)和平行于绳(杆)两个分量,根据沿绳(杆)方向的分速度大小相等求解.常见的模型如图7所示.模型1 绳端速度分解模型例4 质量为m 的物体P 置于倾角为θ1的固定光滑斜面上,轻细绳跨过光滑定滑轮分别连接着P 与小车,P 与滑轮间的细绳平行于斜面,小车以速率v 水平向右做匀速直线运动,重力加速度为g .当小车与滑轮间的细绳和水平方向成夹角θ2时(如图8),下列判断正确的是( ) A .P 的速率为v B .P 的速率为v cos θ2 C .绳的拉力等于mg sin θ1 D .绳的拉力小于mg sin θ1变式4 A 、B 两物体通过一根跨过光滑轻质定滑轮的不可伸长的轻绳相连放在水平面上,现物体A 以v 1的速度向右匀速运动,当绳被拉成与水平面夹角分别是α、β时,如图9所示,物体B 的运动速度为(绳始终有拉力)( )A.v 1sin αsin βB.v 1cos αsin βC.v 1sin αcos βD.v 1cos αcos β模型2 杆端速度分解模型例5 (2019·山东济南市3月模拟)曲柄连杆结构是发动机实现工作循环,完成能量转换的主要运动零件,如图10所示,连杆下端连接活塞Q ,上端连接曲轴P .在工作过程中,活塞Q 在汽缸内上下做直线运动,带动曲轴绕圆心O 旋转,若P 做线速度大小为v 0的匀速圆周运动,则下列说法正确的是( ) A .当OP 与OQ 垂直时,活塞运动的速度等于v 0 B .当OP 与OQ 垂直时,活塞运动的速度大于v 0 C .当O 、P 、Q 在同一直线时,活塞运动的速度等于v 0 D .当O 、P 、Q 在同一直线时,活塞运动的速度大于v 0变式5如图11所示,一根长直轻杆AB在墙角沿竖直墙和水平地面滑动.当AB杆和墙的夹角为θ时,杆的A端沿墙下滑的速度大小为v1,B端沿地面滑动的速度大小为v2,则v1、v2的关系是()A.v1=v2B.v1=v2cos θC.v1=v2tan θD.v1=v2sin θ1.下列关于力与运动的叙述中正确的是()A.物体所受合力方向与运动方向有夹角时,该物体速度一定变化,加速度也变化B.物体做圆周运动,所受的合力一定指向圆心C.物体运动的速率在增加,所受合力方向与运动方向夹角小于90°D.物体在变力作用下有可能做曲线运动,做曲线运动物体一定受到变力作用2.如图1所示,长为L的直杆一端可绕固定轴O无摩擦转动,另一端靠在以水平速度v匀速向左运动、表面光滑的竖直挡板上,当直杆与竖直方向夹角为θ时,直杆端点A的线速度为()A.vsin θB.v sin θ C.vcos θD.v cos θ3.(多选)(2020·广东韶关市质检)在杂技表演中,猴子沿竖直杆向上做初速度为零、加速度为a的匀加速运动,同时人顶着直杆以速度v0水平匀速前进,经过时间t,猴子沿杆向上移动的高度为h,人顶杆沿水平地面移动的距离为x,如图2所示.关于猴子的运动情况,下列说法中正确的是()图2A.相对地面的运动轨迹为直线B.相对地面做匀加速曲线运动C.t时刻猴子相对地面速度的大小为v0+atD.t时间内猴子相对地面的位移大小为x2+h24.(2019·福建厦门市第一次质量检查)在演示“做曲线运动的条件”的实验中,有一个在水平桌面上向右做直线运动的小铁球,第一次在其速度方向上放置条形磁铁,第二次在其速度方向上的一侧放置条形磁铁,如图3所示,虚线表示小铁球的运动轨迹.观察实验现象,以下叙述正确的是()A.第一次实验中,小铁球的运动是匀变速直线运动B.第二次实验中,小铁球的运动类似平抛运动,其轨迹是一条抛物线C.该实验说明做曲线运动物体的速度方向沿轨迹的切线方向D.该实验说明物体做曲线运动的条件是物体受到的合外力的方向与速度方向不在同一直线上5.如图4所示,在灭火抢救过程中,消防队员有时要借助消防车上的梯子爬到高处进行救人或灭火作业.为了节省救援时间,消防队员沿梯子匀加速向上运动的同时消防车匀速后退,则关于消防队员的运动,下列说法正确的是()A.消防队员做匀加速直线运动B.消防队员做匀变速曲线运动C.消防队员做变加速曲线运动D.消防队员水平方向的速度保持不变6.如图5所示,悬线一端固定在天花板上的O点,另一端穿过一张CD光盘的中央小孔后拴着一个橡胶球,橡胶球静止时,竖直悬线刚好挨着水平桌面的边沿.现将CD光盘按在桌面上,并沿桌面边缘以速度v匀速移动,移动过程中,CD光盘中央小孔始终紧挨桌面边线,当悬线与竖直方向的夹角为θ时,小球上升的速度大小为()A.v sin θB.v cos θC.v tan θ D.vtan θ7.如图6所示,河水由西向东流,河宽为800 m,河中各点的水流速度大小为v水,各点到较近河岸的距离为x,v水与x的关系为v水=3400x(m/s)(x的单位为m),让小船船头垂直河岸由南向北渡河,小船划水速度大小恒为v船=4 m/s,则下列说法中正确的是()A.小船渡河的轨迹为直线B.小船在河水中的最大速度是5 m/sC.小船在距南岸200 m处的速度小于在距北岸200 m处的速度D.小船渡河的时间是160 s8.(2019·山东烟台市期中)在一光滑的水平面上建立xOy平面直角坐标系,一质点在水平面上从坐标原点开始运动,沿x方向和y方向的x-t图象和v y-t图象分别如图7甲、乙所示,求:图7(1)运动后4 s内质点的最大速度的大小;(2)4 s末质点离坐标原点的距离.。
关联速度问题

关联速度问题关联速度分解问题指物体拉绳(杆)或绳(杆)拉物体的问题:(1)物体的实际速度一定是合速度.(2)由于绳不可伸长,一根绳两端物体沿绳方向的速度分量大小相等. (3)常见的速度分解模型 情景图示(注:A 沿斜面下滑) 分解图示定量结论 v B =v A cos θ v A cos θ=v 0 v A cos α=v B cos β v B sin α=v A cos α 基本思路 确定合速度(物体实际运动)→分析运动规律→确定分速度方向→平行四边形定则求解阻力恒为F f ,当轻绳与水面的夹角为θ时,船的速度为v ,人的拉力大小为F ,则此时( )A.人拉绳行走的速度大小为v cos θB.人拉绳行走的速度大小为v cos θC.船的加速度大小为F cos θ-F f mD.船的加速度大小为F -F f m【题型2】如图所示, 一根长直轻杆AB 在墙角沿竖直墙和水平地面滑动.当AB 杆和墙的夹角为θ时,杆的A 端沿墙下滑的速度大小为v 1,B 端沿地面滑动的速度大小为v 2,则v 1、v 2的关系是( )A.v 1=v 2B.v 1=v 2cos θC.v 1=v 2tan θD.v 1=v 2sin θ【题型3】人用绳子通过光滑轻质定滑轮拉物体A ,A 穿在光滑的竖直杆上,当以速度v 0匀速地拉绳使物体A 到达如图所示位置时,绳与竖直杆的夹角为θ,则物体A 实际运动的速度大小是( )A.v 0sin θB.v 0 sin θC.v 0cos θD.v 0 cos θ【题型4】如图所示,一根长为L 的轻杆OA ,O 端用铰链固定,轻杆靠在一个高为h 的物块上,某时杆与水平方向的夹角为θ,物块向右运动的速度为v ,则此时A 点速度为( )A.Lv sin θhB.Lv cos θhC.Lv sin 2θhD.Lv cos 2θh【题型5】如图所示,长为L 的直棒一端可绕固定轴O 转动,另一端搁在升降平台上,平台以速度v 匀速上升,当棒与竖直方向的夹角为α时,棒的角速度为( )A.v sin αLB.v L sin αC.v cos αLD.v L cos α针对训练1.如图所示,有人在河面上方20 m 的岸上用跨过定滑轮的长绳拴住一条小船,开始时绳与水面的夹角为30°.人以恒定的速率v =3 m/s 拉绳,使小船靠岸,那么( )A.5 s 时绳与水面的夹角为60°B.5 s 时小船前进了15 mC.5 s 时小船的速率为5 m/sD.5 s 时小船到岸边距离为10 m2.一轻杆两端分别固定质量为m A 和m B 的两个小球A 和B (可视为质点),将其放在一个光滑球形容器中从位置1开始下滑,如图所示,当轻杆到达位置2时,球A 与球形容器球心等高,其速度大小为v 1,已知此时轻杆与水平方向成θ=30°角,球B 的速度大小为v 2,则( )A .v 2=12v 1 B .v 2=2v 1 C .v 2=v 1 D .v 2=3v 13.如图所示,人用轻绳通过定滑轮拉穿在光滑竖直杆上的物块A ,人以速度v 0向左匀速拉绳,某一时刻,绳与竖直杆的夹角为θ,与水平面的夹角为α,此时物块A 的速度v 1为( )A.v 1=v 0sin αcos θB.v 1=v 0sin αsin θC.v 1=v 0cos αcos θD.v 1=v 0cos αcos θ4.一探照灯照射在云层底面上,云层底面是与地面平行的平面,如图所示,云层底面距地面高h ,探照灯以恒定角速度ω在竖直平面内转动,当光束转到与竖直方向夹角为θ时,云层底面上光点的移动速度是( )A .hω B.θωcos h C. θω2cos h D .Hωtan θ5.如图所示,水平面上固定一个与水平面夹角为θ的斜杆A .另一竖直杆B 以速度v 水平向左匀速直线运动,则从两杆开始相交到最后分离的过程中,两杆交点P 的速度方向和大小分别为( )A .水平向左,大小为vB .竖直向上,大小为vtanθC .沿A 杆向上,大小为v/cosθD .沿A 杆向上,大小为vcosθ6.如图所示,细绳一端固定在天花板上的O 点,另一端穿过一张CD 光盘的中央小孔后拴着一个橡胶球,橡胶球静止时,竖直悬线刚好挨着水平桌面的边沿.现将CD 光盘按在桌面上,并沿桌面边缘以速度v 匀速移动,移动过程中,CD 光盘中央小孔始终紧挨桌面边线,当悬线与竖直方向的夹角为θ时,小球上升的速度大小为( )A .v sin θB .v cos θC .v cos θD .v sin θ关联速度问题参考答案【题型1】【答案】 AC【解析】 船的运动产生了两个效果:一是使滑轮与船间的绳缩短,二是使滑轮与船间的绳偏转,因此将船的速度按如图所示(沿绳方向与垂直于绳方向)方式进行分解,人拉绳行走的速度大小v 人=v ∥=v cos θ,选项A 正确,B 错误;绳对船的拉力大小等于人拉绳的力的大小,即绳的拉力大小为F ,与水平方向成θ角,因此F cos θ-F f =ma ,解得a =F cos θ-F f m,选项C 正确,D 错误.【题型2】【答案】C【解析】将A 端的速度沿杆方向和垂直于杆的方向分解,沿杆方向的分速度为v 1∥=v 1cos θ,将B 端的速度沿杆方向和垂直于杆方向分解,沿杆方向的分速度v 2∥=v 2sin θ.由于v 1∥=v 2∥.所以v 1=v 2tan θ,故C 正确,A 、B 、D 错误.【题型3】【答案】D【解析】由运动的合成与分解可知,物体A 参与两个分运动:一个是沿着与它相连接的绳子的运动,另一个是垂直于绳子斜向上的运动.而物体A 的实际运动轨迹是沿着竖直杆向上的,这一轨迹所对应的运动就是物体A 的合运动,它们之间的关系如图所示.由几何关系可得v =v 0 cos θ,所以D 正确.【题型4】【答案】 C【解析】 根据运动的效果可知物块向右运动的速度,如图所示.沿杆和垂直于杆的方向分解成1v 和2v ,根据平行四边形定则可得θθcos cos 1v v v B ==,θθsin sin 2v v v B ==,根据几何关系可得θsin h OB =,由于B 点的线速度为ωθ⋅==OB v v sin 2,所以h v OB v θθω2sin sin ==,所以A 点的线速度hLv L v A θω2sin ==,故C 正确。
高考物理解题模型分类专题讲解9---杆绳速度分解(解析版)

高考物理解题模型分类专题讲解 模型 9 杆绳速度分解1.模型特点 沿绳(或杆)方向的速度分量大小相等。
2.思路与方法 合速度就是物体的实际运动速度 v 分速度 方法:v1 与 v2 的合成遵循平行四边形定则。
【典例 1】(湖北省“荆、襄、宜七校考试联盟”2017 2018 学年高一下学期期中)人 用绳子通过定滑轮拉物体 A,A 穿在光滑的竖直杆上,当以速度 v0 匀速地拉绳使物体 A 到达如图所示位置时,绳与竖直杆的夹角为 θ,则物体 A 实际运动的速率是( B )A.v0cos θv0 B.cosθC.v0sinθv0 D.sinθ【答案】B【解析】物体 A 的运动是由绳的运动和垂直绳子方向的转动合成的,如图,则 v=v0 ,故选 B。
cosθ1 / 16【变式训练 1】如图,人沿平直的河岸以速度 v 行走,且通过不可伸长的绳拖船,船 沿绳的方向行进,此过程中绳始终与水面平行。
当绳与河岸的夹角为 α 时,船的速 率为 ( )A. vsin αv cosαv B. sinαC. vcos αD.【答案】 C 【解析】如图所示,把人的速度沿绳和垂直绳的方向分解,由几何知识有 v 船=vcos α,所以 C 正确,A、B、D 错误。
【典例 2】A、B 两物体通过一根跨过定滑轮的轻绳相连放在水平面上,现物体 A 以 v1 的速度向右匀速运动,当绳被拉成与水平面夹角分别为 α、β 时,如图所示。
物2 / 16体 B 的运动速度 vB 为(绳始终有拉力)( )v1 sin α A. sin βv1 cosα B. sin βv1 sin α C. cos βD.cosα cos βv1【答案】 D 【解析】A、B 两物体的速度分解如图由图可知:v 绳 A=v1cos α v 绳 B=vBcos β 由于 v 绳 A=v 绳 Bcosα 所以 vB= cos β v1 ,故 D 对 【变式训练 2】(多选)如图甲所示,将质量为 2m 的重物悬挂在轻绳的一端,轻绳的另一 端系一质量为 m 的小环,小环套在竖直固定的光滑直杆上,光滑定滑轮与直杆的距离为 d。
高考物理“二级结论”及常见模型

高考物理“二级结论”及常见模型三轮冲刺抢分必备,掌握得越多,答题越快。
一般情况下,二级结论都是在一定的前提下才成立的,因此建议你先确立前提,再研究结论。
一、静力学:1.物体受几个力平衡,则其中任意一个力都是与其它几个力的合力平衡的力,或者说“其中任意一个力总与其它力的合力等大反向”。
2.两个力的合力:F 大+F 小≥F 合≥F 大-F 小。
三个大小相等的共点力平衡,力之间的夹角为120°。
3.力的合成和分解是一种等效代换,分力或合力都不是真实的力,对物体进行受力分析时只分析实际“受”到的力。
4.①物体在三个非平行力作用下而平衡,则表示这三个力的矢量线段必组成闭合矢量三角形;且有312123sin sin sin F F F ααα==(拉密定理)。
②物体在三个非平行力作用下而平衡,则表示这三个力的矢量线段或线段延长线必相交于一点。
5.物体沿斜面不受其它力而自由匀速下滑,则tan μα=。
6.两个原来一起运动的物体“刚好脱离”瞬间:力学条件:貌合神离,相互作用的弹力为零。
运动学条件:此时两物体的速度、加速度相等,此后不等。
7.轻绳不可伸长,其两端拉力大小相等,线上各点张力大小相等。
因其形变被忽略,其拉力可以发生突变,“没有记忆力”。
8.轻弹簧两端弹力大小相等,弹簧发生形变需要时间,因此弹簧的弹力不能发生突变。
9.轻杆能承受拉、压、挑、扭等作用力。
力可以发生突变,“没有记忆力”。
10.两个物体的接触面间的相互作用力可以是:()⎧⎪⎨⎪⎩无一个,一定是弹力二个最多,弹力和摩擦力11.在平面上运动的物体,无论其它受力情况如何,所受平面支持力和滑动摩擦力的合力方向总与平面成N f 1tan tan F ==F αμ。
二、运动学:1.在描述运动时,在纯运动学问题中,可以任意选取参照物;在处理动力学问题时,只能以地为参照物。
2.匀变速直线运动:用平均速度思考匀变速直线运动问题,总是带来方便,思路是:位移→时间→平均速度,且1212222t/s s T++===v v v v 3.匀变速直线运动:时间等分时, 21n n s s aT --= ,这是唯一能判断所有匀变速直线运动的方法;位移中点的即时速度2s/=v , 且无论是加速还是减速运动,总有22s/t/>v v纸带点痕求速度、加速度: 1222t/s s T +=v ,212s s a T -=,()121n s s a n T-=- 4.匀变速直线运动,0v = 0时:时间等分点:各时刻速度之比:1:2:3:4:5各时刻总位移之比:1:4:9:16:25 各段时间内位移之比:1:3:5:7:9位移等分点:各时刻速度之比:1……到达各分点时间之比1……通过各段时间之比1∶)1……5.自由落体(取210m/s g=):n 秒末速度(m/s ): 10,20,30,40,50 =gt n 秒末下落高度(m):5、20、45、80、125 212=gt 第n 秒内下落高度(m):5、15、25、35、452211122n n-=at -at6.上抛运动:对称性:t t 下上=,=v v 下上, 2m 2h g=v7.相对运动:①共同的分运动不产生相对位移。
专题03 关联速度模型-【模型与方法】2023-2024学年高一物理同步模型易点通(人教版2019必

专题03 关联速度模型1.“关联”速度关联体一般是两个或两个以上由轻绳或轻杆联系在一起,或直接挤压在一起的物体,它们的运动简称为关联运动。
一般情况下,在运动过程中,相互关联的两个物体不是都沿绳或杆运动的,即二者的速度通常不同,但却有某种联系,我们称二者的速度为“关联”速度。
2.“关联”速度分解的步骤(ⅰ)确定合运动的方向:物体实际运动的方向就是合运动的方向,即合速度的方向。
(ⅰ)确定合运动的两个效果。
用轻绳或可自由转动的轻杆连接的物体的问题―→⎩⎪⎨⎪⎧效果1:沿绳或杆方向的运动效果2:垂直绳或杆方向的运动相互接触的物体的问题―→⎩⎪⎨⎪⎧效果1:垂直接触面的运动效果2:沿接触面的运动(ⅰ)画出合运动与分运动的平行四边形,确定它们的大小关系。
3.常见的速度分解模型 (1)绳牵联模型单个物体的绳子末端速度分解:如图甲所示,v ⅰ一定要正交分解在垂直于绳子方向,这样v ⅰ的大小就是拉绳的速率,注意切勿将绳子速度分解。
甲 乙两个物体的绳子末端速度分解:如图乙所示两个物体的速度都需要正交分解,其中两个物体的速度沿着绳子方向的分速度是相等的,即v A ⅰ=v B ⅰ。
如图丙所示,将圆环的速度分解成沿绳方向和垂直于绳方向的分速度,B 的速度与A 沿绳方向的分速度相等,即v A ⅰ=v B ⅰ。
丙 丁 (2)杆牵联模型如图丁所示,将杆连接的两个物体的速度沿杆和垂直于杆的方向正交分解,则两个物体沿杆方向的分速度大小相等,即v A ⅰ=v B ⅰ。
【模型演练1】(2024上·甘肃兰州·高一兰州一中校考期末)如图在水平力F 作用下,物体B 沿水平面向左运动,物体A 恰好匀速下降。
以下说法正确的是( )【答案】C【详解】AB .由于绳不可伸长,故B 沿绳方向的分速度等于A 的速度,即B A cos v v α=A 匀速下降过程,α在增大,故B v 增大,即物体B 正向左做加速运动,由三角函数关系可知,并不是匀加速运动,故AB 错误;C .A 匀速下降,绳上拉力T 不变,B 在竖直方向平衡,满足B sin N m g T α=-可知N 减小,由f N μ=可知,地面对B 的摩擦力减小,故C 正确; D .斜绳与水平方向成30°角时,代入关系式B A cos v v α=得示位置时,两绳子与水平面的夹角分别为30β=、60α=则( )A .当β由30增大到45过程中,A 的平均速度小于vB .当β由45增大到60过程中,A 的平均速度大于vC .当β由30增大到45过程中,绳中拉力先减小后增大D .当β由45增大到60过程中,绳中拉力先减小后增大 330tan 45hh h -=-2230sin 60h h h +=+221)0.8445tan 60hh h x --≈>的位移大,故A 的平均速度大于v ,故45增大到60过程中,有30增大到45过程中,.物体B以速度v向右匀速运动,根据平衡条件与53)3730增大到45过程中,绳中拉力先减小后增大,当45增60过程中,绳中拉力一直增大,故正确,D错误。
绳拉船模型的速度分解及其应用

绳拉船模型的速度分解及其应用作者:项其杰来源:《新高考·高一物理》2012年第01期■ 一、问题的由来大家经常会遇到这样的关于速度分解的题目:如图1所示,某人站在岸上通过绕过定滑轮的绳子向岸边拉船,他拉绳子的速率v保持不变,当拉船的绳子与水平面成θ角时,船前进速度u为多大?初次接触这道题目,学生最易出现的速度矢量分解图有两个,见图2、图3,两个图所得到的结论均为u=vcosθ.■ 二、问题的分析图2错误的原因是没有分清哪个是研究对象,哪个速度是合速度. 而是把绳收缩的速度作为合速度,把它按水平和竖直方向正交分解,因小船是沿水平方向运动,所以这样的分解中竖直向上的分速度是没有物理意义的,结论自然也是错误的.图3分解的虽是实际速度,即合速度,但没有正交分解,错误原因是其中的一个分运动并不是竖直向下的,而应是绳以定滑轮O为轴沿顺时针方向的转动,这个分运动的方向应垂直于绳.另外,由刚才两图得到的结论都表明u<v.倘若小船经过一个极短时间Δt从位置A运动到位置B,如图4所示,则AB线段表示小船在这段时间内的位移大小,而OA与OB之差则表示这段时间内绳子收缩的距离,也即人的位移大小,很显然OA与OB之差小于AB,同除以时间Δt应得到u>v,这也与刚才的结论不符合.■ 三、问题的解决其实,当认为绳子不可伸长时,对于用绳联结的两个物体,若速度沿绳方向,则两物体速度必相同,否则绳子就处于松弛状态或者被拉断了;若两物体速度不沿绳子方向,则两物体速度在沿绳方向的分量必定相同. 本题中,人的速度全在沿绳方向上,因此,只要将小船速度沿绳方向和垂直绳子方向进行分解(垂直绳子方向的分量表示小船绕O点的转动),再令两物体沿绳方向的速度相等即可求出. 作出速度矢量的平行四边形. 由图5可知船的速度大小为:u=■.■ 四、模型的应用■ 例1 如图6所示,物块A通过光滑的定滑轮用细绳与圆环B相连,A位于光滑的水平桌面上,B套在光滑的竖直杆上. 当细绳与水平方向的夹角为θ时,A的速度为v,此时B的速度u为多少?■ 解析 B的速度u为“实际速度”,即合速度. 将B的速度分别沿绳的方向和垂直于绳的方向进行分解,如图7所示. 由图可得:u=■.■ 例2 如图8所示,在水平面上小车A通过光滑的定滑轮用细绳拉一物块B,小车A的速度为v1=5 m/s.当细绳与水平方向的夹角分别为30°和60°时,物块B的速度v2为多少?■ 解析将A、B的速度v1、v2都分别沿绳的方向和垂直于绳的方向进行分解,在沿绳的方向上A、B的速度相等,即:v1cos30°=v2cos60°所以v2=5■ m/s.■ 例3 如图9所示,杆OA长为R,可绕过O点的水平轴在竖直平面内转动,其端点A系着一跨过定滑轮B、C的不可伸长的轻绳,绳的另一端系一物块M. 滑轮的半径可忽略,B在O的正上方,OB之间的距离为H. 某一时刻,当绳的BA段与OB之间的夹角为α时,杆的角速度为ω,求此时物块M的速率vM.■ 解析杆的端点A点绕O点做圆周运动,其速度vA的方向与杆OA垂直,在所考察时其速度大小为:vA=ωR.对于速度vA作如图10所示的正交分解,即沿绳BA方向和垂直于BA方向进行分解,沿绳BA方向的分量就是物块M的速率vM,因为物块只有沿绳方向的速度,所以vM=vAcosβ.由正弦定理知,■=■.由以上各式得vM=ωHsinα.■ 五、模型的延伸上面的分解方法对于求解面接触物体的速度问题也是可以的.■ 例4 一个半径为R的半圆柱体沿水平方向向右以速度v0匀速运动. 在半圆柱体上搁置一根竖直杆,此杆只能沿竖直方向运动,如图11所示. 当杆与半圆柱体接触点P与柱心的连线与竖直方向的夹角为θ,求竖直杆运动的速度.■ 解析将两物体的速度分别沿弹力的方向和垂直于弹力的方向进行分解,令两物体沿弹力方向的速度相等即可求出.设竖直杆运动的速度为v1,方向竖直向上,由于弹力方向沿OP方向,所以v0、v1在OP方向的投影相等,即有v0sinθ=v1cosθ,解得v1=v0tanθ.对于连接体中物体之间的速度关系分析思路是:把两物体的速度沿着某一共同的方向进行分解,如例2中的绳子方向,例4中的弹力方向,利用在该方向上的速度分量相等建立关系式进行求解.。
专题04 连接体模型--2024版高三物理培优——模型与方法

2024版高三物理培优——模型与方法专题04连接体模型目录【模型一】平衡中的连接体模型 (1)1.轻杆连接体问题 (1)2.轻环穿杆问题 (2)【模型二】绳杆弹簧加速度问题模型 (8)1.悬绳加速度问题 (8)2.类悬绳加速度问题 (9)【模型三】轻绳相连加速度相同的连接体 (24)【模型四】板块加速度相同的连接体模型 (31)【模型五】轻绳绕滑轮加速度相等----“阿特伍德机”模型 (43)【模型六】弹簧木块分离问题模型 (54)【模型七】“关联速度与机械能守恒”连接体模型 (64)1.绳、杆末端速度分解四步 (64)2.绳杆末端速度分解的三种方法 (64)3.轻绳相连的物体系统机械能守恒模型 (65)方法二、力乘力臂法对m1、m2受力分析,三力平衡可构成矢量三角形,根据正弦定理以整体为研究对象,以圆心为转动轴,两圆弧的支持力的力臂均为零,以整体为研究对象,整体受重力和两圆弧的支持力,根据三力平衡必::根据等腰三角形有:θ1=θ2联立解得m1g sinα=m2g sinβ2=sinβ:sinα轻环穿杆问题F NA.9∶16B.C.3∶4D.根据杠杆原理,由平衡条件得A.需要知道刚性细杆的长度与球面半径的关系C.不需要其他条件,有12:F F=【答案】C分别对小球a 和b 受力分析有11sin sin F G β=根据几何关系有A .2cmB .【答案】C【详解】由于小环是轻质的,故弹簧必将与杆垂直,否则受力不平衡。
对小球受力分析如图所示将各力沿着杆分解,根据平衡条件有解得又弹簧的弹力等于轻绳的拉力,故由胡克定律可得A.定滑轮对钢索的支持力为B.AB段钢索所受到的拉力为C.右臂OB对钢索的支持力为故选A。
【模型演练5】如图所示,竖直放置的光滑圆环,顶端D分别为m1、m2的两小球A、B,两小球用轻绳绕过定滑轮相连,并处于静止状态,且与右侧绳的夹角为θ。
则A、B两小球的质量之比为(A.tanθB.tan【答案】B【解析】对两小球分别受力分析,作出力的矢量三角形,如图所示。
物理一轮复习 专题14 运动的合成与分解(讲)(含解析)

专题14 运动的合成与分解1.掌握曲线运动的概念、特点及条件。
2。
掌握运动的合成与分解法则.1.曲线运动(1)速度的方向:质点在某一点的速度方向,沿曲线在这一点的切线方向.(2)运动的性质:做曲线运动的物体,速度的方向时刻在改变,所以曲线运动一定是变速运动.(3)曲线运动的条件:物体所受合外力的方向跟它的速度方向不在同一条直线上或它的加速度方向与速度方向不在同一条直线上.2.运动的合成与分解(1)基本概念①运动的合成:已知分运动求合运动.②运动的分解:已知合运动求分运动.(2)分解原则:根据运动的实际效果分解,也可采用正交分解.(3)遵循的规律位移、速度、加速度都是矢量,故它们的合成与分解都遵循平行四边形定则.(4)合运动与分运动的关系①等时性合运动和分运动经历的时间相等,即同时开始、同时进行、同时停止.②独立性一个物体同时参与几个分运动,各分运动独立进行,不受其他运动的影响.③等效性各分运动的规律叠加起来与合运动的规律有完全相同的效果.考点一物体做曲线运动的条件及轨迹分析1.条件(1)因为速度时刻在变,所以一定存在加速度;(2)物体受到的合外力与初速度不共线.2.合外力方向与轨迹的关系物体做曲线运动的轨迹一定夹在合外力方向与速度方向之间,速度方向与轨迹相切,合外力方向指向曲线的“凹"侧.3.速率变化情况判断(1)当合外力方向与速度方向的夹角为锐角时,物体的速率增大;(2)当合外力方向与速度方向的夹角为钝角时,物体的速率减小;(3)当合外力方向与速度方向垂直时,物体的速率不变.★重点归纳★做曲线运动的规律小结:(1)合外力或加速度指向轨迹的“凹”(内)侧.(2)曲线的轨迹不会出现急折,只能平滑变化,且与速度方向相切.★典型案例★光滑水平面上有一质量为2kg的物体,在五个恒定的水平共点力的作用下处于平衡状态.现同时撤去大小分别为5N和15N的两个水平力而其余力保持不变,关于此后物体的运动情况的说法中正确的是:()A.一定做匀变速直线运动,加速度大小可能是5m/s2B.可能做匀减速直线运动,加速度大小可能是2m/s2C.一定做匀变速运动,加速度大小可能10m/s2D.可能做匀速圆周运动,向心加速度大小可能是10m/s2【答案】C【名师点睛】本题中物体原来可能静止,也可能做匀速直线运动,要根据物体的合力与速度方向的关系分析物体可能的运动情况。
绳(杆)端速度分解模型
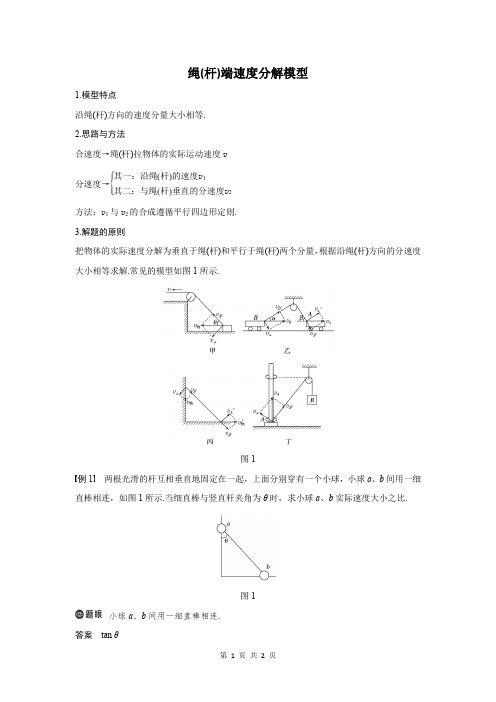
绳(杆)端速度分解模型
1.模型特点
沿绳(杆)方向的速度分量大小相等.
2.思路与方法
合速度→绳(杆)拉物体的实际运动速度v
分速度→⎩⎪⎨⎪⎧
其一:沿绳(杆)的速度v 1其二:与绳(杆)垂直的分速度v 2 方法:v 1与v 2的合成遵循平行四边形定则.
3.解题的原则
把物体的实际速度分解为垂直于绳(杆)和平行于绳(杆)两个分量,根据沿绳(杆)方向的分速度大小相等求解.常见的模型如图1所示.
图1
例1 两根光滑的杆互相垂直地固定在一起,上面分别穿有一个小球,小球a 、b 间用一细直棒相连,如图1所示.当细直棒与竖直杆夹角为θ时,求小球a 、b 实际速度大小之比.
图1
小球a 、b 间用一细直棒相连.
答案 tan θ
解析 根据速度的分解特点,可作出两小球的速度关系如图所示.由图中几何关系可得,a 、b 沿棒方向的分速度分别为v a cos θ和v b sin θ,根据“关联速度”的特点可知,两小球沿棒
的分速度大小相等,即有v a cos θ=v b sin θ,解得:v a v b
=tan θ.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
绳(杆)端速度分解模型
1.人用绳子通过定滑轮拉物体A,A穿在光滑的竖直杆上,当以速度v0匀速地拉绳使物体A到达如图所示位置时,绳与竖直杆的夹角为θ,则物体A实际运动的速度是()
A.v0sinθB.
C.v0cosθD.
2.有一个直角支架AOB,OA水平放置,OB竖直向下,OA上套有小环P,OB
上套有小环Q,两环间由一根质量不计不可伸长的细绳相连,小环P受
水平向右外力作用使其匀速向右平动,在P平动过程中,关于Q的运动
情况以下说法正确的是()
A.Q匀速上升B.Q减速上升
C.Q匀加速上升D.Q变加速上升
3.一辆车通过一根跨过定滑轮的轻绳子提升一个质量为m的重物,开始车在滑轮的正下方,绳子的端点离滑轮的距离是H.车由静止开始向左做匀加速运动,经过时间t绳子与水平方向的夹角为θ,如图所示,则
A.车向左运动的加速度的大小为
B.车向左运动的加速度的大小为
C.重物m在t时刻速度的大小为
D.重物m在t时刻速度的大小为
、B两物体通过一根跨过定滑轮的轻绳相连放在水平面上,现物体A以速度v1向右匀速运动,当绳被拉成与水平面夹角分别为α、β时,如图所示.物
体B的运动速度vB为(绳始终有拉力)()
A.v1sinα/sinβB.v1cosα/sinβ
C.v1sinα/cosβD.v1cosα/cosβ
5.有一竖直放置的T型架,表面光滑,两质量相等的滑块A、B分别套在水平杆与竖直杆上,A、B用一不可伸长的轻细绳相连,A、B可看作质点,如图所示,开始时细绳水平伸直,A、B静止.由静止释放B后,已知当细绳与竖直方向的夹角为60°时,滑块B沿着竖直杆下滑的速度为v,则连接A、B的绳长为()
A.
B.
C.
D.
如图所示,套在竖直细杆上的环A由跨过定滑轮且不可伸长的轻绳与重物B相连,由于B的质量较大,在释放B后,A将沿杆上升,当A运动至与定滑轮的连线处于水平位置时,其上升速度为vA≠0,B未落地,这时B的速度vB=________.
答案解析
1.【答案】D
【解析】由运动的合成与分解可知,物体A参与两个分运动:一个是沿着与它相连接的绳子的运动,另一个是垂直于绳子斜向上的运动.而物体A的实际运动轨迹是沿着竖直杆向上的,这一轨迹所对应的运动就是物体A的合运动,它们之间的关系如图所示.由几何
关系可得v=,所以D项正确.
2.【答案】D
【解析】小环P、小环Q的合运动与分运动的关系如图所示,若细绳与OB的夹角为α,则
v0=vP sinα,而vQ=,所以vQ=vP tanα,由于vP保持不变,α增大,所以vQ增大,Q加速度向上,
但速度不是均匀增大,即Q变加速上升,因此只有选项D正确,选项A,B,C均错误.
3.【答案】A
【解析】汽车在时间t内向左走的位移:
又汽车匀加速运动,所以a,A正确,B错误;
此时汽车的速度
由运动的分解知识可知,汽车速度v汽沿绳的分速度与重物m的速度相等,即得v物=.,CD错误;
故选A
4.【答案】D.
【解析】A、B两物体的速度分解如图.
由图可知:v绳A=v1cosα
v绳B=vB cosβ
由于v绳A=v绳B
所以vB=v1cosα/cosβ,故D对
5.【答案】D
【解析】当绳子与竖直方向的夹角为60°时,设A的速度为v′,绳长为l,将这时A、B的速度均沿绳和垂直绳分解,由沿绳方向的分速度相等得:v′cos 30°=v cos 60°,解出v′=
v.由机械能守恒定律:mv2+mv′2=mgl cos 60°,解出绳长l=.故选项D 对,其余选项均错.
6.【答案】0
【解析】环A沿细杆上升的过程中,任取一位置,此时绳与竖直方向的夹角为α.将A的速度vA沿绳方向和垂直于绳的方向进行分解,如下图,则v1=vA cosα,B下落的速度vB=v1=vA cosα.当环A上升至与定滑轮的连线处于水平位置时α=90°,所以此时B的速度vB=0.。
