理论力学静力学练习
理论力学练习题(静力学)
A.1kN
B.0.5kN
A
B
C. 2 kN
D.2 kN
L
L
题 21 图
22 已知图示斜面的倾角为θ,若要保持物块A静止,则物块与斜
面之间的摩擦因数fs所应满足的条件为:
A.tanθ ≤ f s
B.tanθ ≥ f s
C.cotθ ≤ f s
D.cotθ ≤ f s
23 物块重力为Q,放在粗糙的水平面上,其摩擦角ϕ =200,若力
D.无法判断
B
D
G
C
E
H
题5图
6 已知F1、F2、F3、F4为作用于刚体上的平面汇交力系,
F4
其力矢关系如图所示为平行四边形。由此可知:
F3
A.力系可合成为一个力偶
B.力系可合成为一个力
F1
C.力系简化为一个力和一个力偶 D.力系合力为零,力系平衡
题6图
F2
7 某平面任意力系向O点简化后,得到如图所示的一个主 矢FR′和一个主矩MO,则该力系的最后简化结果为:
P作用于摩擦角之外,并已知α=300,P = Q,物体是否能保持平衡: A.能 B.不能 C.处于临界状态 D.P 与 Q 的值比较小时能保持静止,否则不能
A θ
题 22 图
P α
Q
题 23 图
24 已知 W=100kN,P=80kN,摩擦因数 f = 0.2,物块将: A.向上运动 B.向下运动 C.静止不动 D.无法判断
h
P l
θ B
A
题3图
4 平面汇交力系(F1,F2, F3,F4,F5,)的力多边形如图
所示,则该力系的合力FR等于:
F2
F4
F1
华南理工-理论力学(静力学)随堂练习

理论力学(静力学)一基本概念1.一物体是否被看作刚体,取决于。
(A)变形是否微小(B)变形不起决定因素(C)物体是否坚硬(D是否研究物体的变形答案:B2.平衡是指。
(A)物体相对任何参考体静止不动(B)物体相对任何参考体作匀速直线运动(C)物体只相对地球作匀速直线运动(D物体相对地球静止不动或作匀速直线运动答案:D3.参考答案:BC4.力有两种作用效果:力可以使物体的运动状态发生变化,也可以使物体发生变形。
答案:√5.悬挂的小球静止不动是因为小球对绳向下的拉力和绳对小球向上的拉力相互抵消的缘故。
答案:×6.在任何情况下,体内任意两点的距离保持不变的物体叫刚体。
√7.凡是合力都大于分力。
()答案:×8.二力平衡条件中的两个力作用在同一物体上;作用力和反作用力分别作用在两个物体上。
()答案:√9.理论力学的任务是研究物体作机械运动一般规律的科学。
()答案:√·1.2 静力学公理。
1.参考答案:B2.参考答案:A3.三力平衡定理是。
(A)共面不平行的三个力互相平衡必汇交于一点(B)共面三力若平衡,必汇交于一点(C)三力汇交于一点,则这三个力必互相平衡。
(D)此三个力必定互相平行答案:A4.作用和反作用定律的适用范围是。
(A)只适用于刚体(B)只适用于变形体(C)只适用于处于平衡状态的物体(D)适用于任何物体答案:D5.力的可传性原理。
(A)适用于刚体(B)适用于刚体和弹性体(C)适用于所有物体(D)只适用于平衡的刚体答案:A6.如图所示的三铰刚架,支座A、B处的约束力一定通过。
(A) C 点(B) D点(C) E点(D) F点答案:C7.下列说法正确的是。
(A) 作用力反作用力既可以作用于同一物体,也可以作用于两个不同物体(B) 作用力反作用力肯定作用于两个不同物体(C) 作用反作用定律只适用于平衡刚体(D)作用反作用定律适用于所有刚体答案:BD8.刚体受汇交于一点的三个力作用,肯定能平衡。
理论力学(静力学) 随堂练习

7.(单选题) 如图所示的三铰刚架,支座A、B处的约束力一定通过 ( )。
(A)C点
(B)D点
(C)E点
(D)F点
参考答案:C
8.(单选题) 下列各式中,表示正确的是( )。
(A) (B)
(C) (D)
参考答案:D
9.(单选题) 图示用羊角锤拔钉子,下面四图所示的作用力中,( )是最省力的。
(C)必为一合力偶 (D)为一合力偶或平衡
参考答案:D
5.(单选题) 在刚体上作用3个大小相等的力,其力三角形如图所示,则该力系的简化结果( )。
(A)必为一个力
(B)必为一个力和一个力偶
(C)必为一个力偶
(D)可能平衡或简化为一力偶
参考答案:D
6.(单选题) 平面任意力系简化时若取不同的简化中心,则( )
参考答案:B
3.(单选题) 如图所示,在刚体上的四个点上各作用一个大小相等的力,则该力系的简化结果为 ( )。
(A)一个力
(B)一个力和一个力偶
(C)一个力偶
(D)平衡
参考答案:C
4.(单选题) 某平面力系,其简化结果与简化中心无关,则该力系的简化结果( )。
(A)必为一合力 (B)必平衡
(A)静止 (B)临界平衡
(C)滑动 (D)无法判断
参考答案:A
6.(单选题) 如图所示若尖劈两侧与槽之间的摩擦角均为,则欲使尖劈被打入后不致自动滑出,角应为( )。
(A) (B)
(C) (D)
参考答案Байду номын сангаасC
.(单选题) 圆轮绕固定轴O转动,某瞬时轮缘上一点的速度和加速度如下图所示,则不可能产生的运动情况为( )。
华南理工网络教育理论力学(静力学)随堂练习

参考答案:D5.(单选题) 图示系统受力F作用而平衡。
欲使A支座约束力的作用线与AB成60º角,则斜面的倾角应为()。
(A)0º(B)30º(C)45º(D)60º参考答案:B6.(单选题) 力的可传性原理()。
7.(单选题) 如图所示的两个楔块A、B在m-m处光滑接触,现在其两端沿轴线各加一个大小相等、方向相反的力,则两个楔块的状态为()。
(A)A、B都不平衡(B)A平衡、B不平衡(C)A不平衡、B平衡(D)A、B都平衡参考答案:A8.(单选题) 三力平衡定理是()。
1.(单选题) 如图所示,带有不平行的两条矩形导槽的三角形平板上作用一个力偶M,在槽内各有一个固连于地面、可沿槽滑动的销钉E和H,不计摩擦,则()。
(A)平板保持平衡状态(B)在力偶矩较小时,平板才能平衡(C)平板不可能保持平衡(D)条件不够,无法判断平衡与否参考答案:C2.(单选题) 如图所示,均质杆AB的重为P,D处用绳索悬挂,A端与光滑墙壁接触,现在B端作用一水平力F,则杆AB()。
(A)在力P 很大时才能平衡(B)当力P 大于零时就能平衡(C)当力P为任何值时都能平衡(D)力P为任何值时都不能平衡参考答案:D3.(单选题) 如图所示,带有不平行的两个导槽的矩形平板上作用一力偶,今在槽内插入两个固连于地面的销钉,若不计摩擦,则()。
(A)板必保持平衡状态(B)板不可能保持平衡状态(C)在矩M较小时,板可保持平衡(D)条件不够,无法判断板平衡与否参考答案:B4.(单选题) 均质杆AB长为L,重为P,用一绳索悬吊于光滑槽内,则杆在A、B处受到的约束力的关系为()。
(A)(B)(C)(D)5.(单选题) 已知杆AB和CD的自重不计,且在C处光滑接触,若作用在AB杆上的力偶的矩为m1,则欲使系统保持平衡,作用在CD杆上的力偶的矩m2的转向如图示,其矩值应为()。
(A)m2 = m1 (B)m2 = 4 m1 / 3 (C)m2 = 2 m1 (D)m2 = m1 / 2参考答案:A6.(单选题) 如图结构由O1A、O2B、CD和EF四根杆铰接而成。
《理论力学》静力学典型习题+答案
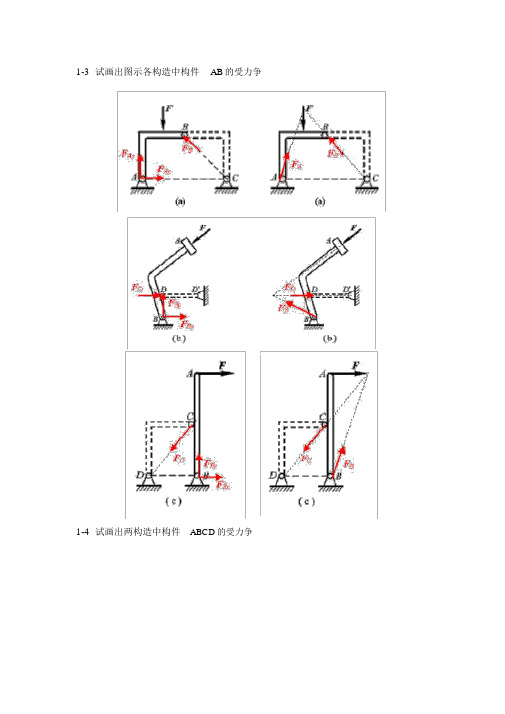
1-3 试画出图示各构造中构件AB的受力争1-4 试画出两构造中构件ABCD的受力争1-5 试画出图 a 和 b 所示刚系统整体各个构件的受力争1-5a1-5b1- 8 在四连杆机构的ABCD的铰链 B 和 C上分别作用有力F1和 F2,机构在图示位置均衡。
试求二力F1和 F2之间的关系。
解:杆 AB,BC, CD为二力杆,受力方向分别沿着各杆端点连线的方向。
解法 1( 分析法 )假定各杆受压,分别选用销钉 B 和 C 为研究对象,受力以下图:yyFBCC xB Fo45BCx30o o F60F2CDF AB F1由共点力系均衡方程,对 B 点有:F x0F2F BC cos4500对 C点有:F x0FBC F1 cos3000解以上二个方程可得:F12 6F2 1.63F23解法 2( 几何法 )分别选用销钉 B 和 C 为研究对象,依据汇交力系均衡条件,作用在 B 和C 点上的力构成关闭的力多边形,以下图。
F F2BCF AB o30o45CD60oFF BC F1对 B 点由几何关系可知:F2F BC cos450对 C 点由几何关系可知:F BC F1 cos300解以上两式可得:F1 1.63F22-3 在图示构造中,二曲杆重不计,曲杆AB 上作用有主动力偶 M。
试求 A 和 C 点处的拘束力。
解: BC为二力杆 ( 受力以下图 ) ,故曲杆 AB 在 B 点处遇到拘束力的方向沿BC 两点连线的方向。
曲杆AB遇到主动力偶M的作用, A 点和 B 点处的拘束力一定构成一个力偶才能使曲杆AB保持均衡。
AB受力以下图,由力偶系作用下刚体的均衡方程有(设力偶逆时针为正):M0 F A10a sin(450 )M 0F A0.354Ma此中:tan 1。
对 BC杆有:F C FB F A0.354M 3aA,C两点拘束力的方向以下图。
2-4解:机构中 AB杆为二力杆,点A,B 出的拘束力方向即可确立。
《理论力学》静力学典型习题+答案00

1-3 试画出图示各结构中构件AB的受力图1-4 试画出两结构中构件ABCD的受力图1-5 试画出图a和b所示刚体系整体各个构件的受力图1-5a1-5b1- 8在四连杆机构的ABCD 的铰链B 和C 上分别作用有力F 1和F 2,机构在图示位置平衡。
试求二力F 1和F 2之间的关系。
解:杆AB ,BC ,CD 为二力杆,受力方向分别沿着各杆端点连线的方向。
解法1(解析法)假设各杆受压,分别选取销钉B 和C 为研究对象,受力如图所示:由共点力系平衡方程,对B 点有:∑=0x F 045cos 02=-BC F F对C 点有:∑=0x F 030cos 01=-F F BC解以上二个方程可得:22163.1362F F F ==解法2(几何法)分别选取销钉B 和C 为研究对象,根据汇交力系平衡条件,作用在B 和C 点上的力构成封闭的力多边形,如图所示。
对B 点由几何关系可知:0245cos BC F F =对C 点由几何关系可知:0130cos F F BC =解以上两式可得:2163.1F F =2-3 在图示结构中,二曲杆重不计,曲杆AB 上作用有主动力偶M 。
试求A 和C 点处的约束力。
解:BC 为二力杆(受力如图所示),故曲杆AB 在B 点处受到约束力的方向沿BC 两点连线的方向。
曲杆AB 受到主动力偶M 的作用,A 点和B 点处的约束力必须构成一个力偶才能使曲杆AB 保持平衡。
AB 受力如图所示,由力偶系作用下刚体的平衡方程有(设力偶逆时针为正):0=∑M 0)45sin(100=-+⋅⋅M a F A θ aM F A 354.0=其中:31tan =θ。
对BC 杆有:aM F F F A B C 354.0=== A ,C 两点约束力的方向如图所示。
2-4FF解:机构中AB杆为二力杆,点A,B出的约束力方向即可确定。
由力偶系作用下刚体的平衡条件,点O,C处的约束力方向也可确定,各杆的受力如图所示。
静力学模拟试题及答案

静力学模拟试题及答案一、选择题1. 静力学中,力的平衡状态是指:A. 物体静止不动B. 物体速度为零C. 物体加速度为零D. 物体受力为零答案:C2. 以下哪项不是静力学中的基本概念?A. 力B. 力矩C. 动量D. 平衡答案:C二、填空题1. 根据牛顿第一定律,物体在不受外力作用时,将保持________状态。
答案:静止或匀速直线运动2. 在静力学中,当物体受到多个力作用时,若这些力的合力为零,则物体处于________状态。
答案:平衡三、简答题1. 解释什么是静力学中的二力平衡,并给出一个生活中的例子。
答案:二力平衡是指两个大小相等、方向相反、作用在同一直线上的力作用在物体上,使得物体保持静止或匀速直线运动的状态。
例如,当一个人站在水平地面上时,其受到的重力和地面的支持力就是一对二力平衡的例子。
2. 描述力矩的三要素,并说明它们是如何影响力矩的大小和方向的。
答案:力矩的三要素包括力的大小、力臂的长度以及力的作用点。
力的大小越大,力臂越长,力矩就越大;力臂长度固定时,力的作用点越远离旋转轴,力矩也越大。
力矩的方向遵循右手定则,即当力的方向从旋转轴指向力的作用点时,拇指指向的方向即为力矩的方向。
四、计算题1. 一个质量为10kg的物体,受到一个水平向右的力F=20N,求物体的加速度。
答案:根据牛顿第二定律,F=ma,所以a=F/m=20N/10kg=2m/s²。
2. 一个杠杆长2m,一端固定,另一端受到一个垂直向下的力G=100N,求杠杆的力臂长度。
答案:由于杠杆平衡,力臂长度等于杠杆长度的一半,即1m。
五、论述题1. 论述静力学在工程学中的应用,并给出至少两个具体的例子。
答案:静力学在工程学中有着广泛的应用,例如:- 在建筑设计中,通过静力学分析可以确定建筑物结构的稳定性和承载能力,确保建筑物的安全。
- 在机械设计中,通过计算零件的受力情况,可以设计出既满足功能需求又具有足够强度的机械结构。
静力学练习题及参考答案

静力学练习题及参考答案1. 问题描述:一根长度为L的均质杆以一端固定在墙上,另一端悬挂一重物。
重物造成的杆的弯曲应力最大为σ。
杆的质量可以忽略不计。
计算重物的质量m。
解答:根据静力学原理,杆的弯曲应力可以用公式计算:σ = M / S,其中M是杆的弯矩,S是杆的截面横截面积。
因为杆是均质杆,所以它的截面横截面积在整个杆上都是相等的。
设杆的截面横截面积为A。
杆的弯矩M可以通过杆的长度L和重物的力矩T计算得到:M = T * (L/2)。
代入上面的公式,我们可以得到:σ = (T * (L/2)) / A。
根据题目的描述,我们可以得到如下等式:σ = (m * g * (L/2)) / A,其中g是重力加速度。
我们可以将这个等式转换成求解未知质量m的方程。
将等式两边的A乘以m,并将等式两边的m乘以g,我们可以得到如下方程:m^2 = (2 * σ * A) / (g * L)解这个方程,我们可以求得未知质量m。
2. 问题描述:一根均质杆的长度为L,质量为M。
杆的一端固定在墙上,另一端悬挂一重物。
杆与地面的夹角为θ。
重物造成的杆的弯曲应力最大为σ。
求重物的质量m。
解答:在这个问题中,除了重物的力矩,还需要考虑到重力对杆的力矩。
由于杆是均质杆,其质量可以均匀分布在整个杆上。
假设杆上的每个微小质量元都受到与其距离一致的力矩。
重物造成的力矩可以用公式计算:M1 = m * g * (L/2) * sinθ,其中g 是重力加速度。
由于杆是均质杆,它的质心位于杆的中点。
因此重力对杆的力矩可以用公式计算:M2 = M * g * (L/2) * cosθ。
根据静力学的原理,杆的弯曲应力可以用公式计算:σ = M / S,其中M是杆的弯矩,S是杆的截面横截面积。
在这个问题中,我们可以将弯曲应力的计算公式推广到杆的中点(也就是质心):σ = (M1 + M2) / S代入上面的公式,我们可以得到:σ = ((m * g * (L/2) * sinθ) + (M *g * (L/2) * cosθ)) / S根据题目的描述,我们可以得到如下等式:σ = ((m * g * (L/2) * sinθ) + (M * g * (L/2) * cosθ)) / (A / 2),其中A是杆的横截面积。
《理论力学》静力学典型习题+答案

1-3 试画出图示各结构中构件AB的受力图1-4 试画出两结构中构件ABCD的受力图1-5 试画出图a和b所示刚体系整体各个构件的受力图1-5a1-5b1- 8在四连杆机构的ABCD 的铰链B 和C 上分别作用有力F 1和F 2,机构在图示位置平衡。
试求二力F 1和F 2之间的关系。
解:杆AB ,BC ,CD 为二力杆,受力方向分别沿着各杆端点连线的方向。
解法1(解析法)假设各杆受压,分别选取销钉B 和C 为研究对象,受力如图所示:由共点力系平衡方程,对B 点有:∑=0x F 045cos 02=-BC F F对C 点有:∑=0x F 030cos 01=-F F BC解以上二个方程可得:22163.1362F F F==解法2(几何法)分别选取销钉B 和C 为研究对象,根据汇交力系平衡条件,作用在B 和C 点上的力构成封闭的力多边形,如图所示。
对B 点由几何关系可知:0245cos BC F F =对C 点由几何关系可知: 0130cos F F BC =解以上两式可得:2163.1F F =2-3 在图示结构中,二曲杆重不计,曲杆AB 上作用有主动力偶M 。
试求A 和C 点处的约束力。
解:BC 为二力杆(受力如图所示),故曲杆AB 在B 点处受到约束力的方向沿BC 两点连线的方向。
曲杆AB 受到主动力偶M 的作用,A 点和B 点处的约束力必须构成一个力偶才能使曲杆AB 保持平衡。
AB 受力如图所示,由力偶系作用下刚体的平衡方程有(设力偶逆时针为正):0=∑M 0)45sin(100=-+⋅⋅M a F A θ aM F A 354.0=其中:31tan=θ。
对BC 杆有:aM F F F A B C 354.0===A ,C 两点约束力的方向如图所示。
2-4FF解:机构中AB杆为二力杆,点A,B出的约束力方向即可确定。
由力偶系作用下刚体的平衡条件,点O,C处的约束力方向也可确定,各杆的受力如图所示。
理论力学静力学题目

例1 平板质量为1m,受水平力F作用而沿水平面运动,板与水平面间的动摩擦系数为f,平板上放一个质量为2m的均匀圆柱,它相对平板只滚动不滑动,求平板的加速度.解:取圆柱分析,建立如图坐标:于是的:取平板分析:例2 已知:均质圆盘R m,F=常量,且很大,使O向右运动,f,初静止。
求:O走过S路程时力的功。
211222112oNm a FF m gm r F rα==-=112212122,213NFF m gm rFa a r amF m aαα===-=-=1、摩擦力d F 的功d W F S ≠,S 是力在空间的位移,不是受力作用点的位移。
例3 长为l ,重为P 的均质杆OA 由球铰链O 固定,并以等角速度ω绕铅直直线转动,如图所示: 如果杆与直线的角度为α,求均质杆的动能解:取出微小段r例4 滑块A 以速度A v 在滑道内滑动,其上铰接一个质量为m ,长为l 的均质杆AB .杆以速度ω绕A 转动。
如图:试求解当杆AB 与铅垂线的夹角为ϕ时,杆的动能。
解:AB 杆作平面运动,其质心C 的速度:C A CA v v v =+例F 所作的功例 7 速度合成矢量图如图,由余弦定理:22222222cos(180)11()2cos 221cos 2C A C A A C A A A A A v v v v v v l v l v l l v ϕωωϕωωϕ=+--=++=++ 杆的动能:222222222211221111(cos )()2221211(cos )22C C A A A A T m v J m v l l v m l m v l l v ωωωϕωωωϕ=+=+++=++。
理论力学 静力学 习题答案
FB 2 y M / a qa
x
' 0 , FB 2 x FCx 0
F
解得
FB 2 x qa / 2
五、研究对象:销钉B,受力如图(d) 六、列方程,求FB1x、FB1y
F
解得
x
0 , FB' 1x FB' 2 x 0
FB' 1x FB' 2 x qa / 2
FT P 1800N
8
2-20 在图a,b 两连续梁中,已知q,M,a 及θ ,不计梁的自重,求各连续梁在A,B,C 三 处的约束力。 解:(a) 一、研究对象:梁BC,受力如图a1所示。 二、列方程,求 FC 该力系为一力偶系,则: FB FC
M
B
0 , FC cos a M 0
2
3
习题:2-3,2-5,2-6,2-8,2-12,2-14,2-18,2-10,2-40 2-3 如图示刚架的点B 作用一水平力F,刚架重量略去不计。求支座A,D 的约束力FA和FD。
解: 一、取刚架为研究对象,画受力图,如图(b)。 二、列平衡方程,求支座 A,D 的约束力 FA 和 FD。 由三力平衡汇交定理,支座A 的约束力FA 必通过点C,方向如图(b) 所示。取坐标系Cxy , 由平衡理论得
注意:本题要求的是求解CD杆上销孔D所受的力, 而不是整体上D点的约束反力。 若不认真审题,极易将本题看成是求解整体上D点 的约束反力,这样也就偏离了本题的题意,解起来很简 单,但不对。
11
2-51 图示结构由AC与CB组成。已知线性分布载荷 q1 3kN/m ,均布载荷 q2 0.5kN/m ,
最后求出Mz,即
M z xFy yFx 150 507 150 169 101.4(Nmm)
理论力学第二章静力学作业

1、图示平面力系,已知:F1=8kN,F2=3kN,M=10kN·m,R=2m,θ=120º。
试求:(1)力系向O点简化的结果;(2)力系的最后简化结果,并示于图上。
2、结构如图,自重不计,已知:F P=4kN,AD=DB,DE段绳处于水平。
试求:A、B处的约束力。
3、图示多跨梁,自重不计。
已知:M、F P、q、L。
试求支座A、B的约束反力及销钉C 对AC梁的作用力。
kN⋅,F =2kN 4、图示多跨梁由AC和CD铰接而成,自重不计。
已知:q =10kN/m,M=40m作用在AB中点,且θ=450,L=2m。
试求支座A、B、D的约束力。
5、图式机构,AB=BC,BD=BE,不计各杆自重,D、E两点用原长为L=0.5m,弹簧常数k=1/6(kN/m)的弹簧连接,设在B处作用一水平力F,已知:F=20N,L1=0.4m,L2=0.6m。
求机构处于平衡时杆AB 与水平面的夹角θ。
6、在图所示机构中,曲柄OA 上作用一力偶,其力偶矩大小为M ,另在滑块D 上作用水平F ,机构尺寸如图所示,各秆重量不计。
求当机构平衡时,力F 与力偶短M 的关系。
7、在如图所示物块中,已知斜面的倾角为θ,接触面间的摩擦角为ϕ f 。
试问:(1)拉力F r 与水平面间的夹角β 等于多大时拉动物块最省力; (2)此时所需拉力F r 的大小为多少?8、两长度相同的均质杆AB ,CD 的重力大小分别为P = 100 N ,P 1 = 200 N ,在点B 用铰链连接,如图所示。
杆BC 的C 点与水平面之间的静滑动摩擦因数f s = 0.3。
已知:θ = 60º,试问:(1)系统能否平衡?并加以证明。
(2)若系统能够平衡,求C 点摩擦力的大小和方向。
理论力学静力学部分

静力学部分小题:简单计算题考点:力偶系平衡问题1. 如图所示平面结构,已知杆AB 和杆CD 的重量不计,且DC 杆在C 点靠在光滑的AB杆上,若作用在杆AB 上的力偶的力偶矩为1m ,则欲使系统保持平衡,求作用在CD 杆上的力偶的力偶矩2m 的大小。
2. 在图示平面结构中,杆AC 和杆BD 为无重杆,在C 处作用一力偶矩为M 的力偶,求A和B 处的约束反力。
3. 如图所示,在三铰拱结构的两半拱上,作用两个等值、反向、力偶矩为M 的力偶,如两半拱的重量不计,试求A 、B 处的约束力。
4. 如图所示平面结构,杆AC 、BC 为无重杆,其上作用两个等值、反向、力偶矩为M 的力偶,试求A 、B 处的约束反力。
5. 外伸梁AC 的尺寸及受力如图所示,已知Q =Q ’=1200N ,M =400m N ,a =1m ,梁的自重不计,求支座A 、B 的约束反力。
6.A 、C 的约束反力。
7. 如图所示平面结构,一力偶矩为M 的力偶作用在直角曲杆ADB 上。
不计杆重,求支座A 、B 对杆的约束反力。
8. 如图所示平面结构,一力偶矩为M 的力偶作用在直角曲杆ADB 上。
不计杆重,求支座A 、B 对杆的约束反力。
9. 在图示平面结构中,已知力偶矩为M ,AC =L ,构件自重不计,求支座A ,C 处的约束反力。
Q '10. 如图所示,已知P =P ’=3.96KN ,构件自重不计,求支座A 、C 的约束反力(AC =1m )。
11. 如图所示平面刚架,已知:123kN m 1kN m m m =⋅=⋅, ,转向如图。
a =1m ,试求图示刚架A 及B 处的约束反力。
12. 平面四连杆机构,在图示位置平衡,3090αβ =,=。
已知:O 1A =6a ,O 2B =8a 。
求此时12/m m 的值。
13. 在图示平面结构中,已知力偶矩M =4KN m ,AC =1m ,构件自重不计,求支座A ,C 的约束反力。
14. 如图所示平面刚架,已知:40kN m M =⋅,F =10kN,q =5kN/m 。
理论力学练习册及答案同济

理论力学练习册及答案同济一、静力学基础1. 题目:一个均匀的木杆,长度为2m,重量为50kg,一端固定在墙上,另一端自由。
求木杆的重心位置。
答案:木杆的重心位于其几何中心,即木杆的中点。
由于木杆均匀,其重心距离固定端1m。
2. 题目:一个质量为10kg的物体,受到三个力的作用:F1=20N向右,F2=30N向上,F3=15N向左。
求物体的合力大小和方向。
答案:合力F = F1 + F2 + F3 = (20N, 0) + (0, 30N) + (-15N, 0) = (5N, 30N)。
合力大小F = √(5² + 30²) = √(25 + 900) = √925 ≈30.41N。
合力方向与水平线的夹角θ满足tanθ = 30N / 5N = 6,所以θ ≈ 80.53°。
二、动力学基础1. 题目:一个质量为2kg的物体,从静止开始沿直线运动,加速度为5m/s²。
求物体在第3秒末的速度和位移。
答案:速度v = at = 5m/s² × 3s = 15m/s。
位移s = 0.5at² = 0.5 × 5m/s² × (3s)² = 22.5m。
2. 题目:一个质量为5kg的物体,以20m/s的初速度沿直线运动,受到一个恒定的阻力,大小为10N。
求物体在第5秒末的速度。
答案:加速度a = F/m = -10N / 5kg = -2m/s²。
速度v = v0 + at = 20m/s - 2m/s² × 5s = 0m/s。
三、转动动力学1. 题目:一个半径为0.5m的均匀圆盘,质量为10kg,绕通过其中心的轴旋转。
若圆盘的角加速度为10rad/s²,求圆盘的转动惯量。
答案:转动惯量I = mr² = 10kg × (0.5m)² = 2.5kg·m²。
理论力学练习册静力学部分

理论力学练习册(静力学部分) 静力学目录第一章 静力学的基本概念和物体的受力分析1-1 概念题 题号1-1-1~1-1-21-2 受力分析 题号 1-2-1~2-1-2第二章 基本力系(汇交力系及力偶系)2-1 思考与判断 题号2-1-1~2-1-22-2 练习题 题号2-2-1~2-2-112-3 选作题 题号2-3-1~2-3-3第三章 平面力系3-1 概念题 题号3-1-1~3-1-43-2练习题 题号3-2-1~3-2-103-3综合练习题 题号3-3-1~3-3-5第四章 考虑摩擦的平衡问题4-1概念题 题号4-1-1~4-1-34-1练习题 题号4-2-1~4-2-9第五章 空间力系5-1概念题 题号5-1-1~5-1-25-2练习题 题号5-2-1~5-2-81-1-1是非题(正确的在括号内画√,错误在画×)。
1.作用于刚体上的力是滑动矢量,作用于变形体上的力是定位矢量。
(√)2.二力构件的约束反力是其作用线的方位沿二受力点的连线,指向可假设。
(√)3.加减平衡力系公理不但适用于刚体,还适用于变形体。
(×)4.若两个力相等,则这个力就等效。
(×)5.作用于A 点共线反向的两个力1F 和2F 且1F >2F ,则合力21F F R -=。
(×)7.两物体在光滑斜面m-n 处接触,不计自重,若力1F 和2F 的大小相等方向相反,且共线,则两个物体都处于平衡状态。
(×)8.力F 可沿其作用线由D 点滑移到E 点。
(×)1-1-2 选择题(将正确答案前面的序号写在括号内)1.二力平衡公理适用于(1)①刚体 ②变形体 ③刚体和变形体2.作用与反作用公理适用于(3)①刚体 ②变形体 ③刚体和变形体3.作用于刚体上三个相互平衡的力,若其中任何两上力的作用线相交于一点,则其余的一个力的作用线必定。
(2)①交于同一点 ②交于同一点,且三个力的作用线共面③不一定交于同一点4.作用于刚体上的平衡力系,如果作用到变形体上,则变形体( 3 )。
理论力学静力学典型习题+答案

1-3试画出图示各结构中构件AB的受力图1-4试画出两结构中构件ABCD勺受力图1-5试画出图a和b所示刚体系整体各个构件的受力图1-5a1-5b1- 8在四连杆机构的ABCD勺铰链B和C上分别作用有力F i和F2,机构在图示位置平衡。
试求二力F1和F2之间的关系。
解:杆AB BC CD为二力杆,受力方向分别沿着各杆端点连线的方向。
解法1(解析法)假设各杆受压,分别选取销钉B和C为研究对象,受力如图所示:由共点力系平衡方程,对B点有:F x 0 F2F BC COS45°0对C点有:F x 0 F BC F1COS300 0解以上二个方程可得:F12 6F 1.63F2解法2(几何法)分别选取销钉B和C为研究对象,根据汇交力系平衡条件,作用在B和C点上的力构成封闭的力多边形,如图所示。
对B点由几何关系可知:F2F BC COS450对C点由几何关系可知:F BC F1 COS300解以上两式可得:F1 1.63F22-3在图示结构中,二曲杆重不计,曲杆AB上作用有主动力偶M试求A和C 点处的约束力。
解:BC为二力杆(受力如图所示),故曲杆AB在B点处受到约束力的方向沿BC 两点连线的方向。
曲杆AB受到主动力偶M的作用,A点和B点处的约束力必须构成一个力偶才能使曲杆AB保持平衡。
AB受力如图所示,由力偶系作用下刚体的平衡方程有(设力偶逆时针为正):M 0 F A 10a sin(450) M 0 F A 0.354M其中:tan -。
对BC杆有:F C F B F A 0.354M3 aA,C两点约束力的方向如图所示。
2-4解:机构中AB 杆为二力杆,点A,B 出的约束力方向即可确定。
由力偶系作用下 刚体的平衡条件,点 0,C 处的约束力方向也可确定,各杆的受力如图所示。
对1313 -6aFFi FjF 2 FiF 3- F i - —Fj2 222F RFi3Fj M A■-3 Fak F R M A V3 d a F R2Fi24d3 a F X 0 PsinFB X0 F y 0 F By P P cos0 F X 04F A X F B X 0F y 0F AyF By0 M A 0 MA F Byl 0求解以上三式可得:M 1 3N m , F ABF OF C 5N ,方向如图所示Psi nAF BxF AxBC 杆有:M 0对AB 杆有: F B F AF B BC sin300 M 2对OA 杆有:M 0 M i F AOA 0F By , MFA X,FAy, FBX, M A 0 N D aG -cos F l coscos2F y 0 N D cosG F 0N D ,arccosf 2(F (2FG)a 卡G)l ]F Ay F By P(1 COS ) M A P(1 cos )1M y O p eta n F BC cos c F BC sin eta n 0 F BC60.6N 2M x' 0 P 1 aF B c F BC S in2a 0 F B100N F y 0 F Z0F Ay,F A;z M x 0 M DE 0 F2COS4500 F20 M AO 0 F6COS45° a F COS450 COS450 a 0 F6 2 F M BH 02F4COS450 a F6COS450 a 0 F4 2F M AD 02F1 a F6COS450 a F sin450 a 0 £ 1 2 F M CD 02F1 a F3 a F sin45°a 0 F3 1F M BC 02F x 0F3 a F5 a F4COS450 a 0 F50 M 1500N cm Fy 0M O0以下几题可看一看!FA , F NA , FB , F NB ,tan3( f sif s2)FNB 0ta n 6002aM cf s2f si2 3F By 2a 0 F ByM H 0 F D y a Fa 0 F Dy FM BF DX a F 2a 0 F DX2FF y 0F AyF DyF By 0F AyF M A0 FD X a FB X 2aFB XFM BF AX 2aFD Xa0 FA XFM c 0 F D bF XF D-F M A0 F B bF XbF i F 2 (F i2Mpcos45° psin45° F 2)DF N 2 N iF i F 2f s N i f s N 2F i ,N i ,F 2,N 2, f s:s 2p D F e f 2M0 f siF By0.223, f s2 4.49 FB x N iP(i _f s2) _2( i —f ;2)f s%.223450F xF yM AT cosAC sinF N T sinF s T cos pT sin AC cosAB . sin 2FN , F s , T, fsf s 0.646a l . a几F NB a Pcos-Psi n 022 3F NA a P cos-Psin a 小 —— 02 2、3 F AF BPsi nM A 0M B 0 F x 0F A F Bf si F NAS 2F NBS24.49 i2MF D )b F ACAyD 2MF (bF 2x)F B F I F AAa b F A F 3 FxAy F i F 3 cos450F 1M2qa F yF 2aF2 Z M r ( 2qa) F x 0 FAXF 3 cos45(F AX(MaaF AyF 2 F 3si n450 P 4qa 0F AyP 4qa M A F 2 a P 2a 4qa 2a F 3S in450 '3aMM A 24qa 2 Pa M M A0 F By 2a F2a 0 F ByF Ay 2a F 2a 0 F A 『FF x 0 F AXFBx FF 32qa) F 0 F EF2 M C 0 F Bx a F By aV 2(MF AX2q x a) a F E sin450 a 0 F BxM eM BF By FF NDF 3 sin450F yM AM B0F BXM AN 13r P 3rcos60020 N i 6.93(N)F xFA XN 1 sin 60°F AX 6(N) F y 0F AyN 1cos600P 0 F Ay 12.5'(N) FN 1cos300 Tcos300 6.93(N)M A F N 2Lsin2P -cos2 M BF N LsinP Lcos F s Lcos2F S P F SFNtan100 F RC ,F RD F RC , F RD F RC , F RD2 2M A 0 F ND aI 0F ND44M A0F NC a F l 0F NC -FF NDaM O 0 F SC R F SD R 0FNCF X 0sinF — ----------- F----- FS D NCN D1 cos 1 cossin 1 costan —, f SD tanFRC,F2 221 cosF RCSDF NDF SD 0tan — 2 I FaFla cos —2PF RCsi n[180°(1800 2,sin ] ftanFl sinISD (Pa Fl )(1 cos )F yF NDP F SC sin F ND PFl ( (cosasin tan —)2f SD tanFl sin(Pa Fl )(1 cos )F B F ACFBF AC tan1 F3(F ND P) R MDF B \M E (P F NE )1RtanF NDM D M E!FRM DF NDBPL FaM AM EF yF x 4 f sP 4f sP } f s ,1 3f s }F SC%F X0 F NC costa nFl sin (Pa Fl )(1 cos )F NCsinF SC cos F SD 0FNDFSDM E 1FFNE F NE F SD tan2FNDF min{ —P,」 P,R R 3 1 F SD F NE F SE F 02P R M DF SE RF SD 3FFSDf s F ND M FM GF SE;FF SE f s F NEF max 0.362.该系统的位置可通过杆OA 与水平方向的夹角B 完全确定,有一个自由度。
静力学练习题及参考答案

静力学复习题1. 某平面任意力系向O 点简化,得到R ˊ=10N ,M 0=10 N·cm ,方向如图所示,求:该力系向A 点简化的结果。
2. 图示三铰刚架受力F 作用,求:A 、B 支座反力的大小。
3. 已知力P = 40 kN ,S =20kN ,物体与地面间的摩擦系数f = 0.5,动摩擦系数f ′= 0.4,求:物体所受的摩擦力。
4. 物块重W ,一外力F 作用在物块上,且作用线在摩擦角外,如图所示,已知ο25=θ,摩擦角ο20=m ϕ,F W =。
试确定物块的运动状态。
5. 力F 通过A (3,4,0),B (0,4,4)两点(长度单位为米),若F =100N ,求/;(1) 该力在y 轴上的投影;(2 )该力对z 轴的矩。
6. 已知力F 的大小,角度ϕ和θ,以及长方体的边长a ,b ,c ,求:(1)力F 在轴z 和y上的投影;(2)力F 对轴x 的矩)(F x m 。
7. 图示正立方体,各边长为a ,四个力1F 、2F 、3F 、4F 大小皆等于F ,如图所示,作用在相应的边上。
求:此力系简化的最终结果并在图中画出。
8. 等边三角形ABC.边长为a.己知四个力的大小相等,即F1=F2=F3=F4=F;力偶矩M=Fa, 则该力系简化的最后结果是什么?9. 图示结构,杆重不计.已知:L=4.5m. q0=3kN/m. P=6kN. M=4.5kNm.求固定端E处的反力.(作业二中4题)10 .图示结构,由杆AB、DE、BD组成,各杆自重不计,D、C、B均为铰链连接,A 端为固定端约束。
已知q(N/m),M=qa2(N·m),P=2qa(N),尺寸如图。
试列四个方程求固定端A的约束反力及BD杆所受的力。
(作业二中3题)11. .图示多跨梁由直杆AD和T字形杆DHG组成.已知:力P=2kN,q=0.5kN/m, M=4kNm,L=4m。
试列二个刚体静力学平衡方程求:支座H和支座C的反力。
静力学试题及答案

静力学试题及答案一、选择题1. 静力学中,力的平衡条件是什么?A. 力的大小相等B. 力的方向相反C. 力的大小相等,方向相反D. 力的大小和方向都相等答案:C2. 以下哪个不是静力学的基本概念?A. 力的合成B. 力的分解C. 力的平衡D. 力的守恒答案:D二、填空题1. 在静力学中,当一个物体处于________时,我们称其为平衡状态。
答案:静止或匀速直线运动2. 根据牛顿第一定律,物体在没有外力作用下,将保持________状态。
答案:静止或匀速直线运动三、简答题1. 简述牛顿第三定律的内容及其在静力学中的应用。
答案:牛顿第三定律指出,作用力和反作用力大小相等,方向相反,作用在两个不同的物体上。
在静力学中,这一定律用于分析物体间的相互作用,确保系统的力平衡。
2. 解释什么是静摩擦力,并说明其在物体保持静止状态时的作用。
答案:静摩擦力是阻止物体滑动的力,其大小与引起滑动的外力相等,但方向相反。
在物体保持静止状态时,静摩擦力与外力平衡,防止物体发生运动。
四、计算题1. 一个质量为10 kg的物体,受到水平方向上的两个力F1和F2的作用,F1 = 50 N,F2 = 30 N,求物体受到的合力。
答案:首先确定两个力的方向,如果F1和F2方向相反,则合力F = F1 - F2 = 50 N - 30 N = 20 N;如果F1和F2方向相同,则合力F = F1 + F2 = 50 N + 30 N = 80 N。
2. 一个斜面上的物体质量为20 kg,斜面与水平面的夹角为30°,求物体受到的重力分量在斜面方向上的分力。
答案:物体受到的重力G = m * g = 20 kg * 9.8 m/s² = 196 N。
在斜面方向上的分力 F = G * sin(θ) = 196 N * sin(30°) = 98 N。
五、分析题1. 一个均匀的直杆,长度为L,固定在水平面上的A点,B点自由悬挂,求直杆的平衡条件。
理论力学练习册(静力学)

文档南昌工程学院工程力学练习册(理论力学静力学部分)姓名:学号:年级、专业、班级:土木与建筑工程学院力学教研室第一章静力学公理和物体的受力分析一、是非题1.力有两种作用效果,即力可以使物体的运动状态发生变化,也可以使物体发生变形。
()2.在理论力学中只研究力的外效应。
()3.两端用光滑铰链连接的构件是二力构件。
()4.作用在一个刚体上的任意两个力成平衡的必要与充分条件是:两个力的作用线相同,大小相等,方向相反。
()5.作用于刚体的力可沿其作用线移动而不改变其对刚体的运动效应。
()6.作用于刚体上的三个力,若其作用线共面且相交于一点,则刚体一定平衡。
( ) 7.平面汇交力系平衡时,力多边形各力应首尾相接,但在作图时力的顺序可以不同。
()8.约束力的方向总是与约束所能阻止的被约束物体的运动方向一致的。
()二、选择题1.若作用在A点的两个大小不等的力F1和F2,沿同一直线但方向相反。
则其合力可以表示为。
①1-2;②2-1;③1+2;2.作用在一个刚体上的两个力A、B,满足A=-B的条件,则该二力可能是。
①作用力和反作用力或一对平衡的力;②一对平衡的力或一个力偶。
③一对平衡的力或一个力和一个力偶;④作用力和反作用力或一个力偶。
3.三力平衡定理是。
①共面不平行的三个力互相平衡必汇交于一点;②共面三力若平衡,必汇交于一点;③三力汇交于一点,则这三个力必互相平衡。
4.已知1、2、3、4为作用于刚体上的平面共点力系,其力矢关系如图所示为平行四边形,由此。
①力系可合成为一个力偶;②力系可合成为一个力;③力系简化为一个力和一个力偶;④力系的合力为零,力系平衡。
5.在下述原理、法则、定理中,只适用于刚体的有。
①二力平衡原理;②力的平行四边形法则;③加减平衡力系原理;④力的可传性原理;⑤作用与反作用定理。
三、填空题1.二力平衡和作用反作用定律中的两个力,都是等值、反向、共线的,所不同的是:。
2.已知力沿直线AB作用,其中一个分力的作用与AB成30°角,若欲使另一个分力的大小在所有分力中为最小,则此二分力间的夹角为度。
