初一下数学拔高题
七年级下数学期末试卷拔高

一、选择题(每题5分,共25分)1. 下列各数中,绝对值最小的是()A. -2B. 3C. -1/2D. 22. 下列方程中,解为整数的是()A. x^2 - 5x + 6 = 0B. x^2 - 4x + 3 = 0C. x^2 - 3x + 2 = 0D. x^2 - 2x + 1 = 03. 下列各数中,有理数的是()A. √2B. πC. 1/3D. √54. 下列函数中,y是x的二次函数的是()A. y = x^2 + 2x + 1B. y = x^2 - 2x + 1C. y = x^2 - 4x + 3D. y = x^2 + 4x + 35. 已知一元二次方程x^2 - 5x + 6 = 0,下列说法正确的是()A. 该方程有两个实数根B. 该方程有两个复数根C. 该方程有一个实数根D. 无法确定二、填空题(每题5分,共25分)6. 已知a > 0,b < 0,则|a| + |b| = ________。
7. 若方程2x - 3 = 5的解为x = 4,则方程4x + 6 = 2的解为x = ________。
8. 已知一元二次方程x^2 - 3x + 2 = 0,则该方程的解为x1 = ________,x2 = ________。
9. 已知二次函数y = x^2 - 2x + 1,则该函数的顶点坐标为( ________,____________)。
10. 已知a、b、c是三角形的三边,且a + b > c,b + c > a,a + c > b,则下列结论正确的是()A. a、b、c能构成三角形B. a、b、c不能构成三角形C. 无法确定三、解答题(每题10分,共40分)11. 已知一元二次方程x^2 - 4x + 3 = 0,求该方程的解。
12. 已知二次函数y = x^2 - 2x + 1,求该函数的顶点坐标。
13. 已知a、b、c是三角形的三边,且a + b > c,b + c > a,a + c > b,求证:a、b、c能构成三角形。
华师大版数学七年级下册_《图形的全等》拔高练习1
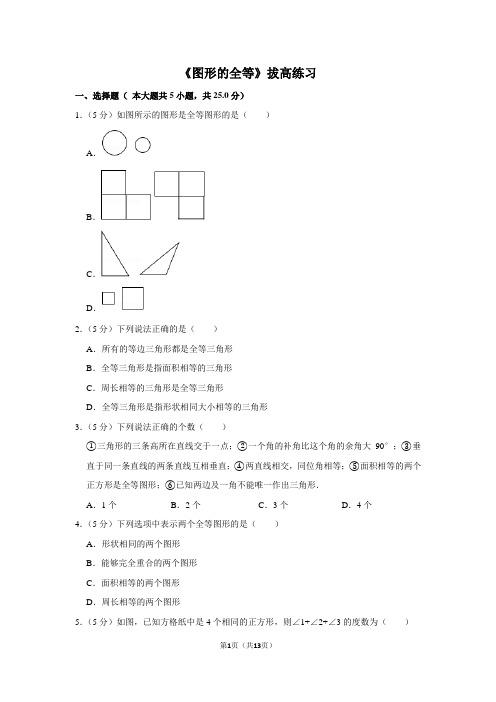
《图形的全等》拔高练习一、选择题(本大题共5小题,共25.0分)1.(5分)如图所示的图形是全等图形的是()A.B.C.D.2.(5分)下列说法正确的是()A.所有的等边三角形都是全等三角形B.全等三角形是指面积相等的三角形C.周长相等的三角形是全等三角形D.全等三角形是指形状相同大小相等的三角形3.(5分)下列说法正确的个数()①三角形的三条高所在直线交于一点;②一个角的补角比这个角的余角大90°;③垂直于同一条直线的两条直线互相垂直;④两直线相交,同位角相等;⑤面积相等的两个正方形是全等图形;⑥已知两边及一角不能唯一作出三角形.A.1个B.2个C.3个D.4个4.(5分)下列选项中表示两个全等图形的是()A.形状相同的两个图形B.能够完全重合的两个图形C.面积相等的两个图形D.周长相等的两个图形5.(5分)如图,已知方格纸中是4个相同的正方形,则∠1+∠2+∠3的度数为()A.90°B.105°C.120°D.135°二、填空题(本大题共5小题,共25.0分)6.(5分)如图为6个边长相等的正方形的组合图形,则∠1﹣∠2+∠3=.7.(5分)如图,在3×3的正方形网格中标出了∠1和∠2,则∠1+∠2=.8.(5分)在如图所示的3×3的正方形网格中,∠1+∠2+∠3的度数为.9.(5分)如图,已知方格纸中是4个相同的正方形,则∠1与∠2的和为.10.(5分)在如图所示的3×3正方形网格中,∠1+∠2+∠3=°.三、解答题(本大题共5小题,共50.0分)11.(10分)如图,某校有一块正方形花坛,现要把它分成4块全等的部分,分别种植四种不同品种的花卉,图中给出了一种设计方案,请你再给出四种不同的设计方案.12.(10分)如图为人民公园中的荷花池,现在测量荷花池两旁A、B两棵大树间的距离(不得直接量得).请你根据图形全等的知识,用一根足够长的绳子及标杆为工具,设计两种不同的测量方案.要求:(1)画出设计的测量示意图;(2)写出测量方案及理由.13.(10分)沿着图中的虚线,用四种不同的方法将下面的图形分成两个全等的图形14.(10分)如图所示,请你在图中画两条直线,把这个“+”图案分成四个全等的图形(要求至少要画出两种方法).15.(10分)试在下列图中,沿正方形的网格线(虚线)把这两个图形分别割成两个全等的图形《图形的全等》拔高练习参考答案与试题解析一、选择题(本大题共5小题,共25.0分)1.(5分)如图所示的图形是全等图形的是()A.B.C.D.【分析】根据能够完全重合的两个图形叫做全等形可得答案.【解答】解:如图所示的图形是全等图形的是B,故选:B.【点评】此题主要考查了全等图形,关键是掌握全等形的定义.2.(5分)下列说法正确的是()A.所有的等边三角形都是全等三角形B.全等三角形是指面积相等的三角形C.周长相等的三角形是全等三角形D.全等三角形是指形状相同大小相等的三角形【分析】直接利用全等图形的定义与性质分析得出答案.【解答】解:A、所有的等边三角形都是全等三角形,错误;B、全等三角形是指面积相等的三角形,错误;C、周长相等的三角形是全等三角形,错误;D、全等三角形是指形状相同大小相等的三角形,正确.故选:D.【点评】此题主要考查了全等图形的性质与判定,正确利用全等图形的性质得出是解题关键.3.(5分)下列说法正确的个数()①三角形的三条高所在直线交于一点;②一个角的补角比这个角的余角大90°;③垂直于同一条直线的两条直线互相垂直;④两直线相交,同位角相等;⑤面积相等的两个正方形是全等图形;⑥已知两边及一角不能唯一作出三角形.A.1个B.2个C.3个D.4个【分析】根据全等图形、三角形的高、互补、垂直以及平行线的性质进行判断即可.【解答】解:①三角形的三条高交于同一点,所以此选项说法正确;②设这个角为α,则这个角的补角表示为180°﹣α,这个角的余角表示为90°﹣α,(180°﹣α)﹣(90°﹣α)=90°,∴一个角的补角比这个角的余角大90°,此选项正确;③垂直于同一条直线的两条直线互相平行,所以此选项不正确;④两直线平行,同位角相等,所以此选项说法不正确;⑤面积相等的两个正方形是全等图形,此选项正确;⑥已知两边及一角不能唯一作出三角形,此选项正确.故选:D.【点评】此题考查全等图形、三角形的高以及平行线的性质等知识,关键是根据全等图形、三角形的高、互补、垂直以及平行线的性质进行判断.4.(5分)下列选项中表示两个全等图形的是()A.形状相同的两个图形B.能够完全重合的两个图形C.面积相等的两个图形D.周长相等的两个图形【分析】直接利用全等图形的定义分析得出答案.【解答】解:A、形状相同的两个图形,不一定是全等图形,故此选项错误;B、能够完全重合的两个图形,一定是全等图形,故此选项正确;C、面积相等的两个图形,不一定是全等图形,故此选项错误;D、周长相等的两个图形,不一定是全等图形,故此选项错误;故选:B.【点评】此题主要考查了全等图形,正确把握全等图形的定义是解题关键.5.(5分)如图,已知方格纸中是4个相同的正方形,则∠1+∠2+∠3的度数为()A.90°B.105°C.120°D.135°【分析】根据对称性可得∠1+∠3=90°,∠2=45°.【解答】解:观察图形可知,∠1所在的三角形与∠3所在的三角形全等,∴∠1+∠3=90°,又∠2=45°,∴∠1+∠2+∠3=135°,故选:D.【点评】主要考查了正方形的性质和全等三角形的判定.充分利用正方形的特殊性质来找到全等的条件从而判定全等后利用全等三角形的性质解题.二、填空题(本大题共5小题,共25.0分)6.(5分)如图为6个边长相等的正方形的组合图形,则∠1﹣∠2+∠3=45°.【分析】观察图形可知∠1与∠3互余,∠2是直角的一半,利用这些关系可解此题.【解答】解:观察图形可知:△ABC≌△BDE,∴∠1=∠DBE,又∵∠DBE+∠3=90°,∴∠1+∠3=90°.∵∠2=45°,∴∠1﹣∠2+∠3=90°﹣45°=45°.故答案为:45°.【点评】此题综合考查角平分线以及全等图形,要注意∠1与∠3互余,∠2是直角的一半,特别是观察图形的能力.7.(5分)如图,在3×3的正方形网格中标出了∠1和∠2,则∠1+∠2=45°.【分析】根据题意,作出合适的辅助线,然后根据勾股定理的逆定理即可解答本题.【解答】解:如右图所示,作CD∥AB,连接DE,则∠2=∠3,设每个小正方形的边长为a,则CD=,DE=a,CE=a,∵CD2+DE2==10a2=CE2,CD=DE,∴△CDE是等腰直角三角形,∠CDE=90°,∴∠DCE=45°,∴∠3+∠1=45°,∴∠1+∠2=45°,故答案为:45°.【点评】本题考查全等图形,解答本题的关键是明确题意,作出合适的辅助线,利用数形结合的思想解答.8.(5分)在如图所示的3×3的正方形网格中,∠1+∠2+∠3的度数为135°.【分析】首先证明△ABC≌△AEF,然后证明∠1+∠2=90°,再根据等腰直角三角形的性质可得∠3=45°,进而可得答案.【解答】解:∵在△ABC和△AEF中,,∴△ABC≌△AEF(SAS),∴∠4=∠2,∵∠1+∠4=90°,∴∠1+∠2=90°,∵AE=DE,∠AED=90°,∴∠3=45°,∴∠1+∠2+∠3=135°,故答案为:135°【点评】此题主要考查了全等三角形的判定和性质,以及等腰直角三角形的性质,关键是掌握全等三角形对应角相等.9.(5分)如图,已知方格纸中是4个相同的正方形,则∠1与∠2的和为90°.【分析】首先证明△ABC≌△AED,根据全等三角形的性质可得∠1=∠AED,再根据余角的定义可得∠AED+∠2=90°,再根据等量代换可得∠1与∠2的和为90°.【解答】解:∵在△ABC和△AED中,∴△ABC≌△AED(SAS),∴∠1=∠AED,∵∠AED+∠2=90°,∴∠1+∠2=90°,故答案为:90°.【点评】此题主要考查了全等图形,关键是掌握全等三角形的判定和性质.10.(5分)在如图所示的3×3正方形网格中,∠1+∠2+∠3=135°.【分析】根据图形判断出∠1、∠3是全等直角三角形的两个互余的锐角,∠2为等腰直角三角形的锐角,然后求解即可.【解答】解:如图,在△ABC和△EGA中,,∴△ABC≌△EGA(SAS),∴∠3=∠BAC,在Rt△ABC中,∠BAC+∠1=90°,∴∠1+∠3=90°,由图可知,△ABD是等腰直角三角形,∴∠2=45°,∴∠1+∠2+∠3=90°+45°=135°.故答案为:135.【点评】本题考查了全等图形,等腰直角三角形的性质,准确识图判断出全等三角形是解题的关键.三、解答题(本大题共5小题,共50.0分)11.(10分)如图,某校有一块正方形花坛,现要把它分成4块全等的部分,分别种植四种不同品种的花卉,图中给出了一种设计方案,请你再给出四种不同的设计方案.【分析】根据正方形的性质,①两条对角线把正方形分成四个全等的三角形;②作一组对边的平行线也能把正方形分成四个全等的矩形;③连接一组对边的中点,把正方形分成两个全等的矩形,再作矩形的对角线就把每个矩形都分成两个全等的三角形,这样就分成了四个全等的三角形;④过正方形的中心做互相垂直的两条线也能把正方形分成四个全等的四边形.【解答】解:设计方案如下:【点评】本题主要考查了全等图形的意义,要利用正方形及全等形的性质解答,方案多种多样,只要是满足要求就可以.12.(10分)如图为人民公园中的荷花池,现在测量荷花池两旁A、B两棵大树间的距离(不得直接量得).请你根据图形全等的知识,用一根足够长的绳子及标杆为工具,设计两种不同的测量方案.要求:(1)画出设计的测量示意图;(2)写出测量方案及理由.【分析】(1)本题属于主观性试题,有多种方案,我们可以构造8字形的全等三角形来测得揽月湖的长度(如下图);(2)根据三角形全等的证明得出对应边相等即可得出答案.【解答】解:(1)如图所示;分别以点A、点B为端点,作AQ、BP,使其相交于点C,使得CP=CB,CQ=CA,连接PQ,测得PQ即可得出AB的长度.(2)理由:由上面可知:PC=BC,QC=AC,又∠PCQ=∠BCA,∴在△PCQ与△BCA中,,∴△PCQ≌△BCA(SAS),∴AB=PQ.【点评】此题考查了全等三角形的应用与证明;此题带有一定主观性,学生要根据已知知识对新问题进行探索和对基础知识进行巩固,这种做法较常见,要熟练掌握.13.(10分)沿着图中的虚线,用四种不同的方法将下面的图形分成两个全等的图形【分析】直接利用图形形状分成全等的两部分即可.【解答】解:如图所示:.【点评】此题主要考查了全等图形,正确把握全等图形的定义是解题关键.14.(10分)如图所示,请你在图中画两条直线,把这个“+”图案分成四个全等的图形(要求至少要画出两种方法).【分析】根据能够完全重合的两个图形叫做全等形画线即可.【解答】解:如图所示:.【点评】此题主要考查了全等图形,关键是掌握全等图形的概念.15.(10分)试在下列图中,沿正方形的网格线(虚线)把这两个图形分别割成两个全等的图形【分析】根据全等形的定义,利用图形的对称性和互补性来分隔成两个全等的图形.【解答】解:如图所示:【点评】本题主要考查了学生的动手操作能力和学生的空间想象能力,重视知识的发生过程,让学生体验学习的过程.。
最新七年级数学下册拔高题

三角形、多边形拔高题一、填空题1、三角形三个内角的比为1:3:5,则最大的内角是_____度2、两根木棒的长分别为cm 3和cm 5,要选择第三根木棒,将它钉成一个三角形,若第三根木棒的长为偶数,则第三根木棒的长是._____cm3、若一个多边形的每一个内角都等于0135,则这个多边形是____边形,它的内角和等于____.二、选择题1、三角形三条高的交点一定在( )A 、三角形的内部B 、三角形的外部C 、三角形的内部或外部.D 、三角形的内部、外部或顶点 2、适合条件C B A ∠=∠=∠21的∆ABC 是( ) A 、锐角三角形 B 、直角三角形 C 、钝角三角形 D 、不能确定 3、直角三角形两锐角的角平分线相交所成的角的度数是( ) A 、045 B 、0135 C 、045或0135 D 、不能确定三、解答题1、已知∆ABC 中,A ∠比2B ∠大040,B ∠比2C ∠少010,求各角的度数.2、如图,090⋅=∠+∠+∠+∠+∠+∠n F E D C B A ,求n ;3、如图,在六边形ABCDEF 中,AF//CD ,AB//DE ,且0080120=∠=∠B A ,,求C ∠ 和D ∠的度数4、已知∆ABC 的三边长分别为c b a ,,,且05|2|2=-++-+)(c b a c b 求b 的取值范围.二元一次方程组拔高题一、填空题1、已知24x y -=,则142______x y -+=.2、若3321m nm n mxny -+-=是关于x 、y 的二元一次方程组,则______mn=. 3、消去方程组235342x ty t=-⎧⎨=+⎩中的t ,得___________.4、当m =_______时,方程组2448x my x y +=⎧⎨+=⎩的解是正整数.5、某学生在n 次考试中,其考试成绩满足条件:如果最后一次考试得97分,则平均为90分,如果最后一次考试得73分,则平均分为87分,则n =_______.6、某商品售价a 元,利润为成本的20%,若把利润提高到30%,售价应提高到_______元.二、选择题1、已知方程组2342x y ax by -=⎧⎨+=⎩与3564x y bx ay -=⎧⎨+=-⎩有相同的解,则a 、b 的值为( )A .21a b =-⎧⎨=⎩B .12a b =⎧⎨=-⎩C .12a b =⎧⎨=⎩D .12a b =-⎧⎨=-⎩2、若方程组()213431kx k y x y +-=⎧⎪⎨+=⎪⎩的解x 和y 互为相反数,则k 的值为( )A .2B .-2C .3D .-33、如果关于x y 、的方程组24x y mx y m +=⎧⎨-=⎩的解是二元一次方程3+214x y =的一个解,那么m 的值( )A .1B .-1C .2D .-24、6年前,A 的年龄是B 的3倍,现在A 的年龄是B 的2倍,A 现在年龄是( ) A .12 B .18 C .24 D .30三、解答题(1)5341134x y x yx y x y +-⎧-=⎪⎪⎨+-⎪+=⎪⎩(2)3221456x y x y x y ++-+==2、某车间有甲、乙两种硫酸的溶液,浓度分别为90%和70%,现将两种溶液混合配制成浓度为80%的硫酸溶液500千克,甲、乙两种溶液各需取多少克?数据的收集、整理与描述拔高题B 校50%20%25%5% 其他水粉画书法剪纸A 校28%22%40%10%其他水粉画书法剪纸1.根据下图提供的信息,甲的圆心角为1200,乙的圆心角为600,丙占30%,丁占20%。
七年级下册数学拔高试卷

一、选择题(每题5分,共25分)1. 下列各数中,属于有理数的是()A. √2B. πC. 0.1010010001...D. -32. 若方程2x-3=5的解为x=a,则a的值为()A. 2B. 3C. 4D. 53. 已知一个正方形的边长为2cm,那么它的面积是()A. 2cm²B. 4cm²C. 8cm²D. 16cm²4. 若等腰三角形的底边长为5cm,腰长为8cm,那么这个三角形的周长是()A. 18cmB. 20cmC. 22cmD. 24cm5. 在平面直角坐标系中,点A(2,3)关于原点对称的点B的坐标是()A.(2,3)B.(-2,-3)C.(-2,3)D.(2,-3)二、填空题(每题5分,共25分)6. 若a、b是相反数,且|a|=3,则a+b=______。
7. 已知x²-5x+6=0,则x=______。
8. 一个圆的半径扩大2倍,那么它的面积扩大______倍。
9. 若一个等边三角形的边长为6cm,那么它的周长是______cm。
10. 在平面直角坐标系中,点P(-3,4)关于x轴的对称点Q的坐标是______。
三、解答题(每题15分,共45分)11. 解下列方程:(1)3x-2=5(2)2(x-3)=612. 某班有男生x人,女生y人,且x+y=30。
若男生人数是女生人数的1.5倍,求男生和女生的人数。
13. 已知一个等腰直角三角形的斜边长为10cm,求这个三角形的面积。
四、拓展题(每题20分,共40分)14. 已知数列{an}的通项公式为an=3n-2,求:(1)数列{an}的前n项和Sn;(2)数列{an}的递推公式。
15. 在平面直角坐标系中,点A(2,3)和点B(-4,5)之间的距离为多少?请写出解题过程。
七年级数学下学期综合拔高练习及答案

七年级数学下学期综练习一、选择题。
1.如图,在数轴上有M ,N ,P ,Q 四点,其中某一点表示无理数2,这个点是( )A .MB .NC .PD .Q 2.下列实数中:36,11,1.414,225,39,π,无理数有( )A .2个B .3个C .4个D .5个3.若点P 在第二象限,且点P 到x 轴的距离为3,到y 轴的距离为2,则点P 的坐标为( ) A .(-3,2) B .(-2,3) C .(3,-2) D .(2,-3) 4.下列说法不正确的是( )A.⎝⎛⎭⎫-142的平方根是±14 B .-5是25的一个平方根C .0.9的算术平方根是0.3 D.3-27=-35.如图,直线a ,b 被直线c 所截,下列条件中,不能判断直线a ,b 平行的是( ) A .∠2=∠3 B .∠1=∠4 C .∠1+∠3=180° D .∠1+∠4=180°6.如图,直线AB ∥CD ,∠C =44°,∠E 为直角,则∠1等于( ) A .132° B .134° C .136° D .138° 7.已知点E (x 0,y 0),F (x 2,y 2),点M (x 1,y 1)是线段EF 的中点,则x 1=x 0+x 22,y 1=y 0+y 22.在平面直角坐标系中有三个点A (1,-1),B (-1,-1),C (0,1),点P (0,2)关于A 的对称点为P 1(即P ,A ,P 1三点共线,且P A =P 1A ),P 1关于B 的对称点为P 2,P 2关于C 的对称点为P 3,按此规律继续以A ,B ,C 为对称点重复前面的操作,依次得到P 4,P 5,P 6,…,则点P 2015的坐标是( )A .(0,0)B .(0,2)C .(2,-4)D .(-4,2)8.若m ,n 满足(m -1)2+n -15=0,则m +n 的平方根是( ) A .±4 B .±2 C .4 D .29.下列命题中:①立方根等于它本身的数有-1,0,1;②负数没有立方根;③36=2;④任何正数都有两个立方根,且它们互为相反数;⑤平方根等于它本身的数有0和1.真命题的个数有( )A .1个B .2个C .3个D .4个10. 若32-a =-3b -3 ,则b -a +3的平方根( ). A. ±1 B. 2±C. 3±D. ±2二、填空题。
人教版七年级数学下册《平移》拔高练习

《平移》拔高练习一、选择题(本大题共5小题,共25.0分)1.(5分)如图,点/为△ABC角平分线交点,AB=8, AC=6, BC=4,将NAC8平移使其顶点C与/重合,则图中阴影部分的周长为()A. 9B. 8C. 6 D, 42.(5分)如图,将△ABC沿8c边上的中线AO平移到△A5C的位置,已知△ABC的面积为18,阴影部分三角形的面积为8.若A4= 1,则A'D等于()A. 3B. 2C. 32D. 233.(5分)某酒店打算在一段楼梯面上铺上宽为2米的地毯,台阶的侧面如图所示,如果这种地毯每平方米售价为80元,则购买这种地毯至少需要()A. 2560 元B. 2620 元C. 2720 元D. 2840 元4.(5分)下列四组图形都含有两个可以重合的三角形,其中可以通过平移其中一个三角形得到另一个三角形的是()B.5.(5分)如图,将△然,沿着由点B到点C的方向平移到已知AB = 7,BC=6, EC=4,那么平移的距离为()二、填空题(本大题共5小题,共25.0分)6.(5分)如图,把沿着BC的方向平移到的位置,它们要登部分的面积是△ABC面积的一半,若BC=,5,则△A8C移动的距离是.7.(5分)如图,图中是重叠的两个直角三角形.现将其中一个直角三角形沿8c方向平移得到如果A8=9a〃,BE=4cm, DH=3cm,则图中阴影部分面积为cm2.8.(5分)如图,将周长为18。
〃的△48C沿8c平移得到△£)£立平移后,如果四边形的周长是21C/H,那么平移的距离是cm.9.(5分)如图,已知N/=70° ,将直线〃,平行移动到直线〃的位置,则N2・10.( 5分)如图,将△A8E向右平移得到△。
尸,如果△相£的周长是12a〃,那么四边形的周长是cm.三、解答题(本大题共5小题,共50.0分)11.(10分)如图,在平面直角坐标系中,△A8C三个顶点的坐标分别为4 (-1,- 2), 5(-2, -4), C ( - 4, - 1).(1)把△48C向上平移4个单位后得到△4BG,请画出△48C1并写出点明的坐标;(2)已知点4与点Th(3, 2)关于直线/成轴对称,请画出直线/及△48C关于直线I对称的并直接写出直线/的函数表达式.12. (10分)如图,三角形ABO 中,A ( -2,-3)、8(2,-1),三角形A'8’O'是三角形A8O 平移之后得到的图形,并且。
七年级下拔高题

七年级下拔高题1、甲乙两人相距6km,若两人同时出发,同向而行,则用3h可追上乙;相向而行,1h相遇。
问:甲、方两人的平均速度各是多少?(请用二元一次方程组解答)2、若关于x、y的方程组x+y=2k,2x-y=4k的解也是方程x-y=2的解,则k的值是多少?3、用白铁皮做盒子,每张铁皮可生产12个盒身或18个盒盖。
现有49张铁皮,怎样安排生产盒身和盒盖的铁皮张数,才使生产的盒身与盒盖配套?(一张铁皮只能生产一种产品,一个盒身配两个盒盖)4、在解方程组ax+by=2、cx-3y=5时,小许正确的解x=1、y=2。
小陈因抄错了c,因此解得的解为x=-3,y=1。
求方程组中的a、b、c的值。
1、某商场计划购买电视机,已知该厂家生产3种不同型号的电视,出厂价分别:甲种每台1500元,乙种每台2100元,丙重每台2500元(1)商场同时购进其中两种不同型号的电视机共50台,用去90000元,请你研究一下商场的进货方案。
(2)以知商场销售一台甲种电视机可获利150元,销售一台乙种电视机可获利200元,销售一台丙种电视机可获利250元,在(1)的方案中,为使销售时获利最多,你选择哪种进货方案?2、某化工厂2006年12月在制定2007年某种化工用品的生产计划时,提供了下列数据:A生产该产品的工人人数不能超过200人B每个工人全年工作时数约2100工时C预计2007年该产品至少可以销售80000袋D每生产1袋化肥需要4工时E每袋需要原料20千克F现在库存原料800吨,本月还需200吨,2007年可以补充1200吨试根据上述数据确定2007年该产品的生产计划。
3、某化肥厂在甲、乙两仓库分别有化肥120t和60t,现要将全部化肥运往李村和张村,其中李村100t,张村80t,每次必须运10t,已知从甲仓库每运10t到李村和张村的运费分别为40元和80元;从乙仓库每运10t到李村和张村的运费分别为30元和50元。
(1)设从乙仓库运往李村化肥为xt,设计一个表格,反映题目所涉及到的调运数量与运费之间的关系(2)若让总运费不超过900元,则有几种调运方安?。
人教版七年级数学下《不等式及其解集》拔高练习

《不等式及其解集》拔高练习一、选择题(本大题共5小题,共25.0分)1.(5分)不等式组的解集在数轴上表示正确的是()A.B.C.D.2.(5分)如图,数轴上表示的是某不等式组的解集,那么这个不等式组可能是()A.B.C.D.3.(5分)据天气预报2018年4月12日大田县的最高气温是32℃,最低气温是21℃,则当天大田县气温t(℃)的变化范围是()A.t>21B.t<32C.21<t<32D.21≤t≤32 4.(5分)若不等式组的解为x<m,则m的取值范围为()A.m≤1B.m=1C.m≥1D.m<15.(5分)若关于x的不等式mx+1>0的解集是x<,则关于x的不等式(m ﹣1)x>﹣1﹣m的解集是()A.x B.x C.x D.x二、填空题(本大题共5小题,共25.0分)6.(5分)已知关于x的不等式(5a﹣2b)x>3b﹣a的解集是x<,则6ax>7b 的解集是.7.(5分)不等式组的解集是3<x<a+2,若a是整数,则a等于.8.(5分)若关于x的不等式(2m﹣n)x+3m﹣4n<0的解集是x>,则关于x 的不等式(m﹣4n)x+2m﹣3n<0的解集是.9.(5分)若不等式组没有解,则m的取值范围是.10.(5分)已知不等式式组无解,则a的取值范围为.三、解答题(本大题共5小题,共50.0分)11.(10分)定义新运算:对于任意有理数a,b,都有a*b=b(a﹣b)﹣b,等式右边是通常的加法、减法及乘法运算,例如:2*5=5×(2﹣5)﹣5=﹣20.(1)求2*(﹣5)的值;(2)若x*(﹣2)的值大于﹣6且小于9,求x的取值范围,并在如图所示的所画的数轴上表示出来.12.(10分)在数轴上表示下列不等式(1)x<﹣1(2)﹣2<x≤3.13.(10分)在数轴上表示下列不等式:(1)x>2(2)﹣2<x≤1.14.(10分)已知不等式≤.(1)求该不等式的解集;(2)该不等式的所有负整数解的和是关于y的方程2y﹣3a=6的解,求a的值.15.(10分)已知关于x的不等式≤的解是x≥,求m的值.《不等式及其解集》拔高练习参考答案与试题解析一、选择题(本大题共5小题,共25.0分)1.(5分)不等式组的解集在数轴上表示正确的是()A.B.C.D.【分析】把不等式的解集表示在数轴上即可.【解答】解:由得不等式组的解集是2<x≤4,在数轴上表示为:故选:C.【点评】把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.2.(5分)如图,数轴上表示的是某不等式组的解集,那么这个不等式组可能是()A.B.C.D.【分析】根据不等式组解集的确定方法:大小小大中间找,可得答案.【解答】解:由数轴上表示的不等式组的解集,得﹣2<x≤3.故选:B.【点评】本题考查了在数轴上表示不等式的解集,不等式的解集,不等式组解集的确定方法:同大取大,同小取小,大小小大中间找,大大小小无处找.3.(5分)据天气预报2018年4月12日大田县的最高气温是32℃,最低气温是21℃,则当天大田县气温t(℃)的变化范围是()A.t>21B.t<32C.21<t<32D.21≤t≤32【分析】直接利用不等式的定义分析得出答案.【解答】解:∵据天气预报2018年4月12日大田县的最高气温是32℃,最低气温是21℃,∴当天大田县气温t(℃)的变化范围是:21≤t≤32.故选:D.【点评】此题主要考查了不等式的定义,正确理解不等式的意义是解题关键.4.(5分)若不等式组的解为x<m,则m的取值范围为()A.m≤1B.m=1C.m≥1D.m<1【分析】先解不等式,然后根据解集为x<m,可得结论.【解答】解:,∵不等式组的解集为x<m,∴m≤1.故选:A.【点评】本题考查了解一元一次不等式组,要遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.5.(5分)若关于x的不等式mx+1>0的解集是x<,则关于x的不等式(m﹣1)x>﹣1﹣m的解集是()A.x B.x C.x D.x【分析】根据不等式mx+1>0的解集,得出m的值,再代入不等式(m﹣1)x >﹣1﹣m中,求解即可.【解答】解:∵关于x的不等式mx+1>0的解集是x<,∴m=﹣5,把m=﹣5代入(m﹣1)x>﹣1﹣m得4x>﹣6,解得x<﹣,故选:A.【点评】本题考查了不等式的解集,掌握不等式的解法是解题的关键.二、填空题(本大题共5小题,共25.0分)6.(5分)已知关于x的不等式(5a﹣2b)x>3b﹣a的解集是x<,则6ax>7b 的解集是x<.【分析】根据不等式的解集,先确定5a﹣2b与0、a与b的关系,代入不等式并求出不等式的解集.【解答】解:∵(5a﹣2b)x>3b﹣a的解集是x<,∴5a﹣2b<0∴x<∴=即24b﹣8a=5a﹣2b∴a=2b当a=2b时,∵5a﹣2b<0即8b<0,∴b<0当a=2b时,不等式6ax>7b可变形为:12bx>7b∴x<故答案为:x<.【点评】本题考查了不等式的解法和不等式的解集.题目难度较大.根据解集确定5a﹣2b<0、a=2b、b<0时解决本题的关键.7.(5分)不等式组的解集是3<x<a+2,若a是整数,则a等于2或3.【分析】根据已知不等式组和不等式组的解集得出关于a的不等式组,求出不等式组的解集即可.【解答】解:∵不等式组的解集是3<x<a+2,∴,解得:1<a≤3,∵a为整数,∴a=2或3,故答案为:2或3.【点评】本题考查了解一元一次不等式组和不等式组的解集,能根据题意得出关于a的不等式组是解此题的关键.8.(5分)若关于x的不等式(2m﹣n)x+3m﹣4n<0的解集是x>,则关于x 的不等式(m﹣4n)x+2m﹣3n<0的解集是x<﹣.【分析】先根据已知不等式的解集得出x>,且2m﹣n<0,=,求出m<0,n<0,在代入求出不等式的解集即可.【解答】解:∵不等式(2m﹣n)x+3m﹣4n<0的解集为x>,∴解不等式(2m﹣n)x+3m﹣4n<0得:x>,且2m﹣n<0,∴=,即n=m,2m﹣m<0,解得:m<0,n<0,∵(m﹣4n)x+2m﹣3n<0,∴(m﹣m)x<﹣2m+m,﹣mx<m,x<﹣,即不等式(m﹣4n)x+2m﹣3n>0的解集是x<﹣,故答案为:x<﹣.【点评】本题考查了一元一次不等式组和解一元一次不等式的应用,解此题的关键是能根据不等式的解集求出m、n的取值范围,题目比较好,难度适中.9.(5分)若不等式组没有解,则m的取值范围是m≥2.【分析】利用不等式组取解集的方法判断即可求出m的范围.【解答】解:∵不等式组没有解,∴m﹣1≥1,解得m≥2.故答案为:m≥2.【点评】此题考查了不等式的解集,熟练掌握不等式取解集的方法是解本题的关键.10.(5分)已知不等式式组无解,则a的取值范围为a≤2.【分析】根据不等式组的解集大大小小无解了,可得答案.【解答】解:∵不等式式组无解,∴a﹣1≤1,解得:a≤2,故答案为:a≤2.【点评】本题考查了不等式的解集,利用了确定不等式的解集的方法.三、解答题(本大题共5小题,共50.0分)11.(10分)定义新运算:对于任意有理数a,b,都有a*b=b(a﹣b)﹣b,等式右边是通常的加法、减法及乘法运算,例如:2*5=5×(2﹣5)﹣5=﹣20.(1)求2*(﹣5)的值;(2)若x*(﹣2)的值大于﹣6且小于9,求x的取值范围,并在如图所示的所画的数轴上表示出来.【分析】(1)根据新定义列式计算可得;(2)根据新定义得出x*(﹣2)=﹣2x﹣2,由“x*(﹣2)的值大于﹣6且小于9”列出关于x的不等式组,解之可得.【解答】解:(1)2*(﹣5)=﹣5×[2﹣(﹣5)]﹣(﹣5)=﹣5×(2+5)+5=﹣35+5=﹣30;(2)x*(﹣2)=﹣2×(x+2)+2=﹣2x﹣4+2=﹣2x﹣2,由题意可得,解得:﹣5.5<x<2,不等式组的解集在数轴上表示为:【点评】本题考查了一元一次不等式组的解法,正确理解运算的定义是关键.12.(10分)在数轴上表示下列不等式(1)x<﹣1(2)﹣2<x≤3.【分析】(1)根据不等式的解集在数轴上表示方法可画出图示.(2)根据不等式的解集在数轴上表示方法可画出图示.【解答】解:(1)将x<﹣1表示在数轴上如下:(2)将不等式组﹣2<x≤3表示在数轴上如下:【点评】本题主要考查在数轴上表示不等式的解集,不等式的解集在数轴上表示出来的方法:“>”空心圆点向右画折线,“≥”实心圆点向右画折线,“<”空心圆点向左画折线,“≤”实心圆点向左画折线.13.(10分)在数轴上表示下列不等式:(1)x>2(2)﹣2<x≤1.【分析】根据不等式的解集在数轴上表示方法可画出图示.【解答】解:(1)将x>2表示在数轴上如下:(2)将﹣2<x≤1表示在数轴上如下:【点评】此题考查了在数轴上表示不等式的解集,把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.14.(10分)已知不等式≤.(1)求该不等式的解集;(2)该不等式的所有负整数解的和是关于y的方程2y﹣3a=6的解,求a的值.【分析】(1)首先去分母,然后去括号、移项、合并同类项,最后把x的系数化为1即可;(2)首先根据不等式的解集确定不等式的解,然后可得y的值,然后再代入即可得到a的值.【解答】解:(1)去分母得:2(2x﹣1)≤9x+8,去括号得:4x﹣2≤9x+8,移项得:4x﹣9x≤8+2,合并同类项得:﹣5x≤10,系数化为1得:x≥﹣2;(2)∵x≥﹣2,∴不等式的所有负整数解为﹣2,﹣1,y=﹣2+(﹣1)=﹣3,把y=﹣3代入2y﹣3a=6得:﹣6﹣3a=6,解得:a=﹣4.【点评】此题主要考查了解不等式,以及一元一次不等式的解,关键是正确确定不等式的解集.15.(10分)已知关于x的不等式≤的解是x≥,求m的值.【分析】不等式组整理后表示出解集,根据已知解集确定出m的值即可.【解答】解:原不等式可化为:4m+2x≤12mx﹣3,即(12m﹣2)x≥4m+3,又因原不等式的解为x≥,则12m﹣2>0,m>,比较得:=,即24m+18=12m﹣2,解得:m=﹣(舍去).故m无值.【点评】此题考查了不等式的解集,熟练掌握运算法则是解本题的关键.。
七年级下册数学试卷拔高

一、选择题(每题4分,共20分)1. 已知二次函数y=ax^2+bx+c的图象开口向上,且a>0,若其对称轴方程为x=-2,且函数在x=1时的值为0,则下列哪个选项可能是该函数的解析式?A. y=x^2-4x+3B. y=x^2+4x+3C. y=x^2-4x-3D. y=x^2+4x-32. 在直角坐标系中,点A(-1,2),点B(2,-1),点C在x轴上,且△ABC为等腰直角三角形,则点C的坐标是()。
A. (1,0)B. (-1,0)C. (-2,0)D. (2,0)3. 若等比数列{an}的前三项分别为a,ar,ar^2,且a+ar+ar^2=12,a^2+ar^2=48,则该数列的公比r是()。
A. 2B. 3C. 4D. 64. 已知函数y=2x-3,若函数y=kx+b与y=2x-3的图象在第二象限内有两个交点,则k和b的取值范围是()。
A. k>0,b>0B. k>0,b<0C. k<0,b>0D. k<0,b<05. 在等边三角形ABC中,点D在BC边上,且AD=BD,若∠ADB=30°,则∠ABC的度数是()。
A. 30°B. 45°C. 60°D. 90°二、填空题(每题5分,共25分)6. 已知一元二次方程x^2-4x+3=0的两个根分别为m和n,则m+n=______,mn=______。
7. 在直角坐标系中,点P(2,3),点Q在y轴上,且PQ=5,则点Q的坐标是______。
8. 若等差数列{an}的前三项分别为3,5,7,则该数列的公差是______。
9. 函数y=3x^2-12x+9在x=______时取得最小值。
10. 在等腰三角形ABC中,若底边AB=8,腰AC=10,则顶角A的度数是______。
三、解答题(共55分)11. (10分)已知一元二次方程x^2-4x+3=0,求:(1)该方程的两个根;(2)若函数y=ax^2+bx+c(a≠0)的图象开口向上,且该函数的图象与x轴有两个交点,这两个交点恰为上述方程的两个根,求a、b、c的值。
七年级数学下册拔高题

三角形、多边形拔高题一、填空题1、三角形三个内角的比为1:3:5,则最大的内角是_____度2、两根木棒的长分别为cm 3和cm 5,要选择第三根木棒,将它钉成一个三角形,若第三根木棒的长为偶数,则第三根木棒的长是._____cm3、若一个多边形的每一个内角都等于0135,则这个多边形是____边形,它的内角和等于____.二、选择题1、三角形三条高的交点一定在( )A 、三角形的内部B 、三角形的外部C 、三角形的内部或外部.D 、三角形的内部、外部或顶点 2、适合条件C B A ∠=∠=∠21的∆ABC 是( ) A 、锐角三角形 B 、直角三角形 C 、钝角三角形 D 、不能确定 3、直角三角形两锐角的角平分线相交所成的角的度数是( ) A 、045 B 、0135 C 、045或0135 D 、不能确定三、解答题1、已知∆ABC 中,A ∠比2B ∠大040,B ∠比2C ∠少010,求各角的度数.2、如图,090⋅=∠+∠+∠+∠+∠+∠n F E D C B A ,求n ;3、如图,在六边形ABCDEF 中,AF//CD ,AB//DE ,且0080120=∠=∠B A ,,求C ∠ 和D ∠的度数4、已知∆ABC 的三边长分别为c b a ,,,且05|2|2=-++-+)(c b a c b 求b 的取值范围.二元一次方程组拔高题一、填空题1、已知24x y -=,则142______x y -+=.2、若3321m n m n mx ny -+-=是关于x 、y 的二元一次方程组,则______mn=. 3、消去方程组235342x ty t=-⎧⎨=+⎩中的t ,得___________.4、当m =_______时,方程组2448x my x y +=⎧⎨+=⎩的解是正整数.5、某学生在n 次考试中,其考试成绩满足条件:如果最后一次考试得97分,则平均为90分,如果最后一次考试得73分,则平均分为87分,则n =_______.6、某商品售价a 元,利润为成本的20%,若把利润提高到30%,售价应提高到_______元.二、选择题1、已知方程组2342x y ax by -=⎧⎨+=⎩与3564x y bx ay -=⎧⎨+=-⎩有相同的解,则a 、b 的值为( )A .21a b =-⎧⎨=⎩B .12a b =⎧⎨=-⎩C .12a b =⎧⎨=⎩D .12a b =-⎧⎨=-⎩2、若方程组()213431kx k y x y +-=⎧⎪⎨+=⎪⎩的解x 和y 互为相反数,则k 的值为( )A .2B .-2C .3D .-33、如果关于x y 、的方程组24x y mx y m +=⎧⎨-=⎩的解是二元一次方程3+214x y =的一个解,那么m 的值( )A .1B .-1C .2D .-24、6年前,A 的年龄是B 的3倍,现在A 的年龄是B 的2倍,A 现在年龄是( ) A .12 B .18 C .24 D .30三、解答题(1)5341134x y x yx y x y +-⎧-=⎪⎪⎨+-⎪+=⎪⎩ (2)3221456x y x y x y ++-+==2、某车间有甲、乙两种硫酸的溶液,浓度分别为90%和70%,现将两种溶液混合配制成浓度为80%的硫酸溶液500千克,甲、乙两种溶液各需取多少克?B 校50%20%25%5% 其他水粉画书法剪纸A 校28%22%40%10%其他水粉画书法剪纸数据的收集、整理与描述拔高题1.根据下图提供的信息,甲的圆心角为1200,乙的圆心角为600,丙占30%,丁占20%。
七年级下拔高试题精编

1有理数的运算(1)1、 计算: ⑴533031232325.031141185348--++-- ⑵32534.14315175.05.2⨯⎪⎭⎫ ⎝⎛-⨯÷⎪⎭⎫ ⎝⎛-⨯⎪⎭⎫ ⎝⎛-⨯÷- ⑶51413121---⑷35217106253121147642321⨯⨯+⨯⨯+⨯⨯⨯⨯+⨯⨯+⨯⨯⑸1263842421729348622431⨯⨯+⨯⨯+⨯⨯⨯⨯+⨯⨯+⨯⨯ ⑹12816413211618141211+++++++⑺201032313131311+++++⑻5121171617815413211+++++⑼201054321++++++ ⑽2010200987654321-++-+-+-+-⑾2010200987654321+++--++--+ ⑿201020091431321211⨯++⨯+⨯+⨯⒀201120091751531311⨯++⨯+⨯+⨯ ⒁7218561742163015201412136121+++++++⒂7217561542133011209127311+-+-+-+ ⒃20332231223213111++++++++⒄20343221241224312114111++++++++++⒅ ⎪⎭⎫ ⎝⎛+++++⎪⎭⎫ ⎝⎛+++⎪⎭⎫ ⎝⎛++98979839816563614341212、2010减去它的21,再减去余下的31,再减去余下的41,……,依次类推,一直到减去余下的20101,那么最后剩下的数是多少?3、2010加上它的21得到一个数,再加上所得数的31,又得到一个数,再加上这次得数的41又得到一个数,……,依次类推,一直加到上一次得数的20101,那么最后得到的数是多少?4、小明进行珠算练习时,用 +++++54321,当加到某个数时和是1000,在验算时发现重复加了一个数,求这个数?2 数轴1、 在数轴上表示数 a 的点到原点的距离为5,则 3 – a =2、 数轴上有两点A 、B ,如果点 A 对应的数是 – 5,且A 、B 两点的距离为4,则点B 对应的数是3、 有理数a 、b 、c 在数轴上的位置如图所示,则化简=----+-+c c a b b a 11第5题第4题第3题DC B A10c b aA B4、 如图:在工作流水线上,A 、B 、C 、D 处各有1名工人,且AB=BC=CD=2 ,现在工作流水线上放一个工具箱,使4个工人到工具箱的距离之和最短,则工具箱应放的位置为5、 如图:数轴上标出若干个点,每相邻两点相距1个单位,点A 、B 、C 、D 对应的数分别是整数a 、b 、c 、d , 且d -2a = 10 ,那么数轴的原点应是 点6、 如图:数轴上有6个点 ,且AB=BC=CD=DE=EF ,则点E 表示的数最接近的整数是第6题13- 4A BCD7、 在数轴上,点 A 、B 分别表示21-和61 ,则线段AB 的中点所表示的数是8、 数轴上有两点A 、B ,如果点 A 与原点的距离为3,且A 、B 两点的距离为4,则满足条件的点B 与原点的距离的和 9、3 绝对值1、b a --9 有最 值,其值为2、 3++b a 有最 值,其值为3、若033=-+-x x , 则 x 的取值范围为4、若()()01=+-x x x , 则 x 的取值范围为5、若a a -= ,则=---a a 216、若2- x ,则=+-x 117、若3- x ,则=+-+x 1238、若03=+b a ,则=-+-21ab b a9、若0 abc ,0=++c b a ,则=+++++cb a ba c ac b10、若0≠abc ,则cc b b a a ++= ;=+++abcabc cc bb aa11、若5=x ,3=y ,且x y y x -=- ,则()=++yx y x12、计算:=-++-+-1212008120091200912010113、若b a b a -=+ ,则=ab 14、若 b a b a +=-,则a 、b 应满足的关系是 15、若a 、b 、c 分别是一个三位数的百位、十位、个位上的数字, 且c b a ≥≥ ,则a c c b b a -+-+-取得的最大值为16、若 9≤-b a ,16≤-d c ,且25=+--d c b a ,则=---c d a b 17、若1-x 与2+y 互为相反数,化简()=+2010y x18、求满足 1=+-ab b a 的非负整数对()b a ,19、若 a 、b 、c 为整数,且1201019=-+-ac b a 求a c c b b a -+-+-20若0201021201021=-+-+-x x x 求20102009432222222x x x x x x+-----4 用字母表示数1、已知 n 为正整数,则“任意正奇数”为2、表示 a 与 b 的差的平方的代数式是3、5个连续的奇数中,第一个数为 a ,最后一个数为 b ,则中间一个数用 a、b 的代数式表示为4、两个数的和为 m ,其中一个因数为2 ,则另一个因数为5、一个三位数的百位、十位个位上的数字分别为1、a 、b ,则这个三位数为6、一件工作甲做 a 天完成,乙做 b 天完成,则两人合做天完成7、某人从甲到乙的速度为 a km/h ,从乙到甲的速度为 b km/h ,则此人来回的平均速度为8、甲、乙、丙、丁四个数的平均数为 a ,甲、乙、丁的平均数为 b ,则丙数为9、一次考试,按成绩排名,前10名的平均数为 a ,前8名的平均数为 b ,第9名一比第10多 c分,则第10名的成绩为分11、把一个两位数的个位数字与十位数字交换后得到一个新数,它与原来的两位数的和恰好是某个自然数的平方,则这个自然数的平方为12、若 m+n 人完成一项工程需要 m天,则 n个人完成这项工程需要天13、求三位数与其数字之和的比值的最大值和最小值5 整式的运算1、代数式x ba xy y z xy xy x ,2,2,51,4,16222-++-+-+中,不是整式的有 个2、化简 222222323321b a ab b a ab b a --+-+并按字母 a 的降幂排列为3、若 832+-y xba 的y x yb a -324 和是单项式,则=+y x4、12-n x b a 与m b a 223- 是同类项 ,则()=-xn m 25、单项式 c b y x 25.0 与单项式 121125.0---n m y x 的和是 m n y ax 625.0,则 =abc6、若0=++c b a ,则()()()=++++abc a c c b b a7、若5,3,2=--=-=-d c c b b a ,则 ()()()=-÷--d a d b c a 8、已知3=+-ba b a ,则()()()=+---+b a b a ba b a 3429、若0223=---x x x ,则=-+-+122234x x x x 10、若0132=+++x x x ,则=+++++2010321x x x x 11、若 012=-+m m ,则 =-+2010223m m12、已知多项式137+++cx bx ax 当2-=x 时,值为2010,则当2=x 时,这个多项式的值为 13、已知等式 ()()()111122+++++=++x c x b x ax x x 是关于 x 的恒等式,则a= ,b= ,c= 14、如果 1322-+x x 与()()c x b x a +-+-112是同一个多项式,则cb a +=15、已知()0122101011111212621a x a x a xa xa xa x x ++++++=+-则=++++12210a a a a , =++++12321a a a a ,=++++12420a a a a ,=-++-+-129101112a a a a a a16、同时都含有字母 a 、b 、c ,且系数为1 的6次单项式共有 个17、若a 、b 、 c 、d 是整数, b 是正整数,且满足 a d c d c b c b a =+=+=+,, ,则d c b a +++ 的最大值是18、已知0=+++d c b a ,则()()()()()()=+++++++++++333333d c d a d b c b c a b a19、已知等式()()121222=--+-+z kk y k x k 与k 值无关,则=x ;=y ;=z6 一元一次方程1、解下列方程: ⑴ 103.02.017.07.0=--xx ⑵16110312=+-+x x⑶03433221=-+++++x x x ⑷2362132432⎪⎭⎫ ⎝⎛+--=+--x x x x x⑸ 0533321212121=-⎭⎬⎫⎩⎨⎧-⎥⎦⎤⎢⎣⎡-⎪⎭⎫⎝⎛-x ⑹526513121=⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛---x x x x⑺200920102009433221=⨯++⨯+⨯+⨯x x x x ⑻()20102009111216121=+++++n n2、解下列关于x 的方程:⑴ x ax +=1 ⑵ ()()m x n x m +=+413⑶ ()132-=-x x k ⑷ ()()111-=+-k x k k ⑸3=--+--+--bac x acb x cba x ⑹cb a x ba c x ac b x cb a x ++=+-++-++-33、8=x 是方程a x x 2433+=- 的解,又是方程 ()[]b x b x x x +=⎥⎦⎤⎢⎣⎡---913131的解,求 b4、小张在解方程1523=-x a (x 为未知数)时,误将 - 2x 看成 2x 得到的解为3=x ,请你求出原来方程的解5、已知关于x 的方程 ()1233+=-x a x 无解,求 a6、已知关于x 的方程()x x k 2124=-+ 无解,求 k7、已知关于x 的方程()0232=+++b ax x b a 有唯一的解,求这个方程的解8、已知关于x 的方程()()b x a x a 3512+-=- 无穷多解,求 a 、b9、已知关于x 的方程 ()()x n x m 121232+=-+无穷多解,求m 、n10、已知关于 x 的方程b x ax -=+23有两个不同的解,求()2010b a +11、已知关于 x 的方程 ()31562-+=+m x x x m 至少有两个解,求 m12、不论k 为何值时,1-=x 总是关于x 的方程1322=--+bkx a kx 的解,求a 、b13、不论 k 为何值时,1=x 总是关于x 的方程6232bk x a kx -+=+ 的解,求a 、b14、关于 x 的方程52-=-x k kx 的解为整数,求整数k15、关于 x 的方程()()11433--=-x m x m 的解为正整数,求整数m16、关于x 的方程 ()x x k 5165-=+-的解为整数,求正整数k17、关于 x 的方程1439+=-kx x 的解为整数,求整数k18、关于x 的方程14285225+=-x a x 有一个正整数解,求最小正整数a19、已知:关于x 的方程()183-=-b x b a 仅有正整数解,并且和关于x 的方程()183-=-a x a b 是同解方程,若 0,022≠+≥b a a ,求这个方程的解7 一次方程的应用(1)1、飞机从甲地飞往乙地,飞机的速度为180km/h ,当飞过路程的一半又120 km后,改为160km/h 的速度飞完全程,所用时间以200 飞完全程所用时间多1小时,求两地距离2、一游泳者沿河逆游而上,在A 处将携带的漂浮物品遗失,在继续游了 20分钟后,发现物品遗失,立即返回顺游,在距 A处2 千米的 B处追到遗失的物品,问水速3、一客轮逆流行驶,船上一乘客掉了一件物品浮在水面上,等到乘客发现后,轮船立即掉头去追所掉的物品,已知轮船从掉头到追上这件物品用了5分钟,问乘客是几分钟后发现所掉的物品的?4、甲骑车从A 到B ,乙骑车从B 到A ,甲每小时比乙多走2千米,两人在上午8点同时出发,到上午10点两人还相距36千米,到中午12点两人又相距36千米,求 A、B两地的距离5、甲地某厂共有80人,现全体员工到40千米处的乙地去,但该厂只有一部可乘40人的汽车,若汽车每小时行36千米,人步行每小时5千米,为了尽快到达乙地,可以让40人现步行,40人乘车,汽车开出一段后让车上的人下车步行,让车掉头来接先步行的人开往乙地,若这些人同时到达乙地,问每人乘车多少千米?6、甲、乙两列客车的长分别为150米和200米,他们相向行驶在平行的轨道上,已知甲车上某乘客测得乙车在他的窗口外经过的时间是10秒,那么乙车上的乘客看见甲车在他的窗口外经过的时间是多少?7、铁路旁的一条平行小路上有一行人与一骑车人同时向东行使,行人速度为 3.6km/h ,骑车人速度为10.8km/h ,如果有一列火车从他们背后开过来,它通过行人用了22秒,通过骑车人用了26秒,问这列火车的车身长为多少米?8、某出租汽车停车站已停有10辆出租车。
七年级下册数学期末拔高试题

七年级下册数学期末拔高试题1. 某家电商场经销A 、B 、C 三种品牌的彩电,5月份共获利48000元,已知A 种品牌的彩电每台可获利100元,B 种品牌的彩电每台可获利144元,C 种品牌的彩电每台可获利360元,请你根据相关信息补全彩电销售台数的条形图和所获利润的百分数的扇形图。
2. 5月12日我国四川汶川县发生里氏级大地震,地震给四川,甘肃,陕西等地造成巨大人员伤亡和财产损失.灾难发生后,某校师生和全国人民一道,迅速伸出支援的双手,为灾区人民捐款捐物.为了支援灾区学校灾后重建,该校决定象灾区捐助床架60个,课桌凳100套.现计划租甲、乙两种货车共8辆将这些物质运往灾区,已知一辆甲货车可装床架5个和课桌凳20套, 一辆乙货车可装床架10个和课桌凳10套.(1)学校如何安排甲、乙两种货车可一次性把这些物资运到灾区有几种方案(2)若甲种货车每辆要付运输费1200元,乙种货车要付运输费1000元,则学校应选择哪种方案,使运输费最少最少运费是多少3. 开学初,小芳和小亮去学校商店购买学习用品,小芳用18元买了一支钢笔和3本笔记本;小亮用31元购买了同样的钢笔2支和笔记本5本.(1)求每支钢笔和每本笔记本的价格;(2)校运会后,班主任拿出200元学校奖励基金交给班长,购买上述价格的钢笔和笔记本共48件作为奖品,奖给校运会中表现突出的同学,要求笔记本数不少于钢笔数,共有多少种购买方案?请你一一写出来.4. 某市公园的门票价格如下表所示: 购票人数1~50人 51~100人 100人以上 票价 10元/人 8元/人5元/人 50多人而乙班不足50人,如果以班为单位购买门票,一共要付920元;如果两个班一起购买门票,一共要付515元.问甲、乙两班分别有多少人?5. 在平面直角坐标系中,设坐标的单位长度为1cm ,整数点P 从原点O 出发,速度为1cm/s ,且点P 只能向上或向右运动,请回答下列问题:P 从O 点出发时间可得到整数点的坐标 可得到整数点的个数 1秒(0,1)、(1,0) 22秒3秒个;(3)当点P 从O 出发________________秒时,可得到整数点(10,5)6. 已知1∠的度数是它补角的3倍,2∠等于45o,那么AB CD ∥吗?为什么? 7. 如图,AB ∥CD ,BN 、DN 分别平分∠ABM 、∠MDC ,试问∠BMD 与∠BND 之 间的数量关系如何?证明你的结论。
初一下数学拔高题

1、三角形的三个外角中,钝角最多有( )。
A :1个 B: 2个 C:3 个 D : 4 个2、直角三角形两锐角的平分线相交所成的钝角是( )。
A :120°B : 135° C:150° D: 165°3、如图所示,在△ABC 中,CD 、BE 分别是AB 、AC 边上的高,并且CD 、BE 交于,点P,若∠A=500 ,则 ∠BPC 等于( )A 、90°B 、130°C 、270°D 、315°4、一个多边形的每一个外角都等于30°,这个多边形的边数是 ,它的内角和是5、如图所示,若∠A =32°,∠B =45°,∠C =38°,则∠DFE 等于( ) A 。
120° B。
115° C。
110° D。
105°6、已知等腰三角形的两边长分别为4cm 和7cm , 它的周长是_________㎝.7、等腰三角形一腰上的中线将这个等腰三角形的周长分成15和6两部分,则这个等腰三角形的三边长是_________________.8、若过m 边形的一个顶点有7条对角线,n 边形没有对角线,k 边形有k 条对角线,求(m -k )n 的值__________。
9、如图,已知∠BOF=120°,则∠A+∠B+∠C+∠D+∠E+∠F=___10、下列正多边形中,与正三角形同时使用能进行镶嵌的是 ( )A.正十二边形 B 。
正十边形 C 。
正八边形 D.正五边形11、如图:小明从A 点出发前进10m ,向右转150,,再前进10m ,右转150……这样一直走下去,他第一次回到出发点A 时,一共走了____m 。
12、过多边形的一个顶点的所有对角线把多边形分成8个三角形,这个多边形的边数是( ) A 、8 B 、9 C 、10 D 、1113、n 边形的每个外角都为24°,则边数n 为( )A 、13B 、14C 、15D 、16(第3题)F E D C B A14、在△ABC 中,若∠C =2(∠A +∠B ),则∠C = 度。
七年级数学下册拔高试卷

1. 若a,b是实数,且a^2 + b^2 = 1,则(a+b)^2的最大值为()A. 2B. 1C. 0D. 32. 在等差数列{an}中,若a1 = 3,公差d = 2,则第10项an =()A. 17B. 18C. 19D. 203. 已知一次函数y = kx + b(k≠0)的图象经过点A(1,3)和B(2,5),则k 的值为()A. 1B. 2C. 3D. 44. 在△ABC中,∠A = 45°,∠B = 60°,则∠C的度数为()A. 45°B. 60°C. 75°D. 90°5. 已知一元二次方程x^2 - 3x + 2 = 0,则它的两个根为()A. 1,2B. 2,1C. 1,-2D. -2,16. 已知一元二次方程x^2 - 4x + 3 = 0的解为x1,x2,则(x1 + x2)^2的值为()A. 7B. 8C. 9D. 107. 在平面直角坐标系中,点P(2,3)关于直线y = x的对称点为()A.(3,2)B.(2,3)C.(-3,-2)D.(-2,-3)8. 已知一次函数y = kx + b(k≠0)的图象与x轴、y轴分别交于点A、B,若OA = 2,OB = 3,则k的值为()A. 3/2B. 2/3C. 3D. 29. 在△ABC中,∠A = 90°,∠B = 30°,则BC的长度为()A. √3B. 2C. 2√3D. 310. 已知一元二次方程x^2 - 2x - 3 = 0的解为x1,x2,则x1^2 + x2^2的值为()A. 5B. 6C. 7D. 811. 若等差数列{an}的首项为a1,公差为d,则第n项an = ________。
12. 已知一次函数y = kx + b(k≠0)的图象与x轴、y轴分别交于点A、B,若OA = 2,OB = 3,则k的值为 ________。
人教版七年级数学下《立方根》拔高练习

《立方根》拔高练习一、选择题(本大题共5小题,共25.0分)1.(5分)下列运算正确的是()A.=±2B.=3+4C.=﹣3D.=2.(5分)下列说法正确的是()A.9的立方根是3B.算术平方根等于它本身的数一定是1C.﹣2是4的平方根D.的算术平方根是23.(5分)下列各式正确的是()A.B.C.D.4.(5分)下列计算正确的是()A.=±3B.=﹣3C.=﹣2D.+=5.(5分)下列各式正确的是()A.(﹣3)2=6B.C.﹣14=﹣1D.二、填空题(本大题共5小题,共25.0分)6.(5分)144的平方根是,﹣125的立方根是.7.(5分)49的平方根是,的立方根是﹣4.8.(5分)若x+17的立方根是3,则3x﹣5的平方根是.9.(5分)化简:±=,=,=.10.(5分)一个正方体,它的体积是棱长为2cm的正方体的体积的8倍,则这个正方体的棱长是cm.三、解答题(本大题共5小题,共50.0分)11.(10分)已知|a|=5,b2=4,c3=﹣8.(1)若a<b,求a+b的值;(2)若abc>0,求a﹣3b﹣2c的值.12.(10分)解方程(1)4(x+1)2﹣289=0(2)8x3﹣125=013.(10分)求下列各式中x的值:①(x+2)2=4;②3+(x﹣1)3=﹣5.14.(10分)已知3a+21的立方根是3,4a﹣b﹣1的算术平方根是2.(1)a的值;(2)求3a+10b的平方根.15.(10分)求下列各式中的x(1)4x2﹣9=0;(2)(2x+1)3=﹣8.《立方根》拔高练习参考答案与试题解析一、选择题(本大题共5小题,共25.0分)1.(5分)下列运算正确的是()A.=±2B.=3+4C.=﹣3D.=【分析】根据立方根和算术平方根的定义逐一判断即可得.【解答】解:A.=2,此选项错误;B.=5≠3+4,此选项错误;C.=﹣3,此选项正确;D.+≠,此选项错误;故选:C.【点评】本题主要考查立方根与算术平方根,解题的关键是掌握立方根和算术平方根的定义.2.(5分)下列说法正确的是()A.9的立方根是3B.算术平方根等于它本身的数一定是1C.﹣2是4的平方根D.的算术平方根是2【分析】根据立方根和算术平方根及平方根的定义逐一判断可得.【解答】解:A.27的立方根是3,此选项错误;B.算术平方根等于它本身的数是1和0,此选项错误;C.﹣2是4的平方根,此选项正确;D.即2的算术平方根,此选项错误;故选:C.【点评】本题主要考查立方根与平方根及算术平方根,解题的关键是掌握立方根和平方根、算术平方根的定义.3.(5分)下列各式正确的是()A.B.C.D.【分析】根据平方根、算术平方根与立方根的定义逐一计算可得答案.【解答】解:A.±=±1,此选项错误;B.=2,此选项错误;C.=6,此选项错误;D.=﹣3,此选项正确;故选:D.【点评】本题主要考查立方根,解题的关键是掌握平方根、算术平方根与立方根的定义.4.(5分)下列计算正确的是()A.=±3B.=﹣3C.=﹣2D.+=【分析】根据算术平方根和立方根的定义逐一判断可得.【解答】解:A.=3,此选项错误;B.=3,此选项错误;C.=﹣2,此选项正确;D.与不是同类二次根式,不能合并,此选项错误;故选:C.【点评】本题主要考查立方根和算术平方根,解题的关键是掌握立方根和算术平方根的定义与性质.5.(5分)下列各式正确的是()A.(﹣3)2=6B.C.﹣14=﹣1D.【分析】根据有理数的乘方,立方根的定义,算术平方根的定义逐一计算即可得.【解答】解:A.(﹣3)2=9,此选项错误;B.=2,此选项错误;C.﹣14=﹣1,此选项正确;D.=3,此选项错误;故选:C.【点评】本题主要考查立方根、算术平方根,解题的关键是掌握立方根和算术平方根的定义及有理数乘方的运算法则.二、填空题(本大题共5小题,共25.0分)6.(5分)144的平方根是±12,﹣125的立方根是﹣5.【分析】根据平方根和立方根的概念求解.【解答】解:∵(±12)2=144,(﹣5)3=﹣125,∴144的平方根是±12,﹣125的立方根是﹣5,故答案为:±12,﹣5.【点评】本题考查了立方根和平方根的知识,解答本题的关键是掌握立方根和平方根的概念.7.(5分)49的平方根是±7,﹣64的立方根是﹣4.【分析】根据平方根和立方根的定义可得.【解答】解:49的平方根是±7,﹣64的立方根是﹣4,故答案为:±7,﹣64.【点评】本题考查了平方根和立方根,关键是能熟练掌握立方根和平方根的定义.8.(5分)若x+17的立方根是3,则3x﹣5的平方根是±5.【分析】直接利用立方根的定义得出x的值,再利用平方根的定义计算即可.【解答】解:∵x+17的立方根是3,∴x+17=27,解得:x=10,则3x﹣5=25的平方根是:±5.故答案为:±5.【点评】此题主要考查了立方根和平方根,正确得出x的值是解题关键.9.(5分)化简:±=±,=﹣4,=5.【分析】根据平方根、立方根和二次根式的性质逐一计算可得.【解答】解:±=±,=﹣4,=5,故答案为:±,﹣4,5.【点评】本题考查了平方根、立方根的定义.如果一个数的平方等于a,这个数就叫做a的平方根,也叫做a的二次方根.如果一个数x的立方等于a,那么这个数x就叫做a的立方根.10.(5分)一个正方体,它的体积是棱长为2cm的正方体的体积的8倍,则这个正方体的棱长是4cm.【分析】直接利用已知得出立方体的体积,进而利用立方根的定义得出答案.【解答】解:棱长为2cm的正方体的体积为:2×2×2=8(cm3),∵一个正方体,它的体积是棱长为2cm的正方体的体积的8倍,∴这个正方体的棱长的体积为:8×8=64(cm3),∴这个正方体的棱长是4cm.故答案为:4.【点评】此题主要考查了立方根,正确把握定义是解题关键.三、解答题(本大题共5小题,共50.0分)11.(10分)已知|a|=5,b2=4,c3=﹣8.(1)若a<b,求a+b的值;(2)若abc>0,求a﹣3b﹣2c的值.【分析】(1)利用绝对值的定义求出a的值,利用平方根的定义求出b的值,利用立方根的定义求c的值,代入即可求出a+b的值;(2)根据ab小于0,得到ab异号,求出a与b的值,代入所求式子中计算即可求出值.【解答】解:(1)∵|a|=5,b2=4,c3=﹣8.∴a=±5,b=±2,c=﹣2,∵a<b,∴a=﹣5,b=±2,∴a+b=﹣5+2=﹣3或a+b=﹣5﹣2=﹣7,即a+b的值为﹣3或﹣7;(2)∵abc>0,c=﹣2,∴ab<0,∴a=5,b=﹣2 或a=﹣5,b=2,∴当a=5,b=﹣2,c=﹣2时,a﹣3b﹣2c=5﹣3×(﹣2)﹣2×(﹣2)=15,当a=﹣5,b=2,c=﹣2时,a﹣3b﹣2c=﹣5﹣3×2﹣2×(﹣2)=﹣7,∴a﹣3b﹣2c=15 或﹣7.【点评】本题考查了代数式求值,涉及的知识有:绝对值及平方根、立方根的定义,求出a与b的值是解本题的关键.12.(10分)解方程(1)4(x+1)2﹣289=0(2)8x3﹣125=0【分析】(1)先移项,再两边都除以4,继而两边开方即可得;(2)先移项,再两边都除以8,再开立方即可得.【解答】解:(1)∵4(x+1)2﹣289=0,∴4(x+1)2=289,∴(x+1)2=,则x+1=±,∴x1=,x2=﹣;(2)∵8x3﹣125=0,∴8x3=125,则x3=,∴x=.【点评】本题主要考查立方根与平方根,解题的关键是掌握立方根与平方根的定义.13.(10分)求下列各式中x的值:①(x+2)2=4;②3+(x﹣1)3=﹣5.【分析】①开方,即可得出两个一元一次方程,求出方程的解即可.②移项、合并后再开立方,即可得出一个一元一次方程,求出方程的解即可.【解答】解:①∵(x+2)2=4,∴x+2=±,即x+2=±2,解得:x1=0,x2=﹣4;②∵3+(x﹣1)3=﹣5,∴(x﹣1)3=﹣8,∴x﹣1=,即x﹣1=﹣2,则x=﹣1.【点评】本题考查了平方根和立方根的应用,关键是能根据平方根和立方根定义得出一元一次方程.14.(10分)已知3a+21的立方根是3,4a﹣b﹣1的算术平方根是2.(1)a的值2;(2)求3a+10b的平方根.【分析】(1)先依据平方根、立方根的定义列出关于a、b的方程,然后可求得a、b的值;(2)先将a,b的值代入计算3a+10b的值,再依据平方根的定义求解即可.【解答】解:(1)∵3a+21的立方根是3,4a﹣b﹣1的算术平方根是2,∴3a+21=27,4a﹣b﹣1=4,∴a=2,b=3,故答案为:2;(2)当a=2,b=3时,3a+10b=3×2+10×3=36,则3a+10b的平方根是±6.【点评】本题主要考查的是平方根、立方根的定义,熟练掌握相关概念是解题的关键.15.(10分)求下列各式中的x(1)4x2﹣9=0;(2)(2x+1)3=﹣8.【分析】(1)先将常数项移到等式右边,再将二次项系数化为1,继而根据平方根的定义求解可得;(2)先根据立方根的定义得到关于x的方程,解之即可得.【解答】解:(1)∵4x2﹣9=0,∴4x2=9,∴x2=,则x=±;(2)∵(2x+1)3=﹣8,∴2x+1=﹣2,则x=﹣.【点评】本题主要考查了利用立方根及平方根解方程,解题的关键是熟记开立方及开平方的定义.。
(精品word)初一下学期数学拔高训练

初一下学期数学拔高训练例题二元一次方程(组)【例1】已知方程组!赛+》尸八的解x, y满足方程5x-y=3,求k的值.如4尸丘+I[【思考与分析】本题有三种解法,前两种为一般解法,后一种为巧解法(1)由已知方程组消去k,得x与y的关系式,再与5x-y=3联立组成方程组求出x,y的值,最后将x, y的值代入方程组中任一方程即可求出k的值.(2)把k当做已知数,解方程组,再根据5x-y=3建立关于k的方程,便可求出k的值•(3)将方程组中的两个方程相加,得5x-y=2k+11 ,又知5x-y=3,所以整体代入即可求出k的值.2兀+3尸匕①3%-4y=k+l I.②5x^=3.③解法一:②得盂-7尸11*④③得M4y=-》2f解得尸-孝杷尸-等代入③,得弘十等=3, 解得絆存把•二:一■ = J代入①,得:厂_厂」:」,解得k=-4.解法二:① X 3—② X2,得17y=k-22 ,解得杷尸特代人①「得2沪3込骨)2 , 昨牛斗铲-杷和r=nr~代入③・得氐哼-_罟_ ◎解得z解法三:①+②,得5x-y=2k+11.又由5x-y=3,得2k+11=3,解得k=-4.【小结】 解题时我们要以一般解法为主,特殊方法虽然巧妙,但是不容易想到, 考巧妙解法的时间, 可能这道题我们已经用一般解法解了一半了, 当然,巧妙解法很容易想到的话,那就应该用巧妙解法了 •【例2】 某种商品价格为每件3 3元,某人身边只带有2元和5元两种面值的人民币 各若干张,买了一件这种商品•若无需找零钱,则付款方式有哪几种 (指付出2元和5元钱 的张数)?哪种付款方式付出的张数最少?【思考与分析】 本题我们可以运用方程思想将此问题转化为方程来求解 •我们先找出问题中的数量关系,再找出最主要的数量关系,构建等式 •然后找出已知量和未知量设元,列方程组求解•最后,比较各个解对应的 x+y 的值,即可知道哪种付款方式付出的张数最少• 解: 设付出2元钱的张数为 x ,付出5元钱的张数为 y ,则x,y 的取值均为自然数•依 题意可得方程:2x+5y=33.因为5y 个位上的数只可能是0或5,所以2x 个位上数应为3或8胱好尸斗尸①【例3】解方程组|N 订尸& ②【思考与分析】本例是一个含字母系数的方程组 •解含字母系数的方程组同解含字母系数的 方程一样,在方程两边同时乘以或除以字母表示的系数时, 也需要弄清字母的取值是否为零。
部编数学七年级下册【期末满分冲刺】综合能力拔高卷(轻松拿满分)(解析版)含答案

人教版七年级数学下册【期末满分冲刺】综合能力拔高卷(轻松拿满分)(考试时间:120分钟试卷满分:100分)学校:___________姓名:___________班级:___________考号:___________本卷试题共三大题,共25小题,单选10题,填空8题,解答7题,限时120分钟,满分100分,本卷题型精选核心常考重难易错典题,具备举一反三之效,覆盖面积广,可充分考查学生双基综合能力!一、单选题(本题共10个小题,每小题3分,共30分)1.点P(−4,3)在平面直角坐标系中所在的象限是()A.第一象限B.第二象限C.第三象限D.第四象限【答案】B【分析】根据点的坐标特征求解即可.【详解】解:点P(−4,3)的横坐标小于0,纵坐标大于0,∴点P(−4,3)所在的象限是第二象限,故选:B.【点睛】本题考查了各象限内点的坐标的符号特征,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).2.实数-5,0.3,3.1415926,227,1.010010001…(相邻两个1之间依次多一个0)中,无理数的个数是()A.1个B.2个C.3个D.4个【答案】B【分析】根据无理数的概念:无限不循环小数判断即可.【详解】解:实数-5,0.3,3.1415926,227,1.010010001…(相邻两个1之间依次多一个0)中,1.010010001…(相邻两个1之间依次多一个0),共2个.故选:B .【点睛】本题考查了无理数,算术平方根,掌握无理数的概念:无限不循环小数是解题的关0.8080080008…(每两个8之间依次多1个0)等形式.3.已知关于x 、y 的方程组21254x y k x y k +=-ìí+=+î的解满足x+y=5,则k 的值为( )A .52B .2C .3D .5【答案】B【分析】首先解方程组,利用k 表示出x 、y 的值,然后代入5x y +=,即可得到一个关于k 的方程,求得k 的值.【详解】解:21254x y k x y k +=-ìí+=+î①②,由´②2-①得399x k =+,解得33x k =+,把33x k =+代入①得3321k y k ++=-,解得2y k =--.5x y +=Q ,3325k k \---=,解得2k =.故选B .【点睛】本题主要考查了二元一次方程组解的定义,以及解二元一次方程组的基本方法.正确解关于x 、y 的方程组是关键.4.不等式组2561x x x £+ìí<î解集在数轴上表示正确的是( )A .B .C .D .【答案】A【分析】分别求出各不等式的解集,再求出其公共解集并在数轴上表示出来即可.【详解】解:2561x x x £+ìí<î由256x x £+解得,2x ³-,故此不等式组的解集为2<1x -£,把此不等式组的解集在数轴上表示为:故选:A .【点睛】本题考查的是解一元一次不等式组,在数轴上表示一元一次不等式组的解集,熟知实心圆点与空心圆点的区别是解答此题的关键.5.如图,已知AB ∥CD ,AF 交CD 于点E ,且BE ⊥AF ,∠BED =50°,则∠A 的度数是( )A .40°B .50°C .80°D .90°【答案】A【分析】本题根据垂直性质求解∠FED ,继而根据两直线平行,同位角相等求解本题.【详解】解:∵,50BE AF BED ^Ð=°,∴∠DEF=40°.又∵AB ∥CD ,∴∠A=∠DEF=40°.故选:A .【点睛】本题考查平行线的性质以及垂直性质,需注意两直线平行,同位角、内错角均相等,同旁内角互补.6.下列说法正确的是( )A 是分数B .16的平方根是4±4=±C .8.30万精确到百分位D ,则1a b =【答案】D 【分析】根据实数的分类、平方根的定义、近似数的定义、算术平方根的非负性逐一判断.【详解】解:A B 、16的平方根是4±,即C 、8.30万精确到百位,故该选项错误;D 、若,∴a=2022,b=-1,则2022(1)1a b =-=,故该选项正确;故选:D .【点睛】本题主要考查实数的有关定义与计算,熟练掌握实数的分类与大小比较及算术平方根、平方根的定义是关键.7.下图中,1Ð与2Ð是同位角的是( )A.B.C.D.【答案】A【分析】根据同位角的意义,结合图形进行判断即可.【详解】解:A.是同位角,故此选项符合题意,故A正确; B.不是同位角,故此选项不符合题意,故B错误; C.不是同位角,故此选项不符合题意,故C错误; D.不是同位角,故此选项不符合题意,故D错误.故选A.【点睛】本题考查同位角的意义,掌握同位角的意义是正确判断的前提.8.如图,围棋棋盘放在某平面直角坐标系内,已知黑棋(甲)的坐标为(﹣2,3),白棋(甲)的坐标为(2,3),则白棋(乙)的坐标为()A.(﹣1,1)B.(﹣2,1)C.(1,1)D.(﹣1,﹣1)【答案】A【分析】先利用黑棋(甲)的坐标为(−2,3),白棋(甲)的坐标为(2,3)画出直角坐标系,然后可写出白棋(乙)的坐标.【详解】解:如图,白棋(乙)的坐标为(−1,1).故选:A.【点睛】此题主要考查了坐标位置的确定,关键是正确确定原点位置.9.如图,将正方形ABCD的一角折叠,折痕为AE,点B落在点B′处,B ADТ比BAEÐ大48°.设BAEÐ和B ADТ的度数分别为x°和y°,那么x和y满足的方程组是( )A.4890y xy x-=ìí+=îB.482y xy x-=ìí=îC.48290x yy x-=ìí+=îD.48290y xy x-=ìí+=î【答案】D【分析】根据由将正方形ABCD的一角折叠,折痕为AE,∠B'AD比∠BAE大48°的等量关系即可列出方程组.【详解】解:.设BAEÐ和B ADТ的度数分别为x°和y°由题意可得:48290 y xy x-=ìí+=î故答案为D.【点睛】本题考查了二元一次方程组的应用,根据翻折变换的性质以及正方形的四个角都是直角寻找等量关系是解答本题的关键.10.2021年春节前夕,学校向2000名学生发出“减少空气污染,少放烟花爆竹”倡议书,并围绕“A类:不放烟花爆竹;B类:少放烟花爆竹;C类:使用电子鞭炮;D类:不会减少烟花爆竹数量”四个选项进行问卷调查(单选),并对100名学生的调查结果绘制成统计图(如图所示)根据抽样结果,估计全校“使用电子鞭炮”的学生有().A .200名B .400名C .600名D .750名【答案】B 【分析】用总人数2000乘以全校“使用电子鞭炮”的学生比例即可得到答案.【详解】解:100(303515)2000400100-++´=(名)故选:B .【点睛】此题考查条形统计图,利用样本中部分的比例求总体中该部分的人数,正确理解统计图是解题的关键.二、填空题(本题共8个小题,每题3分,共24分)11.计算:()23-=______ =______=______.【答案】 9 4 2【分析】负3的平方等于9,16的算术平方根等于4,8的立方根等于2.【详解】解:()239-=4=2=,故答案为:9;4;2.【点睛】本题考查乘方运算,开方运算,注意区分正数平方的相反数与负数的平方之间的区别.12.已知关于x ,y 的二元一次方程组21322x y m x y +=-ìí+=î的解满足x+y =0,则m 的值为__.【答案】1【分析】原方程组可化为:220x y x y +=ìí+=î,解出x 、y ,把y=2,x=-2代入2x+y=1-3m ,求出m .【详解】解:原方程组可化为:220x y x y +=ìí+=î①②,①-②得,y=2,把y=2,代入②得x=-2,把y=2,x=-2代入2x+y=1-3m ,得2×(-2)+2=1-3m ,解得m=1,故答案为:1.【点睛】本题考查了二元一次方程的解、二元一次方程组的解,掌握用加减消元法解二元一次方程组是解题关键.13.当m 的取值范围是______时,关于x 的方程11123x mx -+-=的解不大于11【答案】1m £或32m >【分析】先解方程,再根据解不大于11列出不等式求解即可;【详解】解:11123x mx -+-=,()()31216x mx --+=,33226x mx ---=,()3211m x -=,1132x m=-,根据320m -¹得到32m ¹,根据方程的解不大于11,∴321m -³或320m -<,解得:1m £或32m >;故答案是:1m £或32m >;【点睛】本题主要考查了解一元一次不等式,结合一元一次方程求解是解题的关键.14.关于x 的不等式组36023x x a --<ìí-<î的解集在数轴上如图表示,则a 的值为______.【答案】3【分析】先解不等式组的解集,再结合数轴得出解集得出关于a 的等式,进而得出答案.【详解】解:36023x x a --<ìí-<î①②,解不等式①得2x >-,解②得32a x +<,由数轴可知23x -<<,所以332a +=,解得a=3.故答案为:3.【点睛】此题主要考查了解一元一次不等式组,在数轴上表示不等式的解集,正确得出关于a 的等式是解题关键.15.如图,已知直线a b ∥,点B 是线段AE 的中点,2ABD S =V ,则ACE S =V ______.【答案】4【分析】先根据平行线间的距离可得ABD △的AB 边上的高等于ACE V 的AE 边上的高,再根据线段中点的定义可得2AE AB =,然后根据三角形的面积公式即可得.【详解】解:a b Q P ,ABD \V 的AB 边上的高等于ACE V 的AE 边上的高,Q 点B 是线段AE 的中点,2AE AB \=,2224ACE ABD S S \==´=V V ,故答案为:4.【点睛】本题考查了平行线间的距离、线段中点等知识点,掌握理解平行线间的距离是解题关键.16.在平面直角坐标系中,轰炸机机群的一个飞行队形如图所示,若其中两架轰炸机的坐标分别表示为A (1,3)、B (3,1),则轰炸机C 的坐标是_________.【答案】(1,2)--【分析】直接利用已知点坐标得出原点位置,进而得出答案.【详解】解:如图所示,建立平面直角坐标系,∴轰炸机C 的坐标为(-1,-2),故答案为:(-1,-2).【点睛】此题主要考查了坐标确定位置,正确得出原点位置建立坐标系是解题关键.17.商场购进A 、B 、C 三种商品各100件、112件、60 件,分别按照25%、40%、60%的利润进行标价,其中商品C 的标价为80元,为了促销,商场举行优惠活动:如果同时购买A 、B 商品各两件,就免费获赠三件C 商品.这个优惠活动实际上相当于这七件商品一起打了七五折.那么,商场购进这三种商品一共花了______元..【答案】31800【分析】先求出商品C 的进价为50元.再设商品A 、B 的进价分别为x 元,y 元,表示出商品A 的标价为54x ,商品B 的标价为75y 元,根据“如果同时购买A 、B 商品各两件,就免费获赠三件C 商品.这个优惠活动,实际上相当于把这五件商品各打七五折”列出方程,进而求出1001126050x y ++´的值.【详解】解:由题意,可得商品C 的进价为:80(160%)50¸+=(元).设商品A 、B 的进价分别为x 元,y 元,则商品A 的标价为5(125%)4x x +=(元),商品B 的标价为7(140%)5y y +=(元),由题意,得57572()[2()380]0.754545x y x y +=++´´,\5736045x y +=,5710011280()803602880045x y x y \+=+=´=,100112605031800x y \++´=(元).答:商场购进这三种商品一共花了31800元.故答案为:31800.【点睛】本题考查了二元一次方程的应用,设商品A 、B 的进价分别为x 元,y 元,分别表示出商品A 与商品B 的标价,找到等量关系列出方程是解题的关键.本题虽然设了两个未知数,但是题目只有一个等量关系,根据问题可知不需要求出x 与y 的具体值,这是本题的难点.18.某校图书管理员清理课外书籍时,将其中甲、乙、丙三类书籍的有关数据制成如图不完整的扇形统计图,已知乙类书有90本,则丙类书的本数是__________.【答案】135【分析】根据乙类书籍有90本,占总数的30%即可求得总书籍数,丙类所占的比例是1-25%-30%,所占的比例乘以总数即可求得丙类书的本数.【详解】解:总数是:90÷30%=300(本),丙类书的本数是:300×(1-25%-30%)=300×45%=135(本),故答案为:135.【点睛】本题考查了扇形统计图,从扇形图上可以清楚地看出各部分数量和总数量之间的关系,正确求得书籍总数是关键.三、解答题(本题共7个小题,19-23每题5分,24小题8分,25每题13分,共46分)19.计算:(1)516(8)345æö-´´´-ç÷èø(2)1133æö-¸´-ç÷èø(3)11632æö-´--ç÷èø(4)315606060777-´+´-´(515+(62|【答案】(1)4;(2)19;(3)5;(4)-60;(5)7;(6)8+【分析】(1)直接约分计算即可;(2)将除法转化为乘法,再约分计算;(3)利用乘法分配律展开计算;(4)利用乘法分配律合并计算;(5)先算开方,再算乘法,最后算加减;(6)先算开方,化简绝对值,再算加减.【详解】解:(1)516(8)345æö-´´´-ç÷èø=5168345´´´=4;(2)1133æö-¸´-ç÷èø=11133´´=19;(3)11632æö-´--ç÷èø=11632æö´+ç÷èø=116632´+´=23+=5;(4)315606060777-´+´-´=31560777æö´-+-ç÷èø=()601´-=-60;(515+=19355-+´=61+=7;(62|=732+=8+【点睛】本题考查了实数的混合运算,解题的关键是掌握运算法则和运算顺序.20.解下列方程或方程组:(1)4x-2 =2x+3 (2)13234x x+-= (3)2435x yx y-=ìí-=î【答案】(1)52x=;(2)4x=-;(3)13xy=-ìí=-î【分析】(1)移项、合并同类项、系数化1,即可求解;(2)去分母、去括号、移项、合并同类项、系数化1,即可求解;(3)利用加减消元法求解方程组即可.【详解】(1)解:4x-2=2x+3,移项,得4x-2x=3+2,合并同类项,得2x=5,系数化为1,得52x=;(2)解:x13―3x4=2去分母,得4(x+1)-9x=24,去括号,得4x+4-9x=24,移项,得4x-9x=24-4,合并同类项,得-5x=20,系数化为1,得x=-4;(3)解:2435x y x y -=ìí-=î①②②-①×3,得x=-1,把x=-1代入①,得-1-y=2,解得y=-3,故方程组的解为13-y x =ìíî=- .【点睛】本题考查一元一次方程及二元一次方程组的解法,解题的关键是熟知解题步骤.21.按要求完成下列各题.(1)解不等式组10,53 4.x x x -£ìí>-î(2)解不等式组322,357.33x x x x +>-ìï-í£-ïî并把它的解集在数轴上表示出来.【答案】(1)21x -<£;(2)24x -<£,数轴见解析【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小找不到确定不等式组的解集,第(2)题,再将不等式组的解集表示在数轴上.【详解】解:(1)10,53 4.x x x -£ìí>-î解不等式10x -£,解得1x £,解不等式534x x >-,解得2x >-,\不等式组的解集为:21x -<£;(2)322,357.33x x x x +>-ìï-í£-ïî解不等式322x x +>-,解得2x >-,解不等式35733xx-£-,解得4x£,\不等式组的解集为:24x-<£,不等式的解集表示在数轴上如图:.【点睛】本题考查了解一元一次不等式组,将不等式的解集表示在数轴上,掌握解不等式的方法以及数形结合是解题的关键.22.武汉新冠肺炎疫情发生后,全国人民众志成诚抗疫救灾.某公司筹集了抗疫物资120吨打算运往武汉疫区,现有甲、乙、两三种车型供运输选择,每辆车的运载能力和运费如下表所示: (假设每辆车均满载)车型甲乙丙运载量(吨/辆)5810运费(元/辆)450600700(1)全部物资一次性运送可用甲型车8辆,乙型车5辆,丙型车辆.(2)若全部物资仅用甲、乙两种车型一次性运完,需运费9600元,求甲、乙两种车型各需多少辆?(3)若该公司打算用甲、乙、丙三种车型同时参与运送,已知车辆总数为14辆,且一次性运完所有物资,你能分别求出三种车型的辆数吗?此时的总运费为多少元?【答案】(1)4;(2)甲种车型需8辆,乙种车型需10辆;(3)甲车2辆,乙车5辆,丙车7辆,此时的总运费为8800元.【分析】(1)根据甲型车运载量是5吨/辆,乙型车运载量是8吨/辆,丙型车运载量是10吨/辆,再根据总吨数,即可求出丙型车的车辆数;(2)设甲种车型需x 辆,乙种车型需y 辆,根据运费9600元,总吨数是120,列出方程组,再进行求解即可;(3)设甲车有a 辆,乙车有b 辆,则丙车有(14-a-b )辆,列出等式,再根据a 、b 、14-a-b 均为正整数,求出a ,b 的值,从而得出答案.【详解】解:(1)(120-5×8-5×8)÷10=4(辆).答:丙型车4辆.故答案为:4.(2)设甲种车型需x 辆,乙种车型需y 辆,根据题意得:581204506009600x y x y +=ìí+=î,解得:810x y =ìí=î.答:甲种车型需8辆,乙种车型需10辆.(3)设甲车有a 辆,乙车有b 辆,则丙车有(14-a-b )辆,由题意得5a+8b+10(14-a-b )=120,即a=412b -,∵a 、b 、14-a-b 均为正整数,∴b 只能等于5,∴a=2,14-a-b=7,∴甲车2辆,乙车5辆,丙车7辆,则需运费450×2+600×5+700×7=8800(元),答:甲车2辆,乙车5辆,丙车7辆,此时的总运费为8800元.【点睛】本题考查了二元一次方程组和二元一次方程的应用,将现实生活中的事件与数学思想联系起来,读懂题列出方程即可求解.利用整体思想和未知数的实际意义通过筛选法可得到未知数的具体解,这种方法要掌握.23.晋剧(山西梆子)是我国北方的一个重要戏剧剧种,也叫中路戏,是国家级非物质文化遗产.某校在传统文化活动周期间拟向同学们推介晋剧,并就“你想要听哪部晋剧曲目”调查了部分学生,选择曲目有:A.《打金枝》,B.《战宛城》,C.《杀宫》,D.《火焰驹》,E,《双锁山》,每个学生只能选择一部,根据统计结果绘制了如下不完整的统计图.请根据以上信息,解答下列问题:(1)请补全条形统计图;(2)在扇形统计图中,扇形A的圆心角是多少度?(3)若该校共有2000名学生,请你估计想听《战宛城》的学生有多少人?(4)要从这些被调查的学生中随机抽取一人进行访谈,那么正好抽到想听《火焰驹》的学生的概率是多少?【答案】(1)补图见解析;(2)54°;(3)500人;(4)1 5【分析】(1)根据E的特征,结合两种统计图求出总人数,进而求出B,D组对应的人数即可;(2)先求出A组所占的百分比,再乘以360°即可;(3)用2000乘以B组所占百分比即可;(4)根据概率=D组人数÷总人数即可解题.【详解】解:(1)补全条形统计图如解图;调查学生的总人数为2430%80¸=(人),选择B 的人数为8025%20´=(人),选择D 的人数为80122082416----=(人),据此补全条形统计图.(2)选择A 的人数所占百分比为12100%15%80´=,\扇形A 所对应扇形的圆心角度数为3601554%°°´=.(3)200025%500´=(人),\估计想听《战宛城》的学生有500人;(4)Q 共有80人,其中想听《火焰驹》的有16人,P \(正好抽到想听《火焰驹》的学生)161805==,\随机抽取一人正好抽到想听《火焰驹》的学生的概率是15【点睛】本题考查了统计与概率,用样本信息估计总体信息,属于简单题,找到两种统计图之间的信息关联是解题关键,主要失分原因是: ①找不到扇形统计图和条形统计图中的对应关系;②补全条形统计时作图不规范;③在计算概率时发生错误.24.对于平面直角坐标系xOy 中的图形G 和图形G 上的任意点P (x ,y ),给出如下定义:将点P (x ,y )平移到P'(x+t ,y ﹣t )称为将点P 进行“t 型平移”,点P'称为将点P 进行“t 型平移”的对应点;将图形G 上的所有点进行“t 型平移”称为将图形G 进行“t 型平移”.例如,将点P (x ,y )平移到P'(x+1,y ﹣1)称为将点P 进行“l 型平移”,将点P (x ,y )平移到P'(x ﹣1,y+1)称为将点P 进行“﹣l 型平移”.已知点A (2,1)和点B (4,1).(1)将点A (2,1)进行“l型平移”后的对应点A'的坐标为 .(2)①将线段AB进行“﹣l型平移”后得到线段A'B',点P1(1.5,2),P2(2,3),P3(3,0)中,在线段A′B′上的点是 .②若线段AB进行“t型平移”后与坐标轴有公共点,则t的取值范围是 .(3)已知点C (6,1),D (8,﹣1),点M是线段CD上的一个动点,将点B进行“t型平移”后得到的对应点为B',当t的取值范围是 时,B'M的最小值保持不变.【答案】(1)(3,0);(2)①P1;②42-££-t或1t=;(3)13t££【分析】(1)根据“l型平移”的定义解决问题即可.(2)①画出线段A1B1即可判断.②根据定义求出t 最大值,最小值即可判断.(3)如图2中,观察图象可知,当B′在线段B′B″上时,B'M的最小值保持不变,最小.【详解】解:(1)将点A (2,1)进行“l型平移”后的对应点A'的坐标为(3,0),故答案为:(3,0);(2)①如图1中,观察图象可知,将线段AB进行“﹣l型平移”后得到线段A'B',点P1(1.5,2),P2(2,3),P3(3,0)中,在线段A ′B ′上的点是P 1,故答案为:P 1;②若线段AB 进行“t 型平移”后与坐标轴有公共点,则t 的取值范围是﹣4≤t ≤﹣2或t=1.故答案为:﹣4≤t ≤﹣2或t=1.(3)如图2中,观察图象可知,当B ′在线段B ′B ″上时,B'M 的最小值保持不变,最小,此时1≤t ≤3.故答案为:1≤t ≤3.【点睛】本题属于几何变换综合题,考查了平移变换,“t 型平移”的定义等知识,解题的关键理解题意,灵活运用所学知识解决问题,学会利用图象法解决问题,属于中考创新题型.25.如图,在平面直角坐标系中,已知,点,,,,,满足()0,A a (),0B b ()0,C c a b c(1)直接写出点,,的坐标及的面积;(2)如图2,过点作直线,已知是上的一点,且,求的取值范围;(3)如图3,是线段上一点,①求,之间的关系;②点为点关于轴的对称点,已知,求点的坐标.【答案】(1),,,;(2)的取值范围为;(3)①;②【分析】(1)根据求出a 、b 、c 的值,由此求解即可;(2)分当点在直线上位于轴左侧时和当点在直线上位于轴右侧时讨论求解即可得到答案;(3)①由由得,,由此求解即可;②易得,连接,由得,,化简得,,然后联立求解即可.()28212a b -+-=A B C ABC V C //l AB (),D m n l 152ACD S £△n (),M x y AB x y N M y 21BCN S =△M ()0,8A ()6,0B ()0,2C -30ABC S =V n 40n -££4324x y +=()3,4M ()28212a b -+-=D l y D l y AOB AON BOM S S S =+V V V 1118668222x y ´+´=´´(),N x y -ON NBC CON OBC BON S S S S =++△△△△111226621222x y ´´+´´+´´=315x y +=4324315x y x y +=ìí+=î【详解】解:(1)∵∴,∴,,,∴,,,∴,,,∴AC=10,OB=6,∴;(2)当点在直线上位于轴左侧时,由题意得,,解得,,当时,,结合图形可知,当时,;同理可得,当点在直线上位于轴右侧时,,当时,,,解得,,()28212a b -+-=()282a b -+-80a -=2120b -=20c +=8a =6b =2c =-()0,8A ()6,0B ()0,2C -1302ABC S AC OB ==V g D l y ()()111510222ACD S AC m m =´´-=´´-£△32m ³-32m =-3,02D æö-ç÷èø32m ³-0n £D l y 32m £32m =3,2D n æöç÷èø12//,D D AB Q 22,ACD BCD S S \=V V ()()13113156262222222n n æö´+´--´´-´´--=ç÷èø4n =-结合图形可知,当时,,∴的取值范围为;(3)①由得,,化简得,;②易得,连接,由得,,化简得,,联立方程组,解得,∴32m £4n ³-n 40n -££AOB AOM BOM S S S =+V V V 1118668222x y ´+´=´´4324x y +=(),N x y -ON NBC CON OBC BON S S S S =++△△△△111226621222x y ´´+´´+´´=315x y +=4324315x y x y +=ìí+=î34x y =ìí=î()3,4M坐标与图形,截图的关键在于能够熟练掌握相关是进行求解.。
人教版七年级数学下册《垂线》拔高练习

《垂线》拔高练习一.选择题(本大题共5小题,共25.0分)1. (5分)如图,因为直线丄/于点B, BCAJ于点、B,所以直线佔和BC重合,则其中蕴含的数学原理是()AC11BA. 平面内,过一点有且只有一条直线与已知直线垂直B. 垂线段最短C. 过一点只能作一条垂线D. 两点确定一条直线2. (5分)已知线段CD,点M在线段结合图形,下列说法不正确CA・延长线段A3、CD.相交于点FB. 反向延长线段84、DC,相交于点FC. 过点M画线段A3的垂线,交CD于点ED. 过点M画线段CD的垂线,交CD于点E3. (5分)如图,已知直线AD、BE、CF相交于点O, OG丄AD,且ZBOC=35° ,ZFOG=30Q ,则ZDOE的度数为()B4.(5分)如图,OB丄CD于点O, Z1 = Z2,则Z2与Z3的关系是()BA. Z2=Z3 B・Z2与Z3互补C. Z2与Z3互余D.不确定5. (5分)如图,直线AB与直线CD相交于点O, E是ZCOB内一点,且OE丄AB, ZAOC=35° ,则ZEOD的度数是()1C、2 _______A GA.155°B. 145°C. 135°D. 125°二.填空题本大题共5小题,共25.0分)6. (5分)如图,直线佔与CD相交于点O, EO丄CD于点O, OF平分ZAOC,若ZBOE: ZAOC=4: 5,则ZEOF为 __________ 度.7・(5分)如果两个角的两条边分别垂直,而其中一个角比另一个角的4倍少60° , 则这两个角的度数分别为_ .& (5分)如图,直线AB、CD相交于点O,OE丄AB,垂足是点O, ZBOC=\40Q , 则ZDOE= ________ .9. (5分)已知ZAOB和ZCOD的两边分别互相垂直,且ZCOD比ZAO3的3倍少60°,则ZCOD的度数为_________10. (5分)如图,三条直线AB. CD、EF相交于0,且CD丄EF, ZAOE=6S° .若三、解答题(本大题共5小题,共50.0分)11. (10分)如图1,已知A 、O 、3三点在同一直线上,射线OD 、OE 分别平 分ZAOC 、ZBOC.(1) 求ZDOE 的度数;(2) 如图2,在ZAOD 内引一条射线OF 丄OC,其他不变,设ZDOF=a° (o"/<90°).g 求ZAOF 的度数(用含“的代数式表示);b.若ZBOD 是ZAOF 的2倍,求ZDOF 的度数.(1) ___________________ ZDOE 的补角有 :(2) 若ZDOE : ZAOD=i : 7,求ZAOC 的度数;(3) 射线OF 丄OE.① 当射线OF 在直线AB 上方时,试探究ZBOC 与上DOF 之间的数量关系,并说明理由;O, OE 是ZBOD 的平分线E图1 02②当射线OF在直线AB下方时,ZBOC与ZDOF之间的数量关系是__________ .13.(10分)已知直线AB和CD相交于O点,CO丄OE,OF平分ZAOE, Z2=26° .(1) ___________________________ 写岀图中所有Z4的余角•(2)写出图中相等的三对角:①②③(3)求Z5的度数.14. (10分)已知:如图,AO丄BC, DO丄OE・(1)不添加其他条件情况下,请尽可能多地写出图中有关角的等量关系(至少3个);(2)如果ZCOE=35° ,求ZBOD的度数・15. (10分)若ZA与的两边分别垂直,请判断这两个角的数量关系.(1) ___________________________________ 如图①,ZA与ZB的数量关系是;如图②,ZA与的数量关系是______ .(2)请从图①或图②中选择一种情况说明理山.《相交线》拔高练习参考答案与试题解析一、选择题(本大题共5小题,共25.0分)1. (5分)如图,因为直线A3丄/于点B, BC丄/于点B,所以直线AB和BC重合,则其中蕴含的数学原理是()AC1A. 平面内,过一点有且只有一条直线与已知直线垂直B. 垂线段最短C. 过一点只能作一条垂线D. 两点确定一条直线【分析】根据垂线的性质即可判断.【解答】解:因为直线佔丄/于点B, BC丄/于点B,所以直线AB和3C重合(在平面内,过一点有且只有一条直线与已知直线垂直),故选:A.【点评】本题考查垂线的性质,解题的关键是熟练掌握基本知识,属于中考常考题型.2. (5分)已知线段AB、CD,点M在线段上,结合图形,下列说法不正确CA. 延长线段AB、CD,相交于点FB. 反向延长线段84、DC,相交于点FC. 过点M画线段的垂线,交CD于点ED. 过点M画线段CD的垂线,交CD于点E【分析】根据线段和垂线段的定义,结合图形进行分析即可. 【解答】解:A、延长线段AB、CD,相交于点F,说法正确;B、反向延长线段84、DC,相交于点尺说法正确;C、过点M画线段AB的垂线,交CD于点E,说法正确;D、过点M画线段CD的垂线,交CD于点E,说法错误;故选:D.【点评】此题主要考查了直线、射线、线段,关键是正确掌握三线的特点.3. (5分)如图,已知直线AD、BE、CF相交于点O, OGLAD,且ZBOC=35° ,ZFOG=30Q ,则ZDOE的度数为()【分析】根据对顶角相等,以及垂直的定义求出所求角度数即可.【解答】解:V ZBOC=35° , ZFOG=30° ,A ZEOF=ZBOC=35° ,Z GOE= Z GOF+ Z FOE=65 ° ,TOG 丄AD,A ZGOD=90Q ,A ZDOE=25° ,故选:D.【点评】此题考查了垂线,以及对顶角、领补角,熟练掌握各自的性质是解本题的关键.4・(5分)如图,OB丄CD于点6 Z1 = Z2,则Z2与Z3的关系是()C. Z2与Z3互余D.不确定【分析】根据垂线定义可得Z l +再根据等量代换可得Z2+Z3=90°・【解答】解:、:OB 丄CD,.\Z1+Z3=9O° ,VZ1=Z2,A Z2+Z3=90° ,・・・Z2与Z3互余,故选:C.【点评】此题主要考查了垂线和余角,关键是掌握垂线的定义当两条直线相交所 成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直 线叫做另一条直线的垂线.5. (5分)如图,直线与直线CD 相交于点O, E 是ZCOB 内一点,且OE 丄AB,ZAOC=35° ,则ZEOD 的度数是( )【分析】山对顶角相等可求得ZBOD,根据垂直可求得ZEOB,再利用角的和差 可求得答案.【解答】解:V ZAOC=35° ,r. ZBOD=35° ,':EOLAB,A Z £05=90° ,r. ZEOD=ZEOB+ZBOD=90° +35° =125° , 故选:D.【点评】本题主要考查对项角相等和垂直的定义,掌握对顶角相等是解题的关键, 注意山垂直可得到角为90° .二、填空题(本大题共5小题,共25.0分)6. (5分)如图,直线与CD 相交于点O, EO 丄CD 于点O, OF 平分Z4OC,第28页(共18页)C. 135°D. 125°B. 145°若ZBOE: ZAOC=4: 5,则A EOF为一115 度.【分析】依据ZAOC+ZBOE=90° , ZBOE: ZAOC=4:5,即可得出ZAOC=50° , 根据OF平分ZAOC,可得Z COF=25 ° ,进而得到Z EOF= Z COF+ Z COE=\\5° .【解答】解:•:EO丄CD,;・ZCOE=90° ,r. ZAOC+ZBOE=90° ,又V ZBOE: ZA0C=4: 5,A ZAOC=50° ,乂YOF平分ZAOC,:.ZCOF=25° ,A ZEOF=ZCOF+ZCOE=25° +90° =115° ,故答案为:115.【点评】本题主要考查垂线的定义、角平分线的定义、对顶角的性质、邻补角的性质,关键在于熟练运用各性质定理,推出相关角的度数.7.(5分)如果两个角的两条边分别垂直,而其中一个角比另一个角的4倍少60° ,则这两个角的度数分别为48°、132°或20°、20° ..【分析】分两种悄况进行讨论,依据两个角的两条边分别垂直画出图形,而其中一个角比另一个角的4倍少60°,即可得到这两个角的度数.【解答】解:如图,a+P=180° , 3 =4 a・60° ,解得 a =48° , 3=132°;如图,a 二 B , B =4 a - 60° ,解得a = P =20 _;综上所述,这两个角的度数分别为48°、132°或20°、20° .故答案为:48°、132°或20°、20° .【点评】本题考查了垂线,当两条直线相交所成的四个角中,有一个角是直角时, 就说这两条直线互相垂直.& (5分)如图,直线AB、CD相交于点O,OE丄AB,垂足是点O, ZBOC=\40Q , 则ZDOE= 50°【分析】运用垂线的定义,对顶角的性质进行计算即可.【解答】解:・・•直线AB、CD相交于点O,A ZBOC=ZAOD=\40° ,乂TOE 丄AB,r.ZZ)OE=140o・90° =50° ,故答案为:50° .【点评】本题主要考查了对顶角和垂线的定义,解题的关键是运用对顶角的性质:对顶角相等.9. (5分)已知ZAOB和ZCOD的两边分别互相垂直,且ZCOD比ZAOB的3 倍少60°,则ZCOD的度数为30°或120°【分析】有两种情况:①如图1,根据ZCO£>=90° +90°- ZAOB,列方程可得结论;②如图2, ZAOB+ Z BOD= Z COD+ ZAOC,列方程可得结论.【解答】解:设ZAOB=x° ,则ZCOD=3x° - 60° ,分两种情况:①如图1, -ZAOB和ZCOD的两边分别互相垂直,・•・ ZCOD=90Q +90°・ ZAOB,即3x - 60=90+90 - %,*60° ,.\ZCOD=3X60°・60° =120°;②如图2, TOA丄OC, OB丄OD,・•・ ZAOB+ ZBOD= Z COD+ ZAOC,x+90=3x - 60+90,x=30° ,A ZCOD=30° ,综上所述,ZCOD的度数为30°或120° ,故答案为:30°或120°•【点评】此题主要考查了角的讣算,以及垂直的定义,关键是根据图形理清角之间的和差关系.10. (5分)如图,三条直线AB、CD、EF相交于O,且CD丄EF, ZAOE=68° .若OG 平分ZBOF,则ZDOG= 56 度.c八【分析】直接利用垂直的定义得出ZAOC=ZBOD的度数,再利用角平分线的定义得出答案.【解答】解:•: CD丄EF,ZCOE=90° ,V ZAOE=68° ,A ZAOC=ZBOD=22° , ZBOF=68° ,TOG 平分ZBOF,:.ZBOG=^ZBOF=34° ,2・•・ Z DOG= ZDOB+ ZBOG=56° .故答案为:56.【点评】此题主要考查了垂线以及角平分线的定义和角的计算,正确应用垂直的定义是解题关键.三、解答题(本大题共5小题,共50.0分)11. (10分)如图1,已知A、0、B三点在同一直线上,射线OD、OE分别平分ZAOC、ZBOC.(1)求ZDOE的度数;(2)如图2,在ZAOD内引一条射线OF丄OC,其他不变,设ZDOF=a°(o"<a<90°).g求ZAOF的度数(用含“的代数式表示);b.若ZBOD是ZAOF的2倍,求ZDOF的度数.图1 @2【分析】(1)根据角平分线的性质解答即可;(2) G 根据互余解答即可.b.根据ZBOD 是ZAOF 的2倍,列方程可得a 的值.【解答】解:(1)•・•点A, O, B 在同一条直线上,A ZAOC+ZBOC=\SO° ,•・•射线OD 和射线OE 分别平分ZAOC 和ZBOC,A ZCOD=^ZAOC, ZCOE 丄ZBOC2 2 A ZCOD+ZCOE=^ CZAOC+ZBOC ) =90° , 2r. ZDOE=90° ;(2) a. *:OC 丄OF,r. ZCOF=90° ,I ZDOF= a J:.ZCOD=90° - a ° ,I ZAOD=ZCOD.・•・ ZAOF=ZAOD ・ ZDOF=90° ・a° ・ a ° = (90-2a )b. V ZBOD 是ZAOF 的 2 倍,A180° ・(90 ・ a ) ° =2 (90-2a ) ° , a =18° ,即ZDOF=\S Q.【点评】此题主要考查了垂线和角平分线的定义,熟知从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线是解答此题的关键.(1) ZDOE 的补角有ZAOE 和 ZCOE ;(2) 若ZDOE : ZAOD=\: 7,求ZAOC 的度数;(3) 射线OF 丄OE2 OE 是ZBOD 的平分线①当射线OF在直线AB上方时,试探究ZBOC与ZDOF之间的数量关系,并说明理由;②出射线OF在直线下方时,ZBOC与ZDOF之间的数量关系是—丄ZB0C±2 ZDOF=180°.【分析】(1)根据角平分线的定义可得ZDOE二ZBOE,再根据补角的定义结合图形找出即可;(2)根据角平分线的定义列方程计算即可求出ZBOE,然后根据对顶角相等可得结论;(3 )计算出Z EOF的度数是90° ,设Z BOE=x , Z BOF=y ,则ZCO£>=2v+2y=180o ,可得结论.【解答】解:(1)如图1, TOE是ZBOD的平分线,・•・ ZDOE=ZBOE,由题意得:ZDOE的补角有:ZAOE^IZCOE;故答案为:ZAOE和ZCOE;(2)V ZDOE: ZAOD=\: 7,设ZDOE=x, ZAOD=7x,/.x+x+7.r=180,x=20° ,A ZAOC=ZBOD=2.x=40!3;(3)①如图2, ZDOFAZBOC,理由是:2TOE 丄OF,:.ZEOF=90° ,A ZDOF+ZDOE=90° ,•••上DOE A ZBOD,2・・・ZDOF气ZAOD斗ZBOC;②如图3, L Z B0C+ZDOF=180° ,理山是:2TOE 丄OF,;・ZEOF=90° ,第18页(共18贞)A ZBOF+ZBOE=90° ,••• ZBOF丄ZBOC,2设ZBOE=x, ZBOF=yVZC(?D=2x+2)^180°/.丄ZBOC+ Z DOF=y+2x+y= 180 °・2【点评】此题主要考查了垂线,以及角平分线定义,关键是理清角之间的关系,掌握从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线.13.(10分)已知直线A3和CD相交于O点,CO丄OE,OF平分ZAOE, Z2=26° . (1)写出图中所有Z4的余角Zl, Z5 .(2)写出图中相等的三对角:① Z1二Z5 ② ZAOF=ZEOF③ ZCOE二ZDOE .(3)求Z5的度数・EA6【分析】(1)依据垂直的定义以及对顶角相等,即可得到所有Z4的余角;(2) 依据对顶角相等,角平分线的定义以及垂直的定义,即可得到相等的三对角;(3) 根据垂直的定义可得ZCOE=90° ,然后求出ZEOF,再根据角平分线的定义求出ZAOF,然后求出ZAOC,再根据对顶角相等解答即可.【解答】解:(1) TCO丄OE,:.Z4+Z5=90° ,XVZ1=Z5,r.Zl+Z5=90° ,・・・Z4的余角为Zl, Z5,故答案为:Zl, Z5;(2) •・•直线4B和CD相交于O点,.\Z1=Z5,*:OF平分ZAOE,・•・ ZAOF=ZEOF f•: CO 丄OE,・•・ ZCOE=ZDOE:故答案为:Z1=Z5, ZAOF=ZEOF, ZCOE=ZDOE;(3) *:CO丄OE,・・・ZCOE=90° ,XVZCOF=26° ,A ZEOF=90°・26° =64° ,':OF平分ZAOE,第18贞(共18页)EZAOF=EOF=M° ,6r. ZAOC=64°・26° =38° ,第18贞(共18页)•・• ZAOC与Z5是对顶角,.\Z5=38° .【点评】本题考查了余角和补角的定义,角平分线的定义,准确识图,找出各角度之间的关系是解题的关键.14. (10分)已知:如图,AO丄BC, DO丄OE.(1)不添加其他条件悄况下,请尽可能多地写出图中有关角的等量关系(至少3个);(2)如果ZCOE=35° ,求ZBOD的度数.B O C【分析】(1)已知AO丄BC, DO丄OE,就是已知ZDOE= ZAOB= ZA OC=90° , 利用同角或等角的余角相等,从而得到相等的角.(2)由DO丄OE, ZCOE=35° ,知ZBOD=\SO° ■乙DOE ■乙COE,故可求解.【解答】解:(1) TAO丄BC, DOLOE,A ZDOE=ZAOB=ZAOC=90° , ZBOD+ZAOD=90° , ZAOD+ZAOE=90° ,ZAOE+ZCOE=90° ,:.ZDOA=ZEOC, ZDOB=ZAOE, ZAOB=ZAOC, ZAOB=ZDOE, ZAOC=ZDOE;(2) TDO丄OE, ZCOE=35° ,r.ZBOD= 180°・ ZDOE - ZCOE=90°・ 35° =55° .【点评】本题主要考查了同角或等角的余角相等这一性质,山垂直的定义得出直角是解决本题的关键.15. (10分)若ZA与的两边分别垂直,请判断这两个角的数量关系.(1)如图①,ZA与ZB的数量关系是相等;如图②,ZA与ZB的数量关系是互补 .(2)请从图①或图②中选择一种情况说明理山.D【分析】(1)如果一个角的两边与另一个角的两边分别垂直,那么这两个角的关系是相等或互补;(2)根据垂直的量相等的角都等于90。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、三角形的三个外角中,钝角最多有( )。
A :1个
B : 2个
C :3 个
D : 4 个
2、直角三角形两锐角的平分线相交所成的钝角是( )。
A :120°
B : 135°
C :150°
D : 165°
3、如图所示,在△ABC 中,CD 、BE 分别是AB 、AC 边上的高,并且CD 、BE 交于,点P ,若∠A=500 ,则 ∠BPC 等于( )
A 、90°
B 、130°
C 、270°
D 、315°
4、一个多边形的每一个外角都等于30°,这个多边形的边数是 ,它的内角和是
5、如图所示,若∠A =32°,∠B =45°,∠C =38°,则∠DFE 等于( )
A.120°
B.115°
C.110°
D.105°
6、已知等腰三角形的两边长分别为4cm 和7cm, 它的周长是_________㎝.
7、等腰三角形一腰上的中线将这个等腰三角形的周长分成15和6两部分,则这个等腰三角形的三边长是_________________。
8、若过m 边形的一个顶点有7条对角线,n 边形没有对角线,k 边形有k 条对角线,求(m -k)n 的值__________。
9、如图,已知∠BOF=120°,则∠A+∠B+∠C+∠D+∠E+∠F=___
10、下列正多边形中,与正三角形同时使用能进行镶嵌的是 ( )
A.正十二边形
B.正十边形
C.正八边形
D.正五边形
11、如图:小明从A 点出发前进10m ,向右转150,,再前进10m ,右转150……
这样一直走下去,他第一次回到出发点A 时,一共走了____m.
(第3题)
F E D C B A
12、过多边形的一个顶点的所有对角线把多边形分成8个三角形,这个多边形的边数是( ) A 、8 B 、9 C 、10 D 、11
13、n 边形的每个外角都为24°,则边数n 为( )
A 、13
B 、14
C 、15
D 、16
14、在△ABC 中,若∠C =2(∠A +∠B ),则∠C = 度。
15、如果△ABC 的一个外角等于1500,且∠B =∠C ,则∠A = 。
16、纸片△ABC 中,∠A =650,∠B =750,将纸片的一角折叠,使点C 落在△ABC 内(如图),若∠1=200,则∠2的度数为 。
第8题图
A 2
A 1A 第3题图 D
C B A
17、如图,在△ABC 中,∠A =960,延长BC 到D ,∠ABC 与∠ACD 的平分线相交于1A ,∠1A BC 与∠1A CD 的平分线相交于2A ,依此类推,∠4A BC 与∠4A CD 的平分线相交于5A ,则∠5A 的大小是多少?
18、如果⎩⎨⎧=+=-423y x a y x 的解都是正数,那么a 的取值范围是( )
(A )a <2; (B )34->a ; (C )342<<-a ; (D )3
4
-<a ; 19、关于x 、y 的方程组⎩⎨⎧=-=+m y x m y x 932的解是方程3x +2y =34的一组解,那么m 的值
是( )
(A )2; (B )-1; (C )1; (D )-2;
20、下列方程组中,是二元一次方程组的是( )
(A )⎪⎩⎪⎨⎧=+=+9114
y x y x (B )⎩⎨⎧=+=+75z y y x (C )⎩⎨⎧=-=6231y x x (D )⎩⎨
⎧=-=-1y x xy y x 21、汽车从甲地到乙地,若每小时行驶45千米,就要延误30分钟到达;若每小时行驶50千米,那就可以提前30分钟到达,求甲、乙两地之间的距离及原计划行驶的时间?
22、甲、乙两人在A 地,丙在B 地,他们三人同时出发,甲与乙同向而行,丙与甲、乙相向而行,甲每分钟走100米,乙每分钟走110米,丙每分钟走125米,若丙遇到乙后10分钟又遇到甲,求A 、B 两地之间的距离。
23、如图,在△ABC 中,∠ABC 与∠ACB 的平分线交于点I,根据下列条件求∠BIC 的度数.(1)若∠ABC=50°,∠ACB=80°,则∠BIC=______________________;
(2)若∠ABC+∠ACB=116°,则∠BIC=_______________________;
(3)若∠A=56°,则∠BIC=________________________;
(4)若∠BIC=100°,则∠A=_________________;
(5)通过以上计算,探索出您所发现规律:∠A 与∠BIC 之间的
数量关系是_________________________________。
24、如图所示,在△ABC 中,∠A =α,△ABC 的内角平分线或外角平分线交于点P , 且∠P =β,试探求下列各图中α与β的关系,并选择一个加以说明.
(1)P
C B A
(2)P C B A (3)C B A。
