2018高中全程训练计划·数学(文)仿真考(二) Word版含解析
2018年山东省潍坊高三数学二模试卷(文科)Word版含解析

2018年山东省潍坊高三二模试卷(文科数学)一、选择题:本大题共l0小题.每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.若复数i满足z(1+i)=2i,则在复平面内z对应的点的坐标是()A.(1,1)B.(1,﹣1)C.(﹣1,1)D.(﹣1,﹣1)2.设全集U=R,集合A={x|2x>1},B={x|﹣1≤x≤5},则(∁A)∩B等于()UA.[﹣1,0)B.(0,5] C.[﹣1,0] D.[0,5]3.已知命题p、q,“¬p为真”是“p∧q为假”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件4.若圆C经过(1,0),(3,0)两点,且与y轴相切,则圆C的方程为()A.(x﹣2)2+(y±2)2=3 B.C.(x﹣2)2+(y±2)2=4 D.5.执行如图所示的程序框图,则输出的k的值是()A.3 B.4 C.5 D.66.高三某班有学生56人,现将所有同学随机编号,用系统抽样的方法,抽取一个容量为4的样本,已知5号、33号、47号学生在样本中,则样本中还有一个学生的编号为()A.13 B.17 C.19 D.217.《九章算术》“竹九节”问题:现有一根9节的竹子,自上而下各节的容积成等差数列,上面4节的容积共3升,下面3节的容积共4升,则第5节的容积为( )A .升 B .升 C .升 D .升8.函数y=a |x|与y=sinax (a >0且a ≠1)在同一直角坐标系下的图象可能是( )A .B .C .D .9.三棱锥S ﹣ABC 的所有顶点都在球O 的表面上,SA ⊥平面ABC ,AB ⊥AC ,又SA=AB=AC=1,则球O 的表面积为( )A .B .C .3πD .12π10.设,若函数y=f (x )+k 的图象与x 轴恰有三个不同交点,则k的取值范围是( )A .(﹣2,1)B .[0,1]C .[﹣2,0)D .[﹣2,1)二、填空题:本大题共5小题,每小题5分,共25分.11.已知角α的顶点与原点重合,始边与x 轴的正半轴重合,终边上一点的坐标为(3,4),则cos2α= .12.已知某几何体的三视图如图所示,则该几何体的体积为13.若x、y满足条件,则z=x+3y的最大值是.14.设a>0,b>0,若是4a和2b的等比中项,则的最小值为.15.如图,已知直线l:y=k(x+1)(k>0)与抛物线C:y2=4x相交于A、B两点,点F为抛物线焦点,且A、B两点在抛物线C准线上的射影分别是M、N,若|AM|=2|BN|,则k的值是.三、解答题:本大题共6小题,共75分.应写出证明过程或演算步骤.16.甲、乙两家商场对同一种商品开展促销活动,对购买该商品的顾客两家商场的奖励方案如下:甲商场:顾客转动如图所示圆盘,当指针指向阴影部分(图中四个阴影部分均为扇形,且每个扇形圆心角均为15°,边界忽略不计)即为中奖.乙商场:从装有3个白球3个红球的盒子中一次性摸出2球(球除颜色外不加区分),如果摸到的是2个红球,即为中奖.问:购买该商品的顾客在哪家商场中奖的可能性大?17.已知=(2sinx ,sinx+cosx ),=(cosx ,sinx ﹣cosx ),函数f (x )=•.(Ⅰ)求函数f (x )的单调递减区间;(Ⅱ)在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,且b 2+a 2﹣c 2=ab ,若f (A )﹣m >0恒成立,求实数m 的取值范围.18.如图,底面是等腰梯形的四棱锥E ﹣ABCD 中,EA ⊥平面ABCD ,AB ∥CD ,AB=2CD ,∠ABC=.(Ⅰ)设F 为EA 的中点,证明:DF ∥平面EBC ;(Ⅱ)若AE=AB=2,求三棱锥B ﹣CDE 的体积.19.已知数列{a n }的前n 项和,数列{b n }满足3n ﹣1b n =a 2n ﹣1(I )求a n ,b n ;(Ⅱ)设T n 为数列{b n }的前n 项和,求T n .20.已知函数f(x)=x3﹣x﹣.(Ⅰ)判断的单调性;(Ⅱ)求函数y=f(x)的零点的个数;(Ⅲ)令g(x)=+lnx,若函数y=g(x)在(0,)内有极值,求实数a的取值范围.21.已知双曲线C: =1的焦距为3,其中一条渐近线的方程为x﹣y=0.以双曲线C的实轴为长轴,虚轴为短轴的椭圆记为E,过原点O的动直线与椭圆E交于A、B两点.(Ⅰ)求椭圆E的方程;(Ⅱ)若点P为椭圆的左顶点,,求|的取值范围;(Ⅲ)若点P满足|PA|=|PB|,求证为定值.2018年山东省潍坊高三数学二模试卷(文科)参考答案与试题解析一、选择题:本大题共l0小题.每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.若复数i满足z(1+i)=2i,则在复平面内z对应的点的坐标是()A.(1,1)B.(1,﹣1)C.(﹣1,1)D.(﹣1,﹣1)【考点】复数的基本概念;复数代数形式的乘除运算.【分析】把已知等式两边同时乘以,然后利用复数的除法运算化简,则答案可求.【解答】解:由z(1+i)=2i,得.∴在复平面内z对应的点的坐标是(1,1).故选:A.A)∩B等于()2.设全集U=R,集合A={x|2x>1},B={x|﹣1≤x≤5},则(∁UA.[﹣1,0)B.(0,5] C.[﹣1,0] D.[0,5]【考点】交、并、补集的混合运算.【分析】求出A中不等式的解集确定出A,根据全集U=R求出A的补集,找出A补集与B的交集即可.【解答】解:由A中的不等式变形得:2x>1=20,得到x>0,∴A=(0,+∞),∵全集U=R,∴∁A=(﹣∞,0],U∵B=[﹣1,5],A)∩B=[﹣1,0].∴(∁U故选:C.3.已知命题p、q,“¬p为真”是“p∧q为假”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【考点】必要条件、充分条件与充要条件的判断.【分析】根据复合命题真假之间的关系,以及充分条件和必要条件的定义进行判断即可.【解答】解:若¬p为真,则p且假命题,则p∧q为假成立,当q为假命题时,满足p∧q为假,但p真假不确定,∴¬p为真不一定成立,∴“¬p为真”是“p∧q为假”的充分不必要条件.故选:A.4.若圆C经过(1,0),(3,0)两点,且与y轴相切,则圆C的方程为()A.(x﹣2)2+(y±2)2=3 B.C.(x﹣2)2+(y±2)2=4 D.【考点】圆的标准方程.【分析】由已知圆C经过(1,0),(3,0)两点,且与y轴相切.可得圆心在直线x=2上,且半径长为2.设圆的方程为(x﹣2)2+(y﹣b)2=4.将点(1,0)代入方程即可解得.从而得到圆C的方程.【解答】解:∵圆C经过(1,0),(3,0)两点,∴圆心在直线x=2上.可设圆心C(2,b).又∵圆C与y轴相切,∴半径r=2.∴圆C的方程为(x﹣2)2+(y﹣b)2=4.∵圆C经过点(1,0),∴(1﹣2)2+b2=4.∴b2=3.∴.∴圆C的方程为.故选:D.5.执行如图所示的程序框图,则输出的k的值是()A.3 B.4 C.5 D.6【考点】程序框图.【分析】根据所给数值判定是否满足判断框中的条件,然后执行循环语句,一旦满足条件就退出循环,输出结果.【解答】解:模拟执行程序,可得:k=1,s=1,第1次执行循环体,s=1,不满足条件s>15,第2次执行循环体,k=2,s=2,不满足条件s>15,第3次执行循环体,k=3,s=6,不满足条件s>15,第4次执行循环体,k=4;s=15,不满足条件s>15,第5次执行循环体,k=5;s=31,满足条件s>31,退出循环,此时k=5.故选:C.6.高三某班有学生56人,现将所有同学随机编号,用系统抽样的方法,抽取一个容量为4的样本,已知5号、33号、47号学生在样本中,则样本中还有一个学生的编号为()A.13 B.17 C.19 D.21【考点】系统抽样方法.【分析】根据系统抽样的定义即可得到结论.【解答】解:∵高三某班有学生56人,用系统抽样的方法,抽取一个容量为4的样本,∴样本组距为56÷4=14,则5+14=19,即样本中还有一个学生的编号为19,故选:C.7.《九章算术》“竹九节”问题:现有一根9节的竹子,自上而下各节的容积成等差数列,上面4节的容积共3升,下面3节的容积共4升,则第5节的容积为()A.升B.升C.升D.升【考点】等比数列的通项公式.【分析】设此等差数列为{an },公差d>0,由题意可得:a1+a2+a3+a4=3,a7+a8+a9=4,可得4a1+6d=3,3a1+21d=4,联立解出即可得出.【解答】解:设此等差数列为{an},公差d>0,由题意可得:a1+a2+a3+a4=3,a7+a8+a9=4,则4a1+6d=3,3a1+21d=4,联立解得a1=,d=.∴a5=+4×=.故选:C.8.函数y=a|x|与y=sinax(a>0且a≠1)在同一直角坐标系下的图象可能是()A.B.C.D.【考点】函数的图象.【分析】结合函数图象的对折变换法则和正弦型函数的伸缩变换,分当a>1时和当0<a<1时两种情况,分析两个函数的图象,比照后,可得答案.【解答】解:当a>1时,函数y=a|x|与y=sinax(a>0且a≠1)在同一直角坐标系下的图象为:当0<a<1时,函数y=a|x|与y=sinax(a>0且a≠1)在同一直角坐标系下的图象为:比照后,发现D满足第一种情况,故选D9.三棱锥S﹣ABC的所有顶点都在球O的表面上,SA⊥平面ABC,AB⊥AC,又SA=AB=AC=1,则球O的表面积为()A.B.C.3π D.12π【考点】球的体积和表面积.【分析】根据题意,三棱锥S﹣ABC扩展为正方体,正方体的外接球的球心就是正方体体对角线的中点,求出正方体的对角线的长度,即可求解球的半径,从而可求三棱锥S﹣ABC的外接球的表面积.【解答】解:三棱锥S﹣ABC的所有顶点都在球O的表面上,SA⊥平面ABC,AB⊥AC,又SA=AB=AC=1,三棱锥扩展为正方体的外接球,外接球的直径就是正方体的对角线的长度,∴球的半径R=.球的表面积为:4πR2=4π•()2=3π.故选:C.10.设,若函数y=f(x)+k的图象与x轴恰有三个不同交点,则k的取值范围是()A.(﹣2,1)B.[0,1] C.[﹣2,0)D.[﹣2,1)【考点】函数的图象.【分析】作出函数y=f(x)的图象,由题意可得,函数y=f(x)与y=﹣k的图象有3个交点,结合图象求得结果..【解答】解:设,画出y=f(x)和y=﹣k的图象,如图所示:由图象得:﹣2≤k<1函数y=f(x)与y=﹣k的图象有3个交点,即函数y=f(x)+k的图象与x轴恰有三个公共点;故选:D二、填空题:本大题共5小题,每小题5分,共25分.11.已知角α的顶点与原点重合,始边与x轴的正半轴重合,终边上一点的坐标为(3,4),则cos2α= ﹣.【考点】任意角的三角函数的定义;二倍角的余弦.【分析】根据任意角的三角函数的定义求得cosα=的值,再利用二倍角公式cos2α=2cos2α﹣1,计算求得结果.【解答】解:由题意可得,x=3、y=4、r=5,∴cosα==,∴cos2α=2cos2α﹣1=﹣,故答案为:﹣.12.已知某几何体的三视图如图所示,则该几何体的体积为12【考点】由三视图求面积、体积.【分析】由三视图知几何体为三棱柱,且三棱柱的高为4,底面是直角三角形,且直角三角形的两直角边长分别为3,2,把数据代入棱柱的体积公式计算.【解答】解:由三视图知几何体为三棱柱,且三棱柱的高为4,底面是直角三角形,且直角三角形的两直角边长分别为3,2,∴几何体的体积V=×3×2×4=12.故答案为:12.13.若x、y满足条件,则z=x+3y的最大值是11 .【考点】简单线性规划.【分析】作出不等式对应的平面区域,利用z的几何意义,进行平移即可得到结论.【解答】解:作出不等式组对应的平面区域如图:由z=x+3y得y=,平移直线y=,当直线y=经过点A时,对应的直线的截距最大,此时z也最大,由,解得,即A(2,3),此时z=2+3×3=11,故答案为:1114.设a>0,b>0,若是4a和2b的等比中项,则的最小值为2.【考点】基本不等式;等比数列的通项公式.【分析】是4a和2b的等比中项,可得4a•2b=,2a+b=1.再利用“乘1法”与基本不等式的性质即可得出.【解答】解:是4a和2b的等比中项,∴4a•2b=,∴2a+b=1.又a>0,b>0,则=(2a+b)=5++≥5+2×=9,当且仅当a=b=时取等号.则的最小值为2.故答案为:2.15.如图,已知直线l:y=k(x+1)(k>0)与抛物线C:y2=4x相交于A、B两点,点F为抛物线焦点,且A、B两点在抛物线C准线上的射影分别是M、N,若|AM|=2|BN|,则k的值是.【考点】抛物线的简单性质.【分析】直线y=k(x+1)(k>0)恒过定点P(﹣1,0),由此推导出|OB|=|AF|,由此能求出点B的坐标,从而能求出k的值.【解答】解:设抛物线C:y2=4x的准线为l:x=﹣1直线y=k(x+1)(k>0)恒过定点P(﹣1,0)如图过A、B分别作AM⊥l于M,BN⊥l于N,由|FA|=2|FB|,则|AM|=2|BN|,点B为AP的中点、连接OB,则|OB|=|AF|,∴|OB|=|BF|,点B的横坐标为,∴点B的坐标为B(,),把B(,)代入直线l:y=k(x+1)(k>0),解得k=.故答案为.三、解答题:本大题共6小题,共75分.应写出证明过程或演算步骤.16.甲、乙两家商场对同一种商品开展促销活动,对购买该商品的顾客两家商场的奖励方案如下:甲商场:顾客转动如图所示圆盘,当指针指向阴影部分(图中四个阴影部分均为扇形,且每个扇形圆心角均为15°,边界忽略不计)即为中奖.乙商场:从装有3个白球3个红球的盒子中一次性摸出2球(球除颜色外不加区分),如果摸到的是2个红球,即为中奖.问:购买该商品的顾客在哪家商场中奖的可能性大?【考点】几何概型;列举法计算基本事件数及事件发生的概率.【分析】分别计算两种方案中奖的概率.先记出事件,得到试验发生包含的所有事件,和符合条件的事件,由等可能事件的概率公式得到.【解答】解:如果顾客去甲商场,试验的全部结果构成的区域为圆盘的面积π•R2,阴影部分的面积为,则在甲商场中奖的概率为:;如果顾客去乙商场,记3个白球为a1,a2,a3,3个红球为b1,b2,b3,记(x,y)为一次摸球的结果,则一切可能的结果有:(a1,a2),(a1,a3),(a1,b1),(a1,b2),(a1,b3)(a2,a3),(a2,b1),(a2,b2),(a2,b3),(a3,b1),(a3,b2),(a3,b3),(b1,b2),(b1,b3),(b2,b3),共15种,摸到的是2个红球有(b1,b2),(b1,b3),(b2,b3),共3种,则在乙商场中奖的概率为:P2=,又P1<P2,则购买该商品的顾客在乙商场中奖的可能性大.17.已知=(2sinx,sinx+cosx),=(cosx,sinx﹣cosx),函数f(x)=•.(Ⅰ)求函数f(x)的单调递减区间;(Ⅱ)在△ABC中,内角A,B,C的对边分别为a,b,c,且b2+a2﹣c2=ab,若f(A)﹣m>0恒成立,求实数m的取值范围.【考点】余弦定理;平面向量数量积的运算;三角函数中的恒等变换应用.【分析】(Ⅰ)利用向量的数量积公式,结合辅助角公式,化简函数,利用正弦函数的单调递减区间,求函数f(x)的单调递减区间.(Ⅱ)由已知利用余弦定理可求cosC,由范围C∈(0,π),可求C的值,由题意2sin(2A﹣)>m恒成立,由A∈(0,),可求sin(2A﹣)∈(﹣,1],进而可得m的范围.【解答】解:(Ⅰ)∵=(2sinx,sinx+cosx),=(cosx,sinx﹣cosx),函数f(x)=•.∴f(x)=sin2x+sin2x﹣cos2x=2sin(2x﹣),∵令2kπ+≤2x﹣≤2kπ+,k∈Z,解得:kπ+≤x≤kπ+,k∈Z,∴函数f(x)的单调递减区间为:[kπ+,kπ+],k∈Z.(Ⅱ)∵b2+a2﹣c2=ab,∴cosC===,由C∈(0,π),可得:C=,∵f(A)﹣m=2sin(2A﹣)﹣m>0恒成立,即:2sin(2A﹣)>m恒成立,∵A∈(0,),2A﹣∈(﹣,),∴sin(2A﹣)∈(﹣,1],可得:m≤﹣1.18.如图,底面是等腰梯形的四棱锥E﹣ABCD中,EA⊥平面ABCD,AB∥CD,AB=2CD,∠ABC=.(Ⅰ)设F为EA的中点,证明:DF∥平面EBC;(Ⅱ)若AE=AB=2,求三棱锥B﹣CDE的体积.【考点】棱柱、棱锥、棱台的体积;直线与平面平行的判定.【分析】(Ⅰ)取EB的中点G,连接FG,CG,利用F为EA的中点,证明四边形CDFG为平行四边形,即可证明:DF∥平面EBC;(Ⅱ)等腰梯形ABCD中,作CH⊥AB于H,求出点B到CD的距离,即可求三棱锥B﹣CDE的体积.【解答】(Ⅰ)证明:取EB的中点G,连接FG,CG,∵F为EA的中点,∴FG∥AB,FG=AB,∵AB∥CD,AB=2CD,∴FG∥CD,FG=CD,∴四边形CDFG为平行四边形,∴DF∥CG,∵DF⊄平面EBC,CG⊂平面EBC,∴DF∥平面EBC;(Ⅱ)解:等腰梯形ABCD中,作CH⊥AB于H,则BH=,在Rt△BHC中,∠ABC=60°,则CH=tan60°=,即点C到AB的距离d=,则点B到CD的距离为,∵EA⊥平面ACD,∴三棱锥B﹣CDE的体积为V==.E﹣BDC19.已知数列{a n }的前n 项和,数列{b n }满足3n ﹣1b n =a 2n ﹣1(I )求a n ,b n ;(Ⅱ)设T n 为数列{b n }的前n 项和,求T n . 【考点】数列的求和;数列递推式.【分析】(Ⅰ)当n ≥2时利用a n =S n ﹣S n ﹣1计算即得结论,再代入得到b n =,(Ⅱ)通过错位相减法即可求出前n 项和. 【解答】解:(Ⅰ)∵S n =n 2+2n ,∴当n ≥2时,a n =S n ﹣S n ﹣1=(n 2+2n )﹣(n ﹣1)2﹣2(n ﹣1)=2n+1(n ≥2), 又∵S 1=1+2=3即a 1=1满足上式, ∴数列{a n }的通项公式a n =2n+1; ∴3n ﹣1b n =a 2n ﹣1=2(2n ﹣1)+1=4n ﹣1,∴b n =,(Ⅱ)T n =+++…++,∴T n =+++…++,∴T n =3+4(++…+)﹣=3+4•﹣=5﹣∴T n =﹣20.已知函数f (x )=x 3﹣x ﹣.(Ⅰ)判断的单调性;(Ⅱ)求函数y=f (x )的零点的个数;(Ⅲ)令g (x )=+lnx ,若函数y=g (x )在(0,)内有极值,求实数a 的取值范围.【考点】利用导数研究函数的单调性;利用导数研究函数的极值;利用导数求闭区间上函数的最值.【分析】(Ⅰ)化简,并求导数,注意定义域:(0,+∞),求出单调区间;(Ⅱ)运用零点存在定理说明在(1,2)内有零点,再说明f (x )在(0,+∞)上有且只有两个零点;(Ⅲ)对g (x )化简,并求出导数,整理合并,再设出h (x )=x 2﹣(2+a )x+1,说明h (x )=0的两个根,有一个在(0,)内,另一个大于e ,由于h (0)=1,通过h ()>0解出a 即可.【解答】解:(Ⅰ)设φ(x )==x 2﹣1﹣(x >0),则φ'(x )=2x+>0,∴φ(x )在(0,+∞)上单调递增;(Ⅱ)∵φ(1)=﹣1<0,φ(2)=3﹣>0,且φ(x )在(0,+∞)上单调递增,∴φ(x )在(1,2)内有零点,又f (x )=x 3﹣x ﹣=x•φ(x ),显然x=0为f (x )的一个零点,∴f (x )在(0,+∞)上有且只有两个零点;(Ⅲ)g (x )=+lnx=lnx+,则g'(x )==,设h (x )=x 2﹣(2+a )x+1,则h (x )=0有两个不同的根x 1,x 2,且有一根在(0,)内,不妨设0<x 1<,由于x 1x 2=1,即x 2>e ,由于h (0)=1,故只需h ()<0即可,即﹣(2+a )+1<0,解得a >e+﹣2,∴实数a 的取值范围是(e+﹣2,+∞).21.已知双曲线C :=1的焦距为3,其中一条渐近线的方程为x ﹣y=0.以双曲线C 的实轴为长轴,虚轴为短轴的椭圆记为E ,过原点O 的动直线与椭圆E 交于A 、B 两点. (Ⅰ)求椭圆E 的方程;(Ⅱ)若点P 为椭圆的左顶点,,求|的取值范围;(Ⅲ)若点P 满足|PA|=|PB|,求证为定值.【考点】直线与圆锥曲线的综合问题.【分析】(Ⅰ)由已知条件推导出,,由此能求出椭圆E 的方程.(Ⅱ)由已知条件知P (﹣,0),设G (x 0,y 0),由,推导出G (﹣,0),由此能求出的取值范围.(Ⅲ)由|PA|=|PB|,知P 在线段AB 垂直平分线上,由椭圆的对称性知A ,B 关于原点对称,由此能够证明为定值.【解答】(Ⅰ)解:∵双曲线C : =1的焦距为3,∴c=,∴,①∵一条渐近线的方程为x ﹣y=0,∴,②由①②解得a 2=3,b 2=,∴椭圆E 的方程为.(Ⅱ)解:∵点P 为椭圆的左顶点,∴P (﹣,0),设G (x 0,y 0),由,得(x 0+,y 0)=2(﹣x 0,﹣y 0),∴,解得,∴G(﹣,0),设A(x1,y1),则B(﹣x1,﹣y1),||2+||2=()2++(x1﹣)2+=2+2+=2+3﹣x+=+,又∵x1∈[﹣,],∴∈[0,3],∴,∴的取值范围是[].(Ⅲ)证明:由|PA|=|PB|,知P在线段AB垂直平分线上,由椭圆的对称性知A,B关于原点对称,①若A、B在椭圆的短轴顶点上,则点P在椭圆的长轴顶点上,此时==2()=2.②当点A,B,P不是椭圆的顶点时,设直线l的方程为y=kx(k≠0),则直线OP的方程为y=﹣,设A(x1,y1),由,解得,,∴|OA|2+|OB|2==,用﹣代换k,得|OP|2=,∴==2,综上所述: =2.。
广西2018届高三下学期第二次模拟数学文试题 含答案 精

广西区2018年3月高三年级第二次高考模拟联合考试数学(文科) 第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.复数(13)(1)z i i =-+-在复平面内对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限 2.已知集合2{|20}A x x =->,{|0}B x x =>,则A B =( )A.(0 B .(2)(0)-∞-+∞,, C.)+∞D.((0)-∞+∞,,3.设向量(4)a x =-,,(1)b x =-,,若向量a 与b 同向,则x =( ) A .2- B .2 C .2± D .04.以下关于双曲线M :228x y -=的判断正确的是( ) A .M 的离心率为2 B .M 的实轴长为2 C.M 的焦距为16 D .M 的渐近线方程为y x =±5.某几何体的三视图如图所示,其中俯视图中的圆的半径为2,则该几何体的体积为( )A .51296π-B .296 C.51224π- D .512 6.设x ,y 满足约束条件330280440x y x y x y -+⎧⎪+-⎨⎪+-⎩≥≤≥,则3z x y =+的最大值是( )A .9B .8 C.3 D .47.执行如图所示的程序框图,若输入的11k =,则输出的S =( )A .12B .13 C.15 D .188.我国南宋著名数学家秦九韶发现了三角形三边求三角形面积的“三斜求积公式”,设ABC △三个内角A ,B ,C 所对的边分别为a ,b ,c ,面积为S ,则“三斜求积公式”为S =若2sin 24sin a C A =,2(sin sin )()(27)sin a C B c b a A -+=-,则用“三斜求积公式”求得的S =( )A B9.设D 为椭圆2215y x +=上任意一点,(02)A -,,(02)B ,,延长AD 至点P ,使得PD BD =,则点P 的轨迹方程为( )A .22(2)20x y +-=B .22(2)20x y ++= C.22(2)5x y +-= D .22(2)5x y ++=10.设38a =,0.5log 0.2b =,4log 24c =,则( )A .a c b <<B .a b c << C.b a c << D .b c a <<11.如图,在底面为矩形的四棱锥E ABCD -中,DE ⊥平面ABCD ,F ,G 分别为棱DE ,AB 上一点,已知3CD DE ==,4BC =,1DF =,且FG ∥平面BCE ,四面体ADFG 的每个顶点都在球O 的表面上,则球O 的表面积为( )A .12πB .16π C.18π D .20π 12.将函数sin 2cos2y x x =+的图象向左平移ϕ(02πϕ<<)个单位长度后得到()f x 的图象,若()f x 在5()4ππ,上单调递减,则ϕ的取值范围为( )A .3()88ππ,B .()42ππ, C.3[]88ππ, D .[)42ππ,第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上) 13.若2tan 1α=,tan 2β=-,则tan()αβ+= .14.若m 是集合{1357911},,,,,中任意选取的一个元素,则椭圆2212x y m +=的焦距为整数的概率为 .15.若函数(1)21()52lg 1a x x f x x x -+⎧=⎨-->⎩,,≤是在R 上的减函数,则a 的取值范围是 .16.若函数32()3f x x x a =--(0a ≠)只有2个零点,则a = .三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17. 已知公差不为0的等差数列{}n a 的前n 项和n S ,11S +,3S ,4S 成等差数列,且1a ,2a ,5a 成等比数列.(1)求数列{}n a 的通项公式;(2)若4S ,6S ,10S 成等比数列,求n 及此等比数列的公比.18. 如图,四棱锥P ABCD -的底面ABCD 是正方形,PD ⊥平面ABCD ,且2AB =,3PD =.(1)证明:AB ⊥平面PAD ;(2)设E 为棱PD 上一点,且2D E PE =,记三棱锥C PAB -的体积为1V ,三棱锥P ABE -的体积为2V ,求12V V 的值. 19. “双十一网购狂欢节”源于淘宝商城(天猫)2009年11月11日举办的促销活动,当时参与的商家数量和促销力度均有限,但营业额远超预想的效果,于是11月11日成为天猫举办大规模促销活动的固定日期.如今,中国的“双十一”已经从一个节日变成了全民狂欢的“电商购物日”.某淘宝电商为分析近8年“双十一”期间的宣传费用x (单位:万元)和利润y (单位:十万元)之间的关系,搜集了相关数据,得到下列表格:(1)请用相关系数r 说明y 与x 之间是否存在线性相关关系(当0.81r >时,说明y 与x 之间具有线性相关关系);(2)建立y 关于x 的线性回归方程(系数精确到0.1),预测当宣传费用为20万元时的利润, 附参考公式:回归方程y bx a =+中b 和a 最小二乘估计公式分别为1221ni ii nii x ynx y b xnx==-=-∑∑,a y bx =-,相关系数ni ix ynxyr -=∑参考数据:81241i ii x y==∑,821356i i x ==∑8.256=20. 已知曲线M 由抛物线2x y =-及抛物线24x y =组成,直线l :3y kx =-(0k >)与曲线M 有m (m ∈N )个公共点. (1)若3m ≥,求k 的最小值;(2)若3m =,记这3个交点为A ,B ,C ,其中A 在第一象限,(01)F ,,证明:2FB FC FA ⋅=21. 已知函数()(2)(2)x f x ax e e a =---. (1)讨论()f x 的单调性;(2)当1x >时,()0f x >,求a 的取值范围.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分. 22.选修4-4:坐标系与参数方程在直角坐标系xOy 中,直线l 的参数方程为cos 1sin x t y t αα=⎧⎨=+⎩(t 为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C 的极坐标方程为2sin 0ρθθ-=. (1)写出直线l 的普通方程及曲线C 的直角坐标方程;(2)已知点(01)P ,,点0)Q ,直线l 过点Q 且曲线C 相交于A ,B 两点,设线段AB 的中点为M,求PM的值.23.选修4-5:不等式选讲已知函数()23=-++.f x x x(1)求不等式()15f x≤的解集;(2)若2()-+≤对x∈R恒成立,求a的取值范围.x a f x广西区2018年3月高三年级第二次高考模拟联合考试数学参考答案(文科)一、选择题1-5:ADBDC 6-10:ACDBA 11、12:CC 二、填空题13.34- 14.12 15.[61)-,16.4- 三、解答题17.(1)设数列{}n a 的公差为d由题意可知3142215210S S S a a a d =++⎧⎪=⎨⎪≠⎩,整理得1112a d a =⎧⎨=⎩ ,即112a d =⎧⎨=⎩所以21n a n =-(2)由(1)知21n a n =- ,∴2n S n = ,∴416S = ,836S = , 又248n S S S= ,∴22368116n == ,∴9n = ,公比8494S q S ==18.(1)证明:∵PD ⊥ 平面ABCD ,∴PD AB ⊥ , ∵底面ABCD 是正方形,∴AB AD ⊥ ,又PDAD D = ,∴AB ⊥ 平面PAD .(2)解:∵2DE PE = ,2AD AB == ,3PD = ,∴PAE △ 的面积为11212⨯⨯= , ∴12133P ABE B PAE V V AB --==⨯⨯= 又11232C PAB P ABC V V PD AB BC --==⨯⨯⨯⨯= ∴123V V = 19.解:(1)由题意得6x = ,4y =又81241i ii x y==∑8.25≈6= ,所以88()()8iii ix x yy x yxyr ---=∑∑2418640.990.818.256-⨯⨯≈≈>⨯所以,y 与x 之间具有线性相关关系.(2)因为8182221824186449=0.7235686688i ii i i x yx yb x x==--⨯⨯==≈-⨯-∑∑,40.7260.3a y bx =-=-⨯≈-, (或490.768b =≈ ,49460.368a =-⨯≈- ) 所以y 关于x 的线性回归方程为0.70.3y x =- . 当20x = 时,0.7200.313.7y =⨯-=故可预测当宣传费用为20 万元时的利润为137 万元.20.(1)解:联立2x y =- 与3y kx =- ,得230x kx +-= , ∵21=120k ∆+> ,∴l 与抛物线2x y =- 恒有两个交点. 联立24x y =与3y kx =- ,得24120x kx -+= .∵3m ≥ ,∴22=16480k ∆-≥ ,∵0k > ,∴k ,∴k(2)证明:由(1)知,k =且24120A A x kx -+= ,∴24A x k = ,∴2A x k ==∴24A y = ,∴3A y =易知(01)F ,为抛物线24x y =的焦点,则3142A pFA y =+=+= 设11()B x y , ,22()C x y , ,则12x x k +=-=,123x x =- ,∴1212()69y y k x x +=+-=- ,212121212(3)(3)3()99y y k x kx k x x k x x =--=-++= ∴1212121212(1)(2)()116FB FC x x y y x x y y y y ⋅=+--=+-++= ∵216FA = ,∴2FB FC FA ⋅= 21.解:(1)()(2)xf x ax a e '=-+当0a = 时,()20xf x e '=-< ,∴()f x 在R 上单调递减.当0a > 时,令()0f x '< ,得2a x a -<,令()0f x '> ,得2ax a -> ∴()f x 的单调递减区间为2()a a --∞, ,单调递增区间为2()aa -+∞, , 当0a < 时,令()0f x '< ,得2a x a -> ,令()0f x '> ,得2ax a-<∴()f x 的单调递减区间为2()a a -+∞, ,单调递增区间为2()aa--∞, (2)当0a = 时,()f x 在(1)+∞,上单调递减,∴()(1)0f x f <= ,不合题意. 当0a < 时,222(2)(22)(2)(2)220f a e e a a e e e e =---=--+<,不合题意,当1a ≥ 时,()(2)0x f x ax a e '=-+> ,()f x 在(1)+∞,上单调递增, ∴()(1)0f x f >= ,故 1a ≥满足题意. 当01a << 时,()f x 在2(1)a a -, 上单调递减,在2()aa-+∞, 单调递增, ∴min 2()()(1)0af x f f a-=<= ,故01a << 不满足题意. 综上,a 的取值范围为[1)+∞,22.解:(1)由直线l 的参数方程消去t ,得l 的普通方程为sin cos cos 0x y ααα-+= ,由2sin 0ρθθ-=得22sin cos 0ρθθ-= 所以曲线C的直角坐标方程为2y = (2)易得点P 在l,所以tan 3PQ k α===-,所以56πα= 所以l的参数方程为112x y t ⎧=⎪⎪⎨⎪=+⎪⎩ ,代入2y = 中,得21640t t ++= .设A ,B ,M 所对应的参数分别为1t ,2t ,0t . 则12082t t t +==- ,所以08PM t ==23.解:(1)因为213()532212x x f x x x x --<-⎧⎪=-⎨⎪+>⎩,,≤≤, ,13x <-≤所以当3x <- 时,由()15f x ≤ 得83x -<-≤ ; 当32x -≤≤ 时,由()15f x ≤ 得32x -≤≤ ; 当2x > 时,由()15f x ≤ 得27x <≤综上,()15f x ≤ 的解集为[87]-,(2)(方法一)由2()x a f x -+≤ 得2()a x f x +≤ ,因为()(2)(3)5f x x x --+=≥ ,当且仅当32x -≤≤ 取等号, 所以当32x -≤≤ 时,()f x 取得最小值5 . 所以,当0x = 时,2()x f x + 取得最小值5 ,故5a ≤ ,即a 的取值范围为(5]-∞,(方法二)设2()g x x a =-+ ,则max ()(0)g x g a == , 当32x -≤≤ 时,()f x 的取得最小值5 , 所以当0x = 时,2()x f x + 取得最小值5 , 故5a ≤ ,即a 的取值范围为(5]-∞,。
2018年甘肃高三-高考模拟二文科数学

2018年高考真题模拟卷(含答案)文科数学 2018年高三甘肃省第二次模拟考试文科数学单选题(本大题共12小题,每小题____分,共____分。
)已知集合,,则( )A.B.C.D.函数的图象()A. 关于原点对称B. 关于直线对称C. 关于轴对称D. 关于轴对称一次函数y=-x+的图象同时经过第一、三、四象限的必要不充分条件是( )A. m>1,且n<1B. mn<0C. m>0,且n<0D. m<0,且n<0若,则的值为()A.B.C.D. -圆x2+y2-4x-4y-10=0上的点到直线x+y-14=0的最大距离与最小距离的差是( )A. 30B. 18C. 6D. 5有下列命题:①若直线l平行于平面α内的无数条直线,则直线l∥α;②若直线a在平面α外,则a∥α;③若直线a∥b,b∥α,则a∥α;④若直线a∥b,b∥α,则a平行于平面α内的无数条直线.其中真命题的个数是( )A. 1B. 2C. 3D. 4(其中)的图象如图所示,为了得到的图像,则只要将的图像()A. 向右平移个单位长度B. 向右平移个单位长度C. 向左平移个单位长度D. 向左平移个单位长度把边长为的正方形沿对角线折起,使得平面⊥平面,形成三棱锥的正视图与俯视图如图所示,则侧视图的面积为( )A.B.C.D.已知两点M(2,-3),N(-3,-2),直线l过点P(1,1)且与线段MN相交,则直线l的斜率k的取值范围是( )A. k≥或k≤-4B. -4≤k≤C. ≤k≤4D. -≤k≤4已知函数,且,则以下结论正确的是()A.B.C.D.已知为数列的前项和,且,则数列的通项公式为( )A.B.C.D.三棱锥中,平面,且,则该三棱锥的外接球的表面积是()A.B.C.D.填空题(本大题共4小题,每小题____分,共____分。
)已知点,,,则在方向上的投影为____.m>0,n>0,点(-m,n)关于直线x+y-1=0的对称点在直线x-y+2=0上,那么+的最小值等于________.15.如图所示,在三棱柱ABCA1B1C1中,AA1⊥底面ABC,AB=BC=AA1,∠ABC=90°,点E,F分别是棱AB,BB1的中点,则直线EF和BC1所成的角是________.已知函数,无论去何值,函数在区间上总是不单调,则的取值范围是____简答题(综合题)(本大题共6小题,每小题____分,共____分。
2018《试吧》高中全程训练计划·数学(文)仿真考(二)含解析

仿真考(二)高考仿真模拟冲刺卷(B)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分.考试时间120分钟.第Ⅰ卷(选择题共60分)一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合M={x|-1〈x<1},N={x|x2<2,x∈Z},则( )A.M⊆N B.N⊆M C.M∩N={0}D.M∪N=N2.已知复数z=错误!,其中i为虚数单位,则|z|=()A。
错误!B.1 C.错误!D.23.不等式组错误!的解集记为D,若(a,b)∈D,则z=2a-3b的最小值是( )A.-4 B.-1 C.1 D.44.若f(x)是定义在R上的函数,则“f(0)=0”是“函数f(x)为奇函数”的( )A.必要不充分条件B.充要条件C.充分不必要条件D.既不充分也不必要条件5.若命题“∃x0∈R,x20+(a-1)x0+1<0”是真命题,则实数a的取值范围是( )A.[-1,3] B.(-1,3)C.(-∞,-1]∪[3,+∞) D.(-∞,-1)∪(3,+∞)6.使错误!n(n∈N*)展开式中含有常数项的n的最小值是( )A.3 B.4 C.5 D.67.已知函数f(x)=sin(2x+φ)错误!的图象的一个对称中心为错误!,则函数f(x)的单调递减区间是()A。
错误!(k∈Z) B.错误!(k∈Z)C。
错误!(k∈Z) D.错误!(k∈Z)8.(2017·滨州二模)函数y=错误!,x∈(-π,0)∪(0,π)的图象大致是()9.已知球O的半径为R,A,B,C三点在球O的球面上,球心O 到平面ABC的距离为错误!R,AB=AC=2,∠BAC=120°,则球O 的表面积为( )A.错误!π B。
错误!π C。
错误!π D.错误!π10.如图,网格纸上的小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的体积是( )A.4+6π B.8+6π C.4+12π D.8+12π11.已知抛物线y2=2px的焦点F与双曲线x27-错误!=1的右焦点重合,抛物线的准线与x轴的交点为K,点A在抛物线上且|AK|=错误!|AF|,则△AFK的面积为()A.4 B.8 C.16 D.3212.设定义在(0,+∞)上的函数f(x)满足xf′(x)-f(x)=x ln x,f错误!=错误!,则f(x)()A.有极大值,无极小值B.有极小值,无极大值C.既有极大值,又有极小值D.既无极大值,又无极小值第Ⅱ卷(非选择题共90分)本卷包括必考题和选考题两部分.第13~21题为必考题,每个试题考生都必须作答,第22~23题为选考题,考生根据要求作答.二、填空题:本大题共4小题,每小题5分,共20分.把答案填在题中的横线上.13.高为π,体积为π2的圆柱的侧面展开图的周长为________.14.过点P(3,1)的直线l与圆C:(x-2)2+(y-2)2=4相交于A,B两点,当弦AB的长取最小值时,直线l的倾斜角等于________.15.已知平面向量a与b的夹角为错误!,a=(1,错误!),|a-2b|=2错误!,则|b|=________。
山西省太原市2018届高考二模文科数学试题含答案

太原市2018年高三年级模拟试题(二)文科数学一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合{|12}A x x =-≤≤,B N =,则集合A B 的子集的个数是( )A . 4B . 6C .8D .162.2(2)(1)12i i i+-=-() A .2 B . -2 C .13 D .13- 3.设等比数列{}n a 的前n 项和n S ,则“10a >” 是“32S S >”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要 4.下列函数中,既是奇函数又在(0,)+∞上单调递增的函数是( ) A . x x y e e -=+ B .ln(||1)y x =+ C.sin ||x y x =D .1y x x =-5. 公元263年左右,我国数学家刘徽发现当圆内接正多边形无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”,利用“割圆术”,刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”,如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出n 的值为( )(参考数据:0sin150.2588≈,0sin 7.50.1305≈)A . 6B .12 C. 24 D .486.某班从3名男生和2名女生中任意抽取2名学生参加活动,则抽到2名学生性别相同的概率是( ) A .35 B .25 C. 310 D .127.已知椭圆2222:1(0)x y C a b a b+=>>的半焦距为c ,原点O 到经过两点(,0),(0,)c b 的直线的距离为2c,则椭圆的离心率为( ) A .12 D8. 已知 1.12a =,0.45b =,5ln2c =,则( ) A . b c a >> B .a c b >> C.b a c >> D .a b c >> 9.已知函数()sin f x a x x =的一条对称轴为6x π=-,若12()()4f x f x =-,则12||x x +的最小值为( )A .3π B . 2π C. 23π D .34π10.已知实数,x y 满足00220y x y x y ≥⎧⎪+≤⎨⎪++≤⎩,若10ax y a -+-≥恒成立,则实数a 的取值范围是( )A . (,2]-∞-B . 1(1,]2- C. (,1]-∞- D .1(,]3-∞- 11.某空间几何体的三视图如图所示,则该几何体的体积为( )A .73π B .83π- C.73π- D .83π 12.已知函数32()f x x ax bx =++有两个极值点12,x x ,且12x x <,若10223x x x +=,则函数0()()()g x f x f x =-()A .恰有一个零点B .恰有两个零点 C.恰有三个零点 D .零点个数不确定二、填空题(每题5分,满分20分,将答案填在答题纸上)13.已知非零向量,a b 满足||2||a b =,且()(3)a b a b -⊥+,则向量,a b 的夹角的余弦值为.14.双曲线22221x y a b-=(0,0)a b >> 上一点(3,4)M -关于一条渐近线的对称点恰为双曲线的右焦点2F ,则该双曲线的标准方程为.15.已知菱形ABCD 中,AB =060BAD ∠=,沿对角线BD 折成二面角A BD C --为060的四面体,则四面体ABCD 的外接球的表面积为.16.数列{}n a 中,若12a =,121n n a a +=+,21n n n b a b +=-,*n N ∈,则数列{||}n b 的前n 项和为.三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17. 已知ABC ∆的内角,,A B C 的对边分别为,,a b c ,且tan 3(cos cos )a A c B b C =+. (1)求角A ;(2)若点D 满足2AD AC =,且3BD =,求2b c +的取值范围.18. 按照国家质量标准:某种工业产品的质量指标值落在[100,120)内,则为合格品,否则为不合格品. 某企业有甲乙两套设备生产这种产品,为了检测这两套设备的生产质量情况,随机从两套设备生产的大量产品中各抽取了50件产品作为样本,对规定的质量指标值进行检测.表1是甲套设备的样本频率分布表,图1是乙套设备的样本频率分布直方图.(1)将频率视为概率,若乙套设备生产了5000件产品,则其中的不合格品约有多少件; (2)填写下面列联表,并根据列联表判断是否有90%的把握认为这种产品的质量指标值与甲、乙两套设备的选择有关;(2)根据表1和图1,对甲、乙两套设备的优劣进行比较; 附:19. 四棱锥P ABCD -中,平面PAD ⊥平面ABCD ,底面ABCD 为梯形,//AB CD ,223AB DC ==ACBD F =,PAD ∆与ABD ∆均为正三角形,E 为AD 的中点,G为PAD ∆的重心.(1)求证://GF 平面PDC ; (2)求三棱锥G PCD -的体积.20. 已知以点(0,1)C 为圆心的动圆C 与y 轴负半轴交于点A ,其弦AB 的中点D 恰好落在x 轴上.(1)求点B 的轨迹E 的方程;(2)过直线1y =-上一点P 作曲线E 的两条切线,切点分别为,M N ,求证:直线MN 过定点.21.已知函数()ln (0)xf x m x e m -=-≠.(1)若函数()f x 是单调函数,求实数m 的取值范围;(2)证明:对于任意的正实数,a b ,当a b >时,都有111a ba e e b--->-. 请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分. 22.选修4-4:坐标系与参数方程已知点P 是曲线221:(2)4C x y -+=上的动点,以坐标原点O 为极点,以x 轴正半轴为极轴,建立极坐标系,以极点O 为中心,将点P 逆时针旋转090得到点Q ,设点Q 的轨迹方程为曲线2C .(1)求曲线1C ,2C 的极坐标方程; (2)射线(0)3πθρ=>与曲线1C ,2C 分别交于,A B 两点,定点(2,0)M ,求MAB ∆的面积.23.选修4-5:不等式选讲 已知实数,a b 满足2244a b +=. (1)求证:212a b +≤;(2)若对任意,a b R ∈,|1||3|x x ab +--≤恒成立,求实数x 的取值范围.参考答案一、选择题1-5: CADDC 6-10: BADCC 11、12:BB 二、填空题221520x y -= 15. 156π 16.4(21)n ⨯- 三、解答题17.(1)∵tan cos cos )a A c B b C + ∴sin tan 3(sin cos sin cos )A A C B B C + ∴sin tan 3sin()3sin A A C B A += ∵0A π<<,∴sin 0A ≠ ∴tan 3A =060A =(2)在ABD ∆中,根据余弦定理得:2222cos AD AB BD AD AB A +-=即22(2)92b c bc +-= ∴2(2)96b c bc +-=又222()2b c bc +≤,∴22(2)922()33b c b c bc +-+-≤ ∴2(2)36b c +≤,∴26b c +≤ 又23b c +>,∴326b c <+≤.18.(1)由图1知,乙套设备生产的不合格品率约为750, ∴乙套设备生产的5000件产品中不合格品约为7500070050⨯=(件) (2)根据表1和图1得到列联表:将列联表中的数据代入公式计算得:222()100(487243) 3.053()()()()5050919n ad bc K a b c d a c b d -⨯⨯-⨯==≈++++⨯⨯⨯∵3.053 2.706>,∴有90%的把握认为产品的质量指标值与甲、乙两套设备的选择有关. (3)根据表1和图1可知,甲套设备生产的合格品的概率约为4850,乙套设备生产的合格品的概率约为4350,甲套设备生产的产品的质量指标值主要集中在[105,115)之间,乙套设备生产的产品的质量指标值与甲套设备相比较为分散,因此,可以认为甲套设备生产的合格品的概率更高,且质量指标值更稳定,从而甲套设备优于乙套设备. 19.(1)连接AG 并延长交PD 于H ,连接CH , 梯形ABCD 中,∵//AB CD 且2AB DC =,∴21AE FC = 又G 为PAD ∆的重心,∴21AG GH = 在AHC ∆中,21AG AF GH FC ==,故//GF HC 又HC ⊆平面PCD ,GF ⊄平面PCD ,∴//GF 平面PCD .(2)∵平面PAD ⊥平面ABCD ,PAD ∆与ABD ∆均为正三角形,E 为AD 的中点, ∴PE AD ⊥,∴PE ⊥平面ABCD ,且3PE =,由(1)知,//GF 平面PDC ,∴13G PCD F PCD F CDP CDF V V V PE S ---∆===⨯⨯又由梯形ABCD ,//AB CD 且2AB DC ==13DF BD ==又ABD ∆为正三角形,得060CDF ABD ∠=∠=∴1sin 2CDF S CD DF FDC ∆=⨯⨯⨯∠=∴132P CDF CDF V PE S -∆=⨯⨯=,∴三棱锥G PCD -的体积为220.(1)设(,)B x y ,则AB 的中点(,0)2xD ,0y >, 因为(0,1)C ,则(,1)2x DC =-,(,)2xDB y =, 在圆C 中,因为DC DB ⊥,∴0DC DB ∙=,所以204x y -+=,即24(0)x y y => 所以点B 的轨迹E 的方程为24(0)x y y =>. (2)证明:由已知条件可得曲线E 的方程为24x y = 设点(,1)P t -,11(,)M x y ,22(,)N x y ,∵24x y =,∴'2x y =∴过点,M N 的切线方程分别为111()2x y y x x -=-,222()2xy y x x -=-, 由2114y x =,22224y x =,上述切线方程可化为112()y y x x +=,222()y y x x +=, ∵点P 在这两条切线上,∴112(1)y tx -=,222(1)y tx -=, 即直线MN 的方程为2(1)y tx -=, 故直线2(1)y tx -=过定点(0,1)C . 21.(1)函数()f x 的定义域为(0,)+∞∵()ln xf x m x e -=-,∴'()x x m m xe f x e x x--+=+=∵函数()f x 是单调函数,∴'()0f x ≤在(0,)+∞上恒成立或'()0f x ≥在(0,)+∞上恒成立,①若'()0f x ≤,则0x m xe x-+≤,即0x m xe -+≤,x x x m xe e -≤-=, 令()x x x e ϕ=-,则1'()xx x e ϕ-=,当01x <<时,'()0x ϕ<;当1x >时,'()0x ϕ>则()x ϕ在(0,1)上递减,(1,)+∞上递增,∴min 1()(1)x e ϕϕ==-,∴1m e≤-②若'()0f x ≥,则0x m xe x-+≥,即0x m xe -+≥,x x xm xe e -≥-= 由①得()xxx e ϕ=-在(0,1)上递减,(1,)+∞上递增, 又(0)0ϕ=,x →+∞时,()0x ϕ<,∴0m >综上可知,1m e≤-或0m > (2)由(1)知,当1m e =-时,1()ln xf x x e e-=--在(0,)+∞上递减∵0b a <<,∴()()f b f a >,即11ln ln b ab e a e e e---->--,∴11ln ln a b e e b a --->-要证111a ba e eb --->-,只需证ln ln 1a b a b -≥-,即证ln 1b a a b>-令b t a =,(0,1)t ∈,则需证1ln 1t t >-,令1()ln 1h t t t =+-,则21'()0t h t t-=<∴()h t 在(0,1)上递减,又(1)0h = ∴()0h t >,即1ln 1t t>-,得证.22. (1)曲线1C 的极坐标方程为=4cos ρθ. 设(,)Q ρθ,(,)2P πρθ-,于是4cos()4sin 2πρθθ=-=, 所以,曲线2C 的极坐标方程为4sin ρθ=.(2)M 到射线3πθ=的距离为2sin3d π==||4(sincos )1)33B A AB P P ππ=-=-=,则1||32S AB d =⨯=23. (1)证明:222441||24a b a b a +++≤=≤=.(2)由2244a b +=及2244||a b ab +≥=,可得||1ab ≤,所以1ab ≥-,当且仅当a =b =或a =b =. 因为对任意,a b R ∈,|1||3|x x ab +--≤恒成立,所以|1||3|1x x +--≤-.当1x ≤-时,|1||3|4x x +--=-,不等式|1||3|1x x +--≤-恒成立;当13x -<<时,|1||3|22x x x +--=-,由13221x x -<<⎧⎨-≤-⎩,得112x -<≤;当3x ≥时,|1||3|4x x +--=,不等式|1||3|1x x +--≤-不成立; 综上可得,实数x 的取值范围是12x ≤.。
2018届高考文科数学全国统考仿真试卷二带答案

2018届高考文科数学全国统考仿真试卷(二)带答案绝密★启用前2018年普通高等学校招生全国统一考试仿真卷文科数学(二)本试题卷共8页,23题(含选考题)。
全卷满分150分。
考试用时120分钟。
★祝考试顺利★注意事项:1、答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
用2B铅笔将答题卡上试卷类型A后的方框涂黑。
2、选择题的作答:每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3、填空题和解答题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4、选考题的作答:先把所选题目的题号在答题卡上指定的位置用2B铅笔涂黑。
答案写在答题卡上对应的答题区域内,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
5、考试结束后,请将本试题卷和答题卡一并上交。
第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设是虚数单位,若复数,则的共轭复数为()A.B.C.D.2.若双曲线的一个焦点为,则()A.B.C.D.3.将函数的图像向左平移个单位后,得到函数的图像,则()A.B.C.D.4.函数,的值域为,在区间上随机取一个数,则的概率是()A.B.C.D.15.已知变量和的统计数据如下表:根据上表可得回归直线方程,据此可以预报当时,()A.8.9B.8.6C.8.2D.8.16.一个几何体的三视图如图所示,则该几何体的体积为()A.B.C.D.87.《九章算术》是我国古代的数学名著,书中有如下问题:“今有大夫、不更、簪裹、上造、公士,凡五人,共猎得五鹿,欲以爵次分之,问各得几何?”其意思:“共有五头鹿,5人以爵次进行分配(古代数学中“以爵次分之”这种表述,一般表示等差分配,在本题中表示等差分配).”在这个问题中,若大夫得“一鹿、三分鹿之二”,则簪裹得()A.一鹿、三分鹿之一B.一鹿C.三分鹿之二D.三分鹿之一8.函数的部分图像大致为()A.B.C.D.9.阅读如图所示的程序框图,运行相应程序,输出的结果是()A.12B.18C.120D.12510.设,满足约束条件,若目标函数仅在点处取得最小值,则的取值范围为()A.B.C.D.11.已知抛物线的焦点为,其准线与双曲线相交于,两点,若为直角三角形,其中为直角顶点,则()A.B.C.D.612.若关于的不等式在上恒成立,则实数的取值范围为()A.B.C.D.第Ⅱ卷本卷包括必考题和选考题两部分。
2018年高考数学二模试卷(文科)带答案精讲

2018年高考数学二模试卷(文科)一、选择题(共11小题,每小题5分,满分55分)1.(5分)设等差数列{a n}的前n项和为S n,若a4=9,a6=11,则S9等于()A.180 B.90 C.72 D.102.(5分)在样本的频率分布直方图中,共有5个长方形,若中间一个小长方形的面积等于其它4个小长方形的面积和的,且样本容量为100,则正中间的一组的频数为()A.80 B.0.8 C.20 D.0.23.(5分)在△ABC中,C=60°,AB=,那么A等于()A.135°B.105°C.45°D.75°4.(5分)已知:如图的夹角为的夹角为30°,若等于()A.B.C.D.25.(5分)若集合,B={1,m},若A⊆B,则m的值为()A.2 B.﹣1 C.﹣1或2 D.2或6.(5分)设α、β是两个不同的平面,l、m为两条不同的直线,命题p:若平面α∥β,l⊂α,m⊂β,则l∥m;命题q:l∥α,m⊥l,m⊂β,则β⊥α,则下列命题为真命题的是()A.p或q B.p且q C.¬p或q D.p且¬q7.(5分)已知x,y满足约束条件的最小值是()A.B.C.D.18.(5分)2011年某通讯公司推出一组手机卡号码,卡号的前七位数字固定,后四位数从“0000”到“9999”共10000个号码.公司规定:凡卡号的后四位恰带有两个数字“6”或恰带有两个数字“8”的一律作为“金兔卡”,享受一定优惠政策.如后四位数为“2663”、“8685”为“金兔卡”.则这组号码中“金兔卡”的张数()A.484 B.972 C.966 D.4869.(5分)有三个命题①函数的反函数是y=(x+1)2(x∈R)②函数f(x)=lnx+x﹣2的图象与x轴有2个交点;③函数的图象关于y轴对称.其中真命题是()A.①③B.②C.③D.②③10.(5分)若长度为定值的线段AB的两端点分别在x轴正半轴和y轴正半轴上移动,O为坐标原点,则△OAB的重心、内心、外心、垂心的轨迹不可能是()A.点B.线段C.圆弧D.抛物线的一部分11.(5分)若关于x的不等式|x﹣1|<ax(a≠0)的解集为开区间(m,+∞),其中m∈R,则实数a的取值范围为()A.a≥1 B.a≤﹣1 C.0<a<1 D.﹣1<a<0二、填空题(共5小题,每小题5分,满分25分)12.(5分)一个与球心距离为1的平面截球所得的圆面面积为2π,则球的表面积为.13.(5分)已知二项式展开式中的项数共有九项,则常数项为.14.(5分)已知过椭圆的右焦点在双曲线的右准线上,则双曲线的离心率为.15.(5分)函数,在区间(﹣π,π)上单调递增,则实数φ的取值范围为.16.(5分)在数学中“所有”一词,叫做全称量词,用符号“∀”表示;“存在”一词,叫做存在量词,用符号“∃”表示.设.①若∃x0∈(2,+∞),使f(x0)=m成立,则实数m的取值范围为;②若∀x1∈(2,+∞),∃x2∈(2,+∞)使得f(x1)=g(x2),则实数a的取值范围为.三、解答题(共6小题,满分70分)17.(12分)已知=(cosx+sinx,sinx),=(cosx﹣sinx,2cosx).(I)求证:向量与向量不可能平行;(II)若•=1,且x∈[﹣π,0],求x的值.18.(12分)已知某高中某班共有学生50人,其中男生30人,女生20人,班主任决定用分层抽样的方法在自己班上的学生中抽取5人进行高考前心理调查.(I)求男生被抽取的人数和女生被抽取的人数;(I)若从这5人中选取2人作为重点调查对象,求至少选取1个男生的概率;(II)若本班学生考前心理状态好的概率为0.8,求调查中恰有3人心理状态良好的概率.19.(12分)如图所示,在正方体ABCD﹣A1B1C1D1中,AB=a,E为棱A1D1中点.(I)求二面角E﹣AC﹣B的正切值;(II)求直线A1C1到平面EAC的距离.20.(12分)已知f(x)=tx3﹣2x2+1.(I)若f′(x)≥0对任意t∈[﹣1,1]恒成立,求x的取值范围;(II)求t=1,求f(x)在区间[a,a+3](a<0)上的最大值h(a).21.(12分)已知{a n}是正数组成的数列,a1=1,且点在函数y=x2+1的图象上.数列{b n}满足b1=0,b n+1=b n+3an(n∈N*).(Ⅰ)求数列{a n},{b n}的通项公式;(Ⅱ)若c n=a n b n cosnπ(n∈N*),求数列{c n}的前n项和S n.22.(10分)若圆C过点M(0,1)且与直线l:y=﹣1相切,设圆心C的轨迹为曲线E,A、B为曲线E上的两点,点.(Ⅰ)求曲线E的方程;(Ⅱ)若t=6,直线AB的斜率为,过A、B两点的圆N与抛物线在点A处共同的切线,求圆N的方程;(Ⅲ)分别过A、B作曲线E的切线,两条切线交于点Q,若点Q恰好在直线l 上,求证:t与均为定值.参考答案与试题解析一、选择题(共11小题,每小题5分,满分55分)1.(5分)设等差数列{a n}的前n项和为S n,若a4=9,a6=11,则S9等于()A.180 B.90 C.72 D.10【分析】由a4=9,a6=11利用等差数列的性质可得a1+a9=a4+a6=20,代入等差数列的前n项和公式可求.【解答】解:∵a4=9,a6=11由等差数列的性质可得a1+a9=a4+a6=20故选B【点评】本题主要考查了等差数列的性质若m+n=p+q,则a m+a n=a p+a q和数列的求和.解题的关键是利用了等差数列的性质:利用性质可以简化运算,减少计算量.2.(5分)在样本的频率分布直方图中,共有5个长方形,若中间一个小长方形的面积等于其它4个小长方形的面积和的,且样本容量为100,则正中间的一组的频数为()A.80 B.0.8 C.20 D.0.2【分析】由已知中在样本的频率分布直方图中,共有5个长方形,若中间一个小长方形的面积等于其它4个小长方形的面积和的,我们出该组的频率,进而根据样本容量为100,求出这一组的频数.【解答】解:∵样本的频率分布直方图中,共有5个长方形,又∵中间一个小长方形的面积等于其它4个小长方形的面积和的,则该长方形对应的频率为0.2又∵样本容量为100,∴该组的频数为100×0.2=20故选C【点评】本题考查的知识点是频率分布直方图,其中根据各组中频率之比等于面积之比,求出该组数据的频率是解答本题的关键.3.(5分)在△ABC中,C=60°,AB=,那么A等于()A.135°B.105°C.45°D.75°【分析】由C的度数求出sinC的值,再由c和a的值,利用正弦定理求出sinA 的值,由c大于a,根据大边对大角,得到C大于A,得到A的范围,利用特殊角的三角函数值即可求出A的度数.【解答】解:∵C=60°,AB=c=,BC=a=,∴由正弦定理=得:sinA===,又a<c,得到A<C=60°,则A=45°.故选C【点评】此题考查了正弦定理,三角形的边角关系,以及特殊角的三角函数值,熟练掌握正弦定理是解本题的关键.4.(5分)已知:如图的夹角为的夹角为30°,若等于()A.B.C.D.2【分析】将向量沿与方向利用平行四边形原则进行分解,构造出三角形,由题目已知,可得三角形中三边长及三个角,然后解三角形即可得到答案.【解答】解:如图所示:根据平行四边形法则将向量沿与方向进行分解,则由题意可得OD=λ,CD=μ,∠COD=30°,∠OCD=90°,∠Rt△OCD中,sin∠COD=sin30°===,∴=2,故选D.【点评】对一个向量根据平面向量基本定理进行分解,关键是要根据平行四边形法则,找出向量在基底两个向量方向上的分量,再根据已知条件构造三角形,解三角形即可得到分解结果.5.(5分)若集合,B={1,m},若A⊆B,则m的值为()A.2 B.﹣1 C.﹣1或2 D.2或【分析】由已知中集合,解根式方程可得A={2},结合B={1,m},及A⊆B,结合集合包含关系的定义,可得m的值.【解答】解:∵集合={2}又∵B={1,m}若A⊆B则m=2故选A【点评】本题考查的知识点是集合关系中的参数取值问题,其中解根式方程确定集合A是解答本题的关键,解答中易忽略根成有意义的条件,而错解为A={﹣1}6.(5分)设α、β是两个不同的平面,l、m为两条不同的直线,命题p:若平面α∥β,l⊂α,m⊂β,则l∥m;命题q:l∥α,m⊥l,m⊂β,则β⊥α,则下列命题为真命题的是()A.p或q B.p且q C.¬p或q D.p且¬q【分析】对于命题p,q,只要把相应的平面和直线放入长方体中,找到反例即可.【解答】解:在长方体ABCD﹣A1B1C1D1中命题p:平面AC为平面α,平面A1C1为平面β,直线A1D1,和直线AB分别是直线m,l,显然满足α∥β,l⊂α,m⊂β,而m与l异面,故命题p不正确;﹣p正确;命题q:平面AC为平面α,平面A1C1为平面β,直线A1D1,和直线AB分别是直线m,l,显然满足l∥α,m⊥l,m⊂β,而α∥β,故命题q不正确;﹣q正确;故选C.【点评】此题是个基础题.考查面面平行的判定和性质定理,要说明一个命题不正确,只需举一个反例即可,否则给出证明;考查学生灵活应用知识分析解决问题的能力.7.(5分)已知x,y满足约束条件的最小值是()A.B.C.D.1【分析】本题属于线性规划中的延伸题,对于可行域不要求线性目标函数的最值,而是求可行域内的点与原点(0,0)构成的线段的长度问题,注意最后要平方.【解答】解:先根据约束条件画出可行域,z=x2+y2,表示可行域内点到原点距离OP的平方,点P到直线3x+4y﹣4=0的距离是点P到区域内的最小值,d=,∴z=x2+y2的最小值为故选B.【点评】本题利用直线斜率的几何意义,求可行域中的点与原点的斜率.本题主要考查了用平面区域二元一次不等式组,以及简单的转化思想和数形结合的思想,属中档题.巧妙识别目标函数的几何意义是我们研究规划问题的基础,纵观目标函数包括线性的与非线性,非线性问题的介入是线性规划问题的拓展与延伸,使得规划问题得以深化.8.(5分)2011年某通讯公司推出一组手机卡号码,卡号的前七位数字固定,后四位数从“0000”到“9999”共10000个号码.公司规定:凡卡号的后四位恰带有两个数字“6”或恰带有两个数字“8”的一律作为“金兔卡”,享受一定优惠政策.如后四位数为“2663”、“8685”为“金兔卡”.则这组号码中“金兔卡”的张数()A.484 B.972 C.966 D.486【分析】据题意,对卡号的后4位分3种情况讨论:①、后4位中含有2个8,进而细分为1°其他数字不重复,2°其他数字也相同,由排列、组合数公式可得其情况数目,②、后4位中含有2个6的卡片,同①可得其情况数目,③、含有2个8、2个6,由组合数公式可得其情况数目;最后由事件之间的关心计算可得答案.【解答】解:根据题意,对卡号的后4位分3种情况讨论:①、后4位中含有2个8,1°若其他数字不重复,在其中任取2个其他的数字,与2个8进行全排列,有×A44×C92种情况,2°若其他数字也相同,易得有9×C42种情况,共有×A44×C92+9×C42=486张,②、同理后4位只中含有2个6的卡片有486张,③、后4位中含有2个8、2个6,有C42=6张,共有486+486﹣6=966张;故选C.【点评】本题考查分步计数原理的应用,考查带有约束条件的数字问题,分类讨论时,注意事件之间的关系,要做到不重不漏.9.(5分)有三个命题①函数的反函数是y=(x+1)2(x∈R)②函数f(x)=lnx+x﹣2的图象与x轴有2个交点;③函数的图象关于y轴对称.其中真命题是()A.①③B.②C.③D.②③【分析】对于①,欲求原函数y=﹣1(x≥0)的反函数,即从原函数式中反解出x,后再进行x,y互换,即得反函数的解析式.对于②,利用函数f(x)的单调性,与函数的零点与方程的根判断即可;对于③,通过函数f(x)的奇偶性判断即可.【解答】解:对于①,∵y=﹣1(x≥0),∴x=(y+1)2(y≥﹣1),∴x,y互换,得y=(x+1)2(x≥﹣1).故不正确.对于②,考察f(x)的单调性,lnx和x﹣2在(0,+∞)上是增函数,故f(x)=lnx+x﹣2在(0,+∞)上是增函数,图象与x轴最多有1个交点,故不正确.对于③,函数的定义域为[﹣3,3],所以,函数化简为:y=是偶函数,图象关于y轴对称,正确.故选C.【点评】本小题主要考查函数单调性的应用、函数奇偶性的应用、反函数等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.10.(5分)若长度为定值的线段AB 的两端点分别在x 轴正半轴和y 轴正半轴上移动,O 为坐标原点,则△OAB 的重心、内心、外心、垂心的轨迹不可能是( ) A .点 B .线段 C .圆弧D .抛物线的一部分【分析】本题是个选择题,利用排除法解决.首先由△OAB 的重心,排除C ;再利用△OAB 的内心,排除B ;最后利用△OAB 的垂心,排除A ;即可得出正确选项.【解答】解:设重心为G ,AB 中点为C ,连接OC .则OG=OC (这是一个重心的基本结论).而OC=AB=定值,所以G 轨迹圆弧. 排除C ;内心一定是平分90度的那条角平分线上,轨迹是线段.排除B ;外心是三角形外接圆圆心,对于这个直角三角形,AB 中点C 就是三角形外接圆圆心,OC 是定值, 所以轨迹圆弧,排除C ; 垂心是原点O ,定点,排除A 故选D .【点评】本题考查三角形的重心、内心、外心、垂心、以及轨迹的求法.解选择题时可利用排除法.11.(5分)若关于x 的不等式|x ﹣1|<ax (a ≠0)的解集为开区间(m ,+∞),其中m ∈R ,则实数a 的取值范围为( ) A .a ≥1B .a ≤﹣1C .0<a <1D .﹣1<a <0【分析】在同一坐标系中做出函数 y=|x |和 函数y=ax 的图象,由题意结合图形可得实数a 的取值范围.【解答】解:∵关于x 的不等式|x ﹣1|<ax (a ≠0)的解集为 开区间(m ,+∞),其中m ∈R ,在同一坐标系中做出函数y=|x﹣1|和函数y=ax的图象,如图所示:结合图象可得a≥1.故选:A.【点评】本题主要考查绝对值不等式的解法,体现了数形结合的数学思想,画出图形,是解题的关键,属于中档题.二、填空题(共5小题,每小题5分,满分25分)12.(5分)一个与球心距离为1的平面截球所得的圆面面积为2π,则球的表面积为12π.【分析】求出截面圆的半径,利用勾股定理求出球的半径,然后求出球的表面积.【解答】解:由题意可知截面圆的半径为:r,所以πr2=2π,r=,由球的半径,球心到截面圆的距离,截面圆的半径,满足勾股定理,所以球的半径为:R==.所求球的表面积为:4πR2=12π.故答案为:12π.【点评】本题考查球与球的截面以及球心到截面的距离的关系,是本题的解题的关键,考查计算能力.13.(5分)已知二项式展开式中的项数共有九项,则常数项为1120.【分析】根据展开式中的项数共有九项可求出n的值是8.利用二项展开式的通项公式求出通项,令x的指数为0,求出r,将r的值代入通项求出展开式的常数项.【解答】解:∵二项式展开式中的项数共有九项∴n=8=2r C8r x4﹣r展开式的通项为T r+1令4﹣r=0得r=4所以展开式的常数项为T5=24C84=1120故答案为:1120.【点评】本题考查利用二项展开式的通项公式解决二项展开式的特定项问题,解答关键是求出n的值,属于中档题.14.(5分)已知过椭圆的右焦点在双曲线的右准线上,则双曲线的离心率为.【分析】先由题设条件求出椭圆的焦点坐标和双曲线的准线方程,列出关于b 的方程求出b,从而得到a和c,再利用a和c求出双曲线的离心率.【解答】解:由题设条件可知椭圆的右焦点坐标为(2,0),双曲线的右准线方程为x=,∴,解得b=2.则双曲线的离心率为.故答案为:.【点评】本题是双曲线的椭圆的综合题,难度不大,只要熟练掌握圆锥曲线的性质就行.15.(5分)函数,在区间(﹣π,π)上单调递增,则实数φ的取值范围为.【分析】求出函数的单调增区间,通过子集关系,确定实数φ的取值范围.【解答】解:函数,由2kπ﹣πφ≤2kπ,可得6kπ﹣3π﹣3φ≤x≤6kπ﹣3φ,由题意在区间(﹣π,π)上单调递增,所以6kπ﹣3π﹣3φ≤﹣π 且π≤6kπ﹣3φ,因为0<φ<2π,所以k=1,实数φ的取值范围为;故答案为:【点评】本题是基础题,考查三角函数的单调性的应用,子集关系的理解,考查计算能力.16.(5分)在数学中“所有”一词,叫做全称量词,用符号“∀”表示;“存在”一词,叫做存在量词,用符号“∃”表示.设.①若∃x0∈(2,+∞),使f(x0)=m成立,则实数m的取值范围为(,+∞);②若∀x1∈(2,+∞),∃x2∈(2,+∞)使得f(x1)=g(x2),则实数a的取值范围为不存在.【分析】①先对函数配方,求出其对称轴,判断出其在给定区间上的单调性进而求出函数值的范围,即可求出实数m的取值范围;②先利用单调性分别求出两个函数的值域,再比较即可求出实数a的取值范围.【解答】解:因为f(x)==,(2,+∞),f(x)>f(2)=;g(x)=a x,(a>1,x>2).g(x)>g(2)=a2.①∵∃x0∈(2,+∞),使f(x0)=m成立,∴m;②∵∀x1∈(2,+∞),∃x2∈(2,+∞)使得f(x1)=g(x2),∴⇒a不存在.故答案为:(,+∞):不存在.【点评】本题主要考查函数恒成立问题以及借助于单调性研究函数的值域,是对基础知识的综合考查,属于中档题目.三、解答题(共6小题,满分70分)17.(12分)已知=(cosx+sinx,sinx),=(cosx﹣sinx,2cosx).(I)求证:向量与向量不可能平行;(II)若•=1,且x∈[﹣π,0],求x的值.【分析】(I)先假设两个向量平行,利用平行向量的坐标表示,列出方程并用倍角和两角和正弦公式进行化简,求出一个角的正弦值,根据正弦值的范围推出矛盾,即证出假设不成立;(II)利用向量数量积的坐标表示列出式子,并用倍角和两角和正弦公式进行化简,由条件和已知角的范围进行求值.【解答】解:(I)假设∥,则2cosx(cosx+sinx)﹣sinx(cosx﹣sinx)=0,1+cosxsinx+cos2x=0,即1+sin2x+=0,∴sin(2x+)=﹣3,解得sin(2x+)=﹣<﹣1,故不存在这种角满足条件,故假设不成立,即与不可能平行.(II)由题意得,•=(cosx+sinx)(cosx﹣sinx)+2cosxsinx=cos2x+sin2x=sin (2x+)=1,∵x∈[﹣π,0],∴﹣2π≤2x≤0,即≤,∴=﹣或,解得x=或0,故x的值为:或0.【点评】本题考查了向量共线和数量积的坐标运算,主要利用了三角恒等变换的公式进行化简,对于存在性的题目一般是先假设成立,根据题意列出式子,再通过运算后推出矛盾,是向量和三角函数相结合的题目.18.(12分)已知某高中某班共有学生50人,其中男生30人,女生20人,班主任决定用分层抽样的方法在自己班上的学生中抽取5人进行高考前心理调查.(I)求男生被抽取的人数和女生被抽取的人数;(I)若从这5人中选取2人作为重点调查对象,求至少选取1个男生的概率;(II)若本班学生考前心理状态好的概率为0.8,求调查中恰有3人心理状态良好的概率.【分析】(Ⅰ)根据题意,可得抽取的比例为,由分层抽样的性质,计算可得答案;(Ⅱ)由(Ⅰ)的结论,男生被抽取人数为3人,女生被抽取人数为2人,分析可得“至少选取1个男生”与“没有1个男生”即“选取的都是2个女生”为对立事件;先计算“选取的都是2个女生”的概率,进而由对立事件的概率性质,计算可得答案;(Ⅲ)根据题意,分析可得:本题为在5次独立重复试验中恰有3次发生,由其公式,计算可得答案.【解答】解:(Ⅰ)根据题意,在50人中抽取了5人,抽取的比例为;则抽取男生30×=3,女生20×=2;即男生被抽取人数为3人,女生被抽取人数为2人;(Ⅱ)由(Ⅰ)得,男生被抽取人数为3人,女生被抽取人数为2人,“至少选取1个男生”与“没有1个男生”即“2个女生”为对立事件;选取的两名学生都是女生的概率P==,∴所求的概率为1﹣P=;(Ⅲ)根据题意,本班学生的考前心理状态良好的概率为0.8,则抽出的5人中,恰有3人心理状态良好,即在5次独立重复试验中恰有3次发生,则其概率为C53×()3×()2=.【点评】本题主要考查排列n次独立重复实验中恰有k次发生的概率计算,涉及分层抽样与对立事件的概率计算;需要牢记各个公式,并做到“对号入座”.19.(12分)如图所示,在正方体ABCD﹣A1B1C1D1中,AB=a,E为棱A1D1中点.(I)求二面角E﹣AC﹣B的正切值;(II)求直线A1C1到平面EAC的距离.【分析】(I)取AD的中点H,连接EH,则EH⊥平面ABCD,过H作HF⊥AC与F,连接EF,我们可得∠EFH即为二面角E﹣AC﹣B的补角,解三角形EFH后,即可求出二面角E﹣AC﹣B的正切值;(II)直线A1C1到平面EAC的距离,即A1点到平面EAC的距离,利用等体积法,我们根据=,即可求出直线A 1C1到平面EAC的距离.【解答】解:(I)取AD的中点H,连接EH,则EH⊥平面ABCD,过H作HF⊥AC 与F,连接EF,则EF在平面ABCD内的射影为HF,由三垂线定理得EF⊥AC,,∴∠EFH即为二面角E﹣AC﹣B的补角∵EH=a,HF=BD=∴∠tan∠EFH===2∴二面角E﹣AC﹣B的正切值为﹣2…6分(II)直线A1C1到平面EAC的距离,即A1点到平面EAC的距离d,…8分∵=∴S•d=△EAC∵EF====•AC•EF=•a•=∴S△EAC而=••a=∴•d=•a∴d=∴直线A1C1到平面EAC的距离【点评】本题考查的知识点是二面角的平面角及求法,点到平面的距离,其中(I)的关键是得到∠EFH即为二面角E﹣AC﹣B的补角,(II)中求点到面的距离时,等体积法是最常用的方法.20.(12分)已知f(x)=tx3﹣2x2+1.(I)若f′(x)≥0对任意t∈[﹣1,1]恒成立,求x的取值范围;(II)求t=1,求f(x)在区间[a,a+3](a<0)上的最大值h(a).【分析】(I)f′(x)=3tx2﹣4x,令g(t)=3x2t﹣4x,由,能求出x的取值范围.(II)由f(x)=x3﹣2x2+1,知f′(x)=3x2﹣4x=x(3x﹣4),f′(x)>0,得f(x)在(﹣∞,0)和()为递增函数;令f′(x)<0,得f(x)在(0,)为递减函数.由此进行分类讨论,能求出f(x)在区间[a,a+3](a<0)上的最大值h(a).【解答】解:(I)f′(x)=3tx2﹣4x,令g(t)=3x2t﹣4x,则有,∴,解得.∴x的取值范围是.(II)f(x)=x3﹣2x2+1,f′(x)=3x2﹣4x=x(3x﹣4),令f′(x)>0,得x<0或x>.令f′(x)<0,得0,∴f(x)在(﹣∞,0)和()为递增函数;在(0,)为递减函数.∵f(0)=1,,令f(x)=1,得x=0或x=2.①当a+3<0,即a<﹣3时,f(x)在[a,a+3]单调递增.∴h(a)=f(a+3)=a3+7a2+15a+10.②当0≤a+3≤2,即﹣3≤a≤﹣1时,h(a)=f(0)=1.③当a+3>2,即0>a>﹣1时,h(a)=f(a+3)=a3+7a2+15a+10.∴.【点评】本题考查导数在求最大值和求最小值时的实际应用,考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.综合性强,是高考的重点,易错点是知识体系不牢固.解题时要注意分类讨论思想的灵活运用.21.(12分)已知{a n}是正数组成的数列,a1=1,且点在函数y=x2+1的图象上.数列{b n}满足b1=0,b n+1=b n+3an(n∈N*).(Ⅰ)求数列{a n},{b n}的通项公式;(Ⅱ)若c n=a n b n cosnπ(n∈N*),求数列{c n}的前n项和S n.【分析】(Ⅰ)由题设条件知a n=a n+1,根据等差数列的定义:{a n}是首项为1,+1公差为1的等差数列,从而a n=n,根据b n+1=b n+3an(n∈N*),可得b n+1﹣b n=3n (n∈N*).累加可求和,从而得{b n}的通项公式;(II)根据c n=a n b n cosnπ(n∈N*),可得,再分n为偶数,奇数分别求和即可【解答】解:(Ⅰ)因为点()(n∈N*)在函数y=x2+1的图象上=a n+1所以a n+1根据等差数列的定义:{a n}是首项为1,公差为1的等差数列所以a n=n=b n+3an(n∈N*).∵b n+1∴b n﹣b n=3n(n∈N*).+1∴(II)∵c n=a n b n cosnπ(n∈N*),∴当n为偶数时,S n=(﹣3+2•32+…+n•3n)+3[1﹣2+3﹣4+…+(n﹣1)﹣n]设T n=(﹣3+2•32+…+n•3n),则3T n=﹣32+2•33+…+n•3n+1∴∴当n为奇数时,∴【点评】本题以函数为载体,考查数列的概念和性质及其应用,考查错位相减法求和,解题时要注意公式的灵活运用.22.(10分)若圆C过点M(0,1)且与直线l:y=﹣1相切,设圆心C的轨迹为曲线E,A、B为曲线E上的两点,点.(Ⅰ)求曲线E的方程;(Ⅱ)若t=6,直线AB的斜率为,过A、B两点的圆N与抛物线在点A处共同的切线,求圆N的方程;(Ⅲ)分别过A、B作曲线E的切线,两条切线交于点Q,若点Q恰好在直线l 上,求证:t与均为定值.【分析】(I)由点C到定点M的距离等于到定直线l的距离与抛物线的定义可得点C的轨迹为抛物线所以曲线E的方程为x2=4y.(II)由题得直线AB的方程是x﹣2y+12=0联立抛物线的方程解得A(6,9)和B(﹣4,4),进而直线NA的方程为,由A,B两点的坐标得到线段AB中垂线方程为,可求N点的坐标,进而求出圆N的方程.(III)设A,B两点的坐标,由题意得过点A的切线方程为又Q(a,﹣1),可得x12﹣2ax1﹣4=0同理得x22﹣2ax2﹣4=0所以x1+x2=2a,x1x2=﹣4.所以直线AB的方程为所以t=﹣1.根据向量的运算得=0.【解答】【解】(Ⅰ)依题意,点C到定点M的距离等于到定直线l的距离,所以点C的轨迹为抛物线,曲线E的方程为x2=4y.(Ⅱ)直线AB的方程是,即x﹣2y+12=0.由及知,得A(6,9)和B(﹣4,4)由x2=4y得,.所以抛物线x2=4y在点A处切线的斜率为y'|x=6=3.直线NA的方程为,即.①线段AB的中点坐标为,线段AB中垂线方程为,即.②由①、②解得.于是,圆C的方程为,即.(Ⅲ)设,,Q(a,1).过点A的切线方程为,即x12﹣2ax1﹣4=0.同理可得x22﹣2ax2﹣4=0,所以x1+x2=2a,x1x2=﹣4.又=,所以直线AB的方程为,即,亦即,所以t=1.而,,所以==.【点评】本题主要考查抛物线的定义和直线与曲线的相切问题,解决此类问题的必须熟悉曲线的定义和曲线的图形特征,这也是高考常考的知识点.。
2018届高三下学期第二次模拟考试数学(文)试题 Word版含答案

第Ⅰ卷 选择题一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的4个选项中,只有一项是符合题目要求的.1.设集合{}10|≤≤=x x M ,{}1|||≥=x x N ,则M N =A 、{}10|≤≤x xB 、{}10x x x ≤-≥或C 、{}101|≤≤-≤x x x 或D 、{}12.若复数11iz i-=+,则z = A 、1 B 、1- C 、i D 、i -3.甲乙两名同学6次考试的成绩统计如下图,甲乙两组数据的平均数分别为甲x 、乙x ,标准差分别为甲σ、乙σ,则A 、乙甲乙甲,σσ<<x xB 、乙甲乙甲,σσ><x xC 、乙甲乙甲,σσ<>x xD 、乙甲乙甲,σσ>>x x4.已知数列}{n a 为等差数列,且55=a ,则9S 的值为A 、25B 、45C 、50D 、905.已知2133311,,log 34a b c π⎛⎫⎛⎫=== ⎪⎪⎝⎭⎝⎭,则c b a ,,的大小关系为 A 、c b a >> B 、b c a >> C 、b a c >> D 、a b c >>6.一只蚂蚁在边长为4的正三角形区域内随机爬行,则它在离三个顶点距离都大于2的区域内的概率为A 、3π16-B 、34C 、3π6D 、147.已知某几何体的三视图如图所示,则该几何体的最大边长为A 、5B 、6C 、7D 、228.若函数)(x f 的定义域为R ,其导函数为'()f x .若'()30f x -<恒成立,0)2(=-f ,则()36f x x -<解集为A 、(,2)-∞-B 、)2,2(-C 、)2,(-∞D 、),2(+∞-9.执行如图的程序框图,则输出的S 值为A 、1B 、23 C 、12- D 、010.已知直线134+-=x y 的倾斜角为α,则)sin()45cos(2cos απαπα++的值为A 、22 B 、42 C 、 82 D 、427 11.设函数222)()2cos()(ex e x x x f +++-=ππ的最大值为M ,最小值为N ,则2018)1(-+N M 的值为A 、1B 、2C 、20182D 、2018312. 已知点F 是曲线21:4C y x =的焦点,点P 为曲线C 上的动点,A 为曲线C 的准线与其对称轴的交点,则PFPA 的取值范围是A 、20]2(,B 、2[,12)C 、2[,1]2D 、2[2+∞,)第Ⅱ卷(非选择题共90分)二、填空题:本大题共4小题,每小题5分,共20分,把答案填在题中横线上.13.已知实数y x ,满足约束条件2060230x y x y x y -≥⎧⎪+-≤⎨⎪--≤⎩,则23z x y =-的最小值是 .14.甲、乙、丙三名同学参加某高校组织的自主招生考试的初试,考试成绩采用等级制(分为,,A B C 三个层次),得A 的同学直接进入第二轮考试.从评委处得知,三名同学中只有一人获得A .三名同学预测谁能直接进入第二轮比赛如下:甲说:看丙的状态,他只能得B 或C ; 乙说:我肯定得A ;丙说:今天我的确没有发挥好,我赞同甲的预测.事实证明:在这三名同学中,只有一人的预测不准确,那么得A 的同学是 . 15.在ABC ∆中,内角,,A B C 所对的边分别为,,a b c ,已知()()3a b c a b c ab +-++=,且4=c ,则ABC ∆面积的最大值为 .16.在平面上,12OB OB ⊥ ,且12OB = ,21OB = ,12OP OB OB =+.若12MB MB = ,则PM的取值范围是 .三、解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.第17-21题为必考题,每个试题考生都必须作答.第22,23题为选考题,考生根据要求作答. (一)必考题:共60分 17.(本小题满分12分)已知数列}{n a 的前n 项和为n S ,且满足*4(1),3n n S a n N =-∈. (Ⅰ)求数列}{n a 的通项公式;(Ⅱ)令n n a b 2log =,记数列1(1)(1)n n b b ⎧⎫⎨⎬-+⎩⎭的前n 项和为n T ,证明:21<n T .18.(本小题满分12分)据统计,2017年国庆中秋假日期间,黔东南州共接待游客590.23万人次,实现旅游收入48.67亿元,同比分别增长44.57%、55.22%.旅游公司规定:若公司导游接待旅客,旅游年总收入不低于40(单位:百万元),则称为优秀导游.经验表明,如果公司的优秀导游率越高,则该公司的影响度越高.已知甲、乙两家旅游公司各有导游100名,统计他们一年内旅游总收入,分别得到甲公司的频率分布直方图和乙公司的频数分布表如下:(Ⅰ)求,a b 的值,并比较甲、乙两家旅游公司,哪家的影响度高?(Ⅱ)若导游的奖金y (单位:万元),与其一年内旅游总收入x (单位:百万元)之间的关系为1 202 20403 40x y x x <⎧⎪=≤<⎨⎪≥⎩,求甲公司导游的年平均奖金;(Ⅲ)从甲、乙两家公司旅游收入在[)50,60的总人数中,用分层抽样的方法随机抽取6人进行表彰,其中有两名导游代表旅游行业去参加座谈,求参加座谈的导游中有乙公司导游分组频数1849245[)20,30[)10,20b [)30,40[)40,50[)50,60的概率.19、(本小题满分12分)在四棱锥P ABCD -中,四边形ABCD 是矩形,平面PAB ⊥平面ABCD ,点E 、F 分别为BC 、AP 中点.(1)求证://EF 平面PCD ; (2)若2=12AD AP PB AB ===,求三棱锥P DEF -的体积. 20.(本小题满分12分)已知点)1,0(-A 、)1,0(B ,P 为椭圆C :1222=+y x 上异于点B A ,的任意一点. (Ⅰ)求证:直线PA 、PB 的斜率之积为21-; (Ⅱ)是否存在过点)0,2(-Q 的直线l 与椭圆C 交于不同的两点M 、N ,使得||||BN BM =?若存在,求出直线l 的方程;若不存在,请说明理由.21.(本小题满分12分)已知函数()ln x x f x =,()g x x a =+.(Ⅰ)设()()()h f x x g x =-,求函数()y h x =的单调区间; (Ⅱ)若10a -<<,函数()()()x g x M x f x ⋅=,试判断是否存在0(1,)x ∈+∞,使得0x 为函数()M x 的极小值点.(二)选考题:共10分.请考生在第22,23题中任选一题作答.如果多做,按所做的第一题记分.22.(本小题满分10分)选修4—4:极坐标与参数方程 在平面直角坐标系xOy 中,将曲线1cos :sin x C y θθ=⎧⎨=⎩(θ为参数) 上任意一点(,)P x y 经过伸缩变换'3'2x x y y⎧=⎪⎨=⎪⎩后得到曲线2C 的图形.以坐标原点O 为极点,x 轴的非负半轴为极轴,取相同的单位长度建立极坐标系,已知直线:(2cos sin )8l ρθθ-=.(Ⅰ)求曲线2C 和直线l 的普通方程;(Ⅱ)点P 为曲线2C 上的任意一点,求点P 到直线l 的距离的最大值及取得最大值时点P 的坐标.23.(本小题满分10分)选修4—5:不等式选讲已知函数|3||13|)(k x x x f ++-=,4)(+=x x g . (Ⅰ)当3-=k 时,求不等式()4f x ≥的解集; (Ⅱ)设1->k ,且当⎪⎭⎫⎢⎣⎡-∈31,3k x 时,都有()()f x g x ≤,求k 的取值范围.参考答案一、选择题 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 DCCBDABDDBAC二、填空题13.8- 14.甲 15.43 16.35[,)10+∞三、解答题 17、(12分)解:(I )当1=n 时,有1114(1)3a S a ==-,解得41=a . 当2≥n 时,有)1(3411-=--n n a S ,则 1144(1)(1)33n n n n n a S S a a --=-=---整理得:41=-n na a ∴ 数列}{n a 是以4q =为公比,以41=a 为首项的等比数列.∴ 1*444(n n n a n N -=⨯=∈) 即数列}{n a 的通项公式为:*4()n n a n N =∈. ………………………6分 (II )由(I )有22log log 42n n n b a n ===,则11111=(1)(1)(21)(21)22121n n b b n n n n ⎛⎫=- ⎪+-+--+⎝⎭∴ n T )12)(12(1751531311-++⋅⋅⋅+⨯+⨯+⨯=n n )]121121()7151()5131()3111[(21+--+⋅⋅⋅+-+-+-=n n111(1)2212n =-<+ 故得证. ………………………………………12分18、(12分)解:(I )由直方图知:()0.010.0250.0350.01101a ++++⨯=,有0.02a =, 由频数分布表知:1849245100b ++++=,有4b =.∴ 甲公司的导游优秀率为:()0.020.0110100%30%+⨯⨯=;乙公司的导游优秀率为:245100%29%100+⨯=; 由于30%29%>, 所以甲公司的影响度高. ………………………4分 (II )甲公司年旅游总收入[)10,20的人数为0.011010010⨯⨯=人;年旅游总收入[)20,40的人数为()0.0250.0351010060+⨯⨯=人; 年旅游总收入[)40,60的人数为()0.020.011010030+⨯⨯=人; 故甲公司导游的年平均奖金1106023032.2100y ⨯+⨯+⨯==(万元). ……8分(III )由已知得,年旅游总收入在[)50,60的人数为15人,其中甲公司10人,乙公司5人.按分层抽样的方法甲公司抽取106415⨯=人,记为,,,a b c d ;从乙公司抽取56215⨯=人,记为1,2.则6人中随机抽取2人的基本事件有:()()()()()()()()()()()(),,,,,,,1,,2,,,,,,1,,2,,,,1,,2,a b a c a d a a b c b d b b c d c c()()(),1,,2,1,2d d 共15个.参加座谈的导游中有乙公司导游的基本事件有:(),1a ,(),2a ,(),1b ,(),2b ,(),1c ,(),2c ,(),1d ,(),2d ,()1,2共9个.设事件A 为“参加座谈的导游中有乙公司导游”,则()93155p A == ∴ 所求概率为35. …………………………………………………12分19、(12分)(I )证明:取PD 中点G ,连接,GF GC . 在△PAD 中,有,G F 分别为PD 、AP 中点∴ 1//2GF AD 在矩形ABCD 中,E 为BC 中点∴ 1//2CE AD ∴ //GF EC∴ 四边形ABCD 是平行四边形 ∴ //GC EF而GC ⊂平面PCD ,EF ⊄平面PCD∴ //EF 平面PCD ………………………………………………6分(II )解: 四边形ABCD 是矩形∴ AD AB ⊥,//AD BC平面PAB ⊥平面ABCD ,平面PAB 平面ABCD =AB ,AD ⊂平面PAB ∴ AD ⊥平面PAB∴ 平面PAD ⊥平面PAB ,//BC 平面PAD 2=12AD AP PB AB === ∴ =2AB ,满足222AP PB AB += ∴ AP PB ⊥ ∴ BP ⊥平面PAD //BC 平面PAD∴ 点E 到平面PAD 的距离等于点B 到平面PAD 的距离.而 111112224PDF S PF AD =⨯⨯=⨯⨯= ∴ 1111133412P DEF PDF V S BP -==⨯⨯=∴ 三棱锥P DEF -的体积为112. …………………………………12分20、(12分)解:(I )设点),(y x P ,)0(≠x ,则1222=+y x ,即2212x y =- ∴ 11PA PBy y k k x x -+⋅= 221y x -=22112x x ⎛⎫-- ⎪⎝⎭=12=-故得证. ………………………………5分(II )假设存在直线l 满足题意.显然当直线斜率不存在时,直线与椭圆C 不相交. ①当直线l 的斜率0≠k 时,设直线l 为:)2(+=x k y联立⎪⎩⎪⎨⎧+==+)2(1222x k y y x ,化简得:0288)21(2222=-+++k x k x k由0)28)(21(4)8(2222>-+-=∆k k k ,解得22022k k -<<≠()设点),(11y x M ,),(22y x N ,则212221228128212k x x k k x x k ⎧-+=⎪⎪+⎨-⎪=⎪+⎩∴ 222212121442184)(k kk k k kk x x k y y +=++-=++=+ 取MN 的中点H ,则1212,22x x y y H ++⎛⎫ ⎪⎝⎭,则12122121-=⋅+-+k x x y y 即 22221121412kk k k k -+=--+ ,化简得01222=++k k ,无实数解,故舍去. ②当0=k 时,,M N 为椭圆C 的左右顶点,显然满足||||BN BM =,此时直线l 的方程为0y =.综上可知,存在直线l 满足题意,此时直线l 的方程为0y =. ……………12分21、(12分)解:(I )由题意可知:()ln h x x x x a =--,其定义域为()0,+∞,则x x x h ln 11ln )(=-+='.令0)(>'x h ,得1x >,令()0h x '<,得01x <<.故函数()y h x =的单调递增区间为()1,+∞,单调递减区间为()0,1. …………………………………5分(II )由已知有()ln x aM x x+=,对于(1)x ∈+∞,,有2)(l n 1ln )(x x a x x M --='. 令()ln 1((1,))a q x x x x =--∈+∞,则221()a x a q x x x x+'=+=. 令0)(>'x q ,有a x ->.而10a -<<,所以01a <-<,故当1x >时,0)(>'x q .∴ 函数()q x 在区间(1)+∞,上单调递增. 注意到(1)10q a =--<,()0aq e e=->. 故存在∈0x ()1,e ,使得0'()=0M x ,且当0(1,)x x ∈时,'()0M x <,当0(,)x x e ∈时,'()0M x >,即函数()M x 在区间0(1,)x 上单调递减,在区间0()x +∞,上单调递增.∴ 0x 为函数)(x M 的极小值点.故存在01x ∈+∞(,),使得0x 为函数)(x M 的极小值点.…………………12分 22、(10分)解:(I )由已知有'3cos '2sin x y θθ⎧=⎪⎨=⎪⎩(θ为参数),消去θ得22''134x y +=. 将sin cos x y ρθρθ=⎧⎨=⎩代入直线l 的方程得82:=-y x l∴ 曲线2C 的方程为22''134x y +=,直线l 的普通方程为82:=-y x l . ………5分(II )由(I )可设点P 为)sin 2,cos 3(θθ,[0,2)θπ∈.则点P 到直线l 的距离为:5|8)3sin(4|5|8sin 2cos 32|+-=--=πθθθd 故当sin()13πθ-=,即5=6πθ时d 取最大值5512. 此时点P 的坐标为)1,23(-. ……………………………………10分 23、(10分) 解:(I )当3k =-时,⎪⎪⎪⎩⎪⎪⎪⎨⎧>-≤≤<+-=1 46131 231 46)(x x x x x x f ,,,, 故不等式4)(≥x f 可化为:1644x x >⎧⎨-≥⎩或11324x ⎧≤≤⎪⎨⎪≥⎩或13644x x ⎧<⎪⎨⎪-+≥⎩ 解得:403x x ≤≥或 ∴ 所求解集为:403x x x ⎧⎫≤≥⎨⎬⎩⎭或. ……………………………………5分 (II )当⎪⎭⎫⎢⎣⎡-∈31,3k x 时,由1k >-有:310,30x x k -<+≥ ∴ k x f +=1)(不等式)()(x g x f ≤可变形为:41+≤+x k故3k x ≤+对1,33k x ⎡⎫∈-⎪⎢⎣⎭恒成立,即33k k ≤-+,解得94k ≤ 而1k >-,故914k -<≤.∴ k 的取值范围是:91,4⎛⎤- ⎥⎝⎦ ………………………………………………10分。
2018年高考数学文科(课标版)仿真模拟卷(二)(带答案)

2018高考仿真卷·文科数学(二)(考试时间:120分钟试卷满分:150分)一、选择题(本题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知集合M={x|x(x-1)≥0},N={x|-1<x<1},则M∩N=()A.{x|-1<x≤0}B.{x|-1≤x≤0}C.{x|0≤x<1}D.{x|0≤x≤1}2.=()A.1+iB.1-iC.-1+iD.-1-i3.已知向量a=(-1,2),b=(1,3),则|2a-b|=()A. B.2 C. D.104.设命题p:∀n∈N,n2≤2n,则p为()A.∃n∈N,n2≤2nB.∀n∈N,n2>2nC.∃n∈N,n2>2nD.∀n∈N,n2≥2n5.已知等差数列{a n}的公差为2,且a4是a2与a8的等比中项,则{a n}的通项公式a n=()A.-2nB.2nC.2n-1D.2n+16.下图是1951~2016年中国年平均气温变化图.根据上图,下列结论正确的是()A.1951年以来,我国年平均气温逐年增高B.1951年以来,我国年平均气温在2016年再创新高C.2000年以来,我国年平均气温都高于1981~2010年的平均值D.2000年以来,我国年平均气温的平均值高于1981~2010年的平均值7.古人采取“用臼舂米”的方法脱去稻谷的外壳,获得可供食用的大米,用于舂米的“石臼”由一块正方体石料凿去一部分做成(凿去的部分看成一个简单组合体).一个“石臼”的三视图如图所示,则凿去部分的体积为()A.63πB.72πC.79πD.99π8.定义[x]表示不超过x的最大整数,例如[0.6]=0,[2]=2,[3.6]=3.右面的程序框图取材于中国古代数学著作《孙子算经》.执行该程序框图,则输出a=()A.9B.16C.23D.309.已知函数f(x)=sin ωx的图象关于点π,0对称,且f(x)在0,π上为增函数,则ω=()A. B.3 C. D.610.在长方体ABCD-A1B1C1D1中,AB=AD=2,AA1=1,则点B到平面D1AC的距离等于()A. B. C.1 D.11.若函数f(x)=2x-x2-1,对于任意的x∈Z且x∈(-∞,a),都有f(x)≤0恒成立,则实数a的取值范围为()A.(-∞,-1]B.(-∞,0]C.(-∞,4]D.(-∞,5]12.过抛物线C:y2=2px(p>0)的焦点且倾斜角为锐角的直线l与C交于A,B两点,过线段AB的中点N且垂直于l的直线与C的准线交于点M,若|MN|=|AB|,则l的斜率为()A. B. C. D.1二、填空题(本题共4小题,每小题5分,共20分)13.若变量x,y满足-则z=3x+y的最小值为.14.已知双曲线C:=1(a>0,b>0)的一条渐近线与直线x+2y=0垂直,则C的离心率为.15.将数列{a n}中的所有项按每一行比上一行多1项的规则排成如下数阵:a1a2,a3a4,a5,a6a7,a8,a9,a10……若第11行左起第1个数为a m,则m=.16.已知函数f(x)=-则函数f(x)的零点个数为.-三、解答题(共70分.解答须写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题都必须作答.第22、23题为选考题,考生根据要求作答)(一)必考题:共60分17.(12分)在△ABC中,AC=2,BC=6,∠ACB=150°.(1)求AB的长;(2)延长BC至D,使∠ADC=45°,求△ACD的面积. 18.(12分)某商家为了解“双十一”这一天网购者在其网店一次性购物的情况,从这一天交易成功的所有订单中随机抽取了100份,按购物金额(单位:元)进行统计,得到的频率分布直方图如图所示.(1)该商家决定对这100份订单中购物金额不低于1 000元的订单按区间[1 000,1 200),[1 200,1 400]采用分层抽样的方法抽取6份,对买家进行售后回访,再从这6位买家中随机抽取2位赠送小礼品.求获赠小礼品的2位买家中,至少1位买家购物金额位于区间[1 200,1 400]的概率.(2)若该商家制定了两种不同的促销方案:方案一:全场商品打八折;方案二:全场商品优惠如下表:额 1 1利用直方图中的数据,计算说明哪种方案的优惠力度更大.(同一组中的数据用该组区间的中点值作代表).19.(12分)如图,在三棱锥P-ABC中,∠ABC=90°,平面PAB⊥平面ABC,PA=PB,点D在PC上,且BD⊥平面PAC.(1)证明:PA⊥平面PBC;(2)若AB∶BC=2∶,求三棱锥D-PAB与三棱锥D-ABC的体积比.20.(12分)已知椭圆C:=1(a>b>0)的焦距为4,P2,是C上的点.(1)求椭圆C的方程;(2)O为坐标原点,A,B是椭圆C上不关于坐标轴对称的两点,设,证明:直线AB的斜率与OD的斜率的乘积为定值.21.(12分)已知函数f(x)=ln x+ax2-(2a+1)x-1.(1)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;(2)当x∈(0,1]时,f(x)≤0,求实数a的取值范围.(二)选考题:共10分.请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题记分.22.选修4—4:坐标系与参数方程(10分)在直角坐标系xOy中,已知倾斜角为α的直线l过点A(2,1).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系.曲线C 的极坐标方程为ρ=2sin θ,直线l与曲线C分别交于P,Q两点.(1)写出直线l的参数方程和曲线C的直角坐标方程;(2)若|PQ|2=|AP|·|AQ|,求直线l的斜率k.23.选修4—5:不等式选讲(10分)设函数f(x)=|x-a|+(a≠0,a∈R).(1)当a=1时,解不等式f(x)≤5;(2)记f(x)的最小值为g(a),求g(a)的最小值.2018高考仿真卷·文科数学(二)1.A2.A3.C4.C5.B6.D7.A8.C9.A10.B11.D12.B13.714.15.5616.317.解(1)由余弦定理得AB2=AC2+BC2-2AC·BC cos∠ACB,即AB2=12+36-2×2×6cos 150°=84,所以AB=2.(2)在△ACD中,因为∠ACB=150°,∠ADC=45°,所以∠CAD=105°.由正弦定理得,所以CD=3+,∠∠所以S△ACD=AC·CD·sin∠ACD=×(3+)×2=+1).18.解(1)在这100份订单中,购物金额位于区间[1 000,1 200)的有10份,位于区间[1 200,1 400]的有5份,则购物金额位于区间[1 000,1 400]的订单共有15份.利用分层抽样抽取6份,则位于区间[1 000,1 200)的有4份,用符号X1,X2,X3,X4表示,位于区间[1 200,1 400]的有2份,用符号Y1,Y2表示.从X1,X2,X3,X4,Y1,Y2中抽取2份,结果如下:X1X2,X1X3,X1X4,X2X3,X2X4,X3X4,X1Y1,X1Y2,X2Y1,X2Y2,X3Y1,X3Y2,X4Y1,X4Y2,Y1Y2,共计15个;设事件A表示“获赠小礼品的2位买家中,至少1位买家购物金额位于区间[1 200,1 400]”,所含基本事件如下:X1Y1,X1Y2,X2Y1,X2Y2,X3Y1,X3Y2,X4Y1,X4Y2,Y1Y2,共计9个,则P(A)=.(2)由直方图知,各组的频率依次为0.1,0.2,0.25,0.3,0.1,0.05,方案一:商家最高优惠的平均值为(300×0.1+500×0.2+700×0.25+900×0.3+1 100×0.1+1 300×0.05)×0.2=150(元);方案二:商家最高优惠的平均值为30×0.1+50×0.2+140×0.25+160×0.3+280×0.1+320×0.05=140(元),由于150>140,所以方案一的优惠力度更大.19.解(1)由BD⊥平面PAC,得BD⊥PA,又平面PAB⊥平面ABC,平面PAB∩平面ABC=AB,CB⊥AB,所以CB⊥平面PAB,所以CB⊥PA,所以PA⊥平面PBC.(2)设AB=2,BC=,因为PA⊥平面PBC,所以PA⊥PB,又PA=PB,所以PB=,在直角三角形PBC中解得PC=2,又因为BD⊥PC,所以CD=,PD=.因为三棱锥D-PAB的体积V D-PAB=V A-PBD=S△PBD×PA=×BD×PD×PA,三棱锥D-ABC的体积V D-ABC=V A-BCD=S△BCD×PA=×BD×CD×PA,.所以--三棱锥D-PAB与三棱锥D-ABC的体积比为.20.解(1)椭圆C的焦距2c=4,即c=2,=1,因为P2,在C上,设C:-=1解得a2=5,由-故椭圆C的方程为+y2=1.(2)解法一:设A(x1,y1),B(x2,y2),直线AB的方程为y=kx+n,由得(5k2+1)x2+10knx+5n2-5=0,则x1+x2=-,y1+y2=k(x1+x2)+2n=,由知D(x1+x2,y1+y2),直线AB的斜率为k,直线OD的斜率k OD==-,则k·k OD=-,故直线AB的斜率与OD的斜率的乘积为定值-.,直线OD的斜率k OD=, 解法二:设A(x1,y1),B(x2,y2),则D(x1+x2,y1+y2),直线AB的斜率k AB=--由得(x1+x2)(x1-x2)+(y1+y2)(y1-y2)=0,=-,即--所以k AB·k OD=-.故直线AB的斜率与OD的斜率的乘积为定值-.21.解(1)函数f(x)的定义域为(0,+∞),因为f(x)=ln x+x2-3x-1,所以f'(x)=+2x-3,所以f'(1)=0,而f(1)=-3,所以f(x)在x=1处的切线方程为y=-3.(2)因为f'(x)=-(x>0),当a=0时,f'(x)=≥0,所以函数f(x)在(0,1)上为增函数,所以函数f(x)在(0,1]上的最大值为f(1)=-2<0成立;当a≠0时,由f'(x)=--,令f'(x)=0,得x=或x=1,当<0,即a<0时,函数f(x)在(0,1)上为增函数,所以函数f(x)在(0,1]上的最大值为f(1)=a-(2a+1)-1,则f(1)≤0,所以-2≤a<0;当0<<1,即a>时,函数f(x)在0,上为增函数,在,1上为减函数,所以函数f(x)在(0,1]上的最大值为f,因为f=ln +a·2--1=ln -2<0成立,所以a>;当=1,即a=时,函数f(x)在(0,1)上为增函数,所以函数f(x)在(0,1]上的最大值为f(1)=a-(2a+1)-1=-a-2=-<0成立,所以a=;当>1,即0<a<时,函数f(x)在(0,1)上为增函数,所以函数f(x)在(0,1]上的最大值为f(1)=a-(2a+1)-1=-a-2<0成立,所以0<a<.综上所述,实数a的取值范围为[-2,+∞).22.解(1)直线l的参数方程为(t为参数).曲线C的直角坐标方程为x2+y2=2y.(2)将直线l的参数表达式代入曲线C得:t2+(4cos α)t+3=0,由Δ=(4cos α)2-4×3>0⇒cos2α>,t1+t2=-4cos α,t1·t2=3,又|AP|=|t1|,|AQ|=|t2|,|PQ|=|t1-t2|,由题意知,(t1-t2)2=t1·t2⇒(t1+t2)2=5t1·t2,得(-4cos α)2=5×3,解得cos2α=,满足cos2α>,所以sin2α=,tan2α=,所以k=tan α=±.23.解(1)当a=1时,f(x)=|x-1|+|x+2|,故f(x)=--①当x>1时,由2x+1≤5得x≤2,故1<x≤2;②当-2≤x≤1时,由3≤5得x∈R,故-2≤x≤1;③当x<-2时,由-2x-1≤5得x≥-3,故-3≤x<-2.综上,不等式的解集为[-3,2].(2)f(x)=|x-a|+--,当且仅当(x-a)≤0,即-≤x≤a(a>0)或a≤x≤-(a<0),取“=”,此步对考生不作要求所以,g(a)=,因为=|a|+≥2·=2,当且仅当|a|=,即a=±时,取“=”,所以,g(a)min=g(±)=2.。
2018年高考仿真卷文科数学试卷(二)含解析答案

2018高考仿真卷²文科数学(二)(考试时间:120分钟试卷满分:150分)第Ⅰ卷选择题(共60分)一、选择题(本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知i是虚数单位,则复数=()A.-2+iB.iC.2-iD.-i2.已知集合M={x|x2-4x<0},N=,则M∪N=()A.[-2,4)B.(-2,4)C.(0,2)D.(0,2]3.采用系统抽样的方法从 1 000人中抽取50人做问卷调查,为此将他们随机编号为1,2,3,…,1 000,适当分组后,在第一组中采用简单随机抽样的方法抽到的号码为8.若编号落入区间[1,400]上的人做问卷A,编号落入区间[401,750]上的人做问卷B,其余的人做问卷C,则抽到的人中,做问卷C的人数为()A.12B.13C.14D.154.已知命题p:函数y=ln(x2+3)+的最小值是2;命题q:“x>2”是“x>1”的充分不必要条件.则下列命题是真命题的是()A.p∧qB.(p)∧(q)C.(p)∧qD.p∧(q)5.已知点A是抛物线C1:y2=2px(p>0)与双曲线C2:=1(a>0,b>0)的一条渐近线的交点,若点A 到抛物线C1的焦点的距离为p,则双曲线C2的离心率等于()A. B. C. D.6.某产品的广告费用x(单位:万元)与销售额y(单位:万元)的统计数据如下表:根据表中数据求得回归直线方程为=9.5x+,则等于()A.22B.26C.33.6D.19.57.设a,b,c分别是△ABC的内角A,B,C所对边的边长,则直线sin A²x-ay-c=0与bx+sin B²y+sin C=0的位置关系是()A.平行B.重合C.垂直D.相交但不垂直8.如图,正四棱锥P-ABCD底面的四个顶点A,B,C,D在球O的同一个大圆上,点P在球面上,若V 正四棱锥P-ABCD=,则球O的表面积是()A.4πB.8πC.12πD.16π9.已知变量x,y满足线性约束条件若目标函数z=kx-y仅在点(0,2)处取得最小值,则k的取值范围是()A.k<-3B.k>1C.-1<k<1D.-3<k<110.某几何体的三视图如图所示,当a+b取最大值时,这个几何体的体积为()A. B. C. D.11.已知M是△ABC内一点(不含边界),且=2,∠BAC=30°.若△MBC,△MCA,△MAB的面积分别为x,y,z,记f(x,y,z)=,则f(x,y,z)的最小值为()A.26B.32C.36D.4812.已知集合M={(x,y)|y=f(x)},若对于任意(x1,y1)∈M,存在(x2,y2)∈M,使得x1x2+y1y2=0成立,则称集合M是“商高线”.给出下列四个集合:①M=;②M={(x,y)|y=sin x+1};③M={(x,y)|y=log2x};④M={(x,y)|y=e x-2}.其中是“商高线”的序号是()A.①②B.②③C.①④D.②④第Ⅱ卷非选择题(共90分)二、填空题(本大题共4小题,每小题5分,共20分)13.执行如图所示的程序框图,若输入x=0.1,则输出的m的值是.14.已知f(x)是定义在R上的奇函数,当x≥0时,f(x)=3x+m(m为常数),则f(-log35)的值为.15.关于函数f(x)=2(sin x-cos x)cos x的下列四个结论:①函数f(x)的最大值为;②把函数f(x)=sin 2x-1的图象向右平移个单位后可得到函数f(x)=2(sin x-cos x)²cos x 的图象;③函数f(x)的单调递增区间为,k∈Z;④函数f(x)的图象的对称中心为,k∈Z.其中正确的结论有个.16.已知数列{a n}满足a1=,a n-1-a n=(n≥2),则该数列的通项公式为.三、解答题(本大题共6小题,满分70分,解答须写出文字说明、证明过程或演算步骤)17.(本小题满分12分)在△ABC中,角A,B,C的对边分别为a,b,c,已知A=,sin B=3sin C.(1)求tan C的值;(2)若a=,求△ABC的面积.18.(本小题满分12分)国家教育部要求高中阶段每学年都要组织学生进行“国家学生体质健康数据测试”,方案要求以学校为单位组织实施.某校对高一(1)班的同学按照“国家学生体质健康数据测试”的项目进行了测试,并对测试成绩进行统计,其频率分布直方图如图所示,若分数在[90,100]上的人数为2.(1)请求出分数在[70,80)内的人数;(2)现根据测试成绩从第一组和第五组(从低分段到高分段依次分为第一组,第二组,…,第五组)中任意选出2人,形成搭档小组.若选出的2人成绩差大于30,则称这2人为“互补组”,试求选出的2人为“互补组”的概率.19.(本小题满分12分)如图,在正方体ABCD-A1B1C1D1中,E,F分别为AB,BB1的中点.(1)求证:EF⊥平面A1D1B;(2)若AA1=2,求三棱锥D1-DEF的体积.20.(本小题满分12分)已知椭圆C的中心在原点,焦点在x轴上,长轴长为4,且点在椭圆C 上.(1)求椭圆C的方程;(2)设P是椭圆C长轴上的一个动点,过P作斜率为的直线l交椭圆C于A,B两点,求证:|PA|2+|PB|2为定值.21.(本小题满分12分)设函数f(x)=.(1)求证:f(x)在(0,1)和(1,+∞)内都是增函数;(2)若在函数f(x)的定义域内,不等式af(x)>x恒成立,求a的取值范围.请考生在第22、23两题中任选一题做答,如果多做,则按所做的第一题评分.22.(本小题满分10分)选修4—4:坐标系与参数方程在平面直角坐标系中,以原点为极点,x轴的正半轴为极轴建立极坐标系.已知曲线C:ρcos2θ=2a sin θ(a>0),过点P(-4,-2)的直线l的参数方程为(t为参数),直线l与曲线C分别交于点M,N.(1)写出C的直角坐标方程和l的普通方程;(2)若|PM|,|MN|,|PN|成等比数列,求a的值.23.(本小题满分10分)选修4—5:不等式选讲已知函数f(x)=|x-1|+|x+1|.(1)求不等式f(x)≥3的解集;(2)若关于x的不等式f(x)>a2-x2+2x在R上恒成立,求实数a的取值范围.参考答案2018高考仿真卷²文科数学(二)1.B解析 (方法一)=i.(方法二)=i.2.A解析∵M={x|0<x<4},N={x|-2≤x≤2},∴M∪N=[-2,4).3.A解析若采用系统抽样的方法从1 000人中抽取50人做问卷调查,则需要分为50组,每组20人.若第一组抽到的号码为8,则以后每组抽取的号码分别为28,48,68,88,108,…,所以编号落入区间[1,400]上的有20人,编号落入区间[401,750]上的有18人,所以做问卷C 的有12人.4.C解析因为命题p为假命题,命题q为真命题,所以(p)∧q为真命题.5.C解析因为点A到抛物线C1的焦点的距离为p,所以点A到抛物线准线的距离为p.所以点A的坐标为.所以双曲线的渐近线方程为y=±2x.所以=2,所以b2=4a2.又b2=c2-a2,所以c2=5a2.所以双曲线的离心率为.6.B解析由题意知=2,=45.又由公式,得=26,故选B.7.C解析因为,所以两条直线斜率的乘积为=-1,所以这两条直线垂直.8.D解析连接PO,由题意知,PO⊥底面ABCD,PO=R,S正方形ABCD=2R2.因为V正四棱锥P-ABCD=,所以²2R2²R=,解得R=2,所以球O的表面积是16π.9.D解析如图,作出不等式组所表示的平面区域.由z=kx-y得y=kx-z,要使目标函数z=kx-y仅在点A(0,2)处取得最小值,则阴影部分区域在直线y=kx+2的下方,故目标函数线的斜率k满足-3<k<1.10.D解析由该几何体的三视图可得其直观图为如图所示的三棱锥,且从点A出发的三条棱两两垂直,AB=1,PC=,PB=a,BC=b.可知PA2+AC2=a2-1+b2-1=6,即a2+b2=8.故(a+b)2=8+2ab≤8+2,即a+b≤4,当且仅当a=b=2时,a+b取得最大值,此时PA=,AC=.所以该几何体的体积V=³1³.11.C解析由=2,∠BAC=30°,可得S△ABC=1,即x+y+z=1.故(x+y+z)=1+4+9+≥14+4+6+12=36,当且仅当x=,y=,z=时等号成立.因此,f(x,y,z)的最小值为36.12.D解析若对于函数图象上的任意一点M(x1,y1),在其图象上都存在点N(x2,y2),使OM⊥ON,则函数图象上的点的集合为“商高线”.对于①,若取M(1,1),则不存在这样的点;对于③,若取M(1,0),则不存在这样的点.②④都符合.故选D.13.0解析若输入x=0.1,则m=lg 0.1=-1.因为m<0,所以m=-1+1=0.所以输出的m的值为0.14.-4解析因为f(x)是定义在R上的奇函数,所以f(0)=1+m=0.所以m=-1.所以f(-log35)=-f(log35)=-(-1)=-4.15.2解析因为f(x)=2sin x²cos x-2cos2x=sin 2x-cos 2x-1=sin-1,所以其最大值为-1.所以①错误.因为函数f(x)=sin 2x-1的图象向右平移个单位后得到函数f(x)=sin-1=sin-1的图象,所以②错误.由-+2kπ≤2x-+2kπ,k∈Z,得函数f(x)的单调递增区间为,k∈Z,即为,k'∈Z.故③正确.由2x-=kπ,k∈Z,得x=,k∈Z,故④正确.16.a n= 解析因为a n-1-a n=(n≥2),所以,所以.所以,…,.所以.所以.所以a n=(n≥2).经检验,当n=1时也适合此公式.所以a n=.17.解 (1)∵A=,∴B+C=.∴sin=3sin C.∴cos C+sin C=3sin C.∴cos C=sin C.∴tan C=.(2)由,sin B=3sin C,得b=3c.在△ABC中,由余弦定理得a2=b2+c2-2bc cos A=9c2+c2-2³(3c)³c³=7c2.∵a=,∴c=1,b=3.∴△ABC的面积为S=bc sin A=.18.解 (1)由频率分布直方图可知分数在[50,60)内的频率为0.1,[ 60,70)内的频率为0.25,[80,90)内的频率为0.15,[90,100]上的频率为0.05.故分数在[70,80)内的频率为1-0.1-0.25-0.15-0.05=0.45.因为分数在[90,100]上的人数为2,频率为0.05,所以参加测试的总人数为=40.所以分数在[70,80)内的人数为40³0.45=18.(2)因为参加测试的总人数为=40,所以分数在[50,60)内的人数为40³0.1=4.设第一组[50,60)内的同学为A1,A2,A3,A4;第五组[90,100]上的同学为B1,B2,则从中选出2人的选法有(A1,A2),(A1,A3),(A1,A4),(A1,B1),(A1,B2),(A2,A3),(A2,A4),(A2,B1),(A2,B2),(A3,A4),(A3,B1),( A3,B2),(A4,B1),(A4,B2),(B1,B2),共15种,其中2人成绩差大于30的选法有(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(A4,B1),(A4,B2),共8种, 则选出的2人为“互补组”的概率为.19.(1)证明如图,连接AB1.因为E,F分别为AB与AB1的中点,所以EF∥AB1.因为AB1⊥A1B,所以EF⊥A1B.又因为D1A1⊥平面ABB1A1,平面ABB1A1⊃EF,所以D1A1⊥EF.又因为A1B∩D1A1=A1,所以EF⊥平面A1D1B.(2)解如图,连接DB.因为BB1∥DD1,所以.所以=S△DEB²DD1=³2=.20.(1)解因为2a=4,所以a=2.又因为焦点在x轴上,所以设椭圆方程为=1.将点代入椭圆方程得b2=1,所以椭圆方程为+y2=1.(2)证明设点P(m,0)(-2≤m≤2),可得直线l的方程是y=,由方程组消去y得2x2-2mx+m2-4=0.(*)设A(x1,y1),B(x2,y2),则x1,x2是方程(*)的两个根.所以x1+x2=m,x1x2=.所以|PA|2+|PB|2=(x1-m)2++(x2-m)2+=(x1-m)2+(x1-m)2+(x2-m)2+(x2-m)2=[(x1-m)2+(x2-m)2]=-2m(x1+x2)+2m2]=[(x1+x2)2-2m(x1+x2)-2x1x2+2m2]=[m2-2m2-(m2-4)+2m2]=5.所以|PA|2+|PB|2为定值.21.(1)证明由题意可得f'(x)==(x>0,x≠1).令g(x)=2ln x-,则g'(x)=.当0<x<1时,g'(x) <0,g(x)是减函数,g(x)>g(1)=0.于是f'(x)=g(x)>0,故f(x)在(0,1)内为增函数.当x>1时,g'(x)>0,g(x)是增函数,g(x)>g(1)=0,于是f'(x)=g(x)>0,故f(x)在(1,+∞)内为增函数.(2)解af(x)-x=-x=.令h(x)=-ln x(x>0),则h'(x)=.令φ(x)=ax2-x+a,当a>0,且Δ=1-4a2≤0,即a≥时,此时φ(x)=ax2-x+a>0在(0,1),(1,+∞)内恒成立,所以当a≥时,h'(x)>0在(0,1),(1,+∞)内恒成立,故h(x)在(0,1),(1,+∞)内是增函数,若0<x<1,则h(x)< h(1)=0,所以af(x)-x=h(x)>0;若x>1,则h(x)>h(1)=0,所以af(x)-x=h(x)>0,所以当x>0,x≠1时都有af(x)>x成立.当0<a<时,h'(x)<0,解得<x<,所以h(x)在内是减函数,h(x)<h(1)=0.故af(x)-x=h(x)<0,不符合题意.当a≤0时,x∈(0,1)∪(1,+∞),都有h'(x)<0,故h(x)在(0,1),(1,+∞)内为减函数,同理可知,在(0,1),(1,+∞)内,af(x)-x=h(x)<0,不符合题意.综上所述,a≥,即a的取值范围是.22.解 (1)曲线C的直角坐标方程为x2=2ay(a>0),直线l的普通方程为x-y+2=0.(2)将直线l的参数方程与C的直角坐标方程联立,得t2-2(4+a)t+8(4+a)=0.(*)由Δ=8a(4+a)>0,可设点M,N对应的参数分别为t1,t2,且t1,t2是方程(*)的根,则|PM|=|t1|,|PN|=|t2|,|MN|=|t1-t2|.由题设得(t1-t2)2=|t1t2|,即(t1+t2)2-4t1t2=|t1t2|.由(*)得t1+t2=2(4+a),t1t2=8(4+a)>0.则有(4+a)2-5(4+a)=0,解得a=1或a=-4.因为a>0,所以a=1.23.解 (1)原不等式等价于解得x≤-或x≥.故原不等式的解集为.(2)令g(x)=|x-1|+|x+1|+x2-2x,则g(x)=当x∈(-∞,1]时,g(x)单调递减;当x∈[1,+∞)时,g(x)单调递增.故当x=1时,g(x)取得最小值1.因为不等式f(x)>a2-x2+2x在R上恒成立,所以a2<1,解得-1<a<1.所以实数a的取值范围是(-1,1).。
2018年普通高等学校招生全国统一考试仿真卷文科数学(二)(解析版)

2018年普通高等学校招生全国统一考试仿真卷文科数学(二)(解析版)本试题卷共2页,23题(含选考题)。
全卷满分150分。
考试用时120分钟。
第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.[2018·渭南质检]设i 是虚数单位,则z 的共轭复数为( )A B C D 【答案】D【解析】z 的共轭复数为:D .2.[2018·吉林实验中学]若双曲线221yx m-=的一个焦点为()3,0-,则m =()A .B .8C .9D .64【答案】B【解析】由双曲线性质:21a =,2bm=,219c m ∴=+=,8m=,故选B .3.[2018·菏泽期末]数()f x )A 4B 4C 2D 2【答案】DD .4.[2018·晋城一模]函数()12xf x ⎛⎫= ⎪⎝⎭,()0,x ∈+∞的值域为D ,在区间()1,2-上随机取一个数x ,则x D ∈的概率是( )A .12B .13C .14D .1【答案】B 【解析】0x >,1012x⎛⎫∴<< ⎪⎝⎭,即值域()0,1D =,若在区间()1,2-上随机取一个数x ,x D∈的事件记为A ,则()()101213P A -==--,故选B .5.[2018·菏泽期末]已知变量x 和y 的统计数据如下表:根据上表可得回归直线方程0.7y x a=+,据此可以预报当6x =时,y=( )A .8.9B .8.6C .8.2D .8.1【答案】D 【解析】12345635x +++++==,5566865y++++==,∴60.73a=⨯+, 3.9a=,∴6x=时,0.76 3.98.1y=⨯+=,故选D .6.[2018·昆明一中]一个几何体的三视图如图所示,则该几何体的体积为( )A .83B .163C .203D .8【答案】B【解析】由图可知该几何体底面积为8,高为2的四棱锥,如图所示:∴该几何体的体积116V=⨯⨯=,故选B.82337.[2018·漳州调研]《九章算术》是我国古代的数学名著,书中有如下问题:“今有大夫、不更、簪裹、上造、公士,凡五人,共猎得五鹿,欲以爵次分之,问各得几何?”其意思:“共有五头鹿,5人以爵次进行分配(古代数学中“以爵次分之”这种表述,一般表示等差分配,在本题中表示等差分配).”在这个问题中,若大夫得“一鹿、三分鹿之二”,则簪裹得()A.一鹿、三分鹿之一B.一鹿C.三分鹿之二D.三分鹿之一【答案】B【解析】由题意可知,五人按等差数列进行分五鹿,设大夫得的鹿数为首项a1,且,公差为d,则,解得,所以B.8.[2018·周口期末])A.B.C.D.【答案】Bx≠,即()()≠,1,,,故排除A,11x∈-∞+∞D,当x C,故选B.9.[2018·郴州月考]阅读如图所示的程序框图,运行相应程序,输出的结果是()A .12B .18C .120D .125【答案】C【解析】第一次运行:011a =+=,1i =为奇数,112S =+=,112i =+=;第二次运行:123a =+=,2i=为偶数,326S =⨯=,213i =+=; 第三次运行:336a =+=,3i =为奇数,6612S =+=,314i=+=;第四次运行:6410a=+=,4i =为偶数,1012120S=⨯=,415i =+=;程序终止运行,输出120S =.故选C .10.[2018·济南期末]设x ,y 满足约束条件1122x y x y x y +⎧⎪--⎨⎪-⎩≥≥≤,若目标函数3za x y=+仅在点()1,0处取得最小值,则a 的取值范围为( ) A .()6,3- B .()6,3-- C .()0,3 D .(]6,0-【答案】A【解析】作出约束条件1122x y x y x y +⎧⎪--⎨⎪-⎩≥≥≤,表示的可行域如图所示,将3za x y=+化成33a z y x =-+,当123a -<-<时,33a z yx =-+仅在点()1,0处取得最小值,即目标函数3za x y=+仅在点()1,0A 处取得最小值,解得63a -<<,故选A .11.[2018·武邑中学]已知抛物线22(0)y p x p =>的焦点为F ,其准线与双曲线2213yx-=相交于M ,N 两点,若M N F △为直角三角形,其中F 为直角顶点,则p=( )A.BC. D .6【答案】A【解析】由题设知抛物线22yp x=2213yx-=解得由双曲线的对称性知M N F△为等腰直角三角形,22334p p ∴=+,p ∴=.故选A .12.[2018·滁州期末]若关于x 在()()00-∞+∞,,上恒成立,则实数k 的取值范围为( ) A )25e ⎛+∞ ⎝,B )23e ⎛+∞ ⎝,C 25e ⎫⎛+∞⎪ ⎝,D 23e⎫⎛+∞⎪ ⎝,【答案】A【解析】201e xx x x k >+->令,则e所以当(),1x ∈-∞-时,()0f x '<,当()1,0x ∈-时,()0f x '>,当()0,2x ∈时,()0f x '>,当()2,x ∈+∞时,()0f x '<, 所以()2kf>或()1k f<-或ek<-,故选A .第Ⅱ卷本卷包括必考题和选考题两部分。
黑龙江省2018年普通高等学校招生全国统一考试仿真模拟(二)数学(文科)试题(解析版)

普通高等学校招生全国统一考试仿真模拟(二)文科数学第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知集合,,则()A. B. C. D.【答案】B【解析】试题分析:因,故,应选B.考点:集合的交集运算.2. (2017·桂林市模拟)复数,,是虚数单位.若,则()A. B. C. D.【答案】D【解析】【分析】利用复数的运算法则、模的计算公式即可得出.【详解】z=(a+i)(1﹣i)=a+1+(1﹣a)i,∴|z|=2=,化为a2=1.解得a=±1.故选:D.【点睛】本题考查了复数的运算法则、模的计算公式,考查了推理能力与计算能力,属于基础题.3. (2017·福建质检)某公司为了增加其商品的销售利润,调查了该商品投入的广告费用与销售利润的统计数据如下表:广告费用(万元)销售利润(万元)由表中数据,得线性回归方程:,,则下列结论错误的是()A. B. C. 直线过点 D. 直线过点【答案】D【解析】【分析】求出回归直线方程,根据回归方程进行判断.【详解】=,.∴直线l经过点(4,8).=(﹣2)×(﹣3)+(﹣1)×(﹣1)+1×1+2×3=14.=(﹣2)2+(﹣1)2+12+22=10.∴=,=8﹣1.4×4=2.4.∴回归方程为y=1.4x+2.4.当x=2时,y=1.4×2+2.4=5.2.∴直线l过点(2,5.2)故选:D.【点睛】本题主要考查线性回归方程,属于难题.求回归直线方程的步骤:①依据样本数据画出散点图,确定两个变量具有线性相关关系;②计算的值;③计算回归系数;④写出回归直线方程为;回归直线过样本点中心是一条重要性质,利用线性回归方程可以估计总体,帮助我们分析两个变量的变化趋势.4. 已知数列为等差数列,,,则()A. B. C. D.【答案】A【解析】【分析】利用等差数列的通项公式即可得出.【详解】设等差数列{a n}的公差为d,∵a2+a3=1,a10+a11=9,∴2a1+3d=1,2a1+19d=9,解得a1=﹣,d=.∴a5+a6=2a1+9d=﹣2×+9×=4.故选:A.【点睛】在解决等差、等比数列的运算问题时,有两个处理思路,一是利用基本量,将多元问题简化为一元问题,虽有一定量的运算,但思路简洁,目标明确;二是利用等差、等比数列的性质是两种数列基本规律的深刻体现,应有意识地去应用.但在应用性质时要注意性质的前提条件,有时需要进行适当变形. 在解决等差、等比数列的运算问题时,经常采用“巧用性质、整体考虑、减少运算量”的方法.5. (2017·沈阳市质检)已知函数则()A. B. C. D.【答案】B【解析】【分析】由分段函数的表达式从内向外依次代入求值即可.【详解】f()=log5=﹣2,=f(﹣2)=,故选:B.【点睛】(1)求分段函数的函数值,要先确定要求值的自变量属于哪一段区间,然后代入该段的解析式求值,当出现f(f(a))的形式时,应从内到外依次求值.(2)当给出函数值求自变量的值时,先假设所求的值在分段函数定义区间的各段上,然后求出相应自变量的值,切记要代入检验,看所求的自变量的值是否满足相应段自变量的取值范围.6. 一个几何体的三视图如图所示,则该几何体的表面积为()A. B. C. D.【答案】B【解析】【分析】利用三视图判断几何体为三棱柱,求其面积即可.【详解】三棱柱的表面积为5个面的面积之和,又因为底面是正三角形,边长为2,棱柱的高为:3.所以S=2×+3×2×3=18+2.故选:B.【点睛】思考三视图还原空间几何体首先应深刻理解三视图之间的关系,遵循“长对正,高平齐,宽相等”的基本原则,其内涵为正视图的高是几何体的高,长是几何体的长;俯视图的长是几何体的长,宽是几何体的宽;侧视图的高是几何体的高,宽是几何体的宽.7. (2017·兰州市实战考试)已知直线与圆相交于,,且为等腰直角三角形,则实数的值为()A. 或B.C. 或D.【答案】C【解析】【分析】由题意可得△ABC是等腰直角三角形,可得圆心C(1,﹣a)到直线ax+y﹣1=0的距离等于r•sin45°,再利用点到直线的距离公式求得a的值.【详解】由题意可得△ABC是等腰直角三角形,∴圆心C(1,﹣a)到直线ax+y﹣1=0的距离等于r•sin45°=,再利用点到直线的距离公式可得=,∴a=±1,故选:C.【点睛】这个题目考查的是直线和圆的位置关系,一般直线和圆的题很多情况下是利用数形结合来解决的,联立的时候较少;还有就是在求圆上的点到直线或者定点的距离时,一般是转化为圆心到直线或者圆心到定点的距离,再加减半径,分别得到最大值和最小值。
广东省2018届高三下学期模拟考试(二)数学(文)试题Word版含答案
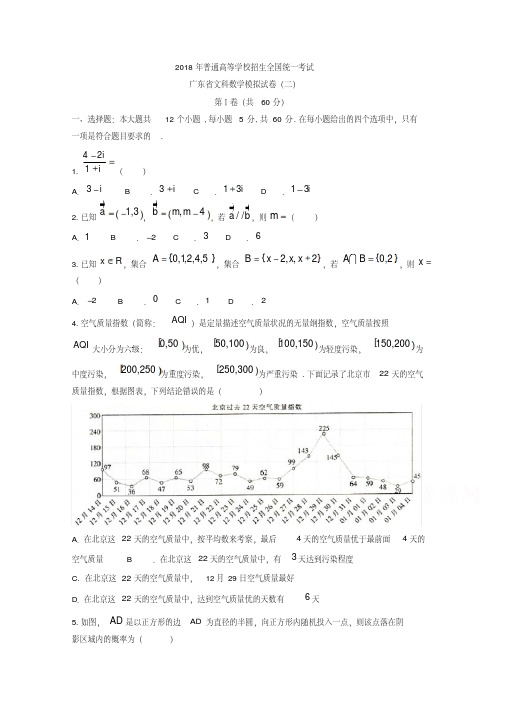
4 天的空气质量优于最前面 4 天的
空气质量
B
.在北京这 22 天的空气质量中,有 3 天达到污染程度
C. 在北京这 22 天的空气质量中, 12 月 29 日空气质量最好
D.在北京这 22 天的空气质量中,达到空气质量优的天数有
6天
5. 如图, AD 是以正方形的边 AD 为直径的半圆,向正方形内随机投入一点,则该点落在阴
影区域内的概率为(
)
A. 16
3 B . 16 C. 4
1 D .4
6. 已知等比数列 an 的首项为 1 ,公比 q 1 ,且 a5 a4 3 a3 a2 ,则 a5 (
)
A. 9
B
. 9 C.
81
D . 81
x2 y2
7. 已知双曲线 C : a2
b2
1a
0, b
0
的一个焦点坐标为
ቤተ መጻሕፍቲ ባይዱ
4,0 ,且双曲线的两条渐近
.
国王问他想要什么,他对国王说: “陛下,请您在这张棋盘的第 1个小格里,赏给我 1 粒麦子,
在第 2 个小格里给 2 粒,第 3 小格给 4 粒,以后每一小格都比前一小格加一倍 . 请您把这样摆
满棋盘上所有的 64 格的麦粒,都赏给您的仆人吧! ”国王觉得这要求太容易满足了,就命令
给他这些麦粒 . 当人们把一袋一袋的麦子搬来开始计数时,国王才发现:就是把全印度甚至
全世界的麦粒全拿来,也满足不了那位宰相的要求
. 那么,宰相要求得到的麦粒到底有多少
AQI 大小分为六级: 0,50 为优, 50,100 为良, 100,150 为轻度污染, 150,200 为
中度污染, 200,250 为重度污染, 250,300 为严重污染 . 下面记录了北京市 22 天的空气
2018年新疆高考数学二模试卷(文科)(解析版)

2018年新疆高考数学二模试卷(文科)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)已知集合M={x|x<1},N={x|2x>1},则M∪N=()A.∅B.{x|0<x<1}C.{x|x<0}D.R2.(5分)a为实数为实数,则a=()A.B.﹣2C.1D.3.(5分)已知A、B、C三点不共线,且点O满足=,则下列结论正确的是()A.B.C.D.4.(5分)若函数的图象向左平移φ(φ>0)个单位后所得的函数为偶函数,则φ的最小值为()A.B.C.D.5.(5分)设等差数列{a n}的前n项和为S n,若S9=54,则2a6+a3=()A.9B.15C.18D.366.(5分)在△ABC中,“A>60°”是“”的()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件7.(5分)已知点(m,8)在幂函数f(x)=(m﹣1)x n的图象上,设,则a,b,c的大小关系为()A.a<c<b B.a<b<c C.b<c<a D.b<a<c8.(5分)某空间几何体的三视图如图所示,则该几何体的外接球的体积为()A.B.C.D.9.(5分)已知实数x,y满足,则使不等式kx﹣y+k≤1恒成立的实数k的取值集合是()A.(﹣∞,1]B.C.D.10.(5分)图中的程序框图所描述的算法称为欧几里得辗转相除法,若输入m=225,n=135则输出的m的值为()A.5B.25C.45D.3511.(5分)设a,b∈R,a2+2b2=6,则a+的最小值为()A.﹣2B.C.﹣3D.12.(5分)抛物线y2=2px(p>0)的焦点为F,其准线经过双曲线﹣=1(a>0,b >0)的左焦点,点M为这两条曲线的一个交点,且|MF|=p,则双曲线的离心率为()A.B.2C.D.+1二、填空题(每题5分,满分20分,将答案填在答题纸上)13.(5分)一个社会调查机构就某地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(如图).为了分析居民的收入与年龄、学历、职业等方面的关系,要从这10000人中再用分层抽样方法抽出100人作进一步调查,则在[2500,3000)(元)月收入段应抽出人.14.(5分)已知函数f(x)是定义在(﹣∞,0)∪(0,+∞)上的奇函数,在(0,+∞)上单调递减,且f(4)=0,若f(x﹣3)≤0,则x的取值范围为.15.(5分)在一次数学测试中,甲、乙、丙、丁四位同学中只有一位同学得了满分,他们四位同学对话如下,甲:我没考满分;乙:丙考了满分;丙:丁考了满分;丁:我没考满分.其中只有一位同学说的是真话,据此,判断考满分的同学是.16.(5分)设函数,其中[x]表示不超过x的最大整数,如[﹣1.2]=﹣2,[1.2]=1,[1]=1,若直线x﹣ky+1=0(k>0)与函数y=f(x)的图象恰好有两个不同的交点,则k的取值范围是.三、解答题(解答应写出文字说明、证明过程或演算步骤.)17.(12分)在等差数列{a n}中,已知a1+a3+a8=9,a2+a5+a11=21.(I)求数列{a n}的通项a n;(II)若,求数列{a n•c n}的前n项和S n.18.(12分)如图,EB垂直于菱形ABCD所在平面,且EB=BC=2,∠BAD=60°,点G、H分别为边CD、DA的中点,点M是线段BE上的动点.(I)求证:GH⊥DM;(II)当三棱锥D﹣MGH的体积最大时,求点A到面MGH的距离.19.(12分)甲、乙两位学生参加数学竞赛培训.现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次.记录如下:甲:82 81 79 78 95 88 93 84乙:92 95 80 75 83 80 90 85(1)画出甲、乙两位学生成绩的茎叶图,指出学生乙成绩的中位数;(2)现要从中选派一人参加数学竞赛,从平均状况和方差的角度考虑,你认为派哪位学生参加合适?请说明理由.20.(12分)已知动点P是圆G:上的任意一点,点P与点的连线段的垂直平分线和GP相交于点Q.(I)求点Q的轨迹C方程;(II)过坐标原点O的直线l交轨迹C于点E,F两点,直线EF与坐标轴不重合.M是轨迹C上的一点,若△EFM的面积是4,试问直线EF,OM的斜率之积是否为定值,若是,求出此定值,否则,说明理由.21.(12分)已知函数f(x)=e x+ax+1(a∈R).若x=0是f(x)的极值点.(I)求a,并求f(x)在[﹣2,1]上的最小值;(II)若不等式kf′(x)<xe x+1对任意x>0都成立,其中k为整数,f′(x)为f(x)的导函数,求k的最大值.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分,作答时请用2B 铅笔在答题卡上把所选题目的题号涂黑.[选修4-4:坐标系与参数方程].22.(10分)在直角坐标系xOy中,曲线C的参数方程为(θ为参数),以坐标原点O为极点,以x轴正半轴为极轴,建立直角坐标系.(I)求曲线C的极坐标方程;(II)过点P(2,0)作斜率为1直线l与曲线C交于A,B两点,试求|P A|+|PB|的值.[选修4-5:不等式选讲]23.设函数f(x)=|x﹣p|.(I)当p=2时,解不等式f(x)≥4﹣|x﹣1|;(II)若f(x)≥1的解集为(﹣∞,0]∪[2,+∞),(m>0,n>1),求证:m+2n≥11.2018年新疆高考数学二模试卷(文科)参考答案与试题解析一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)已知集合M={x|x<1},N={x|2x>1},则M∪N=()A.∅B.{x|0<x<1}C.{x|x<0}D.R【解答】解:N={x|x>0};∴M∪N=R.故选:D.2.(5分)a为实数为实数,则a=()A.B.﹣2C.1D.【解答】解:a为实数,==+i为实数,∴=0,解得a=.故选:D.3.(5分)已知A、B、C三点不共线,且点O满足=,则下列结论正确的是()A.B.C.D.【解答】解:不妨设=(1,0),=(0,1),则=(﹣1,﹣1),∴==(﹣1,1),==(﹣1,﹣2),设=λ+μ,则,解得λ=﹣,μ=﹣.故选:B.4.(5分)若函数的图象向左平移φ(φ>0)个单位后所得的函数为偶函数,则φ的最小值为()A.B.C.D.【解答】解:函数的图象向左平移φ个单位,得y=f(x+φ)=cos[2(x+φ)+]=cos(2x+2φ+)的图象,又函数y为偶函数,∴2φ+=kπ,k∈Z;又φ>0,∴φ的最小值为.故选:D.5.(5分)设等差数列{a n}的前n项和为S n,若S9=54,则2a6+a3=()A.9B.15C.18D.36【解答】解:设等差数列{a n}的公差为d,∵S9=54,∴=9a5=54,可得a5=6,则2a6+a3=3a1+12d=3a5=18.故选:C.6.(5分)在△ABC中,“A>60°”是“”的()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件【解答】解:若“A>60°”成立,则A可能大于120°,此时“”不一定成立,即“A>60°”⇒“”为假命题;在△ABC中,若“”,则60°<A<120°,即“A>60°”一定成立,即“”⇒“A>60°”为真命题;故“A>60°”是“”的必要而不充分条件故选:B.7.(5分)已知点(m,8)在幂函数f(x)=(m﹣1)x n的图象上,设,则a,b,c的大小关系为()A.a<c<b B.a<b<c C.b<c<a D.b<a<c 【解答】解:点(m,8)在幂函数f(x)=(m﹣1)x n的图象上,可得m﹣1=1,即m=2,2n=8,可得n=3,则f(x)=x3,且f(x)在R上递增,由a=f(),b=f(lnπ),c=f(),0<<<1,lnπ>1,可得a<c<b,故选:A.8.(5分)某空间几何体的三视图如图所示,则该几何体的外接球的体积为()A.B.C.D.【解答】解:根据三视图得出几何体为四棱锥,是长方体的一部分,把它镶嵌在长方体中,长宽为4,高为5,宽为3,∴体对角线外接球的半径,∴R==,∴该几何体的外接球的体积为:=π,故选:D.9.(5分)已知实数x,y满足,则使不等式kx﹣y+k≤1恒成立的实数k的取值集合是()A.(﹣∞,1]B.C.D.【解答】解:作出不等式组对应的平面区域如图,则由图象知x≥0,由不等式kx﹣y+k≤1恒成立,得k(x+1)≤1+y,即k≤,设z=,则z的几何意义是区域内的点到定点D(﹣1,﹣1)的斜率,由图象知AD的斜率最小,由得,即A(1,0),此时z的最小值为z==,即k≤,即实数k的取值范围是(﹣∞,],故选:B.10.(5分)图中的程序框图所描述的算法称为欧几里得辗转相除法,若输入m=225,n=135则输出的m的值为()A.5B.25C.45D.35【解答】解:模拟程序框图的运行过程,如下;m=225,n=135,由225÷135=1…90,r=90,m=135,n=90,不满足条件r=0,由135÷90=1…45,r=45,m=90,n=45,不满足条件r=0,由90÷45=2…0,r=0,m=45,n=0,此时,满足条件r=0,退出循环,输出m的值为45.故选:C.11.(5分)设a,b∈R,a2+2b2=6,则a+的最小值为()A.﹣2B.C.﹣3D.【解答】解:由柯西不等式(a2+b2)(c2+d2)≥(ac+bd)2,且a2+2b2=6,则(a2+2b2)=(12+12)(a2+2b2)≥则≤12,即得﹣2≤≤2,所以=﹣2故选:A.12.(5分)抛物线y2=2px(p>0)的焦点为F,其准线经过双曲线﹣=1(a>0,b >0)的左焦点,点M为这两条曲线的一个交点,且|MF|=p,则双曲线的离心率为()A.B.2C.D.+1【解答】解:抛物线y2=2px(p>0)的焦点为F(,0),其准线方程为x=﹣,∵准线经过双曲线﹣=1(a>0,b>0)的左焦点,∴c=;∵点M为这两条曲线的一个交点,且|MF|=p,∴M的横坐标为,代入抛物线方程,可得M的纵坐标为±p,将M的坐标代入双曲线方程,可得=1,∴a=p,∴e=1+.故选:D.二、填空题(每题5分,满分20分,将答案填在答题纸上)13.(5分)一个社会调查机构就某地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(如图).为了分析居民的收入与年龄、学历、职业等方面的关系,要从这10000人中再用分层抽样方法抽出100人作进一步调查,则在[2500,3000)(元)月收入段应抽出25人.【解答】解:由直方图可得[2500,3000)(元)月收入段共有10000×0.0005×500=2500人按分层抽样应抽出人故答案为:2514.(5分)已知函数f(x)是定义在(﹣∞,0)∪(0,+∞)上的奇函数,在(0,+∞)上单调递减,且f(4)=0,若f(x﹣3)≤0,则x的取值范围为[﹣1,3)∪[7,+∞).【解答】解:f(x)为奇函数,在(0,+∞)上单调递减;∴f(x)在(﹣∞,0)上单调递减;又f(4)=0;∴f(﹣4)=0;∵f(x﹣3)≤0;∴①x﹣3>0,即x>3时:f(x﹣3)≤f(4);∵f(x)在(0,+∞)上单调递减;∴x﹣3≥4;∴x≥7;②x﹣3<0,即x<3时:f(x﹣3)≤f(﹣4);∵f(x)在(﹣∞,0)上单调递减;∴x﹣3≥﹣4;∴﹣1≤x<3;综上得,x的取值范围为[﹣1,3)∪[7,+∞).故答案为:[﹣1,3)∪[7,+∞).15.(5分)在一次数学测试中,甲、乙、丙、丁四位同学中只有一位同学得了满分,他们四位同学对话如下,甲:我没考满分;乙:丙考了满分;丙:丁考了满分;丁:我没考满分.其中只有一位同学说的是真话,据此,判断考满分的同学是甲.【解答】解:若甲考满分,则甲、乙、丙说的都是假话,丁说的是真话,符合题意;若乙考满分,则乙、丙说的是假话,甲和丁说的是真话,不合题意;若丙考满分,则甲、乙、丁说的都是真话,丙说的是假话,不合题意;若丁考满分,则甲、丙说的是真话,乙、丁说的是假话,不合题意.综上,甲考满分.故答案为:甲.16.(5分)设函数,其中[x]表示不超过x的最大整数,如[﹣1.2]=﹣2,[1.2]=1,[1]=1,若直线x﹣ky+1=0(k>0)与函数y=f(x)的图象恰好有两个不同的交点,则k的取值范围是2<k≤3.【解答】解:画出函数和函数g(x)=的图象,若直线ky=x+1(k>0)与函数y=f(x)的图象恰有两个不同的交点,结合图象可得:k P A≤<k PC,∵k P A==,k PC==,故≤<,求得2<k≤3,故答案为:2<k≤3.三、解答题(解答应写出文字说明、证明过程或演算步骤.)17.(12分)在等差数列{a n}中,已知a1+a3+a8=9,a2+a5+a11=21.(I)求数列{a n}的通项a n;(II)若,求数列{a n•c n}的前n项和S n.【解答】解:(1)设等差数列{a n}公差为d,∵a1+a3+a8=9,a2+a5+a11=21,∴,解得a1=﹣3,d=2,∴a n=2n﹣5(II)由(I),错位相减得,=,所以.18.(12分)如图,EB垂直于菱形ABCD所在平面,且EB=BC=2,∠BAD=60°,点G、H分别为边CD、DA的中点,点M是线段BE上的动点.(I)求证:GH⊥DM;(II)当三棱锥D﹣MGH的体积最大时,求点A到面MGH的距离.【解答】解:(Ⅰ)证明:连接AC、BD相交于点O.∵BE⊥平面ABCD.而AC⊂平面ABCD,∴BE⊥AC.又∵四边形ABCD为菱形,∴BD⊥AC.∵BD∩BE=B,∴AC⊥平面BDE.∵G、H分别为DC、AD的中点,∴GH∥AC,则GH⊥平面BDE.而DM⊂平面BDE,∴GH⊥DM;(II)菱形ABCD中,∠BAD=60°,得,∠ADC=120°.∵DG=DH=1,∴S△DGH==,∵BE⊥平面ABCD,即BM⊥平面ABCD,∴=.显然,当点M与点E重合时,BM取得最大值2,此时(V D﹣MGH)max=.且MG=MH=,GH=,则,∵H是AD中点,所有A到平面MGH的距离d1等于到平面MGH的距离d2,又V D﹣MGH=V M﹣DGH,∴,得d2=.∴A到平面MGH的距离为.19.(12分)甲、乙两位学生参加数学竞赛培训.现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次.记录如下:甲:82 81 79 78 95 88 93 84乙:92 95 80 75 83 80 90 85(1)画出甲、乙两位学生成绩的茎叶图,指出学生乙成绩的中位数;(2)现要从中选派一人参加数学竞赛,从平均状况和方差的角度考虑,你认为派哪位学生参加合适?请说明理由.【解答】解:(1)茎叶图如下:…(2分)学生乙成绩分别为:75,80,80,83,85,90,92,95,中位数为=84,…(4分)(2)派甲参加比较合适,理由如下:…(5分)=35.5=41…(7分)∴,<∴甲的成绩比较稳定,派甲参加比较合适.…(8分)20.(12分)已知动点P是圆G:上的任意一点,点P与点的连线段的垂直平分线和GP相交于点Q.(I)求点Q的轨迹C方程;(II)过坐标原点O的直线l交轨迹C于点E,F两点,直线EF与坐标轴不重合.M是轨迹C上的一点,若△EFM的面积是4,试问直线EF,OM的斜率之积是否为定值,若是,求出此定值,否则,说明理由.【解答】解:(Ⅰ)由题意,|QP|=|QA|,又∵∴,∴点Q的轨迹是以G、A为焦点的椭圆,其中,∴椭圆C的方程为.(Ⅱ)设直线l的方程为y=k1x,联立,得∴设OM所在直线方程为y=k2x,联立椭圆方程得或,点M到直线EF的距离.∴,即,解得,∴直线EF,OM的斜率之积是定值21.(12分)已知函数f(x)=e x+ax+1(a∈R).若x=0是f(x)的极值点.(I)求a,并求f(x)在[﹣2,1]上的最小值;(II)若不等式kf′(x)<xe x+1对任意x>0都成立,其中k为整数,f′(x)为f(x)的导函数,求k的最大值.【解答】解:(I)f′(x)=e x+a,由x=0是f(x)的极值点,得f′(0)=0,∴a=﹣1.易知f(x)在[﹣2,0]上单调递减,在[0,1]上单调递增,所有当x=0时,f(x)在[﹣2,1]上取得最小值2.(II)由(I)知a=﹣1,此时f′(x)=e x﹣1,∴kf′(x)<xe x+1⇔k(e x﹣1)<xe x+1,∵x>0,∴e x﹣1>0,∴k<,令g(x)=(x>0),则k<g(x)min,g′(x)=(x>0)令h(x)=e x﹣x﹣2,h′(x)=e x﹣1>0,∴h(x)在(0,+∞)单调递增,且h(1)<0,h(2)>0,∴h(x)在(0,+∞)时,g′(x)>0,∴g(x)min=g(x0)=+x0,由g′(x0)=0⇒=x0+2,∴g(x0)=x0+1∈(2,3),又∵k<g(x0),且k∈Z,所以k的最大值为2.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分,作答时请用2B 铅笔在答题卡上把所选题目的题号涂黑.[选修4-4:坐标系与参数方程].22.(10分)在直角坐标系xOy中,曲线C的参数方程为(θ为参数),以坐标原点O为极点,以x轴正半轴为极轴,建立直角坐标系.(I)求曲线C的极坐标方程;(II)过点P(2,0)作斜率为1直线l与曲线C交于A,B两点,试求|P A|+|PB|的值.【解答】解:(I)由曲线C的参数方程为,转化成直角坐标方程为:x2+y2﹣4x+4y=0,转换为极坐标方程为:ρ2=4ρcosθ﹣4ρsinθ,即:.圆C的极坐标方程为.(II)设直线L1的参数方程为(t为参数),A,B两点对应的参数分别为t1,t2,直线l:(t为参数)和圆的方程联立:得:,所以,所以,.[选修4-5:不等式选讲]23.设函数f(x)=|x﹣p|.(I)当p=2时,解不等式f(x)≥4﹣|x﹣1|;(II)若f(x)≥1的解集为(﹣∞,0]∪[2,+∞),(m>0,n>1),求证:m+2n≥11.【解答】解:(I)当p=2时,不等式化为|x﹣2|+|x﹣1|≥4∵∴不等式的解集为(II)根据f(x)≥1得|x﹣p|≥1⇒x≤p﹣1或x≥p+1,∵f(x)≥1的解集为(﹣∞,0]∪[2,+∞),故,所以,∵m>0,n>0,∴,当且仅当m=3,n=4时取等号,∴m+2n≥11.。
2018年黑龙江省普通高等学校招生全国统一考试仿真模拟(二)数学(文科)试题答案

一㊁ 选择题
2 } } , 1. B㊀ ȵT= { x | x <4 x-3 ={ x | 1<x<3
7. C㊀ 由 题 意 知 әA B C 中, C A =C B =1, øA C B= 2 又圆心 ( , ) , 9 0 ʎ ʑ 弦心距为 , C1 - a, 2 | a- a-1 | 2, ʑ = ʑ a=ʃ1. 2 2 2 a +1
������x-2������f( ᶄ( x) x) , f >0 时 , ᶄ( x) = <0 说 明 函 g 3 x 详解答案
1 0 1
数 g( 在( 上 单 调 递 减, 又 f( 为偶函 x) 0, +ɕ ) x) ) 数, 所以 g( 为偶函数 , 又f( 所 以 g( x) 1 =0, 1) =
故选 B.
几何 体 是 一 个 水 平 放 置 的 直 三 6. B㊀ 由三视图可知 , , 棱柱 ( 如图 ) 其 高 为 3, 底 面 是 底 为 2, 高 为 3的 等
2 2 腰三角形 , ʑ 腰 长 为 (3) +1 =2, ʑ底面为等
c 右焦点到渐近 线 y= ʃ bx 的 距 离 为 b = 2 2 a a + b
ç ç ÷ ÷ ç ÷
1ö 1 æ æ1 ö ö æ =f l o =f( -2) = , g 5ø ø 5ø 4 è è2 è 52
l 趋向于与x 轴 平 行 时 , | O B |的 长 度 变 化 越 来 越
快, 斜率越来越陡 , 故排除 C, 选 B. 1 1. C㊀ 双曲线 的 右 焦 点 到 左 顶 点 的 距 离 等 于 a+ c,
1( 1 ) , ) , 2 + 3 + 5 + 6 = 4 5 + 7 + 9 + 1 1 = 8 y= ( 4 4 ( ) ) ) ) - 2 ˑ( - 3 +( - 1 ˑ( - 1 + 1 ˑ 1 + 2 ˑ 3 2 ( ) 2 2 ( ) - 2 + - 12+ 1 + 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
仿真考(二)高考仿真模拟冲刺卷()
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分分.考试时间分钟.
第Ⅰ卷(选择题共分)
一、选择题:本大题共小题,每小题分,在每小题给出的四个选
项中,只有一项是符合题目要求的.
.已知集合={-<<},={<,∈},则( )
.⊆.⊆.∩={} .∪=
.已知复数=,其中为虚数单位,则=( )
...不等式组(\\(-≤,+≥-,-≥-))的解集记为,若(,)
∈,则=-的最小值是( )
.-.-...若()是定义在上的函数,则“()=”是“函数()为奇函数”的(
)
.必要不充分条件.充要条件
.充分不必要条件.既不充分也不必要条件.若命题“∃∈,
+(-)+<”是真命题,则实数的取值范围是( )
.[-] .(-)
.(-∞,-]∪[,+∞) .(-∞,-)∪(,+∞)
.使(∈*)展开式中含有常数项的的最小值是( )
.....已知函数()=(+φ)
的图象的一个对称中心为,则函数()的单调递减区间是( )
(∈) (∈)
(∈) (∈).(·滨州二模)函数=,∈(-π,)∪(,π)的图象大致是( )
.已知球的半径为,,,三点在球的球面上,球心到平面的距
离为,==,∠=°,则球的表面积为( )
π π π π.如图,网格纸上的小正方形的边长为,粗实线画出的是某几
何体的三视图,则该几何体的体积是( )
.+π .+π .+π .+π.已知抛物线=的焦点与双曲线-
=的右焦点重合,抛物线的准线与轴的交点为,点在抛物线上且=
,则△的面积为( )
.....设定义在(,+∞)上的函数()满足′()-()=,=,则()( )
.有极大值,无极小值.有极小值,无极大值.既有极大值,又有极小值.既无极大值,又无极小值
第Ⅱ卷(非选择题共分)
本卷包括必考题和选考题两部分.第~题为必考题,每个试题考
生都必须作答,第~题为选考题,考生根据要求作答.二、填空题:本大题共小题,每小题分,共分.把答案填在题
中的横线上..高为π,体积为π的圆柱的侧面展开图的周长为..过点()的直线与圆:(-)+(-)=相交于,两点,当弦的长取
最小值时,直线的倾斜角等于..已知平面向量与的夹角为,=(,),-=,则=..在△中,,,分别为内角,,的对边,+=,(-)=,则△
的面积的最大值为.三、解答题:本大题共小题,解答应写出文字说明、证明过程或
演算步骤.。
