【原创】R语言Shiny表格数据分析可视化案例报告(附代码数据)
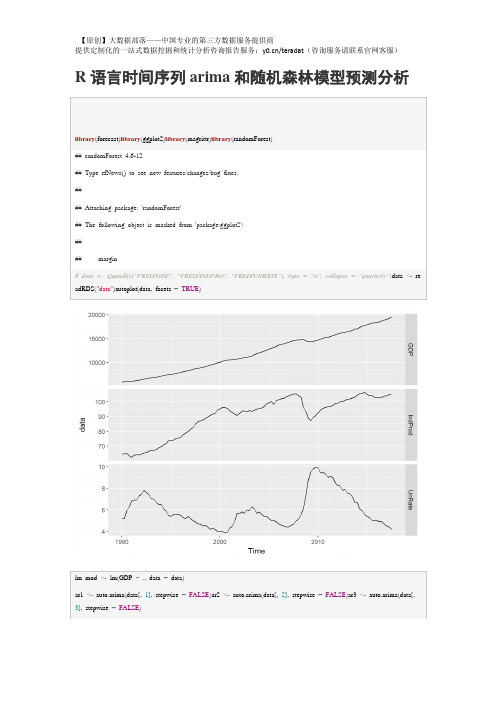
【原创】R语言时间序列arima和随机森林模型预测分析报告(附代码数据)
##
## Model df: 4. Total lags used: 8
checkresiduals(lm_mod)
##
## Breusch-Godfrey test for serial correlation of order up to 10
## Q* = 2.2891, df = 5, p-value = 0.8079
##
## Model df: 3. Total lags used: 8
checkresiduals(arireg)
##
## Ljung-Box test
##
## data: Residuals from Regression with ARIMA(2,2,1) errors
lm_mod<-lm(GDP~.,data=data)
ar1<-auto.arima(data[,1],stepwise=FALSE)ar2<-auto.arima(data[,2],stepwise=FALSE)ar3<-auto.arima(data[,3],stepwise=FALSE)
GDP<-forecast(ar1)$meanIndProd<-forecast(ar2)$meanUnRate<-forecast(ar3)$meanf3<-cbind(IndProd,UnRate)arireg<-auto.arima(data[,1],stepwise=FALSE,xreg=data[,-1])
summary(lm_mod)
##
## Call:
## lm(formula = GDபைடு நூலகம் ~ ., data = data)
【原创】R语言主成分分析因子分析案例报告(完整附数据)

R语言主成分分析因子分析案例报告R语言多元分析系列之一:主成分分析主成分分析(principal components analysis,PCA)是一种分析、简化数据集的技术。
它把原始数据变换到一个新的坐标系统中,使得任何数据投影的第一大方差在第一个坐标(称为第一主成分)上,第二大方差在第二个坐标(第二主成分)上,依次类推。
主成分分析经常用减少数据集的维数,同时保持数据集的对方差贡献最大的特征。
这是通过保留低阶主成分,忽略高阶主成分做到的。
这样低阶成分往往能够保留住数据的最重要方面。
但是在处理观测数目小于变量数目时无法发挥作用,例如基因数据。
R语言中进行主成分分析可以采用基本的princomp函数,将结果输入到summary和plot函数中可分别得到分析结果和碎石图。
但psych扩展包更具灵活性。
1 选择主成分个数选择主成分个数通常有如下几种评判标准:∙根据经验与理论进行选择∙根据累积方差贡献率,例如选择使累积方差贡献率达到80%的主成分个数。
∙根据相关系数矩阵的特征值,选择特征值大于1的主成分。
另一种较为先进的方法是平行分析(parallel analysis)。
该方法首先生成若干组与原始数据结构相同的随机矩阵,求出其特征值并进行平均,然后和真实数据的特征值进行比对,根据交叉点的位置来选择主成分个数。
我们选择USJudgeRatings数据集举例,首先加载psych包,然后使用fa.parallel函数绘制下图,从图中可见第一主成分位于红线上方,第二主成分位于红线下方,因此主成分数目选择1。
fa.parallel(USJudgeRatings[,-1], fa="pc",n.iter=100, show.legend=FALSE)2 提取主成分pc=principal(USJudgeRatings[,-1],nfactors=1)PC1 h2 u21 0.92 0.84 0.15652 0.91 0.83 0.16633 0.97 0.94 0.06134 0.96 0.93 0.07205 0.96 0.92 0.07636 0.98 0.97 0.02997 0.98 0.95 0.04698 1.00 0.99 0.00919 0.99 0.98 0.019610 0.89 0.80 0.201311 0.99 0.97 0.0275PC1SS loadings 10.13Proportion Var 0.92从上面的结果观察到,PC1即观测变量与主成分之间的相关系数,h2是变量能被主成分解释的比例,u2则是不能解释的比例。
【原创】R语言Shiny表格数据分析可视化案例报告(附代码数据)

【原创】R语⾔Shiny表格数据分析可视化案例报告(附代码数据)
R语⾔Shiny表格数据分析可视化案例报告
表格是⼯作和⽣活中常见的数据呈现⽅式,例如公司的很多报表就需要⽤到表格。
当我们展⽰数据的时候,⽤户当然不希望只看到⼀个静态的页⾯,所以就需要⼀些简单的交互功能:排序、查找、筛选等等。
基础的需求并不难实现,但当我们使⽤其他⽹页技术做这件事情的时候,既要做前端,也要做后端,代码量也不会少。
对技术⼩⽩来说,使⽤ R Shiny 做这样的事情就很容易了。
Shiny 是 R 社区⾥⾯⼀个⾮常出名的包,⽤来制作各类交互式⽹络应⽤,我们熟知的谢益辉就是其中的⼀位作者。
先睹为快看看 Shiny 能做出什么样的效果:
可以看出来, Shiny 简直天⽣就是为了交互⽽存在的。
Shiny 也提供了⾮常丰富的 widgets ,⼏乎覆盖了我们对 UI 的全部需求:
DT 也是谢⽼⼤写的包,是 JavaScript DataTables 库的R接⼝,R的数据对象可以直接通过 DT 呈现为HTML的表格。
不仅如此, DT 本⾝还⾃动⽀持筛选、分页、排序等功能,⾮常的强⼤。
⼀⾔以蔽之, Shiny + DT 是交互式呈现表格的⾮常好的⼀个⽅案。
下⾯以我最近做的⼀个表格为例,最终效果是这样的:。
【最新】R语言数据可视化 PPT课件教案讲义(附代码数据)图文

中级图形
basic 3d scatter plot
mpg
25
30
35
500 400 300 200 100 2 3 4 5 6 0
10
15
1
wt
disp
20
中级图形
气泡图 概念:用点的大小表示第三个变量的值 函数:symbols() symbols(x,y,circle=radius)
中级图形
scatter plot matrix via var package
100 200 300 400 2 3 4 5
100 20Leabharlann 300 400dispdrat
5
wt
2
3
4
10
15
20
25
30
3.0
3.5
4.0
4.5
5.0
3.0 3.5 4.0 4.5 5.0
10 15
20
25 30
mpg
中级图形
分组散点图 概念:以某个因子为条件绘制两个变量的散点图
> library(car) > library(ggplot2) > attach(mtcars) > scatterplot(mpg~wt|cyl)
> scatterplot(mpg~wt|cyl,data=mtcars,lwd=2,main="scatter plot of mpg vs. weight by # cylinders",xlab="height of car",ylab="miles per gallon",legend.plot=TRUE,id.method="identity",labels=s(mtcars),bo xplots="xy")
【最新】R语言关联分析模型报告案例附代码数据

【最新】R语⾔关联分析模型报告案例附代码数据【原创】附代码数据有问题到淘宝找“⼤数据部落”就可以了关联分析⽬录⼀、概括 (1)⼆、数据清洗 (1)2.1公⽴学费(NPT4_PUB) (1)2.2毕业率(Graduation.rate) (1)2.3贷款率(GRAD_DEBT_MDN_SUPP) (2)2.4偿还率(RPY_3YR_RT_SUPP) (2)2.5毕业薪⽔(MD_EARN_WNE_P10)。
(3)2.6 私⽴学费(NPT4_PRIV) (3)2.7 ⼊学率(ADM_RATE_ALL) (4)三、Apriori算法 (4)3.1 相关概念 (5)3.2 算法流程 (6)3.3 优缺点 (7)四、模型建⽴及结果 (8)4.1 公⽴模型 (8)4.2 私⽴模型 (11)⼀、概括对7703条样本数据,分别根据公⽴学费和私⽴学费差异,建⽴公⽴模型和私⽴模型,进⾏关联分析。
⼆、数据清洗2.1公⽴学费(NPT4_PUB)此字段,存在4个负值,与实际情况不符,故将此四个值重新定义为NULL。
重新定义后,NULL值的占⽐为75%,占⽐很⼤,不能直接将NULL值删除或者进⾏插补,故将NULL单独作为⼀个取值分组。
对⾮NULL的值按照等⽐原则进⾏分组,分组结果如下:A:[0,5896]B:(5896,7754]C:(7754, 9975]D:(9975, 13819]E:(13819, +]分组后取值分布为:2.2毕业率(Graduation.rate)将PrivacySuppressed值重新定义为NULL,重新定义后,NULL值的占⽐为20%,占⽐较⼤,不适合直接删除或进⾏插补,故将NULL单独作为⼀个取值分组。
对⾮NULL值根据等⽐原则进⾏分组,分组结果如下:A:[0,0.29]B:(0.29,0.47]C:(0.47, 0.61]D:(0.61, 0.75]E:(0.75, +]分组后取值分布为:2.3贷款率(GRAD_DEBT_MDN_SUPP)将PrivacySuppressed值重新定义为NULL,重新定义后,NULL值的占⽐为20%,占⽐较⼤,不适合直接删除或进⾏插补,故将NULL单独作为⼀个取值分组。
【原创】R语言城镇居民人均消费数据主成分,聚类分析报告.pdf(附代码数据)

有问题到百度搜索“大数据部落”就可以了欢迎登陆官网:/datablog我国城镇居民人均消费支出研究有问题到百度搜索“大数据部落”就可以了欢迎登陆官网:/datablog摘要:近年来,随着我们经济的快速发展,居民的消费结构也发生了巨大变化,人们开始根据自身的需求选择多种多样的商品,而且人们在实现物质需求满足的同时,还在不断追求精神需求的满足。
对此,本文先使用R语言对城镇居民人均总消费支出以及恩格尔系数的总体现状进行数据可视化,接着运用主成分和聚类分析法对我国31个省级行政区(不含港澳台)城镇居民消费结构进行综合评价。
共提取2个主成分,分别命名为日常必需品消费成分、非日常必需品成分,并将31个省区市主成分综合得分进行排名和聚类分析,结果分为四类。
最终得出相关结论,体现不同地区的经济发展、城镇居民消费结构、消费偏好的差异性以及其中的联系。
关键词:城镇居民人均消费;数据可视化;主成分分析;聚类分析有问题到百度搜索“大数据部落”就可以了欢迎登陆官网:/datablog有问题到百度搜索“大数据部落”就可以了欢迎登陆官网:/datablog目录一、引言 (4)1.1研究背景及意义 (4)1.2研究方法及数据来源 (4)二、我国城镇居民人均消费支出现状分析 (5)2.1各地区城镇居民人均总消费支出 (5)2.2恩格尔系数分析 (6)三、城镇居民人均消费支出的统计建模分析 (8)3.1主成分分析 (8)3.1.1计算相关矩阵 (8)3.1.2计算相关矩阵的特征值和主成分负荷 (8)3.1.3确定主成分 (9)3.1.4主成分得分 (9)3.1.5计算主成分C1,C2的系数 (10)3.1.6各省、市、自治区的主成分得分排名 (10)3.1.7主成分作图 (12)3.2聚类分析 (13)3.2.1聚类分析结果分析 (13)四、结论及建议 (16)有问题到百度搜索“大数据部落”就可以了欢迎登陆官网:/datablog附录: (17)―、引言1.1研究背景及意义人均消费支出指居民用于满足家庭日常生活消费的全部支出,包括购买实物支出和服务性消费支出。
【原创】r语言层次聚类案例附代码数据

####################################################################### ############ 聚类分析####################################################################### a=cbind(农业总产值 ,林业总产值, 牧业总产值, 渔业总产值, 农村居民家庭拥有生产性固定资产原值, 农村居民家庭经营耕地面积)# ⭞↚⭞Ѡ⭞䠅㚐㊱rownames(a)=mydata$地区detach(mydata)hc1=hclust(dist(scale(a)),"ward.D2")cbind(hc1$merge,hc1$height)### [,1] [,2] [,3]## [1,] -22 -24 0.1562347## [2,] -2 -29 0.4954046## [3,] -12 -20 0.6158525## [4,] -4 1 0.7459837## [5,] -5 -7 0.8431761## [6,] -27 4 0.8502919## [7,] -28 -30 0.9238256## [8,] 2 7 0.9982795## [9,] -1 -9 1.0586066## [10,] -14 3 1.0996796## [11,] -16 -23 1.1292437## [12,] -25 10 1.2758523## [13,] -13 -19 1.4055256## [14,] -3 11 1.4555952## [15,] -21 6 1.6495578## [16,] -10 -17 1.7462669## [17,] 9 15 1.7988319## [18,] -18 12 1.8498860## [19,] -6 -11 1.9536216## [20,] -8 5 2.1881307## [21,] -15 16 2.5009589## [22,] -31 20 2.7312571## [23,] 13 18 3.0129164## [24,] 8 17 3.0616119## [25,] 19 23 3.2580779## [26,] 14 21 4.3774794## [27,] -26 22 5.2122229## [28,] 25 26 6.0403304## [29,] 24 27 8.3310723## [30,] 28 29 11.4082257plot(hc1,hang=-2,ylab="欧氏距离",main="ward ")cutree(hc1,3)## 北京天津河北山西内蒙辽宁吉林黑龙江上海江苏## 1 1 2 1 3 2 3 3 1 2## 浙江安徽福建江西山东河南湖北湖南广东广西## 2 2 2 2 2 2 2 2 2 2## 海南重庆四川贵州云南西藏陕西甘肃青海宁夏## 1 1 2 1 2 3 1 1 1 1## 新疆## 3library(NbClust)# 加载包res<-NbClust(a, distance ="euclidean", min.nc=2, max.nc=8,method ="complete", index ="ch")res$All.index## 2 3 4 5 6 7 8## 22.4859 64.2952 95.0505 91.2070 112.2167 126.6607 125.0580res$Best.nc## Number_clusters Value_Index## 7.0000 126.6607res$Best.partition## 北京天津河北山西内蒙辽宁吉林黑龙江上海江苏## 1 2 2 3 4 5 5 4 6 1## 浙江安徽福建江西山东河南湖北湖南广东广西## 5 1 1 3 2 1 3 3 3 1## 海南重庆四川贵州云南西藏陕西甘肃青海宁夏## 1 1 1 1 2 7 1 2 5 5## 新疆## 4####################################################################### ############ 因子分析####################################################################### x=ascale(x,center=T,scale=T)## 农业总产值林业总产值牧业总产值渔业总产值## 北京 -1.22777296 -0.68966546 -1.0576108 -0.717868590## 天津 -1.20072019 -1.32628581 -1.1287831 -0.587405030## 河北 1.44015787 -0.40768816 1.2735925 -0.276307864## 山西 -0.60736290 -0.39313054 -0.8459665 -0.730089499## 内蒙 -0.31173176 -0.16449038 0.3536925 -0.682760278## 辽宁 0.02317599 0.21376291 1.0886323 0.905582647## 吉林 -0.31664133 -0.16033106 0.3705164 -0.661159286## 黑龙江 0.73000004 0.28496065 0.6928325 -0.543827843## 上海 -1.22304555 -1.24358878 -1.1769433 -0.598687930## 江苏 1.32304764 -0.14014613 0.5106958 2.558246143## 浙江 -0.25945707 0.37842297 -0.4799669 1.088655075## 安徽 0.32193142 1.20245730 0.3549653 0.277626262## 福建 -0.22816878 1.77681021 -0.5790521 1.668371030## 江西 -0.46544975 1.43990544 -0.1820088 0.139953438## 山东 2.22835882 -0.05133246 2.0610374 2.643122498## 河南 2.22683767 0.36264203 2.0166955 -0.521101240## 湖北 0.88705181 -0.13647615 0.6684891 0.925656025## 湖南 1.03609706 1.81987138 0.8945726 -0.002409428## 广东 0.65132842 1.36442604 0.3760463 1.697020485## 广西 0.19109441 1.64358969 0.2862654 0.136415807## 海南 -0.95958625 0.32594217 -0.9698633 -0.119446069## 重庆 -0.61246376 -0.82851329 -0.6191076 -0.632081027## 四川 1.13921636 0.49292656 2.0375425 -0.313747797## 贵州 -0.59146827 -0.69749477 -0.6664339 -0.677051827## 云南 -0.10569354 1.40222691 0.0524867 -0.583545796## 西藏 -1.33060989 -1.32909946 -1.1967954 -0.752065694## 陕西 0.01099770 -0.64550329 -0.4072439 -0.713500151## 甘肃 -0.48272891 -1.11489458 -0.9441448 -0.747831257## 青海 -1.27264229 -1.30451055 -1.0825979 -0.751154486## 宁夏 -1.16021392 -1.24089745 -1.1284759 -0.716850181## 新疆 0.14646191 -0.83389594 -0.5730687 -0.711758136## 农村居民家庭拥有生产性固定资产原值农村居民家庭经营耕地面积## 北京 -0.521919855 -0.69519658 ## 天津 -0.036498322 -0.33578982 ## 河北 0.004069841 -0.23262677 ## 山西 -0.824825602 -0.02962851 ## 内蒙 1.179852466 2.59936535## 辽宁 0.730243656 0.39633505## 吉林 0.724094855 1.89053536## 黑龙江 1.396721068 3.65096289## 上海 -1.404513394 -0.77506475 ## 江苏 -0.340308064 -0.44560856 ## 浙江 0.499884752 -0.68188522 ## 安徽 -0.279565363 -0.23262677 ## 福建 -0.618739413 -0.61865625 ## 江西 -0.805278639 -0.33911766 ## 山东 0.133404538 -0.31582278 ## 河南 -0.500048919 -0.32247846 ## 湖北 -0.721961668 -0.29252790 ## 湖南 -0.917381131 -0.45559208 ## 广东 -0.957062704 -0.68521306 ## 广西 -0.615649655 -0.40567447 ## 海南 -0.663204069 -0.58537785 ## 重庆 -0.570175555 -0.43229719 ## 四川 -0.420353046 -0.48221480 ## 贵州 -0.604823220 -0.46890344 ## 云南 0.118332502 -0.32913414 ## 西藏 3.590383141 -0.23262677 ## 陕西 -0.572497480 -0.35575687 ## 甘肃 0.165991341 0.04358397## 青海 0.415065901 -0.25259382 ## 宁夏 0.655330865 0.36638449## 新疆 1.761431173 1.05524743 ## attr(,"scaled:center")## 农业总产值林业总产值## 1514.206129 111.20612 9## 牧业总产值渔业总产值## 877.092581 280.83903 2## 农村居民家庭拥有生产性固定资产原值农村居民家庭经营耕地面积## 17865.076774 2.58903 2## attr(,"scaled:scale")## 农业总产值林业总产值## 1097.854553 81.74416 7## 牧业总产值渔业总产值## 683.552567 373.13101 0## 农村居民家庭拥有生产性固定资产原值农村居民家庭经营耕地面积## 9767.757883 3.00495 2cor(x)### 农业总产值林业总产值牧业总产值## 农业总产值 1.00000000 0.4304367 0.9148545 ## 林业总产值 0.43043666 1.0000000 0.4593615 ## 牧业总产值 0.91485445 0.4593615 1.0000000 ## 渔业总产值 0.51598365 0.4351225 0.4103977 ## 农村居民家庭拥有生产性固定资产原值 -0.16652881 -0.3495913 -0.1017802## 农村居民家庭经营耕地面积 0.04040478 -0.0961515 0.1426829## 渔业总产值## 农业总产值 0.5159836## 林业总产值 0.4351225## 牧业总产值 0.4103977## 渔业总产值 1.0000000## 农村居民家庭拥有生产性固定资产原值 -0.2131248## 农村居民家庭经营耕地面积 -0.2669966## 农村居民家庭拥有生产性固定资产原值## 农业总产值 -0.1665288 ## 林业总产值 -0.3495913 ## 牧业总产值 -0.1017802 ## 渔业总产值 -0.2131248 ## 农村居民家庭拥有生产性固定资产原值 1.0000000 ## 农村居民家庭经营耕地面积 0.5316341 ## 农村居民家庭经营耕地面积## 农业总产值 0.04040478## 林业总产值 -0.09615150## 牧业总产值 0.14268286## 渔业总产值 -0.26699659## 农村居民家庭拥有生产性固定资产原值 0.53163410## 农村居民家庭经营耕地面积 1.00000000FA=factanal(x,3,scores="regression")FA#### Call:## factanal(x = x, factors = 3, scores = "regression")#### Uniquenesses:## 农业总产值林业总产值## 0.134 0.64 9## 牧业总产值渔业总产值## 0.005 0.00 5## 农村居民家庭拥有生产性固定资产原值农村居民家庭经营耕地面积## 0.005 0.61 0#### Loadings:## Factor1 Factor2 Factor3## 农业总产值 0.902 0.231## 林业总产值 0.460 -0.274 0.253## 牧业总产值 0.989 0.100## 渔业总产值 0.335 -0.172 0.924## 农村居民家庭拥有生产性固定资产原值 -0.185 0.980## 农村居民家庭经营耕地面积 0.120 0.569 -0.227#### Factor1 Factor2 Factor3## SS loadings 2.164 1.396 1.032## Proportion Var 0.361 0.233 0.172## Cumulative Var 0.361 0.593 0.765#### The degrees of freedom for the model is 0 and the fit was 0.0338A=FA$loadings#D=diag(FA$uniquenesses)#cancha=cor(x)-A%*%t(A)-Dsum(cancha^2)## [1] 0.01188033FA$scores## Factor1 Factor2 Factor3## 北京 -0.9595745 -0.700059511 -0.55760316## 天津 -1.0947804 -0.236528598 -0.28377148## 河北 1.3398849 0.269241913 -0.72734450## 山西 -0.6949304 -0.952525400 -0.71168863## 内蒙 0.3022926 1.274620864 -0.61477840## 辽宁 0.9086974 0.898645857 0.80686141## 吉林 0.3617131 0.823049845 -0.69568729## 黑龙江 0.6377695 1.558056539 -0.53064438## 上海 -1.0020542 -1.600313046 -0.58279912## 江苏 0.2978404 -0.338175607 2.58332275## 浙江 -0.6586307 0.351125849 1.47562686## 安徽 0.3633716 -0.220261996 0.12915299## 福建 -0.7017677 -0.799773443 1.90201088## 江西 -0.1252221 -0.843258690 0.03964935## 山东 1.8098550 0.433178408 2.27098864## 河南 2.1841524 -0.072629248 -1.35570609## 湖北 0.6625677 -0.618906179 0.64211420## 湖南 1.0200226 -0.733225411 -0.50075826## 广东 0.3057090 -0.945233885 1.54225085## 广西 0.3420343 -0.562216144 -0.07785160## 海南 -0.9131785 -0.847172077 0.04381513## 重庆 -0.5087268 -0.661768675 -0.62025496## 四川 2.1397385 -0.003827953 -1.11031362## 贵州 -0.5463126 -0.703696201 -0.66210885## 云南 0.1044516 0.146947680 -0.63418799## 西藏 -1.5214222 3.342858193 0.36144124## 陕西 -0.2687306 -0.616728372 -0.78286620## 甘肃 -0.8904189 0.010720625 -0.48059064## 青海 -1.0791206 0.225711752 -0.37974261## 宁夏 -1.1481591 0.456190239 -0.27546552## 新疆 -0.6670714 1.665952673 -0.21307102FA=factanal(x,3,scores="regression")#FA#### Call:## factanal(x = x, factors = 3, scores = "regression")#### Uniquenesses:## 农业总产值林业总产值## 0.134 0.64 9## 牧业总产值渔业总产值## 0.005 0.00 5## 农村居民家庭拥有生产性固定资产原值农村居民家庭经营耕地面积## 0.005 0.61 0#### Loadings:## Factor1 Factor2 Factor3## 农业总产值 0.902 0.231## 林业总产值 0.460 -0.274 0.253## 牧业总产值 0.989 0.100## 渔业总产值 0.335 -0.172 0.924## 农村居民家庭拥有生产性固定资产原值 -0.185 0.980## 农村居民家庭经营耕地面积 0.120 0.569 -0.227#### Factor1 Factor2 Factor3## SS loadings 2.164 1.396 1.032## Proportion Var 0.361 0.233 0.172## Cumulative Var 0.361 0.593 0.765#### The degrees of freedom for the model is 0 and the fit was 0.0338 biplot(FA$scores,FA$loadings)######################################################################## ########## 主成分分析####################################################################### # mydata<-read.csv("cosume.csv",header=TRUE)x=aPCA=princomp(x)# 分分析summary(PCA)## Importance of components:## Comp.1 Comp.2 Comp.3 Comp.4## Standard deviation 9611.2440729 1.248877e+03 3.201426e+02 2.211289e+02## Proportion of Variance 0.9817713 1.657641e-02 1.089277e-03 5.1968 75e-04## Cumulative Proportion 0.9817713 9.983477e-01 9.994370e-01 9.9995 67e-01## Comp.5 Comp.6## Standard deviation 6.377898e+01 2.299907e+00## Proportion of Variance 4.323210e-05 5.621753e-08## Cumulative Proportion 9.999999e-01 1.000000e+00plot(PCA)screeplot(PCA,type="lines")# ⻄⭞ഴPCA$loadings##### Loadings:## Comp.1 Comp.2 Comp.3 Comp.4 Comp. 5## 农业总产值 0.847 0.529 ## 林业总产值 -0.994 ## 牧业总产值 0.510 0.340 -0.786 ## 渔业总产值 0.147 -0.939 -0.304 ## 农村居民家庭拥有生产性固定资产原值 1.000 ## 农村居民家庭经营耕地面积## Comp.6## 农业总产值## 林业总产值## 牧业总产值## 渔业总产值## 农村居民家庭拥有生产性固定资产原值## 农村居民家庭经营耕地面积 1.000#### Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6## SS loadings 1.000 1.000 1.000 1.000 1.000 1.000## Proportion Var 0.167 0.167 0.167 0.167 0.167 0.167## Cumulative Var 0.167 0.333 0.500 0.667 0.833 1.000diag(1/sqrt(diag(cor(x))))%*%eigen(cor(x))$vectors%*%diag(sqrt(eigen(co r(x))$values))# ⭞⭞䠅фѱᡆ分的⭞ީ⭞䱫## [,1] [,2] [,3] [,4] [,5]## [1,] 0.8748914 0.33002393 -0.05962134 -0.2919961 0.03333473## [2,] 0.7199843 -0.09695761 0.39747812 0.5280225 0.18691501## [3,] 0.8358325 0.42778470 0.06215717 -0.2657004 0.10009450## [4,] 0.7239860 -0.13749802 -0.54651176 0.3113087 -0.24595467## [5,] -0.4283184 0.72257821 -0.37626680 0.2240839 0.32017966## [6,] -0.1942551 0.86197649 0.26492953 0.1648656 -0.34904716## [,6]## [1,] 0.189001599## [2,] 0.022088666## [3,] -0.184133750## [4,] -0.029268951## [5,] 0.010900009## [6,] 0.007698218print(-loadings(PCA),cutoff=0.001)#### Loadings:## Comp.1 Comp.2 Comp.3 Comp.4 Comp. 5## 农业总产值 0.019 -0.847 0.041 -0.529 0.027 ## 林业总产值 0.003 -0.026 0.036 0.096 0.994 ## 牧业总产值 0.007 -0.510 -0.340 0.786 -0.077 ## 渔业总产值 0.008 -0.147 0.939 0.304 -0.068 ## 农村居民家庭拥有生产性固定资产原值 -1.000 -0.021 0.006 -0.002 0.002 ## 农村居民家庭经营耕地面积 -0.003 0.003 ## Comp.6## 农业总产值## 林业总产值 0.003## 牧业总产值 0.001## 渔业总产值 -0.002## 农村居民家庭拥有生产性固定资产原值## 农村居民家庭经营耕地面积 -1.000#### Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6## SS loadings 1.000 1.000 1.000 1.000 1.000 1.000## Proportion Var 0.167 0.167 0.167 0.167 0.167 0.167## Cumulative Var 0.167 0.333 0.500 0.667 0.833 1.000####################################################################### ##### 条形图####################################################################### country<-mydata$地区percent<-mydata$农业总产值d<-data.frame(country,percent)# png("d:\\test2.png",width=2048,height=2048)f<-function(name,value) {xsize=200plot(0, 0,xlab="",ylab="",axes=FALSE,xlim=c(-xsize,xsize),ylim=c(-xsize,xsize))for(i in 1:length(name)){info =name[i]percent =value[i]k =(1:(360*percent/100)*10)/10r=xsize*(length(name)-i+1)/length(name)#print(r)x=r*sin(k/180*pi)y=r*cos(k/180*pi)text(-18,r,info,pos=2,cex=0.7)text(-9,r,paste(percent,"%"),cex=0.7)lines(x,y,col="red")}}f(country,percent)####################################################################### ###### 柱状图####################################################################### library(RColorBrewer)pv<-percentid<-countrycol<-c(brewer.pal(9, "YlOrRd")[1:9],brewer.pal(9, "Blues")[1:9]) barplot(pv,col=col,horiz =TRUE,xlim=c(-8000.00,5000))title(main=list("农业总产值",cex=2),sub="",ylab="地区")text(y=seq(from=0.7,length.out=31,by=1.2),x=-450.00,labels=id)legend("topleft",legend=rev(id),pch=10,col=rev(col),ncol=2)。
【原创】R语言通过ARIMA建模进行预测研究实例报告论文(附代码数据)

本文是我们通过时间序列和ARIMA模型预测拖拉机销售的制造案例研究示例的延续。
您可以在以下链接中找到以前的部分:第1部分:时间序列建模和预测简介第2部分:在预测之前将时间序列分解为解密模式和趋势第3部分:ARIMA预测模型简介在本部分中,我们将使用图表和图表通过ARIMA预测PowerHorse拖拉机的拖拉机销售情况。
我们将使用前一篇文章中学到的ARIMA建模概念作为我们的案例研究示例。
但在我们开始分析之前,让我们快速讨论一下预测:诺查丹玛斯的麻烦人类对未来和ARIMA的痴迷 - 由Roopam撰写人类对自己的未来痴迷- 以至于他们更多地担心自己的未来而不是享受现在。
这正是为什么恐怖分子,占卜者和算命者总是高需求的原因。
Michel de Nostredame(又名Nostradamus)是一位生活在16世纪的法国占卜者。
在他的着作Les Propheties (The Prophecies)中,他对重要事件进行了预测,直到时间结束。
诺查丹玛斯的追随者认为,他的预测对于包括世界大战和世界末日在内的重大事件都是不可挽回的准确。
例如,在他的书中的一个预言中,他后来成为他最受争议和最受欢迎的预言之一,他写了以下内容:“饥饿凶猛的野兽将越过河流战场的大部分将对抗希斯特。
当一个德国的孩子什么都没有观察时,把一个伟大的人画进一个铁笼子里。
“他的追随者声称赫斯特暗指阿道夫希特勒诺查丹玛斯拼错了希特勒的名字。
诺查丹玛斯预言的一个显着特点是,他从未将这些事件标记到任何日期或时间段。
诺查丹玛斯的批评者认为他的书中充满了神秘的专业人士(如上所述),他的追随者试图强调适合他的写作。
为了劝阻批评者,他的一个狂热的追随者(基于他的写作)预测了1999年7月世界末日的月份和年份 - 相当戏剧化,不是吗?好吧当然,1999年那个月没有发生任何惊天动地的事情,否则你就不会读这篇文章。
然而,诺查丹玛斯将继续成为讨论的话题,因为人类对预测未来充满了痴迷。
【原创】R语言数据可视化分析报告(附代码数据)
Vis 3这个图形是用另一个数据集菱形建立的,也是内置在ggplot2包中的数据集。
library(ggthemes)
ggplot(diamonds)+geom_density(aes(price,fill=cut,color=cut),alpha=0.4,size=0.5)+labs(title='Diamond Price Density',x='Diamond Price (USD)',y='Density')+theme_economist()
library(ggplot2)
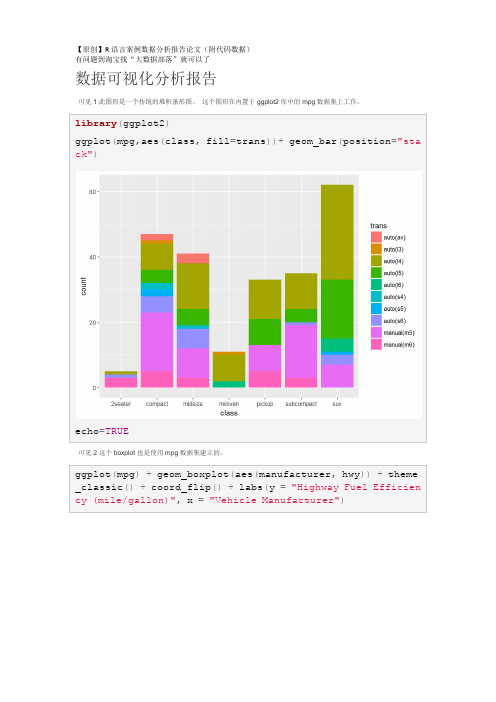
ggplot(mpg,aes(class,fill=trans))+geom_bar(position="stack")
echo=TRUE
可见2这个boxplot也是使用mpg数据集建立的。
ggplot(mpg)+geom_boxplot(aes(manufacturer,hwy))+theme_classic()+coord_flip()+labs(y="Highway Fuel Efficiency (mile/gallon)",x="Vehicle Manufacturer")
echo=TRUE
另外,我正在使用ggplot2软件包来将线性模型拟合到框架内的所有数据上。
ggplot(iris,aes(Sepal.Length,Petal.Length))+geom_point()+geom_smooth(method=lm)+theme_minimal()+theme(panel.grid.major=element_line(size=1),panel.grid.minor=element_line(size=0.7))+labs(title='relationship between Petal and Sepal Length',x='Iris Sepal Length',y='Iris Petal Length')
【原创】R语言用Rshiny探索广义线性混合模型(GLMM)和线性混合模型(LMM)数据分析报告(附代码数据)

咨询QQ:3025393450有问题百度搜索“”就可以了欢迎登陆官网:/datablogR语言用Rshiny探索lme4广义线性混合模型(GLMM)和线性混合模型(LMM)数据分析报告随着lme4软件包的改进,使用广义线性混合模型(GLMM)和线性混合模型(LMM)的工作变得越来越容易。
当我们发现自己在工作中越来越多地使用这些模型时,我们(作者)开发了一套工具,用于简化和加快与的merMod对象进行交互的常见任务lme4。
该软件包提供了那些工具。
安装# development versionlibrary(devtools)install_github("jknowles/merTools")# CRAN version -- coming sooninstall.packages("merTools")咨询QQ:3025393450有问题百度搜索“”就可以了欢迎登陆官网:/datablogRshiny的应用程序和演示演示此应用程序功能的最简单方法是使用捆绑的Shiny应用程序,该应用程序会在此处启动许多指标以帮助探索模型。
去做这个:devtools::install_github("jknowles/merTools")library(merTools)m1 <- lmer(y ~ service + lectage + studage + (1|d) + (1|s), data=InstEval)shinyMer(m1, simData = InstEval[1:100, ]) # just try the first 100 rows of data在第一个选项卡上,该功能提供了用户选择的数据的预测间隔,这些预测间隔是使用predictInterval包中的功能计算得出的。
通过从固定效应和随机效应项的模拟分布中进行采咨询QQ:3025393450有问题百度搜索“”就可以了欢迎登陆官网:/datablog样,并将这些模拟估计值组合起来,可以为每个观测值生成预测分布,从而快速计算出预测间隔。
【原创】R语言NBA数据分析案例附代码数据

Rplot.jpeg写在前面的话莎士比亚说过:“一千个人眼里有一千个哈姆雷特。
” 这就像不同的球迷心中都有自己心爱的球星与球队。
在NBA70多载的历史长河中,演绎过无数次的经典对决,而总决赛的PK更是荡气回肠、精彩绝伦。
作为缔造者,这些伟大的球队更是承载着一代球迷的回忆,如果想要选出最强的球队,无疑是鸡蛋里挑骨头,几乎是一项不可能完成的任务。
然而我们经常会在比如虎扑论坛看到关于最强冠军队伍的讨论,这说明JRs对这个话题的执着热情。
虽然这是一件仁者见仁智者见智的事情,亦或者部分狂热球迷会带着爱屋及乌的那份支持与期待。
实则一场球赛的成败关乎太多因素,有许多LIVE偶然无法预测,作为一个狂热的球迷,结合多年的看比赛及实战经验,同时结合历史上多场经典赛事,今天结合真实数据来揭秘一场球赛成功背后哪些必不可缺少的因素。
接下来且听小编一本正经的胡说八道!!最强冠军球队候选人•时间:公牛王朝元年(90~91赛季)— 1516赛季,因为公牛王朝是绝大多数球迷最初的NBA记忆,而数据方面只记录到1516赛季,所以只能忽略今年这只勇士队了。
•连续两年或者三年内两次打入总决赛的冠军队伍,出于考虑到队伍持久、稳定的竞争力。
候选人登场数据预处理待处理数据•team_season.csv•team_playoff.csv数据处理过程•数据时间太过散乱,不方便进行分类处理,故需要针对时间区间添加“赛季”列•选出上面十个总冠军队伍常规赛、季后赛,球队与对手的各项数据均值•计算冠军队伍的高阶数据:进攻效率值和防守效率值,并实现数据可视化失误=mean(失误,na.rm = TRUE),犯规=mean(犯规,na.rm = TRUE),得分=mean(得分,na.rm = TRUE))return(team_season_General)}#对手赛季数据处理常规赛表现回顾1.jpg•胜负分上双总共有三支队伍:球队赛季胜负分公牛91~92 10.360832 公牛95~96 12.376957 勇士14~15 10.097561 •常规赛战力最差的三支队伍:球队赛季胜负分火箭94~95 1.187669总结乔帮主带队伍是扛扛的,火箭夺冠之路走得确实辛苦,真是一场一场拼出来的,湖人由于伤病再加上自己得意又爱浪的特点,时不时出现注意力不集中,放松的毛病乔丹.jpg 季后赛表现回顾2.jpg•胜负分上双总共有二支队伍:球队赛季胜负分公牛95~96 11.722222 湖人00~01 12.750000•季后赛战力最差的三支队伍:球队赛季胜负分火箭94~95 2.772727 马刺02~03 3.069444总结00-01赛季的湖人常规赛装死,季后赛才露出自己的獠牙,各队被打服,心痛AI一分钟,95-96赛季的公牛队堪称完美,常规赛与季后赛一样大杀四方,乔帮主表示无压力,任凭“手套”垃圾话和全场领防。
【原创】R语言进行分位数回归数据分析报告论文(附代码数据)

欢迎登陆官网:/datablog用R语言进行分位数回归作者的主要贡献有:(1)整理了分位数回归的一些基本原理和方法;(2)归纳了用R语言处理分位数回归的程序,其中写了两个函数整合估计结果;(3)写了一个分位数分解函数来处理MM2005的分解过程;(4)使用一个数据集进行案例分析,完整地展现了分析过程。
第一节分位数回归介绍(一)为什么需要分位数回归?传统的线性回归模型描述了因变量的条件均值分布受自变量X的影响过程。
其中,最小二乘法是估计回归系数的最基本方法。
如果模型的随机误差项来自均值为零、方差相同的分布,那么回归系数的最小二乘估计为最佳线性无偏估计(BLUE);如果随机误差项是正态分布,那么回归系数的最小二乘估计与极大似然估计一致,均为最小方差无偏估计(MVUL)。
此时它具有无偏性、有效性等优良性质。
但是在实际的经济生活中,这种假设通常不能够满足。
例如当数据中存在严重的异方差,或后尾、尖峰情况时,最小二乘法的估计将不再具有上述优良性质。
为了弥补普通最小二乘法(OLS)在回归分析中的缺陷,1818年Laplace[2]提出了中位数回归(最小绝对偏差估计)。
在此基础上,1978年Koenker 和Bassett[3]把中位数回归推广到了一般的分位数回归(Quantile Regression)上。
分位数回归相对于最小二乘回归,应用条件更加宽松,挖掘的信息更加丰富。
它依据因变量的条件分位数对自变量X进行回归,这样得到了所有分位数下的回归模型。
因此分位数回归相比普通的最小二乘回归,能够更加精确第描述自变量X对因变量Y的变化范围,以及条件分布形状的影响。
(二)一个简单的分位数回归模型[4]假设随机变量的分布函数为(1)Y的分位数的定义为满足的最小值,即(2)回归分析的基本思想就是使样本值与拟合值之间的距离最短,对于Y的一组随机样本,样本均值回归是使误差平方和最小,即(3)样本中位数回归是使误差绝对值之和最小,即(4)样本分位数回归是使加权误差绝对值之和最小,即(5)上式可等价表示为:其中,为检查函数(check function),定义为:欢迎登陆官网:/datablog其中,为指示函数(indicator function),z是条件关系式,当z为真时,;当z为假时,。
R语言主成分分析案例 附代码数据

R语言主成分分析案例Question1Q1.1:> print(eigen_values)[1] 2.4802416 0.9897652 0.3565632 0.1734301Q1.2> print(eigen_vectors)[,1] [,2] [,3] [,4][1,] -0.5358995 0.4181809 -0.3412327 0.64922780[2,] -0.5831836 0.1879856 -0.2681484 -0.74340748[3,] -0.2781909 -0.8728062 -0.3780158 0.13387773[4,] -0.5434321 -0.1673186 0.8177779 0.08902432Q1.3> print('variance for each eigen_values')[1] "variance for each eigen_values"> print(scores)Comp.1 Comp.2 Comp.3 Comp.40.9655342206 0.027******* 0.0057995349 0.0008489079Question2:Q2.1:See in codeQ2.2:The result of ordinary linear regression:> OLSCall:lm(formula = Apps ~ ., data = collegeTrainData)Coefficients:(Intercept) Private Accept Enroll Top10perc Top25perc F.Undergrad-8.753e+02 -6.409e+02 1.345e+00 -2.841e-01 4.792e+01 -1.465e+01 1.980e-02P.Undergrad Outstate Room.Board Books Personal PhD Terminal-1.612e-03 -4.370e-02 2.831e-01 2.356e-01 8.284e-02 1.552e-01 -9.877e+00S.F.Ratio perc.alumni Expend Grad.Rate1.547e+01 -6.582e+00 6.118e-02 4.944e+00And the result in terms of MSE and r-squared is;> print(mse)[1] 1454941> print(rsqured)[1] 0.9162122Q2.3:Use the lambda of seq(0, 1, 0.05) in r, which means from 0 to 1 by 0.05,The result by ridge regression of cross validation is:> print(mse)[1] 1464329> print(ridgeRsquared)[1] 0.9156716Which is slightly worse than the ordinary linear regression.Q2.3:Use the lambda of seq(0, 1, 0.05) in r, which means from 0 to 1 by 0.05,The result by lasso regression of cross validation is:> mse[1] 1471047> LassoRsquared[1] 0.9152847And I make the following table to compare the parameters by the three different models:It can found that Lasso set the parameter of “Phd” to 0. Then it can be inferred that the adjusted r-square of Lasso regression is the best among the three models.Question3:Q3.1:> h_1 = sd(F12)*(4/3/length(F12))^(1/5)> h_1[1] 0.3101212Q3.2:> min(F12)[1] -2.995732> max(F12)[1] 7.930889The min value of log_F12 is -2.99, the maximum value is 7.93. Therefore, I choose the sample from -3 to 8 by 0.05, the following is the plot of the estimated density.Q3.3:I choose 4 different bandwidth:h_2 <- 0.1h_3 <- 0.2h_4 <- 0.5h_5 <- 0.7And the following plot can be get:The middle one is the plot by question b.And the numerical summary of the simulated density for the five different bandwidthWe can see that the larger bandwidth will cause a evener gentler distribution.。
原创R语言线性回归案例数据分析可视化报告附代码数据

原创R语言线性回归案例数据分析可视化报告附代码数据在数据分析领域,线性回归是一种常用的数据建模和预测方法。
本文将使用R语言进行一个原创的线性回归案例分析,并通过数据可视化的方式呈现分析结果。
下面是我们的文本分析报告,同时包含相关的代码数据(由于篇幅限制,只呈现部分相关代码和数据)。
请您详细阅读以下内容。
1. 数据概述本次案例我们选用了一个关于房屋价格的数据集,数据包含了房屋面积、房间数量、地理位置等多个维度的信息。
我们的目标是分析这些因素与房屋价格之间的关系,并进行可视化展示。
2. 数据预处理在开始回归分析之前,我们需要对数据进行预处理,包括数据清洗和特征选择。
在这个案例中,我们通过删除空值和异常值来清洗数据,并选择了面积和房间数量两个特征作为自变量进行回归分析。
以下是示例代码:```R# 导入数据data <- read.csv("house_data.csv")# 清洗数据data <- na.omit(data)# 删除异常数据data <- data[data$area < 5000 & data$rooms < 10, ]# 特征选择features <- c("area", "rooms")target <- "price"```3. 线性回归模型建立我们使用R语言中的lm()函数建立线性回归模型,并通过summary()函数输出模型摘要信息。
以下是相关代码:```R# 线性回归模型建立model <- lm(data[, target] ~ ., data = data[, features])# 输出模型摘要信息summary(model)```回归模型摘要信息包含了拟合优度、自变量系数、截距等重要信息,用于评估模型的拟合效果和各个因素对因变量的影响程度。
R----Shiny包介绍学习

R----Shiny包介绍学习为什么⽤ShinyShiny让数据分析师写完分析与可视化代码后,稍微再花⼏⼗分钟,就可以把分析代码⼯程化,将分析成果快速转化为交互式⽹页分享给别⼈。
所以,如果你是⼀名使⽤R的数据分析师,选择Shiny是⾮常明智的,因为它不需要你有新的技能,且开发起来实在太快。
它跟通常我们了解的其他框架不⼀样:其他框架⼀般都是前后端分离,后端提供json,前端根据json绘图绘表,需要若⼲个程序员协同开发完成。
然⽽这种可视化的⼩⼯具往往是得不到研发资源的⽀持,只能本数据分析师⼀⼈操⼑前后端全包。
##########################⼀个时间序列数据可视化栗⼦#########################library(shiny)library(shinyjs)library(DT)library(dplyr)library(tidyr)library(stringr)library(ggplot2)library(scales)library(plotly)run.sql <- function(sql, debug=FALSE) {if(debug==FALSE){df <- XXXXX # ⾃⾏定义函数,根据数据存储位置,执⾏SQL语句}else{# 测试数据group_id <- rep(1, nrow(economics))dt <- paste(as.character(economics$date), "00:00:00")df <- cbind(group_id, dt, economics)}return(df)}ui <- fluidPage(useShinyjs(),titlePanel("时间序列数据可视化⼯具"),# 第⼀部分:SQL命令提交界⾯div(id="download",fluidRow(column(12,textOutput(outputId="download_info"))),fluidRow(column(12,HTML(paste('<textarea id="sql_cmd" rows="10", cols="180">',"select * from xxxx limit 1000;",'</textarea>')))),fluidRow(column(12,actionButton(inputId="refresh_button", label="加载数据", icon=icon("submit"))))),shinyjs::hidden(div(id="table",# 第⼆部分:SQL命令执⾏结果显⽰hr(),dataTableOutput(outputId="sql_tab"),# 第三部分:可视化规则设置hr(),textOutput(outputId="tab_button_message"),sidebarLayout(div(id="table_tool",sidebarPanel(selectInput(inputId="group_fields", label="绘图分组字段", choices=NULL, selected=NULL, multiple=TRUE),selectInput(inputId="x_field", label="设置x轴字段,必须是⽇期时间", choices=NULL, selected=NULL, multiple=FALSE),selectInput(inputId="y_line_fields", label="设置y轴线图字段", choices=NULL, selected=NULL, multiple=TRUE),selectInput(inputId="y_point_fields", label="设置y轴点图字段", choices=NULL, selected=NULL, multiple=TRUE),selectInput(inputId="group_shape_field", label="设置点图形状字段", choices=NULL, selected=NULL, multiple=FALSE),actionButton(inputId="tab_button", label="显⽰分组表格", icon=icon("submit")),width=3)),div(id="group_content",mainPanel(dataTableOutput(outputId="group_tab"),width=9))))),# 第四部分:可视化图形shinyjs::hidden(div(id = "plot",hr(),plotlyOutput(outputId="case_viewer", height="600px"))))server <- function(input, output, session) {observe({# 检查SQL输⼊框if(is.null(input$sql_cmd) | input$sql_cmd == "") {shinyjs::disable("refresh_button")}else{shinyjs::enable("refresh_button")}# 检查可视化规则设置if (input$x_field == "" | (is.null(input$y_line_fields) & is.null(input$y_point_fields)) | is.null(input$group_fields)) {shinyjs::disable("tab_button")} else {shinyjs::enable("tab_button")}})# 执⾏SQL命令获取数据sql_data <- eventReactive(input$refresh_button, {cat(file=stderr(), "#### event log ####: refresh button clicked\n")shinyjs::disable("refresh_button")shinyjs::hide(id = "table", anim = TRUE)shinyjs::hide(id = "plot", anim = TRUE)res <- run.sql(input$sql_cmd, debug=TRUE)updateSelectInput(session, inputId="group_fields", choices=colnames(res))updateSelectInput(session, inputId="x_field", choices=colnames(res))updateSelectInput(session, inputId="y_line_fields", choices=colnames(res))updateSelectInput(session, inputId="y_point_fields", choices=colnames(res))updateSelectInput(session, inputId="group_shape_field", choices=c("⽆",colnames(res)), selected="⽆")shinyjs::enable("refresh_button")shinyjs::show(id = "table", anim = TRUE)shinyjs::hide(id = "group_content", anim = FALSE)return(res)})# SQL命令执⾏状态output$download_info <- renderText({if(input$refresh_button == 0){message <- "请敲⼊SQL select查询语句,点击按钮提交"}else{message <- isolate({paste0("表格下载成功!总⾏数", nrow(sql_data()), ",总列数", ncol(sql_data()), ",更新时间是", as.character(lubridate::now(), format="%Y-%m-%d %H:%M:%S")) })}message})# 显⽰SQL执⾏结果output$sql_tab <- DT::renderDataTable({datatable(sql_data(), filter='top', selection='single')})# 获取绘图分组结果group_data <- eventReactive(input$tab_button, {cat(file=stderr(), "#### event log ####: tab button clicked\n")res <- sql_data() %>%select(one_of(input$group_fields)) %>%distinct()shinyjs::show(id="group_content", anim=TRUE)return(res)})output$tab_button_message <- renderText({if(input$tab_button == 0) {message <- "请在下⽅左侧设置数据可视化规则;点击按钮后,下⽅右侧将以表格显⽰数据分组结果;点击表格的⼀⾏,将在下⽅绘制该⾏所指分组数据的图形"}else {message <- isolate({paste0("绘图分组数", nrow(group_data()), ",更新时间是", as.character(lubridate::now(), format="%Y-%m-%d %H:%M:%S"))})}message})# 显⽰绘图分组结果output$group_tab <- DT::renderDataTable({datatable(group_data(), filter='top', selection='single')})# 显⽰绘图observeEvent(input$group_tab_rows_selected, {cat(file=stderr(), paste0("#### event log ####: group table row ", input$group_tab_rows_selected, " clicked\n"))output$case_viewer <- renderPlotly({s <- input$group_tab_row_last_clickedcat(file=stderr(), "#### event log ####: table row", s, "clicked\n")p <- ggplot()filter_str <- isolate({str_c(group_data()[s, input$group_fields], collapse="_")}) # 使⽤_以配合unite⽅法target_plot_data <- sql_data() %>%unite_("new_var", input$group_fields, remove=FALSE) %>%filter(new_var==filter_str)if(length(input$y_line_fields) > 0) {target_plot_data$dt <- lubridate::ymd_hms(target_plot_data[,input$x_field], tz="UTC-8")line_df <- target_plot_data %>%tidyr::gather(col_name, thresh, one_of(input$y_line_fields)) %>%dplyr::mutate(thresh=as.numeric(thresh))p <- p + geom_line(data=line_df, aes(x=dt,y=thresh,color=col_name))}if(length(input$y_point_fields) > 0) {target_plot_data$dt <- lubridate::ymd_hms(target_plot_data[,input$x_field], tz="UTC-8")point_df <- target_plot_data %>%tidyr::gather(col_name, thresh, one_of(input$y_point_fields)) %>%dplyr::mutate(thresh=as.numeric(thresh))if(input$group_shape_field != "⽆") {point_df[, input$group_shape_field] <- as.factor(point_df[, input$group_shape_field])p <- p + geom_point(data=point_df, aes_string(x="dt",y="thresh",color="col_name", shape=input$group_shape_field))}else{p <- p + geom_point(data=point_df, aes(x=dt,y=thresh,color=col_name))}}p <- pggplotly(p)})shinyjs::show("plot", anim = TRUE)})}shinyApp(ui=ui, server=server)注:为了让⽤户明⽩⼯具的使⽤⽅法,代码采⽤shinyjs在适当的时机隐藏/显⽰对应的组件;在eventReactive事件驱动的计算中,需要保证⾄少⼀个依赖与该reactive的组件处于显⽰状态,否则⽆法触发计算,observeEvent不存在此问题。
【原创】R语言Faithful数据集作探索性数据分析附代码数据

3.数字化探索
describe(faithful) # describe()是Hmisc包中的函数 # 输出数据集的变量个数和观察样本数 # 样本的总数(n),缺失样本书(missing)不同值个数(distinct) # 从0.05到0.95一系列的分位数取值,频率最低和最高的5个水平值
3.数字化探索
2.数据介绍
Description Waiting time between eruptions and the duration of the eruption for the Old Faithful geyser in Yellowstone National Park, Wyoming, USA. A data frame with 272 observations on 2 variables. [,1] eruptions numeric Eruption time in mins [,2] waiting numeric Waiting time to next eruption (in mins)
4.可视化探索 # 绘制箱线图 h <- ggplot(data = faithful) + geom_boxplot(aes(x="eruptions",y=eruptions,colou r="eruptions")) + geom_boxplot(aes(x="waiting",y=waiting/20,colour ="waiting"))+ scale_y_continuous(sec.axis = sec_axis(~.*20))+ scale_colour_manual(values = c("blue","red"),guide=FALSE)+ theme(axis.title.y = element_blank()) h # eruptions 看左纵轴,waiting 看右纵轴,轴的尺 度缩放不一致 # 箱线图能够很好地识别各分位数分布 # sec.axis为了设置第二个轴,即右纵轴 # scale_colour_manual设置颜色标度 # theme设置主题,去掉左纵轴标题
【原创】R语言主成分分析因子分析案例报告(完整附数据)

R语言主成分分析因子分析案例报告R语言多元分析系列之一:主成分分析主成分分析(principal components analysis,PCA)是一种分析、简化数据集的技术。
它把原始数据变换到一个新的坐标系统中,使得任何数据投影的第一大方差在第一个坐标(称为第一主成分)上,第二大方差在第二个坐标(第二主成分)上,依次类推。
主成分分析经常用减少数据集的维数,同时保持数据集的对方差贡献最大的特征。
这是通过保留低阶主成分,忽略高阶主成分做到的。
这样低阶成分往往能够保留住数据的最重要方面。
但是在处理观测数目小于变量数目时无法发挥作用,例如基因数据。
R语言中进行主成分分析可以采用基本的princomp函数,将结果输入到summary和plot函数中可分别得到分析结果和碎石图。
但psych扩展包更具灵活性。
1 选择主成分个数选择主成分个数通常有如下几种评判标准:∙根据经验与理论进行选择∙根据累积方差贡献率,例如选择使累积方差贡献率达到80%的主成分个数。
∙根据相关系数矩阵的特征值,选择特征值大于1的主成分。
另一种较为先进的方法是平行分析(parallel analysis)。
该方法首先生成若干组与原始数据结构相同的随机矩阵,求出其特征值并进行平均,然后和真实数据的特征值进行比对,根据交叉点的位置来选择主成分个数。
我们选择USJudgeRatings数据集举例,首先加载psych包,然后使用fa.parallel函数绘制下图,从图中可见第一主成分位于红线上方,第二主成分位于红线下方,因此主成分数目选择1。
fa.parallel(USJudgeRatings[,-1], fa="pc",n.iter=100, show.legend=FALSE)2 提取主成分pc=principal(USJudgeRatings[,-1],nfactors=1)PC1 h2 u21 0.92 0.84 0.15652 0.91 0.83 0.16633 0.97 0.94 0.06134 0.96 0.93 0.07205 0.96 0.92 0.07636 0.98 0.97 0.02997 0.98 0.95 0.04698 1.00 0.99 0.00919 0.99 0.98 0.019610 0.89 0.80 0.201311 0.99 0.97 0.0275PC1SS loadings 10.13Proportion Var 0.92从上面的结果观察到,PC1即观测变量与主成分之间的相关系数,h2是变量能被主成分解释的比例,u2则是不能解释的比例。
原创R语言多元统计分析介绍数据分析数据挖掘案例报告附代码

原创R语言多元统计分析介绍数据分析数据挖掘案例报告附代码R语言作为一种功能强大的数据分析工具,在数据挖掘领域得到了广泛的应用。
本文将介绍使用R语言进行多元统计分析的方法,并结合实际数据分析案例进行详细分析。
同时,为了便于读者学习和复现,也附上了相关的R代码。
一、多元统计分析简介多元统计分析是指同时考虑多个变量之间关系的统计方法。
在现实生活和研究中,往往会遇到多个变量相互关联的情况,通过多元统计分析可以揭示这些变量之间的联系和规律。
R语言提供了丰富的统计分析函数和包,可以方便地进行多元统计分析。
二、数据分析案例介绍我们选取了一份关于房屋销售数据的案例,来演示如何使用R语言进行多元统计分析。
该数据集包含了房屋的各种属性信息,如房屋面积、卧室数量、卫生间数量等,以及最终的销售价格。
我们的目标是分析这些属性与销售价格之间的关系。
首先,我们需要导入数据集到R中,并进行数据预处理。
预处理包括数据清洗、缺失值处理、异常值检测等。
R语言提供了丰富的数据处理函数和包,可以帮助我们高效地完成这些任务。
接下来,我们可以使用R语言的统计分析函数进行多元统计分析。
常用的多元统计分析方法包括主成分分析(PCA)、因子分析、聚类分析等。
这些方法可以帮助我们从众多的变量中找到重要的变量,对数据集进行降维和聚类,以便更好地理解数据和进行预测。
在本案例中,我们选择主成分分析作为多元统计分析的方法。
主成分分析是一种常用的降维技术,通过线性变换将原始变量转化为一组新的互相无关的变量,称为主成分。
主成分分析可以帮助我们发现数据中的主要模式和结构,从而更好地解释数据。
最后,我们可以通过可视化方法展示多元统计分析的结果。
R语言提供了丰富多样的数据可视化函数和包,可以生成各种图表和图形,帮助我们更直观地理解和传达数据分析的结果。
三、附录:R语言代码下面是进行多元统计分析的R语言代码。
需要注意的是,代码的具体实现可能会因数据集的不同而有所差异,请根据实际情况进行调整和修改。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
R语言Shiny表格数据分析可视化案例报告
表格是工作和生活中常见的数据呈现方式,例如公司的很多报表就需要用到表格。
当我们展示数据的时候,用户当然不希望只看到一个静态的页面,所以就需要一些简单的交互功能:排序、查找、筛选等等。
基础的需求并不难实现,但当我们使用其他网页技术做这件事情的时候,既要做前端,也要做后端,代码量也不会少。
对技术小白来说,使用 R Shiny 做这样的事情就很容易了。
Shiny 是 R 社区里面一个非常出名的包,用来制作各类交互式网络应用,我们熟知的谢益辉就是其中的一位作者。
先睹为快看看 Shiny 能做出什么样的效果:
可以看出来, Shiny 简直天生就是为了交互而存在的。
Shiny 也提供了非常丰富的 widgets ,几乎覆盖了我们对 UI 的全部需求:
DT 也是谢老大写的包,是 JavaScript DataTables 库的R接口,R的数据对象可以直接通过 DT 呈现为HTML的表格。
不仅如此, DT 本身还自动支持筛选、分页、排序等功能,非常的强大。
一言以蔽之, Shiny + DT 是交互式呈现表格的非常好的一个方案。
下面以我最近做的一个表格为例,最终效果是这样的:。
