第四章 平面机构的运动分析
平面机构的运动分析

❖绝对瞬心:运动构件和机架之间的瞬心。
绝对瞬心也就是运动构件上瞬时绝对速度等于零的点。
❖相对瞬心:两个运动构件之间的瞬心。
相对瞬心也就是两个运动构件的同速重合点。
2.机构中瞬心的数目
设机构由K个构件组成,该机构的瞬心的总数为:
N = K(k-1)/2
7
3.机构中瞬心位置的确定
(1)两构件组成运动副 根据瞬心的定义,通过观察直接确定两构件的瞬心位
联接两绝对加速度终点 的矢量代表相应两点间 的相对加速度
c'
P'
e'
30
b' c"
2.组成移动副两活动构件的重合点间的运动关系。
(重合点法) 图示机构中,已知各构件的长度、原动件1的位置1 及等角速度ω1,求机构在图示位置时构件3的速度、 加速度。
31
▪ 活动构件1、2组成移动副, ▪ 作平面复杂运动的构件2上的另一个基本运动副是
vP13 P12
P13
P23 ω3 P34
P14
注意:图解法的特点体现在从“机构位置图”中直
接量出两点之间的距离。
15
提问:
1)如何求构件2的角速度ω2? 2) ω3=0时,构件1的角位置1 ?
P24
P23
P12
P13
P34
16
P14
例2:如图所示为一曲柄滑块机构,已知l AB=30mm, l BC=65mm,原动件1的位置1=145° 及等角速度ω1 = 10rad/s,求机构在该位置时滑块3的速度。
C点
B点
构件2
影像原理
35
E点
2.速度分析
▪
VC = VB + VCB
机械原理-机构运动分析的解析法

l
1
φ θ
2
l
x
a2 x 2l cos al sin a2 y 2l sin al cos
已知:构件的长度L及运动参数角位置θ 、角速度ω 、 角加速度ε ,1点的运动参量。
求: 3点的运动参量。
解: P 3x P 1 x l cos( ) v3 x v1 x l sin( ) P v3 y v1 y l cos( ) 3y P 1 y l sin( )
运 动 副 点 号
要求赋值
构 件 号
构 件 长 度
角位置角速度角加速 度,位置 速度 加速 度 n1
r1
m>0——实线 M<=0——虚线
不赋值
已知: 外运动副N1的位置P、速度v、加速度a,导路上任意参考点 N2的位置P、 速度v、加速度a,构件1的长度及导路的角位置、角速度、角加速度。 求:内运动副N3的运动参量、构件①的运动参量、 r2、vr2、ar2
P 3x P 1x l1 cos 1 P 3y P 1 y l1 sin 1
P 3y P 2y 2 arctan P P 2x 3x
rrrk(m,n1,n2,n3,k1,k2,r1,r2,t,w,e,p,vp,ap)
装 配 模 式
n3 k1 k2 r2 n2 N3’
}
y
3
l
1
φ
l
2
θ
x
bark(n1,n2,n3,k,r1,r2,gam,t,w,e,p,vp,ap)
关 键 点 号 构 n n 件 1 1 号 n n ∠ n3 n1 2 3 间 间 n2 距 距 离 离 角位置角速度 角加速度,位 置 速度 加速度
平面机构的运动分析

曲柄摇杆机构的速度分析
(4-21)
将位移方程式(4-21)对时间求导可得:
l AB1ei (1 / 2) l BC2 ei (2 / 2) l DC 3ei (3 / 2) (4-31)
方向: i (1 / 2) e 大小: l AB 1 意义: VB +
为了消去角,将式(4-22)和(4-23)移项再平方后 相加可得:
2 l BC (l AD l DC cos3 l AB cos1 ) 2 (l DC sin 3 l AB sin 1 ) 2
为了求解φ3,将上式改写为三角方程:
A sin 1
A sin 3 B cos 3 C 0 B l AD / l AB cos1
i ( 2 / 2 )
S (4-13)
.
将速度方程式(4-13)对时间求导可得
l AB e
2 i (1 ) 1
l BC e
2 i ( 2 ) 2
l BC 2 e
i ( 2 / 2 )
S
..
由式(4-19)可得连杆的 角加速度
方向: e i (1 ) 大小: n 意义: aB +
表4-2列出了单位矢量旋转的几种特殊情况。
结果
(φ+π/2) i· eiφ=ei·
(φ+π) i 2· eiφ= - eiφ =ei·
被乘数
作用
i
i2
相当于矢量逆时针转过π/2角
相当于矢量逆时针转过π角
i3
(φ+3π/2) =ei· (φ-π/2) i3· eiφ=- i· eiφ=ei·
相当于矢量逆时针转过3π/2角
e i cos i sin 1
第四章 平面机构的运动分析

概述 机构运动分析的目的和范围 1.机构运动分析的目的:分析现有机构工作性能,检验新机构。 通过轨迹分析,确定构件运动所需空间,判断运动是否干涉。 通过速度分析,确定构件的速度是否合乎要求,为加速度分析和受力分 析提供必要的数据。
通过加速度分析,确定构件的加速度是否合乎要求,为惯性力的计算提
供加速度数据,。 由上述可知,运动分析既是综合的基础,也是力分析的基础。另外,还 为机械系统的动力学分析提供速度和加速度数据。 2.机构运动分析的范围 不考虑引起机构运动的外力,机构构件的弹性变形和机构运动副中间隙 对机构运动的影响,仅仅从几何角度研究在原动件的运动规律已知的情况下,
图4-15
i e c o s i s i n 1 X轴负向的单位矢量
i 3 / 2 3 / 2 e c o s 3 / 2s i i n 3 / 2 i y轴负向的单位矢量
矢量的回转
平面矢量的复数极坐标表示法
e i
若乘以矢量r,相当于把矢量r绕原点旋转了θ角。 表4-2 单位矢量旋转的几种特殊情况
速度瞬心法在平面机构速度分析中的应用
用瞬心法作机构的速度分析
P P 12 24 V P E E 4 14 l 2 P P 1424
已知:构件2的角速度ω2和 长度比例尺μl ; 求:VE和ω4=? 各瞬心如图所示,因在P24点, 构件2和4的绝对速度相等 , 故 ω2 (P24 P12) μl = ω4 (P24 P14) μl ,得:
BE bc BC
n t n t n t a a a a a a C C B B C B C B
2 a a ( p e ) ( / s ) E 4 E 2 2 am
平面机构的运动分析

平面机构的运动分析平面机构是由若干个连杆组成的机械结构,在运动分析中,我们需要研究机构中各个连杆的运动规律,以及机构整体的运动情况。
平面机构常见的类型有四杆机构、曲柄滑块机构、双曲柄滑块机构等。
在运动分析中,我们通常要确定机构的约束条件、求解连杆的角度、速度和加速度等。
首先,我们需要确定机构的约束条件。
约束条件是指机构中各个连杆之间的几何关系,包括定位约束和连杆长度约束。
定位约束是指机构中一些点的位置关系,可以通过坐标方程等方法求解。
连杆长度约束是指连杆的长度是固定的,可以通过连杆长度的几何关系来确定。
然后,我们可以通过运动分析的方法来求解连杆的角度、速度和加速度等。
在运动分析中,可以使用几何法和代数法等不同的方法来求解。
几何法中常用的方法有图解法和模型法。
图解法是通过绘制连杆的运动图来解决问题,可以直观地表示出机构的运动情况。
模型法是将机构模型化为几何图形,然后通过几何关系求解。
这些方法通常适用于简单的机构。
代数法中常用的方法有位置矩阵法和速度矩阵法。
位置矩阵法是通过建立连杆的位移方程来求解连杆的角度。
速度矩阵法是通过建立速度传递关系求解连杆的速度和加速度。
此外,还可以通过数值模拟的方法来进行运动分析。
数值模拟是利用计算机软件对机构进行建模,并进行数值计算得到机构的运动参数。
这种方法可以应用于复杂的机构,但计算量比较大。
总之,平面机构的运动分析是解决机构运动问题的基础,通过确定约束条件和求解连杆的角度、速度和加速度等参数,可以研究机构的运动规律,为机构的设计和优化提供理论依据。
第四章 刚体的平面运动

vB = vA cot ϕ
vA vBA = sin ϕ
vBA vA ωAB = = l l sin ϕ
例2 如图所示平面机构中,AB=BD= DE= l=300mm。在图示位置时,BD∥AE,杆AB的角速度为 ω=5rad/s。 求:此瞬时杆DE的角速度和杆BD中点C的速度。
解:1 、 BD作平面运动
2 2 vC = vB − vCB ≈1.299m s
方向沿BD杆向右
2、速度投影定理
由
r r r vB = vA + vBA
沿AB连线方向上投影
r r ( vB ) AB = ( vA ) AB
同一平面图形上任意两点的速度在这两点连线上 的投影相等。
例5 如图所示的平面机构中,曲柄OA长100mm, 以角速度ω=2rad/s转动。连杆AB带动摇杆CD,并拖 动轮E沿水平面纯滚动。已知:CD=3CB,图示位置 时A,B,E三点恰在一水平线上,且CD⊥ED。 求:此瞬时点E的速度。
由速度投影定理得
vB sin β = vC cos β
vC = vB tan β = rω0 tan β
圆轮瞬心在E 圆轮瞬心在E点
vA = vB = rω0
vC rω0 ωC = = tan β R R
§4-4 用基点法求平面图形内各点的加速度
A :基点
Ax ' y '
:平移坐标系
r r rt rn aB = ae + ar + ar r r rt rn aB = aA + aBA + aBA
va= vB
ve= vA
vr= vAB
r r r v =v +v
B A
BA
平面机构的运动分析习题和答案
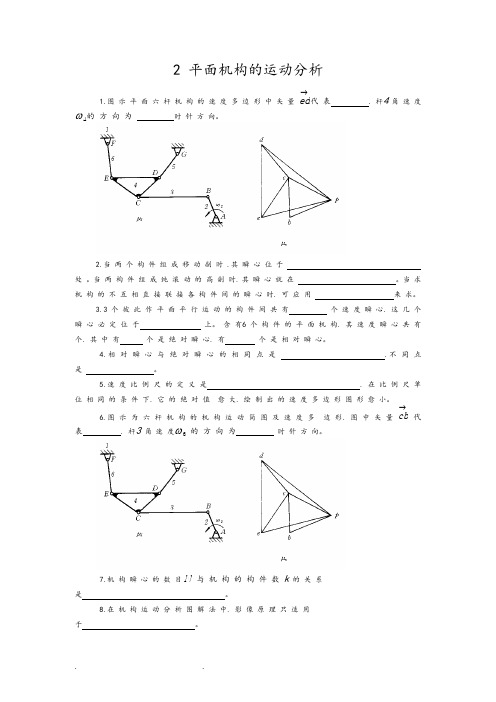
2 平面机构的运动分析1.图 示 平 面 六 杆 机 构 的 速 度 多 边 形 中 矢 量 ed →代 表 . 杆4 角 速 度ω4的 方 向 为时 针 方 向。
2.当 两 个 构 件 组 成 移 动 副 时 .其 瞬 心 位 于 处 。
当 两 构 件 组 成 纯 滚 动 的 高 副 时. 其 瞬 心 就 在 。
当 求 机 构 的 不 互 相 直 接 联 接 各 构 件 间 的 瞬 心 时. 可 应 用 来 求。
3.3 个 彼 此 作 平 面 平 行 运 动 的 构 件 间 共 有 个 速 度 瞬 心. 这 几 个瞬 心 必 定 位 于 上。
含 有6 个 构 件 的 平 面 机 构. 其 速 度 瞬 心 共 有 个. 其 中 有 个 是 绝 对 瞬 心. 有 个 是 相 对 瞬 心。
4.相 对 瞬 心 与 绝 对 瞬 心 的 相 同 点 是 .不 同 点 是 。
5.速 度 比 例 尺 的 定 义 是 . 在 比 例 尺 单 位 相 同 的 条 件 下. 它 的 绝 对 值 愈 大. 绘 制 出 的 速 度 多 边 形 图 形 愈 小。
6.图 示 为 六 杆 机 构 的 机 构 运 动 简 图 及 速 度 多 边 形. 图 中 矢 量 cb →代表 . 杆3 角 速 度ω3 的 方 向 为 时 针 方 向。
7.机 构 瞬 心 的 数 目N 与 机 构 的 构 件 数 k 的 关 系 是 。
8.在 机 构 运 动 分 析 图 解 法 中. 影 像 原 理 只 适 用 于 。
9.当 两 构 件 组 成 转 动 副 时. 其 速 度 瞬 心 在 处; 组 成 移 动 副 时. 其 速 度 瞬 心 在 处; 组 成 兼 有 相 对 滚 动 和 滑 动 的 平 面 高 副 时. 其 速 度 瞬 心 在 上。
10..速 度 瞬 心 是 两 刚 体 上 为 零 的 重 合 点。
11.铰 链 四 杆 机 构 共 有 个 速 度 瞬 心.其 中 个 是 绝 对 瞬 心. 个 是 相 对 瞬 心。
机械设计基础第四章平面机构运动简图及自由度

三、计算机构自由度时应注意的几种情况
1)复合铰链
由三个或三个以上构件组成的轴线重合的转动副称为复合铰链。
由m个构件组成的复合铰链应含有(m-1)个转动副。
两构件用运动副联接后,彼此的相对运动受到某些约束。每个 低副引入两个约束,每个高副引入一个约束。
设某平面机构,除机架外共有n个活动构件,又有pL个 低副和pH个高副,根据自由构件的自由度、运动副引入 的约束,活动构件之间的关系,可以得出平面机构自由 度的计算公式如下:
平面机构的自由度 F = 3n - 2PL – PH
一、构件及其自由度
一个自由构件作平面运动时, 具有三个独立运动;沿x轴和y轴 的移动以及绕垂直于xOy平面内 任一点A转动。
一个作平面运动的自由构件 具有三个自由度。
二、运动副与约束
运动副:机构中两构件直接接触的可动联接。
运动副元素:两构件上参加接触而构成运动的部分, 如点、线、面。 约 束:两构件用运动副联接后,彼此的相对运动受 到某些限制。
b.两构件上某两点间 的距离在运动过程中 始终保持不变时;
c.联接构件与被联接 构件上联接点的轨迹 重合时;
虚约束经常发生的场合:
d.机构中对运动不起作用的对称部分。
e.两构件组成若干个轴线互相重合的转动副.
采用虚约束是为了改善构件的受力情况; 传递较大功率;或满足某种特殊需要。
例题1
n=8 Pl=11 Ph=1 F=1
§4.2.2 平面机构运动简图
机构运动简图是用规定的运动副符号及代表构件的线条来表 示机构的运动特性,并按一定的比例画成的简单图形。并利 用机构运动简图对机构进行结构、运动和动力等分析。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
利用欧拉公式 eiφ=cosφ+i·sinφ, 可将矢量表示为: r=reiφ, 其中eiφ是单位矢量,它表示矢量的方向; leiφl = cos2 sin2 =1,
eiφ表示一个以原点为圆心、以1为半径的圆周上的点。
与坐标轴重合的单位矢量
三心定理
用瞬心法作机构的速度分析
作平面运动的三个构件共有 三个瞬心,它们位于同一直 线上。 设构件1为机架,因构件2和 3均以转动副与构件1相联, 故P12和P13位于转动中心,如 图所示。为了使P23点的构件2 和3的绝对速度的方向相同, P23不可能在M点,只能与P13 和P12位于同一条直线上。
于B1点的相对加速度,其方向平行于 导路。
Ⅱ级机构位置图的确定
运动分析的相对运动图解法
Ⅱ级机构 中,Ⅱ级组的内部 运动副相对于外部运动副的轨 迹不是圆弧,就是直线。 左上图中Ⅱ级组BCD中的内副 C相对于外副B、D的轨迹是圆 弧,故其位置可由两圆弧的交 点确定。 左下图中Ⅱ级组BCD的内副C 相对于外副B的轨迹是圆弧,相 对于外副D的轨迹是直线。故其 位置可由直线与圆弧的交点来 确定。
平面矢量的复数极坐标表示法 与坐标轴重合的单位矢量 矢量的回转 复数极坐标表示的矢量的微分
平面矢量的复数极坐标表示法
平面矢量的复数极坐标表示法
1. 用复数表示平面矢量
若用复数表示平面矢量r, r=rx+i·ry , rx是实部, ry是虚部, r=r(cosφ+isinφ),其中的 φ称为幅角,逆时针为正,
概述 机构运动分析的目的和范围 1.机构运动分析的目的:分析现有机构工作性能,检验新机构。
通过轨迹分析,确定构件运动所需空间,判断运动是否干涉。 通过速度分析,确定构件的速度是否合乎要求,为加速度分析和受力分 析提供必要的数据。 通过加速度分析,确定构件的加速度是否合乎要求,为惯性力的计算提 供加速度数据,。 由上述可知,运动分析既是综合的基础,也是力分析的基础。另外,还 为机械系统的动力学分析提供速度和加速度数据。 2.机构运动分析的范围 不考虑引起机构运动的外力,机构构件的弹性变形和机构运动副中间隙 对机构运动的影响,仅仅从几何角度研究在原动件的运动规律已知的情况下, 如何确定机构其余构件上各点的轨迹、线位移、线速度和线加速度,以及机 构中其余构件的角位移、角速度和角加速度等运动参数。
路平行。
a
k B
2B
为哥氏加速度,其计算公
1
式为:
ak B 2B 1
2ω
VB 2B 1
动点B2的绝对加速度等于相对加速度 、牵连加速度与哥氏加速度三者的矢
量和,即
aB2
aB1
ak B 2B 1
ar B 2B 1
其方向是将相对速度 VB2B1的矢量 箭头绕箭尾沿牵连角速度的方向转 过900
aB1 是牵连加速度;arB2B1为B2点相对
用瞬心法作机构的速度分析 图4-1 速度瞬心
用瞬心法作机构的速度分析
2. 瞬心的种类
1. 绝对瞬心:构成瞬心的两个构件之一固定不动,瞬心点的绝
对速度为零 。
2. 相对瞬心:构成瞬心的两个构件均处于运动中,瞬心点的绝
对速度相等、相对速度为零 。
由此可知,绝对瞬心是相对瞬心的一种特殊情况。
3. 机构中瞬心的数目
a
n C
A方向平行于
AC且由C指向A。
运动分析的相对运动图解法
同一构件上两点间的速度和加速度关系
动点B2的绝对速度等于它的重合点的 牵连速度和相对速度的矢量和,即
VB2 VB1 VB2B1
VB2 VB1 VB2B1
VB1 是牵连速度;VB2B1 为B2点相对 于B1点的相对速度 ,它的方向与导
设机构中有N个(包括机架)构件,每两个进行组合,则该 机构中总的瞬心数目为
K= N(N-1) / 2
(4-1)
用瞬心法作机构的速度分析
机构中通过运动副直接相联的两构件瞬心位置的确定
1.两构件作平面运动时 :
如图4-1所示,作VA2A1 和VB2B1 两 相对速度方向的垂线,它们的交 点(图中的P21)即为瞬心。
的速度和加速度矢量方程,准确地绘出速度和 加速度图,并由此解出待求量。 主要内容 同一构件上两点间的速度和加速度关系 移动副两构件重合点间的速度和加速度关系 Ⅱ级机构位置图的确定 速度分析 加速度分析
运动分析的相对运动图解法
同一构件上两点间的速度和加速度关系
构件AB作平面运动时,可以看作随 其上任一点(基点)A 的牵连运 动和绕基点A 的相对转动。 C的 绝对速度可用矢量方程表示为 :
对于构件2 :VB2=VB1= ω1lAB
VC VB VCB
方向: CD AB CB
大小: ?
l AB 1 ?
be2= (BE) /(BC) bc
对于构件4和5:
VE5 VE4 VE5E4
方向: EF √ ∥ EF
大小: ? √
?
加速度分析
运动分析的相对运动图解法
已知: 各构件的长度和各速度参数 求: aE5 解:对于构件2:
用瞬心法作机构的速度分析
速度瞬心法在平面机构速度分析中的应用
VE
4 P14El
P12 P24 P14 P24
2
已知:构件2的角速度ω2和 长度比例尺μl ;
求:VE和ω4=?
各瞬心如图所示,因在P24点, 构件2和4的绝对速度相等 , 故
ω2 (P24 P12) μl = ω4 (P24 P14) μl ,得:
2.两构件组成移动副:
因相对移动速度方向都平行于移动 副的导路方向(如图4-2 a所示),故 瞬心P12在垂直于导路的无穷远处。
图4-1
图4-2a
用瞬心法作机构的速度分析
3.两构件组成转动副: 两构件 绕转动中心相对转 动,故该转动副的中心便是 它们的瞬心
4.两构件组成纯滚动的高副 其接触点的相对速度为零,所 以接触点就是瞬心。
速度分析
v
真实速度大小 m / s 图中线段长度 mm
vB pb
m/s mm
vC ( pc)v , vCB (bc)v 3 vC / lCD 和 2 vCB / lBC
vE5 ( pe5 )v , vE5E4 (e4e5 )v
运动分析的相对运动图解法
已知:各构件的长和构件1
的位置及等角速度ω1 求:ω2 ,ω3 和VE5 解:1.取长度比例尺画出左图a所 示的机构位置图, 确定解题步骤: 先分析Ⅱ级组BCD,然后再分析4、 5 构件组成的Ⅱ级组。
相当于矢量逆时针转过π/2角
i2
i2·eiφ= - eiφ =ei·(φ+π)
相当于矢量逆时针转过π角
i3 i3·eiφ=- i·eiφ=ei·(φ+3π/2) =ei·(φ-π/2) 相当于矢量逆时针转过3π/2角
或顺时针转π/2角
因eiφ·e-iφ=ei(φ-φ)=1,故e-iφ是eiφ的共轭复数 。
重点:矢量运算法
第二节 用瞬心法作机构的速度分析
学习要求
本节要求全面掌握瞬心的概念,熟练掌握用瞬心法对机 构进行速度分析的方法。
主要内容
瞬心的概念和种类 机构中通过运动副直接相联的两构件瞬心位置的确定 三心定理 速度瞬心法在平面机构速度分析中的应用 本节例题
瞬心的概念和种类
1. 瞬心的概念 瞬心是瞬时等速重合点。瞬时, 是指瞬心的位置随时间而变;等 速,是指在瞬心这一点,两构件 的绝对速度相等(包括大小和方 向)、相对速度为零;重合点, 是指瞬心既在构件1上,也在构件 2上,是两构件的重合点。
4
P12 P24 P14 P24
2
本节例题
用瞬心法作机构的速度分析
已知: 构件2的角速度ω2 和长 度
比例尺μl
求:从动件3 的速度V3;
解:由直接观察法可得P12,由
三心定理可得P13和P23如图所
示v。由瞬心P的P概念可知:
3
2 12 23 l
第三节 运动分析的相对运动图解法
学习要求 掌握相对运动图解法, 能正确地列出机构
平面矢量的复数极坐标表示法
复数极坐标表示的矢量的微分
设r= re i 则对时间的一阶导数为:
dr dt
dr dt
ei
r
d
dt
(iei )
vr ei
rei( / 2)
方向:ei
ei( / 2)
大小: vr
r
式中,vr 是矢量大小的变化率;ω 是角速度; rω 是线速度。 对时间的二阶导数为:
2v e r e re d 2r a ei
VC VA VCA
C点的加速度可用矢量方程式表示为:
aC
aA
aCA
aA
a
n CA
aCt A
a A是牵连加速度,a C A 是C点相对于A点
的相对加速度
,
aCn A是法向加速度,
a
t CA
是切向加速度
式中,VA 牵连速度;VCA 是C点相对
于A点的相对速度 .
其大小为:
,方向如图.
a
t C
A的方向如图,
平面矢量的复数极坐标表示法
与坐标轴重合的单位矢量如表4-1和图4-15所示。
表4-1 与坐标轴重合的单位矢量
图4-15
φ
eiφ
代表的矢量
0 ei0 cos0 i sin0 1
X轴正向的单位矢量
/ 2 ei / 2 cos / 2 i sin / 2 i y轴正向的单位矢量
ei cos i sin 1 X轴负向的单位矢量
3 / 2 ei3 / 2 cos3 / 2 i sin3 / 2 i y轴负向的单位矢量
