C语言实现汉诺塔
汉诺塔游戏-----用C++编的

#ifndef HANIO_H_#define HANIO_Hclass Stack{private:enum{ MAX=50 };int m_node[MAX];int m_top;int m_size;int m_index;public:Stack();~Stack() { };bool Isfull() { return m_top==MAX-1 ;}; //堆栈满则返回TRUE bool Isempty() { return m_top==-1;}; //堆栈空则返回TRUE int Top() { return m_top; };int TopValue() { return m_node[m_top];};int GetDataFromIndex(int i) { return m_node[i]; };int GetIndex() { return m_index; } ;void SetIndex(int index) { m_index = index; };int Size() { return m_top+1; };bool Push(int data);bool Pop(int * pData);int MoveToNext();void OutPrint();};class Hanio{Stack m_stack[3];int m_num; //盘数int m_steps; //移动次数int m_times; //完成所用时间void print(char ch,int n);public:Hanio(int num=3);~Hanio() {};void GameStart();bool MoveFromTo(int x,int y); //从x号盘移动到y号盘void DrawPaletes(char ch='*'); //打印3个堆的盘子bool IsFinished() ; //结束返回TURE;int Solve(char from,char to,char auxiliary,int n); //求解其解法路径};#endif//hanio.cpp#include "hanio.h"#include <iostream>#include<cstdlib>#include<cstring>#include<cctype>#include<windows.h>Stack::Stack(){m_top=-1;m_index=m_top;for(int i=0;i<MAX;i++)m_node[i]=0;}bool Stack::Push(int data){if(Isfull())return false;m_top++;m_node[m_top]=data;m_index=m_top;return true;}bool Stack::Pop(int *pData){if(Isempty())return false;*pData=m_node[m_top];m_node[m_top]=0;m_top--;m_index=m_top;return true;}int Stack::MoveToNext(){int temp=m_index;m_index--;return m_node[temp];}void Stack::OutPrint(){if(m_top!=-1){for(int i=0;i<=m_top;i++)std::cout<<"["<<m_node[i]<<"]";}}///////////////////////////////////////Hanio::Hanio(int num){m_num=num;m_steps=0;m_times=0;for(int i=num;i>=1;i--)m_stack[0].Push(i);//m_stack[0].OutPrint();}void Hanio::print(char ch,int n){for(int i=1;i<=n;i++)std::cout<<ch;}void Hanio::DrawPaletes(char ch){int max;max=m_stack[0].Size()>m_stack[1].Size() ? m_stack[0].Size() : m_stack[1].Size();max=m_stack[2].Size()>max ? m_stack[2].Size() : max;//std::cout<<"Max:"<<max<<std::endl;m_stack[0].SetIndex(max-1);m_stack[1].SetIndex(max-1);m_stack[2].SetIndex(max-1);for(int i=1;i<=max;i++){int data1=m_stack[0].MoveToNext();int data2=m_stack[1].MoveToNext();int data3=m_stack[2].MoveToNext();if(data1==0)print(' ',20);else{print(' ',10-data1);print(ch,2*data1);print(' ',10-data1);}if(data2==0)print(' ',20);else{print(' ',10-data2);print(ch,2*data2);print(' ',10-data2);}if(data3==0)print(' ',20);else{print(' ',10-data3);print(ch,2*data3);print(' ',10-data1);}std::cout<<std::endl;}}bool Hanio::MoveFromTo(int x,int y){m_steps++; //计算所走的步数if(m_stack[x].Isempty()){std::cout<<x<<" pallete is empty ! continue !"<<std::endl; std::cin.get();return false;}if(m_stack[y].Isempty()){int data;m_stack[x].Pop(&data);m_stack[y].Push(data);return true;}else{if(m_stack[x].TopValue()>m_stack[y].TopValue()){std::cout<<"The board can't move from "<<x<<" plate to " <<y<<" plate!"<<std::endl;std::cin.get();return false;}else{int data;m_stack[x].Pop(&data);m_stack[y].Push(data);return true;}}}bool Hanio::IsFinished(){return m_stack[2].Top()==m_num-1;}void Hanio::GameStart(){using namespace std;UINT StartTime=::GetTickCount();UINT EndTime;while(1){system("cls");print('-',80);cout<<"steps: "<<m_steps; print(' ',20);cout<<"Used time: "<<m_times<<endl;print('-',80);cout<<endl; cout<<endl; print(' ',10); cout<<"A";print(' ',19); cout<<"B"; print(' ',19);cout<<"C"<<endl<<endl;Hanio::DrawPaletes();cout<<endl; cout<<endl;print('-',80);//测试游戏是否结束if(Hanio::IsFinished()){cout<<"你好强呀!从今天开始,维护世界和平的任务就交给你那!"<<endl;cin.get();break;}//输入命令并左相应的处理char szCommand[50];cout<<">>";cin.getline(szCommand,50);if(stricmp(szCommand,"QUIT")==0 || stricmp(szCommand,"Q")==0)break;if(stricmp(szCommand,"HELP")==0 || stricmp(szCommand,"H")==0){cout<<" 本游戏说明:"<<endl;cout<<" 该游戏由DAVID用C++编程,花费了一个多下午的时间呢!!!,由命令行来控制铁饼的移动:"<<endl;cout<<" QUIT / Q : 退出程序"<<endl;cout<<" HELP / H : 查看该说明"<<endl;cout<<" XY : X,Y的取值为A,B,C,意思时把X木桩最上面的铁饼移到Y 木桩"<<endl;cout<<" SOLVE / S : 显示求解该问题(移动铁饼)的最优路径..."<<endl; cin.get();}char ch1=toupper(szCommand[0]);char ch2=toupper(szCommand[1]);if( ch1=='A' && ch2=='B')Hanio::MoveFromTo(0,1);else if ( ch1=='A' && ch2=='C')MoveFromTo(0,2);else if ( ch1=='B' && ch2=='A')MoveFromTo(1,0);else if ( ch1=='B' && ch2=='C')MoveFromTo(1,2);else if ( ch1=='C' && ch2=='A')MoveFromTo(2,0);else if ( ch1=='C' && ch2=='B')MoveFromTo(2,1);else{cout<<"Bad command !"<<endl;cin.get();}//统计游戏所用时间EndTime=GetTickCount();m_times=(EndTime-StartTime)/1000;}}int Hanio::Solve(char from,char to,char auxiliary,int n) {if(n==1)return 0;}//main.cpp#include<iostream>#include"hanio.h"#include<cstdlib>using namespace std;int StartPicture();//返回选择的盘数int main(){int number;number=StartPicture();Hanio hanio(number);hanio.GameStart();return 0;}void print(char ch,int n){for(int i=1;i<=n;i++)std::cout<<ch;}int StartPicture(){using namespace std;int number;system("cls");system("color fc");print(' ',20);print('-',25);cout<<endl;print(' ',20);cout<<" Hanio(汉诺塔)"<<endl;print(' ',20);print('-',25);cout<<endl;print(' ',40);print('-',5);cout<<"By David"<<endl;print('=',80);cout<<" 相传在某一座古庙中有3根木桩,有24个铁盘由小到大放置在一根木柱上,庙中流传者一个传说:\"如果能把24个铁盘, 从一根木桩移动到另一个木桩,且必须遵守如下规则:"<<endl;cout<<endl;print(' ',5);cout<<"1. 每天只能动一个盘,而且只能从最上面的铁盘开始搬动."<<endl; print(' ',5);cout<<"2. 必须维持较小的铁盘在上方的原则"<<endl;cout<<endl;cout<<"这两个原则,则当24个铁盘完全般到另一个木桩时,世界就回永久和平!!"<<endl;cout<<"游戏的玩法可以在命令行中输入HELP查看"<<endl;cout<<endl;cout<<endl;cout<<endl;cout<<endl;cout<<endl;cout<<"再此输入你要搬的铁盘数(建议在1--10值间,太多回花费很长时间的)"<<endl;print('=',80);cout<<">>";cin>>number;cin.get();system("cls");return number;}。
C语言实现汉诺塔(图文详解)

C语⾔实现汉诺塔(图⽂详解)⽬录思路:当n=1时:当n=2时:当n=3时:当n=4时:见代码运⾏截图总结汉诺塔的游戏规则:有三根⾦刚⽯柱⼦A、B、C,在A柱⼦上从下往上按照⼤⼩依次减⼩的顺序摞着64⽚黄⾦环。
⼤梵天命令婆罗门把环从下⾯开始按⼤⼩顺序重新摆放在另⼀根柱⼦上。
并且规定,在任何⼀个柱⼦上,⼩环上不能放⼤环,在三根柱⼦之间⼀次只能移动⼀个环。
即将A柱⼦上全部的环通过中间柱⼦B(B柱⼦作为中介)移动到C柱⼦上当A只有⼀个环的时候:A->C当A只有两个环的时候:A->B A->C B->C当A只有三个环的时候:A->C A->B C->B A->C B->A B->C A->C思路:1、将 n-1个环先放到B柱⼦上2、将A柱⼦上的最后⼀个环移动到C柱⼦上3、将n-1个环从B柱⼦移动到C柱⼦上当n=1时:1、将0个环先放到B柱⼦上2、将A柱⼦上的最后⼀个环移动到C柱⼦上:A->C3、将0个环从B柱⼦移动到C柱⼦上当n=2时:1、将1个环先放到B柱⼦上:A->B2、将A柱⼦上的最后⼀个环移动到C柱⼦上:A->C3、将1个环从B柱⼦移动到C柱⼦上:B->C当n=3时:1、将2个环先放到B柱⼦上:使⽤递归将2个环放到B上,因为A柱⼦的最后⼀个环是最⼤的因此可以先不理会,递归重复当n=2时的步骤,不过是从将2个环从A放到C上改为将2个环从A放到B上了2、将A柱⼦上的最后⼀个环移动到C柱⼦上:A->C3、将2个环从B柱⼦移动到C柱⼦上:使⽤递归将2个环从B柱⼦移动到C柱⼦上,此时C柱⼦上已经有了最⼤的⼀个环因此可以不⽤再理会了,递归重复当n=2的步骤,不过是从将2个环从A放到C上改为将2个环从B放到C上了当n=4时:1、将3个环先放到B柱⼦上:递归重复n=3的步骤,不过是从将3个环从A放到C上改为将3个环从A放到B上了2、将A柱⼦上的最后⼀个环移动到C柱⼦上:A->C3、将3个环从B柱⼦移动到C柱⼦上:递归重复当n=3的步骤,不过是从将3个环从A放到C上改为将3个环从B放到C上了见代码#define _CRT_SECURE_NO_WARNINGS 1#include<stdio.h>void move(char X, char Y){printf("%c->%c ", X, Y);}void HanoiTower(int n, char A, char B, char C){if (n == 1)//递归终⽌条件{move(A, C);return;}else{HanoiTower(n - 1, A, C, B);//将n-1个环从A柱⼦放到B柱⼦上,C柱⼦作为中介move(A, C);//将A柱⼦上的最后⼀个环移动到C柱⼦上HanoiTower(n - 1, B, A, C);//将n-1个环从B柱⼦放到C柱⼦上,A柱⼦作为中介}}int main(){printf("请确认A柱⼦上⼀共有多少个环:\n");int n = 0;scanf("%d", &n);HanoiTower(n, 'A','B','C');//将n个环从A柱⼦放到C柱⼦上,B柱⼦作为中介}运⾏截图总结本篇⽂章就到这⾥了,希望能给你带来帮助,也希望您能够多多关注的更多内容!。
汉诺塔问题c语言实现

汉诺塔问题c语言实现汉诺塔问题是一种经典的递归问题,也是计算机算法中的重要问题之一。
本文将介绍如何使用C语言实现汉诺塔问题。
汉诺塔问题的规则是:有三根柱子A、B、C,其中A柱子上有n 个盘子,这些盘子大小不等,大的在下面,小的在上面。
现在要把这n个盘子从A柱子移动到C柱子上,但是每次只能移动一个盘子,并且在移动过程中,任何时候都不能让大盘子放在小盘子上面。
最终要求把所有盘子都移动到C柱子上。
下面是汉诺塔问题的C语言实现代码:#include <stdio.h>void hanoi(int n, char A, char B, char C) {if (n == 1) {printf('%c -> %c', A, C);} else {hanoi(n-1, A, C, B);printf('%c -> %c', A, C);hanoi(n-1, B, A, C);}}int main() {int n;printf('请输入盘子的个数:');scanf('%d', &n);printf('移动的步骤如下:');hanoi(n, 'A', 'B', 'C');return 0;}在上面的代码中,hanoi函数是一个递归函数,用来实现汉诺塔问题的移动过程。
当n等于1时,直接将A柱子上的盘子移动到C柱子上;当n大于1时,将A柱子上的n-1个盘子移动到B柱子上,再将A柱子上的最后一个盘子移动到C柱子上,最后将B柱子上的n-1个盘子移动到C柱子上。
在main函数中,先输入要移动的盘子个数n,然后调用hanoi 函数进行移动,最后输出移动的步骤。
通过上面的代码,我们可以很方便地实现汉诺塔问题的求解。
C语言程序设计课程设计报告---汉诺塔问题

XXXX大学计算机科学与技术学院课程设计报告2012 — 2013学年第一学期课程名称C/C++高级语言程序设计课程设计设计题目小游戏和图形处理汉诺塔问题学生姓名XXX学号XXXXXXX专业班级XXXXXXXXXXX指导教师XX2012 年X 月XX 日目录一、课程设计问题描述 (1)1、课程设计题目 (1)2、设计任务要求 (1)二、总体设计 (1)1、设计思路 (1)2、汉诺塔求解流程图 (2)三、详细设计 (2)1、汉诺塔问题描述 (2)2、算法分析 (3)3、实现递归的条件 (4)4、用C语言实现 (4)四、程序运行结果测试与分析 (4)1、打开Microsoft Visual C++ 6.0操作平台输入以下的源代码 (4)2、编译源代码 (5)3、组建 (5)4、执行 (5)5、运行结果 (6)6、按任意键结束程序 (7)五、结论与心得 (7)六、参考文献 (8)七、附录:程序源代码 (8)一、课程设计问题描述1、课程设计题目汉诺塔问题2、设计任务要求输入盘子数(2个以上有效),移动速度,开始演示汉诺塔移动的步骤,要求:盘子A,B,C柱需要自己绘制,初始时盘子在A柱上通过B柱最终移动到C 柱上,显示出盘子在几个柱之间的移动过程。
二、总体设计1、设计思路对于一个类似的这样的问题,任何一个人都不可能直接写出移动盘子的每一个具体步骤。
可以利用这样的统筹管理的办法求解:我们假设把该任务交给一个僧人,为了方便叙述,将他编号为64。
僧人自然会这样想:假如有另外一个僧人能有办法将63个盘子从一个座移到另一个座,那么问题就解决了,此时僧人A B C64只需这样做:(1).命令僧人63将63个盘子从A座移到C座(2).自己将最底下的最大的一个盘子从A座移到C座(3).再命令僧人63将63个盘子从B座移到C座为了解决将63个盘子从A座移到B座的问题,僧人63又想:如果能再有一个僧人62能将62个盘子移动到另一座,我就能将63个盘子从A座移动到B座。
c语言课程设计汉诺塔

c语言课程设计汉诺塔一、教学目标本节课的教学目标是让学生掌握汉诺塔问题的解法,理解其背后的算法思想,培养逻辑思维能力和编程能力。
具体分为以下三个部分:1.知识目标:使学生了解汉诺塔问题的定义、解法和算法思想,理解递归算法的原理及其在解决汉诺塔问题中的应用。
2.技能目标:培养学生运用C语言实现汉诺塔问题的解决方案,提高编程实践能力。
3.情感态度价值观目标:培养学生独立思考、合作交流的学习习惯,增强对计算机科学的兴趣和热情。
二、教学内容本节课的教学内容主要包括以下几个部分:1.汉诺塔问题的定义和解法:介绍汉诺塔问题的背景,讲解其解法及步骤。
2.递归算法的原理:讲解递归算法的基本概念、特点及其在解决汉诺塔问题中的应用。
3.C语言实现汉诺塔问题:引导学生运用C语言编写汉诺塔问题的解决方案,并进行调试和优化。
4.算法分析和改进:分析汉诺塔问题的算法复杂度,探讨如何优化算法性能。
三、教学方法为了达到本节课的教学目标,采用以下几种教学方法:1.讲授法:讲解汉诺塔问题的定义、解法和递归算法的原理。
2.案例分析法:分析实际案例,让学生了解递归算法在解决汉诺塔问题中的应用。
3.实验法:引导学生动手实践,用C语言实现汉诺塔问题的解决方案。
4.讨论法:学生进行小组讨论,分享算法优化思路,培养合作交流能力。
四、教学资源本节课的教学资源包括以下几个方面:1.教材:选用《C程序设计》等相关教材,为学生提供理论知识的学习参考。
2.参考书:推荐《算法导论》等参考书籍,帮助学生深入了解算法原理。
3.多媒体资料:制作PPT、教学视频等多媒体资料,辅助学生理解和记忆知识点。
4.实验设备:为学生提供计算机、编程环境等实验设备,方便学生动手实践。
五、教学评估本节课的教学评估主要包括以下几个方面:1.平时表现:评估学生在课堂上的参与度、提问回答等情况,占比20%。
2.作业:评估学生完成的汉诺塔问题相关练习,包括C语言代码编写和调试,占比30%。
用C语言解决汉诺塔问题的方法及过程分析

( )将 原 问题 转化 成 新 问题 后 ,能使 求 解算法 的规模减 小. 2
( )递归 有一 个 明显 的 出 口,或称 为递 归的边 界 ,而边 界 问题 的解是显 而 易见 的或 已知 的. 3
3 用 C语 言 编 程
C语 言是 一种 在 国内外 广泛 流行 的高 级程 序设 计语 言 ,它 的语 言 功能 丰富 ,表达 力 强 ,使 用 灵 活 ,应
言 中 ,用 递归 法编 写 条件
2 1 递 归程序 定义 .
《 C程 序设 计 》 数 据结 构 》等教科 书 中 ,都对 递 归 程 序 给 出 了基本 相 同的定 义 ,归纳 如下 :在调 用 、《
一
个 函数 的过 程 中 ,又直接 或 间接地 调用 了该 函数本 身 ,称 为 函数 的递 归调 用 ,使用 了递 归调用 函数 的程
第 3期
{ a ( 一 , o e t r e t ) hn n1 n , h e , wo ;
mo e ( ne, t e ); v o hr e
h n ( 一 ,t a n 1 wo,o e h e ) ) n ,t r e ;)
ma n ( i )
{n i tn;
prn f ( “ e s nt rt mbe ike ” it Pla e e e he nu rofd s s: );
维普资讯
维普资讯
2 0 年 6月 06
河 北 北 方 学 院学 报 ( 自然 科 学 版 )
第 3 期
上操 作 的实质 是把移 动 n个 盘子 的 问题转 化 为移 动 n 一1个盘 .那 一 、三 步 如何解 决 ?事 实 上 ,上述 方法 设盘 子数 为 n ,n可 为任 意数 ,该 法 同样 适 用于 移动 n 1 盘. 因此 ,依 据 上 法 ,可解 决 n 一 个 一1个 盘子从 A杆 移 到 B杆 ( 一 步)或 从 B杆 移到 C杆 ( 第 第三 步 ) 问题 .现 在 ,问题 由移 动 n个 盘 子 的操 作转 化 为 移动 n 一2个 盘子 的操作 .依 据该 原 理 ,层 层递 推 ,即可将 原 问题 转化 为 解 决移 动 n 、n … …3 、 一2 一3 、2 直 到移动 1 盘 的操 作 ,而移 动一 个 盘 的操 作 是可 以 直接 完成 的. 至 此 ,我 们 的任 务 算作 是 真 正完 成 了. 个 而这 种 由繁化 简 ,用简单 的问题 和 已知 的操 作 运算来 解决 复杂 问题 的方 法 ,就是 递归法 . 在计算 机设计 语
汉诺塔问题的程序实现

汉诺塔问题的程序实现汉诺塔问题的程序实现实验⽬的:运⽤程序解决汉诺塔(hanoi)问题。
汉诺塔问题:假设有3个分别命名为A,B,C的塔座,在塔座A上插有n个直径⼤⼩各不相同,依⼩到⼤编号为1,2....,n的圆盘。
现要求将A轴上的n个圆盘移到C并仍按同样顺序叠排,圆盘按以下规则(1)每次只能⼀动⼀个盘⼦(2)圆盘可以插在A,B,C中任⼀个塔座上(3)任何时刻都不能将⼀个较⼤的圆盘压在较⼩的圆盘之上。
A B C实验分析:汉诺塔问题可以规划为⼀个递归的问题予以分析,将n个盘⼦从A针移动到C 针可进⾏3个步骤:(1)将A上n-1的个盘⼦移到B针上;(2)把A针最后1个盘⼦移到C针上;(3)再把B盘⼦上的n-1个移到C针上。
实验过程:#includeusing namespace std;void main(){void hanoi(int m,char A,char B,char C); //A代表初始柱⼦,B代表辅助柱⼦,C代表⽬标柱⼦int m;printf("请输⼊盘⼦的个数:");scanf("%d", &m);printf("当盘⼦的个数为%d时移动的步骤是:\n",m);hanoi(m,'A','B','C');}void hanoi(int n,char X,char Y,char Z){void move(char X,char Z );if(n==1)move(X,Z);else{hanoi(n-1,X,Z,Y);move(X,Z);hanoi(n-1,Y,X,Z);}}void move(char x,char y){printf("%c-->%c\n",x,y);}过程:A代表初始柱⼦,B代表辅助柱⼦,C代表⽬标柱⼦。
⽽a代表第⼀根柱⼦,b代表第⼆根柱⼦,c代表第三根柱⼦。
汉诺塔c语言程序代码

汉诺塔c语言程序代码(通过vc++6.0验证)(附讲解)让我们先看看代码吧#include <stdio.h>int hj(int a,int b, int c,int i){int t;if(i==1)printf("%d->%d\n",a,c);else{t=c;c=b;b=t;hj(a,b,c,i-1);printf("%d->%d\n",a,b);t=a;a=c;c=t;t=b;b=c;c=t;hj(a,b,c,i-1);return 0;}}main(){int a,b,c,i;a=1;b=2;c=3;printf("请输入汉诺塔的盘数");scanf("%d",&i);hj(a,b,c,i);return 0;}以上是汉诺塔的代码,该程序主要是运用了递归的思想,比如数学中的f(x)=f(x-1)+f(x-2),在本程序中为:int hj(int a,int b, int c,int i){int t;if(i==1)printf("%d->%d\n",a,c);else{t=c;c=b;b=t;hj(a,b,c,i-1);也就是说,我们在这个函数中再次调用这个函数,相当于一个循环,而在再次调用的过程中,i的值变成i-1,就类似于f(x-1),这样层层调用,最终就变成当i=1的时候的值,然后通过运算,计算出想要得到的值。
汉诺塔的数值分析:我们可以发现,当只有一个盘的时候,我们只需要做1->3(就是把第一个柱子上的最顶端的盘移动到第三根柱子,以下不再解释)当有两个盘的时候,是1->2 1->3 2->3三个盘子是:1->3 1->2 3->2 1->3 2->1 2->3 1->3分析一下可以得出以下结论:初始值a=1 b=2 c=3一个盘子就是a->c两个盘子与一个盘子的关系是:第一步:b与c交换值,然后打印a->c第二步:打印a->b第三步:a与c交换值,b与c交换值,打印a->c进一步分析,便可以得出以下结论只要盘子数量为i(i大于1),那么它就有三部分第一部分,b与c交换值,然后运行i-1第二部分,打印a->b第三部分,a与c交换值,b与c交换值,然后运行i-1程序表示便是:if(i==1)printf("%d->%d\n",a,c);else{t=c;c=b;(交换值)b=t;hj(a,b,c,i-1);printf("%d->%d\n",a,b);t=a;a=c;c=t;(a c交换)t=b;b=c;c=t;(b c交换)hj(a,b,c,i-1);不明加QQ765233918(请写清备注)如有侵权请联系告知删除,感谢你们的配合!。
c语言取球问题思路

“取球问题”可能有多种含义,因为这可能涉及到许多不同的编程场景和问题。
但是,我将假设你是在提到一个经典的算法问题,即“取球问题”或“汉诺塔问题”。
汉诺塔问题是一个经典的递归问题,它涉及到三个柱子和一堆大小不同的球。
目标是将所有的球从一个柱子移动到另一个柱子,每次只能移动一个球,并且不能将一个较大的球放在一个较小的球上。
解决汉诺塔问题的一种方法是使用递归。
首先,你需要确定一个策略,即如何将问题分解成更小的部分。
然后,你需要编写一个函数来处理这些更小的部分。
在C语言中,你可以使用以下步骤来解决汉诺塔问题:
定义全局变量,包括球的起始柱子、目标柱子和辅助柱子,以及球的数组。
创建一个递归函数,该函数接受球的起始柱子、目标柱子和辅助柱子,以及要移动的球的数量作为参数。
在递归函数中,首先检查如果球的数量为1,那么直接将球从起始柱子移动到目标柱子。
如果球的数量大于1,那么将问题分解为两个较小的部分。
首先,将上面的球移动到辅助柱子。
然后,将下面的球从起始柱子移动到目标柱子。
最后,将辅助柱子上的球移动到目标柱子。
在主函数中调用递归函数,并传递适当的参数。
请注意,解决汉诺塔问题的关键在于理解如何使用递归来分解问题。
因此,理解递归的概念对于解决这个问题非常重要。
同时,还需要理解如何在C语言中创建和调用函数,以及如何使用全局变量在函数之间共享数据。
有趣的c语言代码

有趣的c语言代码在计算机编程领域中,C语言无疑是居于重要地位的一种语言。
它简洁明了,具有高度的灵活性,其语法规范和基本结构也有着非常强的适用性,依旧是很多应用领域的首选语言。
但是,除了作为一门实用的编程语言外,C语言也具备着不少有趣的面向场景和实现思路。
有时候我们不妨放开心态,花一点时间去探索一些优美、神奇或者古怪的代码,或许不仅可以带来好玩的游戏体验,还可以深刻领略计算机编程这一领域的魅力所在。
以下是几个有趣的C语言代码:1. Hello World!这是许多人接触编程时会碰到的第一行代码,既简单又经典。
用C 语言实现只需一行:include <stdio.h>int main(){printf("Hello, World!");return 0;}这段代码的功能很简单,输出 "Hello, World!"。
2. 回文字检测给定一个字符串,判断其是否为回文字符串。
这也是许多入门程序员接触的练手题。
bool isPalindrome(char *s){int len = strlen(s);for (int i = 0; i < len / 2; ++i)if (s[i] != s[len - 1 - i])return false;return true;}这段代码通过比较字符串中左右两端字符是否相同,完成回文检测。
3. 汉诺塔游戏汉诺塔是一个经典的数学谜题,至今仍是计算机课程和聚会游戏的热门选择之一。
在C语言中实现汉诺塔游戏的代码不仅具备实用价值,同时也挑战了程序设计师的算法思考能力。
void hanoi(int n, char A, char B, char C){if (n == 1)printf("%c -> %c\n", A, C);else{hanoi(n - 1, A, C, B);hanoi(1, A, B, C);hanoi(n - 1, B, A, C);}}这段代码通过递归实现了汉诺塔游戏的具体操作,将汉诺塔复杂的问题转化为简单的递归关系。
C语言实现汉诺塔游戏

C语⾔实现汉诺塔游戏操作就是:A B 号码A的塔顶⼀层放在号码B的塔顶。
如1(空格) 3 回车。
话说有⼈能把我这C的代码添加到QT界⾯框架上去么?代码写的不好,维护性不够,只能玩8层的,写完以后发现很难拓展,软件⼯程,设计模式有待提⾼....⾥⾯提⽰输⼊等级的装B⽤了,没有实现,⼤家随便输⼊个个位数就可以玩了。
stackfunc.c#include"STACK.h"#include<stdio.h>extern ceng CENG[SIZE];//数据⼊栈void push_stack(stack*p,int number){p->arr[p->head]=number;p->head++;}//初始化栈1void init_stack1(stack*p){p->head=0;push_stack(p,1);push_stack(p,2);push_stack(p,3);push_stack(p,4);push_stack(p,5);push_stack(p,6);push_stack(p,7);push_stack(p,8);}//初始化栈2 3void init_stack2_3(stack* p1,stack* p2){p1->head=0;p1->arr[p1->head]=0;p2->head=0;p2->arr[p2->head]=0;}//弹出栈顶元素int pop_stack(stack* p){p->head--;return p->arr[p->head];}//访问栈顶元素int top_stack(stack* p){return p->arr[p->head-1];}//⽐较两个栈顶元素的⼤⼩int sizecmp_stack(stack* p1,stack* p2){if(p1->arr[p1->head-1]>p2->arr[p2->head-1])return 1;else if(p1->arr[p1->head-1]<p2->arr[p2->head-1])return -1;else return 0;}//测出栈的⾼度int high_stack(stack* p){return p->head;}//是否为空栈int empty_stack(stack* p){return p->head==0;}//是否栈满int full_stack(stack* p){return p->head==SIZE;}//初始化层1void init_ceng1(ceng* p){p->number=1;p->row=SIZE-1;p->col=0;}//初始化层2void init_ceng2(ceng* p){p->number=2;p->row=SIZE-2;p->col=0;}//初始化层3void init_ceng3(ceng* p){p->number=3;p->row=SIZE-3;p->col=0;}//初始化层4void init_ceng4(ceng* p){p->number=4;p->row=SIZE-4;p->col=0;}//初始化层5void init_ceng5(ceng*p){p->number=5;p->row=SIZE-5;p->col=0;}//初始化层6void init_ceng6(ceng*p){p->number=6;p->row=SIZE-6;p->col=0;}//初始化层7void init_ceng7(ceng*p){p->number=7;p->row=SIZE-7;p->col=0;}//初始化层8void init_ceng8(ceng*p){p->number=8;p->row=SIZE-8;p->col=0;}//移动层void move_ceng(int level,int *nrow,int *ncol,stack*p1,stack* p2,stack* p3,int stdec){stack* arr[3];arr[0]=p1;arr[1]=p2;arr[2]=p3;*nrow=level-1-high_stack(arr[stdec]);*ncol=stdec;}//显⽰图⽚void show_map(void){int i,j;for(i=0;i<SIZE;i++){for(j=0;j<3;j++){if(CENG[0].row==i&&CENG[0].col==j){printf(" | 1 | ");}else if(CENG[1].row==i&&CENG[1].col==j){printf(" | 2 | ");}else if(CENG[2].row==i&&CENG[2].col==j){printf(" | 3 | ");}else if(CENG[3].row==i&&CENG[3].col==j){printf(" | 4 | ");}else if(CENG[4].row==i&&CENG[4].col==j){printf(" | 5 | ");}else if(CENG[5].row==i&&CENG[5].col==j){printf(" | 6 | ");}else if(CENG[6].row==i&&CENG[6].col==j){printf(" | 7 | ");}else if(CENG[7].row==i&&CENG[7].col==j){printf(" |8| ");}else printf(" ");}printf("\n");}printf("=====================================================================\n"); }main.c#include"STACK.h"#include<stdio.h>ceng CENG[SIZE];int main(){int res=1,dec=1;char con;int newrow;int newcol;int step=0;int level=0;while(1){ if (level==0){do{printf("请输⼊游戏等级:\n");scanf("%d",&level);if(level<=0||level>8)printf("等级范围错误,重新输⼊\n");}while(level<=0||level>8);}level=8;newrow=0,newcol=0;stack STACK[3];//初始化3个栈init_stack1(&STACK[0]);init_stack2_3(&STACK[1],&STACK[2]);//初始化8个层init_ceng1(&CENG[0]);init_ceng2(&CENG[1]);init_ceng3(&CENG[2]);init_ceng4(&CENG[3]);init_ceng5(&CENG[4]);init_ceng6(&CENG[5]);init_ceng7(&CENG[6]);init_ceng8(&CENG[7]);while(1){//打印画⾯switch(level){case 1:show_map();break;case 2:show_map();break;case 3:show_map();break;case 4:show_map();break;case 5:show_map();break;case 6:show_map();break;case 7:show_map();break;case 8:show_map();break;}while(1){// printf("游戏等级为:%d\n",level);// printf("源栈最⾼层是%d ......\n",top_stack(&STACK[res]));printf(" ⼀号的⾼度%d ",STACK[0].head);printf(" ⼆号的⾼度%d ",STACK[1].head);printf(" 三号的⾼度%d\n",STACK[2].head);printf("\n已经⾛的步数为 %d \n",step);//选择源⽬标scanf("%d",&res);scanf("%d",&dec);res--;dec-- ;if(!(res>=0&&res<3&&dec>=0&&dec<3))/*||(empty_stack(&STACK[res]))*/{ printf("\n\n输⼊范围超出\n");}else if(empty_stack(&STACK[res])==1){printf("%d\n",STACK[0].head);printf("\n\n源栈空\n");}else if(sizecmp_stack(&STACK[res],&STACK[dec])<0){ printf("\n\n⼤块的不能放在⼩块的上⾯\n");}else{if(dec!=res){printf("\n\n\n正在移动层块....\n");step++;move_ceng(level,&newrow,&newcol,&STACK[0],&STACK[1],&STACK[2],dec); CENG[top_stack(&STACK[res])-1].row=newrow;CENG[top_stack(&STACK[res])-1].col=newcol;push_stack(&STACK[dec],pop_stack(&STACK[res]));break;}else{printf("\n\n\n放轻松\n");}break;}show_map();}if (full_stack(STACK+1)==1||full_stack(STACK+2)==1){printf("完成了汉诺塔!\n");level++;break;}}show_map();printf("是否继续游戏?继续请输⼊y,否则按其它键\n");scanf("%*[^\n]");scanf("%*c");scanf("%c",&con);if(con!='y')break;}return 0;}STACK.h#ifndef __STACK_H__#define __STACK_H__#define SIZE 8typedef struct STACK{int head;int arr[SIZE];}stack;typedef struct CENG{int number;int row;int col;}ceng;extern ceng CENG[SIZE];//⼊栈void push_stack(stack*,int);//初始化栈1void init_stack1(stack*);//初始化栈2和3void init_stack2_3(stack*,stack*);//出栈int pop_stack(stack*);//访问栈顶元素int top_stack(stack*);//⽐较栈顶元素⼤⼩ -1 1int sizecmp_stack(stack*,stack*);//判断栈的⾼度int high_stack(stack*);//判断栈是否为空1 0int empty_stack(stack*);//判断栈是否满1 0int full_stack(stack*);//初始化层1void init_ceng1(ceng*);//初始化层2void init_ceng2(ceng*);//初始化层3void init_ceng3(ceng*);//初始化层4void init_ceng4(ceng*);//初始化层5void init_ceng5(ceng*);//初始化层6void init_ceng6(ceng*);//初始化层7void init_ceng7(ceng*);//初始化层8void init_ceng8(ceng*);//移动层块void move_ceng(int ,int * a,int *b,stack*,stack*,stack*,int k );//打印画⾯void show_map();#endif演⽰图⽚以上所述就是本⽂的全部内容了,希望能够对⼤家学习C语⾔的递归算法有所帮助。
c++汉诺塔问题递归算法

c++汉诺塔问题递归算法汉诺塔问题是经典的递归问题,它可以帮助我们理解和掌握递归算法的思想。
在C++中,我们可以通过递归来解决汉诺塔问题。
汉诺塔问题的描述如下:有三根柱子A、B、C,A柱子上有n 个盘子,盘子的大小不一,大的在下,小的在上。
现在要将A 柱子上的盘子移动到C柱子上,并且每次只能移动一个盘子,并且大的盘子不能放在小的盘子上面。
要求通过借助柱子B来实现移动。
下面我们先给出解决汉诺塔问题的递归代码:```cpp#include <iostream>void hanoi(int n, char A, char B, char C) {if (n == 1) {std::cout << "Move disk 1 from " << A << " to " << C << std::endl;return;}hanoi(n - 1, A, C, B);std::cout << "Move disk " << n << " from " << A << " to " << C << std::endl;hanoi(n - 1, B, A, C);}int main() {int n = 3; // 盘子的个数hanoi(n, 'A', 'B', 'C');return 0;}```上面的代码使用了递归的思想来解决汉诺塔问题。
函数`hanoi()`接受四个参数,n表示盘子的个数,A、B、C表示三根柱子的名称。
当n等于1时,表示只有一个盘子需要移动,直接将它从A柱子移动到C柱子即可。
当n大于1时,我们可以把问题简化为两个步骤:将n-1个盘子从A柱子通过借助C柱子移动到B柱子,然后将最后一个盘子从A柱子移动到C柱子,最后将n-1个盘子从B柱子通过借助A柱子移动到C 柱子。
汉诺塔问题非递归算法

汉诺塔问题非递归算法
汉诺塔问题是一个经典的递归算法问题,但也可以使用非递归的方式解决。
下面是一种非递归算法的实现思路:
1. 创建三个栈,分别命名为A、B、C,表示三个柱子。
2. 对于n个盘子的汉诺塔问题,首先将所有盘子按从大到小的顺序依次压入栈A中。
3. 定义一个变量count,用来记录移动步数,初始值为0。
4. 如果n为奇数,则执行步骤5;如果n为偶数,则执行步骤6。
5. 循环执行以下操作:
5.1 将栈A的栈顶元素弹出,放入栈B中;
5.2 将栈A中剩余的n-1个盘子移到栈C中;
5.3 将栈B中的盘子移到栈C中;
5.4 将栈A作为辅助栈,栈B作为目标栈,栈C作为源栈,重复步骤5.1~5.3,直到栈A为空。
6. 循环执行以下操作:
6.1 将栈A的栈顶元素弹出,放入栈C中;
6.2 将栈A中剩余的n-1个盘子移到栈B中;
6.3 将栈C中的盘子移到栈B中;
6.4 将栈A作为辅助栈,栈C作为目标栈,栈B作为源栈,重复步骤6.1~6.3,直到栈A为空。
通过上述非递归算法,可以按照汉诺塔问题的规则将所有的盘子从栈A移动到栈B,并记录移动的步骤数。
C语言递归调用实例——汉诺塔问题动画实现(附完整代码)

二、程序框架
古人云,不谋全局者,不足谋一域。同样,在编写代码之前,我们必 须得有个大体的思路和整体上的把握。不能一上来就稀里糊涂地乱敲一通。 当然,这里我也只能仅仅谈自己的个人想法,不一定就是最优的解决方案, 还希望能和大家一起相互交流,共同进步。整个程序的框架,我把它分为 动画效果和核心算法两大部分。我首先实现的是动画效果部分,等能够实 现盘子的随意移动后,我才开始研究核心算法的实现。这样一来,在核心 算法部分,我们正好可以利用前面的动画效果来直观地反映出我们的思路, 有助于代码的调试和缩短程序的开发周期。为了尽量减少废话,我们可以 用一张图来进行表示:
图 1-1 移动第一个圆盘..................................................................................................................... 4 图 1-2 移动第二个圆盘...................................................................................................................... 5 图 1-3 移动最后一个圆盘................................................................................................................. 6
能移动一个圆盘,且圆盘在放到棒上时,大的不能放在小的上面。中间的一根
棒作为辅助移动用。” 事实上,对此曾经有人作过分析,按这个规则,众僧耗尽毕生精力也
不可能完成圆盘的移动,因为需要移动圆盘的次数是一个天文数字 18446744073709551615(64 个圆盘需要移动的次数为 2 的 64 次方)。假设 1us 进行一次移动,也需要约一百万年的时间,使用计算机也很难解决 64
汉诺(Hanoi)塔问题(C#版)

汉诺(Hanoi)塔问题(C#版)
⼀个只能⽤递归解决的数学问题;问题描述:古代有⼀个梵塔,塔内有3个座,A、B、C,开始时A座有64个盘,盘⼦⼤⼩不等,⼤的在上,⼩的在下。
有⼀个⽼和尚想把这64个盘⼦从A座移到C座(如图所⽰),但每次只允许移动⼀个盘,且在移动过程中在3个座上始终保持⼤盘在下,⼩盘在上。
在移动地程中可以⾏⽤B座,要求编程序打印出移动的步骤。
逆向推理:1.假如⼀个和尚能把上⾯63个盘⼦先搬到B座,第⼆个和尚再把最⼤的那个移到C,第三个和尚再把63个盘⼦移到C座;⾄此整个⼯作就完成的。
2.问题是怎么才能把63个盘⼦移到B座,按照同样的⽅法,先把62个盘⼦选移到C座
,再把第63个盘⼦移到B座,最后再将62个盘⼦移到B座。
3……如此类推;
4.从上⾯分析可以看出:只有等后⾯那个和尚搬完盘⼦,前⾯的和尚才能够去完成任。
让我们来栈的数据结构:数据的处理只在⼀端处理,且是先进后出。
所以⽤递归的⽅法去处理是正确的。
(汉诺塔图)
汉诺塔问题解决⽅案
如果你发现有什么错误之处,请指出!谢谢了。
基于c#编写汉诺塔游戏讲解
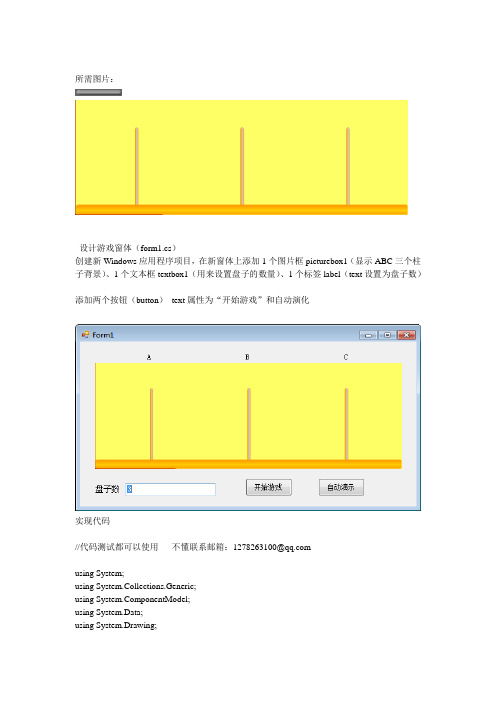
所需图片:设计游戏窗体(form1.cs)创建新Windows应用程序项目,在新窗体上添加1个图片框picturebox1(显示ABC三个柱子背景)、1个文本框textbox1(用来设置盘子的数量)、1个标签label(text设置为盘子数)添加两个按钮(button)text属性为“开始游戏”和自动演化实现代码//代码测试都可以使用不懂联系邮箱:*****************using System;using System.Collections.Generic;using ponentModel;using System.Data;using System.Drawing;using System.Text;using System.Windows.Forms;using System.Collections;namespace 汉诺塔递归{public partial class Form1 : Form{public Form1(){InitializeComponent();}private int i; //移动的次数public PictureBox[] Plate = new PictureBox[11];const int PlateHeight = 17; //盘片厚度private bool isDragging = false;private int x1, y1;private ArrayList A = new ArrayList();private ArrayList B = new ArrayList();private ArrayList C = new ArrayList();//ArrayList 就是数组列表,它位于System.Collections名称空间下,是集合类型。
private int oldx, oldy;private void load_plate(int n){//加载盘片//盘片编号从上往下1,2,...nfor (i = 1; i <= n; i++){Plate[i] = new PictureBox();this.Controls.Add(Plate[i]);Plate[i].Left = 48 + (n - i) * 5;Plate[i].Top = 167 - (n - i + 1) * PlateHeight;Plate[i].Width = 100 - (n - i) * 10;Plate[i].Height = PlateHeight;Plate[i].Tag = i; //设置盘片编号Plate[i].Image = new Bitmap("Plate.bmp"); //盘子图片Plate[i].SizeMode = PictureBoxSizeMode.StretchImage;Plate[i].Parent = pictureBox1;Plate[i].MouseMove += new MouseEventHandler(plate_MouseMove);Plate[i].MouseUp += plate_MouseUp;Plate[i].MouseDown += plate_MouseDown;}for (i = n; i >= 1; i += -1){A.Add(i); //A数组列表添加条目}private void plate_MouseMove(object sender, System.Windows.Forms.MouseEventArgs e){//处理盘子移动的公共事件PictureBox p1;p1 =(PictureBox )sender; //将被点击的PictureBox赋给定义的p1变量if (isDragging){p1.Left = p1.Left - x1 + e.X;p1.Top = p1.Top - y1 + e.Y;}}private void plate_MouseDown(object sender, System.Windows.Forms.MouseEventArgs e){//处理盘子MouseDown的公共事件PictureBox p1;p1 = (PictureBox)sender;//将被点击的PictureBox赋给定义的p1变量int sText;sText = Convert.ToInt16(p1.Tag); //获取盘片编号//首先判断是否不是最上面的盘子if (A.Contains(sText)){foreach (int i in A){if (i < sText){MessageBox.Show("请选择最上面的盘子");return;}}}if (B.Contains(sText)){foreach (int i in B){if (i < sText){MessageBox.Show("请选择最上面的盘子");return;}}if (C.Contains(sText)){foreach (int i in C){if (i < sText){MessageBox.Show("请选择最上面的盘子");return;}}}//最上方的盘片System.Windows.Forms.Cursor.Current = Cursors.Hand;if (e.Button == System.Windows.Forms.MouseButtons.Left){x1 = e.X; y1 = e.Y;oldx = p1.Left; oldy = p1.Top;isDragging = true;}}private void plate_MouseUp(object sender, System.Windows.Forms.MouseEventArgs e){//处理盘子MouseUp的公共事件if (!isDragging) return;isDragging = false;int sText;PictureBox p1;bool cango = false;p1 = (PictureBox)sender; //将被点击的PictureBox赋给定义的p1变量sText = Convert.ToInt16(p1.Tag); //获取盘片编号//盘片移到B柱if ((p1.Left + p1.Width / 2) >= 150 + 80 & (p1.Left + p1.Width / 2) < 320 + 80){if (B.Count == 0 || sText < (int)B[B.Count - 1]){//小于已有盘片B.Add(sText);Plate[sText].Top = 150 - (B.Count - 1) * Plate[sText].Height;if (A.Contains(sText)){ //从A柱到B柱A.Remove(sText);Plate[sText].Left = oldx + 170;}if (C.Contains(sText)){ //从C柱到B柱C.Remove(sText);Plate[sText].Left = oldx - 170;}cango = true;}}//盘片移到C柱if ((p1.Left + p1.Width / 2) >= 320 + 80 & (p1.Left + p1.Width / 2) < 490 + 80) {if (C.Count == 0 || sText < (int)C[C.Count - 1]){//小于已有盘片C.Add(sText);Plate[sText].Top = 150 - (C.Count - 1) * Plate[sText].Height;if (B.Contains(sText)){ //从B柱到C柱B.Remove(sText);Plate[sText].Left = oldx + 170;}if (A.Contains(sText)){ //从A柱到C柱A.Remove(sText);Plate[sText].Left = oldx + 340;}cango = true;}}//盘片移到A柱if ((p1.Left + p1.Width / 2) >= 100 - 80 & (p1.Left + p1.Width / 2) < 150 + 80) {if (A.Count == 0 || sText < (int)A[A.Count - 1]){//小于已有盘片A.Add(sText);Plate[sText].Top = 150 - (A.Count - 1) * Plate[sText].Height;if (B.Contains(sText)){ //从B柱到A柱B.Remove(sText);Plate[sText].Left = oldx - 170;}if (C.Contains(sText)){ //从C柱到A柱C.Remove(sText);Plate[sText].Left = oldx - 340;}cango = true;}}if (cango == false){//盘片恢复到原位址p1.Left = oldx;p1.Top = oldy;}success();}private void success(){if (C.Count == Convert.ToInt16(TextBox1.Text)){MessageBox.Show("你成功了", "祝贺你");}}private void Hanoi(int n, char x, char y, char z){if (n == 1){MoveDisc(x, 1, z);//编号为1的盘子从x到z }else{Hanoi(n - 1, x, z, y); //n-1个盘子从x经z到y,MoveDisc(x, n, z);//编号为n的盘子从x到zHanoi(n - 1, y, x, z); //n-1个盘子从y经x到z,}}private void MoveDisc(char x, int n, char z){int j,t=0;i = i + 1;this.Text = i + ":Move disc " + n + " from " + x + " to " + z;//从源柱对应数组列表中删除盘片nif (x.Equals('A')) A.Remove(n);if (x.Equals('B')) B.Remove(n);if (x.Equals('C')) C.Remove(n);//向目标柱对应数组列表中添加盘片nswitch (z){case 'A':A.Add(n); t = A.Count;break;case 'B':B.Add(n); t = B.Count;break;case 'C':C.Add(n); t = C.Count;break;}//动画效果移动棋子int oldtop,newtop,step1;oldtop = Plate[n].Top;//首先垂直方向向上移动到顶部newtop = 0;for (j = oldtop; j >= newtop; j -= 1){Plate[n].Top = Plate[n].Top -1;System.Windows.Forms.Application.DoEvents();}//其次水平方向移动step1 = (z - x) / Math.Abs( z- x);for (j = 0; j <= Math.Abs(z - x) * 170; j += 1) //柱子之间间隔170像素{Plate[n].Left = Plate[n].Left + step1;System.Windows.Forms.Application.DoEvents();}//再垂直方向向下移动oldtop = 0;newtop = pictureBox1.Height - (t+1) * PlateHeight;// 167 - t * PlateHeight;step1 = (newtop - oldtop) / Math.Abs(newtop - oldtop);for (j = oldtop; j <= newtop; j += step1){Plate[n].Top = Plate[n].Top + step1;System.Windows.Forms.Application.DoEvents();}}private void button1_Click(object sender, System.EventArgs e){//开始游戏int n = Convert.ToInt16(TextBox1.Text);load_plate(n);}private void button2_Click(object sender, System.EventArgs e)//汉诺塔演示动画{int n = Convert.ToInt16(TextBox1.Text);load_plate(n);int Num;char x = 'A';char y = 'B';char z = 'C';i = 0;try{Num = n;Hanoi(Num, x, y, z);}catch (Exception ex){MessageBox.Show ("请输入合适的数量!", "warn");}}private void pictureBox1_MouseMove(object sender, System.Windows.Forms.MouseEventArgs e){//Me.Text = e.X & " " & e.Y}}}。
c语言十大算法案例

c语言十大算法案例C语言是一种广泛应用于编程的高级语言,具有简单、灵活、高效等特点。
在C语言中,有许多经典的算法案例,这些算法案例不仅有助于提高编程能力,还能帮助我们理解计算机科学的基本原理。
下面列举了十个C语言的经典算法案例。
1. 冒泡排序算法:冒泡排序是一种简单但效率较低的排序算法,它通过多次比较和交换相邻元素的方式将最大或最小的元素逐步移动到数组的一端。
2. 快速排序算法:快速排序是一种常用的排序算法,它通过选择一个基准元素,将数组分成两个子数组,然后对子数组进行递归排序。
3. 二分查找算法:二分查找是一种高效的查找算法,它通过将查找范围缩小一半来快速定位目标元素。
4. 链表反转算法:链表反转是一种常见的操作,它可以将链表中的节点顺序逆转。
5. 汉诺塔算法:汉诺塔是一种经典的递归问题,它通过将圆盘从一个柱子移动到另一个柱子来演示递归的思想。
6. 最大公约数算法:最大公约数是指能够同时被两个或多个整数整除的最大正整数,求最大公约数的算法有多种,如辗转相除法和欧几里德算法。
7. 斐波那契数列算法:斐波那契数列是一个数列,其中每个数字都是前两个数字之和,求斐波那契数列的算法有多种,如递归和循环。
8. 图的深度优先搜索算法:深度优先搜索是一种用于遍历图的算法,它通过递归的方式依次访问图中的每个节点。
9. 图的广度优先搜索算法:广度优先搜索也是一种用于遍历图的算法,它通过队列的方式依次访问图中的每个节点。
10. 最短路径算法:最短路径算法用于找到图中两个节点之间的最短路径,常用的最短路径算法有迪杰斯特拉算法和弗洛伊德算法。
这些算法案例涵盖了排序、查找、链表操作、递归、图算法等多个方面,是C语言学习中不可或缺的部分。
通过学习和理解这些经典算法案例,我们可以提高自己的编程能力,并在解决实际问题时能够选择合适的算法。
希望本文能够对读者有所帮助,激发他们对C 语言算法的兴趣,并在编程的道路上不断进步。
汉诺塔问题的程序实现(hanoi塔)

汉诺塔问题的程序实现(hanoi塔)问题重述:有三根柱A、B、C,在柱A上有N块盘⽚,所有盘⽚都是⼤的在下⾯,⼩⽚能放在⼤⽚上⾯。
现要将A上的N块盘⽚移到C柱上,每次只能移动⼀⽚,⽽且在同⼀根柱⼦上必须保持上⾯的盘⽚⽐下⾯的盘⽚⼩,输⼊任意的N,输出移动⽅法。
(注意:这是⼀个古⽼的传说,传说是如果把64个盘⼦由A柱移到了C柱的话,那么世界末⽇就到了,事实上如果要把64个盘⼦从A柱移到C柱的话,即使⽤计算机运算,也要计算数亿年,所以这个预⾔未必不是真实。
)【分析】我们可以这样考虑,当n=1时,我们只要直接将A柱的盘⼦移到C柱,当n>1时,我们可以先把n-1个盘⼦由A柱通过C柱移到B 柱,此时就可以把A柱剩下的最后⼀个盘⼦直接移到C柱,这样接下来只要把n-1个盘⼦通过A柱移到C 柱即可,如果就构成了递归的思路,我们可以定义个移动过程mov(n,a,b,c)表⽰将n个盘⼦从a通过b移到c1.只要求输出搬运的次数#includeusing namespace std;int m=0;void move(){m++;}void I(int n){if(n==1)move();else{I(n-1);move();I(n-1);}}int main(){I(3);cout<cout<<"输出完毕!"<return 0;}更加简单的⽅法!#includeusing namespace std;int fact(int n){if(n==1)return(1);elsereturn((2*fact(n-1)+1));}int main(){cout<}2.不仅要求输出搬运的次数,⽽且要输出每个步骤的详细搬运#includeusing namespace std;int m=0;void Move(int n,char x,char y){cout<<"把"<m++;}void Hannoi(int n,char a,char b,char c){if(n==1)Move(1,a,c);else{Hannoi(n-1,a,c,b);Move(n,a,c);Hannoi(n-1,b,a,c);}}int main(){int i;cout<<"请输⼊圆盘数"<cin>>i;Hannoi(3,'a','b','c');cout<<"总的搬运次数"<cout<<"输出完毕!"<return 0;}}另外⼀种不利⽤递归的解法(很抱歉,我⾃⼰也没调出来,实在太复杂了)#includeusing namespace std;//圆盘的个数最多为64const int MAX = 1;//⽤来表⽰每根柱⼦的信息struct st{int s[MAX]; //柱⼦上的圆盘存储情况int top; //栈顶,⽤来最上⾯的圆盘char name; //柱⼦的名字,可以是A,B,C 中的⼀个int Top()//取栈顶元素{return s[top];}int Pop()//出栈{return s[top--];}void Push(int x)//⼊栈{s[++top] = x;}} ;long Pow(int x, int y); //计算x^yvoid Creat(st ta[], int n); //给结构数组设置初值void Hannuota(st ta[], long max); //移动汉诺塔的主要函数int main(void){int n;cin >> n; //输⼊圆盘的个数st ta[3]; //三根柱⼦的信息⽤结构数组存储Creat(ta, n); //给结构数组设置初值long max = Pow(2, n) - 1;//动的次数应等于2^n - 1 Hannuota(ta, max);//移动汉诺塔的主要函数system("pause");return 0;}void Creat(st ta[], int n){ta[0].name = 'A';ta[0].top = n-1;//把所有的圆盘按从⼤到⼩的顺序放在柱⼦A 上for (int i=0; ita[0].s[i] = n - i;//柱⼦B,C 上开始没有没有圆盘ta[1].top = ta[2].top = 0;for (int j=0; jta[1].s[j] = ta[2].s[j] = 0;//若n 为偶数,按顺时针⽅向依次摆放A B Cif (n%2 == 0){ta[1].name = 'B';ta[2].name = 'C';}else //若n 为奇数,按顺时针⽅向依次摆放A C B {ta[1].name = 'C';ta[2].name = 'B';}}long Pow(int x, int y){long sum = 1;for (int i=0; isum *= x;return sum;}void Hannuota(st ta[], long max){int k = 0; //累计移动的次数int i = 0;int ch;while (k < max){//按顺时针⽅向把圆盘1 从现在的柱⼦移动到下⼀根柱⼦ch = ta[i%3].Pop();ta[(i+1)%3].Push(ch);cout << ++k << ": " <<"Move disk " << ch << " from " << ta[i%3].name <<" to " << ta[(i+1)%3].name << endl;i++;//把另外两根柱⼦上可以移动的圆盘移动到新的柱⼦上if (k < max){ //把⾮空柱⼦上的圆盘移动到空柱⼦上,当两根柱⼦都为空时,移动较⼩的圆if (ta[(i+1)%3].Top() == 0 ||ta[(i-1)%3].Top() > 0 &&ta[(i+1)%3].Top() > ta[(i-1)%3].Top()){ch = ta[(i-1)%3].Pop();ta[(i+1)%3].Push(ch);cout << ++k << ": " << "Move disk "<< ch << " from " << ta[(i-1)%3].name<< " to " << ta[(i+1)%3].name << endl;}else{ch = ta[(i+1)%3].Pop();ta[(i-1)%3].Push(ch);cout << ++k << ": " << "Move disk " << ch << " from " << ta[(i+1)%3].name << " to " << ta[(i-1)%3].name << endl; }}}}补充知识:【典型例题1】求阶乘n!#includeusing namespace std;int fact(int n){if(n==0)return(1);elsereturn(n*fact(n-1)); }int main(){cout<。
汉诺塔问题

汉诺塔问题递归调用的内部执行过程:1.运行开始时,首先为递归调用建立一个工作栈,其结构包括值参,局部变量,和返回地址;2.每次执行递归调用之前,把递归函数的值参和局部变量的当前值及调用后的返回地址入栈;3.每次递归调用结束后,将栈顶元素出栈,使相应的值参和局部变量恢复为调用前的值,然后转向返回地址指定的位置继续执行。
#include <iostream>using namespace std;void Move(char A,char C);void Hanoi(int n,char A,char B,char C);void main(){cout<<"***************汉诺塔问题***************"<<endl;int n;cout<<"输入塔A上原始盘子的数目:";cin>>n;cout<<"^^^^^^^^^^^^^^^^^具体移动过程如下:"<<endl;Hanoi(n,'A','B','C');}void Move(char A,char C){cout<<A<<"--->"<<C<<endl;}void Hanoi(int n,char A,char B,char C){if(n==1)Move(A,C);else{Hanoi(n-1,A,C,B);Move(A,C);Hanoi(n-1,B,A,C);}}。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2、第二部分:把A柱的第n个圆盘移动到C盘
此时直接执行标注为<3>部分的程序move(one,three); 此时打印出A-->C;
3、第三部分:把B柱上的n-1个圆盘借助A移动到C柱
此时执行标志为<4>部分的hannuota((n-1),two,one,three),此时参数为hannuota(2,'B','A','C');
因为n=2>1,执行标志为<2>的代码,此时方法参数为hannuota(1,'B','C','A');因为此时n=1,执行标志为<1>的代码,打印出B-->A;此时,标志为<2>的程序执行完毕,one,two,three的值分别为one=B,two=A,three=C;
继续执行标志<3>的程序move(one,three); 打印出B-->C; 继续执行至标志<4>的代码hannuota((n-1),two,one,three),参数为hannuota(1'A','B','C'),因此n=1,执行标志<1>的代码,打印出A-->C;
# include <stdio.h>
void hannuota(int n,char one,char two,char three);
void move(char x,char y);
int main(void) {
int n;
printf("please input a integer number:");
scanf("%d",&n);
if(n > 10 || n < 0) {
printf("请输入一个0~10范围内的整数!!");
return 0;
}
hannuota(n,'A','B','C');
return 0;
}
void hannuota(int n,char one,char two,char three) {
hannuota((n-1),two,one,three); //<4>
}
}
void move(char x,char y) {
printf("%c ----> %c\n",x,y);
}
为了避免运行需要很长的时间,程序限制了输入的整数大小为0-10,以下是程序执行的顺序:(为了篇幅,假设n的值是3)
if(n == 1) {
move(one,three); //<1>
}
else {
hannuota((n-1),one,three,two); //<2>
பைடு நூலகம் move(one,three); //<3>
返回n=2时程序未执行完的部分,即执行标志为<3>的move方法,因为此时n=1,打印出A-->B,
继续执行标志为<4>的hannuota((n-1),two,one,three)部分,此时参数为hannuota(1,'C','A','B'); 此时n=1,打印出C-->B。到此刻位置标志为<2>部分的 hannuota((n-1),one,three,two)程序执行完毕。
到此为止,程序执行完毕。
程序执行结果如下:
A ----> C
A ----> B
C ----> B
A ----> C
B ----> A
B ----> C
A ----> C
汉诺塔问题主要分为以上三个部分,程序中用到了递归算法,递归要用到栈的知识,就是进栈和出栈,每到递归调用一个系统的子系统时,都会为子系统分配内存单元,把正被调用的子系统压入栈顶,按照先进后出的规则,执行完后就弹出栈,释放为其分配的内存单元。然后继续执行栈中的其他部分,直到整个程序执行完毕。
main方法运行到hannuota(n,'A','B','C')时;该方法里的参数为hannuota(3,'A','B','C');
1、第一部分:把A柱中的n-1个圆盘借助C柱移动到B柱
此时执行hannuota方法,因为n=3>1,因此此时递归执行hantuona方法,此时方法参数为hannuota(2,'A','C','B'),(注意此时hannuota方法的参数改变了,C和B值互换);因为n=2>1,继续递归调用hannuota(1,'A','B','C');(此时hannuota方法的参数改变了,C和B值互换);因为n=1,所以执行move方法,打印出A-->C;
