相似三角形综合试相似与圆(难)

合集下载

【精编版】数学中考专题训练——相似三角形与圆的综合

中考专题训练——相似三角形与圆的综合1．如图，AB是⊙O的直径，C是⊙O上一点，D是的中点，E为OD延长线上一点，且∠CAE＝2∠C，AC与BD交于点H，与OE交于点F．（1）求证：AE是⊙O的切线；（2）若⊙O的半径10，，求线段DH的长．2．如图，AD是⊙O的弦，PO交⊙O于点B，∠ABP＝∠ABD，且AB2＝PB•BD，连接P A．（1）求证：P A是⊙O的切线；（2）若P A＝2PB＝4，求BD的长．3．如图，在⊙O中，直径AB与弦CD相交于点H，点B是弧CD的中点，过点A作AE∥CD，交射线DO于点E，DE与⊙O交于点F，BF与CD交于点G．（1）求证：AE是⊙O的切线．（2）已知AO＝5，AE＝，求BG的长．4．如图，AB是⊙O的直径，C、D是⊙O上两点，且，过点D的直线DE⊥AC交AC的延长线于点E，交AB的延长线于点F，连接AD、OE交于点G．（1）求证：DE是⊙O的切线；（2）若，⊙O的半径为2，求阴影部分的面积．5．某数学小组在研究三角形的内切圆时，遇到了如下问题：如图①，已知等腰△ABC的底边AB为12，底边上的高CD为8，如何在这个等腰三角形中画出其内切圆？小红同学经过计算，在高CD上截取DO＝3，以点O为圆心，以3为半径作的圆即为所求．（1）小红的方法是否正确？如果正确，给出理由；如果不正确，请给出你的方法．（2）如图②，在图①的基础上，以AB为边作一个正方形ABEF，连接FC并延长与BE 交于点G，则BG：GE的值为．6．如图，AB是⊙O的直径，CD是一条弦．过点A作DC延长线的垂线，垂足为点E．连接AC，AD．（1）证明：△ABD∽△ACE．（2）若，BD＝5，CD＝9．①求EC的长．②延长CD，AB交于点F，点G是弦CD上一点，且∠CAG＝∠F，求CG的长．7．如图，△ABC内接于⊙O，BC是直径，AD平分∠BAC交于点D，EF切⊙O于D，BF ⊥AB交EF于F．（1）求证：四边形BCEF为平行四边形．（2）若BF＝，AB＝4，求AE的长．8．如图，AB为⊙O的直径，四边形ABCD内接于⊙O．点D为的中点，对角线AC，BD 交于点E，⊙O的切线AF交BD的延长线于点F，切点为A．（1）求证：AE＝AF；（2）若AB＝4，BF＝5，求sin∠BDC的值．9．如图，在矩形ABCD中，以AB的中点O为圆心，以OA为半径作半圆，连接OD交半圆于点E，在上取点F，使＝，连接BF，DF．（1）求证：DF与半圆相切；（2）如果AB＝10，BF＝6，求矩形ABCD的面积．10．如图，⊙O是△ABC的外接圆，AB是直径，D是AC中点，直线OD与⊙O相交于E，F两点，P在OE延长线上，且满足∠PCA＝∠ABC，连接P A，PC，AF．（1）求证：PC是⊙O的切线；（2）证明：PE•OD＝DE•OE．11．如图，在Rt△ABC中，∠ACB＝90°，以AB为直径作⊙O，过点B的切线交AC延长线于点D，点E为上一点，且BC＝EC，连接BE交AC于点F．（1）求证：BC平分∠DBE；（2）若AB＝2，tan E＝，求EF的长．12．如图，在△ABC中，∠ACB＝90°，点D是AB边的中点，点O在AC边上，⊙O经过点C且与AB边相切于点E，∠F AC＝∠BDC．（1）求证：AF是⊙O的切线；（2）若BC＝6，sin B＝，求⊙O的半径及OD的长．13．如图，在△ABC中，AB＝AC，以AB为直径作⊙O与AC交于点E，过点A作⊙O的切线交BC的延长线于点D．（1）求证：∠D＝∠EBC；（2）若CD＝2BC，AE＝3，求⊙O的半径．14．如图，△ABC内接于⊙O，AB是⊙O的直径，∠BAC的角平分线AF交BC于点D，交⊙O于点E，连接BE和BF，∠F＝∠ABE．（1）求证：BF是⊙O的切线；（2）若AC＝5，AB＝13，求CD的长．15．如图，在△ABC中，AD平分∠BAC交BC于点D，以AD为直径作⊙O交AC于点F，点B恰好落在⊙O上，过D点作⊙O的切线DE交AC于点E，连接DF．（1）求证：∠FDE＝∠CDE；（2）若AB＝12，tan∠C＝，求线段DE的长．16．如图，以△ABC的一边AB为直径作⊙O，交BC于点D，交AC于点E，点D为BE的中点．（1）试判断△ABC的形状，并说明理由；（2）若直线l切⨀O于点D，与AC及AB的延长线分别交于点F、点G．∠BAC＝45°，求的值．17．如图，在Rt△ABC中，∠B＝90°，∠BAC的平分线AD交BC于点D，点E在AC上，以AE为直径的⊙O经过点D．求证：（1）BC是⊙O的切线；（2）CD2＝CE•CA．18．如图，AB是⊙O的直径，点C，D在⊙O上，且弧CD＝弧CB，过点C作CE∥BD，交AB的延长线于点E，连接AC交BD于F．（1）求证：CE是⊙O的切线；（2）过点C作CH⊥AE于H点，CH交BD于M，若CA＝CE＝6，求CH和BF的长．19．如图，⊙O上有A，B，C三点，AC是直径，点D是的中点，连接CD交AB于点E，点F在AB延长线上且FC＝FE．（1）若∠A＝40°，求∠DCB的度数；（2）求证：CF是⊙O的切线；（3）若，BE＝6，求⊙O的半径长．20．已知：如图，AB、AC是⊙O的两条弦，AB＝AC，点M、N分别在弦AB、AC上，且AM＝CN，AM＜AN，联结OM、ON．（1）求证：OM＝ON；（2）当∠BAC为锐角时，如果AO2＝AM•AC，求证：四边形AMON为等腰梯形．21．如图，在△ABC中，∠ACB＝90°，D是AB边上一点，以BD为直径的⊙O与AC相切于点E，连接DE并延长交BC的延长线于点F．（1）求证：BF＝BD；（2）若CF＝1，tan∠EDB＝2，求⊙O的直径．22．如图，边长为6的等边三角形ABC内接于⊙O，点D为AC上的动点（点A、C除外），BD的延长线交⊙O于点E，连接CE．（1）求证：△CED∽△BAD；（2）当DC＝2AD时，求CE的长．23．如图，已知△ABC内接于⊙O，AB是⊙O的直径，∠CAB的平分线交BC于点D，交⊙O于点E，连接EB，作∠BEF＝∠CAE，交AB的延长线于点F．（1）求证：EF是⊙O的切线；（2）若AE＝12，，求⊙O的半径和EF的长．参考答案与试题解析1．如图，AB是⊙O的直径，C是⊙O上一点，D是的中点，E为OD延长线上一点，且∠CAE＝2∠C，AC与BD交于点H，与OE交于点F．（1）求证：AE是⊙O的切线；（2）若⊙O的半径10，，求线段DH的长．【分析】（1）由垂径定理得出OD⊥AC，进而得出∠F AO+∠AOF＝90°，由圆周角定理结合已知条件得出∠AOF＝∠CAE，得出∠F AO+∠CAE＝90°，即∠OAE＝90°，即可证明AE是⊙O的切线；（2）连接AD，利用解直角三角形得出tan B＝＝，设AD＝3x，则BD＝4x，AB＝5x，由⊙O的半径10，得出AB＝5x＝20，求出x＝4，求出AD＝12，BD＝16，继而证明△ADH∽△BDA，利用相似三角形的性质即可求出DH的长．【解答】（1）证明：如图1，∵D是的中点，∴OD⊥AC，∴∠AFO＝90°，∴∠F AO+∠AOF＝90°，∵∠AOF＝2∠C，∠CAE＝2∠C，∴∠AOF＝∠CAE，∴∠F AO+∠CAE＝90°，即∠OAE＝90°，∵OA是半径，∴AE是⊙O的切线；（2）解：如图2，连接AD，∵∠C＝∠B，，tan B＝，∵AB是直径，∴∠ADB＝90°，∴tan B＝＝，设AD＝3x，则BD＝4x，AB＝5x，∵⊙O的半径10，∴AB＝5x＝20，∴x＝4，∴AD＝3×4＝12，BD＝4×4＝16，∵D是的中点，∴AD＝CD＝12，∴∠DAC＝∠C，∵∠B＝∠C，∴∠DAC＝∠B，∵∠ADH＝∠BDA∴△ADH∽△BDA，∴，即，∴DH＝9．2．如图，AD是⊙O的弦，PO交⊙O于点B，∠ABP＝∠ABD，且AB2＝PB•BD，连接P A．（1）求证：P A是⊙O的切线；（2）若P A＝2PB＝4，求BD的长．【分析】（1）延长BO交⊙O于点E，连接AE，先证明△PBA∽△ABD，得出∠P AB＝∠ADB，由圆周角定理得出∠P AB＝∠E，由等腰三角形的性质得出∠OAE＝∠E，进而得出∠P AB＝∠OAE，由圆周角定理得出∠BAE＝∠BAO+∠OAE＝90°，进而得出∠BAO+∠P AB＝∠P AO＝90°，即可证明P A是⊙O的切线；（2）延长BO交⊙O于点E，连接AE，DE，利用勾股定理列方程求出⊙O的半径为3，进而得出OA＝3，OP＝5，BE＝6，再证明△P AO∽△EDB，利用相似三角形的性质即可求出BD的长度．【解答】（1）证明：如图1，延长BO交⊙O于点E，连接AE，∵AB2＝PB•BD，∴，∵∠ABP＝∠ABD，∴△PBA∽△ABD，∴∠P AB＝∠ADB，∵∠ADB＝∠E，∴∠P AB＝∠E，∵OA＝OE，∴∠OAE＝∠E，∴∠P AB＝∠OAE，∵BE为直径，∴∠BAE＝∠BAO+∠OAE＝90°，∴∠BAO+∠P AB＝∠P AO＝90°，∵OA是半径，∴P A是⊙O的切线；（2）解：如图2，延长BO交⊙O于点E，连接AE，DE，∵P A＝2PB＝4，∴PB＝2，设OA＝OB＝x，则OP＝x+2，∵∠P AO＝90°，∴P A2+AO2＝OP2，即42+x2＝（x+2）2，解得：x＝3，∴OA＝3，OP＝2+3＝5，BE＝3+3＝6，∵△PBA∽△ABD，∴∠P＝∠BAD，∵∠BAD＝∠BED，∴∠P＝∠BED，∵BE为直径，∴∠BDE＝90°，∴∠P AO＝∠EDB＝90°，∴△P AO∽△EDB，∴，即，∴BD＝．3．如图，在⊙O中，直径AB与弦CD相交于点H，点B是弧CD的中点，过点A作AE∥CD，交射线DO于点E，DE与⊙O交于点F，BF与CD交于点G．（1）求证：AE是⊙O的切线．（2）已知AO＝5，AE＝，求BG的长．【分析】（1）利用垂径定理的推论得到AB⊥CD，利用平行线的性质和圆的切线的判定定理解答即可；（2）过点F作FM⊥AB于点M，利用勾股定理和相似三角形的判定与性质求出线段OE，OM，MF的长，利用全等三角形的判定与性质求得线段BH的长，利用勾股定理和相似三角形的判定与性质得出比例式即可求得结论．【解答】（1）证明：∵点B是弧CD的中点，AB为⊙O的直径，∴AB⊥CD，∵AE∥CD，∴AE⊥OA．∵OA为⊙O的半径，∴AE是⊙O的切线；（2）解：过点F作FM⊥AB于点M，如图，∵AO＝5，AE＝，AE⊥OA，∴OE＝＝．∵AE⊥AB，FM⊥AB，∴FM∥AE，∴△OMF∽△OAE，∴，∴，∴OM＝3，MF＝4．∴BM＝OB+OM＝5+3＝8，∴BF＝＝4．在△OFM和△ODH中，，∴△OFM≌△ODH（AAS），∴OM＝OH＝3，∴BH＝OB﹣OH＝2．∵FM⊥AB，AB⊥CD，∴CD∥FM，∴△BGH∽△BFM，∴，∴，∴BG＝．4．如图，AB是⊙O的直径，C、D是⊙O上两点，且，过点D的直线DE⊥AC交AC的延长线于点E，交AB的延长线于点F，连接AD、OE交于点G．（1）求证：DE是⊙O的切线；（2）若，⊙O的半径为2，求阴影部分的面积．【分析】（1）连接OD，证明DE是⊙O的切线，关键是证明OD⊥DE；（2）连接BD，根据（1）中OD∥AE得△OGD∽△AEG，从而求出AE的长，再根据△AED∽△ADB求出AD的长，再利用三角函数求出DF的长，利用S阴影＝S△DOF﹣S扇形DOB求出阴影部分的面积．【解答】（1）证明：如图所示，连接OD，∵，∴∠CAD＝∠DAB，∵OA＝OD，∴∠DAB＝∠ODA，∴∠CAD＝∠ODA，∴OD//AE，∵DE⊥AC，∴OD⊥DE，∵OD是⊙O的半径，∴DE是⊙O的切线；（2）解：如图所示，连接BD，∵OD//AE，∴△OGD∽△EGA，∴，∵，⊙O的半径为2，∴，∴AE＝3．∵AB是⊙O的直径，DE⊥AE，∴∠AED＝∠ADB＝90°，∵∠CAD＝∠DAB，∴△AED∽△ADB，∴，即，∴，在Rt△ADB中，，∴∠DAB＝30°，∴∠EAF＝60°，∠DOB＝60°，∴∠F＝30°，∵OD＝2，∴，∴．5．某数学小组在研究三角形的内切圆时，遇到了如下问题：如图①，已知等腰△ABC的底边AB为12，底边上的高CD为8，如何在这个等腰三角形中画出其内切圆？小红同学经过计算，在高CD上截取DO＝3，以点O为圆心，以3为半径作的圆即为所求．（1）小红的方法是否正确？如果正确，给出理由；如果不正确，请给出你的方法．（2）如图②，在图①的基础上，以AB为边作一个正方形ABEF，连接FC并延长与BE 交于点G，则BG：GE的值为．【分析】（1）过点O作OH⊥AC于点H，由等腰三角形的性质得出AD＝BD＝6，OC＝5，由勾股定理得出AC＝10，证明△CHO∽△CDA，，由相似三角形的性质得出OH＝3，继而得出AC是⊙O的切线，同理，BC是⊙O的切线，AB是⊙O的切线，即可得出⊙O是等腰△ABC的内切圆；（2）延长DC交FE于点M，由正方形的性质得出BE＝AB＝12，EF∥AB，由CA＝CB，CD⊥AB，得出AD＝BD＝6，DM⊥EF，继而得出FM＝ME＝6，DM＝BE＝12，由三角形中位线的性质得出GE＝8，进而得出BG＝4，即可求出BG：GE的值．【解答】解：（1）小红的方法正确，理由如下：如图①，过点O作OH⊥AC于点H，∵等腰△ABC的底边AB为12，底边上的高CD为8，OD＝3，∴AD＝BD＝6，OC＝CD﹣OD＝8﹣3＝5，∴AC＝＝＝10，∵∠CHO＝∠CDA＝90°，∠HCO＝∠DCA，∴△CHO∽△CDA，∴，即，∴OH＝3，∵OH⊥AC，∴AC是⊙O的切线，同理，BC是⊙O的切线，∵OD⊥AB，OD＝3，∴AB是⊙O的切线，∴⊙O是等腰△ABC的内切圆；（2）如图②，延长DC交FE于点M，∵四边形ABEF是正方形，AB＝12，∴BE＝AB＝12，EF∥AB，∵CA＝CB，CD⊥AB，∴AD＝BD＝6，DM⊥EF，∴FM＝ME＝6，DM＝BE＝12，∴MC是△EFG的中位线，MC＝DM﹣CD＝12﹣8＝4，∴GE＝2CM＝2×4＝8，∴BG＝BE﹣GE＝12﹣8＝4，∴，故答案为：．6．如图，AB是⊙O的直径，CD是一条弦．过点A作DC延长线的垂线，垂足为点E．连接AC，AD．（1）证明：△ABD∽△ACE．（2）若，BD＝5，CD＝9．①求EC的长．②延长CD，AB交于点F，点G是弦CD上一点，且∠CAG＝∠F，求CG的长．【分析】（1）利用圆内接四边形的性质求得∠ACD+∠ABD＝180°，推出∠ABD＝∠ACE，即可证明；（2）①由△ABD∽△ACE，推出AE＝3CE，在Rt△ADE中，利用勾股定理求解即可；②证明△EAG∽△EDA，利用三角形的性质求解即可．【解答】（1）证明：∵AB是⊙O的直径，AE⊥CE，∴∠AEC＝∠ADB＝90°，∵四边形ABDC是圆内接四边形，∴∠ACD+∠ABD＝180°，又∠ACE+∠ACD＝180°，∴∠ABD＝∠ACE，∴△ABD∽△ACE；（2）解：①在Rt△BDA中，AB＝5，BD＝5，∴AD＝＝15，∵△ABD∽△ACE，∴，即，∴AE＝3CE，在Rt△ADE中，AD2＝AE2+DE2，∴152＝（3CE）2+（9+CE）2，解得：CE＝﹣（舍去）或CE＝3；∴EC的长为3；②∵△ABD∽△ACE，∴∠BAD＝∠CAE，∵∠CAG＝∠F，∠EAG＝∠CAE+∠CAG，∠EDA＝∠BAD+∠F，∴∠EAG＝∠EDA，∴△EAG∽△EDA，∴，∴AE2＝GE•ED，即AE2＝（EC+CG）•ED，∵CE＝3，∴AE＝3CE＝9，∴92＝（3+CG）×12，∴CG＝．7．如图，△ABC内接于⊙O，BC是直径，AD平分∠BAC交于点D，EF切⊙O于D，BF ⊥AB交EF于F．（1）求证：四边形BCEF为平行四边形．（2）若BF＝，AB＝4，求AE的长．【分析】（1）连接OD，证明BF∥AE，BC∥EF，可得结论；（2）根据平行四边形的性质可得CE＝BF＝，如图，连接OD，过点C作CG⊥EF于G，证明四边形CODG是正方形，△ABC∽△GCE，列比例式可得AE的长．【解答】（1）证明：连接OD，∵BF⊥AB，∴∠ABF＝90°，∵BC是⊙O的直径，∴∠BAC＝90°，∴∠BAC+∠ABF＝180°，∴BF∥AE，∵AD平分∠BAC，∴∠BAD＝∠CAD，∴＝，∴BC⊥OD，∵EF切⊙O于D，∴EF⊥OD，∴BC∥EF，∴四边形BCEF为平行四边形；（2）解：由（1）知：四边形BCEF为平行四边形，∴CE＝BF＝，如图，连接OD，过点C作CG⊥EF于G，∴∠COD＝∠ODG＝∠CGD＝90°，∵OC＝OD，∴四边形CODG是正方形，∴CG＝OC，∠BCG＝90°，∴∠ACB+∠ECG＝90°，∵∠ACB+∠ABC＝90°，∴∠ECG＝∠ABC，∵∠CGE＝∠BAC＝90°，∴△ABC∽△GCE，∴＝，设⊙O的半径是r，则BC＝2r，∴＝，∴r＝（负值舍），∴BC＝2，∴AC＝＝＝2，∴AE＝AC+CE＝2+＝．8．如图，AB为⊙O的直径，四边形ABCD内接于⊙O．点D为的中点，对角线AC，BD 交于点E，⊙O的切线AF交BD的延长线于点F，切点为A．（1）求证：AE＝AF；（2）若AB＝4，BF＝5，求sin∠BDC的值．【分析】（1）由点D为的中点，可得∠CBD＝∠ABD，根据AB为⊙O的直径，有∠AEF＝∠BEC＝90°﹣∠CBD，又AF是⊙O的切线，AB为⊙O的直径，有∠F＝90°﹣∠ABD，即得∠AEF＝∠F，AE＝AF；（2）证明△ADF≌△ADE，得AE＝AF，DE＝DF，由勾股定理求得AF，由三角形面积公式求得AD，进而求得DE，BE，再证明△BEC∽△AED，得BC，进而求得sin∠BAC 便可．【解答】（1）证明：∵点D为的中点，∴＝，∴∠CBD＝∠ABD，∵AB为⊙O的直径，∴∠ACB＝90°，∴∠AEF＝∠BEC＝90°﹣∠CBD，∵AF是⊙O的切线，AB为⊙O的直径，∴∠BAF＝90°，∴∠F＝90°﹣∠ABD，∴∠AEF＝∠F，∴AE＝AF；（2）∵AF是⊙O的切线，∴∠F AB＝90°，∵AB是⊙O的直径，∴∠ACB＝∠ADB＝∠ADF＝90°，∴∠ABD+∠BAD＝∠BAD+∠F AD＝90°，∴∠ABD＝∠F AD，∵∠ABD＝∠CAD，∴∠F AD＝∠EAD，∵AD＝AD，∴△ADF≌△ADE（ASA），∴AF＝AE，DF＝DE，在Rt△ADE中，AB＝4，BF＝5，∴AF＝＝3，∴AE＝AF＝3，∵S△ABF＝AB•AF＝BF•AD，∴AD＝＝＝，∴DE＝＝＝，∴BE＝BF﹣2DE＝，∵∠AED＝∠BEC，∠ADE＝∠BCE＝90°，∴△BEC∽△AED，∴＝，∴BC＝＝，∴sin∠BAC＝＝，∵∠BDC＝∠BAC，在Rt△ACB中，∠ACB＝90°∴sin∠BDC＝．9．如图，在矩形ABCD中，以AB的中点O为圆心，以OA为半径作半圆，连接OD交半圆于点E，在上取点F，使＝，连接BF，DF．（1）求证：DF与半圆相切；（2）如果AB＝10，BF＝6，求矩形ABCD的面积．【分析】（1）连接OF，证明△DAO≌△DFO（SAS），可得∠DAO＝90°＝∠DFO，即可得DF与半圆O相切；（2）连接AF，证明△AOD∽△FBA，可得＝，DO＝，在Rt△AOD中，AD＝＝，即可得矩形ABCD的面积是．【解答】（1）证明：连接OF，如图：∵＝，∴∠DOA＝∠FOD，∵OA＝OF，OD＝OD，∴△DAO≌△DFO（SAS），∴∠DAO＝∠DFO，∵四边形ABCD是矩形，∴∠DAO＝90°＝∠DFO，∴OF⊥DF，又OF是半圆O的半径，∴DF与半圆O相切；（2）解：连接AF，如图：∵AO＝FO，∠DOA＝∠DOF，∴DO⊥AF，∵AB为半圆直径，∴∠AFB＝90°，∴BF⊥AF，∴DO∥BF，∴∠AOD＝∠ABF，∵∠OAD＝∠AFB＝90°，∴△AOD∽△FBA，∴＝，即＝，∴DO＝，在Rt△AOD中，AD＝＝＝，∴矩形ABCD的面积为AD•AB＝×10＝，答：矩形ABCD的面积是．10．如图，⊙O是△ABC的外接圆，AB是直径，D是AC中点，直线OD与⊙O相交于E，F两点，P在OE延长线上，且满足∠PCA＝∠ABC，连接P A，PC，AF．（1）求证：PC是⊙O的切线；（2）证明：PE•OD＝DE•OE．【分析】（1）连接OC，根据等腰三角形性质及圆周角定理可得∠PCO＝90°，然后由切线的判定定理可得结论；（2）连接EC，FC，OC，证明Rt△ECD∽Rt△CFD，得出CD2＝DE•DF，继而得出CD2＝DE•OD+DE•OE，同理得出CD2＝OD•DE+OD•PE，进而得出DE•OD+DE•OE＝OD•DE+OD•PE，即可证明PE•OD＝DE•OE．【解答】证明：（1）如图1，连接OC，∵OB＝OC，∴∠OBC＝∠OCB，∵∠PCA＝∠ABC，∴∠PCA＝∠OCB，∵AB是直径，∴∠ACB＝90°，∴∠ACO+∠OCB＝90°，∴∠ACO+∠PCA＝90°，即∠PCO＝90°，∵OC是圆O的半径，∴PC是圆O的切线；（2）如图2，连接EC，FC，OC，∵EF是直径，∴∠ECF＝90°，∴∠CEF+∠CFE＝90°，∵D是AC的中点，EF是直径，∴AC⊥EF，∴∠CEF+∠ECD＝90°，∠EDC＝∠CDF＝90°，∴∠ECD＝∠CFD，∴Rt△ECD∽Rt△CFD，∴，∴CD2＝DE•DF，∴CD2＝DE（OD+OF）＝DE（OD+OE）＝DE•OD+DE•OE，同理Rt△PCD∽Rt△COD，∴，∴CD2＝OD•PD＝OD（PE+DE）＝OD•DE+OD•PE，∴DE•OD+DE•OE＝OD•DE+OD•PE，∴PE•OD＝DE•OE．11．如图，在Rt△ABC中，∠ACB＝90°，以AB为直径作⊙O，过点B的切线交AC延长线于点D，点E为上一点，且BC＝EC，连接BE交AC于点F．（1）求证：BC平分∠DBE；（2）若AB＝2，tan E＝，求EF的长．【分析】（1）因为BD是⊙O的切线，所以∠∠CBD＝∠A，因为BC＝EC，所以∠E＝∠EBC，由同弧所对的圆周角相等可得，∠A＝∠E，所以∠EBC＝∠CBD，即BC平分∠DBE．（2）由（1）可知，tan E＝tan A＝tan∠EBC＝，因为AB为⊙O的直径，所以∠ACB＝90°，所以tan A＝＝，即AC＝2BC，由AB＝2结合勾股定理可得，BC2+AC2＝AB2，即BC2+4BC2＝AB2，解得BC＝2，AC＝4，又因为tan∠EBC＝＝，所以CF＝1，AF＝3，BF＝，易证△ABF∽△ECF，所以AF：EF＝BF：CF，即3：EF＝：1，解之即可．【解答】（1）证明：∵BD是⊙O的切线，∴∠∠CBD＝∠A，∵BC＝EC，∴∠E＝∠EBC，∵∠A＝∠E，∴∠EBC＝∠CBD，即BC平分∠DBE．（2）解：由（1）知，∠A＝∠E＝∠EBC，∴tan E＝tan A＝tan∠EBC＝，∵AB为⊙O的直径，∴∠ACB＝90°，∴tan A＝＝，即AC＝2BC，∵AB＝2，∴BC2+AC2＝AB2，即BC2+4BC2＝AB2，∴BC＝2，AC＝4，∵tan∠EBC＝＝，∴CF＝1，AF＝3，BF＝，∵∠A＝∠E，∠ABF＝∠ECF，∴△ABF∽△ECF，∴AF：EF＝BF：CF，即3：EF＝：1，解得EF＝．12．如图，在△ABC中，∠ACB＝90°，点D是AB边的中点，点O在AC边上，⊙O经过点C且与AB边相切于点E，∠F AC＝∠BDC．（1）求证：AF是⊙O的切线；（2）若BC＝6，sin B＝，求⊙O的半径及OD的长．【分析】（1）作OH⊥F A，垂足为H，连接OE，利用直角三角形斜边上中线的性质得AD ＝CD，再通过导角得出AC是∠F AB的平分线，再利用角平分线的性质可得OH＝OE，从而证明结论；（2）根据BC＝6，sin B＝，可得AC＝8，AB＝10，设⊙O的半径为r，则OC＝OE＝r，利用Rt△AOE∽Rt△ABC，可得r的值，再利用勾股定理求出OD的长．【解答】（1）证明：如图，作OH⊥F A，垂足为H，连接OE，∵∠ACB＝90°，D是AB的中点，∴CD＝AD＝，∴∠CAD＝∠ACD，∵∠BDC＝∠CAD+∠ACD＝2∠CAD，又∵∠F AC＝，∴∠F AC＝∠CAB，即AC是∠F AB的平分线，∵点O在AC上，⊙O与AB相切于点E，∴OE⊥AB，且OE是⊙O的半径，∴OH＝OE，OH是⊙O的半径，∴AF是⊙O的切线；（2）解：如图，在△ABC中，∠ACB＝90°，BC＝6，sin B＝，∴可设AC＝4x，AB＝5x，∴（5x）2﹣（4x）2＝62，∴x＝2，则AC＝8，AB＝10，设⊙O的半径为r，则OC＝OE＝r，∵Rt△AOE∽Rt△ABC，∴，即，∴r＝3，∴AE＝4，又∵AD＝5，∴DE＝1，在Rt△ODE中，由勾股定理得：OD＝．13．如图，在△ABC中，AB＝AC，以AB为直径作⊙O与AC交于点E，过点A作⊙O的切线交BC的延长线于点D．（1）求证：∠D＝∠EBC；（2）若CD＝2BC，AE＝3，求⊙O的半径．【分析】（1）根据切线的性质可得∠DAO＝90°，从而可得∠D+∠ABD＝90°，根据直径所对的圆周角是直角可得∠BEC＝90°，从而可得∠ACB+∠EBC＝90°，然后利用等腰三角形的性质可得∠ACB＝∠ABC，从而利用等角的余角相等即可解答；（2）根据已知可得BD＝3BC，然后利用（1）的结论可得△DAB∽△BEC，从而利用相似三角形的性质可得AB＝3EC，然后根据AB＝AC，进行计算即可解答．【解答】（1）证明：∵AD与⊙O相切于点A，∴∠DAO＝90°，∴∠D+∠ABD＝90°，∵AB是⊙O的直径，∴∠AEB＝90°，∴∠BEC＝180°﹣∠AEB＝90°，∴∠ACB+∠EBC＝90°，∵AB＝AC，∴∠ACB＝∠ABC，∴∠D＝∠EBC；（2）解：∵CD＝2BC，∴BD＝3BC，∵∠DAB＝∠CEB＝90°，∠D＝∠EBC，∴△DAB∽△BEC，∴＝＝3，∴AB＝3EC，∵AB＝AC，AE＝3，∴AE+EC＝AB，∴3+EC＝3EC，∴EC＝1.5，∴AB＝3EC＝4.5，∴⊙O的半径为2.25．14．如图，△ABC内接于⊙O，AB是⊙O的直径，∠BAC的角平分线AF交BC于点D，交⊙O于点E，连接BE和BF，∠F＝∠ABE．（1）求证：BF是⊙O的切线；（2）若AC＝5，AB＝13，求CD的长．【分析】（1）由圆周角定理得出∠ACB＝∠AEB＝90°，进而得出∠F+∠FBE＝90°，由∠F＝∠ABE，得出∠ABE+∠FBE＝90°，即∠ABF＝90°，即可证明BF是⊙O的切线；（2）连接OE交BC于点G，由∠ACB＝∠AEB＝90°，AC＝5，AB＝13，得出BC＝12，，由圆周角定理得出，进而得出OE垂直平分BC，即可求出，OG是△ABC的中位线，得出，求出EG＝4，由∠CAE＝∠CBE，得出tan∠CAD＝tan∠EBG，得出，即可求出．【解答】（1）证明：如图1，∵AB是直径，∴∠ACB＝∠AEB＝90°，∴∠F+∠FBE＝90°，∵∠F＝∠ABE，∴∠ABE+∠FBE＝90°，即∠ABF＝90°，∴AB⊥BF，∵AB是⊙O的直径，∴BF是⊙O的切线；（2）解：如图2，连接OE交BC于点G，∵∠ACB＝∠AEB＝90°，AC＝5，AB＝13，∴BC＝＝＝12，，∵AF平分∠BAC，∴∠CAE＝∠BAE，∴，∴OE垂直平分BC，∴，OG是△ABC的中位线，∴，∴EG＝OE﹣OG＝﹣＝4，∵∠CAE＝∠CBE，∴tan∠CAD＝tan∠EBG，∴，即，∴．15．如图，在△ABC中，AD平分∠BAC交BC于点D，以AD为直径作⊙O交AC于点F，点B恰好落在⊙O上，过D点作⊙O的切线DE交AC于点E，连接DF．（1）求证：∠FDE＝∠CDE；（2）若AB＝12，tan∠C＝，求线段DE的长．【分析】（1）由切线的性质及圆周角定理得出∠ADF+∠FDE＝90°，∠ADB+∠CDE＝90°，证明△F AD≌△BAD，得出∠ADF＝∠ADB，即可证明∠FDE＝∠CDE；（2）由解直角三角形得出BC＝16，由勾股定理得出AC＝20，由全等三角形的性质得出AF＝AB＝12，进而得出CF＝8，由解直角三角形得出DF＝6，进而得出BD＝DF＝6，由勾股定理得出AD＝6，证明△EAD∽△DAB，由相似三角形的性质得出AE＝15，再利用勾股定理即可求出DE＝3．【解答】（1）证明：∵DE是⊙O的切线，AD为直径，∴AD⊥DE，∴∠ADF+∠FDE＝90°，∠ADB+∠CDE＝90°，∵AD是直径，∴∠AFD＝∠ABD＝90°∵AD平分∠BAC，∴∠F AD＝∠BAD，在△F AD和△BAD中，，∴△F AD≌△BAD（AAS），∴∠ADF＝∠ADB，∴∠FDE＝∠CDE；（2）解：在Rt△ABC中，AB＝12，tan∠C＝，∴BC＝＝＝16，∴AC＝＝＝20，∵△F AD≌△BAD，∴AF＝AB＝12，∴CF＝AC﹣AF＝20﹣12＝8，在Rt△CDF中，DF＝CF•tan∠C＝8×＝6，∴BD＝DF＝6，∴AD＝＝＝6，∵∠ABD＝∠ADE＝90°，∠EAD＝∠DAB，∴△EAD∽△DAB，∴，即，∴AE＝15，∴DE＝＝＝3．16．如图，以△ABC的一边AB为直径作⊙O，交BC于点D，交AC于点E，点D为BE的中点．（1）试判断△ABC的形状，并说明理由；（2）若直线l切⨀O于点D，与AC及AB的延长线分别交于点F、点G．∠BAC＝45°，求的值．【分析】（1）连接AD，由AB为⊙O的直径可得出AD⊥BC，由点D为弧BE的中点利用圆周角定理可得出∠BAD＝∠DAC，利用等角的余角相等可得出∠ABD＝∠ACD，进而可证出△ABC为等腰三角形；（2）连接OD，则OD⊥GF，由OA＝OD可得出∠ODA＝∠BAD＝∠DAC，利用“内错角相等，两直线平行”可得出OD∥AC，根据平行线的性质可得出＝、∠GOD ＝∠BAC＝45°，根据等腰直角三角形的性质可得出GO＝DO＝BO，进而可得出＝＝＝．【解答】解：（1）△ABC是等腰三角形，理由如下：连接AD，如图1所示．∵AB为⊙O的直径，∴AD⊥BC．∵点D为弧BE的中点，∴＝，∴∠BAD＝∠DAC，∴∠ABD＝∠ACD，∴△ABC为等腰三角形．（2）连接OD，如图2所示．∵直线l是⊙O的切线，点D是切点，∴OD⊥GF．∵OA＝OD，∴∠ODA＝∠BAD＝∠DAC，∴OD∥AC，∴＝，∠GOD＝∠BAC＝45°，∴△GOD为等腰直角三角形，∴GO＝DO＝BO，∴＝＝＝．∴＝．17．如图，在Rt△ABC中，∠B＝90°，∠BAC的平分线AD交BC于点D，点E在AC上，以AE为直径的⊙O经过点D．求证：（1）BC是⊙O的切线；（2）CD2＝CE•CA．【分析】（1）连接OD，证DO∥AB，得出∠ODB＝90°即可得出结论；（2）连接DE，证△CDE∽△CAD，根据线段比例关系即可得出结论．【解答】证明：（1）连接OD，∵AD是∠BAC的平分线，∴∠DAB＝∠DAO，∵OD＝OA，∴∠DAO＝∠ODA，∴∠DAO＝∠ADO，∴DO∥AB，而∠B＝90°，∴∠ODB＝90°，∵OD是⊙O的半径，∴BC是⊙O的切线；（2）连接DE，∵BC是⊙O的切线，∴∠CDE＝∠DAC，∠C＝∠C，∴△CDE∽△CAD，∴，∴CD2＝CE•CA．18．如图，AB是⊙O的直径，点C，D在⊙O上，且弧CD＝弧CB，过点C作CE∥BD，交AB的延长线于点E，连接AC交BD于F．（1）求证：CE是⊙O的切线；（2）过点C作CH⊥AE于H点，CH交BD于M，若CA＝CE＝6，求CH和BF的长．【分析】（1）连接OC，由垂径定理的推论得出OC⊥BD，由CE∥BD，得出OC⊥CE，即可证明CE是⊙O的切线；（2）连接OC，BC，由等腰三角形的性质得出∠CAB＝∠E，由圆周角定理得出∠BOC ＝2∠E，由OC⊥CE，得出∠BOC+∠E＝90°，求出∠E＝30°，进而求出CH＝3，EH ＝3，由等腰三角形的性质得出∠CAB＝30°，AE＝6，由圆周角定理得出∠ACB ＝90°，由解直角三角形求出AB＝4，由CE∥BD，得出，代入计算即可求出BF＝4，得出答案．【解答】（1）证明：如图1，连接OC，∵弧CD＝弧CB，OC是半径，∴OC⊥BD，∵CE∥BD，∴OC⊥CE，∵OC是半径，∴CE是⊙O的切线；（2）解：如图2，连接OC，BC，∵CA＝CE＝6，∴∠CAB＝∠E，∵∠BOC＝2∠BAC，∴∠BOC＝2∠E，∵OC⊥CE，∴∠BOC+∠E＝90°，∴2∠E+∠E＝90°，∴∠E＝30°，∵CH⊥AE，∴CH＝CE＝×6＝3，EH＝＝＝3，∵CA＝CE＝6，CH⊥AE，∴∠CAB＝∠E＝30°，AE＝2EH＝6，∵AB为直径，∴∠ACB＝90°，∴cos∠CAB＝，∴AB＝＝＝＝4，∵CE∥BD，∴，即，∴BF＝4，∴CH的长为3，BF的长为4．19．如图，⊙O上有A，B，C三点，AC是直径，点D是的中点，连接CD交AB于点E，点F在AB延长线上且FC＝FE．（1）若∠A＝40°，求∠DCB的度数；（2）求证：CF是⊙O的切线；（3）若，BE＝6，求⊙O的半径长．【分析】（1）由圆周角定理得出∠ABC＝90°，由∠A＝40°，得出∠ACB＝50°，由点D是的中点，即可求出∠DCB＝∠ACB＝25°；（2）由圆周角定理得出∠BCD+∠CEF＝90°，由点D是的中点，得出∠DCB＝∠DCA，由等腰三角形的性质得出∠FCE＝∠FEC，进而得出∠ACF＝90°，即可证明CF 是⊙O的切线；（3）由解直角三角形得出＝，设BC＝4x，则CF＝5x，BF＝5x﹣6，由勾股定理得出方程（4x）2+（5x﹣6）2＝（5x）2，解方程求出x＝3，得出BC＝12，CF＝15，BF＝9，再证明△CFB∽△AFC，利用相似三角形的性质求出AC＝20，即可求出⊙O的半径长为10．【解答】（1）解：∵AC是直径，∴∠ABC＝90°，∵∠A＝40°，∴∠ACB＝90°﹣∠A＝90°﹣40°＝50°，∵点D是的中点，∴∠DCB＝∠DCA＝∠ACB＝×50°＝25°；（2）证明：∵AC是直径，∴∠ABC＝90°，∴∠BCD+∠CEF＝90°，∵点D是的中点，∴∠DCB＝∠DCA，∵FC＝FE，∴∠FCE＝∠FEC，∴∠DCA+∠FCE＝90°，即∠ACF＝90°，∴AC⊥CF，∵AC是直径，∴CF是⊙O的切线；（3）解：在Rt△CBF中，sin∠F＝，∵，BE＝6，∴＝，∴设BC＝4x，则CF＝5x，BF＝5x﹣6，∵BC2+BF2＝CF2，∴（4x）2+（5x﹣6）2＝（5x）2，解得：x＝3或（不符合题意，舍去），∴BC＝12，CF＝15，BF＝9，∵∠CBF＝∠ACF＝90°，∠CFB＝∠AFC，∴△CFB∽△AFC，∴，即，∴AC＝20，∴OA＝AC＝×20＝10，∴⊙O的半径长为10．20．已知：如图，AB、AC是⊙O的两条弦，AB＝AC，点M、N分别在弦AB、AC上，且AM＝CN，AM＜AN，联结OM、ON．（1）求证：OM＝ON；（2）当∠BAC为锐角时，如果AO2＝AM•AC，求证：四边形AMON为等腰梯形．【分析】（1）过点O作OE⊥AB于点E，OF⊥AC于点F，利用圆心角，弦，弧，弦心距之间的关系定理可得OE＝OF，AE＝CF＝AB，利用等式的性质可得EM＝FN，再利用全等三角形的判定与性质解答即可；（2）连接OB，利用相似三角形的判定与性质得到∠AOM＝∠B，利用同圆的半径线段，等腰三角形的性质和角平分线性质定理的逆定理得到∠AOM＝∠OAC，则得OM∥ON，利用等腰梯形的定义即可得出结论．【解答】证明：（1）过点O作OE⊥AB于点E，OF⊥AC于点F，如图，∵AB＝AC，OE⊥AB，OF⊥AC，∴OE＝OF，AE＝CF＝AB．∵AM＝CN，∴AE﹣AM＝FC﹣CN，即：EM＝FN．在△OEM和△OFN中，，∴△OEM≌△OFN（SAS）．∴OM＝ON；（2）连接OB，如图，∵AO2＝AM•AC，AC＝AB，∴AO2＝AM•AB，∴．∵∠MAO＝∠OAB，∴△OAM∽△BAO，∴∠AOM＝∠B．∵OA＝OB，∴∠OAB＝∠B，∴∠OAB＝∠AOM，∴OM＝AM．∵OM＝ON，∴AM＝ON．∵OE＝OF，OE⊥AB，OF⊥AC，∴∠OAB＝∠OAC，∴∠AOM＝∠OAC，∴OM∥AN．∵AM＜AN，∴OM＜AN，∴四边形AMON为梯形，∵AM＝ON，∴四边形AMON为等腰梯形．21．如图，在△ABC中，∠ACB＝90°，D是AB边上一点，以BD为直径的⊙O与AC相切于点E，连接DE并延长交BC的延长线于点F．（1）求证：BF＝BD；（2）若CF＝1，tan∠EDB＝2，求⊙O的直径．【分析】（1）连接OE，利用圆的切线的性质定理，平行线的判定与性质，同圆的半径相等和等腰三角形的判定定理解答即可；（2）连接BE，利用直径所对的圆周角为直角，直角三角形的边角关系定理和相似三角形的判定与性质解答即可．【解答】（1）证明：连接OE，如图，∵AC是⊙O的切线，∴OE⊥AC．∵AC⊥BC，∴OE∥BC，∴∠OED＝∠F．∵OD＝OE，∴∠ODE＝∠OED，∴∠BDE＝∠F，∴BD＝BF；（2）解：连接BE，如图，∵∠BDE＝∠F，∴tan∠BDE＝tan∠F＝2，∵CF＝1，tan∠F＝，∴CE＝2．∵BD是⊙O直径，∴∠BED＝90°，∴BE⊥EF．∵EC⊥BF，∴△ECF∽△BCE，∴，∴EC2＝BC•CF．∴BC＝4．∴BF＝BC+CF＝5．∴BD＝BF＝5，即⊙O的直径为5．22．如图，边长为6的等边三角形ABC内接于⊙O，点D为AC上的动点（点A、C除外），BD的延长线交⊙O于点E，连接CE．（1）求证：△CED∽△BAD；（2）当DC＝2AD时，求CE的长．【分析】（1）由对顶角的性质，圆周角定理得出∠CDE＝∠BDA，∠A＝∠E，即可证明△CED∽△BAD；（2）过点D作DF⊥EC于点F，由等边三角形的性质得出∠A＝60°，AC＝AB＝6，由DC＝2AD，得出AD＝2，DC＝4，由相似三角形的性质得，得出EC＝3DE，由含30°角的直角三角形的性质得出DE＝2EF，设EF＝x，则DE＝2x，DF＝x，EC＝6x，进而得出FC＝5x，利用勾股定理得出一元二次方程（x）2+（5x）2＝42，解方程求出x的值，即可求出EC的长度．【解答】（1）证明：如图1，∵∠CDE＝∠BDA，∠A＝∠E，∴△CED∽△BAD；（2）解：如图2，过点D作DF⊥EC于点F，∵△ABC是边长为6等边三角形，∴∠A＝60°，AC＝AB＝6，∵DC＝2AD，∴AD＝2，DC＝4，∵△CED∽△BAD，∴，∴EC＝3DE，∵∠E＝∠A＝60°，DF⊥EC，∴∠EDF＝90°﹣60°＝30°，∴DE＝2EF，设EF＝x，则DE＝2x，DF＝x，EC＝6x，∴FC＝5x，在Rt△DFC中，DF2+FC2＝DC2，∴（x）2+（5x）2＝42，解得：x＝或﹣（不符合题意，舍去），∴EC＝6x＝．23．如图，已知△ABC内接于⊙O，AB是⊙O的直径，∠CAB的平分线交BC于点D，交⊙O于点E，连接EB，作∠BEF＝∠CAE，交AB的延长线于点F．（1）求证：EF是⊙O的切线；（2）若AE＝12，，求⊙O的半径和EF的长．【分析】（1）连接OE，根据直径所对的圆周角是直角可得∠AEB＝90°，从而可得∠AEO+∠OEB＝90°，再利用角平分线和等腰三角形的性质可得∠CAE＝∠AEO，从而可得∠BEF＝∠AEO，然后可得∠BEF+∠OEB＝90°，从而求出∠OEF＝90°，即可解答；（2）利用（1）的结论可得∠BEF＝∠EAO，从而可证△FEB∽△F AE，然后利用相似三角形的性质可求出BE的长，再在Rt△ABE中利用勾股定理求出AB的长，从而求出EF 的长，即可解答．【解答】（1）证明：连接OE，∵AB是⊙O的直径，∴∠AEB＝90°，∴∠AEO+∠OEB＝90°，∵OA＝OE，∴∠EAO＝∠AEO，∵AE平分∠CAB，∴∠EAO＝∠CAE，∴∠CAE＝∠AEO，∵∠BEF＝∠CAE，∴∠BEF＝∠AEO，∴∠BEF+∠OEB＝90°，∴∠OEF＝90°，∵OE是⊙O的半径，∴EF是⊙O的切线；（2）解：∵∠BEF＝∠AEO，∠EAO＝∠AEO，∴∠BEF＝∠EAO，∵∠F＝∠F，∴△FEB∽△F AE，∴＝＝，∴＝＝，∴BE＝6，∴AB＝＝＝30，∴＝，∴EF＝20，∴⊙O的半径为15，EF的长为20．。

相似三角形重难点题型(附参考答案)

经典练习题相似三角形（附答案）一．解答题（共30小题）1．如图，在△ABC中，DE∥BC，EF∥AB，求证：△ADE∽△EFC．2．如图，梯形ABCD中，AB∥CD，点F在BC上，连DF与AB的延长线交于点G．（1）求证：△CDF∽△BGF；（2）当点F是BC的中点时，过F作EF∥CD交AD于点E，若AB=6cm，EF=4cm，求CD的长．3．如图，点D，E在BC上，且FD∥AB，FE∥AC．求证：△ABC∽△FDE．4．如图，已知E是矩形ABCD的边CD上一点，BF⊥AE于F，试说明：△ABF∽△EAD．5．已知：如图①所示，在△ABC和△ADE中，AB=AC，AD=AE，∠BAC=∠DAE，且点B，A，D在一条直线上，连接BE，CD，M，N分别为BE，CD的中点．（1）求证：①BE=CD；②△AMN是等腰三角形；（2）在图①的基础上，将△ADE绕点A按顺时针方向旋转180°，其他条件不变，得到图②所示的图形．请直接写出（1）中的两个结论是否仍然成立；（3）在（2）的条件下，请你在图②中延长ED交线段BC于点P．求证：△PBD∽△AMN．6．如图，E是▱ABCD的边BA延长线上一点，连接EC，交AD于点F．在不添加辅助线的情况下，请你写出图中所有的相似三角形，并任选一对相似三角形给予证明．7．如图，在4×3的正方形方格中，△ABC和△DEF的顶点都在边长为1的小正方形的顶点上．（1）填空：∠ABC=_________ °，BC= _________ ；（2）判断△ABC与△DEC是否相似，并证明你的结论．8．如图，已知矩形ABCD的边长AB=3cm，BC=6cm．某一时刻，动点M从A点出发沿AB方向以1cm/s 的速度向B点匀速运动；同时，动点N从D点出发沿DA方向以2cm/s的速度向A点匀速运动，问：（1）经过多少时间，△AMN的面积等于矩形ABCD面积的？（2）是否存在时刻t，使以A，M，N为顶点的三角形与△ACD相似？若存在，求t的值；若不存在，请说明理由．39．如图，在梯形ABCD中，若AB∥DC，AD=BC，对角线BD、AC把梯形分成了四个小三角形．（1）列出从这四个小三角形中任选两个三角形的所有可能情况，并求出选取到的两个三角形是相似三角形的概率是多少；（注意：全等看成相似的特例）（2）请你任选一组相似三角形，并给出证明．10．如图△ABC中，D为AC上一点，CD=2DA，∠BAC=45°，∠BDC=60°，CE⊥BD于E，连接AE．（1）写出图中所有相等的线段，并加以证明；（2）图中有无相似三角形？若有，请写出一对；若没有，请说明理由；（3）求△BEC与△BEA的面积之比．11．如图，在△ABC中，AB=AC=a，M为底边BC上的任意一点，过点M分别作AB、AC的平行线交AC 于P，交AB于Q．（1）求四边形AQMP的周长；（2）写出图中的两对相似三角形（不需证明）；（3）M位于BC的什么位置时，四边形AQMP为菱形并证明你的结论．12．已知：P是正方形ABCD的边BC上的点，且BP=3PC，M是CD的中点，试说明：△ADM∽△MCP．513．如图，已知梯形ABCD中，AD∥BC，AD=2，AB=BC=8，CD=10．（1）求梯形ABCD的面积S；（2）动点P从点B出发，以1cm/s的速度，沿B⇒A⇒D⇒C方向，向点C运动；动点Q从点C出发，以1cm/s的速度，沿C⇒D⇒A方向，向点A运动，过点Q作QE⊥BC于点E．若P、Q两点同时出发，当其中一点到达目的地时整个运动随之结束，设运动时间为t秒．问：①当点P在B⇒A上运动时，是否存在这样的t，使得直线PQ将梯形ABCD的周长平分？若存在，请求出t的值；若不存在，请说明理由；②在运动过程中，是否存在这样的t，使得以P、A、D为顶点的三角形与△CQE相似？若存在，请求出所有符合条件的t的值；若不存在，请说明理由；③在运动过程中，是否存在这样的t，使得以P、D、Q为顶点的三角形恰好是以DQ为一腰的等腰三角形？若存在，请求出所有符合条件的t的值；若不存在，请说明理由．14．已知矩形ABCD，长BC=12cm，宽AB=8cm，P、Q分别是AB、BC上运动的两点．若P自点A出发，以1cm/s的速度沿AB方向运动，同时，Q自点B出发以2cm/s的速度沿BC方向运动，问经过几秒，以P、B、Q为顶点的三角形与△BDC相似？15．如图，在△ABC中，AB=10cm，BC=20cm，点P从点A开始沿AB边向B点以2cm/s的速度移动，点Q从点B开始沿BC边向点C以4cm/s的速度移动，如果P、Q分别从A、B同时出发，问经过几秒钟，△PBQ与△ABC相似．16．如图，∠ACB=∠ADC=90°，AC=，AD=2．问当AB的长为多少时，这两个直角三角形相似．717．已知，如图，在边长为a的正方形ABCD中，M是AD的中点，能否在边AB上找一点N（不含A、B），使得△CDM与△MAN相似？若能，请给出证明，若不能，请说明理由．18．如图在△ABC中，∠C=90°，BC=8cm，AC=6cm，点Q从B出发，沿BC方向以2cm/s的速度移动，点P从C出发，沿CA方向以1cm/s的速度移动．若Q、P分别同时从B、C出发，试探究经过多少秒后，以点C、P、Q为顶点的三角形与△CBA相似？19．如图所示，梯形ABCD中，AD∥BC，∠A=90°，AB=7，AD=2，BC=3，试在腰AB上确定点P的位置，使得以P，A，D为顶点的三角形与以P，B，C为顶点的三角形相似．20．△ABC和△DEF是两个等腰直角三角形，∠A=∠D=90°，△DEF的顶点E位于边BC的中点上．（1）如图1，设DE与AB交于点M，EF与AC交于点N，求证：△BEM∽△CNE；（2）如图2，将△DEF绕点E旋转，使得DE与BA的延长线交于点M，EF与AC交于点N，于是，除（1）中的一对相似三角形外，能否再找出一对相似三角形并证明你的结论．21．如图，在矩形ABCD中，AB=15cm，BC=10cm，点P沿AB边从点A开始向B以2cm/s的速度移动；点Q沿DA边从点D开始向点A以1cm/s的速度移动．如果P、Q同时出发，用t（秒）表示移动的时间，那么当t为何值时，以点Q、A、P为顶点的三角形与△ABC相似．22．如图，路灯（P点）距地面8米，身高1.6米的小明从距路灯的底部（O点）20米的A点，沿OA所在的直线行走14米到B点时，身影的长度是变长了还是变短了？变长或变短了多少米？23．阳光明媚的一天，数学兴趣小组的同学们去测量一棵树的高度（这棵树底部可以到达，顶部不易到达），他们带了以下测量工具：皮尺，标杆，一副三角尺，小平面镜．请你在他们提供的测量工具中选出所需工具，设计一种测量方案．9（1）所需的测量工具是：_________ ；（2）请在下图中画出测量示意图；（3）设树高AB的长度为x，请用所测数据（用小写字母表示）求出x．24．问题背景在某次活动课中，甲、乙、丙三个学习小组于同一时刻在阳光下对校园中一些物体进行了测量．下面是他们通过测量得到的一些信息：甲组：如图1，测得一根直立于平地，长为80cm的竹竿的影长为60cm．乙组：如图2，测得学校旗杆的影长为900cm．丙组：如图3，测得校园景灯（灯罩视为球体，灯杆为圆柱体，其粗细忽略不计）的高度为200cm，影长为156cm．任务要求：（1）请根据甲、乙两组得到的信息计算出学校旗杆的高度；（2）如图3，设太阳光线NH与⊙O相切于点M．请根据甲、丙两组得到的信息，求景灯灯罩的半径．（友情提示：如图3，景灯的影长等于线段NG的影长；需要时可采用等式1562+2082=2602）25．阳光通过窗口照射到室内，在地面上留下2.7m宽的亮区（如图所示），已知亮区到窗口下的墙脚距离EC=8.7m，窗口高AB=1.8m，求窗口底边离地面的高BC．26．如图，李华晚上在路灯下散步．已知李华的身高AB=h，灯柱的高OP=O′P′=l，两灯柱之间的距离OO′=m．（1）若李华距灯柱OP的水平距离OA=a，求他影子AC的长；（2）若李华在两路灯之间行走，则他前后的两个影子的长度之和（DA+AC）是否是定值请说明理由；（3）若李华在点A朝着影子（如图箭头）的方向以v1匀速行走，试求他影子的顶端在地面上移动的速度v2．27．如图①，分别以直角三角形ABC三边为直径向外作三个半圆，其面积分别用S1，S2，S3表示，则不难证明S1=S2+S3．（1）如图②，分别以直角三角形ABC三边为边向外作三个正方形，其面积分别用S1，S2，S3表示，那么S1，S2，S3之间有什么关系；（不必证明）11（2）如图③，分别以直角三角形ABC三边为边向外作三个正三角形，其面积分别用S1、S2、S3表示，请你确定S1，S2，S3之间的关系并加以证明；（3）若分别以直角三角形ABC三边为边向外作三个一般三角形，其面积分别用S1，S2，S3表示，为使S1，S2，S3之间仍具有与（2）相同的关系，所作三角形应满足什么条件证明你的结论；（4）类比（1），（2），（3）的结论，请你总结出一个更具一般意义的结论．28．已知：如图，△ABC∽△ADE，AB=15，AC=9，BD=5．求AE．29．已知：如图Rt△ABC∽Rt△BDC，若AB=3，AC=4．（1）求BD、CD的长；（2）过B作BE⊥DC于E，求BE的长．30．（1）已知，且3x+4z﹣2y=40，求x，y，z的值；（2）已知：两相似三角形对应高的比为3：10，且这两个三角形的周长差为560cm，求它们的周长．13参考答案与试题解析一．解答题（共30小题）1．如图，在△ABC中，DE∥BC，EF∥AB，求证：△ADE∽△EFC．2．如图，梯形ABCD中，AB∥CD，点F在BC上，连DF与AB的延长线交于点G．（1）求证：△CDF∽△BGF；（2）当点F是BC的中点时，过F作EF∥CD交AD于点E，若AB=6cm，EF=4cm，求CD的长．153．如图，点D，E在BC上，且FD∥AB，FE∥AC．求证：△ABC∽△FDE．4．如图，已知E是矩形ABCD的边CD上一点，BF⊥AE于F，试说明：△ABF∽△EAD．5．已知：如图①所示，在△ABC和△ADE中，AB=AC，AD=AE，∠BAC=∠DAE，且点B，A，D在一条直线上，连接BE，CD，M，N分别为BE，CD的中点．（1）求证：①BE=CD；②△AMN是等腰三角形；（2）在图①的基础上，将△ADE绕点A按顺时针方向旋转180°，其他条件不变，得到图②所示的图形．请直接写出（1）中的两个结论是否仍然成立；（3）在（2）的条件下，请你在图②中延长ED交线段BC于点P．求证：△PBD∽△AMN．176．如图，E是▱ABCD的边BA延长线上一点，连接EC，交AD于点F．在不添加辅助线的情况下，请你写出图中所有的相似三角形，并任选一对相似三角形给予证明．19解答：解：相似三角形有△AEF∽△BEC；△AEF∽△DCF；△BEC∽△DCF．（3分）如：△AEF∽△BEC．在▱ABCD中，AD∥BC，∴∠1=∠B，∠2=∠3．（6分）∴△AEF∽△BEC．（7分）7．如图，在4×3的正方形方格中，△ABC和△DEF的顶点都在边长为1的小正方形的顶点上．（1）填空：∠ABC=135°°，BC= ；（2）判断△ABC与△DEC是否相似，并证明你的结论．21分析：（1）观察可得：BF=FC=2，故∠FBC=45°；则∠ABC=135°，BC==2；（2）观察可得：BC 、EC 的长为2、，可得，再根据其夹角相等；故△ABC∽△DEC．解答：解：（1）∠ABC=135°，BC=；（2）相似；∵BC=，EC==； ∴，； ∴；又∠ABC=∠CED=135°，∴△ABC∽△DEC．8．如图，已知矩形ABCD 的边长AB=3cm ，BC=6cm ．某一时刻，动点M 从A 点出发沿AB 方向以1cm/s 的速度向B 点匀速运动；同时，动点N 从D 点出发沿DA 方向以2cm/s 的速度向A 点匀速运动，问：（1）经过多少时间，△AMN 的面积等于矩形ABCD 面积的？（2）是否存在时刻t ，使以A ，M ，N 为顶点的三角形与△ACD 相似？若存在，求t 的值；若不存在，请说明理由．分析：（1）关于动点问题，可设时间为x，根据速度表示出所涉及到的线段的长度，找到相等关系，列方程求解即可，如本题中利用，△AMN的面积等于矩形ABCD面积的作为相等关系；（2）先假设相似，利用相似中的比例线段列出方程，有解的且符合题意的t值即可说明存在，反之则不存在．解答：解：（1）设经过x秒后，△AMN的面积等于矩形ABCD面积的，则有：（6﹣2x）x=×3×6，即x2﹣3x+2=0，（2分）解方程，得x1=1，x2=2，（3分）经检验，可知x1=1，x2=2符合题意，所以经过1秒或2秒后，△AMN的面积等于矩形ABCD面积的．（4分）（2）假设经过t秒时，以A，M，N为顶点的三角形与△ACD相似，由矩形ABCD，可得∠CDA=∠MAN=90°，因此有或（5分）即①，或②（6分）解①，得t=；解②，得t=（7分）经检验，t=或t=都符合题意，所以动点M，N同时出发后，经过秒或秒时，以A，M，N为顶点的三角形与△ACD相似．（8分）9．如图，在梯形ABCD中，若AB∥DC，AD=BC，对角线BD、AC把梯形分成了四个小三角形．（1）列出从这四个小三角形中任选两个三角形的所有可能情况，并求出选取到的两个三角形是相似三角形的概率是多少；（注意：全等看成相似的特例）（2）请你任选一组相似三角形，并给出证明．解答：解：（1）任选两个三角形的所有可能情况如下六种情况：①②，①③，①④，②③，②④，③④（2分）其中有两组（①③，②④）是相似的．∴选取到的二个三角形是相似三角形的概率是P=（4分）证明：（2）选择①、③证明．在△AOB与△COD中，∵AB∥CD，∴∠CDB=∠DBA，∠DCA=∠CAB，∴△AOB∽△COD（8分）选择②、④证明．∵四边形ABCD是等腰梯形，23点评：此题考查概率的求法：如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m 种结果，那么事件A的概率P（A）=，即相似三角形的证明．还考查了相似三角形的判定．10．附加题：如图△ABC中，D为AC上一点，CD=2DA，∠BAC=45°，∠BDC=60°，CE⊥BD于E，连接AE．（1）写出图中所有相等的线段，并加以证明；（2）图中有无相似三角形？若有，请写出一对；若没有，请说明理由；（3）求△BEC与△BEA的面积之比．解答：解：（1）AD=DE，AE=CE．∵CE⊥BD，∠BDC=60°，∴在Rt△CED中，∠ECD=30°．∴CD=2ED．∵CD=2DA，∴AD=DE，∴∠DAE=∠DEA=30°=∠ECD．∴AE=CE．（2）图中有三角形相似，△ADE∽△AEC；∵∠CAE=∠CAE，∠ADE=∠AEC，∴△ADE∽△AEC；（3）作AF⊥BD的延长线于F，设AD=DE=x，在Rt△CED中，可得CE=，故AE=．∠ECD=30°．在Rt△AEF中，AE=，∠AED=∠DAE=30°，∴sin∠AEF=，∴AF=AE•sin∠AEF=．25∴．11．如图，在△ABC中，AB=AC=a，M为底边BC上的任意一点，过点M分别作AB、AC的平行线交AC 于P，交AB于Q．（1）求四边形AQMP的周长；（2）写出图中的两对相似三角形（不需证明）；（3）M位于BC的什么位置时，四边形AQMP为菱形并证明你的结论．∵AB=AC，∴∠B=∠C，∴∠PMC=∠QMB．∴BQ=QM，PM=PC．∴四边形AQMP的周长=AQ+AP+QM+MP=AQ+QB+AP+PC=AB+AC=2a．（2）∵PM∥AB，∴△PCM∽△ACB，∵QM∥AC，∴△BMQ∽△BCA；（3）当点M中BC的中点时，四边形APMQ是菱形，∵点M是BC的中点，AB∥MP，QM∥AC，∴QM，PM是三角形ABC的中位线．∵AB=AC，∴QM=PM=AB=AC．又由（1）知四边形APMQ是平行四边形，∴平行四边形APMQ是菱形．12．已知：P是正方形ABCD的边BC上的点，且BP=3PC，M是CD的中点，试说明：△ADM∽△MCP．27解答：证明：∵正方形ABCD，M为CD中点，∴CM=MD=AD．∵BP=3PC，∴PC=BC=AD=CM．∴．∵∠PCM=∠ADM=90°，∴△MCP∽△ADM．13．如图，已知梯形ABCD中，AD∥BC，AD=2，AB=BC=8，CD=10．（1）求梯形ABCD的面积S；（2）动点P从点B出发，以1cm/s的速度，沿B⇒A⇒D⇒C方向，向点C运动；动点Q从点C出发，以1cm/s的速度，沿C⇒D⇒A方向，向点A运动，过点Q作QE⊥BC于点E．若P、Q两点同时出发，当其中一点到达目的地时整个运动随之结束，设运动时间为t秒．问：①当点P在B⇒A上运动时，是否存在这样的t，使得直线PQ将梯形ABCD的周长平分？若存在，请求出t的值；若不存在，请说明理由；②在运动过程中，是否存在这样的t，使得以P、A、D为顶点的三角形与△CQE相似？若存在，请求出所有符合条件的t的值；若不存在，请说明理由；③在运动过程中，是否存在这样的t，使得以P、D、Q为顶点的三角形恰好是以DQ为一腰的等腰三角形？若存在，请求出所有符合条件的t的值；若不存在，请说明理由．29解答：解：（1）过D作DH∥AB交BC于H点，∵AD∥BH，DH∥AB，∴四边形ABHD是平行四边形．∴DH=AB=8；BH=AD=2．∴CH=8﹣2=6．∵CD=10，∴DH2+CH2=CD2∴∠DHC=90°．∠B=∠DHC=90°．∴梯形ABCD是直角梯形．∴S ABCD=（AD+BC）AB=×（2+8）×8=40．（2）①∵BP=CQ=t，∴AP=8﹣t，DQ=10﹣t，∵AP+AD+DQ=PB+BC+CQ，∴8﹣t+2+10﹣t=t+8+t．∴t=3＜8．∴当t=3秒时，PQ将梯形ABCD周长平分．②第一种情况：0＜t≤8若△PAD∽△QEC则∠ADP=∠C∴tan∠ADP=tan∠C==∴=，∴t=若△PAD∽△CEQ则∠APD=∠C∴tan∠APD=tan∠C==，∴=∴t=第二种情况：8＜t≤10，P、A、D三点不能组成三角形；第三种情况：10＜t≤12△ADP为钝角三角形与Rt△CQE不相似；∴t=或t=时，△PAD与△CQE相似．③第一种情况：当0≤t≤8时．过Q点作QE⊥BC，QH⊥AB，垂足为E、H．∵AP=8﹣t，AD=2，∴PD==．∵CE=t，QE=t，∴QH=BE=8﹣t，BH=QE=t．∴PH=t﹣t=t．∴PQ==，DQ=10﹣t．Ⅰ：DQ=DP，10﹣t=，31解得t=8秒．Ⅱ：DQ=PQ，10﹣t=，化简得：3t2﹣52t+180=0解得：t=，t=＞8（不合题意舍去）∴t=第二种情况：8≤t≤10时．DP=DQ=10﹣t．∴当8≤t＜10时，以DQ为腰的等腰△DPQ恒成立．第三种情况：10＜t≤12时．DP=DQ=t﹣10．∴当10＜t≤12时，以DQ为腰的等腰△DPQ恒成立．综上所述，t=或8≤t＜10或10＜t≤12时，以DQ为腰的等腰△DPQ成立．14．已知矩形ABCD，长BC=12cm，宽AB=8cm，P、Q分别是AB、BC上运动的两点．若P自点A出发，以1cm/s的速度沿AB方向运动，同时，Q自点B出发以2cm/s的速度沿BC方向运动，问经过几秒，以P、B、Q为顶点的三角形与△BDC相似？33（1）当∠1=∠2时，有：，即；（2）当∠1=∠3时，有：，即，∴经过秒或2秒，△PBQ∽△BCD．15．如图，在△ABC中，AB=10cm，BC=20cm，点P从点A开始沿AB边向B点以2cm/s的速度移动，点Q从点B开始沿BC边向点C以4cm/s的速度移动，如果P、Q分别从A、B同时出发，问经过几秒钟，△PBQ与△ABC相似．即（10﹣2t）：10=4t：20，解得t=2.5（s）（6分）当△QBP∽△ABC时，有BQ：AB=BP：BC，即4t：10=（10﹣2t）：20，解得t=1．所以，经过2.5s或1s时，△PBQ与△ABC相似（10分）．解法二：设ts后，△PBQ与△ABC相似，则有，AP=2t，BQ=4t，BP=10﹣2t分两种情况：（1）当BP与AB对应时，有=，即=，解得t=2.5s（2）当BP与BC对应时，有=，即=，解得t=1s所以经过1s或2.5s时，以P、B、Q三点为顶点的三角形与△ABC相似．16．如图，∠ACB=∠ADC=90°，AC=，AD=2．问当AB的长为多少时，这两个直角三角形相似．解答：解：∵AC=，AD=2，∴CD==．要使这两个直角三角形相似，有两种情况：35（1）当Rt△ABC∽Rt△ACD时，有=，∴AB==3；（2）当Rt△ACB∽Rt△CDA时，有=，∴AB==3．故当AB的长为3或3时，这两个直角三角形相似．17．已知，如图，在边长为a的正方形ABCD中，M是AD的中点，能否在边AB上找一点N（不含A、B），使得△CDM与△MAN相似？若能，请给出证明，若不能，请说明理由．分析：两个三角形都是直角三角形，还只需满足一对角对应相等或夹直角的两边对应成比例即可说明两个三角形相似．若DM与AM对应，则△CDM与△MAN全等，N与B重合，不合题意；若DM与AN对应，则CD：AM=DM：AN，得AN=a，从而确定N的位置．解答：证明：分两种情况讨论：①若△CDM∽△MAN，则=．∵边长为a，M是AD的中点，∴AN=a．②若△CDM∽△NAM，则．∵边长为a，M是AD的中点，∴AN=a，即N点与B重合，不合题意．所以，能在边AB上找一点N（不含A、B），使得△CDM与△MAN相似．当AN=a时，N点的位置满足条件．18．如图在△ABC中，∠C=90°，BC=8cm，AC=6cm，点Q从B出发，沿BC方向以2cm/s的速度移动，点P从C出发，沿CA方向以1cm/s的速度移动．若Q、P分别同时从B、C出发，试探究经过多少秒后，以点C、P、Q为顶点的三角形与△CBA相似？解答：解：设经过x秒后，两三角形相似，则CQ=（8﹣2x）cm，CP=xcm，（1分）∵∠C=∠C=90°，∴当或时，两三角形相似．（3分）（1）当时，，∴x=；（4分）37（2）当时，，∴x=．（5分）所以，经过秒或秒后，两三角形相似．（6分）19．如图所示，梯形ABCD中，AD∥BC，∠A=90°，AB=7，AD=2，BC=3，试在腰AB上确定点P的位置，使得以P，A，D为顶点的三角形与以P，B，C为顶点的三角形相似．解答：解：（1）若点A，P，D分别与点B，C，P对应，即△APD∽△BCP，∴=，∴=，∴AP2﹣7AP+6=0，∴AP=1或AP=6，检测：当AP=1时，由BC=3，AD=2，BP=6，∴=，又∵∠A=∠B=90°，∴△APD∽△BCP．当AP=6时，由BC=3，AD=2，BP=1，又∵∠A=∠B=90°，∴△APD∽△BCP．（2）若点A，P，D分别与点B，P，C对应，即△APD∽△BPC．∴=，∴=，∴AP=．检验：当AP=时，由BP=，AD=2，BC=3，∴=，又∵∠A=∠B=90°，∴△APD∽△BPC．因此，点P的位置有三处，即在线段AB距离点A的1、、6处．20．△ABC和△DEF是两个等腰直角三角形，∠A=∠D=90°，△DEF的顶点E位于边BC的中点上．（1）如图1，设DE与AB交于点M，EF与AC交于点N，求证：△BEM∽△CNE；（2）如图2，将△DEF绕点E旋转，使得DE与BA的延长线交于点M，EF与AC交于点N，于是，除（1）中的一对相似三角形外，能否再找出一对相似三角形并证明你的结论．39解答：证明：（1）∵△ABC是等腰直角三角形，∴∠MBE=45°，∴∠BME+∠MEB=135°又∵△DEF是等腰直角三角形，∴∠DEF=45°∴∠NEC+∠MEB=135°∴∠BEM=∠NEC，（4分）而∠MBE=∠ECN=45°，∴△BEM∽△CNE．（6分）（2）与（1）同理△BEM∽△CNE，∴．（8分）又∵BE=EC，∴，（10分）则△ECN与△MEN中有，又∠ECN=∠MEN=45°，∴△ECN∽△MEN．（12分）21．如图，在矩形ABCD中，AB=15cm，BC=10cm，点P沿AB边从点A开始向B以2cm/s的速度移动；点Q沿DA边从点D开始向点A以1cm/s的速度移动．如果P、Q同时出发，用t（秒）表示移动的时间，那么当t为何值时，以点Q、A、P为顶点的三角形与△ABC相似．解答：解：以点Q、A、P为顶点的三角形与△ABC相似，所以△ABC∽△PAQ或△ABC∽△QAP，①当△ABC∽△PAQ时，，41所以，解得：t=6；②当△ABC∽△QAP时，，所以，解得：t=；③当△AQP∽△BAC时，=，即=，所以t=；④当△AQP∽△BCA时，=，即=，所以t=30（舍去）．故当t=6或t=时，以点Q、A、P为顶点的三角形与△ABC相似．22．如图，路灯（P点）距地面8米，身高1.6米的小明从距路灯的底部（O点）20米的A点，沿OA所在的直线行走14米到B点时，身影的长度是变长了还是变短了？变长或变短了多少米？解答：解：∵∠MAC=∠MOP=90°，∠AMC=∠OMP，∴△MAC∽△MOP．∴，即，解得，MA=5米；同理，由△NBD∽△NOP，可求得NB=1.5米，∴小明的身影变短了5﹣1.5=3.5米．23．阳光明媚的一天，数学兴趣小组的同学们去测量一棵树的高度（这棵树底部可以到达，顶部不易到达），他们带了以下测量工具：皮尺，标杆，一副三角尺，小平面镜．请你在他们提供的测量工具中选出所需工具，设计一种测量方案．（1）所需的测量工具是：；（2）请在下图中画出测量示意图；（3）设树高AB的长度为x，请用所测数据（用小写字母表示）求出x．43解答：解：（1）皮尺，标杆；（2）测量示意图如图所示；（3）如图，测得标杆DE=a，树和标杆的影长分别为AC=b，EF=c，∵△DEF∽△BAC，∴，∴，∴．（7分）24．问题背景在某次活动课中，甲、乙、丙三个学习小组于同一时刻在阳光下对校园中一些物体进行了测量．下面是他们通过测量得到的一些信息：甲组：如图1，测得一根直立于平地，长为80cm的竹竿的影长为60cm．乙组：如图2，测得学校旗杆的影长为900cm．丙组：如图3，测得校园景灯（灯罩视为球体，灯杆为圆柱体，其粗细忽略不计）的高度为200cm，影长为156cm．任务要求：（1）请根据甲、乙两组得到的信息计算出学校旗杆的高度；（2）如图3，设太阳光线NH与⊙O相切于点M．请根据甲、丙两组得到的信息，求景灯灯罩的半径．（友情提示：如图3，景灯的影长等于线段NG的影长；需要时可采用等式1562+2082=2602）解答：解：（1）由题意可知：∠BAC=∠EDF=90°，∠BCA=∠EFD．∴△ABC∽△DEF．∴，即，（2分）∴DE=1200（cm）．所以，学校旗杆的高度是12m．（3分）45（2）解法一：与①类似得：，即，∴GN=208．（4分）在Rt△NGH中，根据勾股定理得：NH2=1562+2082=2602，∴NH=260．（5分）设⊙O的半径为rcm，连接OM，∵NH切⊙O于M，∴OM⊥NH．（6分）则∠OMN=∠HGN=90°，又∵∠ONM=∠HNG，∴△OMN∽△HGN，∴（7分），又ON=OK+KN=OK+（GN﹣GK）=r+8，∴，解得：r=12．∴景灯灯罩的半径是12cm．（8分）解法二：与①类似得：，即，∴GN=208．（4分）设⊙O的半径为rcm，连接OM，∵NH切⊙O于M，∴OM⊥NH．（5分）则∠OMN=∠HGN=90°，又∵∠ONM=∠HNG，∴△OMN∽△HGN．∴，即，（6分）∴MN=r，又∵ON=OK+KN=OK+（GN﹣GK）=r+8．（7分）在Rt△OMN中，根据勾股定理得：r2+（r）2=（r+8）2即r2﹣9r﹣36=0，解得：r1=12，r2=﹣3（不合题意，舍去），∴景灯灯罩的半径是12cm．（8分）25．（2007•白银）阳光通过窗口照射到室内，在地面上留下2.7m宽的亮区（如图所示），已知亮区到窗口下的墙脚距离EC=8.7m，窗口高AB=1.8m，求窗口底边离地面的高BC．47分析：因为光线AE、BD是一组平行光线，即AE∥BD，所以△ECA∽△DCB，则有，从而算出BC的长．解答：解：∵AE∥BD，∴△ECA∽△DCB，∴．∵EC=8.7m，ED=2.7m，∴CD=6m．∵AB=1.8m，∴AC=BC+1.8m，∴，∴BC=4，即窗口底边离地面的高为4m．26．如图，李华晚上在路灯下散步．已知李华的身高AB=h，灯柱的高OP=O′P′=l，两灯柱之间的距离OO′=m．（1）若李华距灯柱OP的水平距离OA=a，求他影子AC的长；（2）若李华在两路灯之间行走，则他前后的两个影子的长度之和（DA+AC）是否是定值请说明理由；（3）若李华在点A朝着影子（如图箭头）的方向以v1匀速行走，试求他影子的顶端在地面上移动的速度v2．解答：解：（1）由已知：AB∥OP，∴△ABC∽△OPC．∵，∵OP=l，AB=h，OA=a，∴，∴解得：．（2）∵AB∥OP，∴△ABC∽△OPC，∴，即，即．∴．同理可得：，∴=是定值．（3）根据题意设李华由A到A'，身高为A'B'，A'C'代表其影长（如图）．由（1）可知，即，∴，同理可得：，∴，49由等比性质得：，当李华从A走到A'的时候，他的影子也从C移到C'，因此速度与路程成正比∴，所以人影顶端在地面上移动的速度为．27．如图①，分别以直角三角形ABC三边为直径向外作三个半圆，其面积分别用S1，S2，S3表示，则不难证明S1=S2+S3．（1）如图②，分别以直角三角形ABC三边为边向外作三个正方形，其面积分别用S1，S2，S3表示，那么S1，S2，S3之间有什么关系；（不必证明）（2）如图③，分别以直角三角形ABC三边为边向外作三个正三角形，其面积分别用S1、S2、S3表示，请你确定S1，S2，S3之间的关系并加以证明；（3）若分别以直角三角形ABC三边为边向外作三个一般三角形，其面积分别用S1，S2，S3表示，为使S1，S2，S3之间仍具有与（2）相同的关系，所作三角形应满足什么条件证明你的结论；。

圆与相似三角形相关的证明题

圆与相似三角形相关的证明题1. 在图中，已知PC=PD，PD切圆O于D，PB交圆O于A，连结AC和BC。

要证明AC·PB=PC·BC。

证明：由于PD是圆O的切线，所以∠PDC=∠ACB。

又因为PC=PD，所以∠PCD=∠PDC。

因此，∠ACB=∠PCD。

又因为∠BCP=∠PBD，所以三角形PBD和PBC相似。

因此，PB·PC=PD2。

由于三角形ACD和BDC相似，所以AC·BD=CD2。

将BD替换为PD+PC，得到AC·(PD+PC)=CD2，即AC·PB=PC·BC。

因此，原命题成立。

2. 在图中，已知AB∥CD，DC延长线交EB延长线于F，EB与圆O相交于F，DF交圆O于G。

要证明AD·ED=BE·DF。

证明：由于AB∥CD，所以∠___∠EAD。

又因为EB是圆O的切线，所以∠___∠EDF。

因此，∠___∠EAD。

又因为AB是圆O的直径，所以∠EAB=90°。

因此，三角形EAB和EDF相似。

因此，AD·ED=BE·DF。

因此，原命题成立。

3. 在图中，___于P，PE⊥AB于E，AC⊥CD，BD⊥CD。

要证明①PE：AC=PB：PA，②PE2=AC·BD。

证明：①由于PE⊥AB，所以∠APE=90°。

又因为AC⊥CD，所以∠ACP=90°。

因此，∠APE=∠ACP。

又因为∠APB=90°，所以三角形APE和APB相似。

因此，PE：AC=PB：PA。

②由于PE⊥AB，所以∠APE=90°。

又因为BD⊥CD，所以∠___°。

因此，四边形AEPD和BEPC是直角四边形。

因此，PE2=AE2-AP2=AC·BD。

因此，原命题成立。

4. 在图中，ABC是内接于圆O的三角形，BD是圆O的直径，AF⊥BD于F，AF延长线与BC交于G。

2020春浙教版九年级中考数学复习测试：6.20圆与相似三角形的结合

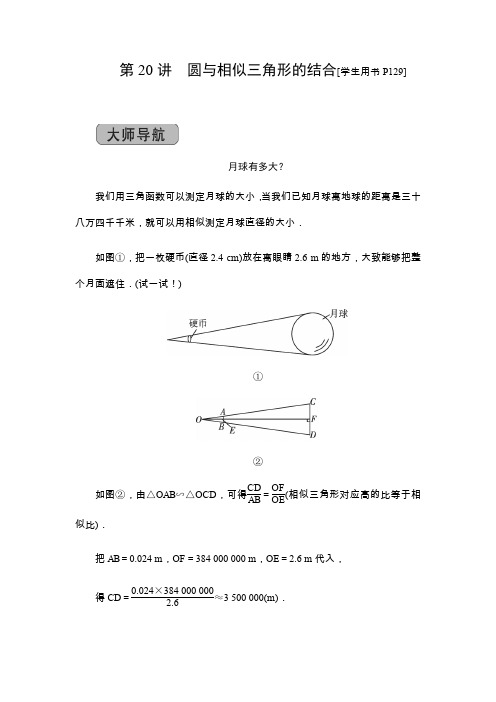
第20讲圆与相似三角形的结合[学生用书P129]月球有多大？我们用三角函数可以测定月球的大小，当我们已知月球离地球的距离是三十八万四千千米，就可以用相似测定月球直径的大小．如图①，把一枚硬币(直径2.4 cm)放在离眼睛2.6 m的地方，大致能够把整个月面遮住．(试一试！)①②如图②，由△OAB∽△OCD，可得CDAB＝OFOE(相似三角形对应高的比等于相似比)．把AB＝0.024 m，OF＝384 000 000 m，OE＝2.6 m代入，得CD＝0.024×384 000 0002.6≈3 500 000(m)．就是说，月球的直径约是3 500 km.类型之一圆的基本性质与相似三角形例1[2018·南京中考]如图，在正方形ABCD中，E是AB上一点，连结DE.过点A作AF⊥DE，垂足为F.⊙O经过点C，D，F，与AD相交于点G.(1)求证：△AFG∽△DFC；(2)若正方形ABCD的边长为4，AE＝1，求⊙O的半径．【思路生成】(1)欲证明△AFG∽△DFC，只要证明∠F AG＝∠FDC，∠AGF ＝∠FCD；(2)首先证明CG是直径，再求CG长度即可解决问题；解：(1)证明：在正方形ABCD中，∠ADC＝90°，∴∠CDF＋∠ADF＝90°，∵AF⊥DE，∴∠AFD＝90°，∴∠DAF＋∠ADF＝90°，∴∠DAF＝∠CDF，∵四边形GFCD是⊙O的内接四边形，∴∠FCD＋∠DGF＝180°，又∵∠FGA＋∠DGF＝180°，∴∠FGA＝∠FCD，∴△AFG∽△DFC；(2)如答图，连结CG.答图∵∠EAD＝∠AFD＝90°，∠EDA＝∠ADF，∴△EDA∽△ADF.∴EAAF＝DADF，即EADA＝AFDF.∵△AFG∽△DFC，∴AGDC＝AF DF.∴AGDC＝EADA.在正方形ABCD中，DA＝DC，∴AG＝EA＝1，DG＝DA－AG＝4－1＝3. ∴CG＝DG2＋DC2＝32＋42＝5.∵∠CDG＝90°，∴CG是⊙O的直径．∴⊙O的半径为5 2.圆与相似三角形的综合运用主要体现在以下几个方面：(1)证明圆中的比例式或等积式；(2)运用相似的性质进行圆的有关计算；(3)运用相似证明圆的切线．判定圆中的相似三角形(1)圆中的角主要有圆心角和圆周角，特别是直径所对的圆周角都是直角，利用圆心角、圆周角等寻找或构造相似三角形是基本思路；(2)利用圆的切线的判定或性质，或切线长定理寻找或构造相似三角形也是重要的方法．1．[太原竞赛]如图，已知△ABC中，∠C＝90°，AC＝11，BC＝5，以C为圆心，BC为半径作圆交BA的延长线于D，则AD的长为__73__．答图【解析】如答图，延长AC与圆相交于E，F，则AF＝5－11，AE＝5＋11，又AB＝6，由相交弦定理AD·AB＝AE·AF得AD＝AE·AFAB＝（5－11）（5＋11）6＝73.2．[第19届江苏竞赛]如图，AB为圆的直径，若AB＝AC＝5，BD＝4，则AE BE＝__724__．【解析】如答图，连结AD，答图∵AB为圆的直径，∴∠E＝90°，AD⊥BC，而AB＝AC＝5，BD＝4，则AD＝3，BD＝DC，∴BC＝2BD＝8，∵∠ACD＝∠BCE，∴Rt△CDA∽Rt△CEB，∴ADBE＝CDCE＝CABC，即3BE＝4CE＝58，所以BE＝245，CE＝325，则AE＝CE－AC＝325－5＝75，所以AEBE＝724.3．[苏州中考]如图，已知△ABC内接于⊙O，AB是直径，点D在⊙O上，OD∥BC，过点D作DE⊥AB，垂足为E ，连结CD 交OE 于点F .(1)求证：△DOE ∽△ABC ； (2)求证：∠ODF ＝∠BDE ；(3)连结OC ，设△DOE 的面积为S 1，四边形BCOD 的面积为S 2，若S 1S 2＝27，求OEOD 的值．解：(1)证明：∵AB 是⊙O 的直径，∴∠ACB ＝90°. ∵DE ⊥AB ，∴∠DEO ＝90°.∴∠DEO ＝∠ACB . ∵OD ∥BC ，∴∠DOE ＝∠ABC ，∴△DOE ∽△ABC ；(2)证明：∵△DOE ∽△ABC ，∴∠ODE ＝∠A .∵∠A 和∠BDC 是BC ︵所对的圆周角，∴∠A ＝∠BDC ，∴∠ODE ＝∠BDC .∴∠ODF ＝∠BDE ；(3)∵△DOE ∽△ABC ，∴S △DOE S △ABC ＝⎝ ⎛⎭⎪⎫OD AB 2＝14，即S △ABC ＝4S △DOE ＝4S 1， ∵OA ＝OB ，∴S △BOC ＝12S △ABC ，即S △BOC ＝2S 1.∵S 1S 2＝27，S 2＝S △BOC ＋S △DOE ＋S △DBE ＝2S 1＋S 1＋S △DBE ，∴S △DBE ＝12S 1，∴BE ＝12OE ，即OE ＝23OB ＝23OD ，∴OE OD ＝23.4．[2018·宁波中考]如图1，直线l ：y ＝－34x ＋b 与x 轴交于点A (4，0)，与y 轴交于点B ，点C 是线段OA 上一动点⎝ ⎛⎭⎪⎫0<AC <165，以点A 为圆心，AC 长为半径作⊙A 交x 轴于另一点D ，交线段AB 于点E .连结OE 并延长交⊙A 于点F .(1)求直线l 的函数表达式和tan ∠BAO 的值． (2)如图2，连结CE ，当CE ＝EF 时． ①求证：△OCE ∽△OEA ； ②求点E 的坐标．(3)当点C 在线段OA 上运动时，求OE ·EF 的最大值．解：(1)∵直线l ：y ＝－34x ＋b 与x 轴交于点A (4，0)， ∴－34×4＋b ＝0，∴b ＝3，∴直线l 的函数表达式为y ＝－34x ＋3， ∴B (0，3)，∴OA ＝4，OB ＝3，在Rt△AOB中，tan∠BAO＝OBOA＝3 4.(2)①证明：如答图①，连结DE，DF，∵CE＝EF，∴∠CDE＝∠FDE，∴∠CDF＝2∠CDE，∵∠OAE＝2∠CDE，∴∠OAE＝∠ODF，∵四边形CEFD是⊙O的圆内接四边形，∴∠OEC＝∠ODF，∴∠OEC＝∠OAE，∵∠COE＝∠EOA，∴△COE∽△EOA；②如答图①，过点E作EM⊥OA于M，由①知，tan∠OAB＝3 4，设EM＝3m，则AM＝4m，∴OM＝4－4m，AE＝5m，∴E(4－4m，3m)，AC＝5m，∴OC＝4－5m，由①知，△COE∽△EOA，∴OCOE＝OEOA，∴OE2＝OA·OC＝4(4－5m)＝16－20m，∵E(4－4m，3m)，∴(4－4m)2＋9m2＝16－20m，解得m ＝0(舍)或m ＝1225，∴4－4m ＝5225，3m ＝3625， ∴E ⎝ ⎛⎭⎪⎫5225，3625.(3)如答图②，设⊙A 的半径为r ，设射线EA 与⊙A 相交于H ，过点O 作OG ⊥AB 于G ，连结FH ，答图①答图②∵A (4，0)，B (0，3)，∴OA ＝4，OB ＝3， ∴AB ＝5，∴12AB ×OG ＝12OA ×OB ，∴OG ＝125， ∴AG ＝OG tan ∠OAB＝125×43＝165， ∴EG ＝AG －AE ＝165－r ，∵EH 是⊙A 直径， ∴EH ＝2r ，∠EFH ＝90°＝∠EGO ， ∵∠OEG ＝∠HEF ，∴△OEG ∽△HEF ， ∴OE HE ＝EG EF ，∴OE ·EF ＝HE ·EG ＝2r ⎝ ⎛⎭⎪⎫165－r ＝－2⎝ ⎛⎭⎪⎫r －852＋12825，∴r ＝85时，OE ·EF 取最大值为12825.类型之二圆的切线与相似三角形例2 [2018·成都]如图，在Rt △ABC 中，∠C ＝90°，AD 平分∠BAC 交BC 于点D ，O 为AB 上一点，经过点A ，D 的⊙O 分别交AB ，AC 于点E ，F ，连结OF 交AD 于点G .(1)求证：BC 是⊙O 的切线；(2)设AB ＝x ，AF ＝y ，试用含x ，y 的代数式表示线段AD 的长； (3)若BE ＝8，sin B ＝513，求DG 的长．【思路生成】(1)连结OD ，由AD 为角平分线得到一对角相等，再由等边对等角得到一对角相等，等量代换得到内错角相等，进而得到OD 与AC 平行，得到OD 与BC 垂直，即可得证；(2)连结DF ，由(1)得到BC 为⊙O 的切线，由弦切角等于夹弧所对的圆周角，进而得到△ABD 与△ADF 相似，由相似得比例，即可表示出AD ；(3)连结EF ，设圆的半径为r ，由sin B 的值，利用锐角三角函数定义求出r 的值，由直径所对的圆周角为直角，得到EF 与BC 平行，得到sin ∠AEF ＝sin B ，进而求出DG 的长即可．解：(1)证明：如答图，连结OD ，答图∵AD为∠BAC的平分线，∴∠BAD＝∠CAD，∵OA＝OD，∴∠ODA＝∠OAD，∴∠ODA＝∠CAD，∴OD∥AC，∵∠C＝90°，∴∠ODC＝90°，∴OD⊥BC，又⊙O过点D，∴BC为⊙O的切线；(2)如答图，连结DF，由(1)知BC为⊙O的切线，∴∠FDC＝∠DAF，∴∠CDA＝∠CFD，∴∠AFD＝∠ADB，∵∠BAD＝∠DAF，∴△ABD∽△ADF，∴ABAD＝ADAF，即AD2＝AB·AF＝xy，则AD＝xy；(3)如答图，连结EF，在Rt△BOD中，sin B＝ODOB＝513，设圆的半径为r，可得rr＋8＝513，解得r＝5，∴AE＝10，AB＝18，∵AE是直径，∴∠AFE＝∠C＝90°，∴EF ∥BC ，∴∠AEF ＝∠B ，∴sin ∠AEF ＝AF AE ＝513，∴AF ＝AE ·sin ∠AEF ＝10×513＝5013，∵AF ∥OD ，∴AG DG ＝AF OD ＝50135＝1013，即DG ＝1323AD ，∴AD ＝AB ·AF ＝18×5013＝301313，则DG ＝1323×301313＝301323.5．[2018·淄博中考]如图，以AB 为直径的⊙O外接于△ABC ，过A 点的切线AP 与BC 的延长线交于点P .∠APB 的平分线分别交AB ，AC 于点D ，E ，其中AE ，BD (AE <BD )的长是一元二次方程x 2－5x ＋6＝0的两个实数根．(1)求证：P A ·BD ＝PB ·AE ；(2)在线段BC 上是否存在一点M ，使得四边形ADME 是菱形？若存在，请给予证明，并求其面积；若不存在，说明理由．解：(1)证明：∵AP 为⊙O 的切线，AB 是直径，∴∠BAP ＝90°，即∠BAC ＋∠EAP ＝90°，∵AB 为直径，∴∠ACB ＝90°，即∠BAC ＋∠DBP ＝90°，∴∠EAP＝∠DBP，又∵PD平分∠APB，∴∠APE＝∠BPD，∴△APE∽△BPD，∴P AAE＝PBBD，∴P A·BD＝PB·AE；(2)存在．如答图，过点D作DM⊥BC于点M，连结EM，答图∵PD平分∠APB，又AD⊥P A，DM⊥PM，∴DM＝DA，∵∠AED＝∠EAP＋∠APE，∠ADE＝∠DBP＋∠BPD，又由(1)知∠EAP＝∠DBP，∠APE＝∠BPD，∴∠AED＝∠ADE，∴AD＝AE，∴DM＝AE，∵DM⊥BC，AC⊥BC，∴DM∥AC，∴四边形ADME为菱形，易得x2－5x＋6＝0的两个根为2，3，∵AE<BD，∴BD＝3，AE＝2，∵四边形ADME为菱形，∴DM＝AE＝AD＝2，在Rt△BDM中，BD＝3，DM＝2，∴BM＝32－22＝5，∵DM∥AC，∴BDDA＝BM MC，∴32＝5MC，∴MC＝253，∴S菱形ADME ＝AE·MC＝2×235＝453.6．[2018·遂宁中考]如图，过⊙O外一点P作⊙O的切线P A切⊙O于点A，连结PO并延长，与⊙O交于C，D两点，M是半圆CD的中点，连结AM交CD于点N，连结AC，CM.(1)求证：CM2＝MN·MA；(2)若∠P＝30°，PC＝2，求CM的长．解：(1)证明：∵在⊙O中M点是半圆CD的中点，∴∠CAM＝∠DCM，又∵∠M是公共角，∴△CMN∽△AMC，∴CMAM＝MNMC，∴CM2＝MN·MA；(2)如答图，连结OA，DM，答图∵P A是⊙O的切线，∴∠P AO＝90°，又∵∠P＝30°，∴OA＝12PO＝12(PC＋CO)，设⊙O的半径为r，∵PC＝2，∴r＝12(2＋r)，解得r＝2，又∵CD是直径，∴∠CMD＝90°，∵M点是半圆CD的中点，∴CM＝DM，∴△CMD是等腰直角三角形，∴在Rt△CMD中，由勾股定理得CM2＋DM2＝CD2，∴2CM2＝(2r)2＝16，解得CM＝2 2.类型之三证明圆中的比例式或乘积式例3[天津竞赛]如图，BC是半圆O的直径，D是弧AC的中点，四边形ABCD的对角线AC，BD交于点E.(1)求证：AC·BC＝2BD·CD；(2)若AE＝3，CD＝25，求弦AB和直径BC的长．【思路生成】(1)连结OD交AC于点F，由于D是弧AC的中点，∠ACD＝∠ABD＝∠CBD，由垂径定理知，AF＝CF＝12AC.∠CFD＝∠BDC＝90°，则有△CDF∽△BCD；(2)延长BA，CD交于点G，易得Rt△CDE∽Rt△CAG，由比例线段解得CE ＝5，在Rt△ACG中，由勾股定理得AG＝4，由割线定理知，GA·GB＝GD·GC，即4(AB＋4)＝25×45，解得AB＝6.在Rt△ABC中，由勾股定理可求得BC的值．解：(1)证明：如答图，连结OD交AC于点F，答图∵D是弧AC的中点，∴∠ACD＝∠ABD＝∠CBD，且AF＝CF＝12AC.∵BC为直径，∴∠BDC＝90°，又∵∠CFD＝90°，∴△CDF∽△BCD.∴CFBD＝CDBC，∴CF·BC＝BD·CD.∴AC·BC＝2BD·CD；(2)如答图，延长BA，CD交于点G，由(1)得∠ABD＝∠CBD，∠BDC＝90°，∴△BCG为等腰三角形，∴BD平分CG，∴CG＝2CD＝45，∴Rt△CDE∽Rt△CAG，∴CECG＝CDCA，即CE45＝25CE＋3，解得CE＝5或CE＝－8(舍去)．在Rt△ACG中，由勾股定理得AG＝CG2－AC2＝（45）2－（3＋5）2＝4，∵GA·GB＝GD·GC，即4(AB＋4)＝25×45，解得AB＝6.在Rt△ABC中，由勾股定理得BC＝AB2＋AC2＝62＋（3＋5）2＝10.7．如图，已知四边形ABCD为圆的内接四边形，求证：AB·CD＋AD·BC＝AC·BD.答图证明：如答图，在BD上取一点E，使∠BCE＝∠ACD，即得△BEC∽△ADC，可得BE BC ＝AD AC ，即AD ·BC ＝BE ·AC ，①又∵∠ACB ＝∠DCE ，可得△ABC ∽△DEC ，即得AB AC ＝DE DC ，即AB ·CD ＝DE ·AC ，②由①＋②，可得AB ·CD ＋AD ·BC ＝AC (BE ＋DE )＝AC ·BD .8．[江苏竞赛]如图，AB ，AC ，AD 是圆中的三条弦，点E 在AD 上，且AB ＝AC ＝AE .请你说明以下各式成立的理由：(1)∠CAD ＝2∠DBE ；(2)AD 2－AB 2＝BD ·DC .证明：(1)如答图，延长BE 交圆于点F ，连结AF ，则∠DBF ＝∠DAF ，答图∵AB ＝AE ，∴∠ABE ＝∠AEB ＝∠DAF ＋∠F ，∴AF ︵＝AC ︵＋CF ︵＝AB ︵＋DF ︵，∵AB ＝AC ，∴AB ︵＝AC ︵，∴CF ︵＝DF ︵，即点F 是CD ︵的中点，∴∠CAD ＝2∠DAF ＝2∠DBE ；(2)如答图，连结BC 交AD 于点G ，∵AB ＝AC ，∴∠ADB ＝∠ABC ，∠BAG ＝∠DAB ，∴△BAG ∽△DAB .∴AB AG ＝AD AB ，即AB 2＝AG ·AD .∴AD 2－AB 2＝AD 2－AG ·AD ＝AD (AD －AG )＝AD ·DG ，∵∠BDA ＝∠ADC ，∠DBG ＝∠DAC ，∴△BDG ∽△ADC .∴BD AD ＝DG DC ，∴AD ·DG ＝BD ·DC .∴AD 2－AB 2＝BD ·DC .相似三角形解决圆中计算问题作辅助线构造直角是证明圆中三角形相似的常见方法．圆中三角形的相似常见的基本图形如下图所示．类型之四利用相似三角形解决圆中的计算问题例4 [2018·武汉中考]如图，P A 是⊙O 的切线，A 是切点，AC 是直径，AB 是弦，连结PB ，PC ，PC交AB 于点E ，且P A ＝PB .(1)求证：PB 是⊙O 的切线；(2)若∠APC ＝3∠BPC ，求PE CE 的值．【思路生成】(1)连结OB ，OP ，△OAP 与△OBP 三边对应相等，这两个三角形全等，得∠OBP ＝∠OAP ＝90°，故PB 是⊙O 的切线；(2)连结BC ，AB 与OP 交于点H ，易证OP ⊥AB ，∠OPC ＝∠PCB ＝∠CPB ，由△OAH ∽△CAB 得OH CB ＝12；由△HPB ∽△BPO ，求得HP OH ；再由△HPE ∽△BCE ，可得PE CE 的值．解：(1)证明：如答图，连结OB ，OP ，在△OAP 和△OBP 中，⎩⎪⎨⎪⎧OA ＝OB ，OP ＝OP ，AP ＝BP ，∴△OAP ≌△OBP (SSS )，∴∠OBP ＝∠OAP ，∵P A 是⊙O 的切线，∴∠OBP ＝∠OAP ＝90°，∴PB 是⊙O 的切线；(2)如答图，连结BC ，AB 与OP 交于点H ，答图∵∠APC ＝3∠BPC ，设∠BPC ＝x ，则∠APC ＝3x ，∠APB ＝x ＋3x ＝4x ，由(1)知∠APO ＝∠BPO ＝2x ，∴∠OPC ＝∠CPB ＝x ，∵AC 是⊙O 的直径，∴∠ABC ＝90°，由P A ＝PB ，∠APH ＝∠BPH 可得OP ⊥AB ，∴∠AHO ＝∠ABC ＝90°，即OP ∥BC ，∴∠OPC ＝∠PCB ＝∠CPB ＝x ，∴CB ＝BP ，易证△OAH∽△CAB，∴OHCB＝OAAC＝12，设OH＝a，则CB＝BP＝2a，易证△HPB∽△BPO，∴HPBP＝BPOP，设HP＝ya，则ya2a＝2aa＋ya，解得y1＝－1－172(舍)或y2＝－1＋172，∵OP∥CB，易证△HPE∽△BCE，∴PECE＝HPCB＝ya2a＝－1＋174.9．[2018·鄂州中考]如图，四边形ABCD内接于⊙O，BC为⊙O的直径，AC 与BD交于点E，P为CB延长线上一点，连结P A，且∠P AB＝∠ADB.(1)求证：AP是⊙O的切线；(2)若AB＝6，tan∠ADB＝34，求PB的长；(3)在(2)的条件下，若AD＝CD，求△CDE的面积．解：(1)证明：如答图，连结OA，∵OA＝OC，∴∠OCA＝∠OAC，又∵∠P AB＝∠ADB，∠OCA＝∠ADB，∴∠OAC＝∠P AB，∵BC为⊙O的直径，∴∠CAB＝90°，∴∠OAC＋∠OAB＝90°，∴∠P AB＋∠OAB＝90°，即OA⊥AP，∴AP是⊙O的切线；(2)如答图，过点B作BF⊥AP于点F，答图∵∠ACB＝∠P AB＝∠ADB，AB＝6，tan∠ADB＝3 4，∴BC＝10，BFAF＝34，设BF＝3a，AF＝4a，又∵AB＝6，∴(3a)2＋(4a)2＝62，∴a＝65，∴BF＝3a＝185，AF＝4a＝245，∵OA⊥AP，BF⊥AP，∴BF∥OA，∴BFOA＝BPOP，即1855＝BPBP＋5，解得PB＝907；(3)如答图，连结OD交AC于点G，∵CD＝AD，∴OD⊥AC，并且CG＝AG＝12AC＝4，在Rt△COG中，由勾股定理可得OG＝OC2－CG2＝52－42＝3，∴DG＝OD－OG＝5－3＝2，S△CDG＝12CG·DG＝12×4×2＝4.显然Rt△CDG∽Rt△CED，∴S△CDES△CDG＝⎝⎛⎭⎪⎫CDCG2＝⎝⎛⎭⎪⎫2542＝54，∴S△CDE ＝54S△CDG＝54×4＝5.圆与相似三角形的综合运用(1)证明圆的切线的常用辅助线是作过切点的半径，证明直线与这条半径垂直；(2)运用切线的性质时，常连结切点和圆心．类型之五圆与相似三角形的综合运用例5 [2017·温州中考]如图，已知线段AB ＝2，MN ⊥AB 于点M ，且AM ＝BM ，P 是射线MN 上一动点，E ，D 分别是P A ，PB 的中点，过点A ，M ，D 的圆与BP 的另一交点为C (点C 在线段BD 上)，连结AC ，DE .(1)当∠APB ＝28°时，求∠B 和CM ︵所对的圆心角的度数．(2)求证：AC ＝AB .(3)在点P 的运动过程中．①当MP ＝4时，取四边形ACDE 一边的两端点和线段MP 上一点Q ，若以这三点为顶点的三角形是直角三角形，且Q 为锐角顶点，求所有满足条件的MQ 的值；②记AP 与圆的另一个交点为F ，将点F 绕点D 旋转90°得点G ，当点G 恰好落在MN 上，连结AG ，CG ，DG ，EG ，直接写出△ACG 与△DEG 的面积比．【思路生成】(1)根据三角形ABP 是等腰三角形，可得∠B 的度数，再连结MD ，根据MD 为△P AB 的中位线，可得∠MDB ＝∠APB ＝28°；(2)由等角的补角相等，得∠ACB ＝∠B ，则AC ＝AB ；(3)①由垂直平分线的性质，分类讨论符合条件的点Q 的个数，利用相似和勾股定理分别求出MQ 的长度；②利用旋转的性质，平行四边形的性质，锐角三角比求出各边的长度，用面积公式求出比值．解：(1)∵MN ⊥AB ，AM ＝BM ，∴P A ＝PB ，∴∠P AB ＝∠B ，答图①∵∠APB ＝28°，∴∠B ＝76°，如答图①，连结MD ，∵MD 为△P AB 的中位线，∴MD ∥AP ，∴∠MDB ＝∠APB ＝28°，∴CM ︵所对的圆心角的度数为2∠MDB ＝56°.(2)证明：∵∠BAC ＝∠MDC ＝∠APB ，又∵∠BAP ＝180°－∠APB －∠B ，∠ACB ＝180°－∠BAC －∠B ， ∴∠BAP ＝∠ACB ，∵∠BAP ＝∠B ，∴∠ACB ＝∠B ，∴AC ＝AB .(3)①记MP 与圆的另一个交点为R ，∵MD 是Rt △MBP 的中线，∴DM ＝DP ，∴∠DPM＝∠DMP＝∠RCD，∴RC＝RP，∵∠ACR＝∠AMR＝90°，∴AM2＋MR2＝AR2＝AC2＋CR2，∴12＋MR2＝22＋PR2，∴12＋(4－PR)2＝22＋PR2，∴PR＝138，∴MR＝198，Ⅰ.当∠ACQ＝90°时，AQ为圆的直径，∴Q与R重合，∴MQ＝MR＝19 8；Ⅱ.如答图②，当∠QCD＝90°时，在Rt△QCP中，由PR＝CR可知PQ＝2PR＝134，∴MQ＝34；答图②答图③Ⅲ.如答图③，当∠QDC＝90°时，∵BM＝1，MP＝4，∴BP＝17，∴DP＝12BP＝172，∵△PBM∽△PQD，∴MPPB＝DPPQ，∴PQ＝178，∴MQ＝158；Ⅳ.如答图④，当∠AEQ＝90°时，答图④由AE＝PE，可得AQ＝PQ，设MQ＝x，则x2＋1＝(4－x)2，解得x＝15 8，∴MQ＝15 8；综上所述，MQ的值为198或34或158；②△ACG和△DEG的面积之比为6－233.理由：如答图⑤，过C作CH⊥AB于H，答图⑤∵DM∥AF，DE∥AB，∴四边形AMDE 是平行四边形，四边形AMDF 是等腰梯形，∴DF ＝AM ＝DE ＝1，又由对称性可得GE ＝GD ，并且DG ＝DF ，∴△DEG 是等边三角形， ∴∠EDF ＝90°－60°＝30°，∴∠DEF ＝75°＝∠MDE ，∴∠GDM ＝75°－60°＝15°，∴∠GMD ＝∠PGD －∠GDM ＝15°， ∴∠GMD ＝∠GDM ，∴GM ＝GD ＝1，由∠B ＝∠BAP ＝∠DEF ＝75°，得∠BAC ＝30°，从而CH ＝12AC ＝12AB ＝1＝MG ，AH ＝3，∴CG ＝MH ＝3－1，∴S △ACG ＝12CG ×CH ＝3－12，∵S △DEG ＝34，∴S △ACG ∶S △DEG ＝6－233.10．[2018·温州中考]如图，已知P 为锐角∠MAN内部一点，过点P 作PB ⊥AM 于点B ，PC ⊥AN 于点C ，以PB 为直径作⊙O ，交直线CP 于点D ，连结AP ，BD ，AP 交⊙O 于点E .(1)求证：∠BPD ＝∠BAC .(2)连结EB ，ED ，当tan ∠MAN ＝2，AB ＝25时，在点P 的整个运动过程中．①若∠BDE ＝45°，求PD 的长；②若△BED 为等腰三角形，求所有满足条件的BD 的长．(3)连结OC ，EC ，OC 交AP 于点F ，当tan ∠MAN ＝1，OC ∥BE 时，记△OFP的面积为S 1，△CFE 的面积为S 2，请写出S 1S 2的值．解：(1)证明：∵PB ⊥AM ，PC ⊥AN ，∴∠ABP ＝∠ACP ＝90°，∴∠BAC ＋∠BPC ＝180°，又∠BPD ＋∠BPC ＝180°，∴∠BPD ＝∠BAC .(2)①如答图①，∵∠APB ＝∠BDE ＝45°，∠ABP ＝90°，∴BP ＝AB ＝25，∵∠BPD ＝∠BAC ，∴tan ∠BPD ＝tan ∠BAC ，∴BD DP ＝2，∴BP ＝5PD ，∴PD ＝2；②Ⅰ.当BD ＝BE 时，∠BED ＝∠BDE ，∴∠BPD ＝∠BED ＝∠BDE ＝∠BPE ＝∠BAC ，∴tan ∠BPE ＝2， ∵AB ＝25，∴BP ＝5，∴BD ＝2；Ⅱ.当BE ＝DE 时，∠EBD ＝∠EDB ，∵∠APB＝∠BDE，∠DBE＝∠APC，∴∠APB＝∠APC，∴AC＝AB＝25，如答图①过点B作BG⊥AC于点G，则四边形BGCD是矩形，答图①∵AB＝25，tan∠BAC＝2，∴AG＝2，∴BD＝CG＝25－2；Ⅲ.当BD＝DE时，∠DEB＝∠DBE＝∠APC，∵∠DEB＝∠DPB＝∠BAC，∴∠APC＝∠BAC，设PD＝x，则BD＝2x，∴ACPC＝2，而AG＝2，CD＝BG＝4，∴2x＋24－x＝2，∴x＝32，∴BD＝2x＝3，综上所述，当BD＝2，3或25－2时，△BDE为等腰三角形．(3)如答图②，过点O作OH⊥DC于点H，答图②∵tan∠BPD＝tan∠MAN＝1，∴BD＝PD，设BD＝PD＝2a，PC＝2b，则OH＝a，CH＝a＋2b，AC＝4a＋2b，∵OC∥BE且∠BEP＝90°，∴∠PFC＝90°，∴∠P AC＋∠APC＝∠OCH＋∠APC＝90°，∴∠OCH＝∠P AC，∴△ACP∽△CHO，∴OHCH＝PCAC，即OH·AC＝CH·PC，∴a(4a＋2b)＝2b(a＋2b)，∴a＝b，即CP＝2a，CH＝3a，则OC＝10a，∵△CPF∽△COH，∴CFCH＝CPOC，即CF3a＝2a10a，则CF＝3105a，OF＝OC－CF＝2105a，∵BE∥OC且BO＝PO，∴OF为△PBE的中位线，∴EF＝PF，∴S1S2＝OFCF＝23.例6[全国数学联赛题]如图，已知四边形ABCD外接圆O的半径为2，对角线AC与BD的交点为E，AE＝EC，AB＝2AE，且BD＝23，求四边形ABCD的面积．【思路生成】先求△ABD的面积，再证△ABD与△BCD的面积相等即可．解：如答图，连结AO，交BD于H，连结OB，答图∵AE＝EC，AB＝2AE，∴AB2＝2AE2＝AE·AC，∴ABAC＝AEAB，又∠EAB＝∠BAC，∴△ABE∽△ACB，∴∠ABE＝∠ACB＝∠ADB，∴AB＝AD.∵AB ＝AD ，∴AO ⊥BD ，∴BH ＝HD ，∵BO ＝2，BD ＝23，∴BH ＝HD ＝ 3.∴OH ＝OB 2－BH 2＝4－3＝1，AH ＝OA －OH ＝2－1＝1.∴S △ABD ＝12BD ·AH ＝12×23×1＝3，∵E 是AC 的中点，∴S △ABE ＝S △BCE ，S △ADE ＝S △CDE ，∴S △ABD ＝S △BCD ，∴S 四边形ABCD ＝2S △ABD ＝2 3.[学生用书P67]【思维入门】1．[余姚自主招生]如图，AB 是半圆的直径，点C 是AB ︵的中点，点E 是AC ︵的中点，连结EB ，CA 交于点F ，则EF BF ＝( D )A.13B.14C.1－22 D.2－12【解析】连结AE ，CE ，作AD ∥CE ，交BE 于点D ，答图∵点E 是AC ︵的中点，设AE ＝CE ＝x ，根据平行线的性质得∠ADE ＝∠CED ＝45°，∴△ADE 是等腰直角三角形，则AD ＝2x ，又∠DAF ＝∠ACE ＝∠CAE ＝∠CBE ，而∠CAB ＝∠CBA ＝45°，∴∠DAB ＝∠DBA ，∴BD ＝AD ＝2x ，∴BE ＝(2＋1)x .∵∠EAC ＝∠ABE ，∠AEF ＝∠BEA ，∴△AEF ∽△BEA ，∴AE BE ＝EF EA ，∴EF ＝(2－1)x ，BF ＝2x .∴EF BF ＝2－12.2．[雨花区自主招生]如图，BC 是半圆O 的直径，EF ⊥BC 于点F ，BF FC ＝5，又AB ＝8，AE ＝2，则AD 的长为( B )A ．1＋ 3 B.1＋32 C.32 D ．1＋ 2 【解析】如答图，连结BE .答图∵BC是直径．∴∠AEB＝∠BEC＝90°，在Rt△ABE中，根据勾股定理可得BE2＝AB2－AE2＝82－22＝60.∵BFFC＝5，∴设FC＝x，则BF＝5x，BC＝6x，又∵BE2＝BF·BC，即30x2＝60，解得x＝2，∴EC2＝FC·BC＝6x2＝12，∴EC＝23，∴AC＝AE＋EC＝2＋23，∵AD·AB＝AE·AC，∴AD＝AE·ACAB＝2（2＋23）8＝1＋32.3．[天津中考]如图，已知△ABC为等腰直角三角形，D为斜边BC的中点，经过点A，D的⊙O与边AB，AC，BC分别相交于点E，F，M.对于如下五个结论：①∠FMC＝45°；②AE＋AF＝AB；③EDEF＝BABC；④2BM2＝BE·BA；⑤四边形AEMF为矩形．其中正确结论的个数是(C)A．2个B．3个C．4个D．5个【解析】如答图，连结AM，根据等腰三角形的三线合一，得AD⊥BC，答图再根据90°的圆周角所对的弦是直径，得EF，AM是直径，根据对角线相等且互相平分的四边形是矩形，得四边形AEMF是矩形，∴①根据等腰直角三角形ABC的底角是45°，易得∠FMC＝45°，正确；②根据矩形和等腰直角三角形的性质，得AE＋AF＝AB，正确；③连结FD，可以证明△EDF是等腰直角三角形，则③中左右两边的比都是等腰直角三角形的直角边和斜边的比，正确；④根据BM＝2BE，得左边＝4BE2，故需证明AB＝4BE，根据已知条件它们之间不一定有这种关系，错误；⑤正确．所以①②③⑤共4个正确．4．[麻城自主招生]如图，⊙O与Rt△ABC的斜边AB相切于点D，与直角边AC相交于点E，且DE∥BC.已知AE＝22，AC＝32，BC＝6，则⊙O的半径是(D)A．3 B．4C．4 3 D．2 3【解析】如答图，延长EC交⊙O于点F，连结DF.则根据90°的圆周角所对的弦是直径，得DF是直径，答图∵DE∥BC，∴△ADE∽△ABC.∴DEBC＝AEAC.则DE＝4.由Rt△ADE∽Rt△DFE，得EF＝DE2AE＝4 2.根据勾股定理，得DF＝DE2＋EF2＝16＋32＝43，则圆的半径是2 3.5．[淮安自主招生]如图，△ABC中，∠C＝90°，O为AB上一点，以O为圆心，OB为半径的圆与AB相交于点E，与AC相切于点D，已知AD＝2，AE＝1，那么BC＝__125__．答图【解析】如答图，连结OD ，∵AC 为⊙O 的切线，∴OD ⊥AC ，在Rt △ADO 中，设OD ＝R ，∵AD ＝2，AE ＝1，∴22＋R 2＝(R ＋1)2，解得R ＝32，∴AO ＝52，AB ＝4，又∵∠C ＝90°，∴OD ∥BC ，∴△AOD ∽△ABC ，∴OD BC ＝OA AB ，即BC ＝4×3252＝125.6．[2018·柳州]如图，△ABC 为⊙O 的内接三角形，AB 为⊙O 的直径，过点A 作⊙O 的切线交BC 的延长线于点D .(1)求证：△DAC ∽△DBA ；(2)过点C 作⊙O 的切线CE 交AD 于点E ，求证：CE ＝12AD ；(3)若点F 为直径AB 下方半圆的中点，连结CF 交AB于点G，且AD＝6，AB＝3，求CG的长．解：(1)证明：∵AB是⊙O直径，∴∠ACD＝∠ACB＝90°，答图∵AD是⊙O的切线，∴∠BAD＝90°，∴∠ACD＝∠DAB＝90°，∵∠D＝∠D，∴△DAC∽△DBA；(2)证明：∵EA，EC是⊙O的切线，∴AE＝CE，∴∠DAC＝∠ECA，∵∠ACD ＝90°，∴∠ACE ＋∠DCE ＝90°，∠DAC ＋∠D ＝90°，∴∠D ＝∠DCE ，∴DE ＝CE ，∴AD ＝AE ＋DE ＝CE ＋CE ＝2CE ，∴CE ＝12AD ；(3)如答图，过点G 作GH ⊥BD 于H ，在Rt △ABD 中，AD ＝6，AB ＝3，∴tan ∠ABD ＝AD AB ＝2，∴tan ∠ABD ＝GH BH ＝2，∴GH ＝2BH ，∵点F 是直径AB 下方半圆的中点，∴∠BCF ＝45°，∴∠CGH ＝90°－∠BCF ＝45°，∴CH ＝GH ＝2BH ，∴BC ＝BH ＋CH ＝3BH ，在Rt △ABC 中，tan ∠ABC ＝AC BC ＝2，∴AC ＝2BC ，根据勾股定理得，AC 2＋BC 2＝AB 2，∴4BC 2＋BC 2＝9，∴BC ＝355，∴3BH ＝355，∴BH ＝55，∴GH＝2BH＝25 5，在Rt△CHG中，∠BCF＝45°，∴CG＝2GH＝2105.【思维拓展】7．[瓯海区自主招生]如图，已知：P A切⊙O于A，若AC为⊙O的直径，PBC为⊙O的割线，E为弦AB的中点，PE的延长线交AC于F，且∠FPB＝45°，点F到PC的距离为5，则FC的长为(C)A．10 B．12 C．5 5 D．5 6【解析】设PB＝x，∵P A切⊙O于A，∴AP⊥AC，∴∠P AC＝90°，∵AC为⊙O的直径，∴∠ABC＝90°，∵∠FPB＝45°，∴BE＝PB＝x，AB＝2x，PH＝FH＝5，∵∠C＋∠BAC＝90°，∠P AB＋∠BAC＝90°，∴∠C＝∠P AB，∴△APB∽△CAB，∴AB BC ＝PB AB ，即2x BC ＝x 2x ，解得BC ＝4x ，∴CH ＝PC －PH ＝PB ＋BC －PH ＝5x －5，∵FH ∥AB ，∴△CFH ∽△CAB ，∴FH AB ＝CH CB ，即52x ＝5x －54x ，解得x ＝3，∴CH ＝5x －5＝10，在Rt △CFH 中，CF ＝FH 2＋CH 2＝52＋102＝5 5.8．[成都自主招生]如图，过⊙O 直径AB 上的点C 作AB 的垂线交⊙O 于点D ，再过D 点作圆的切线l ，然后过C 点作l 的垂线交l 于点E ，若AC ＝a ，CB ＝b ，那么CE长为( A )A.2ab a ＋bB.abC.a ＋b 2D. a 2＋b 22 【解析】如答图，连结OD ，答图∵AB ＝AC ＋BC ＝a ＋b ，∴OD＝12(a＋b)，∴OC＝OA－AC＝12(a＋b)－a＝12(b－a)，∵CD⊥AB，∴∠DCO＝90°，在Rt△DCO中，CD＝OD2－OC2＝ab，∵l与⊙O相切于点D，∴OD⊥l，∵CE⊥l，∴OD∥CE，∴∠ODC＝∠ECD，∴Rt△ODC∽Rt△DCE，∴CDCE＝ODCD，即abCE＝12（a＋b）ab，∴CE＝2ab a＋b.9．[第23届“希望杯”竞赛]如图，已知A，B，C三点在同一圆上，并且AB是⊙O的直径，若点C到AB的距离CD＝5，则⊙O的直径最小值是__10__．【解析】AD·DB＝CD2＝25，AB2＝(AD＋BD)2＝(AD －BD)2＋4AD·BD≥4AD·BD＝100，当AD＝BD时，AB取得最小值10.10．[成都中考]如图，在半径为5的⊙O 中，弦AB＝8，P 是弦AB 所对的优弧上的动点，连结AP ，过点A作AP 的垂线交射线PB 于点C ，当△P AB 是等腰三角形时，线段BC 的长为__8或5615或853__．【解析】 Ⅰ.当BA ＝BP 时，则AB ＝BP ＝BC ＝8，即线段BC 的长为8.Ⅱ.当AB ＝AP 时，如答图①，延长AO 交PB 于点D ，过点O 作OE ⊥AB 于点E ，则AD ⊥PB ，AE ＝12AB ＝4，∴BD ＝DP ，答图①在Rt △AEO 中，AE ＝4，AO ＝5，∴OE ＝3，∵∠OAE ＝∠BAD ，∠AEO ＝∠ADB ＝90°，∴△AOE ∽△ABD ，∴AO AB ＝OE BD ，∴BD ＝245，∴BD ＝PD ＝245，即PB ＝485，∵AB＝AP＝8，∴∠ABD＝∠P，∵∠P AC＝∠ADB＝90°，∴△ABD∽△CP A，∴BDAB＝P ACP，∴CP＝403，∴BC＝CP－BP＝403－485＝5615；Ⅲ.当P A＝PB时，如答图②，连结PO并延长，交AB于点F，过点C作CG⊥AB，交AB的延长线于点G，连结OB，则PF⊥AB，答图②∴AF＝FB＝4，在Rt△OFB中，OB＝5，FB＝4，∴OF＝3，∴FP＝8，∵∠P AF＝∠ABP＝∠CBG，∠AFP＝∠CGB＝90°，∴△PFB∽△CGB，∴PFFB＝CGBG＝21，设BG＝t，则CG＝2t，∵∠CAG＝∠APF，∠AFP＝∠AGC＝90°，∴△APF∽△CAG，∴AFPF＝CGAG，∴2t8＋t＝12，解得t＝83，在Rt△BCG中，BC＝5t＝85 3，综上所述，当△P AB是等腰三角形时，线段BC的长为8或5615或853.11．如图，已知AB是⊙O的直径，BC是⊙O的切线，OC平行于弦AD，过点D作DE⊥AB于E，交AC于点P，求证：点P平分线段DE.答图证明：如答图，连结OD，∵OC∥AD，∴∠COD＝∠ADO，∠COB＝∠DAO，∵OA＝OD，∴∠ADO＝∠DAO，∴∠COD＝∠COB，∵OD＝OB，OC＝OC，∴△ODC≌△OBC，∴∠ODC＝∠OBC.∵OB是⊙O的半径，BC是⊙O的切线，∴BC⊥OB.∴∠OBC＝90°，∴∠ODC＝90°，∴CD⊥OD，∴CD是⊙O的切线．过A作⊙O的切线AF，交CD的延长线于点F，则F A⊥AB. ∵DE⊥AB，CB⊥AB，∴F A∥DE∥CB，∴FDFC＝AEAB.在△F AC中，∵DP∥F A，∴DPF A＝DCFC，即DPDC＝F AFC.∵F A，FD是⊙O的切线，∴F A＝FD，。

第20讲圆与相似三角形的结合复习课件(共38张PPT)

在 Rt△ADC 中，∵∠ACD＝30°，∴AD＝1，CD＝ 3， S 阴影＝S 梯形 OCDA－S 扇形 AOC＝12(1＋2)× 3－60·3π60·22＝ 323－2π3 .
全效优等生
大师导航归类探究自主招生交流平台思维训练
圆与类似三角形的综合运用 (1)证明圆的切线的常用辅助线是作过切点的半径，证明直线与这条半径垂直； (2)运用切线的性质时，常连结切点和圆心．
CD＝235.
又∵CF＝FD，∴CF＝12CD＝12×235＝265，
∴EF＝CF－CE＝265－3＝76，
7
∴在 Rt△AFE 中，sin∠EAF＝EAFE＝63＝178.
全效优等生
大师导航归类探究自主招生交流平台思维训练
2．如图6－20－4，在△ABC中，BA＝ BC，以AB为直径作半圆O，交AC于点D.连结DB，过点D作DE⊥BC，垂足为点E.
∴AD＝3，BD＝
3.∴B2E＝
33，∴BE＝23
3 .
全效优等生
大师导航归类探究自主招生交流平台思维训练
(3)如答图②，当 E 与 A 重合时，∵AB 是直径，AD⊥CD， ∴∠ADB＝∠ADC＝90°，∴C，D，B 共线．
∵AC⊥AB，∴在 Rt△ABC 中，AB＝2 3，AC＝2， ∴tan∠ABC＝AACB＝ 33，∴∠ABC＝30°， ∴α＝∠DAB＝90°－∠ABC＝60°，当E′在BA的延长线上时，可得∠D′AB>∠DAB＝60°， ∵0°<α<90°，∴α的取值范围是60°<α<90°.
全效优等生
大师导航归类探究自主招生交流平台思维训练
判定圆中的类似三角形例1 如图6－20－1，AC是⊙O的直径，弦BD交AC于点E. (1)求证：△ADE∽△BCE； (2)如果AD2＝AE•AC，求证：CD＝CB.

中考数学圆与相似-经典压轴题

（2）当点 E 在线段 AC 上运动时，点 F 也随着运动，若四边形 ABFC 的面积为，求 AE 的长；（3）如图 2，当点 E 在 AC 的延长线上运动时，CF、BE 相交于点 D，请你探求△ ECD 的面积 S1 与△ DBF 的面积 S2 之间的数量关系，并说明理由；
（4）如图 2，当△ ECD 的面积 S1＝时，求 AE 的长．【答案】（1）解：现点 E 沿边 AC 从点 A 向点 C 运动过程中，始终有△ ABE≅△ CBF. 由图 1 知，△ ABC 与△ EBF 都是等边三角形，∴ AB=CB，BE=BF，∠ ABC=∠ EBF=60°， ∴ ∠ CBF=∠ ABE=60°-∠ CBE，∴ △ ABE≅△ CBF. （2）解：由（1）知点 E 在运动过程中始终有△ ABE≅△ CBF，因四边形 BECF 的面积等于三角形 BCF 的面积与三角形 BCE 的面积之和， ∴ 四边形 BECF 的面积等于 △ ABC 的面积，因 △ ABC 的边长为 2 ，则
∴ 在 Rt△ ABC 中，BC=
（2）在 Rt△ ABC 中，AB= 如图 2，当点 D 在线段 BC 上时，此时只有 GF=GD
又∠ CBF=∠ ABE=60°+∠ CBE，∴ △ ABE≅△ CBF，
∴
，∴
，
则
，则
（4）解：由（3）知
，即
，
由
得
，∵ △ ABE≅△ CBF，
∴ AE=CF，∠ BAE=∠ BCF=60°，
又∠ BAE=∠ ABC=60°，得∠ ABC=∠ BCF，∴ CF∥ AB，则△ BDF 的边 CF 上的高与△ ABC 的高
四边形 ACDB 是菱形，又∵ ∠ ACD 与△ FCE 中的∠ FCE 重合，它的对角∠ ABD 顶点在 EF 上， ∴ 四边形 ACDB 为△ FEC 的亲密菱形. （2）解：设菱形 ACDB 的边长为 x，∵ CF=6,CE=12, ∴ FA=6-x，又∵ AB∥ CE, ∴ △ FAB∽ △ FCE,

中考数学专题复习圆与相似的综合题及答案

中考数学专题复习圆与相似的综合题及答案一、相似1．如图所示，△ABC中，AB=AC，∠BAC=90°，AD⊥BC，DE⊥AC，△CDE 沿直线 BC 翻折到△ CDF，连结 AF交 BE、DE、DC分别于点 G、H、I．1）求证： AF⊥ BE；2）求证： AD=3DI．答案】（1）证明：∵在△ ABC中， AB=AC，∠ BAC=90°， D 是 BC的中点，∴AD=BD=CD，∠ACB=45，°∵在△ ADC中， AD=DC，DE⊥AC，∴AE=CE，∵△ CDE沿直线 BC翻折到△CDF，∴△ CDE≌ △CDF，∴CF=CE，∠ DCF=∠ACB=45 ，° ∴CF=AE，∠ACF=∠DCF+∠ACB=90 ，°在△ ABE与△ACF中，∴△ ABE≌ △ ACF（SAS），∴∠ ABE=∠FAC，∵∠ BAG+∠ CAF=90 ，°∴∠ BAG+∠ ABE=90 ，°∴∠ AGB=90 ，°∴AF⊥BE2）证明：作 IC的中点 M，连接 EM，由（ 1）∠DEC=∠ECF=∠ CFD=90°∴四边形 DECF是正方形，∴EC∥DF，EC=DF，∴∠ EAH=∠HFD，AE=DF，在△ AEH与△FDH中∴△ AEH≌△FDH（AAS），∴EH=DH，∵∠ BAG+∠ CAF=90 ，°∴∠ BAG+∠ ABE=90 ，°∴∠ AGB=90 ，°∴AF⊥BE，∵M 是 IC的中点， E 是 AC的中点，∴EM∥AI，∴DI=IM，∴CD=DI+IM+MC=3DI，∴AD=3DI【解析】【分析】（ 1）根据翻折的性质和 SAS 证明△ABE≌△ACF，利用全等三角形的性质得出∠ABE=∠FAC，再证明∠AGB=9°0 ，可证得结论。

（2）作 IC 的中点 M ，结合正方形的性质，可证得∠EAH=∠HFD，AE=DF，利用AAS 证明△AEH 与△FDH全等，再利用全等三角形的性质和中位线的性质解答即可。

2.几何综合提高专题(相似、圆) 优录选拔综合训练(二)

ED CBANMEDCBAEDCBAE DCBAl3l2l1C/B/A/CBAl3l2l1C/B/A/CBA基础知识归纳1、相似三角形中几个的基本图形2、由相似三角形得到的几个常用定理定理1 平行于三角形一边的直线截得的三角形与原三角形形似.如图，若DE∥BC,则AD AE DEAB AC BC==,或AD BDAE CE=.定理2 平行切割定理如图，,D E分别是ABCD的边,AB AC上的点，过点A的直线交,DE BC于,M N,若DE∥MN,则DM BNME NC=定理3 （平行线分线段成比例定理）两条直线被一组平行线截得的对应线段成比例.如图，若1l∥2l∥3l，则AB BC ACA B B C A C==ⅱⅱⅱ,定理4（角平分线性质定理）如图，,AD AE分别是ABCD的内角平分线与外角平分线，则DB EB ABDC EC AC==.定理5 射影定理直角三角形斜边上的高分原三角形成两个直角三角形，这两个三角形与原三角形相似.定理6 相交弦定理：圆内两弦相交，交点分得的两条线段的乘积相等。

即：在⊙O 中，∵弦AB 、CD 相交于点P ，∴PA PB PC PD ⋅=⋅定理7 推论：如果弦与直径垂直相交，那么弦的一半是它分直径所成的两条线段的比例中项。

即：在⊙O 中，∵直径AB CD ⊥， ∴2CE AE BE =⋅定理8 切割线定理：从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项。

即：在⊙O 中，∵PA 是切线，PB 是割线 ∴ 2PA PC PB =⋅定理9 割线定理：从圆外一点引圆的两条割线，这一点到每条割线与圆的交点的两条线段长的积相等（如上图）。

即：在⊙O 中，∵PB 、PE 是割线 ∴PC PB PD PE ⋅=⋅基础能力检测1. 如图，点D 为△ABC 的外心，DE 平分ADB ∠，DE=DA ，CE 交DB 于点F ，∠ADB=120°，∠DBC=50°，则∠DFC 的度数为（） A ．50° B ．70° C ．80° D ．100°考点：本题考查了三角形的外心；等腰三角形的性质；构造辅助圆；圆的垂径定理；圆周角定理。

圆与相似三角形综合题解题技巧

圆与相似三角形综合题解题技巧
圆与相似三角形的综合题是高中数学中的重点难点之一。

一般来说，这类题目需要我们掌握以下的解题技巧：
一、圆相关定理
1.圆的性质：圆周上任意两点距离相等，圆心到圆周上任意一点的距离相等。

2.圆心角定理：圆周上两点的连线所对的圆心角是不变量。

3.圆的切线定理：切线与半径垂直，切点在圆心角的平分线上。

二、相似三角形相关定理
1.角度相等定理：若两个角分别相等，则两个三角形相似。

2.比例定理：若两个角分别相等，则两个三角形对应边的长度成比例。

3.三角形内角和定理：一个三角形内角的度数和是180度。

基于以上的定理，我们可以通过以下步骤解决圆与相似三角形的综合题：
1.根据圆心角定理，求出圆心角。

2.根据角度相等定理或比例定理，确定相似三角形的相似比例。

3.利用三角形内角和定理，求出三角形另一个角的度数。

4.根据三角形内角和定理和已知角度，求出第三个角的度数。

5.利用已知角度和比例定理，求出相似三角形的边长。

6.应用圆的切线定理、圆心角定理或其他定理，求出需要求解的量。

需要注意的是，在解题过程中，我们需要注意角度单位是否一致，如角度一般用度数表示，而弧度制需要换算。

同时，我们还需要注意图形的几何位置关系，如切线与圆周、圆心角的平分线等。

综上所述，圆与相似三角形的综合题需要我们掌握相关的定理和解题技巧，同时需要注意单位和几何位置关系。

数学《圆与相似三角形、三角函数综合题》专题训练(含答案)

2020-2021学年中考数学培优训练讲义（七）《圆与相似三角形、三角函数综合题》专题训练班级姓名座号成绩1.如图，过正方形ABCD顶点B，C的⊙O与AD相切于点P，与AB，CD分别相交于点E、F，连接PF．若tan∠FBC＝，DF＝，则PF的长为．2.如图AB是⊙O的直径，点C是的中点，连接AC并延长至点D，使CD＝AC，点E是OB上一点，且＝，CE的延长线交DB的延长线于F，AF交⊙O于点H，当OB＝2时，则BH的长为．（第1题图）（第2题图）（第3题图）3.如图，PA是⊙O的切线，切点为A，AC是⊙O的直径，连接OP交⊙O于E．过A点作AB⊥PO于点D，交⊙O于B，连接BC、PB，若cos∠PAB＝，BC＝1，则PO的长．4.已知：在△ABC中，AB＝BC，以AB为直径的⊙O交AC于点D，交BC于点E．（1）如下左图，过点D作弦DF⊥AB垂足为H，连接EF交AB于G，求证：EF∥AC；（2）如下右图，在（1）的条件下，过点G作GN⊥BC垂足为N，若OG＝3，EN＝4，求线段DH的长．5.如图，AB是⊙O的直径，弦CD⊥AB于H，G为⊙O上一点，连接AG交CD于K，在CD的延长线上取一点E，使EG＝EK，EG的延长线交AB的延长线于F．（1）求证：EF是⊙O的切线；（2）连接DG，若AC∥EF时．①求证：KG2＝KD•KE；②若cos C＝，AK＝，求BF的长．作业思考：1. 如图，四边形ABCD内接于⊙O，且对角线AC⊥BD，垂足为点E，过点C作CF⊥AB于点F，交BD于点G．（1）如图①，连接EF，若EF平分∠AFG，求证：AE＝GE；（2）如图②，连接CO并延长交AB于点H，若CH为∠ACF的平分线，AD＝3，且tan∠FBG＝，求线段AH长．参考答案：1．如图，过正方形ABCD顶点B，C的⊙O与AD相切于点P，与AB，CD分别相交于点E、F，连接EF．（1）求证：PF平分∠BFD．（2）若tan∠FBC＝，DF＝，求EF的长．【分析】（1）根据切线的性质得到OE⊥AD，由四边形ABCD的正方形，得到CD⊥AD，推出OE∥CD，根据平行线的性质得到∠EFD＝∠OEF，由等腰三角形的性质得到∠OEF＝∠OFE，根据角平分线的定义即可得到结论；（2）连接PF，由BF是⊙O的直径，得到∠BPF＝90°，推出四边形BCFP是矩形，根据tan∠FBC ＝，设CF＝3x，BC＝4x，于是得到3x+＝4x，x＝，求得AD＝BC＝4，推出DF∥OE ∥AB于是得到DE：AE＝OF：OB＝1：1即可得到结论．【解答】解：（1）连接OE，BF，PF，∵∠C＝90°，∴BF是⊙O的直径，∵⊙O与AD相切于点E，∴OE⊥AD，∵四边形ABCD的正方形，∴CD⊥AD，∴OE∥CD，∴∠EFD＝∠OEF，∵OE＝OF，∴∠OEF＝∠OFE，∴∠OFE＝∠EFD，∴EF平分∠BFD；（2）连接PF，∵BF是⊙O的直径，∴∠BPF＝90°，∴四边形BCFP是矩形，∴PF＝BC，∵tan∠FBC＝，设CF＝3x，BC＝4x，∴3x+＝4x，x＝，∴AD＝BC＝4，∵点E是切点，∴OE⊥AD∴DF∥OE∥AB∴DE：AE＝OF：OB＝1：1∴DE＝AD＝2，∴EF＝＝10．【点评】本题考查了切线的性质，正方形的性质，圆周角定理，等腰三角形的性质，平行线的性质，切割线定理，正确的作出辅助线是解题的关键．2.如图，AB是⊙O的直径，点C是的中点，连接AC并延长至点D，使CD＝AC，点E是OB上一点，且＝，CE的延长线交DB的延长线于点F，AF交⊙O于点H，连接BH．（1）求证：BD是⊙O的切线；（2）当OB＝2时，求BH的长．【分析】（1）先判断出∠AOC＝90°，再判断出OC∥BD，即可得出结论；（2）先利用相似三角形求出BF，进而利用勾股定理求出AF，最后利用面积即可得出结论．【解答】证明：（1）连接OC，∵AB是⊙O的直径，点C是的中点，∴∠AOC＝90°，∵OA＝OB，CD＝AC，∴OC是△ABD是中位线，∴OC∥BD，∴∠ABD＝∠AOC＝90°，∴AB⊥BD，∵点B在⊙O上，∴BD是⊙O的切线；解：（2）由（1）知，OC∥BD，∴△OCE∽△BFE，∴，∵OB＝2，∴OC＝OB＝2，AB＝4，，∴，∴BF＝3，在Rt△ABF中，∠ABF＝90°，根据勾股定理得，AF＝5，∵S△ABF＝AB•BF＝AF•BH，∴AB•BF＝AF•BH，∴4×3＝5BH，∴BH＝．【点评】此题主要考查了切线的判定和性质，三角形中位线的判定和性质，相似三角形的判定和性质，求出BF＝3是解本题的关键．3．如图，PA是⊙O的切线，切点为A，AC是⊙O的直径，连接OP交⊙O于E．过A点作AB⊥PO于点D，交⊙O于B，连接BC，PB．（1）求证：PB是⊙O的切线；（2）求证：E为△PAB的内心；（3）若cos∠PAB＝，BC＝1，求PO的长．【分析】（1）连接OB，根据圆周角定理得到∠ABC＝90°，证明△AOP≌△BOP，得到∠OBP＝∠OAP，根据切线的判定定理证明；（2）连接AE，根据切线的性质定理得到∠PAE+∠OAE＝90°，证明EA平分∠PAD，根据三角形的内心的概念证明即可；（3）根据余弦的定义求出OA，证明△PAO∽△ABC，根据相似三角形的性质列出比例式，计算即可．【解答】（1）证明：连接OB，∵AC为⊙O的直径，∴∠ABC＝90°，∵AB⊥PO，∴PO∥BC∴∠AOP＝∠C，∠POB＝∠OBC，OB＝OC，∴∠OBC＝∠C，∴∠AOP＝∠POB，在△AOP和△BOP中，，∴△AOP≌△BOP（SAS），∴∠OBP＝∠OAP，∵PA为⊙O的切线，∴∠OAP＝90°，∴∠OBP＝90°，∴PB是⊙O的切线；（2）证明：连接AE，∵PA为⊙O的切线，∴∠PAE+∠OAE＝90°，∵AD⊥ED，∴∠EAD+∠AED＝90°，∵OE＝OA，∴∠OAE＝∠AED，∴∠PAE＝∠DAE，即EA平分∠PAD，∵PA、PB为⊙O的切线，∴PD平分∠APB∴E为△PAB的内心；（3）解：∵∠PAB+∠BAC＝90°，∠C+∠BAC＝90°，∴∠PAB＝∠C，∴cos∠C＝cos∠PAB＝，在Rt△ABC中，cos∠C＝＝＝，∴AC＝，AO＝，∵△PAO∽△ABC，∴，∴PO＝＝＝5．【点评】本题考查的是三角形的内切圆和内心、相似三角形的判定和性质、切线的判定，掌握切线的判定定理、相似三角形的判定定理和性质定理是解题的关键．4.已知：在△ABC中，AB＝BC，以AB为直径的⊙O交AC于点D，交BC于点E．（1）如图1，求证：AD＝CD；（2）如图2，过点D作弦DF⊥AB垂足为H，连接EF交AB于G，求证：EF∥AC；（3）如图3，在（2）的条件下，过点G作GN⊥BC垂足为N，若OG＝3，EN＝4，求线段DH的长．【分析】（1）如图1中，连接BD，利用等腰三角形的三线合一的性质证明即可．（2）如图2中，连接BD，想办法证明∠ADF＝∠DFE即可．（3）连接AE．设OA＝OB＝r，则AB＝BC＝2r，BG＝3+r，利用平行线分线段成比例定理，构建方程求出r，即可解决问题．【解答】（1）证明：如图1中，连接BD．∵AB是直径，∴∠ADB＝90°，∴BD⊥AC，∵BA＝BC，∴AD＝CD．（2）证明：如图2中，连接BD．∵AB⊥DF，∴＝，∴∠ADF＝∠ABD，∵∠DFE＝∠ABD，∴∠ADF＝∠DFE，∴EF∥AC．（3）解：如图3中，连接AE．设OA＝OB＝r，则AB＝BC＝2r，BG＝3+r，∵EG∥AC，∴＝，∵BC＝BA，∴BE＝BG＝3+r，∴BN＝3+r﹣4＝r﹣1，∵AB是直径，GN⊥BC∴∠AEB＝∠GNB＝90°，∴GN∥AE，∴＝，∴＝，解得r＝9或﹣1（舍弃），∴BG＝12，BN＝8，∴NG＝＝＝4，∴EG＝＝＝2，∵GN∥AE，∴＝，∴＝，∴AE＝6，∵∠C＝∠DAH，∠AEC＝∠AHD＝90°，∴△AEC∽△DHA，∴＝＝2，∴DH＝3．【点评】本题属于圆综合题，考查了垂径定理，解直角三角形，平行线分线段成比例定理，等腰三角形的判定和性质等知识，教育的关键是学会添加常用辅助线，属于中考压轴题．5．如图，AB是⊙O的直径，弦CD⊥AB于H，G为⊙O上一点，连接AG交CD于K，在CD的延长线上取一点E，使EG＝EK，EG的延长线交AB的延长线于F．（1）求证：EF是⊙O的切线；（2）连接DG，若AC∥EF时．①求证：△KGD∽△KEG；②若cos C＝，AK＝，求BF的长．【分析】（1）连接OG，由EG＝EK知∠KGE＝∠GKE＝∠AKH，结合OA＝OG知∠OGA＝∠OAG，根据CD⊥AB得∠AKH+∠OAG＝90°，从而得出∠KGE+∠OGA＝90°，据此即可得证；（2）①由AC∥EF知∠E＝∠C＝∠AGD，结合∠DKG＝∠CKE即可证得△KGD∽△KGE；②连接OG，由设CH＝4k，AC＝5k，可得AH＝3k，CK＝AC＝5k，HK＝CK﹣CH＝k．利用AH2+HK2＝AK2得k＝1，即可知CH＝4，AC＝5，AH＝3，再设⊙O半径为R，由OH2+CH2＝OC2可求得，根据知，从而得出答案．【解答】解：（1）如图，连接OG．∵EG＝EK，∴∠KGE＝∠GKE＝∠AKH，又OA＝OG，∴∠OGA＝∠OAG，∵CD⊥AB，∴∠AKH+∠OAG＝90°，∴∠KGE+∠OGA＝90°，∴EF是⊙O的切线．（2）①∵AC∥EF，∴∠E＝∠C，又∠C＝∠AGD，∴∠E＝∠AGD，又∠DKG＝∠GKE，∴△KGD∽△KEG；②连接OG，∵，AK＝，设，∴CH＝4k，AC＝5k，则AH＝3k∵KE＝GE，AC∥EF，∴CK＝AC＝5k，∴HK＝CK﹣CH＝k．在Rt△AHK中，根据勾股定理得AH2+HK2＝AK2，即，解得k＝1，∴CH＝4，AC＝5，则AH＝3，设⊙O半径为R，在Rt△OCH中，OC＝R，OH＝R﹣3k，CH＝4k，由勾股定理得：OH2+CH2＝OC2，即（R﹣3）2+42＝R2，∴，在Rt△OGF中，，∴，∴．【点评】本题是圆的综合问题，解题的关键是掌握等腰三角形的性质、平行线的性质，圆周角定理、相似三角形的判定与性质及切线的判定等知识点．作业思考：1．如图，四边形ABCD内接于⊙O，且对角线AC⊥BD，垂足为点E，过点C作CF⊥AB于点F，交BD于点G．（1）如图①，连接EF，若EF平分∠AFG，求证：AE＝GE；（2）如图②，连接CO并延长交AB于点H，若CH为∠ACF的平分线，AD＝3，且tan∠FBG＝，求线段AH长．【分析】（1）由垂直的定义，角平分线的定义，角的和差证明EF＝EI，同角的余角相等得∠AEF＝∠GEI，四边形的内角和，邻补角的性质得∠FAE＝∠IGE，最后根据角角边证明△AEF≌△GEI，其性质得AE＝GE；（2）由圆周角定理，等角的三角函数值相等求出⊙O的半径为，根据平行线的性质，勾股定理，角平分线的性质定理，三角形相似的判定与性质，一元二次方程求出t的值为，最后求线段AH的长为．【解答】证明：（1）过点E作EI⊥EF交CF于点I，如图①所示：∵CF⊥AB，∴∠AFG＝90°，又∵EF平分∠AFG，∴∠EFA＝∠EFI＝45°，又∵EF⊥EI，∴∠FEI＝90°，又∵∠EFI+∠EIF＝90°，∴∠EIF＝45°，∴EF＝EI，又∵∠EAF+∠AFG+∠FGE+∠GEA＝360°，∠AFG＝∠AEG＝90°，∴∠EGF+∠FAE＝180°，又∵∠EGF+∠EGI＝180°，∴∠EGI＝∠FAE，又∵∠AEB＝∠AEF+∠FEG，∠FEI＝∠GEI+∠FEG，∴∠AEF＝∠GEI，在△AEF和△GEI中，，∴△AEF≌△GEI（AAS），∴AE＝GE；（2）连接DO并延长，交⊙O于点P，连接AP，如图②甲所示：∵∠ABD与∠P是⊙O上弧AD所对的圆周角，∴∠ABD＝∠P，又∵DP为⊙O的直径，∴∠PAD＝90°，又∵tan∠FBG＝，∴tan∠P＝＝，又∵AD＝3，∴AP＝4，PD＝5，∴OD＝，过点H作HJ⊥AC于点J，过点O作OK⊥AC于点K，设AJ＝3t，CF＝x，如图②乙所示，∵HJ⊥AC，BD⊥AC，∴HJ∥BD，∴∠ABD＝∠AHJ，又∵tan∠ABD＝∴tan∠AHJ＝，又∵AJ＝3t，∴HJ＝4t，在Rt△AHJ中，由勾股定理得：AH＝＝＝5t，又∵CH是∠ACF的平分线，且HF⊥CF，HJ⊥AC，∴HF＝HJ＝4t，∴AF＝AH+HF＝9t，又∵CF＝x，∴CJ＝x，又∵∠BFG＝∠GEC，∠FGB＝∠EGC，∴△FBG∽△ECG，∴∠FBG＝∠ECG，∴tan∠FCJ＝＝＝，解得：x＝12t，∴CF＝CJ＝12t，∴AC＝15t，∴CK＝t，又∵OK∥HJ，∴＝，∴OK＝＝＝t，∴在Rt△OCK中，由勾股定理得：OK2+KC2＝OC2，即（t）2+（t）2＝（）2，解得：t＝，或t＝﹣（舍去），∴AH＝5t＝．【点评】本题综合考查了垂线的定义，平行线的性质，全等三角形的判定与性质，相似三角形的判定与性质，勾股定理，解直角三角形，一元二次方程等相关知识，重点掌握相似三角形的判定与性质，难点是辅助线构建全等三角形，圆周角和相似三角形．。

中考数学圆与相似(大题培优易错难题)

中考数学圆与相似(大题培优易错难题)一、相似1．如图1，在矩形ABCD中，AB=6cm，BC=8cm，E、F分别是AB、BD的中点，连接EF，点P从点E出发，沿EF方向匀速运动，速度为1cm/s，同时，点Q从点D出发，沿DB方向匀速运动，速度为2cm/s，当点P停止运动时，点Q也停止运动．连接PQ，设运动时间为t（0＜t＜4）s，解答下列问题：（1）求证：△BEF∽△DCB；（2）当点Q在线段DF上运动时，若△PQF的面积为0.6cm2，求t的值；（3）如图2过点Q作QG⊥AB，垂足为G，当t为何值时，四边形EPQG为矩形，请说明理由；（4）当t为何值时，△PQF为等腰三角形？试说明理由．【答案】（1）解：证明：∵四边形是矩形，在中，分别是的中点，（2）解：如图1，过点作于，（舍）或秒（3）解：四边形为矩形时,如图所示：解得：（4）解：当点在上时，如图2，当点在上时，如图3，时，如图4，时，如图5，综上所述，或或或秒时，是等腰三角形．【解析】【分析】（1）根据矩形的性质可证得AD∥BC，∠A=∠C，根据中位线定理可证得EF∥AD，就可得出EF∥BC，可证得∠BEF=∠C，∠BFE=∠DBC，从而可证得结论。

（2）过点Q作QM⊥EF，易证QM∥BE，可证得△QMF∽△BEF，得出对应边成比例，可求出QM的值，再根据△PQF的面积为0.6cm2，建立关于t的方程，求解即可。

（3）分情况讨论：当点 Q 在 DF 上时，如图2， PF=QF；当点 Q 在 BF 上时， PF=QF，如图3；PQ=FQ 时，如图4；PQ=PF 时，如图5，分别列方程即可解决问题。

2．已知，如图，AB是⊙O的直径，点C为⊙O上一点，OF⊥BC于点F，交⊙O于点E，AE与BC交于点H，点D为OE的延长线上一点，且∠ODB=∠AEC．（1）求证：BD是⊙O的切线；（2）求证：CE2=EH•EA；（3）若⊙O的半径为，sinA= ，求BH的长．【答案】（1）证明：如图，∵∠ODB=∠AEC，∠AEC=∠ABC，∴∠ODB=∠ABC，∵OF⊥BC，∴∠BFD=90°，∴∠ODB+∠DBF=90°，∴∠ABC+∠DBF=90°，即∠OBD=90°，∴BD⊥OB，∴BD是⊙O的切线（2）证明：连接AC，如图2所示：∵OF⊥BC，∴，∴∠CAE=∠ECB，∵∠CEA=∠HEC，∴△CEH∽△AEC，∴，∴CE2=EH•EA（3）解：连接BE，如图3所示：∵AB是⊙O的直径，∴∠AEB=90°，∵⊙O的半径为，sin∠BAE= ，∴AB=5，BE=AB•sin∠BAE=5× =3，∴EA= =4，∵，∴BE=CE=3，∵CE2=EH•EA，∴EH= ，∴在Rt△BEH中，BH= .【解析】【分析】（1）要证BD是⊙O的切线，只需证∠OBD=90°，因为∠OBC+∠BOD=90°，所以只须证∠ODB=∠OBC即可。

相似三角形与圆的综合题

相似三角形与圆的综合考题1、已知：如图，AB是⊙O的直径，E是AB延长线上一点，过E作⊙O的切线ED，切点为C，AD⊥ED交ED于点D，交⊙O于点F，CG⊥AB交AB于点G．求证：BG•AG=DF•DA．2、已知：如图，AB为⊙O的直径，AB⊥AC，BC交⊙O于D，E是AC的中点，ED与AB的延长线相交于点F．(1)求证：DE为⊙O的切线．(2)求证：AB：AC=BF：DF．3、(南通)已知：如图，AB是⊙O的直径，AB=AC，BC交⊙O于点D，DE⊥AC，E为垂足．(1)求证：∠ADE=∠B；(2)过点O作OF∥AD，与ED的延长线相交于点F，求证：FD•DA=FO•DE．4、如图，AB为⊙O的直径，BF切⊙O于点B，AF交⊙O于点D，点C在DF上，BC交⊙O于点E，且∠BAF=2∠CBF，CG⊥BF于点G，连接AE．(1)直接写出AE与BC的位置关系；(2)求证：△BCG∽△ACE；(3)若∠F=60°，GF=1，求⊙O的半径长．5、如图，AB、AC分别是⊙O的直径和弦，点D为劣弧AC上一点，弦DE⊥AB分别交⊙O于E，交AB于H，交AC于F．P是ED延长线上一点且PC=PF．(1)求证：PC是⊙O的切线；(2)点D在劣弧AC什么位置时，才能使AD2=DE•DF，为什么？(3)在(2)的条件下，若OH=1，AH=2，求弦AC的长．6、如图，AB、AC分别是⊙O的直径和弦，点D为劣弧AC上一点，弦DE⊥AB分别交⊙O于E，交AB于H，交AC于F．P是ED延长线上一点且PC=PF．(1)求证：PC是⊙O的切线；(2)点D在劣弧AC什么位置时，才能使AD2=DE•DF，为什么？(3)在(2)的条件下，若OH=1，AH=2，求弦AC的长．7、如是⊙O的直径，CB、CD分别切⊙O于B、D两点，点E在CD的延长线上，且CE=AE+BC；(1)求证：AE是⊙O的切线；(2)过点D作DF⊥AB于点F，连接BE交DF于点M，求证：DM=MF．8、已知：如图，AB是⊙O的直径，D是⊙O上一点，连结BD并延长，使CD=BD，连结AC。

(完整版)相似三角形与圆综合题

相似三角形与圆综合第一部分：例题分析例1、已知：如图,BC为半圆O的直径,AD⊥BC，垂足为D,过点B作弦BF交AD于点E，交半圆O于点F，弦AC与BF交于点H,且AE=BE。

求证：（1）错误!=错误!;（2)AH·BC=2AB·BE。

例2、如图，PA为圆的切线，A为切点，PBC为割线，∠APC的平分线交AB于点D,交AC于点E，求证：（1）AD=AE；（2）AB·AE=AC·DB．例3、AB是⊙O的直径,点C在⊙O上，∠BAC＝60°，P是OB上一点，过P作AB的垂线与AC的延长线交于点Q，连结OC，过点C作CD⊥OC交PQ于点D．（1)求证：△CDQ是等腰三角形； (2)如果△CDQ≌△COB，求BP∶PO的值．例4、△ABC内接于圆O，∠BAC的平分线交⊙O于D点，交⊙O的切线BE于F，连结BD，CD．求证:（1）BD平分∠CBE；（2)AB·BF＝AF·DC．例3、⊙O内两弦AB，CD的延长线相交于圆外一点E，由E引AD的平行线与直线BC交于F,作切线FG，G 为切点,求证：EF＝FG．第二部分:当堂练习1．如图，AB是⊙O直径，ED⊥AB于D，交⊙O于G，EA交⊙O于C，CB交ED于F，求证：DG2＝DE•DF2．如图，弦EF ⊥直径MN 于H ，弦MC 延长线交EF 的反向延长线于A ，求证：MA •MC ＝MB •MDDCBAOMN EH3．如图,AB 、AC 分别是⊙O 的直径和弦，点D 为劣弧AC 上一点，弦ED 分别交⊙O 于点E ，交AB 于点H ，交AC 于点F ，过点C 的切线交ED 的延长线于点P ．(1)若PC =PF ,求证：AB ⊥ED ;（2）点D 在劣弧AC 的什么位置时,才能使AD 2=DE ·DF ，为什么？4．如图（1），AD 是△ABC 的高,AE 是△ABC 的外接圆直径，则有结论：AB · AC =AE · AD 成立，请证明．如果把图（1）中的∠ABC 变为钝角，其它条件不变，如图（2），则上述结论是否仍然成立? 5．如图，AD 是△ABC 的角平分线，延长AD 交△ABC 的外接圆O 于点E ，过点C 、D 、E 三点的⊙O 1与AC 的延长线交于点F ，连结EF 、DF ．（1）求证：△AEF ∽△FED ； (2)若AD =8，DE =4,求EF 的长． 6．如图，PC 与⊙O 交于B ，点A 在⊙O 上，且∠PCA =∠BAP ．（1)求证：PA 是⊙O 的切线． (2)△ABP 和△CAP 相似吗？为什么？ (3)若PB ：BC =2：3,且PC =20,求PA 的长．DCBAOE F7．已知：如图， AD 是⊙O 的弦，OB ⊥AD 于点E ，交⊙O 于点C ,OE =1,BE =8，AE ：AB =1：3．（1）求证:AB 是⊙O 的切线；(2）点F 是ACD 上的一点,当∠AOF =2∠B 时,求AF 的长．8．如图，⊿ABC 内接于⊙O ，且BC 是⊙O 的直径，AD ⊥BC 于D ，F 是弧BC 中点,且AF 交BC 于E ,AB ＝6，AC ＝8,求CD ，DE ，及EF 的长．ACPED H FO9．已知：如图，在Rt ABC △中,90ACB ∠=，4AC =,43BC =,以AC 为直径的O 交AB 于点D ，点E 是BC 的中点，连结OD ，OB 、DE 交于点F ．(1）求证：DE 是O 的切线; （2）求EF ：FD 的值．ABCD E FO10．如图,A 是以BC 为直径的O 上一点，AD BC ⊥于点D ，过点B 作O 的切线，与CA 的延长线相交于点E G ，是AD 的中点,连结CG 并延长与BE 相交于点F ，延长AF 与CB 的延长线相交于点P ． (1)求证：BF EF =； (2）求证：PA 是O 的切线；（3)若FG BF =,且O 的半径长为32，求BD 和FG 的长度．第三部分课后作业1．已知⊙O 的半径为35厘米,⊙O '的半径为5厘米．⊙O 与⊙O '相交于点D 、E ．若两圆的公共弦DE 的长是6厘米（圆心O 、O '在公共弦DE 的两侧），则两圆的圆心距O O '的长为（）（A ）2厘米 (B)10厘米（C ）2厘米或10厘米（D)4厘米2．如图,两个等圆⊙O 和⊙O '的两条切线OA 、OB ，A 、B 是切点，则∠AOB 等于（）（A ） 30 (B ） 45 (C ） 60 （D ） 903．如图，在△ABC 中，∠BAC ＝ 90，AB ＝AC ＝2，以AB 为直径的圆交BC 于D ，则图中阴影部分的面积为（）（A ）1 (B ）2 （C)1+4π （D ）2－4π4．已知圆的内接正六边形的周长为18,那么圆的面积为（）（A)18π （B ）9π （C ）6π （D ）3πOD GCAEFB5、如图△ABC 是等边三角形，被一平行于BC 的矩形所截 AB 被截成三等分则图中阴影部分的面积是△ABC的面积的（ )6．已知，如图，以△ABC 的边AB 作直径的⊙O ，分别并AC 、BC 于点D 、E ，弦FG ∥AB ,S △CDE ︰S △ABC ＝1︰4，DE ＝5cm ，FG ＝8cm ，求梯形AFGB 的面积．7．如图，在两个半圆中，大圆的弦MN 与小圆相切，D 为切点,且MN ∥AB ，MN ＝a ，ON 、CD 分别为两圆的半径,求阴影部分的面积．8．如图，在Rt ABC △中，斜边1230BC C =∠=，°，D 为BC 的中点,ABD △的外接圆O ⊙与AC 交于F 点，过A 作O ⊙的切线AE 交DF 的延长线于E 点．（1）求证:AE DE ⊥；（2）计算：AC AF ·的值．9．如图，在直角梯形ABCD 中，AB CD ∥，90B ∠=,AB =AD ，∠BAD 的平分线交BC 于E ，连接DE ．（1）说明点D 在△ABE 的外接圆上;（2）若∠AED =∠CED ，试判断直线CD 与△ABE 外接圆的位置关系，并说明理由．10、如图,在Rt ABC △中，90A ∠=，6AB =,8AC =,D E ，分别是边AB AC ，的中点，点P 从点D 出发沿DE 方向运动,过点P 作PQ BC ⊥于Q ，过点Q 作QR BA ∥交AC 于R ，当点Q 与点C 重合时,点P 停止运动．设BQ x =，QR y =． (1)求点D 到BC 的距离DH 的长;（2）求y 关于x 的函数关系式(不要求写出自变量的取值范围）;（3)是否存在点P ，使PQR △为等腰三角形？若存在，请求出所有满足要求的x 的值；若不存在，请说明AB CDERPH QAE FODB理由．。

相似三角形难题集锦(含答案)

一、相似三角形中的动点问题1.如图，在Rt△ABC中，∠ACB=90°，AC=3，BC=4，过点B作射线BB1∥AC．动点D从点A出发沿射线AC方向以每秒5个单位的速度运动，同时动点E从点C沿射线AC 方向以每秒3个单位的速度运动．过点D作DH⊥AB于H，过点E作EF⊥AC交射线BB1于F，G是EF中点，连接DG．设点D运动的时间为t秒．（1）当t为何值时，AD=AB，并求出此时DE的长度；（2）当△DEG与△ACB相似时，求t的值．2.如图，在△ABC 中，ABC＝90°，AB=6m，BC=8m，动点P以2m/s的速度从A点出发，沿AC向点C移动．同时，动点Q以1m/s的速度从C点出发，沿CB向点B移动．当其中有一点到达终点时，它们都停止移动．设移动的时间为t秒．（1）①当t=2.5s时，求△CPQ的面积；②求△CPQ的面积S（平方米）关于时间t（秒）的函数解析式；（2）在P，Q移动的过程中，当△CPQ为等腰三角形时，求出t的值．3.如图1，在Rt△ABC 中，ACB＝90°，AC＝6，BC＝8，点D在边AB上运动，DE 平分CDB交边BC于点E，EM⊥BD，垂足为M，EN⊥CD，垂足为N．（1）当AD＝CD时，求证：DE∥AC；（2）探究：AD为何值时，△BME与△CNE相似？4.如图所示，在△ABC中，BA＝BC＝20cm，AC＝30cm，点P从A点出发，沿着AB以每秒4cm的速度向B点运动；同时点Q从C点出发，沿CA以每秒3cm的速度向A点运动，当P点到达B点时，Q点随之停止运动．设运动的时间为x．（1）当x为何值时，PQ∥BC？（2）△APQ与△CQB能否相似？若能，求出AP的长；若不能说明理由．5.如图，在矩形ABCD中，AB=12cm，BC=6cm，点P沿AB边从A开始向点B以2cm/s的速度移动；点Q沿DA边从点D开始向点A以1cm/s的速度移动．如果P、Q同时出发，用t（s）表示移动的时间（0＜t＜6）。

2024中考备考重难点重难点相似三角形模型及其综合题综合训练(11大题型+满分技巧+限时分层检测)

重难点02 相似三角形模型及其综合题综合训练中考数学中《相似三角形模型及其综合题综合训练》部分主要考向分为五类：一、K型相似二、8字图相似三、A字图相似四、母子型相似五、手拉手相似相似三角形的综合题中各种相似模型的掌握是解决对应压轴题的便捷方法，所以本专题是专门针对相似三角形模型压轴题的，对提高类型的学生可以自主训练。

考向一：K型相似1．（2023•锡山区校级四模）如图，矩形ABCD中，AB＝10，BC＝8．点P在AD上运动（点P不与点A、D重合）将△ABP沿直线翻折，使得点A落在矩形内的点M处（包括矩形边界），则AP的取值范围是，连接DM并延长交矩形ABCD的AB边于点G，当∠ABM＝2∠ADG时，AP的长是．2．（2023•福田区模拟）综合与探究在矩形ABCD的CD边上取一点E，将△BCE沿BE翻折，使点C恰好落在AD边上的点F处．（1）如图①，若BC＝2BA，求∠CBE的度数；（2）如图②，当AB＝5，且AF•FD＝10时，求EF的长；（3）如图③，延长EF，与∠ABF的角平分线交于点M，BM交AD于点N，当NF＝AN+FD时，请直接写出的值．3．（2023•桐柏县一模）【初步探究】（1）把矩形纸片ABCD如图①折叠，当点B的对应点B'在MN的中点时，填空：△EB'M△B'AN （“≌”或“∽”）．【类比探究】（2）如图②，当点B的对应点B'为MN上的任意一点时，请判断（1）中结论是否成立？如果成立，请写出证明过程；如果不成立，请说明理由．【问题解决】（3）在矩形ABCD中，AB＝4，BC＝6，点E为BC中点，点P为线段AB上一个动点，连接EP，将△BPE沿PE折叠得到△B'PE，连接DE，DB'，当△EB'D为直角三角形时，BP的长为．考向二：8字图相似1．（2023•海州区校级二模）“关联”是解决数学问题的重要思维方式．角平分线的有关联想就有很多……【问题提出】（1）如图①，PC是△P AB的角平分线，求证：．小明思路：关联“平行线、等腰三角形”，过点B作BD∥P A，交PC的延长线于点D，利用“三角形相似”．小红思路：关联“角平分线上的点到角的两边的距离相等”，过点C分别作CD⊥P A交P A于点D，作CE⊥PB交PB于点E，利用“等面积法”．请根据小明或小红的思路，选择一种并完成证明．【理解应用】（2）如图②，在Rt△ABC中，∠BAC＝90°，D是边BC上一点．连接AD，将△ACD沿AD所在直线折叠，使点C恰好落在边AB上的E点处，落AC＝1，AB＝2，则DE的长为．【深度思考】（3）如图③，△ABC中，AB＝6，AC＝4，AD为∠BAC的角平分线．AD的垂直平分线EF交BC延长线于点F，连接AF，当BD＝3时，AF的长为．【拓展升华】（4）如图④，PC是△P AB的角平分线，若AC＝3，BC＝1，则△P AB的面积最大值是．2．（2023•衢州二模）如图1，在正方形ABCD中，点E在线段BC上，连接AE，将△ABE沿着AE折叠得到△AFE，延长EF交CD于点G．（1）求证：DG＝FG；（2）如图2，当点E是BC中点时，求tan∠CGE的值；（3）如图3，当时，连接CF并延长交AB于点H，求的值．考向三：A字图相似1．（2023•宿城区一模）如图，在矩形ABCD中，AB＝5，AD＝3，先将△ABC沿AC翻折到△AB′C处，再将△AB'C沿翻折到△AB'C'处，延长CD交AC′于点M，则DM的长为．2．（2023•沙坪坝区校级模拟）如图，△ABC中，D在AB上，E在BC上，∠AED＝∠ABC，F在AE上，EF＝DE．（1）如图1，若CE＝BD，求证：BE＝CF；（2）如图2，若CE＝AD，G在DE上，∠EFG＝∠EFC，求证：CF＝2GF；（3）如图3，若CE＝AD，EF＝2，∠ABC＝30°，当△CEF周长最小时，请直接写出△BCF的面积．3．（2023•中山区模拟）如图，在平面直角坐标系中，直线y＝﹣x+4与x轴，y轴分别交于点A、B，点P为射线AO上的一个动点，过点P作PQ⊥AB于点Q，将沿PQ翻折得到R．设△PQR与△AOB重合部分的面积为S，点P的坐标为（m，0）．（1）求AR的长．（用含m的代数式表示）（2）求S关于m的函数解析式，并直接写出自变量m的取值范围．考向四：母子型相似1．（2023•樊城区模拟）【基础巩固】（1）如图1，在△ABC中，D为AB上一点，∠ACD＝∠B．求证：AC2＝AD•AB．【尝试应用】（2）如图2，在▱ABCD中，E为BC上一点，F为CD延长线上一点，∠BFE＝∠A．若BF ＝6，AD＝9，求CE的长．【拓展提高】（3）如图3，在菱形ABCD中，E是AB上一点，F是△ABC内一点，EF∥AC，AC＝2EF，连接DE、DF分别交AC于M，N，∠EDF＝∠BAD，DF＝AE，若MN＝18，求EF的值．2．（2023•润州区二模）如图1，在△ABC中，点D在边AB上，点P在边AC上，若满足∠BPD＝∠BAC，则称点P是点D的“和谐点”．（1）如图2，∠BDP+∠BPC＝180°．①求证：点P是点D的“和谐点”；②在边AC上还存在某一点Q（不与点P重合），使得点Q也是点D的“和谐点”，请在图2中仅用圆规作图，找出点Q的位置，并写出证明过程．（保留作图痕迹）（2）如图3，以点A为原点，AB为x轴正方向建立平面直角坐标系，已知点B（6，0），C（2，4），点P在线段AC上，且点P是点D的“和谐点”．①若AD＝1，求出点P的坐标；②若满足条件的点P恰有2个，直接写出AD长的取值范围是．考向五：手拉手相似1．（2023•宝安区校级三模）【问题背景】已知D、E分别是△ABC的AB边和AC边上的点，且DE∥BC，则△ABC∽△ADE，把△ADE绕着A逆时针方向旋转，连接BD和CE．①如图2，找出图中的另外一组相似三角形；②若AB＝4，AC＝3，BD＝2，则CE＝；【迁移应用】在Rt△ACB中，∠BAC＝90°，∠C＝60°，D、E，M分别是AB、AC、BC中点，连接DE和CM．①如图3，写出CE和BD的数量关系；②如图4，把Rt△ADE绕着点A逆时针方向旋转，当D落在AM上时，连接CD和CE，取CD中点N，连接MN，若，求MN的长．【创新应用】如图5：，BC＝4，△ADE是直角三角形，∠DAE＝90°，tan∠ADE＝2，将△ADE绕着点A旋转，连接BE，F是BE上一点，，连接CF，请直接写出CF的取值范围．2．（2023•东港市二模）（1）问题发现：如图1，已知正方形ABCD，点E为对角线AC上一动点，将BE绕点B顺时针旋转90°到BF处，得到△BEF，连接CF．填空：①＝；②∠ACF的度数为；（2）类比探究：如图2，在矩形ABCD和Rt△BEF中，∠EBF＝90°，∠ACB＝∠EFB＝60°，连接CF，请分别求出的值及∠ACF的度数；（3）拓展延伸：如图3，在（2）的条件下，将点E改为直线AC上一动点，其余条件不变，取线段EF 的中点M，连接BM，CM，若，则当△CBM是直角三角形时，请直接写出线段CF的长．3．（2023•晋中模拟）综合与实践问题情境：（1）如图1，在△ABC和△ADE中，AB＝AC，AD＝AE．如图2，将△ABC绕顶点A按逆时针方向旋转15°得到△AB'C'，连接B′D，C′E，求证：B′D＝C′E．深入研究：（2）①如图3，在正方形ABCD和正方形CEFG中，已知点B，C，E在同一直线上，连接DE，AF，交于点P，求AF：DE的值；②如图4，若将正方形CEFG绕点C按顺时针方向旋转一定角度，AF：DE的值变化吗？请说明理由．拓展应用：（3）如图5，若把正方形ABCD和正方形CEFG分别换成矩形ABCD和矩形CEFG，且AD：AB＝CG：CE＝k，请直接写出此时AF：DE的值．（建议用时：150分钟）1．（2023•菏泽）（1）如图1，在矩形ABCD中，点E，F分别在边DC，BC上，AE⊥DF，垂足为点G．求证：△ADE∽△DCF．【问题解决】（2）如图2，在正方形ABCD中，点E，F分别在边DC，BC上，AE＝DF，延长BC到点H，使CH＝DE，连接DH．求证：∠ADF＝∠H．【类比迁移】（3）如图3，在菱形ABCD中，点E，F分别在边DC，BC上，AE＝DF＝11，DE＝8，∠AED＝60°，求CF的长．2．（2023•济南）在矩形ABCD中，AB＝2，AD＝2，点E在边BC上，将射线AE绕点A逆时针旋转90°，交CD延长线于点G，以线段AE，AG为邻边作矩形AEFG．（1）如图1，连接BD，求∠BDC的度数和的值；（2）如图2，当点F在射线BD上时，求线段BE的长；（3）如图3，当EA＝EC时，在平面内有一动点P，满足PE＝EF，连接P A，PC，求P A+PC的最小值．3．（2023•武汉）问题提出如图（1），E是菱形ABCD边BC上一点，△AEF是等腰三角形，AE＝EF，∠AEF＝∠ABC＝α（α≥90°），AF交CD于点G，探究∠GCF与α的数量关系．问题探究（1）先将问题特殊化，如图（2），当α＝90°时，直接写出∠GCF的大小；（2）再探究一般情形，如图（1），求∠GCF与α的数量关系．问题拓展将图（1）特殊化，如图（3），当α＝120°时，若，求的值．4．（2023•内蒙古）已知正方形ABCD，E是对角线AC上一点．（1）如图1，连接BE，DE．求证：△ABE≌△ADE；（2）如图2，F是DE延长线上一点，DF交AB于点G，BF⊥BE．判断△FBG的形状并说明理由；（3）在第（2）题的条件下，BE＝BF＝2．求的值．5．（2023•湖州）【特例感知】（1）如图1，在正方形ABCD中，点P在边AB的延长线上，连结PD，过点D作DM⊥PD，交BC的延长线于点M．求证：△DAP≌△DCM．【变式求异】（2）如图2，在Rt△ABC中，∠ABC＝90°，点D在边AB上，过点D作DQ⊥AB，交AC于点Q，点P在边AB的延长线上，连结PQ，过点Q作QM⊥PQ，交射线BC于点M．已知BC＝8，AC＝10，AD ＝2DB，求的值．【拓展应用】（3）如图3，在Rt△ABC中，∠BAC＝90°，点P在边AB的延长线上，点Q在边AC上（不与点A，C重合），连结PQ，以Q为顶点作∠PQM＝∠PBC，∠PQM的边QM交射线BC于点M．若AC＝mAB，CQ＝nAC（m，n是常数），求的值（用含m，n的代数式表示）．6．（2023•鞍山）如图，在△ABC中，AB＝AC，∠BAC＝α，点D是射线BC上的动点（不与点B，C重合），连接AD，过点D在AD左侧作DE⊥AD，使AD＝kDE，连接AE，点F，G分别是AE，BD的中点，连接DF，FG，BE．（1）如图1，点D在线段BC上，且点D不是BC的中点，当α＝90°，k＝1时，AB与BE的位置关系是，＝．（2）如图2，点D在线段BC上，当α＝60°，k＝时，求证：BC+CD＝2FG．（3）当α＝60°，k＝时，直线CE与直线AB交于点N，若BC＝6，CD＝5，请直接写出线段CN的长．7．（2023•益阳）如图，在Rt△ABC中，∠ACB＝90°，AC＞BC，点D在边AC上，将线段DA绕点D按顺时针方向旋转90°得到DA′，线段DA′交AB于点E，作A′F⊥AB于点F，与线段AC交于点G，连接FC，GB．（1）求证：△ADE≌△A′DG；（2）求证：AF•GB＝AG•FC；（3）若AC＝8，tan A＝，当A′G平分四边形DCBE的面积时，求AD的长．8．（2023•福建）如图1，在△ABC中，∠BAC＝90°，AB＝AC，D是AB边上不与A，B重合的一个定点．AO ⊥BC于点O，交CD于点E．DF是由线段DC绕点D顺时针旋转90°得到的，FD，CA的延长线相交于点M．（1）求证：△ADE∽△FMC；（2）求∠ABF的度数；（3）若N是AF的中点，如图2，求证：ND＝NO．9．（2022•湖北）问题背景：一次数学综合实践活动课上，小慧发现并证明了关于三角形角平分线的一个结论．如图1，已知AD是△ABC的角平分线，可证＝．小慧的证明思路是：如图2，过点C作CE∥AB，交AD的延长线于点E，构造相似三角形来证明＝．尝试证明：（1）请参照小慧提供的思路，利用图2证明：＝；应用拓展：（2）如图3，在Rt△ABC中，∠BAC＝90°，D是边BC上一点．连接AD，将△ACD沿AD所在直线折叠，点C恰好落在边AB上的E点处．①若AC＝1，AB＝2，求DE的长；②若BC＝m，∠AED＝α，求DE的长（用含m，α的式子表示）．10．（2022•宁波）【基础巩固】（1）如图1，在△ABC中，D，E，F分别为AB，AC，BC上的点，DE∥BC，BF＝CF，AF交DE于点G，求证：DG＝EG．【尝试应用】（2）如图2，在（1）的条件下，连结CD，CG．若CG⊥DE，CD＝6，AE＝3，求的值．【拓展提高】（3）如图3，在▱ABCD中，∠ADC＝45°，AC与BD交于点O，E为AO上一点，EG∥BD交AD于点G，EF⊥EG交BC于点F．若∠EGF＝40°，FG平分∠EFC，FG＝10，求BF的长．11．（2023•广州）如图，AC是菱形ABCD的对角线．（1）尺规作图：将△ABC绕点A逆时针旋转得到△ADE，点B旋转后的对应点为D（保留作图痕迹，不写作法）；（2）在（1）所作的图中，连接BD，CE．①求证：△ABD～△ACE；②若tan∠BAC＝，求cos∠DCE的值．。

圆与相似三角形综合问题

NMEDCBAEDCBAE DCBA学生：科目：数学教师：谭前富知识框架相似三角形的性质是几何证明的重要工具，是证明线段和差问题、相等问题、比例问题、角相等问题的重要方法,尤其在圆中,相似三角形有着极其重要的作用.1、相似三角形的性质相似三角形的对应边成比例，对应角相等，对应边上的中线，角平分线，高线，周长之比等于相似比，面积之比等于相似比的平方.2、相似三角形的判定方法（1）三边对应成比例的两个三角形相似（2）两边对应成比例，夹角相等的两个三角形相似（3）两组角对应相等的两个三角形相似.3、相似三角形中几个的基本图形4、由相似三角形得到的几个常用定理定理1 平行于三角形一边的直线截得的三角形与原三角形形似.如图，若DE∥BC,则AD AE DEAB AC BC,或AD BDAE CE.定理2 平行切割定理如图，,D E分别是ABC的边,AB AC上的点，过点A的直线交,DE BC于,M N,若DE∥MN,则DM BNME NC定理3 （平行线分线段成比例定理）两条直线被一组平行线截得的对应线段成比例.EDCBAl 3l 2l 1C /B /A /CBA l 3l 2l 1C /B /A /CB A如图，若1l ∥2l ∥3l ，则 AB BC ACA B B C A C,定理4（角平分线性质定理）如图，,AD AE 分别是ABC 的内角平分线与外角平分线，则DB EB AB DC EC AC.定理5 射影定理直角三角形斜边上的高分原三角形成两个直角三角形，这两个三角形与原三角形相似.定理6 相交弦定理：圆内两弦相交，交点分得的两条线段的乘积相等。

即：在⊙O 中，∵弦AB 、CD 相交于点P ， ∴PA PB PC PD ⋅=⋅定理7 推论：如果弦与直径垂直相交，那么弦的一半是它分直径所成的两条线段的比例中项。

圆与相似三角形、三角函数专题(含答案)

圆与相似三角形、解直角三角形及二次函数的综合类型一：圆与相似三角形的综合1．如图，BC是⊙A的直径，△DBE的各个顶点均在⊙A上，BF⊥DE于点F.求证：BD·BE＝BC·BF.2．如图，在Rt△ABC中，∠ACB＝90°，以AC为直径的⊙O与AB边交于点D，过点D作⊙O的切线，交BC于点E.(1)求证：点E是边BC的中点；(2)求证：BC2＝BD·BA；(3)当以点O，D，E，C为顶点的四边形是正方形时，求证：△ABC是等腰直角三角形．解：(1)连结OD，∵DE为切线，∴∠EDC＋∠ODC＝90°.∵∠ACB＝90°，∴∠ECD＋∠OCD＝90°.又∵OD＝OC，∴∠ODC＝∠OCD，∴∠EDC＝∠ECD，∴ED＝EC.∵AC为直径，∴∠ADC＝90°，∴∠BDE＋∠EDC＝90°，∠B＋∠ECD＝90°，∴∠B＝∠BDE，∴ED＝EB，∴EB＝EC，即点E为边BC的中点(2)∵AC为直径，∴∠ADC＝∠ACB＝90°.又∵∠B＝∠B，∴△ABC∽△CBD，∴ABBC＝BCBD，∴BC2＝BD•BA(3)当四边形ODEC为正方形时，∠OCD＝45°.∵AC为直径，∴∠ADC＝90°，∴∠CAD＝90°－∠OCD＝90°－45°＝45°，∴Rt△ABC为等腰直角三角形类型二：圆与解直角三角形的综合3．如图，在△ABC中，以AC为直径作⊙O交BC于点D，交AB于点G，且D是BC的中点，DE⊥AB，垂足为点E，交AC的延长线于点F.(1)求证：直线EF是⊙O的切线；(2)已知CF＝5，cosA＝25，求BE的长．解：(1)连结OD.∵CD＝DB，CO＝OA，∴OD是△ABC的中位线，∴OD∥AB，AB＝2OD.∵DE⊥AB，∴DE⊥OD，即OD⊥EF，∴直线EF是⊙O的切线(2)∵OD∥AB，∴∠COD＝∠A，∴cos∠COD＝cosA＝25.在Rt△DOF中，∵∠ODF＝90°，∴cos∠FOD＝ODOF＝25.设⊙O的半径为r，则rr＋5＝25，解得r＝103，∴AB＝2OD＝AC ＝203.在Rt△AEF中，∵∠AEF＝90°，∴cosA＝AEAF＝AE5＋203＝25，∴AE＝143，∴BE ＝AB－AE＝203－143＝24．(2015·资阳)如图，在△ABC中，BC是以AB为直径的⊙O的切线，且⊙O与AC相交于点D，E为BC的中点，连结DE.(1)求证：DE是⊙O的切线；(2)连结AE，若∠C＝45°，求sin∠CAE的值．解：(1)连结OD，BD，∵OD＝OB，∴∠ODB＝∠OBD.∵AB是直径，∴∠ADB＝90°，∴∠CDB ＝90°.∵E为BC的中点，∴DE＝BE，∴∠EDB＝∠EBD，∴∠ODB＋∠EDB＝∠OBD＋∠EBD，即∠EDO＝∠EBO.∵BC是以AB为直径的⊙O的切线，∴AB⊥BC，∴∠EBO＝90°，∴∠ODE ＝90°，∴DE是⊙O的切线(2)过点E作EF⊥CD于点F，设EF＝x，∵∠C＝45°，∴△CEF，△ABC都是等腰直角三角形，∴CF＝EF＝x，∴BE＝CE＝2x，∴AB＝BC＝22x.在Rt△ABE中，AE＝AB2＋BE2＝10x，∴sin∠CAE＝EFAE＝10105．如图，△ABC内接于⊙O，直径BD交AC于点E，过点O作FG⊥AB，交AC于点F，交AB于点H，交⊙O于点G.(1)求证：OF·DE＝OE·2OH；(2)若⊙O的半径为12，且OE∶OF∶OD＝2∶3∶6，求阴影部分的面积．(结果保留根号)解：(1)∵BD是直径，∴∠DAB＝90°.∵FG⊥AB，∴DA∥FO，∴△FOE∽△ADE，∴FOAD＝OEDE，即OF•DE＝OE•AD.∵O是BD的中点，DA∥OH，∴AD＝2OH，∴OF•DE＝OE•2OH (2)∵⊙O的半径为12，且OE∶OF∶OD＝2∶3∶6，∴OE＝4，ED＝8，OF＝6，∴OH＝6.在Rt△OBH中，OB＝2OH，∴∠OBH＝30°，∴∠BOH＝60°，∴BH＝BO•sin60°＝12×32＝63，∴S阴影＝S扇形GOB－S△OHB＝60×π×122360－12×6×63＝24π－183类型三：圆与二次函数的综合6．如图，在平面直角坐标系中，已知A(－4，0)，B(1，0)，且以AB为直径的圆交y轴的正半轴于点C(0，2)，过点C作圆的切线交x轴于点D.(1)求过A，B，C三点的抛物线的解析式；(2)求点D的坐标；(3)设平行于x轴的直线交抛物线于E，F两点，问：是否存在以线段EF为直径的圆，恰好与x轴相切？若存在，求出该圆的半径，若不存在，请说明理由．解：(1)y＝－12x2－32x＋2(2)以AB为直径的圆的圆心坐标为O′(－32，0)，∴O′C＝52，O′O＝32.∵CD为圆O′的切线，∴O′C⊥CD，∴∠O′CO＋∠DCO＝90°.又∵∠CO′O＋∠O′CO＝90°，∴∠CO′O＝∠DCO，∴△O′CO∽△CDO，∴O′OOC＝OCOD，∴322＝2OD，∴OD＝83，∴点D的坐标为(83，0) (3)存在．抛物线的对称轴为直线x＝－32，设满足条件的圆的半径为|r|，则点E的坐标为(－32＋r，r)或F(－32－r，r)，而点E在抛物线y＝－12x2－32x＋2上，∴r＝－12(－32＋|r|)2－32(－32＋|r|)＋2，∴r1＝－1＋292，r2＝－1－292(舍去)．故存在以线段EF为直径的圆，恰好与x轴相切，该圆的半径为－1＋2927．如图，抛物线y＝ax2＋bx－3与x轴交于A，B两点，与y轴交于点C，经过A，B，C 三点的圆的圆心M(1，m)恰好在此抛物线的对称轴上，⊙M的半径为.设⊙M与y轴交于点D，抛物线的顶点为E.(1)求m的值及抛物线的解析式；(2)设∠DBC＝α，∠CBE＝β，求sin(α－β)的值；(3)探究坐标轴上是否存在点P，使得以P，A，C为顶点的三角形与△BCE相似？若存在，请指出点P的位置，并直接写出点P的坐标；若不存在，请说明理由．解：(1)由题意，可知C(0，－3)，－b2a＝1，∴抛物线的解析式为y＝ax2－2ax－3(a＞0)．过点M作MN⊥y轴于点N，连结CM，则MN＝1，CM＝5，∴CN＝2，于是m＝－1.同理，可求得B(3，0)，∴a×32－2a×3－3＝0，解得a＝1.∴抛物线的解析式为y＝x2－2x－3 (2)由(1)得，A(－1，0)，E(1，－4)，D(0，1)，∴△BCE为直角三角形，BC＝32，CE＝2，∴OBOD＝31＝3，BCCE＝322＝3，∴OBOD＝BCCE，即OBBC＝ODCE，∴Rt△BOD∽Rt △BCE，得∠CBE＝∠OBD＝β，因此sin(α－β)＝sin(∠DBC－∠OBD)＝sin∠OBC＝COBC＝22(3)显然Rt△COA∽Rt△BCE，此时点O(0，0)．过点A作AP2⊥AC交y轴的正半轴于点P2，由Rt△CAP2∽Rt△BCE，得P2(0，13)．过点C作CP3⊥AC交x轴的正半轴于点P3，由Rt△P3CA∽Rt△BCE，得P3(9，0)．故在坐标轴上存在三个点P1(0，0)，P2(0，13)，P3(9，0)，使得以P，A，C为顶点的三角形与△BCE相似。

相似三角形综合试相似与圆(难)

【精编版】数学中考专题训练——相似三角形与圆的综合

相似三角形重难点题型(附参考答案)

圆与相似三角形相关的证明题

2020春浙教版九年级中考数学复习测试：6.20圆与相似三角形的结合

第20讲圆与相似三角形的结合复习课件(共38张PPT)

中考数学圆与相似-经典压轴题

中考数学专题复习圆与相似的综合题及答案

2.几何综合提高专题(相似、圆) 优录选拔综合训练(二)

圆与相似三角形综合题解题技巧

数学《圆与相似三角形、三角函数综合题》专题训练(含答案)

中考数学圆与相似(大题培优 易错 难题)

相似三角形与圆的综合题

(完整版)相似三角形与圆综合题

相似三角形难题集锦(含答案)

2024中考备考重难点重难点相似三角形模型及其综合题综合训练(11大题型+满分技巧+限时分层检测)

圆与相似三角形综合问题

圆与相似三角形、三角函数专题(含答案)

中考数学圆与相似(大题培优易错难题)