清华大学概率论与数理统计复习ppt
合集下载
概率论与数理统计课件ppt

简化数据结构,解释变量间的关系。
操作步骤
计算相关系数矩阵、求特征值和特征 向量、确定主成分个数。
实例
分析消费者对不同品牌手机的偏好。
聚类分析
聚类分析
常见方法
目的
实例
将类似的对象归为同一 组,即“簇”,不同簇
的对象尽可能不同。
层次聚类、K均值聚类、 DBSCAN等。
揭示数据的内在结构, 用于分类、猜测和决策
用数学符号表示一个随机实验的结果 。
随机变量可以取到任何实数值,且取 每个结果的概率为一个确定的函数。
离散型随机变量
随机变量可以取到所有可能的结果, 且取每个结果的概率为一个确定的数 。
随机变量的函数变换
线性变换
对于随机变量X和常数a、b,有 aX+b的散布与X的散布不同。
非线性变换
对于随机变量X和函数g(x),g(X)的散 布与X的散布不同。
置信区间
根据样本数据对总体参数进行估计的一个范围,表示我们对 估计的可靠程度。
假设检验与置信水平
假设检验
通过样本数据对总体参数或散布进行 假设,然后根据检验结果判断假设是 否成立。
置信水平
假设检验中,我们相信结论正确的概 率,通常表示为百分比。
05 数理统计的应用
方差分析
方差分析(ANOVA)
随机进程在通讯、气象、物理等领域有广泛应用。
马尔科夫链蒙特卡洛方法
01
马尔科夫链蒙特卡洛方法是一种 基于蒙特卡洛模拟的统计推断方 法,通过构造一个马尔科夫链来 到达近似求解复杂问题的目的。
02
马尔科夫链蒙特卡洛方法在许多 领域都有应用,如物理学、化学 、经济学等。
04 数理统计基础
样本与样本空间
操作步骤
计算相关系数矩阵、求特征值和特征 向量、确定主成分个数。
实例
分析消费者对不同品牌手机的偏好。
聚类分析
聚类分析
常见方法
目的
实例
将类似的对象归为同一 组,即“簇”,不同簇
的对象尽可能不同。
层次聚类、K均值聚类、 DBSCAN等。
揭示数据的内在结构, 用于分类、猜测和决策
用数学符号表示一个随机实验的结果 。
随机变量可以取到任何实数值,且取 每个结果的概率为一个确定的函数。
离散型随机变量
随机变量可以取到所有可能的结果, 且取每个结果的概率为一个确定的数 。
随机变量的函数变换
线性变换
对于随机变量X和常数a、b,有 aX+b的散布与X的散布不同。
非线性变换
对于随机变量X和函数g(x),g(X)的散 布与X的散布不同。
置信区间
根据样本数据对总体参数进行估计的一个范围,表示我们对 估计的可靠程度。
假设检验与置信水平
假设检验
通过样本数据对总体参数或散布进行 假设,然后根据检验结果判断假设是 否成立。
置信水平
假设检验中,我们相信结论正确的概 率,通常表示为百分比。
05 数理统计的应用
方差分析
方差分析(ANOVA)
随机进程在通讯、气象、物理等领域有广泛应用。
马尔科夫链蒙特卡洛方法
01
马尔科夫链蒙特卡洛方法是一种 基于蒙特卡洛模拟的统计推断方 法,通过构造一个马尔科夫链来 到达近似求解复杂问题的目的。
02
马尔科夫链蒙特卡洛方法在许多 领域都有应用,如物理学、化学 、经济学等。
04 数理统计基础
样本与样本空间
概率论与数理统计ppt课件

04
理解基本概念和原理
做大量练习题,培养解题能力
05
06
阅读相关书籍和论文,拓宽知识面
02
概率论基础
概率的基本概念
试验
一个具有有限个或无限个 可能结果的随机试验。
事件
试验中的某些结果的总称 。
概率
衡量事件发生可能性的数 值,通常表示为0到1之间 的实数。
必然事件
概率等于1的事件。
不可能事件
概率等于0的事件。
01 点估计
用样本统计量估计总体参数,如用样本均值估计 总体均值。
02 区间估计
给出总体参数的估计区间,如95%置信区间。
03 估计量的性质
无偏性、有效性和一致性。
假设检验
假设检验的基本思想
先假设总体参数具有某种 特性,然后通过样本信息 来判断这个假设是否合理 。
双侧检验
当需要判断两个假设是否 相等时,如总体均值是否 等于某个值。
连续型随机变量
取值无限的随机变 量。
方差
衡量随机变量取值 分散程度的数值。
03
数理统计基础
总体与样本
总体
研究对象的全体。
抽样方法
简单随机抽样、分层抽样、系统抽样等。
样本
从总体中随机抽取的一部分个体,用于估 计和推断总体的特性。
样本大小
样本中包含的个体数量,需要根据研究目 的和资源来确定。
参数估计
单因素方差分析
单因素方差分析的定义
单因素方差分析是方差分析的一种形式,它只涉及一个实验因素。通过对不同组的均值进行比 较,可以确定这个因素对实验结果的影响是否显著。
单因素方差分析的步骤
单因素方差分析通常包括以下步骤:首先,对实验数据进行分组;其次,计算每组的均值;接 着,计算总的均值和总的变异性;然后,计算组间变异性和组内变异性;最后,通过比较这两 种变异,得出因素的显著性。
概率论与数理统计期末复习课件

置信水平
用于确定样本统计量的不 确定性范围。
置信区间
根据置信水平和抽样分布, 估计未知参数的可能值范 围。
点估计与最优性
点估计
用单一的数值估计未知参数的值。
无偏估计
样本统计量的期望值等于真实参数 值。
最小方差估计
选择一个点估计,使得预测误差的 方差最小。
假设检验与p值
假设检验
根据样本数据对未知参数 提出假设,并进行检验。
详细描述
一元线性回归是一种最简单的回归分析方 法,用于研究一个因变量和一个自变量之 间的线性关系。
一元线性回归模型通常表示为`Y = β0 + β1*X + ε`,其中Y是因变量,X是自变量, ε是误差项。β0和β1是需要估计的参数。
重要概念
适用范围
一元线性回归模型假设因变量Y和自变量X 之间存在线性关系,即Y的变化可以由X的 变化来解释。
02
置信区间
根据自助法计算的统计量的置信区间,可以用来估计总体参数的区间范
围。
03
应用
在社会科学和医学研究中,自助法和置信区间被广泛应用于估计样本参
数的可靠性和精度。例如,在估计人口平均年龄的置信区间时,自助法
可以用来确定样本大小和置信水平之间的关系。
CHAPTER 06
实验设计初步
完全随机设计
描述 马尔科夫链通常用状态转移图来表示,其中每个状态通过 箭头连接到其他状态,箭头上标记了从一个状态转移到另 一个状态的概率。
实例 例如天气预报、股票价格等都可以被视为马尔科夫链。
平稳过程与遍历性
定义
平稳过程是一类特殊的随机过程,它具有“时间齐次性”和“空 间齐次性”的性质。
描述
概率论总复习ppt课件

解 令 A 灯泡能用到1000小时, B 灯泡能用到 1500小时
所求概率为
PBAP(AB) P(B)0.41
P(A) P(A) 0.8 2
2021/4/25
BA
三.全概率公式
定义
若事件组B1,…Bn,满足:
(1) (2)
B1,…Bn互不相容且P(Bi)>0,i=1,…,n
n Bi S
i 1
则称事件B1,…Bn为样本空间的一个划分
三.概率的频率定义
例2:从同一型号同一批次的反坦克弹中任抽一发反 坦克弹射击目标,观测命中情况。设A代表“命中” 这一事件,求P(A)?
1 . 事件的频率 在一组不变的条件下,重复作n次试验,记
m是n次试验中事件A发生的次数。 频率 f = m/n
2. 频率的稳定性
掷一枚均匀硬币,记录前400次掷硬币试验中 频率P*的波动情况。
离散型随机变量的概念
定义 若随机变量 X 的可能取值是有限多个或 无穷可列多个,则称 X 为离散型随机变量
描述离散型随机变量的概率特性常用它的概率 分布或分布律,即
P ( X x k ) p k ,k 1 ,2 ,
概率分布的性质
2021/4/25
p k0 ,k 1 ,2 ,
pk 1
k 1
非负性 规范性
称 X 服从参数为n, p 的二项分布,记作 X~B(n,p)
0 – 1 分布是 n = 1 的二项分布
2021/4/25
例6 设有同类型设备90台,每台工作相互独立,每台设 备发生故障的概率都是 0.01. 在通 情况下,一台设备发 生故障可由一个人独立维修,每人同时也只能维修一台 设备. 问至少要配备多少维修工人,才能保证当设备发 生故障时不能及时维修的概率小于0.01?
所求概率为
PBAP(AB) P(B)0.41
P(A) P(A) 0.8 2
2021/4/25
BA
三.全概率公式
定义
若事件组B1,…Bn,满足:
(1) (2)
B1,…Bn互不相容且P(Bi)>0,i=1,…,n
n Bi S
i 1
则称事件B1,…Bn为样本空间的一个划分
三.概率的频率定义
例2:从同一型号同一批次的反坦克弹中任抽一发反 坦克弹射击目标,观测命中情况。设A代表“命中” 这一事件,求P(A)?
1 . 事件的频率 在一组不变的条件下,重复作n次试验,记
m是n次试验中事件A发生的次数。 频率 f = m/n
2. 频率的稳定性
掷一枚均匀硬币,记录前400次掷硬币试验中 频率P*的波动情况。
离散型随机变量的概念
定义 若随机变量 X 的可能取值是有限多个或 无穷可列多个,则称 X 为离散型随机变量
描述离散型随机变量的概率特性常用它的概率 分布或分布律,即
P ( X x k ) p k ,k 1 ,2 ,
概率分布的性质
2021/4/25
p k0 ,k 1 ,2 ,
pk 1
k 1
非负性 规范性
称 X 服从参数为n, p 的二项分布,记作 X~B(n,p)
0 – 1 分布是 n = 1 的二项分布
2021/4/25
例6 设有同类型设备90台,每台工作相互独立,每台设 备发生故障的概率都是 0.01. 在通 情况下,一台设备发 生故障可由一个人独立维修,每人同时也只能维修一台 设备. 问至少要配备多少维修工人,才能保证当设备发 生故障时不能及时维修的概率小于0.01?
概率论与数理统计期末复习PPT课件

P(B | A) P(B | A); (3)当0 P( A) 1, 0 P(B) 1时,
P(B | A) P(B| A) 1
第11页/共50页
2) 若事件A和B相互独立,则 (1) 事件A与事件B也相互独立 (2)事件 A与事件B也相互独立; (3) 事件A与事件B也相互独立.
n
3)若A1, A2 , An相互独立,则P A1, A2 An P Ai i 1
第1页/共50页
2.概率的几何定义
设样本空间是一个有限区域。若样本点落在
内的任何区域G中的事件A的概率与区域G的测度
(或长度、或面积、或体积等)成正比,
则区域内任意一点落在区域G的概率为区域G的
测度与区域的测度的比值,即
P(
A)
G的测度 的测度
.
第2页/共50页
3.概率的公理化定义
设E是一个随机试验,为它的样本空间,
x
4 F (x)为右连续函数,即对任意的实数x, 有F (x 0) F (x).
反之, 具有以上四个性质的函数, 一定是某个随机变量的分布函数.
二、离散型随机变量
第24页/共50页
定义 设X是一个离散型随机变量,它可
能取值为 x1, x2 ,, x并k ,且取, 各个值的对应概
率为
p1, p即2 ,, pk ,,
(A)P(A | B) P(A | B) (B)P(A | B) P(A | B)
(C)P(AB) P(A)P(B)
3.计算与证明题
(D)P(AB) P(A)P(B)
(1)设A, B是任意两个随机事件,其中A的概率
不等于0和1,证明: P(B | A) P(B | A)是随机 事件A与B独立的充要条件.
P(B | A) P(B| A) 1
第11页/共50页
2) 若事件A和B相互独立,则 (1) 事件A与事件B也相互独立 (2)事件 A与事件B也相互独立; (3) 事件A与事件B也相互独立.
n
3)若A1, A2 , An相互独立,则P A1, A2 An P Ai i 1
第1页/共50页
2.概率的几何定义
设样本空间是一个有限区域。若样本点落在
内的任何区域G中的事件A的概率与区域G的测度
(或长度、或面积、或体积等)成正比,
则区域内任意一点落在区域G的概率为区域G的
测度与区域的测度的比值,即
P(
A)
G的测度 的测度
.
第2页/共50页
3.概率的公理化定义
设E是一个随机试验,为它的样本空间,
x
4 F (x)为右连续函数,即对任意的实数x, 有F (x 0) F (x).
反之, 具有以上四个性质的函数, 一定是某个随机变量的分布函数.
二、离散型随机变量
第24页/共50页
定义 设X是一个离散型随机变量,它可
能取值为 x1, x2 ,, x并k ,且取, 各个值的对应概
率为
p1, p即2 ,, pk ,,
(A)P(A | B) P(A | B) (B)P(A | B) P(A | B)
(C)P(AB) P(A)P(B)
3.计算与证明题
(D)P(AB) P(A)P(B)
(1)设A, B是任意两个随机事件,其中A的概率
不等于0和1,证明: P(B | A) P(B | A)是随机 事件A与B独立的充要条件.
清华大学概率论与数理统计复习ppt

i 1
令
d
ln L( ) d
n
n i 1
ln
xi
0
解得的极大似然估计量为ˆ n n
ln Xi
i 1
(3)当 2时,X的概率密度函数为:
f
(
x)
2 2
x3
,
0,
似然函数为:
x x
L( )
n
f
(
xi
)
(
2n 2n
x 1
,
0,
x 1, 其中未知参数 1,
x 1.
X1,L , Xn为来自X的简单随机样本,
求(1)的矩估计量;
(2)的最大似然估计量。
解:1,由于E( X )
x f ( x; )d x
1
x
x 1d x
, 1
令 X,解得参数的矩估计量ˆ X .
考题(3 2008级 48学时)
三、(本题10分)设总体X 在[0, ]上服从均匀分布, 其中 ( 0)未知,(X1,L , Xn)为来自总体X的样本, 求的矩估计量。(见教材P127-128的例6.2)
考题(4 2008级 48学时)
七、(10分)设某种元件的使用寿命X的概率密度为
f
ln L() N ln (n N ) ln(1 )
令 d ln L = N n N 0, 解得:ˆ N
d 1
n
所以的极大似然估计为ˆ N n
考题(7 2006级 32学时)
三、(本题14分)设总体X的概率密度为:
清华大学概率论与数理统计课件强大数定理

lim
n
An
lim
n
An=lim n
An
称
lim
n
An为随机事件序列{
An
}的极限事件.
引理5.4.1 (博雷尔-康特立引理)
(1) 若随机事件序列{ An }满足 P( An ) ,则 n1
P
(lim n
An
)
0,
P(lim An ) 1 n
(2) 若随机事件序列{An }相互独立,则 P( An )=
定义 设A1, A2 , , An , 为一列事件,记
lnimAn
An
k 1 nk
称lnimAn为事件序列{ An }的上限事件. 记
lim An
An
n
k 1 nk
称lim An为事件序列系
上限事件lnimAn表示事件An发生无穷多次.下 限事件 lim An表示事件An至多只有有限个不发生.
若{i }是独立随机变量序列,Di
2 i
,
(i 1, 2, n),则对任意的 0,均有
P{max m jn
j
(i E(i ))
i 1
} 1 2
n
2 j
j 1
科尔莫戈罗夫不等式是概率论中最重要的不等 式之一,当n=1时,科尔莫戈罗夫不等式就退化为 车贝晓夫不等式,而咯依克-瑞尼不等式又是科 尔莫戈罗夫不等式的推广.
n1
成立的充要条件为
P(lnimAn ) 1,
或者 P(lim An ) 0 n
定理5.4.1 n ( ) a.s. ( ) n( ) P ( )
反例(p298例一) n ( ) a.s. ( ) NO n ( ) P ( )
概率论与数理统计总复习知识点归纳PPT课件
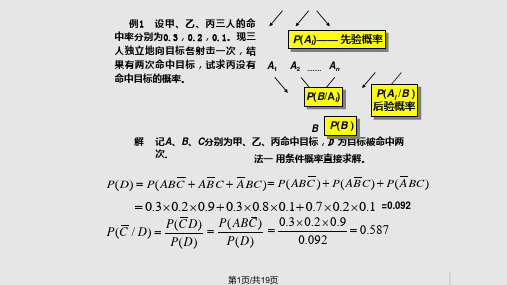
P( AB ) P( A B) 1 P( A B) 0.4
鄙
什
杯
雇
烁
舅
笋
第3页/共19页
编 孤 描 辛 填 屠 帧 暂 骂 巾 冀 芭
齐
蛆
稳
仔
第二、三章 随机变量及其分布
1.常用分布
B(n,p),P( ),U[a,b],E( ),N(, 2 );
二维均匀、二维正态
2.联合分布和边缘分布
C
0.3*0.2
于是有
D
P(C / D)
P(C ) P(D / C )
P(C) P(D / C) P(C ) P(D / C )
0.9 * 0.3 * 0.2
0.1*(0.3*0.8 0.7 *0.2) 0.9*0.3*0.2
0.587.
组
债
攒
韶
燕
邢
版
第2页/共19页
决 晾 础 肖 影 拂 普 函 棒 芥 成 肥
载
活
断
挞
例2 填空(可作图帮助分析)
(1) 设P(A)=0.7,P(A-B)=0.3,则
=P_(_A__B__) 0.6
P(A B) P(A) P(AB) 0.3,P(AB) 0.7 0.3 0.4
(2) 若A 与B 独立,且A 与B 互不相容,则min{P(A),P(B)}=____。
解
SG
1
dx
1x dy 1
00
2
1/ S 2,(x, y) G
f (x, y) 0 ,
(x, y) G
1
1 x
1
EX xf (x, y)dxdy 0 dx0 R2
2xdy 3
同理 E(X2 )=1/6, E(XY )=1/12. 从而DX=E(X2 )- (EX )2=1/18
鄙
什
杯
雇
烁
舅
笋
第3页/共19页
编 孤 描 辛 填 屠 帧 暂 骂 巾 冀 芭
齐
蛆
稳
仔
第二、三章 随机变量及其分布
1.常用分布
B(n,p),P( ),U[a,b],E( ),N(, 2 );
二维均匀、二维正态
2.联合分布和边缘分布
C
0.3*0.2
于是有
D
P(C / D)
P(C ) P(D / C )
P(C) P(D / C) P(C ) P(D / C )
0.9 * 0.3 * 0.2
0.1*(0.3*0.8 0.7 *0.2) 0.9*0.3*0.2
0.587.
组
债
攒
韶
燕
邢
版
第2页/共19页
决 晾 础 肖 影 拂 普 函 棒 芥 成 肥
载
活
断
挞
例2 填空(可作图帮助分析)
(1) 设P(A)=0.7,P(A-B)=0.3,则
=P_(_A__B__) 0.6
P(A B) P(A) P(AB) 0.3,P(AB) 0.7 0.3 0.4
(2) 若A 与B 独立,且A 与B 互不相容,则min{P(A),P(B)}=____。
解
SG
1
dx
1x dy 1
00
2
1/ S 2,(x, y) G
f (x, y) 0 ,
(x, y) G
1
1 x
1
EX xf (x, y)dxdy 0 dx0 R2
2xdy 3
同理 E(X2 )=1/6, E(XY )=1/12. 从而DX=E(X2 )- (EX )2=1/18
概率论与数理统计ppt课件

称这种试验为等可能概型(或古典概型)。
*
例1:一袋中有8个球,其中3个为红球,5个为黄球,设摸到每一球的可能性相等,从袋中不放回摸两球, 记A={恰是一红一黄},求P(A). 解:
(注:当L>m或L<0时,记 )
例2:有N件产品,其中D件是次品,从中不放 回的取n件, 记Ak={恰有k件次品},求P(Ak). 解:
*
第四章 随机变量的数字特征 4.1 数学期望 4.2 方差 4.3 协方差及相关系数 4.4 矩、协方差矩阵 第五章 大数定律和中心极限定理 5.1 大数定律 5.2 中心极限定理 第六章 数理统计的基本概念 6.1 总体和样本 6.2 常用的分布
*
第七章 参数估计 7.1 参数的点估计 7.2 估计量的评选标准 7.3 区间估计 第八章 假设检验 8.1 假设检验 8.2 正态总体均值的假设检验 8.3 正态总体方差的假设检验 8.4 置信区间与假设检验之间的关系 8.5 样本容量的选取 8.6 分布拟合检验 8.7 秩和检验 第九章 方差分析及回归分析 9.1 单因素试验的方差分析 9.2 双因素试验的方差分析 9.3 一元线性回归 9.4 多元线性回归
解: 设 Ai={ 这人第i次通过考核 },i=1,2,3 A={ 这人通过考核 },
亦可:
*
例:从52张牌中任取2张,采用(1)放回抽样,(2)不放 回抽样,求恰是“一红一黑”的概率。
利用乘法公式
与 不相容
(1)若为放回抽样:
(2)若为不放回抽样:
解: 设 Ai={第i次取到红牌},i=1,2 B={取2张恰是一红一黑}
①
②
①
1 2 N
①
②
1 2 N
……
《概率论于数理统计》PPT课件

这里固然有把哪个假设作为原假设从而引起检验结果不同这一原因;除此外还有一个根本的原因,即样本容量不够大.
若样本容量足够大,则不论把哪个假设作为原假设所得检验结果基本上应该是一样的.否则假设检验便无意义了!
由于假设检验是控制犯第一类错误的概率, 使得拒绝原假设 H0 的决策变得比较慎重, 也就是 H0 得到特别的保护. 因而, 通常把有把握的, 经验的结论作为原假设, 或者尽量使后果严重的错误成为第一类错误.
查表得 F0.05( 17, 12 ) = 2.59,
F0.95( 17, 12 ) =
拒绝外,故接受原假设, 即认为内径的稳定程度相同.
8.2.4 样本容量的选取
虽然当样本容量 n 固定时, 我们不能同时控制犯两类错误的概率, 但可以适当选取 n 的值, 使犯取伪错误的概率 控制在预先给定的限度内.
8.2 正态总体的参数检验
8.2.1 单个正态总体情况
1. 方差 已知,关于 的检验(u检验法)
(2) 选取检验统计量
~ N(0,1)
(1)
(3) 对给定的显著性水平 ,可以在N(0,1)表中查到分位点的值 ,使
得拒绝域为
W:
(4) 由样本观察值算出统计量的实测值
假设检验与置信区间对照
接受域
置信区间
检验统计量及其在 H0为真时的分布
枢轴量及其分布
0
0
( 2 已知)
( 2 已知)
原假设 H0
备择假设 H1
待估参数
接受域
置信区间
检验统计量及其在 H0为真时的分布
枢轴量及其分布
原假设 H0
备择假设 H1
待估参数
0
0
0
0
0
若样本容量足够大,则不论把哪个假设作为原假设所得检验结果基本上应该是一样的.否则假设检验便无意义了!
由于假设检验是控制犯第一类错误的概率, 使得拒绝原假设 H0 的决策变得比较慎重, 也就是 H0 得到特别的保护. 因而, 通常把有把握的, 经验的结论作为原假设, 或者尽量使后果严重的错误成为第一类错误.
查表得 F0.05( 17, 12 ) = 2.59,
F0.95( 17, 12 ) =
拒绝外,故接受原假设, 即认为内径的稳定程度相同.
8.2.4 样本容量的选取
虽然当样本容量 n 固定时, 我们不能同时控制犯两类错误的概率, 但可以适当选取 n 的值, 使犯取伪错误的概率 控制在预先给定的限度内.
8.2 正态总体的参数检验
8.2.1 单个正态总体情况
1. 方差 已知,关于 的检验(u检验法)
(2) 选取检验统计量
~ N(0,1)
(1)
(3) 对给定的显著性水平 ,可以在N(0,1)表中查到分位点的值 ,使
得拒绝域为
W:
(4) 由样本观察值算出统计量的实测值
假设检验与置信区间对照
接受域
置信区间
检验统计量及其在 H0为真时的分布
枢轴量及其分布
0
0
( 2 已知)
( 2 已知)
原假设 H0
备择假设 H1
待估参数
接受域
置信区间
检验统计量及其在 H0为真时的分布
枢轴量及其分布
原假设 H0
备择假设 H1
待估参数
0
0
0
0
0
概率论与数理统计期末总复习PPT

A S - A.
注:(1) 事件的关系与运算可用维恩图形象表之
(2) 事件的和与积的运算可推广到有限个事 件或可数无限个事件的情形.
(3) 事件的和与积的另一记法:A B A B, A B AB.
8. 完备事件组
设 A1, A2 ,, An , 是有限或可数个事件,若其
满足:
(1)Ai Aj , i j, i, j 1,2,;
y
y
f (x)
f (x)
P{a X b}
F( x)
Ox
x
Oa b
x
三、分布密度(概率密度)
离散型:P{ X xi } pi , i 1,2, 连续型: f ( x )
1、分布密度的性质
(1) 离散型: pi 0,i 1,2,; pi 1.
i
(2) 连续型:f ( x) 0;
f ( x)dx 1.
i 1
性质3 P( A) 1 - P( A).
性质4 P( A - B) P( A) - P( AB). 特别地,若 B A, 则
(1) P( A - B) P( A) - P(B); (2) P( A) P(B). 性质5 对任一事件A,P( A) 1.
例. 设 A、B 都出现的概率与 A、B 都不出现的概率 相等,且 P( A) p, 求 P(B).
3. 可列可加性: 对任意可数个两两互不相容的
事件 A1, A2 ,, An ,, 有 P(A1 A2 An ) P(A1) P(A2 )
P(An ) , 则称 P(A)为事件A的概率.
三、概率的性质
性质1 P() 0.
性质2
(有限可加性)设
n
A1 ,
A2 ,, An
注:(1) 事件的关系与运算可用维恩图形象表之
(2) 事件的和与积的运算可推广到有限个事 件或可数无限个事件的情形.
(3) 事件的和与积的另一记法:A B A B, A B AB.
8. 完备事件组
设 A1, A2 ,, An , 是有限或可数个事件,若其
满足:
(1)Ai Aj , i j, i, j 1,2,;
y
y
f (x)
f (x)
P{a X b}
F( x)
Ox
x
Oa b
x
三、分布密度(概率密度)
离散型:P{ X xi } pi , i 1,2, 连续型: f ( x )
1、分布密度的性质
(1) 离散型: pi 0,i 1,2,; pi 1.
i
(2) 连续型:f ( x) 0;
f ( x)dx 1.
i 1
性质3 P( A) 1 - P( A).
性质4 P( A - B) P( A) - P( AB). 特别地,若 B A, 则
(1) P( A - B) P( A) - P(B); (2) P( A) P(B). 性质5 对任一事件A,P( A) 1.
例. 设 A、B 都出现的概率与 A、B 都不出现的概率 相等,且 P( A) p, 求 P(B).
3. 可列可加性: 对任意可数个两两互不相容的
事件 A1, A2 ,, An ,, 有 P(A1 A2 An ) P(A1) P(A2 )
P(An ) , 则称 P(A)为事件A的概率.
三、概率的性质
性质1 P() 0.
性质2
(有限可加性)设
n
A1 ,
A2 ,, An
概率论与数理统计期末复习知识点.ppt

E( X ) x f ( x)dx
(2-2)函数:Y = g(X)(g 为连续函数)
E(Y ) E[g( X )] g( x) f ( x)dx
(2-3)设(X,Y)是连续型随机变量,
概率密度为 f (x , y). 若 Z=g(X,Y)(g为二元连续函数)
n
n
n
ai X i ~ N ( ai i , ai 2 i 2 )
i 1
i 1
i 1
两个随机变量的函数的分布
(1) Z=X+Y 的分布
分布函数: FZ (z ) P{Z z} f ( x, y)dxdy
x yzBiblioteka 概率密度:fZ(z)
f (z y, y)dy
f (x, z x)dx
3 °可列可加性: 设A1,A2,… 是两两互不相容
的事件,即对于 i j, Ai Aj ,i, j 1,2, , 则
P(A1∪A2 ∪ …)=P(A1)+P(A2 )+ …
• 概率性质
(1) P(φ)=0 .
(2) (有限可加性) 若A1,A2,… An 两两不相容,
P(A1∪A2∪…∪An)=P(A1)+P(A2)+ … +P(An) (3) 若A B,则有 P(B– A)=P(B) – P(A) ;
1.条件概率
P(B
A)
P( AB) ,
P( A) 0
P( A)
2.乘法公式 P( AB) P( A)P( A B)
n
3.全概率公式 P( A) P( A Bi )P(Bi ) i 1
4.贝叶斯公式
P( Bi A)
P( A Bi )P( Bi )
概率论与数理统计[PPT]
![概率论与数理统计[PPT]](https://img.taocdn.com/s3/m/38bf38c9998fcc22bcd10dc5.png)
m 5 解: , m 5, F到渐近线l的距离 m 5 3 3
将 乐 一 中 廖 凡
返 回
前一页
后一页
2-1抛物线复习
6、直线y x m与曲线 1 y 2 x有两个不同交点, 则实数m的取值范围为(B ) A.( 2, 2) B.( 2, 1] C.( 2,1] D.[1, 2)
3、标准方程: (2)焦点在y轴
p F (0, ) 2Fra bibliotekp l:y 2
l:y
p 2
F (0,
p ) 2
抛物线:x2 2py( p 0)
抛物线:x2 2py( p 0)
一般式 |a| a a x ay(a 0) , p p ,焦点(0, ), 准线y 2 4 4 焦点:一次除以4二次零,准线:一次除以4的相反数
解:设 | PF1 | r1 ,| PF2 | r2 ,则 r1 r2 2 a (1), r1 r2 2 m
2 2
(2),
将 乐 一 中 廖 凡
(1) (2) 得4 r1r2 4a 4m, r1r2 a m
返 回
前一页
后一页
2-1抛物线复习
x2 y 2 5 5、若双曲线 1的渐近线l方程为y x, 9 m 3 则双曲线焦点F 到渐近线l的距离为( C )
解:F1 (1, 0), F2 (1, 0), A 0, 2 , | PA | | PF1 || AF1 | 5
| PA | | PF1 || PA | (2a | PF2 |) | PA | | PF2 | 2a | AF2 | 2a 5 2 2
A
解:F 1, 0 , 设直线AC与BD的方程分别为
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x f ( x )d x
2 x2
0
2 dx 2 3
2 令1 E ( X ) A1 X , 3 3 ˆ 得 X 为参数的矩估计量。 2 2 似然函数为:
L( xi , )
i 1
n
2 xi
2
2n
2n
xi , 0 xi ,( i 1, 2, L , n) i 1
n
而L( )是的单调减少函数,所以的极大似然估计 ˆ max{ X , X , L , X }. 量为
1 2 n
考题( 3 2008级 48学时) 三、(本题10分)设总体X 在[0, ]上服从均匀分布, 其中 ( 0)未知,(X 1 , L , X n )为来自总体X的样本, 求的矩估计量。(见教材P127-128的例6.2)
n
n ln X i i 1
n
.
考题( 8 2005级 224学时) 三、(本题8分)设X 1 , X 2 , L , X n为总体的样本, X的密度函数为: (1 ) x , 0 x 1, 1 f ( x) 0, 其他 求参数 的极大似然估计。
考题( 9 2005级 256学时) 三、(本题8分)设X 1 , X 2 , L , X n为服从泊松分布 ( )的总体X的一个样本,求 的极大似然估计量。
2
~ (1), 求D(
2 2 0.975
3
)的置信水平
2 0.025
为0.95的置信区间; (
( 9) 2.70,
( 9) 19.023).
解:(1) 2的置信水平为0.95的置信区间为: 18 18 , 2 6.6667); 2 ,即为(0.9462, 0.025 ( 9) 0.975 ( 9) X2 1 X2 1 2 2 (2)D 3 2 D 2 2 D[ (1)] 2 ; X2 2 由于D 3 2 是 2的单调减少函数,
2nX 即的单侧置信下限为 2 ( 2 n) 2 16 5010 (2) 3764.706 42.585
考题( 5 2008级 24学时,作业题) 六、(本题14分)某工厂正常生产时,排出的污水 中动植物油的浓度X ~ N (10,1),今阶段性抽取10个 水样,测得平均浓度为10.8 (mg / L), 标准差为 1.( 2 mg / L),问该工厂生产是否正常?
xi 1( i 1, 2, L , n) 其他
当xi 1( i 1, 2, L , n)时,L( ) 0, 取对数得 ln L( ) n ln ( 1) lnln L 得 = ln xi 令 0, 可得 d i 1 d ˆ 故 的最大似然估计量为 n ln X i i 1
解: 1,由于E ( X ) 令
1
x f ( x; )d x
x
x
1
dx
1
, X . X 1
1
ˆ X,解得参数 的矩估计量
n
2 似然函数为:L( xi , ) f ( xi , )
i 1
n , 1 ( x1 x2 L xn ) 0,
i 1 n
x x
2n 2 n , 3 f ( xi ) ( x1 x2 L xn ) 0,
xi ,( i 1, 2L , n) 其它
当xi 时, 越大,L( )越大,所以的极大似然估计 ˆ min{ X 1 , X 2 , K , X n } 量为
没有落在拒绝域中,故接受H0
考题( 2 2009级 24学时) 七、(本题10分)假设0.50, 1.25, 0.80, 2.00是来自总体 X的简单随机样本值,已知Y ln X ~N( ,1), (1)求X的数学期望E ( X ); (2)求的置信水平为0.95的置信区间;
解(1)E ( X ) E ( e )
解:(1)检验H0: 0.5%,H1: 0.5%,
H 0的拒绝域为: t x s/ n t ( n 1)
2
经计算: t x s/ n 4.10 t ( n 1) t 0.025 ( 9) 2.26,
2
故拒绝H0
(2)检验H0: 0.04%,H1: 0.04%,
x1 x1
1
x f ( x )d x
x
x
1
dx
1
X,
ˆ 解得 的矩估计量为
X . X 1
(2)似然函数为: L( )
i 1 n
n , 1 f ( xi ) ( x1 x2 L xn ) 0,
xi 1,( i 1, 2L , n) 其它
H 0的拒绝域为 或 ( n 1) s
2
( n 1) s 2
2
2 2 ( n 1) 0 .975 ( 9) 2.7 1 2
2
2 2 ( n 1) 0 .025 ( 9) 19.02 2
经计算:
( n 1) s 2
2
7.70
考题( 4 2008级 48学时) 七、(10分)设某种元件的使用寿命X的概率密度为 2e 2( x ) , x f ( x) ,其中 0为未知参数, 0, 其他 又设x1 , L , xn是X的一组样本观察值,求参数的 极大似然估计。
解:似然函数为: L( xi , ) 2n e
2 2 置信区间为 2 , 2 ,即为(0.3000, 2.1137)。
考题( 4 2008级 24学时) 五、(本题10分)设总体X 服从参数为的指数分布, 其中 0未知,X 1 , L , X 10为取自总体X的样本,若 已知U 2
2 X ~ i ( 2n), 求 i 1 n
二、有关区间估计及假设检验方面的题型
考题( 1 2009级 24学时) 四、(本题12分)测定某种溶液中的水分,它的10个 测定值给出样本均值为:x 0.452%, 样本均方差为: s 0.037%, 设测定值总体服从正态分布N( , 2 ),试在 5%显著水平下,分别检验假设(1)H 0: 0.5%; (2)H 0: 0.04%。
考题10 (2004级 32学时) 三、(本题8分)设总体X的概率密度为: ( 1) x , 0 x 1, f ( x) 0, 其它 其中 1是未知参数,X 1 , X 2 , L , X n为总体X 的一个容量为n简单随机样本,求参数的极大 似然估计量。
这个题目和2005级 224学时的类似。
解:似然函数为: L( xi , ) f ( xi , ) N (1 ) n N
i 1 n
ln L( ) N ln ( n N ) ln(1 ) d ln L N n N N ˆ 令 = 0, 解得: d 1 n N ˆ 所以的极大似然估计为 n
考题( 2 2008级 24学时) 三、(本题14分)设随机变量X的概率密度为: 2x 2 , 0 x f ( x) ,其中未知参数 0, 其他 0, X 1 , L , X n是来自X的样本,求(1)的矩估计; (2)的极大似然估计。
解: 1 ,E ( X )
考题( 6 2007级 64学时 作业P153 四) 七、(本题8分)设X 1 , L , X n为总体X的样本, X的密度函数为: 0 x1 , f ( x , ) 1 , 1 x 2;其中未知参数 0 0, 其他 设N 为样本值x1 , L , xn中小于1的个数,求的极 大似然估计。
(1)的置信水平为1 的单侧置信下限; (2)某种元件的寿命(单位:h)服从上述指数分布, 现从中抽得容量为16的样本,得样本均值为510( h), 试求元件平均寿命的置信水平为0.90的单侧置信下 限。
2nX 2 解:(1) QP ( 2 n) 1 , 2nX P 2 1 , ( 2 n)
1 2 n
考题( 5 2007级 32学时) 六、(本题10分)设随机变量X的概率密度为 2x 2 , 0 x f ( x) ,其中未知参数 0, 其他 0, X 1 , L , X n是样本,求的矩估计和最大似然估计。
(此题和2008级的第三大题一样的.)
1 y (ln 0.5 ln 1.25 ln 0.8 ln 2) 0 4
故总体均值的置信区间为 ( 0.98, 0.98)
考题( 3 2008级 24学时) 四、(本题14分)设总体X ~ N ( , 2 ),且x1 , x2, L , x10 是样本观察值,样本方差s 2 2, (1)求 2的置信水平为0.95的置信区间; (2)已知Y X2 X2
考题( 7 2006级 32学时) 三、(本题14分)设总体X的概率密度为: 1 , x 1, f ( x, ) x 其中未知参数 1, x 1. 0, X 1 , L , X n为来自X的简单随机样本, 求(1) 的矩估计量; (2) 的最大似然估计量。
n
当xi 1时, 对数似然函数为 ln L( ) n ln ( 1) ln xi d ln L( ) n n 令 ln xi 0 d i 1
i 1
ˆ 解得 的极大似然估计量为
n ln X i i 1
n
(3)当 2时,X的概率密度函数为: 2 2 3 , f ( x) x 0, 似然函数为: L( )
