逐步回归matlab程序
matlab回归建模过程

matlab回归建模过程摘要:一、回归建模概述- 回归分析的定义- 回归建模的目的和意义二、MATLAB 回归建模过程- 一元线性回归- 数学模型定义- 模型参数估计- 检验、预测及控制- 多元线性回归- 数学模型定义- 模型参数估计- 多元线性回归中检验与预测- 逐步回归分析三、MATLAB 回归建模应用案例- 案例一:一元线性回归分析- 案例二:多元线性回归分析- 案例三:逐步回归分析正文:一、回归建模概述回归分析是一种研究变量之间关系的统计方法,通过建立一个数学模型,描述自变量与因变量之间的线性关系。
回归建模在实际应用中有着广泛的应用,如经济学、生物学、社会学等学科的研究中,可以帮助我们更好地理解变量之间的关系,并对未来趋势进行预测和控制。
MATLAB 是一种广泛应用于科学计算和数据分析的编程语言,提供了丰富的回归建模工具箱,可以帮助我们快速、高效地进行回归建模分析。
二、MATLAB 回归建模过程1.一元线性回归一元线性回归是最简单的回归分析方法,适用于只有一个自变量和一个因变量的情况。
在MATLAB 中,我们可以使用回归分析工具箱中的`regress`函数进行一元线性回归建模。
(1)数学模型定义一元线性回归的数学模型可以表示为:y = a + bx其中,y 表示因变量,x 表示自变量,a 和b 分别表示回归系数。
(2)模型参数估计在MATLAB 中,我们可以使用`regress`函数对模型参数进行估计。
函数的原型为:b = regress(y, x)其中,y 表示因变量向量,x 表示自变量向量,b 表示回归系数向量。
(3)检验、预测及控制在得到回归系数向量b 后,我们可以进行回归检验、预测以及控制。
2.多元线性回归多元线性回归适用于有多个自变量和因变量的情况。
在MATLAB 中,我们可以使用回归分析工具箱中的`polyfit`函数进行多元线性回归建模。
(1)数学模型定义多元线性回归的数学模型可以表示为:y = a0 + a1x1 + a2x2 + ...+ anxn其中,y 表示因变量,x1、x2、...、xn 表示自变量,a0、a1、a2、...、an 分别表示回归系数。
matlab多元线性回归与逐步回归实验1
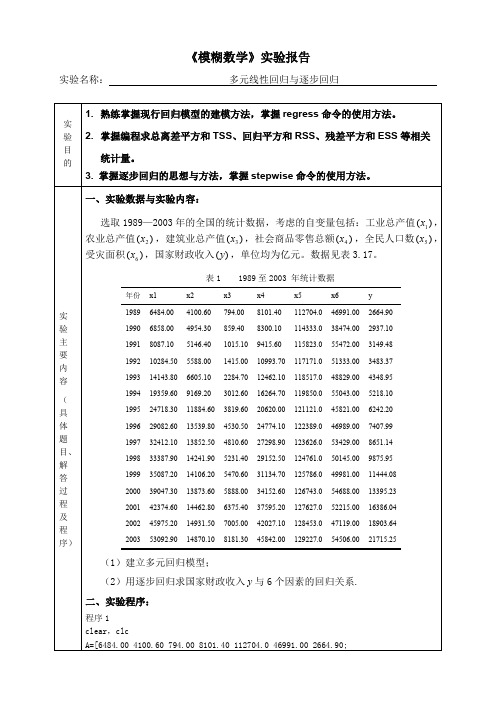
《模糊数学》实验报告实验名称:多元线性回归与逐步回归实验目的1.熟练掌握现行回归模型的建模方法,掌握regress命令的使用方法。
2.掌握编程求总离差平方和TSS、回归平方和RSS、残差平方和ESS等相关统计量。
3. 掌握逐步回归的思想与方法,掌握stepwise命令的使用方法。
实验主要内容(具体题目、解答过程及程序)一、实验数据与实验内容:选取1989—2003年的全国的统计数据,考虑的自变量包括:工业总产值,)(1x农业总产值,建筑业总产值,社会商品零售总额,全民人口数,)(2x)(3x)(4x)(5x受灾面积,国家财政收入,单位均为亿元。
数据见表3.17。
)(6x)(y表1 1989至2003 年统计数据年份x1x2x3x4x5x6y19896484.004100.60794.008101.40112704.046991.002664.9019906858.004954.30859.408300.10114333.038474.002937.1019918087.105146.401015.109415.60115823.055472.003149.48199210284.505588.001415.0010993.70117171.051333.003483.37199314143.806605.102284.7012462.10118517.048829.004348.95199419359.609169.203012.6016264.70119850.055043.005218.10199524718.3011884.603819.6020620.00121121.045821.006242.20199629082.6013539.804530.5024774.10122389.046989.007407.99199732412.1013852.504810.6027298.90123626.053429.008651.14199833387.9014241.905231.4029152.50124761.050145.009875.95199935087.2014106.205470.6031134.70125786.049981.0011444.08200039047.3013873.605888.0034152.60126743.054688.0013395.23200142374.6014462.806375.4037595.20127627.052215.0016386.04200245975.2014931.507005.0042027.10128453.047119.0018903.64200353092.9014870.108181.3045842.00129227.054506.0021715.25(1)建立多元回归模型;(2)用逐步回归求国家财政收入与6个因素的回归关系.y二、实验程序:程序1clear,clcA=[6484.00 4100.60 794.00 8101.40 112704.0 46991.00 2664.90;6858.00 4954.30859.40 8300.10 114333.038474.00 2937.10;8087.105146.401015.109415.60115823.055472.003149.48;10284.505588.001415.0010993.70117171.051333.003483.37; 14143.806605.102284.7012462.10118517.048829.004348.95; 19359.609169.203012.6016264.70119850.055043.005218.10; 24718.3011884.603819.6020620.00121121.045821.006242.20; 29082.6013539.804530.5024774.10122389.046989.007407.99; 32412.1013852.504810.6027298.90123626.053429.008651.14; 33387.9014241.905231.4029152.50124761.050145.009875.95; 35087.2014106.205470.6031134.70125786.049981.0011444.08; 39047.3013873.605888.0034152.60126743.054688.0013395.23; 42374.6014462.806375.4037595.20127627.052215.0016386.04; 45975.2014931.507005.0042027.10128453.047119.0018903.64; 53092.9014870.108181.3045842.00129227.054506.0021715.25];%自变量数据[m,n]=size(A);subplot(3,2,1),plot(A(:,1),A(:,7),'+')xlabel('x1(工业总产值)')ylabel('y(国家财政收入)')subplot(3,2,2),plot(A(:,2),A(:,7),'*')xlabel('x2(农业总产值)')ylabel('y(国家财政收入)')subplot(3,2,3),plot(A(:,3),A(:,7),'o')xlabel('x3(建筑业总产值)')ylabel('y(国家财政收入)')subplot(3,2,4),plot(A(:,4),A(:,7),'+')xlabel('x4(社会商品零售总额)')ylabel('y(国家财政收入)')subplot(3,2,5),plot(A(:,5),A(:,7),'*')xlabel('x5(全民人口数)')ylabel('y(国家财政收入)')subplot(3,2,6),plot(A(:,6),A(:,7),'o')xlabel('x6(受灾面积)')ylabel('y(国家财政收入)')x=[ones(m,1),A(:,1),A(:,2),A(:,3),A(:,4),A(:,5),A(:,6)];%构造设计矩阵y=A(:,7);[n,p]=size(x);%矩阵x0的行数即样本容量[db,dbint,dr,drint,dstats]=regress(y,x)%调用多元回归分析命令TSS=y'*(eye(n)-1/n*ones(n,n))*y%计算TSSH=x*inv((x'*x))*x';%计算对称幂等矩阵ESS=y'*(eye(n)-H)*y%计算ESSRSS=y'*(H-1/n*ones(n,n))*y%计算RSSMRS=RSS/p%计算MRSMSE=ESS/(n-p-1)%计算MSE%F检验F0=(RSS/p)/(ESS/(n-p-1))%计算F0。
MATLAB统计工具箱中的回归分析命令

1. 对回归模型建立M文件model.m如下: function yy=model(beta0,X) a=beta0(1); b=beta0(2); c=beta0(3); d=beta0(4); e=beta0(5); f=beta0(6); x1=X(:,1); x2=X(:,2); x3=X(:,3); x4=X(:,4); x5=X(:,5); x6=X(:,6); yy=a*x1+b*x2+c*x3+d*x4+e*x5+f*x6;
回 归 系
残 差
置 信 区
数
间
显著性水平 (缺省时为0.05)
的
用于检验回归模型的统计量,
区
有三个数值:相关系数r 2、
间 估
F值、与F 对应的概率p
计
相关系数 r2 越接近 1,说明回归方程越显著;
F > F1-α (k,n-k-1)时拒绝 H0,F 越大,说明回归方程越显著;
与 F 对应的概率 p 时拒绝 H0,回归模型成立.
例3 设某商品的需求量与消费者的平均收入、商品价格的统计数 据如下,建立回归模型,预测平均收入为1000、价格为6时 的商品需求量.
需求量 100 75
80
70
50
65
90
100 110 60
收入 1000 600 1200 500 300 400 1300 1100 1300 300
利用MATLAB进行回归分析
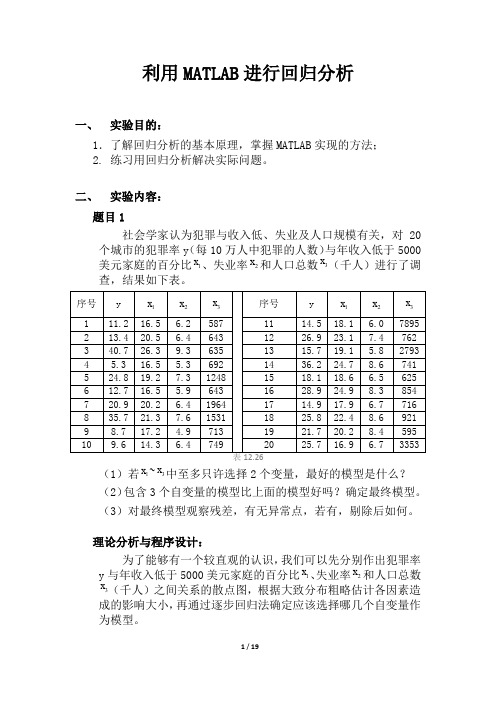
利用MATLAB进行回归分析一、实验目的:1.了解回归分析的基本原理,掌握MATLAB实现的方法;2. 练习用回归分析解决实际问题。
二、实验内容:题目1社会学家认为犯罪与收入低、失业及人口规模有关,对20个城市的犯罪率y(每10万人中犯罪的人数)与年收入低于5000美元家庭的百分比1x、失业率2x和人口总数3x(千人)进行了调查,结果如下表。
(1)若1x~3x中至多只许选择2个变量,最好的模型是什么?(2)包含3个自变量的模型比上面的模型好吗?确定最终模型。
(3)对最终模型观察残差,有无异常点,若有,剔除后如何。
理论分析与程序设计:为了能够有一个较直观的认识,我们可以先分别作出犯罪率y与年收入低于5000美元家庭的百分比1x、失业率2x和人口总数x(千人)之间关系的散点图,根据大致分布粗略估计各因素造3成的影响大小,再通过逐步回归法确定应该选择哪几个自变量作为模型。
编写程序如下:clc;clear all;y=[11.2 13.4 40.7 5.3 24.8 12.7 20.9 35.7 8.7 9.6 14.5 26.9 15.736.2 18.1 28.9 14.9 25.8 21.7 25.7];%犯罪率(人/十万人)x1=[16.5 20.5 26.3 16.5 19.2 16.5 20.2 21.3 17.2 14.3 18.1 23.1 19.124.7 18.6 24.9 17.9 22.4 20.2 16.9];%低收入家庭百分比x2=[6.2 6.4 9.3 5.3 7.3 5.9 6.4 7.6 4.9 6.4 6.0 7.4 5.8 8.6 6.5 8.36.7 8.6 8.4 6.7];%失业率x3=[587 643 635 692 1248 643 1964 1531 713 749 7895 762 2793 741 625 854 716 921 595 3353];%总人口数(千人)figure(1),plot(x1,y,'*');figure(2),plot(x2,y,'*');figure(3),plot(x3,y,'*');X1=[x1',x2',x3'];stepwise(X1,y)运行结果与结论:犯罪率与低收入散点图犯罪率与失业率散点图犯罪率与人口总数散点图低收入与失业率作为自变量低收入与人口总数作为自变量失业率与人口总数作为自变量在图中可以明显看出前两图的线性程度很好,而第三个图的线性程度较差,从这个角度来说我们应该以失业率和低收入为自变量建立模型。
matlab数据拟合回归分析

返回
二、模型参数估计
1、回归系数的最小二乘估计
有 n 组独立观测值, 1,y1)(x2,y2) (x , ,„, n,yn) (x
yi 0 1 x i i , i 1,2,..., n 设 E i 0, D i 2 且 1 2, n 相 互 独 立 ...,
y与x2的散点图
y 0 1 x1 2 x2 3 x3
回归系数0, 1, 2, 3 由数据估计, 是随机误差
MATLAB 统计工具箱常用命令(1)
多元线性回归 y 0 1 x1 ... p x p
1、确定回归系数的点估计值:
b=regress( Y, X )
固定的未知参数 0 、 1 称为回归系数,自变量 x 也称为回归变量.
Y 0 1 x ,称为 y 对 x 的回归直线方程.
一元线性回归分析的主要任务是:
1、用试验值(样本值)对 0 、 1 和 作点估计; 2、对回归系数 0 、 1 作假设检验; 3、在 x= x0 处对 y 作预测,对 y 作区间估计.
1 n 2 1 n xi , xy xi yi . n i 1 n i 1
(经验)回归方程为:
ˆ ˆ ˆ ˆ y 0 1 x y 1 ( x x )
2 的无偏估计 2、
ˆ ˆ 记 Qe Q( 0 , 1 ) ˆ y
n i 1 i 0
默认值是
0.05
[b, bint, r, rint, stats] = regress(Y, X, alpha)
1 x11 x1m 相关系数R2,F-统计量和与F(1,n-2) 分布大于 回归系数beta以及它们的置信区间 y1 残差向量r=Y-Y及它们的置信区间 X , Y F值的概率p,p<时回归模型有效. 1 x n1 x nm yn
天大matlab大作业逐步回归方法分析

逐步回归分析方法在实际中,影响Y的因素很多,这些因素可能存在多重共线性(相关性),这就对系数的估计带来不合理的解释,从而影响对Y的分析和预测。
“最优”的回归方程就是包含所有对Y有影响的变量, 而不包含对Y 影响不显著的变量回归方程。
选择“最优”的回归方程有以下几种方法:(1)从所有可能的因子(变量)组合的回归方程中选择最优者;(2)从包含全部变量的回归方程中逐次剔除不显著因子;(3)从一个变量开始,把变量逐个引入方程;(4)“有进有出”的逐步回归分析。
以第四种方法,即逐步回归分析法在筛选变量方面较为理想.逐步回归分析法的思想:从一个自变量开始,视自变量Y作用的显著程度,从大到小地依次逐个引入回归方程。
当引入的自变量由于后面变量的引入而变得不显著时,要将其剔除掉。
引入一个自变量或从回归方程中剔除一个自变量,为逐步回归的一步。
对于每一步都要进行Y值检验,以确保每次引入新的显著性变量前回归方程中只包含对Y作用显著的变量。
这个过程反复进行,直至既无不显著的变量从回归方程中剔除,又无显著变量可引入回归方程时为止。
原理:1、最优选择的标准设n 为观测样本数,},,,{21m x x x X为所有自变量构成的集合,li i i x x x A ,,,21 为X 的子集。
(1)均方误差s2最小达到最小(2)预测均方误差最小A S l n l n A J E 11)(达到最小(3)统计量最小准则nl m n S A S A C EE p21达到最小(4)AIC 或BIC 准则n lA S A AIC E 2ln )(或n n l A S A BIC E ln ln )( 达到最小 (5)修正R 2准则)1(122R l n in R 达到最大2、选择最优回归子集的方法(1)选择最优子集的简便方法:逐步筛选法(STEPWISE)向前引入法或前进法(FORWARD)向后剔除法或后退法(BACKWARD)(2)计算量最大的全子集法:R2选择法(RSQUARE)Cp选择法(CP)修正R2选择法(ADJRSQ)。
MATLAB程序设计之算法回归分析54页PPT

15.08.2021
故 T t 1 ( n 2 ) , 拒 绝 H 0 , 否 则 就 接 受 H 0 .
2 n
n
其 L x 中 x (x i x )2x i2 n x 2
i 1
i 1
11
(Ⅲ)r检验法
n
( x i x ) y i ( y )
记 r i 1
n
n
( x i x ) 2( y i y ) 2
n
n
记Q Q (0,1) i2 yi01xi2
i 1
i 1
最 小 二 乘 法 就 是 选 择 0和 1的 估 计 ˆ0, ˆ1 使 得
Q (ˆ0,ˆ1)m 0,1Q i(n0, 1)
15.08.2021
7
ˆ
0
y
ˆ1x
ˆ1
xy x2
xy x2
n x i x y i y
8
2 2
n
记 Qe Q(ˆ0,ˆ1)
yi ˆ0 ˆ1xi 2 n (yi yˆi )2
i1
i1
称Qe为残差平方和或剩余平方和.
2 的无偏估计为 ˆe2 Qe (n2)
称ˆe2
为剩余方差(残差的方差),ˆ
2 e
分别与ˆ0ˆ1、 独立。
ˆe 称为剩余标准差.
15.08.2021
返回
9
三、检验、预测与控制
和 ˆ 1 t 1 2 ( n 2 ) ˆ e /L x ,ˆ x 1 t 1 2 ( n 2 ) ˆ e /L x x
2 的 置 信 水 平 为 1 - 的 置 信 区 间 为 1 2 2 Q ( n e 2 ) , 2 2 ( Q n e 2 )
i 1
i 1
用MATLAB求解回归分析

(2)非线性回归命令:nlintool(x,y,’model’, beta0,alpha) ) 2、预测和预测误差估计: 、预测和预测误差估计: [Y,DELTA]=nlpredci(’model’, x,beta,r,J) 求nlinfit 或nlintool所得的回归函数在x处的预测值Y及预测值的显 著性为1-alpha的置信区间Y ± DELTA.
4、预测及作图: [;,x',beta,r ,J); plot(x,y,'k+',x,YY,'r')
例5 财政收入预测问题:财政收入与国民收入、工业总产值、 农业总产值、总人口、就业人口、固定资产投资等因素有关。 下表列出了1952-1981年的原始数据,试构造预测模型。
得结果:b = -16.0730 0.7194 stats = 0.9282 180.9531 0.0000 bint = -33.7071 0.6047 1.5612 0.8340
ˆ ˆ ˆ ˆ 即 β 0 = −16.073, β 1 = 0.7194 ; β 0 的置信区间为[-33.7017,1.5612], β 1 的置信区间为[0.6047,0.834];
回 归 系 数 的 区 间 估 计 F 检验回归模型的 计 数 : 系数r2、 、 F 的 p 差 区 间 时 为 水 0 平 05 ) . 性 残 信 省 著 置 (缺 显
系数 r2 F > F1F k 的 n-k-1
1
回归 H0 F H0 回归模型 回归 .
p< α
3、 、
区间: 区间:
rcoplot
r2=0.9282, F=180.9531, p=0.0000 p<0.05, 可知回归模型 y=-16.073+0.7194x 成立.
3.3 逐步回归

方法2:逐步引入法—只进不出
3.3.1最优回归方程的选择
•思想:所有可能自变量集合{X1,
X2,…,XM},从一个变量开始 ,按重要性把变量逐个引入回归方程 .
计算M个变量Xi与Y的相关系数,将绝对值最大的变量Xi1引入 方程,并对{Y,Xi1}回归模型进行显著性检验,若显著则引入; 找出余下M-1个自变量中与Y偏相关系数最大变量Xi2引入方程 ,检验{Y,Xi1,Xi2}回归显著性,显著则引入,否则停止,不引入; 剩下的M-2个变量中选择与Y偏相关系数最大变量Xi3 ,检验 {Y,Xi1,Xi2,Xi3}显著性,...,直至得到“最优”回归方程为止 .
3.3 逐步回归分析
Y f ( X1 , X 2 ,, X p )
因变量 确定函数关系 自变量,回归变量
随机误差项
Y 0 1 X1 2 X 2 p X p
0 , 1 , p ----待定常数,回归系数
3.3 逐步回归
1 最优回归方程选择 逐步回归Matlab方法
程序执行后得到下列逐步回归的窗口(如图3.23所示):
图3.23 逐步回归窗口
图中蓝色行显示变量x1、x2、x3、x4均保留在模型中,窗口 右侧按钮上方提示:将变量x3剔除回归方程(Move x3 out).
1.点击Next Step进行下一步运算,将第3列数据对应变量x3剔除回 归方程;点击Next Step,剔除的变量x3对应行用红色表示,同时又得 到提示:将变量x4剔除回归方程(Move x4 out);
~ ~ ~ 剔除X k 后模型 Y 0 1 X1 2 X 2 l X l (*) 变为集A,SSE(A)
绝对贡献
SSR( X k | A) SSE( A) SSE( A, X k ) - -剔除后残差增加量
(完整)逐步回归matlab程序

function stepregress(x,y,F)x=zscore(x,1);%数列标准化y=zscore(y,1);%数列标准化r=corrcoef([x,y]);l=0; %消去的次数L=0; %引入变量的个数[n,m]=size(x); %m为变量的个数,n为观测的次数k=ones(m);q=1; %判断逐步回归是否继续while(q==1)q=0;for i=1:mv(i)=r(i,m+1)^2/r(i,i); %计算各因子的方差贡献endmax=1;min=1;for i=1:mif((max==1)&&(k(i)==1)&&(k(1)==0))||((v(i)>v(max))&&(k(i)==1)) max=i;endif((min==1)&&(k(i)==0)&&(k(1)==1))||((v(i)〈v(min))&&(k(i)==0)) min=i;endendif(l〈3)&&(L+1<=m)F1=v(max)/((r(m+1,m+1)—v(max))/(n—l—2));if(F1>F)disp( [ '引入第', num2str(max),’个变量']);k(max)=0;L=L+1;l=l+1;r=matdel(max,m+1,r); %matdel为消去变换程序q=1;endelseF2=v(min)/(r(m+1,m+1)/(n-l—1));if((F2<F)&&(k(min)==0))disp( [ '剔除第’, num2str(min), ’个变量']);k(min)=1;L=L-1;l=l+1;r=matdel(min,m+1,r);q=1;elseF1=v(max)/((r(m+1,m+1)—v(max))/(n—l—2));if(F1>F)disp( [ ’引入第', num2str(max), ’个变量’]);k(max)=0; %如果变量i引入,则对应的k变为0L=L+1;l=l+1;r=matdel(max,m+1,r);q=1;endendendenddisp('没有可剔除或引入的变量,逐步回归结束’);a=zeros(L);j=1;for i=1:mif (k(i)==0)a(j)=i;j=j+1;end;end;xx=x(:,a(1));for i=2:Lxx=[xx x(:,a(i))];end;b=regress(y,xx);%回归系数R=sqrt(1-r(m+1,m+1));%复相关系数yyy=xx*b; %y的估计值ymean=mean(y); %y平均值Q=(y—yyy)'*(y—yyy); %剩余平方和U=(yyy-ymean)’*(yyy-ymean); %回归平方和rs=Q/(n—L-1); %剩余方差f=U/L/(Q/(n—L—1)); %F统计量fid=fopen(’result',’w');ss=['引入第’,num2str(a(1))];for i=2:Lss=[ss,’,’,num2str(a(i))];endss=[ss,'个变量’];ss1=[’y=(',num2str(b(1)),'x’,num2str(a(1)),')'];for i=2:Lss1=[ss1,’+(',num2str(b(i)),'x’,num2str(a(i)),’)'];end;ss2=[’复相关系数=’,num2str(R)];ss3=[’剩余方差=',num2str(rs)];ss4=[’F统计量=',num2str(f)];ss5=[’剩余平方和=’,num2str(Q)];fprintf(fid,'%s\n’,ss);fprintf(fid,’%s\n’,ss1);fprintf(fid,’%s\n',ss2);fprintf(fid,’%s\n’,ss3);fprintf(fid,'%s\n',ss4); fprintf(fid,’%s’,ss5);fclose(fid);end。
用数学软件MATLAB求解回归分析问题

0.9702
40.6656
0.0005
返回
非线性回 归 1.回归:
事先用M文件定义的非线 性函数
(1)确定回归系数的命令: [beta,r,J]=nlinfit(x,y,’model’,beta0)
将左边图形下方方框中的“800”改成1000,右边图形下方的方框 中仍输入6.则画面左边的“Predicted Y”下方的数据由原来的“86.3791” 变为88.4791,即预测出平均收入为1000.价格为6时的商品需求量为 88.4791. 在画面左下方的下拉式菜单中选”all”, 则beta.rmse和residuals都 传送到MATLAB工作区中.
回 归 系 数 的 区 间 估 计
残 差
置 信 区 间 用于检验回归模型的统计量, 有三个数值:相关系数r 2、 F值、与F 对应的概率p
显著性水平 (缺省时为0.05)
相关系数 r2 越接近 1,说明回归方程越显著; F > F1-α (k,n-k-1)时拒绝 H0,F 越大,说明回归方程越显著; 与 F 对应的概率 p 时拒绝 H0,回归模型成立.
在MATLAB工作区中输入命令: beta, rmse
得结果:beta = 110.5313 0.1464 -26.5709 -0.0001 1.8475 rmse = 4.5362 2 2 故回归模型为: y 110.5313 0.1464x1 26.5709x 2 0.0001 x1 1.8475x 2 剩余标准差为 4.5362, 说明此回归模型的显著性较好.
MATLAB统计工具箱中回归分析命令

MATLAB统计工具箱中回归分析命令
相关关系的测度
(相关系数取值及其意义)
完全负相关
无线性相关
完全正相关
-1.0 -0.5 0 +0.5 +1.0
r
负相关程度增加 正相关程度增加
MATLAB统计工具箱中回归分析命令
统计工具箱中的回归分析命令
1.多元线性回归 2.多项式回归 3.非线性回归 4.逐步回归
回
残
置
归
差
信
系
区
显著性水平 (缺省时为0.05)
数
间 用于检验回归模型的统计量,
的
有三个数值:相关系数r 2、
区
F值、与F 对应的概率p
间
估
计
相关系数 r2 越接近 1,说明回归方程越显著;
F > F1-α(k,n-k-1)时拒绝 H0,F 越大,说明回归方程越显著;
与 F 对应的概率 p 时拒绝 H0,回归模型成立.
3. 当变量 x 取某个值时,变 量 y 的取值可能有几个
4. 各观测点分布在直线周围
x
MATLAB统计工具箱中回归分析命令
变量间的关系
(相关关系)
相关关系的例子
▪ 商品的消费量(y)与居民收入(x)之间的关系 ▪ 商品销售额(y)与广告费支出(x)之间的关系 ▪ 粮食亩产量(y)与施肥量(x1) 、降雨量(x2) 、
得回归模型为 :
s ˆ 4.8 29 t2 4 6.8 6 58 t 9 9 .16 329
To MATLAB(liti21)
MATLAB统计工具箱中回归分析命令
法二
化为多元线性回归:
t=1/30:1/30:14/30;
利用 Matlab作回归分析

利用 Matlab 作回归分析一元线性回归模型:2,(0,)y x N αβεεσ=++求得经验回归方程:ˆˆˆyx αβ=+ 统计量: 总偏差平方和:21()n i i SST y y ==-∑,其自由度为1T f n =-; 回归平方和:21ˆ()n i i SSR y y ==-∑,其自由度为1R f =; 残差平方和:21ˆ()n i i i SSE y y ==-∑,其自由度为2E f n =-;它们之间有关系:SST=SSR+SSE 。
一元回归分析的相关数学理论可以参见《概率论与数理统计教程》,下面仅以示例说明如何利用Matlab 作回归分析。
【例1】为了了解百货商店销售额x 与流通费率(反映商业活动的一个质量指标,指每元商品流转额所分摊的流通费用)y 之间的关系,收集了九个商店的有关数据,见下表1.试建立流通费率y 与销售额x 的回归方程。
表1 销售额与流通费率数据【分析】:首先绘制散点图以直观地选择拟合曲线,这项工作可结合相关专业领域的知识和经验进行,有时可能需要多种尝试。
选定目标函数后进行线性化变换,针对变换后的线性目标函数进行回归建模与评价,然后还原为非线性回归方程。
【Matlab数据处理】:【Step1】:绘制散点图以直观地选择拟合曲线x=[1.5 4.5 7.5 10.5 13.5 16.5 19.5 22.5 25.5];y=[7.0 4.8 3.6 3.1 2.7 2.5 2.4 2.3 2.2];plot(x,y,'-o')输出图形见图1。
510152025图1 销售额与流通费率数据散点图根据图1,初步判断应以幂函数曲线为拟合目标,即选择非线性回归模型,目标函数为:(0)b y ax b =< 其线性化变换公式为:ln ,ln v y u x == 线性函数为:ln v a bu =+【Step2】:线性化变换即线性回归建模(若选择为非线性模型)与模型评价% 线性化变换u=log(x)';v=log(y)';% 构造资本论观测值矩阵mu=[ones(length(u),1) u];alpha=0.05;% 线性回归计算[b,bint,r,rint,states]=regress(v,mu,alpha)输出结果:b =[ 2.1421; -0.4259]表示线性回归模型ln=+中:lna=2.1421,b=-0.4259;v a bu即拟合的线性回归模型为=-;y x2.14210.4259bint =[ 2.0614 2.2228; -0.4583 -0.3934]表示拟合系数lna和b的100(1-alpha)%的置信区间分别为:[2.0614 2.2228]和[-0.4583 -0.3934];r =[ -0.0235 0.0671 -0.0030 -0.0093 -0.0404 -0.0319 -0.0016 0.0168 0.0257]表示模型拟合残差向量;rint =[ -0.0700 0.02300.0202 0.1140-0.0873 0.0813-0.0939 0.0754-0.1154 0.0347-0.1095 0.0457-0.0837 0.0805-0.0621 0.0958-0.0493 0.1007]表示模型拟合残差的100(1-alpha)%的置信区间;states =[0.9928 963.5572 0.0000 0.0012] 表示包含20.9928SSR R SST==、 方差分析的F 统计量/963.5572//(2)R E SSR f SSR F SSE f SSE n ===-、 方差分析的显著性概率((1,2))0p P F n F =->≈; 模型方差的估计值2ˆ0.00122SSE n σ==-。
matlab经典算法程序---回归分析教学资料

Y a bx; ~ N(0, 2)
或
需要解决的问题:
Y~N(ab,x2)
1) 在回归模型中如何估计参数a、b和σ2?
2) 模型的假设是否正确?需要检验。 3)利用回归方程对试验指标y进行预测或控制? 估y ˆ0 计 a ˆ b ˆx 量 0 , 区间 (y ˆ0 d ,估 y ˆ0 d )计
参数估计
设观测值为(xi, yi)(i=1,2,…,n), 代入模型中, yi = a + bxi +εi
最小二乘法:
n
mQ in (a,b) [yi (abix)2] i1
解出的参数记为 aˆ , bˆ 则回归方程: yˆ aˆ bˆx
yˆi a ˆbˆxi yi yˆi残差值
回归模型的假设检验
模型:Y = a + bx +ε
在工作空间中,输入yhat,回车,得到预测值。
实验内容
1、确定企业年设备能力与年劳动生产率的关系
某市电子工业公司有14个所属企业,各企业 的年设备能力与年劳动生产率统计数据如下表。 试分析企业年设备能力与年劳动生产率的关系。 若该公司计划新建一个设备能力为9.2千瓦/人的 企业,估计劳动生产率将为多少?
y=[698 872 988 807 738 1025 1316 1539 1561 1765 1762 1960 1902 2013 2446 2736 2825];
X=[ones(size(x')),x'],pause [c,cint,r,rint,stats]=regress(y',X,0.05),pause rcoplot(r,rint)
3000
y=a+bx
2500
2000
matlab实现多元逐步回归算法

自己编写的多元逐步回归分析算法matlab程序,在matlab工具箱中已经提供了一个可视化的图形界面分析窗口,但是一些具体的参数还不能直接得到,这里自己编写了一个小程序,希望对需要的能够提供一定的帮助。
共两个文件:dyzbhg.m和xiaoqu.m第一个函数dyzbhg.mfunction dyzbhg(xy)%多元逐步回归分析%作者:唐世星%2006.11.20%xy为待输入的原始数据,按照先x后y按列排列的数组%如:x1 x2 x3 x4 y等等%clc;%clear all;%计算离差阵R(m,m)[n,m]=size(xy);%F1=0;F2=0;%disp('均值为:')xy_aver=mean(xy)%求均值for i=1:mfor j=1:iR(i,j)=0;for k=1:nR(i,j)=R(i,j)+(xy(k,i)-xy_aver(i))*(xy(k,j)-xy_aver(j));endR(j,i)=R(i,j);endSR(i)=sqrt(R(i,i));%计算对角线元素的平方根end%disp('************ Deviation Matrix & Value of SR (离差阵R&SR) ***********') %输出离差阵R,及SR%[R SR']%计算相关系数R(m,m)for i=1:mfor j=1:iR(i,j)=R(i,j)/(SR(i)*SR(j));R(j,i)=R(i,j);endend%disp('********** Correlation Coefficient Matrix (相关系数阵R) **********')%输出相关系数阵R %Rflag=1;%是否重复进行逐步回归的标志while(flag)disp('******** Stepwise Regression Analysis Start *************')F1=input('剔除门坎值:F1=');F2=input('引入门坎值:F2=');S=0;%计算步数L=0;%引入方程的自变量个数FQ=n-1;%残差平方和的自由度disp('************** Discriminant Value of Contribution V **************')Imin(1)=0;Imax=1:m-1;%定义已引入(最小)和未引入(最大)变量的序号inn=0;outt=0;%引入和剔除的变量的顺序号while(1)% pauseVN=1E+08;%已引入方程的自变量贡献的最小值VX=0;%未引入方程的自变量贡献的最大值IN=0;%贡献最小的已引入的自变量序号IX=0;%贡献最大的未引入的自变量序号S=S+1;disp(['--------- step = ' int2str(S) '------------'])%输出步骤数for i=1:m-1if R(i,i)<1E-08continueend% disp(['VMAX=' int2str(VX) '; IMAX=' int2str(IX)]) %输出Vmax=VX;Imax=IX;V(i)=R(m,i)^2/R(i,i);%计算已引入的变量的方差贡献if V(i)>=0if V(i)>VX %寻找未引入变量方差贡献的最大值for in=1:length(Imax)if i==Imax(in)VX=V(i);IX=i;endendendendif abs(V(i))for out=1:length(Imin)if i==Imin(out)VN=abs(V(i));IN=i;endendend%disp(['方差贡献:V=' num2str(V(i)) 'VX=' num2str(VX) 'IX=' int2str(IX) 'VN=' num2str(VN) 'IN=' int2 str(IN)])end% Imax(inn+1)=IX;inn=inn+1;t=find(Imax==IX);Imax(t)=[];disp(['******** 方差贡献V **********' num2str(V)])disp(['VMAX=' num2str(VX) '; IMAX=' int2str(IX)]) %输出Vmax=VX;Imax=IX;% disp(['VMIN=' num2str(VN) '; IMIN=' int2str(IN)]) %输出Vmin=VN;Imin=IN; if S==1disp(['S=' int2str(S)]) %输出S=1elsedisp(['VMIN=' num2str(VN) '; IMIN=' int2str(IN)]) %输出Vmin=VN;Imin=IN; endif S==1%||S==2||S==3FE=VX*(n-L-2)/(R(m,m)-VX);disp(['FE=' num2str(FE)]) %输出FEif FE<F1if L~=0disp('Neither Delete Out Nor Select In!')elsedisp('May Be Smaller F1 And F2')disp('The Stepwise Regression Analysis End!')break;%程序结束endelseL=L+1;FQ=FQ-1;K=IX;disp(['X' int2str(K) ' Be Selected In'])Imin(outt+1)=IX;outt=outt+1;disp(['L = ' int2str(L) ])R=xiaoqu(R,K) %调用子函数,执行消去变换if L~=m-1continue;enddisp('Already Selecting End')break;endelse%计算剔除变量的F检验值FT=VN*(n-L-1)/R(m,m);disp(['剔除变量的F检验值' num2str(FT)])if FT>=F2FE=VX*(n-L-2)/(R(m,m)-VX);disp(['***FE=' num2str(FE)]) %输出FEif FE<F1if L~=0disp('Neither Delete Out Nor Select In!')disp('The Stepwise Regression Analysis End!')break;%程序结束elsedisp('May Be Smaller F1 And F2')disp('The Stepwise Regression Analysis End!')break;%程序结束endelseL=L+1;FQ=FQ-1;K=IX;disp(['X' int2str(K) ' Be Selected In'])disp(['L = ' int2str(L) ])Imin(outt+1)=IX;outt=outt+1;R=xiaoqu(R,K) %调用子函数,执行消去变换if L~=m-1continue;enddisp('Already Selecting End')break;endelseL=L-1;FQ=FQ+1;K=IN;disp(['X' int2str(K) ' Be Deleted Out'])disp(['L = ' int2str(L) ' (No. of Variable Selected)'])R=xiaoqu(R,K) %调用子函数continueendendend%输出相应的计算结果for i=1:m-1kk=R(i,m)*R(m,i);if kk<0B(i)=R(i,m)*SR(m)/SR(i);elseB(i)=0;endendB0=xy_aver(m);for i=1:m-1B0=B0-B(i)*xy_aver(i);enddisp(['回归系数为:' num2str(B0) ' ' num2str(B)])disp('回归方程为:')disp(['Y=' num2str(B0)])for i=1:m-1if B(i)~=0if B(i)>0disp(['+' num2str(B(i)) 'X' int2str(i)]);elsedisp([num2str(B(i)) 'X' int2str(i)]);endendendQ=SR(m)^2*R(m,m);%残差平方和disp(['Sum of SQuares of Residual Error(残差平方和) Q = ' num2str(Q)])S=SR(m)*sqrt(R(m,m)/FQ);%剩余标准差disp(['Standard Deviation(剩余标准差,即模型误差的均方根) S = ' num2str(S)])RR=sqrt(1-R(m,m));%复相关系数disp(['Multiple Correlation Coefficient(复相关系数) R = ' num2str(RR)])FF=FQ*(1-R(m,m))/(L*R(m,m));%回归方程显著性检验的F值disp(['F Value for Test of Regression(回归方程显著性检验,即回归模型的统计量) F = ' num2str(FF)]) %F=SH*(m-n-1)/(SX*n);%F-统计量%PROB = 1 - fcdf(FF,m,n-length(Imin)-1)%与统计量F对应的概率Pfor i=1:m-1CC=R(i,i)*R(m,m);T(i)=R(i,m)/sqrt(CC/FQ);%各回归系数的t检验值R1(i)=R(i,m)/sqrt(CC+R(i,m)^2);%各自变量的偏相关系数enddisp(['t Test Value of Argument(各回归系数的t检验值):' num2str(T)])disp(['Partial Corre.Coeffi.Ofargu.(各自变量的偏相关系数):' num2str(R1)])%for i=1:n% y(i)=B0;% for j=1:m-1% y(i)=y(i)+B(j)*xy(i,j);% end% E(i)=xy(i,m)-y(i);% PC(i)=E(i)/xy(1,m)*100;%end%x=1:length(xy);%disp(' No. 回归值误差误差百分比%') %[x' y' E' PC']flag=input('是否重新进行逐步回归分析(1:是;0:否):'); end第二个函数xiaoqu.mfunction R=xiaoqu(R,k)%多元逐步回归分析%对R作消去变换%作者:唐世星%2006.11.20G=1/R(k,k);m=length(R);for i=1:mfor j=1:mif i~=k&j~=kR(i,j)=R(i,j)-R(i,k)*R(k,j)*G;endendendfor i=1:mR(k,i)=R(k,i)*G;R(i,k)=-R(i,k)*G;endR(k,k)=G;。
MATLAB 回归分析regress,nlinfit,stepwise函数

回归分析1.多元线性回归在Matlab统计工具箱中使用命令regress()实现多元线性回归,调用格式为b=regress(y,x)或[b,bint,r,rint,statsl = regess(y,x,alpha)其中因变量数据向量y和自变量数据矩阵x按以下排列方式输入对一元线性回归,取k=1即可。
alpha为显著性水平(缺省时设定为0.05),输出向量b,bint为回归系数估计值和它们的置信区间,r,rint为残差及其置信区间,stats是用于检验回归模型的统计量,有三个数值,第一个是R2,其中R是相关系数,第二个是F统计量值,第三个是与统计量F对应的概率P,当P<α时拒绝H0,回归模型成立。
画出残差及其置信区间,用命令rcoplot(r,rint)实例1:已知某湖八年来湖水中COD浓度实测值(y)与影响因素湖区工业产值(x1)、总人口数(x2)、捕鱼量(x3)、降水量(x4)资料,建立污染物y的水质分析模型。
(1)输入数据x1=[1.376, 1.375, 1.387, 1.401, 1.412, 1.428, 1.445, 1.477]x2=[0.450, 0.475, 0.485, 0.500, 0.535, 0.545, 0.550, 0.575]x3=[2.170 ,2.554, 2.676, 2.713, 2.823, 3.088, 3.122, 3.262]x4=[0.8922, 1.1610 ,0.5346, 0.9589, 1.0239, 1.0499, 1.1065, 1.1387]y=[5.19, 5.30, 5.60,5.82,6.00, 6.06,6.45,6.95](2)保存数据(以数据文件.mat形式保存,便于以后调用)save data x1 x2 x3 x4 yload data (取出数据)(3)执行回归命令x =[ones(8,1),];[b,bint,r,rint,stats] = regress得结果:b = (-16.5283,15.7206,2.0327,-0.2106,-0.1991)’stats = (0.9908,80.9530,0.0022)即= -16.5283 + 15.7206xl + 2.0327x2 - 0.2106x3 + 0.1991x4R2 = 0.9908,F = 80.9530,P = 0.00222.非线性回归非线性回归可由命令nlinfit来实现,调用格式为[beta,r,j] = nlinfit(x,y,'model’,beta0)其中,输人数据x,y分别为n×m矩阵和n维列向量,对一元非线性回归,x 为n维列向量model是事先用m-文件定义的非线性函数,beta0是回归系数的初值,beta是估计出的回归系数,r是残差,j是Jacobian矩阵,它们是估计预测误差需要的数据。
用MATLAB做逐步回归

我们对同时选取三个自变量的模型进行分析:
得出结论:
以上是用 stepwise( )命令完成逐步回归,进而求得最
优的方程模型。最后我们用多元回归程序检验一下求得线性
方程的显著性,即用相关系数法来测定它的拟合优度。
编写程序如下:
y=[11.2 13.4 40.7 5.3 24.8 12.7 20.9 35.7 8.7 9.6 14.5 26.9 15.7 36.2 18.1 28.9 14.9 25.8 21.7 25.7];
犯罪率与低收入散点图犯罪率与失业率散点图犯罪率与人口总数散点图低收入与失业率作为自变量低收入与人口总数作为自变量失业率与人口总数作为自变量由上图可以看出
逐步回归法
C
“”
班级:研1614 学生:秦培歌
序号
1
11.2
16.5
6.2
587
2
13.4
20.5
6.4
643
3
40.7
26.3
9>clc; >>clear all; >>y=[11.2 13.4 40.7 5.3 24.8 12.7 20.9 35.7 8.7 9.6 14.5 26.9 15.7 36.2 18.1 28.9 14.9 25.8 21.7 25.7]; >>%犯罪率(人/十万人) >> x1=[16.5 20.5 26.3 16.5 19.2 16.5 20.2 21.3 17.2 14.3 18.1 23.1 19.1 24.7 18.6 24.9 17.9 22.4 20.2 16.9]; >> %低收入家庭百分比 >> x2=[6.2 6.4 9.3 5.3 7.3 5.9 6.4 7.6 4.9 6.4 6.0 7.4 5.8 8.6 6.5 8.3 6.7 8.6 8.4 6.7]; >> %失业率 >> x3=[587 643 635 692 1248 643 1964 1531 713 749 7895 762 2793 741 625 854 716 921 595 3353]; >> %总人口数(千人) >> figure(1),plot(x1,y,'*'); >> figure(2),plot(x2,y,'*'); >>figure(3),plot(x3,y,'*'); >>X1=[x1',x2',x3']; >> stepwise(X1,y)
回归分析(4)多元逐步回归程序

4 6 10 18 13 10 15 16 27 36 46 47 48 60 96 191 186 195
309 400 454 520 516 459 531 558 607 541 597 558 619 618 742 805 859 855
打开数据文件dd2data.mat,将因变量数据录入一 解 打开数据文件 , 维数据矩阵Y1× 中 将自变量数据录入m× 维数据 维数据矩阵 ×n中,将自变量数据录入 ×n维数据 矩阵Xm×n中。执行程序如下: 矩阵 × 中 执行程序如下: >>load dd2data >> stepwise(X,Y) 计算机运行结果如下(见图2.1至图 至图2.3): 计算机运行结果如下(见图 至图 ):
图 2.1
图 2.2
图 2.3
说明: . 说明:1.图2.1中包含各变量的回归系数 中包含各变量的回归系数 置信区间( (Parameter)及其 )及其95%置信区间([lower, 置信区间 upper]),另外还有均方差(REMS),回归 ),另外还有均方差 ),回归 ),另外还有均方差( ), 系数平方( ),F值 系数平方(R–square), 值(F)和显著性概 ), ) 率值( )。 率值(p)。 2.图2.2中为回归模型的均方差示意图,用黄 中为回归模型的均方差示意图, . 中为回归模型的均方差示意图 色填充的小圆圈表示对应模型的均方差。 色填充的小圆圈表示对应模型的均方差。
3.图2.3 中用误差条图表示各变量的系数值。 . 中用误差条图表示各变量的系数值。 图中的填充圆圈表示对应变量的系数值, 图中的填充圆圈表示对应变量的系数值,用两 侧延伸的点虚线表示对应系数值的置信区间。 侧延伸的点虚线表示对应系数值的置信区间。 通过单击图中的圆圈或点线, 通过单击图中的圆圈或点线,可以转换对应变 量的引入或剔除状态。利用“ 量的引入或剔除状态。利用“Export”下拉式 下拉式 列表框,可以确定有关信息的输出, 列表框,可以确定有关信息的输出,包括回归 系数(这时用beta表示)、回归系数的置信区 表示)、 系数(这时用 表示)、回归系数的置信区 ),引入变量 )、剔除变量 间(betaci),引入变量(in)、剔除变量 ),引入变量( )、 (out)。 )。
MATLAB中基本的统计和回归命令

返回:h = 1,sig = 0.0083,ci =[-5.8,-0.9].
检验结果:1. 布尔变量h=1, 表示拒绝零假设. 说明提出的 假设“油价均值相同”是不合理的.
2. 95%的置信区间为[-5.8,-0.9],说明一月份油 价比二月份油价约低1至6分.
3. sig-值为0.0083, 远小于0.5, 不能接受“油价均 相同”假设.
例 3. 计算标准正态分布的概率 P{-1<X<1}.
命令为:P=normcdf(1)-normcdf(-1)
结果为:P =0.6827
To MATLAB(liti3)
3、逆概率分布:x=norminv(P,mu,sigma). 即求出x ,使得 P{X<x}=P.此命令可用来求分位数.
例 4 取 0.05 ,求u 1 2
2、其它分布的参数估计
有两种处理办法: 一.取容量充分大的样本(n>50),按中心极限定理,它近似地
服从正态分布;
二.使用Matlab工具箱中具有特定分布总体的估计命令.
(1)[muhat, muci] = expfit(X,alpha)----- 在显著
性水平alpha下,求指数分布的数据X的均值的点估计及其区间估
计.
(2)[lambdahat, lambdaci] = poissfit(X,alpha)-
---- 在显著性水平alpha下,求泊松分布的数据X 的参数的点
估计及其区间估计.
(3)[phat, pci] = weibfit(X,alpha)----- 在显著性
水平alpha下,求Weibull分布的数据X 的参数的点估计及其区
u1 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
~
function stepregress(x,y,F)
x=zscore(x,1); %数列标准化
y=zscore(y,1); %数列标准化
r=corrcoef([x,y]);
l=0; %消去的次数
L=0; %引入变量的个数
[n,m]=size(x); %m为变量的个数,n为观测的次数
k=ones(m);
?
q=1; %判断逐步回归是否继续
while(q==1)
q=0;
for i=1:m
v(i)=r(i,m+1)^2/r(i,i); %计算各因子的方差贡献
end
max=1;
min=1;
>
for i=1:m
if((max==1)&&(k(i)==1)&&(k(1)==0))||((v(i)>v(max))&&(k(i)==1)) max=i;
end
if((min==1)&&(k(i)==0)&&(k(1)==1))||((v(i)<v(min))&&(k(i)==0)) min=i;
end
end
《
if(l<3)&&(L+1<=m)
F1=v(max)/((r(m+1,m+1)-v(max))/(n-l-2));
if(F1>F)
disp( [ '引入第', num2str(max), '个变量']);
k(max)=0;
L=L+1;
l=l+1;
¥
r=matdel(max,m+1,r); %matdel为消去变换程序
q=1;
end
else
F2=v(min)/(r(m+1,m+1)/(n-l-1));
if((F2<F)&&(k(min)==0))
disp( [ '剔除第', num2str(min), '个变量']);
k(min)=1;
…
L=L-1;
l=l+1;
r=matdel(min,m+1,r);
q=1;
else
F1=v(max)/((r(m+1,m+1)-v(max))/(n-l-2));
if(F1>F)
disp( [ '引入第', num2str(max), '个变量']); /
k(max)=0; %如果变量i引入,则对应的k变为0 L=L+1;
l=l+1;
r=matdel(max,m+1,r);
q=1;
end
end
end
…
end
disp('没有可剔除或引入的变量,逐步回归结束');
a=zeros(L);
j=1;
for i=1:m
if (k(i)==0)
a(j)=i;
、
j=j+1;
end;
end;
xx=x(:,a(1));
for i=2:L
xx=[xx x(:,a(i))];
end;
b=regress(y,xx); %回归系数
!
R=sqrt(1-r(m+1,m+1)); %复相关系数
yyy=xx*b; %y的估计值
ymean=mean(y); %y平均值
Q=(y-yyy)'*(y-yyy); %剩余平方和
U=(yyy-ymean)'*(yyy-ymean); %回归平方和
rs=Q/(n-L-1); %剩余方差
f=U/L/(Q/(n-L-1)); %F统计量
fid=fopen('result','w');
/
ss=['引入第',num2str(a(1))];
for i=2:L
ss=[ss,',',num2str(a(i))];
end
ss=[ss,'个变量'];
ss1=['y=(',num2str(b(1)),'x',num2str(a(1)),')'];
for i=2:L
ss1=[ss1,'+(',num2str(b(i)),'x',num2str(a(i)),')']; }
end;
ss2=['复相关系数=',num2str(R)];
ss3=['剩余方差=',num2str(rs)];
ss4=['F统计量=',num2str(f)];
ss5=['剩余平方和=',num2str(Q)];
fprintf(fid,'%s\n',ss);
fprintf(fid,'%s\n',ss1);
fprintf(fid,'%s\n',ss2);
<
fprintf(fid,'%s\n',ss3);
fprintf(fid,'%s\n',ss4);
fprintf(fid,'%s',ss5);
fclose(fid);
end。
