最短路问题复习课程
八年级上第08讲 最短路径问题 讲义+练习

轴对称:最短路径问题【知识导图】1.两点之间,线段最短。
2.三角形两边之和大于第三边,两边之差小于第三边。
3.线段垂直平分线上的点与这条线段两个端点的距离相等。
求直线异侧的两点到直线上一点距离的和最小的问题讲解内容:只要连接这两点,所得线段与直线的交点即为所求的位置。
讲解内容:只要找到其中一个点关于这条直线的对称点,连接对称点与另一个点,所得线段与该直线的交点即为所求的位置。
如图所示,点A ,B 分别是直线l 同侧的两个点,在l 上找一个点C ,使CA +CB 最短【答案】作点B 关于直线l 的对称点B',连接AB'与l 交于点C ,则点C 为所求的点。
【解析】在直线l 上任取不同于C 点的C'点,连接AC’,BC’∵点B 和B'关于直线l 对称∴CB=CB’、C'B=C'B'∴CA+CB=CA+CB'=AB'∵CA+CB’<C'A+C'B'∴AB'=CA+CB<C'A+C'B'一、导入考点1 二、知识讲解考点2 三 、例题精析例题1如图,A和B两地在一条河的两岸,现要在河上造一座桥MN,桥造在何处可使从A到B的路径AM+NB最短?(假定河的两岸是平行的直线,桥要与河垂直)【答案】1.将点A沿垂直与河岸的方向平移一个河宽到A',2.连接A'B交河对岸于点N,则点N为建桥的位置,MN为所建的桥。
【解析】由平移的性质,得 AM∥A'N且AM=A'N, MN=M'N',AM'∥A'N',AM'=A'N' 所以A、B两地的距:AM+MN+BN=AA'+A'N+NB=AA'+A'B若桥的位置建在M'N'处,则AB两地的距离为: AM'+M'N'+N'B=A'N'+M'N'+N'B 在△A'N'B中,∵A'N'+N'B>A'B ,M'N'=AA'∴M'N'+A'N'+N'B>AA'+A'B所以桥的位置建在MN处,AB两地的路程最短。
最短路径问题PPT课件

A
·
C′ C
B
·
l
B′
问题1 归纳
B A
l
解决实 际问题
B
A
C
l
B′
抽象为数学问题 用旧知解决新知
B
A
C
l
联想旧知
A
C
l
B
尝试应用:
1.如图,直线l是一条河,P、Q是两个村庄.欲在l上的某处修建
一个水泵站,向P、Q两地供水,现有如下四种铺设方案,图中
实线表示铺设的管道,则所需要管道最短的是( D )
A
·
l C
B′
问题3 你能用所学的知识证明AC +BC最短吗? 证明:如图,在直线l 上任取一点C′(与点C 不
重合),连接AC′,BC′,B′C′.
由轴对称的性质知,
BC =B′C,BC′=B′C′. ∴ AC +BC
= AC +B′C = AB′, AC′+BC′
= AC′+B′C′. 在△AB′C′中,
从图中的A 地出发,到一条笔直的河边l 饮马,然 后到B 地.到河边什么地方饮马可使他所走的路线全程 最短?
B A
l
将A,B 两地抽象为两个点,将河流l 抽象为一条直 线.
·B A·
l
你能用自己的语言说明这个问题的意思, 并把它抽象为数学问题吗?
(1)从A 地出发,到河流l边 饮马,然后到B 地;
AM+NB+MN.
问题3:还有其他的方法选两点M,N,使得 AM+MN+NB的和最小吗?试一试。
a
b
A
M
N
B
问题2 归纳
解决实 际问题
《最短路问题》课件

3 最短路问题的历史
渊源
最短路问题最早由荷兰 数学家 Edsger Dijkstra 在 1956 年提出。
最短路问题的定义
图论中的最短路问 题指什么?
在无向连通图或有向连通图 中,从某一起点到其余各顶 点的最短路径。
什么是路径长度?
路径长度是指路径上边或弧 的权值之和。
什么是无环图?
无环图指不存在环的图,可 以用拓扑排序求解最短路。
《最短路问题》PPT课件
欢迎来到最短路问题的世界。在本课件中,我们将介绍四种最短路算法及其 应用,并分析它们的优缺点。
问题背景
1 什么是最短路问题? 2 为什么需要解决最
短路问题?
最短路问题是计算从源 节点到目标节点的最短 路径的问题。它是图论 中的一个经典算法问题。
很多实际问题都涉及到 最短路径的计算,比如 电网、交通、通信等领 域。
Floyd-Warshall算法解决的是所有点对之间 的最短路径问题,可以处理有向图或负边权 图。
Bellman-Ford算法
Bellman-Ford算法解决的是有向图中含有负 权边的单源最短路径问题。
A*算法
A*算法综合了贪心和广度优先搜索,在启发 函数的帮助下,可以高效解决带权图上的单 源最短路径问题。
算法示例
1
Step 1
假设我们要求从 A 点到其他各点的最
Step 2
2
短路径。
首先初始化 A 点到其他各点的距离为
无穷大,A 点到自身的距离为 0。
3
Step 3
找到 A 点的直接邻居,更新其距离值。
Step 4
4
重复 Step 3,直到所有节点的距离值 都已经更新。
总结
运筹学课件 最短路、最大流、邮路

最短路径问题的应用
例 设备更新问题
把求总费用最小问题化为最短路径问题。用点 i (i=1,2,3,4,5)表示第 i 年买进一台新 设备。增设一点 6 表示第五年末。从i点到i+1,……, 6 各画一条弧,弧(i , j)表示在 第 i 年买进的设备一直使用到第 j 年年初(第 j -1年年末)。求1点到6点的最短路径。 路径的权数为购买和维修费用。 弧(i , j)的权数为第i年的购置费ai+从第i年使用至第j-1年末的维修费之和。 从第i年使用至第j-1年末的维修费:b1+…+bj-i
1 1 2 3 4 5 2 16 3 22 16
(使用寿命为j-i年) 具体权数计算结果如下:
5 41 30 23 17 6 59 41 31 23 18
如:(2-4)权数为:a2+b1+b2=11+5+6=22
4 30 22 17
通过一个网络的最短路径
例 设备更新问题 :
2 16 30 22 41 4 23
最大流问题
两个重要结论: 1、任何一个可行流的流量都不会超过任一截集的容量。 2、若对于一个可行流f *,网络中有一个截集( V1*,V1*), 使v( f *)=C(V1*,V1 *),则f *必是最大流,而( V1*, V1 *)必是所有截集中容量最小的一个,即最小截集。
定理:可行流f *是最大流,当且仅当不存在关于f *的增广链。 于是有如下结论:最大流量最小截量定理:任一个网络中,从vs 到vt的最大流量等于分离vs,vt的最小截集的容量。
数学建模最短路问题PPT课件

实现Kruskal算法的MATLAB程序: %加权图的存储结构采用边权矩阵[b(i,j)]m×3 b=[1 1 1 2 2 3 3 4
24535455 8 1 5 6 7 9 10 3]; [B,I]=sortrows(b’,3); B=B’; m =size(b,2); n=5; t=1:n; k=0; T=[ ]; c = 0;
1
8
5
1
55
3
44
9
22
7
6 10
33
51 1 421 1 4 22 3 34 5 5 78 inf 196 5 3
第16页/共54页
实现Prim算法的MATLAB程序: a=[0 8 inf 1 5;8 0 6 inf 7;inf 6 0 9 10;1 inf 9 0 3;…
5 7 10 3 0]; T=[ ]; e=0; v=1; n=5; sb=2:n; %1代表第一个红点,sb代表 白点集。 for j=2:n %构造初始候选边的集合
0
7
9
W
0 5 1 2 0 3 9
0 4 6
0
3 0
因 G 是无向图,故 W 是对称矩阵.
第27页/共54页
迭代 次数
1 2 3 4 5 6 7 8
最后标记:
l (v) z (v)
u1
u2
0
02
2
l(ui )
u3 u4
u5
18
8
8
3
8
7
02 17
3
u1 u1
u1 u6
u2
u6 u7
因此, 可采用树生长的过程来求指定顶点到其余顶点 的最短路.
复习课-最短路径问题

●
N
★思考:本题运用了 两点之间,线段最短, 图形的平移、 .
拓广探索
最短路径问题
温故而知新 温故而知新
温故而知新 回顾课本 探究(一) 基本类型
探究(二) 随堂练习 探究(二) 拓展探索 范例学习 中考链接 课堂小结 课堂小结 巩固练习
1. 如图,点A、B位于直线L同侧,定长为a的线段MN在 直线L上滑动,请问当MN滑到何处时,折线AMNB长度 最短?。 B1
这节课培养的核心素养:图形对称美 转化能力 模型思想 归纳能力
巩固练习
最短路径问题
温故而知新 温故而知新
如图,已知点P是直线x=1上的一动点,点A 的坐 标为(0,-2),若△OPA的周长最小,试在图中 确定点P的位置。
温故而知新 回顾课本 探究(一) 基本类型
●
O’
探究(二) 随堂练习
●
P
探究(二) 拓展探索 范例学习 中考链接 课堂小结 课堂小结 巩固练习
A
P P B
●
D
M
C
回顾课本
最短路径问题
架桥问题:如图,A、B两地在一条河的两岸,现要在河上 两岸是平行的直线,桥要与河垂直。)
造
温故而知新 温故而知新
一座桥MN,桥造在何处可使从A到B的路径AMNB最短?(假定河的
温故而知新 回顾课本 基本类型 探究(一)
●
M A’
●
探究(二) 随堂练习 探究(二) 拓展探索 范例学习 中考链接 课堂小结 课堂小结 巩固练习
图 Z8-3
基础题型
最短路径问题
实例引入 回顾课本
在公路两侧有两村庄A.B,现要在公路l旁修建 一所候车亭P,要使候车亭到两村庄的距离之和最 短,候车亭P的位置应该建在哪呢?(PA+PB最小)
人教版八年级上册教材数学1专题:最短路径问题复习 课件演示

牵出马,先到草地边某一处牧马,再到河边饮马,然 后回到帐篷,请你帮他确定这一天的最短路线。
作法:1.作点C关于直线 OA的对称点点F,
2.作点D关于直线OB 的对称点点E,
F
G
O
A
·C
H
D·
E
3.连接EF分别交直线OA.OB于点G.H, B
则CG+GH+DH最短
MO
BO),AO桌面上摆满了橘子,OB桌面
C
N
上摆满了糖果,站在C处的学生小明先 拿橘子再拿糖果,然后到D处座位上, 请你帮助他设计一条行走路线,使其所
A′ D
B
走的总程最短.
人教版八 年级上 册教材 数学1专 题:最 短路径 问题复 习 课 件演示
13
人教版八 年级上 册教材 数学1专 题:最 短路径 问题复 习 课 件演示
C
E F
∟
A
M
B
D
人教版八 年级上 册教材 数学1专 题:最 短路径 问题复 习 课 件演示
12
人教版八 年级上 册教材 数学1专 题:最 短路径 问题复 习 课 件演示
知识点一:利用轴对称解决最短路径问题
典例讲评
C 桌子摆成如图所示两直排(图中的AO, A
图的主要步骤,并标明你所确定的点.(要求画出草图,保留作图
作痕法迹:) 1、分别作点A关于 OM、ON的对称点A′,A′′;
A′ M
2、连接A′A′′ ,分别交OM、 ON于B、C ;
B A
∟
人教版八 年级上 册教材 数学1专 题:最 短路径 问题复 习 课 件演示
O
C
初二数学最短路径问题知识归纳+练习
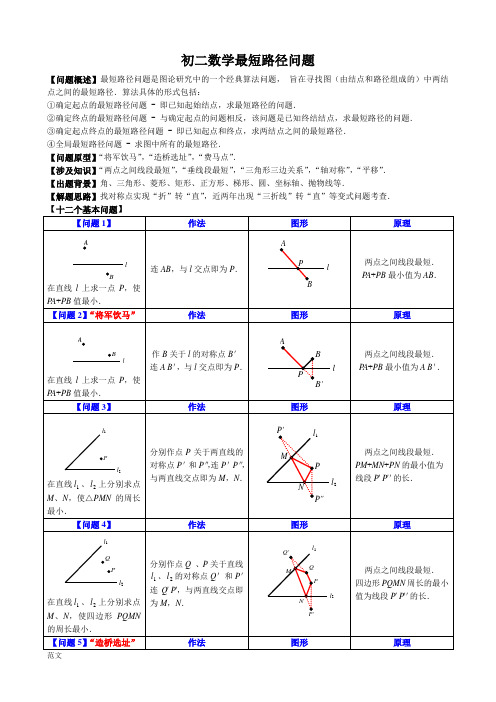
初二数学最短路径问题【问题概述】最短路径问题是图论研究中的一个经典算法问题,旨在寻找图(由结点和路径组成的)中两结点之间的最短路径.算法具体的形式包括:①确定起点的最短路径问题 - 即已知起始结点,求最短路径的问题.②确定终点的最短路径问题 - 与确定起点的问题相反,该问题是已知终结结点,求最短路径的问题.③确定起点终点的最短路径问题 - 即已知起点和终点,求两结点之间的最短路径.④全局最短路径问题 - 求图中所有的最短路径.【问题原型】“将军饮马”,“造桥选址”,“费马点”.【涉及知识】“两点之间线段最短”,“垂线段最短”,“三角形三边关系”,“轴对称”,“平移”.【出题背景】角、三角形、菱形、矩形、正方形、梯形、圆、坐标轴、抛物线等.【解题思路】找对称点实现“折”转“直”,近两年出现“三折线”转“直”等变式问题考查.在直线l 上求一点P ,使PB PA -的值最大.作直线AB ,与直线l 的交点即为P .三角形任意两边之差小于第三边.PB PA -≤AB .PB PA -的最大值=AB .【问题11】 作法图形 原理在直线l 上求一点P ,使PB PA -的值最大.作B 关于l 的对称点B '作直线A B ',与l 交点即为P .三角形任意两边之差小于第三边.PB PA -≤AB '. PB PA -最大值=AB '.【问题12】“费马点” 作法图形 原理△ABC 中每一内角都小于120°,在△ABC 内求一点P ,使P A +PB +PC 值最小.所求点为“费马点”,即满足∠APB =∠BPC =∠APC =120°.以AB 、AC 为边向外作等边△ABD 、△ACE ,连CD 、BE 相交于P ,点P 即为所求.两点之间线段最短. P A +PB +PC 最小值=CD .【精品练习】1.如图所示,正方形ABCD 的面积为12,△ABE 是等边三角形,点E 在正方形ABCD 内,在对角线AC 上有一点P ,使PD +PE 的和最小,则这个最小值为( )A .3B .26C .3D 62.如图,在边长为2的菱形ABCD 中,∠ABC =60°,若将△ACD 绕点A 旋转,当AC ′、AD ′分别与BC 、CD 交于点E 、F ,则△CEF 的周长的最小值为( ) A .2B .32C .32+D .4lBAlPABl ABlBPAB'ABCPEDCBAADEPB C3.四边形ABCD 中,∠B =∠D =90°,∠C =70°,在BC 、CD 上分别找一点M 、N ,使△AMN 的周长最小时,∠AMN +∠ANM 的度数为( )A .120°B .130°C .110°D .140°4.如图,在锐角△ABC 中,AB =42,∠BAC =45°,∠BAC 的平分线交BC 于点D ,M 、N 分别是AD 和AB 上的动点,则BM +MN 的最小值是 .5.如图,Rt △ABC 中,∠C =90°,∠B =30°,AB =6,点E 在AB 边上,点D 在BC 边上(不与点B 、C 重合), 且ED =AE ,则线段AE 的取值范围是 .6.如图,∠AOB =30°,点M 、N 分别在边OA 、OB 上,且OM =1,ON =3,点P 、Q 分别在边OB 、OA 上,则MP +PQ +QN 的最小值是_________.(注“勾股定理”:直角三角形中两直角边的平方和等于斜边的平方,即Rt △ABC 中,∠C =90°,则有222AB BC AC =+)7.如图,三角形△ABC 中,∠OAB =∠AOB =15°,点B 在x 轴的正半轴,坐标为B (36,0).OC 平分∠AOB ,点M 在OC 的延长线上,点N 为边OA 上的点,则MA +MN 的最小值是______. DEABCD MABMN8.已知A (2,4)、B (4,2).C 在y 轴上,D 在x 轴上,则四边形ABCD 的周长最小值为 ,此时 C 、D 两点的坐标分别为 .9.已知A (1,1)、B (4,2).(1)P 为x 轴上一动点,求PA +PB 的最小值和此时P 点的坐标;(2)P 为x 轴上一动点,求PB PA 的值最大时P 点的坐标;(3)CD 为x 轴上一条动线段,D 在C 点右边且CD =1,求当AC +CD +DB 的最小值和此时C 点的坐标;10.点C 为∠AOB 内一点.(1)在OA 求作点D ,OB 上求作点E ,使△CDE 的周长最小,请画出图形;(2)在(1)的条件下,若∠AOB =30°,OC =10,求△CDE 周长的最小值和此时∠DCE 的度数.图①12.荆州护城河在CC'处直角转弯,河宽相等,从A处到达B处,需经过两座桥DD'、EE',护城河及两桥都是东西、南北方向,桥与河岸垂直.如何确定两座桥的位置,可使A到B点路径最短?。
13.4最短路径问题(第一课时)课件人教版

距离最短,在图中画出该点的位置.
C
在AB上求作一点P,
使得PC+PD最短.
D
A
B
初中数学
在AB上求作一点P,使得PC+PD最短.
C
作法:
D
(1)作点C关于AB的对称点C′;
A
PB
(2)连接DC′交AB于点P;
(3)则点P即为所求的点.
C′
初中数学
初中数学
练习
有两棵树位置如图,树的底部分别为A,B,地上 有一只昆虫沿着A—B的路径在地面上爬行.小树 顶D处一只小鸟想飞下来抓住小虫后,再飞到大 树的树顶C处.问小鸟飞至AB之间何处时,飞行 距离最短,在图中画出该点的位置.
总结:① 将实际问题抽象成数学 ①分析题目中的定点和动点,转化为我们熟悉的最短路径问题.
有两棵树位பைடு நூலகம்如图,树的底部分别为A,B,地上有一只昆虫沿着A—B的路径在地面上爬行.小树顶D处一只小鸟想飞下来抓住小虫后,再飞到大树的树顶C处.问小鸟飞至AB之间何
处时,飞行距离最短,在图中画出该点的位置.
问题,用数学语言表达. (2)连接CD′交AB于点P;
如图,已知点D,点E分别是等边三角形ABC中BC、AB边的中点,AD=5,点F是AD边上的动点,则BF+EF的最小值为__________.
如图,在直线 l 上求作一点C,使得CA+CB最短.
③ 用符号语言证明结论. 有两棵树位置如图,树的底部分别为A,B,地上有一只昆虫沿着A—B的路径在地面上爬行.小树顶D处一只小鸟想飞下来抓住小虫后,再飞到大树的树顶C处.问小鸟飞至AB之间何
一点M,使PM+MQ最短. 有两棵树位置如图,树的底部分别为A,B,地上有一只昆虫沿着A—B的路径在地面上爬行.小树顶D处一只小鸟想飞下来抓住小虫后,再飞到大树的树顶C处.问小鸟飞至AB之间何
最短路问题专业知识讲座

5
0
5
V2
38
6 6 5 5 V6
V1 4
7 2
V4 7
1
6
8
V5 4
V3
V7
4
9
(7) 找出全部与v1,v2,v3,v4,v5,v6相邻旳未标识旳点v7, 求出从v1经过v5到这些点旳距离(v1->v2->v6->v5->v7:13) 以及经过v6到这些点旳距离(v1->v2->v6->v7:14)找出这些 距离中最短旳途径为v1->v2->v6->v5->v7,最短距离为 L15=13,将v7标识为13。至此全部点都已标识,即求出 了v1到全部其他点旳最短途径
5
5
0
5
V2
3
6 5 5 V6
V1 4
7 2
V4 7
1
6
8
V5 4
V3
V7
4
(4)找出全部与v1,v2,v3相邻旳未标识旳点v4,v5,v6,求出
从v1直接到这些点旳距离(v1->v4:7)以及经过v2到这些点 旳距离(v1->v2->v4:11;v1->v2->v5:10;v1->v2->v6:8)以及 经过v3到这些点旳距离(v1->v3->v4:6;v1->v3->v5:12)找出 这些距离中最短旳途径为v1->v3->v4,最短距离为L14=6, 将v4标识为6
数学模型
目的函数: P : min z
ij fij
(vi ,v j )A
fij 0或1, (vi , v j ) A
s.t.
fij f ji 1, i s
运筹学-最短路问题

V1 0 V2 2 V3 5 D = V4 − V5 − V6 − V7 −
பைடு நூலகம்
v2
2 0 2 4 6 − −
v3
5 2 0 1 − 3 −
v4
− 4 1 0 4 1 4
v5
− 6 − 4 0 − 1
v6
− − 3 1 − 0 2
v7
− − − 4 1 2 0
二、最短路算法: 最短路算法:
1. D氏标号法(Dijkstra) 氏标号法(Dijkstra) (1)求解思路 求解思路——从始点出发,逐步顺序 从始点出发, 从始点出发 逐步顺序 地向外探寻,每向外延伸一步都要求是最 地向外探寻,每向外延伸一步都要求是最 短的。 短的。 (2)使用条件 使用条件——网络中所有的弧权均 网络中所有的弧权 网络中所有的弧权均 非负, 非负,即 wij ≥ 0 。
(4) 计算步骤及例:
第三步:若网络图中已无T标号点 标号点, 第三步:若网络图中已无 标号点,停止 计算。否则 令 计算。否则,令 二步。 二步。 此时,要注意将第二步中的 此时,
T ( v j0 ) =
min {T ( v )}
v j ∈s j
,
然后将 标号改成P 然后将 v j0 的T 标号改成 标号 ,转入第
步骤 考察点 T标号点集 标号点集 v1 0
标 v2
标号) 号( 表P标号) 标号 v3 v4 v5 v6 v7
1 2 3 4 5 6
v1 v2 v3 v4 v6 v5
{v2,…,v7} , {v3,…,v7} , {v4,…,v7} , {v5,v6,v7} {v5,v7} {v7}
2
5 2+2 4
第三节 最短路问题PPT课件

DijksTra算法的步骤:
第一步(初始化)
令k=0, S(0) ={vs}(S是永久标号点的集合), T(0)={vs,v1…vn}(T是临时标号点的集合)d(0)(vs) =0, d(0) (vi) =∞ (d(vi)是vi点被赋予的路长的初始标号, i=1,2,…n )。
λ(vi) = vs (λ(vi) )是λ(vi)点被赋予的vs→vi路径的vi先驱 点 号,resent= vs ( resent用于表示最新获得永久标号 的顶 点)。
3
vv81, ∞
9
图上标号法:
v2 v1,6 1
6 2
v1
3 v3v1,3
0,0
6
1
2
10
v4
v1,1
v5
v1, ∞ 2
6
3
4 10
4
v6 2
v7
v1, ∞
v1, ∞
v9 v1, ∞
3
vv81, ∞
10
图上标号法:
v2 v1,6 1
6 2
v1
3 v3v1,3
0,0
6
1
2
10
v4
v1,1
v5
v1, ∞ 2
第3节 最短路问题
7.3.1 最短路定义
例 下图为单行线交通网,每弧旁的数字表示通过这条
线所需的费用。现在某人要从v1出发,通过这个交
通网到v8去,求使总费用最小的旅行路线。
v2 1
v5
2
v9
6 2
6
3
v1
3 v3 6
3 4 10
1
2
v4
10
4
v6 2 v7
v8
运筹学-最短路问题[课件参考]
![运筹学-最短路问题[课件参考]](https://img.taocdn.com/s3/m/199eaa4c5727a5e9846a6140.png)
Page 10
1、最短路算法基于以下原理:
一个最优策略的任一子策略也是最优策略.
若P是从vs到vt间的最短路, vi是P中的一个点,则vs到vi的最
短路就是从vs 沿P到vi的那条路。 v2
v4
v1
v3
v5
v1 →v2 →v3一定是v1 →v3的最短路,
v2 →v3 →v4也一定是v2 →v4的最短路。
2.设节点 vi 为刚得到P标号的点,考虑点vj,其中 (vi , v j ) E ,且vj为T标号。对vj的T标号进行如下修改:
T (v j ) min[T (v j ) , P(vi ) wi j ]
3.比较与vi相邻的所有具有T标号的节点,把最小者改为P 标号,即: P(vk ) min[T (vi )]
精选课件
Chapter8 图与网络优化
本章主要内容:
§8.1 图的基本概念 §8.2 树 §8.3 最短路问题 §8.4 网络最大流问题 §8.5 最小费用最大流问题 §8.6 中国邮递员问题
精选课件
Page 3
§8.3 最短路问题
The Shortest-Path Problem
精选课件
§8.3 最短路问题
Page 17
解 :(1)首先给v1以P标号,给其余所有点T 标号。
P(v1) 0,T (vi ) (i 2, 3, , 8),(v1) 0;
(2) T (v2 ) min{T (v2 ), P(v1 ) w12 } min{ , 0 3} 3
T (v4 ) min{T (v4 ), P(v1 ) w14 } min{ , 0 7} 7
精选课件
§8.3 最短路问题
第15讲 最短线路 植树问题 枚举法综合复习
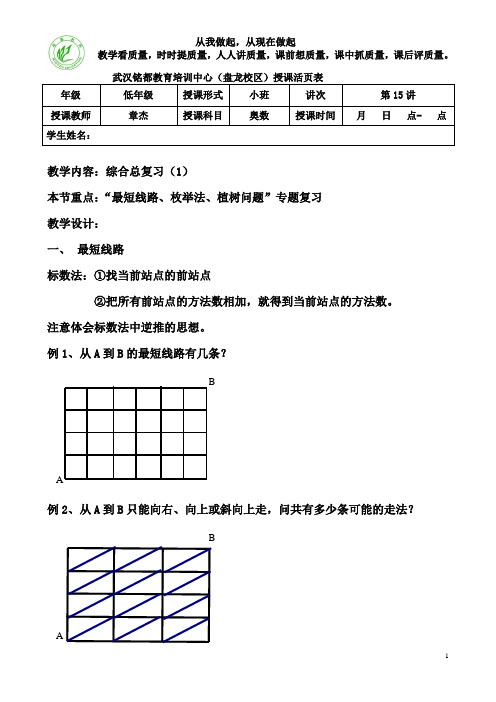
武汉铭都教育培训中心(盘龙校区)授课活页表年级低年级授课形式小班讲次第15讲授课教师章杰授课科目奥数授课时间月日点- 点学生姓名:教学内容:综合总复习(1)本节重点:“最短线路、枚举法、植树问题”专题复习教学设计:一、最短线路标数法:①找当前站点的前站点②把所有前站点的方法数相加,就得到当前站点的方法数。
注意体会标数法中逆推的思想。
例1、从A到B的最短线路有几条?BA例2、从A到B只能向右、向上或斜向上走,问共有多少条可能的走法?BA例3、如图,某城市的街道由5条东西向马路和7条南北向马路组成,现在要从西南角的处沿最短的路线走到东北角出,由于修路,十字路口不能通过,那么共有____种不同走法.例4、如图为一幅街道图,从A出发经过十字路口B,但不经过C走到D的不同的最短路线有条.二、枚举法枚举法就是把所要计数的对象一一列举出来,并做到无一重复、无一遗漏,然后计算其总和。
枚举的关键就是“有条有理”。
例5、把一个整数表示成若干个小于它的自然数值和,叫做整数的拆分。
整数4有多少种不同的拆分方法?例6、用一台天平和重1克、3克、9克的砝码各一个(不再用其他物品当砝码),当砝码只能放在同一个盘内时,可以称出的重量有多少种?例7、课外小组组织30人做游戏,按1~30号排队报数。
第一次报数后,单号全部站出来,然后每次余下的人中第一个开始站出来,隔一人站出来一个人,到第几次这些人全部站出来?最后站出的人应该是第几号?例8、如图所示,数字1处有一颗棋子,现移动这颗棋子到数字5处。
规定每次只能移动到邻近一格,且总是向右移动,例如1→2→4→5就是一条路线。
问有多少种不同的移动路线?三、 植树问题在一定长度的线路上,等距离地安排若干个点植树。
植树的棵数、间隔(相邻两棵树之间的距离)之间存在某种数量关系,研究这种数量关系的问题通常被称为植树问题。
1、 直线型两端植树2、 直线型一段植树3、 直线型两端都不植树4、 封闭型植树问题例9、同学们在全长100米的小路一边植树,每隔5米栽一棵(两端要栽)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
v2 -,-
+
-,-
+(-1))
=4
……… …
依此类推… vs
vs
v1
反向追踪过程: 寻求一点vk,使 dkl1wk tdtl ,本题中vk 即为v1,所以找到弧(v1,vt);
再寻求一点vi ,使 dil1wi1d4l ,这里, vi即为vs ,所以找到弧( vs,v1);
于是得最短路线 vs v1vt
求 min{T(vj )}
v k 满足 T(vk)m vj inS{T(vj)}
令:P(vk)T(vk)
比较v1到所有其它节点的最短距离,找到 节点vk,并将最小的距离记录在P(vk)中。
③如果已经搜索到最后一个节点即
已经求出了v 1 到 v n 的最短距离 P ( v
vk
n)
vn ;
,那么就
否则,令 i k ,从 S 中删去 v k ,转①继续搜索。
反向追踪寻找最短路线,得:
最短路线为 vs v1vt,最短路权为5。
计算过程详示:
d( j1 )w 1j js,1 ,2 ,3 ,t
d(2) s
m i (idni(1)wis)
=min(0+0,4+ -,1+(-1),- + -,- + -)
=0
d(2) 1
=mm iin((idn0i(1+)4,wi41)+0,1+
d d k min
j
i
k 1
j
wij
j2,3,,N
其中,
d
k
j
表示从起点 v 1 到点 v
j 走k步
的最短距离;
③当迭代到第 l步,有
d d l l1时,收敛;
Hale Waihona Puke jjdl
j
就是从起点
v
1
到各点的最短距离;
④反向追踪求出最短路线。
例5-4:计算下图中从vs到vt的最短路 线和最短路长
v1
-1 4
把k赋给i,从搜索节点集合中去掉vk,重新搜索 vk(将vk作为vi)到其余节点的最短距离。
算法思想示意图
ik
v1
T (v j)
i k T (v j )
vj S
vj S
vk vn
T (v j)
T (v j)
ik vj S
vj S
例5-3 用狄克斯拉算法 求解图5-1所示最短路问题。
v2
6
v5
2
5-2. 最 短 路 问 题
一、问题的提法及应用背景
(1)问题的提法——寻求网络中两点间 的最短路就是寻求连接这两个点的边的 总权数为最小的通路。(注意:在有向 图中,通路——开的初等链中所有的弧 应是首尾相连的。)
(2)应用背景——管道铺设、线路安排、 厂区布局、设备更新等。
二、最短路算法:
1. D氏标号法(Dijkstra) (1)求解思路——从始点出发,逐步顺序
2 v1
v3 -5
v2 3
网络中有负权 时,D氏标号 法失效
2. 列表法(Ford算法)
求从点v 1
到任何一点v
(
j
j2,3,,N)
的最短路。
(1)使用条件—没有负回路
(2)步骤:
①
令
d1 j
w1j,j2,3,,N,其中
w
1
j 为起点v 1
到 v j 的弧(v 1 , v j )的权;
②用下列递推公式进行迭代:
4 4
1
v1
2
5
v4
1
1
4
v7
2
v3
3
v6
图5-1 例5-3网络图
解:先将图5-1的网络用矩阵形式表示出来:
v1 v2 v 3 v4 v 5 v 6 v 7
V10 2 5 V22 0 2 4 6
DV V4 3 5
2 4
0 1
1 0
4
3 1
4
V5
6
4
0
1
V6 3 1 0 2
V7 4 1 2 0
vs
-2
-1 1
v2 3
1
6
vt
2
v3
vs v1
v2
v3
vt
d
(1) j
d
(2) j
d
(3) j
vs 0 4 1 --- --- 0 0 0
v1 --- 0 -2 6 1 4 4 4
v2 -1 --- 0 3 --- 1 1 1
v3 --- --- --- 0 2 --- 4 4
vt --- -1 --- --- 0 --- 5 5
则
d
(0) ij
是指vi到vj的一步距离;
当
d
( ij
m
1
)已知时,令
di(m j)m k1~n{d ii(n m k1)dk(m j1)}
则当m=1时,d
(1 ij
是) vi到vj走两步的最小距离;
当m=2时,d
( ij
2
) 是vi
到vj走四步的最小距离;
一般,d
(m ij
)是vi
到vj
走2m步的最小距离;
8+1 8
如果选择v7, 则k=7=n,迭代结束。
T (v j)
8
{8}
反向追踪,得到最优路线: v1 v2 v3 v4 v6 v7
v5
讨论:若先把v7的标号改为永久性标号, 会怎样?
(5) D氏标号法(Dijkstra)的 优缺点(获得的附加信息):
v 能得到从 1 (起点)到各点的最短
路线和最短路长。
地向外探寻,每向外延伸一步都要求是最 短的(两层最小化的含义)。 (2)使用条件——网络中所有的弧权均
非负,即 wij 0 。
(3)选用符号的意义:
①标号 P(固定标号或永久性标号)
——从始点到该标号点的最短路权。
②标号 T(临时性标号)
——从始点到该标号点的最短路权上界。
②在v1到所有其他节点的最短距离中选择最小的距 离,找到节点 vk,使下式满足:
vj
v1
初始值 T ( v j ) {0}
第一次 迭代
P(v1) l1 j
T (v j)
第二次 迭代
P(v2) l2 j
T (v j)
第三次 迭代
P(v3) l3 j
T (v j)
第四次 迭代
P(v4) l4 j
T (v j)
第五次 迭代
P(v6) l6 j
v2
v3
v4
v5
v6
v7
∞ ∞ ∞ ∞ ∞∞
0+2 0+5 ∞ ∞ ∞ ∞
{2} 5 ∞ ∞ ∞ ∞
2+2 2+4 2+6 ∞ ∞
{4} 6 8 ∞ ∞
4+1 4+∞ 4+3 ∞
{5} 8 7 ∞
5+4 5+1 5+4
8 {6} 9
6+∞
6+2
vj
v1
v2
v3
v4
v5
v6
v7
T (v j)
{8}
8
第6次 迭代
P(v5) l5 j T (v j)
当对所有I,j有:
d(m) ij
di(jm1)
时,则
d
( ij
m
)
是vi到vj的最短距离。
由于最短路线上最多有n-1条边,因此,当
2m
②优点:可以在有负权的情况下,寻求从
起点到各个点的最短路线和最短路长。
3. 海斯算法
(1)算法思想:
利 用 vi 到 vj 的 一 步 距 离 求 出 vi 到 vj 的两步距离,再由两步距离求出四步 距离,经有限步迭代即可求得vi到vj的 最短路线和最短距离。
(2)算法步骤:
令 di(0 j)lij i1 ,2 , ,n
