下面的图形可以一笔画成吗
趣味数学300题 第三章 画来画去。移来移去……
趣味数学300题第三章画来画去。
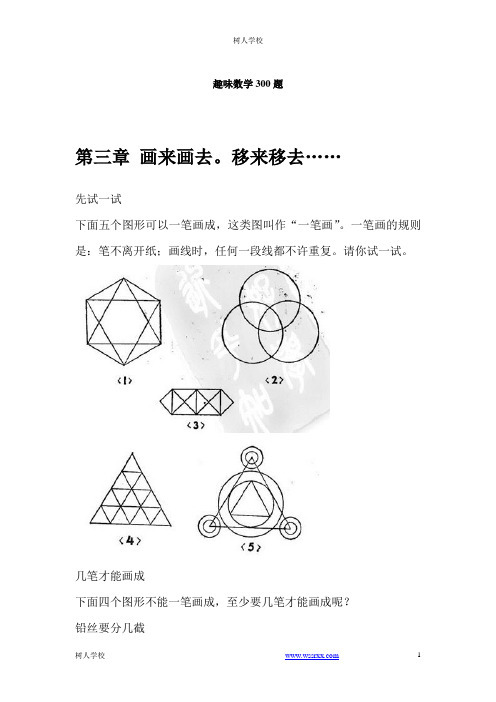
移来移去……先试一试下面五个图形可以一笔画成,这类图叫作“一笔画”。
一笔画的规则是:笔不离开纸;画线时,任何一段线都不许重复。
请你试一试。
几笔才能画成下面四个图形不能一笔画成,至少要几笔才能画成呢?铅丝要分几截在下面三个架子中,有一个只用一根铅丝就可以构成,而另外两个,要把铅丝分成几段才能构成。
请在每一个架子下注明,是用几根铅丝构成的。
擦掉哪一根线下图不能一笔画,可是,只要擦去一根线,图形就可以一笔画成。
应该擦掉哪一根线,你知道吗?走遍所有的门下图是一座房屋的平面图。
每两个相邻房间之间,都有一个门相通;除中间两个房间E和F 以外,每个房间都有门通向室外。
你能够不重复地穿过每一道门吗?提示:把每一个房间设想成一个点,室外也用一个点表示。
如果两个房间这间有门相通,设想相应的两点之间有线段连接。
画出这个图,上述问题就相当于一个“一笔画”。
十五座桥下图中有A、B、C、D、E、F六个小岛,各岛之间共有十五座桥(桥已编号)。
现在要从A 岛出发,不重复地走遍十五座桥,该怎么走呢?你是不是已经看出,这也是一笔画问题?十八世纪伟大的数学家欧拉从哥尼斯堡城的七桥入手,研究了“一笔画”问题。
因此,现代的图论著作和书籍中,都把“一笔画”称为欧拉问题,把能不重复走遍的路,称为欧拉路。
别致的画廊公园里布置了一个很别致的画廊(请看图)。
画廊分为25段,每段画廊两头的圆圈是休息处。
A处为入口,B处是出口,H处设有小吃部。
现在有一个人要不重复地看遍所有画廊,并且打算在看了8段画廊后恰好到小吃部(H处),吃点东西后,再看9段,又恰好回到小吃部(H处),最后看完剩下的8段画廊,从B处出来。
请你替这个人安排一条参观的路线。
最短路线下图是一些街道的平面图,中间九个方格是一些建筑物。
有一辆洒水车从A点出发,要往每一条街道上洒水最后仍回到A点。
洒水车在街道上必然有重复行驶,可是精心地选择行驶路线,能使重复行驶的路程尽可能少。
第2讲 五颜六色B(学生版)
【课前测【课前测【课前测【例题【例题【例题A.18B.20C.22D.24A.16B.17C.18D.19【例题4】用小正方体拼成了一个如下图的模型,然后把它粘在地上喷上红色油漆,这堆正方体中共有几个小正方形没有被喷上颜色.A.27B.28C.29D.30【例题5】薇儿用小正方体拼成了一个如下图的图形,然后把它粘在地上喷上绿色油漆,这堆正方体中共有几个小正方形没有被喷上颜色.【例题6】下图是一个正方体木块,在它的表面涂上蓝色,然后沿正方体上面直线垂直切开.切成了()个三棱柱.这些三棱柱一共有()个面没有被涂色.A.8;14B.8;16C.10;16D.10;20A.2 B.3 C.4 D.5【例题7】用10个小正方体摆成一个“工”字形(如下图),然后又将表面都涂成黄色,最后又把小正方体分开,数一数:(1)3面涂成黄色的小正方体有()个.A.2B.3C.4D.5【例题8】用10个小正方体摆成一个“工”字形(如下图),然后又将表面都涂成黄色,最后又把小正方体分开,数一数:(2)4面涂成黄色的小正方体有()个.【例题9】用10个小正方体摆成一个“工”字形(如下图),然后又将表面都涂成黄色,最后又把小正方体分开,数一数:(3)5面涂成黄色的小正方体有()个.A.2B.3C.4D.5挑战题A.3B.4C.5D.6【例题10】一个大正方体的表面上都涂上绿色,然后切成27个小正方体(切线如下图所示).在这些切成的小正方体中,问:(1)1面涂成绿色的有()个.A.6B.8C.10D.12【例题11】一个大正方体的表面上都涂上绿色,然后切成27个小正方体(切线如下图所示).在这些切成的小正方体中,问:(2)2面涂成绿色的有()个.【例题12】一个大正方体的表面上都涂上绿色,然后切成27个小正方体(切线如下图所示).在这些切成的小正方体中,问:A.6B.8C.10D.12(3)3面涂成绿色的有()个.A.0B.1C.2D.4【例题13】一个大正方体的表面上都涂上绿色,然后切成27个小正方体(切线如下图所示).在这些切成的小正方体中,问:(4)0面涂成绿色的有()个.A.24B.48C.72D.80【例题14】一堆小正方体堆成了如下图的空心大正方体(正中间一列从上到下是空心),再把大正方体放进染缸里染上蓝色,现在没有染色的小正方形共有多少个?。
【三套试卷】小学三年级数学上册第七单元教材检测卷含答案(3)
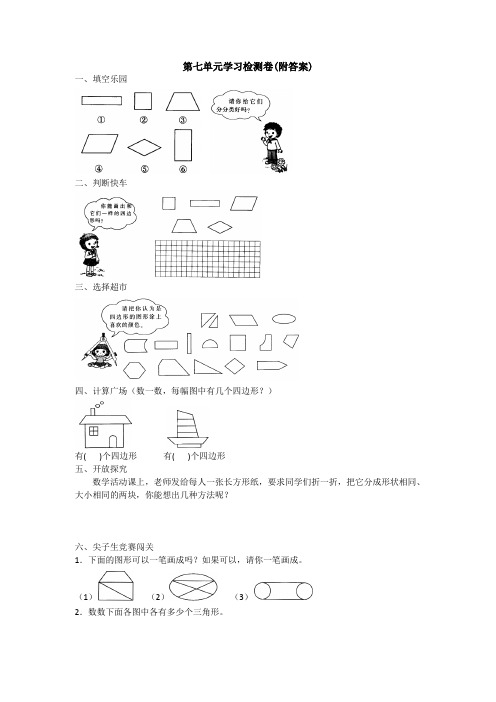
第七单元学习检测卷(附答案)一、填空乐园二、判断快车三、选择超市四、计算广场(数一数,每幅图中有几个四边形?)有( )个四边形有( )个四边形五、开放探究数学活动课上,老师发给每人一张长方形纸,要求同学们折一折,把它分成形状相同、大小相同的两块,你能想出几种方法呢?六、尖子生竞赛闯关1.下面的图形可以一笔画成吗?如果可以,请你一笔画成。
(1)(2)(3)2.数数下面各图中各有多少个三角形。
有( )个三角形有( )个三角形3.下图中有A、B、C、D、E、F6个小岛,各岛之间共有15座桥(见编号)。
现在要从A岛出发,不重复地走遍15座桥,该怎样走?四边形认识四边形一、第一类:①②⑥第二类:③④⑤或第一类:①②④⑤⑥第二类:③二、三、四边形:四、12 12五、六、1.(1)(2)能一笔画(3)有4个单数点,不能一笔画成 2. 42 73.将A、B、C、D、E、F6个小岛用点表示(如下图)。
从图中看A、F是奇顶点,B、C、D、E是偶顶点,只要从A或F出发.回到F或A就可以走遍15座桥。
第七单元达标检测卷(附答案)一、单选题1.四条线段首尾顺次连接的图形叫()A. 三角形B. 四边形C. 圆形2.长方形长7米,比宽多2米,宽是()A. 7+2=9(米)B. 7-2=5(米)C. 7×2=14(米)D. 7+2+2=11(米)3.数学课本的封面是()A. 三角形B. 长方形C. 正方形4.正方形的两组对边分别()。
A. 平行B. 垂直C. 相交D. 重合5.一个梯形只有()对边平行A. 一组B. 两组C. 三组6.属于四个边的图形的是()A. B. C. D.7.用23根长度相同的小棒摆正方形,最多能摆成()个独立的正方形.A. 4B. 5C. 6二、判断题8.因为一张长方形有4个直角,所以剪去1个直角后还剩下3个直角,对吗?9.四边形的四个角都是直角。
10.一个图形有4个直角,它可能是长方形,也可能是正方形.11.长方形、正方形和平行四边形都是四边形.12.两个完全相等的梯形可以拼成一个平行四边形三、填空题13.长方形和正方形都是________形,它们都有________条边,都有________个直角。
小学奥数 奇妙的一笔画 精选练习例题 含答案解析(附知识点拨及考点)

所谓图的一笔画,指的就是:从图的一点出发,笔不离纸,遍历每条边恰好一次,即每条边都只画一次,不准重复.从图中容易看出:能一笔画出的图首先必须是连通图.但是否所有的连通图都可以一笔画出呢?下面,我们就来探求解决这个问题的方法.什么样的图形能一笔画成呢?这就是一笔画问题,它是一种有名的数学游戏.我们把一个图形中与偶数条线相连接的点叫做偶点.相应的把与奇数条线相连接的点叫做奇点. 一笔画问题:(1)能一笔画出的图形必须是连通的图形;(2)凡是只由偶点组成的连通图形.一定可以一笔画出.画时可以由任一偶点作为起点.最后仍回到这点; (3)凡是只有两个奇点的连通图形一定可以一笔画出.画时必须以一个奇点作为起点,以另一个奇点为终点; (4)奇点个数超过两个的图形,一定不能一笔画. 多笔画问题:我们把不能一笔画成的图,归纳为多笔画.多笔画图形的笔画数恰等于奇点个数的一半.事实上,对于任意的连通图来说,如果有2n 个奇点(n 为自然数),那么这个图一定可以用n 笔画成.模块一、判断奇偶点【例 1】 我们把一个图形上与偶数条线相连的点叫做偶点,与奇数条线相连的点叫做奇点.下图中,哪些点是偶点?哪些点是奇点?J O I H G FED CBA【考点】一笔画问题 【难度】2星 【题型】解答【解析】 奇点: D H J O 偶点:A B C E F G I 【答案】奇点: D H J O 偶点:A B C E F G I【例 2】 同学们野营时建了9个营地,连接营地之间的道路如图所示,贝贝要给每个营地插上一面旗帜,要求相邻营地的旗帜色彩不同,则贝贝最少需要 种颜色的旗子,如果贝贝从某营地出发,不走重复路线就 (填“能”或“不能”)完成任务.【考点】一笔画问题 【难度】2星 【题型】填空例题精讲知识点拨4-1-5.奇妙的一笔画【关键词】华杯赛,六年级,初赛,第10题【解析】最少需要3种颜色的旗子。
因为中间的三点连成一个三角形,要使这三点所代表营地两粮相邻,要使相邻营地没有相同颜色的旗子,必须各插一种与其它两点不同颜色的旗子。
举一反三——一笔画成

2.下面图形可以一笔画成吗?说明理由
奇点数有4个,不能一笔画成。
奇点数有2个,能一笔画成。
练习:下面个图能否一笔画成?如果能,请画出
奇点数有0个,可以一笔画成
3.将下图加最少的线改成一笔画成图形
4.将下图去掉最少的线改成一笔画成图形
5.下图中的线段代表小路,请同学们想一想:能够不重复地爬遍小路的是 甲蚂蚁还是乙蚂蚁?该怎么爬?
6.下图是儿童乐园平面图,出入口应该设在哪里才能不重复地走遍每条路?
练习:下图是商场的平面图,顾客可以从A,B,C,D,E,F六个门进入商城,怎样 才能不重复地逛完商场。
加微信,可定做
高斯小学奥数含答案二年级(下)第08讲 一笔画

第八讲一笔画前续知识点:二年级第一讲;XX模块第X讲后续知识点:X年级第X讲;XX模块第X讲把里面的人物换成相应红字标明的人物.这里是小区平面图,我从哪个入口进去,才能一次不重复地走遍小区的所有小路,尽快地把口罩送给每个朋友呢?由于空气污染严重,哥哥让我给朋友们去送口罩,以防大家得病。
墨莫墨莫一笔画,是指从连通图的一点出发,笔不离纸,每条线都只画一次,不能重复.一笔画能解决很多实际问题.那么什么样的图形能够一笔画成,什么样的图形不能一笔画成呢?试着画一画下面的图形吧!例题1观察下列图形,能一笔画成的打“√”,不能一笔画成的打“×”.()()()()()()【提示】动手画一画,你知道什么样的图形一定不能一笔画成吗?练习1观察下列图形,能一笔画成的打“√”,不能一笔画成的打“×”.()()()()()()()()我们画了这么多图形,不难发现,不连通的图形一定不能一笔画成,能一笔画成的图形必定是连通图.连通图,指的是如果一个图形中的任意两点都是连通的,那么这个图形就是连通图.一个图形可以一笔画成,除了必须是连通图,还有没有其它的规律和特点呢?我们一起找找吧!首先,我们先来认识下面的两个名词:从一点出发的线条数目是奇数,如1、3、5、7、……我们称它为奇点. 从一点出发的线条数目是偶数,如2、4、6、8、……我们称它为偶点.奇点、偶点的个数与一个图形能否一笔画成有什么关系呢?我们来看一看下面的题目吧!【例题2】下面的各个图形都是由点和线组成的.请你仔细观察后回答,各图中的交叉点分别有几个奇点?几个偶点?能否一笔画成?能的在“( )”里打“√”,不能的在“( )”里打“×”.【提示】从某一点发出奇数条线,这个点是奇点;从某一点发出偶数条线,这个点是偶点.【练习2】下面的各个图形都是由点和线组成的.请你仔细观察后回答,各图中的交叉点分别有几个奇点?几个偶点?能否一笔画成?能的在“( )”里打“√”,不能的在“( )”里打“×”.(1) (2) (3)(4) 奇点数: ( ) ( ) ( ) ( ) 偶点数: ( ) ( ) ( ) ( ) 能否一笔画成:( ) ( ) ( ) ( )奇点数: ( ) ( ) ( ) ( ) 偶点数: ( ) ( ) ( ) ( )能否一笔画成:( ) ( ) ( ) ( )(1) (2)(3) (4)通过对上题的观察,相信大家都发现了规律.有0个奇点的连通图能够一笔画成.画时可以以任一点为起点,最后一定能以这个点为终点画完此图. 有2个奇点的连通图能够一笔画成.画时必须以一个奇点为起点,另一个奇点为终点画完此图. 有2个以上奇点的连通图不能一笔画成.根据以上规律,我们可以通过奇点个数来正确判断哪些图形能一笔画成,哪些图形不能一笔画成.我们就用学到的知识来解决生活中的一笔画问题吧!例题3草地上有许多小路,丁丁和月月分别站在A 、B 两个路口.谁能够一次不重复地走遍所有小路?【提示】谁的出发点是奇点?练习3花园里有许多崎岖的小路,小乖要浇花,它想一次不重复地走完每条小路.该从哪个路口出发呢?AB CDE例题4小河中有4个小岛,小岛之间建有六座桥.淘淘能一次不重复地走遍所有的小桥吗?【提示】先把实际地图画成“点线图”,然后数数奇点的个数吧!练习4蘑菇园的小朋友们要去游乐场玩,他们可以从6个入口进出游乐场.他们从哪个入口出发,才能一次不重复地走遍游乐场内的所有小路?我们已经可以正确判断哪些图形可以一笔画成,哪些不能一笔画成.如果不能一笔画成,可不可以通过增添或删除一些线的方法,让它变成可以一笔画成的图形呢?例题5AB C D EFG下面的“蝴蝶”能一笔画成吗?如果不能,按照如下要求把它改成能一笔画成的图形.(1)在图1中,去掉一条线;(2)在图2中,添加一条线.图1图2【提示】在两个奇点之间去掉或添加线.例题6甲乙两个不同公司的快递员去送货,两人都要以同样的速度走遍所有的街道(阴影部分),甲从A点出发,乙从B点出发,最后都回到C点.如果都选择最短的线路,谁先回到C点?ABC【提示】先把实际道路图画成“点线图”,再判断各个交叉点中有哪些是奇点.课堂内外七桥问题德国有一个城市叫哥尼斯堡.城中有一条小河,河中有两个小岛,还有7座桥把这两个小岛和陆地连接起来,如下图所示.人们经常在这里游玩,他们在游玩的时候提出这样一个问题:能不能一次不重复地走遍所有的小桥呢?作业1. 观察下列图形,能一笔画成的打“√”,不能一笔画成的打“×”.2. 下面每幅图中的交叉点分别有几个奇点?能否一笔画成呢?能的在“( )”里打“√”,不能的在“( )”里打“×”.( ) ( ) ( )( ) ( ) ( )小岛 小岛3. 菲菲周末去郊外的公园玩,公园里有许多崎岖的小路.她想不重复地一次走完每条小路,可以从哪个路口出发?4. 小熊、灰鼠、小象和小猪要分别从东、南、西、北四个入口去果园采果子,谁能不重复地一次走遍所有小路?5. 下面的图形能一笔画成吗?如果不能,按照如下要求将其改成能一笔画成的图形.(1)在图1中去掉一条线;(2)在图2中添加一条线.图1图2北CD E F G HBA 奇点数: ( ) ( ) ( ) ( ) 能否一笔画:( ) ( ) ( ) ( )(1) (2) (3) (4)第八讲 一笔画1.例题1答案:×,√,√,×,×,√详解:第(1)个图形是非连通图,不能一笔画;其它都是连通图,依次尝试判断即可. 2.例题2答案:如图所示:详解:把交叉点是奇点的圈起来,如图所示:有0个奇点和2个奇点的连通图能够一笔画成;2个奇点以上的连通图不能一笔画成.一个图形能否一笔画成与偶点数无关. 3.例题3 答案:月月详解:图中B 点和E 点是奇点,其它交叉点都是偶点.有2个奇点的图形,一笔画的特征是:从图形的一个奇点出发,回到另一个奇点.只有从奇点的路口出发,才能一次不重复地走遍所有小路.美羊羊站在B 点的路口上,所以能够一次不重复地走遍所有小路. 4.例题4 答案:不能详解:把图中的小岛看成点,把桥看成线,得到“点线图”,如图所示,有4个交叉点,这4个交叉点都是奇点,这个图形不能一笔画成.所以淘淘不能一次不重复地走遍所有的小桥.5.例题5答案:如图所示:(答案不唯一)奇点数: (0) (2) (2) (4) 偶点数: (4) (4) (5) (5) 能否一笔画成: (√) (√) (√) (×)详解:图中有4个奇点,不能一笔画成.去掉或添加一条线使得奇点个数减少,那么就在2个奇点之间去掉或添加线. 6.例题6 答案:甲详解:先把这个送货路线图画成“点线图”,如图所示,A 、C 是奇点.所以,甲从A 点出发回到C 点,可以一次不重复的走遍所有的街道;而乙要走遍所有的街道,其中必有重复.所以甲先回到C 点.7.练习1答案:√,√,√,×,×,√,√简答:第2个图形和第5个图形是非连通图,不能一笔画成;其它是连通图,依次尝试判断即可. 8.练习2答案:如图所示:简答:先把交叉点是奇点的圈起来,一一数出来,再判断能否一笔画成.(1) (2)(3)(4)奇点数: (0) (2) (2) (6) 偶点数: (3) (2) (3) (1) 能否一笔画成: (√) (√) (√) (×)9. 练习3答案:A 点或F 点简答:图中A 点和F 点是奇点,其它交叉点都是偶点.有2个奇点的图形,一笔画的特征是:从图形的一个奇点出发,回到另一个奇点.只有从奇点的路口出发,才能一次不重复地走遍所有小路.所以小乖应该从A 点或F 点出发.10. 练习4答案:C 或D简答:把图中的平面图画成“点线图”,如图所示,C 点和D 点是奇点,所以蘑菇园的小朋友们从C 或D 入口出发,才能一次不重复地走遍游乐场内的所有小路.11. 作业1 答案:×,×,√,×,√,√简答:第1个图形是非连通图,不能一笔画成;其它是连通图,依次尝试判断即可.12. 作业2答案:如图所示:简答:先把交叉点是奇点的圈起来,一一数出来,再判断能否一笔画成.13. 作业3答案:A 或B简答:观察图形可知,图中只有A 和B 两个奇点,其余的都是偶点.走时必须从一个奇点出发到另一个奇点结束,也就是从A 出发,从B 离开,或者从B 出发,从A 离开.14. 作业4答案:灰鼠和小熊简答:先根据果园的平面图画出点线图,如下图所示.观察下图中共有9个交叉点,其中7个点是偶点,只有两奇点数: (2) (4) (0) (4) 能否一笔画: (√) (×) (√) (×)(1) (2) (3) (4)E个点(北、西)是奇点,所以只有在北门和西门的小动物可以不重复地一次走遍所有的小路.15.作业5答案:不能简答:在任意两个奇点之间添一条线或去一条线,如下图所示,都可以改成能一笔画成的图形(答案不唯一).小猪(东)小象(南)。
奇点偶段法求经典例题

奇点偶段法求经典例题一、一笔画相关例题例1- 题目:判断下面图形是否能够一笔画成。
(图形为一个“日”字形状)- 解析:- 首先确定奇点个数。
对于“日”字,它有2个奇点(中间一横的两个端点)。
- 根据奇点偶段法,当奇点个数为0或2时,图形可以一笔画成。
所以“日”字可以一笔画成。
例2- 题目:判断下面图形是否能够一笔画成。
(图形为一个“田”字形状)- 解析:- 找出“田”字的奇点个数。
“田”字有4个奇点(四个小正方形的四个角点)。
- 由于奇点个数不是0或2,所以“田”字不能一笔画成。
例3- 题目:下面是一个连通图,判断能否一笔画成,如果能,怎样画?(图形为一个简单的五角星形状)- 解析- 计算五角星的奇点个数。
五角星的每个顶点的度数都是偶数,所以奇点个数为0。
- 因为奇点个数为0,所以这个图形可以一笔画成。
可以从任意一点出发,最后回到这个点。
例如从五角星的一个角点出发,沿着边依次经过其他点,最后回到起始点。
例4- 题目:在一个公园的平面图中,道路连接各个景点,判断游客能否不重复地走遍所有道路?(简化后的图形为一个有多个交叉点和线段的连通图,有2个奇点)- 解析- 由于图形有2个奇点。
- 根据奇点偶段法,有2个奇点的连通图可以一笔画成,所以游客能够不重复地走遍所有道路。
可以从其中一个奇点出发,到另一个奇点结束。
例5- 题目:判断下面这个复杂的连通图形能否一笔画成。
(图形是由多个三角形和四边形组合而成,有一些交叉点)- 解析- 仔细分析图形的奇点个数。
经过逐一检查交叉点的度数,发现有0个奇点。
- 因为奇点个数为0,所以这个复杂的连通图形可以一笔画成。
二、邮递员问题相关例题(利用奇点偶段法优化路线)例6- 题目:某邮递员要投递信件的区域街道图如下(简单的街区连通图,有4个奇点),他从邮局出发,要走遍所有街道且最后回到邮局,怎样走路线最短?- 解析- 由于有4个奇点,不能一笔画成回到原点。
- 我们要把奇点个数变为0。
小学奥数教程:奇妙的一笔画_全国通用(含答案)

所谓图的一笔画,指的就是:从图的一点出发,笔不离纸,遍历每条边恰好一次,即每条边都只画一次,不准重复.从图中容易看出:能一笔画出的图首先必须是连通图.但是否所有的连通图都可以一笔画出呢?下面,我们就来探求解决这个问题的方法.什么样的图形能一笔画成呢?这就是一笔画问题,它是一种有名的数学游戏.我们把一个图形中与偶数条线相连接的点叫做偶点.相应的把与奇数条线相连接的点叫做奇点. 一笔画问题:(1)能一笔画出的图形必须是连通的图形;(2)凡是只由偶点组成的连通图形.一定可以一笔画出.画时可以由任一偶点作为起点.最后仍回到这点; (3)凡是只有两个奇点的连通图形一定可以一笔画出.画时必须以一个奇点作为起点,以另一个奇点为终点; (4)奇点个数超过两个的图形,一定不能一笔画. 多笔画问题:我们把不能一笔画成的图,归纳为多笔画.多笔画图形的笔画数恰等于奇点个数的一半.事实上,对于任意的连通图来说,如果有2n 个奇点(n 为自然数),那么这个图一定可以用n 笔画成.模块一、判断奇偶点【例 1】 我们把一个图形上与偶数条线相连的点叫做偶点,与奇数条线相连的点叫做奇点.下图中,哪些点是偶点?哪些点是奇点?J O I H G FED CBA【考点】一笔画问题 【难度】2星 【题型】解答 【解析】 奇点: D H J O 偶点:A B C E F G I 【答案】奇点: D H J O 偶点:A B C E F G I【例 2】 同学们野营时建了9个营地,连接营地之间的道路如图所示,贝贝要给每个营地插上一面旗帜,要求相邻营地的旗帜色彩不同,则贝贝最少需要 种颜色的旗子,如果贝贝从某营地出发,不走重复路线就 (填“能”或“不能”)完成任务.【考点】一笔画问题 【难度】2星 【题型】填空 【关键词】华杯赛,六年级,初赛,第10题 【解析】 最少需要3种颜色的旗子。
因为中间的三点连成一个三角形,要使这三点所代表营地两粮相邻,要使相邻营地没有相同颜色的旗子,必须各插一种与其它两点不同颜色的旗子。
一年级一笔画数学题

一年级一笔画数学题
题目1:
下面这些图形,哪些可以一笔画成?(人教版一年级数学一笔画相关)
(1)正方形。
(2)圆形。
(3)“十”字形状。
解析:
对于正方形,它有4个顶点,都是偶数条线相连(每个顶点连接2条线),所以可以一笔画成。
圆形没有顶点这种概念,但它是一个封闭的曲线,我们可以从圆上任意一点开始,沿着圆周画一圈就能一笔画成。
对于“十”字形状,中间的交点连接了4条线,是偶数条线相连,所以也可以一笔画成。
题目2:
观察下面的图形,能一笔画成的在()里打“√”,不能的打“×”。
(人教版一年级数学一笔画相关)
图形1:三角形()
图形2:两个不相连的圆形()
图形3:“Z”字形()
解析:
三角形有3个顶点,每个顶点连接2条线,都是偶数条线相连,所以能一笔画成,(√)。
两个不相连的圆形,因为是两个独立的图形,不能一笔同时画出这两个不相连的图形,所以(×)。
“Z”字形有2个端点和2个转折点,端点连接1条线(可视为奇数条线相连),所以不能一笔画成,(×)。
奥数-03一笔画+答案

【例 8】 如图 A 所示,两条河流的交汇处有两个岛,有七座桥连接这两个岛及河 岸。问:一个散步者能否一次不重复地走遍这七座桥?
解析:通过画图,把一个实际问题转化为一个几何图形(如图 B),成为一笔画 的问题了,而图 B 中有 2 个奇点,所以能一笔画出。 练习四 1、右边各图至少要用几笔画完?
1
【例 1】 右图中,哪些点是偶点?哪些点是奇点? 解析:我们把一个图形上与偶数条线相连的点叫
做偶点,与奇数条线相连的点叫做奇点。奇点有 J、D、 H,偶点有 A、B、C、E、F、G、I。
【例 2】 下面图形能不能一笔画成?如果能,应该怎样画?
解析:图 1 能一笔画,因为图中只有两个奇点。图 2 也能一笔画,因为图中全 是偶点,图 3 不能一笔画,因为有 4 个奇点。
条线,将其改成成可一笔画的图形。
G
H
A
I
J
F
B
K
L
E
C
图b
D
【例 2】 右图是某展览厅的平面图,它由五个展室组 成,任两展室之间都有门相通,整个展览厅还有一个进 口和一个出口,问游人能否从入口进,从出口出,并且 一次不重复地穿过所有的门?
解析:将图形中的 6 个区域看成 6 个点,每个门看 成连结他们的线段,显然 6 个点都是偶点,所以游人能 一次不重复的走过所有的门。
2
【例 4】 右图中的线段表示小路,请你仔细观 察,认真思考,能够不重复地爬遍小路的是甲蚂 蚁还是乙蚂蚁?该怎样爬?
解析:要想不重复爬遍小路,需要图形能 一笔画出,由于图中有两个奇点,所以应该从 奇点出发才能一笔画出图形,所以甲蚂蚁能够。
学而思-数学一笔画及答案
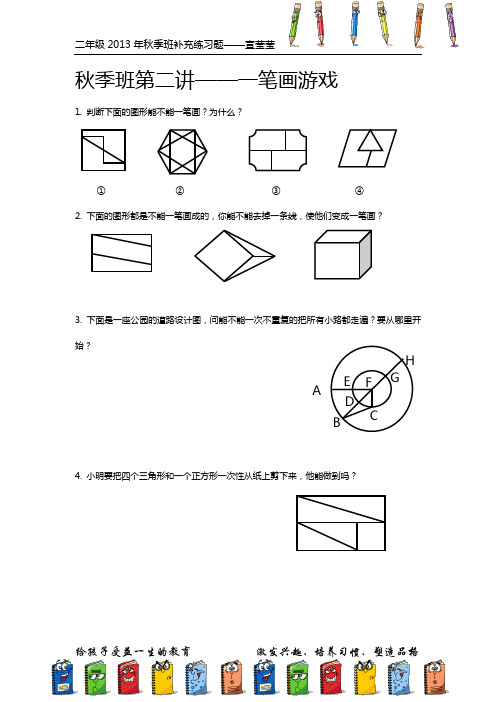
秋季班第二讲——一笔画游戏1. 判断下面的图形能不能一笔画?为什么?① ② ③ ④ 2. 下面的图形都是不能一笔画成的,你能不能去掉一条线,使他们变成一笔画?3. 下面是一座公园的道路设计图,问能不能一次不重复的把所有小路都走遍?要从哪里开始?4. 小明要把四个三角形和一个正方形一次性从纸上剪下来,他能做到吗?A5. 下面是超市的货架摆放位置,丽丽去逛超市,请帮她设计一条路线能够一次不重复地逛遍所有的货架。
6. 平安小镇上有两个邮递员,甲邮递员喜欢从A 点出发开始送信,乙邮递员喜欢从B 点出发开始送信,他们俩都选择最优路线,谁能更快的跑遍多有的街道呢?7. 抗日战争时期,中国人发明了地道战对付日本侵略者,下面是一次地道战的地道分布图,有一次团长下了一个命令,要求传令兵以最快的速度传遍地道里的所有战士,请你帮他设计一条路线。
8. 幸福乡有四个村庄,幸福河从村庄间流过,村民们在河上一共建了5座桥,问来到幸福乡的人能不能一次不重复地走遍所有的桥。
A BCDE【答案】:1. ①0个单数点,可以一笔画;②0个单数点,可以一笔画;③4个单数点,不可以一笔画;④2个单数点,可以一笔画2. 答案不唯一。
3. 图中有两个单数点A和H,从A或H开始就能一笔画。
4. 有两个单数点,可以一次性剪下所有的图形。
5. H→G→E→F→A→L→K→J→I→H→D→I→K→B→A→B→C→D→E6. 图中有两个单数点A和E,从单数点出发可以不重复地跑遍所有街道,从B点出发必须要重复才能跑遍多有街道,所以从A点出发的甲邮递员更快。
7. C→E→B→F→H→B→A→H→G→F→E→D→C→B8.。
三年级奥数专题:一笔画

三年级奥数专题:一笔画(一)如果一个图形可以用笔在纸上连续不断而且不重复地一笔画成,那么这个图形就叫一笔画。
显然,在下面的图形中,(1)(2)不能一笔画成,故不是一笔画,(3)(4)可以一笔画成,是一笔画。
同学们可能会问:为什么有的图形能一笔画成,有的图形却不能一笔画成呢?一笔画图形有哪些特点?关于这个问题有一个著名的数学故事——哥尼斯堡七桥问题。
哥尼斯堡是立陶宛共和国的一座城市,布勒格尔河从城中穿过,河中有两个岛,18世纪时河上共有七座桥连接A,B两个岛以及河的两岸C,D(如下图)。
所谓七桥问题就是:一个散步者要一次走遍这七座桥,每座桥只走一次,怎样走才能成功?当时的许多人都热衷于解决七桥问题,但是都没成功。
后来,这个问题引起了大数学家欧拉(1707-1783)的兴趣,许多人的不成功促使欧拉从反面来思考问题:是否根本就不存在这样一条路线呢?经过认真研究,欧拉终于在1736年圆满地解决了七桥问题,并发现了一笔画原理。
欧拉是怎样解决七桥问题的呢?因为岛的大小,桥的长短都与问题无关,所以欧拉把A,B两岛以及陆地C,D用点表示,桥用线表示,那么七桥问题就变为右图是否可以一笔画的问题了。
我们把一个图形上与偶数条线相连的点叫做偶点,与奇数条线相连的点叫做奇点。
如下图中,A,B,C,E,F,G,I是偶点,D,H,J,O是奇点。
欧拉的一笔画原理是:(1)一笔画必须是连通的(图形的各部分之间连接在一起);(2)没有奇点的连通图形是一笔画,画时可以以任一偶点为起点,最后仍回到这点;(3)只有两个奇点的连通图形是一笔画,画时必须以一个奇点为起点,以另一个奇点为终点;(4)奇点个数超过两个的图形不是一笔画。
利用一笔画原理,七桥问题很容易解决。
因为图中A,B,C,D 都是奇点,有四个奇点的图形不是一笔画,所以一个散步者不可能不重复地一次走遍这七座桥。
顺便补充两点:(1)一个图形的奇点数目一定是偶数。
因为图形中的每条线都有两个端点,所以图形中所有端点的总数必然是偶数。
奥数第九讲作业
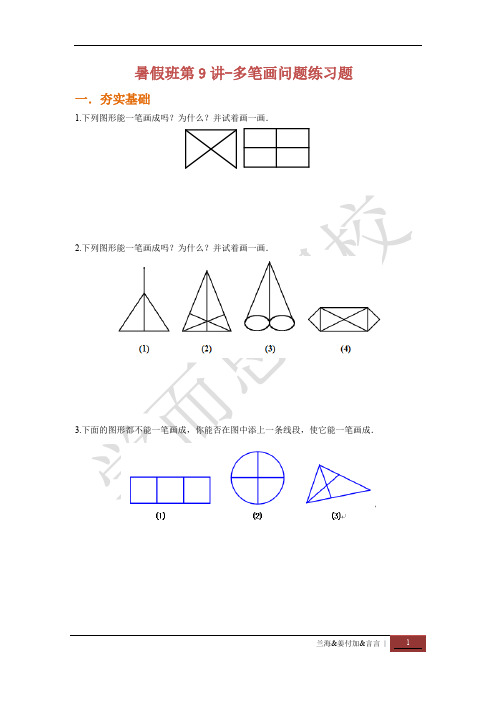
7.解析:把每个展室看作一个点,整个展厅的外部也看作一个点,两室之间有门相通,可以 看作两点之间有线相连.这样,展厅的平面图就转化成 b 图,一个实际问题也就转 化为这个图能否一笔画成的问题了,即能否从 A 出发,一笔画完此图,最后再回到 A .图( b )中,所有的点都是偶点,因此,一定可以以 A 作为起点和终点而一笔画 完此图. 即游人可以从入口进, 一次不重复地穿过所有的门, 最后从出口出来. 下 面仅给出一种参观路线: A E B C E F C D F A .
9.下图为某邮递员负责的邮区街道图,图中交叉点为邮户,每个小长方形的长为 180 米、宽 为 150 米. 如果邮递员每分钟行 200 米, 在每个邮户停留半分钟, 从邮局出发走遍所有邮户, 再回到邮局,最少要用 分钟.
150 邮局 180
兰海&姜付加&言言 |
3
四.杯赛演练:
10. “春蕾杯”小学数学邀请赛决赛 下面的图形,要求画过的线段不能重复画,那么这个图形最少 笔才能画出.
50m 60m 70m 300m 100m 图1 400m
A
兰海&姜付加&言言 |
6
11.(中国台湾小学数学竞赛选拔赛复赛) 有一个城市的街道图是由一些矩形所构成,如下图.一位警察要从 A 点出发巡逻,行经每一 条路段至少一次后回到 A 点.请问他至少要行走多少米?50m 60m 70m 30m 100m 第12题 400m
A
兰海&姜付加&言言 |
4
答案: 1.解析:第一个图形可以一笔画,第二个图形有 4 个奇点不可以一笔画。 2.解析:⑴、⑷可以,⑵、⑶不可以;其实我们不必把所有奇点都找出来,只要发现图中的 奇点多于 2 个就不能一笔画成了. 3.解析:⑴ 图中有四个点是奇点,所以不能一笔画成,要想使这个图形一笔画成,就要添 加一笔,使这个图形的奇点变成两个.如下图: (答案不唯一)
小学数学一笔画问题(格尼斯堡七桥问题)

例1.判断下列各图是否 能一笔画出来。
例1.判断下列各图是否 能一笔画出来。
●1 4●
●1
一对奇点 可以一笔画!
例1.判断下列各图是 否能一笔画出来。
没有奇点可以一笔画!
例2. 填空:
图(1)中有( )个奇点,有( )个偶点; 图(2)中有( )个奇点,有( )个偶点; 图(3)中有( )个奇点,有( )个偶点.
(1)
(2)
(3) (4)
下面各图能否一笔画成?
(1)
(2)
(3)
A
D
B
C
一笔画问题:
(1)必须是连通的图形;
(2)只由偶点组成的。画时可以由任一 偶点作为起点.最后仍回到这点;
(3)只有两个奇点的。画时必须以一个 奇点为起点,以另一个奇点为终点;
(4)奇点个数超过两个的图形,一定 不能一笔画.
一笔画问题
小朋友们,你们能把下面的 图形一笔画出来吗?Fra bibliotek一笔画
指的就是:从图的一点出发, 笔不离纸,遍历每条边恰好一 次,即每条边都只画一次,不 准重复。
下面这些图形,哪个能一笔画? 哪个不能一笔画?
(1) (2) (3) (4)
我们把一个图形中连着双数 条线的点叫做偶点;相应的把 连着单数条线的点叫做奇点.
例3.哥尼斯堡七桥问题 18世纪的哥尼斯堡,有一条河流从这个城 市穿过,河中有两个小岛A、B,河上有七 座桥连结两个小岛及河的两岸(如下图
a),那里的居民在星期日有散步的习
惯.那么能不能一次走遍七座桥,每座桥 只走过一次,最后回到出发点呢?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二年级秋季班第九讲一笔画习题
基础班
1. 下面的图形可以一笔画成吗?如果可以,请你用一笔画成。
2. 判断下列各图能否一笔画出,并说明理由。
※3. 邮递员要从邮局出发,走遍左下图(单位:千米)中所有街道,最后回到邮局,怎样走路程最短?全程多少千米?
4. 有一个邮局,负责21个村庄的投递工作,右上图中的点表示村庄,线段表示道路。
邮
递员从邮局出发,怎样才能不重复地经过每一个村庄,最后回到邮局?
5. 一只木箱的长、宽、高分别为5,4,3厘米(见右图),有一只甲虫从A点出发,沿棱爬行,每条棱不允许重复,则甲虫回到A点时,最多能爬行多少厘米?
6.下图是商场的平面图,顾客可以从六个门进出商场,怎样走才能不重复地走遍商场的每
条通道?
7.一只蚂蚁由A点出发,到达B点,必须不重复地经过每一条线,你能想出好办法吗?
8.一辆清洁车清扫街道,每段街道长1千米,清洁车由A点出发,走遍所有的街道再回
到A点,怎样走路程最短,全程多少千米?
9.游人在林间小路上(见图)散步,问能否一次不重复地走遍所有的路线后回到出发点?
如不能,应选择怎样的路线才能使全程最短?最短路程是多少?(单位:千米)
10.一张纸上画有如下所示的图,你能否用剪刀连续剪下图中的三个正方形和两个三角形?
※11.上图是某个花房的平面图,它由六间展室组成,每相邻两室有一门相同,请你设计一个出口,使参观者能够从入口处进去,一次不重复地经过所有的门,最后由出口走出花房。
习题答案
1 .2.答案略
3.50千米,走法见左下图。
4.见下图。
5.最多爬行34厘米。
提示:8个点都是奇点,故至少要少爬4条棱。
少爬3厘米的棱和4厘米的棱各两条是最合理的(见右图)。
6 只有C、D两点是单数点,因此能从C门进,D门出。
或从D门进,C门出,才能不重复地走遍商场的每条通道.
7 蚂蚁可以这样走:
8图中有8个单数点,两个单数点之间线段要重复走,清洁车至少必须重复走4段1千米的街道,所走的路线如下图所示,全程最短路线是28千米。
9图中有6个单数点,因此游人不能一次不重复的走遍所有路线后返回出发点,他至少必须重复走三段长为1千米的小路,才能使全程最短,最短路程为2×3+4×3+1×6=24(千米)
10图中G、F两点都是奇数点,要一次连续剪下图中的三个正方形和两个三角形,所走路线可以是F→I→E→H→I→G,也可以是G→I→H→E→I→F。
11把原图转化为右图,如果添一条与A相连的边,此图就能成为以A点为起点一笔画出,所以,应连接A、F,把出口处开在花房F处.
二年级秋季班第九讲一笔画习题
提高班
1. 下面的图形可以一笔画成吗?如果可以,请你用一笔画成。
2. 判断下列各图能否一笔画出,并说明理由。
※3. 邮递员要从邮局出发,走遍左下图(单位:千米)中所有街道,最后回到邮局,怎样走路程最短?全程多少千米?
4. 有一个邮局,负责21个村庄的投递工作,右上图中的点表示村庄,线段表示道路。
邮递员从邮局出发,怎样才能不重复地经过每一个村庄,最后回到邮局?
5. 一只木箱的长、宽、高分别为5,4,3厘米(见右图),有一只甲虫从A点出发,沿棱爬行,每条棱不允许重复,则甲虫回到A点时,最多能爬行多少厘米?
11.下图是商场的平面图,顾客可以从六个门进出商场,怎样走才能不重复地走遍商场的每
条通道?
12.一只蚂蚁由A点出发,到达B点,必须不重复地经过每一条线,你能想出好办法吗?
13.一辆清洁车清扫街道,每段街道长1千米,清洁车由A点出发,走遍所有的街道再回
到A点,怎样走路程最短,全程多少千米?
14.游人在林间小路上(见图)散步,问能否一次不重复地走遍所有的路线后回到出发点?
如不能,应选择怎样的路线才能使全程最短?最短路程是多少?(单位:千米)
15.一张纸上画有如下所示的图,你能否用剪刀连续剪下图中的三个正方形和两个三角形?
※11.上图是某个花房的平面图,它由六间展室组成,每相邻两室有一门相同,请你设计一个出口,使参观者能够从入口处进去,一次不重复地经过所有的门,最后由出口走出花房。
习题答案
1 .2.答案略
3.50千米,走法见左下图。
4.见下图。
5.最多爬行34厘米。
提示:8个点都是奇点,故至少要少爬4条棱。
少爬3厘米的棱和4厘米的棱各两条是最合理的(见右图)。
6 只有C、D两点是单数点,因此能从C门进,D门出。
或从D门进,C门出,才能不重复地走遍商场的每条通道.
7 蚂蚁可以这样走:
12图中有8个单数点,两个单数点之间线段要重复走,清洁车至少必须重复走4段1千米的街道,所走的路线如下图所示,全程最短路线是28千米。
13图中有6个单数点,因此游人不能一次不重复的走遍所有路线后返回出发点,他至少必须重复走三段长为1千米的小路,才能使全程最短,最短路程为2×3+4×3+1×6=24(千米)
14图中G、F两点都是奇数点,要一次连续剪下图中的三个正方形和两个三角形,所走路线可以是F→I→E→H→I→G,也可以是G→I→H→E→I→F。
15把原图转化为右图,如果添一条与A相连的边,此图就能成为以A点为起点一笔画出,所以,应连接A、F,把出口处开在花房F处.。
