广东省广州市海珠区2020-2021学年高二上学期期末考试数学试卷 (含解析)
广东省广州市海珠区2020-2021学年第一学期期末联考高一数学试题

海珠区2020学年第一学期期末联考试题高一数学本试卷共4页,共22小题,满分150分,考试用时120分钟。
注意事项:1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上. 2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上无效.3.考试结束后,将本试卷和答题卡一并交回.一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合{2,3,4,5,6}A =,{|21,}B x x k k ==+∈Z ,则AB =A .{2,3}B .{3,4}C .{3,5}D .{3,6}2.已知角α的终边与单位圆的交点为43(,)55−,则sin cos sin cos αααα−=+A .7−B .17−C .17D .73.命题“x ∀∈R ,10x +≥”的否定是A .x ∀∈R ,10x +≤B .x ∀∈R ,10x +<C .x ∃∈R ,10x +≤D .x ∃∈R ,10x +<4.sin15cos75cos15sin 75−= A .12−B .32−C .12D .325.大西洋鲑鱼每年都要逆流而上,游回产地产卵.研究鲑鱼的科学家发现鲑鱼的游速v (单位:/m s )与耗氧量单位数O 的函数关系式为31log 2Ov k=(k 为常数).若一条鲑鱼静止时耗氧量O 为100个单位数,那么鲑鱼的耗氧量O 是8100个单位数时,它的游速为A .1/m sB .3/2m s C .2/m s D .9/2m s 6.已知函数()ln cos f x x x =−的零点为0x ,则0x 所在的区间是A .(0,1)B .(1,2)C .(2,3)D .(3,4) 7.已知π12π2πsin(),31363αα+=<<,则cos α的值为 A .123526 B .123526− C .125326− D .125326−+ 8.已知正数,a b 9273a b =,则ab 的最小值为A .6B .12C .18D .242021.01.20FED C BA二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得3分. 9. 若,,a b c 为实数,则下列命题正确的是A .若a b >,c d >,则a c b d −>−B .若a b <,则22a b <C .若a b >,则b aa b < D .若a b >,则22(1)(1)a c b c +>+ 10.“不等式2304kx kx ++>对一切实数x 都成立”的充分不必要条件是A . 03k k <>或B . 03k ≤<C . 03k <<D . 0k = 11.下图是函数()sin()(0,0π)f x A x ωϕωϕ=+><<的部分图象,则A .函数解析式为()π3sin(2)4f x x =+B .函数()f x 的图象的两条相邻对称轴的距离为π4C .将函数()f x 的图象向右平移π8个单位长度,得到 的图象的对应函数是奇函数 D .将函数()f x 的图象向左平移π8个单位长度,得到的图象的对应函数是偶函数 12.已知函数()||33x f x a =−+(01)a <<,则A .函数()f x 有最大值,且在(,0)−∞上是增函数B .函数()f x 有最小值,且在(,0)−∞上是减函数C .方程()0f x m −=有两个实数根时,m 的取值范围为(0,3)D .不等式()0f x m −<在x ∈R 上恒成立时,m 的取值范围为(3,)+∞三、填空题:本题共4小题,每小题5分,共20分. 13.函数()ln 12f x x x=−的定义域为 . 14.已知集合{|1,A x x =<或5}x >,{|0}B x x a =<<,若A B ⊆R,则实数a 的取值范围为 .15. 已知定义域为R 的函数()f x 在(,0]−∞上单调递增,且()()0f x f x −−=,若()112f =−,则不等式()1212f x −≤−的解集为 .16.如图,在矩形ABCD 中,5AD =,20AB =,点E 在DC 上,点F 在AB 上, AE EF ⊥,则AEF ∆的面积的最小值是 .四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤. 17.(10分)在①sincos227αα=,②24cos27α=,③2tan21tan 2αα=−补充在下面问题中,并对其求解.问题:若锐角α满足 ,求sin(2π)cos(π)αα−−+的值. 注:如果选择多个条件分别解答,按第一个解答计分.18. (12分)已知函数1()f x x x=−. (1)证明:函数()f x 在区间(0,)+∞上单调递减;(2)已知322(0.2),(log 3),(log 5)a f b f c f ===,试比较三个数,,a b c 的大小,并说明理由.19.(12分)已知函数2()cos 2sin 1f x x x x =−+. (1)求函数)(x f 的最小正周期; (2)求函数)(x f 的单调递减区间; (3)在ABC ∆中,若()22A f =,ππ62B ≤≤,求cos cos BC +的取值范围.20.(12分)已知()1log (2)a f x x =++(01)a a >≠,且,()(2)g x f x =− (1)若函数()f x 的图象恒过定点A ,求点A 的坐标; (2)若函数()g x 在区间[],2a a 上的最大值比最小值大12,求a 的值.21.(12分)某电动摩托车企业计划在2021年投资生产一款高端电动摩托车.经市场调研测算,生 产该款电动摩托车需投入设备改造费1000万元,生产该款电动摩托车x 万台需投入资金()P x 万元,且222600,04,()5001501025, 4.mx x x P x x x x x ⎧+<<⎪=⎨−+≥⎪⎩生产1万台该款电动摩托车需投入资金3000万元;当该款电动摩托车售价为5000(单位:元/台)时,当年内生产的 该款摩托车能全部销售完.(1)求2021年该款摩托车的年利润()F x (单位:万元)关于年产量x (单位:万台)的函数解析式;(2)当2021年该款摩托车的年产量x 为多少时,年利润()F x 最大?最大年利润是多少?(年利润=销售所得−投入资金−设备改造费)22.(12分)已知函数2()2f x x x k =−+与2()ln h x x x k x =−+有相同的定义域. (1)解关于x 的不等式()0f x >;(2)若方程()0f x =有两个相异实数根12,x x (120x x <<),且()h x 在区间12[,]x x(参考结论:ln 1((0,1)x x x <−∈)海珠区2020学年第一学期期末联考高一数学参考答案与评分标准评分说明:1.参考答案与评分标准给出了一种或几种解法供参考,如果考生的解法与参考答案不同,可根据试题主要考查的知识点和能力对照评分标准给以相应的分数.2.对解答题中的计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的得分,但所给分数不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.3.解答右端所注分数,表示考生正确做到这一步应得的累加分数. 4.只给整数分数,选择题和填空题不给中间分.一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得3分.三、填空题:本题共4小题,每小题5分,共20分.13. 1(0,)214.(5,)+∞ 15.{|0x x ≤,或1}x ≥ 16.25 四、解答题:本大题共6小题,满分70分.解答应写出文字说明,证明过程或演算步骤. 17.(10分) 解:选择条件①:由条件①,得2sin cos227αα=,所以sin 7α=. 由22sin cos 1αα+=, 得21cos49α=, 因为α是锐角,所以cos 0α>,所以1cos 7α=. 因为sin(2π)sin αα−=−,cos(π)cos αα+=−,所以sin(2π)cos(π)αα−−+sin cos αα=−+=. 选择条件②:由条件②,得1cos 427α+=, 所以1cos 7α=.由22sin cos 1αα+=, 得248sin49α=, 因为α是锐角,所以sin 0α>,所以sin 7α=. 因为sin(2π)sin αα−=−,cos(π)cos αα+=−,所以sin(2π)cos(π)αα−−+sin cos αα=−+17−=. 选择条件③:由条件③,得22tan21tan 2αα=−所以tan α=所以sin cos αα=. 由22sin cos 1αα+=, 得248sin49α=,21cos 49α=, 因为,αβ是锐角,所以sin 0α>,cos 0α>,所以sin 7α=,1cos 7α=. 因为sin(2π)sin αα−=−,cos(π)cos αα+=−,所以sin(2π)cos(π)αα−−+sin cos αα=−+17−=. [说明]求出sin α=,1cos 7α=各得3分,其中22sin cos 1αα+=记1分.18. (12分)解:(1)证明:12,(0,)x x ∀∈+∞,且12x x <,则12122112121111()()()()()()f x f x x x x x x x x x −=−−−=−+− 21212112121()()()(1)x x x x x x x x x x −=−+=−+. 由12,(0,)x x ∈+∞,得120,0x x >>,所以12110x x +>, 由12x x <,得210x x −>, 所以21121()(1)0x x x x −+>, 所以12()()0f x f x −>,即12()()f x f x >, 所以,函数()f x 在区间(0,)+∞上单调递减. (2)因为300.21<<,21log 3<, 所以2log 330.2>.又因为函数()f x 在区间(0,)+∞上单调递减, 所以32(log 3)(0.2)f f <. 因为22log 5log 3>,函数()f x 在区间(0,)+∞上单调递减, 所以22(log 5)(log 3)f f <, 综上所述:c b a <<. 19.(12分)解:因为2()cos 2sin 1f x x x x =−+2cos (12sin )x x x =+−2cos 2x x =+ π2sin(2)6x =+.(1)所以)(x f 的最小正周期为2ππ2T ==. (2)令ππ3π2π22π262k x k +≤+≤+, 得π2πππ63k x k +≤≤+, 所以函数)(x f 的单调递减区间为π2π[π,π]()63k k k ++∈Z . (3)因为()22A f =,所以2sin()26A π+=,sin()16A π+=,因为在ABC ∆中,0πA <<,所以ππ7π666A <+<, 由ππ62A +=,得π3A =, 所以π2ππ33B C +=−=,所以2πcos cos cos cos()3B C B B +=+−1cos 22B B =+ πsin()6B =+.因为ππ62B ≤≤,所以ππ2π363B ≤+≤,sin()16B π≤+≤,所以cos cos B C +的取值范围为[2.20.(12分)解:(1)当21x +=,即1x =−时,1log 11a y =+=, 所以点A 的坐标为(1,1)−.(2)因为()1log (2)a f x x =++,所以()1log a g x x =+.当01a <<时,函数()g x 在区间[]2a a ,上是减函数, 所以当x a =时,函数()g x 有最大值,且max ()2g x =, 当2x a =时,函数()g x 有最小值,且min ()1log 2a g x a =+,因为max min 1()()2g x g x −=, 所以12(1log 2)2a a −+=,所以14a =.当1a >时,函数()g x 在区间[]2a a ,上是增函数, 所以当x a =时,函数()g x 有最小值,且min ()2g x =, 当2x a =时,函数()g x 有最大值,且max ()1log 2a g x a =+,因为max min 1()()2g x g x −=, 所以1(1log 2)22a a +−=,所以4a =.综上所述:14a =或4a =. 21.(12分)解:(1)由题意2(1)126003000P m =⨯+=,所以400m =, 当04x <<时,()22()50004002600100040024001000F x x x x x x =−+−=−+−;当4x ≥时,225001501025401025()50001000x x x x F x x x x−+−+−=−−=, 所以2240024001000,04,()401025, 4.x x x F x x x x x ⎧−+−<<⎪=⎨−+−≥⎪⎩(2)当04x <<时,2()400(3)2600F x x =−−+, 所以当3x =时,max ()2600F x =.当4x ≥时,24010252525()40104010x x F x x x x x x −+−⎛⎫==−−+=−++ ⎪⎝⎭,因为4x ≥,所以2510x x+≥=, 当且仅当25x x=时,即5x =时等号成立, 所以()1040104000F x ≤−+=,所以当5x =时,max ()4000F x =, 因为26004000<,所以,当2021年该款摩托车的年产量为5万台时,年利润()F x 最大,最大年利润是4000万元.22.(12分)解:(1)已知函数()f x 与()h x 有相同的定义域, 所以()f x 与()h x 的定义域都是(0,)+∞. 方程2()20f x x x k =−+=的判别式18k ∆=−.①当180k ∆=−<即18k >时,()0f x >在(0,)+∞上恒成立. ②当180k ∆=−=即18k =时,()0f x =的根为14x =,所以()0f x >的解集为{|0,x x >且1}4x ≠.③当180k ∆=−>即18k <时,()0f x=的两根为114x=,214x =,若108k <<,则120x x <<,所以()0f x >的解集为1{|0,x x x <<或2}x x >;若0k ≤,则120x x ≤<,所以()0f x >的解集为2{|}x x x >.{|x x >; 的解集为1{|0,4x x <<或1}4x >;{|0,x x >且1}4x ≠;{|0}x x >.()0f x =有两个相异实数根12,x x (120x x <<),则08k <<,且121211,22x xx x k +==.因为()h x 在12[,]x x 上是减函数,所以()()12h x h x >,1()x 2()h x −2111(ln )x x k x =−+2222(ln )x x k x −−+121212((ln ln )k x x =+−11221()ln 2x x x k x =−−+12111(ln 244xk x +=−−+12ln 4x k x =+. 因为(0,1)x ∈时,ln 1x x <−,又1201xx <<,所以1122ln 1x xx x <−.因为121281118x k x k −−−−=−=− 12=−=−,且108k <<,所以1ln x k x <124k −.112244k k −−=−,。
2020-2021学年广东省高二上学期期末数学试卷及答案解析

第 1 页 共 20 页2020-2021学年广东省高二上学期期末数学试卷一.选择题(共12小题,满分60分,每小题5分)1.已知命题P :∃x 0≥1,x 02+x 0+1≤0,则命题P 的否定为( )A .∃x ≥1,x 2+x +1>0B .∀x ≥1,x 2+x +1≤0C .∀x <1,x 2+x +1>0D .∀x ≥1,x 2+x +1>02.过双曲线x 2a 2−y 2b 2=1(a >0,b >0)的一个焦点作实轴的垂线,交双曲线于A ,B 两点,若线段AB 的长度恰等于焦距,则双曲线的离心率为( ) A .√5+12B .√102C .√17+14D .√2243.已知数列{a n }满足a n +1﹣2a n =0,且a 1+a 3+a 5=21,那么a 3+a 5+a 7=( ) A .212B .33C .42D .844.△ABC 中,a cosA=b cosB=c cosC,则△ABC 一定是( )A .直角三角形B .钝角三角形C .等腰三角形D .等边三角形5.准线方程为y =2的抛物线的标准方程是( ) A .x 2=16yB .x 2=8yC .x 2=﹣16yD .x 2=﹣8y6.若抛物线y 2=2px (p >0)的焦点是双曲线x 23p−y 2p=1的一个焦点,则p =( )A .2B .4C .8D .167.设a >0,b >0,则“b >a ”是“椭圆x 2a +y 2b =1的焦点在y 轴上”的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件8.已知双曲线C :y 2a −x 2b =1(a >b >0)的一条渐近线与直线3x ﹣2y ﹣5=0垂直,则此双曲线的离心率为( ) A .√133B .√132C .√153 D .√1529.在△ABC 中,D 为BC 的中点,满足∠BAD +∠C =π2,则△ABC 的形状一定是( ) A .直角三角形B .等腰三角形C .等边三角形。
2020-2021学年广东省广州市白云区、海珠区高一(下)期末数学试卷

2020-2021学年广东省广州市白云区、海珠区高一(下)期末数学试卷(i为虚数单位),则|z|=()1.(单选题,5分)若复数z= 13−4iA. 15B.1C.5D. 352.(单选题,5分)已知向量a⃗ =(2,3),b⃗⃗ =(x,-6),且a⃗⊥ b⃗⃗,则x=()A.-9B.9C.-4D.43.(单选题,5分)高一年级有男生510人,女生490人,小明按男女比例进行分层随机抽样,总样本量为100.则在男生中抽取的样本量为()A.48B.51C.50D.494.(单选题,5分)如图,△A'B'C'是水平放置的△ABC的斜二测直观图,△A'B′C′为等腰直角三角形,其中O′与A′重合,A'B′=6,则△ABC的面积是()A.9B.9 √2C.18D.18 √25.(单选题,5分)已知| a⃗ |=6,| b⃗⃗ |=4,a⃗与b⃗⃗的夹角为60°,则(a⃗ +2 b⃗⃗)•(a⃗ -3 b⃗⃗)=()A.-72B.72C.84D.-846.(单选题,5分)某学校开展“学党史,颂党恩,跟党走“学习活动,刘老师去购书中心购买了一批书籍作为阅读学习之用,其中一类是4本不同的红色经典小说类书籍,另一类是2本不同的党史类书籍,两类书籍合计共6本.现刘老师从这6本书中随机抽取2本阅读,则这两本书恰好来自同一类书籍的概率是( ) A. 115 B. 215 C. 715D. 8157.(单选题,5分)如图,已知 OA ⃗⃗⃗⃗⃗⃗ = a ⃗ , OB ⃗⃗⃗⃗⃗⃗ = b⃗⃗ ,任意点M 关于点A 的对称点为S ,点M 关于点B 的对称点为N ,则向量 NS ⃗⃗⃗⃗⃗⃗ =( )A. 12 ( a ⃗ + b⃗⃗ ) B.2( a ⃗ + b⃗⃗ ) C. 12 ( a ⃗ - b ⃗⃗ ) D.2( a ⃗ - b⃗⃗ ) 8.(单选题,5分)已知图1是棱长为1的正六边形ABCDEF ,将其沿直线FC 折叠成如图2的空间图形F′A′E′-C′B′D′,其中A′E′= √62 ,则空间几何体F'A'E'-CB'D'的体积为( )A. 38B. 716C. 12D. 789.(多选题,5分)某士官参加军区射击比赛,打了6发子弹,报靶数据如下:7,8,9,10,6,8,(单位:环),下列说法正确的有( )A.这组数据的平均数是8B.这组数据的极差是4C.这组数据的中位数是8.5D.这组数据的方差是210.(多选题,5分)已知复数z=cosα+( √3 sinα)i (α∈R )(i 为虚数单位),下列说法正确的有( )A.当α=- π3 时,复平面内表示复数z 的点位于第二象限B.当α= π2 时,z 为纯虚数C.|z|最大值为 √3D.z 的共轭复数为 z =-cosα+( √3 sinα)i (α∈R )11.(多选题,5分)某班级到一工厂参加社会实践劳动,加工出如图所示的圆台O 1O 2,在轴截面ABCD 中,AB=AD=BC=2cm ,且CD=2AB ,下列说法正确的有( )A.该圆台轴截面ABCD 面积为3 √3 cm 2B.该圆台的体积为 7√3π3 cm 3C.该圆台的母线AD 与下底面所成的角为30°D.沿着该圆台表面,从点C 到AD 中点的最短距离为5cm12.(多选题,5分)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,点O 为△ABC 所在平面内点,满足x OA ⃗⃗⃗⃗⃗⃗ +y OB ⃗⃗⃗⃗⃗⃗ +z OC ⃗⃗⃗⃗⃗⃗ =0,下列说法正确的有( )A.若x=y=z=1,则点O 为△ABC 的重心B.若x=y=z=1,则点O 为△ABC 的外心C.若x=a ,y=b ,z=c ,则点O 为△ABC 的内心D.若x=a ,y=b ,z=c ,则点O 为△ABC 的垂心13.(填空题,5分)有10种不同的零食,每100克可食部分包含的能量(单位:k )如下: 100,120,125,165,430,190,175,234,425,310这10种零食每100克可食部分的能量的第60百分位数为 ___ .14.(填空题,5分)天气预报元旦假期甲地的降雨概率是0.2,乙地的降雨概率是0.3,假定在这段时间内两地是否降雨相互之间没有影响,则在这段时间内甲,乙两地只有一个地方降雨的概率是 ___ .15.(填空题,5分)如图,在三棱锥V-ABC 中,VA=VB=AB=AC=BC=4,VC=2,则二面角A-VC-B 的余弦值为 ___ .16.(填空题,5分)如图,△ABC是边长为1的正三角形,M,N分别为线段AC,AB上一点,满足AM:MC=1:2,AN:NB=1:3,CN与BM的交点为P,则线段AP的长度为 ___ .17.(问答题,10分)现有两个红球(记为R1,R2),两个白球(记为W1,W2),采用不放回简单随机抽样从中任意抽取两球.(1)写出试验的样本空间;(2)求恰好抽到一个红球一个白球的概率.18.(问答题,12分)已知角A是△ABC的内角,若a⃗ =(√3 sinA,cosA),b⃗⃗ =(1,-1).(1)若a⃗∥b⃗⃗,求角A的值;(2)设f(x)= a⃗•b⃗⃗,当f(x)取最大值时,求a⃗在b⃗⃗上的投影向量(用坐标表示).19.(问答题,12分)如图,直三棱柱ABC-A'B'C'中,D是AB的中点.(1)求证:直线BC′ || 平面A'CD;(2)若AC=CB,求异面直线AB'与CD所成角的大小.20.(问答题,12分)2021年五一假期,各高速公路车流量大,交管部门在某高速公路区间测速路段随机抽取40辆汽车进行车速调查,将这40辆汽车在该区间测速路段的平均车速(km/h)分成六段[90,95),[95,100),[100,105),[105,110),[110,115),[115,120],得到如图的频率分布直方图.(1)根据频率分布直方图估计出这40辆汽车的平均车速的中位数;(2)现从平均车速在区间[90,100)的车辆中任意抽取2辆汽车,求抽取的2辆汽车的平均车速都在区间[95,100)上的概率;(3)出于安全考虑,测速系统对平均车速在区间[115,120]的汽车以实时短信形式对车主进行安全提醒,确保行车安全.假设每辆在此区间测速路段行驶的汽车平均车速相互不受影响,以此次调查的样本频率估计总体概率,求连续2辆汽车都收到短信提醒的概率?21.(问答题,12分)如图,PA垂直于⊙O所在的平面,AC为⊙O的直径,AB=3,BC=4,PA=3 √2,AE⊥PB,点F为线段BC上一动点.(1)证明:平面AEF⊥平面PBC;(2)当点F移动到C点时,求PB与平面AEF所成角的正弦值.22.(问答题,12分)为响应国家“乡村振兴”号召,农民王大伯拟将自家一块直角三角形地按如图规划成3个功能区:△BNC区域为荔枝林和放养走地鸡,△CMA区域规划为“民宿”供游客住宿及餐饮,△MNC区域规划为小型鱼塘养鱼供休闲垂钓.为安全起见,在鱼塘△MNC周围筑起护栏.已知AC=40m,BC=40 √3 m,AC⊥BC,∠MCN=30°(1)若AM=20m时,求护栏的长度(△MNC的周长);倍,求∠ACM;(2)若鱼塘△MNC的面积是“民宿”△CMA的面积的√62(3)当∠ACM为何值时,鱼塘△MNC的面积最小,最小面积是多少?。
2020-2021学年广东省珠海市高二上学期期末数学试题(解析版)

2020-2021学年广东省珠海市高二上学期期末数学试题一、单选题1.命题“00x ∃>,200230x x -+<”的否定是( ) A .00x ∃≤,200230x x -+<B .0x ∀≤,2230x x -+<C .00x ∃>,200230-+≥x xD .0x ∀>,2230x x -+≥【答案】D【分析】直接利用特称命题的否定是全称命题求解即可.【详解】因为特称命题的否定是全称命题,否定特称命题时既要改变量词又要否定结论,所以命题“00x ∃>,200230x x -+<”的否定是0x ∀>,2230x x -+≥,故选:D.2.某公司将180个产品,按编号为001,002,003,…,180从小到大的顺序均匀的分成若干组,采用系统抽样方法抽取一个样本进行检测,若第一组抽取的编号是003,第二组抽取的编号是018,则样本中最大的编号应该是( ) A .168 B .167C .153D .135【答案】A【分析】先求样本间隔,然后根据抽查样本容量,结合系统抽样的定义进行求解即可. 【详解】样本间隔为18﹣3=15, 即抽取样本数为180÷15=12, 则最大的样本编号为3+15×11=168, 故选:A .3.在空间直角坐标系中,点(4,1,9)A ---与点(10,1,6)B --的距离是( ) A .5 B .6C .7D .8【答案】C【分析】由A ,B 的坐标求出AB 的坐标,求其模可得A 与B 的距离. 【详解】点(4,1,9)A ---,点(10,1,6)B --,∴(6,2,3)AB =-,则||||(7AB AB ==-=. 故选:C .4.命题“[1,2]x ∀∈,2x a ≤”成立的一个充分不必要条件是( ) A .1a > B .1a ≥C .4a ≥D .4a >【答案】D【分析】先找出命题为真命题的充要条件{}4a a ≥,从集合的角度充分不必要条件应为{}4a a ≥的真子集,由选项得出答案.【详解】[]1,2x ∀∈,214x ≤≤,∴要使2x a ≤恒成立,即4a ≥, 本题求的是充分不必要条件,结合选项,只有D 符合. 故选:D.【点睛】结论点睛:充分不必要条件一般可根据如下规则判断:(1)若p 是q 的必要不充分条件,则q 对应集合是p 对应集合的真子集; (2)p 是q 的充分不必要条件, 则p 对应集合是q 对应集合的真子集; (3)p 是q 的充分必要条件,则p 对应集合与q 对应集合相等; (4)p 是q 的既不充分又不必要条件,q 对的集合与p 对应集合互不包含.5.方程211(1)x y -=--表示的曲线是( ) A .一个圆 B .一个椭圆C .两个圆D .半圆【答案】D【分析】原方程两边平方,等价于22(1)(1)1(1)x y x -+-=,从而可得出结论. 【详解】方程211(1)x y -=--等价于22(1)(1)1(1)x y x -+-=,∴表示的曲线是半个圆.故选:D .6.如图所示茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分),已知甲组数据的中位数为17,乙组数据的平均数为17.4,则x 、y 的值分别为A .7、8B .5、7C .8、5D .7、7【答案】D【分析】根据中位数和平均数的公式分别进行计算即可.【详解】组数据的中位数为17,x 7∴=,乙组数据的平均数为17.4,()19161610y 2917.45∴+++++=, 得80y 87+=, 则y 7=, 故选D .【点睛】本题主要考查茎叶图的应用,根据中位数和平均数的公式是解决本题的关键.中位数即最中间的数据,平均数即将所有数据加到一起,除以数据个数. 7.根据如表数据,得到的回归方程为y b x 9=+,则b (= )A .2B .1C .0D .1-【答案】D【分析】由题意可得样本中心点,代入回归直线可得b 值,即可得答案. 【详解】由题意可得()14567865x =++++=,()15432135y =++++=, 回归方程为9y b x =+且回归直线过点()6,3,369b ∴=+,解得1b =-,故选D .【点睛】本题考查线性回归方程,涉及平均值的计算和回归方程的性质,属基础题.在一组具有相关关系的变量的数据间,这样的直线可以画出许多条,而其中的一条能最好地反映x 与Y 之间的关系,这条直线过样本中心点.线性回归方程适用于具有相关关系的两个变量,对于具有确定关系的两个变量是不适用的, 线性回归方程得到的预测值是预测变量的估计值,不是准确值.8.若样本数据1x ,2x ,…,10x 的标准差为4,则数据112x -,212x -,…,1012x -的标准差为( ) A .4 B .8C .16D .8-【答案】B【分析】首先设原数据的平均数为x ,则新数据的平均数为12x -,然后结合原数据的方差,利用方差的公式计算得出新数据的方差,再求出标准差即可. 【详解】设原数据的平均数为x ,则新数据的平均数为12x -, 则原数据的方差为22211021[()()()]1610x x x x x x -+-+⋯+-=, 则新数据的方差为:11[(121210x --+22)(1212x x +--+102)(1212x x +⋯+--+2)]x 222121014[()()()10]x x x x x x =⨯-+-+⋯+- 41664=⨯=.故数据112x -,212x -,…,1012x -的标准差为:8. 故选:B .9.从[0]2,中任取一个数x ,从[0]3,中任取一个数y ,则使224x y ≤+的概率为( )A .12B .π9C .π3D .π6【答案】D【分析】在平面直角坐标系中作出图形,则x ∈[0,2],y ∈[0,3]的平面区域为矩形,符合条件x 2+y 2≤4的区域为以原点为圆心,2为半径的扇形内部,则扇形面积与矩形面积的比为概率【详解】在平面直角坐标系中作出图形,如图所示, 则x ∈[0,2],y ∈[0,3]的平面区域为矩形OABC , 符合条件x 2+y 2≤4的区域为以原点为圆心, 2为半径的扇形OAD 内部, ∴P (x 2+y 2≤4)2124236S S ππ⨯===⨯扇形矩形;故选D .【点睛】本题考查了几何概型的概率计算,正确作出几何图形是解题的关键.10.过椭圆()2222:10x y C a b a b+=>>的左焦点F 的直线过C 的上端点B ,且与椭圆相交于点A ,若3BF FA =,则C 的离心率为( ) A .13B .33C 3D .22【答案】D【分析】首先设出点的坐标,然后利用点在椭圆上即可求得椭圆的离心率. 【详解】由题意可得()()0,,,0B b F c -,由3BF FA =, 得4,33b A c ⎛⎫-- ⎪⎝⎭,点A 在椭圆上,则:22224331b c a b ⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭+=,整理可得:2222216812,,9922c c e e a a ⋅=∴===. 故选D.【点睛】椭圆的离心率是椭圆最重要的几何性质,求椭圆的离心率(或离心率的取值范围),常见有两种方法:①求出a ,c ,代入公式ce a=; ②只需要根据一个条件得到关于a ,b ,c 的齐次式,结合b 2=a 2-c 2转化为a ,c 的齐次式,然后等式(不等式)两边分别除以a 或a 2转化为关于e 的方程(不等式),解方程(不等式)即可得e (e 的取值范围).11.已知椭圆:22142x y +=,过点()1,1M 的直线与椭圆相交于,A B 两点,且弦AB 被点M 平分,则直线AB 的方程为( ) A .230x y +-= B .230x y +-=C .20x y +-=D .210x y -+=【答案】B【详解】设()11A x y ,,()22B x y ,则22112222142142x y x y ⎧+=⎪⎪⎨⎪+=⎪⎩ ()()()()12121212042x x x x y y y y +-+-∴+=则()()121212122142x x y y x x y y -+-==--+ 即直线AB 的斜率为12-则直线AB 的方程为()1112y x -=-- 即230x y +-= 故选B12.给出下列命题:①命题“若220a b +=,则a ,b 全为0”的否命题是“若220a b +≠,则a ,b 全不为0”; ②命题“已知,x y ∈R ,若3x y +≠,则2x ≠或1y ≠”的逆否命题是真命题; ③设,x y ∈R ,则“1x ≠或2y ≠”是“2xy ≠”的充分不必要条件;④已知双曲线22221(0,0)x y a b a b-=>>的一条渐近线经过点(1,2),则该双曲线的离心率其中是真命题的有( ) A .①② B .②④C .①③D .②③④【答案】B【分析】根据否命题的定义判断①;求出逆否命题判断②命;根据充分条件与必要条件的定义判断③;求出双曲线的离心率判断④.【详解】①命题“若220a b +=,则a ,b 全为0”的否命题应该是“若220a b +≠,则a ,b 不全为0”,故①错误;②命题“已知,x y ∈R ,若3x y +≠,则2x ≠或1y ≠”的逆否命题是“已知,x y ∈R ,若2x =且1y =,则3x y +=”,故②正确; ③取112x =≠,42y =≠,但是2xy =,即“1x ≠或2y ≠”不能推出“2xy ≠”,所以“1x ≠或2y ≠”不是“2xy ≠”的充分不必要条件,故③错误;④双曲线22221(0,0)x y a b a b -=>>的一条渐近线经过点(1,2),则有2b a=,则离心率2215c b e a a==+=,故④正确故选:B .二、填空题13.某社会爱心组织面向全市征召义务宣传志愿者.现从符合条件的志愿者中随机抽取100名按年龄分组:第1组[20,25),第2组[25,30),第3组[30,35),第4组[35,40),第5组[40,45),得到的频率分布直方图如图所示.若从第3,4,5组中用分层抽样的方法抽取6名志愿者参与广场的宣传活动,应从第3组抽取__________名志愿者.【答案】3【分析】先分别求出这3组的人数,再利用分层抽样的方法即可得出答案. 【详解】第3组的人数为10050.0630⨯⨯=, 第4组的人数为10050.0420⨯⨯=, 第5组的人数为1000.02510⨯⨯=, 所以这三组共有60名志愿者,所以利用分层抽样的方法在60名志愿者中抽取6名志愿者,第三组应抽取306360⨯=名, 故答案为:3.【点睛】关键点点睛:该题考查的是有关频率分布直方图的识别以及分层抽样某层抽取个数的问题,正确解题的关键是掌握在抽取过程中每个个题被抽到的机会均等. 14.在平面直角坐标系xOy 中,抛物线22x y =的焦点到准线的距离为__________. 【答案】1【分析】求出抛物线22x y =的焦点坐标与准线方程,从而可得答案. 【详解】由22x y =可得1p =,抛物线22x y =的焦点坐标为10,2⎛⎫ ⎪⎝⎭,准线方程为12y, 所以抛物线22x y =的焦点到准线的距离为11122⎛⎫--= ⎪⎝⎭, 故答案为:1.15.某学校羽毛球校队进行扩招,共2个名额,现有2名男生和3名女生报名,从报名学生中任选2名学生,则恰好选中2名女生的概率为__________. 【答案】310【分析】从2名男同学和3名女同学中任选2人,共有2510C =种,其中全是女生的有233C =种,根据概率公式计算即可【详解】从2名男同学和3名女同学中任选2人,共有2510C =种,其中全是女生的有233C =种,故选中的2人都是女同学的概率310P =, 故答案为:310.16.若双曲线的渐近线方程为3y x =±,它的一个焦点的坐标为,则该双曲线的标准方程为____________________.【答案】2219y x -=.【解析】解:由双曲线渐近线方程可知b /a =3 ①因为它的一个的焦点为(10,0),所以c=10 ② 又c2=a 2+b 2③联立①②③,解得a 2=1,b 2=9, 所以双曲线的方程为x 2- y 2/9 =1. 故答案为为x 2- y 2/9 =1.17.正方体1111ABCD A B C D -的棱长为2,点M 和N 分别是11B D 和11B C 的中点,则异面直线AM 和CN 所成角的余弦值为__________.【答案】3010【分析】以D 为原点,DA 为x 轴,DC 为y 轴,1DD 为z 轴,建立空间直角坐标系,求出(1,1,2)AM =-,(1,0,2)CN =,利用空间向量夹角余弦公式可得答案.【详解】以D 为原点,DA 为x 轴,DC 为y 轴,1DD 为z 轴,建立空间直角坐标系, 则(2,0,0)A ,(1,1,2)M ,(0,2,0)C ,(1,2,2)N ,(1,1,2)AM =-,(1,0,2)CN =,设异面直线AM 和CN 所成角为θ, 则||30cos ||||65AM CN AM CN θ⋅===⋅⨯.∴异面直线AM 和CN 30.30.18.一个动圆与圆221():31Q x y ++=外切,与圆222:()381Q x y +=-内切,则这个动圆圆心的轨迹方程为:______.【答案】2212516x y += 【分析】设动圆的圆心为(),Q x y ,半径为R ,根据动圆与圆221():31Q x y ++=外切,与圆222:()381Q x y +=-内切,得到121,9QQ R QQ R =+=-,两式相加得到1212106QQ QQ QQ +=>=,再根据椭圆的定义求解.【详解】设动圆的圆心为(),Q x y ,半径为R ,因为动圆与圆221():31Q x y ++=外切,与圆222:()381Q x y +=-内切,所以121,9QQ R QQ R =+=-, 所以1212106QQ QQ QQ +=>=,所以动圆圆心的轨迹为以12,Q Q 为焦点的椭圆, 所以2210,5,3,16a a c b ====,所以动圆圆心的轨迹方程为2212516x y +=, 故答案为:2212516x y += 【点睛】本题主要考查圆与圆的位置关系以及椭圆的定义,还考查了运算求解的能力,属于中档题.19.如图所示,在长方体1111ABCD A B C D -中11AD AA ==,3AB =,点E 是棱AB 的中点,则点E 到平面1ACD 的距离为__________.【答案】319【分析】以D为坐标原点,直线DA ,DC ,1DD 分别为x ,y ,z 轴,建立空间直角坐标系,求出平面1ACD 的法向量,利用向量法能求出点E 到平面1ACD 的距离. 【详解】以D 为原点,DA 为x 轴,DC 为y 轴,1DD 为z 轴,建立空间直角坐标系,31,,02E ⎛⎫⎪⎝⎭,(1,0,0)A ,(0,3,0)C ,1(0,0,1)D , (1,3,0)AC =-,1(1,0,1)AD =-,30,,02AE ⎫⎛= ⎪⎝⎭,设平面1ACD 的法向量(,,)n x y z =,则1300n AC x y n AD x z ⎧⋅=-+=⎪⎨⋅=-+=⎪⎩,取1y =,得(3,1,3)n =, ∴点E 到面1ACD 的距离:||319||38AE n d n ⋅==, 故答案为:31938.【点睛】方法点睛:利用法向量求解空间角与距离的关键在于“四破”: 第一,破“建系关”,构建恰当的空间直角坐标系; 第二,破“求坐标关”,准确求解相关点的坐标; 第三,破“求法向量关”,求出平面的法向量; 第四,破“应用公式关”.20.如图,在一个直二面角AB αβ--的棱上有两点A ,B ,AC ,BD 分别是这个二面角的两个面内垂直于AB 的线段,且4AB =,6AC =,8BD =,则CD =__________.【答案】229【分析】求CD 的长转为求||CD ,而CD CA AB BD =++,按照向量的模长求法,即可求解.【详解】由已知,可得AC AB ⊥,BD AB ⊥,AC BD ⊥,CD CA AB BD AB AC BD =++=-+,22()CD AB AC BD ∴=-+22222AB AC BD AB AC AB BD =++-⋅+⋅2163664116AC BD -⋅=++=, ||229CD ∴=.故答案为229.三、解答题21.已知命题p :“关于x 的方程2x 2x m 0-+=有实数根”,命题q :“23m -<<”,命题r :“1t m t <<+”.(1)若p q ∧是真命题,求m 的取值范围; (2)若r 是q 的充分不必要条件,求t 的取值范围. 【答案】(1)21m -<≤;(2)22t -≤≤. 【分析】(1)由p 为真可得1m ,从而123m m ≤⎧⎨-<<⎩,进而可得答案;(2)由r 是q 的充分不必要条件,可得213t t ≥-⎧⎨+≤⎩(等号不同时成立),进而可得答案.【详解】(1)若p 为真:440m ∆=-≥,解得1m 若“p q ∧”是真命题,则p ,q 均为真命题即123m m ≤⎧⎨-<<⎩,解得21m -<≤.m ∴的取值范围21m -<≤(2)由r 是q 的充分不必要条件, 可得(,1)t t +是(2,3)-的真子集,即213t t ≥-⎧⎨+≤⎩(等号不同时成立),解得22t -≤≤. t ∴的取值范围22t -≤≤22.某校为了解学生对安全知识的重视程度,进行了一次安全知识答题比赛.随机抽取的100名学生的笔试成绩(满分200分),分成[160,165),[165,170),……,[180,185)共五组后,得到的频率分布表如下所示:(1)请先求出频率分布表中①、②位置的相应数据,再完成频率分布直方图(用阴影表示);(2)为能更好了解学生的知识掌握情况,学校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面答,最终从6位学生中随机抽取2位参加市安全知识答题决赛,求抽到的2位学生不同组的概率.【答案】(1)答案见解析;(2)11 15.【分析】(1)依据频数与频率公式求得相应数据,再根据数据完成频率分布直方图;(2)利用分层抽样求得第3、4、5组中的人数,再用列举法求得相应概率.【详解】(1)第2组的频数为1000.30030⨯=人,所以①处应填的数为10人,②处应填的数为0.300,频率分布直方图如图所示,(2)因为第3、4、5组共有60名选手,所以利用分层抽样在60名选手中抽取6名选手进入第二轮面试,每组抽取的人数分别为:第3组:306360⨯=人,第4组:206260⨯=人,第5组:106160⨯=人,所以第3、4、5组分别抽取3人、2人、1人进入第二轮面答.设第3组的3位学生为1A,2A,3A,第4组的2位学生为1B,2B,第5组的1位学生为1C,则从这6位学生中抽取2位学生有:()12,A A ,()13,A A ,()11,A B ,()12,AB ,()11,AC ,()23,A A ,()21,A B ,()22,A B ,()21,A C ,()31,A B ,()32,A B ,()31,A C ,()12,B B ,()11,B C ,()21,B C ,共15种情况.抽到的2位学生不同组的有:()11,A B ,()12,A B ,()11,A C ,()21,A B ,()22,A B ,()21,A C ,()31,A B ,()32,A B ,()31,A C ,()11,B C ,()21,B C ,共11种情况.所以抽到的2位学生不同组的概率为1115. 【点睛】有关古典概型的概率问题,关键是正确求出基本事件总数和所求事件包含的基本事件数,基本事件总数较少时,用列举法把所有基本事件一一列出时,要做到不重复、不遗漏.23.(1)已知等轴双曲线22221(0,0)y x a b a b-=>>的上顶点到一条渐近线的距离为1,求此双曲线的方程;(2)已知抛物线24y x =的焦点为F ,设过焦点F 且倾斜角为45︒的直线l 交抛物线于A ,B 两点,求线段AB 的长.【答案】(1)22122y x -=;(2)8. 【分析】(1)由等轴双曲线的一条渐近线方程为0y x +=,再由点到直线距离公式求解即可;(2)求得直线方程代入抛物线,结合焦点弦长求解即可.【详解】(1)由等轴双曲线的一条渐近线方程为0y x +=,且顶点(0,)a 到渐近线的距离为1,可得1a b=⎧=,解得a b ⎧=⎪⎨=⎪⎩22122y x -=(2)抛物线24y x =的焦点为(1,0)F直线l 的方程为0tan 45(1)y x -=︒⋅-,即1y x =-.与抛物线方程联立,得214y x y x=-⎧⎨=⎩,消y ,整理得2610x x -+=,设其两根为1x ,2x ,且126x x +=. 由抛物线的定义可知,12||628AB x x p =++=+=. 所以,线段AB 的长是8.【点睛】(1)直线与抛物线的位置关系和直线与椭圆、双曲线的位置关系类似,一般要用到根与系数的关系;(2)有关直线与抛物线的弦长问题,要注意直线是否过抛物线的焦点,若过抛物线的焦点,可直接使用公式|AB |=x 1+x 2+p ,若不过焦点,则必须用一般弦长公式. 24.如图①所示,在直角梯形EFCD 中,//CF DE ,EF DE ⊥,BA DE ⊥,224AE AD EF BC ====.现以AB 为折痕将四边形AEFB 折起,使点E 在平面ABCD 的投影恰好为点A ,如图②.(1)求证://CF 平面ADE ;(2)求平面CDF 与平面AEFB 所成锐二面角的余弦值. 【答案】(1)证明见解析;(2)23. 【分析】(1)取线段AD 的中点M ,连结CM ,EM ,由平面几何证得四边形CMEF 为平行四边形,再由线面平行的判定可得证;(2)由已知以A 为坐标原点,建立空间直角坐标系A xyz -,运用二面角的向量求解方法可求得平面CDF 与平面AEFB 所成锐二面角的余弦值. 【详解】(1)取线段AD 的中点M ,连结CM ,EM ,则//AM BC=,∴四边形ABCM 为平行四边形,//AB MC∴=,四边形ABEF 为矩形//AB EF ∴=,//MC EF∴=, ∴四边形CMEF 为平行四边形,//CF EM∴=, 又CF ⊂/平面ADE ,ME ⊂平面ADE ,//CF ∴平面ADE ;(2)点E 在平面ABCD 的投影恰好为点A .EA ∴⊥平面ABCD ,如图,以A 为坐标原点,建立空间直角坐标系A xyz -,则(2,2,0)C ,(0,4,0)D ,(2,0,4)F ,(0,4,0)AD ∴=,(2,2,0)CD =-,(0,2,4)CF =-设(,,)n x y z =是平面CDF 的一个法向量,则00n CD n CF ⎧⋅=⎨⋅=⎩即020x y y z -=⎧⎨-=⎩,令2y =,解得21x z =⎧⎨=⎩,(2,2,1)n ∴=, 又AD 是平面AEFB 的一个法向量,2cos ,3||||n AD n AD n AD ⋅∴〈〉==⋅,∴平面CDF 与平面AEFB 所成锐二面角的余弦值为23.【点睛】方法点睛:向量法求二面角的步骤:建、设、求、算、取.1、建:建立空间直角坐标系.以三条互相垂直的垂线的交点为原点,没有三垂线时需做辅助线;建立右手直角坐标系,让尽量多的点落在坐标轴上.2、设:设所需点的坐标,并得出所需向量的坐标.3、求:求出两个面的法向量.4、算:运用向量的数量积运算,求两个法向量的夹角的余弦值;5、取:根据二面角的范围()0π,和图示得出的二面角是锐角还是钝角,再取值.25.已知椭圆2222:1(0)x y C a b a b+=>>的离心率为13,右焦点为F ,右顶点为A ,以椭圆四个顶点为顶点的四边形面积为122.(1)求椭圆C的方程;(2)过点F的直线l(不与x轴重合)交椭圆C于点M、N,直线MA、NA分别与直线9x=交于点P、Q,且P、Q中点为G,求证:1||||2FG PQ=.【答案】(1)22198x y;(2)证明见解析.【分析】(1)根据离心率及菱形的面积联立方程求出,a b,即可求解;(2)设直线方程为1x ty=+,表示出,P Q点的坐标,利用向量可证明FP FQ⊥,根据直角三角形斜边中线的性质得证.【详解】(1)由题意得132122caab⎧=⎪⎨⎪=⎩,解得3a=,1c=,22b =,所以椭圆C 的方程为22198x y;(2)如图,设直线l的方程为1x ty=+,设点()11,M x y、()22,N x y,联立221198x tyx y=+⎧⎪⎨+=⎪⎩,消去x得()228916640t y ty++-=,则0∆>恒成立,由韦达定理得1221689ty yt+=-+,1226489y yt=-+,设点(9,)P m,(3,0)A,则()()11113,2,AM x y ty y=-=-,(6,)AP m=,由AM//AP→得()1162y m ty=-,可得1162y m ty =-,即点1169,2y P ty ⎫⎛⎪ -⎝⎭,同理可得点2269,2y Q ty ⎫⎛⎪ -⎝⎭,1168,2y FP ty ⎫⎛∴=⎪ -⎝⎭,2268,2y FQ ty ⎫⎛=⎪ -⎝⎭, ()()1212366422y y FP FQ ty ty ∴⋅=+--()1221212366424y y t y y t y y =+-++2222236648964643248989t t t t t ⨯+=+-++++()222366464646406432489t t t -⨯=+=-=-+++ 因此,FP FQ ⊥.又因为P 、Q 中点为G ,所以1||||2FG PQ =. 【点睛】关键点点睛:设点()11,M x y 、()22,N x y ,点(9,)P m ,根据向量AM //AP →,转化出点1169,2y P ty ⎫⎛⎪ -⎝⎭,2269,2y Q ty ⎫⎛⎪-⎝⎭,利用向量0FP FQ ⋅=,证明FP FQ ⊥是证明结论的关键所在,属于中档题.。
广东省广州市海珠区2020-2021学年高二下学期期末数学试题
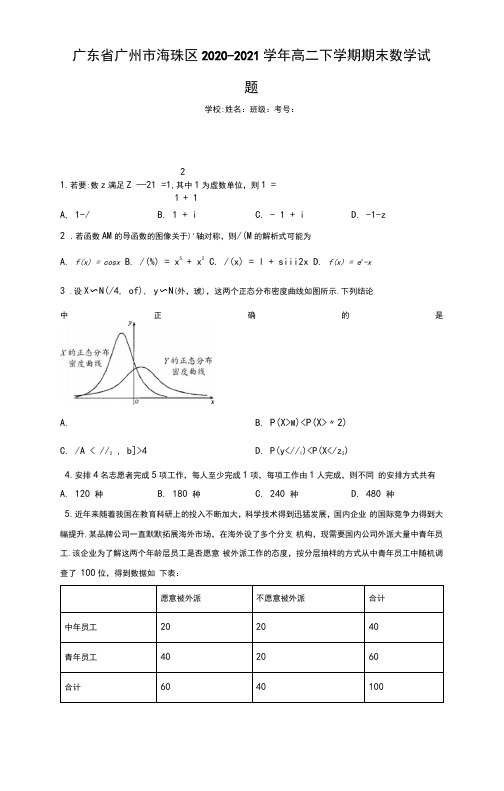
广东省广州市海珠区2020-2021学年高二下学期期末数学试题学校:姓名:班级:考号:21.若要:数z满足Z —21 =1,其中1为虚数单位,则1 =1+ 1A, 1-/ B. 1 + i C. - 1 + i D. -1-z2.若函数AM的导函数的图像关于)'轴对称,则/(M的解析式可能为A. f(x) = cosxB. /(%) = x5 + x2C. /(x) = l + siii2xD. f(x) = e x-x3.设X〜N(/4, of), y〜N(外,琥),这两个正态分布密度曲线如图所示.下列结论中正确的是A. B. P(X>M)<P(X>〃2)C. /A < //2 , b]>4D. P(y<//1)<P(X</z2)4.安排4名志愿者完成5项工作,每人至少完成1项,每项工作由1人完成,则不同的安排方式共有A. 120 种B. 180 种C. 240 种D. 480 种5.近年来随着我国在教育科研上的投入不断加大,科学技术得到迅猛发展,国内企业的国际竞争力得到大幅提升.某品牌公司一直默默拓展海外市场,在海外设了多个分支机构,现需要国内公司外派大量中青年员工.该企业为了解这两个年龄层员工是否愿意被外派工作的态度,按分层抽样的方式从中青年员工中随机调查了100位,得到数据如下表:7 .在5张扑克牌中有3张“红心”和2张“方块' 如果不放回地依次抽取2张牌,则在第一次抽到“红心”的条件下,第二次抽郅。
红心”的概率为C-I8 .“杨辉三角”是中国占代重要的数学成就,在南宋数学家杨辉所著的《详解九章算法》一书中出现,它比西方的“帕斯卡三角形”早了 300多年,如图是杨辉三角数阵,记。
“为 图中第"行各个数之和,s ”为{凡}的前〃项和,则S 】on(ad-bc)2(a + b)(c + d)(a + c)(b + d)并参照附表,得到的正确结论是A, 在犯错误的概率不超过10%的前提下,认为“是否愿意外派与年龄有关”; B. 在犯错误的概率不超过10%的前提下,认为“是否愿意外派与年龄无关”; C. 有99%以上的把握认为“是否愿意外派与年龄有关”; D. 有99%以上的把握认为“是否愿意外派与年龄无关 6.]x_2y )的展开式中的系数是(A, -20 B. -5 C.D. 20B-A. 1024B. 1023C. 512D. 511附表:( 1 \ 19.若函数/(刈二山]一]+51-〃1—5至少有1个零点,则实数。
2019-2020广州海珠区高二上册期末数学【试卷+答案】

( 3 )当 且
时,求函数 的零点.
/
2019~2020学年广东广州海珠区高二上学期期末数学试 卷(答案)
一、选择题
1. C
2. D
3. D
4. C
5. B
6. B
7. C
8. B
9. C
10. D
11. B
12. A
二、填空题
13.
14.
15.
16.
三、解答题
( ) 17. 1
.
( 2 ) 的最大值为 , 或 .
15. 已知 , 是椭圆
的左,右焦点,点 为 上一点, 为坐标原
点, 为正三⻆形,则 的离心率为 .
16. 如图,平行六面体
中, ,则
, .
三、解答题
(本大题共6题,共计70分。)
记 17. 为公差不为零的等差数列 的前 项和,已知 , . ( 1 )求 的通项公式. ( 2 )求 的最大值及对应 的大小.
A.
,使 B.
,都有 C.
,使 D.
,都有
5. 若 , , , 为实数,则下列命题正确的是( ).
若 A. ,则
若 B.
,则 若 C. , , 若 D. , ,
则
则
6. 已知 为平面 的一个法向量, 为一条直线,则“ 是” “ ”的( ).
A. 充分不必要条件
B. 必要不充分条件
C. 充要条件
D. 既不充分也不必要条件
C.
D.
10. 双曲线
的右焦点为 ,点 在 的一条渐近线上, 为坐标原点
B.
C.
D.
11. 为不断满足人⺠日益增⻓的美好生活需要,实现群众对舒适的居住条件、更优美的环境、更丰富 的精神文化生活的追求,某大型广场正计划进行升级改造.改造的重点工程之一是新建一个⻓方 形音乐喷泉综合体 ,该项目由⻓方形核心喷泉区 (阴影部分)和四周绿化带组 成.规划核心喷泉区 的面积为 ,绿化带的宽分别为 和 (如图所示).当整 个项目占地 面积最小时,则核心喷泉区 的边⻓为( ).
2020-2021学年高二上学期期末考试数学试卷(含解析)

2020-2021学年高二上学期期末考试数学试卷学校:___________姓名:___________班级:___________考号:___________一、单选题1.若3324A 10A n n =,则n =( )A .1B .8C .9D .102.期末考试结束后,某班要安排6节课进行试卷讲评,要求课程表中要排入语文、数学、英语、物理、化学、生物共六节课,如果第一节课只能排语文或数学,最后一节不能排语文,则不同的排法共有( ) A .192种B .216种C .240种D .288种3.一台X 型号自动机床在一小时内不需要工人照看的概率为0.8,有4台这种型号的自动机床各自独立工作,则在一小时内至多2台机床需要工人照看的概率是( ) A .0.1536B .0.1808C .0.5632D .0.97284.某市气象部门根据2021年各月的每天最高气温平均值与最低气温平均值(单位:℃)数据,绘制如下折线图:那么,下列叙述错误的是( )A .各月最高气温平均值与最低气温平均值总体呈正相关B .全年中,2月份的最高气温平均值与最低气温平均值的差值最大C .全年中各月最低气温平均值不高于10℃的月份有5个D .从2021年7月至12月该市每天最高气温平均值与最低气温平均值都呈下降趋势5.若()2N 1,X σ~,则()0.6827P X μσμσ-<≤+=,(22)0.9545P X μσμσ-<≤+=,已知()21,3X N ~,则(47)P X <≤=( )A .0.4077B .0.2718C .0.1359D .0.04536.为了评价某个电视栏目的改革效果,在改革前后分别从居民点抽取了100位居民进行调查,经过计算()200.01P K k ≥=,根据这一数据分析,下列说法正确的是( )A .有1%的人认为该栏目优秀;B .有1%的把握认为该栏目是否优秀与改革有关系;C .有99%的把握认为电视栏目是否优秀与改革有关系;D .没有理由认为电视栏目是否优秀与改革有关系.7.若1021001210)x a a x a x a x =++++,则012310a a a a a -+-++的值为.A 1B 1C .101)D .101)8.关于()72x +的二项展开式,下列说法正确的是( ) A .()72x +的二项展开式的各项系数和为73B .()72x +的二项展开式的第五项与()72x +的二项展开式的第五项相同C .()72x +的二项展开式的第三项系数为4372CD .()72x +的二项展开式第二项的二项式系数为712C9.如图,某建筑工地搭建的脚手架局部类似于一个3×2×3的长方体框架,一个建筑工人欲从A 处沿脚手架攀登至B 处,则其最近的行走路线中不连续向上攀登的概率为( )A .528B .514C .29D .1210.三棱锥P ABC -中P A 、PB 、PC 两两互相垂直,4PA PB +=,3PC =,则其体积( ) A .有最大值4B .有最大值2C .有最小值2D .有最小值4二、填空题11.最小二乘法得到一组数据(),(1,2,3,4,5)i i x y i =的线性回归方程为ˆ23yx =+,若5125ii x==∑,则51i i y ==∑___________.12.某班举行的联欢会由5个节目组成,节目演出顺序要求如下: 节目甲不能排在第一个,并且节目甲必须和节目乙相邻.则该班联欢会节目演出顺序的编排方案共有____种. 13.若随机变量X 的概率分布如表,则表中a 的值为______.14.设随机变量ξ~B (2,p ),若P (ξ≥1)=59,则D (ξ)的值为_________.15.已知等差数列{}n a 中,33a =,则1a 和5a 乘积的最大值是______.16.某次知识竞赛规则如下:在主办方预设的5个问题中,选手若能连续正确回答出两个问题,即停止答题,晋级下一轮假设某选手正确回答每个问题的概率都是0.8,且每个问题的回答结果相互独立,则该选手恰好回答了5个问题就晋级下一轮的概率为___________.17.经统计,在银行一个营业窗口每天上午9点钟排队等候的人数及相应概率如下:则该营业窗口上午9点钟时,至少有2人排队的概率是_____.18.点A ,B ,C 在球O 表面上,2AB =,BC =90ABC ∠=︒,若球心O 到截面ABC的距离为___________.19.如图,在三棱柱111ABC A B C -中,四边形11AAC C 是边长为4的正方形,平面ABC ⊥平面11AAC C ,3AB =,5BC =.(℃)求证:1AA ⊥平面;(℃)若点E 是线段的中点,请问在线段是否存在点E ,使得面11AAC C ?若存在,请说明点E 的位置,若不存在,请说明理由; (℃)求二面角的大小.20.四根绳子上共挂有10只气球,绳子上的球数依次为1,2,3,4,每枪只能打破一只球,而且规定只有打破下面的球才能打上面的球,则将这些气球都打破的不同打法数是________.三、解答题21.已知集合(){}()12,,,|,1,2,,1nn i R x x x x R i n n =∈=≥,定义n R 上两点()12,,,n A a a a ,()12,,,n B b b b 的距离()1,ni i i d A B a b ==-∑.(1)当2n =时,以下命题正确的有__________(不需证明): ℃若()1,2A ,()4,6B ,则(),7d A B =;℃在ABC 中,若90C =∠,则()()()222,,,d A C d C B d A B ⎡⎤⎡⎤⎡⎤+=⎣⎦⎣⎦⎣⎦; ℃在ABC 中,若()(),,d A B d A C =,则B C ∠=∠;(2)当2n =时,证明2R 中任意三点A B C ,,满足关系()()(),,,d A B d A C d C B ≤+;(3)当3n =时,设()0,0,0A ,()4,4,4B ,(),,P x y z ,其中x y z Z ∈,,,()()(),,,d A P d P B d A B +=.求满足P 点的个数n ,并证明从这n 个点中任取11个点,其中必存在4个点,它们共面或者以它们为顶点的三棱锥体积不大于83.22.今年4月,教育部办公厅印发了《关于加强义务教育学校作业管理的通知》,规定初中学生书面作业平均完成时长不超过90分钟.某市为了更好地贯彻落实“双减”工作要求,作教育决策,该市教育科学研究院就当前全市初三学生每天完成书面作业时长抽样调查,结果是学生书面作业时长(单位:分钟)都在区间[]50,100内,书面作业时长的频率分布直方图如下:(1)若决策要求:在国家政策范围内,若当前初三学生书面作业时长的中位数估计值大于或等于平均数(计算平均数时,同一组中的数据用该区间的中点值代表)估计值,则减少作业时长;若中位数估计值小于平均数,则维持现状.请问:根据这次调查,该市应该如何决策?(2)调查统计时约定:书面作业时长在区间[]90,100内的为A 层次学生,在区间[)80,90内的为B 层次学生,在区间[70,80)内的为C 层次学生,在其它区间内的为D 层次学生.现对书面作业时长在70分钟以上(含70分钟)的初三学生,按作业时长出现的频率用分层抽样的方法随机抽取8人,再从这8人中随机抽取3人作进一步调查,设这3人来自X 个不同层次,求随机变量X 的分布列及数学期望.23.国家文明城市评审委员会对甲、乙两个城市是否能入围“国家文明城市”进行走访调查.派出10人的调查组.先后到甲、乙两个城市的街道、社区进行问卷调查,然后打分(满分100分).他们给出甲、乙两个城市分数的茎叶图如图所示:(1)请你用统计学的知识分析哪个城市更应该入围“国家文明城市”,请说明理由;(2)从甲、乙两个城市的打分中各抽取2个,在已知有大于80分的条件下,求抽到乙城市的分数都小于80分的概率;(3)从对乙城市的打分中任取2个,设这2个分数中不小于80分的个数为X,求X的分布列和期望.参考答案:1.B【分析】根据排列数的运算求解即可.【详解】由332A 10A n n =得,2(21)(22)10(1)(2)n n n n n n --=--,又3,n n *≥∈N ,所以2(21)5(2)n n -=-,解得8n =, 所以正整数n 为8. 故选:B. 2.B【分析】对第一节课的安排进行分类讨论,结合分步乘法计数原理和分类加法计数原理可得结果.【详解】分以下两种情况讨论:℃若第一节课安排语文,则后面五节课的安排无限制,此时共有55A 种;℃若第一节课安排数学,则语文可安排在中间四节课中的任何一节,此时共有444A 种.综上所述,不同的排法共有54544216A A +=种.故选:B. 3.D【详解】设在一个小时内有ξ台机床需要工人照看,则ξ~B (4,0.2),所以P (ξ≤2)=04C (0.8)4+14C (0.8)3×0.2+24C (0.8)2×(0.2)2=0.972 8. 故选D 4.D【分析】利用折线图可以判断选项ABC 正确,从2021年7月至12月该市每天最高气温平均值与最低气温平均值,先上升后下降,所以选项D 错误.【详解】解:由2021年各月的每天最高气温平均值和最低气温平均值(单位:C)︒数据,绘制出的折线图,知:在A 中,各月最高气温平均值与最低气温平均值为正相关,故A 正确;在B 中,全年中,2月的最高气温平均值与最低气温平均值的差值最大,故B 正确; 在C 中,全年中各月最低气温平均值不高于10C ︒的月份有1月,2月,3月,11月,12月,共5个,故C 正确;在D 中,从2021年7月至12月该市每天最高气温平均值与最低气温平均值,先上升后下降,故D 错误. 故选:D . 5.C【分析】由题意,得(47)(2)P X P X μσμσ<≤=+<≤+,再利用3σ原则代入计算即可.【详解】℃()21,3X N ~,由()0.6827P X μσμσ-<≤+=,(22)0.9545P X μσμσ-<≤+=,℃1(47)(2)(0.95450.6827)0.13592P X P X μσμσ<≤=+<≤+=-=.故选:C 6.C【分析】利用独立性检验的基本原理即可求出答案.【详解】解:℃()200.01P K k ≥=表示“电视栏目是否优秀与改革没有关系”的概率,℃有99%的把握认为电视栏目是否优秀与改革有关系, 故选:C .【点睛】本题主要考查独立性检验的基本应用,准确的理解判断方法是解决本题的关键,属于基础题. 7.D【详解】分析:令1021001210())f x x a a x a x a x ==++++,再求f(-1)的值得解.详解:令1021001210())f x x a a x a x a x ==++++,1001210(1)1)f a a a a -==-+++.故答案为D .点睛:(1)本题主要考查二项式定理中的系数求法问题,意在考查学生对这些基础知识 的掌握水平.(2) 二项展开式的系数0123,,,,n a a a a a ⋅⋅⋅的性质:对于2012()?··n n f x a a x a x a x =++++,0123(1)n a a a a a f ++++⋅⋅⋅+=, 0123(1)(1)n n a a a a a f -+-+⋅⋅⋅+-=-.8.A【分析】利用赋值法求出展开式各项系数和,即可判断A ,根据二项式展开式的通项,即可判断B 、C 、D ;【详解】解:()72x +展开式的通项为7172rrr r T C x -+=⋅⋅,故第二项的二项式系数为177C =,故D 错误; 第三项的系数为2572C ⋅,故C 错误;()72x +的展开式的第五项为43472C x ⋅⋅,()72x +的展开式的第五项为44372C x ⋅⋅,故B 错误; 令1x =则()7723x +=,即()72x +的二项展开式的各项系数和为73,故A 正确; 故选:A 9.B【解析】将问题抽象成“向左三次,向前两次,向上三次”,计算出总的方法数,然后利用插空法计算出最近的行走路线中不连续向上攀登的事件数,最后根据古典概型概率计算公式,计算出所求概率.【详解】从A 的方向看,行走方向有三个:左、前、上. 从A 到B 的最近的行走线路,需要向左三次,向前两次,向上三次,共8次.所以从A 到B 的最近的行走线路,总的方法数有88332332560A A A A =⋅⋅种. 不连续向上攀登的安排方法是:先将向左、向前的安排好,再对向上的方法进行插空.故方法数有:53563232200A C A A ⨯=⋅.所以最近的行走路线中不连续向上攀登的概率为200556014=. 故选:B【点睛】本小题主要考查古典概型的计算,考查有重复的排列组合问题,考查插空法,属于中档题. 10.B【分析】依题意可得1113332P ABC PABV PC SPA PB -=⋅=⨯⨯⋅再利用基本不等式计算可得; 【详解】解:依题意21111132332222P ABCPABPA PB V PC S PA PB PA PB -+⎛⎫=⋅=⨯⨯⋅=⋅≤= ⎪⎝⎭,当且仅当2PA PB ==时取等号,所以()max 2P ABC V -=, 故选:B11.65【分析】由最小二乘法得到的线性回归方程过点(),x y ,代入即可解决 【详解】由5125i i x ==∑可知,数据的平均数2555x ==, 又线性回归方程ˆ23yx =+过点(),x y , 所以25313y =⨯+=,故51551365i i y y ===⨯=∑故答案为:65 12.42【分析】由题意可知,甲可排在第二、三、四、五个,再根据甲、乙相邻,分别计算. 【详解】由题意可知,甲可排在第二、三、四、五个,当甲排在第二、三、四个时,甲乙相邻,有22A 种排法,将甲乙当做一个整体,剩下三个节目全排列,共3×22A ×33A =36种当甲排在第五个时,甲乙相邻,只有一种排法,剩下三个节目全排列,共33A =6种 综上,编排方案共36+6=42种【点睛】本题考查了分类计数原理,分类时要注意不重不漏;解决排列问题时,相邻问题常用捆绑法,特殊位置要优先考虑. 13.0.2【解析】利用概率和为1可求出答案. 【详解】由随机变量X 的概率分布表得: 0.20.30.31a +++=,解得0.2a =. 故答案为:0.2【点睛】本题考查的是分布列的性质,较简单. 14.49【分析】由二项分布的特征,先求出13p =,套公式即可求出D (ξ). 【详解】因为随机变量ξ~B (2,p ),且P (ξ≥1)=59,所以P (ξ≥1)=()11P ξ-<= ()10P ξ-==()25119p --=. 解得:13p =. 所以D (ξ)()12412339np p =-=⨯⨯=.故答案为:4915.9【分析】设出公差,根据等差数列的性质,表示出15,a a ,再列式即可求得结果. 【详解】因为{}n a 是等差数列,设公差为d ,可得13532,2a a d a a d =-=+,于是得()()2153322949a a a d a d d =-+=-≤,当且仅当d =0,即153a a ==时,取得最大值. 故答案为:9.【点睛】本题考查等差数列的下标和性质,属基础题. 16.1443125##0.04608 【分析】认真分析该选手所有可能的答题情况,是本题的关键【详解】由该选手恰好回答了5个问题就晋级下一轮,说明他第4、第5两个问题是连续答对的,第3个问题没有答对,第1和第2两个问题也没有全部答对,即他答题结果可能有三种情况:⨯⨯⨯√√或⨯√⨯√√或√⨯⨯√√,根据独立事件同时发生的概率公式,可得该选手恰好回答了5个问题就晋级下一轮的概率为0.20.20.20.80.8+0.20.80.20.80.8+0.80.20.20.80.8=0.04608⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯故答案为:0.04608 17.0.74【详解】试题分析:x 表示人数,(2)(2)(3)(4)(5)P x P x P x P x P x ≥==+=+=+≥0.30.30.10.040.74=+++=.考点:互斥事件的概率.18.【分析】根据截面圆性质,先求出截面圆半径,然后由求得球半径,从而求得体积.【详解】因为2AB =,BC =90ABC ∠=︒,所以4AC ==,所以三角形外接圆半径22ACr ==,又球心O 到截面ABC 的距离为R =球体积为(334433V R ππ==⨯=.故答案为:.19.(℃)(℃)(℃)见解析【详解】试题分析:(℃)由正方形的性质得1AC AA ⊥,然后由面面垂直的性质定理可证得结果;(℃)当点E 是线段1AB 的中点时,利用中位线定理可得1DE AC ,进而得出DE 面11AAC C ;(℃)利用二面角的定义先确定11C AC ∠是二面角111C A B C --的平面角,易求得11tan C A C ∠,从而求得二面角的平面角为的度数.试题解析:(℃)因为四边形11AAC C 为正方形,所以1AC AA ⊥. 因为平面ABC ⊥平面11AAC C ,且平面ABC ⋂平面11AAC C AC =, 所以1AA ⊥平面ABC .(℃)当点E 是线段1AB 的中点时,有DE 面11AAC C , 连结1AB 交1AB 于点E ,连结BC ,因为点E 是1AB 中点,点⊄是线段DE 的中点,所以1DE AC . 又因为BC ⊂面11AAC C ,11A C 面11AAC C ,所以DE 面11AAC C .(℃)因为1AA ⊥平面ABC ,所以.又因为,所以面11AAC C ,所以11A B ⊥面11AAC C ,所以11A B ⊥1A C ,11A B ⊥11A C ,所以11C AC ∠是二面角111C A B C --的平面角, 易得,所以二面角111C A B C --的平面角为45°.考点:1、线面垂直的判定;2、线面平行的判定;2、二面角.【方法点睛】立体几何中的探索性问题主要是对平行、垂直关系的探究,对条件和结论不完备的开放性问题的探究.解决这类问题时一般根据探索性问题的设问,假设其存在并探索出结论,然后在假设下进行推理,若得到合乎情理的结论就肯定假设,若得到矛盾就否定假设. 20.12600【详解】问题等价于编号为1,2,3,10的10个小球排列,其中2,3号,4,5,6号,7,8,9,10号的排列顺序是固定的,据此可得:将这些气球都打破的不同打法数是101023423412600A A A A =⨯⨯. 21.(1)℃;(2)证明见解析;(3)125n =,证明见解析.【解析】(1)℃根据新定义直接计算.℃根据新定义,写出等式两边的表达式,观察它们是否相同,即可判断;℃由新定义写出等式()(),,d A B d A C =的表达式,观察有无AB AC =; (2)由新定义,写出不等式两边的表达式,根据绝对值的性质证明;(3)根据新定义,及绝对值的性质得P 点是以AB 为对角线的正方体的表面和内部的整数点,共125个,把它们分布在五个平面(0,1,2,3,4)z =上,这五个面一个面取3个点,相邻面上取一个点,以它们为顶点构成三棱锥(能构成时),棱锥的体积不超过83,然后任取11点中如果没有4点共面,但至少有一个平面内有3个点.根据这3点所在平面分类讨论可得. 【详解】(1)当2n =时,℃若()1,2A ,()4,6B ,则(),41627d A B =-+-=,℃正确;℃在ABC 中,若90C =∠,则222AC BC AB +=,设112233(,),(,),(,)A x y B x y C x y ,所以222222131323231212()()()()()()x x y y x x y y x x y y -+-+-+-=-+-而()2221212121221212()()()2)),((x x y y x x y y d A x B x y y =⎡⎤⎣-+-+⎦=--+--, ()()22,,d A C d C B ⎡⎤⎡⎤+=⎣⎦⎣⎦22221313232313132323()()()()2()()2()()x x y y x x y y x x y y x x y y -+-+-+-+--+--,但1313232312122()()2()()2()()x x y y x x y y x x y y --+--=--不一定成立,℃错误; ℃在ABC 中,若()(),,d A B d A C =,在℃中的点坐标,有12121313x x y y x x y y -+-=-+-,但1212131322x x y y x x y y -⋅-=-⋅-不一定成立,因此AB AC =不一定成立,从而B C ∠=∠不一定成立,℃错误.空格处填℃(2)证明:设112233(,),(,),(,)A x y B x y C x y ,根据绝对值的性质有132312x x x x x x -+-≥-,132312y y y y y y -+-≥-,所以(,)(,)(,)d A C d B C d A B +≥.,(3)(,)12d A B =,44,44,44x x y y z z +-≥+-≥+-≥,所以(,)(,)12d A P d B P +≥,当且仅当以上三个等号同时成立,(,)(,)12d A P d B P +=又由已知()()(),,,d A P d P B d A B +=,℃04,04,04x y z ≤≤≤≤≤≤, 又,,x y z Z ∈,℃,,0,1,2,3,4x y z =,555125⨯⨯=,点P 是以AB 为对角线的正方体内部(含面上)的整数点,共125个,125n =. 这125个点在0,1,2,3,4z z z z z =====这五面内.这三个平面内,一个面上取不共线的3点,相邻面上再取一点构成一个三棱锥.则这个三棱锥的体积最大为118441323V =⨯⨯⨯⨯=,现在任取11个点,若有四点共面,则命题已成立,若其中无4点共面,但11个点分在5个平面上至少有一个平面内有3个点(显然不共线),若这三点在1,2,3z z z ===这三个平面中的一个上,与这个面相邻的两个面上如果有一点,那么这一点与平面上的三点这四点可构成三棱锥的四个顶点,其体积不超过83,否则还有8个点在平面0z =和4z =上,不合题意,若这三个点在平面0z =或5z =上,不妨设在平面0z =,若在平面1z =在一个点,则同样四点构成的三棱锥体积不超过83,否则剩下的8个点在2,3,4z z z ===三个平面上,只能是3,3,2分布,不管哪一种分布都有四点构成的三棱锥体积不超过83,综上,任取11个点,其中必存在4个点,它们共面或者以它们为顶点的三棱锥体积不大于83.【点睛】关键点点睛:本题新定义距离(,)d A B ,解题关键是利用新定义转化为绝对值,利用绝对值的性质解决一些问题.本题还考查了抽屉原理,11个放在5个平面上,至少有一个平面内至少有3点,由此分类讨论可证明结论成立. 22.(1)该市应该作出减少作业时长的决策; (2)分布列见解析;期望为167.【分析】(1)根据题意,结合频率分布直方图,分别求出中位数和平均数,即可求解; (2)根据题意,结合分层抽样以及离散型随机变量的分布列与期望求法,即可求解. (1)作业时长中位数的估计值为直方图中等分面积的线对立的值,设为x .0.01100.01100.02100.5⨯+⨯+⨯<. 0.01100.01100.02100.03100.5⨯+⨯+⨯+⨯>,()0.01100.01100.02100.03800.5x ∴⨯+⨯+⨯+⨯-=.解得2503x =,即中位数的故计值2503分钟.又作业时长平均数估计值为0.0110550.0110650.021075⨯⨯+⨯⨯+⨯⨯ 2500.0310850.031095813+⨯⨯+⨯⨯=<. 因为中位数的估计值2503分钟大于平均数估计值81分钟, 所以,根据这次调查,该市应该作出减少作业时长的决策. (2)由题,作业时长在70分钟以上(含70分钟)为[90.100],[80,90),[70,80)三个区间,其频率比为3:3:2,分别对应A ,B ,C 三个层次.根据分层抽样的方法,易知各层次抽取的人数分别为3,3,2, 因此X 的所有可能值为1,2,3.因为333821(1)28C P X C ⨯===,111233389(3)28C C C P X C ⋅⋅===, 121221333232382229(2)14C C C C C C P X C ⨯⋅+⨯⋅+⨯⋅===, 所以X 的分在列为:故数学期望19916()1232814287E X =⨯+⨯+⨯=. 23.(1)乙城市更应该入围“国家文明城市”.理由见解析. (2)425; (3)分布列见解析,期望为1.【分析】(1)根据得分的平均值与方差说明,极差最值也可用来说明;(2)记抽到的数据中有大于80分为事件A ,甲城市抽到的分数有大于80分为事件B ,乙城市抽到的分数有大于80分为事件C ,由()()(|)()()P AC P C P C A P A P A ==计算; (2)X 的可能值是0,1,2,分别求得概率得概率分布列,由期望公式计算出期望. (1)乙城市更应该入围“国家文明城市”. 理由如下:由茎叶图,计算两个城市的得分的均值为 甲:6365987910x +++==,乙:6568927910y +++==,均值相等,方差为甲:222211[(16)(14)19]13610s =-+-++=, 乙:222221[(14)(11)13]59.810s =-+-++=,甲的方差远大于乙的方差,说明乙的得分较稳定,甲极其不稳定,因此乙城市更应该入围“国家文明城市”. (2)记抽到的数据中有大于80分为事件A ,甲城市抽到的分数有大于80分为事件B ,乙城市抽到的分数有大于80分为事件C ,262102()13C P B C =-=,252107()19C P C C =-=,2725()1(1)(1)3927P A =--⨯-=,7()()9P AC P C ==, 所以()()()()749(|)1(|)111252527P AC P C P C A P C A P A P A =-=-=-=-=;(3)乙城市10个人中5个大于80分,5个小于80,X 的可能是0,1,2,252102(0)9C P X C ===,11552105(1)9C C P X C ===,252102(2)9C P X C ===,所以X 的分布列为:52()12199E X =⨯+⨯=.。
2020-2021广州市高二数学上期末试题(及答案)

2020-2021广州市高二数学上期末试题(及答案)一、选择题1.如图,ABC ∆和DEF ∆都是圆内接正三角形,且//BC EF ,将一颗豆子随机地扔到该圆内,用A 表示事件“豆子落在ABC ∆内”,B 表示事件“豆子落在DEF ∆内”,则(|)P B A =( )A .334πB .32πC .13D .232.气象意义上的春季进入夏季的标志为连续5天的日平均温度不低于022C .现有甲、乙、丙三地连续5天的日平均气温的记录数据(记录数据都是正整数): ①甲地:5个数据是中位数为24,众数为22; ②乙地:5个数据是中位数为27,总体均值为24;③丙地:5个数据中有一个数据是32,总体均值为26,总体方差为10.8 则肯定进入夏季的地区有( ) A .①②③B .①③C .②③D .①3.如果数据121x +、221x +、、21n x +的平均值为5,方差为16,则数据:153x -、253x -、、53n x -的平均值和方差分别为( )A .1-,36B .1-,41C .1,72D .10-,1444.若执行如图所示的程序框图,则输出S 的值为( )A .10072015B .10082017C .10092019D .101020215.日本数学家角谷静夫发现的“31x + 猜想”是指:任取一个自然数,如果它是偶数,我们就把它除以2,如果它是奇数我们就把它乘3再加上1,在这样一个变换下,我们就得到了一个新的自然数.如果反复使用这个变换,我们就会得到一串自然数,猜想就是:反复进行上述运算后,最后结果为1,现根据此猜想设计一个程序框图如图所示,执行该程N ,则输出i值为()序框图输入的6A.6B.7C.8D.96.执行如图所示的程序框图,输出的S值为()A.1B.-1C.0D.-27.某工厂对一批新产品的长度(单位:mm)进行检测,如下图是检测结果的频率分布直方图,据此估计这批产品的中位数与平均数分别为( )A .20,22.5B .22.5,25C .22.5,22.75D .22.75,22.758.高二某班共有学生60名,座位号分别为01, 02, 03,···, 60.现根据座位号,用系统抽样的方法,抽取一个容量为4的样本.已知03号、18号、48号同学在样本中,则样本中还有一个同学的座位号是( ) A .31号 B .32号C .33号D .34号9.为了解某社区居民的家庭年收入和年支出的关系,随机调查了该社区5户家庭,得到如下统计数据表: 收入x 万 8.3 8.6 9.9 11.1 12.1 支出y 万5.97.88.18.49.8根据上表可得回归直线方程ˆˆˆybx a =+,其中0.78b ∧=,a y b x ∧∧=-元,据此估计,该社区一户收入为16万元家庭年支出为( ) A .12.68万元B .13.88万元C .12.78万元D .14.28万元10.甲、乙两位同学在高一年级的5次考试中,数学成绩统计如茎叶图所示,若甲、乙两人的平均成绩分别是12,x x ,则下列叙述正确的是( )A .12x x >,乙比甲成绩稳定B .12x x >,甲比乙成绩稳定C .12x x <,乙比甲成绩稳定D .12x x <,甲比乙成绩稳定11.我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”,如40337=+.(注:如果一个大于1的整数除1和自身外无其他正因数,则称这个整数为素数.)在不超过11的素数中,随机选取2个不同的数,其和小于等于10的概率是( ) A .12B .13C .14D .1512.2路公共汽车每5分钟发车一次,小明到乘车点的时刻是随机的,则他候车时间不超过两分钟的概率是( ) A .25B .35C .23D .15二、填空题13.若正方体1111ABCD A B C D -的棱长为3,E 为正方体内任意一点,则AE 的长度大于3的概率等于_________.14.已知2件次品和3件正品放在一起,现需要通过检测将其区分,每次随机检测一件产品,检测后不放回,直到检测出2件次品或者检测出3件正品时检测结束,则恰好检测四次停止的概率为_____(用数字作答).15.执行如图所示的伪代码,若输出的y 的值为10,则输入的x 的值是________.16.下图是华师一附中数学讲故事大赛7位评委给某位学生的表演打出的分数的茎叶图.记分员在去掉一个最高分和一个最低分后,算得平均分为91分,复核员在复核时,发现有一个数字(茎叶图中的x )无法看清,若记分员计算无误,则数字x 应该是____________.17.某公司的广告费支出x 与销售额y (单位:万元)之间有下列对应数据:由资料显示y 对x 呈线性相关关系。
2020-2021学年广东省广州市白云区、海珠区高一(下)期末数学试卷(解析版)

2020-2021学年广东省广州市白云区、海珠区高一(下)期末数学试卷一、选择题(共8小题,每小题5分,共40分).1.若复数z=(i为虚数单位),则|z|=()A.B.1C.5D.2.已知向量=(2,3),=(x,﹣6),且⊥,则x=()A.﹣9B.9C.﹣4D.43.高一年级有男生510人,女生490人,小明按男女比例进行分层随机抽样,总样本量为100.则在男生中抽取的样本量为()A.48B.51C.50D.494.如图,△A'B'C'是水平放置的△ABC的斜二测直观图,△A'B′C′为等腰直角三角形,其中O′与A′重合,A'B′=6,则△ABC的面积是()A.9B.9C.18D.185.已知||=6,||=4,与的夹角为60°,则(+2)•(﹣3)=()A.﹣72B.72C.84D.﹣846.某学校开展“学党史,颂党恩,跟党走“学习活动,刘老师去购书中心购买了一批书籍作为阅读学习之用,其中一类是4本不同的红色经典小说类书籍,另一类是2本不同的党史类书籍,两类书籍合计共6本.现刘老师从这6本书中随机抽取2本阅读,则这两本书恰好来自同一类书籍的概率是()A.B.C.D.7.如图,已知=,=,任意点M关于点A的对称点为S,点M关于点B的对称点为N,则向量=()A.(+)B.2(+)C.(﹣)D.2(﹣)8.已知图1是棱长为1的正六边形ABCDEF,将其沿直线FC折叠成如图2的空间图形F′A′E′﹣C′B′D′,其中A′E′=,则空间几何体F'A'E'﹣CB'D'的体积为()A.B.C.D.二、选择题:本题共4小题,每小题5分,共20分在每小题给出的选项中,有多项符合题目要求全部选对的得5分,有选错的得0分,部分选对的得2分.9.某士官参加军区射击比赛,打了6发子弹,报靶数据如下:7,8,9,10,6,8,(单位:环),下列说法正确的有()A.这组数据的平均数是8B.这组数据的极差是4C.这组数据的中位数是8.5D.这组数据的方差是210.已知复数z=cosα+(sinα)i(α∈R)(i为虚数单位),下列说法正确的有()A.当α=﹣时,复平面内表示复数z的点位于第二象限B.当α=时,z为纯虚数C.|z|最大值为D.z的共轭复数为=﹣cosα+(sinα)i(α∈R)11.某班级到一工厂参加社会实践劳动,加工出如图所示的圆台O1O2,在轴截面ABCD中,AB=AD=BC=2cm,且CD=2AB,下列说法正确的有()A.该圆台轴截面ABCD面积为3cm2B.该圆台的体积为cm3C.该圆台的母线AD与下底面所成的角为30°D.沿着该圆台表面,从点C到AD中点的最短距离为5cm12.在△ABC中,角A,B,C所对的边分别为a,b,c,点O为△ABC所在平面内点,满足x+y+z=0,下列说法正确的有()A.若x=y=z=1,则点O为△ABC的重心B.若x=y=z=1,则点O为△ABC的外心C.若x=a,y=b,z=c,则点O为△ABC的内心D.若x=a,y=b,z=c,则点O为△ABC的垂心三、填空题:本题共4小题,每小题5分,共20分.13.有10种不同的零食,每100克可食部分包含的能量(单位:k)如下:100,120,125,165,430,190,175,234,425,310这10种零食每100克可食部分的能量的第60百分位数为.14.天气预报元旦假期甲地的降雨概率是0.2,乙地的降雨概率是0.3,假定在这段时间内两地是否降雨相互之间没有影响,则在这段时间内甲,乙两地只有一个地方降雨的概率是.15.如图,在三棱锥V﹣ABC中,VA=VB=AB=AC=BC=4,VC=2,则二面角A﹣VC﹣B的余弦值为.16.如图,△ABC是边长为1的正三角形,M,N分别为线段AC,AB上一点,满足AM:MC=1:2,AN:NB=1:3,CN与BM的交点为P,则线段AP的长度为.四、解答题:本题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤. 17.现有两个红球(记为R1,R2),两个白球(记为W1,W2),采用不放回简单随机抽样从中任意抽取两球.(1)写出试验的样本空间;(2)求恰好抽到一个红球一个白球的概率.18.已知角A是△ABC的内角,若=(sin A,cos A),=(1,﹣1).(1)若,求角A的值;(2)设f(x)=,当f(x)取最大值时,求在上的投影向量(用坐标表示).19.如图,直三棱柱ABC﹣A'B'C'中,D是AB的中点.(1)求证:直线BC′∥平面A'CD;(2)若AC=CB,求异面直线AB'与CD所成角的大小.20.2021年五一假期,各高速公路车流量大,交管部门在某高速公路区间测速路段随机抽取40辆汽车进行车速调查,将这40辆汽车在该区间测速路段的平均车速(km/h)分成六段[90,95),[95,100),[100,105),[105,110),[110,115),[115,120],得到如图的频率分布直方图.(1)根据频率分布直方图估计出这40辆汽车的平均车速的中位数;(2)现从平均车速在区间[90,100)的车辆中任意抽取2辆汽车,求抽取的2辆汽车的平均车速都在区间[95,100)上的概率;(3)出于安全考虑,测速系统对平均车速在区间[115,120]的汽车以实时短信形式对车主进行安全提醒,确保行车安全.假设每辆在此区间测速路段行驶的汽车平均车速相互不受影响,以此次调查的样本频率估计总体概率,求连续2辆汽车都收到短信提醒的概率?21.如图,PA垂直于⊙O所在的平面,AC为⊙O的直径,AB=3,BC=4,PA=3,AE ⊥PB,点F为线段BC上一动点.(1)证明:平面AEF⊥平面PBC;(2)当点F移动到C点时,求PB与平面AEF所成角的正弦值.22.为响应国家“乡村振兴”号召,农民王大伯拟将自家一块直角三角形地按如图规划成3个功能区:△BNC区域为荔枝林和放养走地鸡,△CMA区域规划为“民宿”供游客住宿及餐饮,△MNC区域规划为小型鱼塘养鱼供休闲垂钓.为安全起见,在鱼塘△MNC周围筑起护栏.已知AC=40m,BC=40m,AC⊥BC,∠MCN=30°(1)若AM=20m时,求护栏的长度(△MNC的周长);(2)若鱼塘△MNC的面积是“民宿”△CMA的面积的倍,求∠ACM;(3)当∠ACM为何值时,鱼塘△MNC的面积最小,最小面积是多少?参考答案一、选择题(共8小题,每小题5分,共40分).1.若复数z=(i为虚数单位),则|z|=()A.B.1C.5D.解:∵z=,∴|z|=||=,故选:A.2.已知向量=(2,3),=(x,﹣6),且⊥,则x=()A.﹣9B.9C.﹣4D.4解:∵,∴,解得x=9.故选:B.3.高一年级有男生510人,女生490人,小明按男女比例进行分层随机抽样,总样本量为100.则在男生中抽取的样本量为()A.48B.51C.50D.49解:高一年级共有510+490=1000人,所以男生抽取的人数为人.故选:B.4.如图,△A'B'C'是水平放置的△ABC的斜二测直观图,△A'B′C′为等腰直角三角形,其中O′与A′重合,A'B′=6,则△ABC的面积是()A.9B.9C.18D.18解:在斜二测直观图中,由△A'B′C′为等腰直角三角形,A'B′=6,可得A'C′=,还原原图形如图:则AB=6,AC=6,则=.故选:D.5.已知||=6,||=4,与的夹角为60°,则(+2)•(﹣3)=()A.﹣72B.72C.84D.﹣84解:∵||=6,||=4,与的夹角为60°,∴=,则(+2)•(﹣3)==36﹣12﹣6×16=﹣72.故选:A.6.某学校开展“学党史,颂党恩,跟党走“学习活动,刘老师去购书中心购买了一批书籍作为阅读学习之用,其中一类是4本不同的红色经典小说类书籍,另一类是2本不同的党史类书籍,两类书籍合计共6本.现刘老师从这6本书中随机抽取2本阅读,则这两本书恰好来自同一类书籍的概率是()A.B.C.D.解:从6本书中随机抽取2本,共有种取法,若两本书来自同一类书籍则有种取法,所以两本书恰好来自同一类书籍的概率是.故选:C.7.如图,已知=,=,任意点M关于点A的对称点为S,点M关于点B的对称点为N,则向量=()A.(+)B.2(+)C.(﹣)D.2(﹣)解:∵=,=,任意点M关于点A的对称点为S,点M关于点B的对称点为N,∴AB是△MNS的中位线,∴=2=2(﹣)=2(﹣).故选:D.8.已知图1是棱长为1的正六边形ABCDEF,将其沿直线FC折叠成如图2的空间图形F′A′E′﹣C′B′D′,其中A′E′=,则空间几何体F'A'E'﹣CB'D'的体积为()A.B.C.D.解:如图,过A′作A′G⊥C′F′,垂足为G,连接E′G,则E′G⊥C′F′,过B′作B′H⊥C′F′,垂足为H,连接D′H,则D′H⊥C′F′,可得平面A′GE′∥平面B′HD′,即三棱柱A′GE′﹣B′HD′为直三棱柱.∵A′F′=1,∠A′F′G=60°,可得,,同理求得,,又A′E′=,∴A′G2+E′G2=A′E′2,∴空间几何体F'A'E'﹣CB'D'的体积为V==.故选:C.二、选择题:本题共4小题,每小题5分,共20分在每小题给出的选项中,有多项符合题目要求全部选对的得5分,有选错的得0分,部分选对的得2分.9.某士官参加军区射击比赛,打了6发子弹,报靶数据如下:7,8,9,10,6,8,(单位:环),下列说法正确的有()A.这组数据的平均数是8B.这组数据的极差是4C.这组数据的中位数是8.5D.这组数据的方差是2解:对于A,这组数据的平均数是(7+8+9+10+6+8)=8,故A正确;对于B,这组数据的极差是10﹣6=4,故B正确;对于C,这组数据从小到大为6,7,8,8,9,10,∴这组数据的中位数是8,故C错误;对于D,这组数据的方差是S2=[(7﹣8)2+(8﹣8)2+(9﹣8)2+(10﹣8)2+(6﹣8)2+(8﹣8)2]=,故D错误.故选:AB.10.已知复数z=cosα+(sinα)i(α∈R)(i为虚数单位),下列说法正确的有()A.当α=﹣时,复平面内表示复数z的点位于第二象限B.当α=时,z为纯虚数C.|z|最大值为D.z的共轭复数为=﹣cosα+(sinα)i(α∈R)解:对于A,当α=﹣时,z=cos()+[sin()]i=﹣,复平面内表示复数z的点位于第四象限,故A错误;对于B,当α=时,z=cos+(sin)i=,为纯虚数,故B正确;对于C,,最大值为,故C正确;对于D,z的共轭复数为=cosα﹣(sinα)i,故D错误.故选:BC.11.某班级到一工厂参加社会实践劳动,加工出如图所示的圆台O1O2,在轴截面ABCD中,AB=AD=BC=2cm,且CD=2AB,下列说法正确的有()A.该圆台轴截面ABCD面积为3cm2B.该圆台的体积为cm3C.该圆台的母线AD与下底面所成的角为30°D.沿着该圆台表面,从点C到AD中点的最短距离为5cm解:由AB=AD=BC=2cm,且CD=2AB,可得CD=4,高O1O2==,则圆台轴截面ABCD面积为(2+4)×=3cm2,故A正确;圆台的体积为V=π(1+4+2)×=πcm3,故B正确;圆台的母线AD与下底面所成的角为∠ADO1,其正弦值为,所以∠ADO1=60°,故C错误;由圆台补成圆锥,可得大圆锥的母线长为4cm,底面半径为2cm,侧面展开图的圆心角为θ==π,设AD的中点为P,连接CP,可得∠COP=90°,OC=4,OP=2+1=3,则CP==5,所以沿着该圆台表面,从点C到AD中点的最短距离为5cm,故D正确.故选:ABD.12.在△ABC中,角A,B,C所对的边分别为a,b,c,点O为△ABC所在平面内点,满足x+y+z=0,下列说法正确的有()A.若x=y=z=1,则点O为△ABC的重心B.若x=y=z=1,则点O为△ABC的外心C.若x=a,y=b,z=c,则点O为△ABC的内心D.若x=a,y=b,z=c,则点O为△ABC的垂心解:若x=y=z=1则,∴.取AC中点D,连接OD,∴.∴O在△ABC的中线BD上,同理可得O在其它两边的中线上,∴O是△ABC的重心.若x=a,y=b,z=c,则有,延长CO交AB于D,则,,∴a()+b()+c=,设=k,则(ka+kb+c)+(a+b)=,∵与共线,与,不共线,∴ka+kb+c=0,a+b=,∴,∴CD为∠ACB的平分线,同理可证其它的两条也是角平分线.∴O是△ABC的内心.故选:AC.三、填空题:本题共4小题,每小题5分,共20分.13.有10种不同的零食,每100克可食部分包含的能量(单位:k)如下:100,120,125,165,430,190,175,234,425,310这10种零食每100克可食部分的能量的第60百分位数为212.解:根据题意,将10个数据从小到大排列:100,120,125,165,175,190,234,310,425,430;10×60%=6,则该组数据的第60百分位数为=212,故答案为:212.14.天气预报元旦假期甲地的降雨概率是0.2,乙地的降雨概率是0.3,假定在这段时间内两地是否降雨相互之间没有影响,则在这段时间内甲,乙两地只有一个地方降雨的概率是0.38.解:根据题意,设事件A表示甲地下雨,事件B表示乙地下雨,P(A)=0.2,P(B)=0.3,甲,乙两地只有一个地方降雨的概率P=P(A)+P(B)=0.2×(1﹣0.3)+(1﹣0.2)×0.3=0.38;故答案为:0.38.15.如图,在三棱锥V﹣ABC中,VA=VB=AB=AC=BC=4,VC=2,则二面角A﹣VC﹣B的余弦值为.解:取VC的中点D,连接AD、BD,因为VA=VB=AC=BC=4,所以AD⊥VC,BD⊥VC,所以∠ADB即为二面角A﹣VC﹣B的平面角,因为VA=VB=AC=BC=4,VC=2,所以AD=BD=,而AB=4,在△ABD中,由余弦定理可得cos∠ADB==,故答案为:.16.如图,△ABC是边长为1的正三角形,M,N分别为线段AC,AB上一点,满足AM:MC=1:2,AN:NB=1:3,CN与BM的交点为P,则线段AP的长度为.解:以A为原点,AB为x轴,建立如图所示的平面直角坐标系,则A(0,0),B(1,0),C(,),M(,),N(,0),所以直线BM的方程为y=(x﹣1),即x+5y﹣=0,直线CN的方程为y=(x﹣),即4x﹣4y﹣=0,联立,解得,即P(,),所以AP==.故答案为:.四、解答题:本题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤. 17.现有两个红球(记为R1,R2),两个白球(记为W1,W2),采用不放回简单随机抽样从中任意抽取两球.(1)写出试验的样本空间;(2)求恰好抽到一个红球一个白球的概率.解:(1)两个红球(记为R1,R2),两个白球(记为W1,W2),采用不放回简单随机抽样从中任意抽取两球,则试验的样本空间Ω={(R1,R2),(R1,W1),(R1,W2),(R2,W1),(R2,W2),(W1,W2)}.(2)试验的样本空间Ω={(R1,R2),(R1,W1),(R1,W2),(R2,W1),(R2,W2),(W1,W2)},包含6个样本点,其中恰好抽到一个红球一个白球包含4个样本点,∴恰好抽到一个红球一个白球的概率P==.18.已知角A是△ABC的内角,若=(sin A,cos A),=(1,﹣1).(1)若,求角A的值;(2)设f(x)=,当f(x)取最大值时,求在上的投影向量(用坐标表示).解:(1)∵角A是△ABC的内角,∴0<A<π,又=(sin A,cos A),=(1,﹣1)且,∴﹣,即2(sin A+)=0,∴sin(A+)=0,∵0<A<π,∴<A+<,则A+=π,即A=;(2)f(x)===,∵<A﹣<,∴要使f(x)取得最大值,则,即A=.∴=(,cos)=(,﹣),∴在上的投影向量为=•(1,﹣1)=(2,﹣2).19.如图,直三棱柱ABC﹣A'B'C'中,D是AB的中点.(1)求证:直线BC′∥平面A'CD;(2)若AC=CB,求异面直线AB'与CD所成角的大小.解:(1)证明:连接AC′,交AC于点O,连接DO,∵直三棱柱ABC﹣A'B'C'中,ACC′A′是矩形,∴O是AC′中点,∵D是AB的中点,∴OD∥BC′,∵BC′⊄平面A'CD,OD⊂平面A'CD,∴直线BC′∥平面A'CD;(2)解法一:∵AC=CB,D是AB的中点,∴CD⊥AB,∵直三棱柱ABC﹣A'B'C'中,AA′⊥平面ABC,∴CD⊂平面ABC,∴AA′⊥CD,∵AB∩AA′=A,∴CD⊥平面ABB′A′,∵AB′⊂平面ABB′A′,∴AB′⊥CD,∴异面直线AB'与CD所成角的大小为90°.解法二:∵AC=CB,D是AB的中点,∴CD⊥AB,以D为原点,DB为x轴,DC为y轴,过D作平面ABC的垂线为z轴,建立空间直角坐标系,设CD=c,AB=a,AA′=b,则A(﹣,0,0),B′(,0,b),C(0,c,0),D(0,0,0),=(a,0,b),=(0,﹣c,0),∵•=0,∴AB′⊥CD,∴异面直线AB'与CD所成角的大小为90°.20.2021年五一假期,各高速公路车流量大,交管部门在某高速公路区间测速路段随机抽取40辆汽车进行车速调查,将这40辆汽车在该区间测速路段的平均车速(km/h)分成六段[90,95),[95,100),[100,105),[105,110),[110,115),[115,120],得到如图的频率分布直方图.(1)根据频率分布直方图估计出这40辆汽车的平均车速的中位数;(2)现从平均车速在区间[90,100)的车辆中任意抽取2辆汽车,求抽取的2辆汽车的平均车速都在区间[95,100)上的概率;(3)出于安全考虑,测速系统对平均车速在区间[115,120]的汽车以实时短信形式对车主进行安全提醒,确保行车安全.假设每辆在此区间测速路段行驶的汽车平均车速相互不受影响,以此次调查的样本频率估计总体概率,求连续2辆汽车都收到短信提醒的概率?解:(1)设平均车速的中位数的估值为x,则0.01×5+0.02×5+0.04×5+0.06×(x﹣105.0)=0.5x=107.5故平均车速的中位数为107.5.(2)车速在[90,95)内的有0.01×40×5=2,车速在[95,100)的有0.02×40×5=4,故抽取的2辆汽车的平均车速都在区间[95,100)上的概率.(3)设事件A为“汽车收到短信提醒”,则,∵汽车的速度不受影响,∴连续两辆汽车都收到短信体现的概率P=.21.如图,PA垂直于⊙O所在的平面,AC为⊙O的直径,AB=3,BC=4,PA=3,AE ⊥PB,点F为线段BC上一动点.(1)证明:平面AEF⊥平面PBC;(2)当点F移动到C点时,求PB与平面AEF所成角的正弦值.【解答】(1)证明:因为PA垂直于⊙O所在的平面,即PA⊥平面ABC,BC⊂平面ABC,所以PA⊥BC,又AC为⊙O的直径,所以AB⊥BC,因为PA∩AB=A,所以BC⊥平面PAB,又AE⊂平面PAB,所以BC⊥AE,因为AE⊥PB,BC∩PB=B,所以AE⊥平面PBC,又AE⊂平面AEF,所以平面AEF⊥平面PBC.(2)解:因为AB=3,PA=3,所以PB==3,又AE⊥PB,所以AE==,由AB2=BE•PB,可得BE=,如图,过点E作EG∥PA交AB于点G,则=,可得EG=,又BC=4,所以EC==,所以S△ABC=AB•BC=6,S△AEC=AE•EC=,设点B到平面AEC的距离为h,由V E﹣ABC=V B﹣AEC,可得S△ABC•EG=S△AEC•h,解得h=,所以当点F移动到C点时,PB与平面AEF所成角的正弦值为=.22.为响应国家“乡村振兴”号召,农民王大伯拟将自家一块直角三角形地按如图规划成3个功能区:△BNC区域为荔枝林和放养走地鸡,△CMA区域规划为“民宿”供游客住宿及餐饮,△MNC区域规划为小型鱼塘养鱼供休闲垂钓.为安全起见,在鱼塘△MNC周围筑起护栏.已知AC=40m,BC=40m,AC⊥BC,∠MCN=30°(1)若AM=20m时,求护栏的长度(△MNC的周长);(2)若鱼塘△MNC的面积是“民宿”△CMA的面积的倍,求∠ACM;(3)当∠ACM为何值时,鱼塘△MNC的面积最小,最小面积是多少?解:(1)∵AC=40m,BC=40m,AC⊥BC,∴tan B==,∴B=30°,∴A=60°,∴AB=2AC=80,在△ACM中,由余弦定理可得CM2=AC2+AM2﹣2AC•AM•cos A=1600+400﹣2×40×20×=1200,则CM=20,∴AC2=AM2+CM2,∴CM⊥AB,∵∠MCN=30°,∴MN=CM tan30°=20,∴CN=2MN=40,∴护栏的长度(△MNC的周长)为20+40+20=60+20;(2)设∠ACM=θ(0°<θ<60°),因为鱼塘△MNC的面积是“民宿”△CMA的面积的倍,所以,即CN=40sinθ,…在△CAN中,由,得CN=,…从而40sinθ=,即sin2θ=,由0°<2θ<120°,得2θ=45°,所以θ=22.5°,即∠ACM=22.5°.…(3)设∠ACM=θ(0°<θ<60°),由(2)知CN=,又在△ACM中,由,得CM=,…所以S△CMN==,…所以当且仅当2θ+60°=90°,即θ=15°时,△CMN的面积取最小值为km2.…(16分)。
2020-2021学年广东省广州市海珠区高二(上)期末数学试卷

2020-2021学年广东省广州市海珠区高二(上)期末数学试卷一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)已知集合{|33}A x x =-<<,集合2{|340}B x x x =--,则(A B = )A .(3-,1]B .[2-,3)C .(3-,2]-D .(3-,1]-2.(5分)已知椭圆2212516x y +=,则该椭圆的离心率为( )A .45B .1625C .35D .9253.(5分)已知命题:0p a ∃,20a a +<,则命题p ⌝为( )A .0a ∀,20a a +B .0a ∀,20a a +<C .0a ∀,20a a +D .0a ∃<,20a a +< 4.(5分)等比数列{}n a 中,已知1236a a a ++=,4563a a a ++=-,则789(a a a ++= ) A .24B .32C .34D .278-5.(5分)某几何体的三视图如图所示,则该几何体的体积为( )A .2π+B .323π+ C .236π+ D .236π+ 6.(5分)设正数m ,n 满足111m n+=,则94m n +的最小值为( ) A .9B .16C .25D .267.(5分)椭圆22221(0)x y m n m n +=>>和双曲线22221(0,0)x y a b a b-=>>有相同的焦点1F ,2F ,点P 是这两曲线的一个交点,则12||||PF PF ⋅的值为( ) A .22m a -B .1()2m a -C m aD .m a -8.(5分)几何体结构素描是学习素描最重要的一个阶段,某同学在画“切面圆柱体”(用不平行于圆柱底面的平面去截圆柱,圆柱底面与截面之间的部分叫做切面圆柱体)的过程中,发现“切面”是一个椭圆,若切面所在平面与底面成30︒角,则该椭圆的离心率为( )A 23B 3C 6D .12二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得3分.9.(5分)已知命题p :若0x y <<,则x y ->-,命题q :若x y <,则22x y <,则下列命题中真命题( ) A .p q ∧ B .p q ∨C .()p q ∧⌝D .()p q ⌝∨10.(5分)已知110a b<<,则下列不等式正确的是( ) A .11a b ab<+ B .||0a b +> C .22lna lnb >D .11a b a b->- 11.(5分)已知直线1l 、2l 的方向向量分别是(2AB =,4,)x ,(2CD =,y ,2),若||6AB =且12l l ⊥,则x y +的值可以是( ) A .3-B .1-C .1D .312.(5分)已知椭圆C 的中心为坐标原点,焦点1F ,2F 在y 轴上,短轴长等于2,离心率61F 作y 轴的垂线交椭圆C 于P 、Q 两点,则下列说法正确的是( ) A .椭圆C 的方程为2213y x +=B .椭圆C 的方程为2213x y += C .23||PQ =D .△2PF Q 的周长为43三、填空题:本题共4小题,每小题5分,共20分.13.(5分)已知x,y满足条件10301x yx yy-+⎧⎪+-⎨⎪>⎩,则32z x y=-+的最小值为.14.(5分)数列{}na的前n项和为nS,已知2(2)nan n=+,则4S=.15.(5分)如图,长方体1111ABCD A B C D-中,2AB AD==,122AA=,若M 是1AA 的中点,则BM与平面11B D M所成角的正弦值是.16.(5分)过双曲线22221(0,0)x ya ba b-=>>的右顶点且斜率为3的直线,与双曲线的左、右两支分别相交,则此双曲线的离心率的取值范围是.(用区间表示)四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.(10分)①454a a+=-,②266a a+=-,③714S=这三个条件中任选一个,补充在下面的问题中,若问题中的存在,求的值;若不存在,说明理由.问题:等差数列{}na前n项和为nS,73a=,若____,是否存在,使得1S S->且1S S+<?18.(12分)在平面直角坐标系xOy中,已知点P到两点(3,0)M,(3,0)N的距离之和等于4,设点P的轨迹为曲线C.(1)求曲线C的方程;(2)若直线2y x=+与曲线C有公共点,求实数的取值范围.19.(12分)某公司进行技术创新,将原本直接排放进大气中的二氧化碳转化为固态形式的化工产品,从而实现“变废为宝、低碳排放”.经过生产实践和数据分析,在这种技术下,该公司二氧化碳月处理成本y(元)与二氧化碳月处理量([300x x∈,600],单位:吨)之间满足函数关系21300800002y x x=-+,假设每处理一吨二氧化碳得到的化工产品的收入为200元.(1)该公司二氧化碳月处理量为多少吨时,每吨的平均处理成本最低,最低平均成本是多少?(2)该公司利用这种技术处理二氧化碳的最大月收益是多少? (月收益=月收入-月处理成本)20.(12分)如图,正三棱柱111ABC A B C -中,D 是AC 的中点. (1)求证:1//AB 平面1DBC ;(2)若11AB BC ⊥,求二面角1D BC C --的余弦值.21.(12分)已知数列{}n a 满足11a =,1133(*)n n n a a n N ++=+∈. (1)求证:数列{}3n n a 是等差数列;(2)求数列{}n a 的通项公式;(3)设数列{}n a 的前n 项和为n S ,求证:37324n n S n >-. 22.(12分)已知点(1,0)A ,E ,F 为直线1x =-上的两个动点,且AE AF ⊥,动点P 满足//EP OA ,//FO OP (其中O 为坐标原点). (1)求动点P 的轨迹C 的方程;(2)若直线l 与轨迹C 相交于两不同点M ,N ,如果4OM ON ⋅=-,证明直线l 必过一定点,并求出该定点的坐标.2020-2021学年广东省广州市海珠区高二(上)期末数学试卷参考答案与试题解析一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)已知集合{|33}A x x =-<<,集合2{|340}B x x x =--,则(A B = )A .(3-,1]B .[2-,3)C .(3-,2]-D .(3-,1]-【解答】解:集合{|33}A x x =-<<, 集合2{|340}{|1B x x x x x =--=-或4}x , {|31}(3AB x x ∴=-<-=-,1]-.故选:D .2.(5分)已知椭圆2212516x y +=,则该椭圆的离心率为( )A .45B .1625 C .35D .925【解答】解:椭圆2212516x y +=,5a ∴=,4b =,3c =, ∴该椭圆的离心率为35c e a ==. 故选:C .3.(5分)已知命题:0p a ∃,20a a +<,则命题p ⌝为( )A .0a ∀,20a a +B .0a ∀,20a a +<C .0a ∀,20a a +D .0a ∃<,20a a +< 【解答】解:特称命题:0p a ∃,20a a +<,由特称命题的否定是全称命题,则命题p ⌝为0a ∀,20a a +. 故选:C .4.(5分)等比数列{}n a 中,已知1236a a a ++=,4563a a a ++=-,则789(a a a ++= ) A .24B .32C .34D .278-【解答】解:等比数列{}n a 中, 由等比数列的性质得:n S ,2n n S S -,32n n S S -成等比数列,由1236a a a ++=,4563a a a ++=-, 得:78933362a a a -++=-⨯=. 故选:B .5.(5分)某几何体的三视图如图所示,则该几何体的体积为( )A .2π+B .323π+ C .236π+ D .236π+ 【解答】解:由题意可知几何体的是组合体,下部是圆柱,上标是四棱锥,圆柱的高为1,四棱锥的高为1, 圆柱的底面半径为12, 所以组合体的体积为:21321122133V ππ+=⋅⋅+=. 故选:B .6.(5分)设正数m ,n 满足111m n+=,则94m n +的最小值为( ) A .9B .16C .25D .26【解答】11494994(94)()1313225n m n m m n m n m n m n m n∴+=+⋅+=+++⋅=, 当且仅当32m n =时等号成立. 故选:C .7.(5分)椭圆22221(0)x y m n m n +=>>和双曲线22221(0,0)x y a b a b-=>>有相同的焦点1F ,2F ,点P 是这两曲线的一个交点,则12||||PF PF ⋅的值为( )A .22m a -B .1()2m a -C .m a -D .m a -【解答】解:由题意,不妨设P 在双曲线的右支上,则12||||2PF PF m +=,12||||2PF PF a -= 1||PF m a ∴=+,2||PF m a =-2212||||PF PF m a ∴⋅=- 故选:A .8.(5分)几何体结构素描是学习素描最重要的一个阶段,某同学在画“切面圆柱体”(用不平行于圆柱底面的平面去截圆柱,圆柱底面与截面之间的部分叫做切面圆柱体)的过程中,发现“切面”是一个椭圆,若切面所在平面与底面成30︒角,则该椭圆的离心率为( )A 23B 3C 6D .12【解答】解:椭圆的长轴为2a ,短轴的长为2b ,“切面”是一个椭圆,若“切面”所在平面与底面成30︒角, 可得2cos302ba=︒32a b =,所以22212c a b e a a -===. 故选:D .二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得3分.9.(5分)已知命题p :若0x y <<,则x y ->-,命题q :若x y <,则22x y <,则下列命题中真命题( ) A .p q ∧B .p q ∨C .()p q ∧⌝D .()p q ⌝∨【解答】解:若0x y <<,则0x y ->->,即命题p 是真命题,当1x =-,0y =时,满足x y <,但22x y <,不成立,即命题q 是假命题,则p q ∨为真命题,p q ∧为假命题,()p q ∧⌝是真命题,()p q ⌝∨为假命题, 故选:BC . 10.(5分)已知110a b<<,则下列不等式正确的是( ) A .11a b ab<+ B .||0a b +> C .22lna lnb > D .11a b a b->- 【解答】解:由110a b<<,可得0a b >>. 所以11a b ab<+,故A 正确; 因为0a b <-<-,所以||a b <-,即||0a b +<,故B 错误;由0a b <-<-,可得22a b <,所以22lna lnb <,故C 错误; 由110a b <<,可得11a b->-,又a b >, 所以11a b a b->-,故D 正确. 故选:AD .11.(5分)已知直线1l 、2l 的方向向量分别是(2AB =,4,)x ,(2CD =,y ,2),若||6AB =且12l l ⊥,则x y +的值可以是( ) A .3-B .1-C .1D .3【解答】解:直线1l 、2l 的方向向量分别是(2AB =,4,)x ,(2CD =,y ,2),||6AB =且12l l ⊥,∴64420y x ++=⎪⎩,解得216220x x y ⎧=⎨++=⎩,∴43x y =⎧⎨=-⎩或41x y =-⎧⎨=⎩,1x y ∴+=或3x y +=-.故选:AC .12.(5分)已知椭圆C 的中心为坐标原点,焦点1F ,2F 在y 轴上,短轴长等于2,离心率1F 作y 轴的垂线交椭圆C 于P 、Q 两点,则下列说法正确的是( )A.椭圆C的方程为2213yx+=B.椭圆C的方程为2213xy+= C.23||3PQ=D.△2PF Q的周长为43【解答】解:由已知得,22b=,1b=,63ca=,又222a b c=+,解得23a=.∴椭圆方程为2213yx+=.如图:2223||3bPQa∴===,△2PF Q的周长为443a=.故选:ACD.三、填空题:本题共4小题,每小题5分,共20分.13.(5分)已知x,y满足条件10301x yx yy-+⎧⎪+-⎨⎪>⎩,则32z x y=-+的最小值为2-.【解答】解:由约束条件10301x yx yy-+⎧⎪+-⎨⎪>⎩作出可行域如图,联立301x y y +-=⎧⎨=⎩,解得(2,1)A ,化目标函数32z x y =-+为32y x z =+,由图可知,当直线32y x z =+过A 时,直线在y 轴上的截距最小,z 有最小值为2-. 故答案为:2-.14.(5分)数列{}n a 的前n 项和为n S ,已知2(2)n a n n =+,则4S = 1715.【解答】解:已知211(2)2n a n n n n ==-++, 则1111111111111132435112212n S n n n n n n =-+-+-+⋯+-+-=+---++++, 所以411117125615S =+--=. 故答案为:1715. 15.(5分)如图,长方体1111ABCD A B C D -中,2AB AD ==,122AA =,若M 是1AA 的中点,则BM 与平面11B D M 所成角的正弦值是63.【解答】解:由勾股定理知,2211246B M D M BM AM BM ===+=+=,112B D = ∴112211111111()226222222B D MSB D B M B D =-⨯- 设点B 到平面11B D M 的距离为h , 1111B B D M M BB D V V --=, ∴1111111113322B D Mh S AC BB B D ⋅=⋅⋅⋅, 即122222222h ⋅=⋅2h ∴=,设BM 与平面11B D M 所成角为θ,则1sin h B M θ===, 故BM 与平面11B D M16.(5分)过双曲线22221(0,0)x y a b a b-=>>的右顶点且斜率为3的直线,与双曲线的左、右两支分别相交,则此双曲线的离心率的取值范围是) .(用区间表示)【解答】解:过双曲线22221(0,0)x y a b a b-=>>的右顶点且斜率为3的直线,与双曲线的左、右两支分别相交, 双曲线的一条渐近线的斜率b a 必大于3,即3ba>,因此该双曲线的离心率c e a === 故答案为:)+∞.四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤. 17.(10分)①454a a +=-,②266a a +=-,③714S =这三个条件中任选一个,补充在下面的问题中,若问题中的存在,求的值;若不存在,说明理由. 问题:等差数列{}n a 前n 项和为n S ,73a =,若 ____,是否存在,使得1S S ->且1S S+<?【解答】解:若存在,使得1SS ->且1S S+<,则0a <,10a+>,设等差数列{}n a 首项为1a ,公差为d ,若选择条件①:由74534a a a =⎧⎨+=-⎩,可得1163274a d a d +=⎧⎨+=-⎩,解得192a d =-⎧⎨=⎩,所以92(1)211n a n n =-+-=-,*n N ∈, 由0n a <,可得112n <, 所以当5=时,满足50a <,60a >.若选择条件②:由72636a a a =⎧⎨+=-⎩,可得1163266a d a d +=⎧⎨+=-⎩,解得192a d =-⎧⎨=⎩,所以92(1)211n a n n =-+-=-,*n N ∈, 由0n a <,可得112n <, 所以当5=时,满足50a <,60a >.若选择条件③:由77314a S =⎧⎨=⎩,可得116372114a d a d +=⎧⎨+=⎩,可得1113a d =⎧⎪⎨=⎪⎩,所以1121(1)333n a n n =+-=+,*n N ∈,易知0n a >恒成立, 所以不存在满足条件的.18.(12分)在平面直角坐标系xOy 中,已知点P到两点M,(N 的距离之和等于4,设点P 的轨迹为曲线C . (1)求曲线C 的方程;(2)若直线2y x =+与曲线C 有公共点,求实数的取值范围. 【解答】解:(1)由已知可得||||4||PM PN MN +=>=,由椭圆的定义可知点P 的轨迹C 是以M ,N为焦点,焦距长为4的椭圆, 所以2a =,c =,则2431b =-=,所以轨迹C 的方程为2214x y +=;(2)联立方程22214y x x y =+⎧⎪⎨+=⎪⎩,消去y 整理可得:22(14)16120x x +++=,因为直线与椭圆有公共点,则△2225648(14)0=-+,解得33kk -或,故实数的取值范围为3(,[,)-∞+∞. 19.(12分)某公司进行技术创新,将原本直接排放进大气中的二氧化碳转化为固态形式的化工产品,从而实现“变废为宝、低碳排放”.经过生产实践和数据分析,在这种技术下,该公司二氧化碳月处理成本y (元)与二氧化碳月处理量([300x x ∈,600],单位:吨)之间满足函数关系21300800002y x x =-+,假设每处理一吨二氧化碳得到的化工产品的收入为200元.(1)该公司二氧化碳月处理量为多少吨时,每吨的平均处理成本最低,最低平均成本是多少?(2)该公司利用这种技术处理二氧化碳的最大月收益是多少? (月收益=月收入-月处理成本)【解答】解:(1)设每吨的平均处理成本为t 元, 由已知可得18000300,[300,600]2y t x x x x==+-∈, 所以1800018000300230022t x x x =+-⨯ 400300100=-=,当且仅当180002x x=,即400x =时取等号, 故二氧化碳月处理量400吨时,每吨的平均处理成本取到最低值100元; (2)设公司利用这种技术处理二氧化碳的月收益是U 元, 由已知可得21200(3008000)2U x x x =--+,[300x ∈,600],所以22115008000(500)4500022U x x x =-+-=--+, 当500x =时,45000max U =, 当300x =时,25000min U =,故当[300x ∈,600]时,[25000U ∈,45000],所以该公司利用这种技术处理二氧化碳的最大月收益是45000元,此时二氧化碳的月处理量为500吨.20.(12分)如图,正三棱柱111ABC A B C -中,D 是AC 的中点. (1)求证:1//AB 平面1DBC ;(2)若11AB BC ⊥,求二面角1D BC C --的余弦值.【解答】解:(1)证明:连接1B C ,交1BC 于E ,连接DE , 由已知得四边形11BB C C 为矩形,E ∴是1B C 中点, 在△1AB C 中,D 为AC 中点,1//AB DE ∴, 1AB ⊂/平面1DBC ,DE ⊂平面1DBC , 1//AB ∴平面1DBC .(2)设E 、F 分别为1B C 、BC 的中点,连接EF ,AF , 由已知得AF BC ⊥,AF EF ⊥,EF BC ⊥,以F 为原点,分别以FB ,EF ,FA 所在直线为x ,y ,z 轴,建立空间直角坐标系, 设1BB a =,2BC b =,则(0A ,03)b ,(B b ,0,0),1(B b ,a -,0),(C b -,0,0),1(C b -,a -,0), ∴1(AB b =,a -,3)b ,1(2BC b =-,a -,0),11AB BC ⊥,∴221120AB BC b a ⋅=-+=,解得2b =,∴1(2C B a =,a ,0), D 是AC 中点,∴2a ,06a ,∴32(a DB =,0,6a , (0n =,0,1)是平面1CBC 的法向量.设平面1DBC 的法向量(m x =,y ,)z ,则1203260m C B ax ay a a m DB ⎧⋅=+=⎪⎨⋅=-=⎪⎩,取1z =,得36(,m =, 2cos ,||||2m n m n m n ⋅∴<>===⋅∴二面角1D BC C --的余弦值为2.21.(12分)已知数列{}n a 满足11a =,1133(*)n n n a a n N ++=+∈. (1)求证:数列{}3n n a 是等差数列;(2)求数列{}n a 的通项公式;(3)设数列{}n a 的前n 项和为n S ,求证:37324n n S n >-. 【解答】证明:(1)数列{}n a 满足11a =,1133(*)n n n a a n N ++=+∈, 整理得11133n nn na a ++-=(常数), 当1n =时,11133a =, 所以数列{}3n n a 是以13为首项,1为公差的等差数列.解:(2)由于数列{}3n n a 是以13为首项,1为公差的等差数列,所以2()33n n a n =-⨯.证明:(3)由于2()33n n a n =-⨯,故12222(1)3(2)3()3333n n S n =-⨯+-⨯+⋯+-⨯①,2312223(1)3(2)3()3333n n S n +=-⨯+-⨯+⋯+-⨯②,②-①得:111239772()31()33262n n n n S n n +++-=-⨯--=-⨯+,故177()32124n n n S +=-⨯+,所以17()3737737212()3343244324n n n n n n n S n n +-⨯=+=-+>-⨯⨯.22.(12分)已知点(1,0)A ,E ,F 为直线1x =-上的两个动点,且AE AF ⊥,动点P 满足//EP OA ,//FO OP (其中O 为坐标原点). (1)求动点P 的轨迹C 的方程;(2)若直线l 与轨迹C 相交于两不同点M ,N ,如果4OM ON ⋅=-,证明直线l 必过一定点,并求出该定点的坐标.【解答】解:(1)设(,)P x y ,(1,)E a -,(1,)F m -,则(2,),(2,)AE a AF m =-=-,(1,),(1,0),(1,),(,)EP x y a OA FO m OP x y =+-==-=, 由AE AF ⊥,则有(2-,)(2a ⋅-,)0m =且点E ,F 不在x 轴上, 故4am =-,且0a ≠,0m ≠, 由//EP OA ,可得0y a -=,即y a =, 由//FO OP ,可得0mx y +=,即y mx =-, 所以24y amx x =-=-,故动点P 的轨迹C 的方程为24(0)y x x =≠; (2)根据题意可设直线l 的方程为(0)x ty b b =+≠, 由24x ty b y x=+⎧⎨=⎩,可得2440y ty b --=, 设1(M x ,1)y ,2(N x ,2)y , 则124y y t +=,124y y b =-,故22222212121212(1)()4(1)44OM ON x x y y t y y bt y y b b t bt b b b ⋅=+=++++=-+++=-,由4OM ON ⋅=-,解得2b =,故直线l 的方程为2x ty =+,恒过定点(2,0).。
广东省省实、广雅、执信、二中、六中五校2020-2021学年高二上学期期末联考试题 数学 pdf版

∴ y 0.04 0.004 ······4 分 10
1
由题意,80%分位数在[70,80]组内,······5 分
则(0.016+0.032)×10+(t-70)×0.04=0.80······6 分
解得 t=78
∴估计 t 的最小值为 78 分······7 分
cos B
sin B
即(cos A-2cos C)sin B=(2sin C-sin A)cos B,
化简可得 sin(A+B)=2sin(B+C).······2 分
因为 A+B+C=π,所以 sin C=2sin A. ······3 分
因此sin C=2.······4 分 sin A
(2)由sin C=2,得 c=2a.······5 分由余弦定理 b2=a2+c2-2accos B 及 cos B=1,b=2,
12. 已知三棱柱 ABC A1B1C1 的侧棱和底面垂直,且所有顶点都在球 O 的表面上,侧面 BCC1B1 的面积为 4 3 .则正确的结论是( * ) A.若 B1C1 的中点为 E,则 AC1 // 平面 A1BE B.若三棱柱 ABC A1B1C1 的体积为 4 3 ,则 A1 到平面 BCC1B1 的距离为 3
B. ,0 1, 2 D. 1, 2
2. 已知 a 0.3 , b 20.3, c 0.30.2 则 a, b, c 三者的大小关系是( * )
A. b c a
B. b a c C. a b c
D. c b a
3. 已知直线 m、n 和平面α,在下列给定的四个结论中,m//n 的一个必要但不充分条件是
零点,求 a 1 的最小值. a
广州海珠区2020-2021学年高二上学期期末联考试题

广州海珠区2020-2021学年高二上学期期末联考试题一、阅读理解1. Around the Mount Rushmore area of South Dakota, there are many things that you can do with the family. Below is a list of tours we can provide.Tour 1This tour brings visitors to the Holy Terror Mini Golf course. Since it is located on the side of a hill, you get to experience the fresh South Dakota air and enjoy the great outdoors. The course features three different types of turf that simulates (模拟) a real golf course and it features many slopes and stairs, Therefore, it is a challenging course for those who love a little competition.Available between Mar 15&Oct 31Tour2Take a fun train tour to find out how people used to travel in the days before modern cars. Experience travel the way it was in the 19th century with the 1880 Train, a completely restored authentic steam engine train, as you explore the beautiful Black Hills area of South Dakota.Available between May 9&Sept 30Tour 3This is an 8-hour guided sightseeing bus tour. You’ll see Mount Rushmore Nati onal Memorial, Crazy Horse Memorial, Custer State Park, as well as other beautiful sights along the way for a great introduction into American history. Lunch and hotel pickup are included. The tour runs daily and is disabled-accessible.Available between May 13&Sept 15Tour 4This tour gives visitors the chance to tour an authentic gold mine—Big Thunder Gold Mine. The museum is a fascinating and informative site with displays showing what lite was like for those who really “went for the gold”. There is no additional charge to get in the museum, guests are encouraged to try and pan for gold and other riches.Available between May 25&Oct 111. Where can visitors go in April?A.Crazy Horse Memorial.B.Big Thunder Gold Mine.C.The Holly Terror Mini Golf course.D.Mount Rushmore National Memorial.2. Which tour is friendly to people with disabilities?A.Tour 1. B.Tour 2. C.Tour 3. D.Tour4.3. What is special about Tour 4?A.Visitors can try their hand at mining.B.Visitors can take part in a competition.C.It offers visitors free hotel pickup.D.It is a steam train guided tour.2. Each country has its own set of national impression, but perhaps the most famous is Britain’s love of tea. According to the BBC, they drink over 60 billion cups each year. The most popular tea type in the UK is black tea. It’s a simple recipe: You find a mug, add a tea bag, pour boiling water, add milk and sugar (according to your taste) and finish by stirring.Usually,the only debate is whether milk should be added before or after the boiling water. But a recent popular video has made Britons annoved, American TikTok user, Sophie, posted her version of “British tea”, which involved microwaving cold water, then adding milk, sugar and an instant teabag containing powdered lemonade, cinnamon and clove leaves.Mainstream media called the method “deeply disturbed”, and a Twitter user even wrote, “I would rather see tea wasted into the Boston harbor than drink this.”As you can tell, tea is a precious part of British l ife, whether you’re having afternoon tea at a fancy hotel or drinking it in a takeaway cup.“Rosie Lee”, a common slang term for tea, first came to Britain in the mid-1600s from China. Since then, the country’s love for it has not declined.Types of tea can even indicate someone’s social class, according to anthropologist Kate Fox. In her book, she notes that “teas get progressively weaker as one goes up the social ladder”, like black tea served during afternoon tea. Fox added, “Taking sugar in your tea is a lower-class indicator: More than one and you are lower-middle at best; more than two and you are definitely working class.”Despite the argument on what makes a perfect “cuppa”, Britons can at least agree on the saying, “No matter what is happening in your life, you always offer tea.”1. What do we know about tea drinking in UK?A.The British drink over 60 billion cups each month.B.The British pour boiling water over the tea bag.C.“Rosie Lee” is Britons’ favorite tea type.D.Its history dates back to the 16th century.2. Why did Sophie’s video anger Britons?A.She criticized the way Britons drink tea.B.She added milk after the boiling water.C.She used a strange tea bag.D.Her way of making tea was against their tradition3. What does the underlined word “this” refer to in paragraph 3?A.Tea made by Sophie.B.A mixture of sugar and milk.C.Microwaved lemonade with teabag.D.Cold water with teabag.4. What is the text mainly about ?A.Tea drinking culture in the UK.B.The debate on how to make perfect tea.C.The influence of tea drinking on Britons’lives.D.British tea traditions among different social classes.3. Reviewing photos fresh from the printer and discussing new ideas in the meeting room, I express my creative side by translating real-world trends and topics into the print in the SHSID, the school magazine of Shanghai High School International Division.I was first interested in visuals and design because of their power to communicate ideas. Throughout my three and a half year s in the design department of the SHSID, I’ve faced the ongoing challenge of translating ideas into visuals that are not only appealing, but also informative.In the early days of my participation as a freshman designer, every issue of the magazine came with frustration from struggling over the difficulties of Photoshop to seeing my designs changed completely by the editors working above me. However, after constant experiments and many long months of practicing, I finally started to understand the key elements of the position. Two years later, I was offered the job of creative director.The newly earned position came with unique challenges. Unlike a normal art piece or design, spread, designing a bimonthly (双月刊), 52-page magazine is really challenging.The finished product must contain not only my ideas, but also those of other department directors and the 20 members of my team. Through waves of differing opinions over the years, I’ve learned much about negotiation, leadership, and compromise.Applying these lessons still produces a sense of accomplishment: the feeling of joy as repostsof our video projects fill everyone’s news feeds; the satisfaction as fellow designers come up with ideas of inspiration; the excitement whenever others offer the magazine praise. These moments make the long nights of frozen computer screens and staying up late completely worth it.By the September/October 2017 issue, the magazine had achieved all that I’d hoped for. Through authentic and catching photo spreads, illustrations (插画) and articles, we’ve done everything from communicating ideas on shifting pop culture identity to building a greater appreciation for Chinese culture in our school community.1. What does the author do now?A.A director. B.An editor. C.A photographer. D.A designer. 2. What made the author feel frustrated at the beginning?A.He couldn’t use some software well.B.He couldn’t stand others changing his design.C.He didn’t do many experiments and practice.D.He didn’t get the key factors of his position.3. The author thought his newly position was challenging, because he needed to_____. A.negotiate with other department directorsB.combine his ideas with other directorsC.compromise on the ideasD.widely cooperate with others4. How did the author feel after the bimonthly magazine came out?A.Annoyed. B.Confused. C.Satisfied. D.Inspired.4. Before its first planned observations of the universe, the Large Synoptic Survey Telescope (LSST) has received a new name. In an announcement made at the 235th annual meeting of the American Astronomical Society (AAS), officials declared that the facility, set to achieve first light in October 2020, would be known as the NSF Vera C. Rubin Observatory (VRO). The change marks the first time a national United States Observatory has been named for a woman.Naming the observatory after Rubin is an especially fitting way to honor her work. Since the observatory’s construction was first put forward nearly 20 years ago, researchers have eagerly awaited the day the telescope begins to explore the universe for dark matter, the substance thought to hold galaxies to gether. Rubin’s pioneering studiesin the 1970s offered some of the first evidence of dark matter’s existence. She helped the world realize that the universe was dominated not by visible matter, but by something humans have not observed directly.“Her discoveries constituted (构成) one of the most important contributions to science in the past century, not only for astronomy, but also for fundamental physics,” Steve Kahn, the VRO director, said in a statement.In addition to studying dark matter, the VRO will also study near-Earth asteroids (小行星),search for interstellar (星际的) objects and continue the ongoing project to map the Milky Way.Even as our knowledge of the universe expands, Rubin’s name will serve as a reminder that there’s still plenty of work to do right here on Earth. Rubin spent her career measuring the forces of the universe she could not see. But her reach included a far more visible change as well: her fight, for gender equality in the sciences. In a letter to one of her own female scienti fic friends, Rubin once wrote, “From you we have learned. . .that it’s all right to be charming, brilliant, and to be concerned for others as we make our way in the world of science. A woman too can rise to great heights as an astronomer.”1. The opening paragraph is mainly intended to________.A.provide some key facts about the LSSTB.introduce the main idea of the passageC.attract the readers’ interest in the subjectD.show great contribution the LSST has made2. What does the underlined word “dominated” mean in paragraph2? A.Connected. B.Protected. C.Reminded. D.Mastered.3. Rubin’s achievement includes________.①finding the evidence of the dark matter②realizing the domination of the universe③making contributions to astronomy and physics④searching for stars in the Milky WayA.①②④B.②③④C.①②③D.①③④4. Which of the following would Rubin probably NOT agree with?A.There is still lots of work to do with the space.B.Women should concern more about others than themselves.C.Women can be a great astronomer as well.D.Women need to care about appearance.二、七选五5. If you see a black cat crossing your path, is this lucky or unlucky? Or if you walk under aladder? And how do you feel about the number 13 or 7? 1 “Looking on the bright side of life” really does make you lucky.Psychologists now think they have proved your luck has nothing to do with what you are wearing or what you are carrying in your pocket. 2 As Shakespeare almost put it, “It’s not in t he stars —it’s in ourselves.”3 It was carried out by Professor Wiseman at the University of Herefordshire. He found that most people believed that good or bad things happened to them for no reason, and called this “having good or bad luck”.4 He conducted a simple experiment. He asked people to look through a newspaper, and tell him how many photographs there were inside. Halfway through the newspaper there was a very clear message, taking up half a page, stating in large letters:“Report that you have seen this and win $250.” Those who thought that they were unlucky tended to miss this message completely. 5 Professor Wiseman concluded that this is because “unlucky” people are people who worry more. This anxiety interferes with their a bility to notice things, so they miss the chances that “lucky” people always spot. He began to realize that people made their own luck by thinking in certain ways.A.It is more a question of how you think about yourself.B.Whatever you believe, luck is just a matter of the way you think about things. C.The ones who already felt lucky had become even luckier.D.Most people feel either lucky or unlucky, and every country has its superstitions about this.E.Actually, it was a question of how they thought about themselves and how they behaved.F.But the ones who believed themselves to be lucky tended to notice it.G.This might sound rather obvious, but some recent research has thrown some interesting light upon the subject.三、完形填空6. Imagine your favourite song. Now________the way it makes you feel. Chances are, if you asked a friend how that same song made them feel, they would have the same ________.Alan Cowen wanted to know whether people who lived in ________ countries would respond that way, too. He thought it was ________that music Americans consider angry would be considered scary by people who lived somewhere else.Cowen is a researcher. He ________ a study of more than 2500 people in the United States and China. He and his fellow researchers________them many kinds of music.They found that everyone had pretty much the same________response to the music. For example, “The Star-Spangled Banner” made people feel pride, ________Ed Sheeran’s “Shape of You” made them feel joyful. But even though peo ple in China and the United States felt angry while listening to a________song, says Cowen. “They differed in whether they thought that________was good or bad.”Past research by other scientists has shown that people across cultures________as many as six basic emotions: fear, anger, surprise, disgust, sadness and happiness. But Cowen’s study identified motional responses or ________ “felt through the language of music”. Perhaps coolest of all, the researchers ________an interactive map of those musical emotions.Teachers around the world are using this map in their________. It is helping students find newwords to describe their emotions. This ability could help them control their own emotions or better ________ other people’s feelings.1.A.depend on B.compare with C.think about D.laugh at2.A.response B.direction C.responsibility D.purpose3.A.native B.nearby C.faraway D.different4.A.necessary B.possible C.convenient D.clear5.A.considered B.required C.organized D.proved6.A.played B.booked C.taught D.awarded7.A.negative B.strange C.helpful D.emotional8.A.so B.if C.though D.while9.A.complete B.particular C.same D.familiar10.A.experience B.program C.arrangement D.progress11.A.mix B.demand C.share D.separate12.A.feelings B.abilities C.questions D.interests13.A.created B.printed C.downloaded D.recognized14.A.homes B.offices C.playgrounds D.classrooms15.A.admit B.affect C.understand D.decide四、用单词的适当形式完成短文7. 阅读下面短文,在空白处填入一个适当的单词或括号内单词的正确形式。
海珠区高二文科第一学期期末联考试题和详细答案

海珠区第一学期期末联考试题高二数学(文科)本试卷共6页,22小题,满分150分.考试用时120分钟.注意事项:1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的学校、考号、姓名填写在答题卡相应的位置,将条型码粘在相应的条形码区。
2.回答选择题时,选出每小题答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷 (选择题 共60分)一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.椭圆22143x y +=的离心率是A .2B .12C .2D .142.已知命题:p x y <若,则22x y <;命题:q x y >若,则x y -<-;在命题: ①p q ∧;②p q ∨;③()p q ⌝∧; ④()p q ∨⌝中,真命题是A .①③B . ①④C .②③D . ②④3. 设平面α、β,直线a 、b ,a α⊂,b α⊂,则“//a β,//b β”是“//αβ”的 A .充分不必要条件 B .必要不充分条件 C .充要条件D .既不充分也不必要条件4.若函数()()0,1xf x a a a =>≠且是定义域为R 的减函数,则函数()()log 1a f x x =-的图象大致是5. 为了了解本市居民的生活成本,甲、乙、丙3名同学利用假期分别对3个社区进行了“家庭每月日常消费额”的调查.他们将调查所得到的数据分别绘制成频率分布直方图(如图所示),记甲、乙、丙所调查数据的标准差分别为123,,s s s ,则它们的大小关系为A .321s s s <<B .231s s s <<C .312s s s <<D .213s s s <<6. 已知向量()=cos ,1x a ,()cos ,1x -b =, 设函数()f x =⋅a b ,则A .()f x 为偶函数且最小正周期为πB .()f x 为奇函数且最小正周期为πC .()f x 为偶函数且最小正周期为2πD .()f x 为奇函数且最小正周期为2π 7. 已知数列{}n a 满足13132n n a a ++=+,且11a =,则5a =A. 52- B. 125C. 61D. 238-8. 如图所示的茎叶图记录了甲、乙 两组各5名学生在一次英语听力测 试中的成绩.已知甲组数据的中位 数为15,乙组数据的平均数为16.8, 则,x y 的值分别为A .25,B .5,5C .5,8D .88,9.如图所示,圆锥的底面半径为1,母线长为2,在圆锥上方嵌入一个半径为r 的球,使圆锥的母线与球面相切,切点为圆锥母线的端点,则该球的表面积为 A .23πB .3πC .4πD .163π第8题图 第9题图元元丙第5题图10. 若正整数N 除以正整数m 后的余数为r ,则记为()mod N r m =,例如()102mod4= .下列程序框图的算法源于我国古代算术《中国剩余定理》,则执行该程序框图输出的i 等于 A .2 B .4C .8D .1111.已知正三棱柱111ABC A B C -中,12AB BB ==,则异面直线1AB 与1BC所成角的余弦值为AB .12C .14-D .1412.已知函数()1,02ln ,0xx f x x x ⎧⎛⎫≤⎪ ⎪=⎨⎝⎭⎪>⎩,若函 数()()g x f x k =-有两个零点, 则实数k 的取值范围为A .()0+∞,B .[)1+∞,C .()01,D .()1+∞,第Ⅱ卷 (非选择题 共90分)二、填空题: 本大题共4小题,每小题5分,共20分。
2020-2021学年广东省广州市海珠实验中学高二数学理上学期期末试题含解析

2020-2021学年广东省广州市海珠实验中学高二数学理上学期期末试题含解析一、 选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的 1. 已知直线的点斜式方程是,那么此直线的倾斜角为参考答案: C,,故选.2. 已知方程,它们所表示的曲线可能是 ( )A .B .C .D .参考答案:B3. 随机变量X 的分布列如右表,若,则( )A .B .C .D .参考答案:B4. 春天来了,某学校组织学生外出踏青.4位男生和3位女生站成一排合影留念,男生甲和乙要求站在一起,3位女生不全站在一起,则不同的站法种数是( ) A .964 B .1080C .1152D .1296参考答案:C【考点】D8:排列、组合的实际应用.【分析】根据题意,先用捆绑法分析“甲和乙站在一起”的情况数目,再其中求出“甲和乙站在一起且女生全站在一起”的情况数目,用“甲和乙站在一起”的情况数目减去“甲和乙站在一起且女生全站在一起”的情况数目即可得答案.【解答】解:根据题意,男生甲和乙要求站在一起,将2人看成一个整体,考虑2人的顺序,有A 22种情况,将这个整体与其余5人全排列,有A 66种情况, 则甲和乙站在一起共有A 22A 66=1440种站法,其中男生甲和乙要求站在一起且女生全站在一起有A 22A 33A 44=288种; 则符合题意的站法共有1440﹣288=1152种; 故选:C .5. 不等式|x +1|·(2x -1)≥0的解集为A .{}B .{}C .{}D.{参考答案:C6. 在中,分别是的对边,已知成等比数列,且,则的值为 ( )(A) (B) (C)(D)参考答案:C7. 对任意非零实数,定义的算法原理如上右侧程序框图所示。
设为函数的最大值,为双曲线的离心率,则计算机执行该运算后输出结果是 ( )A、 B、 C、 D、参考答案:B略8. 已知椭圆上的一点到椭圆一个焦点的距离为,则到另一焦点距离为()A. B. C. D.参考答案:D9. 命题p:不等式ax2+2ax+1>0的解集为R,命题q:0<a<1,则p是q成立的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件参考答案:B【考点】必要条件、充分条件与充要条件的判断.【分析】求出命题的等价条件,结合充分条件和必要条件的定义进行判断即可.【解答】解:当a=0时,不等式ax2+2ax+1>0的解集为R,满足条件.当a≠0时,则满足,即,即0<a<1时,综上,不等式ax2+2ax+1>0的解集为R时,0≤a<1,则p是q成立必要不充分条件,故选:B.【点评】本题主要考查充分条件和必要条件的判断,根据不等式的性质是解决本题的关键.10. 下列命题中:(1)、平行于同一直线的两个平面平行;(2)、平行于同一平面的两个平面平行;(3)、垂直于同一直线的两直线平行;(4)、垂直于同一平面的两直线平行.正确的是()A、(1)(2)B、(2)(4)C、(2)(3)D、(3)(4)参考答案:B二、填空题:本大题共7小题,每小题4分,共28分11. 命题“如果点M的坐标满足双曲线C的方程,则点M在双曲线C的图象上”的逆否命题是_______________________________________________________________参考答案:_如果点M不在双曲线C上,则点M的坐标不满足双曲线C的方程略12. 已知椭圆:的一个焦点是, 两个焦点与短轴的一个端点构成等边三角形, 则椭圆的方程是ks5u参考答案:13. 在等差数列中,,,则= .参考答案:2n-314. 已知f (x )是定义在[﹣2,2]上的奇函数,当x∈(0,2]时,f (x )=2x﹣1,函数g (x )=x 2﹣2x+m .如果对于?x 1∈[﹣2,2],?x 2∈[﹣2,2],使得g (x 2)=f (x 1),则实数m 的取值范围是 .参考答案:[﹣5,﹣2]【考点】指数函数综合题;特称命题.【分析】求出函数f (x )的值域,根据条件,确定两个函数的最值之间的关系即可得到结论. 【解答】解:∵f(x )是定义在[﹣2,2]上的奇函数,∴f(0)=0, 当x∈(0,2]时,f (x )=2x ﹣1∈(0,3], 则当x∈[﹣2,2]时,f (x )∈[﹣3,3],若对于?x 1∈[﹣2,2],?x 2∈[﹣2,2],使得g (x 2)=f (x 1), 则等价为g (x )max ≥3且g (x )min ≤﹣3,∵g(x )=x 2﹣2x+m=(x ﹣1)2+m ﹣1,x∈[﹣2,2], ∴g(x )max =g (﹣2)=8+m ,g (x )min =g (1)=m ﹣1, 则满足8+m≥3且m ﹣1≤﹣3, 解得m≥﹣5且m≤﹣2, 故﹣5≤m≤﹣2, 故答案为:[﹣5,﹣2]15. 如果方程表示双曲线,那么实数的取值范围是 .参考答案:或略16. 已知直线y=x+1与曲线相切,则α的值为参考答案: 2解:设切点,则,又.17. 设平面区域是由双曲线的两条渐近线和抛物线的准线所围成的三角形(含边界与内部).若点,则目标函数的最大值与最小值之和为 .参考答案:3 略三、 解答题:本大题共5小题,共72分。
广东省珠海市2020-2021学年高二上学期期末数学试题及答案

第四,破“应用公式关”.
20.
【分析】
求 的长转为求 ,而 ,按照向量的模长求法,即可求解.
【详解】
由已知,可得 , , ,
,
,
.
故答案为 .
21.(1) ;(2) .
【分析】
(1)由 为真可得 ,从而 ,进而可得答案;
(2)由 是 的充分不必要条件,可得 (等号不同时成立),进而可得答案.
17.正方体 的棱长为 ,点 和 分别是 和 的中点,则异面直线 和 所成角的余弦值为__________.
18.一个动圆与圆 外切,与圆 内切,则这个动圆圆心的轨迹方程为:______.
19.如图所示,在长方体 中 , ,点 是棱 的中点,则点 到平面 的距离为__________.
20.如图,在一个直二面角 的棱上有两点 , , , 分别是这个二面角的两个面内垂直于 的线段,且 , , ,则 __________.
则最大的样本编号为3+15×11=168,
故选:A.
3.C
【分析】
由 , 的坐标求出 的坐标,求其模可得 与 的距离.
【详解】
点 ,点 ,
,
则 .
故选:C.
4.D
【分析】
先找出命题为真命题的充要条件 ,从集合的角度充分不必要条件应为 的真子集,由选项得出答案.
【详解】
, ,∴要使 恒成立,即 ,
本题求的是充分不必要条件,结合选项,只有D符合.
三、解答题
21.已知命题 :“关于 的方程 有实数根”,命题 :“ ”,命题 :“ ”.
(1)若 是真命题,求 的取值范围;
(2)若 是 的充分不必要条件,求 的取值范围.
广东省广州市职业高级中学2020-2021学年高二数学理期末试卷含解析

广东省广州市职业高级中学2020-2021学年高二数学理期末试卷含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 已知全集为R,集合,,则集合A.B.C.D.参考答案:C2. 某大学的大门蔚为壮观,有个学生想搞清楚门洞拱顶D到其正上方A点的距离,他站在地面C处,利用皮尺量得BC=9米,利用测角仪测得仰角∠ACB=45°,测得仰角∠BCD后通过计算得到sin∠ACD=,则AD的距离为()A.2米B.2.5米C.3米D.4米参考答案:C【考点】解三角形的实际应用.【专题】计算题;应用题;解三角形.【分析】根据已知条件求出AB=BC=9米,再根据在Rt△BDC中,BD=tan(45°﹣∠ACD)?BC,求出BD 的值,最后根据AD=AB﹣BD,即可得出答案.【解答】解:∵Rt△ACB中,∠ACB=45°,∴BC=AB=9,∵sin∠ACD=,∴可解得cos∠ACD=,tan∠ACD=,∵在Rt△BDC中,BD=tan(45°﹣∠ACD)?BC=9×=6,∴AD=AB﹣BD=9﹣6=3(米),∴AD的距离为3米.故选:C.【点评】本题考查仰角的定义,以及解直角三角形的实际应用问题.此题难度不大,解题的关键是要求学生能借助仰角构造直角三角形并解直角三角形,注意当两个直角三角形有公共边时,利用这条公共边进行求解是解此类题的常用方法.3. 平面上动点P到定点F与定直线l的距离相等,且点F与直线l的距离为1.某同学建立直角坐标系后,得到点P的轨迹方程为x2=2y-1,则它的建系方式是参考答案:C4. 圆与直线没有公共点的充要条件是()A. B.C. D.参考答案:A5. 已知点是边长为1的等边三角形ABC的中心,则( )A. B. C. D.参考答案:D6. 在⊿ABC中,,则此三角形为()A.直角三角形; B. 等腰直角三角形 C. 等腰三角形 D. 等腰或直角三角形参考答案:C略7. 已知向量,,分别是直线、的方向向量,若,则()A., B., C.,D.,参考答案:D∵l1∥l2,∴,∴。
广东省广州市海珠区2019-2020学年高二上学期期末联考数学试题Word版含答案

广州市海珠区2021-2021学年高二上学期期末联考数学一、选择题:在每题所给的四个选项中,只有一个是正确的.1.设集合A ={x |x 2+3x -4<0},B ={x |2x +3≥0},那么A ∩B =A .34,2⎛⎤-- ⎥⎝⎦B .3,12⎡⎫--⎪⎢⎣⎭C .3,12⎡⎫-⎪⎢⎣⎭D .3,42⎡⎫⎪⎢⎣⎭2.向量(3,1,2)a =-,(6,2,)b t =-,且a b ∥,那么t =A .10B .-10C .4D .-43.双曲线C 的方程为:221169x y -=,那么双曲线的焦距长为 AB. C .5 D .104.设命题p :∀x ∈[0,1],都有x 2-1≤0,那么¬p 为A .∃x 0∈[0,1],使x 02-1≤0B .∀x ∈[0,1],都有x 2-1≥0C .∃x 0∈[0,1],使x 02-1>0D .∀x ∈[0,1],都有x 2-1>05.假设a ,b ,c ,d 为实数,那么以下命题正确的选项是A .假设a <b ,那么a |c |<b |c |B .假设ac 2<bc 2,那么a <bC .假设a <b ,c <d ,那么a -c <b -dD .假设a <b ,c <d ,那么ac <bd6.n 为平面α的一个法向量,l 为一条直线,那么“l n ⊥〞是“l ∥α〞的A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件7.在长方体ABCD -A 1B 1C 1D 1中,AB =BC =a,1AA =,那么异面直线AC 1与CD 1所成角的余弦值为A .15BCD8.各项均为正数的数列{a n }为等比数列,S n 是它的前n 项和,假设S 3=7a 3,且a 2与a 4的等差中项为5,那么S 5=A .29B .31C .33D .359.命题“假设{a n }是等比数列,那么*()n n k n k na a n k n k a a +-=>∈N 且、〞的逆命题、否命题与逆否命题中,假命题的个数为A .0B .1C .2D .310.双曲线C :2213y x -=的右焦点为F ,点P 在C 的一条渐近线上,O 为坐标原点,假设PO ⊥PF ,那么△PFO 的面积为 ABC .12D11.为不断满足人民日益增长的美好生活需要,实现群众对舒适的居住条件、更优美的环境、更丰富的精神文化生活的追求,某大型广场正方案进行升级改造.改造的重点工程之一是新建一个长方形音乐喷泉综合体A 1B 1C 1D 1,该工程由长方形核心喷泉区ABCD 〔阴影局部〕和四周绿化带组成.规划核心喷泉区ABCD 的面积为1000m 2,绿化带的宽分别为2m 和5m 〔如下图〕.当整个工程占地A 1B 1C 1D 1面积最小时,那么核心喷泉区BC 的边长为A .20mB .50mC .1010mD .100m 12.在三棱锥D -ABC 中,22AB BC ==,DA =DC =AC =4,平面ADC ⊥平面ABC ,点M 在棱BC 上,且DC 与平面DAM 所成角的正弦值为34,那么AM = A .453 B .10 C .23 D .2263二、填空题 13.实数x ,y 满足约束条件10,10330,x x y x y -≥⎧⎪-+≥⎨⎪--≤⎩,那么z =2x +y 的最大值为________.14.某学校启动建设一个全新的信息化“未来报告厅〞,该报告厅的座位按如下规那么排列:从第二排起,每一排都比前一排多出相同的座位数,且规划第7排有20个座位,那么该报告厅前13排的座位总数是________.15.F 1,F 2是椭圆C :22221(0)x y a b a b+=>>的左,右焦点,点P 为C 上一点,O 为坐标原点,△POF 2为正三角形,那么C 的离心率为___________.16.如图,平行六面体ABCD -A 1B 1C 1D 1中,AB =AD =AA 1=1,∠BAD =∠DAA 1=∠BAA 1=60°,那么BD 1=________.三、解答题:解容许写出文字说明,证明过程或演算步骤.17.记S n 为公差不为零的等差数列{a n }的前n 项和,a 12=a 92,S 6=18.〔1〕求{a n }的通项公式;〔2〕求S n 的最大值及对应n 的大小.18.抛物线C 的顶点在原点,对称轴是x 轴,并且经过点(1,-2),抛物线C 的焦点为F ,准线为l .〔1〕求抛物线C 的方程;〔2〕过F 3h 与抛物线C 相交于两点A 、B ,过A 、B 分别作准线l 的垂线,垂足分别为D 、E ,求四边形ABED 的面积.19.如图,四棱锥P -ABCD 中,底面ABCD 是菱形,PB =PD .〔1〕证明:平面APC ⊥平面BPD ;〔2〕假设PB ⊥PD ,∠DAB =60°,AP =AB =2,求二面角A -PD -C 的余弦值.20.数列{a n }的前n 项和为S n ,且S n =n 2(n ∈N *),数列{b n }满足b 1=2,b n =3b n -1+2(n ≥2,n ∈N *).〔1〕求数列{a n }的通项公式;〔2〕求证:数列{b n +1}是等比数列;〔3〕设数列{c n }满足1n n n a c b =+,其前n 项和为T n ,证明:T n <1. 21.如图,圆A :(x +1)2+y 2=16,点B (1,0)是圆A 内一个定点,点P 是圆上任意一点,线段BP 的垂直平分线l 1和半径AP 相交于点Q .当点P 在圆上运动时,点Q 的轨迹为曲线C . 〔1〕求曲线C 的方程;〔2〕设过点D(4,0)的直线l2与曲线C相交于M,N两点〔点M在D,N两点之间〕.是否存在直线l2使得2?假设存在,求直线l2的方程;假设不存在,请说明理由.DN DM22.函数f(x)=x2-mx+(m+n)(m,n∈R).〔1〕假设关于x的不等式f(x)<0的解集为(-3,1),求实数m,n的值;〔2〕设m=-2,假设不等式f(x)>-n2+3n对∀x∈R都成立,求实数n的取值范围;〔3〕当n=3且x∈(1,+∞)时,求函数f(x)的零点.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
广东省广州市海珠区2020-2021学年高二(上)期末考试数学试卷一、选择题(共8小题).1.已知集合A={x|﹣3<x<3},集合B={x|x2﹣3x﹣4≥0},则A∩B=()A.(﹣3,1] B.[﹣2,3)C.(﹣3,﹣2] D.(﹣3,﹣1] 2.已知椭圆,则该椭圆的离心率为()A.B.C.D.3.已知命题p:∃a≥0,a2+a<0,则命题¬p为()A.∀a≥0,a2+a≤0B.∀a≥0,a2+a<0C.∀a≥0,a2+a≥0D.∃a<0,a2+a<04.等比数列{a n}中,已知a1+a2+a3=6,a4+a5+a6=﹣3,则a7+a8+a9=()A.24 B.C.D.5.某几何体的三视图如图所示,则该几何体的体积为()A.π+2 B.C.D.6.设正数m,n满足=1,则9m+4n的最小值为()A.9 B.16 C.25 D.267.椭圆和双曲线有相同的焦点F1,F2,点P是这两曲线的一个交点,则|PF1|⋅|PF2|的值为()A.m2﹣a2B.(m﹣a)C.D.m﹣a8.几何体结构素描是学习素描最重要的一个阶段,某同学在画“切面圆柱体”(用不平行于圆柱底面的平面去截圆柱,圆柱底面与截面之间的部分叫做切面圆柱体)的过程中,发现“切面”是一个椭圆,若切面所在平面与底面成30°角,则该椭圆的离心率为()A.B.C.D.二、选择题(共4小题).9.已知命题p:若x<y<0,则﹣x>﹣y,命题q:若x<y,则x2<y2,则下列命题中真命题()A.p∧q B.p∨q C.p∧(¬q)D.(¬p)∨q 10.已知,则下列不等式正确的是()A.B.|a|+b>0 C.lna2>lnb2D.11.已知直线l1、l2的方向向量分别是=(2,4,x),=(2,y,2),若||=6且l1⊥l2,则x+y的值可以是()A.﹣3 B.﹣1 C.1 D.312.已知椭圆C的中心为坐标原点,焦点F1,F2在y轴上,短轴长等于2,离心率为,过焦点F1作y轴的垂线交椭圆C于P、Q两点,则下列说法正确的是()A.椭圆C的方程为+x2=1 B.椭圆C的方程为+y2=1C.|PQ|=D.△PF2Q的周长为4三、填空题:本题共4小题,每小题5分,共20分.13.已知x,y满足条件,则的最小值为.14.数列{a n}的前n项和为S n,已知a n=,则S4=.15.如图,长方体ABCD﹣A1B1C1D1中,AB=AD=2,,若M是AA1的中点,则BM与平面B1D1M所成角的正弦值是.16.过双曲线的右顶点且斜率为3的直线,与双曲线的左、右两支分别相交,则此双曲线的离心率的取值范围是.(用区间表示)四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.①a4+a5=﹣4,②a2+a6=﹣6,③S7=14这三个条件中任选一个,补充在下面的问题中,若问题中的k存在,求k的值;若k不存在,说明理由.问题:等差数列{a n}前n项和为S n,a7=3,若____,是否存在k,使得S k﹣1>S k且S k<S k+1?18.在平面直角坐标系xOy中,已知点P到两点M(),N()的距离之和等于4,设点P的轨迹为曲线C.(1)求曲线C的方程;(2)若直线y=kx+2与曲线C有公共点,求实数k的取值范围.19.某公司进行技术创新,将原本直接排放进大气中的二氧化碳转化为固态形式的化工产品,从而实现“变废为宝、低碳排放”.经过生产实践和数据分析,在这种技术下,该公司二氧化碳月处理成本y(元)与二氧化碳月处理量x(x∈[300,600],单位:吨)之间满足函数关系y=﹣300x+80000,假设每处理一吨二氧化碳得到的化工产品的收入为200元.(1)该公司二氧化碳月处理量为多少吨时,每吨的平均处理成本最低,最低平均成本是多少?(2)该公司利用这种技术处理二氧化碳的最大月收益是多少?(月收益=月收入﹣月处理成本)20.如图,正三棱柱ABC﹣A1B1C1中,D是AC的中点.(1)求证:AB1∥平面DBC1;(2)若AB1⊥BC1,求二面角D﹣BC1﹣C的余弦值.21.已知数列{a n}满足a1=1,a n+1=3a n+3n+1(n∈N*).(1)求证:数列是等差数列;(2)求数列{a n}的通项公式;(3)设数列{a n}的前n项和为S n,求证:.22.已知点A(1,0),E,F为直线x=﹣1上的两个动点,且,动点P满足,(其中O为坐标原点).(1)求动点P的轨迹C的方程;(2)若直线l与轨迹C相交于两不同点M,N,如果,证明直线l必过一定点,并求出该定点的坐标.广东省广州市海珠区2020-2021学年高二(上)期末考试数学试卷参考答案一、选择题(共8小题).1.已知集合A={x|﹣3<x<3},集合B={x|x2﹣3x﹣4≥0},则A∩B=()A.(﹣3,1] B.[﹣2,3)C.(﹣3,﹣2] D.(﹣3,﹣1] 解:∵集合A={x|﹣3<x<3},集合B={x|x2﹣3x﹣4≥0}={x|x≤﹣1或x≥4},∴A∩B={x|﹣3<x≤﹣1}=(﹣3,﹣1].故选:D.2.已知椭圆,则该椭圆的离心率为()A.B.C.D.解:∵椭圆,∴a=5,b=4,c=3,∴该椭圆的离心率为e==.故选:C.3.已知命题p:∃a≥0,a2+a<0,则命题¬p为()A.∀a≥0,a2+a≤0B.∀a≥0,a2+a<0C.∀a≥0,a2+a≥0D.∃a<0,a2+a<0解:特称命题p:∃a≥0,a2+a<0,由特称命题的否定是全称命题,则命题¬p为∀a≥0,a2+a≥0.故选:C.4.等比数列{a n}中,已知a1+a2+a3=6,a4+a5+a6=﹣3,则a7+a8+a9=()A.24 B.C.D.解:等比数列{a n}中,由等比数列的性质得:S n,S2n﹣S n,S3n﹣S2n成等比数列,由a1+a2+a3=6,a4+a5+a6=﹣3,得:a7+a8+a9=﹣3×=.故选:B.5.某几何体的三视图如图所示,则该几何体的体积为()A.π+2 B.C.D.解:由题意可知几何体的是组合体,下部是圆柱,上标是四棱锥,圆柱的高为1,四棱锥的高为1,圆柱的底面半径为1,正四棱锥的底面边长为,所以组合体的体积为:V=π•12•1+=.故选:B.6.设正数m,n满足=1,则9m+4n的最小值为()A.9 B.16 C.25 D.26【解答】∴9m+4n=(9m+4n)•()=13+≥13+2=25,当且仅当3m=2n时等号成立.故选:C.7.椭圆和双曲线有相同的焦点F1,F2,点P是这两曲线的一个交点,则|PF1|⋅|PF2|的值为()A.m2﹣a2B.(m﹣a)C.D.m﹣a解:由题意,不妨设P在双曲线的右支上,则|PF1|+|PF2|=2m,|PF1|﹣|PF2|=2a∴|PF1|=m+a,|PF2|=m﹣a∴|PF1|•|PF2|=m2﹣a2故选:A.8.几何体结构素描是学习素描最重要的一个阶段,某同学在画“切面圆柱体”(用不平行于圆柱底面的平面去截圆柱,圆柱底面与截面之间的部分叫做切面圆柱体)的过程中,发现“切面”是一个椭圆,若切面所在平面与底面成30°角,则该椭圆的离心率为()A.B.C.D.解:椭圆的长轴为2a,短轴的长为2b,“切面”是一个椭圆,若“切面”所在平面与底面成30°角,可得=cos30°,即a=2b,所以e===.故选:D.二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得3分.9.已知命题p:若x<y<0,则﹣x>﹣y,命题q:若x<y,则x2<y2,则下列命题中真命题()A.p∧q B.p∨q C.p∧(¬q)D.(¬p)∨q 解:若x<y<0,则﹣x>﹣y>0,即命题p是真命题,当x=﹣1,y=0时,满足x<y,但x2<y2,不成立,即命题q是假命题,则p∨q为真命题,p∧q为假命题,p∧(¬q)是真命题,(¬p)∨q为假命题,故选:BC.10.已知,则下列不等式正确的是()A.B.|a|+b>0 C.lna2>lnb2D.解:由,可得0>a>b.所以,故A正确;因为0<﹣a<﹣b,所以|a|<﹣b,即|a|+b<0,故B错误;由0<﹣a<﹣b,可得a2<b2,所以ln a2<ln b2,故C错误;由,可得﹣>﹣,又a>b,所以a﹣>b﹣,故D正确.故选:AD.11.已知直线l1、l2的方向向量分别是=(2,4,x),=(2,y,2),若||=6且l1⊥l2,则x+y的值可以是()A.﹣3 B.﹣1 C.1 D.3解:∵直线l1、l2的方向向量分别是=(2,4,x),=(2,y,2),||=6且l1⊥l2,∴,解得,∴或,∴x+y=1或x+y=﹣3.故选:AC.12.已知椭圆C的中心为坐标原点,焦点F1,F2在y轴上,短轴长等于2,离心率为,过焦点F1作y轴的垂线交椭圆C于P、Q两点,则下列说法正确的是()A.椭圆C的方程为+x2=1B.椭圆C的方程为+y2=1C.|PQ|=D.△PF2Q的周长为4解:由已知得,2b=2,b=1,,又a2=b2+c2,解得a2=3.∴椭圆方程为.如图:∴|PQ|=,△PF2Q的周长为4a=4.故选:ACD.三、填空题:本题共4小题,每小题5分,共20分.13.已知x,y满足条件,则的最小值为﹣2.解:由约束条件作出可行域如图,联立,解得A(2,1),化目标函数为y=,由图可知,当直线y=过A时,直线在y轴上的截距最小,z有最小值为﹣2.故答案为:﹣2.14.数列{a n}的前n项和为S n,已知a n=,则S4=.解:已知a n==,则=1+,所以=.故答案为:.15.如图,长方体ABCD﹣A1B1C1D1中,AB=AD=2,,若M是AA1的中点,则BM与平面B1D1M所成角的正弦值是.解:由勾股定理知,B1M=D1M=BM===,B1D1=,∴=B1D1•=×2×=2,设点B到平面B1D1M的距离为h,∵=,∴h•=•AC•BB1•B1D1,即h•2=••2•2,∴h=2,设BM与平面B1D1M所成角为θ,则sinθ===,故BM与平面B1D1M所成角的正弦值为.故答案为:.16.过双曲线的右顶点且斜率为3的直线,与双曲线的左、右两支分别相交,则此双曲线的离心率的取值范围是(,+∞).(用区间表示)解:过双曲线的右顶点且斜率为3的直线,与双曲线的左、右两支分别相交,双曲线的一条渐近线的斜率必大于3,即>3,因此该双曲线的离心率e===>.故答案为:(,+∞).四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.①a4+a5=﹣4,②a2+a6=﹣6,③S7=14这三个条件中任选一个,补充在下面的问题中,若问题中的k存在,求k的值;若k不存在,说明理由.问题:等差数列{a n}前n项和为S n,a7=3,若____,是否存在k,使得S k﹣1>S k且S k<S k+1?解:若存在k,使得S k﹣1>S k且S k<S k+1,则a k<0,a k+1>0,设等差数列{a n}首项为a1,公差为d,若选择条件①:由,可得,解得,所以a n=﹣9+2(n﹣1)=2n﹣11,n∈N*,由a n<0,可得n<,所以当k=5时,满足a5<0,a6>0.若选择条件②:由,可得,解得,所以a n=﹣9+2(n﹣1)=2n﹣11,n∈N*,由a n<0,可得n<,所以当k=5时,满足a5<0,a6>0.若选择条件③:由,可得,可得,所以a n=1+(n﹣1)=n+,n∈N*,易知a n>0恒成立,所以不存在满足条件的k.18.在平面直角坐标系xOy中,已知点P到两点M(),N()的距离之和等于4,设点P的轨迹为曲线C.(1)求曲线C的方程;(2)若直线y=kx+2与曲线C有公共点,求实数k的取值范围.解:(1)由已知可得|PM|+|PN|=4=|MN|,由椭圆的定义可知点P的轨迹C是以M,N为焦点,焦距长为2,长轴长为4的椭圆,所以a=2,c=,则b2=4﹣3=1,所以轨迹C的方程为;(2)联立方程,消去y整理可得:(1+4k2)x2+16kx+12=0,因为直线与椭圆有公共点,则△=256k2﹣48(1+4k2)≥0,解得k,故实数k的取值范围为(﹣]).19.某公司进行技术创新,将原本直接排放进大气中的二氧化碳转化为固态形式的化工产品,从而实现“变废为宝、低碳排放”.经过生产实践和数据分析,在这种技术下,该公司二氧化碳月处理成本y(元)与二氧化碳月处理量x(x∈[300,600],单位:吨)之间满足函数关系y=﹣300x+80000,假设每处理一吨二氧化碳得到的化工产品的收入为200元.(1)该公司二氧化碳月处理量为多少吨时,每吨的平均处理成本最低,最低平均成本是多少?(2)该公司利用这种技术处理二氧化碳的最大月收益是多少?(月收益=月收入﹣月处理成本)解:(1)设每吨的平均处理成本为t元,由已知可得t=,所以t==400﹣300=100,当且仅当,即x=400时取等号,故二氧化碳月处理量400吨时,每吨的平均处理成本取到最低值100元;(2)设公司利用这种技术处理二氧化碳的月收益是U元,由已知可得U=200x﹣(,x∈[300,600],所以U=﹣=﹣0,当x=500时,U max=45000,当x=300时,U min=25000,故当x∈[300,600]时,U∈[25000,45000],所以该公司利用这种技术处理二氧化碳的最大月收益是45000元,此时二氧化碳的月处理量为500吨.20.如图,正三棱柱ABC﹣A1B1C1中,D是AC的中点.(1)求证:AB1∥平面DBC1;(2)若AB1⊥BC1,求二面角D﹣BC1﹣C的余弦值.解:(1)证明:连接B1C,交BC1于E,连接DE,由已知得四边形BB1C1C为矩形,∴E是B1C中点,在△AB1C中,D为AC中点,∴AB1∥DE,∵AB1⊄平面DBC1,DE⊂平面DBC1,∴AB1∥平面DBC1.(2)设E、F分别为B1C、BC的中点,连接EF,AF,由已知得AF⊥BC,AF⊥EF,EF⊥BC,以F为原点,分别以FB,EF,FA所在直线为x,y,z轴,建立空间直角坐标系,设BB1=a,BC=2b,则A(0,0,),B(b,0,0),B1(b,﹣a,0),C(﹣b,0,0),C1(﹣b,﹣a,0),∴=(b,﹣a,﹣),=(﹣2b,﹣a,0),∵AB1⊥BC1,∴=﹣2b2+a2=0,解得b=,∴=(,a,0),∵D是AC中点,∴,0,),∴=(,0,﹣),=(0,0,1)是平面CBC1的法向量.设平面DBC1的法向量=(x,y,z),则,取z=1,得=(),∴cos<>===,∴二面角D﹣BC1﹣C的余弦值为.21.已知数列{a n}满足a1=1,a n+1=3a n+3n+1(n∈N*).(1)求证:数列是等差数列;(2)求数列{a n}的通项公式;(3)设数列{a n}的前n项和为S n,求证:.【解答】证明:(1)数列{a n}满足a1=1,a n+1=3a n+3n+1(n∈N*),整理得(常数),当n=1时,,所以数列是以为首项,1为公差的等差数列.解:(2)由于数列是以为首项,1为公差的等差数列,所以.证明:(3)由于,故①,3②,②﹣①得:=,故,所以=.22.已知点A(1,0),E,F为直线x=﹣1上的两个动点,且,动点P满足,(其中O为坐标原点).(1)求动点P的轨迹C的方程;(2)若直线l与轨迹C相交于两不同点M,N,如果,证明直线l必过一定点,并求出该定点的坐标.解:(1)设P(x,y),E(﹣1,a),F(﹣1,m),则,,由,则有(﹣2,a)•(﹣2,m)=0且点E,F不在x轴上,故am=﹣4,且a≠0,m≠0,由,可得y﹣a=0,即y=a,由,可得mx+y=0,即y=﹣mx,所以y2=﹣amx=﹣4x,故动点P的轨迹C的方程为y2=4x(x≠0);(2)根据题意可设直线l的方程为x=ty+b(b≠0),由,可得y2﹣4ty﹣4b=0,设M(x1,y1),N(x2,y2),则y1+y2=4t,y1y2=﹣4b,故=,由,解得b=2,故直线l的方程为x=ty+2,恒过定点(2,0).。
