理论力学基础(北师大)习题知识讲解
【理论力学课件@北师大】8-2广义动量积分和广义能量积分

s
∂T1 α = T1 , q ∑ α α =1 ∂q
s
∂T0 α = 0 q ∑ α α =1 ∂q
s
所以
∑p
α =1
s
α
α = 2T2 + T1 q
得
H = T2 − T0 + V
∂ r 若坐标 变换 方程不显含时 间 , 即 i / ∂t = 0 ,
则 T0 = 0 , T = T2 , H = T2 + V = E , 广义能量 H 为系统的 机械 能 . 系统的 机械 能守恒是广义能量 守恒的一种特殊情况. 例题 3 质量为 m 的小环 P 被限制在一个半径 为 R 的 光滑大圆 环上 , 大圆 环 绕 过 大 环 中 心 的 铅 垂轴以 ω 的角速度均匀转动. 已知初始时小环在大 环的 最高 点 , 相 对 大 环 静止 , 然 后 无初 速 滑 下 . 试 通过存在的第一积分 建立小 环 相 对 大 环的 运 动 微分方程. 解 以 小 环 作 为研究对 象 , 它 的 自 由度为 1, 选择图中的 θ 角为广义坐标. 质点的动能用球坐标
因 ∂L / ∂x = 0 , 所以
px =
∂L − maϕ sin ϕ = C (常量) = mx ∂x
表示在水平方向杆的动量守恒. =0 , 则 =0, ϕ 根据初始条件, t = 0 时, x C = 0 . 由上式得 = aϕ sin ϕ x 又因 ∂L / ∂t = 0 , 且 T = T2 , 所以杆的机械能守恒.
T = T2 + T1 + T0
∂ r 可 看出 , i / ∂t 是 否为 零 , 直接影响到 T1 和 T0
理论力学知识点总结(15篇)

理论力学知识点总结第1篇xxx体惯性力系的简化:在任意瞬时,xxx体惯性力系向其质心简化为一合力,方向与质心加速度(也就是刚体的加速度)的方向相反,大小等于刚体的质量与加速度的乘积,即。
平面运动刚体惯性力系的简化:如果刚体具有质量对称面,并且刚体在质量对称面所在的平面内运动,则刚体惯性力系向质心简化为一个力和一个力偶,这个力的作用线通过该刚体质心,大小等于刚体的质量与质心加速度的乘积,方向与质心加速度相反;这个力偶的力偶矩等于刚体对通过质心且垂直于质量对称面的轴的转动惯量与刚体角加速度的乘积,其转向与角加速度的转向相反。
即(10-3)定轴转动刚体惯性力系的简化:如果刚体具有质量对称面,并且转轴垂直于质量对称面,则刚体惯性力系向转轴与质量对称面的交点O简化为一个力和一个力偶,这个力通过O点,大小等于刚体的质量与质心加速度的乘积,方向与质心加速度的方向相反;这个力偶的力偶矩等于刚体对转轴的转动惯量与角加速度的乘积,其转向与角加速度的转向相反。
即(10-4)理论力学知识点总结第2篇定点运动刚体的动量矩。
定点运动刚体对固定点O的动量矩定义为:(12-6)其中:分别为刚体上的质量微团的矢径和速度,为刚体的角速度。
当随体参考系的三个轴为惯量主轴时,上式可表示成(12-7)(2)定点刚体的欧拉动力学方程。
应用动量矩定理可得到定点运动刚体的欧拉动力学方程(12-8)(3)陀螺近似理论。
绕质量对称轴高速旋转的定点运动刚体成为陀螺。
若陀螺绕的自旋角速度为,进动角速度为,为陀螺对质量对称轴的转动惯量,则陀螺的动力学方程为(12-9)其中是作用在陀螺上的力对O点之矩的矢量和。
理论力学知识点总结第3篇牛顿第二定律建立了在惯性参考系中,质点加速度与作用力之间的关系,即:其中:分别表示质点的质量、质点在惯性参考系中的加速度和作用在质点上的力。
将上式在直角坐标轴上投影可得到直角坐标形式的质点运动微分方程(6-2)如果已知质点的运动轨迹,则利用牛顿第二定律可得到自然坐标形式的质点运动微分方程(6-3)对于自由质点,应用质点运动微分方程通常可研究动力学的两类问题。
北大理论力学第一章 静力学基础知识PPT课件

FOy
FBx FBy
例1-5:A处是固定支座,B处为活动支座,D处
是与园盘连结的销钉,作各杆受力图。
C
FCB
C [二力杆]
FAy A
G
FAx F
F
D
[整] E
B
FB F
C FGx
FCB’
FGy G
[CD]
D
FBC B
F FD` y’
[盘]
E
F
P
P
FDx
FDy
FDx’ FD` y’ D FDx
A
FDx’
FAx FAy
FDy [销钉]
FBC’
G FGx’
B
FGy’
FB
[AB]
结束语
当你尽了自己的最大努力时,失败也是伟大的, 所以不要放弃,坚持就是正确的。
When You Do Your Best, Failure Is Great, So Don'T Give Up, Stick To The End
14
谢谢大家
荣幸这一路,与你同行
It'S An Honor To Walk With You All The Way
演讲人:XXXXXX
时 间:XX年XX月XX日
15
F
5).无重链杆
二 力 杆
F1 F1
F2 F2
§1-4 受力分析、受力图
例1-2:作托架受力图
W
[托架]
FC
FCx
FCy
FBA’
C
FC
A
FAB
W
[整体]
B
FBA
1.取研究对像
三力汇交
FAB
理论力学完整讲义
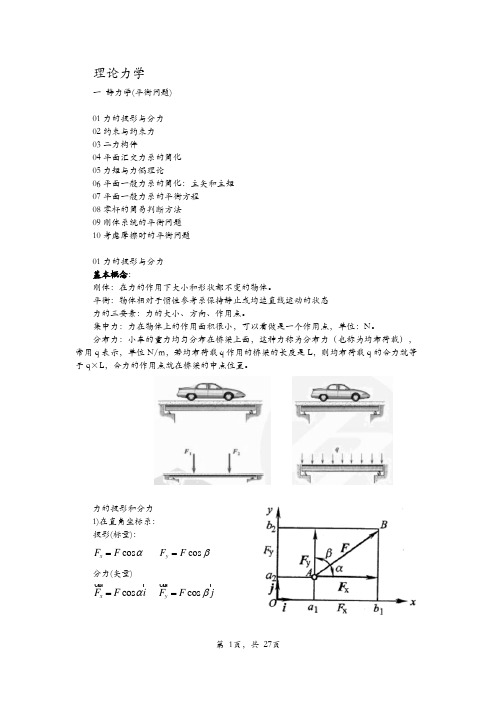
理论力学一 静力学(平衡问题)01力的投影与分力 02约束与约束力 03二力构件04平面汇交力系的简化 05力矩与力偶理论06平面一般力系的简化:主矢和主矩 07平面一般力系的平衡方程 08零杆的简易判断方法 09刚体系统的平衡问题 10考虑摩擦时的平衡问题01力的投影与分力 基本概念:刚体:在力的作用下大小和形状都不变的物体。
平衡:物体相对于惯性参考系保持静止或均速直线运动的状态 力的三要素:力的大小、方向、作用点。
集中力:力在物体上的作用面积很小,可以看做是一个作用点,单位:N 。
分布力:小车的重力均匀分布在桥梁上面,这种力称为分布力(也称为均布荷载),常用q 表示,单位N/m ,若均布荷载q 作用的桥梁的长度是L ,则均布荷载q 的合力就等于q ×L ,合力的作用点就在桥梁的中点位置。
力的投影和分力 1)在直角坐标系: 投影(标量):cos x F F α= cos y F F β=分力(矢量)cos x F F i α=u u r r cos y F F j β=u u r r2)在斜坐标系: 投影(标量):cos x F F α= cos()y F F ϕα=-分力(矢量)(cos sin cot )x F F F i ααϕ=-u u r rsin sin y F F j αβ=u u r r02约束与约束力约束:对于研究对象起限制作用的其他物体。
约束力方向:总是与约束所能阻止物体运动的方向相反,作用在物体和约束的接触点处。
约束力大小:通常未知,需要根据平衡条件和主动力求解。
(1)柔索约束:柔索约束:由绳索、皮带、链条等各种柔性物体所形成的约束,称为柔索约束。
特点:只能承受拉力,不能承受压力。
约束力:作用点位接触点,作用线沿拉直方向,背向约束物体。
(2)光滑面约束光滑面约束:由光滑面所形成的约束称为光滑面约束。
约束性质:只能限制物体沿接触面公法线趋向接触面的位移。
特点:只能受压不能受拉,约束力F 沿接触面公法线指向物体。
北师大理论力学习题答案2第二章思考题

图s2.3第二章 刚体运动学思2.1 答:0R θ=-=A C υυi ,并不能说明0=A a 。
因为0R θ=-=A C υυi 所表示的A υ是A 在一定特定位置,即与地面接触点时的速度,下一时刻与地面的接触点就换为别的质点了,所以不是同一质点速度的表达式。
若要通过对υ求时间的导数去求A a ,必须先将A υ表示成时间的函数式()t A υ,()()d d t t t=A A υa ,然后将在与地面接触时的时刻t 代入()t A a ,才能求得A a 。
思2.2 答:对R θυ=并不能求得R a θ=。
因为按加速度定义=a υ,应该是对速度矢量求导得加速度矢量。
正确的方法应该是:R θυ=R υθ==C υi iR θ==C C a υi又已知a =-C a iR a θ∴=-思2.3 解:设当圆柱A 位于圆柱B 顶部时,''P 与'P 点接触。
由于A 与B 间无滑动,所以弧长'''PP PP =,故无滑条件可写为r R ϕθ=。
选'O 为基点,绕基点的转动可以用由过基点方向固定的直线(称之为定线,'OQ )到过基点且和刚体固连的运动直线(称之为动线,'''O P )的夹角ψ来描述,刚体的角速度ωψ=。
由于'OO 方向不固定,所以刚体的角速度ωϕ≠。
思2.4 答:以瞬心为基点,设作为瞬心的那个点(基点)的瞬时加速度为0a ,则刚体上任一点的加速度为:20r r ωω=++n t a a e e思2.5 答:定点运动中的定点应是与刚体固连(可在刚体之外)且固定不动的点。
由于B 点不是与刚体固连的点,所以B 点不是定点。
根据瞬时轴的定义,因为B 点与刚体不固连,故BQ 和OB 均不是瞬时轴。
思2.6 答:解题时根据题目要求选择参考系,再根据具体情况建立适当的静止和运动坐标系。
例题3中选择地面做参考系,并在地面参考系中写出了相应的矢量表达式,只是为了计算方便才选择了动坐标系做矢量投影,所以P υ和P a 均是相对水平面的速度和加速度。
理论力学1知识点总结

理论力学1知识点总结一、牛顿定律牛顿定律是理论力学的基础,它描述了物体在受力作用下的运动规律。
牛顿第一定律也称惯性定律,它指出一个物体如果受到合外力为零的作用,将保持匀速直线运动或静止状态。
牛顿第二定律描述了物体所受合外力与它的加速度之间的关系,即F=ma,其中F为合外力,m为物体的质量,a为物体的加速度。
牛顿第三定律表明了物体间的相互作用力一定是相等而反向的。
二、动量与能量动量是描述物体运动状态的物理量,它等于物体的质量乘以其速度,即p=mv。
动量守恒定律指出,在一个系统内,如果没有合外力作用,系统总的动量将保持不变。
能量守恒定律则表明在一个封闭系统内,能量的总量是恒定的,能量可以相互转化,但总能量不会增加或减少。
三、碰撞和弹性碰撞碰撞是指两个或多个物体间发生的瞬时交互作用,碰撞可以分为完全弹性碰撞和非完全弹性碰撞。
在完全弹性碰撞中,动能和动量守恒定律都成立,碰撞前后系统的总动能和总动量均不变;而在非完全弹性碰撞中,只有动量守恒定律成立。
四、角动量角动量是描述物体旋转运动状态的物理量,它等于物体的转动惯量乘以其角速度,即L=Iω。
角动量守恒定律表明在一个封闭系统内,如果没有合外力矩作用,系统总的角动量将保持不变。
综上所述,理论力学是物理学中非常重要的一门学科,它揭示了自然界中物体运动的规律和特性。
牛顿定律、动量与能量、碰撞和弹性碰撞以及角动量是理论力学中的重要知识点,它们对于理解和应用物体运动规律具有重要意义。
通过学习这些知识点,可以更好地理解物体的运动行为,对于解决相关问题和开展科学研究都具有重要意义。
北京大学出版社理论力学部分习题解答

16 ΣM C = 0 ⇒ RD × 3 = 2× 4× 2 ⇒ RD = 3 kN ΣM A = 0 ⇒ RB × 4 + 6 + RD × 9 = 10 × 6 + 2 × 4 ×8 ⇒ RB = 17.5kN
29 ΣFy = 0 ⇒ RAy + RD + RB = 10 + 2 × 4 ⇒ RAy = − 6 kN
示:
2 ΣFx = 0 ⇒ F1 + F2 × 2 + FGH = 0
2 ΣFy = 0 ⇒ 50 Байду номын сангаас F2 × 2 = RE ΣM D = 0 ⇒ GGH = RE = 87.5 ∴ F1 = −125kN ; F2 = 37.5 2kN
F1 D 5 0 k N
E
F2
H RE FGH
对 H 点采用节点法;
反力。
ΣFx = 0 ⇒ N A = NB
ΣFy = 0 ⇒ T = G
ΣM = 0 ⇒ N A (orNB ) × 9 = G(orT ) × 2
∴ NA
=
NB
=
1000 3
N
习题 2.28 试求如图 3.40 所示多跨梁的支座反力。
(a):
ΣM B = 0 ⇒ RA × 4 = 5× 4 × 2 ⇒ RA = 10kN ΣFy = 0 ⇒ RCy + RA = 5×8 +12 ⇒ RCy = 42kN ΣM C = 0 ⇒ M C + 5×8× 6 +12× 2 = 10 ×10 ⇒ M C = −164kN • m
s
联立可得:
tan θ
=
P2 P1
θ
北师大理论力学习题答案6第六章思考题

图s6.1 图s6.4图s6.5 第六章 质点组动力学思6.1答:这个说法不对。
应注意质心是空间的一个位置矢量为i iC m M=∑r r 的几何点,质心速度为几何点的速度,并不是位于质心处的质点的速度。
O 为固定点,只说明位于O 的质点速度为零,此时质心速度并不为零。
思6.2答:从本质上说, 质心是一个空间几何点,不是一个具有一定质量的质点。
另一方面,我们为了使质点组整体运动的图像比较清晰和简化动量、角动量、动能的计算,我们假想一个质量为i M m =∑的质点位于质心,具有速度c υ。
这个假想质点的运动遵从质心运动定理,它的动量即为质点组的总动量,它对固定点的角动量为c c M ⨯r υ,并具有动能12c M υ。
引入假想质点是一种手段,它不反映问题的实质,所以并不意味着真有一个质点位于质心。
思6.3解:系统质心即为球心,按定义可知系统总动量 m =p υ思6.4答:由于半圆柱在水平方向不受力,质心的初速度为0,所以质心C 的运动轨迹是一条沿竖直方向的直线。
思6.5答:初始时系统对Oz 轴的总动量0z L =,从开始跑动后,人绕Oz 轴作圆周运动,角速度为11ω=ωk ,盘则沿相反的方向转动,其角速度22ω=-ωk 。
圆盘开始转动后,系统受轴承施与的摩擦力矩0z M >(系统所受其余外力对Oz轴力矩均为零)。
在外力矩z M 的作用下,系统动量矩z L 由零开始逐渐增大,到人停止跑动之时,z L 达最大值。
人在停止跑动过程中,圆盘也逐渐停止转动,人停止跑动后,人与盘一起将继续沿人跑动的方向绕Oz 轴转动。
人停止跑动后,圆盘的转动方向改变了,所以受到的摩擦力矩的方向也变为0z M '<,这时系统在外力矩z M '图s6.10 的作用下,总角动量逐渐减小而趋向于零,因此,人与圆盘一起将逐渐趋于静止。
思6.6答: 由于圆盘与轴间的相互作用比较复杂, 把轴包括在质点组内, 这样轴和盘之间的相互作用就可看作是内力。
《理论力学》第一章基本概念及基本原理

第一章 基本概念及基本原理[习题1-1] 支座受力F ,已知kN F 10=,方向如图所示, 求力沿y x ,轴及沿'',y x 轴分解的结果,并求力F 在各轴上的投影.解:(1)F 沿y x ,轴分解的结果把F 沿y x ,轴分解成两个分力,如图所示. →→→→=⨯==i i i F F x 66.8866.01030cos 0)(kN →→→→=⨯==j j j F F y 55.01030sin 0)(kN (2)F 沿'',y x 轴分解的结果把F 沿'',y x 轴分解成两个分力,如图所示. 由图可知,力三角形是等腰三角形.故:→→→==''10'i i F F x )(kN→→→-=⨯-=''018.575cos 102'j j F y )(kN (3) F 在y x ,轴上的投影)(66.8866.01030cos 0kN F F x =⨯==)(55.01030sin 0kN F F y =⨯== (4) F 在'',y x 轴上的投影)(66.8866.01030cos 0'kN F F x =⨯==)(59.275cos 1075cos 00'kN F F y -=-=-=[习题1-2] 已知N F 1001=,N F 502=,N F 603=N F 804=,各力方向如图所示,试分别求各力在x 轴y 轴上的投影. 解:)(6.86866.010030cos 011N F F x =⨯==)(505.010030sin 011N F F y =⨯==)(305350cos 222N F F x =⨯==α力沿x,y 轴的分解图力沿x ’,y ’轴的分解图力沿x ’,y ’轴的投影图xF yFy 'x F ')(405450sin 222N F F y -=⨯-=-=α 0060cos 333=⨯==αF F x)(60160sin 333N F F y =⨯==α)(57.56135cos 80cos 0444N F F x -===α)(57.56135sin 80sin 0444N F F y ===α[习题1-3] 计算图中321,,F F F 三个力分别在z y x ,,轴上的投影.已知kN F 21=,kN F 12= , kN F 33=. 解:)(2.16.025311kN F F x -=⨯-=⨯-= )(6.18.025411kN F F y =⨯=⨯=01=z F)(424.05345sin 1cos sin 02222kN F F x =⨯⨯==θγ )(566.05445sin 1sin sin 02222kN F F y=⨯⨯==θγ)(707.045cos 1cos 0222kN F F z =⨯==γ03=x F03=y F)(333kN F F z ==[习题1-4] 已知kN F T 10=,求T F 分别在z y x ,,轴上的投影. 解:(591.75353510sin 22222F F T Txy =+++⨯==γ)(51.6355591.7cos 22kN F F Txy Tx =+⨯==θ题1-2图)3,)0,)(91.3353591.7sin 22kN F F Txy Ty =+⨯==θ)(51.6535510cos 222kN F F T Tz -=++⨯-=-=γ[习题1-5] 力F 沿正六面体的对角线AB 作用,kN F 100=,求F 在ON 上的投影. 解:如图所示,F 在AC 线上的投影为:)(345.88400300400400400100cos 22222kN CAB F F F OB AC =+++⨯===5.0400200tan ==NOD 057.265.0arctan ==NOD 00043.1857.2645=-=BONF 在ON 线上的投影为:)(811.8343.18cos 345.88cos 0kN BON F F O B O N ===[习题1-6] 已知N F 10=,其作用线通过A(4,2,0),B(1,4,3)两点,如图所示.试求力F 在沿CB 的T 轴上的投影. 解: 61.313)42()14(22==-+-=AD69.413361.322==+=AB 2361.322=-=DGF 在AD 上的投影为:M)(697.769.461.310cos N BAD F F AD =⨯== )(40.669.4310sin N BAD F F z =⨯==)(264.461.32697.7cos N ADG F F AD y =⨯==)(396.661.33697.7sin N ADG F F AD x =⨯==F 在T 轴上的投影为:)(251.75340.654264.4cos cos kN ECB F BCD F F z y T =⨯+⨯=+= [习题1-7] 图中圆轮在力F 和矩为M 的力偶作用下保持平衡,这是否说明一个力可与一个力偶平衡? 解:图中圆轮在力F 和矩为M 的力偶作用下保持平衡,这不能说明一个力可与一个力偶平衡.因为轮子的圆心处 有支座,该支座反力R 与F 构成一力偶,力偶矩),(F R M 与M 等值,共面,反向,故圆轮保持平衡.[习题1-8] 试求图示的力F 对A 点之矩,已知m r 2.01=m r 5.02=,N F 300=.010012030cos 60sin )30sin (60cos )(r F r r F F M A ⋅+--=)(15232.023300)5.02.05.0(5.0300)(m N F M A ⋅-=⨯⨯⨯+⨯-⨯-= [习题1-9] 试求图示绳子张力T F 对A 点及对B 点的矩.已知kN F T 10=,m l 2=,m R 5.0=,030=α.解:)(530sin 10sin 0kN F F T Tx ===α)(66.830cos 10cos 0kN F F T Ty ===α )(732.1866.0260sin 0m l OC =⨯==)(15.0260cos 0m l AC =⨯==)()()(Ty A Tx A T A F M F M F M +=)30cos 5.01(66.8)30sin 5.0732.1(500+⨯+-⨯-=)(5m kN ⋅=)()()(Ty B Tx B T B F M F M F M +=)30cos 5.01(66.8)30sin 5.0732.1(500-⨯--⨯-=)(320.12m kN ⋅-=[习题1-10] 已矩正六面体的边长为c b a ,,,沿AC 作用一力F ,试求力F 对O 点的矩矢量表达式. 解:zy xF F F c bak j iF M →→→=)(0式中,2222222222cos cos c b a Fa b a a c b a b a F F F x ++-=+⋅+++⋅-=⋅-=θγ2222222222sin cos cb a Fb ba b cb a b a F F F y ++-=+⋅+++⋅-=⋅-=θγ222222sin cb a Fc cb ac F F F z ++=++⋅==γ故cb ac b ak j i c b a FF M --++=→→→2220)(cc bak j i c b a F200222→→→++=baj ic c b a F→→⋅++=2222)(2222→→-++=j a i b c b a cF[习题1-11] 钢绳AB 中的张力kN F T 10=.写出该张力T F 对O 点的矩的矢量表达式.解:2)21()01(22=-+-=BC2318)04()12()10(222==-+-+-=ABzy xF F F k j iF M 42)(0→→→=式中,)(357.22123210cos cos kN F F T Tx =⋅⋅=⋅=θγ )(357.22123210sin cos kN F F T Ty -=⋅⋅-=⋅-=θγ)(428.923410sin kN F F T Tz -=⋅-=-=γ故428.9357.2357.2420)(0--=→→→k j i F M 357.2357.24428.9357.22---=→→→→jiki)(357.24)357.2428.9(2→→→→--⨯---=j i k i →→→-+-=k j i 714.4428.9428.9[习题1-12] 已知力→→→→+-=k j i F 32,其作用点的位置矢→→→→++=k j i r A 423,求力F 对位置矢为→→→→++=k j i r B 的一点B 的矩(力以N 计,长度m 以计).A解:→→→→→⨯-=⨯=F r r F r F M B A AB B )()(式中,→→→→++=k j i r A 423,→→→→++=k j i r B ,=-→→)(B A r r →→→++k j i 312 →→→→+-=k j i F 32故, =)(F M B ⨯++→→→)312(k j i )32(→→→+-k j i=-=→→→132312k j i=--→→→240312k j i 23522---→→→→k k j i 5222---=→→→k j i)425(2→→→+---=k j i→→→-+=k j i 8410 )(m N ⋅[习题1-13] 工人启闭闸门时,为了省力,常常用一根杆子插入手轮中,并在杆的一端C 施加力,以转动手轮.设手轮直径m AB 6.0=,AC 轩长m l 2.1=,在C 端用N F C 100=的力能将闸门开启,若不借用杆子而直接在手轮A,B 施加力偶),('F F ,问F 至少应多大才能开启闸门? 解:支座O 反力O R 与C F 构成一力偶),(0C F R 若要闸门能打开,则),('F F 与),(0C F R 必须 等效,即它们的力偶矩相等:)3.02.1(1006.0-⨯=⨯F )(150N F =[习题1-14] 作下列指定物体的示力图.物体重量,除图上已注明者外,均略去不计.假设接触处都是光滑的.。
北师大理论力学习题答案3第三章思考题

图s3.2(c )图s3.2(d )第三章 质点动力学思3.1答:我们知道f N μ=正,把N 正叫正压力。
当质点被约束在一曲面上运动时,N 正等于曲面施于质点的约束反力在曲面法线方向的投影,而当质点被约束在一曲线上运动时,N 正应等于曲线施于质点的约束反力在曲线法线平面内的投影,即n N n e 与b b N e 矢量和的大小,N =正1)、(2)、(3)式是错误的。
至于(4)式还要进一步分析,我们研究滑动摩擦,若珠子沿弧长正方向运动的情况。
这时运动方向与t e 一致,f 方向与t e 方向相反,故f应取负值,正确的表达式为f =-向与弧长正方向相反时,则运动方向与t e 方向相反,f 与t e 方向相同,此时f的表达式为f =(4)式表达不完整。
思3.2答:角度的正向必须用从定线(铅垂线)到动线(摆线)来规定,故乙的作法是错误的。
乙若也以逆时针方向为θ正向,则应按图(c)标出,这样就可以看出此时θ为第四象限角,应有sin 0θ<,考虑到m g 沿θe 方向投影应为正值,故到方程时仍应表示为sin ml mg θθ=-。
若如图(d )规定θ正向,则m g 沿θe 方向投影应为负值,故到方程时仍应表示为sin ml mg θθ=-。
我们知道受力状况的分析,应在质点的任意位置上进行,这个任意位置应取于何处?这有一点技巧,在可能的条件下,应把这个位置取在直角 图s3.1(a)图s3.1(b )图s3.3(a )图s3.3(b ) 坐标系的第一象限,涉及角度时应使该角度在02π范围内.这时各坐标量(),,x y z ,角度及角的三角函数均取正值,这将给分析问题带来方便。
思 3.3答:不管坐标系如何建立,质点速度均应表示为y =υj ,故阻力均应表示为k ky =-=-f υj ,可见甲列出的方程是错误的,而乙是正确的。
思3.4答:动量部分守恒只有对固定方向才能成立,而径向、横向均不是固定方向,所以上述看法不对。
理论力学基础北师大习题知识讲解

<<<<<<精品资料》》》》》第一章思考题u h向左开行岸上有汽车拉着绳子以匀速率, 岸距水面高为,, 1.1. 如思考题1.1图所示?s BA. 小船到岸的距离为绳与水面交角为则绳子另一端通过滑轮, 连于小船上,?u s的关系为与:????????u?u cos u cos ss?cos?u??s cos s?(1)(4) ;(3) ;(2) ;思考题1.1图??e e随质点位置变化而1.2. 在参考系上建立一个与之固连的极坐标系, 但其单位矢量和?r?是否说明极坐标系是动坐标系这是否与固连相矛盾? 改变, ?v Ox试求质点运图所示. , 正交的直线以做匀速运动如思考题1.31.3. 质点沿一与极轴0a a.动加速度在极坐标系中的分量和?r图思考题1.3??m uOOA沿相对杆以匀速1.4. 杆在平面内绕固定端以匀角速转动. 杆上有一滑块,a a m=0,(1) =0, 的运动有如下结论: 有人认为研究杆滑动, 如思考题1.4图所示. ?r?OOAOa试分析所以在自然坐标法中向心加速度指向. 故=0; (2) 为点转动中心,.上述结论是否正确思考题1.4图第一章习题?1?OA?10s转动, 已知长度柄所如1.1. 题1.1图示,曲连杆以匀角速________0t?cm,?OAAB?80??AOB?AB的中点的运动学方程、轨道、速. 求连杆时. 度和加速度》》》》精品资料》<<<<<<》<<<<<<精品资料》》》》图题1.1220y?2mx?nx?nm,c一质点沿圆锥曲线1.2. . 为常数), 运动 (其速率为常量求x. 分量分量和质点速度的y???λrλ试证其径向与横向加速). (1.3. 一质点的径向与横向速度分别为为常量, 和22???2?????r?(rr和度分别为).v?vb0b?b,径向速度亦为常量(1.4. ), 求质一质点做平面运动, 其速率为常量, 00r?r?0??0t时设.点的轨道方程. ,0)0(c?v?c;其径向加速度为, 1.5. 一质点做平面曲线运动, 其径向速度为正值常量r2b)0(b?a??r3r.求质点的运动学方程并与到极点的距离的三次方成反比, . 负值,????rr??0?t0?,设, , . 且运动中时00?OOA端的竖绕过其保持其与竖直方向的夹角不变, 1.6. 如题1.6图所示,已知一直管??O加速度的大小为点开始沿管做匀加速运动做均匀转动. 一质点从, 直轴以角速度a并用球坐标系求质点试用柱坐标系求质点对地面的速度和加速度, , 初速度为零..对地的速度1.6图题)0(c?Oxycy试证质点其速度的, 分量为正值常量1.7. 一质点的轨道曲线在平面内, 3v?a??cv., 加速度的大小可表示为, 其中为轨道曲率半径为速率v?r保, 初速度为, 其加速度矢量与速度矢量间的夹角1.8. 质点沿半径为的圆周运动0. 求质点速率随时间的变化规律持不变,p?r?p)e cos(1?e为正值和, 如题1.91.9. 已知质点运动的轨道为圆锥曲线图所示.?2?ccr?即圆锥曲已知试证质点加速度的方向必指向原点. , (亦为正值常量. 常量2r.), 线的一个焦点其大小与成反比》》》》精品资料》<<<<<<》》<<<<<<精品资料》》》图题1.9xyO中质点运动的中, 描绘教材中第一章例题1.10. 试用数值计算方法, 在直角坐标系12.情况., 描绘教材中第一章例题3中质点运动的情况1.11. 试用数值计算方法第二章思考题0a?A?2.1. 教材中第二章例题1中(2)式是否说明点加速度A???aR??1中对(3)式求时间导数是否可以得到教材中第二章例题2.2.BRAr由最高点无滑动地半径为沿半径为的圆柱的固定圆柱2.3. 如思考题2.3图所示, ??????Rrr?R????PPPP?由于弧长, 所以无滑条件可表示为对, 求导数滚下, ????????rr?R?RA?的角速度为上述各结论是否正确, 可得所以圆柱,图思考题2.3所以刚体, : 由于每瞬时刚体的平面平行运动都可以看成是绕瞬心的纯转动2.4. 有人认为???r2???erea??r为该点到上任一点的加速度由向心加速度和切向加速度组成, , tn?? 为什么瞬心的距离. 这种看法是否正确BB又因故, 为定点2.16, 甲认为: “, 为固定不动的点32.5. 参见教材中第二章例题图OOBO B,由于: 乙认为“我看定点应为点点不动, 点速度为零所以, 为瞬时轴.”OB.试指出甲、乙二人的错误”所以为瞬时轴.??av Oxyz是甲认为求出的和中的坐标系为动坐标系. 图2.6. 教材中第二章例题32.16PP Oxyz所, . 乙认为题中要求的是相对水平面的速度和加速度相对系的速度和加速度?. 你认为如何以选用动坐标系是不合适的???v新概念物理教赵凯华. , 罗蔚茵(, 角速度是极矢量2.7. 速度, 是轴矢量阅读参考书. 说明它们的共性与差异程·力学),第二章习题》》》》精品资料》<<<<<<》》》<<<<<<精品资料》》Rr线无滑地绕中部绕线轴的半径为2.1. 半径为, 的线轴在水平面上沿直线做无滑滚动, ?Cu A的轴心如题2.1图所示. 求: (1)在轴上, 线端点以不变速度沿水平方向运动,B.的加速度速度和线轴的角速度; (2) 线轴与水平面接触点2.1图题a b,的小圆盘在一半径为两圆盘在水平面内半径为的固定大圆盘的边缘上运动,2.2.?Oxy??x OO夹角的时间导数轴与两圆心连线图所示为固定直角坐标系, 如题2.2.小圆盘上某一确定半径的空间指向不: (1) 已知, 求下列3种情况中小圆盘的角速度O.点小圆盘上某一确定半径始终指向; (3) 小圆盘在大圆盘上做无滑滚动变;(2)图题2.2?ODOAOAOBAB运借助连杆以匀角速度沿轨道绕推动滑块点转动2.3. 曲柄, 曲柄?l?OA?rABOADOt AB的角速求杆与2.3动. 设夹角为图所示, . , 如题,B.点的速度度和2.3图题??vv,a如两板分别以不变的速度, 反向运动2.4. 半径为的圆柱夹在互相平行的两板间, 21圆柱上与上板的接(2): (1) 瞬心位置;, 题2.4图所示. 设圆柱与两板间均无滑动求A. 触点的加速度题2.4图??vv Oxy l AB如题的大小和方向已知, , 且知道的方向的细杆2.5. 长为,在平面内运动BA???v v?C刚好沿杆上某点, 的位置(2)的大小;: (1) . 2.5图所示求杆的角速度及CB. 杆的方向》》》》精品资料》<<<<<<》<<<<<<精品资料》》》》图题2.5????CDCD O AB轴2.6. 圆盘以角速度绕水平轴轴又以角速度转动, 绕过盘心的竖直21???????s?5radsrad?3??.2.6图所示. 及, 求圆盘角速度已知, 转动, 如题21图题2.6??OEODOD AB以绕竖直线轴以角速度转动2.7. 转轮, 绕过轮心且与轮面垂直的而1?????EODb?CBaOC?., 如题, 2.7图所示, 转动角速度. 已知转轮半径2?v.试求转轮最低点速度B图题2.7???2h绕竖直2.8. 高为, 顶角为的圆锥在水平面上做无滑滚动, 若此圆锥以不变角速度?OP的速圆锥底面最高点 (2) . , 轴转动如题2.8图所示试求: (1) 圆锥角速度;?aav P. 和度; (3) 点的转动加速度和向轴加速度的量值21图2.8题第三章思考题》》》》精品资料》<<<<<<》》<<<<<<精品资料》》》m珠采用自然坐标法描述有一质量为. 的珠子, 沿一根置于水平面内的铁丝滑动, 3.1. ???????e?FFe?FeF?eFg?mW铁丝施与的约束力, .即为滑动子受重力tNtNNttNnnNbb摩擦力???F FFF??mg?Nbfff;试判断下列各式正误: (1)(2), 设动摩擦因数为.22??F?FF?FF?NbfNnNnf;)(4)(3?得到动力学方角正向图(a)规定, 某甲如思考题3.2. 用极坐标系描述单摆的运动.3.2????sin mlmg???到则得正向规题程3.2图(b)定, 角;某乙如思考????sin mg?ml??. 你认为谁的做法正确(b)(a) 图思考题3.2?F m f比例, 的质点, 由静止开始自高处自由落下. 设空气阻力质量为3.3.与速度成正比???m?kyy??mg k. (a), 得到方程为. 某甲建立竖直向上的坐标如思考题3.3图系数为???mkyy?mg?他们列出的.某乙建立竖直向下的坐标如思考题3.3图(b), 得到方程为?方程对吗(a) (b)3.3思考题0?F,, 如果, 则沿径向动量守恒3.4. 有人认为: 用极坐标系讨论质点的平面运动时r F?0?p??mr?常量;若. 则沿横向动量守恒这种看法对吗, ?r3.5. 试判断以下二论断是否正确:OO点的任意固定轴的角动量守恒.则对过的角动量守恒, (1) 若质点对固定点(2) 若质点对固定轴的角动量守恒, 则对该轴上任一固定点的角动量守恒.3.6. 一质点动量守恒, 它对空间任一固定点的角动量是否守恒? 如质点对空间某一固定点角动量守恒, 该质点动量是否守恒?3.7. 当质点做匀速直线运动时, 其动量是否守恒? 角动量是否守恒? ????v?vi?vj?vk Oxyzm zxy, 的质点的速度所受合在固定的直角坐标系中, 质量为3.8. ??1????2)?F?mv d(d r kFjFiFF???x2zyx轴方向投. 能否将质点的动能定理力为向》》》》精品资料》<<<<<<精品资料》》》》》<<<<<<12xmv d)?F d(xx2?该方程是否正确影而得出分量方程?第三章习题x度场强已动. 知电的振荡电场中的电3.1. 研究自由子在沿运轴??????i?E?E cos()t,E,me?即当, . ,电子电量为. 初始时, 质量为为常量00????ir?xiv?v0t?时, . 忽略重力及阻力求电子的运动学方程. , 0000?v求自地球表面竖直上抛一质点3.2. 以很大的初速度, 设地球无自转并忽略空气阻力, 0?gR.地球表面处重力加速度为质点能达到的最大高度. 已知地球半径为,22gvmkF?m.其大小, 设空气阻力与速度平方成正比, 3.3. 将质量为的质点竖直上抛R22v?kv?v1v00.试证该质点落回抛出点时的速率如上抛初速度为, 0????B?BEE电的均匀稳定电磁场中入射一电子磁感应强度为. 已知, 3.4. 向电场强度为、???vBE设电子电量为试求电子的运动规律. 3.4图所示. 子初速与和均垂直, 如题0e?.图3.4题a的圆轮在直线上做无滑滚动时轮缘上一图所示, 可理解为一半径为3.5. 旋轮线如题3.5???)?cos?a(x?a(1?sin)y yP设点的轨迹, 其参数方程为, , . 在重力场中O点运动周期绕,试证质点运动具有等时性(轴竖直向上, 一质点沿光滑旋轮线滑动).与振幅无关题3.5图m绳的另可在光滑水平桌面上滑动一小球质量为. , 系在不可伸长的轻绳之一端, 3.6. a如题握在一个人的手中使它向下做匀速运动, 速率为, 一端穿过桌面上的小孔,R其初速度在垂直绳方向, 设初始时绳是拉直的3.6图所示. , 小球与小孔的距离为v.上的投影为试求小球的运动规律及绳的张力. 0》》》》精品资料》<<<<<<》》》<<<<<<精品资料》》图题3.6m R设珠子的圆环水平放置的铁丝做成的圆环上, 3.7. 一质量为. 的珠子串在一半径为v?根 (, 初始速率为, 珠子与圆环间动摩擦因数为求珠子经过多少弧长后停止运动0).据牛顿第二定律求解am b此椭圆弧在竖直3.8. 质量为, 的小球沿光滑的、半长轴为的椭圆弧滑下、半短轴为求小球达到. . 设小球自长轴端点开始运动时其初速度为零平面内且短轴沿竖直方向).根据牛顿第二定律求解椭圆弧最低点时对椭圆弧的压力 (??FFBA图所3.9和上分别作用在长方体的顶角, 和长方体的尺寸和坐标系如题3.9. 力21??FF O.及3示. 试计算和个坐标轴的力矩对原点21题3.9图??tr cossin ty?xm?r,, 3.10. 已知质量为的质点做螺旋运动, 其运动学方程为000?k,r,ktz?tt时刻质点对,试求:(1)(2) 时刻质点对坐标原点的角动量;为常量. 0),c(a,bP)nl,m,(.过方向余弦为的轴的角动量点,m l BA端与轴, 图所示质量为端的小球安装在长为, 的细轻杆的杆的3.11. 如题3.11OOOOOO.和轴做定轴转动, 轴承是光滑的垂直地固连. 小球在液体中可绕211122???mF??设初始角速度为为常量转动中小球所受液体阻力与角速度成正比, ,. R?以及在这段时间内小球所转圈,, 试求经多少时间后, 角速度减小为初始值的一半0.)忽略杆的质量及所受阻力数.(图题3.11kt sin by?m kta cos x? , 其运动学方程为, 3.12. 质量为的质点沿椭圆轨道运动?k4t?kb,a,0t?. 为常量). 时间内所做的功用两种方法计算质点所受合力在到(》》》》精品资料》<<<<<<精品资料》》》》》<<<<<<.3.13. 试用动能定理求解3.7题m螺旋沿如题3.14图所示的光滑的水平的对数螺旋线轨道滑动有一小球质量为3.14. . , ??a?ver?r?a0?求轨道对, 时为常数. 已知当极角,小球初速为. 线轨道方程为00???F e?v方向间夹为小球的水平约束力的大小. (用角动量及动能定理求解, 图中与?N?a tg?.)角,题3.14图?zy?axF?a?azaxF?a?ay?F23y2122个分量为的3,,3.15. 已知质点所受力x131112)3a(i,j?1,2,azaF?ax?y?a ijij满足什么条件时与这些都是常量系数,. 333132z?F.力相关的势能存在? 在这些条件被满足的条件下, 计算其势能q为的力子电偶极的有3.16. 一带场中所电受荷的质点在3?3rF?pq sin?r cos F?2pq p r.,为偶极距, ,为质点到偶极子中心的距离?r试证此力场为有势场.Oxy AB均以与距离成正静止中心和图所示, 自由质点在平面内运动, 3.17. 如题3.17k M. 试证明势能存在并求出质点的势能比例系数为比的力吸引质点.,题3.17图3.18. 试用机械能守恒定律求解3.8题.n次方成正比, 求有阻力抛体运动微分方程数值解设空气阻力与速率的, 并描绘其3.19.运动情况.3.20. 求带电粒子在均匀稳定电磁场中运动微分方程数值解, 并描绘其运动情况.3.21. 求大摆角单摆运动微分方程数值解, 并研究周期与摆角的关系.第四章思考题4.1. 线性振动与非线性振动有什么根本区别?4.2. 基频与固有频率有何不同?4.3. 用小参量级数展开方法求解非线性振动问题时, 什么情况下会出现长期项? 应如何处理长期项?4.4. 如何理解吸引子的概念? 你知道有哪些类型的吸引子?4.5. 如何理解混沌运动? 如何判断混沌运动?》》》》精品资料》<<<<<<》》》》<<<<<<精品资料》第四章习题4.1. 试用微扰法求方程22????0x?xx??0?A0)?x(x)?0(00?t, 设初始条件为. , 时. 准确到第二级的解F?m0x?x?0时受到恒力, 的作用, 当4.2. 做一维运动的质点的质量为当时受到恒0FF??mE力和总能量的作用. 画出描述此运动的相图, 计算运动的周期(以表,00A.. 不考虑阻尼示)和振幅除了已介绍过的4.3. 在非线性动力学发展过程中有三大著名的方程起了重大作用,在研它是由E. N. Lorenz还有洛伦茨方程和Van.der.pol方程外, (Lorenz)方程, Duffing经他在对此方程进行数值计算研究中首次发现混沌现象. 究大气对流问题中引进的,:Lorenz方程是一个三阶的无量纲的常微分方程组过许多简化后得到的x d?y10?10x???t d?y d?xz?28x?y??t d?8z d?xyz????t d3?). Lorenz吸引子试用计算机数值计算方法作出它的相图(通常称为具有精确到一德·4.4. 试用近似计算方法证明教材中第四章方程(4.5.1)(即范·波尔方程)1?x)级的稳态周期解(其中取0????)33sin tt cos x?2?t?sin(?4并证明???0??2T?.与初始条件无关其周期为近于常数,第五章思考题?为什么这种说法是否正确? 5.1. 有人说“牵连运动就是动坐标系的运动”, ???t dd v??sv系的速度, : “它的存在5.2. 是质点相对某习题要求求出. 于是有人提出疑问??????ss vv v s的时间变率为什么可以对系求系的速度是而不是. 依赖于系. 质点相对呢?”你能解决他的疑虑吗?a O处放一光滑小球, 点距离为初始时盘与小球有一光滑水平圆盘5.3. , 在其上离中心O点的竖直轴做均匀转动后, 当圆盘绕过有人认为“小球并未被盘带着运动,均静止.所以它的牵连速度与牵连加速度均为零”. 他的看法正确吗??as O系以地面为,点的加速度为. 一竖直圆盘沿水平直线轨道做无滑滚动5.4. , 其盘心0Oxyz?sO P的绝对加为原点建立平动为图所示系, 如思考题5.4. 以则轮边上一点??????????????r?a??a?(?r)速度为试问 . 0???(1)是绝对变率还是相对变率?(2) 等式右方三项各是什么加速度?》》》》精品资料》<<<<<<<<<<<<精品资料》》》》》图思考题5.4???zOxy?s为, 5.4中若以与圆盘固连的此时系5.5. 在思考题?????????????)a?a?r?r???(0?等式右方三项又各是什么加速度是否还能成立? ??OMR,的圆环, 绕过中心的竖直轴以匀角速度在环上5.6. 水平面内半径为转动. 小虫?su s试说明, 系系, 以地为, 如思考题5.6图所示. 相对于环以匀速率圆环为爬行等式2uu22????u?R(2?)?RRR.左右两端每一项的物理意义思考题5.6图???????r?a?r2??r2中有人认为极坐标加速度公式是科氏加速度. 你以为如何?5.7. ??, 小球是否受惯性力作用5.8. 小球静止于地面, 现以匀加速上升的电梯为参考系这种, 5.9. 有人说“牵连加速度是由牵连惯性力产生的科氏加速度是由科氏力产生的”.?为什么说法对吗?第五章习题??O管内有一质点相对管的速率为5.1. 一直管在水平面内绕其端以匀角速度转动.?at?vv?vOxyzsa O与管固连的方向背离点向外, , ,以地面为常量. 系为, 00???????t d t d?v d v d zOxy?s;(1) 求. 试: ;(2)示图题为, 系如5.1所???dt d a?a d t?d;(4). (3)》》》》精品资料》<<<<<< <<<<<<精品资料》》》》》图题5.1??PR在与固定轴等半径为5.2. 的记录器滚筒绕水平固定轴以角速度转动. 记录器笔尖?v P先以地, 如题相对滚筒的速率求笔尖.(5.2图所示. 高的水平线上, 以速度运动0ss.) 系, 系, 再以滚筒为为分别用两种方法求解5.2题图???质点半顶角为的圆锥以匀角速度圆锥表面有一沿母线的细槽. 绕对称轴转动,5.3. ??vP求运动到图所示如题5.3由圆锥顶点开始, 相对圆锥以速度. 沿槽做匀速运动,s tP).系时刻, (点绝对加速度的量值以地面为5.3图题l P所在平面绕竖直杆和2小球图所示, 瓦特节速器的4根连杆长度均为, 45.4. 如题5.4????)(?t)t?(试求其中一个连杆与转轴间夹角的变化规律为轴转动的规律为, ..小球对地面的加速度5.4图题v R. 的车轮在竖直平面内沿一直线轨道做无滑滚动, 已知轮心的速率为常量5.5. 一半径为》》》》精品资料》<<<<<<》》<<<<<<精品资料》》》v., 轮缘上有一质点以与轮心速率相等的速率相对车轮沿轮缘顺着车轮滚动方向运动.(2) 质点相对地面的加速度求: (1) 质点相对车轮的加速度;??m绕过其一端的, 此管以匀角速度5.6. 在一内壁光滑的水平直管中有一质量为的小球a而管的总长球相对管的速率为零. 如开始时小球到转动轴的距离为, , 竖直轴转动a2小球从小球刚要离开管口时相对管的速度和相对地面的速度;(2) . 求度为: (1).开始运动到离开管口所需的时间)xy?f(m O,的光滑钢丝上, , 穿在曲线方程为此钢丝通过坐标原点5.7. 小环质量为?y?如欲使小环在钢丝的任何位置上都处于相对曲线. 并绕竖直的轴以匀角速度转动.曲线钢丝对小环的约束力求: (1) 钢丝的曲线方程; (2) 钢丝平衡的状态. ??m O R的小环套转动, 5.8. 一半径为有一质量为的圆环绕过环心的竖直轴以匀角速度?O,. 初始时小环和点连线与竖直轴夹角为在此圆环上, 并可在其上无摩擦地滑动0试求小环相对圆环的角速度以及圆环对小环的约束. 如题5.8图所示相对圆环静止,.力题5.8图mm a绳的劲度系数为的弹性轻绳相连和, 的两个质点, 用一原长为5.9. 质量分别为212?(mm?m)?k2m. 如将此系统放在一内壁光滑的水平管中, 水平管绕管上2211??两质点间的距离. 初始时两质点均相对水平管静止, 某点以匀角速度绕竖直轴转动a.. 试求任一时刻两质点间的距离为证明该物体运动轨, 给放置在光滑水平面上的物体一个水平初速度5.10. , 考虑地球自转. 迹是一个圆, 并求出圆半径及水平面所受物体的压力???v忽略空, 5.11. 如在北纬处, 以仰角自地面向正东方发射一炮弹, 炮弹发射速度为试证明炮弹落地时的横向偏离为气阻力但计及地球自转,2v42????cossin d?sin??2g?.式中为地球自转角速度v?h忽. , 处从地面竖直上抛, 达到复落至地面高度后5.12. 一质点如以初速度在北纬0并通过物理图, . 试求质点落至地面时相对抛出点的偏差略空气阻力, 考虑地球自转.象说明结果的合理性., 用计算机研究落体偏东现象5.13. 求教材中第五章(5.4.6)式数值解., 研究在不同初始条件下傅科摆的运动情况求教材中第五章(5.4.11)式数值解5.14.第六章思考题AOBOOO点转动.相同的两匀质杆, 和用铰链连接于固定点并可在水平面内绕6.1.?AOB转动, 如思考题6.1图所示. 某时刻二杆以同样大小的角速度位于同一直线上,OO点为固定点, 故此时质心速度为零, .”此时质心为“以二杆为系统有人认为:, 点》》》》精品资料》<<<<<<》》》<<<<<<精品资料》》?这种说法对吗6.1图思考题1??2vmv?mr ct O2这是否说明质心有时称点的角动量, 为质心的动能称. 6.2. 为质心对ctc??rmv?、位置矢量为、速度为的质点是一个质量为ctc?m v R球旋转角速某时刻球心速度为,6.3. 有一半径为的匀质圆球被旋转抛出, 质量为. ??., 求此时圆球的动量度为求图所示位置, 6.4. 将一半圆柱置于一光滑水平面上, 初始时半圆柱静止于如思考题6.4C.的运动轨迹质心图思考题6.4z., 可绕过其圆心的竖直轴轴转动, 轴承处有较小但不可忽略的摩擦力6.5. 有一水平圆台之后人沿台边跑一段, 如思考题6.5图所示.有人站在台边上, 初始时圆台与人均静止以人、人与圆台将如何运动? 在整个过程中, 又停止跑动时间后, . 问人停止跑动后,z?轴总角动量如何变化, 其对圆台和轴为质点系思考题6.5图? , 把轴包括在质点系内, 这样做有何好处6.6. 思考题6.5中?如轴承是光滑的, 情况又当如何思考题6.7. 6.5中,人与盘运动状态的改变是由人跑动引起的. 而质点系的角动量定6.8. 思考题6.5中,?质点系角动量的变化与内力无关. 这两者之间是否发生矛盾理指出,. 若质点系总动量为零, 则质点系对任意固定点的总角动量均相等6.9. 试证明:OO和有两个形状相同的匀质齿轮位于同一竖直面内6.10. 可绕过各自中心的水平轴, 21?O?I, 如思考题6.10图所示. 开始时轮1绕固定轴转动, 转动惯量同为以角速度转1O向下移动使二齿轮啮合. . 之后可沿竖直线移动的轴已知齿轮啮合后静止动, 轮22?2. 有人说: 转动角速度的大小均为“以二齿轮为质点组, 所受外力对轮轴力矩均???I?I??I??I22, . 为零且啮合前总角动量为, 啮合后总角动量仍为可见啮合过.程角动量守恒.”试分析该说法是否正确》》》》精品资料》<<<<<<》精品资料》》》》<<<<<<6.10图思考题初始时给其中一小球以静止地放在光滑水平面上. 6.11. 质量相同的两小球用轻杆相连, ?v.垂直于杆的水平初速度, 试证两球各自的轨道均为旋轮线0??FF ff这个摩擦力, 其动量变化靠的是地面对后轮向前的摩擦力, 6.12. 自行车由静到动?自行车向前移动距离)(?WF?f?对自行车做的功是否为?????Lmv??L?r????zxyO式代替质动一般的坐标系心和系, 关系以6.13. ???OtOOO12?T?T?mv?L?????zOyx Ot?O2T能点的角动量和动能系中对和(分别为质点系在)?O?否成立如思考初始时杆静止于竖直位置6.14. 一匀质细杆可绕过端点的水平轴无摩擦地转动, , 以小球和杆为质点题6.14图所示. 之后一小球沿水平方向飞来与杆做完全弹性碰撞.?, 在碰撞过程中系统动量、角动量和机械能是否守恒系6.14图思考题m l绕过其中点的竖直轴以角速度在光滑水平面上有一长为、质量为, 的匀质细杆6.15. ??A以杆为现突然将杆的, 端按住. 转动, 但其中心不固定, 如思考题6.15图所示0AAA点的过程但在按住, 系统在点受外力作用, 有人认为研究对象, :“用手按住点A?”你认为这样的看法正确吗, 所以杆的机械能守恒.中,点无位移故该外力不做功6.15图思考题第六章习题》》》》精品资料》<<<<<<》<<<<<<精品资料》》》》mmm2B,A OC AB,为椭质圆规尺, 质量为套管, 曲柄质量为量6.1. 211??lOC?AC?CB?z,绕轴转动, 尺和曲柄的质心均位于其中点, 曲柄以匀角速度.如题6.1图所示. 求此机构总动量的大小和方向题6.1图mmA并可沿直角三棱的不可伸长的轻绳相连和, 的重物以跨过滑轮6.2. 质量分别为21已知三棱柱质量. 三棱柱底面放在光滑水平面上, 如题6.2图所示. 柱的斜面滑动mm?4m?16m.10三棱柱沿水平时求当重物下降高度为初始时各物体均静止, , 21.面的位移题6.2图?mv?m.向前跳出, 此人以与地面成角的初速度6.3. 质量为的人手持质量为的物体00?u,. 问由于物体的抛出当他跳到最高点时, 将物体以相对自己的速度水平向后抛出?跳的距离增加了多少mmAAB质点有水平初, 质量分别为和, 初始时位于同一竖直线上6.4. 两个质点和BA?v hlBABABB在间距离为点的上方速度, 质点静止, , 点高度为. , 点在和0BABA(2) 两质点间没有相互作用;的质心轨迹. (1) 以下3种情况中求质点和和BAAB.和; (3) 以万有引力相互作用质点间以轻杆相连和???t?cos m O其质心规律转动点的水平轴按,6.5. 质量为的薄板在竖直面内, 绕过0a OC.. 离求在任一瞬时水平轴对板的约束力点的距离为图所示, 如题6.56.5图题m l?OA?OB BA初始二球质量均为, . 6.66.6. 瓦特节速器装置如题图, 二杆长和???BA。
理论力学基础(北师大)习题

第一章思考题1.1. 如思考题 1.1图所示, 岸距水面高为h , 岸上有汽车拉着绳子以匀速率u 向左开行,绳子另一端通过滑轮A 连于小船B 上, 绳与水面交角为θ, 小船到岸的距离为s . 则u 与s的关系为: (1)θcos su =;(2) θcos s u -= ;(3)θcos u s = ;(4) θcos u s -=思考题1.1图 1.2. 在参考系上建立一个与之固连的极坐标系, 但其单位矢量r e 和θe 随质点位置变化而改变, 这是否与固连相矛盾? 是否说明极坐标系是动坐标系? 1.3. 质点沿一与极轴Ox 正交的直线以0v 做匀速运动, 如思考题1.3图所示. 试求质点运动加速度在极坐标系中的分量r a 和θa .思考题1.3图 1.4. 杆OA 在平面内绕固定端O 以匀角速ω转动. 杆上有一滑块m , 相对杆以匀速u 沿杆滑动, 如思考题1.4图所示. 有人认为研究m 的运动有如下结论: (1) r a =0, θa =0, 故a =0; (2) O 为OA 转动中心, 所以在自然坐标法中向心加速度指向O 点. 试分析上述结论是否正确.思考题1.4图第一章习题1.1. 如题 1.1图所示,曲柄连杆OA 以匀角速110-=s ω转动, 已知长度0 cm,80________===t AB OA 时α=∠AOB . 求连杆AB 的中点的运动学方程、轨道、速度和加速度.题1.1图 1.2. 一质点沿圆锥曲线0222=--nx mx y 运动 (n m ,为常数), 其速率为常量c . 求质点速度的x 分量和y 分量.1.3. 一质点的径向与横向速度分别为r λ和μθ(λ, μ为常量). 试证其径向与横向加速度分别为r r 222θμλ-和r μλμθ+().1.4. 一质点做平面运动, 其速率为常量0v , 径向速度亦为常量b (0>b ,0v b <), 求质点的轨道方程. 设0=t 时0r r =,0=θ. 1.5. 一质点做平面曲线运动, 其径向速度为正值常量, )0( >=c c v r ;其径向加速度为负值, 并与到极点的距离的三次方成反比, )0( 32>-=b r b a r . 求质点的运动学方程.设0=t 时,0r r =, 0θθ=, 且运动中0>θ . 1.6. 如题1.6图所示,已知一直管OA 保持其与竖直方向的夹角α不变, 绕过其O 端的竖直轴以角速度ω 做均匀转动. 一质点从O 点开始沿管做匀加速运动, 加速度的大小为a , 初速度为零. 试用柱坐标系求质点对地面的速度和加速度, 并用球坐标系求质点对地的速度.题1.6图1.7. 一质点的轨道曲线在Oxy 平面内, 其速度的y 分量为正值常量)0(>c c , 试证质点加速度的大小可表示为ρc v a 3=, 其中v 为速率, ρ为轨道曲率半径.1.8. 质点沿半径为r 的圆周运动, 初速度为0v , 其加速度矢量与速度矢量间的夹角α保持不变, 求质点速率随时间的变化规律.1.9. 已知质点运动的轨道为圆锥曲线)cos 1(θe p r +=, 如题1.9图所示. p 和e 为正值常量. 已知c r =θ 2, c 亦为正值常量. 试证质点加速度的方向必指向原点(即圆锥曲线的一个焦点), 其大小与2r 成反比.题1.9图1.10. 试用数值计算方法, 在直角坐标系xy O 2中, 描绘教材中第一章例题1中质点运动的情况.1.11. 试用数值计算方法, 描绘教材中第一章例题3中质点运动的情况.第二章思考题2.1. 教材中第二章例题1中(2)式是否说明A 点加速度0=A a ?2.2. 教材中第二章例题1中对(3)式求时间导数是否可以得到a R =θ ?2.3. 如思考题2.3图所示, 半径为r 的圆柱A 沿半径为R 的固定圆柱B 由最高点无滑动地滚下, 由于弧长P P P P ''=', 所以无滑条件可表示为θϕR r =, 对θϕR r =求导数可得θϕ R r =, 所以圆柱A 的角速度为r R θϕ =, 上述各结论是否正确?思考题2.3图2.4. 有人认为: 由于每瞬时刚体的平面平行运动都可以看成是绕瞬心的纯转动, 所以刚体上任一点的加速度由向心加速度和切向加速度组成, t n e r e r a ωω+=2, r 为该点到瞬心的距离. 这种看法是否正确? 为什么?2.5. 参见教材中第二章例题3图2.16, 甲认为: “B 为固定不动的点, 故B 为定点, 又因O 点速度为零, 所以OB 为瞬时轴.” 乙认为: “我看定点应为点O , 由于B 点不动, 所以OB 为瞬时轴.” 试指出甲、乙二人的错误. 2.6. 教材中第二章例题3图2.16中的坐标系Oxyz 为动坐标系. 甲认为求出的P v 和P a 是相对Oxyz 系的速度和加速度. 乙认为题中要求的是相对水平面的速度和加速度, 所以选用动坐标系是不合适的. 你认为如何?2.7. 速度v 是极矢量, 角速度ω 是轴矢量, 阅读参考书(赵凯华, 罗蔚茵. 新概念物理教程·力学), 说明它们的共性与差异.第二章习题2.1. 半径为R 的线轴在水平面上沿直线做无滑滚动, 中部绕线轴的半径为r , 线无滑地绕在轴上, 线端点A 以不变速度u 沿水平方向运动, 如题2.1图所示. 求: (1)轴心C 的速度和线轴的角速度; (2) 线轴与水平面接触点B 的加速度.题2.1图2.2. 半径为b 的小圆盘在一半径为a 的固定大圆盘的边缘上运动,两圆盘在水平面内,Oxy 为固定直角坐标系, 如题2.2图所示.x 轴与两圆心连线O O '夹角的时间导数θ已知, 求下列3种情况中小圆盘的角速度: (1) 小圆盘上某一确定半径的空间指向不变;(2) 小圆盘上某一确定半径始终指向O 点; (3) 小圆盘在大圆盘上做无滑滚动.题2.2图2.3. 曲柄OA 以匀角速度ω绕O 点转动, 曲柄OA 借助连杆AB 推动滑块B 沿轨道OD 运动. 设r OA =, l AB =, DO 与OA 夹角为t ω, 如题2.3图所示. 求杆AB 的角速度和B 点的速度.题2.3图 2.4. 半径为a 的圆柱夹在互相平行的两板间, 两板分别以不变的速度21,v v 反向运动, 如题2.4图所示. 设圆柱与两板间均无滑动, 求: (1) 瞬心位置;(2)圆柱上与上板的接触点A 的加速度.题2.4图2.5. 长为l 的细杆AB 在Oxy 平面内运动,A v 的大小和方向已知, 且知道B v 的方向, 如题2.5图所示. 求: (1) 杆的角速度ω 及B v 的大小;(2)杆上某点C 的位置, C v 刚好沿杆的方向.题2.5图 2.6. 圆盘以角速度1ω 绕水平轴CD 转动, CD 轴又以角速度2ω 绕过盘心O 的竖直AB 轴转动, 如题2.6图所示. 已知rad 51=ω , rad 32=ω , 求圆盘角速度ω 及ω .题2.6图2.7. 转轮AB 绕过轮心且与轮面垂直的OD 轴以角速度1ω 转动, 而OD 绕竖直线OE 以角速度2ω 转动. 已知转轮半径a CB =, b OC =, θ=∠EOD , 如题 2.7图所示. 试求转轮最低点速度B v .题2.7图2.8. 高为h , 顶角为α2的圆锥在水平面上做无滑滚动, 若此圆锥以不变角速度ω 绕竖直ζO 轴转动, 如题2.8图所示. 试求: (1) 圆锥角速度; (2) 圆锥底面最高点P 的速度v ; (3) P 点的转动加速度和向轴加速度的量值1a 和2a .题2.8图第三章思考题3.1. 有一质量为m 的珠子, 沿一根置于水平面内的铁丝滑动, 采用自然坐标法描述. 珠子受重力g m W =, 铁丝施与的约束力b Nb n Nn t Nt Ne F e F e F F ++=.t Nt e F 即为滑动摩擦力f F , 设动摩擦因数为μ. 试判断下列各式正误: (1) mg F f μ=; (2) Nb f F F μ=(3)Nn f F F μ=;(4) 22Nb Nn f F F F +=μ3.2. 用极坐标系描述单摆的运动. 某甲如思考题 3.2图(a)规定θ角正向, 得到动力学方程θθsin mg ml -= ; 某乙如思考题 3.2图(b)规定θ角正向, 则得到θθsin mg ml += . 你认为谁的做法正确?(a) (b)思考题3.2图 3.3. 质量为m 的质点, 由静止开始自高处自由落下. 设空气阻力f F 与速度成正比, 比例系数为k . 某甲建立竖直向上的坐标如思考题3.3图(a), 得到方程为y k mg y m+-=. 某乙建立竖直向下的坐标如思考题3.3图(b), 得到方程为y k mg y m-=.他们列出的方程对吗?(a) (b)思考题3.33.4. 有人认为: 用极坐标系讨论质点的平面运动时, 如果0≡r F , 则沿径向动量守恒,==rm p r 常量;若0≡θF , 则沿横向动量守恒. 这种看法对吗? 3.5. 试判断以下二论断是否正确:(1) 若质点对固定点O 的角动量守恒, 则对过O 点的任意固定轴的角动量守恒.(2) 若质点对固定轴的角动量守恒, 则对该轴上任一固定点的角动量守恒.3.6. 一质点动量守恒, 它对空间任一固定点的角动量是否守恒? 如质点对空间某一固定点角动量守恒, 该质点动量是否守恒?3.7. 当质点做匀速直线运动时, 其动量是否守恒? 角动量是否守恒?3.8. 在固定的直角坐标系Oxyz 中, 质量为m 的质点的速度k v j v i v v z y x ++=, 所受合力为k F j F i F F z y x ++=. 能否将质点的动能定理r F mv d )21(d 2⋅=向x 轴方向投影而得出分量方程x F mv x x d )21(d 2=? 该方程是否正确?第三章习题3.1. 研究自由电子在沿x 轴的振荡电场中的运动. 已知电场强度i t E E )c o s (0ϕω+=,ϕω,,0E 为常量. 电子电量为e -, 质量为m . 初始时, 即当0=t 时i x r 00=, i v v 00=. 忽略重力及阻力, 求电子的运动学方程. 3.2. 以很大的初速度0v 自地球表面竖直上抛一质点, 设地球无自转并忽略空气阻力, 求质点能达到的最大高度. 已知地球半径为R , 地球表面处重力加速度为g . 3.3. 将质量为m 的质点竖直上抛, 设空气阻力与速度平方成正比, 其大小22gv mk F R =.如上抛初速度为0v , 试证该质点落回抛出点时的速率20201v k v v +=. 3.4. 向电场强度为E 、磁感应强度为B 的均匀稳定电磁场中入射一电子. 已知B E ⊥, 电子初速0v 与E 和B 均垂直, 如题 3.4图所示. 试求电子的运动规律. 设电子电量为e -.题3.4图3.5. 旋轮线如题3.5图所示, 可理解为一半径为a 的圆轮在直线上做无滑滚动时轮缘上一点P 的轨迹, 其参数方程为)sin (ϕϕ+=a x , )cos 1(ϕ-=a y . 在重力场中, 设y 轴竖直向上, 一质点沿光滑旋轮线滑动, 试证质点运动具有等时性(绕O 点运动周期与振幅无关).题3.5图3.6. 一小球质量为m , 系在不可伸长的轻绳之一端, 可在光滑水平桌面上滑动. 绳的另一端穿过桌面上的小孔, 握在一个人的手中使它向下做匀速运动, 速率为a , 如题3.6图所示. 设初始时绳是拉直的, 小球与小孔的距离为R , 其初速度在垂直绳方向上的投影为0v . 试求小球的运动规律及绳的张力.题3.6图3.7. 一质量为m 的珠子串在一半径为R 的铁丝做成的圆环上, 圆环水平放置. 设珠子的初始速率为0v , 珠子与圆环间动摩擦因数为μ, 求珠子经过多少弧长后停止运动 (根据牛顿第二定律求解).3.8. 质量为m 的小球沿光滑的、半长轴为a 、半短轴为b 的椭圆弧滑下, 此椭圆弧在竖直平面内且短轴沿竖直方向. 设小球自长轴端点开始运动时其初速度为零. 求小球达到椭圆弧最低点时对椭圆弧的压力 (根据牛顿第二定律求解). 3.9. 力1F 和2F分别作用在长方体的顶角A 和B 上, 长方体的尺寸和坐标系如题3.9图所示. 试计算1F 和2F 对原点O 及3个坐标轴的力矩.题3.9图3.10. 已知质量为0m 的质点做螺旋运动, 其运动学方程为t r x ωcos 0=, t r y ωsin 0=,kt z =,k r ,,0ω为常量. 试求: (1)t 时刻质点对坐标原点的角动量;(2) t 时刻质点对过),,(c b a P 点, 方向余弦为),,(n m l 的轴的角动量.3.11. 如题 3.11图所示, 质量为m 的小球安装在长为l 的细轻杆的A 端, 杆的B 端与轴21O O 垂直地固连. 小球在液体中可绕21O O 轴做定轴转动, 轴承1O 和2O 是光滑的. 转动中小球所受液体阻力与角速度成正比, ωαm F R =,α为常量. 设初始角速度为0ω, 试求经多少时间后, 角速度减小为初始值的一半,以及在这段时间内小球所转圈数.(忽略杆的质量及所受阻力.)题3.11图3.12. 质量为m 的质点沿椭圆轨道运动, 其运动学方程为kt a x cos =, kt b y sin =(k b a ,,为常量). 用两种方法计算质点所受合力在0=t 到k t 4π=时间内所做的功.3.13. 试用动能定理求解3.7题.3.14. 有一小球质量为m , 沿如题3.14图所示的光滑的水平的对数螺旋线轨道滑动. 螺旋线轨道方程为θa e r r -=0, a 为常数. 已知当极角0=θ时,小球初速为0v . 求轨道对小球的水平约束力N F 的大小. (用角动量及动能定理求解, 图中δ为θe 与v 方向间夹角,a =δtg .)题3.14图3.15. 已知质点所受力F 的3个分量为z a y a x a F x131211++=,z a y a x a F y 232221++=, z a y a x a F z 333231++=,系数)3,2,1,(=j i a ij 都是常量. 这些ij a 满足什么条件时与力F相关的势能存在? 在这些条件被满足的条件下, 计算其势能.3.16. 一带有电荷q 的质点在电偶极子的场中所受的力为3cos 2r pq F r θ=,3sin r pq F θθ=,p 为偶极距, r 为质点到偶极子中心的距离.试证此力场为有势场.3.17. 如题3.17图所示, 自由质点在Oxy 平面内运动, 静止中心A 和B 均以与距离成正比的力吸引质点M , 比例系数为k . 试证明势能存在并求出质点的势能.题3.17图3.18. 试用机械能守恒定律求解3.8题.3.19. 设空气阻力与速率的n 次方成正比, 求有阻力抛体运动微分方程数值解, 并描绘其运动情况.3.20. 求带电粒子在均匀稳定电磁场中运动微分方程数值解, 并描绘其运动情况.3.21. 求大摆角单摆运动微分方程数值解, 并研究周期与摆角的关系.第四章思考题4.1. 线性振动与非线性振动有什么根本区别?4.2. 基频与固有频率有何不同?4.3. 用小参量级数展开方法求解非线性振动问题时, 什么情况下会出现长期项? 应如何处理长期项?4.4. 如何理解吸引子的概念? 你知道有哪些类型的吸引子?4.5. 如何理解混沌运动? 如何判断混沌运动?第四章习题4.1. 试用微扰法求方程0220=-+x x x εω 准确到第二级的解. 设初始条件为0=t 时, A x =)0(, 0)0(=x. 4.2. 做一维运动的质点的质量为m , 当0<x 时受到恒力0F +的作用, 当0>x 时受到恒力0F -的作用. 画出描述此运动的相图, 计算运动的周期(以m ,0F+和总能量E 表示)和振幅A . 不考虑阻尼.4.3. 在非线性动力学发展过程中有三大著名的方程起了重大作用, 除了已介绍过的Duffing 方程和Van.der.pol 方程外, 还有洛伦茨(Lorenz )方程, 它是由E. N. Lorenz 在研究大气对流问题中引进的, 他在对此方程进行数值计算研究中首次发现混沌现象. 经过许多简化后得到的Lorenz 方程是一个三阶的无量纲的常微分方程组: ⎪⎪⎪⎩⎪⎪⎪⎨⎧+-=--=+-= 38d d 28d d 1010d d xy z t z xz y x t y y x t x 试用计算机数值计算方法作出它的相图(通常称为Lorenz 吸引子).4.4. 试用近似计算方法证明教材中第四章方程(4.5.1)(即范·德·波尔方程)具有精确到一级的稳态周期解(其中取10=x ))3sin sin 3(4cos 2t t t x ωωωμω-+=并证明 0ωω≈ 其周期为ωπ2=T 近于常数,与初始条件无关.第五章思考题5.1. 有人说“牵连运动就是动坐标系的运动”, 这种说法是否正确? 为什么? 5.2. 某习题要求求出t v d d '. 于是有人提出疑问: “v ' 是质点相对s '系的速度, 它的存在依赖于s '系. 质点相对s 系的速度是v 而不是v ' . 为什么可以对s 系求v ' 的时间变率呢?”你能解决他的疑虑吗?5.3. 有一光滑水平圆盘, 在其上离中心O 点距离为a 处放一光滑小球, 初始时盘与小球均静止. 当圆盘绕过O 点的竖直轴做均匀转动后, 有人认为“小球并未被盘带着运动, 所以它的牵连速度与牵连加速度均为零”. 他的看法正确吗?5.4. 一竖直圆盘沿水平直线轨道做无滑滚动, 其盘心O 点的加速度为0a . 以地面为s 系, 以O 为原点建立平动Oxyz 为s '系, 如思考题5.4图所示. 则轮边上一点P 的绝对加速度为)(0r r a a '⨯⨯+'⨯+= ωωω. 试问 (1)ω 是绝对变率还是相对变率?(2) 等式右方三项各是什么加速度?思考题5.4图5.5. 在思考题5.4中若以与圆盘固连的z y x O '''为s '系, 此时)(0r r a a '⨯⨯+'⨯+= ωωω是否还能成立? 等式右方三项又各是什么加速度? 5.6. 水平面内半径为R 的圆环, 绕过中心O 的竖直轴以匀角速度ω转动. 小虫M 在环上,相对于环以匀速率u 爬行, 如思考题 5.6图所示. 以地为s 系, 圆环为s '系, 试说明等式 R u u R R u R 2222)(+-=-ωωω左右两端每一项的物理意义.思考题5.6图 5.7. 有人认为极坐标加速度公式θθθ r r a 2+=中θr2是科氏加速度. 你以为如何? 5.8. 小球静止于地面, 现以匀加速上升的电梯为参考系, 小球是否受惯性力作用?5.9. 有人说“牵连加速度是由牵连惯性力产生的, 科氏加速度是由科氏力产生的”. 这种说法对吗? 为什么?第五章习题5.1. 一直管在水平面内绕其O 端以匀角速度ω 转动. 管内有一质点相对管的速率为at v v +='0, 方向背离O 点向外, 0v ,a 为常量. 以地面Oxyz 为s 系, 与管固连的z y x O '''为s '系, 如题 5.1图所示. 试求: (1) t v d d ';(2)t v d d '*; (3)dt a ' d ;(4)t a d d '* .题5.1图 5.2. 半径为R 的记录器滚筒绕水平固定轴以角速度ω 转动. 记录器笔尖P 在与固定轴等高的水平线上, 以速度0v 运动, 如题5.2图所示. 求笔尖P 相对滚筒的速率.(先以地为s 系, 再以滚筒为s 系, 分别用两种方法求解.)题5.2图5.3. 半顶角为α的圆锥以匀角速度ω 绕对称轴转动, 圆锥表面有一沿母线的细槽. 质点P 由圆锥顶点开始, 相对圆锥以速度v '沿槽做匀速运动, 如题5.3图所示. 求运动到t 时刻, P 点绝对加速度的量值(以地面为s 系).题5.3图5.4. 如题5.4图所示, 瓦特节速器的4根连杆长度均为l , 4杆和2小球P 所在平面绕竖直轴转动的规律为)(t ϕϕ=, 连杆与转轴间夹角的变化规律为)(t θθ=. 试求其中一个小球对地面的加速度.题5.4图5.5. 一半径为R 的车轮在竖直平面内沿一直线轨道做无滑滚动, 已知轮心的速率为常量v .轮缘上有一质点以与轮心速率相等的速率v , 相对车轮沿轮缘顺着车轮滚动方向运动. 求: (1) 质点相对车轮的加速度; (2) 质点相对地面的加速度. 5.6. 在一内壁光滑的水平直管中有一质量为m 的小球, 此管以匀角速度ω 绕过其一端的竖直轴转动. 如开始时小球到转动轴的距离为a , 球相对管的速率为零, 而管的总长度为a 2. 求: (1) 小球刚要离开管口时相对管的速度和相对地面的速度;(2) 小球从开始运动到离开管口所需的时间.5.7. 小环质量为m , 穿在曲线方程为)(x f y =的光滑钢丝上, 此钢丝通过坐标原点O , 并绕竖直的y 轴以匀角速度ω 转动. 如欲使小环在钢丝的任何位置上都处于相对曲线钢丝平衡的状态. 求: (1) 钢丝的曲线方程; (2) 曲线钢丝对小环的约束力. 5.8. 一半径为R 的圆环绕过环心O 的竖直轴以匀角速度ω 转动, 有一质量为m 的小环套在此圆环上, 并可在其上无摩擦地滑动. 初始时小环和O 点连线与竖直轴夹角为0θ,相对圆环静止, 如题5.8图所示. 试求小环相对圆环的角速度以及圆环对小环的约束力.题5.8图5.9. 质量分别为1m 和2m 的两个质点, 用一原长为a 的弹性轻绳相连, 绳的劲度系数为)221221m m m m k +=ω. 如将此系统放在一内壁光滑的水平管中, 水平管绕管上某点以匀角速度ω 绕竖直轴转动. 初始时两质点均相对水平管静止, 两质点间的距离为a . 试求任一时刻两质点间的距离.5.10. 给放置在光滑水平面上的物体一个水平初速度, 考虑地球自转, 证明该物体运动轨迹是一个圆, 并求出圆半径及水平面所受物体的压力.5.11. 如在北纬λ处, 以仰角α自地面向正东方发射一炮弹, 炮弹发射速度为v, 忽略空气阻力但计及地球自转, 试证明炮弹落地时的横向偏离为 ααλωcos sin sin 4222⋅⋅=g v d式中ω为地球自转角速度. 5.12. 一质点如以初速度0v在北纬λ处从地面竖直上抛, 达到h 高度后, 复落至地面. 忽略空气阻力, 考虑地球自转. 试求质点落至地面时相对抛出点的偏差, 并通过物理图象说明结果的合理性.5.13. 求教材中第五章(5.4.6)式数值解, 用计算机研究落体偏东现象.5.14. 求教材中第五章(5.4.11)式数值解, 研究在不同初始条件下傅科摆的运动情况. 第六章思考题6.1. 相同的两匀质杆AO 和BO 用铰链连接于固定点O , 并可在水平面内绕O 点转动.某时刻AOB 位于同一直线上, 二杆以同样大小的角速度ω转动, 如思考题6.1图所示. 有人认为:“以二杆为系统, 此时质心为O 点, O 点为固定点, 故此时质心速度为零.”这种说法对吗?思考题6.1图6.2. 有时称c t c v m r ⨯为质心对O 点的角动量, 称221c t v m 为质心的动能. 这是否说明质心是一个质量为t m 、位置矢量为c r 、速度为c v 的质点? 6.3. 有一半径为R , 质量为m 的匀质圆球被旋转抛出. 某时刻球心速度为v ,球旋转角速度为ω , 求此时圆球的动量.6.4. 将一半圆柱置于一光滑水平面上, 初始时半圆柱静止于如思考题6.4图所示位置, 求质心C 的运动轨迹.思考题6.4图6.5. 有一水平圆台, 可绕过其圆心的竖直轴z 轴转动, 轴承处有较小但不可忽略的摩擦力.有人站在台边上, 初始时圆台与人均静止, 如思考题6.5图所示.之后人沿台边跑一段时间后, 又停止跑动. 问人停止跑动后, 人与圆台将如何运动? 在整个过程中, 以人、圆台和轴为质点系, 其对z 轴总角动量如何变化?思考题6.5图6.6. 思考题6.5中, 把轴包括在质点系内, 这样做有何好处?6.7. 思考题6.5中, 如轴承是光滑的, 情况又当如何?6.8. 思考题6.5中, 人与盘运动状态的改变是由人跑动引起的. 而质点系的角动量定理指出, 质点系角动量的变化与内力无关. 这两者之间是否发生矛盾?6.9. 试证明: 若质点系总动量为零, 则质点系对任意固定点的总角动量均相等.6.10. 有两个形状相同的匀质齿轮位于同一竖直面内, 可绕过各自中心的水平轴1O 和2O 转动, 转动惯量同为I , 如思考题6.10图所示. 开始时轮1绕固定轴1O 以角速度ω 转动, 轮2静止. 之后可沿竖直线移动的轴2O 向下移动使二齿轮啮合. 已知齿轮啮合后转动角速度的大小均为2ω. 有人说: “以二齿轮为质点组, 所受外力对轮轴力矩均为零. 且啮合前总角动量为ω I , 啮合后总角动量仍为ωωωI I I =+⋅22, 可见啮合过程角动量守恒.”试分析该说法是否正确.思考题6.10图6.11. 质量相同的两小球用轻杆相连, 静止地放在光滑水平面上. 初始时给其中一小球以垂直于杆的水平初速度0v , 试证两球各自的轨道均为旋轮线.6.12. 自行车由静到动, 其动量变化靠的是地面对后轮向前的摩擦力f F , 这个摩擦力f F 对自行车做的功是否为自行车向前移动距离)(⨯=f F W ?6.13. 以一般的动坐标系z y x O ''''代替质心系, 关系式O O t O OL v m r L ''''+⨯= 和T v m T O t '+='221(O L ''和T 分别为质点系在z y x O ''''系中对O '点的角动量和动能)能否成立?6.14. 一匀质细杆可绕过端点的水平轴无摩擦地转动, 初始时杆静止于竖直位置, 如思考题6.14图所示. 之后一小球沿水平方向飞来与杆做完全弹性碰撞. 以小球和杆为质点系, 在碰撞过程中系统动量、角动量和机械能是否守恒?思考题6.14图6.15. 在光滑水平面上有一长为l 、质量为m 的匀质细杆, 绕过其中点的竖直轴以角速度0ω 转动, 但其中心不固定, 如思考题6.15图所示. 现突然将杆的A 端按住, 以杆为研究对象, 有人认为:“用手按住A 点, 系统在A 点受外力作用, 但在按住A 点的过程中A 点无位移,故该外力不做功, 所以杆的机械能守恒.”你认为这样的看法正确吗?思考题6.15图第六章习题6.1. 椭圆规尺AB 质量为12m , 曲柄OC 质量为1m , 套管B A ,质量为2m ,l CB AC OC ===, 尺和曲柄的质心均位于其中点, 曲柄以匀角速度ω 绕z 轴转动,如题6.1图所示. 求此机构总动量的大小和方向.题6.1图 6.2. 质量分别为1m 和2m 的重物以跨过滑轮A 的不可伸长的轻绳相连, 并可沿直角三棱柱的斜面滑动. 三棱柱底面放在光滑水平面上, 如题 6.2图所示. 已知三棱柱质量21164m m m ==初始时各物体均静止, 求当重物下降高度为m 1.0时, 三棱柱沿水平面的位移.题6.2图 6.3. 质量为0m 的人手持质量为m 的物体, 此人以与地面成α角的初速度0v 向前跳出.当他跳到最高点时, 将物体以相对自己的速度u 水平向后抛出. 问由于物体的抛出, 跳的距离增加了多少?6.4. 两个质点A 和B 质量分别为A m 和B m , 初始时位于同一竖直线上, A 质点有水平初速度0v , B 质点静止, B 点高度为h , A 点在B 点的上方, A 和B 间距离为l . 在以下3种情况中求质点A 和B 的质心轨迹. (1) A 和B 两质点间没有相互作用;(2) 质点A 和B 以万有引力相互作用; (3) A 和B 间以轻杆相连.6.5. 质量为m 的薄板在竖直面内, 绕过O 点的水平轴按t ωθθcos 0=规律转动, 其质心C 离O 点的距离为a , 如题6.5图所示. 求在任一瞬时水平轴对板的约束力.题6.5图6.6. 瓦特节速器装置如题6.6图, 二杆长l OB OA ==, A 和B 二球质量均为m . 初始时A 和B 二球被一根线连结, 装置以角速度0ω 绕竖直轴转动, 杆的张角为0θ. 自某一时刻线被烧断, 求角速度ω 与张角θ的关系. 设轴承光滑, 不受主动力矩, 杆的质量均可忽略不计. 若杆的质量不可忽略, 但各杆质量分布均匀, 结果又当如何?题6.6图6.7. 一质量为0m 、底半径为R 的匀质圆锥, 它的光滑固定对称轴沿竖直方向, 圆锥尖端向上, 在圆锥表面上有一沿母线的细槽. 初始时, 圆锥绕其对称轴以角速度0ω转动, 同时有一质量为m 的小球开始自槽的顶端沿槽自由下滑. 试求小球滑出槽口时圆锥的角速度. 若此槽不是沿母线的直线, 试问此槽曲线应满足什么条件, 才能使小球滑出槽口时圆锥角速度与槽为沿母线的直线情况相同.6.8. 质量为1m 和2m 的二质点, 用一根长为l 的不可伸长的轻绳相连. 初始时1m 被握在手中不动, 2m 以匀速率0v 绕1m 做圆周运动. 在某瞬时将1m 放手, 试求以后二质点的运动, 并证明绳内张力l m m v m m F T )212021+=. 不考虑重力及质点间引力作用, 并已知绳一直是张紧的.6.9. 传送机由两个相同的滑轮B 和C 和套在其上的传送带构成, 每个滑轮质量为1m 、半径为R , 均可视为匀质圆盘, 传送带质量为2m , 相对水平面倾角为α, 被传送物体质量为3m . 初始时各物体均静止, 在B 上施加一不变力矩M , 如题6.9图所示. 设滑轮轴承处光滑, 传送带与滑轮及传送带与被传送物体间均无滑动, 传送带在EF 间为直线. 试求当被传送物体在EF 间运动时, 传送带运行速率v 与运行距离s 间的关系.题6.9图6.10. 一炮弹质量为21m m +, 发射时水平及竖直速度分别为Ox v 和Oy v . 当炮弹达到最高点时, 其内部炸药爆炸产生能量E , 使此炮弹分为1m 和2m 两部分, 开始时两部分均沿原方向飞行, 不计空气阻力, 试求炮弹的两部分落地时相距的距离.6.11. 质量为0m 、半径为R 的光滑半球, 其底面放在光滑水平面上, 有一质量为m 的质点沿球面滑下. 初始时二物体均静止, 质点初位置与球心连线和竖直向上的直线间夹角为α.求质点滑到它与球心连线和竖直向上直线间夹角为θ时θ的值.6.12. 轻杆AB 长为l ,两端固定有质量分别为1m 和2m 的质点A 和B , 杆只能在竖直平面内运动, 某瞬时A 点速度为1v , B 速度为2v , 分别与杆夹角1α和2α, 如题 6.12图。
北大理论力学作业详解
2.2. 在地球上以第三宇宙速度v3正对太阳发射 一星体(正对太阳是指星体基本上飞出地球 的引力作用后,相对于地球的速度矢量正好 指向太阳),求其轨道方程(地球轨道近似 看成园)。
2.3. 把地球和金星绕太阳运动的轨道都近似 看成在同一平面的园,半径分别为R和0.7R, 现从地面发射一个如图中轨道所示的人造行 星去考查金星,发射速度最小为多少? (Fig. 6)。
z
ω
lθ l
2
45o O
A
l
l
C
FIG. 5:
FIG. 4:
1.7. 证明带电粒子在稳定外电磁场中的能量 积分是T + eϕ = const。
1.8. 一 质 量 为m的 质 点 限 于 一 光 滑 的 曲
线y = y(x), z = z(x)上 运 动 , 质 点 受 到
的 主 动 力 为Fx = ϕ(x),Fy = ψ(x), 和 重 力Fz = −mg。1. 求 该 质 点 的Lagrange 方 程 。2. 如 曲 线 方 程 为y = 0, z = −x; Fx = ϕ(x) = mgx/2c, Fy = ψ(x) = 0,其中c > 0。 由 “1.” 写 出 该 情 形 下 的Lagrange方 程 ,
FIG. 2:
m 1
1.3. 一质点在半径为a的园环上运动。园环平 面保持竖直,并绕其过圆心的竖直轴以匀角 速度ω转动。写出质点在重力作用下的运动方 程和初级分。ω小于何值才能使质点不在底部 的另一处平衡,并求此位置。
O
m 2 FIG. 3:
1.4. 一小球m1在光滑水平桌上运动。另一个 小球m2通过桌上小孔用一根用一根不能伸长 的轻绳与m1 连接。写出该体系的拉氏量和初 级分(Fig. 3)。
CUGB理论力学习题解答PPT课件

40
FRy F1 sin1 F2 sin2 F3
50 F3 F4
x FRy 20N
MO 30F1 sin1 40F1 cos1 20F2 sin2 60F2 cos2 50F4 2000
MO 1000Nmm
3-1 已知:F1
50 N
,1
arctan
3 4
,
F2
30
2N ,2 45o
2
55.80kN
2-16 在一钻床上水平放置工件,在工件上同时钻四个等直径
的孔,每个钻头的力偶矩为 m1 m2 m3 m4 15N m 求工件的总切削力偶矩和A 、B端水平反力?
解: 各力偶的合力偶距为
n
FA
M Mi
i 1
M m1 m2 m3 m4
FB
4 (15) 60N m
求:力系的主矢和对O点的主矩。 z
MOy M y
b
c F1
e
b b2
c2
F1d
d
O
x
e
F2
y
e2 d 2 F2d
d e2
d2
F2 b
e
M Oy
0.3 0.5
100
0.3
1 10 5
5 0.2
2 10 5
5 0.2
6Nm
1-4 已知:F1= 100N,F2=10√5N, b= 0.3m , c= 0.4m , d = 0.2m , e= 0.1m 。
Mo
M
2 x
M
2 y
M
2 z
2
674 52Nm
arccos 40 39.7o 105.2o 54.8o
52
高一物理下学期力学复习北师大版

高一物理下学期力学复习知识总结归纳1. 牛顿运动定律的应用(1)牛顿第二定律是在实验基础上总结出的,定量揭示了物体的加速度与力和质量的关系。
(2)理解该定律时应注意:瞬时对应关系、矢量关系(3)问题分类应用牛顿运动定律解决问题的方法可分两类:根据物体受力及初状态分析物体运动情况,或根据物体运动情况分析受力情况。
解题的基本方法是一致的。
(4)解题思路①根据题设条件正确选取研究对象。
②对研究对象进行受力分析,画出受力示意图,对于连接体问题,要将研究对象隔离,分别进行受力分析。
③分析研究对象的运动情况。
尤其要重视对加速度a 的分析,它是将运动学和动力学连在一起的桥梁。
④根据牛顿运动定律列出动力学方程,在统一单位的条件下求解。
⑤对求解内容进行必要的分析和讨论。
2. 曲线运动、圆周运动、万有引力定律及其应用(1)运动条件①物体做曲线运动的条件:物体所受合外力的方向跟它的速度方向不在一条直线上。
注意:曲线上某点的切线方向就是物体在该点时的瞬时速度的方向。
由于曲线运动中速度方向不断变化,因此曲线运动是变速运动,一定具有加速度。
②匀速圆周运动的运动条件:做匀速圆周运动的物体所受合外力大小不变,方向总是和速度方向垂直并指向圆心。
(2)描述圆周运动的运动学物理量①圆周运动的运动学物理量有线速度v 、角速度ω、周期T 、转速n 、向心加速度a 等。
它们之间的关系大多是用半径r 联系在一起的。
如:T r r v πω2=⋅=,22224T r r r v a πω===。
要注意转速n 的单位为r/min ,它与周期的关系为n T 60=。
②向心加速度的表达式中,对匀速圆周运动和非匀速圆周运动均适用的公式有:ωωv r r v a ===22,公式中的线速度v 和角速度ω均为瞬时值。
只适用于匀速圆周运动的公式有:224T r a π=,因为周期T 和转速n 没有瞬时值。
(3)描述圆周运动的动力学物理量—向心力①向心力来源:向心力是做匀速圆周运动的物体所受外力的合力。
【理论力学课件@北师大】1-5

轨道曲线上无限接近的 3 个点所决定的圆称为 曲 率圆 , 曲 率圆 在密切面 内 . 曲 率圆 的 圆心 称为 曲率中心, 曲率圆的半径 ρ 称为曲率半径, 曲率半 径的倒数 κ = 1 ρ 称为曲率. 设弧长 PP′ = ds , 显然 κ = 1 ρ = dϕ ds , 曲率 κ 越大则 曲线 弯 曲程 度越大 . 当 轨道为平面曲线 y = y ( x) 时, 可利用数学分析中的公式
et v = v t et = s . v = v = vt = s 速度的大小
速度和加速度表达式. 速度沿切线指向运动的前方, 所以 vn = vb = 0 . 考 > 0 时 v 与 et 同向, 故 虑到 s
dv d de et ) = t a= = (s set + s dt dt dt 当 ϕ 的 正 向 与 弧 长 s 正 向 一 致 时 , ds = ρdϕ , 故
hω = − Rω sin ωti + Rω cos ωtj + k (1) 2π i + j + k a= x y z 2 2 = − Rω cosωti − Rω sin ωtj (2)
x = R cosωt y = R sin ωt h z= ωt 2π
《理论力学》第六章 刚体的基本运动习题全解

第六章 刚体的基本运动 习题全解[习题6-1] 物体绕定轴转动的运动方程为334t t -=ϕ(ϕ以rad 计,t 以s 计)。
试求物体内与转动轴相距m r 5.0=的一点,在00=t 与s t 11=时的速度和加速度的大小,并问物体在什么时刻改变它的转向? 解:角速度: 2394)34(t t t dt ddt d -=-==ϕω 角加速度:t t dtddt d 18)94(2-=-==ωα速度: )94(2t r r v -==ω)/(2)094(5.0|20s m r v t =⨯-⨯===ω)/(5.2)194(5.0|21s m v t -=⨯-⨯==切向加速度:rt t r a t 18)18(-=-==ρα法向加速度:22222)94()]94([t r rt r v a n -=-==ρ 加速度: 422222222)94(324])94([)18(t t r t r rt n a a n t -+=-+-=+=)/(8165.0)094(0324|24220s m r a t =⨯=⨯-+⨯== )/(405.1581.305.0)194(1324|24221s m r a t =⨯=⨯-+⨯== 物体改变方向时,速度等于零。
即:0)94(2=-=t r v )(667.0)(32s s t ==[习题6-2] 飞轮边缘上一点M,以匀速v=10m/s运动。
后因刹车,该点以)/(1.02s m t a t =作减速运动。
设轮半径R=0.4m,求M点在减速运动过程中的运动方程及t=2s时的速度、切向加速度与法向加速度。
解:t dtd a t 1.04.022-===ϕρα (作减速运动,角加速度为负)t dt d 25.022-=ϕ12125.0C t dtd +-=ϕ2130417.0C t C t ++-=ϕ12124.005.0)125.0(4.0C t C t dtd R v +-=+-⨯==ϕ104.0005.0|120=+⨯-==C v t图题46-251=C0000417.0|2130=+⨯+⨯-==C C t ϕ 02=C ,故运动方程为: t t 250417.03+=ϕt t t t R s 100167.0)250417.0(4.033+-=+-==ϕ速度方程:1005.02+-=t v)/(8.910205.0|22s m v t =+⨯-== 切向加速度:)/(2.021.01.0|22s m t a t t -=⨯-=-== 法向加速度:222)25125.0(4.0+-⨯==t a n ρω)/(1.240)252125.0(4.0|2222s m a t n =+⨯-⨯==[习题6-3] 当起动陀螺罗盘时,其转子的角加速度从零开始与时间成正比地增大。
北师大版物理八年级上册第三章力学知识归纳(含练习)

北师大版物理八年级上册第三章力学知识归纳(含练习)力学是物理学的一个重要分支,研究物体的运动和受力情况。
本文档将对北师大版物理八年级上册第三章力学知识进行归纳,同时提供相关练。
一、直线运动1. 直线运动是物体在一条直线上的运动。
物体的位置、速度和加速度是直线运动的基本概念。
2. 位移($s$)是物体从初始位置到最终位置的距离,与路径无关。
- 位移的计算公式:$s = s_2 - s_1$3. 速度($v$)是物体运动的快慢程度。
- 平均速度的计算公式:$v_{\text{avg}} = \frac{s}{t}$4. 加速度($a$)是物体速度变化的快慢程度。
- 平均加速度的计算公式:$a_{\text{avg}} = \frac{v}{t}$二、力的作用和相互作用1. 力是物体之间相互作用的结果,是引起物体产生位移和形状改变的原因。
2. 作用力和反作用力的大小相等,方向相反,且作用在两个不同的物体上。
3. 牛顿第三定律:作用力与反作用力之间满足作用反作用原理。
三、力的效果1. 力对物体可能产生以下效果:- 使物体改变速度- 使物体改变方向- 使物体形状发生变化2. 物体的质量对力的效果有影响。
- 物体质量越大,相同大小的力对其引起的加速度越小。
四、题练1. 一个物体以10 m/s 的速度向前直线运动,经过5秒后,物体的位移是多少?2. 一辆车从静止开始向前加速行驶,经过10秒后速度达到36 km/h。
求这段时间内车的加速度。
3. 如果两个力的大小分别为10N和20N,且作用在不同的物体上,求两个力的反作用力的大小。
4. 一个重物和一个轻物被推动,相同大小的力作用在两个物体上,哪个物体的加速度更大?5. 物体的质量为2kg,受到10N的力作用,求物体的加速度。
参考答案1. 50m2. 1 m/s²3. 10N4. 轻物的加速度更大5. 5 m/s²希望本文档对学习北师大版物理八年级上册第三章力学知识有所帮助。
北大理论力学课件第五章 点的运动和刚体的基本运动

0
角加速度为常量:
二个独立方程
0 t;
1 2 (ω 0 ) t;
1 2
t ;
2
θ θ0
0 2 ( 0 ).
理论力学
转动刚体上各点速度、加速度
S=R v=R
aτ dv dt d dt Rω R
2
y M
ds d t
A
k’
rA`
j’
y
x
i’
波桑公式
理论力学
本章结束
理论力学
例5-3: 销钉A由导杆B带动沿固定圆弧槽运动。导杆B沿轴螺 旋立柱以不变的速度v0 =2m/s向上运动。试计算当θ=300 时,销 钉A的切向和法向加速度。
解: 建立弧坐标s和直角坐标0xy如图。
v 因:s=Rθ, 故: s Rθ ,
又:y=Rsinθ,将上式对时间求导,
y R cos ,
2
v ρ
2
)
2
tan
;
;
理论力学
例5-2:汽车以匀速度v=10m/s过拱桥,桥面曲线 y=4fx(L–x)/L2, f=1m求:车到桥最高点时的加速度。
解:
at dv dt
3 '2
;
an
v
2
2
;
y
8 f L
2
(1 y d
) dy y
2
2
2
;
d
y
2
an
;
f x
dt
L=32m
2 2 2
cos
x r
; cos
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.6. 教材中第二章例题3图2.16中的坐标系 为动坐标系. 甲认为求出的 和 是相对 系的速度和加速度. 乙认为题中要求的是相对水平面的速度和加速度, 所以选用动坐标系是不合适的. 你认为如何?
题1.9图
1.10. 试用数值计算方法, 在直角坐标系 中, 描绘教材中第一章例题1中质点运动的情况.
1.11. 试用数值计算方法, 描绘教材中第一章例题3中质点运动的情况.
第二章思考题
2.1. 教材中第二章例题1中(2)式是否说明 点加速度 ?
2.2. 教材中第二章例题1中对(3)式求时间导数是否可以得到 ?
2.3. 如思考题2.3图所示, 半径为 的圆柱 沿半径为 的固定圆柱 由最高点无滑动地滚下, 由于弧长 , 所以无滑条件可表示为 , 对 求导数可得 , 所以圆柱 的角速度为 , 上述各结论是否正确?
思考题2.3图
2.4. 有人认为: 由于每瞬时刚体的平面平行运动都可以看成是绕瞬心的纯转动, 所以刚体上任一点的加速度由向心加速度和切向加速度组成, , 为该点到瞬心的距离. 这种看法是否正确? 为什么?
1.3. 质点沿一与极轴 正交的直线以 做匀速运动, 如思考题1.3图所示. 试求质点运动加速度在极坐标系中的分量 和 .
思考题1.3图
1.4. 杆 在平面内绕固定端 以匀角速 转动. 杆上有一滑块 , 相对杆以匀速 沿杆滑动, 如思考题1.4图所示. 有人认为研究 的运动有如下结论: (1) =0, =0, 故 =0; (2) 为 转动中心, 所以在自然坐标法中向心加速度指向 点. 试分析上述结论是否正确.
2.7. 速度 是极矢量, 角速度 是轴矢量, 阅读参考书(赵凯华, 罗蔚茵. 新概念物理教程·力学), 说明它们的共性与差异.
第二章习题
2.1. 半径为 的线轴在水平面上沿直线做无滑滚动, 中部绕线轴的半径为 , 线无滑地绕在轴上, 线端点 以不变速度 沿水平方向运动, 如题2.1图所示. 求: (1)轴心 的速度和线轴的角速度; (2) 线轴与水平面接触点 的加速度.
思考题1.4图
第一章习题
1.1. 如题1.1图所示,曲柄连杆 以匀角速 转动, 已知长度 时 . 求连杆 的中点的运动学方程、轨道、速度和加速度.
题1.1图
1.2. 一质点沿圆锥曲线 运动 ( 为常数), 其速率为常量 . 求质点速度的 分量和y分量.
1.3. 一质点的径向与横向速度分别为 和 ( , 为常量). 试证其径向与横向加速度分别为 和 ).
题2.4图
2.5. 长为 的细杆 在 平面内运动, 的大小和方向已知, 且知道 的方向, 如题2.5图所示. 求: (1) 杆的角速度 及 的大小;(2)杆上某点 的位置, 刚好沿杆的方向.
题2.5图
2.6. 圆盘以角速度 绕水平轴 转动, 轴又以角速度 绕过盘心 的竖直 轴转动, 如题2.6图所示. 已知 , , 求圆盘角速度 及 .
第一章思考题
1.1. 如思考题1.1图所示, 岸距水面高为 , 岸上有汽车拉着绳子以匀速率 向左开行, 绳子另一端通过滑轮 连于小船 上 绳与水面交角为 , 小船到岸的距离为 . 则 与 的关系为:
(1) ;(2) ;(3) ;(4)
思考题1.1图
1.2. 在参考系上建立一个与之固连的极坐标系, 但其单位矢量 和 随质点位置变化而改变, 这是否与固连相矛盾? 是否说明极坐标系是动坐标系?
1.4. 一质点做平面运动, 其速率为常量 , 径向速度亦为常量 ( , ), 求质点的轨道方程. 设 时 , .
1.5. 一质点做平面曲线运动, 其径向速度为正值常量, ;其径向加速度为负值, 并与到极点的距离的三次方成反比, . 求质点的运动学方程. 设 时, , , 且运动中 .
1.6. 如题1.6图所示,已知一直管 保持其与竖直方向的夹角 不变, 绕过其 端的竖直轴以角速度 做均匀转动. 一质点从 点开始沿管做匀加速运动, 加速度的大小为 , 初速度为零. 试用柱坐标系求质点对地面的速度和加速度, 并用球坐标系求质点对地的速度.
题1.6图
1.7. 一质点的轨道曲线在 平面内, 其速度的 分量为正值常量 , 试证质点加速度的大小可表示为 , 其中 为速率, 为轨道曲率半径.
1.8. 质点沿半径为 的圆周运动, 初速度为 , 其加速度矢量与速度矢量间的夹角 保持不变, 求质点速率随时间的变化规律.
1.9. 已知质点运动的轨道为圆锥曲线 , 如题1.9图所示. 和 为正值常量. 已知 , 亦为正值常量. 试证质点加速度的方向必指向原点(即圆锥曲线的一个焦点), 其大小与 成反比.
题2.2图
2.3. 曲柄 以匀角速度 绕 点转动, 曲柄 借助连杆 推动滑块 沿轨道 运动. 设 , , 与 夹角为 , 如题2.3图所示. 求杆 的角速度和 点的速度.
题2.3图
2.4. 半径为 的圆柱夹在互相平行的两板间, 两板分别以不变的速度 反向运动, 如题2.4图所示. 设圆柱与两板间均无滑动, 求: (1) 瞬心位置;(2)圆柱上与上板的接触点 的加速度.
题2.1图
2.2. 半径为 的小圆盘在一半径为 的固定大圆盘的边缘上运动,两圆盘在水平面内, 为固定直角坐标系, 如题2.2图所示. 轴与两圆心连线 夹角的时间导数 已知, 求下列3种情况中小圆盘的角速度: (1) 小圆盘上某一确定半径的空间指向不变;(2) 小圆盘上某一确定半径始终指向 点; (3) 小圆盘在大圆盘上做无滑滚动.
题2.6图
2.7. 转轮 绕过轮心且与轮面垂直的 轴以角速度 转动, 而 绕竖直线 以角速度 转动. 已知转轮半径 , , , 如题2.7图所示. 试求转轮最低点速度 .
题2.7图
2.8. 高为 , 顶角为 的圆锥在水平面上做无滑滚动, 若此圆锥以不变角速度 绕竖直 轴转动, 如题2.8图所示. 试求: (1) 圆锥角速度; (2) 圆锥底面最高点 的速度 ; (3) 点的转动加速度和向轴加速度的量值 和 .
