等边三角形的判定PPT教学课件
合集下载
等边三角形优秀PPT课件

数学研究中
等边三角形是数学研究中的重要对 象之一,与三角函数、数列等领域 有密切联系。
03
等边三角形面积与周长计算
面积计算公式推导
等边三角形面积公式
S = (a^2 * sqrt(3)) / 4,其中a为等边三角形的边长。
公式推导
等边三角形可以划分成两个等腰直角三角形,每个直角三角形的面积为(1/2) * a * (a * sqrt(3) / 2),因此等边三角形面积为2 * (1/2) * a * (a * sqrt(3) / 2) = (a^2 * sqrt(3)) / 4。
05
等边三角形相关数学问题探讨
等腰直角三角形与等边三角形关系探讨
定义与性质 等腰直角三角形是两边相等的直角三角形,等边三角形则 是三边都相等的三角形。两者都属于特殊三角形,具有一 些独特的性质。
关联与转化 等腰直角三角形可以通过添加辅助线转化为等边三角形, 从而利用等边三角形的性质解决问题。反之,等边三角形 也可以转化为等腰直角三角形进行求解。
三边相等判定法
定义
判定方法
三边长度相等的三角形称为等边三角 形。
通过测量三角形的三边长度,判断是 否相等来确定是否为等边三角形。
判定定理
若三角形三边长度分别为a、b、c, 且满足a=b=c,则该三角形为等边三 角形。
两角相等判定法
定义
有两个内角相等的三角形 称为等腰三角形,若这两 个内角均为60度,则为等 边三角形。
特点
等边三角形的三个内角均为60°, 具有对称性。
与其他三角形关系
01
02
03
与等腰三角形关系
等边三角形是特殊的等腰 三角形,其中两腰长度相 等且等于第三边。
与直角三角形关系
等边三角形是数学研究中的重要对 象之一,与三角函数、数列等领域 有密切联系。
03
等边三角形面积与周长计算
面积计算公式推导
等边三角形面积公式
S = (a^2 * sqrt(3)) / 4,其中a为等边三角形的边长。
公式推导
等边三角形可以划分成两个等腰直角三角形,每个直角三角形的面积为(1/2) * a * (a * sqrt(3) / 2),因此等边三角形面积为2 * (1/2) * a * (a * sqrt(3) / 2) = (a^2 * sqrt(3)) / 4。
05
等边三角形相关数学问题探讨
等腰直角三角形与等边三角形关系探讨
定义与性质 等腰直角三角形是两边相等的直角三角形,等边三角形则 是三边都相等的三角形。两者都属于特殊三角形,具有一 些独特的性质。
关联与转化 等腰直角三角形可以通过添加辅助线转化为等边三角形, 从而利用等边三角形的性质解决问题。反之,等边三角形 也可以转化为等腰直角三角形进行求解。
三边相等判定法
定义
判定方法
三边长度相等的三角形称为等边三角 形。
通过测量三角形的三边长度,判断是 否相等来确定是否为等边三角形。
判定定理
若三角形三边长度分别为a、b、c, 且满足a=b=c,则该三角形为等边三 角形。
两角相等判定法
定义
有两个内角相等的三角形 称为等腰三角形,若这两 个内角均为60度,则为等 边三角形。
特点
等边三角形的三个内角均为60°, 具有对称性。
与其他三角形关系
01
02
03
与等腰三角形关系
等边三角形是特殊的等腰 三角形,其中两腰长度相 等且等于第三边。
与直角三角形关系
等边三角形的性质和判定PPT教学课件

1.5
5140 9766
1.5
6130
1164 7
2.2
7070
1343 3
2.2
8010
1521 9
28
2.2
8950
1700 5
30
2.2
9890
1879 1
➢ 上图采用周边传动刮泥机结构 主要由中心支座、桁架、传动装置、刮板等部分组成,
该机为全桥(或半桥)周边传动刮泥,传动是由电机经行 星摆线针轮减速机直接或通过链条驱动滚轮,以中心支座 为圆心在池壁顶做圆周运行。 ------结构简单,耗电省,运行可靠,目前已广泛推广
3.在△ABC中,∠A=∠B=∠C,你能得到AB=BC=CA 吗?为什么? 你从中能得到什么结论? 三个角都相等的三角形是等边三角形. 4.在△ABC中,AB=AC,∠A=60°.(1)求证:△ABC是 等边三角形; (2)如果把∠A=60°改为∠B=60°或∠C=60°,那么结论 还成立吗? (3)由上你可以得到什么结论? 有一个角是60°的等腰三角形是等边三角形.
将污泥与3-4倍污泥量的水混合而进行沉降分离 (仅适用于消化污泥)
目的:降低污泥中的碱度和粘度,以节省混凝 剂的用量,提高浓缩效果,缩短浓缩时间。
过程:泥水混合—淘洗—沉淀
三、加热加压调理
可使部分有机物分解,亲水性有机胶体物质水解,颗粒 结构改变,从而改善污泥的浓缩与脱水性能
(一)高温加压调理 流程 图5-6
第五章 污泥的浓缩与脱水
第一节 概述 一、污泥的种类
按来源分: 生活污水污泥、工业废水污泥、给水污泥
按污泥从水中的分离过程分: 沉淀污泥(初沉池污泥、混凝沉淀污泥、化学沉
淀污泥)及生物污泥(包括腐殖污泥、剩余活性污泥 )
等边三角形的性质及判定ppt课件
名 称 等 边 三 角 形B
图形
A C
性质 三条边都相等 三个角都相等,且都为60° 三线合一
轴对称图形,有三条对称轴
认 识 到 了 贫 困户贫 困的根 本原因 ,才能 开始对 症下药 ,然后 药到病 除。近 年来国 家对扶 贫工作 高度重 视,已 经展开 了“精 准扶贫 ”项目
等边三角形的判定:
B
A
N
认 识 到 了 贫 困户贫 困的根 本原因 ,才能 开始对 症下药 ,然后 药到病 除。近 年来国 家对扶 贫工作 高度重 视,已 经展开 了“精 准扶贫 ”项目
2、在Rt△ABC 中, 如果∠BCA= 90° , ∠A= 30 °,CD 是高,
(1)BD=1,则BC、AB各等于多少;
(2)求证:BD=1/2BC=1/4AB
解(1)由已知可求得
C
∠BCD= 30 °
于是在Rt△ADC 与Rt△BDC 中用本定理得BC=2,AB=4
A
DB
(2)在Rt△ADC 与Rt△BDC运用本定理
BD=1/2BC
BC=1/2AB
∴ BD=1/2BC=1/4AB
认 识 到 了 贫 困户贫 困的根 本原因 ,才能 开始对 症下药 ,然后 药到病 除。近 年来国 家对扶 贫工作 高度重 视,已 经展开 了“精 准扶贫 ”项目
认 识 到 了 贫 困户贫 困的根 本原因 ,才能 开始对 症下药 ,然后 药到病 除。近 年来国 家对扶 贫工作 高度重 视,已 经展开 了“精 准扶贫 ”项目
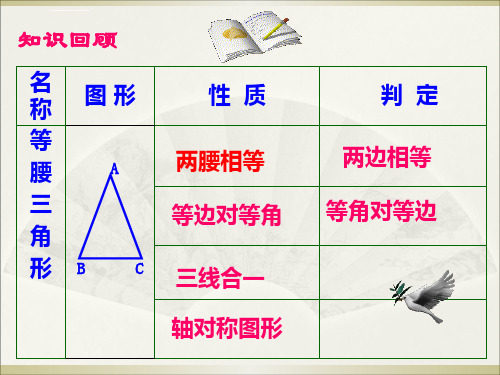
知识回顾
名 称
图形
性质
等
腰
A
两腰相等
三
等边对等角
角
形B
C 三线合一
轴对称图形
《等边三角形的判定》证明课件ppt文档

在△ABC中,∵∠ACB=900,∠A=300(已知),B
CD
∴∠B=600(直角三角形两锐角互余).
又∵ ∠ACB=900, (已知),
∴∠ACD=900(平角意义).
在△ABC与△ADC中
∵BC=DC(作图),
∠ACB=∠ACD(已证),
AC=AC(公共边), ∴△ABC≌△ADC(SAS).
驶向胜利 的彼岸
具体做法.
600
C
我能行 1
命题的证明
定理:有一个角是600的等腰三角形是等边三角形.
已知:如图,在△ABC中AB=AC,∠B=600. A 求证:△ABC是等边三角形.
证明:∵AB=AC, ∠B=600(已知), 600
∴∠C=∠B=600.(等边对等角). B
C
∴∠A=600(三角形内角和定理).
等的三角形是等边三角形).
600
C
这又是一个判定靠边三角形的根据之一.
驶向胜利 的彼岸
我能行 3
命题的猜想
1 操作:用两个含有300角的三角
尺,你能拼成一个怎样的三角形?
300
300 300 300
300
300
能拼出一个等边三角形吗?说说你的理由.
由此你想到,在直角三角形中, 300角所对的 直角边与斜边有怎样的大小关系?
∴∠A=∠B(等式性质).
∴ AC=CB(等角对等边).
∴AB=BC=AC(等式性质).
∴ △ABC是等边三角形(等边三角形 意义).
驶向胜利 的彼岸
回顾反思 1
几何的三种语言
定理:有一个角是600的等腰三角形是等边三角形.
在△ABC中,
A
∵AB=AC,∠B=600(已知).
等边三角形PPT优秀课件

∵ DE∥BC
B
图13.3-7
C
∴∠ADE=∠B,∠AED=∠C
∴∠A=∠ADE=∠AED
∴⊿ADE是等边三角形
试一试
课本的证明是用判定方法二证明的,你能用判 定方法三来证明例4吗?(提示:先证明有一个 角是60 °,再证明它是等腰三角形)
巩固练习
1.等边三角形是轴对称图形吗?如果是,指
出它的对称轴.
等边三角形PPT优秀课件
☻等边三角形的定义:
三边都相等的三角形叫等边三角 形(也叫正三角形) 。
☻等边三角形的性质
等腰三角形是有两边相等的三角形,而 等边三角形是一种三边都相等的特殊的等 腰三角形。
等边三角形性质与等腰三角形性质有紧 密的联系,可以从中类比而得出。采用类 比这种方法学习新知识,可以进一步了解 新旧知识的联系,更加方便于理解、记忆 和应用。
B
等边 三角形
C
求证:有一个角是60 °的等腰三角形是等边三角形。
假若AB=AC.则∠ B= ∠ C (1)当顶角∠A=60 °时,∠ B= ∠ C= 60 ° ∴ ∠A= ∠ B= ∠ C=60 ° ∴ △ABC是等边三角形.(判定方法2)
(2)当底角∠ B= 60°时,∠ C=60 °, ∠A=180 -60 °x2=60 ° ∴ ∠A= ∠ B= ∠ C=60 ° ∴ △ABC是等边三角形. (判定方法2)
归纳:怎样判断一个三角形是等边三角形?
A
方法一:三角形的三边相等;
方法二:三角形的三角相等;
B
C
方法三:有一个角等于60°的等腰三角形 是等边三角形。
例4:如图,⊿ABC是等边三角形,DE∥BC,
交AB、AC于D、E,
A
等边三角形PPT课件

回头看了一眼,朝独自跪在那里的人最后投去悲哀的一瞥。因为挨了四鞭,那人的背还在火辣辣的痛,他的膝盖也跪疼了。不过,这个老人会带着尊严死去,或至少是抱着这样的想法死去。 (节选自《偷书贼》第七章P265~267,略有删改) 致中国读者的信 亲爱的中国读者: ? 谢谢您阅读了这
本《偷书贼》。 ? 我小时候长听故事。我的爸爸妈妈经常在厨房里,把他们小时候的故事告诉我的哥哥、两个姐姐和我,我听了非常着迷,坐在椅子上动都不动。他们提到整个城市被大火笼罩,炸弹掉在他们家附近,还有童年时期建立的坚强友谊,连战火、时间都无法摧毁的坚强友谊。 ? 其中有
所以∠B=600
2
从而∠B=300
B
C
6
逆定理
在直角三角形中锐角是30°。
A
∵ AC⊥BC , BC= 1AB
2
∴ ∠A= 30°
B
C
2021/4/8
7
例1 如图,是屋架设计图的一部分,点D是斜梁
AB的中点,立柱BC、DE垂直于横梁AC,AB=7.4 m ∠A= 30°,立柱BC、DE要多长?
;单创:/c/7radcKIT9fA
;
本文以小红包为线索,两次设置悬念,把小说情节推向高潮;小说的结尾安排巧妙,出人意料却又在情理之中,引人入胜. 【点评】本题考查对文本、故事情节的理解分析能力和对句子含义、作者感情的理解分析能力.其中第(2)题是重点题目,学生解答时,在理解文章内容主旨的基础上,结合
2
如图,将两个含30°角的三角尺摆放在一起。 你能借助这个图形,找到Rt △ABC的直角 边BC与斜边AB之间的数量关系吗?
A
另证:在BA上截取BE=BC,连接EC
30 ° 30 °
则△BCE是等边三角形,所以
《等边三角形》PPT优质课件

∴∠DBE= 1 ∠ABC=30°.
2
∵DE=DB,∴∠E=∠DBE=30°.
B
D CE
∵∠ACB=∠CDE+∠E,∴∠CDE=∠ACB-∠E=30°.
探索新知
知识点1 等边三角形的性质 【变式】如图,等边三角形ABC的边长为3,点D是AC的中点,点E在BC 的延长线上,若DE=DB,求CE的长.
知识点1 等边三角形的性质
A
BC边上的中线,高和所对角的平分线“三线合一”.
AB边上的中线,高和所对角的平分线“三线合一”.
B
C AC边上的中线,高和所对角的平分线“三线合一”.
等边三角形每条边上的中线、高和所对角的平分线相互重 合,即“三线合一”.
探索新知
知识点1 等边三角形的性质
思考3 把等腰三角形的对称性用于等边三角形,能得到什么结 论?
知识点1 等边三角形的性质
图形 性边 质角
三线 合一
等腰三角形
两条边相等 两个底角相等
底边上的中线、高和顶角 的平分线互相重合
对称 性
1条对称轴
等边三角形
三条边都相等 三个角都相等, 且都是60º 每一边上的中线、高和这一边 所对的角的平分线互相重合
3条对称轴
探索新知
知识点1 等边三角形的性质 例1 如图,△ABC是等边三角形,BD平分∠ABC,延长BC到点E,使 得CE=CD.求证:BD=DE.
有一个角是60°的等腰 三角形是等边三角形.
探索新知
知识点2 等边三角形的判定
例2 如图,△ABC是等边三角形,DE∥BC,分别交AB,AC于点D,E.
求证:△ADE是等边三角形.
证明:∵△ABC是等边三角形,∴∠A=∠B=∠C.
等边三角形ppt课件

图形
等
A 60°
边
三
角
形
60°
B
判定方法(从边看) 判定方法(从角看)
1.有两边相等的三 2.有两个角相等的三角
角形是等腰三角形 形是等腰三角形
(定义)
(等角对等边)
1.三边都相等的 三角形是等边三
2.三个角都相等的三 角形是等边三角形
角形 (定义)
3.有一个角是60°的 等腰三角形是等边三
C
角形
A
等边三角形
☻等边三角形的定义:
三边都相等的三角形叫等边三角 形(也叫正三角形) 。
等腰三角形是有两边相等的三角形,而 等边三角形是一种三边都相等的特殊的等 腰三角形。
等边三角形性质与等腰三角形性质有紧 密的联系,可以从中类比而得出。采用类 比这种方法学习新知识,可以进一步了解 新旧知识的联系,更加方便于理解、记忆 和应用。
归纳:怎样判断一个三角形是等边三角形?
A
方法一:三角形的三边相等;
方法二:三角形的三角相等;
B
C
方法三:有一个角等于60°的等腰三角形 是等边三角形。
例4:如图,⊿ABC是等边三角形,DE∥BC,
交AB、AC于D、E,
A
求证: ⊿ADE是等边三角形。
证明: ∵ ⊿ABC是等边三角形, D
E
∴∠A=∠B=∠C
角形是等腰三角形 形是等腰三角形
(定义)
(等角对等边)
1.三边都相等的 三角形是等边三
2.三个角都相等的三 角形是等边三角形
角形 (定义)
3.有一个角是60°的 等腰三角形是等边三
C
角形
A
等腰 三角形
一个内角为60 °
等边三角形的性质和判定PPT课件(华师大版)(1)

解:∵△ABC是等边三角形, ∴∠A=∠B=∠C=60°.
∵DE⊥AC,EF⊥BC,DF⊥AB,
∴∠AED=∠EFC=∠FDB=90°, ∴∠ADE=90°-∠A=90°-60°=30°, ∴∠EDF=180°-30°-90°=60°. 同理可得∠DEF=∠EFD=60°. 即△DEF各个内角的度数都是60°.
例5 AB=AC,∠BAC=120°,AD⊥AB,AE⊥AC. (1)∠C=________,∠B=________; (2)求证:△ADE是等边三角形.
导引:(1)由AB=AC,∠BAC=120°, 可求出∠B,∠C 的度数为30°. (2)三个角都是60°的三角形是等 边三角形.
解:(1)30°;30°. (2)∵AD⊥AB,AE⊥AC(已知), ∴∠BAD=∠EAC=90°(垂直的定义). ∴∠B=∠C=30°(已知), ∴∠ADB=∠AEC=60°(直角三角形的两个锐角 互余). ∴∠ADB=∠AEC=∠EAD=60°. ∴△ADE是等边三角形(三个角都相等的三角形是 等边三角形).
要点精析:(1)它是特殊的等腰三角形,具备等腰三 角 形的所有性质;(2)它是特殊的等腰三角形,任意两边都 可作为腰,任意一个角都可以作为顶角.
(来源于教材)
2.等边三角形的性质:(1)等边三角形的三条边 都相等;(2)等边三角形的三个内角都相等,并且每一 个角都等于60°.(3)等边三角形是轴对称图形,它有 三条对称轴,分别为三边的垂直平分线;(4)各边上的 高、中线、对应的角平分线重合,且长度相等.
例1 如图13.3-5, △ABC是等边三角形,D,E,
F分别是三边AB,AC,BC上的点,且
DE⊥AC,EF⊥BC,DF⊥AB,计算△DEF
各个内角的度数.
等边三角形的性质与判定(共14张PPT)

∴ AB =BC =AC.
证明:∵ △ABC 是等边三角形,
证明:∵ △ABC 是等边三角形, 2.能运用等边三角形的性质和判定进行计算和证
∴ ∠B =∠D,∠C =∠E.
∴ ∠EAD =∠D =∠E.
∴ BC =AC,BC =AB. ∴ AB =BC =AC.
∴ ∠A =∠B =∠C =60°.
A
∵ ∠A=∠B =∠C ,
∴ ∠A =∠B,∠A =∠C . 追问 本题还有其他证法吗?
∴ AB =BC =AC.
∴ BC =AC,BC =AB.
∴ ∠A =∠B =∠C . ∵ DE∥BC,
证明: ∵ △ABC 是等边三角形,
∵ ∠A +∠B +∠C =180°,
∴ ∠A =60°.
B
C
∴ ∠A =∠B =∠C =60°.
等边三角形的性质与判定
课件说明
• 学习目标:
1.探索等边三角形的性质和判定. 2.能运用等边三角形的性质和判定进行计算和证
明. • 学习重点:
探索等边三角形的性质与判定.
变式1 若点D、E 在边AB、AC 的延长线上,且
图形 ∴ BC =AC,BC =AB.
边
是
∴ ∠A =∠ABC =∠ACB =60°.
A
∵ DE∥BC,
∴ ∠B =∠ADE,∠C =∠AED.
∴ ∠A=∠ADE =∠AED. ∴ △ADE 是等边三角形. D
E
追问 本题还有其他证法吗? B
C
动脑思考,变式训练
变式1 若点D、E 在边AB、AC 的延长线上,且
DE∥BC,结论还成立吗?
证明:∵ △ABC 是等边三角形,
等边三角形PPT课件

②得出300 角所对的直角边与斜边之间的数量关系,说明理由.
第34页/共50页
• 探究2
操 作探 究
①当将两个同样大小的三角板(含30 °和60 °的角)摆在一起,
新得到的三角形是特殊的三角形吗?请说明理由;
②得出300 角所对的直角边与斜边之间的数量关系,说明理由.
第35页/共50页
验证:我们可以用两个同样大小的三角尺
二、 等边三角形的判定
1.三个边都相等的三角形是等边三角形; 2.三个角都相等的三角形是等边三角形; 3.有一个内角等于60 °的等腰三角形是等边三角形.
第31页/共50页
• 探究1
操 作探 究
用直尺量一量含30°角的直角三角板的最短直角边(即300 角所
对的直角边)与斜边,记录下数据,你有什么发现?
第14页/共50页
(3)等边三角形各边上中线,高
A
和所对角的平分线都三线合一. D
E
O
(4)等边三角形是轴对称 B F C
图形,有三条对称轴.
A
B
C
第15页/共50页
△ABC是等边三角形,D为AC的中点,延长BC到 E,使CE=CD, 求证:BD=DE A
证明:∵ △ABC是等边三角形
∴ AB=AC=BC,
B
C
第25页/共50页
1.三边都相等的三角形是等边三角形.(定义)
A ∵AB=BC=AC
一般三角形
∴△ABC是等边三角形 等边三角形
B
C
2. 三个角都相等的三角形是 ∵ ∠A= ∠ B= ∠ C
等边三角形.
A
∴△ABC是等边三角形
等腰三角形
等边三角形
B
等边三角形PPT课件2024新版

03
等边三角形面积与 周长计算
面积计算公式推导
01
02
等边三角形面积公式: $S = frac{sqrt{3}}{4}a^{2}$ ,其中 $a$ 为等边三角 形的边长。
推导过程
03
04
05
将等边三角形划分为三 个全等的直角三角形。
利用勾股定理求出直角 三角形的高 $h = frac{sqrt{3}}{2}a$。
等边三角形外心、内心及重心问题
外心性质
等边三角形的外心位于 三条边的垂直平分线的 交点上,且外心到三个 顶点的距离相等。
内心性质
等边三角形的内心位于 三条内角平分线的交点 上,且内心到三边的距 离相等。
重心性质
等边三角形的重心位于 三条中线的交点上,且 重心将每条中线分为两 段,比例为2:1。
等边三角形与圆的关系
06
等边三角形拓展知 识介绍
黄金分割与等边三角形关系
黄金分割点
在等边三角形中,可以通过特定方式 找到黄金分割点,该点将一条边分为 两段,其中较长段与较短段之比等于 整条边与较长段之比。
黄金三角形
等边三角形与黄金分割密切相关,通 过连接等边三角形的各边中点,可以 得到一个较小的等边三角形,这两个 三角形构成黄金三角形。
解:根据面积公式 $S = frac{sqrt{3}}{4}a^{2}$,代入 $S = 16sqrt{3}$cm²,得 $frac{sqrt{3}}{4}a^{2} = 16sqrt{3}$,解得 $a = 8$cm。
解:根据面积公式 $S = frac{sqrt{3}}{4}a^{2}$,代入 $a = 5$cm,得 $S = frac{sqrt{3}}{4} times 5^{2} = frac{25sqrt{3}}{4}$cm²。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
a2=b2+c2-bc,b2=c2+a2-ca,c2=a2+b2-ab,
则△ABC是( D )
A.钝角三角形
B.直角三角形
C.等腰直角三角形 D.等边三角形
2020/12/10
13
3.如图,点D是等边△ABC的边BC上一点, ∠ADE=60°,则∠BAD与∠CDE的大小关系
是( B )
A. ∠BAD>∠CDE B. ∠BAD=∠CDE C. ∠BAD<∠CDE D. 无法确定
定理:有两个角等于60度的三角形 是等边三角形。
2020/12/10
5
练习:如图,△ABC,
(1)如果AB=AC,∠A=60°, △ABC是等边三角形吗?
A
(2)如果AB=AC,∠B=60°,
△ABC是等边三角形吗?
(3)如果AB=AC,∠C=60°,
△ABC是等边三角形吗? B
C
你能用一句话概括上面得到的结论吗?
在△ABE和△DBC中, 在△ABM和△DBN中,
AB=DB
∠BAE=∠BDC
∠ABE=∠DBC BE=BC ∴△ABE≌△DBC
∴∠BAE=∠BDC
2020/12/10
AB=DB ∠ABM=∠DBN=60° ∴△ABM≌△DBN ∴BM=BN ∵∠MBN=60°
∴△BMN是等边三角形。 9
例2:如图,△ABC中,D、E是BC上的点, 且BD=DE=EC=AD=AE,求∠BAC的度数。
2020/12/10
14
4.如图,△ABC中,AB=AC,D、E在BC、 AC上,且AD=AE,∠1=40°,
则∠2=____2_0__°.
此题的一般结论: ∠1=2∠2
2020/12/10
15
PPT教学课件
谢谢观看
Thank You For Watching
16
3
证明:三个角都相等的三角形是等边三角形。
已知:如图,△ABC中,∠A= ∠B=∠C。
A
求证:AB=BC=CA。
证明:∵∠A=∠B,
∴BC=AC
(等角对等边)
B
C
∵∠B=∠C
∴AC=AB
∴AB=BC=AC
2020/12/10
4
定理:三个角都相等的三角形是等 边三角形。
思考:如果一个三角形有两个角等于60°, 那么这个三角形是等边三角形吗?
定理:有一个角等于60度的等腰三角形 是等边三角形。
2020/12/10
6
概括:等边三角形的判定:
1.三边都相等的三角形是等边三角形; 2.三个角都相等的三角形是等边三角形; 3.有两个角等于60度的三角形是等边三
角形。 4.有一个角等于60度的等腰三角形是等
边三角形。
2020/12/10
7
三、例解应用
20例4,例5
2020/12/10
11
四、练习
1.如图,把等腰直角△ABC沿BD折叠,使点 A落在边BC上的点E处.下面结论错误的是
(B )
A.AB=BE
B.AD=DC C.AD=DE D.AD=EC
2020/12/10
12
2.若△ABC的三边长为a,b,c,且满足
13.3.2 等边三角形的判定
2020/12/10
2013.11
1
一、复习
什么叫做等边三角形?它有什么性 质?
2020/12/10
2
二、新知探究
什么样的三角形会是等边三角形? 1.三条边都相等的三角形是等边三角形。 2.猜想:三个角都相等的三角形是等边三角
形。 你能证明这个猜想吗?
2020/12/10
例1:如图,点B是线段AC上一点,分别以 AB,BC为边在线段AC的同侧作等边三角 形ABD和等边三角形BCE,求证:△BMN 是等边三角形。
2020/12/10
8
证明:在等边△ABD和等边 △BCE中,
AB=DB,BE=BC
∠ABD=∠CBE=60°
∴∠MBN=60°,∠ABE=∠DBC=120°
