正弦量的三要素
正弦量的三要素和有效值

如Im 、Um。
首页
2.角频率、周期、频率 正弦量在单位时间内所经历的电角度,称为角频率,用ω 表示,单位是弧度/秒,即
t
正弦量完成一次周期变化所需要的时间,称为周期,用T 表示,单位是秒。
正弦量在1秒钟内完成周期性变化的次数,称为频率,用 f 表示,单位是赫兹。
选零点为计时起点,则初相ψ =0,如图3-7所示是不同初相时
几种正弦电流的解析式和波形图。
首页
i
Im
i Im sint
0
t
a)
i i Im sin(t π 6)
i
i Im sin(t π 2)
0
t
b)
i i Im sin(t π 6)
0
t
0
t
π/6
π/6
首页
例3-3 两个同频率正弦电流的波形如图3-6所示,试写出 它们的解析式,并计算二者之间的相位差。
解 解析式
i/A 10 i1
i1
10 s in(314t
π )A 4
8
i2
i2
8 s in(314t Nhomakorabeaπ )A 4
0
4
4
0.02s
相位差
ωt/rad
i1
i2
π 4
(
c)
d)
图3-3 初相不同的几种正弦电流的波形图 a)初相为0; b)初相为π/2; c)初相为π/6; d)初相为-π/6
首页
注意:正弦量的初相、相位以及解析式都与参考方向有 关。改变参考方向,就是将正弦量的初相加上或减去π。
3-1正弦量的表示方法

已知: i = 141.4 sin( 314t +
u = 311.1sin(314t −
π
6
) A
π
3 求: i 、u 的相量表达式及相量图。
) V
i = 141.4 sin( 314t +
u = 311.1sin(314t −
解:
π
π
6
3
) A
) V
I
141.4 j 30 j 30 I= e = 100e = 100∠ 30 A 2
u = 5 2 sin(ω t − 126 ⋅ 9 )
b. 复数的四则运算
已知:
jθ 1 A1 = a1 + jb1 = A1e
jθ 2 A2 = a 2 + jb2 = Ae
±A = ( a ± a ) + j( b ± b ) 加减:A 1 2 1 2 1 2
乘除:
⋅A = A ⋅ A e j ( θ 1 +θ 2 ) A 1 2 1 2
Im = 2
同理
Um U= 2
Em E= 2
•相位和初相位
i
i = 2 I sin (ω t + ϕ )
ωt
ϕ
相位(相位角): ωt + ϕ
单位:弧度( rad)、度( )
初相位: t = 0 时的相位,即 ϕ
相位差 两个同频率正弦量间的相位差(初相差)
i1
ϕ2
i2
ϕ1
ωt
i1 = I m 1 sin(ω t + ϕ 1 )
30 60
311.1 − j 60 U= e = 220∠ − 60 V 2 相位哪一个超前? 哪一个滞后?
正弦量的三要素及相量表示法基尔霍夫

正弦电流电路导论
内容提要
1.正弦量的相量表示法; 2.两类约束的相量形式; 3.正弦电流电路的分析计算; 4.正弦电流电路的功率。
5.1 正弦量电压和电流的基本概念
一 时变的电压和电流 ◆ 时变电压和电流:随时间变动的电压和电流。
第五章
正弦电流电路
u(t )
◆瞬时值:时变电压和电流在任一时刻的数值,用 和 i (t ) 表示。
2π u2 =100 2sin(100t )V 3
3
0
6
I1
解:
π I1 =50 A 6 π U1 =100 V 3 2π U 2 =100- V 3
2 3
U 2
相量图
第三章 正弦电流电路
四 用相量求正弦量的和与差
i1 (t ) 70.7 2 sin(ωt 45 )A i2 (t ) 42.4 2 sin(ωt 30 )A
③角频率ω:每秒变化的弧度。单位:弧度/秒(rad/s)
第五章 正弦电流电路
三者间的关系:
1 f T
2 2 f T
* 电网频率(工频):我国:50Hz;美国和日本:60Hz * 无线通信频率: 30 kHz ~ 30GMHz ◆ 相位和初相位 ①相位:正弦波的 (ωt ψ ) 。 ②初相位 :t =0 时的相位。 ③规定:初相位的绝对值不超过π。
第五章 正弦电流电路
三 用相量表示正弦量
相量:表示正弦量的复数称为相量。
相量表示法:用模值等于正弦量的最大值(或有效值)、
辐角等于正弦量的初相的复数对应地表示相应的正弦量。
即:相量 Im (或 I )
j
模用最大值表示时,为最 I ψ 大值相量,即 I m m
正弦量的瞬时值、幅值和有效值(精)

正弦量的瞬时值、幅值和有效值
3.2 正弦量的三要素
u U m sin(t u ) i I m sin(t i )
其中u、i分别为电压和电流的瞬时值; Um、Im分别为 电压和电流的幅值(或最大值); ω为角频率; φu, φi分别
为电压和电流的初相角, 如图所示。
注意: 交流电压、电流表测量数据为有效值 交流设备名牌标注的电压、电流均为有效值
u ~
i
R
+ U _
I
R
பைடு நூலகம்
通入正弦交流电,T时 间内,电流热效应:
T
通入直流电,T时间内, 电流热效应:
Q = I2 RT
Q
2 i Rdt 0
则有: 同理:
I
Im 2
U U m 2
E
Em 2
1.瞬时值、最大值、有效值
i I m sin t
母u, i, e 表示 。 母带下标m表示, 如:Im, 有效值。以大写字母I、U、
瞬时值 : 描述正弦量在任一瞬间的值 ,以小写字 最大值 :瞬时值中的最大数值,也称幅值 ,以大写字 Um, Em. 有效值 : 与交流热效应相等的直流定义为交流电的 E表示 。
7 正弦量与相量

C B
ϕb ϕb ϕa + ϕb A
C=A/B
+j
A
B
B jA A
-jB
+1 O C
+1
ϕ a- ϕ b
O 旋转因子示意 +1
O 复数的乘法
复数的除法
7.4 正弦量的相量表示法
一、正弦稳态电路的特点
1、角频率不变性:在线性电路中,如 角频率不变性:在线性电路中, 果电路的所有激励都是同频率的正弦量, 果电路的所有激励都是同频率的正弦量, 激励都是同频率的正弦量 则电路中各支路的稳态响应也为同频率 稳态响应也为 则电路中各支路的稳态响应也为同频率 的正弦量。 ( P208) 的正弦量。 2、计算的复杂性:在列写VCR、KCL、 计算的复杂性:在列写VCR、KCL、 KVL方程的时候会遇到微分、积分和 KVL方程的时候会遇到微分、积分和和 方程的时候会遇到微分 差化积的问题 的问题。 差化积的问题。
二、复数的四则运算
1、加减运算 1)定量运算 1)定量运算------用代数形式计算 定量运算------用代数形式计算
F1 ± F2 = (a1 + jb1 ) ± (a2 + jb2 ) = (a1 ± a2 ) + j (b1 ± b2 )
法则:实部加减,虚部加减。 法则:实部加减,虚部加减。
7 正弦量与相量
重点
1、正弦量的三要素 2、复数的几种表示形式的转换及计算 3、 KCL、KVL 、VCR的相量表示 KCL、 VCR的相量表示
难点
相量图的绘制
本章作业
P217 7.1 7.2 7.5 7.7 7.10 7.12
电路试题库(三)+答案

电路试题库(三)+答案一、填空题(建议较易填空每空0.5分,较难填空每空1分)1、正弦交流电的三要素是指正弦量的 最大值 、 角频率 和 初相 。
2、反映正弦交流电振荡幅度的量是它的 最大值 ;反映正弦量随时间变化快慢程度的量是它的 频率 ;确定正弦量计时始位置的是它的 初相 。
3、已知一正弦量A )30314sin(07.7︒-=t i ,则该正弦电流的最大值是 7.07 A ;有效值是 5 A ;角频率是 314 rad/s ;频率是 50 Hz ;周期是 0.02 s ;随时间的变化进程相位是 314t-30°电角 ;初相是 -30° ;合 -π/6 弧度。
4、正弦量的 有效 值等于它的瞬时值的平方在一个周期内的平均值的 开方 ,所以 有效 值又称为方均根值。
也可以说,交流电的 有效 值等于与其 热效应 相同的直流电的数值。
5、两个 同频率 正弦量之间的相位之差称为相位差, 不同 频率的正弦量之间不存在相位差的概念。
6、实际应用的电表交流指示值和我们实验的交流测量值,都是交流电的 有效 值。
工程上所说的交流电压、交流电流的数值,通常也都是它们的 有效 值,此值与交流电最大值的数量关系为: 最大值是有效值的1.414倍 。
7、电阻元件上的电压、电流在相位上是 同相 关系;电感元件上的电压、电流相位存在 正交 关系,且电压 超前 电流;电容元件上的电压、电流相位存在 正交 关系,且电压 滞后 电流。
8、 同相 的电压和电流构成的是有功功率,用P 表示,单位为 W ; 正交 的电压和电流构成无功功率,用Q 表示,单位为 Var 。
9、能量转换中过程不可逆的功率称 有 功功率,能量转换中过程可逆的功率称 无 功功率。
能量转换过程不可逆的功率意味着不但 有交换 ,而且还有 消耗 ;能量转换过程可逆的功率则意味着只 交换 不 消耗 。
10、正弦交流电路中,电阻元件上的阻抗z = R ,与频率 无关 ;电感元件上的阻抗z = X L ,与频率 成正比 ;电容元件上的阻抗z = X C ,与频率 成反比 。
正弦交流电路习题课

0 由KCL, I1 I 2 I 3 j 2 1 2.263.4 A
U 40 在电压三角形中, arctg arctg 53.130 U2 30
I00 解:设 I
P 1 V1 I cos 1
Z1 Z1 1
240 171 4 cos 1
1 69.460 171 Z1 69.460 42.75 69.460 4 V V2 Z 2 2 60 2 Z1 Z 2 25 I I
提高功率因数的意义方法
• 提高功率因数能使电源设备的容量得到充 分利用; • 提高功率因数能减小线路功耗和电压损耗。 • 提高功率因数的方法通常是在感性负载 两端并联一个电容器,称之为补偿电容 器。补偿电容器的容量为:
正弦稳态电路的分析
• 用相量法分析电路时,线性电阻电路的 各种分析方法和电路定理可推广用于线 性电路的正弦稳态分析,差别仅在于所 得的电路方程是以相量形式表示的代数 方程以及用相量形式描述的电路定理, 而计算则为复数运算。
U I XC
U I XL
I CU
基尔霍夫定律的相量式
• 基尔霍夫定律的相量式与三种基本电路 元件伏安特性的相量形式,是分析正弦 交流电路的基础。 0 U
I 0
• 应用基尔霍夫定律及单一参数电路所得 出的结论,对R、L、C串联、并联电路 进行了分析,分别引出了阻抗Z和导纳Y 的概念。
正弦稳态电路的分析
习题总结课
正弦量及其三要素
1、随时间按正弦规律变化的电流、电压、 电动势等统称为正弦量。 2、正弦量的有效值(振幅)、频率(周期 或角频率)和初相是正弦量的三要素。 三要素是确定一个正弦量的充要条件。 3、直流电的大小和方向恒定不变,在直流 计算时只考虑其大小即可。而在交流电 的分析与计算时,除了考虑大小外,还 要考虑其相位。
正弦量的三要素及相量表示法基尔霍夫

三 相位差
第五章
正弦电流电路
相位差 :两个同频率正弦量间的相位之差,即初相位 之差。
i
u
如:
u
t
i
u U m sin t u
i I m sin t i 则相位差为:
t u t i u i
第五章 正弦电流电路 两个正弦量的相位关系
上述相量图是根据平行四边形法则进行加、减获得的。实际上, 可采用三角形法则作图。如下图所示。
I1
0
I2
I I1 I 2
0
I2
I1
I I1 I 2
两相量相加
两相量相减
第五章 正弦电流电路
5.4基尔霍夫定律的相量形式
一 基尔霍夫电流定律(KCL) 瞬时值形式:
i 0
0 相量形式(同频率的正弦量) : I
◆周期量:每个值在经过相等的时间间隔后循环出现的 时变电压和电流。 ◆交流量:一个循环内波形面积平均值为零的周期量。
u i i
O
t
时变电压
O
t
周期量
O
t
交流量
第五章 正弦电流电路 二 正弦量的三要素
正弦量:按正弦规 律变化的交流量。 设正弦电流
Im
i
O
T
2
t
i I m sin(ωt ψ )
二 基尔霍夫电压定律(KVL)
瞬时值形式:
u 0
相量形式(同频率的正弦量) : U 0
第五章 正弦电流电路 二 旋转矢量与正弦量 设正弦量: i I m sin(ωt ψ )
j B ω t1
0
i
Im
正弦电路的电压电流及相量表示

解:电压u(t)与电流i1(t)的相位差为
=(-180o)-(- 45o )= -135o<0
所以u(t)滞后i1(t)135o 。
电压u(t)与电流i2(t)的相位差为
= -180o - 60o = -240o 由于规定||≤π,所以u(t)与i2(t)的相位 差应为 = -240o+360o = 120o>0,因此u(t)超前 i2(t)120o 。
四、正弦量的有效值 有效值的提出: 正弦量的有效值是根据它的热效应确定的。以正 弦电压u(t)为例,它加在电阻R两端,如果在一个 周期T内产生的热量与一个直流电压U加在同一电阻上 产生的热量相同,则定义该直流电压值为正弦电压 u (t)的有效值。用大写字母“U”表示。 有效值的定义式:
1 U T
本讲作业
1、复习本讲内容;
2、预习下一讲内容——正弦电路的相量分析法; 3、书面作业:习题8-1,8-2,8-4,8-5。
8.2 正弦量的相量表示
一、相量表示法的提出 前面学过的解析式(三角函数表示法)和正弦量 的波形图(正弦曲线表示法)都不便于分析计算正弦 电路。为了解决这个问题,引入了正弦量的第三种表 示方法——相量表示法。 二、相量表示法采用的形式 相量表示法,实际上采用的是复数表示形式。
三、相量表示方法 模等于正弦量的有效值(或振幅),幅角等于 正弦量的初相的复数,称为该正弦量的相量。相量 用该正弦量的符号上加一圆点“ · ”来表示,说明它 是时间的函数,以便与一般复数相区别。 振幅相量 相量的模为正弦量的振幅,称振幅相量,以 I m 、 Um 等表示。其振幅相量表达式为
将u3(t)的解析式整理如下: u3(t)= 5cos(100πt + 60o) = 5sin(100πt + 60o + 90o) = 5sin(100πt + 150o )V 所以得到
电工学试题库

第二章 正弦交流电路 习题参考答案一、填空题:1. 表征正弦交流电振荡幅度的量是它的 最大值 ;表征正弦交流电随时间变化快慢程度的量是 角频率ω ;表征正弦交流电起始位置时的量称为它的 初相 。
三者称为正弦量的 三要素 。
2.电阻元件上任一瞬间的电压电流关系可表示为 u = iR;电感元件上任一瞬间的电压电流关由上述三个关系式可得, 电阻 元件为即时元件; 电感 和 电容 元件为动态元件。
3. 在RLC 串联电路中,已知电流为5A ,电阻为30Ω,感抗为40Ω,容抗为80Ω,那么电路的阻抗为 50Ω ,该电路为 容 性电路。
电路中吸收的有功功率为 450W ,吸收的无功功率又为 600var 。
二、 判断题:1. 正弦量的三要素是指最大值、角频率和相位。
(错)2. 电感元件的正弦交流电路中,消耗的有功功率等于零。
(对)3. 因为正弦量可以用相量来表示,所以说相量就是正弦量。
(错)4. 电压三角形是相量图,阻抗三角形也是相量图。
(错)5. 正弦交流电路的视在功率等于有功功率和无功功率之和。
(错)6. 一个实际的电感线圈,在任何情况下呈现的电特性都是感性。
(错)7. 串接在正弦交流电路中的功率表,测量的是交流电路的有功功率。
(错)8. 正弦交流电路的频率越高,阻抗越大;频率越低,阻抗越小。
(错)三、选择题:1. 某正弦电压有效值为380V ,频率为50Hz ,计时始数值等于380V ,其瞬时值表达式为( B ) A 、V ;B 、V ;C 、V 。
2. 一个电热器,接在10V 的直流电源上,产生的功率为P 。
把它改接在正弦交流电源上,使其产生的功率为P /2,则正弦交流电源电压的最大值为( D ) A 、7.07V ; B 、5V ; C 、14V ; D 、10V 。
3. 提高供电电路的功率因数,下列说法正确的是( D )A 、减少了用电设备中无用的无功功率;B 、减少了用电设备的有功功率,提高了电源设备的容量;C 、可以节省电能;D 、可提高电源设备的利用率并减小输电线路中的功率损耗。
第3章 正弦交流电路

3.3.1 单一参数的正弦交流电路
1.纯电阻电路 (1) 电压与电流的关系
+
u iR
u
i I m sin t
_
u iR I m R sin t U m sin t
i R
对于正弦交流电路中的电阻电路(又称纯电阻 电路),一般结论为:
1)电压、电流均为同频率的正弦量。
2)电压与电流初相位相同,即两者同相。
y
i
ω
Im
i1
ωt1 φ
Im
i0
90
o
x
o
ωt1
ωt
φ
t t1 i1 I m sin(t 1)
对于一个正弦量可以找到一个与其对应的旋转矢量,反之, 一个旋转矢量也都有一个对应的正弦量。
3.2.2 复数及复数的运算 1、复数
A a jb
A r cos r sin
e j cos j sin
作相量图时要注意: 只有同频率的正弦量才 能画在一个相量图上,不 同频率的正弦量不能画在 一个相量图上。
+j
U
Φu
o
Φi
+1
I
3.3正弦交流电路的简单分析与运算
电阻元件、电感元件与电容元件都是组成 电路模型的理想元件。
所谓理想元件,就是突出元件的主要电磁 性质,而忽略其次要因素。如电阻元件具 有消耗电能的性质(电阻性),其它的电 磁性质如电感性、电容性等忽略不计。。
f = 1/T T = 1/f
i
角频率是指交流电在1s内变化的电 Im
角度。正弦量每经过一个周期T,
o
对应的角度变化了2π弧度,所以
φ
ωt
T
2f 2
4-3电路定律的向量形式
I
u i
U
3)电阻的uR (t )的相位 iR (t ) 的相位同相;
4 ) 振幅关系 U Rm RI Rm
u (t )
i (t )
R
时域模型
例2:在正弦稳态电路中,
i ( t ) 2cos(100t 30 )A 流过10Ω电阻的电流
求: u (t )
10 2 cos(100t 30 )V
k 1 k
n
对于线性时不变的正弦稳态电路(单一频率激 励)各支路电压、电流为同频率的正弦量。 设:
n
jωt ik (t ) I km cos(ωt ik ) Re[ I km e ]
n
n jωt jωt ik (t ) Re[I km e ] Re I kme k 1 k 1 k 1
0 I
元件 电阻 电感 相量模型
I
0 U
伏安关系 相量图
R
U
I
jL
U
I
1 jC
电容
U
例 4:
u (t )
4H电感端电压 u (t ) 8 2cos(t 50 )V 100rad/s 求 i (t )
i(t )
解:1)画出电路的相量模型
i3
i1 i2
求:
i3 (t )
解:方法1)由KCL的时域形式: 1060
0
6.236.2
10 60 5 90 I3 I1 I 2
5 90
相量图
10 cos 60 10 j sin 60 j5
5 j3.66 6.236.2 A
正弦量的三要素

i
t
如果 u i 180o
称电压与电流反相。
例1:已知:i(t)=100sin(6280t-/4)mA (1)说明它的Im,I,,f,T, (2)画出波形图。 解:(1) I m 100mA I 100 /
2 70.7mA
6280rad / s 6280 f 1000 Hz 2 2 3.14Fra bibliotek 45
o
i 2 30
o
i1 i 2 o o o 12 45 (30 ) 75
2. 正弦量的计时起点 ——初相位与相位差
对于已知的正弦量:
相位:称(ωt+ψi) 为正弦交流电流的相位角,简称相位。 在不同的时刻正弦量的相位也不同,交流电流的大小 和方向也不同。 初相位:称t = 0时的相位角ψ i为初相角,简称初相位。 初相位用来确定交流电初始瞬时状态。 i i O o i I m sin(t 90 ) i I m sin(t 90 )
Im 2 0.707 I m
0.707U m
T 1 T dt cos( 2t 2 )dt 0 2 2
I
同理
U
Um 2
Em E 0.707 Em 2
正弦交流电的有效值等于 它的最大值除以 2 , 而与 其频率及初相无关。 有效值与最大值之间的 2 关系不适用于其他非正 弦交流量
Im
i ( t )
i
t
t3
0
t1 t2
.
t4 t
i (t )
T
t
有效值:若有一交流电流 i 通过电阻R,在一个周期时 间内消耗的电能,与直流电流I在同样时间内通过同一 电阻所消耗的电能相等,则该直流电流I的数值称为该 交流电流 i 的有效值。 在工程中,正弦电压与电流的计量不是瞬时值也 不是幅值,而是有效值。
电工学 第二章正弦交流电路

(1-2)
. 一、正弦量的三要素
二、同频率正弦量的相位差
三、正弦量的有效值
(1-3)
一、正弦量的三要素
i = Im sin (wt + j ) i
Im
j
wt Im:电流幅值(最大值)
三要素
w: 角频率(弧度/秒)
.
U Z = I
j = j u - ji
结论:Z的模为电路总电压和总电流有效值之比, 而Z的幅角则为总电压和总电流的相位差。
(1-46)
Z 和电路性质的关系
Z = R+ j (XL- XC )
阻抗角
j = ju- ji = arctg
(1-39)
以电流为 参考量时
正 误 判 断
在电阻电路中:
瞬时值
有效值
U I= R
?
U i= R
?
u ? i = R
(1-40)
正 误 判 断
在电感电路中:
u i= XL
?
U I= ωL
u i= ωL
?
?
& U = XL & I
U = jω L I
?
?
(1-41)
第四节
RLC串、并联电路及功率因数的提高 一、RLC串联的正弦交流电路
& I U=&R
& I & U
(1-25)
相量图
总结功率关系
因为:
i= Im sinwt u =Ri=R Im sinwt p=u·=R·2=u2/R i i
小写,瞬时值功率
所以:
i
u
wt
正弦量基础

u
0
t
T
7.1 正弦量
正弦交流电路
由同频正弦激励、线性电阻、线性电容和线性 电感组成的的电路称为正弦交流电路。
正弦交流电路特点:各支路产生的电流、电压均为
和激励同频变化的正弦交流电。
7.1 正弦量
正弦交流电运用非常 广泛,主要原因有以下几点:
1、可以利用变压器升高或降低,这种变换方式 既灵活又经济。 2、正弦量经过加、减、求导、积分等数学运算 后,仍为正弦量,这在电工技术上有重大意义。 3、正弦量变化平滑,在正常情况下不会引起过 电压而破坏电器的绝缘设备。
Im
0
i
t
I m :电流幅值(最大值)
特征量:
:角频率(弧度/秒) :初相角
7.1 正弦量
正弦量三要素之一 —— 振幅(amplitude)
i I m cos t
Im
为正弦电流的最大值
最大值
电量名称必须大写,下标加 m。 如:Um、Im
7.1 正弦量
正弦量三要素之二 —— 角频率(angular frequency)
] I m cos(t )
7.3
相量法的基本概念
Re[ I m e
j( t )
] I m cos( t )
j t
Re[ I m e e ] I m cos( t )
旋转因子——同一个电路中, 每个正弦量所对应的复指数函 数中的旋转因子均相同
1 I 0.707A 2
幅度: 频率:
I m 1A
1000 rad/s 1000
f 2π 2π
159 Hz
初相位:
30
正弦交流电路_习题参考答案[1]
![正弦交流电路_习题参考答案[1]](https://img.taocdn.com/s3/m/3e722542844769eae009edea.png)
第二章 正弦交流电路 习题参考答案一、填空题:1. 表征正弦交流电振荡幅度的量是它的 最大值 ;表征正弦交流电随时间变化快慢程度的量是 角频率ω ;表征正弦交流电起始位置时的量称为它的 初相 。
三者称为正弦量的 三要素 。
2. 电阻元件上任一瞬间的电压电流关系可表示为 u = iR ;电感元件上任由上述三个关系式可得, 电阻 元件为即时元件; 电感 和 电容 元件为动态元件。
3. 在RLC 串联电路中,已知电流为5A ,电阻为30Ω,感抗为40Ω,容抗为80Ω,那么电路的阻抗为 50Ω ,该电路为 容 性电路。
电路中吸收的有功功率为 750W ,吸收的无功功率又为 1000var 。
二、 判断题:1. 正弦量的三要素是指最大值、角频率和相位。
(错)2. 电感元件的正弦交流电路中,消耗的有功功率等于零。
(对)3. 因为正弦量可以用相量来表示,所以说相量就是正弦量。
(错)4. 电压三角形是相量图,阻抗三角形也是相量图。
(错)5. 正弦交流电路的视在功率等于有功功率和无功功率之和。
(错)6. 一个实际的电感线圈,在任何情况下呈现的电特性都是感性。
(错)7. 串接在正弦交流电路中的功率表,测量的是交流电路的有功功率。
(错)8. 正弦交流电路的频率越高,阻抗越大;频率越低,阻抗越小。
(错)三、选择题:1. 某正弦电压有效值为380V ,频率为50Hz ,计时始数值等于380V ,其瞬时值表达式为( B )A 、t u 314sin 380=V ;B 、)45314sin(537︒+=t u V ;C 、)90314sin(380︒+=t u V 。
2. 一个电热器,接在10V 的直流电源上,产生的功率为P 。
把它改接在正弦交流电源上,使其产生的功率为P /2,则正弦交流电源电压的最大值为( D )A 、;B 、5V ;C 、14V ;D 、10V 。
3. 提高供电电路的功率因数,下列说法正确的是( D )A 、减少了用电设备中无用的无功功率;B 、减少了用电设备的有功功率,提高了电源设备的容量;C 、可以节省电能;D 、可提高电源设备的利用率并减小输电线路中的功率损耗。
正弦量的三要素公式

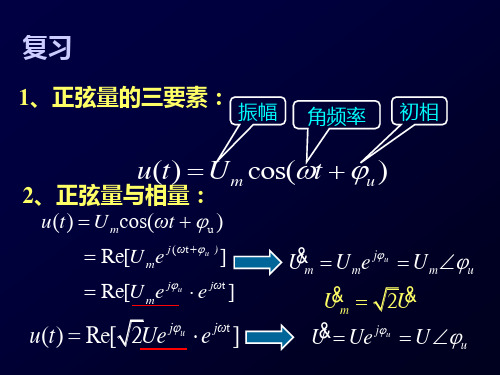
正弦量的三要素
ⅈ=√2I sⅈn(ωt+φ)
正弦量的三要素分别是:振幅、角频率、初相位
1、最大值(峰值或幅值)[U m]
最大值是指最大瞬时值,在一个正弦周期内,必定出现一个最大和最小瞬时值;
2、角频率(ω)
在单位时间内正弦量变化的角度称为角频率,它反应了正弦量变化的快慢程度;
3、初相位或相位差
初相位就是正弦量在起始时间的相位。
在波形图上,初相位规定为正半波的起点与坐标原点之间的夹角。
当φ=0时,正半波起点正好落在原点O上;当φ>0时,则正半波起点在原点O的左边;当φ<0时,正半波起点在原点O的右边。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
设一交变电流i通过电阻R,在一个周期内该电阻消耗的 电能是:
W~ = ∫ i Rdt = R∫ i dt
2 2 0 0
T
T
i
R
如果有一个直流电流I通过同一电阻R,在同一时间T内 所消耗的电能为:
W = I RT
2
I
R
在一个周期时间内,W~=W—, 于是
R∫ i dt = I RT
2 2 0
T
1 T 2 I= ∫0 i dt T
最大值(幅值) 最大值(幅值):在一个周期里 最大的瞬时值叫最大值, 最大的瞬时值叫最大值,它是交 流电的振幅,通常用大写字母并 流电的振幅, 加注下标m表示。 加注下标m表示。如Im、Um及Em。 可见, 可见,最大值实际上就是最大的 瞬时值,也是与时间有关的量。 瞬时值,也是与时间有关的量。
Im
ω
= 2πf
Um
ψu
e = Em sin( ωt +ψe )V
Em
ψe
相位差:两个同频率的正弦交流电在相位上的差值 定义位相位差,用φ表示。
ui = (ωt +ψu ) (ωt +ψi ) =ψu ψi
同频率的两个正弦交流电的相位差等于它们的 初相之差。 i, u i, u
ψi ψu
0
t
ψu 0
Im i t4 t
t3 0 t1 t2
.
每秒时间内重复变化的周期数称 T 为频率,用字母 表示,它的单位是赫 为频率 用字母 f 表示 它的单位是赫 简称赫,周期和频率互为倒数 兹(Hz),简称赫 周期和频率互为倒数 简称赫 周期和频率互为倒数, 1 2π 即有 f = ωT = 2π ω = = 2πf T T 的交流电(称为工频交流电),其角 例如频率 f =50Hz的交流电 称为工频交流电 其角 的交流电 称为工频交流电 频率和周期分别为: 频率和周期分别为 ω=2π f=314 rad/s T=0.02s
1. 周期与频率 周期与频率——变化的快慢 变化的快慢 交流电往复变化一周需要的时间 称为周期, 称为周期,它是波形再次重复出现所 需的最短时间间隔, 需的最短时间间隔,通常用字母 T 表示,如图所示,它的单位是秒(s) (s)。 表示,如图所示,它的单位是秒(s)。
i = Im sin( ωt)
2.1.2 正弦量的三要素 设正弦电流为:
正弦函数或余弦函数 (正弦量)
i = Im sin( ωt +ψ )
周期与频率 初相位
幅值与有效值
1. 正弦量的快慢——周期与频率 正弦量的快慢——周期与频率 2. 正弦量的大小 正弦量的大小——幅值与有效值 幅值与有效值 3. 正弦量的起点 正弦量的起点——初相位 初相位 任何一个正弦量都是由它的三个要素——频率、 频率、 任何一个正弦量都是由它的三个要素 频率 幅值与初相位完全确定,或者说,正弦量一经确定, 幅值与初相位完全确定,或者说,正弦量一经确定, 其三要素也就是唯一的,所以, 其三要素也就是唯一的,所以,可以通过理解三要 素来解决正弦量的表示与计算的问题。 素来解决正弦量的表示与计算的问题。
2. 正弦量的计时起点 ——初相位与相位差 初相位与相位差
对于已知的正弦量:
相位: 相位:称(ωt+ψi) 为正弦交流电流的相位角,简称相位。 在不同的时刻正弦量的相位也不同,交流电流的大小 和方向也不同。 初相位: 0时的相位角 为初相角,简称初相位。 时的相位角ψ 初相位:称t = 0时的相位角ψi为初相角,简称初相位。 初相位用来确定交流电初始瞬时状态。 初相位用来确定交流电初始瞬时状态。 i i o i = I m sin(ωt 90O ) i = I m sin(ωt + 90 )
ψi
t
如果 = ui =ψu ψi > 0
称电压超前电流φ角。
如果 = ui =ψu ψi < 0
称电压滞后电流φ角。
i, u t
i, u t
o
ψu 0 ψi
ψu
ψi 0
如 =ψu ψi = 0 果
称电压与电流同相。 i, u t
如果 =ψu ψi = 90
称电压与电流正交。
如果 =ψu ψi = 180o
i1
= 45
oБайду номын сангаас
ψi 2 = 30
o
ψ ∴ i1 >ψi 2 o o o 12 = 45 (30 ) = 75
在相位上,i1超前 i275o
2. 正弦量的大小 正弦量的大小——瞬时值、幅值与有效值 瞬时值、 瞬时值
i
t′
在t’时刻的 时刻的 值为i( ) 值为 (t’) 正弦交流电流、电压和电动势的大小可表示如下: 正弦交流电流、电压和电动势的大小可表示如下:
i = Im sin( ωt +ψi ) A u = Um sin(在t’’时刻的 )V ωt时刻的 +ψu 值为i( ) 值为 (t’’) e = Em sin( ωt +ψe )V
1 T = = 0.001s f
ψ = = 45o
4
π
(2)画出波形图。
i
Im
5π 4
0
π
4
3π 4
9π 7π 4 2π 4
ωt
T
例2:已知:i1=15sin(314t+45o)A, i2=10sin(314t-30o)A, (1)试问i1与i2的相位差是多少? (2)在相位上i1与i2谁超前,谁滞后。 解(1):∵ ψ
ψu
i = Im sin ωt +ψi ) A (
0
t
0
ψi
t
对一个正弦交流电量来说,如果知道它的角频率、初 相位以及振幅就可以把它唯一确定了。通常把这三个量 叫做交流电的三要素。 例如: 角频率 幅值 初相位
i = Im sin( ωt +ψi ) A
Im
ψi
u = Um sin( ωt +ψu )V
i(t′)
i
t′
t3 0 t1 t2
.
t4 t
i(t′′)
T
′ t′
有效值: 通过电阻R, R,在一个周期时 有效值:若有一交流电流 i 通过电阻R,在一个周期时 间内消耗的电能,与直流电流I 间内消耗的电能,与直流电流I在同样时间内通过同一 电阻所消耗的电能相等,则该直流电流I 电阻所消耗的电能相等,则该直流电流I的数值称为该 的有效值。 交流电流 i 的有效值。 在工程中, 在工程中,正弦电压与电流的计量不是瞬时值也 不是幅值,而是有效值。 不是幅值,而是有效值。
Im
i(t′)
t3 0 t1 t2
.
t4 t
i(t′′)
T
′ t′
瞬时值:任一时刻交流电量值的大小就叫瞬时值, 瞬时值 任一时刻交流电量值的大小就叫瞬时值,都用 任一时刻交流电量值的大小就叫瞬时值 小写拉丁字母表示, 它们都是时间的函数, 小写拉丁字母表示, i、u、e它们都是时间的函数,不 它们都是时间的函数 同时刻其量值也不同。 同时刻其量值也不同。
ψu
0
ψi
称电压与电流反相。
例1:已知:i(t)=100sin(6280t-π/4)mA (1)说明它的Im,I,ω,f,T,ψ (2)画出波形图。 解:(1) Im = 100mA I = 100/
2 = 70.7mA
ω = 6280rad / s 6280 ω f= = =1000Hz 2π 2×3.14
1 T 2 同 : 压u的 效 U = 理 电 有 值 ∫0 u dt T
对于正弦交流电流
i = Im sin( ωt +ψi ) A
1 T 2 1 T 2 I= i dt = Im sin 2 (ωt +ψ )dt 0 0 T∫ T∫
T 1 T ∫0 sin (ωt +ψ )dt =∫0 2dt ∫0cos(2ωt + 2ψ )dt = 2 Im 正弦交流电的有效值等于 I= = 0.707I m 2 它的最大值除以 2 , 而与 其频率及初相无关。 其频率及初相无关。 Um 同理 U= = 0.707Um 有效值与最大值之间的 2 2 关系不适用于其他非正 Em E= = 0.707Em 弦交流量 2 T 2 T
