浙教版八年级竞赛培优训练第25讲 矩形、菱形
《5.1矩形》期末复习培优提升训练2020-2021学年浙教版八年级数学下册
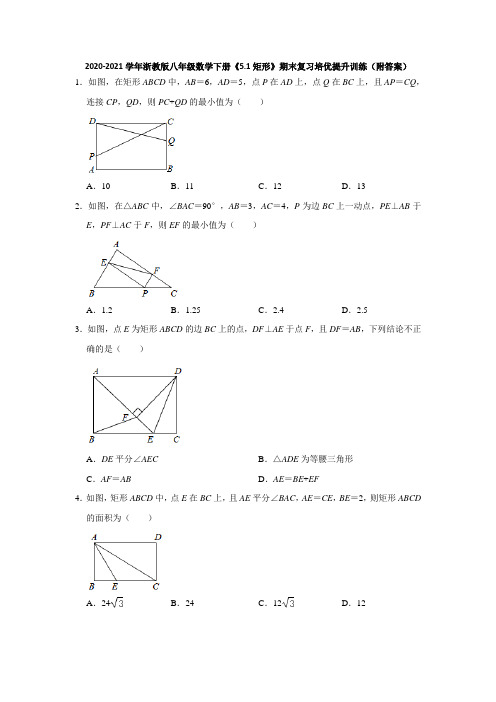
2020-2021学年浙教版八年级数学下册《5.1矩形》期末复习培优提升训练(附答案)1.如图,在矩形ABCD中,AB=6,AD=5,点P在AD上,点Q在BC上,且AP=CQ,连接CP,QD,则PC+QD的最小值为()A.10B.11C.12D.132.如图,在△ABC中,∠BAC=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,则EF的最小值为()A.1.2B.1.25C.2.4D.2.53.如图,点E为矩形ABCD的边BC上的点,DF⊥AE于点F,且DF=AB,下列结论不正确的是()A.DE平分∠AEC B.△ADE为等腰三角形C.AF=AB D.AE=BE+EF4.如图,矩形ABCD中,点E在BC上,且AE平分∠BAC,AE=CE,BE=2,则矩形ABCD 的面积为()A.24B.24C.12D.125.如图,在矩形ABCD中,AB=5,AD=12,对角线BD的垂直平分线分别与AD,BC边交于点E、F,则四边形BFDE的面积为()A.B.C.D.6.如图,在矩形OABC中,点B的坐标是(2,5),则A,C两点间的距离是()A.B.3C.D.57.如图,点P是Rt△ABC中斜边AC(不与A,C重合)上一动点,分别作PM⊥AB于点M,作PN⊥BC于点N,连接BP、MN,若AB=6,BC=8,当点P在斜边AC上运动时,则MN的最小值是()A.1.5B.2C.4.8D.2.48.如图所示,△ABC的面积为1cm2,AP垂直∠ABC的平分线BP于点P,则与△BPC的面积相等的长方形是()A.B.C.D.9.如图,点P是矩形ABCD的对角线AC上一点,过点P作EF∥BC,分别交AB,CD于E、F,连接PB、PD.若AE=2,PF=6,则图中阴影部分的面积为()A.10B.12C.16D.1810.如图,在Rt△ABC中,∠A=90°,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,动点P从点B出发,沿着BC匀速向终点C运动,则线段EF的值大小变化情况是()A.一直增大B.一直减小C.先减小后增大D.先增大后减少11.在▱ABCD中,E、F分别是AB、CD的中点,连接AF、CE.连接AC,当CA=CB时,判断四边形AECF是()A.平行四边形B.矩形C.菱形D.正方形12.如图,在△ABC中,AB=3,AC=4,BC=5,P为边BC上一动点,PE⊥AB于E,PF ⊥AC于F,M为EF中点,则AM的最小值为()A.B.C.D.13.如图,将矩形纸片ABCD沿BE折叠,使点A落在对角线BD上的A'处.若∠DBC=24°,则∠A'EB等于()A.66°B.60°C.57°D.48°14.如图,将长方形ABCD纸片沿BD折叠,使点C落在点C′处,BC′交AD于点E,若∠DBC=22.5°,则在不添加任何辅助线的情况下,图中等腰三角形的个数(虚线也视为角的边)共有()A.2个B.3个C.4个D.5个15.如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,则重叠部分△AFC的面积为()A.12B.10C.8D.616.如图,矩形ABCD沿AE折叠,使D点落在BC边上的F点处,如果∠BAF=60°,则∠AEF=()A.60°B.70°C.75°D.80°17.如图,四边形ABCD为矩形纸片,把纸片ABCD折叠,使点B恰好落在CD边的中点E 处,折痕为AF,若CD=6,则AF等于()A.B.C.D.818.将矩形ABCD沿AE折叠,得到如图所示的图形,已知∠CED′=60°,则∠AED的大小是()A.60°B.50°C.75°D.55°19.如图,在矩形纸片ABCD中,边AB=12,AD=5,点P为DC边上的动点(点P不与点D,C重合),将纸片沿AP折叠,则CD′的最小值为.20.如图,四边形OABC是矩形,点A的坐标为(4,0),点C的坐标为(0,2),把矩形OABC沿OB折叠,点C落在点D处,则点D的坐标为.21.如图,把长方形纸片OABC放入平面直角坐标系中,使OA,OC分别落在x轴、y轴上,连接AC,将纸片OABC沿AC折叠,使点B落在点D的位置,AD与y轴交于点E,若B(2,4),则OE的长为.22.如图,在平面直角坐标系中,矩形ABCO的边CO、OA分别在x轴、y轴上,点E在边BC上,将该矩形沿AE折叠,点B恰好落在边OC上的F处.若OA=6,AB=10,则点E的坐标是.23.如图,在平面直角坐标系中,矩形ABCO的边CO、OA分别在x轴的负半轴、y轴的正半轴上,点D在边BC上,将该矩形沿AD折叠,点B恰好落在边OC上的E处,且△CDE为等腰直角三角形,若OA=4,则点D的坐标是.24.如图,矩形ABCD中,E为BC的中点,将△ABE沿直线AE折叠,使点B落在点F处,连接FC,若∠DAF=18°,则∠DCF=度.25.如图,把一张长方形纸片ABCD沿EF折叠,若∠DEF为x°,∠GFN为y°,x与y 的关系为.26.如图,在平面直角坐标系中有一个长方形ABCO,C点在x轴上,A点在y轴上,B点坐标(8,4),将长方形沿EF折叠,使点B落到原点O处,点C落到点D处,M是y 轴上的一点,且MF=6,则M点的坐标是.27.如图,在平面直角坐标系中,将矩形AOCD沿直线AE折叠(点E在边DC上),折叠后顶点恰好落在边OC上的点F处,若点D的坐标为(10,8).(1)求CE的长;(2)写出点E的坐标.28.(1)如图,把一矩形ABCD的纸片,沿EF折叠后,点D、C分别落在D′、C′的位置上,ED′与BC的交点为G,若∠EFG=55°,求∠1、∠2的度数.(2)如图,把一矩形纸片ABCD,沿EF折叠后,点D和点B重合,点C落在C′位置,若AB=4cm,AD=12cm,求BE的长度.参考答案1.解:如图,连接BP,在矩形ABCD中,AD∥BC,AD=BC,∵AP=CQ,∴AD﹣AP=BC﹣CQ,∴DP=QB,DP∥BQ,∴四边形DPBQ是平行四边形,∴PB∥DQ,PB=DQ,则PC+QD=PC+PB,则PC+QD的最小值转化为PC+PB的最小值,在BA的延长线上截取AE=AB=6,连接PE,∵P A⊥BE,∴P A是BE的垂直平分线,∴PB=PE,∴PC+PB=PC+PE,连接CE,则PC+QD=PC+PB=PC+PE≥CE,∵BE=2AB=12,BC=AD=5,∴CE==13.∴PC+PB的最小值为13.故选:D.2.解:连接AP,如图:∵PE⊥AB,PF⊥AC,∴∠AEP=∠AFP=90°,∵∠BAC=90°,∴四边形AFPE是矩形,∴EF=AP,要使EF最小,只要AP最小即可,当AP⊥BC时,AP最短,∵∠BAC=90°,AB=3,AC=4,∴BC===5,∵△ABC的面积=×4×3=×5×AP,∴AP=2.4,即EF=2.4,故选:C.3.解:∵四边形ABCD是矩形,∴∠C=∠ABE=90°,AD∥BC,AB=CD,∵DF=AB,∴DF=CD,∵DF⊥AE,∴∠DF A=∠DFE=90°,在Rt△DEF和Rt△DEC中,,∴Rt△DEF≌Rt△DEC(HL),∴∠FED=∠CED,∴DE平分∠AEC;故A正确;∵AD∥BC,∴∠AEB=∠DAF,在△ABE和△AFD中,,∴△ABE≌△DF A(AAS),∴AE=AD,∴△ADE为等腰三角形;故B正确;∵△ABE≌△DF A,∴不存在AF=AB,故C错误;∵△ABE≌△DF A,∴BE=F A,∴AE=AF+EF=BE+EF.故D正确.故选:C.4.解:∵四边形ABCD是矩形,∴∠B=90°,∴∠BAC+∠BCA=90°,∵AE平分∠BAC,AE=CE,∴∠BAE=∠EAC=∠ECA,∴∠BAE+∠EAC+∠ECA=90°,∴∠BAE=∠EAC=∠ECA=30°,∴AE=CE=2BE=4,AB=2,∴BC=BE+CE=6,∴矩形ABCD面积=AB×BC=2×6=12;故选:C.5.解:∵四边形ABCD是矩形,∴AD∥BC,∴∠DEO=∠BFO,∠EDO=∠FBO,∵对角线BD的垂直平分线分别与AD,BC边交于点E、F,∴BO=DO,EF⊥BD,∴△DEO≌△BFO(AAS),∴EO=FO,∵BO=DO,∴四边形BEDF是平行四边形,∵EF⊥BD,∴平行四边形BEDF是菱形,∴BE=DE,设DE=x,则AE=12﹣x,在Rt△AEB中,AB2+AE2=BE2,即52+(12﹣x)2=x2,∴x=,∴DE=,∴S菱形EBDF=DE•AB=.故选:A.6.解:如图,连接AC,OB,∵四边形AOCB是矩形,∴AC=OB,∵点B的坐标是(2,5),点O(0,0),∴OB==,∴A,C两点间的距离为,故选:C.7.解:∵∠ABC=90°,AB=6,BC=8,∴AC===10,∵PM⊥AB,PN⊥BC,∠C=90°,∴四边形BNPM是矩形,∴MN=BP,由垂线段最短可得BP⊥AC时,线段MN的值最小,此时,S△ABC=BC•AB=AC•BP,即×8×6=×10•BP,解得:BP=4.8,即MN的最小值是4.8,故选:C.8.解:延长AP交BC于点E,如图所示:∵AP垂直∠B的平分线BP于P,∴∠ABP=∠EBP,∠APB=∠EPB=90°,在△ABP和△EBP中,,∴△ABP≌△EBP(ASA),∴S△ABP=S△BEP,AP=PE,∴△APC和△CPE等底同高,∴S△APC=S△PCE,∴S△BPC=S△PBE+S△PCE=S△ABC=(cm2),选项中只有B的长方形面积为cm2,故选:B.9.解:作PM⊥AD于M,交BC于N.则有四边形AEPM,四边形DFPM,四边形CFPN,四边形BEPN都是矩形,∴S△ADC=S△ABC,S△AMP=S△AEP,S△PBE=S△PBN,S△PFD=S△PDM,S△PFC=S△PCN,∵MP=AE=2∴S△DFP=S△PBE=×2×6=6,∴S阴=6+6=12,故选:B.10.解:如图,连接AP.∵∠A=90°,PE⊥AB,PF⊥AC∴四边形AFPE是矩形,∴EF=AP,由垂线段最短可得AP⊥BC时,AP最短,则线段EF的值最小,∴动点P从点B出发,沿着BC匀速向终点C运动,则线段EF的值大小变化情况是先减小后增大.故选:C.11.四边形AECF是矩形;证明:连接AC,∵四边形ABCD是平行四边形,∴AB=CD,∵E、F分别是AB、CD的中点,∴AE=CF,∵四边形ABCD是平行四边形,∴AB∥CD,∴AE∥CF,∵AE=CF,∴四边形AECF是平行四边形,∵AC=BC,E是AB的中点,∴CE⊥AB,∴∠AEC=90°,∴平行四边形AECF是矩形.故选:B.12.解:设Rt△ABC的斜边BC上的高为h.∵在△ABC中,AB=3,AC=4,BC=5,∴h==,∴AB2+AC2=BC2,即∠BAC=90°.又∵PE⊥AB于E,PF⊥AC于F,∴四边形AEPF是矩形,∴EF=AP.∵M是EF的中点,∴AM=EF=AP.因为AP的最小值即为直角三角形ABC斜边上的高,即等于,∴AM的最小值是.故选:D.13.解:∵四边形ABCD是矩形,∴∠A=∠ABC=90°,由折叠的性质得:∠BA'E=∠A=90°,∠A'BE=∠ABE,∴∠A'BE=∠ABE=(90°﹣∠DBC)=(90°﹣24°)=33°,∴∠A'EB=90°﹣∠A'BE=90°﹣33°=57°;故选:C.14.解:由矩形的性质得:∠ABC=∠A=∠C=90°,AD∥BC,∴∠BDE=∠DBC=22.5°,由折叠的性质得:∠C'BD=∠DBC=22.5°,∠C'=∠C=90°,∴∠CBC'=45°,∠C'BD=∠BDE,∴∠ABE=45°,∴△ABE、△BDE是等腰三角形,∴∠C'ED=∠AEB=45°,∴△C'DE是等腰直角三角形,∴图中的等腰三角形有3个.即:△ABE,△C'DE,△BDE.故选:B.15.解:∵△AD′C≌△CBA,∴△AD′F≌△CBF,∴△AD′F与△CBF面积相等,设BF=x,则(8﹣x)2=x2+42,64﹣16x+x2=x2+16,16x=48,解得x=3,∴△AFC的面积=×4×8﹣×3×4=10.故选:B.16.解:∵∠EAF是∠DAE折叠而成,∴∠EAF=∠DAE,∠ADC=∠AFE=90°,∠EAF===15°,在△AEF中∠AFE=90°,∠EAF=15°,∠AEF=180°﹣∠AFE﹣∠EAF=180°﹣90°﹣15°=75°.故选:C.17.解:由折叠的性质得BF=EF,AE=AB,因为CD=6,E为CD中点,故ED=3,又因为AE=AB=CD=6,所以∠EAD=30°,则∠F AE=(90°﹣30°)=30°,设FE=x,则AF=2x,在△AEF中,根据勾股定理,(2x)2=62+x2,x2=12,x1=2,x2=﹣2(舍去).AF=2×2=4.故选:A.18.解:∵∠AED′是△AED沿AE折叠而得,∴∠AED′=∠AED.又∵∠DEC=180°,即∠AED′+∠AED+∠CED′=180°,又∠CED′=60°,∴∠AED==60°.故选:A.19.解:连接AC,当点D'在AC上时,CD'有最小值,∵四边形ABCD是矩形,AB=12,AD=5,∴∠D=∠B=90°,AD=BC,∴AC=,由折叠性质得:AD=AD'=5,∠AD'P=∠D=90°,∴CD'的最小值=AC﹣AD'=13﹣5=8,故答案为:8.20.解:设BD与OA交于点E,作DF⊥OA于点F,∵点A的坐标为(4,0),点C的坐标为(0,2),∴OC=2,OA=4,∵四边形ABCD是矩形,∴BC∥OA,∴∠CBO=∠AOB,由翻折变换的性质可知,∠DBO=∠CBO,∴∠OBD=∠AOB,∴BE=OE,在Rt△EAB中,设BE=OE=x,则AE=4﹣x,由勾股定理得22+(4﹣x)2=x2,解得x=,即BE=,∴OE=BE=,在Rt△ODE中,OD=OC=2,DE=BD﹣BE=4﹣=,由OE•DF=OD•DE得וDF=×2×,∴DF=,在Rt△ODF中,由勾股定理得OF2=OD2﹣DF2=22﹣()2=,∴OF=,∴点D的坐标为(,﹣),故答案为:(,﹣).21.解:∵四边形OABC是矩形,∴OC∥AB,∴∠ECA=∠CAB,根据题意得:∠CAB=∠CAD,∠CDA=∠B=90°,∴∠ECA=∠EAC,∴EC=EA,∵B(2,4),∴AD=AB=4,设OE=x,则AE=EC=OC﹣OE=4﹣x,在Rt△AOE中,AE2=OE2+OA2,即(4﹣x)2=x2+4,解得:x=,∴OE=,故答案为:.22.解:设CE=a,则BE=6﹣a,由题意可得,EF=BE=6﹣a,由对折知,AF=AB=10,∴,∴CF=OC﹣OF=10﹣8=2,∵∠ECF=90°,∴a2+22=(6﹣a)2,解得,a=,∴点E的坐标为(10,),故答案为(10,).23.解:由折叠可得,∠B=∠AED=90°,∵△CDE是等腰直角三角形,∴∠DEC=45°,∴∠AEO=45°,又∵∠AOE=90°,∴∠EAO=∠AEO,∴AO=EO=4,∴AE=,由折叠可得,AB=AE=,∵四边形ABCO的矩形,∴CO=,∴CE=CO﹣EO=,∴CD=,∵点D在第二象限,∴D(﹣4,),故答案为:(﹣4,).24.解:∵四边形ABCD是矩形,∴∠BAD=∠B=∠BCD=90°,由折叠的性质得:FE=BE,∠F AE=∠BAE,∠AEB=∠AEF,∵∠DAF=18°,∴∠BAE=∠F AE=(90°﹣18°)=36°,∴∠AEF=∠AEB=90°﹣36°=54°,∴∠CEF=180°﹣2×54°=72°,∵E为BC的中点,∴BE=CE,∴FE=CE,∴∠ECF=(180°﹣72°)=54°,∴∠DCF=90°﹣∠ECF=36°;故答案为:36.25.解:∵四边形ABCD是矩形,∴AD∥BC,∴∠DEF+∠EFC=180°,∠DEF=∠EFG=x°,∴∠EFC=180°﹣x°,∵把一张长方形纸片ABCD沿EF折叠,∴∠EFC=∠EFN=180°﹣x°,∵∠EFN=∠EFG+∠GFN,∴180°﹣x°=x°+y°,∴2x+y=180,故答案为:2x+y=180.26.解:在Rt△ODF中,DF2+OD2=OF2,即(8﹣OF)2+42=OF2,解得OF=5,在Rt△OMF中,OM==.故M点的坐标是(0,),(0,﹣).故答案为:(0,),(0,﹣).27.解:(1)∵四边形AOCD为矩形,D的坐标为(10,8),∴AD=OC=10,DC=AO=8,∵矩形沿AE折叠,使D落在BC上的点F处,∴AD=AF=10,DE=EF,在Rt△AOF中,OF==6,∴FC=10﹣6=4,设EC=x,则DE=EF=8﹣x,在Rt△CEF中,EF2=EC2+FC2,即(8﹣x)2=x2+42,解得x=3,即EC的长为3.(2)∵EC的长为3,∴点E的坐标为(10,3).28.(1)解:∵在矩形ABCD中,AD∥BC,∴∠DEF=∠EFB,∠1+∠2=180°.又∵∠EFG=55°,由对称性可知∠GEF=∠DEF=55°.∴∠1=180°﹣∠GEF﹣∠DEF=70°.∴∠2=180°﹣∠1=110°.(2)解:设DE=xcm,则有DE=BE=x.∵AD=12cm,∴AE=(12﹣x)cm.在Rt△ABE中,BE2=AB2+AE2,即x2=42+(12﹣x)2,x2=16+144﹣24x+x224x=160.解得x=,∴BE的长为cm.。
浙教版八年级下册数学期末专区课件-第25讲矩形、菱形

大师导航 归类探究 自主招生交流平台 思维训练
菱形的判定方法 (1)一组邻边相等+平行四边形=菱形; (2)四边都相等+四边形=菱形; (3)对角线互相垂直+平行四边形=菱形; (4)对角线互相垂直平分+四边形=菱形. 这些判定方法中:(1)(3)是从平行四边形出发的;对于判 定方法(4),根据对角线互相平分,可以第一判定它是平行四边 形,这样(4)与(3)就等价了.
ቤተ መጻሕፍቲ ባይዱ全效优等生
图8-25-9
大师导航 归类探究 自主招生交流平台 思维训练
【思路生成】(1)根据两直线平行,内错角相等可得 ∠AEB=∠EAD,根据等边对等角可得∠ABE=∠AEB;
(2)求出∠ABD=∠ADB,再根据等角对等边求出AB =AD,然后利用邻边相等的平行四边形是菱形.
全效优等生
大师导航 归类探究 自主招生交流平台 思维训练
全效优等生
大师导航 归类探究 自主招生交流平台 思维训练
3.如图8-25-5,在△ABC中,点O是边AC上一个动
点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交
∠ACB的外角平分线于点F.
(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC
的长;
(3)当点O在边AC上运动到什么
全效优等生
大师导航 归类探究 自主招生交流平台 思维训练
5.如图8-25-8,在菱形ABCD中,AB=5,对角线AC
=6,过点A作AE⊥BC,垂足为E,则AE的长为
(C )
A.4
全效优等生
图8-25-8
12
24
B. 5
C. 5
D.5
大师导航 归类探究 自主招生交流平台 思维训练
2020—2021年浙教版八年级数学下册《矩形》讲练互动及答案解析精品试卷.docx

5.1 矩形(2)(讲练互动)姓名班级【要点预习】1.矩形的判定:定理1:有三个角是的四边形是矩形;定理2:对角线的平行四边形是矩形【课前热身】1. 矩形具有一般平行四边形不具有的性质是……………………………………………()A. 对边相互平行B. 对角线相等C. 对角线相互平分D. 对角相等2.矩形是轴对称图形,它至少有条对称轴.3.如图,在四边形ABCD中,AD∥BC,∠D=90°,若再添加一个条件,就能推出四边形ABCD 是矩形,你所添加的条件是.(写出一种情况即可)4. 在平面直角坐标系中,点A,B的坐标分别是(0,4),(6,0),点C在第一象限.若四边形AOBC是矩形,则点C的坐标是.【讲练互动】【例1】如图,四边形ABCD的对角线互相平分,要使它变为矩形,需要添加的条件是…………………()A.AB=CDB.AD=BCC.AB=BCD.AC=BD【绿色通道】要证一个四边形是矩形共有三种方法:一是根据定义,证明平行四边形加一个直角;二是根据判定定理1,证明三个直角;三是根据判定定理2,证明平行四边形加对角线相等.【变式训练】1. 只用一把刻度尺检查一张四边形纸片是否是矩形,下列操作中最为恰当的是………()A.先测量两对角线是否互相平分,再测量对角线是否相等B.先测量两对角线是否互相平分,再测量是否有一个直角C.先测量两组对边是否相等,再测量对角线是否相等D.先测量两组对边是否互相平行,再测量对角线是否相等【例2】已知,如图,在矩形ABCD中,E,F分别是AB,CD的中点.求证:四边形AEFD是矩形.【变式训练】2.已知,如图,在Rt ΔABC 中,∠C=Rt ∠,点D ,E ,F 分别是AB ,BC ,CA 边上的中点.求证:四边形CEDF 是矩形.【例3】如图,在平行四边形ABCD 中,E 为BC 的中点,连接AE 并延长交DC 的延长线于点F .(1)求证:CF AB ;(2)当BC 与AF 满足什么数量关系时,四边形ABFC 是矩形,并说明理由.【变式训练】3. 如图,在平行四边形ABCD 中,对角线AC 与BD 交于点O ,OM ⊥BC 于点M ,且BM=CM. 求证:平行四边形ABCD 是矩形.FE DC B A参考答案【要点预习】1.矩形的判定:定理1:有三个角是的四边形是矩形;定理2:对角线的平行四边形是矩形【课前热身】4. 在平面直角坐标系中,点A,B的坐标分别是(0,4),(6,0),点C在第一象限.若四边形AOBC是矩形,则点C的坐标是.答案:(6,4)【讲练互动】【例1】如图,四边形ABCD的对角线互相平分,要使它变为矩形,需要添加的条件是…………………()A.AB=CDB.AD=BCC.AB=BCD.AC=BD解析:由于四边形ABCD的对角线互相平分,故四边形ABCD是平行四边形,要使它变为矩形,只需添加条件对角线相等或有一个内角为直角即可.答案:D【绿色通道】要证一个四边形是矩形共有三种方法:一是根据定义,证明平行四边形加一个直角;二是根据判定定理1,证明三个直角;三是根据判定定理2,证明平行四边形加对角线相等.【变式训练】2.已知,如图,在RtΔABC中,∠C=Rt∠,点D,E,F分别是AB,BC,CA边上的中点.求证:四边形CEDF是矩形.证明:∵点D,E,F分别是AB,BC,CA边上的中点,∴DF∥BC,DE∥AC,∴四边形CEDF是平行四边形.∵∠C=Rt∠,∴四边形CEDF是矩形.【例3】如图,在平行四边形ABCD中,E为BC的中点,连接AE并延长交DC的延长线于点F.(1)求证:CFAB ;(2)当BC与AF满足什么数量关系时,四边形ABFC是矩形,并说明理由.(1)证明:∵四边形ABCD是平行四边形,∴AB∥CD,∴∠BAF=∠AFC,∠ABC=∠BCF.又∵E为BC的中点,∴BE=EC.∴△ABE≌△FCE(AAS),∴AB=CF.(2) BC=AF.证明:∵AB ∥CF,∴四边形ABFC是平行四边形.∵BC=AF,∴四边形ABFC是矩形.FEDCBA。
初中八年级数学竞赛培优讲义全套专题19 平行四边形、矩形、菱形_答案[精品]
![初中八年级数学竞赛培优讲义全套专题19 平行四边形、矩形、菱形_答案[精品]](https://img.taocdn.com/s3/m/f52e7cf3bb4cf7ec4afed050.png)
专题19 平行四边形、矩形、菱形例1 75° 例2 A 只有命题③正确.例3 (1)△BEF 为正三角形 提示:由△ABD 和△BCD 为正三角形,可证明△BDE ≌△BCF , 得:BE=BF ,∠DBE =∠CBF .∵∠DBC=∠CBF +∠DBF =∠DBE +∠DBF =60°,即∠EBF=60°,故△BEF 为等边三角形.(2)设BE BF EF x ===,则可得:24S x =,当BE ⊥AD 时,x .∴2minS ==当BE 与AB 重合时,x 有最大值为2,∴()2max 2S =⨯=S ≤≤例4 提示:PC=EF=PD ,4545CPB PFC EPG GPA BPD ︒︒∠=+∠=+∠=∠=∠,可证明 △CPB ≌△DPB .例5 (1)略 (2)45° (3)60°如图,延长AB 至H ,使AH=AD ,连DH ,则 △AHD 是等边三角形. ∵AH=AD=DF ,∴BH=GF , 又∠BHD=∠GFD=60°,DH=DF , ∴△DBH ≌△DGF ,∠BDH=∠GDF ,∴()1206060BDG ADC ADB GDF ADC ADB BDH ︒︒︒∠=∠-∠-∠=∠-∠+∠=-=例6 如图过M 作ME AN ,连NE ,BE ,则四边形AMEN 为平行四边形,得NE=AM ,ME ⊥BC . ∵ME=CM ,∠EMB=∠MCA=90°,BM=AC .∴△BEM ≌△AMC ,得BE=AM=NE ,∠1=∠2,∠3=∠4. ∵∠1+∠3=90°,∴∠2+∠4=90°且BE=NE . ∴△BEN 为等腰直角三角形,∠BNE=45°. ∵AM ∥NE ,∴∠BPM=∠BNE=45°.A 级1. 2α3. 26° 提示:作FG 边上中线,连接EC ,则EF=EC=AC .4. 20° 提示:连接AC ,则△AFC ≌△AEB ,△AEF 为等边三角形.5.C6.B7.D8. A 提示:E 、F 分别为AB 、BC 中点.9.从6个条件中任取2个,只有15种组合,其中能推出四边形ABCD 是平行四边形的有以下9种 情形:①与③;②与④;⑤与⑥;①与②;③与④;①与⑤;①与⑥;③与⑤;③与⑥. 10. 提示:(2)当D 为BC 中点时,满足题意.11. 提示:连AM ,证明△AMF ≌△BME ,可证△MEF 为等腰直角三角形.12. 6 提示:由△ABC ≌△DBF ,△ABC ≌△EFC 得:AC=DF=AE ,AB=EF=AD .故四边形AEFD 为平行四边形.又∠BAC=90°,则∠DAE =360°-90°-60°-60°=150°,则∠ADF=∠AEF=30°,则F 到AD 的距离为2,故326AEFDS=⨯=.B 级1. 92cm2. 提示:可以证明2222PA PC PB PD +=+. 3.152cm 4. 10 提示:可先证:AF=CF .设AF CF x ==,则8BF x =-, ∴()22284x x =-+. ∴5x =. ∴11541022AFC S AF BC ∆==⨯⨯=. 5.6013提示:过A 作AG ⊥BD 于G 可证PE+PF=AG , 由AG BD AB AD =可得:512601313AG ⨯==.6. 提示:A ,C 关于BD 对称,连AE 交BD 于P . ∴PE+PC=AE .又∵AE ⊥BC 且∠BAE=30°,∴AE =. 7. B8. B 提示:取DE 中点为G ,连结AG ,则AG=DG=EG .9. C10.(1)=;图略 (2)1;图略 (3)3;图略 (4)以AB 为边的矩形周长最小,用面积法证明.11.证明:连AC ,如图,则易证△ABC 与△ADC 都为等边三角形. (1)若∠MAN =60°,则△ABM ≌△ACN . ∵AM =AN ,∠MAN =60°, ∴△AMN 为等边三角形.(2)∠AMN =60°,过M 作CA 的平行线交AB 于P . ∵∠BPM =∠BAC =60°,∠B =60°,∴△BPM 为等边三角形,BP =BM ,BA =BC .∴AP =MC . 又∠APM =120°=∠MCN .∠PAM =∠AMC -∠B =∠AMC -60°=∠AMC -∠AMN =∠CMN , ∴△PAM ≌△CMN .∴AM =MN ,又∠AMN =60°. 故△AMN 为等边三角形.12.提示:如图,分别过点A 作AM ∥EF ,过点C 作CP ∥AB ,过点E 作EN ∥AF ,它们分别交于N ,M ,P 点,得□ABCM 、□CDEP 、□EFAN ,则EF =AN ,AB=CM ,CD =PE ,BC =AM ,CP =DE ,AF =NE ,由条件得△NMP 为等边三角形,可推得六边形的每个内角均为120°.AMNPBDA B CD EP N MF。
八年级数学尖子生培优竞赛专题辅导专题03菱形

专题03菱形专题解读】菱形既是轴对称图形,可以把菱形看成是由等腰三角形沿底边翻折而成:菱形又是中心对称图形,可以看成是由直角三角形以直角顶点为对称中心旋转180°而成,所以在处理菱形类问题时,等腰三角形和直角三角形的图形特征往往是我们尝试的突破口。
思维索引例1. (1)如图1,菱形ABCD和菱形BEFG的边长分别是5和2, ZA=60° ,连结DF,则DF的长为__________(2)如图2是由6个形状大小完全相同菱形组成的网格,若菱形的边长为1, 一个内角(Z0)为60° ,A ABC的各顶点都在格点上,则BC边上的高为___________(3)如图3,在菱形ABCD中,对角线AC与BD相交于点0, AC二8, BD二6, 0E丄AD于点E,交BC于点F,则EF的长为 __________ .(4)如图4, F是萎形ABCD的边AD的中点,AC与BF相交于E, EG丄AB于G,已知Z1=Z2,则下列结论:①AE二BE:②BF丄AD:③AC二2BF:④CE二BF+BG•其中正确的结论是(图4)(郎)2 例2•将矩形OABC如图所示放置在第一象限,点B的坐标为(3, 4), —次函数y=—x+b的图象3与边OC、AB分别交于点D、E,并且满足0D二BE,点M是线段DE上的一个动点。
(1)求b的值:(2)设点N是x轴上方平而内的一点,以0、D、M. N为顶点的四边形是萎形,求点N的坐标。
交0D于点F•若AB=2, ZABC二60°,则AE的长为D. 2y!2素养提升1 •如图,在菱形ABCD中,ZBCD二110°,AB的垂直平分线交对角线AC于点F, E为垂足,连接DF,则ZCDF等于A. 15°B. 25°C. 45°D. 55°2•如图,菱形ABCD的对角线相交于点0,过点D作DE〃AC,且DE二丄AC,连接CE、0E,连接AE,2B. V5DUE3. 如图,菱形ABCD 中,ZABC 二60° , AB 二4,对角线AC. BD 交于点0, E 是线段BO 上一动点,F 是射线DC 上一动点,若ZAEF 二120° ,则线段EF 的长度的整数值的个数有( ) A.1个 B.2个 C.3个 D.4个4. 如图,将三角形纸片ABC 沿DE 折叠,使点A 落在BC 边上的点F 处,且DE 〃BC,下列结论: ①ABDF 是等腰三角形:②DE 二丄BC :③四边形ADFE 是菱形;④ZBDF+ZFEC 二2ZA, 2其中一定正确的结论是( )A.①③④B.②③④C.①②④D.①②③5. 如图,A 、B 两点的坐标分别为(6, 0)、(0, 6),连结AB.点P 从点A 出发,沿AB 方向以每秒迈 个单位的速度向终点B 运动;同时动点Q 从点B 出发沿B0方向以每秒1个单位的速度向终点0运动,将 △PQO 沿B0翻折,记点P 的对应点为点C,若四边形QPOC 为菱形,则点C 的坐标为 _____________ ・6•我们规圧:将一个平而图形分成而积相等的两部分的直线叫做该平而图形的“等积线”,等积线被 这个平面图形截得的线段叫做该图形的“等枳线段”(例如三角形的中线就是三角形的等积线段).已知 菱形的边长为4.且有一个内角为60°,设它的等积线段长为叫则m 的取值范围是 _________________・A (第3题〉 (第5题)(第7题) (第8题)7•如图,在平而直角坐标系xOy中,菱形OABC的边长为2,点A在第一象限,点C在x轴正半轴上,ZAOC二60° ,若将菱形OABC绕点0顺时针旋转75° ,得到四边形OABC ,则点B的对应点3的坐标为8•如图,在菱形ABCD中,AB二BD,点E、F分别在BC、CD上,且BE二CF,连接BF. DE交于点延长ED到H使DH=BM,连接AM, AH,则以下四个结论:©AABD^ADCE;②ZBMD二120° :③△AMH 是等边三角形:④S“昨AM'其中正确结论的是________ (填写序号).9.在如图直角坐标系内,四边形AOBC是边长为2的菱形,E为边0B的中点,连结AE与对角线0C交于点D,且ZBCO二ZEAO,求点D坐标.10.如图,在ZkABC中,ZABC二90° , BD为AC的中线,过点C作CE丄BD于点E,过点才作BD的平行线, 交CE的延长线于点F,在AF的延长线上截取FG二BD,连接BC、DF.若CF二6, AC二AF+2,求四边形BDFG的周长.11•如图1,矩形OABC的两条边OA、0C分别在y轴和x轴上,已知点A (0, 3)、点C (-4, 0).(1)若把矩形OABC沿直线DE折叠,使点C落在点A处,直线DE与OC、AC、AB的交点分别为D、F、E,请根据题意画出图形,并求折痕DE的长;(2)若点P在x轴上,在平面内是否存在点Q,使以P、D、E、Q为顶点的四边形是菱形?若存在,则请求出点Q的坐标;若不存在,请说明理由:(3)如图2,若M为AC边上的一动点,在0A上取一点N (0, 1),将矩形OABC绕点0顺时针旋转一周,在族转的过程中,M的对应点为、L,请直接写出NNL的最大值和最小值.(图1)12•如图,直线li:y=- —x+b分别与x轴、y轴交于A、B两点,与直线b:y=kx-6交于点C (4, 2).2(1)点A坐标为(_____ ) , B为( _____ ):(2)在线段BC上有一点E,过点E作y轴的平行线交直线h于点F,设点E的横坐标为m,当m 为何值时,四边形OBEF是平行四边形;(3)若点P为x轴上一点,则在平而直角坐标系中是否存在一点Q,使得P、Q、A、B四个点能构成一个菱形。
浙教版数学八年级下册 5.2.1 菱形 说课课件(共27张PPT)

关系.
2.探索并证明菱形的性质定理: 符号语言).
2.探索并证明菱形的性质 菱形的四条边相等.
2.学生能说出菱形的四条边相等,并
定理:菱形的四条边相等, 3.探索并证明菱形的性质定理: 给出证明.
对角线互相垂直.
对角线互相垂直,并每条对角 3. 猜想、验证、证明、归纳出菱形
3.探索菱形的轴对称性. 线平分一组对角.
对角线互相垂直,并每条对角线平分
4.探索菱形的轴对称性.
一组对角.
4.学生通过折、剪、拼明确菱形是轴
对称图形,并能说出它的对称轴.
03 教 学 问 题 诊 断 分 析
已经具备的基础
三角形的分类 和特殊三角形
的性质
平行四边形和 矩形的性质、 判定、应用
能够从边和角 考虑图形的特 殊化,知道从 边、角、对角 线和对称性研 究图形性质.
线平分一组对角.
分一组对角.
4.探索菱形的轴对称性.
菱形轴对称性难以理解
课时目标
1.理解菱形的概念, 以及菱形与平行四边 形的关系.
2.探索并证明菱形的 性质定理:菱形的四 条边相等.
3.探索并证明菱形的 性质定理:对角线互 相垂直,并且每条对 角线平分一组对角.
可能问题
教师引导
忽视菱形作为平 行四边形所具备 的一般性质.
Байду номын сангаас定性判 应 义质定 用
菱形
本节课的教学重点:探索并证明菱形的性质
02目标及目标解析
对照 课标 要求
目标确定
课标要求
课时目标
目标解析
1.理解菱形的概念,以及 1.理解菱形的概念,以及菱形 1.学生能说出菱形与平行四边形的关
菱形与平行四边形之间的 与平行四边形的关系.
第25课矩形与菱形中考数学一轮复习教学市公开课一等奖课件名师大赛获奖课件

(1)求证:四边形 ABCD 是矩形;
证明:∵AO=OC,BO=OD, ∴四边形 ABCD 是平行四边形. ∵∠AOB=∠DAO+∠ADO=2∠OAD, ∴∠DAO=∠ADO. ∴AO=DO. ∴AC=BD. ∴四边形 ABCD 是矩形.
(2)若∠AOB∶∠ODC=4∶3,求∠ADO 的度数.
解:∵四边形 ABCD 是矩形, ∴AB∥CD. ∴∠ABO=∠CDO. ∵∠AOB∶∠ODC=4∶3, ∴∠AOB∶∠ABO=4∶3. ∴∠BAO∶∠AOB∶∠ABO=3∶4∶3. ∴∠ABO=54°. ∵∠BAD=90°, ∴∠ADO=90°-54°=36°.
11.(2017·广东)如图所示,已知四边形 ABCD, ADEF 都是菱形,∠BAD=∠FAD,∠BAD 为锐 角.
(1)求证:AD⊥BF;
证明:∵四边形 ABCD,ADEF 都是菱形, ∴AB=BC=CD=DA,AD=DE=EF=FA. ∴AB=AF. ∵∠BAD=∠FAD, ∴AD⊥BF(等腰三角形三线合一).
二、填空题 5.(2020·铜仁模拟)已知一个菱形的两条对角线长分别 为 6 cm 和 8 cm,则这个菱形的面积为___2_4__cm2.
6.(2019·徐州)如图,矩形 ABCD 中,AC、BD 交于点 O,M、N 分别为 BC、OC 的中点.若 MN=4,则 AC 的长为__1_6___.
C.对角线相等
D.对角线互相垂直
3.(2019·贵阳)如图,菱形 ABCD 的周长是 4 cm,∠ ABC=60°,那么这个菱形的对角线 AC 的长是( A ) A.1 cm B .2 cm C.3 cm D .4 cm
4.(2018·遵义)如图,点 P 是矩形 ABCD 的对角线 AC 上一点,过点 P 作 EF∥BC,分别交 AB,CD 于 E、 F,连接 PB、PD.若 AE=2,PF=8.则图中阴影部分的 面积为( C ) A.10 B .12 C.16 D .18
《5.2菱形》期末复习培优提升训练(附答案)2020-2021年八年级数学浙教版下册
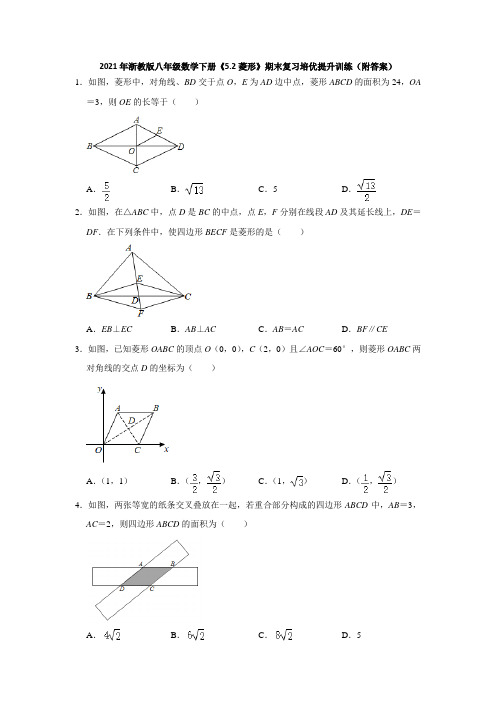
2021年浙教版八年级数学下册《5.2菱形》期末复习培优提升训练(附答案)1.如图,菱形中,对角线、BD交于点O,E为AD边中点,菱形ABCD的面积为24,OA =3,则OE的长等于()A.B.C.5D.2.如图,在△ABC中,点D是BC的中点,点E,F分别在线段AD及其延长线上,DE=DF.在下列条件中,使四边形BECF是菱形的是()A.EB⊥EC B.AB⊥AC C.AB=AC D.BF∥CE3.如图,已知菱形OABC的顶点O(0,0),C(2,0)且∠AOC=60°,则菱形OABC两对角线的交点D的坐标为()A.(1,1)B.(,)C.(1,)D.(,)4.如图,两张等宽的纸条交叉叠放在一起,若重合部分构成的四边形ABCD中,AB=3,AC=2,则四边形ABCD的面积为()A.B.C.D.55.如图,菱形ABCD的边长为10,对角线AC=16,点E、F分别是边CD、BC的中点,连接EF并延长与AB的延长线相交于点G,则EG长为()A.13B.10C.12D.56.如图,在菱形ABCD中,点E,F分别在AB,CD上,且AE=CF,连接EF交BD于点O,连接AO.若∠DBC=25°,则∠OAD的度数为()A.50°B.55°C.65°D.75°7.如图,在菱形ABCD中,E是对角线AC上的一点,过点E作FH∥AD,GI∥AB,点F,G,H,I分别在AB,BC,CD,DA上.若AC=a,∠B=60°,则图中阴影部分的周长为()A.2B.4a C.2a D.6a8.如图,四边形ABCD是菱形,AB=6,∠ABC=120°,点M,N是对角线AC上的三等分点,若点P是菱形ABCD边上的动点,则满足PM+PN=6的点P有()A.4个B.6个C.8个D.12个9.如图,在菱形ABCD中,AB=6,∠ABC=60°,AE⊥BC于点E,交BD于点F.若P是菱形ABCD边上的一动点,当△AFP的面积是9时,DP的长为.10.如图,在▱ABCD中,点E,F分别是AB,CD边上的点,且∠ADE=∠CBF,连接BD,EF.补充一个条件,可使四边形EBFD是菱形,这个条件是.11.如图,A(0,4),B(8,0),点C是x轴正半轴上一点,D是平面内任意一点,若以A、B、C、D为顶点的四边形是菱形,则点D的坐标为.12.如图,四边形ABCD是菱形,点M,N分别在AB,AD上,且BM=DN,MG∥AD,NF∥AB,点F,G分别在BC,CD上,MG与NF相交于点E.若∠A=120°,AB=a (a>0),AB:MB=3:1,则四边形CFEG的面积是.(用含a 的式子表示)13.如图,在菱形ABCD中,AB=8,点E,F分别在AB,AD上,且AE=AF,过点E作EG∥AD交CD于点G,过点F作FH∥AB交BC于点H,EG与FH交于点O.当四边形AEOF与四边形CGOH的周长之差为12时,则AE的值为.14.如图,在菱形ABCD中,∠B=45°,BC=2,E,F分别是边CD,BC上的动点,连接AE,EF,G,H分别为AE,EF的中点,连接GH,则GH的最小值为.15.如图,在▱ABCD中,点E、F分别是AD、BC的中点,分别连接BE、DF、BD.(1)求证:△AEB≌△CFD;(2)当△ABD满足什么条件时,四边形EBFD是菱形,请说明理由.16.如图,在Rt△ABC中,∠ACB=90°,D,E分别是边AB,BC的中点,连接DE并延长到点F,使EF=DE,连接CF,BF.(1)求证:四边形CFBD是菱形;(2)连接AE,若CF=,DF=2,求AE的长.17.如图,E和F分别是菱形ABCD的边AB和AD的中点,且AB=10,AC=12.(1)判断△OEF的形状,并说明理由.(2)求线段EF的长.18.如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.(1)求证:CE=AD;(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由.19.在平行四边形ABCD中,点P是AB上一点(不与A、B重合),连接DP交对角线AC 于点E,连接BE.(1)如图1,若∠EBC=∠EP A,EC平分∠DEB,证明:四边形ABCD为菱形.(2)如图2,对角线AC与BD交于点O,当P是AB的中点时,请直接写出与△ADP 面积相等的三角形(其中不含以AD为边的三角形).20.如图所示,在边长为1的菱形ABCD中,∠DAB=60°,M是AD上不同于A,D两点的一动点,N是CD上一动点,且AM+CN=1.(1)证明:无论M,N怎样移动,△BMN总是等边三角形;(2)求△BMN面积的最小值.参考答案1.解:∵菱形的对角线、BD交于点O,OA=3,∴AC=2AO=6,∵菱形ABCD的面积为24,∴=24,∴BD=8,DO=4,又∵AC⊥BD,∴AD===5,又∵E为AD边中点,∴OE=AD=,故选:A.2.解:∵BD=DC,DE=DF,∴四边形BECF是平行四边形,要使得四边形BECF是菱形,对角线必须垂直,只有AB=AC时,∵BD=CD,∴AD⊥BC,∴此时四边形BECF是菱形,故选:C.3.解:如图,过点A作AE⊥OC于E,∵点O(0,0),C(2,0),∴OC=2,∵四边形ABCO是菱形,∴OA=OC=2,AD=CD,∵∠AOC=60°,AE⊥OC,∴∠OAE=30°,∴OE=AO=1,AE=OE=,∴点A(1,),∵AD=CD,∴点D(,),故选:B.4.解:过点A作AE⊥CD于E,AF⊥BC于F,连接AC,BD交于点O,∵两条纸条宽度相同,∴AE=AF.∵AB∥CD,AD∥BC,∴四边形ABCD是平行四边形.∵S▱ABCD=BC•AF=CD•AE.又∵AE=AF.∴BC=CD,∴四边形ABCD是菱形,∴AO=CO=1,BO=DO,AC⊥BD,∴BO===2,∴BD=4,∴四边形ABCD的面积==4,故选:A.5.解:连接BD,交AC于点O,如图:∵菱形ABCD的边长为10,点E、F分别是边CD、BC的中点,∴AB∥CD,AB=BC=CD=DA=10,EF∥BD,∵AC、BD是菱形的对角线,AC=16,∴AC⊥BD,AO=CO=8,OB=OD,又∵AB∥CD,EF∥BD,∴DE∥BG,BD∥EG,∴四边形BDEG是平行四边形,∴BD=EG,在△COD中,DO===6,∴BD=2OD=12,∴EG=BD=12,故选:C.6.方法一:解:如图,连接EC,OC,AF.在菱形ABCD中,∠EBC=∠ADF,∠ADB=∠DBC=25°,AB=CD,BC=DA.∵AE=CF,∴AB﹣AE=CD﹣CF,即BE=DF.在△EBC与△FDA中,.∴△EBC≌△FDA(SAS)∴EC=AF.又AE=CF,∴四边形AECF是平行四边形,∴EF与AC平分,∴在菱形ABCD中,AO⊥BD,∴∠OAD=90°﹣∠ADB=90°﹣25°=65°.方法二:解:∵ABCD是菱形,AE=CF,∴AB∥CD,AB=CD,∴BE=DF,∠OBD=∠ODF,在△OEB和△OFD中,∴△OEB≌△ODF(AAS).∴OB=OD,∴AO⊥BD,∴∠OAD=90°﹣∠ADB=90°﹣25°=65°.故选:C.7.解:∵四边形ABCD是菱形,∠B=60°,AB=BC,∴AB=BC=AC=a,又∵FH∥AD,GI∥AB,∴四边形BFEG和四边形EHDI是平行四边形,∴FE=BG,FB=EG,EH=ID,EI=HD,∴阴影部分的周长=AF+FE+EI+AI+EG+CG+CH+EH=AF+BF+BG+CG+CH+HD+AI+ID=AB+BC+CD+AD=4a.故选:B.8.解:作点E关于AD的对称点E',连接EF交AD与点P,连接AE',EE',作E'K垂直于AC于点K,∵∠ABC=120°,∴∠BAD=60°,∠DAC=BAD=30°,∵BD=AB=6,∴DO=BD=3,∴AD=BD=6,AO=BO=3,AC=2AO=6,∴AE=EF=FC=AC=2,∵AE=AE',∠E'AE=2∠DAO=60°,∴△E'AE为等边三角形,K为AE中点,KE=AE=,∴KE'=KE=3,KF=KE+EF=3,在Rt△E'KF中,由勾股定理得,E'F==6,∴PE+PF的最小值为6.由对称性可知,每条边上都有一个点P符合条件,故选:A.9.解:∵AB=6,∠ABC=60°,AE⊥BC,∴∠BAE=30°,BE=AB=3,AE=BE=9,∴EC=3,∵四边形ABCD是菱形,∴∠ABD=∠CBD=30°,AD∥BC,∴BE=EF,BF=2EF,∠DAF=∠AEB=90°,∴EF=3,BF=6,∴AF=6,∵△AFP的面积是9,∴9=×AF×点P到AF的距离,∴点P到AF的距离为3,∴点P与点B或点C重合,当点P与点C重合,∴PD=6,当点P与点B重合时,∵∠ADB=30°,∠DAF=90°,∴DF=2AF=12,∴PD=6+12=18;当点P在AD上时,AP=3,∴PD=3,综上所述:PD=6或3或18,故答案为6或3或18.10.解:添加BD⊥EF,理由如下:∵四边形ABCD是平行四边形,∴AD=CB,∠A=∠C,AB∥CD,AB=CD,在△ADE和△CBF中,,∴△ADE≌△CBF(ASA),∴AE=CF,∴AB﹣AE=CD﹣CF,即BE=DF,又∵BE∥DF,∴四边形EBFD是平行四边形,∵BD⊥EF,∴四边形EBFD是菱形.故答案为:BD⊥EF.11.解:当AB为菱形的对角线时,如图1,设菱形的边长为m,∵A(0,4),B(8,0),∴OA=4,OB=8,∵四边形ABCD为菱形,∴CA=AD=BC,AD∥BC,∴CA=CB=8﹣m,在Rt△AOC中,42+(8﹣m)2=m2,解得m=5,∴D(5,4);当AB为菱形的边时,如图2,AB==4,∵四边形ABCD为菱形,∴BC=AB=AD=4,AD∥BC,∴D(4,4),综上所述,D点坐标为(5,4)或(4,4).故答案为(5,4)或(4,4).12.解:如图,连接CE,AE,∵四边形ABCD是菱形,∠A=120°,∴AB∥CD,AD∥BC,AB=BC=a,∠B=60°,∵MG∥AD,NF∥AB,∴AB∥FN∥CD,MG∥BC∥AD,∠B=∠EFC=60°,∴四边形EFCG是平行四边形,四边形BMGC是平行四边形,四边形DNFC是平行四边形,∴DN=FC,BM=CG,∴CG=CF,∴四边形CFEG是菱形,∴EF=FC,∴△EFC是等边三角形,∵AB:MB=3:1,∴EF=a,∴四边形CFEG的面积=2S△EFC=2××(a)2=a2,故答案为:a2.13.解:∵四边形ABCD是菱形,∴AD=BC=AB=CD,AD∥BC,AB∥CD,∵EG∥AD,FH∥AB,∴四边形AEOF与四边形CGOH是平行四边形,∴AF=OE,AE=OF,OH=GC,CH=OG,∵AE=AF,∴OE=OF=AE=AF,∵AE=AF,∴BC﹣BH=CD﹣DG,即OH=HC=CG=OG,∴四边形AEOF与四边形CGOH是菱形,∵四边形AEOF与四边形CGOH的周长之差为12,∴4AE﹣4(8﹣AE)=12,解得:AE=5.5,故答案为:5.5.14.解:连接AF,如图所示:∵四边形ABCD是菱形,∴AB=BC=2,∵G,H分别为AE,EF的中点,∴GH是△AEF的中位线,∴GH=AF,当AF⊥BC时,AF最小,GH得到最小值,则∠AFB=90°,∵∠B=45°,∴△ABF是等腰直角三角形,∴AF=AB=×2=,∴GH=,即GH的最小值为,故答案为:.15.1)证明:∵四边形ABCD是平行四边形,∴∠A=∠C,AD=BC,AB=CD.∵点E、F分别是AD、BC的中点,∴AE=DE=AD,BF=FC=BC.∴AE=CF.在△AEB与△CFD中,,∴△AEB≌△CFD(SAS);(2)解:当△ABD满足∠ABD=90°,四边形EBFD是菱形,理由如下:由(1)得:BF=DE,BF∥DE,∴四边形EBFD是平行四边形,∵∠ABD=90°,点E是AD的中点,∴BE=AD=DE,∴平行四边形EBFD是菱形.16.证明:(1)∵点E为BC的中点,∴CE=BE,又∵EF=DE,∴四边形CFBD是平行四边形,∵D,E分别是边AB,BC的中点,∠ACB=90°,∴DE∥AC,∴∠DEB=∠ACB=90°,即DF⊥CB,∴四边形CFBD是菱形;(2)∵D,E分别是边AB,BC的中点,∴AC=2DE,∵DF=2DE=2EF,DF=2,∴AC=2,EF=1,∵CF=,四边形CFDB是菱形,∴∠CEF=90°,∴CE===3,∵∠ACE=90°,∴AE===,即AE的长是.17.解:(1)△OEF是等腰三角形,理由如下:∵四边形ABCD是菱形,∴BC=CD,∵E、F分别是AB、AD的中点,∴OE是△ABC的中位线,OF是△ACD的中位线,∴OE=BC,OF=CD,∴OE=OF,∴△OEF是等腰三角形;(2)∵四边形ABCD是菱形,∴OA=OC=AC=6,OB=OD,AC⊥BD,∴∠AOB=90°,∴OB=,∴BD=2OB=16,∵E、F分别是AB、AD的中点,∴EF是△ABD的中位线,∴EF=BD=8.18.1)证明:∵DE⊥BC,∴∠DFB=90°,∵∠ACB=90°,∴∠ACB=∠DFB,∴AC∥DE,∵MN∥AB,即CE∥AD,∴四边形ADEC是平行四边形,∴CE=AD;(2)解:四边形BECD是菱形,理由如下:∵D为AB中点,∴AD=BD,∵CE=AD,∴BD=CE,∵BD∥CE,∴四边形BECD是平行四边形,∵∠ACB=90°,D为AB中点,∴CD=BD,∴四边形BECD是菱形.19.1)证明:∵四边形ABCD是平行四边形,∴AB∥CD,∴∠EDC=∠EP A,∵∠EBC=∠EP A,∴∠EBC=∠EDC,∵EC平分∠DEB,∴∠DEC=∠BEC,在△CED和△CEB中,,∴△CED≌△CEB(AAS),∴CD=CB,∵四边形ABCD为平行四边形,∴平行四边形ABCD为菱形;(2)解:与△ADP面积相等的三角形(不包括以AD为边的三角形)为△AOB、△BOC、△COD、△DPB;理由如下:∵四边形ABCD是平行四边形,∴OA=OC,OB=OD,∴△AOB的面积=△BOC的面积=△COD的面积=△ABD的面积,∵点F是AB的中点,∴△ADP的面积=△DPB的面积=△ABD的面积,∴△AOB的面积=△BOC的面积=△COD的面积=△DPB的面积=△ADP的面积.20.1)证明:如图所示,连接BD,在菱形ABCD中,∠DAB=60°,∴∠ADB=∠NDB=60°,故△ADB是等边三角形,∴AB=BD,又AM+CN=1,DN+CN=1,∴AM=DN,在△AMB和△DNB中,,∴△AMB≌△DNB(SAS),∴BM=BN,∠MBA=∠NBD,又∠MBA+∠DBM=60°,∴∠NBD+∠DBM=60°,即∠MBN=60°,∴△BMN是等边三角形;(2)解:过点B作BE⊥MN于点E.设BM=BN=MN=x,则,故,∴当BM⊥AD时,x最小,此时,,.∴△BMN面积的最小值为.。
八年级数学竞赛培优 矩形、菱形 含解析

矩形、菱形【思维入门】1.如图8-25-1所示,菱形ABCD 中,对角线AC ,BD 相交于点O ,H 为AD 边的中点,菱形ABCD 的周长为28,则OH 的长等于 ( )A .3.5B .4C .7D .142.有4个命题:(1)一组对边相等,一组对角相等的四边形是平行四边形; (2)一组对边平行,一组对角相等的四边形是平行四边形;(3)O 是四边形ABCD 内一点,若AO =BO =CO =DO ,则四边形ABCD 是矩形; (4)若四边形的两条对角线互相垂直,则这个四边形是菱形. 其中正确的命题个数是( )A .0B .1C .2D .33.如图8-25-2,在▱ABCD 中,添加下列条件之一能使它成为菱形的是 ()图8-25-2①AC ⊥BD ;②∠BAD =90°; ③AB =BC ;④AC =BD . A .①或③ B .②或③ C .③或④D .①或②或③4.如图8-25-3,在矩形ABCD 中,边AB 的长为3,点E ,F 分别在AD ,BC 上,连结BE ,DF ,EF ,BD ,若四边形BEDF 是菱形,且EF =AE +FC ,则边BC 的长为()图8-25-3A .2 3B .33图8-25-1C.6 3 D.92 35.如果菱形的两条对角线的长为a和b,且a,b满足(a-1)2+b-4=0,那么菱形的面积等于____.6.已知:如图8-25-4,在▱ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF.(1)求证:△DOE≌△BOF;(2)当∠DOE等于多少度时,四边形BFDE为菱形?请说明理由.图8-25-4【思维拓展】7.如图8-25-5,在矩形ABCD中,点E,F分别在边AB,BC上,且AE=13AB.将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连结BP交EF于点Q.对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是()图8-25-5A.①②B.②③C.①③D.①④8.如图8-25-6,矩形ABCD中,AB=60,BD=BC+23CD,则BC=______.图8-25-69.如图8-25-7,已知矩形ABCD,把矩形沿直线AC折叠,点B落在点E处,连结DE ,BE ,若△ABE 是等边三角形,则S △DCES △ABE=____.图8-25-710.如图8-25-8,在△ABC 中,AD 是BC 边上的中线,E 是AD 的中点,过点A 作BC 的平行线交BE 的延长线于点F ,连结CF . (1)求证:AF =DC ;(2)若AB ⊥AC ,试判断四边形ADCF 的形状,并证明你的结论.图8-25-811.某校九年级学习小组在探究学习过程中,用两块完全相同的且含60°角的直角三角板ABC 与AFE 按如图8-25-9①所示位置放置,现将Rt △AEF 绕A 点按逆时针方向旋转角α(0°<α<90°),如图8-25-9②,AE 与BC 交于点M ,AC 与EF 交于点N ,BC 与EF 交于点P . (1)求证:AM =AN ;(2)当旋转角α=30°时,四边形ABPF 是什么样的特殊四边形?并说明理由.图8-25-912.定义:我们把三角形被一边中线分成的两个三角形叫做“友好三角形”. 性质:如果两个三角形是“友好三角形”,那么这两个三角形的面积相等. 理解:如图8-25-10①,在△ABC 中,CD 是AB 边上的中线,那么△ACD 和△BCD 是“友好三角形”,并且S △ACD =S △BCD .应用:如图8-25-10②,在矩形ABCD中,AB=4,BC=6,点E在AD上,点F 在BC上,AE=BF,AF与BE交于点O.(1)求证:△AOB和△AOE是“友好三角形”;(2)连结OD,若△AOE和△DOE是“友好三角形”,求四边形CDOF的面积.探究:在△ABC中,∠A=30°,AB=4,点D在线段AB上,连结CD,△ACD和△BCD是“友好三角形”,将△ACD沿CD所在直线翻折,得到△A′CD,若△A′CD与△ABC重合部分的面积等于△ABC面积的14,请直接写出△ABC的面积.图8-25-10【思维升华】13.菱形的两条对角线之和为L,面积为S,则它的边长为()A.12L2-4S B.12L2-2SC.122L-4S D.124S-L214.如图8-25-11,四边形ABCD中,∠BAD=60°,∠ABC=30°,AB=6,AD=CD,AB∥CD,那么BD的长度是()图8-25-11A.7 B.4C.27 D.4 215.如图8-25-12,将两个长为8,宽为2的矩形透明塑料片交叉摆放,重叠部分是菱形ABCD,当两个塑料片不重合但有一条对角线重合时,菱形ABCD的周长最大,这个最大值是____.图8-25-1216.如图8-25-13,在平面直角坐标系xOy中,多边形OABCDE的顶点坐标分别是O(0,0),A(0,6),B(4,6),C(4,4),D(6,4),E(6,0).若直线l经过点M(2,3),且将多边形OABCDE分割成面积相等的两部分,则直线l的函数表达式是____.图8-25-13【思维入门】1.如图8-25-1所示,菱形ABCD 中,对角线AC ,BD 相交于点O ,H 为AD 边的中点,菱形ABCD 的周长为28,则OH 的长等于 ( A ) A .3.5 B .4 C .7D .142.有4个命题:(1)一组对边相等,一组对角相等的四边形是平行四边形;(2)一组对边平行,一组对角相等的四边形是平行四边形;(3)O 是四边形ABCD 内一点,若AO =BO =CO =DO ,则四边形ABCD 是矩形; (4)若四边形的两条对角线互相垂直,则这个四边形是菱形. 其中正确的命题个数是( B ) A .0B .1C .2D .3【解析】 (1)一组对边相等,一组对角相等的四边形是平行四边形,不能证明另一组对边也相等或平行,故(1)错误;(2)一组对边平行,一组对角相等的四边形是平行四边形,可证出另一组对边也平行,故(2)正确;(3)O 是四边形ABCD 内一点,若AO =BO =CO =DO ,则四边形ABCD 是矩形,只有点O 是四边形ABCD 对角线的交点时,上述说法才成立,故(3)错误; (4)若四边形的两条对角线平分且互相垂直,则这个四边形是菱形,故(4)错误. 3.如图8-25-2,在▱ABCD 中,添加下列条件之一能使它成为菱形的是 ( A)图8-25-2①AC ⊥BD ;②∠BAD =90°; ③AB =BC ;④AC =BD . A .①或③ B .②或③ C .③或④D .①或②或③4.如图8-25-3,在矩形ABCD 中,边AB 的长为3,点E ,F 分别在AD ,BC 上,连结BE ,DF ,EF ,BD ,若四边形BEDF 是菱形,且EF =AE +FC ,则边BC 的长为( B)图8-25-1图8-25-3A .2 3B .3 3C .6 3D.92 3【解析】 ∵四边形ABCD 是矩形, ∴∠ABC =90°, ∵四边形BEDF 是菱形, ∴EF ⊥BD ,∠EBO =∠DBF .∵EF =AE +FC ,AE =CF ,EO =FO , ∴AE =EO =CF =FO .∴AB =BO =3,∠ABE =∠EBO ,∴∠ABE =∠EBD =∠DBC =30°,BE =2 3. ∴BF =BE =2 3. ∴CF =AE = 3. ∴BC =BF +CF =3 3.5.如果菱形的两条对角线的长为a 和b ,且a ,b 满足(a -1)2+b -4=0,那么菱形的面积等于__2__.【解析】 由题意,得a -1=0,b -4=0,解得a =1,b =4. ∵菱形的两条对角线的长为a 和b , ∴菱形的面积=12×1×4=2.6.已知:如图8-25-4,在▱ABCD 中,O 为对角线BD 的中点,过点O 的直线EF 分别交AD ,BC 于E ,F 两点,连结BE ,DF . (1)求证:△DOE ≌△BOF ;(2)当∠DOE 等于多少度时,四边形BFDE 为菱形?请说明理由.图8-25-4解:(1)证明:∵在▱ABCD 中,O 为对角线BD 的中点,∴BO =DO ,∠EDB =∠FBO , 在△DOE 和△BOF 中,⎩⎨⎧∠EDO =∠FBO ,DO =BO ,∠EOD =∠FOB ,∴△DOE ≌△BOF (ASA ).(2)当∠DOE =90°时,四边形BFDE 为菱形. 理由:∵△DOE ≌△BOF , ∴BF =DE , 又∵BF ∥DE ,∴四边形EBFD 是平行四边形. ∵BO =DO ,∠EOD =90°, ∴EB =DE .∴四边形BFDE 为菱形.【思维拓展】7.如图8-25-5,在矩形ABCD 中,点E ,F 分别在边AB ,BC 上,且AE =13AB .将矩形沿直线EF 折叠,点B 恰好落在AD 边上的点P 处,连结BP 交EF 于点Q .对于下列结论:①EF =2BE ;②PF =2PE ;③FQ =4EQ ;④△PBF 是等边三角形.其中正确的是( D )图8-25-5A .①②B .②③C .①③D .①④8.如图8-25-6,矩形ABCD中,AB=60,BD=BC+23CD,则BC=__25____.图8-25-69.如图8-25-7,已知矩形ABCD,把矩形沿直线AC折叠,点B落在点E处,连结DE,BE,若△ABE是等边三角形,则S△DCES△ABE=__13__.图8-25-7【解析】如答图,过E作EM⊥AB于M,交DC于N.第9题答图∵四边形ABCD是矩形,∴DC=AB,DC∥AB,∠ABC=90°.∴MN=BC,EN⊥DC.∵沿AC折叠,B和E重合,△AEB是等边三角形,∴∠EAC=∠BAC=30°.设AB=AE=BE=2a,则BC=2a3=233a,即MN=233a.∵△ABE是等边三角形,EM⊥AB,∴AM=a,由勾股定理得EM=(2a)2-a2=3a,∴△DCE的面积是12×DC×NE=12×2a×⎝⎛⎭⎪⎫3a-233a=33a2.△ABE的面积是12AB×EM=12×2a×3a=3a2.∴S△DCES△ABE=33a23a2=13.10.如图8-25-8,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连结CF.(1)求证:AF=DC;(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.图8-25-8解:(1)证明:∵E是AD的中点,∴AE=ED.∵AF∥BC,∴∠AFE=∠DBE,∠F AE=∠BDE,∴△AFE≌△DBE.∴AF=DB.∵AD是BC边上的中线,∴DB=DC,∴AF=DC.(2)四边形ADCF是菱形.理由:由(1)知,AF=DC.∵AF∥CD,∴四边形ADCF是平行四边形.又∵AB⊥AC,∴△ABC是直角三角形,∵AD是BC边上的中线,∴AD=12BC=DC.∴平行四边形ADCF是菱形.11.某校九年级学习小组在探究学习过程中,用两块完全相同的且含60°角的直角三角板ABC 与AFE 按如图8-25-9①所示位置放置,现将Rt △AEF 绕A 点按逆时针方向旋转角α(0°<α<90°),如图8-25-9②,AE 与BC 交于点M ,AC 与EF 交于点N ,BC 与EF 交于点P . (1)求证:AM =AN ;(2)当旋转角α=30°时,四边形ABPF 是什么样的特殊四边形?并说明理由.图8-25-9解:(1)证明:∵∠α+∠EAC =90°,∠NAF +∠EAC =90°, ∴∠α=∠NAF .又∵∠B =∠F ,AB =AF , ∴△ABM ≌△AFN , ∴AM =AN .(2)四边形ABPF 是菱形.理由:∵∠α=30°,∠EAF =90°, ∴∠BAF =120°, 又∵∠B =∠F =60°.∴∠B +∠BAF =60°+120°=180°, ∠F +∠BAF =60°+120°=180°. ∴AF ∥BC ,AB ∥EF , ∴四边形ABPF 是平行四边形. 又∵AB =AF ,∴▱ABPF 是菱形.12.定义:我们把三角形被一边中线分成的两个三角形叫做“友好三角形”. 性质:如果两个三角形是“友好三角形”,那么这两个三角形的面积相等. 理解:如图8-25-10①,在△ABC 中,CD 是AB 边上的中线,那么△ACD 和△BCD 是“友好三角形”,并且S △ACD =S △BCD .应用:如图8-25-10②,在矩形ABCD 中,AB =4,BC =6,点E 在AD 上,点F 在BC 上,AE =BF ,AF 与BE 交于点O .(1)求证:△AOB 和△AOE 是“友好三角形”;(2)连结OD ,若△AOE 和△DOE 是“友好三角形”,求四边形CDOF 的面积. 探究:在△ABC 中,∠A =30°,AB =4,点D 在线段AB 上,连结CD , △ACD 和△BCD 是“友好三角形”,将△ACD 沿CD 所在直线翻折,得到 △A ′CD ,若△A ′CD 与△ABC 重合部分的面积等于△ABC 面积的14,请直接写出△ABC 的面积.图8-25-10解:(1)证明:∵ 四边形ABCD 为矩形, ∴AD ∥BC , ∴∠EAO =∠BFO ,又∵∠AOE =∠FOB ,AE =BF , ∴△AOE ≌△FOB , ∴EO =BO .∴△AOB 和△AOE 是“友好三角形”. (2)∵△AOE 和△DOE 是“友好三角形”, ∴S △AOE =S △DOE ,AE =ED =12AD =3. ∵△AOB 和△AOE 是“友好三角形”, ∴S △AOB =S △AOE . ∵△AOE ≌△FOB , ∴S △AOE =S △FOB , ∴S △AOD =S △ABF ,∴S 四边形CDOF =S 矩形ABCD -2S △ABF =4×6-2×12×4×3 =12.探究:2或2 3.【思维升华】13.菱形的两条对角线之和为L,面积为S,则它的边长为(A)A.12L2-4S B.12L2-2SC.122L-4S D.124S-L2【解析】设边长为m,一条对角线为2a,另外一条为2b,则a+b=12L,2ab=S.∵m2=a2+b2=(a+b)2-2ab=14L2-S.∴m=12L2-4S.14.如图8-25-11,四边形ABCD中,∠BAD=60°,∠ABC=30°,AB=6,AD=CD,AB∥CD,那么BD的长度是(C)图8-25-11A.7 B.4C.27 D.4 2【解析】如答图,过点C作CE∥AD交AB于E,过点D作DF⊥AB于F,则四边形ADCE是菱形,第14题答图∠CEB=∠A=60°.∵∠ABC=30°∴AD=EC=DC=AE=12BE.∵AB=6,∴AD=EC=DC=AE=2.∴AF=1,DF=3,BF=5.由勾股定理得BD=27.15.如图8-25-12,将两个长为8,宽为2的矩形透明塑料片交叉摆放,重叠部分是菱形ABCD,当两个塑料片不重合但有一条对角线重合时,菱形ABCD的周长最大,这个最大值是__17__.图8-25-12【解析】当两个塑料片如答图所示放置时,菱形周长最大,设这时菱形的边长为x,在Rt△AEB中,第15题答图由勾股定理得x2=(8-x)2+22,解得x=17 4.∴4x=17.即菱形的最大周长为17.16.如图8-25-13,在平面直角坐标系xOy中,多边形OABCDE的顶点坐标分别是O(0,0),A(0,6),B(4,6),C(4,4),D(6,4),E(6,0).若直线l经过点M(2,3),且将多边形OABCDE分割成面积相等的两部分,则直线l的函数表达式是__y=-1 3x+113__.图8-25-13【解析】 如答图,延长BC 交x 轴于点F ,连结OB ,AF ,连结CE ,DF 相交于点N .第16题答图由已知得点M (2,3)是OB ,AF 的中点,即点M 为矩形ABFO 的中心,所以直线l 把矩形ABFO 分成面积相等的两部分.又因为点N (5,2)是矩形CDEF 的中心,所以过点N (5,2)的直线把矩形CDEF 分成面积相等的两部分.于是,直线MN 即为所求的直线l .设直线l 的函数表达式为y =kx +b ,则 ⎩⎨⎧2k +b =3,5k +b =2, 解得 ⎩⎪⎨⎪⎧k =-13,b =113.故所求直线l 的函数表达式为y =-13x +113.。
2020-2021学年浙教版八年级下数学培优——矩形与菱形

第21讲 菱形与矩形考点·方法·破译1.理解并掌握菱形的定义、性质和判定方法,并运用它们进行计算与证明; 2.理解并掌握矩形的定义、性质和判定方法,并运用它们进行计算与证明; 3.理解“直角三角形斜边上的中线等于斜边的一半”并会应用.经典·考题·赏析【例1】如图,四边形ABCD 是矩形,△PBC 和△QCD 都是等边三角形,且点P 在矩形上方,点Q 在矩形内.求证:PA =PQ .【变式题组】01.如图,在矩形ABCD 中,点E 是BC 上一点,AE =AD ,DF ⊥AE 与F ,连接DE .求证:DF =DC .02.如图,矩形ABCD 中,DP 平分∠ADC 交BC 于点P ,将一个直角三角板的直角顶点放在P 点处,且使它的一条直角边过A 点,另一条直角边交CD 于E .找出图中与PA 相等的线段.并说明理由.ABCDEFABCD QP03.如图,矩形ABCD 的对角线相交于O ,AE 平分∠BAD 交BC 于E ,∠CAE =15°,求∠BOE 的度数.【例2】已知:如图,在矩形ABCD 中,点E 在AD 边上,AE >DE ,BE =BC ,点O 是线段CE 的中点.⑴试说明CE 平分∠BED ;⑵若AB =3,BC =5,求BO 的长;⑶在直线AD 上是否存在点F ,使得以B 、C 、E 、F 为顶点的四边形是菱形?如果存在,试画出点F 的位置,并作适当的说明;如果不存在,请说明理由.ABCED PABC EDOABCE DO【变式题组】01.如图,在平面直角坐标系中,点O 为原点,菱形OABC 的对角线OB 在x 轴上,顶点A 在反比例函数y =2x的图像上,菱形的面积为_________.02.两个全等的直角三角形ABC 和DEF 重叠在一起,其中∠A =60°,AC =1.固定△ABC不动,将△DEF 进行如下操作:⑴如图1,△DEF 沿线段AB 向右平移(即D 点在线段AB 内移动),连接DC 、CF 、FB ,四边形CDBF 的形状在不断的变化,但它的面积不变化,请求出其面积; ⑵如图2,当D 点移到AB 的中点时,请你猜想四边形CDBF 的形状,并说明理由.ABCFE D图1FCE BD A图2AB COxy【例3如图,在矩形ABCD 中,已知AD =12,AB =5,P 是AD 边上任意一点,PE ⊥BD ,PF ⊥AC ,E 、F 分别是垂足,则PE +PF =__________.【变式题组】01.⑴观察与发现:讲矩形纸片AOCB 折叠,使点C 与点A 重合,点B 落在点B '处(如图1),折痕为EF .小明发现△AEF 为等腰三角形,你同意吗?请说明理由.⑵实验与应用:以点O 为坐标原点,分别以矩形的边OC 、OA 为x 轴、y 轴建立如图所示的直角坐标系,若顶点B 的坐标为(9,3),请求出折痕EF 的长及EF 所在直线的函数关系式.02.如图,将矩形纸片ABCD 沿对角线AC 折叠使点B 落到B '的位置,AB '与CD 交于点E .ABC FE D OPGF E DAPC OB A B CF EB ' OA B CF EB 'Oy x 图1⑴试找出一个与△AED 全等的三角形,并加以证明;⑵若AB =8,DE =3,P 为线段AC 上的任意一点,PG ⊥AE 于G ,PH ⊥EC 于H ,试求PG +PH 的值,并说明理由.【例4】如图1,在△ABC 中,点P 为BC 边中点,直线a 绕顶点A 旋转,若B 、P 在直线a 的异侧,BM ⊥直线a 于点M ,CN ⊥直线a 于点N ,连接PM 、PN ;⑴延长MP 交CN 于点E (如图2).①求证:△BPM ≌△CPE ;②求证:PM =PN ; ⑵若直线a 绕点A 旋转到图3的位置时,点B 、P 在直线a 的同侧,其他条件不变,此时PM =PN 还成立吗?若成立,请给予证明;若不成立,请说明理由;⑶若直线a 绕点A 旋转到与BC 边平行的位置时,其他条件不变.请直接判断四边形MBCN 的形状及此时PM =PN 还成立吗?不必说明理由.AB CE DHGPB '.【变式题组】01.如图,一副三角板拼在一起,O 为AD 的中点,AB =a .将△ABO 沿BO 对折于△A ’BO ,M 为BC 上一动点,则A ’M 的最小值为________.A BC MNP a A BCMNP a EAaN PM BC 图1图2图3ABC DOMA '60°45°02.如图1,P 是线段AB 上的一点,在AB 的同侧作△APC 和△BPD ,使PC =PA ,PD =PB ,∠APC =∠BPD ,连接CD ,点E 、F 、G 、H 分别是AC 、AB 、BD 、CD 的中点,顺次连接E 、F 、G 、H .⑴猜想四边形EFGH 的形状,直接回答,不必说明理由;、⑵当点P 在线段AB 的上方时,如图2,在△APB 的外部作△APC 和△BPD ,其他条件不变,⑴中的结论还成立吗?说明理由.⑶如果⑵中,∠APC =∠BPD =90°,其他条件不变,先补全图3,再判定四边形EFGH 的形状,并说明理由.AB C HG F E DPAB CH G FE D P AB P图1 图2图303如图所示,一根长为2a 的木棍(AB ),斜靠在与地(OM )垂直的墙(ON )上,设木棍的中点为P .若木棍A 端沿墙下滑,且B 端沿地面向右滑行.⑴请判断木棍滑动的过程中,点P 到点O 的距离是否变化,并简述理由;⑵在木棍滑动的过程中,当滑动到什么位置时,△AOB 的面积最大?简述理由,并求出面积的最大值.演练巩固 反馈提高01.将矩形纸片ABCD 按如图所示的方式折叠,AE 、EF 为折痕,∠BAE =30°,AB =3,ABOP MN折叠后,点C 落在AD 边上的C 1处,并且点B 落在EC 1边上的B 1处.则BC 的长为( )A . 3B .2C .3D .2 302.菱形OABC 在平面直角坐标系中的位置如图所示,∠AOC =45°,OC =2,则点B的坐标为( )A .(2,1)B .(1,2)C .(2+1,1)D .(1,2+1)03.如图,在△ABC 中,AB >AC ,D 、E 分别是AB 、AC 上的点,△ADE 沿线段DE 翻折,使点A 落在边BC 上,记为A ’,若四边形ADA ’E 是菱形,则下列说法正确的是( )A .DE 是△ABC 的中位线B .AA ’是BC 边上的中线 C .AA ’是BC 边上的高D .AA ’是△ABC 的角平分线04.如图,菱形ABCD 中,∠B =60°,AB =2,E 、F 分别是BC 、CD 的中点,连接AE 、EF 、AF ,则△AEF 的周长为( ) A .2 3B .3 3C .4 3D .305.一次数学课上,老师让大家在一张长12cm 、宽5cm 的矩形纸片内,折出一个菱形.甲同学按照取两组对边中点的方法折出菱形EFGH (见方案一),乙同学沿矩形的对角线AC 折出∠CAE =∠DAC ,∠ACF =∠ACB 的方法得到菱形AECF (见方案二),请你通过计算,OA BC xyC 1D ABCFEB 1ABC EDA '第3题图第2题图第1题图ACD EF BA BCFED HG A BCDEFAB C F EDOH第4题图 第5题图第6题图(方案一)(方案二)比较这两种折法中,菱形面积较大的是( )A .甲B .乙C .甲乙相等D .无法判断06.在矩形ABCD 中,AB =1,AD =3,AF 平分∠DAB ,过C 点作CE ⊥BD 于E ,延长AF 、EC 交于点H ,下列结论中:①AF =FH ;②BO =BF ;③CA =CH ;④BE =3ED ,正确的结论为_________________.07.如图,矩形ABCD 中,AB =2,BC =3,对角线AC 的垂直平分线分别交AD 、BC 于点E 、F ,连接CE ,则CE 的长为__________.08.如图,四边形ABCD 为矩形纸片.把纸片ABCD 折叠,使点B 恰好落在CD 边的中点E 处,折痕为AF ,若CD =6,则AF =____________.09.红丝带是关注艾滋病防止问题的国际性标志.将宽为1cm 的红丝带交叉成60°角重叠ABCDF E第8题图60°第9题图ABC DMB '第10题图第7题图C FEDOAB在一起(如图),则重叠四边形的面积为_______cm .10. 如图,一张长方形纸片ABCD ,其长AD 为a ,宽AB 为b (a >b ),在BC 边上选取一点M ,将△ABM 沿AM 翻折后B 至B ’的位置,若B ’为长方形纸片ABCD 的对称中心,则ab的值是__________.11.一种千斤顶利用了四边形的不稳定性.如图,其基本形状是一个菱形,中间通过螺杆连接,转动手柄可改变∠ADC 的大小(菱形的边长不变),从而改变千斤顶的高度(即A 、C 之间的距离).若AB =40cm ,当∠ADC 从60°变为120°时,千斤顶升高了多少?(2=1.414,3=1.732,结果保留整数)12.如图所示,四边形OABC 是矩形,点D 在OC 边上,以AD 为折痕,将△OAD 向上翻折,点O 恰好落在BC 边上的点E 处,若△ECD 的周长为2,△EBA 的周长为6. ⑴矩形OABC 的周长为_______;⑵若点A 坐标为(52,0),求线段AD 所在直线的解析式.ABCD手柄ABC ED Ox y13.如图,△ABC 中,∠ACB =90°,AC =BC ,ME ⊥AC ,MF ⊥BC ,D 是AB 的中点.求证:△DEF 是等腰直角三角形.14.如图,矩形ABCD 中,AC =2AB ,O 为AC 的中点,延长AB 到E ,使BE =AB ,连接EO 并延长交BC 于F ,交AD 于M .求证:四边形AFCM 是菱形.AB CFE DMCFEDOMBA15.如图,矩形ABCD ,E 是CB 延长线上一点,且CE =CA ,F 是AE 的中点.求证:DF⊥BF .16.如图1,在△ABC 中,AB =BC ,P 为AB 边上一点,连接CP ,以PA 、PC 为邻边作□APCD ,AC 与PD 相交于点E ,已知∠ABC =∠AEP =α(0°<α<90°).⑴求证:∠EAP =∠EPA ;⑵□APCD 是否为矩形?请说明理由;⑶如图2,F 为BC 的中点,连接FP ,将∠AEP 绕点E 顺时针旋转适当的角度,得到∠MEN (点M 、N 分别是∠MEN 的两边与BA 、FP 延长线的交点).猜想线段EM 与EN 之间的数量关系,并证明你的结论.ABC FED图1AB DCE P 图2ABDCEPMNF。
最新培优专题7-菱形、矩形、正方形和梯形(含答案)

培优专题和梯形菱形、矩形、正方形都是特殊的平行四边形,它们除了具有平行四边形的性质外,各自都有相应的特性,如菱形四边相等、对角线互相垂直,且平分对角;矩形四个角都是直角且对角线相等;正方形是最特殊的平行四边形,它具有菱形和矩形的所有特性,可以说是菱形、矩形的完美结合体,也是最基本的正多边形之一.梯形是现实生活中比较常见的图形之一,也是考查平行四边形和直角三角形非常好的载体,因此在中考数学测试和初中数学竞赛中这些特殊的四边形都是考查的重要内容.例1 如果将长方形纸片ABCD,沿EF折叠,如图,延长C′E交AD于H,连结GH,那么EF与GH互相垂直平分吗?分析要说明EF与GH互相垂直平分,只须说明四边形FGEH是菱形即可.解:∵FH`∥GE,FG∥EH,∴四边形FGEH为平行四边形,由题意知:△GEF≌△HFE.∴FG=FH,EG=EH.∴四边形GEHF为菱形.∴EF、GH互相垂直平分.练习11.如图1,菱形ABCD中,E、F分别是BC、CD上的点,且∠B=∠EAF=60°,•∠BAE=18°,则∠CEF=________.(1) (2) (3)2.如图2,四边形ABCD是正方形,对角线AC、BD相交于O,四边形BEFD是菱形,若正方形的边长为6,则菱形的面积为________.3.如图3,ABCD是正方形,E为BF上一点,四边形AFEC•恰是一个菱形,•则∠EAB=________.例2 矩形一边长为5,另一边长小于4,将矩形折起来,使两对角顶点重合,•如图,若折痕EF,求另一边长.分析关键弄清“折痕”特点,即在对角线的中垂线上.此问题转化为就矩形ABCD中,已知AD=5,过对角线AC的中点O作AC的垂线EF,分别交AD于F,BC于E,若,求AB的长的问题.解:设AB=x,BE=y,连结AE.则AE=CE=5-y.在Rt△ABE中,AB2+BE2=AE2,即x2+y2=(5-y)2.得y=22510x-,AE=5-y=22510x+.又在Rt△AOE中,AO=12AC=2,EO=12代入AE2=AO2+OE2得,(22510x+)2=(2)2+(2)2.即x4+25x2-150=0.解之得,x2=5,x2=-30(舍去)∴练习21.如图4,矩形纸片ABCD中,AB=3cm,BC=4cm,现将A、C重合,使纸片折叠压平,•设折痕为EF,试确定重叠部分的△AEF的面积是__________.(4) (5)2.如图5所示,把一张长方形的纸条ABCD沿对角线BD将△BCD折成△BDF,DF•交AB于E,若已知AE=2cm,∠BDC=30°,求纸条的长和宽各是________.3.如图,折叠正方形纸片ABCD ,先折出折痕BD ,再折叠使AD 边与对角线BD 重合,得折痕DG ,使AD=2,求AG .例3 如图,E 、F 分别为正方形ABCD 的边BC 、CD 上的一点,AM ⊥EF ,•垂足为M ,AM=AB ,则有EF=BE+DF ,为什么?分析要说明EF=BE+DF ,只需说明BE=EM ,DF=FM 即可,而连结AE 、AF .只要能说明△ABE ≌△AME ,△ADF ≌△AMF 即可.理由:连结AE 、AF .由AB=AM ,AB ⊥BC ,AM ⊥EF ,AE 公用,∴△ABE ≌△AME .∴BE=ME .同理可得,△ADF ≌△AMF .∴DF=MF .∴EF=ME+MF=BE+DF .练习31.如图6,点A 在线段BG 上,四边形ABCD 与DEFG 都是正方形,•其边长分别为3cm 和5cm ,则△CDE 的面积为________c m 2.(6) (7)2.你可以依次剪6张正方形纸片,拼成如图7所示图形.•如果你所拼得的图形中正方形①的面积为1,且正方形⑥与正方形③的面积相等,•那么正方形⑤的面积为________.3.如图,P 为正方形ABCD 内一点,PA=PB=10,并且P 点到CD 边的距离也等于10,求正方形ABCD 的面积?例4 如图,等腰梯形ABCD 中,AD ∥BC ,BD 平分∠ABC ,∠C=30°,求AD :BC 的值. 分析 添加辅助线,使等腰梯形ABCD•的问题转化为平行四边形和等腰三角形的问题. 解:过D 作DF ∥AB 交BC 于F ,过D 作DE ⊥BC 于E ,则四边形ABFD 为平行四边形. 设AD=a ,则AD=BF=a .∵BD 平分∠ABC ,∴AD=AB=DF=DC=a .在Rt △DEC 中,∠C=30°,∵DE=2a ,EC=2a . 又∵EC=DF=2a , ∴(a . ∴AD :BC=a :(a=):2练习41.用长为1、4、4、5的线段为边作梯形,那么这个梯形的面积等于_______.2.用一块面积为900cm2的等腰梯形彩纸做风筝,为牢固起见,•用竹条做梯形的对角线,对角线恰好互相垂直,那么梯形对角线至少需______cm.3.如图,一块直角梯形的钢板,两底长分别是4cm、•10cm,•且有一个内角为60°,问是否能将铁板任意翻转,使从一个直径为8.7cm的圆洞中穿过?例5 如图,在矩形ABCD中,已知AD=12,AB=5,P是AD边上任意一点,PE•⊥BD,PE⊥AC,E、F分别是垂足,求PE+PF的长.分析连结PO,则PE、PF可分别看作是OD、OA边上的高,而OA=OD,故只需求出△AOP、△DOP的面积即可.解:连结OP.由矩形ABCD,AD=12,AB=5.∴AC=BD=2OA=2OB=13.∴OA=OD=6.5.而S矩形=12×5=60.∴S△AOD=14×60=15.∴S△AOP +S△DOP =15.即12×OA×PF+12×OD×PE=15.∴12×6.5×(PE+PF)=15.∴PE+PF=60 13.练习51.如图8,等腰梯形ABCD中,上底AD=2,下底BC=8,M是腰AB的中点,若MD⊥CD,•则梯形的面积为________.(8) (9)2.如图9,已知正方形ABCD的面积为35平方厘米,E、F分别为边AB、BC上的点.AF、CE相交于G,并且△ABF的面积为14平方厘米,△BCE的面积为5平方厘米,•那么四边形BEGF的面积是________.3.如图,在ABCD中,在AD、CD上各取一点E、F,使AF=CE,AF与CE相交于P,•则PB平分∠APC.答案:练习11.18° 2.363.连结BD交AC于点O,作EM⊥AC于点M.设正方形边长为a,则a又∵AC∥BF,BO⊥AC,EM⊥AC,∴BO=EM=12BD=2a.在Rt△AEM中,,a.∴∠CAE=30°.则∠EAB=15°.练习21.7516cm2.2.纸条长为6cm,宽为cm.3.作GM⊥BD,垂足为M.由题意可知∠ADG=GDM,则△ADG≌△MDG.∴DM=DA=2. AC=GM又易知:GM=BM.而-2=2-1),∴AG=BM=2-1).练习31.6c m2. 2.36.3.过P作EF⊥AB于F交DC于E.设PF=x,则EF=10+x,BF=12(10+x).由PB2=PF2+BF2.可得:102=x2+14(x+10)2.故x=6.S正方形ABCD=162=256.练习41.10.2.3.过D作DE⊥BC于E,则BE=4,EC=6,由∠C=60°,知CD=2EC=12,由于BC>8.7,DE>8.7,故这两个方向不能穿过圆洞.过B作BF⊥CD,有CF=12BC=5.得=8.7.故沿CD方向可穿过圆洞.练习51.2.42027cm2(面积法).3.连结BF、BE.过B作BM⊥AF于M,BN⊥CE于N.则有S△ABF=S△BCE=12S ABCD.即12×AF×BM=12×CE×BN.∵AF=CE∴BM=BN∴点B在∠APC的平分线上.即PB平分∠APC.练习5-1的详解:方法一:过D作DQ⊥BC于Q,作CD中点N,连结MN,交DQ于S MN为梯形ABCD中位线,∴MN=5,MN‖BC∴MS为梯形ABQD中位线∴MS=7/2,S为DQ中点,∵DQ⊥BC,MN‖BC,∴DQ⊥MN设DS=SQ=a,则MS²+DS²=MD²,则MD²=49/4 + a²,SN为△DQC中位线∴SN=3/2∴DN²=9/4 +a²∵MD⊥CD∴MD²+DN²=MN²∴49/4 + a²+ 9/4 +a²=25 解得a=√21 /2,DQ=√21,S=1/2(2+8)*√21=5√21方法二:延长DM,BC交于点N。
浙教版八年级下矩形、菱形、正方形复习课件

对特例的忽视
详细描述
学生在判断四边形是否为矩形、菱形或正方形时,可能会忽视一些特例。例如,对于矩形和正方形,学生可能会忽视它们的对角线相等且互相平分这一特例,从而在判断时出现错误。
矩形、菱形、正方形判定的易错点
总结词
详细描述
总结词
详细描述
总结词
详细描述
混淆面积计算公式
学生在计算矩形、菱形或正方形的面积时,可能会混淆面积计算公式。例如,将矩形的面积计算公式误记为“长x宽”,而实际上矩形的面积计算公式应为“长x宽”。
对题目信息的理解不准确
详细描述
学生在解决涉及矩形、菱形或正方形的综合问题时,可能会因为对题目信息的理解不准确而出现错误。例如,在解决一个涉及正方形和圆的综合问题时,学生可能会因为对题目中给出的圆的半径理解错误而导致解题思路出现偏差。
总结词
矩形、菱形、正方形综合应用的易错点
解题步骤不规范
总结词
学生在解决涉及矩形、菱形或正方形的综合问题时,可能会因为解题步骤不规范而出现错误。例如,在解决一个涉及矩形和三角形的综合问题时,学生可能会因为解题步骤不规范而导致最后得出的答案错误。
详细描述
矩形、菱形、正方形判定的易错点
总结词
忽视判定定理中的前提条件
详细描述
学生在应用判定定理时,常常会忽视定理中的前提条件。例如,在应用“一组邻边相等的平行四边形是菱形”这一判定定理时,学生可能会忽视“平行四边形”这一前提条件,从而错误地将一组邻边相等的四边形判定为菱形。
矩形、菱形、正方形判定的易错点
邻边相等的矩形是正方形。
对角线相等的菱形是正方形。
一个内角为直角的菱形是正方形。
正方形的性质和判定
02
矩形、菱形、正方形的面积计算
2020-2021学年浙教版八年级数学下册《5.2菱形》期末复习培优提升训练(附答案)

2020-2021学年浙教版八年级数学下册《5.2菱形》期末复习培优提升训练(附答案)1.菱形的两条对角线的长分别为6和8,则菱形的高为()A.B.C.D.2.如图,在菱形ABCD中,∠ADC=72°,AD的垂直平分线交对角线BD于点P,垂足为E,连接CP,则∠CPB的度数是()A.108°B.72°C.90°D.100°3.如图,菱形ABCD的的边长为6,∠ABC=60°,对角线BD上有两个动点E、F(点E 在点F的左侧),若EF=2,则AE+CF的最小值为()A.2B.4C.6D.84.如图,菱形ABCD的边长为2,∠ABC=60°,点E、F在对角线BD上运动,且EF =2,连接AE、AF,则△AEF周长的最小值是()A.4B.4+C.2+2D.65.如图,四边形ABCD为菱形,点A的坐标为(4,0),点C的坐标为(4,4),点D在y 轴上,则点B的坐标为()A.(4,2)B.(2,8)C.(8,4)D.(8,2)6.菱形的周长为8厘米,两相邻角度数比是1:2,则菱形的面积是()平方厘米.A.2B.2C.4D.47.一个菱形的边长为5,两条对角线的长度之和为14,则此菱形的面积为()A.20B.24C.28D.328.在菱形ABCD中,对角线AC、BD交于点O,过点A作AE⊥BC,垂足为E,交BC于点E,若AC=,AE=2,则菱形ABCD的面积为()A.5B.4C.2D.39.如图,点E,F在菱形ABCD的对角线AC上,∠ADC=120°,∠BEC=∠CBF=50°,ED与BF的延长线交于点M.则对于以下结论:①∠BME=30°;②△ADE≌△ABE;③EM=BC;④AE+BM=EM.其中正确结论的个数是()A.1个B.2个C.3个D.4个10.如图,在菱形ABCD中,AB=AC=1,点E、F分别为边AB、BC上的点,且AE=BF,连接CE、AF交于点H,连接DH交AC于点O,则下列结论:①△ABF≌△CAE;②∠FHC=∠B;③△ADO≌△ACH;④S菱形ABCD=;其中正确的结论个数是()A.1个B.2个C.3个D.4个11.如图,菱形ABCD的边长为4,E,F分别是AB,AD边上的动点,BE=AF,∠BAD=120°,则下列结论:①△BEC≌△AFC;②△ECF为等边三角形;③∠AGE=∠AFC;④若AF=1,则.其中正确个数为()A.4个B.3个C.2个D.1个12.如图,在菱形ABCD中,P是对角线AC上一动点,过点P作PE⊥BC于点E.PF⊥AB于点F.若菱形ABCD的周长为20,面积为24,则PE+PF的值为()A.4B.C.6D.13.如图,已知菱形ABCD中,过AD中点E作EF⊥BD,交对角线BD于点M,交BC的延长线于点F.连接DF,若CF=2,BD=4,则DF的长是()A.4B.4C.2D.514.如图,点E在菱形ABCD的AB边上,点F在BC边的延长线上,连接CE,DF,对于下列条件:①BE=CF;②CE⊥AB,DF⊥BC;③CE=DF;④∠BCE=∠CDF.只选取其中一条添加,不能确定△BCE≌△CDF的是()A.①B.②C.③D.④15.如图,四边形ABCD是菱形,E、F分别是BC、CD两边上的点,不能保证△ABE和△ADF一定全等的条件是()A.∠BAF=∠DAE B.EC=FC C.AE=AF D.BE=DF16.如图,已知△ABC,AB=AC,将△ABC沿边BC翻转,得到的△DBC与原△ABC拼成四边形ABDC,则能直接判定四边形ABDC是菱形的依据是()A.一组邻边相等的平行四边形是菱形B.四条边相等的四边形是菱形C.对角线互相垂直的平行四边形是菱形D.对角线互相平分的平行四边形是菱形17.如图,四边形ABCD是菱形,AC=24,BD=10,DH⊥AB于点H,则线段BH的长为.18.如图,菱形ABCD中,AC交BD于O,DE⊥BC于E,连接OE,若∠ABC=140°,则∠OED=.19.如图所示,菱形ABCD中,对角线AC,BD相交于点O,H为AD边中点,菱形ABCD 的周长为24,则OH的长等于.20.平面直角坐标系中,四边形ABCD的顶点坐标分别是A(﹣1,m)、B(﹣4,0)、C(1,0)、D(a,m),且m>0,若以点A、B、C、D为顶点的四边形是菱形,则点D的坐标为.21.如图,将两根等宽的纸条叠放在一起,重叠的部分(图中阴影部分)是一个四边形,对这个四边形的形状,你认为最准确的描述是:这个四边形是一个.22.如图,在菱形ABCD中,对角线AC、BD相交于点O,点E在线段BO上,连接AE,若CD=2BE,∠DAE=∠DEA,EO=1,则线段AE的长为.23.已知菱形的周长为4,两条对角线长的和为6,则菱形的面积为.24.如图,在平面直角坐标系中,△ACE是以菱形ABCD的对角线AC为边的等边三角形,AC=2,点C与点E关于x轴对称,则点D的坐标是.25.如图,在菱形ABCD中,∠B=45°,BC=2,E,F分别是边CD,BC上的动点,连接AE,EF,G,H分别为AE,EF的中点,连接GH,则GH的最小值为.26.如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连接CE.(1)求证:BD=EC;(2)若∠E=68°,求∠BAD的度数.27.如图,菱形ABCD中,∠B=60°,点E,F分别在AB,AD上,且BE=AF.(1)求证:△ECF为等边三角形;(2)连接AC,若AC将四边形AECF的面积分为1:2两部分,当AB=6时,求△BEC 的面积.28.如图,在△ABC中,D是AC的中点.作BE∥AC,且使BE=AC,连接DE,DE与AB交于点F.(1)求证:DE=BC;(2)连接AE、BD,要使四边形AEBD是菱形,△ABC的边或角需要满足什么条件?证明你的结论.29.在菱形ABCD中,∠ABC=60°,E是对角线AC上一点,F是线段BC延长线上一点,且CF=AE,连接BE、EF.(1)若E是线段AC的中点,如图1,易证:BE=EF(不需证明);(2)若E是线段AC或AC延长线上的任意一点,其它条件不变,如图2、图3,线段BE、EF有怎样的数量关系,直接写出你的猜想;并选择一种情况给予证明.30.如图,在平行四边形ABCD中,P是对角线BD上的一点,过点C作CQ∥DB,且CQ =DP,连接AP、BQ、PQ.(1)求证:△APD≌△BQC;(2)若∠ABP+∠BQC=180°,求证:四边形ABQP为菱形.31.如图,D是△ABC的边AB的中点,DE∥BC,CE∥AB,AC与DE相交于点F,连接AB,CD.(1)求证:AD=CE;(2)当△ABC满足什么条件时,四边形ADCE是菱形?请说明理由.32.一张矩形纸ABCD,将点B翻折到对角线AC上的点M处,折痕CE交AB于点E.将点D翻折到对角线AC上的点H处,折痕AF交DC于点F,折叠出四边形AECF.(1)求证:AF∥CE;(2)当∠BAC=度时,四边形AECF是菱形?说明理由.33.两块完全相同的三角板Ⅰ(△ABC)和Ⅱ(△A1B1C1)如图①放置在同一平面上(∠C =∠C1=90°,∠ABC=∠A1B1C1=60°),斜边重合.若三角板Ⅱ不动,三角板Ⅰ在三角板Ⅱ所在的平面上向右滑动,图②是滑动过程中的一个位置.(1)在图②中,连接BC1、B1C,求证:△A1BC1≌△AB1C;(2)三角板Ⅰ滑到什么位置(点B1落在AB边的什么位置)时,四边形BCB1C1是菱形?说明理由.34.将两张宽度相等的矩形纸片叠放在一起得到如图所示的四边形ABCD.(1)求证:四边形ABCD是菱形;(2)如果两张矩形纸片的长都是8,宽都是2.那么菱形ABCD的周长是否存在最大值或最小值?如果存在,请求出来;如果不存在,请简要说明理由.35.如图,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,BE交AC于F,连接DF.(1)证明:∠BAC=∠DAC,∠AFD=∠CFE.(2)若AB∥CD,试证明四边形ABCD是菱形;(3)在(2)的条件下,试确定E点的位置,使得∠EFD=∠BCD,并说明理由.参考答案1.解:由题意知AC=6,BD=8,则菱形的面积S=×6×8=24,∵菱形对角线互相垂直平分,∴△AOB为直角三角形,AO=3,BO=4,∴AB==5,∴菱形的高h==.故选:A.2.解:连接P A,如图所示:∵四边形ABCD是菱形,∴∠ADP=∠CDP=∠ADC=36°,BD所在直线是菱形的对称轴,∴P A=PC,∵AD的垂直平分线交对角线BD于点P,∴P A=PD,∴PD=PC,∴∠PCD=∠CDP=36°,∴∠CPB=∠PCD+∠CDP=72°;故选:B.3.解:如图,连接AC,作AM⊥AC,使得AM=EF=2,连接CM交BD于F,∵AC,BD是菱形ABCD的对角线,∴BD⊥AC,∵AM⊥AC,∴AM∥BD,∴AM∥EF,∵AM=EF,AM∥EF,∴四边形AEFM是平行四边形,∴AE=FM,∴AE+CF=FM+FC=CM,根据两点之间线段最短可知,此时AE+FC最短,∵四边形ABCD是菱形,AB=6,∠ABC=60°∴BC=AB,∴△ABC是等边三角形,∴AC=AB=6,在Rt△CAM中,CM==∴AE+CF的最小值为2.故选:A.4.解:如图作AH∥BD,使得AH=EF=2,连接CH交BD于F,则AE+AF的值最小,即△AEF的周长最小.∵AH=EF,AH∥EF,∴四边形EFHA是平行四边形,∴EA=FH,∵F A=FC,∴AE+AF=FH+CF=CH,∵菱形ABCD的边长为2,∠ABC=60°,∴AC=AB=2,∵四边形ABCD是菱形,∴AC⊥BD,∵AH∥DB,∴AC⊥AH,∴∠CAH=90°,在Rt△CAH中,CH=,∴AE+AF的最小值4,∴△AEF的周长的最小值=4+2=6,故选:D.5.解:连接AC,BD,AC、BD交于点E,∵四边形ABCD是菱形,OA=4,AC=4,∴ED=OA=EB=4,AC=2EA=4,∴点B坐标为(8,2),故选:D.6.解:∵菱形的周长为8cm,∴边长为2cm,∵两相邻角的度数之比为1:2,∴∠ABC=60°,∴△ABC是等边三角形.∴AC=AB=2cm.∴OA=1cm.在直角△AOB中,根据勾股定理可得,OB=(cm),∴BD=2OB=2(cm)∴菱形的面积=2×2÷2=2cm2.故选:A.7.解:如图所示:∵四边形ABCD是菱形,∴AO=CO=AC,DO=BO=BD,AC⊥BD,∵AC+BD=14,∴OD+AO=7①,∵∠AOB=90°,∴OD2+OA2=25②,由①②两式可得49﹣2OD•OA=25,解得:OD•OA=12,∴BD•AC=2OD•2OA=4OD•OA,∴菱形面积=BD•AC=2OD•OA=24.故选:B.8.解:∵四边形ABCD是菱形,∴AC⊥BD,OA=OC=AC=,∵AE⊥BC,∴△ABC的面积=BC×AE=AC×OB,∴==,设BC=x,则OB=2x,在Rt△OBC中,由勾股定理得:(x)2﹣(2x)2=()2,解得:x=,∴BC=,∴菱形ABCD的面积=BC×AE=×2=5;故选:A.9.解:∵四边形ABD是菱形,∠ADC=120°,∴AD=AB=BC=CD,∠BAD=∠BCD=60°,∠DAE=∠BAE,∠DCE=∠BCE=∠BCD=30°,∵∠BFE=∠BCE+∠CBF=30°+50°=80°,∴∠EBF=180°﹣∠BEC﹣∠BFE=180°﹣50°﹣80°=50°,在△CDE和△CBE中,,∴△CDE≌△CBE(SAS),∴∠DEC=∠BEC=50°,∴∠BEM=∠DEC+∠BEC=100°,∴∠BME=180°﹣∠BEM﹣∠EBF=180°﹣100°﹣50°=30°,故①正确;在△ADE和△ABE中,,∴△ADE≌△ABE(SAS),故②正确;∵∠EBC=∠EBF+∠CBF=100°,∴∠BEM=∠EBC,在△BEM和△EBC中,,∴△BEM≌△EBC(AAS),∴BM=EC,EM=BC,故③正确;连接BD交AC于O,如图所示:∵四边形ABCD是菱形,∴OA=OC,AC⊥BD,∵∠DCO=30°,∴OD=CD=BC,OC=OD,∴OC=BC,∴AC=2OC=BC,∵BM=EC,EM=BC,∴AE+BM=AE+EC=AC=BC=EM,故④正确,正确结论的个数是4个,故选:D.10.解:∵四边形ABCD是菱形,∴AB=BC,∵AB=AC,∴AB=BC=AC,即△ABC是等边三角形,∴AB=CA,∠EAC=∠B=60°,同理:△ADC是等边三角形∴∠OAD=60°,在△ABF和△CAE中,,∴△ABF≌△CAE(SAS);∴∠BAF=∠ACE,EC=AF,∵∠FHC=∠ACE+∠F AC=∠BAF+∠F AC=∠BAC=60°,∴∠FHC=∠B,故①正确,②正确;∵∠OAD=60°=∠EAC≠∠HAC,故③△ADO≌△ACH不正确;∵△ABC是等边三角形,AB=AC=1,∴△ABC的面积=AB2=,∴菱形ABCD的面积=2△ABC的面积=,故④不正确;故选:B.11.解:①∵四边形ABCD是菱形,∴AB=AD=4,∠BAC=∠CAD,∵∠BAD=120°,∴∠BAC=∠CAD=60°,∴△ABC和△ACD都是等边三角形,∴∠B=∠CAD=60°,BC=AC,∵BE=AF,∴△BEC≌△AFC(SAS),故①正确;②∵△BEC≌△AFC,∴CE=CF,∠BCE=∠ACF,∵∠BCE+∠ECA=∠BCA=60°,∴∠ACF+∠ECA=60,∴△CEF是等边三角形,故②正确;③∵∠AGE=∠CAF+∠AFG=60°+∠AFG;∠AFC=∠CFG+∠AFG=60°+∠AFG,∴∠AGE=∠AFC,故③正确;④过点E作EM∥BC交AC于点M,∴∠AEM=∠B=60°,∠AME=∠ACB=60°,∴△AEM是等边三角形,∴EM=AE,∵△BEC≌△AFC,∴BE=AF=1,∴AE=AB﹣BE=4﹣1=3,∴EM=AE=3,∵AF∥EM,④正确,正确个数为4个,故选:A.12.解:连接BP,如图,∵四边形ABCD为菱形,菱形ABCD的周长为20,∴BA=BC=5,S△ABC=S菱形ABCD=12,∵S△ABC=S△P AB+S△PBC,∴×5×PE+×5×PF=12,∴PE+PF=,故选:B.13.解:设CD与EF的交点为H,∵四边形ABCD是菱形,∴AD=CD=BC,∠ADB=∠CDB,∵点E是AD中点,∴AE=DE=AD,在△DEM和△DHM中,,∴△DEM≌△DHM(ASA),∴DE=DH,∴DH=CH,∵AD∥BC,∴DE=CF=2,∴AD=4=CD=BC,∴BF=6,∵BD=4,∴BC=CD=BD,∴△BCD是等边三角形,∴∠DBC=60°,∴∠BFM=30°,∴BM=BF=3,MF=BM=3,∴DM=1,∴DF===2,故选:C.14.解:∵四边形ABCD是菱形,∴BC=CD,AB∥CD,①∵添加BE=CF,∴△BCE≌△CDF(SAS),②∵添加CE⊥AB,DF⊥BC,∴∠CEB=∠F=90°,∴△BCE≌△CDF(AAS),③∵添加CE=DF,不能确定△BCE≌△CDF;④∵添加∠BCE=∠CDF,∴△BCE≌△CDF(ASA),故选:C.15.解:A.∵四边形ABCD是菱形,∴AB=AD,∠B=∠D,∵∠BAF=∠DAE,∴∠BAE=∠CAF,∴△ABE≌△ADF(AAS),故选项A不符合题意;B..∵四边形ABCD是菱形,∴AB=AD,∠B=∠D,BC=BD,∵EC=FC,∴BE=DF,∴△ABE≌△ADF(SAS),故选项B不符合题意;C..∵四边形ABCD是菱形,∴AB=AD,∠B=∠D,∵AE=AF,∴△ABE和△ADF只满足两边和一边的对角相等,两个三角形不一定全等,故选项C符合题意;D..∵四边形ABCD是菱形,∴AB=AD,∠B=∠D,∴△ABE≌△ADF(SAS),故选项D不符合题意.故选:C.16.解:如图所示;∵将△ABC延底边BC翻折得到△DBC,∴AB=BD,AC=CD,∵AB=AC,∴AB=BD=CD=AC,∴四边形ABDC是菱形;故选:B.17.解:∵四边形ABCD是菱形,AC=24,BD=10,∴AO=12,OD=5,AC⊥BD,∴AD=AB==13,∵DH⊥AB,∴AO×BD=DH×AB,∴12×10=13×DH,∴DH=,∴BH==.故答案为:.18.解:∵四边形ABCD是菱形,∴DO=OB,∵DE⊥BC于E,∴OE为直角三角形BED斜边上的中线,∴OE=BD,∴OB=OE,∴∠OBE=∠OEB,∵∠ABC=140°,∴∠OBE=70°,∴∠OED=90°﹣70°=20°,故答案为:20°.19.解:∵菱形ABCD的周长等于24,∴AD==6,在Rt△AOD中,OH为斜边上的中线,∴OH=AD=3.故答案为:3.20.解:作AM⊥BC于M,∵A(﹣1,m)、B(﹣4,0)、C(1,0)、D(a,m),且m>0,∴AD∥BC,OB=4,OC=1,OM=1,∴AD=BC=5,BM=3,CM=2,分两种情况:①当点D在y轴的右侧时,如图1所示:∵以点A、B、C、D为顶点的四边形是菱形,∴AB=BC=5,∴AM===4,∴点D的坐标为(4,4);②当点D在y轴的左侧时,如图2所示:∵以点A、B、C、D为顶点的四边形是菱形,∴AD=BC=5,∴AM===,∴点D的坐标为(﹣6,);综上所述,若以点A、B、C、D为顶点的四边形是菱形,则点D的坐标为(4,4)或(﹣6,);故答案为:(4,4)或(﹣6,).21.解:∵四边形ABCD是用两张等宽的纸条交叉重叠地放在一起而组成的图形,∴AB∥CD,AD∥BC,∴四边形ABCD是平行四边形(对边相互平行的四边形是平行四边形);过点D分别作AB,BC边上的高为DE,DF.则DE=DF(两纸条相同,纸条宽度相同);∵平行四边形ABCD中,S△ABD=S△DBC,即AB×DE=BC×DF,∴AB=BC.∴平行四边形ABCD为菱形(邻边相等的平行四边形是菱形).故答案是:菱形.22.解:设BE=x,则CD=2x,∵四边形ABCD为菱形,∴AB=AD=CD=2x,OB=OD,AC⊥BD,∵∠DAE=∠DEA,∴DE=DA=2x,∴BD=3x,∴OB=OD=x,∵OE+BE=BO,∴1+x=x,解得x=2,即AB=4,OB=3,在Rt△AOB中,OA===,在Rt△AOE中,AE===2.故答案为2.23.解:如图所示:∵两条对角线的和为6,∴AC+BD=6,∵菱形的周长为4,∴AB=,AC⊥BD,AO=AC,BO=BD,∴AO+BO=3,∴AO2+BO2=AB2,(AO+BO)2=9,即AO2+BO2=5,AO2+2AO•BO+BO2=9,∴2AO•BO=4,∴菱形的面积=AC•BD=2AO•BO=4;故答案为:4.24.解:如图,∵△ACE是以菱形ABCD的对角线AC为边的等边三角形,AC=2,∴CH=1,∴AH=,∵∠ABO=∠DCH=30°,∴DH=AO=,∴OD=﹣﹣=,∴点D的坐标是(,0).故答案为:(,0).25.解:连接AF,如图所示:∵四边形ABCD是菱形,∴AB=BC=2,∵G,H分别为AE,EF的中点,∴GH是△AEF的中位线,∴GH=AF,当AF⊥BC时,AF最小,GH得到最小值,则∠AFB=90°,∵∠B=45°,∴△ABF是等腰直角三角形,∴AF=AB=×2=,∴GH=,即GH的最小值为,故答案为:.26.解:(1)证明:∵四边形ABCD是菱形,∴DC∥AB,DC=AB.∵BE=AB,∴DC∥BE,DC=BE.∴四边形BDCE为平行四边形.∴BD=EC.(2)∵四边形BDCE为平行四边形,∴BD∥CE.∴∠DBA=∠E=68°.∵菱形ABCD,∴AC⊥BD,AC平分∠BAD,∴∠BAO=90°﹣∠DBA=22°.∴∠BAD=2∠BAO=44°.27.解:(1)证明:连接AC,∵四边形ABCD是菱形,∴BA=BC=AD=DC,又∵∠B=60°,∴△ABC和△ADC都是等边三角形,∴∠CAD=∠ACB=∠ACD=60°,在△CBE和△CAF中,,∴△CBE≌△CAF(SAS),∴CE=CF,∠BCE=∠ACF,∴∠ECF=60°,∴△ECF为等边三角形;(2)由(1)可知△CBE≌△CAF,∴S△CBE=S△CAF,∴S四边形AECF=S△ABC,作AH⊥BC交BC于点H,在△ABH中,∠B=60°,AB=6,∴BH=3,∴AH=3,∴S△ABC=×6×3=9,当S△CBE:S△CAE=1:2时,S△BEC的面积=S△ABC=3;当S△CBE:S△CAE=2:1时,S△BEC的面积=S△ABC=6;综上,△BEC的面积为3或628.(1)证明:∵D是AC的中点,∴CD=AC,∵BE=AC,∴CD=BE,∵BE∥AC,∴四边形BCDE是平行四边形,∴DE=BC;(2)解:当AB⊥BC(或∠ABC=90°)时,四边形AEBD是菱形;理由如下:如图2所示:∵D是AC的中点,∴AD=AC,∵BE=AC,∴AD=BE,∵BE∥AD,∴四边形AEBD是平行四边形,由(1)得,四边形BCDE是平行四边形,∴DE∥CB,当AB⊥BC时,∠ABC=90°,∴∠AFD=∠ABC=90°,即AB⊥DE,∴四边形AEBD是菱形.29.证明:(1)∵四边形ABCD为菱形,∴AB=BC,又∵∠ABC=60°,∴△ABC是等边三角形,∵E是线段AC的中点,∴∠CBE=∠ABC=30°,AE=CE,∵AE=CF,∴CE=CF,∴∠F=∠CEF,∵∠F+∠CEF=∠ACB=60°,∴∠F=30°,∴∠CBE=∠F,∴BE=EF;(2)图2:BE=EF.图3:BE=EF.图2证明如下:过点E作EG∥BC,交AB于点G,∵四边形ABCD为菱形,∴AB=BC,又∵∠ABC=60°,∴△ABC是等边三角形,∴AB=AC,∠ACB=60°,又∵EG∥BC,∴∠AGE=∠ABC=60°,又∵∠BAC=60°,∴△AGE是等边三角形∴AG=AE,∴BG=CE,又∵CF=AE,∴GE=CF,又∵∠BGE=∠ECF=120°,∴△BGE≌△ECF(SAS),∴BE=EF;图3证明如下:过点E作EG∥BC交AB延长线于点G,∵四边形ABCD为菱形,∴AB=BC,又∵∠ABC=60°,∴△ABC是等边三角形,∴AB=AC,∠ACB=60°,又∵EG∥BC,∴∠AGE=∠ABC=60°,又∵∠BAC=60°,∴△AGE是等边三角形,∴AG=AE,∴BG=CE,又∵CF=AE,∴GE=CF,又∵∠BGE=∠ECF=60°,∴△BGE≌△ECF(SAS),∴BE=EF.30.(1)证明:∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC,∴∠ADB=∠DBC,∵CQ∥DB,∴∠BCQ=∠DBC,∴∠ADB=∠BCQ∵DP=CQ,∴△ADP≌△BCQ.(2)证明:∵CQ∥DB,且CQ=DP,∴四边形CQPD是平行四边形,∴CD=PQ,CD∥PQ,∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,∴AB=PQ,AB∥PQ,∴四边形ABQP是平行四边形,∵△ADP≌△BCQ,∴∠APD=∠BQC,∵∠APD+∠APB=180°,∠ABP+∠BQC=180°,∴∠ABP=∠APB,∴AB=AP,∴四边形ABQP是菱形.31.(1)证明:∵DE∥BC,CE∥AB,∴四边形BCED是平行四边形,∴BD=CE,∵D是△ABC的边AB的中点,∴AD=BD,∴AD=CE;(2)解:当△ABC满足△ABC是直角三角形,∠ACB=90°时,四边形ADCE是菱形;理由如下:由(1)得:AD∥CE,AD=CE,∴四边形ADCE是平行四边形,∵∠ACB=90°,D是△ABC的边AB的中点,∴CD=AB=AD,∴四边形ADCE是菱形.32.(1)证明:∵四边形ABCD为矩形,∴AD∥BC,∴∠DAC=∠BCA,由翻折知,∠DAF=∠HAF=∠DAC,∠BCE=∠MCE=∠BCA,∴∠HAF=∠MCE,∴AF∥CE;(2)解:当∠BAC=30°时四边形AECF为菱形,理由如下:∵四边形ABCD是矩形,∴∠D=∠BAD=90°,AB∥CD,由(1)得:AF∥CE,∴四边形AECF是平行四边形,∵∠BAC=30°,∴∠DAC=60°.∴∠ACD=30°,由折叠的性质得∠DAF=∠HAF=30°,∴∠HAF=∠ACD,∴AF=CF,∴四边形AECF是菱形;故答案为:30.33.(1)证明:∵三角板Ⅰ(△ABC)和Ⅱ(△A1B1C1)是两块完全相同的三角板,∴AC=A1C1AB=A1B1∠A=∠A1∴在图②中A1B=AB1∴△A1BC1≌△AB1C.(2)解:点B1落在AB边的中点.理由如下:如图②所示,由已知条件知BC=B1C1,BC∥B1C1∴四边形BCB1C1是平行四边形.要使四边形BCB1C1是菱形,则BC=CB1∵∠ABC=∠A1B1C1=60°,∴△BCB1为等边三角形.∴BB1=B1C=BC,又∵∠A=30°,在直角三角形ABC中,BC=AB,∴BB1=AB,∴点B1落在AB边的中点.34.(1)证明:如图,∵AD∥BC,DC∥AB,∴四边形ABCD是平行四边形.分别过点A、D作AE⊥BC于E,DF⊥AB于F.∵两张矩形纸片的宽度相等,∴AE=DF,又∵AE•BC=DF•AB=S▱ABCD,∴BC=AB,∴▱ABCD是菱形;(2)解:存在最小值和最大值.(7分)①当∠DAB=90°时,菱形ABCD为正方形,周长最小值为8;(8分)②当AC为矩形纸片的对角线时,设AB=x.如图,在Rt△BCG中,BC2=CG2+BG2,即x2=(8﹣x)2+22,x=.∴周长最大值为×4=17.(9分)35.(1)证明:在△ABC和△ADC中,,∴△ABC≌△ADC(SSS),∴∠BAC=∠DAC,在△ABF和△ADF中,,∴△ABF≌△ADF(SAS),∴∠AFD=∠AFB,∵∠AFB=∠CFE,∴∠AFD=∠CFE;(2)证明:∵AB∥CD,∴∠BAC=∠ACD,又∵∠BAC=∠DAC,∴∠CAD=∠ACD,∴AD=CD,∵AB=AD,CB=CD,∴AB=CB=CD=AD,∴四边形ABCD是菱形;(3)当EB⊥CD时,即E为过B且和CD垂直时垂线的垂足,∠EFD=∠BCD,理由:∵四边形ABCD为菱形,∴BC=CD,∠BCF=∠DCF,在△BCF和△DCF中,,∴△BCF≌△DCF(SAS),∴∠CBF=∠CDF,∵BE⊥CD,∴∠BEC=∠DEF=90°,∴∠BCD+∠CBE=∠CDF+∠EFD,∴∠EFD=∠BCD.。
5.2.2 菱形的判定 浙教版八年级下册课件

C
∴四边形ABCD是菱形
∵AC⊥BD ∴平行四边形ABCD是菱形.
菱形的判定方法: 1.一组邻边相等的平行四边形是菱形.
2.四条边相等的四边形是菱形.
三个角是直角
四边形
一组对边平行且相等 两组对边分别相等
两组对边分别平行
对角线互相平分
平行四边形
矩形
四条边都相等
菱形
【牛刀小试】
1.已知,AD是△ABC的角平分线,
DE∥AC交AB于点E,DF∥AB交AC于点F。
求证:四边形AEDF是菱形。
EA F证明:源自∵DE∥AC,DF∥AB,
B
∴四边形AEDF是平行四边形
D
C
∵DE∥AC,
∴∠ADE=∠DAF.
∵AD是△ABC的角平分线, ∴∠DAE=∠DAF.
∴∠DAE=∠ADE. ∴AE=ED.
∴平行四边形AEDF是菱形.
1.(1)已知菱形ABCD的边长为4, ∠DAB=60°,则对角线
BD=___4___,AC=_4__3_,面积S菱形ABCD=___8__3___.
(2)已知菱形ABCD的两条对角线长分别为2cm, 2 2 cm,则菱形ABCD的边长为___3__cm.
A
D
C B
菱形
定义:有一组邻边相等的平行四边形叫做菱形.
(1)必定是平行四边形.
(2)当AB=BC时,围成的四边形是菱形.
(3)当∠B=Rt∠时,围成的四边形是矩形
(4)平行四边形BEFD的面积是△ABC面积的一半;S△ADF=S△FEC等
菱形的判定:
文字语言
图形语言
判定
四边相等的
A
D
法一 四边形是菱形 B
初中数学竞赛奥数培优资料第三辑专题25 平面几何的最值问题

专题25平面几何的最值问题阅读与思考几何中的最值问题是指在一定的条件下,求平面几何图形中某个确定的量(如线段长度、角度大小、图形面积)等的最大值或最小值.求几何最值问题的基本方法有:1.特殊位置与极端位置法:先考虑特殊位置或极端位置,确定最值的具体数据,再进行一般情形下的推证.2.几何定理(公理)法:应用几何中的不等量性质、定理.3.数形结合法等:揭示问题中变动元素的代数关系,构造一元二次方程、二次函数等.例题与求解【例1】在Rt△ABC中,CB=3,CA=4,M为斜边AB上一动点.过点M作MD⊥AC于点D,过M 作ME⊥CB于点E,则线段DE的最小值为.(四川省竞赛试题)解题思路:四边形CDME为矩形,连结CM,则DE=CM,将问题转化为求CM的最小值.【例2】如图,在矩形ABCD中,AB=20cm,BC=10cm.若在AC,AB上各取一点M,N,使BM+MN 的值最小,求这个最小值.(北京市竞赛试题)解题思路:作点B关于AC的对称点B′,连结B′M,B′A,则BM=B′M,从而BM+MN=B′M+MN.要使BM+MN的值最小,只需使B′M十MN的值最小,当B′,M,N三点共线且B′N⊥AB时,B′M+MN的值最小.a ),P为AB边上的一动点,直线DP交CB的延【例3】如图,已知□ABCD,AB=a,BC=b(b长线于Q.求AP+BQ的最小值.(永州市竞赛试题)解题思路:设AP =x ,把AP ,BQ 分别用x 的代数式表示,运用不等式以ab b a 222≥+或a +b ≥2ab(当且仅当a =b 时取等号)来求最小值.【例4】阅读下列材料:问题如图1,一圆柱的底面半径为5dm ,高AB 为5dm ,BC 是底面直径,求一只蚂蚁从A 点出发沿圆柱表面爬行到C 点的最短路线.小明设计了两条路线:路线1:侧面展开图中的线段AC .如图2所示.设路线l 的长度为l 1,则l 12=AC 2=AB 2+BC 2=25+(5π)2=25+25π2.路线2:高线AB 十底面直径BC .如图1所示.设路线l 的长度为l 2,则l 22=(BC +AB )2=(5+10)2=225.∵l 12–l 22=25+25π2-225=25π2-200=25(π2-8),∴l 12>l 22,∴l 1>l 2.所以,应选择路线2.线才能使蚂蚁从点A 出发沿圆柱表面爬行到C 点的路线最短.(衢州市中考试题)解题思路:本题考查平面展开一最短路径问题.比较两个数的大小,有时比较两个数的平方比较简便.比较两个数的平方,通常让这两个数的平方相减.【例5】如图,已知边长为4的正方形钢板,有一个角锈蚀,其中AF =2,BF =1.为了合理利用这块钢板,将在五边形EABCD 内截取一个矩形块MDNP ,使点P 在AB 上,且要求面积最大,求钢板的最大利用率.(中学生数学智能通讯赛试题)解题思路:设DN =x ,PN =y ,则S =xy .建立矩形MDNP 的面积S 与x 的函数关系式,利用二次函数性质求 S 的最大值,进而求钢板的最大利用率.【例6】如图,在四边形ABCD 中,AD =DC =1,∠DAB =∠DCB =90°,BC ,AD 的延长线交于P ,求AB ·S △P AB 的最小值.(中学生数学智能通讯赛试题)解题思路:设PD =x (x >1),根据勾股定理求出PC ,证Rt △PCD ∽Rt △PAB ,得到PCP A CD AB ,求出AB ,根据三角形的面积公式求出y =AB ·S △P AB ,整理后得到y ≥4,即可求出答案.能力训练A 级1.如图,将两张长为8、宽为2的矩形纸条交叉,使重叠部分是一个菱形.容易知道当两张纸条垂直时,菱形的周长有最小值,那么菱形周长的最大值是.(烟台市中考试题)2.D 是半径为5cm 的⊙O 内一点,且OD =3cm ,则过点O 的所有弦中,最短的弦AB =cm .(广州市中考试题)3.如图,有一个长方体,它的长BC =4,宽AB =3,高BB 1=5.一只小虫由A 处出发,沿长方体表面爬行到C 1,这时小虫爬行的最短路径的长度是.(“希望杯”邀请赛试题)第1题图第3题图第4题图第5题图4.如图,在△ABC 中,AB =10,AC =8,BC =6,经过点C 且与边AB 相切的动圆与CB ,CA 分别相交于点E ,F ,则线段EF 长度的最小值是()(兰州市中考试题)A .42B .4.75C .5D .4.85.如图,圆锥的母线长OA=6,底面圆的半径为2.一小虫在圆锥底面的点A处绕圆锥侧面一周又回到点A,则小虫所走的最短距离为()(河北省竞赛试题)A.12B.4πC.62D.636.如图,已知∠MON=40°,P是∠MON内的一定点,点A,B分别在射线OM,ON上移动,当△PAB周长最小时,∠APB的值为()(武汉市竞赛试题)A.80°B.100°C.120°D.140°7.如图,⌒AD是以等边三角形ABC一边AB为半径的四分之一圆周,P为AD上任意一点.若AC=5,则四边形ACBP周长的最大值是()(福州市中考试题)A.15B.20C.15+52D.15+55第6题图第7题图第8题图8.如图,在正方形ABCD中,AB=2,E是AD边上一点(点E与点A,D不重合),BE的垂直平分线交AB于M,交DC与N.(1)设AE=x,四边形ADNM的面积为S,写出S关于x的函数关系式.(2)当AE为何值时,四边形ADNM的面积最大?最大值是多少?(山东省中考试题)9.如图,六边形ABCDEF内接于半径为r的⊙O,其中AD为直径,且AB=CD=DE=FA.(1)当∠BAD=75°时,求⌒BC的长;(2)求证:BC∥AD∥FE;(3)设AB=x,求六边形ABCDEF的周长l关于x的函数关系式,并指出x为何值时,l取得最大值.10.如图,已知矩形ABCD的边长AB=2,BC=3,点P是AD边上的一动点(P异于A、D).Q是BC边上任意一点.连结AQ,DQ,过P作PE∥DQ交于AQ于E,作PF//AQ交DQ于F.(1)求证:△APE∽△ADQ;(2)设AP的长为x,试求△PEF的面积S△PEF关于x的函数关系式,并求当P在何处时,S△PEF取得最大值?最大值为多少?(3)当Q在何处时,△ADQ的周长最小?(须给出确定Q在何处的过程或方法,不必证明)(无锡市中考试题)11.在等腰△ABC中,AB=AC=5,BC=6.动点M,N分别在两腰AB,AC上(M不与A,B重合,N不与A,C重合),且MN∥BC.将△AMN沿MN所在的直线折叠,使点A的对应点为P.(1)当MN为何值时,点P恰好落在BC上?(2)设MN=x,△MNP与等腰△ABC重叠部分的面积为y,试写出y与x的函数关系式,当x为何值时,y的值最大,最大值是多少?(宁夏省中考试题)B级1.已知凸四边形ABCD中,AB+AC+CD=16,且S四边彤ABCD=32,那么当AC=,BD=时,四边形ABCD面积最大,最大值是.(“华杯赛”试题)2.如图,已知△ABC的内切圆半径为r,∠A=60°,BC=23,则r的取值范围是.(江苏省竞赛试题)第2题图第3题图第4题图第5题图3.如图⊙O 的半径为2,⊙O 内的一点P 到圆心的距离为1,过点P 的弦与劣弧⌒AB组成一个弓形,则此弓形面积的最小值为.4.如图,△ABC 的面积为1,点D ,G ,E 和F 分别在边AB ,AC ,BC 上,BD <DA ,DG ∥BC ,DE ∥AC ,GF ∥AB ,则梯形DEFG 面积的最大可能值为.(上海市竞赛试题)5.已知边长为a 的正三角形ABC ,两顶点A ,B 分别在平面直角坐标系的x 轴,y 轴的正半轴上滑动,点C 在第一象限,连结OC ,则OC 的最大值是.(潍坊市中考试题)6.已知直角梯形ABCD 中,AD ∥BC ,AB ⊥BC ,AD =2,BC =DC =5,点P 在BC 上移动,则当PA +PD 取最小值时,△APD 中边AP 上的高为()(鄂州市中考试题)A .17172B .17174C .17178D .3第6题图第7题图第8题图7.如图,正方形ABCD 的边长为4cm ,点P 是BC 边上不与点B ,C 重合的任意一点,连结AP ,过点P 作PQ ⊥AP 交DC 于点Q .设BP 的长为x cm ,CQ 的长为y cm .(1)求点P 在BC 上运动的过程中y 的最大值;(2)当y =41cm 时,求x 的值.(河南省中考试题)8.如图,y 轴正半轴上有两点A (0,a ),B (0,b ),其中a >b >0.在x 轴上取一点C ,使∠ACB 最大,求C 点坐标.(河北省竞赛试题)9.如图,正方形ABCD 的边长为1,点M ,N 分别在BC ,CD 上,使得△CM N 的周长为2.求:(1)∠MAN 的大小;(2)△MAN 的面积的最小值.(“宇振杯”上海市竞赛试题)10,如图,四边形ABCD 中,AD =CD ,∠DAB =∠ACB =90°,过点D 作DE ⊥AC 于F ,DE 与AB 相交于点E .(1)求证:AB ·AF =CB ·CD ;(2)已知AB =15cm ,BC =9cm ,P 是射线DE 上的动点,设DP =x cm(x >0),四边形BCDP 的面积为y cm 2.①求y 关于x 的函数关系式;②当x 为何值时,△PBC 的周长最小?求出此时y 的值.(南通市中考试题)第6题图第7题图第8题图第9题图11.如图,已知直线l :k kx y 42-+=(k 为实数).(1)求证:不论k 为任何实数,直线l 都过定点M ,并求点M 的坐标;(2)若直线l 与x 轴、y 轴的正半轴交于A ,B 两点,求△AOB 面积的最小值.(太原市竞赛试题)12.如图,在Rt△ABC中,∠C=90°,BC=2,AC=x,点F在边AB上,点G,H在边BC上,四边形EFGH是一个边长为y的正方形,且AE=AC.(1)求y关于x的函数解析式;(2)当x为何值时,y取得最大值?求出y的最大值.(上海市竞赛试题)专题25平面几何的最值问题例1125提示:当CM ⊥AB 时,CM 值最小,CM =125AC BC AB ⋅=例2如图,B ′M +MN 的最小值为点B ′到AB 的距离B ′F ,BE =45AB BC AC⋅=cm ,BB ′=85,AE ()222220455AB BE -=-.在△ABB ′中,由12BB ′•AE =12AB •B ′F ,得B ′F =16cm .故BM +MN 的最小值为16cm .例3由△APD ∽△BPQ ,得AP AD BP BQ=,即BQ =()b a x AD BP AP x -⋅=,∴AP +BQ =x +ab b x -.∵x +ab x ≥22ab x ab x ⋅=x =ab x即x ab 时,上式等号成立.故当AP ab AP +BQ 最小,其最小值为ab b .例4⑴22125l π=+,22l =49,l 1<l 2,故要选择路线l 较短.⑵()2221l h r π=+,()2222l h r =+,()2221244l l r r h π⎡⎤-=--⎣⎦.当r =244h π-时,2212l l =,当r >244h π-时,2212l l >,当r <244h π-时,2212l l <.例5设DN =x ,PN =y ,则S =xy ,由△APQ ∽△ABF ,得()41242y x -=--即x =10-2y ,代入S =xy 得S =xy =y (10-2y ),即S =-2252522y ⎛⎫-+ ⎪⎝⎭,因3≤y ≤4,而y =52不在自变量y 的取值范围内,所以y =52不是极值点,当y =3时,S (3)=12,当y =4时,S (4)=8,故S max =12.此时,钢板的最大利用率21214212-⨯⨯=80%.例6设PD =x (x >1),则PC 21x -,由R t △PCD ∽△PAB ,得AB =21CD PA PC x ⋅=-,令y =AB •S △PAB ,则y =12AB ×PA ×AB =()()2121x x +-,求y 的最小值,有下列不同思路:①配方:y =21212242121x x x x --++=+--1221x x -=-x =3时,y 有最小值4.②运用基本不等式:y =122221x x -++≥-322=4,∴当12x -=21x -,即当x =3时,y 有最小值4.③借用判别式,去分母,得x 2+2(1-y )x +1+2y =0,由△=4(1-y )2-4(1+2y )=4y (y -4)≥0,得y ≥4,∴y 的最小值为4.A 级1.17提示:当两张纸条的对角重合时,菱形周长最大.2.83.4.D5.D6.B7.C 提示:当点P 与点D 重合时,四边形ACBP 的周长最大.8.(1)连结ME ,过N 作NF ⊥AB 于F ,可证明Rt △EB A ≌Rt △MNF ,得MF =AE =x.∵ME 2=AE 2+AM 2,故MB 2=x 2+AM 2,即(2-AM )2=x 2+AM 2,AM =1-14x 2,∴S =2AM DN +×AD =2AM AF +×2=AM +AM +MF =2AM +AE =2(1-14x 2)+x =-12x 2+x +2.(2)S =-12(x 2-2x +1)+52=-12(x -1)2+52.故当AE =x =1时,四边形ADNM 的面积最大,此时最大值为52.9.(1) BC 长为23r π.(2)提示:连结BD .(3)过点B 作BM ⊥AD 于M ,由(2)知四边形ABCD 为等腰梯形,从而BC =AD -2AM =2r -2AM .由△BAM ∽△DAB ,得AM =2AB AD =22x r ,∴BC =2r -2x r .同理,EF =2r -2x r .l =4x +2(2r -2x r )=-x r(x -r )2+6r(0<x <r )..当x =r 时,l 取得最大值6r .10.(1)∵∠APE =∠ADQ ,∠AEP =∠AQD ,∴△APE ∽△ADQ .(2)由△APE ∽△ADQ ,△PDF ∽△ADQ ,S △PEF =12S □PEQF ,得S △PEF =-13x 2+x =-13(x -32)2+34.故当x =32时,即P 是AD 的中点时,S △PEF 取得最大值,(3)作A 关于直线BC 的对称点A′,连结DA′交BC 于Q ,则这个Q 点就是使△ADQ 周长最小的点,此时Q 是BC 的中点.11.(1)点P 恰好在BC 上时,由对称性知MN 是△ABC 的中位线,∴当MN =12BC =3时,点P 在BC 上.(2)由已知得△ABC 底边上的高h==4.①当0<x ≤3时,如图1,连结AP 并延长交BC 于点D ,AD 与MN 交于点O.由△AMN ∽△ABC ,得AO =23x ,y =S △PMN =S △AMN =12·x ·23x =13x 2即y =13x 2.当=3时,y 的值最大,最大值是3.②当3<x <6时,如图2,设△PMN 与BC 相交于点E ,F ,AP 与BC 相交于D .由①中知AO =23x ,∴AP =43x ,∴PD =AP -AD =43x -4,∵△PEF ∽△ABC .,∴PEF ABC S S ∆∆=(PD AD )2=(4434x -)2,即PEF ABC S S ∆∆=2-3)9x (.∵S △ABC =12,∴S △PEF =43(x -3)2.∴y =S △AMN -S △PEF =13x 2-43(x -3)2=-x 2+8x -12=-(x -4)2+4.故当x =4时,y 的最大值为4.综上,当x =4时,y 的值最大,最大值为4.B 级1.832提示:当∠CAB =∠ACD =90°时,四边形ABCD 的面积达到最大值.2.0<r ≤1提示:设BC =a ,CA =b ,AB =c ,b +c =r +1),又12bc sin60°=S △ABC =12(a +b +c )r ,即12bc·2=12[+2(r +1)]r ,.bc =4r (r +2).b ,c 为方程x 2-(r +1)x +4r (r +2)=0的两个根,由△≥0,得(r +1)≤22.因r >0,r +1>0,故r +1≤2,即0<r ≤1.3.249π提示:过P 作垂直于OP 的弦AB ,此时弓形面积最小.4.13提示:设AD AB =x ,则BD BA =1-x =CG CA ,ADG ABC S S ∆∆=x 2,BDE ABCS S ∆∆=(1-x )2=CFG ABC S S ∆∆,S 梯形DEFG =1―x 2―2(1-x )2=-3(x -23)2+13.5.12a 提示:当OA =OB 时,OC 的长最大. 6.C 7.(1)由Rt △ABP ∽Rt △PCQ ,得BP CQ =AB CP ,即x y =44x-,y =-14(x -2)2+1(0<x <4).当x =2时,y 最大值=1cm.(2)由14=-14(x -2)2+1,得x =(2)cm 或(2)cm.8.当过A ,B 两点的圆与x 轴正半轴相切时,切点C 为所求.作O′D ⊥A B 于D .,O′D 2=O′B 2-B D 2=2()2a b +-2()2a b -=ab ,O′DC0).9.(1)如图,延长CB 到L ,使BL =DN ,则Rt △ABL ≌Rt △ADN ,得AL =AN ,∠1=∠2,又∵N =2―CN ―CM =DN +BM =BL +BM =ML ,且AM =AM ,∠NAL =∠DAB =90°.∴△AMN ≌△AML ,故∠MAN =∠MAL =902=45°.(2)设CM =x ,CN =y ,MN =z ,则2222222,2,x y z x y z x y z x y z ++==--⎧⎧⇔⎨⎨+=+=⎩⎩,于是,(2―y ―z )2+y 2=z 2.整理得2y 2+(2z -4)y +(4-4z )=0.∵y >0,故△=4(z -2)2-32(1-z )≥0,即(z +2+)(z +2-)≥0.又∵z >0,故z ≥22-2,当且仅当x =y =2-2时等号成立.由于S △AMN =S △AML =12·ML ·AB =12MN ×1=2z ,因此,△AMN 2-1.10.(1)提示:证明△ADF ∽△BAC .(2)①AB =15,BC =9,∠ACB =90°,∴AC 22AB BC -2215912-=,∴CF =AF =6,∴()()19632702y x x x =+⨯=+>.②∵BC =9(定值),∴△PBC 的周长最小,就是PB +PC 最小,由(1)知,点C 关于直线DE 的对称点是点A ,所以PB +PC =PB +PA ,故只要求PB +PA 最小.显然当P 、A 、B 三点共线时PB +PA 最小,此时DP =DE ,PB +PA =AB .由(1),角∠ADF =∠FAE ,∠DFA =∠ACB =90°,得△DAF ∽△ABC .EF ∥BC ,得AE =BE =12AB =152,EF =92.∴AF ∶BC =AD ∶AB ,即6∶9=AD ∶15,∴AD =10.Rt △ADF 中,AD =10,AF =6,∴DF =8.∴DE =DF +FE =8+92=252.∴当x =252时,△PBC 的周长最小,此时y =1292.11.(1)令k =1,得y =x +2;令k =2,得y =2x +6,联立解得x =4,y =2,故定点(4,2).(2)取x =0,得OB =2-4k (k <0),取y =0,得OA =()420k k k-<.于是△ABO 的面积()()114224022k S OA OB k k k -==-< ,化简得()28820k S k +-+=.由()28640S ∆=--≥得2160S S -≥,故S ≥16.将S =16代入上述方程,得k =12-.故当k =12-,S 值最小.12.(1)如图,延长EF 交AC 于点D ,DF ∥BC ,Rt △ADF ∽Rt △ACB ,AE =AC =x ,()2222DE x x y xy y =--=-,22xy y y x y x -+-=,2x -2y -xy=,两边平方整理得(x 2+2x +2)y 2-(x 3+2x 2+4x )y +2x 2=0.解得2222x y x x =++(y =x 舍去).(2)由(1)2122y x x ==++.当且仅当2x x =,即x =时,上式等号成立.故当x =时,y1-.。
初中八年级数学培优竞赛辅导讲义全册(213页)

初中八年级数学培优竞赛辅导讲义(共213页,按住ctrl键点击目录直接跳转到对应章节)第1讲全等三角形的性质与判定 (2)第2讲角平分线的性质与判定 (12)第3讲轴对称及轴对称变换 (17)第4讲等腰三角形 (25)第5讲等边三角形 (37)第06讲实数 (43)第7讲变量与函数 (50)第8讲一次函数的图象与性质 (55)第9讲一次函数与方程、不等式 (64)第10讲一次函数的应用 (69)第11讲幂的运算 (81)第12讲整式的乘除 (87)第13讲因式分解及其应用 (94)第14讲分式的概念•性质与运算 (101)第15讲分式的化简求值与证明 (109)第16讲分式方程及其应用 (118)第17讲反比例函数的图象与性质 (126)第18讲反比例函数的应用 (139)第19讲勾股定理 (146)第20讲平行四边形 (158)第21讲菱形与矩形 (167)第22讲正方形 (175)第23讲梯形 (185)第24讲数据的分析 (194)B AC D EF 第1讲 全等三角形的性质与判定考点·方法·破译1.能够完全重合的两个三角形叫全等三角形.全等三角形的形状和大小完全相同; 2.全等三角形性质:①全等三角形对应边相等,对应角相等;②全等三角形对应高、角平分线、中线相等;③全等三角形对应周长相等,面积相等;3.全等三角形判定方法有:SAS ,ASA ,AAS ,SSS ,对于两个直角三角形全等的判定方法,除上述方法外,还有HL 法;4.证明两个三角形全等的关键,就是证明两个三角形满足判定方法中的三个条件,具体分析步骤是先找出两个三角形中相等的边或角,再根据选定的判定方法,确定还需要证明哪些相等的边或角,再设法对它们进行证明;5..证明两个三角形全等,根据条件,有时能直接进行证明,有时要证的两个三角形并不全等,这时需要添加辅助线构造全等三角形,构造全等三角形常用的方法有:平移、翻折、旋转、等倍延长线中线、截取等等.经典·考题·赏析【例1】如图,AB ∥EF ∥DC ,∠ABC =90°,AB =CD ,那么图中有全等三角形( ) A .5对 B .4对 C .3对 D .2对【解法指导】从题设题设条件出发,首先找到比较明显的一对全等三角形,并由此推出结论作为下面有用的条件,从而推出第二对,第三对全等三角形.这种逐步推进的方法常用到.解:⑴∵AB ∥EF ∥DC ,∠ABC =90. ∴∠DCB =90. 在△ABC 和△DCB 中AB DC ABC DCB BC CB =⎧⎪=⎨⎪=⎩∠∠ ∴△ABC ≌∴△DCB (SAS ) ∴∠A =∠D ⑵在△ABE 和△DCE 中A DAED DEC AB DC =⎧⎪=⎨⎪=⎩∠∠∠∠ ∴△ABE ≌∴△DCE ∴BE =CE ⑶在Rt △EFB 和Rt △EFC 中BE CEEF EF=⎧⎨=⎩ ∴Rt △EFB ≌Rt △EFC (HL )故选C . 【变式题组】 01.(天津)下列判断中错误的是( )A .有两角和一边对应相等的两个三角形全等B .有两边和一角对应相等的两个三角形全等C .有两边和其中一边上的中线对应相等的两个三角形全等A F C E DB D .有一边对应相等的两个等边三角形全等 02.(丽水)已知命题:如图,点A 、D 、B 、E 在同一条直线上,且AD =BE ,∠A =∠FDE ,则△ABC ≌△DEF .判断这个命题是真命题还是假命题,如果是真命题,请给出证明;如果是假命题,请添加一个适当条件使它成为真命题,并加以证明.03.(上海)已知线段AC 与BD 相交于点O , 连接AB 、DC ,E 为OB 的中点,F 为OC 的中点,连接EF (如图所示).⑴添加条件∠A =∠D ,∠OEF =∠OFE ,求证:AB =DC ; ⑵分别将“∠A =∠D ”记为①,“∠OEF =∠OFE ”记为②,“AB =DC ”记为③,添加①、③,以②为结论构成命题1;添加条件②、③,以①为结论构成命题2.命题1是______命题,命题2是_______命题(选择“真”或“假”填入空格).【例2】已知AB =DC ,AE =DF ,CF =FB . 求证:AF =DE .【解法指导】想证AF =DE ,首先要找出AF 和DE 所在的三角形.AF 在△AFB 和△AEF 中,而DE 在△CDE 和△DEF 中,因而只需证明△ABF ≌△DCE 或△AEF ≌△DFE 即可.然后再根据已知条件找出证明它们全等的条件.证明:∵FB =CE ∴FB +EF =CE +EF ,即BE =CF 在△ABE 和△DCF 中, AB DCAE DF BE CF =⎧⎪=⎨⎪=⎩∴△ABE ≌△DCF (SSS ) ∴∠B =∠C在△ABF 和△DCE 中, AB DC B C BF CE =⎧⎪=⎨⎪=⎩∠∠ ∴△ABF ≌△DCE ∴AF =DE【变式题组】01.如图,AD 、BE 是锐角△ABC 的高,相交于点O ,若BO =AC ,BC =7,CD =2,则AO 的长为( ) A .2 B .3 C .4 D .5A B C D O FE A CEFBD02.如图,在△ABC 中,AB =AC ,∠BAC =90°,AE 是过A 点的一条直线,AE ⊥CE 于E ,BD⊥AE 于D ,DE =4cm ,CE =2cm ,则BD =__________. \ 03.(北京)已知:如图,在△ABC 中,∠ ACB =90°,CD ⊥AB 于点D ,点E 在AC 上,CE =BC ,过点E 作AC 的垂线,交CD 的延长线于点F . 求证:AB =FC .【例3】如图①,△ABC ≌△DEF ,将△ABC 和△DEF 的顶点B 和顶点E 重合,把△DEF 绕点B 顺时针方向旋转,这时AC 与DF 相交于点O .⑴当△DEF 旋转至如图②位置,点B (E )、C 、D 在同一直线上时,∠AFD 与∠DCA 的数量关系是________________;⑵当△DEF 继续旋转至如图③位置时,⑴中的结论成立吗?请说明理由_____________.【解法指导】⑴∠AFD =∠DCA⑵∠AFD =∠DCA 理由如下:由△ABC ≌△DEF ,∴AB =DE ,BC =EF , ∠ABC =∠DEF , ∠BAC =∠EDF ∴∠ABC -∠FBC =∠DEF -∠CBF , ∴∠ABF =∠DEC在△ABF 和△DEC 中, AB DE ABF DEC BF EC =⎧⎪=⎨⎪=⎩∠∠∴△ABF ≌△DEC ∠BAF =∠DEC ∴∠BAC -∠BAF =∠EDF -∠EDC , ∴∠FAC =∠CDF∵∠AOD =∠FAC +∠AFD =∠CDF +∠DCA∴∠AFD =∠DCAAFECB DAE第1题图A BCDEBCDO第2题图B (E )OC F 图③DA【变式题组】01.(绍兴)如图,D、E分别为△ABC的AC、BC边的中点,将此三角形沿DE折叠,使点C 落在AB边上的点P处.若∠CDE=48°,则∠APD等于()A.42°B.48°C.52°D.58°02.如图,Rt△ABC沿直角边BC所在的直线向右平移得到△DEF,下列结论中错误的是()A.△ABC≌△DEF B.∠DEF=90°C.AC=DF D.EC=CF03.一张长方形纸片沿对角线剪开,得到两种三角形纸片,再将这两张三角形纸片摆成如下图形式,使点B、F、C、D在同一条直线上.⑴求证:AB⊥ED;⑵若PB=BC,找出图中与此条件有关的一对全等三角形,并证明.【例4】(第21届江苏竞赛试题)已知,如图,BD、CE分别是△ABC的边A C和AB边上的高,点P在BD的延长线,BP=AC,点Q在CE上,CQ=AB.求证:⑴AP=AQ;⑵AP⊥AQ【解法指导】证明线段或角相等,也就是证线段或角所在的两三角形全等.经观察,证AP=AQ,也就是证△APD和△AQE,或△APB和△QAC全等,由已知条件BP=AC,CQ=AB,应该证△APB≌△QAC,已具备两组边对应相等,于是再证夹角∠1=∠2即可. 证AP⊥AQ,即证∠PAQ=90°,∠PAD+∠QAC=90°就可以.证明:⑴∵BD、CE分别是△ABC的两边上的高,∴∠BDA=∠CEA=90°,∴∠1+∠BAD=90°,∠2+∠BAD=90°,∴∠1=∠2.在△APB和△QAC中, 2AB QCBP CA=⎧⎪=⎨⎪=⎩∠1∠∴△APB≌△QAC,∴AP=AQE FBACDG第2题图21ABCPQEFD⑵∵△APB ≌△QAC ,∴∠P =∠CAQ , ∴∠P +∠PAD =90° ∵∠CAQ +∠PAD =90°,∴AP ⊥AQ 【变式题组】01.如图,已知AB =AE ,∠B =∠E ,BA =ED ,点F 是CD 的中点,求证:02.直距离MA 为am ,此时梯子的倾斜角为75°,如果梯子底端不动,顶端靠在对面的墙上,此时梯子顶端距地面的垂直距离NB 为bm ,梯子倾斜角为45°,这间房子的宽度是( )A .2a bm + B .2a bm - C .bm D .am03.如图,已知五边形ABCDE 中,∠ ABC =∠AED =90°,AB =CD =AE =BC +DE =2,则五边形ABCDE 的面积为__________演练巩固·反馈提高01.(海南)已知图中的两个三角形全等,则∠α度数是( )A .72°B .60°C .58°D .50°02.如图,△ACB ≌△A /C /B /,∠ BCB /=30°,则∠ACA /的度数是( )A .20°B .30°C .35°D .40° 03.(牡丹江)尺规作图作∠AOB 的平分线方法如下:以O 为圆心,任意长为半径画弧交OA 、OB 于C 、D ,再分别以点C 、D 为圆心,以大于12CD 长为半径画弧,两弧交于点P ,作射线OP ,由作法得△OCP ≌△ODP 的根据是( )AECBA 75° C45° BNM第2题图第3题图D第1题图a αcca50° b72° 58°A .SASB .ASAC .AASD .SSS 04.(江西)如图,已知AB =AD ,那么添加下列一个条件后,仍无法判定△ABC ≌△ADC 的是( )A . CB =CD B .∠BAC =∠DAC C . ∠BCA =∠DCAD .∠B =∠D =90°05.有两块不同大小的等腰直角三角板△ABC 和△BDE ,将它们的一个锐角顶点放在一起,将它们的一个锐角顶点放在一起,如图,当A 、B 、D 不在一条直线上时,下面的结论不正确的是( )A . △ABE ≌△CBDB . ∠ABE =∠CBDC . ∠ABC =∠EBD =45° D . AC ∥BE06.如图,△ABC 和共顶点A ,AB =AE ,∠1=∠2,∠B =∠E . BC 交AD 于M ,DE 交AC 于N ,小华说:“一定有△ABC ≌△AED .”小明说:“△ABM ≌△AEN .”那么( ) A . 小华、小明都对 B . 小华、小明都不对 C . 小华对、小明不对 D .小华不对、小明对07.如图,已知AC =EC , BC =CD , AB =ED ,如果∠BCA =119°,∠ACD =98°,那么∠ECA 的度数是___________.08.如图,△ABC ≌△ADE ,BC 延长线交DE 于F ,∠B =25°,∠ACB =105°,∠DAC =10°,则∠DFB 的度数为_______.09.如图,在Rt △ABC 中,∠C =90°, DE ⊥AB 于D , BC =BD . AC =3,那么AE +DE =______10.如图,BA ⊥AC , CD ∥AB . BC =DE ,且BC ⊥DE ,若AB =2, CD =6,则AE =_____. 11.如图, AB =CD , AB ∥CD . BC =12cm ,同时有P 、Q 两只蚂蚁从点C 出发,沿CB 方向爬行,P 的速度是0.1cm /s , Q 的速度是0.2cm /s . 求爬行时间t 为多少时,△APB ≌△QDC .DA C .Q P.BA E FB DC 12.如图, △ABC 中,∠BCA =90°,AC =BC ,AE 是BC 边上的中线,过C 作CF ⊥AE ,垂足为F ,过B 作BD ⊥BC 交CF 的延长线于D . ⑴求证:AE =CD ;⑵若AC =12cm , 求BD 的长.13.(吉林)如图,AB =AC ,AD ⊥BC 于点D ,AD 等于AE ,AB 平分∠DAE 交DE 于点F , 请你写出图中三对全等三角形,并选取其中一对加以证明.14.如图,将等腰直角三角板ABC的直角顶点C 放在直线l 上,从另两个顶点A 、B 分别作l 的垂线,垂足分别为D 、E .⑴找出图中的全等三角形,并加以证明; ⑵若DE =a ,求梯形DABE 的面积.(温馨提示:补形法)15.如图,AC ⊥BC , AD ⊥BD , AD =BC ,CE ⊥AB ,DF ⊥AB ,垂足分别是E 、F .求证:CE =DF .16.我们知道,两边及其中一边的对角分别对应相等的两个三角形不一定全等,那么在什么情况下,它们会全等? ⑴阅读与证明:对于这两个三角形均为直角三角形,显然它们全等;对于这两个三角形均为钝角三角形,可证明它们全等(证明略); 对于这两个三角形均为锐角三角形,它们也全等,可证明如下;已知△ABC 、△A 1B 1C 1均为锐角三角形,AB =A 1B 1,BC =B 1C 1,∠C =∠C 1.求证:△ABC ≌△A 1B 1C 1.(请你将下列证明过程补充完整)⑵归纳与叙述:由⑴可得一个正确结论,请你写出这个结论.ABCDA 1B 1C 1D 1D B A C EF A E B F D CAEF C DB 培优升级·奥赛检测01.如图,在△ABC 中,AB =AC ,E 、F 分别是AB 、AC 上的点,且AE =AF ,BF 、CE 相交于点O ,连接AO 并延长交BC 于点D ,则图中全等三角形有( ) A .4对 B .5对 C .6对 D .7对02.如图,在△ABC 中,AB =AC ,OC =OD ,下列结论中:①∠A =∠B ②DE =CE ,③连接DE , 则OE 平分∠AOB ,正确的是( ) A .①② B .②③ C .①③ D .①②③03.如图,A 在DE 上,F 在AB 上,且AC =CE , ∠1=∠2=∠3, 则DE 的长等于()A .DCB . BC C . ABD .AE +AC04.下面有四个命题,其中真命题是( )A .两个三角形有两边及一角对应相等,这两个三角形全等B .两边和第三边上的高对应相等的两个三角形全等C . 有一角和一边对应相等的两个直角三角形全等D . 两边和第三边上的中线对应相等的两个三角形全等05.在△ABC 中,高AD 和BE 所在直线相交于H 点,且BH =AC ,则∠ABC =_______.06.如图,EB 交AC 于点M , 交FC 于点D , AB 交FC 于点N ,∠E =∠F =90°,∠B =∠C , AE=AF . 给出下列结论:①∠1=∠2;②BE =CF ; ③△ACN ≌△ABM ; ④CD =DB ,其中正确的结论有___________.(填序号)07.如图,AD 为在△ABC 的高,E 为AC 上一点,BE 交AD 于点F ,且有BF =AC ,FD =CD .⑴求证:BE ⊥AC ;⑵若把条件“BF =AC ”和结论“BE ⊥AC ”互换,这个命题成立吗?证明你的判定.08.如图,D 为在△ABC 的边BC 上一点,且CD =AB ,∠BDA =∠BAD ,AE 是△ABD 的中线.求证:AC =2AE .09.如图,在凸四边形ABCD 中,E 为△ACD 内一点,满足AC =AD ,AB =AE , ∠BAE +∠BCEABE D CF第6题图2 1AB CE N M3 21ADEBC FADECOA E O BFCD 第1题图B第2题图第3题图AB C DEAEBDC=90°, ∠BAC =∠EAD .求证:∠CED =90°.10.(沈阳)将两个全等的直角三角形ABC 和DBE 按图①方式摆放,其中∠ACB =∠DEB =90°,∠A =∠D =30°,点E 落在AB 上,DE 所在直线交AC 所在直线于点F .⑴求证:AF +EF =DE ;⑵若将图①中△DBE 绕点B 顺时针方向旋转角α,且0°<α<60°,其他条件不变,请在图②中画出变换后的图形,并直接写出(1)中结论是否仍然成立;⑶若将图①中△DBE 绕点B 按顺时针方向旋转角β,且60°<β<180°,其他条件不变,如图③你认为(1)中结论还成立吗?若成立,写出证明过程;若不成立,请写出此时AF 、EF 与DE 之间的关系,并说明理由。
浙教版八年级下册数学第五章特殊平行四边形之 矩形、菱形、正方形(无答案)

初二下数学第9讲---矩形、菱形、正方形一、选择题(A组)1.如图,△ABC是等腰三角形,点D是底边BC上异于BC中点的一个点,∠ADE=∠DAC,DE=AC.运用这个图(不添加辅助线)可以说明下列哪一个命题是假命题()A.一组对边平行,另一组对边相等的四边形是平行四边形B.有一组对边平行的四边形是梯形C.一组对边相等,一组对角相等的四边形是平行四边形D.对角线相等的四边形是矩形第1题第2题第3题第4题2.如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是()A.12B.24C.12D.163.如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,垂足为E,连结DF,则∠CDF 等于()A.50°B.60°C.70°D.80°4.如图,在边长为2的正方形ABCD中,点M为边AD的中点,延长MD至点E,使ME=MC,以DE为边作正方形DEFG,点G在边CD上,则DG的长为()A.-1B.3-C.+1D.-1二、填空题5.如图,▱ABCD的顶点B在矩形AEFC的边EF上,点B与点E,F不重合.若△ACD的面积为3,则图中阴影部分两个三角形的面积和为.6.已知菱形ABCD的两条对角线长分别为6和8,M,N分别是边BC,CD的中点,P是对角线BD上一点,则PM+PN的最小值=.7.如图,四边形ABCD是矩形,点E在线段CB的延长线上,连结DE交AB于点F,∠AED=2∠CED,点G是DF的中点,若BE=1,AG=4,则AB的长为.三、解答题8.已知:如图1,在面积为3的正方形ABCD中,E,F分别是BC和CD边上的两点,AE⊥BF于点G,且BE=1.(1)求证:△ABE≌△BCF.(2)求出△ABE和△BCF重叠部分(即△BEG)的面积.(3)现将△ABE绕点A逆时针方向旋转到△AB′E′(如图2),使点E落在CD边上的点E′处,问△ABE在旋转前后与△BCF重叠部分的面积是否发生了变化?请说明理由.一、选择题(B组)1.如图,把一个长方形的纸片对折两次,然后剪下一个角,为了得到一个钝角为120°的菱形,剪口与第二次折痕所成角的度数应为()A.15°或30°B.30°或45°C.45°或60°D.30°或60°2.如图,矩形ABCD的对角线AC=8cm,∠AOD=120°,则AB的长为()A.cmB.2 cmC.2cmD.4 cm3.如图,已知菱形ABCD的两条对角线相交于点O,若AC=6,BD=4,则菱形ABCD的周长是()A.24B.16C.4D.24.如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF.添加一个条件,仍不能证明四边形BECF为正方形的是()A.BC=ACB.CF⊥BFC.BD=DFD.AC=BF二、填空题5.如图,在四边形ABCD中,对角线AC⊥BD,垂足为O,点E,F,G,H分别为边AD,AB,BC,CD的中点.若AC=8,BD=6,则四边形EFGH的面积为.6.如图,在菱形ABCD中,边AB的垂直平分线与对角线AC相交于点E,∠ABC=140°,∠EDC=.7.如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连结AD1,BC1.若∠ACB=30°,AB=1,CC1=x,△ACD与△A1C1D1重叠部分的面积为S,则下列结论:①△A1AD1≌△CC1B;②当x=1时,四边形ABC1D1是菱形;③当x=2时,△BDD1为等边三角形;其中正确的是(填序号).三、解答题8.如图①,在正方形ABCD中,△AEF的顶点E,F分别在BC,CD边上,高AG与正方形的边长相等,求∠EAF的度数.(2)如图②,在Rt△ABD中,∠BAD=90°,AB=AD,点M,N是BD边上的任意两点,且∠MAN=45°,将△ABM绕点A逆时针旋转90°至△ADH位置,连接NH,试判断MN,ND,DH之间的数量关系,并说明理由.(3)在图①中,连接BD分别交AE,AF于点M,N,若EG=4,GF=6,BM=32,求AG,MN的长.9邻边不相等的平行四边形纸片,剪去一个菱形,余下一个四边形,称为第一次操作;在余下的四边形纸片中再剪去一个菱形,又余下一个四边形,称为第二次操作;……依次类推,若第n次操作余下的四边形是菱形,则称原平行四边形为n阶准菱形.如图1,▱ABCD中,若AB =1,BC =2,则▱ABCD为1阶准菱形.(1)判断与推理:①邻边长分别为2和3的平行四边形是阶准菱形;②小明为了剪去一个菱形,进行如下操作:如图2,把▱ABCD沿BE折叠(点E在AD上),使点A落在BC边上的点F处,得到四边形ABFE.请证明四边形ABFE是菱形.(2)操作、探究与计算:①已知▱ABCD的邻边长分别为1,a(a >1),且是3阶准菱形,请画出▱ABCD及裁剪线的示意图,并在图形下方写出a的值;②已知▱ABCD的邻边长分别为a,b(a>b),满足a=6b+r,b=5r,请写出▱ABCD是几阶准菱形.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第25讲 矩形、菱形【思维入门】1.如图8-25-1所示,菱形ABCD 中,对角线AC ,BD 相交于点O ,H 为AD 边的中点,菱形ABCD 的周长为28,则OH 的长等于 ( )A .3.5B .4C .7D .142.有4个命题:(1)一组对边相等,一组对角相等的四边形是平行四边形; (2)一组对边平行,一组对角相等的四边形是平行四边形;(3)O 是四边形ABCD 内一点,若AO =BO =CO =DO ,则四边形ABCD 是矩形; (4)若四边形的两条对角线互相垂直,则这个四边形是菱形. 其中正确的命题个数是( )A .0B .1C .2D .33.如图8-25-2,在▱ABCD 中,添加下列条件之一能使它成为菱形的是 ()图8-25-2①AC ⊥BD ;②∠BAD =90°; ③AB =BC ;④AC =BD . A .①或③ B .②或③ C .③或④D .①或②或③4.如图8-25-3,在矩形ABCD 中,边AB 的长为3,点E ,F 分别在AD ,BC 上,连结BE ,DF ,EF ,BD ,若四边形BEDF 是菱形,且EF =AE +FC ,则边BC 的长为()图8-25-1图8-25-3 A.2 3 B.3 3C.6 3 D.92 35.如果菱形的两条对角线的长为a和b,且a,b满足(a-1)2+b-4=0,那么菱形的面积等于____.6.已知:如图8-25-4,在▱ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF.(1)求证:△DOE≌△BOF;(2)当∠DOE等于多少度时,四边形BFDE为菱形?请说明理由.图8-25-4【思维拓展】7.如图8-25-5,在矩形ABCD中,点E,F分别在边AB,BC上,且AE=13AB.将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连结BP交EF于点Q.对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是()图8-25-5A.①②B.②③C.①③D.①④8.如图8-25-6,矩形ABCD中,AB=60,BD=BC+23CD,则BC=______.图8-25-69.如图8-25-7,已知矩形ABCD,把矩形沿直线AC折叠,点B落在点E处,连结DE,BE,若△ABE是等边三角形,则S△DCES△ABE=____.图8-25-710.如图8-25-8,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连结CF.(1)求证:AF=DC;(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.图8-25-811.某校九年级学习小组在探究学习过程中,用两块完全相同的且含60°角的直角三角板ABC与AFE按如图8-25-9①所示位置放置,现将Rt△AEF绕A点按逆时针方向旋转角α(0°<α<90°),如图8-25-9②,AE与BC交于点M,AC与EF交于点N,BC与EF交于点P.(1)求证:AM=AN;(2)当旋转角α=30°时,四边形ABPF是什么样的特殊四边形?并说明理由.图8-25-912.定义:我们把三角形被一边中线分成的两个三角形叫做“友好三角形”.性质:如果两个三角形是“友好三角形”,那么这两个三角形的面积相等.理解:如图8-25-10①,在△ABC 中,CD 是AB 边上的中线,那么△ACD 和△BCD 是“友好三角形”,并且S △ACD =S △BCD .应用:如图8-25-10②,在矩形ABCD 中,AB =4,BC =6,点E 在AD 上,点F 在BC 上,AE =BF ,AF 与BE 交于点O . (1)求证:△AOB 和△AOE 是“友好三角形”;(2)连结OD ,若△AOE 和△DOE 是“友好三角形”,求四边形CDOF 的面积. 探究:在△ABC 中,∠A =30°,AB =4,点D 在线段AB 上,连结CD , △ACD 和△BCD 是“友好三角形”,将△ACD 沿CD 所在直线翻折,得到 △A ′CD ,若△A ′CD 与△ABC 重合部分的面积等于△ABC 面积的14,请直接写出△ABC 的面积.图8-25-10 【思维升华】13.菱形的两条对角线之和为L ,面积为S ,则它的边长为( )A.12L 2-4SB.12L 2-2S C.122L -4SD.124S -L 214.如图8-25-11,四边形ABCD 中,∠BAD =60°,∠ABC =30°,AB =6,AD =CD ,AB ∥CD ,那么BD 的长度是 ( )图8-25-11A .7B .4C .27D .4 215.如图8-25-12,将两个长为8,宽为2的矩形透明塑料片交叉摆放,重叠部分是菱形ABCD,当两个塑料片不重合但有一条对角线重合时,菱形ABCD的周长最大,这个最大值是____.图8-25-1216.如图8-25-13,在平面直角坐标系xOy中,多边形OABCDE的顶点坐标分别是O(0,0),A(0,6),B(4,6),C(4,4),D(6,4),E(6,0).若直线l经过点M(2,3),且将多边形OABCDE分割成面积相等的两部分,则直线l的函数表达式是____.图8-25-13第25讲矩形、菱形【思维入门】1.如图8-25-1所示,菱形ABCD中,对角线AC,BD相交于点O,H为AD边的中点,菱形ABCD的周长为28,则OH的长等于(A)A.3.5B.4C.7D.142.有4个命题:(1)一组对边相等,一组对角相等的四边形是平行四边形; (2)一组对边平行,一组对角相等的四边形是平行四边形;(3)O 是四边形ABCD 内一点,若AO =BO =CO =DO ,则四边形ABCD 是矩形; (4)若四边形的两条对角线互相垂直,则这个四边形是菱形. 其中正确的命题个数是( B )A .0B .1C .2D .3【解析】 (1)一组对边相等,一组对角相等的四边形是平行四边形,不能证明另一组对边也相等或平行,故(1)错误;(2)一组对边平行,一组对角相等的四边形是平行四边形,可证出另一组对边也平行,故(2)正确;(3)O 是四边形ABCD 内一点,若AO =BO =CO =DO ,则四边形ABCD 是矩形,只有点O 是四边形ABCD 对角线的交点时,上述说法才成立,故(3)错误; (4)若四边形的两条对角线平分且互相垂直,则这个四边形是菱形,故(4)错误. 3.如图8-25-2,在▱ABCD 中,添加下列条件之一能使它成为菱形的是 ( A)图8-25-2①AC ⊥BD ;②∠BAD =90°; ③AB =BC ;④AC =BD . A .①或③ B .②或③ C .③或④D .①或②或③4.如图8-25-3,在矩形ABCD 中,边AB 的长为3,点E ,F 分别在AD ,BC 上,连结BE ,DF ,EF ,BD ,若四边形BEDF 是菱形,且EF =AE +FC ,则边BC 的长为( B)图8-25-1图8-25-3A .2 3B .3 3C .6 3D.92 3【解析】 ∵四边形ABCD 是矩形, ∴∠ABC =90°,∵四边形BEDF 是菱形, ∴EF ⊥BD ,∠EBO =∠DBF .∵EF =AE +FC ,AE =CF ,EO =FO , ∴AE =EO =CF =FO .∴AB =BO =3,∠ABE =∠EBO ,∴∠ABE =∠EBD =∠DBC =30°,BE =2 3. ∴BF =BE =2 3. ∴CF =AE = 3. ∴BC =BF +CF =3 3.5.如果菱形的两条对角线的长为a 和b ,且a ,b 满足(a -1)2+b -4=0,那么菱形的面积等于__2__.【解析】 由题意,得a -1=0,b -4=0,解得a =1,b =4. ∵菱形的两条对角线的长为a 和b , ∴菱形的面积=12×1×4=2.6.已知:如图8-25-4,在▱ABCD 中,O 为对角线BD 的中点,过点O 的直线EF 分别交AD ,BC 于E ,F 两点,连结BE ,DF . (1)求证:△DOE ≌△BOF ;(2)当∠DOE 等于多少度时,四边形BFDE 为菱形?请说明理由.图8-25-4解:(1)证明:∵在▱ABCD 中,O 为对角线BD 的中点,∴BO =DO ,∠EDB =∠FBO , 在△DOE 和△BOF 中, ⎩⎪⎨⎪⎧∠EDO =∠FBO ,DO =BO ,∠EOD =∠FOB , ∴△DOE ≌△BOF (ASA ).(2)当∠DOE =90°时,四边形BFDE 为菱形. 理由:∵△DOE ≌△BOF , ∴BF =DE , 又∵BF ∥DE ,∴四边形EBFD 是平行四边形. ∵BO =DO ,∠EOD =90°, ∴EB =DE .∴四边形BFDE 为菱形.【思维拓展】7.如图8-25-5,在矩形ABCD 中,点E ,F 分别在边AB ,BC 上,且AE =13AB .将矩形沿直线EF 折叠,点B 恰好落在AD 边上的点P 处,连结BP 交EF 于点Q .对于下列结论:①EF =2BE ;②PF =2PE ;③FQ =4EQ ;④△PBF 是等边三角形.其中正确的是( D )图8-25-5 A.①②B.②③C.①③D.①④8.如图8-25-6,矩形ABCD中,AB=60,BD=BC+23CD,则BC=__25____.图8-25-69.如图8-25-7,已知矩形ABCD,把矩形沿直线AC折叠,点B落在点E处,连结DE,BE,若△ABE是等边三角形,则S△DCES△ABE=__13__.图8-25-7【解析】如答图,过E作EM⊥AB于M,交DC于N.第9题答图∵四边形ABCD是矩形,∴DC=AB,DC∥AB,∠ABC=90°.∴MN=BC,EN⊥DC.∵沿AC 折叠,B 和E 重合,△AEB 是等边三角形, ∴∠EAC =∠BAC =30°. 设AB =AE =BE =2a ,则BC =2a 3=233a ,即MN =233a . ∵△ABE 是等边三角形,EM ⊥AB , ∴AM =a ,由勾股定理得EM =(2a )2-a 2=3a ,∴△DCE 的面积是12×DC ×NE =12×2a ×⎝ ⎛⎭⎪⎫3a -233a=33a 2. △ABE 的面积是12AB ×EM =12×2a ×3a =3a 2. ∴S △DCE S △ABE=33a 23a 2=13.10.如图8-25-8,在△ABC 中,AD 是BC 边上的中线,E 是AD 的中点,过点A 作BC 的平行线交BE 的延长线于点F ,连结CF . (1)求证:AF =DC ;(2)若AB ⊥AC ,试判断四边形ADCF 的形状,并证明你的结论.图8-25-8解:(1)证明:∵E 是AD 的中点, ∴AE =ED . ∵AF ∥BC ,∴∠AFE =∠DBE ,∠F AE =∠BDE , ∴△AFE ≌△DBE . ∴AF =DB .∵AD 是BC 边上的中线,∴AF=DC.(2)四边形ADCF是菱形.理由:由(1)知,AF=DC.∵AF∥CD,∴四边形ADCF是平行四边形.又∵AB⊥AC,∴△ABC是直角三角形,∵AD是BC边上的中线,∴AD=12BC=DC.∴平行四边形ADCF是菱形.11.某校九年级学习小组在探究学习过程中,用两块完全相同的且含60°角的直角三角板ABC与AFE按如图8-25-9①所示位置放置,现将Rt△AEF绕A点按逆时针方向旋转角α(0°<α<90°),如图8-25-9②,AE与BC交于点M,AC与EF交于点N,BC与EF交于点P.(1)求证:AM=AN;(2)当旋转角α=30°时,四边形ABPF是什么样的特殊四边形?并说明理由.图8-25-9解:(1)证明:∵∠α+∠EAC=90°,∠NAF+∠EAC=90°,∴∠α=∠NAF.又∵∠B=∠F,AB=AF,∴△ABM≌△AFN,(2)四边形ABPF 是菱形. 理由:∵∠α=30°,∠EAF =90°, ∴∠BAF =120°, 又∵∠B =∠F =60°.∴∠B +∠BAF =60°+120°=180°, ∠F +∠BAF =60°+120°=180°. ∴AF ∥BC ,AB ∥EF ,∴四边形ABPF 是平行四边形. 又∵AB =AF ,∴▱ABPF 是菱形.12.定义:我们把三角形被一边中线分成的两个三角形叫做“友好三角形”. 性质:如果两个三角形是“友好三角形”,那么这两个三角形的面积相等. 理解:如图8-25-10①,在△ABC 中,CD 是AB 边上的中线,那么△ACD 和△BCD 是“友好三角形”,并且S △ACD =S △BCD .应用:如图8-25-10②,在矩形ABCD 中,AB =4,BC =6,点E 在AD 上,点F 在BC 上,AE =BF ,AF 与BE 交于点O . (1)求证:△AOB 和△AOE 是“友好三角形”;(2)连结OD ,若△AOE 和△DOE 是“友好三角形”,求四边形CDOF 的面积. 探究:在△ABC 中,∠A =30°,AB =4,点D 在线段AB 上,连结CD , △ACD 和△BCD 是“友好三角形”,将△ACD 沿CD 所在直线翻折,得到 △A ′CD ,若△A ′CD 与△ABC 重合部分的面积等于△ABC 面积的14,请直接写出△ABC 的面积.图8-25-10 解:(1)证明:∵四边形ABCD为矩形,∴AD∥BC,∴∠EAO=∠BFO,又∵∠AOE=∠FOB,AE=BF,∴△AOE≌△FOB,∴EO=BO.∴△AOB和△AOE是“友好三角形”.(2)∵△AOE和△DOE是“友好三角形”,∴S△AOE=S△DOE,AE=ED=12AD=3.∵△AOB和△AOE是“友好三角形”,∴S△AOB=S△AOE.∵△AOE≌△FOB,∴S△AOE=S△FOB,∴S△AOD=S△ABF,∴S四边形CDOF=S矩形ABCD-2S△ABF=4×6-2×12×4×3=12.探究:2或2 3.【思维升华】13.菱形的两条对角线之和为L,面积为S,则它的边长为(A)A.12L2-4S B.12L2-2SC.122L-4S D.124S-L2【解析】设边长为m,一条对角线为2a,另外一条为2b,则a+b=12L,2ab=S.∵m 2=a 2+b 2=(a +b )2-2ab =14L 2-S . ∴m =12L 2-4S .14.如图8-25-11,四边形ABCD 中,∠BAD =60°,∠ABC =30°,AB =6,AD =CD ,AB ∥CD ,那么BD 的长度是 ( C )图8-25-11A .7B .4C .27D .4 2【解析】 如答图,过点C 作CE ∥AD 交AB 于E ,过点D 作DF ⊥AB 于F , 则四边形ADCE 是菱形,第14题答图∠CEB =∠A =60°. ∵∠ABC =30°∴AD =EC =DC =AE =12BE . ∵AB =6,∴AD =EC =DC =AE =2. ∴AF =1,DF =3,BF =5. 由勾股定理得BD =27.15.如图8-25-12,将两个长为8,宽为2的矩形透明塑料片交叉摆放,重叠部分是菱形ABCD ,当两个塑料片不重合但有一条对角线重合时,菱形ABCD 的周长最大,这个最大值是__17__.图8-25-12【解析】当两个塑料片如答图所示放置时,菱形周长最大,设这时菱形的边长为x,在Rt△AEB中,第15题答图由勾股定理得x2=(8-x)2+22,解得x=17 4.∴4x=17.即菱形的最大周长为17.16.如图8-25-13,在平面直角坐标系xOy中,多边形OABCDE的顶点坐标分别是O(0,0),A(0,6),B(4,6),C(4,4),D(6,4),E(6,0).若直线l经过点M(2,3),且将多边形OABCDE分割成面积相等的两部分,则直线l的函数表达式是__y=-1 3x+113__.图8-25-13【解析】如答图,延长BC交x轴于点F,连结OB,AF,连结CE,DF相交于点N.第16题答图由已知得点M (2,3)是OB ,AF 的中点,即点M 为矩形ABFO 的中心,所以直线l 把矩形ABFO 分成面积相等的两部分.又因为点N (5,2)是矩形CDEF 的中心,所以过点N (5,2)的直线把矩形CDEF 分成面积相等的两部分.于是,直线MN 即为所求的直线l .设直线l 的函数表达式为y =kx +b ,则 ⎩⎪⎨⎪⎧2k +b =3,5k +b =2,解得 ⎩⎪⎨⎪⎧k =-13,b =113.故所求直线l 的函数表达式为y =-13x +113.。
