试验设计习题与答案
实验设计练习题-1
实例:1. 试验不同配方的减肥药a1和a2,28名肥胖自愿者参与试验。
以服用减肥药4周后体重下降值为观察指标。
采用何种设计方案?试述该设计步骤。
2.欲研究A、B两种高血压病治疗方案的疗效有无差别。
现将20名高血压患者随机分为两组,其中10名患者以A-B-A的顺序接受治疗;另外10名患者则以B-A-B顺序治疗。
采用该种设计?需要考虑哪些问题?3.比较5种不同剂量的甲状腺素对豚鼠甲状腺体重量的影响,考虑到豚鼠种系与体重对结果的影响。
选用何种设计方案,请叙述设计步骤及应用条件,并回答统计分析后能获得哪些结论?4. 利血平可以使小鼠脑中去甲肾上腺素(NE)等递质下降,现考察某种新药MWC是否具有对抗利血平使递质下降的作用,将24只小鼠随机等分为四组,并分别给予蒸馏水、利血平、MWC、利血平+MWC四种不同处理后,测得脑中NE的含量(ng/g湿组织),该资料属于何种设计方案,其统计分析结果可以回答哪些问题?5.某医生欲比较饮食疗法与某种药物疗法对降低血清胆固醇含量的疗效,选择40名高血脂病人,设立四个组:①正常饮食②饮食疗法组③药物组④药物+饮食疗法组。
问:①该设计属何种设计方案?②其统计分析结果可以回答哪些问题?6. 试述正交设计与析因设计的联系与区别。
L18(37)的含义。
正交表中的每列可作哪些安排?7.研究A、B、C三因素的主效应,三个因素均为2水平。
同时要研究交互作用A×C,B×C,请用L8(27)正交表做表头设计(若将第一列作为空列)。
L8(27)正交表列号试验号1 2 3 4 5 6 71 1 1 1 1 1 1 12 1 1 1 2 2 2 23 1 2 2 1 1 2 24 1 2 2 2 2 1 15 2 1 2 1 2 1 26 2 1 2 2 1 2 17 2 2 1 1 2 2 18 2 2 1 2 1 1 2L8(27)二列间的交互作用表列号1 2 3 4 5 6 7列号(1) 3 2 5 4 7 6 (2) 1 6 7 4 5(3)7 6 5 4(4) 1 2 3(5) 3 2(6) 1答:列号 1 2 3 4 5 6 7因素 A B C A×C B×C列号 1 2 3 4 5 6 7因素 C A B A×C B×C8. 试述序贯试验设计的优缺点,哪些情况不适合用序贯试验设计?9.将20名药物依赖患者随机等分为两组,分别用消瘾扶正胶囊和可乐定治疗,每位患者分别在治疗前、治疗后一天、2天、3天、4天、5天测量其舒张压,该资料为何种设计?其统计分析的总变异是如何划分的?10.在某细胞实验研究中,使用两种不同浓度,两种培养温度,两种培养时间,两种培养基,若选择最优实验条件,请回答:(1)可采用何种实验设计?(2)陈述该设计的步骤?(3)该设计的统计分析可获得哪些结论?11.某医生研究肺癌根治手术后采用化学疗法和免疫疗法是否可以提高疗效?何者为优?它们之间有无交互作用?采用何种设计方法?12.选择20名支气管哮喘现症患者,比较舒喘平和舒喘宁的临床平喘效果,用第一秒通气量FEV为观察指标,请问可用哪些设计方案,以何种方案为最理想。
试验设计和数据分析第一次作业习题答案解析

习题答案1.设用三种方法测定某溶液时,得到三组数据,其平均值如下:x1̅=(1.54±0.01)mol/Lx2̅=(1.7±0.2)mol/Lx3̅=(1.537±0.005)mol/L试求它们的加权平均值。
解:根据数据的绝对误差计算权重:w1=10.012,w2=10.22,w3=10.0052因为w1:w2:w3=400:1:1600所以w̅̅̅=1.54×400+1.7×1+1.537×1600400+1+1600=1.5376812.试解释为什么不宜用量程较大的仪表来测量数值较小的物理量。
答:因为用量程较大的仪表来测量数值较小的物理量时,所产生的相对误差较大。
如3.测得某种奶制品中蛋白质的含量为(25.3±0.2)g/L,试求其相对误差。
解:E w=∆ww =0.225.3=0.79%4.在测定菠萝中维生素C含量的测试中,测得每100g菠萝中含有18.2mg维生素C,已知测量的相对误差为0.1%,试求每100g菠萝中含有维生素C的质量范围。
解:E w=∆ww=0.1%,所以∆m=m×E w=18.2×0.1%=0.0182ww所以m的范围为18.1818mg<m<18.2182ww或依据公式w w=w×(1±|w w|)=18.2×(1±0.1%)mg5.今欲测量大约8kPa(表压)的空气压力,试验仪表用1)1.5级,量程0.2MPa 的弹簧管式压力表;2)标尺分度为1mm的U型管水银柱压差计;3)标尺分度为1mm的U形管水柱压差计。
求最大绝对误差和相对误差。
解:1)压力表的精度为1.5级,量程为0.2MPa,则|∆w|www=0.2×1.5%=0.003www=3wwww w=∆ww×100%=38×100%=3.75×10−1=37.5%2)1mm汞柱代表的大气压为0.133KPa,所以|∆w|www=0.133wwww w=∆ww×100%=0.1338×100%=1.6625×10−2=1.6625%3)1mm水柱代表的大气压:ρgh,其中g=9.80665m/s2,通常取g=9.8m/s2则|∆w|www=9.8×10−3wwww w=∆ww×100%=9.8×10−38×100%=1.225×10−36.在用发酵法生产赖氨酸的过程中,对产酸率(%)作6次评定。
实验设计方法课后习题答案46章

▪ 习题不能用正交表78(2)L ,因为会产生混杂。
需选用正交表1516(2)L 。
表头设计如下:▪ 说明:也可有其他不同的表头设计(试验方案)。
▪ 习题 由于1AB C D A B A C B C f f f f f f f ⨯⨯⨯=======, 7f =总,故可选用正交表78(2)L ,且不会产生混杂。
表头设计如下:根据直观分析结果,因素的主次顺序为:AXB AXC C B BXC A D A 与B 的二元表,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,A 与C 的二元表,▪根据A与B的二元表,A1 B2的效果最好;▪根据A与C的二元表,A1 C2的效果最好;▪从直观分析结果可以得到,D1效果最好;▪故最优生产条件为:A1 B2 C2 D1▪(3)方差分析由于没有误差列,故不能对各因素进行显著性检验。
但是,我们选择离差平方和最小的因素D所在的列作为误差列,对各因素进行显著性检验,得到结果如下:因素的主次顺序与直观分析的一样,从显著性来看,只有AXB显著,其他的因素或交互作用都不显著。
▪习题其中A ×B 的离差平方和349.85222.29632.148A B SS SS SS ⨯=+=+=A ×B 的自由度,,,,,,344A B f f f ⨯=+=32.14841.973 5.14024.446A B F ⨯==<故A ×B 不显著。
B ×C 的离差平方和81134.7417.6342.371B C SS SS SS ⨯=+=+=B ×C 的自由度,,,,,,8114B C f f f ⨯=+=42.3714 2.601 5.14024.446B CF ⨯==<故B ×C 不显著。
▪ 因素的主次顺序(根据极差大小或F 值大小) A D F BXC AXB B E C ▪ 最优工艺条件的确定:可以根据直观分析结果选择每个因素的最优水平,得到最优工艺条件为:,,,,,,,,,,,,,,,A1,D1,F1,E0,B0,C0,,.,,,,,,,,,,也可以计算各因素的水平效应 根据水平效应来确定,具体如下: 对于因素A ,,,,115221319ˆ9.148927927A K T a=-=-= 224251319ˆ 1.630927927A K T a =-=-=-333721319ˆ7.519927927A K T a =-=-=-故A 的第1水平的效应最大。
试验设计习题答案

试验设计习题答案试验设计习题答案试验设计是科学研究中非常重要的一部分,它能够帮助研究者确定实验的设计和分析方法,从而得到准确可靠的研究结果。
在本文中,我们将讨论一些试验设计习题,并给出相应的答案。
1. 一个研究人员想要测试一种新的药物对高血压患者的疗效。
他随机选择了100名高血压患者,并将其分为两组,一组接受新药物治疗,另一组接受安慰剂治疗。
研究人员在治疗前和治疗后测量了每个患者的血压水平。
请问,这个实验设计的类型是什么?答案:这个实验设计是一个随机对照试验。
研究人员通过随机选择和分组的方式来进行实验,其中一组接受新药物治疗,另一组接受安慰剂治疗。
通过比较两组患者在治疗前后的血压水平,研究人员可以评估新药物的疗效。
2. 一家汽车制造公司想要测试一种新的发动机油对汽车性能的影响。
他们选择了10辆同型号的汽车,并将其分为两组,一组使用新发动机油,另一组使用传统发动机油。
然后,他们在相同的测试条件下,测量了每辆汽车的油耗和马力输出。
请问,这个实验设计的类型是什么?答案:这个实验设计是一个配对设计。
研究人员选择了同型号的汽车,并将其分为两组,一组使用新发动机油,另一组使用传统发动机油。
通过在相同的测试条件下进行测量,研究人员可以直接比较两种发动机油对油耗和马力输出的影响,消除了其他因素的干扰。
3. 一位心理学家想要研究音乐对人的情绪的影响。
他随机选择了50名志愿者,并将其分为两组,一组听快节奏的音乐,另一组听慢节奏的音乐。
然后,他们填写了一份情绪问卷。
请问,这个实验设计的类型是什么?答案:这个实验设计是一个因子设计。
研究人员通过随机选择和分组的方式来进行实验,其中一组听快节奏的音乐,另一组听慢节奏的音乐。
通过比较两组志愿者在填写情绪问卷时的得分,研究人员可以评估音乐对人的情绪的影响。
4. 一位农学家想要研究不同施肥方法对玉米产量的影响。
他随机选择了100块农田,并将其分为四组,分别使用不同的施肥方法。
然后,他们测量了每块农田的玉米产量。
实验设计与数据处理第三四五章例题及课后习题答案

试验号 x1 1 2 3 4 5 6 7
总和 平均
x2 1 1.4 1.8 2.2 2.6 3 3.4 15.4 2.2
L11
4.48L22252源自L337L12
16.8
L23
10.5
L31
1.4
L1y
0.2404
L2y
0.564
L3y
0.5245
检验线性回归方程的显著性
(1)F检验
SSt
SSr
标准误差 0.001341014 0.006113002
t Stat
P-value
-210.877979 2.86E-16
88.77758147 2.89E-13
例4-8 xi yi
i
xi
1
2
3
4
5
6
7
8
9
SUM
yi 1 3 4 5 6 7 8 9 10 53
1 2
x1 2 7 8 10 11 12 10 9 8 77
L22
800
L33
8
P1
0.315761009
P2
0.412918242
P3
0.850125793
t1
7.505553499
t2
9.814954576
t3
20.20725942
例4-7
p/atm M/(mol/min)
2.01 0.763
1.78 0.715
1.75 0.71
1.73 0.695
x
y
t Stat
P-value
3.941801374 0.016934
7.505553499 0.001686
试验设计及数据分析第一次作业习题答案

习题答案1.设用三种方法测定某溶液时,得到三组数据,其平均值如下:x1̅̅̅=(1.54±0.01)mol/Lx2̅̅̅=(1.7±0.2)mol/Lx3̅̅̅=(1.537±0.005)mol/L试求它们的加权平均值。
解:根据数据的绝对误差计算权重:w1=10.012,w2=10.22,w3=10.0052因为w1:w2:w3=400:1:1600所以w̅=1.54×400+1.7×1+1.537×1600400+1+1600=1.5376812.试解释为什么不宜用量程较大的仪表来测量数值较小的物理量。
答:因为用量程较大的仪表来测量数值较小的物理量时,所产生的相对误差较大。
如3.测得某种奶制品中蛋白质的含量为(25.3±0.2)g/L,试求其相对误差。
解:E w=∆ww =0.225.3=0.79%4.在测定菠萝中维生素C含量的测试中,测得每100g菠萝中含有18.2mg维生素C,已知测量的相对误差为0.1%,试求每100g菠萝中含有维生素C的质量范围。
解:E w=∆ww=0.1%,所以∆m=m×E w=18.2×0.1%=0.0182ww所以m的范围为18.1818mg<m<18.2182ww或依据公式w w=w×(1±|w w|)=18.2×(1±0.1%)mg5.今欲测量大约8kPa(表压)的空气压力,试验仪表用1)1.5级,量程0.2MPa 的弹簧管式压力表;2)标尺分度为1mm的U型管水银柱压差计;3)标尺分度为1mm的U形管水柱压差计。
求最大绝对误差和相对误差。
解:1)压力表的精度为1.5级,量程为0.2MPa,则|∆w|www=0.2×1.5%=0.003www=3wwww w=∆w w×100%=38×100%=3.75×10−1=37.5%2)1mm汞柱代表的大气压为0.133KPa,所以|∆w|www=0.133wwww w=∆w w×100%=0.1338×100%=1.6625×10−2=1.6625%3)1mm水柱代表的大气压:ρgh,其中g=9.80665m/s2,通常取g=9.8m/s2则|∆w|www=9.8×10−3wwww w=∆w w×100%=9.8×10−38×100%=1.225×10−36.在用发酵法生产赖氨酸的过程中,对产酸率(%)作6次评定。
【免费下载】实验设计DOE复习题及答案

DOE Training Test1. 一个32的实验设计意味着我们会有A两个水平, 三个因子B两个水平, 三个因子, 两个中心点C三个水平, 三个因子D三个水平, 两个因子D2.以下哪个不是DOE的目的 ?A,筛选输入变量B,筛选输出变量C,优化输出变量D,确定输入变量的设定范围B3.某个2水平全因子DOE设计包括4个因子(其中之一乃离散属性的)加3个中心点, 6 个复制, 请问如果你执行Minitab 里的Stat >DOE > Factorial > Create Factorial Design .. 你会总共得到多少个运行次数 ?A,99B,100C,98D,102D4.根据以下试验结果,计算AB interaction 的效果(Effect) 为 B Run A B Response15010%12210010%1335020% 9410020%20A ,5B ,10C ,-5D ,0 解答:50,20(9) 100,20 (20) 50,10(12) 100,10(13) AB 交互效果=((12+20)-(9+13))/2=5左对角线之和减去右对角线之和。
B, 时间的main effect 为1.8C,Interaction 为 0.7D, 时间肯定是统计上算显著 A解析:算某个因子的main effect 时,利用它的高水平时的响应值之和减去低水平响应值之和,最后平均。
本例中,temp 高水平950时的响应值为9.9和10.1,低水平850时的响应值为8和12,那么=((9.9+10.1)-(8+12))/2=1.6。
6.与两水平的因子试验相比, 以下哪一个是三水平试验的优点?A.可以评估交互作用B.可以识别曲率C.试验设计可以被扩展(两水平同样可以扩展)D.试验效果的绩效最大B7.以下的哪一种试验设计不能分析交互作用A.部分因子试验设计B.有复制的部分因子试验设计C.有复制的全因子试验设计D.有复制的饱和筛选设计D8. 一个用于优化电子控制模块可靠性的2水平5 因子试验,只复制全因子试验设计次数的一半。
实验设计方法课后习题答案4-6章

▪ 习题4.1不能用正交表78(2)L ,因为会产生混杂。
需选用正交表1516(2)L 。
表头设计如下:▪ 说明:也可有其他不同的表头设计(试验方案)。
▪ 习题4.2 由于1AB C D A B A C B C f f f f f f f ⨯⨯⨯=======, 7f =总,故可选用正交表78(2)L ,且不会产生混杂。
表头设计如下:根据直观分析结果,因素的主次顺序为:AXB AXC C B BXC A D A 与B 的二元表,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,A 与C 的二元表,▪根据A与B的二元表,A1 B2的效果最好;▪根据A与C的二元表,A1 C2的效果最好;▪从直观分析结果可以得到,D1效果最好;▪故最优生产条件为:A1 B2 C2 D1▪(3)方差分析由于没有误差列,故不能对各因素进行显著性检验。
但是,我们选择离差平方和最小的因素D所在的列作为误差列,对各因素进行显著性检验,得到结果如下:因素的主次顺序与直观分析的一样,从显著性来看,只有AXB显著,其他的因素或交互作用都不显著。
▪习题4.3其中A ×B 的离差平方和349.85222.29632.148A B SS SS SS ⨯=+=+=A ×B 的自由度,,,,,,344A B f f f ⨯=+=32.14841.973 5.14024.446A B F ⨯==<故A ×B 不显著。
B ×C 的离差平方和81134.7417.6342.371B C SS SS SS ⨯=+=+=B ×C 的自由度,,,,,,8114B C f f f ⨯=+=42.3714 2.601 5.14024.446B CF ⨯==<故B ×C 不显著。
▪ 因素的主次顺序(根据极差大小或F 值大小) A D F BXC AXB B E C ▪ 最优工艺条件的确定:可以根据直观分析结果选择每个因素的最优水平,得到最优工艺条件为:,,,,,,,,,,,,,,,A1,D1,F1,E0,B0,C0,,.,,,,,,,,,,也可以计算各因素的水平效应 根据水平效应来确定,具体如下: 对于因素A ,,,,115221319ˆ9.148927927A K T a=-=-= 224251319ˆ 1.630927927A K T a =-=-=-333721319ˆ7.519927927A K T a =-=-=-故A 的第1水平的效应最大。
实验设计与数据处理第一章例题及课后习题(附答案)

1、 根据三组数据的绝对误差计算权重:12322211110000,25,400000.010.20.005w w w ====== 因为123::400:1:1600w w w = 所以1.54400 1.71 1.53716001.53840011600pH ⨯+⨯+⨯==++2、 因为量程较大的分度值也较大,用量程大的测量数值较小的物理量会造成很大的系统误差。
3.、含量的相对误差为0.2g ,所以相对误差为:0.20.99790525.3Rx E x ∆===。
4、 相对误差18.20.1%0.0182x mg mg ∆=⨯= 故100g 中维生素C 的质量范围为:18.2±0.0182。
5、1)、压力表的精度为1.5级,量程为0.2,则max 0.2 1.5%0.003330.3758R x MPa KPa x E x ∆=⨯==∆===2)、1的汞柱代表的大气压为0.133,所以max 20.1330.133 1.6625108R x KPax E x -∆=∆===⨯ 3)、1水柱代表的大气压为gh ρ,其中29.8/g m s =则:3max 339.8109.810 1.225108R x KPax E x ---∆=⨯∆⨯===⨯6、样本测定值算术平均值 3.421666667 3.48 几何平均值 3.421406894 3.37 调和平均值 3.421147559 3.47 标准差s 0.046224092 3.38 标准差 0.04219663 3.4 样本方差 0.002136667 3.43 总体方差0.001780556 算住平均误差 0.038333333极差 0.117、依题意,检测两个分析人员测定铁的精密度是否有显著性差异,用F双侧检验。
根据试验值计算出两个人的方差及F值:221221223.733, 2.3033.7331.621232.303s s s F s ===== 而0.9750.025(9,9)0.248386,(9,9) 4.025994F F ==, 所以0.9750.025(9,9)(9,9)F F F <<两个人的测量值没有显著性差异,即两个人的测量方法的精密度没有显著性差异。
试验设计与建模 第二章课后作业答案
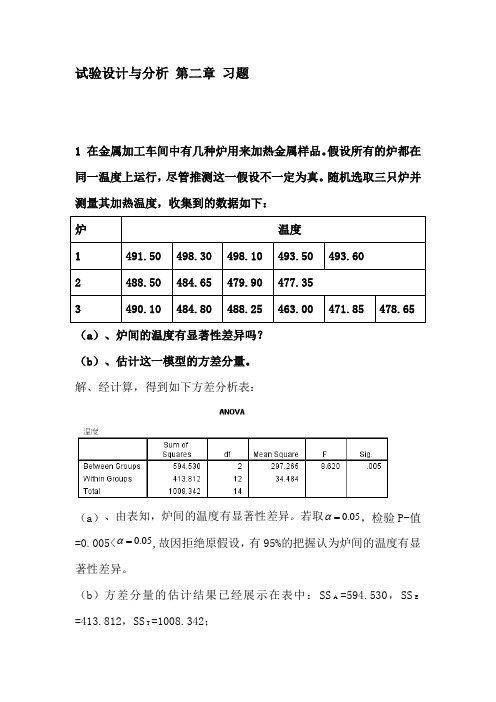
试验设计与分析 第二章 习题1 在金属加工车间中有几种炉用来加热金属样品。
假设所有的炉都在同一温度上运行,尽管推测这一假设不一定为真。
随机选取三只炉并测量其加热温度,收集到的数据如下: 炉 温度1 491.50 498.30 498.10 493.50 493.602 488.50 484.65 479.90 477.353490.10 484.80 488.25 463.00 471.85 478.65(a )、炉间的温度有显著性差异吗? (b )、估计这一模型的方差分量。
解、经计算,得到如下方差分析表:(a )、由表知,炉间的温度有显著性差异。
若取05.0=α,检验P-值=0.005<05.0=α,故因拒绝原假设,有95%的把握认为炉间的温度有显著性差异。
(b )方差分量的估计结果已经展示在表中:SS A =594.530,SS E =413.812,SS T =1008.342;2 纺织厂有很多织布机,设每台织布机每分钟织出同样多的布,为了研究这一假设,随机选取5台织布机并测定它们在不同时间的产量,得出下述数据: 织布机 产量(lb/min) 1 14 14.1 14.2 14 14.1 2 13.9 13.8 13.9 14 143 14.1 14.2 14.1 14 13.9 4 13.6 13.8 14 13.9 13.75 13.813.613.913.814(a )说明为什么这是一种随机效应实验。
这些织布机的产量相等吗?(b )估计织布机间的变异性。
(c )估计实验的误差方差。
(d )给)222σσσττ+(找一个95%的置信区间。
解、(a )因为5台织布机是随机选取的,所以是一种随机效应实验; 经计算,得如下方差分析表:①原假设:H0:织布机不影响产量;H1:织布机影响产量; ②构造统计量:77.5==EMS MS F 处理; ③选定显著性水平:05.0=α;④决策:对于05.0=α,P-值为0.003<05.0=α,故拒绝原假设H0,接受备择假设H1,有95%的把握认为织布机影响产量。
实验设计与数据处理第二章例题及课后习题答案

0
23 23.3 23.6 22.9
30 25 20 15 10 5 0
0
两种高吸水性树脂保水性能比较
5
10
t/h
微波法 常规法
15
10
10
c/(g/L)
η/% He/m
1
系列1
0.1
0
2
4
6
8
10
t/min
例四
qv/(L/s) η/%
0 4 8 12 16 20 24 28 32
He/m
0 24.8 33 24.8 51 24.5 64 23.9 71 23.2 77 21.8 78 20.5 76 18.7 70 16.3
吸附量
/(mg/g)
17.14
AB-8 D-4006 D-101 S-8
NKA-Ⅱ
17.77 1.87 13.71 0.55 13.33 3.67
吸附量/(mg/g)
20 18 16 14 12 10 8 6 4 2 0
DA-201 NKA-9
AB-8 D-4006 D-101 树脂型号
S-8 NKA-Ⅱ
1
5.4
5.8
2
3
4
5
6
5.9
5.8
5.7
24.5 13.3 11.2 10.1
9.5
8.1
ph值
30 25 20 15 10
5 0
0
发酵时间与PH值及残糖量的关系图
5 发酵时间/d
6.1 6 5.9 5.8 5.7 5.6 5.5 5.4 5.3 5.2 10
残糖量 PH值
习题4
树脂型号 DA-201 NKA-9
食品试验设计与统计分析习题答案

2
2
S x1 x2 S1 S 2 =0.2975
n1 n2
t (x1 x2 ) = (x1 x2 ) =6.42
( x1 x2 )
S( x1 x2 )
(4)统计推断。
由α=0.01查附表3, 得t0.01(18)=2.878
实际|u|=6.42>u0.01=2.878, 故P<0.01, 应否定H0, 接 受HA 。说明两种饴糖的还原糖含量有显著差异。
异
HA: μ≠μ0 ,新老工艺有差异
(2)确定显著水平α=0.05
(3)计算统计量t值
t x u0 =0.95 0.91=1.62 自由度 df n 1 8 1 7
Sx
0.07 8
(4)查临界t值,作出统计推断 由df=7,查t值表(附表3)得t0.05(7)=2.365
,因为|t|<t0.05, P>0.05, 故应接受H0, 表明β-胡 萝卜素新老工艺在提取率上无差异。
=1-2Φ(-3) =1-2*0.00135=0.9973
P45/12
设x1~N(70,102), x2~N(85,152), 在x1和x2总体分别随机抽取n1=30和n2=40的两 个样本x 。x求P(∣ 1- 2∣< 10 )=?
x1 - x2 =70-85=-15
x1 - x22
2 1
n1
S=1.2 μg/kg,问这批花生仁的黄曲霉毒素是否超标?
(1) 提出假设。无效假设H0: μ<=μ0= 20μg/kg,即这批花 生仁的黄曲霉毒素没有超标。
备择假设HA: μ>μ0,即这批花生仁的黄曲霉毒素超标。 (2)确定显著水平。α=0.01(单尾概率) (3)构造统计量, 并计算样本统计量值。
试验设计与分析课后习题解答及复习资料

田间试验与统计分析-习题集及解答1.在种田间试验设计方法中,属于顺序排列的试验设计方法为:对比法设计、间比法2.若要控制来自两个方面的系统误差,在试验处理少的情况下,可采用:拉丁方设计3.如果处理内数据的标准差或全距与其平均数大体成比例,或者效应为相乘性,则在进行方差分析之前,须作数据转换。
其数据转换的方法宜采用:对数转换。
4.对于百分数资料,如果资料的百分数有小于30%或大于70%的,则在进行方差分析之前,须作数据转换。
其数据转换的方法宜采用:反正弦转换(角度转换)。
5.样本平均数显著性测验接受或否定假设的根据是:小概率事件实际不可能性原理。
6.对于同一资料来说,线性回归的显著性和线性相关的显著性:一定等价。
7.为了由样本推论总体,样本应该是:从总体中随机地抽取的一部分8.测验回归和相关显著性的最简便的方法为:直接按自由度查相关系数显著表。
9.选择多重比较的方法时,如果试验是几个处理都只与一个对照相比较,则应选择:LSD法。
10.如要更精细地测定土壤差异程度,并为试验设计提供参考资料,则宜采用:空白试验11.当总体方差为末知,且样本容量小于30,但可假设==(两样本所属的总体方差同质)时,作平均数的假设测验宜用的方法为:t测验12.因素内不同水平使得试验指标如作物性状、特性发生的变化,称为:效应13.若算出简单相差系数大于1时,说明:计算中出现了差错。
14.田间试验要求各处理小区作随机排列的主要作用是:获得无偏的误差估计值15.正态分布曲线与轴之间的总面积为:等于1。
16.描述总体的特征数叫:参数,用希腊字母表示;描述样本的特征数叫:统计数,用拉丁字母表示。
17.确定分布偏斜度的参数为:自由度18.用最小显著差数法作多重比较时,当两处理平均数的差数大于LSD0.01时,推断两处理间差异为:极显著19.要比较不同单位,或者单位相同但平均数大小相差较大的两个样本资料的变异度宜采用:变异系数20.选择多重比较方法时,对于试验结论事关重大或有严格要求的试验,宜用:q测验。
实验设计与数据处理习题答案完整版

实验设计与数据处理习题答案完整版实验设计与数据处理是科学研究中非常重要的一环,通过合理的实验设计和数据处理,可以得到准确的实验结果,并从中得出科学结论。
实验设计部分:答:该实验的目的是研究不同光照条件对植物生长的影响。
因变量是植物的生长情况,自变量是光照条件。
实验步骤如下: 1)选择同一种植物作为研究对象。
2)将植物分为三组,分别置于不同的光照条件下:组A为强光照条件,组B为中等光照条件,组C为弱光照条件。
3)每组植物种植在相同的土壤中,并给予相同的水分和养分供应。
4)每天记录植物的生长情况,包括高度、叶片数量等指标。
5)进行一定时间的观察和测量后,比较各组植物的生长情况,得出结论。
数据处理部分:1.对于上述实验,假设我们已经得到了每组植物的生长数据,如何进行数据处理来得出结论?答:首先,我们需要对数据进行描述性统计分析,计算每组植物的平均生长情况、标准差等指标。
然后,我们可以使用方差分析(ANOVA)来比较不同组之间的差异是否显著。
如果ANOVA结果显示差异显著,我们可以进行事后多重比较(如Tukey's HSD test)来确定哪些组之间存在显著差异。
最后,我们可以根据数据和统计分析的结果得出结论,判断不同光照条件对植物生长的影响是否显著。
2.如果实验中有一个组的数据明显偏离其他组,该如何处理?答:如果一个组的数据明显偏离其他组,我们需要先检查该组数据是否存在异常值或错误。
如果没有异常值或错误,我们可以考虑将该组数据排除在统计分析之外,重新进行分析。
如果该组数据确实存在问题,我们可以考虑重新进行实验或者进行更多的观察和测量,以获得更准确的结果。
3.如果实验中的样本量较小,该如何进行数据处理?答:如果实验中的样本量较小,我们可以考虑使用非参数统计方法来进行数据处理。
非参数统计方法不依赖于数据的分布情况,适用于小样本量的情况。
常见的非参数统计方法包括Wilcoxon秩和检验、Mann-Whitney U检验等。
试验设计数据分析第一次作业习题答案

习题答案1.设用三种方法测定某溶液时,得到三组数据,其平均值如下:试求它们的加权平均值.解:根据数据的绝对误差计算权重:由于所以 ----------------------2.试解释为什么不宜用量程较大的仪表来测量数值较小的物理量.答:由于用量程较大的仪表来测量数值较小的物理量时,所产生的相对误差较大.如3.测得某种奶制品中蛋白质的含量为,试求其相对误差.解:- 一4.在测定菠萝中维生素C含量的测试中,测得每100g菠萝中含有18.2mg维生素C,已知测量的相对误差为0.1%,试求每100g菠萝中含有维生素C的质量范围.解: - ,所以所以m的范围为或依据公式5.今欲测量大约8kPa 〔表压〕的空气压力,试验仪表用1〕1.5级,量程0.2MPa的弹簧管式压力表;2〕标尺分度为1mm的U型管水银柱压差计;3〕标尺分度为1mm的U形管水柱压差计.求最大绝对误差和相对误差.解:1〕压力表的精度为1.5级,量程为0.2MPa ,那么2〕 1mm 汞柱代表的大气压为0.133KPa ,所以3〕1mm水柱代表的大气压:,其中,通常取那么6.在用发酵法生产赖氨酸的过程中, 对产酸率〔%〕作6次评定.样本测定值为3.48,3.37 , 3.47, 3.38 , 3.40 , 3.43 ,求该组数据的算术平均值、几何平均值、调和平均值、标准差s、标准差、样本方差、总体方差、算术平均误差和极差.解:数据计算公式计算结果3.48算术平均值-------- 3.4216673.37几何平均值 3.421407调和平均值-------- -----3.473.421148或3.38标准样本差----- -------- --------------- 0.0462243.40总体标准差0.0421973.43样本方差0.002137总体万差0.001781算术平均误差 ----- ------- 0.038333极差0.117.A与B两人用同一种分析方法测定金属钠中的铁,测得铁含量〔〕分别为:分析人员 A : 8.0 , 8.0, 10.0 , 10.0 , 6.0 , 6.0 , 4.0 , 6.0 , 6.0 , 8.0分析人员 B : 7.5 , 7.5, 4.5 , 4.0 , 5.5 , 8.0 , 7.5 , 7.5 , 5.5 , 8.0试问A与B两人测定铁的精密度是否有显著性差异?〔〕解:依题意,检验A与B两人测定铁的精密度是否有显著性差异,采用F双侧检验.根据试验值计算出两种方法的方差以及F值:根据显著性水平, , 查F分布表得, , , .所以, ,,A与B两人测定铁的方差没有显著差异,即两人测定铁的精密度没有显著性差异.分析人员A分析人员B87.587.510 4.51046 5.56847.567.56 5.588F-检验双样本方差分析分析人员A分析人员B平均7.2 6.55力左 3.733333333 2.302778观测值1010df99F 1.621230398P(F<=f)单尾0.24144058F单尾临界 3.1788931048.用新旧两种工艺冶炼某种金属材料,分别从两种冶炼工艺生产的产品中抽样,测定产品中的杂质含量〔%〕,结果如下:旧工艺〔1〕 : 2.69 , 2.28 , 2.57 , 2.30 , 2.23 , 2.42 , 2.61 , 2.64 , 2.72 , 3.02 , 2.45 , 2.95 , 2.51 ;新工艺(2): 2.26 , 2.25 , 2.06 , 2.35 , 2.43 , 2.19 , 2.06 , 2.32 , 2.34 试问新冶炼工艺是否比旧工艺生产更稳定,并检验两种工艺之间是否存在系统误差?〔〕解:工艺的稳定性可用精密度来表征,而精密度可由极差、标准差或方差等表征, 这里依据方差来计算. , ,由于 ,所以新的冶炼工艺比旧工艺生广更稳定.〔依据极差:, ,同样可以得到上述结论〕〔依据标准差, 〕检验两种工艺之间是否存在系统误差,米用t检验法.1〕先判断两组数据的方差是否有显著性差异.根据试验数据计算出各自的平均值和方差:故 _ -------n1=13 , n2=9,那么, ,根据显著性水平,查F分布表得,,两方差有显著差异.旧工艺新工艺2.69 2.262.28 2.252.57 2.062.30 2.352.23 2.432.42 2.192.61 2.062.64 2.322.72 2.343.022.452.952.51F-检验双样本方差分析旧工艺新工艺平均 2.568461538 2.251111111标准差0.242103496 0.128105859方差0.058614103 0.016411111观测值13 9 df 12 8 F 3.571610854P(F<=f)单尾0.039724983F单尾临界 3.283939006t-检验:双样本异方差假设旧工艺新工艺平均 2.568461538 2.251111111力左0.0586141030.016411111观测值139假设平均差0df19t Stat 3.988050168P(T<=t)单尾0.000393697t单尾临界 1.729132812P(T<=t)双尾0.000787395t双尾临界 2.0930240542〕进行异方差t检验根据显著性水平,查单侧t分布表得,所以,那么两种工艺的平均值存在差异,即两种工艺之间存在系统误差.备注:实验方差分析是单侧检验:由于方差分析不像差异显著检验, 方差分析中关心的只是组间均方是否显著大于组内均方或误差均方. 目的是为了区分组间差异是否比组内差异大的多,由于只有大得多,才能证实实验的限制条件是否造成了显著的差异,方差齐性中F检验要用到双侧检验,由于要看的是否有显著性差异,而没有说是要看有差异时到底是谁大于谁,所以没有方向性.9. 用新旧两种方法测得某种液体的黏度〔 〕如下:解:检验新方法是否可行,即检验新方法是否有系统误差,这里采用秩和检验.秩 1234 56.5 6.58 910 11 1213 14 151617 18新 0.730.770.790.810.840.850.870.910.98旧0.74 0.75 0.760.790.800.830.860.920.96此时,n1=9 , n2=9 , n=18 ,对于 ,查秩和临界值表,得 ,,由于 ,故,两组数据无显著差异,新方法无系统误差,可行.新方法:0.73 旧方法:0.760.91 , 0.84 0.92 , 0.860.77, 0.98 0.74 , 0.960.81 , 0.79 0.83 , 0.790.87 , 0.85 0.80 , 0.75其中旧方法无系统误差.试在显著性水平〔 〕时,检验新方法是否可行.T检验成对数据的比拟新方法旧方法di0.730.76-0.030.002075310.910.92-0.010.000653090.840.86-0.020.00126420.770.740.030.000208640.980.960.02 1.9753E-050.810.83-0.020.00126420.790.7900.000241980.870.80.070.00296420.850.750.10.007130860.140.01582222—0.0155560.044472210.34978145n=9 1.04934436计算包括71.38在内的平均值 及标准偏差,查表 法无系统误差,可行. 10 .对同一铜合金,有10个分析人员分析进行分析, 测得其中铜含量〔% 〕的数据为:62.20, 69.49 , 70.30 , 70.65 , 70.82 , 71.03 , 71.22 , 71.25 , 71.33 , 71.38 〔%〕.问这些数据中 哪个〔些〕数据应被舍去,试检验?〔 〕解:1〕拉依达〔P n t 〕检验法 评验62.20计算包括62.20在内的平均值 及标准偏差计算比拟 和,,依据拉依达检验法,当 时,62.20应该舍去.法验69.49计算包括69.49在内的平均值 及标准偏差计算比拟 和, ,依据拉依达检验法,当 时,69.49应该舍去.色院验70.30计算包括70.30在内的平均值 及标准偏差计算比拟 和, ,依据拉依达检验法,当 时,69.49不应该舍去.孕验71.38,即两组数据无显著差异,新方对于2)格拉布斯(Grubbs )检验法⑪验62.20计算包括62.20在内的平均值计算所以62.20应该舍去.聊验69.49计算包括69.49在内的平均值及标准偏差 ,查表得 计算所以69.49应该舍去.验70.30计算包括70.30在内的平均值及标准偏差 ,查表得 计算计算69.49不应该舍去.孕验71.38计算包括71.38在内的平均值及标准偏差 ,查表得 计算计算比拟和, ,依据拉依达检验法,当 时,71.38不应该舍去.及标准偏差 ,查表得计算当时,71.38不应该舍去.3〕狄克逊〔Dixon 〕检验法应用狄克逊双侧情形检验:呵于62.20和71.38 , ,计算当,对于双侧检验,查出临界值,由于 ,且故最小值62.20应该被舍去.须去62.20后,对剩余的9个数据〔n=9〕进行狄克逊双侧检验:当,对于双侧检验,查出临界值,由于 ,且,没有异常值.单侧检验时,查表得到临界值, ,没有异常值.11.将以下数据保存4 位有效数字:3.1459 , 136653 , 2.33050 , 2.7500 , 2.77447解:3.146、1367 X102、2.330、2.750、2.77412.在容量分析中,计算组分含量的公式为,其中V是滴定时消耗滴定液的体积,c是滴定液的浓度.今用浓度为〔1.000也.001 〕mg/mL的标准溶液滴定某试液,滴定时消耗滴定液的体积为〔20.00也.02 〕 mL,试求滴定结果的绝对误差和相对误差.解:根据组分含量计算公式,各变量的误差传递系数分别为所以组分含量的绝对误差为(mg )(mg)最大相对误差为13.在测定某溶液的密度的试验中,需要测定液体的体积和质量,质量测定的相对误差<0.02% ,预使测定结果的相对误差v 0.1%,测量液体体积所允许的最大相对误差为多大? 解:由公式 ,误差传递系数为, -那么绝对误差--——相对误差由于质量的相对误差- ,预使得- ,需要- ,即测量液体体积所允许的最大相对误差为0.08% .。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《试验设计与分析》复习题一、名词解释(15分)1.重复:一个条件值的每一个实现。
或因素某水平值的多次实现。
2.因素:试验中要考虑的可能会对试验结果产生影响的条件。
常用大写字母表示。
3.水平:因素所处的不同状态或数值。
4.处理:试验中各个因素的每一水平所形成的组合 5.响应:试验的结果称为响应;响应函数:试验指标与因素之间的定量关系用模型ε+=),,(1n x x f y Λ表示,其中),,(1n x x f y Λ=是因素的值n x x ,,1Λ的函数,称为响应函数。
6.正交表:是根据均衡分散的思想,运用组合数学理论在拉丁方和正交拉丁方的基础上构造的一种表格。
7.试验指标:衡量试验结果好坏的指标8.随机误差:在试验中总存在一些不可控制的因素,它们的综合作用称为~9.交互作用:一般地说,如果一个因素对试验指标的影响与另一个因素所取的水平有关,就称这两个因素有交互作用。
10.试验设计:是研究如何合理地安排试验,取得数据,然后进行综合的科学分析,从而达到尽快获得最优方案的目的。
11.试验单元:在试验中能施以不同处理的材料单元。
12.拉丁方格:用拉丁字母排列起来的方格,要求每个字母不论在方格的行还是列都只出现一次。
13.综合平衡法:先对各项指标进行分析,找出其较优生产条件,然后将各项指标的较优生产条件综合平衡,找出兼顾各项指标都尽可能好的生产条件的方法。
14.综合评分法:是用评分的方法,将多个指标综合成单一的指标---得分,用每次试验的得分来代表试验的结果,用各号试验的分数作为数据进行分析的方法。
15.信噪比:信号功率与噪声功率之比。
16.并列法:是由相同水平正交表构造水平数不同的正交表的一种方法。
17.拟水平法:是对水平数较少的因素虚拟一些水平使之能排在正交表的多水平列上的一种方法。
18.直和法:是先把一部分因素和水平放在第一正交表上进行试验,如果试验结果达不到要求,再利用第一阶段试验结果提供的信息,在第二正交表上安排下一 阶段的试验,最后再对两正交表上的结果进行统一分析的方法。
19.直积法: 在某些试验设计中,试验因素常可分为几类,为了考察其中某两类因素间的交互作用,常采用的把两类因素所用的两正交表垂直叠在一起进行设计和 分析的一种方法。
20.稳健设计:为了减少质量波动,寻找使得质量波动达到最小的可控因素的水平组合二、简答题(10分)1.试验设计的基本原则是什么?答:一是重复,即一个条件值的每一个实现。
作用是提高估计和检验的精度 二是随机化,是通过试验材料的随机分配及试验顺序的随机决定来实现的 三是区组化,也就是局部控制。
1明确试验目的2选择试验的指标,因素,水平3设计试验方案4实施试验5对获得的数据进行分析和推断。
3.试验设计的相关分析有哪几种?一是相关系数,即用数理统计中的两个量之间的相关程度来分析的一种方法。
二是等级相关,是把数量标志和品质标志的具体体现用等级次序排序,再测定标志等级和标志等级相关程度的一种方法。
有斯皮尔曼等级差相关系数和肯德尔一致相关系数)4.为什么要进行方差分析?方差分析可检验有关因素对指标的影响是否显著,从而可确定要进行试验的因素;另外,方差分析的观点认为,只需对显著因素选水平就行了,不显著的因素原则上可在试验围取任一水平,或由其它指标确定。
5.均匀设计表与正交表,拉丁方设计的关系6.产品的三次设计是什么?产品的三次设计是系统设计,参数设计,容差设计。
三、(15分)1.写出所有3阶拉丁方格,并指出其中的标准拉丁方格和正交拉丁方格再将这六个的第一行不动,分别交换第二,三行又得到六个,共12个。
上面这个是标准拉丁方格,它和由它交换第二,三行得到的拉丁方格是正交的。
2.说明正交试验表中自由度确定的两条原则,并说明3水平因素交互作用列要占几列1正交表每列的自由度等于各列的水平数减一,由于因素和列是等同的,从而每个因素的自由度等于该因素的水平数减一2两因素的交互作用的自由度等于两因素的自由度的乘积。
因此3水平因素交互作用列要占2列3.正交试验设计的常用灵活应用方法有哪三种,说明使用场合。
1.并列法,适用于少量多水平因素和多个相同少水平因素一起用正交表;2.拟水平法:适用于少量少水平因素和多个相同多水平因素一起用正交表;3.拟因素法:适用于水平数较多的因素排入水平数较少的正交表中。
答:1.明确试验目的,确定试验指标,挑因素,选水平;2.用正交表安排试验:选合适的正交表,表头设计,水平翻译,列出试验方案表3.按试验方案进行试验:试验安排好后,严格按各号试验的条件进行试验。
4.试验结果的分析:计算各因素的水平总和,计算各因素的极差,选取较优生产条件,画趋势图5.验证试验:通过验证试验,找出比较稳定的较优生产条件。
四、设计题(10分)1.用拉丁方给出四因素三水平的试验设计方案(5因素4水平)解:先安排两个因素的全面试验,再由两个3阶正交拉丁方安排另两个因素的水平组合,然后将全面试验和上面的水平组合再组合即可。
2.写出一)3(49L 正交试验表并说明这表能进行哪几种试验解:)3(49L 正交试验表如下两因素三水平有两个交互作用的试验3.说明均匀设计表)6(6*6U 是如何构造的?略五、分析题(30分)1由护士和实习生某记录的七个病人的收缩压数据如下: 病 人: 1 2 3 4 5 6 7 护士:105,149,133,160,141,120,152 某:110,140,138,150,130,147,158 计算斯皮尔曼等级差相关系数。
解:先换成等级,再求等级差,然后计算相关系数。
即: 护士:1 5 3 7 4 2 6 某:1 4 3 6 2 5 7等级差:0 1 0 1 2 -3 -1 记为d 代入公式:7143.0)17(71661)1(61222≈-⨯-=--=∑n n d r s2某种产品有十个等级,第一次序为正常次序。
某一检验员判断的等级为第二次序,已知两种次序排列如下:第一次序:1 2 3 4 5 6 7 8 9 10 第二次序:5 2 1 4 3 9 8 10 7 6 计算两者的密切相关程度即肯德尔一致相关系数。
解:第一步:计算颠倒位置数,将相同数用线连起来,得到14个交叉点,即14个颠倒位置数第二步:代入公式计算 38.09101441)1(41≈⨯⨯-=--=∑n n i r k 由计算可知,相关系数太低,表明检验员判断力较低。
3.拉丁方格的直观分析 试验:烟灰砖折断力试验试验目的:寻找用烟灰制砖的最佳工艺条件,观察的指标是折断力,要越大越好 因素和水平数:三因素三水平,且知各因素间无交互作用。
A 因素:成型水份:8,10,12 B 因素:碾压时间:7,10,13 C 因素:碾压料重:340,370,400试验设计与对应数据如下,试用直观分析法对此试验进行分析。
(保留一位小数)直观分析结论:1由C B A R R R <<知对折断力影响从主到次的因素排序为C ,B ,A2由于均值反映了该因素水平对指标的影响,又由于指标值越大越好,由A A A k k k 231<<知,A 因素水平2比其它两个好,故A 选2A ,同理可知,最佳组合为232C B A 33B 处于边界状态,一般还需廷伸数据,如B4为16。
4232C B A 在试验安排中没有,但拉丁方却具备找出末列表试验的组合的能力。
4.正交试验的方差分析 试验:烟灰砖折断力试验试验目的:寻找用烟灰制砖的最佳工艺条件,观察的指标是折断力,要越大越好 因素和水平数:三因素三水平,且知各因素间无交互作用。
A 因素:成型水份:8,10,12 B 因素:碾压时间:7,10,13 C 因素:碾压料重:340,370,400试验数据为:4,5,6,7,6,5,3,6,8 (计算数据保留一位小数)。
要求用正交试验表,在05.0=α下用方差分析法检验各因素对折断力有无显著影响。
2i S 优方案是什么?(4)如果(2)和(3)的最优方案不一致,应如何解释? 答:(1)见表中。
(2)看一看的最优方案是6号试验:1212D C B A (3)算一算的最优方案是2211D C B A (4)如果(2)和(3)的最优方案不一致,一是A ,B 的交互作用太强,二是可能因素D 的作用太不显著。
(1) 用方差分析表检验因素的显著性5.18)2,1(05.0 F ;A2B1较优。
六、1.写出均匀设计表)(??4U 和)(??*4U 要说明问号等于多少。
(10分)2.写出均匀设计表)6(?6U 和)6(?*6U 要说明问号等于多少。
(10分)七、(20分) 1.《试验设计与分析》讲了哪几个基本问题?1验设计的基本概念和作用;2验设计的方差分析和直观分析;3拉丁方试验设计法;4正交试验法;5均匀设计;6其它试验法。
2.谈谈正交试验设计的基本方法。
1明确试验目的,确定试验指标,挑因素,选水平;2用正交表安排试验:选合适的正交表,表头设计,水平翻译,列出试验方案表 3按试验方案进行试验:试验安排好后,严格按各号试验的条件进行试验。
4试验结果的分析:计算各因素的水平总和,计算各因素的极差,选取较优生产条件,画趋势图5验证试验:通过验证试验,找出比较稳定的较优生产条件。
2.响应曲面分析法讲了哪几个基本问题? 一、响应曲面分析法的概念; 二、一阶响应曲面设计法;三、二次响应曲面设计与分析;四、基于多元正交多项式的响应曲面设计 五、二次响应曲面分析3.正交设计中并列法和拟因素法的区别。
4.正交设计中直和法和直积法的区别。
5.你知道的试验设计方法有哪些:拉丁方格设计;正交表设计;均匀设计;参数设计;响应曲面设计等6.你知道的试验设计的分析方法有哪些:方差分析;极差公析;回归分析;相关分析;响应曲面分析等七、附加题:(10分)1、行列式的思想能用于试验设计吗?2、谈谈你学习试验设计与分析的体会。
注:以红色题目为主!这只是参考答案。
