线性代数上机试验

合集下载

线代上机实验报告(3篇)

第1篇一、实验目的1. 掌握线性代数基本概念和基本运算方法。

2. 熟悉MATLAB软件在解决线性代数问题中的应用。

3. 提高实际操作能力和编程能力。

二、实验环境1. 操作系统：Windows 102. 软件环境：MATLAB R2019b3. 实验设备：计算机三、实验内容1. 矩阵的基本运算2. 矩阵的秩3. 矩阵的逆4. 线性方程组的求解5. 特征值和特征向量6. 二次型及其标准形四、实验步骤1. 矩阵的基本运算（1）创建矩阵A：A = [1, 2, 3; 4, 5, 6; 7, 8, 9]（2）计算矩阵A的转置：A_transpose = A'（3）计算矩阵A的行列式：det_A = det(A)（4）计算矩阵A的逆：A_inverse = inv(A)2. 矩阵的秩（1）创建矩阵B：B = [1, 2, 3, 4; 5, 6, 7, 8; 9, 10, 11, 12]（2）计算矩阵B的秩：rank_B = rank(B)3. 矩阵的逆（1）创建矩阵C：C = [1, 2; 3, 4]（2）判断矩阵C是否可逆：is_inverse = rank(C) == size(C, 1)（3）如果可逆，计算矩阵C的逆：C_inverse = inv(C)4. 线性方程组的求解（1）创建矩阵A和B：A = [1, 2; 3, 4]B = [5; 6]（2）使用MATLAB内置函数求解线性方程组：x = A \ B5. 特征值和特征向量（1）创建矩阵D：D = [4, 1; 2, 3]（2）计算矩阵D的特征值和特征向量：[V, D] = eig(D)6. 二次型及其标准形（1）创建矩阵E：E = [2, 1; 1, 3]（2）计算矩阵E的特征值和特征向量：[V, D] = eig(E)（3）将二次型E化为标准形：Q = V D inv(V)五、实验结果与分析1. 矩阵的基本运算（1）矩阵A：1 2 34 5 67 8 9（2）矩阵A的转置：1 4 72 5 83 6 9（3）矩阵A的行列式：（4）矩阵A的逆：-1.5 0.50.5 -0.52. 矩阵的秩矩阵B的秩为2。

东南大学数值分析上机报告完整版

数值分析上机实验报告目录1.chapter1舍入误差及有效数 (1)2.chapter2Newton迭代法 (3)3.chapter3线性代数方程组数值解法-列主元Gauss消去法 (7)4.chapter3线性代数方程组数值解法-逐次超松弛迭代法 (8)5.chapter4多项式插值与函数最佳逼近 (10)1.chapter1舍入误差及有效数1.1题目设S N =∑1j 2−1N j=2，其精确值为)11123(21+--N N 。

（1）编制按从大到小的顺序11131121222-+⋯⋯+-+-=N S N ，计算S N 的通用程序。

（2）编制按从小到大的顺序1211)1(111222-+⋯⋯+--+-=N N S N ，计算S N 的通用程序。

（3）按两种顺序分别计算64210,10,10S S S ,并指出有效位数。

（编制程序时用单精度）（4）通过本次上机题，你明白了什么？ 1.2编写相应的matlab 程序 clear;N=input('please input N:'); AValue=((3/2-1/N-1/(N+1))/2); sn1=single(0); sn2=single(0); for i=2:Nsn1=sn1+1/(i*i-1); %从大到小相加的通用程序% endep1=abs(sn1-AValue); for j=N:-1:2sn2=sn2+1/(j*j-1); %从小到大相加的通用程序% endep2=abs(sn2-AValue);fprintf('精确值为:%f\n',AValue);fprintf('从大到小的顺序累加得sn=%f\n',sn1); fprintf('从大到小相加的误差ep1=%f\n',ep1); fprintf('从小到大的顺序累加得sn=%f\n',sn2); fprintf('从小到大相加的误差ep2=%f\n',ep2); disp('================================='); 1.3matlab 运行程序结果 >> chaper1please input N:100 精确值为:0.740050从大到小的顺序累加得sn=0.740049 从大到小相加的误差ep1=0.000001 从小到大的顺序累加得sn=0.740050 从小到大相加的误差ep2=0.000000 >> chaper1please input N:10000 精确值为:0.749900从大到小的顺序累加得sn=0.749852 从大到小相加的误差ep1=0.000048 从小到大的顺序累加得sn=0.749900 从小到大相加的误差ep2=0.000000please input N:1000000精确值为:0.749999从大到小的顺序累加得sn=0.749852 从大到小相加的误差ep1=0.000147 从小到大的顺序累加得sn=0.749999 从小到大相加的误差ep2=0.0000001.4结果分析以及感悟按照从大到小顺序相加的有效位数为：5,4,3。

数学的上机实验报告

实验题目：线性代数求解方程组一、实验目的1. 理解线性代数中方程组的求解方法。

2. 掌握利用计算机求解线性方程组的算法。

3. 熟悉数学软件（如MATLAB、Python等）在数学问题中的应用。

二、实验内容本次实验主要利用数学软件求解线性方程组。

线性方程组是线性代数中的一个基本问题，其求解方法有很多种，如高斯消元法、矩阵求逆法等。

本实验以高斯消元法为例，利用MATLAB软件求解线性方程组。

三、实验步骤1. 编写高斯消元法算法程序。

2. 输入方程组的系数矩阵和常数项。

3. 调用程序求解方程组。

4. 输出解向量。

四、实验代码及分析1. 高斯消元法算法程序```matlabfunction x = gaussElimination(A, b)[n, m] = size(A);assert(n == m, 'The matrix A must be square.');assert(n == length(b), 'The length of b must be equal to the number of rows in A.');% 初始化解向量x = zeros(n, 1);% 高斯消元for i = 1:n-1% 寻找最大元素[~, maxIdx] = max(abs(A(i:n, i)));maxIdx = maxIdx + i - 1;% 交换行A([i, maxIdx], :) = A([maxIdx, i], :);b([i, maxIdx]) = b([maxIdx, i]);% 消元for j = i+1:nfactor = A(j, i) / A(i, i);A(j, i:n) = A(j, i:n) - factor A(i, i:n); b(j) = b(j) - factor b(i);endend% 回代求解for i = n:-1:1x(i) = (b(i) - A(i, i+1:n) x(i+1:n)) / A(i, i); endend```2. 输入方程组的系数矩阵和常数项```matlabA = [2, 1, -1; 1, 2, 1; -1, 1, 2];b = [8; 5; 2];```3. 调用程序求解方程组```matlabx = gaussElimination(A, b);```4. 输出解向量```matlabdisp('解向量为：');disp(x);```五、实验结果与分析实验结果：```解向量为：2-13```实验分析：通过高斯消元法，我们成功求解了给定的线性方程组。

数值线性代数第二版徐树方高立张平文上机习题第三章实

- 1 -第三章上机习题用你所熟悉的的计算机语言编制利用QR 分解求解线性方程组和线性最小二乘问题的通用子程序，并用你编制的子程序完成下面的计算任务：（1）求解第一章上机习题中的三个线性方程组，并将所得的计算结果与前面的结果相比较，说明各方法的优劣；（2）求一个二次多项式+bt+cy=at 2，使得在残向量的2范数下最小的意义下拟合表3.2中的数据；（3）在房产估价的线性模型111122110x a x a x a x y ++++=中，1121,,,a a a 分别表示税、浴室数目、占地面积、车库数目、房屋数目、居室数目、房龄、建筑类型、户型及壁炉数目，y 代表房屋价格。

现根据表3.3和表3.4给出的28组数据，求出模型中参数的最小二乘结果。

（表3.3和表3.4见课本P99-100）解分析：（1）计算一个Householder 变换H ：由于TTvv I wwI H β-=-=2，则计算一个Householder 变换H 等价于计算相应的v 、β。

其中)/(2,||||12v v e x x v T=-=β。

在实际计算中，为避免出现两个相近的数出现的情形，当01>x 时，令212221||||)(-x x x x v n +++=；为便于储存，将v 规格化为1/v v v =，相应的，β变为)/(221v v v T=β为防止溢出现象，用∞||||/x x 代替（2）QR 分解：利用Householder 变换逐步将n m A n m ≥⨯,转化为上三角矩阵A H HH n n 11-=Λ，则有⎥⎦⎤⎢⎣⎡=0R Q A ，其中n H H H Q 21=，:),:1(n R Λ=。

在实际计算中，从n j :1=，若m j <，依次计算)),:((j m j A x =对应的)1()1()~(+-⨯+-k m k m j H即对应的j v ，j β，将)1:2(+-j m v j 储存到),:1(j m j A +，j β储存到)(j d ，迭代结束后再次计算Q ，有⎥⎥⎦⎤⎢⎢⎣⎡=-~001j j j H I H，n H H H Q 21=（m n =时1-21n H H H Q =）（3）求解线性方程组b Ax =或最小二乘问题的步骤为 i 计算A 的QR 分解；ii 计算b Q c T 11=，其中):1(:,1n Q Q = iii 利用回代法求解上三角方程组1c Rx =（4）对第一章第一个线性方程组，由于R 的结果最后一行为零，故使用前代法时不计最后一行，而用运行结果计算84x 。

线性代数上机作业

线性代数上机作业一、单项选择题。

1、可逆矩阵用用det()函数求行列式判断，选C 代码如下：A = [2 3 0; 0 -2 -3; -6 -5 6];B = [-3 2 3; 2 2 -1; -1 4 2];C = [3 -2 2;3 -1 2 ; 0 -1 -1];D = [2 1 1; -6 -3 -3; 3 -2 2];det(A)ans =>> det(B)ans =1.1102e-15>> det(C)ans =-3>> det(D)ans =Det(B) 可近似为02、用代数余子式求行列式：C>> 1*(-9)+(-5)*2+5*(-6)+(-9)*(-6)ans =53、n阶线性相关即行列式为0：A>> syms x>> A = [-35 56 x -43;-10 17 21 -14;-5 8 9 -6;20 -31 -34 23] A =[ -35, 56, x, -43][ -10, 17, 21, -14][ -5, 8, 9, -6][ 20, -31, -34, 23]>> det(A)ans =5*x - 320>> x = 320/5x =644、f为正定二次型，用特殊值判断t的范围：At=2行列式大于0和t = 5时行列式小于0A =1 -5 4-5 26 184 -22 22>> det(A)ans =82>> A = [1 -5 -10; -5 26 -52; -10 48 22];>> det(A)ans =-282.00005、因特征值与特征向量对应,选D二、填空题：1、147：由行列式互换行列改变符号，所以|B|=7，>> (-3)^3*(-7)-6*7ans =1472、B = [-2 2 0 ] 由B = 2*(A-E)^-1*A得[-6 6 -2][ 0 -2 4]A = [2 -1 -1; 3 -1 -2; 3 -2 0];>> B = 2*(A-eye(3))^-1*AB =-2.0000 2.0000 0-6.0000 6.0000 -2.00000 -2.0000 4.00003、-13 -7 -13 由f(A)=f(λ) f(x) = -x^2+x-1 所以特征值为f(-3)= -13 ;f(3)=-7; f(4)=-134、10 -4 2 化为行最简型：A = [1 4 4; 0 1 4; 0 0 1];>> a = [2 4 2]';>> rref([A a])ans =1 0 0 100 1 0 -40 0 1 25、>> A = [3 0 2 4; 4 4 0 -3; 4 0 4 4; 2 3 1 0];>> B = [4 -3 4 0; 2 0 4 0; 0 2 -1 2; 0 4 3 1];>> (A*B)^2ans =872 100 1197 34338 1128 471 5341032 128 1432 404404 470 710 3566、-3 求行列式直接用det()即可A = [1 3 2 -3 3; 5 0 1 9 -6; 5 3 3 4 -2; 3 5 1 1 6; 0 0 2 -2 -1];>> det(A)-3.00007、3 求秩用rank()函数。

2014线代上机内容及要求

实验内容：
一、利用matlab操作矩阵基本运算，矩阵的初等变换和秩的求解，有关方阵的特征值和特征向量的求解。

注：该题应给出命令及结果
二、下图给出了某城市部分单行街道的交通流量(每小时通过的车辆数)。

图中有6个路口，已有9条街道记录了当天的平均车流量，另有7处的平均车流量未知。

试利用每个路口的进出车流量相等关系来推算这7处的平均车流量。

注：该题应从以下方面给出做题过程：
1、实验问题
2、问题的分析（涉及的理论知识、数学建模与求解的方法等）
3、程序设计
4、问题求解结果与结论
5、问题的进一步拓展与实验
6、实验的总结与体会。

线性代数实验报告

线性代数实验报告一、实验目的线性代数是一门重要的数学基础课程，它在工程、科学、计算机等领域都有着广泛的应用。

本次实验的目的是通过实际操作和计算，加深对线性代数基本概念和方法的理解，提高运用线性代数知识解决实际问题的能力。

二、实验环境本次实验使用了软件名称软件进行计算和绘图。

三、实验内容（一）矩阵的运算1、矩阵的加法和减法给定两个矩阵 A 和 B，计算它们的和 A ＋ B 以及差 A B。

观察运算结果，验证矩阵加法和减法的规则。

2、矩阵的乘法给定两个矩阵 C 和 D，其中 C 的列数等于 D 的行数，计算它们的乘积 CD。

分析乘法运算的结果，理解矩阵乘法的意义和性质。

（二）行列式的计算1、二阶和三阶行列式的计算手动计算二阶和三阶行列式的值，熟悉行列式的展开法则。

使用软件验证计算结果的正确性。

2、高阶行列式的计算选取一个四阶或更高阶的行列式，利用软件计算其值。

观察行列式的值与矩阵元素之间的关系。

（三）线性方程组的求解1、用高斯消元法求解线性方程组给定一个线性方程组，将其增广矩阵通过初等行变换化为行阶梯形矩阵。

求解方程组的解，并验证解的正确性。

2、用矩阵的逆求解线性方程组对于系数矩阵可逆的线性方程组，计算系数矩阵的逆矩阵。

通过逆矩阵求解方程组，并与高斯消元法的结果进行比较。

（四）向量组的线性相关性1、判断向量组的线性相关性给定一组向量，计算它们的线性组合是否为零向量。

根据计算结果判断向量组的线性相关性。

2、求向量组的极大线性无关组对于给定的向量组，通过初等行变换找出极大线性无关组。

（五）特征值和特征向量的计算1、计算矩阵的特征值和特征向量给定一个矩阵，计算其特征值和对应的特征向量。

验证特征值和特征向量的定义和性质。

2、利用特征值和特征向量进行矩阵对角化对于可对角化的矩阵，将其化为对角矩阵。

四、实验步骤（一）矩阵的运算1、首先在软件中输入矩阵 A 和 B 的元素值。

2、然后使用软件提供的矩阵加法和减法功能，计算 A ＋ B 和 A B 的结果。

数值线性代数第二版徐树方高立张平文上机习题第二章实验报告

（1）估计5到20阶Hilbert 矩阵的∞范数条件数（2）设n n R A ⨯∈⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡------=111111111011001ΛΛO O MM M O OΛ,先随机地选取n R x ∈,并计算出x A b n =;然后再用列主元Gauss 消去法求解该方程组,假定计算解为∧x 。

试对n 从5到30估计计算解∧x 的精度,并且与真实相对误差作比较。

解(1)分析:利用for 使n 从5循环到20,利用()hilb 函数得到Hilbert 矩阵A ;先将算法2、5、1编制成通用的子程序,利用算法2、5、1编成的子程序)(B opt v =,对TAB -=求解,得到∞-1A的一个估计值v v =~;再利用inf),(A norm 得到∞A ;则条件数inf),(1A norm v A A K *==∞∞-。

另,矩阵A 的∞范数条件数可由inf),(A cond 直接算出,两者可进行比较。

程序为1 算法2、5、1编成的子程序)(B opt v =function v=opt(B)k=1;n=length(B); x=1、/n*ones(n,1);while k==1 w=B*x;v=sign(w); z=B'*v;if norm(z,inf)<=z'*x v=norm(w,1); k=0; elsex=zeros(n,1);[s,t]=max(abs(z)); x(t)=1; k=1; end end end2 问题(1)求解 ex2_1for n=5:20A=hilb(n);B=inv(A、');v=opt(B);K1=v*norm(A,inf);K2=cond(A,inf);disp(['n=',num2str(n)])disp(['估计条件数为',num2str(K1)])disp(['实际条件数为',num2str(K2)])end计算结果为n=5估计条件数为943656实际条件数为943656n=6估计条件数为29070279、0028实际条件数为29070279、0028n=7估计条件数为985194887、5079实际条件数为985194887、5079n=8估计条件数为33872789099、7717实际条件数为33872789099、7717n=9估计条件数为16、422实际条件数为16、422n=10估计条件数为35353368771750、67实际条件数为35353368771750、67n=11估计条件数为1232433965549344实际条件数为1232433965549344Warning: Matrix is close to singular or badly scaled、Results may be inaccurate、RCOND = 2、547634e-17、> In ex2_1 at 3Warning: Matrix is close to singular or badly scaled、Results may be inaccurate、RCOND = 2、547634e-17、> In cond at 47In ex2_1 at 6n=12估计条件数为3、9245e+16实际条件数为3、9245e+16Warning: Matrix is close to singular or badly scaled、Results may be inaccurate、RCOND = 7、847381e-19、> In ex2_1 at 3Warning: Matrix is close to singular or badly scaled、Results may be inaccurate、RCOND = 7、847381e-19、> In cond at 47In ex2_1 at 6n=13估计条件数为1、2727e+18实际条件数为1、2727e+18Warning: Matrix is close to singular or badly scaled、Results may be inaccurate、RCOND = 2、246123e-18、> In ex2_1 at 3Warning: Matrix is close to singular or badly scaled、Results may be inaccurate、RCOND = 2、246123e-18、> In cond at 47In ex2_1 at 6n=14估计条件数为4、8374e+17实际条件数为4、8374e+17Warning: Matrix is close to singular or badly scaled、Results may be inaccurate、RCOND = 8、491876e-19、> In ex2_1 at 3Warning: Matrix is close to singular or badly scaled、Results may be inaccurate、RCOND = 8、491876e-19、> In cond at 47In ex2_1 at 6n=15估计条件数为4、6331e+17实际条件数为5、234289848563619e+17Warning: Matrix is close to singular or badly scaled、Results may be inaccurate、RCOND = 9、137489e-19、> In ex2_1 at 3Warning: Matrix is close to singular or badly scaled、Results may be inaccurate、RCOND = 9、137489e-19、> In cond at 47In ex2_1 at 6n=16估计条件数为8、3166e+17实际条件数为8、3167e+17Warning: Matrix is close to singular or badly scaled、Results may be inaccurate、RCOND = 6、244518e-19、> In ex2_1 at 3Warning: Matrix is close to singular or badly scaled 、 Results may be inaccurate 、 RCOND = 6、244518e-19、 > In cond at 47 In ex2_1 at 6 n=17估计条件数为1、43e+18 实际条件数为1、43e+18Warning: Matrix is close to singular or badly scaled 、 Results may be inaccurate 、 RCOND = 4、693737e-19、 > In ex2_1 at 3Warning: Matrix is close to singular or badly scaled 、 Results may be inaccurate 、 RCOND = 4、693737e-19、 > In cond at 47 In ex2_1 at 6 n=18估计条件数为2、5551e+18 实际条件数为2、8893e+18Warning: Matrix is close to singular or badly scaled 、 Results may be inaccurate 、 RCOND = 4、264685e-19、 > In ex2_1 at 3Warning: Matrix is close to singular or badly scaled 、 Results may be inaccurate 、 RCOND = 4、264685e-19、 > In cond at 47 In ex2_1 at 6 n=19估计条件数为2、411858563109357e+18 实际条件数为2、411858563109357e+18Warning: Matrix is close to singular or badly scaled 、 Results may be inaccurate 、 RCOND = 1、351364e-19、 > In ex2_1 at 3Warning: Matrix is close to singular or badly scaled 、 Results may be inaccurate 、 RCOND = 1、351364e-19、 > In cond at 47 In ex2_1 at 6 n=20估计条件数为2、31633670586674e+18 实际条件数为6、37335273308473e+18结果分析随着矩阵阶数增加,估计值误差开始出现,20,17,16,15 n 时估计条件数与实际值存在误差;且条件数很大,Hilbert 矩阵为病态的。

上机实习二

上机实习二例1已知 ⎪⎩⎪⎨⎧=+--=-+-=--131581079321321321x x x x x x x x x方程组的准确解为x *= [1，1，1]T，试用迭代法产生向量序列逐步逼近准确解。

解：（1）雅可比（Jacobi ）迭代A=[9 -1 -1;-1 10 -1;-1 -1 15];b=[7;8;13]; x=[0;0;0];y=x; for k=1:4for i=1:3s=0;t=x(i);x(i)=0; for j=1:3s=s+A(i,j)*x(j); end x(i)=t;y(i)=(b(i)-s)/A(i,i); ender=norm(x-y ,1);x=y end（2）塞德尔（Seidel ）迭代A=[9 -1 -1;-1 10 -1;-1 -1 15]; b=[7;8;13];x=[0;0;0]; er=1;k=0; while er>0.01er=0;k=k+1; for i=1:3s=0;t=x(i);x(i)=0; for j=1:3s=s+A(i,j)*x(j); endx(i)=(b(i)-s)/A(i,i); er=max(abs(x(i)-t),er); end xend例2 平面温度场的计算问题。

设有一矩形均匀薄板，它的两面是绝热的，如果四条边界线上温度为已知，它们分别为 10℃、15℃、20℃、18℃（左、上、右、下）.经过一段时间后，板内的各点温度达到平衡状态而不再变化，求板内平衡温度的分布。

解设矩形域上温度函数为 u x y (,).记矩形域为G = {( x ，y ) | 0 ≤ x ≤3，0≤ x ≤2}首先，取 h = 0.5，令 x 0 = 0，y 0 = 0 .x i = x 0 + i h ，i = 0，1，…，6 y j = y 0 + j h ，j = 0，1，…，4两组相互垂直的直线将矩形区域剖分成正方形网格。

直线簇的交点（x i ，y j ）称为网格点或结点。

《线性代数》上机作业

《线性代数》上机作业（一）一、上机目的 1、培养学生运用线性代数的知识解决实际问题的意识、兴趣和能力 2、掌握常用计算方法和处理问题的方法. 二、上机内容 1、求向量组的最大无关组； 2、解线性方程组； 3、解决实际问题举例. 三、上机作业1、设 A=[2 1 2 4; 1 2 0 2; 4 5 2 0; 0 1 1 7];求矩阵A 列向量组的一个最大无关组. 2、用Matlab 解线性方程组|2\ + 4X 2 -= -4參]-+5工？十3屯=10 匕-+ 3x 2 +2x3 - 51、解：在Matlab 中输入:> a=[2 1 2 4; 1 b=rref(a) 解得：b = 1 0 0 0 1 0 0 0 13x-i 41x 262 X 3414x-| 50x 2 3X 3 100 11x 1 38X 2 25X 3501 7];2 0 2; 4 5 2 0; 0 10 0 0 1 所以a1 ，a2,a3,a4 是一个极大无关组2、(1) 解：在Matlab 中输入>> a=[2 4 -6; 1 5 3;1 3 2]; >> b=[-4 10 5]';>> x=a\bx =-321 所以线性方程组的解为x1=-3,x2=2,x3=1 (2) 解：在Matlab 中输入>> a=[3 41 -62;4 50 3;11 38 25]; >> b=[-41 100 50]'; >> x=a\b x = -8.82212.58901.9465>>所以线性方程组的解为x1=-8.8221,x2= 2.5890,x3= 1.9465四、上机心得体会。

大连理工大学线性代数实验上机报告材料

大连理工大学线性代数实验上机报告实验一首先随机生成五阶方阵AA=rand(5)A =0.8147 0.0975 0.1576 0.1419 0.6557 0.9058 0.2785 0.9706 0.4218 0.0357 0.1270 0.5469 0.9572 0.9157 0.8491 0.9134 0.9575 0.4854 0.7922 0.9340 0.6324 0.9649 0.8003 0.9595 0.6787>> B=rand(5)随机生成五阶方阵BB =0.7577 0.7060 0.8235 0.4387 0.4898 0.7431 0.0318 0.6948 0.3816 0.4456 0.3922 0.2769 0.3171 0.7655 0.6463 0.6555 0.0462 0.9502 0.7952 0.7094 0.1712 0.0971 0.0344 0.1869 0.7547>> b=rand(1,5)'随机生成列向量bb =0.27600.67970.65510.16260.1190计算A+B>> A+Bans =1.5725 0.8036 0.9811 0.5806 1.1455 1.6489 0.3103 1.6654 0.8033 0.48130.5192 0.8238 1.2743 1.6813 1.49541.5689 1.0037 1.4356 1.5874 1.6434 0.8035 1.0620 0.8347 1.1464 1.4334 计算A-B>> A-Bans =0.0570 -0.6085 -0.6658 -0.2969 0.1660 0.1627 0.2467 0.2758 0.0402 -0.4099 -0.2652 0.2700 0.6401 0.1502 0.2028 0.2579 0.9113 -0.4648 -0.0030 0.2246 0.4612 0.8678 0.7658 0.7726 -0.0760 计算A*B+B*A>> A*B+B*Aans =3.0288 2.3058 3.1439 2.7276 3.10342.9094 2.19673.0040 3.0737 3.25843.3422 2.1423 3.2104 3.5734 3.90494.1446 2.9794 4.3676 4.2354 4.9170 3.1350 1.7787 3.2289 3.1170 3.2815 求Ax=b的解>> x=A\bx =-0.98502.43963.3124-5.65151.7085验证克莱姆法则>> c=A(:,1)c =0.81470.90580.12700.91340.6324>> d=A(:,2)d =0.09750.5469 0.9575 0.9649>> e=A(:,3)e =0.1576 0.9706 0.9572 0.4854 0.8003>> f=A(:,4)f =0.1419 0.4218 0.91570.9595>> g=A(:,5)g =0.65570.03570.84910.93400.6787>> B1=[b';d';e';f';g']'B1 =0.2760 0.0975 0.1576 0.1419 0.6557 0.6797 0.2785 0.9706 0.4218 0.0357 0.6551 0.5469 0.9572 0.9157 0.8491 0.1626 0.9575 0.4854 0.7922 0.9340 0.1190 0.9649 0.8003 0.9595 0.6787>> B2=[c';b';e';f';g']'B2 =0.8147 0.2760 0.1576 0.1419 0.6557 0.9058 0.6797 0.9706 0.4218 0.0357 0.1270 0.6551 0.9572 0.9157 0.8491 0.9134 0.1626 0.4854 0.7922 0.9340 0.6324 0.1190 0.8003 0.9595 0.6787>> B3=[c';d';b';f';g']'B3 =0.8147 0.0975 0.2760 0.1419 0.6557 0.9058 0.2785 0.6797 0.4218 0.0357 0.1270 0.5469 0.6551 0.9157 0.8491 0.9134 0.9575 0.1626 0.7922 0.9340 0.6324 0.9649 0.1190 0.9595 0.6787>> B4=[c';d';e';b';g']'B4 =0.8147 0.0975 0.1576 0.2760 0.6557 0.9058 0.2785 0.9706 0.6797 0.0357 0.1270 0.5469 0.9572 0.6551 0.8491 0.9134 0.9575 0.4854 0.1626 0.9340 0.6324 0.9649 0.8003 0.1190 0.6787>> B5=[c';d';e';f';b']'B5 =0.8147 0.0975 0.1576 0.1419 0.2760 0.9058 0.2785 0.9706 0.4218 0.6797 0.1270 0.5469 0.9572 0.9157 0.6551 0.9134 0.9575 0.4854 0.7922 0.1626 0.6324 0.9649 0.8003 0.9595 0.1190>> x1=det(B1)/det(A)x1 =-0.9850>> x2=det(B2)/det(A) x2 =2.4396>> x3=det(B3)/det(A) x3 =3.3124>> x4=det(B4)/det(A) x4 =-5.6515>> x5=det(B5)/det(A)x5 =1.7085计算A的行列式>> det(A)ans =-0.0250计算B的行列式>> det(B)ans =0.0647求A的逆>> inv(A)ans =3.1375 -0.8078 -1.8788 -4.21945.1680-8.6076 3.5314 2.8907 13.7204 -14.3665 -6.2824 3.7220 3.6132 10.0084 -12.4190 13.6173 -6.8822 -6.3938 -23.5288 27.5825 -2.5292 1.0729 2.4193 5.8870 -7.2671 求B的逆>> inv(B)ans =-0.4430 3.4997 1.3255 -2.6005 -0.4697 1.4047 -1.1626 0.2422 -0.4475 -0.0119 0.7210 -1.8189 -2.0635 2.4434 0.0765 -0.6122 -0.1837 2.0165 0.0375 -1.2564 0.0384 -0.5157 -0.7370 0.5267 1.7407 求A的秩>> rank(A)ans =5求B的秩>> rank(B)ans =5求A*B的行列式>> det(A*B)ans =-0.0016求A*B的逆>> inv(A*B)ans =-74.0649 35.0433 31.2288 121.5740 -137.3442 6.8291 -1.2718 -2.2922 -8.9951 8.6972 63.9620 -31.4202 -29.5061 -105.6918 122.3246 -9.3196 5.7452 4.6259 11.9660 -15.4028 11.9582 -6.3521 -3.3817 -16.7574 18.6360>> rank(A*B)ans =5>> det(A)*det(B)ans =-0.0016验证（1）>> (A*B)'ans =0.9569 1.5566 1.6237 2.2732 2.25520.6922 0.9401 0.4969 0.9371 0.80900.9461 1.6492 1.6875 2.3563 2.38000.7507 1.5887 1.8840 1.9421 2.14811.1399 1.52122.2149 2.4545 2.4497()()111,,T T T AB B A AB B A AB BA---==≠>> B'*A'ans =0.9569 1.5566 1.6237 2.2732 2.2552 0.6922 0.9401 0.4969 0.9371 0.8090 0.9461 1.6492 1.6875 2.3563 2.38000.7507 1.5887 1.8840 1.9421 2.14811.1399 1.52122.2149 2.4545 2.4497 （2）>> inv(B)*inv(A)ans =-74.0649 35.0433 31.2288 121.5740 -137.3442 6.8291 -1.2718 -2.2922 -8.9951 8.6972 63.9620 -31.4202 -29.5061 -105.6918 122.3246 -9.3196 5.7452 4.6259 11.9660 -15.4028 11.9582 -6.3521 -3.3817 -16.7574 18.6360 （3）>> A*Bans =0.9569 0.6922 0.9461 0.7507 1.13991.5566 0.9401 1.6492 1.5887 1.52121.6237 0.4969 1.6875 1.88402.21492.2732 0.9371 2.3563 1.9421 2.4545 2.2552 0.8090 2.3800 2.1481 2.4497>> B*Aans =2.0719 1.6135 2.1978 1.9769 1.9635 1.3528 1.2566 1.3549 1.4850 1.7372 1.7186 1.6454 1.5229 1.6894 1.6900 1.8714 2.0423 2.0113 2.2932 2.4625 0.8797 0.9697 0.8489 0.9690 0.8317 求矩阵X使得AXB=C首先随机生成五阶方阵C>> C=rand(5)C =0.4984 0.7513 0.9593 0.8407 0.35000.9597 0.2551 0.5472 0.2543 0.19660.3404 0.5060 0.1386 0.8143 0.25110.5853 0.6991 0.1493 0.2435 0.61600.2238 0.8909 0.2575 0.9293 0.4733X=A 的逆*B 的逆>> X=inv(A)*C*inv(B)X =3.8432 -13.8858 2.1418 9.4404 -4.5871-9.3312 41.9602 -7.9101 -28.4683 14.8942-7.8738 35.1218 -5.4107 -22.8861 10.158116.7545 -75.6079 14.6784 49.3951 -24.7450-3.5568 17.0848 -2.9018 -11.2670 5.4559实验二1. 验证：对于一般的方阵A,B,C,D ，首先随机生成方阵A,B,C,D A=rand(5)A BA DB CC D ≠-A =0.8258 0.1067 0.8687 0.4314 0.1361 0.5383 0.9619 0.0844 0.9106 0.8693 0.9961 0.0046 0.3998 0.1818 0.5797 0.0782 0.7749 0.2599 0.2638 0.5499 0.4427 0.8173 0.8001 0.1455 0.1450>> B=rand(5)B =0.8530 0.0760 0.4173 0.4893 0.7803 0.6221 0.2399 0.0497 0.3377 0.3897 0.3510 0.1233 0.9027 0.9001 0.2417 0.5132 0.1839 0.9448 0.3692 0.4039 0.4018 0.2400 0.4909 0.1112 0.0965>> C=rand(5)C =0.1320 0.2348 0.1690 0.5470 0.1835 0.9421 0.3532 0.6491 0.2963 0.3685 0.9561 0.8212 0.7317 0.7447 0.6256 0.5752 0.0154 0.6477 0.1890 0.7802 0.0598 0.0430 0.4509 0.6868 0.0811>> D=rand(5)D =0.9294 0.3063 0.6443 0.9390 0.2077 0.7757 0.5085 0.3786 0.8759 0.3012 0.4868 0.5108 0.8116 0.5502 0.4709 0.4359 0.8176 0.5328 0.6225 0.2305 0.4468 0.7948 0.3507 0.5870 0.8443>> Z=[A,B;C,D]Z =0.8258 0.1067 0.8687 0.4314 0.13610.8530 0.0760 0.4173 0.4893 0.78030.5383 0.9619 0.0844 0.9106 0.86930.6221 0.2399 0.0497 0.3377 0.38970.9961 0.0046 0.3998 0.1818 0.57970.3510 0.1233 0.9027 0.9001 0.24170.0782 0.7749 0.2599 0.2638 0.54990.5132 0.1839 0.9448 0.3692 0.40390.4427 0.8173 0.8001 0.1455 0.14500.4018 0.2400 0.4909 0.1112 0.09650.1320 0.2348 0.1690 0.5470 0.18350.9294 0.3063 0.6443 0.9390 0.20770.9421 0.3532 0.6491 0.2963 0.36850.7757 0.5085 0.3786 0.8759 0.30120.9561 0.8212 0.7317 0.7447 0.62560.4868 0.5108 0.8116 0.5502 0.47090.5752 0.0154 0.6477 0.1890 0.78020.4359 0.8176 0.5328 0.6225 0.23050.0598 0.0430 0.4509 0.6868 0.08110.4468 0.7948 0.3507 0.5870 0.8443求Z的行列式>> det(Z)ans =-0.0295求det(A)*det(D)-det(B)*det(C)>> det(A)*det(D)-det(B)*det(C)ans =1.8656e-004随机生成对角矩阵A>> A=diag([rand rand rand rand rand])A =0.1948 0 0 0 0 0 0.2259 0 0 0 0 0 0.1707 0 0 0 0 0 0.2277 0 0 0 0 0 0.4357 随机生成对角矩阵B>> B=diag([rand rand rand rand rand])B =0.3111 0 0 0 0 0 0.9234 0 0 0 0 0 0.4302 0 0 0 0 0 0.1848 0 0 0 0 0 0.9049 随机生成对角矩阵C>> C=diag([rand rand rand rand rand])C =0.9797 0 0 0 0 0 0.4389 0 0 0 0 0 0.1111 0 0 0 0 0 0.2581 0 0 0 0 0 0.4087 随机生成对角矩阵D>> D=diag([rand rand rand rand rand])D =0.5949 0 0 0 00 0.2622 0 0 00 0 0.6028 0 00 0 0 0.7112 00 0 0 0 0.2217>> Z=[A,B;C,D]Z =0.1948 0 0 0 00.3111 0 0 0 00 0.2259 0 0 00 0.9234 0 0 00 0 0.1707 0 00 0 0.4302 0 00 0 0 0.2277 0 0 0 0 0.1848 00 0 0 0 0.4357 0 0 0 0 0.90490.9797 0 0 0 00.5949 0 0 0 00 0.4389 0 0 00 0.2622 0 0 00 0 0.1111 0 00 0 0.6028 0 00 0 0 0.2581 00 0 0 0.7112 00 0 0 0 0.40870 0 0 0 0.2217计算Z的行列式>> det(Z)ans =-1.1243e-004计算det(A)*det(D)-det(B)*det(C)>> det(A)*det(D)-det(B)*det(C)ans =-9.3107e-005计算A*D-B*C的行列式>> det(A*D-B*C)ans =-1.1243e-004实验三求A列向量组的一个最大无关组，并把不属于极大无关组的向量利用极大无关组表示.N= 200865083;a=83;b=86;c=50;d=88;e=28;f=63;g=83;h=60;>>A=[a,b,c,d,3,4;1,2,3,4,4,3;12,15,22,17,5,7;e,f,g,h, 8,0];>> B=rref(A)B =1.0000 0 0 0 -0.3548 0.46560 1.0000 0 0 -1.4905 -2.00200 0 1.0000 0 0.0473 0.39500 0 0 1.0000 1.79841.3383所以a1,a2,a3,a4是一个极大无关组。

线性代数实验报告

线性代数实验报告
本次实验我们主要学习了线性代数的基础知识，包括向量的表示、矩阵的表示、线性方程组的求解以及线性变换的性质等方面。

在实验中，我们使用MATLAB进行计算及可视化操作。

具体来说，我们学习了以下几个方面的内容：
1. 向量的表示
向量是线性代数的基本概念之一，表示一个有向线段。

而在计算机中，可以通过向量的坐标来表示向量。

本次实验中，我们学习了如何使用MATLAB求出向量的模长、单位向量以及两个向量之间的夹角等。

矩阵是线性代数中的另一个重要概念，常用于表示线性方程组的系数矩阵。

在MATLAB 中，矩阵可以通过嵌套的向量来表示。

我们学习了如何求矩阵的行列式、逆矩阵、特征值等。

3. 线性方程组的求解
线性方程组是线性代数中的一个重要概念，其解法有很多种，包括高斯消元法、LU分解法、Jacobi迭代法等。

本次实验中，我们学习了如何使用MATLAB求解线性方程组，并对几种求解方法进行了比较和分析。

4. 线性变换的性质
线性变换是线性代数中的另一个重要概念，可以将一个向量空间变换成另一个向量空间。

在MATLAB中，可以通过矩阵乘法的方式来表示线性变换。

我们学习了线性变换的一些基本性质，如线性、保持原点等，并通过可视化的方式观察线性变换的效果。

通过本次实验，我们不仅掌握了线性代数的一些基础知识，也学会了使用MATLAB进行线性代数方面的计算和可视化操作。

这对于学习和研究线性代数都有着重要的意义。

数值线性代数上机作业1

0 54.2196 34.8797 23.1669 25.2609 23.2963
0 0 32.4907 -8.9182 -11.2895 -7.9245
0 0 0 7.6283 -3.9114 7.4339
0 0 0 0 3.4197 6.8393
0 0 0 0 0 0.0000
魔方矩阵用matlab内置QR分解：
-0.0710 -0.6424 0.1373 0.4501 0.3329-0.5000
R =
-56.3471 -16.4693 -30.0459 -39.0969 -38.0321 -38.6710
0 -54.2196 -34.8797 -23.1669 -25.2609 -23.2963
0 0 32.4907 -8.9182 -11.2895 -7.9245
-0.0532 -0.5740 -0.4500 -0.2106 -0.64870.0000
-0.5502 0.0011 -0.4460 0.4537 0.20620.5000
-0.1420 -0.4733 0.3763 -0.5034 0.33290.5000
-0.5324 0.0695 0.6287 0.2096 -0.52200.0000
Q =
0.8189 -0.5397 0.1893 -0.0482 0.0090 -0.0011
0.4094 0.3320 -0.7024 0.4489 -0.16170.0332
0.2730 0.4219 -0.1529 -0.5723 0.5854-0.2321
0.2047 0.4067 0.2015 -0.3866 -0.46870.6189
0.2730 0.4219 -0.1529 -0.5723 0.5854-0.2320

线性代数上机作业

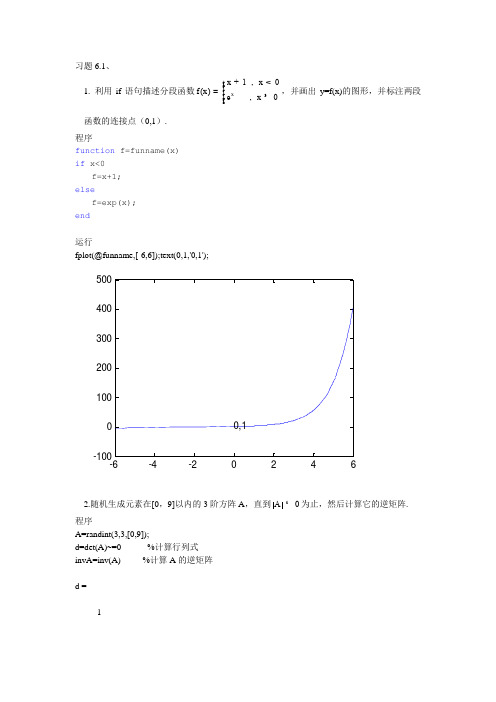
习题6.1、1. 利用if 语句描述分段函数1,0(),0x x x f x e x +<ìïï=íï³ïî，并画出y=f(x)的图形，并标注两段函数的连接点（0,1）.程序function f=funname(x)if x<0f=x+1;elsef=exp(x);end运行fplot(@funname,[-6,6]);text(0,1,'0,1');-6-4-20246-10001002003004005002.随机生成元素在[0，9]以内的3阶方阵A ，直到0A ¹为止，然后计算它的逆矩阵. 程序A=randint(3,3,[0,9]);d=det(A)~=0 %计算行列式invA=inv(A) %计算A 的逆矩阵d =1invA =0.1702 -0.0106 -0.0851-0.0426 0.1277 0.0213-0.0904 -0.1037 0.1702ans =903. 编写一个程序，用以找出10到10000之间的能被5或者17或者47整除的自然数. n=zerosx=10:10000if rem(x,5)|rem(x,17)|rem(x,47)==0n=xend练习 6.21. 下列矩阵为某个线性方程组的增广矩阵，利用MATLAB软件求解该方程组．程序format ratA=[1 2 1 4;2 0 4 3;4 2 2 1;3 1 3 2];b=[13;28;20;6];[R,IP]=rref([A,b])结果R =1 0 0 -3/2 00 1 0 2 00 0 1 3/2 00 0 0 0 1IP =1 2 3 5>> 1 0 0 -3/2 02. 考虑第一章引例3薄板热传导问题，如果希望矩形薄板的左边界温度为0 o C、上边界温度为10 o C、下边界为10 o C、右边界为20 o C，这可能吗？程序format ratA=[4 -1 0 -1 0 0;-1 4 -1 0 -1 0;0 -1 4 0 0 -1;-1 0 0 4 -1 0;0 -1 0 -1 4 -1;0 0 -1 0 -1 4];b=[10;10;30;20;10;30];[U,IP]=rref([A,b])结果U =1 0 0 0 0 0 1212/1610 1 0 0 0 0 1690/1610 0 1 0 0 0 2178/1610 0 0 1 0 0 1548/1610 0 0 0 1 0 1760/1610 0 0 0 0 1 2192/161IP =1 2 3 4 5 63. 已知五个数据点(,cos()),0,0.5,1.0,1.5,2.0t t t=，构造一个四次插值多项式，并计算cos(0.2),cos(0.4),cos(1.4)的近似值．程序A=[0 0 0 0 1;0.0625 0.125 0.25 0.5 1;1 1 1 1 1;5.0625 3.375 2.25 1.5 1;168 4 2 1];b=[1;cos(0.5);cos(1);cos(1.5);cos(2)];[U,IP]=rref([A,b])结果U =1 0 0 0 0 185/85680 1 0 0 0 114/25150 0 1 0 0 -2270/42390 0 0 1 0 67/75400 0 0 0 1 1IP =1 2 3 4 5练习 6.31. 用MA TLAB命令rand随机生成44C D G H，并确定那´的矩阵A和B.求下列指定的,,,些矩阵是相等的.可以利用MATLAB计算两个矩阵的差来测试两个矩阵是否相等.（1）输入：A=randint(4,4,[0,10]);B=randint(4,4,[0,10]);C=A*BD=B*AG=(A'*B')'H=(B'*A')'S1=C-DS2=C-GS3=C-HS4=D-GS5=D-HS6=G-H输出：C =116 48 66 164120 52 50 15677 36 69 126165 128 121 222D =144 124 136 136121 87 126 81145 129 166 12598 60 88 62G =144 124 136 136121 87 126 81145 129 166 12598 60 88 62H =116 48 66 164120 52 50 15677 36 69 126165 128 121 222 S1 =91 13 13 34-13 -34 -51 -894 -53 -82 -2684 61 -45 25 S2 =91 13 13 34-13 -34 -51 -894 -53 -82 -2684 61 -45 25 S3 =0 0 0 00 0 0 00 0 0 00 0 0 0 S4 =0 0 0 00 0 0 00 0 0 00 0 0 0 S5 =-91 -13 -13 -3413 34 51 89-4 53 82 26-84 -61 45 -25S6 =-91 -13 -13 -3413 34 51 89-4 53 82 26-84 -61 45 -25判断是否相等：因为S3=0，S4=0。

数值分析上机实验报告_线性方程组部分实验题1

线性方程组部分实验题11. 问题描述2. 问题分析2.1. Hilbert 矩阵Hilbert 矩阵是一种著名的“坏条件”矩阵，及病态矩阵，该矩阵任意一个元素的微小变化都能引起巨大的误差（如求逆等）。

该矩阵的元素的数学表达式是a(i ，j)=1/(i+j-1)。

这里我们用matlab 自带的产生Hilbert 矩阵的函数hilb(n)计算（n=1、 2......15）。

同时可以用MATLAB 计算。

2.2. Gauss 消去法（LU 分解）和Cholesky 分解方法高斯消去法主要有顺序消去和回代过程，是线性方程最基本的解法之一。

对n n A R ⨯∈，若0detA ≠，0(1,2,,)i i n ∆≠=⋅⋅⋅，则存在唯一的单位下三角形矩阵L 和非奇异上三角形矩阵U 使得A=LU 。

Cholesky 分解方法，也称平方根法。

对n n A R ⨯∈，假设A 对称正定，则存在唯一对角元素为正数的下三角矩阵L ，使得T A=LL 。

2.3. 条件数计算根据条件数定义：1222()n n n cond H H H -= ；12221n i i X x =⎛⎫== ⎪ ⎪⎝⎭∑ 3. 求解方案设计3.1. 线性方程组的求解及误差在这里为了比较，选择n=2、5、8、10、15 五种维数进行计算分析。

按照题意，我们先设x 为分量全1的向量，求出b ，然后将H 和b 作为已知量，求x ，与设定的参考解对比。

Gauss 消去法、Cholesky 分解法的Matlab 实现程序如下：----------------------------------------------------------------------------------------------------------%Guass 法***************************************************************************①Guass.m function guass(n)n=input('请输入系数矩阵的维数n='); %输入nH=hilb(n); %构造Hilbert 矩阵 x_exact=ones(n ，1); %构造x 列向量 b=H*x_exact; %构造b 向量 x=Doolittle(H ，b)a=input('是否继续，继续请按1，结束请按0:'); if a==1clear;clc;close all; guass(n); else end②Doolittle.mfunction x=Doolittle(A ，b) % LU 分解求Ax=b 的解 N=size(A); n=N(1);L=eye(n ，n);%L 的对角元素为1 U=zeros(n ，n); %U 为零矩阵 U(1，1:n)=A(1，1:n)%U 第一行L(1:n，1)=A(1:n，1)/U(1，1)%L第一列for k=2:nfor i=k:nU(k，i)=A(k，i)-L(k，1:(k-1))*U(1:(k-1)，i)endfor j=(k+1):nL(j，k)=(A(j，k)-L(j，1:(k-1))*U(1:(k-1)，k))/U(k，k)endendy=solveDownTriangle(L，b);%调用下三角系数矩阵求解函数x=solveUpTriangle(U，y);%调用上三角系数矩阵求解函数③solveDownTriangle.mfunction x=solveDownTriangle(A，b)%求下三角系数矩阵的线性方程组Ax=bN=size(A);n=N(1);for i=1:nif (i>1)s=A(i，1:(i-1))*x(1:(i-1)，1);elses=0;endx(i，1)=(b(i)-s)/A(i，i);end④solveUpTriangle.mfunction x=solveUpTriangle(A，b)% 求上三角系数矩阵的线性方程组Ax=bN=size(A);n=N(1);for i=n:-1:1if (i<n)s=A(i，(i+1):n)*x((i+1):n，1);elses=0;endx(i，1)=(b(i)-s)/A(i，i);end%Cholosky分解方法******************************************************************** ---------------------------------------------------------------------------------------------------------- %利用对称正定矩阵之Cholesky分解求解线性方程组Ax=bfunction x=Chol_Solve(A，b)clear;clc% A=input('输入A=');% b=input('输入b=');n=input('请输入系数矩阵的维数n=');%定义hilbert矩阵A=hilb(n);x_exact=ones(n，1);b=A*x_exact;n=length(b);l=Cholesky(A);x=ones(n，1);y=ones(n，1);y(1)=b(1)/l(1，1);%求Ly=bfor i=2:nz=0;for k=1:i-1z=z+l(i，k)*y(k);endy(i)=(b(i)-z)/l(i，i);endx(n)=y(n)/l(n，n);%求L'x=yfor i=n-1:-1:1z=0;for k=i+1:nz=z+l(k，i)*x(k);endx(i)=(y(i)-z)/l(i，i);endxwc=x-x_exact %误差计算a=input('是否继续，继续请按1，结束请按0:');if a==1Chol_Solve(A，b);else end%对称正定矩阵之Cholesky分解法：function L=Cholesky(A)% n=input('请输入系数矩阵的维数n=');%定义hilbert矩阵% A=hilb(n);n=length(A);L=zeros(n);for k=1:ndelta=A(k，k);for j=1:k-1delta=delta-L(k，j)^2;endif delta<1e-10return;endL(k，k)=sqrt(delta);for i=k+1:nL(i，k)=A(i，k);for j=1:k-1L(i，k)=L(i，k)-L(i，j)*L(k，j);endL(i，k)=L(i，k)/L(k，k);endend3.2.条件数的计算根据2.3叙述原理，写出条件数的计算程序如下：%tiaojianshu.mm=input ('input m:=') ;N=[1:m];for i=1:mn=N(i);H=hilb(n);k=cond(H);disp('矩阵的阶数')disp(n)disp('矩阵')disp(H)disp('矩阵的条件数')disp(k)end4.结果与误差分析4.1.线性方程组计算结果分别用Gauss法和Cholesky分解法计算线性方程组的结果，并进行误差分析结果如下：4.2.条件数计算结果4.3. 结果分析取不同的n 值，得到如下结果:对于Guass 法，可以看出来，随着n 的增大，求解结果误差变大，这是因为随着n 增大，系数矩阵的条件数变大，微小的扰动就容易造成很大的误差。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

《线性代数》 —上机教学
上机内容
MATLAB的基本知识求向量组的极大无关组求解线性方程组矩阵相关内容：行（列）数、秩、行列式、特征值
上机软件: MATLAB
上机界面
变量及数组输入
a=[1,2,3;4,5,6;7,8,0] %矩阵输入（a为3阶方阵） b=[366;804;351] %列矩阵输入 c=[366;804;351]’ %行矩阵（转置）输入
• 方法是：建立一个M文件，其内容是生成矩阵的命令，在MATLAB的命令窗口中输入此文件名，即将矩阵调入工作空间（写入内存）。
• 用建立M文件的方式生成矩阵 • (1) 建立M文件mydata.m内容如下 • %生成矩阵 • A=[1，2，3；4，5，6；7，8，9] • (2) 运行M文件mydata.m
• 解：在Matlab中输入：
• a=[1,-2,-1,0,2;-2,4,2,6,-6;2,-1,0,2,3;3,3,3,3,4];
• b=rref(a)
• 求得: b =
• 所以
1.0000 0 0 1.0000 00 00
0.3333 0 1.7778
0.6667 0 -0.1111
0 1.0000 -0.3333
r=rank(A),U=rref(A) ⑥ 求欠定线性方程组的基础解系及超定方程解的MATLAB
命令；xb=null(A) ⑦ 矩阵的特征方程、特征根和特征向量的计算命令；
f=poly(A);[P,D]=eig(A) ⑧ 化二次型为标准型的MATLAB命令；yTDy=xTAx; 其中
y=P-1x,
例一、求向量组的最大无关组 • 例1 求下列矩阵列向量组的一个最大无关组.
A = [1,2, 3; 1, 2, 3; 1, 2, 3];
ZR = null(A,'r') ZR = -2 -3
10 01
B=null(A)
B=
0.96362411165943
0
-0.14824986333222 -0.83205029433784
-0.22237479499833 0.55470019622523
• >>mydata • 则生成矩阵A。
求基础解系： Z = null(A) 标准正交基 for the null space of A Z = null(A,'r') "rational" basis for the null space obtained from the reduced row echelon form
• r=•Βιβλιοθήκη 4• >>
例四、求特征值
• >> A=[2,1,-5,1;1,-5,0,7;0,2,1,-1;1,6,-1,-4]; • >> lambda=eig(A);
三.Help
通过M文件创建矩阵
• 当矩阵的规模较大时，直接输入法就力不从心，出现差错也不容易修改。因此可以使用M文件生成矩阵。
0
00
是一个极大无关组,且
3
解：在Matlab中输入：
故
b1
2 3
a1
2 3
a2
a3 , b1
4 3
a1
a2
2 3
a3.
4
例二、解线性方程组
• 直接解法 • 利用左除运算符的直接解法 • 对于线性方程组Ax=b，可以利用左除运
算符“\”求解： x=A\b
例1 用直接解法求解下列线性方程组. 命令如下： A=[2,1,-5,1;1,-5,0,7;0,2,1,-1;1,6,-1,-4]; b=[13,-9,6,0]'; x=A\b
特殊矩阵
随机矩阵rand、单位阵eye、全1阵ones、零矩阵zeros 对角阵diag、魔方阵magic
元素及数组提取
a=A(i,j) b=B(2,:) c=C(:,3) subA=A(1:3,1:3) rowA=A(1:2,:) colA=A(:,1:2)
%提取某个元素 %提取某行 %提取某列 %提取子阵 %提取多行 %提取多列
② 矩阵化为最简行阶梯型的计算命令；[U0,ip]=rref(A) ③ 多元线性方程组MATLAB求解的几种方法；x=inv(A)*b,
U=rref(A) ④ 行列式的几种计算机求解方法；
D=det(A),[L,U]=lu(A);D=prod(diag(L)) ⑤ n个m维向量组的相关性及其秩的计算方法和命令;
N= 200865083共9位
a= 后两位 83 b=第4-5位 86 c=第6-7位 d=第4,8位
a b c d
A
1
2
3
4
12 15 22 17
e
f
g
h
e=第1,8位 f=第5,9位 g=第4,9位 h=第5,7位 60
d e a b
B
1
2
3
4
12 15 22 17
5
7
1
6
求A,B列向量组的一个最大无关组.
MATLAB中基本代数运算符
运算
加法，a+b
减法，a-b
乘法，a×b 除法，a÷b 乘幂，a*a*…*a
符号
+ * / or \ ^
举例
5+3 5-3 5*3 48/4=4\48=12 5^2=25
基本操作
四则运算、转置、求逆、求秩、求行列式、组合、化为行最简形、求特征值
常见任务
① 矩阵的赋值和其加、减、乘、除（求逆）命令；
上机作业
Ax=b的解在下列不同的取值时变化如何？
1 a
b
2
,
A
1
f 12
c
e
b
2 2
15 f
c
3 3
22 g
d
4
4
,
17
h
0.1, 0.2, 0.5, 0.7, 0.9, 0.95
上机作业
N= 201165083共9位 a= 后两位 83 b=第4-5位 86 c=第6-7位 d=第4,8位 e=第1,8位 f=第5,9位 g=第4,9位 h=第5,7位 60
5
• >> A=[2,1,-5,1;1,-5,0,7;0,2,1,-1;1,6,-1,-4]; • b=[13,-9,6,0]'; • x=A\b %不打；则计算机将显示x的值
• x=
• -66.5556 • 25.6667 • -18.7778 • 26.5556
• >>
例三、求秩
• >> A=[2,1,-5,1;1,-5,0,7;0,2,1,-1;1,6,-1,-4];
上机作业
随机生成5阶方阵A,B及5维列向量b
1. A+B,A-B, 2. A*B+B*A 3. Ax=b,Bx=b的解,并验证克莱姆法则 4. A,B的行列式，逆，秩 5. A*B的行列式，逆，秩，
并验证det(A*B)=det(A)*det(B) 6. 求矩阵A+A’,B*B’的特征值
上机作业
• >> r=rank(A);
• >> r=
% = 计算机不显示r的值
• ??? r=
•
|
• Error: Expression or statement is incomplete or incorrect.
• >> rank(A)
%不打；则计算机将显示rank(A)的值
• ans =
•
4
• >> r
a b c d
A
1
2
3
4
12 15 22 17
e
f
g
h
d e a b
B
1
2
3
4
12 15 22 17
5
7
1
6
1
b
2
f
c
A,B特征值，特征向量. A的20次方

线性代数上机试验

线代上机实验报告(3篇)

东南大学数值分析上机报告完整版

数学的上机实验报告

数值线性代数第二版徐树方高立张平文上机习题第三章实

线性代数上机作业

2014线代上机内容及要求

线性代数实验报告

最新线性代数上机作业题答案详解

数值线性代数第二版徐树方高立张平文上机习题第二章实验报告

上机实习二

《线性代数》上机作业

大连理工大学线性代数实验上机报告材料

线性代数实验报告

数值线性代数上机作业1

线性代数上机作业

数值分析上机实验报告_线性方程组部分实验题1