精品 八年级数学下册 函数与变量 正比例函数讲义+同步练习
正比例函数(练习)-2022-2023学年八年级数学下册同步精品课堂(人教版)

19.2.1 正比例函数一、单选题1. 下列问题中,两个变量成正比例的是( )A. 圆的面积和它的半径;B. 长方形的面积一定时,它的长和宽;C. 正方形的周长与边长;D. 三角形的面积一定时,它的一条边长与这条边上的高.2. 下列函数中,正比例函数是( ).A. 25y x = B. 25y x = C. 245y x = D. 25y x =-3. 函数2(1)m y m x =+是正比例函数,则m 的值为( )A. 1±B. 1C. 1-D. 不存在4. 已知y 与x 成正比例,如果x =2时,y =1,那么x =3时,y 为( )A. 32 B. 2 C.3 D. 05. 已知正比例函数()y kx k 0=≠的图象经过点(1,-2),则正比例函数的解析式为( )A. y 2x =B. y 2x =-C. 12y x =D. 1y x 2=-6. 设a 为常数,且()33,1P a a ++,则该点位于正比例函数( )上.A. 3y x =B. 33x y -= C. 13y x = D. 31y x =-7. 当k >0时,正比例函数y =kx 的图象大致是( )A. B. C. D.8. 关于函数12y x =,下列结论正确的是 ( )A. 函数图像必经过点(1,2) B. 函数图像经过二、四象限C. y 随x 的增大而增大D. y 随x 的增大而减小9. 对于正比例函数y kx =,当自变量x 的值增加2时,对应的函数值y 减少6,则k 的值为( )A. 3B. 2-C. 3-D. 0.5-10. ()11,A x y ,()22,B x y 是正比例函数12y x =-图象上的两个点,下列判断中,正确的是( )A. 12y y < B. 12y y >C. 当12x x >时,12y y < D. 当12x x >时,12y y >11. 如图,在同一直角坐标系中,正比例函数1y k x =,2y k x =,3y k x =,4y k x =的图象分别为1l ,2l ,3l ,4l ,则下列关系中正确的是( )A. 1234k k k k <<< B. 2143k k k k <<<C. 1243k k k k <<< D. 2134k k k k <<<12. 如图,直线OA 的解析式为y =x ,点P 1坐标为(1,0),过P 1作PQ 1⊥x 轴交OA 于Q 1,过Q 1作P 2Q 1⊥OA 交x 轴于P 2,过P 2作P 2Q 2⊥x 轴交OA 于Q 2,过Q 2作P 3Q 2⊥OA 交x 轴于P 3,…,按此规律进行下去,则P 100的坐标为( )A. (2100﹣1,0)B. (5050,0)C. (299,0)D. (100,0)二、填空题13. 已知y 与x 成正比例,且当1x =时,2y =,那么当3x =时,y =______.14. 如果正比例函数y =(k -1)x 的图象经过第二、四象限,那么k 的取值范围是__________.15. 若点()1,P n ,()3,6Q n +在正比例函数y kx =的图像上,则k =______.16. 汽车行驶的路程S (千米)与行驶的时间t (时)的函数关系的大致图象如图,那么该汽车行驶的速度是___.17. 如图,过点()2,0A 作x 轴的垂线与正比例函数y x =和3y x =的图象分别相交于点B ,C ,则OCB 的面积为________.18. 放假了,小明和小丽去蔬菜加工厂社会实践,两人同时工作了一段时间后,休息时小明对小丽说:“我已加工了28kg ,你呢?”小丽思考了一会儿说:“我来考考你. 图(1)、图(2)分别表示你和我的工作量与工作时间的关系,你能算出我加工了多少千克吗?”小明思考后回答:“你难不倒我,你现在加工了______kg.”19. 如图,在平面直角坐标系中摆放16个边长为1的正方形,直线l :y =kx 将这16个正方形分成面积相等的两部分,则k 的值是 _____.20. 已知正比例函数()0y kx k =≠,当31x -≤≤时,对应的y 的取值范围是113y -≤≤,且y 随x 的减小而减小,则k 的值为________.21. 在平面直角坐标系中,点(4,2)P --沿与直线y =平行的方向平移4个单位,得到点P '的坐标为__________.22. 如图,已知正方形OABC 的顶点B 在直线2y x =-上,点A 在第一象限.若正方形OABC 的面积是10,则点A 的坐标为______.三、解答题23. 已知y 是x 的正比例函数,并且当2x =-时4y =.(1)求正比例函数的表达式;(2)判断点()0.51A ,和点()36B -,是否在这个函数的图象上.24. 已知正比例函数y kx =图像经过点()2,4-,求:(1)这个函数的解析式;(2)判断点()2,1A -是否在这个函数图像上;(3)图像上两点()11,B x y ,()22,C x y ,如果12x x >,比较1y ,2y 的大小.25. 已知12y y y =+,且13-y 与x 成正比例,2y 与2x -成正比例,当2x =时,7y =,当1x =时,0y =(1)求出y 与x 之间的函数关系式;(2)计算4x =时,y 的值.26. 已知y 与x 成正比例,且当1x =时,3y =.(1)求y 与x 之间的函数解析式;(2)当2<<1x -时,求y 的取值范围.27. 如今餐馆常用一次性筷子,有人说这是浪费资源,破坏生态环境. 已知用来生产一次性筷子的大树的数量(万棵)与加工成一次性筷子的数量(亿双)成正比例关系,且100万棵大树能加工成18亿双一次性筷子.(1)求用来生产一次性筷子的大树的数量y (万棵)与加工成一次性筷子的数量x (亿双)的函数解析式;(2)据统计,我国一年要耗费一次性筷子约450亿双,生产这些一次性筷子约需要多少万棵大树?每1万棵大树占地面积为0.08平方千米,照这样计算,我国的森林面积每年因此将会减少大约多少平方千米?开放探究提优开放探究提优28. 如图,已知正比例函数y=kx 的图象经过点A ,点A 在第四象限,过A 作AH ⊥x 轴,垂足为H ,点A 的横坐标为4,且△AOH 的面积为6.(1)求正比例函数的解析式.(2)在x 轴上是否存在一点P ,使△AOP 的面积为9?若存在,求出点P 的坐标;若不存在,请说明理由.29. 近年来国际石油价格猛涨,我国也受其影响,部分出租车为了降低营运成本进行了改装,改装后的出租车可以用液化气代替汽油. 假设一辆出租车日平均行程为300km.(1)使用汽油的出租车,每升汽油能行驶12km ,汽油价格为4.8元/L ,设行驶时间为t 天时所耗汽油费用为1y 元;使用液化气的出租车,每升液化气能行驶15km ,液化气价格为5元/L ,设行驶时间为t 天时所耗液化气费用为2y 元,分别求出1y 、2y 与t 之间的函数解析式;(2)若改装一辆出租车的费用为8000元,请在(1)的基础上,计算出改装后多少天节省的燃料费用就足够抵消改装费用.30. 已知函数,y =kx (k 为常数且k ≠0);(1)当x =1,y =2时,则函数解析式为 ;(2)当函数图象过第一、三象限时,k ;(3)k ,y 随x 的增大而减小;(4)如图,在(1)的条件下,点A 在图象上,点A 的横坐标为1,点B (2,0),求△OAB 的面积.31. 在平面直角坐标系中,(),P a b 是第一象限内一点,给出如下定义:1a k b =和2k b a=两个值中的最大值叫做点P 的“倾斜系数”k .(1)求点()6,2P 的“倾斜系数”k 的值;(2)①若点(),P a b 的“倾斜系数”2k =,请写出a 和b 的数量关系,并说明理由;②若点(),P a b 的“倾斜系数”2k =,且3a b +=,求OP 的长;(3)如图,边长为2的正方形ABCD 沿直线AC :y x =运动,(),P a b 是正方形ABCD 上任意一点,且点P 的“倾斜系数”k <,请直接写出a 的取值范围.19.2.1 正比例函数一、单选题【1题答案】【答案】C【解析】【分析】先列出函数关系式,然后再根据正比例函数的定义即可解答.【详解】解:A 、圆的面积S =πr 2,不是正比例函数,故此选项不符合题意;B 、长方形的面积S 一定时,它的长a 和宽b 的关系S =ab ,不是正比例函数,故此选项不符合题意;C.正方形的周长C =边长×4=4a ,是正比例函数,故此选项符合题意;D. 三角形的面积S 一定时,它的底边a 和底边上的高h 的关系S =12ah ,不是正比例函数,故此选项不符合题意.故选:C .【点睛】本题考查正比例函数的定义,解题的关键是掌握正比例函数的定义:一般地,两个变量x 、y 之间的关系式可以表示成形如y =kx (k 为常数,且k ≠0)的函数,那么y 就叫做x 的正比例函数.【2题答案】【答案】B【解析】【分析】正比例函数的定义:形如(0)y kx k =≠的函数叫做正比例函数.【详解】根据正比例函数的定义可得:A 、是反比例函数,B 、是正比例函数,C 、是二次函数,D 、是反比例函数.故选B【点睛】本题属于基础应用题,只需学生熟知正比例函数的定义,即可完成.【3题答案】【答案】B【解析】【分析】根据正比例函数的定义,得m2=1,且m+1≠0,求解即可.【详解】解:∵函数y=(m+1)x m2是正比例函数,∴m2=1,且m+1≠0,解得,m=1.故选:B.【点睛】本题主要考查了正比例函数的定义,一般地,形如y=kx,且k≠0,叫正比例函数.【4题答案】【答案】A【解析】【分析】根据y与x成正比例,如果x=4时,y=2,用待定系数法可求出函数关系式.再将x=3代入求出y的值.【详解】解:∵y与x成正比例,∴y=kx,x=4时,y=2,即2=4k,解得12k=,则函数的解析式为12y x=,x=3时,13322 y=⨯=故选A【点睛】本题考查了正比例函数的定义,掌握正比例函数的定义是解题的关键.【5题答案】【答案】B【解析】【分析】利用待定系数法把(1,-2)代入正比例函数y=kx中计算出k即可得到解析式.【详解】根据点在直线上,点的坐标满足方程的关系,将(1,-2)代入y kx=,得:k 2=-,∴正比例函数的解析式为y 2x =-.故选B.【6题答案】【答案】C【解析】【分析】根据题意,设正比例函数为y kx =,将点()33,1P a a ++代入解析式,进而判断即可.【详解】设正比例函数为y kx =,将点()33,1P a a ++代入得,13(1)a k a +=+,解得13k =,∴13y x =.故选:C .【点睛】本题考查了求正比例函数解析式,掌握正比例函数的性质是解题的关键.【7题答案】【答案】A【解析】【分析】正比例函数的图象是一条经过原点的直线,且当k >0时,经过一、三象限.【详解】解:正比例函数的图象是一条经过原点的直线,且当k >0时,经过一、三象限.故选A .【点睛】本题比较简单,主要考查了正比例函数的图象特点:是一条经过原点的直线.【8题答案】【答案】C【解析】【分析】根据正比例函数图象的性质分析.【详解】A 、当x =1时,y =12,错误;B 、因为k >0,所以图象经过第一、三象限,错误;C 、因为k >0,所以y 随x 的增大而增大,C 正确;D 、错误.故选:C .【9题答案】【答案】C【解析】【分析】当自变量为()2x +时,函数值为()6y -,代入解析式化简计算即可.【详解】∵正比例函数y kx =,当自变量x 的值增加2时,对应的函数值y 减少6,∴()()62y k x -=+,∴62y kx k -=+,∴26k =-,解得:3k =-.故选:C .【点睛】本题考查了正比例函数的性质及其解析式的确定,熟练掌握性质是解题的关键.【10题答案】【答案】C【解析】【分析】根据正比例函数的性质,即可求解.【详解】解:∵102-<,∴y 随x 的增大而减小,∴当12x x >时,12y y <,故A ,B ,D 选项错误,不符合题意;C 正确,符合题意.故选:C【点睛】本题主要考查了正比例函数的性质,熟练掌握对于正比例函数()0y kx k =≠,当0k >时,y 随x 的增大而增大,当0k <时,y 随x 的增大而减小是解题的关键.【11题答案】【答案】B【解析】【分析】首先根据直线经过的象限判断k 的符号,再进一步根据直线的陡峭趋势(直线越陡k 越大)判断k 的绝对值的大小,最后判断四个数的大小.【详解】解:根据直线经过的象限,知20k <,10k <,40k >,30k >,根据直线越陡k 越大,知21k k >,43k k <,所以2143k k k k <<<.故选B .【点睛】此题主要考查了正比例函数图象的性质,直线越陡k 越大,熟练掌握正比例函数的性质是解题关键.【12题答案】【答案】C【解析】【分析】根据直线解析式确定,∠AOP 1=45°,再根据等腰直角三角形的判定与性质求得前面几个点的坐标,找出规律即可求解.【详解】解:∵直线OA 的解析式为y =x ,∴∠AOP 1=45°,∵PQ 1⊥x 轴,∴△OP 1Q 1为等腰直角三角形,∵点P 1坐标为(1,0),∴P 1Q 1=OP 1=1,∵P 2Q 1⊥OA ,∴∠P 1Q 1P 2=45°,∴△P 1P 2Q 1为等腰直角三角形,∴P 1P 2=P 1Q 1=1,∴P 2(2,0),同理可得P 3(4,0),P 4(8,0),……,P n (2n ﹣1,0),∴P100(299,0),故选:C.【点睛】此题考查了坐标类规律的探索问题,涉及了正比例函数的性质、等腰直角三角形的性质。
人教版数学八年级下册 同步练习 课件第19章 第33课时 正比例函数图象与性质
y=-2x … 0 -2 …
解:画图略
归纳:函数 y=-2x(k<0)的图象是一条 直直线线 ,它经过 原原 点和(1, --22 ),图象经过 二二、、四四 象限,图象 从左向右下降,即 y 随着 x 增大而 减减小小 .
★三、四基三级练
►答案见:D18
一级 若函数 y=(m-1)x|m|是正比例函数,则该函数的图象经过第
解:存在.∵△AOP 的面积为 5,点 A 的坐标为(3, -2), ∴OP=5.∴点 P 的坐标为(5,0)或(-5,0).
谢谢您的观看与聆听
三级 已知正比例函数 y=kx 的图象过点 P(- 2, 2). (1)写出该函数的解析式;
解:∵正比例函数 y=kx 的图象过点 P(- 2, 2), ∴ 2=- 2k,解得 k=-1. ∴该函数的解析式为 y=-x.
(2)已知点 A(a,-4),B(-2 2,b)都在它的图象上,求 a,b 的值.
(1)求正比例函数的解析式;
解:∵点 A 的横坐标为 3,且△AOH 面积为 3, ∴点 A 的纵坐标为-2, ∴点 A 的坐标为(3,-2). ∵正比例函数 y=kx 经过点 A, ∴3k=-2,解得 k=-23. ∴正比例函数的解析式为 y=-23x.
(2)在 x 轴上能否找到一点 P,使△AOP 的面积为 5?若存在, 求点 P 的坐标;若不存在,请说明理由.
下列不是正比例函数的是( B )
A.y=4x
B.y=-x2
C.y=-2x
D.y=-x
若函数 y=xm-3 是正比例函数,则 m= 44 .
关于 x 的函数 y=(a+1)x 是正比例函数,则 a 满足 aa≠≠--1 1 .
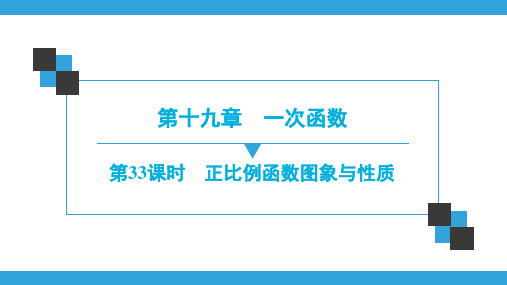
用“描点法”画出 y=1.5x 的图象.
19.2.1 正比例函数 人教版数学八年级下册同步练习(含解析)

第十九章 一次函数19.2 一次函数19.2.1 正比例函数基础过关全练知识点1 正比例函数的定义1.(2022广西南宁期末)下列函数中,是正比例函数的是( )A.y=x2B.y=2xC.y=2x+1D.y=2x2.【易错题】若y=(m-1)x+m2-1是关于x的正比例函数,则m2 023的值为 .知识点2 正比例函数的图象与性质3.(2021山东青岛四校联考)若点A(-4,m)在正比例函数y=-1x的图象上,2则m的值是( )A.2B.-2C.8D.-84.(2021山西临汾三中期末)函数y=mx(m>0)的图象大致是( )A B C D5.【教材变式·P98T2变式】关于正比例函数y=-3x,下列结论中正确的是( )A.函数图象经过点(-3,1)B.y随x的增大而增大C.函数图象经过第二、四象限D.不论x 取何值,总有y <06.【一题多变】设正比例函数y =mx 的图象经过点A (m ,4),且y 的值随x 值的增大而减小,则m 等于 .[变式] 已知在正比例函数y =-2mx 中,函数y 的值随x 值的增大而增大,则点P (m ,4)在第 象限内.7.【新独家原创】当-1≤x ≤3时,正比例函数y =-33x 的最大值是 ,最小值是 .8.已知正比例函数y =(m -1)x 的图象上有A (x 1,y 1),B (x 2,y 2)两点,当x 1<x 2时,y 1>y 2.(1)求m 的取值范围;(2)当m 取最大整数时,画出该函数图象. 知识点3 正比例函数的解析式9.(2022广东广州中考)点(3,-5)在正比例函数y =kx (k ≠0)的图象上,则k 的值为( )A.-15B.15C.-35 D.―5310.(2021湖南衡阳一中月考)对于正比例函数y =kx ,当自变量x 的值增加3时,对应的函数值y 减少6,则k 的值为( )A.2B.-2C.-3D.-0.511.【跨学科·物理】随着海拔的升高,大气压强下降,空气中的含氧量也随之下降,即含氧量y (g/m 3)与大气压强x (kPa )成正比例函数关系.当大气压强为36 kPa 时,含氧量为108 g/m 3,则y 与x 的函数关系式为 .12.已知正比例函数y =kx 的图象经过点(3,-6).(1)求这个函数的解析式;(2)判断点A (4,-2)是否在这个函数图象上;(3)已知图象上两点B (x 1,y 1),C (x 2,y 2),如果x 1>x 2,比较y 1,y 2的大小. 能力提升全练13.(2022福建福州月考,3,★☆☆)如果一个正比例函数的图象经过不同象限的两点A (3,m )、B (n ,-2),那么一定有( )A.m >0,n >0B.m >0,n <0C.m <0,n >0D.m <0,n <014.(2018陕西中考,4,★★☆)如图,在矩形AOBC 中,A (-2,0),B (0,1).若正比例函数y =kx 的图象经过点C ,则k 的值为( )A.-2B.-12C.2D.1215.【易错题】(2022 江苏南京三中月考,5,★★☆)如图,在平面直角坐标系中,已知点A (1,3),B (n ,3),若直线y =2x 与线段AB 有公共点,则n 的值不可能是( )A.54 B.2 C.3 D.416.(2022广东深圳外国语学校期末,5,★★☆)已知点A (x 1,y 1),点B (x 2,y 2)都在正比例函数y =12x 的图象上.若x 2-x 1=3,则y 2-y 1的值为( )A.32 B.23 C.3 D.617.(2022河北石家庄四校联考,18,★★☆)已知正比例函数y =(2m +4)x.(1)m 满足什么条件时,函数图象经过第一、三象限?(2)m 满足什么条件时,y 随x 的增大而减小?(3)m 为何值时,点(1,3)在该函数图象上? 素养探究全练18.【运算能力】已知正比例函数y=kx的图象经过点A,点A在第四象限内,过点A作AH⊥x轴,垂足为点H,点A的横坐标为3,且△AOH的面积为3.(1)求正比例函数的表达式.(2)在x轴上能否找到一点M,使△AOM是等腰三角形?若存在,请求点M的坐标;若不存在,请说明理由.答案全解全析基础过关全练1.B y =x 2不是正比例函数;y =2x 是正比例函数;y =2x +1不是正比例函数;2x 的分母含有字母,y =2x 不是正比例函数,故选B.2. 答案 -1解析 ∵y =(m -1)x +m 2-1是关于x 的正比例函数,∴m 2-1=0且m -1≠0,解得m =-1,∴m 2 023=(-1)2 023=-1.故答案为-1.3.A 将(-4,m )代入y =-12x ,得m =-12×(-4)=2,故选A.4.A 由m >0可知直线经过第一、三象限,故选A .5.C A.当x =-3时,y =9≠1,选项A 不符合题意;B.由k =-3<0可知y 随x 的增大而减小,选项B 不符合题意;C.由k =-3<0可知函数y =-3x 的图象经过第二、四象限,选项C 符合题意;D.由函数y =-3x 的图象可知,当x >0时,y <0,当x <0时,y >0,选项D 不符合题意.故选C.6.答案 -2解析 ∵正比例函数y =mx 的图象经过点A (m ,4),∴4=m 2,解得m =±2.又∵y 的值随x 值的增大而减小,∴m =-2.[变式] 答案 二解析 ∵正比例函数y =-2mx 中,函数y 的值随x 值的增大而增大,∴-2m >0,解得m <0,∴点P (m ,4)在第二象限内.故答案为二.7.答案 33;-1解析 ∵正比例函数y =-33x 中k =―33<0,∴y 的值随x 值的增大而减小,又-1≤x ≤3,∴当x =-1时,正比例函数y =-33x 有最大值,为-33×(-1)=33,当x =3时,正比例函数y =-33x 有最小值,为-33×3=-1.8.解析 (1)∵正比例函数y =(m -1)x 的图象上有A (x 1,y 1),B (x 2,y 2)两点,且当x 1<x 2时,y 1>y 2,∴m -1<0,∴m <1,∴m 的取值范围是m <1.(2)∵m <1,∴m 的最大整数值为0,∴函数解析式为y =-x ,图象如图所示:9.D ∵点(3,-5)在正比例函数y =kx (k ≠0)的图象上,∴-5=3k ,解得k =-53,故选D.10.B 根据题意得y -6=k (x +3),即y -6=kx +3k ,因为y =kx ,所以3k =-6,解得k =-2.故选B.11.答案 y =3x解析 设y 与x 的函数关系式为y =kx (k ≠0),根据题意可得108=36k ,∴k =3,故函数关系式为y =3x.12.解析 (1)∵正比例函数y =kx 的图象经过点(3,-6),∴-6=3k ,解得k =-2,∴这个函数的解析式为y =-2x.(2)将x =4代入y =-2x 得y =-8≠-2,∴点A (4,-2)不在这个函数图象上.(3)∵k =-2<0,∴y 随x 的增大而减小.∵x 1>x 2,∴y 1<y 2.能力提升全练13.B ∵一个正比例函数的图象经过不同象限的两点A (3,m )、B (n ,-2),∴点A ,B 分别在第一、三象限内,∴m >0,n <0.故选B.14.B ∵四边形AOBC 是矩形,A (-2,0),B (0,1),∴AC =OB =1,BC =OA =2,∴点C 的坐标为(-2,1),将点C (-2,1)代入y =kx ,得1=-2k ,解得k =-12,故选B .15.A 当y =3时,有2x =3,解得x =32.∵直线y =2x 与线段AB有公共点,∴n ≥32.故选A.16.A ∵点A (x 1,y 1),点B (x 2,y 2)都在正比例函数y =12x 的图象上,∴y 1=12x 1,y 2=12x 2,∴x 1=2y 1,x 2=2y 2,∵x 2-x 1=3,∴2y 2-2y 1=3,解得y 2-y 1=32,故选A.17.解析 (1)∵函数图象经过第一、三象限,∴2m+4>0,解得m>-2.(2)∵y随x的增大而减小,∴2m+4<0,解得m<-2.(3)∵点(1,3)在该函数图象上,∴2m+4=3,解得m=-1.2素养探究全练18.解析 (1)∵点A的横坐标为3,△AOH的面积为3,点A在第四象限内,∴点A的坐标为(3,-2).,将A(3,-2)代入y=kx,得-2=3k,解得k=-23x.∴正比例函数的表达式为y=-23(2)①当OM=OA时,如图1所示,∵点A的坐标为(3,-2),∴OH=3,AH=2,∴OA=OH2+AH2=13,∴点M的坐标为(-13,0)或(13,0);②当AO=AM时,如图2所示,∵点H的坐标为(3,0),∴点M的坐标为(6,0);③当OM=MA时,设OM=x,则MH=3-x,,∵OM=MA,∴x=(3―x)2+22,解得x=136∴点M,0.综上所述,当点M的坐标为(-13,0)或(13,0)或(6,0),0时,△AOM是等腰三角形.图1图2图3。
2017年春八年级数学下册 19.2.1 正比例函数同步讲义 (新版)新人教版

(1 ) y 3 x
(2 ) y
2 x
(3 ) y
x 2
(4 )s r 2
是,比例系数k=3.
不是.
你能举出一些 正比例函数的
是,比例系数k=
1 2
.
例子吗?
S 不是r的正比例函数,S是 r 2 的正比例函数.
讲授新课
y=kx(k是常数,k≠0)
例1:下列函数中哪些是正比例函数?
√
-3
2.函数y=2x的图象从左到右上升,
-4
经过第一、三象限,即:随着x的
增大y也增大。
3.函数y=-2x的图象从左到右下降,经过第二、四象限, 即:随着x的增大y反而减小。
课时小结
正比例函数的图象特点
(1)正比例函数的图象都是经过坐标原点的直线。
(2)作y=kx的图象时,应先选取两点,通常选点(0,0) 与点(1,k);然后在坐标平面内描点(0,0)与点(1,k);最 后过点(0,0)与点 (1,k)画一条直线。
下册
九章一次函数
19.2.1正比例函 数
复习旧知
1、一般地,在一个变化过程中,如果有两个变量 x
x 与 y ,并且对于 x 的每一个确定的值,y 都有 唯一 确
定的值与其对应,那么我们就说 是自变量, y 是
x 的函数。
2、描点法画函数图象的一般步骤: (1) 列表 ;(2) 描点 ;(3) 连线 . 3、表示函数的三种方法分别为:
2、一般地,形如 y k x(k是常数,k 0)的
函数,叫做_正__比__例__函数,其中 k 叫做_比__例__系__数___。
讲授新课
一般地,形如y=kx(k是常数,k≠0)的函数,
人教版数学八年级下册19.2.1《正比例函数》同步练习(含答案)

15.已知正比例函数的图像经过点 M(-2, 1)、A(x1,y1)、B(x2,y2),如果 x1<x2,那么 y1________y2.(填 “>”、“=”、“<”)
三、解答题
16.已知正比例函数 y=(m﹣1) x5m2 的图象在第二、四象限,求 m 的值.
17.在同一平面直角坐标系中画出函数 y=2x,y=- 1 x,y=-0.6x 的图象 3
人教版数学八年级下册 19.2.1《正比例函数》同步练习
一、选择题
1.对于正比例函数 y=-2x,当自变量 x 的值增加 1 时,函数 y 的值增加( )
A.0.5
B.-0.5
C.2
D.-2
2.若函数 y=(k﹣1)x+b+2 是正比例函数,则( )
A.k≠﹣1,b=﹣2 B.k≠1,b=﹣2 C.k=1,b=﹣2 D.k≠1,b=2
3.设正比例函数 y=mx 的图象经过点 A(m,4),且 y 的值随 x 值的增大而减小,则 m=( )
A.2
B.-2
C.4
D.-4
4.经过以下一组点可以画出函数 y=2x 图象的是( )
A.(0,0)和(2,1) B.(1,2)和(-1,-2) C.(1,2)和(2,1) D.(-1,2)和(1,2)
18.已知 y+3 与 x+2 成正比例,且当 x=3 时,y=7. (1)写出 y 与 x 之间的函数关系式; (2)当 x=﹣1 时,求 y 的值.
2/5
19.已知正比例函数 y=(m-1)x 的图象上有两点 A(x1,y1)、B(x2,y2),当 x1<x2 时,有 y1>y2. (1)求 m 的取值范围; (2)当 m 取最大整数时,画出该函数图象.
【名师点睛】2017年八年级数学下册 同步讲义 正比例函数及同步练习

正比例函数图形性质一次函数定义:正比例函数定义:正比例函数图象性质:例1.写出下列各题中x与y的关系式,并判断y是否是x的正比例函数?(1)电报收费标准是每个字0.1元,电报费y(元)与字数x(个)之间的函数关系;(2)地面气温是28℃,如果每升高1km,气温下降5℃,则气温x(•℃)•与高度y(km)的关系;(3)圆面积y(cm2)与半径x(cm)的关系.例2.根据下列条件求函数的解析式.(1)y与x2成正比例,且x=-2时,y=12.(2)函数y=(k2-4)x2+(k+1)x是正比例函数,且y随x的增大而减小.例3.如图,已知y=mx,正方形ABCD边长为3,A(1,2),若直线y=mx始终与正方形ABCD有交点,求m的取值范围.例4.如图,已知正比例函数的图象经过点P和点Q(﹣m,m+3).(1)求m的值.(2)若A点在坐标轴上,当△OAP的面积为4时,求点A的坐标.(3)若点B在x轴上,△OBP为等腰三角形时,求B点坐标.课堂同步练习:1.下列关系中的两个量成正比例的是()A.从甲地到乙地,所用的时间和速度;B.正方形的面积与边长C.买同样的作业本所要的钱数和作业本的数量;D.人的体重与身高2.下列函数中,y是x的一次函数的是()①y=x-6;②y= -3x –1;③y=-0.6x;④y=7-x.A.①②③B.①③④C.①②③④D.②③④3.下列函数中,y是x的正比例函数的是()A.y=4x+1B.y=2x24.若函数y=(2m+6)x2+(1-m)x是正比例函数,则m的值是()A.m=-3B.m=1C.m=3D.m>-35.下列说法中不成立的是()A.在y=3x-1中y+1与x成正比例B.在y=-0.5中y与x成正比例C.在y=2(x+1)中y与x+1成正比例D.在y=x+3中y与x成正比例6.下列说法正确的是()A.正比例函数是一次函数B.一次函数是正比例函数;C.正比例函数不是一次函数D.不是正比例函数就不是一次函数。
精品 八年级数学下册 一次函数同步讲义+练习01 函数与正比例函数

函数图象与正比例函数函数: 函数的表示方法:(1) ;(2) ;(3) 函数图象画法:正比例函数解析式 图象形状象限分布图象k>0图象k<0图象增减性解析式求法例1.⑴在平面直角坐标系中,A 、B 点的位置如图所示,试写出A 、B 两点的坐标: . (2)若C(-3,-4)、D(3,-3),请在图示坐标系中标出C 、D 两点.(3)试写出A 、B 、C 、D 四点到x 轴和y 轴的距离:A( )到x 轴距离为 ,到y 轴距离为 . B( )到x 轴距离为 ,到y 轴距离为 . C(-3,-4)到x 轴距离为 ,到y 轴距离为 . D(3,-3)到x 轴距离为 ,到y 轴距离为 .(4)分析(3)中点的坐标与该点到坐标轴的距离的关系,利用你所发现的结论写出点P(x,y)到x 轴的距离例2.点P (3,2)关于x 轴对称点是_______,关于y 轴对称点坐标是______,•关于原点对称点的坐标是________.例3.一汽车油箱中有油60升,若每小时耗油6升,则油箱中剩余油量y (升)与时间t (时)之间的函数关系式为 ,其中变量是 ,常量是 。
课堂练习:1.如图,有一游泳池已注满水,使用一段时间后把水排完清洗,然后再注满水使用,则池中存水量Q 随时间t 变化的大致图象是( )2.下列关系中的两个量成正比例的是( )A.从甲地到乙地,所用的时间和速度;B.正方形的面积与边长C.买同样的作业本所要的钱数和作业本的数量;D.人的体重与身高 3.下列函数中,y 是x 的正比例函数的是( )A.y=4x+1B.y=2x 2C.y=-5xD.y=x4.若函数y=(2m+6)x 2+(1-m)x 是正比例函数,则m 的值是( )A.m=-3B.m=1C.m=3D.m>-35.已知(x 1,y 1)和(x 2,y 2)是直线y=-3x 上的两点,且x 1>x 2,则y 1与y 2•的大小关系是( )A.y 1>y 2B.y 1<y 2C.y 1=y 2D.以上都有可能 6.下列说法中不成立的是( )A.在y=3x-1中y+1与x 成正比例;B.在y=-2x中y 与x 成正比例 C.在y=2(x+1)中y 与x+1成正比例; D.在y=x+3中y 与x 成正比例 7.关于函数y=-2x ,下列叙述正确是( )A.函数图象经过点(1,2)B.函数图象经过第二、四象限C.y 随x 的增大而减小D.不论x 取何值,总有y<08.某本书的单价是14元,当购买x 本这种书时,花费为y 元,则用x 表示y 时,应有 ,其中变量是 ,常量是 。
精品 八年级数学下册 函数与变量 正比例函数讲义+同步练习

D.y=2(12-x)
6.已知函数 y=x2-x-2 当 x=2 时,函数值为 7.当 x=
。
时,函数 y=3x-2 与函数 y=5x+1 有相同的函数值。 。 ) C. x 4 且x 1 3 ) D.x≥-1 且 x≠1 D. x 4 3
8.函数 y x 3 的自变量 x 的取值范围是 9.函数 y x 1 中,自变量 x 的取值范围是( 3x 4 A. x 4 3 B. x 1
(2)直角三角形中一个锐角α与另一个锐角β之间的关系.
(3)一盛满 30 吨水的水箱,每小时流出 0.5 吨水,试用流水时间 t(小时)表示水箱中的剩水量 y(吨) .
Байду номын сангаас
(4) 小军用 50 元钱去买单价是 8 元的笔记本,则他剩余的钱 Q(元)与他买这种笔记本的本数 x 之间的关 系
第 1 页 共 12 页
10.函数 y x 2 x 1 的自变量 x 的取值范围为( x 1 A.x≠1 B.x>-1 C.x≥-1
11.汽车由北京驶往相距 120 千米的天津,它的平均速度是 30 千米/时,则汽车距天津的路程 S (千米) 与 行驶时间 t(时)的函数关系及自变量的取值范围是( A.S=120-30t(0≤t≤4) B.S=30t(0≤t≤4) ) C.S=120-30t(t>0) D.S=30t(t=4)
)
4.下图是南昌市某天的温度随时间变化的图像,通过观察可知:下列说法错误的是( A.这天 15 点时温度最高 C.这天最高温度与最低温度的差是 13℃ 5.下列关系式中,变量 x=-1 时,变量 y=6 的是( A.y=3x+3 6.球的体积公式:V= A.4 π B.y=-3x+3 B.这天 3 点时温度最低 D.这天 21 点时温度是 30℃ ) C.y=3x-3 D.y=-3x-3 ) D.π
数学知识点八年级数学下册4.3正比例函数图象和性质(第1课时)同步练习(新版)湘教版含解析

一次函数的图象第 1 课时正比率函数的图象和性质01 课前预习重点感知 1画函数图象的步骤:(1)________ ; (2)________ :成立直角坐标系,以____________ 为横坐标,_______________ _为纵坐标,确立点的坐标;(3)________ .1预习练习 1- 1 画正比率函数 y=2x 的图象,能够过原点和以下哪一点?( )11A.(1 ,2)B. (1 ,- 2)C.(1,2)D. (1 ,-2)重点感知 2正比率函数 y=kx(k为常数, k≠0) 的图象是一条 ________,所以画正比率函数图象时,只需描出图象上的 ________,而后过两点作一条直线即可,这条直线叫作“直线 ________”.预习练习 2- 1 以下各点,不在正比率函数1y=-x 图象上的是 ( )31A.(0 ,0)B.(1 ,- 3)C. ( -3, 1)D. (1 ,-3)重点感知 3正比率函数图象的性质:直线y= kx(k为常数, k≠0) 是一条经过 ________的直线.当 k>0 时,直线 y =kx 经过第 ________象限,从左向右 ________,y 随 x 的增大而 ________;当 k<0 时,直线 y= kx 经过第 ________象限,从左向右________, y 随 x 的增大而 ________.预习练习3- 1以下是正比率函数的图象,且y 随 x 值的增大而减小的是( )2当堂训练知识点 1画正比率函数的图象1.正比率函数y=- 3x 的大概图象是 ( )2.已知正比率函数y= x,请在平面直角坐标系中画出这个函数的图象.知识点 2正比率函数的图象与性质3.已知函数y= kx 的函数值随x 的增大而增大,则函数的图象经过( )A.第一、二象限B.第一、三象限C.第二、三象限D.第二、四象限4. ( 北海中考 ) 正比率函数y= kx 的图象如下图,则k 的取值范围是 ( )A. k> 0C. k> 1D. k< 15.关于函数y=- k2x(k 是常数, k≠ 0) 的图象,以下说法不正确的选项是( )A.其函数图象是一条直线1B.其函数图象过点( k,- k)C.其函数图象经过一、三象限D. y 跟着 x 增大而减小6.函数 y=- 5x 的图象在第 ________象限内, y 随 x 的增大而 ________.知识点 3实质问题中的正比率函数7.一根蜡烛长20 cm ,点燃后每小时焚烧 5 cm,则蜡烛焚烧的长度y(cm) 与焚烧时间x(h) 的函数关系用图象表示为以下图中的 ( )8.小明用16 元零花费购置水果,已知水果单价是每千克 4 元,设买水果x 千克用去的钱为y 元,(1)求买水果用去的钱 y( 元 ) 随买水果的数目 x( 千克 ) 而变化的函数表达式;(2)画出这个函数的图象.3课后作业9.已知正比率函数y=kx(k ≠0) ,当x= 1 时, y=- 2,则它的图象大概是( )10.已知正比率函数y= (3k - 1)x ,若 y 随 x 的增大而增大,则k 的取值范围是( )A. k< 0B. k> 011C. k<3D. k>311. ( 陕西中考 ) 设正比率函数y= mx 的图象经过点A(m, 4) ,且 y 的值随 x 值的增大而减小,则 m= ( )A. 2B.- 2C. 4D.- 412. ( 广州中考 ) 已知正比率函数y= kx(k<0) 的图象上两点 A(x1, y1) 、 B(x 2, y2) ,且 x1<x2,则以下不等式中恒成立的是( )A. y1+ y2>0B. y1+ y2 <0C. y - y >0D. y - y <0121213. ( 德州中考 ) 甲、乙两人在一次百米赛跑中,行程s( 米 ) 与赛跑时间 t( 秒 ) 的关系如下图,则以下说法正确的是 ( )B.甲先抵达终点C.乙用的时间短D.乙比甲跑的行程多14. ( 云南中考 ) 写出一个图象经过一、三象限的正比率函数y=kx(k ≠0) 的表达式 ( 关系式 ) : ________________ .15.当 m=________时,函数 y= mx3m+4是正比率函数,此函数y 随 x 的增大而 ________.16.如图,正比率函数 y= kx ,y=mx,y= n x 在同一平面直角坐标系中的图象如下图.则系数k,m,n 的大小关系是 __ ______.17.已知正比率函数y= (k -2)x.(1) 若函数图象经过第二、四象限,则k 的范围是什么?(2)若函数图象经过第一、三象限,则 k 的范围是什么?18.已知正比率函数y= kx 的图象经过点 ( - 1,2) .(1)求 k 的值;画出这个函数图象;(3)点 (2 ,- 5) 能否在此函数图象上?(4) 若点 A(a, 8) 在这个函数图象上,求点 A 的坐标.挑战自我19.已知正比率函数y= kx 经过点 A,点 A 在第四象限,过点 A 作 AH⊥x轴,垂足为点H,点 A 的横坐标为3,且△ AOH 的面积为 3.在 x 轴上可否找到一点P,使△ AOP的面积为5?若存在,求点P 的坐标;若不存在,请说明原因.参照答案课前预习重点感知 1列表描点自变量值相应的函数值连线预习练习 1- 1C重点感知 2直线两点y= kx预习练习 2- 1B重点感知 3原点一、三上涨增大二、四降落减小预习练习 3- 1C当堂训练1. C 2. 如图: 3.B 4.A 5.C 6. 二、四减小8.(1)依据题意可得y=4x(0 ≤x≤4) .(2) 当 x= 0 时, y= 0;当 x= 4 时, y=16.在平面直角坐标系中画出两点O(0,0) ,A(4 ,16) ,过这两点作线段OA,线段 OA即函数 y=4x(0 ≤x≤4) 的图象,如图.课后作业9. A 10.D 11.B 12.C 13.B 14.y =3x( 答案不独一 ) 15. - 1减小16.k > m>n17.(1)k-2<0,∴k< 2.(2)k - 2>0,∴k>2.18.(1)k=-2.(2)图象如图.(3)将点 (2 ,- 5) 代入,左侧=- 5,右侧=- 4,左侧≠右侧,故点 (2 ,- 5)不在此函数图象上.(4)把 (a , 8) 代入 y=- 2x,得 8=- 2a. 解得 a=- 4. 故点 A 的坐标是 ( - 4,8) .19.(1)∵点A的横坐标为3,且△ AOH的面积为3,∴点 A 的纵坐标为- 2,点 A 的坐标为 (3 ,- 2) .∵正比率函数y= kx 经过点 A,2∴ 3k=- 2. 解得 k=-3.2∴正比率函数的表达式是y=-x.(2)3∵△ AOP的面积为5,点 A 的坐标为 (3 ,- 2) ,∴OP= 5.∴点 P 的坐标为 (5 ,0) 或 ( -5, 0) .。
人教版八年级下册数学一次函数第1课时正比例函数 同步练习
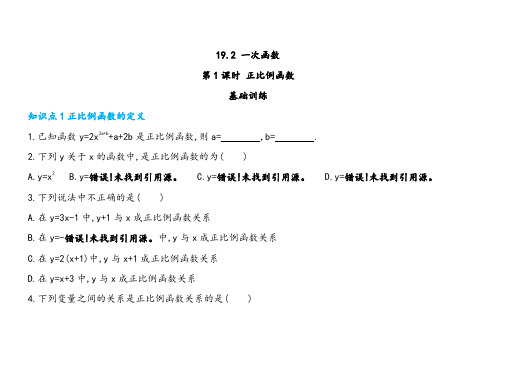
19.2 一次函数第1课时正比例函数基础训练知识点1正比例函数的定义1.已知函数y=2x2a+b+a+2b是正比例函数,则a= ,b= .2.下列y关于x的函数中,是正比例函数的为( )A.y=x2B.y=错误!未找到引用源。
C.y=错误!未找到引用源。
D.y=错误!未找到引用源。
3.下列说法中不正确的是( )A.在y=3x-1中,y+1与x成正比例函数关系B.在y=-错误!未找到引用源。
中,y与x成正比例函数关系C.在y=2(x+1)中,y与x+1成正比例函数关系D.在y=x+3中,y与x成正比例函数关系4.下列变量之间的关系是正比例函数关系的是( )A.矩形的面积固定,长和宽之间的关系B.正方形的面积和边长之间的关系C.三角形的面积一定,底边和底边上的高之间的关系D.匀速运动中,路程和时间之间的关系知识点2求正比例函数的解析式5.根据下表,写出y与x之间的函数解析式: ,这个函数是函数.6.如果每盒圆珠笔有12支,每盒的售价是18元,那么圆珠笔的总售价y(元)与数量x(支)之间的函数解析式为( )A.y=12xB.y=18xC.y=错误!未找到引用源。
xD.y=错误!未找到引用源。
x7.一个正比例函数的图象过点(2,-3),它的解析式为( )A.y=-错误!未找到引用源。
xB.y=错误!未找到引用源。
xC.y=错误!未找到引用源。
xD.y=-错误!未找到引用源。
x易错点忽略比例系数不为零的限制造成错解8.已知函数y=(k-2)x|k|-1(k为常数)是正比例函数,则k的值是.提升训练考查角度1利用正比例函数的定义识别正比例函数9.写出下列各题中y与x之间的关系式,并判断y是否为x的正比例函数.(1)汽车以60 km/h的速度匀速行驶,行驶路程y(km)与行驶时间x(h)之间的关系式;(2)圆的面积y(cm2)与它的半径x(cm)之间的关系;(3)一棵树现在高50 cm,每个月长高2 cm,x月后这棵树的高度为y cm.考查角度2利用求正比例函数解析式解几何问题10.△ABC的底边BC=8 cm,当BC边上的高从小到大改变时,△ABC的面积也随之变化.(1)写出△ABC的面积y(cm2)与BC边上的高x(cm)之间的函数解析式,并指明它是什么函数;(2)列表格表示当x由5 cm变到10 cm时(每次增加1 cm),y的相应值;(3)观察表格,请回答:当x每增加1 cm时,面积y如何变化?参考答案1.错误!未找到引用源。
数学人教版八年级下册第一课时认识 正比例函数同步练习(含答案)

优质资料---欢迎下载19.2.1 第一课时认识正比例函数1.下列变量之间的关系中,一个变量是另一个变量的正比例函数的是 ( ) A .正方形的面积S 随着边长x 的变化而变化B .正方形的周长C 随着边长x 的变化而变化C .水箱有水10 L ,以0.5 L/min 的速度往外放水,水箱中的剩余水量V(L)随着放水时间t(min)的变化而变化D .面积为20的三角形的一边a 随着这边上的高h 的变化而变化2.若y=(m-1)22m x 是正比例函数,则m 的值为( )A .1B .-1C .1或-1D .2-2或3.下列四个函数中,是正比例函数的是 ( )A .y=2x+1B .y=2x ²+1C .y=x2 D .y=2x 4.若在正比例函数y=kx (k ≠0)中,自变量x 的取值每增加1,函数值相应地减小4,则k 的值为( )A .4B .-4C .41D .-41 5.如图19-2-1-2,在矩形AOBC 中,A (-2,0),B(O ,1).若正比例函数y=kx 的图象经过点C ,则k 的值为( )A .-2B .-21C .2D .21 6. 三角形的一边长为6,该边上的高为x ,则三角形的面积S 与x 之间的函数关系式为_____.7.已知正比例函数经过点(-1,2),则该函数解析式为_______.8.已知y 是x 的正比例函数,且函数图象经过点(-3,6).(1)求y 关于x 的函数关系式;(2)当x=-6时,求对应的函数值y ;(3)当x 取何值时,y=32? 9.已知y+2与x+3成正比例,当x=1时,y=2.试求:(1)y 与x 的函数关系式;(2)当x=-3时,求y 的值;(3)当y=5时,求x 的值.答案解析1.B 列出关系式,四个选项分别是S=x ²,C=4x ,y=10-0.5t ,a=h40,只有C=4x 符合正比例函数的定义,故选B .2.B 由题意得2-m ²=1且m-1≠0,解得m=±1且m ≠1,∴m=-1.3.D 根据正比例函数的定义判断:形如y=kx ,其中k 为常数且k ≠0,自变量次数为1,只有y=2x 满足,故选D .4.B 当x 变为x+1时,函数值变为y-4,所以y-4=k(x+1),即y-4=kx+k ,所以kx-4=kx+k ,所以k=-4.故选B .5.B ∵四边形AOBC 是矩形,A (-2,0),B(O ,1),∴AC=OB=1,BC=OA=2,∴点C 的坐标为(-2,1),将点C (-2,1)代入y=kx ,得1=-2k ,解得k=-21,故选B . 6.答案S=3x解析 由三角形的面积公式可得S=21×6x ,即S=3x . 7.答案y=-2x解析 设函数的解析式为y=kx(k ≠O),因为点(-1,2)在该函数图象上,所以-k=2,即k=-2,所以函数的解析式为y=-2x.8.解析 (1)设正比例函数的关系式为y=kx(k ≠0),∴图象经过点(-3,6),∴-3k=6,解得k=-2,所以,此函数的关系式是y=-2x.(2)把x=-6代入函数关系式可得y=-2×(-6)=12.(3)把y=32代入函数关系式可得32=-2x ,解得x=-31. 9.解析(1)由题意,可设y+2=k (x+3)(k ≠O),把x=1,y=2代入,得2+2=4k ,解得k=1,所以y+2=x+3,即y=x+1.(2)当x=-3时,y=-3+1=-2.(3)当y=5时,5=x+1.解得x=4.。
人教版数学八年级下册19.2.1 正比例函数同步练习(解析版)

19.2 一次函数19.2.1 正比例函数基础闯关全练1.下列变量之间的关系中,一个变量是另一个变量的正比例函数的是()A.正方形的面积S随着边长x的变化而变化B.正方形的周长C随着边长x的变化而变化C.水箱有水10 L,以0.5 L/min的速度往外放水,水箱中的剩余水量V(L)随着放水时间t(min)的变化而变化D.面积为20的三角形的一边a随着这边上的高h的变化而变化2.若y=(m-1)22mx 是正比例函数,则m的值为()A.1 B.-1 C.1或-1 D.2-2或3.对于正比例函数y=(1-k)x,若y随x的增大而减小,则k的值可以是()A.-1 B.3 C.0 D.-34.如图19-2-1-1.三个正比例函数的图象分别对应的解析式是④y=ax;②y=bx;③y=cx,则a、b、c的大小关系是()A.a>b>c B.c>b>a C.b>a>c D.b>c>a 5.(1)在同一直角坐标系内画出正比例函数y=-2x与y=0.5x的图象;(2)用量角器量一下这两条直线的夹角,你会发现什么?写出你的猜想.6.三角形的一边长为6,该边上的高为x,则三角形的面积S与x之间的函数关系式为_______.7.已知y是x的正比例函数,且函数图象经过点(-3,6).(1)求y关于x的函数关系式;(2)当x=-6时,求对应的函数值y;(3)当x取何值时,y=32?能力提升全练1.若在正比例函数y=kx(k≠0)中,自变量x的取值每增加1,函数值相应地减小4,则k的值为()A.4 B.-4 C.41 D.-412.已知正比例函数y=kx(k是常数,k≠0),当-3≤x≤1时,对应的y的取值范围是-1≤y≤31,且y随x的减小而减小,则k的值为_______.三年模拟全练一、选择题1.下列四个函数中,是正比例函数的是()A.y=2x+1 B.y=2x²+1 C.y=x2 D.y=2x2.已知函数y=(a-1)•x的图象过第一、三象限,那么a的取值范围是()A.a>1 B.a<1 C.a>0 D.a<03.设正比例函数y=mx的图象经过点A(m,4),且y随x增大而增大,则m=()A.2 B.-2 C.4 D.-4二、填空题4.已知正比例函数经过点(-1,2),则该函数解析式为_______.三、解答题5.已知y+2与x+3成正比例,当x=1时,y=2.试求:(1)y与x的函数关系式;(2)当x=-3时,求y的值;(3)当y=5时,求x的值.五年中考全练一、选择题1.一个正比例函数的图象经过点(2,-1),则它的解析式为()A.y=-2x B.y=2x C.y=-21x D.y=21x2.正比例函数y=2x的大致图象是()A .B .C .D .3.如图19-2-1-2,在矩形AOBC中,A(-2,0),B(O,1).若正比例函数y=kx的图象经过点C,则k的值为()A.-2 B.-21 C.2 D.21二、填空题4.若正比例函数y=kx(k是常数,k≠0)的图象经过第二、第四象限,则k的值可以是_______(写出一个即可).核心素养全练1.如图19-2-1-3,在平面直角坐标系中,点A₁的坐标为(1,2),以点O为圆心,OA₁长为半径画弧,交直线y=21x于点B₁,过B₁点作B₁A₂∥y轴,交直线y=2x于点A₂,以点O为圆心,OA₂长为半径画弧,交直线y=21x于点B₂;过点B₂作B₂A₃∥y轴,交直1x于点B₃;过B₃点作线y=2x于点A3,以点O为圆心,OA₃长为半径画弧,交直线y=21于B₃A₄∥y轴,交直线y=2x于点A₄,以点O为圆心,OA₄长为半径画弧,交直线y=x2点B₄;……,按照此规律进行下去。
人教版八年级数学下册19.2.1正比例函数 同步导学(带答案)

19.2.1正比例函数的图象与性质学习目标1.掌握正比例函数,比例系数等概念; 2.能画出正比例函数的图象并根据图象分析其性质;3.会求正比例函数的解析式.一、变式训练知识点1:形如y=kx(k是常数,k≠0)的函数,叫做正比例函数,其中,k叫做比例系数.1.下列函数中,是正比例函数的是(C)A.y=x2B.y=2 xC.y=x 2D.y=x+1 2知识点2:正比例函数图象与性质正比例函数的图象是一条经过原点的直线.画正比例函数y=kx的图象通常取两个点.2.用“描点法”画出y=1.5x的图象.解:y=1.5x自变量x的取值范围是全体实数x …0 1 …y=1.5x …0 1.5 …归纳:函数y=1.5x(k>0)的图象是一条直线,它经过原点和(1,1.5),图象经过一、三象限,图象从左向右上升,即y随着x增大而增大.画图略知识点3:求正比例函数解析式3.正比例函数y=kx经过点(-2,4),求它的解析式.解:y=-2x4.(1)关于x的函数y=(a+1)x是正比例函数,则a≠-1.(2)关于x的函数y=7x m-2+n-4是正比例函数,则m=3,n=4.5.用“描点法”画出y=-2x的图象.解:y=-2x自变量x的取值范围是全体实数x …0 1 …y=-2x …0 -2 …归纳:函数y=-2x(k<0)的图象是一条直线,它经过原点和(1,-2),图象经过二、四象限,图象从左向右下降,即y随着x增大而减小.画图略6.一个函数的图象是经过原点的直线,并且这条直线经过点(-1,-6),求这个函数解析式.解:y=6x二、基础训练7.下列是正比例函数的是(B)A.y=4x+1B .y =-x3 C .y =-2xD .y =-x 28.下列问题中,是正比例函数的是(D ) A .矩形面积固定,长和宽的关系 B .正方形面积和边长之间的关系C .三角形的面积一定,底边和底边上的高的关系D .匀速运动中,速度固定时,路程和时间的关系 9.关于函数y =13x ,下列结论中,正确的是(C ) A .函数图象经过点(1,3) B .函数图象经过二、四象限 C .y 随x 的增大而增大 D .不论x 为何值,总有y >010.若点A (-5,y 1)和点B (-2,y 2)都在y =-12x 上,则y 1与y 2的大小关系为(A ) A .y 1>y 2 B .y 1=y 2 C .y 1<y 2 D .y 1≤y 211.(2016·眉山)若函数y =(m -1)x |m |是正比例函数,则该函数的图象经过第二、四象限.12.y 与x 成正比例,当x =5时,y =2,则y 关于x 的函数关系式是y=0.4x .13.函数y =-5x 的图象在第二、四象限,经过点(0,0)与点(1,-5),y 随x 的增大而减小.14.已知正比例函数y =(2m +4)x .求: (1)m 为何值时,函数图象经过一、三象限;(2)m为何值时,y随x的增大而减小;(3)m为何值时,点(1,3)在该函数图象上.解:(1)m>-2(2)m<-2(3)m=-1 2三、拓展提升15.写一个图象经过第二、四象限的正比例函数:y=-x(答案不唯一).16.正比例函数y=kx的图象如图所示,则k的取值范围是(A)A.k>0B.k<0C.k>1D.k<117.(2016·陕西)设点A(a,b)是正比例函数y=-32x图象上的任意一点,则下列等式一定成立的是(D)A.2a+3b=0B.2a-3b=0C.3a-2b=0D.3a+2b=018.已知y-2与3x-4成正比例函数关系,且当x=2时,y=3.(1)写出y与x之间的函数解析式;(2)若点P(a,-3)在这个函数的图象上,求a的值;(3)若y取值范围为-1≤y≤1,求x取值范围.解:(1)设y-2=k(3x-4),将x=2,y=3代入,得:2k=1,解得k=1 2,∴y -2=12(3x -4),即y =32x ;(2)将点P (a ,-3)代入y =32x ,得:32a =-3,解得:a =-2;(3)当y =-1时,32x =-1,解得:x =-23,当y =1时,32x =1,解得:x =23,∴-23≤x ≤23.。
2020-2021学年人教版八年级下册数学19.2.1正比例函数 同步练习(含解析)

19.2.1正比例函数同步练习一.选择题1.下列问题中,两个变量之间是正比例函数关系的是()A.汽车以80km/h的速度匀速行驶,行驶路程y(km)与行驶时间x(h)之间的关系B.圆的面积y(cm2)与它的半径x(cm)之间的关系C.某水池有水15m3,我打开进水管进水,进水速度5m3/h,xh后水池有水ym3D.有一个边长为x的正方体,则它的表面积S与边长x之间的函数关系2.已知函数y=3x|m﹣2|是关于x的正比例函数,则常数m的值为()A.3或1B.3C.±1D.13.已知y是x的正比例函数,当x=3时,y=﹣6,则y与x的函数关系式为()A.y=2x B.y=﹣2x C.y=x D.y=﹣x4.已知正比例函数y=kx,当x每增加2时,y减少3,则k的值为()A.﹣B.C.﹣D.5.下列说法中不成立的是()A.在y=3x﹣1中y+1与x成正比例B.在y=﹣中y与x成正比例C.在y=2(x+1)中y与x+1成正比例D.在y=x+3中y与x成正比例6.关于直线y=﹣2x,下列结论正确的是()A.图象必过点(1,2)B.图象经过第一、三象限C.与y=﹣2x+1平行D.y随x的增大而增大7.已知函数y=(m+1)x,y随x的增大而增大,则m的取值范围在数轴上表示正确的是()A.B.C.D.8.已知直线y=k1x,y=k2x,y=k3x的图象如图,则k1、k2、k3的大小关系为()A.k1>k2>k3B.k1>k3>k2C.k3>k2>k1D.k2>k1>k39.关于正比例函数y=﹣2x,下列说法正确的是()A.y随x的增大而增大B.图象是经过第一、第二象限的一条直线C.图象向上平移1个单位长度后得到直线y=﹣2x+1D.点(1,2)在其图象上10.已知正比例函数y=(2t﹣1)x的图象上一点(x1,y1),且x1y1<0,那么t的取值范围是()A.t<0.5B.t>0.5C.t<0.5或t>0.5D.不确定二.填空题11.直线y=x经过第象限.12.某正比例函数的图象经过点(﹣1,2),则此函数关系式为.13.如果正比例函数y=(3k﹣2)x的图象在第二、四象限内,那么k的取值范围是.14.在函数y=x中,若自变量x的取值范围是50≤x≤75,则函数值y的取值范围为.15.如图,直线l的解析式为y=x,点A的坐标为(﹣2,0),AB⊥l于点B,则△ABO的面积为.三.解答题16.已知y与x成正比例,且当x=3时,y=4.(1)求y与x之间的函数解析式;(2)当x=﹣1时,求y的值.17.已知函数y=(k+3)x.(1)k为何值时,函数为正比例函数;(2)k为何值时,函数的图象经过一,三象限;(3)k为何值时,y随x的增大而减小?(4)k为何值时,函数图象经过点(1,1)?18.已知正比例函数y=kx经过点A,点A在第四象限,过点A作AH⊥x轴,垂足为点H,点A 的横坐标为3,且△AOH的面积为3.(1)求正比例函数的表达式;(2)在x轴上能否找到一点P,使△AOP的面积为5?若存在,求点P的坐标;若不存在,请说明理由.参考答案一.选择题1.解:选项A:y=80x,属于正比例函数,两个变量之间成正比例函数关系,符合题意;选项B:y=πx2,属于二次函数,两个变量之间不是成正比例函数关系,不合题意;选项C:y=15+5x,属于一次函数,两个变量之间不是成正比例函数关系,不合题意;选项D:S=6x2,属于二次函数,两个变量之间不是成正比例函数关系,不合题意;故选:A.2.解:∵函数y=3x|m﹣2|是关于x的正比例函数,∴|m﹣2|=1,解得:m=3或1,故选:A.3.解:设y与x之间的函数关系式是y=kx,把x=3,y=﹣6代入得:﹣6=3k,解得:k=﹣2,∴y与x的函数关系式为y=﹣2x,故选:B.4.解:根据题意得:y﹣3=k(x+2),y﹣3=kx+2k,而y=kx,所以2k=﹣3,解得k=﹣.故选:C.5.解:A、∵y=3x﹣1,∴y+1=3x,∴y+1与x成正比例,故本选项正确.B、∵y=﹣,∴y与x成正比例,故本选项正确;C、∵y=2(x+1),∴y与x+1成正比例,故本选项正确;D、∵y=x+3,不符合正比例函数的定义,故本选项错误.故选:D.6.解:A、∵(1,2)不能使y=﹣2x左右相等,因此图象不经过(1,2)点,故此选项错误;B、∵k=﹣2<0,∴图象经过第二、四象限,故此选项错误;C、∵两函数k值相等,∴两函数图象平行,故此选项正确;D、∵k=﹣2<0,∴y随x的增大而减小,故此选项错误;故选:C.7.解:∵一次函数y=(m+1)x,y随x的增大而增大,∴m+1>0,解得,m>﹣1,在数轴上表示为:.故选:C.8.解:由题意得:k1为正数,k2>k3,∴k1,k2,k3的大小关系是k1>k2>k3.故选:A.9.解:A、k=﹣2,y随x的增大而减小,不符合题意;B、图象是经过第二、第四象限的一条直线,不符合题意;C、图象向上平移1个单位长度后得到直线y=﹣2x+1,符合题意;D、当x=1时,y=﹣2,所以点(1,2)不在其图象上,不符合题意;故选:C.10.解:因为x1y1<0,所以该点的横、纵坐标异号,即图象经过二、四象限,则2t﹣1<0,t<.故选:A.二.填空题11.解:由正比例函数y=x中的k=>0知函数y=x的图象经过第一、三象限.故答案是:一、三.12.解:设此函数的解析式为y=kx(k≠0),∵点(﹣1,2)在此函数图象上,∴﹣k=2,解得k=﹣2,∴此函数的关系式为y=﹣2x.故答案为:y=﹣2x.13.解:正比例函数y=(3k﹣2)x的图象经过第二、四象限,∴3k﹣2<0,解得,k<.故答案是:k<.14.解:∵函数y=x的y随x的增大而增大,∴当x=50时,y=×50=120.当x=75时,y=×75=180.则120≤y≤180.故答案是:120≤y≤180.15.解:∵直线l的解析式为y=x,∴∠AOB=45°,设B(a,a),∵AB⊥l于点B,∴△AOB是等腰直角三角形,∴AB=OB=OA,∵点A的坐标为(﹣2,0),∴OA=2,∴AB=OB=,∴△ABO的面积==1,故答案为:1.三.解答题16.解:(1)∵y与x成正比例,∴设y=kx,∵当x=3时,y=4,∴4=3k,解得k=,∴y与x之间的函数关系式为y=x;(2)把x=﹣1代入y=x得y=﹣;17.解:(1)根据题意得k+3≠0,解得k≠﹣3;(2)根据题意得k+3>0,解得k>﹣3;(3)根据题意得k+3<0,解得k<﹣3;(4)把(1,1)代入y=(k+3)x得k+3=1,解得k=﹣2,即k为﹣2时,函数图象经过点(1,1).18.解:(1)∵点A在第四象限,点A的横坐标为3,且△AOH的面积为3.∴点A的纵坐标为﹣2,∴点A的坐标为(3,﹣2).将点A(3,﹣2)代入y=kx,﹣2=3k,解得:k=﹣,∴正比例函数的表达式为y=﹣x.(2)设点P的坐标为(a,0),则S△AOP=|a|×|﹣2|=5,解得:a=±5,∴在x轴上能找到一点P,使△AOP的面积为5,此时点P的坐标为(﹣5,0)或(5,0).。
新人教版数学八下同步练习19.2.1 正比例函数

19.2.1正比例函数知识要点基础练知识点1正比例函数的定义1.下列式子中,表示y是x的正比例函数的是( B)A.y=x-1B.y=2xC.y=2x2D.y2=2x2.若y关于x的函数y=( m-2 )x+n是正比例函数,则m,n应满足的条件是( A)A.m≠2且n=0B.m=2且n=0C.m≠2D.n=03.当m=1时,函数y=( 2m-1 )x3m-2是正比例函数.知识点2正比例函数的图象4.函数y=3x的图象经过( A)A.第一、三象限B.第二、四象限C.第一、二象限D.第三、四象限5.正比例函数y=kx的图象如图所示,则k的值是( B)A.-B.C.-D.知识点3正比例函数的性质6.如图,三个正比例函数的图象对应的解析式为①y=ax,②y=bx,③y=cx,则a,b,c的大小关系( B)A.a>b>cB.c>b>aC.b>a>cD.b>c>a7.已知关于x的正比例函数y=( m+2 )x,若y的值随x值的增大而增大,则m的取值范围是m>-2.综合能力提升练8.已知正比例函数y=kx,当x每增加3,y就减小4,则k的值是( D)A.B.-C.D.-9.已知函数y=( a-1 )x的图象过第一、三象限,那么a的取值范围是( A)A.a>1B.a<1C.a>0D.a<010.如果y=( 1-m)-是正比例函数,且y的值随x值的增大而减小,则m的值是( B)A.-B.C.3D.-311.已知直线y=( 2-3m)x经过点A( x1,y1),B( x2,y2),当x1<x2时,y1>y2,则m的取值范围是m>.12.若点A( m,n)在直线y=kx( k≠0)上,当-1≤m≤1时,-1≤n≤1,则这条直线的函数解析式是y=x或y=-x.13.已知正比例函数y=kx的图象经过点( 3,-6 ).( 1 )求这个函数的解析式;( 2 )判断点A( 4,-2 )是否在这个函数的图象上;( 3 )图象上有两点B( x1,y1),C( x2,y2),如果x1>x2,比较y1,y2的大小.解:( 1 )这个正比例函数的解析式为y=-2x.( 2 )把x=4代入y=-2x,得y=-8≠-2,∴点A( 4,-2 )不在这个函数的图象上.( 3 )∵k=-2<0,∴y随x的增大而减小,∵x1>x2,∴y1<y2.拓展探究突破练14.定义运算“※”:a※b=-( 1 )计算:3※4;( 2 )画出函数y=2※x的图象.解:( 1 )∵4≥0,∴3※4=3×4=12.( 2 )当x≥0时,y=2x;当x<0时,y=-2x.列表如下,描点、连线、作图略.。
人教版-数学-八年级下册《正比例函数》同步练习3

正比例函数1.若y=x+2﹣b是正比例函数,则b的值是()A.0B.-2C.2D.-0.52.下列各选项中的y与x的关系为正比例函数的是()A. 正方形周长y(厘米)和它的边长x(厘米)的关系B. 圆的面积y(平方厘米)与半径x(厘米)的关系C. 如果直角三角形中一个锐角的度数为x,那么另一个锐角的度数y与x间的关系D. 一棵树的高度为60厘米,每个月长高3厘米,x月后这棵的树高度为y厘米3.若函数y=(m﹣3)x|m|﹣2是正比例函数,则m值为()A.3B.-3C. ±3D.不能确定4.已知正比例函数y=(k﹣2)x+k+2的k的取值正确的是()A. k=2B. k≠2C. k=﹣2D. k≠﹣25.已知正比例函数y=kx(k≠0)的图象如图所示,则在下列选项中k值可能是()A.1 B.2 C.3 D.48题图 9题图6.如图所示,在同一直角坐标系中,一次函数y=k1x、y=k2x、y=k3x、y=k4x的图象分别为l1、l2、l3、l4,则下列关系中正确的是()A. k1<k2<k3<k4B. k 2<k1<k4<k3C. k 1<k2<k4<k3D. k2<k1<k3<k47.在直角坐标系中,既是正比例函数y=kx,又是y的值随x的增大而减小的图象是()A. B. C. D.8.若函数y﹦(m+1)x+m2﹣1是正比例函数,则m的值为_________ .9.已知y=(k﹣1)x+k2﹣1是正比例函数,则k= _________ .10.写出一个正比例函数,使其图象经过第二、四象限:_________ .11.请写出直线y=6x上的一个点的坐标:_________ .12.已知正比例函数y=kx(k≠0),且y随x的增大而增大,请写出符合上述条件的k的一个值:_________ .13.若p1(x1,y1) p2(x2,y2)是正比例函数y=﹣6x的图象上的两点,且x1<x2,则y1,y2的大小关系是:y1 _________ y2.点A(-5,y1)和点B(-6,y2)都在直线y= -9x的图像上则y1__________ y214.正比例函数y=(m﹣2)xm的图象的经过第_________ 象限,y随着x的增大而_________ .15.函数y=﹣7x的图象在第_________ 象限内,经过点(1,_________ ),y随x 的增大而_________ .16.已知:如图,正比例函数的图象经过点P和点Q(﹣m,m+3),求m的值.17.已知y+2与x﹣1成正比例,且x=3时y=4.(1)求y与x之间的函数关系式;(2)当y=1时,求x的值.18.已知y=y1+y2,y1与x2成正比例,y2与x﹣2成正比例,当x=1时,y=5;当x=﹣1时,y=11,求y与x之间的函数表达式,并求当x=2时y的值.参考答案1.C2.A3.B4.C5.B6.B7.C8.19.-110.y=﹣x(答案不唯一).11.(0,0)(答案不唯一).12.y=2x.(答案不唯一)13.>14.二、四;减小.15.二、四;﹣7;减小.16.解:设正比例函数的解析式为y=kx(k≠0).∵它图象经过点P(﹣1,2),∴2=﹣k,即k=﹣2.∴正比例函数的解析式为y=﹣2x.又∵它图象经过点Q(﹣m,m+3),∴m+3=2m.∴m=3.17.解:(1)设y+2=k(x﹣1),把x=3,y=4代入得:4+2=k(3﹣1)解得:k=3,则函数的解析式是:y+2=3(x﹣1)即y=3x﹣5;(2)当y=1时,3x﹣5=1.解得x=2.18.解:设y1=kx2,y2=a(x﹣2),则y=kx2+a(x﹣2),把x=1,y=5和x=﹣1,y=11代入得:,k=﹣3,a=2,∴y与x之间的函数表达式是y=﹣3x2+2(x﹣2).把x=2代入得:y=﹣3×22+2×(2﹣2)=﹣12.。
人教版数学2022-2023学年八年级下册第十九章正比例函数同步练习题含答案

人教版数学2022-2023学年八年级下册第十九章正比例函数同步练习题学校:___________姓名:___________班级:_______________一、填空题1.像y =0.5x +10这样,用关于自变量的数学式子表示函数与自变量之间的关系,是描述函数的常用方法.这种式子叫做函数的__________.2.若函数y =(m ﹣2)x +5﹣m 是关于x 的正比例函数,则m =_____. 3.对于正比例函数y=1m mx -,若图像经过第一,三象限,则m=____. 4.已知y 与2x -成正比例,且当1x =时,1y =,则y 与x 之间的函数关系式为______________.5.若两个变量x ,y 间的对应关系可以表示成____的形式,则称y 是x 的一次函数.特别地,当____时,称y 是x 的正比例函数,即____.6.在下列函数中,x 是自变量,y 是因变量,则一次函数有___,正比例函数有___.(将代号填上即可)①1y =+;①22y x x =+;①5y x =;①14y x =-;①1y x= 二、单选题7.下列问题中,两个变量之间成正比例关系的是( ) A .圆的面积S (cm 2)与它的半径r (cm )之间的关系B .某水池有水15m 3,现打开进水管进水,进水速度为5m 3/h ,x h 后这个水池有水y m 3C .三角形面积一定时,它的底边a (cm )和底边上的高h (cm )之间的关系D .汽车以60km/h 的速度匀速行驶,行驶路程y 与行驶时间x 之间的关系 8.下列说法正确的是( )A .面积一定的平行四边形的一边和这边上的高成正比例B .面积一定的平行四边形的一边和这边上的高成反比例C .周长一定的等腰三角形的腰长与它底边的长成正比例D .周长一定的等腰三角形的腰长与它底边的长成反比例 9.正比例函数3y x =-的图象经过( ). A .第一、第二象限 B .第一、第三象限 C .第二、第四象限 D .第三、第四象限10.正比例函数13y x =的图像大致是( )A .B .C .D .11.在同一平面直角坐标系中,函数()20y ax bx a =+≠与y ax b =+的图象可能是( )A .B .C .D .12.下列函数中,正比例函数有( ).(1)2y x =-(2)y =3)1yx =-(4)v =5)213y x =-(6)2y r π=(7)22y x =A .1个B .2个C .3个D .4个三、解答题 13.函数问题:(1)作出y 与x 的函数2y x =的图象①自变量x 的取值范围是____________; ①列表并画出函数图象:①当自变量x 的值从1增加到2时,则函数y 的值增加了____________.(2)在一个变化的过程中,两个变量x 与y 之间可能是函数关系,也可能不是函数关系: 下列各式中, y 是x 的函数的是____________. ①1x y +=; ①1x y +=; ①1xy =; ①221x y +=; 14.用适当的符号表示下列关系: (1)x 的3倍与8的和比x 的5倍大; (2)2x 是非负数;(3)地球上海洋面积大于陆地面积; (4)老师的年龄比你年龄的2倍还大; (5)铅球的质量比篮球的质量大.15.为加强生态文明建设,某市环保局对一企业排污情况进行检测,结果显示:所排污水中硫化物的浓度超标,即硫化物的浓度超过最高允许的1.0mg/L .环保局要求该企业立即整改,在15天内(含15天)排污达标.整改过程中,所排污水中硫化物的浓度y (mg/L )与时间x (天)的变化规律如图所示,其中线段AC 表示前3天的变化规律,第3天时硫化物的浓度降为4.5mg/L .从第3天起,所排污水中硫化物的浓度y 与时间x 满足下面表格中的关系:(1)在整改过程中,当0≤x <3时,硫化物的浓度y 与时间x 的函数表达式;(2)在整改过程中,当x≥3时,硫化物的浓度y与时间x的函数表达式;(3)该企业所排污水中硫化物的浓度能否在15天以内不超过最高允许的1.0mg/L?为什么?参考答案:1.解析式 【解析】略 2.5【分析】直接利用正比例函数的定义进而得出答案.【详解】解:①函数y =(m ﹣2)x +5﹣m 是关于x 的正比例函数, ①50m -= ,20m -≠ , 解得:m =5. 故答案为:5.【点睛】本题主要考查了正比例函数的定义,正确把握定义是解题关键. 3.2【分析】根据正比例函数自变量x 的指数为1,且系数不为0即可求出m 的值,再根据图像经过第一、三象限进而舍去不符合要求的m 值即可.【详解】解:由题意可知:110m m ⎧-=⎨≠⎩,解得:2m =±,又图像经过第一、三象限, ①2m =, 故答案为:2.【点睛】本题考查了正比例函数的定义,正比例函数(0)y kx k =≠要求自变量的指数为1,且自变量前面的系数不为0. 4.2y x =-+##2y x =-【分析】根据题意,可设()()20y k x k =-≠ ,将1x =时,1y =,代入即可求解. 【详解】解:根据题意,可设()()20y k x k =-≠ , ①当1x =时,1y =,①()121k -= ,解得:1k =- ,①y 与x 之间的函数关系式为()22y x x =--=-+ . 故答案为:2y x =-+【点睛】本题主要考查了用待定系数法求函数解析式,正比函数的定义,根据题意()()20y k x k =-≠ 是解题的关键.5. y =k x +b (k ,b 是常数,k ≠0) b =0 y =kx (k ≠0) 【解析】略 6. ①①① ①【分析】根据一次函数及正比例函数的定义,即可一一判定.【详解】解:①1y =+是一次函数,不是正比例函数; ①22y x x =+不是一次函数;①5y x =是正比例函数,因为正比例函数一定是一次函数,所以还是一次函数; ①14y x =-是一次函数;①1y x= 故答案为:①①①,①.【点睛】本题考查了一次函数及正比例函数的定义,熟知正比例函数是一次函数的特例是解决本题的关键. 7.D【分析】分别列出每个选项的解析式,根据正比例函数的定义判断即可. 【详解】解:A 选项,S =πr 2,故该选项不符合题意; B 选项,y =15+5x ,故该选项不符合题意; C 选项,①12ah =S , ①a =2Sh,故该选项不符合题意; D 选项,y =60x ,故该选项符合题意; 故选:D .【点睛】本题考查了正比例函数的定义,掌握形如y =kx (k ≠0)的函数是正比例函数是解题的关键. 8.B【分析】利用正比、反比的性质进行判断即可.【详解】解:面积一定的平行四边形的一边和这边上的高成反比例,故A 错误,B 正确; 周长一定的等腰三角形的腰长与它底边的长成一次函数,故C 、D 错误. 故选:B .【点睛】本题考查了正比、反比的性质,平行四边形的面积公式,等腰三角形的腰、底、周长的关系,解决本题的关键是明确正比与反比的意义. 9.C【分析】根据正比例函数y =k x (k ≠0)k 的符号即可确定正比例函数y =-3x 的图象经过的象限.【详解】解:在正比例函数y =-3x 中, ①k =-3<0,①正比例函数y =-3x 的图象经过第二、四象限, 故选:C【点睛】本题主要考查了正比例函数的性质,熟记“当k <0时,正比例函数y =kx (k ≠0)的图象经过第二、四象限”是解决问题的关键. 10.A【分析】根据正比例函数的图像和性质,即可得出正确选项.【详解】因为正比例函数是一条经过原点的直线,且k >0,经过一三象限,故排除C 、D 选项;当x =1时,13y =,故选A .【点睛】本题考查了正比例函数的图像和性质,熟练掌握性质和图像是本题的关键. 11.A【分析】根据二次函数和一次函数图象的性质依次进行判断即可.【详解】解:函数()20y ax bx a =+≠经过原点(0,0),则B 错误;当a <0时,y ax b =+经过二、四象限,则D 错误; 当02ba->时,b >0, y ax b =+经过一、二、四象限,则C 错误; 当a >0,02ba->时,b <0, y ax b =+经过一、三、四象限,则A 符合题意. 故选:A .【点睛】本题考查二次函数与一次函数的综合,熟练掌握函数图象的性质是解决问题的关键. 12.C【分析】利用正比例函数定义分析即可.【详解】解:(1)2y x =-是正比例函数,(2)y =x 次数不是1,不是正比例函数,(3)1yx =-是反比例函数,不是正比例函数,(4)=v 是正比例函数,(5)213y x =-是一次函数,不是正比例是函数,(6)2y r π=正比例是函数,(7)22y x =是二次函数,不是正比例函数,所以共3个 故选:C .【点睛】此题主要考查了正比例函数定义,关键是掌握形如y=kx (k 是常数,k ≠0)的函数叫做正比例函数.13.(1)①全体实数;①4,2,0,2,4;图见解析;①2 (2)①①【分析】(1)①根据2y x =求出x 的取值范围即可;①根据解析式填出列表,并在坐标系中描出各点,画出函数图象即可; ①把自变量x 的值从1增加到2时,代入函数解析式中求解即可; (2)根据函数的关系式的定义来求解即可. (1)解:①在函数2y x =中,x 的取值范实为全体实数, 故答案为:全体实数; ①列表如下:函数2y x =变形为2y x =或2y x =-,画图如下:①当1x =时,2y =,当2x =时,4y =,所以当自变量x 的值从1增加到2时,则函数y 的值增加了2; (2)解:在①1x y +=,①1x y +=,①1xy =,①221x y +=中,①①中对于x 的每一个值,y 都有唯一确定的值与它对应,①①中对于x 的每一个值,y 都有两个值与它对应,所以①①中y 是x 的函数,①①中y 不是x 的函数. 故答案为:①①.【点睛】本题主要考查了函数关系式,自变量取值范围,函数图象的画法,理解相关知识是解答关键.14.(1)385x x +>;(2)20x ≥;(3)12S S >(1S 表示地球上的海洋面积,2S 表示陆地面积);(4)2x y >(x 表示老师的年龄,y 表示你的年龄);(5)12m m >(1m 表示铅球的质量,2m 表示篮球的质量)【分析】(1)直接利用已知关系得出不等式;(2)直接利用非负数的定义(大于或等于0的数是非负数)得出不等式; (3)利用未知数表示出海洋与陆地面积进而得出答案; (4)利用未知数表示出老师与自己的年龄进而得出答案; (5)利用未知数表示出铅球与篮球的质量进而得出答案. 【详解】解:(1)由题意可得:3x +8>5x ; (2)由题意可得:x 2≥0;(3)设地球上海洋面积为1S ,陆地面积为2S ,根据题意可得:1S >2S ; (4)设老师的年龄为x ,我年龄为y ,根据题意莪哭的:x >2y ; (5)设铅球的质量为1m ,篮球的质量为2m ,根据题意可得:1m >2m .【点睛】此题主要考查了由实际问题抽象出一元一次不等式,正确得出不等关系是解题关键. 15.(1)线段AC 的函数表达式为:y =﹣2.5x +12(0≤x <3); (2)y =13.5x(x ≥3); (3)该企业所排污水中硫化物的浓度可以在15天以内不超过最高允许的1.0mg /L ,理由见解析.【分析】(1)设线段AC 的函数表达式为:y =k x +b ,把A 、C 两点坐标代入求出k 、b 的值即可;(2)设函数的表达式为:y =kx,把C 点坐标代入,求出k 的值即可;(3)根据(2)所得表达式,求出x =15时,y 的值与硫化物浓度允许的最高值比较即可. (1)解:由前三天的函数图像是线段,设函数表达式为:y =kx +b把(0,12)(3,4.5)代入函数关系式,得124.53bk b =⎧⎨=+⎩ , 解得:k =﹣2.5,b =12①当0≤x <3时,硫化物的浓度y 与时间x 的函数表达式为:y =﹣2.5x +12; (2)解:当x ≥3时,设y =kx,把(3,4.5)代入函数表达式,得4.5=3k,解得k =13.5,①当x ≥3时,硫化物的浓度y 与时间x 的函数表达式为:y =13.5x; (3)解:能,理由如下: 当x =15时,y =13.515=0.9, 因为0.9<1,所以该企业所排污水中硫化物的浓度,能在15天以内不超过最高允许的1.0mg /L . 【点睛】本题考查一次函数和反比例函数,熟练掌握根据坐标确定解析式的一次项系数和常数项是解题关键.。
八年级数学(下)第十九章《正比例函数》同步练习题(含答案)

八年级数学(下)第十九章《正比例函数》同步练习(含答案)一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知函数y=(k-1)2k x为正比例函数,则A.k≠±1B.k=±1 C.k=-1 D.k=1【答案】C【解析】由题意得k2=1且k-1≠0,∴k=-1,故选C.2.若y=x+2-b是正比例函数,则b的值是A.0 B.-2 C.2 D.-0.5【答案】C【解析】因为y=x+2-b是正比例函数,所以2-b=0,所以b=2,故选C.3.下列问题中,两个变量成正比例的是A.等腰三角形的面积一定,它的底边和底边上的高B.等边三角形的面积和它的边长C.长方形的一边长确定,它的周长与另一边长D.长方形的一边长确定,它的面积与另一边长【答案】D【解析】A.等腰三角形的面积一定,它的底边和底边上的高成反比例,故本选项错误;B.等边三角形的面积是它的边长的二次函数,故本选项错误;C.长方形的一边长确定,它的周长与另一边长成一次函数,故本选项错误;D.长方形的一边长确定,它的面积与另一边长成正比例,故本选项正确,故选D.4.关于函数y=2x,下列结论中正确的是A.函数图象都经过点(2,1)B.函数图象都经过第二、四象限C.y随x的增大而增大D.不论x取何值,总有y>0【答案】C【解析】A:当x=2时,y=4≠1,∴函数图象不经过(2,1),故错误;B:k=2>0,∴函数图象经过一、三象限,故错误;C:k>0,y随着x的增大而增大,故正确;D:当x<0时,y<0,故错误,故选C.5.正比例函数y=(k-3)x的图象经过一、三象限,那么k的取值范围是A.k>0 B.k>3 C.k<0 D.k<3【答案】B【解析】由正比例函数y=(k-3)x的图象经过第一、三象限,可得:k-3>0,则k>3,故选B.6.在正比例函数y=–3mx中,函数y的值随x值的增大而增大,则P(m,5)在A.第一象限B.第二象限C.第三象限D.第四象限【答案】B【解析】∵y随x的增大而增大,∴-3m>0,解得m<0,∴P(m,5)在第二象限,故选B.7.已知正比例函数y=kx(k≠0),当x=–1时,y=–2,则它的图象大致是A.B.C.D.【答案】C【解析】将x=-1,y=-2代入y=kx(k≠0)中得,k=2>0,∴函数图象经过原点,且经过第一、三象限,故选C.8.如图,三个正比例函数的图象分别对应的解析式是①y=ax,②y=bx,③y=cx,则a、b、c的大小关系是A.a>b>c B.c>b>a C.b>a>c D.b>c>a【答案】C【解析】首先根据图象经过的象限,得a>0,b>0,c<0,再根据直线越陡,|k|越大,则b>a>c.故选C.二、填空题:请将答案填在题中横线上.9.已知正比例函数y =(4m +6)x ,当m __________时,函数图象经过第二、四象限.【答案】<-1.5【解析】∵函数经过第二、四象限,∴4m +6<0,即m <-1.5,故答案为:m <-1.5.10.已知直线y =(2-3m )x 经过点A (x 1,y 1)、B (x 2,y 2),当x 1<x 2时,有y 1>y 2,则m 的取值范围是__________.【答案】m >23【解析】∵直线y =(2-3m )x 经过点A (11x y ,)、B (22x y ,),当12x x <时,有12y y >,∴此函数是减函数,∴2-3m <0,解得m >23,故答案为:m >23. 三、解答题:解答应写出文字说明、证明过程或演算步骤.11.已知y =(k -3)x +2k -9是关于x 的正比例函数,求当x =-4时,y 的值.【解析】当290k -=且30k -≠时,y 是x 的正比例函数,故当k =-3时,y 是x 的正比例函数,∴6y x =-,当x =-4时,y =-6×(-4)=24.12.已知4y +3m 与2x -5n 成正比例,证明:y 是x 的一次函数.【解析】由题意,设4y +3m =k (2x -5n )(k ≠0), ∴1(35)24k y x m kn =⋅-+. ∵k 是不为0的常数.∴2k ,1(35)4m kn -+为常数,且02k ≠, ∴y 是x 的一次函数.13.已知正比例函数y =(2m +4)x ,求:(1)m 为何值时,函数图象经过第一、三象限?(2)m 为何值时,y 随x 的增大而减小?(3)m 为何值时,点(1,3)在该函数的图象上?【解析】(1)∵函数图象经过第一、三象限,∴2m +4>0,∴m >-2.(2)∵y 随x 的增大而减小,∴2m +4<0,∴m <-2.(3)依题意得(2m+4)×1=3,解得12m=-.14.已知正比例函数y=kx经过点A,点A在第四象限,过点A作AH⊥x轴,垂足为点H,点A的横坐标为3,且△AOH的面积为3.(1)求正比例函数的解析式;(2)在x轴上能否找到一点P,使△AOP的面积为5?若存在,求点P的坐标;若不存在,请说明理由.【解析】(1)∵点A的横坐标为3,且△AOH的面积为3∴点A的纵坐标为-2,点A的坐标为(3,-2),∵正比例函数y=kx经过点A,∴3k=-2解得k=-23,∴正比例函数的解析式是y=-23 x.(2)∵△AOP的面积为5,点A的坐标为(3,-2),∴OP=5,∴点P的坐标为(5,0)或(-5,0).。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一次函数第14讲 变量与函数一、变量与函数1.回答(1)----(4)题(1)理解匀速运动中的行程S 与行驶时间t 的关系:S=________. (2)如何探索弹簧的变化规律,l=______________. (3)圆的面积r=_____________________.(4)长方形的面积S=_______________________.2.在一个变化过程中,我们称数值发生变化的量为_________,而始终不变的量称为____________。
3.具体指出(1)--(4)中,那些是变量,哪些是常量? (1)变量是______________,常量是_________________; (2)变量是______________,常量是_________________; (3)变量是______________,常量是_________________; (4)变量是______________,常量是_________________。
巩固训练1.关于r l π2=,下列说法正确的是( )A.2为常量,π,l,r 为变量B.2π为常量,l ,r 为变量C.2,l 为常量,π,r 为变量D.2,r 为常量,π,l 为变量2.摄氏温度C 与华氏温度F 之间的对应关系为5(F-32)9C =℃,则其中的变量是 ,常量是 。
3.在△ABC 中,它的底边是a ,底边上的高是h ,则三角形的面积 ah S 21=,当底边a 的长一定时,在关系式中的常量是 ,变量是 。
4.齿轮每分钟120转,如果n 表示转数,t 表示转动时间,那么用n 表示t 的关系是: ,其中 为变量, 为常量. 能力提升1.写出下列各问题中的关系式,并指出其中的常量与变量。
(1)甲乙两地相距1000千米,一人骑自行车以15千米/小时的速度从甲地前往乙地,用行驶时间t (小时)表示自行车离乙地的距离S (千米).(2)直角三角形中一个锐角α与另一个锐角β之间的关系.(3)一盛满30吨水的水箱,每小时流出0.5吨水,试用流水时间t (小时)表示水箱中的剩水量y (吨).(4)小军用50元钱去买单价是8元的笔记本,则他剩余的钱Q (元)与他买这种笔记本的本数x 之间的关系二、函数【概念】一般地,在一个变化过程中,如果有两个变量x 与y,并且对于x 的每一个确定的值,y 都有 确定的值与其对应,那么我们就说x 是 ,y 是x 的 .如果当x=a 时y=b ,那么b 叫做当自变量的值为a 时的 . 例题讲解【例1】一辆汽车的油箱中现有汽油50L,如果不再加油,那么油箱中的油量y (单位:L )随行驶里程x (单位:km)的增加而减少,平均耗油量为0.1L/km . (1)写出表示y 与x 的函数关系的式子; (2)指出自变量x 的取值范围;(3)汽车行驶200km 时,油箱中还有多少汽油?例2:自变量取值范围: 1.函数5x 1y -=中,自变量x 的取值范围是_________. 2.函数x 2y -=中自变量x 的取值范围是_________. 3.在函数4x 32y -=中,自变量x 的取值范围是_________.4.函数1x xy -=的自变量x 的取值范围是_________. 易错题:下列各式中,y 是x 的函数的有: ①4x-3y=2,②y=∣x ∣,③y=5x,④y 2=2x ,⑤x=∣y ∣ 巩固训练1.全年级每个同学需要一本代数教科书,书的单价为6元,则总金额y (元)与学生数n (个)的关系是 .其中 是 的函数, 是自变量.2.学校计划购买50元的乒乓球,则所购买的乒乓球总数y (个)与单价x (元)的函数关系式是 ;其中 是 的函数, 是自变量.3.已知三角形底边长为4,高为x,三角形的面积为y,则y 与x 的函数关系式为_______________; 其中 是 的函数, 是自变量.4.骆驼被称为“沙漠之舟”,它的体温随时间的变化而变化,在这一问题中,自变量是( ) A.沙漠 B.体温 C.时间 D.骆驼5.长方形的周长为24cm,其中一边为x (其中x>0),面积为y cm 2,则这样的长方形中y 与x 的关系可以写为( )A.y=x 2B.y=(12-x )2C.y=(12-x )xD.y=2(12-x ) 6.已知函数y=x 2-x-2当x=2时,函数值为 。
7.当x= 时,函数y=3x-2与函数y=5x+1有相同的函数值。
8.函数3-=x y 的自变量x 的取值范围是 。
9.函数 431-+=x x y 中,自变量x 的取值范围是( )A.34≠xB.1≠xC.134-≠<x x 且D.34>x10.函数112++--=x x x y 的自变量x 的取值范围为( ) A.x ≠1 B.x>-1 C.x ≥-1 D.x ≥-1且 x ≠1 11.汽车由北京驶往相距120千米的天津,它的平均速度是30千米/时,则汽车距天津的路程S (千米)与行驶时间t (时)的函数关系及自变量的取值范围是( • )A.S=120-30t(0≤t ≤4)B.S=30t(0≤t ≤4)C.S=120-30t(t>0)D.S=30t(t=4) 12.如图,在靠墙(墙长为18m )的地方围建一个矩形的养鸡场,另三边用竹篱笆围成.如果竹篱笆总长为35m,求鸡场的一边长y (m )与另一边长x (m )的函数关系式,并求自变量的取值范围.函数的图像思考:正方形的边长x 与面积S 的 函数关系为 ,其中自变量x 的取值范围是 。
计算并填写下表:如果我们在直角坐标系中,将你所填表格中的自变量x 及对应的函数值S 当作一个点的横坐标与纵坐标,即可在坐标系中得到一些点.对于一个函数,如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象.例1.下图是自动测温仪记录的图象,它反映了北京的春季某天气温T 如何随时间t 的变化而变化.你从图象中得到了哪些信息?例2.下图反映的过程是小明从家去菜地浇水,又去玉米地锄草,然后回家.其中x 表示时间,y 表示小明离他家的距离.小明家,菜地,玉米地在同一条直线上. 1.从家到菜地用了多少时间? 菜地离小明家有多远?2.小明给菜地浇水用了多少时间?3.从菜地到玉米地用了多少时间? 菜地离玉米地有多远?4.小明给玉米地锄草用了多少时间?5.玉米地离家有多远?小明从玉米地回家的平均速度是多少?巩固练习:如果A 、B 两人在一次百米赛跑中,路程s (米)与赛跑的时间t (秒)的 关系如图所示,则下列说法正确的是( ) A.A 比B 先出发 B.A 、B 两人的速度相同 C.A 先到达终点 D.B 比A 跑的路程多例3.画出函数:(1)5.0+=x y (2)xy 6=()0>x 的图像.归纳总结:1.画函数图像步骤: 、 、2.函数三种表示方法::直接给出部分函数值. :表示对应规律; :表示变化趋势。
注:有时为了需要,这三种表达方式交替使用或者同时使用。
例4.一水库的水位在最近5小时内持续上涨,下表记录了这5小时的水位高度.(1) 由记录表推出这5小时中水位高度y (单位:米)随时间t (单位:时)变化的函数解析式,并画出函数图像;(2) 据估计按这种上涨规律还会持续上涨2小时,预测再过2小时水位高度将达到多少米.例5.试判断(2,4)是否在函数 y=2x 的图像上.例6.小明同学骑自行车去郊外春游,下图为表示他离家的距离y (千米)与所用的时间x (时)之间关系的函数图像.(1)根据图象回答:小明到达离家最远的地方需几小时?此时离家多远? (2)求小明出发2.5小时离家多远? (3)求小明出发多长时间距家10千米.练习1.下列各点中,在函数x y =的图像上的是( )A (-2,4)B (4,4)C (2,4)D (1,-1)2.已知函数:(1)xy 1=;(2)12+=x y ;(3)x y =;(4)x y -=2;(5)x y -=.其中图像经过原点的有( )A.1个B.2个C.3个D.4个 3.点A (1,m )在函数x y 2=图像上,则点A 坐标为 4.在高速路上,一辆轿车和一辆货车沿相同路线从A 地到B 地,所经过的路程y(千米)与时间x(小时)的函数关系图像如图所示,试根据图像,回答下列问题: (1)货车比轿车早出发 小时,轿车追上货车时行驶了______千米,A 地到B 地的距离为 千米;(2)货车的速度是 千米/时.课堂同步1.油箱中有油30kg ,油从管道中匀速流出,1小时流完,•求油箱中剩余油量Q (kg)与流出时间t (分钟)间的函数关系式为___________,•自变量的范围是_____________.当Q=10kg 时,t=_________.2.已知函数y=5x+1中,当x=2时,y= ;当y=10时x= .3.已知两个变量x 、y 满足关系2x-3y+1=0.用含x•的式子表示y•为____________.4.从A 地向B 地打长途电话,按时收费,3分钟内收费2.4元,以后每超过1分钟加收1元,若通话t 分钟(3≥t ),则需付电话费y (元)与t (分钟)之间的函数关系式是 ,其中t 的取值范围是 .5.甲、乙两地相距S 千米,某人行完全程所用的时间t (时)与他的速度v (千米/时)满足S=vt,在这个变化过程中,下列判断中错误的是( )A.v 是变量B.t 是变量C.S 是变量D.S 是常量 6.已知函数212+-=x x y 中,当x=a 时的函数值为1,则a 的值是( ) A.-1 B.1 C.-3 D.37.已知两个变量x 、y 满足关系2x-3y-1=0,试问:①y 是x 的函数吗?②x•是y 的函数吗?若是,写出y 与x 的关系式,若不是,说明理由.8. 弹簧挂上物体后会伸长,测得一弹簧的长度y (cm )与所挂物体的质量x (kg )有如下关系:x/kg 0 1 2 3 4 56y/cm1212.51313.51414.5 15(1)请写出弹簧总长y (cm )与所挂物体质量x (kg )之间的函数关系式. (2)当挂重10千克时弹簧的总长是多少?9.已知函数12-=x y ,不画图能否判断点A (-2.5,-4),B(1,3) ,C(2.5,4)在该函数图像上?第14课 函数与变量 测试题日期: 月 日 满分:100分 姓名: 得分:1.在函数3x 1y -=中,自变量x 的取值范围是( )A. x ≠3B. x ≠0C. x>3D. x ≠-32.函数1x y -=中,自变量x 的取值范围是( )A. x ≥1B. x>1C. x>0D. x ≠13.一杯水越晾越凉,下列图象中可以表示这杯水的水温T (℃)与时间t (分)的函数关系( )4.下图是南昌市某天的温度随时间变化的图像,通过观察可知:下列说法错误的是( )A.这天15点时温度最高B.这天3点时温度最低C.这天最高温度与最低温度的差是13℃D.这天21点时温度是30℃ 5.下列关系式中,变量x=-1时,变量y=6的是( )A.y=3x+3B.y=-3x+3C.y=3x-3D.y=-3x-3 6.球的体积公式:V=34πr 3,r 表示球的半径,V 表示球的体积.当r=3时,V=( ) A.4 π B.12π C.36π D.π7.一个容量为100立方米的水池,原有水60立方米,现以每分钟2立方米的速度匀速向水池中注水,设注水时间t 分钟,水池有水Q 立方米,则注满水池的时间t 为( )A.50分钟B.20分钟C.30分钟D.40分钟8.在匀速运动公式S=Vt 中,V 表示速度,t 表示时间,S 表示在时间t 内所走的路程,则变量是 ,常量是 。
