运筹学讲义
运筹学讲义(考研)

研究生入学考试辅导《运筹学讲义》1.线线规划与单纯形法●线性规划问题和数学模型;●线性规划图解法●线性规划解的概念和单纯形法●单纯形法的一些具体问题2.对偶理论与灵敏度分析●线性规划问题的对偶及其变换;●线性规划的对偶定理;●对偶单纯形法;●线性规划的灵敏度分析写出规划模型和标准化问题;指出解的类型;和对偶问题结合的题目;求解的问题;1.某饲料厂用原料A、B、C加工成三种不同牌号的饲料甲、乙、丙。
已知各种牌号饲料中A、B、C含量,原料成本,各种原料的每月限制用量,三种牌号的饲料的单位加工费及售价如【表1-1】所示。
表1-1问该厂每月应生产这三种牌号饲料各多少千克,使该厂获利最大?试建立这个问题的的线性规划的数学模型。
2.有如下线性规划问题,令X6,X7分别为约束条件(1)和(2)的松弛变量,指出下表各组解的类型(可行解、非可行解、基础可行解、基础非可行解),,,,7204234360 22 264242x ax5432154315 432154321≥≤++ +≤+++ +++++xxxxxx xx xxxxx xxxxxxfM)=(3.设某投资者有30000元可供为期四年的投资。
现有下列五项投资机会可供选择:A:在四年内,投资者可在每年年初投资,每年每元投资可获得0.2元,每年获利后可将本利重新投资;B:在四年内,投资者应在第一年年初或第三年年初投资,每年每元获利0.5元,两年后获利。
然后再将本利投资;C:在四年内,投资者应在第一年年初投资,三年后每元获利0.8元。
获利后可将本利重新投资,这项投资最多不超过20000元;D:在四年内,投资者应在第二年投资,两年后获利每元投资可获利0.6元,获利后可将本利和投资,这项投资最多不超过20000元;E:在四年内,投资者应在第一年投资,四年后获利每元1.7元,最大投资不超过20000元;求:四年后,投资获利最大?不求解。
4.某公司计划在三年的计划期内,有四个项目可以投资:项目一从第一年到第三年年初都可以投资,年末可收回本利120%,每年又可以重新将所获本利纳入投资计划;项目二需要在第一年初投资,经过两年可收回本利150%,又可以重新将所获本利纳入投资计划,但用于该项目的最大投资额不得超过20万元;项目三需要在第二年年初投资,经过两年可收回本利160%,但用于该项目的最大投资额不得超过15万元;项目四需要在第三年年初投资,年末可收回本利140%,但用于该项目的最大投资额不得超过10万元。
运筹学讲义

OPERATIONS RESEARCH运筹学Ⅰ——怎样把事情做到最好第一章绪论♦1.1题解Operations 汉语翻译工作、操作、行动、手术、运算Operations Research日本——运用学港台——作业研究中国大陆——运筹学Operational Research原来名称,意为军事行动研究——历史渊源绪论♦1.2 运筹学的历史早期运筹思想:田忌赛马丁渭修宫沈括运粮Erlang 1917 排队论Harris 1920 存储论Levinson 1930 零售贸易康脱洛维奇1939 LP绪论♦1.2运筹学的历史军事运筹学阶段德军空袭防空系统Blackett运输船编队空袭逃避深水炸弹轰炸机编队绪论♦1.2运筹学的历史管理运筹学阶段战后人员三分:军队、大学、企业大学:课程、专业、硕士、博士企业:美国钢铁联合公司英国国家煤炭局运筹学在中国:50年代中期引入华罗庚推广优选法、统筹法中国邮递员问题、运输问题1.3学科性质▪应用学科▪Morse&Kimball定义:运筹学是为决策机构在对其控制的业务活动进行决策时提供的数量化为基础的科学方法。
▪Churchman定义:运筹学是应用科学的方法、技术和工具,来处理一个系统运行中的问题,使系统控制得到最优的解决方法。
▪中国定义:运筹学是应用分析、试验、量化的方法,对经济管理系统中人力、物力、财力等资源进行统筹安排,为决策者提供有依据的最优方案,以实现最有效的管理。
1.4定性与定量♦例:店主进货♦两者都是常用的决策方法♦定性是基础,定量是工具,定量为定性服务。
♦定性有主观性也有有效性,定量有科学性也有局限性。
管理科学的发展,定量越来越多。
但定量不可替代定性。
1.5运筹学的模型♦模型:真实事物的模仿,主要因素、相互关系、系统结构。
♦形象模型:如地球仪、沙盘、风洞♦模拟模型:建港口,模拟船只到达。
学生模拟企业管理系统运行。
♦数学模型:用符号或数学工具描述现实系统。
运筹学讲义(工程硕士)

运筹学应用的成功案例
ቤተ መጻሕፍቲ ባይዱ
联合航空公司(1-2/1986,$600万) 满足乘客需求以最低成本进行订票处和机场工作班次排程 Citgo石油公司(1-2/1987,$7000万) 优化炼油运作以及产品的供应、配送和营销 旧金山警署(1-2/1989,$1100万)
用计算机系统最优排程和巡警设置
荷玛特发展公司(1-2/1987,$4000万) 商业区和办公楼销售的最优化安排
Operations
Research (美国)—简称OR Operational Research(英国) 作业研究(港台) 运筹学(大陆) 管理科学 (Management Science,简称MS)
运筹学的历史
萌芽阶段 二战期间 二战之后
运筹学的应用实例
田忌赛马 盟军轰炸鲁尔水库 美洲航空公司的收益管理
运筹学应用的成功案例
宝洁公司(1-2/1997,$2亿) 重新设计生产和分销系统以降低成本和改进市场进入速度 南非国防部(1-2/1997,$11亿) 国防设施和武器系统规模和状态的重新优化设计 数字设备公司(1-2/1995,$8亿) 重构供应商、工厂、分销中心、潜在厂址和市场区域供应链 雷诺德金属制品公司(1-2/1991,$700万) 自动化超过200个工厂、仓库和供应商的货物装载调度系统 中国政府(1-2/1995,$4.25亿) 为满足国家未来能源需求的大型项目的优选和排程 Delta航空公司(1-2/1994,$1亿) 超过2,500个国内航线的飞机类型配置来最大化利润
授课内容
规划论
线性规划 目标规划 整数规划 动态规划
运筹学讲义

第一章绪论一运筹学的发展历史1学科起源:二战期间英美等国军事部门集中多学科人员,研究提高武器系统效能,如反空袭雷达控制系统,使雷达和高炮相配合。
诺将物理学家布莱克特(Blackett)领导研究小组“Operational Research”,多学科构成(布莱克特马戏团)。
战争结束后专家转移到企业和院校——学科形成。
2我国古代的运筹思想:齐王赛马——齐王“上中下”,田忌“下上中”丁渭修皇宫——北宋真宗宰相丁渭(澶chan州之盟的主和派),主持皇宫失火后的修复。
宫前大街取土、引汴河运料、完工后回填废土。
3我国近代以来:50年代开始钱学森、许志国等引进运筹学理论,华罗庚教授回国后从事优选法和统筹法研究推广(烧茶壶的故事)4翻译:来自汉高祖“夫运筹帷幄之中,决胜千里之外,吾不如子房;填国家,抚百姓,给饷馈,不绝粮道,吾不如萧何;连百万之众,战必胜,攻必取,吾不如韩信。
”台湾地区直译为“运作研究”。
二运筹学的特点运筹学存在多种定义,如“依照给定目标和条件,从众多方案中选择最优方案的最优化技术”,学科特点:最优化、定量化1 多种专家的协作2 科学的方法:从实际情况出发,通过假设的模型打到一个符合实际的结论3 目的在于解决实际问题。
4 需要系统的信息资料5 需要建立模型——运筹学的核心问题就是通过合适的模型分析系统的未来情况6 对于复杂问题,需要计算机三运筹学的模型运筹学的主要特点是通过模型来描述和分析所认定范围内的系统状态。
分析过程包括:1 系统分析和问题描述。
认定问题的实质——社会经济问题复杂性、不可重复性,不同于具有可控性的物理模型(提高企业效益:开发市场?增加设备?加强研发?)。
明确系统的主要目标(利润最大化、市场占有率最大化、销售收入最大化?GDP增长、可持续协调增长?)、找出系统主要变量和参数、变化范围、相互关系及其对目标的影响。
分析问题的可行性:技术可行性—有无现成的运筹学方法?经济可行性—研究的成本和预期的效果,考虑运筹决策的时间和代价,要对研究问题的深度和广度作出一定限制操作可行性—研究人员的配备2 建立数学模型——要尽可能简单;要能完整的描述所研究的系统。
运筹学课件PPT课件

整数规划的解法
总结词
整数规划的解法可以分为精确解法和近似解法两大类。
详细描述
整数规划的解法可以分为两大类,一类是精确解法,另一类是近似解法。精确解法包括割平面法、分支定界法等, 这些方法可以找到整数规划的精确最优解。而近似解法包括启发式算法、元启发式算法等,这些方法可以找到整 数规划的近似最优解,但不一定能保证找到最优解。
模拟退火算法采用Metropolis准则来 判断是否接受一个较差解,即如果新 解的能量比当前解的能量低,或者新 解的能量虽然较高但接受的概率足够 小,则接受新解。
模拟退火算法的应用
01
模拟退火算法在旅行商问题中得到了广泛应用。通过模拟退火算 法,可以求解旅行商问题的最优解,即在给定一组城市和每对城 市之间的距离后,求解访问每个城市恰好一次并返回出发城市的 最短路径。
动态规划的解法
确定问题的阶段和状态
首先需要确定问题的阶段和状态,以便将问 题分解为子问题。
建立状态转移方程
根据问题的特性,建立状态转移方程,描述 状态之间的转移关系。
求解子问题
求解每个子问题,并存储其解以供将来使用。
递推求解
从最后一个阶段开始,通过递推方式向前求 解每个阶段的最优解。
动态规划的应用
线性规划的解法
单纯形法
01
单纯形法是求解线性规划问题的经典方法,通过迭代过程逐步
找到最优解。
对偶理论
02
对偶理论是线性规划的一个重要概念,它通过引入对偶问题来
简化求解过程。
分解算法
03
分解算法是将大规模线性规划问题分解为若干个小问题,分别
求解后再综合得到最优解。
线性规划的应用
生产计划
线性规划可以用于生产计划问题, 通过优化资源配置和生产流程, 提高生产效率和利润。
运筹学讲义完整版

等可能准则
n
max{
i
1 n
Vij
j=1
}
S1 A1 20 A2 9 A3 6
S2
S3
Vi =
1 3
Vij
1 -6
5
80
5
2 3
max=5
2 3
54
5
选 A2
第36页
5.后悔值准则(Savage原则 ) (最小机会损失决策)
定义:称每个方案aj在结局Si下的最大可能 收益与现收益的差叫机会损失,又称后悔值 或遗憾值。记Rij(si,aj)=MaxQij(si,aj)-Qij(si,aj)
第27页
收益矩阵
事件 高
方案
S1
A1
20
A2
9
A3
6
中
低
S2 S3(万元)
1
-6
8
0
5
4
第28页
1.乐观准则(Hurwicz原则、MaxMax ) (冒险型决策)
对于任何行动方案 ,都认为将是最好的状态发 生,即益损值最大的状态发生。然后,比较各 行动方案实施后的结果,取具有最大益损值的 行动为最优行动的决策原则,也称为最大最大 准则。
第39页
(3)在机会损失表中,从每一行选一 个最大的值,即每一方案的最大机会损 失值 Max Rij(si,aj) (4)再在选出的 Max Rij(si,aj)选择最 小者:
第37页
对于任何行动方案aj ,都认为将是 最大的后悔值所对应的状态发生。然后, 比较各行动方案实施后的结果,取具有 最小后悔值的行动为最优行动的决策原 则,称为后悔值准则。记
R (s,aopt) = Min Max Rij(si,aj) ji
运筹学课程讲义

运筹学课程讲义第一部分 线性规划 第一章 线性规划的基本性质 1.1 线性规划的数学模型一、 线性规划问题的特点胜利家具厂生产桌子和椅子两种家具。
桌子售价50元/个,椅子售价30元/个。
生产桌子和椅子需木工和油漆工两种工种。
生产一个桌子需要木工4小时,油漆工2小时。
生产一个椅子需要木工3小时,油漆工1小时。
该厂每月可用木工工时为120小时,油漆工工时为50小时。
问该厂如何组织生产才能使每月的销售收入最大?213050m ax x x z +=⎪⎩⎪⎨⎧≥≤+≤+0,50212034212121x x x x x x 例:某工厂生产某一种型号的机床。
每台机床上需要 2.9m 、2.1m 、1.5m 的轴,分别为1根、2根和1根。
这些轴需用同一种圆钢制作,圆钢的长度为74m 。
如果要生产100台机床,问应如何安排下料,才能用料最省?二、 数学模型的标准型 1. 繁写形式 2. 缩写形式 3. 向量形式 4. 矩阵形式三、 任一模型如何化为标准型?1. 若原模型要求目标函数实现最大化,如何将其化为最小化问题?2. 若原模型中约束条件为不等式,如何化为等式?3. 若原模型中变量x k 是自由变量,如何化为非负变量?4. 若原模型中变量x j 有上下界,如何化为非负变量?⎪⎪⎩⎪⎪⎨⎧≥≤-=--≤+--≥-+----=无约束321321321321321,0,052010651535765max x x x x x x x x x x x x x x x z 令'''3'3''3'331'1,0,,,Z Z x x x x x x x =-≥-=-=⎪⎪⎩⎪⎪⎨⎧≥-=+-++=+-+-=+-+-+--+-++-=0,,,,,,,5201010651533507765min 7654''3'32'17''3'32'15''3'32'164''3'32'1765''3'32'1'x x x x x x x x x x x x x x x x x x x x x x x x Mx Mx x x x x x z 1. 2图解法该法简单直观,平面作图适于求解二维问题。
运筹学教学课件(全)

实用举例
某公司通过市场调研,决定生产高中档新型拉杆箱。 某分销商决定买进该公司3个月内的全部产品。拉杆箱生 产需经过原材料剪裁、缝合、定型、检验和包装4过程。
通过分析生产过程,得出:生产中档拉杆箱需要用 7/10小时剪裁、5/10小时缝合、1小时定型、1/10小时检 验包装;生产高档拉杆箱则需用1小时剪裁、5/6小时缝合、 2/3小时定型、1/4小时检验包装。由于公司生产能力有限, 3月内各部的最大生产时间为剪裁部630小时、缝合部600 小时、定型部708小时、检验包装部135小时。
D {x | Ax b, x (x1,, xi ,, xn ) 0}
是凸集(凸多面体)。
引理2.1:线性规划的可行解 x (x1 ,, xn )T 为基本可行解的 充分必要条件是x的正分量所对应的系数列向量是线性无关的, 即每个正分量都是一个基变量。
定理2.2:线性规划问题的基本可行解x对应于可行域的顶点
通过分析生产过程,得出:生产中档拉杆箱需要用
7/10小时可剪裁以、通5/1过0小线时性缝合规、划1小求时定解型!、1/10小时
检验包装;生产高档拉杆箱则需用1小时剪裁、5/6小时 缝合、2/3小时定型、1/4小时检验包装。由于公司生产 能力有限,3月内各部的最大生产时间为剪裁部630小时、 缝合部600小时、定型部708小时、检验包装部135小时。
x2
L1:x1=6 L3:2x1+3x2=18
B 可行域
L2:x2=4 最优解
x1
4x1+3x2
解的特殊情况——解的特殊情况——无界解
线性规划的基本性质
若线性规划有最 优解,则最优解必在可 行域的顶点上达到。
X
可行域内部的点 • 可行解? 是 • 最优解? 不
运筹学讲义第一章
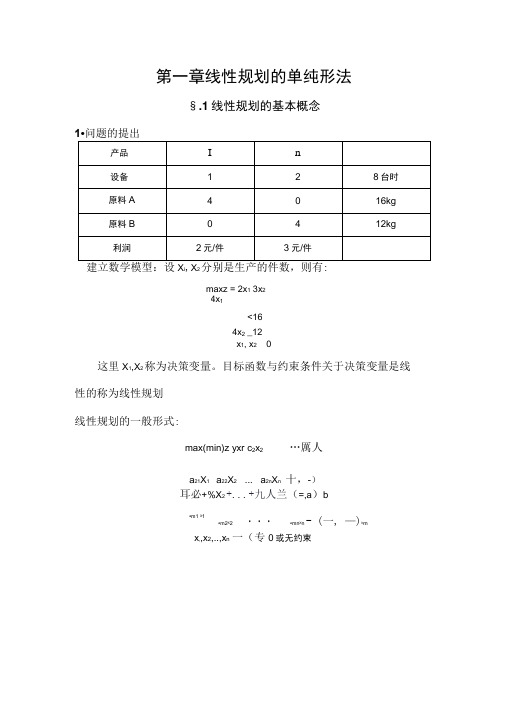
4x 1<164x 2 _12a 21X 1 a 22X 2 ... a 2n X n 十,-)b a m1 X 1第一章线性规划的单纯形法§.1线性规划的基本概念建立数学模型:设X i ,X 2分别是生产的件数,则有:maxz = 2x 1 3x 2x 1, x 2 0这里X 1,X 2称为决策变量。
目标函数与约束条件关于决策变量是线 性的称为线性规划线性规划的一般形式:max(min)z yxr c 2x 2 …厲人耳必+%X 2 +...+九人兰(=,a )ba m2X 2 ・・・ a mn X n - (一, —)bm x ,,x 2,..,x n 一(专0或无约束2. 线性规划的标准形maxz 二C1X1 …Cn X n"a^x, +ai2x2+••• + 印*人=Ra21^ +a22x2+... + a2n x n= b2a m1 为* a m2 X2 * …+ a mn 人=b m捲_ 0,X2_0,...,X n_0特点:目标函数求极大;等式约束;变量非负。
^令c =(G,c2,…,q), X = (X1,X2,…,x n) , A = (a ij )m n,b=(九^,…,b m ) 则线性规划标准形的矩阵表达式为:max z = exAx = bx _0约定:b — 0,m ^ n,秩A=m.如何化标准形:(I)目标函数实现极大化,即min z=cx,令w--z,则m w丸;(II )约束条件为不等式约束条件为“「不等式,则在约束条件的左端加上一个非负的松弛变量;约束条件为“ 一”不等式,则在约束条件的左端减去一个非负的松弛变量。
(III )若存在无约束的变量X k,可令X k = Xk - x k,其中x k 一0,x'k- 0.故有 x^ -B 4b 。
由此,得到Ax -b 的一个解例1.将线性规划min z = -捲 2x 2x-i x 2 x 3 _ 2* X i — X ? + X 3 乏 1论Z0,x 2兰0,x 3无约束化为标准形。
运筹学全册精品完整课件

36
例2-2 考虑例2-1
某工厂拥有A、B、C 三种类型的设备,
生产甲、乙两种产品。每件产品在生产中 需要占用的设备机时数,每件产品可以获 得的利润以及三种设备可利用的时数如下 表所示。问题:工厂应如何安排生产可获 得最大的总利润?
一、线性规划问题的提出
在实践中,根据实际问题的要求,常常 可以建立线性规划问题数学模型。
例2-1 我们首先分析开篇案例提到的问题。 解:设变量 xi 为第 i 种(甲、乙)产品的 生产件数(i=1,2)。根据题意,我们知道 两种产品的生产受到设备能力(机时数)的 限制。对设备A:两种产品生产所占用的机时 数不能超过65,于是我们可以得到不等式:
运筹学是运用科学的方法(如 分析、试验、量化等)来决定如何 最佳地运营和设计各种系统的一门 学科。
4
运筹学概述
运筹学能够对经济管理系统中 的人力、物力、财力等资源进行统 筹安排,为决策者提供有依据的最 优方案,以实现最有效的管理。
通常以最优、最佳等作为决策 目标,避开最劣的方案。
5
运筹学的产生和发展
8பைடு நூலகம்
运筹学在管理中的应用
生产计划:生产作业的计划、日程表的
编排、合理下料、配料问题、物料管 理等。
库存管理:多种物资库存量的管理,库
存方式、库存量等。
运输问题:确定最小成本的运输线路、
物资的调拨、运输工具的调度以及建
厂地址的选择等。
9
运筹学在管理中的应用
• 人事管理:对人员的需求和使用的 预测,确定人员编制、人员合理分 配,建立人才评价体系等。
x1 ,x2 ,… ,xn ≥ 0
运筹学讲义第1章

(2) 和式: max z= cjxj
j=1
n
s.t.
aijxj≤bi (i=1,2,……,m)
j=1
n
xj≥ 0
(j=1,2,……,n)
其中:cj---------表示目标函数系数 aij---------表示约束条件系数 bi ---------表示约束右端项
2007/08
-7-
---第 1 章 线性规划---
起迄时间 2----6 时 6---10 时 10--14 时 14--18 时 18--22 时 22---2 时
2007/08
服务员人数 4 8 10 7 12 4
-18-
---第 1 章 线性规划---
建立线性规划模型要求:
(1)要求决策的量是连续的、可控的量,或 者是可以简化为连续取值的变量;
1
n
xj≥0
(j=1,2,……,n)
(1)可行解:满足所有约束方程和变量符号限制条件的一组变量的 取值。 (2)可行域:全部可行解的集合称为可行域。 (3)最优解:使目标函数达到最优值的可行解。
2007/08 -20-
---第 1 章 线性规划---
(4)基:设A为线性规划模型约束条件系数矩阵(m n,m<n), 而B为其mm子矩阵,若|B|≠0,则称B为该线性规划模型的一个基。
可行解:X=(0,0)T,X=(0,1)T,X=(1/2,1/3)T 等。 x3 x4 ——基变量 x x x x
1 2 3 4
设
A=
1 1
1 2
1
0
0
1
,令 B=
1
0
0
1
,则 | B |=1≠0,
运筹学讲义(复习)

j 1
b
i 1
i
yi
Z bi
yi
• 影子价格不是资源的实际价格,而是资源配置结构的反映, 是在其它数据相对稳定的条件下某种资源增加一个单位导致 的目标函数值的增量变化。 对资源i总存量的评估:购进 or 出让 对资源i当前分配量的评估:增加 or 减少
13
SHUFE
1
SHUFE
线性规划标准型
目标函数极大化, 约束条件为等式, 右端常数项bi≥0, 决策变量非负。
• 标准型
maxZ=c1x1+c2x2+…+cnxn a11x1+a12x2+…+a1nxn =b1 a21x1+a22x2+…+a2nxn =b2 …………… am1x1+am2x2+…+amnxn=bm x1,x2,…,xn ≥0
二、表上作业法 1、确定初始方案:最小元素法、西北角法和Vogel法。 2、解的最优性检验:闭回路法和对偶变量法(位势法) 3、解的改进。 三、进一步讨论 将产销不平衡的问题转换为产销平衡问题。
17
SHUFE
1、已知运输问题的供需关系与单位运价表,试用表上作业 法求最优解
销地 产地
甲
乙
丙
丁
产 量
1
基变量
XS I 0
XB
CB XB Cj-Zj B-1 b I 0
XN
B-1 N CN- CB B-1 N
XS
B-1 I - CB B-1
11
SHUFE
• 二、基本性质(P57) • 1、弱对偶性:极大化原问题的任一可行解的目标函数值, 不大于其对偶问题任意可行解的目标函数值。 • 2、最优性。 • 3、强对偶性。 • 4、互补松弛性。
运筹学基础教学课件PPT

都江堰水利工程
Page 4
川西太守李冰 父子主持修建, 其目标是利用 岷江上游的水 资源灌溉川西 平原,追求的 效益还有防洪 与航运。其总 体构思是系统 思想的杰出运 用
北宋丁谓主持修复皇宫
Page 5
例2、北宋丁谓主持修复皇宫 面临的问题:木材、石材、 砖瓦等建筑材料如何取得?
修建如何进行?
大街 开封 皇宫
2、策略集
策 略:在对策中,局中人在整个决策过程中针对一系 列行动制定的完整行动方案。
策略集:每个局中人策略的全体集合。 局 势:每个局中人从自己的策略集合中选择一个策
略,构成一个局势。
3、赢得函数
利用全部局势集合上的一个实值函数,来描述 每个局势完结后局中人的得失的报酬数值。
对策的分类
Page 23
目标函数: 约束条件:1原材料的限制 2工时的限制 3座椅的限制 4非负限制 数学模型:
图解法
x2
1000
5x1+2.5x2≤2500
x1=400
800
Z=2600
600
400
Z=1800
Page 20
max Z=4x1+3x2
2x1 2x2 1600 5x1x1420.05x2 2500 x1 0、x2 0
线平衡率 秒表法/PTS
动作和方法研究
动改法
成本控制 设施规划
双手操作法 人机配合法
物流分析
防错法
PMP体系
PAC体系
系统设计
……
工作抽样法 流程程序法
五五法 其它
1工程学 2人机学(人因工程学) 3材料学 4管理学 5统计学 6运筹学 7系统工程学 8材料力学 9工程力学 10物流与设施规划
《运筹学》全套课件(完整版)

服务时间分布
负指数分布、确定型分布、一般分布等。
顾客到达和服务时间的独立性
假设顾客到达和服务时间是相互独立的。
单服务台排队系统
M/M/1排队系统
顾客到达服从泊松分布,服务时间服从负指 数分布,单服务台。
M/D/1排队系统
顾客到达服从泊松分布,服务时间服从确定 型分布,单服务台。
投资组合优化
确定投资组合中各种资产的最 优配置比例,以最大化收益或
最小化风险。
03
整数规划
整数规划问题的数学模型
01
整数规划问题的定 义
整数规划是数学规划的一个分支 ,研究决策变量取整数值的规划 问题。
02
整数规划问题的数 学模型
包括目标函数、约束条件和决策 变量,其中决策变量要求取整数 值。
03
Edmonds-Karp算法
介绍Edmonds-Karp算法的原理、步骤和实现方法,以及其与FordFulkerson算法的比较。
网络最大流问题的应用
列举网络最大流问题在资源分配、任务调度等领域的应用案例。
最小费用流问题
最小费用流问题的基本概 念
介绍最小费用流问题的定义、 分类和应用背景。
Bellman-Ford算法
优点是可以求解较大规模的整数规划问题,缺点是计算量较大,需 要较高的计算精度。
割平面法
割平面法的基本思想
通过添加新的约束条件(割平面)来缩小可行域的范围,从而逼 近最优解。
割平面法的步骤
包括构造割平面、求解子问题和更新割平面三个步骤,通过不断 迭代找到最优解。
割平面法的优缺点
优点是可以处理较复杂的整数规划问题,缺点是构造割平面的难 度较大,需要较高的数学技巧。
运筹学讲义

运筹学讲义引言1.年轻的学科:20世纪30年代,英国,美国,加拿大等在防空作战研究上提出的一种方法。
当时叫operational research,缩写为O.R. 是一门年轻的学科。
我国是在56年在中科院力学研究所成立运筹小组,80年成立运筹学会。
2。
应用数学:包括小到日常生活,如出门买东西的线路选择,大到国民经济建设优化组合,无处不在。
例如,我国北宋时代,丁渭修皇宫P 1。
3。
讲授内容:ch1.§1~5;ch3; ch7;ch8;ch12;ch13.第一章 线性规划及单纯型法运筹学的一大分支是数学规划,而线性规划又是数学规划的重要组成部分。
线性规划(linear programming 简写LP )也是运筹学最基本的内容。
相对于其他运筹学分支,LP 理论完善,方法简单,应用广泛,是任何运筹分支首先要阐明的基本知识。
§1 LP 问题及其数学模型 一. 问题的提出及建模例1 美佳公司计划制造Ⅰ,Ⅱ两种家电产品。
已知各制造一件事分别占用的设备A ,B 的台时、调试时间、调试工序及每天可用于这两种家电的能力、各出售一件时的获利情况,如表1-1所示。
问该公司应各制造两种家电各多少件,使获利最大?解:设制造Ⅰ,Ⅱ产品数量为1x ,2x .则利润 z=21x +2x问题是:在现有设备、调试能力的限制下,如何确定产量1x ,2x .可使利润最大? 我们把它数学化:目标函数:z max =21x +2x约 束条件⎪⎪⎩⎪⎪⎨⎧≥≤+≤+≤)4(0,)3(5)2(2426)1(1552121212x x x x x x x其中(1)~(3)资源限制,(4)为非负限制。
下面从数学的角度来归纳线性规划的模型特点:(1) 每一个问题都有一组变量——称之为决策变量,一般记为1x ,2x …n x 。
对决策变量的每一组值:Tn x x x ),,()0()0(2)0(1 代表了一种决策方案。
通常要求决策变量取值非负,即0≥j x (j =1,2,…n ).非负约束调试能力限制 设备A 的限制设备B 的限制(2)每个问题都有决策变量须满足的一组约束条件——线性的等式或不等式。
清华大学MBA课程讲义——运筹学

课程介绍一、运筹学产生的和发展1. 运筹学产生的原因✓科学技术的发展,利用和改造自然的规模扩大,生产规模扩大,生产组织形式复杂,出现了更复杂的管理方面的问题。
管理方面的新问题:如何有效和合理地利用有限的或稀缺的资源,使系统的整体目标达到最优。
2. 运筹学的起源✓运筹学的三个来源:军事、经济、管理✓1981年美国军事运筹学会出版的“System analysis and modeling in defence”一书中称孙武子是世界上第一个军事运筹学家。
✓第二次世界大战期间英、美等国军事部门成立的一些研究小组的研究活动。
最初人们称这类研究为“运作研究”(operational research),或“运作分析”(operational analysis)。
✓研究的特点是集中一批跨多学科的研究人员,有组织地对一特定问题进行系统分析,提出提高某武器系统效率的操作方法和执行策略。
✓二战期间成功的运筹研究案例有:英国防空部门如何布置防空雷达,建立有效的空防预警系统;研究反潜飞机巡逻路线及深水炸弹引爆深度,击沉德军潜艇数提高4倍;研究如何使用机载雷达提高轰炸命中率,两年内使命中率提高3倍;研究船队在受敌机攻击时的躲避策略,使中弹率从47%下降到29%;✓数理经济对运筹学的影响Qusnay 的经济表Walras 提出的经济平衡问题V on Neumann 提出的广义经济平衡模型康托洛维奇(Kantorovich)发表的《生产组织和计划中的数学方法》✓管理科学-- 运筹学的关系✓管理理论中最有影响的三个学派中的两个(古典学派与系统学派)广泛应用定量分析与系统分析的方法。
✓古典学派的代表性人物Taylor, Gantt 等提出的动作分析、甘特图至今还在使用。
3. 运筹学的发展二战结束后运筹学在理论上得到全面的发展;线性规划、非线性规划、动态规划、网络分析、整数规划、对策论、排队论等分枝得到迅速的发展。
运筹学应用从军事部门迅速向工业部门转移。
运筹学讲义

运筹学讲义绪论(2学时)参考教材:(1)运筹学基础教程(魏权龄)(2)管理运筹学(韩伯棠)(3)管理运筹学通论(韩大卫)(4)运筹学(胡运权)先修课程:一元微积分、线性代数、概率统计学时:48+(8)主讲教师:狄军锋一、运筹学发展1、运筹学的产生✧最早与1938年出现于英国,简称OR(operational Research)✧夫运筹帷幄之中,决胜于千里之外,吾不如子房。
---史记✧古代运筹学思想:田忌赛马+丁谓挖沟+沈括运军粮✧二战中的运筹学:反潜艇策略、深水炸弹的起爆深度、诺曼底登陆✧运筹学在我国的发展:①50年代中期,钱学森、许国志等教授将运筹学由西方引入我国。
②管梅谷(1962年,山东师范大学):“中国邮递员问题”③华罗庚:优选法(1970)和统筹法(1965)2、运筹学的定义:管理运筹学是一门应用科学,它广泛应用现有的科学技术和数学方法,解决管理中提出的专门问题,为决策者选择最优或较优的决策提供定量依据。
运筹学是一门新兴的交叉学科,来源于军事、管理和经济。
本课程主要介绍用于解决管理领域问题的运筹学,因此称为管理运筹学,也有人称为管理科学。
二、运筹学解决问题的思路提出问题→建模→求解→结果分析与调整→实施二、运筹学的学科内容:线性规划(LP);*整数规划(IP);*非线性规划(NP);*多目标规划(MP);动态规划(DP);对策论(GT);决策分析(DA);存贮论(IC);排队论(QT);图论(Graph Theory)三、章节安排1、绪论(2学时)2、线性规划(14学时)3、动态规划(6学时)4、存储论(6学时)5、对策论(10学时)6、决策论(6学时)7、统筹方法(2学时)8、总复习(2学时)四、应用举例1、猴子运香蕉2、海盗分宝石3、猜生日第二*主要内容1、线性规划的一般形式、压缩形式、矩阵形式、向量形式2、线性规划问题的图解法(3)3、线性规划问题的标准形式4、单纯形方法(4)5、线性规划问题应用举例(3)6、运输问题的解法(4)§1 线性规划问题的基本模型一、 引例【引例1】某工厂在计划期内要安排生产Ⅰ、Ⅱ两种产品,已知生产单位产品需的设备台时,A 、B 两种原材料的消耗以及每种产品可获利润如下表所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《管理运筹学》1、运筹学的工作步骤(1)提出和形成问题.(2)建立模型.(3)求解.(4)解的检验.(5)解的控制.(6)解的实施.2、运筹学模型三种基本形式:(1)形象模型(2)模拟模型(3)符号或数学模型构模的五种方法和思路: (1)直接分析法 (如线性规划)(2)类比法(手机的普及与电视机的普及)(3)数据分析法(如汽车销售量预测模型)(4)试验分析法(销售量与价格之间的关系模型)(5)想定(构想)法(销售与心理)3、如何将线性规划问题的一般形式化为标准形式:1.如果问题是求目标函数的最小值,求min f=∑Cjxj则可先将目标函数乘(-1),化为求极大值问题,即求 max Z=-f=-∑Cjxj2.如果有某个bk≤0,则可将该等式两边均乘以(-1),使右端常数项bk=-bk≥03.如果第k个约束条件是∑akjxj≤bk,引入松弛变量sk≥0 , 将它写成∑akjxj+sk=bk如果第l个约束条件是∑aljxj≥bl则引入剩余变量(也可称为松弛变量)sl≥0,将它写成∑aljxj—sl=bl 且使松弛变量和剩余变量在目标函数中的系数为零。
4.如果对某个变量xj没有非负限制(这种变量称为自由变量或无约束变量),则引进两个非负变量xj′,xj″,令xj=xj′-xj″代人目标函数和约束条件中,可将它化为对全部变量都有非负限制的问题。
4、①目标函数为变量的线性函数,约束条件也为变量的线性等式或不等式的模型称之为线性规划。
②如果目标函数是变量的非线性函数,或约束条件中含有变量非线性的等式或不等式的数学模型则称之为非线性规划。
③满足所有约束条件的解称为该线性规划的可行解。
④把使得目标函数值最大(即利润最大)的可行解称为该线性规划的最优解,此目标函数值称为最优目标函数值,简称最优值5、图解法的启示1.最优解:如果某一个线性规划问题有最优解,则一定有一个可行域的顶点对应一个最优解。
(一般为封闭可行域凸集)2.无穷多个最优解:若将上例中的目标函数变为求maxZ=50x1+50x2则代表目标函数的直线平移到最优位置后将和直线x1+x2=300重合。
此时不仅顶点B,C都代表了最优解,而且线段BC上的所有点都代表了最优解,这样最优解就有无穷多个了。
最优值 50x1+50x2=15000。
(一般为封闭可行域凸集)3.无界解:即无最优解的情况。
4.无可行解:若在例l的数学模型中再增加4x1+3x2≥1200,显然可见新的线性规划的可行域为空域,也即不存在满足所有约束条件的x1和x2的解,当然更不存在最优解了。
出现这种情况是由于约束条件自相矛盾导致的建模错误。
(无可行域)6、图解法得到的启示①求解线性规划问题时,解的情况有;唯一最优解、无穷多最优解、无界解、无可行解。
②若线性规划问题的可行域存在,则可行域是一个凸集。
凸集:如果集合C中任意两个点X1,X2,其连线上的所有点也都是集合X中的点,称C为凸集。
凸集数学解析式可表为:对任何X1∈C,X2∈C,有a X1+(1-a) X2∈C(0≤a ≤ 1),则称C为凸集③若线性规划问题的最优解存在,则最优解或最优解之一(如果有无穷多的话)一定是可行域的凸集的某个顶点。
④解题思路:先找出凸集的任一顶点,计算在顶点处的目标函数值。
比较周围相邻顶点的目标函数值是否比这个值大,如果为否,则该顶点就是最优解的点或最优解的点之一,否则转到比这个点的目标函数值更大的另一顶点,重复上述过程,一直到找出使目标函数值达到最大的顶点为止。
7、对偶价格总结:在约束条件右边常量增加一个单位而使最优目标函数值得到改进的数量称之为这个约束条件的对偶价格。
当约束条件右边常数增加一个单位时:1)如果对偶价格大于零,则其最优目标函数值得到改进,即求最大值时,变得更大;求最小值时,变得更小。
2)如果对偶价格小于零,则其最优目标函数值变坏了求最大值时变小了;求最小值时变大了。
3)如果对偶价格等于零,则其最优目标函数值不变。
8、几个基本概念:①基:已知A是约束条件的m×n系数矩阵,其秩为m。
若B是A中m×m阶非奇异子矩阵(即可逆矩阵,|B|≠0),则称B是线性规划问题中的一个基。
②基向量:基B中的一列即称为一个基向量。
③非基向量:在A中除了基B之外的一列则称之为基B的非基向量。
④基变量:与基向量Pi相应的变量xi叫基变量。
⑤非基变量:与非基向量Pj相应的变量xj叫非基变量⑥把满足非负条件的一个基本解叫做基本可行解,并把这样的基叫做可行基。
⑦在第一次找可行基时,所找到的基或为单位矩阵或为由单位矩阵的各列向量所组成,称之为初始可行基其相应的基本可行解叫初始基本可行解。
9、线性规划的最优解里有人工变量大于零,则此线性规划无可行解。
无界解是指在约束条件下目标函数值可以任意的大。
在单纯形表中识别线性规划问题是否无界的方法:在某次迭代的单纯形表中,ⅰ如果存在着一个大于零的检验数σj,并且该列的系数向量的每个元素aij(i=1,2,…,m)都小于或等于零,则此线性规划问题是无界的。
ⅱ在一个已得到最优解的单纯形表中,如果存在一个非基变量的检验数σS为零,则此线性规划问题有无穷多最优解。
在单纯形法计算过程中,入基变量所对应列向量与常数项相除有时存在两个以上相同的最小比值,这样在下一次迭代中就有了一个或几个基变量的值等于零,这称之为退化。
10、勃兰特法则(1)在所有检验数大于零的非基变量中,选一个下标最小的作为入基变量。
(2)在存在两个和两个以上最小比值时,选一个下标最小的基变量为出基变量。
11、原问题与对偶问题把求目标函数最大值的线性规划问题看成原问题,则求目标函数最小值的线性规划问题看成对偶问题。
1.求目标函数最大值的线性规划问题中有n个变量m个约束条件,它的约束条件都是小于等于不等式。
而其对偶则是求目标函数为最小值的线性规划问题,有m个变量n个约束条件,其约束条件都为大于等于不等式。
2.原问题的目标函数中的变量系数为对偶问题中的约束条件的右边常数项,并且原问题的目标函数中的第i个变量的系数就等于对偶问题中的第i个约束条件的右边常数项。
3.原问题的约束条件的右边常数项为对偶问题的目标函数中的变量的系数。
并且原问题的第i个约束条件的右边常数项就等于对偶问题的目标函数中的第i个变量的系数。
4.对偶问题的约束条件的系数矩阵且是原问题约束条件的系数矩阵的转置AT &原问题与对偶问题对于两个有对偶关系的线性规划的问题我们只要求得了其中一个最优解,就可以从这个问题的对偶价格而求得其对偶问题的最优解,知道了其中一个最优值也就找到了其对偶问题的最优值,因为这两个最优值相等。
12、对偶单纯形法单纯形法是在保持原问题的所有约束条件的常数大于等于零的情况下,通过迭代,使得所有的检验数都小于等于零,最后求得最优解;对偶单纯形法则是在保持原问题的所有检验数都小于等于零的情况下,通过迭代,使得所有约束条件的常数都大于等于零,最后求得最优解。
13、对偶单纯形法的迭代步骤①找一个基B,使检验系数σj≤0做初始单纯形表。
②若 B-1b≥0,则B-1b就是最优解。
否则进行第三步。
③确定出基变量,在常数列中找到一个最小的负常量,则这个负常量所在行的基变量为出基变量。
14、线性规划问题中某一个约束条件的影子价格表示为,当该约束条件的右端常数增加一个单位时(假设原问题的最优基解不变),原问题目标函数最优值增加的数量。
这是因为互为对偶的线性规划问题的最优值相等。
15、灵敏度分析方法:将变化以后的bi 直接代入原来的最终单纯表看是否满足最优基的要求(可行性、正则性)若满足最优基的要求,则最优基不变;最优解变为B-1b*,若不满足最优基的要求,接原来的最终单纯表进行对偶单纯表换基迭代。
求新解。
总结方法:将变化以后的bi 直接代入原来的最终单纯表看是否满足最优基的要求(可行性、正则性)若满足最优基的要求,则最优基不变;最优解变为B-1b*,若不满足最优基的要求,接原来的最终单纯表进行对偶单纯表换基迭代。
求新解。
16、运输问题:需求假设: 每一个出发地都有一个固定的供应量,所有的供应量都必须配送到目的地。
与之相类似,每一个目的地都有一个固定的需求量,整个需求量都必须由出发地满足,即总供应量=总需求量可行解特性:当且仅当供应量的总和等于需求量的总和时,运输问题才有可行解成本假设:从任何一个出发地到任何一个目的地的货物配送成本和所配送的数量成线性比例关系,因此这个成本就等于配送的单位成本乘以所配送的数量整数解性质:只要它的供应量和需求量都是整数,任何有可行解的运输问题必然有所有决策变量都是整数的最优解。
因此,没有必要加上所有变量都是整数的约束条件17、整数规划:一个数学规划问题,如果对它的某些决策变量或全部决策变量要求取整数,该问题就称为整数规划问题。
若问题的目标函数和约束条件都具有线性特性时,这类问题就称为整数线性规划。
性质:任何求最大目标函数值的纯整数规划或混合整数规划的最大目标函数值小于或等于相应的线性规划的最大目标函数值;任何求最小目标函数值的纯整数规划或混合整数规划的最小目标函数值大于或等于相应的线性规划的最小目标函数值。
18、0-1整数规划的隐枚举法步骤:⑴找出任意一可行解,目标函数值为Z0⑵ 原问题求最大值时,则增加一个约束 ......(*)⑶列出所有可能解,对每个可能解先检验式(*),若满足再检验其它约束,若不满足式(*),则认为不可行,若所有约束都满足,则认为此解是可行解,求出目标值; 11220n n c x c x c x Z +++≥⑷目标函数值最大(最小)的解就是最优解。
19、动态规划是运筹学的一个分支,是求解多阶段决策过程最优化问题的数学方法。
20、动态决策问题的特点:系统所处的状态和时刻是进行决策的重要因素即在系统发展的不同时刻(或阶段)根据系统所处的状态,不断地做出决策;找到不同时刻的最优决策以及整个过程的最优策略。
在多阶段决策过程中,动态规划方法是既把当前一段和未来一段分开,又把当前效益和未来效益结合起来考虑的一种最优化方法。
因此,每段决策的选取是从全局来考虑的,与该段的最优选择答案一般是不同的.21、存贮论的基本概念:1.需求:为了满足生产的需要,需不断地将库存输出给需用单位,需求就是库存的输出。
2.补充订货和提前订货时间(1)补充订货:库存由于需求而不断减少,必须及时进行补充订货。
补充订货相当于库存的输入。
(2)提前订货时间:从开始订货到货物入库为止所需要的办理订货手续、准备货物、运输货物以及到货验收的时间,称为提前订货时间。
3.费用分析存贮系统必须按最经济的原则运行。
存贮系统的费用分析要考虑到订货费、存贮费、缺货损失费等费用。
(1)订货费:订货费是指补充库存,办理一次订货发生的有关费用,包括订货过程中发生的订购手续费、联络通讯费、人工核对费、差旅费、货物检查费、入库验收费等。
