激光散斑的测量讲解
激光散斑

实验题目:激光散斑测量实验目的:通过对激光散斑大小的测量,了解激光散斑的统计特性,学习有关散斑光强分布重要的数据处理方法。
实验器材:氦氖激光器,双偏振片,全反射镜,透镜 ,毛玻璃,CCD ,计算机。
数据处理:1、理论值激光波长λ = 0.0006328mm 常数π = 3.14159265 CCD 像素大小=0.014mm激光器内氦氖激光管的长度d=250mm 会聚透镜的焦距f=50mm激光出射口到透镜距离d 1=700mm 透镜到毛玻璃距离=d 2+P 1=154mm 毛玻璃到CCD 探测阵列面P 2=513mm毛玻璃垂直光路位移量d ξ 和d η, d ξ=4小格=0.04mm ,d η=0 P 1=154mm-53.55mm=100.45mm 其束腰大小为 mm mm 2244.03.141592652500006328.0d W 01=⨯==πλ束腰位置mm ffd d f f55.53)0006328.0502244.0()506501(6505050)W ()1(d 2222'2012'11''2=⨯⨯+---=+---=πλπ束腰大小mm fW fd W W 0173.0)500006328.02244.0()506501(2244.0)()1(22222'2012'120102=⨯⨯+-=+-=πλπmm mm W a 4858.10006328.00173.0220=⨯==πλπ光斑大小mm mm aP W P W 1697.14858.145.10010173.0)1()(21222122101=⎪⎪⎭⎫ ⎝⎛+⨯=+=mm mm P aP P 4636.100)45.1001697.11(45.100)1()(2221211=+⨯=+=ρ散斑的统计半径20.00063285130.09760.0976像素 6.976像素1.16970.014P S mm mm Wλππ⨯=====⨯()像素4.172442.04636.100513104.0112==⎪⎪⎭⎫⎝⎛+⨯=⎪⎪⎭⎫ ⎝⎛+=∆mm mm P P d x ρξ()像素01y 12=⎪⎪⎭⎫⎝⎛+=∆P P d ρη 2、实验数据处理图一 实验装置图表一 实验数据照在毛玻璃上激光光斑的平均半径,毛玻璃的平均实际位移量的计算S 1=(Sx +Sy)/2=(6.5640+7.1428)/2=6.8534 (象素) S 2=(Sx +Sy)/2=(6.6581+7.2277)/2=6.9429 (象素) S 3=(Sx +Sy)/2= (6.6936+8.0257)/2=7.35965 (象素) S ’=(S 1+S 2+S 3)/3= (6.8534+6.9429 +7.35965)/3 =7.05185(像素)()()())像素(06.01232221=-'-+'-+'-=n S S S S S Ss σ68.0),像素(08.032.1u a ==⨯=P s σa b u u <<()7.050.08像素,P 0.68S =±=误差7.05 6.976100%100% 1.06%6.976s s s d s'--=⨯=⨯=毛玻璃的平均实际位移量∆x ’ = (15+19+15+16+16+16+17)/7=16(像素))像素(.73=s σ68.0),像素(532.1u a ==⨯=P s σa b u u <<()x 165像素,P 0.68∆=±=误差1617.4100%100%8.04%17.4x x xd x∆'∆-∆-=⨯=⨯=∆思考题:1、根据什么选择激光散斑测量的光路参数(P 1和P 2)?答:透镜的焦距,散斑大小和 CCD 像元大小的关 系 ,选择恰当的P 1P 2使得散斑的大小适中,图像中散斑数量适中。
激光散斑测量讲解

引言散斑现象普遍存在于光学成像的过程中,很早以前牛顿就解释过恒星闪烁而行星不闪烁的现象。
由于激光的高度相干性,激光散斑的现象就更加明显。
最初人们主要研究如何减弱散斑的影响。
在研究的过程中发现散斑携带了光束和光束所通过的物体的许多信息,于是产生了许多的应用。
例如用散斑的对比度测量反射表面的粗糙度,利用散斑的动态情况测量物体运动的速度,利用散斑进行光学信息处理、甚至利用散斑验光等等。
激光散斑可以用曝光的办法进行测量,但最新的测量方法是利用CCD和计算机技术,因为用此技术避免了显影和定影的过程,可以实现实时测量的目的,在科研和生产过程中得到日益广泛的应用,因此是值得在教学实验中推广的一个实验。
本实验的目的是让学生初步了解激光散斑的特性,学习有关散斑光强分布和散射体表面位移的实时测量方法:相关函数法,通过本实验还可以了解激光光束的基本特点以及CCD光电数据采集系统。
这些都是当代科研和教育技术中很有用的基本技术和知识。
实验原理激光散斑的基本概念:激光自散射体的表面漫反射或通过一个透明散射体(例如毛玻璃)时,在散射表面或附近的光场中可以观察到一种无规分布的亮暗斑点,称为激光散斑(Laser Speckles)或斑纹。
如果散射体足够粗糙,这种分布所形成的图样是非常特殊和美丽的(对比度为1)。
激光散斑是由无规散射体被相干光照射产生的,因此是一种随机过程。
要研究它必须使用概率统计的方法。
通过统计方法的研究,可以得到对散斑的强度分布、对比度和散斑运动规律等特点的认识。
图1 光散斑的产生(图中为透射式,也可以是反射式的情形)图1说明激光散斑具体的产生过程。
当激光照射在粗糙表面上时,表面上的每一点都要散射光。
因此在空间各点都要接受到来自物体上各个点散射的光,这些光虽然是相干的,但它们的振幅和位相都不相同,而且是无规分布的。
来自粗糙表面上各个小面积元射来的基元光波的复振幅互相迭加,形成一定的统计分布。
由于毛玻璃足够粗糙,所以激光散斑的亮暗对比强烈,而散斑的大小要根据光路情况来决定。
大学物理实验---激光散斑

实 验 报 告
3、 做完实验后,思考本实验的用途,觉得它可以用于以下几个方 面: (1)可以用本实验原理测量物体的微小位移量 (2)可以用其他透明物体代替毛玻璃,来测量其粗糙度
思考题:
1. 根据什么选择激光散斑测量的光路参数(P1 和 P2)?
答:首先根据透镜的焦距,其次须考虑散斑大小和 CCD 象元大小 的关系。只有选择适当距离的 P1、P2 才能使 CCD 上可以拍摄到较 多的散斑,而且每个散斑又占据足够多的像元数,并且拍摄到的图 像足够清晰有较好的对比度,这样才能得到对散斑光强分布的良好 结果。
W 02 =
2 ������������02 a= = 1.228566������������ ������
d πW (1 − 1' )2 + ( 01' )2 f λf
=
0.2244032 = 0.015731mm 203.4896818
P 1 =透镜到毛玻璃的距离-d 2 =178-53.282722=124.727178mm ������2 ρ(������1 ) = ������1 �1 + 2 � = 124.739279������������ ������ 1
产生误差的原因经过分析有以下几个方面: (1)
实验心得:
1、 为了减小估算误差,对光斑半径进行估算并输入计算机进行自 相关计算时,应该多取几组,比较这几组的相关度大小,最终 取相关度最大的那一组作为实验数据; 2、 在实验过程中要保证光器具的干净, 不能用手碰光器具的镜面, 在实验结束时应该及时将塑料罩盖回去;
S = λP2 / πW
(3)
因此测量出 S 的大小就可以求出 W。 (2) 两个散斑场光强分布的互相关函数: 假设观察面任意一点Q 1 上的散斑光强分布为I(x 1 ,y 1 ),当散射体发 生一个变化后(如散射体发生一个微小的平移 d 0 = d ξ 2 + dη 2 )观察面任意 一点Q 2 上的散斑光强分布为 I’ (x 2 ,y 2 )我们定义光强分布的互相关函数为: G C (x 1 ,y 1 ;x 2 ,y 2 )=〈I(x 1 ,y 1 ) I’(x 2 ,y 2 ) 〉 两个散斑场的互相关函数为:
激光散斑的测量

W ( Z ) W0 (1 Z 2 / a 2 )1/2 0.01726 1
S P2 / W
632.8 106 555.0 0.07545mm 1.4816
2. x 和y 的计算
P2 555 x d 1 0.1611mm 1 P 0.03 126.96 1 P2 y d 1 P 0 1
答:由于激光光强起伏周期远大于 CCD 采样的周期,激光器光强时整体下降或 者提升的,最终图像上整体光强大小可能会有变化 6、在本实验中若有一均匀的背景光迭加在散斑信号上,对 S 值的测量有影响 吗?试分析原因。 答:观察面上的光强整体上升了,统计平均值显然会上升,但是不会影响统计分 布。即对拟合没有影响,因此对 S 无影响。
W012
f ' d1
2 01 2 '
50mm
(50 650) 53.55mm 650 2 0.22442 2 (1 ) ( ) 50 632.8nm 50mm
W02 (1
d1 2 W012 2 ) ( ) f' f'
0.22442 0.01726mm 650 2 0.22442 2 (1 ) ( ) 50 632.8nm 50
五.思考题
1、激光散斑测量的光路参数(P1,P2)选择是根据什麽? 答: 为了得到较好的图像, 一方面需要考虑图像中散斑个数要多已得到的统计数 据比较可信, 另一方面要使散斑图像尽可能地大以获得精确测量。所以实验中需 要调节(P1,P2)兼顾这两个方面,以获得最佳图像 2、为什麽在本实验中散斑的大小用 CCD 象元,而毛玻璃与 CCD 表面的距离可 以用卷尺(最小刻度为 1 毫米)? 答:CCD 象元由计算机处理,精确度高。有公式 d x
激光散斑测量物体表面粗糙度的研究

激光散斑测量物体表面粗糙度的研究
激光散斑测量物体表面粗糙度是一种常见的非接触式测量方法,它利用激光经过物体表面反射后形成的散斑图案来反映物体表面的粗糙度。
通过分析散斑的形态和强度分布,可以获得物体表面的粗糙度信息。
激光散斑测量一般包括以下几个步骤:
1. 激光照射:将激光束照射到待测物体表面。
激光的波长和功率通常需要根据待测物体的特性来选择。
2. 散斑图案获取:激光束经过物体表面反射后,形成散斑图案。
通过合适的光学设备(如衍射光栅、透镜等)将散斑图案投射到像面上,然后采用相机等图像捕获设备来获取散斑图像。
3. 图像处理:对获取到的散斑图像进行处理,例如去除背景噪声、提取散斑图案等。
常用的处理方法包括傅里叶变换、滤波等。
4. 特征提取:通过分析散斑图案的形态和强度分布,提取与物体表面粗糙度相关的特征参数,例如散斑尺度、形状等。
5. 数据分析:根据特征参数,利用合适的粗糙度评估方法(如均方根粗糙度、自相关函数等),对物体表面的粗糙度进行评估和分析。
激光散斑测量方法具有非接触、快速、高精度等特点,广泛应
用于粗糙度测量、表面质量控制等领域。
在工业制造、材料研究、纳米技术等领域都有重要的应用价值。
激光散斑测量(中国科大实验讲义)

可编辑ppt
19
一维自相关函数图
实验曲线
拟合曲线
可编辑ppt
20
一维互相关函数图
实验曲线
可编辑ppt
21
可编辑ppt
22
激光散斑实验
什麽是激光散斑现象? 激光散斑现象的特点
激光散斑的应用 散斑测量实验的内容 数据处理的方法和结论
可编辑ppt
1
什麽是激光散斑现象?
• 当一束激光照射到具有漫射特性的粗糙表面 上时,在反射光的空间中用一个白色的屏去 接收光总可以看到一些斑点。这就是激光散 斑现象。
• 经透镜成象形成的散斑是主观散斑 。在自由 空间传播形成的 散斑叫做客观散斑。
xdx(1P 2/(P 1))
gc
可编辑ppt
x
17
实验相关函数的计算
• 利用CCD和采集卡(10moons)得到的是BMP格式的图 象文件,调用程序可以将BMP图象文件转化为两维的 数据文件,也就是得到了CCD面阵所在的这一面积上 的光强的值I(i, j)(i,j=1,2…,N0) 。利用这些值就可以 计算散斑场的归一化样本自相关函数和互相关函数。 这些由计算机完成。
可编辑ppt
6
由激光器出射的高斯光束
d
2W0
d=250mm ,=0.0006328mm ,w0=0.2244mm
d 1 w0 ( ) 2
可编辑ppt
7
高斯光束的复振幅表达式:
I I0
W0 0.135I0
u ( x , y , z ) A exp[ ik ( x y ) ] q(z)
S P W
使用激光散斑仪检测物体表面粗糙度的技术介绍

使用激光散斑仪检测物体表面粗糙度的技术介绍随着科学技术的不断发展,精确测量物体表面粗糙度的需求也日益增加。
在工业生产和科研领域中,我们经常需要对材料表面进行粗糙度的测量和分析,以确保产品的质量或研究物体表面的特性。
而使用激光散斑仪来进行粗糙度测量则是一种常见而有效的方法。
激光散斑仪是一种利用激光光源和散斑原理进行测量的仪器。
它通过对物体表面反射的激光光束进行观测,获得散斑图像,并通过对图像的分析来得到物体表面的粗糙度信息。
激光散斑仪的原理相对简单,但其在粗糙度测量中的应用却非常广泛。
在进行粗糙度测量时,首先需要将待测物体放置在激光光束的照射下。
激光光源发出的光束照射到物体表面上,并在表面上产生散斑图像。
这些散斑图像包含了物体表面的微小结构和细节信息。
然后,激光散斑仪通过摄像机或光电二极管等感光元件,将散斑图像转化为电信号。
接下来,电信号被传送到计算机等数据处理设备进行图像处理和分析。
在图像处理和分析过程中,可以利用散斑图像的尺度变化和灰度分布等特征来计算物体表面的粗糙度。
通常,粗糙度的评价参数有均方根值(Ra)、最大峰值高度(Rz)、平均峰值高度(Rp)等。
这些参数可以通过对散斑图像的灰度分布进行统计和计算来得到。
与传统的粗糙度测量方法相比,使用激光散斑仪进行测量具有许多优势。
首先,激光散斑仪可以对各种不同材料的表面进行测量,包括金属、陶瓷、塑料等。
其次,激光散斑仪能够实现非接触测量,无需对物体进行接触或破坏。
这对于某些对表面质量要求严格的物体来说尤为重要。
此外,激光散斑仪的测量速度快,可以实时获取粗糙度信息,并且可以进行自动化控制和数据分析。
激光散斑仪不仅在工业生产中有着广泛的应用价值,还在科学研究领域发挥着重要的作用。
在材料科学、光学、表面物理学等领域中,对物体表面粗糙度的测量和分析是不可或缺的一部分。
激光散斑仪提供了一种快速、准确的非接触式测量方法,为研究人员提供了便利。
总之,使用激光散斑仪进行物体表面粗糙度测量是一种简便、准确、快速的方法。
激光光斑尺寸测量方法

激光光斑尺寸测量方法我折腾了好久激光光斑尺寸测量方法,总算找到点门道。
一开始我真的是瞎摸索。
我最先想到的方法呢,就是拿尺子去量。
你能想象多傻吧,激光打在墙上形成的光斑,模模糊糊的,尺子根本就不精确啊。
这个办法肯定是不行的,这算是我第一个失败的尝试。
然后呢,我就想是不是可以用相机拍照,然后在电脑上根据照片的比例来计算光斑尺寸。
我拿我的普通数码相机就咔咔拍了不少照片。
但是这里就有个大问题,普通相机镜头会有畸变,你根本没法保证拍出来的光斑形状是准的,这就导致计算出来的尺寸误差超级大。
我那时候就意识到,没专业摄影设备这种方法不靠谱。
我后来还试过用一种特制的透明薄膜,想把光斑投射到薄膜上,用标记笔围着光斑边缘画一圈,然后再精确测量这个圈。
结果发现这个薄膜还是会对激光产生折射之类的,搞得光斑边缘乱糟糟的,也不准确。
再后来我就学聪明了点。
我弄来了一个光学传感器,这个就比较高级了。
就像是给光斑找了一个特别细心的小管家,能精确感应到光斑的边界。
但是这里面也有不少要注意的地方呢。
这个传感器要精心调校,就好像你给小管家安排工作,得跟他说清楚规则一样,要精确调整传感器的灵敏度还有扫描范围之类的。
要是没调好,还是会出错。
比如说灵敏度太高,可能就把周围的杂光也当成光斑一部分了;要是太低,又可能测不全光斑边缘。
还有就是如果测量的环境光线有干扰的话,数据可能也不准。
就像你在一个大吵大闹的市场里面听别人说话,容易听错是一个道理。
所以要是能控制环境光就尽量控制,暗一点的环境测量结果会更好。
目前我觉得用光学传感器这个方法还是不错的,但是我知道肯定还有其他更好的办法,我还在继续探索,要是哪天我有了新的发现,肯定第一时间再跟你说说。
激光散斑测量(中国科大实验讲义)

高斯光束的传播公式
高斯光束过程中光束轮廓为绕Z轴旋转的双曲面
( z ) z (1
z w
0
z0 ) 2 z
2
w
2
2 0
(z) w
2 0
(1
z 2 ) 2 z0
高斯光束特性图解
R(z)z处波面曲率半径
W0=0.2244mm
z
准直距离 Z0=2W02 / =499.99mm
高斯光束经透镜后的变换
2W01
2W02
d1
d2
w d a ( ) ( f f f d d f CD是Charge-coupled devices的缩写
CCD的空间分辨率与每个 象元的尺寸和间距以及传输 mA/W 过程有关,本实验中大约为 14微米。 暗电流(主要由热产生) 很高的光电灵敏度, (CCD器件必须避免强光照 射。同学们在每次采样完毕 后应及时合上光窗或挡住 光)。 光谱响应 度
400
1050 波长/nm
实验中的光路参数
2w
2w01
He-Ne
2w02 CCD
d1
d2
p1
p2
实验目的
1)测量散斑的统计半径(通过计算散斑场各点光强 的自相关函数并拟合求出)
P S W
2)测量散斑的位移(通过计算两个散斑场各点光强 的互相关函数并寻峰求出)
P x dx( ) (P )
He-Ne Laser
透镜
客 观 散 斑 场 毛玻璃
CCD
PC
激光的产生
激光工作物质被激活(光、电能等)后产生粒子数反转, 发生受激辐射,能使光得到放大。光在由两片高反射 率的镜片和激活物质组成的谐振腔之间多次的反射形 成激光输出。
激光散斑测量实验报告

激光散斑测量实验报告实验报告一、引言二、实验仪器和原理实验仪器:激光、透镜、狭缝、幕布、尺子、直尺实验原理:1.激光散斑现象:当激光通过光学元件后,由于光的波动性,光束经过屏幕成为一幅杂乱无章的亮暗交替、相互交错的斑图,这种图案被称为散斑。
散斑的出现是由于光的相位随机分布所导致的,故散斑图案是一种统计性质的成像效应。
2.透镜焦距的测量:当激光通过透镜时,如果透镜的焦距为f,则在焦距前后的位置,散斑图案会有明显的变化。
通过观察焦距前后散斑的大小和形状,可以确定透镜的焦距。
3.狭缝宽度的测量:当激光通过狭缝时,经狭缝后的散斑会变得更加明显。
通过观察狭缝前后散斑的大小和形状,可以确定狭缝的宽度。
三、实验步骤1.将激光照射到透镜上,观察透镜前后的散斑图案。
2.移动屏幕,找到焦距前后的位置,观察散斑图案的变化。
3.测量透镜到焦距前后的距离,计算出焦距。
4.将狭缝放在激光路径上,观察狭缝前后的散斑图案。
5.测量狭缝前后散斑的距离,计算出狭缝的宽度。
四、实验结果及数据处理1.透镜焦距的测量:透镜到焦距前后的距离为d1和d2,焦距为f,根据几何关系可得:1/f=1/d1+1/d2根据测量数据计算得到透镜焦距为f = xx mm。
2.狭缝宽度的测量:狭缝前后散斑的距离为l,透镜到屏幕的距离为D,根据几何关系可得:d=f*l/D根据测量数据计算得到狭缝宽度为d = xx mm。
五、实验讨论1.实验中使用的激光是否满足单色条件?可以通过观察散斑图案的颜色变化进行判断。
2.实验中是否考虑了折射和衍射对散斑图案的影响?3.实验中使用的透镜和狭缝是否满足理想条件?是否考虑了它们的光学畸变?5.实验中的结果是否与理论值相符?如果不符合,可能的原因是什么?六、结论通过激光散斑测量实验,测量得到了透镜的焦距和狭缝的宽度。
实验结果表明,激光散斑测量是一种简便有效的方法,可以用来测量光学元件的性能参数。
同时,实验中也发现了一些实验中需要注意的问题,并提出了一些改进的建议。
激光散斑干涉电子测量
激光散斑干涉电子测量技术摘要:激光散斑干涉测量就是根据与物体变形有内在联系的散斑图, 将物体表面位移或变形测量出来。
介绍了激光散斑干涉技术的物理学基础、检测方法及其应用。
说明它是一种非常便捷、先进、并具有发展潜力的光测技术。
1. 引言用相干激光照射表面粗糙的物体, 按照惠更斯的原理, 在物体表面散射的光, 尤如无数新的点光源发出相干子波, 它们相互之间将产生相长或相消干涉。
在物体表面的前方空间出现无数随机分布的亮点与暗点, 形成一幅很复杂的散斑图。
人们发现, 散斑的尺寸和形状, 与物体表面的结构、观察位置、光源和光源到记录装置之间的光程等因素有关。
当物体表面位移或变形时, 其散斑图也随之发生变化, 物体散斑虽为随机分布。
但物体变形前、后散斑有一定规律, 且常有物体表面位移或变形的信息。
散斑干涉计量就是根据与物体变形有内在联系的散斑图, 将物体表面位移或变形测量出来。
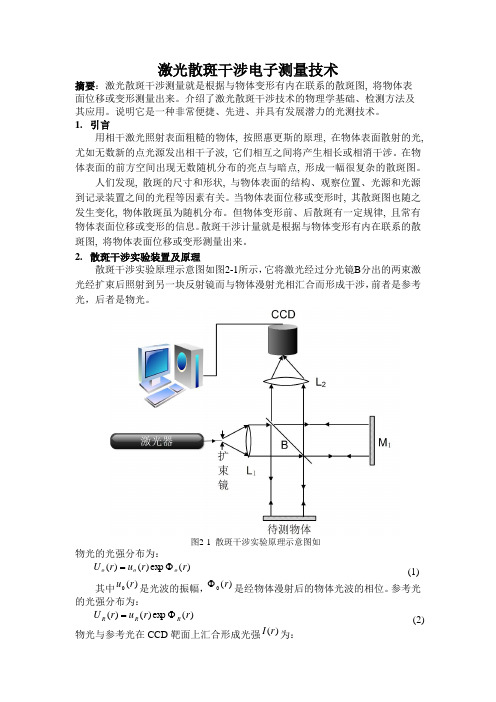
2. 散斑干涉实验装置及原理散斑干涉实验原理示意图如图2-1所示,它将激光经过分光镜B 分出的两束激光经扩束后照射到另一块反射镜而与物体漫射光相汇合而形成干涉,前者是参考光,后者是物光。
图2-1 散斑干涉实验原理示意图如 物光的光强分布为:)(exp )()(r r u r U o o o Φ= (1) 其中)(0r u 是光波的振幅,)(0r Φ是经物体漫射后的物体光波的相位。
参考光的光强分布为:)(exp )()(r r u r U R R R Φ= (2)物光与参考光在CCD 靶面上汇合形成光强)(r I 为:)cos(2)(22R o R o R o u u u u r I φφ-++= (3)当被测物体发生变形后,表面各点的散斑场振幅)(r u o 基本不变,而位相)(r o φ将改变为)()(r r o φφ∆-,即[])()(exp )('r r r u U o o O φφ∆-=(4)其中ΔФ(r )为由于物体变形产生的相位变化。
激光散斑测量讲解

引言散斑现象普遍存在于光学成像的过程中,很早以前牛顿就解释过恒星闪烁而行星不闪烁的现象。
由于激光的高度相干性,激光散斑的现象就更加明显。
最初人们主要研究如何减弱散斑的影响。
在研究的过程中发现散斑携带了光束和光束所通过的物体的许多信息,于是产生了许多的应用。
例如用散斑的对比度测量反射表面的粗糙度,利用散斑的动态情况测量物体运动的速度,利用散斑进行光学信息处理、甚至利用散斑验光等等。
激光散斑可以用曝光的办法进行测量,但最新的测量方法是利用 CCD 和计算机技术,因为用此技术避免了显影和定影的过程,可以实现实时测量的目的,在科研和生产过程中得到日益广泛的应用,因此是值得在教学实验中推广的一个实验。
本实验的目的是让学生初步了解激光散斑的特性,学习有关散斑光强分布和散射体表面位移的实时测量方法:相关函数法,通过本实验还可以了解激光光束的基本特点以及 CCD 光电数据采集系统。
这些都是当代科研和教育技术中很有用的基本技术和知识。
实验原理激光散斑的基本概念:激光自散射体的表面漫反射或通过一个透明散射体(例如毛玻璃)时,在散射表面或附近的光场中可以观察到一种无规分布的亮暗斑点,称为激光散斑(Laser Speckles或斑纹。
如果散射体足够粗糙,这种分布所形成的图样是非常特殊和美丽的(对比度为 1)。
激光散斑是由无规散射体被相干光照射产生的,因此是一种随机过程。
要研究它必须使用概率统计的方法。
通过统计方法的研究,可以得到对散斑的强度分布、对比度和散斑运动规律等特点的认识。
图1光散斑的产生(图中为透射式,也可以是反射式的情形)图1说明激光散斑具体的产生过程。
当激光照射在粗糙表面上时,表面上的每一点都要散射光。
因此在空间各点都要接受到来自物体上各个点散射的光,这些光虽然是相干的,但它们的振幅和位相都不相同,而且是无规分布的。
来自粗糙表面上各个小面积元射来的基元光波的复振幅互相迭加,形成一定的统计分布。
由于毛玻璃足够粗糙,所以激光散斑的亮暗对比强烈,而散斑的大小要根据光路情况来决定。
激光散斑测量技术与应用研究

激光散斑测量技术与应用研究引言激光散斑测量技术是一种基于散斑现象的非接触式测量技术,通过激光照射目标物体表面,利用散斑的特性来获取目标物体表面形貌或者表面变形的信息。
该技术具有测量精度高、测量速度快、适用范围广等优点,在科学研究、工业制造、生物医学等领域具有广泛的应用前景。
散斑现象介绍散斑是指当一束平行光线经过不规则表面或者光束传播介质中的不均匀区域时,由于光的散射而形成的频率和强度的空间变化。
散斑现象的形成原理主要包括两个因素:绕射和干涉效应。
绕射是光线在不规则表面或光束传播介质变化的区域上发生偏折;干涉是不同光线在某一点重新叠加时产生的干涉效应。
通过观察和分析散斑现象,可以获得物体表面形貌、表面变形等信息。
激光散斑测量原理激光散斑测量技术是利用激光的单色性、相干性和定向性,通过激光的投影和散射来实现对目标物体表面形貌或表面变形的测量。
基本的激光散斑测量原理包括以下几个步骤:1.激光照射:将激光照射到目标物体表面,产生散斑现象。
2.散斑记录:使用相机或者其他散斑记录装置记录散斑图像。
3.散斑分析:对散斑图像进行分析,提取目标物体表面形貌或者表面变形的信息。
激光散斑测量技术的应用1. 表面形貌测量激光散斑测量技术可以应用于表面形貌的测量。
通过记录激光照射到目标物体表面的散斑图像,利用散斑图像的信息可以还原出目标物体表面的形貌信息。
这对于制造行业的工件检测、光学元件的表面质量检验等方面具有重要的应用意义。
2. 表面变形测量激光散斑测量技术可以应用于表面变形的测量。
通过记录目标物体在受力或变形作用下的散斑图像,可以分析散斑图像的变化,从而获取目标物体的表面变形信息。
这对于工程结构的应力分析、材料力学性能的研究等方面具有很大的意义。
3. 物体运动测量激光散斑测量技术还可以应用于物体运动的测量。
通过记录目标物体运动过程中的散斑图像,可以利用散斑图像的相位信息提取出物体的运动参数,如速度、加速度等。
这对于机器人导航、运动追踪等领域具有广泛的应用前景。
三级大物实验报告-激光散斑的测量

实验题目:激光散斑测量实验目的:通过对激光散斑大小的测量,了解激光散斑的统计特性,学习有关散斑光强分布重要的数据处理方法。
实验器材:氦氖激光器,双偏振片,全反射镜,透镜 ,毛玻璃,CCD ,计算机。
实验原理:激光散斑是由无规散射体(实验中为毛玻璃)被相干光照射产生的。
散斑场按光路分为两种,一种是在自由空间中传播而形成的客观散斑(本实验研究的情况),另一种是由透镜成象形成的主观散斑。
散斑的大小、位移及运动变化可以反映光路中物体及传播介质的变化。
试验中用的是激光高斯光束,其传播时光场的等振幅线在沿光路方向为双曲线。
光斑最细的位置为束腰。
激光经过凸透镜时其偏角会变化,会产生新的束腰。
毛玻璃离透镜的距离改变时,照在其上的光斑半径也随之改变。
实验是通过用计算机测量散斑的变化来算出光路中毛玻璃的移动情况。
激光散斑光强分布的规律由相关函数来描述。
自相关函数为:G (x 1,y 1;x 2,y 2)=〈I(x 1,y 1) I(x 2,y 2) 〉归一化后为: 其中: 互相关函数为:G C (x 1,y 1;x 2,y 2)=〈I(x 1,y 1) I’(x 2,y 2) 〉归一化后为: )](ex p[1),(222Sy x y x g ∆+∆-+=∆∆})](/1[ex p{})](/1[(ex p{1),(212212S P P d y S P P d x y x g y x C ρρ++∆-++∆-+=∆∆WP S πλ/2=其中实验数据(原始数据纸质提交): N s x /像素 s y /像素 1 8.54 7.94 2 7.62 7.95 3 7.59 7.51 4 8.46 8.28 5 7.77 8.35 6 7.70 7.91 77.747.87))(/1(12P P d x x ρ+-=∆实验装置图 1.氦氖激光器 2.双偏振片 3.全反射镜 4.透镜 5.毛玻璃 D 7.计算机123 4 5 6735cm30cm15cm55cm数据处理:(1)理论值计算:由公式:2101)(πλd w =得激光管口处腰束半径为:mm E w 2244.01415926.398.632*25.001==-=由2'2012'11''2)()1(d fW f dd f f λπ+---=得mm E 55.53)4328.6*502244.0*()506501(6505050d 2222=-+---=π 由公式:2'2012'120102)()1(fW f d W W λπ+-=得:mm E W 01726.0)50*4328.62244.0*()506501(2244.0222202=-+-=πP1=150-53.55mm=96.45mm)(479.110328.6/01726.0/42202mm W a =⨯⨯==-πλπ)(126.1)479.1/45.961(01726.0)/11()1(2/1222/12202mm a p W p W =+⨯=+=)(47.96)45.96/479.11(45.96)1/1(1)1(2222mm p a p p =+⨯=+=ρ)(0984.0)126.1/(55010328.6/42mm W P S =⨯⨯⨯==-ππλ ∆x 和∆y 计算:(这里d ξ=0.06mm)∆x = d ξ (1 + p2 / ρ(P1))=0.06×(1 + 550/ 96.47)mm =0.4021(mm ) ∆y= d η (1 + p2 / ρ(P1))=0mm (2)实验值计算:S1=(Sx +Sy)/2=(8.55+7.95)/2=8.25 (像素) S2=(Sx +Sy)/2= (7.62+7.95)/2=7.78 (像素) S3=(Sx +Sy)/2= (7.59+7.51)/2=7.55 (像素) S4=(Sx +Sy)/2= (8.46+8.28)/2=8.37 (像素) S5=(Sx +Sy)/2= (7.77+8.35)/2=8.06 (像素) S6=(Sx +Sy)/2= (7.70+7.91)/2=7.80 (像素) S7=(Sx +Sy)/2= (7.74+7.87)/2=7.80 (像素) S8=(Sx +Sy)/2= (7.78+7.69)/2=7.74 (像素) 则S =0.014*(S1+S2+S3+S4+S5+S6+S7+S8)/8=0.014*(8.25+7.78+7.55+8.37+8.06+7.80+7.80+7.74)/8=0.1109mm则照在毛玻璃上激光光斑的平均半径为:mm E S P w 9990.01109.0*4328.6*5502=-==ππλ ∆x =0.014*(36+36+37+37+37+35)/6=0.5087mm 毛玻璃的平均实际位移量mm P P x d 076.047.96/55015087.0)(112=+=+∆=ρξ误差分析:1)试验中求得毛玻璃的平均实际位移量为0.076mm ,照在毛玻璃上的光斑半径理论值为0.0984mm ,而实际测得为0.1109mm 。
激光散斑和激光多普勒测量

低可认为是由于光的相干度的降低,表
面粗糙度或散射情况的降低,或者是均匀背景等引起的。
散斑的一阶统计描述了单点光强的涨落,如果需要了解散斑图像中光强从空间一
点到另一点的快速变化,了解散斑的空间结构和散斑的尺寸,则需要进行散斑的二阶
统计。散斑二阶统计的常用方法就是计算散斑强度分布的空间自相关函数和它的功率
激光散斑和激光多普勒测量
从图1.3可知,激光散斑主要应用于微循环的血流监测,这是因为激光散斑测量
法相对于放射性微球技术
[25]
、荧光示踪检测法
[26]
和氢离子稀释
[27]
等方法,具有非接触、
无创伤、能对血流分布快速成像等优点。具有相同优点的另外一种光学检测技术——
激光多普勒速度测量技术,是利用粒子散射光的强度波动引起的多普勒频移来测量散
谱密度。
在静态散斑研究中,散斑光强自相关函数可以帮助了解散斑空间结构的统计性
质。对动态散斑而言,静态散斑光强起伏的自相关函数概念可以推广为动态散斑光强
起伏的空间-时间互相关函数
[34]
。动态散斑的性质与散射物质的运动速度有关,因此
可以使用动态散斑的二阶统计来测量散射物质的运动速度。在照明光(高斯光束束腰
密度函数为指数概率分布,如图1.6所示。
通过对(1.6)式直接积分可得到 为平均光强,此
为空间平均。则(1.6)式可重写为
对于散斑图像,定义散斑衬比为
定义散斑信噪比为
假定由理想单一频率激光照射得到的
散斑图像,其强度变化的标准差等于其
平均强度,散斑衬比为1。实际应用中,
散斑图像的标准差总是小于其平均强
强波动的频移(多普勒频移)和散射粒子的平均速度成正比,比例系数与波长相关,
激光散斑干涉电子测量技术

激光散斑干涉电子测量技术李康华(哈尔滨工业大学威海校区光电科学系,威海 264209)摘要:激光散斑干涉测量是根据与物体变形有内在联系的散斑图, 将物体表面变形测量出来。
本文介绍了激光散斑干涉技术的原理、检测方法及其应用。
从实验检测中,发现其是一种非常便捷、先进、并具有发展潜力的光测技术,能广泛应用在许多领域中,尤其是工业产品生产的领域中。
关键词:激光散斑干涉技术1 引言散斑现象早已被人们所熟悉,但是在激光问世之后才被深刻的了解,并且应用到许多的领域.激光是一种高度相干性的光源,当它照射在具有漫反射性质的物体表面,根据惠更斯理论,物体表面的每一点都可以看成一个点光源,从物体表面反射的光在空间相互叠加,就会在整个空间发生干涉,形成随机分布的,明暗相间的斑点,这些斑点成为激光斑点(speckle)[1].随着科技的发展,对散斑的深入研究,人们发现, 发现这些斑点的大小和位置虽然是随机分布,但是整体上斑点是符合统计学规律的。
在一点范围内,散斑场的运动是与物体表面上各点的运动一一对应的。
散斑的尺寸和形状, 与物体表面的结构、观察位置、光源和光源到记录装置之间的光程等因素有关。
当物体表面位移或变形时, 其散斑图也随之发生变化, 物体散斑虽为随机分布。
但物体变形前、后散斑有一定规律, 且常有物体表面位移或变形的信息。
散斑干涉计量就是根据与物体变形有内在联系的散斑图, 将物体表面位移或变形测量出来。
激光散斑干涉法测量物体变形,除了具备全息干涉法的非接触直观,可以遥感,全场性实时性外,还具备光路简单,对试件表面,实验条件要求不高,计算方便,精度可靠等特点[8-10]。
因此,激光散斑干涉电子测量技术在许多领域上都得到到了广泛的应用。
2 散斑干涉原理散斑干涉计量的全过程分为2 步: 第1 步应用相干光照射目标的粗糙表面, 记录目标表面位移信息的散斑图; 第2 步将记录的散斑图放在某一分析光路( 逐点分析或全场分析光路) 中, 把散斑图中传感的位移或变形信息分离出来, 进行定性或定量分析。
激光散斑测量(268)

实验报告 4+04级11系 姓名:付艳艳 学号:PB04210268 日期:06.03.17实验题目:激光散斑测量实验目的:了解激光散斑的原理及应用,掌握散斑的测量方法以及相关的一些函数关系,性质。
实验原理:激光自散射体的表面漫反射或通过一个透明散射体(例如毛玻璃)时,在散射表面或附近的光场中可以观察到一种无规分布的亮暗斑点,称为激光散斑(laser Speckles )或斑纹。
当激光照射在粗糙表面上时,表面上的每一点都要散射光。
因此在空间各点都要接受到来自物体上各个点散射的光,这些光虽然是相干的,但它们的振幅和位相都不相同,而且是无规分布的。
来自粗糙表面上各个小面积元射来的基元光波的复振幅互相迭加,形成一定的统计分布。
由于毛玻璃足够粗糙,所以激光散斑的亮暗对比强烈。
当单色激光穿过具有粗糙表面的玻璃板,在某一距离处的观察平面上可以看到大大小小的亮斑分布在几乎全暗的背景上,当沿光路方向移动观察面时这些亮斑会发生大小的变化,如果设法改变激光照在玻璃面上的面积,散斑的大小也会发生变化。
由于这些散斑的大小是不一致的,因此这里所谓的大小是指其统计平均值。
它的变化规律可以用相关函数来描述。
可以知道S 与激光高斯光斑半径W (在毛玻璃上的光斑)的关系式为2/S P W l p =。
S 的意义即代表散斑的平均半径。
这是一个以1为底的高斯分布函数。
以下为两个散斑场的互相关函数:实验器材:1.氦氖激光器 2.双偏振片 3.全反射镜 4.透镜 5.毛玻璃 D 7.计算机实验预习数据演算: 光路参数:d1=650mmr 1()P =96.169mm P2=550mm P1=96.45mm激光波长λ = 0.0006328mm2121222(1/())(1/())(,)1exp{[}exp{[}C y d P P x d P P g x y SS h x r r D ++D ++D D =+--常数π = 3.14159265CCD 像素大小=0.014mm激光器内氦氖激光管的长度d=250mm 会聚透镜的焦距f ’=50mm激光出射口到透镜距离d 1=650mm毛玻璃垂直光路位移量d ξ 和d η, d ξ=3小格=0.03mm ,d η=0 d=250mm λ=632.8nm演算过程如下:l p =?2/0.0006328mm 250mm/3.14159265=0.0503566mm d01W ==0.2244mm √ ''12222011''d (1)()f d f W d f f p l -=--+ p l p -=--+-=--+?''12222101''2201d (1)()5065050(1650/50)(/0.000632850)f d f d W f f WP1=150-53.55=96.45mm02W ==0.04096mm20/a W p l =\=?=23.141592650.04096/0.00063288.329a mmr \=+=221()96.45(18.329/96.45)97.169p mm2/S P W l p =221/20()(1/)W Z W Z a =+p \=?221/2010.0006328550/(1/)s mm mm W p a=0.2327mm √转换为像素,结果为:16.62r D =?2d (1 + p /(P1))=0.03mm(1+550/97.169)=0.1998mm x转换为像素,结果为:14.27√∆y= d η (1 + p2 / ρ(P 1))=0实验数据及数据处理a) 求出照在毛玻璃上激光光斑的平均半径 2w Sp = 计算得:0.476mm 即为34像素√ b) 求出毛玻璃的平均实际位移量 211()xd P P x r D =+计算得:0.0299989mm √理论值与实验值比较?。
蜂窝结构激光散斑检测PPT课件

第6页/共11页
• 错位量对NDT检测的影响研究
• 在相同加载方式和载荷大小情况下选取不同错 位量,得出干涉条纹图,研究错位量选取的规 律和方法。由于缺陷为圆形,错位方向对检测 结果影响不大,通过改变错位量大小,获取6种 不同错位量条件下的检测图像进行研究。
• 检测对象是根据航标HB5461-1990《金属蜂窝胶接结构缺陷类 型及试块》制造的蜂窝结构标准样件,大小为 450mm×330mm,蒙皮材料为铝,蒙皮厚度为0.4mm;蜂窝 芯材料为铝。
• 样件预置圆形人工缺陷,直径分别为10mm、15mm、20mm、 30mm四种规格。
第3页/共11页
• 蜂窝结构
第7页/共11页
• 热加载时间对NDT检测的影响研究
• 在选取相同错位量的情况下,分别对物体加热3 秒,5秒,8秒和10秒,加热前物体表面未变形 时获取第一幅散斑干涉图,加热后让试件在室 温下冷却4秒,待物体表面变形达到最大时获取 第二幅散斑干涉图。
第8页/共11页
第四章 结论
• (1)激光错位散斑检测具有非接触、无污染、全场检测、单次 检测面积大、检测速率高,抗干扰能力强等优点。Βιβλιοθήκη 图3 蜂窝结构样件 设计图
图4铝蜂窝样件缺陷
第4页/共11页
实验方案
• 加载方式的选取
• 参考ASTM标准E 2581 – 07.根据检测对象的 材料、结构和缺陷类型选取合适的加载方式, 使被测对象的缺陷部位产生与正常部位不一致 的、适当大小的表面位移。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
激光散斑的测量
By 金秀儒
物理三班
Pb05206218
实验题目:激光散斑的测量
学号:PB05206218
姓名:金秀儒
实验目的:
了解激光散斑的统计特性,学会两种处理激光散斑的重要方法----自相关函数法和互相关函数法。
实验仪器:
氦氖激光器,全反射镜,双偏振片,透镜,毛玻璃, CCD ,计算机。
实验原理:
激光自散射体的表面漫反射或通过一个透明散射体时,在散射体表面或附近的光场中可以观察到一种无规则分布的亮暗斑点,称为激光散斑。
(1)自相关函数
假设观察面任意两点上的散斑光强分布为I 11(x ,y ),22I (x ,y ),
我们定义光强分布的自相关函数为:
G (x1,y1;x2,y2)=〈I(x1,y1) I(x2,y2) 〉 进行归一化处理,可以得到归一化的自相关函数为:
222(,)()/1exp[()/]g x y G x I x y S ∆∆=∆<>=+-∆+∆
(2)两个散斑场光强分布的互相关函数:
假设观察面任意一点Q1上的散斑光强分布为I 11(x ,y ),当散射体发生一个变化后(如散射体发生一个微小的平移220d d d ξη=
+)观察面任意一点Q2上的散斑光强分布为I '11(
x ,y ) 定义光强分布的互相关函数为:11221122GC x ,y ;x ,y )=<I(x ,y ) I'(x ,y ) >(;可以,归一化的互相关函数为:2121222
(1/())
(1/())
(,)1exp{[
]}exp{[
]}C x d P P y d P P g x y S
S
ξηρρ∆++∆++∆∆=+--
实验光路图 1.氦氖激光器 2.双偏振片 3.全反射镜 4.透镜 5.毛玻璃 D 7.计算机
5-
数据处理及结论:
一、原始数据和计算机计算结果:
1、FFT 计算自相关系数:(r=15)
FFT 计算自相关系数:(r=15) 序号 max g
min g max g 位置 min g 位置 散斑半径 SSX 像素 散斑半径
SSY 像素 拟合误差
1 1.775 -62.24610⨯
0 0 11.760 10.767 -35.54410⨯
2 1.760 -63.67810⨯
0 0 11.898 10.737 -35.61010⨯ 3 1.855 -54.55310⨯
0 0 11.416 11.010 -34.81210⨯ 4 1.841 -102.87910⨯
0 0 11.555 11.283 -35.41810⨯ 5 1.809 -75.38510⨯
0 0 11.797 11.795 -35.38710⨯ 6
1.768
-103.25610⨯
0 0 11.196 11.985 -35.71710⨯
2、计算互相关:
FFT 计算互相关系数:
序号 max g
min g max g 位置 min g 位置
(1;2) 1.475 0.346 28 0 (2;3) 1.634 0.347 23 0 (3;4) 1.575 0.370 28 0 (4;5) 1.615 0.365 21 0 (5;6) 1.529
0.355 28
3、相关参数(光路图见实验原理部分,已做必须修改):
相关参数:
光路参数:L1=35.00cm ;L2=30.50cm ;L3=13.40cm ;L4=53.20cm ; 激光波长:=632.8nm λ; 透镜焦距:f=5.00cm ;
1CCD 像素=0.014cm
实验光路图:
此列全为零!为什么?
二、数据处理:
1. 完成实验理论值w 和s 的计算
29
4101632.825.001010 2.24103.1415926
d w m λπ---⨯⨯⨯===⨯;
'22'
2
5
1
2228
22220119''
5103510510 3.501035 2.2410(1)()(1)()5632.810f d d f m w d
f f
ππλ-------⨯-⨯=-=⨯-=⨯⨯⨯-+-+⨯;
242
501
02228
222201192''
(2.2410) 3.501035 2.2410(1)()(1)()5632.810510w w m w d
f f ππλ-----⨯===⨯⨯⨯-+-+⨯⨯⨯; 22213213.4010 5.73107.6710p l d m ---=-=⨯-⨯=⨯;
2
523029
3.1415926(3.5010) 6.0810632.810
w a m πλ---⨯⨯===⨯⨯; 11
2225
4122102232
(7.6710)()(1) 3.5010(1) 4.4310(6.0810)
p w p w m a ----⨯=⨯+=⨯⨯+=⨯⨯; 924
2
4
1632.81053.2010 2.4210() 4.4310
p s m w p λππ----⨯⨯⨯===⨯⨯⨯;
2. 完成实验值的计算
a) 求出照在毛玻璃上激光光斑的平均半径 S
P w πλ=
2
; 散斑半径 SSX 像素 散斑半径
SSY 像素
S= 1/2(SSX+SSY ) 11.760 10.767 11.264 11.898 10.737 11.318 11.416 11.010 10.712 11.555 11.283 11.419 11.797 11.795 11.796 11.196 11.985 11.590 _
11.26411.31810.71211.41911.79611.59011.3506
s +++++==像素;
3411.3500.01410 1.5910m m --=⨯⨯=⨯ ;
因此,_
41.5910s m -=⨯;
92424
632.81053.2010 6.74103.1415926 1.5910
p w m s λπ----⨯⨯⨯===⨯⨯⨯;
b) 求出毛玻璃的平均实际位移量 )
(112P P x
d ρ+∆=ξ;
23222
1122
1(6.0810)()(1)7.6710(1)7.732106.7610
a p p m p ρ----⨯=+=⨯⨯+=⨯⨯; 3428232821280.01410 2.987105
x m --++++∆=⨯⨯=⨯;
0y ∆=;
因此,222
145
53.2010
()7.73102.98710 3.791011p p x d m ξρ----⨯⨯∆⨯===⨯++; 实验中,实际位移应该是5
3.0010d m -=⨯,相差不大;
实验小结及建议:
本实验是一个比较精确的实验,引起误差的主要因素有如下述:仪器方面,光路调整的好坏直接影响到实验的结果;调整光路时应保证各光学元件中心等高,激光束穿过各元件的中心。
调好光路后要将磁性座锁好,以确保其不再发生移动;读数方面,本试验为2人合作,一人看电脑,一人调光路,配合的默契程度也会影响结果;
从本次实验的结果来看,一方面,本实验主要的数据处理已经由计算机完成,就自相关结
果,222(,)1exp[(
)]x y g x y S ∆+∆∆∆=+-(理论公式)和22
2
(,)exp[()]x y g x y S αβ∆+∆∆∆=+-(实验公式)的结果基本是符合的;另一方面,互相关时误差相对而言较大,估计误差是主要
来自用手调节3格时,两人配合不默契,造成的误差;
总的来说,实验结果基本让人满意,在现有实验条件下,实验比较准确。
另,用MathType 编辑公式时,发现有时公式出现斜体,有时则不是,不知道是否有什么技巧加以控制操作?(貌似斜体的比较好看。
)
一般要求斜体,你可以试试,能否变成正体
思考题:
1. 激光散斑测量的光路参数(P1,P2)选择是根据什么? 答:
选择的依据有二:一则根据透镜的焦距,再则必须考虑散斑大小和CCD 象元大小的关系,选择恰当时可以使画面中有足够多的散斑,且图象有足够的像素,这样的采集图片在分析时才能得到较好的统计结果。
2. 为什么在本实验中散斑的大小用CCD 象元,而毛玻璃与CCD 表面的距离可以用卷尺(最小刻度为1毫米)? 答:
因为实验中散斑大小很小,一个象元对应0.014mm ,是尺度较小的长度单位,适合描述散斑的大小,数值更方便运算。
而毛玻璃与CCD 的距离为50厘米左右。
由误差的均分原理,毛玻璃与CCD 的距离的测量误差对最终误差的贡献可以忽略,故 P2的测量直接用米尺即可,而散斑的大小则要用较为精确的CCD 像元来测量。
3. 毛玻璃上高斯光斑半径W=2.5mm ,想使表征激光散斑大小的参数S 在CCD 接收面上为50个象元,毛玻璃距CCD 接收面的距离P2为多少? 答:
由公式2
S W
p λπ=
,可得毛玻璃距CCD 接收面的距离P2: 可得,2P =SW /5014 2.5 3.141590.62388.684m mm m m πλμμ=⨯⨯⨯÷=,即为所求;
物理三班 金秀儒 2007.5.27
报告要及时交。
