《信号与系统》第四章
信号与系统 吴大正 第四章 傅立叶变换和系统的频域分析

4.2 傅里叶级数
3 .f(t)为奇谐函数—f(t) = –f(t±T/2) 此时 其傅里叶级数中只含奇次谐波分量,而不含偶 次谐波分量即 a0=a2=…=b2=b4=…=0
f(t) 0 T/2 T t
4.3 周期信号(Periodic Signal)的频谱
周期信号的频谱 周期矩形脉冲的频谱 从广义上说,信号的某种特征量随信号频率变化的关 系,称为信号的频谱,所画出的图形称为信号的频谱图。 周期信号的频谱是指周期信号中各次谐波幅值、相位 随频率的变化关系,即将An~ω和n~ω的关系分别画在以ω 为横轴的平面上得到的两个图,分别称为振幅频谱图和相 位频谱图。因为n≥0,所以称这种频谱为单边谱。 也可画|Fn|~ω和n~ω的关系,称为双边谱。若Fn为实 数,也可直接画Fn 。
“非周期信号都可用正弦信号的加权积分表示”
——傅里叶的第二个主要论点
4.2 傅里叶级数
周期信号展开的无穷级数成为傅里叶级数,分“三角型傅里 叶级数”和“指数型傅里叶级数”,只有当周期信号满足狄 里赫利条件时,才能展开成傅里叶级数。 狄利赫利条件(Dirichlet condition)
t 0 T
2 T bn 2T f (t )sin(nt ) d t T 2
任意函数f(t)都可分解为奇函数和偶函数两部分, 由于f(-t) = -fod(t) + fev(t) ,所以 f (t ) f (t ) f (t ) f (t ) f e v (t ) f od (t ) 2 2
4.2 傅里叶级数
三角形式 指数形式 奇偶函数的傅里叶级数
e jx e jx 由于 cos x 2
A0 f (t ) An cos( n t n ) 2 n 1
精品文档-信号与系统分析(徐亚宁)-第4章

F2= s/(s^2+w0^2)
第4章 连续时间信号与系统的复频域分析
【例4-10】用MATLAB求解【例4-3】, 设τ=1 解 求解的代码如下: %program ch4-10 R=0.02; t=-2:R:2; f=stepfun(t, 0)-stepfun(t, 1); S1=2*pi*5; N=500; k=0:N; S=k*S1/N; L=f*exp(t′*s)*R; L=real(L);
本例中
和
的ROC均为
Re[s]>0,
极点均在s=0处。但
有一个s=0的零点,
抵消了该处的极点,相应地ROC扩大为整个s平面。
第4章 连续时间信号与系统的复频域分析 4.2.3 复频移(s域平移)特性
【例4-4】
, s0为任意常数 (4-12)
求e-atcosω0tU(t)及e-atsinω0tU(t)的象函数。
第4章 连续时间信号与系统的复频域分析
1. s 借助复平面(又称为s平面)可以方便地从图形上表示 复频率s。如图4-1所示,水平轴代表s Re[s]或σ, 垂直轴代表s的虚部,记为Im[s]或jω, 水平 轴与垂直轴通常分别称为σ轴与jω轴。如果信号f(t)绝 对可积,则可从拉氏变换中得到傅里叶变换:
f= exp(-t)+2*t*exp(-2*t)-exp(-2*t)
第4章 连续时间信号与系统的复频域分析
【例4-9】 用MATLAB求解【例4-2】 解 求解的代码如下:
%program ch4-9 syms w0t; F1=laplace(sin(w0*t)) F2=laplace(cos(w0*t))
(4-2)
(仅供参考)信号与系统第四章习题答案

e −sT
=
−sT
2 − 4e 2
+ 2e −sT
Ts 2
(f) x(t) = sin πt[ε (t)− ε (t − π )]
sin π tε (t ) ↔
π s2 + π 2
L[sin
πtε (t
−π
)]
=
L e jπt
− 2
e− jπt j
ε (t
−π
)
∫ ∫ =
1 2j
∞ π
e
jπt e−st dt
4.3 图 4.2 所示的每一个零极点图,确定满足下述情况的收敛域。
(1) f (t) 的傅里叶变换存在
(2) f (t )e 2t 的傅里叶变换存在
(3) f (t) = 0, t > 0
(4) f (t) = 0, t < 5
【知识点窍】主要考察拉普拉斯变换的零极点分布特性。 【逻辑推理】首先由零极点写出拉普拉斯变换式,再利用反变换求取其原信号,即可求取其收
= cosϕ eω0tj + e−ω0tj − sin ϕ eω0tj − e−ω0tj
2
2j
=
cos 2
ϕ
−
sin 2
ϕ j
e
ω0 t j
+
cosϕ 2
+
sin ϕ 2j
e −ω 0tj
F(s) =
L
cosϕ 2
−
sin ϕ 2j
eω0tj
+
cos 2
ϕ
+
sin ϕ 2j
e
−ω0
t
j
ε
(t
)
∫ ∫ =
信号与系统第四章习题参考答案13

《信号与系统》第四章习题参考答案4-1 解 (1)111()ataL es s a s s a -⎡⎤-=-=⎣⎦++ (2)[]2221221sin 2cos 111s s L t t s s s ++=+++++ (3)()2212tL te s -⎡⎤=⎣⎦+(4)[]21sin(2)4L t s =+,由S 域平移性质,得 ()21s i n (2)14tL e t s -⎡⎤=⎣⎦++ (5)因为1!nn n L t s +⎡⎤=⎣⎦,所以 []2211212s L t s s s++=+= 由S 域平移性质,得 ()()23121ts L t e s -+⎡⎤+=⎣⎦+(6)()2211cos sL at s s a -=-⎡⎤⎣⎦+,由S 域平移性质,得 (){}()2211cos ts L at e s s aβββ-⎡⎤-=-⎣⎦+++ (7)232222L t t s s ⎡⎤+=+⎣⎦ (8)732()327tL t es δ-⎡⎤-=-⎣⎦+ (9)[]22sinh()L t s βββ=-,由S 域平移性质,得()22sinh()atL e t s a βββ-⎡⎤=⎣⎦+-(10)由于()211cos ()cos 222t t Ω=+Ω 所以 222221111c o s ()22424ss L t s s s s ⎛⎫⎡⎤Ω=+∙=+ ⎪⎣⎦+Ω+Ω⎝⎭(11)()()()11111at t L e e a a s a s s a s βββββ--⎡⎤⎛⎫-=-= ⎪⎢⎥--++++⎣⎦⎝⎭ (12)由于()221cos()1ts L e t s ωω-+⎡⎤=⎣⎦++所以 ()()()221cos()1a t a s e L et s ωω--++⎡⎤=⎣⎦++(13)因为(2)(1)(1)(1)(1)(1)t t t te u t e t e e u t ------⎡⎤-=-+-⎣⎦且()(1)(1)2(1)(1)(1)11sst t e e L t eu t L eu t s s ------⎡⎤⎡⎤--=-=⎣⎦⎣⎦++所以 ()(1)(2)2211(2)(1)(1)11s t s s e L teu t e e s s s -----⎡⎤+⎡⎤-=+=⎢⎥⎣⎦+++⎣⎦(14)()(1)tL e f t F s -⎡⎤=+⎣⎦,由尺度变换性质,得(1)ta t L e f aF as a -⎡⎤⎛⎫=+⎢⎥ ⎪⎝⎭⎣⎦(15)()t L f aF as a ⎡⎤⎛⎫=⎪⎢⎥⎝⎭⎣⎦,再由s 域平移性质,得 []2()()at t L e f aF a s a aF as a a -⎡⎤⎛⎫=+=+ ⎪⎢⎥⎝⎭⎣⎦(16)31cos(6)cos (3)cos(3)2t t t -=∙13cos(9)cos(3)44t t =+32213cos (3)48149s s L t s s ⎡⎤=+⎣⎦++由s 域微分性质,得()()22322222213181327cos (3)481494819d s s s s L t t ds s s s s ⎡⎤--⎛⎫⎢⎥⎡⎤=-+=+ ⎪⎣⎦⎢⎥++⎝⎭++⎣⎦(17)[]2cos(2)4sL t s =+,连续两次应用s 域微分性质,有 []()2224cos(2)4s L t t s-=+,()3232224cos(2)4s sL t t s-⎡⎤=⎣⎦+(18)111atL es s a -⎡⎤-=-⎣⎦+,由s 域积分性质,得111111(1)at sL e ds t s s a ∞-⎛⎫⎡⎤-=- ⎪⎢⎥+⎣⎦⎝⎭⎰ln()ln ln s s a s s a ⎛⎫=+-=- ⎪+⎝⎭ (19)351135tt L ee s s --⎡⎤-=-⎣⎦++,由s 域积分性质,得 33111115ln 353t t s e e s L ds t s s s --∞⎛⎫⎡⎤-+⎛⎫=-= ⎪ ⎪⎢⎥+++⎝⎭⎣⎦⎝⎭⎰(20)()22sin aL at s a =⎡⎤⎣⎦+,由s 域积分性质,得()1122211sin 1arctan 21s s at s a s L ds d t s a a a s a π∞∞⎡⎤⎛⎫⎛⎫===-⎢⎥ ⎪ ⎪+⎝⎭⎝⎭⎛⎫⎣⎦+ ⎪⎝⎭⎰⎰ 4-2 解(1)因为()()sin ()2T f t t u t u t ω⎡⎤⎛⎫=--⎪⎢⎥⎝⎭⎣⎦()sin ()sin 22T T t u t t u t ωω⎡⎤⎛⎫⎛⎫=+-- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦ 所以可借助延时定理,得()()sin ()sin 22T T L f t L t u t L t u t ωω⎧⎫⎡⎤⎛⎫⎛⎫=+--⎡⎤⎡⎤⎨⎬ ⎪ ⎪⎢⎥⎣⎦⎣⎦⎝⎭⎝⎭⎣⎦⎩⎭222222221sT T s ee S S S ωωωωωω--⎛⎫=+=+ ⎪+++⎝⎭(2)因为()()()sin sin cos cos sin t t t ωϕωϕωϕ+=+ 所以()222222cos sin cos sin sin s s L t s s s ωϕϕωϕϕωϕωωω++=+=⎡⎤⎣⎦+++ 4-3 解此题可巧妙运用延时性质。
信号与系统(第四版)第四章课后答案

第5-10页
■
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案
4.1 拉普拉斯变换
四、常见函数的单边拉普拉斯变换
1. (t ) 1, 2.( t) 或1 3. ( t ) s, 4. 指数信号e
1
s
, 0
1 s s0
s0t
(t 2)
f1(t) 1 0 1 f2(t) 1 t
例1:e (t 2) e
-t
2
e
(t 2)
e
2
1 s 1
e
2s
-1 0
第5-17页
■
1
t
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案
4.2 拉普拉斯变换性质
1 1e sT
例2: 单边冲激 T(t ) 1 e sT e s 2T 例3: 单边周期信号 fT(t ) (t ) f1(t ) f1(t T ) f1(t 2T ) F1(s )(1 e sT e s 2T )
8 e 2 s
s
f(t ) 1 0 1 y(t ) 2 4 t
二、尺度变换
2s
2
(1 e 2 s 2s e 2 s )
2 e 2 s 2 (1 e 2 s 2s e 2 s ) s
第5-16页
■
0
2
4
t
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案
拉氏逆变换的物理意义
f (t )
2 j 1
j
j
F (s)est ds
信号与系统第4章

正方波为奇谐函数
f (t)
1
OT
2T t
1
f
(t
)
4
sin(t)
1 3
sin(3t)
1 5
sin(5t)
36
傅里叶级数的指数形式
f
(t)
A0 2
n1
An
c os (nt
n)
A0 2
n1
An
1 2
e j (nt n )
e j(nt n )
A0 2
1 2
n1
Ane jn e jnt
t1
(t)
i
(t)dt
0,
i 1,2,, n
则称该函数集为完备正交函数集。函数 ψ (t) 应满足条 件
0 t2 2 (t)dt t1
5
正交的三角函数集 (1)
1, cos 2 1 t , cos 2 2 t ,cos 2 m t ,,
T T
T
sin 2 1 t ,sin 2 2 t ,sin 2 n t ,
1 2
n1
Ane jn e jnt
A0 2
1 2
n1
Ane jn e jnt
1 2
Ane
n1
e j n
jnt
A0 2
1 2
n1
Ane jn e jnt
1 2
Ane
n1
e jn
jnt
1 2
Ane jn e jnt
n
37
傅里叶级数的指数形式
f
(t)
1 2
Ane
n
e j n
jnt
Fne jnt
n
上式中,
《信号与系统》教与学第四章
j n e 3
j n
e3
1 n
sin
n 3
,
n
0, 1,
2,
2
《信号与系统》教与学第四章答案
4.4 周期信号 f (t ) 的双边频谱 Fn 如图所示,求其三角函数表达式。
【知识要点:】本题主要考查周期信号的频谱概念,单边谱与双边谱的关系。
(3)计算信号的功率。
【知识要点:】本题主要考查周期信号的频谱概念应用;帕斯瓦尔功率等式应用。
T
2
;
f
t
A0 2
n1
An
cos
nt n
;P
Fn 2 。
n
【解题方法:】利用已知条件观察求出 ,并带入公式计算求出各次谐波分量;
根据单边幅度谱和双边幅度谱的关系、单边相位谱和双边相位谱的关系画出双
边幅度谱和相位谱;最后利用帕斯瓦尔功率等式计算信号的功率。
解:(1)
x
t
16 cos
20
t
4
6
cos
30
t
6
4
cos
40
t
3
10 (rad/s) ,
T
2
2 10
1 (s) , 5
周期信号所含谐波次数为二次,三次,四次;
求得。
(1) cos( t ) sin 2t
解: T1
《信与系统》教与学

4.14
利用能量等式
f
2 (t )dt
1 2
2
F ( j) d ,计算
sin t
2t
2
dt
。
【解题方法:】先利用门函数常用对和对称性求出 sin(2t) 的傅里叶变换, t
4.11 如下图所示信号, f1 (t ) 的傅立叶变换 F1 ( j ) 已知,求信号 f 2 (t ) 的傅立叶 变换 F2 ( j ) 。
解:
f2 (t ) f1 (t t0 ) f1(t t0 ) f1(t ) F1( j)
f1(t t0 ) F1( j)e jt0
9
《信号与系统》教与学第四章答案
解: T1
2
2(s )
T2
2 2
(s)
故该信号为非周期信号。
(2)
cos(
t)
sin(
t)
2
4
T1 T2
2
为无理数,
解: cos
2
t
,
2
4
(s),
sin
4
t
,
2
8
(s),
2
4
8 (s)。
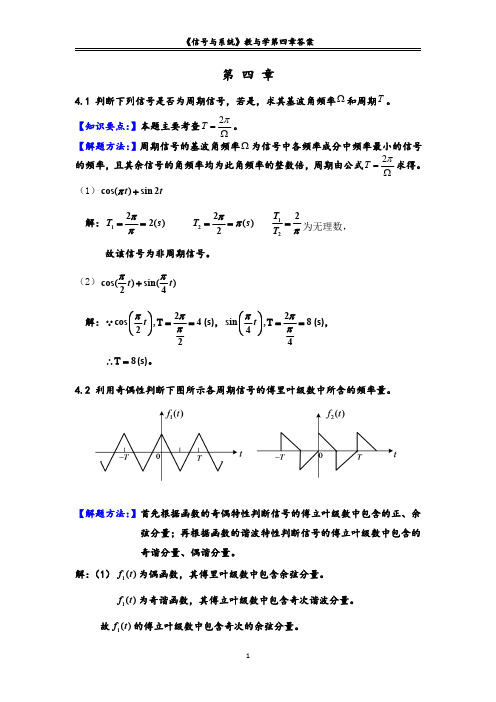
4.2 利用奇偶性判断下图所示各周期信号的傅里叶级数中所含的频率量。
【解题方法:】首先根据函数的奇偶特性判断信号的傅立叶级数中包含的正、余 弦分量;再根据函数的谐波特性判断信号的傅立叶级数中包含的 奇谐分量、偶谐分量。
df (t) ( j ) F ( j ) dt
jt
df (t) dt
d( j) F(
d
j)
jF
(j)
j
dF ( j ) d
4t
df (t dt
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图 两个矢量正交
矢量的分解
c2V2
V
V2
2
o
1
V1
c1V1
图 平面矢量的分解
c3V3
V3
V
o V1
V2
c2V2
c1V1
V c1V1 c2V2 c3V3
图 三维空间矢量的分解
推广到n维空间
1 正交函数的定义
在区间 (t1,t内2 ),函数集 {0 (t),1(t中),的,各N个(t)函} 数间,若满足下列 正交条件:
➢在波形任一周期内,其第二个半波波形与第一个半波波形相同;
x(t) x(t T0 / 2)
➢这时x(t)是一个周期减半为
的周期非正弦波,其基波频率
为
,即其只含有偶次谐T0波2;
20
4.4波形对称性与傅里叶系数
4 奇半波对称
➢在波形任一周期内,其第二个半周波形恰为第一个半周波形的
负值; x(t) x(t T0 / 2)
交函数集 {0 (t),1(t), ,N (t)} 是完备的,即再也找不到一个函数 (t)
能满足
t2
(t)
* m
(t
)dt
0
t1
m 0,1, , N
则在区间 (t1,t2 ) 内,任意函数x(t)可以精确地用N+1个正交函数地加权和
表示:
N
x(t) c00 (t) c11(t) cN N (t) cnn (t)
T0
3 傅里叶级数系数的确定
➢正弦—余弦形式傅里叶级数的系数
2Bk
2 T0
x(t) cos k0tdt
T0
2Dk
2 T0
x(t) sin k0tdt
T0
➢极坐标形式的傅里叶级数的系数
Ak Bk2 Dk2
由正弦—余弦形式傅里叶级数的
tgk Dk Bk
➢另一种求法:
系数确定
Bk Re{ck }, Dk Im{ck }, k 0
根据欧拉公式
ejt=cos(t)+jsin(t) e-jt=cos(t)-jsin(t)
sin(t)=(ejt-e-jt)/(2j) cos(t)=(ejt+e-jt)/2
得 x(t) 1 (1/ 2)cos 2t cos4t (2 / 3)cos6t
X(t)是实信号
因为 x(t) x(t)
2 Dk sin k0t k 1
❖任何 2信D号k x(Tt4)0都0T可0 以2 x分(t)解sin为k偶0函t d数t 和奇函数两部分。
Ev{x(t)} {[ x(t) x(t)]}/ 2 Od{x(t)} {[ x(t) x(t)]}/ 2
4.4波形对称性与傅里叶系数
3 偶半波对称
例4-7
习题1
如图所示信号为周期信号的一个周期,其付氏级数包含 ( ) A. 直流 、 偶次余弦项 B. 直流 、奇 次余弦项 C. 直流 、 偶次正弦项 D. 直流 、 奇次正弦项
习题2
信号如图所示,其三角型付氏级数为( )
A.
n 为奇数
B.
n 为偶数
C.
n 为奇数
D.
n 为偶数
4.5周期信号的频谱与功率谱
4.4波形对称性与傅里叶系数
1 偶对称 x(t) x(t)
❖波形对纵轴对称 ❖奇函数在对称区间积分为零 ❖傅里叶级数中只有常数项和余弦项
x(t) c0 2B1 cos0t 2B2 cos 20t 2Bk cos k0t
c0 2 Bk cos k0t k 1
2Bk
4 T0
T0
第四章 连续时间傅立叶变换
连续时间信号的谱分析和时-频分析
4.1 引言
➢时域中,连续信号的基本信号是冲激函数,离散信号的 基本信号是抽样序列;以冲激(抽样)响应作为基本响 应。
➢频域中以复指数函数或序列作为基本信号。系统响应表 示为不同频率的复指数信号响应的加权或积分。 ➢原因:1)它是LTI系统的特征函数。
➢正弦函数 sin n0t 和余弦函数 cos n0t 在区间 (t1, t1 T0 ) 内是正交函数。
4.3 周期信号的表示 连续时间傅里叶级数
1 用指数函数表示周期信号:复指数形式的傅里叶级数
➢复指数函数集 k e jk0t , k 0,1, ,
加权组合的信号 x(t) ck e jk0t
k 1
3 傅里叶级数系数的确定
➢周期信号的复指数形式的傅里叶级数:
x(t)
ck e jk0t
k
ck
1 T0
x(t )e jk0t dt
T0
➢已知x(t)可以分析出所含的频谱;
➢系数 ck 称为x(t)的傅里叶系数或频谱; ➢系数 c0 是x(t)中的直流或常数分量
1
c0
T0
x(t )d t
2)
c0
1 T0
T0
x(t)dt= 1 T0
T1 / 2 -T1 / 2
A dt
AT1
/ T0
ck
1 T0
x(t )e jk0t dt
T0
1 T0
T1 / 2 Ae jk0t dt
T1 / 2
(2 A / k0T0 ) sin(k0T1 / 2) ( A / k ) sin(kT1 / T0 )
3)
x(t)
ck e jk0t
复指数形式的傅立叶级数
k
正-余弦形式的傅立叶级数
例 4-4 已知 x(t) 7 cos0t 3sin0t 5,求cos其2复0t 指4数sin形2式0t 的傅 立叶级数
解:
x(t) c0 2 [Bk cos k0t Dk sink0t]
k 1
对比
2B1 7, 2D1 3, 2B2 5, 2D2 4, 其余系数2Bk 0, 2Dk 0
k
k 1
将| ck | 和 argck 对k0 的函数关系绘成图,称为复指数频谱 图4-10 (b)
| ck || ck | Ak
argck argck k , k 0
➢为镜像对称方式;
➢这时x(t) 只含有奇次谐波;
0 k为偶数
2Bk
4
T0
T0
2
x(t) cos k0t
dt
0
k为奇数
0 k为偶数
2Dk
4
T0
T0
2
x(t) sin k0t
dt
0
k为奇数
4.4波形对称性与傅里叶系数
5 双重对称
➢X(t)是奇函数或偶函数,同时又具有奇半波对称或偶半波对称; ➢这种波形对与纵轴相隔 的垂线对称,又称为1/4波对称; ➢通过例4-6说明双重对称T0有4与傅里叶系数的关系。 ➢ 表4-1 波形对称性、对称条件及其对应的傅里叶系数; ➢求复杂函数的傅里叶系数时,可以先求其偶部和奇部的傅里叶 系数,然后相加。
k 1
傅里叶级数的 三角函数形式
2 三角函数形式的傅里叶级数
在连续时间情况下,实周期信号的傅里叶级数的三角函数形式:
➢极坐标形式:令 ck Ak e jk
x(t) c0 2 Ak cos(k0t k ) k 1
➢正弦—余弦形式形式:
数学上等效
令 ck Bk jDk
x(t) c0 2 (Bk cos k0t Dk sin k0t)
2
x(t) cos k0t
dt
0
4.4波形对称性与傅里叶系数
2 奇对称 x(t) x(t)
❖波形对原点对称 ❖ x(t) cosk0t 为奇函数,x(t) sin k0t 为偶函数;奇函数 在对称区间积分为零 ❖傅里叶级数中只有正弦项
x(t) 2D1 sin 0t 2D2 sin 20t 2Dk sin k0t
x(t) ck e jk0t
k
两边取共轭 x(t)
ck*e jk0t
k
以-k替代k
x(t)
c-k*e jk0t
k
比较
ck c*k 或 ck* ck
2 三角函数形式的傅里叶级数
x(t)
ck e jk0t
k
重写
x(t) c0 [ck e jk0t ck e jk0t ]
x(t)
ck e jk0t
k 3
式中 c0 1, c1 c1 1/ 4, c2 c2 1/ 2,c3 c3 1/ 3,0 2
求(a)其三角函数表示式;(b)用图解方法表示各谐波分量的
波形及其合成波形x(t).
解: x(t) 1 (e j2t e j2t )/ 4 (e j4t e j4t )/ 2 (e j6t e j6t )/3
➢三角函数形式的傅里叶级数: x(t) c0 2 Ak cos(k0t k ) k 1 将 Ak 对 k0 的函数关系,绘成图,称为振幅频谱图,简称为频谱图; 将 k 对 k0 的函数关系,绘成图,称为相位频谱。
➢ x(t) 频谱 ➢图4-10 (a)
单边频谱
x(t)
ck e jk0t c0 (ck e jk0t ck e jk0t )
2)复指数是正交函数。 3)信号频率和信号本身是现实可观测。
➢信号的谱分析:把信号表示为一组不同频率的复指数函
数或正弦信号的加权和,称为信号的频谱分析或傅里叶
分析。
本章主要内容
4.2 复指数函数的正交性
V2
两矢量V1与V2正时的夹角为
90°。不难得到两正交矢量
的点积为零, 即
90°
o
V1
V1V 2 V1 V2 cos90 0
掌握 式 4-44,4-45,4-46
例 4-2 已知x(t)是一周期的矩形脉冲,如图所示,求其傅 里叶级数。
