2014仿真试题 (1)

合集下载

2014年初中学业水平思想品德仿真试卷

2014年初中学业水平思想品德仿真试卷(一)(全卷三个大题，共32个小题。

共8页；满分l00分，考试用时l00分钟)一、选择题(下列各题的四个选项中，请选出最符合题意的一个答案．并将其字母填写(涂} 在答题卷（卡)相应题号的位置。

每小题2分。

共50分)1．“在大海上航行，没有不带伤口的船；在生命中旅行，没有不受伤的心灵。

”这告诉人们( B )A．保持乐观心态，才能远航B．人生难免有挫折，挫折是人生的一部分C．坚持正确的人生方向，需要坚强的意志D．只要不经历挫折就能避免受伤2．随意践踏地球上的生命，就是破坏我们的地球。

这句话说明( B )①要尊重生命，善待生命②每种生命都有其存在的意义与价值③人的生命具有独特性，只要珍惜人的生命即可④人类是自然界的主宰A．①②③B．①②C．②③④D．①③3．每个人的生命都是有价值的，但是实现生命的价值并不是一蹴而就的，实现人生的意义，追求生命的价值，要脚踏实地，从现在做起，从小事做起。

下列能体现我们人生价值的是( B ) ①在家主动帮父母洗碗、拖地②同学遇到困难时，能尽我最大的努力帮助他们摆脱困境③路上遇到坏人欺负他人时，我会赶快走开，以免惹祸上身④朋友烦恼时，我会开导他们，让他们摆脱不快的阴影A．①②③B．①②④C．①③④D．②③④4．关注他人的尊严，既要从欣赏、鼓励、期望等角度来来善待对方，更要注意不做有损他人的事情。

这样，我们才能得到他人的尊重，与人共享自尊的快乐。

这属于（D ）A．重视他人B．达观C．自尊D．尊重他人5．小明：“虽然我平时成绩很好，但总担心考不进理想的学校。

”小红：“你应该放松点，考试前试着去做一些自己喜欢的事。

”小明产生烦恼的主要原因是( B )A．心胸狭隘B．缺乏自信C．过于自负D．过于依赖他人；6．小鸡孵化出壳时，需要自己吃力地一点点啄破蛋壳，才能爬出来。

有人觉得小鸡可怜，便帮小鸡把蛋壳掰开……可人们很快发现，这些“被”顺利出壳的小鸡过后多是病怏怏的，而那些自己啄破蛋壳艰难出壳的小鸡，却个个强壮。

四川省宜宾市李庄中学2014届高考英语仿真模拟试题试题(1)外研社版

2014年四川高考英语仿真试题第Ⅰ卷注意事项：1、每小题选出答案后，用铅笔将答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号。

2、本卷共55小题，共9分第一部分：英语知识运用（共两节，满分45分）第一节：单项填空（共10小题，每小题1分，满分10分）从A、B、C、D四个选项中，选出可以填入空白处的最佳选项。

1. —Excuse me. How much is the shirt?— _______.A. Extra LargeB. 50 eachC. It sells wellD. Altogether there are 52. New technologies have made ____ possible to turn out new products faster and at a lower cost.A. thatB. thisC. oneD. it3. We are said to be living in ____ Information Age, ____ time of new discoveries and great changes.A. an; theB. 不填; theC. 不填; aD. the; a4. At school, some students are active ______ some are shy, yet they can be good friends with one another.A. whileB. althoughC. soD. as5. It’s surprising that your brother _____ Russian so quickly—he hasn’t lived there very long.A. picked upB. looked upC. put upD. made up6. Tom took a taxi to the airport, only _____ his plane high up in the sky.A. findingB. to findC. being foundD. to have found7. The hotel is almost finished, but it _____ needs one or two weeks to get ready for guests.A. onlyB. alsoC. evenD. still8. I looked up and noticed a snake ______ its way up the tree to catch its breakfast.A. to windB. windC. windingD. wound9. —Did you catch what I said?—Sorry. I ______ a text message just now.A. had answeringB. have answeredC. would answerD. was answering10. He will come to under stand your efforts sooner or later. It’s just a matter of _____.A. luckB. valueC. timeD. fact第二节：完形填空（共20小题：每小题1.5分，满分30分）阅读下面短文，掌握其大意，然后从16～35各题所给出的A、B、C、D四个选项中选出最佳选项。

2014全国新课标高考仿真模拟卷(一)

2014全国新课标高考仿真模拟卷(一)(时间：45分钟满分：90分)一、选择题(本题共6个小题，每小题6分，共36分)1．(2013·北京丰台区5月)下列叙述正确的是()。

A．醋酸菌和酵母菌进行有氧呼吸的主要场所是线粒体B．人体用于维持体温的热能来自于ATP水解释放的能量C．用透气的消毒纱布包扎伤口可抑制破伤风芽孢杆菌增殖D．加酶洗衣粉的去污能力与衣物水洗的温度无明显相关性答案 C2．(2013·浙江重点中学联考)对下列图中有关的生物学意义的描述正确的是()。

A．甲图若在c点切断，则刺激b点后，a点会兴奋，肌肉会收缩B．乙图人体物质交换中体内细胞与B间不能直接物质交换，体内细胞与A 之间才能直接进行物质交换C．丙图中，对向光弯曲的植物而言，若茎背光侧为B对应的生长素浓度，则茎向光侧不可能为C对应的浓度D．图丁中靶细胞裂解与效应T细胞内的溶酶体有关解析甲图若在c点切断，则刺激b点时肌肉不再收缩；乙图中C为血浆、A为组织液、B为淋巴，人体有些细胞如淋巴管壁细胞、淋巴细胞可与B直接进行物质交换；图丁中靶细胞裂解与效应T细胞激活靶细胞内的溶酶体酶有关。

答案 C3．(2013·黄冈质检)下图1表示胰岛素浓度与血糖的补充速率和消耗速率之间的关系，图2表示描述某种生命活动的模型。

下列相关分析错误的是()。

A．曲线甲表示血糖的补充速率，曲线乙表示血糖的消耗速率B．胰岛素作用于肝脏、肌肉等细胞导致曲线甲上升C．若E为调节中枢，a为血糖浓度下降，则b、c可分别代表胰高血糖素和肾上腺素分泌增加D．若E为调节中枢，a为渗透压升高，则b、c可分别代表抗利尿激素分泌增加和产生渴觉解析渴觉形成中枢位于大脑皮层，而不是渗透压感受器所在场所——下丘脑。

答案 D4．正常情况下，神经纤维上某一点受到刺激后电位变化记录如甲图。

在实验装置中加入河豚毒素后，给予该部位同种强度的刺激，结果电位变化如图乙，据图分析河豚毒素的作用可能是()。

2014广东仿真试卷(一)理科综合答案详解

2014年广东省普通高等学校招生全国统一考试仿真模拟试卷（一）理科综合答案详解一、单选题1、C：不能发生质壁分离的细胞可以是活的动物细胞、没有大液泡的植物细胞等2、B：乙烯具有促进茎段细胞横向生长、抑制纵向生长的作用，而高浓度的生长素会促进乙烯的合成从而抑制茎段细胞伸长，故B错。

3、D：内环境的组成包括组织液、血浆、淋巴等，图中未显示淋巴，故A错；③葡萄糖进入肝细胞是主动运输、④氧气跨膜是自由扩散，故B错；肝细胞有氧呼吸在肝细胞内进行，细胞内液不属于内环境组成。

4、D：进行DNA粗提取实验选材应该是DNA含量丰富的实验材料，猪血红细胞不适合作为实验材料，因为哺乳动物成熟的红细胞没有细胞核。

5、B：根据表格F2性状分离比可以知道黑鲤：红鲤（15:1）是属于16组合的异常比例，红鲤鱼基因型为双隐（aabb），故可知鲤鱼的体色遗传受两对等位基因共同控制，遵循自由组合定律。

根据F2出现16组合可知，F1的基因型为AaBb，与红鲤（aabb）测交后代是（AaBb、Aabb、aaBb）：aabb=3:16、C：据图2可知，随着横坐标葡萄糖溶液浓度增加，大肠杆菌增长速率不断增加。

当葡萄糖溶液浓度达到一定值后，大肠杆菌增长速率保持不变，最可能的原因就是细胞膜上运输葡萄糖的载体数量有限，尽管外界葡萄糖浓度增高，但是能够进入细胞的葡萄糖达到了峰值。

二、双选题24、BD：流经（池塘）生态系统的总能量应该是生产者固定的太阳能（有时要根据题意考虑是否有人工添加的化学能，比如投放饲料），故A错；能量从贝类流入下一营养级的传递效率应该是下一营养级的同化量/贝类同化量①，题中的④是下一营养级的摄入量，并不是同化量，故C错。

25、AB：首先必须熟悉果蝇染色体组成，不受“图片旋转”的影响，根据染色体组成可以判断出图中表示的是雄果蝇（其中一条性染色体多一段弯曲成勾），故A错；雄果蝇的次级精母细胞中有可能是只有复制后的Y染色体，X染色体为0，也可能是减Ⅱ前期、中期只有一条复制后的X染色体，也可能是减Ⅱ后期复制后的X染色体着丝点分裂，姐妹染色单体形成两条子X染色体。

2014年高考仿真密卷一

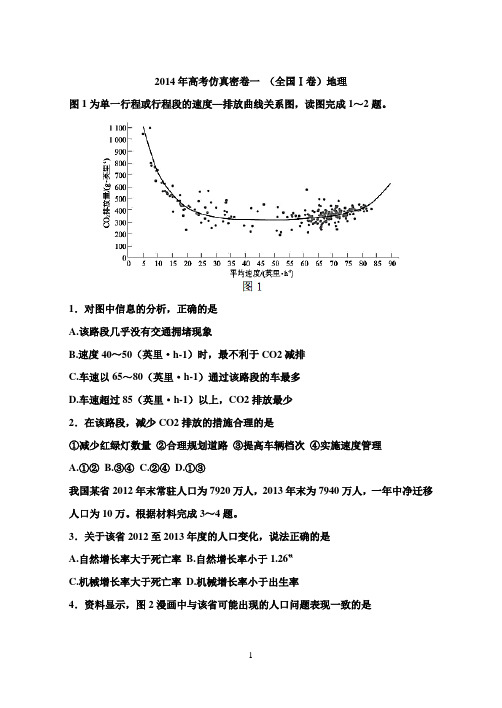
2014年高考仿真密卷一（全国Ⅰ卷）地理图1为单一行程或行程段的速度—排放曲线关系图，读图完成1～2题。

1．对图中信息的分析，正确的是A.该路段几乎没有交通拥堵现象B.速度40～50（英里·h-1）时，最不利于CO2减排C.车速以65～80（英里·h-1）通过该路段的车最多D.车速超过85（英里·h-1）以上，CO2排放最少2．在该路段，减少CO2排放的措施合理的是①减少红绿灯数量②合理规划道路③提高车辆档次④实施速度管理A.①②B.③④C.②④D.①③我国某省2012年末常驻人口为7920万人，2013年末为7940万人，一年中净迁移人口为10万。

根据材料完成3～4题。

3．关于该省2012至2013年度的人口变化，说法正确的是A.自然增长率大于死亡率B.自然增长率小于1.26‟C.机械增长率大于死亡率D.机械增长率小于出生率4．资料显示，图2漫画中与该省可能出现的人口问题表现一致的是资源型城市是以本地区自然资源开采、加工为主导产业的城市类型。

2013年12月03日，国务院正式发布《全国资源型城市可持续发展规划(2013-2020年)》，首次界定了262个“资源型城市”，分为四类：成长型城市、成熟型城市、衰退型城市、再生型城市。

资源型城市数量在各省分布如图3所示，读图文资料，完成5～6题。

5．我国资源型城市的分布特点是A．南方多，北方少B．东部多，西部少C．与经济水平正相关D．与人口密度负相关6．资源型城市的再生发展，合理措施是A．产业链向高端延伸B．扩大规模，提高技术C．提高第一产业比重D．将主导产业向外转移读漫画《枯萎的外表，强大的的内心》（图4），完成7～8题。

7．漫画揭示的地理环境A．降水稀少B．地下水丰富C．地形平坦D．土壤肥沃8．图中景观在我国最典型的地区是A．西藏地区B．华南地区C．西北地区D．东北地区图5为某地等高线示意图，读图完成9～11题。

9．该地最大相对高度可接近A．600米B．650米C．700米D．800米10．图中甲、乙、丙、丁四地有可能形成瀑布的是A．甲处B．乙处C．丙处D．丁处。

2014年高考数学仿真模拟试题新课标

2014年高考数学仿真模拟试题第Ⅰ卷 (选择题共60分)一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中只有一项是符合题目要求的．1.（理）已知集合{34}M x x =-<，集合2{0,}1x N xx Z x +=≤∈-，那么M N =（） A.{11}x x -<≤ B. {1,0}- C ．{0} D ．{0,1} （文）已知集合{34}M x x =-<，集合2{0,}1x N xx Z x +=<∈-，那么M N =（）A.{11}x x -<<B. φ C ．{0} D ．{2}2. 已知→a ＝(cos40︒，sin40︒)，→b ＝(cos80︒，sin80︒)，则→a ·→b = （） A. 1 B.32 C ．12 D ．223.（理）复数2lg(3)(441)()x x z x i x R -=+-+-∈，z 是z 的共轭复数，复数z 在复平面内对应的点位于（） A. 第一象限 B. 第二象限 C ．第三象限 D ．第四象限（文）复数321i z i=-，z 是z 的共轭复数，复数z 在复平面内对应的点位于（）A. 第一象限B. 第二象限 C ．第三象限 D ．第四象限 4.已知()f x 的定义域为R ，()f x 的导函数()f x '的图象如图所示，则 ( ) A ．()f x 在1x =处取得极小值 B ．()f x 在1x =处取得极大值 C ．()f x 是R 上的增函数D ．()f x 是(－∞，1)上的减函数，(1，＋∞)上的增函数5.下列结论错误．．的个数是（） ①命题“若p ，则q ”与命题“若,q ⌝则p ⌝”互为逆否命题；②命题:[0,1],1x p x e ∀∈≥，命题2:,10,q x R x x ∃∈++<则p q ∨为真； ③ “若22,am bm <则a b <”的逆命题为真命题；④若q p ∨为假命题，则p 、q 均为假命题．A. 0B. 1 C ．2 D ．3 6. （理）由曲线1xy =，直线,3y x y ==所围成的平面图形的面积为（）A.329B. 2ln 3- C ．4ln 3+ D ．4ln 3- （文）奇函数()f x 在(0,)+∞上的解析式是()(1)f x x x =-，则在(,0)-∞上()f x 的函数解析式是（）A. ()(1)f x x x =--B. ()(1)f x x x =+C ．()(1)f x x x =-+D ．()(1)f x x x =-7.（理）同时抛掷5枚均匀的硬币80次，设5枚硬币正好出现2枚正面向上，3枚反面向上的次数为ξ，则ξ的数学期望是 ( )A ．20B ．25C ．30D ．40（文）在一个袋子中装有分别标注数字1,2,3,4,5的五个小球，这些小球除标注数字外完全相同，现从中随机取2个小球，则取出的小球标注的数字之和为3或6的概率是( )A ．112B ．110C ．15D ．3108.（理）函数f (x )＝lgsin(π4－2x )的一个增区间为( )A ．(3π8，7π8)B ．(7π8，9π8)C ．(5π8，7π8)D ．(－7π8，－3π8)（文）已知函数y ＝tan ωx 在(－π2，π2)内是减函数，则( )A ．0<ω≤1B ．－1≤ω<0C ．ω≥1D ．ω≤－1 9.（理）如图，正四棱锥P ABCD -底面的四个顶点,,,A B C D 在球O 的同一个大圆上，点P 在球面上，如果163P ABCD V -=，则球O 的体积是（） A ．163πB ．8πC ．16πD ．323π （文）三棱锥P-ABC 的三条侧棱PA 、PB 、PC 两两互相垂直，且长度分别为3、4、5，则三棱锥P-ABC 外接球的体积是（） A．B.6350π 10. 已知双曲线的两个焦点分别为1F (－5，0)，2F (5，0)，P 是双曲线上的一点，1212PF PF PF PF 2⊥⋅且＝，则双曲线方程是( )A.22123x y -= B. 2214x y -= C.22132x y -= D ．2214y x -= 11. 在如图所示的程序框图中，当()*N 1n n ∈>时，函数()n f x 表示函数()n 1f x －的导函数，若输入函数()1f x sinx cosx ＝＋，则输出的函数()n f x 可化为( )A. 2sin(x ＋π4) B ．－2sin(x －π2) C.x －π4) D ．2sin(x ＋π4)12. 已知函数21(0)()(1)(0)x x f x f x x -⎧-≤=⎨->⎩，若方程a x x f +=)(有且只有两个不相等的实数>2014n根，则实数a 的取值范围是（） A.(－∞，1) B.(0,1) C.(－∞，1] D.[0，＋∞)第Ⅱ卷 (非选择题共90分)本卷包括必考题和选考题两部分．第13题～第21题为必考题，每个试题考生都必须做答．第22题～第24题为选考题，考生根据要求做答．二、填空题：本大题共4小题，每小题5分，共20分．把答案填在题中横线上． 13. 如图所示两个立体图形都是由相同的小正方体拼成的．图(1)的正(主)视图与图(2)的________视图相同． 14.（理）若x ，y 满足约束条件⎩⎪⎨⎪⎧x ＋y ≥1，x －y ≥－1，2x －y ≤2，目标函数z ＝ax ＋2y 仅在点(1,0)处取得最小值，则a 的取值范围是 . （文）若实数x ，y 满足100x y x -+≤⎧⎨>⎩，则1yx -的取值范围是．15.已知两点(2,0),(0,2)A B -，点C 是圆0222=-+x y x 上任意一点，则ABC ∆面积的最小值是 .16. （理）在ABC ∆中，c b a ,,分别是C B A ∠∠∠,,的对边长，已知A A cos 3sin 2=.且有mbc b c a -=-222,则实数m = ．（文）在△ABC 中，a 、b 、c 分别为三个内角A 、B 、C 所对的边，设向量m ＝(b －c ，c －a )，n ＝(b ，c ＋a )，若向量m n ⊥，则角A 的大小为．三．解答题：共70分．解答应写出文字说明，证明过程或演算步骤． 17. (本小题满分12分)（理）已知二次函数()y f x =的图像经过坐标原点，其导函数为()62f x x '=-，数列{}n a 的前n 项和为n S ，点*(,)()n n S n ∈N 均在函数()y f x =的图像上．（Ⅰ）求数列{}n a 的通项公式；（Ⅱ）设13,n n n n b T a a +=是数列{}n b 的前n 项和，求使得20n m T <对所有*n N ∈都成立的最小正整数.m（文）已知二次函数()y f x =的图像经过坐标原点，其导函数为()62f x x '=-，数列{}n a 的前n 项和为n S ，点*(,)()n n S n ∈N 均在函数()y f x =的图像上．（Ⅰ）求数列{}n a 的通项公式；（Ⅱ）设13,n n n n b T a a +=是数列{}n b 的前n 项和，求证：12n T <．18. (本小题满分12分)（理）如图所示，在矩形ABCD 中，AB=1，AD=a ， PA ⊥平面ABCD ，且PA=1．（Ⅰ）在BC 边上是否存在点Q ，使得PQ ⊥QD ，说明理由；（Ⅱ）若BC 边上有且仅有一个点Q ，使PQ ⊥QD ，C求AD 与平面PDQ 所成角的正弦大小；（文）如图，AB 为圆O 的直径，点E 、F 在圆O 上，EF AB //，矩形ABCD 所在的平面和圆O 所在的平面互相垂直，且2=AB ，==EF AD （Ⅰ）求证：⊥AF 平面CBF ；（Ⅱ）设FC 的中点为M ，求证：//OM 平面DAF （Ⅲ）设平面CBF 将几何体EFABCD 分成的两个锥体的体积分别为ABCD F V -，CBE F V -，求ABCD F V -F V -:19. (本小题满分12分)（理）某车间在两天内，每天生产10件某产品，其中第一天、第二天分别生产了1件、2件次品，而质检部每天要在生产的10件产品中随意抽取4件进行检查，若发现有次品，则当天的产品不能通过。

2014年物理中考仿真选择题系列(一)及其答案共10页

2014年物理中考仿真选择题系列（一）1．小球从左向右运动，每隔相等时间曝光一次所得到的照片如下图，其中小球做匀速直线运动的是（）2．质量相同的A 、B 两件货物在两台吊车钢索的牵引力作用下竖直向上运动，它们运动的s －t 图像分别如图甲、乙所示，则（）A ．两件货物都做匀速直线运动B ．前6秒A 货物的平均速度小于B 货物的平均速度C ．吊车钢索对A 货物的拉力大于A 货物的重力D ．B 货物在整个运动过程中受到一对平衡力作用3．如图所示，小华在探究液体内部压强的特点时，将压强计的探头放入水中某一深度处，记下U 型管两边液面的高度差h ，下列做法能够使高度差h 减小的是（）A ．将探头向上移动一段距离B ．将探头向下移动一段距离C ．将探头放在食盐水中的同样深度处D ．将探头在原深度处向其他方向任意转动一个角度4．下列关于压强的四幅图中，体现了流体压强与流速关系的是（）5．如图将鼓轻敲一下，然后再重敲一下，两次敲击发出的声音，发生了变化的是（） 0 0 2 4 6 8 10 12 0.2 0.20.40.60.80.4 0.6 0.8 1 2 3 4 5 6 S/m S/mt/st/s 甲乙 A B C DD B A CA ．音调B ．响度C ．音色D ．频率6．如图所示，当吊在弹簧测力计下的物体浸在水中的体积为物体体积的1/3时，弹簧测力计的示数为5.0N ；当物体浸在水中的体积为物体体积的1/2时，弹簧测力计的示数为3.5N 。

从弹簧测力计上取下物体将其缓慢的放入水中（容器足够大，水足够多），则物体静止时受到的浮力为（）A ．9.0NB ．8.5NC ．8.0N D．7.5N7．与所示实物图相对应的电路图是下图中的（）8．CCTV 科教频道曾报道：有一辆小车载人后停在水平放置的地磅上时，左前轮、右前轮、左后轮、右后轮对地磅的压力分别为4750N、4980N 、4040N 、3960N 。

2014中考数学仿真试题一(含答案)

23.（本题 8 分）如图，在梯形 ABCD 中，AD∥BC，AB∥DE，AF∥DC，E、F 两点在边 BC 上，且四边形 AEFD 是平行四边形。（1）AD 与 BC 有何等量关系？请说明理由；（2）当 AB＝DC 时，求证：平行四边形 AEFD 是矩形。
A
D
B
E
F
C
24.（本题 8 分）有红、白、蓝三种颜色的小球各一个，它们除颜色外没有其它任何区别。现将 3 个小球放入编号为①、②、③的三个盒子里，规定每个盒子里放一个，且只能放一个小球。（1）请用树状图或其它适当的形式列举出 3 个小球放入盒子的所有可能情况；（2）求红球恰好被放入②号盒子的概率。 25.（本题 12 分）据调查，连云港市“欣欣”家电商场电视柜，今年一月至六月份销售型号为“HH －2188X”的长虹牌电视机的销量如下：月份销量（台）一 50 二 51 三 48 四 50 五 52 六 49
**10. 如图，动点 P 从点 A 出发，沿线段 AB 运动至点 B 后，立即按原路返回。点 P 在运动过程中速度大小不变。则以点 A 为圆心，线段 AP 长为半径的圆的面积 S 与点 P 的运动时间 t 之间的函数图象大致为（）
S A P B A t B t C t D t S S S
二、填空题（每小题 2 分，共 20 分） 11. 某天早晨的气温是－1℃，中午上升了 4℃，则中午的气温为__________℃。 12. 分解因式 x2－y2－3x－3y＝__________。 13. 函数 y＝（x－2）（3－x）取得最大值时，x＝__________。 x2－x－2 14. 若分式 2 的值为 0，则 x 的值等于__________。 x ＋2x＋1 15.《孙子算经》中有“鸡兔同笼”问题： “今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各几何？”请你回答，笼中有__________只兔。

河北省冀州中学2014届高考数学仿真试题文新人教B版

冀州中学第一次仿真考试数学试题（文科）第I 卷（选择题共60分）一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的。

1．集合Ａ＝｛a ２，a ＋１，－３｝，Ｂ＝｛a －３，a ２＋１，２a －１｝，且ＡＢ＝｛－３｝.则a=（）A ．1-B ．0C ．0 或1-D ．22．设x R ∈,则“1x =”是“复数2(1)(1)z x x i =-++为纯虚数”的（）A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件 3．从装有2个红球和2个黑球的口袋内任取2个球，那么互斥而不对立的两个事件是 A ．“至少有一个黑球”与“都是黑球” B ．“至少有一个黑球”与“都是红球” C ．“至少有一个黑球”与“至少有一个红球” D ．“恰有一个黑球”与“恰有两个黑球4．命题“若022=+b a ，R b a ∈,，则0==b a ”的逆否命题是( ) A ．若0≠≠b a ，R b a ∈,，则022=+b a B ．若0≠=b a ，R b a ∈,，则022≠+b a C ．若0≠a 且0≠b ，R b a ∈,，则022≠+b a D ．若0≠a 或0≠b ，R b a ∈,，则022≠+b a5. 某学校从高三全体500名学生中用系统抽样抽取50名学生作学习状况问卷调查,现将500名学生从1到500进行编号,即每10人抽取一个人,在1至10中随机抽取一个数,如果抽到的是6,则从125至140的数中应抽取的数是（）A ．126B ．136C ．146D ．126和1366. 已知点(,)P a b 与点(1,0)Q 在直线2310x y +-=的两侧，且0, 0a b >>，则2w a b =-的取值范围是( )A ．21[,]32-B ．2(,0)3-C ．21(,)32-D ．1(0,)2 7.已知*,7980N n n n a n ∈--=，则在数列{a n }的前50项中最小项和最大项分别是（）A 、1a ，50aB 、9a ，50aC 、9a ，8aD 、8a ，9a 8．如图所示程序框图中，输出S = ( )A ． 45B ． 55-C ． 66-D ． 669. 偶函数)(x f 满足()()()x f x f x f +-=+111,且在]1,0[∈x 时，2)(x x f =，则关于x 的方程 xx f ⎪⎭⎫⎝⎛=101)(在]3,2[-上的根的个数是（）A ．3B ．4C ．5D ．610.已知P 、M 、N 是单位圆上互不相同的三个点,且满足PM PN =，则PM PN的最小值是（）（）A ．14-B ．12-C ．34-D ．1- 11.已知双曲线22221(0)x y a b a b-=>>的右焦点为F ，过F 的直线l 交双曲线的渐近线于A 、B 两点，且直线l的倾斜角是渐近线OA 倾斜角的2倍，若2AF FB =，则该双曲线的离心率为（） A ．4 B ．3 C ．5．212.在△ABC 中，BC AC =1，以AB 为边作等腰直角三角形ABD （B 为直角顶点，C 、D 两点在直线AB 的两侧）．当C ∠变化时，线段CD 长的最大值为（） A ．1 B ．2 C ．3 D ．4第Ⅱ卷（非选择题共90分）二、填空题：本大题共4小题，每小题5分，共20分，把答案填在答题卡相应位置。

(全国卷)2014届高考数学(文)仿真模拟卷1 Word版含解析]

仿真模拟(一)———————————————————————————————————— 【说明】本试卷分为第Ⅰ、Ⅱ卷两部分，请将第Ⅰ卷选择题的答案填入答题格内，第Ⅱ卷可在各题后直接作答，共150分，考试时间120分钟．第Ⅰ卷 (选择题共60分)只有一项是符合题目要求的)1．复数⎝ ⎛⎭⎪⎫2i 1－i 2(其中i 是虚数单位)的虚部等于( )A ．－iB ．－1C ．1D ．02．已知全集U ＝{0,1,2,3,4}，A ＝{1,2,3}，B ＝{2,4}，则如图阴影部分表示的集合为( )A ．{0,2}B ．{0,1,3}C ．{1,3,4}D ．{2,3,4}3．某几何体的三视图(图中单位：cm)如图所示，则此几何体的体积是( )A ．36 cm 3B ．48 cm 3C ．60 cm 3D ．72 cm 34．在△ABC 中，a ，b ，c 分别是角A ，B ，C 的对边，若a ＝2b ，sin B ＝sin C ，则B 等于( )A ．60°B ．30°C ．135°D ．45°5．设x 1＝18，x 2＝19，x 3＝20，x 4＝21，x 5＝22，将这5个数依次输入下面的程序框图运行，则输出S 的值及其统计意义分别是( )A ．S ＝2，这5个数据的方差B ．S ＝2，这5个数据的平均数C ．S ＝10，这5个数据的方差D ．S ＝10，这5个数据的平均数6．若点P (1,1)是圆x 2＋(y －3)2＝9的弦AB 的中点，则直线AB 的方程为( ) A ．x －2y ＋1＝0 B ．x ＋2y －3＝0 C ．2x ＋y －3＝0D ．2x －y －1＝07．某农场给某种农作物施肥量x (单位：吨)与其产量y (单位：吨)的统计数据如下表：根据上表，得到回归直线方程y ＝9.4x ＋a ，当施肥量x ＝6时，该农作物的预报产量是( )A ．72.0B ．67.7C ．65.5D ．63.68．下列函数中，为偶函数且有最小值的是( ) A ．f (x )＝x 2＋x B ．f (x )＝|ln x | C ．f (x )＝x sin xD ．f (x )＝e x ＋e －x9．已知球的半径为5，球面被互相垂直的两个平面所截，得到的两个圆的公共弦长为23，若其中一个圆的半径为4，则另一个圆的半径为( )A ．3B ．10C ．11D ．2 310．已知实数a ，b 满足⎩⎪⎨⎪⎧0≤a ≤4，0≤b ≤4，x 1，x 2是关于x 的方程x 2－2x ＋b －a ＋3＝0的两个实根，则不等式0＜x 1＜1＜x 2成立的概率是( )A.332 B ．316C ．532D ．91611．已知函数f (x )＝⎩⎪⎨⎪⎧2|x －4|， x ≠4，a ， x ＝4，若函数y ＝f (x )－2有3个零点，则实数a 的值为( )A ．－4B ．－2C ．0D ．212．已知双曲线x 2a 2－y 2b 2＝1(a ＞0，b ＞0)的左、右焦点分别为F 1，F 2，点O 为双曲线的中心，点P 在双曲线右支上，△PF 1F 2内切圆的圆心为Q ，圆Q 与x 轴相切于点A ，过F 2作直线PQ 的垂线，垂足为B ，则下列结论成立的是( )A ．|OA |＞|OB | B ．|OA |＜|OB |C ．|OA |＝|OB |D ．|OA |与|OB |大小关系不确定第Ⅱ卷 (非选择题共90分)本卷包括必考题和选考题两部分，第13～21题为必考题，每个试题考生都必须作答，第22～24题为选考题，考生根据要求作答.13．已知命题p ：直线a ，b 相交，命题q ：直线a ，b 异面，则¬p 是q 的________条件． 14．抛物线y ＝x 2上的点到直线x ＋y ＋1＝0的最短距离为________．15．“求方程⎝⎛⎭⎫35x ＋⎝⎛⎭⎫45x ＝1的解”有如下解题思路：设f (x )＝⎝⎛⎭⎫35x ＋⎝⎛⎭⎫45x ，则f (x )在R 上单调递减，且f (2)＝1，所以原方程有唯一解x ＝2.类比上述解题思路，不等式x 6－(x ＋2)＞(x ＋2)3－x 2的解集是________．16．向量a ，b ，c 满足：|a |＝1，|b |＝2，b 在a 方向上的投影为12，(a －c )·(b －c )＝0，则|c |的最大值是________．三、解答题(本大题共6小题，共70分．解答应写出必要的文字说明、证明过程或演算步骤)17．(本小题满分12分)已知数列{a n }的前n 项和S n ＝n 2(n ∈N *)，等比数列{b n }满足b 1＝a 1,2b 3＝b 4.(1)求数列{a n }和{b n }的通项公式；(2)若c n ＝a n ·b n (n ∈N *)，求数列{c n }的前n 项和T n .18．(本小题满分12分)为了解某市民众对政府出台楼市限购令的情况，在该市随机抽取了50名市民进行调查，他们月收入(单位：百元)的频数分布及对楼市限购令赞成的人数如下表：族”．(1)根据已知条件完成下面的2×2列联表，问能否在犯错误的概率不超过0.01的前提下认为非高收入族赞成楼市限购令？(2)概率．附：K2＝n(ad－bc)2(a＋b)(c＋d)(a＋c)(b＋d)19．(本小题满分12分)如图，在四棱锥P－ABCD中，侧棱P A⊥底面ABCD，底面ABCD为矩形，E为PD上一点，AD＝2AB＝2AP＝2，PE＝2DE.(1)若F为PE的中点，求证：BF∥平面ACE；(2)求三棱锥P－ACE的体积．20.(本小题满分12分)如图，已知椭圆的中心在坐标原点，焦点在x 轴上，长轴长是短轴长的2倍，且经过点M (2,1)，平行于OM 的直线l 在y 轴上的截距为m ，直线l 与椭圆相交于A ，B 两个不同点．(1)求实数m 的取值范围；(2)证明：直线MA ，MB 与x 轴围成的三角形是等腰三角形．21．(本小题满分12分)已知a ，b ∈R ，函数f (x )＝a ＋ln(x ＋1)的图象与g (x )＝13x 3－12x 2＋bx 的图象在交点(0,0)处有公共切线．(1)证明：不等式f (x )≤g (x )对一切x ∈(－1，＋∞)恒成立； (2)设－1＜x 1＜x 2，当x ∈(x 1，x 2)时，证明：f (x )－f (x 1)x －x 1＞f (x )－f (x 2)x －x 2.请考生在第22～24三题中任选一题作答，如果多做，则按所做的第一题记分． 22.(本小题满分10分)选修4－1：几何证明选讲如图，点C 是⊙O 直径BE 的延长线上一点，AC 是⊙O 的切线，A 为切点，∠ACB 的平分线CD 与AB 相交于点D ，与AE 相交于点F .(1)求∠ADF 的值；(2)若AB ＝AC ，求ACBC 的值．23．(本小题满分10分)选修4－4：坐标系与参数方程平面直角坐标系xOy 中，点A (2,0)在曲线C 1：⎩⎪⎨⎪⎧x ＝a cos φ，y ＝sin φ(a ＞0，φ为参数)上．以原点O 为极点，x 轴的正半轴为极轴建立极坐标系，曲线C 2的极坐标方程为ρ＝a cos θ.(1)求曲线C 2的普通方程；(2)已知点M ，N 的极坐标分别为(ρ1，θ)，⎝⎛⎭⎫ρ2，θ＋π2，若点M ，N 都在曲线C 1上，求1ρ21＋1ρ22的值．24．(本小题满分10分)选修4－5：不等式选讲设函数f (x )＝|x ＋1|＋|x －a |(a ＞0)． (1)当a ＝2时，解不等式f (x )≤4；(2)若不等式f (x )≤4对一切x ∈[a,2]恒成立，求实数a 的取值范围．详解答案一、选择题1．B 因为⎝ ⎛⎭⎪⎫2i 1－i 2＝(2i )2(1－i )2＝－2－2i＝－i ，故其虚部为－1，故选B.2．A 由于A ∪B ＝{1,2,3,4}，A ∩B ＝{2}，故阴影部分所示集合为{0,2}，故选A. 3．B 由三视图可知几何体上方是一长方体，下方是一放倒的直四棱柱，且四棱柱底面是等腰梯形，上底长为2 cm ，下底长为6 cm ，高为2 cm ，故几何体的体积是2×2×4＋12×(2＋6)×2×4＝48(cm 3)，故选B.4．D 据正弦定理将角化边可得sin B ＝sin C ⇒b ＝c ，又a ＝2b ，由勾股定理可得三角形为等腰直角三角形，故B ＝45°.5．A 据已知数据可得其均值x ＝18＋19＋20＋21＋225＝20，而框图输出S ＝15[(x 1－20)2＋(x 2－20)2＋…＋(x 5－20)2]＝2，S 的统计意义是此5个数据的方差，故选A.6．A 据题意可知直线AB 与点P 和圆心C (0,3)连线垂直，故k AB ＝－1k CP ＝12，从而得直线AB 方程为y －1＝12(x －1)，整理得直线AB 的方程为x －2y ＋1＝0.7．C 据已知数据可得x ＝3.5，y ＝42，由于回归直线经过点(3.5,42)，代入回归直线方程得42＝9.4×3.5＋a ∧，解得a ∧＝9.1，故回归直线方程为y ∧＝9.4x ＋9.1，当x ＝6时该作物的产量大约为y ∧＝9.4×6＋9.1＝65.5，故选C.8．D 对于A ，注意到f (－1)＝0，f (1)＝2，f (－1)≠f (1)，因此函数f (x )不是偶函数；对于B ，注意到函数f (x )的定义域是(0，＋∞)，因此函数f (x )不是偶函数；对于C ，f (－x )＝f (x )，易知该函数无最小值；对于D ，f (－x )＝f (x )，因此函数f (x )是偶函数，且f (x )≥2 e x ·e －x ＝2，当且仅当x ＝0时取等号，即函数f (x )有最小值．综上所述，故选D.9．D 由已知可得球心到半径为4的圆距离d ＝52－42＝3，因此所求圆圆心到弦的距离为3，故所求圆半径R ＝32＋(3)2＝23，故选D.10．A 由题意基本事件空间可视为Ω＝⎩⎨⎧(a ，b )⎪⎪⎪ ⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫0≤a ≤40≤b ≤4，可用面积为16的正方形面积作为事件的几何度量，其中0＜x 1＜1＜x 2，令f (x )＝x 2－2x ＋b －a ＋3，满足⎩⎪⎨⎪⎧f (0)＝b －a ＋3＞0，f (1)＝b －a ＋2＜0，故0＜x 1＜1＜x 2成立对应事件可表示为A ＝⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫(a ，b )⎪⎪⎪⎩⎪⎨⎪⎧ 0≤a ≤4，0≤b ≤4，b －a ＋3＞0，b －a ＋2＜0，作出不等式组表示的平面区域，由几何概型可知所求概率等于两不等式组表示的平面区域面积之比，即P (A )＝3216＝332，故选A.11．D 如图，当函数y ＝f (x )－2有3个零点时，等价于函数y ＝f (x )的图象和y ＝2的图象有3个交点，此时必有a ＝2，故选D.12．C 由于点Q 为三角形PF 1F 2内切圆的圆心，故过点F 2作PQ 的垂线并延长交PF 1于点N ，易知垂足B 为F 2N 的中点，连接OB ，则|OB |＝12|F 1N |＝12(|F 1P |－|F 2P |)＝a ，又设内切圆与PF 1，PF 2分别切于G ，H ，则由内切圆性质可得|PG |＝|PH |，|F 1G |＝|F 1A |，|F 2A |＝|F 2H |，故|F 1P |－|F 2P |＝|F 1A |－|F 2A |＝2a ，设|OA |＝x ，则有x ＋c －(c －x )＝2a ，解得|OA |＝a ，故有|OA |＝|OB |＝a ，故选C.二、填空题13．解析：依题意得，¬p ：直线a ，b 不相交．由直线a ，b 不相交不能得知直线a ，b 是异面直线；反过来，由直线a ，b 是异面直线可得直线a ，b 不相交．因此，¬p 是q 的必要不充分条件．答案：必要不充分14．解析：由于f ′(x )＝2x ，设与直线x ＋y ＋1＝0平行且与抛物线相切的直线与抛物线切于点A (x 0，y 0)，由导数几何意义可知2x 0＝－1，求得切点为⎝⎛⎭⎫－12，14.切点A ⎝⎛⎭⎫－12，14到直线x ＋y ＋1＝0的距离最小，由点到直线距离公式易得最小值为328.答案：32815．解析：原不等式等价于x 6＋x 2＞(x ＋2)3＋(x ＋2)，令f (x )＝x 3＋x ，易知函数在R 上为单调递增函数，故原不等式等价于x 2＞x ＋2，解得x ＞2或x ＜－1，故原不等式的解集为(－∞，－1)∪(2，＋∞)．答案： (－∞，－1)∪(2，＋∞)16．解析：由投影公式可得b ·a |a |＝b ·a ＝12，∴|b ＋a |2＝|a |2＋|b |2＋2a ·b ＝4⇒|b ＋a |＝2.由(a －c )·(b －c )＝a ·b －c ·(a ＋b )＋c 2＝0，整理得12＋|c |2＝|c |·|a ＋b |cos θ≤2|c |，解不等式12＋|c |2－2|c |≤0，得|c |≤1＋22，即|c |的最大值为1＋22. 答案： 1＋22三、解答题17．解析： (1)∵当n ＝1时，a 1＝S 1＝1；当n ≥2时，a n ＝S n －S n －1＝n 2－(n －1)2＝2n －1， ∴a n ＝2n －1(n ∈N *)，∴b 1＝a 1＝1，设等比数列{b n }的公比为q ，则q ≠0. ∵2b 3＝b 4，∴2q 2＝q 3，∴q ＝2， ∴b n ＝2n －1(n ∈N *)．(2)由(1)可得c n ＝a n ·b n ＝(2n －1)×2n －1(n ∈N *)，∴T n ＝1×20＋3×2＋5×22＋…＋(2n －1)×2n －1，①∴2T n ＝1×2＋3×22＋5×23＋…＋(2n －1)×2n ，② ②－①得T n ＝(2n －1)×2n －(1×20＋2×2＋2×22＋…＋2×2n －1)＝(2n －1)×2n －(1＋22＋23＋…＋2n ) ＝(2n －3)×2n ＋3.18．解析： (1)由题意得列联表如下：则K 2＝n (ad －bc )2(a ＋b )(c ＋d )(a ＋c )(b ＋d )＝50×(29×7－11×3)232×18×40×10＝6.272＜6.635，∴不能在犯错误的概率不超过0.01的前提下认为非高收入族赞成楼市限购令． (2)由题意得月收入在[15,25)中有4人赞成楼市限购令，1人不赞成，将他们分别记为A 1，A 2，A 3，A 4，a ，则从月收入在[15,25)的人群中随机抽取两人的所有结果为(A 1，A 2)，(A 1，A 3)，(A 1，A 4)，(A 1，a )，(A 2，A 3)，(A 2，A 4)，(A 2，a )，(A 3，A 4)，(A 3，a )，(A 4，a )，共10种；其中所抽取的两人都赞成楼市限购令的结果为(A 1，A 2)，(A 1，A 3)，(A 1，A 4)，(A 2，A 3)，(A 2，A 4)，(A 3，A 4)，共6种，∴所抽取的两人都赞成楼市限购令的概率为P ＝0.6. 19．解析： (1)证明：连接BD ，交AC 于点O ，连接OE ，∵底面ABCD 为矩形，∴OB ＝OD . ∵F 为PE 的中点，∴PE ＝2EF . 又∵PE ＝2DE ，∴DE ＝EF ，∴OE ∥BF .又∵BF ⊄平面ACE ，OE ⊂平面ACE ，∴BF ∥平面ACE . (2)∵侧棱P A ⊥底面ABCD ，∴AP ⊥CD . 又∵底面ABCD 为矩形，∴CD ⊥AD . ∵AD ∩AP ＝A ，∴CD ⊥平面P AD . 又∵AD ＝2AB ＝2AP ＝2，∴V P －ACE ＝V C －AEP ＝13×CD ×S △AEP ＝13×CD ×23S △ADP＝19×CD ×AD ×AP ＝29. 20．解析： (1)设椭圆方程为x 2a 2＋y 2b 2＝1(a ＞b ＞0)，由题意得⎩⎪⎨⎪⎧a ＝2b ，4a 2＋1b2＝1，∴⎩⎪⎨⎪⎧a 2＝8，b 2＝2，∴椭圆方程为x 28＋y 22＝1.由题意可得直线l 的方程为y ＝12x ＋m (m ≠0)，设A (x 1，y 1)，B (x 2，y 2)，则点A ，B 的坐标是方程组⎩⎨⎧y ＝12x ＋m ，x 28＋y22＝1的两组解，消去y 得x 2＋2mx ＋2m 2－4＝0.∵Δ＝4m 2－4(2m 2－4)＞0，∴－2＜m ＜2.又∵m ≠0，∴实数m 的取值范围为(－2,0)∪(0,2)．(2)证明：由题意可设直线MA ，MB 的斜率分别为k 1，k 2，只需证明k 1＋k 2＝0即可，由(1)得x 2＋2mx ＋2m 2－4＝0，∴x 1＋x 2＝－2m ，x 1x 2＝2m 2－4，∵k 1＋k 2＝y 1－1x 1－2＋y 2－1x 2－2＝x 1y 2＋x 2y 1－2(y 1＋y 2)－(x 1＋x 2)＋4(x 1－2)(x 2－2) ＝(m －2)(x 1＋x 2)＋x 1x 2＋4(1－m )(x 1－2)(x 2－2)＝－2m (m －2)＋2m 2－4＋4(1－m )(x 1－2)(x 2－2)＝0， ∴直线MA ，MB 与x 轴围成的三角形是等腰三角形．21．证明： (1)由题意得f ′(x )＝1x ＋1，g ′(x )＝x 2－x ＋b ，x ＞－1，则⎩⎪⎨⎪⎧ f (0)＝g (0)，f ′(0)＝g ′(0)，解得⎩⎪⎨⎪⎧a ＝0，b ＝1， ∴f (x )＝ln(x ＋1)(x ＞－1)，g (x )＝13x 3－12x 2＋x . 令h (x )＝f (x )－g (x )＝ln(x ＋1)－13x 3＋12x 2－x (x ＞－1)， ∴h ′(x )＝1x ＋1－x 2＋x －1＝－x 3x ＋1， ∴h (x )在(－1,0)上单调递增，在(0，＋∞)上单调递减，∴h (x )≤h (0)＝0，∴f (x )≤g (x )．(2)当x ∈(x 1，x 2)时，由题意得－1＜x 1＜x ＜x 2，①设u (x )＝(x ＋1)[f (x )－f (x 1)]－(x －x 1)，则u ′(x )＝ln(x ＋1)－ln(x 1＋1)＞0，∴u (x )＞u (x 1)＝0，即(x ＋1)[f (x )－f (x 1)]－(x －x 1)＞0，∴f (x )－f (x 1)x －x 1>11＋x； ②设v (x )＝(x ＋1)[f (x )－f (x 2)]－(x －x 2)，则v ′(x )＝ln(x ＋1)－ln(x 2＋1)＜0，∴v (x )＞v (x 2)＝0，即(x ＋1)[f (x )－f (x 2)]－(x －x 2)＞0，∴f (x )－f (x 2)x －x 2＜11＋x，由①②得f (x )－f (x 1)x －x 1＞f (x )－f (x 2)x －x 2. 22．解析： (1)∵AC 是⊙O 的切线，∴∠B ＝∠EAC .又∵DC 是∠ACB 的平分线，∠ACD ＝∠DCB ，∴∠B ＋∠DCB ＝∠EAC ＋∠ACD ，∴∠ADF ＝∠AFD . ∵BE 是⊙O 的直径，∴∠BAE ＝90°，∴∠ADF ＝45°.(2)∵AB ＝AC ，∴∠B ＝∠ACB ＝∠EAC ，由(1)得∠BAE ＝90°，∴∠B ＋∠AEB ＝∠B ＋∠ACE ＋∠EAC ＝3∠B ＝90°，∴∠B ＝30°.∵∠B ＝∠EAC ，∠ACB ＝∠ACB ，∴△ACE ∽△BCA ， ∴AC BC ＝AE AB ＝tan 30°＝33. 23．解析： (1)∵点A (2,0)在曲线C 1上，∴⎩⎪⎨⎪⎧2＝a cos φ，0＝sin φ， ∵a ＞0，∴a ＝2，∴ρ＝2cos θ，由⎩⎪⎨⎪⎧x ＝ρcos θ，y ＝ρsin θ得(x －1)2＋y 2＝1， ∴曲线C 2的普通方程为(x －1)2＋y 2＝1.(2)由(1)得曲线C 1：⎩⎪⎨⎪⎧x ＝2cos φ，y ＝sin φ，消去参数φ得x 24＋y 2＝1. 由题意得点M ，N 的直角坐标分别为(ρ1cos θ，ρ1sin θ)，⎝⎛⎭⎫ρ2cos ⎝⎛⎭⎫θ＋π2，ρ2sin ⎝⎛⎭⎫θ＋π2. ∵点M ，N 在曲线C 1上，∴ρ21cos 2θ4＋ρ21sin 2θ＝1，ρ22sin 2θ4＋ρ22cos 2θ＝1， ∴1ρ21＋1ρ22＝⎝⎛⎭⎫cos 2θ4＋sin 2θ＋⎝⎛⎭⎫sin 2θ4＋cos 2θ＝54. 24．解析： (1)当a ＝2时，原不等式转化为|x ＋1|＋|x －2|≤4，即⎩⎪⎨⎪⎧ x ≤－1，－(x ＋1)－(x －2)≤4或⎩⎪⎨⎪⎧－1＜x ＜2，(x ＋1)－(x －2)≤4或⎩⎪⎨⎪⎧x ≥2，(x ＋1)＋(x －2)≤4， ∴－32≤x ≤－1或－1＜x ＜2或2≤x ≤52， ∴原不等式的解集为⎣⎡⎦⎤－32，52. (2)当x ∈[a,2]时，原不等式转化为(x ＋1)＋(x －a )≤4， ∴a ≥2x －3.∵(2x －3)max ＝1，∴1≤a ＜2，∴实数a 的取值范围为[1,2)．。

山东省2014届高三高考仿真模拟冲刺考试(一)文综 Word版含答案

绝密★启用前试卷类型A山东省2014年高考仿真模拟冲刺卷（一）文科综合说明：本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，满分300分，考试时间150分钟。

第Ⅰ卷（必做，共140分）一、选择题：（本大题35小题，每小题4分，共140分。

在每小题给出的四个选项中，只有一个是最符合题目要求的。

）2013年3月31日的“地球一小时”熄灯活动，是由世界自然基金会发起应对气候变化、倡导节约能源的集体行动。

下图中①②③是甲乙丙丁四地二分二至日的正午太阳光线。

据此回答1～2题。

1．活动时间是当地20：30～21：30，下列四城市中最早和最晚熄灯的分别是（）A ．乙和甲B ．甲和丁C ．乙和丙D ．丙和丁2．如果只考虑日照条件，则甲乙丙丁四地楼间距最小的是（）A ．甲B ．乙C ．丙D ．丁2013年6月24日，在太平洋马利亚里海沟（下图），我国蛟龙号进行了第四次下潜，蛟龙号首次突破了7000米水深，并且在7020米的最大深度成功坐底，这也创造了世界同类潜水下潜的记录。

读图，完成3~4题。

3．流经图示区域的洋流流向及性质分别是（）A ．自南向北、暖流B ．自南向北、寒流C ．自北向南、寒流D ．自北向南、暖流 4．下列有关马里亚纳海沟形成过程的图示，正确的是（）下图为我国某种工业类型的空间分布图。

读图，回答5～6题。

5．图中黑点代表的工业可能是（）A ．制糖工业B ．畜产品加工C ．风力发电D ．汽车制造 6．这一工业类型布局的主导区位因素是（）A ．原料B ．资金C ．资源D ．技术7．右图为“我国某城市总人口的逐日变化示意图”（2012年11月28日～2013年3月8日），引起春节期间下图城市人口巨大变化的最主要原因是（）A．洪涝灾害B．疾病传播C．旅行度假D．民工返乡8．秦岭没有出现积雪冰川带，主要原因是（）A．纬度低B．相对高度低C．海拔较低D．坡度小2013年中央一号文件提出，鼓励和支持承包土地向专业大户、家庭农场、农民合作社流转。

2014年高考仿真模拟冲刺卷(一)及答案

理综物理试题本试卷分第I卷和第II卷两部分，共4页。

满分110分。

考试用时60分钟。

第Ⅰ卷（必做，共42分）二、选择题（本题包括7小题，共42分。

每小题给出的四个选项中，有的只有一个选项正确，有的有多个选项正确，全部选对的得6分，选对但不全的得3分，有选错的得0分）14．了解物理规律的发现过程，学会像科学家那样观察和思考，往往比掌握知识本身更重要．以下符合史实的是（）A．焦耳发现了电流热效应的规律B．库仑总结出了点电荷间相互作用的规律C．楞次发现了电流的磁效应，拉开了研究电与磁相互关系的序幕D．牛顿将斜面实验的结论合理外推，间接证明了自由落体运动是匀变速直线运动15．如图所示，A为静止于地球赤道上的物体，B为绕地球沿椭圆轨道运行的卫星，绕地心运动的周期相同，相对于地心，下列说法中正确的是（）A．物体A和卫星C具有相同大小的线速度B．物体A和卫星C具有相同大小的加速度C．卫星B在P点的加速度与卫星C在该点的加速度一定相同D．卫星B在P点的线速度与卫星C在该点的线速度一定相同16．如图所示，有一对等量异种电荷分别位于空间中的a点和f点，以a点和f点为顶点作一正立方体．现在各顶点间移动一试探电荷，关于试探电荷受电场力和具有的电势能，以下判断正确的是（）B．在c点和h点受力大小相等，方向相同C．在b点和d点电势能相等D．在c点和h点电势能相等17．按如图所示的电路连接各元件后，闭合开关S ，L 1、L 2两灯泡都能发光．在保证灯泡安全的前提下，当滑动变阻器的滑动头向左移动时，下列判断正确的是（）A ．L 1亮度不变B ．L 1变亮C ．L 2功率变小D ．L 2变亮18．如图，直线a 和曲线b 分别是在平直公路上行驶的汽车a 和b 的位置-时间（x-t ）图线，由图可知（） A ．在时刻t 1，a 车追上b 车B ．在时刻t 2，a 、b 两车运动方向相反C ．在t 1到t 2这段时间内，b 车的速率先减少后增加D ．在t 1到t 2这段时间内，b 车的速率一直比a 车大19．一水平放置的平行板电容器的两极板间距为d ，极板分别与电池两极相连，上极板中心有一小孔（小孔对电场的影响可忽略不计）。

2014年浙江省初中毕业生学业考试仿真模拟卷(word版有答案)

2014年浙江省初中毕业生学业考试仿真模拟卷考生注意：1．全卷满分为160分，考试时间120分钟。

试卷共4大题，38小题2．本卷答案必须做在答卷的相应位置上，做在试卷上无效。

3．本卷可能要用到的数据⑴相对原子质量：H－1C－12O－16Na-23S-32 K-39Cl-35.5 Ba-138⑵本卷的g取10N/kg一、选择题（本题每小题只有一个答案，错选、不选、多选均不得分。

每题3分，共60分。

）1．2013年3月，针对最近出现的人感染禽流感事件，卫生部紧急发布了人感染高致病性禽流感防治知识。

提醒公众特别是儿童应避免密切接触家禽和野禽。

人感染高致病性禽流感主要由甲型流感H7N9病毒引起的急性呼吸道传染病。

下列说法正确的是（▲ ）A.接触公共物品后及时洗手，这一行为只能预防消化道传染病，而对预防流感这类呼吸道传染病是无效的B.侵入人体的甲型流感H7N9病毒是高致病性禽流感的病原体C.将患者进行医学隔离治疗，这一措施属于切断传播途径。

D.高致病性禽流感不具有传染性、流行性和免疫性等特点2．4月20日四川芦山7级地震发生之后，四川电视台播报省中心血库A型血告急，许多市民纷纷到各献血站无偿献血。

下列叙述中不正确的是( ▲ )A．A型血液中含A凝集原和抗A凝集素B．血型是由遗传决定的，一般终生不变C．一次献200毫升一般不会影响健康D．给病人输血时也遵循输同型血为原则3．上海交大教授赵立平通过临床实验发现“阴沟肠杆菌”是造成肥胖元凶之一。

“阴沟肠杆菌”与酵母菌相比，在结构上最主要的区别在于无（▲）A．细胞膜B．细胞质C．细胞核D．细胞壁4．大家在投掷实心球的时候，都有一个感觉，人如果不加以控制，会随着实心球一起越过线，从而造成犯规，这是因为（）A．人受到向前的力的作用B．人受到向前的惯性的作用C．人具有惯性，要保持向前的运动状态D．球具有惯性，将人带了过去5．炎热的夏天，食物很容易腐败变质即变馊，引起食物腐败变质的主要原因是（）A．夏天空气潮湿，化学物质的污染严重B．夏季阳光太强，食物容易分解C．温度较高，食物中的细菌、真菌大量繁殖D．炎热的夏天，食物的水分蒸发过快6．2013年1月份，欧洲东部和美国受到近年来最严重的暴风雪袭击，气温不断创造历史新低。

河北省冀州中学2014届高三高考仿真题数学理含答案

2014高考仿真试题理科数学一、选择题：本大题共l2个小题,每小题5分,共60分．每小题给出的四个选项中只有一项是符合题目要求的． 1．已知集合{}1,A i =-，i 为虚数单位，则下列选项正确的是（）.A 1A i∈.B11iA i-∈+.C 5i A ∈.D i A -∈ 2、已知集合{1,2},{,},aA B a b ==若⎭⎬⎫⎩⎨⎧=⋂21B A ，则A B 为.()A ．1{,1,}2b B ．1{1,}2- C ．1{1,}2D ．1{1,,1}2-3。

数列{}na 的前n 项和为nS ,前n 项积为n ∏，且()()12n n n +∏=,则5S 等于（） A 。

31 B 。

62 C.124 D 。

1264。

给出30个数:1,2,4,7，……其规律是：第1个数是1；第2个数比第1个数大1；第3个数比第2个数大2；第4个数比第3个数大3;……以此类推，要计算这30个数的和,现已给出了该问题的程序框图如图所示,那么框图中判断框①处和执行框②处应分别填入（ ) A. 30;1i p p i ≤=+- B. 29;1i p p i ≤=++ . 31;i p p i ≤=+ D. 30;i p p i ≤=+5.定义在R 上的函数()f x 满足()()2,f x f x +=当[]1,3x ∈,()22f x x =--,则下列结论中正确的是（）A.sin cos 66f f ππ⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭B. ()()sin1cos1f f >C.22cos sin 33f f ππ⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭D. ()()cos2sin2f f >6. 如图，在正方体ABCD-A 1B 1C 1D 1中，点P 是上底面A 1B 1C 1D 1内一动点,则三棱锥 P —BCD 的正视图与侧视图的面积之比为( ）A ．1:1 B. 2：1 C 。

2:3 D. 3:27。

2014年高考数学(理)二轮专练：仿真模拟题(1)及答案解析

仿真模拟题(一)一、选择题(本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的)1．设i 为虚数单位，则复数z ＝2i 31＋i在复平面内对应的点位于( )A ．第一象限B ．第二象限C ．第三象限D ．第四象限2．某雷达测速区规定：凡车速大于或等于80 km/h 的汽车视为“超速”，并将受到处罚．如图是某路段的一个检测点对200辆汽车的车速进行检测所得结果的频率分布直方图，则从图中可以看出被处罚的汽车大约有( ) A ．20辆 B ．40辆 C ．60辆 D ．80辆3．下列函数中，既是偶函数，又在区间(1，2)内是增函数的为( ) A ．y ＝cos 2x －sin 2x B ．y ＝lg|x |C ．y ＝e x－e－x 2D ．y ＝x 34．(2013·高考北京卷)若双曲线x 2a 2－y 2b2＝1的离心率为3，则其渐近线方程为( )A ．y ＝±2xB ．y ＝±2xC ．y ＝±12xD ．y ＝±22x5．(2013·高考安徽卷)如图所示，程序框图(算法流程图)的输出结果是( ) A.16 B.2524 C.34 D.11126．给出下列命题：①如果不同直线m 、n 都平行于平面α，则m 、n 一定不相交； ②如果不同直线m 、n 都垂直于平面α，则m 、n 一定平行；③如果平面α、β互相平行，若直线m ⊂α，直线n ⊂β，则m ∥n ；④如果平面α、β互相垂直，且直线m 、n 也互相垂直，若m ⊥α，则n ⊥β.则真命题的个数是( ) A ．3 B ．2 C ．1 D ．07．设集合A ＝{x |x 2＋2x －3>0}，B ＝{x |x 2－2ax －1≤0，a >0}．若A ∩B 中恰含有一个整数，则实数a 的取值范围是( )A ．(0，34)B ．[34，43)C ．[34，＋∞) D ．(1，＋∞)8．已知变量x ，y 满足⎩⎪⎨⎪⎧x －y ＋6≥0x ＋y ≥0x ≤3，若z ＝ax ＋y 的最大值为3a ＋9，最小值为3a －3，则实数a 的取值范围为( )A ．[－1，0]B ．[－1，1]C ．[0，1]D ．[－1，0)∪(0，1] 9．(2013·高考山东卷)△ABC 的内角A ，B ，C 所对的边分别为a ，b ，c ，若B ＝2A ，a ＝1，b ＝3，则c ＝( ) A ．2 3 B ．2 C. 2 D ．110．若函数f (x )＝x 3－3x 在(a ，6－a 2)上有最小值，则实数a 的取值范围是( ) A ．(－5，1) B ．[－5，1) C ．[－2，1) D ．(－2，1)二、填空题(本大题5小题，考生作答4小题，每小题5分，共20分．) (一)必做题(11～13题)11．已知圆C 的圆心是直线x －y ＋1＝0与x 轴的交点，且圆C 与直线x ＋y ＋3＝0相切，则圆C 的方程为________．12．已知a n ＝cos n π6＋161＋2cos 2n π12(n ∈N *)，则数列{a n }的最小值是________．13．已知函数y ＝f (x )的图象是开口向下的抛物线，且对任意x ∈R ，都有f (1－x )＝f (1＋x )，若向量a ＝(log 12m ，－1)，b ＝(1，－2)，则满足不等式f (a ·b )<f (－1)的实数m 的取值范围是________．(二)选做题(14～15，考生只能从中选做一题)14．(坐标系与参数方程选做题)若直线l 的参数方程为⎩⎨⎧x ＝－22ty ＝6＋22t (t 为参数)，圆C 的极坐标方程为ρ＝4sin θ，则圆心到直线l 的距离为________．15．(几何证明选讲选做题)如图，PQ 为半圆O 的直径，A 为以OQ 为直径的半圆A 的圆心，⊙O 的弦PN 切⊙A 于点M ，PN ＝8，则⊙A 的半径为________．三、解答题(本大题共6小题，共80分．解答应写出文字说明，证明过程或演算步骤)16．(本小题满分12分)函数f (x )＝A sin(ωx ＋φ)(A >0，ω>0，－π2<φ<π2，x ∈R )的部分图象如图所示．(1)求函数y ＝f (x )的解析式；(2)当x ∈[－π，－π6]时，求f (x )的取值范围．17．(本小题满分12分)通过随机询问110名性别不同的大学生是否爱好某项运动，得到如下的列表：(1)(2)如果采用分层抽样的方法从爱好该项运动的大学生中选取6人，组成一个兴趣小组，求被选取的男女生的人数各是多少？(3)在上述6人小组中，随机选定2人去做某件事，求这2人中有女生被选中的概率．数据：公式：K 2＝n ×（ad －bc ）（a ＋b ）（c ＋d ）（a ＋c ）（b ＋d ）18．(本小题满分14分)在数列{a n }中，a 1＝1，a 2＝103，a n ＋1－103a n ＋a n －1＝0(n ≥2，且n ∈N *)．(1)若数列{a n ＋1＋λa n }是等比数列，求实数λ； (2)求数列{a n }的通项公式．19．(本小题满分14分)如图，三棱柱ABC -A 1B 1C 1的侧棱AA 1⊥底面ABC ，∠ACB ＝90°，E 是棱CC 1的中点，F 是AB 的中点，AC ＝BC ＝1，AA 1＝2. (1)求证：CF ∥平面AB 1E ； (2)求三棱锥C -AB 1E 在底面AB 1E 上的高．20．(本小题满分14分)已知椭圆E ：x 2a 2＋y 2b2＝1(a >b >0)以抛物线y 2＝8x 的焦点为顶点，且离心率为12.(1)求椭圆E 的方程；(2)若直线l ：y ＝kx ＋m 与椭圆E 相交于A 、B 两点，与直线x ＝－4相交于Q 点，P 是椭圆E 上一点且满足OP →＝OA →＋OB →(其中O 为坐标原点)，试问在x 轴上是否存在一点T ，使得OP →·TQ →为定值？若存在，求出点T 的坐标及OP →·TQ →的值；若不存在，请说明理由．21．(本小题满分14分)已知函数f(x)＝ax2－e x(a∈R)．(1)当a＝1时，试判断f(x)的单调性并给予证明；(2)若f(x)有两个极值点x1，x2(x1<x2)．①求实数a的取值范围；②证明：－e2<f(x1)<－1.(注：e是自然对数的底数)答案：1．【解析】选C.因为z ＝2i 31＋i ＝－2i1＋i ＝－2i （1－i ）（1＋i ）（1－i ）＝－i(1－i)＝－1－i ，所以复数z ＝2i 31＋i 在复平面内对应的点位于第三象限，故应选C. 2．【解析】选A.由频率分布直方图可得，大于或等于80 km/h 的汽车的频率为0.01×10＝0.1，所以其频数为0.1×200＝20，即被处罚的汽车大约有20辆． 3．【解析】选B.由偶函数排除C 、D ，再由在区间(1，2)内是增函数排除A.故选B.4．【解析】选B.∵e ＝3，∴ca ＝3，即a 2＋b 2a 2＝3，∴b 2＝2a 2，∴双曲线方程为x 2a 2－y22a2＝1，∴渐近线方程为y ＝±2x .5．【解析】选D.s ＝0，n ＝2，2<8，s ＝0＋12＝12；n ＝2＋2＝4，4<8，s ＝12＋14＝34；n ＝4＋2＝6，6<8，s ＝34＋16＝1112；n ＝6＋2＝8，8<8不成立，输出s 的值为1112.6．【解析】选C.当不同直线m 、n 都平行于平面α时，m 、n 的位置不能确定，因此命题①不是真命题；根据直线与平面垂直的性质定理可得命题②是真命题；命题③中m 、n 的位置关系不能确定，因此命题③不是真命题；命题④中的直线n 与平面β的位置关系不确定，因此命题④也不是真命题．故选C. 7．【解析】选B.A ＝{x |x 2＋2x －3>0}＝{x |x >1或x <－3}，因为函数y ＝f (x )＝x 2－2ax －1的对称轴为x ＝a >0，f (－3)＝6a ＋8>0，根据对称性可知，要使A ∩B 中恰含有一个整数，则这个整数解为2，所以有f (2)≤0且f (3)>0，即⎩⎪⎨⎪⎧4－4a －1≤09－6a －1>0，所以⎩⎨⎧a ≥34a <43，即34≤a <43，故选B.8．【解析】选B.作出可行域如图中阴影部分所示，则z 在点A 处取得最大值，在点C 处取得最小值．又k BC ＝－1，k AB ＝1，∴－1≤－a ≤1，即－1≤a ≤1.9．【解析】选B.由正弦定理得：a sin A ＝bsin B，∵B ＝2A ，a ＝1，b ＝3，∴1sin A ＝32sin A cos A. ∵A 为三角形的内角，∴sin A ≠0.∴cos A ＝32.又0<A <π，∴A ＝π6，∴B ＝2A ＝π3.∴C ＝π－A －B ＝π2，∴△ABC 为直角三角形．由勾股定理得c ＝12＋（3）2＝2.10．【解析】选C.f ′(x )＝3x 2－3＝3(x ＋1)·(x －1)，令f ′(x )＝0，得x ＝±1，所以f (x )的图象如图所示，因f (1)＝－2，f (－2)＝－2，若函数f (x )在(a ，6－a 2)上有最小值，则⎩⎪⎨⎪⎧－2≤a <16－a 2>1，解得－2≤a <1. 11．【解析】在x －y ＋1＝0中，令y ＝0得x ＝－1，所以直线x －y ＋1＝0与x 轴的交点为(－1，0)，即圆C 的圆心为(－1，0)．因为直线x ＋y ＋3＝0与圆C 相切，所以圆心到直线的距离等于半径，即r ＝|－1＋0＋3|2＝2，所以圆C 的方程为(x ＋1)2＋y 2＝2.【答案】(x ＋1)2＋y 2＝212．【解析】设t ＝2＋cos n π6，有1≤t ≤3，则a n ＝cos n π6＋162＋cosn π6＝t ＋16t －2.用导数可以证明，函数f (t )＝t ＋16t在1≤t ≤3上是单调递减的，所以当t ＝3，即n ＝12k (k ∈N *)时，a n 取最小值193.【答案】19313．【解析】因为函数y ＝f (x )的图象是开口向下的抛物线，且对任意x ∈R ，都有f (1－x )＝f (1＋x )，所以函数y ＝f (x )为开口向下、以x ＝1为对称轴的二次函数，所以f (－1)＝f (3)．又因为a ·b ＝log 12m ＋2，所以不等式f (a ·b )<f (－1)即为不等式log 12m ＋2<－1或log 12m ＋2>3，解得m >8或0<m <12.【答案】(0，12)∪(8，＋∞)14．【解析】圆C 的直角方程为x 2＋(y －2)2＝4，得圆心坐标为(0，2)；由参数方程为⎩⎨⎧x ＝－22ty ＝6＋22t 消去t 后，得直线方程为x ＋y ＝6，那么圆心到直线l 的距离为|0＋2－6|12＋12＝22；【答案】2 215．【解析】设⊙A 的半径为R ，连接NQ 、MA ，∵∠PNQ ＝90°，∠PMA ＝90°，∴PMPN＝P A PQ ＝34，又PN ＝8，∴PM ＝6，而PM 2＝PO ·PQ ，∴36＝2R ·4R ，∴OA ＝R ＝322.【答案】32216．【解】(1)由图象得A ＝1，T 4＝2π3－π6＝π2，所以T ＝2π，则ω＝1.将(π6，1)代入得1＝sin(π6＋φ)，而－π2<φ<π2，所以φ＝π3，因此函数f (x )＝sin(x ＋π3)．(2)由于x ∈[－π，－π6]，－2π3≤x ＋π3≤π6，所以－1≤sin(x ＋π3)≤12，所以f (x )的取值范围是[－1，12]．17．【解】(1)K 2＝110×（40×30－20×20）260×50×60×50≈7.8>6.635，而P (K 2≥6.635)≈0.010＝1%，即，认为“爱好该项运动与性别没有关系”的概率是1%，∴有99%以上的把握认为“爱好该项运动与性别有关”．(2)应抽取男生人数为660×40＝4人，应抽取女生人数为660×20＝2人．(3)设6人中2个女生分别为A ，B ，4个男生分别为c ，d ，e ，f ，则从6人中随机选定2人去做某件事的基本事件为：AB ，Ac ，Ad ，Ae ，Af ，Bc ，Bd ，Be ，Bf ，cd ，ce ，cf ，de ，df ，ef ，共15个基本事件，其中，有女生被选中的事件为AB ，Ac ，Ad ，Ae ，Af ，Bc ，Bd ，Be ，Bf ，共9个，∴有女生被选中的概率为P ＝915＝35.18．【解】(1)设a n ＋1＋λa n ＝μ(a n ＋λa n －1)(n ≥2)， ∴a n ＋1＋(λ－μ)a n －λμa n －1＝0，∴⎩⎪⎨⎪⎧λ－μ＝－103λμ＝－1，∴λ＝－13或λ＝－3.(2)由(1)知当n ≥2时，a n －13a n －1＝3n －1，①a n －3a n －1＝13n －1，②由①②得a n ＝38(3n －13n )．经验证，n ＝1时也成立，∴a n ＝38(3n －13n )．19．【解】(1)证明：取AB 1的中点G ，连接EG ，FG ， ∵F 、G 分别是AB 、AB 1的中点，∴FG ∥BB 1，FG ＝12BB 1.∵E 为侧棱CC 1的中点， ∴FG ∥EC ，FG ＝EC ，∴四边形FGEC 是平形四边形， ∴CF ∥EG ，∵CF ⊄平面AB 1E ，EG ⊂平面AB 1E ， ∴CF ∥平面AB 1E . (2)∵三棱柱ABC -A 1B 1C 1的侧棱AA 1⊥底面ABC ，∴BB 1⊥平面ABC .又AC ⊂平面ABC ，∴AC ⊥BB 1. ∵∠ACB ＝90°，∴AC ⊥BC .∵BB 1∩BC ＝B ，∴AC ⊥平面EB 1C ，∴AC ⊥CB 1，∴VA EB 1C ＝13S △EB 1C ·AC ＝13×(12×1×1)×1＝16.∵AE ＝EB 1＝2，AB 1＝6，∴S △AB 1E ＝32.∵VC AB 1E ＝VA EB 1C ，∴三棱锥C -AB 1E 在底面AB 1E 上的高为3VC －AB 1E S △AB 1E＝33.20．【解】(1)抛物线y 2＝8x 的焦点为椭圆E 的顶点，即a ＝2. 又c a ＝12，故c ＝1，b ＝ 3. ∴椭圆E 的方程为x 24＋y 23＝1.(2)设A (x 1，y 1)，B (x 2，y 2)．联立⎩⎪⎨⎪⎧y ＝kx ＋m 3x 2＋4y 2＝12，得(4k 2＋3)x 2＋8kmx ＋4m 2－12＝0. 由根与系数的关系，得x 1＋x 2＝－8km 4k 2＋3，y 1＋y 2＝k (x 1＋x 2)＋2m ＝6m4k 2＋3.将P (－8km 4k 2＋3，6m4k 2＋3)代入椭圆E 的方程，得64k 2m 24（4k 2＋3）2＋36m 23（4k 2＋3）2＝1. 整理，得4m 2＝4k 2＋3.设T (t ，0)，Q (－4，m －4k )．∴TQ →＝(－4－t ，m －4k )，OP →＝(－8km 4k 2＋3，6m 4k 2＋3)．即OP →·TQ →＝32km ＋8kmt 4k 2＋3＋6m （m －4k ）4k 2＋3＝6m 2＋8km ＋8kmt 4k 2＋3.∵4k 2＋3＝4m 2，∴OP →·TQ →＝6m 2＋8km ＋8kmt 4m 2＝32＋2k （1＋t ）m.要使OP →·TQ →为定值，只需[2k （1＋t ）m ]2＝4k 2（1＋t ）2m 2＝（4m 2－3）（1＋t ）2m 2为定值，则1＋t ＝0，∴t ＝－1，11 ∴在x 轴上存在一点T (－1，0)，使得OP →·TQ →为定值32. 21．【解】(1)当a ＝1时，f (x )＝x 2－e x ，f (x )在R 上单调递减．f ′(x )＝2x －e x ，只要证明f ′(x )≤0恒成立即可，设g (x )＝f ′(x )＝2x －e x ，则g ′(x )＝2－e x ，当x ＝ln 2时，g ′(x )＝0，当x ∈(－∞，ln 2)时，g ′(x )>0，当x ∈(ln 2，＋∞)时，g ′(x )<0.∴f ′(x )max ＝g (x )max ＝g (ln 2)＝2ln 2－2<0，故f ′(x )<0恒成立，∴f (x )在R 上单调递减．(2)①若f (x )有两个极值点x 1，x 2，则x 1，x 2是方程f ′(x )＝0的两个根，故方程2ax －e x ＝0有两个根x 1，x 2，又x ＝0显然不是该方程的根，∴方程2a ＝e x x有两个根．设φ(x )＝e x x ，得φ′(x )＝e x （x －1）x 2，当x <0时，φ(x )<0且φ′(x )<0，φ(x )单调递减，当x >0时，φ(x )>0，当0<x <1时，φ′(x )<0，φ(x )单调递减，当x >1时，φ′(x )>0，φ(x )单调递增，要使方程2a ＝e x x有两个根，需2a >φ(1)＝e ，故a >e 2且0<x 1<1<x 2，故a 的取值范围为(e 2，＋∞)． ②证明：由f ′(x 1)＝0，得2ax 1－e x 1＝0，故a ＝e x 12x 1，x 1 ∈(0，1)， f (x 1)＝ax 21－e x 1＝e x 12x 1·x 21－e x 1＝e x 1(x 12－1)，x 1∈(0，1)，设φ(t )＝e t (t 2－1)(0<t <1)，则φ′(t )＝e t ·t －12<0， φ(t )在0<t <1上单调递减，故φ(1)<φ(t )<φ(0)，即－e 2<f (x 1)<－1.。

2014湖南省高中学业水平考试数学仿真试题

湖南省高中学业水平考试数学仿真试题1姓名得分一、选择题：本大题共10小题，每小题4分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的。

1. 已知集合{1,2}M =,{2,3}N =，则=N M I ( ) . A. {1},2 B. {2,3} C. {1,3} D. {}2 2. 已知,a b c R >∈，则（）.A. +a c b c >+B. a c b c +<+C. a c b c +≥+D. a c b c +≤+ 3. 下列几何体中，正视图、侧视图和俯视图都不相同的是（）. A .圆柱 B.圆锥 C.球 D.五菱柱4. 已知圆C 的方程为()()42122=+++y x ，则圆C 的圆心坐标和半径r 分别为（）.A. ()1,2,2r =B. ()1,2,2r --=C. ()1,2,4r =D. ()1,2,4r --= 5. 下列函数中，是奇函数的是（）. A. ()f x x =+1 B. 1()f x x=C. 2()f x x =D. ()x x f cos = 6. 如图所示的圆盘由八个全等的扇形构成，指针绕中心旋转，可能随机停止，则指针停止在阴影部分内的概率为（）.A.12 B. 14 C. 16 D. 187.化简：()=-2cos sin αα（）.A . 1sin 2a + B. 1sin a - C. 1sin 2a - D. 1sin a + 8. 在ABC ∆中，若向量0=⋅BC AC ，则ABC ∆一定是（）. A .锐角三角形 B. 直角三角形 C .钝角三角形 D. 等腰三角形 9. 已知函数()(01)x f x a a a 且=>≠，若()211=f ，则函数()f x 的解析式为（）. A. ()4xf x = B. 1()4xf x ⎛⎫= ⎪⎝⎭ C. ()2x f x = D. 1()2xf x ⎛⎫= ⎪⎝⎭10. 在ABC ∆中，,,a b c 分别是ABC ∆的对边，若2,1,120==︒=c a B ，则b 等于（）. A. 1 B.3 C. 2 D.7二、填空题：本大题共5小题，每小题4分，共20分，将正确答案填在题后横线上. 11. 直线1-=x y 的倾斜角=α .12. 已知如图所示的程序框图，若输入的x 的值为11，则输出的y 值为 . 13. 已知点(,)x y 在如图所示的阴影部分内运动，则2z x y =+的最小值为 .14. 已知向量 (4,2),(,3)a b x r r==，若⊥，则实数x 的值为 .15. 张山同学家里开了一个小卖部，为了研究气温对某种冷饮销售量的影响，他收集了一段时间内这种冷饮每天的销售量y （杯）与当天最高气温()x C o 的有关数据，通过描绘散点图，发现y 和x 呈线性相关关系，并求得其回归方程260y x ∧=+如果气象预报某天的最高温度气温为C ︒35，则可以预测该天这种饮料的销售量为杯。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2014年医科基础仿真试题（一）一、选择题（解剖学1-30；生理学31-60。

每小题2分，共120分。

每小题中只有一个选项是正确的，请将正确选项涂在答题卡上）1．将人体分为左、右对称的两部分的切面是（）A．水平面B．冠状面C．矢状面D．正中矢状面2．不属于躯干骨的是（）A．肋骨B．胸骨C．肩胛骨D．椎骨3．颈椎的主要特征是（）A．有肋凹B．有横突孔C．棘突细长D．椎体较大4．与胸骨角相连的是（）A．第1肋软骨B．第2肋软骨C．第3肋软骨D．第2肋骨5．肩胛骨上角平对（）A．第2肋B．第3肋C．第6肋D．第7肋6．下消化道是指（）A．从口腔到食管B．十二指肠以下的消化道C．从口腔到十二指肠D．空肠以下的消化道7．手术时识别空肠起始端的标志是( )Ａ、十二指肠Ｂ、十二指肠悬肌Ｃ、十二指肠纵襞Ｄ、十二指肠大乳头8．下列哪项属于腹膜间位器官 ( )A、脾B、胃C、胆囊D、输尿管9．出入肝门的主要结构有( )A．肝固有动脉、肝门静脉和肝管B．肝管、下腔静脉和肝门静脉C．肝管、胆囊管和肝门静脉D．肝总动脉、肝管和肝门静脉10．唯一完整环形的喉软骨是( )A．甲状软骨B．杓状软骨C．会厌软骨D．环状软骨11．肺下界体表投影在肩胛线上平对（）A、第10肋B、第8肋C、第6肋D、第11肋12．肺（）A．位于胸膜腔内 B．呈圆柱状 C．肺底与膈相贴 D．右肺被水平裂分为上下两叶13．关于肾的描述，正确的是（）A．属于腹膜内位器官B．肾小盏包绕肾乳头C．肾髓质包括肾柱D．肾乳头朝向肾皮质14．在男性，尿道内括约肌环绕于（）A、尿道前列腺 B、尿道膜部 C、尿道海绵体 D、尿道外口15．输卵管结扎的常选部位是（）A．子宫部B．输卵管峡 C．输卵管壶腹D．输卵管漏斗16．左心房（）A、构成心左缘大部分B、有两个入口左右肺静脉口C、收纳有肺回流的静脉血D、出口为左房室口17．室间隔缺损的常见部位是（）A．卵圆窝B．室间隔肌部C．室间隔膜部D．室间隔近心尖处18．上腔静脉（）A．由左、右颈内静脉合成B．在升主动脉左侧下行C．注入右心房D．收集胸腹腔脏器回流的血液19．关于胸导管的描述，错误的是（）A．起于第1腰椎体前方B．起始处的膨大为乳糜池 C．是全身最大的淋巴导管D．注入静脉前收集右颈干、右锁骨下干和右支气管纵隔干20．脉络膜（）Ａ、呈乳白色Ｂ、无色素细胞Ｃ、含丰富的神经末梢Ｄ、由遮光作用21．对咽鼓管描述错误的是（）Ａ、是联通鼓室与咽部的通道Ｂ、是中耳的一部分Ｃ、是维持鼓室内外压力平衡的通道Ｄ、管壁的粘膜与鼓室的粘膜互不相连22．脊髓后角神经元是（）A．运动神经元B．联络神经元C．交感神经元D．感觉神经元23．皮质脊髓束的作用是（）A、传导痛，温觉冲动B、传导本体感觉冲体C、传导内脏运动冲体D、传导躯体运动冲体24．属于脑干腹侧面的结构是（）A．菱形窝B．舌下神经三角C．锥体D．上丘25．与听觉传导有关的是（）A、外侧膝状体B、内侧膝状体C、上丘D、下丘26．颈内动脉的分支是（）A、椎动脉B、脑膜中动脉C、大脑前动脉D、大脑后动脉27．动眼神经损伤的表现是（）A．全部眼球外肌瘫痪 B．上睑下垂 C．眼外上斜视D．瞳孔缩小28．小指感觉功能丧失见于（）损伤A、正中神经B、尺经神C、绕神经D、腋神经29．不受迷走神经支配的是（）A．心B．胃C．食管D．乙状结肠30．甲状腺（）A．仅有两个侧叶组成B．侧叶位于气管和喉的前方C．肿大时可在体表摸到D．分泌甲状腺激素调节钙磷代谢31．神经调节的特点是（）A．作用缓慢B．作用迅速、准确和短暂C．调节幅度小D．作用广泛而持久32．在细胞膜的物质转运中，Na+ 跨膜转运的方式有（）A．单纯扩散和易化扩散B．单纯扩散和主动转运C．易化扩散和主动转运D．易化扩散和出胞33．静息电位的产生是由于（）A．Na+内流B．Na+外流C．K+内流D．K+外流34．细胞膜内电位由-70mV上升至+30mV，称为（）A．极化B．超极化C．去极化D．复极化35．下列红细胞生成的叙述错误的是（）A、红细胞的主要成分是血红蛋白B、促红细胞生成素在肾合成C、生成原料主要是叶酸和维生素B12D、雄激素可使红细胞数增多36．临床上急性炎症时。

血中( )的数量明显增加A、中性粒细胞B、单核细胞C、淋巴细胞D、嗜酸性粒细胞37．启动外源性凝血途径的物质是( )A．因子ⅫB．凝血酶原C．因子ⅢD．Ca2+38．肝素抗凝血的作用机理是( )A．抑制因子Ⅰ激活B．增强抗凝血酶Ⅲ的活性C．去除血浆中Ca2+ D．促进纤维蛋白溶解39．老年人小动脉硬化，大动脉管壁弹性下降，可导致（）A、收缩压降低B、舒张压降低C、脉压增大D、收缩压、舒张压都升高40．房室交界区传导速度减慢可导致（）A、P波增宽B、QRS波群增宽C、P-R间期延长D、ST段延长41．动脉舒张压主要反映的是（）A．搏出量B．大动脉弹性C．外周阻力D．血管充盈的程度42．某患者出现颈静脉怒张，肝肿大和双下肢水肿，最可能的心血管疾病是（）A.右心衰竭 B.左心衰竭 C.肺水肿 D.高血压43．保持潮气量和呼吸频率不变时，增大无效腔可引起（）A．肺泡通气量减少B．肺泡通气量不变 C．肺泡通气量增大D．以上均有可能44．决定肺内气体交换方向的主要因素是（）A、气体的分压差B、气体的分子量C、气体的溶解度D、呼吸膜的通透性45．中枢化学感受器最敏感的刺激因素是（）A、脑脊液H+浓度升高B、脑脊液CO2分压升高C、脑脊液O2分压降低D、动脉血H+浓度升高46．分泌盐酸和内因子的是（）A．主细胞B．壁细胞C．黏液细胞D．胃上皮细胞47．激活胰蛋白酶原的主要物质是（）A．胆汁B．胃酸C．肠致活酶D．糜蛋白酶48．下列哪种情况可导致肾小球滤过率增高（）A、肾交感神经兴奋B、快速静脉滴注生理盐水C、静脉注射高渗葡萄糖液D、注射抗利尿激素49．原尿中葡萄糖被重吸收的部位是（）A．近端小管B．远端小管C．髓袢升支D．集合管50．大量饮清水后尿量增多的主要原因是（）A．血浆晶体渗透压升高，引起抗利尿激素分泌增多B．血浆晶体渗透压降低，引起抗利尿激素分泌减少C．血浆胶体渗透压升高，引起抗利尿激素分泌增多D．血浆胶体渗透压降低，引起抗利尿激素分泌减少51．肾小球滤过率是指（）A．每分钟一侧肾脏生成的原尿量B．每分钟两侧肾脏生成的原尿量C．每分钟一侧肾脏生成的终尿量D．每分钟两侧肾脏生成的终尿量52．眼做最大调节所能看清眼前的最近距离，称为（）A、节点B、焦点C、近点D、远点53．反射弧中，最容易出现疲劳的部位是（）A．感受器、效应器B．传入神经C．反射中枢D．传出神经54．非特异投射系统的主要功能是（）A．调节内脏活动 B．维持睡眠状态C．调节肌紧张D．维持大脑皮质的兴奋状态55．副交感神经兴奋可引起（）A、瞳孔扩大B、糖原分解C、胃肠运动增强D、骨骼肌血管舒张56．脊休克产生的原因是（）A．脊髓横断损伤的刺激B．脊髓运动神经元功能障碍C．脑干网状结构功能障碍D．离断脊髓失去高位中枢控制57．维持身体姿势最基本的反射是（）A．肌紧张B．腱反射C．膝反射D．屈肌反射58．机体在急性失血时，最早出现的代偿反应是（）A、迷走神经兴奋B、交感神经兴奋C、组织液回流增加D、血管紧张素系统作用加强59．地方性甲状腺肿的病因主要是（）A．糖皮质激素分泌增多B．生长激素分泌过多C．食物中缺碘D．促甲状腺激素分泌减少60．糖皮质激素对血细胞的作用，错误的是（）A．使红细胞增多 B．使中性粒细胞增多C．使淋巴细胞增多D．使血小板增多解剖学（70分）二、判断题（每小题2分、共20分）61、下颌骨是颅骨中唯一可移动的骨。

（）62、腮腺导管的开口平对上额第2磨牙的颊黏膜上。

（）63、吸气时胸腔容积因膈肌下降、肋上举而扩大。

（）64、男性的胸膜腔是密闭的，女性的胸膜腔则与外界相通。

（）65、女性腹股沟管内有子宫圆韧带通过。

（）66、颈总动脉是头颈部的主要动脉，均发自主动脉弓。

（）67、心音是指心动周期中，心脏搏动引起机械性振动而产生的声音。

（）68、全部内脏器官都接受交感和副交感神经的双重支配（）69、面神经支配面部的感觉和运动。

（）70、糖皮质激素能促进胃酸和胃蛋白酶原的分泌，故能诱发或加剧消化性溃疡三、名词解释（每小题3分，共12分）71．胸廓72．回盲瓣73．静脉角74．内囊四、简答题（每小题5分，共20分）75、临床上计数肋序数的骨性标志有哪些76、简述胆汁的产生和排出途径。

77、外界光线经过哪些结构才能投射到视网膜上?78、写出躯干、四肢深感觉的传导通路五、综合题（18分）79、肝门静脉受阻时通过什么途径回流到上、下腔静脉？为什么出现呕血或便血？生理学（60分）六、判断题（每小题2分，共20分）80．内环境稳态是指细胞外液的成分和理化性质保持绝对不变。

（）81．影响毛细血管内外水平衡的是血浆胶体渗透压。

（）82．血型是指红细胞膜上特异性抗原的类型。

（）83．给动物静脉注射去甲肾上腺素，将引起血压升高。

（）84．浅而快的呼吸比深而慢的呼吸对机体更有利。

（）85．胃酸可激活胃蛋白酶原。

（）86．人体安静时主要的产热器官是肝脏，运动时的主要产热器官是骨骼肌。

（）87．应激反应时血中促肾上腺皮质激素和糖皮质激素分泌减少。

（）88．糖尿病患者的多尿属于渗透性利尿。

（）89．副交感神经兴奋时，会引起瞳孔扩大，支气管扩张和心脏活动增强。

（）七、名词解释题。

（每小题2分，共8分）90．阈电位91．血液凝固92．胃排空93．牵涉痛八、简答题（每小题5分，共20分）94、简述胆碱能受体的主要分类及相应的受体阻断剂。

95、简述动脉血中CO2分压升高对呼吸的影响，其机制如何？96、何谓牵张反射？有几种类型？各有何生理意义？97、简述生长激素的生理作用。

九、综合题（16分）98、试述心脏射血和充盈过程中压力、瓣膜、血流方向和心室容积的变化。