人教版高中数学必修二第4讲:平面的基本性质与推论(教师版)
最新人教版高中数学必修2第二章《平面的基本性质与推论》

数学人教B必修2第一章1.2.1 平面的基本性质与推论1.理解平面的三个基本性质与三个推论,并会用三种语言表示性质和推论.2.了解异面直线的概念,能用符号语言描述点、直线、平面之间的相互位置关系.3.能进行文字语言与数学图形语言和符号语言间的相互转化与应用.1.空间点和直线的基本性质(1)连接两点的线中,________最短.(2)过________有一条直线,并且只有一条直线.2【做一做1-1】若点B在直线b上,b在平面β内,则B,b,β之间的关系可以记作().A.B∈b∈βB.B∈b⊂βC.B⊂b⊂βD.B⊂b∈β【做一做1-2】若两个不重合的平面有公共点,则公共点的个数是().A.1个B.2个C.1个或无数个D.无数个且在同一条直线上【做一做1-3】如果直线a⊂平面α,直线b⊂平面α,M∈a,N∈b且M∈l,N∈l,那么().A.l⊂αB.l⊄αC.l∩α=M D.l∩α=N3.平面基本性质的推论推论1:经过一条直线和直线外的一点,__________个平面.推论2:经过两条______直线,有且只有一个平面.推论3:经过两条______直线,有且只有一个平面.空间中的几个点或几条直线,如果都在同一平面内,我们就说它们________.【做一做2-1】下列命题正确的是().①一条直线和一个点确定一个平面;②两条相交直线确定一个平面;③两条平行直线确定一个平面;④四个点确定一个平面.A.①③B.②③C.③④D.②③④【做一做2-2】由4条平行直线最多可以确定().A.2个平面B.4个平面C.5个平面D.6个平面A.四边形是平面图形B.有三个公共点的两个平面必重合C.两两相交的三条直线必在同一个平面内D.三角形是平面图形5.异面直线(1)画法:画两条异面直线时,为了充分显示出它们既不________又不______的特点,即________的特点,通常采用平面衬托法,以加强直观性,常见的画法如下图.(2)判断方法:与一平面相交于一点的直线与这个平面内不经过交点的直线是异面直线.【做一做4】在正方体ABCD-A1B1C1D1中,与棱AA1成异面直线的棱有__________条.1.对异面直线的理解剖析:若直线a,b是异面直线,则在空间中找不到一个平面,使其同时经过a,b两条直线.例如,如图所示的长方体ABCD-A1B1C1D1中,棱AB和B1C1所在的直线既不平行又不相交,找不到一个平面同时经过这两条棱所在的直线.要注意分别在两个平面内的直线不一定是异面直线,可以平行,可以相交,也可以异面.2.平面的基本性质的作用剖析:(1)基本性质1的作用.利用基本性质1可以判断一条直线是否在一个平面内.基本性质1给出了判断直线在平面内的方法,引出了直线在平面内的定义,从而说明了在空间中的每个平面内都存在着各种平面图形,在每个平面内都可以用初中的平面几何知识.另外,该基本性质也是判断点在平面内的方法,还可借此用直线来检验平面.(2)基本性质2的作用.作用之一是确定平面,作用之二是可用它来证明点、线共面问题.(3)基本性质3的作用.平面的基本性质3主要说明了两个相交平面的特征,对我们确定两个平面的交线有着重要的作用.其一,它是判定两个平面是否相交的依据,也就是说,只要两个平面有公共点,则这两个平面就相交;其二,它可以证多点共线的问题.若点是某两个平面的公共点,则该点必定在这两个平面的交线上.3.教材中的“思考与讨论”已知两条直线相交,过其中任意一条直线上的一点作另一条直线的平行线,这些平行线是否都共面?为什么?剖析:都共面,如图所示,a∩b=A,过b上任意一点B作c∥a,则a,c可确定一个平面α.因为A∈a,所以A∈α.又因为B∈c,所以B∈α,所以AB⊂α,即b⊂α.所以a,b,c 共面.同理在a上任取一点作b的平行线,都与a,b共面,所以这些平行线都共面.题型一文字语言、图形语言和符号语言的转换【例1】将下面用符号语言表示的关系改用文字语言予以叙述,并且用图形语言予以表示.α∩β=l,A∈l,AB⊂α,AC⊂β.分析:本题实质是数学的三种语言:符号语言、文字语言、图形语言之间的互译.反思:符号语言简洁,层次感强.文字语言比较自然、生动,它能将问题所研究的对象的含义更加明白地叙述出来.教科书上的概念、定理等多以文字语言叙述.图形语言,易引起清晰的视觉形象,它能直观地表达概念、定理的本质以及相互关系,在抽象的数学思维面前起着具体化和加深理解的作用.各种数学语言间的互译可为我们在更广阔的思维领域里寻找问题解决的途径提供方便.题型二共线问题【例2】如图所示,已知△ABC的三边所在的直线分别与平面α交于P,Q,R三点.求证:P,Q,R三点共线.分析:证明P,Q,R三点均在平面ABC与平面α的交线上.反思:证明点共线,可先由两点确定一条直线,再证其他的点也在这一直线上,也可证明所有点都在一条特定直线(两平面交线)上.题型三共面问题【例3】如图所示,已知一直线a分别与两平行直线b,c相交.求证:a,b,c三线共面.分析:有两种方法.(1)先用两平行直线b,c确定一个平面,再证a也在这个平面内;(2)先由两条相交直线a,b确定一个平面,再证c也在这个平面内.反思:本题为我们证明共面问题提供了多角度的思维模式,但整体套路是先用部分对象确定一个平面,后证明剩余对象亦在其中.题型四共点问题【例4】三个平面α,β,γ两两相交于三条直线,即α∩β=c,β∩γ=a,γ∩α=b,若直线a和b不平行,求证:a,b,c三条直线必过同一点.分析:直线过同一点,我们可以这样来思考:先证明两线相交,得一交点,然后证明该点在其余的直线上(或其余的直线经过该点).反思:证明三线共点的思路是:先证两条直线交于一点,再证明第三条直线经过这点,把问题化归到证明点在直线上的问题.题型五交线问题【例5】如图所示,G是正方体ABCD-A1B1C1D1的棱DD1延长线上一点,E,F是棱AB,BC的中点.试分别画出过下列各点、直线的平面与正方体表面的交线.(1)过点G及AC;(2)过三点E,F,D1.分析:找两个平面的两个公共点,则过这两个公共点的直线为两平面的交线.反思:画截面截得正方体的截面图形,关键是利用好公理,找到两个平面上的公共点是解决此类问题的突破口.题型六易错辨析【例6】在空间中,可以确定一个平面的条件的序号有__________.①两两相交的三条直线②三条直线,其中的一条与另外两条直线分别相交③三个点④三条直线,它们两两相交,但不交于同一点错解:①②③④错因分析:不能正确理解确定一个平面所需的条件,往往是疏忽了其中的特殊要求,只记得性质和推论的大概致误.1与“直线l上两点A,B在平面α内”含义不同的是().A.l⊂αB.平面α过直线lC.直线l上只有这两个点在α内D.直线l上所有点都在α内2平面α∩β=l,点A∈α,点B∈α,且C∉l,但C∈β,又AB∩l=R,如图,过A,B,C三点确定的平面为γ,则β∩γ是().A.直线AC B.直线BCC.直线CR D.直线AR3在正方体ABCD-A1B1C1D1中,P,Q,R分别是AB,AD,B1C1的中点,那么在正方体中过P,Q,R的截面图形是().A.三角形B.四边形C.五边形D.六边形4如图所示,请把下面的叙述用符号语言表示出来.(1)点A,B在直线a上:__________;(2)直线a在平面α内:__________,点C在平面α内:__________;(3)点D不在平面α内:__________,直线b不在平面α内:__________.5木匠师傅只需要用三只脚就能将一张圆桌面平稳地固定,为什么?答案:基础知识·梳理1.(1)线段(2)两点2.两点所有点在平面内经过直线l⊂α有且只有确定有一个公共点有且只有交线【做一做1-1】B关键是弄清点与直线是元素与集合之间的关系,直线与平面是集合与集合之间的关系.【做一做1-2】D利用基本性质3可知如果两个平面有一个公共点,则它们就一定有一条交线,而线是由无数个点构成的,所以这两个平面有无数个在同一直线上的交点.【做一做1-3】A因为M∈a,N∈b,a,b⊂α,所以M,N∈α,根据基本性质1可知l⊂α.故选A.3.有且只有一相交平行共面【做一做2-1】B【做一做2-2】D本题从确定平面的条件来考虑即可,要使四条平行直线确定的平面最多,只有当这四条直线中任两条所确定的平面互不相同时即为最多,从而得到结果.由确定平面的条件知,由四条平行直线最多可以确定六个平面,选D.4.有且只有一个在同一平面内异面直线【做一做3】D空间四边形不是平面图形,故选项A说法不正确;若三个公共点在一条直线上,则两个平面不一定重合,选项B也是错误的;选项C中两两相交的三条直线可能会经过同一点,此时三条直线不一定在同一个平面内.故选D.5.(1)平行相交不共面【做一做4】4典型例题·领悟【例1】解:文字语言叙述为:点A在平面α与平面β的交线l上,AB,AC分别在α,β内.图形语言如下图所示.【例2】证明:∵A,B,C是不在同一直线上的三点,∴过A,B,C有一个平面β.又∵AB∩α=P,且AB⊂β,∴点P既在β内又在α内.设α∩β=l,则P∈l.同理可证:Q∈l,R∈l.∴P,Q,R三点共线.【例3】证法一:∵b∥c,则b,c确定一个平面,设为α,如图,令a∩b=A,a∩c=B,∴A∈α,B∈α,∴AB⊂α,即直线a⊂α.∴a,b,c三线共面.证法二:∵a与b是相交直线,则a,b确定一个平面,设为α,如图,设a∩c=A,过A点在α内作直线c′∥b,∵c∥b,c′∥b,∴c∥c′.又∵c与c′相交于点A,∴c与c′重合.∴a,b,c三线共面.【例4】证明:∵α∩γ=b,β∩γ=a,∴a⊂γ,b⊂γ.由于直线a和b不平行,∴a,b必相交,设a∩b=P,如图,则P∈a,P∈b.∵a⊂β,b⊂α,∴P∈β,P∈α.又α∩β=c,∴P∈c,即交线c经过点P.∴a,b,c三条直线相交于同一点.【例5】解:(1)画法:连接GA交A1D1于点M;连接GC交C1D1于点N;连接MN,AC,则MA,CN,MN,AC为所求平面与正方体表面的交线.如图①所示.(2)画法:连接EF交DC的延长线于点P,交DA的延长线于点Q;连接D1P交CC1于点M,连接D1Q交AA1于点N;连接MF,NE,则D1M,MF,FE,EN,ND1为所求平面与正方体表面的交线.如图②所示.【例6】④正解:①中两两相交的三条直线,它们可能交于同一个点,也可能不交于同一个点,若交于同一个点,则三条直线不一定在同一个平面内,故排除①;②中的另外两条直线可能共面,也可能不共面,当另外两条直线不共面时,则三条直线不能确定一个平面,故排除②;对于③来说,三个点的位置可能不在同一直线上,也可能在同一直线上,只有前者才能确定一个平面,故排除③;条件④中的三条直线,它们两两相交且不交于同一点,因而其三个交点不在同一直线上,由基本性质2知其确定一个平面.随堂练习·巩固1.C根据平面的基本性质1,可知只有选项C不正确.2.C由已知条件可知,C∈γ,A,B∈γ,所以AB⊂γ.而R∈AB,所以R∈γ.又因为C,R∈β,故CR=γ∩β.3.D如图所示,延长PQ分别交CB,CD的延长线于M,N,连接MR,交BB1于E,交CC1的延长线于H,连接NH,分别交D1D,D1C1于F,G,则六边形QPERGF为截面图形.4.(1)A∈a,B∈a(2)a⊂αC∈α(3)D∉αb⊄α5.解:根据平面的基本性质2,经过不在同一条直线上的三点,有且只有一个平面.。
人教B版高中数学必修二1.2.1《平面的基本性质与推论》ppt课件

③ 根据老师的提示抓住老师的思路。老师在教学中经常有一些提示用语,如“请注意”、“我再重复一遍”、“这个问题的关键是····”等 等,这些用语往往体现了老师的思路。来自:学习方法网
• [点评] 符号语言是数学中常用的一种语言,要熟练 掌握符号语言、文字语言、图形语言之间的转化.
编后语
老师上课都有一定的思路,抓住老师的思路就能取得良好的学习效果。在上一小节中已经提及听课中要跟随老师的思路,这里再进一步论述听课时如何 抓住老师的思路。
① 根据课堂提问抓住老师的思路。老师在讲课过程中往往会提出一些问题,有的要求回答,有的则是自问自答。一般来说,老师在课堂上提出的 问题都是学习中的关键,若能抓住老师提出的问题深入思考,就可以抓住老师的思路。
•共面问题
•
已知直线m与直线a、直线b分别交于A、B
两点,且a∥b.
• 求证:直线a、b、m共面.
[解析] 如图所示,∵a∥b,∴a、 b 确定一个平面 α,
又∵m∩a=A,m∩b=B, ∵A∈α,B∈α,∴m⊂α,∴直线 a、b、m 共面.
• 已知:a、b、c、d是两两相交且不共点的四条直 线.求证:a、b、c、d共面.
• 3.公理1的作用是__判_定__直__线__在_平__面__内_的__依__据_______,
•
公理2及它的三个推论的作用是 ____________________.
确定平面的依据
• 公理3的作用是 判定两平面相交的依据,也是证明点共 线_或__线__共_点__的__依__据________________________
人教B版高中数学必修二课件:1.2.1《平面的基本性质及推论》

求证 :过直线l和点A有且只 有一个平面.
证明:点A是直线l外一点, 在l上任取两点B, C,
根据公理2,经过不共 线的三点A, B, C有一个
平面α.
因为点B, C在平面α内, 所以根据公理1, 直
线l在平面α内,即平面α是经过直线l 和点A
的平面.
C
Bl
α
A
又因为B, C在l上, 所以任Fra bibliotek经过点A和l 的 平面一定经过点A, B, C,
高中数学课件
灿若寒星整理制作
平面的基本性质
1.平面的表示方法 2.平面的基本性质
公理1:如果一条直线上的两点在一个平面内, 那么这条直线上的所有点都在这个平面内。
公理2:经过不在同一条直线上的三点有且只有 一个平面。(即不共线的三点确定一平面)
公理3:如果两个平面有一个公共点,那么它们还 有其他公共点,这些公共点的集合是一条直线。
平面的基本性质
1.平面的表示方法
α 平面α
β
D
C
A
平面β
B
平面AC
点A在直线a上, 记作_A___a_,点A不在直线a上, 记作_A___a_; 点A在平面α内, 记作_A___α_,点A不在α内, 记作_A___α_; 直线l在平面α内, 记作_l__α__, 直线l不在α内, 记作_l___α_; 直线l和平面α相交于 点A, 记作_l__α____A;
公理1:如果一条直线上的两点在一个平面内, 那么这条直线上的所有点都在这个平面内。
公理3:如果两个平面有一个公共点,那么它们还 有其他公共点,这些公共点的集合是一条直线。 公理2:经过不在同一条直线上的三点有且只有 一个平面。(即不共线的三点确定一平面) 推论1:经过一条直线和这条直线外的一点有且 只有一个平面。 推论2:经过两条相交直线有且只有一个平面。
高中数学人教A版必修2《2.2.4平面与平面的性质》教案4

必修二 2.2.4 平面与平面平行的性质教案一、教学目标1、知识与技能:掌握两个平面平行的性质定理及其应用。
2、过程与方法:学生通过观察与类比,借助实物模型理解性质及应用。
3、情感态度与价值观:进一步提高学生空间想象能力、思维能力,体会类比的作用,渗透等价转化的思想。
二、教学重点:平面与平面平行的性质定理的理解。
难点:面面平行性质定理的证明及正确应用。
三、学法指导:学生借助实物,通过类比、交流等,得出性质及基本应用。
四、教学过程(一)创设情景,揭示课题复习:两个平面平行的判定定理:βαααββ////,//,,,⇒=⊂⊂b a P b a b a I 。
相关性质:1、若两个平面平行,那么一个平面内的任意一条直线都和另一个平面平行。
2、平行于同一个平面的两个平面平行。
问题1:若两个平面平行,则一个平面内的直线与另一个平面内的直线具有什么位置关系?学生借助长方体模型思考、交流得出结论:异面或平行。
问题2:分别在两个平行平面内的两条直线满足什么条件时平行?(共面)问题3:长方体中,平面ABCD 内哪些直线会与直线D B ''平行?怎么样找到这些直线?(平面ABCD 内的直线只要与D B ''共面即可)(二)研探新知例1、如图,已知平面α、β、γ满足b a ==γβγαβαI I ,,//,求证:a // b 。
证明:因为b a ==γβγαI I ,,所以βα⊂⊂b a ,,又因为βα//,所以a ,b 没有公共点,又因为a ,b 同在平面γ内,所以a// b 。
归纳(两个平面平行的性质定理)如果两个平面同时与第三个平面相交,那么它们的交线平行。
符号语言:b a b a //,,//⇒==γβγαβαI I 。
可以由平面与平面平行得出直线与直线平行。
课堂练习1:判断下列命题是否正确。
(1)如果a ,b 是两条直线,且a // b ,那么a 平行于经过b 的任何平面。
(2)如果直线a 和平面α满足a // α,那么a 与α内的任何直线平行。
【B版】人教课标版高中数学必修二教学教案-平面的基本性质及推论2-新版

1.2.1平面基本性质与推论一、教学目标确立依据(一)课程标准要求及解读1、课程标准要求借助长方体模型,解空间点线面的基础上,抽象出空间点线面位置关系的定义,并了解如下可以作为推理依据的公理和定理.基本性质1:如果一条直线上的两点在一个平面内,那么这条直线上的所有的点都在这个平面内.基本性质2:经过不在同一直线上的三点,有且只有一个平面基本性质3:如果不重合的两个平面有一个公共点,那么它们有且只有一条过这个点的公共直线.2、课程标准解读平面的基本性质1给出了判断直线在平面内的方法,引出了直线在平面内的定义. 平面的基本性质2及平面的基本性质的三个推论,说明了怎样的条件可以确定一个平面,从而我们知道什么条件下可以画出确定的平面,什么条件下两个平面互相重合,这些都是研究空间图形时首先需要明确的.平面的基本性质3主要说明了两个相交平面的特征,对我们确定或画出两个平面的交线有重要的指导作用.平面的基本性质的推论用以确定平面的依据.(二)教材分析本节课在必修二中是第一张第二节内容,是整个立体几何的基础和工具.是立体几何的起始课,平面的概念和平面的性质是立体几何全部理论的基础.平面是把三维空间图形转化为二维平面图形的主要媒介,在立体几何平面化的过程中具有重要的桥梁作用.通过对平面基本性质的学习,有助于学生更好的学习立体几何的其他知识本节的重点是平面的基本性质及三种语言的转换.难点是平面的基本性质的理解与应用.课前要充分观察理解教室里的点、线、面,来理解点、线、面及位置关系.知识结构图基本性质1 推论1平面的基本性质基本性质2 推论2基本性质3 推论3(三)学情分析通过第一章空间几何体的学习,学生对于点线面之间的位置关系有初步认识,本节要求学生能够用集合语言表示点线面之间的位置关系,引导学生对空间中点线面的位置关系可各种可能性进行分类和研究.对于证明学生可能感觉难度较大.二、教学目标1、在直观认识和理解空间点线面的基础上,能抽象出空间点线面位置关系的定义.2、图形语言符号语言表示点线面之间的位置关系,3.通过第一节课学习,在掌握平面的三个基本性质的基础上,进一步掌握平面基本性质的三个推论;三、评价设计目标1评价:能说出线不在面内的情况,并用图形表示.能说出两个平面的位置关系.目标2评价:学生对基本性质及推论能说出条件及结论是什么,并会用图形语言及符号语言表示.目标3评价:经过小组讨论会证明平面基本性质的三个推论;四、教学方法学生从直观认识平面到理性的理解平面,有一个抽象的过程.通过这个过程可培养学生的抽象能力.要让学生认识平面的三条基本性质的直观背景.学完这三条基本性质,学生营养成用性质理解平面的习惯,学会用直线和皮面的基本性质进行推理.五、教学过程温故知新,导入新课.1.平面有哪些性质呢?2.一条直线和平面有哪几种关系呢?两个平面呢?教学重点、难点的学习与完成过程师:立体几何中有一些公理,构成一个公理体系.人们经过长期的观察和实践,把平面的三条基本性质归纳成三条公理.请同学们思考下列问题(用幻灯显示).问题1:直线l上有一个点P在平面α内,直线l是否全部落在平面α内?问题2:直线l上有两个点P、Q在平面α内,直线l是否全部落在平面α内?(用竹针穿过纸板演示问题1,用直尺紧贴着玻璃黑板演示问题2,学生思考回答后教师归纳.)【设计意图】:形象直观,学生易于接受.这就是基本性质1:如果一条直线上的两点在一个平面内,那么这条直线上的所有的点都在这个平面内..这里的条件是什么?结论是什么?生:条件是直线(a)上有两点(A、B)在平面(α)内,结论是:直线(a)在平面(α)内.师:把条件表示为A∈a,B∈b且A∈α,B∈α,把结论表示.【设计意图】:学生学会符号语言.这条公理是判定直线是否在平面内的依据,也可用于验证一个面是否是平面,如泥瓦工用直的木条刮平地面上的水泥浆.在这里,我们用平行四边形来表示平面,那么平面是不是只有平行四边形这么个范围呢?生:不是,因为平面是无限延展的.师:对,根据基本性质1,直线是可以落在平面内的,因为直线是无限延伸的,如果平面是有限的,那么无限延伸的直线又怎么能在有限的平面内呢?所以平面具有无限延展的特征.现在我们根据平面的无限延展性来观察一个现象:两个纸板交叉师:两个平面会不会只有一个公共点?生甲:只有一个公共点.生乙:因为平面是无限延展的,应当有很多公共点.师:生乙答得对,正因为平面是无限延展的,所以有一个公共点,必有无数个公共点.那么这无数个公共点在什么位置呢?(教师随手一压,一块纸板随即插入另一块纸板上事先做好的缝隙里).可见,这无数个公共点在一条直线上.这说明,如果不重合的两个平面有一个公共点,那么它们有且只有一条过这个点的公共直线.【设计意图】:形象直观,学生易于接受.此时,就说两平面相交,交线就是公共点的集合这就是基本性质3其条件和结论分别是什么?生:条件是两平面(α、β)有一公共点(A),结论是:它们有且只有一条过这个点的直线.师:条件表示为A∈α,A∈β,结论表示为:α∩β=a,A∈a,图形表示基本性质3判定两平面相交的依据,提供了确定相交平面的交线的方法.下面请同学们思考下列问题(用幻灯显示):问题1:经过空间一个已知点A可能有几个平面?问题2:经过空间两个已知点A、B可能有几个平面?问题3:经过空间三个已知点A、B、C可能有几个平面?【设计意图】:以问题串的形式引出基本性质2.(教师演示给学生看,学生思考后回答,教师归纳).这说明,经过不在同一直线上的三点,有且只有一个平面,即基本性质2其条件、结论分别是什么?生:条件是:不在同一直线上的三点(A、B、C),结论是:过这三点(A、B、C)有且只有一个平面(α).基本性质2是确定平面位置的依据之一.推论师:确定一个平面的依据,除基本性质2外,还有它的三个推论.推论1:经过一条直线和这条直线外的一点,有且只有一个平面.说出推论1的条件和结论并证明.生:条件是:一条直线和直线外一点,结论是:经过这条直线和这一点有且只有一个平面求证:经过a和A有且只有一个平面.∉已知:A l求证:经过点A和直线l有且只有一个平面.【设计意图】:学生学会将文字叙述改写为数学语言.证明:①存在性:如图(1)在直线l上任取两点B,C,据题意A、B、C三点不共线,根据基本性质2,经过不共线的三点A、B、C有一个平面αα∈B ,α∈C ∴α⊂l (基本性质1)所以平面α就是经过直线l 和点A 的平面.②唯一性: B l ∈ ,C l ∈ ,∴ 任何经过点A 和l 的平面一定经过点A 、B 、C ,三点A 、B 、C 不共线,根据基本性质2,这样的平面只有一个,由①②可知:经过一条直线和直线外一点有且只有一个平面.推论2:经过两条相交直线,有且只有一个平面.其条件、结论分别是什么?生:条件是:两条直线相交,结论是:经过这两条直线有且只有一个平面. 师(板书)已知:a ∩b =A求证:经过a 和b 有且只有一个平面.证明:①存在性: 如图(2)在a 上任取一点B ,且B ∉b,根据推论1, 经过一条直线b 和直线外一点B 有一个平面α∵A ∈a ,B ∈a ∴a α⊂所以平面α就是经过相交直线a 和b 的平面.②唯一性:∵B ∈a∴任何经过直线a 和b 的平面一定经过点B 和直线b ,∵根据推论1,这样的平面只有一个,由①②可知:经过两条相交直线,有且只有一个平面.推论3 经过两条平行直线,有且只有一个平面.已知:a∥b求证:经过a和b有且只有一个平面.证明:①存在性:如图(3)∵a∥b∴根据平行线的定义,a和b在同一平面α内.②唯一性:在a上任取一点A,在b上任取一点B,连接点A,B作直线c,∵A∈α,B∈α,∴c在α内,∵a∩c=A,b∩c=B,∴根据推论2 ,a和c在唯一的平面内,b和c在唯一的平面内.又a和b在同一平面内,则a,b,c在唯一的一个平面内.由①②可知:经过两条平行直线,有且只有一个平面.证明线共面例题:已知:a,b,c,d是不共点且两两相交的四条直线,求证:a,b,c,d共面.分析:弄清楚四条直线不共点且两两相交的含义:四条直线不共点,包括有三条直线共点的情况;两两相交是指任何两条直线都相交.在此基础上,根据平面的性质,确定一个平面,再证明所有的直线都在这个平面内.证明1º若当四条直线中有三条相交于一点,不妨设a,b,c相交于一点A∴直线d和A确定一个平面α.又设直线d与a,b,c分别相交于E,F,G,则A,E,F,G∈α.∵A,E∈α,A,E∈a,∴aα.同理可证bα,cα.∴a,b,c,d在同一平面α内.2º当四条直线中任何三条都不共点时,如图.∵这四条直线两两相交,则设相交直线a,b确定一个平面α.设直线c与a,b分别交于点H,K,则H,K∈α.又∵H,K∈c,∴cα.同理可证dα.∴a,b,c,d四条直线在同一平面α内.点评:证明若干条线(或若干个点)共面的一般步骤是:首先由题给条件中的部分线(或点)确定一个平面,然后再证明其余的线(或点)均在这个平面内.本题最容易忽视“三线共点”这一种情况.因此,在分析题意时,应仔细推敲问题中每一句话的含义.证明线共点例题. 如图,已知平面α,β,且α∩β=l.设梯形ABCD中,AD∥BC,且ABα,CDβ,求证:AB,CD,l共点(相交于一点).分析:AB,CD是梯形ABCD的两条腰,必定相交于一点M,只要证明M在l上,而l是两个平面α,β的交线,因此,只要证明M∈α,且M∈β即可.证明:∵梯形ABCD中,AD∥BC,∴AB,CD是梯形ABCD的两条腰.∴AB,CD必定相交于一点,设AB∩CD=M.又∵ABα,CDβ,∴M∈α,且M∈β.∴M∈α∩β.l,∴M∈l,即AB,CD,l共点.又∵α∩β=点评:证明多条直线共点时,与证明多点共线是一样的.当堂检测:1、下列命题是否正确.1.不共线的三点确定一个平面.(√)2.有三个公共点的两个平面重合.(√)3.三角形一定是平面图形.(√)4.平行四边形一定是平面图形.(√)5.四边形一定是平面图形.(×)6.不共线的四点确定一个平面.(×)2、P38练习B组第6题用符号语言表示.3、P38练习B组第2题.【设计意图】:检测基本性质及推论的理解及应用.归纳总结:请同学将3个平面基本性质及3个推论用图形语言及符号语言表述. 【设计意图】:学生会将自然语言、数学语言和符号语言相互转化.。
人教版数学高一人教B必修2讲义平面的基本性质与推论

1.2 点、线、面之间的位置关系1.2.1 平面的基本性质与推论1.了解平面的概念,掌握平面的画法及表示方法.(难点)2.掌握平面的基本性质及推论,能用符号语言描述空间点、直线、平面之间的位置关系.(重点)3.能用图形、文字、符号三种语言描述三个公理,并能解决空间线面的位置关系问题.(难点)[基础·初探]教材整理1平面阅读教材P35的内容,完成下列问题.1.平面的概念几何里所说的“平面”,是从课桌面、黑板面、海面这样的一些物体中抽象出来的.几何里的平面是无限延展的.2.平面的画法(1)水平放置的平面通常画成一个平行四边形,它的锐角通常画成45°,且横边长等于其邻边长的2倍.如图1-2-1①.(2)如果一个平面被另一个平面遮挡住,为了增强它的立体感,把被遮挡部分用虚线画出来.如图1-2-1②.①②图1-2-13.平面的表示法上图中图①的平面可表示为平面α、平面ABCD、平面AC或平面BD.下列说法正确的是()A.生活中的几何体都是由平面组成的B.平面无厚薄,但有边界线C.任何一个平面图形都是一个平面D.平面多边形和圆都可以表示平面【解析】由平面的特性是无限延展性知,选项A、B错误;平面图形和平面是两个完全不同的概念,平面图形是有大小的,不能无限延展,选项C错误;选项D正确.【答案】 D教材整理2平面的基本性质及推论阅读教材P35~P37“思考”以上的内容,完成下列问题.公理内容图形符号基本性质1如果一条直线上的两点在一个平面内,那么这条直线在此平面内A∈l,B∈l,且A∈α,B∈α⇒l⊂α基本性质2过不在一条直线上的三点,有且只有一个平面A,B,C三点不共线⇒存在唯一的平面α使A,B,C∈α基本性质3如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线P∈α,P∈β⇒α∩β=l,且P∈l图1-2-2推论1经过一条直线和直线外的一点,有且只有一个平面(图1-2-2①).推论2经过两条相交直线,有且只有一个平面(图1-2-2②).推论3经过两条平行直线,有且只有一个平面(图1-2-2③).判断(正确的打“√”,错误的打“×”)(1)三点可以确定一个平面.()(2)一条直线和一个点可以确定一个平面.()(3)四边形是平面图形.()(4)两条相交直线可以确定一个平面.()【解析】(1)错误.不共线的三点可以确定一个平面.(2)错误.一条直线和直线外一个点可以确定一个平面.(3)错误.四边形不一定是平面图形.(4)正确.两条相交直线可以确定一个平面.【答案】(1)×(2)×(3)×(4)√教材整理3共面与异面直线阅读教材P37~P38“练习”以上内容,完成下列问题.1.异面直线(1)定义:把不同在任何一个平面内的两条直线叫做异面直线.(2)画法:(通常用平面衬托)图1-2-32.空间两条直线的位置关系⎩⎪⎨⎪⎧共面直线⎩⎨⎧相交直线:同一平面内,有且只有一个公共点.平行直线:同一平面内,没有公共点.异面直线:不同在任何一个平面内,没有公共点.判断(正确的打“√”,错误的打“×”)(1)两条直线无公共点,则这两条直线平行.()(2)两直线若不是异面直线,则必相交或平行.()(3)过平面外一点与平面内一点的连线,与平面内的任意一条直线均构成异面直线.()(4)和两条异面直线都相交的两直线必是异面直线.()【解析】(1)错误.空间两直线无公共点,则可能平行,也可能异面.(2)正确.因空间两条不重合的直线的位置关系只有三种:平行、相交或异面.(3)错误.过平面外一点与平面内一点的连线,和平面内过该点的直线是相交直线.(4)错误.和两条异面直线都相交的两直线也可能是相交直线.【答案】(1)×(2)√(3)×(4)×[小组合作型]文字语言、图形语言、符号语言的相互转化出相应的图形:(1)A∈α,B∉α;(2)l⊂α,m⊄α,m∩α=A,A∉l;(3)P∈l,P∉α,Q∈l,Q∈α.【精彩点拨】解答本题要正确理解立体几何中表示点、线、面之间位置关系的符号“∈”,“∉”,“⊂”,“⊄”,“∩”的意义,在此基础上,由已知给出的符号表示语句,写出相应的点、线、面的位置关系,画出图形.【自主解答】(1)点A在平面α内,点B不在平面α内;(2)直线l在平面α内,直线m与平面α相交于点A,且点A不在直线l上;(3)直线l经过平面α外一点P和平面α内一点Q.图形分别如图(1),(2),(3)所示.图(1)图(2)图(3)1.用文字语言、符号语言表示一个图形时,首先仔细观察图形有几个平面、几条直线且相互之间的位置关系如何,试着用文字语言表示,再用符号语言表示.2.要注意符号语言的意义.如点与直线的位置关系只能用“∈”或“∉”表示,直线与平面的位置关系只能用“⊂”或“⊄”表示.3.由符号语言或文字语言画相应的图形时,要注意实线和虚线的区别.[再练一题]1.根据图形用符号表示下列点、直线、平面之间的关系.图1-2-4(1)点P与直线AB;(2)点C与直线AB;(3)点M与平面AC;(4)点A1与平面AC;(5)直线AB与直线BC;(6)直线AB与平面AC;(7)平面A1B与平面AC.【解】(1)点P∈直线AB;(2)点C∉直线AB;(3)点M∈平面AC;(4)点A1∉平面AC;(5)直线AB∩直线BC=点B;(6)直线AB⊂平面AC;(7)平面A1B∩平面AC=直线AB.点、线共面问题内.【导学号:45722037】【精彩点拨】四条直线两两相交且不共点,可能有两种情况:一是有三条直线共点;二是任意三条直线都不共点,故要分两种情况.【自主解答】已知:a,b,c,d四条直线两两相交,且不共点,求证:a,b,c,d四线共面.证明:(1)若a,b,c三线共点于O,如图所示,∵O∉d,∴经过d与点O有且只有一个平面α.∵A、B、C分别是d与a、b、c的交点,∴A、B、C三点在平面α内.由公理1知a、b、c都在平面α内,故a、b、c、d共面.(2)若a、b、c、d无三线共点,如图所示,∵a∩b=A,∴经过a、b有且仅有一个平面α,∴B、C∈α.由公理1知c⊂α.同理,d⊂α,从而有a、b、c、d共面.综上所述,四条直线两两相交,且不共点,这四条直线在同一平面内.证明点线共面常用的方法1.纳入法:先由部分直线确定一个平面,再证明其他直线也在这个平面内.2.重合法:先说明一些直线在一个平面内,另一些直线在另一个平面内,再证明两个平面重合.[再练一题]2.一条直线与三条平行直线都相交,求证:这四条直线共面.【解】已知:a∥b∥c,l∩a=A,l∩b=B,l∩c=C.求证:直线a,b,c,l共面.证明:法一∵a∥b,∴a,b确定一个平面α,∵l∩a=A,l∩b=B,∴A∈α,B∈α,故l⊂α.又∵a∥c,∴a,c确定一个平面β.同理可证l⊂β,∴α∩β=a且α∩β=l.∵过两条相交直线a、l有且只有一个平面,故α与β重合,即直线a,b,c,l共面.法二由法一得a、b、l共面α,也就是说b在a、l确定的平面α内.同理可证c在a、l确定的平面α内.∵过a和l只能确定一个平面,∴a,b,c,l共面.空间两直线位置关系的判定如图1-2-5,正方体ABCD-A1B1C1D1中,判断下列直线的位置关系:图1-2-5①直线A1B与直线D1C的位置关系是________;②直线A1B与直线B1C的位置关系是________;③直线D1D与直线D1C的位置关系是________;④直线AB与直线B1C的位置关系是________.【精彩点拨】判断两直线的位置关系,主要依据定义判断.【自主解答】根据题目条件知直线A1B与直线D1C在平面A1BCD1中,且没有交点,则两直线“平行”,所以①应该填“平行”;点A1、B、B1在一个平面A1BB1内,而C不在平面A1BB1内,则直线A1B与直线B1C“异面”.同理,直线AB与直线B1C“异面”.所以②④都应该填“异面”;直线D1D与直线D1C 相交于D1点,所以③应该填“相交”.【答案】①平行②异面③相交④异面1.判定两条直线平行与相交可用平面几何的方法去判断.2.判定两条直线是异面直线有定义法和排除法,由于使用定义判断不方便,故常用排除法,即说明这两条直线不平行、不相交,则它们异面.[再练一题]3.若a、b是异面直线,b、c是异面直线,则()A.a∥cB.a、c是异面直线C.a、c相交D.a、c平行或相交或异面【解析】若a、b是异面直线,b、c是异面直线,那么a、c可以平行,可以相交,可以异面.【答案】 D[探究共研型]点共线与线共点问题探究1如图1-2-6,在正方体ABCD-A 1B1C1D1中,设A1C∩平面ABC1D1=E.能否判断点E在平面A1BCD1内?图1-2-6【提示】如图,连接BD1,∵A1C∩平面ABC1D1=E,∴E∈A1C,E∈平面ABC1D1.∵A1C⊂平面A1BCD1,∴E∈平面A1BCD1.探究2上述问题中,你能证明B,E,D1三点共线吗?【提示】由于平面A1BCD1与平面ABC1D1交于直线BD1,又E∈BD1,根据公理3可知B,E,D1三点共线.如图1-2-7,在正方体ABCD-A1B1C1D1中,点M,N,E,F分别是棱CD,AB,DD1,AA1上的点,若MN与EF交于点Q,求证:D,A,Q三点共线.图1-2-7【精彩点拨】欲证D、A、Q三点共线,只需说明三点均在平面AD1和平面AC的交线DA上即可.【自主解答】∵MN∩EF=Q,∴Q∈直线MN,Q∈直线EF,又∵M∈直线CD,N∈直线AB,CD⊂平面ABCD,AB⊂平面ABCD.∴M、N∈平面ABCD,∴MN⊂平面ABCD.∴Q∈平面ABCD.同理,可得EF⊂平面ADD1A1.∴Q∈平面ADD1A1,又∵平面ABCD∩平面ADD1A1=AD,∴Q∈直线AD,即D,A,Q三点共线.点共线与线共点的证明思路1.点共线的思路:证明这些点都分别在两个相交的平面内,因此也在两个平面的交线上.2.线共点的思路:先由两条直线交于一点,再证明该点在第三条直线上.[再练一题]4.如图1-2-8,在四边形ABCD中,已知AB∥CD,直线AB,BC,AD,DC 分别与平面α相交于点E,G,H,F.图1-2-8求证:E,F,G,H四点必定共线.【证明】∵AB∥CD,∴AB,CD确定一个平面β,又∵AB∩α=E,AB⊂β,∴E∈α,E∈β,即E为平面α与β的一个公共点.同理可证F,G,H均为平面α与β的公共点,∵两个平面有公共点,它们有且只有一条通过公共点的公共直线,∴E,F,G,H四点必定共线.1.一条直线与两条异面直线中的一条平行,则它和另一条的位置关系是()A.平行或异面B.相交或异面C.异面D.相交【解析】如图,在正方体ABCD-A1B1C1D1中,AA1与BC是异面直线,又AA1∥BB1,AA1∥DD1,显然BB1∩BC=B,DD1与BC是异面直线,故选B.【答案】 B2.下列说法中正确的个数为()①三角形一定是平面图形;②若四边形的两对角线相交于一点,则该四边形是平面图形;③圆心和圆上两点可确定一个平面;④三条平行线最多可确定三个平面.A.1B.2C.3D.4【解析】圆上两点为直径端点时,它们与圆心共线,此时这三个点不能确定平面,故③不正确,①②④正确,故选C.【答案】 C3.设平面α与平面β交于直线l,A∈α,B∈α,且直线AB∩l=C,则直线AB∩β=________.【导学号:45722038】【解析】∵α∩β=l,AB∩l=C,∴C∈β,C∈AB,∴AB∩β=C.【答案】 C4.有以下三个说法:①平面外的一条直线与这个平面最多有一个公共点;②直线l在平面α内,可以用符号“l∈α”表示;③已知平面α与β不重合,若平面α内的一条直线a与平面β内的一条直线b相交,则α与β相交.其中正确的序号是________.【解析】若直线与平面有两个公共点,则这条直线一定在这个平面内,故①正确;直线l在平面α内用符号“⊂”表示,即l⊂α,②错误;由a与b相交,说明两个平面有公共点,因此一定相交,故③正确.【答案】①③5.如图1-2-9,三个平面α,β,γ两两相交于三条直线,即α∩β=c,β∩γ=a,γ∩α=b,若直线a和b不平行.图1-2-9求证:a,b,c三条直线必过同一点.【证明】∵α∩γ=b,β∩γ=a,∴a⊂γ,b⊂γ.由于直线a和b不平行,∴a、b必相交.设a∩b=P,如图,则P∈a,P∈b.∵a⊂β,b⊂α,∴P∈β,P∈α.又α∩β=c,∴P∈c,即交线c经过点P.∴a、b、c三条直线相交于同一点.。
高B数学必修二课件平面的基本性质与推论

空间向量的线性运算
空间向量的加法运算
空间向量的减法运算
空间向量加法运算遵循平行四边形法 则或三角形法则。两个空间向量相加 ,其和向量也是一个空间向量,其大 小等于两个向量的大小之和,方向遵 循平行四边形法则或三角形法则。
空间向量减法运算遵循三角形法则。 两个空间向量相减,其差向量也是一 个空间向量,其大小等于两个向量的 大小之差,方向遵循三角形法则。
直线在平面内的判定
判定定理
如果一条直线上的两个点在平面内, 则这条直线在平面内。
推论
如果一条直线与一个平面有一个公共 点,且这条直线在平面内,则这条直 线完全在平面内。
直线与平面平行的判定与性质
判定定理
如果一条直线与一个平面没有公共点,则这条直线与这个平 面平行。
性质定理
如果一条直线与一个平面平行,那么过这条直线的任一平面 与这个平面的交线与这条直线平行。
空间向量在平面几何中的拓展应用
01
向量在解析几何中的应用
通过向量的坐标表示和运算,可以建立平面解析几何的基本概念和性质
,如直线的方程、圆的方程等。
02
向量在物理中的应用
向量在物理中有着广泛的应用,如力、速度、加速度等都是向量,通过
向量的运算可以解决物理中的实际问题。
03
向量在计算机图形学中的应用
计算机图形学是研究计算机生成和操作图形的科学,向量在计算机图形
学中有着重要的应用,如向量的线性变换可以实现图形的缩放、旋转和
平移等操作。
06
总结与展望
平面的基本性质与推论的总结
平面的基本性质
平面是无限延展的,没有边界; 平面内任意两点可以确定一条直 线,且该直线在平面内;不在同 一直线上的三点确定一个平面。
高中数学的必修二数学平面的基本性质知识点

高中数学的必修二数学平面的基本性质知识点平面的基本性质教学目标1、知识与能力:(1)巩固平面的基本性质即四条推断出公理和三条推论.(2)能使用公理和推论进行解题.2、过程与方法:(1)体验在空间确定一个平面的过程与方法;(2)掌握利用平面的基本性质证明三点共线、三线共点、多线共面的方法。
3、情感成见与价值观:培养学生认真观察的态度,慎密思考的习惯,提高学生审美能力和空间想象的能力。
教学重点平面的三条基本性质即三条推论.教学难点准确运用三条公理和推论解题.教学过程一、问题情境问题1:空间共点的三条直线二维能确定几个平面?空间互相对角线平行的三条直线呢?问题2:如何判断办公桌的四条腿内则的底端是否在一个平面内?二、温故知新公理1一处如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内.公理2如果两个平面有两个一个公共设施点,那么它们还有其它公用点,这些公共点的集合是经过这个公共给定点的一条直线.公理3经过不在同一条直线上的三点,有且只有一个平面.推论1经过一条直线和这条直线外的一点,有且只有一个平面.推论2经过两条直角直线,有且只有一个平面.推论3经过两条平行平行线,有且只有一个平面.公理4(平行公理)平行于同一条直线的两条直线互相平行.把作出以上各公理及推论进行对比:三、数学运用基础训练:(1)已知:;求证:直线AD、BD、CD共面.证明:——公理3推论1——公理1同理可证,,直线AD、BD、CD共面【解题反思1】1。
逻辑要严谨2.书写要规范3.证明共面的步骤:(1)确定平面——公理3及其3个推论(2)证线“归”面(线在面内如:)——公理1(3)作出结论。
变式1、如果直线两两交汇,那么这三条直线是否共面?(口答)变式2、已知空间不共面的二点,过其中任意三点可以三维空间确定一个平面,由这四个一两个点能确知几个平面?变式3、四条线段顺次首尾连接,所得的图形一定是平面曲面图形吗?(口答)(2)已知直线满足:;求证:直线证明:——公理3推论3——公理1直线共面提高训练:已知,求证:四条直线在同一平面内.思路分析:考虑由直线a,b确定一个平面,再证明直线c,l在此平面上,但十分困难。
平面的基本性质及推论

(2)推论2:
文字语言 :经过两条相交直线,有且只有一 个平面.
图形语言: a是任意一条直线
符号语言: b是任意一条直线
a∩b=A a,b共面于平面α,且α是惟一的 .
(2)推论3: 文字语言 :经过两条平行直线,有且只有一 个平面. 图形语言:
符号语言:a,b是两条直线
a//b a,b共面于平面α,且αБайду номын сангаас惟一的 .
3条直线相交于一点时:
(1)、3条直线共面时 (2)、每2条直线确定一平面时
三条直线相交于一点,用其中的两条确定 平面,可以确定1、3个。
4条直线相交于一点时:
(1)、4条直线 全共面时
(2)、有3条直线 共面时
(3)、每2条直线 都确定一平面时
三条直线相交于一点,用其中的两条 确定平面,可以确定1、4、6个。
把一条直线在面内旋转,固定两个点在面内后, 如果其他点也在面内,则该面为平面。
公理1的作用有三:
一 是可以用来判定一条直线是否在平面内,即 要判定直线在平面内,只需确定直线上两个 点在平面内即可;
二 是可以用来判定点在平面内,即如果直线在 平面内、点在直线上,则点在平面内.
三 是表明平面是“平的”
用手指头将一本书平衡地摆方在空 间某一位置,至少需要几个手指头?
手指的位置需要满足什么条件?
B
αA
C
公理2.过不在同一直线上的三点,有且只有一个平面.
文字语言:
公理2.过不在同一直线上的三点,有且只有一个平面.
图形语言: 符号语言:
B
αA
C
或记为平面ABC
A, B,C三点不共线 有且只有一个平面
点A在直线a上: 记为:A∈a
【高中数学】平面 课件 2022-2023学年高一下学期数学人教A版(2019)必修第二册

四、平面的基本性质
思考:两点可以确定一条直线,那么几个点可以确定一个平面呢?
自行车着地 “站稳”,三脚架
支撑照相机…….由这些事实和
类似经验说明什么?
平面的基本事实1
文字语言:过不在一条直线上的三个点,有且只有一个平面
也可以简单说成:“不共线的三点确定一个平面”.
图形语言:
C
α A
B
符号语言: A,B,C不共线=>存在唯一的平
α
M ,M a
β
题型三:确定平面个数问题
1.【见课本第132页,第7题】
三条直线两两平行且不共面,每两条直线确定一个一个平面,
一共可以确定几个平面?如果三条直线相较于一点,它们最
多可以确定几个平面?
3
A
3
2.不共面的四点可以确定几个平面?
4
D
B
3.空间有5个点,其中有四个点在同一平面内,
但没有任何的三点共线.这样的5个点确定平面
的个数最多可以确定几个平面?
7
C
题型四:点共线、线共点、点共面、线共面问题
1.【见课本第132页,第6题】
如果一条直线与两条平行直线都相交,那么这三条直线共面吗?
题型四:点共线、线共点、点共面、线共面问题
例1.如右图在空间四边形ABCD中,
A
若直线EH和FG相交于K,则K点在
BD上吗,为什么?
E·
H
·
B
F·
D
·
G
C
K
推论1
基本事实1给出了确定一个平面的一种方法,
利用基本事实1和基本事实2,再结合“两点
确定一条直线”,你还能得到一些确定一个
人教版高数必修二第4讲:平面的基本性质与推论(教师版)
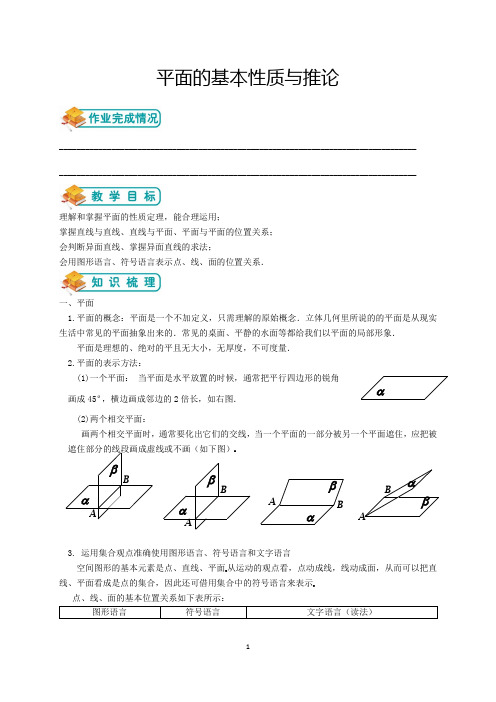
平面的基本性质与推论__________________________________________________________________________________ __________________________________________________________________________________理解和掌握平面的性质定理,能合理运用;掌握直线与直线、直线与平面、平面与平面的位置关系; 会判断异面直线、掌握异面直线的求法;会用图形语言、符号语言表示点、线、面的位置关系.一、平面1.平面的概念:平面是一个不加定义,只需理解的原始概念.立体几何里所说的的平面是从现实生活中常见的平面抽象出来的.常见的桌面、平静的水面等都给我们以平面的局部形象.平面是理想的、绝对的平且无大小,无厚度,不可度量. 2.平面的表示方法:(1)一个平面: 当平面是水平放置的时候,通常把平行四边形的锐角 画成45,横边画成邻边的2倍长,如右图. (2)两个相交平面:画两个相交平面时,通常要化出它们的交线,当一个平面的一部分被另一个平面遮住,应把被遮住部分的线段画成虚线或不画(如下图)3. 运用集合观点准确使用图形语言、符号语言和文字语言空间图形的基本元素是点、直线、平面从运动的观点看,点动成线,线动成面,从而可以把直线、平面看成是点的集合,因此还可借用集合中的符号语言来表示点、线、面的基本位置关系如下表所示:αBAβαABαβαβBAAβαBb A =a α⊂α=∅A α=l β= 二、平面的基本性质1. 公理1 如果一条直线的两点在一个平面内,那么这条直线上的所有点都在这个平面内推理模式:A ABB ααα∈⎫⇒⊂⎬∈⎭. 如图示: 或者:∵,A B αα∈∈,∴AB α⊂ 公理1的作用:①判定直线是否在平面内;②判定点是否在平面内; ③检验面是否是平面.2. 公理2 如果两个平面有一个公共点,那么它们还有其他公共点,且所有这些公共点的集合是一条过这个公共点的直线推理模式:A A l A ααββ∈⎫⇒∈=⎬∈⎭如图示:或者:∵,A A αβ∈∈,∴,l A l αβ=∈公理2的作用:(1)判断两个平面是否相交及交线位置; (2)判断点是否在线上今后所说的两个平面(或两条直线),如无特殊说明,均指不同的平面(直线).(1)以上是确定平面的四个不同的条件,是判断两个平面重合的依据,是证明点线共面的依据,也是作截面、辅助面的依据.(2)有且只有一个”的含义要准确理解.这里的“有”是说图形的存在,“只有一个”是说图形唯一.因此,在证明有关这类语句的命题时,要从“存在性”和“唯一性”两方面来论证. 3. 公理3 经过不在同一条直线上的三点,有且只有一个平面推理模式:,, ,,,,A B C A B C A B C ααβ⎫⎪∈⇒⎬⎪∈⎭不共线与β重合或者:∵,,A B C 不共线,∴存在唯一的平面α,使得,,A B C α∈. 推论1:经过一条直线和这条直线外的一点,有且只有一个平面; 推论2:经过两条相交直线,有且只有一个平面; 推论3:经过两条平行直线,有且只有一个平面.(1)以上是确定平面的四个不同的条件,是判断两个平面重合的依据,是证明点线共面的依据,也是作截面、辅助面的依据.(2)“有且只有一个”的含义要准确理解.这里的“有”是说图形的存在,“只有一个”是说图形唯一.因此,在证明有关这类语句的命题时,要从“存在性”和“唯一性”两方面来论证. 三、空间两直线的位置关系四、平行直线 1. 公理4 平行公理平行于同一条直线的两条直线互相平行推理模式://,////a b b c a c ⇒.(1)它是判断空间两条直线平行的依据; (2)它说明平行关系具有传递性 2.等角定理如果一个角的两边和另一个角的两边分别平行,且方向相同,那么这两个角相等. 由球的半径R 计算球表面积的公式:S 球= .即球面面积等于它的大圆面积的4倍. 五、异面直线 1. 定义:不在任何一个平面内的两条直线叫做异面直线(1)异面直线既不平行,也不相交,永远不存在一个平面能同时包含这两直线; (2)不能把异面直线误认为:分别在不同平面内的两条直线为异面直线 (3)异面直线一般是对两条直线而言的,没有三条异面直线的说法. 2.异面直线的画法画异面直线时,为了充分显示不共面的特点,常常需要以辅助平面为衬托,以加强直观性.bb βb3.异面直线判定定理过平面内一点与平面外一点的直线,和这个平面内不经过该点的直线是异面直线推理模式:l A B B L ααα⊂⎫⎪∉⎪⇒⎬∈⎪⎪∉⎭直线AB 与直线l 是异面直线六、异面直线所成的角 1. 定义:已知a ,b 是两条异面直线,经过空间任意一点O 作直线//,//a a b b '',我们把直线a '和b '所成的锐角(或直角)叫做异面直线a ,b 所成的角.(1)异面直线所成的角与O 点的位置无关.(2)如果两条异面直线所成角是直角,则说这两条异面直线互相垂直,记作a b ⊥. (3)异面直线所成角的范围是0,2π⎛⎤⎥⎝⎦. 2. 求异面直线所成角的步骤(1)恰当选点,由平移构造出一个交角; (2)证平行关系成立;(3)把角放入三角形或其它平面图形中求出;(4)作结论:若求出的角是锐角或直角,则它就是所求异面直线所成的角;若求出的角是钝角,则它的补角才是所求异面直线所成的角. 七、直线、平面的位置关系1.空间直线与平面的位置关系有以下三种:(1)直线在平面内:如果一条直线a 与平面α有两个不同的公共点,那么这条直线就在这个平面内,记作a ⊂α.(2)直线与平面相交:直线a 与平面α只有一个公共点A ,叫做直线与平面相交,记作a ∩α=A ,公共点A 叫做直线a 与平面α的交点.(3)直线与平面平行:如果一条直线a 与平面α没有公共点,叫做直线与平面平行,记作a ∥α. 2.两个平面的位置关系有且只有一下两种: (1)两个平面平行---没有交点 (2)两个平面相交---有一条公共直线3.顺次连接不共面的四点A 、B 、C 、D 所构成的图形,叫做空间四边形.这四个点中的各个点叫做空间四边形的顶点;所连接的相邻顶点间的线段叫做空间四边形的边;连接不相邻的顶点的线段叫做空间四边形的对角线.类型一 平面及其性质例1:对下图的几何图形,下列表示错误的是( )A .l ∈αB .P ∉lC .l ⊂αD .P ∈α解析:由图形可知,l ⊂α,P ∉l ,P ∈α,故选A. 答案:A练习1:判断下列说法是否正确,并说明理由.(1)平面的形状是平行四边形( ) (2)任何一个平面图形都可以表示平面( ) (3)平面ABCD 的面积为10㎡( ) (4)空间图形中,后引的辅助线是虚线( ) 答案: (1)(3)(4)错,(2)正确. 练习2:1、下列说法正确的个数( )①铺的很平的一张纸是一个平面;②可以一个长20cm 、宽30cm 的平面;③通常300页的书要比10页的书厚一些,那么300个平面重合在一起时一定比10个平面重合在一起厚. A 、0个 B 、1个 C 、2个 D 、3个 答案:A练习3:若点Q 在直线b 上,b 在直线平面β内,则,,Q b β之间的关系可记作( B ) A 、Q b β∈∈ B 、Q b β∈⊂ C 、Q b β⊂⊂ D 、Q b β⊂∈ 答案:B例2:如右图,已知,,,E F G H 分别为空间四边形ABCD 各边,,,AB AD BC CD上的点,且EF GH P =,求证:,,B D P 共线.解析:由公理2可判断D 点在交线上. 答案:证明:∵EFGH P = ∴P EF ∈∵EF ⊂平面ABD ∴P ∈平面ABD 同理P ∈平面CBD ∵平面ABD平面CBD BD = ∴P BD ∈∴,,B D P 共线练习1:已知l 与三条平行线,,a b c 都相交,求证:l 与,,a b c 共面. 答案: 证明:如右图所示∵//a b ∴直线a 与直线b 确定一个平面,设为α ∵,la A lb B == ∴,A a B b ∈∈∴,A B αα∈∈ ∴l α⊂PH GF EDC BACB Aαlcba∵//b c ∴直线b 与直线c 确定一个平面,设为β 同理可证l β⊂ ∵,,,,l l b b l b B αβαβ⊂⊂⊂⊂= ∴平面α与平面β重合∴l 与,,a b c 共面练习2:两个不重合的平面有公共点,则公共点的个数是( )A 、2个B 、有无数个且在一条直线上C 、一个或无数个D 、1个 答案:B练习3:下列命题:①公理1可用集合符号叙述为:若,A l B l ∈∈且,A B αα∈∈,则必有l α∈;②四边形的两条对角线必交于一点;③用平行四边形表示的平面,以平行四边形的四边作为平面边界线;④梯形是平面图形.其中正确的命题个数为( )A 、1B 、2C 、3D 、4 答案:D类型二 直线及其位置关系例3:若a 、b 是异面直线,直线c ∥a ,则c 与b 的位置关系是( )A .相交B .异面C .平行D .异面或相交解析:如图,借助正方体可知c 与b 相交或异面. 答案:D 练习1:在长方体ABCD -A 1B 1C 1D 1中,E 、F 分别是BD 和CD 的中点,长方体的各棱中与EF 平行的有( )A .1条B .2条C .3条D .4条答案:如图所示∵E 、F 分别为BD 、CD 的中点, ∴EF ∥BC ,又∵BC ∥B 1C 1,∴EF ∥B 1C 1,同理,EF ∥A 1D 1,EF ∥AD . 故选D .练习2:空间四边形ABCD 中,给出下列说法:①直线AB 与CD 异面; ②对角线AC 与BD 相交; ③四条边不能都相等;④四条边的中点组成一个平行四边形. 其中正确说法的个数是( )A .1个B .2个C .3个D .4个答案:本题主要考查空间四边形,关键要理解空间四边形的概念.由定义知①正确;②错误,否则A 、B 、C 、D 四点共面;③不正确,可将一个菱形沿一条对角线折起一个角度,就成为四边相等的空间四边形;④正确,由平行四边形的判定定理可证.故选B . 练习3:a 、b 、c 是空间中三条直线,下面给出几种说法:①若a ∥b ,b ∥c ,则a ∥c ;②若a 与b 相交,b 与c 相交,则a 与c 也相交;③若a 、b 分别在两个相交平面内,则这两条直线不可能平行. 上述说法中正确的是________(仅填序号). 答案:由基本性质4知①正确.若a 与b 相交,b 与c 相交,则a 与c 可能平行,也可能相交或异面,②错误. 若平面α∩β=l ,a ⊂α,b ⊂β,a ∥l ,b ∥l ,则a ∥b ,③错误.例4:已知正方体1111ABCD A B C D -,E 、F 分别为1AA 、1CC 的中点,求证:1//BF ED 解析:平行四边形是平面图形,若能证得四边形的一组对边平行且相等,那么这个四边形就是平行四边形.答案:证明:如右图,取1BB 中点G ,连结1GC 、GE . ∵F 为1CC 的中点 ∴1//BG C F∴四边形1BGC F 为平行四边形 ∴1//BF GC 又∵111111//,//EG A B C D A B ∴11//EG C D∴ 四边形11EGC D 为平行四边形 ∴11//ED GC ∴1//BF ED练习1:已知棱长为a 正方体1111ABCD A B C D -,M 、N 分别为CD 、AD 的中点, 求证:四边形11MNAC 是梯形答案:证明:如右图 ∵M 、N 分别为CD 、AD 的中点∴1//2MN AC 由正方体的性质知11//AC AC ∴111//2MN A C ∴四边形 11MNAC 是梯形.练习2:已知E 、F 、G 、H 为空间四边形ABCD 的边AB 、BC 、CD 、DA 上的点,若AE AB =AH AD =12,CF CB =CG CD =13,则四边形EFGH 形状为________. 答案:如右图在△ABD 中,∵AE AB =AH AD =12,∴EH ∥BD 且EH =12BD .在△BCD 中,∵CF CB =CG CD =13,∴FG ∥BD 且FG =13BD ,∴EH ∥FG 且EH >FG ,∴四边形EFGH 为梯形.例5:已知E 、1E 分别是正方体1111ABCD A B C D -的棱AD 、11A D 的中点.N D 1C 1B 1MA 1D CBA求证:111BEC B E C ∠=∠解析:由等角定理,证明角的边之间的关系,进而得到角的关系. 答案: 证明:如右图,连结1EE∵E 、1E 分别是AD 、11A D 的中点 ∴11//A E AE ∴四边形11A E EA 为平行四边形 ∴11//A A E E 又∵11//A A B B ∴11//E E B B∴四边形11E EBB 是平行四边形 ∴11//E B EB 同理可证:11//E C EC又111C E B ∠与CEB ∠方向相同 ∴111BEC B E C ∠=∠练习1:如右图,111,,AA BB CC 不共面,且1111//,//BB AA CC AA ,求证:△ABC ≌△111A B C答案:证明:∵11//BB AA ∴四边形11AA B B 是平行四边形 ∴11//AB A B 同理可证:11//AC AC又∵BAC ∠和111B AC ∠方向相同 ∴BAC ∠=111B A C ∠ ∴△ABC 和△111A B C 中有1111111AB A B AC A C BAC B A C=⎧⎪=⎨⎪∠=∠⎩∴△ABC ≌△111A B C练习2:在平行六面体ABCD -A 1B 1C 1D 1中,M 、N 、P 分别是CC 1、B 1C 1、C 1D 1的中点.求证:∠NMP =∠BA 1D.答案:如图,连接CB 1、CD 1,易得 四边形A 1B 1CD 是平行四边形, ∴A 1D ∥B 1C .∵M 、N 分别是CC 1、B 1C 1的中点, ∴MN ∥B 1C ,∴MN ∥A 1D .∴四边形A 1BCD 1是平行四边形, ∴A 1B ∥CD 1.C 1B 1A 1C∵M 、P 分别是CC 1、C 1D 1的中点,∴MP ∥CD 1, ∴MP ∥A 1B ,∴∠NMP 和∠BA 1D 的两边分别平行且方向都相反, ∴∠NMP =∠BA 1D .例6:如右图,已知不共面的直线,,a b c 相交于O 点,M 、P 是直线a 上两点,N 、Q 分别是直线b 、c 上一点.求证:MN 和PQ 是异面直线. 解析:证明其中一点不属于两外三点确定的平面即可. 答案:证明:∵ab O = ∴由a 、c 确定一个面,设为β∵,P a Q c ∈∈ ∴,P Q ββ∈∈∴PQ β⊂且,M M PQ β∈∉ 又∵,,a b c 不共面,N b ∈ ∴N B ∉ ∴MN 和PQ 是异面直线练习1:1、两条异面直线是指( )A 、空间没有公共点的两条直线B 、分别位于两个平面内的直线C 、平面内的一条直线与平面外的一条直线D 、既不平行也不相交的两条直线 答案:D练习2:下列说法正确的有 .①两直线无公共点,则两直线平行;②两直线若不是异面直线,则必相交或平行;③过平面外一点与平面内一点的连线,与平面内的任一直线均构成异面直线;④和两条一面直线都相交的直线的两直线必是异面直线. 答案:② 练习3:已知,,a b a b A αββ=⊂=且,//c c a α⊂,求证:b ,c 为异面直线.答案:证明:如右图 ∵,,c a b A a ααβ⊂== ∴A a α∈⊂而//a c∴A c ∉在直线b 上任取不同于A 的一点B ∵b β⊂ ∴B α∉ ∴AB 与c 是异面直线,即b ,c 为异面直线例7:正四面体A BCD -的棱长为a ,E 、F 分别为棱AD 、BC 的中点,求异面直线AF 和CE 所成角的余弦值.解析:找出其中一条直线的平行线,构造三角形求解.答案:如右图, 连结FD ,在面AFD 内过E 点作//EO AF 交FD 于O ,则OEC ∠ (或其补角)为异面直线AF 与CE 所成的角,且O 是FD 的中点.c baOQPNMEA又∵E 为AD 的中点 ∴1//2EO AF ∵△ABC 和△ACD 均为等边三角形,且边长为a ,AF 、CE 分别是它们的中线∴AF CE ==,则12EO == 在Rt △DFC中,11,242FO FD FC a ===∴4CO a == 在△OEC中,2222222cos 23EO EC OC OEC EO EC ⎫⎫⎫+-⎪⎪⎪⎪⎪⎪+-∠===⨯⨯即异面直线AF 与CE 所成的角的余弦值为23练习1:已知m 、n 为异面直线,m α⊂,n β⊂,l αβ=,则直线l ( )A 、与m 、n 都相交B 、与m 、n 至少一条相交C 、与m 、n 都不相交D 、至多与m 、n 中的一条相交 答案:B练习2:在棱长为1的1111ABCD A B C D -中,M 和N 分别为11A B 和1BB 的中点,那么直线AM 与CN 所成角的余弦值是( )AB、35 D 、25答案:D练习3:如右图,等腰直角三角形ABC中,90,,A BC DA AC DA AB ∠==⊥⊥,若1DA =,且E 为DA 的中点.求异面直线BE 与CD 所成角的余弦值.答案:取AC 的中点F ,连结EF ,在△ACD 中,E 、F 分别为AD 、AC 的中点.∴//EF CD ∴BEF ∠或其补角即为所求异面直线BE 与CD 所成的角在Rt △EAB 中,111,22AB AE AD ===∴BE =在Rt △AEF 中,11,22AF AE ==∴EF = 在Rt △ABF 中,11,2AB AF ==∴2BF = FE D CBA在等腰△EBF中,12cos EF FEB BE ∠== ∴异面直线BE 与CD1.在空间内,可以确定一个平面的条件是( )A 、两两相交的三条直线B 、三条直线,其中的一条与另外两条直线分别相交C 、三个点D 、三条直线,它们两两相交,但不交于同一点E 、两条直线答案:D2.分别和两条异面直线都相交的两条直线的位置关系是( )A .异面B .相交C .平行D .异面或相交答案:D3.一条直线与两条平行线中的一条是异面直线,那么它与另一条的位置关系是( )A 、相交B 、异面C 、平行D 、相交或异面答案:D4.从空间一点P 分别向BAC ∠的两边,AB AC 作垂线,PE PF ,垂足分别为,E F ,则EPF ∠与BAC ∠的关系为( )A 、互补B 、相等C 、互补或相等D 、以上都不对答案: D5.在正四面体A BCD -中,E 为AD 的中点,则AB 与CE 所成角的余弦值为 ._________________________________________________________________________________ _________________________________________________________________________________基础巩固1. 空间有四个点,其中无三点共线,可确定 个平面;若将此四点两两相连,再以所得线段中点为顶点构成一个几何体,则这个几何体至多有 个面.答案:1或4,82、三个两两相交的平面最多可把空间分为 个部分.答案:83、下面6个命题:①四边相等的四边形是菱形;②两组对边相等的四边形是平行四边形;③若四边形有一组对角相等,则该四边形是圆内接四边形;④在空间,过已知直线外一点,引该直线的平行线,可能不只一条;⑤四条直线两两平行,无三线共面,它们共可确定6个平面.其中正确命题的个数是( )A 、0B 、1C 、2D 、3答案:B4. 在正方体1111ABCD A B C D 中,与1AD 成60的面对角线共有( )A 、4条B 、6条C 、8条D 、10条答案:C5. 已已知棱长为a 的正方体ABCD -A ′B ′C ′D ′中,M 、N 分别为CD 、AD 的中点,则MN 与A ′C ′的位置关系是________.答案:平行能力提升6. 如图,点P 、Q 、R 、S 分别在正方体的四条棱上,且是所在棱的中点,则直线PQ 与RS 是异面直线的一个图是________.答案:③. ①中PQ ∥RS ,②中RS ∥PQ ,④中RS 和PQ 相交.7. 若直线a 、b 与直线l 相交且所成的角相等,则a 、b 的位置关系是( )A .异面B .平行C .相交D .三种关系都有可能答案:D8. 如图,在长方体ABCD -A 1B 1C 1D 1中,A 1C 1∩D 1B 1=O ,E 、F 分别是B 1O 和C 1O 的中点,则在长方体各棱中与EF 平行的有________条.答案:∵E 、F 分别是B 1O 与C 1O 的中点,∴EF ∥B 1C 1,又∵在长方体ABCD -A 1B 1C 1D 1中,B 1C 1∥A 1D 1∥BC ∥AD ,∴EF ∥A 1D 1,EF ∥BC ,EF ∥AD .故在长方体的各棱中与EF 平行的有4条.9. 如图,a ∥α,A 是α的另一侧的点,B ,C ,D ∈a ,线段AB ,AC ,AD 分别交平面α于E ,F ,G ,若BD =4,CF =4,AF =5,则EG =________.答案:∵a ∥α,α∩平面ABD =EG ,∴a ∥EG ,即BD ∥EG , ∴EG BD =AF AF +FC ,则EG =AF ·BD AF +FC =5×45+4=209. 10. 如右图,正方体1111ABCD A B C D -中,求AC 与1A D 所成角的大小 答案:(1)连结1B C .由正方体的性质可知,11//A B CD ∴四边形11A DCB 是平行四边形 ∴11//A D B C ∴1BC 与AC 所成的锐角或直角就是异面直线1AD 和AC 所成的角 设正方体的棱长为a ,连结1AB ,在Rt △1B BC中,1B C ===同理可得:1,AC AB ==∴△1AB C 是等边三角形 ∴160B CA ∠= ∴AC 与1A D 所成角为60F E D 1C 1B 1A 1D CB A。
人教版高中数学新教材必修第二册8.4.1《平面》教学课件

⑵直线L在平面α内,直线m不在平面α内;
⑶平面α和β相交于直线L; ⑷直线L经过平面α外一点P和平面α内一点Q .
⑸直线L是平面α和β的交线,直线m在平面 α内,L和m相交于点P 。
巩固
下列四个命题中,正确的是( CD )
A、四边形一定是平面图形 B、空间的三个点确定一个平面 C、梯形一定是平面图形 D、三角形一定是平面图形
文字语言
基本事实3:如果两个不重合的平面有一个公共点, 那么它们有且只有一条过该点的公共直线.
β
图形语言
P ·
l
α
符号语言
p
p
l
l
作用 可用于判别两平面是否相交。
基本事实3告诉我们,如果两个平面有一个公共点,那么这两个平 面一定相交于过这个公共点的一条直线.两个平面相交成一条直线 的事实,使我们进一步认识了平面的“平”和“无限延展”.
如果直线 l 与平面α有一个公共点,直线 是l 否在 平面α内?如果直线 与l 平面α有两个公共点呢?
文字语言
基本事实2:如果一条直线上的两点在一个平面内, 那么这条直线在此平面内.
由点、线、面的关系有
直线 l 在平面α内表示为 l
直线m不在平面α内表示为 l
图形语言
m
. . A
l
·
·B
·
(3)在画图时,如果图形的一部分被另一 部分遮住,可以把遮住部分画成虚线,也 可以不画。
两相交平面的画法:
⑴先画两平面基本线 ⑵画两平面的交线 ⑶分别画三条线的平 行线
⑷把被遮部分的线段画 成虚线或不画。其它为 实线。
β α
上述三个关于平面的基本事实是人们经过长期观察与实践 总结出来的,是几何推理的基本依据,也是我们进一步研究立 体图形的基础.
人教版高中数学【必修二】[知识点整理及重点题型梳理]_平面_提高
![人教版高中数学【必修二】[知识点整理及重点题型梳理]_平面_提高](https://img.taocdn.com/s3/m/b5d7d28dad02de80d5d8407f.png)
人教版高中数学必修二知识点梳理重点题型(常考知识点)巩固练习平面【学习目标】1 .利用生活中的实物对平面进行描述;理解平面的概念,掌握平面的画法及表示方法.2 .重点掌握平面的基本性质.3 .能利用平面的性质解决有关问题.【要点梳理】[空间点线面之间的位置关系知识讲解】要点一、平面的基本概念1 .平面的概念:“平面”是一个只描述而不定义的原始概念,常见的桌面、黑板面、平静的水面等都给我们以平面的形象几何里的平面就是从这些物体中抽象出来的,但是,几何里的平面是无限延展的.要点诠释:(1) “平面”是平的(这是区别“平面”与“曲面”的依据);(2) “平面”无厚薄之分;(3) “平面”无边界,它可以向四周无限延展,这是区别“平面”与“平面图形”的依据.2 .平面的画法:通常画平行四边形表示平面.要点诠释:(1)表示平面的平行四边形,通常把它的锐角画成45 ,横边长是其邻边的两倍;(2)两个相交平面的画法:当一个平面的一部分被另一个平面遮住时,把被遮住的部分的线段画为虚线或者不画:3 .平面的表示法:(1)用一个希腊字母表示一个平面,如平面a、平面0、平面7等;(2)用表示平面的平行四边形的四个字母表示,如平面ABCD ;(3)用表示平面的平行四边形的相对两个顶点的两个字母表示,如平面AC或者平面BD ;4 .点、直线、平面的位置关系:(1)点A在直线a上,记作Awa;点A在直线a外,记作Ac a ;⑵点A在平面a上,记作Asa ;点A在平面a外,记作A氏a ;(3)直线I在平面a内,记作lua:直线I不在平面a内,记作l(za.要点二、平面的基本性质平面的基本性质即书中的三个公理,它们是研究立体几何的基本理论基础.1 .公理1:(1)文字语言表述:如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内;⑵符号语言表述:AeI , B G I , Awa, Bea =>I ca ;(3)图形语言表述:要点诠释:公理1是判断直线在平面内的依据.证明一条直线在某一平面内,只需证明这条直线上有两个不同的点在该平面内.“直线在平面内”是指“直线上的所有点都在平面内”2 .公理2:(1)文字语言表述:过不在一条直线上的三点,有且只有一个平面:(2)符号语言表述:A、B、C三点不共线=有且只有一个平面a ,使得Awa, Bea, Cea;(3)图形语言表述:要点诠释:公理2的作用是确定平面,是把^间问题化归成平面问题的重要依据.它还可用来证明“两个平面重合”.特别要注意公理2中“不在一条直线上的三点”这一条件.“有且只有一个”的含义可以分开来理解.“有”是说明“存在”,“只有一个”说明“唯一”,所以“有且只有一个”也可以说成“存在”并且“唯一”,与确定同义.(4)公理2的推论:①过一条直线和直线外一点,有且只有一个平面:②过两条相交直线,有且只有一个平面;③过两条平行直线,有且只有一个平面.(5)作用:确定一个平面的依据.3 .公理3:(1)文字语言表述:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线:(2)符号语言表述:Pwa nPnanP = l且P E I;(3)图形语言表述:要点诠释:公理3的作用是判定两个平面相交及证明点在直线上的依据.要点三、点线共面的证明所谓点线共面问题就是指证明一些点或直线在同一个平面内的问题.1 .证明点线共面的主要依据:(1)如果一条直线上的两点在一个平面内,那么这条直线上的所有点都在这个平面内(公理1):②经过不在同一条直线上的三点,有且只有一个平面(公理2及期隹论).2 .证明点线共面的常用方法:(1)纳入平面法:先确定一个平面,再证明有关点、线在此平面内;20辅助平面法:先证明有关的点、线确定平面。
高一数学必修2第四课
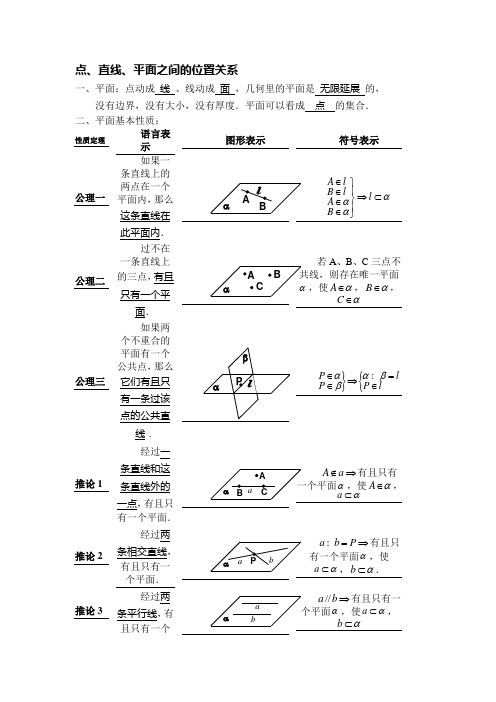
点、直线、平面之间的位置关系一、平面:点动成线、线动成面,几何里的平面是无限延展的,没有边界,没有大小,没有厚度.平面可以看成点的集合.二、平面基本性质:性质定理语言表示图形表示符号表示公理一如果一条直线上的两点在一个平面内,那么这条直线在此平面内.A lB l lABααα∈⎫⎪∈⇒⊂⎬∈⎪∈⎭公理二一条直线上的三点,有且只有一个平面.若A、B、C三点不,使Aα∈,Bα∈,Cα∈公理三个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.}{P lP P lααββ∈=⇒∈∈推论1经过一条直线和这条直线外的一点,有且只有一个平面.A a∉⇒有且只有α,使Aα∈,aα⊂推论2经过两条相交直线,有且只有一个平面.a b P=⇒有且只有一个平面α,使aα⊂,bα⊂.推论3经过两条平行线,有且只有一个平面.baα//a b⇒有且只有一个平面α,使aα⊂,bα⊂公理四平行于同一条直线的两条直线互相平行.αβcb a}//////a b a cb c⇒等角定理:空间中如果两个角的两边分别对应平行,那么这两个角相等或互补.点、直线、平面的位置关系: 三点、直线、平面的位置关系:点与直线 点与平面 共面直线 异面直线 直线与平面 平面与平面 共面与异面直线共面:空间中几个点或几条直线都在同一个面内 异面直线:既不相交又不平行的直线1 如图,在正方体ABCD -A 1B 1C 1D 1中,E ,F 分别是AB ,AA 1的中点. 求证:(Ⅰ)E 、C 、D 1、F 四点共面;(Ⅱ)CE 、DA 、D 1F 三线共点.2.如图1,正方体1111ABCD A BC D -中,1AC 与截面1DBC 交O 点,ACBD ,交M 点,求证:1C O M ,,三点共线.3. 如图,已知平面α,β,且α∩β=l .设梯形ABCD 中,AD ∥BC ,且AB α,CDβ,求证:AB ,CD ,l共点(相交于一点).4.如图3,设P Q R S M N ,,,,,分别为正方体1111ABCD A BC D - 的棱111111AB BC CC C D A D A A ,,,,,的中点,求证:P QR S M N ,,,,,共面.四、空间图形中三种角的定义,取值范围,: 1、异面直线所成的角:(1)异面直线所成的角的取值范围是]90,0(︒︒。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
人教版高中数学 平面的基本性质与推论__________________________________________________________________________________ __________________________________________________________________________________理解和掌握平面的性质定理,能合理运用;掌握直线与直线、直线与平面、平面与平面的位置关系; 会判断异面直线、掌握异面直线的求法;会用图形语言、符号语言表示点、线、面的位置关系.一、平面1.平面的概念:平面是一个不加定义,只需理解的原始概念.立体几何里所说的的平面是从现实生活中常见的平面抽象出来的.常见的桌面、平静的水面等都给我们以平面的局部形象.平面是理想的、绝对的平且无大小,无厚度,不可度量. 2.平面的表示方法:(1)一个平面: 当平面是水平放置的时候,通常把平行四边形的锐角 画成45,横边画成邻边的2倍长,如右图. (2)两个相交平面:画两个相交平面时,通常要化出它们的交线,当一个平面的一部分被另一个平面遮住,应把被遮住部分的线段画成虚线或不画(如下图)3. 运用集合观点准确使用图形语言、符号语言和文字语言空间图形的基本元素是点、直线、平面从运动的观点看,点动成线,线动成面,从而可以把直线、平面看成是点的集合,因此还可借用集合中的符号语言来表示αBAβαABαβαβBAAβαB点、线、面的基本位置关系如下表所示:b A =a α⊂α=∅A α=l β= 二、平面的基本性质1. 公理1 如果一条直线的两点在一个平面内,那么这条直线上的所有点都在这个平面内推理模式:A ABB ααα∈⎫⇒⊂⎬∈⎭. 如图示: 或者:∵,A B αα∈∈,∴AB α⊂ 公理1的作用:①判定直线是否在平面内;②判定点是否在平面内; ③检验面是否是平面.2. 公理2 如果两个平面有一个公共点,那么它们还有其他公共点,且所有这些公共点的集合是一条过这个公共点的直线推理模式:A A l A ααββ∈⎫⇒∈=⎬∈⎭如图示:或者:∵,A A αβ∈∈,∴,l A l αβ=∈公理2的作用:(1)判断两个平面是否相交及交线位置; (2)判断点是否在线上今后所说的两个平面(或两条直线),如无特殊说明,均指不同的平面(直线).(1)以上是确定平面的四个不同的条件,是判断两个平面重合的依据,是证明点线共面的依据,也是作截面、辅助面的依据.(2)有且只有一个”的含义要准确理解.这里的“有”是说图形的存在,“只有一个”是说图形唯一.因此,在证明有关这类语句的命题时,要从“存在性”和“唯一性”两方面来论证. 3. 公理3经过不在同一条直线上的三点,有且只有一个平面推理模式:,, ,,,,A B C A B C A B C ααβ⎫⎪∈⇒⎬⎪∈⎭不共线与β重合或者:∵,,A B C 不共线,∴存在唯一的平面α,使得,,A B C α∈. 推论1:经过一条直线和这条直线外的一点,有且只有一个平面; 推论2:经过两条相交直线,有且只有一个平面; 推论3:经过两条平行直线,有且只有一个平面.(1)以上是确定平面的四个不同的条件,是判断两个平面重合的依据,是证明点线共面的依据,也是作截面、辅助面的依据.(2)“有且只有一个”的含义要准确理解.这里的“有”是说图形的存在,“只有一个”是说图形唯一.因此,在证明有关这类语句的命题时,要从“存在性”和“唯一性”两方面来论证. 三、空间两直线的位置关系四、平行直线 1. 公理4 平行公理平行于同一条直线的两条直线互相平行推理模式://,////a b b c a c ⇒.(1)它是判断空间两条直线平行的依据; (2)它说明平行关系具有传递性 2.等角定理如果一个角的两边和另一个角的两边分别平行,且方向相同,那么这两个角相等. 由球的半径R 计算球表面积的公式:S 球= .即球面面积等于它的大圆面积的4倍. 五、异面直线 1. 定义:不在任何一个平面内的两条直线叫做异面直线(1)异面直线既不平行,也不相交,永远不存在一个平面能同时包含这两直线; (2)不能把异面直线误认为:分别在不同平面内的两条直线为异面直线 (3)异面直线一般是对两条直线而言的,没有三条异面直线的说法. 2.异面直线的画法画异面直线时,为了充分显示不共面的特点,常常需要以辅助平面为衬托,以加强直观性.3.异面直线判定定理过平面内一点与平面外一点的直线,和这个平面内不经过该点的直线是异面直线推理模式:l A B B L ααα⊂⎫⎪∉⎪⇒⎬∈⎪⎪∉⎭直线AB 与直线l 是异面直线六、异面直线所成的角 1. 定义:已知a ,b 是两条异面直线,经过空间任意一点O 作直线//,//a a b b '',我们把直线a '和b '所成的锐角(或直角)叫做异面直线a ,b 所成的角.(1)异面直线所成的角与O 点的位置无关.(2)如果两条异面直线所成角是直角,则说这两条异面直线互相垂直,记作a b ⊥. (3)异面直线所成角的范围是0,2π⎛⎤⎥⎝⎦. 2. 求异面直线所成角的步骤(1)恰当选点,由平移构造出一个交角; (2)证平行关系成立;(3)把角放入三角形或其它平面图形中求出;(4)作结论:若求出的角是锐角或直角,则它就是所求异面直线所成的角;若求出的角是钝角,则它的补角才是所求异面直线所成的角. 七、直线、平面的位置关系1.空间直线与平面的位置关系有以下三种:(1)直线在平面内:如果一条直线a 与平面α有两个不同的公共点,那么这条直线就在这个平面内,记作a ⊂α.(2)直线与平面相交:直线a 与平面α只有一个公共点A ,叫做直线与平面相交,记作a ∩α=A ,公共点A 叫做直线a 与平面α的交点.(3)直线与平面平行:如果一条直线a 与平面α没有公共点,叫做直线与平面平行,记作a ∥α. 2.两个平面的位置关系有且只有一下两种: (1)两个平面平行---没有交点 (2)两个平面相交---有一条公共直线3.顺次连接不共面的四点A 、B 、C 、D 所构成的图形,叫做空间四边形.这四个点中的各个点叫做baαβbaα空间四边形的顶点;所连接的相邻顶点间的线段叫做空间四边形的边;连接不相邻的顶点的线段叫做空间四边形的对角线.类型一 平面及其性质 例1:(2014·邵阳一中月考)对下图的几何图形,下列表示错误的是( )A .l ∈αB .P ∉lC .l ⊂αD .P ∈α解析:由图形可知,l ⊂α,P ∉l ,P ∈α,故选A. 答案:A练习1:判断下列说法是否正确,并说明理由.(1)平面的形状是平行四边形( ) (2)任何一个平面图形都可以表示平面( ) (3)平面ABCD 的面积为10㎡( ) (4)空间图形中,后引的辅助线是虚线( ) 答案: (1)(3)(4)错,(2)正确. 练习2:1、下列说法正确的个数( )①铺的很平的一张纸是一个平面;②可以一个长20cm 、宽30cm 的平面;③通常300页的书要比10页的书厚一些,那么300个平面重合在一起时一定比10个平面重合在一起厚. A 、0个 B 、1个 C 、2个 D 、3个 答案:A练习3:若点Q 在直线b 上,b 在直线平面β内,则,,Q b β之间的关系可记作( B ) A 、Q b β∈∈ B 、Q b β∈⊂ C 、Q b β⊂⊂ D 、Q b β⊂∈ 答案:B例2:如右图,已知,,,E F G H 分别为空间四边形ABCD 各边,,,AB AD BC CD上的点,且EF GH P =,求证:,,B D P 共线.解析:由公理2可判断D 点在交线上. 答案:证明:∵EFGH P = ∴P EF ∈∵EF ⊂平面ABD ∴P ∈平面ABD 同理P ∈平面CBD ∵平面ABD平面CBD BD = ∴P BD ∈∴,,B D P 共线练习1:已知l 与三条平行线,,a b c 都相交,求证:l 与,,a b c 共面. 答案: 证明:如右图所示∵//a b ∴直线a 与直线b 确定一个平面,设为α ∵,la A lb B == ∴,A a B b ∈∈PH GF EDC BACB Aαlcba∴,A B αα∈∈ ∴l α⊂∵//b c ∴直线b 与直线c 确定一个平面,设为β 同理可证l β⊂ ∵,,,,l l b b l b B αβαβ⊂⊂⊂⊂= ∴平面α与平面β重合∴l 与,,a b c 共面练习2:两个不重合的平面有公共点,则公共点的个数是( )A 、2个B 、有无数个且在一条直线上C 、一个或无数个D 、1个 答案:B练习3:下列命题:①公理1可用集合符号叙述为:若,A l B l ∈∈且,A B αα∈∈,则必有l α∈;②四边形的两条对角线必交于一点;③用平行四边形表示的平面,以平行四边形的四边作为平面边界线;④梯形是平面图形.其中正确的命题个数为( )A 、1B 、2C 、3D 、4 答案:D类型二 直线及其位置关系例3:(2014·甘肃嘉峪关市一中高一期末测试)若a 、b 是异面直线,直线c ∥a ,则c 与b 的位置关系是( )A .相交B .异面C .平行D .异面或相交解析:如图,借助正方体可知c 与b 相交或异面. 答案:D 练习1:在长方体ABCD -A 1B 1C 1D 1中,E 、F 分别是BD 和CD 的中点,长方体的各棱中与EF 平行的有( )A .1条B .2条C .3条D .4条答案:如图所示∵E 、F 分别为BD 、CD 的中点, ∴EF ∥BC ,又∵BC ∥B 1C 1,∴EF ∥B 1C 1,同理,EF ∥A 1D 1,EF ∥AD . 故选D .练习2:空间四边形ABCD 中,给出下列说法:①直线AB 与CD 异面; ②对角线AC 与BD 相交; ③四条边不能都相等;④四条边的中点组成一个平行四边形. 其中正确说法的个数是( )A .1个B .2个C .3个D .4个答案:本题主要考查空间四边形,关键要理解空间四边形的概念.由定义知①正确;②错误,否则A 、B 、C 、D 四点共面;③不正确,可将一个菱形沿一条对角线折起一个角度,就成为四边相等的空间四边形;④正确,由平行四边形的判定定理可证.故选B . 练习3:a 、b 、c 是空间中三条直线,下面给出几种说法:①若a ∥b ,b ∥c ,则a ∥c ;②若a 与b 相交,b 与c 相交,则a 与c 也相交;③若a 、b 分别在两个相交平面内,则这两条直线不可能平行. 上述说法中正确的是________(仅填序号). 答案:由基本性质4知①正确.若a 与b 相交,b 与c 相交,则a 与c 可能平行,也可能相交或异面,②错误. 若平面α∩β=l ,a ⊂α,b ⊂β,a ∥l ,b ∥l ,则a ∥b ,③错误.例4:已知正方体1111ABCD A B C D -,E 、F 分别为1AA 、1CC 的中点,求证:1//BF ED 解析:平行四边形是平面图形,若能证得四边形的一组对边平行且相等,那么这个四边形就是平行四边形.答案:证明:如右图,取1BB 中点G ,连结1GC 、GE . ∵F 为1CC 的中点 ∴1//BG C F∴四边形1BGC F 为平行四边形 ∴1//BF GC 又∵111111//,//EG A B C D A B ∴11//EG C D∴ 四边形11EGC D 为平行四边形 ∴11//ED GC ∴1//BF ED练习1:已知棱长为a 正方体1111ABCD A B C D -,M 、N 分别为CD 、AD 的中点, 求证:四边形11MNA C 是梯形答案:证明:如右图 ∵M 、N 分别为CD 、AD 的中点∴1//2MN AC 由正方体的性质知11//AC A C ∴111//2MN A C ∴四边形 11MNA C 是梯形.练习2:已知E 、F 、G 、H 为空间四边形ABCD 的边AB 、BC 、CD 、DA 上的点,若AE AB =AH AD =12,CF CB =CG CD =13,则四边形EFGH 形状为________. 答案:如右图在△ABD 中,∵AE AB =AH AD =12,∴EH ∥BD 且EH =12BD .在△BCD 中,∵CF CB =CG CD =13,∴FG ∥BD 且FG =13BD ,∴EH ∥FG 且EH >FG ,∴四边形EFGH 为梯形.N D 1C 1B 1MA 1D CBA例5:已知E 、1E 分别是正方体1111ABCD A B C D -的棱AD 、11A D 的中点. 求证:111BEC B E C ∠=∠解析:由等角定理,证明角的边之间的关系,进而得到角的关系. 答案: 证明:如右图,连结1EE∵E 、1E 分别是AD 、11A D 的中点 ∴11//A E AE ∴四边形11A E EA 为平行四边形 ∴11//A A E E 又∵11//A A B B ∴11//E E B B∴四边形11E EBB 是平行四边形 ∴11//E B EB 同理可证:11//E C EC又111C E B ∠与CEB ∠方向相同 ∴111BEC B E C ∠=∠练习1:如右图,111,,AA BB CC 不共面,且1111//,//BB AA CC AA ,求证:△ABC ≌△111A B C答案:证明:∵11//BB AA ∴四边形11AA B B 是平行四边形 ∴11//AB A B 同理可证:11//AC A C又∵BAC ∠和111B A C ∠方向相同 ∴BAC ∠=111B A C ∠∴△ABC 和△111A B C 中有1111111AB A B AC A C BAC B A C=⎧⎪=⎨⎪∠=∠⎩∴△ABC ≌△111A B C练习2:在平行六面体ABCD -A 1B 1C 1D 1中,M 、N 、P 分别是CC 1、B 1C 1、C 1D 1的中点.求证:∠NMP =∠BA 1D.答案:如图,连接CB 1、CD 1,易得 四边形A 1B 1CD 是平行四边形, ∴A 1D ∥B 1C .∵M 、N 分别是CC 1、B 1C 1的中点, ∴MN ∥B 1C ,∴MN ∥A 1D .C 1B 1A 1C∴四边形A 1BCD 1是平行四边形, ∴A 1B ∥CD 1.∵M 、P 分别是CC 1、C 1D 1的中点,∴MP ∥CD 1, ∴MP ∥A 1B ,∴∠NMP 和∠BA 1D 的两边分别平行且方向都相反, ∴∠NMP =∠BA 1D .例6:如右图,已知不共面的直线,,a b c 相交于O 点,M 、P 是直线a 上两点,N 、Q 分别是直线b 、c 上一点.求证:MN 和PQ 是异面直线. 解析:证明其中一点不属于两外三点确定的平面即可. 答案:证明:∵ab O = ∴由a 、c 确定一个面,设为β∵,P a Q c ∈∈ ∴,P Q ββ∈∈∴PQ β⊂且,M M PQ β∈∉ 又∵,,a b c 不共面,N b ∈ ∴N B ∉ ∴MN 和PQ 是异面直线练习1:1、两条异面直线是指( )A 、空间没有公共点的两条直线B 、分别位于两个平面内的直线C 、平面内的一条直线与平面外的一条直线D 、既不平行也不相交的两条直线 答案:D练习2:下列说法正确的有 .①两直线无公共点,则两直线平行;②两直线若不是异面直线,则必相交或平行;③过平面外一点与平面内一点的连线,与平面内的任一直线均构成异面直线;④和两条一面直线都相交的直线的两直线必是异面直线. 答案:② 练习3:已知,,a b a b A αββ=⊂=且,//c c a α⊂,求证:b ,c 为异面直线.答案:证明:如右图 ∵,,c a b A a ααβ⊂== ∴A a α∈⊂而//a c∴A c ∉在直线b 上任取不同于A 的一点B ∵b β⊂ ∴B α∉ ∴AB 与c 是异面直线,即b ,c 为异面直线例7:正四面体A BCD -的棱长为a ,E 、F 分别为棱AD 、BC 的中点,求异面直线AF 和CE 所成角的余弦值.解析:找出其中一条直线的平行线,构造三角形求解.c baOQPNMA答案:如右图, 连结FD ,在面AFD 内过E 点作//EO AF 交FD 于O ,则OEC ∠ (或其补角)为异面直线AF 与CE 所成的角,且O 是FD 的中点. 又∵E 为AD 的中点 ∴1//2EO AF ∵△ABC 和△ACD 均为等边三角形,且边长为a ,AF 、CE 分别是它们的中线∴2AF CE a ==,则1224EO a a =⨯= 在Rt △DFC中,11,22FO FD a FC a ===∴CO == 在△OEC中,2222222cos 2342EO EC OC OEC EO EC ⎫⎫⎫+-⎪⎪⎪⎪⎪⎪+-∠===⨯⨯即异面直线AF 与CE 所成的角的余弦值为23练习1:已知m 、n 为异面直线,m α⊂,n β⊂,l αβ=,则直线l ( )A 、与m 、n 都相交B 、与m 、n 至少一条相交C 、与m 、n 都不相交D 、至多与m 、n 中的一条相交 答案:B练习2:在棱长为1的1111ABCD A B C D -中,M 和N 分别为11A B 和1BB 的中点,那么直线AM 与CN 所成角的余弦值是( )AB、35 D 、25答案:D练习3:如右图,等腰直角三角形ABC中,90,,A BC DA AC DA AB ∠==⊥⊥,若1DA =,且E 为DA 的中点.求异面直线BE 与CD 所成角的余弦值.答案:取AC 的中点F ,连结EF ,在△ACD 中,E 、F 分别为AD 、AC 的中点.∴//EF CD ∴BEF ∠或其补角即为所求异面直线BE 与CD 所成的角在Rt △EAB 中,111,22AB AE AD ===∴2BE =在Rt △AEF 中,11,22AF AE ==∴2EF = FE D CBA在Rt △ABF 中,11,2AB AF ==∴BF =在等腰△EBF中,12cos EFFEB BE ∠==∴异面直线BE 与CD1.在空间内,可以确定一个平面的条件是( )A 、两两相交的三条直线B 、三条直线,其中的一条与另外两条直线分别相交C 、三个点D 、三条直线,它们两两相交,但不交于同一点E 、两条直线 答案:D2.分别和两条异面直线都相交的两条直线的位置关系是( )A .异面B .相交C .平行D .异面或相交 答案:D3.一条直线与两条平行线中的一条是异面直线,那么它与另一条的位置关系是( ) A 、相交 B 、异面 C 、平行 D 、相交或异面 答案:D4.从空间一点P 分别向BAC ∠的两边,AB AC 作垂线,PE PF ,垂足分别为,E F ,则EPF ∠与BAC ∠的关系为( )A 、互补B 、相等C 、互补或相等D 、以上都不对答案: D5.在正四面体A BCD -中,E 为AD 的中点,则AB 与CE 所成角的余弦值为 ._________________________________________________________________________________ _________________________________________________________________________________基础巩固1. 空间有四个点,其中无三点共线,可确定 个平面;若将此四点两两相连,再以所得线段中点为顶点构成一个几何体,则这个几何体至多有 个面. 答案:1或4,82、三个两两相交的平面最多可把空间分为 个部分. 答案:83、下面6个命题:①四边相等的四边形是菱形;②两组对边相等的四边形是平行四边形;③若四边形有一组对角相等,则该四边形是圆内接四边形;④在空间,过已知直线外一点,引该直线的平行线,可能不只一条;⑤四条直线两两平行,无三线共面,它们共可确定6个平面.其中正确命题的个数是( ) A 、0 B 、1 C 、2 D 、3 答案:B4. 在正方体1111ABCD A B C D 中,与1AD 成60的面对角线共有( )A 、4条B 、6条C 、8条D 、10条答案:C5. 已已知棱长为a 的正方体ABCD -A ′B ′C ′D ′中,M 、N 分别为CD 、AD 的中点,则MN 与A ′C ′的位置关系是________.答案:平行能力提升6. (2014·山东泰安肥城高一期末测试)如图,点P 、Q 、R 、S 分别在正方体的四条棱上,且是所在棱的中点,则直线PQ 与RS 是异面直线的一个图是________.答案:③. ①中PQ ∥RS ,②中RS ∥PQ ,④中RS 和PQ 相交.7. 若直线a 、b 与直线l 相交且所成的角相等,则a 、b 的位置关系是( )A .异面B .平行C .相交D .三种关系都有可能 答案:D8. 如图,在长方体ABCD -A 1B 1C 1D 1中,A 1C 1∩D 1B 1=O ,E 、F 分别是B 1O 和C 1O 的中点,则在长方体各棱中与EF 平行的有________条.答案:∵E 、F 分别是B 1O 与C 1O 的中点, ∴EF ∥B 1C 1,又∵在长方体ABCD -A 1B 1C 1D 1中,B 1C 1∥A 1D 1∥BC ∥AD , ∴EF ∥A 1D 1,EF ∥BC ,EF ∥AD .故在长方体的各棱中与EF 平行的有4条.9. 如图,a ∥α,A 是α的另一侧的点,B ,C ,D ∈a ,线段AB ,AC ,AD 分别交平面α于E ,F ,G ,若BD =4,CF =4,AF =5,则EG =________.答案:∵a ∥α,α∩平面ABD =EG ,∴a ∥EG ,即BD ∥EG ,∴EG BD =AF AF +FC ,则EG =AF ·BD AF +FC =5×45+4=209. 10. 如右图,正方体1111ABCD A B C D -中,求AC 与1A D 所成角的大小答案:(1)连结1B C .由正方体的性质可知,11//A B CD ∴四边形11A DCB 是平行四边形∴11//A D B C ∴1B C 与AC 所成的锐角或直角就是异面直线1A D 和AC 所成的角 设正方体的棱长为a ,连结1AB ,在Rt △1B BC中,1B C ===同理可得:1,AC AB ==∴△1AB C 是等边三角形∴160B CA ∠= ∴AC 与1A D 所成角为60FED 1C 1B1A 1DCBA。
