重复性公式
GRR计算公式表格
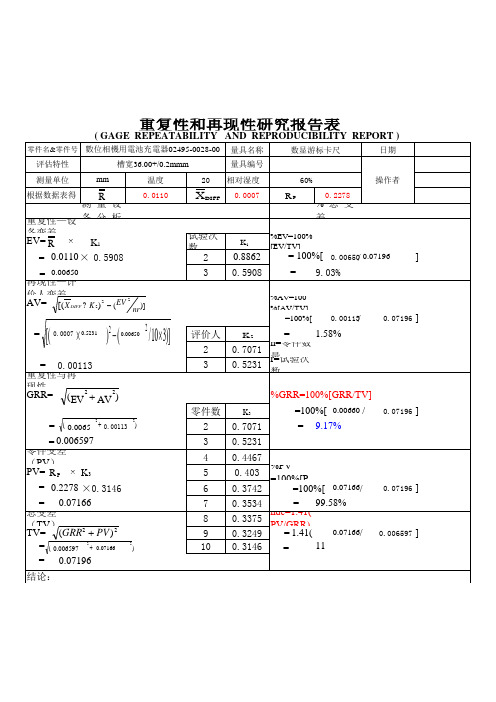
= 0.0110 × 0.5908
0.0110
= 0.00650 再现性—评 价人变差 AV= [(X DIFF ? K 2)2 - (EV 2 nr)]
[( ) -( /103)] =
2 2 0.0007 0.5231
0.00650
= 0.00113 重复性与再 现性 GRR= (EV2 + AV2)
重复性和再现性研究报告表
( GAGE REPEATABILITY AND REPRODUCIBILITY REPORT )
零件名&零件号 數位相機用電池充電器02495-0028-00 量具名称
数显游标卡尺
日期
评估特性
槽宽36.00+/0.2mmm
量具编号
测量单位
mm
温度
20 相对湿度
60%
操作者
根据数据表得 测 量R 设
到30%之间
时,基于应
用的重要性
、测量装置
的成本、维
修的成本等
方面的考
虑,
可能是可接
受的;
误差超过
30%时,认
为是不可接
受的,应该
作出各种努
力改进测量
系统。
过程能力被
测量系统区
分开的分级
数(ndc)应
该大于或等
于5。
审核:
K2
0.7071 0.5231=Leabharlann 1.58%n=零件数
量r=试验次
数
0.07196 ]
零件数 2
%GRR=100%[GRR/TV]
K3
0.7071
=100%[ 0.00660 / = 9.17%
计量标准稳定性和重复性考核的方法探讨

计量标准稳定性和重复性考核的方法探讨摘要:计量标准考核是国家主管部门对计量标准测量能力的评定和利用该标准开展量值传递的资格的确认。
被考核的计量标准不仅要满足相应的技术要求,还必须满足国家法制管理的有关要求。
关键词计量标准计量标准考核计量标准的稳定性计量标准的重复性引言:计量标准是准确度低于计量基准,用于检定或校准其他计量标准,或者工作计量器具的计量器具。
它处于量值传递(溯源)体系的中间环节,起着承上启下的作用。
量值一旦失准,它所传递的其他计量标准或工作计量器具的量值都将失准,结果影响各个方面,严重的会影响到全国量值的一致性和国家量值传递(溯源)体系的安全。
为了保障国家计量单位制的统一和量值传递的一致性、准确性,为国民经济发展以及计量监督管理提供公正、准确的检定、校准数据或结果,国家对一些重要的计量标准实行考核制度。
计量标准的稳定性:是计量标准,保持其计量特性随时间恒定的能力。
计量标准的重复性:在一组重复性测量条件下的测量精密度。
下面就考核工作中计量标准的稳定性和重复性考核加以探讨。
1.计量标准的稳定性考核在计量标准考核中计量标准的稳定性用计量特性在规定时间间隔内发生的变化量表示。
新建的计量标准一般应当经过半年以上的稳定性考核,证明其所复现的量值稳定可靠后,方可申请计量标准考核;已建计量标准一般每年至少进行一次稳定性考核,并通过历年的稳定性考核记录数据比较,证明其计量特性的持续稳定。
有证标准物质有效期内,可以不进行稳定性考核。
计量标准的稳定性应当包括计量标准器的稳定性和配套设备的稳定性。
稳定性的考核应当根据计量标准的具体情况选用适当的考核方法,方法有五种。
a、采用核查标准进行考核。
b、采用高等级的计量标准进行考核。
c、用控制图法进行考核。
d、采用计量检定规程或计量技术规范规定的方法进行考核。
e、采用计量标准器的稳定性考核结果进行考核。
核查标准或核查装置是指用于日常验证测量仪器或测量系统性能的装置。
汽柴油的重复性和再现性公式

汽油质量检验项目的重复性和再现性计算公式1、溶剂洗胶质GB/T8019重复性计算:未洗胶质含量r=0.997X0.4,溶剂洗胶质含量r=1.298X0.3 X—重复测定结果的算术平均值。
再现性计算:未洗胶质含量R=1.928X0.4,溶剂洗胶质含量R=2.494X0.3 X—两个独立结果的算术平均值。
2、荧光硫SH/T0742重复性计算:r= 12 .30 (X + 1 0 )0.1X—重复测定结果的算术平均值。
再现性计算: R =3 6. 26 (X + 10 )0.1X—两个独立结果的算术平均值。
3、紫光硫SH/T0689重复性计算:r=0.1867X0.63X—重复测定结果的算术平均值。
再现性计算:R=0.2217X0.92X—两个独立结果的算术平均值。
4、硫醇硫GB/1792重复性计算:r=0.00007+0.027XX—重复测定结果的算术平均值。
再现性计算:R=0.00031+0.042XX—两个独立结果的算术平均值。
5、馏程GB/T6536 ℃1)手工法回收点重复性r、再现性R的计算:10%回收点:S=0.05(T20%平均回收温度-T初馏点平均回收温度)r=(S+2.46)/2.44R=(S+1.39)/0.7650%回收点:S=0.05(T60%平均回收温度-T40%平均回收温度)r=(S+2.46)/2.44R=(S+1.39)/0.7690%回收点:S=0.1(T90%平均回收温度-T80%平均回收温度)r=(S+2.46)/2.44R=(S+1.39)/0.76终馏点:S=(T终馏点平均回收温度-T95%平均回收温度)/(V终馏点平均体积-95)r=(S+1.82)/2.66R=(S+6.95)/2.242)自动法回收点重复性r、再现性R的计算:10%回收点:S=0.05(T20%平均回收温度-T初馏点平均回收温度)r=1.2+1.42SR=3.0+2.64S50%回收点:S=0.05(T60%平均回收温度-T40%平均回收温度)r=1.2+1.42SR=2.9+3.97S90%回收点:S=0.1(T90%平均回收温度-T80%平均回收温度)r=1.1+1.08SR=2.0+2.53S终馏点:r=3.5R=10.56、烃的重复性和再现性计算(1)不含含氧化合物样品的重复性和再现性%(体积分数)(2)含有含氧化合物样品的重复性和再现性%(体积分数)7、苯、甲苯重复性和再现性计算%(体积分数)8、醇类和醚类中氧含量的重复性和再现性计算%(质量分数)9、汽油中Fe和Mn含量的重复性和再现性计算mg/LFe重复性:0.65X0.48再现性:0.55X0.79Mn重复性:0.42X1/2再现性:1.41X1/2/a/20100427/004567.htm柴油质量检验项目的重复性和再现性计算公式1、闭口闪点GB/T261重复性计算:0.029XX—重复测定结果的算术平均值。
MSA重复性再现性讲解及分析公式省公开课获奖课件说课比赛一等奖课件

鉴定原则
假如Gage R&R不不小于所测零件公差旳10%, 则此系统无问题。
假如Gage R&R不小于所测零件公差旳10%而不 不小于20%,那么此系统是能够接受旳。
假如Gage R&R不小于所测零件公差旳20%而不 不小于30%,则接受旳根据是数据测量系统旳主 要程度和改善所花费旳商业成本。
分析措施
计算公式
UCLr=Rbar*D4
若任何单独旳R值不小于UCLr,就应重新检讨试验 过程,重新试验并改正不正确旳地方,或除掉不 合适旳数据,利用新旳数据重新进行计算R值。 D4值按下表选用。
试验次数
2
3
D4
3.27
2.58
分析措施
计算公式 可反复性——测量仪器(设备)变异( EV) EV=Rbar*K1
分析措施
可反复性及再现性分析数据表
检
验
A
B
C
员
样 本 XA1
XA2
XA3
RA
XB1
XB2
XB3
RB
XC1
XC2
XC3
1
XA11
XA21
XA31
RA1
XB11
XB21
XB31
RB1
XC11
XC21
XC31
2
XA12
XA22
XA32
RA2
XB12
XB22
XB32
RB2
XC12
XC22
XC32
3
XA13
9
4.98 4.97 5.03 0.06 4.97 4.99 5.04 0.07 5.03 5.01 5.04
RC 0.03 0.03 0.02 0.02 0.02 0.06 0.07 0.07 0.03
1.MSA重复性再现性讲解及分析公式

二厂品质部 三厂品质部 16.38万 四厂品质部
编制人数 80
103 73 75
5
客服
15
6
来料
6
7
实验室
10
总计
313
备注:第二阶段激励根据生产计件效 果及品 质第二 阶段减 人情况 确定绩 效激励 方案。
拟制:
审核:
批准:
发生环境变化、电源
优化后编制 66 92 62 62 15 6 10 63
提升绩效金额
当同一零件的同一种特征
由不同的人使用同一量具
进行测量时,在测量平均 值方面的变异的总和。
分析时机
对于需进行GR&R分析的测量系统,一般在以 下三种情况下要进行GR&R分析
品质部第一阶段减人增效激励方案
一、实施目标及基本原则
通过对品质人员实施检验技能培训提 升及通 过系统 管控等 方式达 到减少 人员提 高部门 工作的 整体效 率,前 提是减 人不降 低工作 质量, 通过人 员减少 提高品 质部QC的绩效 工资、 实现公 司与Q C双赢 ,既增 加员工 工资也 能为公 司留住 老员工 ,保证 品质工 作稳定 发展。
三、第一阶段减人绩效激励(QC)
按公司50%+员工50%激励方式进行激 励,预 计每月 激励金 额为:
三人时为每人3次。 序号 1 人均值+523
2 3 4
部门 提升总金额 一厂品质部
二厂品质部 三厂品质部 16.38万 四厂品质部
编制人数 80
103 73 75
提升绩效金额
5
客服
15
6
来料
6
7
实验室
关于化学分析回收率不确定度评估公式的思考

关于化学分析回收率不确定度评估公式的思考占永革;龚剑;黄湘燕【摘要】以化学测量回收率定义及其过程特点为依据,分析了3种流行公式的适用性,认为它们都不是普适公式而各有其适用条件,随意套用获得的结果可靠性较低。
思考了合理评估方法,认为化学回收率不是一个直接测量量,其不确定度是各复合因素合成的结果;平均回收率不确定度只是回收率总不确定度中的一个重复性分量,只有当它占绝对优势时才可代表回收率总不确定度;遵循过程与模型的评估原则可获得针对性强、可靠程度高的评估结果。
%Based on the definition and process feature of recovery percentage , the present authors analyzed the applicability of three popular formulas , it is deemed that these formulas are not universally used while each has specific conditions of application , and the reliability of results obtained by indiscriminately using the formulas is low.The reasonable assessment method is thought aabout , it is found that the recovery percentage in chemical analysis is not a direct measuring quantity , the uncertainty of recovery percentage should be the synthetic result of some composite factors , and the uncertainty of average recovery percentage is just the repetitive components in overall uncertainty of recovery percentage , and average recovery percentage can represent the overall uncer-tainty of recovery percentage only when it is dominated .It is recommended that by complying with the process and the principles of evaluating model , a higher reliability of the result can be obtained .【期刊名称】《广州大学学报(自然科学版)》【年(卷),期】2014(000)003【总页数】7页(P40-46)【关键词】化学分析;回收率;不确定度;公式;探讨【作者】占永革;龚剑;黄湘燕【作者单位】广州大学分析测试中心,广东广州 510006; 广东省放射性核素污染控制与资源化重点实验室,广东广州 510006;广州大学分析测试中心,广东广州510006; 广东省放射性核素污染控制与资源化重点实验室,广东广州 510006;中山市供水有限公司水质检测中心,广东中山 528403【正文语种】中文【中图分类】TB99有复杂前处理的化学检测的方法回收率常偏离100%.环境、食品和给排水等类分析方法,一般不要求对结果偏差进行校正,只要回收率达到方法规定的范围[1-3]就视为准确度满足要求,方法偏差并入测量不确定度后,常成为测量不确定度主要分量之一.方法偏差的不确定度常由回收率的不确定度与回收率偏差的不确定度构成,有时回收率的不确定度远远大于回收率偏差的不确定度,成为方法偏差不确定度的主要贡献者.当检测结果接近符合限时,回收率不确定度评估结果的大小可能影响符合性结论,因而合理评估回收率之不确定度已受到业内人士的日益重视.但在目前流行的3种评估方法中,常见不加选择的使用,使得相同数据使用不同公式得出不同结果而直接影响评估结果的可比性与可靠性,故有必要辨析这些公式的适用条件,思考合理的评估方法.1 几种流行的回收率不确定度评估公式目前主要流行着3种回收率不确定度评估公式:重复性 + 证书标准值公式[4-7],重复性公式[8-12],近似公式[13-17].1.1 重复性+证书标准值公式式中,为回收率的平均值;s(X)为标准物质观测值X的标准差;n为X的个数;XS为标准物质的标准值;根式中的第1项s(X )为n个X的重复性相对不确定度,因有s(X)=XS*s(R),故也是n个回收率R的重复性相对不确定度s(R)/根式中的第2项u(XS)/XS为标准物质证书给定的标准值的相对不确定度.从文献[4]的应用情况看,无论是标样回收法还是加标回收法都使用该公式,且计算的都是平均回收率的不确定度.从文献[4]的应用情况看,无论是标样回收法还是加标回收法都使用该公式,且计算的都是平均回收率的不确定度.1.2 重复性公式式中,为回收率的平均值;s(R)为n个R的标准差.1.3 近似公式式中,u(R)为回收率不确定度;R+为回收率的上界;R-为回收率的下界;上下界从资料获得而非实验所得.2 对回收率及其不确定度的思考考察化学分析中的回收率定义及其实验过程,不难看出存在3个基本特点:(1)回收率结果是间接测量得到的.对于标样回收法,其结果R是分子上的标准物质观测值X与分母上的标准物质标准值XS之比:R=X/XS;对于加标回收法,分子上的标准物质观测值X则是加标样观测值X加标与非加标样观测值X样之差:X=X加标-X样.(2)回收率分子上的标准物质观测值X、加标样观测值X加标、非加标样观测值X样也是间接测量的结果,即 X或 X加标或 X样 =f(x1,x2,…xn),都经历了一个与样品检测相同甚至步骤更多的实验过程.(3)标样回收法是直接观测标物证书的标准值XS0;加标回收法常是观测标物证书标准值经n次稀释后的期望值XSn.第1个特点提示了回收率的不确定度应是与其具有复合函数关系的各因素不确定度合成的结果;第2个特点提示了标准物质观测值的不确定度应是整个实验过程各分量合成的结果,标样回收法与加标回收法的评估模型与过程不同;第3个特点提示了加标回收法标准期望值的不确定度应是有证标准物质稀释过程各分量合成的结果.分析式(1)的推导过程及其各因素的含义认为,该式虽考虑了与回收率R具有函数关系的X和XS因素,但却未考虑与X有函数关系的其他因素;根式中的第1项是数组平均值标准差的计算式,这是一个纯数学算式,它关注的对象是数组的平均值,给出的仅是数组之平均值的分散性,而数组数值本身的分散性并未包含其中;分母中的XS专指标物证书给出的标准值XS0,这对标样回收法是合适的,但对于加标回收法,其分母实际上并不是XS0而是经n次稀释后的XSn,例如,当n=2时,XS2={[(XS0V移1)/V容1)]× V移2}/V容2,如果加标回收法仍用XS0则明显不符合定义,若其中的体积分量大于或相当于u(XS0)则只用u(XS0)不考虑其他也不合适.式(2)既不涉及与回收率R具有函数或者复函数关系的所有因素,也不涉及数组数值本身的分散性,给出的仅是数组之平均值的分散性.从回收率的3个基本特点看,回收率R的不确定度≠回收率平均值或者称平均回收率的不确定度,即u(R)≠u(),u(R)是依据过程和模型的计算结果,包含了与R具有复函数关系的所有因素,或者说依据R的过程及其模型评估的是R值本身的不确定度;u()是对n个R的平均值的计算结果,计算对象是R而不是R;u()只是u(R)中的一个重复性分量,既然是一个分量,它的贡献不一定在任何过程都占绝对优势而完全忽略其他分量.因此若将回收率不确定度的评估固化为式(1)或者式(2),当某些过程的其他分量不能忽略甚至较大时,式(1)或式(2)显然得不到客观合理的评估结果.故式(1)或式(2)并不是适合任何过程的通式,式(1)只适合于重复性分量和标准值分量占绝对优势的条件与场合,式(2)只适合于重复性分量占绝对优势的条件与场合,实际上,仅这两个因素占绝对优势的情况并不多;因此,不加选择地套用公式获得的结果可靠性较低.式(3)适用于回收率不确定度的 B类评定[13],即回收率数据非评估人员实验所得,是直接利用方法等文献资料提供的信息,给出的常是回收率的上下界如“本方法的回收率为93%~104%”.如果1组回收率数据为实验所得,则不应使用式(3)计算,用A类方法评估更客观合理.3 对回收率不确定度严密计算的思考由于回收率与过程及其模型有关,过程不同不确定度的评估结果不同,故难以给出一个既适合任何过程又具体的通式,获得针对性强的评估结果必须遵循具体过程及其模型的评估原则.但对那些方法已标准化、过程重复性强、分量之间大小取舍明确的检测,如能总结一个适合该过程的具体算式,则可大大提高评估工作的效率.根据回收率R为标准物质观测值X与其标准值XS之比的定义,与其不确定度有关的模型为式中,F为总校正因子,F=f1f2f3…fi.R的不确定度为式中3.1 标样回收法对于标样回收法,式(5)中的X是直接观测标准样品所得之值,XS是证书所给之值XS0,即:可视式(6)为标样回收法回收率不确定度计算通式.具体计算时,将X的计算式代入式(6)按不确定度传播律展开整理,便可得到标样回收率不确定度的具体算式.例如,石墨炉原子吸收光谱法测定食品中铅含量 X 的计算式[18]:分析不确定度来源,F主要由配制校准溶液的浓度因子f配制和回收率重复性因子f重复性构成.设相对不确定度最大的校准溶液浓度是对有证标准溶液(浓度标准值CS0)进行2次稀释的结果:将式(7)~(9)代入式(6):u(R)=当式(10)中的体积项和质量项与其他项相比较小可以忽略时,式(10)可简化为u(R)=当R是n次测量的平均值,则式(6)可表达为u(R)=因有s(X)=XS*s(R),故式中的s(R)/也可为s(X)/式(12)则是石墨炉原子吸收光谱法测定食品中铅含量标样回收法回收率不确定度的严密算式.3.2 加标回收法对于加标回收法,式(5)中的X=X加标-X样,XS=XSi,XSi为标准物质的加入浓度,是对有证标准溶液经过i次稀释后的期望值,式(5)变为u(R)=式(13)则为加标回收法回收率不确定度的计算通式.具体计算时,将 X加标、X样和 XSi等的计算式代入式(13)按不确定度传播律展开整理,便可得到加标回收率不确定度的具体算式.仍以石墨炉原子吸收光谱法测定食品中铅含量X的计算式为例:一般当拟合曲线的相关系数r<0.999 9时,体积不确定度u(V)、称量不确定度u(m)与曲线拟合浓度的不确定度u(c)相比可以忽略,则式(13)根式中的第1项可化为设式(13)中的XSi是对有证标准溶液XS0稀释2次的期望值XS2:也设F主要由配制校准溶液的浓度因子f配制和回收率重复性因子f重复性构成. 设相对不确定度最大的校准溶液的浓度CS2是对有证标准溶液CS0稀释2次的结果,即:将式(14)~(16)和式(9)代入式(13):u(R)=当式(17)中的体积项和质量项与其他项相比较小而可忽略时,式(17)可简化为u(R)=当加入的标准物质与配制校准溶液的标准物质相同(XS0=CS0)时,则:u(R)=当R是n次测量的平均值,则式(19)可写为因有s(X)=XS*s(R),故式中的s(R )也可以为s(X)其中的X=X加标-X样.式(20)即为石墨炉原子吸收光谱法测定食品中铅含量加标法回收率不确定度的严密算式.3.3 实例比较3.3.1 数据来源3.3.2 量值计算(1)曲线拟合浓度的不确定度u()、u():将文献[19]表1、表2中的n=6,=35 ng·mL-1,p=7,=20.5 ng·mL-1,=0.016 ng·mL-1代入文献[19]的式(9)~(10),得:sR=0.007 4,u()=0.47 ng·mL-1,u()=0.59 ng·mL-1.则:(2)标样证书铅含量标准值XS0的(XS0):(3)标物证书铅浓度标准值CS0的(CS0):(4)标样回收率重复性的()标样:将式(21)~(24)的计算值代入式(12),计算得:将文献[19]、表2标样回收率的数据代入本文式(3),计算得:3.3.3 讨论式(24)中,标样回收法的重复性分量=3.05×10-4,只占式(25)回收率总不确定度=3.05×10-3的10%,标样标准值的分量)=1.37 ×10-3,占45%,二者之和1.68 ×10-3占55%;用式(1)和式(12)计算之结果的相对偏差:(3.05 -1.68)/[(3.05+1.68)/2]=58%;用式(2)和式(12)计算之结果的相对偏差:(3.05 × 10-3-3.05 × 10-4)/[(3.05 × 10-3+3.05 ×10-4)/2]=164%;用式(3)和式(12)计算之结果的相对偏差:(3.05×10-3-1.56×10-3)/[(3.05×10-3+1.56×10-3)/2]=65%.如果评估加标法的不确定度使用标样法的式(1)计算,计算结果则是文献[19]3.1.2.4 节中的重复性分量u2rel(f重复)=5.00 × 10 -4与 3.1.2.2(3)节中的标准溶液标准值的不确定度分量u2rel(CS0)=1.60×10-5之和(R)=5.16 ×10-4,只占使用加标回收法算式(20)之结果2.99×10-3的17%,二者的相对偏差为(2.99×10-3-5.16×10-4)/[(2.99 ×10-3+5.16 ×10-4)/2] =141%.4 结论(1)“重复性+证书标准值”公式适合于重复性分量和标准值分量占绝对优势的场合;“重复性”公式适合于重复性分量占绝对优势的场合;“近似公式”适合于B类评定的场合.(2)回收率不确定度评估的对象应是回收率值本身,平均回收率的不确定度只是回收率总不确定度中的一个重复性分量,只有当这个分量占绝对优势才可代表回收率总不确定度.(3)化学回收率不是一个直接测量量,其不确定度是与其具有复合函数关系的各因素之不确定度合成的结果;它是一个与过程有关的量,过程不同评估结果不同,难以有一个普适的具体公式,由某一过程导出的具体公式只适合于相同或相似的过程;只有遵循过程与模型的原则才可获得客观合理、针对性强、可靠性高的评估结果. 参考文献:[1]全国认证认可标准化技术委员会.GB/T 27404-2008实验室质量控制规范食品理化检测[S].北京:中国标准出版社,2008.The National Certification and Accreditation Standardization Technical Committee.GB/T 27404-2008 quality control specification on physical and chemical testing laboratory of food[S].Beijing:China Standard Press,2008.[2]国家环保总局.水和废水监测分析方法[M].4版.北京:中国环境科学出版社,2002:82-84.The State Environmental Protection Administration.Water and wastewater monitoring analysis method[M].4th ed.Beijing:China Environmental Science Press,2002:82-84.[3]中华人民共和国卫生部,中国国家标准化管理委员会.GB5750-2006生活饮用水标准检验方法[S].北京:中国标准出版社,2006.The Ministry of Healthof the People's Republic of China,China National Standardization Management Committee.GB5750 -2006 standard inspection method on drinking water[S].Beijing:China Standard Press,2006.[4]北京市环境保护监测中心.环境监测测量不确定度评定[M].北京:中国计量出版社,2009:49-53.Beijing Environmental Protection Monitoring Center.The evaluation of measurement uncertainty on environmentalmonitoring[M].Beijing:China Metrology Publishing House,2009:49-53. [5] PETER R,SHAUN B,RICHARD L,等.标准物质及其在分析化学中的应用[M].李红梅,刘菲,李孟婉,译.李红梅,卢晓华,校.北京:中国计量出版社,2006:118-125.PETER R,SHAUN B,RICHARD L,et al.Standard material and its application in analytical chemistry[M].Translated by LI H M,LIU F,LI M W.Checked by LI H M,LU X H.Beijing:China Metrology Publishing House,2006:118-125.[6]李慎安.回收率及其不确定度[J].中国计量,2007(1):89-90.LI SA.Recovery rate and its uncertainty[J].China Metro,2007(1):89-90. [7]李慎安.JJF1059-1999《测量不确定度评定与表示》讨论之九——测量误差与回收率[J].工业计量,2007,17(1):37-38.LI S A.JJF1059-1999“evaluation and said on measurement uncertainty,”to discuss the nine-measurement error and recovery[J].Indus Metro,2007,17(1):37-38.[8]昃向君,陈世山,刘心同,等.食品安全检测实验室测量不确定度的评定与应用[M].青岛:中国海洋大学出版社,2007:106-111.ZE X J,CHEN S S,LIU X T,et al.Measurement uncertainty evaluation and application on food safety testing laboratory[M].Qingdao:China Ocean University Press,2007:106-111.[9]付登洲,杨雪娇,黄伟.HPLC法测定乳制品中三聚氰胺含量的不确定度评定[J].食品研究与开发,2011,32(2):108-112.FU D Z,YANG X J,HUANG W.Analysis of uncertainty in determination of melamine in dairy products by HPLC[J].Food Res Devel,2011,32(2):108-112.[10]李应东,刘耀敏,张凤枰.高氯酸湿消化-原子荧光光度法测定饲料中总砷的不确定度评定[J].中国粮油学报,2011,26(2):115-119.LI Y D,LIU Y M,ZHANG F P.Uncertainty evaluation of determination of total arsenic in feeds by atomic fluorescence spectrometry after Perchloric acid wet digestion[J].J Chin Cerea Oils Asso,2011,26(2):115-119.[11]魏大伟,程江山,郑玉芝.液相色谱法测定饼干中日落黄含量的测量不确定度评定[J].食品工业科技,2011(6):414-417.WEI D W,CHENG J S,ZHENG Y Z.Uncertainty evaluation for determining concentration of sunset yellow in biscuit by HPLC[J].Sci Tech Food Indus,2011(6):414-417.[12]张蓉,张华琚,王志斌.微波消解-石墨炉原子吸收光谱法测定保健食品中痕量铅的不确定度评定[J].计量学报,2010,31(4):369-373.ZHANG R,ZHANG H J,WANG Z B.Evaluation of uncertainty in determination of lead in health food by microwave digestion-graphite furnace atomic absorption spectrometry[J].Acta Metro,2010,31(4):369-373.[13]国家质量监督检验检疫总局.JJF1059-1999测量不确定度评定与表示[S].北京:中国计量出版社,1999.General Administration of Quality Supervision,Inspection and Quarantine of the People's Republic of China.JJF1059 -1999 evaluation and expression of uncertainty in measurement[S].Beijing:China Metrology Publishing House,1999. [14]冯信平.微波消解ICP-MS测定土壤中铅、镉的不确定度评估[J].热带生物学报,2010,1(1):31-36.FENG X P.Uncertainty evaluation of Pb and Cd in soft measured by ICP-MS after microwave-assisted digestion[J].J Trop Orga,2010,1(1):31-36.[15]杨洋,徐春祥,车文军.高效液相色谱法测定奶粉中的三聚氰胺及其不确定度分析[J].食品科学,2010,31(4):250-253.YANG Y,XU C X,CHE WJ.Uncertainty evaluation of HPLC determination of melamine in milk powderchromatography[J].Food Sci,2010,31(4):250-253.[16]韦新红,魏雅娟,陈永欣,等.电感耦合等离子体质谱(ICP-MS)法测定高纯氧化铟中铜含量的不确定度评定[J].中国无机分析化学,2011,1(2):50-53.WEI X H,WEI Y J,CHEN Y X,et al.The evaluation of the uncertainty of quantitative determination of copper in high purity indium oxide by inductively coupled plasma mass spectrometry[J].Chin J Inor Anal Chem,2011,1(2):50-53.[17]董朝敏,旷运坤.磷钒钼黄分光光度法测定炉水磷酸盐含量的不确定度评定[J].中国计量,2009(10):92-94.DONG C M,KUANG Y K.The uncertainty evaluation of phosphate content in boiler water determinated by Hosphorus Vanadium Molybdenum yellow spectrophotometric method [J].China Metro,2009(10):92-94.[18]中华人民共和国卫生部.GB5009.12-2010食品安全国家标准食品中铅的测定[S].北京:中国标准出版社,2010.The ministry of health of the People's Republic of China.GB5009.12 -2010 national food safety standards on the determination of lead in food[S].Beijing:China Standard Press,2010. [19]占永革,龚剑,黄湘燕.石墨炉原子吸收法检测猪肝中铅回收率不确定度的评估[J].食品科学,2012,33(10):155-160.ZHAN Y G,GONG J,HUANG X Y.Uncertainty evaluation of recovery in the measurement of lead in pigs liver by GF-AAS[J].Food Sci,2012,33(10):155-160.。
MSA GRR计算公式

MSA GRR计算公式
MSAGRR是一种用于衡量测量系统可靠性的方法。
GRR代表了GaugeRepeatabilityandReproducibility,即重复性和再现性。
MSA GRR计算公式是一种用于计算GRR的公式,它可以帮助我们了解测量系统的精度和可靠性。
MSA GRR计算公式包括以下几个要素:
1.测量系统误差:包括重复性误差和再现性误差。
重复性误差是指在相同条件下,同一测量员使用同一测量工具进行多次测量时,所得结果的差异。
再现性误差是指在不同条件下,不同测量员使用同一测量工具进行测量时,所得结果的差异。
2.零件离散程度:用于衡量被测零件的离散程度,其值越大表示测量系统所测量的零件变化范围越大。
3.相对扩大误差(%R&R):用于计算测量系统的可靠性,其值越小表示测量系统越可靠。
MSA GRR计算公式为:
%R&R = (GRR/总变差)× 100%
其中,GRR = 2.5 ×(测量系统误差/零件离散程度)
总变差 = 6 ×(测量系统误差/零件离散程度)
通过这个公式,我们可以计算出测量系统的可靠性水平,以便进行必要的改进和优化。
在实际运用中,我们应该根据实际情况选择合适的数据采集方法和样本数量,以尽可能减小误差和提高测量系统的可靠性。
GR&R研究之测量仪器设备培训 MSA重复性再 性 解及分析公式

分析时机
对于需进行GR&R分析的测量系统,一般在以 下三种情况下要进行GR&R分析 1、首次正式使用前 2、每年2次的保养时/6个月1次 3、故障修复后
分析方法
准备 1、检查员人数:一般为3人。当以前分析时的GR&R值低 于20%时,也可为2人。 2、试验次数:与检查员人数相同,即两人时为每人两次, 三人时为每人3次。 3、零件数量:一般选10个可代表覆盖整个工序变化范围 的样品 。当以前分析时的GR&R值低于20%时,也可选5 个。 4、测量仪器(设备)的精度(分辨率):需比被测量体 要求精度高一个数量级,即如要求测量精度是0.001,测 量仪器的精度要求须是0.0001。
测试条件: 1.测量必须在稳定条件下运行某一测量仪器设备 简单来说:在稳定条件下运行测量系统得到某一特性多次测量的结果
若这些结果与基准值都很“接近”,则表示这个测量系统质量很高 若是与基准值“远离”则表示这个测量系统质量 低
测量时应采用盲测,以排除人为干扰(在实际测量环境下,操作者事先不知 道该测量系统的条件下进行评估
定 义
测量系统 :是指由测量仪器(设备)、测量软件、 测量操作人员和被测量物所组成的一个整体。 测量系统分析 :是指检测测量系统以便更好地了 解影响测量结果的变异来源及其分布的一种方法。 通过测量系统分析可把握当前所用测量系统有无 问题和主要问题出在哪里,以便及时纠正偏差, 使测量精度满足要求。 测量系统误差:由精确度、稳定度、可重复性、 再现性合并而成
5.00
B XA3 4.98 4.98 4.99 4.98 5.05 4.96 5.04 4.95 5.03 4.99 RA 0.03 0.03 0.04 0.03 0.02 0.02 0.07 0.09 0.06 0.04
如何进行计量标准的重复性_稳定性考核和期间核查

如何进行计量标准的重复性、稳定性考核和期间核查How to Check the Repetition,Stability of Measurement Standard王兴东(陕西省计量科学研究院,陕西西安710048)摘 要:本文叙述了计量标准的测量重复性、稳定性考核和期间核查的目的,给出计量标准重复性和稳定性考核以及计量标准的期间核查的方法。
同时给出考核结果的判定原则和考核时应注意的事项。
关键词:计量标准;重复性;稳定性;期间核查;方法;判定 新修订的JJ F1033-2008《计量标准考核规范》都对计量标准的重复性考核,稳定性考核和期间核查提出了要求,根据自己对这两个规范的学习和实际工作谈淡自己的理解。
1 计量标准的测量重复性考核111 计量标准重复性测量的准备工作(1)选择被测对象:选择被测对象一定要具有稳定的性能,并有代表性,的确能反映计量标准的实际情况,容易实现的样品。
重复性测量中“被测量或被检测器具”的选取原则是在计量检定工作中,要求标准设备的不确定度尽可能小到使其对被检仪器的允许误差而言可以忽略不计,以使错判的风险减到最小。
对重复性测量也是一样,应使“被测量或被检测器具”的选取对测量数据的影响尽可能地小。
(2)重复性试验的依据:对计量标准重复性试验,有规程或规范要求的一定要按要求去做重复性试验,如果没有,可参考有关技术资料进行。
(3)环境条件:重复性试验一定要在规定的环境条件下进行,环境条件如温度、相对湿度、振动、磁场等。
如果环境条件无法满足要求时,对重复性试验的结果要进行修正。
(4)量值的溯源:做重复性试验时一定要注意量值的溯源,这样才能保证量值的统一、准确和可靠,如无法溯源的要进行互相比对,这样的计量标准的重复性才有意义。
(5)重复性记录:原始记录保留着做重复性试验数据和有关信息,计量标准的重复性是否满足要求都是来自原始记录,原始记录一定要真实,信息量要大,真实的反映重复性的实际情况。
对饲料检测标准中平行样重复性表示方法的理解

对饲料检测标准中平行样重复性表示方法的理解1、 平行样重复性常用相对偏差表示,通用公式: 平均相对偏差i1100%ni x x nx =-=⨯∑通常都是测定两平行样,x 1,x 2;若x 1<x 2,11d x =-x ,22d x =-x ,12d d =则 平均相对偏差2i1212112100%100%100%100%222i x x x x d d d d x x xx =--+=⨯=⨯=⨯=⨯∑或 2、 平行样重复性又用精密度表示,公式:精密度=12100%x x x-⨯ 显然精密度为平均相对偏差的2倍!3、 平行样重复性还用重复性限表示,因检测项目不同,计算公式不一致;或是直接给出重复性限数值。
计算重复性=12x x -后,与重复性限比较,判断是否超限。
实际重复性限为平均相对偏差或精密度的另一种表示方式。
4、 上世纪80年代、90年代饲料标准大多采用(平均)相对偏差表示,有极少数用精GB/T 6435—2014饲料中水分的测定,则平均相对偏差和重复限并用;近年来国家食品等标准普遍采用精密度表示,新修订饲料标准也逐步向这一方向转变,只是规定描述不太统一规范!5、 食品标准中精密度表述:在重复条件下获得的两次独立测定结果的绝对差值不得超过算术平均值的xx%。
表述:在重复性条件下获得的两次独立测定结果的绝对差值不大于这两个测定值的算术平均值的xx%。
GB/T 13083—2018的限量参数比原GB/T 13083—2002(相对偏差)增加一倍,实际和原标准相同;GB/T 6436—2018的限量参数比原GB/T 6436—2002(相对偏差)增加近一倍,也作了与原标准相当的修改,.比原标准严;GB/T 6437—2018的限量参数与原GB/T 6437—2002(相对偏差)相一致?是否原标准太宽松了,有实验数据的支持,制定的比原标准严一倍?还是没有理解精密度与相对偏差的关系?值的xx%。
这种表述很模糊,实际应该为平均相对偏差,GB/T 6432—2018的限量参数与原GB/T 6432—1994(相对偏差)一致!是否采用精密度?限量参数增大一倍与氟相同;GB/T 13085—2018的限量参数与原GB/T 13085—2005(相对偏差)基本一致!。
测量仪器的重复性评定

一二测量仪器的重复性评定 测量仪器的重复性是指在相同的测量条件下,重复测量同一个被测量,测量仪器提供相近示值的能力,一般可用示值的分散性定量地表示。
下面本文主要根据JJF测量仪器特性评定相关内容介绍测量仪器重复性评定方法及计算。
测量仪器的重复性评定方法--贝塞尔公式法 在重复性条件下,由被评定测量仪器对给定的约定真值或稳定的被测量进行连续多次的测量或比较,有的情况下则是由提供约定真值的测量仪器对被评定测量仪器进行连续多次的测量,用实验标准差来表示被评定测量仪器的重复性。
重复性条件包括测量程序、人员、仪器、环境等,同时为尽可能保证在相同的条件下进行测量,必须在尽量短的时间内完成重复性测量。
实验标准差一般用贝塞尔公式计算: 式中: S——实验标准差,在此即测量仪器的重复性; Xi——第i次观测值,i=1,2,……,n; X——n次观测值的算术平均值; n——测量次数。
注:用贝塞尔公式计算得到的实验标注差s是有不确定度的,其相对标准不确定度可表示为 式中:u(s)为实验标准差s的标准不确定度。
测量次数越多,实验标准差的不确定度越小,实验标准差越可靠。
例如:测量次数为9,由上式计算得到的实验标准差的相对标准不确定度为25%,若s=0.10mm,则u(s)=0.025mm。
测量仪器的重复性评定方法--最大残差法 由每个观测值与算术平均值之差得到残差,从残差中找出最大残差值,按下式计算实验标准差 式中: Vimax——最大残差值;三 Cn——最大残差系数。
Cn的值根据测量次数n从表1中查得。
表1 最大残差系数Cn测量仪器的重复性评定方法--极差法 找出观测值中的最大值和最小值,两者之差为极差,按下式计算实验标准差 式中: Xmax——观测值中的最大值; Xmin——观测值中的最小值; dn——极差系数。
dn的值根据测量次数n从表2中查得。
表2 极差系数dn 在测量次数较少时,一般也可采用极差法。
在实际的重复性评定中应当注意用最大残差法或极差法算得的实验标准差的不确定度,不大于贝塞尔公式计算得的实验标准差的不确定度。
测量重复性计算公式

测量重复性计算公式重复性计算是一种重要的统计技术,它可以帮助我们更好地理解数据的变化趋势。
它可以帮助我们更好地分析数据,从而更好地掌握数据的变化趋势。
重复性计算是一种统计技术,它可以帮助我们更好地分析数据,从而更好地掌握数据的变化趋势。
重复性计算的公式是:重复性=(样本均值-样本中位数)/样本标准差。
其中,样本均值是指样本中所有数据的平均值;样本中位数是指样本中所有数据的中位数;样本标准差是指样本中所有数据的标准差。
重复性计算的公式可以帮助我们更好地分析数据,从而更好地掌握数据的变化趋势。
重复性计算的结果可以帮助我们判断数据的变化趋势是否稳定,从而更好地掌握数据的变化趋势。
重复性计算的公式可以帮助我们更好地分析数据,从而更好地掌握数据的变化趋势。
重复性计算的结果可以帮助我们判断数据的变化趋势是否稳定,从而更好地掌握数据的变化趋势。
重复性计算的公式可以帮助我们更好地分析数据,从而更好地掌握数据的变化趋势。
重复性计算的结果可以帮助我们判断数据的变化趋势是否稳定,从而更好地掌握数据的变化趋势。
此外,重复性计算的结果还可以帮助我们判断数据的变化趋势是否有明显的变化,从而更好地掌握数据的变化趋势。
重复性计算是一种重要的统计技术,它可以帮助我们更好地理解数据的变化趋势。
它可以帮助我们更好地分析数据,从而更好地掌握数据的变化趋势。
重复性计算的公式可以帮助我们更好地分析数据,从而更好地掌握数据的变化趋势。
重复性计算的结果可以帮助我们判断数据的变化趋势是否稳定,从而更好地掌握数据的变化趋势。
因此,重复性计算是一种重要的统计技术,它可以帮助我们更好地理解数据的变化趋势。
MSA测量系统重复性与再现性GRR

M S A测量系统重复性与再现性G R RHessen was revised in January 2021MSA测量系统重复性与再现性GR&R分析摘要:是使用数理统计和图表的方法对测量系统的分辨率和误差进行分析,以评估测量系统的分辨率和误差对于被测量的参数来说是否合适,并确定测量系统误差的主要成分, 而测量系统误差的重复性和再现性由GR&R 研究确定。
由精确度、稳定度、重复性、再现性合并而成,其中重复性跟再现性简称为GR&R,其目的是借助量具量测数据,验证量具是否可靠,是否好用,还可以计算出量具的量测误差;1.重复性(Repeatability ):当同一零件的同一种特征由同一个人进行多次测量时变异的总和。
说明:其实验数据必须符合以下条件:同一人员、同一产品、同一环境、同一位置、同一仪器、短期时间内.2.再现性(Reproducibility ):当同一零件的同一种特征由不同的人使用同一量具进行测量时,在测量平均值方面的变异的总和。
说明:其实验数据必须符合以下条件: 不同人员同一产品、不同环境、不同位置、不同仪器、较长时间段.什么时候才需要进行GR&R分析对于需进行GR&R分析的测量系统,一般在以下三种情况下要进行GR&R分析:首次正式使用前每年一次的保养时故障修复后GR&R分析方法1.准备检查员人数:一般为3人。
当以前分析时的GR&R值低于20%时,也可为2人。
试验次数:与检查员人数相同,即两人时为每人两次,三人时为每人3次。
零件数量:一般选10个可代表覆盖整个工序变化范围的样品。
当以前分析时的GR&R值低于20%时,也可选5个。
2.实施第一名检查员以随机方式对所给的零件进行第一次测量,将测量结果填入表格第二列。
然后第二名检查员同样以随机方式对这些零件进行第一次测量,将测量结果填入表格第六列。
第三名检查员做法相同,将测量结果填入表格第十列。
MSA测量系统重复性与再现性

MSA测量系统重复性与再现性GR&R分析摘要:是使用数理统计和图表的方法对测量系统的分辨率和误差进行分析,以评估测量系统的分辨率和误差对于被测量的参数来说是否合适,并确定测量系统误差的主要成分, 而测量系统误差的重复性和再现性由GR&R 研究确定。
由精确度、稳定度、重复性、再现性合并而成,其中重复性跟再现性简称为GR&R,其目的是借助量具量测数据,验证量具是否可靠,是否好用,还可以计算出量具的量测误差;1.重复性(Repeatability ):当同一零件的同一种特征由同一个人进行多次测量时变异的总和。
说明:其实验数据必须符合以下条件:同一人员、同一产品、同一环境、同一位置、同一仪器、短期时间内.2.再现性(Reproducibility ):当同一零件的同一种特征由不同的人使用同一量具进行测量时,在测量平均值方面的变异的总和。
说明:其实验数据必须符合以下条件: 不同人员同一产品、不同环境、不同位置、不同仪器、较长时间段.什么时候才需要进行GR&R分析对于需进行GR&R分析的测量系统,一般在以下三种情况下要进行GR&R分析:?首次正式使用前?每年一次的保养时?故障修复后GR&R分析方法1.准备检查员人数:一般为3人。
当以前分析时的GR&R值低于20%时,也可为2人。
试验次数:与检查员人数相同,即两人时为每人两次,三人时为每人3次。
零件数量:一般选10个可代表覆盖整个工序变化范围的样品。
当以前分析时的GR&R值低于20%时,也可选5个。
2.实施第一名检查员以随机方式对所给的零件进行第一次测量,将测量结果填入表格第二列。
然后第二名检查员同样以随机方式对这些零件进行第一次测量,将测量结果填入表格第六列。
第三名检查员做法相同,将测量结果填入表格第十列。
重复上述步骤,进行第二次、第三次测量,并将测量结果填入其余空白表格。
3.计算出设备变异EV、人员差异以及 GR&R等百分比,其计算公式如下图所示:4.判异标准如果GR&R小于所测零件公差的10%,则此系统无问题。
汽柴油的重复性和再现性公式

汽油质量检验项目的重复性和再现性计算公式1、溶剂洗胶质GB/T8019重复性计算:未洗胶质含量r=0.997X0.4,溶剂洗胶质含量r=1.298X0.3 X—重复测定结果的算术平均值。
再现性计算:未洗胶质含量R=1.928X0.4,溶剂洗胶质含量R=2.494X0.3 X—两个独立结果的算术平均值。
2、荧光硫SH/T0742重复性计算:r= 12 .30 (X + 1 0 )0.1X—重复测定结果的算术平均值。
再现性计算: R =3 6. 26 (X + 10 )0.1X—两个独立结果的算术平均值。
3、紫光硫SH/T0689重复性计算:r=0.1867X0.63X—重复测定结果的算术平均值。
再现性计算:R=0.2217X0.92X—两个独立结果的算术平均值。
4、硫醇硫GB/1792重复性计算:r=0.00007+0.027XX—重复测定结果的算术平均值。
再现性计算:R=0.00031+0.042XX—两个独立结果的算术平均值。
5、馏程GB/T6536 ℃1)手工法回收点重复性r、再现性R的计算:10%回收点:S=0.05(T20%平均回收温度-T初馏点平均回收温度)r=(S+2.46)/2.44R=(S+1.39)/0.7650%回收点:S=0.05(T60%平均回收温度-T40%平均回收温度)r=(S+2.46)/2.44R=(S+1.39)/0.7690%回收点:S=0.1(T90%平均回收温度-T80%平均回收温度)r=(S+2.46)/2.44R=(S+1.39)/0.76终馏点:S=(T终馏点平均回收温度-T95%平均回收温度)/(V终馏点平均体积-95)r=(S+1.82)/2.66R=(S+6.95)/2.242)自动法回收点重复性r、再现性R的计算:10%回收点:S=0.05(T20%平均回收温度-T初馏点平均回收温度)r=1.2+1.42SR=3.0+2.64S50%回收点:S=0.05(T60%平均回收温度-T40%平均回收温度)r=1.2+1.42SR=2.9+3.97S90%回收点:S=0.1(T90%平均回收温度-T80%平均回收温度)r=1.1+1.08SR=2.0+2.53S终馏点:r=3.5R=10.56、烃的重复性和再现性计算(1)不含含氧化合物样品的重复性和再现性%(体积分数)(2)含有含氧化合物样品的重复性和再现性%(体积分数)7、苯、甲苯重复性和再现性计算%(体积分数)8、醇类和醚类中氧含量的重复性和再现性计算%(质量分数)9、汽油中Fe和Mn含量的重复性和再现性计算mg/LFe重复性:0.65X0.48再现性:0.55X0.79Mn重复性:0.42X1/2再现性:1.41X1/2/a/20100427/004567.htm柴油质量检验项目的重复性和再现性计算公式1、闭口闪点GB/T261重复性计算:0.029XX—重复测定结果的算术平均值。
