岩石力学数值方法(翻译)
一种基于abaqus的岩石力学试验数值仿真方法

一种基于abaqus的岩石力学试验数值仿真方法对于基于Abaqus的岩石力学试验数值仿真方法,以下是一种可能的步骤:1. 建立模型:首先,根据岩石试验的几何形状和尺寸,使用Abaqus软件建立岩石模型。
可以使用几何建模工具创建模型的几何形状,如创建圆柱形、立方体或其他形状的岩石模型。
2. 确定边界条件:在建模过程中,确定加载和边界条件。
例如,如果进行压缩试验,可以将一个表面固定,然后在另一个表面施加压力负荷。
或者,如果进行拉伸试验,可以在两个表面施加拉伸负载。
3. 定义材料特性:根据所使用的岩石材料的力学特性,定义岩石的材料参数。
这些参数可以通过实验获得,也可以从文献中找到。
参数可能包括岩石的弹性模量、泊松比、黏滞性和塑性参数等。
4. 设置模拟参数:在Abaqus中设置数值仿真参数,例如时间步长、迭代次数和收敛准则。
这些参数的选择可以根据岩石试验的特点和需要进行调整。
5. 运行模拟:输入所需的加载项和其他参数,运行岩石数值仿真模拟。
Abaqus将通过求解弹性-塑性和/或黏弹性方程来模拟岩石的行为。
6. 分析结果:在模拟运行完成后,可以分析仿真的结果。
Abaqus提供了一系列分析工具,可以用于查看应力、应变、变形、裂纹扩展等参数的变化情况。
7. 验证模拟结果:为了验证数值仿真的准确性,可以将模拟结果与实际试验结果进行比较。
如果两者吻合较好,则说明数值仿真模型能够准确地模拟岩石试验。
需要注意的是,在进行岩石力学试验数值仿真时,应根据具体的试验需求和岩石特性进行模型和参数的选择和定义。
此外,由于岩石具有非线性和各向异性等特性,需要谨慎选择适合的数值方法和模型进行仿真分析。
常用地岩土和岩石物理力学全参数

(E, ν) 与(K, G)的转换关系如下:)21(3ν-=EK)1(2ν+=EG (7.2)当ν值接近0.5的时候不能盲目的使用公式3.5,因为计算的K 值将会非常的高,偏离实际值很多。
最好是确定好K 值(利用压缩试验或者P 波速度试验估计),然后再用K 和ν来计算G 值。
表7.1和7.2分别给出了岩土体的一些典型弹性特性值。
岩石的弹性(实验室值)(Goodman,1980) 表7.1土的弹性特性值(实验室值)(Das,1980) 表7.2各向异性弹性特性——作为各向异性弹性体的特殊情况,横切各向同性弹性模型需要5中弹性常量:E 1, E 3, ν12,ν13和G 13;正交各向异性弹性模型有9个弹性模量E 1,E 2,E 3, ν12,ν13,ν23,G 12,G 13和G 23。
这些常量的定义见理论篇。
均质的节理或是层状的岩石一般表现出横切各向同性弹性特性。
一些学者已经给出了用各向同性弹性特性参数、节理刚度和空间参数来表示的弹性常数的公式。
表3.7给出了各向异性岩石的一些典型的特性值。
横切各向同性弹性岩石的弹性常数(实验室) 表7.3砂岩 15.7 9.6 0.28 0.21 5.2 石灰石 39.8 36.0 0.18 0.25 14.5 页岩 66.8 49.5 0.17 0.21 25.3 大理石 68.6 50.2 0.06 0.22 26.6 花岗岩10.75.20.200.411.2流体弹性特性——用于地下水分析的模型涉及到不可压缩的土粒时用到水的体积模量K f ,如果土粒是可压缩的,则要用到比奥模量M 。
纯净水在室温情况下的K f 值是2 Gpa 。
其取值依赖于分析的目的。
分析稳态流动或是求初始孔隙压力的分布状态(见理论篇第三章流体-固体相互作用分析),则尽量要用比较低的K f ,不用折减。
这是由于对于大的K f 流动时间步长很小,并且,力学收敛性也较差。
在FLAC 3D中用到的流动时间步长, tf 与孔隙度n ,渗透系数k 以及K f 有如下关系:'f f kK nt ∝∆ (7.3) 对于可变形流体(多数课本中都是将流体设定为不可压缩的)我们可以通过获得的固结系数νC 来决定改变K f 的结果。
第九章 岩石力学的数值模拟分析

Betti互等 定理
解方程组
边界上划分单元
同上
离散单元 法
牛顿运动 定律
显式差分
按结构弱面分布特 征划分单元
岩石中硬以上,低应力水平, 大变形,岩体沿弱面发生非连
续性破坏
非连续变 形法
数值流形 法
拉各朗日 元法
最小势能 原理
最小势能 原理
牛顿运动 定律
解方程组
按主要结构弱面实 际情况划分单元
解方程组 全区域划分单元
在上面4种并行机中,COW和MPP具有类似的地方, 实际上,当前MPP和COW之间的界限正在逐渐模 糊。例如IBM SP格比远优于MPP,系统扩 充方便,网络连接形式多种多样,所以COW是发 展可扩放并行计算的主流趋势。
并行算法及并行程序开发 并行算法是区别于串行算法的另外一大类型的算法,它是适合于 各种并行计算机上求解问题和处理数据的算法。并行程序开发是 对给定算法构造并行程序的活动,它要求算法设计者和计算机系 统的体系结构的设计者进行广泛的交互。
并行程序的设计不仅编程困难,而且调试和分析更加困难。目前, 并行程序设计在各方面都处于一个初级阶段,它不支持一个成熟、 稳定和通用的并行程序开发环境。并行开发环境指的是软件环境, 它对并行计算的影响比一般串行机要大得多。软件对计算性能的 影响的差别可达几个数量级。并行开发环境包括两部分内容:操 作系统、通信平台、编译和调试工具以及性能测试软件等。其中 最主要的是操作系统和通信平台。可以用于并行计算的操作系统 主要有Windows(NT或者2000)和Unix,其中与Unix内核基 本相同的自由软件Linux在并行计算中占优绝对的统治地位,而 比较流行的通信平台有P4、PVM、Express、PARMACS和MPI 等。
岩体力学方法

第5讲 岩体力学方法—数值法
1、计算范围的确定和离散方法 (4)应注意的几个问题(remarks)
1)一个单元各边长相差不能过大,两边夹角不能过小, 各夹角最好尽量相等。
2)一个单元中不能包含两种或两种以上的材料。 3)集中荷载作用点或荷载突变处必须布置节点。 4)如隧道结构和岩体结构具有对称性时取部分计算范围
为边界位移, T为温度。它们可由各种计算模型给出。先将计
算区域离散化,给定, Fx,Fy 等的初值,用有限元法计算域 内应力,求出相应于特定, Fx, Fy等因素的基本初始应力 ,
Fx, Fy ,将其与相应回归系数相乘并迭加,得到初始应力场的 回归方程:
b 1 b 2 F b x 3 y k ( 2 )
进行离散。几何形状和材料特性方面都具有对称性 时,可利用该对称性取部分计算范围进行剖分。
土木工程学院隧道工程系
第5讲 岩体力学方法—数值法
1、计算范围的确定和离散方法 (4)应注意的几个问题(remarks)
5)洞室边缘两侧的对应单元,其大小形状尽量一致。 6)洞室边缘及附近单元的布置应考虑设置锚杆的方向及
土木工程学院隧道工程系
第5讲 岩体力学方法—数值法
二、数值法
(一)隧道工程数值计算模型的建立
1、计算范围的确定和离散方法 (1)计算范围(scope of problem)
大多数隧道工程都涉及无限域或半无限域,而有限元法处理 这类问题通常是在有限区域里进行离散化。为了使这种处理方 法不至于产生过大的误差,离散区域必须有足够的范围,并使 区域外边界条件尽可能接近实际状态。理论分析表明,在均质 弹性无限域中开挖的圆形洞室,由于荷载释放而引起的洞周介 质应力和位移变化,在五倍洞径范围之外将小于l%,三倍洞 径之外约小于5%。
岩石静态力学参数测试方法与数据处理

岩石静态力学参数测试方法与数据处理岩石是地球上常见的天然物质,研究岩石的力学参数对于地质灾害预测、工程设计以及资源勘探等领域具有重要意义。
本文将介绍岩石静态力学参数的测试方法与数据处理。
一、岩石静态力学参数的测试方法1. 岩石抗压强度测试岩石抗压强度是岩石力学参数中的关键指标之一,它反映了岩石的抗压能力。
常用的测试方法包括单轴压缩试验和直接剪切试验。
在单轴压缩试验中,需要使用压力机对岩石样品进行垂直方向的单向加载,同时测量加载过程中岩石的变形和承载能力。
通过绘制应力-应变曲线,可以得到岩石的抗压强度参数。
而直接剪切试验则是将岩石样品切割成一个矩形或圆形的平面,再对这个平面进行横向和纵向的剪切加载,通过测量剪切力和位移来推导出剪切强度。
2. 岩石弹性模量测试岩石的弹性模量是指岩石在受力下能够发生弹性变形的能力,是衡量岩石刚性的重要参数。
常用的测试方法包括弹性波速度法和恒定应力法。
在弹性波速度法中,通过在岩石样品上产生激发弹性波,测量波传播速度来计算岩石的弹性模量。
这种方法常用于实验室条件下对小尺寸岩石样品进行非破坏性测试。
而恒定应力法则是在施加一定大小的应力下,测量岩石样品的应变,通过根据背反映的力学模型计算岩石的弹性模量。
二、岩石静态力学参数的数据处理1. 数据采集与记录在进行试验时,需要对实验过程中产生的数据进行准确的记录。
这些数据包括施加的力、变形量、位移等。
可以使用计算机或数据采集系统来实现自动化的数据记录,以减少因人为操作导致的误差。
2. 数据处理与分析数据处理是在原始数据的基础上进行数据修正、提取有效信息以及统计分析的过程。
在岩石静态力学参数的数据处理中,需要对原始数据进行平滑处理、误差修正,并进行数据拟合和计算。
平滑处理是通过去除噪声和异常值,使得数据更加平滑。
常用的平滑方法有移动平均法、多项式拟合法等。
误差修正是根据实际情况对数据进行校正,主要考虑仪器误差和环境因素。
校正过程中需要参考相关的国际或行业标准。
岩土工程数值方法

岩土工程数值方法摘要:逐渐发展起来的一些岩土分析手段与数学理论,如信息量法、层次分析法、随机模拟法、无网络法、数值流形法、离散元法、分形理论、可靠度分析、人工神经元网络和智能岩石力学等,已经呈现出综合应用的趋势,对于岩体力学研究而言,岩石破坏过程的渐进性、岩体内部初始损伤的存在及块体之间的不连续特征是必须考虑的因素,因此建立在连续介质力学基础上的传统有限单元法具有明显的局限性。
各种新方法的涌现从不同方面推动了岩石力学数值计算方法的进步。
关键词:岩土数值模拟有限元法无网络伽辽金法扩展有限元法数值流形法离散元法Abstract: gradually developed some geotechnical analysis method and mathematical theory, such as information method, the analytic hierarchy process (ahp), random simulation method, the numerical manifold method, no network, discrete element method, fractal theory, reliability analysis, artificial neural network and intelligent rock mechanics etc, has presented a comprehensive application trend, for research in rock mechanics, rock failure process of rock mass progressive, the existence of the internal initial damage and block the discontinuous characteristics between is must consider factors so based on continuum mechanics on the basis of the traditional finite element method has obvious limitation. All kinds of the emerging of the new method from different aspects promote the rock mechanics numerical calculation method of progress.Keywords: geotechnical numerical simulation finite element method without network petro-galerkin method was expanded numerical manifold method finite element method of discrete element method中图分类号:O241 文献标识码:A文章编号:岩土数值模拟是否正确,其解决问题的重要基础仍然是地质工作,“地质体运动真实行为的理解比精确计算更为重要”。
一种基于abaqus的岩石力学试验数值仿真方法

一种基于abaqus的岩石力学试验数值仿真方法(原创版4篇)目录(篇1)1.引言2.岩石力学试验数值仿真的背景和意义3.Abaqus 软件在岩石力学试验数值仿真中的应用4.Abaqus 软件的优点和局限性5.结论正文(篇1)1.引言随着科技的发展,数值仿真已经成为了工程领域中不可或缺的一部分。
在岩石力学试验中,数值仿真方法可以有效地辅助实际试验,提高试验效率和准确性。
本文将介绍一种基于 Abaqus 的岩石力学试验数值仿真方法。
2.岩石力学试验数值仿真的背景和意义岩石力学试验是研究岩石力学性质的重要手段,其目的是为了了解岩石在各种应力条件下的行为。
然而,实际试验受到许多因素的影响,例如试验设备的限制、试验过程的复杂性以及试验结果的可靠性等。
因此,数值仿真方法在岩石力学试验中的应用变得越来越重要。
数值仿真方法可以模拟各种复杂的应力条件,以及岩石在这些条件下的行为。
这种方法不仅可以提高试验效率,还可以降低试验成本。
此外,数值仿真方法还可以为研究者提供更多的信息,例如应力分布、应变分析等。
3.Abaqus 软件在岩石力学试验数值仿真中的应用Abaqus 是一款广泛应用于工程领域的数值仿真软件,它可以模拟各种复杂的力学问题,包括岩石力学问题。
在岩石力学试验数值仿真中,Abaqus 可以模拟岩石的应力、应变、破裂等过程,为研究者提供有关岩石力学性质的重要信息。
4.Abaqus 软件的优点和局限性Abaqus 软件在岩石力学试验数值仿真中具有许多优点,例如:(1)Abaqus 具有强大的模拟能力,可以模拟各种复杂的应力条件和岩石行为。
(2)Abaqus 可以提供详细的应力、应变等信息,有助于研究者深入了解岩石的力学性质。
(3)Abaqus 的图形用户界面简单易用,方便研究者进行模型构建和结果分析。
然而,Abaqus 软件也存在一些局限性,例如:(1)Abaqus 的学习曲线较陡峭,需要研究者投入较多的时间和精力进行学习。
岩石的物理力学指标及其试验方法、强度特性、变形特性、强度理论、工程岩体分级标准

(一)掌握岩石的物理力学指标及其试验方法;了解岩石的强度特性、变形特性、强度理论;掌握工程岩体分级标准。
1.物理力学指标(物理性质指标)
岩石的容重:单位体积内岩石(包括孔隙体积)的重量称为岩石的容重,单位(N/m³)。
干容重:就是指不含水分状态下的容重。
一般用于表示土的压实效果,干容重越大表示压实效果越好。
最大干容重:是在实验室中得到的最密实状态下的干容重。
密度:单位体积所具有的质量称为密度,公式ρ=m/V(kg/m3);单位体积所具有的重量称为容重,公式γ=G/V(N/m3),容重等于密度和重力加速度的乘积,即γ=ρg,单位是牛/立方米(N/m³)。
岩石的比重:岩石的比重就是绝对干燥时岩石固体部分实体积(即不包含孔隙的体积)的重量与同体积水(4℃)的重量之比。
单轴压缩试验试件要求:
端部效应是指试样受压时,两端部受其与试验机承压极间摩擦力的束缚、不能自由侧向膨胀而产生的对强度试验值的影响。
渗透系数
2.物理力学指标(变形性质指标)
弹性模量
变形模量
泊松
弹性模量:单位应变的应力。
3.物理力学指标(强度性质指标)
强度指标:抗压强度、抗剪强度、抗剪断强度、抗切强度、抗拉强度
三轴压缩试验:
岩石的强度特性、变形特性、强度
岩石三轴试验要求尽可能地使岩石处于三轴受力情况下
、。
岩石力学的数值模拟(讲义)

第10章岩石力学的数值模拟随着计算机软硬件技术的迅速发展,使岩石力学有了长足的进步,特别在岩石力学的数值计算和模拟方面发展尤为迅速,使得许多岩石力学解析方法难于解决的问题得以重新认识。
正如钱学森在给中国力学学会“力学——迎接21世纪新的挑战”的一封信中对力学发展趋势总结的那样“今日力学是一门用计算机计算去回答一切宏观的实际科学技术问题,计算方法非常重要”。
岩石力学和其他力学学科一样,需要数值计算方法并推动岩石力学的发展。
岩石介质不同于金属材料,在数值计算方面具有其独特的特点[205]:(1)岩石介质是赋存于地壳中的各向异性天然介质。
(2)岩石介质被众多的节理、裂缝等弱面所切割而呈现高度的非均质性,而其物理、化学及力学性质具有随机性特点。
(3)岩石介质赋存时以受压为主,而且抗压强度远大于抗拉强度。
(4)岩石力学与工程问题在时空分布上较广,从本质上讲都是三维问题。
(5)岩石工程一般无法进行原型试验,而实验室测得的数据不能直接应用于工程设计和计算。
(6)岩石力学与工程具有数据有限问题。
数值计算方法经过几十年的发展,目前已形成许多种岩石力学计算方法,主要有有限元法、边界元法、有限差分法、离散元法、流形元法、拉格朗日元法、不连续变形法及无单元法等。
它们各有优缺点,有限元的理论基础和应用比较成熟,在金属材料和构件的计算中应用十分成功,但它是以连续介质为基础,似乎与岩体的非连续性有一定差距,流形元等数值方法虽然考虑了岩体中节理效应,但其理论基础还不完全成熟。
相信在不久的将来,肯定会出现完全适合于岩体材料和工程的数值计算方法[206~208]。
10.1 岩石力学的有限元分析[209~213]有限元法(finite element method,FEM)是岩石力学数值计算方法中最为广泛应用的一种。
自20世纪50年代发展至今,有限元已成功地求解了许多复杂的岩石力学与工程问题。
被广大岩石力学研究与工程技术人员喻为解决岩石工程问题的有效工具。
岩石力学参数测量与分析方法

岩石力学参数测量与分析方法引言岩石作为地球上最常见的固体物质之一,在地质、矿产资源开发以及工程建设中起着至关重要的作用。
了解岩石的力学性质和参数,对于地质灾害的预测和工程设计的可靠性具有重要意义。
本文将介绍一些常用的岩石力学参数测量与分析的方法,为相关领域的研究人员和工程师提供参考。
一、应力-应变曲线的测量与分析方法应力-应变曲线是描述岩石在外力作用下的变形行为的重要参数。
常用的测量方法包括压力试验、拉伸试验、剪切试验等。
其中,剪切试验是一种常用的测量岩石力学参数的方法。
在剪切试验中,通过施加一个水平剪切力和一个垂直压力,测量岩石样本在剪切力下的变形情况。
然后,根据变形和应力之间的关系,可以得到应力-应变曲线。
曲线的形状和斜率可以反映岩石的强度和变形能力。
二、弹性模量的测量与分析方法弹性模量是岩石力学中最基本的参数之一,它描述了岩石对外力作用下的弹性变形能力。
常用的测量方法包括静力弹性模量测定和动力弹性模量测定。
静力弹性模量测定方法主要是通过施加不同大小的压力或拉伸力,测量岩石样本的应力和应变关系,得到弹性模量。
而动力弹性模量测定方法主要是通过地震波传播的速度和岩石的密度来计算弹性模量。
三、抗压强度的测量与分析方法抗压强度是岩石力学中评价岩石抵抗外力压缩的能力的重要参数。
传统的抗压强度测量方法是在实验室中进行压力试验。
在压力试验中,岩石样本被垂直施加压力,然后记录岩石破裂的压力值。
除了传统方法外,近年来还出现了一些新的测量方法,如非接触式测量方法和声波测量方法。
这些方法不仅提高了测量的准确性,还能够在线实时监测岩石的抗压强度。
四、剪切强度的测量与分析方法剪切强度是岩石力学中评价岩石抵抗剪切破坏的能力的重要参数。
常用的剪切强度测量方法包括剪切试验和直剪试验。
剪切试验是一种常用的测量剪切强度的方法。
在剪切试验中,岩石样本在剪切力的作用下发生破坏,通过记录岩石破坏的剪切力值和剪切位移,可以计算剪切强度。
岩石力学数值实验报告

岩石力学数值实验报告引言岩石力学是地球科学的一个重要分支,研究岩石的力学性质和变形规律。
为了更好地理解岩石的力学行为,科学家们开展了一系列的实验研究。
本实验通过使用数值模拟方法,以岩石样本的应力-应变关系为研究对象,旨在探究岩石的力学特性和变形模式。
实验步骤步骤1:创建数值模型首先,通过计算机软件创建一个岩石样本的数值模型。
模型的构建需要考虑样本的形状和大小、物理属性等因素。
我们选择了一个典型的立方体状样本,并设置了合适的材料参数。
步骤2:施加边界条件为了模拟实际岩石样本的状态,需要施加一些边界条件。
比如,在顶部施加一个垂直向下的载荷,并在侧面施加一定的约束条件,以保持样本的稳定。
步骤3:加载应力在数值模型中,我们可以通过施加不同的载荷形式来模拟实验中的应力加载。
常用的应力加载方式包括均匀加载、递增加载和脉冲加载等。
根据实际需要,我们选择了递增加载方式。
步骤4:模拟应变应变是岩石变形的重要参数之一。
通过在数值模型中测量岩石样本的应变变化,可以了解其力学性质。
在实验中,我们记录了岩石样本在不同应力下的应变情况。
步骤5:分析结果根据实验数据,我们对岩石样本的力学性质进行分析。
包括估计材料的弹性模量、塑性参数等,并绘制出应力-应变曲线。
结果与讨论实验数据分析通过数值模拟实验,我们获得了岩石样本在不同载荷下的应变数据。
利用这些数据,我们可以计算出岩石的应力-应变曲线,并进一步分析岩石的力学性质。
结果展示我们绘制了岩石样本在不同载荷下的应变-应力曲线,并通过计算得到了岩石的弹性模量和塑性参数。
根据曲线的变化趋势,我们可以得出岩石在不同应力下的变形模式。
结果讨论根据实验结果和数据分析,我们可以得出以下结论:1. 岩石样本在低应力下表现出弹性行为,即应力消失时,岩石会完全恢复原状。
2. 随着载荷的增加,岩石样本的应变开始发生塑性变形,不再完全恢复原状。
这表明岩石的塑性变形能力较弱。
3. 在高应力下,岩石样本的变形模式更加明显,出现了破坏和失稳的现象。
岩土物理力学性质指标
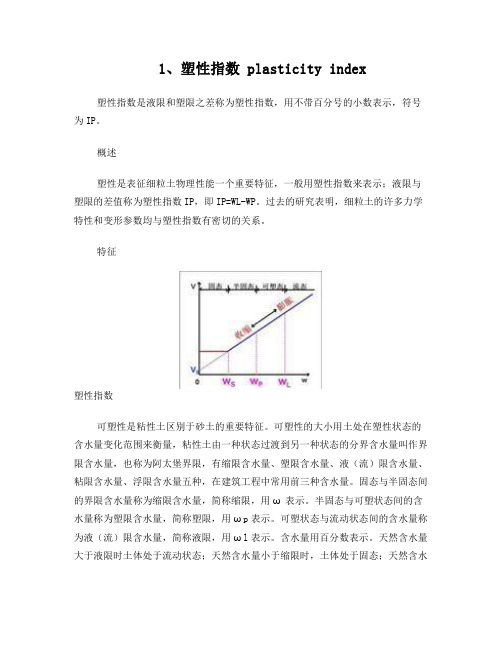
1、塑性指数 plasticity index塑性指数是液限和塑限之差称为塑性指数,用不带百分号的小数表示,符号为IP。
概述塑性是表征细粒土物理性能一个重要特征,一般用塑性指数来表示;液限与塑限的差值称为塑性指数IP,即IP=WL-WP。
过去的研究表明,细粒土的许多力学特性和变形参数均与塑性指数有密切的关系。
特征塑性指数可塑性是粘性土区别于砂土的重要特征。
可塑性的大小用土处在塑性状态的含水量变化范围来衡量,粘性土由一种状态过渡到另一种状态的分界含水量叫作界限含水量,也称为阿太堡界限,有缩限含水量、塑限含水量、液(流)限含水量、粘限含水量、浮限含水量五种,在建筑工程中常用前三种含水量。
固态与半固态间的界限含水量称为缩限含水量,简称缩限,用ω表示。
半固态与可塑状态间的含水量称为塑限含水量,简称塑限,用ωp表示。
可塑状态与流动状态间的含水量称为液(流)限含水量,简称液限,用ωl表示。
含水量用百分数表示。
天然含水量大于液限时土体处于流动状态;天然含水量小于缩限时,土体处于固态;天然含水量大于缩限小于塑限时,土体处于半固态;天然含水量大于塑限小于液限时,土体处于可塑状态。
塑性指数习惯上用不带%的数值表示。
塑性指数是粘土的最基本、最重要的物理指标之一,它综合地反映了粘土的物质组成,广泛应用于土的分类和评价。
因素由于塑性指数在一定程度上综合反映了影响粘性土特征的各种重要因素。
塑性指数愈大,表明土的颗粒愈细,比表面积愈大,土的粘粒或亲水矿物(如蒙脱石)含量愈高,土处在可塑状态的含水量变化范围就愈大。
也就是说塑性指数能综合地反映土的矿物成分和颗粒大小的影响。
因此,在工程上常按塑性指数对黏性土进行分类。
粉土为塑性指数小于等于10且粒径大于0.075的颗粒含量不超过总质量50%的土;黏性土为塑性指数大于10且粒径大于0.075的颗粒含量不超过总质量50%的土,其中:Ip>17 黏土Ip>10 粉质黏土Ip<10或Ip=10 粉土2、液性指数liquid index对黏性土来说,有一个指标叫液性指数,是判断土的软硬状态,表示天然含水率与界限含水率相对关系的指标。
岩石力学特性测试方法及数据分析

岩石力学特性测试方法及数据分析一、引言岩石力学特性测试方法及数据分析是地质学和工程领域中重要的研究内容之一。
通过了解岩石的力学性能,可以为地质灾害预测、岩土工程设计以及矿山开采等提供科学依据。
本文将介绍岩石力学特性测试的一般方法,并对数据的分析与应用进行探讨。
二、岩石力学特性测试方法1. 野外取样:在进行岩石力学特性测试前,需要首先野外进行取样工作。
取样方法包括钻孔取样和露头取样两种。
钻孔取样适用于需要获取深部岩石样本的情况,而露头取样则适用于岩石露头暴露的情况。
2. 实验室测试:在实验室中进行的岩石力学特性测试包括力学性质测试和物理性质测试两个方面。
a. 力学性质测试:包括抗压强度、抗拉强度、剪切强度、弹性模量、泊松比等指标的测试。
其中,抗压强度是最常用的力学参数,可以通过压力载荷下的试验来测定。
b. 物理性质测试:包括密度、孔隙度、饱和度、渗透性等指标的测试。
这些参数主要用于描述岩石材料的含水、渗透和破坏性。
3. 效应测试:岩石在变应力和变变形下的特性测试。
主要包括应力应变关系、岩石的蠕变、岩石的断裂以及破碎过程等。
三、数据分析与应用1. 统计分析:对于得到的测试数据,需要进行合理的统计分析。
常用的统计参数包括平均值、方差、标准差、可信区间等。
通过统计分析,可以了解不同岩石样本的力学特性之间的差异,并基于这些数据为工程设计和实践提供参考依据。
2. 岩石类别划分:通过测试数据的分析,可以将不同的岩石样本划分为不同的类别。
这些类别可以是基于不同力学特性的区分,也可以是基于岩石的结构和成分的区分。
岩石类别的划分对于岩土工程设计和地质灾害预测具有重要意义。
3. 参数拟合与预测:通过对测试数据进行参数拟合,可以建立岩石力学特性与其他参数之间的数学模型。
这些模型可以用于预测未知岩石样本的力学特性,并为实际工程中的决策提供依据。
4. 数值模拟:基于岩石力学特性测试数据,可以进行数值模拟分析。
采用有限元分析等方法,可以模拟真实工程场景下不同岩石样本的应力、应变和破坏过程。
岩石力学数值分析方法

谢谢!!!
3岩石力学数值方法应用中的几个关键点与展望1岩石力学数值计算方法得到迅猛发展使复杂岩石力学工程问题的设计发生了根本性的变化2岩石力学数值计算不仅已基本上取代了传统线弹性力学实验而且也在岩石工程非线性实验中显示出极大的优势3出现了有限差分有限元透界元离散元块体元无限元流形元及其混会应用等各种数值模拟技术4有限元法已不仅由线性发展到高度非线性和大变形同题由二维发展到三维同时还可以考虑粘性流变渗流与应力场耦合损伤断裂以及动力效应5国内出现了一些享有声誉的有限元程序如北京大学nolm83清华大学的tflne西安科技学院ncap2d程序等这些程序均在谗多大型岩石工程中得到了良好应用6不同数值计算方法的结合更能发挥各种数值方法优势互补的作用如有限元边界元的混合有限元离散元的混合有限元无限元和有限元块体元的混合采用等7由于岩体具有非连续非均质各向异性天然初始地应力影响地下水影响及复杂边界条件处理等诸多复杂性使得当前岩石力学数值计算仍然是一个值得探讨的问题
3)单一数值方法的局限性问题
• 各种数值计算方法虽有其优点,但也有许多不足 之处,之前已有阐述。因此,要想利用某种方法 就可解决客观上就极其复杂的岩石力学与工程问 题显然是不现实的。为了吸取各种计算方法的长 处以弥补其不足,近年来涌现出大量的各种数值 方法的耦合计算,这种思路进一步反映了岩体工 程的计算特点。 • 有限元与边界元耦合,可以发挥边界元处理无限 域边界的长处,克服有限元的边界效应,在减小 解题规模方面也有明显的效果。这种方法最先用 于弹塑性分析,后来又发展到流渗分析等,不足 之处是程序编制比较复杂。
3、离散单元法
• 利用离散单元法研究矿山边坡的破坏机理,考虑 了坡体中裂隙水的影响,认为以往用于边坡稳定 性分析或其破坏机理研究的数值计算方法(如有限 元法、边界元法)都只是计算指定区域内或指定边 界上的应力分布和位移值,也就是说,都是从运 动学方面来分析和研究,而未能将坡体破坏的动 力学和运动学有机地结合起来,对于坡体中地下 水的影响,只是考虑其对结构面及充填体剪切强 度的削弱作用,对裂隙中静水水压的影响则估计 不足,因而是欠妥的。离散单元法则具有将动力 学和运动学结合起来对坡体进行研究的特点,故 特别适用于研究节理坡体的变形过程和破坏形态。
论述岩石力学4类研究方法的特点

岩石力学是研究岩石在地质力学作用下的性质和变形规律的学科,是地质学、工程学和岩土力学的交叉学科。
在岩石力学研究中,有四种主要的研究方法,它们分别是实验方法、观测方法、理论分析方法和数值模拟方法。
本文将从这四个方面分别讨论,以便对岩石力学的研究方法进行全面地评估。
一、实验方法1. 特点:实验方法是通过对岩石样本进行实验,来模拟和研究岩石在受力作用下的力学性质和变形规律。
实验方法的特点是能够直接获取岩石的力学参数,如强度、变形模量、裂隙特征等。
实验方法可以控制实验条件,提供可靠的数据支持。
2. 个人观点:实验方法作为岩石力学研究的基础方法,具有重要意义。
通过实验方法,我们能够深入了解岩石的物理力学性质,为工程建设和地质灾害防治提供可靠的依据。
二、观测方法1. 特点:观测方法是通过对岩石体进行现场观测和勘察,获取岩石体的构造、裂隙特征、变形情况等信息。
观测方法的特点是能够直接观察到岩石的实际情况,获取真实的地质信息。
2. 个人观点:观测方法在岩石力学研究中起着至关重要的作用。
通过对岩石体的实地观测,我们能够了解岩石的构造特征、变形程度,为工程设计和地质灾害风险评估提供重要依据。
三、理论分析方法1. 特点:理论分析方法是通过建立岩石力学的理论模型,运用物理力学和力学原理,对岩石在受力作用下的本质进行分析和解释。
理论分析方法的特点是能够揭示岩石力学的基本规律和本质。
2. 个人观点:理论分析方法是对岩石力学研究具有重要意义的方法之一。
通过建立理论模型,我们可以从宏观角度揭示岩石的力学行为规律,为岩石工程设计和地质灾害机理解析提供理论支持。
四、数值模拟方法1. 特点:数值模拟方法是通过数值计算和模拟,对岩石在受力作用下的变形和破坏过程进行模拟和预测。
数值模拟方法的特点是能够模拟复杂的岩石结构和受力情况,为岩石工程和地质灾害预测提供技术支持。
2. 个人观点:数值模拟方法是现代岩石力学研究的重要方法之一,具有重要的应用前景。
岩土工程中的数值模拟方法

岩土工程中的数值模拟方法岩土工程是土壤和岩石力学性质在工程应用中的研究与应用。
在岩土工程领域中,数值模拟方法是解决工程问题的一种重要手段。
本文将介绍岩土工程中常用的数值模拟方法,包括有限元法、边界元法和离散元法。
一、有限元法有限元法是一种广泛应用于岩土工程中的数值模拟方法。
其基本原理是将复杂的工程体系分割成许多简单的几何单元,如三角形、四边形等,然后利用应变能最小的原理构建形函数和位移函数,通过离散化的方式,将原始问题转化为一系列代数方程。
有限元法具有计算精度高、适用范围广、计算速度快等优点,被广泛应用于岩土工程中的稳定性分析、地下工程开挖与支护、地基处理等问题的求解。
二、边界元法边界元法是一种基于边界网格的数值模拟方法,通过将问题的边界离散化,将待求解问题转化为边界上的积分方程。
边界元法适用于具有均匀性边界条件的工程问题,如弹性地基的应力分布、地下水流动与渗流等。
相比于有限元法,边界元法不需要对整个求解域进行离散化,减少了计算量,但其在处理边界条件不均匀或存在突变问题时可能会受到限制。
三、离散元法离散元法是一种能够模拟岩土体内的离散颗粒运动的方法。
该方法将岩土体看作由颗粒组成的离散体系,通过模拟颗粒的运动与相互作用,来研究岩土体在受力下的力学行为。
离散元法适用于模拟土体和岩石的破坏、岩土体变形过程以及地震引起的地质灾害等问题。
离散元法在岩土工程中具有较好的可视化效果,能够更加真实地反映岩土体力学特性,但同时计算量较大,需要考虑离散颗粒的联系与摩擦力等因素。
结论岩土工程中的数值模拟方法包括有限元法、边界元法和离散元法。
这些方法在工程实践中具有广泛的应用,能够帮助工程师评估岩土体的稳定性、分析地下结构施工过程中的变形与破坏以及预测地震对工程的影响等。
随着计算机技术的不断发展,数值模拟方法在岩土工程领域的应用将更加准确、高效,为工程师提供更好的决策依据。
岩石动态力学参数测试方法与数据处理

岩石动态力学参数测试方法与数据处理一、引言岩石动态力学参数测试方法与数据处理是岩石力学领域的重要研究方向。
岩石力学的研究对岩石工程、地质灾害等领域具有重要的实用价值。
本文将介绍岩石动态力学参数的测试方法以及对测试数据的处理方法。
二、岩石动态力学参数测试方法1.冲击试验法冲击试验法是常用的测试岩石动态力学参数的方法之一。
该方法通过施加冲击或冲击波加载,获得岩石的动态强度、动态模量等参数。
冲击试验法包括冲击回弹法、冲击波法等。
2.压杆试验法压杆试验法是另一种测试岩石动态力学参数的常用方法。
该方法通过施加压力加载,测量岩石的瞬态变形与应力,获得岩石的动态参数。
3.声波试验法声波试验法是一种非破坏性的测试岩石动态力学参数的方法。
该方法通过发送声波信号并测量传播速度和衰减来求解岩石的动态弹性模量、泊松比等参数。
三、数据处理方法1.统计分析方法在岩石动态力学参数测试中,通常需要对多组数据进行统计分析。
统计分析方法可以用来处理测试数据中的误差,并得到更加准确可靠的力学参数。
2.数据拟合方法数据拟合方法是一种常用的处理岩石动态力学参数测试数据的方法。
通过拟合实验数据与理论模型,可以得到最佳拟合曲线,并获得更精确的力学参数。
3.数据可视化方法数据可视化方法是将测试数据以图表的形式展示,以便更直观地理解和分析数据。
常用的数据可视化方法包括绘制曲线图、柱状图、散点图等。
四、案例分析以某次岩石动态力学参数测试为例,通过冲击试验法获得了岩石的动态模量和动态强度数据。
在数据处理过程中,首先使用统计分析方法对多组测试数据进行处理,得到平均值和标准差。
然后,使用数据拟合方法拟合实验数据与理论模型,获得了更精确的力学参数。
最后,将处理后的数据通过绘制曲线图的方式进行可视化展示。
五、结论岩石动态力学参数测试方法与数据处理是岩石力学研究的重要环节。
冲击试验法、压杆试验法和声波试验法是常用的测试方法。
在数据处理过程中,统计分析方法、数据拟合方法和数据可视化方法是常用的处理方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
在裂隙单元的相对面上使用位移和牵引边界方程[73,74]。然而,使用两个独立的边界积分方 程进行裂隙分析的原始概念, 一个位移方程和一个带有它的法向导数的位移方程, 最初出现 于文献[41]中。因为应力和位移的奇异性,特殊的裂纹尖端的元素,如文献[75,76]中,应该 在裂缝尖端使用。 边界元法的一个特殊方法,被称为伽辽金边界元法,或 GBEM,由传统的边界积分两 次,乘以一个加权试函数,产生一个对称的系数矩阵,这就是伽辽金意义上的加权余量法。 文献[77]中给出了伽辽金边界元法的最新评论,文献[78]中对岩石力学问题应用也进行了报 道。 在边界元法中,源项的内含物,如潜在问题的体力,热源,汇 /源项等等,会导致域积 分。在考虑初始应力/应变效应和材料非线性行为时这个问题也会出现,如塑性变形。在处 理这类域积分时传统的技术是把域划分为多个内部单元, 基本上消除了边界元法只有边界离 散化的优势。多年来已经开发了克服这个困难的不同技术[79],最显著的是双重互易法[80]。 文献[81]中使用该法解决地下水流动问题。 与有限元法和有限差分法相比较, 边界元法的主要优点是生成更简单的网格, 模型尺寸 减小,因此输入数据准备减少。此外,域内解是连续的,不像利用有限元法和有限差分法得 到的点明智的不连续解。然而,在一般情况下,在处理材料的不均匀性时,边界元法没有有 限元法有效,因为它不像有限元法中的单元那样,有许多子区域。在模拟非线性材料的行为 时,边界元法也没有有限元法有效,如塑性和损伤演化过程,因为域积分往往出现于这些问 题中。边界元法更适合于求解不均匀破裂和线弹性体问题。
2.3. 边界元法以及有关方法
不同于有限单元法和有限差分法,边界元方法最初利用 Betti 互易定理和 Somiglian 不 等式通过推导的积分方程的数值解在全局层面上寻求一个弱解。文献[40,41]中,利用不同阶 的形函数引入等参元, 和在有限元分析中使用相同的方式, 大大提高了边界元法对应力分析 的适用性。 在岩石力学领域边界元法的应用最显著和原始的发展可能要归于文献[42-44]中报道的 早期工程,其他许多人紧随其后[45-48],应用包括地下工程开挖,土-结构相互作用,地下 水流动和破裂过程的一般应力和变形分析。工程中著名的例子如下: � 带有或没有裂隙的地下工程开挖应力分析 [49-55] � 动力学问题[56-58] � 原位应力和弹性材料中的反分析[59,60] � 渗透率测量的井下试验[61] 自 80 年代初以来,一个重要发展涉及 TM 和 HM 耦合过程的边界元法公式,例如文献 [62-64]中报道的工程。 由于边界元法在降低模型尺寸方面的优势, 三维方面的应用也有报道, 特别是采用位移不连续法 (DDM) 进行应力分析, 如在文献[65-67]中报道的。 DDM 方法[68] 最适合于裂缝扩展模拟, 推广应用到岩石二维[69]和三维[70,71]的裂隙问题。 它的相反部分, 虚拟应力方法,也是一种适用于应力模拟的间接边界元法。 为使用标准的边界元法模拟裂缝扩展, 已经提出了两种技术。 一种是将问题域划分成多 个裂隙沿界面的子域,这是一个预先假定的裂隙路径[72];第二种是双重边界元法(DBEM)
2.岩石力学数值方法最新进展
2.1.有限差分法以及有关方法
在有限差分法中, 最基本的技术是通过在相邻网格点定义的差值替代偏导数来实现控制 偏微分方程的离散化。 网格系统是采样点之间获取目标函数的一种简便方式, 在采样点之间, 间距足够小, 以致产生的误差小到可以接受。 用恰当的公式表达, 例如静态或动态松弛技术,
当模拟裂缝发育的过程时,小单元尺寸、裂缝发育连续网格重建、裂隙路径和单元边界 的要求, 对有限元法不利。 这个整体的缺点使得有限元法在处理裂隙问题时比同类边界元法 要低效。然而,现已开发出特殊的算法,试图克服这一缺点,例如对裂隙萌生和扩展的隐式 模拟使用不连续形函数[21],通过分岔理论、‘丰富的有限元法’和‘广义的有限元法’[22–25]。 在单元层面裂隙的处理: 通过设置距离函数定义裂隙面, 使得它们的表征只需要节点函数值, 用试函数里的附加自由度, 沿裂隙的跳跃函数和顶端裂缝函数表示。 使用等值面技术和无预 定义裂隙单元模拟裂隙的运动。在广义的有限元法中,网格可以独立于问题几何形状。在文 献[26]中,丰富的有限元法应用于带位移不连续的裂隙的隧道稳定性分析。 除了裂隙和离散块的处理,广义有限元法在许多方面和‘流形方法’类似[27–29]。流形方 法使用截断的不连续形函数来模拟裂隙和处理连续体、 裂隙体和按统一方式形成的离散块的 集合体, 是连续与离散表征之间的天然桥梁。 该方法是基于节点的星形覆盖系统构造试函数 制定的, 其中节点与覆盖星形相关, 可以是一组有节点的标准有限元法单元或由使用普通形 状的最小二乘核心技术产生。然而,整合,分析地采用单纯形积分技术进行。流形方法也有 独立域几何形状的网格,因此大大简化网格划分任务,模拟裂隙发展过程不需要网格重划。 该技术已被扩展应用于大变形和裂纹扩展的岩石力学问题的[30,31]。 大多数的出版物都包括 在 ICADD1 会议[32-35]的一系列会议记录里。 当把有限元法应用于实际问题时, 具有复杂内部结构和外部边界的网格的生成, 是一项 艰巨的任务。当处理带有复杂几何形状的三维问题时,这个问题是至关重要的。在过去十年 中,‘无网格’法取得了重大进步,它大大简化了网格划分任务。在这个方法里,试函数不再 是标准的,但由不同近似范围影响区域相邻节点产生,如最小二乘技术。该方法的全面概述 在文献[36]中。从纯计算能力的角度看,它尚未超越有限元法技术,但是它有针对一般土木 工程问题的潜力,尤其是岩石力学应用,主要是由于它在处理裂隙时的灵活性,像文献[37] 报道的带块-界面模型的节理岩体的分析和文献[38]报道的混凝土裂隙扩展。在文献[39]中, 接触-识别算法使用无网格技术,为延伸无网格技术到离散块系统建模铺平道路,其概念也 延伸到边界元法。
图 1 四类基本方法,两级,因此形成八种不同方法,可用于岩石力学建模,为岩土工程提供预测[1]
建模和设计工作以图 1 中顶部方框中的目标开始, 接着在中央方框中有八种建模和设计 方法,四列代表着四类主要的建模方法: 方法 A:基于以往经验的设计。 方法 B:基于简化模型的设计。 方法 C:基于试图捕捉多数相关机理而建模的设计。 方法 D:基于包括一切而建模的设计。 在图 1 中央大的方框中有两行,上边的一行,第一级,包括试图实现模型中一对一映射 机理的方法。换句话说,该机理被认为真实发生在岩石中,并被包括在模型中而直接建模, 例如显式应力-应变关系。相反,下边的一行,第二级,包括非完全直接映射机理的方法, 例如岩体分级系统的使用。左手的方框内,一些岩体表征参数将从现场调查获得。然后, 岩 土工程的设计和施工工序从施工循环反馈给建模。 评论指向位于图 1 中间方框中顶部行第一级的方法 C 和 D。重要的一点是,在岩土力 学和工程设计中,一种生活方式是没有足够的数据,而不是一个当地的困难,这是为什么经 验方法,例如分级系统得到发展仍然需要的缘故。因此,我们也将讨论表征单元体 REV, 均质化/放大化,反分析和反算的话题。这些都是与建模有关的基本问题,并与图中所有的 A,B,C 和 D 各类方法有关。 对岩石力学问题最常用的数值方法: (1)连续方法:有限差分法(FDM) ,有限单元法(FEM) ,和边界元法(BEM) 。 (2)离散方法:离散单元法(DEM) ,离散裂缝网络方法(DFN) 。 (3)混合连续/离散方法。 连续或离散方法的选择取决于许多具体问题的因素, 主要取决于问题的规模和裂隙系统 的几何形状。 如果只存在少许裂隙或开口裂隙和完全的块分离不是重要因素, 就可以使用连 续方法。在中等的裂隙岩体中,对连续的裂隙单元方法来说,裂隙的数目太大,或单个块体 的大尺度位移可能发生, 采用离散方法是最合适的。 没有一种方法有绝对的优势超过另一种 方法。然而,通过使用结合连续离散方法的混合模型,每种方法的一些缺点是可以避免的。 在这篇综述中,我们专注于针对岩石力学目的的数值方法的最高水准的能力和实用性, 注重突出问题的解决。 该综述重点是在土木工程中的应用, 但资料适用于所有岩土工程分支, 此处通过广泛的文献参考源获得适量的支持。
岩石力学数值方法(翻译稿)
L. Jing, J.A. Hu于不同环境和不同用途的岩土工程结构设计中, 且不同的建 模技术已经得到发展, 因此我们现在有一个广泛的建模和设计方法。 这些方法以不同的方式 出现,在四类方法和两个层次的基础上,分为八种方法,如图 1 所示(参看英文原稿,图 1 内容不再翻译) 。
2.2. 有限单元法以及有关方法
有限单元法可能是应用最广泛的数值方法,其遍布科学和工程领域。自从 20 世纪 60 年代早期诞生以来,更多的有限单元法发展工作专门针对岩石力学问题 [7-10],这因为它是 第一个足够灵活处理材料非均匀性、变形非线性(主要是塑性) 、复杂边界条件、原岩应力 和重力场的数值方法。在 20 世纪 60 年代晚期和 70 年代早期,当传统的带有规则网格的有 限差分法不能满足岩石力学问题的这些基本需要时,有限单元法出现了。由于这些优势, 它 超越了传统的有限差分法。 20 世纪 60 年代后期以来,在有限元法中岩石裂隙的表征已受到岩石力学需求的激发, 最显著的贡献见于文献[11,12]中。岩石力学中著名的 Goodman 节理单元已经在有限元法代 码中广泛使用,并应用于许多实际的岩土工程问题。然而,这些模型基于连续介质假设而形 成,因此大尺度的开口、滑动和单元的完全脱离是不允许的。由于节理单元大的纵横比(长 度与厚度的比值)Goodman 节理单元的零厚度导致数值病态,在后来的文献[13-20]中节理 单元有所改进。 尽管取得了这些努力, 但裂缝和裂缝发育的处理仍然是有限元法岩石力学问题应用最重 要的制约因素。有限元法存在这样的事实,当许多裂隙单元加入时,整体刚度矩阵表现为病 态。由于有限元法公式中广义连续性假设要求裂隙单元不能被撕开,故其不能处理块旋转、 完全脱离和大尺寸开口裂隙。
不需要组成和求解全局坐标系下的矩阵形式的方程, 方程的组成和求解是局部的, 在计算机 执行时内存和存储方面,会更有效。在采样点的邻域,没有像有限单元法和边界元中那样使 用局部尝试(插值)函数对偏微分方程进行近似。因此,有限差分法是偏微分方程求解的最 直接和直观的方法, 这也对本构复杂材料行为的直接模拟提供了附加的优势, 如塑性和损伤, 没有在使用全局矩阵方程系统的其他数值方法中必须采用的预估校正映射的迭代求解方案, 例如在有限元法和边界元法中。 带有规则网格系统的传统有限差分法也有缺点, 首先在于在处理裂隙、 复杂边界条件和 材料不均匀性时缺乏灵活性, 这使得标准的有限差分法一般不适用于实际岩石力学问题的建 模。然而,有限差分法在不规则网格方面已经有了重大进步,如三角网格或 Voronoi 网格系 统,从而导致出现所谓的控制体积,或有限体积技术。Voronoi 多边形基于点发展填满空间, 与切割平面的线形成的多边形镶嵌,或建立一个源于已存在多边形的镶嵌图案相对立。 有限体积法可以制定基本变量(如位移)在单元(元素)或节点(网格点)中心的非结 构化网格。也可以考虑在不同的单元中具有不同的材料特性。因此,有限体积法在处理材料 的非均匀性、网格生成和带有任意形状非结构化网格的边界条件时,与有限元法一样灵活。 它与有限元法有相似之处, 被认为是有限差分法和有限单元法之间的桥梁。 在有限体积法中 用于应力分析的原始概念和早期代码可以追溯到文献[2]中的工作,使用带有四边形网格的 顶点-中心格式。目前,利用有限体积法/有限差分法的岩土工程问题应力分析的最知名的计 算机代码可能是 FLAC 代码组[3],它有三角形或四边形网格顶点格式。 在有限差分法/有限体积法中显式表达是不容易的, 因为它们需要相邻网格节点之间函 数的连续性。而且,在有限差分法或有限体积法中,和有限单元法一样具有特殊的裂隙单元 是不可能的。事实上,不能进行裂隙的整体显式表达是有限差分法 /有限体积法进行岩石力 学分析的弱点。另一方面,有限差分法/有限体积法模型被用来研究破裂过程机理,如岩石 和土样在实验室条件下剪切带的形成[4],作为构造荷载的结果断层系统的形成[5],这可以 通过模型表面没有裂隙的网格点或单元中心处材料的失效过程或损伤传播获得。 有限体积法是岩土工程中最流行的数值方法之一,其应用几乎覆盖岩石力学的所有方 面,如边坡稳定性,岩体特性表征,构造演化过程和冰川动力学,涉及范围的广泛性可参见 文献[6]。
