锁相环仿真(基于MATLAB)
4阶锁相环matlab

4阶锁相环matlab4阶锁相环是一种广泛应用于通信系统和控制系统中的控制算法,其主要用于抑制信号的相位偏移和频率误差。
本文将以回答关于4阶锁相环在Matlab中的应用为主题,一步一步地介绍相关知识和实例。
第一步:了解锁相环的基本原理要学习和应用4阶锁相环,首先需要了解锁相环的基本原理。
锁相环是一种控制系统,它通过比较输入信号和参考信号的相位差异,并根据差异调整输出信号的相位和频率,使其与参考信号同步。
在一个理想的锁相环中,输出信号的相位和频率将与参考信号完全一致。
第二步:了解4阶锁相环的结构4阶锁相环是一种具有更高精度和更快响应速度的锁相环。
它由相位解调器、低通滤波器、环路滤波器和控制电压产生器等组成。
相位解调器用于将输入信号分解为正弦和余弦分量,低通滤波器用于提取正弦分量,环路滤波器用于对正弦分量进行进一步处理,而控制电压产生器则根据环路滤波器的输出产生对输出信号的调整。
第三步:编写Matlab代码实现4阶锁相环在Matlab中实现4阶锁相环可以通过调用DSP System Toolbox 中的相位锁定环模块来完成。
以下是一个简单的示例代码:matlab设置相关参数omega_n = 2*pi*1e4; 自然频率zeta = 0.707; 阻尼系数Kp = 1; 比例增益Ki = 1; 积分增益创建4阶锁相环loop = dspPLL('PhaseDetectorGain', Kp, ...'LoopBandwidth', omega_n, ...'DampingFactor', zeta, ...'LoopFilterGain', Ki);生成输入信号fs = 1e6; 采样率t = 0:1/fs:1;fin = 1000; 输入信号频率inputSignal = cos(2*pi*fin*t);执行锁相环[outputSignal, controlVoltage] = loop(inputSignal);绘制输出信号和调整电压figure;subplot(2,1,1);plot(t, inputSignal, 'b', t, outputSignal, 'r');xlabel('Time (s)');ylabel('Amplitude');legend('Input Signal', 'Output Signal');subplot(2,1,2);plot(t, controlVoltage, 'g');xlabel('Time (s)');ylabel('Control Voltage');legend('Control Voltage');通过上述代码,可以生成一个包含输入信号、输出信号和调整电压的图形,并显示相应的波形。
06、电力电子技术matlab仿真-锁相环

Thyristor
GTO/IGCT
IGBT
MOSFET
(Base/gate) Driver circuit
Control Circuit
Driver Circuit
From control circuit
+VGG R1 + Rg G + VGS _ D VDC S _
Q1 LM311
MOSFET gate driver
17
西南交通大学
锁相环的应用——APF
主电路板
18
控制路板
西南交通大学
APF静态性能
19
西南交通大学
STATCOM控制系统
STATCOM 控制器
PWM
西南交通大学
20
Modeling and Simulation of Power Electronics System
Modeling and Simulation of Three-phase PLL
• IGCT – Integrated with its driver
西南交通大学
Photos of IGBT
西南交通大学
Power Switches: Power Ratings
1GW 10MW 10MW 1MW 100kW 10k W 1kW 100W 10Hz 1kHz 100kHz 1MHz 10MHz
西南交通大学
Isolation
R1 ig
+
vak
-
R2 Pulse source
iak
Isolation using Pulse Transformer
From control circuit
数字锁相环matlab

数字锁相环matlab摘要:1.数字锁相环的概述2.Matlab 在数字锁相环中的应用3.数字锁相环的实现方法4.结论正文:1.数字锁相环的概述数字锁相环(Digital Phase-Locked Loop,简称DPLL)是一种数字信号处理技术,用于在数字通信系统中实现信号同步。
在数字通信系统中,信号的同步至关重要,因为只有实现信号同步,才能确保接收端正确地解调出原始信号。
数字锁相环通过比较接收信号与本地生成的信号,并根据两者之间的相位差来调整本地信号的相位,从而实现信号的同步。
2.Matlab 在数字锁相环中的应用MATLAB 是一种广泛应用于信号处理和通信系统的软件工具,它可以方便地实现数字锁相环的模型和算法。
使用MATLAB 可以搭建数字锁相环的仿真模型,对锁相环的性能进行分析和评估,以及对锁相环的算法进行优化。
此外,MATLAB 还提供了丰富的通信系统工具箱,如通信系统工具箱、信号处理工具箱等,为数字锁相环的设计和分析提供了强大的支持。
3.数字锁相环的实现方法数字锁相环的实现方法主要包括以下几种:(1)基于滤波器的实现方法:该方法通过设计一个滤波器,使得滤波器的传递函数与输入信号的相位相关,从而实现信号的同步。
(2)基于频率检测的实现方法:该方法通过检测输入信号的频率,并将其与本地信号的频率进行比较,从而实现信号的同步。
(3)基于相位检测的实现方法:该方法通过检测输入信号与本地信号之间的相位差,并根据相位差来调整本地信号的相位,从而实现信号的同步。
(4)基于最大似然估计的实现方法:该方法通过计算输入信号与本地信号之间的最大似然估计,从而实现信号的同步。
4.结论数字锁相环是一种重要的信号处理技术,广泛应用于数字通信系统中。
MATLAB 作为一种强大的信号处理工具,可以方便地实现数字锁相环的模型和算法。
数字锁相环的实现方法有多种,每种方法都有其独特的优点和适用场景。
4阶锁相环环路计算matlab

一、锁相环环路计算的基本原理锁相环(PLL)是一种控制系统,它可以跟踪并锁定一个输入信号的相位和频率。
它通常包括一个相位比较器、一个数字控制环路滤波器、一个控制电压示数器和一个振荡器。
锁相环环路计算就是指计算和分析锁相环系统的环路参数,以实现系统设计和优化。
锁相环环路计算在数字信号处理、通信系统、雷达和仪器仪表等领域都有着广泛的应用。
在锁相环设计过程中,环路计算可以帮助工程师确定合适的环路带宽、相位裕度以及滤波器设计等参数,从而实现系统对输入信号的准确跟踪和稳定锁定。
二、锁相环环路计算的基本步骤1. 确定锁相环的工作频率范围和精度要求。
根据系统的应用需求和输入信号的特性,确定锁相环所需的频率范围和频率精度,这将指导锁相环环路的设计和计算。
2. 分析环路的稳定性和性能指标。
通过传递函数、脉冲响应和频率特性等分析方法,对锁相环环路的稳定性、相位裕度、噪声抑制和跟踪性能等指标进行评估和分析,为后续的计算和优化提供基础。
3. 计算环路滤波器的参数。
根据系统的稳定性要求和性能指标,计算锁相环环路滤波器的参数,包括带宽、阶数、极点位置和增益等,以实现对输入信号的精确跟踪和稳定锁定。
4. 优化振荡器的设计参数。
选择合适的振荡器类型、频率范围和相位噪声等参数,结合锁相环环路的设计要求进行优化,确保锁相环系统的性能达到最佳状态。
5. 模拟仿真和实际测试。
利用matlab等工具进行锁相环环路计算的模拟仿真,验证设计参数的有效性和系统性能的稳定性,然后进行实际测试和调试,对系统进行进一步优化和改进。
三、matlab在锁相环环路计算中的应用matlab是一种强大的数学建模和仿真工具,它在锁相环环路计算中有着广泛的应用。
通过matlab工具箱中的控制系统工具箱和信号处理工具箱,可以方便地进行锁相环环路的建模、分析和计算,为系统设计和优化提供有效的支持。
matlab提供了丰富的控制系统函数和工具,可以实现锁相环环路的传递函数建模、频率响应分析、环路稳定性评估和性能指标计算等功能。
数字锁相放大器原理及其Matlab仿真

数字锁相放大器原理及其Matlab仿真摘要:数字锁相放大器作为一种新型的放大器,其原理和应用逐渐受到人们的关注。
本文主要介绍数字锁相放大器的基本工作原理和Matlab仿真的方法。
基于数字信号处理技术,数字锁相放大器通过数字积分器和数字锁相环的组合实现了高精度的信号放大和相位锁定。
在Matlab环境下,仿真过程首先建立数字锁相放大器的模型,然后进行参数设置和仿真测试。
通过多次调整模型参数,并对仿真结果进行分析,得到最优的数字锁相放大器设计方案。
本文的研究可以为数字锁相放大器的实际应用提供参考。
关键词:数字锁相放大器、数字信号处理、数字积分器、数字锁相环、Matlab仿真正文:一、引言数字锁相放大器作为一种新型的放大器,其应用范围涉及多个领域,如精密测量、生物医学、材料科学等。
与传统的电子放大器相比,数字锁相放大器具有响应速度快、抗干扰性强、精度高等优点。
为了更好地掌握数字锁相放大器的原理和应用,本文通过Matlab仿真的方法进行研究,以期发现数字锁相放大器的最佳设计方案。
二、数字锁相放大器原理数字锁相放大器基于数字信号处理技术实现了高精度的信号放大和相位锁定。
其基本工作原理是:将待放大信号与参考信号做乘积,再将乘积信号通过数字积分器得到直流分量和交流分量。
然后将交流分量输入数字锁相环进行相位锁定,最后从数字锁相放大器的输出端可以获得相位锁定后的信号。
数字锁相放大器的电路图如下所示:图1 数字锁相放大器的电路图其中,$u_i$表示待放大信号,$u_{ref}$为参考信号,$v$为输出端信号,$n_i$,$n_{ref}$,$n$为噪声信号。
数字积分器的计算公式为:$$y(n)=y(n-1)+\frac{T}{2}\left(x(n)+x(n-1)\right)$$其中,$x(n)$为输入信号,$y(n)$为输出信号,$T$为采样周期。
数字锁相环的计算公式为:$$\theta_{n}=\theta_{n-1}+K_{p} \Delta \varphi_{n}+K_{i}\sum_{j=0}^{n} \Delta \varphi_{j}$$其中,$\theta_{n}$为相位偏差,$\Delta \varphi_{n}=2 \pif_{ref} T$为相位差,$K_{p}$和$K_{i}$为比例常数和积分常数。
锁相环设计与MATLAB仿真

锁相环设计与MATLAB仿真锁相环(Phase-Locked Loop,PLL)是一种电路设计技术,用于提取输入信号中的相位信息,并在输出信号中保持输入信号与输出信号的相位差稳定。
PLL广泛应用于通信系统、时钟生成器、频率合成器等领域。
锁相环主要由相位检测器(Phase Detector,PD)、环路滤波器(Loop Filter,LF)、振荡器(Voltage-Controlled Oscillator,VCO)和分频器(Divider)组成。
相位检测器用于比较输入信号和VCO输出信号的相位差,并产生一个低频的误差信号。
传统的相位检测器包括异或门相位检测器(XOR PD)和倍频器相位检测器(Multiplier PD)。
异或门相位检测器适用于窄带相位差测量,倍频器相位检测器适用于宽带相位差测量。
MATLAB提供了用于建模和仿真PLL的工具箱,可以方便地进行相位检测器的设计和性能分析。
环路滤波器用于滤波相位误差信号,根据滤波器的设计方法不同,可以实现不同的环路特性。
传统的环路滤波器包括积分环路滤波器和比例积分环路滤波器。
积分环路滤波器对误差信号进行积分,使得环路系统具有很高的稳定性和抗干扰能力,但响应时间较长。
比例积分环路滤波器在积分环路滤波器的基础上引入比例增益,可以更快地响应相位误差的变化。
振荡器(VCO)根据环路滤波器输出的控制电压来生成输出信号,并提供给分频器进行频率除法操作。
振荡器通常采用压控振荡器(VCO)或电流模式逻辑(Current Mode Logic,CML)结构,可以根据应用需求选择合适的振荡器设计。
分频器用于将振荡器输出的高频信号按照设定的分频比例进行分频,生成与输入信号相位对齐的输出信号。
分频器采用计数器和锁存器设计,计数器用于记录输入信号的周期数,锁存器将计数器的值锁定在一个周期,输出给相位检测器进行相位比较。
锁相环的设计和仿真可以通过MATLAB工具箱进行。
首先,设计相位检测器的传输函数和特性,选择适当的相位检测器类型和设计参数。
基本理论锁相环是一个闭环的相位负...

基于Matlab的锁相环设计摘要随着现代集成电路技术的发展,锁相环已经成为集成电路设计中非常重要的一个部分,所以对锁相环的研究具有积极的现实意义。
锁相环电路是一种输出信号在频率和相位上能够与输入参考信号同步的电路,锁相环由于其具有一系列独特的优良性能,它已经成为通信、雷达、导航、电子仪器仪表等设备中不可缺少的一部分。
所以这些年来锁相环的设计与研究工作也越来越受到人们的重视,人们开始利用人工计算或计算机软件来分析锁相环的性能。
在研究大量资料的基础之上,先对锁相系统的基本工作原理进行了分析,以传统模拟锁相环的结构为基础,分析了锁相环的数学模型,详细描述了锁相环的整体电路以及鉴相器、环路滤波器、压控振荡器等电路模块。
并以此为出发点对锁相环的锁定性能、及稳定性能、等各种性能进行了分析。
在分析和设计的同时,也采用Matlab软件对锁相环电路进行了仿真。
首先分析了一阶锁相环和二阶锁相环的锁定性能,并进行了比较。
其次分析了阻尼系数 对环路稳定性能的影响。
最后介绍了锁相环的调制作用。
从锁相环的仿真结果可知,我们的理论研究结果和实验结果相符,锁相环电路达到了设计指标要求。
关键词锁相环;Matlab;仿真Phase-Locked Loop Design Based on MatlabAbstractWith the development of modern integrated circuit technology, phase locked loop has become a significant component of integrated circuit, which makes the research of phase-locked loop valuable. Phase-locked loop is a kind of circuit that an output signal in the frequency and phase reference signal can be synchronized with the input. Because of a series of uniquely excellent performances, it is becoming an indispensable part of the equipments such as communication, radar, airmanship, electronic instrument etc. People realize the importance of the design and study of PLL , they come to use artificially calculation or software to analyze the property of PLL.After a deep study of the materials about PLL, this thesis starts with the analysis of the fundamental principles of a phase-locked system , then we build the mathematical model based on the traditional of the PLL, describes the overall PLL circuit and phase detector, loop filter, VCO circuit module, etc, and afterwards investigate some of its characters such as locking performance and stability.In the analysis and design, but also we conducted a phase locked loop circuit simulation by Matlab software. First of all, we analyzed the first-order phase lock loop and a second order phase-locked loop lock performance, and on the basis of the comparison. Secondly we analyzed the damping how to stability of the loop. Finally we introduced the modulation of the phase locked loop. From the simulation results, we know that the theory conclusions and the simulation results fit well phase-locked loop circuit to the design requirements.Keywords PLL, simulation, Matlab目录摘要 (I)Abstract (II)第1章绪论 (1)1.1 课题背景及研究意义 (1)1.2 发展历程 (2)1.3 国内外发展现状 (3)1.4 锁相环的应用 (4)1.4.1 频率合成 (5)1.4.2 时钟产生器 (5)1.4.3 时钟恢复电路 (5)1.4.4 偏移减小 (6)1.5 本文的章节安排及主要内容 (6)第2章锁相环理论 (7)2.1 基本理论 (7)2.2 基本模块 (8)2.2.1 鉴相器 (8)2.2.2 环路滤波器 (10)2.2.3 压控振荡器 (11)2.3 环路的相位模型及基本方程 (12)2.4 环路性能 (12)2.4.1 线性化相位模型和传递函数 (13)2.4.2 锁定状态下锁相环的动态特性 (14)2.5 本章小结 (16)第3章锁相环仿真 (17)3.1 Matlab软件介绍 (17)3.2 锁定性能 (18)3.2.1 一阶锁相环 (18)3.2.2 二阶锁相环 (19)3.2.3 一阶锁相环与二阶锁相环比较 (21)3.3 环路性能 (21)3.3.1 鉴相器的输出 (22)3.3.2 低通滤波器的输出 (23)3.3.3 压控振荡器的输出 (24)3.4 稳定性能 (25)3.5 调制作用 (27)3.6 本章小结 (28)结论 (29)致谢 (30)参考文献 (31)附录A (33)附录B (36)第1章绪论1.1课题背景及研究意义在现代集成电路中,锁相环(Phase Locked Loop)是一种广泛应用于模拟、数字及数模混合电路系统中的非常重要的电路模块。
锁相环与MATLAB仿真讲解

目录中文摘要 (3)英文摘要 (4)前言 (6)第一章绪论 (7)1.1 锁相环的发展及国内外研究现状 (7)1.2 本文的主要内容组织 (9)第二章锁相环的基本理论 (10)2.1锁相环的工作原理 (11)2.1.1鉴相器 (11)2.1.2 低通滤波器 (13)2.1.3 压控振荡器 (15)2.2锁相环的工作状态 (15)2.3锁相环的非线性工作性能分析 (17)2.3.1跟踪性能 (18)2.3.2捕获性能 (18)2.3.3失锁状态 (19)2.4锁相环的稳定性 (20)2.5信号流程图 (21)2.6锁相环的优良特性 (21)2.7锁相环的应用 (22)2.7.1锁相环在调制和解调中的应用 (22)2.7.2锁相环在频率合成器中的应用 (23)2.8本章小结 (23)第三章锁相环的噪声分析 (24)3.1锁相环的输入噪声 (24)3.2压控振荡器的噪声 (24)3.3相位噪声的抑制 (26)3.4本章小结 (27)第四章二阶锁相环仿真及结果 (28)4.1仿真介绍 (28)4.2程序代码 (28)4.3仿真结果 (34)4.4本章小结 (36)结论 (38)致谢 (39)参考文献 (40)毕业设计小结 (41)摘要锁相环电路是使一个特殊系统跟踪另外一个系统,更确切的说是一种输出信号在频率和相位上能够与输入参考信号同步的电路,它是模拟及数模混合电路中的一个基本的而且是非常重要的模块。
由于锁相环具有捕获、跟踪和窄带滤波的作用,因此被应用在通信、微处理器、以及卫星等许多领域。
锁相环是通信电路里时钟电路的一个重要模块。
本文详细介绍了锁相环设计中所涉及的各项指标计。
论文首先对锁相环的发展历史和研究现状做了介绍,然后从其基本工作原理出发,以传统锁相环的结构为基础,得到了锁相环的数学模型,对锁相环的跟踪性能、捕获性能、稳定性以及噪声性能等各种性能进行了分析,对锁相环的各项指标参数进行了详细推导,得出了锁相环数学分析的结论。
Matlab中基于dq变换的锁相环仿真研究
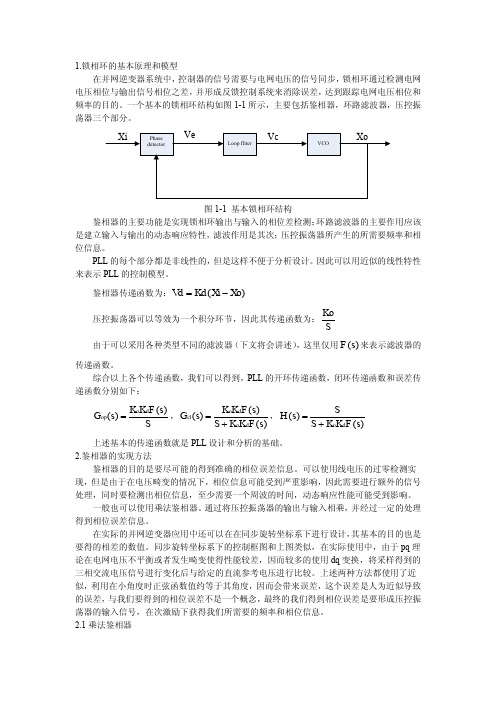
1 Sin(i(t ) o(t )) ,更进一步的,对于较小的相角差 2 1 1 值,我们可以近似认为: Sin(i(t ) o(t )) (i(t ) o(t )) (t ) ,从而得到相角差。 2 2
输入与输出相乘以后得到的结果是: 那么要想只得到右边的直流分量, 可以做个很简单的处理, 将两倍基频分量用低通滤波器滤 除即可。 其控制框图如图 2 所示:
1 1 2 2 变换矩阵为: C 3 3 0 2 1 2 cos 3 sin 2 sin cos
Usa Ud U sin( ) , 因此有 C Usb 要使得系统电压相角 与 PLL 输出相角 U q U cos( ) Usc
U Ki ( Kp ) S S
Gcl (s)
Gop(s) UKpS UKi 2 1 Gop(s) S UKpS UKi
2wnS wn 2 将上述闭环传递函数写成二阶传递函数的标准形式: 2 ,其中 S 2wnS wn 2
wn UKi ,
Kp U 。设 U 220 2 311 V 。对于典型的二阶系统,要取得较优 2 Ki
3.3 RC 积分滤波器 RC 积分滤波器的传递函数为 实零点。其频率响应如图 7 所示
1 1 U 2 (1 2 1 ) S 1 S1
1 ,它就是一个低通滤波器。给原系统增加了一个负 1 S
图 7 RC 积分滤波器的频率响应 PLL 系统的开环和闭环传递函数分别为: Gop( s)
Sin( wit i (t )) Sin( wot o(t )) 1 1 Sin( wit wot i(t ) o(t )) Sin((wi wo)t i(t ) o(t )) 2 2
基于MATLAB数字锁相环仿真设计

本科生毕业设计(申请学士学位)论文题目基于Matlab的数字锁相环的仿真设计作者专业名称电子信息工程指导教师2014年5月学生:(签字)学号:答辩日期:2014 年 5 月24 日指导教师:(签字)目录摘要 (1)Abstract (1)1 绪论 (2)1.1 本文研究背景 (2)1.2 本文研究意义 (2)1.3 锁相环和仿真方式 (2)1.3.1 锁相环 (2) (2)3 2 模拟锁相环Matlab仿真 (3)2.1 模拟锁相环方案 (3)2.1.1 模拟鉴相器 (3)2.1.2 模拟低通滤波器 (6)2.1.3 模拟压控振荡器 (7)2.2 模拟锁相环仿真 (8)2.3 本章小结 (9)3 数字锁相环Matlab仿真 (10)3.1 数字锁相环方案 (10)3.1.1 数字鉴相器 (10)3.1.2 数字滤波器 (12)3.1.3 数字压控振荡器 (13)3.2 数字锁相环仿真 (14)3.3 本章小结 (15)4 总结与展望 (15)参考文献 (16)致 (18)基于Matlab的数字锁相环的仿真设计摘要:锁相环是一种能够自动跟踪信号相位并达到锁频目的的闭环负反馈系统。
数字锁相环在无线电领域得到较广泛的应用和发展。
而且已经成为雷达、通信、导航等各类电子信号产品不可替代的元器件之一。
锁相环的窄带跟踪性能使其得到较广泛应用。
因为锁相技术在实际应用中较为复杂,所以锁相环的设计通常采用仿真设计这种方式。
本次设计采用Matlab这一软件进行辅助仿真设计,完全能达到设计预期的目标。
Matlab中的Simulink仿真软件,具有很强的灵活性和直观性。
本次设计所采用的方法是在simulink中搭建模拟锁相的模型,并对模拟锁相环的组成、结构、设计进行不断的分析和改进。
然后根据模拟锁相环的原理进行改进,并搭建数字锁相环。
关键词:锁相环;自动跟踪;matlab;simulinkSimulative design of digital phase-locked loop based onMatlabAbstract:PLL is the automatic tracking system of close loop atracking signal phase. It is widely used in various fields of radio. It has become an irreplaceable part of radar, communication, navigation and all kinds of electronicsignal device. PLL is able to be widely used. Because, it has unique narrow-band tracking performance. However, because of the complexity of phase lock technique, for the design of PLL have brought great difficulty. This design uses Matlab, the simulative software for design assistance, can completely meet the design expectations. Simulink simulative software on Matlab, has strong flexibility and intuitive. Methods used by this project is to build the analog phase locked in the Simulink model, and the composition, structure, design of analog phase-locked loop of continuous improvement and analysis. It improved according to the principle of analog PLL, build digital phase-locked loop in Simulink, and then reach the simulation design of digitalphase-locked loop based on Matlab the design objective .Key words: PLL, Automatic tracking, Matlab, simulink1 绪论1.1 本文研究背景19世纪30年代法国H.de Bellescize首次提出同步检波这一概念,并且设计出锁相环电路这一划时代的研究成果[1]。
锁相环仿真报告

ωn =
2 BL ; 1 ζ+ 4ζ
τ1 =
Kd Kr
ω
2 n
;
τ2 =
2ζ
ωn
。
2. 仿真分析(使用 Matlab 中的 Simulink)
(1) 仿真参数 3 给定 ζ=0.707,Kd=4V/rad,Kr=24π×10 rad/(V·S),BL=10Hz,计算得 ωn=19rad/s, τ1=848s,τ2=0.075s,环路滤波器传递函数
0
0.1
0.2
0.3
1/ 2
τ ⎛ Kd Kr ⎞ ⎟ , ζ = ωn = 2 ⎜ ⎟ 2 2⎜ ⎝ τ1 ⎠ τ2
1/ 2
它是传递函数的幅频曲线的最高点对应的频率; ζ 为环路阻尼系数, ωn 为自然谐振频率, 它表示了传递函数幅频响应最大值的衰减程度,该值越大,传递函数幅频曲线最高点越小。 环路噪声带宽 BL 可用 ωn 和 ζ 来表示
BL =
ωn
2
(ζ +
1 ) 4ζ
环路噪声带宽是幅频响应下降到 3dB 时的频宽。
二. 锁相环的锁定过程分析
1. 环路捕获过程的几种情况
① 快捕过程
3
起始频差很小,即输入输出的相差 θe(t)动态变化频率很小,使得 Z(t)的变化不超过一个 周期时环路就进入锁定状态。此时 θe(t)的变化不超过 2π,这种捕获过程称为快捕过程。 快捕带:使得 θe(t)在 2π 之内环路就进入锁定的最大起始频差。 ② 频率牵引的捕捉过程 随着起始频差增大, 相位误差 θe(t)的频率增大, 则误差电压信号 ε(t)频率增大, 此时 ε(t) 通过环路滤波器(低通)有衰减。如果衰减后的误差信号不至于使 Z(t)接近于 0,而是对压控 振荡器(VCO)还是有一定的控制作用,则 VCO 输出频率会逐渐向着输入频率靠近,这就使 得误差信号 ε(t)的频率得到降低,通过环路滤波器的衰减变弱,Z(t)变大,对 VCO 的控制作 用逐渐变大,直到最后进入锁定过程。 捕捉带:可以通过频率牵引过程使环路进入锁定状态的最大起始频差。 ③ 环路无法锁定情况 当起始频差很大,使得误差信号 ε(t)不能通过环路滤波器,Z(t)接近于 0,不能对 VCO 进行电压控制,则 VCO 的输出频率和相位不发生变化,环路不能锁定。
锁相环的matlab的仿真程序(PLL matlab simulation program)

锁相环的matlab的仿真程序(PLL matlab simulation program)% phasell。
M%锁相环(PLL),调整一个本地振荡器的相位。
%与输入的调制信号。
这样的阶段%输入信号被锁定,信号解调。
%也用于PM和FM。
我们将使用闭环系统来实现它。
控制系统这里应用了%技术。
%*********************************************************** ***锁相环一阶闭环透过率的%阶跃响应% h(s)= 1;%系统类型号= 1;%道/ thetai(输出/输入阶段)关闭所有千伏= 1;KD=1;DT = 0.01T=0:dt:2u =(1,长度(t))G11 = [ TF([ 2 * pi *千* KD ]、[ 1 2 * pi *千* KD ])]为其传递函数在给定的讲义[ 11 ] = lsim(G11,U,T)图形情节(t,Y11)xlabel(秒的时间)ylabel(幅度标准”)标题(第一阶'step响应闭环率”)%*********************************************************** ****锁相环一阶闭环误差透过率的阶跃响应所有其他因素h(s)等在这里都一样。
%中来/ thetai(相同的解释。
如上)G12 = [([ 1,0 ],TF [ 1 2 * pi *千* KD ])]误差透过讲义中给出[ 12 ] = lsim(G12,U,T)图形情节(t,Y12)xlabel(秒的时间)ylabel(幅度标准”)标题(第一阶'step响应闭环误差率”)%*********************************************************** *****锁相环一阶闭环透过率的%阶跃响应VCO与输入信号相位之间的百分比% h(s)= 1;%系统类型号= 1;% v2 / thetaiKD=1;G13 = [ TF([ 0 ] [ 1 KD,2 * pi *千* KD ])]为压控振荡器的电压和输入信号透过率[ 13 ] = lsim(G13,U,T)图形情节(t,Y13)xlabel(秒的时间)ylabel(幅度标准”)标题(第一阶'step响应闭环透光率的B / W的VCO和输入阶段”)%*********************************************************** *********锁相环二阶闭环透射率的阶跃响应%系统类型号= 2;%道/ thetai= 3.15ζ= sqrt((π*千* KD)/(2 *))omegan = sqrt(2 * pi *伏* KD *)G21 = [([ 2 *泽塔* TF omegan omegan ^ 2 ]、[ 1 2 *泽塔* omegan omegan ^ 2 ])]【Y21 T ] = lsim(G21,U,T)图形情节(t,Y21)xlabel(秒的时间)ylabel(幅度标准”)标题(二阶锁相环的环路闭合'step响应率)%*********************************************************** **********锁相环二阶闭环误差透过率的阶跃响应%系统类型号= 2;% / thetai中来G22 = [([ 0 ] 0 TF 1,[ 1 2 *泽塔* omegan omegan ^ 2 ])]【Y22 T ] = lsim(G22,U,T)图形情节(t,Y22)xlabel(秒的时间)ylabel(幅度标准”)标题(二阶锁相环的环路闭合'step响应误差率)%*********************************************************** **********锁相环二阶闭环透射率的阶跃响应VCO与输入信号相位之间的百分比%系统类型号= 2;% v2 / thetaiG23 = [ TF(KD KD * [ 0 ]、[ 1 2 * pi *千* 2 * pi *千* KD KD ])]【Y23 T ] = lsim(G23,U,T)图形情节(t,Y23)xlabel(秒的时间)ylabel(幅度标准”)标题(二阶'step响应闭环透光率的B / W的VCO和输入阶段”)%*********************************************************** ***************%锁相环。
锁相环matlab代码

锁相环matlab代码锁相环(Phase-Locked Loop,简称PLL)是一种广泛应用于通信系统、控制系统和信号处理系统中的重要电路。
它通过对输入信号的频率、相位进行调整,使得输出信号与参考信号保持同步。
在实际应用中,锁相环常常用于频率合成、时钟恢复、调制与解调等方面。
本文将介绍锁相环的原理及其在MATLAB中的实现。
一、锁相环的原理锁相环由相位比较器(Phase Detector)、低通滤波器(Low-Pass Filter)、控制电压生成器(Voltage-Controlled Oscillator,简称VCO)和反馈电路组成。
其基本原理如下:1. 相位比较器:用于比较参考信号与输出信号的相位差,并将相位差转换为电压信号输出。
2. 低通滤波器:对相位比较器输出的电压信号进行滤波处理,去除高频噪声,得到平滑的控制电压。
3. 控制电压生成器:根据低通滤波器输出的控制电压,调整VCO的频率和相位。
4. 反馈电路:将VCO的输出信号反馈给相位比较器,与参考信号进行比较,形成闭环控制。
二、MATLAB中的锁相环实现在MATLAB中,可以使用DSP System Toolbox提供的相关函数和模块来实现锁相环。
下面以一个简单的频率合成器为例,介绍MATLAB中锁相环的实现步骤:1. 设计参考信号和输入信号:可使用sine函数生成参考信号和输入信号。
2. 设计相位比较器:使用phasedetector函数创建相位比较器对象,并设置相位差量化精度。
3. 设计低通滤波器:使用lowpass函数创建低通滤波器对象,并设置截止频率和阶数。
4. 设计控制电压生成器:使用vco函数创建VCO对象,并设置控制电压范围和频率范围。
5. 设计反馈电路:将VCO的输出信号与参考信号输入相位比较器。
6. 运行锁相环:通过循环控制,不断调整VCO的频率和相位,使输出信号与参考信号同步。
三、锁相环的应用锁相环在通信系统、控制系统和信号处理系统中有着广泛的应用。
锁相环设计及其MATLAB仿真

摘要锁相环是一个能够跟踪输入信号相位变化的闭环自动跟踪系统。
它广泛应用于无线电的各个领域,并且,现在已成为通信、雷达、导航、电子仪器等设备中不可缺少的一部分。
根据虚拟无线电技术的特点和锁相环的基本原理,提出一种适于计算机软件化实现的锁相环数学模型,分析不同参数对锁相环捕获和跟踪性能的影响,得出不同情况下参数设定的基本准则。
计算机仿真结果表明,软件锁相环在加性高斯白噪声信道下具有较好的捕获与跟踪性能。
最后提出软件锁相环在测控系统中实现信号实时处理的优化方借助于MATLAB中的Simulink仿真软件,在Simulink中利用仿真模块搭建了全数字锁相环的仿真模型。
先借助模拟锁相环直观形象、易于理解的特点,通过锁相环在频率合成方面的应用,先对模拟锁相环进行了仿真,对锁相环的工作原理进行了形象的说明。
在模拟锁相环的基础上,重新利用仿真模块搭建了全数字锁相环的仿真模型,通过仿真达到了设计的目的,验证了此全数字锁相环完全能达到模拟锁相环的各项功能要求。
关键词:锁相环,压控振荡器,锁定,MATLAB,Simulink,频率合成,仿真模块ABSTRACTPhase-locked loop is a closed loop frequency control system,which functioning is based on the phase sensitive detection of phase difference between the input and output signals of the controlled oscillator.It has been widely used in all aspects in radio field and ,has becomed a indispensable part in communication、radar、nevigation and electronic equipments.But with the disign complexity of phase-locked loop in works,there will meet a lot of datas and a long simulation time if simulating the PLL with SPICE ,what is worse, which need to simulate several times to extract the disign parameters,at that way,the disign term will be extended.With the help of flexibility and palpability of Matlab’s simulink,the behavioral model of DPLL is builded using the block in simulink based on the frequency systhesis.Through the DPLL applicating in frequency systhesis,the principle of phase-locked loop and the work process is simulated. According to the characteristics of the Virtual Radio technology and the basic theory of the Phase Look Loop ( PLL) ,this paper puts forward the mathematicalmodel of the PLL which is suitable for software realization by the computer. In this paper,the influences of the parameters to the cap ture performance and the tracking performance are analyzed, and the basic p rincip le of the parameter setting in different conditions is given. The results of the simulation p rove that the cap ture performance and the tracking performance of Software PLL in AdditiveWhite Gaussian Noise are good. At the last of the paper, the op timized method of the PLL signal realtime p rocessing in the Tracking, Telemetering and Control System is p resented.KEYWORDS: MATLAB, phase-lockedloop, V oltage-controlledoscillator ,locked,simulink, frequency systhesis, simulationmodel。
锁相环的时域跟踪性能及MATLAB仿真分析

如图1 所示, (- s t0() 假设 t i + ), ) n U(- ono + 0) 0)U ( t0() t sc i o 。
为输入信号的振幅 , 3 为输入信号 的载波角 0f 频率 ; 为输 出信号的振幅 ,1 为输 出信 号的载 波 (0 )
0 引言
锁相环在 日常生 活中具有重要的应用 ,当我们
航 、雷达 、航空航天 、卫星 电视 、遥控遥测 等诸 多 方面。锁相环之 所以有这么多的应用 ,源于它的跟 踪性能 。本文从 定量和定性两方面 ,阐述锁相环最
打开 电视机时 ,立刻会体会到 锁相 环所 带来的好处 , 基本 的时 域跟踪性 能。并用 MA L T AB进 行仿 真分
模拟 锁 相 环 由鉴相 器 (D 、环 路 滤 波 器 ( F 、 环 l P) L) 。 压 控振 荡器 ( c ) v o 3部分 所组 成 。为研 究 问题方 便 ,
PLL r c i r or a e a i e t a k ng pe f m nc nd tm —do a n m i s ul rng a l i A一‘ AB i fa i na ̄ " ofM  ̄ l in m t yssoI… 1I LA
W e ua p n Y a i i Zha ou he g i X n i g, o M nl, ng Zh s n
人们通过进行 电视频道转换 ,可收看到清 晰的画面 和悦耳动听的音乐。此外 ,锁相环也广泛应用于导 析 。从而得 出对 电子设计具有一 定实用价 值的结 论。
巴
锁 相环的时域相位 模型
11锁 相环 的 组成 .
环路 的开环传递函数为 :
H0 ) Kd s K s ( = Ko 、 F() F()
基于Matlab的Costas环仿真设计

clcclear allfs = 12e6; %采样频率ts = 1/fs;num = 2.5e6; %数据长度snr = -15;real_fc = 3563000; %实际信号频率data = sin(2*pi*real_fc*ts*(0:num-1)+pi/4)+sqrt(10^(snr/10))*randn(1, num);%costas环输入数据% data = exp(j*2*pi*real_fc*ts*(0:num-1)+pi/4)+sqrt(10^(snr/10))*(rand n(1,num)+j*randn(1,num));%costas环输入数据fc = 3562800; %本地频率n = fs/1000; %累积时间为1msnn = 0:n-1;nf = floor(length(data)/n); %将输入数据分成1ms的多个数据块wfc = 2*pi*fc; %本地信号phi_prv = 0;temp = 0;frame = 0;carrier_phase = 0;phase = 0;% 环路滤波器的参数c1 = 153.7130;c2 = 6.1498;for frame = 1:nf%产生本地的sin和cos函数expcol = exp(j*(wfc*ts*nn+phase));sine = imag(expcol);cosine = real(expcol);x= data((1:n)+((frame-1)*n));%将数据转换至基带x_sine = x.*sine;x_cosine = x.*cosine;Q = sum(x_sine); %经过滤波器I = sum(x_cosine);%phase_discri(frame) = atan(Q/I); %得到锁相环的输入phase_discri(frame) = (sign(I(i))*Q(i)-sign(Q(i))*I(i)).../(sqrt(2)*abs(I(i)));%锁相环dfrq(frame) = c1*phase_discri(frame)+temp; %经过环路滤波器temp = temp+c2*phase_discri(frame);wfc = wfc - dfrq(frame)*2*pi; %改变本地频率dfrq_frame(frame) = wfc;phase = wfc*ts*n+phase; %得到不同块的相位endplot(dfrq_frame/(2*pi));hold on;plot([1:length(dfrq_frame)], real_fc,'r');% plot(phase_discri);legend('锁相环跟踪','实际的载波频率');gridmean_freq = mean(dfrq_frame/2/pi);p = abs(real_fc-mean_freq)/real_fc;。
matlab锁相环代码

下面是一个简单的MATLAB锁相环(PLL)的代码示例。
此代码是一个非常基础的示例,用于说明如何实现一个基本的PLL。
在实际应用中,PLL通常会更复杂,并需要更多的调整和优化。
matlab复制代码% 参数设置Kp = 1; % 比例增益Ki = 1; % 积分增益Kd = 0.1; % 微分增益set_params(Kp, Ki, Kd); % 设置参数% 初始化phase_error = 0; % 相位误差integral = 0; % 积分项prev_phase_error = 0; % 上一次的相位误差% 模拟输入信号,例如一个正弦波t = 0:0.001:10; % 时间向量input_signal = sin(t); % 正弦波输入信号% 模拟输出信号output_signal = zeros(size(t)); % 初始化输出信号% 循环计算输出信号for i = 2:length(t)% 计算相位误差phase_error = input_signal(i) - output_signal(i-1);% 更新积分项integral = integral + phase_error;% 更新输出信号output_signal(i) = output_signal(i-1) + Kp*phase_error +Ki*integral + Kd*(phase_error - prev_phase_error);% 更新上一次的相位误差prev_phase_error = phase_error;end% 绘制结果figure;subplot(2,1,1); plot(t, input_signal); title('Input Signal');xlabel('Time (s)'); ylabel('Amplitude');subplot(2,1,2); plot(t, output_signal); title('Output Signal');xlabel('Time (s)'); ylabel('Amplitude');此代码中,我们首先设置PLL的参数,然后模拟一个输入信号(例如正弦波)。
锁相环仿真(基于MATLAB)

锁相环仿真1.锁相环的理论分析1.1 锁相环的基本组成锁相环路是一种反馈控制电路,简称锁相环( PLL,Phase-Locked Loop )。
锁相环的特点是:利用外部输入的参考信号控制环路内部振荡信号的频率和相位。
因锁相环可以实现输出信号频率对输入信号频率的自动跟踪,所以锁相环通常用于闭环跟踪电路。
锁相环在工作的过程中,当输出信号的频率与输入信号的频率相等时,输出电压与输入电压保持固定的相位差值,即输出电压与输入电压的相位被锁住,这就是锁相环名称的由来。
锁相环通常由鉴相器(PD,Phase Detector )、环路滤波器( LF,Loop Filter )和压控振荡器( VCO,Voltage Controlled Oscillator )三部分组成,锁相环组成的原理框图如图示:锁相环中的鉴相器又称为相位比较器,它的作用是检测输入信号和输出信号的相位差,并将检测出的相位差信号转换成 u D(t )电压信号输出,该信号经低通滤波器滤波后形成压控振荡器的控制电压 u C(t ),对振荡器输出信号的频率实施控制。
1.2 锁相环的工作原理1.2.1 鉴相器锁相环中的鉴相器(PD)通常由模拟乘法器组成,利用模拟乘法器组成的鉴相器电路如图示:鉴相器的工作原理是:设外界输入的信号电压和压控振荡器输出的信号电压分别为:式中的ω0 为压控振荡器在输入控制电压为零或为直流电压时的振荡角频率,称为电路的固有振荡角频率。
则模拟乘法器的输出电压 u D为:低通滤波器低通滤波器(LF)的将上式中的和频分量滤掉,剩下的差频分量作为压控振荡器的输入控制电压 u C(t )。
即 u C(t )为:式中的ωi 为输入信号的瞬时振荡角频率,θ i (t)和θ O(t)分别为输入信号和输出信号的瞬时位相,根据相量的关系可得瞬时频率和瞬时位相的关系为:即则,瞬时相位差θ d为对两边求微分,可得频差的关系式为上式等于零,说明锁相环进入相位锁定的状态,此时输出和输入信号的频率和相位保持恒定不变的状态, u c(t )为恒定值。
基于MATLAB的锁相环非线性分析

式 中 , K 是 V 0常 数 ,单 位 C
X =A c s nc+ , i n o [ ft ( 】 2 )
而压控 振荡器 的输 出信号表达式假设为
() 1
G
fn)  ̄一 一 i ㈣ 2
( 6 )
X t ~ i 2 r+ ) a= As[ c 】 g n f
【 摘 要 】锁相环通常工作在捕捉和跟踪两种模 式下的一种。在捕捉模式下 ,锁相环试 图使 V O 的输 出信号与输入信号 C 在频 率和相位上 同步。但 是在捕捉模式 下,VC 的输 出信号与输入信 号的相位差可能相 当大,锁相环此 时工作在 非线性状 态, O
需要 用非线性模 型来进行分析 。分析非线性模 型是很 困难的 ,常常需要进行仿 真。利用 MA L B 工具 ,使 用徽分方程法研究 TA 锁 相 环 系统 的 非 线性 特 性 。 【 关键 词】锁相环 ;微分方程法;非线性 ;MAT A LB 【 中图分类号 】T 23 P 7 【 文献标识码】A 【 文章编号】10 — 1 1 O 1o 一 o o 0 08 15 f 1)5 o6 一 2 2 于零。在稳态时,相位 差是否为零取决于输入信号和环路滤
2 " 年第 5期 0 I 总第 1 1 ) 4 期
大 众 科 技
DA Z HONG J KE I
No 5。 0 1 . 2 1
p l .4 】 yNo1 1
基 于 M TA A L B的锁 相 环 非 线 性 分析
刘 科 江
( 电子科技 大学电子工程 学院 ,四川 成都 6 13 ) 17 1
性。
山
由定 义 ,V 0的 输 出频 率 偏 差 与 V O的 输入 信 号成 正 比 , C C 这样
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
锁相环仿真1.锁相环的理论分析1.1锁相环的基本组成锁相环路是一种反馈控制电路,简称锁相环(PLL,Phase-Locked Loop)。
锁相环的特点是:利用外部输入的参考信号控制环路内部振荡信号的频率和相位。
因锁相环可以实现输出信号频率对输入信号频率的自动跟踪,所以锁相环通常用于闭环跟踪电路。
锁相环在工作的过程中,当输出信号的频率与输入信号的频率相等时,输出电压与输入电压保持固定的相位差值,即输出电压与输入电压的相位被锁住,这就是锁相环名称的由来。
锁相环通常由鉴相器(PD,Phase Detector)、环路滤波器(LF,Loop Filter)和压控振荡器(VCO,Voltage Controlled Oscillator)三部分组成,锁相环组成的原理框图如图示:锁相环中的鉴相器又称为相位比较器,它的作用是检测输入信号和输出信号的相位差,并将检测出的相位差信号转换成u(t)电压信号输出,该信号经低通滤D(t),对振荡器输出信号的频率实施波器滤波后形成压控振荡器的控制电压uC控制。
1.2锁相环的工作原理1.2.1鉴相器锁相环中的鉴相器(PD)通常由模拟乘法器组成,利用模拟乘法器组成的鉴相器电路如图示:鉴相器的工作原理是:设外界输入的信号电压和压控振荡器输出的信号电压分别为:为压控振荡器在输入控制电压为零或为直流电压时的振荡角频率,称式中的ω为:为电路的固有振荡角频率。
则模拟乘法器的输出电压uD1.2.2 低通滤波器低通滤波器(LF)的将上式中的和频分量滤掉,剩下的差频分量作为压控振荡器的输入控制电压uC (t)。
即uC(t)为:式中的ωi 为输入信号的瞬时振荡角频率,θi(t)和θO(t)分别为输入信号和输出信号的瞬时位相,根据相量的关系可得瞬时频率和瞬时位相的关系为:即则,瞬时相位差θd为对两边求微分,可得频差的关系式为上式等于零,说明锁相环进入相位锁定的状态,此时输出和输入信号的频率和相位保持恒定不变的状态,uc(t)为恒定值。
当上式不等于零时,说明锁相环的相位还未锁定,输入信号和输出信号的频率不等,uc(t)随时间而变。
1.2.3 压控振荡器压控振荡器(VCO)的压控特性如图示该特性说明压控振荡器的振荡频率ωu 以ω为中心,随输入信号电压uc(t)线性地变化,变化的关系如下:上式说明当uc (t)随时间而变时,压控振荡器(VCO)的振荡频率ωu也随时间而变,锁相环进入“频率牵引”,自动跟踪捕捉输入信号的频率,使锁相环进入锁定的状态,并保持ω0=ωi的状态不变。
2.信号流程图锁相环的原理框图如下:其工作过程如下:(1)压控振荡器的输出Uo经过采集并分频;(2)输出和基准信号同时输入鉴相器;(3)鉴相器通过比较上述两个信号的频率差,然后输出一个直流脉冲电压Ud;(4)Ud进入到滤波器里面,滤除高频成分后得到信息Ue;(5)Ue进入到压控震荡器VCO里面,控制频率随输入电压线性地变化;(6)这样经过一个很短的时间,VCO的输出就会稳定于某一期望值。
3.二阶环仿真源程序代码及仿真结果3.1 程序代码:% File: c6_nltvde.mw2b=0; w2c=0; % initialize integratorsyd=0; y=0; % initialize differential equationtfinal = 50; % simulation timefs = 100; % sampling frequencydelt = 1/fs; % sampling periodnpts = 1+fs*tfinal; % number of samples simulatedydv = zeros(1,npts); % vector of dy/dt samplesyv = zeros(1,npts); % vector of y(t) samples%% beginning of simulation loopfor i=1:nptst = (i-1)*delt; % timeif t<20ydd = 4*exp(-t/2)-3*yd*abs(y)-9*y; % de for t<20elseydd = 4*exp(-t/2)-3*yd-9*y; % de for t>=20endw1b=ydd+w2b; % first integrator - step 1w2b=ydd+w1b; % first integrator - step 2yd=w1b/(2*fs); % first integrator outputw1c=yd+w2c; % second integrator - step 1 w2c=yd+w1c; % second integrator - step 2 y=w1c/(2*fs); % second integrator outputydv(1,i) = yd; % build dy/dt vectoryv(1,i) = y; % build y(t) vectorend % end of simulation loopplot(yv,ydv) % plot phase planexlabel('y(t)') % label x axisylabel('dy/dt') % label y zxis% End of script file.% File: pllpost.m%kk = 0;while kk == 0k = menu('Phase Lock Loop Postprocessor',...'Input Frequency and VCO Frequency',...'Input Phase and VCO Phase',...'Frequency Error','Phase Error','Phase Plane Plot',...'Phase Plane and Time Domain Plots','Exit Program');if k == 1plot(t,fin,'k',t,fvco,'k')title('Input Frequency and VCO Freqeuncy')xlabel('Time - Seconds');ylabel('Frequency - Hertz');pause elseif k ==2pvco=phin-phierror;plot(t,phin,t,pvco)title('Input Phase and VCO Phase')xlabel('Time - Seconds');ylabel('Phase - Radians');pause elseif k == 3plot(t,freqerror);title('Frequency Error')xlabel('Time - Seconds');ylabel('Frequency Error - Hertz');pause elseif k == 4plot(t,phierror);title('Phase Error')xlabel('Time - Seconds');ylabel('Phase Error - Radians');pause elseif k == 5ppplotelseif k == 6subplot(211);phierrn = phierror/pi;plot(phierrn,freqerror,'k');grid;title('Phase Plane Plot');xlabel('Phase Error /Pi');ylabel('Frequency Error - Hertz');subplot(212)plot(t,fin,'k',t,fvco,'k');gridtitle('Input Frequency and VCO Freqeuncy')xlabel('Time - Seconds');ylabel('Frequency - Hertz');subplot(111) elseif k == 7kk = 1;end end % End of script file.% File: pllpre.m%clear all % be safedisp(' ') % insert blank linefdel = input('Enter the size of the frequency step in Hertz > ');fn = input('Enter the loop natural frequency in Hertz > ');lambda = input('Enter lambda, the relative pole offset > ');disp(' ')disp('Accept default values:')disp(' zeta = 1/sqrt(2) = 0.707,')disp(' fs = 200*fn, and')disp(' tstop = 1')dtype = input('Enter y for yes or n for no > ','s');if dtype == 'y'zeta = 1/sqrt(2);fs = 200*fn;tstop = 1;elsezeta = input('Enter zeta, the loop damping factor > ');fs = input('Enter the sampling frequency in Hertz > ');tstop = input('Enter tstop, the simulation runtime > ');end %npts = fs*tstop+1; % number of simulation pointst = (0:(npts-1))/fs; % default time vectornsettle = fix(npts/10); % set nsettle time as 0.1*npts tsettle = nsettle/fs; % set tsettle% The next two lines establish the loop input frequency and phase% deviations.fin = [zeros(1,nsettle),fdel*ones(1,npts-nsettle)];phin = [zeros(1,nsettle),2*pi*fdel*t(1:(npts-nsettle))];disp(' ') % insert blank line% end of script file pllpre.m % File: pll2sin.mw2b=0; w2c=0; s5=0; phivco=0; %initializetwopi=2*pi; % define 2*pitwofs=2*fs; % define 2*fsG=2*pi*fn*(zeta+sqrt(zeta*zeta-lambda)); % set loop gaina=2*pi*fn/(zeta+sqrt(zeta*zeta-lambda)); % set filter parametera1=a*(1-lambda); a2 = a*lambda; % define constants phierror = zeros(1,npts); % initialize vectorfvco=zeros(1,npts); % initialize vector % beginning of simulation loopfor i=1:nptss1=phin(i) - phivco; % phase errors2=sin(s1); % sinusoidal phase detectors3=G*s2;s4=a1*s3;s4a=s4-a2*s5; % loop filter integrator inputw1b=s4a+w2b; % filter integrator (step 1)w2b=s4a+w1b; % filter integrator (step 2)s5=w1b/twofs; % generate fiter outputs6=s3+s5; % VCO integrator inputw1c=s6+w2c; % VCO integrator (step 1)w2c=s6+w1c; % VCO integrator (step 2)phivco=w1c/twofs; % generate VCO outputphierror(i)=s1; % build phase error vectorfvco(i)=s6/twopi; % build VCO input vectorend% end of simulation loopfreqerror=fin-fvco; % build frequency error vector % End of script file.function [] = pplane(x,y,nsettle)% Plots the phase plane with phase in the range (-pi,pi)ln = length(x);maxfreq = max(y);minfreq = min(y);close % Old figure discardedaxis([-1 1 1.1*minfreq 1.1*maxfreq]); % Establish scalehold on % Collect info for new figj = nsettle;while j < lni = 1;while x(j) < pi & j < lna(i) = x(j)/pi;b(i) = y(j);j = j+1;i = i+1;endplot(a,b,'k')a = [];b = [];x = x - 2*pi;endhold offtitle('Phase-Plane Plot')xlabel('Phase Error / Pi')ylabel('Frequency Error in Hertz')grid % End of script file.% File: ppplot.m% ppplot.m is the script file for plotting phase plane plots. If the% phase plane is constrained to (-pi,pi) ppplot.m calls pplane.m.kz = 0;while kz == 0k = menu('Phase Plane Options',...'Extended Phase Plane',...'Phase Plane mod(2pi)',...'Exit Phase Plane Menu');if k == 1phierrn = phierrn/pi;plot(phierrn,freqerror,'k')title('Phase Plane Plot')xlabel('Phase Error /Pi')ylabel('Frequency Error - Hertz')gridpauseelseif k == 2pplane(phierrn,freqerror,nsettle+1)pauseelseif k == 3kz = 1;endend % End of script file.3.2仿真结果:G=30时的仿真图形:Accept the tentative values:the first loop frequency is 5Enter y for yes or n for no > yEnter the loop gain >30 输入环路增益为30Enter the sampling frequency in Hertz > 1200Enter tstop, the simulation runtime > 5 仿真时间为5秒相平面图输入频率和VCO频率图输入相位和VCO相位图频率差图相位差图G=40时的仿真图形:Accept the tentative values:the first loop frequency is 5Enter y for yes or n for no > yEnter the loop gain >40 输入环路增益为40Enter the sampling frequency in Hertz > 1200Enter tstop, the simulation runtime > 5 仿真时间为5秒相平面图输入频率和VCO频率图相位差图频率差图输入频率和VCO频率图输入相位和VCO相位图。
