备战中考数学复习《圆的综合》专项综合练习
中考数学《圆》专项复习综合练习题-附带答案
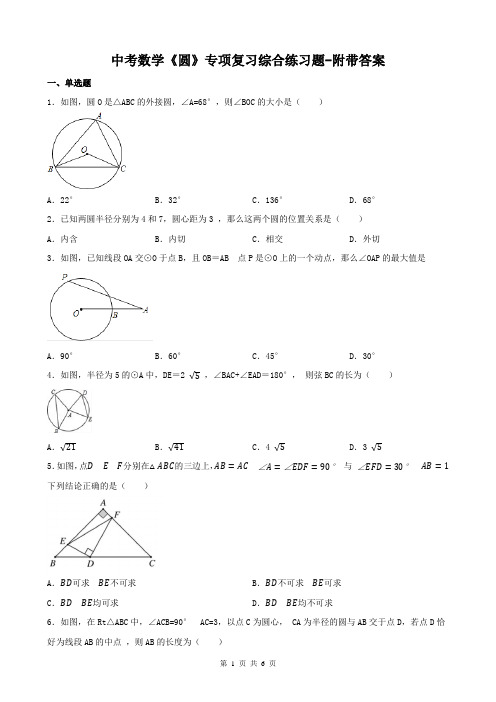
中考数学《圆》专项复习综合练习题-附带答案一、单选题1.如图,圆O是△ABC的外接圆,∠A=68°,则∠BOC的大小是()A.22°B.32°C.136°D.68°2.已知两圆半径分别为4和7,圆心距为3 ,那么这两个圆的位置关系是()A.内含B.内切C.相交D.外切3.如图,已知线段OA交⊙O于点B,且OB=AB 点P是⊙O上的一个动点,那么∠OAP的最大值是A.90°B.60°C.45°D.30°4.如图,半径为5的⊙A中,DE=2 √5,∠BAC+∠EAD=180°,则弦BC的长为()A.√21B.√41C.4 √5D.3 √55.如图,点D E F分别在△ABC的三边上,AB=AC∠A=∠EDF=90°与∠EFD=30°AB=1下列结论正确的是()A.BD可求BE不可求B.BD不可求BE可求C.BD BE均可求D.BD BE均不可求6.如图,在Rt△ABC中,∠ACB=90° AC=3,以点C为圆心, CA为半径的圆与AB交于点D,若点D恰好为线段AB的中点,则AB的长度为()B.3 C.9 D.6A.327.如图,⊙O是△ABC的外接圆,弦BD交AC于点E,AE=DE, BC=CE,过点O作OF⊥AC于点F,延长FO 交BE于点G ,若DE=6,EG=4,则AB的长为()A.4√5B.8√3C.13 D.148.如图,把正六边形各边按同一方向延长,使延长的线段与原正六边形的边长相等,顺次连接这六条线段外端点可以得到一个新的正六边形…,重复上述过程,经过2018次后所得到的正六边形边长是原正六边形边长的()A.(√2)2016倍B.(√3)2017倍C.(√3)2018倍D.(√2)2019倍二、填空题9.如图,PA、PB切⊙O于点A、B ,已知⊙O半径为2 且∠APB=60°,则AB= .10.如图,矩形ABCD中,BC=4 CD=2 以AD为直径的半圆O与BC相切于点E,连接BD,则阴影部分的面积为.(结果保留π)11.如图,两边平行的刻度尺在圆上移动当刻度尺的一边与直径为6.5cm的圆相切时另一边与圆两个交点处的读数恰好为“2”和“8”(单位:cm)则刻度尺的宽为 cm.12.如图,两圆相交于A、B两点小圆经过大圆的圆心O 点C D分别在两圆上若∠ADB=100°则∠ACB的度数为。
备战中考数学复习《圆的综合》专项综合练习及详细答案

一、圆的综合真题与模拟题分类汇编(难题易错题)1.如图,⊙O是△ABC的外接圆,点E为△ABC内切圆的圆心,连接AE的延长线交BC于点F,交⊙O于点D;连接BD,过点D作直线DM,使∠BDM=∠DAC.(1)求证:直线DM是⊙O的切线;(2)若DF=2,且AF=4,求BD和DE的长.【答案】(1)证明见解析(2)23【解析】【分析】(1)根据垂径定理的推论即可得到OD⊥BC,再根据∠BDM=∠DBC,即可判定BC∥DM,进而得到OD⊥DM,据此可得直线DM是⊙O的切线;(2)根据三角形内心的定义以及圆周角定理,得到∠BED=∠EBD,即可得出DB=DE,再判定△DBF∽△DAB,即可得到DB2=DF•DA,据此解答即可.【详解】(1)如图所示,连接OD.∵点E是△ABC的内心,∴∠BAD=∠CAD,∴BD CD=,∴OD⊥BC.又∵∠BDM=∠DAC,∠DAC=∠DBC,∴∠BDM=∠DBC,∴BC∥DM,∴OD⊥DM.又∵OD为⊙O半径,∴直线DM是⊙O的切线.(2)连接BE.∵E为内心,∴∠ABE=∠CBE.∵∠BAD=∠CAD,∠DBC=∠CAD,∴∠BAD=∠DBC,∴∠BAE+∠ABE=∠CBE+∠DBC,即∠BED=∠DBE,∴BD=DE.又∵∠BDF=∠ADB(公共角),∴△DBF∽△DAB,∴DF DBDB DA=,即DB2=DF•DA.∵DF=2,AF=4,∴DA=DF+AF=6,∴DB2=DF•DA=12,∴DB=DE=23.【点睛】本题主要考查了三角形的内心与外心,圆周角定理以及垂径定理的综合应用,解题时注意:平分弦所对一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧;三角形的内心到三角形三边的距离相等;三角形的内心与三角形顶点的连线平分这个内角.2.如图,AB 为⊙O 的直径,点E 在⊙O 上,过点E 的切线与AB 的延长线交于点D ,连接BE ,过点O 作BE 的平行线,交⊙O 于点F ,交切线于点C ,连接AC(1)求证:AC 是⊙O 的切线;(2)连接EF ,当∠D= °时,四边形FOBE 是菱形.【答案】(1)见解析;(2)30.【解析】【分析】(1)由等角的转换证明出OCA OCE ∆∆≌,根据圆的位置关系证得AC 是⊙O 的切线. (2)根据四边形FOBE 是菱形,得到OF=OB=BF=EF ,得证OBE ∆为等边三角形,而得出60BOE ∠=︒,根据三角形内角和即可求出答案.【详解】(1)证明:∵CD 与⊙O 相切于点E ,∴OE CD ⊥,∴90CEO ∠=︒,又∵OC BE ,∴COE OEB ∠=∠,∠OBE=∠COA∵OE=OB ,∴OEB OBE ∠=∠,∴COE COA ∠=∠,又∵OC=OC ,OA=OE ,∴OCA OCE SAS ∆∆≌(), ∴90CAO CEO ∠=∠=︒,又∵AB 为⊙O 的直径,∴AC 为⊙O 的切线;(2)解:∵四边形FOBE 是菱形,∴OF=OB=BF=EF ,∴OE=OB=BE ,∴OBE ∆为等边三角形,∴60BOE ∠=︒,而OE CD ⊥,∴30D ∠=︒.故答案为30.【点睛】本题主要考查与圆有关的位置关系和圆中的计算问题,熟练掌握圆的性质是本题的解题关键.3.如图,AB 为⊙O 的直径,AC 为⊙O 的弦,AD 平分∠BAC ,交⊙O 于点D ,DE ⊥AC ,交AC 的延长线于点E .(1)判断直线DE 与⊙O 的位置关系,并说明理由;(2)若AE =8,⊙O 的半径为5,求DE 的长.【答案】(1)直线DE 与⊙O 相切(2)4【解析】试题分析:(1)连接OD ,∵AD 平分∠BAC ,∴EAD OAD ∠∠=,∵OA OD =,∴ODA OAD ∠∠=,∴ODA EAD ∠∠=,∴EA ∥OD ,∵DE ⊥EA ,∴DE ⊥OD ,又∵点D 在⊙O 上,∴直线DE 与⊙O 相切(2)如图1,作DF ⊥AB ,垂足为F ,∴DFA DEA 90∠∠︒==,∵EAD FAD ∠∠=,AD AD =,∴△EAD ≌△FAD ,∴AF AE 8==,DF DE =,∵OA OD 5==,∴OF 3=,在Rt △DOF 中,22DF 4OD OF -==,∴AF AE 8== 考点:切线的证明,弦心距和半径、弦长的关系点评:本题难度不大,第一小题通过内错角相等相等证明两直线平行,再由两直线平行推出同旁内角相等.第二小题通过求出两个三角形全等,从而推出对应边相等,接着用弦心距和弦长、半径的计算公式,求出半弦长.4.如图,已知△ABC中,AB=AC,∠A=30°,AB=16,以AB为直径的⊙O与BC边相交于点D,与AC交于点F,过点D作DE⊥AC于点E.(1)求证:DE是⊙O的切线;(2)求CE的长;(3)过点B作BG∥DF,交⊙O于点G,求弧BG的长.【答案】(1)证明见解析(2)33)4π【解析】【分析】(1)如图1,连接AD,OD,由AB为⊙O的直径,可得AD⊥BC,再根据AB=AC,可得BD=DC,再根据OA=OB,则可得OD∥AC,继而可得DE⊥OD,问题得证;(2)如图2,连接BF,根据已知可推导得出DE=12BF,CE=EF,根据∠A=30°,AB=16,可得BF=8,继而得DE=4,由DE为⊙O的切线,可得ED2=EF•A E,即42=CE•(16﹣CE),继而可求得CE长;(3)如图3,连接OG,连接AD,由BG∥DF,可得∠CBG=∠CDF=30°,再根据AB=AC,可推导得出∠OBG=45°,由OG=OB,可得∠OGB=45°,从而可得∠BOG=90°,根据弧长公式即可求得BG的长度.【详解】(1)如图1,连接AD,OD;∵AB为⊙O的直径,∴∠ADB=90°,即AD⊥BC,∵AB=AC,∴BD=DC,∵OA=OB,∴OD∥AC,∵DE⊥AC,∴DE⊥OD,∴∠ODE=∠DEA=90°,∴DE为⊙O的切线;(2)如图2,连接BF,∵AB为⊙O的直径,∴∠AFB=90°,∴BF∥DE,∵CD=BD ,∴DE=12BF ,CE=EF , ∵∠A=30°,AB=16,∴BF=8,∴DE=4,∵DE 为⊙O 的切线,∴ED 2=EF•AE , ∴42=CE•(16﹣CE ),∴CE=8﹣43,CE=8+43(不合题意舍去);(3)如图3,连接OG ,连接AD ,∵BG ∥DF ,∴∠CBG=∠CDF=30°,∵AB=AC ,∴∠ABC=∠C=75°,∴∠OBG=75°﹣30°=45°,∵OG=OB ,∴∠OGB=∠OBG=45°,∴∠BOG=90°,∴BG 的长度=908180π⨯⨯=4π.【点睛】本题考查了圆的综合题,涉及了切线的判定、三角形中位线定理、圆周角定理、弧长公式等,正确添加辅助线、熟练掌握相关的性质与定理是解题的关键.5.如图,AB 为⊙O 的直径,点D 为AB 下方⊙O 上一点,点C 为弧ABD 的中点,连接CD ,CA .(1)求证:∠ABD =2∠BDC ;(2)过点C 作CH ⊥AB 于H ,交AD 于E ,求证:EA =EC ;(3)在(2)的条件下,若OH =5,AD =24,求线段DE 的长度.【答案】(1)证明见解析;(2)见解析;(3)92DE =. 【解析】【分析】 (1)连接AD ,如图1,设∠BDC =α,∠ADC =β,根据圆周角定理得到∠CAB =∠BDC =α,由AB 为⊙O 直径,得到∠ADB =90°,根据余角的性质即可得到结论;(2)根据已知条件得到∠ACE =∠ADC ,等量代换得到∠ACE =∠CAE ,于是得到结论; (3)如图2,连接OC ,根据圆周角定理得到∠COB =2∠CAB ,等量代换得到∠COB =∠ABD ,根据相似三角形的性质得到OH =5,根据勾股定理得到AB =22AD BD +=26,由相似三角形的性质即可得到结论.【详解】(1)连接AD .如图1,设∠BDC =α,∠ADC =β,则∠CAB =∠BDC =α,∵点C 为弧ABD 中点,∴AC =CD ,∴∠ADC =∠DAC =β,∴∠DAB =β﹣α,∵AB 为⊙O 直径,∴∠ADB =90°,∴α+β=90°,∴β=90°﹣α,∴∠ABD =90°﹣∠DAB =90°﹣(β﹣α),∴∠ABD =2α,∴∠ABD =2∠BDC ;(2)∵CH ⊥AB ,∴∠ACE +∠CAB =∠ADC +∠BDC =90°,∵∠CAB =∠CDB ,∴∠ACE =∠ADC ,∵∠CAE =∠ADC ,∴∠ACE =∠CAE ,∴AE =CE ;(3)如图2,连接OC ,∴∠COB =2∠CAB ,∵∠ABD =2∠BDC ,∠BDC =∠CAB ,∴∠COB =∠ABD ,∵∠OHC =∠ADB =90°,∴△OCH ∽△ABD ,∴12OH OC BD AB ==, ∵OH =5,∴BD =10,∴AB 22AD BD +,∴AO =13,∴AH =18, ∵△AHE ∽△ADB ,∴AH AE AD AB =,即1824=26AE ,∴AE =392,∴DE =92.【点睛】本题考查了垂径定理,相似三角形的判定和性质,等腰三角形的判定和性质,正确的作出辅助线是解题的关键.6.如图,CD 为⊙O 的直径,点B 在⊙O 上,连接BC 、BD ,过点B 的切线AE 与CD 的延长线交于点A ,AEO C =∠∠,OE 交BC 于点F .(1)求证:OE ∥BD ;(2)当⊙O 的半径为5,2sin 5DBA ∠=时,求EF 的长.【答案】(1)证明见解析;(2)EF 的长为212【解析】 试题分析:(1)连接OB ,利用已知条件和切线的性质证明;(2)根据锐角三角函数和相似三角形的性质,直接求解即可.试题解析:(1)连接OB , ∵CD 为⊙O 的直径 , ∴ 90CBD CBO OBD ∠=∠+∠=︒. ∵AE 是⊙O 的切线,∴ 90ABO ABD OBD ∠=∠+∠=︒. ∴ ABD CBO ∠=∠. ∵OB 、OC 是⊙O 的半径,∴OB=OC . ∴C CBO ∠=∠. ∴C ABD ∠=∠.∵E C ∠=∠,∴E ABD ∠=∠. ∴ OE ∥BD .(2)由(1)可得sin ∠C = ∠DBA= 25,在Rt △OBE 中, sin ∠C =25BD CD =,OC =5, 4BD =∴90CBD EBO ∠=∠=︒∵E C ∠=∠,∴△CBD ∽△EBO .∴BD CD BO EO=∴252EO =. ∵OE ∥BD ,CO =OD ,∴CF =FB .∴122OF BD ==. ∴212EF OE OF =-=7.如图,已知AB 是⊙O 的直径,点C ,D 在⊙O 上,BC=6cm,AC=8cm,∠BAD=45°.点E 在⊙O 外,做直线AE ,且∠EAC=∠D .(1)求证:直线AE 是⊙O 的切线.(2)求图中阴影部分的面积.【答案】(1)见解析;(2)25-504π. 【解析】 分析:(1)根据圆周角定理及推论证得∠BAE=90°,即可得到AE 是⊙O 的切线; (2)连接OD ,用扇形ODA 的面积减去△AOD 的面积即可.详解:证明:(1) ∵AB 是⊙O 的直径,∴∠ACB=90°,即∠BAC+∠ABC=90°,∵∠EAC=∠ADC ,∠ADC=∠ABC ,∴∠EAC=∠ABC∴∠BAC+∠EAC =90°,即∠BAE= 90°∴直线AE 是⊙O 的切线;(2)连接OD∵ BC=6 AC=8∴ 226810AB =+=∴ OA = 5又∵ OD = OA∴∠ADO =∠BAD = 45°∴∠AOD = 90°∴AOD ODA S S S ∆-阴影扇形==90155553602π⨯⨯-⨯⨯ 25504π-= (2cm )点睛:此题主要考查了圆周角定理和圆的切线的判定与性质,关键是利用圆周角定理和切线的判定与性质,结合勾股定理的和弓形的面积的求法求解,注意数形结合思想的应用.8.如图,在△ABC 中,AB =AC ,以AB 为直径的⊙O 与边BC 交于点D ,DE ⊥AC ,垂足为E ,交AB 的延长线于点F .(1)求证:EF 是⊙O 的切线;(2)若∠C =60°,AC =12,求BD 的长.(3)若tan C =2,AE =8,求BF 的长.【答案】(1)见解析;(2) 2π;(3)103. 【解析】 分析:(1)连接OD ,根据等腰三角形的性质:等边对等角,得∠ABC=∠C ,∠ABC=∠ODB ,从而得到∠C=∠ODB ,根据同位角相等,两直线平行,得到OD ∥AC ,从而得证OD ⊥EF ,即 EF 是⊙O 的切线;(2) 根据中点的性质,由AB=AC=12 ,求得OB=OD=12AB =6,进而根据等边三角形的判定得到△OBD 是等边三角形,即∠BOD=600,从而根据弧长公式七届即可; (3)连接AD ,根据直角三角形的性质,由在Rt △DEC 中, tan 2DE C CE == 设CE=x,则DE=2x ,然后由Rt △ADE 中, tan 2AE ADE DE∠== ,求得DE 、CE 的长,然后根据相似三角形的判定与性质求解即可.详解:(1)连接OD ∵AB=AC ∴∠ABC=∠C∵OD=OB ∴∠ABC=∠ODB∴∠C=∠ODB ∴OD ∥AC又∵DE ⊥AC ∴OD ⊥DE ,即OD ⊥EF∴EF 是⊙O 的切线(2) ∵AB=AC=12 ∴OB=OD=12AB =6 由(1)得:∠C=∠ODB=600∴△OBD 是等边三角形 ∴∠BOD=600∴BD =6062180ππ⨯= 即BD 的长2π (3)连接AD ∵DE ⊥AC ∠DEC=∠DEA=900在Rt △DEC 中, tan 2DE C CE== 设CE=x,则DE=2x ∵AB 是直径 ∴∠ADB=∠ADC=900 ∴∠ADE+∠CDE=900 在Rt △DEC 中,∠C+∠CDE=900∴∠C=∠ADE 在Rt △ADE 中, tan 2AE ADE DE ∠== ∵ AE=8,∴DE=4 则CE=2∴AC=AE+CE=10 即直径AB=AC=10 则OD=OB=5∵OD//AE ∴△ODF ∽△AEF∴ OF OD AF AE = 即:55108BF BF +=+ 解得:BF=103 即BF 的长为103. 点睛:此题考查了切线的性质与判定、圆周角定理、等腰三角形的性质、直角三角形以及相似三角形的判定与性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.9.如图,在△ABC 中,以AC 为直径作⊙O 交BC 于点D ,交AB 于点G ,且D 是BC 中点,DE ⊥AB ,垂足为E ,交AC 的延长线于点F .(1)求证:直线EF 是⊙O 的切线;(2)若CF=3,cosA=25,求出⊙O 的半径和BE 的长;(3)连接CG,在(2)的条件下,求CGEF的值.【答案】(1)见解析;(2)2,65(3)CG:EF=4:7【解析】试题分析:(1)连结OD.先证明OD是△ABC的中位线,根据中位线的性质得到OD∥AB,再由DE⊥AB,得出OD⊥EF,根据切线的判定即可得出直线EF是⊙O的切线;(2)先由OD∥AB,得出∠COD=∠A,再解Rt△DOF,根据余弦函数的定义得到cos∠FOD==,设⊙O的半径为R,解方程=,求出R=,那么AB=2OD=,解Rt△AEF,根据余弦函数的定义得到cosA==,求出AE=,然后由BE=AB﹣AE即可求解.试题解析:(1)证明:如图,连结OD.∵CD=DB,CO=OA,∴OD是△ABC的中位线,∴OD∥AB,AB=2OD,∵DE⊥AB,∴DE⊥OD,即OD⊥EF,∴直线EF是⊙O的切线;(2)解:∵OD∥AB,∴∠COD=∠A.在Rt△DOF中,∵∠ODF=90°,∴cos∠FOD==,设⊙O的半径为R,则=,解得R=,∴AB=2OD=.在Rt△AEF中,∵∠AEF=90°,∴cosA===,∴AE=,∴BE=AB﹣AE=﹣=2.【点睛】本题考查了切线的判定,解直角三角形,三角形中位线的性质知识点.要证某线是圆的切线,已知此线过圆上某点,连结圆心与这点(即为半径),再证垂直即可.10.如图1,D是⊙O的直径BC上的一点,过D作DE⊥BC交⊙O于E、N,F是⊙O上的一点,过F的直线分别与CB、DE的延长线相交于A、P,连结CF交PD于M,∠C=12∠P.(1)求证:PA是⊙O的切线;(2)若∠A=30°,⊙O的半径为4,DM=1,求PM的长;(3)如图2,在(2)的条件下,连结BF、BM;在线段DN上有一点H,并且以H、D、C 为顶点的三角形与△BFM相似,求DH的长度.【答案】(1)证明见解析;(2)PM=32;(3)满足条件的DH 63-或1223+【解析】【分析】(1)如图1中,作PH⊥FM于H.想办法证明∠PFH=∠PMH,∠C=∠OFC,再根据等角的余角相等即可解决问题;(2)解直角三角形求出AD,PD即可解决问题;(3)分两种情形①当△CDH∽△BFM时,DH CD FM BF=.②当△CDH∽△MFB时,DH CDFB MF=,分别构建方程即可解决问题;【详解】(1)证明:如图1中,作PH⊥FM于H.∵PD⊥AC,∴∠PHM=∠CDM=90°,∵∠PMH=∠DMC,∴∠C=∠MPH,∵∠C=12∠FPM,∴∠HPF=∠HPM,∵∠HFP+∠HPF=90°,∠HMP+∠HPM=90°,∴∠PFH=∠PMH,∵OF=OC,∴∠C=∠OFC,∵∠C+∠CMD=∠C+∠PMF=∠C+∠PFH=90°,∴∠OFC+∠PFC=90°,∴∠OFP=90°,∴直线PA是⊙O的切线.(2)解:如图1中,∵∠A=30°,∠AFO=90°,∴∠AOF=60°,∵∠AOF=∠OFC+∠OCF,∠OFC=∠OCF,∴∠C=30°,∵⊙O的半径为4,DM=1,∴OA=2OF=8,CD33,∴OD=OC﹣CD=43,∴AD=OA+OD=8+43=123,在Rt△ADP中,DP=AD•tan30°=(123)3=3﹣1,∴PM=PD﹣DM=3﹣2.(3)如图2中,由(2)可知:BF =12BC =4,FM 3BF =3,CM =2DM =2,CD 3, ∴FM =FC ﹣CM =3﹣2, ①当△CDH ∽△BFM 时,DH CD FM BF = , ∴3432=- ,∴DH 63- ②当△CDH ∽△MFB 时,DH CD FB MF =, ∴34432DH =-,∴DH =12311+ , ∵DN ()22443833--=-,∴DH <DN ,符合题意, 综上所述,满足条件的DH 的值为632- 或12311+. 【点睛】本题考查圆综合题、切线的判定、解直角三角形、相似三角形的判定和性质等知识,解题的关键是熟练掌握基本知识,学会用分类讨论的思想思考问题.。
中考数学总复习《圆的综合题》专项测试卷(附答案)

中考数学总复习《圆的综合题》专项测试卷(附答案)一、单选题(共12题;共24分)1.如图,在4×4的方格中(共有16个小方格),每个小方格都是边长为1的正方形,O,A,B分别是小正方形的顶点,则扇形OAB的面积等于()A.2πB.√2πC.2√2πD.√22π2.如图,已知A、B两点的坐标分别为(8,0)、(0,8),点C、F分别是直线x=−5和x轴上的动点,CF=10,点D是线段CF的中点,连接AD交y轴于点E,当△ABE面积取得最小值时,E点的坐标是()A.(0,103)B.(0,83)C.(0,2)D.(0,52)3.下列四边形中一定有外接圆的是()A.平行四边形B.菱形C.矩形D.梯形4.如图,⊙O是四边形ABCD的内切圆,下列结论一定正确的有()个:①AF=BG;②CG=CH;③AB+CD=AD+BC;④BG<CG.A.1B.2C.3D.45.如图,圆内接四边形ABCD中AB=AC,AC⊙BD,则⊙DAC是⊙BAC的()A.12B.13C.23D.256.如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为12,∠B=135°,则AC⌢的长为()A.6πB.12πC.2πD.3π7.如图,⊙ABC内接于⊙O,⊙B=65°,⊙C=70°.若BC=3 √2,则弧BC的长为()A.34πB.32πC.92πD.3 √2π8.如图,四边形ABCD内接于⊙O,F是CD̂上一点,且DF̂= BĈ,连接CF并延长交AD的延长线于点E,连接AC.若⊙ABC=105°,⊙BAC=30°,则⊙E的度数为()A.45°B.50°C.55°D.60°9.如图,A,B,C,D为⊙O的四等分点,动点P从圆心O出发,沿O﹣C﹣D﹣O路线作匀速运动,设运动时间为t(s).⊙APB=y(°),则下列图象中表示y与t之间函数关系最恰当的是()A.B.C.D.10.如图,将半径为2 cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长为()A.2 cm B.√3cm C.2√3 cm D.2√5 cm11.如图的平面直角坐标系中有一个正六边形ABCDEF,其中C、D的坐标分别为(1,0)和(2,0).若在无滑动的情况下,将这个六边形沿着x轴向右滚动,则在滚动过程中这个六边形的顶点A,B,C,D,E,F中会过点(2017,2)的是()A.点A B.点C C.点E D.点F12.如图,AB 为⊙O 的直径,点C 是AB 上方半圆上的一点,点D 是AB 下方半圆的中点,连接AC,BC,AD,过点 D 作DE⊙AB 交CB 的延长线于点 E.若AD= 5 √2,则AC·CE的最大值为()A.50B.50 √2C.100D.75 √2二、填空题(共6题;共6分)13.如图,四边形内接于⊙O,若它的一个外角∠DCE=46°,则∠A的度数为.14.如图,AC与BD交于P,AD、BC延长交于点E,⊙AEC=37°,⊙CAE=31°,则⊙APB的度数为.15.如图,点A、B、C、D均在⊙O上,E为BC延长线上的一点,若∠A=110°,则∠DCE 的度数为°.16.如图,圆内接四边形ABCD的边AB过圆心O,过点C的切线与边AD所在直线垂直于点M,若⊙ABC=65°,则⊙ACD=°.17.如图,已知正⊙ABC的边长为9,⊙O是它的内切圆,则图中阴影部分的面积为.(结果保留π)18.如图,点A,点B,点C在⊙O上,分别连接AB,BC,OC.若AB=BC,⊙B=40°,则⊙OCB =.三、综合题(共6题;共56分)19.如图,AB为⊙O的直径,点C在⊙O上,连接AC,BC,过点O作OD⊥BC于点D,过点C作⊙O的切线交OD的延长线于点E.(1)求证:∠E=∠B;(2)连接AD.若CE=4√5,BC=8求AD的长.20.如图,AB是⊙O的直径,AE是⊙O的切线,点C为直线AE上一点,连接OC交⊙O于点D,连接BD并延长交线段AC于点E.(1)求证:∠CAD=∠CDE(2)若CD=6,tan∠BAD=√2求⊙O的半径.21.如图,在△ABC中AC=BC,以BC为直径作⊙O,交AC于点F,过C点作CD⊥AC交AB延长线于点D,E为CD上一点,且EB=ED.(1)求证:BE为⊙O的切线;(2)若AF=2,tanA=2求BE的长.22.如图,在Rt△ABC中∠C=90°,点O在AB上,以点O为圆心,OA长为半径的圆与AC、AB分别交于点D、E,且∠CBD=∠A.(1)求证:BD是⊙O的切线;(2)若AD:AE=5:6和BC=10求BD的长.23.如图1,在平面直角坐标系xOy中A,B两点的坐标分别为A(x1,y1),B(x2,y2),由勾股定理得AB2=|x2﹣x1|2+|y2﹣y1|2,所以A,B两点间的距离为:AB= √(x2−x1)2+(y2−y1)2我们知道,圆可以看成到圆心距离等于半径的点的集合,如图2,在平面直角坐标系xOy中A (x,y)为圆上任意一点,则A到原点的距离的平方为OA2=|x﹣0|2+|y﹣0|2,当⊙O的半径为r时,⊙O的方程可写为:x2+y2=r2.(1)问题拓展:如果圆心坐标为P(a,b),半径为r,那么⊙P的方程可以写为.(2)综合应用:如图3,⊙P与x轴相切于原点O,P点坐标为(0,6),A是⊙P上一点,连接OA,使⊙POA=30°,作PD⊙OA,垂足为D,延长PD交x轴于点B,连接AB.①证明:AB是⊙P的切线;②是否存在到四点O,P,A,B距离都相等的点Q?若存在,求Q点坐标,并写出以Q为圆心,以OQ为半径的⊙Q的方程;若不存在,说明理由.24.(1)解方程:x(x−4)=−2(x−4)(2)已知:如图,⊙O的直径AB与弦CD(不是直径)交于点F,若FB=2,CF=FD=4,设⊙O的半径为r,求AC的长.参考答案1.【答案】A2.【答案】A3.【答案】C4.【答案】B5.【答案】A6.【答案】A7.【答案】B8.【答案】A9.【答案】C10.【答案】C11.【答案】D12.【答案】C13.【答案】46°14.【答案】99°15.【答案】110°16.【答案】4017.【答案】27√3−9π418.【答案】20°19.【答案】(1)证明:连接OC如图:OD⊙CB∴OB=OC,⊙B=OCD又CE为圆O的切线∴OC⊙CE∴⊙ECD+⊙DCO=⊙ECD+⊙E=90°∴⊙E=⊙DCO=⊙B∴⊙E=⊙B(2)解:连接AD如图∵⊙EDC为Rt⊙∴DE=√EC2−DC2=√(4√5)2−42=8由(1)得⊙E=⊙B又AB为直径∴⊙BCA=90°在⊙CED和⊙ABC中∵{∠B=∠E∠EDC=∠BCAED=BC∴⊙CED⊙⊙ABC(AAS)∴AC=DC=12BC=420.【答案】(1)证明:∵AE是⊙O的切线,点A为切点∴∠OAE=90°,∴∠OAD+∠DAE=90°∵AB是⊙O的直径,∴∠ADB=90°∴∠B+∠OAD=90°,∴∠B=∠DAE∵OB=OD,∴∠B=∠ODB,∴∠ODB=∠DAE∵∠ODB=∠CDE,∴∠CDE=∠CAD;(2)解:∵∠BAD+∠DAE=90°,∠AEB+∠B=90°,∠BAD=∠B ∴∠BAD=∠AED∵tan∠BAD=√2∴tan∠AED =AB AE =AD DE =√2 ∵∠C =∠C ,∠CDE =∠CAD∴ΔCDE ∼ΔCAD∴CA CD =CD CE =AD DE∵CD =6,∴CA 6=6CE=√2 ∴CA =6√2,CE =3√2,∴AE =CA −CE =3√2 ∴AB 3√2=√2,∴AB =6 ∴OB =12AB =3,∴⊙O 的半径为3. 21.【答案】(1)证明:∵AC=BC ,EB=ED ∴⊙A=⊙ABC ,⊙D=⊙EBD∵CD⊙AC∴⊙A+⊙D=90°∴⊙ABC+⊙EBD=90°∴⊙CBE=90°∵BC 是⊙O 的直径.∴BE 是⊙O 的切线.(2)解:连接BF∵BC 是⊙O 的直径.∴⊙BFC=⊙BFA=90° 在Rt⊙ABF 中tanA=BF AF =BF 2=2 ∴BF=4设CF=x ,则AC=BC=x+2在Rt⊙BCF 中即(x +2)2=x 2+42∴x=3∴CF=3,BC=5∵⊙ACB=⊙AFB=90°∴BF⊙CD∴⊙1=⊙2又∵⊙CFB=⊙EBC=90°∴⊙CFB⊙⊙EBC∴FC BE =FB BC∴3BE =45∴BE=15422.【答案】(1)证明:连接OD∵点D 在⊙O 上∴OD =OA∴∠A =∠ADO∵∠C =90°∴∠CDB +∠CBD =90°∵∠CBD =∠A =∠ADO∴∠CDB +∠ADO =90°∴∠ODB =90°,即OD ⊥BD∵点D 在⊙O 上∴BD 是⊙O 的切线;(2)解:连接DE∵∠ADE =90°=∠C ,∠CBD =∠A∴△ADE ∽△BCD∴ADBC=AEBD,即ADAE=BCBD∵ADAE=56,BC=10∴BD=12.23.【答案】(1)(x﹣a)2+(y﹣b)2=r2(2)解:①∵PO=PA PD⊙OA∴⊙OPD=⊙APD在⊙POB和⊙PAB中{PO=PA ∠OPB=∠APB PB=PB∴⊙POB⊙⊙PAB∴⊙PAB=⊙POB=90°∴PA⊙AB∴AB是⊙P的切线②存在到四点O,P,A,B距离都相等的点Q 当点Q在线段BP中点时∵⊙POB=⊙PAB=90°∴QO=QP=QA=QB∴此时点Q到四点O,P,A,B距离都相等∵PB⊙OA,⊙POB=90°,⊙POA=30°∴⊙PBO=30°.∴在Rt⊙POB中OP=6∴OB= √3OP=6 √3,PB=2PO=12∴B点坐标为(6 √3,0)∵Q是PB中点,P(0,6),B(6 √3,0)∴Q点坐标为(3 √3,3)∴OQ= 12PB=6∴以Q为圆心,OQ为半径的⊙Q的方程为(x﹣3 √3)2+(y﹣3)2=36 24.【答案】(1)解:x(x−4)+2(x−4)=0,∴x2−2x−8=0∴(x+2)(x−4)=0解得:x1=−2,x2=4(2)解:连接OC,如图:∵AB是直径∴AB⊥CD∴42+(r−2)2=r2即r=5∴AF=2r−2=8∴由勾股定理得AC=√42+82=4√5.。
人教备战中考数学压轴题专题圆的综合的经典综合题含答案

一、圆的综合真题与模拟题分类汇编(难题易错题)1.如图,在平面直角坐标系xoy中,E(8,0),F(0 , 6).(1)当G(4,8)时,则∠FGE= °(2)在图中的网格区域内找一点P,使∠FPE=90°且四边形OEPF被过P点的一条直线分割成两部分后,可以拼成一个正方形.要求:写出点P点坐标,画出过P点的分割线并指出分割线(不必说明理由,不写画法).【答案】(1)90;(2)作图见解析,P(7,7),PH是分割线.【解析】试题分析:(1)根据勾股定理求出△FEG的三边长,根据勾股定理逆定理可判定△FEG是直角三角形,且∠FGE="90" °.(2)一方面,由于∠FPE=90°,从而根据直径所对圆周角直角的性质,点P在以EF为直径的圆上;另一方面,由于四边形OEPF被过P点的一条直线分割成两部分后,可以拼成一个正方形,从而OP是正方形的对角线,即点P在∠FOE的角平分线上,因此可得P(7,7),PH是分割线.试题解析:(1)连接FE,∵E(8,0),F(0 , 6),G(4,8),∴根据勾股定理,得FG=,EG=,FE=10.∵,即.∴△FEG是直角三角形,且∠FGE=90 °.(2)作图如下:P(7,7),PH是分割线.考点:1.网格问题;2.勾股定理和逆定理;3.作图(设计);4.圆周角定理.2.如图,AB是⊙O的直径,PA是⊙O的切线,点C在⊙O上,CB∥PO.(1)判断PC与⊙O的位置关系,并说明理由;(2)若AB=6,CB=4,求PC的长.【答案】(1)PC是⊙O的切线,理由见解析;(235 2【解析】试题分析:(1)要证PC是⊙O的切线,只要连接OC,再证∠PCO=90°即可.(2)可以连接AC,根据已知先证明△ACB∽△PCO,再根据勾股定理和相似三角形的性质求出PC的长.试题解析:(1)结论:PC是⊙O的切线.证明:连接OC∵CB∥PO∴∠POA=∠B,∠POC=∠OCB∵OC=OB∴∠OCB=∠B∴∠POA=∠POC又∵OA=OC,OP=OP∴△APO≌△CPO∴∠OAP=∠OCP∵PA是⊙O的切线∴∠OAP=90°∴∠OCP=90°∴PC是⊙O的切线.(2)连接AC∵AB是⊙O的直径∴∠ACB=90°(6分)由(1)知∠PCO=90°,∠B=∠OCB=∠POC∵∠ACB=∠PCO∴△ACB∽△PCO∴∴.点睛:本题考查了切线的判定.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.同时考查了勾股定理和相似三角形的性质.3.如图,AB是圆O的直径,射线AM⊥AB,点D在AM上,连接OD交圆O于点E,过点D作DC=DA交圆O于点C(A、C不重合),连接O C、BC、CE.(1)求证:CD是⊙O的切线;(2)若圆O的直径等于2,填空:①当AD=时,四边形OADC是正方形;②当AD=时,四边形OECB是菱形.【答案】(1)见解析;(2)①1;②3.【解析】试题分析:(1)依据SSS证明△OAD≌△OCD,从而得到∠OCD=∠OAD=90°;(2)①依据正方形的四条边都相等可知AD=OA;②依据菱形的性质得到OE=CE,则△EOC为等边三角形,则∠CEO=60°,依据平行线的性质可知∠DOA=60°,利用特殊锐角三角函数可求得AD的长.试题解析:解:∵AM⊥AB,∴∠OAD=90°.∵OA=OC,OD=OD,AD=DC,∴△OAD≌△OCD,∴∠OCD=∠OAD=90°.∴OC⊥CD,∴CD是⊙O的切线.(2)①∵当四边形OADC是正方形,∴AO=AD=1.故答案为:1.②∵四边形OECB是菱形,∴OE=CE.又∵OC=OE,∴OC=OE=CE.∴∠CEO=60°.∵CE∥AB,∴∠AOD=60°.在Rt△OAD中,∠AOD=60°,AO=1,∴AD=.故答案为:.点睛:本题主要考查的是切线的性质和判定、全等三角形的性质和判定、菱形的性质、等边三角形的性质和判定,特殊锐角三角函数值的应用,熟练掌握相关知识是解题的关键.4.如图,在直角坐标系中,⊙M经过原点O(0,0),点A(6,0)与点B(0,-2),点D 在劣弧OA上,连结BD交x轴于点C,且∠COD=∠CBO.(1)求⊙M的半径;(2)求证:BD平分∠ABO;(3)在线段BD的延长线上找一点E,使得直线AE恰为⊙M的切线,求此时点E的坐标.【答案】(1)M的半径r2;(2)证明见解析;(3)点E的坐标为(2632).【解析】试题分析:根据点A和点B的坐标得出OA和OB的长度,根据Rt△AOB的勾股定理得出AB的长度,然后得出半径;根据同弧所对的圆周角得出∠ABD=∠COD,然后结合已知条件得出角平分线;根据角平分线得出△ABE≌△HBE,从而得出2,从而求出OH 的长度,即点E的纵坐标,根据Rt△AOB的三角函数得出∠ABO的度数,从而得出∠CBO 的度数,然后根据Rt△HBE得出HE的长度,即点E的横坐标.试题解析:(1)∵点A6,0),点B为(02)∴62∴根据Rt△AOB的勾股定理可得:2∴M的半径r=122.(2)根据同弧所对的圆周角相等可得:∠ABD=∠COD ∵∠COD=∠CBO ∴∠ABD=∠CBO ∴BD 平分∠ABO(3)如图,由(2)中的角平分线可得△ABE ≌△HBE ∴BH=BA=22∴OH=22-2=2在Rt △AOB 中,3OA OB=∴∠ABO=60° ∴∠CBO=30° 在Rt △HBE 中,HE=263=∴点E 的坐标为(26,2)考点:勾股定理、角平分线的性质、圆的基本性质、三角函数.5.如图,已知AB 是⊙O 的直径,P 是BA 延长线上一点,PC 切⊙O 于点C ,CD ⊥AB ,垂足为D .(1)求证:∠PCA =∠ABC ;(2)过点A 作AE ∥PC 交⊙O 于点E ,交CD 于点F ,交BC 于点M ,若∠CAB =2∠B ,CF 3【答案】(1)详见解析;(2633π-. 【解析】【分析】(1)如图,连接OC ,利用圆的切线的性质和直径对应的圆周角是直角可得∠PCA=∠OCB ,利用等量代换可得∠PCA=∠ABC.(2)先求出△OCA 是等边三角形,在利用三角形的等边对等角定理求出FA=FC 和CF=FM,然后分别求出AM 、AC 、MO 、CD 的值,分别求出0A E S ∆、BOE S 扇形 、ABM S ∆ 的值,利用0A E ABM BOE S S S S ∆∆=+-阴影部分扇形,然后通过计算即可解答.【详解】解:(1)证明:连接OC,如图,∵PC切⊙O于点C,∴OC⊥PC,∴∠PCA+∠ACO=90º,∵AB是⊙O的直径,∴∠ACB=∠ACO+OCB=90º∴∠PCA=∠OCB,∵OC=OB,∴∠OBC=∠OCB,∴∠PCA=∠ABC;(2)连接OE,如图,∵△ACB中,∠ACB=90º,∠CAB=2∠B,∴∠B=30º,∠CAB=60º,∴△OCA是等边三角形,∵CD⊥AB,∴∠ACD+∠CAD=∠CAD+∠ABC=90º,∴∠ACD=∠B=30º,∵PC∥AE,∴∠PCA=∠CAE=30º,∴FC=FA,同理,CF=FM,∴AM=2CF=23,Rt△ACM中,易得AC=23×3=3=OC,∵∠B=∠CAE=30º,∴∠AOC=∠COE=60º,∴∠EOB=60º,∴∠EAB=∠ABC=30º,∴MA=MB,连接OM,EG⊥AB交AB于G点,如图所示,∵OA=OB,∴MO⊥AB,∴MO=3∵△CDO≌△EDO(AAS),∴332∴1332ABM S AB MO ∆=⨯=, 同样,易求934AOE S ∆=, 260333602BOE S ππ⨯==扇形 ∴0A E ABM BOE S S S S ∆∆=+-阴影部分扇形=93363333424ππ-+-=. 【点睛】本题考查了切线的性质、解直角三角形、扇形面积和识图的能力,综合性较强,有一定难度,熟练掌握定理并准确识图是解题的关键.6.如图,在Rt △ABC 中,点O 在斜边AB 上,以O 为圆心,OB 为半径作圆,分别与BC ,AB 相交于点D ,E ,连接AD .已知∠CAD =∠B .(1)求证:AD 是⊙O 的切线;(2)若CD =2,AC =4,BD =6,求⊙O 的半径.【答案】(1)详见解析;(2)35. 【解析】【分析】 (1)解答时先根据角的大小关系得到∠1=∠3,根据直角三角形中角的大小关系得出OD ⊥AD ,从而证明AD 为圆O 的切线;(2)根据直角三角形勾股定理和两三角形相似可以得出结果【详解】(1)证明:连接OD ,∵OB =OD ,∴∠3=∠B ,∵∠B =∠1,∴∠1=∠3,在Rt△ACD中,∠1+∠2=90°,∴∠4=180°﹣(∠2+∠3)=90°,∴OD⊥AD,则AD为圆O的切线;(2)过点O作OF⊥BC,垂足为F,∵OF⊥BD∴DF=BF=12BD=3∵AC=4,CD=2,∠ACD=90°∴AD=22AC CD=25∵∠CAD=∠B,∠OFB=∠ACD=90°∴△BFO∽△ACD∴BFAC = OB AD即34=25∴OB=352∴⊙O的半径为352.【点睛】此题重点考查学生对直线与圆的位置关系,圆的半径的求解,掌握勾股定理,两三角形相似的判定条件是解题的关键7.(问题情境)如图1,点E是平行四边形ABCD的边AD上一点,连接BE、CE.求证:BCE 1S2=S平行四边形ABCD.(说明:S表示面积)请以“问题情境”为基础,继续下面的探究(探究应用1)如图2,以平行四边形ABCD的边AD为直径作⊙O,⊙O与BC边相切于点H,与BD相交于点M.若AD=6,BD=y,AM=x,试求y与x之间的函数关系式.(探究应用2)如图3,在图1的基础上,点F在CD上,连接AF、BF,AF与CE相交于点G,若AF=CE,求证:BG平分∠AGC.(迁移拓展)如图4,平行四边形ABCD中,AB:BC=4:3,∠ABC=120°,E是AB的中点,F在BC上,且BF:FC=2:1,过D分别作DG⊥AF于G,DH⊥CE于H,请直接写出DG:DH的值.【答案】【问题情境】见解析;【探究应用1】18yx=;【探究应用2】见解析;【迁移【解析】【分析】(1)作EF⊥BC于F,则S△BCE=12BC×EF,S平行四边形ABCD=BC×EF,即可得出结论;(2)连接OH,由切线的性质得出OH⊥BC,OH=12AD=3,求出平行四边形ABCD的面积=AD×OH=18,由圆周角定理得出AM⊥BD,得出△ABD的面积=12BD×AM=12平行四边形的面积=9,即可得出结果;(3)作BM⊥AF于M,BN⊥CE于N,同图1得:△ABF的面积=△BCE的面积=12平行四边形ABCD的面积,得出12AF×BM=12CE×BN,证出BM=BN,即可得出BG平分∠AGC.(4)作AP⊥BC于P,EQ⊥BC于Q,由平行四边形的性质得出∠ABP=60°,得出∠BAP=30°,设AB=4x,则BC=3x,由直角三角形的性质得出BP=12AB=2x,BQ=12BE,AP=BP=,由已知得出BE=2x,BF=2x,得出BQ=x,EQ x,PF=4x,QF=3x,QC=4x,由勾股定理求出AF=x,CE,连接DF、DE,由三角形的面积关系得出AF×DG=CE×DH,即可得出结果.【详解】(1)证明:作EF⊥BC于F,如图1所示:则S△BCE=12BC×EF,S平行四边形ABCD=BC×EF,∴12BCE ABCD S S =.(2)解:连接OH ,如图2所示:∵⊙O 与BC 边相切于点H , ∴OH ⊥BC ,OH =12AD =3, ∴平行四边形ABCD 的面积=AD×OH =6×3=18,∵AD 是⊙O 的直径,∴∠AMD =90°,∴AM ⊥BD ,∴△ABD 的面积=12BD×AM =12平行四边形的面积=9, 即12xy =9, ∴y 与x 之间的函数关系式y =18x ; (3)证明:作BM ⊥AF 于M ,BN ⊥CE 于N ,如图3所示:同图1得:△ABF 的面积=△BCE 的面积=12平行四边形ABCD 的面积, ∴12AF×BM =12CE×BN , ∵AF =CE ,∴BM =BN ,∴BG 平分∠AGC . (4)解:作AP ⊥BC 于P ,EQ ⊥BC 于Q ,如图4所示:∵平行四边形ABCD 中,AB :BC =4:3,∠ABC =120°,∴∠ABP =60°,∴∠BAP =30°,设AB =4x ,则BC =3x ,∴BP =12AB =2x ,BQ =12BE ,AP BP =, ∵E 是AB 的中点,F 在BC 上,且BF :FC =2:1,∴BE =2x ,BF =2x ,∴BQ =x , ∴EQ,PF =4x ,QF =3x ,QC =4x ,由勾股定理得:AF =x ,CE , 连接DF 、DE ,则△CDE 的面积=△ADF 的面积=12平行四边形ABCD 的面积,∴AF×DG =CE×DH ,∴DG :DH =CE :AF =19x :27x 19:27=.【点睛】本题是圆的综合题目,考查了圆周角定理、平行四边形的性质、三角形面积公式、含30°角的直角三角形的性质、勾股定理、角平分线的判定等知识;本题综合性强,需要添加辅助线,熟练掌握平行四边形的性质和勾股定理是解题的关键.8.对于平面直角坐标系xoy 中的图形P ,Q ,给出如下定义:M 为图形P 上任意一点,N 为图形Q 上任意一点,如果M ,N 两点间的距离有最小值,那么称这个最小值为图形P ,Q 间的“非常距离”,记作d (P ,Q ).已知点A (4,0),B (0,4),连接AB .(1)d (点O ,AB )= ;(2)⊙O 半径为r ,若d (⊙O ,AB )=0,求r 的取值范围;(3)点C (-3,-2),连接AC ,BC ,⊙T 的圆心为T (t ,0),半径为2,d (⊙T ,△ABC ),且0<d <2,求t 的取值范围.【答案】(1)222)224r ≤≤;(3)25252t -<<-或6<r <8.【解析】【分析】(1)如下图所示,由题意得:过点O 作AB 的垂线,则垂线段即为所求;(2)如下图所示,当d (⊙O ,AB )=0时,过点O 作OE ⊥AB ,交AB 于点E ,则:OB=2, OE=22,即可求解; (3)分⊙T 在△ABC 左侧、⊙T 在△ABC 右侧两种情况,求解即可.【详解】(1)过点O 作OD ⊥AB 交AB 于点D ,根据“非常距离”的定义可知,d (点O ,AB )=OD=2AB =22442+=22; (2)如图,当d (⊙O ,AB )=0时,过点O 作OE ⊥AB,则OE=22,OB=OA=4,∵⊙O 与线段AB 的“非常距离”为0,∴224r ≤≤;(3)当⊙T 在△ABC 左侧时,如图,当⊙T 与BC 相切时,d=0,BC=2236+=35,过点C 作CE ⊥y 轴,过点T 作TF ⊥BC,则△TFH ∽△BEC,∴TF TH BE BC=, 即2=635TH , ∴TH=5,∵HO ∥CE,∴△BHO ∽△BEC,∴HO=2,此时T(-5-2,0);当d=2时,如图,同理可得,此时T (252--);∵0<d <2,∴25252t --<<--;当⊙T 在△ABC 右侧时,如图,当p=0时,t=6,当p=2时,t=8.∵0<d <2,∴6<r <8; 综上,25252t --<<--或6<r <8.【点睛】本题主要考查圆的综合问题,解题的关键是理解并掌握“非常距离”的定义与直线与圆的位置关系和分类讨论思想的运用.9.如图,AB 是半圆⊙O 的直径,点C 是半圆⊙O 上的点,连接AC ,BC ,点E 是AC 的中点,点F 是射线OE 上一点.(1)如图1,连接FA ,FC ,若∠AFC =2∠BAC ,求证:FA ⊥AB ;(2)如图2,过点C 作CD ⊥AB 于点D ,点G 是线段CD 上一点(不与点C 重合),连接FA ,FG ,FG 与AC 相交于点P ,且AF =FG .①试猜想∠AFG 和∠B 的数量关系,并证明;②连接OG ,若OE =BD ,∠GOE =90°,⊙O 的半径为2,求EP 的长.【答案】(1)见解析;(2)①结论:∠GFA =2∠ABC .理由见解析;②PE 3. 【解析】【分析】 (1)证明∠OFA =∠BAC ,由∠EAO +∠EOA =90°,推出∠OFA +∠AOE =90°,推出∠FAO =90°即可解决问题.(2)①结论:∠GFA =2∠ABC .连接FC .由FC =FG =FA ,以F 为圆心FC 为半径作⊙F .因为AG AG =,推出∠GFA =2∠ACG ,再证明∠ACG =∠ABC .②图2﹣1中,连接AG ,作FH ⊥AG 于H .想办法证明∠GFA =120°,求出EF ,OF ,OG 即可解决问题.【详解】(1)证明:连接OC .∵OA=OC,EC=EA,∴OF⊥AC,∴FC=FA,∴∠OFA=∠OFC,∵∠CFA=2∠BAC,∴∠OFA=∠BAC,∵∠OEA=90°,∴∠EAO+∠EOA=90°,∴∠OFA+∠AOE=90°,∴∠FAO=90°,∴AF⊥AB.(2)①解:结论:∠GFA=2∠ABC.理由:连接FC.∵OF垂直平分线段AC,∴FG=FA,∵FG=FA,∴FC=FG=FA,以F为圆心FC为半径作⊙F.∵AG AG,∴∠GFA=2∠ACG,∵AB是⊙O的直径,∴∠ACB=90°,∵CD⊥AB,∴∠ABC+∠BCA=90°,∵∠BCD+∠ACD=90°,∴∠ABC=∠ACG,∴∠GFA=2∠ABC.②如图2﹣1中,连接AG,作FH⊥AG于H.∵BD =OE ,∠CDB =∠AEO =90°,∠B =∠AOE ,∴△CDB ≌△AEO (AAS ),∴CD =AE ,∵EC =EA ,∴AC =2CD .∴∠BAC =30°,∠ABC =60°,∴∠GFA =120°,∵OA =OB =2,∴OE =1,AE =,BA =4,BD =OD =1, ∵∠GOE =∠AEO =90°,∴OG ∥AC , 323DG OG ∴==, 222213AG DG AD ∴=+=, ∵FG =FA ,FH ⊥AG ,∴AH =HG 21∠AFH =60°, ∴AF =27sin 603AH ︒=, 在Rt △AEF 中,EF 2213AF AE -=, ∴OF =OE +EF =43 , ∵PE ∥OG , ∴PE EF OG 0F=, ∴134233=, ∴PE 3. 【点睛】圆综合题,考查了垂径定理,勾股定理,圆周角定理,全等三角形的判定和性质,锐角三角函数,解直角三角形等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题.10.如图,已知在△ABC中,AB=15,AC=20,tanA=12,点P在AB边上,⊙P的半径为定长.当点P与点B重合时,⊙P恰好与AC边相切;当点P与点B不重合时,⊙P与AC边相交于点M和点N.(1)求⊙P的半径;(2)当AP=65时,试探究△APM与△PCN是否相似,并说明理由.【答案】(1)半径为35;(2)相似,理由见解析.【解析】【分析】(1)如图,作BD⊥AC,垂足为点D,⊙P与边AC相切,则BD就是⊙P的半径,利用解直角三角形得出BD与AD的关系,再利用勾股定理可求得BD的长;(2)如图,过点P作PH⊥AC于点H,作BD⊥AC,垂足为点D,根据垂径定理得出MN=2MH,PM=PN,再利用勾股定理求出PH、AH、MH、MN的长,从而求出AM、NC的长,然后求出AMMP、PNNC的值,得出AMMP=PNNC,利用两边对应成比例且夹角相等的两三角形相似即可证明.【详解】(1)如图,作BD⊥AC,垂足为点D,∵⊙P与边AC相切,∴BD就是⊙P的半径,在Rt△ABD中,tanA= 1BD2AD ,设BD=x,则AD=2x,∴x2+(2x)2=152,解得:5∴半径为35; (2)相似,理由见解析, 如图,过点P 作PH ⊥AC 于点H ,作BD ⊥AC ,垂足为点D ,∴PH 垂直平分MN ,∴PM=PN ,在Rt △AHP 中,tanA=12PH AH =, 设PH=y ,AH=2y ,y 2+(2y )2=(65)2解得:y=6(取正数),∴PH=6,AH=12,在Rt △MPH 中,MH=()22356-=3,∴MN=2MH=6,∴AM=AH-MH=12-3=9,NC=AC-MN-AM=20-6-9=5,∴3535AM MP ==,35PN NC =, ∴AM MP =PN NC, 又∵PM=PN ,∴∠PMN=∠PNM ,∴∠AMP=∠PNC ,∴△AMP ∽△PNC.【点睛】本题考查了解直角三角形、垂径定理、相似三角形的判定与性质等,综合性较强,有一定的难度,正确添加辅助线、灵活应用相关的性质与定理是解题的关键.。
中考数学《圆的综合题》专项练习题及答案

中考数学《圆的综合题》专项练习题及答案一、单选题1.如图,在一块正三角形飞镖游戏板上画一个正六边形(图中阴影部分),假设飞镖投中游戏板上的每一点是等可能的(若投中边界或没有投中游戏板,则重投1次),任意投掷飞镖1次,则飞镖投中阴影部分的概率为()A.13B.49C.12D.232.如图,AB为⊙O的直径,弦DC垂直AB于点E,⊙DCB=30°,EB=3,则弦AC的长度为()A.3 √3B.4√3C.5√3D.6√33.如图,AB是⊙O的弦,半径OC⊙AB于点D,且AB=6cm,OD=4cm。
则DC的长为()A.cm B.1cm C.2cm D.5cm4.如图,四边形ABCD内接于⊙ O,AB为⊙ O的直径,∠ABD=20∘,则∠BCD的度数是()A.90°B.100°C.110°D.120°5.如图,点A,B,C,D都在⊙O上,AC,BD相交于点E,则⊙ABD=()A.⊙ACD B.⊙ADB C.⊙AED D.⊙ACB6.如图,在⊙O中,弦AB⊙CD,若⊙ABC=40°,则⊙BOD=()A.20°B.40°C.50°D.80°7.下列判断结论正确的有()(1)直径是圆中最大的弦.(2)长度相等的两条弧一定是等弧.(3)面积相等的两个圆是等圆.(4)同一条弦所对的两条弧一定是等弧.(5)圆上任意两点间的部分是圆的弦.A.1个B.2个C.3个D.4个8.已知如图,PA、PB切⊙O于A,B,MN切⊙O于C,交PB于N;若PA=7.5cm,则⊙PMN的周长是()A.7.5cm B.10cm C.15cm D.12.5cm9.若小李同学掷出的铅球在场地航砸出一个直径为10厘米,深2厘米的小坑,则该铅球的直径为()A.20厘米B.19.5厘米C.14.5厘米D.10厘米10.如图,如果从半径为9cm的圆形纸片剪去13圆周的一个扇形,将留下的扇形(阴影部分)围成一个圆锥(接缝处不重叠),那么这个圆锥的高为()A.6cm B.5√3cm C.8cm D.3√5cm11.如图,△ABC内接于⊙O,∠B=65o,∠C=70o,若BC=2√2,则弧BC长为()A.πB.√2πC.2πD.√2π12.如下图,点B,C,D在⊙O上,若⊙BCD=130°,则⊙BOD的度数是()A.96°B.98°C.102°D.100°二、填空题13.如图,在扇形AOB中,OA=4,⊙AOB=90°,点P是弧AB上的动点,连接OP,点C是线段OP的中点,连接BC并延长交OA于点D,则图中阴影部分面积最小值为.14.如图,在边长为√2的正方形ABCD中,分别以四个顶点为圆心,以边长为半径画弧,分别与正方形的边和对角线相交,则图中阴影部分的面积为(结果保留π).15.如图,⊙ABC的顶点A,B,C均在⊙O上,若⊙ABC+⊙AOC=90°,则⊙AOC的大小是.16.如图:⊙O为⊙ABC的内切圆,⊙C=90°,AO的延长线交BC于点D,AC=4,CD=1,则⊙O的半径为.17.如图,在正八边形ABCDEFGH中,AC、GC是两条对角线,则tan⊙ACG=.18.如图,菱形ABCD中,已知AB=2,∠DAB=60°将它绕着点A逆时针旋转得到菱形ADEF,使AB与AD重合,则点C运动的路线CE⌢的长为.三、综合题19.如图,AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C,点D为AP的中点,连结AC.求证:(1)⊙P=⊙BAC(2)直线CD是⊙O的切线.20.如图,以△ABC的边AB为直径的⊙O交AC于点F,点E是BF⌢的中点,连接BE并延长交AC于点D,若∠CBD=12∠CAB.(1)求证:BC是⊙O的切线;(2)若⊙O的半径为2,cos∠BAC=25,求CD的长.21.如图,⊙O是⊙ABC的外接圆,AC是O的直径,BD=BA=12,BC=5,BE⊙DC,交D的延长线于点E,BD交直径AC于点F.(1)求证:⊙BCA=⊙BAD.(2)求证:BE是⊙O的切线.(3)若BD平分⊙ABC,交⊙O于点D,求AD的长.22.如图,⊙OAB中,OA=OB=10cm,⊙AOB=80°,以点O为圆心,半径为6cm的优弧弧MN分别交OA,OB于点M,N.(1)点P在右半弧上(⊙BOP是锐角),将OP绕点O逆时针旋转80°得OP′.求证:AP=BP′;(2)点T在左半弧上,若AT与弧相切,求A T的长.23.如图,有一直径是√2米的圆形铁皮,现从中剪出一个圆周角是90°的最大扇形ABC,则:(1)AB的长为米;(2)用该扇形铁皮围成一个圆锥,所得圆锥的底面圆的半径为米.⌢的中点,CE⊥AB于点E,BD交CE于点F.24.如图,AB是⊙O的直径,C是BD(1)求证:CF=BF;(2)若CD﹦5,AC﹦12,求⊙O的半径和CE的长.参考答案1.【答案】D2.【答案】D3.【答案】B4.【答案】C5.【答案】A6.【答案】D7.【答案】B8.【答案】C9.【答案】C10.【答案】D11.【答案】A12.【答案】D13.【答案】4π−8√3314.【答案】4-π15.【答案】60°16.【答案】0.817.【答案】118.【答案】2√33π19.【答案】(1)解:证明:∵AB是⊙O的直径∴⊙ACB=90°∴⊙ACP=90°∴⊙P+⊙CAP=90°∵AP⊙O是切线∴⊙BAP=90°即⊙CAP+⊙BAC=90°∴⊙P=⊙BAC;(2)解:∵CD是Rt⊙PAC斜边PA的中线∴CD=AD∴⊙DCA=⊙DAC连接OC∵OC=OA∴⊙OCA=⊙OAC∴⊙DCO=⊙DAO=90°∴CD是⊙O的切线.20.【答案】(1)证明:连接AE,如图所示:∵AB是⊙O的直径∴∠AEB=90°∴∠BAE+∠ABE=90°.∵点E为弧BF的中点∴EF⌢=EB⌢∴∠BAE=∠DAE=12∠CAB.又∵∠CBD=12∠CAB∴∠BAE=∠CBD∴∠CBD+∠ABE=90°∴AB⊥CB∴BC是⊙O的切线.(2)解:∵∠BAE=∠DAE,∠AED=∠AEB=90°∴∠ADE=∠ABE∴AD=AB=2×2=4.∵cos∠BAC=2 5∴在Rt△ABC中即4AC=25,得AC=10∴CD=AC−AD=10−4=6.21.【答案】(1)证明:∵BD=BA ∴∠BDA=∠BAD.∵∠BCA=∠BDA∴∠BCA=∠BAD.(2)证明:连结OB,如图∵∠BCA=∠BAD又∵∠BCE=∠BAD∴∠BCA=∠BCE∵OB=OC∴∠BCO=∠CBO∴∠BCE=∠CBO∴OB//ED.∵BE⊥ED∴EB⊥BO.∴BE是⊙O的切线.(3)解:∵AC是⊙O的直径∴∠ABC=90°∴AC=√AB2+BC2=√122+52=13.∵∠BDE=∠CAB∴△BED∽△CBA∴BDAC=DEAB,即1213=DE12∴DE=14413∴BE=√BD2−DE2=6013∴CE=√BC2−BE2=2513∴CD=DE−CE=119 13∵BD平分⊙ABC ∴∠CBD=∠ABD∴AD=CD=119 13.22.【答案】(1)证明:∵⊙AOB=⊙POP′=80°∴⊙AOB+⊙BOP=⊙POP′+⊙BOP即⊙AOP=⊙BOP′在⊙AOP 与⊙BOP′中 OA=OB ⊙AOP=⊙BOP OP=OP′∴⊙AOP⊙⊙BOP′ ∴AP=BP′(2)解:∵A T 与弧相切,连结OT .∴OT⊙A T在Rt⊙AOT 中,根据勾股定理得,A T= √OA 2−OT 2 ∵OA=10,OT=6 ∴AT=823.【答案】(1)1 (2)1424.【答案】(1)证明:∵AB 是 ⊙O 的直径∴∠ACB =90° ∴∠A +∠ABC =90° 又∵CE ⊥AB ∴∠CEB =90° ∴∠BCE +∠ABC =90° ∴∠BCE =∠A∵C 是 BD ⌢ 的中点 ∴CD⌢=CB ⌢ ∴∠DBC =∠A ∴∠DBC =∠BCE ∴CF =BF(2)解:∵CD⌢=CB ⌢,CD =5 ∴∠DBC =∠BDC∴BC=CD=5∵∠ACB=90°∴AB=√AC2+BC2=√122+52=13∴AO=6.5∵∠BCE=∠A,∠ACB=∠CEB=90°∴△CEB⊙ △ACB∴CE=AC⋅BCAB=12×513=6013故⊙O的半径为6.5,CE的长是6013.第11页共11。
备战中考数学《圆的综合的综合》专项训练附答案解析

一、圆的综合真题与模拟题分类汇编(难题易错题)1.如图,点P在⊙O的直径AB的延长线上,PC为⊙O的切线,点C为切点,连接AC,过点A作PC的垂线,点D为垂足,AD交⊙O于点E.(1)如图1,求证:∠DAC=∠PAC;(2)如图2,点F(与点C位于直径AB两侧)在⊙O上,BF FA=,连接EF,过点F作AD 的平行线交PC于点G,求证:FG=DE+DG;(3)在(2)的条件下,如图3,若AE=23DG,PO=5,求EF的长.【答案】(1)证明见解析;(2)证明见解析;(3)EF=32.【解析】【分析】(1)连接OC,求出OC∥AD,求出OC⊥PC,根据切线的判定推出即可;(2)连接BE交GF于H,连接OH,求出四边形HGDE是矩形,求出DE=HG,FH=EH,即可得出答案;(3)设OC交HE于M,连接OE、OF,求出∠FHO=∠EHO=45°,根据矩形的性质得出EH∥DG,求出OM=12AE,设OM=a,则HM=a,AE=2a,AE=23DG,DG=3a,求出ME=CD=2a,BM=2a,解直角三角形得出tan∠MBO=12MOBM=,tanP=12COPO=,设OC=k,则PC=2k,根据OP=5k=5求出k=5,根据勾股定理求出a,即可求出答案.【详解】(1)证明:连接OC,∵PC为⊙O的切线,∴OC⊥PC,∵AD⊥PC,∴OC∥AD,∴∠OCA=∠DAC,∵OC=OA,∴∠PAC=∠OCA,∴∠DAC=∠PAC;(2)证明:连接BE交GF于H,连接OH,∵FG∥AD,∴∠FGD+∠D=180°,∵∠D=90°,∴∠FGD=90°,∵AB为⊙O的直径,∴∠BEA=90°,∴∠BED=90°,∴∠D=∠HGD=∠BED=90°,∴四边形HGDE是矩形,∴DE=GH,DG=HE,∠GHE=90°,∵BF AF=,∴∠HEF=∠FEA=12∠BEA=1902o⨯=45°,∴∠HFE=90°﹣∠HEF=45°,∴∠HEF=∠HFE,∴FH=EH,∴FG=FH+GH=DE+DG;(3)解:设OC交HE于M,连接OE、OF,∵EH=HF,OE=OF,HO=HO,∴△FHO≌△EHO,∴∠FHO=∠EHO=45°,∵四边形GHED是矩形,∴EH∥DG,∴∠OMH=∠OCP=90°,∴∠HOM=90°﹣∠OHM=90°﹣45°=45°,∴∠HOM=∠OHM,∴HM=MO,∵OM⊥BE,∴BM=ME,∴OM=12 AE,设OM=a,则HM=a,AE=2a,AE=23DG,DG=3a,∵∠HGC=∠GCM=∠GHE=90°,∴四边形GHMC是矩形,∴GC=HM=a,DC=DG﹣GC=2a,∵DG=HE,GC=HM,∴ME=CD=2a,BM=2a,在Rt△BOM中,tan∠MBO=122 MO aBM a==,∵EH∥DP,∴∠P=∠MBO,tanP=12 COPO=,设OC=k,则PC=2k,在Rt△POC中,,解得:在Rt△OME中,OM2+ME2=OE2,5a2=5,a=1,∴HE=3a=3,在Rt△HFE中,∠HEF=45°,∴.【点睛】考查了切线的性质,矩形的性质和判定,解直角三角形,勾股定理等知识点,能综合运用性质进行推理是解此题的关键.2.在平面直角坐标中,边长为2的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上,点O在原点.现将正方形OABC绕O点顺时针旋转,当A点一次落在直线y x=上时停止旋转,旋转过程中,AB边交直线y x=于点M,BC边交x轴于点N(如图).(1)求边OA 在旋转过程中所扫过的面积;(2)旋转过程中,当MN 和AC 平行时,求正方形OABC 旋转的度数;(3)设MBN ∆的周长为p ,在旋转正方形OABC 的过程中,p 值是否有变化?请证明你的结论.【答案】(1)π/2(2)22.5°(3)周长不会变化,证明见解析【解析】试题分析:(1)根据扇形的面积公式来求得边OA 在旋转过程中所扫过的面积; (2)解决本题需利用全等,根据正方形一个内角的度数求出∠AOM 的度数; (3)利用全等把△MBN 的各边整理到成与正方形的边长有关的式子.试题解析:(1)∵A 点第一次落在直线y=x 上时停止旋转,直线y=x 与y 轴的夹角是45°,∴OA 旋转了45°.∴OA 在旋转过程中所扫过的面积为24523602ππ⨯=. (2)∵MN ∥AC ,∴∠BMN=∠BAC=45°,∠BNM=∠BCA=45°.∴∠BMN=∠BNM .∴BM=BN .又∵BA=BC ,∴AM=CN .又∵OA=OC ,∠OAM=∠OCN ,∴△OAM ≌△OCN .∴∠AOM=∠CON=12(∠AOC-∠MON )=12(90°-45°)=22.5°. ∴旋转过程中,当MN 和AC 平行时,正方形OABC 旋转的度数为45°-22.5°=22.5°. (3)在旋转正方形OABC 的过程中,p 值无变化.证明:延长BA 交y 轴于E 点,则∠AOE=45°-∠AOM ,∠CON=90°-45°-∠AOM=45°-∠AOM ,∴∠AOE=∠CON .又∵OA=OC ,∠OAE=180°-90°=90°=∠OCN .∴△OAE ≌△OCN .∴OE=ON ,AE=CN .又∵∠MOE=∠MON=45°,OM=OM ,∴△OME ≌△OMN .∴MN=ME=AM+AE .∴MN=AM+CN ,∴p=MN+BN+BM=AM+CN+BN+BM=AB+BC=4.∴在旋转正方形OABC的过程中,p值无变化.考点:旋转的性质.3.如图,已知△ABC中,AC=BC,以BC为直径的⊙O交AB于E,过点E作EG⊥AC于G,交BC的延长线于F.(1)求证:AE=BE;(2)求证:FE是⊙O的切线;(3)若FE=4,FC=2,求⊙O的半径及CG的长.【答案】(1)详见解析;(2)详见解析;(3).【解析】(1)证明:连接CE,如图1所示:∵BC是直径,∴∠BEC=90°,∴CE⊥AB;又∵AC=BC,∴AE=BE.(2)证明:连接OE,如图2所示:∵BE=AE,OB=OC,∴OE是△ABC的中位线,∴OE∥AC,AC=2OE=6.又∵EG⊥AC,∴FE⊥OE,∴FE是⊙O的切线.(3)解:∵EF是⊙O的切线,∴FE2=FC•FB.设FC=x,则有2FB=16,∴FB=8,∴BC=FB﹣FC=8﹣2=6,∴OB=OC=3,即⊙O的半径为3;∴OE=3.∵OE∥AC,∴△FCG∽△FOE,∴,即,解得:CG=.点睛:本题利用了等腰三角形三线合一定理,三角形中位线的判定,切割线定理,以及勾股定理,还有平行线分线段成比例定理,切线的判定等知识.4.(类比概念)三角形的内切圆是以三个内角的平分线的交点为圆心,以这点到三边的距离为半径的圆,则三角形可以称为圆的外切三角形,可以得出三角形的三边与该圆相切.以此类推,如图1,各边都和圆相切的四边形称为圆外切四边形(性质探究)如图1,试探究圆外切四边形的ABCD两组对边AB,CD与BC,AD之间的数量关系猜想结论:(要求用文字语言叙述)写出证明过程(利用图1,写出已知、求证、证明)(性质应用)①初中学过的下列四边形中哪些是圆外切四边形(填序号)A:平行四边形:B:菱形:C:矩形;D:正方形②如图2,圆外切四边形ABCD,且AB=12,CD=8,则四边形的周长是.③圆外切四边形的周长为48cm,相邻的三条边的比为5:4:7,求四边形各边的长.【答案】见解析.【解析】【分析】(1)根据切线长定理即可得出结论;(2)①圆外切四边形是内心到四边的距离相等,即可得出结论;②根据圆外切四边形的对边和相等,即可求出结论;③根据圆外切四边形的性质求出第四边,利用周长建立方程求解即可得出结论.【详解】性质探讨:圆外切四边形的对边和相等,理由:如图1,已知:四边形ABCD的四边AB,BC,CD,DA都于⊙O相切于G,F,E,H.求证:AD+BC=AB+CD.证明:∵AB,AD和⊙O相切,∴AG=AH,同理:BG=BF,CE=CF,DE=DH,∴AD+BC=AH+DH+BF+CF=AG+BG+CE+DE=AB+CD,即:圆外切四边形的对边和相等.故答案为:圆外切四边形的对边和相等;性质应用:①∵根据圆外切四边形的定义得:圆心到四边的距离相等.∵平行四边形和矩形不存在一点到四边的距离相等,而菱形和正方形对角线的交点到四边的距离相等.故答案为:B,D;②∵圆外切四边形ABCD,∴AB+CD=AD+BC.∵AB=12,CD=8,∴AD+BC=12+8=20,∴四边形的周长是AB+CD+AD+BC=20+20=40.故答案为:40;③∵相邻的三条边的比为5:4:7,∴设此三边为5x,4x,7x,根据圆外切四边形的性质得:第四边为5x+7x﹣4x=8x.∵圆外切四边形的周长为48cm,∴4x+5x+7x+8x=24x=48,∴x=2,∴此四边形的四边为4x=8cm,5x=10cm,7x=14cm,8x=16cm.【点睛】本题是圆的综合题,主要考查了新定义圆的外切的性质,四边形的周长,平行四边形,矩形,菱形,正方形的性质,切线长定理,理解和掌握圆外切四边形的定义是解答本题的关键.5.如图,在⊙O中,直径AB⊥弦CD于点E,连接AC,BC,点F是BA延长线上的一点,且∠FCA=∠B.(1)求证:CF是⊙O的切线; (2)若AE=4,tan∠ACD=12,求AB和FC的长.【答案】(1)见解析;(2) ⑵AB=20 ,403 CF【解析】分析:(1)连接OC,根据圆周角定理证明OC⊥CF即可;(2)通过正切值和圆周角定理,以及∠FCA=∠B求出CE、BE的长,即可得到AB长,然后根据直径和半径的关系求出OE的长,再根据两角对应相等的两三角形相似(或射影定理)证明△OCE∽△CFE,即可根据相似三角形的对应线段成比例求解.详解:⑴证明:连结OC∵AB是⊙O的直径∴∠ACB=90°∴∠B+∠BAC=90°∵OA=OC∴∠BAC=∠OCA∵∠B=∠FCA∴∠FCA+∠OCA=90°即∠OCF=90°∵C在⊙O上∴CF是⊙O的切线⑵∵AE=4,tan ∠ACD12AE EC = ∴CE=8 ∵直径AB ⊥弦CD 于点E∴AD AC =∵∠FCA =∠B∴∠B=∠ACD=∠FCA∴∠EOC=∠ECA∴tan ∠B=tan ∠ACD=1=2CE BE ∴BE=16∴AB=20∴OE=AB÷2-AE=6∵CE ⊥AB∴∠CEO=∠FCE=90°∴△OCE ∽△CFE ∴OC OE CF CE= 即106=8CF ∴40CF 3= 点睛:此题主要考查了圆的综合知识,关键是熟知圆周角定理和切线的判定与性质,结合相似三角形的判定与性质和解直角三角形的知识求解,利用数形结合和方程思想是解题的突破点,有一定的难度,是一道综合性的题目.6.如图,在RtΔABC 中,∠ABC=90°,AB=CB ,以AB 为直径的⊙O 交AC 于点D ,点E 是AB 边上一点(点E 不与点A 、B 重合),DE 的延长线交⊙O 于点G ,DF ⊥DG ,且交BC 于点F.(1)求证:AE=BF ;(2)连接EF ,求证:∠FEB=∠GDA ;(3)连接GF,若AE=2,EB=4,求ΔGFD 的面积.【答案】(1)(2)见解析;(3)9【解析】分析:(1)连接BD,由三角形ABC为等腰直角三角形,求出∠A与∠C的度数,根据AB 为圆的直径,利用圆周角定理得到∠ADB为直角,即BD垂直于AC,利用直角三角形斜边上的中线等于斜边的一半,得到AD=DC=BD=12AC,进而确定出∠A=∠FBD,再利用同角的余角相等得到一对角相等,利用ASA得到三角形AED与三角形BFD全等,利用全等三角形对应边相等即可得证;(2)连接EF,BG,由三角形AED与三角形BFD全等,得到ED=FD,进而得到三角形DEF为等腰直角三角形,利用圆周角定理及等腰直角三角形性质得到一对同位角相等,利用同位角相等两直线平行,再根据平行线的性质和同弧所对的圆周角相等,即可得出结论;(3)由全等三角形对应边相等得到AE=BF=1,在直角三角形BEF中,利用勾股定理求出EF的长,利用锐角三角形函数定义求出DE的长,利用两对角相等的三角形相似得到三角形AED与三角形GEB相似,由相似得比例,求出GE的长,由GE+ED求出GD的长,根据三角形的面积公式计算即可.详解:(1)连接BD.在Rt△ABC中,∠ABC=90°,AB=BC,∴∠A=∠C=45°.∵AB为圆O的直径,∴∠ADB=90°,即BD⊥AC,∴AD=DC=BD=12AC,∠CBD=∠C=45°,∴∠A=∠FBD.∵DF⊥DG,∴∠FDG=90°,∴∠FDB+∠BDG=90°.∵∠EDA+∠BDG=90°,∴∠EDA=∠FDB.在△AED和△BFD中,A FBDAD BDEDA FDB∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△AED≌△BFD(ASA),∴AE=BF;(2)连接EF,BG.∵△AED≌△BFD,∴DE=DF.∵∠EDF=90°,∴△EDF是等腰直角三角形,∴∠DEF=45°.∵∠G=∠A=45°,∴∠G=∠DEF,∴GB∥EF,∴∠FEB=∠GBA.∵∠GBA=∠GDA,∴∠FEB=∠GDA;(3)∵AE=BF,AE=2,∴BF=2.在Rt△EBF中,∠EBF=90°,∴根据勾股定理得:EF 2=EB 2+BF 2.∵EB =4,BF =2,∴EF =2242+=25. ∵△DEF 为等腰直角三角形,∠EDF =90°,∴cos ∠DEF =DE EF . ∵EF =25,∴DE =25×22=10. ∵∠G =∠A ,∠GEB =∠AED ,∴△GEB ∽△AED ,∴GE AE =EB ED ,即GE •ED =AE •EB ,∴10•GE =8,即GE =4105,则GD =GE +ED =9105. ∴1191011092252S GD DF GD DE =⨯⨯=⨯⨯=⨯⨯=.点睛:本题属于圆综合题,涉及的知识有:全等三角形的判定与性质,相似三角形的判定与性质,勾股定理,圆周角定理,以及平行线的判定与性质,熟练掌握判定与性质是解答本题的关键.7.如图1O ,的直径12AB P =,是弦BC 上一动点(与点B C ,不重合)30ABC ,∠=,过点P 作PD OP ⊥交O 于点D .()1如图2,当//PD AB 时,求PD 的长;()2如图3,当DC AC =时,延长AB 至点E ,使12BE AB =,连接DE . ①求证:DE 是O 的切线;②求PC 的长.【答案】(1)262)333①见解析,②.【解析】分析:()1根据题意首先得出半径长,再利用锐角三角函数关系得出OP PD ,的长; ()2①首先得出OBD 是等边三角形,进而得出ODE OFB 90∠∠==,求出答案即可; ②首先求出CF 的长,进而利用直角三角形的性质得出PF 的长,进而得出答案. 详解:()1如图2,连接OD ,//OP PD PD AB ⊥,,90POB ∴∠=, O 的直径12AB =,6OB OD ∴==,在Rt POB 中,30ABC ∠=, 3tan30623OP OB ∴=⋅=⨯=, 在Rt POD 中, 22226(23)26PD OD OP =-=-=;()2①证明:如图3,连接OD ,交CB 于点F ,连接BD ,DC AC =,30DBC ABC ∴∠=∠=,60ABD ∴∠=,OB OD =,OBD ∴是等边三角形,OD FB ∴⊥,12BE AB =,OB BE ∴=,//BF ED ∴,90ODE OFB ∴∠=∠=,DE ∴是O 的切线;②由①知,OD BC ⊥, 3cos306332CF FB OB ∴==⋅=⨯=, 在Rt POD 中,OF DF =, 13(2PF DO ∴==直角三角形斜边上的中线,等于斜边的一半), 333CP CF PF ∴=-=-.点睛:此题主要考查了圆的综合以及直角三角形的性质和锐角三角函数关系,正确得出OBD 是等边三角形是解题关键.8.对于平面直角坐标系xOy 中的线段MN 和点P ,给出如下定义:点A 是线段MN 上一个动点,过点A 作线段MN 的垂线l ,点P 是垂线l 上的另外一个动点.如果以点P 为旋转中心,将垂线l 沿逆时针方向旋转60°后与线段MN 有公共点,我们就称点P 是线段MN 的“关联点”.如图,M (1,2),N (4,2).(1) 在点P 1(1,3),P 2(4,0),P 3(3,2)中,线段MN 的“关联点”有 ;(2) 如果点P 在直线1y x =+上,且点P 是线段MN 的“关联点”,求点P 的横坐标x 的取值范围;(3) 如果点P 在以O (1,1-)为圆心,r 为半径的⊙O 上,且点P 是线段MN 的“关联点”,直接写出⊙O 半径r 的取值范围.【答案】(1)P 1和P 3;(2)3311x -≤≤;(3333 3.r +≤ 【解析】【分析】 (1)先根据题意求出点P 的横坐标的范围,再求出P 点的纵坐标范围即可得出结果;(2)由直线y=x+1经过点M (1,2),得出x≥1,设直线y=x+1与P 4N 交于点A ,过点A 作AB ⊥MN 于B ,延长AB 交x 轴于C ,则在△AMN 中,MN=3,∠AMN=45°,∠ANM=30°,设AB=MB=a ,tan ∠ANM=AB BN ,即tan30°=3a a -,求出a 即可得出结果; (3)圆心O 到P 4的距离为r 的最大值,圆心O 到MP 5的距离为r 的最小值,分别求出两个距离即可得出结果.【详解】(1))如图1所示:∵点A 是线段MN 上一个动点,过点A 作线段MN 的垂线l ,点P 是垂线l 上的另外一个动点,M (1,2),N (4,2),∴点P 的横坐标1≤x≤4,∵以点P 为旋转中心,将垂线l 沿逆时针方向旋转60°后与线段MN 有公共点, 当∠MPN=60°时,PM=60MN tan ︒=3=3, 同理P′N=3,∴点P 的纵坐标为2-3或2+3,即纵坐标2-3≤y≤2+3,∴线段MN 的“关联点”有P 1和P 3;故答案为:P 1和P 3;(2)线段MN 的“关联点”P 的位置如图所示,∵ 直线1y x =+经过点M (1,2),∴ x ≥1.设直线1y x =+与P 4N 交于点A .过点A 作AB ⊥MN 于B ,延长AB 交x 轴于C .由题意易知,在△AMN 中,MN = 3,∠AMN = 45°,∠ANM = 30°.设AB = MB = a ,∴ tan AB ANM BN ∠=,即tan303a a ︒=-, 解得333.a -= ∴ 点A 的横坐标为33333111.22x a --=+=+= ∴331.x -≤ 综上 3311.2x -≤≤(3)点P 在以O (1,-1)为圆心,r 为半径的⊙O 上,且点P 是线段MN 的“关联点”,如图3所示:连接P 4O 交x 轴于点D ,P 4、M 、D 、O 共线,则圆心O 到P 4的距离为r 的最大值,由(1)知:MP 4=NP 53即OD+DM+MP 433圆心O 到MP 5的距离为r 的最小值,作OE ⊥MP 5于E ,连接OP 5,则OE 为r 的最小值,MP 5225MN NP +223(3)+3OM=OD+DM=1+2=3, △OMP 5的面积=12OE•MP 5=12OM•MN ,即12312×3×3, 解得:33 ∴333 【点睛】本题是圆的综合题,考查了旋转、直角三角形的性质、勾股定理、最值等知识,熟练掌握“关联点”的含义,作出关于MN 的“关联点”图是关键.9.如图,在Rt △ABC 中,90C ∠=︒,AD 平分∠BAC ,交BC 于点D ,点O 在AB 上,⊙O 经过A 、D 两点,交AC 于点E ,交AB 于点F .(1)求证:BC 是⊙O 的切线;(2)若⊙O 的半径是2cm ,E 是弧AD 的中点,求阴影部分的面积(结果保留π和根号)【答案】(1)证明见解析 (2)233π- 【解析】【分析】 (1)连接OD ,只要证明OD ∥AC 即可解决问题;(2)连接OE ,OE 交AD 于K .只要证明△AOE 是等边三角形即可解决问题.【详解】(1)连接OD .∵OA =OD ,∴∠OAD =∠ODA .∵∠OAD =∠DAC ,∴∠ODA =∠DAC ,∴OD ∥AC ,∴∠ODB =∠C =90°,∴OD ⊥BC ,∴BC 是⊙O 的切线.(2)连接OE ,OE 交AD 于K .∵AE DE =,∴OE ⊥AD .∵∠OAK =∠EAK ,AK =AK ,∠AKO =∠AKE =90°,∴△AKO ≌△AKE ,∴AO =AE =OE ,∴△AOE是等边三角形,∴∠AOE =60°,∴S 阴=S 扇形OAE ﹣S △AOE 26023360π⋅⋅=-22233π=. 【点睛】本题考查了切线的判定、扇形的面积、等边三角形的判定和性质、平行线的判定和性质、全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,灵活运用所学知识解决问题,属于中考常考题型.10.如图,点B 在数轴上对应的数是﹣2,以原点O 为原心、OB 的长为半径作优弧AB ,使点A 在原点的左上方,且tan ∠AOB 3C 为OB 的中点,点D 在数轴上对应的数为4.(1)S扇形AOB=(大于半圆的扇形);(2)点P是优弧AB上任意一点,则∠PDB的最大值为°(3)在(2)的条件下,当∠PDB最大,且∠AOP<180°时,固定△OPD的形状和大小,以原点O为旋转中心,将△OPD顺时针旋转α(0°≤α≤360°)①连接CP,AD.在旋转过程中,CP与AD有何数量关系,并说明理由;②当PD∥AO时,求AD2的值;③直接写出在旋转过程中,点C到PD所在直线的距离d的取值范围.【答案】(1)103π(2)30(3)①AD=2PC②20+83或20+83③1≤d≤3【解析】【分析】(1)利用扇形的面积公式计算即可.(2)如图1中,当PD与⊙O相切时,∠PDB的值最大.解直角三角形即可解决问题.(3)①结论:AD=2PC.如图2中,连接AB,AC.证明△COP∽△AOD,即可解决问题.②分两种情形:如图3中,当PD∥OA时,设OD交⊙O于K,连接PK交OC于H.求出PC即可.如图④中,当PA∥OA时,作PK⊥OB于K,同法可得.③判断出PC的取值范围即可解决问题.【详解】(1)∵tan∠AOB=3,∴∠AOB=60°,∴S扇形AOB=23002103603ππ⋅⋅=(大于半圆的扇形),(2)如图1中,当PD与⊙O相切时,∠PDB的值最大.∵PD是⊙O的切线,∴OP⊥PD,∴∠OPD=90°,∵21sin 42OP PDO OD ∠=== ∴∠PDB =30°, 同法当DP ′与⊙O 相切时,∠BDP ′=30°,∴∠PDB 的最大值为30°.故答案为30.(3)①结论:AD =2PC .理由:如图2中,连接AB ,AC .∵OA =OB ,∠AOB =60°,∴△AOB 是等边三角形,∵BC =OC ,∴AC ⊥OB ,∵∠AOC =∠DOP =60°,∴∠COP =∠AOD ,∵2AO OD OC OP==, ∴△COP ∽△AOD , ∴2AD AO PC OC==, ∴AD =2PC . ②如图3中,当PD ∥OA 时,设OD 交⊙O 于K ,连接PK 交OC 于H .∵OP =OK ,∠POK =60°,∴△OPK 是等边三角形,∵PD ∥OA ,∴∠AOP=∠OPD=90°,∴∠POH+∠AOC=90°,∵∠AOC=60°,∴∠POH=30°,∴PH=1OP=1,OH=3PH=3,2∴PC=2222+=++=+,PH CH1(13)523∵AD=2PC,∴AD2=4(5+23)=20+83.如图④中,当PA∥OA时,作PK⊥OB于K,同法可得:PC2=12+(3﹣1)2=5﹣23,AD2=4PC2=20﹣83.③由题意1≤PC≤3,∴在旋转过程中,点C到PD所在直线的距离d的取值范围为1≤d≤3.【点睛】本题属于圆综合题,考查了切线的性质,相似三角形的判定和性质,旋转变换,勾股定理,等边三角形的判定和性质等知识,解题的关键是学会用分类讨论的思想思考问题.。
中考数学复习《圆综合》专项检测卷(带答案)

中考数学复习《圆综合》专项检测卷(带答案)学校:___________班级:___________姓名:___________考号:___________一、选择题(本大题共10道小题)1. (2023·苏州模拟)一个扇形的圆心角为120°,扇形的弧长等于4π,则该扇形的面积等于( )A.2πB.πC.12πD.24π2. (2022·宁波期中)下列语句中不正确的有( )①长度相等的弧是等弧;②垂直于弦的直径平分弦;③圆是轴对称图形,任何一条直径都是它的对称轴;④平分弦的直线也必平分弦所对的两条弧;⑤半圆是圆中最长的弧;⑥不在同一条直线上的三个点可以确定一个圆.A.5个B.4个C.3个D.2个3. (2023•淮安)如图所示,点A、B、C在⊙O上,∠ACB=54°,则∠ABO的度数是( )A.54°B.27°C.36°D.108°4. (2023·青岛模拟)已知⊙O的直径为6 cm,M是直线l上一点,且点M与圆心O之间的距离为3 cm,则直线l与⊙O的位置关系是( )A.相切B.相切或相交C.相交D.相离或相切5. (2023秋•永年区期末)如图,△ABC中,∠A=80°,点O是△ABC的内心,则∠BOC的度数为( )A.100°B.160°C.80°D.130°6. (2023•随州)设边长为a的等边三角形的高、内切圆的半径、外接圆的半径分别为h、r、R,则下列结论不正确的是( )A.h=R+rB.R=2rC.r aD.R a7. (2023秋•河东区期末)如图,菱形OABC的顶点A,B,C在⊙O上,过点B作⊙O的切线交OA 的延长线于点D.若⊙O的半径为1,则BD的长为( )A.1B.C.D.28. (2023·浙江绍兴·中考真题)如图.点A,B,C,D,E均在⊙O上.∠BAC=15°,∠CED=30°,则∠BOD的度数为( )A.45°B.60°C.75°D.90°9. (2023·山西中考)如图,在⊙O中,AB切⊙O于点A,连接OB交⊙O于点C,过点A作AD∥OB交⊙O于点D,连接CD.若∠B=50°,则∠OCD为( )A.15°B.20°C.25°D.30°10. (2023·合肥市第四十五中学九年级三模)如图,四边形ABCD内接于⊙O,点I是△ABC的内心,∠AIC=124°,点E在AD的延长线上,则∠CDE的度数为( )A.56°B.62°C.68°D.78°二、填空题(本大题共8道小题)11. (2023·山东初三二模)Rt△ABC中,∠C=90°,若直角边AC=5,BC=12,则此三角形的内切圆半径为________.12. (2023·湖北随州中考)如图,点A,B,C在O上,AD是∠BAC的角平分线,若∠BOC=120o,则∠CAD的度数为_____.13. (2023•太原二模)如图,点A的坐标为(2,0),点B的坐标为(0,23),⊙A与y轴相切,点C是⊙A上的动点,射线BC与x轴交于点D,则BD长的最大值等于.14. (2023•牡丹江)AB 是⊙O 的弦,OM ⊥AB,垂足为M,连接OA.若△AOM 中有一个角是30°,OM =23,则弦AB 的长为 .15. (2023·海口模拟)如图,在△ABC 中,∠B =90°,AB =6,BC =4,点O 在AC 边上,⊙O 与边AB,BC 分别切于点D,E,则CO OA的值为____.16. (2023•延平区模拟)如图,Rt △ABD 中,∠D =90°,AB =8,BD =4,在BD 延长线上取一点D,使得DC =BD,在直线AD 左侧有一动点P 满足∠PAD =∠PDB,连接PC,则线段CP 长的最大值为 .17. (2023·凉山州)如图,等边三角形ABC 的边长为4,⊙C 的半径为3,P 为AB 边上一动点,过点P 作⊙C 的切线PQ,切点为Q,则PQ 的最小值为 .18. (2023•盘锦)如图,在平面直角坐标系xOy 中,点A 在x 轴负半轴上,点B 在y 轴正半轴上,⊙D 经过A,B,O,C 四点,∠ACO =120°,AB =4,则圆心点D 的坐标是 .三、解答题(本大题共6道小题)19. 如图,AB 为⊙O 的直径,BE =CE,CD ⊥AB 于点D,交BE 于点F,连接CB.求证:BC=CF.20. (2023·黔东南州)如图,PA 是以AC 为直径的⊙O 的切线,切点为A,过点A 作AB ⊥OP,交⊙O 于点B.(1)求证:PB 是⊙O 的切线;(2)若AB =6,cos ∠PAB =35,求PO 的长.21. (2022北京平谷)如图,AB 是⊙O 的直径,C 是⊙O 上一点,过C 作⊙O 的切线交AB 的延长线于点D,连接AC 、BC,过O 作OF ∥AC,交BC 于G,交DC 于F.(1)求证:∠DCB =∠DOF;(2)若tan ∠A =12,BC =4,求OF 、DF 的长.22. (2023•贵阳)如图,在⊙O 中,AC 为⊙O 的直径,AB 为⊙O 的弦,点E 是的中点,过点E 作AB 的垂线,交AB 于点M,交⊙O 于点N,分别连接EB,CN.(1)EM与BE的数量关系是;(2)求证:=;(3)若AM=,MB=1,求阴影部分图形的面积.23. (2022北京东直门中学)对于平面直角坐标系xOy中的图形W1和图形W2.给出如下定义:在图形W1上存在两点A,B(点A,B可以重合),在图形W2上存在两点M,N,(点M于点N可以重合)使得AM=2BN,则称图形W1和图形W2满足限距关系(1)如图1,点C(1,0),D(-1,0),E(0,3),点P在线段DE上运动(点P可以与点D,E重合),连接OP,CP.①线段OP的最小值为_______,最大值为_______;线段CP的取值范直范围是_____;②在点O,点C中,点____________与线段DE满足限距关系;(2)如图2,⊙O的半径为1,直线3=+(b>0)与x轴、y轴分别交于点F,G.若线段FG与y x b⊙O满足限距关系,求b的取值范围;(3)⊙O的半径为r(r>0),点H,K是⊙O上的两个点,分别以H,K为圆心,1为半径作圆得到⊙H 和⊙K,若对于任意点H,K,⊙H和⊙K都满足限距关系,直接写出r的取值范围.24. (2023·江苏南京·中考真题)如图①,要在一条笔直的路边l上建一个燃气站,向l同侧的A、B两个城镇分别发铺设管道输送燃气,试确定燃气站的位置,使铺设管道的路线最短.(1)如图②,作出点A关于l的对称点A’,线A’B与直线l的交点C的位置即为所求, 即在点C 处建气站, 所得路线ACB是最短的,为了让明点C的位置即为所求,不妨在l直线上另外任取一点C’,连接AC’,BC’, 证明AC+CB<AC’+C’B, 请完成这个证明.(2)如果在A、B两个城镇之间规划一个生态保护区,燃气管道不能穿过该区域请分别始出下列两种情形的铺设管道的方案(不需说明理由)①生市保护区是正方形区城,位置如图③所示②生态保护区是圆形区域,位置如图④所示.答案一、选择题(本大题共10道小题)1. C2. B3. C4. B5. 故选:D.6. C7. 故选:C.8. D【详解】解:连接BE∵∠BEC=∠BAC=15o,∠CED=30o,∴∠BED=∠BEC+∠CED=45o,∴∠BOD=2∠BED=90o.故选:D.9. B10. C【解析】详解:∵点I是△ABC的内心,∴∠BAC=2∠IAC、∠ACB=2∠ICA,∵∠AIC=124°∴∠B=180°﹣(∠BAC+∠ACB)=180°﹣2(∠IAC+∠ICA)=180°﹣2(180°﹣∠AIC)=68°又四边形ABCD内接于⊙O,∴∠CDE=∠B=68°,故选C.二、填空题(本大题共8道小题)11. 2【详解】解:如图;在Rt △ABC,∠C=90°,AC=5,BC=12; 根据勾股定理: 22AB AC +BC 13== 四边形OECF 中,OE=OF,∠OEC=∠OFC=∠C=90°;∴四边形OECF 是正方形;由切线长定理,得:AD=AE,BD=BF,CE=CF;∴CE=CF=12(AC+BC-AB);即:r=12(5+12-13)=2.故答案为2. 12. 30°13. 故答案为43.BD 最大.14. 12或4.15. 32 16. 故答案为:23+2717. 318. ∵四边形ABOC 为圆的内接四边形∴∠ABO+∠ACO =180°,∴∠ABO =180°-120°=60°,∵∠AOB =90°∴AB 为⊙D 的直径,∴D 点为AB 的中点在Rt △ABO 中,∵∠ABO =60°∴OB =21AB =2,∴OA =3OB =23,∴A(-23,0),B(0,2),∴D 点坐标为(-3,1). 故答案为(-3,1).三、解答题(本大题共6道小题)19. 证明:在题图上连接AE,∵,∴∠A=∠FBC,∵AB 为直径,∴∠E=90°,∴∠A+∠ABE=90°,∵CD ⊥AB 于点D,∴∠FDB=90°,∴∠CFB+∠ABE=90°,∴∠A=∠CFB,∴∠FBC=∠CFB,∴BC=CF.20. (1)证明:连结OB.∵PA 是以AC 为直径的⊙O 的切线,切点为A∴∠PAO =90°.∵OA =OB,AB ⊥OP,∴∠POA =∠POB.在△PAO 和△PBO 中⎩⎪⎨⎪⎧OA =OB ,∠POA =∠POB ,OP =OP ,∴△PAO ≌△PBO(SAS).∴∠PBO =∠PAO =90°,即OB ⊥PB.∴PB 是⊙O 的切线.(2)解:设OP 与AB 交于点D.∵AB ⊥OP,AB =6,∴DA =DB =3,∠PDA =90°.∵cos ∠PAB =35=DA PA ∴PA =5.∴PD =PA 2-DA 2=52-32=4.在Rt △APD 和Rt △APO 中,cos ∠APD =PD PA ,cos ∠APO =PA PO∴PD PA =PA PO .∴PO =PA 2PD =254. 21. (1)见解析(2)5553OF DF ==, (1)解:如图所示,连接OC∵CD 是圆O 的切线,AB 是圆O 的直径∴∠OCD=∠ACB=90°∴∠DCB+∠OCB=∠OCA+∠OCB ∴∠DCB=∠OCA∵OC=OA∴∠OAC=∠OCA=∠DCB∵OF AC ∥∴∠DOF=∠OAC∴∠DOF=∠DCB;(2)解:设OF 与BC 交于点G∵OF//AC,∴△OBG ∽△ABC,∠BGO=∠ACB=90° ∴1==2BG OB OG BC AB AC =,∠CGF=90°∴122BG BC ==,∴CG=2 ∵∠BCD=∠OAC,1tan =2A ∠,∴1tan =tan ===2FG BC FCG A CG AC∠∠ ∴11282GF CG AC BC ====, ∴1=42OG AC = 225CF GF CG =+∴5OF OG GF =+=同理可证△OFD ∽△ACD∴DF OF DC AC =,585DF =+,∴55DF =22. (1)∵AC为⊙O的直径,点E是的中点∴∠ABE=45°,∵AB⊥EN,∴△BME是等腰直角三角形∴BE=2EM,故答案为BE=2EM;(2)连接EO,∵AC是⊙O的直径,E是的中点∴∠AOE=90°,∴∠ABE=∠AOE=45°∵EN⊥AB,垂足为点M,∴∠EMB=90°∴∠ABE=∠BEN=45°∴=,∵点E是的中点,∴=,∴=∴-=-,∴=;(3)连接AE,OB,ON∵EN⊥AB,垂足为点M∴∠AME=∠EMB=90°∵BM=1,由(2)得∠ABE=∠BEN=45°∴EM=BM=1又∵BE=EM,∴BE=∵在Rt△AEM中,EM=1,AM=,∴tan∠EAB==∴∠EAB=30°∵∠EAB=∠EOB∴∠EOB=60°又∵OE=OB∴△EOB是等边三角形∴OE=BE=,又∵=,∴BE=CN∴△OEB≌△OCN(SSS)∴CN=BE=又∵S扇形OCN==,S△OCN=CN×CN=×=∴S阴影=S扇形OCN-S△OCN=-.23. (1)①32 3 32CP ≤≤ ②O;(2)13b ≥;(3)0<r ≤3. (1)①如图1中∵3∴OD=1,3OE =∴3OE tan EDO OD ∠==∴∠EDO=60° 当OP ⊥DE 时,3•60OP OD sin =︒=此时OP 的值最小 当点P 与E 重合时,OP 的值最大,3当CP ⊥DE 时,CP 的值最小,最小值•603CD cos =︒=当点P 与D 或E 重合时,PC 的值最大,最大值为2故答案为3332CP ≤≤. ②根据限距关系的定义可知,线段DE 上存在两点M,N,满足OM=2ON 故点O 与线段DE 满足限距关系.故答案为O.(2)直线3y x b =+与x 轴、y 轴分别交于点F,G(0,b)当0<b <1时,线段FG 在⊙O 内部,与⊙O 无公共点此时⊙O 上的点到线段FG 的最小距离为1-b,最大距离为1+b∵线段FG 与⊙O 满足限距关系∴1+b ≥2(1-b),解得13b ≥,∴b 的取值范围为131b ≤<. 当1≤b ≤2时,线段FG 与⊙O 有公共点,线段FG 与⊙O 满足限距关系 当b >2时,线段FG 在⊙O 的外部,与⊙O 没有公共点此时⊙O 上的点到线段FG 的最小距离为121b -,最大距离为b+1 ∵线段FG 与⊙O 满足限距关系∴11212b b ⎛⎫+≥- ⎪⎝⎭,而11212b b ⎛⎫+≥- ⎪⎝⎭总成立 ∴b >2时,线段FG 与⊙O 满足限距关系,综上所述,b 的取值范围为13b ≥. (3)如图3中,不妨设⊙K,⊙H 的圆心在x 轴上位于y 轴的两侧两圆的距离的最小值为2r-2,最大值为2r+2∵⊙H和⊙K都满足限距关系∴2r+2≥2(2r-2),解得r≤3,故r的取值范围为0<r≤3.24. (1)证明见解析;(2)①见解析,②见解析【详解】(1)证明:如图,连接A’C∵点A、A’关于l对称,点C在l上∴A’C=CA∴CA+CB=A’C+CB=A’B同理AC’+C’B=A’C’+C’B在△A’C’B中,有A’B<A’C’+C’B∴AC+CB<AC’+C’B;(2)解:①在点C处建燃气站,铺设管道的最短路线是AC+CD+DB(如图,其中D是正方形的顶点).②在点C处建燃气站,铺设管道的最短路线是AC+CD++EB(如图,其中CD、BE都与圆相切).第11 页共11 页。
备战中考数学专题训练---圆的综合的综合题分类附答案

一、圆的综合真题与模拟题分类汇编(难题易错题)1.如图1,在Rt△ABC中,AC=8cm,BC=6cm,D、E分别为边AB、BC的中点,连结DE,点P从点A出发,沿折线AD﹣DE运动,到点E停止,点P在AD上以5cm/s的速度运动,在DE上以1cm/s的速度运动,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN.设点P的运动时间为t(s).(1)当点P在线段DE上运动时,线段DP的长为_____cm.(用含t的代数式表示)(2)当正方形PQMN与△ABC重叠部分图形为五边形时,设五边形的面积为S(cm2),求S与t的函数关系式,并写出t的取值范围.(3)如图2,若点O在线段BC上,且CO=1,以点O为圆心,1cm长为半径作圆,当点P 开始运动时,⊙O的半径以0.2cm/s的速度开始不断增大,当⊙O与正方形PQMN的边所在直线相切时,求此时的t值.【答案】(1)t﹣1;(2)S=﹣38t2+3t+3(1<t<4);(3)t=103s.【解析】分析:(1)根据勾股定理求出AB,根据D为AB中点,求出AD,根据点P在AD上的速度,即可求出点P在AD段的运动时间,再求出点P在DP段的运动时间,最后根据DE段运动速度为1c m/s,即可求出DP;(2)由正方形PQMN与△ABC重叠部分图形为五边形,可知点P在DE上,求出DP=t﹣1,PQ=3,根据MN∥BC,求出FN的长,从而得到FM的长,再根据S=S梯形FMHD+S矩形DHQP,列出S与t的函数关系式即可;(3)当圆与边PQ相切时,可求得r=PE=5﹣t,然后由r以0.2c m/s的速度不断增大,r=1+0.2t,然后列方程求解即可;当圆与MN相切时,r=CM=8﹣t=1+0.2t,从而可求得t的值.详解:(1)由勾股定理可知:AB22AC BC.∵D、E分别为AB和BC的中点,∴DE=12AC=4,AD=12AB=5,∴点P在AD上的运动时间=55=1s,当点P在线段DE上运动时,DP段的运动时间为(t﹣1)s.∵DE段运动速度为1c m/s,∴DP=(t﹣1)cm.故答案为t ﹣1.(2)当正方形PQMN 与△ABC 重叠部分图形为五边形时,有一种情况,如下图所示.当正方形的边长大于DP 时,重叠部分为五边形,∴3>t ﹣1,t <4,DP >0,∴t ﹣1>0,解得:t >1,∴1<t <4.∵△DFN ∽△ABC ,∴DN FN =AC BC =86=43. ∵DN =PN ﹣PD ,∴DN =3﹣(t ﹣1)=4﹣t , ∴4t FN -=43,∴FN =344t -(), ∴FM =3﹣344t -()=34t , S =S 梯形FMHD +S 矩形DHQP , ∴S =12×(34t +3)×(4﹣t )+3(t ﹣1)=﹣38t 2+3t +3(1<t <4). (3)①当圆与边PQ 相切时,如图:当圆与PQ 相切时,r =PE ,由(1)可知,PD =(t ﹣1)cm ,∴PE =DE ﹣DP =4﹣(t ﹣1)=(5﹣t )cm .∵r 以0.2c m/s 的速度不断增大,∴r =1+0.2t ,∴1+0.2t =5﹣t ,解得:t =103s . ②当圆与MN 相切时,r =CM .由(1)可知,DP=(t﹣1)cm,则PE=CQ=(5﹣t)cm,MQ=3cm,∴MC=MQ+CQ=5﹣t+3=(8﹣t)cm,∴1+0.2t=8﹣t,解得:t=356s.∵P到E点停止,∴t﹣1≤4,即t≤5,∴t=356s(舍).综上所述:当t=103s时,⊙O与正方形PQMN的边所在直线相切.点睛:本题主要考查的是圆的综合应用,解答本题主要应用了勾股定理、相似三角形的性质和判定、正方形的性质,直线和圆的位置关系,依据题意列出方程是解题的关键.2.在平面直角坐标系xOy中,点M的坐标为(x1,y1),点N的坐标为(x2,y2),且x1≠x2,y1≠y2,以MN为边构造菱形,若该菱形的两条对角线分别平行于x轴,y轴,则称该菱形为边的“坐标菱形”.(1)已知点A(2,0),B(0,23),则以AB为边的“坐标菱形”的最小内角为;(2)若点C(1,2),点D在直线y=5上,以CD为边的“坐标菱形”为正方形,求直线CD 表达式;(3)⊙O的半径为2,点P的坐标为(3,m).若在⊙O上存在一点Q,使得以QP为边的“坐标菱形”为正方形,求m的取值范围.【答案】(1)60°;(2)y=x+1或y=﹣x+3;(3)1≤m≤5或﹣5≤m≤﹣1【解析】分析:(1)根据定义建立以AB为边的“坐标菱形”,由勾股定理求边长AB=4,可得30度角,从而得最小内角为60°;(2)先确定直线CD与直线y=5的夹角是45°,得D(4,5)或(﹣2,5),易得直线CD的表达式为:y=x+1或y=﹣x+3;(3)分两种情况:①先作直线y=x,再作圆的两条切线,且平行于直线y=x,如图3,根据等腰直角三角形的性质分别求P'B=BD=1,PB=5,写出对应P的坐标;②先作直线y=﹣x,再作圆的两条切线,且平行于直线y=﹣x,如图4,同理可得结论.详解:(1)∵点A(2,0),B(0,3∴OA=2,OB3.在Rt△AOB中,由勾股定理得:AB22(),∴∠ABO=30°.223∵四边形ABCD是菱形,∴∠ABC=2∠ABO=60°.∵AB∥CD,∴∠DCB=180°﹣60°=120°,∴以AB为边的“坐标菱形”的最小内角为60°.故答案为:60°;(2)如图2.∵以CD为边的“坐标菱形”为正方形,∴直线CD与直线y=5的夹角是45°.过点C作CE⊥DE于E,∴D(4,5)或(﹣2,5),∴直线CD的表达式为:y=x+1或y=﹣x+3;(3)分两种情况:①先作直线y=x,再作圆的两条切线,且平行于直线y=x,如图3.∵⊙O2,且△OQ'D是等腰直角三角形,∴OD2OQ'=2,∴P'D=3﹣2=1.∵△P'DB是等腰直角三角形,∴P'B=BD=1,∴P'(0,1),同理可得:OA=2,∴AB=3+2=5.∵△ABP是等腰直角三角形,∴PB=5,∴P(0,5),∴当1≤m≤5时,以QP为边的“坐标菱形”为正方形;②先作直线y=﹣x,再作圆的两条切线,且平行于直线y=﹣x,如图4.∵⊙O的半径为2,且△OQ'D是等腰直角三角形,∴OD=2OQ'=2,∴BD=3﹣2=1.∵△P'DB是等腰直角三角形,∴P'B=BD=1,∴P'(0,﹣1),同理可得:OA=2,∴AB=3+2=5.∵△ABP是等腰直角三角形,∴PB=5,∴P(0,﹣5),∴当﹣5≤m≤﹣1时,以QP为边的“坐标菱形”为正方形;综上所述:m的取值范围是1≤m≤5或﹣5≤m≤﹣1.点睛:本题是一次函数和圆的综合题,考查了菱形的性质、正方形的性质、点P,Q的“坐标菱形”的定义等知识,解题的关键是理解题意,学会利用图象解决问题,学会用分类讨论的思想思考问题,注意一题多解,属于中考创新题目.3.矩形ABCD中,点C(3,8),E、F为AB、CD边上的中点,如图1,点A在原点处,点B在y轴正半轴上,点C在第一象限,若点A从原点出发,沿x轴向右以每秒1个单位长度的速度运动,点B随之沿y轴下滑,并带动矩形ABCD在平面内滑动,如图2,设运动时间表示为t秒,当点B到达原点时停止运动.(1)当t=0时,点F的坐标为;(2)当t=4时,求OE的长及点B下滑的距离;(3)求运动过程中,点F到点O的最大距离;(4)当以点F为圆心,FA为半径的圆与坐标轴相切时,求t的值.【答案】(1)F (3,4);(2)8-43;(3)7;(4)t 的值为245或325. 【解析】试题分析:(1)先确定出DF ,进而得出点F 的坐标;(2)利用直角三角形的性质得出∠ABO =30°,即可得出结论; (3)当O 、E 、F 三点共线时,点F 到点O 的距离最大,即可得出结论;(4)分两种情况,利用相似三角形的性质建立方程求解即可.试题解析:解:(1)当t =0时.∵AB =CD =8,F 为CD 中点,∴DF =4,∴F (3,4); (2)当t =4时,OA =4.在Rt △ABO 中,AB =8,∠AOB =90°,∴∠ABO =30°,点E 是AB 的中点,OE =12AB =4,BO =43,∴点B 下滑的距离为843-.(3)当O 、E 、F 三点共线时,点F 到点O 的距离最大,∴FO=OE+EF=7.(4)在Rt △ADF 中,FD 2+AD 2=AF 2,∴AF 22FD AD +,①设AO =t 1时,⊙F 与x 轴相切,点A 为切点,∴FA ⊥OA ,∴∠OAB +∠FAB =90°.∵∠FAD +∠FAB =90°,∴∠BAO =∠FAD .∵∠BOA =∠D =90°,∴Rt △FAE ∽Rt △ABO ,∴AB AO FA FE =,∴1853t =,∴t 1=245,②设AO =t 2时,⊙F 与y 轴相切,B 为切点,同理可得,t 2=325.综上所述:当以点F为圆心,FA为半径的圆与坐标轴相切时,t的值为245或325.点睛:本题是圆的综合题,主要考查了矩形的性质,直角三角形的性质,中点的意义,勾股定理,相似三角形的判定和性质,切线的性质,解(2)的关键是得出∠ABO=30°,解(3)的关键是判断出当O、E、F三点共线时,点F到点O的距离最大,解(4)的关键是判断出Rt△FAE∽Rt△ABD,是一道中等难度的中考常考题.4.如图,AB,BC分别是⊙O的直径和弦,点D为BC上一点,弦DE交⊙O于点E,交AB于点F,交BC于点G,过点C的切线交ED的延长线于H,且HC=HG,连接BH,交⊙O 于点M,连接MD,ME.求证:(1)DE⊥AB;(2)∠HMD=∠MHE+∠MEH.【答案】(1)证明见解析;(2)证明见解析.【解析】分析:(1)连接OC,根据等边对等角和切线的性质,证明∠BFG=∠OCH=90°即可;(2)连接BE,根据垂径定理和圆内接四边形的性质,得出∠HMD=∠BME,再根据三角形的外角的性质证明∠HMD=∠DEB=∠EMB即可.详解:证明:(1)连接OC,∵HC=HG,∴∠HCG=∠HGC;∵HC切⊙O于C点,∴∠OCB+∠HCG=90°;∵OB=OC,∴∠OCB=∠OBC,∵∠HGC=∠BGF,∴∠OBC+∠BGF=90°,∴∠BFG=90°,即DE⊥AB;(2)连接BE,由(1)知DE⊥AB,∵AB是⊙O的直径,∴,∴∠BED=∠BME;∵四边形BMDE内接于⊙O,∴∠HMD=∠BED,∴∠HMD=∠BME;∵∠BME是△HEM的外角,∴∠BME=∠MHE+∠MEH,∴∠HMD=∠MHE+∠MEH.点睛:此题综合性较强,主要考查了切线的性质、三角形的内角和外角的性质、等腰三角形的性质、内接四边形的性质.5.函数是描述客观世界运动变化的重要模型,理解函数的本质是重要的任务。
备战中考数学复习《圆的综合》专项综合练习含答案

一、圆的综合真题与模拟题分类汇编(难题易错题)1.如图,⊙O是△ABC的外接圆,AC为直径,BD=BA,BE⊥DC交DC的延长线于点E(1) 求证:BE是⊙O的切线(2) 若EC=1,CD=3,求cos∠DBA【答案】(1)证明见解析;(2)∠DBA3 5【解析】分析:(1)连接OB,OD,根据线段垂直平分线的判定,证得BF为线段AD的垂直平分线,再根据直径所对的圆周角为直角,得到∠ADC=90°,证得四边形BEDF是矩形,即∠EBF=90°,可得出结论.(2)根据中点的性质求出OF的长,进而得到BF、DE、OB、OD的长,然后根据等角的三角函数求解即可.详解:证明:(1) 连接BO并延长交AD于F,连接OD∵BD=BA,OA=OD∴BF为线段AD的垂直平分线∵AC为⊙O的直径∴∠ADC=90°∵BE⊥DC∴四边形BEDF为矩形∴∠EBF=90°∴BE是⊙O的切线(2) ∵O、F分别为AC、AD的中点∴OF=12CD=32∵BF=DE=1+3=4∴OB=OD=35 422 -=∴cos∠DBA=cos∠DOF=332552OFOD==点睛:此题主要考查了圆的切线的判定与性质,关键是添加合适的辅助线,利用垂径定理和圆周角定理进行解答,注意相等角的关系的转化.2.如图,PA、PB是⊙O的切线,A,B为切点,∠APB=60°,连接PO并延长与⊙O交于C 点,连接AC、BC.(Ⅰ)求∠ACB的大小;(Ⅱ)若⊙O半径为1,求四边形ACBP的面积.【答案】(Ⅰ)60°;(Ⅱ)33【解析】分析:(Ⅰ)连接AO,根据切线的性质和切线长定理,得到OA⊥AP,OP平分∠APB,然后根据角平分线的性质和三角形的外角的性质,30°角的直角三角形的性质,得到∠ACB的度数;(Ⅱ)根据30°角的直角三角形的性质和等腰三角形的性质,结合等底同高的性质求三角形的面积即可.详解:(Ⅰ)连接OA,如图,∵PA、PB是⊙O的切线,∴OA⊥AP,OP平分∠APB,∴∠APO=12∠APB=30°,∴∠AOP=60°,∵OA=OC,∴∠OAC=∠OCA,∴∠ACO=12AOP=30°,同理可得∠BCP=30°,∴∠ACB=60°;(Ⅱ)在Rt△OPA中,∵∠APO=30°,∴AP=3OA=3,OP=2OA=2,∴OP=2OC,而S△OPA=12×1×3,∴S△AOC=12S△PAO=3,∴S△ACP=33,∴四边形ACBP的面积=2S△ACP=332.点睛:本题考查了切线的性质,解直角三角形,等腰三角形的判定,熟练掌握切线的性质是解题的关键.3.如图,△ABC内接于⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC 交AC于点E,交PC于点F,连结AF.(1)判断AF与⊙O的位置关系并说明理由;(2)若AC=24,AF=15,求sin B.【答案】(1) AF与⊙O相切理由见解析;(2)3 5【解析】试题分析:(1)连接OC,先证∠OCF=90°,再证明△OAF≌△OCF,得出∠OAF=∠OCF=90°即可;(2)先求出AE、EF,再证明△OAE∽△AFE,得出比例式OA AEAF EF,可求出半径,进而求出直径,由三角函数的定义即可得出结论.试题解析:解:(1)AF与⊙O相切.理由如下:连接OC.如图所示.∵PC是⊙O的切线,∴OC⊥PC,∴∠OCF=90°.∵OF∥BC,∴∠B=∠AOF,∠OCB=∠COF.∵OB=OC,∴∠B=∠OCB,∴∠AOF=∠COF.在△OAF和△OCF 中,∵OA =OC ,∠AOF =∠COF ,OF =OF ,∴△OAF ≌△OCF (SAS ),∴∠OAF =∠OCF =90°,∴AF 与⊙O 相切;(2)∵△OAF ≌△OCF ,∴∠OAE =∠COE ,∴OE ⊥AC ,AE =12AC =12,∴EF =2215129-=.∵∠OAF =90°,∴△OAE ∽△AFE ,∴OA AE AF EF =,即12159OA =,∴OA =20,∴AB =40,sin B =243405AC AB ==.点睛:本题考查了切线的性质与判定和全等三角形的判定与性质以及相似三角形的判定与性质;熟练掌握切线的证法和三角形相似是解题的关键.4.如图,□ABCD 的边AD 是△ABC 外接圆⊙O 的切线,切点为A ,连接AO 并延长交BC 于点E ,交⊙O 于点F ,过点C 作直线CP 交AO 的延长线于点P ,且∠BCP =∠ACD . (1)求证:PC 是⊙O 的切线;(2)若∠B =67.5°,BC =2,求线段PC ,PF 与弧CF 所围成的阴影部分的面积S .【答案】(1)见解析;(2)14π- 【解析】【分析】(1) 过C 点作直径CM ,连接MB ,根据CM 为直径,可得∠M+∠BCM =90°,再根据AB ∥DC 可得∠ACD =∠BAC ,由圆周角定理可得∠BAC =∠M ,∠BCP =∠ACD ,从而可推导得出∠PCM =90°,根据切线的判定即可得;(2)连接OB ,由AD 是⊙O 的切线,可得∠PAD =90°,再由BC ∥AD ,可得AP ⊥BC ,从而得BE =CE =12BC =1,继而可得到∠ABC =∠ACB =67.5°,从而得到∠BAC =45°,由圆周角定理可得∠BOC=90°,从而可得∠BOE =∠COE =∠OCE = 45°,根据已知条件可推导得出OE =CE =1,PC =OC 22OE CE 2+部分的面积.【详解】(1) 过C 点作直径CM ,连接MB , ∵CM 为直径,∴∠MBC=90°,即∠M+∠BCM=90°,∵四边形ABCD是平行四边形,∴AB∥DC,AD∥BC,∴∠ACD=∠BAC,∵∠BAC=∠M,∠BCP=∠ACD,∴∠M=∠BCP,∴∠BCP+∠BCM=90°,即∠PCM=90°,∴CM⊥PC,∴PC与⊙O相切;(2)连接OB,∵AD是⊙O的切线,切点为A,∴OA⊥AD,即∠PAD=90°,∵BC∥AD,∠AEB=∠PAD=90°,∴AP⊥BC.∴BE=CE=12BC=1,∴AB=AC,∴∠ABC=∠ACB=67.5°,∴∠BAC=180°-∠ABC-∠ACB=45°,∴∠BOC=2∠BAC=90°,∵OB=OC,AP⊥BC,∴∠BOE=∠COE=∠OCE= 45°,∵∠PCM=90°,∴∠CPO=∠COE=∠OCE= 45°,∴OE=CE=1,PC=OC=22OE CE2+=,∴S=S△POC-S扇形OFC=()245π21π221 23604⨯⨯⨯-=-.【点睛】本题考查了切线的判定与性质、圆周角定理、垂径定理、扇形面积等,综合性较强,准确添加辅助线是解题的关键.5.如图1,已知⊙O是ΔADB的外接圆,∠ADB的平分线DC交AB于点M,交⊙O于点C,连接AC,BC.(1)求证:AC=BC;(2)如图2,在图1 的基础上做⊙O的直径CF交AB于点E,连接AF,过点A作⊙O的切线AH,若AH//BC,求∠ACF的度数;(3)在(2)的条件下,若ΔABD的面积为63ΔABD与ΔABC的面积比为2:9,求CD 的长.【答案】(1)证明见解析;(2)30°;(3)233【解析】分析:(1)运用“在同圆或等圆中,弧相等,所对的弦相等”可求解;(2)连接AO并延长交BC于I交⊙O于J,由AH是⊙O的切线且AH∥BC得AI⊥BC,易证∠IAC=30°,故可得∠ABC=60°=∠F=∠ACB,由CF是直径可得∠ACF的度数;(3)过点D作DG⊥AB ,连接AO,知ABC为等边三角形,求出AB、AE的长,在R tΔAEO 中,求出AO的长,得CF的长,再求DG 的长,运用勾股定理易求CD的长.详解:(1)∵DC平分∠ADB,∴∠ADC=∠BDC,∴AC=BC.(2)如图,连接AO并延长交BC于I交⊙O于J∵AH是⊙O的切线且AH∥BC,∴AI⊥BC,∴BI=IC,∵AC=BC,∴IC=1AC,2∴∠IAC=30°,∴∠ABC=60°=∠F=∠ACB.∵FC是直径,∴∠FAC=90°,∴∠ACF=180°-90°-60°=30°. (3)过点D 作DG AB ⊥,连接AO由(1)(2)知ABC 为等边三角形 ∵∠ACF=30°, ∴AB CF ⊥, ∴AE=BE , ∴2ΔABC 33S AB == ∴AB=3 ∴33AE =在RtΔAEO 中,设EO=x ,则AO=2x , ∴222AO AE OE =+, ∴()(222233x x =+,∴x =6,⊙O 的半径为6, ∴CF=12.∵ΔABD 11636322S AB DG DG =⨯⨯=⨯= ∴DG=2.如图,过点D 作DG CF '⊥,连接OD . ∵AB CF ⊥,DG AB ⊥, ∴CF//DG ,∴四边形G ′DGE 为矩形, ∴2G E '=,63211CG G E CE +=++'==',在RtΔOG D '中,5,6OG OD ='=,∴11DG '= ∴2221111233CD DG CG =++=''点睛:本题是一道圆的综合题.考查了圆的基本概念,垂径定理,勾股定理,圆周角定理等相关知识.比较复杂,熟记相关概念是解题关键.6.如图,过⊙O 外一点P 作⊙O 的切线PA 切⊙O 于点A ,连接PO 并延长,与⊙O 交于C 、D 两点,M 是半圆CD 的中点,连接AM 交CD 于点N ,连接AC 、CM . (1)求证:CM 2=MN.MA ;(2)若∠P=30°,PC=2,求CM 的长.【答案】(1)见解析;(2)CM=22. 【解析】 【分析】(1)由CM DM =知CAM DCM ∠=∠,根∠CMA=∠NMC 据证ΔAMC ∽ΔCMN 即可得;(2)连接OA 、DM ,由直角三角形PAO 中∠P=30°知()1122OA PO PC CO ==+,据此求得OA=OC=2,再证三角形CMD 是等腰直角三角形得CM 的长. 【详解】(1)O 中,M 点是半圆CD 的中点, ∴ CM DM =,CAM DCM ∴∠=∠,又CMA NMC ∠=∠, AMC CMN ∽∴∆∆, ∴ CM AM MN CM=,即2·CM MN MA =; (2)连接OA 、DM ,PA 是O 的切线,90PAO ∴∠=︒, 又30P ∠=︒,()1122OA PO PC CO ∴==+,设O 的半径为r ,2PC =,()122r r ∴=+,解得:2r =, 又CD 是直径, 90CMD ∴∠=︒, CM DM =,CMD ∴∆是等腰直角三角形,∴在Rt CMD ∆中,由勾股定理得222CM DM CD +=,即()222216CM r ==,则28CM =,22CM ∴=. 【点睛】本题主要考查切线的判定和性质,解题的关键是掌握切线的性质、圆周角定理、相似三角形的判定和性质等知识点7.如图,在ABC △中,10AC BC ==,3cos 5C =,点P 是BC 边上一动点(不与点,A C 重合),以PA 长为半径的P 与边AB 的另一个交点为D ,过点D 作DE CB ⊥于点E .()1当P 与边BC 相切时,求P 的半径;()2联结BP 交DE 于点F ,设AP 的长为x ,PF 的长为y ,求y 关于x 的函数解析式,并直接写出x 的取值范围;()3在()2的条件下,当以PE 长为直径的Q 与P 相交于AC 边上的点G 时,求相交所得的公共弦的长.【答案】(1)409;(2))25880010x x x y x -+=<<;(3)105- 【解析】 【分析】(1)设⊙P 与边BC 相切的切点为H ,圆的半径为R ,连接HP ,则HP ⊥BC ,cosC=35,则sinC=45,sinC=HPCP=R10R-=45,即可求解;(2)PD∥BE,则EBPD=BFPF,即:2248805x x x yx y--+-=,即可求解;(3)证明四边形PDBE为平行四边形,则AG=GP=BD,即:AB=DB+AD=AG+AD=45,即可求解.【详解】(1)设⊙P与边BC相切的切点为H,圆的半径为R,连接HP,则HP⊥BC,cosC=35,则sinC=35,sinC=HPCP=R10R-=45,解得:R=409;(2)在△ABC中,AC=BC=10,cosC=35,设AP=PD=x,∠A=∠ABC=β,过点B作BH⊥AC,则BH=ACsinC=8,同理可得:CH=6,HA=4,5tan∠()2284x+-2880x x-+25,则525,如下图所示,PA=PD ,∴∠PAD=∠CAB=∠CBA=β,tanβ=2,则cosβ=5,sinβ=5, EB=BDcosβ=(45-25x )×5=4-25x , ∴PD ∥BE ,∴EB PD =BF PF ,即:2248805x x x y x --+-=, 整理得:y=()25x x 8x 800x 103x 20-+<<+; (3)以EP 为直径作圆Q 如下图所示,两个圆交于点G ,则PG=PQ ,即两个圆的半径相等,则两圆另外一个交点为D ,GD 为相交所得的公共弦,∵点Q 时弧GD 的中点,∴DG ⊥EP ,∵AG 是圆P 的直径,∴∠GDA=90°,∴EP ∥BD ,由(2)知,PD ∥BC ,∴四边形PDBE 为平行四边形,∴AG=EP=BD ,∴5设圆的半径为r,在△ADG中,AD=2rcosβ=5,DG=5,AG=2r,5+2r=45,解得:2r=51+,则:DG=5=10-25,相交所得的公共弦的长为10-25.【点睛】本题考查的是圆知识的综合运用,涉及到解直角三角形、勾股定理等知识,其中(3),要关键是根据题意正确画图,此题用大量的解直角三角形的内容,综合难度很大.8.如图,四边形ABCD是⊙O的内接四边形,AC为直径,BD AD=,DE⊥BC,垂足为E.(1)判断直线ED与⊙O的位置关系,并说明理由;(2)若CE=1,AC=4,求阴影部分的面积.【答案】(1)ED与O相切.理由见解析;(2)2=33Sπ-阴影【解析】【分析】(1)连结OD,如图,根据圆周角定理,由BD AD=得到∠BAD=∠ACD,再根据圆内接四边形的性质得∠DCE=∠BAD,所以∠ACD=∠DCE;利用内错角相等证明OD∥BC,而DE⊥BC,则OD⊥DE,于是根据切线的判定定理可得DE为⊙O的切线;(2)作OH⊥BC于H,易得四边形ODEH为矩形,所以OD=EH=2,则CH=HE﹣CE=1,于是有∠HOC=30°,得到∠COD=60°,然后根据扇形面积公式、等边三角形的面积公式和阴影部分的面积=S扇形OCD﹣S△OCD进行计算即可.【详解】(1)直线ED与⊙O相切.理由如下:连结OD,如图,∵BD AD=,∴∠BAD=∠ACD.∵∠DCE=∠BAD,∴∠ACD=∠DCE.∵OC=OD,∴∠OCD=∠ODC,而∠OCD=∠DCE,∴∠DCE=∠ODC,∴OD∥BC.∵DE ⊥BC ,∴OD ⊥DE ,∴DE 为⊙O 的切线;(2)作OH ⊥BC 于H ,则四边形ODEH 为矩形,∴OD =EH .∵CE =1,AC =4,∴OC =OD =2,∴CH =HE ﹣CE =2﹣1=1.在Rt △OHC 中,∵OC =2,CH =1,∠OHC =90°,∠HOC =30°,∴∠COD =60°,∴阴影部分的面积=S 扇形OCD ﹣S △OCD260233604π⋅⋅=-•22 23=π3-.【点睛】本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了扇形面积的计算.9.如图,在△ABC 中,以AC 为直径作⊙O 交BC 于点D ,交AB 于点G ,且D 是BC 中点,DE ⊥AB ,垂足为E ,交AC 的延长线于点F .(1)求证:直线EF 是⊙O 的切线;(2)若CF=3,cosA=25,求出⊙O 的半径和BE 的长;(3)连接CG ,在(2)的条件下,求CG EF的值.【答案】(1)见解析;(2)2,65(3)CG:EF =4:7 【解析】 试题分析:(1)连结OD .先证明OD 是△ABC 的中位线,根据中位线的性质得到OD∥AB,再由DE⊥AB,得出OD⊥EF,根据切线的判定即可得出直线EF是⊙O的切线;(2)先由OD∥AB,得出∠COD=∠A,再解Rt△DOF,根据余弦函数的定义得到cos∠FOD==,设⊙O的半径为R,解方程=,求出R=,那么AB=2OD=,解Rt△AEF,根据余弦函数的定义得到cosA==,求出AE=,然后由BE=AB﹣AE即可求解.试题解析:(1)证明:如图,连结OD.∵CD=DB,CO=OA,∴OD是△ABC的中位线,∴OD∥AB,AB=2OD,∵DE⊥AB,∴DE⊥OD,即OD⊥EF,∴直线EF是⊙O的切线;(2)解:∵OD∥AB,∴∠COD=∠A.在Rt△DOF中,∵∠ODF=90°,∴cos∠FOD==,设⊙O的半径为R,则=,解得R=,∴AB=2OD=.在Rt△AEF中,∵∠AEF=90°,∴cosA===,∴AE=,∴BE=AB﹣AE=﹣=2.【点睛】本题考查了切线的判定,解直角三角形,三角形中位线的性质知识点.要证某线是圆的切线,已知此线过圆上某点,连结圆心与这点(即为半径),再证垂直即可.10.如图,AB是⊙O的直径,∠ACB的平分线交AB于点D,交⊙O于点E,过点C作⊙O 的切线CP交BA的延长线于点P,连接AE.(1)求证:PC=PD;(2)若AC=5cm,BC=12cm,求线段AE,CE的长.【答案】(1)见解析 (2) EC=1722AE=1322【解析】试题分析:(1)如图1中,连接OC、OE.利用等角的余角相等,证明∠PCD=∠PDC即可;(2)如图2中.作EH⊥BC于H,EF⊥CA于F.首先证明Rt△AEF≌Rt△BEH,推出AF=BH,设AF=BH=x,再证明四边形CFEH是正方形,推出CF=CH,可得5+x=12﹣x,推出x=72,延长即可解决问题;试题解析:(1)证明:如图1中,连接OC、OE.∵AB直径,∴∠ACB=90°,∴CE平分∠ACB,∴∠ECA=∠ECB=45°,∴AE=BE,∴OE⊥AB,∴∠DOE=90°.∵PC是切线,∴OC⊥PC,∴∠PCO=90°.∵OC=OE,∴∠OCE=∠OEC.∵∠PCD+∠OCE=90°,∠ODE+∠OEC=90°,∠PDC=∠ODE,∴∠PCD=∠PDC,∴PC=PD.(2)如图2中.作EH⊥BC于H,EF⊥CA于F.∵CE 平分∠ACB ,EH ⊥BC 于H ,EF ⊥CA 于F ,∴EH =EF ,∠EFA =∠EHB =90°.∵AE =BE ,∴AE =BE ,∴Rt △AEF ≌Rt △BEH ,∴AF =BH ,设AF =BH =x .∵∠F =∠FCH =∠CHE =90°,∴四边形CFEH 是矩形.∵EH =EF ,∴四边形CFEH 是正方形,∴CF =CH ,∴5+x =12﹣x ,∴x =72,∴CF =FE =172,∴EC 2CF 172,AE 22EF AF +2217722()()+132 点睛:本题考查了切线的性质、圆周角定理、勾股定理、垂径定理、正方形的判定和性质、全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.。
2025年中考数学总复习培优训第21题圆的综合题专练

以点O为圆心,OC长为半径作⊙O与线段AC交于点D. (1)求证:AB为⊙O的切线;
基础和中档解答题专练
证明:如解图,过点O作OH⊥AB于点H. ∵∠ACB=90°,∴OC⊥BC. ∵BO为△ABC的角平分线,OH⊥AB, ∴OH=OC, 即OH为⊙O的半径. ∴AB为⊙O的切线.
︵
π
AC的长是 3 .
基础和中档解答题专练
5.[2024抚顺顺城区三模]如图,四边形ABCD是⊙O的内接四边 形,AB为⊙O的直径,点D为的中点,连接BD,DF是⊙O的 切线, 交BC的延长线于点F.
(1)求证:DF⊥BC;
基础和中档解答题专练
证明:如解图.连接 OD.
∵DF 是⊙O 的切线,∴DF⊥OD,即∠ODF=90°.
基础和中档解答题专练
基础和中档解答题专练
3.[2024辽阳灯塔一中一模改编]如图1,AB是⊙O的直径,点D 在 AB 的 延 长 线 上 , 点 C , E 是 ⊙ O 上 的 两 点 , CE = CB , ∠BCD=∠CAE,延长AE交BC的延长线于点F.
(1)求证:CD是⊙O的切线; Nhomakorabea基础和中档解答题专练
︵
︵︵
∵D 为AC的中点,∴AD=CD.∴∠ABD=∠CBD.
又∵OB=OD,∴∠ABD=∠ODB.
∴∠CBD=∠ODB.∴OD∥BC.
∴∠ODF+∠DFB=180°.
∴∠DFB=90°.∴DF⊥BC.
(2)若AD=6,BD=8,求CF的长. CF=3.6.
基础和中档解答题专练
基础和中档解答题专练
第二篇 基础和中档解答题专练 第21题 圆的综合题专练
2020-2021备战中考数学综合题专练∶圆的综合及详细答案

2020-2021备战中考数学综合题专练∶圆的综合及详细答案一、圆的综合1.如图,已知△ABC内接于⊙O,BC交直径AD于点E,过点C作AD的垂线交AB的延长线于点G,垂足为F.连接OC.(1)若∠G=48°,求∠ACB的度数;(2)若AB=AE,求证:∠BAD=∠COF;(3)在(2)的条件下,连接OB,设△AOB的面积为S1,△ACF的面积为S2.若tan∠CAF=12,求12SS的值.【答案】(1)48°(2)证明见解析(3)3 4【解析】【分析】(1)连接CD,根据圆周角定理和垂直的定义可得结论;(2)先根据等腰三角形的性质得:∠ABE=∠AEB,再证明∠BCG=∠DAC,可得»»»CD PB PD==,则所对的圆周角相等,根据同弧所对的圆周角和圆心角的关系可得结论;(3)过O作OG⊥AB于G,证明△COF≌△OAG,则OG=CF=x,AG=OF,设OF=a,则OA=OC=2x-a,根据勾股定理列方程得:(2x-a)2=x2+a2,则a=34x,代入面积公式可得结论.【详解】(1)连接CD,∵AD是⊙O的直径,∴∠ACD=90°,∴∠ACB+∠BCD=90°,∵AD⊥CG,∴∠AFG=∠G+∠BAD=90°,∵∠BAD=∠BCD,∴∠ACB=∠G=48°;(2)∵AB=AE,∴∠ABE=∠AEB,∵∠ABC=∠G+∠BCG,∠AEB=∠ACB+∠DAC,由(1)得:∠G=∠ACB,∴∠BCG=∠DAC,∴»»CD PB=,∵AD是⊙O的直径,AD⊥PC,∴»»CD PD=,∴»»»CD PB PD==,∴∠BAD=2∠DAC,∵∠COF=2∠DAC,∴∠BAD=∠COF;(3)过O作OG⊥AB于G,设CF=x,∵tan∠CAF=12=CF AF,∴AF=2x,∵OC=OA,由(2)得:∠COF=∠OAG,∵∠OFC=∠AGO=90°,∴△COF≌△OAG,∴OG=CF=x,AG=OF,设OF=a,则OA=OC=2x﹣a,Rt△COF中,CO2=CF2+OF2,∴(2x﹣a)2=x2+a2,a=34 x,∴OF=AG=34 x,∵OA=OB,OG⊥AB,∴AB=2AG=32x,∴1213··3 22 1·24·2AB OG x xSS x xCF AF===.【点睛】圆的综合题,考查了三角形的面积、垂径定理、角平分线的性质、三角形全等的性质和判定以及解直角三角形,解题的关键是:(1)根据圆周角定理找出∠ACB+∠BCD=90°;(2)根据外角的性质和圆的性质得:»»»CDPB PD ==;(3)利用三角函数设未知数,根据勾股定理列方程解决问题.2.如图,AB 是半圆的直径,过圆心O 作AB 的垂线,与弦AC 的延长线交于点D ,点E 在OD 上DCE B ∠=∠.(1)求证:CE 是半圆的切线;(2)若CD=10,2tan 3B =,求半圆的半径.【答案】(1)见解析;(2)413【解析】分析: (1)连接CO ,由DCE B ∠=∠且OC=OB,得DCE OCB ∠=∠,利用同角的余角相等判断出∠BCO+∠BCE=90°,即可得出结论;(2)设AC=2x ,由根据题目条件用x 分别表示出OA 、AD 、AB ,通过证明△AOD ∽△ACB ,列出等式即可.详解:(1)证明:如图,连接CO .∵AB 是半圆的直径,∴∠ACB =90°.∴∠DCB =180°-∠ACB =90°.∴∠DCE+∠BCE=90°.∵OC =OB ,∴∠OCB =∠B.∵=DCE B ∠∠,∴∠OCB =∠DCE .∴∠OCE =∠DCB =90°.∴OC ⊥CE .∵OC 是半径,∴CE 是半圆的切线.(2)解:设AC =2x ,∵在Rt △ACB 中,2tan 3AC B BC ==, ∴BC =3x .∴AB ==.∵OD ⊥AB ,∴∠AOD =∠A CB=90°.∵∠A =∠A ,∴△AOD ∽△ACB .∴AC AO AB AD=. ∵122OA AB x ==,AD =2x+10, ∴2210x =+. 解得x =8.∴8OA == 则半圆的半径为点睛:本题考查了切线的判定与性质,圆周角定理,相似三角形.3.已知▱ABCD 的周长为26,∠ABC=120°,BD 为一条对角线,⊙O 内切于△ABD ,E ,F ,G 为切点,已知⊙O 的半径为▱ABCD的面积.【答案】【解析】【分析】首先利用三边及⊙O 的半径表示出平行四边形的面积,再根据题意求出AB+AD=13,然后利用切线的性质求出BD的长即可解答.【详解】设⊙O分别切△ABD的边AD、AB、BD于点G、E、F;平行四边形ABCD的面积为S;则S=2S△ABD=2×12(AB·OE+BD·OF+AD·OG)=3(AB+AD+BD);∵平行四边形ABCD的周长为26,∴AB+AD=13,∴S=3(13+BD);连接OA;由题意得:∠OAE=30°,∴AG=AE=3;同理可证DF=DG,BF=BE;∴DF+BF=DG+BE=13﹣3﹣3=7,即BD=7,∴S=3(13+7)=203.即平行四边形ABCD的面积为203.4.如图,PA、PB是⊙O的切线,A,B为切点,∠APB=60°,连接PO并延长与⊙O交于C 点,连接AC、BC.(Ⅰ)求∠ACB的大小;(Ⅱ)若⊙O半径为1,求四边形ACBP的面积.【答案】(Ⅰ)60°;(Ⅱ)33 2【解析】分析:(Ⅰ)连接AO,根据切线的性质和切线长定理,得到OA⊥AP,OP平分∠APB,然后根据角平分线的性质和三角形的外角的性质,30°角的直角三角形的性质,得到∠ACB的度数;(Ⅱ)根据30°角的直角三角形的性质和等腰三角形的性质,结合等底同高的性质求三角形的面积即可.详解:(Ⅰ)连接OA,如图,∵PA、PB是⊙O的切线,∴OA⊥AP,OP平分∠APB,∴∠APO=12∠APB=30°,∴∠AOP=60°,∵OA=OC,∴∠OAC=∠OCA,∴∠ACO=12AOP=30°,同理可得∠BCP=30°,∴∠ACB=60°;(Ⅱ)在Rt△OPA中,∵∠APO=30°,∴33,OP=2OA=2,∴OP=2OC,而S△OPA=123∴S△AOC=12S△PAO3∴S△ACP33,∴四边形ACBP的面积=2S△ACP=332.点睛:本题考查了切线的性质,解直角三角形,等腰三角形的判定,熟练掌握切线的性质是解题的关键.5.如图,一条公路的转弯处是一段圆弧»().AB()1用直尺和圆规作出»AB所在圆的圆心O;(要求保留作图痕迹,不写作法) ()2若»AB的中点C到弦AB的距离为2080m AB m=,,求»AB所在圆的半径.【答案】(1)见解析;(2)50m【解析】分析:()1连结AC 、BC ,分别作AC 和BC 的垂直平分线,两垂直平分线的交点为点O ,如图1;()2连接OA OC OC ,,交AB 于D ,如图2,根据垂径定理的推论,由C 为»AB的中点得到1OC AB AD BD AB 402⊥===,,则CD 20=,设O e 的半径为r ,在Rt OAD V 中利用勾股定理得到222r (r 20)40=-+,然后解方程即可.详解:()1如图1,点O 为所求;()2连接OA OC OC ,,交AB 于D ,如图2,C Q 为»AB 的中点,OC AB ∴⊥,1402AD BD AB ∴===, 设O e 的半径为r ,则20OA r OD OD CD r ==-=-,,在Rt OAD V 中,222OA OD AD =+Q ,222(20)40r r∴=-+,解得50r=,即»AB所在圆的半径是50m.点睛:本题考查了垂径定理及勾股定理的应用,在利用数学知识解决实际问题时,要善于把实际问题与数学中的理论知识联系起来,能将生活中的问题抽象为数学问题.6.如图.在△ABC中,∠C=90°,AC=BC,AB=30cm,点P在AB上,AP=10cm,点E从点P 出发沿线段PA以2c m/s的速度向点A运动,同时点F从点P出发沿线段PB以1c m/s的速度向点B运动,点E到达点A后立刻以原速度沿线段AB向点B运动,在点E、F运动过程中,以EF为边作正方形EFGH,使它与△ABC在线段AB的同侧,设点E、F运动的时间为t (s)(0<t<20).(1)当点H落在AC边上时,求t的值;(2)设正方形EFGH与△ABC重叠部分的面积为S.①试求S关于t的函数表达式;②以点C为圆心,12t为半径作⊙C,当⊙C与GH所在的直线相切时,求此时S的值.【答案】(1)t=2s或10s;(2)①S=2229?(02)75050(210)240400?(1020)t tt t tt t t⎧<≤⎪⎪-+-<≤⎨⎪-+<<⎪⎩;②100cm2.【解析】试题分析:(1)如图1中,当0<t≤5时,由题意AE=EH=EF,即10﹣2t=3t,t=2;如图2中,当5<t<20时,AE=HE,2t﹣10=10﹣(2t﹣10)+t,t=10;(2)分四种切线讨论a、如图3中,当0<t≤2时,重叠部分是正方形EFGH,S=(3t)2=9t2.b、如图4中,当2<t≤5时,重叠部分是五边形EFGMN.c、如图5中,当5<t<10时,重叠部分是五边形EFGMN.d、如图6中,当10<t<20时,重叠部分是正方形EFGH.分别计算即可;②分两种情形分别列出方程即可解决问题.试题解析:解:(1)如图1中,当0<t≤5时,由题意得:AE=EH=EF,即10﹣2t=3t,t=2如图2中,当5<t<20时,AE=HE,2t﹣10=10﹣(2t﹣10)+t,t=10.综上所述:t=2s或10s时,点H落在AC边上.(2)①如图3中,当0<t≤2时,重叠部分是正方形EFGH,S=(3t)2=9t2如图4中,当2<t≤5时,重叠部分是五边形EFGMN,S=(3t)2﹣12(5t﹣10)2=﹣72t2+50t﹣50.如图5中,当5<t<10时,重叠部分是五边形EFGMN,S=(20﹣t)2﹣12(30﹣3t)2=﹣72t2+50t﹣50.如图6中,当10<t<20时,重叠部分是正方形EFGH,S=(20﹣t)2=t2﹣40t+400.综上所述:S=2229?(02)75050(210) 240400?(1020)t tt t tt t t⎧<≤⎪⎪-+-<≤⎨⎪-+<<⎪⎩.②如图7中,当0<t≤5时,12t+3t=15,解得:t=307,此时S=100cm2,当5<t<20时,12t+20﹣t=15,解得:t=10,此时S=100.综上所述:当⊙C与GH所在的直线相切时,求此时S的值为100cm2点睛:本题考查了圆综合题、正方形的性质、等腰直角三角形的性质、切线的性质等知识,解题的关键是灵活运用所学知识解决问题,学会用分类讨论的思想思考问题,注意不能漏解,属于中考压轴题.7.已知A(2,0),B(6,0),CB⊥x轴于点B,连接AC画图操作:(1)在y正半轴上求作点P,使得∠APB=∠ACB(尺规作图,保留作图痕迹)理解应用:(2)在(1)的条件下,①若tan∠APB12=,求点P的坐标②当点P的坐标为时,∠APB最大拓展延伸:(3)若在直线y43=x+4上存在点P,使得∠APB最大,求点P的坐标【答案】(1)图形见解析(2)(0,2),(0,4)(0,23)(3)(953-,1255)【解析】试题分析:(1)以AC为直径画圆交y轴于P,连接PA、PB,∠PAB即为所求;(2)①由题意AC的中点K(4,4),以K为圆心AK为半径画圆,交y轴于P和P′,易知P(0,2),P′(0,6);②当⊙K与y轴相切时,∠APB的值最大,(3)如图3中,当经过AB的园与直线相切时,∠APB最大.想办法求出点P坐标即可解决问题;试题解析:解:(1)∠APB如图所示;(2)①如图2中,∵∠APB=∠ACB,∴tan∠ACB=tan∠APB=12=ABBC.∵A(2,0),B(6,0),∴AB=4,BC=8,∴C(6,8),∴AC的中点K(4,4),以K为圆心AK为半径画圆,交y轴于P和P′,易知P(0,2),P′(0,6).②当⊙K与y轴相切时,∠APB的值最大,此时AK=PK=4,AC=8,∴BC22AC AB-3,∴C(6,3∴K(4,2),∴P(0,3案为:(0,3(3)如图3中,当经过AB的园与直线相切时,∠APB最大.∵直线y=43x+4交x轴于M(﹣3,0),交y轴于N(0,4).∵MP是切线,∴MP2=MA•MB,∴MP5PK⊥OA于K.∵ON∥PK,∴ONPK=OMMK=NMMP,∴4PK=3MK=35,∴PK=1255,MK=95,∴OK=95﹣3,∴P(95﹣3,125).点睛:本题考查了一次函数综合题、直线与圆的位置关系、平行线的性质、切线的判定和性质、勾股定理、锐角三角函数等知识,解题的关键是学会添加常用辅助线解决问题,学会构造辅助圆解决最大角问题,属于中考压轴题.8.如图,AD是△ABC的角平分线,以AD为弦的⊙O交AB、AC于E、F,已知EF∥BC.(1)求证:BC是⊙O的切线;(2)若已知AE=9,CF=4,求DE长;(3)在(2)的条件下,若∠BAC=60°,求tan∠AFE的值及GD长.【答案】(1)证明见解析(2)DE=6(318367-【解析】试题分析:(1)连接OD,由角平分线的定义得到∠1=∠2,得到»»DE DF=,根据垂径定理得到OD⊥EF,根据平行线的性质得到OD⊥BC,于是得到结论;(2)连接DE,由»»DE DF=,得到DE=DF,根据平行线的性质得到∠3=∠4,等量代换得到∠1=∠4,根据相似三角形的性质即可得到结论;(3)过F作FH⊥BC于H,由已知条件得到∠1=∠2=∠3=∠4=30°,解直角三角形得到FH=12DF=12×6=3,3227CF HF-=,根据三角函数的定义得到tan∠AFE=tan∠C=37HFCH=;根据相似三角形到现在即可得到结论.试题解析:(1)连接OD , ∵AD 是△ABC 的角平分线, ∴∠1=∠2,∴»»DEDF =, ∴OD ⊥EF , ∵EF ∥BC , ∴OD ⊥BC , ∴BC 是⊙O 的切线; (2)连接DE ,∵»»DEDF =, ∴DE=DF , ∵EF ∥BC , ∴∠3=∠4, ∵∠1=∠3, ∴∠1=∠4, ∵∠DFC=∠AED , ∴△AED ∽△DFC ,∴AE DE DF CF =,即94DEDE =, ∴DE 2=36, ∴DE=6;(3)过F 作FH ⊥BC 于H , ∵∠BAC=60°,∴∠1=∠2=∠3=∠4=30°,∴FH=12DF=162⨯=3,∴=, ∵EF ∥BC , ∴∠C=∠AFE ,∴tan ∠AFE=tan ∠C=HF CH =; ∵∠4=∠2.∠C=∠C , ∴△ADC ∽△DFC , ∴AD CDDF CF=, ∵∠5=∠5,∠3=∠2, ∴△ADF ∽△FDG ,∴AD DFDF DG=, ∴CD DF CF DG =,即33764DG +=, ∴DG=183675-.点睛:本题考查了切线的判定、圆周角定理、相似三角形的判定与性质、解直角三角形、平行线的性质,正确作出辅助线是解题的关键.9.如图,正三角形ABC 内接于⊙O ,P 是BC 上的一点,且PB <PC ,PA 交BC 于E ,点F 是PC 延长线上的点,CF=PB ,AB=13,PA=4. (1)求证:△ABP ≌△ACF ; (2)求证:AC 2=PA•AE ; (3)求PB 和PC 的长.【答案】(1)证明见解析;(2)证明见解析;(3)PB=1,PC=3.【解析】试题分析:(1)先根据等边三角形的性质得到AB=AC ,再利用圆的内接四边形的性质得∠ACF=∠ABP ,于是可根据“SAS”判断△ABP ≌△ACF ;(2)先根据等边三角形的性质得到∠ABC=∠ACB=60°,再根据圆周角定理得∠APC=∠ABB=60°,加上∠CAE=∠PAC ,于是可判断△ACE ∽△APC ,然后利用相似比即可得到结论;(3)先利用AC 2=PA•AE 计算出AE=134 ,则PE=AP-AE=34,再证△APF 为等边三角形,得到PF=PA=4,则有PC+PB=4,接着证明△ABP ∽△CEP ,得到PB•PC=PE•A=3,然后根据根与系数的关系,可把PB 和PC 看作方程x 2-4x+3=0的两实数解,再解此方程即可得到PB 和PC 的长. 试题解析:(1)∵∠ACP+∠ABP=180°,又∠ACP+∠ACF=180°, ∴∠ABP=∠ACF 在ABP ∆和ACF ∆中,∵AB=AC ,∠ABP=∠ACF , CF PB = ∴ABP ∆≌ACF ∆. (2)在AEC ∆和ACP ∆中, ∵∠APC=∠ABC ,而ABC ∆是等边三角形,故∠ACB=∠ABC=60º, ∴∠ACE =∠APC . 又∠CAE =∠PAC , ∴AEC ∆∽ACP ∆ ∴AC AEAP AC=,即2AC PA AE =⋅. 由(1)知ABP ∆≌ACF ∆, ∴∠BAP=∠CAF , CF PB = ∴∠BAP+∠PAC=∠CAF+∠PAC∴∠PAF=∠BAC=60°,又∠APC =∠ABC =60°. ∴APF ∆是等边三角形 ∴AP=PF∴4PB PC PC CF PF PA +=+=== 在PAB ∆与CEP ∆中, ∵∠BAP=∠ECP , 又∠APB=∠EPC=60°, ∴PAB ∆∽CEP ∆ ∴PB PAPE PC=,即PB PC PA PE ⋅=⋅ 由(2)2AC PA AE =⋅,∴()22AC PB PC PA AE PA PE PA AE PE PA +⋅=⋅+⋅=+= ∴()22AC PB PC PA AE PA PE PA AE PE PA +⋅=⋅+⋅=+=∴22222243PB PC PA AC PA AB ⋅=-=-=-=因此PB 和PC 的长是方程2430x x --=的解.解这个方程,得11x =, 23x =. ∵PB<PB ,∴PB=11x =,PC=23x =, ∴PB 和PC 的长分别是1和3。
中考数学总复习《圆的综合题》专项测试卷-附参考答案

中考数学总复习《圆的综合题》专项测试卷-附参考答案一、单选题(共12题;共24分)1.已知⊙O的半径为5,点P到圆心O的距离为6,那么点P与⊙O的位置关系是A.点P在⊙O上B.点P在⊙O内C.点P在⊙O外D.无法确定2.如图,△ABC内接于⊙O,∠C=46°,连接OA,则∠OAB=()A.44°B.45°C.54°D.67°3.下列命题:①三点确定一个圆;②相等的圆周角所对的弧相等;③平分弦的直径垂直于弦;④等弧所对的圆心角相等;其中真命题的个数是()A.0B.1C.2D.34.若圆锥的底面半径长是5,母线长是13,则该圆锥的侧面面积是()A.60B.60πC.65D.65π5.一块等边三角形的木板,边长为1,现将木板沿水平线翻滚(如图),那么B点从开始至结束所走过的路径长度为()A.3π2B.4π3C.4D.2+ 3π26.下列命题正确的个数有()①长度相等的弧叫做等弧;②三点确定一个圆;③平分弦的直径垂直于弦;④弧相等,则弧所对的圆心角相等.A.1B.2C.3D.47.如图是一个几何体的三视图,则这个几何体的侧面积是()A.πcm2B.2 πcm2C.6πcm2D.3πcm28.如图,AB是⊙O的直径,DB、DE分别切⊙O于点B、C,若⊙ACE=25°,则⊙D的度数是()A.50°B.55°C.60°D.65°9.如图,一条公路的转变处是一段圆弧(即图中弧CD,点O是弧CD的圆心),其中CD=600米,E 为弧CD上一点,且OE⊙CD,垂足为F,OF=300√3米,则这段弯路的长度为A.200π米B.100π米C.400π米D.300π米10.如图,⊙O的直径AB与弦CD交于点,AE=6,BE=2,CD=2 ,则⊙AED的度数是()A.30°B.60°C.45°D.36°11.如图,AB是⊙O的直径,C,D是⊙O上的点,⊙CDB=30°,过点C作⊙O的切线交AB的延长线于点E,则sinE的值为()A.√32B.12C.√33D.√312.如图,⊙O的半径为3,四边形ABCD内接于⊙O,连接OB、OD,若⊙BOD=⊙BCD,则BD̂的长为()A.πB.32πC.2πD.3π二、填空题(共6题;共7分)13.如图,△ABC中AB=2,将△ABC绕点A逆时针旋转60°得到△AB1C1,AB1恰好经过点C,则阴影部分的面积为.14.如图,Rt⊙ABC中⊙C=90°,⊙A=30°,AB=4,以AC上的一点O为圆心OA为半径作⊙O,若⊙O与边BC始终有交点(包括B、C两点),则线段AO的取值范围是.15.如图所示一张圆形光盘,已知光盘内直径为2cm,一个宽为2cm的刻度尺在圆形光盘上移动,当刻度尺的一边与光盘相切时,则另一边与光盘边缘两个交点处的读数恰好是“2”和“10”(单位:cm),那么该光盘的外直径是cm,该光盘的面积是cm2.16.如图,⊙O是△ABC的外接圆OB=√13,BC=4则tanA的值为.R,则AC 17.已知半径为R的半圆O,过直径AB上一点C,作CD⊙AB交半圆于点D,且CD=√32的长为18.如图,在矩形ABCD中AB=2,BC=4点E为BC上一动点,过点B作AE的垂线交AE于点F,连接DF则DF的最小值是.三、综合题(共6题;共60分)19.如图,在△ABC中以△ABC的边AB为直径作⊙O,交AC于点D,DE是⊙O的切线,且DE⊥BC 垂足为点E.(1)求证:AB=BC;(2)若DE=3,CE=6,求直径AB长.20.如图,AB是⊙O的直径,点C在⊙O上,AD垂直于过点C的切线,垂足为D.(1)若⊙BAD=80°,求⊙DAC的度数;(2)如果AD=6,AB=8,求AC的长.21.如图,AB为⊙O的直径,点C是⊙O上的一点,AB=8cm,⊙BAC=30°,点D是弦AC上的一点.(1)若OD⊙AC,求OD长;(2)若CD=2OD,判断△ADO形状,并说明理由.22.如图,以⊙ABC的边AB为直径的⊙O与边AC相交于点D,BC是⊙O的切线,E为BC的中点,连接BD、DE.(1)求证:DE是⊙O的切线;(2)设⊙CDE的面积为S1,四边形ABED的面积为S2,若S2=5S1,求tan⊙BAC的值.23.如图,AB、AC是⊙O的两条弦,且AB=AC,点D是弧BC的中点,连接并延长BD、CD,分别交AC、AB的延长线于点E、F.(1)求证:DF=DE(2)若BD=6,CE=8求⊙O的半径.24.如图,AB是⊙O的直径,AC是弦,D是弧BC的中点,过点D作EF垂直于直线AC,垂足为F,交AB的延长线于点E.(1)求证: EF是⊙O的切线;(2)若AF=6,EF=8,求⊙O的半径.参考答案1.【答案】C 2.【答案】A 3.【答案】B 4.【答案】D 5.【答案】B 6.【答案】A 7.【答案】A 8.【答案】A 9.【答案】A 10.【答案】C 11.【答案】B 12.【答案】C 13.【答案】23π14.【答案】√3≤OA ≤43√3 15.【答案】10;24π 16.【答案】2317.【答案】12R 或32R 18.【答案】√17−119.【答案】(1)证明:连接OD .∵DE 是⊙O 的切线 ∴OD ⊥DE ∵DE ⊥BC ∴OD ∥BC ∴∠ODA =∠C又∵OD=OA∴∠ODA=∠OAD ∴∠OAD=∠C∴AB=BC(2)解:连接BD ∵AB为直径∴∠BDA=90°∴∠BDC=90°∴△DEB∼△CED∴DEBE=CEDE∴3BE=63∴BE=3 2∴BC=15 2∴AB=15 220.【答案】(1)解:如图,连接OC∵DC切⊙O于C∴OC⊙CF∴⊙ADC=⊙OCD=90°∴AD //OC∴⊙DAC=⊙OCA∵OA=OC∴⊙OAC=⊙OCA∴⊙DAC=⊙OAC∵⊙BAD=80°∴⊙DAC=12⊙BAD=12×80°=40°(2)解:连接BC.∵AB是直径∴⊙ACB=90°=⊙ADC ∵⊙DAC=⊙BAC∴⊙ADC⊙⊙ACB∴ACAB=ADAC∵AD=6,AB=8∴AC8=6AC∴AC=4 √3.21.【答案】(1)∵AB为⊙O的直径∴∠ACB=90°∵AB=8cm,⊙BAC=30°∴BC=4∵OD⊙AC∴OD//BC∵OA=OB∴OD=12BC=2(2)△ADO是等腰三角形.理由如下:如图,过O作OQ⊥AC于Q,连接OC,∵AB=8,∠BAC=30°∴AC=AB·cos30°=8×√32=4√3∴CQ=AQ=2√3∴OQ=12OA=2设OD=x,则CD=2OD=2x∴DQ=2x−2√3由勾股定理可得:x2=(2x−2√3)2+22∴(√3x−4)2=0∴x1=x2=4√3 3∴AD=4√3−2×4√33=4√33=OD∴△ADO是等腰三角形.22.【答案】(1)证明:连接OD∵OD=OB∴⊙ODB=⊙OBD.∵AB是直径∴⊙ADB=90°∴⊙CDB=90°.∵E为BC的中点∴DE=BE∴⊙EDB=⊙EBD∴⊙ODB+⊙EDB=⊙OBD+⊙EBD 即⊙EDO=⊙EBO.∵BC是以AB为直径的⊙O的切线∴AB⊙BC∴⊙EBO =90°∴⊙ODE =90°∴DE 是⊙O 的切线(2)解:连接AE∵S 2=5S 1,E 为BC 的中点∴S ⊙ACE =3S 1∴S ⊙ADE =2S 1∴AD =2DC∵⊙CBO =90°,⊙CDB =90° ∴⊙BDC⊙⊙ADB∴AD BD =DB DC∴DB 2=AD •DC ,即 DB =√2DC∴DB AD =√2DC 2DC =√22∴tan⊙BAC = DB AD =√2223.【答案】(1)解: ∵AB =AC AB ⏜=AC ⏜ ∵ 点 D 是 BC ⃗⃗⃗⃗⃗ 的中点∴BD ⏜=CD ⏜∴AB ⏜+BD ⏜=AC ⏜+CD ⏜∴ABD ⏜=ACD ⏜∴∠ACD =∠ABD =90°在 △ACF △ABE 中{∠A =∠A AB =AC ∠ABE =∠ACF∴△ACF ≌△ABE(ASA)∴CF =BE又 ∵BD ⏜=CD ⏜∴BD =CD∴CF −CD =BE −BD ,即 DF =DE (2)解:连接 AD由(1)知 ∠ACD =90°∴AD 是 ⊙O 的直径∴∠DCE =90°又 ∵CD =BD =6在 Rt △DCE 中令 AB =AC =x ,在 Rt △ABE 中由 AB 2+BE 2=AE 2 ,得 x 2+(6+10)2=(x +8)2 解得 x =12 ,即 AC =12在 Rt △ACD 中∴⊙O 的半径为 12AD =3√5 24.【答案】(1)证明:连接OD .∵EF⊙AF∴⊙F =90°.∵D 是 BC⌢ 的中点,∴BD ⌢=CD ⌢ . ∴⊙EOD =⊙DOC = 12⊙BOC ∵⊙A = 12⊙BOC ,∴⊙A =⊙EOD ∴OD⊙AF .∴⊙EDO =⊙F =90°.∴OD⊙EF∴EF 是⊙O 的切线;(2)解:在Rt⊙AFE 中∵AF =6,EF =8 ∴AE =√AF 2+EF 2 = √62+82 =10 设⊙O 半径为r ,∴EO =10﹣r . ∵⊙A =⊙EOD ,⊙E =⊙E∴⊙EOD⊙⊙EAF ,∴OD AF = OE EA ∴r 6=10−r 10 .∴r = 154 ,即⊙O 的半径为 154 .。
2024年中考数学一轮复习综合练习题:圆 含参考答案

2024年中考数学一轮复习综合练习题:圆一、单选题1.两个圆的半径分别为4cm 和3cm ,圆心距是7cm ,则这两个圆的位置关系是()A .内切B .相交C .外切D .外离2.如图,现有一圆心角为90°,半径为8cm 的扇形纸片,用它恰好围成一个圆锥的侧面(接缝忽略不计),则该圆锥底面圆的半径为()A .4cmB .3cmC .2cmD .1cm3.正多边形的一个外角等于60°,则这个正多边形的边数是()A .6B .7C .8D .44.如图,在⊙O 中,∠BOC =50°,则∠A 的度数是()A .50°B .25°C .40°D .35°5.扇形的弧长为20πcm ,面积为240πcm 2,那么扇形的半径是()A .6cmB .12cmC .24cmD .28cm6.如图,BC 是O 的直径,A ,D 是O 上的两点,连接AB ,AD ,BD ,若70ADB ︒∠=,则ABC∠的度数是()A .20°B .70°C .30°D .90°7.如图,螺母的外围可以看作是正六边形ABCDEF ,已知这个正六边形的半径是2,则它的周长是()A .6B .12C .12D .248.如图,正方形的边长为2,以各边为直径在正方形内画半圆,则图中阴影部分的面积()A .π-4B .2π-4C .4-πD .4-2π9.如图,正六边形ABCDEF 中,点P 是边AF 上的点,记图中各三角形的面积依次为12345S S S S S ,,,,,则下列判断正确的是()A .1232S S S +=B .253S S S +=C .2432S S S +=D .153S S S +=10.如图、在Rt △ABC 中,∠C=90°,AC=8,BC=6,两等圆⊙A ,⊙B 外切,那么图中两个扇形(即阴影部分)的面积之和为()A .258πB .254πC .2516πD .2532π二、填空题11.圆内接正六边形的边长为6,则该正六边形的边心距为.12.若⊙O 的直径是4,圆心O 到直线l 的距离为3,则直线l 与⊙O 的位置关系是.13.如图,在Rt △ABC 中,∠ABC=90°,⊙O 的圆心在AB 边上,且分别与AC 、BC 相切于点D 、B ,若AB=6cm ,AC=10cm ,则⊙O 的半径为cm .14.如图,如AE 是⊙O 的直径,半径OD 垂直于弦AB ,垂足为C ,AB=8cm ,CD=2cm ,则BE=.15.已知正六边形的边长为4cm ,分别以它的三个不相邻的顶点为圆心,边长为半径作弧(如图),则所得到的三条弧的长度之和为cm .(结果保留π)三、解答题16.如图,AB 为O 的直径,弦CD AB ⊥于点E ,若26AB =,8EB =,求弦CD 的长.17.如图,圆O 是ABC 的内切圆,其中75AB BC ==,,8AC =,求其内切圆的半径.18.如图,BC 是O 的弦,半径OA BC ⊥,点D 在O 上,且50AOC ∠=︒.求ADB ∠的度数.19.如图,点A 、B 在⊙O 上,直线AC 是⊙O 的切线,OC ⊥OB ,连接AB 交OC 于点D .(1)求证:AC=CD ;(2)如果OD=1,tan ∠OCA=52,求AC 的长.20.已知:AB 是⊙O 的直径,DA 、DC 分别是⊙O 的切线,点A 、C 是切点,连接DO 交弧AC 于点E ,连接AE 、CE .(1)如图1,求证:EA=EC ;(2)如图2,延长DO 交⊙O 于点F ,连接CF 、BE 交于点G ,求证:∠CGE=2∠F ;(3)如图3,在(2)的条件下,DE=12AD ,,求线段CG 的长.答案解析部分1.【答案】C 2.【答案】C 3.【答案】A 4.【答案】B 5.【答案】C 6.【答案】A 7.【答案】C 8.【答案】B 9.【答案】B 10.【答案】B 11.【答案】12.【答案】相离13.【答案】8314.【答案】6cm 15.【答案】8π16.【答案】解:连接OC ,如图所示:∵AB 为O 的直径,CD AB ⊥,∴12CE DE CD ==,1132OC OB AB ===,∴1385OE OB EB =-=-=,在Rt OCE 中,由勾股定理得:12CE ==,∴224CD CE ==.17.【答案】解:过B 作BD ⊥AC 于D ,切点分别为E 、F 、G ,连结OE ,OF ,OG ,设AD=x ,CD=8-x ,其内切圆的半径为r ,根据勾股定理2222AB AD BC CD -=-,即()2222758x x -=--,解方程得112x =,∴==∵圆O 是ABC 的内切圆,∴OE ⊥AC ,OF ⊥AB ,OG ⊥BC ,OE=OF=OG=r ,∴S △ABC=()1111122222AC BD AB OF BC OG AC OE AB BC AC r ⋅=⋅+⋅+⋅=++⋅,∴()AC BD AB BC AC r ⋅=++⋅,∴8220AC BDr AB BC AC⋅===++18.【答案】解:∵BC OA ⊥,OA 为半径,∴ AB=AC,∴11502522ADB AOC ∠=∠=⨯︒=︒.19.【答案】(1)证明:∵直线AC 是⊙O 的切线,∴OA ⊥AC ,∴∠OAC=90°,即∠OAB+∠DAC=90°,∵OC ⊥OB ,∴∠B+∠ODB=90°,∵OA=OB ,∴∠B=∠DAB ,∵∠ODB=∠ADC ,∴∠ADC=∠DAC ,∴AC=CD ;(2)解:在Rt △OAC 中,∠OAC=90°,∵tan ∠OCA=2,∴OA AC =2,∴设AC=2x ,则AO=x ,由勾股定理得:OC=3x ,∵AC=CD ,∴AC=CD=2x ,∵OD=1,∴OC=2x+1,∴2x+1=3x ,解得:x=1,∴AC=2.20.【答案】证明:(1)如图1,连接OC ,∵DA 、DC 分别是⊙O 的切线,点A 、C 是切点,OA 、OC 是半径,∴OA ⊥DA ,OC ⊥DC ,∴∠DAO=∠DCO=90°,在Rt △ODA 和Rt △ODC 中,O =OO =O,∴Rt △ODA ≌Rt △ODC ,∴∠EOA=∠EOC ,∴AE=CE ;(2)证明:如图2,连接OC ,BE ,由(1)证得∠AOE=∠COE ,又∵∠B=12∠AOE ,∠F=12∠COE ,∴∠B=∠F ,∵OB=OE ,∴∠B=∠OEB ,∴∠F=∠OEG ,∵∠EGC 是△EGF 的外角,∴∠EGC=∠F+∠GEF=2∠F ,即∠EGC=2∠F ;(3)解:∵EF 是⊙O 的直径,∴∠ECF=90°∵,∴OA=OE=12∵DE=12AD ,设DE=m ,∴AD=2m ,在Rt △DAO 中,OA 2+DA 2=OD 2,∴()(2222m m +=+,解得m 1=0(舍去),m 2=3,∴DA=43DO=53∴在Rt △ADO 中,tan ∠DOA=DA OA =43,cos ∠DOA=DA OA =35,∵∠EOA=2∠B ,∠EGC=2∠F ,∴∠EGC=∠EOA ,∴tan ∠EGC=43,如图3,过点E 作EH ⊥AB 于点H ,在Rt △EOH 中OH=OE•cos ∠35=35,∴EH=45﹣3525在Rt △EHA 中,EA 2=AH 2+EH 2,∴EA=2,∵AE=CE ,∴EC=2,在Rt △ECG 中,tan ∠EGC=EC GC =2GC =43,∴GC=32.。
中考数学总复习《圆的综合题》专项测试卷(带有答案)

中考数学总复习《圆的综合题》专项测试卷(带有答案)学校:___________班级:___________姓名:___________考号:___________类型一 与圆的性质有关的证明与计算典例精讲例 (一题多设问) 如图,在⊙O 中,AC 为⊙O 的直径,AB 为⊙O 的弦,点E 是AC ︵的中点,过点E 作AB 的垂线,交AB 于点M ,交⊙O 于点N ,分别连接EB ,CN . (1)EM 与BE 的数量关系是________; (2)求证:EB ︵=CN ︵;(3)若AM =3,MB =1,求阴影部分图形的面积.例题图拓展设问(4)若∠BAC =15°,AM =3,求⊙O 的半径及EN 的长.针对演练1.如图,AB是⊙O的直径,弦CD与AB交于点M,过点D作DE⊥CD交⊙O于点E,连接AD,OE,若M为CD的中点.(1)求证:DE∥AB;(2)若OE∥AD①连接AC,求证:AC=DE;②若CD=23,求图中阴影部分的面积.第1题图类型二与切线有关的证明与计算典例精讲例(一题多设问) 如图①,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,交AC于点E,过点D作⊙O的切线DF,与AC交于点F.(1)求证:CF=EF;【思维教练】要证CF=EF,可连接OD、DE,利用切线的性质及AB=AC可证明DF⊥AC,则只需证明△CDE是等腰三角形,利用三线合一的性质即可求证.例题图①(2)如图②,连接BE,求证:DF∥BE;【思维教练】根据AB是⊙O的直径,可以得到BE⊥AC,要证DF∥BE,只需证明DF⊥AC 即可,由(1)即可得知.例题图②(3)如图③,若③O的半径为4,③CDF=30°,求CF的长;【思维教练】要求CF的长,可将其放在Rt△CDF中,利用三角函数求解,连接AD,由⊙O 的半径可得CD的长,即可求解.例题图③(4)如图④,若tan C=2,CE=4,求⊙O的半径;【思维教练】要求⊙O的半径,只需求出AB的长,连接BE,构造出Rt△ABE,在直角三角形中求解即可.例题图④(5)如图③,若③A =45°,AB =4,求阴影部分的面积.【思维教练】要求阴影部分的面积,可将其分为△AOE 、△BOD 及扇形DOE 三部分,利用和差法求解即可.例题图⑤针对演练1. 如图,在Rt △ABC 中,∠C =90°,以点B 为圆心,适当的长为半径作弧,分别交AB 、BC 于点M 、N ,再分别以点M 、N 为圆心,大于12MN 的长为半径作弧,两弧交于点P ,作射线BP ,交AC 于点F .点O 是斜边AB 上一点,以点O 为圆心,OB 的长为半径的圆恰好与AC 相切于点F .第1题图(1)若∠A =30°,求证:△ABF 是等腰三角形;(2)若BC =6,tan A =34,求⊙O 的半径.参考答案类型一 与圆的性质有关的证明与计算典例精讲例 (1)解:BE =2EM ;(2分)【解法提示】∵AC 为⊙O 的直径,E 是AC ︵的中点,∴∠ABE =45°.∵AB ⊥EN ,∴△EMB 为等腰直角三角形,∴BE =2EM . (2)证明:如解图①,连接EO∵AC 是⊙O 的直径,点E 是AC ︵的中点 ∴∠AOE =90°∴∠ABE =12∠AOE =45°.∵EN ⊥AB ,垂足为M ∴∠EMB =90° ∴∠ABE =∠BEN =45° ∴AE ︵=BN ︵. ∵点E 是AC ︵的中点 ∴AE ︵=EC ︵ ∴EC ︵=BN ︵∴EC ︵-BC ︵=BN ︵-BC ︵ ∴EB ︵=CN ︵;(7分)例题解图①(3)解:如解图①,连接AE ,OB ,ON ∵EN ⊥AB ,垂足为M ∴∠AME =∠EMB =90°.∵BM =1,由(2)得∠ABE =∠BEN =45° ∴EM =1,BE = 2.∵在Rt △AEM 中,EM =1,AM =3 ∴tan ∠EAB =13=33∴∠EAB =30°. ∵∠EAB =12∠EOB∴∠EOB =60°. 又∵OE =OB∴△EOB 是等边三角形 ∴OE =BE = 2. 又∵EB ︵=CN ︵∴CN =BE =2,∠CON =∠BOE =60°.又∵S 扇形CON =60π×(2)2360=π3,S △OCN =12CN ·32CN =12×2×32×2=32∴S 阴影=S 扇形CON -S △OCN =π3-32.(12分)拓展设问(4)解:如解图②,连接AE ,AN ,OE ∵点E 是AC ︵的中点 ∴∠AOE =90°.∵OA=OE∴∠EAC=45°.∵∠BAC=15°∴∠EAB=45°-15°=30°.∵EM⊥AB∴在Rt△AEM中,EM=AM·tan30°=3,AE=AMcos30°=23∴在Rt△AOE中,OA=AE·cos45°= 6.∵∠BAN=∠BEN=45°,EM⊥AB∴在Rt△AMN中,MN=AM=3∴EN=EM+MN=3+3∴⊙O的半径为6,EN的长为3+3.例题解图②针对演练1. (1)证明:∵AB是⊙O的直径,CM=DM∴AB⊥CD.∵DE⊥CD∴∠CMB=∠CDE=90°∴DE∥AB;(2)①证明:∵OE∥AD,OA∥DE∴四边形AOED是平行四边形.∵OA=OE∴四边形AOED是菱形∴AD=DE.∵AB⊥CD∴AD=AC∴AC=DE;②解:如解图,连接OC ∵DE ⊥CD∴CE 为⊙O 的直径,即点O 在CE 上. ∵M 为CD 的中点∴CM =12CD =3,AC =AD =OE =OA =OC∴△AOC 是等边三角形∴∠AOC =60°,OC =CMsin ∠AOC =2.∵AD ∥OE∴∠OAD =∠AOC ,∠ADC =∠DCE . ∵AD =OC ∴△ADM ≌△OCM∴S 阴影=S 扇形AOC =60π×22360=2π3.第1题解图类型二 与切线有关的证明与计算典例精讲例 (1)证明:如解图①,连接OD ,DE ∵AB =AC ∴∠ABC =∠ACB . ∵OB =OD ∴∠OBD =∠ODB ∴∠ODB =∠ACB ∴OD ∥AC . ∵DF 是⊙O 的切线 ∴DF ⊥OD ∴DF ⊥AC .∵∠DEC =∠ABC ∴∠DEC =∠ACB ∴DE =CD ∴CF =EF ;例题解图①(2)证明:由(1)知DF ⊥AC ∵AB 是⊙O 的直径 ∴∠AEB =90°,即BE ⊥AC ∴DF ∥BE ;(3)解:如解图②,连接AD ∵∠CDF =30°,DF ⊥AC ∴∠ACB =60°∴∠ABC =∠ACB =60°. ∵AB 是⊙O 的直径 ∴∠ADB =90° ∴BD =CD .在Rt △ABD 中,∵AB =2AO =8 ∴BD =AB ·cos ∠ABC =4 ∴CD =4在Rt △CDF 中,∵∠CDF =30° ∴CF =12CD =2;例题解图②(4)解:如解图③,连接BE∵CE =4,点F 是CE 的中点 ∴CF =2 ∵tan C =DFCF =2∴DF =4 ∴BE =2DF =8设AE =x ,则AB =AC =x +4在Rt △ABE 中,由勾股定理得AB 2=AE 2+BE 2,即(x +4)2=x 2+82 解得x =6 ∴AB =x +4=10 即⊙O 的半径为5;例题解图③(5)解:如解图④,连接OE 、OD ,过点D 作DH ⊥AB 于点H ∵∠A =45°,OA =OE ,AB =AC ∴∠AEO =∠A =45°,∠AOE =90°. ∵AC ∥OD∴∠DOE =∠AEO =45°,∠BOD =∠A =45° ∴DH =22OD =2 ∴S 阴影=S △AOE +S 扇形DOE +S △BOD =12OA 2+45π×22360+12OB ·DH =2+π2+2∴阴影部分的面积为2+π2+ 2.例题解图④针对演练1. (1)证明:∵∠A =30°,∠C =90°第 11 页 共 11 页 ∴∠ABC =60°由作图步骤可知,BP 是∠ABC 的平分线 ∴∠ABF =12∠ABC =30°∴∠A =∠ABF ,即AF =BF∴△ABF 是等腰三角形;(2)解:∵BC =6,tan A =34∴tan A =BC AC =34,即AC =8∴AB =AC 2+BC 2=10如解图,连接OF∵AC 是⊙O 的切线∴∠AFO =90°∴△AOF ∽△ABC∴OF BC =AO AB ,即OF 6=10-OF 10解得OF =154∴⊙O 的半径为154.第1题解图。
哈尔滨备战中考数学压轴题专题复习——圆的综合的综合

哈尔滨备战中考数学压轴题专题复习——圆的综合的综合一、圆的综合1.如图,四边形OABC 是平行四边形,以O 为圆心,OA 为半径的圆交AB 于D ,延长AO 交O 于E ,连接CD ,CE ,若CE 是⊙O 的切线,解答下列问题:(1)求证:CD 是⊙O 的切线;(2)若BC=4,CD=6,求平行四边形OABC 的面积.【答案】(1)证明见解析(2)24【解析】试题分析:(1)连接OD ,求出∠EOC=∠DOC ,根据SAS 推出△EOC ≌△DOC ,推出∠ODC=∠OEC=90°,根据切线的判定推出即可;(2)根据切线长定理求出CE=CD=4,根据平行四边形性质求出OA=OD=4,根据平行四边形的面积公式=2△COD 的面积即可求解.试题解析:(1)证明:连接OD ,∵OD=OA ,∴∠ODA=∠A ,∵四边形OABC 是平行四边形,∴OC ∥AB ,∴∠EOC=∠A ,∠COD=∠ODA ,∴∠EOC=∠DOC ,在△EOC 和△DOC 中,OE OD EOC DOC OC OC =⎧⎪∠=∠⎨⎪=⎩∴△EOC ≌△DOC (SAS ),∴∠ODC=∠OEC=90°,即OD ⊥DC ,∴CD 是⊙O 的切线;(2)由(1)知CD 是圆O 的切线,∴△CDO 为直角三角形,∵S △CDO =12CD•OD , 又∵OA=BC=OD=4,∴S △CDO =12×6×4=12, ∴平行四边形OABC 的面积S=2S △CDO =24.2.已知AB ,CD 都是O e 的直径,连接DB ,过点C 的切线交DB 的延长线于点E . ()1如图1,求证:AOD 2E 180∠∠+=o ;()2如图2,过点A 作AF EC ⊥交EC 的延长线于点F ,过点D 作DG AB ⊥,垂足为点G ,求证:DG CF =;()3如图3,在()2的条件下,当DG 3CE 4=时,在O e 外取一点H ,连接CH 、DH 分别交O e 于点M 、N ,且HDE HCE ∠∠=,点P 在HD 的延长线上,连接PO 并延长交CM 于点Q ,若PD 11=,DN 14=,MQ OB =,求线段HM 的长.【答案】(1)证明见解析(2)证明见解析(3)37【解析】【分析】(1)由∠D +∠E =90°,可得2∠D +2∠E =180°,只要证明∠AOD =2∠D 即可;(2)如图2中,作OR ⊥AF 于R .只要证明△AOR ≌△ODG 即可;(3)如图3中,连接BC 、OM 、ON 、CN ,作BT ⊥CL 于T ,作NK ⊥CH 于K ,设CH 交DE 于W .解直角三角形分别求出KM ,KH 即可;【详解】()1证明:如图1中,O Q e 与CE 相切于点C ,OC CE ∴⊥,OCE 90∠∴=o ,D E 90∠∠∴+=o ,2D 2E 180∠∠∴+=o ,AOD COB ∠∠=Q ,BOC 2D ∠∠=,AOD 2D ∠∠=,AOD 2E 180∠∠∴+=o .()2证明:如图2中,作OR AF ⊥于R .OCF F ORF 90∠∠∠===o Q ,∴四边形OCFR 是矩形,AF//CD ∴,CF OR =,A AOD ∠∠∴=,在AOR V 和ODG V 中,A AOD ∠∠=Q ,ARO OGD 90∠∠==o ,OA DO =,AOR ∴V ≌ODG V ,OR DG ∴=,DG CF ∴=,()3解:如图3中,连接BC 、OM 、ON 、CN ,作BT CL ⊥于T ,作NK CH ⊥于K ,设CH 交DE 于W .设DG 3m =,则CF 3m =,CE 4m =,OCF F BTE 90∠∠∠===o Q ,AF//OC//BT ∴,OA OB =Q ,CT CF 3m ∴==,ET m ∴=,CD Q 为直径,CBD CND 90CBE ∠∠∠∴===o ,E 90EBT CBT ∠∠∠∴=-=o ,tan E tan CBT ∠∠∴=,BT CT ET BT∴=, BT 3m m BT∴=, BT 3m(∴=负根已经舍弃),3m tan E 3∠∴== E 60∠∴=o ,CWD HDE H ∠∠∠=+Q ,HDE HCE ∠∠=,H E 60∠∠∴==o ,MON 2HCN 60∠∠∴==o ,OM ON =Q ,OMN ∴V 是等边三角形,MN ON ∴=,QM OB OM ==Q ,MOQ MQO ∠∠∴=,MOQ PON 180MON 120∠∠∠+=-=o o Q ,MQO P 180H 120∠∠∠+=-=o o , PON P ∠∠∴=,ON NP 141125∴==+=,CD 2ON 50∴==,MN ON 25==,在Rt CDN V 中,2222CN CD DN 501448=-=-=,在Rt CHN V 中,CN 48tan H 3HN HN∠===, HN 163∴=,在Rt KNH V 中,1KH HN 832==,3NK HN 24==, 在Rt NMK V 中,2222MK MN NK 25247=-=-=,HM HK MK 837∴=+=+.【点睛】本题考查圆综合题、全等三角形的判定和性质、平行线的性质、勾股定理、等边三角形的判定和性质、锐角三角函数等知识,添加常用辅助线,构造全等三角形或直角三角形解题的关键.3.如图,△ABC 的内接三角形,P 为BC 延长线上一点,∠PAC=∠B ,AD 为⊙O 的直径,过C 作CG ⊥AD 于E ,交AB 于F ,交⊙O 于G .(1)判断直线PA 与⊙O 的位置关系,并说明理由;(2)求证:AG 2=AF·AB ; (3)若⊙O 的直径为10,AC=25,AB=45,求△AFG 的面积.【答案】(1)PA 与⊙O 相切,理由见解析;(2)证明见解析;(3)3.【解析】试题分析:(1)连接CD ,由AD 为⊙O 的直径,可得∠ACD=90°,由圆周角定理,证得∠B=∠D ,由已知∠PAC=∠B ,可证得DA ⊥PA ,继而可证得PA 与⊙O 相切.(2)连接BG ,易证得△AFG ∽△AGB ,由相似三角形的对应边成比例,证得结论.(3)连接BD ,由AG 2=AF•AB ,可求得AF 的长,易证得△AEF ∽△ABD ,即可求得AE 的长,继而可求得EF 与EG 的长,则可求得答案.试题解析:解:(1)PA 与⊙O 相切.理由如下:如答图1,连接CD ,∵AD 为⊙O 的直径,∴∠ACD=90°.∴∠D+∠CAD=90°.∵∠B=∠D ,∠PAC=∠B ,∴∠PAC=∠D.∴∠PAC+∠CAD=90°,即DA ⊥PA.∵点A 在圆上,∴PA 与⊙O 相切.(2)证明:如答图2,连接BG ,∵AD 为⊙O 的直径,CG ⊥AD ,∴»»AC AD =.∴∠AGF=∠ABG.∵∠GAF=∠BAG ,∴△AGF ∽△ABG.∴AG :AB=AF :AG. ∴AG 2=AF•AB.(3)如答图3,连接BD ,∵AD 是直径,∴∠ABD=90°.∵AG 2=AF•AB ,55∴5∵CG ⊥AD ,∴∠AEF=∠ABD=90°.∵∠EAF=∠BAD ,∴△AEF ∽△ABD. ∴AE AF AB AD =545=,解得:AE=2. ∴221EF AF AE =-=. ∵224EG AG AE =-=,∴413FG EG EF =-=-=.∴1132322AFG S FG AE ∆=⋅⋅=⨯⨯=.考点:1. 圆周角定理;2.直角三角形两锐角的关系;3. 相切的判定;4.垂径定理;5.相似三角形的判定和性质;6.勾股定理;7.三角形的面积.4.如图,已知AB 是⊙O 的直径,点C 为圆上一点,点D 在OC 的延长线上,连接DA , 交BC 的延长线于点E ,使得∠DAC=∠B .(1)求证:DA 是⊙O 切线;(2)求证:△CED ∽△ACD ;(3)若OA=1,sinD=13,求AE 的长.【答案】(1)证明见解析;(22【解析】分析:(1)由圆周角定理和已知条件求出AD ⊥AB 即可证明DA 是⊙O 切线;(2)由∠DAC =∠DCE ,∠D =∠D 可知△DEC ∽△DCA ;(3)由题意可知AO =1,OD =3,DC =2,由勾股定理可知AD =2,故此可得到DC 2=DE •AD ,故此可求得DE 的长,于是可求得AE 的长.详解:(1)∵AB 为⊙O 的直径,∴∠ACB =90°,∴∠CAB +∠B =90°.∵∠DAC =∠B ,∴∠CAB +∠DAC =90°,∴AD ⊥AB .∵OA 是⊙O 半径,∴DA 为⊙O 的切线;(2)∵OB =OC ,∴∠OCB =∠B .∵∠DCE =∠OCB ,∴∠DCE =∠B .∵∠DAC =∠B ,∴∠DAC =∠DCE .∵∠D =∠D ,∴△CED ∽△ACD ;(3)在Rt △AOD 中,OA =1,sin D =13,∴OD =OA sinD =3,∴CD =OD ﹣OC =2. ∵AD =22OD OA -=22. 又∵△CED ∽△ACD ,∴AD CD CD DE =,∴DE =2CD AD=2, ∴AE =AD ﹣DE =22﹣2=2.点睛:本题主要考查的是切线的性质、圆周角定理、勾股定理的应用、相似三角形的性质和判定,证得△DEC ∽△DCA 是解题的关键.5.如图1O e ,的直径12AB P =,是弦BC 上一动点(与点B C ,不重合)30ABC o ,∠=,过点P 作PD OP ⊥交O e 于点D .()1如图2,当//PD AB 时,求PD 的长;()2如图3,当»»DC AC =时,延长AB 至点E ,使12BE AB =,连接DE . ①求证:DE 是O e 的切线;②求PC 的长.【答案】(1)262)333①见解析,②.【解析】分析:()1根据题意首先得出半径长,再利用锐角三角函数关系得出OP PD ,的长; ()2①首先得出OBD V 是等边三角形,进而得出ODE OFB 90∠∠==o ,求出答案即可;②首先求出CF 的长,进而利用直角三角形的性质得出PF 的长,进而得出答案. 详解:()1如图2,连接OD ,//OP PD PD AB ⊥Q ,,90POB ∴∠=o ,O Q e 的直径12AB =,6OB OD ∴==,在Rt POB V 中,30ABC o ∠=, 3tan306233OP OB ∴=⋅=⨯=o , 在Rt POD V 中, 22226(23)26PD OD OP =-=-=;()2①证明:如图3,连接OD ,交CB 于点F ,连接BD ,»»DC AC =Q ,30DBC ABC ∴∠=∠=o ,60ABD o ∴∠=,OB OD =Q ,OBD ∴V 是等边三角形,OD FB ∴⊥,12BE AB =Q , OB BE ∴=,//BF ED ∴,90ODE OFB o ∴∠=∠=,DE ∴是O e 的切线;②由①知,OD BC ⊥,3cos30633CF FB OB ∴==⋅==o在Rt POD V 中,OF DF =, 13(2PF DO ∴==直角三角形斜边上的中线,等于斜边的一半), 333CP CF PF ∴=-=-.点睛:此题主要考查了圆的综合以及直角三角形的性质和锐角三角函数关系,正确得出OBD V 是等边三角形是解题关键.6.已知:AB 是⊙0直径,C 是⊙0外一点,连接BC 交⊙0于点D ,BD=CD,连接AD 、AC .(1)如图1,求证:∠BAD=∠CAD(2)如图2,过点C 作CF ⊥AB 于点F,交⊙0于点E,延长CF 交⊙0于点G.过点作EH ⊥AG 于点H ,交AB 于点K,求证AK=2OF ;(3)如图3,在(2)的条件下,EH 交AD 于点L,若0K=1,AC=CG,求线段AL 的长.图1 图2 图3【答案】(1)见解析(2)见解析(3)12105【解析】试题分析:(1)由直径所对的圆周角等于90°,得到∠ADB =90°,再证明△ABD ≌△ACD 即可得到结论;(2)连接BE .由同弧所对的圆周角相等,得到∠GAB =∠BEG .再证△KFE ≌△BFE ,得到BF =KF =BK .由OF =OB -BF ,AK =AB -BK ,即可得到结论. (3)连接CO 并延长交AG 于点M ,连接BG .设∠GAB =α.先证CM 垂直平分AG ,得到AM =GM ,∠AGC +∠GCM =90°.再证∠GAF =∠GCM =α.通过证明△AGB ≌△CMG ,得到BG =GM =12AG .再证明∠BGC =∠MCG =α.设BF =KF =a , 可得GF =2a ,AF =4a . 由OK =1,得到OF =a +1,AK =2(a +1),AF = 3a +2,得到3a +2=4a ,解出a 的值,得到AF ,AB ,GF ,FC 的值.由tanα=tan ∠HAK =12HK AH =, AK =6,可以求出 AH 的长.再由1tan tan 3BAD BCF ∠=∠= ,利用公式tan ∠GAD =tan tan 1tan tan GAF BAD GAF BAD∠+∠-∠⋅∠,得到∠GAD =45°,则AL 2AH ,即可得到结论.试题解析:解:(1)∵AB 为⊙O 的直径,∴∠ADB =90°,∴∠ADC =90°.∵BD =CD ,∠BDA =∠CDA ,AD =AD ,∴△ABD ≌△ACD ,∴∠BAD =∠CAD .(2)连接BE .∵BG =BG ,∴∠GAB =∠BEG . ∵CF ⊥AB ,∴∠KFE =90°.∵EH ⊥AG ,∴∠AHE =∠KFE =90°,∠AKH =∠EKF ,∴∠HAK =∠KEF =∠BEF . ∵FE =FE ,∠KFE =∠BFE =90°,∴△KFE ≌△BFE ,∴BF =KF =BK .∵ OF =OB -BF ,AK =AB -BK ,∴AK =2OF .(3)连接CO 并延长交AG 于点M ,连接BG .设∠GAB =α.∵AC =CG , ∴点C 在AG 的垂直平分线上.∵ OA =OG ,∴点O 在AG 的垂直平分线上, ∴CM 垂直平分AG ,∴AM =GM ,∠AGC +∠GCM =90°. ∵AF ⊥CG ,∴∠AGC +∠GAF =90°,∴∠GAF =∠GCM =α. ∵AB 为⊙O 的直径,∴∠AGB = 90°,∴∠AGB =∠CMG =90°. ∵AB =AC =CG ,∴△AGB ≌△CMG ,∴BG =GM =12AG .在Rt △AGB 中, 1tan tan 2GB GAB AG α∠=== . ∵∠AMC =∠AGB = 90°,∴BG ∥CM , ∴∠BGC =∠MCG =α. 设BF =KF =a , 1tan tan 2BF BGF GF α∠===,∴GF =2a ,1tan tan 2GF GAF AF α∠=== ,AF =4a .∵OK =1,∴OF =a +1,AK =2OF =2(a +1),∴AF =AK +KF =a +2(a +1)=3a +2,∴3a +2=4a ,∴a =2, AK =6,∴AF =4a =8,AB =AC =CG =10,GF =2a =4,FC =CG -GF =6. ∵tanα=tan ∠HAK =12HK AH =,设KH =m ,则AH =2m ,∴AK 22(2)m m +=6,解得:m=655,∴AH=2m=1255.在Rt△BFC中,1tan3BFBCFFC∠==.∵∠BAD+∠ABD=90°,∠FBC+∠BCF=90°,∴∠BCF=∠BAD,1tan tan3BAD BCF∠=∠=,∴tan∠GAD=tan tan1tan tanGAF BADGAF BAD∠+∠-∠⋅∠=1123111123+=-⨯,∴∠GAD=45°,∴HL=AH,AL=2AH= 12105.7.已知:BD为⊙O的直径,O为圆心,点A为圆上一点,过点B作⊙O的切线交DA的延长线于点F,点C为⊙O上一点,且AB=AC,连接BC交AD于点E,连接AC.(1)如图1,求证:∠ABF=∠ABC;(2)如图2,点H为⊙O内部一点,连接OH,CH若∠OHC=∠HCA=90°时,求证:CH=12DA;(3)在(2)的条件下,若OH=6,⊙O的半径为10,求CE的长.【答案】(1)见解析;(2)见解析;(3)215.【解析】【分析】()1由BD 为O e 的直径,得到D ABD 90∠∠+=o ,根据切线的性质得到FBA ABD 90∠∠+=o ,根据等腰三角形的性质得到C ABC ∠∠=,等量代换即可得到结论;()2如图2,连接OC ,根据平行线的判定和性质得到ACO COH ∠∠=,根据等腰三角形的性质得到OBC OCB ∠∠=,ABC CBO ACB OCB ∠∠∠∠+=+,根据相似三角形的性质即可得到结论;()3根据相似三角形的性质得到AB BD 2OHOC==,根据勾股定理得到22AD BD AB 16=-=,根据全等三角形的性质得到BF BE =,AF AE =,根据射影定理得到212AF 916==,根据相交弦定理即可得到结论.【详解】()1BD Q 为O e 的直径,90BAD ∴∠=o , 90D ABD ∴∠+∠=o ,FB Q 是O e 的切线, 90FBD ∴∠=o , 90FBA ABD ∴∠+∠=o ,FBA D ∴∠=∠, AB AC =Q ,C ABC ∴∠=∠, CD ∠=∠Q ,ABF ABC ∴∠=∠;()2如图2,连接OC ,90OHC HCA ∠=∠=o Q ,//AC OH ∴,ACO COH ∴∠=∠, OB OC =Q ,OBC OCB ∴∠=∠,ABC CBO ACB OCB ∴∠+∠=∠+∠, 即ABD ACO ∠=∠, ABC COH ∴∠=∠,90H BAD ∠=∠=o Q ,ABD ∴V ∽HOC V , 2AD BD CH OC∴==, 12CH DA ∴=; ()3由()2知,ABC V ∽HOC V ,2AB BDOH OC∴==, 6OH =Q ,O e 的半径为10, 212AB OH ∴==,20BD =,16AD ∴==,在ABF V 与ABE V 中,90ABF ABE AB AB BAF BAE ∠=∠⎧⎪=⎨⎪∠=∠=⎩o , ABF ∴V ≌ABE V ,BF BE ∴=,AF AE =, 90FBD BAD ∠=∠=o Q ,2AB AF AD ∴=⋅,212916AF ∴==,9AE AF ∴==,7DE ∴=,15BE ==, AD Q ,BC 交于E , AE DE BE CE ∴⋅=⋅,9721155AE DE CE BE ⋅⨯∴===.【点睛】本题考查了切线的性质,圆周角定理,全等三角形的判定和性质,相似三角形的判定和性质,平行线的性质,勾股定理,射影定理,相交弦定理,正确的识别图形是解题的关键.8.如图①,抛物线y =ax 2+bx+c 经过点A (﹣2,0)、B (4,0)、C (0,3)三点.(1)试求抛物线的解析式;(2)点P 是y 轴上的一个动点,连接PA ,试求5PA+4PC 的最小值;(3)如图②,若直线l 经过点T (﹣4,0),Q 为直线l 上的动点,当以A 、B 、Q 为顶点所作的直角三角形有且仅有三个时,试求直线l 的解析式. 【答案】(1)233384y x x =-++;(2)5PA+4PC 的最小值为18;(3)直线l 的解析式为334y x =+或334y x =--.【解析】 【分析】(1)设出交点式,代入C 点计算即可 (2)连接AC 、BC ,过点A 作AE ⊥BC 于点E ,过点P 作PD ⊥BC 于点D ,易证△CDP ∽△COB ,得到比例式PC PD BC OB =,得到PD=45PC ,所以5PA+4PC =5(PA+45PC )=5(PA+PD ),当点A 、P 、D 在同一直线上时,5PA+4PC =5(PA+PD )=5AE 最小,利用等面积法求出AE=185,即最小值为18 (3)取AB 中点F ,以F 为圆心、FA 的长为半径画圆, 当∠BAQ =90°或∠ABQ =90°时,即AQ 或BQ 垂直x 轴,所以只要直线l 不垂直x 轴则一定找到两个满足的点Q 使∠BAQ =90°或∠ABQ =90°,即∠AQB =90°时,只有一个满足条件的点Q ,∴直线l 与⊙F 相切于点Q 时,满足∠AQB =90°的点Q 只有一个;此时,连接FQ ,过点Q 作QG ⊥x 轴于点G ,利用cos ∠QFT 求出QG ,分出情况Q 在x 轴上方和x 轴下方时,分别代入直接l 得到解析式即可 【详解】解:(1)∵抛物线与x 轴交点为A (﹣2,0)、B (4,0) ∴y =a (x+2)(x ﹣4) 把点C (0,3)代入得:﹣8a =3 ∴a =﹣38∴抛物线解析式为y =﹣38(x+2)(x ﹣4)=﹣38x 2+34x+3 (2)连接AC 、BC ,过点A 作AE ⊥BC 于点E ,过点P 作PD ⊥BC 于点D ∴∠CDP =∠COB =90°∵∠DCP =∠OCB ∴△CDP ∽△COB ∴PC PDBC OB= ∵B (4,0),C (0,3)∴OB=4,OC =3,BC ∴PD =45PC ∴5PA+4PC =5(PA+45PC )=5(PA+PD ) ∴当点A 、P 、D 在同一直线上时,5PA+4PC =5(PA+PD )=5AE 最小 ∵A (﹣2,0),OC ⊥AB ,AE ⊥BC ∴S △ABC =12AB•OC =12BC•AE ∴AE =631855AB OC BC ⨯==n ∴5AE =18∴5PA+4PC 的最小值为18.(3)取AB 中点F ,以F 为圆心、FA 的长为半径画圆 当∠BAQ =90°或∠ABQ =90°时,即AQ 或BQ 垂直x 轴,∴只要直线l 不垂直x 轴则一定找到两个满足的点Q 使∠BAQ =90°或∠ABQ =90° ∴∠AQB =90°时,只有一个满足条件的点Q∵当Q 在⊙F 上运动时(不与A 、B 重合),∠AQB =90° ∴直线l 与⊙F 相切于点Q 时,满足∠AQB =90°的点Q 只有一个 此时,连接FQ ,过点Q 作QG ⊥x 轴于点G ∴∠FQT =90°∵F 为A (﹣2,0)、B (4,0)的中点 ∴F (1,0),FQ =FA =3 ∵T (﹣4,0) ∴TF =5,cos ∠QFT =35FQ TF = ∵Rt △FGQ 中,cos ∠QFT =35FG FQ = ∴FG =35FQ =95∴x Q =1﹣9455=-,QG 125==①若点Q 在x 轴上方,则Q (41255-,)设直线l解析式为:y=kx+b∴40 412 55 k bk b-+=⎧⎪⎨-+=⎪⎩解得:343kb⎧=⎪⎨⎪=⎩∴直线l:334y x=+②若点Q在x轴下方,则Q(41255--,)∴直线l:334y x=--综上所述,直线l的解析式为334y x=+或334y x=--【点睛】本题是二次函数与圆的综合题,同时涉及到三角函数、勾股定理等知识点,综合度比较高,需要很强的综合能力,第三问能够找到满足条件的Q点是关键,同时不要忘记需要分情况讨论9.如图,点B在数轴上对应的数是﹣2,以原点O为原心、OB的长为半径作优弧AB,使点A在原点的左上方,且tan∠AOB3C为OB的中点,点D在数轴上对应的数为4.(1)S扇形AOB=(大于半圆的扇形);(2)点P是优弧AB上任意一点,则∠PDB的最大值为°(3)在(2)的条件下,当∠PDB最大,且∠AOP<180°时,固定△OPD的形状和大小,以原点O 为旋转中心,将△OPD 顺时针旋转α(0°≤α≤360°)①连接CP ,AD .在旋转过程中,CP 与AD 有何数量关系,并说明理由; ②当PD ∥AO 时,求AD 2的值;③直接写出在旋转过程中,点C 到PD 所在直线的距离d 的取值范围.【答案】(1)103π(2)30(3)①AD =2PC ②20+83或20+83③1≤d ≤3 【解析】 【分析】(1)利用扇形的面积公式计算即可.(2)如图1中,当PD 与⊙O 相切时,∠PDB 的值最大.解直角三角形即可解决问题. (3)①结论:AD =2PC .如图2中,连接AB ,AC .证明△COP ∽△AOD ,即可解决问题. ②分两种情形:如图3中,当PD ∥OA 时,设OD 交⊙O 于K ,连接PK 交OC 于H .求出PC 即可.如图④中,当PA ∥OA 时,作PK ⊥OB 于K ,同法可得. ③判断出PC 的取值范围即可解决问题. 【详解】(1)∵tan ∠AOB =3, ∴∠AOB =60°,∴S 扇形AOB =23002103603ππ⋅⋅=(大于半圆的扇形), (2)如图1中,当PD 与⊙O 相切时,∠PDB 的值最大.∵PD 是⊙O 的切线, ∴OP ⊥PD , ∴∠OPD =90°,∵21sin 42OP PDO OD ∠=== ∴∠PDB =30°,同法当DP ′与⊙O 相切时,∠BDP ′=30°,∴∠PDB 的最大值为30°. 故答案为30.(3)①结论:AD =2PC . 理由:如图2中,连接AB ,AC .∵OA =OB ,∠AOB =60°, ∴△AOB 是等边三角形, ∵BC =OC , ∴AC ⊥OB ,∵∠AOC =∠DOP =60°, ∴∠COP =∠AOD ,∵2AO ODOC OP==, ∴△COP ∽△AOD ,∴2AD AOPC OC ==, ∴AD =2PC .②如图3中,当PD ∥OA 时,设OD 交⊙O 于K ,连接PK 交OC 于H .∵OP =OK ,∠POK =60°, ∴△OPK 是等边三角形, ∵PD ∥OA ,∴∠AOP =∠OPD =90°, ∴∠POH +∠AOC =90°, ∵∠AOC =60°, ∴∠POH =30°,∴PH=12OP=1,OH=3PH=3,∴PC=2222PH CH1(13)523+=++=+,∵AD=2PC,∴AD2=4(5+23)=20+83.如图④中,当PA∥OA时,作PK⊥OB于K,同法可得:PC2=12+(3﹣1)2=5﹣23,AD2=4PC2=20﹣83.③由题意1≤PC≤3,∴在旋转过程中,点C到PD所在直线的距离d的取值范围为1≤d≤3.【点睛】本题属于圆综合题,考查了切线的性质,相似三角形的判定和性质,旋转变换,勾股定理,等边三角形的判定和性质等知识,解题的关键是学会用分类讨论的思想思考问题.10.如图,AB为⊙O的直径,且AB=m(m为常数),点C为»AB的中点,点D为圆上一动点,过A点作⊙O的切线交BD的延长线于点P,弦CD交AB于点E.(1)当DC⊥AB时,则DA DBDC+=;(2)①当点D在»AB上移动时,试探究线段DA,DB,DC之间的数量关系;并说明理由;②设CD长为t,求△ADB的面积S与t的函数关系式;(3)当9220PDAC=时,求DEOA的值.【答案】(12;(2)①DA+DB2DC,②S=12t2﹣14m2;(3)242DEOA=.【解析】【分析】(1)首先证明当DC ⊥AB 时,DC 也为圆的直径,且△ADB 为等腰直角三角形,即可求出结果;(2)①分别过点A ,B 作CD 的垂线,连接AC ,BC ,分别构造△ADM 和△BDN 两个等腰直角三形及△NBC 和△MCA 两个全等的三角形,容易证出线段DA ,DB ,DC 之间的数量关系;②通过完全平方公式(DA+DB )2=DA 2+DB 2+2DA•DB 的变形及将已知条件AB =m 代入即可求出结果;(3)通过设特殊值法,设出PD 的长度,再通过相似及面积法求出相关线段的长度,即可求出结果.【详解】解:(1)如图1,∵AB 为⊙O 的直径,∴∠ADB =90°,∵C 为»AB 的中点,∴»»AC BC=, ∴∠ADC =∠BDC =45°,∵DC ⊥AB ,∴∠DEA =∠DEB =90°,∴∠DAE =∠DBE =45°,∴AE =BE ,∴点E 与点O 重合,∴DC 为⊙O 的直径,∴DC =AB ,在等腰直角三角形DAB 中,DA =DB =2AB , ∴DA+DB =2AB =2CD ,∴DA DB DC+=2;(2)①如图2,过点A 作AM ⊥DC 于M ,过点B 作BN ⊥CD 于N ,连接AC ,BC ,由(1)知»»AC BC=,∴AC =BC ,∵AB 为⊙O 的直径,∴∠ACB =∠BNC =∠CMA =90°,∴∠NBC+∠BCN =90°,∠BCN+∠MCA =90°,∴∠NBC =∠MCA ,在△NBC 和△MCA 中,BNC CMA NBC MCA BC CA ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△NBC ≌△MCA (AAS ),∴CN =AM ,由(1)知∠DAE =∠DBE =45°,AM =22DA ,DN=22DB , ∴DC =DN+NC =2DB+2DA =2(DB+DA ), 即DA+DB =2DC ;②在Rt △DAB 中,DA 2+DB 2=AB 2=m 2,∵(DA+DB )2=DA 2+DB 2+2DA•DB ,且由①知DA+DB 2DC 2t ,∴2t )2=m 2+2D A•DB ,∴DA•DB =t 2﹣12m 2, ∴S △ADB =12DA•DB =12t 2﹣14m 2, ∴△ADB 的面积S 与t 的函数关系式S =12t 2﹣14m 2; (3)如图3,过点E 作EH ⊥AD 于H ,EG ⊥DB 于G ,则NE =ME ,四边形DHEG 为正方形,由(1)知»»AC BC =, ∴AC =BC ,∴△ACB 为等腰直角三角形,∴AB =2AC , ∵9220PD AC =, 设PD =92,则AC =20,AB =202,∵∠DBA =∠DBA ,∠PAB =∠ADB ,∴△ABD ∽△PBA ,∴AB BD AD PB AB PA ==, ∴20292202DB =+, ∴DB =162, ∴AD =22AB DB -=122, 设NE =ME =x ,∵S △ABD =12AD•BD =12AD•NE+12BD•ME , ∴12×122×162=12×122•x+12×162•x , ∴x =4827, ∴DE =2HE =2x =967, 又∵AO =12AB =102, ∴96242735102DE OA =⨯=.【点睛】本题考查了圆的相关性质,等腰直三角形的性质,相似的性质等,还考查了面积法及特殊值法的运用,解题的关键是认清图形,抽象出各几何图形的特殊位置关系.11.如图,过⊙O 外一点P 作⊙O 的切线PA 切⊙O 于点A ,连接PO 并延长,与⊙O 交于C 、D 两点,M 是半圆CD 的中点,连接AM 交CD 于点N ,连接AC 、CM .(1)求证:CM 2=MN.MA ;(2)若∠P=30°,PC=2,求CM 的长.【答案】(1)见解析;(2)CM=22. 【解析】【分析】(1)由··CMDM =知CAM DCM ∠=∠,根∠CMA=∠NMC 据证ΔAMC ∽ΔCMN 即可得;(2)连接OA 、DM ,由直角三角形PAO 中∠P=30°知()1122OA PO PC CO ==+,据此求得OA=OC=2,再证三角形CMD 是等腰直角三角形得CM 的长.【详解】 (1)O Q e 中,M 点是半圆CD 的中点,∴ ··CMDM =, CAM DCM ∴∠=∠,又CMA NMC ∠=∠Q ,AMC CMN ∽∴∆∆,∴ CM AM MN CM=,即2·CM MN MA =; (2)连接OA 、DM ,PA Q 是O e 的切线,90PAO ∴∠=︒,又30P ∠=︒Q ,()1122OA PO PC CO ∴==+, 设O e 的半径为r ,2PC =Q ,()122r r ∴=+, 解得:2r =,又CD Q 是直径,90CMD ∴∠=︒,CM DM =Q ,CMD ∴∆是等腰直角三角形,∴在Rt CMD ∆中,由勾股定理得222CM DM CD +=,即()222216CM r ==, 则28CM =, 22CM ∴=.【点睛】本题主要考查切线的判定和性质,解题的关键是掌握切线的性质、圆周角定理、相似三角形的判定和性质等知识点12.(问题情境)如图1,点E 是平行四边形ABCD 的边AD 上一点,连接BE 、CE .求证:BCE 1S 2=V S 平行四边形ABCD .(说明:S 表示面积) 请以“问题情境”为基础,继续下面的探究 (探究应用1)如图2,以平行四边形ABCD 的边AD 为直径作⊙O ,⊙O 与BC 边相切于点H ,与BD 相交于点M .若AD =6,BD =y ,AM =x ,试求y 与x 之间的函数关系式.(探究应用2)如图3,在图1的基础上,点F 在CD 上,连接AF 、BF ,AF 与CE 相交于点G ,若AF =CE ,求证:BG 平分∠AGC .(迁移拓展)如图4,平行四边形ABCD 中,AB :BC =4:3,∠ABC =120°,E 是AB 的中点,F 在BC 上,且BF :FC =2:1,过D 分别作DG ⊥AF 于G ,DH ⊥CE 于H ,请直接写出DG :DH 的值.【答案】【问题情境】见解析;【探究应用1】18y x =;【探究应用2】见解析;【迁移1927【解析】【分析】(1)作EF ⊥BC 于F ,则S △BCE =12BC×EF ,S 平行四边形ABCD =BC×EF ,即可得出结论; (2)连接OH ,由切线的性质得出OH ⊥BC ,OH =12AD =3,求出平行四边形ABCD 的面积=AD×OH =18,由圆周角定理得出AM ⊥BD ,得出△ABD 的面积=12BD×AM =12平行四边形的面积=9,即可得出结果; (3)作BM ⊥AF 于M ,BN ⊥CE 于N ,同图1得:△ABF 的面积=△BCE 的面积=12平行四边形ABCD 的面积,得出12AF×BM =12CE×BN ,证出BM =BN ,即可得出BG 平分∠AGC . (4)作AP ⊥BC 于P ,EQ ⊥BC 于Q ,由平行四边形的性质得出∠ABP =60°,得出∠BAP =30°,设AB =4x ,则BC =3x ,由直角三角形的性质得出BP =12AB =2x ,BQ =12BE ,AP =BP =,由已知得出BE =2x ,BF =2x ,得出BQ =x ,EQ x ,PF =4x ,QF =3x ,QC =4x ,由勾股定理求出AF =x ,CE,连接DF 、DE ,由三角形的面积关系得出AF×DG =CE×DH ,即可得出结果.【详解】(1)证明:作EF ⊥BC 于F ,如图1所示:则S △BCE =12BC×EF ,S 平行四边形ABCD =BC×EF , ∴12BCE ABCD S S =V Y . (2)解:连接OH ,如图2所示:∵⊙O 与BC 边相切于点H ,∴OH ⊥BC ,OH =12AD =3, ∴平行四边形ABCD 的面积=AD×OH =6×3=18,∵AD 是⊙O 的直径,∴∠AMD =90°,∴AM ⊥BD ,∴△ABD 的面积=12BD×AM =12平行四边形的面积=9, 即12xy =9, ∴y 与x 之间的函数关系式y =18x ; (3)证明:作BM ⊥AF 于M ,BN ⊥CE 于N ,如图3所示:同图1得:△ABF 的面积=△BCE 的面积=12平行四边形ABCD 的面积,∴12AF×BM =12CE×BN , ∵AF =CE , ∴BM =BN ,∴BG 平分∠AGC . (4)解:作AP ⊥BC 于P ,EQ ⊥BC 于Q ,如图4所示:∵平行四边形ABCD 中,AB :BC =4:3,∠ABC =120°,∴∠ABP =60°,∴∠BAP =30°,设AB =4x ,则BC =3x ,∴BP =12AB =2x ,BQ =12BE ,AP =3BP =23x , ∵E 是AB 的中点,F 在BC 上,且BF :FC =2:1,∴BE =2x ,BF =2x ,∴BQ =x , ∴EQ =3x ,PF =4x ,QF =3x ,QC =4x ,由勾股定理得:AF =22AP PF +=27x ,CE =22EQ QC +=19x , 连接DF 、DE ,则△CDE 的面积=△ADF 的面积=12平行四边形ABCD 的面积, ∴AF×DG =CE×DH , ∴DG :DH =CE :AF =19x :27x 19:27=.【点睛】本题是圆的综合题目,考查了圆周角定理、平行四边形的性质、三角形面积公式、含30°角的直角三角形的性质、勾股定理、角平分线的判定等知识;本题综合性强,需要添加辅助线,熟练掌握平行四边形的性质和勾股定理是解题的关键.13.如图,在中,,以为直径作,交边于点,交边于点,过点作的切线,交的延长线于点,交于点.(1)求证:;(2)若,,求的半径.【答案】(1)证明见解析;(2)4.【解析】试题分析:(1)连接AD,根据等腰三角形三线合一即可证明.(2)设⊙O的半径为R,则FO=4+R,FA=4+2R,OD=R,连接OD,由△FOD∽△FAE,得列出方程即可解决问题.试题解析:(1)连接AD,∵AB是直径,∴∠ADB=90°,∵AB=AC,AD⊥BC,∴BD=DC.(2)设⊙O的半径为R,则FO=4+R,FA=4+2R,OD=R,连接OD、∵AB=AC,∴∠ABC=∠C,∵OB=OD,∴∠ABC=∠ODB,∴∠ODB=∠C,∴OD∥AC,∴△FOD∽△FAE,∴,∴,整理得R2﹣R﹣12=0,∴R=4或(﹣3舍弃).∴⊙O的半径为4.考点:切线的性质、等腰三角形的性质等知识.14.已知:如图,四边形ABCD为菱形,△ABD的外接圆⊙O与CD相切于点D,交AC于点E.(1)判断⊙O与BC的位置关系,并说明理由;(2)若CE=2,求⊙O的半径r.【答案】(1)相切,理由见解析;(2)2.【解析】试题分析:(1)根据切线的性质,可得∠ODC的度数,根据菱形的性质,可得CD与BC 的关系,根据SSS,可得三角形全等,根据全等三角形的性质,可得∠OBC的度数,根据切线的判定,可得答案;(2)根据等腰三角形的性质,可得∠ACD=∠CAD,根据三角形外角的性质,∠COD=∠OAD+∠AOD,根据直角三角形的性质,可得OC与OD的关系,根据等量代换,可得答案.(1)⊙O与BC相切,理由如下连接OD、OB,如图所示:∵⊙O与CD相切于点D,∴OD⊥CD,∠ODC=90°.∵四边形ABCD为菱形,∴AC垂直平分BD,AD=CD=CB.∴△ABD的外接圆⊙O的圆心O在AC上,∵OD=OB,OC=OC,CB=CD,∴△OBC≌△ODC.∴∠OBC=∠ODC=90°,又∵OB为半径,∴⊙O与BC相切;(2)∵AD=CD,∴∠ACD=∠CAD.∵AO=OD,∴∠OAD=∠ODA.∵∠COD=∠OAD+∠AOD,∠COD=2∠CAD.∴∠COD=2∠ACD又∵∠COD+∠ACD=90°,∴∠ACD=30°.∴OD=12OC,即r=12(r+2).∴r=2.【点睛】运用了切线的判定与性质,利用了切线的判定与性质,菱形的性质,直角三角形的性质.15.如图,直角坐标系中,直线y kx b=+分别交x,y轴于点A(-8,0),B(0,6),C(m,0)是射线AO上一动点,⊙P过B,O,C三点,交直线AB于点D(B,D不重合).(1)求直线AB的函数表达式.(2)若点D在第一象限,且tan∠ODC=53,求点D的坐标.【答案】(1)364y x=+;(2)D(8825,21625).【解析】【分析】(1)把A 、B 两点坐标代入y=kx+b 求出k 、b 的值即可;(2)连结BC ,作DE ⊥OC 于点E ,根据圆周角定理可得∠OBC=∠ODC ,由tan ∠ODC=53可求出OC 的长,进而可得AC 的长,利用∠DAC 的三角函数值可求出DE 的长,即可得D 点纵坐标,代入直线AB 解析式求出D 点横坐标即可得答案.【详解】(1)∵A (-8,0)、B (0,6)在y=kx+b 上,∴086k b b =-+⎧⎨=⎩, 解得346k b ⎧=⎪⎨⎪=⎩,∴直线AB 的函数表达式为y=34x+6. (2)连结BC ,作DE ⊥OC 于点E ,∵∠BOC=90°,∴BC 为⊙P 的直径,∴∠ADC=90°,∵∠OBC=∠ODC ,tan ∠ODC=53, ∴OC 5OB 3=, ∵OB=6,OA=8,∴OC=10,AC=18,AB=10, ∵cos ∠DAC=OA AB =45,sin ∠DAC=OB AB =35, 472AD AC cos DAC 1855∠=⋅=⨯=, 723216DE AD sin DAC 5525∠=⋅=⨯=, ∵D 点在直线AB 上, ∴2163x 6254=+, 解得:88x 25=, ∴D (8825,21625)【点睛】本题考查待定系数法求一次函数解析式、圆周角定理及锐角三角函数的定义,熟练掌握直径所对的圆周角等于90°及正切、正弦、余弦等三角函数的定义是解题关键.。
人教备战中考数学复习《圆的综合》专项综合练习附答案

一、圆的综合 真题与模拟题分类汇编(难题易错题)1.如图,AB 为O 的直径,弦//CD AB ,E 是AB 延长线上一点,CDB ADE ∠=∠. ()1DE 是O 的切线吗?请说明理由;()2求证:2AC CD BE =⋅.【答案】(1)结论:DE 是O 的切线,理由见解析;(2)证明见解析.【解析】【分析】 (1)连接OD ,只要证明OD DE ⊥即可;(2)只要证明:AC BD =,CDB DBE ∽即可解决问题.【详解】()1解:结论:DE 是O 的切线.理由:连接OD .CDB ADE ∠=∠,ADC EDB ∴∠=∠,//CD AB ,CDA DAB ∴∠=∠,OA OD =,OAD ODA ∴∠=∠,ADO EDB ∴∠=∠, AB 是直径,90ADB ∴∠=,90ADB ODE ∴∠=∠=,DE OD ∴⊥,DE ∴是O 的切线.()2//CD AB,ADC DAB∴∠=∠,CDB DBE∠=∠,AC BD∴=,AC BD∴=,DCB DAB∠=∠,EDB DAB∠=∠,EDB DCB∴∠=∠,CDB∴∽DBE,CD DBBD BE∴=,2BD CD BE∴=⋅,2AC CD BE∴=⋅.【点睛】本题考查相似三角形的判定和性质、圆周角定理、切线的判定等知识,解题的关键是学会添加常用辅助线,准确寻找相似三角形解决问题,属于中考常考题型.2.如图1,已知AB是⊙O的直径,AC是⊙O的弦,过O点作OF⊥AB交⊙O于点D,交AC于点E,交BC的延长线于点F,点G是EF的中点,连接CG(1)判断CG与⊙O的位置关系,并说明理由;(2)求证:2OB2=BC•BF;(3)如图2,当∠DCE=2∠F,CE=3,DG=2.5时,求DE的长.【答案】(1)CG与⊙O相切,理由见解析;(2)见解析;(3)DE=2【解析】【分析】(1)连接CE,由AB是直径知△ECF是直角三角形,结合G为EF中点知∠AEO=∠GEC=∠GCE,再由OA=OC知∠OCA=∠OAC,根据OF⊥AB可得∠OCA+∠GCE=90°,即OC⊥GC,据此即可得证;(2)证△ABC∽△FBO得BC ABBO BF=,结合AB=2BO即可得;(3)证ECD∽△EGC得EC EDEG EC=,根据CE=3,DG=2.5知32.53DEDE=+,解之可得.【详解】解:(1)CG与⊙O相切,理由如下:如图1,连接CE,∵AB是⊙O的直径,∴∠ACB=∠ACF=90°,∵点G是EF的中点,∴GF=GE=GC,∴∠AEO=∠GEC=∠GCE,∵OA=OC,∴∠OCA=∠OAC,∵OF⊥AB,∴∠OAC+∠AEO=90°,∴∠OCA+∠GCE=90°,即OC⊥GC,∴CG与⊙O相切;(2)∵∠AOE=∠FCE=90°,∠AEO=∠FEC,∴∠OAE=∠F,又∵∠B=∠B,∴△ABC∽△FBO,∴BC AB,即BO•AB=BC•BF,BO BF∵AB=2BO,∴2OB2=BC•BF;(3)由(1)知GC=GE=GF,∴∠F=∠GCF,∴∠EGC=2∠F,又∵∠DCE=2∠F,∴∠EGC=∠DCE,∵∠DEC=∠CEG,∴△ECD∽△EGC,∴EC ED EG EC =, ∵CE =3,DG =2.5,∴32.53DE DE =+, 整理,得:DE 2+2.5DE ﹣9=0, 解得:DE =2或DE =﹣4.5(舍),故DE =2.【点睛】本题是圆的综合问题,解题的关键是掌握圆周角定理、切线的判定、相似三角形的判定与性质及直角三角形的性质等知识点.3.如图,AB 是半圆O 的直径,半径OC ⊥AB ,OB =4,D 是OB 的中点,点E 是弧BC 上的动点,连接AE ,DE .(1)当点E 是弧BC 的中点时,求△ADE 的面积;(2)若3tan 2AED ∠= ,求AE 的长; (3)点F 是半径OC 上一动点,设点E 到直线OC 的距离为m ,当△DEF 是等腰直角三角形时,求m 的值.【答案】(1)62ADE S =2)1655AE =3)23m =,22m =71m =.【解析】【分析】(1)作EH ⊥AB ,连接OE ,EB ,设DH =a ,则HB =2﹣a ,OH =2+a ,则EH =OH =2+a ,根据Rt △AEB 中,EH 2=AH•BH ,即可求出a 的值,即可求出S △ADE 的值;(2)作DF ⊥AE ,垂足为F ,连接BE ,设EF =2x ,DF =3x ,根据DF ∥BE 故AF AD EF BD=,得出AF =6x ,再利用Rt △AFD 中,AF 2+DF 2=AD 2,即可求出x ,进而求出AE 的长; (3)根据等腰直角三角形的不同顶点进行分类讨论,分别求出m 的值.【详解】解:(1)如图,作EH ⊥AB ,连接OE ,EB ,设DH =a ,则HB =2﹣a ,OH =2+a ,∵点E 是弧BC 中点,∴∠COE =∠EOH =45°,∴EH =OH =2+a ,在Rt △AEB 中,EH 2=AH•BH ,(2+a )2=(6+a )(2﹣a ),解得a =222±-, ∴a =222-,EH=22,S △ADE =1622AD EH =;(2)如图,作DF ⊥AE ,垂足为F ,连接BE设EF =2x ,DF =3x∵DF ∥BE∴AF AD EF BD= ∴622AF x ==3 ∴AF =6x 在Rt △AFD 中,AF 2+DF 2=AD 2(6x )2+(3x )2=(6)2解得x =255AE =8x =1655 (3)当点D 为等腰直角三角形直角顶点时,如图设DH =a由DF=DE,∠DOF=∠EHD=90°,∠FDO+∠DFO=∠FDO+∠EDH,∴∠DFO=∠EDH∴△ODF≌△HED∴OD=EH=2在Rt△ABE中,EH2=AH•BH(2)2=(6+a)•(2﹣a)-解得a=±232m=23当点E为等腰直角三角形直角顶点时,如图同理得△EFG≌△DEH设DH=a,则GE=a,EH=FG=2+a在Rt△ABE中,EH2=AH•BH(2+a)2=(6+a)(2﹣a)解得a=222±-∴m=22当点F为等腰直角三角形直角顶点时,如图同理得△EFM≌△FDO设OF=a,则ME=a,MF=OD=2∴EH=a+2在Rt△ABE中,EH2=A H•BH(a+2)2=(4+a)•(4﹣a)解得a=71m71【点睛】此题主要考查圆内综合问题,解题的关键是熟知全等三角形、等腰三角形、相似三角形的判定与性质.4.如图1,等边△ABC的边长为3,分别以顶点B、A、C为圆心,BA长为半径作AC、CB 、BA ,我们把这三条弧所组成的图形称作莱洛三角形,显然莱洛三角形仍然是轴对称图形,设点l 为对称轴的交点.(1)如图2,将这个图形的顶点A 与线段MN 作无滑动的滚动,当它滚动一周后点A 与端点N 重合,则线段MN 的长为 ;(2)如图3,将这个图形的顶点A 与等边△DEF 的顶点D 重合,且AB ⊥DE ,DE =2π,将它沿等边△DEF 的边作无滑动的滚动当它第一次回到起始位置时,求这个图形在运动过程中所扫过的区域的面积;(3)如图4,将这个图形的顶点B 与⊙O 的圆心O 重合,⊙O 的半径为3,将它沿⊙O 的圆周作无滑动的滚动,当它第n 次回到起始位置时,点I 所经过的路径长为 (请用含n 的式子表示)【答案】(1)3π;(2)27π;(3)3.【解析】试题分析:(1)先求出AC 的弧长,继而得出莱洛三角形的周长为3π,即可得出结论; (2)先判断出莱洛三角形等边△DEF 绕一周扫过的面积如图所示,利用矩形的面积和扇形的面积之和即可;(3)先判断出莱洛三角形的一个顶点和O 重合旋转一周点I 的路径,再用圆的周长公式即可得出.试题解析:解:(1)∵等边△ABC 的边长为3,∴∠ABC =∠ACB =∠BAC =60°,AC BC AB ==,∴AC BC l l ==AB l =603180π⨯=π,∴线段MN 的长为AC BC AB l l l ++=3π.故答案为3π;(2)如图1.∵等边△DEF 的边长为2π,等边△ABC 的边长为3,∴S 矩形AGHF =2π×3=6π,由题意知,AB ⊥DE ,AG ⊥AF ,∴∠BAG =120°,∴S 扇形BAG =21203360π⨯=3π,∴图形在运动过程中所扫过的区域的面积为3(S 矩形AGHF +S 扇形BAG )=3(6π+3π)=27π;(3)如图2,连接BI 并延长交AC 于D .∵I 是△ABC 的重心也是内心,∴∠DAI =30°,AD =12AC =32,∴OI =AI =3230AD cos DAI cos ∠=︒3∴当它第1次回到起始位置时,点I所经过的路径是以O为圆心,OI为半径的圆周,∴当它第n次回到起始位置时,点I所经过的路径长为n•2π•3=23nπ.故答案为23nπ.点睛:本题是圆的综合题,主要考查了弧长公式,莱洛三角形的周长,矩形,扇形面积公式,解(1)的关键是求出AC的弧长,解(2)的关键是判断出莱洛三角形绕等边△DEF 扫过的图形,解(3)的关键是得出点I第一次回到起点时,I的路径,是一道中等难度的题目.5.如图1,在Rt△ABC中,∠ABC=90°,BA=BC,直线MN是过点A的直线CD⊥MN于点D,连接BD.(1)观察猜想张老师在课堂上提出问题:线段DC,AD,BD之间有什么数量关系.经过观察思考,小明出一种思路:如图1,过点B作BE⊥BD,交MN于点E,进而得出:DC+AD= BD.(2)探究证明将直线MN绕点A顺时针旋转到图2的位置写出此时线段DC,AD,BD之间的数量关系,并证明(3)拓展延伸在直线MN绕点A旋转的过程中,当△ABD面积取得最大值时,若CD长为1,请直接写BD的长.【答案】(12;(2)AD﹣2BD;(3)2+1.【解析】【分析】(1)根据全等三角形的性质求出DC,AD,BD之间的数量关系(2)过点B 作BE ⊥BD ,交MN 于点E .AD 交BC 于O ,证明CDB AEB ∆∆≌,得到CD AE =,EB BD =,根据BED ∆为等腰直角三角形,得到2DE BD =, 再根据DE AD AE AD CD =-=-,即可解出答案.(3)根据A 、B 、C 、D 四点共圆,得到当点D 在线段AB 的垂直平分线上且在AB 的右侧时,△ABD 的面积最大.在DA 上截取一点H ,使得CD=DH=1,则易证2CH AH ==,由BD AD =即可得出答案.【详解】解:(1)如图1中,由题意:BAE BCD ∆∆≌,∴AE=CD ,BE=BD ,∴CD+AD=AD+AE=DE ,∵BDE ∆是等腰直角三角形,∴DE=2BD ,∴DC+AD=2BD ,故答案为2.(2)2AD DC BD -=.证明:如图,过点B 作BE ⊥BD ,交MN 于点E .AD 交BC 于O .∵90ABC DBE ∠=∠=︒,∴ABE EBC CBD EBC ∠+∠=∠+∠,∴ABE CBD ∠=∠.∵90BAE AOB ∠+∠=︒,90BCD COD ∠+∠=︒,AOB COD ∠=∠,∴BAE BCD ∠=∠,∴ABE DBC ∠=∠.又∵AB CB =,∴CDB AEB ∆∆≌,∴CD AE =,EB BD =,∴BD ∆为等腰直角三角形,2DE BD =. ∵DE AD AE AD CD =-=-,∴2AD DC BD -=.(3)如图3中,易知A 、B 、C 、D 四点共圆,当点D 在线段AB 的垂直平分线上且在AB 的右侧时,△ABD 的面积最大.此时DG ⊥AB ,DB=DA ,在DA 上截取一点H ,使得CD=DH=1,则易证2CH AH ==, ∴21BD AD ==+.【点睛】 本题主要考查全等三角形的性质,等腰直角三角形的性质以及图形的应用,正确作辅助线和熟悉图形特性是解题的关键.6.如图,在△ABC 中,AB =AC ,以AB 为直径的⊙O 与边BC 交于点D ,DE ⊥AC ,垂足为E ,交AB 的延长线于点F .(1)求证:EF 是⊙O 的切线;(2)若∠C =60°,AC =12,求BD 的长.(3)若tan C =2,AE =8,求BF 的长.【答案】(1)见解析;(2) 2π;(3)103. 【解析】 分析:(1)连接OD ,根据等腰三角形的性质:等边对等角,得∠ABC=∠C ,∠ABC=∠ODB ,从而得到∠C=∠ODB ,根据同位角相等,两直线平行,得到OD ∥AC ,从而得证OD ⊥EF ,即 EF 是⊙O 的切线;(2) 根据中点的性质,由AB=AC=12 ,求得OB=OD=12AB =6,进而根据等边三角形的判定得到△OBD 是等边三角形,即∠BOD=600,从而根据弧长公式七届即可; (3)连接AD ,根据直角三角形的性质,由在Rt △DEC 中, tan 2DE C CE == 设CE=x,则DE=2x ,然后由Rt △ADE 中, tan 2AE ADE DE ∠== ,求得DE 、CE 的长,然后根据相似三角形的判定与性质求解即可.详解:(1)连接OD ∵AB=AC ∴∠ABC=∠C∵OD=OB ∴∠ABC=∠ODB∴∠C=∠ODB ∴OD ∥AC又∵DE ⊥AC ∴OD ⊥DE ,即OD ⊥EF∴EF 是⊙O 的切线(2) ∵AB=AC=12 ∴OB=OD=12AB =6 由(1)得:∠C=∠ODB=600 ∴△OBD 是等边三角形 ∴∠BOD=600∴BD =6062180ππ⨯= 即BD 的长2π (3)连接AD ∵DE ⊥AC ∠DEC=∠DEA=900在Rt △DEC 中, tan 2DE C CE== 设CE=x,则DE=2x ∵AB 是直径 ∴∠ADB=∠ADC=900 ∴∠ADE+∠CDE=900 在Rt △DEC 中,∠C+∠CDE=900∴∠C=∠ADE 在Rt △ADE 中, tan 2AE ADE DE ∠== ∵ AE=8,∴DE=4 则CE=2∴AC=AE+CE=10 即直径AB=AC=10 则OD=OB=5∵OD//AE ∴△ODF ∽△AEF∴ OF OD AF AE = 即:55108BF BF +=+解得:BF=103即BF的长为103.点睛:此题考查了切线的性质与判定、圆周角定理、等腰三角形的性质、直角三角形以及相似三角形的判定与性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.7.如图,AB是半圆⊙O的直径,点C是半圆⊙O上的点,连接AC,BC,点E是AC的中点,点F是射线OE上一点.(1)如图1,连接FA,FC,若∠AFC=2∠BAC,求证:FA⊥AB;(2)如图2,过点C作CD⊥AB于点D,点G是线段CD上一点(不与点C重合),连接FA,FG,FG与AC相交于点P,且AF=FG.①试猜想∠AFG和∠B的数量关系,并证明;②连接OG,若OE=BD,∠GOE=90°,⊙O的半径为2,求EP的长.【答案】(1)见解析;(2)①结论:∠GFA=2∠ABC.理由见解析;②PE=36.【解析】【分析】(1)证明∠OFA=∠BAC,由∠EAO+∠EOA=90°,推出∠OFA+∠AOE=90°,推出∠FAO=90°即可解决问题.(2)①结论:∠GFA=2∠ABC.连接FC.由FC=FG=FA,以F为圆心FC为半径作⊙F.因为AG AG,推出∠GFA=2∠ACG,再证明∠ACG=∠ABC.②图2﹣1中,连接AG,作FH⊥AG于H.想办法证明∠GFA=120°,求出EF,OF,OG即可解决问题.【详解】(1)证明:连接OC.∵OA=OC,EC=EA,∴OF⊥AC,∴FC=FA,∴∠OFA=∠OFC,∵∠CFA=2∠BAC,∴∠OFA=∠BAC,∵∠OEA=90°,∴∠EAO+∠EOA=90°,∴∠OFA+∠AOE=90°,∴∠FAO=90°,∴AF⊥AB.(2)①解:结论:∠GFA=2∠ABC.理由:连接FC.∵OF垂直平分线段AC,∴FG=FA,∵FG=FA,∴FC=FG=FA,以F为圆心FC为半径作⊙F.∵AG AG,∴∠GFA=2∠ACG,∵AB是⊙O的直径,∴∠ACB=90°,∵CD⊥AB,∴∠ABC+∠BCA=90°,∵∠BCD+∠ACD=90°,∴∠ABC=∠ACG,∴∠GFA=2∠ABC.②如图2﹣1中,连接AG,作FH⊥AG于H.∵BD=OE,∠CDB=∠AEO=90°,∠B=∠AOE,∴△CDB≌△AEO(AAS),∴CD =AE ,∵EC =EA ,∴AC =2CD .∴∠BAC =30°,∠ABC =60°,∴∠GFA =120°,∵OA =OB =2,∴OE =1,AE =,BA =4,BD =OD =1, ∵∠GOE =∠AEO =90°,∴OG ∥AC , 33,33DG OG ∴==, 222213AG DG AD ∴=+=, ∵FG =FA ,FH ⊥AG ,∴AH =HG 21∠AFH =60°, ∴AF =27sin 60AH ︒=, 在Rt △AEF 中,EF 2213AF AE -=, ∴OF =OE +EF =43 , ∵PE ∥OG , ∴PE EF OG 0F=, ∴134233=, ∴PE =36. 【点睛】圆综合题,考查了垂径定理,勾股定理,圆周角定理,全等三角形的判定和性质,锐角三角函数,解直角三角形等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题.8.如图,已知等边△ABC ,AB=16,以AB 为直径的半圆与BC 边交于点D ,过点D 作DF ⊥AC ,垂足为F ,过点F 作FG ⊥AB ,垂足为G ,连结GD .(1)求证:DF是⊙O的切线;(2)求FG的长;(3)求tan∠FGD的值.【答案】(1)证明见解析;(2)6;(3).【解析】试题分析:(1)连接OD,根据等边三角形得出∠A=∠B=∠C=60°,根据OD=OB得到∠ODB=60°,得到OD∥AC,根据垂直得出切线;(2)根据中位线得出BD=CD=6,根据Rt△CDF的三角函数得出CF的长度,从而得到AF的长度,最后根据Rt△AFG的三角函数求出FG的长度;(3)过点D作DH⊥AB,根据垂直得出FG∥DH,根据Rt△BDH求出BH、DH的长度,然后得出∠GDH的正切值,从而得到∠FGD的正切值.试题解析:(1)如图①,连结OD,∵△ABC为等边三角形,∴∠C=∠A=∠B=60°,而OD=OB,∴△ODB是等边三角形,∠ODB=60°,∴∠ODB=∠C,∴OD∥AC,∵DF⊥AC,∴OD⊥DF,∴DF是⊙O的切线(2)∵OD∥AC,点O为AB的中点,∴OD为△ABC的中位线,∴BD=CD=6.在Rt△CDF中,∠C=60°,∴∠CDF=30°,∴CF=CD=3,∴AF=AC-CF=12-3=9 在Rt△AFG中,∵∠A=60°,∴FG=AF·sinA=9×=(3)如图②,过D作DH⊥AB于H.∵FG⊥AB,DH⊥AB,∴FG∥DH,∴∠FGD=∠GDH.在Rt△BDH中,∠B=60°,∴∠BDH=30°,∴BH=BD=3,DH=BH=3.∴tan∠GDH===,∴tan∠FGD=tan∠GDH=考点:(1)圆的基本性质;(2)三角函数.9.如图,OA,OD是⊙O半径.过A作⊙O的切线,交∠AOD的平分线于点C,连接CD,延长AO交⊙O于点E,交CD的延长线于点B.(1)求证:直线CD是⊙O的切线;(2)如果D点是BC的中点,⊙O的半径为 3cm,求DE的长度.(结果保留π)【答案】(1)证明见解析;(2)DE的长度为π.【解析】(1)证明:∵AC是⊙O切线,∴OA⊥AC,∴∠OAC=90°,∵CO平分∠AOD,∴∠AOC=∠COD,在△AOC和△DOC中,∴△AOC≌△DOC,∴∠ODC=∠OAC=90°,∴OD⊥CD,∴直线CD是⊙O的切线.(2)∵OD⊥BC,DC=DB,∴OC=OB,∴∠OCD=∠B=∠ACO,∵∠B+∠ACB=90°,∴∠B=30°,∠DOE=60°,∴的长度==π.[来源:]10.如图1,⊙O的直径AB=12,P是弦BC上一动点(与点B,C不重合),∠ABC=30°,过点P作PD⊥OP交⊙O于点D.(1)如图2,当PD∥AB时,求PD的长;(2)如图3,当弧DC=弧AC时,延长AB至点E,使BE=12AB,连接DE.①求证:DE是⊙O的切线;②求PC的长.【答案】(1)6;(2)①证明见解析;33.【解析】试题分析:(1)根据题意首先得出半径长,再利用锐角三角三角函数关系得出OP,PD的长;(2)①首先得出△OBD是等边三角形,进而得出∠ODE=∠OFB=90°,求出答案即可;②首先求出CF的长,进而利用直角三角形的性质得出PF的长,进而得出答案.试题解析:(1)如图2,连接OD,∵OP⊥PD,PD∥AB,∴∠POB=90°,∵⊙O的直径AB=12,∴OB=OD=6,在Rt△POB中,∠ABC=30°,∴OP=OB•tan30°=6×=2,在Rt△POD中,PD===;(2)①如图3,连接OD,交CB于点F,连接BD,∵,∴∠DBC=∠ABC=30°,∴∠ABD=60°,∵OB=OD,∴△OBD是等边三角形,∴OD⊥FB,∵BE=AB,∴OB=BE,∴BF∥ED,∴∠ODE=∠OFB=90°,∴DE是⊙O的切线;②由①知,OD⊥BC,∴CF=FB=OB•cos30°=6×=3,在Rt△POD中,OF=DF,∴PF=DO=3(直角三角形斜边上的中线,等于斜边的一半),∴CP=CF﹣PF=3﹣3.考点:圆的综合题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、圆的综合 真题与模拟题分类汇编(难题易错题)1.(1)如图1,在矩形ABCD 中,点O 在边AB 上,∠AOC =∠BOD ,求证:AO =OB ; (2)如图2,AB 是⊙O 的直径,PA 与⊙O 相切于点A ,OP 与⊙O 相交于点C ,连接CB ,∠OPA =40°,求∠ABC 的度数.【答案】(1)证明见解析;(2)25°.【解析】试题分析: (1)根据等量代换可求得∠AOD=∠BOC ,根据矩形的对边相等,每个角都是直角,可知∠A=∠B=90°,AD=BC ,根据三角形全等的判定AAS 证得△AOD ≌△BOC ,从而得证结论.(2)利用切线的性质和直角三角形的两个锐角互余的性质得到圆心角∠POA 的度数,然后利用圆周角定理来求∠ABC 的度数.试题解析:(1)∵∠AOC=∠BOD∴∠AOC -∠COD=∠BOD-∠COD即∠AOD=∠BOC∵四边形ABCD 是矩形∴∠A=∠B=90°,AD=BC∴AOD BOC ∆≅∆∴AO=OB(2)解:∵AB 是O 的直径,PA 与O 相切于点A , ∴PA ⊥AB ,∴∠A=90°.又∵∠OPA=40°,∴∠AOP=50°,∵OB=OC ,∴∠B=∠OCB.又∵∠AOP=∠B+∠OCB , ∴1252B OCB AOP ∠=∠=∠=︒.2.如图,已知平行四边形OABC 的三个顶点A 、B 、C 在以O 为圆心的半圆上,过点C 作CD ⊥AB ,分别交AB 、AO 的延长线于点D 、E ,AE 交半圆O 于点F ,连接CF . (1)判断直线DE 与半圆O 的位置关系,并说明理由;(2)若半圆O 的半径为6,求AC 的长.【答案】(1)直线CE 与半圆O 相切(2)4π【解析】试题分析:(1)结论:DE 是⊙O 的切线.首先证明△ABO ,△BCO 都是等边三角形,再证明四边形BDCG 是矩形,即可解决问题;(2)只要证明△OCF 是等边三角形即可解决问题,求AC 即可解决问题.试题解析:(1)直线CE 与半圆O 相切,理由如下:∵四边形OABC 是平行四边形,∴AB ∥OC.∵∠D=90°,∴∠OCE=∠D=90°,即OC ⊥DE ,∴直线CE 与半圆O 相切.(2)由(1)可知:∠COF=60°,OC=OF ,∴△OCF 是等边三角形,∴∠AOC=120°∴AC 的长为1206180π⨯⨯=4π.3.已知A (2,0),B (6,0),CB ⊥x 轴于点B ,连接AC画图操作:(1)在y 正半轴上求作点P ,使得∠APB=∠ACB (尺规作图,保留作图痕迹)理解应用:(2)在(1)的条件下,①若tan ∠APB 12=,求点P 的坐标 ②当点P 的坐标为 时,∠APB 最大拓展延伸:(3)若在直线y43=x+4上存在点P,使得∠APB最大,求点P的坐标【答案】(1)图形见解析(2)(0,2),(0,4)(0,23)(3)(953 5-,1255)【解析】试题分析:(1)以AC为直径画圆交y轴于P,连接PA、PB,∠PAB即为所求;(2)①由题意AC的中点K(4,4),以K为圆心AK为半径画圆,交y轴于P和P′,易知P(0,2),P′(0,6);②当⊙K与y轴相切时,∠APB的值最大,(3)如图3中,当经过AB的园与直线相切时,∠APB最大.想办法求出点P坐标即可解决问题;试题解析:解:(1)∠APB如图所示;(2)①如图2中,∵∠APB=∠ACB,∴tan∠ACB=tan∠APB=12=ABBC.∵A(2,0),B(6,0),∴AB=4,BC=8,∴C(6,8),∴AC的中点K(4,4),以K为圆心AK为半径画圆,交y轴于P和P′,易知P(0,2),P′(0,6).②当⊙K与y轴相切时,∠APB的值最大,此时AK=PK=4,AC=8,∴BC22AC AB-3,∴C(6,3∴K(4,2),∴P(0,3案为:(0,3(3)如图3中,当经过AB 的园与直线相切时,∠APB 最大.∵直线y =43x +4交x 轴于M (﹣3,0),交y 轴于N (0,4).∵MP 是切线,∴MP 2=MA •MB ,∴MP =35,作PK ⊥OA 于K .∵ON ∥PK ,∴ON PK =OM MK =NM MP ,∴4PK =3MK =35,∴PK =125,MK =955,∴OK =955﹣3,∴P (955﹣3,1255).点睛:本题考查了一次函数综合题、直线与圆的位置关系、平行线的性质、切线的判定和性质、勾股定理、锐角三角函数等知识,解题的关键是学会添加常用辅助线解决问题,学会构造辅助圆解决最大角问题,属于中考压轴题.4.如图,□ABCD 的边AD 是△ABC 外接圆⊙O 的切线,切点为A ,连接AO 并延长交BC 于点E ,交⊙O 于点F ,过点C 作直线CP 交AO 的延长线于点P ,且∠BCP =∠ACD . (1)求证:PC 是⊙O 的切线;(2)若∠B =67.5°,BC =2,求线段PC ,PF 与弧CF 所围成的阴影部分的面积S .【答案】(1)见解析;(2)14π-【解析】 【分析】(1) 过C 点作直径CM ,连接MB ,根据CM 为直径,可得∠M+∠BCM =90°,再根据AB ∥DC 可得∠ACD =∠BAC ,由圆周角定理可得∠BAC =∠M ,∠BCP =∠ACD ,从而可推导得出∠PCM =90°,根据切线的判定即可得;(2)连接OB ,由AD 是⊙O 的切线,可得∠PAD =90°,再由BC ∥AD ,可得AP ⊥BC ,从而得BE =CE = 12BC =1,继而可得到∠ABC =∠ACB =67.5°,从而得到∠BAC =45°,由圆周角定理可得∠BOC=90°,从而可得∠BOE =∠COE =∠OCE = 45°,根据已知条件可推导得出OE =CE =1,PC =OC 22OE CE 2+部分的面积.【详解】(1)过C点作直径CM,连接MB,∵CM为直径,∴∠MBC=90°,即∠M+∠BCM=90°,∵四边形ABCD是平行四边形,∴AB∥DC,AD∥BC,∴∠ACD=∠BAC,∵∠BAC=∠M,∠BCP=∠ACD,∴∠M=∠BCP,∴∠BCP+∠BCM=90°,即∠PCM=90°,∴CM⊥PC,∴PC与⊙O相切;(2)连接OB,∵AD是⊙O的切线,切点为A,∴OA⊥AD,即∠PAD=90°,∵BC∥AD,∠AEB=∠PAD=90°,∴AP⊥BC.∴BE=CE=12BC=1,∴AB=AC,∴∠ABC=∠ACB=67.5°,∴∠BAC=180°-∠ABC-∠ACB=45°,∴∠BOC=2∠BAC=90°,∵OB=OC,AP⊥BC,∴∠BOE=∠COE=∠OCE= 45°,∵∠PCM=90°,∴∠CPO=∠COE=∠OCE= 45°,∴OE=CE=1,PC=OC=22OE CE2+=,∴S=S△POC-S扇形OFC=()245π21π221 23604⨯⨯⨯-=-.【点睛】本题考查了切线的判定与性质、圆周角定理、垂径定理、扇形面积等,综合性较强,准确添加辅助线是解题的关键.5..如图,△ABC中,∠ACB=90°,∠A=30°,AB=6.D是线段AC上一个动点(不与点A 重合),⊙D与AB相切,切点为E,⊙D交射线..DC于点F,过F作FG⊥EF交直线..BC于点G,设⊙D的半径为r.(1)求证AE=EF;(2)当⊙D与直线BC相切时,求r的值;(3)当点G落在⊙D内部时,直接写出r的取值范围.【答案】(1)见解析,(2)r=3,(3)63 35r<<【解析】【分析】(1)连接DE,则∠ADE=60°=∠DEF+∠DFE,而∠DEF=∠DFE,则∠DEF=∠DFE=30°=∠A,即可求解;(2)如图2所示,连接DE,当圆与BC相切时,切点为F,∠A=30°,AB=6,则BF=3,AD=2r,由勾股定理,即可求解;(3)分点F在线段AC上、点F在线段AC的延长线上两种情况,分别求解即可.【详解】解:设圆的半径为r;(1)连接DE,则∠ADE=60°=∠DEF+∠DFE,而∠DEF=∠DFE,则∠DEF=∠DFE=30°=∠A,∴AE=EF;(2)如图2所示,连接DE,当圆与BC相切时,切点为F∠A=30°,AB=6,则BF=3,AD=2r,由勾股定理得:(3r)2+9=36,解得:r=3; (3)①当点F 在线段AC 上时,如图3所示,连接DE 、DG ,333,3933FC r GC FC r =-==-②当点F 在线段AC 的延长线上时,如图4所示,连接DE 、DG ,333,3339FC r GC FC r ===-两种情况下GC 符号相反,GC 2相同,由勾股定理得:DG 2=CD 2+CG 2,点G 在圆的内部,故:DG2<r2,即:22(332)(339)2r r r +-<整理得:25113180r r -+<6335r <<【点睛】本题考查了圆的综合题:圆的切线垂直于过切点的半径;利用勾股定理计算线段的长.6.如图,已知AB 为⊙O 的直径,AB=8,点C 和点D 是⊙O 上关于直线AB 对称的两个点,连接OC 、AC ,且∠BOC <90°,直线BC 和直线AD 相交于点E ,过点C 作直线CG 与线段AB 的延长线相交于点F ,与直线AD 相交于点G ,且∠GAF =∠GCE(1)求证:直线CG 为⊙O 的切线;(2)若点H 为线段OB 上一点,连接CH ,满足CB =CH ,①△CBH ∽△OBC②求OH +HC 的最大值【答案】(1)证明见解析;(2)①证明见解析;②5.【解析】分析:(1)由题意可知:∠CAB=∠GAF,由圆的性质可知:∠CAB=∠OCA,所以∠OCA=∠GCE,从而可证明直线CG是⊙O的切线;(2)①由于CB=CH,所以∠CBH=∠CHB,易证∠CBH=∠OCB,从而可证明△CBH∽△OBC;②由△CBH∽△OBC可知:BC HBOC BC=,所以HB=24BC,由于BC=HC,所以OH+HC=4−24BC+BC,利用二次函数的性质即可求出OH+HC的最大值.详解:(1)由题意可知:∠CAB=∠GAF,∵AB是⊙O的直径,∴∠ACB=90°∵OA=OC,∴∠CAB=∠OCA,∴∠OCA+∠OCB=90°,∵∠GAF=∠GCE,∴∠GCE+∠OCB=∠OCA+∠OCB=90°,∵OC是⊙O的半径,∴直线CG是⊙O的切线;(2)①∵CB=CH,∴∠CBH=∠CHB,∵OB=OC,∴∠CBH=∠OCB,∴△CBH∽△OBC②由△CBH∽△OBC可知:BC HB OC BC=∵AB=8,∴BC2=HB•OC=4HB,∴HB=24 BC,∴OH=OB-HB=4-24BC ∵CB=CH , ∴OH+HC=4−24BC +BC , 当∠BOC=90°,此时BC=42∵∠BOC <90°, ∴0<BC <42,令BC=x 则CH=x ,BH=24x ()221142544OH HC x x x ∴+=-++=--+ 当x=2时,∴OH+HC 可取得最大值,最大值为5点睛:本题考查圆的综合问题,涉及二次函数的性质,相似三角形的性质与判定,切线的判定等知识,综合程度较高,需要学生灵活运用所知识.7.如图,四边形为菱形,且,以为直径作,与交于点.请仅用无刻度的直尺按下列要求画图.(保留作图痕迹)(1)在如图中,过点作边上的高. (2)在如图中,过点作的切线,与交于点.【答案】(1)如图1所示.(答案不唯一),见解析;(2)如图2所示.(答案不唯一),见解析.【解析】【分析】(1)连接AC 交圆于一点F ,连接PF 交AB 于点E,连接CE 即为所求.(2)连接OF 交BC 于Q ,连接PQ 即为所求.【详解】(1)如图1所示.(答案不唯一)(2)如图2所示.(答案不唯一)【点睛】本题考查作图-复杂作图,菱形和圆的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.8.如图,在中,,以为直径作,交边于点,交边于点,过点作的切线,交的延长线于点,交于点.(1)求证:;(2)若,,求的半径.【答案】(1)证明见解析;(2)4.【解析】试题分析:(1)连接AD,根据等腰三角形三线合一即可证明.(2)设⊙O的半径为R,则FO=4+R,FA=4+2R,OD=R,连接OD,由△FOD∽△FAE,得列出方程即可解决问题.试题解析:(1)连接AD,∵AB是直径,∴∠ADB=90°,∵AB=AC,AD⊥BC,∴BD=DC.(2)设⊙O的半径为R,则FO=4+R,FA=4+2R,OD=R,连接OD、∵AB=AC,∴∠ABC=∠C,∵OB=OD,∴∠ABC=∠ODB,∴∠ODB=∠C,∴OD∥AC,∴△FOD ∽△FAE , ∴, ∴,整理得R 2﹣R ﹣12=0,∴R=4或(﹣3舍弃).∴⊙O 的半径为4.考点:切线的性质、等腰三角形的性质等知识.9.如图,在ABC △中,10AC BC ==,3cos 5C =,点P 是BC 边上一动点(不与点,A C 重合),以PA 长为半径的P 与边AB 的另一个交点为D ,过点D 作DE CB ⊥于点E .()1当P 与边BC 相切时,求P 的半径;()2联结BP 交DE 于点F ,设AP 的长为x ,PF 的长为y ,求y 关于x 的函数解析式,并直接写出x 的取值范围;()3在()2的条件下,当以PE 长为直径的Q 与P 相交于AC 边上的点G 时,求相交所得的公共弦的长. 【答案】(1)409;(2))25880010x x x y x -+=<<;(3)105- 【解析】【分析】(1)设⊙P 与边BC 相切的切点为H ,圆的半径为R ,连接HP ,则HP ⊥BC ,cosC=35,则sinC=45,sinC=HPCP=R10R-=45,即可求解;(2)PD∥BE,则EBPD=BFPF,即:2248805x x x yx y--+-=,即可求解;(3)证明四边形PDBE为平行四边形,则AG=GP=BD,即:AB=DB+AD=AG+AD=45,即可求解.【详解】(1)设⊙P与边BC相切的切点为H,圆的半径为R,连接HP,则HP⊥BC,cosC=35,则sinC=35,sinC=HPCP=R10R-=45,解得:R=409;(2)在△ABC中,AC=BC=10,cosC=35,设AP=PD=x,∠A=∠ABC=β,过点B作BH⊥AC,则BH=ACsinC=8,同理可得:CH=6,HA=4,5tan∠()2284x+-2880x x-+25,则525,如下图所示,PA=PD ,∴∠PAD=∠CAB=∠CBA=β,tanβ=2,则cosβ=5,sinβ=5, EB=BDcosβ=(45-25x )×5=4-25x , ∴PD ∥BE ,∴EB PD =BF PF ,即:2248805x x x y x --+-=, 整理得:y=()25x x 8x 800x 103x 20-+<<+; (3)以EP 为直径作圆Q 如下图所示,两个圆交于点G ,则PG=PQ ,即两个圆的半径相等,则两圆另外一个交点为D ,GD 为相交所得的公共弦,∵点Q 时弧GD 的中点,∴DG ⊥EP ,∵AG 是圆P 的直径,∴∠GDA=90°,∴EP ∥BD ,由(2)知,PD ∥BC ,∴四边形PDBE 为平行四边形,∴AG=EP=BD ,∴5设圆的半径为r,在△ADG中,AD=2rcosβ=5,DG=5,AG=2r,5+2r=45,解得:2r=51,则:DG=5=10-25,相交所得的公共弦的长为10-25.【点睛】本题考查的是圆知识的综合运用,涉及到解直角三角形、勾股定理等知识,其中(3),要关键是根据题意正确画图,此题用大量的解直角三角形的内容,综合难度很大.10.如图,是大半圆的直径,是小半圆的直径,点是大半圆上一点,与小半圆交于点,过点作于点.(1)求证:是小半圆的切线;(2)若,点在上运动(点不与两点重合),设,.①求与之间的函数关系式,并写出自变量的取值范围;②当时,求两点之间的距离.【答案】(1)见解析;(2)①,,②两点之间的距离为或.【解析】【分析】(1)连接CO、CM,只需证到CD⊥CM.由于CD⊥OP,只需证到CM∥OP,只需证到CM 是△AOP的中位线即可.(2)①易证△ODC∽△CDP,从而得到CD2=DP•OD,进而得到y与x之间的函数关系式.由于当点P与点A重合时x=0,当点P与点B重合时x=4,点P在大半圆O上运动(点P不与A,B两点重合),因此自变量x的取值范围为0<x<4.②当y=3时,得到-x2+4x=3,求出x.根据x的值可求出CD、PD的值,从而求出∠CPD,运用勾股定理等知识就可求出P,M两点之间的距离.【详解】(1)连接,如图1所示∵是小半圆的直径,∴即∵∴∵∴∴,∵∴,∴∴.,即∵经过半径的外端,且∴直线是小半圆的切线.(2)①∵,,∴∴∴∽∴∴∵,,,∴当点与点重合时,;当点与点重合时,∵点在大半圆上运动(点不与两点重合),∴∴与之间的函数关系式为,自变量的取值范围是.②当时,解得,Ⅰ当时,如图2所示在中,∵,∴,∴∵,∴是等边三角形∵∴∴.Ⅱ当时,如图3所示,同理可得∵∴∴过点作,垂足为,连接,如图3所示∵,∴同理在中,∵,∴综上所述,当时,两点之间的距离为或.【点睛】考查了切线的判定、平行线的判定与性质、等边三角形的判定与性质、相似三角形的判定与性质、特殊角的三角函数值、勾股定理等知识,综合性比较强.。
