《现代控制理论》实验报告
现代控制理论实训报告

一、前言随着科技的飞速发展,自动化、智能化已成为现代工业生产的重要特征。
为了更好地掌握现代控制理论,提高自己的实践能力,我参加了现代控制理论实训课程。
本次实训以状态空间法为基础,研究多输入-多输出、时变、非线性一类控制系统的分析与设计问题。
通过本次实训,我对现代控制理论有了更深入的了解,以下是对本次实训的总结。
二、实训目的1. 巩固现代控制理论基础知识,提高对控制系统的分析、设计和调试能力。
2. 熟悉现代控制理论在工程中的应用,培养解决实际问题的能力。
3. 提高团队合作意识,锻炼动手能力和沟通能力。
三、实训内容1. 状态空间法的基本概念:状态空间法是现代控制理论的核心内容,通过建立状态方程和输出方程,描述系统的动态特性。
2. 状态空间法的基本方法:包括状态空间方程的建立、状态转移矩阵的求解、可控性和可观测性分析、状态反馈和观测器设计等。
3. 控制系统的仿真与实现:利用MATLAB等仿真软件,对所设计的控制系统进行仿真,验证其性能。
4. 实际控制系统的分析:分析实际控制系统中的控制对象、控制器和被控量,设计合适的控制策略。
四、实训过程1. 理论学习:首先,我对现代控制理论的相关知识进行了复习,包括状态空间法、线性系统、非线性系统等。
2. 实验准备:根据实训要求,我选择了合适的实验设备和软件,包括MATLAB、控制系统实验箱等。
3. 实验操作:在实验过程中,我按照以下步骤进行操作:(1)根据实验要求,建立控制系统的状态空间方程。
(2)求解状态转移矩阵,并进行可控性和可观测性分析。
(3)设计状态反馈和观测器,优化控制系统性能。
(4)利用MATLAB进行仿真,观察控制系统动态特性。
(5)根据仿真结果,调整控制器参数,提高控制系统性能。
4. 结果分析:通过对仿真结果的分析,我对所设计的控制系统进行了评估,并总结经验教训。
五、实训成果1. 掌握了现代控制理论的基本概念和方法。
2. 提高了控制系统分析与设计能力,能够独立完成实际控制系统的设计。
现代控制理论 实验报告
实验三典型非线性环节一.实验要求1.了解和掌握典型非线性环节的原理。
2.用相平面法观察和分析典型非线性环节的输出特性。
二.实验原理及说明实验以运算放大器为基本元件,在输入端和反馈网络中设置相应元件(稳压管、二极管、电阻和电容)组成各种典型非线性的模拟电路。
三、实验内容3.1测量继电特性(1)将信号发生器(B1)的幅度控制电位器中心Y测孔,作为系统的-5V~+5V输入信号(Ui):B1单元中的电位器左边K3开关拨上(-5V),右边K4开关也拨上(+5V)。
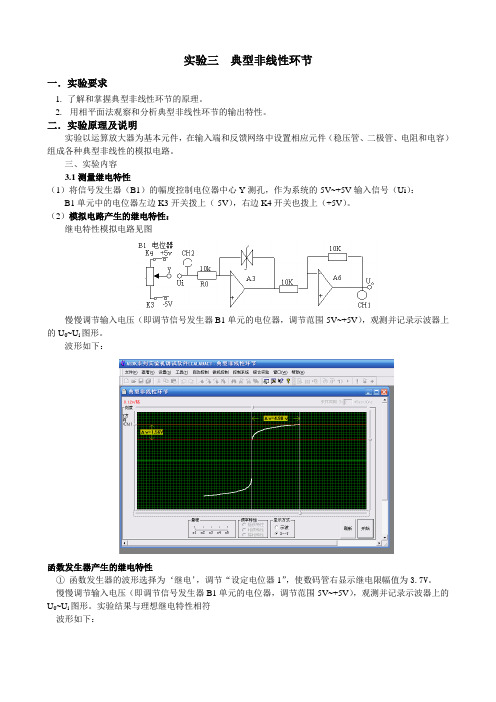
(2)模拟电路产生的继电特性:继电特性模拟电路见图慢慢调节输入电压(即调节信号发生器B1单元的电位器,调节范围-5V~+5V),观测并记录示波器上的U0~U i图形。
波形如下:函数发生器产生的继电特性①函数发生器的波形选择为‘继电’,调节“设定电位器1”,使数码管右显示继电限幅值为3.7V。
慢慢调节输入电压(即调节信号发生器B1单元的电位器,调节范围-5V~+5V),观测并记录示波器上的U0~U i图形。
实验结果与理想继电特性相符波形如下:3.2测量饱和特性将信号发生器(B1)的幅度控制电位器中心Y测孔,作为系统的-5V~+5V输入信号(Ui):B1单元中的电位器左边K3开关拨上(-5V),右边K4开关也拨上(+5V)。
(2)模拟电路产生的饱和特性:饱和特性模拟电路见图3-4-6。
慢慢调节输入电压(即调节信号发生器B1单元的电位器,调节范围-5V~+5V),观测并记录示波器上的U0~U i图形。
如下所示:函数发生器产生的饱和特性①函数发生器的波形选择为‘饱和’特性;调节“设定电位器1”,使数码管左显示斜率为2;调节“设定电位器2”,使数码管右显示限幅值为3.7V。
慢慢调节输入电压(即调节信号发生器B1单元的电位器,调节范围-5V~+5V),观测并记录示波器上的U0~U i图形。
波形如下:。
3.3测量死区特性模拟电路产生的死区特性死区特性模拟电路见图3-4-7。
现代控制理论实验报告

现代控制理论实验指导书实验一:线性系统状态空间分析1、模型转换图1、模型转换示意图及所用命令传递函数一般形式:)()(11101110n m a s a s a s a b s b s b s b s G n n n n m m m m ≤++++++++=----K KMATLAB 表示为:G=tf(num,den),其中num,den 分别是上式中分子,分母系数矩阵。
零极点形式:∏∏==--=n i j mi i ps z s K s G 11)()()( MATLAB 表示为:G=zpk(Z,P ,K),其中 Z ,P ,K 分别表示上式中的零点矩阵,极点矩阵和增益。
传递函数向状态空间转换:[A,B,C,D] = TF2SS(NUM,DEN);状态空间转换向传递函数:[NUM,DEN] = SS2TF(A,B,C,D,iu)---iu表示对系统的第iu个输入量求传递函数;对单输入iu为1;验证教材P438页的例9-6。
求P512的9-6题的状态空间描述。
>> A=[0 1;0 -2];>> B=[1 0;0 1];>> C=[1 0;0 1];>> D=[0 0;0 0];>> [NUM,DEN] = ss2tf(A,B,C,D,1)NUM =0 1 20 0 0DEN =1 2 0>> [NUM,DEN] = ss2tf(A,B,C,D,2)NUM =0 0 10 1 0DEN =1 2 0给出的结果是正确的,是没有约分过的形式P512 9-6>> [A,B,C,D]=tf2ss([1 6 8],[1 4 3])A =-4 -31 0B =1C =2 5D =12、状态方程求解单位阶跃输入作用下的状态响应:G=ss(A,B,C,D);[y,t,x]=step(G);plot(t,x). 零输入响应[y,t,x]=initial(G,x0)其中,x0为状态初值。
现代控制理论基础实验报告

紫金学院计算机系实验报告现代控制理论基础实验报告专业:年级:姓名:学号:提交日期:实验一 系统能控性与能观性分析1、实验目的:1.通过本实验加深对系统状态的能控性和能观性的理解;2.验证实验结果所得系统能控能观的条件与由它们的判据求得的结果完全一致。
2、实验内容:1.线性系统能控性实验;2. 线性系统能观性实验。
3、实验原理:系统的能控性是指输入信号u 对各状态变量x 的控制能力。
如果对于系统任意的初始状态,可以找到一个容许的输入量,在有限的时间内把系统所有的状态变量转移到状态空间的坐标原点。
则称系统是能控的。
系统的能观性是指由系统的输出量确定系统所有初始状态的能力。
如果在有限的时间内,根据系统的输出能唯一地确定系统的初始状态,则称系统能观。
对于图10-1所示的电路系统,设i L 和u c 分别为系统的两个状态变量,如果电桥中4321R R R R ≠,则输入电压u 能控制i L 和u c 状态变量的变化,此时,状态是能控的;状态变量i L 与u c 有耦合关系,输出u c 中含有i L 的信息,因此对u c 的检测能确定i L 。
即系统能观的。
反之,当4321R R =R R 时,电桥中的c 点和d 点的电位始终相等, u c 不受输入u 的控制,u 只能改变i L 的大小,故系统不能控;由于输出u c 和状态变量i L 没有耦合关系,故u c 的检测不能确定i L ,即系统不能观。
1.1 当4321R RR R ≠时u L u i R R R R C R R R R R R R R L R R R R R R C R R R R R R R R L u i C L C L ⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛⨯⎪⎪⎪⎪⎪⎭⎫+++-+-+-⎝⎛+-+-+++-=⎪⎪⎭⎫ ⎝⎛01)11(1)(1)(1)(143214343212143421243432121 (10-1)y=u c =[01]⎪⎪⎪⎭⎫⎝⎛c L u i (10-2)由上式可简写为bu Ax x+= cx y =式中⎪⎪⎭⎫ ⎝⎛=C L u i x ⎪⎪⎪⎪⎪⎭⎫+++-+-+-⎝⎛+-+-+++-=)11(1)(1)(1)(143214343212143421243432121R R R R C R R R R R R R R L R R R R R R C R R R R R R R R L A⎪⎪⎪⎭⎫⎝⎛=01L b 1] [0=c由系统能控能观性判据得][Ab brank =2 2=⎥⎦⎤⎢⎣⎡cA c rank故系统既能控又能观。
现代控制理论实验

现代控制理论实验华北电力大学实验报告||实验名称状态空间模型分析课程名称现代控制理论基础||专业班级:自动化1203 学生姓名:孟令虎学号:201209020216 成绩:指导教师:刘鑫屏老师实验日期: 2015.4.24一、实验目的l.加强对现代控制理论相关知识的理解;2.掌握用 matlab 进行系统李雅普诺夫稳定性分析、能控能观性分析; 二、实验仪器与软件 1. MATLAB7.6 环境三、实验内容1、 模型转换例 1.把传递函数模型转化为状态空间模型3248G s =81912s s s s ++++()。
解:程序如下num=[4 8]; den=[1 8 19 12];[A,B,C,D]=tf2ss(num,den); G=ss(A,B,C,D) 运行结果: A =-8 -19 -12 1 0 0 0 1 0 B = 1 0 0 C =0 4 8 D =0 结果为112233-8 -19 -1211 0 010 1 00x x x x u x x ∙∙∙⎡⎤⎢⎥⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎢⎥⎣⎦,[]1230 4 8x y x x ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦例2.把状态空间模型转化为传递函数模型A=0 1 00 0 1-6 -11 -6⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦B=001⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦C= []2 3 0 D=0。
解:程序如下:clearA=[0 1 0;0 0 1;-6 -11 -6]; B=[0;0;1]; C=[3 2 0]; D=0; iu=1;[num,den] = ss2tf(A,B,C,D,iu); sys=tf(num,den) 运行结果为:Transfer function: 2 s + 3---------------------- s^3 + 6 s^2 + 11 s + 62、 状态方程状态解和输出解例1.单位阶跃输入作用下的状态响应A=0 1 00 0 1-6 -11 -6⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦B=001⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦C=[]2 3 0 D=0。
中北大学现代控制理论实验报告

中北大学计算机与控制工程学院实验报告《现代控制理论》专业电气工程与智能控制班级XX070541学号XX070541XX姓名XX辅导老师成绩实验日期2017.04.25 实验时间8:30—11:30实验名称单级倒立摆系统控制特性分析实验目的1、旋转倒立摆线性模型建立与分析;2、利用MATLAB 分析线性定常系统的可控性、可观性与稳定性;3、线性模型与非线性模型对比;实验内容(1)根据实验原理中提供的单级倒立摆模型及可控、可观、稳定性判定方法,自编写程序判断倒立摆系统中占空比δ→旋转臂角位移α,占空比δ→摆杆角位移q 两通道的可控性,求解两通道系统的变换矩阵Qc;(2)自编写程序判断倒立摆系统中占空比δ→旋转臂角位移α,占空比δ→摆杆角位移q 两通道的可观性,求解两通道系统的变换矩阵Qo;(3)自编写程序判断倒立摆系统中占空比δ→旋转臂角位移α,占空比δ→摆杆角位移q 两通道的稳定性;实验原理或流程图实验过程或源代码J=0.0423m=0.404辅导老师成绩实验日期2017.04.25 实验时间8:30—11:30 实验名称单级倒立摆极点配置控制系统设计实验目的1. 根据设计指标获取理想极点位置;2.利用MATLAB 基于极点配置方法求解状态反馈矩阵;实验内容实验原理或流程图实验过程或源代码引用实验1的全部程序并附加以下程序disp('原系统的极点');p=eig(A)' %求矩阵A的全部特征根P=[-100;-101;-7.07+10*sqrt(-1/2);-7.07-10*sqrt(-1/2)]; K=place(A,B,P) %对系统进行极点配置disp('配置后系统的极点为')p=eig(A-B*K)'Simulink仿真输出结果显示系统稳定。
实验心得:学会了如何进行系统极点配置。
在simulink仿真模型中,可直接引用矩阵ABCD,一个系统的输入输出维数应相等。
现代控制理论基础实验报告

现代控制理论基础实验报告专业:年级:姓名:学号:提交日期:实验一系统能控性与能观性分析1、实验目的:1. 通过本实验加深对系统状态的能控性和能观性的理解;2. 验证实验结果所得系统能控能观的条件与由它们的判据求得的结果完全一致。
2、实验内容:1•线性系统能控性实验 2.线性系统能观性实验。
3、实验原理:系统的能控性是指输入信号u 对各状态变量x 的控制能力。
如果对于系统任意的初始状态,可以找到一个容许的输入量,在有限的时间内把系统所有的状态变量转移到状态空间的坐标原 点。
则称系统是能控的。
系统的能观性是指由系统的输出量确定系统所有初始状态的能力。
如果在有限的时间内,根据 系统的输出能唯一地确定系统的初始状态,则称系统能观。
(10-1)i Ly=U c =[01]U c由上式可简写为x Ax bU y cxR 3对于图10-1所示的电路系统,设i L 和u c 分别为系统的两个状态变量,如果电桥中旦R 2 &则输入电压U 能控制i L 和U c 状态变量的变化,此时,状态是能控的;状态变量i L 与U c 有耦合关系, 输出U c 中含有i L 的信息,因此对U c 的检测能确定i L 。
即系统能观的。
R 1 R 3反之,当」时, R 2 R 4变i L 的大小,故系统不能控; 即系统不能观。
Ri R 31.1当13时R 2 R 4电桥中的由于输出R 31( R 1R 2 L (R , R 2R 3 R 4R3R4R 2c 点和d 点的电位始终相等,U c 不受输入U 的控制,u 只能改U c 和状态变量i L 没有耦合关系,故 U c 的检测不能确定i L ,丄(亠亠)C R R 2R 3 R 41 ( R 1R2 L (R R 2R 3 R 4R3R4I L U C(10-2)I LR 2R 1 R 2 i L式中X U C1 (L R 1 R 21 R2 ( —— C R 1 R 2 R3 R 4)R3 R 4R 3 R 4R 1 R 2 1 (L R 1 R 21 1 -( CR 1R 2R3 R 4) R 4 1 )R 3 R 4[0 1]由系统能控能观性判据得 ran k[b Ab] =2c rank cA 故系统既能控又能观。
现代理论控制实验3

ans =3,所以系统是能控的
由Vo=obsv(a,c);rank(Vo)得
ans =3,所以系统是能观的
(2)
a.
选取K=[0 3 0] 为状态反馈矩阵,解得闭环ห้องสมุดไป่ตู้统的零点、极点和传递函数如下
由a=[-3 0 0;0 2 0;0 0 -1];b=[1 1 1]';k=[0 3 0];a1=a+b*k得
三、实验过程及结果
1. 已知系统
(1)求解系统的零点、极点和传递函数,并判断系统的能控性和能观测性。
(2)分别选取K=[0 3 0],K=[1 3 2],K=[0 16 /3–1/3]为状态反馈矩阵,求解闭环系统的零点、极点和传递函数,判断闭环系统的能控性和能观测性。它们是否发生改变?为什么?
(3)任选三个输出反馈矩阵,求解闭环系统的零点、极点和传递函数,并判断系统的能控性和能观测性。它们是否发生改变? 为什么?
[xo,x,t]=simobsv(g1,l);plot(t,x,'-k',t,xo,':r')
观测器观测到的状态如下
其中l=
(4)
三、实验结果
1(1)
系统的零点、极点和传递函数如下
由a=[-3 0 0;0 2 0;0 0 -1];b=[1 1 1]';c=[0.4 0.2667 0.3333];g1=ss(a,b,c,0);g1=tf(g1)得
g1=
由g1=zpk(g1)得
系统的零点为1,-2;系统的极点为-3,-1,2
系统的能控性和能观性判断如下
ans =3,所以系统是能控的
由Vo=obsv(a,c);rank(Vo)得
现代控制理论实验报告

现代控制理论实验院系:计算机与电子信息学院班级:电气09-1姓名:学号:指导老师:禹柳飞实验一线性控制系统状态空间法分析第一部分线性控制系统状态空间模型的建立及转换一、实验目的1 掌握线性控制系统状态空间模型的建立方法。
2 掌握MATLAB中的各种模型转换函数。
二、实验项目1 已知系统的传递函数求取其状态空间模型。
2 MATLAB中各种模型转换函数的应用。
3 连续时间系统的离散化。
三、实验设备与仪器1、计算机2、MATLAB软件四、实验原理及内容(一)系统数学模型的建立1、传递函数模型—tf功能:生成传递函数,或者将零极点模型或状态空间模型转换成传递函数模型。
格式:G=tf(num,den)其中,(num,den)分别为系统的分子和分母多项式系数向量。
返回的变量G为传递函数对象。
【例】:已知G(S)=错误!未找到引用源。
用MA TLAB语句将上述传递函数表示出来。
编程如下:num=[2 9];den=[1 2 4 6];Sys=tf(num,den)MATLAB中运行结果如下图所示:2、状态方程模型—ss功能:生成状态方程,或者将零极点模型或传递函数模型转换成状态方程模型。
格式:G=ss(A,B,C,D)其中,A,B,C,D分别为状态方程的系统矩阵、输入矩阵、输出矩阵和前馈矩阵。
【例】:已知系统状态空间模型为编程如下:>>A=[0 1;-1 -2];>>B=[0;1];>>C=[1,3]; D=1];>>G=ss(A,B ,C ,D)运行结果如下图:3、零极点模型—zpk功能:生成零极点模型,或将状态方程模型或传递函数模型转换成零极点模型。
格式:G=zpk(z, p, K)其中,z,p,K分别表示系统的零点、极点和增益。
【例】:G(s)=6(s+3)/(s+1)(s+2)(s+5)使用MATLAB 语句将上述零极点增益模型表示出来。
编程如下:z=[-3];p=[-1,-2,-5];k=[6];G=zpk(z,p,k)(二)连续时间系统离散化函数名称:c2d格式:G=c2d(G1,Ts),其中Ts 为采样周期。
《现代控制理论》实验报告

.现代控制理论实验报告组员:院系:信息工程学院专业:指导老师:年月日实验1 系统的传递函数阵和状态空间表达式的转换[实验要求]应用MATLAB 对系统仿照[例1.2]编程,求系统的A 、B 、C 、阵;然后再仿照[例1.3]进行验证。
并写出实验报告。
[实验目的]1、学习多变量系统状态空间表达式的建立方法、了解系统状态空间表达式与传递函数相互转换的方法;2、通过编程、上机调试,掌握多变量系统状态空间表达式与传递函数相互转换方法。
[实验内容]1 设系统的模型如式(1.1)示。
p m n R y R u R x DCx y Bu Ax x ∈∈∈⎩⎨⎧+=+= (1.1)其中A 为n ×n 维系数矩阵、B 为n ×m 维输入矩阵 C 为p ×n 维输出矩阵,D 为传递阵,一般情况下为0,只有n 和m 维数相同时,D=1。
系统的传递函数阵和状态空间表达式之间的关系如式(1.2)示。
D B A SI C s den s num s G +-==-1)()()(()( (1.2)式(1.2)中,)(s num 表示传递函数阵的分子阵,其维数是p ×m ;)(s den 表示传递函数阵的按s 降幂排列的分母。
2 实验步骤① 根据所给系统的传递函数或(A 、B 、C 阵),依据系统的传递函数阵和状态空间表达式之间的关系如式(1.2),采用MATLA 的file.m 编程。
注意:ss2tf 和tf2ss 是互为逆转换的指令;② 在MATLA 界面下调试程序,并检查是否运行正确。
③ [1.1] 已知SISO 系统的状态空间表达式为(1.3),求系统的传递函数。
,2010050010000100001043214321u x x x x x x x x ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-+⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡ []⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=43210001x x x x y (1.3)程序:A=[0 1 0 0;0 0 -1 0;0 0 0 1;0 0 5 0]; B=[0;1;0;-2]; C=[1 0 0 0]; D=0;[num,den]=ss2tf(A,B,C,D,1)程序运行结果:num =0 -0.0000 1.0000 -0.0000 -3.0000 den =1.0000 0 -5.0000 0 0从程序运行结果得到:系统的传递函数为:24253)(ss s S G --= ④ [1.2] 从系统的传递函数式求状态空间表达式。
现代控制理论实验报告

现代控制理论实验报告实验⼀线性定常系统模型⼀实验⽬的1. 掌握线性定常系统的状态空间表达式。
学会在MATLAB 中建⽴状态空间模型的⽅法。
2. 掌握传递函数与状态空间表达式之间相互转换的⽅法。
学会⽤MATLAB 实现不同模型之间的相互转换。
3. 熟悉系统的连接。
学会⽤MA TLAB 确定整个系统的状态空间表达式和传递函数。
4. 掌握状态空间表达式的相似变换。
掌握将状态空间表达式转换为对⾓标准型、约当标准型、能控标准型和能观测标准型的⽅法。
学会⽤MATLAB 进⾏线性变换。
⼆实验内容1. 已知系统的传递函数,(1)建⽴系统的TF 或ZPK 模型。
(a) )3()1(4)(2++=s s s s G(b) 3486)(22++++=s s s s s G(2)将给定传递函数⽤函数ss( )转换为状态空间表达式。
再将得到的状态空间表达式⽤函数tf( )转换为传递函数,并与原传递函数进⾏⽐较2. 已知系统的状态空间表达式(a) u x x+--=106510 []x y 11= (1)建⽴给定系统的状态空间模型。
⽤函数eig( ) 求出系统特征值。
⽤函数tf( ) 和zpk( )将这些状态空间表达式转换为传递函数,记录得到的传递函数和它的零极点。
⽐较系统的特征值和极点是否⼀致,为什么?给定系统的状态空间模型⽤函数eig( ) 求出系统特征值⽤函数tf( ) 将状态空间表达式转换为传递函数⽤函数zpk( ) 将状态空间表达式转换为传递函数(b) u x x ??+---=7126712203010 []111=y 给定系统的状态空间模型⽤函数tf( ) 和zpk( )将状态空间表达式转换为传递函数实验⼆线性定常系统状态⽅程的解⼀、实验⽬的1. 掌握状态转移矩阵的概念。
学会⽤MA TLAB 求解状态转移矩阵。
2. 掌握线性系统状态⽅程解的结构。
学会⽤MATLAB 求解线性定常系统的状态响应和输出响应,并绘制相应曲线。
现代控制理论课程设计实验报告

现代控制理论课程设计实验报告现代控制理论课程设计系别机电⼯程系专业⾃动化⼀、题⽬:⼆、技术指标:三、设计内容第1章线性系统状态空间表达式建⽴1-1由开环系统的传递函数结构图建⽴系统的状态结构图。
1-2由状态结构图写出状态空间表达式。
第2章理论分析计算系统的性能2-1稳定性分析⽅法与结论。
2-2能控性与能观测性分析⽅法与结论。
第3章闭环系统的极点配置3-1极点配置与动态质量指标关系。
3-2极点配置的结果(闭环特征多项式)。
第4章由状态反馈实现极点配置4-1通过状态反馈可任意配置极点的条件。
4-2状态反馈增益阵的计算。
第5章⽤MATLAB编程研究状态空间表达式描述的线性系统5-1由传递函数结构图建⽴状态空间表达式。
5-2由状态空间表达式分析稳定性、能控性、能观测性。
5-3根据极点配置要求,确定反馈增益阵。
5-4求闭环系统阶跃响应特性,并检验质量指标。
第6章⽤模拟电路实现三阶线性系统6-1系统模拟电路图。
6-2各运算放⼤电路的电阻、电容值的确定。
6-3模拟实验结果及参数的修改。
课程设计⼩结1、收获。
2、经验教训与建议。
⼀、⽬的要求⽬的:1、通过课程设计,加深理解现代控制理论中的⼀些基本概念;2、掌握⽤状态⽅程描述的线性系统的稳定性、能控性、能观性的分析计算⽅法;3、掌握对线性系统能进⾏任意极点配置来表达动态质量要求的条件,并运⽤状态反馈设计⽅法来计算反馈增益矩阵和⽤模拟电路来实现。
达到理论联系实际,提⾼动⼿能⼒。
要求:1、在思想上重视课程设计,集中精⼒,全⾝⼼投⼊,按时完成个阶段设计任务。
2、重视理论计算和MATLAB 编程计算,提⾼计算机编程计算能⼒。
3、认真写课程设计报告,总结经验教训。
⼆、设计题⽬及技术指标题⽬:⽤现代控制理论中状态反馈设计三阶线性控制系统技术指标:1、已知线性控制系统开环传递函数为:0G 012K (s)=s(Ts+1)(T s+1),其中T1= 0.1 秒,T2=1.0秒,K 0=1结构图如图所⽰:2、质量指标要求:% =4.32% ,p t =1秒,ss e =0 ,ssv e = 0.1三、设计报告正⽂第1章线性系统状态空间表达式建⽴1-1由开环系统的传递函数结构图建⽴系统的状态结构图由系统结构图可得变换后的系统结构图如下:1-2由状态结构图写出状态空间表达式。
现代控制理论实验报告
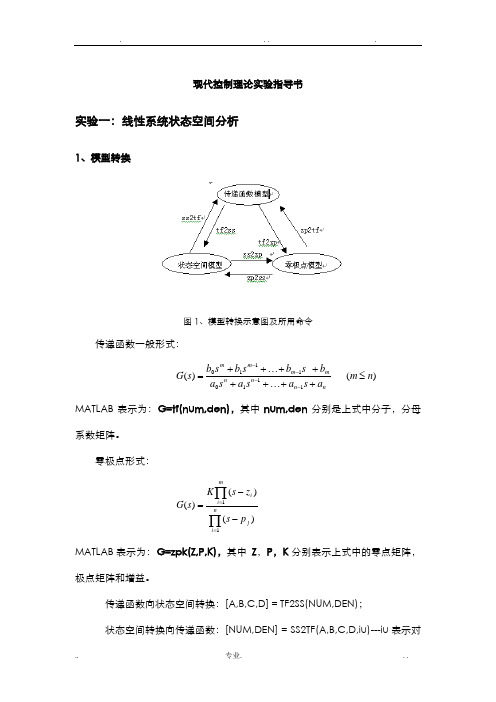
现代控制理论实验指导书实验一:线性系统状态空间分析1、模型转换图1、模型转换示意图及所用命令传递函数一般形式:)()(1111110nmasasasabsbsbsbsGnnnnmmmm≤++++++++=----MATLAB表示为:G=tf(num,den),其中num,den分别是上式中分子,分母系数矩阵。
零极点形式:∏∏==--=nijmiipszsKsG11)()()(MATLAB表示为:G=zpk(Z,P,K),其中Z,P,K分别表示上式中的零点矩阵,极点矩阵和增益。
传递函数向状态空间转换:[A,B,C,D] = TF2SS(NUM,DEN);状态空间转换向传递函数:[NUM,DEN] = SS2TF(A,B,C,D,iu)---iu表示对系统的第iu个输入量求传递函数;对单输入iu为1;验证教材P438页的例9-6。
求P512的9-6题的状态空间描述。
>> A=[0 1;0 -2];>> B=[1 0;0 1];>> C=[1 0;0 1];>> D=[0 0;0 0];>> [NUM,DEN] = ss2tf(A,B,C,D,1)NUM =0 1 20 0 0DEN =1 2 0>> [NUM,DEN] = ss2tf(A,B,C,D,2)NUM =0 0 10 1 0DEN =1 2 0给出的结果是正确的,是没有约分过的形式P512 9-6>> [A,B,C,D]=tf2ss([1 6 8],[1 4 3])A =-4 -31 0B =1C =2 5D =12、状态方程求解单位阶跃输入作用下的状态响应:G=ss(A,B,C,D);[y,t,x]=step(G);plot(t,x).零输入响应[y,t,x]=initial(G,x0)其中,x0为状态初值。
验证P435的例9-4,P437的例9-5。
9-4A=[0 1;-2 -3];B=[0;0];C=[0 0];D=[0];G=ss(A,B,C,D);[y,t,x]=initial(G,[1;2]);plot(t,x)(设初始状态为[1 ;2])零输入响应00.20.40.60.81 1.2 1.4 1.6 1.82-1-0.50.511.529-5零输入响应A=[0 1;-2 -3];B=[0;1];C=[0 0];D=[0];G=ss(A,B,C,D);[y,t,x]=initial(G,[1;2]);plot(t,x)00.20.40.60.81 1.2 1.4 1.6 1.82-1-0.50.511.52零状态响应,阶跃信号激励下>> A=[0 1;-2 -3];B=[0;1];C=[0 0];D=[0];>> G=ss(A,B,C,D);[y,t,x]=step(G);plot(t,x)00.20.40.60.81 1.2 1.4 1.6 1.8200.050.10.150.20.250.30.350.4总响应>> A=[0 1;-2 -3];B=[0;1];C=[0 0];D=[0];G=ss(A,B,C,D);[y1,t1,x1]=step(G);[y2,t2,x2]=initial(G,[1;2]);>> x=x1+x2;>> plot(t1,x)00.20.40.60.81 1.2 1.4 1.6 1.82-0.500.511.523、系统可控性和可观测性可控性判断:首先求可控性矩阵:co=ctrb(A ,B)。
现代控制理论课程设计实验报告

现代控制理论课程设计目录第1章线性系统状态空间表达式建立1.1由开环系统的传递函数结构图建立系统的状态结构图1.2由状态结构图写出状态空间表达式第2章理论分析计算系统的性能2.1稳定性分析方法与结论2.2能控性与能观测性分析方法与结论第3章闭环系统的极点配置3.1极点配置与动态质量指标关系3.2极点配置的结果(闭环特征多项式)第4章由状态反馈实现极点配置4.1通过状态反馈可任意配置极点的条件4.2状态反馈增益阵的计算第5章用MATLAB编程研究状态空间表达式描述的线性系统5.1由传递函数结构图建立状态空间表达式5.2由状态空间表达式分析稳定性、能控性、能观测性5.3根据极点配置要求,确定反馈增益阵5.4求闭环系统阶跃响应特性,并检验质量指标课程设计小结第1章 线性系统状态空间表达式建立1.1由开环系统的传递函数结构图建立系统的状态结构图由已知条件得线性控制系统开环传递函数结构图如图所示:系统开环传递函数结构框图图1-1已知线性控制系统开环传递函数为G 012K (s)=s(T s+1)(T s+1),根据系统对具体参数的要求(见表1-1),可得系统参数如下:K0=1,T1=0.4S,T2=3.3S ,则系统的开环传递函数如下为:1G (s)=s(0.4s+1)(3.3s+1)320.758G 2.7560.758s s ++(s)=系统参数要求 表1-1由系统的结构框图1-1经过变换得到系统的结构图如下1-2:系统结构图图1-21.2由状态结构图写出状态空间表达式根据系统的状态结构图得:()()⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧==-=-=-=-==3303232232121121.300.31 2.52.51x x k y x x x x T x x x x x T x u x 系统的状态空间方程和输出方程如下:⎩⎨⎧+=+=D Cx y B Ax x 其中A,B,C,D 矩阵分别为:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=0.3-.30002.5-2.5000A ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=001B []100=C0=D第2章 理论分析计算系统的性能2.1稳定性分析方法与结论稳定性是控制系统能否正常工作的前提条件:系统的稳定性与系统的结构和参数有关,与外界初始条件无关,与外界扰动大小无关;非线性系统的稳定性与系统的结构和参数有关,与外界初始条件有关,与外界扰动大小有关。
现代控制理论实验报告

现代控制理论实验报告学院:机电学院学号:XXXXX姓名:XXXXX班级:XXXX实验一 系统的传递函数阵和状态空间表达式的转换一、实验目的1.熟悉线性系统的数学模型、模型转换。
2.了解MATLAB 中相应的函数 二、实验内容及步骤 1.给定系统的传递函数为1503913.403618)(23++++=s s s s s G 要求(1)将其用Matlab 表达;(2)生成状态空间模型。
2.在Matlab 中建立如下离散系统的传递函数模型y (k + 2) +5y (k +1) +6y (k ) = u (k + 2) + 2u (k +1) +u (k ) 3.在Matlab 中建立如下传递函数阵的Matlab 模型⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+++++++++++=726611632256512)(2322s s s s s s s s s s s s G 4.给定系统的模型为)4.0)(25)(15()2(18)(++++=s s s s s G求(1)将其用Matlab 表达;(2)生成状态空间模型。
5.给定系统的状态方程系数矩阵如下:[]0,360180,001,0100011601384.40==⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=D C B A用Matlab 将其以状态空间模型表示出来。
6.输入零极点函数模型,零点z=1,-2;极点p=-1,2,-3 增益k=1;求相应的传递函数模型、状态空间模型。
三、实验结果及分析 1. 程序代码如下:num = [18 36];den = [1 40.3 391 150]; tf(num,den) ss(tf(num,den))Transfer function:18 s + 36----------------------------s^3 + 40.3 s^2 + 391 s + 150a =x1 x2 x3x1 -40.3 -24.44 -2.344x2 16 0 0x3 0 4 0b =u1x1 1x2 0x3 0c =x1 x2 x3y1 0 1.125 0.5625d =u1y1 0Continuous-time model.2.2.程序代码如下:num=[1 2 1];den=[1 5 6];tf(num,den,-1)运行结果:Transfer function:z^2 + 2 z + 1-------------z^2 + 5 z + 6Sampling time: unspecified3.程序代码如下:num={[1 2 1],[1 5];[2 3],[6]};den={[1 5 6],[1 2];[1 6 11 6],[2 7]};tf(num,den)Transfer function from input 1 to output...s^2 + 2 s + 1#1: -------------s^2 + 5 s + 62 s + 3#2: ----------------------s^3 + 6 s^2 + 11 s + 6Transfer function from input 2 to output...s + 5#1: -----s + 26#2: -------2 s + 74. 程序代码如下:sys=zpk(-2,[-15 -25 -0.4],18)ss(sys)运行结果:1)Zero/pole/gain:18 (s+2)---------------------(s+15) (s+25) (s+0.4)2)a =x1 x2 x3x1 -0.4 1.265 0x2 0 -15 1x3 0 0 -25b =u1x1 0x2 0x3 8c =x1 x2 x3y1 2.846 2.25 0d =u1y1 0Continuous-time model.5.程序代码如下:A=[-40.4 -138 -160;1 0 0;0 1 0];B=[1 0 0]';C=[0 18 360];D=0;ss(A,B,C,D)运行结果:a =x1 x2 x3x1 -40.4 -138 -160x2 1 0 0x3 0 1 0b =u1x1 1x2 0x3 0c =x1 x2 x3y1 0 18 360d =u1y1 0Continuous-time model.6. 程序代码如下:sys=zpk([1 -2],[-1 2 -3],1) tf(sys)ss((sys)运行结果:Zero/pole/gain:(s-1) (s+2)-----------------(s+1) (s+3) (s-2)Transfer function:s^2 + s - 2---------------------s^3 + 2 s^2 - 5 s - 6a =x1 x2 x3x1 -1 2.828 1.414x2 0 2 2x3 0 0 -3b =u1x1 0x2 0x3 2c =x1 x2 x3y1 -0.7071 1 0.5d =u1y1 0Continuous-time model.四、实验总结本次实验主要是熟悉利用matlab建立线性系统数学模型以及模型间的相应转换(如状态空间、传递函数模型等)、并了解matlab中相应函数的使用,如tf、ss、zp2ss、ss2tf等。
现代控制理论试验报告

实验七 状态空间表达与求解的Matlab 实现1、 实验目的了解和熟悉Matlab 关于矩阵运算和状态空间表达及相关运算的常用命令和使用方法,以便在学习过程中能有效地应用Matlab 这个工具解决复杂系统的相关设计运算工作。
2、 实验内容(1)熟悉并使用以下常用的矩阵运算命令及运算符:det; eig; rank; inv; diag(v)和diag(v,k); poly; poly2symexp(A)和expm(A)A^n; A./B ; A.*B; A\B; A\B; A.’; A ’;(注:A ,B 均指任意矩阵)(2)熟悉系统的状态空间表达的Matlab 实现方法(SS 函数与tf 函数的应用和相互转换),并将相应的状态模型在Simulink 中表达成模拟结构图。
(3)利用实验(1)中的相关命令练习将一般的状态空间模型转换为约旦(Jordan )标准型;直接应用函数Jordan(A)求解状态空间的转换矩阵。
(4)利用符号变量和前述的相关函数计算状态方程的非齐次解,解题思路如下:若某系统的状态方程为:u B x A x +=,求系统在单位阶跃作用下的状态响应解,设初始状态为)0(x ,输入量为:)(1)(t t u = ,应用Matlab 的求解过程为:Syms t sExp1=expm(A*t)*x0;Exp2=int(expm(a*(t-s))*B*u,s,0,t);最后的总解:X=Exp1+Exp2;(5) 若只需知道已知系统各状态量随时间的响应曲线,则可以直接应用Simulink 进行仿真,也可以通过直接建立SS 模型,再利用系统响应函数(如:step,initial,lsim )获取状态响应值(曲线),后者代码可如下操作:已知系统为: u B x A x +=,u D x C y +=G=ss(A,B,C,D); [y,t,x]=lsim(G,u,t); //求任意输入响应,注:A,B,C,D,u,t 等应先赋值 G=ss(A,B,C,D); [y,t,x]=step(G,t); //阶跃响应G=ss(A,B,C,D); [y,t,x]=initial(G,x0,t); //零输入响应,x0为初始状态plot(t,x) //画出状态响应曲线实验报告(七)——状态空间表达于求解的Matlab 实现班级 自动化92 姓名 杨孝凌 学号32209209一、 已知系统的状态空间表达为:u x x ⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡--=023120 ,⎥⎦⎤⎢⎣⎡=11)0(x 试用Matlab 求出系统单位阶跃下的状态解,写出实现过程的相应代码。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
.现代控制理论实验报告组员:院系:信息工程学院专业:指导老师:年月日实验1 系统的传递函数阵和状态空间表达式的转换[实验要求]应用MATLAB 对系统仿照[例1.2]编程,求系统的A 、B 、C 、阵;然后再仿照[例1.3]进行验证。
并写出实验报告。
[实验目的]1、学习多变量系统状态空间表达式的建立方法、了解系统状态空间表达式与传递函数相互转换的方法;2、通过编程、上机调试,掌握多变量系统状态空间表达式与传递函数相互转换方法。
[实验内容]1 设系统的模型如式(1.1)示。
p m n R y R u R x DCx y Bu Ax x ∈∈∈⎩⎨⎧+=+= (1.1)其中A 为n ×n 维系数矩阵、B 为n ×m 维输入矩阵 C 为p ×n 维输出矩阵,D 为传递阵,一般情况下为0,只有n 和m 维数相同时,D=1。
系统的传递函数阵和状态空间表达式之间的关系如式(1.2)示。
D B A SI C s den s num s G +-==-1)()()(()( (1.2)式(1.2)中,)(s num 表示传递函数阵的分子阵,其维数是p ×m ;)(s den 表示传递函数阵的按s 降幂排列的分母。
2 实验步骤① 根据所给系统的传递函数或(A 、B 、C 阵),依据系统的传递函数阵和状态空间表达式之间的关系如式(1.2),采用MATLA 的file.m 编程。
注意:ss2tf 和tf2ss 是互为逆转换的指令;② 在MATLA 界面下调试程序,并检查是否运行正确。
③ [1.1] 已知SISO 系统的状态空间表达式为(1.3),求系统的传递函数。
,2010050010000100001043214321u x x x x x x x x ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-+⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡ []⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=43210001x x x x y (1.3)程序:A=[0 1 0 0;0 0 -1 0;0 0 0 1;0 0 5 0]; B=[0;1;0;-2]; C=[1 0 0 0]; D=0;[num,den]=ss2tf(A,B,C,D,1)程序运行结果:num =0 -0.0000 1.0000 -0.0000 -3.0000 den =1.0000 0 -5.0000 0 0从程序运行结果得到:系统的传递函数为:24253)(ss s S G --= ④ [1.2] 从系统的传递函数式求状态空间表达式。
程序:num =[0 0 1 0 -3]; den =[1 0 -5 0 0]; [A,B,C,D]=tf2ss(num,den)程序运行结果:A =0 5 0 0 1 0 0 0 0 1 0 00 0 1 0B =1C =0 1 0 -3D =⑤ [1.3] 对上述结果进行验证编程%将[1.2]上述结果赋值给A、B、C、D阵;A=[0 5 0 0;1 0 0 0;0 1 0 0;0 0 1 0];B=[1;0;0;0];C=[0 1 0 -3];D=0;[num,den]=ss2tf(A,B,C,D,1)实验结果:num =0 0.0000 1.0000 0.0000 -3.0000den =1.0000 0 -5.0000 0 0程序运行结果与[1.1]完全相同。
[实验分析]当已知系统的状态空间表达式,我们可以求得系统的传递函数。
当已知系统的传递函数式,我们也可以求得状态空间表达式。
由于一个系统的状态空间表达式并不唯一,所以程序运行结果有可能不等于原式中的矩阵,但该结果与原式是等效的。
验证结果证明了这个结论。
实验2 状态空间控制模型系统仿真及状态方程求解[实验要求]1、进行模型间的相互转换。
2、绘出系统单位阶跃及脉冲曲线。
[实验目的]1、熟悉线性定常离散与连续系统的状态空间控制模型的各种表示方法。
2、熟悉系统模型之间的转换功能。
3、利用MATLAB 对线性定常系统进行动态分析 [实验内容]1、 给定系统125.032)(2323++++++=s s s s s s s G ,求系统的零极点增益模型和状态空间模型,并求其单位脉冲响应及单位阶跃响应。
2、 已知离散系统状态空间方程:[]⎪⎪⎩⎪⎪⎨⎧=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=+)(021)()(102)(101110221)1(k x k y k u k x k x 采样周期s T s 05.0=。
在Z 域和连续域对系统性能进行仿真、分析。
[实验结果及分析] 1、 程序:num=[1 2 1 3]; den=[1 0.5 2 1]; sys=tf(num,den)[z,p,k]=tf2zp(num,den) [A,B,C,D]=tf2ss(num,den) impulse(sys),hold on step(sys)程序运行结果:Transfer function:s^3 + 2 s^2 + s + 3-----------------------s^3 + 0.5 s^2 + 2 s + 1z =-2.17460.0873 + 1.1713i0.0873 - 1.1713ip =0 + 1.4142i0 - 1.4142i-0.5000k =1A =-0.5000 -2.0000 -1.0000 1.0000 0 00 1.0000 0B =1C =1.5000 -1.00002.0000D =1单位脉冲响应/单位阶跃响应:2、程序:g=[-1 -2 2;0 -1 1;1 0 -1];h =[2;0;1];c =[1 2 0];d=0;u=1;sysd=ss(g,h,c,d,0.05) dstep(g,h,c,d,u)程序运行结果:a =x1 x2 x3x1 -1 -2 2x2 0 -1 1x3 1 0 -1b =u1x1 2x2 0x3 1c =x1 x2 x3y1 1 2 0d =u1y1 0Sampling time: 0.05 Discrete-time model.Z域性能仿真图形:连续域仿真曲线:sysc=d2c(sysd,'zoh')step(sysc)和连续系统不同,离散系统中各部分的信号不再都是时间变量t的连续函数。
实验3 能控能观判据及稳定性判据[实验目的]1、利用MATLAB 分析线性定常及离散系统的可控性与可观性。
2、利用MATLAB 进行线性定常及离散系统的李雅普诺夫稳定性判据。
[实验内容]1、已知系统状态空间方程:(1) ⎪⎪⎩⎪⎪⎨⎧⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=u x x 111001342100010(2)[]⎪⎪⎩⎪⎪⎨⎧-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=x y x x 0312025016200340 对系统进行可控性、可观性分析。
2、 已知系统状态空间方程描述如下:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----=0100001000011263A ,⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=0001B ,[]1100=C试判定其稳定性,并绘制出时间响应曲线来验证上述判断。
[实验结果及分析](1)能控性分析程序:A=[0 1 0;0 0 1;-2 -4 -3]B=[1 0;0 1;-1 1]Qc=ctrb(A,B)rank(Qc)程序运行结果:A =0 1 00 0 1-2 -4 -3B =1 00 1-1 1Qc =1 0 0 1 -1 10 1 -1 1 1 -7-1 1 1 -7 1 15ans =3系统满秩,故系统能控。
系统的状态可控性描述了输入对状态的控制能力(2)能观性分析程序:A=[0 4 3;0 20 16;0 -25 -20]C=[-1 3 0]rank(obsv(A,C))程序运行结果:A =0 4 30 20 160 -25 -20C =-1 3 0ans =3系统满秩,故系统能观。
系统的状态可观性描述了通过输出可以观测状态的能力2、程序:A=[-3 -6 -2 -1;1 0 0 0;0 1 0 0;0 0 1 0];B=[1;0;0;0];C=[0 0 1 1];D=[0];[z,p,k]=ss2zp(A,B,C,D,1);Flagz=0;n=length(A);for i=1:nifreal(p(i))>0Flagz=1;endenddisp('系统的零极点模型为');z,p,k程序运行结果:系统的零极点模型为z =-1.0000p =-1.3544 + 1.7825i-1.3544 - 1.7825i-0.1456 + 0.4223i-0.1456 - 0.4223ik =1程序:if Flagz==1disp('系统不稳定');else disp('系统是稳定的');endstep(A,B,C,D);程序运行结果为:系统是稳定的程序:step(A,B,C,D);程序运行结果为:051015202530354000.20.40.60.811.21.4Step ResponseTime (sec)A m p l i t u d e从图中可以看出,系统是稳定的实验4 状态反馈及状态观测器的设计[实验要求] 1、求出系统的状态空间模型;2、依据系统动态性能的要求,确定所希望的闭环极点P ;3、利用上面的极点配置算法求系统的状态反馈矩阵K ;4、检验配置后的系统性能。
[实验目的]1、熟悉状态反馈矩阵的求法。
2、熟悉状态观测器设计方法。
[实验内容]1、 某控制系统的状态方程描述如下:[]242471,0001,01000010000124503510=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----=C B A 通过状态反馈使系统的闭环极点配置在P=[-30,-1.2,-2.4±4i 位置上,求出状态反馈阵K,并绘制出配置后系统的时间响应曲线。
2、考虑下面的状态方程模型:[]0,001,10000,100008.20980010==⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=D C B A 要求选出合适的参数状态观测器(设观测器极点为op=[-100;-102;-103])。
[实验结果及分析]1、程序:A=[-10 -35 -50 -24;1 0 0 0;0 1 0 0;0 0 1 0];B=[1;0;0;0];C=[1 7 24 24];D=[0];disp('原系统的极点为');p=eig(A)' %求原系统极点转置np=[-30;-1.2;-2.4+sqrt(-16);-2.4-sqrt(-16)]K=place(A,B,np) %求反馈K值disp('极点配置后的闭还系统为');sysnew=ss(A-B*K,B,C,D) %配置后新系统disp('配置后系统的极点为');pp=eig(A-B*K)' %求新系统极点step(sysnew/dcgain(sysnew)) %dcgain为求最大增益,使得最后结果在0—1程序运行结果:原系统的极点为p =-4.0000 -3.0000 -2.0000 -1.0000np =-30.0000-1.2000-2.4000 + 4.0000i-2.4000 - 4.0000iK =26.0000 172.5200 801.7120 759.3600极点配置后的闭还系统为a =x1 x2 x3 x4x1 -36 -207.5 -851.7 -783.4x2 1 0 0 0x3 0 1 0 0x4 0 0 1 0b =u1x1 1x2 0x3 0x4 0c =x1 x2 x3 x4y1 1 7 24 24d =u1y1 0Continuous-time model.配置后系统的极点为pp =-30.0000 -2.4000 - 4.0000i -2.4000 + 4.0000i -1.20002、程序:A=[0 1 0;980 0 -2.8;0 0 -100];B=[0;0;100];C=[1 0 0];D=[0];op=[-100;-102;-103];disp('原系统为');sysold=ss(A,B,C,D)disp('原系统的闭还极点为');p=eig(A)n=length(A); %求A阵维度Q=zeros(n); % 为n维0阵Q(1,:)=C; %C阵为Q第一行for i=2:nQ(i,:)=Q(i-1,:)*A;endm=rank(Q);if m==nH=place(A',C',op')';elsedisp('系统不是状态完全可观测') enddisp('状态观测器模型');est=estim(sysold,H)disp('配置后观测器的极点为');p=eig(est)程序运行结果:原系统为a =x1 x2 x3x1 0 1 0x2 980 0 -2.8x3 0 0 -100b =u1x1 0x2 0x3 100c =x1 x2 x3y1 1 0 0u1y1 0Continuous-time model.原系统的闭还极点为p =31.3050-31.3050-100.0000状态观测器模型a =x1 x2 x3 x1 -205 1 0 x2 -1.051e+004 0 -2.8 x3 0 0 -100 b =u1x1 205x2 1.149e+004x3 0c =x1 x2 x3y1 1 0 0y2 1 0 0y3 0 1 0y4 0 0 1d =u1y1 0y2 0y3 0y4 0Input groups:Name ChannelsMeasurement 1Output groups:Name ChannelsOutputEstimate 1StateEstimate 2,3,4Continuous-time model.配置后观测器的极点为-103.0000 -102.0000 -100.0000。
