北京邮电大学计算机学院离散数学下半学期
国家开放大学《离散数学》综合练习题参考答案

国家开放大学《离散数学》综合练习题参考答案一、单项选择题1.若集合A ={ a ,{a },{1,2}},则下列表述正确的是()。
A .{a ,{a }}∈AB .{1,2}∉AC .{a }⊆AD .∅∈A2.若集合A ={1,2},B ={1,2,{1,2}},则下列表述正确的是()。
A .A ⊂B ,且A ∈B B .B ⊂A ,且A ∈BC .A ⊂B ,且A ∉BD .A ⊄B ,且A ∈B3.若集合A ={ a ,{1}},则下列表述正确的是( )。
A .{1}∈AB .{1}⊆AC .{a }∈AD .∅∈A4.设集合A = {1, a },则P (A ) = ()。
A .{{1}, {a }}B .{,{1}, {a }}C .{,{1}, {a }, {1, a }}D .{{1}, {a }, {1, a }}5.若集合A 的元素个数为10,则其幂集的元素个数为()。
A .10B .100C .1024D .16.集合A ={1, 2, 3, 4, 5, 6, 7, 8}上的关系R ={<x ,y >|x +y =10且x , y A },则R 的性∅∅∈质为( )。
A .自反的B .对称的C .传递且对称的D .反自反且传递的7.设集合A ={1 , 2 , 3 , 4}上的二元关系R = { 1 , 1, 2 , 2, 2 , 3, 4 , 4},S = { 1 , 1, 2 , 2, 2 , 3, 3 , 2, 4 , 4}, 则S 是R 的()闭包。
A .自反B .传递C .对称D .以上都不对8.设A ={1, 2, 3, 4, 5, 6, 7, 8},R 是A 上的整除关系,B ={2, 4, 6},则集合B 的最大元、最小元、上界、下界依次为 ()A .8、2、8、2B .8、1、6、1C .6、2、6、2D .无、2、无、29.设A ={a , b },B ={1, 2},R 1,R 2,R 3是A 到B 的二元关系,且R 1={<a ,2>, <b ,2>},R 2={<a ,1>, <a ,2>, <b ,1>},R 3={<a ,1>, <b ,2>},则( )不是从A到B 的函数。
最新国家开放大学电大《离散数学》形考任务1试题及答案

最新国家开放大学电大《离散数学》形考任务1试题及答案最新国家开放大学电大《离散数学》形考任务1试题及答.形考任务1(集合论部分概念及性质)单项选择.题目.若集合A=.a, {a}, {1, 2}}, 则下列表述正确的是().选择一项:A.{a, {a}}.B..C.{1, 2..D.{a..题目.设函数f: N→N, f(n)=n+1, 下列表述正确的是.).选择一项: A.f是满射.B.f存在反函.C.f是单射函.D.f是双射.题目.设集合A={1, 2, 3, 4, 5}, 偏序关系是A上的整除关系, 则偏序集<A, >上的元素5是集合A的.).选择一项:A.极小.B.极大.C.最大.D.最小.题目.设A={a, b}, B={1, 2}, C={4, 5}, 从A到B的函数f={<a,1>.<b, 2>}, 从B到C的函数g={<1, 5>.<2, 4>}, 则下列表述正确的是.).选择一项:A.g..={<a, 5>.<b, 4>.B.g..={<5, .>.<4, .>.C.f°.={<5, .>.<4, .>.D.f°.={<a, 5>.<b, 4>.题目.集合A={1.2.3.4}上的关系R={<x, y>|x=y且x.yA}, 则R的性质为.).选择一项:A.传递.B.不是对称.C.反自.D.不是自反.题目.设集合..{1..}, 则P(A...).选择一项:A.{{1}.{a}.{1..}.B.{{1}.{a}.C.{,{1}.{a}.D.{,{1}.{a}.{1..}.题目.若集合A={1, 2}, B={1, 2, {1, 2}},则下列表述正确的是.).选择一项:A.AB, 且A.B.AB, 且A.C.BA, 且A.D.AB, 且A.题目.设集合A={1.2.3}, B={3.4.5}, C={5.6.7},则A∪B–.=.).选择一项:A.{1.2.3.4.B.{4.5.6.7.C.{2.3.4.5.D.{1.2.3.5.题目.设集合..{1.2.3.4.5}上的偏序关系的哈斯图如右图所示, 若A的子集..{3.4.5}, 则元素3为B的.).选择一项:A.最小上.B.下.C.最大下.D.最小.题目1.如果R1和R2是A上的自反关系, 则R1∪R2, R1∩R2, R1-R2中自反关系有.)个.选择一项:A..B..C..D..以下资料为赠送资料:《滴水之中见精神》主题班会教案活动目的: 教育学生懂得“水”这一宝贵资源对于我们来说是极为珍贵的, 每个人都要保护它, 做到节约每一滴水, 造福子孙万代。
第9讲 函数 北京大学计算机系离散数学讲义(ppt版)

2020/9/26
《集合论与图论》第9讲
12
例2(解(2))
例2: (2) A2={a,b,c}, B2={1,2}, 解: (2) A2B2中无单射,无双射,满射6个:
f1={<a,1>,<b,1>,<c,2>}, f2={<a,1>,<b,2>,<c,1>}, f3={<a,2>,<b,1>,<c,1>}, f4={<a,1>,<b,2>,<c,2>}, f5={<a,2>,<b,1>,<c,2>}, f6={<a,2>,<b,2>,<c,1>}.
2020/9/26
《集合论与图论》第9讲
26
定理3(证明)
证明: (2) dom(f○g) = A. 显然dom(f○g)A,下证Adom(f○g),
x, xA !y(yBxgy) !y!z(yBzCxgyyfz) !z(zCx(f○g)z) xdom(f○g).
2020/9/26
《集合论与图论》第9讲
第9讲 函数
内容提要 函数,偏函数,全函数,真偏函数 单射,满射,双射,计数问题 象,原象 常数函数,恒等函数,特征函数,单调函数,
自然映射 合成(复合),反函数,单边逆(左逆,右逆) 构造双射(有穷集,无穷集)
2020/9/26
《集合论与图论》第9讲
1
函数(function),映射(mapping)
2020/9/26
《集合论与图论》第9讲
21
特殊函数
常数函数: f:AB, bB, xA, f(x)=b
国家开放大学电大《离散数学》期末题库及答案

最新国家开放大学电大《离散数学》期末题库及答案《离散数学》题库及答案一一、单项选择题(每小题3分,本题共15分)1.若集合A = (l,2,3,4),则下列表述不正确的是()•A.16AB. {1,2,3}CAC. (1.2.3J6AD. 0UA2.若R和R?是A上的对称关系,则中对称关系有(〉个・A. 1B. 2C. 3D. 43.设G为连通无向图,则])时,G中存在欧拉回路・A. G不存在奇数度数的结点B. G存在偶数度数的结点C. G存在一个奇数度数的结点D. G存在两个奇数度数的结点4.无向图G是棵树,边数是10,则G的结点度数之和是().A.20B. 9C. 10D. 115.设个体域为整数集,则公式V z3y(x+y = 0)的解释可为().A-存在一整数z有整数丁满足x+y = 0B.对任意整数z存在整数財满足x+y = 0C.存在一整数z对任意整数'满足工+y・0D.任意整数工对任意整数,满足x+y=0得分评卷人--------------- 二、填空題(毎小通3分,本題共15分)6.设集合A = {1.2,3),B = (2,3,4}.C=(3.4.5,则A (J (C - B )等于7-设 A = (2,3},B-{l,2}.C-{3,4}.从 A 到 B 的函ft/-{<2,2>,<3,1>}.从 B 到C 的函数R = <V1.3>,V2.4>),则Dom(g")等于.8.已知图G中共有】个2度结点,2个3度结点,3个4度结点,则G的边数是・9.设G是连通平面分别衰示G的結点数.边数和面数,u值为5/值为4,则r的值为・-10-设个体域D = (1.2.3,4hA(x)为七大于5”,则调词公式(Vz)AGr)的真值为11. 将语句“学生的主要任务是学习”翻译成命题公式. 12.将语句“今天天暗,昨天下雨.”翻译成命题公式.四、判斷说明題(判断各题正误,并说明理由.每小题7分,本题共1413. 空集的圳:集是空集. 14.完全图K,不是平面图.15.设集合A = <1,2,3,4}上的关系:R-«1.2>.<2.3>.<3,4>}.S = (<1.1>,<2,2>,<3,3>), 试计算(DR • S t (2)7? (3)r(J?nS).16.图 G=<V,E>.其中 V=S ,6,c,d}.E=((a,6),S,c),(a,d),(5,c),0,d),(c,d)},对应边的权值依次为2、3、4、5、6及7,试(1)画出G 的图形, (2)写岀G 的邻接矩阵;(3)求出G 权最小的生成树及其权值. 17.求PTQPR )的析取范式与主合取范式.18.试证明:r -1 (P-*Q) An R A(QfR)=>i P.试题答案及评分标准仅供參考一、单项选择题(毎小题3分,本题共15分)l.C2.D3. A4. A5. B2OZZ«r-2O23^ttM三、逻辑公式翻译(毎小題6分,本题共】2分)分)五、计鼻16(每小JS 12分,本贓共36分)六、证明85(本楚共8分)2022集・2U23年股*二、壊空題(每小题3分,本题共15分)6. {1,2,3,5)7. {2,3}(或 A)8.109.110. 假(或F,或0)三、逻辑公式B!译(毎小题6分,本題共12分)11.设P :学生的主要任务是学习. 则命题公式为:P.12.设今天夭晴,Q :昨天下雨. 则命题公式为:PAQ.四、判断说明題(每小題7分,本题共14分)13.借误.空集的專集不为空集,为{0}. 14. 错误.完全图K,是平面图, 如K,可以如下图示嵌入平面.五、计算题(每小题12分,本題共36分)15. 解:(!)/? • S = (V1,2>,V2,3>* (2)J?-* = «2,1>,<3,2>,<4,3>}» (3)r(RnS)={Vl,l>,V2,2>,V3,3>,V4,4>} 16. 解.(DG 的图形表示为:《7分)(2)邻接矩阵:(3分)(6分)(2分)(6分) (2分) (6分)(3分)(4分) (8分)2022 集-2U23 年股*(3)粗线与结点表示的是最小生成树,(10 分)权值为9 (12分)17.解:P-(QAR)PV(QAR) 析取范式(2分)PVQ)A(q PVR) (5 分)g PVQ〉V(RA")A("VR) (7 分)PVQ)V(R A-i R)A(i PVR)V(QAr Q) (9 分)«(n PVQVR) A("VQV")A(i P VRVQ)A("VRVr Q)⑴分)PVQVR) A(i PVQV-i R) A(n P Vn QVR) 主合取范式 (12 分)六、证明JH(本■共8分)18.证明:(1)n □ (P-*Q) P(1 分)(2)P-*Q T(1)E (3 分)(3)(Q々) P(4 分)(On R P(5 分)(5>-| Q T(3)(4)7 (6 分)(6)n P T(2)(5)r (8 分)说明:(1)因证明过程中,公式引用的次序可以不同,一般引用前提正确得1分,利用两个公式得.出有效结论得1或2分,最后得岀靖论得2或1分.(2)另,可以用真值表验证.《陽散数学〉题库及答案二的关系R = {<=,3>M£A,3£B,且工+ » = 5}.则R=( ).A・(V1,2>,V1,3>,V2,3>} B. (VI,4>,V2,3>,V3,2>}C. (<1,1>,<2,2>,<3,2>}D. (<3.2>,<2,4>,<3,4»2.若集合A = {a,6,c,d},则下列表述正确的是( )•B. (a}£AD・("匕A2DZZ 邮-2023 邮3.设个体域为整数集期公式(七)(功)(工一,・2)的解释可为()•A.存在一整数1有整数,満足工一》=2R存在一整散工对任意整數:,満足工一>・2G对任一整数工存在整数:y满足上一y=2D.任一整数]对任意幣数》满足x-y-24.”阶无向完全图K.的边數及每个结点的度数分别是()・A. n(n —1)与mB. n(n —1)与C.n — 1 与nD. n(n —1)/2 与“一】5.设G为连通无向ffl.MC 〉时,G中存在欧拉回路•A.G不存在奇数度数的靖点B・G存在一个奇数度數的靖点C.G存在两个奇数度数的结点D.G存在偶数度数的结点得分|评卷人二、壊空順(毎小H 3分.本顕共15分)6.设集合A = {x|x是小于4的正整数).用集合的列挙法A=・7.设 A = U,2),B-{a.6}.C-{l,2).从 A 到 B 的函»/= {<1 .a>.<2,6>).从 B 到C的函数g-«a.2>,<6,l>),则复合函数g./- ・8.设G = <V,E>是一个图,结点度数之和为30,MG的边数为・9.设G是具有r,个結点责条边4个面的连通平面图.JRn+4-2-・10.设个体域D-(2,3.4},A(x )为—小于3■,则调词公式< Vx)A(x>的真值为得分评卷人三、遂梅公式翻译(毎小題6分,本■共12分)11-将语句•如果今天下頂•那么明天的比賽就要延期译成命,公式.12.将语句•地球是圆的,太阳也是圆的.”翻洋成命題公式.得分呼卷人----- 四、判断说明題(判斷各IH正讓•井说明理由.毎小願7分.本■共 14 分)13.设A = {a,6.c.</}.R-«a.6>,<6,a>,<a ,a>,<b,b> ,<(.€>}.则R是等价关系.2OZZ«r-2O23^ttM14.<Vz)(P(x)AQ(y»-R(x)中量伺V 的辖域为(PGr〉AQ(y)).得分评卷人-------------- 五、计算题(每小題12分,本題共36分)15.设集合A^{a,b,c}t B^{b t c,d}t试计算(DAUB; (2) A-Bi(3MXB.16.设G = VV,E>,V= {vi. v a. vj»v4).E =* ((vi»)» (vi»v s)» (t>i»v4). (v,,v>)»(V1 ,。
北邮 智能专业培养方案
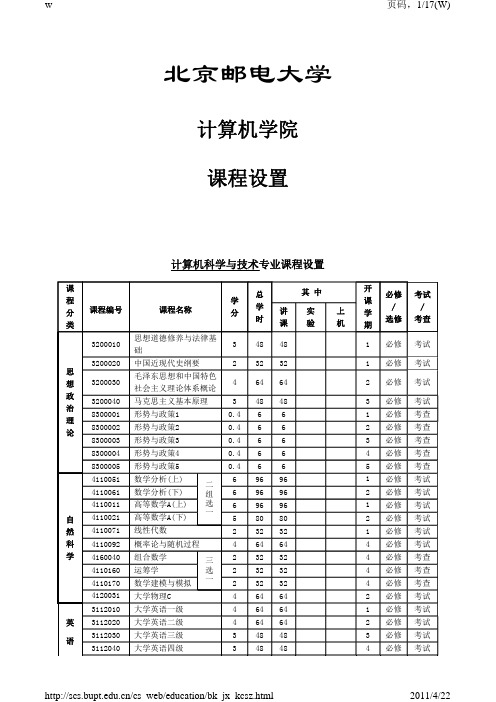
64 64
政 3200040 马克思主义基本原理 治
8300001 形势与政策1 理 论 8300002 形势与政策2
3 48 48
0.4 6
6
0.4 6
6
8300003 形势与政策3
0.4 6
6
1 必修 考试
2 必修 考试
3 必修 考试 1 必修 考查 2 必修 考查 3 必修 考查
8300004 形势与政策4
开
必修 考试
课
/
/
学
选修 考查
期
7 选修 考试
7 选修 考试
7 选修 考查
7 选修 考查
7 选修 考试 7 选修 考试 7 选修 考查
7 选修 考查
7 选修 考试 7 选修 考试 7 选修 考查 7 选修 考查
7 选修 考试 7 选修 考试 7 选修 考查
7 选修 考查
5 选修 考查 5 选修 考查 6 选修 考查 6 选修 考查
二
6
96 96
4110061 数学分析(下)
组 6 96 96
4110011 高等数学A(上) 选 6 96 96
自
4110021 高等数学A(下)
一
5
80 80
然 4110071 线性代数
2 32 32
科 4110092 概率论与随机过程
4 64 64
学 4160040 组合数学
三
2
32 32
4110160 运筹学
16 5 必修 考试
1321030 计算机网络
4 64 48 16
5 必修 考试
1313050 微机系统与接口技术 专 1321040 现代交换原理 业 基 1311030 数据库系统原理 础 1312050 软件工程
离散数学第二版答案(6-7章)

离散数学第二版答案(6-7章)LT第六章 代数系统6.1第129页1. 证明:任取,x y I ∈,(,)*(,)g y x y x y x yx x y xy g x y ==+-=+-=,因此,二元运算*是可交换的; 任取,,x y z I ∈,(,(,))*(*)*()()g x g y z x y z x y z yz x y z yz x y z yz x y z xy xz yz xyz==+-=++--+-=++---+((,),)(*)*()*()(,(,))g g x y z x y z x y xy zx y xy z x y xy z x y z xy xz yz xyz g x g y z ==+-=+-+-+-=++---+=因此,运算*是可结合的。
该运算的么元是0,0的逆元是0,2的逆元是2,其余元素没有逆元。
2.证明:任取,,x y N x y ∈≠,由*,*x y x y x y x ==≠知,**y x x y ≠,*运算不是可交换的。
任取,,x y z N ∈,由(*)**x y z x z x ==,*(*)*x y z x y x ==知,(*)**(*)x y z x y z =,*运算是可结合的。
任取x N ∈,*x x x =,可知N 中的所有元素都是等幂的。
*运算有右么元,任取,x y N ∈,*x y x =,知N 中的所有元素都是右么元。
*运算没有左么元。
证明:采用反证法。
假定e 为*运算的左么元,取,b N b e ∈≠,由*的运算公式知*e b e =,由么元的性质知,*e b b =,得e b =,这与b e ≠相矛盾,因此,*运算没有左么元。
3.解: ① 任取y x I y x ≠∈,,的最小公倍数和y x y x =*的最小公倍数和的最小公倍数和y x x y x y ==*因此对于任意的y x I y x ≠∈,,都有x y y x **=,即二元运算*是可交换的。
北邮离散数学期末复习题

北邮离散数学期末复习题第一章集合论一、判断题(1)空集是任何集合的真子集. ( 错 )(2){}φ是空集. ( 错 ) (3){}{}a a a },{∈ ( 对 ) (4)设集合{}{}{}{}AA 22,1,2,1,2,1⊆=则. ( 对 ) (5)如果B A a ⋃∉,则A a ∉或B a ∉. ( 错 )解 B A a ⋃∉则B A B A a ⋂=⋃∈,即A a ∈且B a ∈,所以A a ∉且B a ∉(6)如果A ∪.,B A B B ⊆=则 ( 对 )(7)设集合},,{321a a a A =,},,{321b b b B =,则},,,,,{332211><><><=⨯b a b a b a B A ( 错 )(8)设集合}1,0{=A ,则}1},0{,0},0{,1,,0,{><><><><=φφρ是A2到A 的关系. ( 对 )解 A 2}},1{},0{,{A φ=, =⨯A A 2}1,,0,,1},1{,0},1{,1},0{,0},0{,1,,0,{><><><><><><><><A A φφ(9)关系的复合运算满足交换律. ( 错 )(10).条件具有传递性的充分必要上的关系是集合ρρρρA = ( 错 )(11)设.~,上的传递关系也是则上的传递关系是集合A A ρρ ( 对 ) (12)集合A 上的对称关系必不是反对称的. ( 错 )(13)设21,ρρ为集合A 上的等价关系, 则21ρρ⋂也是集合A 上的等价关系( 对 )(14)设ρ是集合A 上的等价关系, 则当ρ>∈<b a ,时, ρρ][][b a = ( 对 )(15)设21,ρρ为集合 A 上的等价关系, 则 ( 错 )二、单项选择题(1)设R 为实数集合,下列集合中哪一个不是空集 ( A )A. {}R x x x ∈=-且,01|2 B .{}R x x x ∈=+且,09|2C. {}R x x x x ∈+=且,1|D. {}R x x x ∈-=且,1|2(2)设B A ,为集合,若φ=B A \,则一定有 ( C )A. φ=B B .φ≠B C. B A ⊆ D. B A ⊇(3)下列各式中不正确的是 ( C )A. φφ⊆ B .{}φφ∈ C. φφ⊂ D. {}}{,φφφ∈ (4)设{}}{,a a A =,则下列各式中错误的是 ( B )A. {}A a 2∈ B .{}A a 2⊆ C. {}A a 2}{∈ D. {}Aa 2}{⊆ (5)设{}2,1=A ,{}c b a B ,,=,{}d c C ,=,则)(C B A ⨯为 ( B ) A. {}><><c c ,2,1, B .{}><><c c ,2,,1C. {}><><2,,,1c cD. {}><><2,,1,c c(6)设{}b A ,0=,{}3,,1b B =,则B A 的恒等关系为 ( A ) A. {}><><><><3,3,,,1,1,0,0b b B .{}><><><3,3,1,1,0,0C. {}><><><3,3,,,0,0b bD. {}><><><><0,3,3,,,1,1,0b b(7)设{}c b a A ,,=上的二元关系如下,则具有传递性的为 ( D )A. {}><><><><=a b b a a c c a ,,,,,,,1ρB . {}><><=a c c a ,,,2ρC. {}><><><><=c b a b c c b a ,,,,,,,3ρD. {}><=a a ,4ρ(8)设ρ为集合A 上的等价关系,对任意A a ∈,其等价类[]ρa 为 ( B )A. 空集; B .非空集; C. 是否为空集不能确定; D. }|{A x x ∈.(9)映射的复合运算满足 ( B )A. 交换律 B .结合律 C. 幂等律 D. 分配律(10)设A ,B 是集合,则下列说法中( C )是正确的.A .A 到B 的关系都是A 到B 的映射B .A 到B 的映射都是可逆的C .A 到B 的双射都是可逆的D .B A ⊂时必不存在A 到B 的双射(11)设A 是集合,则( B )成立.A .A A #22#=B .A X X A⊆↔∈2 C .{}A2∈φ D .{}AA 2∈ (12)设A 是有限集(n A =#),则A 上既是≤又是~的关系共有(B ).A .0个B .1个C .2个D .n 个三、填空题1. 设}}2,1{,2,1{=A ,则=A2____________.填}}},2,1{,2{}},2,1{,1{},2,1{}},2,1{{},2{},1{,{2A A φ=2.设}}{,{φφ=A ,则A 2= . 填}}},{{},{,{2A A φφφ=3.设集合B A ,中元素的个数分别为5#=A ,7#=B ,且9)(#=⋃B A ,则集合B A ⋂中元素的个数=⋂)(#B A .34.设集合}4,1001|{Z x x x x A ∈≤≤=的倍数,是,}5,1001|{Z x x x x B ∈≤≤=的倍数,是,则B A 中元素的个数为 .405.设 },{b a A =, ρ 是 A2 上的包含于关系,,则有ρ= .},,},{,}{},{,},{,}{},{,,,}{,,}{,,,{><><><><><><><><><A A A b b b A a a a A b a φφφφφ6.设21,ρρ为集合 A 上的二元关系, 则=21ρρ .~1~2ρρ7.集合A 上的二元关系ρ为传递的充分必要条件是 .ρρρ⊆8. 设集合{}{}><><==0,2,2,02,1,01ρ上的关系A 及集合A 到集合{}4,2,0=B 的关系=2ρ{><b a ,|><b a ,A b a B A ∈⨯∈,且∩}=21,ρρ 则B ___________________.填 }2,2,0,2,2,0,0,0{><><><><四、解答题1. 设 A d c b a A },,,,{=上的关系 },,,,,,,,,,,,,,,{><><><><><><><><=c d d c a b b a d d c c b b a a ρ(1)写出ρ的关系矩阵;(2)验证ρ是A 上的等价关系;(3)求出A 的各元素的等价类。
离散数学(第二版)最全课后习题答案详解

-
(10)
p:天下大雨
q:他乘车上班
-
(11)
p:下雪
q:路滑
r:他迟到了
(12)
p:2 是素数
q:4 是素数
-
(13)
p:2 是素数
q:4 是素数
-
15.设 p:2+3=5. q:大熊猫产在中国. r:太阳从西方升起. 求下列符合命题的真值:
(1)
(2)
(3) (4) 解:p 真值为 1,q 真值为 1,r 真值为 0. (1)0,(2)0,(3)0,(4)1 16.当 p,q 的真值为 0,r,s 的真值为 1 时,求下列各命题公式的真值: (1) (2) (3) (4)
24.已知 的类型.
解:∵
是重言式,试判断公式
及
是重言式,而要使该式为重言式,其成真赋值只有
11,∴ 25.已知
解:∵
的类型.
都是重言式。
Hale Waihona Puke 是矛盾式,试判断公式及
是矛盾式,而要使该式为矛盾式,其成假赋值
只有 00,∴
都是重言式。
26. 已 知 解:
是重言式, 及
是矛盾式,试判断 的类型.
是矛盾式。
是重言式。
q:老王是河北人
-
(3)
p:天气冷
p:王欢与李乐组成
(4)
一个小组
p:李辛与李末是兄
(5)
弟
q:我穿羽绒服 -
-
p:王欢与李乐组成一个
-
小组
-
p:李辛与李末是兄弟
(6) p:王强学过法语
q:刘威学过法语
-
(7)
p:他吃饭
q:他听音乐
-
北京邮电大学计算机学院离散数学下半学期

Examples
(Z, +) is a commutative semigroup.
The set P(S), where S is a set, together with the operation of union is a commutative semigroup.
The set Z with the binary operation of subtraction is not a semigroup, since subtraction is not associative.
Subsemigroup – 子半群
Let
(S, *) be a semigroup and T be a subset of S.
if T is closed under the operation *, then
(T, *) is called a subsemigroup of (S, *).
Powers of a
Suppose
(S, *) is a semigroup, a ∈ S n ∈ Z+
Define the powers of an recursively as follows:
al = a, an = an-1 * a, n ≥2.
a0 = e
if (S, *) is a monoid
if it is a one-to-one correspondence from S to T, and f(a*b) = f(a)*'f(b) for all a and b in S.
Note
If f is an isomorphism from (S, *) to (T, *'), then, since f is a one-to-one correspondence, f-1 exists and is a one-toone correspondence from T to S.
育明考博-北京邮电大学计算机学院考博资料保录报录比难度经验复习方法

北京邮电大学计算机学院考博报考资料分析一、北邮计算机学院简介北京邮电大学计算机学院是全校规模大、综合实力强的学院之一。
学院下设计算机科学与技术系、智能科学与网络工程系、信息安全系等三个系。
拥有优秀的生源、出色的师资、完整的本科-硕士-博士-博士后人才培养体系。
学院现有教职工130余人,其中院士2人,国家级教学名师1人,北京市教学名师3人,博士生导师21人,教授23人,副教授51人,具有博士学位的教师80余人。
据统计,院具有博士生招生专业4个,研究方向35个,指导教师28位。
二、2014年北邮计算机学院博士录取人数及考试科目三、2014年公开招考博士生初试合格标准1、单科不低于35分,总分不限。
2、初试成绩有一科或两科成绩低于35分,低于部分累计不超过10分(含),复试成绩优异且获得省部级(含)以上科研学术奖励;或作为第一作者发表的论文被SCI、EI、CSSCI 收录;或获得发明专利以及其它反映考生科研创新能力的获奖证明等。
符合第2条考生须经拟录取导师推荐,学院招生领导小组审议通过后提交学校研究生招生委员会讨论。
四、北邮计算机学院考博的专业课参考书专业招生方式初试考试科目汇总复试内容081200计算机科学与技术录取总数37人公开招考23人硕博连读11人本科直博3人①1101英语②2201概率论与随机过程③2205近世代数④2206离散数学⑤3308数字信号处理⑥3311信息论基础⑦3312软件工程⑧3313计算机网络⑨3314现代密码学①外国语听力②外国语口语③综合面试(总分100分)0812Z1★信息安全0812Z2★智能科学与技术110505密码学同等学力考生初试加考政治理论,复试须加试两门所报专业硕士学位主干课程。
最终成绩=初试成绩+复试成绩五、北京邮电大学考博英语题型快速阅读(主观)≥1500词深度阅读(客观)1选词填空2篇章阅读理解综合运用(客观)300~400词1英汉互译英原文≥250词汉原文≥150字2英译汉英原文≥800词汉译文≤600字作文300~400词10题10分1、10题10分2、25题25分20题10分1、10分2、15分20分考试科目参考书目2201概率论与随机过程1、《概率论·数理统计·随机过程》(第1~5章,第10~12章),胡细宝、孙洪祥、王丽霞,北京邮电大学出版社(第1版)2、《随机过程》孙洪祥,机械工业出版社,20083、《概率论与随机过程》王玉孝,孙洪祥,北京邮电大学出版社,20052205近世代数1、《近世代数及其应用(第二版)》阮传概,孙伟,北京邮电大学出版社,2005年。
北京邮电大学计算机学院智能科学与技术专业课程设置

服务科学与服务工程概论
2
32
32
7
选修
考查
专业课 合计 9 学分; 必修 1 学分, 最低选修 8 学分
理论教学 总合计149 学分;必修 112 学分,占75 %;最低选修 37 学分、占25 %
注:1.开课学期用1、2、3、…8分别表示一年级~四年级的8个学期。
2.智能游戏、计算智能为双语课程。
必修
考查
1302030
面向对象程序设计与实践(C++)1
2
2周
3
必修
考查
1302050
通信认识实习
1
1周
4
必修
考查
1302020
数据结构课程设计
2
32
32
4
必修
考查
1302040
面向对象程序设计与实践(C++)2
2
2周
4
必修
考查
1302060
计算机组成原理课程设计
二选一
2
2周
5
必修
考查
1302070
2
2周
7
必修
考查
1302001
毕业设计
16
16周
8
必修
考查
实践环节合计38学分必修 38学分
32
5
必修
考试
1321010
网络技术导论
2
32
32
4
必修
考试
1312040
形式语言与自动机
2
32
32
4
必修
考查
1204012
电路与电子学实验
离散数学北京邮电大学

• §3.5: Primes and Greatest Common Divisors • §3.6: Integers & Algorithms
– Alternate bases, algorithms for basic arithmetic
Algorithm Characteristics
Some important general features of algorithms: • Input. Information or data that comes in. • Output. Information or data that goes out. • Definiteness. Algorithm is precisely defined. • Correctness. Outputs correctly relate to inputs. • Finiteness. Won‟t take forever to describe or run. • Effectiveness. Individual steps are all do-able. • Generality. Works for many possible inputs. • Efficiency. Takes little time & memory to run.
– Example assignment statement: v := 3x+7 (If x is 2, changes v to 13.)
• In pseudocode (but not real code), the expression might be informally stated:
(精华版)国家开放大学电大本科《离散数学》网络课形考网考作业及答案

(精华版)国家开放大学电大本科《离散数学》网络课形考网考作业及答案(精华版)国家开放大学电大本科《离散数学》网络课形考网考作业及答案 100%通过考试说明:2020年秋期电大把该网络课纳入到“国开平台”进行考核,该课程共有5个形考任务,针对该门课程,本人汇总了该科所有的题,形成一个完整的标准题库,并且以后会不断更新,对考生的复习、作业和考试起着非常重要的作用,会给您节省大量的时间。
做考题时,利用本文档中的查找工具,把考题中的关键字输到查找工具的查找内容框内,就可迅速查找到该题答案。
本文库还有其他网核及教学考一体化答案,敬请查看。
课程总成绩 = 形成性考核×30% + 终结性考试×70% 形考任务1 单项选择题题目1 若集合A={ a,{a},{1,2}},则下列表述正确的是().选择一项:题目2 若集合A={2,a,{ a },4},则下列表述正确的是( ).选择一项:题目3 设集合A={1 , 2 , 3 , 4}上的二元关系R={<1, 1>,<2, 2>,<2, 3>,<4, 4>},S={<1, 1>,<2, 2>,<2, 3>,<3, 2>,<4, 4>},则S是R的()闭包.选择一项:B. 对称题目4 设集合A={1, 2, 3},B={3, 4, 5},C={5, 6, 7},则A∪B–C=( ).选择一项:D. {1, 2, 3, 4} 题目5 如果R1和R2是A上的自反关系,则R1∪R2,R1∩R2,R1-R2中自反关系有()个.选择一项:C. 2 题目6 集合A={1, 2, 3, 4}上的关系R={<x,y>|x=y且x, y∈A},则R的性质为().选择一项:D. 传递的题目7 若集合A={1,2},B={1,2,{1,2}},则下列表述正确的是( ).选择一项:题目8 设A={a,b,c},B={1,2},作f:A→B,则不同的函数个数为().选择一项:C. 8 题目9 设A={1, 2, 3, 4, 5, 6, 7, 8},R是A上的整除关系,B={2, 4, 6},则集合B的最大元、最小元、上界、下界依次为 ( ).选择一项:B. 无、2、无、2 题目10 设集合A ={1 , 2, 3}上的函数分别为:f = {<1, 2>,<2, 1>,<3, 3>},g = {<1, 3>,<2, 2>,<3, 2>},h = {<1, 3>,<2,1>,<3, 1>},则h =().选择一项:D. f◦g 判断题题目11 设A={1, 2}上的二元关系为R={<x, y>|xA,yA, x+y =10},则R的自反闭包为{<1, 1>, <2, 2>}.()选择一项:对题目12 空集的幂集是空集.()选择一项:错题目13 设A={a, b},B={1, 2},C={a, b},从A到B的函数f={<a, 1>, <b, 2>},从B到C的函数g={<1, b>, <2, a >},则g° f ={<1,2 >, <2,1 >}.()选择一项:错题目14 设集合A={1, 2, 3, 4},B={2, 4, 6, 8},下列关系f = {<1, 8>, <2, 6>,<3, 4>, <4, 2,>}可以构成函数f:.()选择一项:对题目15 设集合A={1, 2, 3},B={2, 3, 4},C={3, 4, 5},则A∩(C-B )= {1, 2, 3, 5}.()选择一项:错题目16 如果R1和R2是A上的自反关系,则、R1∪R2、R1∩R2是自反的.()选择一项:对题目17 设集合A={a, b, c, d},A上的二元关系R={<a, b>, <b, a>, <b, c>, <c, d>},则R具有反自反性质.()选择一项:对题目18 设集合A={1, 2, 3},B={1, 2},则P(A)-P(B )={{3},{1,3},{2,3},{1,2,3}}.()选择一项:对题目19 若集合A = {1,2,3}上的二元关系R={<1, 1>,<1, 2>,<3, 3>},则R是对称的关系.()选择一项:错题目20 设集合A={1, 2, 3, 4 },B={6, 8, 12}, A到B的二元关系R=那么R-1={<6, 3>,<8,4>}.()选择一项:对形考任务2 单项选择题题目1 无向完全图K4是().选择一项:C. 汉密尔顿图题目2 已知一棵无向树T中有8个顶点,4度、3度、2度的分支点各一个,T的树叶数为( ).选择一项:D. 5 题目3 设无向图G的邻接矩阵为则G的边数为( ).选择一项:A. 7 题目4 如图一所示,以下说法正确的是 ( ) .选择一项:C. {(d, e)}是边割集题目5 以下结论正确的是( ).选择一项:C. 树的每条边都是割边题目6 若G是一个欧拉图,则G一定是( ).选择一项:B. 连通图题目7 设图G=<V, E>,v∈V,则下列结论成立的是 ( ) .选择一项:题目8 图G如图三所示,以下说法正确的是 ( ).选择一项:C. {b, c}是点割集题目9 设有向图(a)、(b)、(c)与(d)如图五所示,则下列结论成立的是( ).选择一项:A. (a)是强连通的题目10 设有向图(a)、(b)、(c)与(d)如图六所示,则下列结论成立的是( ).选择一项:D. (d)只是弱连通的判断题题目11 设图G是有6个结点的连通图,结点的总度数为18,则可从G中删去4条边后使之变成树.( ) 选择一项:对题目12 汉密尔顿图一定是欧拉图.( ) 选择一项:错题目13 设连通平面图G的结点数为5,边数为6,则面数为4.( ) 选择一项:错题目14 设G是一个有7个结点16条边的连通图,则G为平面图.( ) 选择一项:错题目15 如图八所示的图G存在一条欧拉回路.( ) 选择一项:错题目16 设图G如图七所示,则图G的点割集是{f}.( ) 选择一项:错题目17 设G是一个图,结点集合为V,边集合为E,则( ) 选择一项:对题目18 设图G是有5个结点的连通图,结点度数总和为10,则可从G中删去6条边后使之变成树.( ) 选择一项:错题目19 如图九所示的图G不是欧拉图而是汉密尔顿图.( ) 选择一项:对题目20 若图G=<V, E>,其中V={ a, b, c, d },E={ (a, b), (a, d),(b, c), (b, d)},则该图中的割边为(b, c).( ) 选择一项:对形考任务3 单项选择题题目1 命题公式的主合取范式是( ).选择一项:题目2 设P:我将去打球,Q:我有时间.命题“我将去打球,仅当我有时间时”符号化为( ).选择一项:题目3 命题公式的主析取范式是( ).选择一项:题目4 下列公式成立的为( ).选择一项:题目5 设A(x):x是书,B(x):x是数学书,则命题“不是所有书都是数学书”可符号化为().选择一项:题目6 前提条件的有效结论是( ).选择一项:B. ┐Q 题目7 命题公式(P∨Q)→R的析取范式是 ( ).选择一项:D. (┐P∧┐Q)∨R 题目8 下列等价公式成立的为( ).选择一项:题目9 下列等价公式成立的为( ).选择一项:题目10 下列公式中 ( )为永真式.选择一项:C. ┐A∧┐B ↔ ┐(A∨B) 判断题题目11 设个体域D={1, 2, 3},A(x)为“x小于3”,则谓词公式(∃x)A(x) 的真值为T.( ) 选择一项:对题目12 设P:小王来学校, Q:他会参加比赛.那么命题“如果小王来学校,则他会参加比赛”符号化的结果为P→Q.( ) 选择一项:对题目13 下面的推理是否正确.( ) (1) (∀x)A(x)→B(x) 前提引入(2) A(y)→B(y) US (1) 选择一项:错题目14 含有三个命题变项P,Q,R的命题公式P∧Q的主析取范式(P∧Q∧R)∨(P∧Q∧┐R).( ) 选择一项:对题目15 命题公式P→(Q∨P)的真值是T.( ) 选择一项:对题目16 命题公式┐P∧P的真值是T.( ) 选择一项:错题目17 谓词公式┐(∀x)P(x)(∃x)┐P(x)成立.( ) 选择一项:对题目18 命题公式┐(P→Q)的主析取范式是P∨┐Q.( ) 选择一项:错题目19 设个体域D={a, b},则谓词公式(∀x)(A(x)∧B(x))消去量词后的等值式为(A(a)∧B(a))∧(A(b)∧B(b)).( ) 选择一项:对题目20 设个体域D={a, b},那么谓词公式(∃x)A(x)∨(∀y)B(y)消去量词后的等值式为A(a)∨B(b).( ) 选择一项:错形考任务4 要求:学生提交作业有以下三种方式可供选择:1. 可将此次作业用A4纸打印出来,手工书写答题,字迹工整,解答题要有解答过程,完成作业后交给辅导教师批阅. 2. 在线提交word文档. 3. 自备答题纸张,将答题过程手工书写,并拍照上传形考任务 5 网上学习行为(学生无需提交作业,占形考总分的10%)附:元宇宙(新兴概念、新型虚实相融的互联网应用和社会形态)元宇宙(Metaverse)是整合了多种新技术而产生的新型虚实相融的互联网应用和社会形态,通过利用科技手段进行链接与创造的,与现实世界映射与交互的虚拟世界,具备新型社会体系的数字生活空间。
国开放大学电大本科《离散数学》《社会保障学》网络课形考网考作业(合集)答案

案形考任务 1单项选择题题目 1若集合 A={ a,{a},{1,2}},则下列表述正确的是().选择一项:题目 2若集合A={2,a,{ a },4},则下列表述正确的是( ).选择一项:题目 3设集合 A={1 , 2 , 3 , 4}上的二元关系 R={<1, 1>,<2, 2>,<2, 3>,<4, 4>},S={<1, 1>,<2, 2>,<2, 3>,<3, 2>,<4, 4>},则S 是R 的()闭包.选择一项:A. 传递B. 对称C. 自反和传递D. 自反题目 4设集合A={1, 2, 3},B={3, 4, 5},C={5, 6, 7},则A∪B–C =( ).选择一项:A. {1, 2, 3, 5}B. {4, 5, 6, 7}C. {2, 3, 4, 5}D. {1, 2, 3, 4}R2,R1-R2 中自反关系有()个.选择一项:A. 1B. 3C. 2D. 0题目 6集合A={1, 2, 3, 4}上的关系R={<x,y>|x=y 且x, y∈A},则R 的性质为().选择一项:A. 不是对称的B. 反自反C. 不是自反的D. 传递的题目 7若集合A={1,2},B={1,2,{1,2}},则下列表述正确的是().选择一项:题目 8设A={a,b,c},B={1,2},作f:A→B,则不同的函数个数为().选择一项:A. 3B. 2C. 8D. 6题目 9设A={1, 2, 3, 4, 5, 6, 7, 8},R 是A 上的整除关系,B={2, 4, 6},则集合B 的最大元、最小元、上界、下界依次为 ( ).选择一项:A. 6、2、6、2= {<1, 2>,<2, 1>,<3, 3>},g = {<1, 3>,<2, 2>,<3, 2>},h = {<1, 3>,<2, 1>,<3, 1>},则h =().选择一项:A. f◦fB. g◦fC. g◦gD. f◦g判断题题目 11设A={1, 2}上的二元关系为R={<x, y>|xA,yA, x+y =10},则R 的自反闭包为{<1, 1>, <2, 2>}.()选择一项:对错题目 12空集的幂集是空集.()选择一项:对错题目 13设A={a, b},B={1, 2},C={a, b},从A 到B 的函数f={<a, 1>, <b, 2>},从B 到C 的函数g={<1, b>, <2, a >},则g° f ={<1,2 >, <2,1 >}.()选择一项:对错题目 14设集合 A={1, 2, 3, 4},B={2, 4, 6, 8},下列关系 f = {<1, 8>, <2, 6>, <3, 4>, <4, 2,>}可以构成函数f:.(){1, 2, 3, 5}.()选择一项:对错题目 16如果R1 和R2 是A 上的自反关系,则、R1∪R2、R1∩R2是自反的.()选择一项:对错题目 17设集合A={a, b, c, d},A 上的二元关系R={<a, b>, <b, a>, <b, c>, <c, d>},则R 具有反自反性质.()选择一项:对错题目 18设集合A={1, 2, 3},B={1, 2},则P(A)-P(B )= {{3},{1,3},{2,3},{1,2,3}}.()选择一项:对错题目 19若集合A = {1,2,3}上的二元关系R={<1, 1>,<1, 2>,<3, 3>},则R 是对称的关系.()选择一项:对错题目 20设集合A={1, 2, 3, 4 },B={6, 8, 12}, A 到B 的二元关系R=那么R-1={<6, 3>,<8,4>}.()选择一项:对错一项:A. 树B. 欧拉图C. 汉密尔顿图D. 非平面图题目 2已知一棵无向树T 中有8 个顶点,4 度、3 度、2 度的分支点各一个,T 的树叶数为().选择一项:A. 4B. 8C. 3D. 5题目 3设无向图 G 的邻接矩阵为则G 的边数为().选择一项:A. 7B. 14C. 6D. 1题目 4如图一所示,以下说法正确的是 () .选择一项:A. {(a, e) ,(b, c)}是边割集B. {(a, e)}是边割集C. {(d, e)}是边割集有 n 个结点 n-1 条边的无向图都是树B. 无向完全图都是平面图C. 树的每条边都是割边D. 无向完全图都是欧拉图题目 6若G 是一个欧拉图,则G 一定是().选择一项:A. 汉密尔顿图B. 连通图C. 平面图D. 对偶图题目 7设图G=<V, E>,v∈V,则下列结论成立的是 () .选择一项:题目 8图G 如图三所示,以下说法正确的是 ().选择一项:A. {b, d}是点割集B. {c}是点割集C. {b, c}是点割集D. a 是割点题目 9设有向图(a)、(b)、(c)与(d)如图五所示,则下列结论成立的是().选择一项:A. (a)是强连通的(b)、(c)与(d)如图六所示,则下列结论成立的是().选择一项:A. (b)只是弱连通的B. (c)只是弱连通的C. (a)只是弱连通的D.(d)只是弱连通的判断题题目 11设图G 是有6 个结点的连通图,结点的总度数为18,则可从G 中删去4 条边后使之变成树.( ) 选择一项:对错题目 12汉密尔顿图一定是欧拉图.( )选择一项:对错题目 13设连通平面图G 的结点数为5,边数为6,则面数为4.( )选择一项:对错题目 14设G 是一个有7 个结点16 条边的连通图,则G 为平面图.( )选择一项:对错题目 15如图八所示的图G 存在一条欧拉回路.( )题目 17设G 是一个图,结点集合为V,边集合为E,则( )选择一项:对错题目 18设图G 是有5 个结点的连通图,结点度数总和为10,则可从G 中删去6 条边后使之变成树.( )选择一项:对错题目 19如图九所示的图G 不是欧拉图而是汉密尔顿图.( )选择一项:对错题目 20若图G=<V, E>,其中V={ a, b, c, d },E={ (a, b), (a, d),(b, c), (b, d)},则该图中的割边为(b, c).( )选择一项:对错形考任务 3单项选择题题目 1命题公式的主合取范式是( ).时间时”符号化为().选择一项:题目 3命题公式的主析取范式是().选择一项:题目 4下列公式成立的为().选择一项:题目 5设A(x):x 是书,B(x):x 是数学书,则命题“不是所有书都是数学书”可符号化为().选择一项:题目 67命题公式(P∨Q)→R的析取范式是 ().选择一项:A. (P∨Q)∨RB. ┐(P∨Q)∨RC. (P∧Q)∨RD. (┐P∧┐Q)∨R题目 8下列等价公式成立的为().选择一项:题目 9下列等价公式成立的为().选择一项:题目 10下列公式中 ( )为永真式.选择一项:A. ┐A∧┐B ↔ ┐(A∧B)B. ┐A∧┐B ↔A∨BC. ┐A∧┐B ↔┐(A∨B)D. ┐A∧┐B ↔ ┐A∨┐B选择一项:对错题目 12设P:小王来学校, Q:他会参加比赛.那么命题“如果小王来学校,则他会参加比赛”符号化的结果为P→Q.( ) 选择一项:对错题目 13下面的推理是否正确.( )(1) (∀x)A(x)→B(x)(2) A(y)→B(y)前提引入US (1)选择一项:对错题目 14含有三个命题变项P,Q,R 的命题公式P∧Q的主析取范式(P∧Q∧R)∨(P∧Q∧┐R).( ) 选择一项:对错题目 15命题公式P→(Q∨P)的真值是T.( )选择一项:对错题目 16命题公式┐P∧P的真值是T.( )选择一项:对错的主析取范式是P∨┐Q.( )选择一项:对错题目 19设个体域D={a, b},则谓词公式(∀x)(A(x)∧B(x))消去量词后的等值式为(A(a)∧B(a))∧(A(b)∧B(b)).( )选择一项:对错题目 20设个体域D={a, b},那么谓词公式(∃x)A(x)∨(∀y)B(y)消去量词后的等值式为A(a)∨B(b).( )选择一项:对错形考任务 4要求:学生提交作业有以下三种方式可供选择:1. 可将此次作业用 A4 纸打印出来,手工书写答题,字迹工整,解答题要有解答过程,完成作业后交给辅导教师批阅.2. 在线提交 word 文档.3. 自备答题纸张,将答题过程手工书写,并拍照上传形考任务 5网上学习行为(学生无需提交作业,占形考总分的 10%)《社会保障学》网络课答案形考任务 1思考题:请你谈谈 2015 年的两会在退休、养老、就医等社会保障方面有什么政策变化?对你的生活有何影响?(形成书面作业,字数为 300---500 字)二届全国人大三次会议上的专场新闻发布会答记者问时回应了当前延长退休、推进基层公务员职务与职级并行、养老金全国统筹和取消公费医疗等备受关注的公共政策。
电大-离散数学-形考作业答案3-5-7合集

电大离散数学作业答案3-7合集Array离散数学作业3离散数学集合论部分形成性考核书面作业本课程形成性考核书面作业共3次,内容主要分别是集合论部分、图论部分、数理逻辑部分的综合练习,基本上是按照考试的题型(除单项选择题外)安排练习题目,目的是通过综合性书面作业,使同学自己检验学习成果,找出掌握的薄弱知识点,重点复习,争取尽快掌握。
本次形考书面作业是第一次作业,大家要认真及时地完成集合论部分的综合练习作业。
要求:将此作业用A4纸打印出来,手工书写答题,字迹工整,解答题要有解答过程,要求2010年11月7日前完成并上交任课教师(不收电子稿)。
并在03任务界面下方点击“保存”和“交卷”按钮,完成并上交任课教师。
一、填空题1.设集合{1,2,3},{1,2}A B==,则P(A)-P(B )= {{3},{1,3},{2,3},{1,2,3}} ,A⨯ B= {<1,1>,<1,2>,<2,1>,<2,2>,<3,1>,<3.2>} .2.设集合A有10个元素,那么A的幂集合P(A)的元素个数为1024.3.设集合A={0, 1, 2, 3},B={2, 3, 4, 5},R是A到B的二元关系,∈x∈R⋂<且=且y∈>{B,,xAyAyBx}则R的有序对集合为{<2, 2>,<2, 3>,<3, 2>},<3,3> .4.设集合A={1, 2, 3, 4 },B={6, 8, 12},A到B的二元关系R=}yyx∈=<>∈x2,x,,{ByA那么R-1={<6,3>,<8,4>}5.设集合A={a, b, c, d},A上的二元关系R={<a, b>, <b, a>, <b, c>, <c, d>},则R具有的性质是没有任何性质.6.设集合A={a, b, c, d},A上的二元关系R={<a, a >, <b, b>, <b, c>, <c, d>},若在R中再增加两个元素{<c,b>,<d,c>},则新得到的关系就具有对称性.7.如果R1和R2是A上的自反关系,则R1∪R2,R1∩R2,R1-R2中自反关系有 2 个.8.设A={1, 2}上的二元关系为R={<x, y>|x∈A,y∈A, x+y =10},则R的自反闭包为{<1,1>,<2,2>} .9.设R是集合A上的等价关系,且1 , 2 , 3是A中的元素,则R中至少包含<1,1>,<2,2>,<3,3> 等元素.10.设A ={1,2},B ={a ,b },C ={3,4,5},从A 到B 的函数f ={<1, a >, <2, b >},从B 到C 的函数g ={< a ,4>, < b ,3>},则Ran(g ︒ f )= {3,4} .二、判断说明题(判断下列各题,并说明理由.)1.若集合A = {1,2,3}上的二元关系R={<1, 1>,<2, 2>,<1, 2>},则 (1) R 是自反的关系; (2) R 是对称的关系.(1) 错误。
北京邮电大学网络教育学院课程教材信息
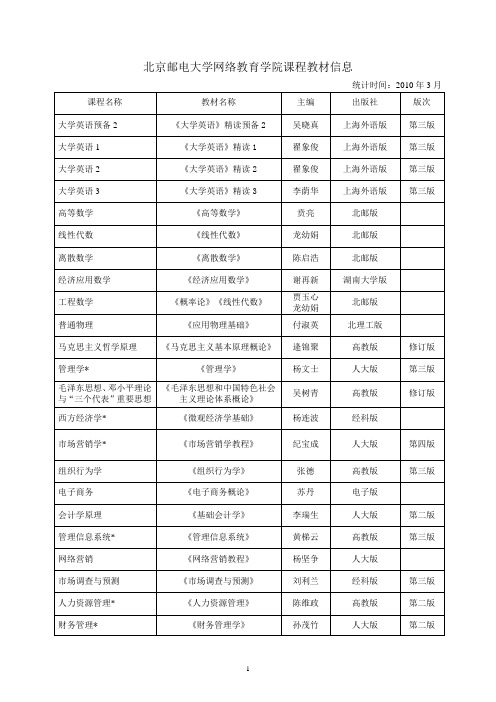
统计时间:2010年3月
课程名称
教材名称
主编
出版社
版次
大学英语预备2
《大学英语》精读预备2
吴晓真
上海外语版
第三版
大学英语1
《大学英语》精读1
翟象俊
上海外语版
第三版
大学英语2
《大学英语》精读2
翟象俊
上海外语版
第三版
大学英语3
《大学英语》精读3
李荫华
上海外语版
第三版
高等数学
第十四版
统计学原理*
《统计学》
邱东
高教版
货币银行学
《货币银行学》
蔡则祥
高教版
质量管理学
《质量管理学》
李晓春
北邮版
第三版
公共关系学
《公共关系学》
熊源伟
安徽人民版
第三版
应用文写作
《应用文写作》
曾爱波
北邮版
品牌管理与决策
《品牌战略与决策》
余鑫炎
东北财经版
消费者行为学
《消费者行为学》
符国群
武汉大学版
第二版
客户关系管理*
人大版
第三版
毛泽东思想、邓小平理论与“三个代表”重要思想
《毛泽东思想和中国特色社会主义理论体系概论》
吴树青
高教版
修订版
西方经济学*
《微观经济学基础》
杨连波
经科版
市场营销学*
《市场营销学教程》
纪宝成
人大版
第四版
组织行为学
《组织行为学》
张德
高教版
第三版
电子商务
《电子商务概论》
苏丹
北京邮电大学 计算机学院 离散数学 2.5- Cardinality of sets-2014

2015-2-6
College of Computer Science & Technology, BUPT
5
Cardinality: Formal Definition
For any two (possibly infinite) sets A and B, we say that A and B have the same cardinality (written |A|=|B|) iff there exists a bijection (bijective function) from A to B. When A and B are finite, it is easy to see that such a function exists iff A and B have the same number of elements nN.
2015-2-6
College of Computer Science & Technology, BUPT -- © Copyright Yang Juan
Countable versus Uncountable
For any set S, if S is finite or if |S|=|N|, we say S is countable. Else, S is uncountable. Intuition behind “countable:” we can enumerate (sequentially list) elements of S in such a way that any individual element of S will eventually be counted in the enumeration. Examples: N, Z. Uncountable means: No series of elements of S (even an infinite series) can include all of S’s elements. Examples: R, R2, P(N)
离散数学教程

二、提高 [4] Kenneth H. Rosen. Discrete Mathematics and its Applications. (4th, 5th Edition). 机械工业出版 社, McGraw-Hill. (中、英文版)
本书第4版是全球500多所大学的指定教材, 获得了极大的成功。中文版也已被国内大学广泛 采用为教材。第5版在前四版的基础上做了大量的 改进,使其成为更有效的教学工具。
/*集合论题集,经典习题,集合基础*/
五 定义1.4(全集):在取定一个集合U以 后,对于U的任何子集而言,称U为全集。
定理1.2:
(1)A (2) AA (3) AU
1.2 集合的子集——证明的方法
证明:(1)A (2) AA (3) AU (1)反证法:假设结论不成立,导出矛盾 结果。 不是A的子集,导致矛盾 (2,3)基本法:由子集定义 x左x右,则左右
第十二章
生成函数与递推关系
掌握:用生成函数和递推关系解决组合计数 问题的方法,以及求解递推关系的生成函数方法。 了解:求解递推关系的特征根方法。
教学内容与要求----图论
第五章 图的基本概念
掌握:图的基本术语,路、回路和连通的基本概念, 求最短路的算法及算法正确性证明,欧拉图和哈密顿图的 基本概念、判别方法以及有关定理。
理论计算机科学经典网站
国内: 国际: /~suresh/theory/the ory-home.html
命题说明和题型
1 填空题:基本概念的理解和掌握 2 判断题:概念的掌握与应用 3 计算、证明题:概念的综合应用,数学 方法的运用
北邮电信工程学院课程简介
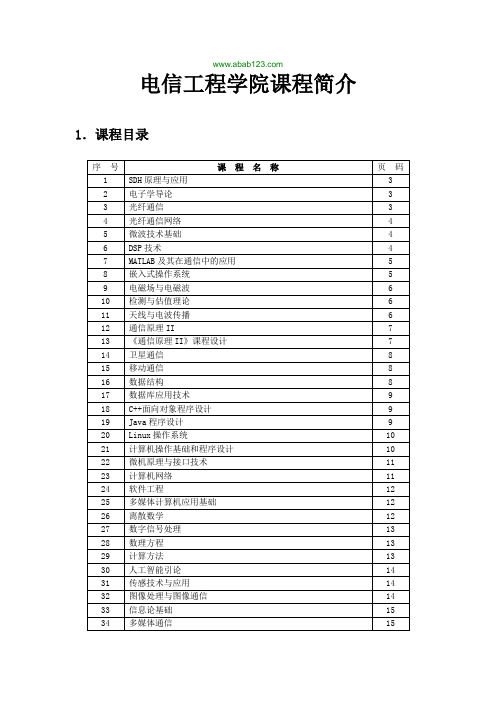
电信工程学院课程简介1.课程目录2.专业基础、专业课程简介课程编号:412·01103课程名称:SDH原理与应用SDH Technology and Its Applications课程性质:选修先修课程:《数字通信》、《现代通信技术》开课学期及学分/学时:四秋(2/34)内容提要:本课程属于通信工程、电子信息工程及相关信息类专业的专业课。
SDH技术是传送网的支撑技术之一,在现代信息传输网络中占据重要地位。
它是一个将复接、线路传输及交叉连接功能融为一体的、并由统一网管系统操作的综合信息传送网络,可实现诸如网络的有效管理、开业务时的性能监视、动态网络维护、不同供应厂商设备之间的互通等多项功能。
《SDH原理与应用》主要以传输体制与相关技术为主线,讲述SDH帧结构与段开销、同步复用和映射原理、SDH网络中的基本网元、SDH自愈网原理、光传送网技术以及一些典型SDH系统的原理与应用。
使用教材:《SDH原理与技术》,肖萍萍吴键学周芳胡春琳,2002年3月,北京邮电大学出版社《光同步数字传送网》(2版,修订版),韦乐平,1998年12月,人民邮电出版社课程编号:322·01807课程名称:电子学导论Introduction to Electronics课程性质:选修先修课程:大学物理学中的近代物理,电磁场理论与微波技术,半导体物理,电子电路基础,数字系统与逻辑设计开课学期及学分/学时:三春(2/34)内容提要:大规模集成电路、通信电子电路与光电器件的迅速发展对电子学知识的掌握提出了越来越高的要求。
本课程主要内容包括:介绍半导体物理知识、半导体工艺、集成电路工艺、新的SOC(片内系统)理论;介绍电子系统的设计方法、电子电路的仿真软件及仿真方法、电路原理图与印刷版图的设计、电子电路的调试,以及最新的高速电子通信技术;介绍通信系统中常见的激光光源、光检测器、光波导器件的基本原理与应用。
使用教材:教师自选合适中英文教材及讲义课程编号:323·01101课程名称:光纤通信Optical Fiber Communications课程性质:专业选修课先修课程:通信原理Ⅰ开课学期及学分/学时:3春(3/51)内容提要:课程全面系统地介绍光纤的传输理论;半导体激光器的工作原理、性质、光源的直接调制和间接调制;光检测器的原理、性质、光接收机的组成、噪声的分析和光接收机灵敏度的计算;光纤通信系统的组成、性能指标及其分配以及系统的总体设计;光纤通信测量技术;还介绍了光纤通信新技术和新型系统,如掺铒光纤放大器、密集波分复用系统、色散补偿技术以及非线性光学效应等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
f-1 is an isomorphism
Let a' and b' be any elements of T. Since f is onto, there exist a and b in S such
that
f(a) = a' and f(b) = b'. Then a = f-1(a') and b = f-1(b'). f-1(a' *' b') = f-1(f(a)*'f(b))= f-1(f(a*b)) = (f-1f) (a*b)
Example 4
Let S be a fixed nonempty set, and let Ss be the set of all functions f : S→S. If f and g are elements of Ss, we define f *g as fg, the composite function.
= a*b = f-1(a') * f-1(b').
generated by a(由a生成的)
Isomorphism – 同构映射 Homomorphism – 同态映射
Let (S, *) and (T, *') be two semigroups. A function f : S→T
is called an isomorphism from (S, *) to (T, *')
Example 6
• is an associative binary operation, and (A*, •) is a semigroup.
The semigroup (A*, • ) is called the free semigroup generated by A(由A生成的自由 半群).
Note
The associative property holds in any subset of a semigroup so that a subsemigroup (T, *) of a semigroup (S, *) is itself a semigroup.
Similarly, a submonoid of a monoid is itself a monoid.
Semigroup and Groups
9.1 二元运算/Binary Operations Revisited 9.2 半群/Semigroups 9.3 乘积半群与商半群/Products and Quotients of Semigroups 9.4 群Groups 9.5 乘积群与商群Products and Quotients of Groups
Proof are omitted
Note
Theorem 1 shows that the products
((al*a2)*a3)*a4 al*(a2*(a3*a4)) (al*(a2*a3))*a4 are all equal.
If al, a2,..., an are elements in a semigroup (S, *), then the product can be written as
Subsemigroup – 子半群
Let
(S, *) be a semigroup and T be a subset of S.
if T is closed under the operation *, then
(T, *) is called a subsemigroup of (S, *).
Theorem 1
If al, a2,..., an, n ≥3, are arbitrary elements of a semigroup, then all products of the elements al, a2,..., an that can be formed by inserting meaningful parentheses arbitrarily are equal.
The catenation is a binary operation •on A*.
if α = ala2...an and β= blb2…bk
α • β= ala2...anblb2…bk
if α, β, and γ are any elements of A*,
α •(β• γ ) = (α • β) • γ .
identity Λ, the empty sequence, since
α• Λ = Λ •α = α for all α∈ A* .
The set of all relations on set A is a monoid under the operation of composition. The identity element is the equality relation Δ.
Denote the semigroup by (S, *) or S. a*b is referred as the product of a and b. The
semigroup (S, *) is said to be commutative if * is a commutative operation.
If (S, *) is a semigroup, then (S, *) is a subsemigroup of (S, *).
Similarly, let (S,*) be a monoid, then (S, *) is a submonoid of (S, *), and
If T= {e}, then (T, *) is also a submonoid of (S, *)
Example 8,9
The number 0 is an identity in the semigroup (Z, +). The semigroup (Z+, +) has no identity element
Monoid – 独异点、含幺半群
A monoid is a semigroup (S, *) that has an identity.
* is a binary operation on Ss * is associative. (Ss, *) is a semigroup. The semigroup Ss is not commutative.
Example 6
Let
A = {al, a2,..., an} be a nonempty set. A* is the set of all finite sequences of elements of A. α and βbe elements of A*.
Examples
If T is the set of all even integers, then (T, *) is a subsemigroup of the monoid (Z, *), where * is ordinary multiplication, but it is not a submonoid since the identity of Z, the number l, does not belong to T.
Example 10
The semigroup P(S) defined in Example 2 has the
identity , since for any element A P(S).
*A = ∪A = A = A∪ = A* Hence P(S) is a monoid.
Example 11,12,13
if m and n are nonnegative integers, then
am * an = am+n
Example 16
If (S, *) is a semigroup, a S, and T = {ai|i ∈Z+}, then (T, *) is a subsemigroup of (S, *). If (S, *) is a monoid, a ∈ S, and T = {ai| i ∈ Z+ or i = 0}, then (T, *) is a submonoid of (S, *).
if it is a one-to-one correspondence from S to T, and f(a*b) = f(a)*'f(b) for all a and b in S.
Note
If f is an isomorphism from (S, *) to (T, *'), then, since f is a one-to-one correspondence, f-1 exists and is a one-toone correspondence from T to S.
Definition Isomorphism and
Homomorphism
定义1 一代数系统 S , , 若
S 非空且 是封闭的, 则称
S , 为广群. 定义2 一代数系统 S , ,若
S 非空且 是封闭的, 可结合
的,则称 S , 为半群.
Semigroup – 半群
A semigroup is a nonempty set S together with an associative binary operation * defined on S.
Powers of a
Suppose
(S, *) is a semigroup, a ∈ S n ∈ Z+
Define the powers of an recursively as follows:
