苏科版中考数学专题17 相似三角形及应用含答案

合集下载

中考数学复习专题17：三角形及其性质(含中考真题)

专题17 三角形及其性质☞解读考点知识点名师点晴三角形的重要线段中线、角平分线、高线理解三角形有关的中线、角平分线、高线，并会作三角形的中线、角平分线、高线三角形的中位线理解并掌握三角形的中位线的性质三角形的三边关系两边之和大于第三边，两边之差小于第三边理解三角形的三边关系，并能确定三角形第三边的取值范围三角形的内角和定理三角形的内角和等于180°掌握三角形的内角和定理，并会证明三角形的内角和定理三角形的外角三角形的外角的性质能利用三角形的外角进行角的有关计算与证明☞2年中考【题组】1．（崇左）如果一个三角形的两边长分别是2和5，则第三边可能是（）A．2 B．3 C．5 D．8【答案】C．【解析】试题分析：设第三边长为x，则由三角形三边关系定理得5﹣2＜x＜5+2，即3＜x＜7．故选C．考点：三角形三边关系．2．（来宾）如图，△ABC中，∠A=40°，点D为延长线上一点，且∠CBD=120°，则∠C=（）A．40° B．60° C．80° D．100°【答案】C．【解析】试题分析：由三角形的外角性质得，∠C=∠CBD﹣∠A=120°﹣40°=80°．故选C．考点：三角形的外角性质．3．（柳州）如图，图中∠1的大小等于（）A．40° B．50° C．60° D．70°【答案】D ．考点：三角形的外角性质．4．（南通）下列长度的三条线段能组成三角形的是（）A ．5，6，10B ．5，6，11C ．3，4，8D ．4a ，4a ，8a （a ＞0）【答案】A ．【解析】试题分析：A ．∵10﹣5＜6＜10+5，∴三条线段能构成三角形，故本选项正确； B ．∵11﹣5=6，∴三条线段不能构成三角形，故本选项错误； C ．∵3+4=7＜8，∴三条线段不能构成三角形，故本选项错误； D ．∵4a+4a=8a ，∴三条线段不能构成三角形，故本选项错误．故选A ．考点：三角形三边关系．5．（宿迁）若等腰三角形中有两边长分别为2和5，则这个三角形的周长为（） A ．9 B ．12 C ． 7或9 D ．9或12 【答案】B ．【解析】试题分析：当腰为5时，根据三角形三边关系可知此情况成立，周长=5+5+2=12；当腰长为2时，根据三角形三边关系可知此情况不成立；所以这个三角形的周长是12．故选B ．考点：1．等腰三角形的性质；2．三角形三边关系；3．分类讨论．6．（雅安）已知等腰三角形的腰和底的长分别是一元二次方程2430x x -+=的根，则该三角形的周长可以是（）A ．5B ．7C ．5或7D ．10 【答案】B ．考点：1．解一元二次方程-因式分解法；2．三角形三边关系；3．等腰三角形的性质；4．分类讨论．7．（绵阳）如图，在△ABC 中，∠B 、∠C 的平分线BE ，CD 相交于点F ，∠ABC=42°，∠A=60°，则∠BFC=（）A ．118°B ．119°C ．120°D ．121° 【答案】C ．【解析】试题分析：∵∠A=60°，∴∠ABC+∠ACB=120°，∵BE ，CD 是∠B 、∠C 的平分线，∴∠CBE=21∠ABC ，∠BCD=21∠BCA ，∴∠CBE+∠BCD=21（∠ABC+∠BCA ）=60°，∴∠BFC=180°﹣60°=120°，故选C ．考点：三角形内角和定理．8．（广州）已知2是关于x 的方程2230x mx m -+=的一个根，并且这个方程的两个根恰好是等腰三角形ABC 的两条边长，则三角形ABC 的周长为（）A ．10B ．14C ．10或14D ．8或10 【答案】B ．考点：1．解一元二次方程-因式分解法；2．一元二次方程的解；3．三角形三边关系；4．等腰三角形的性质；5．分类讨论．9．（北海）三角形三条中线的交点叫做三角形的（） A ．内心 B ．外心 C ．中心 D ．重心【答案】D ．【解析】试题分析：三角形的重心是三角形三条中线的交点．故选D ．考点：三角形的重心．10．（百色）下列图形中具有稳定性的是（）A ．正三角形B ．正方形C ．正五边形D ．正六边形【答案】A ．【解析】试题分析：∵三角形具有稳定性，∴A 正确，B ．C 、D 错误．故选A ．考点：三角形的稳定性．11．（百色）△ABC 的两条高的长度分别为4和12，若第三条高也为整数，则第三条高的长度是（）A ．4B ．4或5C ．5或6D ．6 【答案】B ．【解析】试题分析：设长度为4、12的高分别是a ，b 边上的，边c 上的高为h ，△ABC 的面积是S ，那么a=24S ，b=212S ，c=2S h ，又∵a ﹣b ＜c ＜a+b ，∴22222412412S S S S Sh -<<+，即2233S S Sh <<，解得3＜h ＜6，∴h=4或h=5，故选B ．考点：1．一元一次不等式组的整数解；2．三角形的面积；3．三角形三边关系；4．综合题．12．（广安）下列四个图形中，线段BE 是△ABC 的高的是（）A ．B ．C ．D ．【答案】D ．考点：三角形的角平分线、中线和高．13．（宜昌）下列图形具有稳定性的是（）A ．正方形B ．矩形C ．平行四边形D ．直角三角形【答案】D ．【解析】试题分析：直角三角形具有稳定性．故选D ．考点：1．三角形的稳定性；2．多边形．14．（长沙）如图，过△ABC 的顶点A ，作BC 边上的高，以下作法正确的是（）A ．B ．C ．D ．【答案】A ．【解析】试题分析：为△ABC 中BC 边上的高的是A 选项．故选A ．考点：三角形的角平分线、中线和高．15．（鄂尔多斯）如图，A ．B 是边长为1的小正方形组成的网格上的两个格点，在格点中任意放置点C ，恰好能使△ABC 的面积为1的概率是（）A ．256B ．51C ．254D ．257【答案】A ．考点：1．概率公式；2．三角形的面积．16．（淄博）如图，在四边形ABCD 中，DC ∥AB ，CB ⊥AB ，AB=AD ，CD=12AB ，点E 、F 分别为AB 、AD 的中点，则△AEF 与多边形BCDFE 的面积之比为（）A．17 B ．16 C．15 D．14【答案】C．考点：1．相似三角形的判定与性质；2．三角形的面积；3．三角形中位线定理；4．综合题．17．（淮安）将一副三角尺按如图所示的方式放置，使含30°角的三角尺的短直角边和含45°角的三角尺的一条直角边重合，则∠1的度数是．【答案】75°．【解析】试题分析：如图，∵含30°角的三角尺的短直角边和含45°角的三角尺的一条直角边重合，∴AB ∥CD ，∴∠3=∠4=45°，∴∠2=∠3=45°，∵∠B=30°，∴∠1=∠2+∠B=30°+45°=75°，故答案为：75°．考点：1．三角形的外角性质；2．三角形内角和定理．18．（宜宾）如图，AB ∥CD ，AD 与BC 交于点E ．若∠B=35°，∠D=45°，则∠AEC= ．【答案】80°．考点：1．平行线的性质；2．三角形的外角性质．19．（巴中）若a 、b 、c 为三角形的三边，且a 、b 满足229(2)0a b -+-=，则第三边c 的取值范围是．【答案】1＜c ＜5．【解析】试题分析：由题意得，290a -=，20b -=，解得a=3，b=2，∵3﹣2=1，3+2=5，∴1＜c ＜5．故答案为：1＜c ＜5．考点：1．三角形三边关系；2．非负数的性质：偶次方；3．非负数的性质：算术平方根． 20．（南充）如图，点D 在△ABC 边BC 的延长线上，CE 平分∠ACD ，∠A=80°，∠B=40°，则∠ACE 的大小是度．【答案】60．【解析】试题分析：∵∠ACD=∠B+∠A ，而∠A=80°，∠B=40°，∴∠ACD=80°+40°=120°，∵CE 平分∠ACD ，∴∠ACE=60°，故答案为：60．考点：三角形的外角性质．21．（佛山）各边长度都是整数、最大边长为8的三角形共有个．【答案】10．【解析】试题分析：∵各边长度都是整数、最大边长为8，∴三边长可以为：1，8，8；2，7，8；2，8，8；3，6，8；3，7，8；3，8，8；4，5，8；4，6，8；4，7，8；4，8，8；故各边长度都是整数、最大边长为8的三角形共有10个．故答案为：10．考点：三角形三边关系．22．（广东省）如图，△ABC 三边的中线AD 、BE 、CF 的公共点为G ，若ABC 12S =△，则图中阴影部分的面积是．【答案】4．考点：1．三角形的面积；2．综合题．23．（长春）如图，点E 在正方形ABCD 的边CD 上．若△ABE 的面积为8，CE=3，则线段BE 的长为．【答案】5．【解析】试题分析：过E 作EM ⊥AB 于M ，∵四边形ABCD 是正方形，∴AD=BC=CD=AB ，∴EM=AD ，BM=CE ，∵△ABE 的面积为8，∴12×AB×EM=8，解得：EM=4，即AD=DC=BC=AB=4，∵CE=3，由勾股定理得：BE=22BC CE +=2243+=5，故答案为：5．考点：1．正方形的性质；2．三角形的面积；3．勾股定理．24．（昆明）如图，△ABC是等边三角形，高AD、BE相交于点H，BC=43，在BE上截取BG=2，以GE为边作等边三角形GEF，则△ABH与△GEF重叠（阴影）部分的面积为．【答案】53 2．考点：1．等边三角形的判定与性质；2．三角形的重心；3．三角形中位线定理；4．综合题；5．压轴题．25．（临沂）如图，在△ABC 中，BD ，CE 分别是边AC ，AB 上的中线，BD 与CE 相交于点O ，则OBOD = ．【答案】2．【解析】试题分析：∵△ABC 的中线BD 、CE 相交于点O ，∴点O 是△ABC 的重心，∴OBOD =2．故答案为：2．考点：1．三角形的重心；2．相似三角形的判定与性质．26．（六盘水）如图，已知， l1∥l2，C1在l1上，并且C1A ⊥l2，A 为垂足，C2，C3是l1上任意两点，点B 在l2上，设△ABC1的面积为S1，△ABC2的面积为S2，△ABC3的面积为S3，小颖认为S1＝S2＝S3，请帮小颖说明理由．【答案】理由见试题解析．考点：1．平行线之间的距离；2．三角形的面积．27．（达州）化简2221432a a a a a a +⋅----，并求值，其中a 与2、3构成△ABC 的三边，且a 为整数．【答案】13a -，1．【解析】试题分析：原式第一项约分后，两项通分并利用同分母分式的减法法则计算得到结果，把a 的值代入计算即可求出值．考点：1．分式的化简求值；2．三角形三边关系．28．（青岛）【问题提出】用n根相同的木棒搭一个三角形（木棒无剩余），能搭成多少种不同的等腰三角形？【问题探究】不妨假设能搭成m种不同的等腰三角形，为探究m与n之间的关系，我们可以先从特殊入手，通过试验、观察、类比、最后归纳、猜测得出结论．【探究一】（1）用3根相同的木棒搭一个三角形，能搭成多少种不同的等腰三角形？此时，显然能搭成一种等腰三角形．所以，当n=3时，m=1．（2）用4根相同的木棒搭一个三角形，能搭成多少种不同的等腰三角形？只可分成1根木棒、1根木棒和2根木棒这一种情况，不能搭成三角形．所以，当n=4时，m=0．（3）用5根相同的木棒搭一个三角形，能搭成多少种不同的等腰三角形？若分成1根木棒、1根木棒和3根木棒，则不能搭成三角形．若分成2根木棒、2根木棒和1根木棒，则能搭成一种等腰三角形．所以，当n=5时，m=1．（4）用6根相同的木棒搭一个三角形，能搭成多少种不同的等腰三角形？若分成1根木棒、1根木棒和4根木棒，则不能搭成三角形．若分成2根木棒、2根木棒和2根木棒，则能搭成一种等腰三角形．所以，当n=6时，m=1．n 3 4 5 6m 1 0 1 1【探究二】（1）用7根相同的木棒搭一个三角形，能搭成多少种不同的三角形？（仿照上述探究方法，写出解答过程，并将结果填在表②中）（2）用8根、9根、10根相同的木棒搭一个三角形，能搭成多少种不同的等腰三角形？（只需把结果填在表②中）n 7 8 9 10m你不妨分别用11根、12根、13根、14根相同的木棒继续进行探究，…【问题解决】：用n根相同的木棒搭一个三角形（木棒无剩余），能搭成多少种不同的等腰三角形？（设n分别等于4k﹣1，4k，4k+1，4k+2，其中k是正整数，把结果填在表③中）表③n 4k﹣1 4k 4k+1 4k+2m【问题应用】：用根相同的木棒搭一个三角形（木棒无剩余），能搭成多少种不同的等腰三角形？（写出解答过程），其中面积最大的等腰三角形每腰用了根木棒．（只填结果）【答案】【探究二】：2；1；2；2；【问题解决】：k；k﹣1；k；k；【问题应用】：672．考点：1．作图—应用与设计作图；2．三角形三边关系；3．等腰三角形的判定与性质；4．探究型．【题组】1.（福建南平）下列每组数分别表示三根木棒的长，将它们首尾连接后，能摆成三角形的一组是（）A．1，2，1 B．1，2，2 C．1，2，3 D．1，2，4【答案】B．【解析】试题分析：根据三角形的三边关系：三角形两边之和大于第三边，计算两个较小的边的和，看看是否大于第三边即可：A、1+1=2，不能组成三角形，故此选项错误；B、1+2＞2，能组成三角形，故此选项正确；C、1+2=3，不能组成三角形，故此选项错误；D、1+2＜4，能组成三角形，故此选项正确．故选B．考点：三角形的三边关系．2.（浙江台州）如图，跷跷板AB的支柱OD经过它的中点O，且垂直于地面BC，垂足为D，OD＝50cm，当它的一端B着地时，另一端A离地面的高度AC为（）A．25cm B．50cm C．75cm D．100cm【答案】D．考点：三角形的中位线．3．（•北海）如图△ABC中，D、E分别是边AB、AC的中点，已知DE=5，则BC的长为（）A．8 B．9 C．10 D．11【答案】C．【解析】试题分析：∵D、E分别是边AB、AC的中点，∴DE是△ABC的中位线，∴BC=2DE=2×5=10．故选C．考点：三角形中位线定理．4.（•营口）如图，在△ABC中，点D、E分别是边AB、AC的中点，∠B=50°，∠A=26°，将△ABC沿DE折叠，点A的对应点是点A′，则∠AEA′的度数是（）A．145°B．152°C．158°D．160°【答案】B．考点：翻折变换（折叠问题）；三角形中位线定理．5.（•威海）如图，在△ABC中，∠ABC=50°，∠ACB=60°，点E在BC的延长线上，∠ABC的平分线BD与∠ACE的平分线CD相交于点D，连接AD，下列结论中不正确的是（）A．∠BAC=70°B．∠DOC=90°C．∠BDC=35°D．∠DAC=55°【答案】B．【解析】试题分析：根据三角形的内角和定理列式计算即可求出∠BAC=70°，再根据角平分线的定义求出∠ABO，然后利用三角形的内角和定理求出∠AOB再根据对顶角相等可得∠DOC=∠AOB，根据邻补角的定义和角平分线的定义求出∠DCO，再利用三角形的内角和定理列式计算即可∠BDC，判断出AD为三角形的外角平分线，然后列式计算即可求出∠DAC．试题解析：∵∠ABC=50°，∠ACB=60°，∴∠BAC=180°-∠ABC-∠ACB=180°-50°-60°=70°，故A选项正确，∵BD平分∠ABC，∴∠ABO=12∠ABC=12×50°=25°，在△ABO中，∠AOB=180°-∠BAC-∠ABO=180°-70°-25°=85°，∴∠DOC=∠AOB=85°，故B选项错误；∵CD平分∠ACE，∴∠ACD=12（180°-60°）=60°，∴∠BDC=180°-85°-60°=35°，故C选项正确；∵BD、CD分别是∠ABC和∠ACE的平分线，∴AD是△ABC的外角平分线，∴∠DAC=12（180°-70°）=55°，故D选项正确．故选B．考点：角平分线的性质；三角形内角和定理．6.（江苏淮安）若一个三角形三边长分别为2，3，x，则x的值可以为（只需填一个整数）【答案】4（答案不唯一）．考点：三角形的三边关系．7、（广东广州）△ABC中，已知∠A=60°，∠B=80°，则∠C的外角的度数是___________°．【答案】140．．【解析】试题分析：∵∠A=60°，∠B=80°，∴∠C的外角=∠A+∠B=60°+80°=140°．考点：三角形的外角的性质．8.（湖北随州）将一副直角三角板如图放置，使含30°角的三角板的直角边和含45°角的三角板的一条直角边重合，则∠1的度数为度．【答案】75．【解析】试题分析：如答图．∵∠3=60°，∠4=45°，∴∠1=∠5=180°﹣∠3﹣∠4=75°．考点：1．三角形内角和定理；2．对顶角的性质．☞考点归纳归纳 1：三角形的有关线段基础知识归纳：中线：连接一个顶点与它对边中点的线段，三角形的三条中线的交点叫做三角形的重心高线：从三角形一个顶点到它对边所在直线的垂线段．角平分线：一个内角的平分线与这个角的对边相交，顶点与交点之间的线段中位线：连接三角形两边中点的线段基本方法归纳：三角形的中位线平行线于第三边，且等于第三边的一半注意问题归纳：三角形的中线将三角形分成面积相等的两部分【例1】如图，EF是△ABC的中位线，BD平分∠ABC交EF于点D，若AB＝4，BC＝6，则DF＝_____．【答案】1．考点：1．三角形中位线定理；2．等腰三角形的判定与性质．归纳 2：三角形的三边关系基础知识归纳：三角形两边的和大于第三边，两边的差小于第三边．基本方法归纳：三角形的三边关系是判断三条线段能否构成三角形的依据，并且还可以利用三边关系列出不等式求某些量的取值范围．注意问题归纳：三角形的三边关系是中考的热点问题之一，是解决三角形的边的有关问题的重要依据．【例2】已知三角形两边长分别为3和8，则该三角形第三边的长可能是（）A．5 B．10 C．11 D．12【答案】B．考点：三角形三边关系．归纳 3：内角和定理基础知识归纳：三角形三个内角的和等于180°．基本方法归纳：在同一个三角形中，大边对大角，小边对小角．注意问题归纳：三角形的内角和定理是求三角形一个角的度数或证明角相等的重要工具．【例3】如图，在△ABC中，∠B=46°，∠C=54°，AD平分∠BAC，交BC于D，DE∥AB，交AC于E，则∠ADE的大小是（）A．45°B．54°C．40°D．50°【答案】C．【解析】试题分析：∵∠B=46°，∠C=54°，∴∠BAC=180°-∠B-∠C=180°-46°-54°=80°，∵AD平分∠BAC，∴∠BAD=12∠BAC=×80°=40°，∵DE∥AB，∴∠ADE=∠BAD=40°．故选C．考点：平行线的性质；三角形内角和定理．归纳 4：三角形的外角基础知识归纳：（1）三角形的外角等于与它不相邻的两个内角的和．（2）三角形的一个外角大于任何一个和它不相邻的内角．基本方法归纳：三角形的外角等于与它不相邻的两个内角的和．注意问题归纳：三角形的外角是解决角的计算与角的大小比较的重要工具．【例4】如图，AB∥CD，AD与BC相交于点O，∠B=30°，∠D=40°，则∠AOC的度数为（）A．60°B．70°C．80°D．90°【答案】B．考点：1．平行线的性质；2．三角形的外角性质．☞1年模拟1．（北京市平谷区中考二模）如图，将三角板的直角顶点放在直尺的一边上，若∠1=65°，则∠2的度数为（）A．10° B．15° C．20° D．25°【答案】D．【解析】试题分析：根据平行线的性质及三角形的内角和定理，有图像可知∠1与∠2互余，因此∠2=90°-65°=25°．故选D．考点：1．平行线的性质；2．三角形内角和定理．2．（安徽省安庆市中考二模）如图所示，AB∥CD，∠D=26°，∠E=35°，则∠ABE的度数是（）A．61° B．71° C．109° D．119°【答案】A ．考点：1．平行线的性质；2．三角形的外角性质．3．（山西省晋中市平遥县九年级下学期4月中考模拟）如图，直线a∥b，直角三角形如图放置，∠DCB=90°．若∠1+∠B=70°，则∠2的度数为（）A．20° B．40° C．30° D．25°【答案】A．【解析】试题分析：由三角形的外角性质，∠3=∠1+∠B=70°，∵a∥b，∠DCB=90°，∴∠2=180°﹣∠3﹣90°=180°﹣70°﹣90°=20°．故选A．考点：1．三角形的外角性质；2．平行线的性质．4．（广东省佛山市初中毕业班综合测试）如图，将△ABC三个角分别沿DE、HG、EF翻折，三个顶点均落在点O处，则∠1+∠2的度数为（）A． 120° B． 135° C． 150° D． 180°【答案】D．考点：1．翻折变换（折叠问题）；2．三角形内角和定理．5．（山东省济南市平阴县中考二模）如图，△ABC的各个顶点都在正方形的格点上，则sinA的值为（）A55255225105【答案】A．【解析】试题分析：如图所示：延长AC交网格于点E，连接BE，∵55，AB=5，∴AE2+BE2=AB2，∴△ABE是直角三角形，∴sinA=55BEAB，故选A．考点：1．锐角三角函数的定义；2．三角形的面积；3．勾股定理；4．表格型．6．（山东省威海市乳山市中考一模）如图，已知S△ABC=8m2，AD平分∠BAC，且AD⊥BD于点D，则S△ADC= m2．【答案】4．考点：1．等腰三角形的判定与性质；2．三角形的面积．7．（四川省成都市外国语学校中考直升模拟）长为1、2、3、4、5的线段各一条，从这5条线段中任取3条，能构成钝角三角形的概率是．【答案】1 5．【解析】试题分析：从长度分别为1，2，3，4，5的五条线段中，任取三条，所有的情况共有10种，其中，取出的三边能构成钝角三角形时，必须最大边的余弦值小于零，即：较小的两个边的平方和小于第三边的平方，故满足构成钝角三角形的取法只有：2、3、4 和2、4、5两种，故取出的三条线段为边能构成钝角三角形的概率是21105 ．考点：1．列表法与树状图法；2．三角形三边关系．8．（广东省佛山市初中毕业班综合测试）如图，已知△ABC 中，∠A=40°，剪去∠A 后成四边形，则∠1+∠2= 度．【答案】220．考点：1．三角形的外角性质；2．三角形内角和定理．9．（湖北省黄石市6月中考模拟）如图，点A1，A2，A3，A4，…，An 在射线OA 上，点B1，B2，B3，…，Bn ﹣1在射线OB 上，且A1B1∥A2B2∥A3B3∥…∥An ﹣1Bn ﹣1，A2B1∥A3B2∥A4B3∥…∥AnBn ﹣1，△A1A2B1，△A2A3B2，…，△An ﹣1AnBn ﹣1为阴影三角形，若△A2B1B2，△A3B2B3的面积分别为1、4，则△A1A2B1的面积为__________；面积小于的阴影三角形共有__________个．【答案】12；6．【解析】试题分析：由题意得，△A2B1B2∽△A3B2B3，因此可知2132A B A B =212323A B B A B B S S=12，2233A B A B =212323A B B A B B SS=12，再由考点：1．相似三角形的判定与性质；2．平行线的性质；3．三角形的面积；4．规律型．。

初三数学相似三角形典例及练习(含答案)

初三数学相似三角形（一）相似三角形是初中几何的一个重点，同时也是一个难点，本节复习的目标是：1。

理解线段的比、成比例线段的概念，会根据比例线段的有关概念和性质求线段的长或两线段的比，了解黄金分割.2. 会用平行线分线段成比例定理进行有关的计算、证明，会分线段成已知比。

3. 能熟练应用相似三角形的判定和性质解答有关的计算与证明题。

4. 能熟练运用相似三角形的有关概念解决实际问题本节的重点内容是相似三角形的判定定理和性质定理以及平行线分线段成比例定理。

本节的难点内容是利用判定定理证明两个三角形相似以及相似三角形性质的应用。

相似三角形是平面几何的主要内容之一,在中考试题中时常与四边形、圆的知识相结合构成高分值的综合题,题型常以填空、选择、简答或综合出现，分值一般在10%左右，有时也单独成题,形成创新与探索型试题；有利于培养学生的综合素质。

（二）重要知识点介绍： 1。

比例线段的有关概念：在比例式：：中，、叫外项，、叫内项，、叫前项，a b cda b c d a d b c a c ==() b 、d 叫后项，d 叫第四比例项，如果b=c ，那么b 叫做a 、d 的比例中项。

把线段AB 分成两条线段AC 和BC,使AC 2=AB ·BC ，叫做把线段AB 黄金分割，C 叫做线段AB 的黄金分割点。

2. 比例性质: ①基本性质：a b cdad bc =⇔= ②合比性质：±±a b c d a b b c d d=⇒= ③等比性质：……≠……a b c d m n b d n a c m b d n a b===+++⇒++++++=()03。

平行线分线段成比例定理：①定理：三条平行线截两条直线，所得的对应线段成比例，如图：l 1∥l 2∥l 3。

则，，，…AB BC DE EF AB AC DE DF BC AC EFDF===②推论：平行于三角形一边的直线截其他两边(或两边的延长线）所得的对应线段成比例。

苏科版数学中考专题复习：图形的相似综合压轴题专项练习题汇编(Word版,含答案)

苏科版数学中考专题复习：图形的相似综合压轴题专项练习题汇编1．已知四边形ABCD中，M，N两点分别在AB，BD上，且满足∠MCN＝∠BDC．（1）如图1，当四边形ABCD为正方形时，①求证：△ACM∽△DCN；②求证：DN+BM＝CD；（2）如图2，当四边形ABCD为菱形时，若∠BAD＝120°，试探究DN，BM，CD的数量关系．2．在△ABC中，CA＝CB＝m，在△AED中，DA＝DE＝m，请探索解答下列问题．【问题发现】（1）如图1，若∠ACB＝∠ADE＝90°，点D，E分别在CA，AB上，则CD与BE的数量关系是，直线CD与BE的夹角为；【类比探究】（2）如图2，若∠ACB＝∠ADE＝120°，将△AED绕点A旋转至如图2所示的位置，则CD与BE之间是否满足（1）中的数量关系？说明理由．【拓展延伸】（3）在（1）的条件下，若m＝2，将△AED绕点A旋转过程中，当B，E，D三点共线．请直接写出CD的长．3．已知四边形ABCD中，E、F分别是AB、AD边上的点，DE与CF交于点G．问题发现：（1）①如图1，若四边形ABCD是正方形，且DE⊥CF于G，则＝；②如图2，当四边形ABCD是矩形时，且DE⊥CF于G，AB＝m，AD＝n，则＝；拓展研究：（2）如图3，若四边形ABCD是平行四边形，且∠B+∠EGC＝180°时，求证：；解决问题：（3）如图4，若BA＝BC＝5，DA＝DC＝10，∠BAD＝90°，DE⊥CF于G，请直接写出的值．4．在等边△ABC中，D，E分别是AC，BC上的点，且AD＝CE，连接BD、AE相交于点F．（1）如图1，当时，＝；（2）如图2，求证：△AFD∽△BAD；（3）如图3，当时，猜想AF与BF的数量关系，并说明理由．5．如图1，点D是△ABC中AB边上一点，∠ACD＝∠B，BC2＝AB•BD．（1）求证：∠ADC＝∠ACB；（2）求∠ACB的度数；（3）将图1中的△BCD绕点C顺时针旋转得到△ECF，BD的对应边EF经过点A（如图2所示），若AC＝2，求线段CD的长．6．在矩形ABCD中，AB＝6，AD＝4，点M为AB边上一个动点，连接DM，过点M作MN ⊥DM，且MN＝DM，连接DN．（1）如图①，连接BD与BN，BD交MN于点E．①求证：△ABD∽△MND；②求证：∠CBN＝∠DNM；（2）如图②，当AM＝4BM时，求证：A，C，N三点在同一条直线上．7．在△EFG中，∠EFG＝90°，EF＝FG，且点E，F分别在矩形ABCD的边AB，AD上，AB＝8，AD＝6．（1）如图1，当点G在CD上时，求AE+DG的值；（2）如图2，FG与CD相交于点N，连接EN，当EF平分∠AEN时，求证：EN＝AE+DN；（3）如图3，EG，FG分别交CD于点M，N，当MG2＝MN•MD时，求AE的值．8．【问题背景】如图1，在Rt△ABC和Rt△ADE中，AB＝AC，AD＝AE，由已知可以得到：①△≌△；②△∽△．【尝试应用】如图2，在△ABC和△ADE中，∠ACB＝∠AED＝90°，∠ABC＝∠ADE ＝30°，求证：△ACE∽△ABD．【问题解决】如图3，在△ABC和△ADE中，∠BAC＝∠DAE＝90°，∠ABC＝∠ADE ＝30°，AC与DE相交于点F，点D在BC上，，求的值．9．已知正方形ABCD中，点E是边CD上一点（不与C、D重合），将△ADE绕点A顺时针旋转90°得到△ABF，如图1，连接EF分别交AC、AB于点P、G．（1）请判断△AEF的形状；（2）求证：P A2＝PG•PF；（3）如图2，当点E是边CD的中点时，PE＝1，求AG的长．10．如图，等边△ABC的边长为12，点D，E分别在边AB，AC上，且AD＝AE＝4，点F 为BA延长线上一点，过点F作直线l∥BC，G为射线BC上动点，连接GD并延长交直线l于点H，连接FE并延长交BC于点M，连接HE并延长交射线BC于点N．（1）若AF＝4，当BG＝4时，求线段HF和EH的长；（2）若AF＝a（a＞0），点G在运动过程中，请判断△HGN的面积是否改变．若不变，求出其值（用含a的代数式表示）；若改变，请说明理由．11．在△ABC中，∠ACB＝90°，AC＝8，BC＝6．（1）如图1，点D为AC上一点，DE∥BC交AB边于点E，若＝，求AD及DE的长；（2）如图2，折叠△ABC，使点A落在BC边上的点H处，折痕分别交AC、AB于点G、F，且FH∥AC．①求证：四边形AGHF是菱形；②求菱形的边长；（3）在（1）（2）的条件下，线段CD上是否存在点P，使得△CPH∽△DPE？若存在，求出PD的长；若不存在，请说明理由．12．如图①，AB∥MH∥CD，AD与BC相交于点M，点H在BD上．求证：．小明的部分证明如下：证明：∵AB∥MH，∴△DMH∽△DAB，∴．同理可得：＝，…．（1）请完成以上的证明（可用其他方法替换小明的方法）；（2）求证：；（3）如图②，正方形DEFG的顶点D、E分别在△ABC的边AB、AC上，E、F在边BC 上，AN⊥BC，交DG于M，垂足为N，求证：．13．【问题情境】如图1，在Rt△ABC中，∠ACB＝90°，CD⊥AB，垂足为D，我们可以得到如下正确结论：①CD2＝AD•BD；②AC2＝AB•AD；③BC2＝AB•BD，这些结论是由古希腊著名数学家欧几里得在《几何原本》最先提出的，我们称之为“射影定理”，又称“欧几里德定理”．（1）请证明“射影定理”中的结论③BC2＝AB•BD．【结论运用】（2）如图2，正方形ABCD的边长为6，点O是对角线AC、BD的交点，点E在CD上，过点C作CF⊥BE，垂足为F，连接OF．①求证：△BOF∽△BED．②若CE＝2，求OF的长．14．如图①，在正方形ABCD中，点P为线段BC上的一个动点，连接AP，将△ABP沿直线AP翻折得到△AEP，点Q是CD的中点，连接BQ交AE于点F，若BQ∥PE．（1）求证：△ABF∽△BQC；（2）求证：BF＝FQ；（3）如图②，连接DE交BQ于点G，连接EC，GC，若FQ＝6，求△GBC的面积．15．如图1，已知等边△ABC的边长为8，点D在AC边上，AD＝2，点P是AB边上的一个动点．（1）连接PC、PD．①当AP＝时，△APD∽△ACP；②若△APD与△BPC相似，求AP的长度；（2）已知点Q在线段PB上，且PQ＝2．①如图2，若△APD与△BQC相似，则∠ACQ与∠PDC之间的数量关系是；②如图3，若E、F分别是PD、CQ的中点，连接EF，线段EF的长是否是一个定值，若是，求出EF的长，若不是，说明理由．16．（1）如图①，点E，F分别在正方形边AB，BC上，且AF⊥DE，请直接写出AF与DE的关系．（2）如图②，点E，F，G分别在矩形ABCD的边AB，BC，CD上，且AF⊥EG，求证：．（3）如图③，在（2）的条件下，连接AG，过点G作AG的垂线与CF交于点H，已知BH＝3，HG＝5，GA＝7.5，求的值．17．【问题背景】正方形ABCD和等腰直角三角形CEF按如图①所示的位置摆放，点B，C，E在同一条直线上，其中∠ECF＝90°．【初步探究】（1）如图②，将等腰直角三角形CEF绕点C按顺时针方向旋转，连接BF，DE，请直接写出BF与DE的数量关系与位置关系：；【类比探究】（2）如图③，将（1）中的正方形ABCD和等腰直角三角形CEF分别改成矩形ABCD和Rt△CEF，其中∠ECF＝90°，且，其他条件不变．①判断线段BF与DE的数量关系，并说明理由；②连接DF，BE，若CE＝6，AB＝12，求DF2+BE2的值．18．在相似的复习课中，同学们遇到了一道题：已知∠C＝90°，请设计三种不同方法，将Rt△ABC分割成四个小三角形，使每个小三角形与原三角形相似．（1）甲同学设计了如图1分割方法：D是斜边AB的中点，过D分别作DE⊥AC，DF ⊥BC，请判断甲同学的做法是否正确，并说明理由．（2）乙同学设计了如图2分割方法，过点D作FD⊥AB，DE⊥BC，连结EF，易证△ADF∽△ACB，△DEB∽△ACB，但是只有D在AB特殊位置时，才能证明另两个三角形与原三角形相似，李老师通过几何画板，发现∠A＝30°时，，∠A＝45°时，，∠A＝60°时，．猜测对于任意∠A，当＝（用AC，BC或AB相关代数式表示），结论成立．请补充条件并证明．（3）在普通三角形中，显然连结三角形中位线分割成四个小三角形与原三角形相似．你能参考乙同学的分割方法找到其他分割方法吗？请做出示意图并作适当分割说明（不要求证明过程）．19．△ABC中，∠BAC＝90°，AB＝AC，点D在AB边上，点E在AC边上，连接DE，取BC边的中点O，连接DO并延长到点F，使OF＝OD，连接CF，EF，令＝＝k．（1）①如图1，若k＝1，填空：＝；△ECF是三角形．②如图2，将①中△ADE绕点A旋转，①中的结论是否仍然成立？若成立，请仅就图2所示情况给出证明；若不成立，请说明理由．（2）如图3，若k＝，AB＝AD，将△ADE由图1位置绕点A旋转，当点C，E，D三点共线时，请直接写出sin∠1的值．20．【基础探究】如图1，四边形ABCD中，∠ADC＝∠ACB，AC为对角线，AD•CB＝DC•AC．（1）求证：AC平分∠DAB．（2）若AC＝8，AB＝12，则AD＝．【应用拓展】如图2，四边形ABCD中，∠ADC＝∠ACB＝90°，AC为对角线，AD•CB ＝DC•AC，E为AB的中点，连结CE、DE，DE与AC交于点F．若CB＝6，CE＝5，请直接写出的值．参考答案1．（1）①证明：∵四边形ABCD为正方形∴∠ACD＝∠BDC＝∠BAC＝45°，又∵∠MCN＝∠BDC，∴∠MCN＝∠ACD＝45°，∴∠MCA+∠ACN＝∠ACN+∠DCN，∴∠MCA＝∠DCN，∴△ACM∽△DCN．②证明：由①可知：△ACM∽△DCN，∴，∴DN＝AM，∴AM+BM＝AB＝CD，∴DN+BM＝CD．（2）解：如图所示：连接AC，在DN上取一点P使∠PCD＝∠PDC＝30°，过P作PQ ⊥CD于Q，∴∠PCD＝∠PDC＝30°，∴∠NPC＝60°，又∵四边形ABCD为菱形且∠BAD＝120°，∴∠BAC＝60°，∴∠NPC＝∠BAC，又∵∠ACP＝∠ACD﹣∠PCD＝30°，∠MCN＝∠BDC＝30°，∵∠MCN＝∠ACP，∴∠MCA+∠ACN＝∠ACN+∠NCP，∴∠MCA＝∠NCP，∴△AMC∽△PNC，∴，∵，∴CD＝CP，∴，∴AM，∴AM＝PN，∴AM+MB＝AB＝CD，∴PN+MB＝CD，∴（DN﹣DP）+MB＝CD，∴（DN﹣CD）+MB＝CD，即DN﹣CD+MB＝CD，∴DN+MB＝2CD．2．解：（1）∵∠ACB＝∠ADE＝90°，CA＝CB，DA＝DE，∴∠A＝∠B＝∠DEA＝45°，∴AB＝AC＝m，AE＝AD＝m，∴CD＝AC﹣AD＝m，BE＝AB﹣AE＝m，∴BE＝CD，∵∠A＝45°，∴直线CD与BE的夹角为45°，故答案为：BE＝CD，45°；（2）不满足，BE＝CD，直线CD与BE的夹角为30°，理由如下：如图2，过点C作CH⊥AB于H，延长CD、BE交于点F，∵CA＝CB，∴AH＝HB，∵∠ACB＝∠ADE＝120°，CA＝CB，DA＝DE，∴∠CAB＝∠CBA＝30°，∠DAE＝∠DEA＝30°，∴AC＝2CH，∠CAD＝∠BAE，由勾股定理得：AH＝AC，∴AB＝AC，同理可得：AE＝AD，∵∠CAD＝∠BAE，∴△CAD∽△BAE，∴＝＝，∠ACD＝ABE，∴BE＝CD，∠F＝∠CAB＝30°，∴BE＝CD，直线CD与BE的夹角为30°；（3）如图3，点E在线段BD上，∵m＝2，∴AD＝DE＝1，AB＝2，由勾股定理得：BD＝＝，∴BE＝BD﹣DE＝﹣1，∴CD＝BE＝，如图4，点D在线段BE上，BE＝BD+DE＝+1，∴CD＝BE＝，综上所述：当B，E，D三点共线．CD的长为或．3．（1）解：①∵四边形ABCD是正方形，∴AD＝CD，∠BAD＝∠ADC＝90°，∵DE⊥CF，∴∠DGF＝90°＝∠ADC，∴∠ADE+∠EDC＝90°＝∠EDC+∠DCF，∴∠ADE＝∠DCF，∴△ADE≌△DCF（ASA），∴DE＝CF，故答案为：1；②解：∵四边形ABCD是矩形，∴∠A＝∠FDC＝90°，AB＝CD＝m，∵CF⊥DE，∴∠DGF＝90°，∴∠ADE+∠CFD＝90°，∠ADE+∠AED＝90°，∴∠CFD＝∠AED，∵∠A＝∠CDF，∴△AED∽△DFC，∴＝，故答案为：；（2）证明：如图所示，∠B+∠EGC＝180°，∠EGC+∠EGF＝180°，∴∠B＝∠EGF，在AD的延长线上取点M，使CM＝CF，则∠CMF＝∠CFM，∵AB∥CD，∴∠A＝∠CDM，∵AD∥BC，∴∠B+∠A＝180°，∵∠B＝∠EGF，∴∠EGF+∠A＝180°，∴∠AED＝∠CFM＝∠CMF，∴△ADE∽△DCM，∴，即；（3）解：过C作CN⊥AD于N，CM⊥AB交AB延长线于M，连接BD，设CN＝x，∵∠BAD＝90°，即AB⊥AD，∴∠A＝∠M＝∠CNA＝90°，∴四边形AMCN是矩形，∴AM＝CN，AN＝CM，在△BAD和△BCD中，，∴△BAD≌△BCD（SSS），∴∠BCD＝∠A＝90°，∴∠ABC+∠ADC＝180°，∵∠ABC+∠CBM＝180°，∴∠MBC＝∠ADC，∵∠CND＝∠M＝90°，∴△BCM∽△DCN，∴，∴，∴CM＝x，在Rt△CMB中，CM＝x，BM＝AM﹣AB＝x﹣5，由勾股定理得：BM2+CM2＝BC2，∴（x﹣5）2+（x）2＝52，解得：x1＝0（舍去），x2＝8，∴CN＝8，∵∠A＝∠FGD＝90°，∴∠AED+∠AFG＝180°，∵∠AFG+∠NFC＝180°，∴∠AED＝∠CFN，∵∠A＝∠CNF＝90°，∴△AED∽△NFC，∴＝＝．4．解：（1）如图，∵∠ABC＝∠C＝60°，∴△ABC是等边三角形，∴AB＝AC＝BC，∠BAC＝∠ABC＝∠ACB＝60°，∵AD＝CE，∴△ABD≌△CAE（SAS），∴∠EAC＝∠DBA，∵，∴点D是AC中点，且△ABC是等边三角形，∴∠DBA＝30°，∴∠EAC＝30°，∴∠BAE＝∠DBA＝30°，∴AF＝BF，∴，故答案为：1；（2）由（1）可得△ABD≌△CAE，∴∠EAC＝∠DBA，∵∠ADF＝∠BDA，∴△AFD∽△BAD；（3）由（1）可得△ABD≌△CAE，∴BD＝AE，∠EAC＝∠DBA，∴∠BFE＝∠DBA+∠BAF＝∠EAC+∠BAF＝∠BAD＝60°，设AF＝x，BF＝y，AB＝AC＝BC＝n，AD＝CE＝1，BD＝AE＝m，∵∠EAC＝∠DBA，∠ADB＝∠ADB，∴△ADF∽△BDA，∴，∴①，∵∠BFE＝∠C＝60°，∠DBC＝∠DBC，∴△BFE∽△BCD，∴，∴②，①÷②得：，∴，∵，即n＝4，∴．5．（1）证明：∵∠ACD＝∠B，∠A＝∠A，∴△ADC∽△ACB．∴∠ADC＝∠ACB．（2）解：∵BC2＝AB•BD，∴．又∵∠B＝∠B，∴△ABC∽△CBD．∴∠ACB＝∠CDB．∵∠ADC+∠CDB＝180°，∠ADC＝∠ACB，∴∠ACB＝∠CDB＝∠ADC＝90°．（3）解：∵△BCD绕点C顺时针旋转得到△ECF，∴CE＝BC，∠E＝∠B．∵∠ACD＝∠B，∴∠ACD＝∠E．∴AC＝AE．∵∠ADC＝90°，∴CE⊥AB．∴CD＝DE＝CE．∴∵△ADC∽△ACB，∴．∴AD＝•AC＝1，在Rt△ADC中，．6．证明：（1）①∵四边形ABCD为矩形，DM⊥MN，∴∠A＝∠DMN＝90°，∵AB＝6，AD＝4，MN＝DM，∴，∴△ABD∽△MND；②∵四边形ABCD为矩形，DM⊥MN，∴∠ABC＝∠DMN＝90°，∴∠ABD+∠CBD＝90°，由①得△ABD∽△MND，∴∠ABD＝∠DNM，又∵∠MEB＝∠DEN，∴△MBE∽△DNE，∴，又∵∠MED＝∠BEN，∴△DME∽△NBE，∴∠NBE＝∠DME＝90°，∴∠CBN+∠CBD＝90°，∴∠CBN＝∠DNM；（2）如图②，过点N作NF⊥AB，交AB延长线于点F，连接AC，AN，则∠NF A＝90°，∵四边形ABCD为矩形，AD＝4，AB＝6，∴∠A＝∠ABC＝90°，BC＝AD＝4，，则∠ADM+∠AMD＝90°，∵AM＝4BM，AB＝6，∴AM＝AB＝，又∵DM⊥MN，∴∠DMN＝90°，∴∠AMD+∠FMN＝90°，∴∠ADM＝∠FMN，∴△ADM∽△FMN，∴，，∴MF＝6，FN＝，∴，∴，∵∠ABC＝∠AFN＝90°，∴△ABC∽△AFN，∴∠BAC＝∠F AN，∴A，C，N三点在同一条直线上．7．（1）解：∵四边形ABCD是矩形，∴∠A＝∠D＝90°，EF＝FG，∵∠EFG＝90°，∴∠AFE+∠DFN＝90°，∠AFE+∠AEF＝90°，∴∠DFN＝∠AEF．∴△DFG≌△AEF（AAS），∴AF＝DG，AE＝DF，∴AE+DG＝AF+DF＝AD＝6；（2）证明：如图，延长NF，EA相交于H，∴∠HFE＝90°，∠HAF＝90°，∵∠HFE＝∠NFE，EF＝EF，∠HEF＝∠NEF，∴△HFE≌△NFE（ASA），∴FH＝FN，HE＝NE，∵∠AFH＝∠DFN，∠HAF＝∠D，∴△HF A≌△NFD（AAS），∴AH＝DN，∵EH＝AE+AH＝AE+DN，∴EN＝AE+DN；（3）解：如图，过点G作GP⊥AD交AD的延长线于P，∴∠P＝90°，∵MG2＝MN•MD，∴＝，∵∠GMN＝∠DMG，∴△MGN∽△MDG，∴∠GDM＝45°，∠PDG＝45°，∴△PDG是等腰直角三角形，PG＝PD，∵∠AFE+∠PFG＝90°，∠AFE+∠AEF＝90°，∴∠PFG＝∠AEF，∵∠A＝∠P＝90°，EF＝FG，∴△PFG≌△AEF（AAS），∴AF＝PG，AE＝PF，∴AE＝PD+DF＝AF+DF＝AD＝6．8．【问题背景】∵△ABC和△ADE是等腰直角三角形，∴△ABC∽△ADE．∠BAC＝∠DAE，∴∠BAD＝∠CAE，∵AB＝AC，AD＝AE，∴△ABD≌△ACE，故答案为：①△ABD≌△ACE；②△ABC∽△ADE．【尝试应用】∵△ABC∽△ADE，∴，∠CAB＝∠EAD，∴∠CAE＝∠BAD，∴△ACE∽△ABD；【问题解决】连接CE，由【尝试应用】知，△ABD∽△ACE，∴∠ACE＝∠ABD＝∠ADE＝30°，∵∠AFD＝∠EFC，∴△ADF∽△ECF，∴，∵，∴，∵，∴．9．（1）解：△AEF是等腰直角三角形，理由如下：由旋转的性质可知：AF＝AE，∠F AE＝90°，∴△AEF是等腰直角三角形；（2）证明：∵四边形ABCD是正方形，∠CAB＝45°，由（1）知∠AFE＝45°，∴∠P AG＝∠AFP＝45°，又∵∠APG＝∠FP A，∴△APG∽△FP A，∴，∴P A2＝PG•PF；（3）解：设正方形的边长为2a，∵将△ADE绕点A顺时针旋转90°得到△ABF，∴∠ABF＝∠D＝90°，DE＝BF，∵∠ABC＝90°，∴∠FBC＝180°，∴F，B，C三点共线，∵DE＝EC＝BF＝a，BC＝2a，∴CF＝3a，EF＝＝＝a，∵BG∥EC，∴BG：EC＝FB：CF＝FG：FE＝1：3，∴BG＝，AG＝，GE＝a，∵∠GAP＝∠EG＝45°，∠AGP＝∠EGA，∴△AGP∽△EGA，∴，∴AG2＝GP•GE，∴（）2＝（）×，∴a＝或a＝0（舍去），∴AG＝．10．解：（1）如图1，由题意可得：BD＝DF＝8，∵HF∥BC，∴∠HFD＝∠B，在△HFD和△GBD中，，∴△HFD≌△GBD（ASA），∴HF＝BG＝4，连接DE，∵△ABC是等边三角形，∴∠B＝∠BAC＝60°，∵AD＝AE＝4，∴△ADE是等边三角形，∴DE＝AD＝4，∠ADE＝60°，∴∠ADE＝∠B，∴DE∥BC，∴DE∥FH，∵FH＝DE＝4，∴四边形DEFH是平行四边形，∴HE和DF互相平分，∵DA＝AF，∴HE经过点A，∴HE＝2AE＝8；（2）如图2，面积不变，理由如下：连接DE，作FK⊥BC于K，在Rt△BFK中，∠B＝60°，BF＝12+a，∴FK＝BF•sin60°＝，由（1）得，DE∥FH＝BC，∴△HDE∽△HGN，△HFD∽△GBD，∴，，∴，∴，∴，∴GN＝，∴S△HGN＝＝＝，11．解：（1）∵DE∥BC，∴△ADE∽△ABC，∴，∴，∴AD＝2，；（2）①由翻折不变性可知：AF＝FH，AG＝GH，∠AFG＝∠GFH，∵FH∥AC，∴∠AGF＝∠GFH，∴∠AGF＝∠AFG，∴AG＝AF，∴AG＝AF＝FH＝HG，∴四边形AGHF是菱形；②∵FH∥AC，∴△FBH∽△ABC，∴，又∵BC＝6，AC＝8，AB＝10，∴BH：FH：BF＝3：4：5，∴设BH＝3a，则FH＝AF＝4a，BF＝5a，∴4 a+5a＝10，∴，∴FH＝，即菱形的边长为；（3）在点P使得△CPH∽△DPE，理由如下：∵△CPH∽△DPE，∴，∵BH＝，∴CH＝，∴，∴．12．证明：（1）∴＝，两边都除以MH，得，；（2）如图1，作AE⊥BD于E，MF⊥BD于F，CG⊥BD于G，∴AE∥MF∥CG，∴，∵HH∥AB，∴，∴，同理可得：，由（1）得，，两边乘以，得，（3）如图2，∵DG∥BC，∴△ADG∽△ABC，∴，∵，∴，∵四边形DEFG是正方形，∴MN＝DE＝DG，∴，两边都除以DG，得，．13．（1）证明：∵CD⊥AB，∴∠BDC＝90°＝∠ACB，∵∠CBD＝∠ABC，∴△CBD∽△ABC，∴，∴BC2＝AB•BD；（2）①证明：∵四边形ABCD是正方形，∴OC⊥BO，∠BCD＝90°，∴BC2＝BO•BD，∵CF⊥BE，∴BC2＝BF•BE，∴BO•BD＝BF•BE，即，∵∠OBF＝∠EBD，∴△BOF∽△BED；②解：在Rt△BCE中，∵BC＝6，CE＝2，∴BE＝＝2，∴DE＝4，BO＝3，由①知△BOF∽△BED，∴，∴，∴OF＝．14．（1）证明：如图①中，∵四边形ABCD是正方形，∴∠ABC＝∠C＝90°，AB∥CD，∴∠ABF＝∠CQB，由翻折的性质可知，∠E＝∠ABC＝90°∵PE∥BQ，∴∠AFB＝∠E＝90°，∴△AFB∽△BCQ；（2）证明：如图①中，设AB＝BC＝CD＝AD＝2a，∵Q是CD的中点，∴CQ＝QD＝a，∵∠C＝90°，∴BQ＝＝＝a，∵△AFB∽△BCQ，∴＝，∴＝，∴BF＝a，∴QF＝a，∴＝＝，∴BF＝QF；（3）解：如图②，建立如图平面直角坐标系，过点E作EH⊥AB于点T．∵BF＝FQ，FQ＝6，∴BF＝4，∴BQ＝BF+FQ＝4+6＝10，∴CQ＝2，AB＝BC＝CD＝AD＝4，∴Q（4，2），∴直线BQ的解析式为y＝x，∵∠EAT＝∠CBQ，∠ATE＝∠BCQ＝90°，∴△ATE∽△BCQ，∴＝＝，∴＝＝，∴AT＝8，ET＝4，∴BT﹣AB﹣AT＝4﹣8，∴E（4，4﹣8），∵D（4，4），∴直线DE的解析式为：y＝x+2﹣10，由，解得，∴G（4﹣4，2﹣2），∴S△BCG＝××（2﹣2）＝20﹣4．15．解：（1）①∵等边△ABC的边长为8，∴AC＝8，∵△APD∽△ACP，∴，∵AD＝2，∴，∴AP＝4，故答案为4；②∵△ABC为等边三角形，∴AB＝BC＝8，∠A＝∠B＝60°，∵△APD与△BPC相似，∴△APD∽△BPC或△APD∽△BCP，Ⅰ、当△APD∽△BPC时，，∴，∴AP＝，Ⅱ、当△APD∽△BCP时，，∴，∴AP＝4，即△APD与△BPC相似时，AP的长度为或4；（2）①∵△ABC为等边三角形，∴AB＝BC＝8，∠A＝∠B＝∠ACB＝60°，∵△APD与△BQC相似，∴△APD∽△BQC或△APD∽△BCQ，Ⅰ、当△APD∽△BQC时，∠APD＝∠BQC，∴∠PDC＝∠A+∠APD＝60°+∠APD＝60°+∠BQC，∴∠BQC＝∠PDC﹣60°，∴∠ACQ＝∠ACB﹣∠BCQ＝60°﹣（180°﹣∠B﹣∠BAC）＝∠B+∠BQC﹣120°＝60°+∠PDC﹣60°﹣120°＝∠PDC﹣120°，∴∠PDC+∠ACQ＝120°；Ⅱ、当△APD∽△BCQ时，∠APD＝∠BCQ，∴∠PDC＝∠A+∠APD＝60°+∠APD＝60°+∠BCQ，∴∠BCQ＝∠PDC﹣60°，∴∠ACQ＝∠ACB﹣∠BCQ＝60°﹣（∠PDC﹣60°）＝120°﹣∠PDC，∴∠ACQ+∠PDC＝120°，即满足条件的∠ACQ与∠PDC之间的数量关系是∠ACQ+∠PDC＝120°或∠PDC﹣∠ACQ＝120°；②线段EF的长是一个定值，为．如图，连接AE并延长至G，使AE＝GE，连接PG，QG，∵点E是DP的中点，∴DE＝PE，∵∠AED＝∠GEP，∴△AED≌△GEP（SAS），∴AE＝GE，PG＝AD＝2，∠ADE＝∠GPE，∴PG∥AD，∴∠QPG＝∠BAC＝60°，∵PQ＝2＝PG，∴△PQG为等边三角形，∴QG＝2，∠PQG＝60°＝∠B，∴QG∥BC，连接GF并延长交BC于H，∴∠FQG＝∠FCH，∵点F是CQ的中点，∴FQ＝FC，∵∠QFG＝∠CFH，∴△QFG≌△CFH（ASA），∴FG＝FH，CH＝QG＝2，连接AH，过点A作AM⊥BC于M，∴∠AMC＝90°，CM＝BC＝4，在Rt△AMC中，AC＝8，根据勾股定理得，AM2＝AC2﹣CM2＝82﹣42＝48，在Rt△AMH中，MH＝CM﹣CH＝2，根据勾股定理得，AH＝＝＝2，∵AE＝GE，FG＝FH，∴EF是△AHG的中位线，∴EF＝AH＝，即线段EF的长是一个定值．16．解：（1）∵AF⊥DE，∴∠ADE+∠DAF＝90°，∵∠ADE+∠AED＝90°，∴∠DAF＝∠AED，∵∠ADE＝∠ABF＝90°，AD＝AB，∴△ADE≌△DAF（AAS），∴AF＝DE；（2）过点G作GM⊥BA交于点M，∵AF⊥EG，∴∠F AB+∠AEG＝90°，∵∠F AB+∠AFB＝90°，∴∠AEG＝∠AFB，∵∠GME＝∠ABF＝90°，∴△GME∽△ABF，∴＝，∵AD＝GM，∴；（3）连接AH，∵AG⊥GH，∴△AGH是直角三角形，∵HG＝5，GA＝7.5，∴AH＝，在Rt△ABH中，BH＝3，AH＝，∴AB＝，∵∠AGH＝90°，∴∠DGA+∠CGH＝90°，∵∠DGA+∠GAD＝90°，∴∠GAD＝∠CGH，∴△DAG∽△CGH，∴＝＝，∴＝＝，∴AD＝6，由（2）知，∴＝＝．17．解：（1）如图②，BF与CD交于点M，与DE交于点N，∵四边形ABCD是正方形，∴BC＝DC，∠BCD＝90°，∵△ECF是等腰直角三角形，∴CF＝CE，∠ECF＝90°，∴∠BCD＝∠ECF，∴∠BCD+∠DCF＝∠ECF+∠DCF，∴∠BCF＝∠DCE，∴△BCF≌△DCE（SAS），∴BF＝DE，∠CBF＝∠CDE，∵∠BMC＝∠DMF，∠CBF+∠BMC＝90°，∴∠CDE+∠DMF＝90°，∴∠BND＝90°，∴BF⊥DE，故答案为：BF＝DE，BF⊥DE；（2）①如图③，，理由：∵四边形ABCD是矩形，∴∠BCD＝90°，∵∠ECF＝90°，∴∠BCD+∠DCF＝∠ECF+∠DCF，∴∠BCF＝∠DCE，∵，∴△BCF∽△DCE，∴＝；②如图③，连接BD，∵△BCF∽△DCE，∴∠CBF＝∠CDE，∵四边形ABCD是矩形，∴CD＝AB＝12，∵CE＝6，，∴＝，∴CF＝8，BC＝16，∵∠DBO+∠CBF+∠BDC＝∠BDO+∠CDE+∠BDC＝∠DBO+∠BDO＝90°，∴∠BOD＝90°，∴∠DOF＝∠BOE＝∠EOF＝90°，在Rt△DOF中，DF2＝OD2+OF2，在Rt△BOE中，BE2＝OB2+OE2，在Rt△DOB中，DB2＝OD2+OB2，在Rt△EOF中，EF2＝OE2+OF2，∴DF2+BE2＝OD2+OF2+OB2+OE2＝DB2+EF2，在Rt△BCD中，BD2＝BC2+CD2＝162+122＝400，在Rt△CEF中，EF2＝EC2+CF2＝62+82＝100，∴BD2+EF2＝400+100＝500，∴DF2+BE2＝500．18．解：（1）甲的做法正确，理由如下：∵DE⊥AC，DF⊥BC，∴∠DEC＝∠DFC＝90°，∵∠C＝90°，∴四边形DECF是矩形，∴∠EDF＝90°，DE∥BC，DF∥AC，∴，△AED∽△ACB，△BFD∽△BCA，即：AE＝CE，同理可得：BF＝CF，∴DF∥AC，EF∥AB，∴四边形AEFD是平行四边形，△CEF∽△CAB，同理可得：四边形DEFB是平行四边形，∴∠EFD＝∠A，∵∠AED＝∠EDF，∴△AED∽△FDE，∴四个小三角形与△ABC相似；（2）当时，△EDF∽△AFD∽△FEC，理由如下：∵△ADF∽△ACB，△DEB∽△ACB，∴①，②，得，，∴DE＝EF，∵DE∥AF，∴四边形ADFE是平行四边形，由（1）可得，△DEF和△CEF与△ABC相似，故答案是：；（3）如图，根据和AC和AB及AB的长度找出点D的位置，然后作DE∥AC交BC于E，作EF∥AB交AC于F，连接DF即可．19．解：（1）①∵O是BC的中点，∴OB＝OC，在△BOD和△COF中，，∴△BOD≌△COF（SAS），∴CF＝BD，∠OCF＝∠B，∵AD＝AE，AB＝AC，∴BD＝CE，∴CE＝CF，即：，∵∠B+∠ACB＝90°，∴∠OCF+∠ACB＝90°，∴∠ECF＝90°，∴△ECF是等腰直角三角形，故答案是：1，等腰直角三角形，解：（2）如图1，仍然成立，理由如下：连接BD，由（1）得：CF＝BD，CF∥BD，∴∠CFO＝∠DBO，∵∠BAC＝∠DAE＝90°，∴∠BAC﹣∠BAE＝∠DAE﹣∠BAE，∴∠CAE＝∠BAD，在△CAE和△BAD中，，∴△CAE≌△BAD（SAS），∴CE＝BD，∠ACE＝∠ABD，∴CE＝CF，∵∠ACB+∠ABC＝90°，∴∠ACE+∠EAO+∠ABC＝90°，∴∠ABD+∠EAO+∠ABC＝90°，∴∠EAO+∠DBO＝90°，∴∠EAO+∠CFO＝90°，∴∠FCE＝90°，∴＝1，△ECF是等腰直角三角形；（3）如图2，连接BD，作AG⊥CD于G，设AD＝a，则AB＝，AC＝a，AE＝，由（2）得：∠CAE＝∠BAD，CF＝BD，∵，∴△CAE∽△BAD，∴，∠ACD＝∠ABD，∴，同理（2）得：∠CEF＝90°，∴∠ECF＝∠EAD＝90°，∴点C、A、B、D共圆，∴∠1＝∠ACG，∵AD＝a，AE＝，∠DAE＝90°，∴DE＝，由S△ADE＝得，AG＝a，∴sin∠ACD＝＝＝，∴sin∠1＝．20．（1）证明：∵∠ADC＝∠ACB，，∴△ADC∽△ACB，∴∠DAC＝∠CAB，∴AC平分∠DAB；（2）解：∵△ADC∽△ACB，∴，∴AC2＝AB×AD，∵AC＝8，AB＝12，∴64＝12AD，∴AD＝，故答案为：；（3）解：∵∠ACB＝90°，点E为AB的中点，∴AB＝2CE＝10，∴AC＝8，∵△ADC∽△ACB，∴AD＝＝6.4，由（1）知∠DAC＝∠EAC，∵CE＝AE，∴∠ECA＝∠EAC，∴∠DAC＝∠ECA，∴△AFD∽△CFE，∴．。

初中数学经典相似三角形练习题(附参考答案)(K12教育文档)

初中数学经典相似三角形练习题(附参考答案)(word版可编辑修改) 编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（初中数学经典相似三角形练习题(附参考答案)(word版可编辑修改)）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为初中数学经典相似三角形练习题(附参考答案)(word版可编辑修改)的全部内容。

相似三角形一．解答题（共30小题）1．如图，在△ABC中，DE∥BC，EF∥AB，求证:△ADE∽△EFC．2．如图,梯形ABCD中，AB∥CD，点F在BC上，连DF与AB的延长线交于点G．(1）求证：△CDF∽△BGF;（2）当点F是BC的中点时，过F作EF∥CD交AD于点E，若AB=6cm，EF=4cm，求CD的长．3．如图，点D,E在BC上，且FD∥AB，FE∥AC．求证：△ABC∽△FDE．4．如图，已知矩形ABCD的边长AB=3cm，BC=6cm．某一时刻，动点M从A点出发沿AB方向以1cm/s的速度向B点匀速运动;同时，动点N从D点出发沿DA方向以2cm/s的速度向A点匀速运动，问:（1）经过多少时间，△AMN的面积等于矩形ABCD面积的？（2）是否存在时刻t,使以A，M,N为顶点的三角形与△ACD相似？若存在,求t的值；若不存在,请说明理由．5．已知：P是正方形ABCD的边BC上的点，且BP=3PC，M是CD的中点，试说明:△ADM∽△MCP．6．已知矩形ABCD,长BC=12cm,宽AB=8cm，P、Q分别是AB、BC上运动的两点．若P自点A出发，以1cm/s的速度沿AB方向运动，同时,Q自点B出发以2cm/s的速度沿BC方向运动，问经过几秒，以P、B、Q为顶点的三角形与△BDC相似？7．如图，∠ACB=∠ADC=90°，AC=，AD=2．问当AB的长为多少时,这两个直角三角形相似．8．如图在△ABC中,∠C=90°,BC=8cm，AC=6cm,点Q从B出发，沿BC方向以2cm/s的速度移动，点P从C出发,沿CA方向以1cm/s的速度移动．若Q、P分别同时从B、C出发，试探究经过多少秒后，以点C、P、Q为顶点的三角形与△CBA相似？9．如图所示，梯形ABCD中，AD∥BC，∠A=90°，AB=7，AD=2，BC=3，试在腰AB上确定点P 的位置,使得以P，A，D为顶点的三角形与以P，B，C为顶点的三角形相似．10．如图，在矩形ABCD中，AB=15cm，BC=10cm,点P沿AB边从点A开始向B以2cm/s的速度移动；点Q沿DA边从点D开始向点A以1cm/s的速度移动．如果P、Q同时出发，用t（秒）表示移动的时间，那么当t为何值时,以点Q、A、P为顶点的三角形与△ABC相似．11．如图，路灯（P点)距地面8米，身高1.6米的小明从距路灯的底部（O点）20米的A点，沿OA所在的直线行走14米到B点时，身影的长度是变长了还是变短了?变长或变短了多少米？12．阳光通过窗口照射到室内，在地面上留下2.7m宽的亮区（如图所示）,已知亮区到窗口下的墙脚距离EC=8.7m，窗口高AB=1.8m，求窗口底边离地面的高BC．13．如图，李华晚上在路灯下散步．已知李华的身高AB=h,灯柱的高OP=O′P′=l,两灯柱之间的距离OO′=m．（1）若李华距灯柱OP的水平距离OA=a,求他影子AC的长；（2）若李华在两路灯之间行走，则他前后的两个影子的长度之和(DA+AC）是否是定值请说明理由;（3）若李华在点A朝着影子（如图箭头）的方向以v1匀速行走，试求他影子的顶端在地面上移动的速度v2．14．已知：如图,△ABC∽△ADE，AB=15,AC=9，BD=5．求AE．15．已知:如图Rt△ABC∽Rt△BDC，若AB=3，AC=4．（1）求BD、CD的长;（2)过B作B E⊥DC于E，求BE的长．相似三角形一．解答题（共30小题)1．如图，在△ABC中，DE∥BC，EF∥AB，求证：△ADE∽△EFC．2．如图，梯形ABCD中，AB∥CD，点F在BC上，连DF与AB的延长线交于点G．(1）求证：△CDF∽△BGF；（2）当点F是BC的中点时,过F作EF∥CD交AD于点E,若AB=6cm，EF=4cm，求CD的长．分析：（1）利用平行线的性质可证明△CDF∽△BGF．（2）根据点F是BC的中点这一已知条件,可得△CDF≌△BGF，则CD=BG，只要求出BG的长即可解题．3．如图，点D，E在BC上,且FD∥AB,FE∥AC．求证：△ABC∽△FDE．点评:本题很简单，考查的是相似三角形的判定定理：（1）如果两个三角形的两个角对应相等，那么这两个三角形相似；（2）如果一个三角形的两条边和另一个三角形的两条边对应成比例，并且夹角相等，那么这两个三角形相似；(3）如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似．4．如图，已知矩形ABCD的边长AB=3cm，BC=6cm．某一时刻，动点M从A点出发沿AB方向以1cm/s的速度向B点匀速运动；同时，动点N从D点出发沿DA方向以2cm/s的速度向A点匀速运动，问：（1)经过多少时间，△AMN的面积等于矩形ABCD面积的？（2)是否存在时刻t，使以A，M，N为顶点的三角形与△ACD相似？若存在，求t的值；若不存在，请说明理由．分析：（1）关于动点问题，可设时间为x，根据速度表示出所涉及到的线段的长度，找到相等关系，列方程求解即可，如本题中利用,△AMN的面积等于矩形ABCD面积的作为相等关系;（2）先假设相似，利用相似中的比例线段列出方程，有解的且符合题意的t值即可说明存在，反之则不存在．解答：（1)设经过x秒后,（6﹣2x）x=×3×6,得x1=1，x2=2，（2)假设经过t秒时,以A,M，N为顶点的三角形与△ACD相似，由矩形ABCD,可得∠CDA=∠MAN=90°，因此有或即①,或②解①，得t=;解②，得t=经检验，t=或t=都符合题意12．已知：P是正方形ABCD的边BC上的点，且BP=3PC,M是CD的中点,试说明：△ADM∽△MCP．分析：欲证△ADM∽△MCP,通过观察发现两个三角形已经具备一组角对应相等,即∠D=∠C,此时，再求夹此对应角的两边对应成比例即可．6．已知矩形ABCD，长BC=12cm，宽AB=8cm，P、Q分别是AB、BC上运动的两点．若P自点A 出发，以1cm/s的速度沿AB方向运动，同时，Q自点B出发以2cm/s的速度沿BC方向运动，问经过几秒,以P、B、Q为顶点的三角形与△BDC相似？分析：要使以P、B、Q为顶点的三角形与△BDC相似，则要分两两种情况进行分析．分别是△PBQ∽△BDC或△QBP∽△BDC，从而解得所需的时间．解答：解：设经x秒后，△PBQ∽△BCD,由于∠PBQ=∠BCD=90°，(1）当∠1=∠2时,有：,即；（2）当∠1=∠3时，有:,即,∴经过秒或2秒，△PBQ∽△BCD．7．如图,∠ACB=∠ADC=90°,AC=，AD=2．问当AB的长为多少时，这两个直角三角形相似．解答：解：∵AC=，AD=2，∴CD==．要使这两个直角三角形相似，有两种情况：（1)当Rt△ABC∽Rt△ACD时，有=，∴AB==3；（2)当Rt△ACB∽Rt△CDA时,有=,∴AB==3．8．如图在△ABC中，∠C=90°,BC=8cm,AC=6cm，点Q从B出发，沿BC方向以2cm/s的速度移动，点P从C出发，沿CA方向以1cm/s的速度移动．若Q、P分别同时从B、C出发,试探究经过多少秒后，以点C、P、Q为顶点的三角形与△CBA相似?解答：解：设经过x秒后，两三角形相似，则CQ=（8﹣2x）cm，CP=xcm，∵∠C=∠C=90°，当或时，两三角形相似．（1）当时，，∴x=;（2）当时，，∴x=．19．如图所示,梯形ABCD中，AD∥BC，∠A=90°，AB=7，AD=2,BC=3，试在腰AB上确定点P的位置，使得以P，A,D为顶点的三角形与以P,B，C为顶点的三角形相似．解答：解：（1）若点A，P,D分别与点B，C，P对应，即△APD∽△BCP，∴=，=,AP2﹣7AP+6=0,AP=1或AP=6，检测：当AP=1时,由BC=3，AD=2，BP=6，∴=，又∵∠A=∠B=90°，∴△APD∽△BCP．当AP=6时，由BC=3,AD=2，BP=1，又∵∠A=∠B=90°，△APD∽△BCP．(2)若点A，P,D分别与点B，P，C对应，即△APD∽△BPC．∴=，∴=，∴AP=．检验：当AP=时，由BP=,AD=2，BC=3，=，∵∠A=∠B=90°，∴△APD∽△BPC．此，点P的位置有三处，即在线段AB距离点A的1、、6处．10．如图，在矩形ABCD中，AB=15cm,BC=10cm，点P沿AB边从点A开始向B以2cm/s的速度移动；点Q沿DA边从点D开始向点A以1cm/s的速度移动．如果P、Q同时出发，用t（秒）表示移动的时间，那么当t为何值时,以点Q、A、P为顶点的三角形与△ABC相似．分析：若以点Q、A、P为顶点的三角形与△ABC相似,有四种情况：①△APQ∽△BAC,此时得AQ：BC=AP:AB;②△APQ∽△BCA，此时得AQ：AB=AP:BC；③△AQP∽△BAC,此时得AQ：BA=AP：BC；④△AQP∽△BCA，此时得AQ：BC=AP：BA．可根据上述四种情况所得到的不同的对应成比例线段求出t的值．11．如图，路灯(P点）距地面8米，身高1.6米的小明从距路灯的底部(O点）20米的A点，沿OA所在的直线行走14米到B点时,身影的长度是变长了还是变短了？变长或变短了多少米？分析：如图,由于AC∥BD∥OP,故有△MAC∽△MOP,△NBD∽△NOP即可由相似三角形的性质求解．12．阳光通过窗口照射到室内，在地面上留下2。

三角形全等、相似及综合应用模型(6大模型+解题技巧)—2024年中考数学(全国通用)(解析版)

三角形全等、相似及综合应用模型题型解读｜模型构建｜通关试练三角形基础知识部分多以选择或者填空题形式，考察其三边关系、内角和/外角和定理、“三线”基本性质等。

特殊三角形的性质与判定也是考查重点，年年都会考查，最为经典的“手拉手”模型就是以等腰三角形为特征总结的，且等腰三角形单独出题的可能性还是比较大。

直角三角形的出题类型可以是选择填空题这类小题，也可以是各类解答题，以及融合在综合压轴题中，作为问题的几何背景进行拓展延伸。

模型01 与三角形有关的线段应用高（AD）中线（AD）角平分线（AD）中位线（DE）模型02 与三角形有关的角的应用（1）三角形的内角：（1）三角形内角的概念：三角形内角是三角形三边的夹角．每个三角形都有三个内角，且每个内角均大于0°且小于180°．（2）三角形内角和定理：三角形内角和是180°．（3）三角形内角和定理的证明证明方法，不唯一，但其思路都是设法将三角形的三个内角移到一起，组合成一个平角．在转化中借助平行线．（4）三角形内角和定理的应用主要用在求三角形中角的度数．①直接根据两已知角求第三个角；②依据三角形中角的关系，用代数方法求三个角；③在直角三角形中，已知一锐角可利用两锐角互余求另一锐角．（2）三角形的外角：（1）三角形外角的定义：三角形的一边与另一边的延长线组成的角，叫做三角形的外角．三角形共有六个外角，其中有公共顶点的两个相等，因此共有三对．（2）三角形的外角性质：①三角形的外角和为360°．②三角形的一个外角等于和它不相邻的两个内角的和．③三角形的一个外角大于和它不相邻的任何一个内角．（3）若研究的角比较多，要设法利用三角形的外角性质②将它们转化到一个三角形中去．（4）探究角度之间的不等关系，多用外角的性质③，先从最大角开始，观察它是哪个三角形的外角．模型03 三角形全等的判定及应用（1）全等三角形的定义：全等的图形必须满足：（1）形状相同；（2）大小相等能够完全重合的两个三角形叫做全等三角形。

2020—2021年新苏科版九年级数学下册《图形的相似-相似三角形的性质》专题练习及答案.docx

2017-2018学年苏科版（新课标）九年级下册第六章《图形的相似》（相似三角形的性质）一．选择题1．如果两个相似三角形的面积比是1：4，那么它们的周长比是（）A．1：16 B．1：4 C．1：6 D．1：22．△ABC与△DEF的相似比为1：4，则△ABC与△DEF的周长比为（）A．1：2 B．1：3 C．1：4 D．1：163．如图是由边长相同的小正方形组成的网格，A，B，P，Q四点均在正方形网格的格点上，线段AB，PQ相交于点M，则图中∠QMB的正切值是（）A．B．1 C． D．24．已知△ABC∽△DEF，若△ABC与△DEF的相似比为，则△ABC与△DEF对应中线的比为（）A．B．C．D．5．在四边形ABCD中，∠B=90°，AC=4，AB∥CD，DH垂直平分AC，点H为垂足．设AB=x，AD=y，则y关于x的函数关系用图象大致可以表示为（）A．B．C．D．6．如图，D、E分别是△ABC的边AB、BC上的点，且DE∥AC，AE、CD相交于点O，若S△DOE：S△COA=1：25，则S△BDE与S△CDE的比是（）A．1：3 B．1：4 C．1：5 D．1：257．如图，矩形ABCD的边长AD=3，AB=2，E为AB的中点，F 在边BC上，且BF=2FC，AF分别与DE、DB相交于点M，N，则MN的长为（）A．B．C．D．8．如图，在△ABC中，AD和BE是高，∠ABE=45°，点F是AB 的中点，AD与FE、BE分别交于点G、H，∠CBE=∠BAD．有下列结论：①FD=FE；②AH=2CD；③BC•AD=AE2；④S △ABC=4S△ADF．其中正确的有（）A．1个B．2 个C．3 个D．4个9．如图的△ABC中有一正方形DEFG，其中D在AC上，E、F在AB上，直线AG分别交DE、BC于M、N两点．若∠B=90°，AB=4，BC=3，EF=1，则BN的长度为何？（）A．B．C．D．10．如图，CB=CA，∠ACB=90°，点D在边BC上（与B、C不重合），四边形ADEF为正方形，过点F作FG⊥CA，交CA的延长线于点G，连接FB，交DE于点Q，给出以下结论：①AC=FG；②S△FAB：S四边形CBFG=1：2；③∠ABC=∠ABF；④AD2=FQ•AC，其中正确的结论的个数是（）A．1 B．2 C．3 D．411．如图，P为平行四边形ABCD边AD上一点，E、F分别是PB、PC（靠近点P）的三等分点，△PEF、△PDC、△PAB的面积分别为S1、S2、S3，若AD=2，AB=2，∠A=60°，则S1+S2+S3的值为（）A．B．C．D．412．如图，在正方形网格中，每个小正方形的边长均相等．网格中三个多边形（分别标记为①，②，③）的顶点均在格点上．被一个多边形覆盖的网格线中，竖直部分线段长度之和记为m，水平部分线段长度之和记为n，则这三个多边形中满足m=n的是（）A．只有②B．只有③C．②③D．①②③二．填空题13．如图，已知△ADE∽△ABC，若∠ADE=37°，则∠B= °．14．如图，在平行四边形ABCD中，点E是边AD的中点，EC交对角线BD于点F，若S△DEC=3，则S△BCF= ．15．如图，AC⊥BC，AC=BC，D是BC上一点，连接AD，与∠ACB的平分线交于点E，连接BE．若S△ACE=，S△BDE=，则AC= ．16．如图，已知点C为线段AB的中点，CD⊥AB且CD=AB=4，连接AD，BE⊥AB，AE是∠DAB的平分线，与DC相交于点F，EH⊥DC于点G，交AD于点H，则HG的长为．17．如图，已知△ABC和△DEC的面积相等，点E在BC边上，DE∥AB交AC于点F，AB=12，EF=9，则DF的长是．18．如图，在△ABC中，D、E分别是边AB、AC上的点，且DE ∥BC，若△ADE与△ABC的周长之比为2：3，AD=4，则DB= ．19．如图，已知△ABC、△DCE、△FEG、△HGI是4个全等的等腰三角形，底边BC、CE、EG、GI在同一直线上，且AB=2，BC=1，连接AI，交FG于点Q，则QI= ．20．如图，矩形EFGH内接于△ABC，且边FG落在BC上，若AD⊥BC，BC=3，AD=2，EF=EH，那么EH的长为．21．如图，在矩形纸片ABCD中，AB=6，BC=10，点E在CD上，将△BCE沿BE折叠，点C恰落在边AD上的点F处；点G在AF 上，将△ABG沿BG折叠，点A恰落在线段BF上的点H处，有下列结论：①∠EBG=45°；②△DEF∽△ABG；③S△ABG=S△FGH；④AG+DF=FG．其中正确的是．（把所有正确结论的序号都选上）三．解答题22．如图，在平面直角坐标系xOy中，直线y=﹣x+3与x轴交于点C，与直线AD交于点A（，），点D的坐标为（0，1）（1）求直线AD的解析式；（2）直线AD与x轴交于点B，若点E是直线AD上一动点（不与点B重合），当△BOD与△BCE相似时，求点E的坐标．23．从三角形（不是等腰三角形）一个顶点引出一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中一个为等腰三角形，另一个与原三角形相似，我们把这条线段叫做这个三角形的完美分割线．（1）如图1，在△ABC中，CD为角平分线，∠A=40°，∠B=60°，求证：CD为△ABC的完美分割线．（2）在△ABC中，∠A=48°，CD是△ABC的完美分割线，且△ACD为等腰三角形，求∠ACB的度数．（3）如图2，△ABC中，AC=2，BC=，CD是△ABC的完美分割线，且△ACD是以CD为底边的等腰三角形，求完美分割线CD的长．24．如图，△ABC中，AB=AC，E在BA的延长线上，AD平分∠CAE．（1）求证：AD∥BC；（2）过点C作CG⊥AD于点F，交AE于点G，若AF=4，求BC 的长．25．如图，△ABC为锐角三角形，AD是BC边上的高，正方形EFGH的一边FG在BC上，顶点E、H分别在AB、AC上，已知BC=40cm，AD=30cm．（1）求证：△AEH∽△ABC；（2）求这个正方形的边长与面积．26．如图，在△ABC中，点D，E分别在边AB，AC上，∠AED=∠B，射线AG分别交线段DE，BC于点F，G，且．（1）求证：△ADF∽△ACG；（2）若，求的值．27．如图，在菱形ABCD中，G是BD上一点，连接CG并延长交BA的延长线于点F，交AD于点E．（1）求证：AG=CG．（2）求证：AG2=GE•GF．28．如图，在Rt△ABC中，∠ACB=90°，AC=5cm，∠BAC=60°，动点M从点B出发，在BA边上以每秒2cm的速度向点A匀速运动，同时动点N从点C出发，在CB边上以每秒cm的速度向点B匀速运动，设运动时间为t秒（0≤t≤5），连接MN．（1）若BM=BN，求t的值；（2）若△MBN与△ABC相似，求t的值；（3）当t为何值时，四边形ACNM的面积最小？并求出最小值．29．如图①，△ABC与△CDE是等腰直角三角形，直角边AC、CD在同一条直线上，点M、N分别是斜边AB、DE的中点，点P 为AD的中点，连接AE、BD．（1）猜想PM与PN的数量关系及位置关系，请直接写出结论；（2）现将图①中的△CDE绕着点C顺时针旋转α（0°＜α＜90°），得到图②，AE与MP、BD分别交于点G、H．请判断（1）中的结论是否成立？若成立，请证明；若不成立，请说明理由；（3）若图②中的等腰直角三角形变成直角三角形，使BC=kAC，CD=kCE，如图③，写出PM与PN的数量关系，并加以证明．30．【探究证明】（1）某班数学课题学习小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究，提出下列问题，请你给出证明．如图1，矩形ABCD中，EF⊥GH，EF分别交AB，CD于点E，F，GH分别交AD，BC于点G，H．求证：=；【结论应用】（2）如图2，在满足（1）的条件下，又AM⊥BN，点M，N分别在边BC，CD上，若=，则的值为；【联系拓展】（3）如图3，四边形ABCD中，∠ABC=90°，AB=AD=10，BC=CD=5，AM⊥DN，点M，N分别在边BC，AB上，求的值．参考答案与解析一．选择题1．（2016•临夏州）如果两个相似三角形的面积比是1：4，那么它们的周长比是（）A．1：16 B．1：4 C．1：6 D．1：2【分析】根据相似三角形周长的比等于相似比，相似三角形面积的比等于相似比的平方解答即可．【解答】解：∵两个相似三角形的面积比是1：4，∴两个相似三角形的相似比是1：2，∴两个相似三角形的周长比是1：2，故选：D．【点评】本题考查的是相似三角形的性质，掌握相似三角形周长的比等于相似比，相似三角形面积的比等于相似比的平方是解题的关键．2．（2016•重庆）△ABC与△DEF的相似比为1：4，则△ABC 与△DEF的周长比为（）A．1：2 B．1：3 C．1：4 D．1：16【分析】由相似三角形周长的比等于相似比即可得出结果．【解答】解：∵△ABC与△DEF的相似比为1：4，∴△ABC与△DEF的周长比为1：4；故选：C．【点评】本题考查了相似三角形的性质；熟记相似三角形周长的比等于相似比是解决问题的关键．3．（2016•淄博）如图是由边长相同的小正方形组成的网格，A，B，P，Q四点均在正方形网格的格点上，线段AB，PQ相交于点M，则图中∠QMB的正切值是（）A．B．1 C． D．2【分析】根据题意得出△PAM∽△QBM，进而结合勾股定理得出AP=3，BQ=，AB=2，进而求出答案．【解答】解：连接AP，QB，由网格可得：∠PAB=∠QBA=90°，又∵∠AMP=∠BMQ，∴△PAM∽△QBM，∴=，∵AP=3，BQ=，AB=2，∴=，解得：AM=，∴tan∠QMB=tan∠PMA===2．故选：D．【点评】此题主要考查了勾股定理以及相似三角形的判定与性质以及锐角三角函数关系，正确得出△PAM∽△QBM是解题关键．4．（2016•兰州）已知△ABC∽△DEF，若△ABC与△DEF的相似比为，则△ABC与△DEF对应中线的比为（）A．B．C．D．【分析】根据相似三角形的对应中线的比等于相似比解答．【解答】解：∵△ABC∽△DEF，△ABC与△DEF的相似比为，∴△ABC与△DEF对应中线的比为，故选：A．【点评】本题考查的是相似三角形的性质，相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方；相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比．5．（2016•金华）在四边形ABCD中，∠B=90°，AC=4，AB∥CD，DH垂直平分AC，点H为垂足．设AB=x，AD=y，则y关于x的函数关系用图象大致可以表示为（）A．B．C．D．【分析】由△DAH∽△CAB，得=，求出y与x关系，再确定x的取值范围即可解决问题．【解答】解：∵DH垂直平分AC，∴DA=DC，AH=HC=2，∴∠DAC=∠DCH，∵CD∥AB，∴∠DCA=∠BAC，∴∠DAN=∠BAC，∵∠DHA=∠B=90°，∴△DAH∽△CAB，∴=，∴=，∴y=，∵AB＜AC，∴x＜4，∴图象是D．故选D．【点评】本题科学相似三角形的判定和性质、相等垂直平分线性质、反比例函数等知识，解题的关键是正确寻找相似三角形，构建函数关系，注意自变量的取值范围的确定，属于中考常考题型．6．（2016•随州）如图，D、E分别是△ABC的边AB、BC上的点，且DE∥AC，AE、CD相交于点O，若S△DOE：S△COA=1：25，则S△BDE与S△CDE的比是（）A．1：3 B．1：4 C．1：5 D．1：25【分析】根据相似三角形的判定定理得到△DOE∽△COA，根据相似三角形的性质定理得到=，==，结合图形得到=，得到答案．【解答】解：∵DE∥AC，∴△DOE∽△COA，又S△DOE：S△COA=1：25，∴=，∵DE∥AC，∴==，∴=，∴S△BDE与S△CDE的比是1：4，故选：B．【点评】本题考查的是相似三角形的判定和性质，掌握相似三角形的面积比等于相似比的平方是解题的关键．7．（2016•泸州）如图，矩形ABCD的边长AD=3，AB=2，E为AB的中点，F在边BC上，且BF=2FC，AF分别与DE、DB相交于点M，N，则MN的长为（）A．B．C．D．【分析】过F作FH⊥AD于H，交ED于O，于是得到FH=AB=2，根据勾股定理得到AF===2，根据平行线分线段成比例定理得到OH=AE=，由相似三角形的性质得到==，求得AM=AF=，根据相似三角形的性质得到==，求得AN=AF=，即可得到结论．【解答】解：过F作FH⊥AD于H，交ED于O，则FH=AB=2 ∵BF=2FC，BC=AD=3，∴BF=AH=2，FC=HD=1，∴AF===2，∵OH∥AE，∴==，∴OH=AE=，∴OF=FH﹣OH=2﹣=，∵AE∥FO，∴△AME∽FMO，∴==，∴AM=AF=，∵AD∥BF，∴△AND∽△FNB，∴==，∴AN=AF=，∴MN=AN﹣AM=﹣=，故选B．【点评】本题考查了相似三角形的判定与性质，矩形的性质，勾股定理，比例的性质，准确作出辅助线，求出AN与AM的长是解题的关键．8．（2016•丹东）如图，在△ABC中，AD和BE是高，∠ABE=45°，点F是AB的中点，AD与FE、BE分别交于点G、H，∠CBE=∠BAD．有下列结论：①FD=FE；②AH=2CD；③BC•AD=AE2；④S△ABC=4S△ADF．其中正确的有（）A．1个B．2 个C．3 个D．4个【分析】由直角三角形斜边上的中线性质得出FD=AB，证明△ABE是等腰直角三角形，得出AE=BE，证出FE=AB，延长FD=FE，①正确；证出∠ABC=∠C，得出AB=AC，由等腰三角形的性质得出BC=2CD，∠BAD=∠CAD=∠CBE，由ASA证明△AEH≌△BEC，得出AH=BC=2CD，②正确；证明△ABD～△BCE，得出=，即BC•AD=AB•BE，再由等腰直角三角形的性质和三角形的面积得出BC•AD=AE2；③正确；由F是AB的中点，BD=CD，得出S△ABC=2S△ABD=4S△ADF．④正确；即可得出结论．【解答】解：∵在△ABC中，AD和BE是高，∴∠ADB=∠AEB=∠CEB=90°，∵点F是AB的中点，∴FD=AB，∵∠ABE=45°，∴△ABE是等腰直角三角形，∴AE=BE，∵点F是AB的中点，∴FE=AB，∴FD=FE，①正确；∵∠CBE=∠BAD，∠CBE+∠C=90°，∠BAD+∠ABC=90°，∴∠ABC=∠C，∴AB=AC，∵AD⊥BC，∴BC=2CD，∠BAD=∠CAD=∠CBE，在△AEH和△BEC中，，∴△AEH≌△BEC（ASA），∴AH=BC=2CD，②正确；∵∠BAD=∠CBE，∠ADB=∠CEB，∴△ABD～△BCE，∴=，即BC•AD=AB•BE，∵AE2=AB•AE=AB•BE，BC•AD=AC•BE=AB•BE，∴BC•AD=AE2；③正确；∵F是AB的中点，BD=CD，∴S△ABC=2S△ABD=4S△ADF．④正确；故选：D．【点评】本题考查了相似三角形的判定与性质、全等三角形的判定与性质、直角三角形斜边上的中线性质、等腰三角形的判定与性质；本题综合性强，有一定难度，证明三角形相似和三角形全等是解决问题的关键．9．（2016•台湾）如图的△ABC中有一正方形DEFG，其中D在AC上，E、F在AB上，直线AG分别交DE、BC于M、N两点．若∠B=90°，AB=4，BC=3，EF=1，则BN的长度为何？（）A．B．C．D．【分析】由DE∥BC可得求出AE的长，由GF∥BN可得，将AE的长代入可求得BN．【解答】解：∵四边形DEFG是正方形，∴DE∥BC，GF∥BN，且DE=GF=EF=1，∴△ADE∽△ACB，△AGF∽△ANB，∴①，②，由①可得，，解得：AE=，将AE=代入②，得：，解得：BN=，故选：D．【点评】本题主要考查正方形的性质及相似三角形的判定与性质，根据相似三角形的性质得出AE的长是解题的关键．10．（2016•深圳）如图，CB=CA，∠ACB=90°，点D在边BC 上（与B、C不重合），四边形ADEF为正方形，过点F作FG⊥CA，交CA的延长线于点G，连接FB，交DE于点Q，给出以下结论：①AC=FG；②S△FAB：S四边形CBFG=1：2；③∠ABC=∠ABF；④AD2=FQ •AC，其中正确的结论的个数是（）A．1 B．2 C．3 D．4【分析】由正方形的性质得出∠FAD=90°，AD=AF=EF，证出∠CAD=∠AFG，由AAS证明△FGA≌△ACD，得出AC=FG，①正确；证明四边形CBFG是矩形，得出S△FAB=FB•FG=S四边形CBFG，②正确；由等腰直角三角形的性质和矩形的性质得出∠ABC=∠ABF=45°，③正确；证出△ACD∽△FEQ，得出对应边成比例，得出D•FE=AD2=FQ•AC，④正确．【解答】解：∵四边形ADEF为正方形，∴∠FAD=90°，AD=AF=EF，∴∠CAD+∠FAG=90°，∵FG⊥CA，∴∠C=90°=∠ACB，∴∠CAD=∠AFG，在△FGA和△ACD中，，∴△FGA≌△ACD（AAS），∴AC=FG，①正确；∵BC=AC，∴FG=BC，∵∠ACB=90°，FG⊥CA，∴FG∥BC，∴四边形CBFG是矩形，∴∠CBF=90°，S△FAB=FB•FG=S四边形CBFG，②正确；∵CA=CB，∠C=∠CBF=90°，∴∠ABC=∠ABF=45°，③正确；∵∠FQE=∠DQB=∠ADC，∠E=∠C=90°，∴△ACD∽△FEQ，∴AC：AD=FE：FQ，∴AD•FE=AD2=FQ•AC，④正确；故选：D．【点评】本题考查了相似三角形的判定与性质、全等三角形的判定与性质、正方形的性质、矩形的判定与性质、等腰直角三角形的性质；熟练掌握正方形的性质，证明三角形全等和三角形相似是解决问题的关键．11．（2016•日照）如图，P为平行四边形ABCD边AD上一点，E、F分别是PB、PC（靠近点P）的三等分点，△PEF、△PDC、△PAB的面积分别为S1、S2、S3，若AD=2，AB=2，∠A=60°，则S1+S2+S3的值为（）A．B．C．D．4【分析】先作辅助线DH⊥AB于点D，然后根据特殊角的三角函数值可以求得DH的长度，从而可以求得平行四边形的面积，然后根据三角形的相似可以求得S1+S2+S3的值．【解答】解：作DH⊥AB于点H，如右图所示，∵AD=2，AB=2，∠A=60°，∴DH=AD•sin60°=2×=，∴S ▱ABCD=AB•DH=2=6，∴S2+S3=S△PBC=3，又∵E、F分别是PB、PC（靠近点P）的三等分点，∴，∴S△PEF=×3=，即S1=，∴S1+S2+S3=+3=，故选A．【点评】本题考查相似三角形的判定与性质、平行四边形的性质，解题的关键是明确题意，找出所求问题需要的条件，画出合适的辅助线，利用数形结合的思想解答问题．12．（2016•江西）如图，在正方形网格中，每个小正方形的边长均相等．网格中三个多边形（分别标记为①，②，③）的顶点均在格点上．被一个多边形覆盖的网格线中，竖直部分线段长度之和记为m，水平部分线段长度之和记为n，则这三个多边形中满足m=n的是（）A．只有②B．只有③C．②③D．①②③【分析】利用相似三角形的判定和性质分别求出各多边形竖直部分线段长度之和与水平部分线段长度之和，再比较即可．【解答】解：假设每个小正方形的边长为1，①：m=1+2+1=4，n=2+4=6，则m≠n；②在△ACN中，BM∥CN，∴=，∴BM=，在△AGF中，DM∥NE∥FG，∴=，=，得DM=，NE=，∴m=2+=2.5，n=+1++=2.5，∴m=n；③由②得：BE=，CF=，∴m=2+2++1+=6，n=4+2=6，∴m=n，则这三个多边形中满足m=n的是②和③；故选C．【点评】本题考查了相似多边形的判定和性质，对于有中点的三角形可以利用三角形中位线定理得出；本题线段比较多要依次相加，做到不重不漏．二．填空题13．（2016•宁德）如图，已知△ADE∽△ABC，若∠ADE=37°，则∠B= 37 °．【分析】根据相似三角形的对应角相等，可得答案．【解答】解：由△ADE∽△ABC，若∠ADE=37°，得∠B=∠ADE=37°，故答案为：37．【点评】本题考查了相似三角形的性质，熟记相似三角形的性质是解题关键．14．（2016•梅州）如图，在平行四边形ABCD中，点E是边AD 的中点，EC交对角线BD于点F，若S△DEC=3，则S△BCF= 4 ．【分析】根据平行四边形的性质得到AD∥BC和△DEF∽△BCF，由已知条件求出△DEF的面积，根据相似三角形的面积比是相似比的平方得到答案．【解答】解：∵四边形ABCD是平行四边形，∴AD∥BC，AD=BC，∴△DEF∽△BCF，∴，=（）2，∵E是边AD的中点，∴DE=AD=BC，∴=，∴△DEF的面积=S△DEC=1，∴=，∴S△BCF=4；故答案为：4．【点评】本题考查的是平行四边形的性质、相似三角形的判定和性质；掌握三角形相似的判定定理和性质定理是解题的关键，注意：相似三角形的面积比是相似比的平方．15．（2016•遵义）如图，AC⊥BC，AC=BC，D是BC上一点，连接AD，与∠ACB的平分线交于点E，连接BE．若S△ACE=，S △BDE=，则AC= 2 ．【分析】设BC=4x，根据面积公式计算，得出BC=4BD，过E作AC，BC的垂线，垂足分别为F，G；证明CFEG为正方形，然后在直角三角形ACD中，利用三角形相似，求出正方形的边长（用x表示），再利用已知的面积建立等式，解出x，最后求出AC=BC=4x即可．【解答】解：过E作AC，BC的垂线，垂足分别为F，G，设BC=4x，则AC=4x，∵CE是∠ACB的平分线，EF⊥AC，EG⊥BC，∴EF=EG，又S△ACE=，S△BDE=，∴BD=AC=x，∴CD=3x，∵四边形EFCG是正方形，∴EF=FC，∵EF∥CD，∴=，即=，解得，EF=x，则×4x×x=，解得，x=，则AC=4x=2，故答案为：2．【点评】本题考查的是相似三角形的性质、角平分线的性质，掌握相似三角形的对应边的比相等、角的平分线上的点到角的两边的距离相等是解题的关键．16．（2016•山西）如图，已知点C为线段AB的中点，CD⊥AB 且CD=AB=4，连接AD，BE⊥AB，AE是∠DAB的平分线，与DC相交于点F，EH⊥DC于点G，交AD于点H，则HG的长为3﹣．【分析】根据AB=CD=4、C为线段AB的中点可得BC=AC=2、AD=2，再根据EH⊥DC、CD⊥AB、BE⊥AB得EH∥AC、四边形BCGH为矩形，BC=GE=2，继而由AE是∠DAB的平分线可得∠DAE=∠HEA即HA=HE，设GH=x得HA=2+x，由△DHG∽△DAC得=，列式即可求得x．【解答】解：∵AB=CD=4，C为线段AB的中点，∴BC=AC=2，∴AD=2，∵EH⊥DC，CD⊥AB，BE⊥AB，∴EH∥AC，四边形BCGH为矩形，∴∠HEA=∠EAB，BC=GE=2，又∵AE是∠DAB的平分线，∴∠EAB=∠DAE，∴∠DAE=∠HEA，∴HA=HE，设GH=x，则HA=HE=HG+GE=2+x，∵EH∥AC，∴△DHG∽△DAC，∴=，即=，解得：x=3﹣，即HG=3﹣，故答案为：3﹣．【点评】本题主要考查勾股定理、平行线的性质和判定、等腰三角形的判定与性质、矩形的判定与性质及相似三角形的判定与性质等知识点，根据相似三角形的性质得出对应边成比例且表示出各边长度是关键．17．（2016•舟山）如图，已知△ABC和△DEC的面积相等，点E在BC边上，DE∥AB交AC于点F，AB=12，EF=9，则DF的长是7 ．【分析】根据题意，易得△CDF与四边形AFEB的面积相等，再根据相似三角形的相似比求得它们的面积关系比，从而求DF的长．【解答】解：∵△ABC与△DEC的面积相等，∴△CDF与四边形AFEB的面积相等，∵AB∥DE，∴△CEF∽△CBA，∵EF=9，AB=12，∴EF：AB=9：12=3：4，∴△CEF和△CBA的面积比=9：16，设△CEF的面积为9k，则四边形AFEB的面积=7k，∵△CDF与四边形AFEB的面积相等，∴S△CDF=7k，∵△CDF与△CEF是同高不同底的三角形，∴面积比等于底之比，∴DF：EF=7k：9k，∴DF=7．故答案为：7．【点评】此题考查了相似三角形的判定与性质，解题的关键是会用割补法计算面积．18．（2016•乐山）如图，在△ABC中，D、E分别是边AB、AC 上的点，且DE∥BC，若△ADE与△ABC的周长之比为2：3，AD=4，则DB= 2 ．【分析】由DE∥BC，易证△ADE∽△ABC，由相似三角形的性质即可求出AB的长，进而可求出DB的长．【解答】解：∵DE∥BC，∴△ADE∽△ABC，∵△ADE与△ABC的周长之比为2：3，∴AD：AB=2：3，∵AD=4，∴AB=6，∴DB=AB﹣AD=2，故答案为：2．【点评】此题主要考查的是相似三角形的性质：相似三角形的一切对应线段（包括对应边、对应中线、对应高、对应角平分线等）的比等于相似比，面积比等于相似比的平方．19．（2016•黄冈）如图，已知△ABC、△DCE、△FEG、△HGI 是4个全等的等腰三角形，底边BC、CE、EG、GI在同一直线上，且AB=2，BC=1，连接AI，交FG于点Q，则QI= ．【分析】由题意得出BC=1，BI=4，则=，再由∠ABI=∠ABC，得△ABI∽△CBA，根据相似三角形的性质得=，求出AI，根据全等三角形性质得到∠ACB=∠FGE，于是得到AC∥FG，得到比例式==，即可得到结果．【解答】解：∵△ABC、△DCE、△FEG是三个全等的等腰三角形，∴HI=AB=2，GI=BC=1，BI=4BC=4，∴==，=，∴=，∵∠ABI=∠ABC，∴△ABI∽△CBA；∴=，∵AB=AC，∴AI=BI=4；∵∠ACB=∠FGE，∴AC∥FG，∴==，∴QI=AI=．故答案为：．【点评】本题主要考查了平行线分线段定理，以及三角形相似的判定，正确理解AB∥CD∥EF，AC∥DE∥FG是解题的关键．20．（2016•安顺）如图，矩形EFGH内接于△ABC，且边FG落在BC上，若AD⊥BC，BC=3，AD=2，EF=EH，那么EH的长为．【分析】设EH=3x，表示出EF，由AD﹣EF表示出三角形AEH 的边EH上的高，根据三角形AEH与三角形ABC相似，利用相似三角形对应边上的高之比等于相似比求出x的值，即为EH的长．【解答】解：如图所示：∵四边形EFGH是矩形，∴EH∥BC，∴△AEH∽△ABC，∵AM⊥EH，AD⊥BC，∴，设EH=3x，则有EF=2x，AM=AD﹣EF=2﹣2x，∴，解得：x=，则EH=．故答案为：．【点评】此题考查了相似三角形的判定与性质，以及矩形的性质，熟练掌握相似三角形的判定与性质是解本题的关键．21．（2016•安徽）如图，在矩形纸片ABCD中，AB=6，BC=10，点E在CD上，将△BCE沿BE折叠，点C恰落在边AD上的点F 处；点G在AF上，将△ABG沿BG折叠，点A恰落在线段BF上的点H处，有下列结论：①∠EBG=45°；②△DEF∽△ABG；③S△ABG=S△FGH；④AG+DF=FG．其中正确的是①③④．（把所有正确结论的序号都选上）【分析】由折叠性质得∠1=∠2，CE=FE，BF=BC=10，则在Rt △ABF中利用勾股定理可计算出AF=8，所以DF=AD﹣AF=2，设EF=x，则CE=x，DE=CD﹣CE=6﹣x，在Rt△DEF中利用勾股定理得（6﹣x）2+22=x2，解得x=，即ED=；再利用折叠性质得∠3=∠4，BH=BA=6，AG=HG，易得∠2+∠3=45°，于是可对①进行判断；设AG=y，则GH=y，GF=8﹣y，在Rt△HGF中利用勾股定理得到y2+42=（8﹣y）2，解得y=3，则AG=GH=3，GF=5，由于∠A=∠D和≠，可判断△ABG与△DEF不相似，则可对②进行判断；根据三角形面积公式可对③进行判断；利用AG=3，GF=5，DF=2可对④进行判断．【解答】解：∵△BCE沿BE折叠，点C恰落在边AD上的点F 处，∴∠1=∠2，CE=FE，BF=BC=10，在Rt△ABF中，∵AB=6，BF=10，∴AF==8，∴DF=AD﹣AF=10﹣8=2，设EF=x，则CE=x，DE=CD﹣CE=6﹣x，在Rt△DEF中，∵DE2+DF2=EF2，∴（6﹣x）2+22=x2，解得x=，∴ED=，∵△ABG沿BG折叠，点A恰落在线段BF上的点H处，∴∠3=∠4，BH=BA=6，AG=HG，∴∠2+∠3=∠ABC=45°，所以①正确；HF=BF﹣BH=10﹣6=4，设AG=y，则GH=y，GF=8﹣y，在Rt△HGF中，∵GH2+HF2=GF2，∴y2+42=（8﹣y）2，解得y=3，∴AG=GH=3，GF=5，∵∠A=∠D，==，=，∴≠，∴△ABG与△DEF不相似，所以②错误；∵S△ABG=•6•3=9，S△FGH=•GH•HF=×3×4=6，∴S△ABG=S△FGH，所以③正确；∵AG+DF=3+2=5，而GF=5，∴AG+DF=GF，所以④正确．故答案为①③④．【点评】本题考查了相似形综合题：熟练掌握折叠和矩形的性质、相似三角形的判定方法；会运用勾股定理计算线段的长．三．解答题22．（2016•广州）如图，在平面直角坐标系xOy中，直线y=﹣x+3与x轴交于点C，与直线AD交于点A（，），点D的坐标为（0，1）（1）求直线AD的解析式；（2）直线AD与x轴交于点B，若点E是直线AD上一动点（不与点B重合），当△BOD与△BCE相似时，求点E的坐标．【分析】（1）设直线AD的解析式为y=kx+b，用待定系数法将A（，），D（0，1）的坐标代入即可；（2）由直线AD与x轴的交点为（﹣2，0），得到OB=2，由点D的坐标为（0，1），得到OD=1，求得BC=5，根据相似三角形的性质得到或，代入数据即可得到结论．【解答】解：（1）设直线AD的解析式为y=kx+b，将A（，），D（0，1）代入得：，解得：．故直线AD的解析式为：y=x+1；（2）∵直线AD与x轴的交点为（﹣2，0），∴OB=2，∵点D的坐标为（0，1），∴OD=1，∵y=﹣x+3与x轴交于点C（3，0），∴OC=3，∴BC=5∵△BOD与△BEC相似，∴或，∴==或，∴BE=2，CE=，或CE=，∵BC•EF=BE•CE，∴EF=2，CF==1，∴E（2，2），或（3，）．【点评】本题考查了相似三角形的性质，待定系数法求函数的解析式，正确的作出图形是解题的关键．23．（2016•宁波）从三角形（不是等腰三角形）一个顶点引出一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中一个为等腰三角形，另一个与原三角形相似，我们把这条线段叫做这个三角形的完美分割线．（1）如图1，在△ABC中，CD为角平分线，∠A=40°，∠B=60°，求证：CD为△ABC的完美分割线．（2）在△ABC中，∠A=48°，CD是△ABC的完美分割线，且△ACD为等腰三角形，求∠ACB的度数．（3）如图2，△ABC中，AC=2，BC=，CD是△ABC的完美分割线，且△ACD是以CD为底边的等腰三角形，求完美分割线CD的长．【分析】（1）根据完美分割线的定义只要证明①△ABC不是等腰三角形，②△ACD是等腰三角形，③△BDC∽△BCA即可．（2）分三种情形讨论即可①如图2，当AD=CD时，②如图3中，当AD=AC时，③如图4中，当AC=CD时，分别求出∠ACB即可．（3）设BD=x，利用△BCD∽△BAC，得=，列出方程即可解决问题．【解答】解：（1）如图1中，∵∠A=40°，∠B=60°，∴∠ACB=80°，∴△ABC不是等腰三角形，∵CD平分∠ACB，∴∠ACD=∠BCD=∠ACB=40°，∴∠ACD=∠A=40°，∴△ACD为等腰三角形，∵∠DCB=∠A=40°，∠CBD=∠ABC，∴△BCD∽△BAC，∴CD是△ABC的完美分割线．（2）①当AD=CD时，如图2，∠ACD=∠A=48°，∵△BDC∽△BCA，∴∠BCD=∠A=48°，∴∠ACB=∠ACD+∠BCD=96°．②当AD=AC时，如图3中，∠ACD=∠ADC==66°，∵△BDC∽△BCA，∴∠BCD=∠A=48°，∴∠ACB=∠ACD+∠BCD=114°．③当AC=CD时，如图4中，∠ADC=∠A=48°，∵△BDC∽△BCA，∴∠BCD=∠A=48°，∵∠ADC＞∠BCD，矛盾，舍弃．∴∠ACB=96°或114°．（3）由已知AC=AD=2，∵△BCD∽△BAC，∴=，设BD=x，∴（）2=x（x+2），∵x＞0，∴x=﹣1，∵△BCD∽△BAC，∴==，∴CD=×2=﹣．【点评】本题考查相似三角形的判定和性质、等腰三角形的性质等知识，解题的关键是理解题意，学会分类讨论思想，属于中考常考题型．24．（2016•泰州）如图，△ABC中，AB=AC，E在BA的延长线上，AD平分∠CAE．（1）求证：AD∥BC；（2）过点C作CG⊥AD于点F，交AE于点G，若AF=4，求BC 的长．【分析】（1）由AB=AC，AD平分∠CAE，易证得∠B=∠DAG=∠CAG，继而证得结论；（2）由CG⊥AD，AD平分∠CAE，易得CF=GF，然后由AD∥BC，证得△AGF∽△BGC，再由相似三角形的对应边成比例，求得答案．【解答】（1）证明：∵AD平分∠CAE，∴∠DAG=∠CAG，∵AB=AC，∴∠B=∠ACB，∵∠CAG=∠B+∠ACB，∴∠B=∠CAG，∴∠B=∠DAG，∴AD∥BC；（2）解：∵CG⊥AD，∴∠AFC=∠AFG=90°，在△AFC和△AFG中，，∴△AFC≌△AFG（ASA），∴CF=GF，∵AD∥BC，∴△AGF∽△BGC，∴GF：GC=AF：BC=1：2，∴BC=2AF=2×4=8．【点评】此题考查了等腰三角形的性质、全等三角形的判定与性质以及相似三角形的判定与性质．注意证得△AGF∽△BGC是关键．25．（2016•怀化）如图，△ABC为锐角三角形，AD是BC边上的高，正方形EFGH的一边FG在BC上，顶点E、H分别在AB、AC上，已知BC=40cm，AD=30cm．（1）求证：△AEH∽△ABC；（2）求这个正方形的边长与面积．【分析】（1）根据EH∥BC即可证明．（2）如图设AD与EH交于点M，首先证明四边形EFDM是矩形，设正方形边长为x，再利用△AEH∽△ABC，得=，列出方程即可解决问题．【解答】（1）证明：∵四边形EFGH是正方形，∴EH∥BC，∴∠AEH=∠B，∠AHE=∠C，∴△AEH∽△ABC．（2）解：如图设AD与EH交于点M．∵∠EFD=∠FEM=∠FDM=90°，∴四边形EFDM是矩形，∴EF=DM，设正方形EFGH的边长为x，∵△AEH∽△ABC，∴=，∴=，∴x=，∴正方形EFGH的边长为cm，面积为cm2．【点评】本题考查正方形的性质、相似三角形的判定和性质等知识，解题的关键是利用相似三角形的相似比对于高的比，学会用方程的思想解决问题，属于中考常考题型．26．（2016•杭州）如图，在△ABC中，点D，E分别在边AB，AC上，∠AED=∠B，射线AG分别交线段DE，BC于点F，G，且．（1）求证：△ADF∽△ACG；（2）若，求的值．【分析】（1）欲证明△ADF∽△ACG，由可知，只要证明∠ADF=∠C即可．（2）利用相似三角形的性质得到=，由此即可证明．【解答】（1）证明：∵∠AED=∠B，∠DAE=∠DAE，∴∠ADF=∠C，∵=，∴△ADF∽△ACG．（2）解：∵△ADF∽△ACG，∴=，又∵=，∴=，∴=1．【点评】本题考查相似三角形的性质和判定、三角形内角和定理等知识，记住相似三角形的判定方法是解决问题的关键，属于基础题中考常考题型．27．（2016•大庆）如图，在菱形ABCD中，G是BD上一点，连接CG并延长交BA的延长线于点F，交AD于点E．（1）求证：AG=CG．（2）求证：AG2=GE•GF．【分析】根据菱形的性质得到AB∥CD，AD=CD，∠ADB=∠CDB，推出△ADG≌△CDG，根据全等三角形的性质即可得到结论；（2）由全等三角形的性质得到∠EAG=∠DCG，等量代换得到∠EAG=∠F，求得△AEG∽△FGA，即可得到结论．【解答】解：（1）∵四边形ABCD是菱形，∴AB∥CD，AD=CD，∠ADB=∠CDB，∴∠F=∠FCD，在△ADG与△CDG中，，∴△ADG≌△CDG，∴∠EAG=∠DCG，∴AG=CG；（2）∵△ADG≌△CDG，∴∠EAG=∠F，∵∠AGE=∠AGE，∴△AEG∽△FGA，∴，∴AG2=GE•GF．【点评】本题考查了相似三角形的判定和性质，菱形的性质，全等三角形的判定和性质，熟练掌握各定理是解题的关键．28．（2016•梅州）如图，在Rt△ABC中，∠ACB=90°，AC=5cm，∠BAC=60°，动点M从点B出发，在BA边上以每秒2cm的速度向点A匀速运动，同时动点N从点C出发，在CB边上以每秒cm的速度向点B匀速运动，设运动时间为t秒（0≤t≤5），连接MN．（1）若BM=BN，求t的值；（2）若△MBN与△ABC相似，求t的值；（3）当t为何值时，四边形ACNM的面积最小？并求出最小值．【分析】（1）由已知条件得出AB=10，．由题意知：BM=2t，，，由BM=BN得出方程，解方程即可；（2）分两种情况：①当△MBN∽△ABC时，由相似三角形的对应边成比例得出比例式，即可得出t的值；②当△NBM∽△ABC时，由相似三角形的对应边成比例得出比例式，即可得出t的值；（3）过M作MD⊥BC于点D，则MD∥AC，证出△BMD∽△BAC，得出比例式求出MD=t．四边形ACNM的面积y=△ABC的面积。

相似三角形中的动点问题—2023-2024学年九年级数学下册(苏科版)(解析版)

相似三角形中的动点问题【典例1】如图，在矩形ABCD中，AB=4，AD=2，动点P从点A开始以每秒2个单位长度沿AB向终点B运动，同时，动点Q从点C开始沿C−D−A以每秒3个单位长度向终点A运动，它们同时到达终点．连接PQ交AC于点E．过点E作EF⊥PQ，交直线CD于点F．（1）当点Q在线段CD上时，求证：CEAE =32．（2）当DQ=1时，求△APE的面积．（3）在P，Q的运动过程中，是否存在某一位置，使得以点E，F，Q为顶点的三角形与△ABC相似？若存在，求BP的长；若不存在，请说明理由．（1）证明△CQE∽△APE（2）①当点Q在CD上时，如图1，CQ=CD−DQ=3．过点E作AB的垂线交AB于点M，交CD于点N．②当点Q在AD上时，如图2，作EM⊥AB于点M，设EM=ℎ，再利用相似三角形的性质求解三角形的高，再利用面积公式计算即可；（3）分三种情况讨论：①当点Q在CD上时，设CQ=3t，则AP=2t，若点F在Q的右侧，如图3，当△FEQ∽△ABC，则∠1=∠2，作PH⊥CD于点H，而∠B=∠PHQ=90°，∴△ABC∽△PHQ，则PHQH =ABBC=2，从而可得答案；若点F在Q的左侧，如图4，△FEQ∽△ABC，点F与点C重合，从而可得答案；②当点Q在AD上时，如图5，△FEQ∽△ABC，EFEQ =BABC=2，∠FEG=∠B=90°，作EN⊥CD于点N，EG⊥AD于点G．，则∠NEQ=90°，再结合相似三角形的性质建立方程可得答案．（1）当点Q在线段CD上时，由题意可得：AB∥CD，CQ=3t，AP=2t，∴△CQE∽△APE，∴CE AE =CQAP=32．（2）①当点Q在CD上时，如图1，CQ=CD−DQ=3．过点E作AB的垂线交AB于点M，交CD于点N．由CQAP =V点QV点P=32，得AP=2．由△CQE∽△APE，得ENEM =CEAE=32，∴EM=25MN=45，∴S△APE=12AP⋅EM=12×2×45=45．②当点Q在AD上时，如图2，作EM⊥AB于点M，设EM=ℎ．AQ=AD−DQ=1，AP=23(CD+DQ)=103．同理：△AME∽△ABC，∴EM AM =BCAB=12，∴AM=2EM=2ℎ．同理：△PME∽△PAQ，得EMPM =AQPA=1103=310，∴PM=103EM=103ℎ．∴AP=PM+AM=103ℎ+2ℎ=103，解得ℎ=58，∴S△APE=12AP⋅EM=12×103×58=2524．∴△APE 的面积为45或2524．（3）①当点Q 在CD 上时，设CQ =3t ，则AP =2t ．若点F 在Q 的右侧，如图3，当△FEQ∽△ABC ，则∠1=∠2．作PH ⊥CD 于点H ，而∠B =∠PHQ =90°， ∴△ABC ∽△PHQ ，则PHQH =ABBC =2， ∴QH =12PH =1．∵HD =AP =2t ，∴CD =CQ +QH +HD =3t +1+2t =4，解得t =35．∴BP =4−2t =4−65=145．若点F 在Q 的左侧，如图4，△△ABC ，点F 与点C 重合．∵AC =√AB 2+BC 2=√42+22=2√5，又∵CEAE =32 ∴AE =25AC =4√55． ∵由△FEQ∽△ABC 结合对顶角可得：∠AEP =∠B =90°，而∠PAE =∠BAC ， ∴△AEP∽△ABC ，∴AE AB =APAC ，即4√554=2√5，则AP =2，∴BP =AB −AP =2．②当点Q 在AD 上时，如图5，△FEQ∽△ABC ，EFEQ =BABC =2，∠FEG =∠B =90°，作EN ⊥CD 于点N ，EG ⊥AD 于点G ．，则∠NEQ =90°，由∠FEQ =∠NEG =90°，得∠FEN =∠QEG ， ∴Rt △FEN∽Rt △QEG ， ∴ENEG =EFEQ =2．同理可得：AGEG =BCAB=12，设AG =k ，则EG =2AG =2k ，EN =2EG =4k ． ∴DG =EN =4k ，AD =AG +DG =5k ，由AD =2，得5k =2，k =25， ∴AG =25，EG =45．由题意，AQ BP =V 点Q V 点P=6−3t 4−2t=32，设AQ =3x ，则BP =2x ，AP =4−2x ，QG =AQ −AG =3x −25，由△QGE∽△QAP ，得EGAP =QGQA ，即454−2x =3x−253x，化简，得15x 2−26x +4=0，解得x 1=13+√10915（舍去），x 2=13−√10915．∴BP =2x =26−2√10915．综上所述，BP 的长为145或2或26−2√10915．1．（2023秋·江苏常州·九年级常州市第二十四中学校考阶段练习）如图，在平面直角坐标系中，A、B两点的坐标分别为(20,0)和(0,15)，动点P从点A出发在线段AO上以每秒2cm的速度向原点O运动，动直线EF从x轴开始以每秒1cm的速度向上平行移动(即EF∥x轴)，分别与y轴、线段AB交于点E、F，连接EP、FP，设动点P与动直线EF同时出发，运动时间为t秒．（1）求t=9时，△PEF的面积；（2）直线EF、点P在运动过程中，是否存在这样的t使得△PEF的面积等于40cm2？若存在，请求出此时t的值；若不存在，请说明理由；（3）当t为何值时，△EOP与△BOA相似．【思路点拨】（1）由于EF//x轴，则S△PEF=12⋅EF⋅OE,t=9时，OE=9，关键是求EF.易证△BEF∽△BOA，则EFOA=BEBO，从而求出EF的长度，得出△PEF（2）假设存在这样的t，使得△PEF的面积等于40cm2，则根据面积公式列出方程，由根的判别式进行判断，得出结论；（3）如果△EOP与△BOA相似，由于∠EOP=∠BOA=90°，则只能点O与点O对应，然后分两种情况分别讨论：①点P与点A对应；②点P与点B对应．即可得解．【解题过程】（1）∵EF//OA，∴∠BEF=∠BOA又∵∠B=∠B，∴△BEF∽△BOA，∴EFOA =BEBO，当t=9时，OE=9，OA=20，OB=15，BE=OB−OE=15−9=6，∴EF=20×615=8，∴S△PEF=12EF⋅OE=12×8×9=36(cm2)；（2）不存在．理由：∵△BEF∽△BOA，∴EF=BE⋅OABO =(15−t)⋅2015=43(15−t)，∴12×43(15−t)×t=40，整理，得t2−15t+60=0，∵△=152−4×1×60<0，∴方程没有实数根．∴不存在使得△PEF的面积等于40cm2的t值；（3）当∠EPO=∠BAO时，△EOP∽△BOA，∴OPOA =OEOB，即20−2t20=t15，解得t=6；当∠EPO=∠ABO时，△EOP∽△AOB，∴OPOB =OEOA，即20−2t15=t20，解得t=8011．∴当t=6s或t=8011s时，△EOP与△BOA相似．2．（2022·四川·九年级专题练习）如图1，已知矩形ABCD的边长AB=3cm，BC=6cm．某一时刻，动点M从点A出发，沿AB以1cm/s的速度向点B匀速运动：同时点N从点D出发，沿DA方向以2cm/s的速度向点A匀速运动，点N运动到点A时停止运动，运动时间为t．（1）若△AMN是等腰直角三角形，则t=___________（直接写出结果）．（2）是否存在时刻t，使以A、M、N为顶点的三角形与△ACD相似？若存在，求t的值，若不存在，请说明理由．（3）如图2，连接CN 、CM ，试求CN +2CM 的最小值．【思路点拨】（1）根据题意可知只有AM =AN 时，△AMN 是等腰直角三角形，再根据题意可用t 表示出AM =t ，AN =6−2t ，列出等式，解出t 即可；（2）分类讨论①当△ACD ∼△NMA 时和②当△CAD ∼△NMA 时，列出比例式，代入数据，即可求解；（3）取CN 中点E ，作E 点关于CD 的对称点E ′，连接CE ′．作M 点关于BC 的对称点M ′，连接CM ′，E ′M ′．根据作图可知CE ′=CE ，CM ′=CM ，即可知当CE ′+CM ′最小时CN +2CM 最小，即最小值为E ′M ′的长．连接E ′E 并延长，交CD 于点F ，AB 于点G ．由作图结合题意易求出E ′G =E ′F +AD =t +6，BG =12AB =32，BM ′=BM =AB −AM =3−t ，从而可求出GM ′=BG +BM ′=92−t ．在Rt △E ′GM ′中，利用勾股定理可求出E ′M ′=√E ′G 2+GM ′2=√2(t +34)2+4418，最后根据二次函数的性质，即得出t =0时，√2(t +34)2+4418最小，即此时E ′M ′=152，故可求出CN +2CM 的最小值为15．【解题过程】（1）∵∠MAN =90°，∴若△AMN 是等腰直角三角形时，只有AM =AN ．根据题意可知AM =t ，DN =2t AN =AD −DN =6−2t ， ∴t =6−2t ，解得t =2，故答案为：2．（2）∵∠MAN =∠ADC =90°，∴以A 、M 、N 为顶点的三角形与△ACD 相似分为两种情况， ①当△ACD ∼△NMA 时，有ADAN =CDAM ，即66−2t =3t ，解得：t =32；②当△CAD ∼△NMA 时，有ADAM =CDAN ，即6t =36−2t ，解得：t =125．当t =32或t =125时，以A 、M 、N 为顶点的三角形与△ACD 相似；（3）如图，取CN中点E，作E点关于CD的对称点E′，连接CE′．作M点关于BC的对称点M′，连接CM′，E′M′．根据作图可知CE′=CE，CM′=CM，∴CN+2CM=2(CE+CM)=2(CE′+CM′)，∴当CE′+CM′最小时CN+2CM最小，∵CE′+CM′≥E′M′，∴CE′+CM′的最小值为E′M′的长，即CN+2CM的最小值为2E′M′的长．如图，连接E′E并延长，交CD于点F，AB于点G．∵作E点关于CD的对称点E′，∴E′F//AD，E′F=EF．又∵E为中点，∴E′F=EF=12DN=t，G为AB中点，∴E′G=E′F+AD=t+6，BG=12AB=32．∵作M点关于BC的对称点M′，∴BM′=BM=AB−AM=3−t，∴GM′=BG+BM′=32+3−t=92−t．在Rt△E′GM′中，E′M′=√E′G2+GM′2=√(6+t)2+(92−t)2=√2(t+34)2+4418，∵t≥0，2>0∴t=0时，√2(t+34)2+4418最小，即E′M′=√2×(34)2+4418=152．∴CN+2CM=2E′M′=15．3．（2022秋·江苏泰州·九年级校联考阶段练习）如图1，四边形ABCD是矩形，点P是对角线AC上的一个动点（不与A、C重合），过点P作PE⊥CD于点E，连接PB，已知AD＝3，AB＝4，设AP＝m．（1）当m＝1时，求PE的长；（2）连接BE，试问点P在运动的过程中，能否使得△P AB≌△PEB？请说明理由；（3）如图2，过点P作PF⊥PB交CD边于点F，设CF＝n，试判断5m+4n的值是否发生变化，若不变，请求出它的值；若变化，请说明理由．【思路点拨】（1）根据勾股定理得出AC，进而利用相似三角形的判定和性质解答即可；（2）根据全等三角形的性质和勾股定理解答即可；（3）根据相似三角形的判定和性质以及勾股定理解答即可．【解题过程】解：（1）连接BE，由已知：在Rt△ADC中，AC＝√AD2+DC2=√32+42=5，当AP＝m＝1时，PC＝AC﹣AP＝5﹣1＝4，∵PE⊥CD，∴∠PEC＝∠ADC＝90°，∵∠ACD＝∠PCE，∴△ACD∽△PCE，∴AD PE =ACPC，即3PE=54，∴PE＝125；（2）如图1，当△P AB≌△PEB时，∴P A ＝PE ，∵AP ＝m ，则PC ＝5﹣m ，由（1）得：△ACD ∽△PCE ， ∴3PE =55−m， ∴PE ＝3(5−m)5，由P A ＝PE ，即3(5−m)5=m ，解得：m ＝158， ∴EC ＝√PC 2−PE 2=√(5−158)2−(158)2=52，∴BE ＝√EC 2+BC 2=√(52)2+32=√312≠AB ，∴△P AB 与△PEB 不全等， ∴不能使得△P AB ≌△PEB ；（3）如图2，延长EP 交AB 于G ，∵BP ⊥PF ， ∴∠BPF ＝90°， ∴∠EPF +∠BPG ＝90°， ∵EG ⊥AB ， ∴∠PGB ＝90°， ∴∠BPG +∠PBG ＝90°， ∴∠PBG ＝∠EPF ， ∵∠PEF ＝∠PGB ＝90°， ∴△BPG ∽△PFE ，∴BG PE =PGEF，由（1）得：△PCE∽△ACD，PE＝3(5−m)5，∴EC DC =PCAC，即EC4=5−m5，∴EC＝4(5−m)5，∴BG＝EC＝4(5−m)5，∴3−3(5−m)54(5−m)5−n=4(5−m)3(5−m)=43，∴5m+4n＝16．4．（2023秋·河北保定·九年级统考期末）如图（1），在矩形ABCD中，AB=6cm，tan∠ABD=43，E、F 分别是AB、BD中点，连接EF，点P从点E出发，沿EF方向匀速运动，速度为1cm/s，同时，点Q从点D 出发，沿DB方向匀速运动，速度为2cm/s，当点P停止运动时，点Q也停止运动，连接PQ，设运动时间为ts（0<t<4），解答下列问题：∴t=1（1）当0<t<2.5时，FQ=______．（用含有t的式子表示）（2）当点Q在线段DF上运动时，若△PQF的面积为0.6cm2，求t的值；（3）当t为______时，△PQF为等腰三角形?（直接写出结果）．【思路点拨】（1）先由题目条件求出AD，再利用勾股定理求出DF，当0<t<2.5时，接着判断出点Q的位置，即可求解．（2）先判断出△QMF∽△BEF，进而得出，再利用面积公式建立方程求解即可．（3）分点Q在DF和BF上，利用相似三角形的性质建立方程求解即可得出结论．【解题过程】（1）在矩形ABCD中，∠A=90°∴在直角三角形DBA中tan∠ABD=ADAB =AD6=43∴AD=8∵E、F分别是AB、BD中点，∴EF=12AD=4∵BD=√AB2+AD2=10∴DF=12BD=5∴Q从D到F的时间为52=2.5当0<t<2.5时，Q在线段DF上，∴FQ=DF−DQ=5−2t．故答案为：5−2t．（2）过点Q作QM⊥EF交EF延长线于点M，可知：QM∥BE，∴△QMF∽△BEF，∴QM BE =QFBF，∴QM3=5−2t5，可得QM=35(5−2t)，∴S△PFQ=12×PF⋅QM=12×(4−t)×35(5−2t)=0.6=35，解得：t=92（舍去）或t=2，∴当t=2时，△PQF的面积为0.6cm2；故答案为：t=2．（3）当点Q在DF上时，如图PF=QF∴4−t=5−2t∴t=1当点Q在BF上时，如图PF=QF∴4−t=2t−5∴t=3当PQ=FQ时，如图∴12(4−t)2t−5=45∴t=207当PF=PQ时，如图∴12(2t−5)4−t=45∴t=19 6所以t=1或3或207或196时，△PQF为等腰三角形．故答案为：t=1或3或207或196．5．（2023秋·山东青岛·九年级山东省青岛第五十九中学校考阶段练习）如图，在Rt△ABC中，∠ACB=90°，AC=8，BC=6，CD⊥AB于点D．点P从点D出发，沿线段DC向点C运动，点Q从点C出发，沿线段CA向点A运动，两点同时出发，速度都为每秒1个单位长度，当点P运动到C时，两点都停止运动．设运动时间为t秒．（1）用含t的代数式分别表示线段CP=_______________、CQ=_______________．（2）在运动过程中是否存在某一时刻t，使得S△CPQ:S△ABC=9:100？若存在，求出t的值；若不存在，请说明理由．（3）是否存在某一时刻t，使得△CPQ为直角三角形？若存在，求出所有满足条件的t的值；若不存在，请说明理由．【思路点拨】（1）利用勾股定理可求出AB长，再用等积法就可求出线段CD的长，据此求解即可；（2）过点P作PH⊥AC，垂足为H，通过三角形相似即可用t的代数式表示PH，从而可以求出S与t之间的函数关系式；利用S△CPQ:S△ABC=9:100建立t的方程，解方程即可解决问题；（3）分两种情况，利用相似三角形得出比例式建立方程求解，即可得出结论．【解题过程】（1）解：如图1，∵∠ACB=90°，AC=8，BC=6，∴AB =√62+82=10，∵CD ⊥AB ，∴S △ABC =12BC ⋅AC =12AB ⋅CD ， ∴CD =BC·AC AB =6×810=245，由题意得CQ =PD =t ，∴CP =245−t故答案为：t ，245−t ；（2）解：过点P 作PH ⊥AC ，垂足为H ，如图2所示．由题可知CQ =PD =t ，CP =245−t ，∵∠ACB =∠CDB =90°，∴∠HCP =90°−∠DCB =∠B ，∵PH ⊥AC ，∴∠CHP =90°，∴∠CHP =∠ACB ，∴△CHP ∽△BCA ，∴ PH AC =PC AB ， ∴ PH 8=4.8−t 10，∴PH =9625−45t ，∴S △CPQ =12CQ ⋅PH =12t (9625−45t)=−25t 2+4825t ；存在某一时刻t ，使得S ΔCPQ :S ΔABC =9:100，∵S ΔABC =12×6×8=24，且S △CPQ :S △ABC =9:100，∴(−25t 2+4825t):24=9:100，整理得：5t 2−24t +27=0，即(5t −9)(t −3)=0，解得：t =95或t =3，∵0≤t ≤245， ∴当t =95秒或t =3秒时，S ΔCPQ :S ΔABC =9:100；（3）解：由（2）知∠ACD =∠B ①当∠CPQ =∠BCA =90°时，∴△CPQ ∽△BCA ，∴CP BC =CQ AB ，∴245−t 6=t 10， ∴t =3；②当∠CQP =∠BCA =90°时，∴△CQP ∽△BCA ，∴CP AB =CQ BC ，∴245−t 10=t 6∴t=95，即：t为3秒或95秒时，△CPQ为直角三角形．6．（2022·山东青岛·统考一模）如图，在矩形ABCD中，BD是对角线，AB=6cm，BC=8cm．点E从点D 出发，沿DA方向匀速运动，速度是2cm/s；点F从点B出发，沿BD方向匀速运动，速度是1cm/s，MN 是过点F的直线，分别交AB、BC于点M、N，且在运动过程中始终保持MN⊥BD．连接EM、EN、EF，两点同时出发，设运动时间为t（s）（0＜t＜3．6），请回答下列问题：（1）求当t为何值时，△EFD～△ABD？（2）设四边形BMEN的面积为S（cm2），求S关于t之间的函数关系式；（3）求当t为何值时，△EFD为等腰三角形；（4）将△EMN沿直线MN t的值；若不存在，请说明理由；【思路点拨】（1）由题意得，DE=2t，BF=t，在Rt△ABD中，BD=10，DF=BD=BF=10-t，当△ABD∼△EFD，利用对应边成比例，即可求出t值；（2）证得△BFM∼△BAD，可求出BM=53t，BN=54t，AM=AB-BM=6-53t，代入面积表达式，即可求出关系式；（3）分种情况进行讨论即可，注意结果是否符合；（4）假设t值存在，则四边形EKCD为矩形，利用勾股定理表示出EN2=EK2+NK2=16916t2−52t+100，EM2=AM2+AE2=616t2−52t+100，可知t=0，不符合题意，可知不存在符合的t值．【解题过程】（1）解：由题意得，DE=2t，BF=t，∵四边形ABCD为矩形，∴∠BAD=90°，在Rt△ABD中，BD=√AB2+AD2=√62+82=10，∴DF=BD=BF=10-t，当△ABD∼△EFD时，则EDAD =DFDB，即2t8=10−t10，解得：t=207．即当t为207时，△EFD～△ABD；（2）∵MN⊥BD，∴∠MFB=90°，∵∠MBF=∠MBF，∴△BFM∼△BAD，∴BF AB =BMBD，即t6=BM10，∴BM=53t，同理BN=54t，∴AM=AB-BM=6-53t，S=S梯形ABNE −S△AME=(8−2t+54t)×62−(8−2t)×(6−53t)2=−53t2+12512t，即S关于t之间的函数关系式为：S=−53t2+12512t；（3）ED=DF时，则2t=10-t，解得：t=103；ED=EF时，过点E作EG⊥BF于G，∵ED=EF，∴△EFD为等腰三角形，又∵EG⊥DF，∴DG=12DF=10−t2，∵∠EDG=∠BDA，∠EGD=∠BAD=90°，∴△EGD∼△BAD，∴DG AD =EDBD，即10−t28=2t10，∴t=5021；EF=FD时，过点F作FH⊥AD，∵EF=FD，∴△EFD为等腰三角形，又∵FH⊥ED，∴HD=12ED=t，∵∠ADB=∠HDF，∠BAD=∠FHD，∴△DHF∼△DAB，即t8=10−t10，∴t=409＞3.6（舍去）；综上所述，当t=103或5021时，△EFD为等腰三角形；（4）假设存在符合题意的t，则EM=EN，过点E作EK⊥BC交BC于K，则四边形EKCD为矩形，∴ED=CK=2t，EK=CD=6，NK=BC-BN-CK=8−54t−2t=8−134t，∴EN2=EK2+NK2=62+(842=16916t2−52t+100，EM2=AM2+AE2=(6−53t)2+(8−2t)2=616t2−52t+100，∴169 16t2−52t+100=619t2−52t+100，即t1=t2=0，∵t=0不符合题意，∴不存在符合题意的t．7．（2023春·山东青岛·九年级专题练习）已知，在菱形ABCD中，对角线AC，BD相交于点O，AC=6cm，BD=8cm.延长BC至点E，使CE=BC，连接ED，点F从点E出发，沿ED方向向点D运动，速度为1cm s⁄，过点F作FG⊥ED垂足为点F交CE于点G；点H从点A出发，沿AD方向向点D运动，速度为1cm s⁄，过点H作HP∥AB，交BD于点P，当F点停止运动时，点H也停止运动.设运动时间为t(0<t≤3)，解答下列问题：（1）求证：∠BDE=90°；（2）是否存在某一时刻t，使G点在ED的垂直平分线上?若存在，求出t值；若不存在，请说明理由.（3）设六边形PCGFDH的面积为S(cm2)，求S与t的函数关系式；（4）连接HG，是否存在某一时刻t，使HG∥AC?若存在，求出t值；若不存在，请说明理由.【思路点拨】（1）根据菱形和等腰三角形的性质，得四边形ACED为平行四边形、∠E=∠CDE，从而完成证明；（2）根据平行四边形和垂直平分线的性质分析，即可得到答案；（3）根据菱形和勾股定理的性质，得CE；延长CP，交AD于点M，根据相似三角形的性质，得MD；设AD和BC的距离为ℎ，根据三角形面积的性质，得ℎ=245cm，根据相似三角形的性质得S△GFES△BDE=t6，通过计算即可得到答案；（4）根据相似三角形的性质，得GE=5t3cm，根据平行四边形和一元一次方程的性质计算，即可得到答案．【解题过程】（1）∵菱形ABCD，∴AC⊥BD，AD=BC，AD//BC，AO=CO=12AC，BO=DO=12BD，∴∠CBD+∠ACB=90°，∠CBD=∠CDB，∵CE=BC，∴AD=CE，CD=CE，∴四边形ACED为平行四边形，∠E=∠CDE，∴AC//DE，∴∠ACB=∠E，∴∠CDB+∠CDE=90°，即∠BDE=90°；（2）∵四边形ACED为平行四边形，∴DE=AC=6cm，∵FG⊥ED，∴当EF=DF=12DE时，使G点在ED的垂直平分线上，∴t=12DE1cm s⁄=3s；（3）∵点F从点E出发，沿ED方向向点D运动，速度为1cm s⁄，点H从点A出发，沿AD方向向点D运动，速度为1cm s⁄，∴AH=EF=t(cm)，∵AC⊥BD，AC=6cm，BD=8cm，AO=CO=12AC，BO=DO=12BD，∴CE=BC=CD=AD=√(12AC)2+(12BD)2=5cm，∴DH=AD−AH=5−t(cm)，∵菱形ABCD，∴∠ADP=∠CDP，∵HP，∴∠HPD=∠CDP，∴∠ADP=∠HPD，∴PH=DH，如图，延长CP，交AD于点M，∵HP，∴∠MHP=∠MDC，∵∠PMH=∠CMD，∴△MPH∽△MCD，∴S△MPH S△MCD =PHCD=DHCD=5−t5，MHMD=MHMH+DH=PHCD=5−t5，∴MH MH+5−t =5−t5，∴MH=(5−t)2t，∴MD=MH+DH=(5−t)2t +5−t=5(5−t)t，设AD和BC的距离为ℎ，∴S△ACD=12AC×OD=12AD×ℎ，∴ℎ=245cm，∵∠BDE=90°，FG⊥ED，∴△GFE∽△BDE，∴S△GFE S△BDE =EFDE=t6，∴六边形PCGFDH的面积，=S△MCD−S△MPH+S△CDE−S△GFE=S△MCD−5−t5×S△MCD+S△CDE−t6×S△BDE=t5×S△MCD+S△CDE−t6×S△BDE=t5×12×MD×ℎ+12×CE×ℎ−t6×12×(BC+CE)×ℎ=t5×12×5(5−t)t×245+12×5×245−t6×12×10×245=12−12t5+12−4t=24−32t5cm，∴S=24−32t5(0<t≤3)；（4）∵△GFE∽△BDE，∴GE BE =EFDES，∴GE=EF×BEDE =t×(BC+CE)6=t×106=5t3cm，∵DH=AD−AH=5−t(cm)，当GE=DH时，得5t3=5−t，∴t=158，∵AD//BE，GE=DH，∴四边形HGED为平行四边形，∴HG//DE，∵AC//DE，∴HG//AC，∴当t=158时，HG//AC．8．（2022秋·山西运城·九年级校考阶段练习）如图，已知梯形ABCD中，AD∥BC，AD=1，AB=BC=4，CD=5．（1）求梯形ABCD的面积S；（2）动点P从点B出发，以1cm/s的速度，沿B→A→D→C方向，向点C运动：动点Q从点C出发，以1cm/s 的速度，沿C→D→A方向，向点A运动，过点Q作QE⊥BC于点E．若P、Q两点同时出发，当其中一点到达目的地时整个运动随之结束，设运动时间为t秒．问：①在运动过程中，是否存在这样的t P、D、Q为顶点的三角形恰好是以DP为底的等腰三角形？若存在，请求出所有符合条件的t的值；若不存在，请说明理由．②在运动过程中，是否存在这样的t，使得以P、A、D为顶点的三角形与△COE相似？若存在，请求出所有符合条件的t的值；若不存在，请说明理由．【思路点拨】（1）作DF∥AB交BC于F，即易证四边形ABFD是平行四边形，从而可求出DF=AB=3，BF=AD=1，CF=3．再利用勾股定理逆定理即可证∠ABC=∠DFC=90°，最后利用梯形的面积公式计算即可；（2）①在图1的基础上作QG⊥AB于G，易证四边形BEQG是矩形，即得出BG=EQ，QG=BE．又易证△CEQ∽△CFD，得出EQDF =CECF=CQCD，从而可用t表示出CE=35t，EQ=45t，BG=45t，QG=BE=4−35t．PG=t5，即可利用勾股定理得出PQ2=(15t)2+(4−35t)2，最后根据等腰三角形的定义列出等式，解出t即可；②分类讨论当△PAD∽△QEC时和当△PAD∽△CEQ时，根据对应边成比例计算即可．【解题过程】（1）如图1，作DF∥AB交BC于F，∵AD∥BC，∴四边形ABFD是平行四边形，∴DF=AB=3，BF=AD=1，∴CF=BC−BF=3．∵32+42=52，即CF2+DF2=CD2，∴∠DFF=90°，∴∠ABC=∠DFC=90°，∴S梯形ABCD =12(1+4)×4=10；（2）①如图2，在图1的基础上作QG⊥AB于G，由题意可知t≤6．∵∠B=∠QEB=90°，∴四边形BEQG是矩形，∴BG=EQ，QG=BE．∵EQ∥DF，∴△CEQ∽△CFD，∴EQ DF =CECF=CQCD，∴EQ 4=CE 3=t 5， ∴CE =35t ，EQ =45t ，∴BG =45t ，QG =BE =BC −CE =4−35t ．在Rt △PQG 中，PG =BP −BG =t −45t =t 5， ∴PQ 2=PG 2+QG 2=(15t)2+(4−35t)2，由PQ 2=DQ 2得，(15t)2+(4−35t)2=(5−t)2，解得：t 1=13−√1092，t 2=13+√1092(舍去)， ∴当t =13−√1092时，使得以P 、D 、Q 为顶点的三角形恰好是以DP 为底的等腰三角形；②如图3，当△PAD∽△QEC 时，∵∠A =∠QEC =90°，∴PA AD =QE CE，即AP 1=43， ∴AP =43，∴t =4−43=83；当△PAD∽△CEQ 时，∴PA AD =CE QE ，即PA 1=34，∴PA =34，∴t =4−34=134．综上所述：t =83或134．9．（2022秋·陕西咸阳·九年级期末）在平面直角坐标系中，过原点O及点A（8，0），C（0，6）作矩形OABC，连接OB，点D为OB的中点，点E是线段AB上的动点，连接DE，作DF⊥DE，交OA于点F，连接EF．已知点E从A点出发，以每秒1个单位长度的速度在线段AB上移动，设移动时间为t秒．（1）如图①，当t＝3时，求DF的长；（2）如图②，当点E在线段AB上移动的过程中，DFDE的大小是否发生变化？若变化，请说明理由；若不变，请求出DFDE的值；（3）连接AD，当AD将△DEF分成的两部分的面积之比为1：2时，求相应的t＜3时的值．【思路点拨】（1）当t=3时，可知DE//OA，DE=12OA=4，则四边形DFAE是矩形，得DF=AE=3；（2）作DM⊥OA于点M，DN⊥AB N，根据两个角相等，可证明ΔDMF∽ΔDNE，得DFDE =DMDN=34；（3）作DM⊥OA于点M，DN⊥AB于点N，则点G为EF的三等分点，利用（2）同理可得E、F的坐标，从而得出点G的坐标，代入直线AD的解析式即可解决问题．【解题过程】（1）当t=3时，E为AB的中点，∵A(8,0)，C(0,6)，∴OA=8，OC=6，∵点D为OB的中点，∴DE//OA，DE=12OA=4，∵四边形OABC是矩形，∴OA⊥AB，∴DE⊥AB，∴∠OAB=∠DEA=90°，又∵DF⊥DE，∴∠EDF=90°，∴四边形DFAE是矩形，∴DF=AE=3；（2）DFDE的大小不变，理由如下：如图，作DM⊥OA于点M，DN⊥AB于点N，∵四边形OABC是矩形，∴OA⊥AB，∴四边形DMAN是矩形，∴∠MDN=90°，DM//AB，DN//OA，∴BDDO =BNNA,DOBD=OMMA，∵点D是OB的中点，∴M，N分别是OA，OB的中点，∴DM=12AB=3,DN=12OA=4，∵∠EDF=90°，∴∠FDM=∠EDN，又∵∠DMF=∠DNE=90°，∴ΔDMF∽ΔDNE，∴DFDE =DMDN=34；（3）作DM⊥OA于点M，DN⊥AB于点N，若AD将ΔDEF的面积分成1:2的两部分，设AD交EF于点G，则点G为EF的三等分点，如图，NE=3−t，由ΔDMF∽ΔDNE得，MF=34(3−t)，∴AF=4+MF=−34t+254，∵点G为EF的三等分点，∴G(3t+7112,23 t)，设直线AD的表达式为y=kx+b，将A(8,0)，D(4,3)代入得{8k+b=04k+b3，解得{k=−34b=6，∴直线AD的表达式为y=−34x+6，将G(3t+7112,23t)代入得：t=7541，∴当t<3时的值为t=7541．10．（2022秋·河北邯郸·九年级邯郸市第二十三中学校考期末）如图（1），在四边形ABCD中，AB∥DC，CB⊥AB，AB=14cm，BC=CD=6cm，动点P从点D开始沿DA边匀速运动，动点Q从点A开始沿AB边匀速运动，它们的运动速度均为1cm/s．点P和点Q同时出发，设运动的时间为t(s)，0<t<10．（1）用含t的代数式表示AP；（2）当以点A、P、Q为顶点的三角形与△ABD相似时，求t的值；（3）如图（2），延长QP、BD，两延长线相交于点M，当ΔQMB为直角三角形时，直接写出．．．．t的值．【思路点拨】（1）作DH⊥AB于H，得矩形DHBC，则CD=BH=6cm，DH=BC=6cm，AH=8cm，由勾股定理可求得AD的长，从而可得AP；（2）分两种相似情况加以考虑，根据对应边成比例即可完成；（3）分∠QMB=90°和∠MQB=90°两种情况考虑即可，再由相似三角形的性质即可求得t的值．【解题过程】（1）如图，作DH⊥AB于H则四边形DHBC是矩形∴CD=BH=6cm，DH=BC=6cm∴AH=8cm在RtΔADH中，由勾股定理得AD=√DH2+AH2=√62+82=10(cm)∵DP=tcm∴AP=AD−DP=(10−t)cm（2）①当ΔAPQ∽ΔADB时则有APAQ =ADAB∴10−tt =1014解得：t=356②当ΔAPQ∽ΔABD时则有APAQ =ABAD∴10−tt =1410解得：t=256综上所述，当t=356或256时，以点A、P、Q为顶点的三角形与△ABD相似；（3）①当∠QMB=90°时，ΔQMB为直角三角形如图，过点P作PN⊥AB于N，DH⊥AB于H∴∠PNQ=∠BHD∵∠QMB=90°∴∠PQN+∠DBH=90°∵∠PQN+∠QPN=90°∴∠QPN=∠DBH∴ΔPNQ∽ΔBHD∴QN PN =DHBH=66=1即QN=PN∵PN∥DH∴ΔAPN∽ΔADH∴PN AP =DHAD=610=35，ANAP=AHAD=810=45∴PN=35AP=35(10−t)，AN=45AP=45(10−t)∴QN=AN−AQ=45(10−t)−t=8−95t由QN=PN得：8−95t=35(10−t)解得：t=53②当∠MQB=90°时，ΔQMB为直角三角形，如图则PQ∥DH∴ΔAPQ∽ΔADH∴AQ AP =AHAD=45∴AQ=45AP即t=45(10−t)解得：t=409综上所述，当t=53或409时，ΔQMB是直角三角形．11．（2022秋·山东青岛·九年级统考期中）如图1，在RtΔABC中，∠ACB=90°，AC=8，BC=6，CD⊥AB 于点D．点P从点D出发，沿线段DC向点C运动，点Q从点C出发，沿线段CA向点A运动，两点同时出发，速度都为每秒1个单位长度，当点P运动到C时，两点都停止．设运动时间为t秒．（1）当ΔPQC 是等腰三角形时，请直接写出t 值为．（2）如图2，在运动过程中是否存在某一时刻t ，使得沿PC 翻折ΔCPQ 所得到的四边形CQPM 是菱形？若存在，求出t 的值；若不存在，请说明理由；（3）如图3，连接BP ，设四边形BPQC 的面积为S ．求S 与t 之间的函数关系式；（4）是否存在某一时刻t ，使得P 、Q 、B 三点共线？若存在，求出t 的值；若不存在，请说明理由．【思路点拨】（1）根据勾股定理及等面积法可求CD ，由等腰三角形的性质分PC =QC 、PC =QP 、PQ =CQ 三种情况讨论即可求解；（2）根据菱形的性质可知，当PQ =CQ 时复合题意，过点Q 作QF ⊥CD ，证ΔABC ∼ΔQCF ，得CF =35t ，由PC =2×35t =245−t ，即可求解；（3）过点Q 作QH ⊥CD ，证ΔABC ∼ΔQCH ，得10t=8QH，即QH =45t ，证ΔABC ∼ΔBCD ，得BD =185，由S =S Δ⬚PCQ +S ΔBPC =12PC ⋅QH +12PC ⋅BD 即可求解；（4）过点P 作PG ⊥BC ，可得，ΔABC ∼ΔCPG ，得245−t 10=CG8，即CG =45(245−t)，BG =6−45(245−t)，由S ΔPBC =12PC ⋅BD =12BC ⋅PG 可得PG =35(245−t)，由CQPG =66−45(245−t)，当ΔBCQ ∼ΔBGP 时，B 、P 、Q 三点共线，得t35(245−t)=66−45(245−t)，即可求解；【解题过程】（1）解：∵∠ACB =90°，AC =8，BC =6， ∴AB =√AC 2+BC 2=√82+62=10， ∵CD ⊥AB ， ∴CD =AC⋅BC AB=6×810=245，∵ΔPQC 是等腰三角形，①当PC =QC 时，即245−t =t ，解得：t =125；②当PC =QP 时，如图，过点P 作PE ⊥AC ，∵PC =QP ，PE ⊥AC ， ∴QE =CE ，∵PE ⊥AC ，CD ⊥AB ，∠ACB =90°， ∴∠A =∠ACD ， ∴ΔABC ∼ΔPCE ， ∴AB PC=BC EC，即，10245−t=612t，解得：t =14455．③当PQ =CQ 时，过点Q 作QF ⊥CD ，∵∠A =∠ACD ， ∴ΔABC ∼ΔQCF ， ∴ABQC =BCCF，即10t =6CF ， ∴CF =35t ，∵PQ =CQ ，QF ⊥CD ， ∴CF =PF =35t ， ∴PC =2×35t =245−t ，解得：t=2411，故当ΔPQC是等腰三角形时，t值为125或14455或2411．（2）当PQ=CQ时，四边形CQPM是菱形，过点Q作QF⊥CD，∵∠A=∠ACD，∴ΔABC∼ΔQCF，∴AB QC =BCCF，即10t=6CF，∴CF=35t，∵PQ=CQ，QF⊥CD，∴CF=PF=35t，∴PC=2×35t=245−t，解得：t=2411，（3）如图，过点Q作QH⊥CD，∵∠A=∠ACD，∴ΔABC∼ΔQCH，∴AB QC =ACQH，即10t=8QH，∴QH =45t ，易证ΔABC ∼ΔBCD ，AB BC=BC BD ，即106=6BD ，解得：BD =185．S =S Δ⬚PCQ +S ΔBPC =12PC ⋅QH +12PC ⋅BD =12×(245−t)(45t +185)=−25t 2+325t +21625；（4）如图过点P 作PG ⊥BC ，可得，ΔABC ∼ΔCPG ，∴CPAB =CGAC ，即245−t 10=CG 8，∴CG =45(245−t)， ∴BG =6−45(245−t)，∵S ΔPBC =12PC ⋅BD =12BC ⋅PG ， ∴PG =PC⋅BD BC =(245−t)×1856=35(245−t)，∴CQPG =t 35(245−t)，BCBG =66−45(245−t)，当ΔBCQ ∼ΔBGP 时，B 、P 、Q 三点共线，所有t35(245−t)=66−45(245−t)，解得：t 1=12√6−185，t 2=−12√6−185（舍去）， ∴当t =12√6−185时，P 、Q 、B 三点共线．12．（2023秋·浙江金华·九年级统考期末）如图1，在矩形ABCD 中，AB =6，BC =3，动点P 从点A 出发，沿AB 边以每秒2个单位的速度向点B 运动，同时，动点Q 从点B 出发，沿BC −CD 匀速向终点D 运动，点P 、Q 同时到达终点，BD 与PQ 交于点E ．过点B 作BF ⊥PQ 于点F ．设点P 、Q 的运动时间为t 秒．（1）求点Q的运动速度．（2）如图2，当点Q与点C重合时，求BE的长．（3）在点P、Q的运动过程中，是否存在某一时刻，使得以B、E、F为顶点的三角形与△BCD相似？若存在，求运动时间t的值；若不存在，请说明理由．【思路点拨】（1）求出点P运动的时间即Q运动的时间计算解题即可；（2）当点Q与点C重合时，求出BD长，利用△EPB∽△ECD解题即可；（3）分①点Q在BC边上，②点Q在DC边上，点Q在P的右侧时，③点Q在DC边上，点Q在P的左侧时三种情况利用三角形相似解题即可．【解题过程】（1）解：由题可知点P运动的时间为62=3s，点Q运动的速度为：3+63=3，（2）如图，当点Q与点C重合时，∴t=33=1∴BP=AB−AP=6−2×1=4，在Rt△BDC中，BD=√BC2+CD2=√32+62=3√5，∵AB∥CD∴△EPB∽△ECD∴BE ED =BPCD即3√5−BE=46解得：BE =65√5（3）解：∵BF ⊥PQ ∴∠BFE =∠C =90°，当△BEF ∽△BDC 时，则∠BEF =∠BDC ∴PQ ∥CD 不符合题意，当△BEF ∽△DBC 时， ∴∠BEF =∠DBC , 当点Q 在BC 边上∴BQ =EQ =3t ，EP =PQ −3t 过点Q 作QH ∥CD 交BD 于点H ，则AB ∥CD ∥QH ,∴HQBP =EQ EP ,HQCD=BQ BC∴HQ =EQ×BP EP =3t(6−2t)PQ−3t,∴3t(6−2t)PQ−3t6=3t 3，解得：PQ =2t +3，在Rt △PQB 中，PB 2+BQ 2=PQ 2 即(2t +3)2=(6−2t)2+(3t)2, 解得：t =1或t =3(舍去)当点Q 在DC 边上，点Q 在P 的右侧时，如图，过Q 作QH ∥BC 交AB 、BD 于点H 、M ，则HB=QC=3t−3，DQ=9−3t ∵QH∥BC，BC∥AD∴QH∥BC∥AD，∴△BMH∽△BDA∴HM AD =HBAB即3t−36=HM3解得HM=32t−32，∴QE=MQ=3−(32t−32)=92−32t，PH=6−2t−(3t−3)=9−5t∵AB∥CD∴△BPE∽△DQE∴PB DQ =PEEQ即6−2t9−3t =PE92−32t，解得PE=3−t∴PQ=PE+EQ=3−t+92−32t=152−52t在Rt△PQH中，PH2+HQ2=PQ2即(152−52t)2=(9−5t)2+32解得t=95或t=1(舍去)；如图，当点Q在P的左侧时，过Q作QH∥BC交AB、BD于点H、M，则∠PEB=∠EDQ=∠DEQ=∠PBE∴PE=PB=6−2t，EQ=QD=9−3t，∴PQ=6−2t+9−3t=15−5t在Rt △PQH 中，PH 2+HQ 2=PQ 2 即(15−5t)2=(9−5t)2+32 解得t =94综上所述，当t =1或t =95或t =94时，以B 、E 、F 为顶点的三角形与△BCD 相似13．（2023秋·江苏无锡·九年级无锡市南长实验中学校考阶段练习）如图，在平面直角坐标系中，点B (6,5)，过点B 作x 轴的垂线，垂足为A ，作y 轴的垂线，垂足为C ．点D 从O 出发，沿y 轴正方向以每秒1个单位长度运动；点E 从O 出发，沿x 轴正方向以每秒3个单位长度运动；点F 从B 出发，沿BA 方向以每秒2个单位长度运动．当E 点运动到点A 时，三点随之停止运动．运动过程中△ODE 关于直线DE 的对称图形是△O ′DE ，设运动时间为t ．（1）用含t 的代数式分别表示点E ，点F 的坐标；（2）若△ODE 与以点A ，E ，F 为顶点的三角形相似，求t 的值；（3）是否存在这样的t ，使得以D ，E ，F ，O′所围成的四边形中有一组对边平行?若存在，求出t 的值；若不存在，请说明理由．【思路点拨】（1）由题可得OE =3t ，OD =t ，BF =2t ，易证四边形OABC 是矩形，从而得到AB =OC ，BC =OA ，即可求出AF ， OE ，即可求出点E ，点F 的坐标（2）只需两种情况讨论①当△ODE ∽△AEF ，②当△ODE ∽△AFE ，然后运用相似三角形的性质即可求解；（3）过点O′作x轴的平行线与y轴交于点M，与过点E的y轴的平行线交于点N，如图1，易得△MDO′∽△NO′E，设MO′=a，根据相似三角形的性质可得出a=35t，然后分两种情况讨论即可求解．【解题过程】（1）由题可得OE=3t，OD=t，BF=2t，∵BA⊥x轴，BC⊥y轴，∠AOC=90°，∴∠AOC=∠BAO=∠BCO=90°，∴四边形OABC是矩形，∴AB=OC，BC=OA，∵B(12,10)，∴BC=OA=12，AB=OC=10，∴AF=10−2t，OE=12−3t，∴点E的坐标为(3t,0)，点F的坐标为(12,10−2t)；（2）①当△ODE∽△AEF时，则有ODAE =OEAF，∴t 12−3t =3t10−2t，解得t1=0(舍去)，t2=267，②当△ODE∽△AFE时，则有ODAF =OEAE，∴t 10−2t =3t12−3t，解得t1=0(舍去)，t2=6，∵点E运动到点A时，三点随之停止运动，∴3t≤12，∴t≤4，∴t=6舍去，综上所述：t的值为267；（3）过点O′作x轴的平行线与y轴交于点M，与过点E的y轴的平行线交于点N，如图1，则有∠DMN=90°，∠N=90°，由折叠可得：DO′=DO=t，O′E=OE=3t，∠DO′E=∠DOE=90°，∴∠DMO′=∠N=90°，∠MDO′=90°−∠MO′D=∠NO′E，∴△MDO′∽△NO′E，∴MO′NE =MDNO′=O′DEO′=t3t=13，∴NE=3MO′，NO′=3MD，设MO′=a，则有OM=NE=3a，NO′=3t−a，MD=3a−t，∴3t−a=3(3a−t)，解得：a=35t，∴MO′=35t，OM=95t，∴点O′的坐标为(35t,95t)，①若DO′∥EF，如图2，延长O′D交x轴于S，则有O′M∥OS，∠DSE=∠FEA，∴∠MO′D=∠DSE=∠FEA，∵∠O′MD=∠EAF=90°，∴∠O ′MD ∽∠EAF ，∴MO ′AE =MD AF ， ∴35t 6−3t =95t−t 5−2t ，解得：t 1=0(舍去)，t 2=32，经检验：t =32是分式方程的解， ②若OF∥DE ，如图3，过点O ′作x 轴的平行线与AB 交于点Q ，延长DE 交 BA 的延长线于点T ，同①可得：△DOE ∽△FQO ′，∴OD QF =OE QO ′，t95t−(5−2t )=3t 6−35t ，解得t 1=0(舍去)，t 2=74，综上所述：t 的值为32或74． 14．（2023秋·吉林长春·九年级长春市解放大路学校校考阶段练习）如图，在Rt △ABC 中，∠C =90°，AC =3，AB =5，点D 为边AB 上一点且BD =2．动点P 从点A 出发，沿AB 以每秒1个单位长度的速度向终点B 运动，且点P 不与点A 、B 、D 重合．过动点P 作PQ ⊥AB 交折线AC −CB 于点Q ，作点P 关于点D 的对称点E ，连结QE ．设点P 的运动时间为t 秒．（1）当点Q 与点C 重合时，t =________；（2）用含t的代数式表示PE的长；（3）当△PEQ∽△CAB时，求t的值；（4）当Q在BC上运动时，若△BEQ为等腰三角形，直接写出此时t的值．【思路点拨】（1）利用面积计算即可；（2）分两种情况讨论即可；（3）由△PEQ∽△CAB可得PEAC =PQBC，代入线段计算即可；（4）画出图形，分类讨论即可．【解题过程】（1）∵∠C=90°，AC=3，AB=5，∴BC=√AB2−AC2=4，当点Q与点C重合时，S△ABC=12AC⋅BC=12PQ⋅AB∴S△ABC=12×3×4=12PQ×5∴PQ=125，∴PA=√AC2−PQ2=95，∴t=PA÷1=95，故答案为：95；（2）由题意可得，PA=t，PB=AB−PA=5−t，AD=AB−BD=3∵点P关于点D的对称点E，∴PD=DE，∴PE=2PD，当点P在点D的右边时，0<t<3，此时PD=AD−PA=3−t=DE，∴PE=2PD=6−2t，当点P在点D的左边时，3<t<5，此时PD=PA−AD=t−3=DE，∴PE=2PD=2t−6，综上所述，PE ={6−2t(0<t <3)2t −6(3<t <5)（3）当0<t ≤95时，点Q 在AC 边上，点P 在点D 的右边，PE =6−2t ∵∠APQ =∠ACB =90°∴△PAQ ∽△CAB ，∴PA AC=PQ BC ， ∴t 3=PQ 4∴PQ =43t ∵△PEQ ∽△CAB∴PE AC =PQ BC ∴6−2t 3=43t 4 ∴t =2（舍）当95<t <3时，点Q 在BC 边上，点P 在点D 的右边，PE =6−2t ，∵∠BPQ =∠ACB =90°∴△PBQ ∽△CBA ，∴BP BC =PQ AC =BQ AB ， ∴5−t 4=PQ 3=BQ 5 ∴PQ =34(5−t)，BQ =54(5−t)∵△PEQ ∽△CAB∴PE AC =PQ BC ∴6−2t 3=34(5−t)4t =5123，当3<t<5时，点Q在BC边上，点P在点D的左边，此时PQ=34(5−t)，PE=2t−6∵△PEQ∽△CAB∴PE AC =PQBC∴2t−63=34(5−t)4t=141 41综上，当△PEQ∽△CAB时，t=5123，t=14141（4）当当Q在BC上运动时，95<t<5，当95<t<3时，点Q在BC边上，点P在点D的右边，PE=6−2t，PQ=34(5−t)此时△BEQ为钝角三角形，若△BEQ为等腰三角形，则EB=EQ=AB−PE−PA=5−(6−2t)−t=t−1，在Rt△PQE中，PQ2+PE2=QE2，∴[34(5−t)]2+(6−2t)2=(t−1)2，此方程无解当3<t<5时，点Q在BC边上，点P在点D的左边，PE=2t−6，PQ=34(5−t)，BE=PA−PE=t−(2t−6)=6−t，BQ=54(5−t)。

2023年九年级数学中考专题：二次函数综合压轴题(相似三角形问题)(含简单答案)

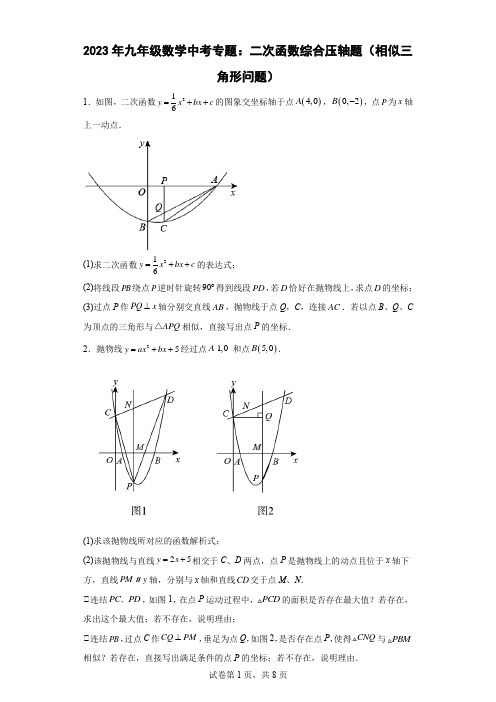
2023年九年级数学中考专题：二次函数综合压轴题（相似三角形问题）1．如图，二次函数216y x bx c =++的图象交坐标轴于点()4,0A ，()0,2B -，点P 为x 轴上一动点．(1)求二次函数216y x bx c =++的表达式； (2)将线段PB 绕点P 逆时针旋转90︒得到线段PD ，若D 恰好在抛物线上，求点D 的坐标； (3)过点P 作PQ x ⊥轴分别交直线AB ，抛物线于点Q ，C ，连接AC ．若以点B 、Q 、C 为顶点的三角形与APQ △相似，直接写出点P 的坐标． 2．抛物线25y ax bx =++经过点1,0A 和点()5,0B ．(1)求该抛物线所对应的函数解析式；(2)该抛物线与直线25y x =+相交于C 、D 两点，点P 是抛物线上的动点且位于x 轴下方，直线PM y ∥轴，分别与x 轴和直线CD 交于点M 、N ．①连结PC PD 、，如图1，在点P 运动过程中，PCD 的面积是否存在最大值？若存在，求出这个最大值；若不存在，说明理由；①连结PB ，过点C 作CQ PM ⊥，垂足为点Q ，如图2，是否存在点P ，使得CNQ 与PBM 相似？若存在，直接写出满足条件的点P 的坐标；若不存在，说明理由．3．已知抛物线24y ax ax b =-+与x 轴交于A ，B 两点，（A 在B 的左侧），与y 轴交于C ，若OB OC =，且03C （，）．(1)求抛物线的解析式；(2)设抛物线的顶点为D ，点P 在抛物线的对称轴上，且APD ACB ∠=∠，求点P 的坐标； (3)在抛物线上是否存在一点M ，过M 作MN x ⊥轴于N ，以A 、M 、N 为顶点的三角形与AOC ∆相似，若存在，求出所有符合条件的M 点坐标，若不存在，请说明理由． 4．如图．在平面直角坐标系中．抛物线212y x bx c =++与x 轴交于A 、B 两点，与y 轴交于点C ．点A 的坐标为()1,0-，点C 的坐标为()0,2-．已知点(),0E m 是线段AB 上的动点（点E 不与点A ，B 重合）．过点E 作PE x ⊥轴交抛物线于点P ，交BC 于点F ．(1)求该抛物线的表达式；(2)若:1:2EF PF =，请求出m 的值；(3)是否存在这样的m ，使得BEP △与ABC 相似？若存在，求出此时m 的值；若不存在，请说明理由；(4)当点E 运动到抛物线对称轴上时，点M 是x 轴上一动点，点N 是抛物线上的动点，在运动过程中，是否存在以C 、B 、M 、N 为顶点的四边形是平行四边形？若不存在，请说明理由；若存在，请直接写出点M 的坐标．5．如图，二次函数212y x bx c =-++图像交x 轴于点A ，B （A 在B 的左侧），与y 轴交于点(0,3)C ，CD y ⊥轴，交抛物线于另一点D ，且5CD =，P 为抛物线上一点，PE y轴，与x 轴交于E ，与BC ，CD 分别交于点F ，G ．(1)求二次函数解析式；(2)当P 在CD 上方时，是否存在点P ，使得以C ，P ，G 为顶点的三角形与FBE 相似，若存在，求出CPG △与FBE 的相似比，若不存在，说明理由．(3)点D 关于直线PC 的对称点为D ，当点D 落在抛物线的对称轴上时，此时点P 的坐标为________．6．如图，抛物线22y ax bx =++与x 轴交于点A ，B ，与y 轴交于点C ，已知A ，B 两点坐标分别是(1,0)A ，(4,0)B -，连接,AC BC ．(1)求抛物线的表达式；(2)将ABC ∆沿BC 所在直线折叠，得到DBC ∆，点A 的对应点D 是否落在抛物线的对称轴上？若点D 在对称轴上，请求出点D 的坐标；若点D 不在对称轴上，请说明理由；(3)若点P 是抛物线位于第二象限图象上的一动点，连接AP 交BC 于点Q ，连接BP ，BPQ ∆的面积记为1S ，ABQ ∆的面积记为2S ，求12S S 的值最大时点P 的坐标． 7．已知，二次函数23y ax bx =+-的图象与x 轴交于A ，B 两点（点A 在点B 的左边），与y 轴交于C 点，点A 的坐标为()1,0-，且OB OC =．(1)求二次函数的解析式；(2)当04x ≤≤时，求二次函数的最大值和最小值分别为多少？(3)设点C '与点C 关于该抛物线的对称轴对称．在y 轴上是否存在点P ，使PCC '△与POB 相似，且PC 与PO 是对应边？若存在，求出点P 的坐标；若不存在，请说明理由．8．已知菱形OABC 的边长为5，且点(34)A ，，点E 是线段BC 的中点，过点A ，E 的抛物线2y ax bx c =++与边AB 交于点D ，(1)求点E 的坐标；(2)连接DE ，将BDE △沿着DE 翻折痕．①当B 点的对应点B '恰好落在线段AC 上时，求点D 的坐标；①连接OB ，BB '，若BB D '△与BOC 相似，请直接写出此时抛物线二次项系数=a ______． 9．如图，抛物线22(0)y ax x c a =-+≠与x 轴交于A 、()3,0B 两点，与y 轴交于点()0,3C -，抛物线的顶点为D ．(1)求抛物线的解析式；(2)已知点M 是x 轴上的动点，过点M 作x 轴的垂线交抛物线于点G ，是否存在这样的点M ，使得以点A 、M 、G 为顶点的三角形与BCD △相似，若存在，请求出点M 的坐标；若不存在，请说明理由．(3)在直线BC 下方抛物线上一点P ，作PQ 垂直BC 于点Q ，连接CP ，当CPQ 中有一个角等于ACO ∠时，求点P 的坐标．10．如图，抛物线顶点D 在x 轴上，且经过(0,3)-和(4,3)-两点，抛物线与直线l 交于A 、B 两点．(1)直接写出抛物线解析式和D 点坐标；(2)如图1，若()03A ，-，且 94ABDS ＝，求直线l 解析式； (3)如图2，若90ADB ∠=︒，求证：直线l 经过定点，并求出定点坐标．11．如图1，已知抛物线2=23y x x --与x 轴交于A 、B 两点（点A 在点B 的左侧），与y 轴交于点C ，连接BC ，点P 是线段BC 下方抛物线上一动点，过点P 作∥PE BC ，交x 轴于点E ，连接OP 交BC 于点F ．(1)直接写出点A ，B ，C 的坐标以及抛物线的对称轴； (2)当点P 在线段BC 下方抛物线上运动时，求BFPE取到最小值时点P 的坐标； (3)当点P 在y 轴右边抛物线上运动时，过点P 作PE 的垂线交抛物线对称轴于点G ，是否存在点P ，使以P 、E 、G 为顶点的三角形与①AOC 相似？若存在，来出点P 的坐标；若不存在，请说明理由．12．如图，抛物线212ax ax b =-+y 经过()1,0A -，32,2C ⎛⎫⎪⎝⎭两点，与x 轴交于另一点B ．(1)求此抛物线的解析式；(2)若抛物线的顶点为M ，点P 为线段OB 上一动点(不与点B 重合)，点Q 在线段MB 上移动，且2PM MQ MB =⋅，设线段OP x =，2MQ y =，求2y 与x 的函数关系式，并直接写出自变量x 的取值范围；并直接写出PM APPQ BQ-的值；(3)在同一平面直角坐标系中，两条直线x m =，x n =分别与抛物线交于点E ，G ，与（2）中的函数图象交于点F ，.H 问四边形EFHG 能否为平行四边形？若能，求m ，n 之间的数量关系；若不能，请说明理由．13．已知抛物线213222y x x =-++交x 轴于A 、B 两点，A 在B 的左边，交y 轴于点C ．(1)求抛物线顶点的坐标；(2)如图1，若10,2E ⎛⎫- ⎪⎝⎭，P 在抛物线上且在直线AE 上方，PQ AE ⊥于O ，求PQ 的最大值；(3)如图2，点(),3D a （32a <）在抛物线上，过A 作直线交抛物线于第四象限另一点F ，点M 在x 轴上，以M 、B 、D 为顶角的三角形与AFB △相似，求点M 的坐标． 14．如图，抛物线23y ax bx =+-与x 轴交于点()1,0A 、()3,0B ，与y 轴交于点C ，联结AC 、BC ．(1)求该抛物线的表达式及顶点D 的坐标；(2)如果点P 在抛物线上，CB 平分ACP ∠，求点P 的坐标：(3)如果点Q 在抛物线的对称轴上，DBQ 与ABC 相似．求点Q 的坐标．15．如图，抛物线23y ax x c =-+与x 轴交于(4,0)A -，B 两点，与y 轴交于点(0,4)C ，点D 为x 轴上方抛物线上的动点，射线OD 交直线AC 于点E ，将射线OD 绕点O 逆时针旋转45︒得到射线OP ，OP 交直线AC 于点F ，连接DF ．(1)求抛物线的解析式； (2)当点D 在第二象限且34DE EO =时，求点D 的坐标； (3)当ODF △为直角三角形时，请直接写出点D 的坐标．16．如图①，抛物线与x 轴交于A ，B 两点，与y 轴交于点C （0，3），顶点为D （4，-1），对称轴与直线BC 交于点E ，与x 轴交于点F ．(1)求二次函数的解析式；(2)点M 在第一象限抛物线的对称轴上，若点C 在BM 的垂直平分线上，求点M 的坐标； (3)如图①，过点E 作对称轴的垂线在对称轴的右侧与抛物线交于点H ，x 轴上方的对称轴上是否存在一点P ，使以E ，H ，P 为顶点的三角形与EFB △相似，若存在，求出P点坐标；若不存在，请说明理由．17．如图，在平面直角坐标系xOy 中，已知抛物线2y ax x c =++经过()2,0A -，()0,4B 两点，直线3x =与x 轴交于点C ．(1)求a ，c 的值；(2)经过点O 的直线分别与线段AB ，直线3x =交于点D ，E ，且BDO △与OCE △的面积相等，求直线DE 的解析式；(3)P 是抛物线上位于第一象限的一个动点，在线段OC 和直线3x =上是否分别存在点F ，G ，使B ，F ，G ，P 为顶点的四边形是以BF 为一边的矩形？若存在，求出点F的坐标；若不存在，请说明理由．18．如图1，抛物线2y ax bx c =++与x 轴交于A ，B （点A 在点B 左侧），与y 轴负半轴交于C ，且满足2OA OB OC ===．(1)求抛物线的解析式；(2)如图2，D 为y 轴负半轴上一点，过D 作直线l 垂直于直线BC ，直线l 交抛物线于E ，F 两点（点E 在点F 右侧），若3DF DE =，求D 点坐标； (3)如图3，点M 为抛物线第二象限部分上一点，点M ，N 关于y 轴对称，连接MB ，P 为线段MB 上一点（不与M 、B 重合），过P 点作直线x t =（t 为常数）交x 轴于S ，交直线NB 于Q ，求QS PS -的值（用含t 的代数式表示）．参考答案：1．(1)211266y x x =-- (2)()3,1D -或()8,10D -(3)点P 的坐标为()011-，或()10，．2．(1)265y x x =-+ (2)37,24⎛⎫- ⎪⎝⎭或()3,4-3．(1)243y x x =-+ (2)()2,2P 或()2,2-(3)存在符合条件的M 点，且坐标为：110(3M ，7)9-，()26,15M ，38(3M ，5)9-4．(1)213222y x x =--； (2)2m =；(3)存在，m 的值为0或3；(4)存在，M 点的坐标为()7,0或()1,0M 或⎫⎪⎪⎝⎭或⎫⎪⎪⎝⎭．5．(1)215322y x x =-++；(2)存在点P ，使得以C ，P ，G 为顶点的三角形与FBE 相似，CPG △与FBE 的相似比为2或25；(3)P 点横坐标55．6．(1)213222y x x =--+(2)点D 不在抛物线的对称轴上， (3)(2,3)-7．(1)2=23y x x --(2)函数的最大值为5，最小值为4- (3)存在，(0,9)P -或9(0,)5P -8．(1)13(2)2E ， (2)①11(4)2D ，或23(4)6D ，；①47-9．(1)2=23y x x --(2)()0,0，()6,0，8,03⎛⎫ ⎪⎝⎭，10,03⎛⎫⎪⎝⎭(3)57,24⎛⎫- ⎪⎝⎭或者315,24⎛⎫- ⎪⎝⎭10．(1)()2324y x =--，()2,0D (2)334y x =-或1534y x =- (3)证明见解析，定点坐标为423⎛⎫- ⎪⎝⎭，11．(1)A （﹣1，0），B （3，0），C （0，﹣3），对称轴为直线x ＝1(2)当t ＝32时，BF PE 最小，最小值为47，此时P （32，﹣154）．(3)存在，点P 的坐标为（2，﹣3）12．(1)211322y x x =-++(2)22150322y x x x =-+≤<（），PM AP PQ BQ -的值为0 (3)m 、n 之间的数量关系是2(1)m n m +=≠13．(1)（32，258）答案第3页，共3页(3)（2，0）或（-5，0）或13,07⎛⎫ ⎪⎝⎭或2205⎛⎫- ⎪⎝⎭，14．(1)2=+43y x x --，(21)D ， (2)111639⎛⎫ ⎪⎝⎭，- (3)(2，−2)或12,3⎛⎫ ⎪⎝⎭15．(1)234y x x =--+(2)(1,6)D -或(3,4)D -(3)(3,4)-或(0,4)或2⎫⎪⎪⎝⎭或2⎫⎪⎪⎝⎭16．(1)21234y x x =-+(2)(4,3(3)存在P 1)或(4,1)，使以E ，H ，P 为顶点的三角形与EFB △相似，17．(1)12a =-，4c = (2)23y x =- (3)存在这样的点F ，点F 的坐标为(2,0)或18．(1)2122y x =- (2)()0,1D -或190,8D ⎛⎫- ⎪⎝⎭， (3)24QS PS t -=-+。

【2022】苏教版中考数学精编专题《相似三角形及应用》(含答案解析)

【苏教版】中考数学精编专题汇编专题1 相似三角形及应用学校：___________姓名：___________班级：___________1.【江苏省南通市九年级上学期期末】下列条件不能判定△ABC 与△DEF 相似的是（）A ．B ． ,C ． ∠A=∠D ，∠B=∠E D ．，∠B=∠E【考点定位】相似三角形的判定．2. 【江苏省徐州市中考模拟】直线l 1∥l 2∥l 3，且l 1与l 2的距离为1，l 2与l 3的距离为3，把一块含有45°角的直角三角形如图放置，顶点A ，B ，C 恰好分别落在三条直线上，AC 与直线l 2交于点D ，则线段BD 的长度为（）A ．B ．C ．D ．【答案】A ．【解析】分别过点A 、B 、D 作AF ⊥l 3，BE⊥l 3，DG⊥l 3，先根据全等三角形的判定定理得出△BCE≌△ACF，故可得出CF 及CE 的长，在Rt△ACF 中根据勾股定理求出AC 的长，再由相似三角形的判定得出△CDG∽△CAF，故可得出CD 的长，在Rt△BCD 中根据勾股定理即可求出BD 的长．分别过点A 、B 、D 作AF⊥l 3，BE⊥l 3，DG⊥l 3，AB BC AC DE EF DF ==AB BCDE EF=A D ∠=∠AB BCDE EF=254253203154∵△ABC 是等腰直角三角形，∴AC=BC，∵∠EBC+∠BCE=90°，∠BCE+∠ACF=90°，∠ACF+∠CAF=90°，∴∠EBC=∠ACF，∠BCE=∠CAF，在△BCE 与△ACF 中，，【考点定位】1.相似三角形的判定与性质；2.平行线之间的距离；3.全等三角形的判定与性质；4.等腰直角三角形．3.【江苏省淮安市中考】如图，l 1∥l 2∥l 3，直线a ，b 与l 1、l 2、l 3分别相交于A 、B 、C 和点D 、E 、F ．若，DE =4，则EF 的长是（）A．B ．C ．6D ．10 【答案】C ．EBC ACF BC ACBCE CAF ∠=∠⎧⎪=⎨⎪∠=∠⎩32=BC AB 38320【考点定位】平行线分线段成比例．4.【江苏省南京市中考】如图所示，△ABC 中，DE ∥BC ，若，则下列结论中正确的是（） A ．B ．C ．D ．【答案】C ．【考点定位】相似三角形的判定与性质．5.【江苏省南通市九年级上学期期末】若△ABC∽△A′B′C′，相似比为1：3，则△ABC 与△A′B′C′的面积之比为．【答案】1：9．【解析】∵△ABC ∽△A′B′C′，相似比为1：3，∴△A BC 与△A′B′C′的面积之比为1：9．故答案为：1：9．【考点定位】相似三角形的性质．6.【江苏省扬州市中考】如图，练习本中的横格线都平行，且相邻两条横格线间的距离都相等，同一条直线上的三个点A 、B 、C 都在横格线上，若线段AB =4 cm ，则线段BC = c m【答案】1212AD DB =12AE EC =12DE BC =1=3ADE ABC △的周长△的周长1=3ADE ABC △的面积△的面积【考点定位】平行线分线段成比例7.【江苏省常州市中考】如图，在△ABC 中，DE ∥BC ，AD ：DB =1：2，DE =2，则BC 的长是．【答案】6．【考点定位】相似三角形的判定与性质．8.【江苏省无锡市中考】已知：如图，AD 、BE 分别是△ABC 的中线和角平分线，AD ⊥BE ，AD ＝BE ＝6，则AC的长等于．【答案】952BACDE故答案为：952【考点定位】全等三角形的判定及性质；相似三角形的判定及性质；勾股定理.9.【江苏省苏州中考一模】如图，在平面直角坐标系中，已知点A （0，6），B （8，0）．点P 从A 点出发，以每秒1个单位的速度沿AO 运动；同时，点Q 从O 出发，以每秒2个单位的速度沿OB 运动，当Q 点到达B 点时，P 、Q 两点同时停止运动．（1）求运动时间t 的取值范围；（2）t 为何值时，△POQ 的面积最大？最大值是多少？（3）t 为何值时，以点P 、0、Q 为顶点的三角形与Rt △AOB 相似？【答案】(1) 0≤t ≤4；(2) 当t=3时，△POQ 的面积最大，最大值是9．(3) 当t 为或时，以点P 、0、Q 为顶点的三角形与Rt △AOB 相似．【解析】试题分析：（1）由点Q 从O 出发，以每秒2个单位的速度沿O B 运动，当Q 点到达B 点时，P 、Q 两点同时停止运动，可得：2t=8，解得：t=4，进而可得：0≤t ≤4；1251811（2）先根据三角形的面积公式，用含有t 的式子表示△POQ 的面积=-t 2+6t ，然后根据二次函数的最值公式解答即可；试题解析：（1）∵点A （0，6），B （8，0），∴OA=6，OB=8，∵点Q 从O 出发，以每秒2个单位的速度沿OB 运动，当Q 点到达B 点时，P 、Q 两点同时停止运动， ∴2t=8，解得：t=4， ∴0≤t ≤4；（2）根据题意得：经过t 秒后，AP=t ，OQ=2t ，∴OP=OA-AP=6-t ， ∵△POQ 的面积=•OP •OQ ，即△POQ 的面积=×（6-t ）×2t=-t 2+6t ． ∵a=-1＜0，∴△POQ 的面积有最大值，当t=-=3时，△POQ 的面积的最大值==9，即当t=3时，△POQ 的面积最大，最大值是9．（3）①若Rt △POQ ∽Rt △AOB 时， ∵Rt △POQ ∽R t △AOB ，∴，即，解得：t= ②若Rt △QOP ∽Rt △AOB 时， ∵Rt △QOP ∽Rt △AOB ，∴，即，解得：t=．所以当t 为或时，以点P 、0、Q 为顶点的三角形与Rt △AOB 相似．【考点定位】相似三角形与一次函数综合题．10.【江苏省南京市中考】如图，△ABC 中，CD 是边AB 上的高，且．（1）求证：△ACD ∽△CBD ；（2）求∠ACB 的大小．12122ba244ac b a - PO OQ AO OB =6268t t -=125 PO OQ OB AO =6286t t -=18111251811AD CDCD BD=【答案】（1）证明见试题解析；（2）90°．【解析】【考点定位】相似三角形的判定与性质．专题2 圆的有关计算及圆的综合学校：___________姓名：___________班级：___________1.【江苏省南通市九年级上学期期末】如图，⊙O 中，OA ⊥BC ，∠A OB=52°，则∠ADC 的度数为（）A ．36°B ．26°C ． 38°D ．46°【答案】D ．【解析】故选D.【考点定位】1.圆周角定理；2.垂径定理.2.【江苏省江阴市九年级下学期期中】一个圆锥底面直径为2，母线为4，则它的侧面积为（） A ． B．C ．D ．【答案】C.【解析】根据圆锥的侧面积公式S=πrl 可得这个圆锥的侧面积为π×1×4=4π.故选C. 【考点定位】圆锥的侧面积公式.3.【江苏省苏州市区中考】如图，⊙O 上A 、B 、C 三点，若∠B=50，∠A=20°，则∠AOB 等于（） A 、30° B 、50° C 、70° D 、60°【答案】D ．2π12π4π8π【解析】先根据圆周角定理得出∠ACB=∠AOB ，再由三角形内角和定理即可得出结论．∵∠AOB 与∠ACB是同弧所对的圆心角与圆周角，∠B=50，∠A=20°，∴∠ACB=∠AOB ．∴180°-∠AOB-∠A=180°-∠ACB-∠B ，即180°-∠AOB-20°=180°-∠AOB-50°，解得∠AOB=60°．故选D ．【考点定位】圆周角定理．4.【江苏省南通市九年级上学期期末】某个圆锥的侧面展开图形是一个半径为6cm ，圆心角为120°的扇形，则这个圆锥的底面半径为（）cm ． A 、2B 、3C 、4D 、5【答案】A ．故选A.【考点定位】弧长的计算.5.【江苏省苏州市中考一模】如图，AB 是⊙O 的切线，切点为B ，AO 交⊙O 于点C ，且AC=OC ，若⊙O 的半径为5，则图中阴影部分的面积是 .．【解析】直接利用切线的性质结合勾股定理得出AB 的长，再利用锐角三角函数关系得出∠BOC 的度数，结合阴影部分的面积为：S △OBA -S 扇形BOC 求出即可．连接OB ，∵AB 是⊙O 的切线，切点为B ，∴∠OBBA=90°，∵AC=OC ，⊙O 的半径为5，∴AC=5，AB=5，∴∠A=30°，则∠BOC=60°，∴图中阴影部分的面积为：S △OBA -S 扇形BOC =×BO ×AB-．故答案为：121212625π312605360π⨯536225π. 【考点定位】1.扇形面积的计算；2.切线的性质．6.【江苏省徐州中考】13.圆锥底面圆的半径为3m ，其侧面展开图是半圆，则圆锥母线长为 m．【答案】6．【考点定位】圆锥的计算．7.【江苏省中考】已知扇形的圆心角为120°，弧长为6π，则扇形的面积是．【答案】27π．【考点定位】扇形面积的计算．8.【江苏省南京市中考二模】已知等腰△ABC 中，AB=AC=13cm ，BC=10cm ，则△ABC 的内切圆半径为 cm ．【答案】. 【解析】如图，设△ABC 的内切圆半径为r ，由勾股定理得AD=12，再由切线长定理得AE=8，根据勾股定理求得r 即可．如图，∵AB=AC=13cm ，BC=10cm ，∴BD=5cm ，∴AD=12cm ，根据切线长定理，AE=AB-BE=AB-BD=13-5=8，设△ABC 的内切圆半径为r ，∴AO=12-r ，∴（12-r ）2-r 2=64，解得r=.故答案为：. 【考点定位】1.三角形的内切圆与内心；2.等腰三角形的性质．9.【江苏省苏州中考一模】如图所示，D 是以AB 为直径的半圆O 上的一点，C 是弧AD 的中点，点M 在AB 上，AD 与CM 交于点N ，CN=AN ．625π103103103（1）求证：CM⊥AB；（2）若BD=2，求半圆的直径．【答案】（1）证明见解析；（2）6．【解析】试题解析：（1）证明：如图1，连接BC，则∠ACB=90°，∵CN=AN，∴∠NCA=∠NAC，∴∠MCA=∠DAC，∵C是弧AD的中点，∴∠ABC=∠DAC，∴∠MCA=∠ABC，∵∠CAB=∠BAC，∴△ABC∽△ACM，∴∠AMC=90°，∴CM⊥AB；（2）解：如图2，连接CD，作CE⊥BD，交BD的延长线于E，在△CMB与△BCE中，，【考点定位】1.相似三角形的判定与性质；2,全等三角形的判定与性质；2.圆周角定理．10.【江苏省无锡市中考】已知：如图，AB 为⊙O 的直径，点C 、D 在⊙O 上，且BC ＝6cm ，AC ＝8cm ，∠ABD ＝45º．（1）求BD 的长；（2）求图中阴影部分的面积．【答案】(1)BD ＝52cm;(2)S 阴影＝25π－504cm 2．【解析】MBC CBE CMB CEB BC BC ∠=∠∠=∠=⎧⎪⎨⎪⎩【考点定位】圆周角定理的推论；勾股定理；扇形的面积公式.专题3 图形的变换、视图与投影学校：___________姓名：___________班级：___________1. 【江苏省苏州市中考一模】下列腾讯QQ表情中，不是轴对称图形的是（）【答案】C．【解析】根据轴对称图形的概念求解．A、是轴对称图形，故本选项错误；B、是轴对称图形，故本选项错误；C、不是轴对称图形，故本选项正确；D、是轴对称图形，故本选项错误．故选C．【考点定位】轴对称图形．2.【江苏省徐州市中考模拟】下列图形中，既是中心对称图形又是轴对称图形的是（）【答案】D．【考点定位】1.中心对称图形；2.轴对称图形．3. 【江苏省淮安市中考】如图所示物体的主视图是（）A． B． C． D．【答案】C．【考点定位】简单组合体的三视图．4.【江苏省常州市中考】下列“慢行通过，注意危险，禁止行人通行，禁止非机动车通行”四个交通标志图（黑白阴影图片）中为轴对称图形的是（）A． B． C． D．【答案】B．故选B.【考点定位】轴对称图形．5.【江苏省常州市中考】将一张宽为4cm的长方形纸片（足够长）折叠成如图所示图形，重叠部分是一个三角形，则这个三角形面积的最小值是【答案】8cm2 .故答案为：8cm 2.【考点定位】1．翻折变换（折叠问题）；2．最值问题．6.【江苏省江阴市中考】如图，Rt ΔABC 中，AB=9，BC=6，∠B=900，将ΔABC 折叠，使A 点与BC 的中点D 重合，折痕为MN ，则线段BN的长为【答案】 4. 【解析】故答案为：4.【考点定位】翻折变换；勾股定理. 7.【江苏省苏州市区中考】在R t △ABC 中，斜边AB=4，∠B=60°，将△ABC 绕点B 旋转60°，顶点C 运动的路线长是（结果保留π）．【答案】.【解析】将△ABC 绕点B 旋转60°，顶点C 运动的路线长是就是以点B 为圆心，B C 为半径所旋转的弧，根据弧长公式即可求得．∵AB=4，∴BC=2，所以弧长=.故答案为：. 【考点定位】1.弧长的计算；2.旋转的性质．8.【江苏省扬州市2015年中考数学试题】如图，已知Rt △ABC 中，∠ABC =90°，AC =6，BC =4，将△ABC 绕直角顶点C 顺时针旋转90°得到△DEC ，若点F 是DE 的中点，连接AF ，则AF = 23π602180π⨯=23π23π【答案】5【考点定位】旋转的性质9.【江苏省徐州市中考】如图，在方格纸上建立平面直角坐标系，每个小正方形的边长为1．（1）画出△AOB关于x轴对称的△A1OB1．（2）画出将△AOB绕点O顺时针旋转90°的△A2OB2，并判断△A1OB1和△A2OB2在位置上有何关系？若成中心对称，请直接写出对称中心坐标；如成轴对称，请直接写出对称轴的函数关系式．（3）若将△AOB绕点O旋转360°，试求出线段AB扫过的面积．【答案】（1）画图见解析；（2）画图见解析；△A1OB1和△A2OB2是轴对称关系，对称轴为：y=﹣x．（3）2.5π．【解析】试题解析：（1）如图所示：．（2）如图所示：△A1OB1和△A2OB2是轴对称关系，对称轴为：y=﹣x．（3）过点O作OE⊥AB，线段AB2﹣π（）2=5π﹣2.5π=2.5π．【考点定位】1.作图-旋转变换；2.扇形面积的计算；3.作图-轴对称变换．10.【江苏省南京市中考二模试题】△ABC 中，AB=AC=10，BC=12，矩形DEFG 中，EF=4，FG ＞12．（1）如图①，点A 是FG 的中点，FG ∥BC ，将矩形DEFG 向下平移，直到DE 与BC 重合为止．要研究矩形DEFG 与△ABC 重叠部分的面积，就要进行分类讨论，你认为如何进行分类，写出你的分类方法（无需求重叠部分的面积）．（2）如图②，点B 与F 重合，E 、B 、C 在同一直线上，将矩形DEFG 向右平移，直到点E 与C 重合为止．设矩形DEFG 与△ABC 重叠部分的面积为y ，平移的距离为x ．①求y 与x 的函数关系式，并写出自变量的取值范围；②在给定的平面直角坐标系中画出y 与x 的大致图象，并在图象上标注出关键点坐标．2【考点定位】几何变换综合题．。

苏科版九年级数学下册相似三角形题型归纳(含隐圆、动点、最值、拓展、压轴)(无答案)

相似三角形（相似动点）分类涉及隐圆问题、最值问题、分类讨论题型、动点题型、压轴题、拓展题题型分类：一、相似三角形的判定定理①平行于三角形一边的直线和其他两边或其延长线相交，所得的三角形与原三角形相似；②三边对应成比例的两个三角形相似；③两角对应相等的两个三角形相似；④两边对应成比例且夹角相等的两个三角形相似。

二、相似三角形解题思路：(1)相似三角形有公共角或对顶角时，公共角或对顶角是最明显的对应角；相似三角形中最大的角(或最小的角)一定是对应角；相似三角形中，一对相等的角是对应角，对应角所对的边是对应边，对应角的夹边是对应边；(2)相似三角形中，一对最长的边(或最短的边)一定是对应边；对应边所对的角是对应角；对应边所夹的角是对应角．2、常见的相似三角形的基本图形：三角形相似的判定，要与三角形全等的判定相比较，把证明三角形全等的思想方法迁移到相似三角形中来；对一些出现频率较高的图形，要善于归纳和记忆；对相似三角形的判定思路要善于总结，形成一整套完整的判定方法．如：(1)“平行线型”相似三角形。

(2)“相交线型”相似三角形。

(3)“旋转型”相似三角形。

三、相似模型1．A字、8字模型。

2.共边共角模型（扭屁股模型）。

3.一线三等角模型。

4.倒数模型（较难）5.圆中的相似。

6.平行线分线段成比例。

类型一、线段比例问题1. （构造平行）如图1，在Rt△ABC中，∠BAC=90°，AD⊥BC于点D，点O是AC边上一点，连接BO交AD于F，OE⊥OB交BC边于点E．（1）求证：△ABF∽△COE；（2）当O为AC的中点，=2时，如图2，求的值；（3）当O为AC边中点，=n时，请直接写出的值．2.如图1 ,DE是⊙O的直径，点A、C是直径DE上方半圆上的两点，且AO⊥OC.连接AE，CD相交于点F.点B是直径DE下方半圆上的任意一点，连接AB交CD 于点G，连接CB交AE于点H.(1)求∠ABC的度数;(2)证明: △CFH∽△CBG;(3)若弧DB为半圆的三分之一，把∠AOC绕着点O旋转，使点C、O、B在一直线上时，如图2.①证明FH：BG=1：2;②若⊙O的半径为4，直接写出FH的长.3. 已知抛物线(3)(1)y a x x =+-（a ≠0），与x 轴从左至右依次相交于A 、B 两点，与y 轴相交于点C ，经过点A 的直线y=-x+b 与抛物线的另一个交点为D ．（1）若点D 的横坐标为2，求抛物线的函数解析式；（2）若在第三象限内的抛物线上有点P ，使得以A 、B 、P 为顶点的三角形与△ABC 相似，求点P 的坐标；（3）在（1）的条件下，设点E 是线段AD 上的一点（不含端点），连接BE ．一动点Q 从点B 出发，沿线段BE 以每秒1个单位的速度运动到点E ，再沿线段ED 以每秒个单位的速度运动到点D 后停止，问当点E 的坐标是多少时，点Q 在整个运动过程中所用时间最少？二、相似比乘积处理方法（逆向和正向分析找解题思路）1.如果四边形ABCD 的对角线交于O ，过O 作直线OG ∥AB 交BC 于E ，交AD 于F ，交CD的延长线于G ，求证：OG 2=GE ·GF.2.如图，在平面直角坐标系中，函数（x>0，k 是常数）的图像经过A （2，6），B （m,n ），其中m>2．过点A 作X 轴垂线，垂足为C ，过点B 作y 轴垂线，垂足为D ，AC 与BD 交于点E ，连结AD 、DC 、CB 。

2019年江苏苏教版中考相似三角形专题培优汇编真题（含答案）

2019年江苏苏教版中考相似三角形专题培优汇编真题（含答案）2019年江苏中考相似三角形培优汇编1.（2019扬州）如图，在△ABC 中，AB=5，AC=4，若进行一下操作，在边BC 上从左到右一次取点D 1、D 2、D 3、D 4…；过点D1作AB 、AC 的平行线分别交于AC 、AB 与点E 1、F 1；过点D 2作AB 、AC 的平行线分别交于AC 、AB 于点E 2、F 2；过点D 3作AB 、AC 的平行线分别交于AC 、AB 于点E 3、F 3…，则4（D 1E 1+D 2E 2+…+D 2019E 2019）+5（D 1F 1+D 2F 2+…+D 2019F 2019）= ．解：∵D 1E 1∥AB D 1F 1∥AC ∴CB CD AB E D 111=BCBD AC F D 11=∵AB=5 AC=4 ∴CB CD E D 1115= BC BD F D 114= ∴14511111==+=+BCBCBC BD CB C D F D E D ∴4D 1E+5D 1F=20有2019组，即2019×20=403802.（2019扬州）如图，平面内的两条直线l 1、l 2,点A 、B 在直线l 2上，过点A 、B 两点分别作直线l 1的垂线，垂足分别为A 1、B1，我们把线段A 1B 1叫做线段AB 在直线l 2上的正投影，其长度可记作T （AB ，CD ）或T （AB ，l 2）,特别地，线段AC 在直线l 2上的正投影就是线段A 1C 请依据上述定义解决如下问题（1）如图1，在锐角△ABC 中，AB=5，T （AC ，AB ）=3，则T （BC ，AB ）= ；（2）如图2，在Rt △ABC 中，∠ACB=90°，T （AC ，AB ）=4，T （BC ，AB ）=9，求△ABC 的面积；（3）如图3，在钝角△ABC 中，∠A=60°，点D 在AB 边上，∠ACD=90°，T （AB ，AC ）=2，T （BC ，AB ）=6，求T （BC ，CD ）.解：(1)过C 作CE ⊥AB ，垂足为E∴由T （AC ，AB ）=3投影可知AE=3∴BE=2即T （BC ，AB ）=2 (2)过点C 作CF ⊥AB 于F∵∠ACB=90°CF ⊥AB ∴△ACF ∽△CBF ∴CF 2=AF ·BF ∵T （AC ，AB ）=4，T （BC ，AB ）=9∴AF=4 BF=9即CF=6 △ABC =2，T =6∴AC=2 BM=63.（2019泰州）如图，⊙O 的半径为5，点P 在⊙O 上，点A 在⊙O 内，且AP ＝3,过点A 作AP 的垂线交于⊙O 点B 、C.设PB=x,PC=y,则y 与x 的函数表达式为．解：如图，连接PO 并延长交⊙O 于点N ，连接BN ，∵PN 是直径，∴∠PBN=90°. ∵AP ⊥BC,C∴∠PAC =90°，∴∠PBN=∠PAC ，又∵∠PNB=∠PCA ，∴△PBN ∽△PAC ，∴PA PB =PCPN , ∴3x =y10 ∴y=x 30.故答案为：y=x30. 4.（2019无锡）如图，在△ABC 中，AB ＝AC ＝5，BC＝D 为边AB 上一动点（B 点除外），以CD 为一边作正方形CDEF ，连接BE ，则△BDE 面积的最大值为．5.（2019宿迁）．如图①，在钝角△ABC中，∠ABC＝30°，AC＝4，点D为边AB中点，点E为边BC中点，将△BDE绕点B逆时针方向旋转α度（0≤α≤180）．（1）如图②，当0＜α＜180时，连接AD、CE．求证：△BDA∽△BEC；（2）如图③，直线CE、AD交于点G．在旋转过程中，∠AGC的大小是否发生变化？如变化，请说明理由；如不变，请求出这个角的度数；解：（1）如图②中，由图①，∵点D为边AB中点，点E为边BC中点，∴DE∥AC，∴＝，∴＝，∵∠DBE＝∠ABC，∴∠DBA＝∠EBC，∴△DBA∽△EBC．（2）∠AGC的大小不发生变化，∠AGC＝30°．理由：如图③中，设AB交CG于点O．∵△DBA∽△EBC，∴∠DAB＝∠ECB，∵∠DAB +∠AOG +∠G ＝180°，∠ECB +∠COB +∠ABC ＝180°，∠AOG ＝∠COB ，∴∠G ＝∠ABC ＝30°．6.（2019连云港）如图，在平面直角坐标系xOy 中，抛物线L 1：2y x bx c =++过点C (0，﹣3)，与抛物线L 2：213222y x x =--+的一个交点为A ，且点A 的横坐标为2，点P 、Q 分别是抛物线L 1、抛物线L 2上的动点．（1）求抛物线L 1对应的函数表达式；（2）设点R 为抛物线L 1上另一个动点，且CA 平分∠PCR ，若OQ ∥PR ，求出点Q 坐标．详解：（1）将2x =代入213222y x x =--+，得3y =-，故点A 的坐标为()23-，. 将()()2303A C --，，，代入2y x bx c =++，得2322300b c c-=++?-=++?，解得23b c =-??=-?.所以抛物线1L 对应的函数表达式为223y x x =--.（2）当点P 在y 轴左侧时，抛物线1L 不存在动点R 使得CA 平分PCR ∠.的当点P 在y 轴右侧时，不妨设点P 在CA 的上方，点R 在CA 的下方，过点P 、R 分别作y 轴的垂线，垂足分别为S T 、，过点P 作PH TR ⊥，垂足为H ，则有90PSC RTC ∠=∠=?. 由CA 平分PCR ∠，得PCA RCA ∠=∠，则PCS RCT ∠=∠，故PSC RTC ??∽，所以PS TR CS TC=. 设点P 坐标为()211123x x x --，，点R 坐标为()222223x x x --，，所以有()()12221122233323x x x x x x =--------，整理得124x x +=.在Rt PRH 中，.过点Q 作QK x ⊥轴，垂足为K .设点Q 坐标为213222m m m ??--+，. 若OQ PR ∥，则需QOK PRH ∠=∠.所以2132222m m m =--+.解得m =.所以点Q 坐标为7-?或7-?.7.（2019连云港）问题情境：如图1，在正方形ABCD中，E为边BC上一点（不与点B、C重合），垂直于AE的一条直线MN分别交AB、AE、CD于点M、P、N．判断线段DN、MB、EC之间的数量关系，并说明理由．问题探究：在“问题情境”的基础上，（1）如图2，若垂足P恰好为AE的中点，连接BD，交MN于点Q，连接EQ，并延长交边AD于点F．求∠AEF的度数；（2）如图3，当垂足P在正方形ABCD的对角线BD上时，连接AN，将△APN沿着AN翻折，点P落在点P'处．若正方形ABCD的边长为4 ，AD的中点为S，求P'S的最小值．问题拓展：如图4，在边长为4的正方形ABCD 中，点M 、N 分别为边AB 、CD 上的点，将正方形ABCD 沿着MN 翻折，使得BC 的对应边B'C '恰好经过点A ，C'N 交AD 于点F ．分别过点A 、F 作AG ⊥MN ，FH ⊥MN ，垂足分别为G 、H ．若AG ＝52，请直接写出FH 的长．解：问题情境：因为四边形ABCD 是正方形，所以90ABE BCD AB BC CD DC AB ∠=∠=?==，，∥. 过点B 作BF MN ∥分别交AE CD 、于点G F 、. 所以四边形MBFN 为平行四边形.所以NF MB =.所以90BF AE BGE ∠=?⊥，，所以90CBF AEB ∠+∠=?，又因为90BAE AEB ∠+∠=?，所以CBF BAE ∠=∠.ABE BCF △△≌，所以BE CF =.因为DN NF CF BE EC ++=+，所以DN NF EC +=，所以DN MB EC +=.问题探究：（1）连接AQ ，过点Q 作HI AB ∥，分别交AD BC 、于点H I 、.易得四边形ABIH 为矩形. 所以HI AD HI BC ⊥⊥，且HI AB AD ==.因为BI 是正方形ABCD 的对角线，所以45BDA ∠=?. 所以DHQ 是等腰直角三角形，HD HQ =.所以AH QI =.因为MN 是AE 的垂直平分线，所以AQ QE =.所以Rt Rt AHQ QIE △≌△.所以AQH QEI ∠=∠.所以90AQH EQI ?∠+∠=.所以90AQE ∠=?.所以AQE 是等腰直角三角形，45EAQ AEQ ∠=∠=?，即45AEF ∠=?.（2）如图所示，连接AC 交BD 于点O ，由题意易得APN 的直角顶点P 在OB 上运动. 设点P 与点B 重合，则点P '与点D 重合；设P 与点O 重合，则点P 的落点为O '.易知45ADO '∠=?.当点P 在线段BO 上运动时，过点P 作CD 的垂线，垂足为G ，过点P '作P H CD '⊥，垂足为点H .易证：Rt PGN Rt NHP '△△≌，所以PG NH G H P N '==，，因为BD 是正方形ABCD 的对角线，所以45PDG ∠=?，易得PG GD =，所以GN DH =. 所以DH H P '=.所以45P DH '∠=?，故45P DA '∠=?. 所以点P '在线段DO '上运动.过点S 作SK DO '⊥，垂足为K ，因为点S 为AD 的中点，所以2DS =，则P S '.问题拓展：解：延长AG 交BC 于E ，交DC 的延长线于Q ，延长FH 交CD 于P ，如图4：则EG＝AG＝52，PH＝FH，∴AE＝5，在Rt△ABE中，BE3，∴CE＝BC﹣BE＝1，∵∠B＝∠ECQ＝90°，∠AEB＝∠QEC，∴△ABE∽△QCE，∴1520 QE AE,AQ AE QE333===+=∵AG⊥MN，∴∠AGM＝90°＝∠B，∵∠MAG＝∠EAB，∴△AGM∽△ABE，∴AM AGAE AB=，即5254AM=，解得：25 AM8=，由折叠的性质得：AB'＝EB＝3，∠B'＝∠B＝90°，∠C'＝∠BCD＝90°，∴B'M7,AC1 8'==，∵∠BAD＝90°，∴∠B'AM＝∠C'FA，∴△AFC'∽△MAB'，∴''1,25788 AF AC AFAM MB==，解得：25253 AF,DF4777 ==-=∵AG⊥MN，FH⊥MN，∴AG∥FH，∴AQ∥FP，∴△DFP∽△DAQ，∴FP DFAQ DA=，即372043FP=，解得：FP＝57，∴FH＝15 FP214=．8.（2019南通）如图，矩形ABCD中，AB=2,AD=4,E,FF分别在AD,BC上，点A与点C关于EF所在的直线对称，P 是边DC上的一动点，（1）连接AF，CE，求证四边形AFCE是菱形；（2）当PEF ?的周长最小时，求CPDP的值；（3）连接BP 交EF 于点M ，当?=∠45EMP 时，求CP 的长。

相似三角形重要模型之母子型(共边共角模型)-2024年中考数学常见几何模型及参考答案

相似三角形重要模型之母子型(共边共角模型)相似三角形是初中几何中的重要的内容，常常与其它知识点结合以综合题的形式呈现，其变化很多，是中考的常考题型。

在相似三角形中存在众多的相似模型，其中“母子型”相似模型应用较为广泛，深入理解模型内涵，灵活运用相关结论可以显著提高解题效率，本专题重点讲解相似三角形的“母子”模型。

母子相似证明题一般思路方法:①由线段乘积相等转化成线段比例式相等；②分子和分子组成一个三角形、分母和分母组成一个三角形；③第②步成立，直接从证这两个三角形相似，逆向证明到线段乘积相等；④第②步不成立，则选择替换掉线段比例式中的个别线段，之后再重复第③步。

模型1.“母子”模型(共边角模型)【模型解读与图示】“母子”模型的图形(通常有一个公共顶点和另外一个不是公共的顶点，由于小三角形寓于大三角形中，恰似子依母怀)，也是有一个“公共角”，再有一个角相等或夹这个公共角的两边对应成比例就可以判定这两个三角形相似．图1图2图3图41)“母子”模型(斜射影模型)条件：如图1，∠C=∠ABD；结论：△ABD∽△ACB，AB2=AD·AC.2)双垂直模型(射影模型)条件:如图2，∠ACB=90o，CD⊥AB；结论：△ACD∽△ABC∽△CBD；CA2=AD·AB，BC2=BD·BA，CD2=DA·DB.3)“母子”模型(变形)条件:如图3，∠D=∠CAE，AB=AC；结论：△ABD∽△ECA；4)共边模型条件:如图1，在四边形ABCD中，对角线BD平分∠ABC，∠ADB=∠DCB，结论：BD2=BA⋅BC；1(2022·贵州贵阳·中考真题)如图，在△ABC中，D是AB边上的点，∠B=∠ACD，AC:AB=1:2，则△ADC与△ACB的周长比是()A.1:2B.1:2C.1:3D.1:42(2022春·江苏·九年级专题练习)如图，在Rt△ABC中，∠ACB=90°，点D在AB上，且ADAC=ACAB．(1)求证△ACD∽△ABC；(2)若AD=3，BD=2，求CD的长．3(2022.山西九年级期中)如图，点C，D在线段AB上，△PCD是等边三角形，且∠APB=120°，求证：(1)△ACP∽△PDB，(2)CD2=AC•BD．证明：(1)∵△PCD是等边三角形，∴∠PCD=∠PDC=∠CPD=60°，∴∠ACP=∠PDB=120°，∵∠APB=120°，∴∠APC+∠BPD=60°，∵∠CAP+∠APC=60°∴∠BPD=∠CAP，∴△ACP∽△PDB；(2)由(1)得△ACP∽△PDB，∴ACPD =PC BD，∵△PCD是等边三角形，∴PC=PD=CD，∴ACCD =CDBD，∴CD2=AC•BD．4(2023·湖南·统考中考真题)在Rt△ABC中，∠BAC=90°，AD是斜边BC上的高．(1)证明：△ABD∽△CBA；(2)若AB=6，BC=10，求BD的长．5(2023.浙江中考模拟)如图，在△ABC中，∠ACB=90°，CD⊥AB．(1)图1中共有对相似三角形，写出来分别为(不需证明)：(2)已知AB=5，AC=4，请你求出CD的长：(3)在(2)的情况下，如果以AB为x轴，CD为y轴，点D为坐标原点O，建立直角坐标系(如图2)，若点P 从C点出发，以每秒1个单位的速度沿线段CB运动，点Q出B点出发，以每秒1个单位的速度沿线段BA运动，其中一点最先到达线段的端点时，两点即刻同时停止运动；设运动时间为t秒是否存在点P，使以点B、P、Q为顶点的三角形与△ABC相似？若存在，请求出点P的坐标；若不存在，请说明理由．6(2022·陕西汉中·九年级期末)如图，CD是等腰直角△ABC斜边AB的中线，以点D为顶点的∠EDF绕点D旋转，角的两边分别与AC、BC的延长线相交，交点分别为点E、F，DF与AE交于点M，DE与BC 交于点N，且∠EDF=45°．(1)如图1，若CE=CF，求证：DE=DF；(2)如图2，若CE≠CF，求证：CD2 =CE⋅CF；(3)如图2，过D作DG⊥BC于点G，若CD=2，CF=2，求DN的长．7(2023·浙江·九年级期末)(1)如图1，在△ABC中，D为AB上一点，AC2=AD⋅AB．求证：∠ACD=∠B．(2)如图2，在▱ABCD中，E是AB上一点，连接AC，EC．已知AE=4，AC=6，CD=9．求证：2AD =3EC．(3)如图3，四边形ABCD内接于O，AC、BD相交于点E．已知O的半径为2，AE=CE，AB=2AE，BD=23，求四边形ABCD的面积．8(2022春·广东深圳·九年级校考期中)【基础巩固】(1)如图1，在四边形ABCD中，对角线BD平分∠ABC，∠ADB=∠DCB，求证：BD2=BA⋅BC；【尝试应用】(2)如图2，四边形ABCD为平行四边形，F在AD边上，AB=AF，点E在BA延长线上，连结EF，BF，CF，若∠EFB=∠DFC，BE=4，BF=5，求AD的长；【拓展提高】(3)如图3，在△ABC 中，D 是BC 上一点，连结AD ，点E ，F 分别在AD ，AC 上，连结BE ，CE ，EF ，若DE =DC ，∠BEC =∠AEF ，BE =16，EF =7，CE BC =34，求AF FC的值．课后专项训练1(2023成都市九年级期中)如图，矩形ABCD 中，F 是DC 上一点，BF ⊥AC ，垂足为E ，AD AB =12，△CEF 的面积为S 1，△AEB 的面积为S 2，则S 1S 2的值等于()A.116B.15C.14D.1252(2022·浙江衢州·统考中考真题)如图，在△ABC 中，AB =AC ,∠B =36°．分别以点A ，C 为圆心，大于12AC 的长为半径画弧，两弧相交于点D ，E ，作直线DE 分别交AC ，BC 于点F ，G ．以G 为圆心，GC 长为半径画弧，交BC 于点H ，连结AG ,AH ．则下列说法错误的是()A.AG =CGB.∠B =2∠HABC.△CAH ≅△BAGD.BG 2=CG ⋅CB3(2023·湖北恩施·校考模拟预测)如图，在Rt △ABC 中，∠ACB =90°，CD ⊥AB 于D 点，下列关系中不正确的是()A.BC 2=BD ⋅ABB.CD 2=AD ⋅BDC.AC 2=CD ⋅ABD.AC 2-BC 2=AD 2-BD 24(2023·山东济南·统考中考真题)如图，在△ABC中，AB=AC，∠BAC=36°，以点C为圆心，以BC为半径作弧交AC于点D，再分别以B，D为圆心，以大于12BD的长为半径作弧，两弧相交于点P，作射线CP交AB于点E，连接DE．以下结论不正确的是()A.∠BCE=36°B.BC=AEC.BEAC =5-12D.S△AECS△BEC=5+125(2023·云南临沧·统考三模)如图，在△ABC中，D是AB上的点，∠B=∠ACD，AC=1，AB=2，则△ACD与△BCD的面积比为()A.1:2B.1:2C.1:3D.1:46(2023·山东东营·统考中考真题)如图，在△ABC中，以点C为圆心，任意长为半径作弧，分别交AC，BC于点D，E；分别以点D，E为圆心，大于12DE的长为半径作弧，两弧交于点F；作射线CF交AB于点G，若AC=9，BC=6，△BCG的面积为8，则△ACG的面积为．7(2020·山西·统考中考真题)如图，在RtΔABC中，∠ACB=90°，AC=3，BC=4，CD⊥AB，垂足为D，E为BC的中点，AE与CD交于点F，则DF的长为．8(2022·河北邢台·校考二模)如图1，在△ABC中，AB=AC，BC=24，tan C=512，点P为BC边上一点，则点P与点A的最短距离为．如图2，连接AP，作∠APQ，使得∠APQ=∠B，PQ交AC于Q，则当BP=11时，AQ的长为．9(2023·内蒙古·统考中考真题)如图，AC,AD,CE是正五边形ABCDE的对角线，AD与CE相交于点F．下列结论：①CF平分∠ACD； ②AF=2DF； ③四边形ABCF是菱形； ④AB2=AD⋅EF 其中正确的结论是．(填写所有正确结论的序号)10(2020·广东广州·统考中考真题)如图，正方形ABCD中，ΔABC绕点A逆时针旋转到ΔAB C ，AB ，AC 分别交对角线BD于点E,F，若AE=4，则EF⋅ED的值为．11(2021·四川南充·中考真题)如图，在△ABC中，D为BC上一点，BC=3AB=3BD，则AD:AC的值为．12(2022·四川宜宾·九年级期末)如图，在△ABC中，点D在BC边上，点E在AC边上，且AD=AB，∠DEC=∠B．(1)求证：△AED∽△ADC；(2)若AE=1，EC=3，求AB的长．13(2022·江苏盐城·中考真题)如图，在△ABC与△A B C 中，点D、D 分别在边BC、B C 上，且△ACD∽△A C D ，若，则△ABD∽△A B D ．请从①BDCD =B DC D；②ABCD=A BC D；③∠BAD=∠B A D 这三个选项中选择一个作为条件(写序号)，并加以证明．14(2023·湖南·统考中考真题)在Rt△ABC中，∠BAC=90°，AD是斜边BC上的高．(1)证明：△ABD∽△CBA；(2)若AB=6，BC=10，求BD的长．15(2023·宁夏·统考中考真题)综合与实践问题背景：数学小组发现国旗上五角星的五个角都是顶角为36°的等腰三角形，对此三角形产生了极大兴趣并展开探究．探究发现：如图1，在△ABC 中，∠A =36°，AB =AC ．(1)操作发现：将△ABC 折叠，使边BC 落在边BA 上，点C 的对应点是点E ，折痕交AC 于点D ，连接DE ，DB ，则∠BDE =°，设AC =1，BC =x ，那么AE =(用含x 的式子表示)；(2)进一步探究发现：底BC 腰AC =5-12，这个比值被称为黄金比．在(1)的条件下试证明：底BC 腰AC=5-12；拓展应用：当等腰三角形的底与腰的比等于黄金比时，这个三角形叫黄金三角形．例如，图1中的△ABC 是黄金三角形．如图2，在菱形ABCD 中，∠BAD =72°，AB =1．求这个菱形较长对角线的长．16(2023·广东·九年级专题练习)定义：如图，若点P 在三角形的一条边上，且满足∠1=∠2，则称点P 为这个三角形的“理想点”．(1)如图①，若点D 是△ABC 的边AB 的中点，AC =22，AB =4，试判断点D 是不是△ABC 的“理想点”，并说明理由；(2)如图②，在Rt △ABC 中，∠C =90°，AB =5，AC =4，若点D 是△ABC 的“理想点”，求CD 的长．17(2022·江西·统考中考真题)如图，四边形ABCD 为菱形，点E 在AC 的延长线上，∠ACD =∠ABE ．(1)求证：△ABC∽△AEB；(2)当AB=6,AC=4时，求AE的长．18(2022·湖北武汉·校考模拟预测)已知，点D在△ABC的边BC上，连接AD．(1)如图1，若∠BAD =∠C．求证：BA2=BD⋅BC；(2)如图2，若AD⊥BC，BD=5，CD=3，tan∠BAC=43．求线段AD的长；(3)如图3，M、N分别是AC、AB上的两点，连接MN交AD于点P，当AB=AC，BD:BA:BC=2:5:6时，若∠APN=∠C，直接写出MPMN的值．19(2022·湖南长沙·校考三模)约定：若三角形一边上的中线将三角形分得的两个小三角形中有一个三角形与原三角形相似，我们则称原三角形为关于该边的“华益美三角”．例如，如图1，在△ABC中，AD为边BC上的中线，△ABD与△ABC相似，那么称△ABC为关于边BC的“华益美三角”．(1)如图2，在△ABC中，BC=2AB，求证：△ABC为关于边BC的“华益美三角”；(2)如图3，已知△ABC为关于边BC的“华益美三角”，点D是△ABC边BC的中点，以BD为直径的⊙O 恰好经过点A．①求证：直线CA与⊙O相切；②若⊙O的直径为26，求线段AB的长；(3)已知△ABC为关于边BC的“华益美三角”，BC=4，∠B=30°，求△ABC的面积．20(2022·浙江台州·统考一模)已知在▱ABCD，AB=23，BC=10，∠B=60°，E是边BC上的动点，以AE为一边作▱AEFG，且使得直线FG经过点D．(1)如图1，EF与AD相交于H，若H是EF的中点．①求证：GF=DF；②若GF⊥CD，求GD的长；(2)如图2，设AE=x，AG=y，当点E在边BC上移动时，始终保持∠AEF=45°，①求y关于x的函数关系式，并求函数y的取值范围；②连接ED，当△AED是直角三角形时，求DF的值．21(2023·山西临汾·统考二模)阅读与思考请阅读下列材料，并完成相应的任务．规定：在一个三角形中，若一个内角是另一个内角度数的n倍，则称三角形为“n倍角三角形”．当n=1时，称为“1倍角三角形”，显然等腰三角形是“1倍角三角形”；当n=2时，称为“2倍角三角形”，小康通过探索后发现：“2倍角三角形”的三边有如下关系．如图，在△ABC中，∠BAC，∠B，∠C所对的边分别为a，b，c，若∠BAC=2∠B，则a2-b2=bc．下面是小康对“2倍角三角形”的结论的两种探索证明过程：证法1：如图1，作∠BAC的平分线AD，∴∠BAD=∠CAD=12∠BAC．∵∠BAC=2∠B，∴∠BAD=∠CAD=∠B∵∠ACD=∠BCA，∴△ACD∼△BCA∴ACBC =DCAC=ADAB设DC=x，则AD=BD=a-x．∵AC=b，BC=a，AB=c∴ba =xb=a-xc∴b2=ax，a2-ax=bc∴a2-b2=bc证法2：如图2，延长CA到点D，使得AD=AB=c，连接BD，⋯⋯任务：(1)上述材料中的证法1是通过作辅助线，构造出三角形来加以证明的(填“全等”或“相似”)．(2)请补全证法2剩余的部分．22(2022·安徽·校联考三模)在△ABC中，∠ABC=2∠ACB，BD平分∠ABC．(1)如图1，若AB=3，AC=5，求AD的长．(2)如图2，过A分别作AE⊥AC交BC于E，AF⊥BD于F．①求证：∠ABC=∠EAF；②求BFAC的值．23(2023春·山东淄博·八年级统考期末)如图，已知△ABP，点C，D在边AB上，连接PC，PD，使∠ADP=60°，且△ACP∽△PDB．(1)请判定△PCD的形状，并说明理由；(2)若AC=2，BD=3，求△ABP的面积．24(2023·湖南娄底·统考中考真题)鲜艳的中华人民共和国国旗始终是当代中华儿女永不褪色的信仰，国旗上的每颗星都是标准五角星．为了增强学生的国家荣誉感、民族自豪感等．数学老师组织学生对五角星进行了较深入的研究．延长正五边形的各边直到不相邻的边相交，得到一个标准五角星．如图，正五边形ABCDE的边BA、DE的延长线相交于点F，∠EAF的平分线交EF于点M．(1)求证：AE2=EF⋅EM．(2)若AF=1，求AE的长．(3)求S正五边形ABCDES△AEF的值．25(2022·江苏苏州·统考中考真题)(1)如图1，在△ABC中，∠ACB=2∠B，CD平分∠ACB，交AB于点D，DE⎳AC，交BC于点E．①若DE=1，BD=32，求BC的长；②试探究ABAD-BEDE是否为定值．如果是，请求出这个定值；如果不是，请说明理由．(2)如图2，∠CBG和∠BCF是△ABC的2个外角，∠BCF=2∠CBG，CD平分∠BCF，交AB的延长线于点D，DE⎳AC，交CB的延长线于点E．记△ACD的面积为S1，△CDE的面积为S2，△BDE的面积为S3．若S1⋅S3=916S22，求cos∠CBD的值．相似三角形重要模型之母子型(共边共角模型)相似三角形是初中几何中的重要的内容，常常与其它知识点结合以综合题的形式呈现，其变化很多，是中考的常考题型。

中考数学三角形相似专题测试题及答案

《三角形相似》学号：____姓名：_______________三角形的相似是解决数学中图形问题的重要的工具，也是初中数学的重点内容，因此也是中考的重要考查内容。

主要考查以下几方面的内容：1．会运用三角形相似的性质与判定进行有关的计算和推理。

2．能运用三角形相似的知识解决相关的实际问题。

3．能探索解决一些与三角形相似有关的综合性题型。

一、基础训练 1、（07宁德）若23a b =，则a b b+=． 2、若如图所示的两个四边形相似，则α∠的度数是（）A ．87B ．60C ．75D ．1203、如果两个相似三角形的相似比为2：3,那么这两个相似三角形周长比为________；对应角平分线的比为_______，对应高的比为__________，对应中线的比为__________，面积比为。

4、（08海珠）若梯形的上底为3cm ，下底为5㎝，则此梯形的中位线长为㎝.5、（08越秀）如图，D 是ABC ∆的重心，则下列结论正确的是（） A ．DE AD =2 B ．DE AD 2= C ．DE AD 23= D ．DE AD 3=6、如图，已知DE ∥BC ，EC=6cm ，DE=5cm ，AE=3cm ，AB=14cm ，求AD 、BC 的长．•二、例题分析：例1、如图5所示为农村一古老的捣碎器，已知支撑柱AB 的高为0.3米，踏板DE 长为1.6米，支撑点A 到踏脚D 的距离为0.6米，现在从捣头点E 着地的位置开始，让踏脚(2007南京)如图,在梯形ABCD 中，AD BC ∥，6AB DC AD ===，60ABC ∠=，点E F ，分别在线段AD DC ，上（点E 与点A D ，不重合），且120BEF ∠=，设AE x =，DF y =．⑴ 求y 与x 的函数表达式；⑵ 当x 为何值时，y 有最大值，最大值是多少？着地，则捣头点E 上升了米．6075α60138第2题图ABCD E·（第5题图）Ｃ图3ABDO第2题例2、三、巩固练习：（Ａ组）1．如图1，若DE ∥BC ，且AD=2cm ，AB=4cm ，AC=3cm ，则AE=_______．2、如图，在梯形ABCD 中，AD ∥BC ，AC 、BD 交于O 点，S △AOD :S △COB ＝1:9，则OD:OB ＝。

中考数学专题训练：相似三角形(附参考答案)

中考数学专题训练：相似三角形（附参考答案）1.若a3＝b2，则a+bb的值为( )A．32B．53C．52D．232.如图，在△ABC中，DE∥BC，AD＝2，BD＝3，AC＝10，则AE的长为( )A．3 B．4C．5 D．63.如图，AD∥BE∥FC，直线l1，l2分别与三条平行线交于点A，B，C和点D，E，F.若AB＝3，BC＝5，DF＝12，则EF的长为( )A．4.5 B．6C．7.5 D．84.如图，小雅同学在利用标杆BE测量建筑物的高度时，测得标杆BE高1.2 m，又知AB∶BC＝1∶8，则建筑物CD的高是( )A．9.6 m B．10.8 mC．12 m D．14 m5.如图，在平面直角坐标系中，△ABC的三个顶点分别为A(1，2)，B(2，1)，C(3，2).现以原点O为位似中心，在第一象限内作与△ABC的相似比为2的位似图形△A′B′C′，则顶点C′的坐标是( )A．(2，4) B．(4，2)C．(6，4) D．(5，4)6.如图(单位：mm)，小明探究课本“综合与实践”板块“制作视力表”的相关内容：当测试距离为5 m时，标准视力表中最大的“E”字高度为72.7 mm，当测试距离为3 m时，最大的“E”字高度为( )A．121.17 mm B．43.62 mmC．29.08 mm D．4.36 mm7.如图，AC是□ABCD的对角线，点E在CD的延长线上，连接BE分别交AC，AD 于点F，G，则下列式子一定正确的是( )A．AFCF ＝AGDGB．ABCE＝CFAFC．BFFG ＝EFBFD．ADDG＝ABDE8.如图，在△ABC中，D，E分别为边AB，AC上的点，试添加一个条件：________________________，使得△ADE与△ABC相似．(任意写出一个满足的条件即可)9.如图，已知在梯形ABCD中，AD∥BC，S△ABDS△BCD ＝12，则S△BOCS△BCD＝______．10.如图，在矩形ABCD中，若AB＝3，AC＝5，AFFC ＝14，则AE的长为_____.11.如图，为了测量山坡的护坡石坝高，把一根长为4.5 m 的竹竿AC斜靠在石坝旁，量出竿上AD长为1 m时，它离地面的高度DE为0.6 m，则坝高CF为________m.12.已知在平面直12角坐标系中，△AOB的顶点分别为A(2，1)，B(2，0)，O(0，0)．若以原点O为位似中心，相似比为2，将△AOB放大，则点A的对应点的坐标为__________________________．13.如图，在△ABC中，点D，E分别是AB，AC的中点．若S△ADE＝2，则S△ABC＝_____．14.如图，在平面直角坐标系中，△ABC与△ODE是位似图形，则它们位似中心的坐标是____________.15.如图，在△ABC和△DEC中，∠A＝∠D，∠BCE＝∠ACD.(1)求证：△ABC∽△DEC；(2)若S△ABC∶S△DEC＝4∶9，BC＝6，求EC的长．16.如图，在△ABC中，AB＝4，BC＝5，点D，E分别在BC，AC上，CD＝2BD，CE ＝2AE，BE交AD于点F，则△AFE面积的最大值是______．17.小孔成像的示意图如图所示，光线经过小孔O，物体AB在幕布前形成倒立的实像CD(点A，B的对应点分别是C，D)．若物体AB的高为6 cm，小孔O到物体和实像的水平距离BE，CE分别为8 cm，6 cm，则实像CD的高度为________cm.18.如图，在正方形ABCD中，点E是边CD上一点，连接BE，以BE为对角线作正方形BGEF，边EF与正方形ABCD的对角线BD相交于点H，连接AF，有以下五个结论：①∠ABF＝∠DBE；②△ABF∽△DBE；③AF⊥BD；④2BG2＝BH·BD；⑤若CE∶DE＝1∶3，则BH∶DH＝17∶16.你认为其中正确的是____________．(填写序号)19.已知，如图1，若AD是△ABC中∠BAC的内角平分线，通过证明可得ABAC ＝BDCD，同理，若AE是△ABC中∠BAC的外角平分线，通过探究也有类似的性质．请你根据上述信息，求解如下问题：如图2，在△ABC中，BD＝2，CD＝3，AD是△ABC的内角平分线，则△ABC的BC边上的中线长l的取值范围是_____________．20.如图，在等腰三角形ABC中，AB＝AC，点E，F在线段BC上，点Q在线段AB 上，且CF＝BE，AE2＝AQ·AB.求证：(1)∠CAE＝∠BAF；(2)CF·FQ＝AF·BQ.21.在等腰三角形ABC中，AB＝AC，点D是边BC上一点(不与点B，C重合)，连接AD.(1)如图1，若∠C＝60°，点D关于直线AB的对称点为点E，连接AE，DE，则∠BDE＝________．(2)若∠C＝60°，将线段AD绕点A顺时针旋转60°得到线段AE，连接BE.①在图2中补全图形；②探究CD与BE的数量关系，并证明．(3)如图3，若ABBC ＝ADDE＝k，且∠ADE＝∠C，试探究BE，BD，AC之间满足的数量关系，并证明．参考答案1．C 2．B 3．C 4．B 5．C 6．B 7．C8．ADAB ＝AEAC(答案不唯一) 9．2310．1 11．2.712．(4，2)或(－4，－2)13．8 14．(4，2) 15．(1)证明略(2)EC＝916．43 17．4.5 18．①②③④ 19．12<l<25220．(1)证明略(2)证明略21．(1)30°(2)①图略②CD与BE的数量关系为CD＝BE，证明略(3)AC＝k(BD＋BE)，证明略。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

苏科版中考数学专题17 相似三角形及应用含答案
20分钟
1.【江苏省南通市海安县2015届九年级上学期期末考试数学试题】下列条件不能判定△ABC与△DEF相似的是（）
A．AB BC AC
DE EF DF
==B．
AB BC
DE EF
=,A D
∠=∠
C．∠A=∠D，∠B=∠E D．AB BC
DE EF
=，∠B=∠E
【考点定位】相似三角形的判定．
2. 【江苏省徐州市市区、铜山县2015届九年级中考模拟数学试题】直线l1∥l2∥l3，且l1与l2的距离为1，l2与l3的距离为3，把一块含有45°角的直角三角形如图放置，顶点A，B，C恰好分别落在三条直线上，AC 与直线l2交于点D，则线段BD的长度为（）
A．25
4
B．
25
3
C．
20
3
D．
15
4
【答案】A．
【解析】分别过点A 、B 、D 作AF ⊥l 3，BE ⊥l 3，DG ⊥l 3，先根据全等三角形的判定定理得出△BCE ≌△ACF ，故可得出CF 及CE 的长，在Rt △ACF 中根据勾股定理求出AC 的长，再由相似三角形的判定得出△CDG ∽△CAF ，故可得出CD 的长，在Rt △BCD 中根据勾股定理即可求出BD 的长．分别过点A 、B 、D 作AF ⊥l 3，BE ⊥l 3，DG ⊥l 3，
∵△ABC 是等腰直角三角形，∴AC=BC ，
∵∠EBC+∠BCE=90°，∠BCE+∠ACF=90°，∠ACF+∠CAF=90°，∴∠EBC=∠ACF ，∠BCE=∠CAF ，
在△BCE 与△ACF 中，
EBC ACF BC AC
BCE CAF ∠=∠⎧⎪=⎨⎪∠=∠⎩
，
【考点定位】1.相似三角形的判定与性质；2.平行线之间的距离；3.全等三角形的判定与性质；4.等腰直角三角形．
3.【江苏省淮安市2015年中考数学试题】如图，l 1∥l 2∥l 3，直线a ，b 与l 1、l 2、l 3分别相交于A 、B 、C 和点D 、E 、F ．若3
2=BC AB ，DE =4，则EF 的长是（）
A ．38
B ．3
20 C ．6 D ．10 【答案】C ．
【考点定位】平行线分线段成比例．
4.【江苏省南京市2015年中考数学试题】如图所示，△ABC 中，DE ∥BC ，若
12
AD DB =，则下列结论中正确的是（） A ．12AE EC = B ．12DE BC = C ．1=3
ADE ABC △的周长△的周长 D ．1=3ADE ABC △的面积△的面积【答案】C ．
【考点定位】相似三角形的判定与性质．
5.【江苏省南通市海安县2015届九年级上学期期末考试数学试题】若△ABC ∽△A ′B ′C ′，相似比为1：3，则△ABC 与△A ′B ′C ′的面积之比为．
【答案】1：9．
【解析】∵△ABC ∽△A ′B ′C ′，相似比为1：3，∴△A BC 与△A ′B ′C ′的面积之比为1：9．故答案为：1：9．
【考点定位】相似三角形的性质．
6.【江苏省扬州市2015年中考数学试题】如图，练习本中的横格线都平行，且相邻两条横格线间的距离都
相等，同一条直线上的三个点A、B、C都在横格线上，若线段AB=4 cm，则线段BC= c m
【答案】12
【考点定位】平行线分线段成比例
7.【江苏省常州市2015年中考数学试题】如图，在△ABC中，DE∥BC，AD：DB=1：2，DE=2，则BC的长是．
【答案】6．
【考点定位】相似三角形的判定与性质．
8.【江苏省无锡市2015年中考数学试题】已知：如图，AD 、BE 分别是△ABC 的中线和角平分线，AD ⊥BE ，AD ＝BE ＝6，则AC 的长等于．
【答案】
952
故答案为：95
2
【考点定位】全等三角形的判定及性质；相似三角形的判定及性质；勾股定理.
9.【江苏省苏州市吴中、相城、吴江区2015届九年级中考一模数学试题】如图，在平面直角坐标系中，已知点A （0，6），B （8，0）．点P 从A 点出发，以每秒1个单位的速度沿AO 运动；同时，点Q 从O 出发，B
A
C D E
以每秒2个单位的速度沿OB运动，当Q点到达B点时，P、Q两点同时停止运动．（1）求运动时间t的取值范围；
（2）t为何值时，△POQ的面积最大？最大值是多少？
（3）t为何值时，以点P、0、Q为顶点的三角形与Rt△AOB相似？
【答案】(1) 0≤t≤4；(2) 当t=3时，△POQ的面积最大，最大值是9．(3) 当t为12
5
或
18
11
时，以点P、0、
Q为顶点的三角形与Rt△AOB相似．
【解析】
试题分析：（1）由点Q从O出发，以每秒2个单位的速度沿OB运动，当Q点到达B点时，P、Q两点同时停止运动，可得：2t=8，解得：t=4，进而可得：0≤t≤4；
（2）先根据三角形的面积公式，用含有t的式子表示△POQ的面积=-t2+6t，然后根据二次函数的最值公式解答即可；
试题解析：（1）∵点A（0，6），B（8，0），∴OA=6，OB=8，
∵点Q从O出发，以每秒2个单位的速度沿OB运动，当Q点到达B点时，P、Q两点同时停止运动，∴2t=8，解得：t=4，
∴0≤t≤4；
（2）根据题意得：经过t秒后，AP=t，OQ=2t，∴OP=OA-AP=6-t，
∵△POQ 的面积=12•OP •OQ ，即△POQ 的面积=12
×（6-t ）×2t=-t 2+6t ． ∵a=-1＜0，∴△POQ 的面积有最大值，
当t=-2b a
=3时，△POQ 的面积的最大值=244ac b a -=9，即当t=3时，△POQ 的面积最大，最大值是9．
（3）①若Rt △POQ ∽Rt △AOB 时，
∵Rt △POQ ∽R t △AOB ，∴ PO OQ AO OB =，即6268t t -=，解得：t=125
②若Rt △QOP ∽Rt △AOB 时，
∵Rt △QOP ∽Rt △AOB ，∴
PO OQ OB AO =，即6286t t -=，解得：t=1811．所以当t 为125或1811
时，以点P 、0、Q 为顶点的三角形与Rt △AOB 相似．【考点定位】相似三角形与一次函数综合题．
10.【江苏省南京市2015年中考数学试题】如图，△ABC 中，CD 是边AB 上的高，且AD CD CD BD
=．
（1）求证：△ACD ∽△CBD ；
（2）求∠ACB 的大小．
【答案】（1）证明见试题解析；（2）90°．
【解析】
【考点定位】相似三角形的判定与性质．。