第三章矿井风流流动的能量方程及其应用
矿井通风课件: 能量方程在矿井通风中的应用

3
d0 ed
d1 d2
流程 4
二、通风系统能量(压力)坡度线
2、坡度线的分析
(1)能量(压力)坡度线( a-b-c-d )清楚地反映了风 流在流动过程中,沿程各断面上全能量与通风阻力hR之间 的关系。全能量沿程逐渐下降,从入风口至某断面的通风 阻力就等于该断面上全能量的下降值(如b0b),任意两 断面间的通风阻力等于这两个断面全能量下降值的差。
0
1
压力Pa
全压线 p0 静压线
2 3 45 6 7 8 9
h全
h阻12
h阻78
扩散器 10
流程
一、水平风道的通风能量(压力)坡度线
风流的边界条件
入口断面处: 风流入口断面处的绝对全压等于大气压(可用能量方程加以证明,
对入口断面的内外侧列能量方程并忽略极小的入口流动损失) 出口断面处 :
风流出口断面处的绝对静压等于大气压(可用能量方程加以证明, 对出口断面的内外侧列能量方程并忽略极小的出口流动损失)
二、通风系统能量(压力)坡度线
1、坡度线的绘制
以下图所示简化通风系统为例,说明矿井通风系统中有高度变 化的风流路线上能量(压力)坡度线的画法。
1
4
2
3
二、通风系统能量(压力)坡度线
作图步骤:
(1)确定基准面。一般地,以最低水
平(如2-3)为基准面。
压 能
(2)测算出各断面的总压能(包括静压、
动压和相对基准面的位能)。
-6-4线路上各对应点风流的全能量。所以工作面Ⅰ通过其采空区向工作面
Ⅱ漏风,如果工作面Ⅰ或其采空区发生火灾时其有害气体将会流向工作面Ⅱ,
影响工作面Ⅱ的安全生产。
Ⅰ Ⅰ
43
采矿风流的能量与能量方程

采矿风流的能量与能量方程引言在采矿行业中,能源是至关重要的资源。
采矿工程通常需要大量的能量来驱动设备、实现提炼过程以及满足运输需求。
因此,了解矿山中的能量来源和能量转化过程对于优化能源利用、提高效率至关重要。
本文将讨论采矿风流的能量以及能量方程的应用。
采矿风流的能量类型采矿风流中存在着多种能量类型,包括动能、势能和热能。
这些能量类型相互转化,驱动着采矿过程中的各种机械设备。
动能动能是指物体由于其运动而具有的能量。
在采矿风流中,动能主要来自于风流的流动速度。
风流通过管道或通道时,其动能可以用以下公式表示:$$ E_k = \\frac{1}{2}mv^2 $$其中,E k表示动能,m表示风流中空气的质量,v表示风流的流速。
势能势能是指物体由于其位置而具有的能量。
在采矿风流中,势能的存在主要来自于风流的位置高度。
势能可以用以下公式表示:E p=mgℎ其中,E p表示势能,m表示风流中空气的质量,g表示重力加速度,ℎ表示风流的垂直高度。
热能热能是指物体由于其温度而具有的能量。
在采矿风流中,热能主要来自于风流的温度。
热能可以用以下公式表示:$$ E_t = mc\\Delta T $$其中,E t表示热能,m表示风流中空气的质量,c表示空气的比热容,$\\Delta T$表示风流的温度变化。
能量转化与能量方程在采矿过程中,能量的转化是一个复杂的过程。
各种能量类型之间可以相互转化,通过不同的设备和机械实现能量的利用。
能量转化过程可以通过能量方程来描述。
能量方程表示能量的守恒原理,即能量在系统内的转化和储存总量不变。
在采矿风流中,能量方程可以写作:$$ E_{\\text{in}} - E_{\\text{out}} = \\Delta E_{\\text{sys}} $$其中,$E_{\\text{in}}$表示能量输入,$E_{\\text{out}}$表示能量输出,$\\Delta E_{\\text{sys}}$表示系统内能量的变化。
动压与静压

第二章 风流的能量与能量方程井下风流的流动遵循能量守恒及转换定律。
本章结合矿井风流流动的特点,介绍了空气的主要物理参数,风流的能量与压力, 压力测量方法及压力之间的关系,重点阐述了矿井通风中的能量方程及其应用。
第一节 空气的主要物理参数与矿井通风密切相关的物理参数除了反映气候条件的温度、湿度以外,还有密度、比容、压力、粘性等。
一、空气的密度单位体积空气所具有的质量称为空气的密度,用ρ来表示。
即:V M =ρ (2-1) 式中 ρ——空气的密度,kg/m3;M ——空气的质量,m ;V ——空气的体积,m3。
一般来说,空气的密度是随温度、湿度和压力的变化而变化的。
在标准大气状况下(P =101325Pa ,t =O ℃,ϕ=O%),干空气的密度为1.293 kg/m3。
湿空气密度的计算公式为:ρ湿=0.003484T P (1-0.378P P 饱ϕ) (2-2) 式中 P ——空气的压力,Pa ;T ——热力学温度(T =273+t ),K ;t ——空气的温度,℃;ϕ——相对湿度,%;P 饱——温度为t (℃)时的饱和水蒸气压力(见表1-9),pa 。
由上式可见,压力越大,温度越低,空气密度越大。
当压力和温度一定时,湿空气的密度总是小于干空气的密度。
在矿井通风中,由于通风系统内的空气温度、湿度、压力各有不同,空气的密度也有所变化,但变化范围有限。
在研究空气流动规律时,要根据具体情况考虑是否忽略这种变化。
一般将空气压力为101325Pa ,温度为20℃,相对湿度为60%的矿井空气称为标准矿井空气,其密度为1.2kg/m3。
二、空气的比容单位质量空气所占有的体积叫空气的比容,用υ(m3/kg )表示,比容和密度互为倒数,它们是一个状态参数的两种表达方式。
即:ρυ1==M V (2-3)三、空气的压力(压强)矿井通风中,习惯将压强称为空气的压力。
由于空气分子的热运动,分子之间不断碰撞,同时气体分子也不断地和容器壁碰撞,形成了气体对容器壁的压力。
3运动能量方程解读

(p1 p2) m1 gz1 m2 gz2 h12
上式表明,在断面相同的垂直或 倾斜巷道中,两断面间的静压差与
2
2
位压差之和,等于井巷的通风阻力。
1 精密气压计得P1,P2 , 丈 量Z1,Z2 ,计算ρm ; 2 用比托管和压差计,直接测 出 ∆p ,即为h12。
4.3.1 有扇风机工作时的能量方程式 4.3.2 通风动力与阻力之间的关系
2019/2/23
11
4.3.1
1
有扇风机工作时的能量方程式(1)
Energy Equation with Fan 1’ 2’ 2
1
1’
2’
2
在所研究的1-2断面间有扇风机工作,则断面1的全能 量加上扇风机的全压,应等于断面2的全能量加1,2断面 间的通风阻力,则单位体积流体的能量方程式为:
(p1 p 2) (
1v1 2 2 v2 2
2
) m1 gz1 m2 gz2 h12
上式的物理意义为1,2两断面之间的压能、动能、位能之差的总和, 等于风流由断面1到断面2克服井巷阻力所损失的能量。
2019/2/23 4
风流的能量关系
Energy Relationship of Airflow 1
H f =(p 2 -p )+(
,
, 1
2 v22
2
—
1 v 1 2
2
)
上式表明,扇风机的全压等于扇风机出风口与入风口之间 静压差与动压差之和。
2019/2/23 13
4.3.2
通风动力与阻力之间的关系
the Relationship between Ventilation Power and Resistance
矿井风流流动的能量方程及其应用

二、抽出式通风矿井的能量互换关系 A、B两点的能量互换关系为:
三、主要扇风机安设在井下的能量互换关系 从地表到扇风机入口A的通风阻力为h1,其能量互换关系为:
式中: 同理,从扇风机出口B到地表的通风阻力为h2,其能量互换关系为: 式中
整个矿井的通风阻力为上述两段阻力之和,即h=h1+h2,即
实际上 以hc表示,则:
(2)风流流动必须是稳定流,即断面上的参数不随时间的变化而变 化;所研究的始、末断面要选在缓变流场上。
(3)风流总是从总能量(机械能)大的地方流向总能量小的地方。在 判断风流方向时,应用始末两断面上的总能量来进行,而不能只看 其中的某一项。如不知风流方向,列能量方程时,应先假设风流方 向,如果计算出的能量损失(通风阻力)为正,说明风流方向假设 正确;如果为负,则风流方向假设错误。
2)风流具有的内能 风流的内能是风流内部储存能的简称,它是风流内部所 具有的分子内动能与分子位能之和。
2.风流流动过程中能量分析 风流在如图所示的井巷中流动,设1、2断面的参数分别 为风流的绝对静压P1、P2(Pa);风流的平均流速为v1、 v2(m/s);风流的密度(kg/m3)距基准面的高程H(m)。 可得单位体积流体的能量方程:
二、关于能量方程使用的几点说明
从能量方程的推导过程可知,方程是在一定的条件下导出的, 并对它做了适当的简化。因此,在应用能量方程时应根据矿井的实 际条件,正确理解能量方程中各参数的物理意义,灵活应用。
(1)能量方程的意义是,表示单位体积空气由1断面流向2断面的过 程中所消耗的能量(通风阻力)等于流经1、2断面间空气总机械能 (压能、位能、动能)的变化量。
就是井下这台扇风机的全压,
得出的结论,仍然和主要扇风机安装在地表是一样的。
矿井通风阻力

3.3 摩擦风阻与阻力
一、摩擦阻力 摩擦阻力概念 摩擦阻力约占井巷通风总阻力的80-90%。 二、摩擦阻力的计算 L 2 计算公式(达西公式):
hf
得:
LP
8 S
hf
v
2
d 2
v
因矿内空气密度变化不大,令
LP 2 hf 3 Q S
8 同时 : v Q / S
例1:某梯形巷道断面S=6m2,平均 风速 v=1.2m/s,问该巷道的风流状态是层流还是紊流? 若要使风流为层流,平均风速应是多少? 解: Re=vd/ν d=4S/P=4S/4.16*S1/2=2.35 (m) 所以:Re=1.2*2.35/(15*10-6)=188000>2300 为紊流。 要为层流,则 v≤2320ν/d=2320*(15*10-6)/2.35 =0.01468(m/s)
Re
vd
ν—运动粘性系数,m2/s;受流体的温度和压力影 响,矿内风流ν=14.4× 10-6 m2/s进行计算。
等值直径是与风流流过的巷道净断面积相等的圆 的直径,用公式表示:
S d 4 P
→
4vS Re P
U是巷道的周边长,用近似计算: 梯形断面: P=4.16 S0.5 三心拱断面:P=4.10 S0.5 半圆拱断面:P=3.84 S0.5 规定:Re=2300为临界(层流与紊流)雷诺数
雷诺数Re的关系,如下图所示:
坐标:
纵坐标轴:lg(100λ);横坐标轴:lgRe 根据λ值随Re变化特征,图中曲线分为五个区:
•Ⅰ区——层流区:Re<2320(即lgRe<3.36) •在此区,不论管道粗糙度如何,其实验结果都集中分布 于直线Ⅰ上。 •这表明λ与相对糙度无关,只与Re有关,且λ=64/Re。与 相对粗糙度无关。
矿井空气流动基本理论

矿井空气流动基本理论第一节 空气的主要物理参数一、大气压力:它是指空气分子热运动对器壁碰撞的宏观表现。
P=2/3n(1/2mv 2)矿井常用压强单位:Pa 、mmHg 、mmH20、mmbar 、bar 、atm 等。
换算关系:1atm =760mmHg=1013.25mmbar=101325Pa 1mmbar=100Pa=10.2mmH20, 1mmHg=13.6mmH 2O=133.32Pa 1bar=100mmbar 二、相对湿度单位体积空气中实际含有的水蒸汽量(ρV )与其同温度下的饱和水蒸汽含量(ρS )之比称为空气的相对湿度 φ=ρV /ρS反映空气中所含水蒸汽量接近饱和的程度。
三、粘性流体抵抗剪切力的性质。
当流体层间发生相对运动时,在流体内部两个流体层的接触面上,便产生粘性阻力(内摩擦力)以阻止相对运动,流体具有的这一性质,称作流体的粘性。
其大小主要取决于温度。
正是由于流体具有粘性,因此,风流流动时才会产生阻力,产生能量损失。
四、密度单位体积空气所具有的质量称为空气的密度,kg/m 3式中:P 为大气压,单位:Pa ;Psat 为饱和水蒸汽压,单位:Pa ; φ为相对湿度;T为空气绝对温度,T=t+273,K 。
)1(003484.0378.0PP TP satφρ-=第二节风流的能量与压力一、风流的能量与压力:①巷道某断面风流的压力可分为:静压、动压、位压,三者可互相转化。
②相应的巷道某断面风流的能量可分为:静压能、动压能、位能,三者也可互相转化。
③单位体积风流具有的各种能量与风流在该断面上表现的压力大小具有相同的量,因此,在矿井通风中对应的能量与压力用同一符号表示;其区别在于压力有方向性,而能量没有方向性,是标量。
1.静压能-静压(1)产生的机理:由分子热运动产生的。
空气分子无时无刻不在作无序热运动。
(2)静压特点a.无论静止的空气还是流动的空气都具有静压力;b.风流中任一点的静压各向同值,且垂直于作用面;(3)根据静压的测算基准不同,可分为:绝对压力和相对压力。
4-1矿井风流运动的能量方程式及其应用PPT

4.1 矿井风流运动的能量方程式及其应用
(4)正确选择基准面。
(5)在始、末断面间有压源(扇风机)时,压源的作用方 向与风流的方向一致,压源为正,说明压源对风流做功; 如果两者方向相反,压源为负,则压源成为通风阻力。
(6)单位质量或单位体积流量的能量方程只适用1、2断面 间流量不变的条件,对于流动过程中有流量变化的情况, 应按总能量的守恒与转换定律列方程。
《矿井通风与空气调节》
中南大学 资源与安全工程学院
第4章 矿井风流流动的能量方程及其 应用
• 4.1 矿井风流运动的能量方程式及其应用 • 4.2 能量方程在分析通风动力与阻力关系
上的应用
4.1 矿井风流运动的能量方程式 及其应用
4.1.1 空气流动方程
4.1 矿井风流运动的能量方程式及其应用
如果用皮托管的静 压端和压差计直接 测定两断面间的压 差时,压差计上的 示度即为井巷的通 风阻力,无需再计 算两断面的位能差。
△P
压差计在井巷 中所摆的位置 不会影响测定
结果。
4.1 矿井风流运动的能量方程式及其应用
4. 断面变化的垂直或倾斜巷道 当垂直或倾斜巷道两端断面不相同时,欲测这 段巷道的通风阻力,必须全面测定两断面的静压 差、动压差和位能差,然后根据能量方程式的一 般形式,计算通风阻力。 如果用皮托管的静压端和压差计测定时,压差 计的读数等于两断面间的静压差与位能差之和, 此时,只要再加上动压差即可求得通风阻力
1v12 2v22 ——断面1、2处单位体积的动能,Pa;
2
2
m1gZ1 m2gZ2 ——断面1、2处单位体积风流的位能,Pa。
4.1 矿井风流运动的能量方程式及其应用
能量方程表明: 两断面之间的压能、动能与位能之差的总和等于风流由断
第三章矿井风流流动能量方程及其应用

• 根据压力(p)、温度(可T见)空和气比的容内(能v)是之空间气关系
u f (T, p)
状态参数的函数。
3.1 矿井风流运动的能量方程式及其 • 3.1.2单位质量流量能应量方用程
• 2.风流流动过程中能量分析
1断面上,1 kg空气
所具有的能量为:
2
3.1 矿井风流运动的能量方程式及其
• 实际多变过程中其值应是变用化的。在深井通风中,如
果其值变化较大时,可分成若干段(各段的值均不
相等),在每一段中的值可近似认为不变。当对式
• (3-16) pvn const 微分,则有:
• npvn1dv vndp 0 或 dp n dv 0
据能量守恒定律,空气从第一断面流向第二个断面时
p1
1v12
2
m1gZ1
p2
2v22
2
m2 gZ2
h12
实际矿井内空气流动
时,同一断面上各 点风速不是均匀一 致的,常以断面平 均风速来计算。风 • 流的图总地3-是方2风由 流流总 向的能 总能量能量大量关系 小的地方。
3.1 矿井风流运动的能量方程式及其
空气的内能并使空气膨胀做功
3.1 矿井风流运动的能量方程式及其
ቤተ መጻሕፍቲ ባይዱ
• 3.可压缩空气单位质应量用流量的能量方程
• 当风流在井巷中做一维稳定流动时
p1
1
v12 2
gZ1
u1
qR
q
p2
2
v22 2
gZ2
u2
第3章 矿内风流的能量方程

2013-1-2
1
2
第3章 矿内风流运动的能量方程
两种特例: (I) 若 S1=S2
1=
,
2,
则 则
ρ
1
V1 = ρ
2
V2
; 。
(II) 若ρ
ρ
V1 S1 = V2 S2
对于不可压缩流体,通过任一断面的体积流量相等,即 Q=viSi=const
2013-1-2
第3章 矿内风流运动的能量方程
二、 运动微分方程
2013-1-2
H f Hn h
v
2 4
第3章 矿内风流运动的能量方程
本章习题 3-9 3-10 3-13 3-15 3-17 3-19
2013-1-2
第3章 矿内风流运动的能量方程
3-1 矿井通风中的能量方程是什么?从能量 和压力观点讲,分别代表什么含义? 3-2 为什么说风流在有高差变化的井巷中流 动时,其静压和位压之间可以相互转化?
2013-1-2
第3章 矿内风流运动的能量方程
二、通风动力与阻力之间助关系
把全矿通风系统视为连续风流,可应用能量方程说 明不同情况下通风动力与阻力之间的关系。 1、压入式通风 如图所示,压入式扇风机工作时,任风内硐断面1处风流 的静压为p1,平均风速为v1,在出风井断面2处的静压等 于地表大气压力P,平均风速为V2。列1、2两断面间能量 方程式(下页)
一、有扇风机工作时的能量方程式
如图所示,在1、2两断面间如果有扇风机工作,则断面1全能量如 上扇风机的全压应等于断面2的全能量加上1、2两个断面间的通风阻 力。此时,单位体积流体的能量方程式可写成如下形式
2013-1-2
第3章 矿内风流运动的能量方程
矿井空气流动的基本理论能量方程在矿井通风中的应用

∴ 通风机全压是用以克服风道通风阻力和出口动能损失。
第四讲 能量方程在矿井通风中的应用
通风机静压 通风机用于克服风道阻力的那一部分能量叫通风机的静压Hs。 Hs = hR1~11
(4-8)
通风机全压与静压关系 Ht= Hs+hv11
(4-9)
通风机的全压等于通风机的静压和出口动能损失之和。
第二章 矿井空气流动的基本理论
第四讲 能量方程在矿井通风中的应用
第四讲 能量方程在矿井通风中的应用
一、能量(压力)坡度线的作法 通风能量(压力)坡度线是对能量方程的图形描述。从图形上比较 直观地反映了空气在流动过程中能量(压力)沿程的变化规律、通 风能量(压力)和通风阻力之间的相互关系以及相互转换。
即:入口至任意断面i的通风阻力(hR1~i)就等于该断面的相对 全压(hti)的绝对值。 压入段 求任意断面i至出口的通风阻力:
hRi~11 hti ht10 hti hv11 (h11 0) (4-3)
即:压入段任意断面i至出口的通风阻力(hRi~11)等于该断面
的相对全压(hti)减去出口断面的动压(hv11)。
(4-6)
第四讲 能量方程在矿井通风中的应用
通风机全压Ht与风道通风阻力、出口动能损失的关系 由能量方程和能量(压力)坡度线可以看出:
hR6~11 = Pt7-Pt11
hR1~6 = Pt1-Pt6
∴
∴
Pt7 = hR7~11+Pt11,
Pt6 = Pt1-hR1~6,
Ht = Pt7-Pt6 = hR7~11+Pt11-(Pt1-hR1~6) =hR7~11+P1+hv11-(P1-hR1~6)=hR7~11+hv11+hR1~6 Ht= hR1~11+hv11
3.风流能量方程及其在矿井通风中的应用
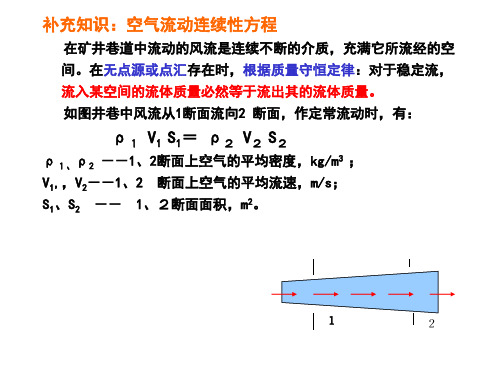
在矿井巷道中流动的风流是连续不断的介质,充满它所流经的空 间。在无点源或点汇存在时,根据质量守恒定律:对于稳定流, 流入某空间的流体质量必然等于流出其的流体质量。
如图井巷中风流从1断面流向2 断面,作定常流动时,有:
ρ1 V1 S1 = ρ2 V2 S2
ρ1、ρ2 --1、2断面上空气的平均密度,kg/m3 ;
上式表明,断面相同的水平巷道。两断面间的静压差即该 段巷道的通风阻力。
2
断面不同的水平巷道
1 2
1
因为 Z1=Z2
2
则ρm1=ρm2 , 由(3-8)式,得
(p1 p 2) (
1v1 2 2 v2 2
2
) h12
1 测出静压P1,P2 ,测出风速v1,v2 ,计算动压; 2 测出静压差和动压差(比托管,压差计).
2v22
2
上式说明,压入式通风时,扇风机的静压与动压之和与自 然风压共同作用,克服矿井阻力,并在出风井口造成动压损 失。
为了使通风阻力与扇风机的全压联系起来,再列出1-0断
面的能量方程,h10=0,P0=pa(大气压),V0=0。
2015/12/19 2015/12/19
32 32
压 入 式 通 风(3)
3.2能量方程
• 方程式(3-8)表明:风流在起末两断面间的压能差 、动能差和位能差之和,等于风流在起末断面间 为克服通风阻力而损失的能量。或者说,这项能 量损失就是风流在起末两断面上的总能量之差, 这项总能量之差叫做通风压力。风流沿井巷的流 动过程,实质就是通风压力与通风阻力之间相互 转化的过程。所以,通风压力和通风阻力同时产 生,互相依存,大小相等,方向相反。为了克服 通风阻力,必须满足相应的通风压力,风流从总 能量大的断面流向总能量小的断面。
第3章-通风阻力

➢ 风流流动时,必须具有一定的能量(通风压力),用以克服 井巷及空气分子之间的摩擦对风流所产生的阻力。通风 压力克服通风阻力,两者因次相同,数值相等,方向相 反。知道通风阻力的大小就能确定所需通风压力的大小。 在矿井通风中,存在着摩擦阻力和局部阻力,必须分析 研究它们的特性、测定方法以及降低措施等,从而作为 选择通风设备,进行通风管理与设计的依据。这在通风 设计中尤其重要。
第 4 节 通风阻力定律和特性
1、井巷风阻及其阻力特性
➢ 在矿井巷道中,任何井巷的通风阻力,不管它是摩擦阻力、 局部阻力或系两者同时具有的阻力,其阻力公式均可写成 通式:
h=RQ2
2、井巷等积孔
当研究井巷通风阻力时,为了在概念上更形象化,有时采 用井巷等积孔来代替井巷风阻。等积孔就是用一个与井巷 风阻值相当的理想孔的面积值来衡量井巷通风的难易程度。 设想将一个矿井的入风口到出风口,沿着井下主要巷道进 行均匀压缩,最后形成一个薄片,在这个薄片上将形成一 个孔口,这个孔口面积A使得薄片的两端作用有矿井的风 压差P时,通过孔口的风量正好为该矿井的风量Q,这时, 该孔口面积即为矿井的等积孔。
第 1 节 风流的流动状态
➢ 流体产生的阻力与流体流动过程中的状态有关。流体流动 时有两种状态;一种是流体呈层状流动,各层间流体互不 混合,流体质点流动的轨迹为直线或有规则的平滑曲线, 这一状态称为层流。在流速很小、管径很小、或粘性较大 的流体流动时会发生层流。
➢ 另一种是流体流动时,各部分流体强烈地互相混合,流体 质点的流动轨迹是极不规则的。除了有沿流体总方向的位 移外,还有垂直于液流总方向的位移,流体内部存在着时 而产生时而消灭的漩涡,这种状态称为紊流。研究层流与 紊流的主要意义在于两种流态有着不同的阻力定律。
《矿井通风与空气调节》习题解答_OK

1.2kg/m3,1、2两断
面处的绝对静压分
别为760 mmHg与
7(16mh31mm2HmgH=g1p313.322p2
v12
2
v22
2
gZ
Pa)。求=该10段13巷24道.72的-101724.69+1.2×22÷2
通风阻力。-1.2×1.672÷2+1.2×9.81×50=189.36(Pa)
2021/8/10
21
第p三1=章760矿×井13风3.3流22流动的能量方程及其应用
=101324.72(Pa)
p2=763×133.322
解=1:01724.69(Pa)
v1=Q/60/S1
=600/60/5
=2(m/s)
v2=Q/60/S2
==h6510/023/=610./6p761(m/sp) 2
(氡)及其子体(RaA~RaD),开采汞、砷的矿井
还有可能混入Hg和As的蒸气。
2021/8/10
4
第一章 矿井空气
⊙ (5)供人员呼吸及其他需要所消耗的氧气 量可折算成每人30 L/min,求每人所需新鲜空 气量为多少?
解:矿井新鲜空气含O2量不低于20%, 则所 需新鲜空气量为:
30 150 (L/min)
0.04%,则
0.04%x 5.52
0.5%
x=1200x(m3/min)
2021/8/10
6
第一章 矿井空气 ⊙ (9)说明井下氡的来源。 答: ①矿岩壁析出的氡; ②爆下矿石析出的氡; ③地下水析出的氡; ④地面空气中的氡随入风风流进入井下,这决定于
所处地区的自然本底浓度。一般来说,它在数量上 是极微小的,可忽略不计。 以上是矿井空气中氡的来源,在一些老矿山,由于 开采面积较大,崩落区多,采空区中积累的氡有时 也会成为氡的主要来源。
(二)风流的能量与能量方程

风 流 的 能 量 与 能 量 方 程
2、风流的能量与压力
矿井通风系统中,风流在井巷某断面上所具有的总机械能(包括 静压能、动能和位能)及内能之和叫做风流的能量。风流之所以能够 流动,其根本原因是系统中存在着能量差,所以风流的能量是风流流 动的动力。单位体积空气所具有的能够对外做功的机械能就是压力。 能量与压力即有区别又有联系,除了内能是以热的形式存在于风流中
功MgZ(J),物体因而获得了相同数量的位能,即:
E位 = mgZ
风 流 的 能 量 与 能 量 方 程
2、风流的能量与压力
例:
如图,井口断面对第一水平和第二水平标高的位压 是不相等的,如果求1-1断面对2-2断面的位能,可 取2-2断面为基准面,1-1断面的位压为: 1 1 Z1a
a·
Zab b· Zb2 2 2 Z12
p位12 12 Z12 g
实测时,应在两个断面之间布置多个测点,分别测 出各点和各段的平均密度,再由下式计算。
p12 1a Z1a g ab Zab g b2 Zb2 g ij Zij g
图2.2 立井位压计算图
测点布置的越多,测段垂直距离越小,计算结果越精确。
风 流 的 能 量 与 能 量 方 程
2、风流的能量与压力
特点:
(1)位压只相对于基准面存在,是该断面相对于基准面的位压差。基准面的选 取是任意的,因此位压可为正值,也可为负值。为了便于计算,一般将基准面 设在所研究系统风流的最低水平。 (2)位压是一种潜在的压力,不能在该断面上呈现出来。在静止的空气中,上 断面相对于下断面的位压,就是下断面比上断面静压的增加值,可通过测定静 压差来得知。 (3)在倾斜或垂直巷道中,空气位压和静压可以相互转化。 (4)不论空气是否流动,上断面相对于下断面的位压总是存在的。
第3次课 风流能量与压力

第3次课风流能量与压力一、风流能量与压力(注[1])(一)静压能与静压1、静压能:由分子热运动产生的分子动能的一部分转化的能够对外做功的机械能叫静压能。
E P(J/m3)2、静压力:分子热运动撞击到器壁上的单位面积上的力叫静压力。
P(N/m2,Pa)3、矿井通风中压力与物理学中压强的关系:矿井通风中压力的的概念与物理学中压强的概念相同。
都是单位面积上受到的垂直作用力。
4、矿井通风中静压能与静压力的关系:在矿井通风中,静压能与静压力单位不同,数值相等。
如风流压力为101332 Pa,则指1 m3风流具有101332J的静压能。
5、静压特点(1)静止和流动空气均具有静压力(2)风流中任一点的静压各向同值,且垂直于作用面。
6、压力的二种测算基准(1)绝对压力:以真空为零点测得的压力,注[1]:风流能量与压力是通风工程中二个最基本概念。
用P 表示。
(2)相对压力:以当地同标高大气压为零点测得的压力,用h 表示。
7、绝对压力与相对压力的区别关系:00h P P h h =-><时为正压时为负压(二)重力位能1、重力位能:因物体在地球重力场中位置不同而具有的一种能量,用E P0表示。
0P E M g Z =g g2、重力位能计算 (1)数学定义式130122,/P i i E gZ J m ρ=⎰(2)多测点分段平均密度法30121122,/P a a ab ab b b ij ij E Z g Z g Z g Z g J m ρρρρ=++=∑g g图见PPT图见PPT3、势能:矿井通风中某点的静压能与重力位能之和称为势能4、位能的特点:(1)位能是相对于某一基准面而具有的能量,随基准面的变化而变化。
(2)位能是一种潜在的能量,不能测量,只能计算。
(3)位能与静压能可相互转化,空气由标高高的地方向标高低的地方流动,位能转化为静压能;反之,静压能转化为位能。
(三)动能—动压1、动能:空气做定向流动是时所具有的运动能。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.1 矿井风流运动的能量方程式及其 应用 • 3.1.2单位质量流量能量方程 单位质量流量能量方程
• 2.风流流动过程中能量分析 . 1断面上,1 kg空气 断面上, 断面上 空气 所具有的能量为: 所具有的能量为:
v12 + + gZ1 + u1 ρ1 2 p1
流经1 断面 断面, 流经 2断面,到 1kg空气由 断面流至 断面时,克 空气由1断面流至 断面时, 空气由 断面流至2断面时 另外还有地温(通过井巷壁面或淋 达2断面时 断面时 另外还有地温 井巷中的风流 图3-3 通过井巷壁面或淋 服流动阻力消耗能量为L 服流动阻力消耗能量为 R(这 2 水等其他途径)、 水等其他途径 、机电设备等传给 p2 v2 部分被消耗能量将转化成热能 + + gZ 2 + u2 ρ2 2 1kg空气热量 。这些热量将增加 空气热量q。 q空气热量 仍存在于空气中)。 R,仍存在于空气中)。 空气的内能并使空气膨胀做功
2 2
u uds ∫ u 3 ds 2 Kv = s = s 3 2 v vS ρ vS 2
∫ρ
2
Kv =
ui3 si ∑
i =1
n
v3 S
3.1 矿井风流运动的能量方程式及其 应用 • 在进行了上述两项简化处理后,单位体积流体的能 在进行了上述两项简化处理后,
量方程可近似地写成式( 量方程可近似地写成式(3-30)和(3-31): ) ):
• 由于水平巷道中,空气密度又近似相等,因此 由于水平巷道中,空气密度又近似相等,
h 1− 2 = ( p1 − p2 ) + (
ρ1v12
2
−
2 ρ 2 v2
2
)
断面积均匀不变的水平巷道有 Z1 = Z 2
h1− 2 = ( p1 − p2 )
• 图3-1 一元稳定流连续性分析图
3.1 矿井风流运动的能量方程式及其 应用 • 3.1.1空气流动连续性方程 空气流动连续性方程
• 2.风流运动的能量方程 . 据能量守恒定律, 据能量守恒定律,空气从第一断面流向第二个断面时 2 ρ1v12 ρ 2v2 p1 + + ρ m1 gZ1 = p2 + + ρ m 2 gZ 2 + h1− 2
3.1 矿井风流运动的能量方程式及其应用 3.2 能量方程在分析通风动力与阻力关系 上的应用 3.3 有分支风路的能量方程式
3.1 矿井风流运动的能量方程式及其 任一过流断面质量流量M 任一过流断面质量流量 i (kg/s)为常数 ,即 ) 即 应用 • 3.1.1空气流动连续性方程 空气流动连续性方程 Mi=常数 常数 • 1.连续性方程 . 对于不可压缩流体(密度为常数), ),则 对于不可压缩流体(密度为常数),则 • 两个过流断面的空气质量流量相等,即 两个过流断面的空气质量流量相等, Q=viSi=常数 常数 空气在矿井巷道中的流动可近似地认为是一元稳定 ρ1v1S1 = ρ2v2S2 这在工程应用中是满足要求的。 流,这在工程应用中是满足要求的。
2 v12 v2 hR ≈ p1 − p2 + ( ρ1 − ρ 2 ) + g ( ρ m1Z1 − ρ m 2 Z 2 ) 2 2
2 v12 v2 hR ≈ p1 − p2 + ( ρ1 − ρ 2 ) + g ( ρ m1Z1 − ρ m 2 Z 2 ) + H t 2 2
3.1 矿井风流运动的能量方程式及其 应用 • 3.1.4 断面不同的水平巷道能量方程
断面流至2断面的过程中的静压能变化, 断面流至 断面的过程中的静压能变化,它与空气 断面的过程中的静压能变化 流动过程的状态密切相关。对于多变过程, 流动过程的状态密切相关。对于多变过程,过程指 数为n(可以在0~ 数为 (可以在 ~±∞范围内变化 )时,n = const 范围内变化 pv • n =0时, = const ,即为定压过程, vdp = 0 时 p 即为定压过程, ∫ ∫ vdp • n =1时, = const ,即为等温过, = p v 即为等温过, 时 pv
• 1.能量组成 . • 在井巷通风中,风流的能量由机械能和内能组成, 在井巷通风中,风流的能量由机械能和内能组成, 常用1kg空气或 m3空气所具有的能量表示。 空气或1 空气所具有的能量表示。 常用 空气或 • 风流具有的机械能包括静压能、动压能和位能。风 风流具有的机械能包括静压能、动压能和位能。 流具有的内能是风流内部储存能的简称, 流具有的内能是风流内部储存能的简称,它是风流 内部所具有的分子内动能与分子位能之和。 内部所具有的分子内动能与分子位能之和。 • 用表示 用表示1kg空气所具有的内能(J/kg),则 空气所具有的内能( ),则 空气所具有的内能 ), 空气的比容,m3/kg u = f (T ,υ ) 空气的比容, • 根据压力(p)、温度(T)和比容(v)之间关系 根据压力( )、温度( )和比容( ) )、温度 可见空气的内能是空气 状态参数的函数。 状态参数的函数。 u = f (T , p )
=
ρ
n 2
= L = const
3.1 矿井风流运动的能量方程式及其 • 将式 q + q = (u − u ) + ∫ pdv应用 代入积分项并由积分公式
2 R
• •
∫ x dx =
µ
x
µ +1
2
1
µ +1
+c
1
积分得: 积分得:
∫
1
2
vdp =
n p1 p2 ( − ) n − 1 ρ1 ρ 2
LR =
p1 − p2
ρm
2 v12 v2 + ( − ) + g ( Z1 − Z 2 ) 2 2 ,
LR =
p1 − p2
ρm
2 v12 v2 + ( − ) + g ( Z1 − Z 2 ) + Lt 2 2
3.1 矿井风流运动的能量方程式及其 这就是单位体积流体的能量方程。 这就是单位体积流体的能量方程。 应用 断面的标高差较大的情况下, 当1、2断面的标高差较大的情况下, 、 断面的标高差较大的情况下 • 3.1.3单位体积流量能量方程 单位体积流量能量方程
3.1 矿井风流运动的能量方程式及其 应用 • 3.可压缩空气单位质量流量的能量方程 .
• 当风流在井巷中做一维稳定流动时 2 2
ρ1
p1 + v1 p v + gZ1 + u1 + qR + q = 2 + 2 + gZ 2 + u2 + LR 2 ρ2 2
这就是单位质量可压缩空气在无压 • 根据热力学第一定律,传给空气的热量,一部分用 根据热力学第一定律,传给空气的热量, 单位质量可压缩空气1、 断面间有 单位质量可压缩空气 、2断面间有 源的井巷中流动时能量方程的一 于增加空气的内能, 于增加空气的内能,一部分使空气膨胀对外做功 压源(如局部通风机等)存在, 压源(如局部通风机等)存在, 2 般形式 u ) + pdv qR + q =则其能量方程为 (u2 − 1 ∫ 1 p p • 又因为: 又因为: − = p v − p v = ∫ d ( pv) = ∫ pd (v) + ∫ vd ( p ) ρ ρ • 整理得: 2 2 整理得: 2 v v v v LR = − ∫ vdp + ( 1 − 2 ) + g ( Z1 − Z 2 ) = ∫ vdp + ( − ) + g ( Z − Z ) 2 2 2 2 1 v v • L = ∫ vdp + ( − ) + g ( Z − Z ) + L 2 2
2 n p1 p2 v12 v2 这就是单位质量可压缩空气在无压 = ( − ) + ( − ) + g (Z 、 得: LR单位质量可压缩空气在 1 − Z 22断面间 单位质量可压缩空气在1、 )断面间 n − 1 ρ1 ρ 2 2 2
源的井巷中流动时能量方程又可 存在 有压源(如局部通风机等) 有压源(如局部通风机等) n 表示为 ( p − p ) + ( v − v 有可表示为 L = 时能量方程为 ) + g ( Z − Z ) + L
后一个是有压源H 时的能量方程。 后一个是有压源 t时的能量方程。 由于井巷断面上风速分布的不均匀性,用断面平 由于井巷断面上风速分布的不均匀性, 该项数值在方程中往往占有很大 • 在考虑空气的可压缩性时,那么 3空气流动过程 在考虑空气的可压缩性时,那么1m 均风速计算出来的断面总动能与断面实际总动 的比重, 的比重,必须准确测算。 中的能量损失可由l kg空气流动过程中的能量损失 中的能量损失可由必须准确测算。 空气流动过程中的能量损失 实际测算动能系数时,把断 实际测算动能系数时, 能不等,需用动能系数K 加以修正。 能不等,需用动能系数 v加以修正。动能系数 LR乘以按流动过程状态考虑计算的空气密度ρm,即: 乘以按流动过程状态考虑计算的空气密度 面分成若干微小面积( 面分成若干微小面积(分 是断面实际总动能与用断面平均风速计算出的 断面上风速分布愈不均匀, 断面上风速分布愈不均匀,K • h = L ρ 。代入式(3-24)、( 分别测出 v 代入式( )、(3-25) )、( 得越小越好), ),分别测出 得越小越好), )得: 总动能的比 R R m 的值愈大。在矿井条件下, 的值愈大。在矿井条件下, 每一微小面积上的u 每一微小面积上的 i和si, 2 v12 一般为 v2 一般为1.02~1.05。 hR = p1 − p2 + (Kv− ) ρ m + g ρ m (~− Z 2 ) 。由于动 Z1 测出断面平均风速v和断面 测出断面平均风速 和断面 微小面积ds上的 微小面积 上的 2 2 能差项很小, 能差项很小,在应用能量方 2 风速 v12 积S,用下式计算 v2 , hR = p1 − p2 + ( 程时,Kg可取为 2 ) + H t − ) ρm ρ m ( Z1 − Z 。 程时, + v可取为1。
