传感器与测试技术-形考作业4(第7-8章,15%)-国开(内蒙古)-参考资料

合集下载

特殊字符大全

特殊字符大全汉字大全(1 2 3 4) 按部首查询字符大全! " # $ % & ' ( ) * + , - . / 0 1 2 3 4 5 6 7 8 9 : ; < = > @ A B C D E F G H I J K L M N O P Q R S T U V W X Y Z [ \ ] ^ _ ` a b c d e f g h i j k l m n o p q r s t u v w x y z { | } ~ •￠￡¤ ￥| § ¨ a - ˉ ° ± 2 3 ′ μ · 1 o à á è é ê ì í D ò ó × ù ú ü Y T à á a è é ê ì í e ò ó ÷ ù ú ü y t ā ā ē ē ě ě ī ī ń ň ō ō ū ū ∥ ǎ ǎ ǐ ǐ ǒ ǒ ǔ ǔ ǖ ǖ ǘ ǘ ǚ ǚ ǜ ǜ ɑ ɡ ˇ ˉ ˊ ˋ ˙ Α Β Γ Δ Ε Ζ Η Θ Ι Κ Λ Μ Ν Ξ Ο Π Ρ Σ Τ Υ Φ Χ Ψ Ω α β γ δ ε ζ η θ ι κ λ μ ν ξ ο π ρ σ τ υ φ χ ψ ω Ё А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ъ Ы Ь Э Ю Я а б в г д е ж з и й к л м н о п р с т у ф х ц ч ш щ ъ ы ь э ю я ё‐ –—― ‖‘ ’ “ ” ‥ … ‰ ′ ″ ‵ ※ ￣€ ℃ ℅ ℉ № ℡ Ⅰ Ⅱ Ⅲ Ⅳ Ⅴ Ⅵ Ⅶ Ⅷ Ⅸ Ⅹ Ⅺ Ⅻ ⅰ ⅱ ⅲ ⅳ ⅴ ⅵ ⅶ ⅷ ⅸ ⅹ ← ↑ → ↓ ↖ ↗ ↘ ↙ ∈ ∏ ∑ ∕ ° √ ∝ ∞ ∟ ∠ ∣ ∥ ∧ ∨ ∩ ∪ ∫ ∮ ∴ ∵ ∶ ∷ ～∽ ≈ ≌ ≒ ≠ ≡ ≤ ≥ ≦ ≧ ≮ ≯ ⊕ ⊙ ⊥ ⊿ ⌒ ① ② ③ ④ ⑤ ⑥ ⑦ ⑧ ⑨ ⑩ ⑴ ⑵ ⑶ ⑷ ⑸ ⑹ ⑺ ⑻ ⑼ ⑽ ⑾ ⑿ ⒀ ⒁ ⒂ ⒃ ⒄ ⒅ ⒆ ⒇ ⒈ ⒉ ⒊ ⒋ ⒌ ⒍ ⒎ ⒏ ⒐ ⒑⒒ ⒓ ⒔ ⒕ ⒖ ⒗ ⒘ ⒙ ⒚ ⒛ ─ ━ │ ┃ ┄ ┅ ┆ ┇ ┈ ┉ ┊ ┋ ┌ ┍ ┎ ┏ ┐ ┑ ┒ ┓ └ ┕ ┖ ┗ ┘ ┙ ┚ ┛ ├ ┝ ┞ ┟ ┠ ┡ ┢ ┣ ┤ ┥ ┦ ┧ ┨ ┩ ┪ ┫ ┬ ┭ ┮ ┯ ┰ ┱ ┲ ┳ ┴ ┵ ┶ ┷ ┸ ┹ ┺ ┻ ┼ ┽ ┾ ┿ ╀ ╁ ╂ ╃ ╄ ╅ ╆ ╇ ╈ ╉ ╊ ╋ ═ ║ ╒ ╓ ╔ ╕ ╖ ╗ ╘ ╙ ╚ ╛ ╜ ╝ ╞ ╟ ╠ ╡ ╢ ╣ ╤ ╥ ╦ ╧ ╨ ╩ ╪ ╫ ╬ ╭ ╮ ╯ ╰ ╱ ╲ ╳ ▁ ▂ ▃ ▄ ▅ ▆▇ █ ▉ ▊ ▋ ▌ ▍ ▎ ▏ ▓ ▔ ▕ ■ □ ▲ △ ▼ ▽ ◆ ◇ ○ ◎ ● ◢ ◣ ◤ ◥ ★ ☆ ☉ ♀♂、。

腾云联盟2023-2024学年度上学期高三年级10月联考化学试卷及答案

2023—2024学年度上学期高三年级十月联考化学试卷试卷满分：100分＊祝考试顺利＊注意事项：1答题前，先将自己的姓名、准考证号填写在试卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。

2选择题的作答：每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑。

写在试卷、草稿纸和答题卡上的非答题区域均无效。

3非选择题的作答：用黑色签字笔直接答在答题卡上对应的答题区域内。

写在试卷、草稿纸和答题卡上的非答题区域均无效。

4考试结束后，请将本试卷和答题卡一并上交。

可能用到的相对原子质量：H1 N 14 0 16 F 19 Mg 24-S 32 K 39 Fe 56 Ni 59 一、选择题：本题共15小题，每小题3分，共45分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

l．生活中处处有化学。

下列说法正确的是A.食用白糖的主要成分：庶糖B.水煤气的主要成分：甲烧C.84消毒液的主要成分：次氯酸钙D.植物油的主要成分：高级脂肪酸2.湖北大冶铁矿素有江南“聚宝盆”的美称。

下列说法正确的是A.生铁属于碳素钢B.，铁元素位千d区c.铁强化酱油中铁为单质 D.常用KSCN检验Fe2+3.2016年IUPAC将117号元素命名为础(Ts)。

下列关于帘Ts和帘Ts的说法正确的是A.二者互为同位素B.都含有117个中子C.含有不同的电子数D.分别含有176个和177个质子4.两种有机物的分子式均为C3压o,二者的沸点信息如下图所示。

：丙醇：91.2·c 下列说法错误的是A.二者互为同分异构体c.一氯代物均有4种甲乙酸：10.8-CB.碳原子均为sp3杂化D.丙醇分子间存在氢键化学试卷第1.页（共8页）5.制备过氧化锡晶体的原理为S产＋H心计8H20=Sr02·8比Ot+2H.，装置如下图所示。

下列说法错误的是A.该反应为氧化还原反应B.仪器X的作用是防倒吸C.氨气的作用是中和H+D.冰水混合液可减少Sr02·8比0分解6.设凡为阿伏加德罗常数的值。

聚四氟乙烯材料力学性能参数表

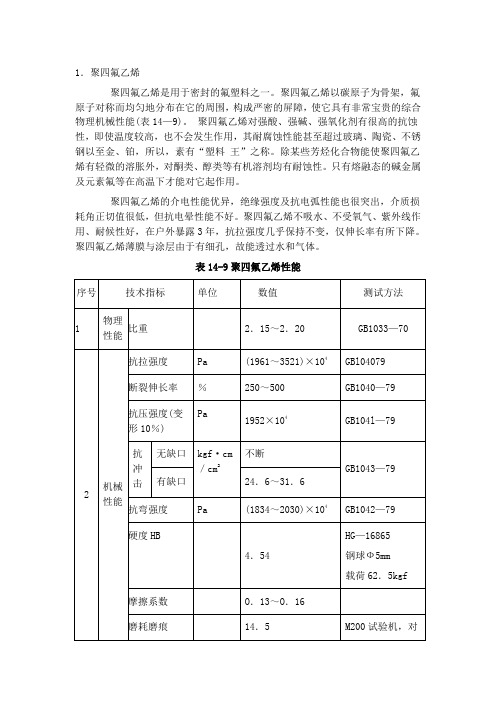
1．聚四氟乙烯聚四氟乙烯是用于密封的氟塑料之一。

聚四氟乙烯以碳原子为骨架，氟原子对称而均匀地分布在它的周围，构成严密的屏障，使它具有非常宝贵的综合物理机械性能(表14—9)。

聚四氟乙烯对强酸、强碱、强氧化剂有很高的抗蚀性，即使温度较高，也不会发生作用，其耐腐蚀性能甚至超过玻璃、陶瓷、不锈钢以至金、铂，所以，素有“塑料王”之称。

除某些芳烃化合物能使聚四氟乙烯有轻微的溶胀外，对酮类、醇类等有机溶剂均有耐蚀性。

只有熔融态的碱金属及元素氟等在高温下才能对它起作用。

聚四氟乙烯的介电性能优异，绝缘强度及抗电弧性能也很突出，介质损耗角正切值很低，但抗电晕性能不好。

聚四氟乙烯不吸水、不受氧气、紫外线作用、耐候性好，在户外暴露3年，抗拉强度几乎保持不变，仅伸长率有所下降。

聚四氟乙烯薄膜与涂层由于有细孔，故能透过水和气体。

表14-9聚四氟乙烯性能聚四氟乙烯在200℃以上，开始极微量的裂解，即使升温到结晶体熔点327℃，仍裂解很少，每小时失重为万分之二。

但加热至400℃以上热裂解速度逐渐加快，产生有毒气体，因此，聚四氟乙烯烧结温度一般控制在375～380℃。

聚四氟乙烯分子间的范德华引力小，容易产生键间滑动，故聚四氟乙烯具有很低的摩擦系数及不粘性，摩擦系数在已知固体材料中是最低的。

聚四氟乙烯的导热系数小，该性能对其成型工艺及应用影响较大。

其不但导热性差，且线膨胀系数较大，加入填充剂可适当降低线膨胀系数。

在负荷下会发生蠕变现象，亦称作“冷流”，加入填充剂可减轻蠕变程度。

聚四氟乙烯可以添加不同的填充剂，选择的填充剂应基本满足下述要求：能耐380℃高温即四氟制品的烧结温度；与接触的介质不发生反应；与四氟树脂有良好的混入性；能改善四氟制品的耐磨性、冷流性、导热性及线膨胀系数等。

常用的填充剂有无碱无蜡玻璃纤维、石墨、碳纤维、MoS2、A123、CaF2、焦炭粉及各种金属粉。

如填充玻璃纤维或石墨，可提高四氟制品的耐磨、耐冷流性，填充MoS2可提高其润滑性，填充青铜、钼、镍、铝、银、钨、铁等，可改善导热性，填充聚酰亚胺或聚苯酯，可提高耐磨性，填充聚苯硫醚后能提高抗蠕变能力，保证尺寸稳定等。

自动控制原理+第五版课后习题答案

C(s ) G 1G 2 G 3 = R ( s ) 1 + G 1 H 1 + G 2 H 2 + G 3 H 3 + G 1 H 1G 3 H 3
C(s ) G 1G 2G 3 = G4 + R (s ) 1 + G 2 H 1 G 1G 2 H 1 + G 2G 3 H 2
(f)
C(s) (G 1 + G 3 )G 2 = R(s ) 1 + G 1G 2 H 1
C(s ) G 3G 2 (1 + G 1G 2 H1 ) = N(s ) 1 + G 1G 2 + G 1G 2 H1
C(s ) G4 = N (s ) 1 + G 2 G 4 + G 3 G 4
2-18(a) (b)
C(s ) G 1G 2 = R(s ) 1 + G 1G 2 + G 1G 2 H1
& = f1 f 2 &&i ( t ) + ( f1k 2 + f 2 k1 ) x i ( t ) + k1k 2 x i ( t ) x 2-4(a) R1 R2 Cuo ( t ) + ( R1 + R2 )uo ( t ) = R1 R2 Cui ( t ) + R2 ui ( t ) & &
&& & & & m xo ( t ) = f1[ xi ( t ) - xo ( t )] - f 2 xo ( t )
&& & = R1 R2C1C 2 ui ( t ) + ( R1C1 + R2C 2 )ui ( t )

服装号型,尺寸换算对照表

全面实用的服装号型，尺码换算对照表" ]" o8 K6 N/ k6 Z% Z2 Z: x9 b4 H0 ^/ M& ?3 T2 l9 S. r" d! ]) L ?一．吊牌上的执行标准的意思; @" i' ~+ |% r; @3 F0 B- hA类，B类，C类的含义：这是国标中对甲醛含量的规定，A类是婴糼儿用品，B类是直接接触皮肤，C类是非直接接触皮肤1 M L) }5 ?6 r' Q; F9 [6 J) L) I/ r& Y% A5 T( E二．常见的服装生产国家标准: u" n7 _, H0 w) ?GB/T2664-2001男西服，大衣 GB/T2665-2001女西服GB/T2666-2001男女西裤 GB/T2660-1999衬衫 GB/T2662-1999棉服装 FZ/T81004-2003连衣裙，裙套。

FZ/T81006-1992牛仔服装FZ/T81007-2003男女单服装FZ/T81008-1994茄克衫GB/T8878-2002棉针织内衣FZ/T73008-2002针织T恤衫 FZ/T73010-1998针织工艺衫FZ/T73003-1991精梳毛针织品FZ/T73004-1991粗梳毛针织品GB1103-1999棉花细绒棉GB/T14272-2002羽绒服- L/ D6 B- x$ R$ ~) M三．国家服装号型的含义$ T# t) p) g y$ `号型定义：“号”指人体的身高，以cm为单位，是设计和选购服装长短的依据；“型”指人体的胸围和腰围，以cm为单位，是设计和选购服装肥瘦的依据。

体型分类：以人体的胸围与腰围的差数为依据来划分体型，并将体型分为四类，体型分类代号分别为Y(偏瘦)、A（正常）、B（偏胖）、C（肥胖）9 [5 ~- L8 H/ ` r/ j( ~: ?& O) ~" j4 W- P号型标志：号型的表示方法为号与型之间用斜线分开，后接体型分类代号。

一元一次方程-七年级数学上册课件(浙教版)

程叫做解方程.
x
x
思考：x=420是 1方程的解吗?
60 70
420 420
解：当x=420时，方程左边= - =7-6=1，右边=1，左边=右边，
60 70
所以x=420是此方程的解.
例3 x=1000和x=2000中哪一个是方程 0.52x-(1-0.52)x=80的解？
解：当x=1000时，方程左边=0.52×1000-(1-0.52)×1000=520-480=40，
由题意列方程为5x+4(5-x)=21．
【点睛】本题考查了列一元一次方程，找准等量关系是解题关键．
14
3
2+0.3x 5
问题1:每个方程中，各含有几个未知数？ 1个
问题2:说一说每个方程中未知数的次数.
1次
问题3:等号两边的式子有什么共同点？
都是整式
一元一次方程的概念
只含有一个未知数,未知数的次数都是1,等号两边都是整式，
这样的方程叫做一元一次方程.
练一练
下列哪些是一元一次方程？
（1） 2 x 1 ；
(1) 2 5 3 ( × )
(2) 3x 1 7
( √ )
(3) 2a b
(× )
(4) x 3
( ×)
(5) x y 8
(√ )
(6) 2 x 2 5 x 1 0 ( √ )
含有未知数的等式叫做方程.
知识点一一元一次方程的概念
请用已学知识，根据下列问题中的条件分别列出方程.
9．只列方程，不解方程
(1)某班有男生25人，比女生的2倍少15人，这个班女生有多少人？
(2)小明买苹果和梨共5千克，用去21元，其中苹果每千克5元，梨每

2024-2025学年四川省成都市第十二中学(四川大学附属中学)八年级上学期10月考数学试卷含详解

八年级（上）10月学情反馈数学试卷注意事项：1．全卷分A 卷和B 卷,A 卷满分100分,B 卷满分50分,时间120分钟．2．考生使用答题卡作答,保持答题卡清洁,不得折叠,污染,破损等．3．选择题部分必须使用2B 铅笔填涂,非选择题部分必须使用0.5毫米黑色签字笔书写,字体工整,笔迹清楚4．请按照题号在答题卡上各题目对应的答题区域内作答,超出答题区域书写的答案无效．A 卷（100分）一,选择题（共8小题每题4分共32分）1.在下列实数234,π4,134.070070007-⋯（相邻两个7之间依次多一个0）中,无理数有（）A.1个 B.2个 C.3个 D.4个2.一个直角三角形的一条直角边和斜边的长分别为3和5,则另一条直角边的长为（）A.B. C.4 D.4或3.下列计算正确的是（）A.23=B.3=C.4=± D.3=-4.已知12x y =⎧⎨=⎩是关于x ,y 的方程,x ＋ky ＝3的一个解,则k 的值为（）A.－1 B.1 C.2 D.35.ABC V 的三边长分别为a ,b ,c ,由下列条件不能判断ABC V 为直角三角形的是（）A.90B C ∠+∠=︒B.::3:4:5A B C ∠∠∠=C.6a =,8b =,10c = D.222c a b -=6.有意义,则x 的取值范围是（）A.1x ≥-B.1x ≤-C.1x >- D.1x <-7.若1a a <<+,则22a -的值为（）A.3B.7C.8D.98.如图所示,将一根24cm 的筷子,置于底面直径为15cm ,高8cm 的圆柱形水杯中,设筷子露在杯子外面的长度h cm ,则h 的取值范围是（）A.17cm h ≤B.8cm h ≥C.15cm 16cm h <≤D.7cm 16cmh ≤≤二,填空题（共5小题每题4分共20分）9.若实数x ,y|2|0y +=,则x +y 的值为__________．10.如图,长方形ABCD 的边AB 落在数轴上,A ,B 两点在数轴上对应的数分别为1-和1,1BC =,连接BD ,以B 为圆心,BD 为半径画弧交数轴于点E ,则点E 在数轴上所表示的数为_________．11.下列几组数：①8,15,17,②1,20.3,0.4,0.5,④16,18,110,⑤12,16,20．其中是勾股数的有______．（填序号）12.若2325m n m n +=⎧⎨+=⎩．则m n +的值为______．13.如图,在ABC V 中,90ACB ∠=︒,34AC BC ==，,点D 在边AB 上,AD AC AE CD =⊥，,垂足为F ,与BC 交于点E ,则BE 的长是___________．三,解答题（共5小题14题10分,15题12分,16题8分,17题8分,18题10分共48分）14.计算（1()202431-+-+（2）)222-．15.解下列方程组（1）1342x y x y =+⎧⎨-=-⎩.（2）11233210x y x y +⎧-=⎪⎨⎪+=⎩．16.如图,在四边形ABCD 中,90B Ð=°,3AB =,4BC =,点D 是Rt ABC △外一点,连接CD ,AD ,且12CD =,13AD =．求四边形ABCD 的面积17.如图,实数,,a b c 在数轴上对应点的位置如图所示,化简b a +--的结果．18.如图①,在长方形ABCD 中,已知AB ＝10,AD ＝6,动点P 从点D 出发,以每秒2个单位的速度沿线段DC 向终点C 运动,运动时间为t 秒,连接AP ,把△ADP 沿着AP 翻折得到△AEP ．（1）如图②,射线PE 恰好经过点B ,试求此时t 的值．（2）当射线PE 与边AB 交于点Q 时,是否存在这样的t 的值,使得QE ＝QB ？若存在,请求出所有符合题意的t 的值,若不存在,请说明理由．B 卷（50分）一,填空题（共5小题每题4分共20分）19.比较大小：12-_____12．20.已知a 的值为__________．21.关于x ,y 的二元一次方程()()32290m x m y m ++-+-=,不论m 取何值,方程总有一组固定不变的解,这组解为__________．22.如图,在四边形ABCD 中和,6AB BC ==,60ABC ∠=︒,90ADC ∠=︒．对角线AC 与BD 相交于点E ,若3BE DE =,则ED =__________．23.【阅读材料】平面几何中的费马问题是十七世纪法国数学家皮埃尔·德·费马提出的一个著名的几何问题：给定不在一条直线上的三个点A ,B ,C ,求平面上到这三个点的距离之和最短的点P 的位置,费马问题有多种不同的解法,最简单快捷的还是几何解法．如图1,我们可以将BPC 绕点B 顺时针旋转60°得到BDE V ,连接PD ,可得BPD △为等边三角形,故PD PB =,由旋转可得DE PC =,因PA PB PC PA PD DE ++=++,由两点之间线段最短可知,PA PB PC ++的最小值与线段AE 的长度相等．【解决问题】如图2,在直角三角形ABC 内部有一动点P ,90BAC ∠=︒,30ACB ∠=︒,连接PA ,PB ,PC ,若3AB =,求PA PB PC ++的最小值______．二,解答题（共3小题24题8分,25题10分,26题12分共30分）24.如图,在一条笔直的东西方向的公路上有A ,B 两地,相距500米,且离公路不远处有一块山地C 需要开发,已知C 与A 地的距离为300米,与B 地的距离为400米,在施工过程中需要实施爆破,为了安全起见,爆破点C 周围半径260米范围内不得进入．（1）山地C 距离公路的垂直距离为多少米？（2）在进行爆破时,A ,B 两地之间的公路是否有危险需要暂时封锁？若需要封锁,请求出需要封锁的公路长．25.科华数学之星在解决问题：已知a =,求2281a a -+的值．他是这样分析与解决的：2a ===2a ∴-=2(2)3a ∴-=,2443a a -+=.241a a ∴-=-.()222812412(1)11a a a a ∴-+=-+=⨯-+=-．请你根据小明的分析过程,解决如下问题：（1=,=．（2+ ．（3）若a =,请按照小明的方法求出2481a a -+的值．26.数学活动课上,老师出示两个大小不一样的等腰直角ABC 和ADE 摆在一起,其中直角顶点A 重合,AB AC =,AD AE =,90BAC DAE ∠=∠=︒．（1）用数学的眼光观察．如图1,连接B ,C ,判断B 与C 的数量关系,并说明理由.（2）用数学的思维思考．如图2,连接BE ,B ,若F 是BE 中点,判断AF 与B 的数量关系,并说明理由.（3）用数学的语言表达．如图3,延长C 至点F ,满足AF AC =,然后连接DF ,BE ,当AB =,1AD =,ADE 绕A 点旋转得到D E F，，三点共线时,求线段EF 的长．八年级（上）10月学情反馈数学试卷A卷（100分）一,选择题（共8小题每题4分共32分）1.在下列实数234,π4,134.070070007-⋯（相邻两个7之间依次多一个0）中,无理数有（）A.1个B.2个C.3个D.4个【答案】C【分析】本题考查无理数,根据无理数是无限不循环小数,进行判断即可．【详解】解：在234,π4,134.070070007-⋯（相邻两个7之间依次多一个0）中,无理数有,π4,134.070070007-⋯（相邻两个7之间依次多一个0）,共3个.故选C．2.一个直角三角形的一条直角边和斜边的长分别为3和5,则另一条直角边的长为（）A.B. C.4 D.4或【答案】C【分析】本题考查勾股定理求线段长,根据题意,利用勾股定理列式即可得到答案,熟练掌握勾股定理求线段长是解决问题的关键．【详解】解：一个直角三角形的一条直角边和斜边的长分别为3和5.∴由勾股定理可得另一条直角边的长为4=.故选：C．3.下列计算正确的是（）A.23=B.3=C.4=± D.3=-【答案】A【分析】根据二次根式的性质进行化简,然后分析作出判断即可．【详解】A.23=,故A正确,符合题意.B.3=±,故B错误,不符合题意.4=,故C错误,不符合题意.3=,故D错误,不符合题意．故选：A．a=,2a=,是解题的关键．4.已知12x y =⎧⎨=⎩是关于x ,y 的方程,x ＋ky ＝3的一个解,则k 的值为（）A.－1 B.1 C.2 D.3【答案】B【分析】把x 与y 的值代入方程计算即可求出k 的值．【详解】解：∵12x y =⎧⎨=⎩是关于x ,y 的方程x +ky ＝3的一个解.∴把12x y =⎧⎨=⎩代入到原方程,得1+2k ＝3.解得k ＝1.故选：B ．【点睛】本题主要考查了二元一次方程的解的定义,解一元一次方程,熟知方程的解是使方程两边相等的未知数的值是解题的关键．5.ABC V 的三边长分别为a ,b ,c ,由下列条件不能判断ABC V 为直角三角形的是（）A.90B C ∠+∠=︒B.::3:4:5A B C ∠∠∠=C.6a =,8b =,10c = D.222c a b -=【答案】B【分析】本题考查勾股定理的逆定理的应用和三角形的内角和定理．根据三角形内角和定理可分析出A ,B 的正误,根据勾股定理逆定理可分析出C ,D 的正误．【详解】解：A ,90B C ∠+∠=︒ ,180A B C ∠+∠+∠=︒.90A ∴∠=︒.∴ABC V 为直角三角形,故A 选项不符合题意.B ,设3A x ∠=︒,4B x ∠=︒,5C x ∠=︒.345180x x x ++=.解得：15x =.则575x ︒=︒.∴ABC V 不是直角三角形,故B 选项符合题意.C ,∵6a =,8b =,10c =.222c a b ∴=+.∴能构成直角三角形,故C 选项不合题意.D ,222c a b -= .222a b c ∴+=.∴能构成直角三角形,故D 选项不合题意.故选：B ．6.有意义,则x 的取值范围是（）A.1x ≥- B.1x ≤- C.1x >- D.1x <-【答案】A【分析】本题考查的是二次根式有意义的条件,即二次根式中的被开方数是非负数．根据二次根式有意义的条件列出关于x 的不等式,求出x 的取值范围即可．【详解】解：有意义.10x ∴+≥,解得1x ≥-．故选：A ．7.若1a a <<+,则22a -的值为（）A.3B.7C.8D.9【答案】B【分析】此题主要考查了估算无理数的大小,正确得出接近无理数的整数是解题关键．根据题意得出34<<,进而求出3a =,然后代入22a -即可得出答案．【详解】∵91216<<∴34<<∵1a a <<+∴3a =∴222327a -=-=．故选：B ．8.如图所示,将一根24cm 的筷子,置于底面直径为15cm ,高8cm 的圆柱形水杯中,设筷子露在杯子外面的长度h cm ,则h 的取值范围是（）A.17cmh ≤ B.8cm h ≥ C.15cm 16cm h <≤ D.7cm 16cmh ≤≤【答案】D 【分析】本题主要考查了勾股定理的实际应用,如图,当筷子的底端在A 点时,筷子露在杯子外面的长度最短,当筷子的底端在D 点时,筷子露在杯子外面的长度最长．然后分别利用已知条件根据勾股定理即可求出h 的取值范围．【详解】解：如图1所示,当筷子的底端在D 点时,筷子露在杯子外面的长度最长.24816cm h ∴=-=最大.如图2所示,当筷子的底端在A 点时,筷子露在杯子外面的长度最短.在Rt ABD △中,15cm AD =,8cm BD =.17cm AB ∴==.∴此时24177cm h =-=最小.∴h 的取值范围是7cm 16cm h ≤≤．故选：D ．二,填空题（共5小题每题4分共20分）9.若实数x ,y |2|0y +=,则x +y 的值为__________．【答案】1【分析】根据非负数的性质列出方程求出x,y 的值,代入所求代数式计算即可．【详解】根据题意得：x−3＝0,y+2=0.解得：x ＝3,y ＝−2.则x+y=3-2=1．故答案是：1．【点睛】本题考查了非负数的性质：几个非负数的和为0时,这几个非负数都为0．10.如图,长方形ABCD 的边AB 落在数轴上,A ,B 两点在数轴上对应的数分别为1-和1,1BC =,连接BD ,以B 为圆心,BD 为半径画弧交数轴于点E ,则点E 在数轴上所表示的数为_________．【答案】1-1+【分析】根据勾股定理求得BD ,进而根据数轴上的两点距离即可求得点E 在数轴上所表示的数．【详解】解：四边形ABCD 是长方形,A ,B 两点在数轴上对应的数分别为1-和1,1BC =.1,2AD BC AB ∴===依题意BE BD ===.设点E 在数轴上所表示的数为x,则1x -=解得1x =-故答案为：1【点睛】本题考查了勾股定理,实数与数轴,掌握勾股定理求得BD 是解题的关键．11.下列几组数：①8,15,17,②1,20.3,0.4,0.5,④16,18,110,⑤12,16,20．其中是勾股数的有______．（填序号）【答案】①⑤##⑤①【分析】本题考查了勾股数的定义,注意：作为勾股数的三个数必须是正整数,一组勾股数扩大相同的整数倍得到三个数仍是一组勾股数．根据勾股数的定义,逐一判断即可求解．【详解】解：①22281517+= .∴8,15,17是勾股数.1,2不是勾股数.③0.3,0.4,0.5不是整数,故0.3,0.4,0.5不是勾股数.④16,18,110不是整数,故16,18,110不是勾股数.⑤ 222121620+=.∴12,16,20是勾股数.故答案为：①⑤．12.若2325m n m n +=⎧⎨+=⎩．则m n +的值为______．【答案】83##223【分析】本题考查了求代数式的值,解二元一次方程组,能根据代数式的特点,选择整体代数法,从而将两个方程相加是解题的关键．【详解】解：2325m n m n +=⎧⎨+=⎩①②．由①+②得：3335m n +=+.即83m n +=.故答案为：8313.如图,在ABC V 中,90ACB ∠=︒,34AC BC ==，,点D 在边AB 上,AD AC AE CD =⊥，,垂足为F ,与BC 交于点E ,则BE 的长是___________．【答案】52【分析】此题考查了垂直平分线的判定和性质,全等三角形的判定和性质,勾股定理等知识,证明AE 是CD 的垂直平分线,则CE DE =,证明()SSS ACE ADE ≌,则90ADE ACB ∠=∠=︒,在Rt ABC △中,由勾股定理得5AB =,则2BD AB AD =-=,根据ABC ACE ABE S S S =+△△△求出32=DE ,在Rt BDE △中,由勾股定理即可得到BE 的长．【详解】解：连接DE .∵3AD AC AE CD ==⊥，.∴AE 是CD 的垂直平分线.∴CE DE =.∴()SSS ACE ADE ≌∴90ADE ACB ∠=∠=︒.在Rt ABC △中,由勾股定理得：5AB ==.∴2BD AB AD =-=.∵ABC ACE ABE S S S =+△△△.∴AC BC AC CE AB DE ⨯=⨯+⨯.∴3435CE DE ⨯=+.∴32=DE .在Rt BDE △中,由勾股定理得：52BE===,故答案为：52．三,解答题（共5小题14题10分,15题12分,16题8分,17题8分,18题10分共48分）14.计算（1()202431-+-+（2）)222-．【答案】（1）（2）4+【分析】本题考查了二次根式的混合运算,乘方和立方根,掌握相关运算法则是解题关键．（1）先化简绝对值,二次根式,乘方和立方根,再计算加减法即可.（2）先根据完全平方公式和平方差公式展开,再计算加减法即可．【小问1详解】20243(1)+-+3214=+--=.【小问2详解】解：)222-32(54)=++--51=+-4=+．15.解下列方程组（1）1342x yx y=+⎧⎨-=-⎩.（2）11233210x yx y+⎧-=⎪⎨⎪+=⎩．【答案】（1）65xy=⎧⎨=⎩（2）312x y =⎧⎪⎨=⎪⎩【分析】本题考查解二元一次方程组.（1）把①代入②得()3142y y +-=-,求出y ,再把y 的值代入①求出y 即可.（2）整理后①＋②得618x =,求出x ,②－①得42y =,再求出y 即可.把二元一次方程组转化成一元一次方程是解题的关键,解二元一次方程组的方法有代入消元法和加减消元法两种．【小问1详解】解：1342x y x y =+⎧⎨-=-⎩①②.把①代入②,得：()3142y y +-=-.解得：5y =.把5y =代入①,得：516x =+=.∴方程组的解是65x y =⎧⎨=⎩.【小问2详解】整理得：3283210x y x y -=⎧⎨+=⎩①②.①＋②,得：618x =.解得：3x =.②－①,得：42y =.解得：12y =.∴方程组的解是312x y =⎧⎪⎨=⎪⎩．16.如图,在四边形ABCD 中,90B Ð=°,3AB =,4BC =,点D 是Rt ABC △外一点,连接CD ,AD ,且12CD =,13AD =．求四边形ABCD的面积【答案】36【分析】本题考查了勾股定理及其逆定理,熟练掌握定理是解题的关键．根据勾股定理计算AC ,根据勾股定理的逆定理判定ADC △是直角三角形,根据面积公式计算即可．【详解】∵90B Ð=°,3AB =,4BC =.∴5AC ===.故AC 得长为5．∵12CD =,13AD =,5AC =.且22222251213CD AC AD +=+==.∴=90ACD ∠︒.∴四边形ABCD 面积为：1122BC AC DC AD + =11512343622⨯⨯+⨯⨯=．17.如图,实数,,a b c 在数轴上对应点的位置如图所示,化简b a +--的结果．【答案】3a b c-+-【分析】本题主要考查了整式的加减混合运算,立方根的性质,算术平方根的性质．观察数轴可得0a b c <<<,再根据立方根的性质,算术平方根的性质化简,然后计算,即可求解．【详解】解：观察数轴得：0a b c <<<.b a +-()a b a a b bc =+--+--()()()a b a a b c b =-+--+--a b a a b c b=-+----+3a b c =-+-．18.如图①,在长方形ABCD 中,已知AB ＝10,AD ＝6,动点P 从点D 出发,以每秒2个单位的速度沿线段DC 向终点C 运动,运动时间为t 秒,连接AP ,把△ADP 沿着AP 翻折得到△AEP ．（1）如图②,射线PE 恰好经过点B ,试求此时t 的值．（2）当射线PE 与边AB 交于点Q 时,是否存在这样的t 的值,使得QE ＝QB ？若存在,请求出所有符合题意的t 的值,若不存在,请说明理由．【答案】（1）1t s =,（2）存在,0.9t s =或5.t s =【分析】（1）先证明∠APD =∠EPA =∠PAB ,得AB =PB =10,根据勾股定理得PC =8,由PD =2=2t ,可得结论,（2）分两种情况：点E 在矩形的内部时,先求解5+,AQ t =再过点P 作PH ⊥AB 于H ,过点Q 作QG ⊥CD 于G ,求解29t PG t -=,2992,t AQ PD PG t t t t-=+=+=+再建立方程求解即可,当点E 在矩形的外部,可得AB =2t ,从而可得答案.【详解】解：（1）如图1, 长方形ABCD ,,AB CD \∥∴∠DPA =∠PAB ,由轴对称得：∠DPA =∠EPA ,∴∠EPA =∠PAB ,∴BP =AB =10,在Rt △PCB 中,由勾股定理得：228,PC PB BC =-=∴PD =2=2t ,∴t =1,（2）存在,分两种情况：当点E 在矩形ABCD 内部时,如图,∵QE =PQ -PE =PQ -DP =PQ -2t ,而QE =QB ,由（1）同理可得：PQ =AQ ,∴QB =AQ -2t ,∵AQ +BQ =AB =10,∴AQ +AQ -2t =10,∴AQ =5+t ,如图,过点P 作PH ⊥AB 于H ,过点Q 作QG ⊥CD 于G ,∴PH =QG =AD =6.而222222636PQ PG QG PG PG =+=+=+,∴2236AQ PG =+,∵AQ =DG =DP +PG ,∴()2236DP PG PG +=+,∵PD =2t ,∴()22236t PG PG +=+,解得：29t PG t-=,∴2992,t AQ PD PG t t t t-=+=+=+∴910t t t∴+=+,解得：0.9t =.经检验,符合题意,当点E 在矩形ABCD 的外部时,如图,∵QE =PE -PQ =DP -PQ =2t -PQ ,同理：AQ PQ =.∵QE =QB ,∴BQ =2t -AQ ,∴AB -AQ =2t -AQ ,∴AB =2t ,∴152t AB ==,（此时P 与C 重合）,综上,存在这样的t 值,使得QE =QB ,t 的值为0.9秒或5秒．【点睛】本题考查长方形的性质,几何动点问题,轴对称的性质,勾股定理的应用,等腰三角形的判定等知识,解题的关键是学会正确画出图形,学会分类讨论,充分利用轴对称的性质解决问题．B 卷（50分）一,填空题（共5小题每题4分共20分）19.比较大小：612-_____12．【答案】>6的大小,然后再比较无理数的大小即可．642>=.611->.∴61122->.故答案为：>．【点睛】本题考查了实数的比较大小,无理数的估算,解题关键是正确掌握实数比较大小的法则．20.已知a 4933113a a a a +---的值为__________．【答案】39223310a -≥130a -≥,求出13a =,再代入求值即可．0≥0≥.∴13a =.∴原式==+393=+.故答案为：393+．21.关于x ,y 的二元一次方程()()32290m x m y m ++-+-=,不论m 取何值,方程总有一组固定不变的解,这组解为__________．【答案】13x y =-⎧⎨=⎩【分析】本题考查了解决含字母参数的二元一次方程组的能力,准确理解题意并能用特殊值法求解时解题关键．分别求出320m +=和20m -=时m 的值,再代入方程求出x ,y 的值即可．【详解】解：()()32290m x m y m ++-+-=.当320m +=时,32m =-.将32m =-代入方程得：3329022y ⎛⎫⎛⎫--+--= ⎪ ⎪⎝⎭⎝⎭.解得：2y =.当20m -=时,2m =.将2m =代入方程得：()322920x +⨯+-=.解得：1x =-.∴不论m 取何值,方程总有一组固定不变的解,这组解为13x y =-⎧⎨=⎩.故答案为：13x y =-⎧⎨=⎩．22.如图,在四边形ABCD 中和,6AB BC ==,60ABC ∠=︒,90ADC ∠=︒．对角线AC 与BD 相交于点E ,若3BE DE =,则ED =__________．【答案】36【分析】过点B 作BM AC ⊥于点M ,过点D 作DN BM ⊥于点N ,连接DM 并延长到H,使得MH MD =,连接AH ,先证明ABC ∴ 为等边三角形,得到6AC AB ==,再由三线合一定理得到132CM AM AC ===．则由勾股定理可得2233BM BC CM =-=,证明()SAS AHM CDM ≌,得到AH CD MAH MCD ==，∠∠,再证明ADH DAC △≌△,得到DH AC =,则132DM AC ==,由3BE DE =,得到34BE BD =,则132142BM ME BM DN ⋅=⋅,据此得到34ME DN =,设3434ME x DN x BE y BD y ====，，，在Rt BME △中,由勾股定理得222BE ME BM -=,可推出223y x -=.在Rt BDN △中,由勾股定理得222161648BN y x =-=,则3BN =,3MN =．利用勾股定理得到226DN DM MN =-=．则2236BD BN DN +=．【详解】解：过点B 作BM AC ⊥于点M ,过点D 作DN BM ⊥于点N ,连接DM 并延长到H,使得MH MD =,连接AH.6AB BC == ,60ABC ∠=︒.ABC ∴ 为等边三角形.6AC AB ∴==.BM AC ⊥ .132CM AM AC ∴===．2233BM BC CM ∴=-=.∵AM CM AMH CMD HM DM ===，∠∠，.∴()SAS AHM CDM ≌.∴AH CD MAH MCD ==，∠∠.∵90ADC ∠=︒.∴90ACD CAD ∠+∠=︒.∴90CAD CAH +=︒∠∠.∴90DAH ADC =︒=∠.又∵AD DA =.∴ADH DAC △≌△.∴DH AC =.∴132DM AC ==.∵3BE DE =.∴34BE BD =.∴34BDM BME S BE S BD ==△△.∴132142BM ME BM DN ⋅=⋅.∴34ME DN =.设3434ME x DN x BE y BD y ====，，，.在Rt BME △中,由勾股定理得222BE ME BM -=.∴229927y x -=.∴223y x -=.在Rt BDN △中,由勾股定理得222BN BD DN =-.∴222161648BN y x =-=.∴BN =MN ∴=．DN ∴==．BD ∴===．故答案为：．【点睛】本题主要考查了全等三角形的性质与判定,等边三角形的性质与判定,勾股定理等等,正确作出辅助线构造全等三角形是解题的关键．23.【阅读材料】平面几何中的费马问题是十七世纪法国数学家皮埃尔·德·费马提出的一个著名的几何问题：给定不在一条直线上的三个点A ,B ,C ,求平面上到这三个点的距离之和最短的点P 的位置,费马问题有多种不同的解法,最简单快捷的还是几何解法．如图1,我们可以将BPC 绕点B 顺时针旋转60°得到BDE V ,连接PD ,可得BPD △为等边三角形,故PD PB =,由旋转可得DE PC =,因PA PB PC PA PD DE ++=++,由两点之间线段最短可知,PA PB PC ++的最小值与线段AE 的长度相等．【解决问题】如图2,在直角三角形ABC 内部有一动点P ,90BAC ∠=︒,30ACB ∠=︒,连接PA ,PB ,PC ,若3AB =,求PA PB PC ++的最小值______．【答案】【分析】将ABP 绕点B 顺时针旋转60︒得到EBF △,连接,PF CE ,作EH CA ⊥交CA 的延长线于点H ,首先证明PA PB PC CE ++≥,求出CE 的值即可解决问题．【详解】解：将ABP 绕点B 顺时针旋转60︒得到EBF △,连接,PF CE ,作EH CA ⊥交CA 的延长线于点H .在Rt ABC △中,∵30ACB ∠=︒,3AB =.∴26,BC AB AC ====.由旋转的性质可知：PA EF =,PBF △,ABE 是等边三角形.∴PF PB =.∴PA PB PC EF FP PC ++=++.∵EF FP PC CE ++≥.∴当C P F E 、、、共线时,PA PB PC ++的值最小.∵90BAC ∠=︒,60=︒∠BAE .∴180906030HAE ∠=︒-︒-︒=︒.∵,3EH AH AE AB ⊥==.∴1322EH AE ==,2AH ==.∴CE ==.∴PA PB PC ++的最小值为故答案为：【点睛】本题考查了费马点求最值问题,涉及到的知识点有旋转的性质,等边三角形的判定与性质,勾股定理,以及两点之间线段最短等知识点,读懂题意,理由旋转作出正确的辅助线是解本题的关键．二,解答题（共3小题24题8分,25题10分,26题12分共30分）24.如图,在一条笔直的东西方向的公路上有A ,B 两地,相距500米,且离公路不远处有一块山地C 需要开发,已知C 与A 地的距离为300米,与B 地的距离为400米,在施工过程中需要实施爆破,为了安全起见,爆破点C 周围半径260米范围内不得进入．（1）山地C 距离公路的垂直距离为多少米？（2）在进行爆破时,A ,B 两地之间的公路是否有危险需要暂时封锁？若需要封锁,请求出需要封锁的公路长．【答案】（1）240m（2）需要,200m【分析】本题考查了勾股定理及其逆定理的应用.（1）过C 作CD AB ⊥,因为222300400500+=,由勾股定理的逆定理得ABC V 是直角三角形,通过三角形的面积转化,即可求解.（2）以点C 为圆心,260m 为半径画弧,交AB 于点E ,F ,连接CE ,CF ,由等腰三DE DF =,比较CD 与CE 的大小即可判断,由勾股定理得DE =,即可求解．掌握勾股定理及其逆定理,能作出适当的辅助线,将实际问题转化为勾股定理及其逆定理是解题的关键．【小问1详解】解：由题意得500m AB =,300m AC =,400m BC =.如图,过C 作CD AB ⊥,222300400500+=.222AC BC AB ∴+=.ABC ∴ 是直角三角形,且90ACB ∠=︒,1122AC BC AB CD ∴⋅=⋅.1130040050022CD ∴⨯⨯=⨯⋅.解得：240CD =.答：山地C 距离公路的垂直距离为240m .【小问2详解】解：公路AB 有危险需要暂时封锁,理由如下：如图,以点C 为圆心,260m 为半径画弧,交AB 于点E ,F ,连接CE ,CF .则260EC FC ==.CD AB ⊥ .DE DF ∴=.由（1）可知,240CD =.240260< .∴有危险需要暂时封锁.在Rt CDE △中.22DE CE CD =-22260240=-100=.2200EF DE ∴==.即需要封锁的公路长为200m ．25.科华数学之星在解决问题：已知123a =+,求2281a a -+的值．他是这样分析与解决的：2a ===2a ∴-=2(2)3a ∴-=,2443a a -+=.241a a ∴-=-.()222812412(1)11a a a a ∴-+=-+=⨯-+=-．请你根据小明的分析过程,解决如下问题：（1=,=．（2+ ．（3）若a =,请按照小明的方法求出2481a a -+的值．【答案】（1-,2-（2）4（3）5【分析】本题考查了二次根式的化简求值,分母有理化．熟练掌握分母有理化,整体代入法求代数式的值,是解决本题的关键．（1）根据例题可得：对每个式子的分子和分母同时乘以分母的有理化因式化简即可.（2）将式子中的每一个分式进行分母有理化,问题随之得解.（3）根据小明的分析过程,1a -=221a a -=,可求出代数式的值．【小问1详解】==.2==．,2-．【小问2详解】原式11(311)422=--=-+=．【小问3详解】∵1a ==.1a ∴-=．2(1)2a ∴-=,2212a a -+=．221a a ∴-=．∴原式()24214115a a =-+=⨯+=．26.数学活动课上,老师出示两个大小不一样的等腰直角ABC 和ADE 摆在一起,其中直角顶点A 重合,AB AC =,AD AE =,90BAC DAE ∠=∠=︒．（1）用数学的眼光观察．如图1,连接B ,C ,判断B 与C 的数量关系,并说明理由.（2）用数学的思维思考．如图2,连接BE ,B ,若F 是BE 中点,判断AF 与B 的数量关系,并说明理由.（3）用数学的语言表达．如图3,延长C 至点F ,满足AF AC =,然后连接DF ,BE ,当AB =,1AD =,ADE 绕A 点旋转得到D E F ，，三点共线时,求线段EF 的长．【答案】（1）BD CE =,理由见解析（2）2CD AF =,理由见解析（3）2或622+【分析】本题考查全等三角形的判定与性质,等腰直角三角形的性质,勾股定理等知识,灵活运用三角形的判定来判定三角形全等是解题的关键．（1）利用SAS 证明BAD CAE ≌,从而得解.（2）点B 作BQ AE ∥交AF 的延长线于点Q ,证明()AAS FAE FBQ ≌得到AF FQ =12=AQ ,再证明()SAS DAC QAB ≌,得到2CD BQ AF ==,即得证.（3）分①当点D E 、在直线AC 下方时,②当点D E 、在直线AC 上方时两种情况讨论即可得解．【小问1详解】解：BD CE =,理由：∵AE DA =,90BAD BAC CAD CAD EAD CAD CAE ∠=∠+∠=︒+∠=∠+∠=∠,AB AC =,∴()SAS BAD CAE ≌.∴BD CE =.【小问2详解】2CD AF =,理由：点B 作BQ AE ∥交AF 的延长线于点Q .∴Q EAF ∠=∠,EFA QFB ∠=∠.∵F 是BE 中点,则FE FB =.∴()AAS FAE FBQ ≌.∴AF FQ =12=AQ ,BQ AE AD ==.∵BQ EA ∥.∴180QBA EAB ∠+∠=︒.∵360180DAC EAB DAE BAC ∠+∠=︒-∠-∠=︒.∴DAC QBA ∠=∠.∵AB AC =.∴()SAS DAC QAB ≌.∴2CD BQ AF ==.【小问3详解】ADE 旋转得到D E F ，，三点共线.①当点D E 、在直线AC 下方时,如图所示,过点A 作1AM D F ^于M .∵Rt ADE 是等腰三角形,111AD AE AD AE ====,1AM D F ^.∴11D E ==,1AM D M =12=11D E 2=.在Rt AFM 中,AF AB ==.∴62MF ===.∴11D F MF D M =-622=.即ADE 旋转得到D E F ，，三点共线时,DF 622=.②当点D E 、在直线AC 上方时,如图所示,过点A 作2AN D F ^于N .同理,22D F MF D M =-2=.即ADE 旋转得到D E F ，，三点共线时,DF 622+=.综上所述,线段DF 的长为：622或622+．。

上海卷01(高考仿真模拟) (金榜题名)决战2023年高考数学黑马逆袭卷附答案

2023年高考数学黑马逆袭卷（上海专用卷01)数学（考议时间：120分钟议卷满分：150分）注意事项：1.答卷前，考生务必将自己的姓名、准考证号填写在答是E卡上。

2.回答选择题时，逃出每小题答案后，用铅笔把答是里卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

回答非选择题时，将答案写在答；题卡上。

写在本试卷上无效。

3.考试结束后，将本试卷和答是E卡－并交回。

一、填空题〈本大题共12题，1-6每题4分，7-12＜！事题5分，共54分〉1.函数y= ./2i+J.+log2 (2-x）的定义域为2定义A-B＝｛对xeA且X!e B），若A={l,3,5,7,9},B = {2,3,5｝，则J(A-B)v(B-A）＝一－3四（吨的展开式中第坷的撒切翩翩之比山则n.＝4.已知向量a=(-1,2），向最b=(-3,4），则向量。

在b方向上的投影向量为一一一·5若复数z＝字型（i为应数单位〉在复平而上对应的点在第四象｜坝，则实敛。

的取值范围l+LI为·6.i谱写出－组由6个不同的自然数从小到大排列的数据，这组数据要满足以下两个条件：①第70百分位数为6，②极差为6.－7.如图，己知正三梭校ABC-A,B,C，的底而边长为lcm，高为5cm，一质点自A点出发，沿莉三棱校的侧丽绕行两周到达A，点的；最短路线的长为’Ai l飞U～，，，，c,B8.非空集合A中所有元素乘积记为T(A).己失11综合M= {l,4,5,7,8），从综合M的所有非空子集中任选－个子如，贝I J T(A）为偶数的概率是（结果用最简分数表示）9.设A(2,0）为平面上一定点，Pl s in[ 2t－王j,co s[ 2t－王l I为动点，则当t由0变化到旦时，l l 3) l 3JJ线段AP 扫过的面积是一一一－－10.叫窒αb c, (i =与－b 的夹角为0』，若对于任意，，，/2 > 0，总有k >!cos向－co吗｜，贝忱的毅小值为11.费马点是指位于三角形内旦到三角形三个T§j点距离之和最小的点。

慧净电子-单片机学习板原理图

�
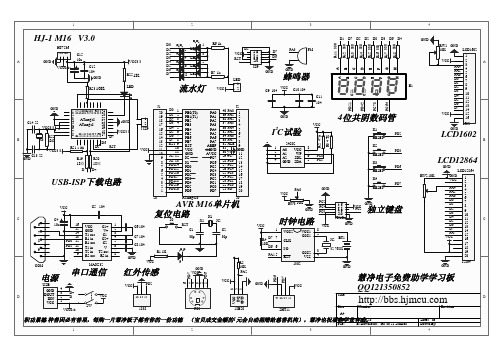
D7 R13 330
D5 R14 330
D2 R15 330
D0 R16 330
D3 R17 330
D6 R18 330
D4
GND RW1 GND 10K VCC LCD1602 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 1602 A
A
D
G
LED
CS1
CS2
CS3
1
2
3
4
HJ-1 M16 V3.0
HT7536 1 2 3 C15 10u C12 104 GND R23 10K A GND VCCusb VCC3.3 D0 D1 D2 D3 D4 D5 D6 D7 1 2 4 LED 3 LED 5 6 LED 7 8 LED
D1 R11 330 R12 330 R6 1k D5 VCC RST 16 27 38 49 5 10 ISP R7 1k LED 1 2 GND D7 D6 PA3 FM
USB-ISP下载电路
VCC
AVR M16单片机复位电路 X1 S0
X1 X2 RST C1 30p C2 30p
独立键盘
16 15 14 13 PD0 12 PD1 11 10 9
VCC C1+ GND V+ T1 out C1R1 in C2+ R1 out C2T1 in VT2 in T2 out R2 out R2 in MAX232
1 2 3 4 5 6 7 8
C6 104 C7 104 C8 104 R1 1K GND VCC 9
VCC 1 R4 D7 7 10K D6 6 PA1 5 R5 10K PA2 PD6 VCC 3 2 1 GND

摩托车车辆识别代号VIN

Q/ZS 宗申产业集团有限公司企业标准Q/ZSJJ 3-2006代替Q/ZSJJ 3-2006摩托车车辆识别代号（VIN）编制规则2006-12-15发布2006-12-20 实施宗申产业集团有限公司发布前言本标准与Q/ZSJJ 3-2006《摩托车车辆识别代号（VIN）编制规则》（2006年8月26日发布）的异同：——将4.3.5.1中及表6中的“改进次数代码”删除；——将电动摩托车驱动电机额定功率规格代码按驱动电机的额定功率范围进行编号。

本标准由宗申产业集团有限公司提出。

本标准由宗申产业集团有限公司技术中心统一归口管理。

本标准由宗申产业集团有限公司技术中心主任吴健批准。

本标准起草单位：宗申产业集团有限公司技术中心。

本标准主要起草人：龙腾明。

本标准所代替标准的历次版本发布情况为:——Q/ZSJ 93-2001；——Q/ZSJJ 3-2004：——Q/ZSJJ 3-2006（2006年8月26日发布）。

Ⅰ摩托车车辆识别代号（VIN）编制规则1范围本标准规定了宗申产业集团有限公司所生产的轻便摩托车和摩托车车辆识别代号（VIN）的编制规则、标示要求。

本标准适用于宗申产业集团有限公司（以下简称“集团”）所生产的轻便摩托车和摩托车（以下简称“车辆”）车辆识别代号（VIN）的编制。

2规范性引用文件下列文件中的条款通过本标准的引用而成为本标准的条款。

凡是注日期的引用文件，其随后所有的修改单（不包括勘误的内容）或修订版均不适用于本标准，然而，鼓励根据本标准达成协议的各方研究是否可使用这些文件的最新版本。

凡是不注日期的引用文件，其最新版本适用于本标准。

GB 16735-2004 道路车辆车辆识别代号（VIN）3术语和定义GB 16735-2004中的术语和定义适用于本标准。

4编制规则4.1 车辆识别代号（VIN）的基本构成车辆识别代号（VIN）由世界制造厂识别代号（WMI）、车辆说明部分（VDS）、车辆指示部分（VIS）3部分17位字码组成（见图1）。

F G H J K代表的年份

F G H J K代表的年份
代表车架号生产日期的是车架号第十位的字符，代表年份的字符为1、2、3、4、5、6、7、8、9、A、B、C、D、E、F、G、H、J、K、L、M、N、P、R、S、T、V、W、X、Y这30个字符，30年一个轮回周期，从2001年起为1。

比如说，车架号第十位如果是F G H J K的话，对应年份就是2015、2016、2017、2018、2019。

代表年份的英文字母“I”、“O”、“Q”、“Z”“U”在车架号上都不被使用，是为了避免与1、0、2、V混淆。

车辆识别号码（Vehicle Identification Number,或车架号码），简称VIN，是一组由十七个英数组成，用于汽车上的一组独一无二的号码，可以识别汽车的生产商、引擎、底盘序号及其他性能等资料。

VIN中的每个字符都具有特定的含义，而且整个VIN分为多个部分。

第一位标识原产国/地区，第二位分标识车辆的制造商，接下来的三位对所有制造商都是一致的，第九位始终为校验位，第十位是车型年码（每年都有一个代码字符），地第十一位是工厂代码（表示车辆的组装工厂），最后六位是产品序列号。

STC15F2K60S2系列单片机总体介绍

STC15F2K60S2系列单片机总体介绍1.STC15F2K60S2系列单片机简介STC15F2K60S2系列单片机是STC 生产的单时钟/机器周期(1T)的单片机，是高速/高可靠/低功耗/超强抗干扰的新一代8051单片机，��代��技术，��，指�代��代��技术，��，指�代��指�代��容传统8051,但速度快8-12倍。

��高�度��高�度R/C 时钟(±0.3%)，±1%温飘(-40℃~+85℃)，常温下温飘±0.6%(-20℃~+65℃)，ISP 编程时5MHz~35MHz 宽范围可设置，可彻底省掉外�昂贵的晶振和外�复位电路(��已��高可靠复位电路，ISP 编程时8级复位门槛电压可选)。

3路CCP/PWM/PCA ，8路高速10位A/D 转换(30万次/秒)，�置2K 字节大容量SRAM ，2组超高速异步串行通信端口(UART1/UART2，可在5组管脚之间进行切换，分时复�可作5组串口使�)，1组高速同步串行通信端口SPI ，��串行口通信��串行口通信�串行口通信/电机控制/强干扰场合。

在 Ke�lC Ke�l C 开发环境中，选择 Intel 8052 编译，头文件包含<reg51.h>即可现STC15系列单片机��STC-Y5超高速CPU �核，在相同的时钟频率下，速度又比STC 早期的1T 系列单片机(如STC12系列/STC11系列/STC10系列)的速度快20%.1.增强型 8051 CPU ，1T ，单时钟/机器周期，速度比普通8051快8-12倍2.工作电压：STC15F2K60S2 系列工作电压：5.5V - 4.5V （5V 单片机）STC15L2K60S2 系列工作电压：3.6V - 2.4V （3V 单片机）3.8K/16K/24K/32K/40K/48K/56K/60K/61K/63.5K 字节片�Flash 程序存储器，可擦写次数10万次以上4.片�大容量�大容量2048字节的的SRAM ，包括常规的256字节RAM <�data> 和��扩展的1792字节XRAM <xdata>5.大容量片�EEPROM ，擦写次数10万次以上6.ISP/IAP ，在系统可编程/在应�可编程，�需编程器，�需仿真器7.共8通道10位高速ADC ，速度可达30万次/秒，3路PWM 还可当3路D/A 使�8.共3通道捕获/比较单元(CCP/PWM/PCA)----也可�来再实现3个定时器或3个外�中断(支持上升沿/下降沿中断)或3路D/A9.利�CCP/PCA高速脉冲输出功能可实现3路9 ~ 16位PWM (每通道占�系统时间小于0.6%)10.利�定时器T0、T1或T2的时钟输出功能可实现高�度的8 ~ 16位PWM (占�系统时间小于0.4%)11.��高可靠复位，ISP编程时8级复位门槛电压可选，可彻底省掉外�复位电路12.工作频率范围：0MHz ~ 28MHz，相当于普通8051的0MHz～336MHz13.��高�度R/C时钟(±0.3%)，±1%温飘(-40℃~+85℃)，常温下温飘±0.6%(-20℃~+65℃)，ISP编程时��时钟从5MHz~28MHz可设(5.5296MHz / 11.0592MHz / 22.1184MHz)14.不需外�晶振和外�复位，还可�外输出时钟和低电平复位信号15.两组超高速异步串行通信端口(可同时使�)，可在5组管脚之间进行切换，分时复�可当5组串口使�：串口1(RxD/P3.0, TxD/P3.1)可以切换到(RxD_2/P3.6, TxD_2/P3.7),还可以切换到(RxD_3/P1.6, TxD_3/P1.7)；串口2(RxD2/P1.0, TxD2/P1.1)可以切换到(RxD2_2/P4.6, TxD2_2/P4.7)注意：建议�户将串口1放在 P3.6/P3.7 或 P1.6/ P1.7 (P3.0/P3.1 作下载/仿真�)；若�户不想切换，坚持使� P3.0/P3.1 或作为串口1进行通信，则务必在下载程序时，在软件上勾选“下次冷启动时，P3.2/P3.3为0/0时才可以下载程序”。

广东省惠州市2024-2025学年高三上学期第二次调研考试数学含解析

惠州市2025届高三第二次调研考试试题数学全卷满分150分，时间120分钟．2024.10注意事项：1答题前，考生务必将自己的姓名、准考证号、座位号、学校、班级等考生信息填写在答题卡上．2．作答单项及多项选择题时，选出每个小题答案后，用2B铅笔把答题卡上对应题目的答案信息点涂黑如需改动，用橡皮擦干净后，再选涂其它答案，写在本试卷上无效．3非选择题必须用黑色字迹签字笔作答，答案必须写在答题卡各题指定的位置上，写在本试卷上无效一、单项选择题：本题共8小题，每小题满分5分，共40分．在每小题给出的四个选项中，只有一项符合题目要求，选对得5分，选错得0分l已知集合A={�2�x<5}，集合B={xl x2-4x<O}，则A^B=( ）A.(o,s)B.[2,4) c.(4,5) o.(-00,O)u[2,+oo)2已知复数z满足z2+l = 0,则lz+ll=( )A.3B.2C.l D．五3已知等差数列{a,,}前9项的和为27，如＝8，则a.oo= ()A.100B.99C.98 0.974在正方体ABCD-'4iB1Cp1中，棱BC,A戊的中点分别为E,F，则直线E F与平面ABBA所成角的正弦值为（）石 B. 森2石 D. 痀5已知向凳a,b满足：a=(✓3,1)，叫＝石，（兹－b ）·6=3，则向豐6在向榄五上的投影向榄为（）A胃气）B[竿i)C［告）叶亨订6已知函数f(x)=log2厅－2ax),aeR,则“a:s;O"是“函数f(x)在(1，七吩上单调递增＂的（）A充分不必要条件B必要不充分条件C充要条件D既不充分也不必要条件7已知“水滴＂的表面是一个由圆锥的侧面和部分球面（常称为“球冠”)所围成的几何体如图所示，将“水滴＂的轴截面看成由线段AB,AC 和优弧BC所围成的平面图形，其中点B,C 所在直线与水平面平行，AB和AC与圆弧相切已知“水滴＂的“竖直高度”与“水平宽度”(“水平宽度”指的是平行千水4平面的直线截轴截面所得线段的长度的最大值）的比值为－，则sin乙BAC=<A3416 24A.-B .- C.—D .—55252538在统计某学校所有选择理科和文科的学生数据中，发现理科生多千文科生，女生多千男生，则关千本次学生样本的数据中，结论一定成立的是（）A理科男生多千文科女生B文科女生多千文科男生C理科女生多干文科男生D理科女生多于理科男生二、多选题：本题共3小题，每小题6分，共18分．在每小题给出的四个选项中，有多项符合题目要求全部选对的得6分，部分选对的得部分分，有选错的得0分9某公司为保证产品生产质量，连续10天监测某种新产品生产线的次品件数，得到关千每天出现的次品的件数的一组样本数据：3,4, 3, 1,5, 3, 2,5, 1, 3则关千这组数据的结论正确的是（）A极经是4B众数小千平均数c ．方差是2D数据的第80百分位数为4.510函数f (x) =A sin (cvx+ <p)(A> O,a> > 0树<§）的部分图象如图所示，现将f(x )的图象向左平移巴6个单位长度，得到函数g(x)的图象，则下列结论正确的是(2亡7兀X12兀A.<p =－一6B.(i)=2c ．函数）1= xf (x ＋王）是奇函数12 D.g (x )=2c os （2x -¾)II 如图，心形曲线L:x 2+(y -|入扩＝1与Y 轴交于A ,B 两点，点P 是L 上的一个动点，则（）ypXBA点［孚叩11(-1,1.）均在L 上B.IO月的最大值和最小值之和为3C 点P 的纵坐标的最大值为J5D.I PAl+IPB 怍2石三、填空题：本题共3小题，每小题5分，共15分．12．在（x+1)5的二项展开式中，各项的系数和为13椭圆于fi =l (a >b>O )的左、右顶点分别是A 、B ，左、右焦点分别是R 、F2，若I A F.I ,I F.Fzl,IF.纠成等比数列，则此椭圆的离心率e=.14若关千X的方程ln(ax4)＝[二了有实根，则a江护的最小值为四、解答题：本题共5小题，共77分解答应写出必要的文字说明、证明过程或演算步骤15（本题满分13分）已知函数f(x)=�X 2一x-2ln x(l)求曲线y=f(x)在点(l,f(1)）处的切线方程：(2)求函数f(x)在区间[1,e]上的晟小值16（木题满分15分）如图，四棱锥P-ABCD中，PA J_底面ABCD,AB II CD,AD=CD=l.乙BAD=120'，乙ACB=90°.D C(l)求证：BC上平面PAC:(2)若PA＝石，求平面PCD与平面PCA夹角的余弦值l7 （本题满分15分）已知双曲线C:x2-y2=l及直线l:y＝虹－1(])若l与C有两个不同的交点，求实数K的取值范围：(2)若l与C交千A,B两点，O是坐标原点，且t:.OAB的面积为J5，求实数K的值18（本题满分17分）记t:,.ABC的内角A,B,C的对边分别为a,b,c,已知a<b<c且tanA,tanB, t anC均为整数(I)求tanA,tanB, t anC的值，(2)设AC的中点为D,求乙CDB的余弦值19（本题满分17分）若数列{a,,}(1 s n s k, n E N*, k EN*）满足a,，叶0,1}，则称数列{a,,｝为K项0-1数列，由所有k项0-1数列组成集合M ks4)时，a,,=0,求数列{(-l)飞，｝的所有(])若伈｝是12项0-1数列，当且仅当n=3p(p E N*,p项的和；(2)从梊合M人．中仔意取出两个数列｛动，｛丸｝，记X=区|a,－b/|i=I＠求随机变量X的分布列，并证明：E(X)＞一：k2＠若用某软件产生k(k2'.:2)项0-1数列，记事件A =“第一次产生数字1"'B=“第二次产生数字l"'且0<P(A ) <1,0<P (B) <l若P(BIA)<P(B区），比较P(Al B)与P(AI B )的大小惠州市2025届高三第二次调研考试试题高三数学参考答案与评分细则一、单项选择题：本题共8小题，每小题满分5分，共40分．题号2345 678答案BDc BAADcl 【解析】因为B ={xl O < x <4}，所以A nB={xl 2�x<4}故选：B 2【解析】因为z 2+l=O,即z 2= -1,所以z ＝土，所以卜＋11=11士11=f言75了＝J5故选：D.的公妇为d，由已知得：｛9a, +36d =273【解析】设等劳数列{a ,,}，解得a,= -1, cl = 1,a, +9d =8所以a 100=a , + 99d = -1 + 99 = 98故选：C.4【解析】连接FB ，在正方体ABCD -f\B ,C 1D 1中，BC..l 平面A BB A ，棱BC 的中点为E,则BE..l 平面A BB I A ，而BFc 平面A BB A ，故BE..l BF,则乙EFB 即为迎线EF 与平面A BB I A 所成角，设正方体棱长为2,则BE=l,BF=.JB I F 2+B阻＝j了I ＝心，BE1✓6则EF =✓BF 2+BE 2＝拆，故sin乙E FB =－－＝－－＝一－故选：BEF拆6A lni ,DI L ,“K ,＇,'…,'} ，夕,j A5【解析】由例＝石，（2ii-b)·b =3,得2li·b -lbi 2=2li·b -2=3,即a 6=－525由已知得la:1=2,所以向摄6在向量a上的投影向量为彗向＝＼卢＝｀石，l)＝厂产，i)故选：A .as l6【解析】若函数f(x)在（l，切）上单调递增，则｛，解得a5-，Il-2a之02所以“a�O"是＂函数f(x)在(1.冲~)上单调递增”的充分不必要条件．故选：A7【解析】设优弧BC 所在圆的圆心为O,半径为R,连接OA ,OB ,OC 易知“水滴＂的＂竖直商度”为OA +R, OA +R 45 “水平宽度”为2R,由题意知＝一，解得OA=－R 因为AB 与圆弧相切千点B ,2R 3 3OB R 3 所以B 在Rt 心ABO 中，sin乙BAO =—=—=－冗OA 5 :::...R5，又乙BAO e l 0，一，（』4所以COS乙BAO=.Jl-sm 汔BAO ＝一，由对称性知，5乙BAO ＝乙CA O,则乙BAC=2乙BAO,3 4 24所以sin 乙BAC=2sin 乙BAOcos 乙BA0=2x-=-x-=—故选：D.5 5 258【解析】根据已知条件设理科女生有x 1人，理科男生有X 2人：文科女生有）'1人，文科男生有）5人；根据题意可知：X 1 + X 2 > Y i + Y 2'X i +Y i > X 2 + Y 2'根据同向不等式可加的性质有：X 1 + X 2 + X 1 + Y 1 > Y 1 + Y 2 + X 2 + Y 2'即X 1> Y 2，所以理科女生多千文科男生，C正确其他选项没有足够证据论证故选：C .二、多项选择题：本题共3小题，每小题满分6分，共18分．在每小题给出的四个选项中，有多项符合题目要求全部选对得6分，部分选对得部分分，有选错的得0分．题号I 9 I 10 I 11全部正确选项I A D I ABO I ACD9【解析】数据从小到大排列为：1,1, 2, 3, 3, 3, 3, 4, 5, 5对千A,该组数据的极差为5-1=4,故A正确：对于B,众数为3,平均数为lx2+2+3x4+4+5x210=3,两者相等，故B错误；对干C,方差为而伈－3)2x2+(2-3)2xl+(3-3)2x4+(4-3)2xl+(S-3)2x2] = 1.8,故C错误，对千D,10x80%=8,这组数据的第80百分位数为第8个数和第9个数的平均数4.5,故D正确故选：AD.10【解析】由图像可知：f(x)ma x = 2, A= 2:又f(0)=2s叩＝－l,故sinrp＝一L，又lrp|＜巴，所以rp＝－巴，所以A项正确，2 2 6已知f（气＝2sin（五0－勹＝0,由五点作图法可知：卫坛－巴＝亢，解得：OJ=2'所以B项正l2 12 6 l2 6确；故f(x) =2sin（三）则xj.（咕）＝2xsin2x设h(x)=xf.（咕）＝2xsin2x则h(-x)= 2(-x)sin(-2x) =2.xsin2x= h(x)，所以函数y=.-1;小号）是偶函数，故C项错误g(x)=f(x十艺）＝2s i n[2(x+：)－去］＝2s i n(2x＋艺）＝2c o s[�-(2x＋艺）］=2cos甘－2x)=2cos（三），所以D项正确故选：ABD.五II【解析】A选项，经验算，点(—,0和(-1,1)的坐标满足曲线L的方程x2 +(y-lxl)2 =L所以` o)和(-l,l）均在L上故2A项：确B 选项，I OP l ＝心三了，因为曲线L:x江(y-I 入扩＝l 关千Y 轴对称，当x 以0时，x 2 +(y-x)2 =l,设x=cos0, y-x= s in0,0e[－豆］，2 2.l+co s20 所以IOPl 2=.,\,:2+y 2=cos 20+(cos0+sin0)2 =l+�+sin20 23 1 3森l =-＋sin20+－cos20=－＋—sin (20 + rp ),其中tanrp ＝一，2 22 22 所以OP l min =[工石－�,10P 1m ax =[工石＋12 2 2 2 2 2，所以10月的最大值和最小值之和为石，故B项错误；C 选项，因为曲线L:x 2+(y -l x 忙＝1关千Y 轴对称，当x习0时，x 2+(y-x)2 =I ,则(y-x)2 =1-.,\,，2，所以y =x 土』7了因求，占P 的纵坐标的最大值，故取y =x+.[i':了，2又y 2=(x ＋石二了）＝1+2x../I 二了＝1+2[x.了7平1+.,\,;2+(l －入＂2)=2（当且仅当x 2＝上时等号2成立），所以y�.,fi ，故C项正确；x -D 选项，IPA I +I P B� 2✓3等价千点P 在椭圆上－＋—＝1内（包含椭圆），由B 项可知，即满足：322(cos0+sin0)2 +3cos 20 � 6,即2(l+sin20)+3(1+cos20)�6，整理得：23 4sin20 + 3cos20 � 5,即5sin(20+/3）�5'其中其中tan/3＝－，即sin(20+/3）�l 恒成立，则故D4项正确故选：A BD .三、填空题：本题共3小题，每小题5分，共15分．12.32五5314.e i12.【解析】当x =l 时，二项式展升式各项的系数和为25=32故答案为：3213【解析】由题意知I Mi l =a-c,I F;Fz l =2c,IF;科＝c+a,且三者成等比数列，则IFiFi l 2= IAF;I .I F;BIl石石即4c 2= (c-a )(c +a )= c 2 -a 2,所以e 2=－，所以e =—故答案为：—－55514【解析】设方程ln （釭＋勹＝k的实根为X。

光学玻璃

光学玻璃
由于具有良好的光学性能，诸如光线的高透过率和环境的稳定性，光学玻璃因此成为制作光学产品最为常见的材料。

不同的光学部件需要不同的光学玻璃材料，下列图表为市面上常见的光学玻璃材料的折射率和色散系数的汇总。

具体的选择取决于光学性能的要求、环境适宜性、可加工性和成本。

光学玻璃材料主要参考以下两个参数：折射率及其色散指数(阿贝数)。

当你在选择定制部件的材料时，可能需要参考一些特定参数，下列数据将有助于你选择正确的玻璃材料，我们的工程师将根据客户产品的应用领域为客户选择材料提供力所能及的帮助以及参考建议，下列数据来源于成都光明、肖特、豪雅、小原四大玻璃材料生产商，你可以点击链接以获取更为详细的数据。

对比数据
代码折射率色散系数CHINESE SCHOTT OHARA HOYA QK 系列
470668 1.47047 66.83 H-QK1FK1 FSL1 FC1 487700 1.48746 70.04 H-QK3
487704 1.48749 70.44 H-QK3L N-FK5 S-FSL5 FC5
K 系列
500621 1.49967 62.07 K1 K11
500660 1.50047 66.02 H-K2BK4 BSL4 BSC4 505647 1.50463 64.72 H-K3 BK5
508611 1.50802 61.05 K4A ZKN7 ZSL7 ZNC7 510634 1.51007 63.36 H-K5BK1 BSL1 BSC1 511605 1.51112 60.46 H-K6K7 NSL7 C7。

2025中考数学二次函数压轴题专题练习22 胡不归模型(学生版+解析版)

专题22胡不归模型一、知识导航在前面的最值问题中往往都是求某个线段最值或者形如PA+PB最值，除此之外我们还可能会遇上形如“PA+kP矿这样的式子的最值，此类式子一般可以分为两类问题：（1)胡不归问题，（2)阿氏固．本文简单介绍“胡不归“模型【故丰介绍l从前有个少年外出求学，某天不幸得知老父亲病危的消息，便立即赶路回家．根据＇，两点之间线段最短＂，虽然从他此刻位置A到家B之间是一片砂石地，但他义无反顾踏上归途，当赶到家时，老人刚咽了气，小伙子追悔莫及失声痛哭邻居告诉小伙子说，老人弥留之际不断念叨着“胡不归？胡不归？(“胡“同“何”)而如果先沿着驿道AC先走一段，再走砂石地，会不会更早些到家？A VZ R驿道［棋型建立）如图，一动点P在直线MN外的运动速度为VI'在直线MN上运动的速度为忆，且冈＜忆，A、BAC BC为定点，点C在直线MN上，确定点C的位置使－－＋—－的值最小V2 V,MBA V2 CN（问题分析）AC B C l V V了三(B C+t AC]，记k=t即求BC+kAC的最小值．（问题解决I构造射线AD使得sin乙D儿'V=k,CH/ A C=k, CH=kAC.M A勺、＂、、,'CCH、、、令si11a＝一＝k H、、AC、、、、、、忽CH=kAC BN将问题转化为求B C+CH最小值，过B点作BH上AD交J\1N于点C,交A D于H，点，此时BC+CH取到最小值，即BC+kAC最小．B，，，，M A义”、、、、、、、'佥H、、、、、艾N（棋型总结】在求形如“PA+kP矿的式子的最值问题中，关键是构造与kPB相等的线段，将“1刃＋肘功”型问题转化为“PA+PC'型．而这里的PB必须是一条方向不变的线段，方能构造定角利用三角函数得到kPB的等线段石如图， 6.ABC中，AB=AC=IO,ta叭＝2,BE_I_AC于点E,D是线段BE上的一个动点，则CD+—-BD的晟5小值是A8c乔（分析）本题关键在于处理”__:_BD",考虑tanA:o2,t,. ABE三边之比为1:2✓5,石上AB交AB于H点，则DH=－-BD,5石sin乙钮E—，故作D H5A Ac8c问题转化为CD+DH最小值，故C、D、H共线时值最小，此时CD+DH=CH= 8£=4✓5【小结1本题简单在于题目已经将B A线作出来，只需分析角度的三角函数值，作出垂线D H即可斛决问题，若稍作改变，将图形改造如下·B二三则需自行构造a,如下图，这一步正是解决“胡不归”问题关锭所在．B二三渗石，l sina＝一－B夕AIII、、I、$IIIIIIHIIcI三、中考真题演练I.(2023山东中考真题）已知抛物线y=-x2+b入＋c与x轴交于A,B两点，与y轴交千点C(0,4)，其对称轴为x=－一．3y A｀l�l(1)求抛物线的表达式：(3)如图2,动点P在直线AC上方的抛物线上，过点P作直线AC的垂线，分别交直线AC,线段BC千点E,图2F，过点F作FG..lx轴，垂足为G,求FG＋丘F P的最大值．2.(2023黑龙汀绥化中考真题）如困，抛物线Y,＝少:2+bx+c的图象经过A(-6,0),8(-2,0), C(0,6)三点，且一次函数y＝虹＋6的图象经过点B.-8 -7l广X-8-7I 2(l)求抛物线和一次函数的解析式．(3将抛物线Y,=a.,\2 +bx+c的图象向右平移8个单位长度得到抛物线Y2，此抛物线的图象与X轴交于M,N两点(M点在N点左侧）．点P是抛物线Y2上的一个动点且在过线NC下方已知点P的横坐标为m.过点P作PD上NC于点D求m为何值时，CD+�PD有最大值，最大值是多少？2(2023四川内江中考真题）如图，在平面丑角坐标系中，抛物线y=w.2+b入＋c与x轴交千B(4,0),C(-2,0) 两点与y轴交于点A(0,-2)I •(I)求该抛物线的函数表达式；(2)若点P是直线AB下方抛物线上的一动点，过点P作轴的平行线交AB千点K,过点P作y轴的平行线l交r轴于点D,求与－PK+PD的最大值及此时点P的坐标；24.(2023天津中考真题）已知抛物线y=-入2+bx+c(b,c为常数，c>I)的顶点为P,与X轴相交于A,bB两点（点A在点B的左侧），与Y轴相交于点C,抛物线上的点M的横坐标为m,且－c<m＜一，过点M2作C,垂足为N(I)若b=-2,c=3.＠求点P和点A的坐标；＠当仙V＝石时，求点M的坐标；(2)若点A的坐标为（气',0)，且MPII A C,当A N+3M N=9✓2时，求点M的坐标k5. (2023福建泉州模拟预测）如图，已知抛物线y=�(x+2)(x-4)(k为常数，且k>O)与X轴从左至右8§依次交千A,8两点，与Y轴交于点C,经过点B的宜线y=－—-x+b与抛物线的另一交点为D.y yX备用图(I)若点D的横坐标为－5,求抛物线的函数表达式；(2)在（l)条件下，设F为线段BD上一点（不含端点），连接AF,一动点M从点A出发，沿线段AF以每秒l个单位的速度运动到F,再沿线段FD以每秒2个单位的速度运动到D后停止．当点F的坐标是多少时，点M在整个运动过程中用时最少？6.(2023广西柳州二模）已知抛物线y＝少:2+b入＋c(a丑0)过点A(LO),8(3,0)两点，与Y轴交于点C, OC=3,。

基本偏差值

-2
-4
-6
0
0
+2
+4
+6
+10
+14
+18
+20
+26
+32
+40
+60
3
6
-270
-140
-70
-46
-30
-20
-14
-10
-6
-4
0
-2
-4
+1
0
+4
+8
+12
+15
+19
+23
+28
+35
+42
+50
+80
6
10
-280
-150
-80
-56
-40
-25
-18
-13
-8
-5
0
-2
-5
+1
0
表1-3 基本尺寸≤500mm孔的基本偏差数值（摘自GB/T 1800.3—1998）（m）注：①1mm以下各级A和B均不采用。②标准公差≤IT8级的K、M、N及≤IT7级的P到ZC时，从表的右侧选取△值。例：在
基本尺寸/㎜
基本偏差数值
Δ值
下偏差EI
上偏差ES
所有标准公差等级
IT6
IT7
IT8
≤IT8
-540
-660
-820
-1000
-1250
-1600
-2100
-2600
18mm～30mm之间的P7，△=8m，因此ES=-22+8=-14m。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

传感器与测试技术-形考作业4（第7-8章，15%）--00236国开（内蒙古）-参考资料
请认真阅读一下说明然后下载：题库有可能会换，不保证全部都有！请仔细核对是不是您需要的题目再下载！！！！
本文档的说明：如果题目顺序和你的试卷不一样，按CTRL+F在题库中逐一搜索每一道题的答案，预祝您取得好成绩百！
第1题
与一般传感器相比，智能传感器成本低但不具备编程自动化能力。
对
错
参考答案是：“错”。
第2题
压阻式微传感器是在单晶半导体膜片适当部位扩散形成力敏电阻而构成的。
对
错
参考答案是：“对”。
第3题
压力微传感器广泛应用于汽车电子：如tpms（轮胎压力监测系统）、发动机机油压力传感器、汽车刹车系统等。
对
错
参考答案是：“对”。
对
错
参考答案是：“对”。
第16题
电子鼻能分辨气体的种类和浓度，有时比人鼻还灵敏，而且，有的气体比如一氧化碳（俗称煤气），人的鼻子是闻不到的，而电子鼻却能感觉到。
对
错
参考答案是：“对”。
第17题
实现味觉传感器的一种有效方法是使用类似于生物系统的材料作为传感器的敏感膜。
对
错
参考答案是：“对”。
第18题
虚拟仪器技术的三大组成部分包括：灵活高效的软件、模块化i/o硬件和用于集成的软硬件平台。
对
错
参考答案是：“对”。
第10题
虚拟仪器技术所具有的特点是开发时间长。
对
错
参考答案是：“错”。
第11题
目前的固体图像传感器主要有三种类型：第一种是电视摄像机mos（金属氧化物半导体）图像传感器，又称为sspa（自扫描光电二极管阵列），第二种是ccd图像传感器，第三种是cid（电荷注入器件）图像传感器。
对ห้องสมุดไป่ตู้
错
参考答案是：“对”。
第12题
机器人触觉传感器主要有检测和识别功能。
对
错
参考答案是：“对”。
第13题
现代机器人的“皮肤”主要有两方面的感觉：冷热和软硬。
对
错
参考答案是：“对”。
第14题
常见的人工嗅觉系统一般由气敏传感器阵列和分析处理器构成。
对
错
参考答案是：“对”。
第15题
金属半导体传感器是目前使用最为广泛的嗅觉传感器。
第4题
谐振式微传感器是利用某种谐振子的振动力随被测量的变化而变化来进行测量的一种传感器。
对
错
参考答案是：“错”。
第5题
thinkpad手提电脑能够动态的监测出笔记本在使用中的振动，并根据这些振动数据，系统会智能地选择关闭硬盘还是让其继续运行，因为其内置了压力传感器。
对
错
参考答案是：“错”。
第6题
微机械陀螺的工作原理是基于经典力学的牛顿第2定律，通过一定形式的装置产生并检测哥氏加速度。
对
错
参考答案是：“对”。
第19题
常见的智能传感器有微型传感器、模糊传感器和网络传感器三种。
对
错
参考答案是：“对”。
第20题
听觉传感器是将声源通过空气振动产生的声波转换成电信号的换能设备。
对
错
参考答案是：“对”。
对
错
参考答案是：“错”。
第7题
视觉传感器是将景物的电信号转换成光信号的器件，固态图像传感器是现在视觉信息获取的一种基础器件。
对
错
参考答案是：“错”。
第8题
虚拟仪器技术是利用高性能的模块化硬件，结合高效灵活的软件来完成各种测试、测量和自动化的应用。
对
错
参考答案是：“对”。
第9题
虚拟仪器技术所具有的特点是集成性强、扩展性强。