c应用贪心算法求解背包问题
贪心算法-01背包问题

贪⼼算法-01背包问题1、问题描述:给定n种物品和⼀背包。
物品i的重量是wi,其价值为vi,背包的容量为C。
问:应如何选择装⼊背包的物品,使得装⼊背包中物品的总价值最⼤?形式化描述:给定c >0, wi >0, vi >0 , 1≤i≤n.要求找⼀n元向量(x1,x2,…,xn,), xi∈{0,1}, ∋ ∑ wi xi≤c,且∑ vi xi达最⼤.即⼀个特殊的整数规划问题。
2、最优性原理:设(y1,y2,…,yn)是 (3.4.1)的⼀个最优解.则(y2,…,yn)是下⾯相应⼦问题的⼀个最优解:证明:使⽤反证法。
若不然,设(z2,z3,…,zn)是上述⼦问题的⼀个最优解,⽽(y2,y3,…,yn)不是它的最优解。
显然有∑vizi > ∑viyi (i=2,…,n)且 w1y1+ ∑wizi<= c因此 v1y1+ ∑vizi (i=2,…,n) > ∑ viyi, (i=1,…,n)说明(y1,z2, z3,…,zn)是(3.4.1)0-1背包问题的⼀个更优解,导出(y1,y2,…,yn)不是背包问题的最优解,⽭盾。
3、递推关系:设所给0-1背包问题的⼦问题的最优值为m(i,j),即m(i,j)是背包容量为j,可选择物品为i,i+1,…,n时0-1背包问题的最优值。
由0-1背包问题的最优⼦结构性质,可以建⽴计算m(i,j)的递归式:注:(3.4.3)式此时背包容量为j,可选择物品为i。
此时在对xi作出决策之后,问题处于两种状态之⼀:(1)背包剩余容量是j,没产⽣任何效益;(2)剩余容量j-wi,效益值增长了vi ;使⽤递归C++代码如下:#include<iostream>using namespace std;const int N=3;const int W=50;int weights[N+1]={0,10,20,30};int values[N+1]={0,60,100,120};int V[N+1][W+1]={0};int knapsack(int i,int j){int value;if(V[i][j]<0){if(j<weights[i]){value=knapsack(i-1,j);}else{value=max(knapsack(i-1,j),values[i]+knapsack(i-1,j-weights[i]));}V[i][j]=value;}return V[i][j];}int main(){int i,j;for(i=1;i<=N;i++)for(j=1;j<=W;j++)V[i][j]=-1;cout<<knapsack(3,50)<<endl;cout<<endl;}不使⽤递归的C++代码:简单⼀点的修改//3d10-1 动态规划背包问题#include <iostream>using namespace std;const int N = 4;void Knapsack(int v[],int w[],int c,int n,int m[][10]);void Traceback(int m[][10],int w[],int c,int n,int x[]);int main(){int c=8;int v[]={0,2,1,4,3},w[]={0,1,4,2,3};//下标从1开始int x[N+1];int m[10][10];cout<<"待装物品重量分别为:"<<endl;for(int i=1; i<=N; i++){cout<<w[i]<<" ";}cout<<endl;cout<<"待装物品价值分别为:"<<endl;for(int i=1; i<=N; i++){cout<<v[i]<<" ";}cout<<endl;Knapsack(v,w,c,N,m);cout<<"背包能装的最⼤价值为:"<<m[1][c]<<endl;Traceback(m,w,c,N,x);cout<<"背包装下的物品编号为:"<<endl;for(int i=1; i<=N; i++){if(x[i]==1){cout<<i<<" ";}}cout<<endl;return 0;}void Knapsack(int v[],int w[],int c,int n,int m[][10]){int jMax = min(w[n]-1,c);//背包剩余容量上限范围[0~w[n]-1] for(int j=0; j<=jMax;j++){m[n][j]=0;}for(int j=w[n]; j<=c; j++)//限制范围[w[n]~c]{m[n][j] = v[n];}for(int i=n-1; i>1; i--){jMax = min(w[i]-1,c);for(int j=0; j<=jMax; j++)//背包不同剩余容量j<=jMax<c{m[i][j] = m[i+1][j];//没产⽣任何效益}for(int j=w[i]; j<=c; j++) //背包不同剩余容量j-wi >c{m[i][j] = max(m[i+1][j],m[i+1][j-w[i]]+v[i]);//效益值增长vi }}m[1][c] = m[2][c];if(c>=w[1]){m[1][c] = max(m[1][c],m[2][c-w[1]]+v[1]);}}//x[]数组存储对应物品0-1向量,0不装⼊背包,1表⽰装⼊背包void Traceback(int m[][10],int w[],int c,int n,int x[]){for(int i=1; i<n; i++){if(m[i][c] == m[i+1][c]){x[i]=0;}else{x[i]=1;c-=w[i];}}x[n]=(m[n][c])?1:0;}运⾏结果:算法执⾏过程对m[][]填表及Traceback回溯过程如图所⽰:从m(i,j)的递归式容易看出,算法Knapsack需要O(nc)计算时间; Traceback需O(n)计算时间;算法总体需要O(nc)计算时间。
C++贪心算法实现部分背包问题
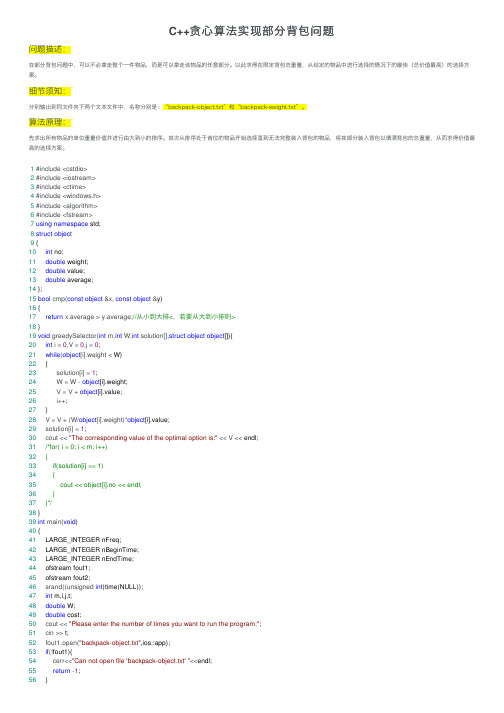
C++贪⼼算法实现部分背包问题问题描述:在部分背包问题中,可以不必拿⾛整个⼀件物品,⽽是可以拿⾛该物品的任意部分。
以此求得在限定背包总重量,从给定的物品中进⾏选择的情况下的最佳(总价值最⾼)的选择⽅案。
细节须知:分别输出到同⽂件夹下两个⽂本⽂件中,名称分别是:“backpack-object.txt”和“backpack-weight.txt”。
算法原理:先求出所有物品的单位重量价值并进⾏由⼤到⼩的排序。
其次从排序处于⾸位的物品开始选择直到⽆法完整装⼊背包的物品,将其部分装⼊背包以填满背包的总重量,从⽽求得价值最⾼的选择⽅案。
1 #include <cstdio>2 #include <iostream>3 #include <ctime>4 #include <windows.h>5 #include <algorithm>6 #include <fstream>7using namespace std;8struct object9{10int no;11double weight;12double value;13double average;14};15bool cmp(const object &x, const object &y)16{17return x.average > y.average;//从⼩到⼤排<,若要从⼤到⼩排则>18}19void greedySelector(int m,int W,int solution[],struct object object[]){20int i = 0,V = 0,j = 0;21while(object[i].weight < W)22 {23 solution[i] = 1;24 W = W - object[i].weight;25 V = V + object[i].value;26 i++;27 }28 V = V + (W/object[i].weight)*object[i].value;29 solution[i] = 1;30 cout << "The corresponding value of the optimal option is:" << V << endl;31/*for( i = 0; i < m; i++)32 {33 if(solution[i] == 1)34 {35 cout << object[i].no << endl;36 }37 }*/38}39int main(void)40{41 LARGE_INTEGER nFreq;42 LARGE_INTEGER nBeginTime;43 LARGE_INTEGER nEndTime;44 ofstream fout1;45 ofstream fout2;46 srand((unsigned int)time(NULL));47int m,i,j,t;48double W;49double cost;50 cout << "Please enter the number of times you want to run the program:";51 cin >> t;52 fout1.open("backpack-object.txt",ios::app);53if(!fout1){54 cerr<<"Can not open file 'backpack-object.txt' "<<endl;55return -1;56 }57 fout1.setf(ios_base::fixed,ios_base::floatfield); //防⽌输出的数字使⽤科学计数法58 fout2.open("backpack-weight.txt",ios::app);59if(!fout2){60 cerr<<"Can not open file 'backpack-weight.txt' "<<endl;61return -1;62 }63 fout2.setf(ios_base::fixed,ios_base::floatfield); //防⽌输出的数字使⽤科学计数法64for (j = 0;j < t;j++)65 {66 cout << "——————————————————The "<< j + 1 << "th test —————————————————"<<endl;67 m = 1 + rand()%100000; //物品个数68 W = 10 + rand()%100000; //背包总重量69 fout1 << m << ",";70 fout2 << (int)W << ",";71int solution[m];72object object[m];73for( i = 0;i < m;i++)74 {75object[i].no = i + 1;76object[i].value = 1 + rand()%10000;77object[i].weight = 1 + rand()%10000;78object[i].average = object[i].value/object[i].weight;79 }80 QueryPerformanceFrequency(&nFreq);81 QueryPerformanceCounter(&nBeginTime);82 sort(object,object + m,cmp);83 greedySelector(m,W,solution,object);84 QueryPerformanceCounter(&nEndTime);85 cost=(double)(nEndTime.QuadPart - nBeginTime.QuadPart) / (double)nFreq.QuadPart;86 fout1 << cost << endl;87 fout2 << cost << endl;88 cout << "The running time is:" << cost << " s" << endl;89 }90 fout1.close();91 fout2.close();92 cout << endl;93 cout << "Success!" << endl;94return0;95 }程序设计思路:① 数据结构:结构体中存储物品序号、物品的重量、物品的价值、物品的单位重量价值;② 利⽤C++⾃带的sort函数对结构体按照物品的单位重量价值进⾏降序排列;③ 从排序处于⾸位的物品开始选择直到⽆法完整装⼊背包的物品,将其部分装⼊背包以填满背包的总重量,从⽽求得价值最⾼的选择⽅案。
贪心法求解01背包问题

贪心法的关键是度量标准,这个程序的度量标准有三个占用空间最小物品效益最大物品效益/占用空间最大程序实现如下:至于文件的操作不加论述。
#include <stdio.h>#include <stdlib.h>typedef struct{char name[10];int weight;int price;}Project;Project *Input(Project *wp,int TotalNum,int TotalWeight) {int i,j,Way,GoBack,RealWeight,RealPrice,TotalPrice;Project temp;do{printf("请选择:\n");printf(" 1.空间最优\n");printf(" 2.价格最优\n");printf(" 3.价格空间比最优\n");scanf("%d",&Way);switch(Way){case 1:for(i=0;i<TotalNum;i++)for(j=0;j<TotalNum-i-1;j++){if(wp[j].weight>wp[j+1].weight){temp=wp[j];wp[j]=wp[j+1];wp[j+1]=temp;}}break;case 2:for(i=0;i<TotalNum;i++)for(j=0;j<TotalNum-i-1;j++){if(wp[j].price<wp[j+1].price){temp=wp[j];wp[j]=wp[j+1];wp[j+1]=temp;}}break;case 3:for(i=0;i<TotalNum;i++)for(j=0;j<TotalNum-i-1;j++){if((float)wp[j].price/(float)wp[j].weight<(float)wp[j+1].price/(float)wp[j+1].weight){temp=wp[j];wp[j]=wp[j+1];wp[j+1]=temp;}}break;default:{printf("输入错误!\n");exit(1);}}i=0;RealWeight=wp[0].weight;TotalPrice=wp[0].price;printf("被装入背包的物品是:\n(物品名价格重量)\n");while(RealWeight<TotalWeight&&i<TotalNum){printf("%s %d %d\n",wp[i].name,wp[i].price,wp[i].weight);i++;RealWeight+=wp[i].weight;TotalPrice+=wp[i].price;}RealWeight-=wp[i].weight;TotalPrice-=wp[i].price;printf("求解结束!背包所装物品总重量:%d,总价值:%d\n",RealWeight,TotalPrice);printf("退出本次测试请按0!\n");scanf("%d",&GoBack);}while(GoBack!=0);return wp;}void main(){int InputWay,TotalNum,i,TotalWeight,RealWeight,Goon,TotalPrice;Project *Array;FILE *fp;do{printf("请选择数据录入方式!\n");printf(" 1.文件读入\n");printf(" 2.键盘输入\n");scanf("%d",&InputWay);switch(InputWay){case 1:printf("请输入背包最大容量:");scanf("%d",&TotalWeight);fp=fopen("data.txt","r");fscanf(fp,"%d\n",&TotalNum);if((Array=(Project*)malloc(TotalNum*sizeof(Project)))==NULL){printf("内存已满,申请空间失败!\n");exit(1);}else{for(i=0;i<TotalNum;i++){fscanf(fp,"%s %d %d\n",&Array[i].name,&Array[i].price,&Array[i].weight);}}fclose(fp);Array=Input(Array,TotalNum,TotalWeight);break;case 2:printf("请输入物品数量及背包容量\n");scanf("%d%d",&TotalNum,&TotalWeight);if((Array=(Project*)malloc(TotalNum*sizeof(Project)))==NULL){printf("内存已满,申请空间失败!\n");exit(1);}else{printf("请输入:物品名价格重量\n");for(i=0;i<TotalNum;i++)scanf("%s%d%d",&Array[i].name,&Array[i].price,&Array[i].weight);}Array=Input(Array,TotalNum,TotalWeight);break;default:{printf("输入错误!\n");exit(1);}}printf("继续其他数据测试请按1\n");scanf("%d",&Goon);}while(Goon==1);delete Array;}。
贪心法解决背包问题

算法分析实验报告贪心法解决背包问题学生姓名:专业:班级:学号:指导教师:2017年6月12日目录一、实验题目 (2)二、实验目的 (2)三、实验要求 (2)四、实现过程 (3)1、实验设计: (3)2、调试分析 (5)3、运行结果: (6)4、实验总结: (6)五、参考文献 (6)一、实验题目贪心法解决背包问题二、实验目的1)以背包问题为例,掌握贪心法的基本设计策略。
2)熟练掌握各种贪心策略情况下的背包问题的算法并实现;其中:量度标准分别取:效益增量v、物品重量w、v/ w比值;3) 分析实验结果来验证理解贪心法中目标函数设计的重要性。
三、实验要求1.[问题描述]:给定n种物品和一个背包。
物品i的重量是Wi,其价值为Vi,背包的容量为C。
应如何选择装入背包的物品,使得装入背包中物品的总价值最大? 与0-1背包问题类似,所不同的是在选择物品i装入背包时,可以选择物品i的一部分,而不一定要全部装入背包,但不可以重复装入。
2.[算法]:贪心法的基本思路:从问题的某一个初始解出发逐步逼近给定的目标,以尽可能快的地求得更好的解。
当达到某算法中的某一步不能再继续前进时,算法停止。
该算法存在问题:1)不能保证求得的最后解是最佳的;2)不能用来求最大或最小解问题;3)只能求满足某些约束条件的可行解的范围。
四、实现过程1、实验设计:1.用贪心法求解背包问题的关键是如何选定贪心策略,使得按照一定的顺序选择每个物品,并尽可能的装入背包,直至背包装满。
至少有三种看似合理的贪心策略:1)按物品价值v降序装包,因为这可以尽可能快的增加背包的总价值。
但是,虽然每一步选择获得了背包价值的极大增长,但背包容量却可能消耗太快,使得装入背包得物品个数减少,从而不能保证目标函数达到最大。
2)按物品重量w升序装包,因为这可以装入尽可能多的物品,从而增加背包总价值。
但是,虽然每一步选择使背包得容量消耗得慢了,但背包价值却没能保证迅速增长,从而不能保证目标函数达到最大。
c语言算法--贪婪算法---01背包问题

c语言算法--贪婪算法---0/1背包问题在0 / 1背包问题中,需对容量为c 的背包进行装载。
从n 个物品中选取装入背包的物品,每件物品i 的重量为wi ,价值为pi 。
对于可行的背包装载,背包中物品的总重量不能超过背包的容量,最佳装载是指所装入的物品价值最高,即n ?i=1pi xi 取得最大值。
约束条件为n ?i =1wi xi≤c 和xi?[ 0 , 1 ] ( 1≤i≤n)。
在这个表达式中,需求出xt 的值。
xi = 1表示物品i 装入背包中,xi =0 表示物品i 不装入背包。
0 / 1背包问题是一个一般化的货箱装载问题,即每个货箱所获得的价值不同。
货箱装载问题转化为背包问题的形式为:船作为背包,货箱作为可装入背包的物品。
例1-8 在杂货店比赛中你获得了第一名,奖品是一车免费杂货。
店中有n 种不同的货物。
规则规定从每种货物中最多只能拿一件,车子的容量为c,物品i 需占用wi 的空间,价值为pi 。
你的目标是使车中装载的物品价值最大。
当然,所装货物不能超过车的容量,且同一种物品不得拿走多件。
这个问题可仿照0 / 1背包问题进行建模,其中车对应于背包,货物对应于物品。
0 / 1背包问题有好几种贪婪策略,每个贪婪策略都采用多步过程来完成背包的装入。
在每一步过程中利用贪婪准则选择一个物品装入背包。
一种贪婪准则为:从剩余的物品中,选出可以装入背包的价值最大的物品,利用这种规则,价值最大的物品首先被装入(假设有足够容量),然后是下一个价值最大的物品,如此继续下去。
这种策略不能保证得到最优解。
例如,考虑n=2, w=[100,10,10], p =[20,15,15], c = 1 0 5。
当利用价值贪婪准则时,获得的解为x= [ 1 , 0 , 0 ],这种方案的总价值为2 0。
而最优解为[ 0 , 1 , 1 ],其总价值为3 0。
另一种方案是重量贪婪准则是:从剩下的物品中选择可装入背包的重量最小的物品。
贪婪法求解背包问题

贪婪法求解背包问题-CAL-FENGHAI.-(YICAI)-Company One1实验二贪婪法一、实验目的1)理解和掌握贪婪算法的基本思想;2)使用贪婪算法求解背包问题以及最小花费生成树问题。
二、方法原理贪心算法就是做出一系列选择,使原问题达到最优解。
在每一个决策点,都是做出当前看来的最优选择。
三、实验设备PC机一台,C语言、PASCAL语言、Matlab任选四、方法原理贪心算法就是做出一系列选择,使原问题达到最优解。
在每一个决策点,都是做出当前看来的最优选择。
五、实验内容1)利用贪婪法求如下背包问题的最优解:n=5,M=100,价值P={20,30,66,40,60 },重量为w={10,20,30,40,50}。
六、实验要求1)认真分析题目的条件和要求,复习相关的理论知识,选择适当的解决方案和算法;2)编写上机实验程序,作好上机前的准备工作;3)上机调试程序,并试算各种方案,记录计算的结果(包括必要的中间结果);4)分析和解释计算结果;5)按照要求书写实验报告;源代码:#include<stdio.h>#include<stdlib.h>#include<iostream>using namespace std;#define n 5#define M 100typedef struct {int s;float p;//价值float w;float t;//价值重量比float x;}OBJECT;OBJECT obj[n];void swap(float &x, float &y) {float t;t = x;x = y;y = t;}float divide_and_conquer(OBJECT obj[], int low, int high) { int k, i = low;float z = obj[low].t;for (k = low + 1; k <= high; k++) {if (obj[k].t>z) {i += 1;if (i != k)swap(obj[i], obj[k]);}}swap(obj[low], obj[i]);return i;}void quick_sort(OBJECT obj[], int low, int high) {int k;if (low < high) {k = divide_and_conquer(obj, low, high);quick_sort(obj, low, k - 1);quick_sort(obj, k + 1, high);}}void sort_recover(OBJECT obj[]) {int i, j,temp;for (i = 0; i < n-1; i++) {for (j = 0; j < n - 1 - i; j++) {if (obj[j].s > obj[j + 1].s)swap(obj[j], obj[j + 1]);}}}float knapsack_greedy(OBJECT obj[]) {int i;float m,r=0;for(i=0;i<n;i++){obj[i].t=obj[i].p/obj[i].w;obj[i].x = 0;}quick_sort(obj,0,4);m = M;printf(" 物体价值重量价值重量比结果\n");printf("=========================================\n");for (i = 0; i < n; i++) {if (obj[i].w <= m) {obj[i].x = 1;m -= obj[i].w;r += obj[i].p;}else {obj[i].x = m / obj[i].w;r += obj[i].x * obj[i].p;break;}}return r;}void main() {int i;float r;//float x[] = { 0 };float s[] = { 1,2,3,4,5 };float p[]={ 20,30,66,40,60 };float w[]={ 10,20,30,40,50 };for (i = 0; i < n; i++) {obj[i].s = s[i];obj[i].p = p[i];obj[i].w = w[i];}r = knapsack_greedy(obj);sort_recover(obj);for (i = 0; i < n; i++) {printf(" %d %2.0f %2.0f %2.1f %1.1f\n", obj[i].s, obj[i].p, obj[i].w, obj[i].t, obj[i].x);}printf("\n最大价值为:%f\n",r );printf("背包问题的解向量:X={");for (i = 0; i < n; i++) {printf("%1.1f",obj[i].x);if(i<4)printf(",");}printf("}");system("pause");}结果:。
背包问题C语言程序设计

1 问题要求及任务描述1.1 题目要求假设有一个能装入总体积为T的背包和n件体积分别为w1 , w2 , … , wn 的物品,能否从n件物品中挑选若干件恰好装满背包,即使w1 +w2 + … + wn=T,要求找出所有满足上述条件的解。
例如:当T=10,各件物品的体积{1,8,4,3,5,2}时,可找到下列4组解:(1,4,3,2)(1,4,5)(8,2)(3,5,2)。
1.2 主要任务在给定物品数量,物品各自体积和背包体积的前提下,找出物体组合后的总体积与背包体积相等的物体组合2 解决问题的主要思路和方法2.1 关键问题如何选择第i件物品:(1)考虑物品i被选择,这种可能性仅当包含它不会超过方案总重量限制时才是可行的。
选中后,继续去考虑其余物品的选择。
(2)考虑物品i不被选择,这种可能性仅当不包含物品i也有可能会找到价值更大的方案的情况。
2.2 拟采用解决问题的方法可利用回溯法的设计思想来解决背包问题。
首先将物品排成一列,然后顺序选取物品装入背包,假设已选取了前i 件物品之后背包还没有装满,则继续选取第i+1件物品,若该件物品"太大"不能装入,则弃之而继续选取下一件,直至背包装满为止。
但如果在剩余的物品中找不到合适的物品以填满背包,则说明"刚刚"装入背包的那件物品"不合适",应将它取出"弃之一边",继续再从"它之后"的物品中选取,如此重复,直至求得满足条件的解,或者无解。
2.3 主要算法和处理流程图1.输入物品总个数2.依次输入各物品的体积3.输入背包总体积4.将物品排成一列,按顺序选取物品装入背包中,当物品太大不能装入时则弃之继续选取下一件,直到背包装满为止,5.出现在剩余的物品中找不到合适的物品填满背包的情况是说明刚刚装入背包的那件物品不适合,将它取出后继续选取后面的物品。
6.重复步骤4和5直至求出满足条件的解或者无解。
c应用贪心算法求解背包问题

实验五应用贪心算法求解背包问题学院:计算机科学与技术专业:计算机科学与技术学号:班级:姓名:一、实验内容:背包问题指的是:有一个承重为W的背包和n个物品,它们各自的重量和价值分别是n,假设Wwi和vi(1i n)wi1i,求这些物品中最有价值的一个子集。
如果每次选择某一个物品的时候,只能全部拿走,则这一问题称为离散(0-1)背包问题;如果每次可以拿走某一物品的任意一部分,则这一问题称为连续背包问题。
二、算法思想:首先计算每种物品单位重量的价值Vi/Wi,然后,依贪心选择策略,将尽可能多的单位重量价值最高的物品装入背包。
若将这种物品全部装入背包后,背包内的物品总重量未超过C,则选择单位重量价值次高的物品并尽可能多地装入背包。
依此策略一直地进行下去,直到背包装满为止。
三、实验过程:#include <iostream>using namespace std;struct goodinfo{float p; //物品效益float w; //物品重量float X; //物品该放的数量int flag; //物品编号};//物品信息结构体void Insertionsort(goodinfo goods[],int n)//插入排序,按pi/wi价值收益进行排序,一般教材上按冒泡排序{int j,i;for(j=2;j<=n;j++){goods[0]=goods[j];i=j-1;while (goods[0].p>goods[i].p){}goods[i+1]=goods[0];}}//按物品效益,重量比值做升序排列goods[i+1]=goods[i];i--;void bag(goodinfo goods[],float M,int n){float cu;int i,j;for(i=1;i<=n;i++)goods[i].X=0;cu=M;//背包剩余容量for(i=1;i<n;i++){if(goods[i].w<cu)//若不超过容量,尽量增加物品{goods[i].X=1;cu-=goods[i].w;//确定背包新的剩余容量}else{goods[i].X=0;}for(j=2;j<=n;j++) /*按物品编号做降序排列*/ {goods[0]=goods[j];while (goods[0].flag<goods[i].flag){goods[i+1]=goods[i];i--;}}goods[i+1]=goods[0];}cout<<"最优解为:"<<endl;for(i=1;i<=n;i++){cout<<"第"<<i<<"件物品要放:";cout<<goods[i].X<<endl;}}void main(){cout<<"|--------运用贪心法解背包问题---------|"<<endl; int j,n;float M;goodinfo *goods;//定义一个指针{cout<<"请输入物品的总数量:";cin>>n;goods=new struct goodinfo [n+1];//cout<<"请输入背包的最大容量:";cin>>M;cout<<endl;int i;for(i=1;i<=n;i++){goods[i].flag=i;cout<<"请输入第"<<i<<"件物品的重量:";cin>>goods[i].w;cout<<"请输入第"<<i<<"件物品的效益:";cin>>goods[i].p;goods[i].p=goods[i].p/goods[i].w;//得出物品的效益,重量比cout<<endl;}Insertionsort(goods,n);bag(goods,M,n);cout<<"press <1> to run agian"<<endl;cout<<"press <0> to exit"<<endl;cin>>j;}}四、实验结果:对于0-1背包问题,贪心选择之所以不能得到最优解是因为在这种情况下,它无法保证最终能将背包装满,部分闲置的背包空间使每公斤背包空间的价值降低了。
算法设计和分析实验四:贪心算法求解背包问题

实验五:贪心算法求解背包问题实验内容应用贪心算法求解离散背包问题,分析时间复杂度。
有一个承重为W的背包和n个物品,它们各自的重量和价值分别是wi和vi (1<=i<=n),设求这些物品中最有价值的一个子集。
如果每次选择某一个物品的时候,只能全部拿走,则这一问题称为离散(0-1)背包问题;如果每次可以拿走某一物品的任意一部分,则这一问题称为连续背包问题。
算法思想•动态规划的思想:–对较小的子问题进行一次求解,并把结果记录下来,然后利用较小问题的解,求解出较大问题的解,直到求解出最大问题的解。
–引进一个二维数组ch[MAX][MAX],用ch[i][j]记录CH1与CH2的LCS的长度,b[i][j]记录ch[i][j]是通过哪一个子问题的值求得的,以决定搜索的方向。
我们是自底向上进行递推计算,那么在计算ch[i,j]之前,ch[i-1][j-1],ch[i-1][j]与ch[i][j-1]均已计算出来。
此时我们根据CH1 [i] = CH2[j]还是CH1[i] !=CH2[j],就可以计算出ch[i][j]。
算法length(string CH1,string CH2,int b[MAX][MAX])//用于构建动态数组//输入:两字符窜//输出:最长公共子序列for(i=1;i<=ch1Len;i++)//二重循环求解for(int j=1;j<=ch2Len;j++){if(CH1[i-1]==CH2[j-1])//相等字符{ch[i][j]=ch[i-1][j-1]+1;b[i][j]=0;}else if(ch[i-1][j]>=ch[i][j-1])//上比较大{ch[i][j]=ch[i-1][j];b[i][j]=1;}else//左比较大{ch[i][j]=ch[i][j-1];b[i][j]=-1;}}printCS(int b[MAX][MAX],string x,int i,int j) //回溯求出最长子序列输出//输入:标记数组//输出:最长子序列if(i == 0 || j == 0)//边界,返回return;if(b[i][j] == 0){printCS(b, x, i-1, j-1);//左上cout<<x[i-1]<<" ";}else if(b[i][j] == 1)printCS(b, x, i-1, j);//上elseprintCS(b, x, i, j-1);//左源程序//应用贪心算法求解离散背包问题#include<iostream>using namespace std;#define MAX 100//结构体struct Elem{double W;double V;double P;int number;};//顺序表struct SqList{Elem *elem;int length;int listsize;};//构造一个空的线性顺序表void InitList_Sq(SqList &L){L.elem=(Elem *)malloc(100*sizeof(Elem)); L.length=0;L.listsize=100;}//******************************** //构造背包,顺序表//******************************void input(SqList &L){cout<<"请输入物品的个数:";cin>>L.length;for(int i=0;i<L.length;i++){cout<<"请输入第"<<i+1<<"个物品的重量和价值:";cin>>L.elem[i].W>>L.elem[i].V;L.elem[i].P=L.elem[i].V/L.elem[i].W;cout<<"价值比为:"<<L.elem[i].P<<endl;L.elem[i].number=i+1;}}//*********************************//插入排序由大到小//*******************************void inser(SqList &L){Elem inserter;int index;//inserter待插入合适位置的元素,index指示插入位置for(int pass=1;pass<L.length;pass++){//共比较size-1轮inserter=L.elem[pass];//第pass轮时,待插入的对象是a[pass] index=pass-1;while(index>=0&&inserter.P>L.elem[index].P){ //寻找插入位置L.elem[index+1]=L.elem[index];index--;//指针前移,再比较}L.elem[index+1]=inserter;//跳出while时,找到插入位置}//end of forcout<<"按照价值比由大到小排列的顺序为:";for(pass=0;pass<L.length;pass++)cout<<L.elem[pass].number<<" ";cout<<endl;}//*************************************************8 //背包程序//采用贪心算法//根据价值和重量的比来实现贪心算法//************************************************ void bag(SqList L){double w,sumV=0,sumW=0;int list[MAX],a=0;cout<<"请输入背包承重量W:";cin>>w;inser(L);for(int i=0;i<L.length;i++){while(sumW+L.elem[i].W<=w){sumW=sumW+L.elem[i].W;sumV=sumV+L.elem[i].V;list[a++]=L.elem[i].number;}}cout<<"最后包里的总重量为:"<<sumW<<endl; cout<<"最后包里的总价值为:"<<sumV<<endl; cout<<"放到背包中的物品的序号列表为:"; for(i=0;i<a;i++){cout<<list[i]<<" ";}}int main(){cout<<"贪心算法求解背包问题"<<endl;SqList L;InitList_Sq(L);input(L);bag(L);return 0;}实验结论1、运行截图查找最长公共子序列长度时的动态规划两个for循环,时间复杂度为O(n*n)。
贪心算法实现01背包问题

贪心算法实现01背包问题算法思想:贪心原则为单位价值最大且重量最小,不超过背包最大承重量为约束条件。
也就是说,存在单位重量价值相等的两个包,则选取重量较小的那个背包。
具体实现过程是:首先可以设置一个备份pvu类型的数组,在不破环原数据的情况下,对此备份数组按单位重量价值从大到小的排序。
依次设立两个指针i,j(其中i表示当前应该参与最佳pv值的元素指针,j表示符合约束条件的指针(单位重量价值PV最大,重量最小,不超过最大承重量约束)代码实现如下:#include <iostream>using namespace std;typedef struct{int v;int w;float pv;}pvu;void sortByPv(pvu [],int );int zeroneBags(pvu[],int,int,int * );void print(pvu a[],int n){for (int i=0;i<n;i++){cout<<a[i].w<<" "<<a[i].v<<" "<<a[i].pv<<endl;}cout<<endl;}int main(){int i,maxw;int w[]={1,2,3,2};int v[]={9,10,15,6};int n=sizeof(w)/sizeof(int );const int N=n;pvu arr[N];for (i=0;i<n;i++){arr[i].v=v[i];arr[i].w=w[i];arr[i].pv=v[i]*1.0/w[i];}int remained;cout<<"输入背包的最大承重量:\n";cin>>maxw;cout<<"最大价值为:"<<zeroneBags(arr,n,maxw,&remained)<<"\n还剩"<<remained<<"公斤空间未使用"<<endl;return 0;}void sortByPv(pvu arr[] ,int n){pvu t;int i,j;for (i=0;i<n-1;i++)for (j=0;j<n-1-i;j++)if (arr[j].pv<arr[j+1].pv){t=arr[j];arr[j]=arr[j+1];arr[j+1]=t;}}int zeroneBags(pvu arr[],int n,int maxw,int *e){int i=0,j,minw,totalv=0;int avail=maxw;sortByPv(arr,n); //按最大单位重量价值PV从大到小的排序while (avail&&i<n){minw=i;for (j=0;j<n;j++)if (arr[i].pv==arr[j].pv){if (arr[i].w>arr[j].w&&j>i){minw=j;}}if (arr[minw].w<=avail){avail-=arr[minw].w;totalv+=arr[minw].v;i++;}elsei++;}*e=avail;return totalv; }运行结果截图:。
贪心算法背包问题

《算法设计与分析》实验报告2015-2016年第2学期实验班级:学生姓名:学号:指导老师:信息工程学院实验项目名称:贪心算法背包问题实验日期:2016年4月12日一、实验类型:□√验证性□设计性二、实验目的1、掌握背包问题的算法2、初步掌握贪心算法三、实验内容及要求问题描述:与0-1背包问题相似,给定n种物品和一个背包。
物品i的重量是wi,其价值为vi,背包的容量为c。
与0-1背包问题不同的是,在选择物品i装入背包时,背包问题的解决可以选择物品i的一部分,而不一定要全部装入背包,1< i < n。
四、实验步骤#include "iostream.h"#include "stdio.h"#include <cstdlib>struct stone{ int name;int weight;//物品的剩余重量int weight_t;//物品的重量float benefit;//物品的价值//float b;};void sort(stone *data,int num){if(num<1)return;int low=0,high=num;stone key_s=data[low];float key=(float)key_s.benefit/key_s.weight;int empty=low;while(low<high){ if(low==empty){ while((data[high].benefit/data[high].weight<key) &&(high>low)){ high--;}if(data[high].benefit/data[high].weight>=key){ data[low]=data[high];empty=high;}}else if(high==empty) {while((data[low].benefit/data[low].weight>=key)&&(low<h igh)){ low++; }if(data[low].benefit/data[low].weight<key){ data[high]=data[low];empty=low; }}}data[empty]=key_s;if(empty>1)sort(data,empty-1);if(num-empty-1>0)sort(data+empty+1,num-empty-1);}void inputstone(stone *bag,int num){ for(int i=0;i<num;i++){ bag[i].name=i+1;printf("请输入第%d号物品的重量:",i+1); scanf("%d",&bag[i].weight);if (bag[i].weight<=0){printf("物品的重量必须大于0!\n");} printf("请输入第%d号物品的价值:",i+1); scanf("%f",&bag[i].benefit);if (bag[i].benefit<=0){printf("物品的价值必须大于0!\n");}bag[i].weight_t=bag[i].weight;}}int main(int argc, char* argv[]){ int i;int num=0;int weight=0;float benefit=0;stone *bag;do{ printf("请输入背包可容纳的重量:"); scanf("%d",&weight);if (weight<=0)printf("背包可容纳的重量必须大于0!\n"); }while(weight<=0);do{ printf("请输入物品的数量:");scanf("%d",&num);if (num<=0)printf("物品数量必须大于0!\n");}while(num<=0);bag=new stone[num];inputstone(bag,num);sort(bag,num-1);for(i=0;i<num&&weight>0;i++){ stone *temp=bag+i;if(weight>=temp->weight){ weight-=temp->weight;temp->weight=0;benefit+=temp->benefit;continue;}else{ temp->weight-=weight;weight=0;benefit+=(temp->benefit*(1-(float)temp->weight/temp->we ight_t));break;} }printf("物品种类放入的比例每单位效益\n");for(i=0;i<num;i++){ stone *temp=bag+i;printf("%d类物品",temp->name);printf("\t\t%.2f\t\t",(temp->weight_t-temp->weight)/(fl oat)temp->weight_t);printf(" %.4f\n",temp->benefit/(float)temp->weight_t) ;}printf("总效益:%.2f",benefit);delete bag;getchar();system("PAUSE");return EXIT_SUCCESS;return 0;}五、实验结果1、实验图形2、结果分析如上面第一个图所示当输入背包可容纳的重要为21,输入物品的数量为3,输入第1号物品的重量为8,输入第1号物品的价值为12,输入第2号物品的重量为9,输入第2号物品的价值为16,输入第3号物品的重量为4,输入第3号物品的价值为15,则可以得出总效益为43.00。
最佳装载背包问题--贪心算法

贪心法求解最佳装载背包问题描述:对于容量为c的背包进行装载,从n个物品中选择装入背包的物品,每个物品i的重量和价值分别为wi和pi。
在背包中物品的总重量不超过背包容量的前提下,求装入物品价值最高的装载法。
输入:5 20 //物品的数量和背包的容量6 3 //第一个物品的重量和价值2 5 //…3 810 67 4输出:1110.714286算法如下:#include <stdio.h>#include <stdlib.h>struct goodinfo//物品结构体{float p;//价值float w;//重量float x;//数量int flag;//标志变量};void Insertionsort(struct goodinfo goods[],int n)//将物品根据价值排序{int i,j;for(j=2;j<=n;j++){goods[0]=goods[j];//保存比较的对象i=j-1;while(goods[0].p>goods[i].p)//找到位置后退出{goods[i+1]=goods[i];//错位i--;}goods[i+1]=goods[0];//找到位置后将比较的对象覆盖}}void bag(struct goodinfo goods[],float M,int n){float cu;//剩余空间int i,j;for(i=1;i<=n;i++)goods[i].x=0;//初始化cu=M;//初始化for(i=1;i<=n;i++){if(goods[i].w>cu)break;goods[i].x=1;cu=cu-goods[i].w;}if(i<=n)goods[i].x=cu/goods[i].w;//将物品分割for(j=2;j<=n;j++)//按照物品的编号排序,便于输出goods[0]=goods[j];i=j-1;while(goods[0].flag<goods[i].flag){goods[i+1]=goods[i];i--;}goods[i+1]=goods[0];}printf("最优解为:\n");for(i=1;i<=n;i++){printf("第%d件物品要放:%f\n",i,goods[i].x);}}int main(){int j=1,n,i;float M;while(j)system("cls");printf("输入物品的总数:");scanf("%d",&n);struct goodinfo goods[n+1];//动态定义结构体数组的大小printf("背包最大容量:");scanf("%f",&M);for(i=1;i<=n;i++){goods[i].flag=i;printf("weight input:");scanf("%f",&goods[i].w);printf("price input:");scanf("%f",&goods[i].p);goods[i].p/=goods[i].w;}Insertionsort(goods,n);bag(goods,M,n);printf("press <1> to run again\npress <0> to exit\n请输入操作码:");scanf("%d",&j);}return 0; }。
贪心法求解背包问题

问题描述
•
已知有n种物品和一个可容纳M重量的背包,每种物品i的重 量为。假定将物品i的一部分放入背包就会得到的效益,这里,, 。显 然,由于背包容量是M,因此,要求所有选中要装入背包的物品总重 量不得超过M.。如果这n件物品的总重量不超过M,则把所有物品装 入背包自然获得最大效益。现需解决的问题是,在这些物品重量的和 大于M的情况下,该如何装包,使得得到更大的效益值。由以上叙述, 可将这个问题形式表述如下: p i xi • 极 大 化目标函数 1i n • 约束条件 wi xi M • 1i n
0 xi 1, pi 0, wi 0,1 i n
算法分析
•
首先需确定最优的量度标准。这里考虑三种策略: • 策略1:按物品价值p降序装包, • 策略2:按物品重w升序装包 • 策略3:按物品价值与重量比值p/w的降序装包 分别以上面三种策略分别求以下情况背包问题的解: • n=7,M=15, 7 • ( p1 ,, p) =(10,5,15,7,6,18,3) • ( w1 ,, w7)=(2,3,5,7,1,4,1)
结果
The end,thank you!
请提问!
与其他算法比较
• 1.贪心法:处理问题的速度快,思想简单。使用该方法的 必要条件是寻找好的贪心法则。不足之处在于很多时候它 只能求的似优解,却不能求的最优解 • 2.动态规划法:可以求解最优解,重点在于徐兆最优决策 序列但是速度较慢。 • 3.分支限界法:可以求解最优解,重点在于寻找限界值。 易求最优解,但是空间花费较高,效率不是很高。 • பைடு நூலகம்择哪一种算法,不仅要根据问题本身还需要考虑到其他 因素,例如时间复杂度,空间复杂度,易求解等等因素。
贪心算法 背包问题

17 if (temp < tempArray[j])
18 {
19 temp = tempArray[j];
20 index = j;
22 {
23 temp = tempArray[j];
24 index = j;
25 }
26 }
27
28 if (sortResult[index] == 0)
17 index = i;
18
19 for (j = i; j < n; j++)
20 {
21 if ((temp < tempArray[j]) && (sortResult[j] == 0))
temp = sortResult[i];//得到取物体的顺序
if (w[temp] > cu)
{
break;
}
x[temp] = 1;//若合适则取出
cu -= w[temp];//将容量相应的改变
}
if (i <= n)//使背包充满
1 -107374176.000000 1 1.600000 2 1.600000
after arithmetic data: x[i]
0.000000 0.333333 0.000000
可以看到其效益为x[3] = {1.4, 1.6, 1.5},于是在M = 20的情况下,其预想中的输出结果是0,1,0.5。然而事实上是不是就这样呢?
问题就在这里了!排序后的w[i] = {1.6, 1.6, 1.5},因此对w[i]排序后就既改变了w[i]的原有顺序,还改变了w[i]的原来值!
背包问题

背包问题(贪心算法)一、实验目的与要求1、掌握背包问题的算法2、初步掌握贪心算法二、实验题:问题描述:有一个背包容量为C,输入N个物品,每个物品有重量W,以及物品放入背包中所得的收益P。
问选择放入的物品,不超过背包的容量,且得到的收益最好。
三、实验代码#include<iostream>using namespace std;struct _Object//物品结构体{int Value;//物品价值int Weight;//物品重量int AveValue;//物品单位价值float Num;//物品可以放入的数量};void knaspsack(int n,float M,_Object object[]){ //n为物品个数,M为背包容量int i;float C=M;for(i=0;i<n;i++){object[i].Num=0;//初始化放入背包的物品为0if(object[i].Weight>C)break;//当物品重量大于背包容量时else//小于时{object[i].Num=1;//物品i放入一件C-=object[i].Weight;//背包容量减小}}if(i<=n)//当不能放入整个物品时,选取物品一部分放入object[i].Num=C/object[i].Weight;for(i=0;i<n;i++){if(object[i].Num>0)cout<<"重量为: "<<object[i].Weight<<" 价值为: "<<object[i].Value<<" 的物品放入"<<object[i].Num<<" 件"<<endl;}}void SortObject(_Object object[],int n)//将各个物品按单位价值进行排序{int j;_Object temp;int i;for(i=0;i<n;i++)object[i].AveValue=object[i].Value/object[i].Weight;//各个物品的单位价值for(i=0;i<n-1;i++)//根据物品的单位价值对物品进行从大到小的冒泡排序{for(j=0;j<n-i-1;j++){if(object[j].AveValue<object[j+1].AveValue){temp=object[j];object[j]=object[j+1];object[j+1]=temp;}}}}int main(){_Object object[4];//4个物品int M=9;//背包容量为15object[0].Weight=2;object[0].Value=3;object[1].Weight=3;object[1].Value=4;object[2].Weight=4;object[2].Value=5;object[3].Weight=5;object[3].Value=7;SortObject(object,4);knaspsack(4,M,object);}四、实验结果。
贪心算法求解背包问题C语言描述

贪心算法求解背包问题:#include<stdio.h>#define maxnumber 20typedef struct node{float w;float v;int i;}Object;float find(Object wp[],int n,float M) {float x[maxnumber];int i;float maxprice=0;for(i=1;i<=n;i++)//初始化x[n];{x[i]=0.0;}i=0;while(wp[i].w < M){x[wp[i].i]=1;M=M-wp[i].w;i++;}x[wp[i].i]=M/wp[i].w;//输出解向量printf("解向量是:\n");for(i=1;i<=n;i++){printf("x[%d]=%f",i,x[i]);}printf("\n");//计算最大价值for(i=0;i<n;i++){maxprice=maxprice+wp[i].v*x[wp[i].i];}return maxprice;}void main(){Object wp[maxnumber];int i,j,n;float C;//背包的重量int flag;float maxprice,temp;printf("请输入物品的种数:");scanf("%d",&n);printf("请输入背包的重量:");scanf("%f",&C);printf("\n请输入物品的序号、重量和价值:");for(i=0;i<n;i++){scanf("%d",&wp[i].i);scanf("%f",&wp[i].w);scanf("%f",&wp[i].v);}printf("\n输入的物品是:\n");//输出物品for(i=0;i<n;i++){printf(" %d",wp[i].i);printf(" %f",wp[i].w);printf(" %f",wp[i].v);printf("\n");}//用冒泡排序对物品按照单位价值进行降序排序for(i=1;i<n;i++){flag=0;for(j=n-1;j>=i;j--){if(wp[j-1].v/wp[j-1].w < wp[j].v/wp[j].w){temp=wp[j-1].i;wp[j-1].i=wp[j].i;wp[j].i=temp;temp=wp[j-1].w;wp[j-1].w=wp[j].w;wp[j].w=temp;temp=wp[j-1].v;wp[j-1].v=wp[j].v;wp[j].v=temp;flag=1;}if(flag==0)break;}}printf("\n排序后的物品是:\n");//输出物品for(i=0;i<n;i++){printf(" %d",wp[i].i);printf(" %f",wp[i].w);printf(" %f",wp[i].v);printf("\n");}maxprice=find(wp,n,C);printf("\n物品的重价值为:%f",maxprice);}。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验五应用贪心算法求解背包问题
学院:计算机科学与技术专业:计算机科学与技术
学号:班级:姓名:
、
实验内容:
背包问题指的是:有一个承重为W的背包和n个物品,它们各自的重量和价值分别是n
,假设W
w
i和v
i(1 i n)w
i 1i,求这些物品中最有价值的一个子集。
如果每次选择某一个物品的时候,只能全部拿走,则这一问题称为离散(0-1)背包问题;如果每次可以拿走某一物品的任意一部分,则这一问题称为连续背包问题。
二、算法思想:
首先计算每种物品单位重量的价值Vi/Wi,然后,依贪心选择策略,将尽可能多的单位重量价值最高的物品装入背包。
若将这种物品全部装入背包后,背包内的物品总重量未超过C,则选择单位重量价值次高的物品并尽可能多地装入背包。
依此策略一直地进行下去,直到背包装满为止。
三、实验过程:
#in elude <iostream>
using n amespace std;
struct goodi nfo
{
float p; // 物品效益
float w; // 物品重量
float X; // 物品该放的数量
int flag; // 物品编号
};// 物品信息结构体
void Insertionsort(goodinfo goods[],int n)// 插入排序,按pi/wi 价值收益进行排序,一般教材上按冒泡排序
{
int j,i;
for(j=2;j<=n;j++)
{
goods[0]=goods[j];
i=j-1;
while (goods[0].p>goods[i].p)
{
}
goods[i+1]=goods[0];
}
}// 按物品效益,重量比值做升序排列goods[i+1]=goods[i];
i--;
void bag(goodinfo goods[],float M,int n)
{
float cu;
int i,j;
for(i=1;i<=n;i++)
goods[i].X=0;
cu=M;// 背包剩余容量for(i=1;i<n;i++)
{
if(goods[i].w<cu)// 若不超过容量,尽量增加物品{ goods[i].X=1;
cu-=goods[i].w;// 确定背包新的剩余容量
}
else
{
goods[i].X=0;
}
for(j=2;j<=n;j++) /* 按物品编号做降序排列*/
{
goods[0]=goods[j];
i=j-1;
while (goods[0].flag<goods[i].flag)
{
goods[i+1]=goods[i];
i--;
}}
goods[i+1]=goods[0];
}
coutvv"最优解为:"<<endl;
for(i=1;i<=n;i++)
{
coutvv"第"<<i<<'件物品要放:"; cout<<goods[i].X<<endl; }
}
void main()
{
coutvv"| ------- 运用贪心法解背包问题
|"vvendl;
int j,n;
float M;
goodinfo *goods;// 定义一个指针
while(j)
{
cout<<" 请输入物品的总数量:";
cin>>n;
goods=new struct goodinfo [n+1];//
coutvv"请输入背包的最大容量:";
cin>>M;
cout<<endl;
int i;
for(i=1;i<=n;i++)
{
goods[i].flag=i;
coutvv"请输入第"vvivv"件物品的重量:";
cin>>goods[i].w;
coutvv"请输入第"vvivv"件物品的效益:";
cin>>goods[i].p;
goods[i].p=goods[i].p/goods[i].w;// 得出物品的效益,重量比coutvvendl;
}
Insertionsort(goods,n); bag(goods,M,n);
cout<<"press <1> to run agian"<<endl;
cout<<"press <0> to exit"<<endl;
cin>>j;
}
}
四、实验结果:
对于0-1 背包问题,贪心选择之所以不能得到最优解是因为在这种情况下,它无法保证最终能将背包装满,部分闲置的背包空间使每公斤背包空间的价值降低了。
以上算法的时间和空间复杂度为O(n*n) ,其中时间复杂度基本已经不能再优化了,但空间复杂度可以优化到O(n)。
