编译原理龙书课后部分答案(英文版)
编译原理课后习题答案

第一章1.典型的编译程序在逻辑功能上由哪几部分组成?答:编译程序主要由以下几个部分组成:词法分析、语法分析、语义分析、中间代码生成、中间代码优化、目标代码生成、错误处理、表格管理。
2. 实现编译程序的主要方法有哪些?答:主要有:转换法、移植法、自展法、自动生成法。
3. 将用户使用高级语言编写的程序翻译为可直接执行的机器语言程序有哪几种主要的方式?答:编译法、解释法。
4. 编译方式和解释方式的根本区别是什么?答:编译方式:是将源程序经编译得到可执行文件后,就可脱离源程序和编译程序单独执行,所以编译方式的效率高,执行速度快;解释方式:在执行时,必须源程序和解释程序同时参与才能运行,其不产生可执行程序文件,效率低,执行速度慢。
第二章1.乔姆斯基文法体系中将文法分为哪几类?文法的分类同程序设计语言的设计与实现关系如何?答:1)0型文法、1型文法、2型文法、3型文法。
2)2. 写一个文法,使其语言是偶整数的集合,每个偶整数不以0为前导。
答:Z→SME | BS→1|2|3|4|5|6|7|8|9M→ε | D | MDD→0|SB→2|4|6|8E→0|B3. 设文法G为:N→ D|NDD→ 0|1|2|3|4|5|6|7|8|9请给出句子123、301和75431的最右推导和最左推导。
答:N⇒ND⇒N3⇒ND3⇒N23⇒D23⇒123N⇒ND⇒NDD⇒DDD⇒1DD⇒12D⇒123N⇒ND⇒N1⇒ND1⇒N01⇒D01⇒301N⇒ND⇒NDD⇒DDD⇒3DD⇒30D⇒301N⇒ND⇒N1⇒ND1⇒N31⇒ND31⇒N431⇒ND431⇒N5431⇒D5431⇒75431N⇒ND⇒NDD⇒NDDD⇒NDDDD⇒DDDDD⇒7DDDD⇒75DDD⇒754DD⇒7543D⇒75431 4. 证明文法S→iSeS|iS| i是二义性文法。
答:对于句型iiSeS存在两个不同的最左推导:S⇒iSeS⇒iiSesS⇒iS⇒iiSeS所以该文法是二义性文法。
编译原理第六章到第十一章课后习题答案
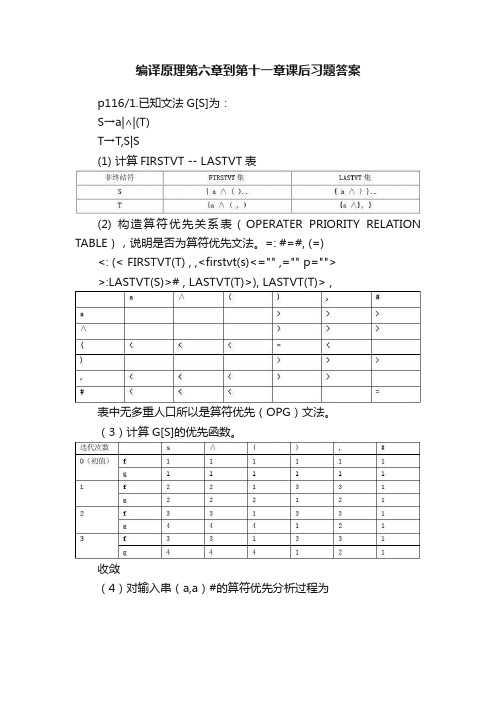
编译原理第六章到第十一章课后习题答案p116/1.已知文法G[S]为:S→a|∧|(T)T→T,S|S(1) 计算FIRSTVT -- LASTVT表(2) 构造算符优先关系表(OPERATER PRIORITY RELATION TABLE),说明是否为算符优先文法。
=: #=#, (=)<: (< FIRSTVT(T) , ,<firstvt(s)<="" ,="" p="">>:LASTVT(S)># , LASTVT(T)>), LASTVT(T)> ,表中无多重人口所以是算符优先(OPG)文法。
(3)计算G[S]的优先函数。
收敛(4)对输入串(a,a)#的算符优先分析过程为Success!3.有文法G(S):s->Vv->T/ViTT->F/T+FF->)V*|((1)(+(i(的规范推导S=>V=>ViT=>ViF=>Vi(=>Ti(=>T+Fi(=>T+(i(=>F+(i(=>(+(i((2)F+Fi(的短语、句柄、素短语。
短语S: F+Fi(T1:F+F (素短语)T2:F (句柄)F:( (素短语)(3) G(S)是否为OPG?若是,给出(1)中句子的分析过程!S’->#S# S->V V->T/ViT T->F/T+F F->)V*|(算符优先关系表(OPERATER PRIORITY RELATION TABLE)对输入串(+(I(的算符优先分析过程为:p152/2文法:S→L.L|LL→LB|BB→0|1拓广文法为G′,增加产生式S′→SI3若产生式排序为:0 S' →S1 S →L.L2 S →L3 L →LB4 L →B5 B →06 B →1由产生式知:First (S' ) = {0,1}First (S ) = {0,1}First (L ) = {0,1}First (B ) = {0,1}Follow(S' ) = {#}Follow(S ) = {#}Follow(L ) = {.,0,1,#}Follow(B ) = {.,0,1,#}G′的LR(0)项目集族及识别活前缀的DFA如下图所示:I5B →.0和B →.1为移进项目,S →L.为归约项目,存在移进-归约冲突,因此所给文法不是LR(0)文法。
编译原理课后习题答案

(a) 0 ( 0 | 1)* 0
由0和1组成且以0开始和结束的符号串全体. (b) ( ( | 0 ) 1* ) * 由0和1组成的符号串全体.
(c) ( 0 | 1 )* 0 ( 0 | 1) ( 0 | 1) 由0和1组成且以000,001,010或011结束的符号串全体. 长度大于等于3且倒数第3个字符为0的01符号串全体.
R R ‘|’ S | S S ST | T T U* | U U (R) | a | b
a
a
a
28
4.5 dangling-else文法: stmt if expr then stmt | matched-stmt matched-stmt if expr then matched-stmt else stmt | other 试说明此文法是二义性的。 句子 if e1 then if e2 then s1 else if e3 then s2 else s3 if e1 then if e2 then s1 else if e3 then s2 else s3
0|1 B 1 D E 0 ABDE ABDE ABCDE ABDE 1 ABCDE ABCDE
start
A
1
C
NFA 0
start A' 1
0
B'
0
1
start
A'
1
最小化DFA
24
DFA
3.8 给定右线性文法G: S 0S | 1S | 1A | 0B A 1C |1 B 0C | 1 C 0C | 1C | 0 | 1 试求一个等价的左线性文法G’.
20
3.6 给出接受下列在字母表{0,1}上的DFA。 (a)所有以00结束的符号串的集合; (1|0)*00
编译原理课后答案-第二版
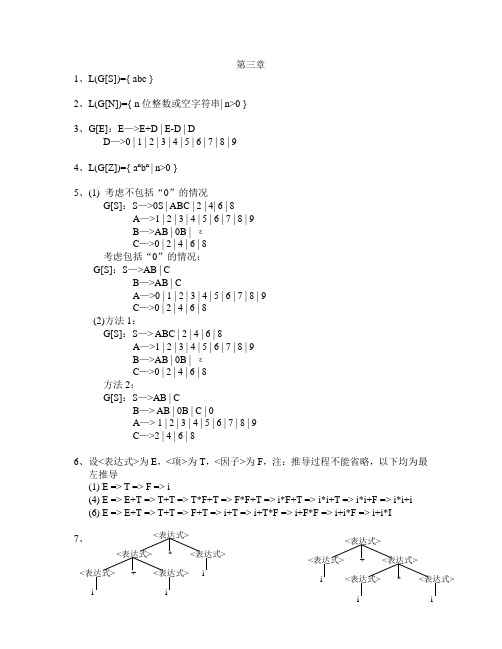
第三章1、L(G[S])={ abc }2、L(G[N])={ n位整数或空字符串| n>0 }3、G[E]:E—>E+D | E-D | DD—>0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 94、L(G[Z])={ a n b n | n>0 }5、(1) 考虑不包括“0”的情况G[S]:S—>0S | ABC | 2 | 4| 6 | 8A—>1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9B—>AB | 0B | εC—>0 | 2 | 4 | 6 | 8考虑包括“0”的情况:G[S]:S—>AB | CB—>AB | CA—>0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9C—>0 | 2 | 4 | 6 | 8(2)方法1:G[S]:S—> ABC | 2 | 4 | 6 | 8A—>1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9B—>AB | 0B | εC—>0 | 2 | 4 | 6 | 8方法2:G[S]:S—>AB | CB—> AB | 0B | C | 0A—> 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9C—>2 | 4 | 6 | 86、设<表达式>为E,<项>为T,<因子>为F,注:推导过程不能省略,以下均为最左推导(1) E => T => F => i(4) E => E+T => T+T => T*F+T => F*F+T => i*F+T => i*i+T => i*i+F => i*i+i(6) E => E+T => T+T => F+T => i+T => i+T*F => i+F*F => i+i*F => i+i*I7、<表达式><表达式>*<表达式><表达式>+<表达式>i i i<表达式><表达式>+<表达式>i <表达式>*<表达式>i i8、是有二义性的,因为句子abc 有两棵语法树(或称有两个最左推导或有两个最右推导)最左推导1:S => Ac => abc 最左推导2:S => aB => abc 9、(1)(2) 该文法描述了变量a 和运算符+、*组成的逆波兰表达式10、(1) 该文法描述了各种成对圆括号的语法结构(2) 是有二义性的,因为该文法的句子()()存在两种不同的最左推导: 最左推导1:S => S(S)S => (S)S => ()S => ()S(S)S => ()(S)S => ()()S => ()()最左推导2:S => S(S)S => S(S)S(S)S => (S)S(S)S=> ()S(S)S => ()(S)S => ()()S => ()()11、(1) 因为从文法的开始符E 出发可推导出E+T*F ,推导过程如下:E => E+T =>E+T*F ,所以E+T*F 是句型。
《编译原理》课后习题答案第三章第3章文法和语言第1

《编译原理》课后习题答案第三章第3 章文法和语言第1 题文法G=({A,B,S},{a,b,c},P,S)其中P 为:S→Ac|aBA→abB→bc写出L(G[S])的全部元素。
答案:L(G[S])={abc}第2 题文法G[N]为:N→D|NDD→0|1|2|3|4|5|6|7|8|9G[N]的语言是什么?答案:G[N]的语言是V+。
V={0,1,2,3,4,5,6,7,8,9}N=>ND=>NDD.... =>NDDDD...D=>D......D或者:允许0 开头的非负整数?第3题为只包含数字、加号和减号的表达式,例如9-2+5,3-1,7等构造一个文法。
答案:G[S]:S->S+D|S-D|DD->0|1|2|3|4|5|6|7|8|9第4 题已知文法G[Z]:Z→aZb|ab写出L(G[Z])的全部元素。
盛威网()专业的计算机学习网站 1《编译原理》课后习题答案第三章答案:Z=>aZb=>aaZbb=>aaa..Z...bbb=> aaa..ab...bbbL(G[Z])={anbn|n>=1}第5 题写一文法,使其语言是偶正整数的集合。
要求:(1) 允许0 打头;(2)不允许0 打头。
答案:(1)允许0 开头的偶正整数集合的文法E→NT|DT→NT|DN→D|1|3|5|7|9D→0|2|4|6|8(2)不允许0 开头的偶正整数集合的文法E→NT|DT→FT|GN→D|1|3|5|7|9D→2|4|6|8F→N|0G→D|0第6 题已知文法G:<表达式>::=<项>|<表达式>+<项><项>::=<因子>|<项>*<因子><因子>::=(<表达式>)|i试给出下述表达式的推导及语法树。
(5)i+(i+i)(6)i+i*i盛威网()专业的计算机学习网站 2 《编译原理》课后习题答案第三章答案:<表达式><表达式> + <项><因子><表达式><表达式> + <项><因子>i<项><因子>i<项><因子>i( )(5) <表达式>=><表达式>+<项>=><表达式>+<因子>=><表达式>+(<表达式>)=><表达式>+(<表达式>+<项>)=><表达式>+(<表达式>+<因子>)=><表达式>+(<表达式>+i)=><表达式>+(<项>+i)=><表达式>+(<因子>+i)=><表达式>+(i+i)=><项>+(i+i)=><因子>+(i+i)=>i+(i+i)<表达式><表达式> + <项><项> * <因子><因子> i<项><因子>ii(6) <表达式>=><表达式>+<项>=><表达式>+<项>*<因子>=><表达式>+<项>*i=><表达式>+<因子>*i=><表达式>+i*i=><项>+i*i=><因子>+i*i=>i+i*i盛威网()专业的计算机学习网站 3《编译原理》课后习题答案第三章第7 题证明下述文法G[〈表达式〉]是二义的。
编译原理龙书第四章答案

编译原理龙书第四章答案编译原理是计算机科学中的一门基础课程,是用于教授计算机程序的设计、构建和优化的学科,常常被用于编写编译器和解释器。
在编译原理课程中,龙书(Compilers: Principles, Techniques, and Tools)是一本经典的教材,其中第四章主要讲述了词法分析器的设计和实现。
以下是第四章的答案,按照列表划分:1. 什么是词法分析器?词法分析器(Lexical Analyzer)是编译器的组成部分之一,它用于将程序中的字符序列转换为一系列单词或词法单元(Lexeme),以便后续的语法分析和语义分析使用。
2. 词法分析器的工作流程是什么?词法分析器的工作流程如下:(1)读入字符序列。
(2)将字符序列划分为一个个词法单元,或者检查字符序列是否合法。
(3)生成一个词法单元序列,并将其传递给语法分析器。
3. 词法单元的定义是什么?词法单元是编程语言中的一个基本单元,它是对代码中的一个单一概念进行编码的基本方式。
例如,在C语言中,词法单元包括关键字(如int,if,while等)、标识符(Identifier,即自定义变量名)、运算符和特殊符号等。
4. 有哪些方法可以实现词法分析器?可以使用正则表达式、自动机等方法实现词法分析器。
其中,正则表达式可以表示字符串的集合,因此可以将其用于识别单词类别;自动机是根据输入字符序列转换状态的一种计算模型,因此可以用于实现有限自动机(Deterministic Finite Automaton)和非确定有限自动机(Nondeterministic Finite Automaton)等。
5. DFA和NFA分别是什么?DFA和NFA都是有限自动机的一种,但在转换动作上有所不同。
DFA 是确定的有限自动机,即在状态转换时只有唯一的一个选择;而NFA 是非确定的有限自动机,即在状态转换时可以有多个选择。
6. DFA和NFA之间有什么关系?DFA和NFA虽然在转换动作上不同,但它们可以互相转化。
编译原理 龙书答案

第四章部分习题解答Aho:《编译原理技术与工具》书中习题(Aho)4.1 考虑文法S → ( L ) | aL → L, S | Sa)列出终结符、非终结符和开始符号解:终结符:(、)、a、,非终结符:S、L开始符号:Sb)给出下列句子的语法树i)(a, a)ii)(a, (a, a))iii)(a, ((a, a), (a, a)))c)构造b)中句子的最左推导i)S(L)(L, S) (S, S) (a, S) (a, a)ii)S(L)(L, S) (S, S) (a, S) (a, (L)) (a, (L, S)) (a, (S, S)) (a, (a, S) (a, (a, a))iii)S(L)(L, S) (S, S) (a, S) (a, (L)) (a, (L, S)) (a, (S, S)) (a, ((L), S)) (a, ((L, S), S)) (a, ((S, S), S)) (a, ((a, S), S))(a, ((a, a), S)) (a, ((a, a), (L))) (a, ((a, a), (L, S))) (a, ((a, a), (S, S))) (a, ((a, a), (a, S))) (a, ((a, a), (a, a)))d)构造b)中句子的最右推导i)S(L)(L, S) (L, a) (S, a) (a, a)ii)S(L)(L, S) (L, (L)) (L, (L, S)) (L, (L, a)) (L, (S, a)) (L, (a, a)) (S, (a, a)) (a, (a, a))iii)S(L)(L, S) (L, (L)) (L, (L, S)) (L, (L, (L))) (L, (L, (L, S))) (L, (L, (L, a))) (L, (L, (S, a))) (L, (L, (a, a))) (L, (S,(a, a))) (L, ((L), (a, a))) (L, ((L, S), (a, a))) (L, ((L, a), (a,a))) (L, ((S, a), (a, a))) (L, ((a, a), (S, S))) (S, ((a, a), (a,a))) (a, ((a, a), (a, a)))e)该文法产生的语言是什么解:设该文法产生语言(符号串集合)L,则L = { (A1, A2, …, A n) | n是任意正整数,A i=a,或A i∈L,i是1~n之间的整数}(Aho)4.2考虑文法S→aSbS | bSaS |a)为句子构造两个不同的最左推导,以证明它是二义性的S aSbS abS abaSbS ababS ababS aSbS abSaSbS abaSbS ababS ababb)构造abab对应的最右推导S aSbS aSbaSbS aSbaSb aSbab ababS aSbS aSb abSaSb abSab ababc)构造abab对应语法树d)该文法产生什么样的语言?解:生成的语言:a、b个数相等的a、b串的集合(Aho)4.3 考虑文法bexpr→bexpr or bterm | btermbterm→bterm and bfactor | bfactorbfactor→not bfactor | ( bexpr ) | true | falsea)试为句子not ( true or false)构造分析树解:b)试证明该文法产生所有布尔表达式证明:一、首先证明文法产生的所有符号串都是布尔表达式变换命题形式——以bexpr、bterm、bfactor开始的推导得到的所有符号串都是布尔表达式最短的推导过程得到true、false,显然成立假定对步数小于n的推导命题都成立考虑步数等于n 的推导,其开始推导步骤必为以下情况之一bexpr bexpr or btermbexpr btermbterm bterm and bfactorbexpr bfactorbfactor not bfactorbfactor ( bexpr )而后继推导的步数显然<n,因此由归纳假设,第二步句型中的NT推导出的串均为布尔表达式,这些布尔表达式经过or、and、not运算或加括号,得到的仍是布尔表达式因此命题一得证。
编译原理(龙书)课后习题解答(详细)

编译原理(龙书)课后习题解答(详细)编译原理(龙书)课后题解答第一章1.1.1 :翻译和编译的区别?答:翻译通常指自然语言的翻译,将一种自然语言的表述翻译成另一种自然语言的表述,而编译指的是将一种高级语言翻译为机器语言(或汇编语言)的过程。
1.1.2 :简述编译器的工作过程?答:编译器的工作过程包括以下三个阶段:(1) 词法分析:将输入的字符流分解成一个个的单词符号,构成一个单词符号序列;(2) 语法分析:根据语法规则分析单词符号序列中各个单词之间的关系,确定它们的语法结构,并生成抽象语法树;(3) 代码生成:根据抽象语法树生成目标程序(机器语言或汇编语言),并输出执行文件。
1.2.1 :解释器和编译器的区别?答:解释器和编译器的主要区别在于执行方式。
编译器将源程序编译成机器语言或汇编语言等,在运行时无需重新编译,程序会一次性运行完毕;而解释器则是边翻译边执行,每次执行都需要进行一次翻译,一次只执行一部分。
1.2.2 :Java语言采用的是解释执行还是编译执行?答:Java一般是编译成字节码的形式,然后由Java虚拟机(JVM)进行解释执行。
但是,Java也有JIT(即时编译器)的存在,当某一段代码被多次执行时,JIT会将其编译成机器语言,提升代码的执行效率。
第二章2.1.1 :使用BNF范式定义简单的加法表达式和乘法表达式答:<加法表达式> ::= <加法表达式> "+" <乘法表达式> | <乘法表达式><乘法表达式> ::= <乘法表达式> "*" <单项式> | <单项式><单项式> ::= <数字> | "(" <加法表达式> ")"2.2.3 :什么是自下而上分析?答:自下而上分析是指从输入字符串出发,自底向上构造推导过程,直到推导出起始符号。
编译原理课后答案-第二版

第三章1、L(G[S])={ abc }2、L(G[N])={ n位整数或空字符串| n>0 }3、G[E]:E—>E+D | E-D | DD—>0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 94、L(G[Z])={ a n b n | n>0 }5、(1) 考虑不包括“0”的情况G[S]:S—>0S | ABC | 2 | 4| 6 | 8A—>1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9B—>AB | 0B | εC—>0 | 2 | 4 | 6 | 8考虑包括“0”的情况:G[S]:S—>AB | CB—>AB | CA—>0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9C—>0 | 2 | 4 | 6 | 8(2)方法1:G[S]:S—> ABC | 2 | 4 | 6 | 8A—>1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9B—>AB | 0B | εC—>0 | 2 | 4 | 6 | 8方法2:G[S]:S—>AB | CB—> AB | 0B | C | 0A—> 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9C—>2 | 4 | 6 | 86、设<表达式>为E,<项>为T,<因子>为F,注:推导过程不能省略,以下均为最左推导(1) E => T => F => i(4) E => E+T => T+T => T*F+T => F*F+T => i*F+T => i*i+T => i*i+F => i*i+i(6) E => E+T => T+T => F+T => i+T => i+T*F => i+F*F => i+i*F => i+i*I7、<表达式><表达式>*<表达式><表达式>+<表达式>i i i<表达式><表达式>+<表达式>i <表达式>*<表达式>i i8、是有二义性的,因为句子abc 有两棵语法树(或称有两个最左推导或有两个最右推导)最左推导1:S => Ac => abc 最左推导2:S => aB => abc 9、(1)(2) 该文法描述了变量a 和运算符+、*组成的逆波兰表达式10、(1) 该文法描述了各种成对圆括号的语法结构(2) 是有二义性的,因为该文法的句子()()存在两种不同的最左推导: 最左推导1:S => S(S)S => (S)S => ()S => ()S(S)S => ()(S)S => ()()S => ()()最左推导2:S => S(S)S => S(S)S(S)S => (S)S(S)S=> ()S(S)S => ()(S)S => ()()S => ()()11、(1) 因为从文法的开始符E 出发可推导出E+T*F ,推导过程如下:E => E+T =>E+T*F ,所以E+T*F 是句型。
(完整版)编译原理课后答案

第二章2.3叙述由下列正规式描述的语言(a) 0(0|1)*0在字母表{0, 1}上,以0开头和结尾的长度至少是2的01串(b) ((ε|0)1*)*在字母表{0, 1}上,所有的01串,包括空串(c) (0|1)*0(0|1)(0|1)在字母表{0, 1}上,倒数第三位是0的01串(d) 0*10*10*10*在字母表{0, 1}上,含有3个1的01串(e) (00|11)*((01|10)(00|11)*(01|10)(00|11)*)*在字母表{0, 1}上,含有偶数个0和偶数个1的01串2.4为下列语言写正规定义C语言的注释,即以 /* 开始和以 */ 结束的任意字符串,但它的任何前缀(本身除外)不以 */ 结尾。
[解答] other → a | b | … other指除了*以外C语言中的其它字符other1 → a | b | …other1指除了*和/以外C语言中的其它字符 comment → /* other* (* ** other1 other*)* ** */(f) 由偶数个0和偶数个1构成的所有0和1的串。
[解答]由题目分析可知,一个符号串由0和1组成,则0和1的个数只能有四种情况:x 偶数个0和偶数个1(用状态0表示); x 偶数个0和奇数个1(用状态1表示); x 奇数个0和偶数个1(用状态2表示); x 奇数个0和奇数个1(用状态3表示);所以,x 状态0(偶数个0和偶数个1)读入1,则0和1的数目变为:偶数个0和奇数个1(状态1)x 状态0(偶数个0和偶数个1)读入0,则0和1的数目变为:奇数个0和偶数个1(状态2)x 状态1(偶数个0和奇数个1)读入1,则0和1的数目变为:偶数个0和偶数个1(状态0)x 状态1(偶数个0和奇数个1)读入0,则0和1的数目变为:奇数个0和奇数个1(状态3)x 状态2(奇数个0和偶数个1)读入1,则0和1的数目变为:奇数个0和奇数个1(状态3)x 状态2(奇数个0和偶数个1)读入0,则0和1的数目变为:偶数个0和偶数个1(状态0)x 状态3(奇数个0和奇数个1)读入1,则0和1的数目变为:奇数个0和偶数个1(状态2)x 状态3(奇数个0和奇数个1)读入0,则0和1的数目变为:偶数个0和奇数个1(状态1)因为,所求为由偶数个0和偶数个1构成的所有0和1的串,故状态0既为初始状态又为终结状态,其状态转换图:由此可以写出其正规文法为:S0 → 1S1 | 0S2 | ε S1 → 1S0 | 0S3 | 1 S2 → 1S3 | 0S0 | 0 S3 → 1S2 | 0S1在不考虑S0 →ε产生式的情况下,可以将文法变形为: S0 = 1S1 + 0S2 S1 = 1S0 + 0S3 + 1 S2 = 1S3 + 0S0 + 0S3 = 1S2 + 0S1 所以: S0 = (00|11) S0 + (01|10) S3 + 11 + 00(1) S3 = (00|11) S3 + (01|10) S0 + 01 + 10(2) 解(2)式得: S3 = (00|11)* ((01|10) S0 + (01|10)) 代入(1)式得:S0 = (00|11) S0 + (01|10) (00|11)*((01|10) S0 + (01|10)) + (00|11) => S0 = ((00|11) + (01|10) (00|11)*(01|10))S0 + (01|10) (00|11)*(01|10) + (00|11) => S0 = ((00|11)|(01|10) (00|11)*(01|10))*((00|11) + (01|10) (00|11)* (01|10)) => S0 = ((00|1 1)|(01|10) (00|11)* (01|10))+因为S0→ε所以由偶数个0和偶数个1构成的所有0和1的串的正规定义为: S0 → ((00|11)|(01|10) (00|11)* (01|10))* (g) 由偶数个0和奇数个1构成的所有0和1的串。
编译原理课后习题答案

编译原理课后习题答案第三章N=>D=> {0,1,2,3,4,5,6,7,8,9}N=>ND=>NDDL={a |a(0|1|3..|9)n且 n>=1}(0|1|3..|9)n且 n>=1{ab,}a nb n n>=1第6题.(1) <表达式> => <项> => <因子> => i(2) <表达式> => <项> => <因子> => (<表达式>) => (<项>)=> (<因子>)=>(i)(3) <表达式> => <项> => <项>*<因子> => <因子>*<因子> =i*i(4) <表达式> => <表达式> + <项> => <项>+<项> => <项>*<因子>+<项>=> <因子>*<因子>+<项> => <因子>*<因子>+<因子> = i*i+i (5) <表达式> => <表达式>+<项>=><项>+<项> => <因子>+<项>=i+<项> => i+<因子> => i+(<表达式>) => i+(<表达式>+<项>)=> i+(<因子>+<因子>)=> i+(i+i)(6) <表达式> => <表达式>+<项> => <项>+<项> => <因子>+<项> => i+<项> => i+<项>*<因子> => i+<因子>*<因子> = i+i*i第7题第9题语法树ss s* s s+aa a推导: S=>SS*=>SS+S*=>aa+a* 11. 推导:E=>E+T=>E+T*F语法树:E*短语: T*F E+T*F直接短语: T*F句柄: T*F12.短语:直接短语:句柄:13.(1)最左推导:S => ABS => aBS =>aSBBS => aBBS => abBS => abbS => abbAa => abbaa最右推导:S => ABS => ABAa => ABaa => ASBBaa => ASBbaa => ASbbaa => Abbaa => a1b1b2a2a3 (2) 文法:S ABSS Aa S ε A aB b(3) 短语:a1 , b1 , b2, a2 , , bb , aa , abbaa,直接短语: a1 , b1 , b2, a2 , , 句柄:a114 (1)S ABA aAb | εB aBb | ε (2)S 1S0 S AA 0A1 |ε第四章1. 1. 构造下列正规式相应的DFA (1) 1(0|1)*101NFA123114(2) 1(1010*|1(010)*1)*0 NFA(3)NFA(4)NFA2.解:构造DFA 矩阵表示b其中0 表示初态,*表示终态用0,1,2,3,4,5分别代替{X} {Z} {X,Z} {Y} {X,Y} {X,Y,Z}得DFA状态图为:3.解:构造DFA矩阵表示构造DFA的矩阵表示其中表示初态,*表示终态替换后的矩阵4.(1)解构造状态转换矩阵:{2,3} {0,1}{2,3}a={0,3} {2},{3},{0,1}{0,1}a={1,1} {0,1}b={2,2}(2)解:首先把M 的状态分为两组:终态组{0},和非终态组{1,2,3,4,5} 此时G=( {0},{1,2,3,4,5} ) {1,2,3,4,5}a ={1,3,0,5} {1,2,3,4,5}b ={4,3,2,5}由于{4}a ={0} {1,2,3,5}a ={1,3,5}因此应将{1,2,3,4,5}划分为{4},{1,2,3,5} G=({0}{4}{1,2,3,5}) {1,2,3,5}a ={1,3,5} {1,2,3,5}b ={4,3,2}因为{1,5}b ={4} {23}b ={2,3}所以应将{1,2,3,5}划分为{1,5}{2,3} G=({0}{1,5}{2,3}{4}){1,5}a ={1,5} {1,5}b ={4} 所以{1,5} 不用再划分{2,3}a ={1,3} {2,3}b ={3,2}因为 {2}a ={1} {3}a ={3} 所以{2,3}应划分为{2}{3} 所以化简后为G =( {0},{2},{3},{4},{1,5})7.去除多余产生式后,构造NFA 如下确定化,构造DFA 矩阵G={(0,1,3,4,6),(2,5)} {0,1,3,4,6}a={1,3}{0,1,3,4,6}b={2,3,4,5,6}所以将{0,1,3,4,6}划分为 {0,4,6}{1,3} G={(0,4,6),(1,3),(2,5)}{0,4,6}b={3,6,4} 所以划分为{0},{4,6} G={(0),(4,6),(1,3),(2,5)}不能再划分,分别用0,4,1,2代表各状态,构造DFA 状态转换图如下;b8.代入得S = 0(1S|1)| 1(0S|0) = 01(S|ε) | 10(S|ε) = (01|10)(S|ε) = (01|10)S | (01|10)= (01|10)*(01|10)构造NFA由NFA可得正规式为(01|10)*(01|10)=(01|10)+9.状态转换函数不是全函数,增加死状态8,G={(1,2,3,4,5,8),(6,7)}(1,2,3,4,5,8)a=(3,4,8) (3,4)应分出(1,2,3,4,5,8)b=(2,6,7,8)(1,2,3,4,5,8)c=(3,8)(1,2,3,4,5,8)d=(3,8)所以应将(1,2,3,4,5,8)分为(1,2,5,8), (3,4)G={(1,2,5,8),(3,4),(6,7)}(1,2,5,8)a=(3,4,8) 8应分出(1,2,5,8)b=(2,8)(1,2,5,8)c=(8)(1,2,5,8)d=(8)G={(1,2,5),(8),(3,4),(6,7)}(1,2,5)a=(3,4,8) 5应分出G={(1,2), (3,4),5, (6,7) ,(8) }去掉死状态8,最终结果为 (1,2) (3,4) 5,(6,7) 以1,3,5,6代替,最简DFA为b正规式:b*a(da|c)*bb*第五章1.S->a | ^ |( T )T -> T , S | S(a,(a,a))S => ( T ) => ( T , S ) => ( S , S ) => ( a , S) => ( a, ( T )) =>(a , ( T , S ) ) => (a , ( S , S )) => (a , ( a , a ) )S=>(T) => (T,S) => (S,S) => ( ( T ) , S ) => ( ( T , S ) , S ) => ( ( T , S , S ) , S ) => ( ( S , S , S ) , S )=> ( ( ( T ) , S , S ) , S ) => ( ( ( T , S ) , S , S ) , S ) =>( ( ( S , S ) ,S , S ) , S ) => ( ( ( a , S ) , S , S ) , S )=> ( ( ( a , a ) , S , S ) , S ) => ( ( ( a , a ) , ^ , S ) , S ) => ( ( ( a , a ) , ^ , ( T ) ) , S )=> ( ( ( a , a ) , ^ , ( S ) ) , S ) => ( ( ( a , a ) , ^ , ( a ) ) , S ) => ( ( ( a , a ) , ^ , ( a ) ) , a )S->a | ^ |( T )T -> T , ST -> S消除直接左递归:S->a | ^ |( T )T -> S T’T’ -> , S T’ | ξSELECT ( S->a) = {a}SELECT ( S->^) = {^}SELECT ( S->( T ) ) = { ( }SELECT ( T -> S T’) = { a , ^ , ( }SELECT ( T’ -> , S T’ ) = { , }SELECT ( T’ ->ξ) = FOLLOW ( T’ ) = FOLLOW ( T ) = { ) } 构造预测分析表分析符号串( a , a )#分析栈剩余输入串所用产生式#S ( a , a) # S -> ( T )# ) T ( ( a , a) # ( 匹配# ) T a , a ) # T -> S T’# ) T’ S a , a ) # S -> a# ) T’ a a , a ) # a 匹配# ) T’,a) # T’ -> , S T’# ) T’ S , , a ) # , 匹配# ) T’ S a ) # S->a# ) T’ a a ) # a匹配# ) T’) # T’ ->ξ# ) ) # )匹配# # 接受2.E->TE’ E’->+E E’->ξ T->FT’ T’->T T’->ξ F->PF’ F’->*F’ F’->ξP->(E) P->a P->b P->∧SELECT(E’->+E)={+}SELECT(E’->ε)=FOLLOW(E’)= {#,)}SELECT(T->FT’)=FIRST(F)= {(,a,b,^}SELECT(T’ —>T)=FIRST(T)= {(,a,b,^)SELECT(T’->ε)=FOLLOW(T’)= {+,#,)}SELECT(F ->P F’)=FIRST(F)= {(,a,b,^}SELECT(F’->*F’)={*}SELECT(F’->ε)=FOLLOW(F’)= {(,a,b,^,+,#,)}3. S->MH S->a H->Lso H->ξ K->dML K->ξ L->eHf M->K M->bLMFIRST ( S ) =FIRST(MH)= FIRST ( M ) ∪ FIRST ( H ) ∪ {ξ} ∪ {a}= {a, d , b , e ,ξ}FIRST( H ) = FIRST ( L ) ∪ {ξ}= { e , ξ}FIRST( K ) = { d , ξ}FIRST( M ) = FIRST ( K ) ∪ { b } = { d , b ,ξ}FOLLOW ( S ) = { # , o }FOLLOW ( H ) = FOLLOW ( S ) ∪ { f } = { f , # , o }FOLLOW ( K ) = FOLLOW ( M ) = { e , # , o }FOLLOW ( L ) ={ FIRST ( S ) –{ξ} } ∪{o} ∪ FOLLOW ( K )∪ { FIRST ( M ) –{ξ} } ∪ FOLLOW ( M )= {a, d , b , e , # , o }FOLLOW ( M ) ={ FIRST ( H ) –{ξ} } ∪ FOLLOW ( S )∪{ FIRST ( L ) –{ξ} } = { e , # , o }SELECT ( S-> M H) = ( FIRST ( M H) –{ξ} ) ∪ FOLLOW ( S )= ( FIRST( M ) ∪ FIRST ( H ) –{ξ} ) ∪ FOLLOW ( S )= { d , b , e , # , o }SELECT ( S-> a ) = { a }SELECT ( H->L S o ) = FIRST(L S o) = { e }SELECT ( H ->ξ ) = FOLLOW ( H ) = { f , # , o }SELECT ( K-> d M L ) = { d }SELECT ( K->ξ ) = FOLLOW ( K ) = { e , # , o }SELECT ( L-> e H f ) = { e }SELECT ( M->K ) = ( FIRST( K ) –{ξ} ) ∪ FOLLOW ( M ) = {d,e , # , o }SELECT ( M -> b L M )= { b }构造LL( 1 ) 分析表4 . 文法含有左公因式,变为S->C $ { b, a }C-> b A { b }C-> a B { a }A -> b A A { b }A-> a A’ { a }A’-> ξ { $ , a, b }A’-> C { a , b }B->a B B { a }B -> b B’ { b }B’->ξ { $ , a , b }B’-> C { a, b }5. <程序> --- S <语句表>――A <语句>――B <无条件语句>――C <条件语句>――D <如果语句>――E<如果子句> --FS->begin A end S->begin A end { begin }A-> B A-> B A’ { a , if }A-> A ; B A’-> ; B A’ { ; }A’->ξ { end }B-> C B-> C { a }B-> D B-> D { if }C-> a C-> a { a }D-> E D-> E D’ { if }D-> E else B D’-> else B { else }D’->ξ {; , end }E-> FC E-> FC { if }F-> if b then F-> if b then { if }非终结符是否为空S-否 A-否A’-是 B-否 C-否 D-否D’-是 E-否 F-否FIRST(S) = { begin }FIRST(A) = FIRST(B) ∪ FIRST(A’) ∪ {ξ} = {a , if , ; , ξ}FIRST(A’) ={ ; , ξ}FIRST(B) = FIRST(C) ∪ FIRST(D) ={ a , if }FIRST(C) = {a}FIRST(D) = FIRST(E)= { if }FIRSR(D’) = {else , ξ}FIRST(E) = FIRST(F) = { if }FIRST(F) = { if }FOLLOW(S) = {# }FOLLOW(A) = {end}FOLLOW(A’) = { end }FOLLOW(B) = {; , end }FOLLOW (C) = {; , end , else }FOLLOW(D) = {; , end }FOLLOW( D’ ) = { ; , end }FOLLOW(E) = { else , ; end }FOLLOW(F) = { a }S A A’ B C D D’ E F if then else begin end a b ;6. 1.(1) S -> A | B(2) A -> aA|a(3)B -> bB |b提取(2),(3)左公因子(1) S -> A | B(2) A -> aA’(3) A’-> A|ξ(4) B -> bB’2.(1) S->AB(2) A->Ba|ξ(3) B->Db|D(4) D-> d|ξ提取(3)左公因子(1) S->AB(2) A->Ba|ξ(3) B->DB’(4) B’->b|ξ(5) D-> d|ξ3.(1) S->aAaB | bAbB(2) A-> S| db(3) B->bB|a4(1)S->i|(E)(2)E->E+S|E-S|S提取(2)左公因子(1)S->i|(E)(2)E->SE’(3)E’->+SE’|-SE’ |ξ5(1)S->SaA | bB(2)A->aB|c(3)B->Bb|d消除(1)(3)直接左递归(1)S->bBS’(2)S’->aAS’|ξ(4) B -> dB’(5)B’->bB’|ξ6.(1) M->MaH | H(2) H->b(M) | (M) |b消除(1)直接左递归,提取(2)左公因子(1)M-> HM’(2)M’-> aHM’ |ξ(3)H->bH’ | ( M )(4)H’->(M) |ξ7. (1)1)A->baB2)A->ξ3)B->Abb4)B->a将1)、2)式代入3)式1)A->baB2)A->ξ3)B->baBbb4)B->bb5)B->a提取3)、4)式左公因子1)A->baB2)A->ξ3)B->bB’4)B’->aBbb | b5)B->a(3)1)S->Aa3)A->SB4)B->ab将3)式代入1)式1)S->SBa2)S->b3)A->SB4)B->ab消除1)式直接左递归1)S->bS’2)S’->BaS’ |ξ3)S->b4)A->SB5)B->ab删除多余产生式4)1)S->bS’2)S’->BaS’ |ξ3)S->b4)B->ab(5)1)S->Ab2)S->Ba3)A->aA4)A->a5)B->a提取3) 4)左公因子1)S->Ab2)S->Ba3)A->aA’4)A’-> A |ξ将3)代入1) 5)代入21)S->aA’b2)S->aa3)A->aA’4)A’-> A |ξ5)B->a提取1) 2)左公因子1)S-> aS’2)S’->A’b | a3)A->aA’4)A’-> A |ξ5)B->a删除多余产生式5)1)S-> aS’2)S’->A’b | a3)A->aA’4)A’-> A |ξA A’ S’ S将3)代入4)1)S-> aS’2)S’->A’b | a3)A->aA ’4)A’-> aA’ |ξ将4)代入2)1)S-> aS’2)S’->aA’b3)S’->a4)S’->b5)A->aA ’6)A’-> aA’ |ξ对2)3)提取左公因子1)S->aS’2)S’->aS’’3)S’’->A’b|ξ4)S’->b5)A->aA ’6)A’-> aA’ |ξ删除多余产生式5)1)S->aS’2)S’->aS’’3)S’’->A’b|ξ4)S’->b5)A’-> aA’ |ξ第六章1S a | ∧ | ( T )T T , S | S解:(1) 增加辅助产生式S’#S#求 FIRSTVT集FIRSTVT(S’)= {#}FIRSTVT(S)={a ∧ ( }={ a ∧ ( } FIRSTVT (T) ={,} ∪ FIRSTVT( S ) = { , a ∧ ( }求 LASTVT集LASTVT(S’)= { # }LASTVT(S)={ a ∧ )}LASTVT (T) ={ , a ∧ )}(2)算符优先关系表a∧(),# a·>·>·>∧·>·>·> (<·<·<·=·<·)·>·>·>,<·<·<··>·>#<·<·<·=·因为任意两终结符之间至多只有一种优先关系成立,所以是算符优先文法(3)a ∧( ) , #F 1 1 1 1 1 1g 1 1 1 1 1 1f 2 2 1 3 2 1g 2 2 2 1 2 1f 3 3 1 3 3 1g 4 4 4 1 2 1f 3 3 1 3 3 1g 4 4 4 1 2 1(4)栈优先关系当前符号剩余输入串移进或规约#<· ( a,a)# 移进#( <· a ,a)# 移进# (a ·> , a)# 规约#(T <· , a)# 移进#(T,<· a )# 移进#(T,a ·> ) # 规约#(T,T ·> ) # 规约#(T =· ) # 移进#(T) ·> #规约#T =·#接受4.扩展后的文法S’#S# S S;G S G G G(T) G H H a H(S)T T+S T S(1)FIRSTVT(S)={;}∪FIRST VT(G) = {; , a , ( }FIRSTVT(G)={ ( }∪FIRSTVT(H) = {a , ( }FIRSTCT(H)={a , ( }FIRSTVT(T) = {+} ∪FIRSTVT(S) = {+ , ; , a , ( }LASTVT(S) = {;} ∪LASTVT(G) = { ; , a , )}LASTVT(G) = { )} ∪ LASTVT(H) = { a , )}LASTVT(H) = {a, )}LASTVT(T) = {+ } ∪LASTVT(S) = {+ , ; , a , ) };()a+#;·><··><··>·> (<·<·=·<·<·)·>·>·>·>·> a·>·>·>·>·> +<·<··><··>#<·<·<·=·因为任意两终结符之间至多只有一种优先关系成立,所以是算符优先文法(2)句型a(T+S);H;(S)的短语有:a(T+S);H;(S) a(T+S);H a(T+S) a T+S (S) H直接短语有: a T+S H (S)句柄: a素短语:a T+S (S)最左素短语:a(3)分析a;(a+a)(4)不能用最右推导推导出上面的两个句子。
compiler-龙书-习题解答-学生

3.7.6 ............ p166 3.6节的练习 ............ p103 Exercise 3.7.1 练习3.6.1NFA确定化NFA确定化‘+’代表终态3.9.9 ............ p186Exercise 3.9.4a)补充已知正则表达式,构造最小化自动机a) (a|b)*a(a|b)最小化:Π0: {1,2} {3,4}Π1: {1} {2} {3,4} 将1和2分开的原因: 1遇到a 转移到{1,2}; 2遇到a 转移到{3,4} Π2: {1} {2} {3} {4} 将3和4分开的原因: 3遇到a 转移到{3,4}; 4遇到a 转移到{2} 所以, 最小化结果与确定化结果相同S ABa abbNFAChapter 44.2.8 ............ p2064.2节的练习 ............ p119Exercise 4.2.1练习4.2.1推导、语法树、二义、语言答案 略……Exercise 4.2.3练习4.2.3设计文法a)* b)*1)* 2)*a)G: S → 1S | 0A | ε A → 1S b)G: S → 0S0 | 1S1 | ε4.3.6 ............ p2164.3节的练习 ............ p126Exercise 4.3.1练习4.3.1 提左公因子,消左递归,LL1判别a) ...... b) ......c) 消除左递归E → TE ’E ’→ +TE ’ | ε T → FT ’ T ’→ FT ’ | εF → PF ’ F ’→ *F ’ | ε P → a | bExercise 4.3.2练习4.3.2 提左公因子,消左递归,LL1判别a) ......1) ......AS4.4.6 ............ p231 4.4节的练习 ............ p136 Exercise 4.4.1练习4.4.1预测分析表d) e) 4) 5)d) S →S+S | S S | (S) | S* | a消除左递归G’: S → (S)B | aBB → +SB | SB | *B | εe) S → (L) | aL → L,S | S消除左递归G’: S → (L) | aL → SL’L’→ ,SL’ | εExercise 4.4.3练习4.4.3First集合、Follow集Exercise 4.4.4练习4.4.4First集合、Follow集b) c) f) g) 2) 3) 6) 7)f) S → aSbS | bSaS | εg)将文法简写为:E → E o T | TT → T a F | FF → n F | (E) | t | f4.5.5 ............ p2404.5节的练习 ............ p141Exercise 4.5.1练习4.5.1句柄a) 010********* 句柄: 0311 b) 0102S1112 句柄: 02S11Exercise 4.5.2练习4.5.2句柄a) c)1) 3)a) S 1S 2S 3+a++ 句柄: S 2S 3+ c) a 1a 2a 3*a 4++句柄: a 14.6.6 ............ p2574.6节的练习 ............ p153Exercise 4.6.1练习4.6.1描述文法的活前缀a)1)a) S → 0S1 | 01构造识别文法所有活前缀的自动机:活前缀的正则表达式:S | 00*S1 | 00*1I 0:S ’ → • S S → • 0S1 S → • 01I 1:S ’ → S •SI 2:S →0 • S1 S →0 • 1 S → • 0S1 S → • 01 0I 3:S →0S • 1S1I 4:S →01 •1I 5:S →0S1 • SS11S → SS+ | SS* | aG ’ : S ’→ S (0) S → SS+ (1) S → SS* (2) S → a(3)FIRST FOLLOW $ a + *$I 0:S ’ → • S S → • SS+ S → • SS* S → • a I 1:S ’ → S • S → S • S+ S → S • S* S → • SS+ S → • SS* S → • a Sa I 2:S → a •r3SI 3:S → SS • + S → SS • * S → S • S+ S → S • S* S → • SS+ S → • SS* S → • aa+I 4:S → SS+ • r1 *I 5:S → SS* •r2 Sar0Exercise 4.6.5练习4.6.5LL(1)判别、SLR判别G’ : S’→ S (0)S → AaAb (1)S → BbBa (2)A →ε(3)LL(1)文法。
编译原理龙书课后部分答案(英文版)

1) What is the difference between a compiler and an interpreter?∙ A compiler is a program that can read a program in one language - the source language - and translate it into an equivalent program in another language – the target language and report any errors in the source program that it detects during the translation process.∙ Interpreter directly executes the operations specified in the source program on inputs supplied by the user.2) What are the advantages of:(a) a compiler over an interpretera. The machine-language target program produced by a compiler is usually much faster than an interpreter at mapping inputs to outputs.(b) an interpreter over a compiler?b. An interpreter can usually give better error diagnostics than a compiler, because it executes the source program statement by statement.3) What advantages are there to a language-processing system in which the compiler produces assembly language rather than machine language?The compiler may produce an assembly-language program as its output, becauseassembly language is easier to produce as output and is easier to debug.4.2.3 Design grammars for the following languages:a) The set of all strings of 0s and 1s such that every 0 is immediately followed by at least 1.S -> SS | 1 | 01 | ε4.3.1 The following is a grammar for the regular expressions over symbols a and b only, using + in place of | for unions, to avoid conflict with the use of vertical bar as meta-symbol in grammars:rexpr -> rexpr + rterm | rtermrterm -> rterm rfactor | rfactorrfactor -> rfactor * | rprimaryrprimary -> a | ba) Left factor this grammar.rexpr -> rexpr + rterm | rtermrterm -> rterm rfactor | rfactorrfactor -> rfactor * | rprimaryrprimary -> a | bb) Does left factoring make the grammar suitable for top-down parsing?No, left recursion is still in the grammar.c) In addition to left factoring, eliminate left recursion from the original grammar.rexpr -> rterm rexpr‟rexpr‟ -> + rterm rexpr | εrterm -> rfactor rterm‟rterm‟ -> rfactor rterm | εrfactor -> rprimary rfactor‟rfactor‟ -> * rfactor‟ | εrprimary -> a | bd) Is the resulting grammar suitable for top-down parsing?Yes.Exercise 4.4.1 For each of the following grammars, derive predictive parsers and show the parsing tables. You may left-factor and/or eliminate left-recursion from your grammars first.A predictive parser may be derived by recursive decent or by the table driven approach. Either way you must also show the predictive parse table.a) The grammar of exercise 4.2.2(a).4.2.2 a) S -> 0S1 | 01This grammar has no left recursion. It could possibly benefit from left factoring. Here is the recursive decent PP code.s() {match(…0‟);if (lookahead == …0‟)s();match(…1‟);}OrLeft factoring the grammar first:S -> 0S‟S‟ -> S1 | 1s() {match(…0‟); s‟();}s‟() {if (lookahead == …0‟)s(); match(…1‟);elsematch(…1‟);}Now we will build the PP tableS -> 0S‟S‟ -> S1 | 1First(S) = {0}First(S‟) = {0, 1}Follow(S) = {1, $}The predictive parsing algorithm on page 227 (fig4.19 and 4.20) can use this table for non-recursive predictive parsing.b) The grammar of exercise 4.2.2(b).4.2.2 b) S -> +SS | *SS | a with string +*aaa.Left factoring does not apply and there is no left recursion to remove.s() {if(lookahead == …+‟)match(…+‟); s(); s();else if(lookahead == …*‟)match(…*‟); s(); s();else if(lookahead == …a‟)match(…a‟);elsereport(“syntax error”);}First(S) = {+, *, a}Follow(S) = {$, +, *, a}The predictive parsing algorithm on page 227 (fig4.19 and 4.20) can use this table for non-recursive predictive parsing.5.1.1 a, b, c: Investigating GraphViz as a solution to presenting trees5.1.2: Extend the SDD of Fig. 5.4 to handle expressions as in Fig. 5.1:1.L -> E N1.L.val = E.syn2. E -> F E'1. E.syn = E'.syn2.E'.inh = F.val3.E' -> + T Esubone'1.Esubone'.inh = E'.inh + T.syn2.E'.syn = Esubone'.syn4.T -> F T'1.T'.inh = F.val2.T.syn = T'.syn5.T' -> * F Tsubone'1.Tsubone'.inh = T'.inh * F.val2.T'.syn = Tsubone'.syn6.T' -> epsilon1.T'.syn = T'.inh7.E' -> epsilon1.E'.syn = E'.inh8. F -> digit1. F.val = digit.lexval9. F -> ( E )1. F.val = E.syn10.E -> T1. E.syn = T.syn5.1.3 a, b, c: Investigating GraphViz as a solution to presenting trees5.2.1: What are all the topological sorts for the dependency graph of Fig. 5.7?1.1, 2, 3, 4, 5, 6, 7, 8, 92.1, 2, 3, 5, 4, 6, 7, 8, 93.1, 2, 4, 3, 5, 6, 7, 8, 94.1, 3, 2, 4, 5, 6, 7, 8, 95.1, 3, 2, 5, 4, 6, 7, 8, 96.1, 3, 5, 2, 4, 6, 7, 8, 97.2, 1, 3, 4, 5, 6, 7, 8, 98.2, 1, 3, 5, 4, 6, 7, 8, 99.2, 1, 4, 3, 5, 6, 7, 8, 910.2, 4, 1, 3, 5, 6, 7, 8, 95.2.2 a, b: Investigating GraphViz as a solution to presenting trees5.2.3: Suppose that we have a production A -> BCD. Each of the four nonterminals A, B, C, and D have two attributes: s is a synthesized attribute, and i is an inherited attribute. For each of the sets of rules below, tell whether (1) the rules are consistent with an S-attributed definition (2) the rules are consistent with an L-attributed definition, and (3) whether the rules are consistent with any evaluation order at all?a) A.s = B.i + C.s1.No--contains inherited attribute2.Yes--"From above or from the left"3.Yes--L-attributed so no cyclesb) A.s = B.i + C.s and D.i = A.i + B.s1.No--contains inherited attributes2.Yes--"From above or from the left"3.Yes--L-attributed so no cyclesc) A.s = B.s + D.s1.Yes--all attributes synthesized2.Yes--all attributes synthesized3.Yes--S- and L-attributed, so no cyclesd)∙ A.s = D.i∙ B.i = A.s + C.s∙ C.i = B.s∙ D.i = B.i + C.i1.No--contains inherited attributes2.No--B.i uses A.s, which depends on D.i, which depends on B.i (cycle)3.No--Cycle implies no topological sorts (evaluation orders) using the rules5.3.1: Below is a grammar for expressions involving operator + and integer or floating-point operands. Floating-point numbers are distinguished by having a decimal point.1. E -> E + T | T2.T -> num . num | numa) Give an SDD to determine the type of each term T and expression E.1. E -> Esubone + T1. E.type = if (E.type == float || T.type == float) { E.type = float } else{ E.type = integer }2. E -> T1. E.type = T.type3.T -> numsubone . numsubtwo1.T.type = float4.T -> num1.T.type = integerb) Extend your SDD of (a) to translate expressions into postfix notation. Use the binary operator intToFloat to turn an integer into an equivalent float.Note: I use character ',' to separate floating point numbers in the resulting postfix notation. Also, the symbol "||" implies concatenation.1. E -> Esubone + T1. E.val = Esubone.val || ',' || T.val || '+'2. E -> T1. E.val = T.val3.T -> numsubone . numsubtwo1.T.val = numsubone.val || '.' || numsubtwo.val4.T -> num1.T.val = intToFloat(num.val)5.3.2 Give an SDD to translate infix expressions with + and * into equivalent expressions without redundant parenthesis. For example, since both operators associate from the left, and * takes precedence over +, ((a*(b+c))*(d)) translates into a*(b+c)*d. Note: symbol "||" implies concatenation.1.S -> E1. E.iop = nil2.S.equation = E.equation2. E -> Esubone + T1.Esubone.iop = E.iop2.T.iop = E.iop3. E.equation = Esubone.equation || '+' || T.equation4. E.sop = '+'3. E -> T1.T.iop = E.iop2. E.equation = T.equation3. E.sop = T.sop4.T -> Tsubone * F1.Tsubone.iop = '*'2. F.iop = '*'3.T.equation = Tsubone.equation || '*' || F.equation4.T.sop = '*'5.T -> F1. F.iop = T.iop2.T.equation = F.equation3.T.sop = F.sop6. F -> char1. F.equation = char.lexval2. F.sop = nil7. F -> ( E )1.if (F.iop == '*' && E.sop == '+') { F.equation = '(' || E.equation || ')' }else { F.equation = E.equation }2. F.sop = nil5.3.3: Give an SDD to differentiate expressions such as x * (3*x + x * x) involving the operators + and *, the variable x, and constants. Assume that no simplification occurs, so that, for example, 3*x will be translated into 3*1 + 0*x. Note: symbol "||" implies concatenation. Also, differentiation(x*y) = (x * differentiation(y) + differentiation(x) * y) and differentiation(x+y) = differentiation(x) + differentiation(y).1.S -> E1.S.d = E.d2. E -> T1. E.d = T.d2. E.val = T.val3.T -> F1.T.d = F.d2.T.val = F.val4.T -> Tsubone * F1.T.d = '(' || Tsubone.val || ") * (" || F.d || ") + (" || Tsubone.d || ") * (" ||F.val || ')'2.T.val = Tsubone.val || '*' || F.val5. E -> Esubone + T1. E.d = '(' || Esubone.d || ") + (" || T.d || ')'2. E.val = Esubone.val || '+' || T.val6. F -> ( E )1. F.d = E.d2. F.val = '(' || E.val || ')'7. F -> char1. F.d = 12. F.val = char.lexval8. F -> constant1. F.d = 02. F.val = constant.lexval。
编译原理英文版第四章答案

Chapter 4 Answers - Compiler Principles Exercise 1Question:Consider the following context-free grammar (CFG):S → a | BB → a1.Is the language generated by this CFG ambiguous? Justify your answer.2.If the CFG is ambiguous, provide a string that can be generated in twodifferent ways.Answer:1.The language generated by this CFG is not ambiguous. In order toprove this, we need to show that for every valid string in the language, there isa unique deriv ation tree. Let’s analyze the grammar to determine thisuniqueness:•The production rule S → a is a direct derivation from the start symbol S, resulting in the terminal symbol a. Since this is the only possible derivation from S, it is unambiguous.•The production rule S → B has B as its right-hand side. The production rule B → a is the only production rule for B, so B will eventually derive theterminal a. Therefore, the derivation from S to the single terminal a is unique.Hence, we can conclude that the language generated by this CFG is not ambiguous because there is a unique derivation for every valid string.2.Since the language is not ambiguous, we cannot provide a string thatcan be generated in two different ways, as every valid string has only onederivation.Exercise 2Question:Consider the following context-free grammar (CFG):E → E + E | E * E | id1.Starting with the non-terminal symbol E, apply the productions of thegrammar to generate the string id + id * id.2.Draw a parse tree for the string id + id * id using the abovegrammar.Answer:1.To generate the string id + id * id, we can apply the productions ofthe grammar as follows:E (Starting with E)E + E (Using E → E + E)E + E * E (Using E → E * E)id + id * id (Using E → id)2.The parse tree for the string id + id * id is as follows:E_____|_____| | |E + E| |E E| |id __|__| |E *| |E id|idExercise 3Question:Provide a context-free grammar (CFG) for the language of palindromes over the alphabet {a, b}.Answer:We can define a context-free grammar (CFG) to generate palindromes over the alphabet {a, b} as follows:S → ε | a | b | aSa | bSbExplanation: - The production rule S → ε generates an empty string (epsilon). - The production rules S → a and S → b generate single characters a and b respectively. - The production rules S → aSa and S → bSb generate palindromes. Here, the recursive non-terminal S is enclosed between the same terminal symbols a or b.This CFG covers all possible palindromes over the alphabet {a, b}, including empty strings, single characters, and palindromic strings of various lengths.Exercise 4Question:Consider the following context-free grammar (CFG):S → AaBA → ε | aAB → ε | bB1.What is the language generated by this CFG?2.Determine if the CFG is ambiguous. If so, provide a string that can begenerated in two different ways.Answer:1.The language generated by this CFG consists of strings with a prefix ofa and a suffix of b. The generated language can be represented as:L = {anbm | n ≥ 0, m ≥ 0}Where an represents zero or more a and bn represents zero or more b.2.The CFG is ambiguous. Here is an example of a string that can begenerated in two different ways: aab.Possible derivations:•Derivation 1:S (Start with S)AaB (Using S → AaB)aaABb (Using A → aA)aaBb (Using A → ε)aab (Using B → bB)•Derivation 2:S (Start with S)AaB (Using S → AaB)AaaBBb (Using A → aA)aaBBb (Using A → ε)aaBb (Using B → ε)aab (Using B → bB)Thus, the string aab can be derived in two different ways, making the grammar ambiguous.Exercise 5Question:Consider the following context-free grammar (CFG):E → E + D | DD → D * F | FF → idStarting with the non-terminal symbol E, apply the productions of the grammar to generate the string id + id * id.Answer:To generate the string id + id * id, we can apply the productions of the grammar as follows:E (Starting with E)E + D (Using E → E + D)D + D (UsingE → D)D + D * F (Using D → D * F)F + D * F (Using D → F)id + D * F (Using F → id)id + D * id (Using F → id)id + D * id * F (Using D → F)id + id * F (Using F → id)id + id * id (Using F → id)Hence, the string id + id * id can be generated by applying the productions of the given grammar starting with the non-terminal symbol E.。
编译原理第章答案

编译原理第章答案 IMB standardization office【IMB 5AB- IMBK 08- IMB 2C】第四章词法分析1.构造下列正规式相应的DFA : (1)1(0|1)*101(2)1(1010*|1(010)*1)*0 (3)a((a|b)*|ab *a)*b (4)b((ab)*|bb)*ab 解:(1)1(0|1)*101对应的NFA 为下表由子集NFA 转换法将DFA :为下表由子集法将NFA转换为DFA:(3)a((a|b)*|ab*a)*b(略)(4)b((ab)*|bb)*ab(略)0,12.已知NFA=({x,y,z},{0,1},M,{x},{z})其中:M(x,0)={z},M(y,0)={x,y},M(z,0)={x,z},M(x,1)={x},M(y,1)=φ,M(z,1)={y},构造相应的DFA 。
解:根据题意有NFA 图如下下面将该DFA 最小化:(1) 首先将它的状态集分成两个子集:P 1={A,D,E},P 2={B,C,F}(2) 区分P 2:由于F(F,1)=F(C,1)=E,F(F,0)=F 并且F(C,0)=C,所以F ,C 等价。
由于F(B,0)=F(C,0)=C,F(B,1)=D,F(C,1)=E,而D ,E 不等价(见下步),从而B 与C ,F 可以区分。
有P 21={C,F},P 22={B}。
(3)区分P1:由于A ,E 输入0到终态,而D 输入0不到终态,所以D 与A ,E 可以区分,有P 11={A,E},P 12={D}。
(4)由于F(A,0)=B,F(E,0)=F,而B ,F 不等价,所以A ,E 可以区分。
(5)综上所述,DFA 可以区分为P={{A},{B},{D},{E},{C ,F}}。
所以最小化的DFA 如下:3.0 0 F1 1 0 C B 0 0 10 1解:下表由子集法将NFA 转换为DFA :4.把图的(a)和(b)分别确定化和最小化:(a)(b) 解: (a):下表由子集法将NFA 转换为DFA :化,即:删除B ,将原来引向B 的引线引向与其等价的状态A ,有图(a2)。
编译原理龙书答案
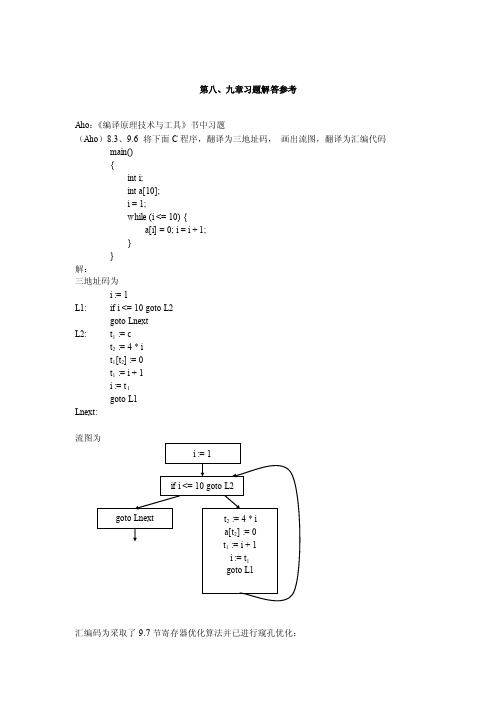
第八、九章习题解答参考Aho:《编译原理技术与工具》书中习题(Aho)8.3、9.6 将下面C程序,翻译为三地址码,画出流图,翻译为汇编代码main(){int i;int a[10];i = 1;while (i <= 10) {a[i] = 0; i = i + 1;}}解:三地址码为i := 1L1: if i <= 10 goto L2goto LnextL2: t1 := ct2 := 4 * it1[t2] := 0t1 := i + 1i := t1goto L1Lnext:汇编码为采取了9.7节寄存器优化算法并已进行窥孔优化:MOV 1, R0L1:CMP R0, 10J<= L2GOTO LnextL2: MOV 4, R1MUL R0, R1MOV 0, a(R1)MOV i, R1ADD 1, R1MOV R1, R0GOTO L1Lnext: 文案编辑词条B 添加义项?文案,原指放书的桌子,后来指在桌子上写字的人。
现在指的是公司或企业中从事文字工作的职位,就是以文字来表现已经制定的创意策略。
文案它不同于设计师用画面或其他手段的表现手法,它是一个与广告创意先后相继的表现的过程、发展的过程、深化的过程,多存在于广告公司,企业宣传,新闻策划等。
基本信息中文名称文案外文名称Copy目录1发展历程2主要工作3分类构成4基本要求5工作范围6文案写法7实际应用折叠编辑本段发展历程汉字"文案"(wén àn)是指古代官衙中掌管档案、负责起草文书的幕友,亦指官署中的公文、书信等;在现代,文案的称呼主要用在商业领域,其意义与中国古代所说的文案是有区别的。
在中国古代,文案亦作" 文按"。
公文案卷。
《北堂书钞》卷六八引《汉杂事》:"先是公府掾多不视事,但以文案为务。
"《晋书·桓温传》:"机务不可停废,常行文按宜为限日。
编译原理课后作业参考答案

作业参考答案第二章 高级语言及其语法描述6、(1)L (G 6)={0,1,2,......,9}+(2)最左推导:N=>ND=>NDD=>NDDD=>DDDD=>0DDD=>01DD=>012D=>0127 N=>ND=>DD=>3D=>34N=>ND=>NDD=>DDD=>5DD=>56D=>568 最右推导:N=>ND =>N7=>ND7=>N27=>ND27=>N127=>D127=>0127 N=>ND=>N4=>D4=>34N=>ND=>N8=>ND8=>N68=>D68=>568 7、G:S →ABC | AC | CA →1|2|3|4|5|6|7|8|9B →BB|0|1|2|3|4|5|6|7|8|9C →1|3|5|7|98、(1)最左推导:E=>E+T=>T+T=>F+T=>i+T=>i+T*F=>i+F*F=>i+i*F=>i+i*iE=>T=>T*F=>F*F=>i*F=>i*(E)=>i*(E+T)=>i*(T+T)=>i*(F+T)=>i*(i+T)=>i*(i+F)=>i*(i+i) 最右推导:E=>E+T=>E+T*F=>E+T*i=>E+F*i=>E+i*i=>T+i*i=>F+i*i=>i+i*iE=>T=>T*F=>T*(E)=>T*(E+T)=>T*(E+F)=>T*(E+i)=>T*(T+i)=>T*(F+i)=>T*(i+i)=>F*(i+i)=>i*(i+i) (2)9、证明:该文法存在一个句子iiiei 有两棵不同语法分析树,如下所示,因此该文法是二义的。
编译原理(龙书)习题答案(chap2,3)

DFA的状态图:
4) (a | b) * abb(a | b) * 根据算法3.25得到NFA:
DFA的转换表:
状态 -A{0} B{0,1} C{0,2} +D{0,3} +E{0,1,3} +F{0,2,3} a B B B E E E b A C D D F D
DFA的状态图:
括号的匹配,包括空串
4)
S a S b S |b S a S |
由相同数目的a和b组成பைடு நூலகம்字符串的集合,或者空串 5)
S a | S S | S S | S | ( S )
以a为变量,包括+,连接,*和括号四种运算的表 达式的集合
2.2.3 练习2.2.2中哪些文法具有二义性? 3) 4) 5)具有二义性。 以5)为例进行说明: 给定字符串 a+a+a ,对应着两棵分析树:
包含3个b的a,b字符串的集合
5) (aa | bb) * ((ab | ba)(aa | bb) * (ab | ba)(aa | bb)*)* 包含偶数个a和偶数个b的a,b字符串的集合
3.2.5 试写出下列语言的正则定义: 1)包含5个元音的所有小写字母串,这些串中的元音按 顺序出现。 X:除五个元音外的所有小写字母的集合。
8)所有由a和b组成且不含子串abb的串。
b * (a | ab) *
9)所有由a和b组成且不含子序列abb的串。
b * a * (b | )a * b * a * (a | b)a* |
X:[^*"] Y:[^/] Z:[^"]
3.6.1 将下图中的NFA转换为DFA。
DFA的转换表:
第二章 一个简单的语法制导翻译器
编译原理课后习题解答(2)

2/7
西北大学 Gong Xq
龙书本科教学版习题解答
仅供教学参考
解答:文法 3) 、4) 、5)有二义性。 证明:3)对文法的句子()(),存在两棵不同的语法分析树如下:
S S
S
(
S ε
)
S ε
S ε
( ε
S
)
S
S ε
(
S ε
)
S ε
S ε
(
S ε
)
S ε
所以文法是二义的。 4)对文法的句子 abab,存在两棵不同的语法分析树如下:
5/7
西北大学 Gong Xq
龙书本科教学版习题解答
仅供教学参考
2.3 节 语法制导翻译
产生式
翻译方案 { E.pre = '+' || E1.pre || T.pre } { E.pre = '-' || E1.pre || T.pre } { E.pre = T.pre } { T.pre = '*' || T1.pre || F.pre } { T.pre = '/' || T1.pre || F.pre } { T.pre = F.pre } {F.pre = id.lexeme} {F.pre = num.value} {F.pre = E.pre} E pre =-9* 52
1)证明:对语法分析树的结点数目使用数学归纳法。 ①归纳基础:当语法分析树有两个结点时,形如
num 11
num 1001
生成的串分别为 11 和 1001,表示的值为 3 和 9,能被 3 整除。 ②归纳步骤: 假设语法分析树的结点数目少于 n 时生成的二进制串的值能被 3 整除, 那么当 结点数目等于 n 时,语法分析树的根有下面两种可能的形式:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1) What is the difference between a compiler and an interpreterA compiler is a program that can read a program in one language - the source language - and translate it into an equivalent program in another language – the target language and report any errors in the source program that it detects during the translation process.Interpreter directly executes the operations specified in the source program on inputs supplied by the user.2) What are the advantages of:(a) a compiler over an interpretera. The machine-language target program produced by a compiler is usually much faster than an interpreter at mapping inputs to outputs.(b) an interpreter over a compilerb. An interpreter can usually give better error diagnostics than a compiler, because it executes the source program statement by statement.,3) What advantages are there to a language-processing system in which the compiler produces assembly language rather than machine languageThe compiler may produce an assembly-language program as its output, becauseassembly language is easier to produce as output and is easier to debug.4.2.3 Design grammars for the following languages:a) The set of all strings of 0s and 1s such that every 0 is immediately followed by at least 1.<S -> SS | 1 | 01 |4.3.1 The following is a grammar for the regular expressions over symbols a and b only, using + in place of | for unions, to avoid conflict with the use of vertical bar as meta-symbol in grammars:rexpr -> rexpr + rterm | rtermrterm -> rterm rfactor | rfactorrfactor -> rfactor * | rprimaryrprimary -> a | ba) Left factor this grammar.?rexpr -> rexpr + rterm | rtermrterm -> rterm rfactor | rfactorrfactor -> rfactor * | rprimaryrprimary -> a | bb) Does left factoring make the grammar suitable for top-down parsingNo, left recursion is still in the grammar.c) In addition to left factoring, eliminate left recursion from the original grammar.rexpr -> rterm rexpr’;r expr’ -> + rterm rexpr |rterm -> rfactor rterm’rterm’ -> rfactor rterm |rfactor -> rprimary rfactor’rfactor’ -> * rfactor’ |rprimary -> a | bd) Is the resulting grammar suitable for top-down parsingYes.》Exercise 4.4.1 For each of the following grammars, derive predictive parsers and show the parsing tables. You may left-factor and/or eliminate left-recursion from your grammars first.A predictive parser may be derived by recursive decent or by the table driven approach. Either way you must also show the predictive parse table.a) The grammar of exercise 4.2.2(a).4.2.2 a) S -> 0S1 | 01This grammar has no left recursion. It could possibly benefit from left factoring. Here is the recursive decent PP code.s() {match(‘0’);。
if (lookahead == ‘0’)s();match(‘1’);}Or《Left factoring the grammar first: S -> 0S’S’ -> S1 | 1s() {match(‘0’); s’();}(s’() {if (lookahead == ‘0’)s(); match(‘1’);elsematch(‘1’);}Now we will build the PP tableS -> 0S’S’ -> S1 | 1】First(S) = {0}First(S’) = {0, 1}Follow(S) = {1, $}The predictive parsing algorithm on page 227 and can use this table for non-recursive predictive parsing.b) The grammar of exercise 4.2.2(b).4.2.2 b) S -> +SS | *SS | a with string +*aaa.Left factoring does not apply and there is no left recursion to remove.{s() {if(lookahead == ‘+’)match(‘+’); s(); s();else if(lookahead == ‘*’)match(‘*’); s(); s();else if(lookahead == ‘a’)match(‘a’);elsereport(“syntax error”);—}First(S) = {+, *, a}Follow(S) = {$, +, *, a}The predictive parsing algorithm on page 227 and can use this table for non-recursive predictive parsing.}5.1.1 a, b, c: Investigating GraphViz as a solution to presenting treesExtend the SDD of Fig. to handle expressions as in Fig. :1.L -> E N1.=2. E -> F E'1.= E'.syn2.E'.inh =3.E' -> + T Esubone'1.、2.Esubone'.inh = E'.inh +3.E'.syn = Esubone'.syn4.T -> F T'1.T'.inh =2.= T'.syn5.T' -> * F Tsubone'1.Tsubone'.inh = T'.inh *2.T'.syn = Tsubone'.syn6.T' -> epsilon1.T'.syn = T'.inh7.~8.E' -> epsilon1.E'.syn = E'.inh9. F -> digit1.=10.F -> ( E )1.=11.E -> T1.=5.1.3 a, b, c: Investigating GraphViz as a solution to presenting treesWhat are all the topological sorts for the dependency graph of Fig.1.1, 2, 3, 4, 5, 6, 7, 8, 92.(3.1, 2, 3, 5, 4, 6, 7, 8, 94.1, 2, 4, 3, 5, 6, 7, 8, 95.1, 3, 2, 4, 5, 6, 7, 8, 96.1, 3, 2, 5, 4, 6, 7, 8, 97.1, 3, 5, 2, 4, 6, 7, 8, 98.2, 1, 3, 4, 5, 6, 7, 8, 99.2, 1, 3, 5, 4, 6, 7, 8, 910.2, 1, 4, 3, 5, 6, 7, 8, 911.2, 4, 1, 3, 5, 6, 7, 8, 95.2.2 a, b: Investigating GraphViz as a solution to presenting treesSuppose that we have a production A -> BCD. Each of the four nonterminals A, B, C, and D have two attributes: s is a synthesized attribute, and i is an inherited attribute. For each ofthe sets of rules below, tell whether (1) the rules are consistent with an S-attributed definition (2) the rules are consistent with an L-attributed definition, and (3) whether the rules are consistent with any evaluation order at all?a) = +1.·2.No--contains inherited attribute3.Yes--"From above or from the left"4.Yes--L-attributed so no cyclesb) = + and = +1.No--contains inherited attributes2.Yes--"From above or from the left"3.Yes--L-attributed so no cyclesc) = +1.Yes--all attributes synthesized2.Yes--all attributes synthesized3.…4.Yes--S- and L-attributed, so no cyclesd)== +== +1.No--contains inherited attributeses , which depends on , which depends on (cycle)3.No--Cycle implies no topological sorts (evaluation orders) using the rulesBelow is a grammar for expressions involving operator + and integer or floating-point operands. Floating-point numbers are distinguished by having a decimal point.1.,2. E -> E + T | T3.T -> num . num | numa) Give an SDD to determine the type of each term T and expression E.1. E -> Esubone + T1.= if == float || == float) { = float } else { = integer }2. E -> T1.=3.T -> numsubone . numsubtwo1.= float4.T -> num1.…2.= integerb) Extend your SDD of (a) to translate expressions into postfix notation. Use the binary operator intToFloat to turn an integer into an equivalent : I use character ',' to separate floating point numbers in the resulting postfix notation. Also, the symbol "||" implies concatenation.1. E -> Esubone + T1.= || ',' || || '+'2. E -> T1.=3.T -> numsubone . numsubtwo1.= || '.' ||4.T -> num1.= intToFloat`5.3.2 Give an SDD to translate infix expressions with + and * into equivalent expressions without redundant parenthesis. For example, since both operators associate from the left, and * takes precedence over +, ((a*(b+c))*(d)) translates into a*(b+c)*d. Note: symbol "||" implies concatenation.1.S -> E1.= nil2.=2. E -> Esubone + T1.=2.=3.= || '+' ||4.= '+'3. E -> T1.*2.=3.=4.=4.T -> Tsubone * F1.= '*'2.= '*'3.= || '*' ||4.= '*'5.T -> F1.=2.&3.=4.=6. F -> char1.=2.= nil7. F -> ( E )1.if == '*' && == '+') { = '(' || || ')' } else { = }2.= nil5.3.3: Give an SDD to differentiate expressions such as x * (3*x + x * x) involving the operators + and *, the variable x, and constants. Assume that no simplification occurs, so that, for example, 3*x will be translated into 3*1 + 0*x. Note: symbol "||" implies concatenation. Also, differentiation(x*y) = (x * differentiation(y) + differentiation(x) * y) and differentiation(x+y) = differentiation(x) + differentiation(y).1.S -> E1.=2. E -> T1.=2.=3.T -> F1.=2.=4.T -> Tsubone * F1.= '(' || || ") * (" || || ") + (" || || ") * (" || || ')'2.= || '*' ||5. E -> Esubone + T1.= '(' || || ") + (" || || ')'2.= || '+' ||6. F -> ( E )1.=2.= '(' || || ')'7. F -> char1.= 12.=8. F -> constant1.= 02.=。
