成都锦江区2020-2021-2018级初三一诊试题与答案_20210121161650
2021年四川省成都市锦江区中考英语一诊试卷

锦江区中考英语一诊试卷六、选择填空.(共10小题,计分20分)A.从各题的A,B,C三个选项中选择正确答案,(共10小题,每小题1分,计10分)1.(1分)This winter vacation,Cindy will go to France which is _____European country.()A.a B.an C.the2.(1分)﹣﹣﹣Jack,may I use your phone?﹣﹣﹣Sorry,it doesn't work.You can ask Mary for____.()A.it B.his C.hers3.(1分)﹣﹣Who cleaned the classroom?﹣﹣It ______be Mary.She took out the rubbish just now.()A.must B.can't C.might not4.(1分)﹣Who is the _____one,Lucy or Lily?﹣Lucy.()A.tall B.taller C.tallest5.(1分)Great changes ______in Macao since its return io China.()A.take place B.have taken placeC.took place6.(1分)It is raining heavily.The sports meeting ______if it keeps raining()A.puts off B.was put offC.will be put off7.(1分)I _____walk to school,but now I like riding a bike.It's more convenient.()A.used to B.was used toC.didn't use to8.(1分)My people,My country is a great movie _____almost every Chinese loves.()A.who B.that C.what9.(1分)﹣Could you please tell me______?﹣Sure.The bookstore closes at 1.00 p.m today.()A.where I can buy a dictionaryB.how I can get to the bookstoreC.If I can buy a dictionary in the bookstore now10.(1分)Students are not supposed to enter the teachers' office_____.()A.unless they are allowed toB.if they want to ask questionsC.when they are asked to come inB.补全对话.根据对话内容,从下边方框中选出适当的选项补全对话.(共1小题,每小题10分计10分)11.(10分)A:What are you going to do this weekend?B:(1).Have you got any good advice ?A:How about shopping with me?I hear that a shopping center is having a big sale.B:Emm,but I don't want to stay indoors.(2)A:Then let's go to the Wangjiang Park.We can take some nice photos there.B:That's a good idea.(3)A:But how are we going there?B:Let me see.(4)A:OK.(5)B:Let's make it early.How about 10:00 a.m.A:OK.See you then.B:See you.A:The air isn't fresh.B:I haven't got any ideas.C.I am going to bring my camera.D.We can take the No.19 bus there.E.When are we going to meet at the bus stop?七、完形填空.阅读下面两篇短文,根据短文内容,从A、B、C三个选项中选出可填入空白处的最佳答案.(共2小题,计20分.A篇每小题10分,计10分:B篇每小题10分,计10分.)12.(10分)Tom and Sam were twin brothers.They were totally (1)﹣except for their appearance.Tom had no friends,(2)for Sam,the world was full of friends.Tom was mean,but Sam was not.As their father got old,he wanted to divide his money into halves for his sons.However,Tom disagreed.He argued that whoever was smarter and stronger should get more money.Their father decided to organize a (3)between the two.The two sons had to walk as long as they could and return home before sunset.Whoever covered the longer distance(距落)would get more money.Sam walked as usual,but Tom started to run at once.At noon,Sam decided to (4)so that he could reach home on time.But Tom,to(5)more money,did not go back home.He decided to return as evening fell.Unluckily,he wasn't even halfway home by the time the moon rose.(1)A.the same B.outgoing C.different(2)A.therefore B.while C.so(3)A.competition B.party C.game(4)A.return B.eat C.run(5)A.spend B.manage C.get13.(10分)I was eleven years old standing outside in just my underwear while I watched the house that I grew up in rapidly burn to the ground,A few minutes(1)I had been in a deep sleep in my nice,warm bed when a shout woke me up.Jenny's(2)was just next to mine and my brother's.A fire(3)there and woke her up.(4)her,my older brother began to take action.While I stumbled(跌跌撞撞)in the (5)and darkness,he ran from room to room quickly waking everyone in the house.The house,however,was over 50 years old and made of wood.Before we could do anything the fire took it down.I stood there shaking while the fire burnt my books,clothes and toys.I watched(6)while my Mom criedand my Dad shouted.I wondered what was going to happen to us now that we had lost all of our things.As I looked around,though,1 realized something for the first time:The things that(7)are not things but our life.Everything that was important had survived(幸免于)the fire.Our lives would continue.I still think of that fire in the(8).It helped me to become who I am today.It showed me for the veryfirst time what is truly (9)in life.It helped me to learn(10)love is far more important than the things we own.Love others.Help everyone.Let the love inside of you make this world a warmer place.Let your soul shine brightly.(1)A.later B.earlier C.sooner(2)A.living room B.bedroom C.dining room(3)A.gave out B.went out C.broke out(4)A.Understanding B.Seeing C.Hearing(5)A.smoke B.cloud C.noise(6)A.helplessly B.uselessly C.carelessly(7)A.fail B.matter C.go(8)A.morning B.afternoon C.night(9)A.important B.convenient C.patient(10)A.what B.how C.that八、第三部分阅读理解,阅读下面短文,据短文内容判断句子的正误.正确的涂“A”,错误的涂“B”.(共5 小题,每小题10分:计10分)14.(10分)Basketball is widely loved in China.You can find people playing basketball almost everywhere,from cities to the countryside,from schools to factories.Here is a look at how the sport has developed in this country.The sport was introduced to China by American missionaries(传教士)in 1895,just four years after its invention in Springfield,Massachusetts.Soon,it was very popular in the country.Even during the Second World War,basketball was still loved by the soldiers during their free time because of its need for teamwork and hard work.In the years following Deng Xiaoping's reform and opening up,Chinese basketball began to see a fast growth thanks to the USA's National Basketball Association,or NBA.Under the direction of NBA official David Stern in 1987,the NBA began giving away free recorded games to CCTV Two years later,that agreement changed into a live﹣broadcasting deal.In 1995 ,the Chinese Basketball Association (or CBA)was founded.The CBA is now a choice for many American and European players who miss the chance to the NBA ,something that was unimaginable 20Today,more than 300 million people in China play basketball,and China's CBA has grown to include 20 men's teams.Basketball has become a part of everyday life and entertainment in China.(1)Basketball was invented in 1891(2)The soldier loved this game because they had free time during the World War.(3)Chinese basketball has been developing very fast since Chinese people could watch NBA games.(4)European basketball players tried to play basketball in the CBA in 1995.(5)The passage is mainly about how the CBA has developed in China.九、阅读下面两篇短文,根据短文内容选择正确答案.(共10小题,每小题10分:计20分)15.(10分)Do you use the apps in your smartphone everyday?We know smartphone apps have many useful functions (功能).Here are two apps.Warning:Earthquake is coming!A new app called EAS(Earthquake Alert System)gives users all the first﹣hand information about earthquakesaround the world.It also provides a guide for self﹣rescue(自救)in case an earthquake happens near you.But the best part of the app is that you can turn on its alarm system(警报系统)before you go to sleep.If an earthquake happens during he night,you'll be woken up by your phone and have a chance to get to safety You can buy this app on Apple's app store for only 2 yuan per month,which seems a small price to pay to protect your life.But It's a pity that it can't be used on Android phones,such as Samsung phones and Huawei phones.Snail Sleep ﹣gives you a better sleep!Snail Sleep ﹣An app that improves your sleep,spends the night with you and helps you develop a good sleeping habit.It records your sleep information and gives a report to help you learn more about your sleep.The smart alarm clock wakes you up at your light sleep.If you find it difficult to fall asleep at night,Snail Sleep can play soft sleep music to help you relax and bring you a good sleep.It will stop once you fall asleep.In the morning ,the soft ,cheerful music will make it easy for you to get up.This app will help you learn more about your sleep habits by recording your sleep talks and snores.(1)The app EAS can be used on smartphones.B.SamsungC.iPhone(2)How much does the app EAS cost if you want to use the app for a year?A.2 yuanB.12 yuanC.24 yuan(3)When an earthquake happens near you,.A.your phone will find a safe place for youB.the app EAS will guide you to save yourselfC.all the smarphone Users can get the first﹣hand information(4)Snail Sleep won't stop playing music until.A.you fall asleepB.you are at a light sleepC.you find it hard to fall asleep(5)What can we learn from the two passages?A.The app EAS can stop the earthquake.B.The smartphone apps can make our daily life easier and less boring.C.Both apps EAS and Snail Sleep can help you learn more about your sleep.16.(10分)A picture is worth a thousand words,but it can't always tell the whole story.The sailor in the classical photo VJ Day in Times Square,George Mendonsa,died last month at age 95.On Aug 14,1945,Japan surrendered to the United States,ending World War I American photojournalist Alfred Eisenstaedt took his camera to the streets of New York.In Times Square,people were celebrating the victory everywhere."I saw a sailor running along the street taking hold of any and every girl he met.Whether she was a grandmother,heavy,thin,old,didn't make a difference" Eisenstaedt saidHe then took the photo,which later became one of the most famous photos in history.But Eisenstaedt forgot to ask for the pair's names!Since then,many have come to Eisenstaedt to say they are the pair in the photo.One book,The Kissing Sailor,describes every detail of the photo,as well as interviews with all the people in the background of the photo.The authors stated that Greta Zimmer Friedman,a nurse,was the woman pictured.Mendonsa described what happened that day.According to him,he and his friends were in a theater at the time.People rushed in,shouting that the war was over.They then ran out and joined the street celebration in Times Square.Although it was quite sudden,Friedman,who died in 2016,said she didn't mind the kiss."It was just somebody really celebrating …it wasn't a romantic (浪漫的)event.It was just …"thank God the war is over."(1)The kissing pair in the photo were.A.George and AlfredB.Mendonsa and FriedmanC.Friedman and Eisenstaedt(2)What is TRUE about the pair in the picture?A.They didn't know each other at all.B.The man fell in love with the woman.C.The man was asking the girl for marriage.(3)The sailor would celebrate the victory by kissing he met.A.any beautyB.any grandmotherC.any female(4)What happened after the picture got its fame?A.Eisenstaedt wrote a book about it.B.People in it were all interviewed.C.Mendonsa tried to find the woman.(5)What would be the best title for the passage?A.A sailor's kissing makes history.B.Who were the pair in the picture?C.A great way to celebrate the victory.根据首字母填写单词.(共5小题r 每小题1分;计5分)17.(1分)With the help of GPS,you can find the p of a place easily.18.(1分)Only when children's mistakes are punished,will they learn to behave c19.(1分)The movie Better Days r the real problems of teenagers' school life.20.(1分)Six times he failed,but he still wanted to make his e for the last time.21.(1分)All the students love Mr.Smith because his classes are the l of all the teachers' at school.二、完成对话在对话空格中填上适当的单词,使对话完整正确.每空一词(含缩写词).(共1小题,每小题10分;计10分)22.(10分)A:Hey,Jason,what's up?You look so serious.B:It's the news about Godfrey Gao.A:You mean the Canadian﹣born actor who died from heart arrest during the(1)of filming the sports reality show Chase Me on Wednesday?B:Yes,his death has made people shocked and they also doubted whether the first﹣aid rescuing services were provided in time and in a (2)way when the accident happened.A:People think it's the mistake of Zhejiang TV station.B:The news says Chase Me has already been asked to(3).Another TV show has taken its place.Many people started to think about what's behind the (4)of reality TV shows these years.You know people are getting crazy about them.There is a hot(5)online about the dark side of reality TV shows like Chase Me.A:The dark side?I only know Chase Me gets two teams(6)each other in different challenges.B:Yeah,you are right.But this is what I just read in Weibo.It says the competitors who are usually singers,actors and models have to not only compete (7)like sportsmen but also challenge themselves mentally (脑力地).The activities would put them at a great (8)of getting hurt.A:Well,it's not hard for me to understand that the TV stations want higher television viewing rating(收视率),so they just find all the ways to (9)the strange taste of the audience(观众).But I wonder why the famous people want to join these shows.B:That's because the reality TV shows offer them an easy way to get more social (10)and become more popular.A:I think the TV stations should provide us with something positive.B:Probably this is what Gao's event exactly reminds us.三、短文填空从下面方框中选出10个单词并使用其适当形式填入短文空格内,使短文意思正确、通顺(每词限用一次).(共10小题,每小题10分:计10分)23.(10分)cause comfortable control especial fool fun include introduce it providereason solveAround the world,artificial intelligence (AI)has slowly become a part of our everyday lives.One of the biggest implementations (实施)is facial recognition (FR)technology.After enabling people to make payments,FR has now been put to use in the subway of Zhengzhou,Henan province.(1)in September,FR is available to passenger who link their online payment systems to the smartphone app of the subway.China Daily reports that other cities in China,(2)Beijing,are testing a similar system.It's not hard to set why FR technology could help speed up security checks meaningfully.Yuan Xiaoqin,a park manager in Hangzhou,told China Central Television the reason the park changed(3)entry system:"Facial recognition can help a visitor enter the park in two or three seconds.Fingerprint information sometimes isn't sensitive (灵敏的),(4)in cases of being hurt or when the fingers are too dry to be recognized." Before,the park used a fingerprint entry system.However,the use of facial recognition(5)some problems about security hidden danger so far.Many people feel (6)using facial recognition.They doubt the necessity of using facial details and worry the information could be let out.Their worries are (7).In August,a face﹣changing app called Zao allowed users to imitate famous stars from films and TV through the use of facial recognition.(8)as it was,users worried that the app was collecting a large amount of personal information.Sometimes people can refuse the app if they don't want their facial information disclosed,but sometimes people don't have a choice.Once this information is let out,it's hard to take useful actions.There is no law in China (9)the use and collection of facial information.App operators,public service (10)and government departments should be more careful in preventing use of the technology disorderly.四、阅读表达(共1小题:计10分)A.补全短文.据短文内容,从短文后的A~F选项中选出适当的选项补全短文,并将代表句子的字母填涂在答题卡相应题号的位置上.(共5 小题,每小题5分:计5分)24.(5分)As my family and I drive to my grandmother's house,my dad point out all the houses he lived in as a kid.I count 12,probably missing one or two along the way.(1)At 16,my dad had to drop out of high school to support his mom,sisters and brothers.One time,he came home from school to find an empty house and a notice that his family would have to move out of the house.We start to understand why he has no pictures of his younger self.His dad spent all his money on gambling (赌博).There is no anger in my dad's words.(2).His little sister would cry at birthday parties because she could never have one of her own at home.(3)My brothers and I have had one every year.We couldn't imagine it any other way.(4)We've heard it so much that sometimes we roll our eyes ,but his words now are still in my head,and I find new meanings every time I recall them:"There's nothing you can't do if you stay in school and work hard."I wonder how differently my father's life could have turned out if he'd had just one person saying those words to him.My dad works 16 hours a day He's gone just as I'm falling asleep.He works hard so we can have a good home and do the things he never could.(5)For 18 years,my dad has always told me this,but now it's my turn:I am so proud of you,Dad.A.However,his dad lost everything he had.B.He tells us to work hard and stay in school.C.He tells my brothers and me stories of when he was at our age.D.We threw my dad his first birthday party when he was at least 40.E.It makes me think the world is at my hands and nothing is impossibleF.Instead,there is a sense of longing (渴望)as he recalls the very little time with his father.B.完成表格.阅读下面短文,根据其内容,完成表格中所缺的信息,并将答案填写在答题卡相应的题号位置上.(共1小题,每小题5分:计5分)25.(5分)Have you noticed that many of the clothes on the high street look the same these days?So how do young people manage to express their own style?We interviewed some people in different parts of the UK."Young creative people in the UK have always come up with ways to express their personality through clothes.They like to add some accessories(配件)on their clothes.Punks added zippers and safety pins(别针),and skaters buy chains from hardware shops to hang from their trousers.You don't need money﹣you need be imaginative."said Alexi,an art student.Printing your own T﹣shirt is the easiest and most common way to customize(定制)clothes.You don't have to make a T﹣shirt.You can buy a cheap one and add some pictures of your choice."I used to make customized,colorful T﹣shirts for my friends using cloth paints.They looked a bit messy but sort of col.A couple of years ago,my mate Simon made one with a picture of Spider﹣Man.He still wears it in fact.It looks great," said John,25.Everyone knows that students don't have a lot of money.That doesn't have to be a problem if you have the ability to have new and exciting ideas."I used to make clothes sometimes when I was a student.Once I found a pair of trousers in a shop that I really liked,but I couldn't afford them.I drew a picture of it in a notebook,then I bought some cloth in the same color and copied the trousers using my mum's sewing machine (缝纫机).I loved it when people didn't believe I had made them myself," said Corrine,31.Second﹣hand or"vintage" clothes are very popular among young people.They consider them as a symbol of fashion."Sometimes a little change of my own old clothes makes a difference,because I know that they will fit and they'll look good.I like to go shopping in second﹣hand shops for jackets,trousers and dresses.You can be sure you will always have something original (原始的)as well as cheap." said Helen,26.Purpose:to (1)wearing the same clothes on the streetsCustomizing clothesWays Detailsadding accessories ●Punks add zippers and safety pins.●Skaters buy chains from hardware shops to hang from their trousersprintingsome pictures(2) cloth paints to make customized , colorful T ﹣shirts . makingby themselves Make (3) clothes they like but can't afford on their own .(4) old clothes ●Second ﹣hand or "vintage" clothes are very popular .●A small change of their own old clothes makes a difference .Conclusion :(5) can help young people to express themselves with customized clothes .五、书面表达.(计 15分) (请直接书写在答题卡的相应位置)26.(15分)假如你是李阳,将在今年寒假到美国参加为期一个月的 Study Tour 活动,美方提供了两个家庭供你选择居住,请阅读以下信息,根据两个家庭提供的居住条件和要求,分析利弊,给出你最终的决定,并给对方联系人Mr . Black 写封电子邮件回复.The Smiths The Whitesa middle ﹣aged couple who knowabout China well● a junior school boy and girl●a house with a garden , a little farfrom New York●﹩220 per month●Wanted : A kid who can liveindependently●an old couple who know little about China●no children but two dogs●a flat , in the center of New York●﹩320 per month●Wanted:A kid who can speak English well注意:1.包含选中家庭至少三条优点,并逐条阐明原因:没选中家庭两条不足,屏逐条阐明原因:2.词数要求110词左右:3.注意写作格式:4.作文中不得提及有关考生个人身份的任何信息,如校名、人名等.________________.锦江区中考英语一诊试卷参考答案六、选择填空.(共10小题,计分20分)A.从各题的A,B,C三个选项中选择正确答案,(共10小题,每小题1分,计10分)1.A;2.C;3.A;4.B;5.B;6.C;7.A;8.B;9.C;10.A;B.补全对话.根据对话内容,从下边方框中选出适当的选项补全对话.(共1小题,每小题10分计10分)11.B;A;C;D;E;七、完形填空.阅读下面两篇短文,根据短文内容,从A、B、C三个选项中选出可以填入空白处的最佳答案.(共2小题,计20分.A篇每小题10分,计10分:B篇每小题10分,计10分.)12.C;B;A;A;C;13.B;B;C;C;A;A;B;C;A;B;八、第三部分阅读理解,阅读下面短文,根据短文内容判断句子的正误.正确的涂“A”,错误的涂“B”.(共5 小题,每小题10分:计10分)14.F;T;F;F;T;九、阅读下面两篇短文,根据短文内容选择正确答案.(共10小题,每小题10分:计20分)15.C;C;B;A;B;16.B;A;C;B;A;根据首字母填写单词.(共5小题r 每小题1分;计5分)17.osition;18.orrectly;19.eflects;20.ffort;21.iveliest;二、完成对话在对话空格中填上适当的单词,使对话完整正确.每空一词(含缩写词).(共1小题,每小题10分;计10分)22.process;correct/ right;stop;popularity;discussion;competing;physically;risk;satisfy/ meet;attention;三、短文填空从下面方框中选出10个单词并使用其适当形式填入短文空格内,使短文意思正确、通顺(每词限用一次).(共10小题,每小题10分:计10分)23.Introduced;including;its;especially;has caused;uncomfortable;reasonable;Fun;to control;providers;四、阅读表达(共1小题:计10分)A.补全短文.根据短文内容,从短文后的A~F选项中选出适当的选项补全短文,并将代表句子的字母填涂在答题卡相应题号的位置上.(共5 小题,每小题5分:计5分)24.C;F;D;B;E;B.完成表格.阅读下面短文,据其内容,完成表格中所缺的信息,并将答案填写在答题卡相应的题号位置上.(共1小题,每小题5分:计5分)25.avoid;Use;whatever;Reusing;Different ways;五、书面表达.(计15分)(请直接书写在答题卡的相应位置)26.;。
2018年四川成都锦江区初三一模语文试卷

(3) 对文中划线句子翻译正确的一项是
A. “惩山北之塞,出入之迂也”意思是:苦于山区北部的关塞,出来进去都要绕远。 B. “指通豫南,达于汉阴”意思是:一过通向豫州的南部,到达汉水的北岸。 C. “叩石垦壤,箕畚运于渤海之尾”意思是:凿石头,挖土,用箕畚运到渤海边上。 D. “汝之心固,固不可彻”意思是:你思想顽固,顽固到了不可谓不彻底的程度。 (4) 下列对文章理解和分析有误的—项是 A. 选文开篇交代故事背景,指出太行、王屋二山的面积、高度和地理位置,衬托了移山
雍南。自此,冀之南,汉之阴,无陇断焉。
(1) 下面语句中加粗的词语解释有误的一项是
A. 杂然相许
许:赞同
B. 荷担者三夫 荷:扛
C. 操蛇之神
操:操作
D. 无陇断焉
断:隔绝
(2) 下列语句中加粗词的意义和用法相同的一项是
A. 笑而跪之/长跪而谢之
B. 以君之力/悉以咨之
C. 汝之不惠/时人莫之许也
D. 其如土石何/吾视其辙乱
4 2018年四川成都锦江区初三下学期初三一模第4题 下列语句中没有语病的一项是 A. 能否不断促进人的全面发展,对推动人类命运共同体建设,共同创造人类美好未来具 有重大 意乂。 B. “乐享成都,跑出乐趣”纪念卡,展现了一幅选择公共交通工具出行,让生活变得更环保、更快 捷。 C. 这则通讯报道了宁夏一位代课教师,在没有校舍的情况下,挤出自家一间房坚持办学的感人事 迹。 D. “英语广播讲座”之所以能给我很大的帮助,我认为把讲课和练习结合起来是它突出的优点。
瑞智 正心
歇斯底里 阔然无累
答案 A
解析 本题考查字形的正确书写,正确写法为:B睿智;C陨落;D廓然无累。
考点
语言文字运用 基础知识
2018年四川省成都市锦江区中考数学一诊试卷及答案

2018年四川省成都市锦江区中考数学一诊试卷A卷一、选择题(共10小题,每小题3分,满分30分)1.(3分)如图所示的几何体,其主视图是()A.B.C.D.2.(3分)已知=,则的值为()A.B.C.﹣D.﹣3.(3分)如图,线段AB两个端点的坐标分别为A(2,2)、B(3,1),以原点O为位似中心,在第一象限内将线段AB扩大为原来的2倍后得到线段CD,则端点C的坐标分别为()A.(3,1)B.(3,3)C.(4,4)D.(4,1)4.(3分)如图,在菱形ABCD中,AB=2,∠ABC=120°,则对角线BD等于()A.2B.4C.6D.85.(3分)如图,A、B、C三点在正方形网格线的交点处,若将△ABC绕着点A逆时针旋转得到△AC′B′,则tan B′的值为()A.B.C.D.6.(3分)如图,在▱ABCD中,AD=18,点E、F分别是BD、CD上的点,EF∥BC,且=,则EF 等于()A.6B.8C.9D.187.(3分)小明家2015年年收入20万元,通过合理理财,2017年年收入达到25万元,求这两年小明家年收入的平均增长率,设这两年年收入的平均增长率为x,根据题意所列方程为()A.20x2=25B.20(1+x)=25C.20(1+x)2=25D.20(1+x)+20(1+x)2=258.(3分)如图所示的暗礁区,两灯塔A,B之间的距离恰好等于圆的半径,为了使航船(S)不进入暗礁区,那么S对两灯塔A,B的视角∠ASB必须()A.大于60°B.小于60°C.大于30°D.小于30°9.(3分)如图所示,在矩形ABCD中,AD=6,AB=10,若将矩形ABCD沿DE折叠,使点C落在AB边上的点F处,则线段CE的长为()A.B.C.D.1010.(3分)如图,菱形OBAC的边OB在x轴上,点A(8,4),tan∠COB=,若反比例函数y=(k ≠0)的图象经过点C,则反比例函数解析式为()A.y=B.y=C.y=D.y=二、填空题(本大题共4小题,每小题4分,满分16分)11.(4分)课间休息,小亮与小明一起玩“五子棋”游戏,他们决定通过“剪刀、石头、布”游戏赢者开棋,若小亮出“石头”,则小亮开棋的概率是.12.(4分)如图,AC是正方形ABCD的对角线,∠DCA的平分线交BA的延长线于点E,若AB=3,则AE=13.(4分)关于x的一元二次方程(k﹣2)x2+2kx+k=0有实数根,则k的取值范围是14.(4分)如图,⊙O的直径为10,弦AB=8,P是弦AB上一动点,那么OP长的取值范围是.三、解答题(共18分)15.(12分)(1)计算:+6cos30°﹣(+2)0(2)解方程:(x+2)(x+3)=2x+16.16.(6分)为传递爱心,传播文明,某中学团委倡议全校同学在寒假期间选择参加志愿者活动(每人只能参加一种活动),活动项目有:敬老助残(A)、环境保护(B)、关爱留守儿童(C)、团委筹备小组在校门口随机调查50位同学,发现这50位同学选择三种活动项目(A、B、C)的人数之比为3:3:4.(1)若该校有1200名同学,请估计参加环境活动项目的同学有多少人?(2)请用画树状图或列表的方法,求九年级一班班长和团委书记两位同学都选择参加关爱留守儿童(C)的概率17.(8分)如图,AC是▱ABCD的对角线,在AD边上取一点F,连接BF交AC于点E,并延长BF交CD 的延长线于点G.(1)若∠ABF=∠ACF,求证:CE2=EF•EG;(2)若DG=DC,BE=6,求EF的长.18.(8分)如图,一辆滴滴快车在笔直公路上由西向东行驶,行驶至A处时接到正东方B处乘客订单,但师傅发现油量不足,马上左拐30°,沿AC行驶1200米到达加油站C处加油,加油用时5分钟,加油后再沿CB行驶1000米到B处接到乘客,假设滴滴快车的平均速度是每分钟360米,其他情况忽略不计,滴滴快车让乘客多等了多少时间?(结果保留整数≈1.414,≈1.732,≈2.236)19.(10分)如图,一次函数y1=kx+b的图象与反比例函数y2=的图象交于点A、B两点,与x轴、y轴交于C、D两点,且点C、D刚好是线段AB的三等分点,OD=2,tan∠DCO=(1)求一次函数与反比例函数的解析式;(2)求△AOB的面积;(3)若y1≤y2,请直接写出相应自变量x的取值范围20.(10分)如图,在△ABC中,∠ABC=90°,⊙O是△ABC外接圆,点D是圆上一点,点D、B分别在AC两侧,且BD=BC,连接AD、BD、OD、CD,延长CB到点P,使∠APB=∠DCB.(1)求证:AP为⊙O的切线;(2)若⊙O的半径为1,当△OED是直角三角形时,求△ABC的面积;(3)若△BOE、△DOE、△AED的面积分别为a、b、c,试探究a、b、c之间的等量关系式,并说明理由.B卷六、填空题(每小题4分,共20分)21.(4分)已知m、n是方程x2﹣2x﹣7=0的两个根,那么m2+mn+2n=.22.(4分)如图,小明周末晚上陪父母在锦江绿道上散步,他由灯下A处前进4米到达B处时,测得影子BC长为1米,已知小明身高1.6米,他若继续往前走4米到达D处,此时影子DE长为米.23.(4分)如图,点A是反比例函数y=(x>0)图象上的一点,点B是反比例函数y=﹣(x<0)图象上的点,连接OA、OB、AB,若∠AOB=90°,则sin∠A=24.(4分)如图,二次函数y=ax2+bx+c(a≠0)的图象过点(﹣1,2),下列结论:①abc>0;②a+b+c >0;③2a+b<0;④b<﹣1;⑤b2﹣4ac<8a,正确的结论是(只填序号)25.(4分)如图,⊙O的半径为6,∠AOB=90°,点C是上一动点(不与点B、A重合),过点C作CD⊥OB于点D,CE⊥OA于点E,连接ED,点F是OD的中点,连接CF交DE于点P,则CE2+3CP2等于.26.(8分)科技驱动新零售商业变革的时代已经来临,无人超市的经营模式已在全国各地兴起,某家无人超市开业以来,经测算,为销售A型商品每天需固定支出的费用为400元,若A型商品每件的销售利润不超过9元,每天销售A型商品的数量为280件,若A型商品每件的销售利润超过9元,则每超过1元,每天销售A型商品的数量减少10件,设该家无人超市A型商品的销售利润为x元/件,A型商品的日净收入为y元(日净收入=A型商品每天销售的总利润﹣A型商品每天固定的支出费用):(1)试求出该超市A型商品的日净收入为y(元)与A型商品的销售利润x(元/件)之间的关系式;(2)该超市能否实现A型商品的销售日净收入3000元的目的?如能实现,求出A型商品的销售利润为多少元/件?如不能实现,请说明理由;(3)请问该超市A型商品的销售利润为多少元/件时,能获得A型商品的最大日净收入?八、解答题(10分)27.(10分)如图,在△ABC中,CA=CB,AB=10,0°<∠C<60°,AF⊥BC于点F,在FC上截取FD =FB,点E是AC上一点,连接DA、DE,且∠ADE=∠B.(1)求证:ED=EC(2)若∠C=30°,求BD长;(3)在(2)的条件下,将图1中△DEC绕点D逆时针旋转得到△DE′C′,请问在旋转的过程中,以点D、E、C′、E′为顶点的四边形可以构成平行四边形吗?若可以,请求出该平行四边形的面积;若不可以,请说明理由.28.(12分)如图,在平面直角坐标系中,抛物线y=x2+bx+c的图象与x轴交于点A(2,0)、B(﹣4,0),与y轴交于点D.(1)求抛物线的解析式;(2)连接BD,点P在抛物线的对称轴上,以Q为平面内一点,以点P、B、D、Q为顶点的四边形能否成为矩形?若能,请求出点P的坐标;若不能,请说明理由;(3)在抛物线上有一点M,过点M、A的直线MA交y轴于点C,连接BC,若∠MBO=∠BCO,请直接写出点M的坐标.参考答案与试题解析一、选择题(共10小题,每小题3分,满分30分)1.(3分)如图所示的几何体,其主视图是()A.B.C.D.【解答】解:从正面看第一层是三个小正方形,第二层左边一个小正方形,右边一个小正方形,故选:B.2.(3分)已知=,则的值为()A.B.C.﹣D.﹣【解答】解:设x=2k,y=5k,则==﹣.故选:D.3.(3分)如图,线段AB两个端点的坐标分别为A(2,2)、B(3,1),以原点O为位似中心,在第一象限内将线段AB扩大为原来的2倍后得到线段CD,则端点C的坐标分别为()A.(3,1)B.(3,3)C.(4,4)D.(4,1)【解答】解:∵以原点O为位似中心,在第一象限内将线段AB扩大为原来的2倍后得到线段CD,∴A点与C点是对应点,∵C点的对应点A的坐标为(2,2),位似比为:1:2,∴点C的坐标为:(4,4)故选:C.4.(3分)如图,在菱形ABCD中,AB=2,∠ABC=120°,则对角线BD等于()A.2B.4C.6D.8【解答】解:∵四边形ABCD为菱形,∴AD∥BC,AD=AB,∴∠A+∠ABC=180°,∴∠A=180°﹣120°=60°,∴△ABD为等边三角形,∴BD=AB=2,故选:A.5.(3分)如图,A、B、C三点在正方形网格线的交点处,若将△ABC绕着点A逆时针旋转得到△AC′B′,则tan B′的值为()A.B.C.D.【解答】解:过C点作CD⊥AB,垂足为D.根据旋转性质可知,∠B′=∠B.在Rt△BCD中,tan B==,∴tan B′=tan B=.故选:B.6.(3分)如图,在▱ABCD中,AD=18,点E、F分别是BD、CD上的点,EF∥BC,且=,则EF等于()A.6B.8C.9D.18【解答】解:∵四边形ABCD是平行四边形,∴BC=AD=18,∵EF∥BC,且=,∴EF=BC=×18=6.故选:A.7.(3分)小明家2015年年收入20万元,通过合理理财,2017年年收入达到25万元,求这两年小明家年收入的平均增长率,设这两年年收入的平均增长率为x,根据题意所列方程为()A.20x2=25B.20(1+x)=25C.20(1+x)2=25D.20(1+x)+20(1+x)2=25【解答】解:设这两年年收入的平均增长率为x,由题意得:20(1+x)2=25,故选:C.8.(3分)如图所示的暗礁区,两灯塔A,B之间的距离恰好等于圆的半径,为了使航船(S)不进入暗礁区,那么S对两灯塔A,B的视角∠ASB必须()A.大于60°B.小于60°C.大于30°D.小于30°【解答】解:连接OA,OB,AB,BC,如图所示:∵AB=OA=OB,即△AOB为等边三角形,∴∠AOB=60°,∵∠ACB与∠AOB所对的弧都为,∴∠ACB=∠AOB=30°,又∠ACB为△SCB的外角,∴∠ACB>∠ASB,即∠ASB<30°.故选:D.9.(3分)如图所示,在矩形ABCD中,AD=6,AB=10,若将矩形ABCD沿DE折叠,使点C落在AB边上的点F处,则线段CE的长为()A.B.C.D.10【解答】解:由折叠是性质可知,DF=DC=AB=10,在Rt△ADF中,AF==8,∴BF=AB﹣AF=2,设CE=x,则BE=6﹣x,由折叠是性质可知,EF=CE=x,在Rt△BEF中,EF2=BF2+BE2,即x2=22+(6﹣x)2,解得,x=,故选:C.10.(3分)如图,菱形OBAC的边OB在x轴上,点A(8,4),tan∠COB=,若反比例函数y=(k ≠0)的图象经过点C,则反比例函数解析式为()A.y=B.y=C.y=D.y=【解答】解:如图,过点A作AE⊥x轴于点E,过点C作CF⊥OB于点F,∵四边形OCAB为菱形,∴OC∥BA,则tan∠COB=tan∠ABE==,∵点A(8,4),∴AE=4,则BE=3,∴OC=AB==5,设CF=4x,则OF=3x,根据OF2+CF2=OC2即(3x)2+(4x)2=52,解得x=1,则OF=3、CF=4,即点C坐标为(3,4),所以反比例函数解析式为y=,故选:B.二、填空题(本大题共4小题,每小题4分,满分16分)11.(4分)课间休息,小亮与小明一起玩“五子棋”游戏,他们决定通过“剪刀、石头、布”游戏赢者开棋,若小亮出“石头”,则小亮开棋的概率是.【解答】解:若小亮出“石头”,则小明出的手势情况为剪刀、石头、布这3种,其中小明出布时,小亮获胜,所以小亮开棋的概率是,故答案为:.12.(4分)如图,AC是正方形ABCD的对角线,∠DCA的平分线交BA的延长线于点E,若AB=3,则AE=3【解答】解:∵AC是正方形ABCD的对角线,AB=3,∴AC=3,∵正方形ABCD,∠DCA的平分线交BA的延长线于点E,∴∠DCE=∠ECA,DC∥EB,∴∠CEA=∠DCE,∴∠E=∠ECA,∴AE=AC=3,故答案为:313.(4分)关于x的一元二次方程(k﹣2)x2+2kx+k=0有实数根,则k的取值范围是k≥0且k≠2【解答】解:∵关于x的一元二次方程(k﹣2)x2+2kx+k=0有实数根,∴,解得:k≥0且k≠2.故答案为:k≥0且k≠2.14.(4分)如图,⊙O的直径为10,弦AB=8,P是弦AB上一动点,那么OP长的取值范围是3≤OP≤5.【解答】解:如图:连接OA,作OM⊥AB与M,∵⊙O的直径为10,∴半径为5,∴OP的最大值为5,∵OM⊥AB与M,∴AM=BM,∵AB=8,∴AM=4,在Rt△AOM中,OM=,OM的长即为OP的最小值,∴3≤OP≤5.三、解答题(共18分)15.(12分)(1)计算:+6cos30°﹣(+2)0(2)解方程:(x+2)(x+3)=2x+16.【解答】解:(1)+6cos30°﹣(+2)0=2﹣2+6×﹣1=5﹣3;(2)(x+2)(x+3)=2x+16,x2+5x+6=2x+16,x2+3x﹣10=0,(x﹣2)(x+5)=0,解得x1=2,x2=﹣5.16.(6分)为传递爱心,传播文明,某中学团委倡议全校同学在寒假期间选择参加志愿者活动(每人只能参加一种活动),活动项目有:敬老助残(A)、环境保护(B)、关爱留守儿童(C)、团委筹备小组在校门口随机调查50位同学,发现这50位同学选择三种活动项目(A、B、C)的人数之比为3:3:4.(1)若该校有1200名同学,请估计参加环境活动项目的同学有多少人?(2)请用画树状图或列表的方法,求九年级一班班长和团委书记两位同学都选择参加关爱留守儿童(C)的概率【解答】解:(1)1200×=360(人),答:估计参加环境活动项目的同学有360人;(2)如图所示:,一共有9种可能,两位同学都选择参加关爱留守儿童的可能有1种,故两位同学都选择参加关爱留守儿童的概率为:.四、解答题(每小题8分,共16分)17.(8分)如图,AC是▱ABCD的对角线,在AD边上取一点F,连接BF交AC于点E,并延长BF交CD 的延长线于点G.(1)若∠ABF=∠ACF,求证:CE2=EF•EG;(2)若DG=DC,BE=6,求EF的长.【解答】解:(1)∵AB∥CG,∴∠ABF=∠G,又∵∠ABF=∠ACF,∴∠ECF=∠G,又∵∠CEF=∠CEG,∴△ECF∽△EGC,∴,即CE2=EF•EG;(2)∵平行四边形ABCD中,AB=CD,又∵DG=DC,∴AB=CD=DG,∴AB:CG=1:2,∵AB∥CG,∴,即,∴EG=12,BG=18,∵AB∥DG,∴,∴BF=BG=9,∴EF=BF﹣BE=9﹣6=3.18.(8分)如图,一辆滴滴快车在笔直公路上由西向东行驶,行驶至A处时接到正东方B处乘客订单,但师傅发现油量不足,马上左拐30°,沿AC行驶1200米到达加油站C处加油,加油用时5分钟,加油后再沿CB行驶1000米到B处接到乘客,假设滴滴快车的平均速度是每分钟360米,其他情况忽略不计,滴滴快车让乘客多等了多少时间?(结果保留整数≈1.414,≈1.732,≈2.236)【解答】解:如图作CH⊥AB于H.在Rt△ACH中,AC=1200,∠A=30°,∴CH=AC=600,AH=CH≈1039.2,在Rt△BCH中,BH===800,∴AB=1893,AC+BC=2200,∴滴滴快车让乘客多等的时间=5+≈6(分钟),五、解答题(每小题10分,共20分)19.(10分)如图,一次函数y1=kx+b的图象与反比例函数y2=的图象交于点A、B两点,与x轴、y轴交于C、D两点,且点C、D刚好是线段AB的三等分点,OD=2,tan∠DCO=(1)求一次函数与反比例函数的解析式;(2)求△AOB的面积;(3)若y1≤y2,请直接写出相应自变量x的取值范围【解答】解:(1)∵OD=2,tan∠DCO==,∴,∴OC=3,∴D(0,2),C(﹣3,0),把D(0,2),C(﹣3,0)代入y1=kx+b中得:,解得:,∴一次函数的解析式为:y1=x+2;过A作AE⊥x轴于E,∵点C、D刚好是线段AB的三等分点,∴AC=CD=BD,∵∠AEC=∠COD=90°,∠ECA=∠OCD,∴△AEC≌△DOC,∴EC=OC=3,AE=OD=2,∴A(﹣6,﹣2),∴m=﹣6×(﹣2)=12,∴反比例函数的解析式为:y2=;(2)同理得:B(3,4),∴S△AOB=S△BOC+S△ACO,=•|y B|+•|y A|,=+×3×2,=9;(3)由图象得:当x≤﹣6或0<x≤3时,y1≤y2.20.(10分)如图,在△ABC中,∠ABC=90°,⊙O是△ABC外接圆,点D是圆上一点,点D、B分别在AC两侧,且BD=BC,连接AD、BD、OD、CD,延长CB到点P,使∠APB=∠DCB.(1)求证:AP为⊙O的切线;(2)若⊙O的半径为1,当△OED是直角三角形时,求△ABC的面积;(3)若△BOE、△DOE、△AED的面积分别为a、b、c,试探究a、b、c之间的等量关系式,并说明理由.【解答】(1)证明:∵BD=BC,∴∠BDC=∠BCD,∵∠P=∠BCD,∠BAC=∠BDC,∴∠P=∠BAC,∵AC是直径,∴∠ABC=∠ABP=90°,∴∠P+∠BAP=90°,∴∠BAP+∠BAC=90°,∴∠OAP=90°,∴OA⊥P A,∴P A是⊙O的切线.(2)解:①当∠OED=90°时,CB=CD=BD,△ABC是等边三角形,可得∠ACB=30°,∵AC=2,∴AB=1,BC=,∴S△ABC=.②当∠DOE=90°时,作BH⊥AC于H.∵BD=BC,BO=BO,OC=OD,∴△BOC≌△BOD(SSS),∴∠OBC=∠OBD=∠OCB=22.5°,∴∠BOH=45°,∴BH=,∴S△ABC=×2×=(3)解:∵BD=BC,OD=OC,BO=BO,∴△BOD≌△BOC,∴∠OBD=∠OBC,∵OB=OD=CO,∴∠OBD=∠OBC=∠ODB=∠OCB,∵∠ADB=∠OCB,∴∠ADB=∠OBD,∴AD∥OB,∴△AED∽△OEB,∴=()2,∵==,∴=()2,∴b2=ac.六、填空题(每小题4分,共20分)21.(4分)已知m、n是方程x2﹣2x﹣7=0的两个根,那么m2+mn+2n=4.【解答】解:∵m、n是方程x2﹣2x﹣7=0的两个根,∴m+n=2,mn=﹣7,m2﹣2m﹣7=0,∴m2=2m+7,∴m2+mn+2n=2m+7+mn+2n=7+2×2+(﹣7)=4.故答案为:4.22.(4分)如图,小明周末晚上陪父母在锦江绿道上散步,他由灯下A处前进4米到达B处时,测得影子BC长为1米,已知小明身高1.6米,他若继续往前走4米到达D处,此时影子DE长为2米.【解答】解:由FB∥AP可得,△CBF∽△CAP,∴,即,解得AP=8,由GD∥AP可得,△EDG∽△EAP,∴,即,解得ED=2,故答案为:2.23.(4分)如图,点A是反比例函数y=(x>0)图象上的一点,点B是反比例函数y=﹣(x<0)图象上的点,连接OA、OB、AB,若∠AOB=90°,则sin∠A=【解答】解:如图作AE⊥x轴于E,BF⊥x轴于F.设A(a,),B(b,﹣),∵∠AOB=∠OFB=∠AEO=90°,∴∠BOF+∠AOE=90°,∠AOE+∠OAE=90°,∴∠BOF=∠OAE,∴△BOF∽△OAE,∴=,∴=,∴a2b2=5,∵AB2=OB2+OA2=b2++a2+=6b2+,∴AB=,OB=,∴sin∠A===,故答案为.24.(4分)如图,二次函数y=ax2+bx+c(a≠0)的图象过点(﹣1,2),下列结论:①abc>0;②a+b+c >0;③2a+b<0;④b<﹣1;⑤b2﹣4ac<8a,正确的结论是①④⑤(只填序号)【解答】解:①∵抛物线开口向上,∴a>0,∵x=﹣>0,∴b<0,又∵抛物线与y轴交于负半轴,∴c<0,∴abc>0.故①正确;②∵x=1时,y<0,∴a+b+c<0,故②错误;③∵a>0,0<﹣<1,∴﹣b<2a,∴2a+b>0.故③错误;④∵抛物线过点(﹣1,2),∴a﹣b+c=2∴a+c=b+2∵a+b+c<0,∴b+2+b<0∴b<﹣1故④正确;∵>﹣2且a>0∴4ac﹣b2>﹣8a∴b2﹣4ac<8a成立,故⑤正确.故答案为:①④⑤.25.(4分)如图,⊙O的半径为6,∠AOB=90°,点C是上一动点(不与点B、A重合),过点C作CD⊥OB于点D,CE⊥OA于点E,连接ED,点F是OD的中点,连接CF交DE于点P,则CE2+3CP2等于48.【解答】解:设DF=OF=a,CD=b,连接OC.∵CD⊥OB于点D,CE⊥OA于点E,∴∠EOD=∠CDO=∠CEO=90°,∴四边形CDOE是矩形,∴CE=OD=2a,CD=OE=b,∵EC∥DF,∴==,∴PC=2PF,PC=CF=,∴EC2+3CP2=4a2+(a2+b2)=(4a2+b2),在Rt△OCE中,∵EC2+OE2=OC2,∴4a2+b2=36,∴EC2+3CP2=48.故答案为48七、解答题(8分)26.(8分)科技驱动新零售商业变革的时代已经来临,无人超市的经营模式已在全国各地兴起,某家无人超市开业以来,经测算,为销售A型商品每天需固定支出的费用为400元,若A型商品每件的销售利润不超过9元,每天销售A型商品的数量为280件,若A型商品每件的销售利润超过9元,则每超过1元,每天销售A型商品的数量减少10件,设该家无人超市A型商品的销售利润为x元/件,A型商品的日净收入为y元(日净收入=A型商品每天销售的总利润﹣A型商品每天固定的支出费用):(1)试求出该超市A型商品的日净收入为y(元)与A型商品的销售利润x(元/件)之间的关系式;(2)该超市能否实现A型商品的销售日净收入3000元的目的?如能实现,求出A型商品的销售利润为多少元/件?如不能实现,请说明理由;(3)请问该超市A型商品的销售利润为多少元/件时,能获得A型商品的最大日净收入?【解答】解:(1)由题意可得,当0<x≤9时,y=280x﹣400,当x>9时,y=[280﹣(x﹣9)×10]x﹣400=﹣10x2+370x﹣400,由上可得,该超市A型商品的日净收入为y(元)与A型商品的销售利润x(元/件)之间的关系式是:y=;(2)∵当0<x≤9时,y=280x﹣400≤2120,∴令y=3000代入y=﹣10x2+370x﹣400,解得,x1=17,x2=20,答:该超市能实现A型商品的销售日净收入3000元的目的,A型商品的销售利润为17元/件或20元/件;(3)∵当0<x≤9时,y=280x﹣400≤2120,当x>9时,y=﹣10x2+370x﹣400=﹣10(x﹣)2+3022.5,∵x>9且x为整数,∴当x=18或19时,y取得最大值,此时y=3020,答:该超市A型商品的销售利润为18元/件或19元/件时,能获得A型商品的最大日净收入.八、解答题(10分)27.(10分)如图,在△ABC中,CA=CB,AB=10,0°<∠C<60°,AF⊥BC于点F,在FC上截取FD =FB,点E是AC上一点,连接DA、DE,且∠ADE=∠B.(1)求证:ED=EC(2)若∠C=30°,求BD长;(3)在(2)的条件下,将图1中△DEC绕点D逆时针旋转得到△DE′C′,请问在旋转的过程中,以点D、E、C′、E′为顶点的四边形可以构成平行四边形吗?若可以,请求出该平行四边形的面积;若不可以,请说明理由.【解答】解:(1)∵AC=BC,∴∠ABC=∠BAC,∴∠C=180°﹣∠ABC﹣∠BAC=180°﹣2∠ABC,∵AF⊥BC,BF=DF,∴AB=AD,∴∠ADB=∠ABC,∵∠ADE=∠ABC,∴∠CDE=180°﹣∠ADE﹣∠ADB=180°﹣2∠ABC,∴∠CDE=∠C,∴DE=CE;(2)∵∠C=30°,∴∠ABC=∠ADB=∠BAC=∠ADE=75°,∴∠BAD=30°,过点B作BG⊥AD于G,如图1,在Rt△ABG中,AB=10,∠BAD=30°,∴BG=5,AG=5,∴DG=AD﹣AG=10﹣5=5(2﹣),在Rt△BDG中,BD==10=5﹣5;(3)可以,①理由:如图2;∵DE=CE,∴∠EDC=∠C=30°,由旋转知,∠E'DC'=∠E'C'D=∠C=30°∵四边形DEC'E'是平行四边形,∴C'E'∥DE,∴∠C'DE=30°,∴∠C'DC=60°,∴C'D⊥AC于H,在Rt△ADH中,AD=10,∠DAH=∠BAC﹣∠BAD=45°,∴DH=5,在Rt△DEH中,∠AED=∠ACB+∠CDE=60°,∴∠EDH=30°,∴DE=,∴CE=,∴S▱DEC'E'=2S△CDE=2×CE×DH=×5=.②理由:如图3,由①知,S△CDE=S△C'DE'=,∴S▱DEC'E'=2S△CDE=2×CE×DH=×5=.九、解答题(12分)28.(12分)如图,在平面直角坐标系中,抛物线y=x2+bx+c的图象与x轴交于点A(2,0)、B(﹣4,0),与y轴交于点D.(1)求抛物线的解析式;(2)连接BD,点P在抛物线的对称轴上,以Q为平面内一点,以点P、B、D、Q为顶点的四边形能否成为矩形?若能,请求出点P的坐标;若不能,请说明理由;(3)在抛物线上有一点M,过点M、A的直线MA交y轴于点C,连接BC,若∠MBO=∠BCO,请直接写出点M的坐标.【解答】解:(1)由题意,解得,∴抛物线的解析式为y=x2+x﹣4.(2)如图1中,当BD为矩形的边时,∵直线BD的解析式为y=﹣x﹣4,∴直线BP的解析式为y=x=4,直线DP′的解析式为y=x﹣4,可得P(﹣1,3),P′(﹣1,﹣5).当BD为矩形的对角线时,设P(﹣1,m),BD的中点N(﹣2,﹣2),由BN=P″N,可得12+(m+2)2=(2)2,解得m=﹣2+或﹣2﹣,∴P″(﹣1,﹣2+),或(﹣1.﹣2﹣),∴要使四边形PBQD能成为矩形,满足条件的点P坐标为(﹣1,﹣2+)或(﹣1.﹣2﹣).综上所述,满足条件的P的坐标为(﹣1,3)或(﹣1,﹣5)或(﹣1,﹣2+)或(﹣1.﹣2﹣).(3)设M(m,m2+m﹣4),设直线AM的解析式为y=kx+b,则有,解得,∴直线AM的解析式为y=x﹣m﹣4,∴C(0,﹣m﹣4).①点M在第二象限显然不可能,当点M在第三象限时,如图2中,作MN⊥OB于N.∵∠MBN=∠BCO,∠MNB=∠BOC=90°,∴△MNB∽△BOC,∴=,∴=,∴m=﹣2或0.∴M(﹣2,﹣4)或(0,﹣4)(舍弃)②当点M在y轴上时,可得M(0,﹣4);③当点M在第一象限时,同法可得=,整理得:m2+2m﹣16=0,∴m=﹣1+或﹣1﹣(舍弃),∴M(﹣1+,4),④当点M在第四象限时,不存在,综上所述,满足条件的点M坐标(﹣2,﹣4)或(0,﹣4)或(﹣1+,4).。
2020年四川省成都市锦江区中考数学一诊试卷含答案

2020年四川省成都市锦江区中考数学一诊试卷A卷(共100分)一、选择题(共10个小题,每小题3分,满分30分)在下列小题中,均给出四个答案,其中有且只有一个正确答案,请将正确答案的字母代号在答题卡上涂黑,涂错或不涂均为零分1.(3分)下列立体图形中,主视图是三角形的是()A.B.C.D.2.(3分)如图,在Rt△ABC中,∠C=90°,AB=13,cos A=,则AC的长为()A.5B.8C.12D.133.(3分)用配方法解一元二次方程x2﹣4x﹣1=0,配方后得到的方程是()A.(x﹣2)2=1B.(x﹣2)2=4C.(x﹣2)2=3D.(x﹣2)2=54.(3分)如图,双曲线y=的一个分支为()A.①B.②C.③D.④5.(3分)在一个不透明的布袋中装有9个白球和若干个黑球,它们除颜色不同外,其余均相同.若从中随机摸出一个球,摸到白球的概率是,则黑球的个数为()A.3B.12C.18D.276.(3分)如图,MN所在的直线垂直平分线段AB,利用这样的工具,可以找到圆形工件的圆心.如果使用此工具找到圆心,最少使用次数为()A.1B.2C.3D.47.(3分)如图,在△ABC中,AB=AC=6,D为AC上一点,连接BD,且BD=BC=4,则DC为()A.2B.C.D.58.(3分)若点A(﹣3,y1),B(﹣1,y2),C(1,y3)在反比例函数y=的图象上,则y1,y2,y3的大小关系是()A.y1<y2<y3B.y2<y1<y3C.y3<y1<y2D.y3<y2<y19.(3分)如图,在菱形ABCD中,点E,F分别在AB,CD上,且AE=CF,连接EF交BD于点O,连接AO.若∠DBC=25°,则∠OAD的度数为()A.50°B.55°C.65°D.75°10.(3分)已知y关于x的函数表达式是y=ax2﹣4x﹣a,下列结论不正确的是()A.若a=﹣1,函数的最大值是5B.若a=1,当x≥2时,y随x的增大而增大C.无论a为何值时,函数图象一定经过点(1,﹣4)D.无论a为何值时,函数图象与x轴都有两个交点二、填空题(共4个小题,每小题4分,满分16分)11.(4分)如图,将∠AOB放在边长为1的小正方形组成的网格中,若点A,O,B都在格点上,则tan∠AOB=.12.(4分)已知关于x的方程x2+(2k+1)x+k2=0有两个实数根,则实数k的取值范围为.13.(4分)如图,在矩形ABCD中,AB=3,AD=4,对角线AC,BD交于点O,点M,N分别为OB,OC 的中点,则△OMN的面积为.14.(4分)如图,BA,BC是⊙O的两条弦,以点B为圆心任意长为半径画弧,分别交BA,BC于点M,N;分别以点M,N为圆心,以大于MN为半径画弧,两弧交于点P,连接BP并延长交⊙O于点D;连接OD,OC.若∠COD=70°,则∠ABD等于.三、解答题(共6个小题,满分54分)15.(12分)(1)计算:(﹣)﹣1+﹣6sin45°﹣|3﹣|(2)解方程:x(x﹣3)+2x﹣6=016.(6分)为全面贯彻党的教育方针,坚持“健康第一”的教育理念,促进学生健康成长,提高体质健康水平,成都市调整体育中考实施方案:分值增加至60,男1000米(女800米)必考,足球、篮球、排球“三选一”…,从2019年秋季新入学的七年级起开始实施.某中学为了解七年级学生对三大球类运动的喜爱情况,从七年级学生中随机抽取部分学生进行调查问卷,通过分析整理绘制了如下两幅统计图.请根据两幅统计图中的信息回答下列问题:(1)求参与调查的学生中,喜爱排球运动的学生人数,并补全条形图;(2)若该中学七年级共有400名学生,请你估计该中学七年级学生中喜爱篮求运动的学生有多少名?(3)若从喜爱足球运动的2名男生和2名女生中随机抽取2名学生,确定为该校足球运动员的重点培养对象,请用列表法或画树状图的方法求抽取的两名学生为一名男生和一名女生的概率.17.(8分)近日,国产航母山东舰成为了新晋网红,作为我国本世纪建造的第一艘真正意义上的国产航母,承载了我们太多期盼,促使我国在伟大复兴路上加速前行.如图,山东舰在一次测试中,巡航到海岛A 北偏东60°方向P处,发现在海岛A正东方向有一可疑船只B正沿BA方向行驶.山东舰经测量得出:可疑船只在P处南偏东45°方向,距P处50海里.山东舰立即从P沿南偏西30°方向驶岀,刚好在C处成功拦截可疑船只.求被拦截时,可疑船只距海岛A还有多少海里?(≈1.414,≈1.732,结果精确到0.1海里)18.(8分)在▱ABCD中,E,F分别是AB,DC上的点,且AE=CF,连接DE,BF,AF.(1)求证:四边形DEBF是平行四边形;(2)若AF平分∠DAB,AE=3,DE=4,BE=5,求AF的长.19.(10分)如图,在直角坐标系中,点B的坐标为(2,1),过点B分别作x轴、y轴的垂线,垂足分别是C,A,反比例函数y=(x>0)的图象交AB,BC分别于点E,F.(1)求直线EF的解析式;(2)求四边形BEOF的面积;(3)若点P在y轴上,且△POE是等腰三角形,请直接写出点P的坐标.20.(10分)如图1,△ABD内接于⊙O,AD是直径,∠BAD的平分线交BD于H,交⊙O于点C,连接DC并延长,交AB的延长线于点E,(1)求证:AE=AD;(2)若=,求的值;(3)如图2,连接CB并延长,交DA的延长线于点F,若AH=HC,AF=6,求△BEC的面积.B卷(共50分)一、填空题(共5个小题,每小题4分,满分20分)B卷(50分)21.(4分)若a,b是一元二次方程x2﹣2x+1=0的两根,则=.22.(4分)光线从空气射入水中会发生折射现象,发生折射时,满足的折射定律如图①所示:折射率n=(α代表入射角,β代表折射角).小明为了观察光线的折射现象,设计了图②所示的实验:通过细管可以看见水底的物块,但从细管穿过的直铁丝,却碰不上物块.图③是实验的示意图,点A,C,B在同一直线上,测得BC=7cm,BF=12cm,DF=16cm,则光线从空气射入水中的折射率n等于.23.(4分)如图,在平面直角坐标系中,正方形ABCD的面积为20,顶点A在y轴上,顶点C在x轴上,顶点D在双曲线y=(x>0)的图象上,边CD交y轴于点E,若CE=ED,则k的值为.24.(4分)如图,已知△ABC中,CA=CB=4,∠C=45°,D是线段AC上一点(不与A,C重合),连接BD,将△ABD沿AB翻折,使点D落在点E处,延长BD与EA的延长线交于点F.若△BEF是直角三角形,则AF的长为.25.(4分)如图,在▱ABCD中,BC=6,对角线BD=10,tan∠DBC=,点E是线段BC上的动点,连接DE,过点D作DP⊥DE,在射线DP上取点F,使得∠DFE=∠DBC,连接CF,则△DCF周长的最小值为.二、解答题(共3个小题,满分30分)26.(8分)非洲猪瘟疫情发生以来,猪肉市场供应阶段性偏紧和猪价大幅波动时有发生.为稳定生猪生产,促进转型升级,增强猪肉供应保障能力,国务院办公厅于2019年9月印发了《关于稳定生猪生产促进转型升级的意见》.某生猪饲养场积极响应国家号召,努力提高生产经营管理水平,稳步扩大养殖规模,增加猪肉供应量.该饲养场2019年每月生猪产量y(吨)与月份x(1≤x≤12,且x为整数)之间的函数关系如图所示.(1)请直接写出当0<x≤4(x为整数)和4<x≤12(x为整数)时,y与x的函数关系式;(2)若该饲养场生猪利润p(万元/吨)与月份x(1≤x≤12,且x为整数)满足关系式:p=﹣x+.请问:该饲养场哪个月的利润最大?最大利润是多少?27.(10分)如图1,在矩形ABCD中,点P是BC边上一点,连接AP交对角线BD于点E,BP=BE.作线段AP的中垂线MN分别交线段DC,DB,AP,AB于点M,G,F,N.(1)求证:∠BAP=∠BGN;(2)若AB=6,BC=8,求;(3)如图2,在(2)的条件下,连接CF,求tan∠CFM的值.28.(12分)如图,在平面直角坐标系中,抛物线y=ax2+bx+c的图象与x轴交于A(4,0),B两点,与y 轴交于点C(0,2),对称轴x=与x轴交于点H.(1)求抛物线的函数表达式;(2)直线y=kx+1(k≠0)与y轴交于点E,与抛物线交于点P,Q(点P在y轴左侧,点Q在y轴右侧),连接CP,CQ,若△CPQ的面积为,求点P,Q的坐标;(3)在(2)的条件下,连接AC交PQ于G,在对称轴上是否存在一点K,连接GK,将线段GK绕点G逆时针旋转90°,使点K恰好落在抛物线上,若存在,请直接写出点K的坐标;若不存在,请说明理由.参考答案A卷一、选择题(共10个小题,每小题3分,满分30分)在下列小题中,均给出四个答案,其中有且只有一个正确答案,请将正确答案的字母代号在答题卡上涂黑,涂错或不涂均为零分1.D;2.A;3.D;4.D;5.C;6.B;7.C;8.B;9.C;10.D;二、填空题(共4个小题,每小题4分,满分16分)11.2;12.k≥;13.;14.35°;三、解答题(共6个小题,满分54分)15.解:(1)原式=﹣3+2﹣6×﹣3+=﹣3+2﹣3﹣3+=﹣6;(2)∵x(x﹣3)+2(x﹣3)=0,∴(x﹣3)(x+2)=0,∴x﹣3=0或x+2=0,解得x=3或x=﹣2.16.解:(1)由题意可知调查的总人数=12÷20%=60(人),所以喜爱排球运动的学生人数=60×35%=21(人)补全条形图如图所示:(2)∵该中学七年级共有400名学生,∴该中学七年级学生中喜爱篮求运动的学生有400×(1﹣35%﹣20%)=180名;(3)画树状图为:共有12种等可能的结果数,其中抽取的两人恰好是一名男生和一名女生结果数为8,所以抽取的两人恰好是一名男生和一名女生概率==.17.解:如图所示,过点P作PD⊥AB于点D,由题意知,∠BPD=45°,∠CPD=30°,∠P AC=30°,PB=50,在Rt△BPD中,PD=BD=PB sin∠BPD=50×=50,在Rt△CPD中,∵cos∠CPD=,∴PC===,∵∠PCD=60°、∠P AC=30°,∴∠P AC=∠APC=30°,∴AC=PC=≈57.7(海里),答:被拦截时,可疑船只距海岛A还有57.7海里.18.(1)证明:∵四边形ABCD是平行四边形,∴∠A=∠C,AD=CB,在△DAE和△BCF中,∴△DAE≌△BCF(SAS),∴DE=BF,∵AB=CD,AE=CF,∴DF=BE,∴四边形DEBF是平行四边形;(2)解:∵AB∥CD,∴∠DF A=∠BAF,∵AF平分∠DAB,∴∠DAF=∠BAF,∴∠DAF=∠AFD,∴AD=DF,∵四边形DEBF是平行四边形,∴DF=BE=5,BF=DE=4,∴AD=5,∵AE=3,DE=4,∴AE2+DE2=AD2,∴∠AED=90°,∵DE∥BF,∴∠ABF=∠AED=90°,∴AF===4.19.解:(1)∵点B的坐标为(2,1),过点B分别作x轴、y轴的垂线,垂足分别是C,A,∴点A,点E纵坐标为1,点C,点F的横坐标为2,∵点E,点F在反比例函数y=(x>0)的图象上,∴点E(1,1),点F(2,),设直线EF的解析式的解析式为:y=kx+b,∴∴∴直线EF的解析式的解析式为:y=﹣x+;(2)∵四边形BEOF的面积=S四边形ABCO﹣S△AOE﹣S△OCF,∴四边形BEOF的面积=2﹣﹣=1;(3)∵点E(1,1),∴OE=,若OE=OP=,则点P(0,)或(0,﹣),若OE=EP,且AE⊥AO,∴OA=AP=1,∴点P(0,2)若OP=PE,∴点P在OE的垂直平分线上,即点P(0,1),综上所述:当点P(0,)或(0,﹣)或(0,2)或(0,1)时,△POE是等腰三角形.20.解:(1)∵AD是直径,∴∠ACD=90°,即AC⊥ED,BD是∠BAD的平分线,故AE=AD;(2)=,则设BE=3a,AB=2a,AD=AE=5a,O交BD于点G,BD是∠BAD的平分线,则,则OC⊥BD,故OC∥AB,则OC是△ADE的中位线,则OG=AB=a,OC=AD=,则CG=OC﹣OG=,∵CG∥AB,则=;(3)设:OG=m,则AB=2m,当AH=HC时,由(2)知,△AHB≌△CHG(AAS),则AB=CG=2m,则OC=3m,即圆的半径为3m,∵AB∥CO,则,即,解得:m=1,故AB=2,AD=6,BE=4,则BD==4,∵EC=DC,则△BEC的面积=S△EBD=×BE×BD=×4×4=4.B卷一、填空题(共5个小题,每小题4分,满分20分)B卷(50分)21.2;22.;23.4;24.4或4﹣4;25.2+10;二、解答题(共3个小题,满分30分)26.解:(1)当0<x≤4(x为整数)时,y与x的函数关系式为:y=140,(0<x≤4)(x为整数);当4<x≤12(x为整数)时,设y与x的函数关系式为:y=kx+b,∴,解得:,∴y与x的函数关系式为:y=;(2)设该饲养场每月的利润为w,∵利润p(万元/吨)与月份x(1≤x≤12,且x为整数)满足关系式:p=﹣x+,∴当0<x≤4,w=400×(﹣x+)=﹣20x+600,∴当x=1时,w最大=580万元,当4<x≤12时,w=py=(﹣x+)(10x+100)=﹣x2+10x+150=﹣(x﹣5)2+200,∴当x=5时,w最大=200,∴当x=1时,w最大=580万元,答:该饲养场1月的利润最大,最大利润是580万元.27.(1)证明:如图1中,∵四边形ABCD是矩形,∴∠ABC=90°,∴∠BAP=∠APB=90°∵BP=BE,∴∠APB∠BEP=∠GEF,∵MN垂直平分线段AP,∴∠GFE=90°,∴∠BGN+∠GEF=90°,∴∠BAP=∠BGN.(2)解:∵四边形ABCD是矩形,∴∠BAD=∠ABP=90°,AD∥BC,AD=BC=8,∴BD===10,∵AD∥BC,∴∠DAE=∠APB,∵∠APB=∠BEP=∠DEA,∴∠DAE=∠DEA,∴DA=DE=8,∴BE=BP=BD﹣DE=10﹣8=2,∴P A===2,∵MN垂直平分线段AP,∴AF=PF=,∵PB∥AD,∴===,∴PE=P A=,∴EF=PF﹣PE=﹣=,∴==.(3)解:如图3中,连接AM,MP.设CM=x.∵四边形ABCD是矩形,∴∠ADM=∠MCP=90°,AB=CD=6,AD=BC=8,∵MN垂直平分线段AP,∴MA=MP,∴AD2+DM2=PC2+CM2,∴82+(6﹣x)2=62+x2,∴x=,∵∠PFM=∠PCM=90°,∴P,F,M,C四点共圆,∴∠CFM=∠CPM,∴tan∠CFM=tan∠CFM===.28.解:(1)对称轴x=,则点B(﹣1,0),则抛物线的表达式为:y=a(x+1)(x﹣4)=a(x2﹣3x﹣4),即﹣4a=2,解得:a=﹣,故抛物线的表达式为:y=x2+x+2;(2)设直线PQ交y轴于点E(0,1),点P、Q横坐标分别为m,n,△CPQ的面积=×CE×(n﹣m)=,即n﹣m=,联立抛物线于直线PQ的表达式并整理得:x2+(﹣k)x+1=0…①,m+n=3﹣2k,mn=﹣2,n﹣m===,解得:k=0(舍去)或3;将k=3代入①式并解得:x=,故点P、Q的坐标分别为:(,﹣2﹣)、(,﹣2+);(3)设点K(,m),联立PQ和AC的表达式并解得:x=,故点G(,)过点G作x轴的平行线交函数对称轴于点N,交过点R与y轴的平行线于点M,则△KNG≌△GMR(AAS),GN=﹣==MR,NK=﹣m,故点R的纵坐标为:,则点R(m﹣,)将该坐标代入抛物线表达式解得:x=,故m=,故点K(,).。
2021年四川省成都市中考数学一诊试卷(附答案详解)

2021年四川省成都市中考数学一诊试卷(附答案详解)1.下列关于防范“新冠肺炎”的标志中既是轴对称图形,又是中心对称图形的是()A。
B。
C。
D.2.我国古代著作《九章算术》在世界数学史上首次正式引入负数。
若气温升高3℃时,气温变化记作+3℃,那么气温下降10℃时,气温变化记作()A。
-13℃ B。
-10℃ C。
-7℃ D。
+7℃3.下列计算正确的是()A。
$a^2\cdot a^4=a^8$ B。
$a^{-2}=-a^2$ C。
$(a^2)^4=a^8$ D。
$a^4\div a^4=a^0$4.如图,在△ABC中,点D是AB上一点,DE//BC交AC于点E,AD=3,BD=2,则AE与EC的比是()A。
9:4 B。
3:5 C。
9:16 D。
3:25.如图所示,点B、C都在⊙O上,∠ACO=30°,若∠ABO=20°,则∠BOC=()A。
100° B。
110° C。
125° D。
130°6.如图所示的几何体是由两个相同的正方体和一个圆锥搭建而成,其左视图是()A。
B。
C。
D.7.___提出了五年“精准扶贫”的战略构想,意味着每年要减贫约xxxxxxxx人,将数据xxxxxxxx用科学记数法表示为()A。
1.16×106 B。
1.16×107 C。
1.16×108 D。
11.6×1068.一个足球队23名队员的年龄统计结果如下表所示,这个足球队队员年龄的众数,中位数分别是()年龄/岁人数/人 12 2 13 4 14 5 15 7 16 5 A。
14,15 B。
14,14 C。
15,13 D。
15,159.若点A(m,y1),点B(m+a/2+1,y2)都在一次函数y=5x+4的图象上,则()A。
y1y2 D。
y1=y210.二次函数y=ax^2+bx+c的图象如图,下列结论:①a<0;②2a+b=0;③b^2-4ac<0;④4a+2b+c<0.其中正确的有()A。
锦江区2020-2021学年九年级(上)期末数学试卷(一诊)

2020-2021学年四川省成都市锦江区九年级(上)期末数学试卷(一诊)一、选择题(共10个小题,每小题3分,满分30分)在下列小题中,均给出四个答案,其中有且只有一个正确答案,请将正确答案的字母代号在答题卡上涂黑,涂错或不涂均为零分.1.如图所示的几何体的俯视图是()A.B.C.D.2.如图,在Rt△ABC中,∠C=90°,sin A=,BC=3,则AC的长为()A.3B.4C.5D.63.为满足人们对防疫物资的需求,某口罩加工厂增加设备,努力提高口罩生产量.2020年10月份该工厂的口罩产量为500万个,12月份产量为720万个,若口罩产量平均每月增长率为x,则可列方程为()A.500(1+2x)=720B.720(1﹣x)2=500C.500(1+x2)=720D.500(1+x)2=7204.如图,在△ABC中,点D,E分别是边AB,AC的中点,若S△ADE=4.则四边形BDEC的面积为()A.4B.8C.12D.165.已知点(x1,y1),(x2,y2)都在反比例函数y=的图象上,且0<x1<x2,则y1与y2的大小关系为()A.y1>y2B.y1≥y2C.y1<y2D.y1≤y26.如图,在⊙O上有三点A,B,C,连接OA,OC,BA,BC,若∠ABC=110°,则∠AOC的大小为()A.70°B.110°C.130°D.140°7.已知,将△ABC沿AD折叠,点B的对应点B'落在边AC上(如图a),再将∠CAD对折,点A的对应点为A',折痕为EF(如图b),再沿A'E所在直线剪下,则阴影部分展开后的形状为()A.等腰三角形B.矩形C.菱形D.正方形8.将二次函数y=x2﹣2x+1的图象向上平移3个单位长度,再向左平移2个单位长度,得到的抛物线的表达式为()A.y=x2﹣2x+3B.y=x2﹣2x+4C.y=x2+2x+3D.y=x2+2x+49.如图,矩形ABCD的对角线AC,BD相交于点0,且∠AOD=120°.过点A作AE⊥BD于点E,则BE:ED等于()A.1:3B.1:4C.2:3D.2:510.二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,下列结论:①abc<0;②9a+3b+c<0;③a>;④若方程ax2+bx+c=0两个根x1和x2,则3<|x1﹣x2|<4,其中正确的结论有()A.①②③B.①②④C.①③④D.②③④二、填空题(共4个小题,每小题4分,满分16分)11.如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则tan C=.12.已知关于x的一元二次方程x2﹣2(k﹣1)x+k2﹣1=0有两个不相等的实数根,则k的取值范围是.13.用图中两个可自由转动的转盘做“配紫色”游戏:分别旋转两个转盘,若转盘a转出红色,转盘b转出蓝色即可配成紫色,则配成紫色的概率为.14.如图,四边形ABCD是正方形,按如下步骤操作:①分别以点A,D为圆心,以AD长为半径画弧,两弧交于点P,连接AP,DP;②连接BP,CP,则∠BPC=.三、解答题(共6个小题,满分54)15.(1)计算:﹣tan60°+()﹣1﹣|1﹣2cos30°|.(2)解方程:x2﹣4x﹣1=0.16.“青年大学习”是共青团中央为组织引导广大青年,深入学习宣传贯彻习近平新时代中国特色社会主义思想和党的十九大精神的青年学习行动.某校为了解九年级同学学习“青年大学习”的情况,随机抽取部分九年级同学进行了问卷调查,按照调查结果,将学习情况分为优秀、良好、合格、较差四个等级.学校绘制了如下不完整的统计图,根据图中信息解答下列问题:(1)将上面的条形统计图补充完整;(2)若该校九年级有800名学生,请估计九年级学生“青年大学习”学习情况为“优秀”和“良好”的一共有多少名?(3)该校某班有3名同学(1名男同学、2名女同学)在调查中获得“优秀”等级,班主任将从这3名同学中随机选取2名同学,代表班级参加学校组织的“青年大学习”演讲大赛.请用列表或画树状图的方法,求所选两位同学恰好是1名男同学和1名女同学的概率.17.如图,在水平地面上,有一盏垂直于地面的路灯AB,在路灯前方竖立有一木杆CD.已知木杆长CD=2.65米,木杆与路灯的距离BD=5米,并且在C点测得灯源A的仰角为44°.(结果保留1位小数:参考数据:sin44°≈0.69,cos44°≈0.72,tan44°≈0.97)(1)求路灯高AB大约是多少米?(2)请在图中画出木杆CD在灯光下的影子(用线段表示),并求出影长.18.如图1,在平行四边形ABCD中,过点A作AE⊥BC交BC于点E,连接ED,且ED平分∠AEC.(1)求证:AE=BC;(2)如图2,过点C作CF⊥DE交DE于点F,连接AF,BF,猜想△ABF的形状并证明.19.如图,直线y=﹣x+4与x轴交于点A,与y轴交于点B,反比例函数y1=(x>0)的图象经过线段AB的中点C.(1)求反比例函数的表达式;(2)将直线y=﹣x+4向右平移4个单位长度后得到直线y2=ax+b,直线y2交x轴于点D,交反比例函数y1=(x>0)的图象于点E,F,连接CE,CF,求△CEF的面积;(3)请结合图象,直接写出不等式y1<y2的解集.20.如图,在△ABC中,AB=AC,以边BC为直径作⊙O,交AC于点D,连接AO,交BD于点E,交⊙O 于点F,连接DF.(1)求证:∠CAO=∠CBD;(2)求证:=;(3)当△DEF为等腰三角形时,若BC=4,求△DEF的面积.四、填空题(共5个小题,每小题4分,满分20分)21.设x1,x2是一元二次方程x2﹣3x﹣2=0的两个实数根,则x12+3x1x2+x22的值为.22.如图,菱形ABCD的边长AB=3,对角线BD=4,点E,F在BD上,且BE=DF=,连接AE,AF,CE,CF.则四边形AECF的周长为.23.如图,点A,B是反比例函数y=(x>0)的图象上的两点,过点A作AC⊥x轴于点C,交直线OB 于点D,连接OA.若点A的坐标为(3,1),OB=BD,则sin∠AOD=.24.黄金分割是指把一条线段分割为两部分,使较短线段与较长线段的比等于较长线段与原线段的比,其比值等于.如图,在正方形ABCD中,点G为边BC延长线上一动点,连接AG交对角线BD于点H,△ADH的面积记为S1,四边形DHCG的面积记为S2.如果点C是线段BG的黄金分割点,则的值为.25.如图1,点是等边△ABC的边BC上一点(不与点B,C重合),连接AE.以AE为边向右作等边△AEP,连接CF.若△ECF的面积(S)与BE的长(x)之间的函数关系如图2所示(P为图象顶点),则等边△ABC的边长AB=.五、解答题(第26题满分30分,第27题满分30分,第28题满分30分)26.近年来,西部某民族聚居区扶贫工作小组结合当地实际,大力开发乡村旅游扶贫项目,积极挖掘乡村生态休闲、旅游观光、文化教育价值,发展乡村民宿某民宿建有40个房间供游客居住,当每个房间的定价为每天180元时,房间会全部住满;当每个房间每天的定价每增加10元时,就会有一个房间空闲,如果游客居住房间,宾馆每天需对每个房间支出40元的各种费用,设每个房间的定价为x元,相应的住房数为y间.(1)求y与x的函数关系式;(2)求每个房间定价为多少元时,该民宿当天利润W最大?最大利润是多少?27.如图,在△ABC中,AB=AC,∠BAC=90°,BC=14,过点A作AD⊥BC于点D,E为腰AC上一动点,连接DE,以DE为斜边向左上方作等腰直角△DEF,连接AF.(1)如图1,当点F落在线段AD上时,求证:AF=EF;(2)如图2,当点F落在线段AD左侧时,(1)中结论是否仍然成立?若成立,请证明;若不成立,请说明理由;(3)在点E的运动过程中,若AF=,求线段CE的长.28.抛物线y=ax2+bx﹣3(a≠0)的图象与x轴交于点B(﹣3,0),C(1,0),与y轴交于点A.(1)求抛物线的表达式和顶点坐标;(2)抛物线上是否存在一点D(不与点A,B,C重合),使得直线DA将四边形DBAC的面积分为3:5两部分,若存在,求出点D的坐标;若不存在,请说明理由;(3)点P是抛物线对称轴上一点,在抛物线上是否存在一点Q,使以点P,Q,A,B为顶点的四边形是平行四边形?若存在,直接写出点Q的坐标;若不存在,请说明理由.。
成都2021年九上期末(一诊)B卷

成都市锦江区初2018级学业质量专项监测工具B 卷(共50分)一、填空题(本大题共5个小题,每小题4分,共20分,答案写在答题卡上)21.设1x ,2x 是一元二次方程2320x x --=的两个实数根,则2211223x x x x ++的值为______.22.如图,菱形ABCD 的边长AB =3,对角线BD =,点E ,F 在BD上,且BE DF ==,连接AE ,AF ,CE ,CF .则四边形AECF 的周长为______.第22题图第23题图第24题图23.如图,点A ,B 是反比例函数k y x=(0x >)的图象上的两点,过点A 作AC ⊥x 轴于点C ,交直线OB 于点D ,连接OA .若点A 的坐标为(3,1),OB =BD ,则sin AOD ∠=______.24.黄金分割是指把一条线段分割成两部分,使较短线段与较长线段的比等于较长线段与原线段的比,其比.如图,在正方形ABCD 中,点G 为边BC 延长线上一动点,连接AG 交对角线BD 于点H ,△ADH 的面积记为1S ,四边形DHCG 的面积记为2S .如果点C 是线段BG 的黄金分割点,则12S S 的值为______.25.如图1,点E 是等边△ABC 的边BC 上一点(不与点B ,C 重合),连接AE ,以AE 为边向右作等边AEF △,连接CF .若△ECF 的面积(S )与BE 的长(x )之间的函数关系如图2所示(P 为图象顶点),则等边△ABC 的边长AB =______.图1图2二、解答题(本大题共3个小题,共30分,解答过程写在答题卡上)26.(本小题满分8分)近年来,西部某民族聚居区扶贫工作小组结合当地实际,大力开发乡村旅游扶贫项目,积极挖掘乡村生态休闲、旅游观光、文化教育价值,发展乡村民宿.某民宿建有40个房间供游客居住,当每个房间的定价为每天180元时,房间会全部住满;当每个房间每天的定价每增加10元时,就会有一个房间空闲,如果游客居住房间,宾馆每天需对每个房间支出40元的各种费用,设每个房间的定价为x元,相应的住房数为y间.(1)求y与x的函数关系式;(2)求每个房间定价为多少元时,该民宿当天利润W最大?最大利润是多少?如图,在△ABC 中,AB =AC ,∠BAC =90°,BC =14,过点A 作AD ⊥BC 于点D ,E 为腰AC 上一动点,连接DE ,以DE 为斜边向左上方作等腰直角△DEF ,连接AF .(1)如图1,当点F 落在线段AD 上时,求证:AF =EF ;(2)如图2,当点F 落在线段AD 左侧时,(1)中结论是否仍然成立?若成立,请证明;若不成立,请说明理由;(3)在点E 的运动过程中,若AF ,求线段CE 的长.图1图2图3抛物线2y ax bx c =++(0a ≠)的图象与x 轴交于点(3,0)B -,(1,0)C ,与y 轴交于点A .(1)求抛物线的表达式和顶点坐标;(2)抛物线上是否存在一点D (不与点A ,B ,C 重合),使得直线DA 将四边形DBAC 的面积分为3:5的两部分,若存在,求出点D 的坐标;若不存在,请说明理由;(3)点P 是抛物线对称轴上一点,在抛物线上是否存在一点Q ,使以点P ,Q ,A ,B 为顶点的四边形是平行四边形?若存在,直接写出点Q 的坐标;若不存在,请说明理由.备用图成都市金牛区2020~2021学年度(上)期末B 卷(共50分)一、填空题(本大题共5个小题,每小题4分,共20分,答案写在答题卡上)21.若m 、n 是一元二次方程2320210x x +-=的两个实数根,则22m n mn ++的值为______.22.如图所示,在平面直角坐标系中,正方形OABC 的顶点O 与原点重合,顶点A 、C 分别在x 轴、y 轴上,双曲线k y x=(0k ≠,0x >)经过AB 、BC 的中点N 、F ,连接ON 、OF 、NF .若3BFN S =△,则k =______.第22题图第24题图23.现有牌面编码为1-,1,2的三张卡片,背面向上,从中随机抽取一张卡片,记其数字为k ,将抽到的卡片背面朝上,放回打乱后,再抽一张记其数字为m ,则事件:“关于a 、b 的方程组2122a b k a b +=+⎧⎨+=⎩的解满足01a b -≤≤,且二次函数22y x x m =-+的图象与x 轴恰有2个交点”成立的概率为______.24.如图,Rt △ABC 中,∠ACB =90°,AC =BC =8,F 为AC 中点,D 是线段AB 上一动点,连接CD ,将线段CD 绕点C 沿逆时针方向旋转90°得到线段CE ,连接EF ,则点D 在运动过程中,EF 的最大值为______,最小值为______.25.如图所示,在平面直角坐标系中,抛物线2y =++的顶点为A ,并与x 轴正半轴交于点B ,在y 轴上存在点C ,使∠ACB =30°.则点C 的坐标是______.二、解答题(本大题共3个小题,共30分,解答过程写在答题卡上)26.(本小题满分8分)某经销商经过市场调查,整理出某种商品在2020年10月的第x天(130≤≤)的售价与销量的相关信x息如下表:售价(元/件)日销售量(件)x+60200-5x已知该商品的进价为50元/件.(1)销售该商品第几天时,销售该商品的日销售利润为2280元;(2)销售该商品第几天时,日销售利润最大?最大日销售利润为多少元?如图所示,在矩形ABCD 中,将矩形ABCD 沿EF 折叠,使点D 落在AB 边上的点G 处,点C 落在点H 处,GH 交BC 于点K ,连接DG 交EF 于点O ,DG =2EF .(1)求证:DE DA DO DG ⋅=⋅;(2)探索AB 与BC 的数量关系,并说明理由;(3)连接BH ,3sin 5BFH ∠=,EF =BFH 的周长.已知:如图1,在平面直角坐标系中,抛物线2y x bx c =++与x 轴交于A 、B 两点,与y 轴交于点(0,6)D -,直线123y x =-+交x 轴于点B ,与y 轴交于点C .(1)求抛物线的函数解析式;(2)抛物线上点E 位于第四象限,且在抛物线的对称轴的右侧,当△BCE 的面积为32时,过点E 作平行于y 轴的直线交x 轴于Q ,交BC 于点F ,在y 轴上是否存在点K ,使得以K 、E 、F 三点为顶点的三角形是直角三角形.若存在,求出点K 的坐标;若不存在,请说明理由;(3)如图2,在线段OB 上有一动点P BP +的最小值和此时点P 的坐标.图1图2成都市青羊区2020~2021学年度上期期末B 卷(共50分)一、填空题(本大题共5个小题,每小题4分,共20分,答案写在答题卡上)21.已知二次函数2y x x a =++的图象与x 轴交于1(,0)A x 、2(,0)B x 两点,且2212113x x +=,则a 的值为______.22.将一个棱长为4的正方体的表面涂成灰色,再把它分割成棱长为1的小正方体,从中任取一个小正方体,则取得的小正方体恰有三个面涂有灰色的概率为______.第22题图第23题图23.如图,已知⊙O 的半径为6,PA 是⊙O 的一条切线,切点为A ,连接PO 并延长,交⊙O 于点B ,过点A 作AC ⊥PB 交⊙O 于点C ,交PB 于点D .当∠P =30°时,弦AC 的长为______.24.如图,在平面直角坐标系中,M 、N 、C 三点的坐标分别为1(,1)4,(3,1),(3,0),点A 为线段MN 上的一个动点,连接AC ,过点A 作AB ⊥AC 交y 轴于点B ,当点A 从M 运动到点N 时,点B 随之运动.设点B 的坐标为(0,)b ,则b 的最小值为______.25.如图,在正方形ABCD 中,E 是线段CD 上一点,连接AE ,将△ADE 沿AE 翻折至△AEF ,连接BF 并延长BF 交AE 延长线于点P ,当22PF =时,DE CD=______.二、解答题(本大题共3个小题,共30分,解答过程写在答题卡上)26.(本小题满分8分)某旅馆有客房120间,每间房的日租金为160元,每天都客满,装修后,市场调查发现,如果每间客房的日租金每增加10元,那么客房每天出租数会减少6间,假设日租金提高x元.(1)直接写出装修后日出租房间数y与x的关系式;(2)不考虑其他因素,旅馆将每间客房的日租金提高到多少元时,客房日租金的总收入最高?比装修前日租金的总收入增加多少元?已知在菱形ABCD 中,∠BAD =120°,点E 为射线BC 上的一个动点,AE 与边CD 交于点G .(1)如图1,连接对角线BD 交AE 于点F ,连接CF ,若2AF CG CD =⋅,试求∠CFE 的度数;(2)如图2,点F 为AE 上一点,且∠ADF =∠AED ,若菱形的边长为2,则当DE ⊥BC 时,求△CFE 的面积;(3)如图3,当点E 在射线BC 上运动时,试求DE AE 的最小值.图1图2图3如图1,抛物线1C :2y ax bx c =++经过(1,0)A -,(5,0)B ,(0,C 三点,直线DF 为该抛物线的对称轴,连接线段AC ,∠CAB 的平分线AE 交抛物线1C 于点E .(1)求抛物线1C 的表达式;(2)如图1,作点C 关于x 轴的对称点'C ,将原抛物线沿对称轴向下平移经过点'C 得到抛物线2C ,在射线AE 上取点Q ,连接CQ ,将射线QC 绕点Q 逆时针旋转120°交抛物线2C 于点P ,当△CAQ 为等腰三角形时,求点P 的横坐标;(3)如图2,将抛物线1C 沿一定方向平移,使顶点'D 落在射线AE 上,平移后的抛物线3C 与线段CB 相交于点M 、N ,线段CB 与DF 相交于点H ,当点H 恰好为线段MN 的中点时,求抛物线3C 的顶点坐标.图1图2成都市武侯区2020~2021学年度上期期末B 卷(共50分)一、填空题(本大题共5个小题,每小题4分,共20分,答案写在答题卡上)21.已知a ,b 是关于x 的一元二次方程2220220x x --=的两个实数根,则ab a b ++的值为______.22.一个盒子中装有分别写上数字1,2,4-的三个大小形状相同的白球,现摇匀后从中随机摸出一个球,将上面的数字记作a ,不放回.再从中随机摸出一个球,将上面的数字记作b ,则a ,b 的值使得抛物线23y ax bx =++的对称轴在y 轴右侧的概率为______.23.如图,在矩形ABCD 中,AB =3,BC =4,点M 为AD 的中点,点N 为AB 上一点,连接MN ,CN ,将△AMN 沿直线MN 折叠后,点A 恰好落在CN 上的点P 处,则CN 的长为______.第23题图第24题图24.如图,在平面直角坐标系xOy 中,点A ,B 在反比例函数3y x=的图象上(点A 在第一象限),且线段AB 经过点O ,将线段AB 绕点A 逆时针旋转60°得到线段AC ,线段AC 交x 轴于点D ,若13AD AC =,则点C 的坐标是______.25.如图,在△ABC 中,BC =9,AC =12,AB =15,D 为直线AB 上方一点,连接AD ,BD ,且∠ADB =90°,过D 作直线BC 的垂线,垂足为E ,则线段BE 的长度的最大值为______.二、解答题(本大题共3个小题,共30分,解答过程写在答题卡上)26.(本小题满分8分)春节即将来临,某电商平台准备销售一批服装,已知购进时的单价是150元.调查发现:销售单价是200元时,月销售量是100件,而销售单价每降低1元,月销售量就增加10件.每件服装的售价不能低于进价,设该服装的销售单价在200元的基础上降低x元时(x为正整数),月销售利润为y元.(1)求y与x的函数关系式;(2)该服装的销售单价为多少元时,月销售利润最大?最大的月销售利润是多少?在△ABC中,AB=AC=5,BC=6,点D为线段AB上一动点(点D不与A,B重合),连接CD,分别以AC,DC为斜边向右侧作等腰直角三角形ACE和等腰直角三角形DCF,连接EF.(1)当点F在△ABC的外部时,求证:△ACD∽△ECF;(2)如图1,当D,F,E三点共线时,求△ECF的面积;(3)如图2,当点D在BA的延长线上时,其它条件不变,连接DE,若DE∥AC,且AD的长.图1图2如图,在平面直角坐标系xOy 中,直线3y x =-+与y 轴交于点A ,与x 轴交于点B ,抛物线经过A ,B 两点,并与x 轴交于另一点C ,抛物线的对称轴为直线2x =,顶点为点D .(1)求抛物线的函数表达式;(2)点E 为对称轴右侧的抛物线上的点.ⅰ)点F 在抛物线的对称轴上,且EF ∥x 轴,若以点D ,E ,F 为顶点的三角形与△ABD 相似,求出此时点E 的坐标;ⅱ)点G 在平面内,则以点A ,B ,E ,G 为顶点的四边形能否成为矩形?若能,求出此时点E 的坐标;若不能,请说明理由.备用图成都市高新区2020~2021学年上期期末B 卷(共50分)一、填空题(本大题共5个小题,每小题4分,共20分,答案写在答题卡上)21.已知a ,b 是方程230x x --=的两个实数根,则21a b ++的值为______.22.在Rt △ABC 中,∠BCA =90°,CD 是AB 边上的中线,BC =8,CD =5,则tan ∠ACD =______.23.在平面直角坐标系中,△ABC 的顶点坐标分别是(1,1)A ,(4,2)B ,(3,5)C ,以点A 为位似中心,相似比为1:2,把△ABC 缩小,得到△11AB C ,则点C 的对应点1C 的坐标为______.24.如图,平面直角坐标系xOy 中,在反比例函数4k y x =(0k >,0x >)的图象上取点A ,连接OA ,与k y x =的图象交于点B ,过点B 作BC ∥x 轴交函数4k y x =的图象于点C ,过点C 作CE ∥y 轴交函数k y x=的图象于点E ,连接AC ,OC ,BE ,OC 与BE 交于点F ,则CEF ABCS S =△△______.25.如图,在矩形ABCD 中,AB =4,BC =M 为BC 边中点,E 为AD 边上的一动点,过点A 作BE的垂线,垂足为F ,连接FM ,则FM 的最小值为______.在线段FM 上取点G ,使34GM FM =,将线段GM 绕点M 顺时针旋转60°得到NM ,连接GN ,CN ,则CN 的最小值为______.二、解答题(本大题共3个小题,共30分,解答过程写在答题卡上)26.(本小题满分8分)某旅馆有客房120间,经市场调查发现,客房每天的出租数量y(间)与每间房的日租金x(元)的关系如图所示,为保证旅馆的收益,每天出租的房间数不少于90间.(1)结合图象,求出客房每天的出租的房间数y(间)与每间房的日租金x(元)之间的函数关系式和自变量的取值范围;(2)设客房的日租金总收入W(元),不考虑其它因素,将旅馆每间客房的日租金定为多少元时,客房的日租金定为多少元时,客房的日租金总收入最高?最高总收入为多少?如图,在菱形ABCD 中,AB =2tan 3BAC ∠=.点E 在射线BC 上,连接DE ,DE 绕点D 顺时针旋转,旋转后得到的线段与对角线AC 交于点F ,旋转角∠EDF =∠BAC .射线DE 与射线AC 交于点P .(1)如图1,当点E 在线段BC 上时,求证:△FDP ∽△FCD ;(2)如图2,已知点E 在线段BC 的延长线上,当DF =5时,求线段CE 的长;(3)如图3,连接EF ,当EF ∥AB 时,求线段EF 的长.如图1,在平面直角坐标系xOy 中,已知抛物线212y x bx c =-++与x 轴交于点(4,0)A -,(2,0)B ,与y 轴交于点C .(1)求抛物线的解析式;(2)如图2,沿直线AC 平移抛物线212y x bx c =-++,使得A 、C 两点的对应点E 、F 始终在直线AC 上.①设在平移过程中抛物线与y 轴交于点M ,求点M 纵坐标的最大值;②试探究抛物线在平移过程中,是否存在这样的点E ,使得以A 、E 、B 为顶点的三角形与△ABF 相似.若存在,请直接写出此时点E 的坐标;若不存在,请简要说明理由.图1图2备用图成都市天府新区2020~2021学年度上期期末B 卷(共50分)一、填空题(本大题共5个小题,每小题4分,共20分,答案写在答题卡上)21.若2310a a -+=,则2392020a a -+=______.22.对于任意实数a ,b ,定义:22a b a ab b *=++.若方程(2)50x *-=的两根记为m ,n ,则(3)(3)m n ++=______.23.在一个不透明的盒子里装有4个标有1,2,3,4的小球,它们形状、大小完全相同.小明从盒子里随机取出一个小球,记下球上的数字,作为点P 的横坐标x ,放回.然后再随机取出一个小球,记下球上的数字,作为点P 的纵坐标y ,则点P 在以原点为圆心,5为半径的圆内的概率为______.24.以矩形OABC 的顶点O 为坐标原点建立平面直角坐标系,使点A ,C 分别在x ,y 轴的正半轴上,双曲线k y x=(0x >)的图象经过BC 的中点D ,且与AB 交于点E ,过OC 边上一点F ,把△BCF 沿直线BF 翻折,使点C 落在矩形内部的一点'C 处,且'C E ∥BC ,若点'C 的坐标(2,4),则BF 的长为______.25.如图,正方形ABCD 的边长为8,E 为BC 上一点,且BE =2.5,F 为AB 边上的一个动点,连接EF ,以EF 为边向右侧作等边△EFG ,连接CG ,则CG 的最小值为______.二、解答题(本大题共3个小题,共30分,解答过程写在答题卡上)26.(本小题满分8分)2020年,新型冠状病毒肆虐,给人们的生活带来许多不便,网络销售成为这个时期最重要的一种销售方式.某乡镇农贸公司新开设了一家网店,销售当地农产品.其中一种当地特产在网上试销售,其成本为每千克2元,公司在试销售期间,调查发现,每天销售量y(kg)与销售单价x(元)满足如图所示的函数关系(其中210<≤).x(1)求y与x之间的函数关系式;(2)销售单价x为多少元时,每天的销售利润最大?最大利润是多少元?问题背景:如图1,已知△ABC ∽△ADE ,求证:△ABD ∽△ACE ;尝试运用:如图2,在△ABC 中,点D 是BC 边上一动点,∠BAC =∠DAE =90°,且∠ABC =∠ADE ,AB =4,AC =3,AC 与DE 相交于点F ,在点D 运动的过程中,当1tan 2EDC ∠=,求DE 的长度;拓展创新:如图3,D 是△ABC 内一点,∠BAD =∠CBD ,1tan 2BAD ∠=,∠BDC =90°,AB =4,AC =,求AD 长.图1图2图3如图,抛物线2y x bx c =-++与x 轴交于A ,B 两点(B 在A 的右侧),且与直线1l :2y x =+交于A ,D 两点,已知B 点的坐标为(6,0).(1)求抛物线的函数表达式;(2)过点B 的直线2l 与线段AD 交于点E ,且满足16DE AE =,与抛物线交于另一点C .①若点P 为直线2l 上方抛物线2y x bx c =-++上一动点,设点P 的横坐标为t ,当t 为何值时,△PEB 的面积最大;②过E 点向x 轴作垂线,交x 轴于点F ,在抛物线上是否存在一点N ,使得∠NAD =∠FEB ,若存在,求出N 的坐标;若不存在,请说明理由.备用图。
四川成都锦江区初三一模数学试卷
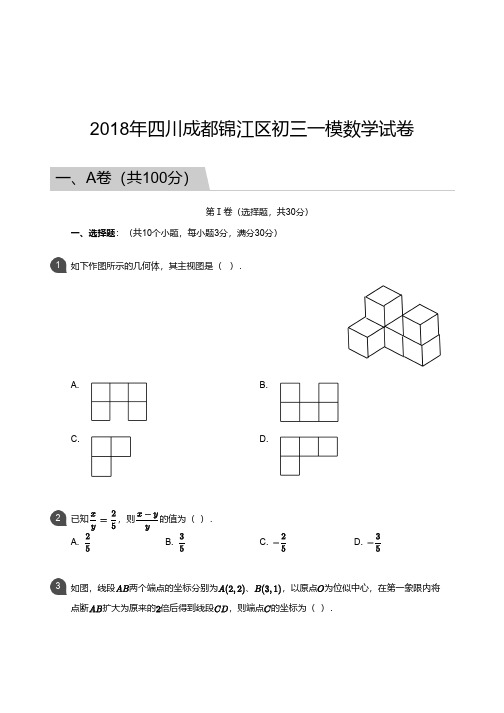
点断 扩大为原来的 倍后得到线段 ,则端点 的坐标为( ).
A.
B.
4 如图,在菱形
中,
,
C.
D.
,则对角线 等于( ).
A.
B.
C.
D.
5 如图, 、 、 三点在正方形网格线的交点处,若将
,则
的值为( ).
绕着点 逆时针旋转得到
A.
B.
C.
D.
6 如图,在平行四边形
中,
,则 等于( ).
,点 、 分别是 、 上的点,
,请直接写出点 的坐标.
三、解答题:(15小题每小题6分,16小题6分,共18分)
15 计算:
.
16 解方程:
.
17 为传递爱心,传播文明,某中学团委倡议全校同学在寒假期间选择参加志愿者活动(每人只能参
加一种活动),活动项目有:敬老助残( )、环境保护( )、关爱留守儿童( ).团委筹备
小组在校门口随机调查 位同学,发现这 位同学选择三种活动项目
四、解答题(12分)
29 如图,在平面直角坐标系中,抛物线 轴交于点 .
的图象与 轴交于点
,
,与
(1) 求抛物线的解析式.
(2) 连接 ,点 在抛物线的对称轴上,点 为平面内一点,四边形
能否成为矩形?
若能,请求出点 的坐标;若不能,请说明理由.
(3) 在抛物线上有一点 ,过点 , 的直线 交 轴于点 ,连接 ,若
(1) 若 (2) 若
,求证:
.
,
,求 的长.
19 如图,一辆滴滴快车在笔直公路上由西向东行驶,行驶至 处时接到正东方 处乘客订单,但师
傅发现油量不足,马上左拐 ,沿 行驶 米到达加油站 处加油,加油用时 分钟,加油后
2021届锦江区一诊语文试卷和答案

56““”““3.C 【点拨】徙:调动4. (1)(扬雄)家产不角 除A 、C 、D 选项的负闲适;C 项表达内心的渴望;D 项表达�·的储备,(却)安然E (2)等到王莽第位, 封爵的谈说者很多封侯。
A 项表达作者内心的但更表达对建功立业僮憬和对故土的依恋.穷得没有一两石余粮物赞美其功德而获得因未赞其德)仍不被活的开始, “我”对它寄予奔向未来的热悄,@5百行车见证了岁月的变迁和“我” 的成长,“我“对有它陪伴的岁月充满怀念。
9. A 。
Cl)"热辣的阳光” 符合初秋景物特点,烘托出“我“迎接新生活的热情。
@“心也是热的“既照应前文父母之爱引发的感动,又与后文“我”蓄势待发的殷切心情相呼应。
10. Cl)这辆自行车既寄托父母之爱.又促使“我”产生奔向新生活的使命感,它被偷走,令人感伤。
色) 【说明】(D 基础等级评分以题意、 ft 容、语言、 文体为疵点,全面衡壁。
符合文体,指符合考生根据题意和ft 容自选的文体要求s <D 两篇文章都推崇扬雄的安贫乐道.《陋室铭》中 扬雄虽生活贫闲但安贫乐道;本文中扬雄对穷闲生活安然自如,不愿为名利而攀附权贵.@本文 自行车丢失后“我”不但有了机会买当时流行的 新车,还有卸却负担的轻松和生活将有所改变的兴奋,使人欣喜。
@这句话写出逐渐长大的 我”。
还推崇扬雄的博学多思、文才斐然他博览群书,既习惯被呵护,又渴望独立自主的矛盾心情。
@发展等级评分,依据评分点,不要求全面,以 点突出者按内容评分,直至满分。
@缺题目扣2分;不足字数,每少50字扣1分。
@每个错别字扣 1 分,相同错别字不或复扣分,扣满 3 分为止;书写潦草 、卷面不整洁扣 1-2 分(最高扣 2 分) 。
@确认为抄袭的作文, 基础等级 在四等之ft 偏后评分, 发展等级 不给分。
思考深远;创作诸多辞赋,文才及作品受到高度评 价。
(或:本文还推崇扬雄顺势而为、 乐天安命的思想。
初2018届成都市锦江区中考数学九年级一诊数学试卷(含答案)

初2018届成都市锦江区中考数学九年级一诊试卷(考试时间:120分钟满分150分)A卷(共100分)一、选择题:(共10个小题,每小题3分,满分30分)1.如图所示的几何体,其主视图是()A.B.C.D.2.已知=,则的值为()A.B.C.﹣D.﹣3.如图,线段AB两个端点的坐标分别为A(2,2)、B(3,1),以原点O为位似中心,在第一象限内将线段AB扩大为原来的2倍后得到线段CD,则端点C的坐标分别为()A.(3,1)B.(3,3)C.(4,4)D.(4,1)4.如图,在菱形ABCD中,AB=2,∠ABC=120°,则对角线BD等于()A.2 B.4 C.6 D.85.如图,A、B、C三点在正方形网格线的交点处,若将△ABC绕着点A逆时针旋转得到△AC′B′,则tanB′的值为()A.B.C.D.6.如图,在▱ABCD中,AD=18,点E、F分别是BD、CD上的点,EF∥BC,且=,则EF等于()A.6 B.8 C.9 D.187.小明家2015年年收入20万元,通过合理理财,2017年年收入达到25万元,求这两年小明家年收入的平均增长率,设这两年年收入的平均增长率为x,根据题意所列方程为()A.20x2=25 B.20(1+x)=25C.20(1+x)2=25 D.20(1+x)+20(1+x)2=258.如图所示的暗礁区,两灯塔A,B之间的距离恰好等于圆的半径,为了使航船(S)不进入暗礁区,那么S对两灯塔A,B的视角∠ASB必须()A.大于60°B.小于60°C.大于30°D.小于30°9.如图所示,在矩形ABCD中,AD=6,AB=10,若将矩形ABCD沿DE折叠,使点C落在AB边上的点F处,则线段CE的长为()A.B.C.D.1010.如图,菱形OBAC的边OB在x轴上,点A(8,4),tan∠COB=,若反比例函数y=(k≠0)的图象经过点C,则反比例函数解析式为()A.y=B.y=C.y=D.y=二、填空题:(本大题共4个小题,每小题4分,满分16分)11.课间休息,小亮与小明一起玩“五子棋”游戏,他们决定通过“剪刀、石头、布”游戏赢者开棋,若小亮出“石头”,则小亮开棋的概率是.12.如图,AC是正方形ABCD的对角线,∠DCA的平分线交BA的延长线于点E,若AB=3,则AE=13.关于x的一元二次方程(k﹣2)x2+2kx+k=0有实数根,则k的取值范围是14.如图,⊙O的直径为10,弦AB=8,P是弦AB上一动点,那么OP长的取值范围是.三、简答题(15小题每小题12分,16小题6分,共18分)15.(12分)(1)计算:+(﹣)﹣1+6cos30°﹣(+2)0(2)解方程:(x+2)(x+3)=2x+1616.(6分)为传递爱心,传播文明,某中学团委倡议全校同学在寒假期间选择参加志愿者活动(每人只能参加一种活动),活动项目有:敬老助残(A)、环境保护(B)、关爱留守儿童(C)、团委筹备小组在校门口随机调查50位同学,发现这50位同学选择三种活动项目(A、B、C)的人数之比为3:3:4.(1)若该校有1200名同学,请估计参加环境活动项目的同学有多少人?(2)请用画树状图或列表的方法,求九年级一班班长和团委书记两位同学都选择参加关爱留守儿童(C)的概率17.(8分)如图,AC是▱ABCD的对角线,在AD边上取一点F,连接BF交AC于点E,并延长BF交CD的延长线于点G.(1)若∠ABF=∠ACF,求证:CE2=EF•EG;(2)若DG=DC,BE=6,求EF的长.18.(8分)如图,一辆滴滴快车在笔直公路上由西向东行驶,行驶至A处时接到正东方B处乘客订单,但师傅发现油量不足,马上左拐30°,沿AC行驶1200米到达加油站C处加油,加油用时5分钟,加油后再沿CB行驶1000米到B处接到乘客,假设滴滴快车的平均速度是每分钟360米,其他情况忽略不计,滴滴快车让乘客多等了多少时间?(结果保留整数≈1.414,≈1.732,≈2.236)19.(10分)如图,一次函数y1=kx+b的图象与反比例函数y2=的图象交于点A、B两点,与x轴、y轴交于C、D两点,且点C、D刚好是线段AB的三等分点,OD=2,tan∠DCO=(1)求一次函数与反比例函数的解析式;(2)求△AOB的面积;(3)若y1≤y2,请直接写出相应自变量x的取值范围20.(10分)如图,在△ABC中,∠ABC=90°,⊙O是△ABC外接圆,点D是圆上一点,点D、B分别在AC 两侧,且BD=BC,连接AD、BD、OD、CD,延长CB到点P,使∠APB=∠DCB.(1)求证:AP为⊙O的切线;(2)若⊙O的半径为1,当△OED是直角三角形时,求△ABC的面积;(3)若△BOE、△DOE、△AED的面积分别为a、b、c,试探究a、b、c之间的等量关系式,并说明理由.B卷(共50分)一、填空题:(每小题4分,共20分)21.已知m、n是方程x2﹣2x﹣7=0的两个根,那么m2+mn+2n=.22.如图,小明周末晚上陪父母在锦江绿道上散步,他由灯下A处前进4米到达B处时,测得影子BC长为1米,已知小明身高1.6米,他若继续往前走4米到达D处,此时影子DE长为米.23.如图,点A是反比例函数y=(x>0)图象上的一点,点B是反比例函数y=﹣(x<0)图象上的点,连接OA、OB、AB,若∠AOB=90°,则sin∠A=24.如图,二次函数y=ax2+bx+c(a≠0)的图象过点(﹣1,2),下列结论:①abc>0;②a+b+c>0;③2a+b<0;④b<﹣1;⑤b2﹣4ac<8a,正确的结论是(只填序号)25.如图,⊙O的半径为6,∠AOB=90°,点C是上一动点(不与点B、A重合),过点C作CD⊥OB于点D,CE⊥OA于点E,连接ED,点F是OD的中点,连接CF交DE于点P,则CE2+3CP2等于.二、解答题(8分)26.(8分)科技驱动新零售商业变革的时代已经来临,无人超市的经营模式已在全国各地兴起,某家无人超市开业以来,经测算,为销售A型商品每天需固定支出的费用为400元,若A型商品每件的销售利润不超过9元,每天销售A型商品的数量为280件,若A型商品每件的销售利润超过9元,则每超过1元,每天销售A型商品的数量减少10件,设该家无人超市A型商品的销售利润为x元/件,A型商品的日净收入为y元(日净收入=A型商品每天销售的总利润﹣A型商品每天固定的支出费用):(1)试求出该超市A型商品的日净收入为y(元)与A型商品的销售利润x(元/件)之间的关系式;(2)该超市能否实现A型商品的销售日净收入3000元的目的?如能实现,求出A型商品的销售利润为多少元/件?如不能实现,请说明理由;(3)请问该超市A型商品的销售利润为多少元/件时,能获得A型商品的最大日净收入?27.(10分)如图,在△ABC中,CA=CB,AB=10,0°<∠C<60°,AF⊥BC于点F,在FC上截取FD=FB,点E是AC上一点,连接DA、DE,且∠ADE=∠B.(1)求证:ED=EC(2)若∠C=30°,求BD长;(3)在(2)的条件下,将图1中△DEC绕点D逆时针旋转得到△DE′C′,请问在旋转的过程中,以点D、E、C′、E′为顶点的四边形可以构成平行四边形吗?若可以,请求出该平行四边形的面积;若不可以,请说明理由.28.(12分)如图,在平面直角坐标系中,抛物线y=x2+bx+c的图象与x轴交于点A(2,0)、B(﹣4,0),与y轴交于点D.(1)求抛物线的解析式;(2)连接BD,点P在抛物线的对称轴上,以Q为平面内一点,以点P、B、D、Q为顶点的四边形能否成为矩形?若能,请求出点P的坐标;若不能,请说明理由;(3)在抛物线上有一点M,过点M、A的直线MA交y轴于点C,连接BC,若∠MBO=∠BCO,请直接写出点M的坐标.参考答案与试题解析1.【解答】解:从正面看第一层是三个小正方形,第二层左边一个小正方形,右边一个小正方形,故选:B.2.【解答】解:设x=2k,y=5k,则==﹣.故选:D.3.【解答】解:∵以原点O为位似中心,在第一象限内将线段AB扩大为原来的2倍后得到线段CD,∴A点与C点是对应点,∵C点的对应点A的坐标为(2,2),位似比为:1:2,∴点C的坐标为:(4,4)故选:C.4.【解答】解:∵四边形ABCD为菱形,∴AD∥BC,AD=AB,∴∠A+∠ABC=180°,∴∠A=180°﹣120°=60°,∴△ABD为等边三角形,∴BD=AB=2,故选:A.5.【解答】解:过C点作CD⊥AB,垂足为D.根据旋转性质可知,∠B′=∠B.在Rt△BCD中,tanB==,∴tanB′=tanB=.故选:B.6.【解答】解:∵四边形ABCD是平行四边形,∴BC=AD=18,∵EF∥BC,且=,∴EF=BC=×18=6.故选:A.7.【解答】解:设这两年年收入的平均增长率为x,由题意得:20(1+x)2=25,故选:C.8.【解答】解:连接OA,OB,AB,BC,如图所示:∵AB=OA=OB,即△AOB为等边三角形,∴∠AOB=60°,∵∠ACB与∠AOB所对的弧都为,∴∠ACB=∠AOB=30°,又∠ACB为△SCB的外角,∴∠ACB>∠ASB,即∠ASB<30°.故选:D.9.【解答】解:由折叠是性质可知,DF=DC=AB=10,在Rt△ADF中,AF==8,∴BF=AB﹣AF=2,设CE=x,则BE=6﹣x,由折叠是性质可知,EF=CE=x,在Rt△BEF中,EF2=BF2+BE2,即x2=22+(6﹣x)2,解得,x=,故选:C.10.【解答】解:如图,过点A作AE⊥x轴于点E,过点C作CF⊥OB于点F,∵四边形OCAB为菱形,∴OC∥BA,则tan∠COB=tan∠ABE==,∵点A(8,4),∴AE=4,则BE=3,∴OC=AB==5,设CF=4x,则OF=3x,根据OF2+CF2=OC2即(3x)2+(4x)2=52,解得x=1,则OF=3、CF=4,即点C坐标为(3,4),所以反比例函数解析式为y=,故选:B.二、填空题:(本大题共4个小题,每小题4分,满分16分)11.【解答】解:若小亮出“石头”,则小明出的手势情况为剪刀、石头、布这3种,其中小明出布时,小亮获胜,所以小亮开棋的概率是,故答案为:.12.【解答】解:∵AC是正方形ABCD的对角线,AB=3,∴AC=3,∵正方形ABCD,∠DCA的平分线交BA的延长线于点E,∴∠DCE=∠ECA,DC∥EB,∴∠CEA=∠DCE,∴∠E=∠ECA,∴AE=AC=3,故答案为:313.【解答】解:∵关于x的一元二次方程(k﹣2)x2+2kx+k=0有实数根,∴,解得:k≥0且k≠2.故答案为:k≥0且k≠2.14.【解答】解:如图:连接OA,作OM⊥AB与M,∵⊙O的直径为10,∴半径为5,∴OP的最大值为5,∵OM⊥AB与M,∴AM=BM,∵AB=8,∴AM=4,在Rt△AOM中,OM=,OM的长即为OP的最小值,∴3≤OP≤5.三、简答题(15小题每小题12分,16小题6分,共18分)15.【解答】解:(1)原式=2﹣2+6×﹣1,=2﹣2+3﹣1,=5﹣3.(2)(x+2)(x+3)=2x+16,x2+5x+6=2x+16,x2+3x﹣10=0,(x﹣2)(x+5)=0,解得x1=2,x2=﹣5.16.【解答】解:(1)1200×=360(人),答:估计参加环境活动项目的同学有360人;(2)如图所示:,一共有9种可能,两位同学都选择参加关爱留守儿童的可能有1种,故两位同学都选择参加关爱留守儿童的概率为:.四、简答题:(每小题8分,共16分)17.【解答】解:(1)∵AB∥CG,∴∠ABF=∠G,又∵∠ABF=∠ACF,∴∠ECF=∠G,又∵∠CEF=∠CEG,∴△ECF∽△EGC,∴,即CE2=EF•EG;(2)∵平行四边形ABCD中,AB=CD,又∵DG=DC,∴AB=CD=DG,∴AB:CG=1:2,∵AB∥CG,∴,即,∴EG=12,BG=18,∵AB∥DG,∴,∴BF=BG=9,∴EF=BF﹣BE=9﹣6=3.18.【解答】解:如图作CH⊥AB于H.在Rt△ACH中,AC=1200,∠A=30°,∴CH=AC=600,AH=CH≈1039.2,在Rt△BCH中,BH===800,∴AB=1893,AC+BC=2200,∴滴滴快车让乘客多等的时间=5+≈6(分钟),五、简答题:(每小题10分,共20分)19.【解答】解:(1)∵OD=2,tan∠DCO==,∴,∴OC=3,∴D(0,2),C(﹣3,0),把D(0,2),C(﹣3,0)代入y1=kx+b中得:,解得:,∴一次函数的解析式为:y1=x+2;过A作AE⊥x轴于E,∵点C、D刚好是线段AB的三等分点,∴AC=CD=BD,∵∠AEC=∠COD=90°,∠ECA=∠OCD,∴△AEC≌△DOC,∴EC=OC=3,AE=OD=2,∴A(﹣6,﹣2),∴m=﹣6×(﹣2)=12,∴反比例函数的解析式为:y2=;(2)同理得:B(3,4),∴S△AOB=S△BOC+S△ACO,=•|y B|+•|y A|,=+×3×2,=9;(3)由图象得:当x≤﹣6或0<x≤3时,y1≤y2.20.【解答】(1)证明:∵BD=BC,∴∠BDC=∠BCD,∵∠P=∠BCD,∠BAC=∠BDC,∴∠P=∠BAC,∵AC是直径,∴∠ABC=∠ABP=90°,∴∠P+∠BAP=90°,∴∠BAP+∠BAC=90°,∴∠OAP=90°,∴OA⊥PA,∴PA是⊙O的切线.(2)解:①当∠OED=90°时,CB=CD=BD,△BCD是等边三角形,可得∠ACB=30°,∵AC=2,∴AB=1,BC=,∴S△ABC=.②当∠DOE=90°时,作BH⊥AC于H.∵BD=BC,BO=BO,OC=OD,∴△BOC≌△BOD(SSS),∴∠OBC=∠OBD=∠OCB=22.5°,∴∠BOH=45°,∴BH=,∴S△ABC=×2×=(3)解:∵BD=BC,OD=OC,BO=BO,∴△BOD≌△BOC,∴∠OBD=∠OBC,∵OB=OD=CO,∴∠OBD=∠OBC=∠ODB=∠OCB,∵∠ADB=∠OCB,∴∠ADB=∠OBD,∴AD∥OB,∴△AED∽△OEB,∴=()2,∵==,∴=()2,∴b2=ac.一、填空题:(每小题4分,共20分)21.【解答】解:∵m、n是方程x2﹣2x﹣7=0的两个根,∴m+n=2,mn=﹣7,m2﹣2m﹣7=0,∴m2=2m+7,∴m2+mn+2n=2m+7+mn+2n=7+2×2+(﹣7)=4.故答案为:4.22.【解答】解:由FB∥AP可得,△CBF∽△CAP,∴,即,解得AP=8,由GD∥AP可得,△EDG∽△EAP,∴,即,解得ED=2,故答案为:2.23.【解答】解:如图作AE⊥x轴于E,BF⊥x轴于F.设A(a,),B(b,﹣),∵∠AOB=∠OFB=∠AEO=90°,∴∠BOF+∠AOE=90°,∠AOE+∠OAE=90°,∴∠BOF=∠OAE,∴△BOF∽△OAE,∴=,∴=,∴a2b2=5,∵AB2=OB2+OA2=b2++a2+=6b2+,∴AB=,OB=,∴sin∠A===,故答案为.24.【解答】解:①∵抛物线开口向上,∴a>0,∵x=﹣>0,∴b<0,又∵抛物线与y轴交于负半轴,∴c<0,∴abc>0.故①正确;②∵x=1时,y<0,∴a+b+c<0,故②错误;③∵a>0,0<﹣<1,∴﹣b<2a,∴2a+b>0.故③错误;④∵抛物线过点(﹣1,2),∴a﹣b+c=2∴a+c=b+2∵a+b+c<0,∴b+2+b<0∴b<﹣1故④正确;∵>﹣2且a>0∴4ac﹣b2>﹣8a∴b2﹣4ac<8a成立,故⑤正确.故答案为:①④⑤.25.【解答】解:设DF=OF=a,CD=b,连接OC.∵CD⊥OB于点D,CE⊥OA于点E,∴∠EOD=∠CDO=∠CEO=90°,∴四边形CDOE是矩形,∴CE=OD=2a,CD=OE=b,∵EC∥DF,∴==,∴PC=2PF,PC=CF=,∴EC2+3CP2=4a2+(a2+b2)=(4a2+b2),在Rt△OCE中,∵EC2+OE2=OC2,∴4a2+b2=36,∴EC2+3CP2=48.故答案为48二、简答题(8分)26.【解答】解:(1)由题意可得,当0<x≤9时,y=280x﹣400,当x>9时,y=[280﹣(x﹣9)×10]x﹣400=﹣10x2+370x﹣400,由上可得,该超市A型商品的日净收入为y(元)与A型商品的销售利润x(元/件)之间的关系式是:y=;(2)∵当0<x≤9时,y=280x﹣400≤2120,∴令y=3000代入y=﹣10x2+370x﹣400,解得,x1=17,x2=20,答:该超市能实现A型商品的销售日净收入3000元的目的,A型商品的销售利润为17元/件或20元/件;(3)∵当0<x≤9时,y=280x﹣400≤2120,当x>9时,y=﹣10x2+370x﹣400=﹣10(x﹣)2+3022.5,∵x>9且x为整数,∴当x=18或19时,y取得最大值,此时y=3020,答:该超市A型商品的销售利润为18元/件或19元/件时,能获得A型商品的最大日净收入.27.【解答】解:(1)∵AC=BC,∴∠ABC=∠BAC,∴∠C=180°﹣∠ABC﹣∠BAC=180°﹣2∠ABC,∵AF⊥BC,BF=DF,∴AB=AD,∴∠ADB=∠ABC,∵∠ADE=∠ABC,∴∠CDE=180°﹣∠ADE﹣∠ADB=180°﹣2∠ABC,∴∠CDE=∠C,∴DE=CE;(2)∵∠C=30°,∴∠ABC=∠ADB=∠BAC=∠ADE=75°,∴∠BAD=30°,过点B作BG⊥AD于G,如图1,在Rt△ABG中,AB=10,∠BAD=30°,∴BG=5,AG=5,∴DG=AD﹣AG=10﹣5=5(2﹣),在Rt△BDG中,BD==10=5﹣5;(3)可以,①理由:如图2;∵DE=CE,∴∠EDC=∠C=30°,由旋转知,∠E'DC'=∠E'C'D=∠C=30°∵四边形DEC'E'是平行四边形,∴C'E'∥DE,∴∠C'DE=30°,∴∠C'DC=60°,∴C'D⊥AC于H,在Rt△ADH中,AD=10,∠DAH=∠BAC﹣∠BAD=45°,∴DH=5,在Rt△DEH中,∠AED=∠ACB+∠CDE=60°,∴∠EDH=30°,∴DE=,∴CE=,∴S▱DEC'E'=2S△CDE=2×CE×DH=×5=.②理由:如图3,由①知,S△CDE=S△C'DE'=,∴S▱DEC'E'=2S△CDE=2×CE×DH=×5=.四、简答题(12分)28.【解答】解:(1)由题意,解得,∴抛物线的解析式为y=x2+x﹣4.(2)如图1中,当BD为矩形的边时,∵直线BD的解析式为y=﹣x﹣4,∴直线BP的解析式为y=x=4,直线 DP′的解析式为y=x﹣4,可得P(﹣1,3),P′(﹣1,﹣5).当BD为矩形的对角线时,设P(﹣1,m),BD的中点N(﹣2,﹣2),由BN=P″N,可得12+(m+2)2=(2)2,解得m=﹣2+或﹣2﹣,∴P″(﹣1,﹣2+),或(﹣1.﹣2﹣),∴要使四边形PBQD能成为矩形,满足条件的点P坐标为(﹣1,﹣2+)或(﹣1.﹣2﹣).综上所述,满足条件的P的坐标为(﹣1,3)或(﹣1,﹣5)或(﹣1,﹣2+)或(﹣1.﹣2﹣).(3)设M(m,m2+m﹣4),设直线AM的解析式为y=kx+b,则有,解得,∴直线AM的解析式为y=x﹣m﹣4,∴C(0,﹣m﹣4).①点M在第二象限显然不可能,当点M在第三象限时,如图2中,作MN⊥OB于N.∵∠MBN=∠BCO,∠MNB=∠BOC=90°,∴△MNB∽△BOC,∴=,∴=,∴m=﹣2或0.∴M(﹣2,﹣4)或(0,﹣4)(舍弃)②当点M在y轴上时,可得M(0,﹣4);③当点M在第一象限时,同法可得=,整理得:m2+2m﹣16=0,∴m=﹣1+或﹣1﹣(舍弃),∴M(﹣1+,4),④当点M在第四象限时,不存在,综上所述,满足条件的点M坐标(﹣2,﹣4)或(0,﹣4)或(﹣1+,4)。
2023年四川省成都市锦江区中考一模试题(解析版)

B.Maybe you shouldn’t spend too much time watching the games.
C.In Qatar, a desert country in the Middle East.
A.placedB.placingC.to place
【答案】A
【解析】
【详解】句意:由于烟雾报警器放在卧室外面,格林一家被及时叫醒,阻止了这场可怕的火灾。
考查非谓语动词。空前的“ the smoke alarm”和place有被动关系,表示烟雾报警器“被放置”在教室外,所以用过去分词表示被动。故选A。
A.aB.anC.the
【答案】B
【解析】
【详解】句意:作为一名交换生,劳拉发现餐桌礼仪似乎是她最大的挑战。
考查冠词的用法。根据“As ... exchange student,”可知,此处表示泛指一名交换生,用不定冠词,exchange是以元音音素开头的单词,不定冠词用an。故选B。
2.—Which is the ________ park? Dong’anhu Sports Park or Qinglonghu Wetland Park?
考查定语从句先行词辨析。where在哪里,关系副词,表地点;which那个,关系代词,指代物;when什么时候,关系副词,表时间。此题空处需填一个关系代词,作从句的主语,指代“Jingsha Site Museum”。故选B。
10.With the smoke alarm ________ outside the bedroom, the Greens were woken up in time to stop the terrible fire.
四川省成都市锦江区中考化学一诊试卷(含解析)

2021年四川省成都市锦江区中考化学一诊试卷一.选择题节日期间的商场里人头攒动,常常会让人感觉闷热缺氧.此时,测定出氧气的体积分数可能是〔〕A.1% B.75% C.25% D.19%2.以下物质在实际应用中出现错误的选项是〔〕A、食品包装充氮气防腐B、活性炭用于净水C、填充稀有气体制霓虹灯D、二氧化碳气体肥料A.A B.B C.C D.D3.以下做法不是为了隔绝空气中氧气的是〔〕A.自行车支架外表喷漆B.用灯帽盖灭酒精灯火焰C.生石灰需要密封保存D.白磷浸没在冷水中保存4.下表是元素周期表的一局部,那么以下答复不正确的选项是〔〕+2A.12号元素的离子符号 MgB.硫原子的核外电子排布为C.硅元素位于周期表的第三周期D.13号元素是地壳中含量最多的金属元素5.化学是以实验为根底的学科,以下有关实验现象的描述中,正确的选项是〔〕A.硫粉在空气中燃烧产生明亮的蓝紫色火焰B.电解水实验中正极与负极产生的气体体积比是1:8C.氧气复原铜丝外表的氧化铜,铜丝外表由黑色变红色D.将铁钉浸到硫酸铜溶液中,铁钉外表会有红色固体生成,溶液变成无色6.某反响的微观示意图如图,用“〞与“〞代表A、B两种元素的原子.以下说法不正确的选项是〔〕A.该反响属于化合反响B.反响前后原子的种类不发生变化C.反响前后物质的化学性质不发生变化D.该反响的化学方程式表示为A2+3B2═2AB37.某外控型食品保鲜剂以淀粉、二氧化硅〔SiO2〕为载体,吸附酒精制作而成.保鲜原理是酒精缓慢挥发,某食品周围形成一定浓度的气体保护层.以下说法不正确的选项是〔〕A.SiO2中硅元素化合价为+4 B.该保鲜剂不能与明火接触C.起保鲜作用的物质是酒精D.酒精挥发时分子体积变大8.比拟、推理是化学学习常用的方法,以下是根据一些反响事实推导出的影响化学反响的因素,其中推理合理的是:〔〕序号化学反响事实影响化学反响的因素①硫在氧气中燃烧,比在空气中燃烧更剧烈反响物浓度②碳在常温下不与氧气发生,而在点燃时能与氧气反响物温度③过氧化氢溶液在常温下较难分解,而在参加二氧化锰后迅速分解催化剂④铁丝在空气中很难燃烧,而在氧气中能剧烈燃烧反响物种类⑤碳充分燃烧时生成二氧化碳,不充分燃烧时生成一氧化碳反响物的量A.2个B.3个C.4个D.5个2+ ﹣9.在化学符号①NO2②2CO③Ca④H2O2⑤2OH⑥SO4中,关于数字“2〞的意义,以下说法错误的选项是〔〕A.表示分子个数的是②B.表示离子所带电荷数的是③⑤C.表示化合价数值的是⑥D.表示一个分子中所含某种原子个数的是①④10.用于区别以下气体的方法中,不可行的是〔〕A.O2和CO2分别通过灼热氧化铜B.CO和CO2分别通入澄清石灰水C.H2和CO2分别通入紫色石蕊试液2D.CO和O2分别通过灼热氧化铜11.一定条件下,甲、乙、丙、丁四种物质在密闭容器中反响,测得反响前后各物质的质量分数如图所示,以下说法正确的选项是〔〕①丁可能是该反响的催化剂②该反响的根本反响类型属于分解反响③该反响中的甲、丙物质的质量比为7:10④该反响中的乙、丙物质的质量比为3:17⑤甲、乙物质的质量之和一定等于生成的丙物质的质量.A.①⑤B.②③C.③④D.①④12.以下验证不能成功的是〔〕A、证明呼出气体含有CO2B、检验该瓶气体是 CO2C、验证分子在不断运动D、水电解实验A.A B.B C.C D.D13.以下是小吴同学对所学知识的整理归纳,完全正确的选项是〔〕A、物质在微观上都是由粒子构成的,如:B、气体的性质决定了收集方法,如:C、物质的性质决定了它的用途,如:D、物质因组成结构差异,在性质上表现不同,如:A.A B.B C.C D.D14.在“创新实验装置〞的竞赛中,某化学兴趣小组设计了如下图的装置〔夹持一起已略去〕,引起同学们的兴趣.如图是四位同学对实验中的局部现象进行的预测,预测正确的选项是〔〕3A.B.C.D.二.计算题〔此题有1小题,共6分〕可能用到的相对原子质量:C-12O-16Cu-64.15.〔6分〕将25g木炭粉和氧化铜粉末的混合物在高温下加热一段时间后,剩余固体混合物为,求反响中生成的铜的质量是多少克?〔假设反响过程中生成的气体只有二氧化碳,请写出解答过程.〕三.填空题16.用数学或化学用语符号填空〔可能用到的相对原子质量:O﹣16 Fe﹣56〕〔1〕2个氮分子;〔2〕3个硝酸根离子;〔3〕人体含量最多的元素;〔4〕算出氧化铁中铁元素的质量分数;〔5〕画出硅原子的结构示意图;〔6〕硫酸铵的化学式.17.化学与生活息息相关,请用学过的化学知识解决以下问题.4〔1〕2021年11月份起我国多地被雾霾笼罩,成都市到达重度污染,其中主要污染物.是指大气中直径小于或等于μm的颗粒物.雾霾天气导致呼吸系统病人增多,因为雾霾使空气中增加大量的可吸入颗粒物.〔2〕为减少污染、治理雾霾.提高煤的利用率,可将煤转化为可燃性气体,其主要反响有:①2C+O2CO ②C+H2O CO+H2③CO+H2O H2+CO2反响①的根本反响类型是;反响②和反响③中,C和CO均表现出具有性;此外,反响②和反响③还有的相同点是〔填序号〕.A.都属于置换反响B.水都发生了复原反响C.生成物都是可燃性气体D.反响后碳元素的化合价都升高〔3〕燃料在使用的过程中的碳循环示意图如图:①除了燃料燃烧释放大量CO2外,常见释放CO2的途径还有,空气中的CO2含量增多导致的后果是;②利用海水进行碳储存,可以缓解空气中CO2过多的问题,写出海水吸收CO2时发生反响的化学方程式:;③科学家采取“组合转化〞技术,将CO2转化为化工原料,其反响的化学方程式:2CO+6X C2H4+4H2O,那么X的化学式为;④生物燃料〔如酒精〕可来源于植物体,写出酒精燃烧的化学方程式:;结合如图信息,从碳循环角度说出生物燃料的优点有.〔写出一条即可〕18.有A﹣F六种物质,A、B、C三种固体含有同种金属元素,A是大理石、石灰石的主要成分,B是一种氧化物能与E反响放出大量的热,D、E、F含有同种非金属元素,E通常状况下为液体,D、F通常状况下为气体,且F为单质.它们的转化关系如图〔局部产物已略去〕.温馨提示:图中“→〞表示箭尾的物质可转化为箭头的物质;“﹣〞表示两端的物质能发生化学反响.〔1〕写出A、E物质的名称: A ;E5〔2〕写出C→A的化学方程式:〔3〕写出E→F的化学方程式:.四.实验题19.根据图甲答复有关问题.〔1〕仪器D的名称为,仪器F的名称为.〔2〕图A﹣C是常见实验根本操作.其中操作正确的选项是〔填序号〕;请选择一个有错误的操作写出,改正方法:.〔3〕选择仪器D﹣I完成以下实验操作:①用KMnO4制备O2的发生装置,应选仪器〔填序号〕,其化学反响方程式为;②用大理石与稀盐酸反响制备 CO2时,并使反响随时发生或停止的发生装置,应选仪器〔填序号〕,其化学反响方程式为.〔4〕图乙是用过氧化氢溶液制备氧气,并用排水法收集的装置.请把图中缺失局部补画完整.五.流程题20.根据有关报道,美国宇航局科学探测发现月球储存有一定数量的冰尘混合物、甲醛和钛铁矿〔主要成分FeTiO3〕资源.人类有望利用月球上的水资源,并通过电解获取氢气为火箭提供燃料,获取的氧气可逐渐形成可供呼吸的大气层,用来满足植物和人类所需.根据科学家设想的有关人类利用月球资源的流程图,如下图:6〔1〕得到净化水的过程中,加絮凝剂的目的是.〔2〕该流程图中,可循环利用的物质是.〔3〕推测流程图中的“金属单质〞是.〔4〕根据流程图的信息,写出一氧化碳和氢气发生反响的化学方程式〔5〕FeTiO3的名称读作“钛酸亚铁〞,那么其中钛元素的化合价为;求其中铁、氧元素的质量比为.〔相对原子质量:O﹣16Fe﹣56〕六、探究题21.选修课上,某化学兴趣小组在老师的帮助下,开展了以下的相关探究:探究一:氢气的燃烧实验〔1〕用锌和稀硫酸制取氢气,从图甲中选择仪器组装一套随开随停的发生装置,所需仪器为〔填编号〕;反响的化学方程式为.7〔2〕按图乙操作研究氢气的燃烧实验,需用试管收集不同体积比的氢气与空气的混合物,现用〔1〕中组装的正确装置制取氢气,如何用试管〔假设试管容积为10mL〕收集氢气与空气体积比为4:1的混合气体,写出其操作方法:.〔3〕用不同体积比的混合气体做氢气的燃烧实验,结果如表:序号1234567氢气与空气体积9:18:27:35:53:71:9:比点燃现象安静安静弱的强的强的弱的不燃烧燃烧燃烧爆鸣声爆鸣声爆鸣声爆鸣声不爆鸣分析上表信息,你对燃烧或燃烧条件的新认识是.探究二:该化学兴趣小组的同学们在一次课外实验中发现一种淡黄色的粉末可以杀菌、消毒和漂白,于是想探究该固体的成分.提出问题]该淡黄色固体的化学成分是什么?[查阅资料]1〕硫单质是一种淡黄色固体,难溶于水.在空气中点燃硫单质,生成一种无色、有刺激性气味的气体.2〕过氧化钠〔Na2O2〕是一种淡黄色固体,能与水反响,生成气体并放出大量的热.[设计实验方案]方案一:取少量该固体粉末于试管中,加2mL水,振荡并观察现象.方案二:在燃烧匙里放少量该固体,在酒精灯上加热,观察现象.比拟以上两方案,你认为的最正确方案是,理由是〔从环保或操作角度分析〕.[实验验证并得出结论]兴趣小组中甲同学向盛有少量该固体的试管中参加 2mL水,立刻观察到有无色气泡产生,并且验证出该反响同时生成了氢氧化钠〔NaOH〕.通过实验验证,确定该淡黄色粉末为过氧化钠.甲同学对生成的气体成分判断.他提出了以下三种假设:①该气体是CO②该气体是O2.你认为上述假设哪个更合理〔填“①〞、“②〞或“③〞〕;理由是.[分析]过氧化钠与水反响的化学方程式为.[交流讨论]兴趣小组中乙同学在查阅资料时发现过氧化钠还能与二氧化碳反响,产生一种无色气体.为了验证该结论,该小组同学用图丙所示的装置进行实验,一段实验后,将带火星的木条伸入试管中,发现木条复燃.〔温馨提示两点:a.浓硫酸具有吸水性; b.氢氧化钠溶液能与二氧化碳8反响.〕B装置能否省去?你的理由是;D装置中的氢氧化钠溶液的作用是.92021年四川省成都市锦江区中考化学一诊试卷参考答案与试题解析一.选择题节日期间的商场里人头攒动,常常会让人感觉闷热缺氧.此时,测定出氧气的体积分数可能是〔〕A.1% B.75% C.25% D.19%【考点】空气的成分及各成分的体积分数.【专题】空气与水.【分析】根据空气中氧气的体积分数为21%,进行分析判断.【解答】解:空气中氧气的体积分数为21%,节日期间的商场里顾客很多,有人会感觉到闷热缺氧,那么氧气的体积分数应略小于21%,应选D【点评】此题难度不大,了解空气中氧气的体积分数〔21%〕是正确解答此题的关键.2.以下物质在实际应用中出现错误的选项是〔〕A、食品包装充氮气防腐B、活性炭用于净水C、填充稀有气体制霓虹灯D、二氧化碳气体肥料A.A B.B C.C D.D【考点】常见气体的用途;碳单质的物理性质及用途.【专题】物质的性质与用途.【分析】物质的性质决定物质的用途,根据常见气体的性质和永和用途分析判断.【解答】解:A、食品包装充氮气防腐,正确;B、活性炭用于净水,正确;C、填充稀有气体制霓虹灯,正确;D、氮气作气体肥料,错误;10应选D【点评】掌握物质性质,并能依据其性质分析其用途.3.以下做法不是为了隔绝空气中氧气的是〔〕A.自行车支架外表喷漆B.用灯帽盖灭酒精灯火焰C.生石灰需要密封保存D.白磷浸没在冷水中保存【考点】金属锈蚀的条件及其防护;生石灰的性质与用途;灭火的原理和方法.【专题】化学与能源;金属与金属材料;常见的碱碱的通性.【分析】物质的性质决定物质的用途,根据已有的物质的性质、实验操作方法进行分析解答即可.【解答】解:A、自行车支架外表喷漆是为了隔绝氧气防止生锈;B、用灯帽盖灭酒精灯火焰是为了隔绝氧气而灭火;C、生石灰需要密封保存是为了防止与水接触;D、白磷浸没在冷水中保存是为了防止与氧气反响;应选C.【点评】掌握物质的性质是正确解答此题的关键.4.下表是元素周期表的一局部,那么以下答复不正确的选项是〔〕+2A.12号元素的离子符号 MgB.硫原子的核外电子排布为C.硅元素位于周期表的第三周期D.13号元素是地壳中含量最多的金属元素【考点】元素周期表的特点及其应用;原子结构示意图与离子结构示意图.【专题】化学用语和质量守恒定律.【分析】A.根据离子符号的写法来分析;B.根据原子结构示意图的画法来分析;C.根据硅元素的原子核外电子层数来分析;D.根据地壳中元素的含量来分析.11【解答】解:号元素是镁元素,由离子的表示方法,在表示该离子的元素符号右上角,标出该离子所带的正负电荷数,数字在前,正负符号在后,带1个电荷时,1要省略.镁离子可表示为:2+Mg,故错误;B.硫元素是16号元素,原子核外有16个电子,第一层2个、第二层8个,最外层6个,故正确;C.硅元素是14号元素,原子核外有3个电子层,所以位于第三周期,故正确;D.由地壳中元素含量较多的前四位依次是,氧、硅、铝、铁可知,含量最多的金属元素是铝元素,故正确.应选A.【点评】此题考查学生根据元素周期律和地壳中含量最多的金属元素是铝进行分析解题的能力.5.化学是以实验为根底的学科,以下有关实验现象的描述中,正确的选项是〔〕A.硫粉在空气中燃烧产生明亮的蓝紫色火焰B.电解水实验中正极与负极产生的气体体积比是1:8C.氧气复原铜丝外表的氧化铜,铜丝外表由黑色变红色D.将铁钉浸到硫酸铜溶液中,铁钉外表会有红色固体生成,溶液变成无色【考点】金属的化学性质;氧气与碳、磷、硫、铁等物质的反响现象;电解水实验;氢气的化学性质与燃烧实验.【专题】实验现象的观察和记录.【分析】A、根据硫粉在空气中燃烧产生淡蓝色火焰进行分析;B、根据电解水实验中正极与负极产生的气体体积比是1:2进行分析;C、根据氧化铜和氢气在加热的条件下生成铜和水进行分析;D、根据铁和硫酸铜反响生成硫酸亚铁和铜进行分析.【解答】解:A、硫粉在空气中燃烧产生淡蓝色火焰,故A错误;B、电解水实验中,正氧负氢,正极与负极产生的气体体积比是1:2,故B错误;C、氧化铜和氢气在加热的条件下生成铜和水,所以氢气复原铜丝外表的氧化铜,铜丝外表由黑色变红色,故 C正确;D、铁和硫酸铜反响生成硫酸亚铁和铜,所以铁钉外表会有红色固体生成,溶液变成浅绿色,故D错误.应选:C.【点评】此题难度不大,掌握碱与金属的化学性质、电解水的实验现象、常见物质燃烧的现象即可12正确解答,在描述实验现象时,需要注意生成物的颜色.6.某反响的微观示意图如图,用“〞与“〞代表A、B两种元素的原子.以下说法不正确的选项是〔〕A.该反响属于化合反响B.反响前后原子的种类不发生变化C.反响前后物质的化学性质不发生变化D.该反响的化学方程式表示为A2+3B2═2AB3【考点】微粒观点及模型图的应用;反响类型的判定.【专题】化学反响模拟图型.【分析】此题应从分子的原子构成和反响前后粒子的变化角度入手.从模拟图可看出,反响物中共有两种原子,其中每种原子构成一种分子,生成物是一种由不同原子构成的分子,据此逐项分析即可.【解答】解:A、观察微观示意图,该反响由两种物质生成了一种物质,属于化合反响,故说法正确;B、由微粒的变化可知,反响前后原子的种类不发生变化,故说法正确;C、由微粒的变化可知,反响前后的分子发生了改变,因此化学性质也发生了改变,故说法不正确;D、由微粒的构成及微粒变化的数目关系可以可出,该反响的化学方程式表示为:A2+3B2═2AB3,故说法正确.应选项为:C.【点评】此题是有关微观示意图的考查,学会利用微观的观点及微观示意图的意义对反响根本类型判断及化学变化的微观信息的获取等是解题的关键,难度不大.7.某外控型食品保鲜剂以淀粉、二氧化硅〔SiO2〕为载体,吸附酒精制作而成.保鲜原理是酒精缓慢挥发,某食品周围形成一定浓度的气体保护层.以下说法不正确的选项是〔〕A.SiO2中硅元素化合价为+4 B.该保鲜剂不能与明火接触C.起保鲜作用的物质是酒精D.酒精挥发时分子体积变大【考点】化学式的书写及意义;甲烷、乙醇等常见有机物的性质和用途;分子的定义与分子的特性;13有关元素化合价的计算.【专题】化学用语和质量守恒定律.【分析】A.根据在化合物中正负化合价代数和为零,进行分析判断.B.根据酒精具有可燃性,进行分析判断.C.根据题意,某外控型食品保鲜剂以淀粉、二氧化硅〔SiO2〕为载体,吸附酒精制作而成.保鲜原理是酒精缓慢挥发,在食品周围形成一定浓度的气体保护层,进行分析判断.D.根据分子的根本性质,进行分析判断.【解答】解:A.氧元素显﹣2价,设硅元素的化合价是x,根据在化合物中正负化合价代数和为零,可得:x+〔﹣2〕×2=0,那么x=+4价,应选项说法正确.B.酒精具有可燃性,属于易燃物,该保鲜剂不能与明火接触,应选项说法正确.C.某外控型食品保鲜剂以淀粉、二氧化硅〔SiO2〕为载体,吸附酒精制作而成.保鲜原理是酒精缓慢挥发,在食品周围形成一定浓度的气体保护层,起保鲜作用的物质是酒精,应选项说法正确.D.酒精挥发时没有新物质生成,酒精分子没有发生改变,只是分子间的间隔发生了改变,应选项说法错误.应选D.【点评】此题难度不大,理解题意,掌握化合价的原那么、分子的根本性质、酒精具有可燃性等是正确解答此题的关键.8.比拟、推理是化学学习常用的方法,以下是根据一些反响事实推导出的影响化学反响的因素,其中推理合理的是:〔〕序号化学反响事实影响化学反响的因素①硫在氧气中燃烧,比在空气中燃烧更剧烈反响物浓度②碳在常温下不与氧气发生,而在点燃时能与氧气反响物温度③过氧化氢溶液在常温下较难分解,而在参加二氧化锰后迅速分解催化剂④铁丝在空气中很难燃烧,而在氧气中能剧烈燃烧反响物种类⑤碳充分燃烧时生成二氧化碳,不充分燃烧时生成一氧化碳反响物的量A.2个B.3个C.4个D.5个【考点】实验探究物质变化的条件和影响物质变化的因素.【专题】科学探究.【分析】影响化学反响的因素有:温度,温度越高,反响越快;反响物的接触面积,物质间的接触14面积越充分,反响速度越快;反响物颗粒的大小,颗粒越小,反响速度越快;通常反响物的浓度越大,反响速度越快;参加催化剂可以改变其反响速率等;据此结合事实进行分析解答.【解答】解:①硫在氧气中燃烧,比在空气中燃烧更剧烈,是因为氧气的浓度不同,说明增大反响物的浓度影响化学反响的发生,应选项推理合理.②碳在常温下不与氧气发生,而在点燃时能与氧气,说明反响的温度影响化学反响的发生,应选项推理合理.③过氧化氢溶液在常温下较难分解,而在参加二氧化锰后迅速分解,说明了使用催化剂,可以改变化学反响的速率,应选项推理合理.④铁丝在空气中很难燃烧,而在氧气中能剧烈燃烧,是因为氧气的浓度不同,说明增大反响物的浓度影响化学反响的发生,应选项推理不合理.⑤碳充分燃烧时生成二氧化碳,不充分燃烧时生成一氧化碳,说明反响物的量影响化学反响的生成物,应选项推理合理.故推理合理有4个.应选:C.【点评】此题难度不是很大,了解影响化学反响的因素即可正确解答此题,可从温度、反响物的接触面积、反响物颗粒的大小、反响物的浓度及催化剂等方面进行分析考虑.2+ ﹣9.在化学符号①NO2②2CO③Ca④H2O2⑤2OH⑥SO4中,关于数字“2〞的意义,以下说法错误的选项是〔〕A.表示分子个数的是②B.表示离子所带电荷数的是③⑤C.表示化合价数值的是⑥D.表示一个分子中所含某种原子个数的是①④【考点】化学符号及其周围数字的意义.【专题】化学用语和质量守恒定律.【分析】A、标在分子符号前面的数字表示分子的个数.B、标在元素符号右上角的数字表示离子所带电荷数.C、标在元素符号正上方的数字表示该元素化合价的数值.D、标在化学式中元素右下角的数字表示一个分子中所含原子的数目.15【解答】解:A、标在分子符号前面的数字表示分子的个数,②2CO中的“2〞表示一氧化碳分子的个数为2,应选项说法正确.B、标在元素符号右上角的数字表示离子所带电荷数,③Ca2+中的“2〞表示一个钙离子带有两个单位﹣的正电荷,⑤2OH中的“2〞表示氢氧根离子的个数为2,应选项说法错误.C、标在元素符号正上方的数字表示该元素化合价的数值,⑥SO4中的“2〞表示硫酸镁中镁元素的化合价为+2价,应选项说法正确.D、标在化学式中元素右下角的数字表示一个分子中所含原子的数目,表示示一个分子中含有某种原子个数的是①NO2、④H2O2,应选项说法正确.应选:B.【点评】此题难度不大,主要考查了元素符号不同位置的数字表示的意义,掌握标在元素符号不同位置的数字所表示的意义是正确解答此类题的关键所在.10.用于区别以下气体的方法中,不可行的是〔〕A.O2和CO2分别通过灼热氧化铜B.CO和CO2分别通入澄清石灰水C.H2和CO2分别通入紫色石蕊试液D.CO和O2分别通过灼热氧化铜【考点】常见气体的检验与除杂方法.【专题】物质的鉴别题;物质的检验、鉴别与推断.【分析】鉴别两种气体,要求根据两种气体性质的不同,设计的方案能出现两种明显不同的实验现象,才能到达到达一次鉴别出两种气体的目的.【解答】解:A、O2和CO2都不能与灼热氧化铜反响,均无明显变化,不能鉴别,应选项正确.B、二氧化碳能使澄清的石灰水变浑浊,一氧化碳不能,可以鉴别,应选项错误.C、分别通入紫色石蕊溶液中,能使紫色石蕊溶液变红色的是二氧化碳,无变化的是氢气,可以鉴别,应选项错误.D、一氧化碳能与灼热的氧化铜反响生成铜和二氧化碳,氧气不能,根据红色粉末是否变红色可以鉴别,应选项错误.应选:A.【点评】此题考查了常见气体的鉴别方法,解题的关键是利用所要鉴别气体的性质的差异,根据实16验中是否出现明显的不同现象判断能否鉴别.11.一定条件下,甲、乙、丙、丁四种物质在密闭容器中反响,测得反响前后各物质的质量分数如图所示,以下说法正确的选项是〔〕①丁可能是该反响的催化剂②该反响的根本反响类型属于分解反响③该反响中的甲、丙物质的质量比为7:10④该反响中的乙、丙物质的质量比为3:17⑤甲、乙物质的质量之和一定等于生成的丙物质的质量.A.①⑤B.②③C.③④D.①④【考点】质量守恒定律及其应用;催化剂的特点与催化作用;反响类型的判定.【专题】化学用语和质量守恒定律.【分析】此题可分析甲~丁四种物质反响前后各物质的质量分数,确定是反响物还是生成物,据此结合题意进行分析判断即可.【解答】解:由四种物质反响前后各物质的质量分数可知,反响前丙的质量分数为1﹣70%﹣14%﹣10=6%,反响后乙的质量分数为1﹣42%﹣40%﹣10%=8%;反响前后甲的质量分数减少了70%﹣42%=28%,故甲是反响物;同理可以通过图示确定乙的质量分数减少了14%﹣8%=6%,故乙是反响物;丙的质量分数增加了40%﹣6%=34%,丙是生成物;丁的质量分数不变,可能作该反响的催化剂,也可能没有参加反响.①丁的质量分数不变,可能作该反响的催化剂,也可能没有参加反响,正确;②该反响的反响物为甲和乙,生成物是丙,符合“多变一〞的特征,属于化合反响,错误;③该反响中的甲、丙物质的质量比为:28:34=14:17,错误;④该反响中的乙、丙物质的质量比为:6:34=3:17,正确;⑤参加反响的甲、乙物质的质量之和一定等于生成的丙物质的质量,错误.应选D.【点评】此题难度不大,考查的是质量守恒定律的应用,解题的关键是分析图中数据,灵活运用质17。
2020-2021学年四川省成都市中考数学一诊试卷及答案解析

四川省成都市中考数学一诊试卷一、选择题(本大题共10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.4的平方根是()A.±2 B.2 C.± D.2.已知点P(3,﹣2)与点Q关于x轴对称,则Q点的坐标为()A.(﹣3,2)B.(﹣3,﹣2)C.(3,2)D.(3,﹣2)3.今年3月5日,温家宝总理在《政府工作报告》中,讲述了六大民生新亮点,其中之一就是全部免除了细部地区和部分中部地区农村义务教育阶段约52 000 000名学生的学杂费.这个数据保留三个有效数字用科学记数法表示为()A.5.2×107B.52×108C.5.2×108D.5.20×1074.如图所示的几何体是由几个相同的小正方体搭成的一个几何体,它的俯视图是()A.B.C.D.5.如图,已知a∥b,∠1=40°,则∠2=()A.140°B.120°C.40°D.50°6.若一个多边形的内角和是900°,则这个多边形的边数是()A.5 B.6 C.7 D.87.不等式组的解集的情况为()A.x<﹣1 B.x< C.﹣1<x<D.无解8.在Rt△ABC中,∠C=90°,BC=2,AB=4,则cosA=()A.B.C.D.9.如图,图中正方形ABCD的边长为4,则图中阴影部分的面积为()A.16﹣4πB.32﹣8πC.8π﹣16 D.无法确定|10.如图,在△ABC中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与CA、CB分别相交于点P、Q,则线段PQ长度的最小值是()A.4.75 B.4.8 C.5 D.4二、填空题(本大题共4个小题,每小题4分,共16分)11.如图,AB是⊙O的直径,点C在⊙O上,OD∥BC,若OD=1,则BC的长为.12.某班开展为班上捐书活动.共捐得科技、文学、教辅、传记四类图书,分别用A、B、C、D 表示,如图是未制作完的捐书数量y(单位:百本)与种类x(单位:类)关系的条形统计图,若D类图书占全部捐书的10%,则D类图书的数量(单位:百本)是.13.写出一个图象位于二、四象限的反比例函数的表达式,y= .14.如图,AD是△ABC的高,AD=h,点R在AC边上,点S在AB边上,SR⊥AD,垂足为E.当SR=BC时,则DE= .三、解答题(本大题共6个小题,共54分.解答应写出必要的文字说明、证明过程或演算步骤.)15.(1)计算:(2)解方程:.16.先化简,后求值:,其中x=﹣.17.过原点的直线交反比例函数y=图象于A、B两点,BD⊥x轴于点D,AE⊥y轴于点E.问:(1)直线AB与直线ED的位置关系是什么?并说明理由.(2)四边形ABDE的面积等于多少?18.某市今年的信息技术结业考试,采用学生抽签的方式决定自己的考试内容.规定:每位考生先在三个笔试题(题签分别用代码B1、B2、B3表示)中抽取一个,再在三个上机题(题签分别用代码J1、J2、J3表示)中抽取一个进行考试.小亮在看不到题签的情况下,分别从笔试题和上机题中随机地抽取一个题签.(1)用树状图或列表法表示出所有可能的结果;(2)求小亮抽到的笔试题和上机题的题签代码的下标(例如“B1”的下标为“1”)为一个奇数一个偶数的概率.19.如图所示,山坡上有一棵与水平面垂直的大树,一场台风过后,大树被刮倾斜后折断倒在山坡上,树的顶部恰好接触到坡面.已知山坡的坡角∠AEF=23°,量得树干倾斜角∠BAC=38°,大树被折断部分和坡面所成的角∠ADC=60°,AD=8m.(1)求∠CAE的度数;(2)求这棵大树折断前的高度?(结果精确到个位,参考数据:=1.4,=1.7,=2.4).20.在△ABC中,∠BAC=90°,AB<AC,∠PMQ是直角,且直角顶点M是BC边的中点,MN⊥BC 交AC于点N.PM边上动点P从点B出发沿射线BA以每秒2cm的速度运动,同时,MQ边上动点Q从点N出发沿射线NC运动,设运动时间为t秒(t>0).(1)求证:△PBM∽△QNM;(2)探求BP2、PQ2、CQ2三者之间的数量关系,并说明理由.(3)若∠ABC=60°,BC=8cm.①求动点Q的运动速度;②设△APQ的面积为S(平方厘米),求S与t的函数关系式;一、填空(本大题5个小题,每小题4分,共20分.)21.如果关于x的一元二次方程x2﹣4x+3m=0有两个不相等的实数根,则m的取值范围是.22.如图,在△ABC中,AC=BC=2,∠ACB=90°,D是BC边的中点,E是AB边上一动点,则EC+ED 的最小值是.23.如图,已知一次函数y=x+1的图象与反比例函数的图象在第一象限相交于点A,与x轴相交于点C,AB⊥x轴于点B,△AOB的面积为1,则AC的长为(保留根号).24.如图,已知A(2,0)、B(0,5),⊙C的圆心坐标为C(﹣1,0),半径为1,若D是⊙C 上一个动点,线段DA与y轴交于点E,则△ABE面积的最小值是.25.用火柴棒按下图中的方式搭图形,按照这种方式搭下去,搭第2015个图形需根火柴棒.二、解答题(本大题共3个小题,共30分.解答题应写出必要的文字说明,证明过程或演算步骤.)26.据我们调查,成都市某家电商场今年一月至六月份销售型号为“JSQ20﹣H”的海尔牌热水器的销量如下:月份一二三四五六销量(台)50 51 48 50 52 49(1)求上半年销售型号为“JSQ20﹣H”的海尔牌热水器销售量的平均数、中位数、众数.(2)由于此型号的海尔牌热水器的价格适中,消费者满意度很高,商场计划八月份销售此型号的热水器72台,与上半年平均月销售量相比,七、八月销售此型号的热水器平均每月的增长率是多少?27.如图,已知⊙O的直径AB垂直于弦CD于点E,过C点作CG∥AD交AB的延长线于点G,连接CO并延长交AD于点F,且CF⊥AD.(1)试问:CG是⊙O的切线吗?说明理由;(2)求证:E为OB的中点;(3)若AB=10,求CD的长.28.如图,在直角坐标系中有一直角三角形AOB,O为坐标原点,OB=6,tan∠ABO=,将此三角形绕原点O逆时针旋转90°,得到△DOC,抛物线y=ax2+bx+c经过点A、B、C.(1)求抛物线的解析式;(2)若点P是第二象限内抛物线上的动点,其横坐标为t,①设抛物线对称轴l与x轴交于一点E,连接PE,交CD于F,若△CEF∽△COD,求t的值;②是否存在一点P,使△PCD得面积最大?若存在,求出△PCD的面积的最大值;若不存在,请说明理由.参考答案与试题解析一、选择题(本大题共10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.4的平方根是()A.±2 B.2 C.± D.【考点】平方根.【分析】根据平方根的定义,求数a的平方根,也就是求一个数x,使得x2=a,则x就是a的平方根,由此即可解决问题.【解答】解:∵(±2)2=4,∴4的平方根是±2.故选:A.【点评】本题考查了平方根的定义.注意一个正数有两个平方根,它们互为相反数;0的平方根是0;负数没有平方根.2.已知点P(3,﹣2)与点Q关于x轴对称,则Q点的坐标为()A.(﹣3,2)B.(﹣3,﹣2)C.(3,2)D.(3,﹣2)【考点】关于x轴、y轴对称的点的坐标.【分析】利用关于x轴对称的两点,横坐标相同,纵坐标互为相反数的性质来求解.【解答】解:根据轴对称的性质,得点P(3,﹣2)关于x轴对称的点的坐标为(3,2).故选:C.【点评】熟记关于x轴对称的两点,横坐标相同,纵坐标互为相反数,关于y轴对称的两点,横坐标互为相反数,纵坐标相同,关于原点对称的两点,横坐标和纵坐标均互为相反数.3.今年3月5日,温家宝总理在《政府工作报告》中,讲述了六大民生新亮点,其中之一就是全部免除了细部地区和部分中部地区农村义务教育阶段约52 000 000名学生的学杂费.这个数据保留三个有效数字用科学记数法表示为()A.5.2×107B.52×108C.5.2×108D.5.20×107【考点】科学记数法与有效数字.【专题】应用题.【分析】科学记数法就是将一个数字表示成a×10的n次幂的形式,其中1≤|a|<10,n表示整数.n 为整数位数减1,即从左边第一位开始,在首位非零的后面加上小数点,再乘以10的n次幂.而保留三个有效数字,要观察第4个有效数字,四舍五入,不足的补0.【解答】解:52 000 000=5.20×107.故选D.【点评】本题考查学生对科学记数法的掌握.科学记数法要求前面的部分是大于或等于1,而小于10,小数点向左移动7位,应该为5.20×107.4.如图所示的几何体是由几个相同的小正方体搭成的一个几何体,它的俯视图是()A.B.C.D.【考点】简单组合体的三视图.【分析】俯视图是从上面看到的图形.【解答】解:从上面看,左边和中间都是2个正方形,右上角是1个正方形,故选D.【点评】本题考查了三视图的知识,关键是找准俯视图所看的方向.5.如图,已知a∥b,∠1=40°,则∠2=()A.140°B.120°C.40°D.50°【考点】平行线的性质;对顶角、邻补角.【专题】计算题.【分析】如图:由a∥b,根据两直线平行,同位角相等,可得∠1=∠3;又根据邻补角的定义,可得∠2+∠3=180°,所以可以求得∠2的度数.【解答】解:∵a∥b,∴∠1=∠3=40°;∵∠2+∠3=180°,∴∠2=180°﹣∠3=180°﹣40°=140°.故选A.【点评】此题考查了平行线的性质:两直线平行,同位角相等以及邻补角互补.6.若一个多边形的内角和是900°,则这个多边形的边数是()A.5 B.6 C.7 D.8【考点】多边形内角与外角.【分析】根据多边形的内角和公式(n﹣2)•180°,列式求解即可.【解答】解:设这个多边形是n边形,根据题意得,(n﹣2)•180°=900°,解得n=7.故选:C.【点评】本题主要考查了多边形的内角和公式,熟记公式是解题的关键.7.不等式组的解集的情况为()A.x<﹣1 B.x< C.﹣1<x<D.无解【考点】解一元一次不等式组.【分析】由题意分别解出不等式组中的两个不等式,再根据求不等式组解集的口诀:同大取大,同小取小,大小小大中间找,大大小小找不到(无解)来求出不等式的解集.【解答】解:由移项整理,得x<﹣1,由3x﹣2<0移项,得3x<2,∴x<,∴不等式的解集:x<﹣1,故选A.【点评】主要考查了一元一次不等式组解集的求法,考不等式组解集的口诀,还考查学生的计算能力.8.在Rt△ABC中,∠C=90°,BC=2,AB=4,则cosA=()A.B.C.D.【考点】锐角三角函数的定义.【分析】根据勾股定理求出AC,根据余弦的定义计算即可.【解答】解:∵∠C=90°,BC=2,AB=4,∴AC==2,∴cosA===,故选:D.【点评】本题考查锐角三角函数的定义及运用:在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.9.如图,图中正方形ABCD的边长为4,则图中阴影部分的面积为()A.16﹣4πB.32﹣8πC.8π﹣16 D.无法确定|【考点】扇形面积的计算.【专题】压轴题.【分析】根据图形,知阴影部分的面积即为直径为4的圆面积的2倍减去边长为4的正方形的面积.【解答】解:根据图形,得阴影部分的面积=2×π×22﹣4×4=8π﹣16.故选C.【点评】此题关键是能够看出阴影部分的面积的整体计算方法.10.如图,在△ABC中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与CA、CB分别相交于点P、Q,则线段PQ长度的最小值是()A.4.75 B.4.8 C.5 D.4【考点】切线的性质.【专题】压轴题.【分析】设QP的中点为F,圆F与AB的切点为D,连接FD,连接CF,CD,则有FD⊥AB;由勾股定理的逆定理知,△ABC是直角三角形,FC+FD=PQ,由三角形的三边关系知,FC+FD>CD;只有当点F在CD上时,FC+FD=PQ有最小值,最小值为CD的长,即当点F在直角三角形ABC的斜边AB的高CD上时,PQ=CD有最小值,由直角三角形的面积公式知,此时CD=BC•AC÷AB=4.8.【解答】解:如图,设QP的中点为F,圆F与AB的切点为D,连接FD、CF、CD,则FD⊥AB.∵AB=10,AC=8,BC=6,∴∠ACB=90°,FC+FD=PQ,∴FC+FD>CD,∵当点F在直角三角形ABC的斜边AB的高CD上时,PQ=CD有最小值,∴CD=BC•AC÷AB=4.8.故选:B.【点评】本题利用了切线的性质,勾股定理的逆定理,三角形的三边关系,直角三角形的面积公式求解.二、填空题(本大题共4个小题,每小题4分,共16分)11.如图,AB是⊙O的直径,点C在⊙O上,OD∥BC,若OD=1,则BC的长为 2 .【考点】三角形中位线定理;圆的认识.【分析】首先证明OD是△ABC的中位线,根据三角形的中位线定理即可求解.【解答】解:∵OD∥BC,且O是AB的中点.∴OD是△ABC的中位线.∴BC=2OD=2.故答案是:2.【点评】本题主要考查了三角形的中位线定理,正确证明OD是中位线是解题的关键.12.某班开展为班上捐书活动.共捐得科技、文学、教辅、传记四类图书,分别用A、B、C、D 表示,如图是未制作完的捐书数量y(单位:百本)与种类x(单位:类)关系的条形统计图,若D类图书占全部捐书的10%,则D类图书的数量(单位:百本)是10本.【考点】条形统计图.【分析】首先设D地车票有x张,根据去D地的车票占全部车票的10%列方程即可求得去D地的车票的数量.【解答】解:设D类图书数量为x,则x=(x+20+40+30)×10%,解得x=10.即D类书有10本.故答案为:10本.【点评】此题考查条形统计图,关键是读懂统计图,会分析数据进行解答问题.13.写出一个图象位于二、四象限的反比例函数的表达式,y= 答案不唯一,如y=﹣x等.【考点】正比例函数的性质.【专题】开放型.【分析】根据正比例函数的系数与图象所过象限的关系,易得答案.【解答】解:根据正比例函数的性质,其图象位于第二、四象限,则其系数k<0;故只要给出k小于0的正比例函数即可;答案不唯一,如y=﹣x等.【点评】解题关键是掌握正比例函数的图象特点.14.如图,AD是△ABC的高,AD=h,点R在AC边上,点S在AB边上,SR⊥AD,垂足为E.当SR=BC时,则DE= h .【考点】相似三角形的判定与性质.【分析】根据AD⊥BC,SR⊥AD可得出SR∥BC,故△ASR∽△ABC,再由相似三角形的性质可得出AE的长,进而可得出结论.【解答】解:∵AD⊥BC,SR⊥AD,SR=BC,AD=h,∴SR∥BC,∴△ASR∽△ABC,∴=,即=,解得AE=h,∴DE=AD﹣AE=h﹣h=h.故答案为:h.【点评】本题考查的是相似三角形的判定与性质,熟知相似三角形对应高的比等于相似比是解答此题的关键.三、解答题(本大题共6个小题,共54分.解答应写出必要的文字说明、证明过程或演算步骤.)15.(1)计算:(2)解方程:.【考点】实数的运算;零指数幂;负整数指数幂;解分式方程;特殊角的三角函数值.【专题】实数;分式方程及应用.【分析】(1)原式第一项利用负整数指数幂法则计算,第二项利用二次根式性质化简,第三项利用零指数幂法则计算,最后一项利用特殊角的三角函数值计算即可得到结果;(2)分式方程整理后,去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.【解答】解:(1)原式=4﹣3+1﹣2×=4﹣3+1﹣2=0;(2)原方程可化为:=+,去分母得:1=3x﹣1+43x﹣1=﹣3,解得:x=﹣,经检验x=﹣是原方程的解.【点评】此题考查了实数的运算,熟练掌握运算法则是解本题的关键.16.先化简,后求值:,其中x=﹣.【考点】分式的化简求值.【分析】先根据分式混合运算的法则把原式进行化简,再把x的值代入进行计算即可.【解答】解:原式=+•=+•=+=,当x=﹣时原式==﹣=﹣.【点评】本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.17.过原点的直线交反比例函数y=图象于A、B两点,BD⊥x轴于点D,AE⊥y轴于点E.问:(1)直线AB与直线ED的位置关系是什么?并说明理由.(2)四边形ABDE的面积等于多少?【考点】反比例函数与一次函数的交点问题.【分析】(1)根据题意得出A、B关于原点对称,得出AE=OD,AE∥OD,从而证得四边形OAED 是平行四边形,即可证得AB∥ED.(2)根据反比例函数系数k的几何意义即可求得.【解答】解:(1)AB∥ED;理由如下:∵过原点的直线交反比例函数y=图象于A、B两点,∴A、B关于原点对称,∴AE=OD,∵AE⊥y轴于点E.∴AE∥x轴,∴AE∥OD,∴四边形OAED是平行四边形,∴AB∥ED.(2)∵四边形OAED是平行四边形,∴S△AOE =S△EOD,根据反比例函数系数k的几何意义:S△AOE =S△BOD=×12=6,∴四边形ABDE的面积=3×6=18.【点评】本题考查了反比例函数和一次函数的交点问题,平行四边形的判定和性质以及反比例函数系数k的几何意义.18.某市今年的信息技术结业考试,采用学生抽签的方式决定自己的考试内容.规定:每位考生先在三个笔试题(题签分别用代码B1、B2、B3表示)中抽取一个,再在三个上机题(题签分别用代码J1、J2、J3表示)中抽取一个进行考试.小亮在看不到题签的情况下,分别从笔试题和上机题中随机地抽取一个题签.(1)用树状图或列表法表示出所有可能的结果;(2)求小亮抽到的笔试题和上机题的题签代码的下标(例如“B1”的下标为“1”)为一个奇数一个偶数的概率.【考点】列表法与树状图法.【分析】(1)首先根据题意画出树状图,然后由树状图求得所有等可能的结果;(2)由(1)中的树状图可求得小亮抽到的笔试题和上机题的题签代码的下标(例如“B1”的下标为“1”)为一个奇数一个偶数的情况,然后直接利用概率公式求解即可求得答案.【解答】解:(1)画树状图:则共有9种等可能的结果;(2)∵由树状图或表可知,所有可能的结果共有9种,其中笔试题和上机题的题签代码下标为一奇一偶的有4种,∴题签代码下标为一奇一偶的概率是.【点评】此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.19.如图所示,山坡上有一棵与水平面垂直的大树,一场台风过后,大树被刮倾斜后折断倒在山坡上,树的顶部恰好接触到坡面.已知山坡的坡角∠AEF=23°,量得树干倾斜角∠BAC=38°,大树被折断部分和坡面所成的角∠ADC=60°,AD=8m.(1)求∠CAE的度数;(2)求这棵大树折断前的高度?(结果精确到个位,参考数据:=1.4,=1.7,=2.4).【考点】解直角三角形的应用-坡度坡角问题.【分析】(1)延长BA交EF于点G.根据三角形内角和定理求出∠CAE的度数;(2)过点A作AE⊥CD,根据余弦和正弦的概念分别求出DH和AH的长,根据等腰直角三角形的性质计算即可.【解答】解:(1)延长BA交EF于点G.在Rt△AGE中,∠E=23°,∴∠GAE=67°,又∵∠BAC=38°,∴∠CAE=180°﹣67°﹣38°=75°.(2)过点A作AE⊥CD,垂足为H.在△ADH中,∠ADC=60°,AD=8,cos∠ADC=,∴DH=4,sin∠ADC=,∴.在Rt△ACH中,∠C=180°﹣75°﹣60°=45°,∴,.∴(米).答:这棵大树折断前高约20米.【点评】本题考查的是解直角三角形的应用﹣坡度坡角问题,正确标注坡角、倾斜角、灵活运用锐角三角函数的概念是解题的关键,注意特殊角的三角函数值的应用.20.在△ABC中,∠BAC=90°,AB<AC,∠PMQ是直角,且直角顶点M是BC边的中点,MN⊥BC 交AC于点N.PM边上动点P从点B出发沿射线BA以每秒2cm的速度运动,同时,MQ边上动点Q从点N出发沿射线NC运动,设运动时间为t秒(t>0).(1)求证:△PBM∽△QNM;(2)探求BP2、PQ2、CQ2三者之间的数量关系,并说明理由.(3)若∠ABC=60°,BC=8cm.①求动点Q的运动速度;②设△APQ的面积为S(平方厘米),求S与t的函数关系式;【考点】相似形综合题.【专题】综合题;图形的相似.【分析】(1)根据MQ垂直于MP,MN垂直于BC,利用等式的性质得到一对角相等,再利用同角的余角相等得到一对角相等,利用两角相等的三角形相似即可得证;(2)PQ2=BP2+CQ2,理由如下:如图1,延长QM至D,使MD=MQ,连结BD、PD,利用SAS得到三角形BDM与三角形CQM全等,利用全等三角形的对应角相等,对应边相等得到一对内错角相等,进而确定出BD与CQ平行且相等,利用两直线平行同旁内角互补,得到∠PBD为直角,利用勾股定理列出关系式,等量代换即可得证;(3)由M为BC中点,求出CM的长,在直角三角形MNC中,利用锐角三角函数定义求出MN 的长,①设Q点的运动速度为vcm/s,如图1,当0≤t<2时,由(1)知△PBM∽△QNM,由相似得比例求出Q速度,如图2,易知当t≥2时,Q的速度;②由AC﹣NC表示出AN,如图1,当0≤t<2时,根据AP,AQ,表示出S;如图2,当t≥2时,同理表示出AP,AQ,进而表示出S即可.【解答】(1)证明:如图1,∵MQ⊥MP,MN⊥BC,∴∠PMB+∠PMN=90°,∠QMN+∠PMN=90°,∴∠PMB=QMN,∵∠PBM+∠C=90°,∠QNM+∠C=90°,∴∠PBM=∠QNM,∴△PBM∽△QNM;(2)解:PQ2=BP2+CQ2,理由如下:如图1,延长QM至D,使MD=MQ,连结BD、PD,∵BC、DQ互相平分,∴BM=CM,DM=QM,在△BDM和△CQM中,,∴△BDM≌△CQM(SAS),∴∠CQM=∠BDM,BD=CQ,∴BD∥CQ,∵∠BAC=90°,∴∠PBD=90°,∴PD2=BP2+BD2=BP2+CQ2,∵PM垂直平分DQ,∴PQ=PD,则PQ2=BP2+CQ2;(3)解:∵BC=8cm,M为BC的中点,∴BM=CM=4cm,∵∠ABC=60°,∠C=30°,∴MN=CM=cm;①设Q点的运动速度为vcm/s,如图1,当0≤t<2cm时,由(1)知△PBM∽△QNM,∴=,即=,∴v=cm/s;如图2,易知当t≥2时,v=cm/s,综上所述,Q点运动速度为cm/s;②∵BC=8cm,AB=4cm,AC=4cm,NC=cm,∴AN=AC﹣NC=4﹣=cm,∴如图1,当0≤t<2cm时,AP=(4﹣2t)cm,AQ=AN+NQ=(+t)cm,∴S=AP•AQ=(4﹣2t)(+t)=(﹣t2+)cm2;如图2,当t≥2cm时,AP=(2t﹣4)cm,AQ=AN+NQ=(+t)cm,∴S=AP•AQ=(2t﹣4)(+t)=(t2﹣)cm2.【点评】此题属于相似形综合题,涉及的知识有:相似三角形的判定与性质,全等三角形的判定与性质,以及勾股定理,利用了分类讨论的思想,熟练掌握相似三角形的判定与性质是解本题的关键.一、填空(本大题5个小题,每小题4分,共20分.)21.如果关于x的一元二次方程x2﹣4x+3m=0有两个不相等的实数根,则m的取值范围是m<.【考点】根的判别式.【分析】根据题意一元二次方程有两不相等实根,则有△=b2﹣4ac=16﹣12m>0,然后解得m的取值范围.【解答】解:∵关于x的一元二次方程x2﹣4x+3m=0有两个不相等的实数根,∴△>0,即△=16﹣12m>0,∴m<,故答案为:m<.【点评】本题主要考查了利用一元二次方程根的判别式(△=b2﹣4ac)判断方程的根的情况.一元二次方程ax2+bx+c=0(a≠0)的根与△=b2﹣4ac有如下关系:①当△>0时,方程有两个不相等的两个实数根;②当△=0时,方程有两个相等的两个实数根;③当△<0时,方程无实数根.22.如图,在△ABC中,AC=BC=2,∠ACB=90°,D是BC边的中点,E是AB边上一动点,则EC+ED 的最小值是.【考点】轴对称-最短路线问题.【专题】压轴题;动点型.【分析】首先确定DC′=DE+EC′=DE+CE的值最小.然后根据勾股定理计算.【解答】解:过点C作CO⊥AB于O,延长CO到C′,使OC′=OC,连接DC′,交AB于E,连接CE,此时DE+CE=DE+EC′=DC′的值最小.连接BC′,由对称性可知∠C′BE=∠CBE=45°,∴∠CBC′=90°,∴BC′⊥BC,∠BCC′=∠BC′C=45°,∴BC=BC′=2,∵D是BC边的中点,∴BD=1,根据勾股定理可得DC′==.故答案为:.【点评】此题考查了线路最短的问题,确定动点E何位置时,使EC+ED的值最小是关键.23.如图,已知一次函数y=x+1的图象与反比例函数的图象在第一象限相交于点A,与x轴相交于点C,AB⊥x轴于点B,△AOB的面积为1,则AC的长为(保留根号).【考点】反比例函数与一次函数的交点问题;反比例函数系数k的几何意义;勾股定理.【专题】压轴题.【分析】由于△AOB的面积为1,根据反比例函数的比例系数k的几何意义可知k=2,解由y=x+1与联立起来的方程组,得出A点坐标,又易求点C的坐标,从而利用勾股定理求出AC的长.【解答】解:∵点A在反比例函数的图象上,AB⊥x轴于点B,△AOB的面积为1,∴k=2.解方程组,得,.∴A(1,2);在y=x+1中,令y=0,得x=﹣1.∴C(﹣1,0).∴AB=2,BC=2,∴AC==2.【点评】本题考查函数图象交点坐标的求法及反比例函数的比例系数k与其图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系,即S=|k|.24.如图,已知A(2,0)、B(0,5),⊙C的圆心坐标为C(﹣1,0),半径为1,若D是⊙C 上一个动点,线段DA与y轴交于点E,则△ABE面积的最小值是5﹣.【考点】一次函数综合题.【分析】△ABE的BE边上高为OA=2,当AD与⊙C相切时,BE最短,此时,△ABE的面积最小,由勾股定理求相切时,AD的长,利用三角形相似求OE,再求BE,由三角形面积公式求面积的最小值.【解答】解:如图,当AD与⊙C相切于D点时,△ABE的面积最小,连接CD,则△ACD为直角三角形,由勾股定理,得AD===2,∵∠CDA=∠EOA=90°,∠CAD=∠EAO,∴△CAD∽△EAO,∴=,即=,解得OE=,BE=OB﹣OE=5﹣,=×(5﹣)×2=5﹣.S△ABE故答案为:5﹣.【点评】本题考查了一次函数的综合运用.关键是根据动点的变化情况,找出使△ABE的面积最小时,D点的位置,利用相似比求OE.25.用火柴棒按下图中的方式搭图形,按照这种方式搭下去,搭第2015个图形需12096 根火柴棒.【考点】规律型:图形的变化类.【分析】由图可知:第一个图形用了12根火柴;即12=6×(1+1);第二个图形用了18根火柴;即18=6(2+1);…由此得出搭第n个图形需6n+6根火柴.进一步代入求得答案即可.【解答】解:∵搭第1个图形需12根火柴;搭第2个图形需12+6×1=18根;搭第3个图形需12+6×2=24根;…∴搭第n个图形需12+6(n﹣1)=6n+6根;∴搭第2015个图形需2015×6+6=12096根火柴棒.故答案为:12096.【点评】此题考查图形的变化规律,找出图形的变化规律:后面的图形总比前面的图形多6根火柴棒,由此规律解决问题.二、解答题(本大题共3个小题,共30分.解答题应写出必要的文字说明,证明过程或演算步骤.)26.据我们调查,成都市某家电商场今年一月至六月份销售型号为“JSQ20﹣H”的海尔牌热水器的销量如下:月份一二三四五六销量(台)50 51 48 50 52 49(1)求上半年销售型号为“JSQ20﹣H”的海尔牌热水器销售量的平均数、中位数、众数.(2)由于此型号的海尔牌热水器的价格适中,消费者满意度很高,商场计划八月份销售此型号的热水器72台,与上半年平均月销售量相比,七、八月销售此型号的热水器平均每月的增长率是多少?【考点】一元二次方程的应用;算术平均数;中位数;众数.【专题】增长率问题.【分析】(1)根据平均数、中位数、众数的概念求解;(2)根据增长率问题的公式:6月份生产台数×(1+增长率)n=72,列方程求解.【解答】解:(1),中位数为:,众数为:50;(2)设七、八月份销售量的平均增长率为x,依题意,得:50(1+x)2=72,解得:x1=0.2,x2=﹣(不合题意,舍去).答:七、八月销售此型号的热水器平均每月的增长率是20%.【点评】考查了一元二次方程的应用及有关统计量的意义,解题的关键是能够了解增长率问题的解法,难度不大.27.如图,已知⊙O的直径AB垂直于弦CD于点E,过C点作CG∥AD交AB的延长线于点G,连接CO并延长交AD于点F,且CF⊥AD.(1)试问:CG是⊙O的切线吗?说明理由;(2)求证:E为OB的中点;(3)若AB=10,求CD的长.【考点】切线的判定;勾股定理;相似三角形的判定与性质.【分析】(1)由CG∥AD,CF⊥AD,易得CF⊥CG,即可证得CG是⊙O的切线;(2)首先连接BD,易证得△BDE∽△OCE,然后由相似三角形的对应边成比例,证得E为OB的中点;(3)首先由E为OB的中点,AB=10,求得OE的长,然后由勾股定理求得CE的长,继而求得答案.【解答】(1)解:CG是⊙O的切线.理由:∵CG∥AD,∴∠FCG+∠CFD=180°,∵CF⊥AD,∴∠CFD=90°,∴∠FCG=90°,即OC⊥CG,又∵OC为⊙O的半径,∴CG是⊙O的切线;(2)证明:连接BD,。
2023年四川省成都市锦江区九年级一诊数学试题(含答案解析)

2023年四川省成都市锦江区九年级一诊数学试题学校:___________姓名:___________班级:___________考号:___________一、单选题1.如图,是一个由长方体截去一部分后得到的几何体,其主视图是()A .B .C .D .2.下列函数中,y 是x 的反比例函数的是()A .4y x=B .1y x =+C .3x y =D .2y x =3.若关于x 的一元二次方程x 2﹣2x +m =0有一个解为x =﹣1,则另一个解为()A .1B .﹣3C .3D .44.如图所示的两个四边形相似,则下列结论不正确的是()A .a =B .2m n =C .2x =D .60α∠=︒5.如图,已知在平面直角坐标系中,四边形ABCD 是菱形,其中点B 的坐标是()62,,点D 的坐标是()02,,点A 在x 轴上,则点C 的坐标是()A .()32,B .()33,C .()34,D .()24,6.一个不透明的箱子里共装有m 个球,其中红球5个,这些球除颜色不同外其余都相同.每次搅拌均匀后,任意摸出一个球记下颜色后再放回,大量重复试验发现,摸到红球的频率稳定在0.2附近,则可以估算出m 的值为()A .1B .5C .20D .257.如图,在方格纸上,以点O 为位似中心,把线段AB 缩小到原来的12,则点A 的对应点为()A .点D 或点GB .点E 或点FC .点D 或点F D .点E 或点G8.如图,在矩形ABCD 中,6AB =,8BC =,对角线AC ,BD 相交于点O ,点E ,F 分别是AO ,AD 的中点,连接EF ,则AEF △的周长为()A .6B .7C .8D .9二、填空题9.若2ba=则b a b +=_____.10.关于x 的一元二次方程2(1)1x a -=+有两个不相等的实数根,则a 的取值范围是__________.11.已知点11(,)A x y ,22(,)B x y 都在反比例函数3y x=的图象上,且120x x <<,则1y 和2y 的大小关系为__________.12.小颖将能够活动的菱形学具活动成为图1所示形状,并测得5AC =,=60B ∠︒.接着,她又将这个学其活动成为图2所示正方形,此时A C ''的长为__________.13.如图,在ABC 中,AB =C 为圆心,以适当的长为半径作弧,交CB 于点D ,交CA 于点E ,连接DE ;②以点B 为圆心,以CD 长为半径作弧,交BA 于点F ;③以点F 为圆心,以DE 的长为半径作弧,在ABC 内与前一条弧相交于点G ;④连接BG 并延长交AC 于点H ,若H 恰好为AC 的中点,则AC 的长为__________.三、解答题14.(1()11233-⎛⎫--- ⎪⎝⎭;(2)解方程:()21310x x -++=.15.中国共产党第二十次全国代表大会于10月16日至22日在北京举行,这是一次具有里程碑意义的大会,必将对中国和世界产生深远影响.某校积极组织学生学习二十大相关会议精神,并组织了二十大知识问答赛,将比赛结果分为A ,B ,C ,D 四个等级,根据如下不完整的统计图解答下列问题:(1)求该校参加知识问答赛的学生人数;(2)求扇形统计图中C 级所对应的圆心角的度数;(3)现准备从结果为A 级的4人(两男两女)中随机抽取两名同学参加二十大宣讲,请用列表或画树状图的方法,求恰好抽到一名男生和一名女生参加宣讲活动的概率.16.【学科融合】如图1,在反射现象中,反射光线,入射光线和法线都在同一个平面内:反射光线和入射光线分别位于法线两例;入射角i 等于反射角r .这就是光的反射定律.【问题解决】如图2,小红同学正在使用手电筒进行物理光学实验,地面上从左往右依次是墙,木板和平面镜,手电筒的灯泡在点G 处,手电筒的光从平面镜上点B 处反射后,恰好经过木板的边缘点F ,落在墙上的点E 处,点E 到地面的高度 3.5m DE =,点F 到地面的高度 1.5m CF =,灯泡到木板的水平距离 5.4m AC =,木板到墙的水平距离为4m CD =.图中A ,B ,C ,D 在同一条直线上.(1)求BC 的长;(2)求灯泡到地面的高度AG .17.如图1,ABCD Y 的各内角的平分线分别相交于点E ,F ,G ,H .(1)求证:四边形EFGH 为矩形;(2)如图2,当ABCD Y 为矩形时,①求证:四边形EFGH 为正方形;②若10AD =,四边形EFGH 的面积为8,求AB 的长.18.如图1,已知反比例函数(0)ky k x=≠的图象与一次函数1y x =-的图象相交于A (2,a ),B两点.(1)求反比例函数的表达式及A ,B 两点的坐标;(2)M 是x 轴上一点,N 是y 轴上一点,若以A ,B ,M ,N 为顶点的四边形是以AB 为边的平行四边形,求点M 的坐标;(3)如图2,反比例函数ky x=的图象上有P ,Q 两点,点P 的横坐标为(2)m m >,点Q 的横坐标与点P 的横坐标互为相反数,连接AP ,AQ ,BP ,BQ .若ABQ 的面积是ABP 的面积的3倍,求m 的值.四、填空题19.已知一元二次方程2320230x x --=的两个根为12x x ,,则1212x x x x +的值为__________.20.如图,矩形ABCD 的对角线AC ,BD 相交于点O ,过点O 作OE BD ⊥,交AD 于点E ,若20ACB ∠=︒,则AOE ∠的大小为__________.21.如图,在平面直角坐标系xOy 中,AOB 的顶点A 在函数4(0)y x x=>的图象上,顶点B 在x 轴正半轴上,边AO ,AB 分别交的数1(0)y x x=>,4(0)y x x=>的图象于点M ,N .连接MN ,若MN x ∥轴,则AOB 的面积为__________.22.如图,在矩形ABCD 中,6AB =,12BC =,点P 是DC 上一点,且5DP =,点E ,F 分别是AD BC ,上的动点,连接EF AP ,,始终满足EF AP ⊥.连接AF PF PE ,,,记四边形AEPF 的面积为1S ,记ABF △的面积为2S ,记FCP 的面积为3S ,记EDP △的面积为4S ,则1423S S S S =++__________.23.如图,在平面直角坐标系xOy 中,正方形ABCD 的顶点A ,C 的坐标分别为(1,1)A -,(1,1)C -.已知线段MN 的端点M ,N 的坐标分别为(3,3)M ,73(,)22N ,平移线段MN ,使得平移后的线段的两个端点均落在正方形ABCD 的边上,此时正方形ABCD 被该线段分为两部分,其中三角形部分的面积为__________;已知线段PQ 的端点坐标分别为11(,)P x y ,22(,)Q x y ,且12x x ≠,12y y ≠,2PQ =.平移线段PQ ,使得平移后的线段P Q ''的两个端点均落在正方形ABCD 的边上,且线段P Q ''将正方形的ABCD 面积分为6:19两部分,取P Q ''的中点H ,连接OH ,则OH 的长为__________.五、解答题24.电影《长津湖》是一部讲述抗美援朝题材影片,该片以朝鲜长津湖战役为背景,讲述一个志愿军连队在极寒严酷环境下坚守阵地奋勇杀敌、为战役胜利作出重要贡献的故事,2021年8月首映,深受人们的喜爱.2022年清明节来临之际某电影院开展“清明祭英烈共铸中华魂”系列活动,对团体购买该电影票实行优惠,决定在原定零售票价基础上每张降价16元,这样按原定票价需花费2000元购买的门票张数,现在只花费了1200元.(1)求每张零售电影票的原定价;(2)为了弘扬爱国主义精神,该影院决定对网上购票的个人也采取优惠,原定零售票价经过连续两次降价后票价为每张32.4元,求原定零售票价平均每次的下降率.25.已知在平面直角坐标系xOy 中,点(1,)a ,1(2,2a -在反比例函数k y x =的图像上.(1)求k 的值;(2)将反比例函数ky x=的图像中x 轴下方部分沿x 轴翻折,其余部分保持不变,得到新的函数图像如图1所示,新函数记为函数F .①如图2,直线y x b =+与函数F 的图像交于A ,B 两点,点A 横坐标为1x ,点B 横坐标为2x ,且120x x <<,124x x =.点P 在y 轴上,连接AP ,BP .当AP BP +最小时,求点P 的坐标;②已知一次函数2(0)y nx n n =-+≠)的图像与函数F 的图像有三个不同的交点,直接写出n 的取值范围.26.【问题背景】如图1,在矩形ABCD 中,点M ,N 分别在边BC ,AD 上,且1BM MC m=,连接BN ,点P 在BN 上,连接PM 并延长至点Q ,使1PM MQ m=,连接CQ .【尝试初探】求证:CQ BN ∥;【深入探究】若AN BM AB ==,2m =,点P 为BN 中点,连接NC ,NQ ,求证:NC NQ =;【拓展延伸】如图2,在正方形ABCD 中,点P 为对角线BD 上一点,连接PC 并延长至点Q ,使1(1)PC n QC n =>,连接DQ ,若22222(1)n BP DQ n AB +=+,求BPBD的值(用含n 的代数式表示)参考答案:1.C【分析】从正面看,确定主视图即可.【详解】解:几何体的主视图为:故选C .【点睛】本题考查三视图.熟练掌握三视图的确定方法,是解题的关键.注意,存在看不见的用虚线表示.2.A【分析】根据反比例函数的定义,即可判断.【详解】解:A 、4y x=,y 是x 的反比例函数,故A 符合题意;B 、1y x =+,y 不是x 的反比例函数,故B 不符合题意;C 、3xy =,y 不是x 的反比例函数,故C 不符合题意;D 、2y x =,y 不是x 的反比例函数,故D 不符合题意;故选:A .【点睛】本题考查了反比例函数的定义,熟练掌握正比例函数的定义是解题的关键,一般地,形如()0ky k x=≠且k 是常数的函数叫做反比例函数.3.C【分析】设方程的另一个解为x 1,根据两根之和等于﹣ba,即可得出关于x 1的一元一次方程,解之即可得出结论.【详解】设方程的另一个解为x 1,根据题意得:﹣1+x 1=2,解得:x 1=3,故选C .【点睛】本题考查了根与系数的关系以及一元二次方程的解,牢记两根之和等于﹣ba、两根之积等于ca是解题的关键.4.B【分析】由相似三角形的性质:对应角相等,对应边成比例,即可求解.【详解】因为两个图形相似:244m x a n ===解得:a =A 选项正确,不符合题意;2n m =B 选项错误,符合题意;2x =C 选项正确,不符合题意;360904516560α∠=︒-︒-︒-︒=︒,D 选项正确,不符合题意;故选:B .【点睛】本题考查了相似多边形的性质;根据性质求出对应边和对应角是解题的关键.5.C【分析】首先连接AC 、BD 相交于点E ,由在菱形ABCD 中,点A 在x 轴上,点B 的坐标为()62,,点D 的坐标为()02,,可求得点E 的坐标,继而求得答案.【详解】解:连接AC ,BD 相交于点E ,四边形ABCD 是菱形,AE CE ∴=,BE DE =,AC BD ⊥,点A 在x 轴上,点B 的坐标为()62,,点D 的坐标为()02,,6BD =∴,BD y ⊥轴,2AE ∴=,13242DE BD AC AE ∴====,,∴点C 的坐标为:()34,.故选:C .【点睛】本题考查了菱形的性质以及坐标与图形的性质,解题的关键是注意菱形的对角线互相平分且垂直.6.D【分析】用红球的数量除以红球的频率即可.【详解】解:50.225÷=(个),所以可以估算出m的值为25,故选:D.【点睛】本题主要考查利用频率估计概率,大量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率.7.A【分析】作射线AO,根据位似中心的概念、线段的位似比解答即可.【详解】解:作射线AO,,射线AO经过点D和点G,且1 2OD OA=,12OG OA=,∴点A的对应点为点D或点G,故选:A.【点睛】本题考查位似变换,正确记忆位似图形的特征是解题关键.8.D【分析】利用勾股定理算出AC 的长度,根据矩形的性质即可得出OA OD =的长度,再根据中位线的性质求出周长即可.【详解】在矩形ABCD 中,6AB =,8BC =,10AC =,对角线AC ,BD 相交于点O ,152OA OD AC ===,点E ,F 分别是AO ,AD 的中点,EF ∴是AOD △的中位线,1522EF OD ∴==,1522AE OA ∴==,142AF AD ==,AEF ∴ 的周长为:554922AE AF EF ++=++=,故选:D .【点睛】本题考查矩形的性质和中位线的应用,关键在于根据矩形的性质转变边长,中位线的性质求出边长.9.23【分析】将2b a=变形为2b a =,然后代入b a b +计算即可.【详解】解:∵2b a =∴2b a=将2b a =代入b a b+得2223a a a =+故答案为:23【点睛】本题考查了已知式子值,求代数式值,分式化简求值,熟练分式化简求值是解题关键.【分析】先将一元二次方程2(1)1x a -=+可转化为一般形式220x x a --=,再根据一元二次方程解的根的判别式的意义得到()4410a ∆=-⨯⨯->,然后求出a 的取值范围.【详解】一元二次方程2(1)1x a -=+可转化为220x x a --=,∵关于x 的一元二次方程2(1)1x a -=+有两个不相等的实数根∴()4410a ∆=-⨯⨯->∴440a +>∴1a >-【点睛】本题考查一元二次方程解的根的判别式的意义,解题的关键是掌握当0∆>时,方程有两个不相等的实数根;当Δ0=时,方程有两个相等的实数根;当Δ0<时,方程无实数根.11.12y y >##21y y <【分析】根据反比例函数的图象和性质进行判断即可,由于点()11,A x y ,()22,B x y 都在反比例函数3y x=的图象上,若120x x <<,在第三象限,y 随x 的增大而减小,进而得出答案.【详解】解:由于点()11,A x y ,()22,B x y 都在反比例函数3y x =的图象上,且120x x <<,由在第三象限内,y 随x 的增大而减小可得,12y y >.故答案为:12y y >或21y y <.【点睛】本题考查反比例函数的图象和性质,理解并掌握当0k >时,在每个象限内y 随x 的增大而减小的性质是正确解答的关键.12.【分析】根据菱形的性质和=60B ∠︒,求出AB BC =的长度,然后再运用勾股定理求解即可.【详解】由题意可知ABCD 是菱形,AB BC ∴==60B ∠︒ ,ABC ∴ 是等边三角形,5AC =A B C D ''''是正方形,5A B B C ''''∴==A C ='='故答案为:【点睛】本题考查了菱形、正方形的、等边三角形的性质以及勾股定理;灵活运用性质正确计算是解题的关键.13.【分析】连接FG ,如图所示,先证明()SSS BFG CDE △≌△得到ABH ACB =∠∠,进一步证明ABH ACB ∽得到AH AB AB AC=,再由H 是AC 的中点,得到2AC AH =,由此即可得到答案.【详解】解:连接FG ,如图所示,由题意得BF BG CD CE FG DE ====,,∴()SSS BFG CDE △≌△,∴ABH ACB =∠∠,又∵A A ∠=∠,∴ABH ACB ∽,∴AH AB AB AC =,∵H 是AC 的中点,∴2AC AH =,∴222AH AB =,∴AH =,∴2AC AH ==故答案为:【点睛】本题主要考查了全等三角形的性质与判定,相似三角形的性质与判定,证明()SSS BFG CDE △≌△得到ABH ACB =∠∠,进一步证明ABH ACB ∽是解题的关键.14.(14;(2)11x =-,22x =-【分析】(1)根据实数的混合计算法则,零指数幂和负整数指数幂的计算法则求解即可;(2)先把方程化为一般式,然后利用因式分解法解方程即可.【详解】解:(1)原式2321=-+-4=;(2)∵()21310x x -++=,∴21330x x -++=,∴2320x x ++=,∴()()120x x ++=,∴10x +=或20x +=,解得11x =-,22x =-.【点睛】本题主要考查了实数的混合计算,解一元二次方程,零指数幂和负整数指数幂,正确计算是解题的关键.15.(1)40,(2)108︒,(3)23.【分析】(1)根据A 在频数统计图数据除以扇形统计图中的数据即可;(2)根据(1)和频数统计图求出C 级人数,然后用360︒乘以C 的总人数所占的比例即可;(3)画树状图,求出所有可能和符合条件数,根据概率公式求解即可.【详解】(1)解:总人数为:410%40÷=(人);(2)C 级人数为:40416812---=(人),C 级所对应的圆心角的度数为:1236010840︒⨯=︒;(3)画树状图如下:从两男两女中随机抽取两名同学共有12种可能,恰好抽到一名男生和一名女生有8种可能,恰好抽到一名男生和一名女生的概率为:82123P ==.【点睛】本题考查了统计和随机抽样的概率;根据题意求出总人数、正确画出树状图并按照公式求解是解题的关键.16.(1)3m(2)1.2m .【分析】(1)先证明BFC BED ∽ ,再利用相似三角形的性质得出BC FC BD DE =,代入数据即可求BC 的长;(2)先证明BGA BFC ∽ ,再利用相似三角形的性质得出AG FC AB BC=,代入数据即可求AG 的长.【详解】(1)解:(1)由题意可得:FC DE ∥,则BFC BED ∽ ,∴BC FC BD DE =,∴ 1.54 3.5BC BC =+,解得:3BC =,答:BC 的长为3m ;(2)解:∵ 5.4m AC =,∴()5.43 2.4m AB =-=,∵光在镜面反射中的入射角等于反射角,∴FBC GBA ∠=∠,又∵FCB GAB ∠=∠,∴BGA BFC ∽ ,∴AG FC AB BC =,∴ 1.52.43AG =,解得: 1.2m AG =,答:灯泡到地面的高度AG 为1.2m .【点睛】此题主要考查了相似三角形的应用,正确得出相似三角形是解题关键.17.(1)证明见解析(2)①证明见解析;②6【分析】(1)根据平行四边形的邻角互补,以及角平分线平分角,得到四边形EFGH 的四个内角均为90︒,即可得证;(2)①由(1)可知,四边形EFGH 为矩形,根据矩形的性质以及角平分线平分角,得到,,,ABE AFD CDG BHC 均为等腰直角三角形,进而推出EH HG =,得到四边形EFGH 为正方形;②根据正方形的面积为8,得到正方形的边长为的性质,求出AF 的长,进而求出AE 的长,再利用勾股定理和等腰三角形的性质,求出AB 的长.【详解】(1)解:∵四边形ABCD 为平行四边形,∴180,180,ABC DAB ABC BCD ∠+∠=︒∠+∠=︒180,180BCD CDA CDA DAB ∠+∠=︒∠+∠=︒,∵ABCD Y 的各内角的平分线分别相交于点E ,F ,G ,H ,∴()1902EAB EBA DAB ABC ∠+∠=∠+∠=︒,即:90AEB ∠=︒,同理可得:90AFD BHC CGD ∠=∠=∠=︒,∵90AEB ∠=︒,∴90HEF ∠=︒,∴四边形EFGH 为矩形;(2)解:①同(1)法可得:四边形EFGH 为矩形;∵ABCD Y 为矩形,∴45EAB EBA ∠=∠=︒,∴ABE 为等腰直角三角形,∴AE EB ==,同理可得:,22AF DF AD BH CH BC ====,∵AD BC =,∴BH AF =,∴BH BE AF AE -=-,即:EH EF =,又∵四边形EFGH 为矩形,∴四边形EFGH 为正方形;②由①得:2AF AD ==∵四边形EFGH 的面积为8,∴28EF =,∴EF =∴AE AF EF =-=∵2AE AB ==,∴6AB =.【点睛】本题考查平行四边形的性质,矩形的判定和性质,正方形的性质,等腰三角形的判定和性质,勾股定理.熟练掌握平行四边形的邻角互补,是解题的关键.18.(1)2y x=,A (2,1),()1,2B --(2)()3,0或()3,0-(3)1m =【分析】(1)将A (2,a ),代入一次函数解析式,求出a 值,再求出反比例函数的解析式,联立两个解析式,求出B 点坐标;(2)根据平行四边形的性质,对边平行且相等,利用平移思想进行求解即可;(3)分别用含m 的式子表示出ABQ ,ABP 的面积,再利用ABQ 的面积是ABP 的面积的3倍,列式计算即可.【详解】(1)解:反比例函数(0)k y k x=≠的图象与一次函数1y x =-的图象相交于A (2,a ),B 两点,将A (2,a ),代入1y x =-,得:211a =-=,∴A (2,1),∴212k =⨯=,∴2y x =,联立,得:12y x y x =-⎧⎪⎨=⎪⎩,整理,得:220x x --=,解得:121,2x x =-=,当=1x -时,112y =--=-,∴()1,2B --;(2)解:设(),0M x ,()0,N y ,∵A (2,1),()1,2B --,∴点B 是由点A 先向左平移3个单位,再向下平移3个单位得到的;∵以A ,B ,M ,N 为顶点的四边形是以AB 为边的平行四边形,①将点(),0M x 先向左平移3个单位,再向下平移3个单位,得到()0,N y ,则:30x -=,即:3x =,033y =-=-,∴()3,0M ;②将点()0,N y 先向左平移3个单位,再向下平移3个单位,得到(),0M x ,则:033x =-=-,30y -=,即:3y =,∴()3,0M -;综上:当M 点坐标为()3,0或()3,0-时,以A ,B ,M ,N 为顶点的四边形是以AB 为边的平行四边形;(3)如图,过点B 作BE x ⊥轴交AQ 于点E ,过点A 作AF x ⊥轴交BP 于点F ,由题意,可知:22(,),(,)P m Q m m m--,设直线AQ 的解析式为()0y kx b k =+≠,将()2,1A ,2(,)Q m m--代入()0y kx b k =+≠,则:12,2k b mk b m =+⎧⎪⎨-=-+⎪⎩解得:12k m m b m ⎧=⎪⎪⎨-⎪=⎪⎩则直线AQ 的解析式为12m y x m m -=+当1x =时,123(1)m m y m m m --=⨯-+=,则3(1,m E m --;∵()1,2B --∴333(2)m m BE m m--=--=,∴11()()22ABQ EBA EBQ B Q A B S S S BE x x BE x x =+=⨯-+⨯- 1()2A Q BE x x =⨯-133(2)2m m m-=⨯⨯+23362m m m+-=;设直线BP 的解析式为()0y ax z a =+≠将()1,2B --,2(,)P m m代入()0y ax z a =+≠得:2,2a z ma z m -=-+⎧⎪⎨=+⎪⎩解得:222a m m z m ⎧=⎪⎪⎨-⎪=⎪⎩则直线BP 的解析式为222m y x m m -=+当2x =时,222622,m m y m m m --=⨯+=则:622,m F m -⎛⎫ ⎪⎝⎭,∵()2,1A ,∴62361m m AF m m--=-=,11()()22ABP AFB APP A B P A S S S AF x x AF x x ∆∆∆=+=⨯-+⨯-1()2P B AF x x =⨯-136(1)2m m m-=⨯⨯+23362m m m--=;∵3ABQ ABP S S = ,∴22336336322m m m m m m+---=⨯,解得:11m =21m =,又∵m>2,∴1m =【点睛】本题考查反比例函数与一次函数的综合应用,反比例函数与几何的综合应用.正确的求出函数解析式,利用数形结合,分类讨论的思想进行求解,是解题的关键.19.32023-【分析】根据一元二次方程根与系数的关系求出1212x x x x +,的值即可得到答案.【详解】解:∵一元二次方程2320230x x --=的两个根为12x x ,,∴121232023x x x x =-+=,,121232023x x x x +=-,故答案为:32023-.【点睛】本题主要考查根与系数的关系,解题的关键是熟记两根之和与两根之积与系数之间的关系.20.50︒##50度【分析】根据矩形的性质,得到OBC OCB ∠=∠,利用三角形外角求出AOB ∠,利用垂直可求出结果.【详解】∵四边形ABCD 是矩形,OA OB OC OD ∴===,20ACB ∠=︒ ,20OBC OCB ∴∠=∠=︒,40AOB OBC OCB ∴∠=∠+∠=︒,OE BD ⊥ ,90BOE \Ð=°,904050AOE BOE AOB ∴∠=∠-∠=︒-︒=︒,故答案为:50︒.【点睛】本题考查了矩形的性质;灵活运用矩形的性质求解是解题的关键.21.6【分析】设M 点的坐标为1,b b ⎛⎫ ⎪⎝⎭,N 点的坐标为4,b b ⎛⎫ ⎪⎝⎭,表示出3MN b =,根据相似,求出6OB b=,2AF b =,进而求出AOB 的面积.【详解】∵MN x ∥轴,∴AMN AOB ∽,点M ,N 的纵坐标相同,设M 点的坐标为1,b b ⎛⎫ ⎪⎝⎭,N 点的坐标为4,b b ⎛⎫ ⎪⎝⎭,∴3MN b=,如图,过点M 作ME x ⊥轴,点A 作AF x ⊥轴,∴MOE AOF ∽,根据反比例函数与三角形的面积关系可得:2AOF S = ,0.5MOE S = ,∴0.5124MOE AOF S S == ,∵相似三角形中面积比等于相似比的平方,∴12OM OA =,∴12AM OA =,∵AMN AOB ∽,∴12AM MN OA OB ==,即312b OB =,∴6OB b=,∵M 点的坐标为4,b b ⎛⎫ ⎪⎝⎭,∴ME b =,∴2AF b =,∴1162622AOB S OB AF b b =鬃=创=,故答案为:6.【点睛】本题考查反比例函数与三角形面积的关系,解题的关键是根据题意作出相应的辅助线,并通过设坐标法进行求解.22.169119【分析】根据题意假设当当点E 和点D 重合时,首先证明出ADP DCF V V ∽,根据相似三角形的性质得到52FC =,然后根据三角形面积公式表示出1S ,2S ,3S 的大小求解即可.【详解】∵点E ,F 分别是AD BC ,上的动点,∴假设当点E 和点D 重合时,如图所示,∴40S =,∵在矩形ABCD 中,6AB =,12BC =,∴12,6AD BC CD AB ====,∵5DP =,∴1CP CD DP =-=,∵90AOD ADC ∠=∠=︒,∴DAP ADO CDF ADO ∠+∠=+∠,∴DAP CDF ∠=,又∵ADP DCF ∠=,∴ADP DCF V V ∽,∴AD DP CD FC=,即1256FC =,解得52FC =∴5191222BF BC FC =-=-=,∴3115512224S FC CP =⨯⨯=⨯⨯=,∴211195762222S AB BF =⨯⨯=⨯⨯=,∵6AB =,12BC =,∴矩形ABCD 的面积61272AB AD =⨯=⨯=,∴123575169=7272244S S S --=--=∴31421691694575119024S S S S ==++++.故答案为:169119【点睛】此题考查了矩形的性质,相似三角形的性质和判定等知识,解题的关键是熟练掌握以上知识点.23.38【分析】明确三角形部分与EMN 形状大小完全相同,即可求解;明确P Q ''的长度定了,不管怎么放,三角形部分,形状大小完全一样,OH 长度一样,即可求解.【详解】MN 平移之后,如图所示,三角形部分与EMN 形状大小完全相同,∴三角形部分的面积1733332228⎛⎫⎛⎫=⨯-⨯-= ⎪ ⎪⎝⎭⎝⎭,2PQ =,平移后两端点落在正方形边上,∵12x x ≠,12y y ≠,∴P Q ''不垂直四条边,P Q ''把正方形分成两部分为三角形部分和另一部分多边形,两部分的面积为6:19,可得62461925S S ==+正方形三角形,P Q ''的长度定了,P Q D S '' 的面积确定了,不管怎么放,三角形部分,形状大小完全一样,则OH 长度一样,令P Q ''在如图位置,且P D DQ '≥',221242254P D DQ P D DQ ⎧⋅'='''⎪⎨⎪+=⎩解得 1.61.2P D DQ ''=⎧⎨=⎩,∴P '的坐标为(0.6,1)-,Q '的坐标为(1,0.2)-,∴中点H 的坐标为0.6110.2(,)22-+-,即H 的坐标为(0.2,0.4),∴5OH ===故答案为:38【点睛】本题考查四边形的综合题和移动线段问题,解题的关键是理解题意,画出图形,学会利用特殊点解决问题.24.(1)每张零售电影票的原定价为40元.(2)原定零售票价平均每次的下降率为10%.【分析】(1)设每张零售电影票的原定价为x 元,根据“在原定零售票价基础上每张降价16元,这样按原定票价需花费2000元购买的门票张数,现在只花费了1200元”列方程,即可求解;(2)设原定零售票价平均每次的下降率为m ,根据“原定零售票价经过连续两次降价后票价为每张32.4元”列方程求解即可.【详解】(1)解:设每张零售电影票的原定价为x 元,则题意可得,2000120016x x =-,解得,40x =,经检验,40x =是原方程的根且符合题意,答:每张零售电影票的原定价为40元.(2)解:设原定零售票价平均每次的下降率为m ,由题意得,()240132.4m -=,解得10.1m =,2 1.9m =(不合题意,舍去),即原定零售票价平均每次的下降率为10%.答:原定零售票价平均每次的下降率为10%.【点睛】此题考查了分式方程和一元二次方程的实际应用,读懂题意,正确列出方程是解题的关键.25.(1)1k =;(2)①170,20P ⎛⎫ ⎪⎝⎭,②0n <或04n <<-.【分析】(1)用待定系数法,将点带入求解即可;(2)结合题意求出新函数解析式,设B 的横坐标为()0m m ->,表示出A ,B 的坐标,然后找到找()1,1B -关于y 轴的对称点()1,1C ,连接AC ,则AC 与y 轴的交点为P 为所求;一次函数和反比例函数联立方程,方程有两个不相等的实数根即可.【详解】(1)解:点(1,)a ,1(2,2a -在反比例函数k y x =的图像上,∴1122k a k a ⎧=⎪⎪⎨⎪-=⎪⎩,解得:11a k =⎧⎨=⎩,反比例函数解析式为:1y x=;(2)①依题意的新函数解析式为:1y x =,即:()()1010x x y x x⎧>⎪⎪=⎨-⎪<⎪⎩,120x x << ,124x x =,设B 的横坐标为()0m m ->,则A 的横坐标为()40m m ->,结合函数解析式:1,B m m ⎛⎫∴- ⎪⎝⎭,14,4A m m ⎛⎫- ⎪⎝⎭,∴1144m b m m b m ⎧=-+⎪⎪⎨⎪=-+⎪⎩,解得:1m =或1m =-,0m > ,1m ∴=,2b ∴=,14,4A ⎛⎫∴- ⎪⎝⎭,()1,1B -,找()1,1B -关于y 轴的对称点()1,1C ,连接AC ,则AC 与y 轴的交点为P ,设AC 所在直线解析式为11y k x b =+,则11111144k b k b =+⎧⎪⎨=-+⎪⎩,解得:113201720k b ⎧=⎪⎪⎨⎪=⎪⎩,3172020y x =+,与y 轴的交点为170,20P ⎛⎫ ⎪⎝⎭;②一次函数2(0)y nx n n =-+≠)的图像与函数F 的图像有三个不同的交点,20n ∴-+>2n ∴<当02n <<,2y nx n =-+与1y x=恒有一个交点,故2y nx n =-+与1y x -=有两个交点,此时12nx n x -=-+,即()2210nx n x +-++=,()22410n n -+-⨯>,2840n n -+>,当2840n n -+=,4n =或4n =-,∵284y n n =-+的图像开口向上,2840n n ∴-+>的解为:4n <-或4n >;02n <<04n ∴<<-当0n <,2y nx n =-+与1y x -=恒有一个交点,故2y nx n =-+与1y x =有两个交点,此时12nx n x=-+,即()2210nx n x +-+-=,()22410n n -++⨯>,240n +>,恒成立,所以0n <,综上所述:0n <或04n <<-.【点睛】本题考查了反比例函数、一次函数的综合运用以及一元二次方程解的情况;理解函数图像的交点就是方程的解是解题的关键.26.(1)见解析;(2)见解析;(3)12BP n BD n-=.【分析】(1)根据相似三角形的判定定理进行判定即可;(2)连接,,,NC BQ NM BQ ,证ABMN 是正方形,得PM 垂直平分BN ,BQ NQ =在证明CQBN 是平行四边形,利用平行四边形的性质判定即可;在矩形ABCD 中;(3)过Q 作QM BD 交BC 的延长线于M ,DG 于N ,连接DM ,结合题意用勾股定理逆定理证DQM 是直角三角形,然后借助45︒和相似三角形解决.【详解】(1)由题意可知在CQM 与BPM △中,CMQ BMP ∠=∠ ,1BM PM MC m MQ==,CQM BPM ∴~ ,CQM BPM ∴∠=∠,CQ BN ∴ ;(2)如图:连接,,,NC BQ NM BQ ,在矩形ABCD 中,90A ∠=︒AN BM ∥,AN BM AB == ,ABMN 是正方形,P 为BN 中点,PM ∴垂直平分BN ,2BN BP =,BQ NQ ∴=,由CQM BPM ~ 和2m =可知,12BP PM CQ CQ ∴==,2CQ BP ∴=,CQ BN ∴=,CQ BN ,CQBN ∴是平行四边形,BQ CN ∴=,NC NQ ∴=;(3)过Q 作QM BD 交BC 的延长线于M ,DG 于N ,连接DM ,在正方形ABCD 中,QM BD ,CBP CMQ ∴~ ,45DBC CMQ ∠=∠=︒,1BP BC PC QM CM CQ n∴===,1BP QM n ∴=,CM nBC nAB ==,222DM CD CM =+ ,()()222221DM AB nAB n AB ∴=+=+,()()2222222QM DQ nBP DQ n BP DQ ∴+=+=+,22222(1)n BP DQ n AB +=+ ,222QM DQ DM ∴+=,DQM ∴ 是直角三角形,90DQM ∴∠=︒,QM BD ,90DQM BDQ ∴∠=∠=︒,45BDC NDQ ∴∠=∠=︒,45DNC ∴∠=︒,NC BC∴=,()1MN nBC BC n BC ∴=-=-,在Rt MQN中,45CMQ∠=︒,QM nBP=,)12nQN QM BC-∴===,)111·2nBP QM BCn n-==,)11·122nBCBP nnBD n--=,【点睛】本题考查了相似三角形的判定和性质、正方形的判定和性质、矩形的性质、勾股定理的逆定理;三角形相似的证明和性质的应用是解题的关键.。
锦江区初2018届第一次诊断测试题

四川成都锦江区初三2019届第一次诊断测试题物理全卷分A卷和B卷,A卷满分100分,B卷满分20分,全卷共120分;考试时间90分钟A卷(共100分)第I卷(选择题,共30分一、单项选择题(每小题2分,共30分)1.下列物品,通常情况下属于导体的是()2.通过一些可直接感知的现象,经过合理的推测来认识无法直接感知的事实,是常用的一种物理方法。
下列推测既合理又符合事实的是()A.现象:水和酒精混合后体积变小推测:分子之间没有间隙B.现象:磁铁吸住了很多铁屑推测:分子间有引力作用C.现象:钢棒很难被压缩推测:分子之间存在斥力D.现象:轻质球a、b靠近时相互吸引推测:a、b两球一定带异种电荷3.关于磁场的知识,以下说法正确的是()A.磁感线是磁体发出的实际曲线B.奥斯特实验说明通电导线周围存在磁场C.任何物体在磁体或电流的作用下都会获得磁性D地球的南、北极与地磁场的南、北极是重合的4.如图所示的四个电路中,开关均闭合后,通过两个灯泡的电流一定相等的是()5关于家底电路和安全用电的说法中正确的是()A.电路中出现“跳”现象,一定是过载引起的B.洗衣机的外壳可以不用接地C发现有人轴电后,立即用手把电人拉离电D.高压触电的两种情形包括电弧触电和跨步电压触电6.下列关于热现象的说法中正确的()A.热机消耗的燃料越多,效率就越低B热传递中温度总是从热的物体传给冷的物体C.0℃的水变成0℃的冰,温度不变,内能减小D.火箭使用液态作燃料,是因为它含有的热量多7.对下列物理量的估测中,最接近实际的是()A.一节新干电池的电压约为2VB 家用电冰箱的电流大约为1AC.教室里一盏日光灯的功率约为100wD.对人体的安全电压不高于220V8.如图所示是汽油机工作时各个冲程的示意图,其中将机械能转化为内能的是( )9.关于电压,电流和电阻,下列说法正确的是( )A.电路中有电流时它两端一定有电B 绝缘体在任何情况下都不能导电C.两灯泡接入电路,亮度大的灯泡通过的电流大D.电荷移动就能形成电流10.如图所示是某种“测重仪”的原理图,A 为托盘,P 为金属滑片,且固定在轻质弹簧上并能随轻质弹簧一起上下滑动,R 0为保护电阻,托盘中物体的质量大小可由电表的示数来显示,当物体的质量越大时,电表的示数就越大,符合这一要求的电路是( )11.如图所示,电电压为3V 保持不变,两灯都标有“3W 0.6V ”字样,要使两灯泡 都能正常发光,下列措施可行的是()A .闭合S 1,同时断开S 2和S 3B. 闭合S 2,同时断开S 1和S 3C. 闭合S 3,同时断开S 1和S 2D. 闭合S 2,同时闭合S 1和S 312.如图所示,GMR 是一个巨磁电阻,其特性是电阻子磁场中会急剧减小,且磁场越强电阻越小,闭合开关S 2后,下列四种情况相比较,指示灯最亮的是( )A .S 1断开,滑片P 在图示位置B .S 1闭合,滑片P 在图示位置C .S 1闭合,滑片P 在滑动变阻器最右端D .S 1闭合,滑片P 在滑动变阻器最左端13.如图所示电路中,闭合开关后,发现两灯都不亮,电流表指针几平指在”0”刻度线不动,电压表指针则有明量偏转且接近于电源电压,该电路故障可能是()A.电流表被烧坏了的灯丝断了B.灯泡L1C.两个灯泡都断路D.灯泡L的灯丝断了214.在如图所示的电路中,电源电压保持不变,闭合开关S.滑动变阻器的滑片P 向左滑动时,下列判断正确的是( )A.电流表的示数减小,电压表的示数增大B.电流表的示数增大,电压表的示数减小C.定值电阻R消耗的电功率增大D电路消耗的总功率不变15.甲、乙两地相距10km,在甲、乙两地之网沿直线架设了两条输电线,已知所用的输电线每千米的电阻为0.2Ω,现输电线在某处发生了短路,为确定短路位置,检员在甲地利用电压表、电流表、定值电阻R和电源接成如图所示电路进行测量,当电压表的示数为3.0V,电流表的示数为0.3A时,则短路位置离甲地的距离为()A.7.5kmB.15kmC.25kmD.30km第II卷(非选择题,共70分二填空题(每空2分,共3分)16.人们在公步,闻到梅花发出的清香,这是________现象,人们泡温泉时身体会变热,这是通过__________的方式改变了身体的内能的缘故。
成都市锦江区2020届九年级语文第一次诊断考试试卷

锦江区初2020届第一次诊断测试题语文A卷第Ⅰ卷(选择题)一、基础知识1.下面加下划线字注音有误的一项是()A.灰烬(jìn)拮据(jū)矫揉造作(jiǎo)B.冠冕(guān)恪守(gè)不省人事(xǐng)C.撩逗(liáo)逞能(chěng)间不容发(jiān)D.愧赧(nǎn)箴言(zhēn)自吹自擂(léi)2.下列语句中书写正确的一项是()A.若爱比恨多,小屋就光明温暖,像一座金色池塘,有红色的鲤鱼游戈,那是你的福气。
B.在国难危急时,各地一定有许多口头的消息,要知道实际情形,只能靠自己亲身视查。
C.关公曰:“兄长两次亲往拜遏,其礼太过矣。
想诸葛亮有虚名而无实学,故避而不敢见。
”D.一个男人跟朋友和熟人见面时彬彬有礼,可是在家里却对妻子儿女动不动就大发雷霆。
3.下列语句中加下划线的成语使用有误的一项是()A.骆宾王才华绝世却际遇坎坷,他的书信大都怀古伤今,苍凉飘逸,令人感慨万分。
B.几十年来,文静老师一直在语文教学的道路上默默无闻地奉献,孜孜不倦地研究。
C.他内心并不十分认可对方观点,但为了不让矛盾加剧,只好言不及义地表示赞同。
D.民国时期,军阀张宗昌才疏学浅却喜欢附庸风雅,经常吟诗作赋甚至出版作品集。
4.下列语句中没有语病的一项是()A.为了确保低收入群众的正常生活不因物价上涨而受到影响,多省开始发放临时补贴。
B.本届成都国际非遗节邀请了近百个不同国家和地区的嘉宾及传承人进行展示与交流。
C.十月一日的阅兵仪式全面展示了中国军队的风采,感受到了国之大典的隆重与庄严。
D.在四小时跨年演讲中,罗振宇分享了自己在过去一年里的学习心得与社会发展趋势。
二、文言文阅读阅读下面文言文,完成5~8题。
甲若夫淫雨霏霏,连月不开,阴风怒号,浊浪排空,日星隐曜,山岳潜形,商旅不行,樯倾楫摧,薄暮冥冥,虎啸猿啼。
登斯楼也,则有去国怀乡,忧谗畏讥,满目萧然,感极而悲者矣。
