SMPS
开关电源(SMPS)的发展趋势

开关电源(SMPS)的发展趋势
(1)高频化技术:随着开关频率的提高,开关变换器的体积也随之减少,功率密度也得到大幅提升,动态响应得到改善。
小功率DC-DC变换器的开关频率将上升到MHz。
但随着开关频率的不断提高,开关元件和无源元件损耗的增加、高频寄生参数以及高频EMI等新的问题也将随之产生。
(2)软开关技术:为提高变换器的变换效率,各种软开关技术应用而生,具有代表性的是无源软开关技术和有源软开关技术,主要包括零电压开关/零电流开关(ZVS/ZCS)谐振、准谐振、零电压/零电流脉宽调制技术(ZVS/ZCS-PWM)以及零电压过渡/零电流过渡脉宽调制(ZVT/ZCT-PWM)技术等。
采用软开关技术可以有效的降低开关损耗和开关应力,有助于变换器变换效率的提高。
(3)功率因数校正技术(PFC)。
目前PFC技术主要分为有源PFC技术和无源PFC技术两大类,采用PFC技术可以提高AC-DC变化器输入端功率因数,减少对电网的谐波污染。
(4)模块化技术。
采用模块化技术可以满足分布式电源系统的需要,提高系统的可靠性。
(5)低输出电压技术。
随着半导体制造技术的不断发展,微处理器和便携式电子设备的工作越来越低,这就要求未来的DC-DC变换器能够提供低输出电压以适应微处理器和便携式电子设备的供电要求。
SMPS1004H-I整流模块

第一章简介SMPS1002H-I、SMPS1004H-I整流模块(以下简称SMPS1000H-I系列整流模块),是珠江电信设备制造有限公司自主设计生产的高频开关电源模块。
该模块采用了APFC有源功率因数校正、ZVS相移谐振软开关技术、直流输出恒功率控制等先进技术。
APFC技术的应用使整流模块的功率因数可接近于1,极大的降低市电电流波形的失真,最大限度地降低电源设备的接入对电网质量的影响;相移谐振软开关技术极大地减小整流设备中大功率开关器件的开关损耗和开关应力,有效地提高产品的效率和运行的可靠性。
SMPS1000H-I系列整流模块具有很宽的交流输入电压适应范围:100V~ 310V,其性能指标更适合国内的使用环境和用户的要求。
SMPS1000H-I系列整流模块的产品规格:SMPS1002H-I:输出电压为直流21.5V~29V,输出电流标称值60ASMPS1004H-I:输出电压为直流43V~59V,输出电流标称值30ASMPS1000H-I系列整流模块可应用于中小型通信系统、中等容量的程控交换局、数字环路系统、移动通信系统、光纤传输系统、铁路中间站或通信站、微波通信系统、无人值守机站等,具有高效率、宽输入电压范围、高功率因数、结构紧凑等特点,性能价格比高。
第二章安全注意事项为了遵守已公布的安全标准规范,使用SMPS1000H-I系列整流模块时请注意以下事项:2.1 SMPS1000H-I系列整流模块是装入通信机房内的专用机架使用的嵌入式设备(IP20),为热插拔方式,工作时将通过整流模块后部专用的热插拔插头与机架的插座(配电)连接。
2.2在使用整流模块前,请仔细阅读本说明书,将有助于安装与维护。
只有通过专业培训的技术人员才可以安装与维护。
2.3 由于整流模块是装入专用的机架与其他设备配合使用的,整流模块的工作及送出功率是通过整流模块的输入输出插头与机架的插座连接来实现的,因此,安装机架电源时必须遵守IEC60950-1999;EN 60950-2000有关的安全规定,尤其是满足初级对地、初级对次级(SELV)之间的:爬电距离、电气间隙与穿透距离(固体绝缘)的绝缘要求。
SMPS选择和测试要领的分析

SMPS选择和测试要领的分析在现代电子产品中,开关电源(SMPS)被普遍选择用为来提供各种不同的直流电源,因它对于提高DC-DC电源转换系统的效率和可靠性是必不可少。
然而在这设计和应用过程中对于了解与掌握高效率SMPS的选择和测试要领很为重要,为此本文将对SMPS的选择和测试要领作分析说明。
1、选择SMPS基本要领1.1从开关电源(SMPS)系统基本特征说起大多数现代系统中主流的直流电源体系结构是开关电源系统,它因为能够有效地应对变化负载而众所周知。
典型SMPS的电能“信号通路”包括无源器件、有源器件和磁性元件。
SMPS尽可能少地使用损耗性元器件(如电阻和线性晶体管),而主要使用(理想情况下)无损耗的元器件:开关晶体管、电容和磁性元件。
SMPS设备还有一个控制部分,其中包括脉宽调节器、脉频调节器以及反馈环路等组成部分。
控制部分可能有自己的电源。
图1是简化的SMPS示意图,图中显示了电能转换部分,包括有源器件、无源器件以及磁性元件。
绝大部分的电气直流负载由标准电源供电。
但是,标准电源的电压可能不符合微处理器、电机、LED或其他负载的电压要求,尤其当标准电源本身的输出电压并不稳定时。
电池供电设备就是一个最好的例子:标准的Li+电池或NiMH电池组的典型电压对于大多数应用而言,不是过高就是过低,或者随着放电过程电压下降的过多。
1.2选择要领拓扑结构很多有通用性幸运的是,SMPS的通用性帮我们解决了这一难题,它将标准电源电压转换成合适的、符合规定的电源电压。
SMPS拓扑结构有很多,但可以划分为几种基本的类型,不同类型的转换器可以对输入电压实现升压、降压、反转以及升/降压变换。
与线性稳压器只能对输入电压进行降压不同的是,可以选择不同拓扑的SMPS来满足任何输出电压的需求,这也正是SMPS极具吸引力的原因。
如上所述,根据电路拓扑的不同,SMPS可以将(DC-DC)直流输入电压转换成不同的直流输出电压。
实际应用中存在多种拓扑结构,比较常见有三种非隔离式DC-DC拓扑结构,按照功能划分为:降压(buck 图2a所示)、升压(boost图2b所示)、升/降压(buck-boost或反转图2c所示)。
形状记忆高分子材料

形状记忆高分子材料引言形状记忆高分子材料(SMP)作为一类智能材料,因其可以在适当的刺激条件(如温度、光、电磁或溶剂等)下,响应环境变化,而相应发生形状转变的能力,为解决科学技术难题带来了一种新的方法。
1950年,第一次报道了具有形状记忆效应的交联聚乙稀聚合物,并在文中描述了具体的表征方法。
这类形状记忆高分子材料与其它形状记忆材料如形状记忆合金和陶瓷相比,具有变形量大、赋形容易、响应温度易于调整,质量轻、价格低、以及易加工成型等优点。
而且易于设计成具有良好的生物相容性、可生物降解性的生物材料,比如手术缝合线、支架、心脏瓣膜、组织工程、药物释放、矫形术及光学治疗等。
1.形状记忆高分子材料的分类SMPs根据刺激响应的不同可分为热致型,电磁致型,光致型,化学型以及水致型,其中热致型是研究最广也是研究最成熟的一种高分子材料。
热致型SMPs 由固定相和可逆相两部分组成,其中固定相通常是由化学交联或物理交联点构成,其可以决定初始形变;可逆相通常由结晶结构构成,可随温度变化而进行可逆的软硬化转变。
1.1 热致型SMP热致型SMP是指材料在初始条件下开始受热,当加热温度达到相转变温度时,同时给材料施加外应力,然后再外力不变的情况下,将温度迅速下降至室温,材料会保持暂时形状,即使在撤去外应力后材料依旧可保持这种状态,直到再次在无应力条件下加热,温度再次达到相转变温度时,材料才会自发地恢复到初始形状。
以聚氨酯为例其可以通过改变嵌段共聚物的成分和比例,来改变聚氨酯材料物理化学性质、生物相容性、组织相容性,以及可生物降解性质。
形状记忆聚氨酯由软段和硬段组成,其中硬段主要由二异氰酸酯和扩链剂组成,因此刚度比较大,抑制了材料变形过程中大分子链的塑性滑移;软段主要由聚酯多元醇或聚醚多元醇等线性分子组成,因此能够进行较大的形变.一般情况下,在温度增加到软段的转变温度之上时形状记忆聚氨酯材料处于高弹态,而且软段微观布朗运动的加剧,致使材料容易变形,此时因为硬段还处于玻璃态,所以阻止了分子链滑移的同时产生了一个内部的回弹力;当温度从冷却的温度增加到软段的转变温度以上时,硬段储存的应力释放,进而导致了材料能够回复到初始形变。
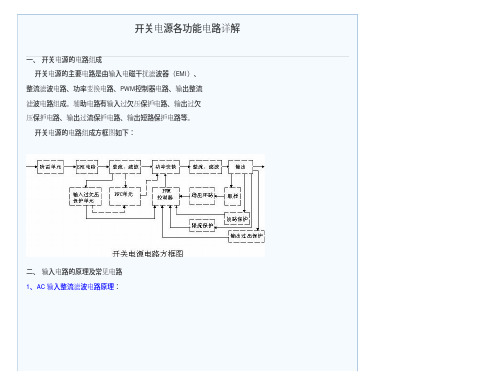
SMPS各功能电路解说
Q1
5
驱 T2为驱
压 压 T1为
换 压 TR1为 环
滤 1
T1为
压 L1为续 C4 L2 C5组 π
D1为 滤
D2为续
R1
C1
R2
C2为
2
T1为 负载 3
压 C4 L2 C5组 π 滤
D1为
R1
C1为
L1为续
R2为
压 Q1
级
为
时 压 级 C6
C2 为 L1
R5 时
R6
R7
Q2导 C3 R4 R1 R2 C1 Q1导 R9
RT1 RT1 z 纹 2 DC 滤 滤
热 RT1 压 负 这时 C5滤
BRG1
x 对 y R1 Q2
滤
C1 时
L1
C2组 产
π
滤 频杂 R5 Q2
络 对 RT1 Z1
对 C3 C7组 稳压 Q2 时Q2导 压 导 C4 为 规
杂 L2
进 L3为 C6
R2 导
R3
Z1
C6 RT1
Q1
Z2
R4 C6
Q2 为 Q1为续 C4为 Q2
L2为续
C7组
π
滤
五、 稳压环路原理 1、反馈电路原理图:
2、工作原理: 当输出 U0升高,经取样电阻R7、R8、R10、VR1分压后,U1③脚电压升高,当其超过U1②脚基准电压后 U1①脚输出高电平,使Q1导通,光耦OT1发光二极管发光,光电三极管导通,UC3842①脚电位相应变低,从 而改变U1⑥脚输出占空比减小,U0降低。 当输出 U0降低时,U1③脚电压降低,当其低过U1②脚基准电压后 U1①脚输出低电平,Q1不导通,光耦OT1发光二极管不发光,光电三极管不导通,UC3842①脚电位升高,从 而改变U1⑥脚输出占空比增大,U0降低。周而复始,从而使输出电压保持稳定。调节VR1可改变输出电压 值。 反馈环路是影响开关电源稳定性的重要电路。如反馈电阻电容错、漏、虚焊等,会产生自激振荡,故障现 象为:波形异常,空、满载振荡,输出电压不稳定等。 六、短路保护电路 1、在输出端短路的情况下,PWM控制电路能够把输出电流限制在一个安全范围内,它可以用多种方法来实现 限流电路,当功率限流在短路时不起作用时,只有另增设一部分电路。
记忆材料

形状记忆高分子材料 SMPs
SMA 原理
马氏体相变的可逆性 热弹性马氏体相变高低温相互变化
从图示,,温度升高时材料马氏体相同步缩小, 反 之温度下降时马氏体晶核同步长大,其数量随 温度变化,从而出现形状记忆效应
SMPs 发展历程
1959年 Charlesby 首 次对 辐 射 交联 聚 乙 烯 所 具有的形状记忆现象进行了描述。 20 世纪 70 年代中期 随着美国国家航空航天局对其在航空航天领域的开发应用,对不同型号的辐射
THANKS FOR YOUR TIME
SMPs 记忆效应
很大一部分 SMPs为热致感应型 即在一定温度下 SMPs 受应力变 形,并能在室温( 或较低温度) 固 定形变并长期保存,当升温至某 一特定响应温度时,SMPs 又能 回复至初始形状。
SMPs 生物医学的应用
药物缓释
将材料加工成图3中的永久形状,装载药物颗粒后,加热至玻璃化转变温度以上, 对其施加外力,使其成为图3中的暂时形状,然后通过微创手术植入到人体病灶部 位,在体温的热驱动下发生形状记忆效应,形状回复到起始展开的状态,将药物 释放出来。材料可在人体内自行降解,无需二次手术取出。
交联聚乙烯的记忆特性进行了仔细研究,才引起人们的广泛关注。
PUT THE NAME OF YOUR COMPANY HERE
SMPs 分类
回复响应条件
o热致感应型 o光致 感应型 o化学 感应型 o电 /磁致感应型
o 热塑性 SMPs( 固定
相为物理交联结构)
o 热固性 SMPs( 固定
相为化学交联结构)
SMPs 生物医学的应用
防止血管阻塞器材
• 制作材料可以是聚氨酯、聚降冰 片烯或聚异戊二烯等。
形状记忆聚合物及其多功能复合材料

形状记忆聚合物及其多功能复合材料形状记忆聚合物及其多功能复合材料形状记忆聚合物(shape memory polymers,SMPs)是一种聚合物材料,具有特殊的自修复能力和形状记忆特性。
SMPs的基本特征是具有两种形态:一种是高温下的一种形态,是低弹性模量和高分子链密度的形态;另一种是低温下的一种形态,是高弹性模量和低分子链密度的形态。
SMPs的自修复能力是指在破坏或变形后,该材料可以通过热处理或其他方式恢复原来的形状和性能。
这种自修复能力使得SMPs在医学和航空航天等领域具有广泛的应用前景。
例如,SMPs可以用作医学中的生物医学材料,如微型支架、人工骨骼等,也可以用于制作机器人或机械手等。
SMPs的形状记忆特性是指该材料可以在一定的温度范围内,从一种形态转变为另一种形态,然后随着温度的变化再次恢复原来的形状。
这种形状记忆特性使得SMPs在多种领域具有重要的应用。
例如,SMPs可以用于制作自适应材料,在不同的环境中改变形状,在安全和保护等方面具有良好的应用前景。
在多功能复合材料中,SMPs可以与其他材料相结合,形成一种多功能的复合材料。
这种复合材料具有SMPs的形状记忆特性和其他材料的特点,如导电性、抗菌性和阻燃性等。
例如,SMPs可以与碳纤维相结合,形成一种具有形状记忆特性的复合材料,具有先进的机械性能和良好的导电性能,可以用于制作太空船的结构材料。
总之,形状记忆聚合物及其多功能复合材料在医学、航空航天等领域具有广泛的应用前景。
随着科技的发展和应用的不断推广,形状记忆聚合物及其复合材料将会更加完善和多样化,为我们的生活带来更多的便利和创新。
SMPS性能指标定义

一.描述输入电压影响输出电压的几个指标形式。 1. 绝对稳压系数。 A.绝对稳压系数:表示负载不变时,稳压电源输出直流变 化量△U0与输入电网变化量△Ui之比。既: K=△U0/△Ui。 B. 相对稳压系数:表示负载不变时,稳压器输出直流电压 Uo的相对变化量△Uo与输出电网Ui的相对变化量△Ui之比。 即: S=△Uo/Uo / △Ui/Ui 2. 电网调整率。 它表示输入电网电压由额定值变化+-10%时,稳压电源输出电压的相对变化量,有时也以绝对值表示。 3. 电压稳定度。 负载电流保持为额定范围内的任何值,输入电压在规定的范围内变化所引起的输出电压相对变化△Uo/Uo(百 分值),称为稳压器的电压稳定度。 二.负载对输出电压影响的几种指标形式。 1. 负载调整率(也称电流调整率)。 在额定电网电压下,负载电流从零变化到最大时,输出电压的最大相对变化量,常用百分数表示,有时也用绝 对变化量表示。 2. 输出电阻(也称等效内阻或内阻)。 在额定电网电压下,由于负载电流变化△IL引起输出电压变化△Uo,则输出电阻为
这是交流稳压器特有的。是指输出波形不是正 波形,产生波形畸变,称为畸变。 十三.噪声。 按30HZ——18kHZ的可听频率规定,这对开关电源的转换频率不成问题,但对带风扇的电源要根据需要加以规 定。 十四.输入噪声。 为使开关电源工作保持正常状态,要根据额定输入条件,按由允许输入外并叠加于工业用频率的脉冲状电压 (0——peak)制定输入噪声指标。一般外加脉冲宽度为100——800us,外加电压1000V。 十五.浪涌。 这是在输入电压,以1分钟以上的间隔按规定次数加一种浪涌电压,以避免发生绝缘破坏、闪络、电弧等异常 现象。通信设备等规定的数值为数千伏,一般为1200V。 十六.静电噪声。 指在额定输入条件下,外加到电源框体的任意部分时,全输出电路能保持正常工作状态的一种重复脉冲状的静 电。一般保证5——10KV以内。 十七.稳定度。 允许使用条件下,输出电压最大相对变化△Uo/Uo 。 十八.电气安全要求(GB 4943-90)。 1. 电源结构的安全要求。 1) 空间要求。UL、CSA、VDE安全规范强调了在带电部分之间和带电部分与非带电金属部分之间的表面、空 间的距离要求。UL、CSA要求:极间电压大于等于250VAC的高压导体之间,以及高压导体与非带电金属部分 之间(这里不包括导线间),无论在表面间还是在空间,均应有0.1英寸的距离;VDE要求交流线之间有3mm 的徐变或2mm的净空隙;IEC要求:交流线间有3mm的净空间隙及在交流线与接地导体间的4mm的净空间 隙。另外,VDE、IEC要求在电源的输出和输入之间,至少有8mm的空间间距。
SMPS功率器件性能分析比较说明书

SMPS 功率器件性能分析比较Analysis and Comparison on SMPS Power Devices Characteristic赵忠礼 Zhao Zhongli北京时代新晨电子技术有限公司 100080 北京 Beijing Brilliance Time Electronic Technology Co., Ltd摘要:本文对SMPS 功率器件性能和一定应用条件下的sm f 和j T 的计算分析。
给出了器件选择和应用的原则。
Abstract : This article introduces SMPS Power Device characteristics and the calculation as well as the analysis of sm f and j T under specific condition. It also gives out the rule of the selection and application of the devices.关键词:SMPS 功率器件,分析和比较Keywords : SMPS Power Devices, Analysis and Comparison 引言:SMPS (Switching Mode Power Supply )朝着高频、高效、高可靠,高功率因数和低成本的方向发展。
功率器件则要求高速、高可靠、低损耗和低成本。
目前所用功率器件主要是MOSFET 和IGBT 。
功率MOSFET 的发展是围绕降低高压MOSFET 的导通电阻()DS ON R 的,为此出现了IGBT 和COOLMOS 。
IGBT 是在MOSFET 的漏极加一P +层,注入少子空穴实现电导调制作用,从而降低导通电压。
COOLMOS 则是利用P 型镶条的插入和降低漂移区的电阻实现电荷补偿作用达到降低()DS ON R 的目的。
在高速、低损耗MOS7的工艺基础上生产的MOS7-IGBT ,实现了高速、低损耗、低成本及短拖尾时间。
smps结构与基本原理

开关电源工作原理
通过高频开关技术将输入的较高的交流电压(AC)转 换为PC电脑工作所需要的较低的直流电压(DC)
开关电源的中心思想:用提高工作频率等手段来提 高电源的功率密度,进而达到减少变压器的体积和重量 的目的。采用开关变换的显著优点是大大提高了电能的 转换效率,典型的PC电源效率为70%-75%,而相应的线 性稳压电源的效率仅有50%左右。 输出电压的稳定则是依赖对脉冲宽度的改变来实现, 这就叫做脉宽调制PWM。
R138
7 5K 0 80 5
R137
1 00 K 08 05
R155
1 K 0 6 03
R148
R102
1 0 1 20 6
3 0K 0 60 3
R141
C41
16 17
R135
3 0K 0 80 5
R134
UV
3 .9K 0 60 3
C51
2 .2u ,5 0V
R152
1 K 0 6 03
3 0K 0 80 5 1 03 ,50 V
F R1 04
1 12 06
1 02 50 V 0 80 5
Q5
R91
8 7 6 5
R166
1 0 1 /8 W
1 00 ,1/2W
1 N4 14 8 SM D
1 0u F,5 0V
2 ,12 0 6
D2
R30-33
1 0u F/5 0V
1 00 12 06
Tex t
1 61 6A
D28
C12 D31
D23 U3
S G6 10 5B 1 N4 14 8 SMD
4 70 08 05
1 0K 0 80 5
开关电源(SMPS)的拓扑结构(第一部分)

前馈控制
在降压转换器中,输入电压变化在电压输出端产生的影 响通常可通过输入电压前馈控制降到最低。与模拟控制 方式相比,使用具有输入电压检测功能的数字信号控制 器能轻易实现前馈控制。在前馈控制方法中,数字信号 控制器一旦检测到输入电压的变化,在输入变化对输出 参数造成实际影响之前就将开始采取自适应措施进行相 应的处理。
AN1114
开关电源 (SMPS)的拓扑结构 (第一部分)
作者: Mohammad Kamil Microchip Technology Inc.
简介
工业驱动向更小、更轻和更高效的电子设备的发展趋势 促 进 了 开 关 电 源 (Switch Mode Power Supply, SMPS)的发展。通常可采用几种不同的拓扑结构实现 SMPS。
DS01114A_CN 第 2 页
2008 Microchip Technology Inc.
图 2:
(A)
降压转换器 IIN
Q1 VIN
D1
L
+ IL -
IOUT VOUT
AN1114
(B) Q1GATE
t
(C)
VL
VIN - VOUT
t
-VOUT
(VIN - VOUT)/L
(D)
IIN
t
-VOUT/L IL2
输入和输出电容的设计取决于每一个转换器的开关频率 乘以并联转换器的个数。从输出电容的角度来看纹波电 流减少 “n”倍。与图 2 (D)中所示的单一转换器相 比,多相同步降压转换器汲取的输入电流是连续的且纹 波较少,如图 3 (E)所示。因此,对于多相同步降压 转换器来说,较小的输入电容能满足设计要求。
SMPS 扫描电迁移率粒径谱仪

U-SMPS 扫描电迁移率粒径谱仪Palas® U-SMPS(Uuniversal Scanning Mobility Particle Sizer扫描电迁移率粒径谱仪)用于亚微米颗粒粒径分布研究。
颗粒大小和浓度的测量在健康领域广为研究,如吸入治疗、工作环境评价,同时在环境监测领域也广为关注。
Palas® U-SMPS由一个DMA静电迁移率分析仪和CPC凝聚核粒子计数器,DMA静电迁移率分析仪又称为DEMC 差分粒子电迁移器。
气溶胶颗粒根据他们在电场中的性质不同而被分离,然后被CPC凝聚核粒子计数器计数或Palas® Charme®气溶胶静电计检测,软件将以上数据反演为气溶胶粒径和浓度分布图。
用户可以自行设置粒径范围,最快30秒可以扫描一次。
用户也可以设置电压,获得更好的分离效果。
系统触摸屏图形化的用户界面,测量值线性和对数显示,内存数据管理。
数据评价软件,可用于数据进一步处理。
系统为嵌入式操作系统,也可外接电脑进行操作。
特点:• 气溶胶粒径分布, 3 nm to 1.2 μm•可连续快速操作• 高分辨率: 64 size channels/decade• 测量浓度可达 to 108 particles/cm3• 图形化显示测量值• 7”触摸屏,引导式操作• 内置数据记录功能• 可远程操作应用:• 过滤材料测试• 气溶胶研究• 大气环境研究• 吸入和暴露研究• 室内和工作环境测量技术参数DEMC:• 粒径范围: DEMC 1000 dp = 3 nm – 350 nmDEMC 2000 dp = 5 nm – 1,200 nm• 通道数: 1 – 64• 浓度范围: up to 108 particles/cm3• 样气流速 /鞘气流速: 0 – 4 l/min / 0 – 8 l/min• 嵌入式操作系统: 触摸屏 800 x 480 pixels处理器 1.6 GHz Intel Atom TM内存:2 GB• 接口: USB, WLAN, Ethernet, RS‐232/485• 供电: 115/230 V; 50/60 Hz• 控制单元尺寸: 33 x 38 x 24 cm (H x W x D)• 柱体尺寸: 15 x 57 cm (ø at base x H)• 控制单元重量: 12.9 kg• 柱体重量: 9.3 kgUF-CPC颗粒粒径范围: dp = 5 nm – 10,000 nm浓度范围:UF‐CPC 100 CNmax ≤ 50,000 P/cm3 (single counting)CNmax < 107 P/cm3 (nephelometric mode) UF‐CPC 200 CNmax ≤ 1,000,000 P/cm3 (single counting)CNmax < 107 P/cm3 (nephelometric mode)浓度精度: 5% (single counting),10% (photometric mode)工作流体: Butanol, isopropanol, water 或其他可选气溶胶流速: Adjustable 0.30 to 0.60 L/min数字信号:detection: 20 MHz Processor256 Raw data channels光源:LED 寿命长稳定性高尺寸(HxWxD): 33 x 38 x 24 cm (13 x 15 x 9.5 in)重量: 10 kg (22 lbs)设备可选的组合SMPS+C可广泛应用于室内/室外纳米气溶胶检测,如汽车尾气排放检测以及交通实时监测、环境网络和气候研究。
SMPS设计验证准则

1.目的:
1.1.藉由該準則來規範設計工程師,使產品符合客戶要求
1.2.為使整個設計評估計畫能達到最佳的客戶滿意度
1.3.達到產品及零件標準化
2.範圍:
2.1.帛漢新開發的Power Supply 機種
3.參考資料:
3.1.ISO9001
4.權責單位:
由設計工程師執行,工程部經理或主管驗證,若因實際PC板空間限制或開發時間無法達到要求時,需與工程部經理或主管討論,必要時可委託品管工程師或協力廠幫忙做相關測試並提供資料作為佐證,務必使產品符合規格要求
5.內容:
5.1.基本設計原則:
5.1.1.線路簡單 --------- 設計越簡單越好,結構愈複雜,可靠度愈差
5.1.2.標準零件 --------- 建立標準零件庫,標準線路,使設計時間縮短,交貨時間更快
5.2.零件選用:
根據所要的操作功能、環境,選取適當零件,並需考慮減額度( Derating ),以獲得更好的可靠度要求,現將其列表如下:
減額度表 ( Derating ):
*零件種類將隨日後的增加而隨時加入。
5.3.電氣特性:
通常客戶會提供電氣規格,基本設計務必符合要求,現僅就工程師常會忽略的事項做列表,以便逐
*其他關於安規、CE等測試項目,則依客戶不同的需求而委託安規工程師代測之,設計工程師協辦
5.4.機構:
由於機構的內容相當廣泛,現僅列舉常遇到的項目作為考,待日後逐項增列之:。
开关电源工作原理如何理解及其电路图详细解析

开关电源工作原理如何理解及其电路图详细解析开关模式电源(Switch Mode Power Supply,简称SMPS),又称交换式电源、开关变换器,是一种高频化电能转换装置,是电源供应器的一种。
其功能是将一个位准的电压,透过不同形式的架构转换为用户端所需求的电压或电流。
开关电源的输入多半是交流电源(例如市电)或是直流电源,而输出多半是需要直流电源的设备,例如个人电脑,而开关电源就进行两者之间电压及电流的转换。
开关模式电源(Switch Mode Power Supply,简称SMPS),又称交换式电源、开关变换器,是一种高频化电能转换装置,是电源供应器的一种。
其功能是将一个位准的电压,透过不同形式的架构转换为用户端所需求的电压或电流。
开关电源的输入多半是交流电源(例如市电)或是直流电源,而输出多半是需要直流电源的设备,例如个人电脑,而开关电源就进行两者之间电压及电流的转换。
开关电源不同于线性电源,开关电源利用的切换晶体管多半是在全开模式(饱和区)及全闭模式(截止区)之间切换,这两个模式都有低耗散的特点,切换之间的转换会有较高的耗散,但时间很短,因此比较节省能源,产生废热较少。
理想上,开关电源本身是不会消耗电能的。
电压稳压是透过调整晶体管导通及断路的时间来达到。
相反的,线性电源在产生输出电压的过程中,晶体管工作在放大区,本身也会消耗电能。
开关电源的高转换效率是其一大优点,而且因为开关电源工作频率高,可以使用小尺寸、轻重量的变压器,因此开关电源也会比线性电源的尺寸要小,重量也会比较轻。
若电源的高效率、体积及重量是考虑重点时,开关电源比线性电源要好。
不过开关电源比较复杂,内部晶体管会频繁切换,若切换电流尚加以处理,可能会产生噪声及电磁干扰影响其他设备,而且若开关电源没有特别设计,其电源功率因数可能不高。
主要用途开关电源产品广泛应用于工业自动化控制、军工设备、科研设备、LED照明、工控设备、通讯设备、电力设备、仪器仪表、医疗设备、半导体制冷制热、空气净化器,电子冰箱,液晶显示器,LED灯具,通讯设备,视听产品,安防监控,LED灯带,电脑机箱,数码产品和仪器类等领域。
SMPS-反激变压器设计

开关电源设计——反激变压器设计Flock fai liu2012-02-23学习除了努力,还需要方法!一、电流纹波率在设计之前,先引入SMPS最基本也是影响最广的一个设计参数——电流纹波率(K RP)。
它的设定非常重要,一旦设定好了它,几乎所有参数都已确定。
它会影响功率器件(开关管、输出整流二极管),输出滤波电容的电流应力和损耗,变压器几何尺寸。
所以不了解它,就无法开展变压器的设计。
电流纹波率定义初级纹波电流(△I)与电流有效值(I P)的比值。
即:K RP=△II P ; △I=V DCmin∗T ONL p; I p=I O∗1n1−D MaxK RP的有效范围为0—2,CCM<1,DCM=1,BCM=2 (电感电流的三种工作模式,自参阅书籍),若将它设为0,△I必为0,根据电感方程V=L*△I△t表明此时电感量为无穷大,所以实际中不可能。
从铜损跟铁损的折中考虑、变压器的几何尺寸以及EMI等综合折中;根据输出功率或特性的不同,将K RP设定在0.4—1之间进行调整,低压大电流和大功率输出选择偏低;高压小电流和小功率输出选择偏大。
当V INmin增加时,K RP相对应偏大。
当然任何情况下如果将K RP设定偏小,允许选择更大的磁蕊,效果是非常好的。
但从商业角度来说,控制成本,体积等原因,大多情况下只是空谈吧了。
不过认识这一点是很有帮助的。
当然有时也会有,这时可相对应偏小。
我们必须要深刻了解K RP的设定给设计结果带来的影响。
设置过小,会增大变压器尺寸以及高频铜损问题,当然会减小峰值电流、功率器件、电容的损耗。
CCM模式会使输出整流二极管发热增加。
然而设置过大自然与上述相反了,它还会影响EMI。
然而我们从低压时设计的CCM并不意味着它会一直工作在CCM模式。
它会随着电压的升高或负载的减小,使K RP=1后进入DCM模式,此时在输出整流二极管反向恢复之前电感电流刚好为0,给DIODE提供一个很好的工作条件,但此时再次提醒,K RP越大的缺点。
SMPS中光耦接法

流Ic增大,电阻R4上的电压降增大,com引脚电压下降,占空比减小,输出电压减小;反之,当输出电压降低 时,调节过程类似。 常见的第2种接法,如图2所示。与第1种接法不同的是,该接法中光耦的第4脚直接接到芯片的误差放大器 输出端,而芯片内部的电压误差放大器必须接成同相端电位高于反相端电位的形式,利用运放的一种特性 —— 当运放输出电流过大(超过运放电流输出能力)时,运放的输出电压值将下降,输出电流越大,输出电压下 降越多。因此,采用这种接法的电路,一定要把PWM 芯片的误差放大器的两个输入引脚接到固定电位上,且 必须是同向端电位高于反向端电位,使误差放大器初始输出电压为高。
功率大约为30 w。实际测得的光耦4脚电压(此电压与芯片三角波相比较,从而决定驱动占空比)波形,如图9 所示。对应的驱动信号波形,如图10所示。 图10的驱动波形有负电压部分,是由于上、下管的驱动绕在一个驱动磁环上的缘故。可以看出,驱动信号 的占空比比较大,大约为0.7。
对于第2种接法,一般芯片内部的电压误差放大器,其最大电流输出能力为3 mA左右,超过这个电流值, 误差放大器输出的最高电压将下降。所以,该接法中,如果电源稳态占空比较大,那么电流Ic比较小,其值可 能仅略大于3 mA,对应图7,Ib为2 mA左右。由图6可知,Ib值较小时,微小的Ib变化将引起Ic剧烈变化,光 耦的增益非常大,这将导致闭环网络不容易稳定。而如果电源稳态占空比比较小,光耦的4脚电压比较小,对 应电压误差放大器的输出电流较大,也就是Ic比较大(远大于3 mA),则对应的Ib也比较大,同样对应于图6, 当Ib值较大时,对应的光耦增益比较适中,闭环网络比较容易稳定。 同样,对于上面的半桥辅助电源电路,用接法2代替接法1,闭环不稳定,用示波器观察光耦4脚电压波形, 有明显的振荡。光耦的4脚输出电压(对应于UC3525的误差放大器输出脚电压),波形如图11所示,可发现明显 的振荡。这是由于这个半桥电源稳态占空比比较大,按接法2则光耦增益大,系统不稳定而出现振荡。
SMPS-基本概念-X1-011024

*課程內容:(一).交換式電源(以下簡稱SMPS)之用途(二).SMPS常用之架構和種類(三).常見之規格內容及名詞解釋(四).如何設計SMPS及成本考量(五).SMPS 製造流程(六).SMPS 測試設備1.SMPS之用途:我們先以日常生活中會用到的電器用品來說明,清早起來打開電子式日光燈或電子式檯燈,刷牙時,充電式電動牙刷之充電器,用遙控器打開電視機看新聞,用電磁爐或微波爐加熱早餐,出門搭電梯下樓,進入辦公室時,放眼望去每一種需插電的事務機器,電話、傳真。
,大致可以說需用到電的產品,就是SMPS的可能用途。
所需的規格要求及線路架構則隨使用場所,價格上會有極大差異。
以一般我們選用的電子零件,其溫度範圍就可分為:●商業用( 0 ~ 70 ℃)●工業用 (-25 ~ 125 ℃)●軍事用 (-40 ~ 125 ℃)而SMPS也會因為使用的周圍環境溫度範圍,而區分不同的等級:●商業用( 0 ~ 40 ℃)------ 一般日常生活所接觸到的電器用品,如電腦、影印機所使用者●工業用 (-20 ~ 71 ℃) ------ 工業產品所使用的POWER,如SMD機器、CNC機器中的POWER即是●軍事用 (-40 ~ 125 ℃) ------ 軍事用途,如飛彈、戰艦、坦克中所用到的POWER不同的溫度範圍,所選用的零件就不相同,其價格當然也不同2.SMPS 常用之架構和種類:2.1.依輸出 / 輸入使用的電壓高低可分為:(適用於非隔離的環境*)*所謂非隔離的環境:如同下列所提的環境,都是自己形成一個系統,輸入與輸出共地,不會與其他的系統連線,而且接地良好,不會對使用者有漏電的危險,例如其中所提的系統輸入都屬於低電壓輸入,而且使用者接觸的機殼都是接地(GROUND),沒有被電到的危險。
(a).降壓式 (Buck) : 輸入比輸出高 ,例如卡車之車用冰箱中的POWER將24V轉12VFig. 2-1(b).升壓式 (Boost) : 輸入比輸出低,例如電擊棒將電池電壓9V升高為1000VFig. 2-2(c).降升壓式 (Buck-Boost) : 輸入比輸出低或高 ,例如汽車充電器充筆記型電腦19V電池,而汽車電池有轎車12V及卡車24V兩種Fig. 2-3(線路動作原理請參見相關SMPS基本原理說明)2.2.一般常用架構可分為:(適用於需隔離的環境*)*所謂需隔離的環境:用專業術語來說就是──輸入與輸出不共地,例如帛漢的DC/DC使用於網路卡,而網路連線就是一個典型的隔離環境,因為兩部電腦的輸入接地不一定相同(插頭不一定插同一方向),如果使用非隔離的電源,將會天下大亂,而且會有因兩部電腦地的電位不同,造成兩部電腦間大電流流動,而使保險絲燒毀。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
d (s )
G m (s )
1 Vm
V c (s )
Vm為鋸齒波的最大振幅
轉換器系統之穩定度分析
圖6-6中,系統方塊圖中H(s)為回授分壓網絡之轉移函數, 其電路型態如圖6-7所示。
轉換器系統之穩定度分析
圖6-7中,可以得知各類型的轉移函數。
由圖6-7(a)得知其轉移函數為
V 1 (s )
超前補償:
超前之意,即指輸出信號之相位會領先輸入信號,電路中加入超前補 償,會對轉換器之影響為: 1.增加系統之頻代寬度,導致較快的暫態響應,但容易受雜訊干擾。
2.降低overshoot現象,與改善系統相對穩定性。
3.增加了轉換器系統之增益交越頻率(0dB時的頻率)。
4.增加轉換器系統之相位邊限(P.M.)。
5.需要額外的增益放大器來補強超前網路在低頻之衰減。 6.超前補償對穩態響應只做有限之改進。
1. 振幅之大小以分貝(dB)為單位對 log 或 log f 的圖形。
2. 相位以度為單位對 log 或 log f 的圖形。
波德圖的特色
1. 振幅大小是以分貝表示,因此在轉移函數中含乘與除 的項取對數變成加與減;相位也是各項的相位加減取
得。
2. 系統的行為可以廣泛的表現出來,即可表現出系統的
C (s ) G (s ) R (s ) H (s )G (s )C (s )
(6-7)
最後,由(6-7)式,可以求得閉迴路轉移函數之表示式:
C (s ) R (s ) G (s ) 1 G (s ) H (s )
穩定度準則
特性方程式之解為
F (s ) 1 G (s ) H (s ) 0
G (s)
bn s
(6-1)
R(s)為輸入驅動信號 C(s)為輸出信號 C(s)/R(s)之比值,則定義為轉移函數G(s)
G(s)即表示為轉換器系統輸出信號之拉普拉斯轉換對輸入 驅動信號之拉普拉斯轉和之比。
頻率響應
如圖6-1所示,而由此函數即可得知,其結合了增益大小 與相位之特性。
頻率響應
在(6-1)方程式中,一般定義C(s) = 0的根稱之系統的零點, 而R(s) =0的根則稱之系統極點,轉移函數一可表示為
i i
G (s )
在此將Z1~ Zm或1/T1~1/Tm稱為零點的轉角頻率或轉折頻率。而 P1~Pn或1/Ta~1/Tn稱為極點的轉角頻率或是轉折頻率。
頻率響應
若要決定增益大小漸進線之變化率,可以用八度或是十 進來表示。
八度乃指2:1的頻率範圍,即每八度有6dB的斜率。 十進則指10:1的頻率範圍,即每十進有-20dB的斜率。
R
2 2
V o (s )
R1 R
H (s )
由圖6-7(b)得知其轉移函數為
V 1 (s )
R
2 2
V o (s )
R1 R
(1 SC 1 R 1 ) 1 SC 1 R 1 R R1 R
2
H (s )
2
從上式中,零點比極點更接近原點,所以可視為領前網路,其頻 率響應會隨著頻率的變化而改變。
G
m
(s )G d (s )G p (s ) H (s )
轉換器系統之穩定度分析
爲了使系統更穩定,則須加入迴授補償網路G1(s),一般 補償網路都是配合運算放大器來達成。
轉移函數之表示式為
V c (s )
Zf Z in
G 1 (s )
V 1 (s )
V ref ( s ) 0
系統方塊各個轉移函數都求得,即可求出轉換器迴路增益轉移函 數為
4
4
)S
7
V c (s )
) S ( 2 . 34 10
)S
2
其波德圖頻率響應結果,如圖6-9與圖6-10所示,由此頻率響應曲線 可看出其斜率為-2(-40dB/sec),至於曲線中轉折頻率分別為:
f Z1 1 2R cC
1 2 LC
1590 Hz ( R
c
25 m )
高低頻的行為。
3. 可以完全依據波德圖設計補償器。
4. 可提供其他頻域圖所需資料,如極座標圖或大小相位
圖。
頻率響應
若要表現出轉換器在頻域中的形式,則可將時域中的這些 方程式以拉普拉斯轉換。
C (s) R (s) am s
m n
a m 1 s b n 1 s
m 1 n 1
... a 1 s a 0 ... b 1 s b 0
圖6-6所示;此圖中Gd(s)Gp(s)為工作週期至輸出轉移函 數 ( V o ( s ) / d ( s )) ,可以利用狀態空間平均法求得此部分,亦可 推導出輸入至輸出 ( V o ( s ) / V in ( s )) 之轉移函數Gi(s)Gp(s)。
轉換器系統之穩定度分析
圖6-6中,系統方塊圖中Gm(s)為調變器的轉移函數,在 PWM系統中,誤差信號會與鋸齒波做比較;若誤差信號準 位等於鋸齒波電壓時,則工作週期為100%。則調變器轉移 函數可以表示為
交換式電源供給器報告
第六章 穩定度之分析與迴授補償控制器之 設計
交換式電源供給器之理論與實務設計 梁適安 編著
內容大綱
前言 頻率響應 轉換器之迴授原理與穩定度準據 轉換器系統之穩定度分析 迴授補償網路之結構與設計
前言
在交換式電源轉換器之系統中,整個架構可視為負迴授 型式,因此可使用頻率響應(frequency response)法來決定穩 定度之程度。而一個系統的頻率響應就是系統饋入正弦輸入 信號時的穩定狀態響應,其輸出信號和系統內各處信號都是 正弦的,它們和輸入信號只是大小(magnitude)和相位(phase) 的不同而已。
轉換器之迴授原理
圖6-3閉迴路回授控制系統方塊圖
轉換器之迴授原理
可由圖6-3推導出閉迴路轉移函數
C (s ) G (s ) E (s ) B (s ) H (s )C (s ) E (s ) R (s ) B (s )
(6-4) (6-5)
(6-6)
將(6-4)式、(6-5)式代入(6-6)式,則可得
f P 1, P 2
325 Hz
迴授補償網路之結構與設計
圖6-9所示為在波德圖上工作週期至輸出之頻率響應曲線
迴授補償網路之結構與設計
圖6-10所示為在波德圖上控制至輸出之頻率響應曲線
迴授補償網路之結構與設計
當輸入電壓改變時,轉換器之工作週期也會隨之變化; 因此,其控制至輸出之響應曲線,如圖6-11~13所示。
穩定度準則
有時增益定義相位邊限來補充增益邊限的不足。
相位邊限:當閉迴路系統到不穩定之前,其迴路內所能容許增加的 相位。 閉迴路系統之增益邊限定義為 相位邊限(P.M.)
G ( j g ) H ( j g ) ( 180 )
對於穩定系統系統而言,F(s)之根或是其零點都是在S平面的半邊; 或是閉迴路轉移函數之極點都是位於S平面的左半邊,若是位於 虛軸上或S平面的右半邊,系統就變的不穩定了。
特性方程式中的G(s)H(s)項一般稱為迴路轉移函數, G(s)H(s)包含所有關於閉迴路極點的訊息,且也表示出誤差 信號與回授信號之間所有迴路之方塊的轉移函數。
迴授補償網路之結構與設計
將參數代入(6-22)式與(6-23)式,並考慮最大輸入電壓與最大負載,
可得
V o (s )
60
1 (10 1 ( 3 . 44 10
4
4
)S
7
d (s )
) S ( 2 . 34 10
)S
2
且
V o (s )
12
1 (10 1 ( 3 . 44 10
增益大小之頻率響應曲線中,遇到極點其響應曲線之斜 率是向下轉折的。至於在頻率中的零點,其波德圖的斜率是 向上轉折。
轉換器之迴授原理
由圖6-2可知電源轉換器可視為閉迴路之負迴授系統。
H(s) : 迴授分壓網路 G1(s):誤差放大器與補償網路 G2(s):脈波寬度調變器與高頻轉換器 G3(s):低通濾波器
穩定度準則
穩定度準則
穩定度準則
對於交換式電源轉換器系統而言,若要獲得穩定且不 振盪的結果,則迴路增益轉移函數的頻率響應需滿足:
1.增益交越頻率之增益為 0dB,此時曲線斜率為 -1,且相 移不可低於 -180度。
2.相位交越頻率之處,其增益大小必須小於 0dB,也就是增 益邊限必須大於零。
轉換器系統之穩定度分析
穩定度準則
在波德圖中,為了分析相對穩定度常利用增益邊限 和相位邊限。
增益邊限:當閉迴路系統到不穩定之前,其迴路內所能容許增加的 迴路增益(以分貝-dB表示)。 閉迴路系統之增益邊限定義為 增益邊限(G.M.)
1
10
20log
G ( j c ) H ( j c )
(dB)
c:相位交越頻率
迴授補償網路之結構與設計
迴授補償網路之結構與設計
迴授補償網路之結構與設計
補償補路之結構可以區分為三種:
(1)超前補償(lead compensation) (2)落後補償(lag compensation) (3)超前-落後補償(lead-lag compensation)
迴授補償網路之結構與設計
頻率響應特色
優點: 1. 容易取得各種不同頻率範圍和大小的正弦信號,所以 利用實驗方法則可容易獲致系統的頻率響應。
2. 系統正弦穩定行為的轉移函數容易求得,只要將系統 轉移函數中的 S 用 j 來取代即可。
