巴特沃兹有源低通滤波器设计
【完整版毕业论文】巴特沃斯有源低通滤波器的设计

巴特沃斯有源低通滤波器的设计摘要随着社会科学技术的飞速发展,各种科技产品在人类社会中随处可见,极大的丰富了人们的日常生活。
物联设备、可穿戴设备以及虚拟仪器产品在各种应用和消费场合变得极为普遍。
就目前而言,在几乎所有的电子产品中,各种增益、带宽以及高性能的滤波器都发挥着至关重要的作用,例如可穿戴设备的语音信号输入系统中,运用高性能的低通滤波器进行语音信号的降噪、滤波、回声消除,来提高系统的音质和语音识别精准度等。
本论文通过对各种低通滤波器的通频带、增益和截止频率的分析,采用通频带最大扁平度技术(巴特沃斯技术)来设计实现四阶高性能低通滤波器,通过Multisum仿真软件,验证了设计的正确性。
在这基础上,本文还对如何提高该滤波器的响应速度进行了研究,提出了一种有效的提高响应速度的方案,并通过仿真软件得以验证。
这在低通滤波器的理论以及实际工程应用中,都具有非常重要的意义。
关键词:有源低通滤波器,巴特沃斯,运算放大器Design of Butterworth Active Low Pass FilterABSTRACTWith the rapid development of social science and technology, various technological products can be seen everywhere in human society, which greatly enriches people's daily lives. IoT devices, wearable devices, and virtual instrument products have become extremely common in various applications and consumer occasions. For now, in almost all electronic products, various gains, bandwidths, and high-performance filters play a vital role. For example, in the voice signal input system of wearable devices, the use of high-performance low-pass The filter performs noise reduction, filtering, and echo cancellation of the speech signal to improve the sound quality of the system and the accuracy of speech recognition.In this paper, through the analysis of the passband, gain and cutoff frequency of various low-pass filters, the maximum flatness of the passband technology (Butterworth technology) is used to design and implement a fourth-order high-performance low-pass filter, through Multisum simulation software To verify the correctness of the design. On this basis, this paper also studies how to improve the response speed of the filter, and puts forward an effective scheme to improve the response speed, which is verified by simulation software. This is of great significance in the theory of low-pass filters and in practical engineering applications.KEYWORDS:active low-pass filter,butterworth,amplifier1绪论1.1 引言在近现代的科技发展中,滤波器作为一种必不可少的组成成分,在仪器仪表、智能控制、计算机科学、通信技术、电子应用技术和现代信号处理等领域有着十分重要的作用。
【完整版毕业论文】巴特沃斯有源低通滤波器的设计

巴特沃斯有源低通滤波器的设计摘要随着社会科学技术的飞速发展,各种科技产品在人类社会中随处可见,极大的丰富了人们的日常生活。
物联设备、可穿戴设备以及虚拟仪器产品在各种应用和消费场合变得极为普遍。
就目前而言,在几乎所有的电子产品中,各种增益、带宽以及高性能的滤波器都发挥着至关重要的作用,例如可穿戴设备的语音信号输入系统中,运用高性能的低通滤波器进行语音信号的降噪、滤波、回声消除,来提高系统的音质和语音识别精准度等。
本论文通过对各种低通滤波器的通频带、增益和截止频率的分析,采用通频带最大扁平度技术(巴特沃斯技术)来设计实现四阶高性能低通滤波器,通过Multisum仿真软件,验证了设计的正确性。
在这基础上,本文还对如何提高该滤波器的响应速度进行了研究,提出了一种有效的提高响应速度的方案,并通过仿真软件得以验证。
这在低通滤波器的理论以及实际工程应用中,都具有非常重要的意义。
关键词:有源低通滤波器,巴特沃斯,运算放大器Design of Butterworth Active Low Pass FilterABSTRACTWith the rapid development of social science and technology, various technological products can be seen everywhere in human society, which greatly enriches people's daily lives. IoT devices, wearable devices, and virtual instrument products have become extremely common in various applications and consumer occasions. For now, in almost all electronic products, various gains, bandwidths, and high-performance filters play a vital role. For example, in the voice signal input system of wearable devices, the use of high-performance low-pass The filter performs noise reduction, filtering, and echo cancellation of the speech signal to improve the sound quality of the system and the accuracy of speech recognition.In this paper, through the analysis of the passband, gain and cutoff frequency of various low-pass filters, the maximum flatness of the passband technology (Butterworth technology) is used to design and implement a fourth-order high-performance low-pass filter, through Multisum simulation software To verify the correctness of the design. On this basis, this paper also studies how to improve the response speed of the filter, and puts forward an effective scheme to improve the response speed, which is verified by simulation software. This is of great significance in the theory of low-pass filters and in practical engineering applications.KEYWORDS:active low-pass filter,butterworth,amplifier1绪论1.1 引言在近现代的科技发展中,滤波器作为一种必不可少的组成成分,在仪器仪表、智能控制、计算机科学、通信技术、电子应用技术和现代信号处理等领域有着十分重要的作用。
设计一个巴特沃斯模拟低通滤波器

1. 设计一个巴特沃斯模拟低通滤波器,要求通带截止频率为Hz f p 25=,通带最大衰减dB a p 3=,阻带起始频率Hz f s 50=,阻带最小衰减dB a s 25=。
解:根据已知条件确定巴特沃斯低通滤波器的阶数N :053.01010202520===--s a s δ()()2355.46021.05502.22lg 21053.01lg lg211lg 22==⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛-≥p s s ΩΩδN取N =5。
低通滤波器3dB 截止频率为)/(157502s rad πf πΩΩp p c ====则五阶巴特沃斯滤波器的传输函数为:1021.010719.110095.110326.510048.111236.3236.4236.4236.31)(2436495112345++⨯+⨯+⨯+⨯=+⎪⎪⎭⎫⎝⎛+⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛=----s s s s s Ωs Ωs Ωs Ωs Ωs s H c c ccc2. 设计一个切比雪夫模拟低通滤波器,要求通带截止频率为kHz f p 3=,通带最大衰减dB a p 2.0=,阻带起始频率kHz f s 12=,阻带最小衰减dB a s 50=。
解:由()2.01lg 20-=-p δ,求得9772.0101202.0==--p δ。
则2171.019772.011)1(122=-=--=p δε 由50lg 20-=s δ,求得0032.0102050==-s δ,则23.31610032.011122=-=-=s δδ 所需滤波器的阶数为:()()()()8604.30634.29770.7312arccos 2171.0/23.316arccos arccos arccos ===≥h h ΩΩh εδh N p s取N =4。
则该模拟低通滤波器的幅度表示为:⎪⎭⎫ ⎝⎛⨯⨯+=⎪⎪⎭⎫⎝⎛+=32422210322171.01111)(πΩC ΩΩC εΩj H p Na归一化的系统函数表示为:∏∏==--=-⋅=Nk k Nk k N a p p p p εp H 111)(7368.11)(21)(其中极点k p 为:0715.14438.01j p +-=,4438.00715.12j p +-=,4438.00715.13j p --=,0715.14438.01j p --=将)(p H a 去归一化,求得实际滤波器的系统函数)(s H a()()()8428426414107790.4100394.4107791.4106731.1102687.77368.1)()(⨯+⨯+⨯+⨯+⨯=-==∏==s s s s p Ωs Ωp H s H k k p pΩs p a a p3. 设计一个巴特沃斯模拟高通滤波器,要求通带截止频率为kHz f p 20=,通带最大衰减dB a p 3=,阻带起始频率kHz f s 10=,阻带最小衰减dB a s 15=。
LC低通滤波器设计(巴特沃斯低通滤波器归一化)讲解

C1 1.84776F C2 0.76537F
1NEW
0.76537 K 0.76537 4 12.29μH 5 M 2.512 10
L2NEW
1.84776 K 1.84776 4 29.42μH 5 M 2.512 10
待设计LPF的电容参数为 :
(1 2 )Hz
特征阻抗变换K 4 4 1 四阶Butterworth低通滤波器的电感电容参 数
2018/10/24
只因准备不足,才导致失败
7
四阶Butterworth低通滤波器的归一化LPF基 准滤波器的参数,设 L1 0.76537H L2 1.84776H 得:L
1.84776 1.84776 C1NEW 1.84 μF 5 M K 4 2.512 10 0.76537 0.76537 C2NEW 0.76μF 5 M K 4 2.512 10
2018/10/24 只因准备不足,才导致失败 8
电感采用无损磁芯及细包漆线绕制而成,其 电感值可用数字电桥测量仪器测量得到。
2018/10/24
只因准备不足,才导致失败
1
对滤波器截止角频率的变换是通过先求出待 设计滤波器截止角频率与基准角频率的比值 M,再用这个M去除滤波器中的所有元件值 来计算所需参数,其计算公式如下:
待设计滤波器的截止频 率 M 基准滤波器的截止频率
C (base) Cm(new) M
2018/10/24
5. 低通滤波器设计
1)归一化LPF设计方法 归一化低通滤波器设计数据,指的是特征阻 1 抗为 1 且截止频率为 0.159Hz 的基准 低通滤波器的数据。 2 在设计巴特沃思型的归一化LPF的情况下, 以巴特沃思的归一化LPF设计数据为基准滤 波器,将它的截止频率和特征阻抗变换为待 设计滤波器的相应值。
用MATLAB设计巴特沃斯低通滤波器

⽤MATLAB设计巴特沃斯低通滤波器⽤MATLAB 设计巴特沃斯低通滤波器1 巴特沃斯低通滤波器的特性⼀个理想低通滤波器的幅频特性如图3-80的阴影部分所⽰。
为了实现这个理想低通特性,需要在从0~ωC 的整个频带内增强增益,在ω>ωC 增益要降到0。
实际上,理想滤波器是不可能实现的。
图3-78是实际滤波器的幅频特性。
但是实际滤波器的特性愈接近理想特性愈好,巴特沃斯(Butterworth )滤波器就是解决这个问题的⽅法之⼀。
巴特沃斯滤波器以巴特沃斯函数来近似滤波器的系统函数,巴特沃斯的低通模平⽅函数为:221|()|1,2,,1(/)NC H j N j j ωωω==+ (3-138)式中以C ω是滤波器的电压-3dB 点或半功率点。
不同阶次的巴特沃斯滤波器特性如图3-79(a)所⽰。
4阶巴特沃斯滤波器的极点分布如图3-79(b)所⽰。
巴特沃斯滤波器幅频响应有以下特点:最⼤平坦性:在0=ω附近⼀段范围内是⾮常平直的,它以原点的最⼤平坦性来逼近理想低通滤波器。
通带、阻带下降的单调性。
这种滤波器具有良好的相频特性。
3dB 的不变性:随着N 的增加,频带边缘下降越陡峭,越接近理想特性。
但不管N 是多少,幅频特性都通过-3dB 点。
极点配置在半径为ωC 的圆上,并且均匀分布。
左半平⾯上的N 个极点是)(s H 的极点,右半平⾯上的N 个极点是)(s H -的极点。
2 巴特沃斯低通滤波器的实现为使巴特沃斯滤波器实⽤,我们必须能够实现它。
⼀个较好的⽅法是将巴特沃斯滤波器函数化成若⼲⼆阶节级联,其中每⼀节实现⼀对共轭复极点。
通过将极点以共轭复数的形式配对,对所有的每⼀个⼆阶节都具有实系数。
1图3-78 低通滤波器的幅频特性图3-80所⽰运算放⼤器电路为实现⼀对共轭极点提供了很好的⽅法。
电路的系统函数为202202121121122121)(1)11(1)(ωωω++=+++=s Qs C C R R s C R C R s C C R R s H (3-139)式中,ω0是S 平⾯原点与极点之间的距离,Q 被称为电路的“品质因数”,它提供了对响应峰值尖锐程度的⼀种度量。
巴特沃斯低通滤波器的设计
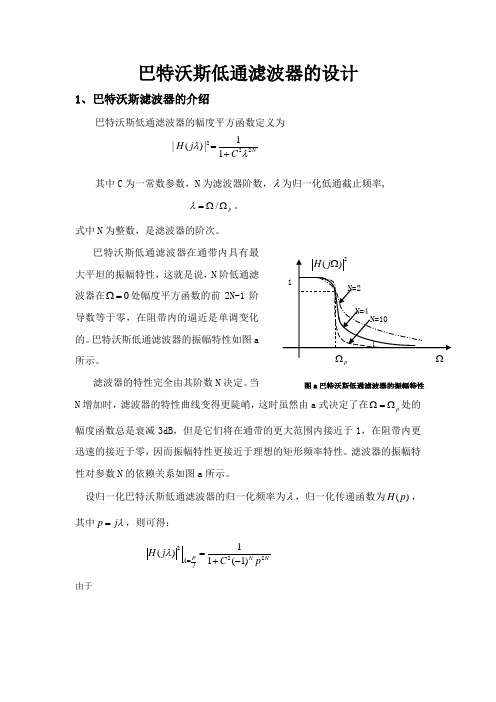
巴特沃斯低通滤波器的设计1、巴特沃斯滤波器的介绍巴特沃斯低通滤波器的幅度平方函数定义为2221|()|1NH j C λλ=+其中C 为一常数参数,N 为滤波器阶数,λ为归一化低通截止频率,/p λ=ΩΩ。
式中N 为整数,是滤波器的阶次。
巴特沃斯低通滤波器在通带内具有最大平坦的振幅特性,这就是说,N 阶低通滤波器在0Ω=处幅度平方函数的前2N-1阶导数等于零,在阻带内的逼近是单调变化的。
巴特沃斯低通滤波器的振幅特性如图a 所示。
滤波器的特性完全由其阶数N 决定。
当N 增加时,滤波器的特性曲线变得更陡峭,这时虽然由a 式决定了在p Ω=Ω处的幅度函数总是衰减3dB ,但是它们将在通带的更大范围内接近于1,在阻带内更迅速的接近于零,因而振幅特性更接近于理想的矩形频率特性。
滤波器的振幅特性对参数N 的依赖关系如图a 所示。
设归一化巴特沃斯低通滤波器的归一化频率为λ,归一化传递函数为()H p ,其中p j λ=,则可得:2221()1(1)N NpjH j C pλλ==+- 由于p图a 巴特沃斯低通滤波器的振幅特性221()()()1()a a jsNcH s H s A s j Ω=--=Ω=+Ω所以巴特沃斯滤波器属于全极点滤波器。
2、常用设计巴特沃斯低通滤波器指标p λ:通带截止频率; p α:通带衰减,单位:dB ;s λ:阻带起始频率;s α:阻带衰减,单位:dB 。
说明:(1)衰减在这里以分贝(dB )为单位;即222110lg10lg 1()NC H j αλλ⎡⎤==+⎣⎦(2)当3dB α=时p C Ω=Ω为通常意义上的截止频率。
(3)在滤波器设计中常选用归一化的频率/C λ=ΩΩ,即1,p sp s ppλλΩΩ===ΩΩ图b 为巴特沃斯低通滤波器指标3、设计巴特沃斯低通滤波器的方法如下:(1)计算归一化频率1p p pλΩ==Ω,ss pλΩ=Ω。
(2) 根据设计要求按照210101pC α=-和lg lg saN λ=其中a =特沃斯滤波器的参数C 和阶次N ;注意当3p dB α=时 C=1。
巴特沃斯低通滤波器课程设计

电路基础课程设计巴特沃斯低通滤波器设计目标:通带边界频率ωc=4396rad/s (f c=700Hz);通带最大衰减αmax=3dB;阻带边界频率ωs=26376rad/s(f s=4200Hz); 阻带最小衰减αmin=30dB;1.设计步骤⑴设计电压转移函数①将给定的电压衰减技术指标进行频率归一化选取归一化角频率ωr=ωc,这样通带边界频率Ωc=ωc/ ωr=1,阻带边界频率Ωs=ωs/ ωr=ωs/ωc。
②根据归一化的技术指标求出电压转移函数巴特沃斯低通滤波器的阶数n=Log(100.1αmin−1) 2Log(Ωs)带入数据求得n=1.93 取整得n=2由a k=2sin(2k−1)π2n,b k=1和H(s)=U out(s)U in(s)=∏A ks2+a k s+b kn2k=1可得到电压转移函数H(s)=U out(s)U in(s)=1s2+√2s+1将转移函数进行反归一化,即另s=sωc 得到实际转移函数H(s)=U out(s)U in(s)=1s243962+√2s4396+1⑵转移函数的实现选取下图作为实现转移函数的具体电路:列节点方程求解转移函数节点1 U1(1R1+1R2+s∗C1)−1R1U in−1R2−s∗C1∗U2=0节点2 (1R2+s∗C2)U2−1R2U1=0又有U out=U3解得H(s)=U outU in=11+(R2+R2)s∗C2+C1C2R1R2s2对比解得的电压转移函数和推得的电压转移函数里各项的系数并且令R1= R2,C1=1μF,可以得到C1=11000000F=1μFR1=250000√21099Ω=321.705ΩR2=250000√21099Ω==321.705ΩC2=12000000F=0.5μF因实验室没有0.5μF的电容因此取C2=0.47μF2.计算机仿真⑴软件环境:Multisim 10⑵电路图:⑶仿真结果:①700Hz下的波形图②4200Hz下的波形图③波特图◎700Hz下衰减2.673dB◎4200Hz下衰减30.491dB3.实验室实际操作因实验室没有0.5μF的电容和321.705Ω的电阻,因此取C2=0.47μFR1=R2=330Ω实际连电路时,选取集成电路块的第1、2、3引脚分别作为放大器的输出端、负端和正端,第4和11引脚作为供电端,C2一端连接电压源的接地线。
低通滤波器 实验报告

1.概述低通滤波器LPF是滤除噪声用得最多的滤波器。
由于高阶有源低通滤波器的每个滤波节皆由二阶滤波器和一阶滤波器组成。
我们设计一个巴特沃兹二阶有源低通滤波器。
并使用电子电路仿真软件进行性能仿真。
(2)巴特沃斯低通滤波器的幅频特性为: n c uo u A j A 211)(⎪⎪⎭⎫ ⎝⎛+=ωωω . . . . . . (1)其中Auo 为通带内的电压放大倍数,ωC 为截止角频率,n 称为滤波器的阶。
从(1)式中可知,当ω=0时,(1)式有最大值1;ω=ωC 时,(1)式等于0.707,即Au 衰减了 3dB ;n 取得越大,随着ω的增加,滤波器的输出电压衰减越快,滤波器的幅频特性 越接近于理想特性。
当 ω>>ωC 时, n c uo u A j A ⎪⎪⎭⎫ ⎝⎛≈ωωω1)( . . . . . . (2) 两边取对数,得:lg 20cuo u n A j A ωωωlg 20)(-≈ . . . . . . (3) 此时阻带衰减速率为: -20ndB/十倍频或-6ndB/倍频,该式称为计算公式。
2.工作原理图图2-1低通滤波器原理图2-2低通滤波器原理图工作原理:(1)滤波器是具有频率选择作用的电路或运算处理系统。
滤波处理可以利用模拟电路实现,也可以利用数字运算处理系统实现。
滤波器的工作原理是当信号与噪声分布在不同频带中时,可以在频率与域中实现信号分离。
在实际测量系统中,噪声与信号的频率往往有一定的重叠,如果重叠不严重,仍可利用滤波器有效地抑制噪声功率,提高测量精度。
任何复杂地滤波网络,可由若干简单地、相互隔离地一阶与二阶滤波电路级联等效构成。
一阶滤波电路只能构成低通和高通滤波器,而不能构成带通和带阻。
可先设计一个一阶滤波电路来熟悉电路设计思路以及器件使用要求和软件地进一步学习。
有源滤波器地设计,主要包括确定传递函数,选择电路结构,选择有源器件与计算无源元件参数四个过程。
巴特沃斯滤波器的特点是通频带内的频率响应曲线最大限度平坦,没有起伏,而在阻频带则逐渐下降为零。
有源低通滤波器的课程设计-四阶巴特沃斯滤波器

电气工程学院有源低通滤波器课程设计设计题目:有源低通滤波器设计学号:姓名:同组人:指导教师:设计时间:2012年11月20号设计地点:电气学院实验中心指导教师签字:年月日学生姓名:指导教师:一、课程设计题目:有源低通滤波器设计二、课程设计要求1. 根据具体设计课题的技术指标和给定条件,独立进行方案论证和电路设计,要求概念清楚、方案合理、方法正确、步骤完整;2. 查阅有关参考资料和手册,并能正确选择有关元器件和参数,对设计方案进行仿真;3. 完成预习报告,报告中要有设计方案,设计电路图,还要有仿真结果;4. 进实验室进行电路调试,边调试边修正方案;5. 撰写课程设计报告——最终的电路图、调试过程中遇到的问题和解决问题的方法。
三、进度安排2.执行要求课程设计共5个选题,每组不得超过2人,要求学生在教师的指导下,独力完成所设计的详细电路(包括计算和器件选型)。
严禁抄袭,严禁两篇设计报告雷同。
摘要滤波器用于对信号的频率具有选择性的电路,它的功能是使特定频率范围内的信号通过,有源滤波器被广泛用于信息处理、数据传送等电路中。
在对二阶有源低通滤波器的原理进行分析的基础上,采用2个2阶低通滤波电路级联的方案,设计了基于巴特沃斯逼近的4阶有源低通滤波器。
在Multisim软件中使用虚拟示波器、波特图示仪等设备,对设计的滤波器的交流特性进行仿真,并对仿真结果进行了分析,其交流特性符合理论设计,具有一定的参考价值。
关键词:滤波器,有源低通,巴特沃斯,multisimAbstractAbstract:Filter is the circuit which has a selective for the frequency of signals,its function is to make a specific range offrequency through.Source filter is widely used for information processing and data transmission circuit.Based on the analysis of principle of 2nd Source low passed filter,by using the Scheme of cascading two 2nd source low-passed filter and themethod of examining the table,the 4nd source low-passed filter based on Butterworth is designed.By using the oscilloscopeand Bode plotter in Multisim ,the AC Features of this Filter was Simulated,and the sim ulation results were analyzed,it SAC features met with theory design and has certain reference value.Key words: Source low—passed filter,Butterworth,Multisim目录摘要 (3)Abstract (3)目录 (4)第一章系统方案设计 (1)1.1 滤波器介绍 (1)1.2 有源低通滤波器的设计要求 (1)1.2.1设计内容 (1)1.2.2设计要求 (1)1.2.3元器件 (1)1.2.4考核标准 (1)1.3芯片介绍 (2)1.4有源低通滤波器的设计原理 (2)1.5有源低通滤波器的设计方案 (3)第二章仿真 (5)2.1仿真电路图 (5)2.2 仿真结果分析 (5)2.2.1瞬态特性分析 (5)2.2.2频率特性分析 (7)第三章电路调试 (10)3.1实物面包板图 (10)3.2调试最终元器件阻值 (11)3.3 PCB制版 (12)第四章结论 (13)第五章心得体会与建议 (14)参考文献 (15)附录1:元器件清单 (16)第一章系统方案设计1.1 滤波器介绍滤波器用于对信号的频率具有选择性的电路,它的功能是使特定频率范围内的信号通过,而阻止其他频率的信号通过。
巴特沃斯低通滤波器的设计精编资料

巴特沃斯低通滤波器的设计巴特沃斯低通滤波器的设计1、巴特沃斯滤波器的介绍巴特沃斯低通滤波器的幅度平方函数定义为2221|()|1NH j C λλ=+其中C 为一常数参数,N 为滤波器阶数,λ为归一化低通截止频率,/p λ=ΩΩ。
式中N 为整数,是滤波器的阶次。
巴特沃斯低通滤波器在通带内具有最大平坦的振幅特性,这就是说,N 阶低通滤波器在0Ω=处幅度平方函数的前2N-1阶导数等于零,在阻带内的逼近是单调变化的。
巴特沃斯低通滤波器的振幅特性如图a 所示。
滤波器的特性完全由其阶数N 决定。
当N 增加时,滤波器的特性曲线变得更陡峭,这时虽然由a 式决定了在p Ω=Ω处的幅度函数总是衰减3dB ,但是它们将在通带的更大范围内接近于1,在阻带内更迅速的接近于零,因而振幅特性更接近于理想的矩形频率特性。
滤波器的振幅特性对参数N 的依赖关系如图a 所示。
设归一化巴特沃斯低通滤波器的归一化频率为λ,归一化传递函数为()H p ,其中p j λ=,则可得:2221()1(1)N Np jH j C pλλ==+-p 图a 巴特沃斯低通滤波器的振幅特性由于221()()()1()a a jsNcH s H s AsjΩ=--=Ω=+Ω所以巴特沃斯滤波器属于全极点滤波器。
2、常用设计巴特沃斯低通滤波器指标pλ:通带截止频率;pα:通带衰减,单位:dB;sλ:阻带起始频率;sα:阻带衰减,单位:dB。
说明:(1)衰减在这里以分贝(dB)为单位;即222110lg10lg1()NCH jαλλ⎡⎤==+⎣⎦(2)当3dBα=时p CΩ=Ω为通常意义上的截止频率。
(3)在滤波器设计中常选用归一化的频率/Cλ=ΩΩ,即1,p sp sp pλλΩΩ===ΩΩ图b 为巴特沃斯低通滤波器指标3、设计巴特沃斯低通滤波器的方法如下:(1)计算归一化频率1p p pλΩ==Ω,ss pλΩ=Ω。
(2) 根据设计要求按照210101pC α=-和lg lg saN λ=其中a =特沃斯滤波器的参数C 和阶次N ;注意当3p dB α=时 C=1。
巴特沃斯低通滤波器

带最小衰减α =30dB,按照以上技术指标设计巴特沃斯低通滤波器。 0.1a s
1a p
1a s
2.4
0242 4.25, 2.4
2.4 10 1 2 f lg 0.0242 lg 0.0242 NN 2 4.25, 55 lgf 2.4 4.25, N N s sp lg 2.4 2.4 2 f p
H( a s)
N c
(s s
k 0
N 1
k
)
7 j 3
• 例如N=3, 通过下式可以计算出6个极点 5 2 4 j j j j s 3 c 3 s 2 c 3 s 0 c 3 s1 c
s 4 c
j2
s 5 c
要求
f i g u r e ; p l o t ( Q , H a s ) ; a x i s ( [ 0 5]);xlabel('f(kHz)'),ylabel('20lg(abs(H_{a}(j{\Omega})))(dB)');
3 0
- 7 0
• • • • •
L=length(Ha); Yt=Xt(1:L).*Ha; figure;plot(Q,abs(Yt));axis([0 60 0 150]); yt=ifft(Yt); figure;plot(Q,yt);
• 模拟低通滤波器的设计指标 • 构造一个逼近设计指标的传输函数Ha(s) • Butterworth(巴特沃斯)低通逼近
模拟低通滤波器的设计指标及逼近方法(续)
• 模拟低通滤波器的设计指标有αp, Ωp,αs和Ωs。 • Ωp;通带截止频率 • Ωs:阻带截止频率
Butterworth (巴特沃斯)滤波器设计参考

可以看出 fc@1000Hz 有-3dB 的衰减。
6
3. 1 阶 Butterworth HPF 设计
1 z 1 s C1 1 z 1 1 z 1 1 H ( z) , set G (C1 1) (C1 1) z 1 C1 1 1 H (s) , s 1 G Gz 1 H ( z) 1 G (C1 1) z 1 B0 G, A0 1, B1 B0 , B2 0 A2 0
多项式因子
1 2 3 4 5 6 7 8
(Note: 参考 维基百科 “巴特沃斯滤波器”)
1
由此得到 d0=a0=aN=1 情况下的 Butterworth 多项式展开的系数表:
H (s)
d0 , a0 a N d 0 1 a 0 a1 s a 2 s 2 a N s N
Butterworth (巴特沃斯)滤波器设计参考
-- By Water 在嵌入式音频产品开发过程中经常会到 LPF(Low Pass Filter 低通滤波器)和 HPF(High Pass Filter 高通滤 波器),一般情况下都是离线用工具(如: Matlab)设计好滤波器的参数(Filter Coefficients)再应用到产品中 去。但有些状况下需要用户自己根据需求来实时(Real-time)调整 Filter Frequency Response (滤波器频率响应), 这种情形下就需要在嵌入式系统中实时根据客户的设定需求来产生相应的 Filter Coefficients。 下文就汇总出了 N 阶 IIR LPF & HPF Butterworth 滤波器系数的设计方法, 具体的算法原理推导可以参考陈佩 青《数字信号处理教程》一书,此处只给出工程上可以应用的结论。
巴特沃斯低通滤波器设计

巴特沃斯低通滤波器一、设计要求(1)设计一巴特沃斯数字低通滤波器,在0.3π通带频率范围内,通带幅度波动小于1dB ,在0.5π~πrad 阻带频率范围内,阻带衰减大于12dB 。
二.设计过程巴特沃斯双线性变换法(1)数字指数:p w =0.3π,s w =0.5π,(2)求p Ω,s Ω利用频率预畸变公式得:p Ω=2T tan 2p w =2T tan 320π=1.019⨯1Ts Ω=2T tan 2s w =2T tan 4π=2T (3)确定滤波器阶数sp λ=s p ΩΩ=211.019TT ⨯=1.963 sp k≈0.132 N=—lg lg sp sp k λ=—lg 0.132lg1.963≈3.0023 N=4 (4)确定系统函数G(p)= 43212.613 3.4142 2.61311p p p p ++++ c Ω=p Ω()10.12101p a N --=1.019⨯1T⨯()10.1124101-⨯⨯-=1.2065T P=11211c s z s T z ---=Ω+=1c Ω⨯2T ⨯1111z z ---+=11211.20651z z ---+ H(z)=G(p)=12341234146434.1675441.3465432.542711.06234 1.69864z z z z z z z z--------++++-+-+三.软件仿真(1)将分子分母带入Matlab 验证b=[1 4 6 4 1];a=[34.16754 -41.34654 32.5427 -11.06234 1.69864];[H,w]=freqz(b,a,1000);plot(w,20*log10(abs(H)/max(H)),'-');grid;xlabel('frequency');ylabel('magnitude');-250-200-150-100frequency m a g n i t u d e图(a )频率——幅度衰减图0.3π≈0.940.9250.930.9350.940.9450.950.955frequency m a g n i t u d e图(b)0.5π≈1.57frequency m a g n i t u d e图(c)(2)用Matlab 直接仿真出低通滤波器wp=2*tan(0.3*pi/2)*1000;ws=2*tan(0.5*pi/2)*1000;ap=1;as=12;[n,wn]=buttord(wp,ws,ap,as,'s');[b,a]=butter(n,wn,'s');[bn,an]=bilinear(b,a,1000);[H,w]=freqz(bn,an);plot(w,abs(H),'-');grid;xlabel('frequency');ylabel('magnitude');legend('双线性变化法');figure(2);plot(w,20*log10(abs(H)/max(H)),'-');grid;00.51 1.522.533.5frequency m a g n i t u d e0.3π≈0.94图(d)0.5π≈1.57图(e)四.分析将计算得出的低通滤波器系统函数H(z)的分子分母各项系数用Matlab验证,得图(a)幅频关系图。
一阶巴特沃斯低通滤波器电路图
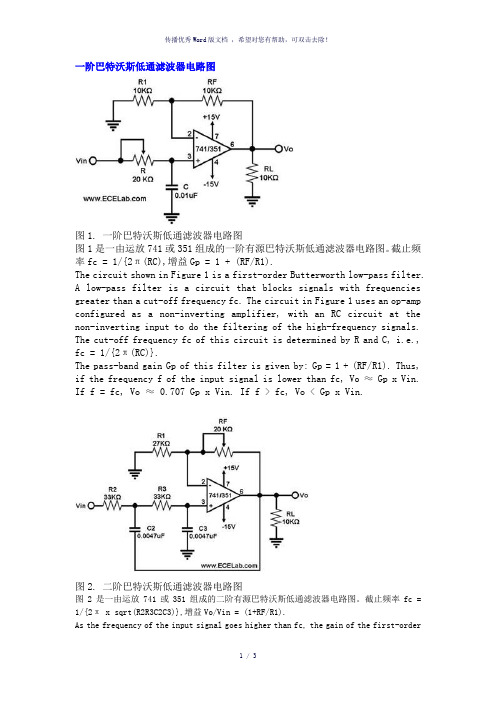
一阶巴特沃斯低通滤波器电路图图1. 一阶巴特沃斯低通滤波器电路图图1是一由运放741或351组成的一阶有源巴特沃斯低通滤波器电路图。
截止频率fc = 1/{2π(RC),增益Gp = 1 + (RF/R1).The circuit shown in Figure 1 is a first-order Butterworth low-pass filter.A low-pass filter is a circuit that blocks signals with frequencies greater than a cut-off frequency fc. The circuit in Figure 1 uses an op-amp configured as a non-inverting amplifier, with an RC circuit at the non-inverting input to do the filtering of the high-frequency signals. The cut-off frequency fc of this circuit is determined by R and C, i.e., fc = 1/{2π(RC)}.The pass-band gain Gp of this filter is given by: Gp = 1 + (RF/R1). Thus, if the frequency f of the input signa l is lower than fc, Vo ≈ Gp x Vin. If f = fc, Vo ≈ 0.707 Gp x Vin. If f > fc, Vo < Gp x Vin.图2. 二阶巴特沃斯低通滤波器电路图图2是一由运放741或351组成的二阶有源巴特沃斯低通滤波器电路图。
一种巴特沃斯低通滤波器构成的PWM转DAC设计

一种巴特沃斯低通滤波器构成的P WM 转D A C设计*龙顺宇,何程,杨伟,吴建奇(海南热带海洋学院海洋信息工程学院,三亚572022)*基金项目:海南省2020年教育发展专项资金项目(H n j g202091);海南热带海洋学院2020年校级教育教学改革研究项目(R H Y j gz d 202004);海南热带海洋学院2019年校级教改项目(R H Y J G 201908)㊂摘要:本文提出一种巴特沃斯有源低通滤波器构成的P WM 转D A C 设计,利用S T C 8单片机片内12位分辨率的P WM发生器产生了频率为10k H z ㊁占空比可变的P WM 信号㊂将信号送入巴特沃斯低通滤波器后,P WM 信号转换为直流电压,电压幅度与P WM 信号占空比呈正比变化,转换得到的直流电压纹波小于0.2m V ,转换分辨率可达1/12位㊂转换电路线性度较高㊁纹波小㊁谐波抑制比较高㊂相比于专用D A C 芯片或P A C 芯片而,该方案性价比高,可以适配于分辨率要求高㊁建立时间要求一般的应用场景㊂关键词:脉宽调制;数/模转换器;P A C 转换器;巴特沃斯滤波器中图分类号:T P 31 文献标识码:AP WM t o D A C D e s i g n C o m p o s e d o f B u t t e r w o r t h L o w -pa s s F i l t e r L o n g S h u n y u ,H e C h e n g ,Y a n g W e i ,W u J i a n qi (C o l l e g e o f O c e a n o g r a p h i c I n f o r m a t i o n E n g i n e e r i n g ,H a i n a n T r o p i c a l O c e a n U n i v e r s i t y ,S a n ya 572022,C h i n a )Ab s t r ac t :I n t h e p a p e r ,a P WM t o D A Cde s i g n i s p r o p o s e d ,w h i c h i s c o m p o s e d of B u t t e r w o r t h a c t i v e l o w -pa s s f i l t e r .I t u s e s t h e 12b i t r e s -o l u t i o n P WM g e n e r a t o r o n t h e S T C 8m ic r o c o n t r o l l e r t o g e n e r a t e a P WM s i g n a l w i t h a f r e q u e n c y o f 10k H z a nd a v a r i a b le d u t y c yc l e .A f -t e r s e nd i n g t he s i g n a l t o t h e B u t t e r w o r t h l o w -p a s sf i l t e r ,t h e P WM s ig n a l i s c o n v e r t e d i n t o a D C v o l t a g e ,a n d th e v o l t a g e a m pl i t u d e c h a n -g e s i n p r o p o r t i o n t o t h e P WM s i g n a l d u t y c y c l e .T h e c o n v e r t e d D C v o l t a g e r i p pl e i s l e s s t h a n 0.2m V ,a n d t h e c o n v e r s i o n r e s o l u t i o n c a n r e a c h 1/12b i t .T h e c o n v e r s i o n c i r c u i t h a s h i g h l i n e a r i t y ,s m a l l r i p p l e a n d h i g h h a r m o n i c s u p p r e s s i o n .C o m pa r e d w i t h a d e d i c a t e d D A C c h i p o r a P A C c h i p ,t h i s s o l u t i o n i s c o s t -e f f e c t i v e a n d c a nb e a d a p t e d t o a p p l ic a t i o n s c e n a r i o s w i t h h i g h r e s o l u t i o n r e q u i r e m e n t s a nd ge n e r -a l s e t u p t i m e r e qu i r e m e n t s .K e yw o r d s :P WM ;D A C ;P A C c o n v e r t e r ;B u t t e r w o r t h f i l t e r 0 引 言通用型8位㊁16位㊁32位微控制器芯片中通常不带D A C 资源,无法凭借芯片自身实现数/模转换[1-2]㊂若需要程控输出高精度模拟电压,大多采用专用D A C 芯片,该类专用芯片在价格㊁分辨率㊁建立时间㊁内部结构㊁电压范围㊁输出通道数量及通信接口形式上存在较大差异,价格不低甚至超过了主控单片机的成本[3-4]㊂基于此类场景的实际需求,将P WM 信号转换为D A C 的方法得以广泛使用,只需将P WM 信号通过一阶R C 或L C 低通滤波器即可得到直流电压,此类电路虽然简单但转换质量不高,无源滤波形式下会严重影响D A C建立时间指标,导致输出信号滞后,线性度差[5-6]㊂故而本文改进了滤波器形式,选用M C P 6002运算放大器设计一种巴特沃斯低通滤波器,在此基础上采用了S T C 8增强型P WM 资源,对转换原理㊁过程㊁实现进行探究,使得系统指标满足一般场景的需求㊂1 P WM 转D A C 的基本原理以单极性P WM 信号为例,从时域上进行分析,该信号的周期保持固定,只是高/低电平所占的脉宽(即占空比)发生了改变,理论研究时可以将P WM 信号进行时域分解,变成一个直流分量加平均幅值为零的方波形式,直流分量幅值与占空比呈正比变化[7-8]㊂若占空比变化,则直流分量也会跟随改变,若在P WM 输出后级连接低通滤波器就可以衰减交流成分,得到幅值随占空比变化而变化的模拟电压,虽然交流成分不可能完全去除,但得到的模拟电压已经较为平滑,其转换过程如图1所示㊂若从频域理解P WM 信号,可以结合傅里叶级数的相关方法㊂将周期不变㊁占空比变动的P WM 信号进行分图1 P WM 转D A C 基本原理解,可以将其看作是基波频率和无限多个整数倍谐波的总和,信号函数f (t)级数展开之后有:f (t )=U 0+ðɕn =1U n ˑc o s 2πn t T+V n ˑs i n 2πn t T(1) 式中,U 0为PWM 信号的直流分量,数值等于P WM 信号的实际幅度与占空比的积:U 0=12T ʏT-Tf (t )d t (2) 式中,U n 和V n 就是PWM 信号的交流分量,数值等于P WM 信号的载波频率乘以整数倍之后的高频谐波,可以将其表达为:U n =12T ʏT-T f (t )c o s 2πn tTd t (3)V n=12TʏT-T f (t )s i n 2πn tT d t (4) 设U m 代表P WM 信号的幅度,D 为P WM 信号的占空比,代入式(2)~式(4),可以得到此时P WM 信号的直流分量U 0为:U 0=U m ˑD(5) 此时P WM 信号的交流分量U n 和V n 为:U n =U m ˑ1n πs i n (n πD )-si n2n π1-D2(6)V n =0(7) 式(5)和式(6)中的D 必须合理取值,只有在合适的占空比范围内才能得到细分电压,U n 和V n 是P WM 信号的整数倍正弦高次谐波,对于输出的模拟电压而言是应该去除的成分,所以应用中需要设计低通滤波器(L P F ),L P F 尽可能衰减谐波导致的纹波,只保留直流分量,即P WM 转换后输出电压U D A C 应该为:U D A C =U m ˑD(8)2 硬件L P F 单元设计将P WM 信号转换为D A C 本质就是尽可能地去除交流分量,处理得到的直流分量部分与占空比大小呈正比变化,这样就能用P WM 信号占空比调节间接得到直流电压的幅度调节,最终实现P A C 转换(即P WM 到D A C 的转换)㊂通常情况下,硬件采用一阶或多阶R C ㊁L C 低通滤波器,此类无源滤波电路较为简单,但输出阻抗较大,对于多阶的组成形式而言阻抗更大,P WM 信号虽然可以得到处理,但是输出的直流电压带载能力大大降低,很容易被拉低幅值,影响使用㊂而用运算放大器构成的L P F 有很大改善,不存在负载驱动问题,还可以方便地扩展为多阶滤波形式,其线性度㊁频幅特性以及抗干扰性都更好㊂在设计具体硬件滤波器之前需确定相关参数,设定供电电压U m 为5V ,即P WM 信号高电平幅值为5V ,低电平为0V ㊂实验中单片机系统时钟为27MH z ,P WM 信号输出分辨率为12位,若要求输出电压精度为12位,则P WM 信号的输出频率应配置为单片机系统时钟除以输出电压精度再除以2分频系数,即27MH z /212/2=3.3k H z ㊂然后根据傅里叶级数计算L P F 所需的衰减倍数,当P WM 信号占空比D 为0.5时,基波的幅度U 0最大,此时L P F 能将基波以上的多次谐波幅度衰减至1/2个L S B 以下㊂在P WM 信号的交流分量中,n =1时的基波频率最低,将n =1代入式(6),可得基波幅度:U n =1=2ˑU m π=2ˑ5π=3.18309886V ʈ3.1831V (9) 则L P F 所需的最低衰减倍数U f 为:U f =12ˑU m 212ˑ1U n =1=52ˑ4096ˑ3.1831=0.0001917(10) 结合式(9)和式(10)可知,输出12位精度的直流电压时,L P F 衰减倍数U f 应为0.0001917,约-74.34d B ㊂从理论上计算至少需要4阶L P F 单元,可采用两级两阶巴特沃斯L P F 滤波器级联得到㊂按照相关计算在L T s pi c e 软件中进行电路仿真,取交流1V ㊁相位0ʎ㊁10H z~10k H z 扫描频率范围,得到的频率响应如图2所示,在3.3k H z 处的衰减约为-81d B ,满足大于-74.34d B 的需求,这样就可以留有一些裕量去衰减高频谐波,输出相位滞后于输入P WM 信号相位约400ʎ,因输出信号为直流电压,故相位滞后不产生实际影响㊂得到必要的参数后即可设计硬件电路,综合考虑运算放大器带宽㊁成本及电路复杂度之后,实际使用了一级三阶巴特沃斯L P F 滤波器构成所需电路,电路原理如图3所示㊂电路由单5V 供电,P WM _I N 为P WM 信号输入端子(由S T C 8产生),经施密特触发器74L V C 1G 14芯片整形㊁去毛刺之后送入由M C P 6002运放构成的三阶巴特沃斯L P F 滤波器,最后得到的D C _O U T 端子即为输出电压㊂3 系统软件设计实验中选取S T C 8A 8K 64S 4A 12产生了频率为图2 两级两阶巴特沃斯L P F滤波器频率响应图3 三阶巴特沃斯低通L P F 滤波器电路原理图10k H z ㊁分辨位数12位㊁占空比可在0至100%变化的P WM 信号㊂因设计具有通用性,单片机的选择并无特殊要求,有的单片机具备高级定时/计数器单元㊁P C A 单元或者增强型P WM 发生器,产生的P WM 信号支持4㊁6㊁8㊁12㊁16乃至32位(如意法半导体公司生产的S TM 32F 334可产生32位分辨率高精度P WM 信号),此类微控制器产生的P WM 信号就更加细分,从原理上分析,转换后的D A C 精度会更高,但在实际应用中也要考虑运放性能㊁干扰等实际原因,从而进行合理选择㊂为了方便控制P WM 输出脉宽,单片机系统中分配3个I /O 口用作P WM 信号输出使能(K 1按键)㊁P WM 信号脉宽增加(K 2按键)㊁P WM 信号脉宽减小(K 3按键),其软件流程如图4所示㊂当K 1按键按下时,单片机使能P WM 信号输出,所得P WM 占空比默认为50%,在此基础上按下K 2或K 3按键即可分别控制脉宽的增加或减小,P WM 配置部分源码如下:v o i d m a i n (){ //主函数 P _S W 2=0x 80;//访问扩展寄存器P WM C K S =0x 00;//系统时钟图4 软件控制P WM 调整流程图 P WM C =0x 0400;//设置P WM 周期 P WM 0C R=0x 80;//使能P WM 输出 P _S W 2=0x 00;//关闭访问扩展寄存器P WM C R=0x C 0; //启动P WM 模块 W h i l e (1){K E Y _I n i t();}//循环按键处理}4 系统测试与分析按照图4所示硬件电路原理图绘制P C B并打样贴片后可以得到实物样式如图5所示,由于M C P 6002芯片内部自带两个运算放大器单元,为此做了图5 设计实物样式双通道P WM 信号转D A C 单元㊂模块实物做好后用锂电池组为其供电,实测供电电压为4.8V ,然后将S T C 8A 8K 64S 4A 12产生的P WM 信号送入模块相关端子并测量输出电压,P WM 信号占空比与输出电压的实测数据如表1所列㊂从数据误差上看,转换后的D A C 线性度优于1%㊂该模块参数与12位精度的专用P A C 芯片G P 8500(即客益电子生产的P WM 信号转换为D A C 的专用芯片)以及专用的D A C 芯片T L C 5618(即T I 公司生产的12位D A C )做了指标对比,结果如表2所列㊂表1P WM信号占空比及输出电压数据表表2三种不同方案的D A C指标对比指标项P WM转D A C模块(本设计)G P8500芯片(P A C专用芯片)T L C5618芯片(D A C专用芯片)P WM信号频率10H z~300k H z50H z~50k H z-P WM信号占空比0~100%0~100%-建立时间4~10m s<20μs<2.5μs分辨率约12位12位12位从指标项的对比结果看,本设计中的P WM信号转D A C模块在分辨率上接近于专用芯片,性价比也有明显优势,但在D A C的建立时间指标项上还是相对较慢,比较适合做低速非隔离型D A C应用㊂5结语本设计作为单片机类电子工艺实训项目在实际实验中取得了较好的效果,在实测中发现了P WM信号载波频率及谐波分量会影响D A C的分辨率,若贸然降低P WM信号的载波频率,则基波频率和谐波频率也会发生变化㊂应先确定L P F参数,再考虑P WM信号配置,合理设计L P F结构才能达到指标要求㊂L P F阶数会影响D A C建立时间参数及输出线性度,因此需要根据实际需求进行设计适配㊂参考文献[1]吴财源,周华,钟球盛,等.基于双通信的多通道P WM式D A C模块设计[J].机电工程技术,2017,46(6):710.[2]陈启武,吴新春,王飞.基于S TM32的P WM D A C实现精密程控电压源的设计[J].今日电子,2016(6):5457.[3]游乙龙.基于单片机的P WM转D A C实现通用变频器的自动控制[J].机电工程技术,2015,44(6):9092.[4]赵月丽.P WM模拟D A C的关键参数分析[J].微型机与应用,2014,33(18):2022.[5]吴桂清,李泓霖,戴瑜兴,等.微控制器P WM接口实现高分辨率D/A转换器方法研究[J].电子学报,2012,40(8):16311634.[6]辛德环.传统数模转换器的优缺点分析及高性能P WMD A C的基本设计思想[J].机械工程师,2011(10):2933.[7]W S t e p h e n W o o d w a r d.几乎没有纹波的快速稳定同步P WM D A C滤波器[J].电子设计技术,2008(8):101.[8]秦健.一种基于P WM的电压输出D A C电路设计[J].现代电子技术,2004(14):8183.龙顺宇(实验师),主要研究方向为嵌入式应用㊁单片机智能㊁物联网技术应用㊂通信作者:龙顺宇,t l o n g s y@163.c o m㊂(责任编辑:薛士然收稿日期:2020-11-02)4结语为提高工地信息化管理水平,降低安全生产施工发生率,依托于智慧工地建设理念开展了基于人脸识别和检测的工地管理系统平台研究㊂智慧工地系统平台应紧密结合工程实际操作流程,尽量减少人工干预的可能性;同时,人脸识别数据采集应智能化,并且集成自动分析㊁自动记录功能㊁证据备份和检索功能㊂参考文献[1]吉林省住房和城乡建设厅关于推进智慧工地建设的指导意见[J].北方建筑,2020,5(5):8182.[2]王瑜,叶子明.基于B I M技术的智慧工地平台方案架构探讨[J].江西建材,2020(9):181182.[3]樊则森.建筑工业化与智能建造融合发展的几点思考[J].中国勘察设计,2020(9):2527.[4]谢佳霓,黄玉贤,沈玉香.智慧工地平台管控中B I M技术的应用研究[J].低温建筑技术,2020,42(8):124126.[5]黄凯,张梅,王涛,等.大型综合体项目智慧工地信息化平台建设关键技术[J].施工技术,2020,49(16):3639.[6]杜黎明,王燃.物联网技术在智慧工地中的应用研究[J].核动力工程,2020,41(S1):9295.[7]王淮.5G与人工智能在航道建设智慧监管上的应用[J].珠江水运,2020(15):1516.[8]王秋茗,孙广玲,陆小锋,等.智慧工地中低分辨率的安全帽状态识别[J].电子测量技术,2020,43(15):6367.[9]陈巨坤.智慧工地中的智能安全帽及其管理平台研究[D].广州:华南理工大学,2019.[10]董荣.基于智慧工地理念的塔机租赁公司定制化E R P设计[D].北京:中国矿业大学,2019.李建奎㊁陈阳㊁黄小星(工程师),李辉(助理工程师):主要研究方向为建筑工程项目管理㊂通信作者:李建奎,t k j g j i h d u9852@163.c o m㊂(责任编辑:薛士然收稿日期:2020-10-29)。
巴特沃斯滤波器设计
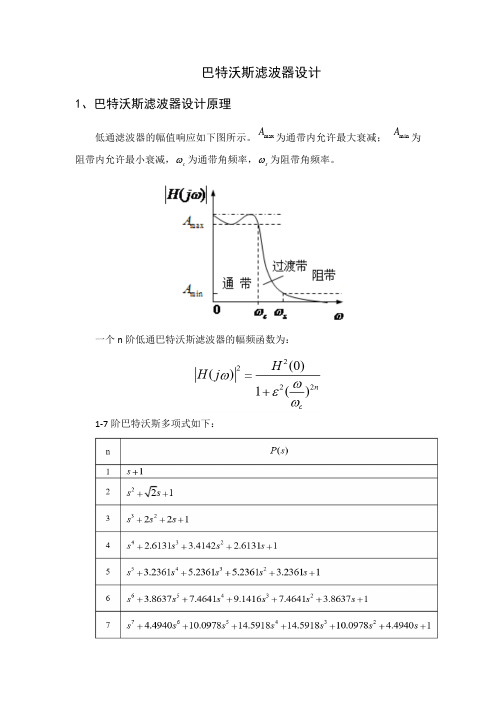
巴特沃斯滤波器设计1、巴特沃斯滤波器设计原理低通滤波器的幅值响应如下图所示。
maxA 为通带内允许最大衰减;minA 为阻带内允许最小衰减,c ω为通带角频率,s ω为阻带角频率。
一个n 阶低通巴特沃斯滤波器的幅频函数为:1-7阶巴特沃斯多项式如下:常数ε的作用是调整通带内允许的最大衰减,使其可小于3dB。
逼近过程中,A 需要确定的参数为ε和巴特沃斯多项式的阶数n,其中,通带内允许最大衰减maxA。
首先,推导确定了ε的大小;阶数n的大小取决于阻带内允许的最小衰减minε。
习惯上,多用衰减(分贝数)表示幅频特性。
因此,巴特沃斯低通响应为:ωω时,产生通带内最大衰减,即当=c解上式,可得:ωω时,产生阻带内最小衰减当=s上式可写为:对上式求解,可得:把 的表达式带入,可得:例子:用matlab 重复以上计算过程:wp=90*pi; ws=150*pi; Rp=3; Rs=10;N_true=(10^(Rp/10)-1)/(10^(Rs/10)-1);%真数 Num_Base=wp/ws;%底数N=ceil(log10(N_true)/log10(Num_Base)/2); wc=ws/((10^(Rs/10)-1)^(1/(2*N)));附加:Matlab 计算对数的时候,没有以a 为底b 的对数的函数,因此需要通过lgblog lg b a a改为以10为底的对数或者自然对数进行计算。
来源:https:///view/06e71fc5c67da26925c52cc58bd63186bceb92ca.html2、matlab 的巴特沃斯滤波器设计matlab 中提供了函数进行巴特沃斯滤波器设计同样对应上边的例子,通带90πHz ,通带最大衰减3dB ,阻带150πHz ,阻带最小衰减10 dB 。
Matlab 计算方法如下:229010lg 1315010lg 110nc nc πωπω⎧⎡⎤⎛⎫⎪⎢⎥+= ⎪⎪⎢⎥⎝⎭⎪⎣⎦⎨⎡⎤⎪⎛⎫⎢⎥+=⎪⎪⎢⎥⎝⎭⎪⎣⎦⎩20.32901010.995261501019nc nc πωπω⎧⎛⎫⎪=-= ⎪⎪⎝⎭⎨⎛⎫⎪=-= ⎪⎪⎝⎭⎩两式相除有:2290150900.99526/0.110581509nncc πππωωπ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭ 整理得:()20.60.11058n=因此,0.110580.61log 2.15532n ==取3n =,带入215010lg 110n c πω⎡⎤⎛⎫⎢⎥+= ⎪⎢⎥⎝⎭⎣⎦,即21509nc πω⎛⎫= ⎪⎝⎭计算得:1/6150326.7388/9c rad s πω== 3n =,查表得对应的巴特沃斯滤波器,并去归一化:7323232711 3.488210221653.5 2.135 3.488210221c c c s s s s s s s s s ωωω⨯==++++++⨯⎛⎫⎛⎫⎛⎫+++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭Matlab 代码如下: wp=90*pi; ws=150*pi; Rp=3; Rs=10;[N,wc]=buttord(wp,ws,Rp,Rs,'s');[B,A]=butter(N,wc,'s');f=1:300;w=2*pi*f;H=freqs(B,A,w);figure(1)plot(f,20*log10(abs(H)));grid on,xlabel('频率(Hz)'),ylabel('幅度(dB)')title('巴特沃斯模拟滤波器')设计滤波器幅值响应如下:3、pscad和matlab关于滤波器的配合设计的滤波器的系数经常很大,连续的滤波器在pscad中用s的传递函数实现,pscad中该元件系数有限制要在-810之间,实际的滤波器不满足该条件。
巴特沃斯低通滤波器设计

L1'
2
600 1.304 104
0.7654H
5.61mH
C2
1 c RS
C2'
2
1 1.304 104
600
1.8478F
0.038uF
L3
RS c
L'3
2
600 1.304 104
1.8478H
13.53mH
C4
1 c RS
C4'
2
1 1.304 104
600
0.7654F
0.016uF
设计实现电路
巴特沃斯低通滤波器迅速设计总结
一:根据滤波器性
能指标(通带内旳
最大衰减 c ,阻带
内旳最小衰减 s ,
截至频率 c ,阻带
起始频率 s )利用
公式
N
lg
1
s2
-1
2 lg s / c
求巴特沃斯低通滤波 器旳阶次N。
二:根据阶次N和考尔 型电路
RS' 1
L1' 0.7654
L'3 1.8478
一般情况下,电路是在匹配情况下工作,所以取
信源内阻 Rs 和负载电阻 RL 相等。
此时满足
Ha ( j0)
RL RS RL
1 2
根据反射系数公式
(s)
(
s)=1- 4RS RL
s' s
H
a
s
H
a
-s
j
达林顿电路构造
Rs 源电阻 RL 负载电阻
RS
I1
Es
V1
1
2
LC
I2
无损
五阶巴特沃斯有源低通滤波器的设计

222
一线技术
浅谈静电的危害及其消除
文⊙ 陈中银 盛宗生(南阳理工学院)
静电防灾己发展成为专门的科学,它 不 仅 限 于 静 电 工 程 学 ,而 且 广 泛 地 涉 及 到 燃 烧 化 学 工 程 学 、环 境 工 程 学 、材 料 工 程 学 和 系 统 工 程 学 。静 电 危 害 的 实 质 将 随 着 科 学 技 术 的 发 展 而 变 化 。所 以 ,了 解 静 电 的 危 害 ,熟 悉 静 电 的 消 除 方 法 显 得 越 来 越 重要了。 一、静电的危害 大家知道,物体带了静电,其周围空 间 即 存 在 静 电 场 。在 电 场 力 作 用 下 ,可以 产 生 种 种 物 理 现 象 。这 些 物 理 现 象 ,有的 有 利 ,有 的 有 危 害 。由 静 电 引 起 的 危 害 主 要有三个方面: (一)静电对生产的危害 由于静电对轻小物体有明显的力学作 用,因 而 在 某 些 生 产 部 门 中 会 引 起 严 重 的 障碍。如 在 某 些 粉 末 状 物 体 生 产 过 程 中 , 静 电 力 能 使 筛 孔 或 管 道 堵 塞;静 电 吸 引 灰 尘,使纺织品颜色灰暗,丝 质 脆 而 易 断; 感 光 胶 片 涂 膜 不 匀 ,出 现 拉 丝 、划痕;在 薄 膜 、纸 品 生 产 中 ,静 电 斥 力 能 使 产 品 离 散 而 无 法 整 理 ,而 静 电 引 力 又 能 使 产 品 互 相吸附而无法分离;静电力能吸引尘埃, 因而会严重影响某些电器外壳的喷涂质 量,也 会 影 响 某 些 超 净 工 作 场 所 环 境 的 净 化;车 间 工 人 由 于 在 地 面 上 行 走 、操 作 绝 缘 材 料 、在 椅 凳 和 工 作 台 面 上 移 动 、接近 或 触 及 其 它 带 电 体 、沾 附 带 电 粉 体 或 液 滴 等活动而带电,且人体充电电位一般为 1 k V 左右,最高可达 5 0 k V ,这足以影响比 较 精 密 的 电 器 设 备 、微 电 子 元 件 、计 算 机 等正常生产与工作。例如: 较新的集成电 路采用 H M O S 、S O S 等工艺,其静电敏感 度只有 3 0 ~4 0 V ,因而在制造和应用集成 电路时,必须从生产、运输、保管、组装、 调试、维修等场合采用一系列的保护措 施,防 止 人 体 静 电 电 位 的 产 生 而 带 来 的 影 响。 美国一家公司认为,一个价值 5 0 美分 (上接 222 页) 的集成电路,如果在生产和调测时忽略了 防静电措施,它将会出现极不稳定的特 性,因而大大降低了设备的可靠性,这时 的维修费用将会是 5 0 0 美元,即需要用原 旧件的一千倍的代价才能挽回质量和信 誉。美国的一些公司在采取防静电措施 后,元件失效率降低了 1 0 0 / n 。节约了上 百万的资金,其效益是投资购买防静电器 材的 1 0 倍以上。 (二)静电泄放的危害 对于电阻率特别大( ρ> 1 0 1 2 Ω m ) 的物 质,静电电荷不易散逸,静电电位越积越 高,在一定条件下导致火花放电瞬时功率 可达几十千瓦。把电能转变成热能,使易 燃易爆物引燃引爆,是十分危险的。例如: 干燥的制粉厂由于防尘设备不好,粉尘飞 扬,往往就会引燃粉尘,造成强烈爆炸,甚 至因拖擦车间地面油渍,使拖把因磨擦起 电而放电,引起充满汽油气的车间爆炸。 国内外因静电引起火灾、爆炸等事故屡见 不鲜。据有关资料统计,1 9 6 2 年~1 9 7 1 年 间,日本由于静电引起的火灾平均每年达 1 0 0 起;1 9 6 7 年~1 9 7 1 年间,加拿大空军 由于静电引起的燃油和油车着火达 1 1 次; 1 9 6 9 年 1 2 月份的两个星期内,连续发生 在英国、荷兰、挪威三国三艘 2 0 万吨级油 轮,因为冲洗船舱的水滴喷离水管或货油 流离油管时所带的电荷放电,引起严重的 爆炸事故,震惊了世界航运界。我国石油 工业从 6 0 年代以来迅猛发展,伴随而来的 因静电引起的火灾、爆炸等也时有发生。 在火化工厂里,静电事故率约为 1 0 % 。 (三)静电放电引起电击的危害 人在绝缘良好的地毯上行走,可带上 3 ~5 k V 的静电。一按触门把,使人感受到 电击而有惊悸和痛感;在其它生产现场, 如卷绕绝缘薄膜,收送印刷品、粉体装袋 作业等,都会发生电击伤害事故;静电电 击虽难以直接致人死亡,但由此而引起的 此外为了减少输入偏置电流及其漂移 对电路的影响,应使: 与 联立求解,可得: 恐怖情绪会使生产效率下降,精神受到 损。此 外 ,静 电 电 击 引 起 的 二 次 伤 害 事 故 也是不可忽视的。 二、消除静电的方法 为了防止电荷的积累,避免给国家和 个 人 生 活 带 来 的 严 重 危 害 ,就 必 须 采 取 行 之有效的措施,消除静电。其基本方法有: (一)接地法消除静电 如消除人体静电积累,将人体予以接 地,使人体电位不超过规定的 l 0 V 以下的 安 全 值 。人 体 接 地 的 主 要 方 法 要 看 地 面 的 导 电 性 ,一 般 水 泥 砂 浆 、大 理 石 、菱 苦 土 地 面 均 属 导 电 地 面;其 次 是 人 着 导 电 鞋 和 导 电 的 工 作 衣 、工 装 用 器 件 等 。在 操 作 高 静 电 敏 感 的 火 工 品 或 电 子 元 件 的 场 所 ,还 需要用电镯套,以降低人体电位至安全 值。人 在 操 作 时 动 作 要 小 心 谨 慎 ,严 禁 突 发 性 的 活 动 与 磨 擦 。对 于 存 在 金 属 外 壳 的 容 器 、设 备 、管 道 来 讲 ,也 要 采 取 接 地 或 跨接( 即各容器、管道、与设备之间用金属 线相连) 的方法消除静电。 (二)采取先进技术手段消除静电 各种高分子合成纤维材料是优良的绝 缘 材 料 ,容 易 积 累 静 电 ,现 今 我 国 已 研 制 出 各 种 新 型 的 抗 静 电 合 成 化 纤 材 料 。如为 防 止 石 油 输 送 过 程 中 ,由 于 石 油 在 管 道 内 流 动 摩 擦 而 产 生 的 电 荷 积 累 ,可 以 控 制 流 速 和 改 变 加 油 方 式 ,避 免 水 、空 气 和 油 品 的混合等措施减少摩擦产生的电荷积累, 同时采用抗静电添加剂。 (三)湿度控制法除静电 考虑到工作中的环境因素,应注意提 高空气湿度,使相对湿度控制在 4 5 % ~ 7 0 % 范围内,以减小物体表面的电阻率,增 加物体的漏电能力,防止电火花的产生; 减 少 粉 末 、纤 维 等 的 不 必 要 吸 附 。在 某 些 特 殊 环 境 条 件 工 作 的 设 备 上 ,还 应 安 装 放 电 尖 端 ,及 时 泄 漏 电 荷 的 积 累 ,防 止 产 生 电火花而引起火灾或爆炸事故。 三、仿真结果 使用 M u l t i s i m 进行仿真,很容易就可 以得到电路幅频特性和相频特性。在 B o d e P l o t t e r 仪表 I N 接系统输入端,O U T 接系 统 输 出 端 。打 开 仿 真 运 行 器 即 可 看 到 响 应 曲线。在 G r a p h e r 查看器中可以看到曲线 细节部分。 四、结束语 传统滤波器设计都是按照固定的模式 进 行 的 。本 文 就 给 出 了 一 个 低 通 滤 波 器 实 现 的 实 例 。但 经 典 滤 波 器 设 计 理 论 在 处 理 一 些 如 算 术 对 称 滤 波 器 的 设 计 、线 性 相 位 与 理 想 低 通 衰 减 相 结 合 等 问 题 时 ,却 存 在 较 大 困 难 。为 此 ,通 过 计 算 机 优 化 进 行 滤 波器设计的方法得到越来越广泛的应用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
巴特沃兹有源低通滤波器设计
李彦哲 关恩明
(中国电子科技集团第49研究所,黑龙江 哈尔滨 150001)
摘要:给出了二阶巴特沃兹有源低通滤波器的设计方法和设计实例,通过multisim 电路仿真试验能够得到一个性能优良的二阶有源低通滤波器。
关键词:有源;低通滤波器;设计 1 概述
低通滤波器LPF是滤除噪声用得最多的滤波器。
由于高阶有源低通滤波器的每个滤波节皆由二阶滤波器和一阶滤波器组成。
我们设计一个巴特沃兹二阶有源低通滤波器。
并使用电子电路仿真软件进行性能仿真。
2 设计方法 2.1频率特性
巴特沃斯低通滤波器的幅频特性为:
n
c
uo
u A j A 211)
(⎪⎪⎭
⎫ ⎝⎛+=ωωω . . . . . . (1)
其中Auo 为通带内的电压放大倍数,ωC 为截止角频率,n 称为滤波器的阶。
从(1)式中可知,当ω=0时,(1)式有最大值1;ω=ωC 时,(1)式等于0.707,即Au 衰减了 3dB ;n 取得越大,随着ω的增加,滤波器的输出电压衰减越快,滤波器的幅频特性 越接近于理想特性。
当 ω>>ωC 时,
n
c uo u A j A ⎪⎪⎭
⎫
⎝⎛≈ωωω1
)( . . . . . . (2) 两边取对数,得:
lg
20c
uo u n A j A ωω
ωlg 20)(-≈ . . . . . . (3) 此时阻带衰减速率为: -20ndB/十倍频或-6ndB/倍频,该式称为衰减估算式。
任何高阶滤波器都可由一阶和二阶滤波器级联而成。
对于n 为偶数的高阶滤波器,可以由
2n 节二阶滤波器级联而成;而n 为奇数的高阶滤波器可以由2
1
-n 节二阶滤波器和一节一阶滤波器级联而成,因此一阶滤波器和二阶滤波器是高阶滤波器的基础。
2.2设计步骤
有源滤波器的设计,就是根据所给定的指标要求,确定滤波器的阶数n ,选择具体的电路形式,算出电路中各元件的具体数值,安装电路和调试,使设计的滤波器满足指标要求,以巴特沃斯响应的二阶滤波器的设计为例。
具体步骤如下:
1)根据阻带衰减速率要求,确定滤波器的阶数。
2)选择具体的电路形式。
3)根据电路的传递函数和归一化滤波器传递函数的分母多项式,建立起系数的方 程组。
4)解方程组求出电路中元件的具体数值。
5)安装电路并进行调试,使电路的性能满足指标要求。
3 设计实例
设计一个有源低通滤波器,指标为:截止频率 f C =1kHz ,通带电压放大倍数:A uo =2,在f = 10f c 时,要求幅度衰减大于30dB 。
3.1设计步骤
1)由衰减估算式:-20ndB/+倍频,算出n = 2。
2)选择Sallen-Key 电路作为低通滤波器的电路形式。
R 3 R 4
u o
图1 压控电压源二阶有源低通滤波器
该电路的传递函数:
2
22
)(c c
c uo u s Q
s A s A ωωω++
=
. . . . . . (4)
其归一化函数:
1
1)(2
++=
L L uo
L u s Q
s A s A . . . . . . (5)
将上式分母与表1归一化传递函数的分母多项式比较得:
21
=Q
通带内的电压放大倍数:
3
4
1R R A A f uo +
===2. . . . . . (6) 滤波器的截止角频率:
c c f C C R R πω212
121==
=3102⨯π. . . . . . (7)
则:
2
212111
)
1(11C R A C R C R Q
uo c
-++=
ω21023⨯⨯=π. . . . . .(8) 4321//R R R R =+. . . . . . (9) 在上面四个式子中共有六个未知数,三个已知量,因此有许多元件组可满足给定特性的
要求,这就需要先确定某些元件的值,元件的取值有几种:
1) 当A f =1时,先取R 1=R 2=R ,然后再计算C 1和C 2。
2) 当A f ≠1时,取R 1=R 2=R ,C 1=C 2=C 。
3) 先取C 1=C 2=C ,然后再计算R 1和R 2。
此时C 必须满足:)(10
21F f C C C c
μ=== 4) 先取C 1,接着按比例算出C 2=KC 1,然后再算出R 1和R 2的值。
其中K 必须满足条件:K ≤A f -1+
2
41Q
对于本例,由于A f =2,因此先确定电容C 1=C 2的值,即取: F F F f C C C μμμ01.0)(10
10
)(103021===
==, 将C 1=C 2=C 代入(7)和(8)式,可分别求得: Ω⨯=⨯⨯⨯⨯==
3
16
311026.111001.021021πωC Q R c Ω⨯=⨯⨯⨯=
=
-36
321052.2210
01.01022
1πωC
Q R c Ω⨯=⨯+⨯=+=3
3
2141056.6710)52.2226.11(2)(R R A R f
Ω⨯=-⨯=-=33
431056.671
21056.671f A R R
3.2仿真结果
通过multisim 电路仿真试验能够得到一个性能优良的巴特沃兹二阶有源低通滤波器。
1Hz 时 6.02dB, 1kHz 时3dB, 10kHz 时-33.989dB,满足设计要求。
4结论
通过设计的二阶有源低通滤波器,给出了设计有源低通滤波器的基本设计方法,步骤,经过电路仿真我们设计的二阶有源低通滤波器性能优良。
参考文献
[1]童诗白,华成英模拟电子技术基础高等教育出版社1980;
[2]邵毅全,马耀庭三阶有源低通滤波器设计与仿真研究内江师范学院学报200908;。
