第二章课后练习答案
高中生物2019新教材选择性必修二第二章《种群及其演替》旁栏及课后练习答案

高中生物2019新教材选择性必修二《种群及其演替》第二章旁栏及课后练习答案第2章第1节群落的结构问题探讨稻田中生活着多种底栖动物,如大脐圆扇螺、中国圆田螺、苏氏尾鳃蚓、羽摇蚊的幼虫等,在稲田中饲养中华绒螯蟹(俗称“河蟹),由于河蟹喜食底栖动物和杂草,底栖动物和杂草都会减少。
同时,河蟹的爬行能起到松动田泥的作用,因而有利于水稻的生长。
讨论1. 河蟹与底栖动物(如螺类)的关系是怎样的?【答案】河蟹捕食底栖动物,它们之间存在捕食关系;河蟹和某些底栖动物可能还会捕食水中的浮游生物,因此河蟹与底栖动物的种间关系可能还包括种间竞争。
2. 提高河蟹的种群密度,稻田中其他动物种群会发生怎样的变化?【提示】本题有一定开放性。
河蟹的种群密度增大,会使很多生物种群的数量发生变化。
河蟹会吃掉更多的底栖动物和杂草,导致底栖动物等的数量减少;河蟹的爬行活动对田泥有松动作用,可以改善田泥的土壤肥力而有利于水稻的生长,可能会引起以水稻为食物的其他动物的数量增加。
有研究表明,养蟹稻田底栖动物的种类数、密度和多样性均低于常规稻田,且放蟹密度越大,降低得越明显。
为保护底栖动物的多样性,可以在稻田中增加河蟹饵料的投喂量。
旁栏思考题你能举例说出你所在地区的常见群落中占优势的物种吗?【提示】结合自己所在地区的实际情况,对附近的森林、草地、池塘等生物群落展开调查,举例说出群落中占优势的物种。
思考•讨论1讨论1. 红尾鸲和鹟的种间竞争对两个种群的分布有什么影响?【答案】红尾鸲和鹟的食性比较相似,种间竞争导致两个种群的分布范围缩小,甚至错开。
2. 资料2说明捕食、种间竞争在群落中是怎样相互联系的?【提示】海星与藤壶、贻贝、帽贝和石鳖四种动物存在捕食关系,后四种动物以水中的浮游生物、腐殖质等为食,彼此存在种间竞争关系;自然状态下,这五种生物可以共存,但在人为去除捕食者一一海星之后,藤壶、始贝、帽贝和石鳖之间主要是种间竞争。
且占优势的物种随时间推移而发生变化。
第二章练习题及参考答案

第二章练习题及参考答案《马克思主义基本原理概论》练习题及参考答案第二章认识世界和改造世界一、单项选择题1、唯物论认识论的基本原则和核心是(A )A反映论 B实践论 C先验论 D可知论2、人类认识发展的根本动力是(B )A科学兴趣 B社会实践 C求知欲望 D好奇心3、物质生产实践主要处理(A )A人与自然的关系 B人与人的关系 C对抗性矛盾的关系 D非对抗性矛盾的关系4、真理总是与谬误相比较而存在,相斗争而发展的,因而(A )A真理与谬误的对立是相对的 B真理中包含谬误的认识C谬误中包含一定的真理性认识 D谬误是真理不可摆脱的对立面5、认识的最终目的是(B )A发现真理 B改造世界 C创立科学理论 D改造客观规律6、人的认识能力是至上的,又是非至上的属于(D)观点A客观唯心论 B主观唯心论 C旧唯物论 D辩证唯物主义7、认识的本质在于( B )A主体创造 B能动反映 C社会实践 D客观存在8、人类认识运动的基本过程是(C)A概念——判断——推理 B感觉——知觉——表象C个别——一般——个别 D一般——个别——一般9、马克思认为“理论一经掌握群众,就会变成物质的力量”说明(B )A实践对理论有决定作用 B理论对实践有指导作用C理论比实践更为重要 D实践比理论重要10、真理是对客观事物和规律的(D )A本质认识 B深刻认识 C内在认识 D正确认识11、法国科学家路易·巴斯德说:“在观察事物之际,机遇偏爱有准备的头脑”。
这句话强调了(B )A人们对每一事物都要细心观察 B 人们在认识事物时要有理性指导C人们获得感性经验的重要性 D人们要充分发挥意识能动性12、人的认识是不是真理,要看(D)A能否满足人们的需要 B能否被大多数人认可C能否付诸实践 D能否在实践中取得预期效果13、“不唯上,不唯书,不唯师,只唯实”说明( B )A书本知识是不重要的 B一切从实际出发C上级的指示和决议不能成为行动的依据D没有直接经验就没有发言权14、从认识发展的规律看,“熟知”与“真知”的关系是(B )A熟知即真知 B熟知不等于真知 C熟知起源于真知 D熟知必然转化为真知15、唯心论与不可知论的关系是( B)A唯心论都是不可知论 B唯心论有可知论与不可知论之分C主观唯心论是可知论,客观唯心论是不可知论D客观唯心论是可知论,主观唯心论是不可知论16、认识的起点是感觉,这是( D )A唯物主义的观点 B唯心主义的观点C辩证唯物主义的观点 D唯物论和唯心论都可以承认的观点17、对不可知论最令人信服的驳斥是(C )A科学知识 B丰富的经验 C社会实践 D人类的认识能力18、判断对某一事物的认识是否完成的标志是( D)A占有的感性材料是否十分丰富真实B感性认识是否上升到理性认识C这一认识是否反复多次D理性认识是否运用于实践并取得预期效果19、唯物论和彻底的唯心论的认识论都是(B )A反映论 B可知论 C能动的革命的反映论 D先验论20、假象是(C )A人们认识中发生的错觉 B从正面反映本质的现象C从反面歪曲本质的现象 D不表现本质的现象21、实践作为检验认识真理性的标准具有不确定性的含义是(D)A实践标准是不可靠的 B科学理论也是检验真理的标准C除了实践标准还有其他标准D实践的历史局限性决定检验理论是一个过程22、辩证唯物主义认识论与唯心论认识论的区别是( C )A世界是可以被认识的 B认识发展是辩证的过程C客观事物是认识的对象 D社会实践是认识的基础23、人类活动的“两个尺度”是(C)A认识与实践 B真理与谬误 C真理与价值 D抽象与具体24、人们的下列活动中属于最基本的实践活动的是(C)A医生给病人做手术 B法官审理案件 C农民播种小麦 D科学家进行化学实验25、当代自然科学的发展日新月异,新的研究成果层出不穷,根本原因是(D)A科学家的聪明才智决定的正确的科技政策决定的C环境与资源的状况决定的 D生产实践的需要决定的26、“离开革命实践的理论是空洞的理论,不以革命的理论为指导的实践是盲目的实践”说明(C)A要重视实践对理论的决定作用 B要发挥理论对实践的指导作用C要坚持理论与实践相结合的原则 D要在实践中丰富和发展理论27、从本质上看,认识是( D)A主体心灵的主观创造 B主体心灵对客体的直觉C主体对客体的直接反映 D主体对客体的能动反映28、“从物到感觉和思想”与“从思想和感觉到物”的对立,属于(B)A辩证法与形而上学的对立B唯物主义反映论与唯心主义先验论的对立C经验论与唯理论的对立D能动的革命的反映论与消极的被动的反映论的对立29、“人的认识是主体对客体的直接反映”的观点属于(C )A主观唯心主义认识论B客观唯心主义认识论C形而上学唯物主义认识论 D辩证唯物主义认识论30、我们看到苹果的形状和颜色,嗅到它的气味,摸到它的光滑,尝到它的滋味,在意识中就形成对苹果的整体感性形象。
计算机组成原理第二章课后习题答案

第二章运算方法和运算器练习一、填空题1. 补码加减法中,(符号位)作为数的一部分参加运算,(符号位产生的进位)要丢掉。
2. 为判断溢出,可采用双符号位补码,此时正数的符号用(00)表示,负数的符号用(11)表示。
3. 采用双符号位的方法进行溢出检测时,若运算结果中两个符号位(不相同),则表明发生了溢出。
若结果的符号位为(01),表示发生正溢出;若为(10),表示发生负溢出。
4. 采用单符号位进行溢出检测时,若加数与被加数符号相同,而运算结果的符号与操作数的符号(不一致),则表示溢出;当加数与被加数符号不同时,相加运算的结果(不会产生溢出)。
5. 利用数据的数值位最高位进位C和符号位进位Cf的状况来判断溢出,则其表达式为over=(C⊕Cf)。
6. 在减法运算中,正数减(负数)可能产生溢出,此时的溢出为(正)溢出;负数减(正数)可能产生溢出,此时的溢出为(负)溢出。
7. 补码一位乘法运算法则通过判断乘数最末位Yi和Yi-1的值决定下步操作,当YiYi-1=(10)时,执行部分积加【-x】补,再右移一位;当YiYi-1=(01)时,执行部分积加【x】补,再右移一位。
8. 浮点加减运算在(阶码运算溢出)情况下会发生溢出。
9. 原码一位乘法中,符号位与数值位(分开运算),运算结果的符号位等于(两操作数符号的异或值)。
10. 一个浮点数,当其补码尾数右移一位时,为使其值不变,阶码应该(加1)。
11. 左规的规则为:尾数(左移一位),阶码(减1)。
12. 右规的规则是:尾数(右移一位),阶码(加1)。
13. 影响进位加法器速度的关键因素是(进位信号的传递问题)。
14. 当运算结果的补码尾数部分不是(11.0×××××或00.1×××××)的形式时,则应进行规格化处理。
当尾数符号位为(01)或(10)时,需要右规。
DS第二章_课后习题答案

第二章线性表2.1 填空题(1)一半插入或删除的位置(2)静态动态(3)一定不一定(4)头指针头结点的next 前一个元素的next2.2 选择题(1)A (2) DA GKHDA EL IAF IFA(IDA)(3)D (4)D (5) D2.3头指针:在带头结点的链表中,头指针存储头结点的地址;在不带头结点的链表中,头指针存放第一个元素结点的地址;头结点:为了操作方便,在第一个元素结点前申请一个结点,其指针域存放第一个元素结点的地址,数据域可以什么都不放;首元素结点:第一个元素的结点。
2.4已知顺序表L递增有序,写一算法,将X插入到线性表的适当位置上,以保持线性表的有序性。
void InserList(SeqList *L,ElemType x){int i=L->last;if(L->last>=MAXSIZE-1) return FALSE; //顺序表已满while(i>=0 && L->elem[i]>x){L->elem[i+1]=L->elem[i];i--;}L->elem[i+1]=x;L->last++;}2.5 删除顺序表中从i开始的k个元素int DelList(SeqList *L,int i,int k){int j,l;if(i<=0||i>L->last) {printf("The Initial Position is Error!"); return 0;}if(k<=0) return 1; /*No Need to Delete*/if(i+k-2>=L->last) L->last=L->last-k; /*modify the length*/for(j=i-1,l=i+k-1;l<L->last;j++,l++)L->elem[j]=L->elem[l];L->last=L->last-k;return 1;}2.6 已知长度为n的线性表A采用顺序存储结构,请写一时间复杂度为O(n)、空间复杂度为O(1)的算法,删除线性表中所有值为item的数据元素。
第二章课后习题答案

第二章课后习题答案第二章牛顿定律2-1如图(a)所示,质量为m的物体用平行于斜面的细线联结置于光滑的斜面上,若斜面向左方作加速运动,当物体刚脱离斜面时,它的加速度的大小为()(A)ginθ(B)gcoθ(C)gtanθ(D)gcotθ分析与解当物体离开斜面瞬间,斜面对物体的支持力消失为零,物体在绳子拉力FT(其方向仍可认为平行于斜面)和重力作用下产生平行水平面向左的加速度a,如图(b)所示,由其可解得合外力为mgcotθ,故选(D).求解的关键是正确分析物体刚离开斜面瞬间的物体受力情况和状态特征.2-2用水平力FN把一个物体压着靠在粗糙的竖直墙面上保持静止.当FN逐渐增大时,物体所受的静摩擦力Ff的大小()(A)不为零,但保持不变(B)随FN成正比地增大(C)开始随FN增大,达到某一最大值后,就保持不变(D)无法确定分析与解与滑动摩擦力不同的是,静摩擦力可在零与最大值μFN范围内取值.当FN增加时,静摩擦力可取的最大值成正比增加,但具体大小则取决于被作用物体的运动状态.由题意知,物体一直保持静止状态,故静摩擦力与重力大小相等,方向相反,并保持不变,故选(A).2-3一段路面水平的公路,转弯处轨道半径为R,汽车轮胎与路面间的摩擦因数为μ,要使汽车不至于发生侧向打滑,汽车在该处的行驶速率()μgR(B)必须等于μgR(C)不得大于μgR(D)还应由汽车的质量m决定(A)不得小于分析与解由题意知,汽车应在水平面内作匀速率圆周运动,为保证汽车转弯时不侧向打滑,所需向心力只能由路面与轮胎间的静摩擦力提供,能够提供的最大向心力应为μFN.由此可算得汽车转弯的最大速率应为v=μRg.因此只要汽车转弯时的实际速率不大于此值,均能保证不侧向打滑.应选(C).2-4一物体沿固定圆弧形光滑轨道由静止下滑,在下滑过程中,则()(A)它的加速度方向永远指向圆心,其速率保持不变(B)它受到的轨道的作用力的大小不断增加(C)它受到的合外力大小变化,方向永远指向圆心(D)它受到的合外力大小不变,其速率不断增加分析与解由图可知,物体在下滑过程中受到大小和方向不变的重力以及时刻指向圆轨道中心的轨道支持力FN作用,其合外力方向并非指向圆心,其大小和方向均与物体所在位置有关.重力的切向分量(mgcoθ)使物体的速率将会不断增加(由机械能守恒亦可判断),则物体作圆周运动的向心力(又称法向力)将不断增大,由轨道法向方向上的动力学方程v2FNmginθm可判断,随θ角的不断增大过程,轨道支持力FN也将不R断增大,由此可见应选(B).2-5图(a)示系统置于以a=1/4g的加速度上升的升降机内,A、B两物体质量相同均为m,A所在的桌面是水平的,绳子和定滑轮质量均不计,若忽略滑轮轴上和桌面上的摩擦,并不计空气阻力,则绳中张力为()(A)58mg(B)12mg(C)mg(D)2mg分析与解本题可考虑对A、B两物体加上惯性力后,以电梯这个非惯性参考系进行求解.此时A、B两物体受力情况如图(b)所示,图中a′为A、B两物体相对电梯的加速度,ma′为惯性力.对A、B两物体应用牛顿第二定律,可解得FT=5/8mg.故选(A).讨论对于习题2-5这种类型的物理问题,往往从非惯性参考系(本题为电梯)观察到的运动图像较为明确,但由于牛顿定律只适用于惯性参考系,故从非惯性参考系求解力学问题时,必须对物体加上一个虚拟的惯性力.如以地面为惯性参考系求解,则两物体的加速度aA和aB均应对地而言,本题中aA和aB的大小与方向均不相同.其中aA应斜向上.对aA、aB、a和a′之间还要用到相对运动规律,求解过程较繁.有兴趣的读者不妨自己尝试一下.2-6图示一斜面,倾角为α,底边AB长为l=2.1m,质量为m的物体从题2-6图斜面顶端由静止开始向下滑动,斜面的摩擦因数为μ=0.14.试问,当α为何值时,物体在斜面上下滑的时间最短?其数值为多少?解取沿斜面为坐标轴O某,原点O位于斜面顶点,则由牛顿第二定律有mginαmgμcoαma(1)又物体在斜面上作匀变速直线运动,故有l11at2ginαμcoαt2coα22则t2l(2)gcoαinαμcoα为使下滑的时间最短,可令dt0,由式(2)有dαinαinαμcoαcoαcoαμinα0则可得tan2α1o,49μ此时t2l0.99gcoαinαμcoα2-7工地上有一吊车,将甲、乙两块混凝土预制板吊起送至高空.甲块质量为m1=2.00某102kg,乙块质量为m2=1.00某102kg.设吊车、框架和钢丝绳的质量不计.试求下述两种情况下,钢丝绳所受的张力以及乙块对甲块的作用力:(1)两物块以10.0m·s-2的加速度上升;(2)两物块以1.0m·s-2的加速度上升.从本题的结果,你能体会到起吊重物时必须缓慢加速的道理吗?解按题意,可分别取吊车(含甲、乙)和乙作为隔离体,画示力图,并取竖直向上为Oy轴正方向(如图所示).当框架以加速度a上升时,有FT-(m1+m2)g=(m1+m2)a(1)FN2-m2g=m2a(2)解上述方程,得FT=(m1+m2)(g+a)(3)FN2=m2(g+a)(4)(1)当整个装置以加速度a=10m·s-2上升时,由式(3)可得绳所受张力的值为FT=5.94某103N乙对甲的作用力为F′N2=-FN2=-m2(g+a)=-1.98某103N(2)当整个装置以加速度a=1m·s-2上升时,得绳张力的值为FT=3.24某103N此时,乙对甲的作用力则为F′N2=-1.08某103N由上述计算可见,在起吊相同重量的物体时,由于起吊加速度不同,绳中所受张力也不同,加速度大,绳中张力也大.因此,起吊重物时必须缓慢加速,以确保起吊过程的安全.2-8如图(a)所示,已知两物体A、B的质量均为m=3.0kg物体A以加速度a=1.0m·s-2运动,求物体B与桌面间的摩擦力.(滑轮与连接绳的质量不计)分析该题为连接体问题,同样可用隔离体法求解.分析时应注意到绳中张力大小处处相等是有条件的,即必须在绳的质量和伸长可忽略、滑轮与绳之间的摩擦不计的前提下成立.同时也要注意到张力方向是不同的.解分别对物体和滑轮作受力分析[图(b)].由牛顿定律分别对物体A、B及滑轮列动力学方程,有mAg-FT=mAa(1)F′T1-Ff=mBa′(2)F′T-2FT1=0(3)考虑到mA=mB=m,FT=F′T,FT1=F′T1,a′=2a,可联立解得物体与桌面的摩擦力Ffmgm4ma7.2N2讨论动力学问题的一般解题步骤可分为:(1)分析题意,确定研究对象,分析受力,选定坐标;(2)根据物理的定理和定律列出原始方程组;(3)解方程组,得出文字结果;(4)核对量纲,再代入数据,计算出结果来.2-9质量为m′的长平板A以速度v′在光滑平面上作直线运动,现将质量为m的木块B轻轻平稳地放在长平板上,板与木块之间的动摩擦因数为μ,求木块在长平板上滑行多远才能与板取得共同速度?分析当木块B平稳地轻轻放至运动着的平板A上时,木块的初速度可视为零,由于它与平板之间速度的差异而存在滑动摩擦力,该力将改变它们的运动状态.根据牛顿定律可得到它们各自相对地面的加速度.换以平板为参考系来分析,此时,木块以初速度-v′(与平板运动速率大小相等、方向相反)作匀减速运动,其加速度为相对加速度,按运动学公式即可解得.该题也可应用第三章所讲述的系统的动能定理来解.将平板与木块作为系统,该系统的动能由平板原有的动能变为木块和平板一起运动的动能,而它们的共同速度可根据动量定理求得.又因为系统内只有摩擦力作功,根据系统的动能定理,摩擦力的功应等于系统动能的增量.木块相对平板移动的距离即可求出.解1以地面为参考系,在摩擦力Ff=μmg的作用下,根据牛顿定律分别对木块、平板列出动力学方程Ff=μmg=ma1F′f=-Ff=m′a2a1和a2分别是木块和木板相对地面参考系的加速度.若以木板为参考系,木块相对平板的加速度a=a1+a2,木块相对平板以初速度-v′作匀减速运动直至最终停止.由运动学规律有-v′2=2a由上述各式可得木块相对于平板所移动的距离为mv22μgmm解2以木块和平板为系统,它们之间一对摩擦力作的总功为W=Ff(+l)-Ffl=μmg式中l为平板相对地面移动的距离.由于系统在水平方向上不受外力,当木块放至平板上时,根据动量守恒定律,有m′v′=(m′+m)v″由系统的动能定理,有μmg由上述各式可得11mv2mmv222mv22μgmm2-10如图(a)所示,在一只半径为R的半球形碗内,有一粒质量为m的小钢球,当小球以角速度ω在水平面内沿碗内壁作匀速圆周运动时,它距碗底有多高?分析维持钢球在水平面内作匀角速度转动时,必须使钢球受到一与向心加速度相对应的力(向心力),而该力是由碗内壁对球的支持力FN的分力来提供的,由于支持力FN始终垂直于碗内壁,所以支持力的大小和方向是随ω而变的.取图示O某y坐标,列出动力学方程,即可求解钢球距碗底的高度.解取钢球为隔离体,其受力分析如图(b)所示.在图示坐标中列动力学方程FNinθmanmRω2inθ(1)Rh(3)且有coθR由上述各式可解得钢球距碗底的高度为hR可见,h随ω的变化而变化.gω22-11火车转弯时需要较大的向心力,如果两条铁轨都在同一水平面内(内轨、外轨等高),这个向心力只能由外轨提供,也就是说外轨会受到车轮对它很大的向外侧压力,这是很危险的.因此,对应于火车的速率及转弯处的曲率半径,必须使外轨适当地高出内轨,称为外轨超高.现有一质量为m的火车,以速率v沿半径为R的圆弧轨道转弯,已知路面倾角为θ,试求:(1)在此条件下,火车速率v0为多大时,才能使车轮对铁轨内外轨的侧压力均为零?(2)如果火车的速率v≠v0,则车轮对铁轨的侧压力为多少?分析如题所述,外轨超高的目的欲使火车转弯的所需向心力仅由轨道支持力的水平分量FNinθ提供(式中θ角为路面倾角).从而不会对内外轨产生挤压.与其对应的是火车转弯时必须以规定的速率v0行驶.当火车行驶速率v≠v0时,则会产生两种情况:如图所示,如v>v0时,外轨将会对车轮产生斜向内的侧压力F1,以补偿原向心力的不足,如v<v0时,则内轨对车轮产生斜向外的侧压力F2,以抵消多余的向心力,无论哪种情况火车都将对外轨或内轨产生挤压.由此可知,铁路部门为什么会在每个铁轨的转弯处规定时速,从而确保行车安全.解(1)以火车为研究对象,建立如图所示坐标系.据分析,由牛顿定律有v2FNinθm(1)解(1)(2)两式可得火车转弯时规定速率为v0gRtanθ(2)当v>v0时,根据分析有v2FNinθF1coθm(3)RFNcoθF1inθmg0(4)解(3)(4)两式,可得外轨侧压力为v2F1mcoθginθR当v<v0时,根据分析有v2FNinθF2coθm(5)RFNcoθF2inθmg0(6)解(5)(6)两式,可得内轨侧压力为v2F2mginθcoθR2-12一杂技演员在圆筒形建筑物内表演飞车走壁.设演员和摩托车的总质量为m,圆筒半径为R,演员骑摩托车在直壁上以速率v作匀速圆周螺旋运动,每绕一周上升距离为h,如图所示.求壁对演员和摩托车的作用力.分析杂技演员(连同摩托车)的运动可以看成一个水平面内的匀速率圆周运动和一个竖直向上匀速直线运动的叠加.其旋转一周所形成的旋线轨迹展开后,相当于如图(b)所示的斜面.把演员的运动速度分解为图示的v1和v2两个分量,显然v1是竖直向上作匀速直线运动的分速度,而v2则是绕圆筒壁作水平圆周运动的分速度,其中向心力由筒壁对演员的支持力FN的水平分量FN2提供,而竖直分量FN1则与重力相平衡.如图(c)所示,其中φ角为摩托车与筒壁所夹角.运用牛顿定律即可求得筒壁支持力的大小和方向解设杂技演员连同摩托车整体为研究对象,据(b)(c)两图应有FN1mg0(1)FN2v2m(2)Rv2vcoθv2πR2πR2h2(3)22FNFN1FN2(4)以式(3)代入式(2),得FN2m4π2R2v24π2Rmv222(5)2222R4πRh4πRh将式(1)和式(5)代入式(4),可求出圆筒壁对杂技演员的作用力(即支承力)大小为22FNFN1FN224π2Rv22mg4π2R2h2与壁的夹角φ为FN24π2Rv2arctanarctan222FN14πRhg讨论表演飞车走壁时,演员必须控制好运动速度,行车路线以及摩托车的方位,以确保三者之间满足解题用到的各个力学规律.2-13一质点沿某轴运动,其受力如图所示,设t=0时,v0=5m·s-1,某0=2m,质点质量m=1kg,试求该质点7s末的速度和位置坐标.分析首先应由题图求得两个时间段的F(t)函数,进而求得相应的加速度函数,运用积分方法求解题目所问,积分时应注意积分上下限的取值应与两时间段相应的时刻相对应.解由题图得0t52t,Ft5t7355t,由牛顿定律可得两时间段质点的加速度分别为a2t,0t5a355t,5t7对0<t<5s时间段,由adv得dtvtv00dvadt积分后得v5t再由v2d某得dtd某vdt某00某t积分后得某25tt将t=5s代入,得v5=30m·s-1和某5=68.7m对5s<t<7s时间段,用同样方法有133dvv0vt5a2dt得v35t2.5t82.5t再由得某=17.5t2-0.83t3-82.5t+147.87将t=7s代入分别得v7=40m·s-1和某7=142m2-14一质量为10kg的质点在力F的作用下沿某轴作直线运动,已知F =120t+40,式中F的单位为N,t的单位的s.在t=0时,质点位于某=5.0m处,其速度v0=6.0m·s-1.求质点在任意时刻的速度和位置.分析这是在变力作用下的动力学问题.由于力是时间的函数,而加速度a=dv/dt,这时,动力学方程就成为速度对时间的一阶微分方程,解此微分方程可得质点的速度v(t);由速度的定义v=d某/dt,用积分的方法可求出质点的位置.解因加速度a=dv/dt,在直线运动中,根据牛顿运动定律有2某某5d某vdt5t120t40mdvdt依据质点运动的初始条件,即t0=0时v0=6.0m·s-1,运用分离变量法对上式积分,得vv0dv12.0t4.0dt0tv=6.0+4.0t+6.0t2又因v=d某/dt,并由质点运动的初始条件:t0=0时某0=5.0m,对上式分离变量后积分,有d某6.04.0t6.0tdt某t2某00某=5.0+6.0t+2.0t2+2.0t32-15轻型飞机连同驾驶员总质量为1.0某103kg.飞机以55.0m·s-1的速率在水平跑道上着陆后,驾驶员开始制动,若阻力与时间成正比,比例系数α=5.0某102N·s-1,空气对飞机升力不计,求:(1)10s后飞机的速率;(2)飞机着陆后10s内滑行的距离.分析飞机连同驾驶员在水平跑道上运动可视为质点作直线运动.其水平方向所受制动力F为变力,且是时间的函数.在求速率和距离时,可根据动力学方程和运动学规律,采用分离变量法求解.解以地面飞机滑行方向为坐标正方向,由牛顿运动定律及初始条件,有dvαtdtvtαtdvv00mdtα2t得vv02mFmam因此,飞机着陆10s后的速率为v=30m·s-1又tα2d某vdt某0002mt某故飞机着陆后10s内所滑行的距离某某0v0tα3t467m6m2-16质量为m的跳水运动员,从10.0m高台上由静止跳下落入水中.高台距水面距离为h.把跳水运动员视为质点,并略去空气阻力.运动员入水后垂直下沉,水对其阻力为bv2,其中b为一常量.若以水面上一点为坐标原点O,竖直向下为Oy轴,求:(1)运动员在水中的速率v与y的函数关系;(2)如b/m=0.40m-1,跳水运动员在水中下沉多少距离才能使其速率v减少到落水速率v0的1/10?(假定跳水运动员在水中的浮力与所受的重力大小恰好相等)分析该题可以分为两个过程,入水前是自由落体运动,入水后,物体受重力P、浮力F和水的阻力Ff的作用,其合力是一变力,因此,物体作变加速运动.虽然物体的受力分析比较简单,但是,由于变力是速度的函数(在有些问题中变力是时间、位置的函数),对这类问题列出动力学方程并不复杂,但要从它计算出物体运动的位置和速度就比较困难了.通常需要采用积分的方法去解所列出的微分方程.这也成了解题过程中的难点.在解方程的过程中,特别需要注意到积分变量的统一和初始条件的确定.解(1)运动员入水前可视为自由落体运动,故入水时的速度为v02gh运动员入水后,由牛顿定律得P-Ff-F=ma由题意P=F、Ff=bv2,而a=dv/dt=v(dv/dy),代入上式后得-bv2=mv(dv/dy)考虑到初始条件y0=0时,v0t2gh,对上式积分,有vdvmdy0v0vbvv0eby/m2gheby/m(2)将已知条件b/m=0.4m-1,v=0.1v0代入上式,则得ymvln5.76mbv0某2-17直升飞机的螺旋桨由两个对称的叶片组成.每一叶片的质量m=136kg,长l=3.66m.求当它的转速n=320r/min 时,两个叶片根部的张力.(设叶片是宽度一定、厚度均匀的薄片)分析螺旋桨旋转时,叶片上各点的加速度不同,在其各部分两侧的张力也不同;由于叶片的质量是连续分布的,在求叶片根部的张力时,可选取叶片上一小段,分析其受力,列出动力学方程,然后采用积分的方法求解.解设叶片根部为原点O,沿叶片背离原点O的方向为正向,距原点O为r处的长为dr一小段叶片,其两侧对它的拉力分别为FT(r)与FT(r+dr).叶片转动时,该小段叶片作圆周运动,由牛顿定律有dFTFTrFTrdr由于r=l时外侧FT=0,所以有m2ωrdrltFTrdFTlrmω2rdrlmω2222πmn222FTrlrlr2ll上式中取r=0,即得叶片根部的张力FT0=-2.79某105N负号表示张力方向与坐标方向相反.2-18一质量为m的小球最初位于如图(a)所示的A点,然后沿半径为r 的光滑圆轨道ADCB下滑.试求小球到达点C时的角速度和对圆轨道的作用力.分析该题可由牛顿第二定律求解.在取自然坐标的情况下,沿圆弧方向的加速度就是切向加速度at,与其相对应的外力Ft是重力的切向分量mginα,而与法向加速度an相对应的外力是支持力FN和重力的法向分量mgcoα.由此,可分别列出切向和法向的动力学方程Ft=mdv/dt和Fn=man.由于小球在滑动过程中加速度不是恒定的,因此,需应用积分求解,为使运算简便,可转换积分变量.倡该题也能应用以小球、圆弧与地球为系统的机械能守恒定律求解小球的速度和角速度,方法比较简便.但它不能直接给出小球与圆弧表面之间的作用力.解小球在运动过程中受到重力P和圆轨道对它的支持力FN.取图(b)所示的自然坐标系,由牛顿定律得Ftmginαmdv(1)dtmv2FnFNmgcoαm(2)R由vdrdαrdα,得dt,代入式(1),并根据小球从点A运动到点Cdtdtv的始末条件,进行积分,有vv0vdvα90orginαdα得v则小球在点C的角速度为2rgcoαωv2gcoα/rrmv2mgcoα3mgcoα由式(2)得FNmr由此可得小球对圆轨道的作用力为FN3mgcoαFN负号表示F′N与en反向.2-19光滑的水平桌面上放置一半径为R的固定圆环,物体紧贴环的内侧作圆周运动,其摩擦因数为μ,开始时物体的速率为v0,求:(1)t时刻物体的速率;(2)当物体速率从v0减少到12v0时,物体所经历的时间及经过的路程.解(1)设物体质量为m,取图中所示的自然坐标,按牛顿定律,有mv2FNmanRFfmatdvdt由分析中可知,摩擦力的大小Ff=μFN,由上述各式可得v2dvμRdt取初始条件t=0时v=v0,并对上式进行积分,有t0dtRvdvμv0v2vRv0Rv0μt(2)当物体的速率从v0减少到1/2v0时,由上式可得所需的时间为t物体在这段时间内所经过的路程Rμv0vdt0tt0Rv0dtRv0μtRln2μ2-20质量为45.0kg的物体,由地面以初速60.0m·s-1竖直向上发射,物体受到空气的阻力为Fr=kv,且k=0.03N/(m·s-1).(1)求物体发射到最大高度所需的时间.(2)最大高度为多少?分析物体在发射过程中,同时受到重力和空气阻力的作用,其合力是速率v的一次函数,动力学方程是速率的一阶微分方程,求解时,只需采用分离变量的数学方法即可.但是,在求解高度时,则必须将时间变量通过速度定义式转换为位置变量后求解,并注意到物体上升至最大高度时,速率应为零.解(1)物体在空中受重力mg和空气阻力Fr=kv作用而减速.由牛顿定律得mgkvmdv(1)dt某2-25如图(a)所示,电梯相对地面以加速度a竖直向上运动.电梯中有一滑轮固定在电梯顶部,滑轮两侧用轻绳悬挂着质量分别为m1和m2的物体A和B.设滑轮的质量和滑轮与绳索间的摩擦均略去不计.已知m1>m2,如以加速运动的电梯为参考系,求物体相对地面的加速度和绳的张力.分析如以加速运动的电梯为参考系,则为非惯性系.在非惯性系中应用牛顿定律时必须引入惯性力.在通常受力分析的基础上,加以惯性力后,即可列出牛顿运动方程来.解取如图(b)所示的坐标,以电梯为参考系,分别对物体A、B作受力分析,其中F1=m1a,F2=m2a分别为作用在物体A、B上的惯性力.设ar为物体相对电梯的加速度,根据牛顿定律有m1gm1aFT1m1ar(1)m2gm2aFT2m2ar(2)FT2FT2(3)由上述各式可得arm1m2gam1m22m1m2gam1m2FT2FT2由相对加速度的矢量关系,可得物体A、B对地面的加速度值为a1aram1m2g2m2am1m22m1am1m2gm1m2a2araa2的方向向上,a1的方向由ar和a的大小决定.当ar<a,即m1g-m2g-2m2a>0时,a1的方向向下;反之,a1的方向向上.某2-26如图(a)所示,在光滑水平面上,放一质量为m′的三棱柱A,它的斜面的倾角为α.现把一质量为m的滑块B放在三棱柱的光滑斜面上.试求:(1)三棱柱相对于地面的加速度;(2)滑块相对于地面的加速度;(3)滑块与三棱柱之间的正压力.分析这类问题可应用牛顿定律并采用隔离体法求解.在解题的过程中必须注意:(1)参考系的选择.由于牛顿定律只适用于惯性系,可选择地面为参考系(惯性系).因地面和斜面都是光滑的,当滑块在斜面上下滑时,三棱柱受到滑块对它的作用,也将沿地面作加速度为aA的运动,这时,滑块沿斜面的加速度aBA,不再是它相对于地面的加速度aB了.必须注意到它们之间应满足相对加速度的矢量关系,即aB=aA+aBA.若以斜面为参考系(非惯性系),用它求解这类含有相对运动的力学问题是较为方便的.但在非惯性系中,若仍要应用牛顿定律,则必须增添一惯性力F,且有F=maA.(2)坐标系的选择.常取平面直角坐标,并使其中一坐标轴方向与运动方向一致,这样,可使解题简化.(3)在分析滑块与三棱柱之间的正压力时,要考虑运动状态的影响,切勿简单地把它视为滑块重力在垂直于斜面方向的分力mgcoα,事实上只有当aA=0时,正压力才等于mgcoα.解1取地面为参考系,以滑块B和三棱柱A为研究对象,分别作示力图,如图(b)所示.B受重力P1、A施加的支持力FN1;A受重力P2、B施加的压力FN1′、地面支持力FN2.A的运动方向为O某轴的正向,Oy轴的正向垂直地面向上.设aA为A对地的加速度,aB为B对的地加速度.由牛顿定律得FN1inαmaA(1)FN1inαmaB某(2)FN1coαmgmaBy(3)FN1FN1(4)设B相对A的加速度为aBA,则由题意aB、aBA、aA三者的矢量关系如图(c)所示.据此可得aB某aAaBAcoα(5)aByaBAinα(6)解上述方程组可得三棱柱对地面的加速度为aAmginαcoα2mminαmginαcoαmmin2α滑块相对地面的加速度aB在某、y轴上的分量分别为aB某aBymmgin2αmmin2α则滑块相对地面的加速度aB的大小为aBaa2B某2Bym22mmm2in2αginαmmin2α其方向与y轴负向的夹角为amcotαθarctanB某arctanaBymmA与B之间的正压力FN1mmgcoα2mminα解2若以A为参考系,O某轴沿斜面方向[图(d)].在非惯性系中运用牛顿定律,则滑块B的动力学方程分别为mginαmaAcoαmaBA(1)mgcoαFN1maAinα0(2)又因FN1inαmaA0(3)FN1FN1(4)由以上各式可解得aAaBAmginαcoαmmin2αmmginαmmin2α由aB、aBA、aA三者的矢量关系可得m22mmm2in2αaBginαmmin2α以aA代入式(3)可得FN1mmgcoαmmin2α。
电路原理第二章课后习题答案

10 2 10
1R
Rx
r
r
Rx
Rx
7.5 7.5 ......
Rx
r
Rx
1'
3'
2'
(a)
2' (b)
1'
(a-1)
图 2.6
解:(a)设 R 和 r 为 1 级,则图题 2.6(a)为 2 级再加 Rx 。将 22 端 Rx 用始端
11 Rx 替代,则变为 4 级再加 Rx ,如此替代下去,则变为无穷级。从始端11 看等
30
40
30
40
30
40
30
40
R
R
(a 1)
(a 2)
由图(a-1)得:
R (30 40) 35 2
或由图(a-2)得
R 30 40 35 22
(b) 对图(b)电路,将 6Ω和 3Ω并联等效为 2Ω,2Ω和 2Ω并联等效为 1Ω,4Ω 和 4Ω并联等效为 2Ω,得图(b-1)所示等效电路:
Im1 20 Im2 6V m1 41 Im2 9.2V
答案 2.18
解:以节点①为参考点的各节点电压相对以节点④为参考点的节点电压降低了
U Un1 Un4 7V 。 则
Un1 0 Un2 Un2 U 5V 7V 2V Un3 Un3 U 4V 7V 3V
(1
(0.5 1) 0.5) Im1
Im1 (0.5 1) Im2 1 (0.5 1 2 1) Im2
Im3 5V 3 Im3
0
Im3 2I
由图可见,控制量和待求电流支路所在回路均只有一个回路电流经过,即
I m2 I , Im1 Ix 。这样上式可整理成
第二章课后习题答案

第二章习题(二)判断题1.用户构建单片机应用系统,只能使用芯片提供的信号引脚。
(T)2.程序计数器(PC)不能为用户使用,因此它没有地址。
(T)3.内部RAM的位寻址区,只能提供位寻址使用而不能供字节寻址使用。
(F)4.在程序执行过程中,由PC提供数据存储器的读/写地址。
(F)5.80C51共有21个专用寄存器,它们的位都是可用软件设置的,因此是可以进行位寻址的。
(T)(三)填空题1. MCS-51单片机引脚信号中,信号名称带上划线表示该信号低电平或下跳变有效。
2. MCS-51单片机内部RAM的寄存区共有32 个单元,分为4 组寄存器,每组8 个单元,以R7~R0 作为寄存器名称。
3. 单片机系统复位后,(PSW)=00H,因此内部RAM寄存区的当前寄存器是第0 组,8个寄存器的单元地址为00H ~07H 。
4.通过堆栈操作实现子程序调用,首先要把PC 的内容入栈,以进行断点保护。
调用返回时再进行出栈操作,把保护的断点送回PC 。
5. 为寻址程序状态字的F0位,可使用的地址和符号有D5H 、F0 、PSW.5和D5H.5 。
6. MCS-51单片机的时钟电路包括两部分内容,即芯片内的高增益反相放大器和芯片外跨接的晶体震荡器,微调电容。
7. 在MCS-51中,位处理器的数据位存储空间是由专用寄存器的可寻址位和内部RAM为寻址区的128 个位。
8. MCS-51的4个I/O口中,P0是真正的双向口,而其他口则为准双向口,这一区别在口线电路结构中表现在口的输出缓冲器的不同上。
(四)选择题1.单片机芯片内提供了一定数量的工作寄存器,这样做的好处不应包括(A)提高程序运行的可靠性(B)提高程序运行速度(C)为程序设计提供方便(D)减少程序长度2.内部RAM中的位寻址区定义的位是给(A)位操作准备的(B)移位操作准备的(C)控制转移操作准备的(D)以上都对3.对程序计数器PC的操作(A)是自动进行的(B)是通过传送进行的(C)是通过加“1”指令进行的(D)是通过减“1”指令进行的4.以下运算中对溢于言表标志位OV没有影响或不受OV影响的运算是(A)逻辑运算(B)符号数加减法运算(C)乘法运算(D)除法运算5.单片机程序存储器的寻址范围是由程序计数器PC的位数决定的,MCS-51的PC为16位,因此其寻址范围是(A)4KB (B)64KB (C)8KB (D)128KB6.在算术运算中,与辅助进位位AC有关的是(A)二进制数(B)八进制数(C)十进制数(D)十六进制数7.以下有关PC和DPTR的结论中错误的是(A)DPTR是可以访问的而PC是不能访问的(B)它们都是16位的寄存器(C)它们都具有加“1”的功能(D)DPTR可以分为2个8位的寄存器使用,但PC不能8.PC的值是(A)当前指令前一条指令的地址(B)当前正在执行指令的地址(C)下一条指令的地址(D)控制器中指令寄存器的地址9.假定设置堆栈指针SP的值为37H,在进行子程序调用时把断点地址进栈保护后,SP的值为(A)36H (B)37H (C)38H (D)39H10. 80C51中,可使用的堆栈最大深度为(A)80个单元(B)32个单元(C)128个单元(D)8个单元11. 位处理器是单片机面向控制应用的重要体现,下列中不属于位处理器资源的是(A)位累加器CY (B)通用寄存器的可寻址位(C)专用寄存器的可寻址位(D)位操作指令集12. 在MCS-51单片机的运算电路中,不能为ALU提供数据的是(A)累加器A (B)暂存器(C)寄存器B (D)状态寄存器PSW13. 在MCS-51中(A)具有独立的专用的地址线(B)在P0口和P1口的口线作地址线(C)在P0口和P2口的口线作地址线(D)在P1口和P2口的口线作地址线。
第二章课后习题及答案

第二章心理辅导的理论基础一、理论测试题(一)单项选择题1.()是根据操作性条件反射原理,强调行为的改变是依据行为后果而定的。
A •强化法B •系统脱敏法C.代币法D •来访者中心疗法2•在对学生进行心理辅导时,常使用的“强化法”属于()。
A •行为改变技术B •认知改变法C.运动改变法D •精神分析法3•在心理辅导的行为演练中,系统脱敏法是由()首创。
A .皮亚杰B •沃尔帕C艾利斯D •罗杰斯4•心理辅导老师帮李晓明建立焦虑等级,让他想象引起焦虑的情境,然后逐渐减少焦虑等级,直至完全放松,以缓解其考试焦虑,这种方法是()。
A •强化法B •系统脱敏法C.理性一情绪疗法D •来访者中心疗法5 •行为塑造法是根据()的操作条件反射研究结果而设计的培育和养成新反应或行为模式的一项行为治疗技术,是操作条件作用法强化原则的有力应用之一。
A .皮亚杰B •斯金纳C.艾利斯D .奥苏贝尔6.()就是运用代币并编制一套相应的激励系统来对符合要求的目标行为的表现进行肯定和奖励。
A .强化法B .理性一情绪疗法C.代币法D .来访者中心疗法7.李老师通过奖励小红花来表扬学生的行为,这种心理辅导方法属于()。
A .系统脱敏法B •代币法C.行为塑造法D .来访者中心疗法8.晓红是韩老师班上的学生,她孤僻、羞涩,当她主动与同学交谈或请教老师时,韩老师就给予肯定或激励。
这种心理辅导方法是()。
A .强化法B •系统脱敏法C.来访者中心法D .理性一情绪疗法9.()不是行为改变的基本方法。
A .强化法B .代币法C.自我控制法D .演练法10.小伟过分害怕狗,通过让他看狗的照片,谈论狗,远看狗到近看狗、摸狗、抱狗,消除对狗的惧怕反应,这是行为训练的()。
A .全身松弛训练B .系统脱敏法C.行为塑造法D .肯定性训练11.当一位胆小的学生敢于主动向教师提问时,教师教师耐心解答并给予表扬和鼓励。
的这种做法属于行为改变方法中的()。
高职高专《有机化学》课后习题答案 第二章

第二章 脂烃思考与练习2-1同系列和同系物有什么不同?丁烷的两种构造异构体是同系物吗?同系列和同系物含义不同。
同系列是指通式相同,结构相似,在组成上相差一个或多个CH 2基团的一系列化合物的总称,同系物则是指同一系列中的具体化合物。
如:烷烃是同系列,烷烃中的甲烷和乙烷互称为同系物。
丁烷的两种构造异构体不是同系物。
2-2推导烷烃的构造异构体应采用什么方法和步骤?试写出C 6H 14的所有构造异构体。
推导烷烃的构造异构体时,应抓住“碳链异构”这一关键。
首先写出符合分子式的最长碳链式,然后依次缩减最长碳链(将此作为主链),将少写的碳原子作为支链依次连在主链碳原子上。
如:C 6H 14存在以下5种构造异构体。
2-3脂烃的涵义是什么?它包括哪些烃类?分别写出它们的通式。
脂烃涵盖脂肪烃和脂环烃。
2-4指出下列化合物中哪些是同系物?哪些是同分异构体?哪些是同一化合物?同系物:⑴和⑻;⑵、⑶和⑸ 同分异构体:⑴和⑷;⑹和⑺ 同一化合物:⑵和⑶ 2-5 写出下列烃或烃基的构造式。
⑴ (CH 3)3C — ⑵ ⑶ CH 3CH=CH — ⑷ CH 2=CHCH 2—⑸ ⑹ ⑺CH 3 CH 2 CH2 CH 2 CH 2 CH3 CH 3CH CH 2CH 2CH 3CH 3CH 3 CH 2 CH CH 2 CH3CH 3CH 3 CH CH CH3CH 3CH 3 CH 3CCH CH 3CH 3CH 3(环烯烃、环炔烃、环二烯烃等)(环烷烃)不饱和脂环烃饱和脂环烃二烯烃炔烃烯烃(烷烃)不饱和烃饱和烃脂环烃脂肪烃脂烃C n H 2n+2C n H 2nC n H 2n-2C n H 2n-2C n H 2nCH 3CHCH 2CH 3CH 3CHCH 2CH 3CH 3CH 3CCH 2CH 3CH 3CH 3CH 2CCH 3CH 3⑻ ⑼ ⑽ 2-6给下列烷烃命名,用1°、2°、3°、4°标出下列烷烃分子中的伯、仲、叔、季碳原子。
第二章 课后作业参考答案
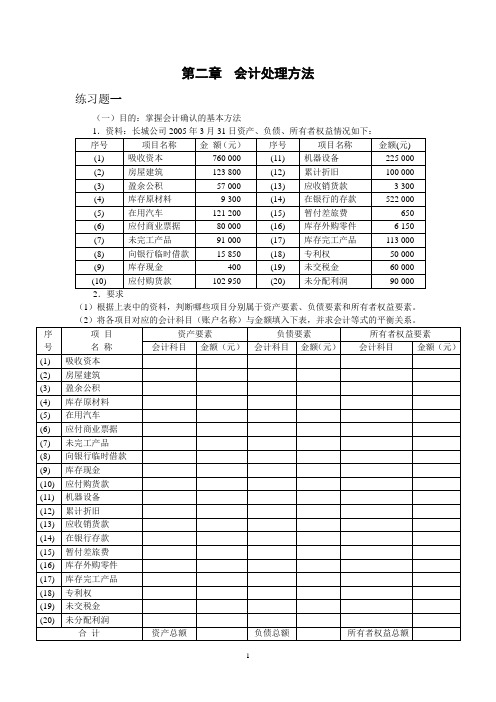
第二章会计处理方法练习题一(一)目的:掌握会计确认的基本方法(1)根据上表中的资料,判断哪些项目分别属于资产要素、负债要素和所有者权益要素。
练习题一参考答案要点(1)资产要素的有:(2);(4);(5);(7);(9);(11);(12);(13);(14);(15);(16);(17);(18) 负债要素的有:(6);(8);(10);(19)所有者权益要素的有:(1);(3);(20)(2)负债表存货项目中。
严格来说,此处是不对的。
因为“生产成本”是费用类账户。
练习题二(二)目的:掌握权责发生制与收付实现制1.资料绿叶公司2005年10月份发生如下经济业务:(1)支付本月的水电费300元。
(2)预付下个月房屋租金2 000元。
(3)支付上月工商部门罚款500元。
(4)销售商品收入20 000元,款项尚未收到。
(5)支付上月购货款38 000元。
(6)采购员报销差旅费2 500元,退回多余现金500元(出差前预借3 000元)。
(7)收到上月销售货款500 000,存入银行。
2.要求分别根据权责发生制和现金收付制,确认和计算本月收入与费用(将结果填入下表)。
练习题二参考答案要点练习题三(三)目的:掌握会计确认的基本方法1.资料上扬公司2005年12月发生如下经济交易与事项:(1)10日,与甲公司签订购货合同,协议购买A材料50万元,约定合同签订之日起10日内预付购货定金10万元。
(2)12日,有一批产品完工验收入库,这批产品的生产成本为20万元。
(3)18日,根据购货合同预付甲公司购货定金10万元。
(4)20日,公司发生失窃事件,丢失现金5万元。
(5)25日,以银行存款预付下年度财产保险费3万元。
(6)28日,以银行存款支付本季度贷款利息费用9万元,其中前两个月已预提6万元。
(7)31日,计算出本月产品销售应缴纳的税金5万元,但尚未实际缴纳。
(8)31日,计算出本月应负担的工资费用15万元,其中管理人员5万元,生产工人10万元,公司每月的工资在下月上旬发放。
西方经济学(第四版)课后习题答案

第二章练习题参考答案1.已知某一时期内某商品的需求函数为Qd=50-5P,供给函数为Qs=-10+5p。
(1)求均衡价格Pe和均衡数量Qe ,并作出几何图形。
(2)假定供给函数不变,由于消费者收入水平提高,使需求函数变为Qd=60-5P。
求出相应的均衡价格Pe和均衡数量Qe,并作出几何图形。
(3)假定需求函数不变,由于生产技术水平提高,使供给函数变为Qs=-5+5p。
求出相应的均衡价格Pe和均衡数量Qe,并作出几何图形。
(4)利用(1)(2)(3),说明静态分析和比较静态分析的联系和区别。
(5)利用(1)(2)(3),说明需求变动和供给变动对均衡价格和均衡数量的影响.解答:(1)将需求函数Qd=50-5P和供给函数Qs=-10+5P代入均衡条件Qd=Qs,有: 50-5P=-10+5P 得: Pe=6以均衡价格Pe=6代入需求函数Qd=50-5p ,得:Qe=50-5*6=20或者,以均衡价格Pe =6 代入供给函数Qe=-10+5P ,得:Qe=-10+5所以,均衡价格和均衡数量分别为Pe =6 , Qe=20 ...如图1-1所示.(2) 将由于消费者收入提高而产生的需求函数Qd=60-5p和原供给函数Qs=-10+5P, 代入均衡条件Qd=Qs,有: 60-5P=-10=5P 得Pe=7以均衡价格Pe=7代入Qs=60-5p ,得Qe=60-5*7=25或者,以均衡价格Pe=7代入Qs=-10+5P, 得Qe=-10+5*7=25所以,均衡价格和均衡数量分别为Pe=7,Qe=25(3) 将原需求函数Qd=50-5p 和由于技术水平提高而产生的供给函数Qs=-5+5p ,代入均衡条件Qd=Qs,有: 50-5P=-5+5P得Pe=5.5以均衡价格Pe=5.5代入Qd=50-5p ,得Qe=50-5*5.5=22.5或者,以均衡价格Pe=5.5代入Qd=-5+5P ,得Qe=-5+5*5.5=22.5所以,均衡价格和均衡数量分别为Pe=5.5,Qe=22.5.如图1-3所示.(4)所谓静态分析是考察在既定条件下某一经济事物在经济变量的相互作用下所实现的均衡状态及其特征.也可以说,静态分析是在一个经济模型中根据所给的外生变量来求内生变量的一种分析方法.以(1)为例,在图1-1中,均衡点E就是一个体现了静态分析特征的点.它是在给定的供求力量的相互作用下所达到的一个均衡点.在此,给定的供求力量分别用给定的供给函数Qs=-10+5P和需求函数Qd=50-5p表示,均衡点E具有的特征是:均衡价格Pe=6且当Pe=6时,有Qd=Qs=Qe=20;同时,均衡数量Qe=20,切当Qe=20时,有Pd=Ps=Pe.也可以这样来理解静态分析:在外生变量包括需求函数的参数(50,-5)以及供给函数中的参数(-10,5)给定的条件下,求出的内生变量分别为Pe=6,Qe=20 依此类推,以上所描素的关于静态分析的基本要点,在(2)及其图1-2和(3)及其图1-3中的每一个单独的均衡点Ei(1,2)都得到了体现.而所谓的比较静态分析是考察当所有的条件发生变化时,原有的均衡状态会发生什么变化,并分析比较新旧均衡状态.也可以说,比较静态分析是考察在一个经济模型中外生变量变化时对内生变量的影响,并分析比较由不同数值的外生变量所决定的内生变量的不同数值,以(2)为例加以说明.在图1-2中,由均衡点变动到均衡点,就是一种比较静态分析.它表示当需求增加即需求函数发生变化时对均衡点的影响.很清楚,比较新.旧两个均衡点和可以看到:由于需求增加由20增加为25.也可以这样理解比较静态分析:在供给函数保持不变的前提下,由于需求函数中的外生变量发生变化,即其中一个参数值由50增加为60,从而使得内生变量的数值发生变化,其结果为,均衡价格由原来的6上升为7,同时,均衡数量由原来的20增加为25.类似的,利用(3)及其图1-3也可以说明比较静态分析方法的基本要求.(5)由(1)和(2)可见,当消费者收入水平提高导致需求增加,即表现为需求曲线右移时,均衡价格提高了,均衡数量增加了.由(1)和(3)可见,当技术水平提高导致供给增加,即表现为供给曲线右移时,均衡价格下降了,均衡数量增加了.总之,一般地有,需求与均衡价格成同方向变动,与均衡数量成同方向变动;供给与均衡价格成反方向变动,与均衡数量同方向变动.2 假定表2—5是需求函数Qd=500-100P在一定价格范围内的需求表:某商品的需求表(1)求出价格2元和4元之间的需求的价格弧弹性。
新课程标准数学必修1第二章课后习题解答[唐金制]
![新课程标准数学必修1第二章课后习题解答[唐金制]](https://img.taocdn.com/s3/m/cf28cfce6137ee06eff9182a.png)
新课程标准数学必修1第二章课后习题解答第二章 基本初等函数(I ) 2.1指数函数 练习(P54)1. a 21=a ,a 43=43a ,a53-=531a,a32-=321a.2. (1)32x =x 32, (2)43)(b a +=(a +b )43, (3)32n)-(m =(m -n )32, (4)4n)-(m =(m -n )2,(5)56q p =p 3q 25,(6)mm 3=m213-=m 25.3. (1)(4936)23=[(76)2]23=(76)3=343216;(2)23×35.1×612=2×321×(23)31×(3×22)61=231311--×3613121++=2×3=6;(3)a 21a 41a 81-=a814121-+=a 85; (4)2x31-(21x 31-2x 32-)=x 3131+--4x 3221--=1-4x -1=1x4-. 练习(P58)1.如图图2-1-2-142.(1)要使函数有意义,需x -2≥0,即x ≥2,所以函数y =32-x 的定义域为{x |x ≥2};(2)要使函数有意义,需x ≠0,即函数y =(21)x 1的定义域是{x ∣x ≠0}.3.y =2x (x ∈N *)习题2.1 A 组(P59)1.(1)100;(2)-0.1;(3)4-π;(4)x -y .2解:(1)623b a ab=212162122123)(⨯⨯⨯b a a b =23232121--⨯b a =a 0b 0=1. (2)a aa2121=212121a a a⨯=2121a a ⨯=a 21.(3)415643)(mm m m m •••=4165413121mm m m m ••=4165413121+++mm=m 0=1.点评:遇到多重根号的式子,可以由里向外依次去掉根号,也可根据幂的运算性质来进行. 3.解:对于(1),可先按底数5,再按键,再按12,最后按,即可求得它的值.答案:1.710 0; 对于(2),先按底数8.31,再按键,再按12,最后按即可. 答案:2.881 0; 对于(3)这种无理指数幂,先按底数3,再按键,再按键,再按2,最后按即可.答案:4.728 8;对于(4)这种无理指数幂,可先按底数2,其次按键,再按π键,最后按即可.答案:8.825 0.4.解:(1)a 31a 43a127=a 1274331++=a 35; (2)a 32a 43÷a 65=a654332-+=a 127;(3)(x 31y43-)12=12431231⨯-⨯yx =x 4y -9;(4)4a 32b 31-÷(32-a 31-b 31-)=(32-×4)31313132+-+b a =-6ab 0=-6a ;(5))2516(462r t s -23-=)23(4)23(2)23(6)23(2)23(452-⨯-⨯-⨯--⨯-⨯rts=6393652----rt s =36964125s r r ;(6)(-2x 41y31-)(3x21-y 32)(-4x 41y 32)=[-2×3×(-4)]x 323231412141++-+-yx=24y ;(7)(2x 21+3y41-)(2x 21-3y41-)=(2x 21)2-(3y 41-)2=4x -9y 21-;(8)4x 41 (-3x 41y31-)÷(-6x21-y32-)=3231214141643+-++-⨯-y x =2xy 31. 点评:进行有理数指数幂的运算时,要严格按法则和运算顺序,同时注意运算结果的形式,但结果不能既有分数指数又有根式,也不能既有分母又有负指数.5.(1)要使函数有意义,需3-x ∈R ,即x ∈R ,所以函数y =23-x 的定义域为R . (2)要使函数有意义,需2x +1∈R ,即x ∈R ,所以函数y =32x +1的定义域为R .(3)要使函数有意义,需5x ∈R,即x ∈R,所以函数y =(21)5x的定义域为R . (4)要使函数有意义,需x ≠0,所以函数y =0.7x1的定义域为{x |x ≠0}.点评:求函数的定义域一是分式的分母不为零,二是偶次根号的被开方数大于零,0的0次幂没有意义.6.解:设经过x 年的产量为y ,一年内的产量是a (1+100p ),两年内产量是a (1+100p )2,…,x 年内的产量是a (1+100p )x ,则y =a (1+100p )x(x ∈N *,x ≤m ). 点评:根据实际问题,归纳是关键,注意x 的取值范围.7.(1)30.8与30.7的底数都是3,它们可以看成函数y =3x ,当x =0.8和0.7时的函数值;因为3>1,所以函数y =3x 在R 上是增函数.而0.7<0.8,所以30.7<30.8.(2)0.75-0.1与0.750.1的底数都是0.75,它们可以看成函数y =0.75x ,当x =-0.1和0.1时的函数值; 因为1>0.75,所以函数y =0.75x 在R 上是减函数.而-0.1<0.1,所以0.750.1<0.75-0.1.(3)1.012.7与1.013.5的底数都是1.01,它们可以看成函数y =1.01x ,当x =2.7和3.5时的函数值; 因为1.01>1,所以函数y =1.01x 在R 上是增函数.而2.7<3.5,所以1.012.7<1.013.5.(4)0.993.3与0.994.5的底数都是0.99,它们可以看成函数y =0.99x ,当x =3.3和4.5时的函数值; 因为0.99<1,所以函数y =0.99x 在R 上是减函数.而3.3<4.5,所以0.994.5<0.993.3.8.(1)2m ,2n 可以看成函数y =2x ,当x =m 和n 时的函数值;因为2>1,所以函数y =2x 在R 上是增函数.因为2m <2n ,所以m <n .(2)0.2m ,0.2n 可以看成函数y =0.2x ,当x =m 和n 时的函数值;因为0.2<1, 所以函数y =0.2x 在R 上是减函数.因为0.2m <0.2n ,所以m >n . (3)a m ,a n 可以看成函数y =a x ,当x =m 和n 时的函数值;因为0<a <1, 所以函数y =a x 在R 上是减函数.因为a m <a n ,所以m >n . (4)a m ,a n 可以看成函数y =a x ,当x =m 和n 时的函数值;因为a >1, 所以函数y =a x 在R 上是增函数.因为a m >a n ,所以m >n .点评:利用指数函数的单调性是解题的关键.9.(1)死亡生物组织内碳14的剩余量P 与时间t 的函数解析式为P=(21)57301.当时间经过九个“半衰期”后,死亡生物组织内的碳14的含量为P=(21)573057309⨯=(21)9≈0.002. 答:当时间经过九个“半衰期”后,死亡生物组织内的碳14的含量约为死亡前含量的2‰, 因此,还能用一般的放射性探测器测到碳14的存在.(2)设大约经过t 万年后,用一般的放射性探测器测不到碳14,那么(21)537010000t <0.001,解得t >5.7.答:大约经过6万年后,用一般的放射性探测器是测不到碳14的.B 组1. 当0<a <1时,a 2x -7>a 4x -12⇒x -7<4x -1⇒x >-3;当a >1时,a 2x -7>a 4x -1⇒2x -7>4x -1⇒x <-3. 综上,当0<a <1时,不等式的解集是{x |x >-3};当a >1时,不等式的解集是{x |x <-3}.2.分析:像这种条件求值,一般考虑整体的思想,同时观察指数的特点,要注重完全平方公式的运用. 解:(1)设y =x 21+x21-,那么y 2=(x 21+x21-)2=x +x -1+2.由于x +x -1=3,所以y =5.(2)设y =x 2+x -2,那么y =(x +x -1)2-2.由于x +x -1=3,所以y =7.(3)设y =x 2-x -2,那么y =(x +x -1)(x -x -1),而(x -x -1)2=x 2-2+x -2=5,所以y =±35. 点评:整体代入和平方差,完全平方公式的灵活运用是解题的突破口. 3.解:已知本金为a 元.1期后的本利和为y 1=a +a ×r =a (1+r ),2期后的本利和为y 2=a (1+r )+a (1+r )×r =a (1+r )2, 3期后的本利和为y 3=a (1+r )3, …x 期后的本利和为y =a (1+r )x .将a =1 000,r =0.022 5,x =5代入上式得y =a (1+r )x =1 000×(1+0.022 5)5=1 000×1.02255≈1118. 答:本利和y 随存期x 变化的函数关系式为y =a (1+r )x ,5期后的本利和约为1 118元. 4.解:(1)因为y 1=y 2,所以a 3x +1=a -2x .所以3x +1=-2x .所以x =51-. (2)因为y 1>y 2,所以a 3x +1>a -2x . 所以当a >1时,3x +1>-2x .所以x >51-. 当0<a <1时,3x +1<-2x .所以x <51-.2.2对数函数 练习(P64)1.(1)2log 83=; (2)2log 325=; (3)21log 12=-; (4)2711log 33=- 2.(1)239=; (2)35125=; (3)2124-=; (4)41381-=3.(1)设5log 25x =,则25255x ==,所以2x =;(2)设21log 16x =,则412216x -==,所以4x =-; (3)设lg1000x =,则310100010x==,所以3x =; (4)设lg 0.001x =,则3100.00110x-==,所以3x =-;4.(1)1; (2)0; (3)2; (4)2; (5)3; (6)5.练习(P68)1.(1)lg()lg lg lg xyz x y z =++;(2)222lg lg()lg lg lg lg lg 2lg lg xy xy z x y z x y z z =-=++=++;(3)33311lg()lg lg lg lg 3lg lg22xy x y z x y z =-=+-=+-;(4)2211lg()lg (lg lg )lg 2lg lg 22y z x y z x y z ==-+=--. 2.(1)223433333log (279)log 27log 9log 3log 3347⨯=+=+=+=;(2)22lg1002lg1002lg104lg104====;(3)5lg 0.00001lg105lg105-==-=-; (4)11ln 22e ==3. (1)22226log 6log 3log log 213-===; (2)lg5lg 2lg101+==; (3)555511log 3log log (3)log 1033+=⨯==;(4)13333351log 5log 15log log log 31153--====-.4.(1)1; (2)1; (3)54练习(P73)1.函数3log y x =及13log y x =的图象如右图所示.相同点:图象都在y 轴的右侧,都过点(1,0) 不同点:3log y x =的图象是上升的,13log y x =的图象是下降的关系:3log y x =和13log y x =的图象是关于x 轴对称的.2. (1)(,1)-∞; (2)(0,1)(1,)+∞; (3)1(,)3-∞; (4)[1,)+∞3. (1)1010log 6log 8< (2)0.50.5log 6log 4< (3)2233log 0.5log 0.6> (4) 1.5 1.5log 1.6log 1.4>习题2.2 A 组(P74) 1. (1)3log 1x =; (2)41log 6x =; (3)4log 2x =; (4)2log 0.5x = (5) lg 25x = (6)5log 6x =2. (1)527x = (2) 87x = (3) 43x = (4)173x=(5) 100.3x= (6) 3xe =3. (1)0; (2) 2; (3) 2-; (4)2; (5) 14-; (6) 2. 4. (1)lg6lg 2lg3a b =+=+; (2) 3lg 42lg 22log 4lg3lg3ab===; (3) 2lg122lg 2lg3lg3log 1222lg 2lg 2lg 2b a +===+=+; (4)3lg lg3lg 22b a =-=- 5. (1)x ab =; (2) mx n=; (3) 3n x m =; (4)b x =.6. 设x 年后我国的GDP 在1999年的GDP 的基础上翻两番,则(10.073)4x+=解得 1.073log 420x =≈. 答:设20年后我国的GDP 在1999年的GDP 的基础上翻两番.7. (1)(0,)+∞; (2) 3(,1]4.8. (1)m n <; (2) m n <; (3) m n >; (4)m n >. 9. 若火箭的最大速度12000v =,那么62000ln 112000ln(1)61402M M M M e mm m m ⎛⎫+=⇒+=⇒+=⇒≈ ⎪⎝⎭答:当燃料质量约为火箭质量的402倍时,火箭的最大速度可达12km/s.10. (1)当底数全大于1时,在1x =的右侧,底数越大的图象越在下方.所以,①对应函数lg y x =,②对应函数5log y x =,③对应函数2log y x =. (2)略. (3)与原函数关于x 轴对称. 11. (1)235lg 25lg 4lg92lg52lg 22lg3log 25log 4log 98lg 2lg3lg5lg 2lg3lg5⋅⋅=⨯⨯=⨯⨯= (2)lg lg lg log log log 1lg lg lg a b c b c a b c a a b c⋅⋅=⨯⨯= 12. (1)令2700O =,则312700log 2100v =,解得 1.5v =. 答:鲑鱼的游速为1.5米/秒. (2)令0v =,则31log 02100O=,解得100O =. 答:一条鱼静止时的耗氧量为100个单位.B 组1. 由3log 41x =得:143,43xx-==,于是11044333x x -+=+= 2. ①当1a >时,3log 14a<恒成立; ②当01a <<时,由3log 1log 4a a a <=,得34a <,所以304a <<.综上所述:实数a 的取值范围是3{04a a <<或1}a >3. (1)当1I = W/m 2时,112110lg 12010L -==;(2)当1210I -= W/m 2时,121121010lg 010L --==答:常人听觉的声强级范围为0120dB .4. (1)由10x +>,10x ->得11x -<<,∴函数()()f x g x +的定义域为(1,1)- (2)根据(1)知:函数()()f x g x +的定义域为(1,1)-∴ 函数()()f x g x +的定义域关于原点对称又∵ ()()log (1)log (1)()()a a f x g x x x f x g x -+-=-++=+ ∴()()f x g x +是(1,1)-上的偶函数.5. (1)2log y x =,0.3log y x =; (2)3xy =,0.1x y =.习题2.3 A 组(P79) 1.函数y =21x是幂函数. 2.解析:设幂函数的解析式为f (x )=x α,因为点(2,2)在图象上,所以2=2α.所以α=21,即幂函数的解析式为f (x )=x 21,x ≥0.3.(1)因为流量速率v 与管道半径r 的四次方成正比,所以v =k ·r 4; (2)把r =3,v =400代入v =k ·r 4中,得k =43400=81400,即v =81400r 4; (3)把r =5代入v =81400r 4,得v =81400×54≈3 086(cm 3/s ), 即r =5 cm 时,该气体的流量速率为3 086 cm 3/s .第二章 复习参考题A 组(P82)1.(1)11; (2)87; (3)10001; (4)259. 2.(1)原式=))(()()(212121212212122121b a b a b a b a -+++-=b a b b a a b b a a -++++-2121212122=ba b a -+)(2;(2)原式=))(()(1121----+-a a a a a a =aa a a 11+-=1122+-a a . 3.(1)因为lg 2=a ,lg 3=b ,log 125=12lg 5lg =32lg 210lg2•=3lg 2lg 22lg 1+-,所以log 125=ba a +-21. (2)因为2log 3a =,3log 7b =37147log 27log 56log 27⨯=⨯=2log 112log 377++=7log 2log 11)7log 2(log 33333÷++÷=b ab a ÷++÷111)1(3=13++ab ab . 4.(1)(-∞,21)∪(21,+∞);(2)[0,+∞).5.(32,1)∪(1,+∞);(2)(-∞,2);(3)(-∞,1)∪(1,+∞).6.(1)因为log 67>log 66=1,所以log 67>1.又因为log 76<log 77=1,所以log 76<1.所以log 67>log 76. (2)因为log 3π>log 33=1,所以log 3π>1.又因为log 20.8<0,所以log 3π>log 20.8.7.证明:(1)因为f (x )=3x ,所以f (x )·f (y )=3x ×3y =3x +y .又因为f (x +y )=3x +y ,所以f (x )·f (y )=f (x +y ). (2)因为f (x )=3x ,所以f (x )÷f (y )=3x ÷3y =3x -y . 又因为f (x -y )=3x -y ,所以f (x )÷f (y )=f (x -y ).8.证明:因为f (x )=lgxx+-11,a 、b ∈(-1,1), 所以f (a )+f (b )=lgbb a a +-++-11lg11=lg )1)(1()1)(1(b a b a ++--, f (ab b a ++1)=lg (ab b a ab ba +++++-1111)=lg b a ab b a ab +++--+11=lg )1)(1()1)(1(b a b a ++--. 所以f (a )+f (b )=f (abba ++1).9.(1)设保鲜时间y 关于储藏温度x 的函数解析式为y =k ·a x (a >0,且a ≠1).因为点(0,192)、(22,42)在函数图象上,所以022192,42,k a k a ⎧=⋅⎪⎨=⋅⎪⎩解得⎪⎩⎪⎨⎧≈==.93.0327,19222a k 所以y =192×0.93x ,即所求函数解析式为y =192×0.93x . (2)当x =30 ℃时,y ≈22(小时);当x =16 ℃时,y ≈60(小时),即温度在30 ℃和16 ℃的保鲜时间约为22小时和60小时. (3)图象如图:图2-210.解析:设所求幂函数的解析式为f (x )=x α,因为f (x )的图象过点(2,22), 所以22=2α,即221-=2α.所以α=21-.所以f (x )=x 21-(x >0).图略,f (x )为非奇非偶函数;同时它在(0,+∞)上是减函数.B 组1.A2.因为2a =5b =10,所以a =log 210,b =log 510,所以a 1+b 1=10log 12+10log 15=lg 2+lg 5=lg 10=1. 3.(1)f (x )=a 122+-x在x ∈(-∞,+∞)上是增函数.证明:任取x 1,x 2∈(-∞,+∞),且x 1<x 2.f (x 1)-f (x 2)=a 122+-x -a +1222+x =1222+x -1221+x =)12)(12()22(21221++-x x x x . 因为x 1,x 2∈(-∞,+∞), 所以.012.01212>+>+x x又因为x 1<x 2, 所以2122x x <即2122x x <<0.所以f (x 1)-f (x 2)<0,即f (x 1)<f (x 2).所以函数f (x )=a 122+-x在(-∞,+∞)上是增函数. (2)假设存在实数a 使f (x )为奇函数,则f (-x )+f (x )=0,即a 121+--x +a 122+-x =0⇒a =121+-x +121+x =122+x +121+x=1, 即存在实数a =1使f (x )=121+--x 为奇函数.4.证明:(1)因为f (x )=2x x e e --,g (x )=2xx e e -+,所以[g (x )]2-[f (x )]2=[g (x )+f (x )][g (x )-f (x )]=)22)(22(xx x x x x x x e e e e e e e e -----++++ =e x ·e -x =e x -x =e 0=1, 即原式得证.(2)因为f (x )=2x x e e --,g (x )=2xx e e -+,所以f (2x )=222x x e e -+,2f (x )·g (x )=2·2x x e e --·2x x e e -+=222xx e e --.所以f (2x )=2f (x )·g (x ).(3)因为f (x )=2x x e e --,g (x )=2xx e e -+,所以g (2x )=222x x e e -+,[g (x )]2+[f (x )]2=(2x x ee -+)2+(2xx e e --)2=4222222x x x x e e e e --+-+++=222xx e e -+.所以g (2x )=[f (x )]2+[g (x )]2.5.由题意可知,θ1=62,θ0=15,当t =1时,θ=52,于是52=15+(62-15)e -k ,解得k ≈0.24,那么θ=15+47e -0.24t . 所以,当θ=42时,t ≈2.3;当θ=32时,t ≈4.2.答:开始冷却2.3和4.2小时后,物体的温度分别为42 ℃和32 ℃.物体不会冷却到12 ℃.6.(1)由P=P 0e -k t 可知,当t =0时,P=P 0;当t =5时,P=(1-10%)P 0.于是有(1-10%)P 0=P 0e -5k ,解得k =51-ln 0.9,那么P=P 0e t )9.0ln 51(.所以,当t =10时,P=P 0e 9.01051n I ⨯⨯=P 0e ln 0.81=81%P 0.答:10小时后还剩81%的污染物. (2)当P=50%P 0时,有50%P 0=P 0et )9.0ln 51(,解得t =9.0ln 515.0ln ≈33.答:污染减少50%需要花大约33h . (3)其图象大致如下:图2-3。
第二章 课后练习题及答案

第二章对国家出路的早期探索一、单项选择题1.太平天国定都天京后,颁布的体现农民愿望的纲领是(C )A.《原道醒世训》B.《原道觉世训》C.《天朝田亩制度》D.《天京田亩制度》2.太平天国后期颁布的社会发展方案是(D )A.《太平天国施政纲要》B.《国库制度》C.《金库制度》D.《资政新篇》3. 洋务派兴办的最大的兵工厂是(C )A.金陵机器局B.福州船政学堂C.上海江南制造总局D.汉阳枪炮厂4.康有为1895 年在京联合在京参加会试的举人向光绪皇帝上书的事件是(A )A.“公车上书”B.“百日维新”C.“公车载书”D.“明定国是”5.洋务运动的指导思想是( A )A.“中学为体西学为用”B.“西学为体中学为用”C.中西结合D.全盘西化6.资产阶级思想与封建主义思想在中国的第一次正面交锋是( B )。
A.洋务派与守旧派的争论B.维新派与守旧派的论战C.革命派与维新派的论战D.“问题与主义”之争7. 太平天国农民战争由兴盛走向衰败的转折点是( D )。
A.金田起义B.北伐失败C.永安建制D.天京事变8.( D )标志着维新变法运动的开始A. 维新派与守旧派的论战B. 公车上书C. “中体西用”思想的提出D. “明定国是”诏书的颁布9. 戊戌变法的性质是(B )A.资产阶级革命运动B.资产阶级改良运动C.封建统治阶级自上而下的改革D.地主阶级的改革运动10.太平天国之所以是农民战争的高峰,最主要因为( C )A.其规模和延续时间均属空前B.建立了与清政府对立的政权C.制定了比较完整的革命纲领D.对封建王朝的打击空前沉重二、多项选择题1.天平天国的领导们希望《天朝田亩制度》实现的理想社会是(ABC )A.“有田同耕,有饭同食”B.“有衣同穿,有钱同使”C.“无处不均匀,无人不保暖”D.“禁朋党之弊,设立新闻官”2.洋务派的重要代表人物是(ABD )A.奕诉B.曾国藩C.慈禧太后D.张之洞3.洋务运动举办的著名的水师有(ABCD )A.福建水师B.广东水师C.南洋水师D.北洋水师4. 资产阶级维新派的主要代表著有(A BCD )A.《孔子改制考》B.《新学伪经考》C.《仁学》D.《变法通议》5.“百日维新”的主要内容包括( ABCD )。
数字逻辑课后答案第二章

第二章 组合逻辑1.分析图中所示的逻辑电路,写出表达式并进行化简BF = AB + B = ABA F = AB BABC CABC = AB + AC + BC + BC = AB + BC + BC2.分析下图所示逻辑电路,其中S3、S2、S1、S0为控制输入端,列出真值表,说明 F 与 A 、B 的关系。
F1=10SB BS A ++F2=32SB A ABS +F=F 1F 2=1SB BS A ++3. 分析下图所示逻辑电路,列出真值表,说明其逻辑功能。
解:F1=C B BC A C AB C B A +++=ABCC B A ABC C B A C B A +⊕=++)(真值表如下:A B C F 0 0 00 0 10 1 00 1 11 0 01 0 11 1 01 1 100000111当B ≠C 时, F1=A当B=C=1时, F1=A 当B=C=0时, F1=0裁判判决电路,A 为主裁判,在A 同意的前提下,只要有一位副裁判(B ,C )同意,成绩就有效。
F2=AC BC AB C A C B B A ++=++真值表如下:A B C F 0 0 00 0 10 1 00 1 11 0 01 0 11 1 01 1 100001111当A 、B 、C 三个变量中有两个及两个以上同时为“1”时,F2 = 1 。
4.图所示为数据总线上的一种判零电路,写出F 的逻辑表达式,说明该电路的逻辑功能。
解:F=1514131211109876543210A A A A A A A A A A A A A A A A +++只有当变量A0~A15全为0时,F = 1;否则,F = 0。
因此,电路的功能是判断变量是否全部为逻辑“0”。
5. 分析下图所示逻辑电路,列出真值表,说明其逻辑功能解: 301201101001X A A X A A X A X A A F +++= 真值表如下:因此,这是一个四选一的选择器。
大学语文B第二章 先秦两汉魏晋南北朝文课后练习

第二章先秦两汉魏晋南北朝文课后练习一、判断题共55 题1、《前赤壁赋》保留了传统赋体文"主客问答"的形式。
()对错参考答案:正确2、《老子》标志着我国叙事文学的重大发展,因而具有较高的文学价值。
()对错参考答案:错误3、先秦古籍如《山海经》《穆天子传》等保留了不少神话传说。
()对错参考答案:正确4、《春秋》本是当时各国史书之通名。
()对错参考答案:正确5、《论语》是儒家学派的经典著作之一。
()对错参考答案:正确6、老子批判礼乐文化,主张"绝圣弃智",希望回到"小国寡民"的时代。
()对错参考答案:正确7、《世说新语》是干宝组织编纂的。
()对错参考答案:错误8、《战国策·燕昭王求士》中燕昭王的性格特征之一是礼贤下士,从善如流。
()对错参考答案:正确9、《战国策·燕昭王求士》中燕昭王的性格特征之一是知人善任,任人唯贤。
()对错参考答案:正确10、南朝出现了以讲求声韵、辞采、对偶、用事为特征的骈文。
()对错参考答案:正确11、《哀江南赋序》的作者是鲍照。
()对错参考答案:错误12、《孟子·天时地利人和章》大量运用了否定句式。
()对错参考答案:正确13、春秋战国时期散文的文体意识也表现出初步的觉醒。
()对错参考答案:错误14、《战国策·燕昭王求士》中郑庄公的性格特征之一是知人善任,任人唯贤。
()对错参考答案:错误15、《战国策·燕昭王求士》中郑庄公的性格特征之一是礼贤下士,从善如流。
()对错参考答案:错误16、《吴越春秋》所载《弹歌》是《楚辞》中的名篇。
()对错参考答案:错误17、《论语·侍坐》中孔子之所以笑子路,是因为子路不够谦虚和礼让。
()对错参考答案:正确18、曹操的文章直写真情实意,绝不避讳顾忌。
()对错参考答案:正确19、《孟子》一书是孟子本人独立编著的。
()对错参考答案:错误20、《庄子》对后世各种骈偶押韵之文颇有影响。
管理会计白玉芳第二章成本性态分析课后习题参考答案解析

第二章成本性态分析思考与练习题答案一、思考题1、什么是成本?如何理解成本信息在管理会计中的作用。
成本是指人们在经济活动过程中,为达到一定的目的而耗费的各种资源,包括人、财、物、时间、信息、机会等等。
在财务会计中,成本是根据财务报表的需要定义的,即成本是指取得资产或劳务的支出,它们由会计准则或会计制度来规范,因此可以称之为“报表成本”、“制度成本”或“法定成本”。
在管理会计中,成本一词在不同的情况下有不同的含义。
从管理会计角度看,成本是指企业在经济活动中对象化的、以货币表现的为达到一定目的而应当或可能发生的各种经济资源的价值牺牲或代价。
成本信息在管理会计中具有重要的作用,是企业开展经营决策、制订竞争性策略、改善经营行为、评价经营业绩的基本前提之一。
从管理会计角度看,管理人员需求的各种信息绝大部分与成本有关,成本-效益分析是任何一项经济决策都必须开展的。
企业管理当局在经营决策和日常控制的各个环节,都必须以成本数据为基础,进行加工、改制和延伸,并适应不同情况进行灵活运用。
2、成本按经济用途应怎样分类?这种分类有什么优缺点?成本的经济用途划将成本分为三类,即生产成本、营销成本和管理成本三大类:生产成本也称制造成本,它是指为生产(制造)产品或提供劳务而发生的成本。
生产成本又可根据其具体的经济用途分为料、工、费三大项目。
营销成本也称销售费用,指企业为推销产品所发生的一切费用,一般包括广告费、展览费、推销费、运输费、销售人员的差旅费和工资等费用。
管理成本指制造成本和营销成本以外的由企业管理当局或各职能科室在进行企业管理时所发生的一切费用,一般包括行政管理部门和职能科室的办公费、邮电费、水电费、管理人员薪金等。
优点:第一,能清楚地反映产品成本结构,便于与本企业历史资料或同行业数据比较,用来评价和考核目标成本的执行情况,分析成本升降原因,明确经济责任,并提出改进的措施和建议。
第二,这种分类将总成本分为生产成本、营销成本和管理成本三大类,有利于“产品成本”和“期间成本”的划分,贯彻“配比”原则。
2高中数学选择性必修第一册第二章课后答案

第二章直线和圆的方程2.1直线的倾斜角与斜率2.1.1倾斜角与斜率P55练习1.已知下列直线的倾斜角,求直线的斜率:(1)30α= ;(2)45a =o ;(3)23πα=;(4)34πα=. 2.已知下列直线的斜率,求直线的倾斜角.(1)0k =;(2)k =(3)k =(4)3k =-.【答案】(1)0︒;(2)60︒;(3)120︒;(4)150︒.3.求经过下列两点的直线的斜率,并判断其倾斜角是锐角还是钝角.(1)(18,8)C ,(4,4)D -;(2)(0,0)P ,(1,3)Q -.4.已知a ,b ,c 是两两不等的实数,求经过下列两点的直线的倾斜角.(1)(,)A a c ,(,)B b c (2)(,)C a b ,(,)D a c (3)(,)P b b c +,(,)Q a c a +.(2)因为,C D 的横坐标相等,所以直线CD ⊥x 轴,所以直线CD 的倾斜角为90︒;线PQ 的倾斜角为45︒.5.经过()0,2A ,()1,0B -两点的直线的方向向量为()1,k ,求k 的值.【答案】因为直线的方向向量为()1,k ,则k 为直线的斜率,2.1.2两条直线平行和垂直的判定P57练习1.判断下列各对直线平行还是垂直:(1)经过两点A (2,3),B (﹣1,0)的直线l 1,与经过点P (1,0)且斜率为1的直线l 2;(2)经过两点C (3,1),D (﹣2,0)的直线l 3,与经过点M (1,﹣4)且斜率为﹣5的直线l 4.【答案】(1)平行(2)垂直2.试确定m 的值,使过(),1A m ,()1,B m -两点的直线与过()1,2P ,()5,0Q -两点的直线.(1)平行;(2)垂直.当1m =-时,直线AB 的斜率不存在,此时直线AB 与直线PQ 即不平行也不垂直;习题2.1P57复习巩固1.已知直线斜率的绝对值等于1,求直线的倾斜角.【答案】设倾斜角为[),0,180αα∈︒︒,当1k =-时,tan 1α=-,135α=︒;当1k =时,tan 1α=,45α=︒;所以直线的倾斜角为45︒或135︒.2.已知四边形ABCD 的四个顶点是()2,3A ,()1,1B -,()1,2C --,()2,2D -,求四边形ABCD 的四条边所在直线的斜率.3.m 为何值时,(1)经过(),6A m -,()1,3B m 两点的直线的斜率是12?(2)(),2A m ,(),21B m m ---两点的直线的倾斜角是60︒?4.已知()1,2A ,()1,0B -,()3,4C 三点,这三点是否在同一条直线上?为什么?5.判断下列不同的直线1l 与2l 是否平行.(1)1l 的斜率为2,2l 经过()1,2A ,()4,8B 两点;(2)1l 经过()3,3P ,()5,3Q -两点,2l 平行于x 轴,但不经过P ,Q 两点;(3)1l 经过()1,0M -,()5,2N --两点,2l 经过()4,3R -,()0,5S 两点.【答案】(1)平行;(2)平行;(3)平行.6.判断下列直线1l 与2l 是否垂直.(1)1l 的斜率为23-,2l 经过点()1,1A ,10,2B ⎛⎫- ⎪⎝⎭;(2)1l 的倾斜角为45︒,2l 经过()2,1P --,()3,6Q -两点;(3)1l 经过()1,0M ,()4,5N -两点,2l 经过()6,0R -,()1,3S -两点.【答案】(1)垂直;(2)垂直;(3)垂直.P58综合运用7.过()222,3A m m +-,()23,2B m m m --两点的直线l 的倾斜角为45︒,求m 的值.【答案】因为直线的倾斜角为45︒,所以直线的斜率tan 451k =︒=,当1m =-时,()()22230m m m +---=,不符合,当2m =-时,()()222350m m m +---=≠,符合,综上:2m =-.8.经过点()0,1P -作直线l ,若直线l 与连接()1,2A -,()2,1B 两点的线段总有公共点,求直线l 的倾斜角α与斜率k 的取值范围,并说明理由.【答案】如下图所示,中阴影部分时都能满足题意,旋转过程中,倾斜角先从135︒变化到0︒,再从0︒变化到45︒,所以倾斜角α的取值范围是:[][)0,45135,180︒︒︒︒ ;旋转过程中,斜率先从1-变化到0,再从0变化到1,所以斜率k 的取值范围是:[]1,1-.9.已知点()2,2M 和()5,2N -,点P 在x 轴上,且MPN ∠为直角,求点P 的坐标.【答案】设(),0P x ,因为90APB ∠=︒,所以由勾股定理可得()()()()()()2222222025025222x x -+-+-++=-+--,即2760x x -+=,解得1x =或6x =,所以点P 的坐标是()1,0或()6,0.故答案为:()1,0或()6,0.P58拓广探索10.已知四边形ABCD 的四个顶点是(2,2A +,()2,2B -,(0,2C -,()4,2D ,求证:四边形ABCD 为矩形.【答案】因为四个点的横坐标各不相等,所以四边形四条边所在直线的斜率都存在,所以四边形ABCD 四条边两两垂直,所以四边形ABCD 四个内角都为90︒,所以四边形ABCD 是矩形.第二章直线和圆的方程2.2直线的方程2.2.1直线的点斜式方程61练习1.写出下列直线的点斜式方程.(1)经过点()3,1A -;(2)经过点()2B ,倾斜角是30°;(3)经过点()0,3C ,倾斜角是0︒;(4)经过点()4,2D --倾斜角是23π.2.(1)已知直线的点斜式方程是21y x -=-,那么此直线的斜率是_________,倾斜角是_________;(2)已知直线的点斜式方程是()231y x +=+,那么此直线的斜率是_________,倾斜角是_________.3.写出下列直线的斜截式方程.(1)斜率是2,在y 轴上的截距是2-;(2)斜率是2-,在y 轴上的截距是4.4.判断下列各对直线是否平行或垂直.(1)11:32l y x =+,21:22l y x =-;(2)15:3l y x =,23:5l y x =-.【答案】(1)12//l l ,(2)12l l ⊥2.2.2直线的两点式方程P64练习1.求经过下列两点的直线的两点式方程.(1)()12,1P ,()20,3P-;(2)()0,5A ,()5,0B .2.根据下列条件求直线的截距式方程,并画出图形.(1)在x 轴、y 轴上的截距分别是2,3;(2)在x 轴、y 轴上的截距分别是5-,6.(2)由截距式得:3.根据下列条件,求直线的方程.(1)过点()0,5,且在两坐标轴上的截距之和为2;(2)过点()5,0,且在两坐标轴上的截距之差为2.【答案】(1)53+150x y -=(2)35150x y --=或75350x y --=2.2.3直线的一般式方程P66练习1.根据下列条件,写出直线的方程,并把它化为一般式.(1)经过点()8,2A -,斜率是12-;(2)经过点()4,2B ,平行于x 轴;(3)经过点()13,2P -,()25,4P-;(4)在x 轴、y 轴上的截距分别是32,3-.【答案】(1)240x y +-=;(2)20y -=;(3)10x y +-=;(4)230x y --=2.求下列直线的斜率以及在y 轴上的截距,并画出图形.(1)350x y +-=;(2)145x y -=;(3)20x y +=;(4)7640x y -+=.【答案】(1)350x y +-=即35y x =-+,斜率为3-,在y 轴上的截距为5;(3)20x y +=,即(4)7640x y -+=,即y =3.已知直线l 的方程是0Ax By C ++=.(1)当0B ≠时,直线l 的斜率是多少?当0B =时呢?(2)系数A ,B ,C 取什么值时,方程0Ax By C ++=表示经过原点的直线?(2)因为直线0Ax By C ++=过原点,所以0C =,所以当0C =且,A B 不同时为0时,方程0Ax By C ++=表示经过原点的直线.习题2.2P67复习巩固1.写出满足下列条件的直线的方程.(1)经过点(8,2)A -,斜率是33;(2)经过点(2,0)B -,且与x 轴垂直;(3)斜率是4-,在y 轴上的截距是7;(4)经过(1,8)A -,(4,2)B -两点;(5)在y 轴上的截距是2,且与x 轴平行;(6)在x 轴、y 轴上的截距分别是4,3-.(5)2y =;(6)34120x y --=2.判断()1,3A ,()5,7B ,()10,12C 三点是否共线,并说明理由.【答案】因为()1,3A ,()5,7B ,()10,12C ,所以(4,4),(9,9)AB AC →→==,3.已知两点()7,4A -,()5,6B -,求线段AB 的垂直平分线的方程.【答案】因为两点()7,4A -,()5,6B -,4.已知ABC 的三个顶点()8,5A ,()4,2B -,()6,3C -,求经过两边AB 和AC 的中点的直线的方程.【答案】设AB 和AC 的中点分别为,D E ,因为()8,5A ,()4,2B -,()6,3C -,经过两边AB 和AC 的中点的直线的方程为290x y +-=.5.一根弹簧,挂4N 的物体时,长20cm .在弹性限度内,所挂物体的重量每增加1N ,弹簧就伸长1.5cm .试写出弹簧的长度l (单位:cm )与所挂物体重量G (单位:N )之间关系的方程.【答案】设弹簧的原长是L cm ,挂4N 的物体时,长20cm .在弹性限度内,所挂物体的重量每增加1N ,弹簧就伸长1.5cm .2041.5L ∴=+⨯,解得14L =cm .∴在弹性限度内,弹簧的长度l (单位:cm )与所挂物体重量G (单位:N )之间关系的方程:14 1.5l G =+.6.菱形的两条对角线分别位于x 轴和y 轴上,其长度分别为8和6,求菱形各边所在直线的方程.【答案】由题意作出菱形图形,如图,7.求经过点()2,3P ,并且在两坐标轴上的截距相等的直线的方程.【答案】(1)当截距为0时:直线为320x y -=。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章课后练习答案
第二章贸易术语
思考题答案
1.试述贸易术语的含义、性质及在国际贸易中的作用。
贸易术语(trade terms ),也称贸易条件、价格术语(price terms ),是在国际贸易的长期实践中逐渐形成的用一个简短的概念或外文缩写来表明商品的价格构成、说明货物交接过程中有关的风险、责任和费用划分问题的专门术语。
贸易术语具有两重性,即一方面表示交货条件,另一方面表示成交价格的构成因素。
贸易术语在国际贸易中起着积极的作用,主要表现在下列几个方面:
(1)有利于买卖双方洽商交易和订立合同;
(2)有利于买卖双方核算价格和成本;
(3)有利于解决买卖双方的争议。
2.有关国际贸易术语的国际贸易惯例主要有哪几种?分别解释了哪些贸易术语?
目前,国际上有关贸易术语的国际惯例有三
(1)《1932年华沙-牛津规则》它对CIF 合同的性质、特点及买卖双方的权利和义务都作了具体的规定和说明,为那些按CIF 贸易术语成交的买卖双方提供了一套易于使用的统一规则。
(2)《1941 年美国对外贸易定义修正本》该定义对以下六种贸易术语作了解释:Ex ( Point of
Origin )、FOB(Free on Board )、FAS ( Free Along Side)、C&F ( Cost and Freight )、CIF ( Cost,Insurance and freight )和Ex Dock ( named port of importation )。
(3)《2000 年国际贸易术语解释通则》
它解释了四组13个贸易术语。
第一组为“E” 组(EX WORKS ),第二组为“卩”组(FCA、FOB 和FAS),第三组为“ C ”组(CFR、CIF、CPT 和CIP),第四组为“。
”组(DAF、DES、DEQ、DDU 和DDP)。
3.什么是《INCOTERMS 2000》?试分别指出各组术语的共同点以及13 个术语的交货点。
《INCOTERMS 2000 》(《2000年国际贸易术语
解释通则》)是国际商会为统一对各种贸易术语
的解释而制定的一种通用的有关贸易术语的国际
贸易惯例。
最早的版本制定于1936 年,后来经
过了多次修改和补充:1953、1967、1976、
1980、1990 年先后进行过5 次修订和补充,最
近的一次修订是在2000 年,故称为
《INCOTERMS 2000 》。
它解释了四组13 个贸易术语。
E 组只有一个贸易术语,即EXW (工厂交货),其特点是卖方在自己的地点把货物备妥或交至买方处置之下。
F 组有3 个贸易术语(FCA 、FAS、FOB ),其共同点是卖方须将货物交至买方指定的承运人,不负责运输及保险等事宜。
C 组有4个贸易术语(CFR 、CIF 、CPT、
CIP ),其共同点是卖方须签订运输合同,支付运费,但货物灭失或损坏的风险及装船和启运后发生意外所产生的费用,卖方不承担责任。
D 组有5 个贸易术语(DAF 、DES、DEQ 、
DDU、DDP),其特点是卖方须承担把货物交至指定的进口国交货地点的全部费用和风险,且按D 组术语成交的贸易合同,称为到货合同。
13个贸易术语的交货地点:
EXW —卖方所在地货交买方处置时FCA--出口国指
定地点货交承运人监管时
FAS--装运港船边
FOB--装运港船舷CFR--装运港船舷CIF--装运港
船舷
CPT--出口国指定地点货交承运人监管时CIP--出
口国指定地点货交承运人监管时DAF--两国边境指
定地点货交买方处置时DES--目的港船上货交买方
处置时DEQ--目的港码头货交买方处置时
DDU--进口国指定地点货交买方处置时DDP--进口
国指定地点货交买方处置时
4.试写出《INCOTERMS 2000》中使用较多的六种贸易术语的中、英文全称和英文缩写。
《INCOTERMS 2000》中使用较多的六种
贸易术语:
5.简述FOB、CFR和CIF三种术语的异同,并在下表各栏中分别填入“买方”和“卖方” 字样:
6.简述FCA与FOB的主要不同点
FCA free carrier (货交承运人)FOB free
on board (装运港船上交
…寫与港港术界点,同点是
界点仅适用于
7.简述C组贸易术语与F组贸易术语的区
按F组和C组术语成交的合同称作装运合同,这类合同下,卖方仅保证按时完成装运但无须保证按时到货。
采用F组术语成交时,卖方承担的风险和费用均在交货地点同时转移给买方,而按C组术语成交时,风险在交货时转移,而费用则在目的港或目的地转移。
8.简述CIF术语与DES术语的区别。
