关于圆的切线的练习题经典

合集下载

初三圆的切线试题及答案

初三圆的切线试题及答案
一、选择题
1. 下列说法正确的是（）
A. 圆的切线垂直于过切点的半径
B. 圆的切线与过切点的半径垂直
C. 圆的切线与过切点的直径垂直
D. 圆的切线与过切点的弦垂直
答案：B
2. 经过圆外一点作圆的切线，下列说法正确的是（）
A. 只能作一条
B. 能作两条
C. 能作无数条
D. 不能作
答案：B
二、填空题
3. 已知圆的半径为5，圆心到切线的距离为3，则切线的长度为______。

答案：4√2
4. 圆的直径为10，切线与直径的夹角为30°，则切线的长度为______。

答案：5√3
三、解答题
5. 已知圆O的半径为2，点A在圆外，OA=4，求经过点A的圆O的切
线长。

答案：首先，连接OA，设切点为B。

由题意知，OA=4，OB=2。

在直角
三角形OAB中，根据勾股定理，AB²=OA²-OB²=4²-2²=12，所以
AB=2√3。

由于切线与半径垂直，所以切线长为2√3。

6. 圆的半径为3，圆心到切线的距离为2，求切线与圆心的夹角。

答案：设切线与圆心的夹角为θ，根据切线的性质，圆心到切线的距
离等于半径乘以sinθ，即2=3sinθ。

解得sinθ=2/3。

由于θ在0°到90°之间，所以θ=arcsin(2/3)。

圆的切线和切线长练习题

练习题1、过圆上一点可以作圆的_______条切线；过圆外一点可以作圆的________条切线；过_____点不存在圆的切线。

2、等腰直角三角形ABC 的腰长为5cm ，D 为斜边AB 的中点，则以D 为圆心，以______cm 为半径的圆经过A 、 B 、C ；以D 为圆心，以_______cm 为半径的圆与直线AC 、BC 相切。

当半径_______cm 时，⊙D 和直线AB 、BC 、AC 都相交。

3、已知圆中最大的弦长为8，一条直线与此圆相交，设圆心到直线的距离为d ，则d 的取值范围为______。

4、在射线OA 上取一点P ，使OP=4cm ，以P 为圆心作直径为4cm 的圆，若⊙P 与射线OB 相交，则锐角AOB 的取值范围为_________。

5、Rt △ABC 的斜边AB 为4，直角边AC=2，若AB 与⊙C 相切，则⊙C 的半径为___________。

6、PA 切⊙O 于A 点，PO 交⊙O 于B ，OB=PB=1，则PA 等于______________。

7、⊙O 的两条切线L 1∥L 2，⊙O 的半径为4，则L 1与L 2的距离为____________。

8、在直角坐标系中，⊙M 的圆心坐标为(m ，0)，半径是2，如果⊙M 与y 轴所在的直线相切，那m 等于______，若⊙M 与y 轴所在的直线相交，那么m 的取值范围是__________。

9、OA 平分∠BOC ，P 是OA 上任一点(O 除外)，若以P 为圆心的⊙P 与OC 相离，那么⊙P 与OB 的位置关系是（）A 、相离B 、相切C 、相交D 、相交或相切10、菱形对角线交于O 点，以O 为圆心，O 到菱形一边的距离为半径的⊙O 与其他边的位置关系是（）A 、相交B 、相离C 、相切D 、无法确定11、以三角形一边为直径的圆切三角形的另一边，则该三角形为（）A 、锐角三角形B 、钝角三角形C 、直角三角形D 、等边三角形12、平面直角坐标系中有点A （3，4），以A 为圆心，5为半径画圆，在同一坐标系中直线y =－x 与⊙A 的位置关系是（）A 、相离B 、相切C 、相交D 、以上情况都有可能13、已知△ABC 中，∠C=90°，AB=13，AC=12，则以B 为圆心，以6为半径的圆与直线AC 的位置关系是_____。

3.7 切线长定理(练习)(解析版)

第三章圆第七节切线长定理精选练习一、单选题1．（2021·北京九年级专题练习）如图，PA ，PB 为⊙O 的两条切线，点A ，B 是切点，OP 交⊙O 于点C ，交弦AB 于点D ．下列结论中错误的是（）A ．PA ＝PBB ．AD ＝BDC ．OP ⊥ABD ．∠PAB ＝∠APB【答案】D【分析】利用切线长定理、等腰三角形的性质即可得出答案．【详解】解：由切线长定理可得：∠APO =∠BPO ，PA =PB ，从而AB ⊥OP ，AD =BD ．因此A ．B ．C 都正确．无法得出∠PAB =∠APB ，可知：D 是错误的．综上可知：只有D 是错误的．故选：D ．【点睛】本题考查了切线长定理、等腰三角形的性质，关键是利用切线长定理、等腰三角形的性质解答．2．（2021·全国九年级课时练习）如图，AB 是⊙O 的直径，点P 在BA 的延长线上，PA ＝AO ，PD 与⊙O 相切于点D ，BC ⊥AB 交PD 的延长线于点C ，若⊙O 的半径为1，则BC的长是（）A ．1.5B ．2CD 【答案】D【分析】连接OD ，根据切线的性质求出∠ODP ＝90°，根据勾股定理求出PD ，证明BC 是⊙O 的切线，根据切线长定理得出C D ＝BC ，再根据勾股定理求出BC 即可．【详解】连接OD ，如图所示∵PC 切⊙O 于D ∴∠ODP ＝90°∵⊙O 的半径为1，PA ＝AO ，AB 是⊙O 的直径 ∴PO ＝1+1＝2，PB ＝1+1+1＝3，OD ＝1∴由勾股定理得：PD ==∵BC ⊥AB ，AB 过O ∴BC 切⊙O 于B ∵PC 切⊙O 于D ∴CD ＝BC设CD ＝CB ＝x 在Rt △PBC 中，由勾股定理得：PC 2＝PB 2+BC 2即222)3x x +=+ 解得：x 即BC故选：D【点睛】本题考查了切线的性质和判定，及切线长定理，切线的性质定理为：圆的切线垂直于过切点的半径，切线长定理为：从圆外一点可以引圆的两条切线，它们的切线长相等，这一点和圆心的连线平分两条切线的夹角．同时考查了利用勾股定理解直角三角形．3．（2021·湖北武汉市·九年级一模）如图，经过A 、C 两点的⊙O 与△ABC 的边BC 相切，与边AB 交于点D ，若∠AD C ＝105°，BC ＝CD ＝3，则AD 的值为（）A ．B ．CD 【答案】A【分析】连接OC 、OD ，作OE AB ^于点E ．易求出75CBD CDB Ð=Ð=°，30BCD Ð=°．再由切线的性质，即可求出60OCD Ð=°，即三角形OCD 为等边三角形．得出结论60ODC Ð=°，3OC OD CD ===．从而即可求出45ADO Ð=°，即三角形OED 为等腰直角三角形，由此即可求出DE 的长，最后根据垂径定理即可求出AD 的长．【详解】如图，连接OC 、OD ，作OE AB ^于点E ．∵BC CD =，∴CBD CDB Ð=Ð，∵105ADC Ð=°，∴75CBD CDB Ð=Ð=°，∴18027530BCD Ð=°-´°=°．由题意可知OC BC ^，即90OCB Ð=°，∴903060OCD OCB BCD Ð=Ð-Ð=°-°=°，∵OD =OC ，∴三角形OCD 为等边三角形．∴60ODC Ð=°，3OC OD CD ===．∴1056045ADO ADC ODC Ð=Ð-Ð=°-°=°，∴三角形OED 为等腰直角三角形，∴3DE ===∴22AD DE ===故选：A ．本题考查切线的性质，等腰三角形的性质，三角形外角的性质，等腰直角三角形与等边三角形的判定和性质以及垂径定理，综合性强．正确的连接辅助线是解答本题的关键．4．如图，直线AB，BC，CD分别与⊙O相切于E，F，G，且AB//CD，若OB=3cm，OC=4cm，则四边形EBCG的周长等于（）A．5cm B．10cm C．745cm D．625cm【答案】C【分析】连接OF，利用切线性质和切线长定理可证明BE=BF，CG=CF，∠OBE=∠OBF，∠OCG=∠OCF，OF⊥BC，再根据平行线的性质证得∠BOC=90°，进而由勾股定理求得BC长，根据三角形的面积公式求得OF，进而可求得四边形的周长．【详解】解：连接OF，∵直线AB，BC，CD分别与⊙O相切于E，F，G，∴BE=BF，CG=CF，∠OBE=∠OBF，∠OCG=∠OCF，OF⊥BC，∵AB∥CD，∴∠ABC+∠DCB=180°，∴∠OBF+∠OCF=90°，即∠BOC=90°，∴在Rt△BOC中，OB=3cm，OC=4cm，由勾股定理得：BC==，由1122OB OC BC OF××=××得：OF=341255´=cm，∴OE=OG=OF= 125cm，∴四边形EBCG的周长为BE+BC+CG+EG=2OE+2BC=2×125+2×5=745cm，【点睛】本题考查切线的性质、切线长定理、平行线的性质、勾股定理、三角形的面积公式，熟练掌握切线长定理的运用，证得∠BOC =90°和利用等面积法求出OF 是解答的关键．5．（2021·山西吕梁市·九年级月考）如图，四边形ABCD 内接于⊙O ，AB ＝BC ．AT 是⊙O 的切线，∠BAT ＝55°，则∠D 等于（）A ．110°B ．115°C ．120°D ．125°【答案】A【分析】连接AC ，OA ，OB ，先结合切线的性质以及圆的性质求得ACB BAT Ð=Ð，再结合等腰三角形的性质以及圆的内接四边形的性质求得2D ACB Ð=Ð即可．【详解】如图所示，连接AC ，OA ，OB ，则()11802AOB OBA OAB =°-ÐÐÐ=，∵2AOB ACB Ð=Ð，∴90ACB OAB =°-ÐÐ，∴90ACB OAB Ð=°-Ð，∵AT 是⊙O 的切线，∴90BAT OAB Ð=°-Ð，∴55ACB BAT Ð=Ð=°，∵AB BC =，∴1802ABC ACB Ð=°-Ð，根据圆的内接四边形可得：180D ABC Ð=°-Ð，∴2110D ACB Ð=Ð=°，故选：A ．【点睛】本题考查圆的综合问题，理解圆的切线的性质以及内接四边形的性质是解题关键．6．（2021·浙江九年级专题练习）如图，⊙O 的弦AB ＝8，M 是弦AB 上的动点，若OM 的最小值是3，则⊙O 的半径是（）A ．4B ．5C ．6D ．7【答案】B【分析】过O 点作OH ⊥AB 于H ，连接OA ，如图，根据垂径定理得到AH ＝BH ＝4，利用垂线段最短得到OH ＝3，然后利用勾股定理计算出OA 即可．【详解】解：过O 点作OH ⊥AB 于H ，连接OA ，如图，∵OH ⊥AB ，∴AH ＝BH ＝12AB ＝12×8＝4，∵OM 的最小值是3，∴OH ＝3，在Rt △OAH 中，OA ＝5，即⊙O 的半径是5．故选：B ．【点睛】本题考查了垂径定理：直于弦的直径平分这条弦，并且平分弦所对的两条弧．也考查了勾股定理．7．（2020·聊城市茌平区实验中学九年级月考）如图，P 为O 外一点，PA 、PB 分别切O 于点A 、B ，CD 切O 于点E 且分别交PA 、PB 于点C ，D ，若PA =4，则△PCD 的周长为( )A ．5B ．7C ．8D ．10【答案】C【分析】根据切线长定理求解即可【详解】解：∵PA 、PB 分别切O 于点A 、B ，CD 切O 于点E ，PA=4，∴PA=PB=4，AC=CE ，BD=DE ，∴△PCD 的周长为PC+CE+DE+PD=PC+AC+BD+PD=PA+PB=4+4=8，故选：C ．【点睛】本题考查切线长定理，熟练掌握切线长定理及其应用是解答的关键．8．（2021·北京九年级专题练习）如图，ABC D 的内切圆O e 与A B ，BC ，CA 分别相切于点D ，E ，F ，且2AD =，ABC D 的周长为14，则BC 的长为（）A ．3B ．4C ．5D ．6【答案】C 【分析】根据切线长定理得到AF =AD =2，BD =BE ，CE =CF ，由△ABC 的周长为14，可求BC 的长．【详解】解：O Qe 与A B ，BC ，CA 分别相切于点D ，E ，F2AF AD \==，BD BE =，CE CF =，ABC D Q 的周长为14，14AD AF BE BD CE CF \+++++=2()10BE CE \+=5BC \=故选：C ．【点睛】本题考查了三角形的内切圆与内心，切线长定理，熟练掌握切线长定理是解题的关键．二、填空题9．如图，PA 、PB 、CD 是⊙O 的切线，A 、B 、E 是切点，CD 分别交PA 、PB 于C 、D 两点，若∠COD =70°，则∠AP B =_______.【答案】40°【分析】先利用切线长定理，得出∠BDO =∠CDO ，∠ACO =∠DCO ，再利用三角形内角和求出∠CDO +∠DCO 后得到∠BDC+∠A CD 的值，最后利用三角形外角的性质得到关于∠P 的方程，解方程即可得出答案．【详解】解：∵PA 、PB 、CD 是⊙O 的切线，∴∠BDO =∠CDO ，∠ACO =∠DCO ，∵∠COD =70°，∴∠CDO +∠DCO =180°－70°=110°，∴∠BDC +∠ACD =2（∠CDO +∠DCO ）=2 ×110°=220°，∵∠BDC =∠DCP +∠P ，∠ACD =∠CDP +∠P ，∴∠DCP +∠P +∠CDP +∠P =220°，即180°+∠P =220°，∴∠P =40°，即∠APB =40°，故答案为：40°．【点睛】本题综合考查了圆的切线长定理、三角形的内角和定理、三角形外角的性质等，解决本题的关键是要牢记各定理与性质的内容，能灵活运用它们进行不同的角之间的转化，考查了学生推理分析的能力．10．（2021·浙江九年级其他模拟）如图，已知AD 是BAC Ð的平分线，以线段AB 为直径作圆，交BAC Ð和角平分线于C ，D 两点．过D 向AC 作垂线DE 垂足为点E ．若24DE CE ==，则直径AB =_______．【答案】10【分析】连接CD 、OD 、OC 、BD ，运用勾股定理求得CD 的长,再证明DE 是圆O 的切线，运用全等三角形的判定与性质以及余角的性质得出∠CDE =∠BAD ,易得BD =CD ，然后再根据正切函数求得AD ，最后根据勾股定理解答即可．【详解】解：如图：连接CD 、OD 、OC 、BD∵AE ⊥DE , 24DE CE ==∴CD =∵OA =OD∴∠OAD =∠ODA∴∠BOD =∠OAD +∠ODA = 2∠OAD∵∠ODA =∠OAD∴∠EAD =∠ODA∴OD //AE∴OD ⊥DE ，即DE 是圆O 的切线∴∠CDE +∠ODC =90°∵AB是直径∴∠BAD+∠B=90°在△BOD和△DOC中OC=OB,DO=DO,BD=CD ∴△BOD≌△DOC∴∠ODC=∠OBD∴∠CDE=∠BAD∵∠BAD=∠DAC∴∠COD=∠BOD∴BD=CD=∵tan∠BAD=BDAD= tan∠CDE=12CEDE=,∴AD=∴AB10=．故填10．【点睛】本题主要考查了三角形的性质、圆的切线的判定与性质、勾股定理、三角函数等知识点，灵活应用相关知识成为解答本题的关键．11．（2020·湖北孝感市·九年级月考）如图，PA、PB是⊙O的切线，A、B为切点，点C、D在⊙O上．若∠P＝108°，则∠B+∠D＝_____．【答案】216°【分析】连接AB，根据切线得出PA＝PB，求出∠PBA＝∠PAB＝36°，根据圆内接四边形的对角互补得出∠D+∠CBA＝180°，再求出答案即可．【详解】解：连接AB，∵PA、PB是⊙O的切线，A、B为切点，∴PA＝PB，∴∠PAB＝∠PBA，∵∠APB＝108°，∴∠PBA＝∠PAB＝12×（180°﹣∠APB）＝36°，∵A、D、C、B四点共圆，∴∠D+∠CBA＝180°，∴∠PBC+∠D＝∠PBA+∠CBA+∠D＝36°+180°＝216°，故答案为：216°．【点睛】本题考查了切线长定理，圆周角定理，等腰三角形的性质，三角形内角和定理，圆内接四边形等知识点，能综合运用知识点进行推理和计算是解此题的关键．12．（2021·河北石家庄市·石家庄外国语学校九年级月考）已知△ABC中，⊙I为△ABC的内切圆，切点为H，若B C＝6，AC＝8，AB＝10，则点A到圆上的最近距离等于_____．-【答案】2【分析】连接IA，IA与⊙I半径的差即为点A到圆上的最近距离，只需求出IA和⊙I半径即可得答案．【详解】解：连接IA，设AC、BC分别切⊙I于E、D，连接IE、ID，如图：∵BC＝6，AC＝8，AB＝10，∴BC2+AC2＝AB2∴∠C＝90°∵⊙I为△ABC的内切圆，∴∠IEC＝∠IDC＝90°，IE＝ID，∴四边形IDCE是正方形，设它的边长是x，则IE＝EC＝CD＝ID＝IH＝x，∴AE＝8﹣x，BD＝6﹣x，由切线长定理可得：AH＝8﹣x，BH＝6﹣x，而AH+BH＝10，∴8﹣x+6﹣x＝10，解得x＝2，∴AH＝6，IH＝2，∴IA，∴点A到圆上的最近距离为﹣2，故答案为：﹣2．【点睛】本题考查勾股定理、切线长定理、三角形的内切圆等知识，是重要考点，难度较易，掌握相关知识是解题关键．三、解答题13．（2021·浙江温州市·九年级一模）如图，点C ，D 在以AB 为直径的半圆O 上， AD BC=，切线DE 交AC 的延长线于点E ，连接OC ．（1）求证：∠ACO ＝∠ECD ．（2）若∠CDE ＝45°，DE ＝4，求直径AB 的长．【答案】（1）证明见详解；（2）【分析】（1）由 AD BC=，可得∠A ＝∠B ，内接四边形可得出∠ECD=∠B ，进而得出∠ACO ＝∠ECD ；（2））连接OD ，由切线的性质可得出∠ODE ＝90°，进而得出∠CDO ＝∠DCO=45°，再根据已知条件计算出∠E=∠ECD ，得到CD=DE ＝4，再利用勾股定理求出半径，进而得出答案；【详解】（1）证明：∵ AD BC=，∴∠A ＝∠B ；∵ABDC 是内接四边形∴∠ECD=∠B∴∠ECD=∠A∵AO ＝CO ；∴∠ACO ＝∠A∴∠ACO ＝∠ECD（2）连接OD∵DE 是圆的切线∴∠ODE ＝90°，∵∠CDE ＝45°，OC=OD∴∠CDO ＝∠DCO =45°，∴∠COD ＝90°，∵ AD BC=，∴ AC DC=，∴∠AOC ＝∠DOB=45°，∴AO ＝OC ，∴∠ACO ＝∠A=1804567.52°-°=° ；∵∠DCO =45°，∴∠ECD =180°-45°-67.5°=67.5°，∵∠E=180°-∠CDE -∠ECD =180°-45°-67.5°=67.5°，∴∠E=∠ECD∴CD=DE ＝4，∵∠COD ＝90°，∴222CD OC OD =+∴2216OC OD +=，即28OC =∴OC= 故⊙O 的半径为∴直径AB 的长，【点睛】本题属于圆综合题，考查了圆周角定理，内接四边形，切线性质定理，等腰三角形的判定与性质，勾股定理等知识，熟练掌握性质及定理是解决本题的关键．14．（2021·江苏无锡市·九年级期中）如图，AB 为⊙O 的直径，PD 切⊙O 于点C ，与BA 的延长线交于点D ，DE ⊥P O 交PO 延长线于点E ，连接PB ，∠EDB ＝∠EPB ．（1）求证：PB 是⊙O 的切线．（2）若PB ＝3，tan ∠PDB ＝34，求⊙O 的半径．【答案】（1）见解析；（2）32【分析】（1）根据三角形的内角和定理可证E PBO Ð=Ð，然后根据垂直定义可得90E Ð=°，从而得出半径CB PB ^，根据切线的判定定理即可证出结论；（2）连接OC ，根据题意求出45BD PD ==，，再结合切线长定理得到3PC =，2CD =，从而设O e 的半径是r ，利用勾股定理求解即可．【详解】（1）,EDB EPB DOE POB Ð=ÐÐ=ÐQ ，E PBO \Ð=Ð，DE PO ^Q ，90E \Ð=°，90PBO \Ð=°，\半径CB PB ^，PB \是O e 的切线．（2）如图，连接OC ，33tan 904PB PDB PBD =Ð=Ð=°Q ，，tan 45BD PB PDB PD \=Ð===g ，．PB Q 和PC 是O e 的切线，3PC PB \==，2CD PD PC \=-=，设O e 的半径是r ，则4OD DB OB r =-=-，PD Q 切O e 于点C ，OC PD \^，222CD OC OD \+=，()22224r r \+=-，32r \=．【点睛】本题考查圆的综合问题，理解切线的判定与性质定理以及正切函数的定义是解题关键．15．（2021·天津九年级学业考试）已知AB 为O e 的直径，点C ，D 为O e 上的两点，AD 的延长线于BC 的延长线交于点P ，连接CD ，30CAB Ð=°．（Ⅰ）如图①，若 2=CBCD ，4AB =，求AD 的长；（Ⅱ）如图②，过点C 作O e 的切线交AP 于点M ，若6CD AD ==，求CM 的长．【答案】（1）AD =；（2）CM = ．【分析】（1）根据弧、圆周角之间的关系可求得∠BAD =45°，连接BD ，可得△ABD 为等腰直角三角形，求解即可；（2）根据弦、圆心角之间关系、等边对等角以及三角形外角的性质可求得∠PDM =60°，OC //AP ，再根据切线的性质定理易得△CDM 为直角三角形，解直角三角形即可．【详解】解：（1）∵ 2=CBCD ，30CAB Ð=°，∴1152CAD CAB Ð=Ð=°,∴∠BAD =45°，连接BD ，∵AB 为直径，∴∠BDA =90°，∴cos45AD AB =×°=（2）连接OD 、OC ，∵30CAB Ð=°，∴∠COB =60°，∠AOC =120°，∵6CD AD ==，∴∠AOD =∠COD =60°，∴∠ACD =∠CAD =30°，∠BAP =∠CAD +∠CAB =60°=∠COB ，∴OC //AP ，∠CDP =∠ACD +∠CAD =60°，∵CM 为O e 的切线，∴∠OCM =90°，∴∠AMC =180°-∠OCM =90°，在Rt △CDM 中，sin 60CM CD =×°=．【点睛】本题考查切线的性质定理，等腰三角形等边对等角，弧、圆心角、圆周角、弦之间的关系，解直角三角形．正确作出辅助线是解题关键．。

圆的切线练习题

圆的切线练习题一、选择题1. 已知圆的半径为5，点P到圆心的距离为10，则点P与圆的位置关系是（）。

A. 点P在圆内B. 点P在圆上C. 点P在圆外2. 圆的切线与圆相切于点A，若切线与圆心的距离为6，则圆的半径是（）。

A. 3B. 6C. 12D. 9二、填空题1. 若圆的半径为r，点P到圆心的距离为d，当d等于r时，点P与圆的位置关系是________。

2. 已知圆的切线在圆上与点A相切，若切线与圆心的距离为d，圆的半径为r，则切线与圆心的距离d等于________。

三、计算题1. 已知圆的半径为7，圆上一点A的坐标为(3,4)，求过点A的圆的切线方程。

2. 圆心坐标为(0,0)，半径为5，求过点(3,3)的圆的切线方程。

四、证明题1. 证明：圆的切线垂直于经过切点的半径。

2. 证明：若两圆相切于点A，且两圆的半径分别为r1和r2，点P在两圆的公共切线上，且PA=PB，则PA=PB=r1+r2。

五、应用题1. 一个圆的半径为10，圆心在原点(0,0)，求过点(6,8)的圆的切线方程。

2. 已知两圆外切，圆心分别为O1(-3,0)和O2(3,0)，半径分别为5和3，求两圆的公共切线方程。

六、综合题1. 在平面直角坐标系中，圆C的圆心在(1,2)，半径为3。

点A的坐标为(4,0)，求过点A的圆C的切线方程。

2. 圆心在(2,3)的圆与x轴相切，求圆的半径，并求出切点坐标。

七、探索题1. 探索：若圆的半径为定值，当圆上一点到圆心的距离逐渐增大时，过该点的圆的切线数量会如何变化？2. 探索：若两圆相切，且已知一圆的半径和两圆心的距离，如何求另一圆的半径？八、开放性问题1. 若圆的切线与圆心构成一个直角三角形，求切线的长度与圆的半径之间的关系。

2. 设想一个实际问题，其中涉及到圆的切线，并尝试构建一个数学模型来解决这个问题。

请注意，以上题目仅为示例，具体题目应根据实际教学大纲和学生水平进行适当调整。

圆的切线综合练习题与答案完整版

圆的切线综合练习题与答案HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】切线的判定与性质练习题一、选择题（答案唯一，每小题3分）1．下列说法中，正确的是( )A．与圆有公共点的直线是圆的切线 B．经过半径外端的直线是圆的切线C．经过切点的直线是圆的切线 D．圆心到直线的距离等于半径的直线是圆的切线2. 如图，AB是⊙O的直径，AC切⊙O于A，BC交⊙O于点D，若∠C＝70°，则∠AOD的度数为( )A．70° B．35° C．20° D．40°第2题第3题第4题第5题3. 如图，线段AB是⊙O的直径，点C，D为⊙O上的点，过点C作⊙O的切线交AB的延长线于点E，若∠E＝50°，则∠CDB等于( )A．20° B．25° C．30° D．40°4.如图，等腰直角三角形ABC中，AB＝AC＝8，O为BC的中点，以O为圆心作半圆，使它与AB，AC都相切，切点分别为D，E，则⊙O的半径为( )A．8 B．6 C．5 D．45.如图，CD是⊙O的直径，弦AB⊥CD于点G，直线EF与⊙O相切于点D，则下列结论中不一定正确的是( )A．AG＝BG B．AB∥EF C．AD∥BC D．∠ABC＝∠ADC二．填空题（每小题3分）6．如图，在⊙O中，弦AB＝OA，P是半径OB的延长线上一点，且PB＝OB，则PA与⊙O的位置关系是_________．第6题第7题第8题7.如图，△ABC的一边AB是⊙O的直径，请你添加一个条件，使BC是⊙O的切线，你所添加的条件为________________．8.如图，AB是⊙O的直径，O是圆心，BC与⊙O切于点B，CO交⊙O于点D，且BC＝8，CD＝4，那么⊙O的半径是______．9. 如图，若以平行四边形一边AB为直径的圆恰好与对边CD相切于点D，则∠C＝_______度．第9题第10题第11题10. 如图，AB为⊙O的直径，直线l与⊙O相切于点C，AD⊥l，垂足为D，AD交⊙O于点E，连接OC，BE.若AE＝6，OA＝5，则线段DC的长为______．11．如图，已知△ABC内接于⊙O，BC是⊙O的直径，MN与⊙O相切，切点为A，若∠MAB＝30°，则∠B＝________度．三、解答题（写出详细解答或论证过程）12.（7分）如图，在Rt△ABC中，∠C＝90°，BD是角平分线，点O在AB上，以点O为圆心，OB为半径的圆经过点D，交BC于点E.求证：AC是⊙O的切线．第12题第13题第14题13.（7分）如图，AB是⊙O的直径，点C在AB的延长线上，CD与⊙O相切于点D，CE⊥AD，交AD的延长线于点E.求证：∠BDC＝∠A.14.（7分）如图，在Rt△ABC中，∠ABC＝90°，∠BAC的平分线交BC于D，以D为圆心，DB长为半径作⊙D，求证：AC与⊙D相切．15.（10分）如图，AB为⊙O的直径，PD切⊙O于点C，交AB的延长线于点D，且∠D＝2∠CAD.(1)求∠D的度数；(2)若CD＝2，求BD的长．第15题第16题16．（12分）已知△ABC内接于⊙O，过点A作直线EF.(1)如图①，若AB为⊙O的直径，要使EF成为⊙O的切线，还需要添加的一个条件是(至少说出两种)：__________________________或者_______________________；(2)如图②，如果AB是不过圆心O的弦，且∠CAE＝∠B，那么EF是⊙O的切线吗？试证明你的判断．17.（12分）如图，已知直线PA交⊙O于A，B两点，AE是⊙O的直径，点C为⊙O上一点，且AC平分∠PAE，过C作CD⊥PA，垂足为D.(1)求证：CD为⊙O的切线；(2)若DC＋DA＝6，⊙O的直径为10，求AB的长．答案：DDADC 6. 相切 7. ∠ABC＝90°不排除等效答案 8. 6 9. 45 10. 4 11. 6012. 解：连接OD，∵BD为∠ABC平分线，∴∠OBD＝∠CBD，∵OB＝OD，∴∠OBD＝∠ODB，∴∠CBD＝∠ODB，∴OD∥BC，∵∠C＝90°，∴∠ODA＝90°，则AC为⊙O的切线13. 解：连接OD，∵CD是⊙O的切线，∴∠ODC＝90°，∴∠ODB＋∠BDC＝90°，∵AB是⊙O的直径，∴∠ADB＝90°，即∠ODB＋∠ADO＝90°，∴∠BDC＝∠ADO，∵OA＝OD，∴∠ADO＝∠A，∴∠BDC＝∠A14. 解：过D作DH⊥AC于H，由角平分线的性质可证DB＝DH，∴AC与⊙D相切15. 解：(1)∵∠COD＝2∠CAD，∠D＝2∠CAD，∴∠D＝∠COD.∵PD与⊙O相切于点C，∴OC⊥PD，即∠OCD＝90°，∴∠D＝45°(2)由(1)可知△OCD是等腰直角三角形，∴OC＝CD＝2，由勾股定理，得OD＝22＋22＝22，∴BD＝OD－OB＝22－216. (1) ∠BAE＝90°∠EAC＝∠ABC(2) (2)EF是⊙O的切线．证明：作直径AM，连接CM，则∠ACM＝90°，∠M＝∠B，∴∠M＋∠CAM＝∠B＋∠CAM＝90°，∵∠CAE＝∠B，∴∠CAM＋∠CAE＝90°，∴AE⊥AM，∵AM为直径，∴EF是⊙O的切线17. 解：(1)连接OC，证∠DAC＝∠CAO＝∠ACO，∴PA∥CO，又∵CD⊥PA，∴CO⊥CD，∴CD为⊙O 的切线(2)过O作OF⊥AB，垂足为F，∴四边形OCDF为矩形．∵DC＋DA＝6，设AD＝x，则OF＝CD＝6－x，AF＝5－x，在Rt△AOF中，有AF2＋OF2＝OA2，即(5－x)2＋(6－x)2＝25，解得x1＝2，x2＝9，由AD＜DF知0＜x＜5，故x＝2，从而AD＝2，AF＝5－2＝3，由垂径定理得AB＝2AF＝6。

圆的切线的判定与性质练习题

圆的切线的判定与性质一、若直线l过⊙O上某一点A，证明l是⊙O的切线，只需连OA，证明OA⊥l就行了，简称“连半径，证垂直”，难点在于如何证明两线垂直.例1如图，在△ABC中，AB=AC，以AB为直径的⊙O交BC于D，交AC于E，B为切点的切线交OD延长线于F.求证：EF与⊙O相切.例2如图，AD是∠BAC的平分线，P为BC延长线上一点，且PA=PD. 求证：PA与⊙O相切.二、若直线l与⊙O没有已知的公共点，又要证明l是⊙O的切线，只需作OA⊥l，A为垂足，证明OA是⊙O的半径就行了，简称：“作垂直；证半径”例3 如图，AB=AC，D为BC中点，⊙D与AB切于E点.求证：AC与⊙D相切.例3已知：如图，AC，BD与⊙O切于A、B，且AC∥BD，若∠COD=900.求证：CD是⊙O的切线.练习题1.如图，AB=AC，AB是⊙O的直径，⊙O交BC于D，DM⊥AC于M求证：DM与⊙O相切.3（2008黄冈市）已知：如图，在△ABC中，AB=AC，以AB为直径的⊙O交BC于点D，过点D作DE⊥AC于点E．求证：DE是⊙O的切线．4. 如图，ABCD是正方形，G是BC延长线上一点，AG交BD于E，交CD于F.求证：CE与△CFG的外接圆相切.5.如图，AB是⊙O的直径，∠BAC=30°，M是OA上一点，过M作AB的垂线交AC于点N，交BC 的延长线于点E，直线CF交EN于点F，且∠ECF=∠E.（1）证明CF是⊙O的切线；（2）设⊙O的半径为1，且AC=CE，求MO的长.6．如图，已知⊙O1与⊙O2交于A，B，⊙O1的半径为17，⊙O 2的半径为10，O 1O 2=21，求AB 的长．7．如图，已知⊙O 1与⊙O 2交于A ，B 两点，过A 的直线交两圆于C ，D 两点，•G•为CD 的中点，BG 及其延长线交⊙O 1，⊙O 2于E ，F ，连结DF ，CE ，求证：CE=DF ．8.某人用如下方法测一钢管的内径:将一小段钢管竖直放在平台上,向内放入两个半径为5cm 的钢球,测得上面一个钢球顶部高DC=16cm(钢管的轴截面如图所示), 求钢管的内直径AD 的长9．如图，⊙O 1和⊙O 2交于A 、B ，⊙O 1弦交⊙O 2于E ，⊙O 2弦AD 交⊙O 1于F ，若∠CAB=∠DAB ，求证：CE=DF 。

初中圆切线试题及答案

初中圆切线试题及答案一、选择题1. 圆的切线与过切点的半径垂直，这是圆的切线性质中的哪一条？A. 切线与半径垂直B. 切线与直径垂直C. 切线与切点垂直D. 切线与圆心垂直答案：A2. 已知圆的半径为5，圆心到直线的距离为3，则直线与圆的位置关系是：A. 相离B. 相切C. 相交D. 无法确定答案：C3. 圆的切线与圆的交点个数是：A. 0个B. 1个C. 2个D. 3个答案：B二、填空题4. 圆的切线与过切点的半径垂直，因此圆的切线与_________垂直。

答案：过切点的半径5. 如果圆的半径为r，圆心到直线的距离为d，那么直线与圆相切的条件是_________。

答案：d = r三、解答题6. 已知圆O的半径为4，圆心O到直线l的距离为3，求证：直线l是圆O的切线。

证明：由题意知，圆心O到直线l的距离d=3，圆的半径r=4。

因为d=r，所以直线l与圆O相切。

7. 已知圆的半径为6，圆心到直线的距离为5，求圆与直线的交点个数。

解：由于圆心到直线的距离d=5小于圆的半径r=6，所以直线与圆相交，交点个数为2个。

四、计算题8. 已知圆的方程为(x-2)^2 + (y-3)^2 = 25，直线方程为3x + 4y - 15 = 0，求直线与圆的切线方程。

解：首先求圆心坐标，圆心为(2, 3)。

计算圆心到直线的距离d，利用点到直线距离公式：\[ d = \frac{|3*2 + 4*3 - 15|}{\sqrt{3^2 + 4^2}} = \frac{|6 + 12 - 15|}{5} = 1 \]由于d=1，直线与圆相切。

设切线方程为3x + 4y + c = 0，将圆心坐标代入得：\[ 3*2 + 4*3 + c = 0 \]\[ 6 + 12 + c = 0 \]\[ c = -18 \]所以切线方程为3x + 4y - 18 = 0。

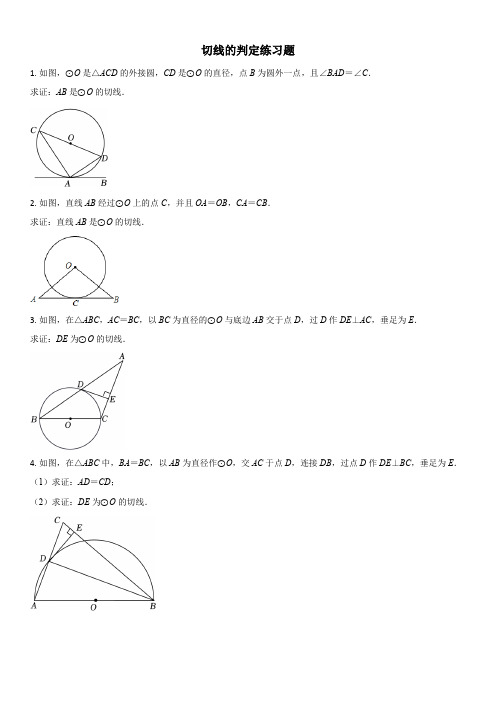
圆的切线的判定练习题2024~2025学年人教版数学九年级上册++

切线的判定练习题1.如图，⊙O是△ACD的外接圆，CD是⊙O的直径，点B为圆外一点，且∠BAD＝∠C．求证：AB是⊙O的切线．2.如图，直线AB经过⊙O上的点C，并且OA＝OB，CA＝CB．求证：直线AB是⊙O的切线．3.如图，在△ABC，AC＝BC，以BC为直径的⊙O与底边AB交于点D，过D作DE⊥AC，垂足为E．求证：DE为⊙O的切线．4.如图，在△ABC中，BA＝BC，以AB为直径作⊙O，交AC于点D，连接DB，过点D作DE⊥BC，垂足为E．（1）求证：AD＝CD；（2）求证：DE为⊙O的切线．5.如图，AB为⊙O的直径，点C，D在⊙O上，AĈ=CD̂=DB̂，DE⊥AC．求证：DE是⊙O的切线．6.如图，AB为⊙O的直径，AC平分∠BAD交⊙O于点C，CD⊥AD，垂足为点D．求证：CD是⊙O的切线．7.如图△ABC中，∠ABC＝90°，CD平分∠ACB交AB于点D，以点D为圆心，BD为半径作⊙D交AB于点E．（1）求证：⊙D与AC相切；（2）若AC＝5，BC＝3，试求AE的长．8.如图，在△ABC中，AB＝BC，以AB为直径的⊙O与AC交于点D，过D作DF⊥BC，交AB的延长线于E，垂足为F．求证：直线DE是⊙O的切线．9.如图，在△ABC中，CA＝CB，O为AB上一点．以O为圆心，OB长为半径的⊙O过点C，交AB于另一点D．若D是OA的中点，求证：AC是⊙O的切线．10.如图所示，AB为半圆O的直径，C是半圆上一点，AD平分∠CAB交半圆于点D，过点D作DE⊥AC，DE交AC的延长线于点E．（1）求证：DE是⊙O的切线；（2）若⊙O的半径为2，DE=√3，求线段AC的长．11.如图，在△ABC中，AB＝AC，D为AC上一点，以CD为直径的⊙O交BC于点F，FG⊥AB，垂足为G，求证：FG是⊙O的切线．12.如图，已知AB＝AC，以AB为直径的圆O交边BC于点D，过点D作DE⊥AC，垂足为点E．（1）求证：DE是圆O的切线；（2）如果∠BAC＝120°，求证：DE=14BC．13.如图，已知AB是⊙O的直径，D是⊙O上一点，且∠A＝∠CDB＝∠COB．求证：CB是⊙O的切线．14.如图，在Rt△ABC中，∠ABC＝90°，AC＝10，BC＝6，∠ACB的平分线CO交AB于点O，以OB为半径作⊙O．（1）请判断AC与⊙O的位置关系，并说明理由；（2）求⊙O的半径．。

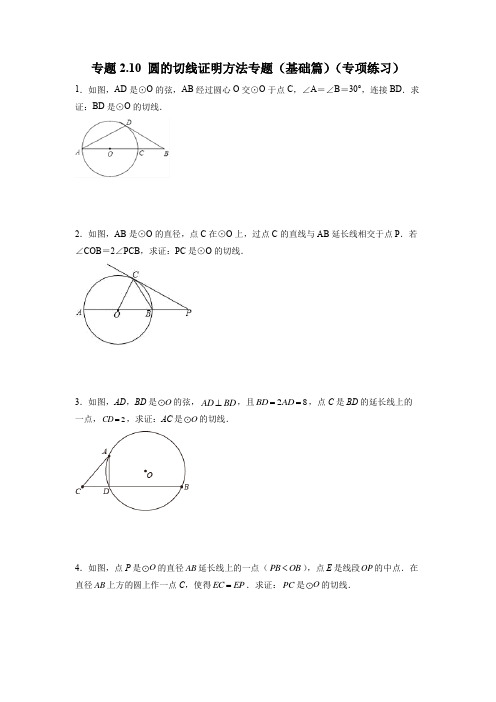
圆的切线证明方法专题(基础篇)(专项练习)

专题2.10 圆的切线证明方法专题（基础篇）（专项练习） 1．如图，AD 是⊙O 的弦，AB 经过圆心O 交⊙O 于点C ，∠A ＝∠B ＝30°，连接BD ．求证：BD 是⊙O 的切线．2．如图，AB 是⊙O 的直径，点C 在⊙O 上，过点C 的直线与AB 延长线相交于点P ．若∠COB ＝2∠PCB ，求证：PC 是⊙O 的切线．3．如图，AD ，BD 是O 的弦，AD BD ⊥，且28BD AD ==，点C 是BD 的延长线上的一点，2CD =，求证：AC 是O 的切线．4．如图，点P 是O 的直径AB 延长线上的一点（PB OB <），点E 是线段OP 的中点．在直径AB 上方的圆上作一点C ，使得EC EP =．求证：PC 是O 的切线．5．如图，在△ABC 中，∠A=45°，以AB 为直径的⊙O 交于AC 的中点D ，连接CO ，CO 的延长线交⊙O 于点E ，过点E 作EF ⊥AB ，垂足为点G ．（1）求证：BC 时⊙O 的切线；（2）若AB=2，求线段EF 的长．6．如图，AB 是O 的直径，CD 是O 的切线，切点为C ，BE CD ⊥，垂足为E ，连接,AC BC .（1）求证：BC 平分ABE ∠；（2）若60A ∠=︒，2OA =，求CE 的长.7．如图，AB是⊙O的直径，弦CD⊥AB于点E，AM是△ACD外角∠DAF的平分线.(1)求证：AM是⊙O的切线.(2)若C是优弧ABD的中点，AD＝4，射线CO与AM交于N点，求ON的长.8．如图，在△ABC中，AB＝AC，O是边AC上的点，以OC为半径的圆分别交边BC、AC 于点D、E，过点D作DF⊥AB于点F．（1）求证：直线DF是⊙O的切线；（2）若OC＝1，∠A＝45°，求劣弧DE的长．9．如图，已知△ABC内接于⊙O，点D在OC的延长线上，CD＝CB，∠D＝∠A（1）求证：BD是⊙O的切线；（2）若BC＝2，求BD的长．10．已知：如图，AB是O的直径，点C在O上，BD平分 ABC，AD＝AE，AC与BD 相交于点E．(1) 求证：AD是O的切线．(2) 若AD＝DE＝2，求BC的长．11．如图，已知AB是⊙O的直径，BD是⊙O的弦，延长BD到C，使DC=BD，连接AC，过点D作DE⊥AC，垂足为E．（1）求证：AB=AC；（2）求证：DE是⊙O的切线；（3）若⊙O的半径为6，∠BAC=60°，则DE=________．12．已知AB是⊙O的直径，点C在AB的延长线上，AB＝4，BC＝2，P是⊙O上半部分的一个动点，连接OP，CP．(1) 如图①，△OPC的最大面积是________；(2) 如图②，延长PO交⊙O于点D，连接DB，当CP＝DB时，求证：CP是⊙O的切线．13．如图，在Rt ABC △中，90ACB ∠=︒，延长CA 到点D ，以AD 为直径作O ，交BA 的延长线于点E ，延长BC 到点F ，使BF EF =．(1) 求证：EF 是O 的切线；(2) 若9OC =，4AC =，8AE =，求BE 的长．14．如图，AB 是⊙O 的直径，弦CD ⊥AB 于点E ，且DC ＝AD ．过点A 作⊙O 的切线，过点C 作DA 的平行线，两直线交于点F ，FC 的延长线交AB 的延长线于点G ．(1) 求证：FG 与⊙O 相切；(2) 连接EF ，若AF ＝2，求EF 的长．15．如图，Rt △ABC ，∠ABC =90°，点O 在AB 上，AD ⊥CO 交CO 延长线于点D ，∠DAO =∠ACO ，以点O 为圆心，OB 为半径作圆．(1) 求证：AC 是⊙O 的切线；(2) 已知68CB AB ==，，求OC 的长？16．如图所示，AB 为⊙O 的直径，在△ABC 中，AB =BC ，AC 交⊙O 于点D ，过点D 作DE ⊥BC ，垂足为点E ．(1) 证明DE 是⊙O 的切线；(2) AD =8，P 为⊙O 上一点，P 到弦AD 的最大距离为8．① 尺规作图作出此时的P 点，保留作图痕迹；② 求DE 的长．17．如图，线段AB 经过O 的圆心O ，交圆O 于点A ，C ，1BC =，AD 为O 的弦，连接BD ，30BAD ABD ∠=∠=︒，连接DO 并延长交O 于点E ，连接BE 交O 于点M ．(1) 求证：直线BD 是O 的切线；(2) 求线段BM 的长．18．如图，Rt ABC △中，90C ∠=︒，点O 在AC 上，以OA 为半径的半圆O 分别交AB ，AC 于点D ，E ，过点D 作半圆O 的切线DF ，交BC 于点F ．(1) 求证：BF DF =；(2) 若4AO CE ==，1CF =，求BF 的长．19．如图，在Rt △AOB 中，∠AOB ＝90°，⊙O 与AB 相交于点C ，与AO 相交于点E ，连接CE ，已知∠AOC ＝2∠ACE ．(1) 求证：AB 为⊙O 的切线；(2) 若AO ＝20，BO ＝15，求AE 的长．20．如图，ABC 内接于O ，AC 是O 的直径，点D 是O 上一点，连接CD 、AD ，过点B 作BE AD ⊥，交DA 的延长线于点E ，AB 平分CAE ∠．(1) 求证：BE 是O 的切线；(2) 若30ACB ∠=︒，O 的半径为6，求BE 的长．21．如图，在Rt △ABC 中，∠ABC ＝90°，∠BAC 的平分线交BC 于点O ，D 为AB 上的一点，OD ＝OC ，以O 为圆心，OB 的长为半径作⊙O ．(1) 求证：AC 是⊙O 的切线；(2) 若AB ＝6，BD ＝2，求线段AC 的长．22．如图，在△ABC中，AB=AC，以AB为直径的⊙O与BC相交于点D，过点D作DE⊥AC交AC于点E．(1) 试判断直线DE与⊙O的位置关系，并说明理由；(2) 若⊙O的半径为5，BC=16，求DE的长．∠=︒，以AC为直径作O，交AB于点D，E为BC的23．如图，在Rt ABC中，ACB中点，连接DE并延长交AC的延长线于点E．(1)求证：DF是O的切线；(2)若2CF=，4DF=，求O的半径．24．如图，AB为⊙O的直径，点C在⊙O上，点P在BA的延长线上，连接BC，OC，PC．若AB＝6，AC的长为π．(1) 求∠AOC的度数；(2) 若BC＝PC，求证：直线PC与⊙O相切．参考答案1．证明见分析【分析】连接OD，求出∠ODB＝90°，根据切线的判定推出即可．解：如图，连接OD，∵OD＝OA，∴∠ODA＝∠DAB＝30°，∴∠DOB＝∠ODA+∠DAB＝60°，∴∠ODB＝180°﹣∠DOB﹣∠B＝180°﹣60°﹣30°＝90°，即OD⊥BD，∴直线BD与⊙O相切．【点拨】此题主要考查了切线的判定，三角形的内角和以及三角形的外角性质，关键是证明OD⊥BD．2．证明见分析．【分析】利用半径OA＝OC可得∠COB＝2∠A，然后利用∠COB＝2∠PCB即可证得结论，再根据圆周角定理，易得∠PCB＋∠OCB＝90°，即OC⊥CP；故PC是⊙O的切线．解：连接AC，∵OA＝OC，∴∠A＝∠ACO．∴∠COB＝2∠ACO．又∵∠COB＝2∠PCB，∴∠ACO＝∠PCB．∵AB是⊙O的直径，∴∠ACO+∠OCB＝90°．∴∠PCB+∠OCB＝90°，即OC⊥CP．∵OC是⊙O的半径，∴PC是⊙O的切线．【点拨】此题主要考查了圆的切线的判定及圆周角定理的运用，关键是利用半径OA ＝OC 可得∠COB ＝2∠A ．3．证明见分析．【分析】先由勾股定理的逆定理证明垂直，再由切线的判断进行解答即可．证明：连接AB ，∵AD BD ⊥，且28BD AD ==∴AB 为直径，AB 2=82+42=80，∵CD =2，AD =4∴AC 2=22+42=20∵CD =2，BD =8,∴BC 2=102=100∴222AC AB CB +=，∴90BAC ∠=︒∴AC 是O 的切线．【点拨】本题考查切线的判定，圆周角定理的推论，勾股定理的逆定理，解题关键是作出辅助线构造直角三角形．4．证明见分析【分析】连接OC ，根据线段中点的定义得到OE ＝EP ，求得OE ＝EC ＝EP ，得到∠COE ＝∠ECO ，∠ECP ＝∠P ，利用三角形内角和定理求出90ECO ECP ∠+∠=︒，根据切线的判定定理即可得到结论．证明：连接OC ，∵点E 是线段OP 的中点，∴OE EP =，∵EC EP =，∴OE EC EP ==，∴COE ECO ∠=∠，ECP P ∠=∠，∵180COE ECO ECP P ∠+∠+∠+∠=︒，∴90ECO ECP ∠+∠=︒，∴OC PC ⊥，∵OC 是O 的半径，∴PC 是O 的切线．【点拨】本题考查了切线的判定，等边对等角，三角形内角和定理，熟练掌握切线的判定定理是解题的关键．5．（1）证明参见分析；（2 试题分析：（1）连接BD ，由圆周角性质定理和等腰三角形的性质以及已知条件证明∠ABC=90°即可；（2）根据AB=2，则圆的直径为2，所以半径为1，即OB=OE=1，利用勾股定理求出CO 的长，再通过证明△EGO ∽△CBO 得到关于EG 的比例式可求出EG 的长，进而求出EF 的长．解：（1）如图：连接BD ，∵AB 为⊙O 的直径，∴∠ADB=90°，∴BD ⊥AC ，∵AD=CD ，∴AB=BC ，∴∠A=∠ACB=45°，∴∠ABC=90°，∴BC 是⊙O 的切线；（2）∵AB=2，∴BO=1，∵AB=BC=2，∴EF ⊥AB ，BC ⊥AB ，∴EF ∥BC ，∴△EGO ∽△CBO ，∴EG EOBC CO =，∴2EG =，∴考点：1.切线的判定；2.相似三角形的判定与性质；3.勾股定理的运用.6．（1）详见分析；（2）CE 【分析】（1）利用切线的性质得OC ⊥DE ，再证明OC ∥BE 得到∠OCB ＝∠CBE ，加上∠OCB ＝∠CBO ，所以∠OBC ＝∠CBE ；（2）利用圆周角定理得到∠ACB ＝90°，再证明△OAC 等边三角形得到AC ＝OA ＝2，再利用勾股定理可计算出BC ＝Rt △CBE 中利用含30度的直角三角形三边的关系求CE 的长．（1）证明：∵CD 是O 的切线，∴OC DE ⊥，又∵BE DE ⊥，∴OC BE ，∴OCB CBE ∠=∠，∴OBC CBE ∠=∠，即BC 平分ABE ∠；（2）解：∵AB 为O 的直径，∴90ACB ∠=︒，∵60A ∠=︒，∴OAC 是等边三角形，2AC OA ==.∴24AB OA ==，∴BC =∵1302OBC AOC ∠=∠=︒，且OBC CBE ∠=∠， ∴30CBE ∠=︒.∴12CE BC ==【点拨】本题考查了切线的性质：经过半径的外端且垂直于这条半径的直线是圆的切线；常常“遇到切点连圆心得半径”．7．(1)证明见分析；(2)ON . 【分析】(1)根据垂径定理得到AB 垂直平分CD ，根据线段垂直平分线的性质得到AC ＝AD ，得到∠BAD ＝12∠CAD ，由AM 是△ACD 的外角∠DAF 的平分线，得到∠DAM ＝12∠FAD ，于是得到结论；(2)证明△ACD 是等边三角形，得到CD ＝AD ＝4，根据直角三角形的性质即可得到结论.(1)证明：∵AB 是⊙O 的直径，弦CD ⊥AB 于点E ，∴AB 垂直平分CD ，∴AC ＝AD ，∴∠BAD ＝12∠CAD ，∵AM 是△ACD 的外角∠DAF 的平分线，∴∠DAM ＝12∠FAD ，∴∠BAM ＝12(∠CAD+∠FAD)＝90°，∴AB ⊥AM ，∴AM 是⊙O 的切线；(2)解：∵AC ＝AD ，C 是优弧ABD 的中点，∴AC ＝AD ＝CD ，∴△ACD 是等边三角形，∴CD ＝AD ＝4，60CAD ACD ︒∠=∠=由（1）知AB 垂直平分CD ，则AB 平分CAD ∠∴CE ＝DE ＝2，1302CAE CAD ︒∠=∠= OC OA =30ACO CAE ︒∴∠=∠=30OCE ACD ACO ︒∴∠=∠-∠=在Rt OCE 中，设OC x =，则12OE x = 根据勾股定理得222OE CE OC +=，即2221()22x x +=解得x =∴OC ＝OA ∵∠ANO ＝∠OCE ＝30°，∴ON ＝2OA . 【点拨】本题是圆与三角形的综合题，涉及的知识点主要有切线的判定、垂径定理、等边三角形的判定与性质、直角三角形30度角的性质，灵活利用圆与三角形的相关性质是解题的关键.8．（1）详见分析；（2）34π．【分析】（1）连结OD ，根据等腰三角形的性质得到OD ∥AB ，根据平行线的性质得到∠ODF ＝90°，根据切线的判定定理证明；（2）根据平行线的性质得到∠AOD ＝180°﹣45°＝135°，根据弧长公式计算即可．证明：如图，连结OD ，∵AB＝AC，∴∠B＝∠ACB，∵OC＝OD，∴∠ODC＝∠ACB，∴∠B＝∠ODC，∴OD∥AB，∵DF⊥AB，∴∠ODF＝∠BFD＝90°，∵OD为半径，∴直线DF是⊙O的切线；（2）解：∵∠A＝45°，OD∥AB，∴∠AOD＝180°﹣45°＝135°，∴劣弧DE的长为1353 1804ππ⨯=．【点拨】本题主要考查了切线的判定及弧长的计算，熟练掌握切线的判定定理及弧长的计算公式是解题的关键.9．（1）见分析；（2）BD＝【分析】（1）由等腰三角形的性质得出∠CBD+∠OBC＝90°，则∠OBD＝90°，可得出结论；（2）证明△OBC为等边三角形，得出∠BOC＝60°，根据直角三角形的性质可得出答案．（1）证明：∵OB＝OC，∴∠OBC＝∠OCB，∴∠BOC+2∠OBC＝180°，∵∠BOC＝2∠A，∴∠A+∠OBC＝90°，又∵BC＝CD，∴∠D＝∠CBD，∵∠A＝∠D，∴∠CBD+∠OBC＝90°，∴∠OBD＝90°，∴OB⊥BD，∴BD是⊙O的切线；（2）解：∵∠OBD＝90°，∠D＝∠CBD，∴∠OBC＝∠BOC，∴OC＝BC，又∵OB＝OC，∴△OBC为等边三角形，∴∠BOC＝60°，∵BC＝2，∴OB＝2，∴BD＝【点拨】本题考查切线的判定，等腰三角形的性质，圆周角定理，直角三角形的性质，等边三角形的判定与性质，熟练掌握切线的判定是解题的关键．10．(1)见分析【分析】（1）根据AB是O的直径，可得∠C＝90°，由BD平分∠ABC，可得∠CBD＝∠ABD，根据AD＝AE，可得∠CEB＝∠DEA，进而可得∠BAD＝90°，即可得证；（2）连接AF，根据等腰三角形的性质可得DF＝12DE＝1，勾股定理求得AF，证明△AEF≌△BEC，即可求解．（1）∵AB是O的直径，∴∠C＝90°，∴∠CBE＋∠CEB＝90°，∵BD平分∠ABC，∴∠CBD＝∠ABD，∵AD＝AE，∴∠D＝∠AED，∵∠CEB＝∠DEA，∴∠ABD＋∠D＝∠CBE ＋∠CEB＝90°，即∠BAD＝90°，∴AD是⊙O的切线，（2）连接AF，如图，∵AB是O的直径，∴∠AFB＝90°，即AF BD⊥，∵AD＝DE＝2，∴DF＝12DE＝1，在Rt ADF∆中，AD＝2，DF＝1，∴AF＝41-＝3，∵∠DBA＋∠D＝∠EAB＋∠DAE＝90°，∠D＝∠DAE＝60°，∴∠DBA＝∠EAB，∴AE＝BE，又∠AFE＝∠C＝90°，∠AEF＝∠CEB，∴△AEF≌△BEC（AAS），∴BC＝AF【点拨】本题考查了直径所对的圆周角是直角，切线的判定，勾股定理，全等三角形的性质与判定，掌握以上知识是解题的关键．11．（1）见分析；（2）见分析；（3）【分析】（1）连接AD，由直径所对的圆周角度数及中点可证AD是BC的垂直平分线，根据线段垂直平分线的性质可得结论；（2）连接OD，由中位线的性质可得OD∥AC，由平行的性质与切线的判定可证；（3）易知ABC是等边三角形，由等边三角形的性质可得CB长及C∠度数，利用直角三角形30度角的性质及勾股定理可得结果.解：（1）连接AD．∵AB是⊙O的直径，∴∠ADB=90°．∴⊥AD BC又∵DC=BD，∴AD是BC的垂直平分线∴AB=AC．（2）连接OD．∵DE⊥AC，∴∠CED=90°．∵O为AB中点，D为BC中点，∴OD∥AC．∴∠ODE=∠CED=90°．∴DE是⊙O的切线．=（3）由（1）得AC AB60BAC ∠=︒ABC ∴是等边三角形60,2612C BC AB ︒∴∠===⨯=162DC BD BC ∴=== 在Rt CED 中，906030CDE ︒︒︒∠=-=132CE CD ∴== 根据勾股定理得222CE DE CD +=DE ∴【点拨】本题考查了圆与三角形的综合，涉及的知识点主要有圆的切线的判定、圆周角定理的推论、垂直平分线的性质、等边三角形与直角三角形的性质，灵活的将图形与已知条件相结合是解题的关键.12．(1)4(2)见分析【分析】（1）因为OC 长度确定，所以当点P 到OC 的距离最大时△OPC 的面积最大，当OP ⊥OC 时，当点P 到OC 的距离最大，等于圆O 的半径，求出此时的△OPC 的面积即可；（2）连接AP ，BP ，利用同圆中，相等的圆心角所对的弦相等，可得AP =DB ，因为CP ＝DB ，所以AP =CP ，可证△APB ≌△CPO （SAS ），得到∠OPC ＝90°，即可证明CP 是切线．(1)解：∵AB ＝4，∴OB ＝2，OC ＝OB +BC ＝4．在△OPC 中，设OC 边上的高为h ，∵S △OPC 12=OC •h ＝2h ， ∴当h 最大时，S △OPC 取得最大值．作PH ⊥OC ，如图①，则PO PH >，当OP ⊥OC 时，PO PH =，此时h 最大，如答图1所示：此时h ＝半径＝2，14242OPC S ⨯⨯＝＝．∴△OPC 的最大面积为4，故答案为：4．(2)证明：如答图②，连接AP ，BP ．∵∠AOP ＝∠BOD ，∴AP ＝BD ，∵CP ＝DB ，∴AP ＝CP ，∴∠A ＝∠C ，在△APB 与△CPO 中，AP CP A C AB CO =⎧⎪∠=∠⎨⎪=⎩，∴△APB ≌△CPO （SAS ），∴∠APB ＝∠OPC ，∵AB 是直径，∴∠APB ＝90°，∴∠OPC ＝90°，∴DP ⊥PC ，∵DP 经过圆心，∴PC 是⊙O 的切线．【点拨】本题考查了圆，熟练掌握圆的半径、切线、弦与圆心角的关系等知识是解题的关键．13．(1)见分析(2)13【分析】（1）连接OE ，根据等边对等角可得OEA OAE ∠=∠，FEB B ∠=∠，根据对顶角相等，等量代换后可得90OEA FEB ∠+∠=︒即可得证；（2）过点O 作OG BE ⊥，根据垂径定理可得4AG AC ==，由945AO OC AC =-=-=，证明AOG ≌ABC ，可得5AB =，根据BE EA AB =+即可求解．（1）如图，连接OE ，Rt ABC △中，90ACB ∠=︒，90CAB B ∴∠+∠=︒，OE OA =，OEA OAE ∴∠=∠，OAE CAB ∠=∠，90OEA B ∴∠+∠=︒，BF EF =，FEB B ∴∠=∠，90OEA FEB ∴∠+∠=︒，即90FEO ∠=︒，OE 是半径，∴EF 是O 的切线；（2）如图，过点O 作OG BE ⊥，8AE =，124EG AG AE ∴===，9OC =，4AC =，945AO OC AC ∴=-=-=，在AOG 与ABC 中，904OGA BCA AG AC GAO CAB ∠=∠=︒⎧⎪==⎨⎪∠=∠⎩∴AOG ≌ABC ，5AB AO ∴==，5813BE BA AE ∴=+=+=，【点拨】本题考查了切线的判定定理，垂径定理，掌握以上知识是解题的关键． 14．(1)见分析(2)EF =【分析】（1）连接OC ，AC ．先证明△ACD 为等边三角形．可得∠ACO =∠OAC =30°．再由FG ∥DA ，可得∠ACF =∠DAC =60°．从而得到∠OCF =90°．即可求证；（2）根据AD ∥FG ，可得∠AGF =∠DAE =30°．再根据直角三角形的性质可得FG =2AF =4，AG ADE ≌△GCE ．可得AE=GE即可求解．(1)证明：连接OC，AC．∵AB是⊙O的直径，CD⊥AB，∴CE=DE，AD=AC．∵DC=AD，∴DC=AD=AC．∴△ACD为等边三角形．∴∠D=∠DCA=∠DAC=60°．∴∠AOC=30°，∵OA=OC，∴∠ACO=∠OAC=30°．∵FG∥DA，∴∠ACF=∠DAC=60°．∴∠OCF=90°．∴OC⊥FG．∵OC为半径，∴FG与⊙O相切．(2)解：∵AD∥FG，∴∠AGF=∠DAE=30°．∵AF为⊙O的切线，∴∠F AG=90°，∴FG=2AF=4，∴AG=在△ADE和△GCE中，∵∠AGF=∠DAE=30°．∠CEG=∠AED，DE=CE，∴△ADE≌△GCE．∴AE=GE∴EF【点拨】本题主要考查了垂径定理，切线的性质和判定，直角三角形的性质，等边三角形的判定和性质，全等三角形的判定和性质，勾股定理，熟练掌握垂径定理，切线的性质和判定，直角三角形的性质，等边三角形的判定和性质，全等三角形的判定和性质是解题的关键．15．(1)见分析(2)OC=【分析】（1）证明∠BCO=∠ACO，推出OE=OB，即可证明AC是⊙O的切线；（2）证明△OBC≌△OEC，利用勾股定理求得AC=10，在Rt△AOE中，利用勾股定理列式计算可求得圆的半径，进一步求解即可．(1)证明：作OE⊥AC，垂足为E，∵AD⊥CO，∴∠ADO=90°，∴∠ADO=∠ABC=90°，∵∠AOD=∠BOC，∴∠DAO=∠BCO，∵∠DAO=∠ACO，∴∠BCO=∠ACO，∵OB⊥BC，OE⊥AC，∵OE=OB，∵OB是半径，∴AC是⊙O的切线；(2)解：∵OBC=∠OEC，∠BCO=∠ACO，OC=CO，∴△OBC≌△OEC，∴BC=EC=6，在Rt△ABC中，10AC=，∴AE=AC−EC=10−6=4，在Rt△AOE中，设半径为R，∵AE2+OE2=OA2，∴42+R2=(8−R)2，∴R=OC=3，∴在Rt△OBC中，OC==【点拨】本题考查了切线的判定和性质，勾股定理，全等三角形的判定和性质，熟练掌握切线的判定和性质是解题的关键．16．(1)见分析(2)①见分析；②DE=4.8【分析】（1）连接OD、BD，求出BD⊥AC，可得AD=DC，根据三角形的中位线得出OD∥BC，推出OD⊥DE，根据切线的判定推出即可；（2）①利用垂径定理作出AD的垂直平分线即可；②根据垂径定理以及勾股定理求得⊙O的半径和FO，再根据中位线中位线定理求得BD，然后根据三角形面积公式即可求解．(1)证明：连接OD，BD，∵AB为⊙O的直径，∴BD⊥AD，又∵AB=BC，△ABC是等腰三角形，∴BD又是AC边上的中线，∴OD是△ABC的中位线，∴OD∥BC，又DE⊥BC，∴DE⊥OD，∵OD是⊙O的半径，∴DE是⊙O的切线；(2)解：①如图，作AD的垂直平分线与☉O相交于点P，点P即为所求．②如图，AD 的垂直平分线与AD 相交于点F ，连接BD ，∵PF ⊥AD ，∴AF =12AD =4，设☉O 的半径为r ，在Rt △AFO 中，AF 2+FO 2=AO 2，即42+(8−r ) 2=r 2，解得r =5．∴FO =PF −PO =3，∵FO 是△ABD 的中位线，∴BD =2FO =6，∵AB 为⊙O 的直径，∴BD ⊥AC ，又∵AB =BC ，△ABC 是等腰三角形，∴AD =DC =8，∴BC =AB =10，在Rt △BDC 中，S △BDC =12BD ⋅CD =12BC ⋅DE ， ∴DE =4.8．【点拨】本题考查了切线的判定和性质，等腰三角形的性质，垂径定理，勾股定理，三角形中位线等知识点的综合运用．17．(1)见分析【分析】（1）根据圆周角定理可得260BOD BAD ∠=∠=︒，从而得到90ODB ∠=︒ ，即可求证；（2）连接DM ，Rt △BOD 中，根据直角三角形的性质可得 BO =2OD ，从而得到1OD OC ==，BD =DE O 为的直径，可得2DE =，90DME ∠=︒，从而得到BE =1122BDE S BD DE BE DM =⋅=⋅△，可得DM =，再由勾股定理，即可求解．(1)证明：∵∠BOD =2∠BAD ，∴260BOD BAD ∠=∠=︒，又∵30ABD ∠=︒，∴90ODB ∠=︒ ，即OD BD ⊥，又∵OD 为O 的半径，∴直线BD 是O 的切线；(2)解：如图，连接DM ，Rt △BOD 中，30DBO ∠=︒，∴2BO OD OC BC ==+，又1BC =，OD OC =，∴1OD OC ==，∴BD =∵DE O 为的直径，∴2DE =，90DME ∠=︒，在Rt △BDE 中，BE == ∵1122BDE S BD DE BE DM =⋅=⋅△，∴BD DE DM BE ⋅==在Rt △BDM 中，BM = 【点拨】本题主要考查了切线的判定，圆周角定理，直角三角形的性质，勾股定理等知识，熟练掌握切线的判定，圆周角定理，直角三角形的性质，勾股定理是解题的关键． 18．(1)见分析(2)7(1) 连接OD ，得到OAD ADO ∠=∠，利用余角的性质得到B BDF ∠=∠，得出结果；(2) 连接OF ，构造直角三角形，利用勾股定理求解．(1)证明：连接OD ，如图，∵半圆O 的切线DF ，∴90ODF ∠=︒．∴90ADO BDF ∠+∠=︒．∵90C ∠=︒，∴90OAD B ∠+∠=︒．∵OA OD =，∴OAD ADO ∠=∠．∴B BDF ∠=∠．∴BF DF =．(2)解：连接OF ．∵4AO CE ==，AO OE =，∴8OC =．∵9090C ODF ∠=︒=∠=︒，1CF =，∴2222265OF OC CF OD DF =+=+=．又∵4OD =，∴7DF BF ==．【点拨】本题考查切线的性质、等腰三角形的判定以及勾股定理，遇切线连接圆心和切点时解决问题的关键．19．(1)见分析(2)8（1）根据OC ＝OE ，得到∠OCE ＝∠OEC ，再根据∠AOC ＝2∠ACE ，得到∠OCA ＝∠OCE +∠ACE ＝12（∠OCE +∠OEC +∠AOC ）＝11802⨯＝90°，即有OC ⊥AB ，结论得证；（2）利用勾股定理求出AB ，在根据三角形的面积的不同算法可求出OC ，即AE 可求．(1)证明：∵OC ＝OE ，∴∠OCE ＝∠OEC ，∵∠AOC ＝2∠ACE ，∴∠OCA ＝∠OCE +∠ACE ＝12（∠OCE +∠OEC +∠AOC ）＝11802⨯＝90°， ∴OC ⊥AB ，∴AB 为⊙O 的切线；(2)∵AO ＝20，BO ＝15，∴25AB ， ∵1122OA OB AB OC ⨯⨯=⨯⨯，即1120152522OC ⨯⨯=⨯⨯， ∴OC ＝12，∴AE ＝OA ﹣OE ＝20﹣12＝8.【点拨】本题考查了切线的判定与性质、勾股定理以及三角形面积的知识，利用勾股定理解直角三角形是解答本题的关键．20．(1)见分析；(2)【分析】（1）根据切线的判定定理证明即可；（2）证明ABO 是等边三角形，利用30所对的直角边等于斜边的一半证明132AE AB ==，再由勾股定理，得BE (1)证明：连接BO ．∵OA OB =，∴OAB OBA ∠=∠．∵AB 平分CAE ∠，∴OAB BAE ∠=∠，∴OBA BAE ∠=∠．∴OB AE ∥，∴18090EBO E ∠=︒-∠=︒，即BE OB ⊥，又∵OB 是O 的半径，∴BE 是O 的切线．(2)解：30ACB ∠=︒，∴60AOB ∠=︒．又∵OA OB =，∴ABO 是等边三角形，∴60OBA ∠=︒，6OA OB AB ===，∴30ABE ∠=︒， ∴132AE AB ==．由勾股定理，得BE =【点拨】本题考查切线的判定定理，等边三角形的判定及性质，30所对的直角边等于斜边的一半，勾股定理，解题的关键是熟练掌握以上知识点．21．(1)见分析(2)8【分析】（1）过O 作OE ⊥AC 于E ，先证Rt △ABO ≌Rt △AEO ，OB ＝OE ，即OE 为圆的半径，即可求证；（2）利用切线的性质可得AB =AE ，再证Rt △BOD ≌Rt △COE ，即有BD ＝CE ＝2，则AC 可求．(1)证明：过O 作OE ⊥AC 于E ．∵AO 平分∠BAC ，且∠ABC ＝90°，OE ⊥AC ，∴OB ＝OE ，即OE 为圆的半径，∴AC 是⊙O 的切线；(2)∵∠ABC ＝90°，OB 为⊙O 半径，∴AB 是⊙O 的切线，又由（1）AC 是⊙O 的切线，∴AB ＝AE ＝6，在Rt △BOD 和Rt △COE 中，OB OE OD OC =⎧⎨=⎩， ∴Rt △BOD ≌Rt △COE ，∴BD ＝CE ＝2，∴AC ＝AE +CE ＝8【点拨】本题考查了切线的判定与性质，角平分线的性质定理，在OE ⊥AC 的条件下证得OE 为圆的半径是解答本题的关键．22．(1)DE 是⊙O 的切线，理由见分析；(2)DE 的长为245．【分析】（1）连接OD ，根据等边对等角性质和平行线的判定和性质证得OD ⊥DE ，从而证得DE 是⊙O 的切线；（2）由等腰三角形的性质求出BD =CD =8，由勾股定理求出AD 的长，根据三角形的面积得出答案．(1)解：DE 是⊙O 的切线，理由如下：连接OD ，∵OB =OD ，∵AB=AC，∴∠B=∠C，∴∠ODB=∠C，∴OD∥AC，∵DE⊥AC，∴OD⊥DE，∴DE是⊙O的切线；(2)解：连接AD，∵∠ADB=90°，AB=AC，∴BD=CD，∵⊙O的半径为5，BC=16，∴AC=AB=10，CD=8，∴AD= 6，∵S△ADC=12AC•DE=12AD•CD，∴DE=6824105 AD CDAC⋅⨯==．【点拨】本题考查了切线的判定与性质，圆周角定理，等腰三角形的性质和判定，三角形的内角和定理，勾股定理，三角形的面积等知识，掌握切线的判定与性质是解题的关键．23．(1)见分析(2)3【分析】（1）连接OD、CD，由AC为⊙O的直径知△BCD是直角三角形，结合E为BC的中点知∠CDE=∠DCE，由∠ODC=∠OCD且∠OCD+∠DCE=90°可得答案；（2）设⊙O的半径为r，由OD2+DF2=OF2，即r2+42=（r+2）2可得r=3，即可得出答案．(1)解：如图，连接OD、CD．∵AC为⊙O的直径，∴∠ADC=90°，∴∠CDB=90°，即△BCD是直角三角形，∵E为BC的中点，∴∠CDE =∠DCE ，∵OD =OC ，∴∠ODC =∠OCD ，∵∠ACB =90°，∴∠OCD +∠DCE =90°，∴∠ODC +∠CDE =90°，即OD ⊥DE ，∴DE 是⊙O 的切线；(2)解：设⊙O 的半径为r ，∵∠ODF =90°，∴OD 2+DF 2=OF 2，即r 2+42=（r +2）2，解得：r =3，∴⊙O 的半径为3．【点拨】本题主要考查了圆切线的判定与性质，等腰三角形的性质与判定，直角三角形斜边上的中线，勾股定理等等，熟知圆切线的性质与判定是解题的关键．24．(1)60︒(2)见分析【分析】（1）由直径为6，求得⊙O 的周长，再由AC 的长为π，求得AOC ∠的度数．（2）由（1）知60AOC ∠=︒，由于OB OC =，可得1302OBC AOC ∠=∠=︒，再由BC PC =推出30P ∠=︒，从而证得OC CP ⊥，直线PC 与⊙O 相切．(1)解：∵6AB =，∴⊙O 的周长为6π．∵AC 的长为π， ∴1360606AOC ∠=⨯︒=︒． (2)证明：∵AB 为⊙O 的直径，点C 在⊙O 上，∴OB OC =， ∴12OBC OCB AOC ∠=∠=∠．∵60AOC ∠=︒， ∴1302OBC OCB AOC ∠=∠=∠=︒． ∵BC PC =，∴30CBO P ∠=∠=︒．在COP 中，∵60COA ∠=︒，30P ∠=︒，∴180180603090OCP COA P ∠=︒-∠-∠=︒-︒-︒=︒，∴OC CP ⊥，又∵点C 在⊙O 上，∴直线PC 与⊙O 相切．【点拨】本题考查了圆的相关性质，切线的判定，综合运用圆的性质确定相关角度是解题关键．。

圆的切线试题(经典版)

10．如图，已知AB为⊙O的弦，C为⊙O上一点，∠C=∠BAD，且BD⊥AB于B.
（1）求证：AD是⊙O的切线；
（2）若⊙O的半径为3，AB=4，求AD的长.
11．已知：如图，在△ABC中，AB=AC，点D是边BC的中点．以BD为直径作圆O，交边AB于点P，联结PC，交AD于点E．
（1）求证：AD是圆O的切线；
（1）求证:AC是⊙O的切线;
（2）联结EF，求的值.
15
如图，四边形ABCD内接于，BD是的直径，于E，
DA平分 .
（1）求证：AE是的切线；
（2）若
16.如图，是⊙O的直径，⊙O交的中点
于，，E是垂足.
（1）求证：是⊙O的切线；
（2）如果AB=5,tan∠B= ,求CE的长.
（1）求证：BD是⊙O的切线；
（2）若点E是劣弧BC上一点，弦AE与BC相交
于点F，且CF＝9，cos∠BFA＝，求EF的长．
9已知：如图，⊙O的直径 =8cm，是延长线上的一点，过点作⊙O的切线，切点为，连接．
(1)若，求阴影部分的面积；
(2)若点在的延长线上运动，的平分线交于点，∠ 的大小是否发生变化？若变化，请说明理由；若不变，求出∠ 的度数．
（2）若PC是圆O的切线，BC= 8，求DE的长．
12已知：如图，△ABC中，AB=AC=5，BC=6，以AB为直径作⊙O交AC于点D，交BC于点E，EF⊥AC于F交AB的延长线于G.
（1）求证：FG是⊙O的切线；
（2）求AD的长.
（1）证明：
13
已知：在⊙O中，AB是直径，AC是弦，OE⊥AC
于点E，过点C作直线FC，使∠FCA＝∠AOE，交

圆切线练习题(含答案)

圆切线问题典型问题例1. 已知半径为3的⊙O上一点P和圆外一点Q，如果OQ＝5，PQ＝4，则PQ 和圆的位置关系是（）A. 相交B. 相切C. 相离D. 位置不定例2. 在△ABC中，∠C＝90°，∠B＝30°，O为AB上一点，AO＝m，⊙O的半径，问m在什么范围内取值时，AC与圆：（1）相离；（2）相切；（3）相交。

例3. 已知：在△ABC中，AD为∠BAC的平分线，以C为圆心，CD为半径的半圆交BC的延长线于点E，交AD于点F，交AE于点M，且∠B＝∠CAE，FE：FD＝4：3。

求证：AF＝DF；例4. 已知⊙O中，AB是直径，过B点作⊙O的切线，连结CO，若AD∥OC 交⊙O于D，求证：CD是⊙O的切线。

例5. 如图所示，△ABC为等腰三角形，O是底边BC的中点，⊙O与腰AB 相切于点D。

求证：AC与⊙O相切。

点悟：显然AC与⊙O的公共点没有确定，故用“d＝r”证之。

而AB与⊙O 切于D点，可连结OD，则OD⊥AB。

例6. 已知⊙O的半径OA⊥OB，点P在OB的延长线上，连结AP交⊙O于D，过D作⊙O的切线CE交OP于C，求证：PC＝CD。

例7. 在△ABC中，∠A＝70°，点O是内心，求∠BOC的度数。

圆切线问题典型问题答案例1 解：∵OP＝3，PQ＝4，OQ＝5，∴，∴△OPQ是直角三角形，且∠OPQ＝90°，∴PQ⊥OP。

即圆心O到PQ的距离等于圆的半径。

∴PQ和圆的位置关系相切，故选B。

点拨：在没有明确知道圆心到直线的距离和半径的关系时，通过已有的知识进行推证。

本题也可以通过切线的判定定理求解，即通过半径的外端并且垂直于这条半径的直线是圆的切线。

例2.点悟：要判定直线与圆的位置关系，只要比较圆心到直线的距离与半径的大小。

解：如图所示，过O作OD⊥AC垂足为D，，∴（1）当，即，也即时，则AC与⊙O相离；（2）当，即，也即时，AC与⊙O相切；（3）当，即，也即时，AC与⊙O相交。

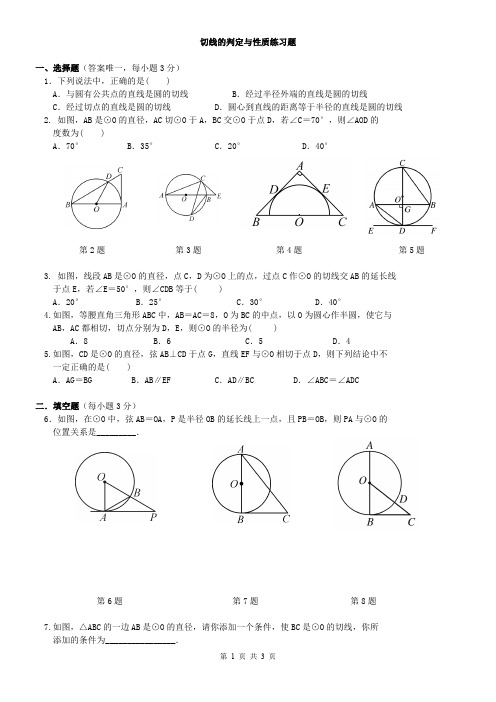
(完整版)圆的切线综合练习题与答案(2018)

切线的判定与性质练习题一、选择题（答案唯一，每小题3分）1．下列说法中，正确的是( )A．与圆有公共点的直线是圆的切线 B．经过半径外端的直线是圆的切线C．经过切点的直线是圆的切线 D．圆心到直线的距离等于半径的直线是圆的切线2. 如图，AB是⊙O的直径，AC切⊙O于A，BC交⊙O于点D，若∠C＝70°，则∠AOD的度数为( )A．70° B．35° C．20° D．40°第2题第3题第4题第5题3. 如图，线段AB是⊙O的直径，点C，D为⊙O上的点，过点C作⊙O的切线交AB的延长线于点E，若∠E＝50°，则∠CDB等于( )A．20° B．25° C．30° D．40°4.如图，等腰直角三角形ABC中，AB＝AC＝8，O为BC的中点，以O为圆心作半圆，使它与AB，AC都相切，切点分别为D，E，则⊙O的半径为( )A．8 B．6 C．5 D．45.如图，CD是⊙O的直径，弦AB⊥CD于点G，直线EF与⊙O相切于点D，则下列结论中不一定正确的是( )A．AG＝BG B．AB∥EF C．AD∥BC D．∠ABC＝∠ADC二．填空题（每小题3分）6．如图，在⊙O中，弦AB＝OA，P是半径OB的延长线上一点，且PB＝OB，则PA与⊙O的位置关系是_________．第6题第7题第8题7.如图，△ABC的一边AB是⊙O的直径，请你添加一个条件，使BC是⊙O的切线，你所添加的条件为________________．8.如图，AB 是⊙O 的直径，O 是圆心，BC 与⊙O 切于点B ，CO 交⊙O 于点D ，且BC ＝8，CD ＝4，那么⊙O 的半径是______．9. 如图，若以平行四边形一边AB 为直径的圆恰好与对边CD 相切于点D ，则∠C＝_______度．第9题第10题第11题10. 如图，AB 为⊙O 的直径，直线l 与⊙O 相切于点C ，AD⊥l ，垂足为D ，AD 交⊙O 于点E ，连接OC ，BE.若AE ＝6，OA ＝5，则线段DC 的长为______．11．如图，已知△ABC 内接于⊙O，BC 是⊙O 的直径，MN 与⊙O 相切，切点为A ，若∠MAB＝30°，则∠B＝________度．三、解答题（写出详细解答或论证过程）12.（7分）如图，在Rt △ABC 中，∠C＝90°，BD 是角平分线，点O 在AB 上，以点O 为圆心，OB 为半径的圆经过点D ，交BC 于点E.求证：AC 是⊙O的切线．第12题第13题第14题13.（7分）如图，AB 是⊙O 的直径，点C 在AB 的延长线上，CD 与⊙O 相切于点D ，CE⊥AD，交AD 的延长线于点E.求证：∠BDC＝∠A.14.（7分）如图，在Rt △ABC 中，∠ABC＝90°，∠BAC 的平分线交BC 于D ，以D 为圆心，DB 长为半径作⊙D，求证：AC 与⊙D 相切．15.（10分）如图，AB 为⊙O 的直径，PD 切⊙O 于点C ，交AB 的延长线于点D ，且∠D＝2∠CAD.(1)求∠D 的度数；(2)若CD ＝2，求BD的长．第15题第16题g se16．（12分）已知△ABC 内接于⊙O，过点A 作直线EF.(1)如图①，若AB 为⊙O 的直径，要使EF 成为⊙O 的切线，还需要添加的一个条件是(至少说出两种)：__________________________或者_______________________；(2)如图②，如果AB 是不过圆心O 的弦，且∠CAE＝∠B，那么EF 是⊙O 的切线吗？试证明你的判断．17.（12分）如图，已知直线PA 交⊙O 于A ，B 两点，AE 是⊙O 的直径，点C 为⊙O 上一点，且AC 平分∠PAE，过C 作CD⊥PA，垂足为D.(1)求证：CD 为⊙O 的切线；(2)若DC ＋DA ＝6，⊙O 的直径为10，求AB 的长．答案：DDADC 6. 相切 7. ∠ABC＝90°不排除等效答案 8. 6 9. 45 10. 4 11. 6012. 解：连接OD ，∵BD 为∠ABC 平分线，∴∠OBD＝∠CBD，∵OB＝OD ，∴∠OBD＝∠ODB，∴∠CBD＝∠ODB，∴OD∥BC，∵∠C＝90°，∴∠ODA＝90°，则AC 为⊙O 的切线13. 解：连接OD ，∵CD 是⊙O 的切线，∴∠ODC＝90°，∴∠ODB＋∠BDC＝90°，∵AB 是⊙O 的直径，∴∠ADB＝90°，即∠ODB＋∠ADO＝90°，∴∠BDC＝∠ADO，∵OA＝OD ，∴∠ADO＝∠A，∴∠BDC＝∠A 14. 解：过D 作DH⊥AC 于H ，由角平分线的性质可证DB ＝DH ，∴AC 与⊙D 相切15. 解：(1)∵∠COD＝2∠CAD，∠D＝2∠CAD，∴∠D＝∠COD.∵PD 与⊙O 相切于点C ，∴OC⊥PD，即∠OCD＝90°，∴∠D＝45°(2)由(1)可知△OCD 是等腰直角三角形，∴OC＝CD ＝2，由勾股定理，得OD ＝＝2，∴BD＝OD －OB ＝2－222＋222216. (1) ∠BAE＝90° ∠EAC＝∠ABC (2) (2)EF 是⊙O 的切线．证明：作直径AM ，连接CM ，则∠ACM＝90°，∠M＝∠B，∴∠M＋∠CAM＝∠B＋∠CAM＝90°，∵∠CAE＝∠B，∴∠CAM＋∠CAE＝90°，∴AE⊥AM，∵AM 为直径，∴EF 是⊙O 的切线17. 解：(1)连接OC ，证∠DAC＝∠CAO＝∠ACO，∴PA∥CO，又∵CD⊥PA，∴CO⊥CD，∴CD 为⊙O 的切线(2)过O 作OF⊥AB，垂足为F ，∴四边形OCDF 为矩形．∵DC＋DA ＝6，设AD ＝x ，则OF ＝CD ＝6－x ，AF ＝5－x ，在Rt △AOF 中，有AF 2＋OF 2＝OA 2，即(5－x)2＋(6－x)2＝25，解得x 1＝2，x 2＝9，由AD ＜DF 知0＜x ＜5，故x ＝2，从而AD ＝2，AF ＝5－2＝3，由垂径定理得AB ＝2AF ＝6。

证明圆的切线经典例题

证明圆的切线方法及例题证明圆的切线常用的方法有：一、若直线l过⊙O上某一点A，证明l是⊙O的切线，只需连OA，证明OA⊥l 就行了，简称“连半径，证垂直”，难点在于如何证明两线垂直.例1如图，在△ABC中，AB=AC，以AB为直径的⊙O交BC于D，交AC于E，B为切点的切线交OD延长线于F.求证：EF与⊙O相切.证明：连结OE，AD.∵AB是⊙O的直径，∴AD⊥BC.又∵AB=BC，∴∠3=∠4.⌒⌒∴BD=DE，∠1=∠2.又∵OB=OE，OF=OF，∴△BOF≌△EOF（SAS）.∴∠OBF=∠OEF.∵BF与⊙O相切，∴OB⊥BF.∴∠OEF=900.∴EF与⊙O相切.说明：此题是通过证明三角形全等证明垂直的例2 如图，AD是∠BAC的平分线，P为BC延长线上一点，且PA=PD. 求证：PA与⊙O相切.证明一：作直径AE，连结EC.∵AD是∠BAC的平分线，∴∠DAB=∠DAC.∵PA=PD，∴∠2=∠1+∠DAC.∵∠2=∠B+∠DAB，∴∠1=∠B.又∵∠B=∠E，∴∠1=∠E∵AE是⊙O的直径，∴AC⊥EC，∠E+∠EAC=900.∴∠1+∠EAC=900.即OA⊥PA.∴PA与⊙O相切.证明二：延长AD交⊙O于E，连结OA，OE.∵AD是∠BAC的平分线，⌒⌒∴BE=CE，∴OE⊥BC.∴∠E+∠BDE=900.∵OA=OE，∴∠E=∠1.∵PA=PD，∴∠PAD=∠PDA.又∵∠PDA=∠BDE,∴∠1+∠PAD=900即OA⊥PA.∴PA与⊙O相切说明：此题是通过证明两角互余，证明垂直的，解题中要注意知识的综合运用. 例3 如图，AB=AC，AB是⊙O的直径，⊙O交BC于D，DM⊥AC于M求证：DM与⊙O相切.证明一：连结OD.∵AB=AC，∴∠B=∠C.∵OB=OD，∴∠1=∠B.∴∠1=∠C.∴OD∥AC.∵DM⊥AC，∴DM⊥OD.∴DM与⊙O相切证明二：连结OD，AD.∵AB是⊙O的直径，∴AD⊥BC.又∵AB=AC,∴∠1=∠2.∵DM⊥AC，∴∠2+∠4=900∵OA=OD，∴∠1=∠3.∴∠3+∠4=900. DC即OD⊥DM.∴DM是⊙O的切线说明：证明一是通过证平行来证明垂直的.证明二是通过证两角互余证明垂直的，解题中注意充分利用已知及图上已知.例4 如图，已知：AB是⊙O的直径，点C在⊙O上，且∠CAB=300，BD=OB，D在AB的延长线上.求证：DC是⊙O的切线证明：连结OC、BC.∵OA=OC，∴∠A=∠1=∠300.∴∠BOC=∠A+∠1=600.D 又∵OC=OB，∴△OBC是等边三角形.∴OB=BC.∵OB=BD，∴OB=BC=BD.∴OC⊥CD.∴DC是⊙O的切线.说明：此题是根据圆周角定理的推论3证明垂直的，此题解法颇多，但这种方法较好.例5 如图，AB是⊙O的直径，CD⊥AB，且OA2=OD·OP.求证：PC是⊙O的切线.证明：连结OC∵OA2=OD·OP，OA=OC，∴OC2=OD·OP，OC OP OD OC . 又∵∠1=∠1，∴△OCP ∽△ODC.∴∠OCP=∠ODC.∵CD ⊥AB ，∴∠OCP=900.∴PC 是⊙O 的切线.说明：此题是通过证三角形相似证明垂直的例6 如图，ABCD 是正方形，G 是BC 延长线上一点，AG 交BD 于E ，交CD 于F.求证：CE 与△CFG 的外接圆相切.分析：此题图上没有画出△CFG 的外接圆，但△CFG 是直角三角形，圆心在斜边FG 的中点，为此我们取FG 的中点O ，连结OC ，证明CE ⊥OC 即可得解.证明：取FG 中点O ，连结OC.∵ABCD 是正方形，∴BC ⊥CD ，△CFG 是Rt △∵O 是FG 的中点，∴O 是Rt △CFG 的外心.∵OC=OG ，∴∠3=∠G ，∵AD ∥BC ，∴∠G=∠4.∵AD=CD ，DE=DE ，∠ADE=∠CDE=450，∴△ADE ≌△CDE （SAS ）∴∠4=∠1，∠1=∠3.∵∠2+∠3=900,∴∠1+∠2=900.即CE⊥OC.∴CE与△CFG的外接圆相切二、若直线l与⊙O没有已知的公共点，又要证明l是⊙O的切线，只需作OA⊥l，A为垂足，证明OA是⊙O的半径就行了，简称：“作垂直；证半径”例7 如图，AB=AC，D为BC中点，⊙D与AB切于E点.求证：AC与⊙D相切.证明一：连结DE，作DF⊥AC，F是垂足.∵AB是⊙D的切线，∴DE⊥AB.∵DF⊥AC，∴∠DEB=∠DFC=900.∵AB=AC，∴∠B=∠C.又∵BD=CD，∴△BDE≌△CDF（AAS）∴DF=DE.∴F在⊙D上.∴AC是⊙D的切线证明二：连结DE，AD，作DF⊥AC，F是垂足.∵AB与⊙D相切，∴DE⊥AB.∵AB=AC，BD=CD，∴∠1=∠2.∵DE ⊥AB ，DF ⊥AC ，∴DE=DF.∴F 在⊙D 上. ∴AC 与⊙D 相切.说明：证明一是通过证明三角形全等证明DF=DE 的，证明二是利用角平分线的性质证明DF=DE 的，这类习题多数与角平分线有关.例8 已知：如图，AC ，BD 与⊙O 切于A 、B ，且AC ∥BD ，若∠COD=900. 求证：CD 是⊙O 的切线.证明一：连结OA ，OB ，作OE ⊥CD ，E 为垂足.∵AC ，BD 与⊙O 相切，∴AC ⊥OA ，BD ⊥OB. ∵AC ∥BD ，∴∠1+∠2+∠3+∠4=1800.∵∠COD=900，∴∠2+∠3=900，∠1+∠4=900.∵∠4+∠5=900.∴∠1=∠5.∴Rt △AOC ∽Rt △BDO.∴OD OC OB AC =.∵OA=OB ， ∴OD OC OA AC =. 又∵∠CAO=∠COD=900，∴△AOC ∽△ODC ，∴∠1=∠2. 又∵OA ⊥AC ，OE ⊥CD,O∴OE=OA.∴E点在⊙O上.∴CD是⊙O的切线.证明二：连结OA，OB，作OE⊥CD于E，延长DO交CA延长线于F.∵AC，BD与⊙O相切，∴AC⊥OA，BD⊥OB.∵AC∥BD，∴∠F=∠BDO.又∵OA=OB，∴△AOF≌△BOD（AAS）∴OF=OD.∵∠COD=900，∴CF=CD，∠1=∠2.又∵OA⊥AC，OE⊥CD，∴OE=OA.∴E点在⊙O上.∴CD是⊙O的切线.证明三：连结AO并延长，作OE⊥CD于E，取CD中点F，连结OF.∵AC与⊙O相切，∴AC⊥AO.∵AC∥BD，∴AO⊥BD.∵BD与⊙O相切于B，∴AO的延长线必经过点B.∴AB是⊙O的直径.∵AC∥BD，OA=OB，CF=DF，∴OF ∥AC ，∴∠1=∠COF.∵∠COD=900，CF=DF ，∴CF CD OF ==21.∴∠2=∠COF.∴∠1=∠2.∵OA ⊥AC ，OE ⊥CD ，∴OE=OA.∴E 点在⊙O 上. ∴CD 是⊙O 的切线说明：证明一是利用相似三角形证明∠1=∠2，证明二是利用等腰三角形三线合一证明∠1=∠2.证明三是利用梯形的性质证明∠1=∠2，这种方法必需先证明A 、O 、B 三点共线.以上介绍的是证明圆的切线常用的两种方法供同学们参考.。

圆的切线试题专项训练

圆的切线试题专项训练一．选择题（共6小题）1．已知OA平分∠BOC，P是OA上一点，以P为圆心的⊙P与OC相切，则⊙P与OB的位置关系为（）A．相离B．相切C．相交D．不能确定2．如图，P为⊙O的直径BA延长线上的一点，PC与⊙O相切，切点为C，点D是⊙上一点，连接PD．已知PC=PD=BC．下列结论：（1）PD与⊙O相切；（2）四边形PCBD是菱形；（3）PO=AB；（4）∠PDB=120°．其中正确的个数为（） A.4 B.3 C.2 D.1 3．如图，线段AB是⊙O的直径，⊙O交线段BC于D，且D是BC中点，DE⊥AC于E，连接AD，则下列结论正确的个数是（）①CE•CA=CD•CB；②∠EDA=∠B；③OA=1/2AC；④DE是⊙O的切线；⑤AD2=AE•AB．A．2个B．3个C．4个D．5个4．如图，直线AB、CD相交于点O，∠AOD=30°，半径为1cm的⊙P的圆心在射线OA上，且与点O的距离为6cm．如果⊙P以1cm/s的速度沿由A向B的方向移动，那么（）秒钟后⊙P与直线CD相切． A.4 B.8 C.4 或6 D.4 或85．如图，直线AC∥BD，⊙O与AC和BD分别相切于点A和点B．点M和点N分别是AC 和BD上的动点，MN沿AC和BD平移．⊙O的半径为1，∠1=60°．下列结论错误的是（）A．直线AC和BD的距离为2 B．若∠MON=90°，则MN与⊙O相切C．若MN与⊙O相切，则AM= D．MN=6．如图，在梯形ABCD中，AB∥DC．①若∠A=90°，AB+CD=BC，则以AD为直径的圆与BC 相切；②若∠A=90°，当以AD为直径的圆与BC相切，则以BC为直径的圆也与AD相切；③若以AD为直径的圆与BC相切，则AB+CD=BC；④若以AD为直径的圆与BC相切，则以BC 为直径的圆与AD相切．以上判断正确的个数有（） A.1 B.2 C.3 D.47.如图，在Rt△AOB中，OA=OB=3，⊙O的半径为1，点P是AB边上的动点，过点P作⊙O 的一条切线PQ（点Q为切点），则线段PQ的最小值为（）8．如图，AB是⊙O的直径，C、D是⊙O上的点，∠CDB=30°，过点C作⊙O的切线交AB 的延长线于E，则sin∠E的值为（）A.1/2 B.3/2 C. 2 D.39.在等腰直角三角形ABC中，AB=AC=4，点O为BC的中点，以O为圆心作⊙O交BC于点M、N，⊙O与AB、AC相切，切点分别为D、E，则⊙O的半径和∠MND的度数分别为（）A．2，22.5°B．3，30°C．3，22.5°D．2，30°二．填空题1.如图，等腰△ABC中，∠ACB=90°，I为△ABC的内心，AI的延长线交BC于E．若IE=1，则AI= .2．三角形的内切圆（1）定义：与三角形各边都的圆叫做三角形的内切圆．内切圆的圆心叫三角形的．（2）三角形的内心是三角形的交点，它到三角形的距离相等，都等于该三角形．（3）如图，若△ABC的三边分别为AB=c，BC=a，AC=b，其内切圆⊙O分别切BC、CA、AB于D、E、F．则AF=AE= ，BD=BF= ，CD=CE= ．∠BOC与∠A 的关系是，∠EDF与∠A的关系是△ABC的面积S与内切圆半径r的关系是（4）直角三角形的外接圆半径等于，内切圆半径等于．3.如图，边长为4的正方形ABCD内接于⊙O，点E是弧AB上的一动点（不与点A、B重合），点F是弧BC上的一点，连接OE，OF，分别与交AB，BC于点G，H，且∠EOF＝90°，连接GH，有下列结论：①弧AE＝弧BF；②△OGH是等腰直角三角形；③四边形OGBH 的面积随着点E位置的变化而变化；④△GBH周长的最小值为4+2√2.其中正确的是 .（把你认为正确结论的序号都填上）4．如图，已知AB是⊙O的直径，AD、BD是半圆的弦，∠PDA=∠PBD，∠BDE=60°，若PD=√3 ，则PA的长为5．如图，AB是⊙O的直径，经过圆上点D的直线CD恰使∠ADC=∠B．过点A作直线AB 的垂线交BD的延长线于点E，且AB=√5 ，BD=2，则线段AE的长为.6．如图，在△ABC中，∠BAC=90°，D为BC上的中点，O是线段AD上一点，以点O为圆心，OA长为半径的⊙O交AC于点E，EF⊥BC于点F，则EF ⊙O的切线．（填“是”或“不是”）7．如图，△ACD内接于⊙O，CB垂直于过点D的切线，垂足为B，如果BC=3，sin∠A=3/4，那么⊙O的半径为8．如图，矩形ABCD中，AB=2√3 ，AD=2，以AB为弦在矩形内部画一条120°的弧，过点C 作直线CE，与弧ＡＢ切于点F，与AD边交于点E，那么DE的长是9．如图，在⊙O中，直径AB=2，CA切⊙O于A，BC交⊙O于D，若∠C=45°，则阴影部分的面积为三．解答题1．如图，O为正方形ABCD对角线AC上一点，以O为圆心，OA长为半径的⊙O与BC相切于点M．（1）求证：CD与⊙O相切；（2）若⊙O的半径为1，求正方形ABCD的边长．2．如图：已知AB是⊙O的直径，BC是⊙O的切线，OC与⊙O相交于点D，连接AD并延长，与BC相交于点E．（1）若BC=，CD=1，求⊙O的半径；（2）取BE的中点F，连接DF，求证：DF是⊙O的切线．3．如图，已知AB是OD的直径，AM和BN是⊙O的两条切线，点E是⊙O上一点，点D 是AM上一点，连接DE并延长交BN于点C，连接OD、BE，且OD∥BE．（1）求证：DE是⊙O的切线；（2）若AD=l，BC=4，求直径AB的长．4．如图，⊙O是Rt△ABC的外接圆，∠ABC=90°，点P是圆外一点，PA切⊙O于点A，且PA=PB．（1）求证：PB是⊙O的切线；（2）已知PA= 3，∠ACB=60°，求⊙O的半径．5．如图，在平面直角坐标系中，以点O为圆心，半径为2的圆与y轴交于点A，点P（4，2）是⊙O外一点，连接AP，直线PB与⊙O相切于点B，交x轴于点C．（1）证明PA是⊙O 的切线；（2）求点B的坐标．6．如图，PB切⊙O于B点，直线PO交⊙O于点E，F，过点B作PO的垂线BA，垂足为点D，交⊙O于点A，延长AO交⊙O于点C，连接BC，AF．（1）求证：直线PA为⊙O的切线；（2）若BC=6，AD：FD=1：2，求⊙O的半径的长．7．如图，AB是⊙O的直径，CA是⊙O的切线，在⊙O上取点D，连接CD，使得AC=DC，延长CD交直线AB于点E．（1）求证：CD是⊙O的切线；（2）作AF⊥CD于点F，交⊙O于点G，若⊙O的半径是6cm，ED=8cm，求GF的长．8．如图，PB为⊙0的切线，B为切点，直线PO交⊙于点E、F，过点B作PO的垂线BA，垂足为点D，交⊙O于点A，延长AO9．在平面直角坐标系xOy中，已知点A（6，0），点B（0，6），动点C在以半径为3的⊙O 上，连接OC，过O点作OD⊥OC，OD与⊙O相交于点D（其中点C、O、D按逆时针方向排列），连接AB．（1）当OC∥AB时，∠BOC的度数为45°或135°；（2）连接AC，BC，当点C 在⊙O上运动到什么位置时，△ABC的面积最大？并求出△ABC的面积的最大值．（3）连接AD，当OC∥AD时，①求出点C的坐标；②直线BC是否为⊙O的切线？请作出判断，并说明理由．10．在⊙O中，AB为直径，点C为圆上一点，将劣弧沿弦AC翻折交AB于点D，连结CD．（1）如图1，若点D与圆心O重合，AC=2，求⊙O的半径r；（2）如图2，若点D与圆心O不重合，∠BAC=25°，请直接写出∠DCA的度数．11．如图，在Rt△ABC中，∠ACB=90°，AC=6cm，BC=8cm．P为BC的中点，动点Q从点P 出发，沿射线PC方向以2cm/s的速度运动，以P为圆心，PQ长为半径作圆．设点Q运动的时间为t s．（1）当t=1.2时，判断直线AB与⊙P的位置关系，并说明理由；（2）已知⊙O 为△ABC的外接圆．若⊙P与⊙O相切，求t的值．12．如图，点A，B在直线MN上，AB=11厘米，⊙A，⊙B的半径均为1厘米．⊙A以每秒2厘米的速度自左向右运动，与此同时，⊙B的半径也不断增大，其半径r（厘米）与时间t （秒）之间的关系式为r=1+t（t≥0）．（1）试写出点A、B之间的距离d（厘米）与时间t（秒）之间的函数表达式；（2）问点A出发后多少秒两圆相切？13．已知矩形纸片ABCD，AB=2，AD=1，将纸片折叠，使顶点A与边CD上的点E重合．（1）如果折痕FG分别与AD、AB交于点F、G（如图1），AF= 2/3，求DE的长；（2）如果折痕FG分别与CD、AB交于点F、G（如图2），△AED的外接圆与直线BC相切，求折痕FG的长．14．如图，在矩形ABCD中，AB=20cm，BC=4cm，点P从A开始沿折线A-B-C-D以4cm/s的速度移动，点Q从C开始沿CD边以1cm/s的速度移动，如果点P、Q分别从A、C同时出发，当其中一点到达D时，另一点也随之停止运动．设运动时间为t（s）．（1）t为何值时，四边形APQD为矩形；（2）如图，如果⊙P和⊙Q的半径都是2cm，那么t为何值时，⊙P和⊙Q外切．15．如图，AB是半圆O的直径，AC⊥AB，CD切半圆于点D，BF⊥AB，交AD的延长线于F，交CD的延长线于E．（1）若∠C=80°，求∠F的度数；（2）求证：BE=EF；（3）若AC=6，BE=4，求AB的长．16．如图，在△ABC中，AB=AC，以AC为直径作⊙O交BC于点D，过点D作⊙O的切线EF，交AB和AC的延长线于E、F．（1）求证：FE⊥AB；（2）当AE=6，sin∠CFD=3/5 时，求EB 的长．17．已知，AB为⊙O的直径，C为⊙O上一点，若直线CD与⊙O相切于点C，AD⊥CD，垂足为D．（1）如图①，AB=10，AD=2，求AC的长；（2）如果把直线CD向下平行移动，如图（2），直线CD交⊙O于C，G两点，若题目中的其他条件不变，且AG=4，BG=3，求AD/AC 的值．18．如图，AB为⊙O的直径，D、T是圆上的两点，且AT平分∠BAD，过点T作AD的延长线的垂线PQ，垂足为C．（1）求证：PQ是⊙O的切线；（2）已知⊙O的半径为2，若过点O 作OE⊥AD，垂足为E，OE=√3 ，求弦AD的长．19．如图，△ABC为等边三角形，以边BC为直径的半圆与边AB，AC分别交于D，F两点，过点D作DE⊥AC，垂足为点E．（1）判断DE与⊙O的位置关系，并证明你的结论；（2）过点F作FH⊥BC，垂足为点H，若AB=4，求FH的长（结果保留根号）．20．已知：如图，△ABC中，AB=AC，AD平分∠BAC，BE平分∠ABC交AD于点E．经过B、E两点的⊙O交AB于点F，交BC于点G，BF恰为⊙O的直径．（1）求证：AD与⊙O相切；（2）若BC=4，cos C＝1/3 ，求⊙O的半径长．21．如图，在Rt△ABC中，∠C=90°，BE平分∠ABC交AC于点E，点D在AB边上且DE⊥BE．（1）判断直线AC与△DBE外接圆的位置关系，并说明理由；（2）若AD=4，AE=4√2 ，求BC的长．22．如图，⊙D交y轴于A、B，交x轴于C，过点C的直线：y=-2 √2x-8与y轴交于P．（1）求证：PC是⊙D的切线；（2）判断在直线PC上是否存在点E，使得S△EOP=4S△CDO，若存在，求出点E的坐标；若不存在，请说明理由；（3）当直线PC绕点P转动时，与劣弧AC 交于点F（不与A、C重合），连接OF，设PF=m，OF=n，求m、n之间满足的函数关系式，并写出自变量n的取值范围．。

圆的切线综合练习题与答案

切线的判定与性质练习题一、选择题（答案唯一，每小题3分）1．下列说法中，正确的是( )A．与圆有公共点的直线是圆的切线 B．经过半径外端的直线是圆的切线C．经过切点的直线是圆的切线 D．圆心到直线的距离等于半径的直线是圆的切线2. 如图，AB是⊙O的直径，AC切⊙O于A，BC交⊙O于点D，若∠C＝70°，则∠AOD的度数为( )A．70° B．35° C．20° D．40°第2题第3题第4题第5题3. 如图，线段AB是⊙O的直径，点C，D为⊙O上的点，过点C作⊙O的切线交AB的延长线于点E，若∠E＝50°，则∠CDB等于( )A．20° B．25° C．30° D．40°4.如图，等腰直角三角形ABC中，AB＝AC＝8，O为BC的中点，以O为圆心作半圆，使它与AB，AC都相切，切点分别为D，E，则⊙O的半径为( )A．8 B．6 C．5 D．45.如图，CD是⊙O的直径，弦AB⊥CD于点G，直线EF与⊙O相切于点D，则下列结论中不一定正确的是( )A．AG＝BG B．AB∥EF C．AD∥BC D．∠ABC＝∠ADC二．填空题（每小题3分）6．如图，在⊙O中，弦AB＝OA，P是半径OB的延长线上一点，且PB＝OB，则PA与⊙O的位置关系是_________．第6题第7题第8题7.如图，△ABC的一边AB是⊙O的直径，请你添加一个条件，使BC是⊙O的切线，你所添加的条件为________________．8.如图，AB是⊙O的直径，O是圆心，BC与⊙O切于点B，CO交⊙O于点D，且BC＝8，CD＝4，那么⊙O的半径是______．9. 如图，若以平行四边形一边AB为直径的圆恰好与对边CD相切于点D，则∠C＝_______度．第9题第10题第11题10. 如图，AB为⊙O的直径，直线l与⊙O相切于点C，AD⊥l，垂足为D，AD交⊙O于点E，连接OC，BE.若AE＝6，OA＝5，则线段DC的长为______．11．如图，已知△ABC内接于⊙O，BC是⊙O的直径，MN与⊙O相切，切点为A，若∠MAB＝30°，则∠B＝________度．三、解答题（写出详细解答或论证过程）12.（7分）如图，在Rt△ABC中，∠C＝90°，BD是角平分线，点O在AB上，以点O为圆心，OB为半径的圆经过点D，交BC于点E.求证：AC是⊙O的切线．第12题第13题第14题13.（7分）如图，AB是⊙O的直径，点C在AB的延长线上，CD与⊙O相切于点D，CE⊥AD，交AD的延长线于点E.求证：∠BDC＝∠A.14.（7分）如图，在Rt△ABC中，∠ABC＝90°，∠BAC的平分线交BC于D，以D为圆心，DB长为半径作⊙D，求证：AC与⊙D相切．15.（10分）如图，AB为⊙O的直径，PD切⊙O于点C，交AB的延长线于点D，且∠D＝2∠CAD.(1)求∠D的度数；(2)若CD＝2，求BD的长．第15题第16题16．（12分）已知△ABC内接于⊙O，过点A作直线EF.(1)如图①，若AB为⊙O的直径，要使EF成为⊙O的切线，还需要添加的一个条件是(至少说出两种)：__________________________或者_______________________；(2)如图②，如果AB是不过圆心O的弦，且∠CAE＝∠B，那么EF是⊙O的切线吗试证明你的判断．17.（12分）如图，已知直线PA交⊙O于A，B两点，AE是⊙O的直径，点C为⊙O上一点，且AC平分∠PAE，过C作CD⊥PA，垂足为D.(1)求证：CD为⊙O的切线；(2)若DC＋DA＝6，⊙O的直径为10，求AB的长．答案：DDADC 6. 相切 7. ∠ABC＝90°不排除等效答案 8. 6 9. 45 10. 4 11. 60 12. 解：连接OD，∵BD为∠ABC平分线，∴∠OBD＝∠CBD，∵OB＝OD，∴∠OBD＝∠ODB，∴∠CBD＝∠ODB，∴OD∥BC，∵∠C＝90°，∴∠ODA＝90°，则AC为⊙O的切线13. 解：连接OD，∵CD是⊙O的切线，∴∠ODC＝90°，∴∠ODB＋∠BDC＝90°，∵AB是⊙O的直径，∴∠ADB＝90°，即∠ODB＋∠ADO＝90°，∴∠BDC＝∠ADO，∵OA＝OD，∴∠ADO＝∠A，∴∠BDC＝∠A14. 解：过D作DH⊥AC于H，由角平分线的性质可证DB＝DH，∴AC与⊙D相切15. 解：(1)∵∠COD＝2∠CAD，∠D＝2∠CAD，∴∠D＝∠COD.∵PD与⊙O相切于点C，∴OC⊥PD，即∠OCD＝90°，∴∠D＝45°(2)由(1)可知△OCD是等腰直角三角形，∴OC＝CD＝2，由勾股定理，得OD＝22＋22＝22，∴BD ＝OD－OB＝22－216. (1) ∠BAE＝90°∠EAC＝∠ABC(2) (2)EF是⊙O的切线．证明：作直径AM，连接CM，则∠ACM＝90°，∠M＝∠B，∴∠M＋∠CAM＝∠B＋∠CAM＝90°，∵∠CAE＝∠B，∴∠CAM＋∠CAE＝90°，∴AE⊥AM，∵AM为直径，∴EF是⊙O的切线17. 解：(1)连接OC，证∠DAC＝∠CAO＝∠ACO，∴PA∥CO，又∵CD⊥PA，∴CO⊥CD，∴CD为⊙O的切线(2)过O作OF⊥AB，垂足为F，∴四边形OCDF为矩形．∵DC＋DA＝6，设AD＝x，则OF＝CD＝6－x，AF＝5－x，在Rt△AOF中，有AF2＋OF2＝OA2，即(5－x)2＋(6－x)2＝25，解得x1＝2，x2＝9，由AD＜DF知0＜x＜5，故x＝2，从而AD＝2，AF＝5－2＝3，由垂径定理得AB＝2AF＝6。

中考数学考点《圆的切线的证明》专项练习题-附答案

中考数学考点《圆的切线的证明》专项练习题-附答案学校:班级:姓名:考号:1．如图，在Rt△ABC中，∠ABC=90°，∠BAC的平分线交BC于D，以D为圆心，DB长为半径作⊙D．求证：AC与⊙D相切.2．已知AB是⊙O的直径，CD是⊙O的弦，AB与CD交于E，CE=DE，过B作BF∥CD，交AC的延长线于点F，求证：BF是⊙O的切线．3．如图，点C在以AB为直径的⊙O上，弧AC＝1弧BC，经过点C与⊙O相切的直线CE交BA的延长线2于点D，连接BC，过点D作DF∥BC．求证：DF是⊙O的切线．4．如图，Rt△ABC中∠C=90°，点O是AB边上一点，以OA为半径作⊙O，与边AC交于点D，连接BD，若∠DBC=∠A，求证：BD是⊙O的切线．5．如图，在△ABC中，AB=BC，以AB为直径的⊙O交AC于点D，DE⊥BC，垂足为E．（1）求证：DE是⊙O的切线；（2）若DG⊥AB，垂足为点F，交⊙O于点G，∠A=35°，⊙O半径为5，求劣弧DG的长．（结果保留π）6．如图，AB是⊙O的直径，弦CD⊥AB于点H，点G在弧BD上，连接AG，交CD于点K，过点G的直线交CD延长线于点E，交AB延长线于点F，且EG=EK．（1）求证：EF是⊙O的切线；（2）若⊙O的半径为13，CH=12，AC∥EF，求OH和FG的长．7．如图，已知△ABC内接于⊙O，点D在OC的延长线上，∠B＝∠CAD＝30°.（1）AD是⊙O的切线吗？为什么？（2）若OD⊥AB，BC=5，求⊙O的半径.8．如图在Rt△ABC中，∠C＝90°，点D是AC的中点，且∠A＋∠CDB＝90°，过点A、D作⊙O，使圆心O 在AB上，⊙O与AB交于点E.(1)求证：直线BD与⊙O相切；(2)若AD：AE＝4：5，BC＝6，求⊙O的直径．9．如图，四边形ABCD内接于⊙O，BD是⊙O的直径，AE⊥CD，垂足为E，DA平分∠BDE．（1）求证：AE是⊙O的切线；（2）若∠DBC=30°，DE=1cm，求BD的长．10．如图，AB为⊙O的直径，AD平分∠BAC交⊙O于点D，DE⊥AC交AC的延长线于点E，FB是⊙O的切线交AD的延长线于点F.（1）求证：DE是⊙O的切线（2）若DE=3，⊙O的半径为5，求BF的长11．如图，△ABC内接于⊙O，点D在半径OB的延长线上，∠BCD=∠A=30°．（1）试判断直线CD与⊙O的位置关系，并说明理由；（2）若⊙O的半径长为1，求由弧BC、线段CD和BD所围成的阴影部分面积．（结果保留π和根号）12．如图，AB是⊙O的弦，OP⊥OA交AB于点P，过点B的直线交OP的延长线于点C，且CP=CB．（1）求证：BC是⊙O的切线；（2）若⊙O的半径为√5，OP=1，求BC的长．13．如图，点B、C、D都在半径为4的⊙O上，过点C作AC∥BD交OB的延长线于点A，连接CD，已知∠CDB=∠OBD=30°．（1）求证：AC是⊙O的切线；（2）求弦BD的长．14．如图，⊙O的直径为AB，点C在圆周上（异于A，B），AD⊥CD．（1）若BC=3，AB=5，求AC的值；（2）若AC是∠DAB的平分线，求证：直线CD是⊙O的切线．15．如图，△ABC的边AB为⊙O的直径，BC与⊙O交于点D，D为BC的中点，过点D作DE⊥AC于E．（1）求证：DE是⊙O的切线；（2）若AB=13，BC=10，求CE的长．16．如图，AB是⊙O的直径，点C，D在⊙O上，且AD平分∠CAB，过点D作AC的垂线，与AC的延长线相交于点E，与AB的延长线相交于点F．（1）求证：EF与⊙O相切；（2）若AB=6，AD=4 √2，求EF的长．17．如图，AB是⊙O直径，D为⊙O上一点，AT平分∠BAD交⊙O于点T，过T作AD的垂线交AD的延长线于点C．（1）求证：CT为⊙O的切线；（2）连接BT，若⊙O半径为1，AT= √3，求BT的长．18．如图，点A是⊙O直径BD延长线上的一点，C在⊙O上，AC=BC，AD=CD（1）求证：AC是⊙O的切线；（2）若⊙O的半径为2，求△ABC的面积．19．如图，已知⊙O是以AB为直径的△ABC的外接圆，OD∥BC，交⊙O于点D，交AC于点E，连接BD，BD 交AC于点F，延长AC到点P，连接PB．（1）若PF=PB，求证：PB是⊙O的切线；（2）如果AB=10，BC=6，求CE的长度．答案解析1．证明：过点D作DF⊥AC于F，如图所示：∵AB为⊙D的切线∴∠B=90°∴AB⊥BC∵AD平分∠BAC，DF⊥AC∴BD=DF∴AC与⊙D相切．2．【解答】证明：∵AB是⊙O的直径，CD是⊙O的弦，AB与CD交于E，CE=DE ∴AB⊥CD∵BF∥CD∴BF⊥AB∴BF是⊙O的切线．3．解：连接OC，过点O作OG⊥DF，垂足为G弧BC∵弧AC =12∴∠AOC=13∠AOB=60°∴∠ABC=12∠AOC=30°∵CE切⊙O于点C∴OC⊥CE，即∠DCO=90°∴在ΔDOC中∵DF//CB∴∠ABC=∠GDO=30°∴∠CDO=∠GDO，即DO平分∠CDG∵OC⊥CE,OG⊥DF ∴OC=OG（角平分线性质）∴OG是⊙O的半径∴DF是⊙O的切线（垂径定理）.4．证明：如图，连接OD．∵OA=OD∴∠A=∠ADO．∵∠C=90°∴∠CBD+∠CDB=90°又∵∠CBD=∠A∴∠ADO+∠CDB=90°∴∠ODB=180°﹣（∠ADO+∠CDB）=90°．∴直线BD与⊙O相切．5．（1）证明：如图1，连接BD、OD∵AB是⊙O直径∴BD ⊥AC∵AB=BC∴AD=DC∵AO=OB∴OD 是△ABC 的中位线∴DO ∥BC∵DE ⊥BC∴DE ⊥OD∵OD 为半径∴DE 是⊙O 切线；（2）解：如图2所示，连接OG ，OD∵DG ⊥AB ，OB 过圆心O∴弧BG=弧BD∵∠A=35°∴∠BOD=2∠A=70°∴∠BOG=∠BOD=70°∴∠GOD=140°∴劣弧DG 的长是140π×5180=359π．6．解：（1）证明：连接OG∵弦CD ⊥AB 于点H∴∠HKA+∠KAH=90°∵EG=EK∴∠EGK=∠EKG∵∠HKA=∠GKE∴∠HAK+∠KGE=90°∵AO=GO∴∠OAG=∠OGA∴∠OGA+∠KGE=90°∴GO⊥EF∴EF是⊙O的切线；（2）解：连接CO，在Rt△OHC中∵CO=13，CH=12∴HO=5∴AH=8∵AC∥EF∴∠CAH=∠F∴tan∠CAH=tan∠F=128=32在Rt△OGF中，∵GO=13∴FG=13tan∠E =263．7．解：（1）AD是⊙O的切线，理由如下：连接OA∵∠B=30°∴∠O=60°∵OA=OC∴∠OAC=60°∵∠CAD=30°∴∠OAD=90°又∴点A在⊙O 上∴AD是⊙O的切线；（2）∵∠OAC=∠O=60°∴∠OCA=60°∴△AOC是等边三角形∵OD⊥AB∴OD垂直平分AB∴AC=BC=5∴OA=5即⊙O的半径为5．8．(1)证明：连接OD，在△AOD中，OA＝OD∴∠A＝∠ODA又∵∠A＋∠CDB＝90°∴∠ODA＋∠CDB＝90°∴∠BDO＝180°－90°＝90°，即OD⊥BD ∴BD与⊙O相切．(2)解：连接DE，∵AE是⊙O的直径∴∠ADE＝90°∴DE∥BC.又∵D是AC的中点，∴AE＝BE.∴△AED∽△ABC.∴AC∶AB＝AD∶AE.∵AC∶AB＝4∶5令AC＝4x，AB＝5x，则BC＝3x.∵BC＝6，∴AB＝10∴AE＝5，∴⊙O的直径为5.9．（1）连接OA∵DA平分∠BDE∴∠BDA=∠EDA．∵OA=OD∴∠ODA=∠OAD∴∠OAD=∠EDA∴OA∥CE．∵AE⊥DE∴∠AED=90°．∴∠OAE=∠DEA=90°．∴AE⊥OA．∴AE是⊙O的切线；（2）∵BD是直径∴∠BCD=∠BAD=90°．∵∠DBC=30°，∠BDC=60°∴∠BDE=120°．∵DA平分∠BDE∴∠BDA=∠EDA=60°．∴∠ABD=∠EAD=30°．∵在Rt△AED中，∠AED=90°，∠EAD=30°∴AD=2DE．∵在Rt△ABD中，∠BAD=90°，∠ABD=30°∴BD=2AD=4DE．∵DE的长是1cm∴BD的长是4cm．10．（1）证明：如图(1)连接OD.∵AD平分∠BAC，∴∠1=∠2.又∵OA="OD" ，∴∠1=∠3.∴∠2="∠3."∴OD∥AE.∵DE⊥AE∴DE⊥OD.而D在⊙O上∴DE是⊙O的切线.(2)过D作DG⊥AB 于G.∵DE⊥AE ，∠1=∠2.∴DG="DE=3" ，半径OD=5.在Rt△ODG中，根据勾股定理： OG＝＝＝4 ∴AG=AO+OG=5+4=9.∵FB是⊙O的切线， AB是直径∴FB⊥AB.而DG⊥AB∴DG∥FB. △ADG∽△AFB∴∴.∴BF=.11．（1）解：直线CD与⊙O相切∵在⊙O中，∠COB=2∠CAB=2×30°=60°又∵OB=OC∴△OBC是正三角形∴∠OCB=60°又∵∠BCD=30°∴∠OCD=60°+30°=90°∴OC ⊥CD又∵OC 是半径∴直线CD 与⊙O 相切．（2）解：由（1）得△OCD 是Rt △，∠COB=60° ∵OC=1∴CD= √3∴S △COD = 12 OC •CD= √32又∵S 扇形OCB = π6∴S 阴影=S △COD ﹣S 扇形OCB = √32−π6=3√3−π6 ．12．（1）证明：连接OB ，如图∵OP ⊥OA∴∠AOP=90°∴∠A+∠APO=90°∵CP=CB∴∠CBP=∠CPB而∠CPB=∠APO∴∠APO=∠CBP∵OA=OB∴∠A=∠OBA∴∠OBC=∠CBP+∠OBA=∠APO+∠A=90° ∴OB ⊥BC∴BC 是⊙O 的切线；（2）解：设BC=x ，则PC=x在Rt △OBC 中，OB= √5 ，OC=CP+OP=x+1 ∵OB 2+BC 2=OC 2∴（ √5 ）2+x 2=（x+1）2解得x=2即BC 的长为2．13．（1）证明：连接OC，OC交BD于E∵∠CDB=30°∴∠COB=2∠CDB=60°∵∠CDB=∠OBD∴CD∥AB又∵AC∥BD∴四边形ABDC为平行四边形∴∠A=∠D=30°∴∠OCA=180°﹣∠A﹣∠COB=90°，即OC⊥AC 又∵OC是⊙O的半径∴AC是⊙O的切线（2）解：由（1）知，OC⊥AC．∵AC∥BD∴OC⊥BD∴BE=DE∵在直角△BEO中，∠OBD=30°，OB=4∴BE=OBcos30°=2 √3∴BD=2BE=4 √314．（1）解：∵AB是⊙O直径，C在⊙O上∴∠ACB=90°又∵BC=3，AB=5∴由勾股定理得AC=4（2）解：证明：连接OC∵AC是∠DAB的角平分线∴∠DAC=∠BAC又∵AD⊥DC∴∠ADC=∠ACB=90°∴△ADC∽△ACB∴∠DCA=∠CBA又∵OA=OC∴∠OAC=∠OCA∵∠OAC+∠OBC=90°∴∠OCA+∠ACD=∠OCD=90°∴DC是⊙O的切线．15．（1）证明：连接OD∵D为BC的中点，O为AB的中点∴OD∥AC；∵DE⊥AC∴DE⊥OD∴DE是圆O的切线（2）解：连接 AD∵AB是直径∴AD⊥BC；∵D为BC的中点∴AD 是BC 的垂直平分线∴AC=AB=13；∵∠C=∠C ，∠DEC=∠ADC=90°∴△CDE ∽△CAD∴EC CD = DC AD ，而AC=AB=13，CD= 12 BC=5 ∴CE= 2513 ．16．（1）证明：连接OD∵AD 平分∠CAB∴∠OAD=∠EAD ．∵OD=OA∴∠ODA=∠OAD ．∴∠ODA=∠EAD ．∴OD ∥AE ．∵∠ODF=∠AEF=90°且D 在⊙O 上 ∴EF 与⊙O 相切．（2）证明：连接BD ，作DG ⊥AB 于G∵AB 是⊙O 的直径∴∠ADB=90°∵AB=6，AD=4 √2∴BD= √AB 2−AD 2 =2∵OD=OB=3设OG=x ，则BG=3﹣x∵OD 2﹣OG 2=BD 2﹣BG 2，即32﹣x 2=22﹣（3﹣x ）2 解得x= 73∴OG= 73∴DG= √OD2−OG2 = 43√2∵AD平分∠CAB，AE⊥DE，DG⊥AB∴DE=DG= 43√2∴AE= √AD2−DE2 = 163∵OD∥AE∴△ODF∽△AEF∴DFEF =ODAE，即EF−EDEF=ODAE∴EF−43√2EF=3163∴EF= 6421√2．17．（1）证明：连接OT，如图1所示：∵OA=OT∴∠OAT=∠OTA又∵AT平分∠BAD∴∠DAT=∠OAT∴∠DAT=∠OTA∴OT∥AC又∵CT⊥AC∴CT⊥OT∴CT为⊙O的切线（2）解：连接BT，如图2所示：∵AB是⊙O直径∴AB=2，∠ATB=90°∴BT= √AB2−AT2 = √22+(√3)2 =1．18．（1）解：连接OC ．∵AC=BC ，AD=CD ，OB=OC∴∠A=∠B=∠1=∠2．∵∠ACO=∠DCO+∠2∴∠ACO=∠DCO+∠1=∠BCD又∵BD 是直径∴∠BCD=90°∴∠ACO=90°又C 在⊙O 上∴AC 是⊙O 的切线（2）解：由题意可得△DCO 是等腰三角形 ∵∠CDO=∠A+∠2，∠DOC=∠B+∠1∴∠CDO=∠DOC ，即△DCO 是等边三角形． ∴∠A=∠B=∠1=∠2=30°，CD=AD=2 在直角△BCD 中BC= √BD 2−CD 2 = √42−22 =2 √3 ．又AC=BC∴AC=2 √3 ．作CE ⊥AB 于点E ．在直角△BEC 中，∠B=30°∴CE= 12 BC= √3∴S △ABC = 12 AB •CE= 12 ×6× √3 =3 √3 ．19．（1）证明：∵PF=PB∴∠PFB=∠PBF又∵∠DFE=∠PFB∴∠DFE=∠PBF∵AB 是圆的直径∴∠ACB=90°，即AC ⊥BC ．又∵OD ∥BC∴OD ⊥AC ．∴在直角△DEF 中，∠D+∠DFE=90° 又∵OD=OB∴∠D=∠DBO∴∠DBO+∠PBE=90°，即PB ⊥AB ∴PB 是⊙O 的切线；（2）解：∵OD ∥BC ，OA=OB ∴OE= 12 BC= 12 ×6=3．∵OD ⊥AB∴EC=AE ．∵在直角△OAE 中，OA= 12 AB= 12 ×10=5∴AE= √OA 2−OE 2 = √52−32 =4． ∴EC=4。

圆的切线综合练习题与答案(2018)

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

圆的切线
一、1、直线和圆的位置关系有三种：相交、相切、相离.
　用数量关系表示是：如果⊙O 的半径为r ，圆心O 到直线l 的距离为d ，那么：（1）直线l 和⊙O 相交d<r （2）直线l 和⊙O 相切
d=r ；（3）直线l 和⊙O 相离
d>r.
2、切线的判定定理经过半径的外端并且垂直于这条半径的直线是圆的切线.
3、切线的性质定理及其推论切线的性质定理　圆的切线垂直于经过切点的半径.　推论1　经过圆心且垂直于切线的直线必经过切点.　推论2　经过切点且垂直于切线的直线必经过圆心.二、1、直线和圆的位置关系2、切线的判定定理
例1、已知如图所示，AB 为⊙O 的直径，C 、D 是直径AB 同侧圆周上两点，且，过
D 作DE⊥AC 于点
E ，求证：DE 是⊙O 的切线.
例2、（1）如图所示，△ABC 内接于⊙O，如果过点A 的直线AE 和AC 所成的角∠EAC=∠B，那么EA 是⊙O 的切线.
3、切线的性质及其推论
例3如图，已知AB 是⊙O 的直径，AC 是弦，CD 切⊙O 于点C ，交AB 的延长线于点
D ，
∠ACD=120°，BD=10．（1）求证：CA=CD ；
（2）求⊙O 的半径．
例4、已知：如图所示，AB 为半圆O 的直径，直线MN 切半圆于点C ，AD⊥MN 于点D ，BE⊥MN 于点E ，BE 交半圆于点F ，AD=3cm ，BE=7cm ，
（1）求⊙O 的半径；（2）求线段DE 的长.
例5、如图所示，AB 为⊙O 的直径，BC 、CD 为⊙O 的切线，B 、D 为切点，
求证：AD∥OC，.
例6、已知如图所示，在梯形ABCD 中，AD∥BC，∠D=90°，AD ＋BC=AB ，以AB 为直径作⊙O，求证：⊙O 和CD 相切.
例7如图，AB 是半圆O 的直径，AD 为弦，∠DBC=∠A ．（1）求证：
BC 是半圆
O 的切线；
（2）若OC
∥AD ，OC 交BD 于E ，BD=6，CE=4，求AD 的长．
例8、如图，AB 为⊙O 的直径，弦CD ⊥AB 于点M ，过点B 作BE ∥CD ，交AC 的延长
线于点E ，连结BC ．
（1）求证：BE 为⊙O 的切线；
（2）如果CD=6，tan ∠BCD=
，求⊙O 的直径．1
2
例9如图，AB 为⊙O 的直径，BC 切⊙O 于B ，AC 交⊙O 于P ，CE=BE ，E 在BC 上. 求证：PE 是⊙O 的切线．
例10、已知:如图,在Rt△ABC 中,∠ACB=90°,以AC 为直径的⊙O 交
AB 于点D,过点D 作⊙O 的切线DE 交BC 于点E.求证:BE=CE.
例11如图，P 为⊙O 外一点，
PO 交⊙O 于C ，过⊙O 上一点A 作弦AB ⊥PO 于E ，
若∠EAC=∠CAP ，求证：PA 是⊙O 的切线．
例12在△ABC 中，∠C＝90°，∠B＝30°，O 为AB 上一点，AO ＝m ，⊙O 的半径，r 12
问m 在什么范围内取值时，AC 与圆：（1）相离；（2）相切；（3）相交。

例13经过⊙O 上的点T 的切线和弦AB 的延长线相交于点C ，求证：∠ATC=∠TBC
例14已知：AD 是∠BAC 的平分线，BDC 例15、如图1，AB 是⊙O 的直径，BC 是⊙O 的切线，B 为切点，OC 平行于弦AD ，连接CD 。

求证：DC 是⊙O 的切线。