06_分析力学基础_第二类拉格朗日方程
合集下载
第二类拉格朗日方程的初积分PPT课件

j 1
L q j
q j
L ) 0 q j
②
式②代入到式①
d
dt
k
(q j
j 1
L q j
)
dL dt
0
d
dt
[
k j 1
(q j
L q j
)
L]
0
得:
k j 1
(q j
L q j
)
L
常量
③
将L=T-V=T2+T1+T0-V代入式③
第4页/共29页
其中:
k
j 1
(q j
T2 q j
)
2T2
V mg(R r) cosj
因为 L T V L(j,j,q)
q为循环坐标,有
L
q
(J
2 3
mr2 )q
2 5
m(R
r)Rj
C1
又L中不显含时间t,且T=T2,存在能量积分,由
T2 V C2
即:
1 2
(JO
2 5
mR2
)q2
1 2
7 5
m(R
r)j
2
保守系统
2 m(R r)Rjq mg(R r) cosj 0
哈密尔顿力学是哈密尔顿于1833年 建立的经典力学的重新表述。它由拉格 朗日力学演变而来,那是经典力学的另 一表述,由拉格朗日于1788年建立。但 它可以使用辛空间不依赖于拉格朗日力 学表述。
第13页/共29页
哈密顿原理
哈密顿原理是一种积分形式的变分原理,是哈密顿于1834年建立的。
哈密顿原理为:在相同的 始终位置、相同,约束条件下, 完整、主动力有势的系统在所 有的可能运动中,真实运动使 哈密顿作用量取驻值。
L q j
q j
L ) 0 q j
②
式②代入到式①
d
dt
k
(q j
j 1
L q j
)
dL dt
0
d
dt
[
k j 1
(q j
L q j
)
L]
0
得:
k j 1
(q j
L q j
)
L
常量
③
将L=T-V=T2+T1+T0-V代入式③
第4页/共29页
其中:
k
j 1
(q j
T2 q j
)
2T2
V mg(R r) cosj
因为 L T V L(j,j,q)
q为循环坐标,有
L
q
(J
2 3
mr2 )q
2 5
m(R
r)Rj
C1
又L中不显含时间t,且T=T2,存在能量积分,由
T2 V C2
即:
1 2
(JO
2 5
mR2
)q2
1 2
7 5
m(R
r)j
2
保守系统
2 m(R r)Rjq mg(R r) cosj 0
哈密尔顿力学是哈密尔顿于1833年 建立的经典力学的重新表述。它由拉格 朗日力学演变而来,那是经典力学的另 一表述,由拉格朗日于1788年建立。但 它可以使用辛空间不依赖于拉格朗日力 学表述。
第13页/共29页
哈密顿原理
哈密顿原理是一种积分形式的变分原理,是哈密顿于1834年建立的。
哈密顿原理为:在相同的 始终位置、相同,约束条件下, 完整、主动力有势的系统在所 有的可能运动中,真实运动使 哈密顿作用量取驻值。
分析力学基础-拉格朗日方程

支持。
其他应用领域
要点一
机器人学
在机器人学中,拉格朗日方程被用于描述机器人的运动规 律。通过建立机器人运动的拉格朗日方程,可以求解出机 器人的关节角度和速度,为机器人的运动控制提供理论依 据。
要点二
生物力学
在生物力学中,拉格朗日方程也被应用于描述生物体的运 动规律。例如,在分析动物的运动行为或人体姿势控制时 ,可以使用拉格朗日方程来描述生物体的运动状态和变化 规律。
解析解法的优缺点分析
优点
解析解法可以得到系统的精确解,适用 于简单模型和特定条件下的复杂模型。
VS
缺点
对于复杂模型,解析解法可能非常困难甚 至无法求解,需要借助数值方法或其他近 似方法。
04
拉格朗日方程的数值解法
数值解法的概念和步骤
概念
数值解法是一种通过数学计算来求解数学问 题的方法,它通过将问题离散化,将连续的 问题转化为离散的问题,然后使用计算机进 行计算求解。
步骤
1.建立数学模型:根据实际问题建立数学模 型,将实际问题转化为数学问题。2.离散化 :将连续的问题离散化,将连续的时间和空 间划分为若干个小的单元,每个单元称为一 个网格点或节点。3.求解离散化后的方程: 使用数值方法求解离散化后的方程,得到每 个网格点的数值解。4.后处理:对计算结果 进行后处理,提取所需的信息,并进行分析
分析力学基础-拉格 朗日方程
目录
• 引言 • 拉格朗日方程的推导 • 拉格朗日方程的解析解法 • 拉格朗日方程的数值解法 • 拉格朗日方程的应用领域
01
引言
拉格朗日方程的背景和重要性
背景
拉格朗日方程是分析力学中的基 本方程,它描述了系统的运动规 律。
重要性
拉格朗日方程在理论物理、工程 技术和科学研究等领域有着广泛 的应用,是理解和研究复杂系统 运动行为的关键工具。
其他应用领域
要点一
机器人学
在机器人学中,拉格朗日方程被用于描述机器人的运动规 律。通过建立机器人运动的拉格朗日方程,可以求解出机 器人的关节角度和速度,为机器人的运动控制提供理论依 据。
要点二
生物力学
在生物力学中,拉格朗日方程也被应用于描述生物体的运 动规律。例如,在分析动物的运动行为或人体姿势控制时 ,可以使用拉格朗日方程来描述生物体的运动状态和变化 规律。
解析解法的优缺点分析
优点
解析解法可以得到系统的精确解,适用 于简单模型和特定条件下的复杂模型。
VS
缺点
对于复杂模型,解析解法可能非常困难甚 至无法求解,需要借助数值方法或其他近 似方法。
04
拉格朗日方程的数值解法
数值解法的概念和步骤
概念
数值解法是一种通过数学计算来求解数学问 题的方法,它通过将问题离散化,将连续的 问题转化为离散的问题,然后使用计算机进 行计算求解。
步骤
1.建立数学模型:根据实际问题建立数学模 型,将实际问题转化为数学问题。2.离散化 :将连续的问题离散化,将连续的时间和空 间划分为若干个小的单元,每个单元称为一 个网格点或节点。3.求解离散化后的方程: 使用数值方法求解离散化后的方程,得到每 个网格点的数值解。4.后处理:对计算结果 进行后处理,提取所需的信息,并进行分析
分析力学基础-拉格 朗日方程
目录
• 引言 • 拉格朗日方程的推导 • 拉格朗日方程的解析解法 • 拉格朗日方程的数值解法 • 拉格朗日方程的应用领域
01
引言
拉格朗日方程的背景和重要性
背景
拉格朗日方程是分析力学中的基 本方程,它描述了系统的运动规 律。
重要性
拉格朗日方程在理论物理、工程 技术和科学研究等领域有着广泛 的应用,是理解和研究复杂系统 运动行为的关键工具。
2_拉格朗日方程
O
(x1,y1)
A
P1
(x2,y2) B(x3,y3)
P2
F
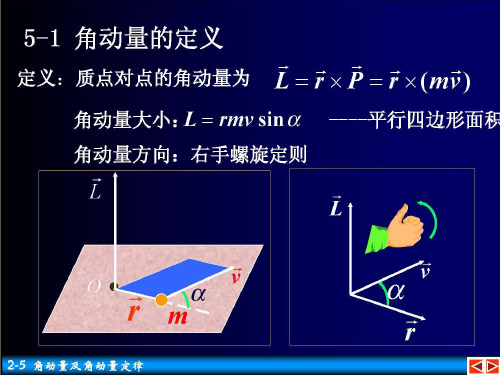
(1)
由已知条件可得
x1
1 2
l1 sin 1 l 2 sin (2)
x 2 l1 sin
2 y 3 l1 cos l 2 cos
把(2) 式代入(1) 式得
P1 (
1 2
l1 sin ) P2 ( l1 sin
x i x i ( q1 , q 2 , , q s , t ) y i y i ( q1 , q 2 , , q s , t ) z i z i ( q1 , q 2 , , q s , t )
或 式中
( i 1, 2 , , n , s 3 n )
ri ri ( q 1 , q 2 , , q s , t )
以上分量式若改用s 个独立广义坐标表示,然后令s 个独立的 虚位移前的乘数等于零,则可得出所求的平衡条件。 若求约束力,则要利用拉格朗日未定乘数。 广义坐标下 ri 的虚位移为
ri
n
s
ri
由此得广义坐标下的平衡方程是
W
Q
1
q
q 0
s
F
i 1 s
n
i n
i 1
虚功原理:受理想约束的力学体系平衡的充要条件是此力学 体系的诸主动力在任意虚位移中所做的元功之和为零。这就 是虚功原理,也叫虚位移原理。是1717年伯努利首先发现。 对于理想约束体系,利用虚功原理可以方便的求出主动力满 足的平衡条件,但无法求出约束反力。 由于约束,3n 个坐标不独立,即作用在任一质点上的合外 力在虚位移方向上的投影,一般不会全令之为零。否则就可 能变成n 个自由质点的平衡方程。
第2章 拉格朗日方程

z
O
l
2
x2 y2 z 2 l 2 0
x
M m
x vt
2
y z l 0
2 2
y
x2 y2 z 2 l 2 0
拉格朗日科学研究所涉及的领域极其广泛。他在数学上最突出的贡献是使数学分析与几何与力学脱离开来,使数学的独立性更为清楚, 从此数学不再仅仅是其他学科的工具。 拉格朗日总结了18世纪的数学成果,同时又为19世纪的数学研究开辟了道路,堪称法国最杰出的数学大师。同时,他的关于月球 运动(三体问题)、行星运动、轨道计算、两个不动中心问题、流体力学等方面的成果,在使天文学力学化、力学分析化上,也起到了 历史性的作用,促进了力学和天体力学的进一步发展,成为这些领域的开创性或奠基性研究。 在柏林工作的前十年,拉格朗日把大量时间花在代数方程和超越方程的解法上,作出了有价值的贡献,推动了代数学的发展。他 提交给柏林科学院两篇著名的论文:《关于解数值方程》和《关于方程的代数解法的研究》 。把前人解三、四次代数方程的各种解法, 总结为一套标准方法,即把方程化为低一次的方程(称辅助方程或预解式)以求解。 他试图寻找五次方程的预解函数,希望这个函数是低于五次的方程的解,但未获得成功。然而,他的思想已蕴含着置换群概念,对后 来阿贝尔和伽罗华起到启发性作用,最终解决了高于四次的一般方程为何不能用代数方法求解的问题。因而也可以说拉格朗日是群论 的先驱。 在数论方面,拉格朗日也显示出非凡的才能。他对费马提出的许多问题作出了解答。如,一个正整数是不多于4个平方数的和的问 题等等,他还证明了圆周率的无理性。这些研究成果丰富了数论的内容。 在《解析函数论》以及他早在1772年的一篇论文中,在为微积分奠定理论基础方面作了独特的尝试,他企图把微分运算归结为代数运 算,从而抛弃自牛顿以来一直令人困惑的无穷小量,并想由此出发建立全部分析学。但是由于他没有考虑到无穷级数的收敛性问题, 他自以为摆脱了极限概念,其实只是回避了极限概念,并没有能达到他想使微积分代数化、严密化的目的。不过,他用幂级数表示函 数的处理方法对分析学的发展产生了影响,成为实变函数论的起点。 拉格朗日也是分析力学的创立者。拉格朗日在其名著《分析力学》中,在总结历史上各种力学基本原理的基础上,发展达朗贝尔、 欧拉等人研究成果,引入了势和等势面的概念,进一步把数学分析应用于质点和刚体力学,提出了运用于静力学和动力学的普遍方程, 引进广义坐标的概念,建立了拉格朗日方程,把力学体系的运动方程从以力为基本概念的牛顿形式,改变为以能量为基本概念的分析 力学形式,奠定了分析力学的基础,为把力学理论推广应用到物理学其他领域开辟了道路。他还给出刚体在重力作用下,绕旋转对称 轴上的定点转动(拉格朗日陀螺)的欧拉动力学方程的解,对三体问题的求解方法有重要贡献,解决了限制性三体运动的定型问题。拉 格朗日对流体运动的理论也有重要贡献,提出了描述流体运动的拉格朗日方法。 拉格朗日的研究工作中,约有一半同天体力学有关。他用自己在分析力学中的原理和公式,建立起各类天体的运动方程。在天体 运动方程的解法中,拉格朗日发现了三体问题运动方程的五个特解,即拉格朗日平动解。此外,他还研究了彗星和小行星的摄动问题, 提出了彗星起源假说等。 近百余年来,数学领域的许多新成就都可以直接或间接地溯源于拉格朗日的工作。所以他在数学史上被认为是对分析数学的发展 产生全面影响的数学家之一。被誉为“欧洲最大的数学家”。
拉格朗日方程

拉格朗日函数为
L 1 m( x 2 y 2 ) 1 m(l r )22 (1)
2
2
将
L
m(l r )
和 L mr(l r )2 代入拉氏方程得质点的运动微分方
程为
积分得
(l r ) r2 0
d [(l r )] 0
V 0 , 1,2,, s
q
(2.19)
(2.18)和(2.19)式即是体系的拉格朗日平衡方程。
[例3] 求体系的平衡位置
教材:P.46 [例1]
解:体系自由度:2,广义坐标: 1 , 2
x1
l1 2
si n 1
,
y1
l1 2
cos1 ,
x2
l1
si n 1
l2 2
si n 2
,
y2
l1
cos1
l2 2
cos 2
x2
l1
si n 1
l2 2
si n 2
,
y2
l1
cos1
l2 2
第2章 拉格朗日方程
内容: • 基本概念 • 理想完整系的拉格朗日方程 • 对称性和守恒定律
重点: 完整保守系的拉格朗日方程 难点: 拉格朗日方程的推导
牛顿力学理论几乎都以力 F 为基础,因此它的应用只局限于纯力 学问题的范畴,运算也比较烦琐。18世纪伯努利、达朗贝尔、欧拉 等人发展了经典力学的分析形式。1788年拉格朗日发表了名著《分 析力学》,建立了经典力学的拉格朗日形式,用体系的动能和势能 取代了牛顿形式的加速度和力,将力学的研究和应用范围开拓到整 个物理学。
拉格朗日第二类方程
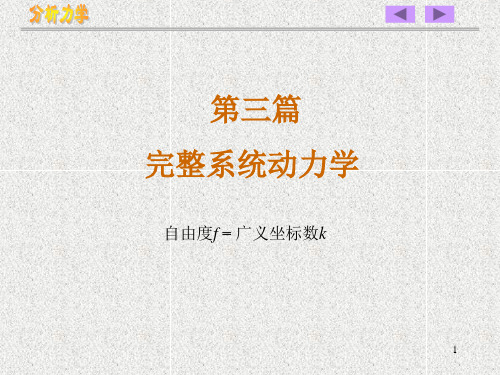
代入初始条件,t =0 时, 0 0 , 0 0 得 C1 C2 0
故:
3M
gt 2
(2P9Q)( Rr)2
20
[例]图示系统,物块C质量为m1 ,均质轮A、B质量均为m2, 半径均为R,A作纯滚动,求系统的运动微分方程。 解:系统具有一自由度,保守
系统。以物块C的平衡位置为
原点,取x为广义坐标:
AF q j
(4)不含约束力。
二、保守系统的拉格朗日方程
如果作用于质点系的力是有势力,则:
Qj
V q j
而拉氏方程为:
15
d dt
T q j
T q j
V q j
由于V=V(q1,q2,...,qk),不含广义速度,所以
V q j
0,
d dt
V q j
0
上式为:
d dt
T q j
T q j
d dt
V q j
V q j
或:d dt
(T V q j
)
(T V q j
)
0
令L=T-V——拉格朗日函数
d dt
(
L q j
)
L q j
0 ( j1,2,,k )
保守系统的拉格朗日第二类方程。
16
应用拉氏方程解题的步骤:
1. 判定质点系的自由度 f,选取适宜的广义坐标。必须注意: 不能遗漏独立的坐标,也不能有多余的(不独立)坐标。
Q
A
M
T
1 2P 6
9Q (R g
r ) 2
;
d T
dt
1 2P 9Q (R r)2
6
g
;
T 0
19
理论力学:第二类拉格朗日方程的总结

θ&&(θ ) = ? x&(θ ) = ?
L中无 x, t
∂T ∂x&
=
5 2
mx& +
1 2
mLθ& cosθ
=
C
&x&(θ ) = ?
5 mx&2 + 1 mL2θ&2 + 1Lmg(1− cosθ ) = E
4
6
2
2014-3-25
8
理论力学
习题课
∂T ∂x&
2014-3-25
根据对z轴的动量矩守恒和初始条件,可得关系式: ϕ&
=
1
sin2 θ
15
理论力学
习题课
问题:B 点的运动轨迹?
θ0
=
π
4
=
0.7854,ϕ0
=
0,θ&0
=
0,ϕ&0
=
2.0rad/s
m = 1kg L = 1m k = 10N/m
∂T
∂ϕ&
=
1 mL2 3
sin2 θϕ&
=
C1
2014-3-25
mL&x&cosθ
+
1 mL2θ&&+
3
1 2
mgL sinθ
=
0
2014-3-25
10
理论力学
习题课
x
A
aA
θ&&= −15 2 g,
17L
&x&
=3g 17
求地面的约束力
F
aCt A
第1章 分析力学基础 1-6拉格朗日第二类方程的积分汇总

解:研究楔形体与圆柱体组成 的系统。系统受理想、完整、 定常约束,具有两个自由度。 取广义坐标为x, s ;各坐标原点 均在初始位置。
M1-8
我们已知道系统动能和势能为
V
1 3
Ph
Q(h
s sin
r cos )
T
1 2
P
g
Q
x&2
3 4
Q g
s&2
Q g
x&s&cos
1 2
P
g
Q
x&2
3 4
M1-10
[例] 一均质圆柱体可绕其垂直中心轴自由
转动,圆柱表面刻有倾角为 的螺旋槽。
小球M自静止沿槽下滑,已知小球质量为 m1圆柱体质量为m2,半径为R, 试求:小球下降高度为h时,小球相对圆
柱体的速度,圆柱体的角速度。 解:系统受理想、完整、定常约束,
具有两个自由度。取广义坐标为, s ;
各坐标原点均在初Leabharlann 位置。当ssin =h ,得
2m12 sin2 m2 s&2 2gh 0
(2m1 m2 )
s&
(2m1 m2 )2gh
2m1 sin2 m2
& 2m1 cos
R
2gh
(2m1 m2 )(2m1 sin2 m2)
q&k
L qk
q&k
0
N k 1
d dt
L q&k
q&k
L q&k
q&&k
L qk
q&k
d dt
N
k 1
L q&k
q&k
M1-8
我们已知道系统动能和势能为
V
1 3
Ph
Q(h
s sin
r cos )
T
1 2
P
g
Q
x&2
3 4
Q g
s&2
Q g
x&s&cos
1 2
P
g
Q
x&2
3 4
M1-10
[例] 一均质圆柱体可绕其垂直中心轴自由
转动,圆柱表面刻有倾角为 的螺旋槽。
小球M自静止沿槽下滑,已知小球质量为 m1圆柱体质量为m2,半径为R, 试求:小球下降高度为h时,小球相对圆
柱体的速度,圆柱体的角速度。 解:系统受理想、完整、定常约束,
具有两个自由度。取广义坐标为, s ;
各坐标原点均在初Leabharlann 位置。当ssin =h ,得
2m12 sin2 m2 s&2 2gh 0
(2m1 m2 )
s&
(2m1 m2 )2gh
2m1 sin2 m2
& 2m1 cos
R
2gh
(2m1 m2 )(2m1 sin2 m2)
q&k
L qk
q&k
0
N k 1
d dt
L q&k
q&k
L q&k
q&&k
L qk
q&k
d dt
N
k 1
L q&k
q&k
分析力学基础-第二类拉格朗日方程

广义坐标vA 。(Rr)
A
vA r
R r
r
M1-16
T
1 2
JO&2
1 2
Q g
v
2 A
1 2
J AA2
1 2
1 3
P g
(R
r)2&2
1 2
Q g
(R
r)2&2
1 2
1 2
Q g
r2
(R
r)2 r2
&2
1 2P 9Q (R r)2&2
12 g
W ( ) M
Q
W ( )
M
T&
1 6
2P
得
(m1 m2 )&x&1 m2l&&cos m2l&2 sin 0
M1-14
同理:
T& m2l2& m2lx&1 cos
T
m2lx&in
d dt
T x&1
m2l(l&&
cos &x&1
x&1&sin )
由拉格朗日方程d
dt
(
T q&k
)
T qk
Qk
得
m2l(l&& cos&x&1 x&1&sin) m2gl sin
)
M1-13
系统势能:(选质点 M2 在最低位置为零势能位
置)
V m2gl(1 cos)
求导运算可得:
T x&1
(m1
m2
)
x&1
06分析力学基础第二类拉格朗日方程

将Qk代入拉格朗日方程式,得
d dt
(
T qk
)
T qk
V qk
0
势能V不包含广义速度,引入拉格朗日函数
L T V L(qk , qk , t)
为拉格朗日函数(动势),是表征体系约束运动状态和相互作用 等性质的特征函数。
保守体系的拉格朗日方程为:
d dt
(
L qk
)
系统的运动微分方程。
(m1 m2 )x m2l kx 0 x l g 0
上式为系统在平衡位置(x =0, =0)附近微幅运动的微分方程。
M1-23
M1-24
变换 1.
ri qk
ri qk
由 ri ri (q1, q2, qN , t) (i 1, 2, n)
d dt
n i1
mi ri
ri qk
qk
n i1
1 2
mi
ri
ri
d dt
qk
n1 2
i1
mivi2
qk
n i1
1 2
mivi2
d dt
T qk
T qk
M1-3
由
Qk
n
miri
i1
ri qk
k 1, 2, N
可得
d dt
T qk
T qk
Qk
k 1, 2, N
为理想完整系的拉格朗日方程,方程数等于质点系的自由度数。 其中:
Qk
分析动力学1-第二类拉格朗日方程 - 2019

例4
本题也可以将力偶M视为 有势力,则系统势能函数 为
V mgR cos 0 Md
L=T–V
d dt
L
L
0
d dt
L
L
0
解
M
y
O
x
R
R
m
第8章 第 二 类 拉 格 朗 日 方 程 及 其 应 用
例6
Q
设倾角为的质量为M的三角块可以沿着水平
面自由运动,质量为 m的小物块沿着三角块 运动,并以刚度系数为 k的弹簧与三角块相 连,如图所示。求该系统的运动微分方程。
用
xr :
3 2
mxr
mx cos
mg
sin
0
第8章 第 二 类 拉 格 朗 日 方 程 及 其 应 用
例4
半径为R的圆环在力偶 矩为M的力偶作用下转 动,质量为m的小环可 在圆环上自由滑动。 已知圆环对y轴的转动 惯量为J,忽略摩擦力。 求为使圆环匀角速转 动所需施加的力偶矩M。
M
y
O
x
R
m
第8章 第 二 类 拉 格 朗 日 方 程 及 其 应 用
)(r1
r2
)2
2
A=M Q M
T
1 6
(2m
9m2
)(
r1
r2
)
2
T
0
d dt
T
T
Q
1 6
(2m
9m2 )(r1
r2 )2
M
(2m
6M 9m2 )(r1
r2 )2
第8章 第 二 类 拉 格 朗 日 方 程 及 其 应 用
例3
M
用拉格朗日方程列写系统的运动微分方程(假 定小球纯滚动)。
06-分析力学基础-第二类拉格朗日方程资料

保守体系的拉格朗日方程为:
d dt
(qLk)qLk
0
想一想:上式的成立、适用条件是什么?
M1-6
3. 对拉格朗日方程的评价
(1) 拉氏方程的特点(优点): 是一个二阶微分方程组,方程个数与体系的自由度相同。形式简 洁、结构紧凑。而且无论选取什么参数作广义坐标,方程形式不变。 方程中不出现约束反力,因而在建立体系的方程时,只需分析已 知的主动力,不必考虑未知的约束反力。体系越复杂,约束条件越 多,自由度越少,方程个数也越少,问题也就越简单。
M1-10
系统动能:
T1 2m 1x21 2JBB 21 2JI
2 A
1 2 m 1 x 2 1 2 1 2 m 2 R 2B 2 1 2 2 3 m 2 R 2A 2
m1
2m2 2
x2
系统的拉格朗日函数(动势)
LTV m 1 2 2 m 2x 2 1 2 k (0 x )2 m 1 g x
5. 求出上述一组微分方程的积分。
M1-9
[例] 物块C的质量为m1,A,B两轮 皆为均质圆轮,半径R,质量为m2, 求系统的运动微分方程。
解:图示机构只有一个自由度,所受
约束皆为完整、理想、定常的,以物 块平衡位置为原点,取x 为广义坐标。
系统势能: (以弹簧原长为弹性势能零点)
V1 2k(0x)2m1gx
2. 计算质点系的动能T,表示为广义速度和广义坐标的函数。
3. 计算广义力 Q j(j 1 ,2 , ,k),计算公式为:
Q j i n1(Xi q xijYi q yijZi q zij) 或
Qj
W ( j) qj
若主动力为有势力,也可将势能 V 表示为广义坐标的函数。
理论力学(Ⅱ)—拉格朗日方程

B
B
解:以系统为研究对象,系统所 受的主动力有圆柱的重力。设两轮的 角加速度为 1 、 2 ,轮B质心的加速 度为 a 。假想加上惯性力,如图。
1 其中 M mR 21 2
g A
C
2
yC
1 2
mg
g MB
a
2
g FBg ma M B mR 2 2
此系统具有两个自由度,取轮A、轮B的转 角1 、 2 为广义坐标。给系统一组虚位移,如图。
q (q1 , q2 , , q N )
ri ri (q1 , q2 , , qN , t )
由动力学普遍方程,得
F δ r m a δ r 0
i 1 i i i 1 i i i
(m1 m2 ) g m1lcos
2
例题3 质量为m 的三棱柱ABC 1
通过滚轮搁置在光滑的水平面上。 质量为m2、半径为R的均质圆轮沿 三棱柱的斜面AB无滑动地滚下。
求:1、三棱柱后退的加速度a1; 2、圆轮质心C2相对于三棱 柱加速度ar。 解:1、分析运动 三棱柱作平动,加速度为 a1。 y D ae a1 C1
引
言
本章是将达朗伯原理和虚位移原理结合起来 推导出动力学普遍方程和拉格朗日方程。动力学 普遍方程中系统的运动是直角坐标来描述的,而 拉格朗日方程是用广义坐标来描述系统的运动, 两者都是用来解决非自由质点系的动力学问题, 它是用分析的方法解决动力学问题的出发点,因 此它是分析力学的基础。对于解决复杂的非自由 质点系的动力学问题,应用拉格朗日方程往往要 比用动力学普遍方程简便得多。
2 aC g sin 3
0
mgsin x - FIR x M IC
B
解:以系统为研究对象,系统所 受的主动力有圆柱的重力。设两轮的 角加速度为 1 、 2 ,轮B质心的加速 度为 a 。假想加上惯性力,如图。
1 其中 M mR 21 2
g A
C
2
yC
1 2
mg
g MB
a
2
g FBg ma M B mR 2 2
此系统具有两个自由度,取轮A、轮B的转 角1 、 2 为广义坐标。给系统一组虚位移,如图。
q (q1 , q2 , , q N )
ri ri (q1 , q2 , , qN , t )
由动力学普遍方程,得
F δ r m a δ r 0
i 1 i i i 1 i i i
(m1 m2 ) g m1lcos
2
例题3 质量为m 的三棱柱ABC 1
通过滚轮搁置在光滑的水平面上。 质量为m2、半径为R的均质圆轮沿 三棱柱的斜面AB无滑动地滚下。
求:1、三棱柱后退的加速度a1; 2、圆轮质心C2相对于三棱 柱加速度ar。 解:1、分析运动 三棱柱作平动,加速度为 a1。 y D ae a1 C1
引
言
本章是将达朗伯原理和虚位移原理结合起来 推导出动力学普遍方程和拉格朗日方程。动力学 普遍方程中系统的运动是直角坐标来描述的,而 拉格朗日方程是用广义坐标来描述系统的运动, 两者都是用来解决非自由质点系的动力学问题, 它是用分析的方法解决动力学问题的出发点,因 此它是分析力学的基础。对于解决复杂的非自由 质点系的动力学问题,应用拉格朗日方程往往要 比用动力学普遍方程简便得多。
2 aC g sin 3
0
mgsin x - FIR x M IC
第六章_Lagranger第二类方程

使用广义坐标表示动能的优点: 1)可以将位形坐标的数目减到最少,最适用于所讨论的问题; 2)建立的各种方程式有很大的一般性,适用于各种广义坐标,而无 需要事先规定用哪一组特定的坐标。
应用力学研究所 李永强
第7页
§6.1 动量的广义坐标表达式 例6-1 质量为m的无约束的质点的动能用直角坐标表示为 T m x2 y 2 z2 2 。
应用力学研究所 李永强
第15页
§6.2 Lagranger第二类方程
例6-3 半径为R、质量为m的圆环挂在一半径为r的固定圆 柱上。设圆环与圆柱间有足够大的摩擦力阻止相对滑动, 试写出圆环的运动微分方程,并求微幅摆动的周期。
A
R
O
解:圆环具有一个自由度,是完整系统,取θ为广义坐标
T
1 2
mvO2
司方程和惠特克方程 §6.5 耗散系统
应用力学研究所 李永强
第4页
§6.1 动量的广义坐标表达式
n个质点假的设系统ri 对,受于dq个i和理t是想二完整阶ri 约可束r微i ,q的1取,,qk2个则,广义, q坐k ,r标it q1j、k1 q2qr、ij q… j 、 qkrti( k=3n-d ),则
T
T2
1 2
kk
a j q j q
j1 1
即动能是广义速度的二次齐次函数,此时动能是正定的,是速度的正二次型。
2)c为非负的
因为
c
n i 1
mi
ri t
ri
t
而 mi 0
ri ri 0 t t
应用力学研究所 李永强
第6页
§6.1 动量的广义坐标表达式
3)由于T2为正定的,T0为非负的,T为正定的,故T必为非负的。 由定义可知c ≥0, T ≥ 0,bj 可能是负的,但决不可能使T成为负的。
应用力学研究所 李永强
第7页
§6.1 动量的广义坐标表达式 例6-1 质量为m的无约束的质点的动能用直角坐标表示为 T m x2 y 2 z2 2 。
应用力学研究所 李永强
第15页
§6.2 Lagranger第二类方程
例6-3 半径为R、质量为m的圆环挂在一半径为r的固定圆 柱上。设圆环与圆柱间有足够大的摩擦力阻止相对滑动, 试写出圆环的运动微分方程,并求微幅摆动的周期。
A
R
O
解:圆环具有一个自由度,是完整系统,取θ为广义坐标
T
1 2
mvO2
司方程和惠特克方程 §6.5 耗散系统
应用力学研究所 李永强
第4页
§6.1 动量的广义坐标表达式
n个质点假的设系统ri 对,受于dq个i和理t是想二完整阶ri 约可束r微i ,q的1取,,qk2个则,广义, q坐k ,r标it q1j、k1 q2qr、ij q… j 、 qkrti( k=3n-d ),则
T
T2
1 2
kk
a j q j q
j1 1
即动能是广义速度的二次齐次函数,此时动能是正定的,是速度的正二次型。
2)c为非负的
因为
c
n i 1
mi
ri t
ri
t
而 mi 0
ri ri 0 t t
应用力学研究所 李永强
第6页
§6.1 动量的广义坐标表达式
3)由于T2为正定的,T0为非负的,T为正定的,故T必为非负的。 由定义可知c ≥0, T ≥ 0,bj 可能是负的,但决不可能使T成为负的。
§14.2、第二类拉格朗日方程

v1 r55 v4 v2 r44 r55 v3 r44 r55 1 1 1 2 2 2 2 T m1r5 5 m2 (r4 4 r55 ) m3 (r4 4 r55 ) 2 2 2 w 5 (m1 m2 m3 ) gr5 3) 确定广义力; Q5 5 w 4 m2 g r4 4 m3 g r4 4 Q4 (m2 m3 ) gr4 4 4
x r cos (r L) sin y r sin (r L) cos
1 2 2 T m(r L) 2
12
w m g y Q m g(r L) sin
4) 列拉格朗日方程;
3) 确定广义力;
(m1 m2 )a2 m1ar cos 0 2(m1 m2 ) sin 5) 联立求解; ar g 2 m1 2m1 sin 3m2
2
3) 确定广义力;
10
m1 sin( 2 ) a2 g 2 m1 2m1 sin 3m2
评论,在应用第二类拉格朗日方程求解动力学问题 时,解题思路/解题步骤都相同: 第一步、确定系统的自由度数与相应的系统参数 即广义坐标; 第二步、进行速度分析,确定系统动能; 第三步、确定各系统参数(广义坐标) 的广义力; 第四步、依次列各广义坐标对应的拉格朗日方程; 第五步、联立求解;
1) 确定系统参数:轮1轮心O点相对位移和三角 块向左的位移(xr /xe);
9
wxr m1 g sin xr wx 2 m1 g sin Qx 2 0 Qxr xr xr x2 T 3 4) 列拉格朗日方程; m1vr m1v2 cos vr 2 T 3 0 m1ar m1a2 cos m1 g sin xr 2 T T 0 (m1 m2 )v2 m1vr cos x2 v
分析力学基础 第二类拉格朗日方程

2. 计算质点系的动能T,表示为广义速度和广义坐标的函数。
3. 计算广义力 Q j(j 1 ,2 ,L,k),计算公式为:
Q j i n1(Xi q xijYi q yijZi q zij) 或
Qj
W ( j) qj
若主动力为有势力,也可将势能 V 表示为广义坐标的函数。
4. 建立拉氏方程并加以整理,得出k个二阶常微分方程。
i n1(F im i& r& i) q rik0 k1,2,LN
M1-2
变换
1.
ri qk
r&i q&k
2.
d dt
ri qk
r&i qk
3. i n 1m i& r & i q r ik i n 1m id d t r & i q r ik i n 1m ir & id d t q r ik
T
n
1 2
mivi2
——体系相对惯性系的动能
i1
pk
T q&k
——广义动量,可为线动量、角动量或其他物理量
M1-4
2. 保守体系的拉格朗日方程
如果主动力都是保守力,即 FV,则为广义力
Q k i n 1 F ri q r r ik i n 1 V r r i q r r ik q V k Q k i n 1F ri q r r ik i n 1 F ix q x k i F iy q y k i F iz q z k i
两边再对 q&k 求偏导即可得
ri qk
r&i q&k
3—5 第二类拉格朗日方程
1. 基本形式的拉格朗日方程
质点 i 的虚位移
拉格朗日第二类方程
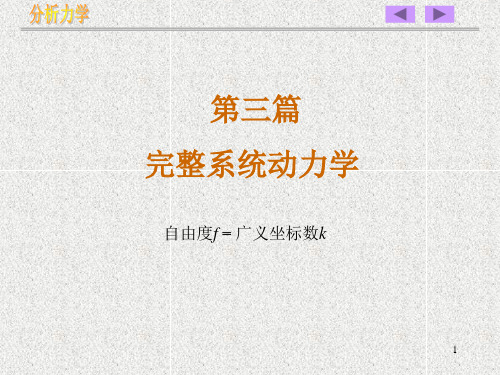
n 1 1 2 2 ( m v ) ( m v i i i i ) k d i 1 2 i 1 2 [ ]q j j q q j j 1 dt n
d T T [ ]q j j q j j 1 dt q
k
( m)
13
将(d)(m)代入(c)得:
9
j — 广义速度 式中:q
ri ri , 由(a)知 只是广义坐标和时间的函数,与广义速 q j t
j 求偏导: 度无关,故将上式对q
ri vi j q j q
②将(g)对任一广义坐标ql 求偏导:
( h)
k k vi 2 ri 2 ri ri ri j j ( )q ( ) q ql j 1 ql q j ql t tql j 1 ql q j
故:
3M 2 gt ( 2 P 9Q )( R r ) 2
20
[例]图示系统,物块C质量为m1 ,均质轮A、B质量均为m2, 半径均为R,A作纯滚动,求系统的运动微分方程。 解:系统具有一自由度,保守 系统。以物块C的平衡位置为 原点,取x为广义坐标:
1 1 1 1 2 2 2 2 T m1 x J A A m2 v A J B B 2 2 2 2 2 1 2 11 2 1 11 x x 2 2 2 x m1 x m2 R ( ) m2 ( ) m2 R ( ) 2 22 2R 2 2 22 R 1 2 (8m1 7m2 ) x 16
v A ( R r ) vA Rr A r r
18
1 1Q 2 1 2 2 T J O v A J A A 2 2g 2 2 11 P 1 Q 1 1 Q ( R r ) 2 2 2 (R r)2 (R r)2 r2 23 g 2g 2 2g r2 1 2 P 9Q 2 (R r)2 12 g
d T T [ ]q j j q j j 1 dt q
k
( m)
13
将(d)(m)代入(c)得:
9
j — 广义速度 式中:q
ri ri , 由(a)知 只是广义坐标和时间的函数,与广义速 q j t
j 求偏导: 度无关,故将上式对q
ri vi j q j q
②将(g)对任一广义坐标ql 求偏导:
( h)
k k vi 2 ri 2 ri ri ri j j ( )q ( ) q ql j 1 ql q j ql t tql j 1 ql q j
故:
3M 2 gt ( 2 P 9Q )( R r ) 2
20
[例]图示系统,物块C质量为m1 ,均质轮A、B质量均为m2, 半径均为R,A作纯滚动,求系统的运动微分方程。 解:系统具有一自由度,保守 系统。以物块C的平衡位置为 原点,取x为广义坐标:
1 1 1 1 2 2 2 2 T m1 x J A A m2 v A J B B 2 2 2 2 2 1 2 11 2 1 11 x x 2 2 2 x m1 x m2 R ( ) m2 ( ) m2 R ( ) 2 22 2R 2 2 22 R 1 2 (8m1 7m2 ) x 16
v A ( R r ) vA Rr A r r
18
1 1Q 2 1 2 2 T J O v A J A A 2 2g 2 2 11 P 1 Q 1 1 Q ( R r ) 2 2 2 (R r)2 (R r)2 r2 23 g 2g 2 2g r2 1 2 P 9Q 2 (R r)2 12 g
理论力学(Ⅱ)—拉格朗日方程

(m1 m2 ) g m1lcos
2
例题3 质量为m 的三棱柱ABC 1
通过滚轮搁置在光滑的水平面上。 质量为m2、半径为R的均质圆轮沿 三棱柱的斜面AB无滑动地滚下。
求:1、三棱柱后退的加速度a1; 2、圆轮质心C2相对于三棱 柱加速度ar。 解:1、分析运动 三棱柱作平动,加速度为 a1。 y D ae a1 C1
yC R1 R 2 (1)
由动力学普遍方程得
g A g B g B
1
O
g MA
A
M 1 M 2 (mg F )yC 0
1 mg g FB
C
B
2
g 2 将惯性力及(1)式代入上式,得 MB a 1 1 2 mR 1 1 mR 2 2 2 (mg ma ) R( 1 2 ) 0 2 2 1 1 2 (mgR maR mR 1 ) 1 (mgR maR mR 2 2 ) 2 0
2 aC g sin 3
0
mgsin x - FIR x M IC
x
R
例 题 2
离心调速器
FIA m1g l
C
O1
l l
A
x1
FIB l m1g
已知: m1-球A、B 的质量; m2-重锤C 的质量; l-杆件的长度; - O1 y1轴的旋转角速度。 求: - 的关系。
i 1
n i 1
即
( Fi mi ai ) ri 0
将上式写成解析式,则有
( X
i 1
n
i
i ) xi (Yi mi i ) yi ( Z i mi i ) zi 0 mi x y z
2
例题3 质量为m 的三棱柱ABC 1
通过滚轮搁置在光滑的水平面上。 质量为m2、半径为R的均质圆轮沿 三棱柱的斜面AB无滑动地滚下。
求:1、三棱柱后退的加速度a1; 2、圆轮质心C2相对于三棱 柱加速度ar。 解:1、分析运动 三棱柱作平动,加速度为 a1。 y D ae a1 C1
yC R1 R 2 (1)
由动力学普遍方程得
g A g B g B
1
O
g MA
A
M 1 M 2 (mg F )yC 0
1 mg g FB
C
B
2
g 2 将惯性力及(1)式代入上式,得 MB a 1 1 2 mR 1 1 mR 2 2 2 (mg ma ) R( 1 2 ) 0 2 2 1 1 2 (mgR maR mR 1 ) 1 (mgR maR mR 2 2 ) 2 0
2 aC g sin 3
0
mgsin x - FIR x M IC
x
R
例 题 2
离心调速器
FIA m1g l
C
O1
l l
A
x1
FIB l m1g
已知: m1-球A、B 的质量; m2-重锤C 的质量; l-杆件的长度; - O1 y1轴的旋转角速度。 求: - 的关系。
i 1
n i 1
即
( Fi mi ai ) ri 0
将上式写成解析式,则有
( X
i 1
n
i
i ) xi (Yi mi i ) yi ( Z i mi i ) zi 0 mi x y z
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
求导:
x2 x1 l cos y1 0 y2 l sin
系统动能:
T
1 2
m1x12
1 2
m2
(
x22
y22 )
1 2
(m1
m2
) x12
m2l 2
(l
2
2 x1
cos
)
M1-13
系统势能:(选质点 M2 在最低位置为零势能位置)
V m2gl(1 cos)
求导运算可得:
T x1
(m1
m2 ) x1
5. 求出上述一组微分方程的积分。
M1-9
[例] 物块C的质量为m1,A,B两轮 皆为均质圆轮,半径R,质量为m2, 求系统的运动微分方程。
解:图示机构只有一个自由度,所受
约束皆为完整、理想、定常的,以物 块平衡位置为原点,取x 为广义坐标。
系统势能: (以弹簧原长为弹性势能零点)
V
1 2
k
(
0
x)2
规律,描述了力学系统的动力学规律,为解决体系的动力学问题 提供了统一的程序化的方法,不仅在力学范畴有重要的理论意义 和实用价值,而且为研究近代物理学提供了必要的物理思想和数 学技巧。
M1-8
应用拉氏方程解题的步骤:
1. 判定质点系的自由度k,选取适宜的广义坐标。必须注意: 不能遗漏独立的坐标,也不能有多余的(不独立)坐标。
2. 计算质点系的动能T,表示为广义速度和广义坐标的函数。
3. 计算广义力 Q j ( j 1,2, ,k ),计算公式为:
Qj
n
(X i
i 1
xi q j
Yi
yi q j
Zi
zi q j
)
或
Qj
W ( j) qj
若主动力为有势力,也可将势能 V 表示为广义坐标的函数。
4. 建立拉氏方程并加以整理,得出k个二阶常微分方程。
等性质的特征函数。
保守体系的拉格朗日方程为:
d dt
(
L qk
)
L qk
0
想一想:上式的成立、适用条件是什么?
M1-6
3. 对拉格朗日方程的评价
(1) 拉氏方程的特点(优点): 是一个二阶微分方程组,方程个数与体系的自由度相同。形式简 洁、结构紧凑。而且无论选取什么参数作广义坐标,方程形式不变。 方程中不出现约束反力,因而在建立体系的方程时,只需分析已 知的主动力,不必考虑未知的约束反力。体系越复杂,约束条件越 多,自由度越少,方程个数也越少,问题也就越简单。
3—5 第二类拉格朗日方程
1. 基本形式的拉格朗日方程
质点 i 的虚位移
ri
N k 1
ri qk
qk
i 1, 2,3, n
将上式代入动力学普遍方程(3-15)式:
n (Fi
i1
mi
ri
)
N k 1
ri qk
qk
Nn
[ (Fi
k 1 i1
mi
ri
)
ri qk
]qk
0
因qk是独立的,所以
m2l
cos
T x1
0
Qx1
V x1
0
d dt
T x1
(m1
m2 ) x1
m2l cos
m2l 2 sin
由拉格朗日方程
d dt
(
T qk
)
T qk
Qk
mi ri
d dt
ri qk
n i1
mi
d dt
ri
ri qk
n i1
mi ri
ri qk
d dt
n i1
mi ri
ri qk
qk
n
1 2
mi ri
ri
i1
d dt
qk
n1 2
i1
mivi2
qk
n1 2
i1
mivi2
d dt
T qk
T qk
M1-3
由
Qk
n
mi ri
➢ 拉氏方程是从能量的角度来描述动力学规律的,能量是整个物理 学的基本物理量而且是标量,因此拉氏方程为把力学规律推广到其 他物理学领域开辟了可能性,成为力学与其他物理学分支相联系的 桥梁。
M1-7
3. 对拉格朗日方程的评价
(2) 拉氏方程的价值 拉氏方程在理论上、方法上、形式上和应用上用高度统一的
M1-11
注意到 k0 m1g
可得系统的运动微分方程 (m1 2m2 )x kx 0
M1-12
已知:M1的质量为m1, M2的质量为m2, 杆长为l。
试建立此系统的运动微分方程。
解:图示机构为两个自由度,取x1,
为广义坐标,则有。
x2 x1 l sin y1 0 y2 l cos
m1gx
M1-10
系统动能:
T
1 2
m1x
2
1 2
J BB2
1 2
J IA2
1 2
m1 x 2
1 2
1 2
m2 R 2B2
1 2
3 2
m2
R
2
2 A
m1
2m2 2
x2
系统的拉格朗日函数(动势)
L
T
V
m1
2m2 2
x2
1 2
k (0
x)2
m1gx
代入拉格朗日方程
d dt
(
L qk
)
L qk
0
(m1 2m2 )x k(0 x) m1g 0
zi qk
n i 1
V xi
xi qk
V yi
yi qk
V zi
zi qk
Hale Waihona Puke V qkM1-52. 保守体系的拉格朗日方程
将Qk代入拉格朗日方程式,得
d dt
(
T qk
)
T qk
V qk
0
势能V不包含广义速度,引入拉格朗日函数
L T V L(qk , qk , t)
为拉格朗日函数(动势),是表征体系约束运动状态和相互作用
pk
T qk
——广义动量,可为线动量、角动量或其他物理量
M1-4
2. 保守体系的拉格朗日方程
如果主动力都是保守力,即 F V,则为广义力
Qk
n i 1
Fi
ri qk
n V i1 ri
ri qk
V qk
Qk
n i 1
Fi
ri qk
n i 1
Fix
xi qk
Fiy
yi qk
Fiz
n
i1
(Fi
mi ri
)
ri qk
0
注意广义力可得
k 1, 2, N
M1-1
注意到广义力可得
Qk
n
mi ri
i1
ri qk
k 1, 2, N
上式中的第二项与广义力相对应,称为广义惯性力。
上式应用起来很不方便。我们要作变换
拉格朗日改造动力学普遍方程的第一步:就是把主动力的虚功改 造为广义力虚功。
拉格朗日改造动力学普遍方程的第二步:就是改造惯性虚功项,
使之与系统的动能的变化联系起来。
n
i1
(Fi
mi ri
)
ri qk
0
k 1, 2, N
M1-2
变换
1.
ri qk
ri qk
2.
d dt
ri qk
ri qk
3.
n i1
mi ri
ri qk
n
mi
i1
d dt
ri
ri qk
n i1
i1
ri qk
k 1, 2, N
可得
d dt
T qk
T qk
Qk
k 1, 2, N
为理想完整系的拉格朗日方程,方程数等于质点系的自由度数。 其中:
Qk
n i1
Fi
ri qk
——主动力的广义力,可以是力、力矩或其他力学量 (不包含约束反力)
T
n
1 2
mivi2
——体系相对惯性系的动能
i1
x2 x1 l cos y1 0 y2 l sin
系统动能:
T
1 2
m1x12
1 2
m2
(
x22
y22 )
1 2
(m1
m2
) x12
m2l 2
(l
2
2 x1
cos
)
M1-13
系统势能:(选质点 M2 在最低位置为零势能位置)
V m2gl(1 cos)
求导运算可得:
T x1
(m1
m2 ) x1
5. 求出上述一组微分方程的积分。
M1-9
[例] 物块C的质量为m1,A,B两轮 皆为均质圆轮,半径R,质量为m2, 求系统的运动微分方程。
解:图示机构只有一个自由度,所受
约束皆为完整、理想、定常的,以物 块平衡位置为原点,取x 为广义坐标。
系统势能: (以弹簧原长为弹性势能零点)
V
1 2
k
(
0
x)2
规律,描述了力学系统的动力学规律,为解决体系的动力学问题 提供了统一的程序化的方法,不仅在力学范畴有重要的理论意义 和实用价值,而且为研究近代物理学提供了必要的物理思想和数 学技巧。
M1-8
应用拉氏方程解题的步骤:
1. 判定质点系的自由度k,选取适宜的广义坐标。必须注意: 不能遗漏独立的坐标,也不能有多余的(不独立)坐标。
2. 计算质点系的动能T,表示为广义速度和广义坐标的函数。
3. 计算广义力 Q j ( j 1,2, ,k ),计算公式为:
Qj
n
(X i
i 1
xi q j
Yi
yi q j
Zi
zi q j
)
或
Qj
W ( j) qj
若主动力为有势力,也可将势能 V 表示为广义坐标的函数。
4. 建立拉氏方程并加以整理,得出k个二阶常微分方程。
等性质的特征函数。
保守体系的拉格朗日方程为:
d dt
(
L qk
)
L qk
0
想一想:上式的成立、适用条件是什么?
M1-6
3. 对拉格朗日方程的评价
(1) 拉氏方程的特点(优点): 是一个二阶微分方程组,方程个数与体系的自由度相同。形式简 洁、结构紧凑。而且无论选取什么参数作广义坐标,方程形式不变。 方程中不出现约束反力,因而在建立体系的方程时,只需分析已 知的主动力,不必考虑未知的约束反力。体系越复杂,约束条件越 多,自由度越少,方程个数也越少,问题也就越简单。
3—5 第二类拉格朗日方程
1. 基本形式的拉格朗日方程
质点 i 的虚位移
ri
N k 1
ri qk
qk
i 1, 2,3, n
将上式代入动力学普遍方程(3-15)式:
n (Fi
i1
mi
ri
)
N k 1
ri qk
qk
Nn
[ (Fi
k 1 i1
mi
ri
)
ri qk
]qk
0
因qk是独立的,所以
m2l
cos
T x1
0
Qx1
V x1
0
d dt
T x1
(m1
m2 ) x1
m2l cos
m2l 2 sin
由拉格朗日方程
d dt
(
T qk
)
T qk
Qk
mi ri
d dt
ri qk
n i1
mi
d dt
ri
ri qk
n i1
mi ri
ri qk
d dt
n i1
mi ri
ri qk
qk
n
1 2
mi ri
ri
i1
d dt
qk
n1 2
i1
mivi2
qk
n1 2
i1
mivi2
d dt
T qk
T qk
M1-3
由
Qk
n
mi ri
➢ 拉氏方程是从能量的角度来描述动力学规律的,能量是整个物理 学的基本物理量而且是标量,因此拉氏方程为把力学规律推广到其 他物理学领域开辟了可能性,成为力学与其他物理学分支相联系的 桥梁。
M1-7
3. 对拉格朗日方程的评价
(2) 拉氏方程的价值 拉氏方程在理论上、方法上、形式上和应用上用高度统一的
M1-11
注意到 k0 m1g
可得系统的运动微分方程 (m1 2m2 )x kx 0
M1-12
已知:M1的质量为m1, M2的质量为m2, 杆长为l。
试建立此系统的运动微分方程。
解:图示机构为两个自由度,取x1,
为广义坐标,则有。
x2 x1 l sin y1 0 y2 l cos
m1gx
M1-10
系统动能:
T
1 2
m1x
2
1 2
J BB2
1 2
J IA2
1 2
m1 x 2
1 2
1 2
m2 R 2B2
1 2
3 2
m2
R
2
2 A
m1
2m2 2
x2
系统的拉格朗日函数(动势)
L
T
V
m1
2m2 2
x2
1 2
k (0
x)2
m1gx
代入拉格朗日方程
d dt
(
L qk
)
L qk
0
(m1 2m2 )x k(0 x) m1g 0
zi qk
n i 1
V xi
xi qk
V yi
yi qk
V zi
zi qk
Hale Waihona Puke V qkM1-52. 保守体系的拉格朗日方程
将Qk代入拉格朗日方程式,得
d dt
(
T qk
)
T qk
V qk
0
势能V不包含广义速度,引入拉格朗日函数
L T V L(qk , qk , t)
为拉格朗日函数(动势),是表征体系约束运动状态和相互作用
pk
T qk
——广义动量,可为线动量、角动量或其他物理量
M1-4
2. 保守体系的拉格朗日方程
如果主动力都是保守力,即 F V,则为广义力
Qk
n i 1
Fi
ri qk
n V i1 ri
ri qk
V qk
Qk
n i 1
Fi
ri qk
n i 1
Fix
xi qk
Fiy
yi qk
Fiz
n
i1
(Fi
mi ri
)
ri qk
0
注意广义力可得
k 1, 2, N
M1-1
注意到广义力可得
Qk
n
mi ri
i1
ri qk
k 1, 2, N
上式中的第二项与广义力相对应,称为广义惯性力。
上式应用起来很不方便。我们要作变换
拉格朗日改造动力学普遍方程的第一步:就是把主动力的虚功改 造为广义力虚功。
拉格朗日改造动力学普遍方程的第二步:就是改造惯性虚功项,
使之与系统的动能的变化联系起来。
n
i1
(Fi
mi ri
)
ri qk
0
k 1, 2, N
M1-2
变换
1.
ri qk
ri qk
2.
d dt
ri qk
ri qk
3.
n i1
mi ri
ri qk
n
mi
i1
d dt
ri
ri qk
n i1
i1
ri qk
k 1, 2, N
可得
d dt
T qk
T qk
Qk
k 1, 2, N
为理想完整系的拉格朗日方程,方程数等于质点系的自由度数。 其中:
Qk
n i1
Fi
ri qk
——主动力的广义力,可以是力、力矩或其他力学量 (不包含约束反力)
T
n
1 2
mivi2
——体系相对惯性系的动能
i1
