沪教版七年级数学(上)因式分解专题训练(一)
12.2因式分解的方法(运用完全平方公式因式分解)(课件)-七年级数学上册(沪教版2024)

2
即( x -3 y ) =0.∴ x -3 y =0.∴ x =3 y .∴ =3.
16. 将下列各式进行因式分解.
(1)简便计算: 8002-1 600×798+7982;
【解】原式=8002-2×800×798+7982=(800-798)2
=4.
(2) b2-4 a2-1+4 a ;
【解】原式= b2-(4 a2-4 a +1)= b2-(2 a -1)2
的大小关系为( B
)
A. M > N
B. M ≥ N
C. M ≤ N
D. 不能确定
4. [2023太原期末]已知一个圆的面积为9π a2+6π ab +π b2( a >0, b
>0),则该圆的半径是(
A )
A. 3 a + b
B. 9 a + b
C. 3 ab
D. 3π a +π b
5. 将多项式4 x2+1加上一项,使它能化成( a + b )2的形式,
= 8 + 2 .
2
2 −
2
− 10 2 − + 25.
解: 2 − 2 − 10 2 − + 25
= 2 − 2 − 2 • 2 − • 5 + 52
= 2 − − 5 2 .
分层练习-基础
1.下列可以用完全平方公式因式分解的是(
C )
A. 4 a2-4 a -1
课堂练习
课堂练习12.2 3
1. 口答 下列整式能用完全平方公式因式分解吗?为什么?
1
2 + 4 + 16;
解:不能.
3
9 2 − 24 + 16;
解:能.
初一数学专题训练(乘法公式+因式分解)(含答案)

初一数学专题训练(乘法公式+因式分解)(一) 巧用乘法公式进行计算类型一 巧用乘法公式的变形求式子的值1.阅读下面的材料,解答相应问题:数学知识随着人类文明的起源而产生,人类祖先为我们留下了许多珍贵的原始贵料, 古巴比伦泥板上记载了两种利用平方数表计算两数乘积的公式:221[()()]4ab a b a b =+--①; 221[()2ab a b a =+- ]②. (1)补全材料中公式②中的空缺部分.(2)验证材料中的公式①.(3)当5,7a b a b +=-=时,利用公式①计算ab 的值.类型二 巧用乘法公式进行简便计算2.化简:6X (7+1) X(72+1) X(74+1) X(78+1)X (716+1)+1.3.观察下列等式:22()()a b a b a b -+=-;2233()()a b a ab b a b -++=-;322344()()a b a a b ab b a b -+++=-;…利用你发现的规律解决下列问题:(1)计算: 432234()()a b a a b a b ab b -++++= .(2)计算: 123221()()n n n n n a b a a b a b ab b ------+++⋅⋅⋅++= .(3)利用(2)中得出的结论求20192018266661++⋅⋅⋅+++的值.类型三 巧用乘法公式解决整除问题4.当n 为自然数时,22(5)(3)n n +--能被16整除吗?请说明理由.5.当n 为自然数时,22(7)(5)n n +--能被24整除吗?请说明理由.(二) 常见因式分解的方法类型一 提公因式法1.分解因式(1) 2222464x y x z -= .(2) 2222898a b ab -+== .(3) 323612ma ma ma -+-= .(4) 2(1)(32)(23)x x x --+-= . 类型二 公式法2.分解因式:(1) 2244816x y x y -- = .(2) 2222(328)(28)a a a a +----= .类型三 分组分解法3.观察“探究性学习”小组的甲、乙两名同学进行的因式分解:甲: 244x xy x y -+-=2()(44)x xy x y -+-)=()4()x x y x y -+-=()(4)x y x -+.乙: 2222a b c bc --+=222(2)a b c bc -+- =22()a b c --=()()a b c a b c +--+请你在他们解法的启发下,分解因式: 22441x x y +-+.类型四 配方法4.阅读与思考:对于形如222x ax a ++这样的二次三项式,可以用公式法将它分解成2()x a +的形式.但 对于二次三项式2223x ax a +-,就不能直接运用公式了.此时,我们可以在二次三项式 2223x ax a +-中先加上一项2a ,使它与22x ax +的和成为一个完全平方式,再减去2a ,整个式子的值不变,于是有2223x ax a +-=2222(2)3x ax a a a ++--=22()(2)x a a +- =(2)(2)x a a x a a +++-=(3)()x a x a +-.像这样,先添一适当项,使式中一出现完全 平方式,再减去这个项,使整个式子的值不变的方法称为“配方法”.利用“配方法’,分 解因式:(1) 268a a -+= .(2) 21213x x +-= .类型五 十字相乘法5.阅读与思考:整式乘法与因式分解是方向相反的变形,由2()()()x p x q x p q x pq ++=+++,得 2()()()x p q x pq x p x q +++=++.利用这个式子可以将某些二次项系数是1的二次三 项式分解因式.例如将式子26x x --分解因式,这个式子的常数项-6=2X(-3),一次项 系数-1=2+(-3),这个过程可用“十字相乘”的形式形象地表示:先分解二次项系数,分 别写在十字交叉线的左上角和左下角;再分解常数项,分别写在干字交叉线的右上有和右 下角;然后交叉相乘,求代数和;使其等于一次项系数(如图),这种分解二次三项式的方法 叫“十字相乘法”.请同学们认真观察,分析理解后,解答下面的问题:(1)分解因式: 2718x x +-.(2)若28x px +-可分解为两个一次因式的积,则整数p 的所有可能值是 .参考答案(一) 巧用乘法公式进行计算1.(1)2b -(2)略(3)6ab =-2. 原式327=3. (1) 55a b -(2) n n a b - (3)原式2020615-= 4. 能点拨:22(5)(3)16(1)n n n +--=+5. 能点拨:22(7)(5)24(1)n n n +--=+(二) 常见的因式分解方法1.(1) 24()()x y z y z +-(2) 22(7)ab -(3) 23(424)ma a a --+(4) (32)(2)x x x --2.(1)22(2)(2)x y x y -+-(2)28(2)(2)a a a +-3. 22441(21)(21)x x y x y x y +-+=+++-4.(1)(2)(4)a a --(2)(13)(1)x x +-5. (1)2718(9)(2)x x x x +-=+-(2)7,7,2,2--。
上海初中七上因式分解260题(学生版)

【因式分解方法总览】版块一 基本方法因式分解的四种基本方法:一提二代三组四叉1. 【提】提公因式法:一次提净,注意符号确定公因式的方法:系数——取多项式各项系数的最大公约数;字母(或多项式因式)——取各项都含有的字母(或多项式因式)的最低次幂. 2. 【代】公式法因式分解中常用的公式:⑴平方差公式:22()()a b a b a b −=+− ⑵完全平方公式:2222()a ab b a b ±+=±⑶三元平方公式:2222222()a b c ab ac bc a b c +++++=++ ⑷三次方公式:①3322()()a b a b a ab b +=+−+;3322()()a b a b a ab b −=−++ ②3223333()a a b ab b a b +++=+;3223333()a a b ab b a b −+−=− ③()()3332223a b c abc a b c a b c ab bc ca ++−=++++−−− ⑸n 次方公式:①()()12321n n n n n n n a b a b a a b a b ab b −−−−−−=−+++++(n 为正整数) ②()()12321n n n n n n n a b a b a a b a b ab b −−−−−−=+−+−+−(n 为正偶数) ③()()12321n n n n n n n a b a b a a b a b ab b −−−−−+=+−+−−+(n 为正奇数)3. 【组】分组分解法分组分解法:通过分组,各组内可以用提公因式法或者公式法进行因式分解. 4. 【叉】十字相乘法与双十字相乘法⑴十字相乘法:适用范围:形如2ax bx c ++的二次三项式设()()21122ax bx c a x c a x c ++=++,则:12a a a =,12c c c =,1221a c a c b +=; 写成十字交叉的形式,即:12a x a x 12c c ; 口诀:降幂排列,首尾分解,交叉相乘,求和凑中.【注】若24b ac −不是一个平方数,那么二次三项式2ax bx c ++就不能在有理数范围内分解.⑵双十字相乘法适用范围:形如22Ax Bxy Cy Dx Ey F +++++的二次多项式 条件:①12A a a =,12C c c =,12F f f =②1221a c a c B +=,1221c f c f E +=,1221a f a f D += 即: 1a x 1c y 1f2a x 2c y 2f则()()22111222Ax Bxy Cy Dx Ey F a x c y f a x c f +++++=++++步骤:①用十字相乘法分解二次三项式()()221122Ax Bxy Cy a x c y a x c y ++=++,用十字交叉线表示(共两列);②用十字相乘法分解二次三项式()()21122Cy Ey F c y f c y f ++=++,继续用十字交叉线表示,即把常数项F 分解成两个因式填在第三列上;③用十字相乘法分解二次三项式2Ax Dx F ++,检验是否等于()()1122a x f a x f ++,若相等,则双十字相乘法分解因式成功.应用情况:⑴二元二次式(22Ax Bxy Cy Dx Ey F +++++);⑵三元二次齐次式(222Ax Bxy Cy Dxz Eyz Fz +++++); ⑶四次五项式(43243210a x a x a x a x a ++++).版块二 拓展方法因式分解的六种拓展方法:拆添项与配方、主元、换元、试根、待定系数、轮换对称式 1. 拆添项与配方法⑴拆、添项⇒分组⇒提、代; ⑵配方法⇒配完全平方式⇒平方差公式 2. 主元法步骤:选(二次三项式)→排(降幂排列)→叉(十字相乘法) 3. 换元法整体思想:化繁为简,本质不变4. 因式定理与试根法⑴余数定理:x c −除()f x ,余数为()f c ;⑵因式定理:若()0f c =,则x c −为()f x 的因式;若x c −为()f x 的因式,则()0f c =;⑶试根法:设()1110n n n n f x a x a x a x a −−=++++为整系数多项式若存在有理数c 满足()0f c =,则pc q=;其中:p 为0a 的因数,q 为n a 的因数;()f x 含有因式()qx p −;特别地,当1n a =时,c p =为整数.【注】常见技巧:若多项式各项系数和为0,则1一定为根. 5. 待定系数法步骤:设(待定系数)→(展)→等(对应项系数相等) 【注】待定系数法往往会有多种情况,需逐一验证. 6. 轮换对称式⑴判定多项式是否为轮换对称式;⑵试根:选定一个字母为主元,利用因式定理确定因式,并写出相关同型式 对于关于x ,y ,z 的轮换对称式,最常见的试根情况有:常见的齐次轮换对称式:【基础篇】1. 分解因式:22462x xy y +−2. 分解因式:242ab a b a bm an −++3. 分解因式:26312m mn mn −−4. 分解因式:()()32226a b c a c b −−−5. 分解因式:22223a b abc ab c −+−6. 分解因式:44332232722436x y z x y z x y z +−7. 分解因式:()()23262x a b xy a b +−+8. 分解因式:()()221n n x a b y b a +−+−9. 解方程:()()()()45303315453033160x x x x ++−++=11. 分解因式:()()()()22x y x y x y x y +−++−12. 分解因式:23361412abc a b a b −−+13. 分解因式:32461512a a a −+−14. 分解因式:4325286x y z x y −15. 分解因式:322618m m m −+−16. 分解因式:22224()x a x a x +−−17. 分解因式:2316()56()m m n n m −+−18. 分解因式:3223224612x y x y x y −+−20. 分解因式:(23)(2)(32)(2)a b a b a b b a +−−+−21. 分解因式:()()()213223x x x −−+− 22. 分解因式:2121()()m m p q q p +−−+−23. 分解因式:429ax ay −24. 分解因式:322x x x ++25. 分解因式:()2m p q p q −−+26. 分解因式:()()229m n m n +−−27. 分解因式:2229166824a b c ab ac bc ++−+−28. 分解因式:322333x x y xy y +++29. 分解因式:()222224a b a b +−30. 计算:2221999100033⎛⎫⎛⎫− ⎪ ⎪⎝⎭⎝⎭31. 计算:()22221052100595−⨯−+32. 计算:22221111111123410⎛⎫⎛⎫⎛⎫⎛⎫−−−− ⎪⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭33. 分解因式:()()()33x y x y xy y x −−−−−34. 已知5a b +=,3ab =,求代数式32232a b a b ab −+的值.35. 分解因式:()()22924a b a b +−−36. 分解因式:53182a a −+37. 分解因式:()()22229a a b x y +−+38. 分解因式:8881a b −39. 分解因式:322206045x x y xy −+−40. 分解因式:()2222224x y z x y +−−41. 分解因式:338a b +42. 分解因式:75()()a b b a −+−43. 分解因式:2243()27()x x y y x −−−44. 分解因式:22(5)2(5)(3)(3)m n n m n m n m +−+−+−45. 分解因式:44244()4p q p q +−46. 分解因式:222()4()4x x x x +−++47. 分解因式:22(23)9(1)x x +−−48. 分解因式:22223(2)27a a b a b +−49. 分解因式:222222(35)(53)a b a b −−+−50. 分解因式:22222(91)36a b a b +−−51. 分解因式:1xy x y −+−52. 分解因式:2ma mb m mn na nb −+++−53. 分解因式:434164a a a +−−54. 分解因式:26432xy yz x xz −+−55. 分解因式:322288a a b b a −+−56. 分解因式:3223636x x y x z xyz +−−57. 分解因式:ax by bx ay −−+58. 分解因式:32acx bcx adx bd +++59. 分解因式:42244a x ax a −+−60. 分解因式:()()22ax by bx ay ++−61. 分解因式:()()2221ab x x a b +++62.分解因式:()()()211y y m m −−−+63.分解因式:32232x x xy y y −+−−64.分解因式:3254222x x x x x −−++−65. 分解因式:()()2222ab x y xy a b −+−66. 已知3210x x x +++=,求20082000199625x x x ++的值.67. 分解因式:()()22114m n mn −−+68. 分解因式:()()()222222a b b c c a a b c +++++−−−69. 分解因式:22(1)12a b b b −−+−70. 分解因式:(1)(2)6x x x −−−72. 分解因式:241194n n m x x y +−+73. 分解因式:5544()x y x y xy +−+74. 分解因式:2222()()()()a b a c c d b d +++−+−+75. 分解因式:325153x x x −−+76. 分解因式:2226923ax a xy xy ay −+−77. 分解因式:222221x y z x z y z −−+78. 分解因式:22221a b a b −−+79. 分解因式:251539a m am abm bm −+−81. 分解因式:2910x x −−82. 分解因式:()238x x −−83. 分解因式:2367928x x −+84. 分解因式:21166x x −−+85. 分解因式:()()222211224x x x x −−−+86. 分解因式:2222360x y xyz z −+87. 分解因式:222536x y xyz z −−89. 分解因式:22310x xy y +−90. 分解因式:2672x x −+91. 分解因式:2121115x x −−92. 分解因式:256x x −++93. 分解因式:26136x x −+94. 分解因式:2273x x ++95. 分解因式:2253x x −+96. 分解因式:222064xy y x −++98. 分解因式:2273320x x −−99. 分解因式:2612x x −+−100. 分解因式:2214425x y xy +−101. 分解因式:22672x xy y −+102. 分解因式:22121115x xy y −−103. 分解因式:2358x x +−104. 分解因式:2212197x xy y −+105. 分解因式:2212()11()()2()x y x y x y x y +++−+−107. 分解因式:2(2)8(2)12a b a b −−−+108. 分解因式:222()14()24x x x x +−++109. 分解因式:()233x m n x mn +++110. 分解因式:2()()x a b c x a b c +++++【提高篇】1. 分解因式:321246n n n y y y +++−+−2. 分解因式:222232284163915a b x a x a b −−3. 分解因式:()()()()2223326a b x y b c a b x y b c ++−++4.分解因式:()()()()56m x y a b c n y x b a c −−++−−−5.分解因式:()()()()()()22322132212123x x x x x x x −+−−+++−6.计算:20.1737 2.017530201.7⨯+⨯+7.分解因式:()()()()()21222n n n x y x z x y y x y z +−−−−+−−8. 分解因式:8684279a a −9. 分解因式:32233111248x y x y x y −+−10. 分解因式:()()2232p p q p p q +−+11. 分解因式:()()()()322522322n n x y x y −−−−−12. 分解因式:()()()1232n n n a x y b y x c y x ++−−−+−13. 分解因式:()()13122n n n x x x x +−−−14. 分解因式:23229632x y x y xy ++15.分解因式:3222524261352xy z xy z x y z −++16.分解因式:212146n m n m a b a b ++−−(m 、n 为大于1的自然数)17.分解因式:23423232545224()20()8()x y z a b x y z a b x y z a b −−−+−18.分解因式:()()2121510n n a a b ab b a +−−−(n 为正整数)19.分解因式:2122()()()2()()n n n x y x z x y y x y z +−−−−+−−(n 为正整数)20. 分解因式:322()()()()()x x y z y z a x z z x y x y z x y x z a +−+−+−−+−−−−21. 分解因式:229312554a ab b −+22. 分解因式:2222()4()4()m n m n m n +−−+−23. 分解因式:()()()24c a b c a b −−−−24. 分解因式:()()24422a a b c b c −+++25. 分解因式:()()222122x x x x −++−26. 分解因式:()()24222222x a b x a b −++−27. 分解因式:77x y xy −28. 分解因式:5131214242n n n n n n x y x y x y −−+−+−+−29. 分解因式:3333a b c abc ++−30. 分解因式:3223332x x y xy y +++31. 分解因式:()()()()333333ax by ay bx a b x y +++−++32. 分解因式:()()2222224c b d a ab cd −+−−−33. 已知2471−可被40到50之间的两个整数整除,求这两个数.34. 求证:22823x xy y −−是两个整系数多项式的平方差.35. 分解因式:222139x xy y −+−36. 分解因式:444222222222a b c a b b c c a ++−−−37. 分解因式:81644x −38. 计算:()12351721n −⨯⨯⨯+39.分解因式:44()()a x a x +−−40.分解因式:2224244a b c ab ac bc +++−−41.分解因式:()()()()ab c d c d cd a b a b +−++−42.分解因式:()()3211x y xy x y ++−−−43.分解因式:2222x yz axyz yz xy xz az ++−−−44. 分解因式:()()222x b c d y d b c c d b +−−−−−+−45. 分解因式:322222422x x z x y xyz xy y z −−++−46. 分解因式:()()3322332a b a b a b ++++++47. 分解因式:432234a a a b ab b b ++++−48. 分解因式:()()()bc b c ca c a ab a b ++−++49. 分解因式:()222231b a x ab x +−−50. 分解因式:224632x xy ax a x y +−+−−51. 分解因式:222221x y z xy z +−−−−52. 分解因式:()222223691x y x y −+−53.分解因式:2222224x y x z y z z −−+54.分解因式:232232a b abc d ab cd c d −+−55.分解因式:22224946a b c d ac bd −+−++56.分解因式:221x ax x ax a +++−−57.分解因式:222332154810ac cx ax c +−−58.分解因式:22abx bxy axy y +−−59.分解因式:()()x x z y y z +−+60. 分解因式:333333()()()a b b c c a a b c ++++++++61.分解因式:3322()()ax y b by bx a y +++62.分解因式:2231()b a x abx +−−63.分解因式:22(3)(43)x ab x a b −+−64.分解因式:2222()()ab c d a b cd −−−65.分解因式:3254222x x x x x −−++−66.分解因式:222(1)()ab x x a b +++67.分解因式:222222()()ax by ay bx c x c y ++−++68.分解因式:()()()bc b c ca c a ab a b ++−−+69. 分解因式:()222124m x mx m −−−+70.分解因式:2222(48)3(48)2x x x x x x ++++++71.分解因式:2222()abcx a b c x abc +++72.分解因式:2222(4)8(4)15x x x x x x ++++++73.分解因式:2222222(61)5(61)(1)2(1)x x x x x x ++++++++74.分解因式:2()2a b x ax a b −+++75.分解因式:2222()3103x a b x a ab b ++−+−76.分解因式:()221999199911999x x −−−77.分解因式:22276212x xy y x y −++−−78.分解因式:22121021152x xy y x y −++−+79.分解因式:22534x y x y −+++80.分解因式:226731385x xy y x y −−++−81.分解因式:224434103x xy y x y −−−+−82.分解因式:22344883x xy y x y +−+−−83.分解因式:2265622320x xy y x y −−++−84.分解因式:226136222320x xy y x y −++−+85.分解因式:22223345a b c ab ac bc +++++86.分解因式:222311642x xy y xz yz z −+−−−87.分解因式:222695156x xy y xz yz z −+−++88.分解因式:2222372x y z xy yz xz −−+++89.分解因式:22265622320x xy y xz yz z −−−−−90.分解因式:222695156x xy y xz yz z −+−++91.分解因式:332x x ++92.分解因式:3234x x +−93.分解因式:9633x x x ++−94.分解因式:432433x x x x ++++95. 分解因式:432234232a a b a b ab b ++++96. 分解因式:444a b +97. 分解因式:44x +98. 分解因式:12631x x −+99. 分解因式:841x x ++100. 分解因式:422411x x y y −+101. 分解因式:4224(1)(1)(1)x x x ++−+−102. 分解因式:22(1)(1)4m n mn −−+103. 分解因式:412323x x −+104. 分解因式:42511x x −+105. 分解因式:444m n +106. 分解因式:422241x x ax a −++−107. 分解因式:2284025a ax xy y −−−108. 分解因式:22a ax xy y ++−109. 分解因式:2232x mx mx x −+−+110. 分解因式:()2232x a x a b b −−+−111. 分解因式:()()()2212121a a b a a b −−+−−112. 分解因式:22226x ax bx a ab b +−−−+113. 分解因式:4222x ax x a a −++−114. 分解因式:()32322x x a x a −++−115. 分解因式:222232x y x y xy xy x y ++++++116. 分解因式:22222a b ab ab a b ++−−−117. 分解因式:3222222x x y x z xz xyz y z yz −+−−++118. 分解因式:()()()2222abc a b c b c a c a b ++++++119. 分解因式:32539x x x ++−120. 分解因式:32256x x x +−−121. 分解因式:32694x x x −+−122. 分解因式:3210x x x +−−123. 分解因式:3487x x −−124. 分解因式:432262x x x x −−−+125. 分解因式:343115x x −+126. 分解因式:3292624x x x +++127. 分解因式:32252x x x −−−128. 分解因式:22(1)(2)12x x x x ++++−129. 分解因式:2222(48)3(48)2x x x x x x ++++++130. 分解因式:222(231)22331x x x x −+−+−131. 分解因式:2(2)(3)(4)(6)42x x x x x ++++−132. 分解因式:4(1)(21)(31)(41)6x x x x x ++−−+133. 分解因式:()()22216112a a a a a ++−++134. 分解因式:()()2254272x x x x −+−−−135. 分解因式:2244661124864x y x y x y −+−136. 分解因式:168243528x x y y −−137. 分解因式:()()222224x xy y xy x y ++−+138. 求证:(2016)(2017)(2018)(2019)1n n n n +++++是一个完全平方数.139. 计算:(472)(692)(8112)...(199419972)(362)(582)(7102) (199319962)⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+140. 计算:44444444(1064)(1864)(2664)(3464)(664)(1464)(2264)(3064)++++++++141. 分解因式:432227447x x x x −−−+142. 分解因式:435159x x x ++−143. 多项式32226x x x k +−+有一个因式是21x +,求k 的值.144. 若()()x a x b k −−−中含有因式x b +,求用a 、b 表示k 的式子.145. 21y x −+是2244xy x y k −−−的一个因式,求k 的值.146. 设多项式324715ax bx x +−−含有因式31x +、23x −,试试将此多项式因式分解.147. 已知关于x 、y 的二次式22754324x xy my x y ++−+−可分解为两个一次因式的乘积,求m 的值.148. 多项式2256x axy by x y ++−++的一个因式是2x y +−,试确定a b +的值.149. 已知225x x ++是42x ax b ++的一个因式,求a b +的值.150. 若多项式432511x x x mx n −+++能被2(1)x −整除,求m n +的值.。
沪教版(上海)七年级上册数学 第九章 第五节 因式分解(含解析)

第五节 因式分解一、单选题1.(2020·上海浦东新区初一期末)下列各多项式中,能用平方差公式分解因式有是( ) A .﹣x 2+16 B .x 2+9 C .﹣x 2﹣4 D .x 2﹣2y【答案】A 【解析】−x 2+16=(4+x )(4−x ),而B 、C 、D 都不能用平方差公式分解因式,故选:A . 2.(2020·上海市静安区实验中学初三专题练习)下列各式可以用完全平方公式分解因式的是( ) A .296y y -+ B .2144m m -+C .2224a ab b -+D .222x xy y --【答案】A 【解析】A 、22(963)y y y =--+,故A 正确;B 、221142(2)42m m m -+=+,故B 错误; C 、22244(2)a ab b a b -+=-,故C 错误;D 、2222()x xy y x y -+=-,故D 错误; 故选择:A.3.(2020·上海市卢湾中学初一期末)将下列多项式分解因式,结果中不含因式1x -的是( ) A .2x x +B .21x -C .221x x -+D .(2)(2)x xx【答案】A 【解析】2(1)x x x x +=+,A 项正确;()()2111x x x -=+-,B 项错误;()22211x x x -+=-,C 项错误;(2)(2)21x xx xx,D 项错误.故答案选A4.(2020·上海闵行初一期末)下列多项式能用公式法分解因式的有( )①221x x -- ①214xx -+ ①22a b -- ①22a b -+ ①2244x xy y -+A .1个B .2个C .3个D .4个【答案】C 【解析】①221x x --不能用公式法因式分解;②原式=2112x ⎛⎫- ⎪⎝⎭, ①22a b --不能用公式法因式分解; ④原式=(b -a )(b+a ), ⑤原式=()22x y - 故选:C .5.(2020·上海杨浦复旦二附中初一月考)下列式子从左到右的变形是因式分解的是① ① A .①x ①2①①x –2①①x 2①4 B ..x 2①4①3x ①①x ①2①①x –2①①3x C .x 2①3x ①4①①x ①4①①x ①1① D .x 2①2x ①3①①x ①1①2①4 【答案】C【解析】试题分析:A 、是整式的乘法,不是因式分解;B 、右边不是因式的积的形式,不是因式分解;C 、把多项式化成因式的积的形式,是因式分解;D 、右边不是因式的积的形式,不是因式分解.故选C .6.(2020·湖南邵阳初三一模)把8a 3①8a 2+2a 进行因式分解,结果正确的是( ① A .2a ①4a 2①4a +1① B .8a 2①a ①1① C .2a ①2a ①1①2 D .2a ①2a +1①2【答案】C 【解析】 8a 3①8a 2+2a =2a(4a 2①4a+1) =2a(2a①1)2①①①C.7.(2020·广西兴宾初一期中)对多项式2()2a b a b +--进行因式分解的结果是( )A .(22)()a b a b ++B .2242a ab b a b ++--C .)()21(2a b a b ++-D .())21(2a b a b +++【答案】C 【解析】原式=()()()()()()2=212212a b a b b a b a b a a b -+++-=++-⎡⎤⎣⎦+. 故选:C .8.(2020·甘肃平川区四中初二期末)多项式:①16x 2﹣8x ;②(x ﹣1)2﹣4(x ﹣1)+4;③(x+1)4﹣4x (x+1)2+4x 2;④﹣4x 2﹣1+4x 分解因式后,结果中含有相同因式的是( ) A .①和② B .③和④C .①和④D .②和③【答案】C 【解析】①16x 2−8x =8x (2x−1);②(x−1)2−4(x−1)+4=(x−1−2)2=(x−3)2;③(x +1)4−4x (x +1)2+4x 2=[(x +1)2−2x]2=(x 2+1)2; ④−4x 2−1+4x =−(2x−1)2; ∴结果中含有相同因式的是①和④; 故选:C .9.(2020·湖南湘潭电机子弟中学初二月考)因式分解x 2+mx ①12①①x +p ①①x +q ),其中m ①p ①q 都为整数,则这样的m 的最大值是( ) A .1 B .4C .11D .12【答案】C 【解析】①(x①p)(x①q)= x 2①①p+q①x+pq= x 2①mx①12①p+q=m①pq=-12.①pq=1×①-12①=①-1①×12=①-2①×6=2×①-6①=①-3①×4=3×①-4①=-12①m=-11或11或4或-4或1或-1.∴m的最大值为11.故选C.10.(2020·扬州市江都区第三中学初一期中)已知a①b①c是三角形的三边,那么代数式a2-2ab+b2-c2的值① ①A.大于零B.等于零C.小于零D.不能确定【答案】C【解析】a2-2ab+b2-c2=①a-b①2-c2=①a+c-b①[a-①b+c①]①①a①b①c是三角形的三边.①a+c-b①0①a-①b+c①①0①①a2-2ab+b2-c2①0①故选C①11.(2020·安徽蚌埠初一期末)已知a=2012x+2011①b=2012x+2012①c=2012x+2013,那么a2+b2+c2—ab①bc①ca 的值等于( )A.0 B.1 C.2 D.3【答案】D【解析】a2+b2+c2①ab①bc①ac①a2①ab+b2①bc+c2①ac①a ①a ①b ①+b ①b ①c ①+c ①c ①a ①当a ①2012x +2011①b ①2012x +2012①c ①2012x +2013时①a -b =①1①b ①c =①1①c ①a =2①原式=(2012x +2011①×①①1①+①2012x +2012①×①①1①+①2012x +2013①×2 ①①2012x ①2011①2012x ①2012+2012x ×2+2013×2 ①3① 故选D①12.(2020·全国初二课时练习)①2017重庆市兼善中学八年级上学期联考①在日常生活中如取款、上网等都需要密码.有一种用“因式分解法”产生的密码方便记忆,如:对于多项式44x y -,因式分解的结果是()()()22x y x y x y -++,若取9x =① 9y =时,则各个因式的值为()0x y -=① ()18x y +=①()22162xy +=,于是就可以把“018162”作为一个六位数的密码.对于多项式32x xy -,取20x①10y =时,用上述方法产生的密码不可能...是( ① A .201030 B .201010C .301020D .203010【答案】B 【解析】x 3-xy 2=x①x 2-y 2①=x①x+y①①x -y①① 当x=20①y=10时,x=20①x+y=30①x -y=10① 组成密码的数字应包括20①30①10① 所以组成的密码不可能是201010① 故选B①二、填空题13.(2020·温州市南浦实验中学初三二模)因式分解:249m -=________.【答案】()()2323m m +- 【解析】249m -=()()2323m m +-.故答案为:()()2323m m +-14.(2020·广东高州初二期末)如果2x Ax B ++因式分解的结果为()()35x x -+,则A B +=_______. 【答案】-13 【解析】()()22=531521535x x x x x x x ++--+--=∴A=2,B=-15 ∴A+B=-13 故答案为:-13.15.(2020·东北师大附中明珠学校初三其他)把多项式因式分解22a b ab b -+的结果是__________.【答案】2(1)b a -【解析】()()2222211a b ab b b a a b a -+=-+=-.故答案为: ()21b a -.16.(2020·上海市静安区实验中学初三专题练习)分解因式:3244a a a -+=__________.【答案】2(2)a a -; 【解析】3244a a a -+=a(a 2-4a+4)=a(a -2)2.故答案是:a(a -2)2.17.(2020·陕西西安初二期末)多项式2ax a -与多项式2242x x -+的公因式分别是______.【答案】x-1 【解析】多项式2ax a -=a (x +1)(x -1) 2x 2-4x +2=2(x -1)2所以两个多项式的公因式是x -118.(2020·山东东明初三一模)已知a ﹣b =5,ab =1,则a 2b ﹣ab 2的值为_____. 【答案】5 【解析】∵a ﹣b =5,ab =1,∴a 2b ﹣ab 2=ab (a ﹣b )=5×1=5; 故答案为:5.19.(2020·杭州市文澜中学初一期中)若多项式429n n k ++可化为()2a b +的形式,则单项式k 可以是__________.【答案】36n 或36n -或814或636n①当4n 和29n 作为平方项,k 作为乘积项,则多项式429n n k ++可化为:()223±n n ,即42224329(3)69++=±=±+n n k n n n n n ,∴36=±k n ;②当4n 和k 作为平方项,29n 作为乘积项,则多项式429n n k ++可化为:(22+n,即4222429(++=+=++nn k n n k ,∴229=n ,解得:814=k ; ③当29n 和k 作为平方项,4n 作为乘积项,则多项式429n n k ++可化为:(23n ,即42229(39++=+=++nn k n n k ,∴4=n ,解得:636=n k ;故答案为:36n 或36n -或814或636n .20.(2020·全国初一课时练习)通过计算几何图形的面积,可表示一些代数恒等式,如图所示,我们可以得到恒等式:2232a ab b ++=______.【答案】()()2a b a b ++.由面积可得:()()22a 3ab 2b a 2b a b ++=++.故答案为()()a 2b a b ++.21.(2020·黑龙江龙凤初一期末)2222111111......112319992000⎛⎫⎛⎫⎛⎫⎛⎫---- ⎪⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭=_______. 【答案】20014000【解析】2222111111......112319992000⎛⎫⎛⎫⎛⎫⎛⎫---- ⎪⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭=111111111111......111122331999199920002000⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫-+-+-+-+ ⎪⎪⎪⎪ ⎪⎪⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭=1341998200019992001 (223319991999200022000)⨯⨯⨯⨯⨯⨯⨯⨯=1200122000⨯=2001400022.(2020·全国初一课时练习)若a, b, c 满足2223331,2,3a b c a b c a b c ++=++=++=,则444a b c ++=________【答案】146【解析】因为1,a b c ++=所以()21a b c ++= ,即22221ab c ab ac bc因为2222a b c ++=所以12ab ac bc =-++ 因为()()2222a b c a b c++++=所以3332ab c ab abbc b c ac a c因为3331,3a b c a b c ++=++=所以31112ab c bc a ac b即332abbaacabc13322abc16abc因为()()3333a b c a b c++++=即4442222223ab c ab a b ac a c bc b c4442222223a b c ab c ac b bc a 44423a b c abbcacabc abc4441136a b c444146a b c故答案为:146三、解答题23.(2020·江苏高港初一期中)因式分解 ①-2x 2+8;②3222x x y xy -+;③222(4)16x x +-.【答案】①()()222x x -+-;②2()x x y -;③22(2)(2)x x +-【解析】 分析:①首先提取公因式2-,再利用平方差公式进行二次分解; ②首先提取公因式x ,再利用完全平方公式进行二次分解; ③先利用平方差公式分解,再利用完全平方公式进行二次分解. ①228x -+()224x =--()()222x x =-+-;②3222x x y xy -+22(2)x x xy y =-+ 2()x x y =-;③222(4)16x x +-22(44)(44)x x x x =+++- 22(2)(2)x x =+-.24.(2020·江苏射阳初一期中)因式分解 (1)2126ab c ab -(2)269a a -+- (3)2464x -【答案】(1)()621ab bc -;(2)()23a --;(3)()()444x x +-【解析】 分析:(1)直接提取公因式即可求解; (2)根据完全平方公式即可求解; (3)先提取4,再根据平方差公式即可求解.()1解:原式()621ab bc =- ()2解:原式()269a a =--+()23a =--()3解:原式()2416x =-=4(x+4)(x -4).25.(2020·山东定陶初一期末)分解因式(1)2425x - (2)22363ax axy ay -+(3)()()222ma m a -+- (4)()()251101a a ---【答案】(1)()()2525x x +-;(2)()23-a x y ;(3)()()21m a m -- ;(4)()()511a a -+ 【解析】 分析:(1)原式根据平方差公式分解;(2)原式先提取公因式,再利用完全平方公式分解; (3)原式利用提公因式法分解; (4)原式利用提公因式法分解. 解:(1)2425x -=()()2525x x +-;(2)22363ax axy ay -+=()2232a x xy y-+=()23-a x y ; (3)()()222ma m a -+-=()()222ma m a ---=()()21m a m --;(4)()()251101a a --- =()()251101a a -+-=()()5112a a --+ =()()511a a -+.26.(2020·广西江州初一期中)已知x -y=-2,xy=12,求代数式x 3y -2x 2 y 2+xy 3的值. 【答案】xy (x -y )2,2 【解析】 分析:首先根据x -y=2,xy=12,应用完全平方公式,求出(x -y )2的值是多少;然后根据因式分解的方法,求出x 3y -2x 2 y 2+xy 3的值是多少即可. 解:∵x -y=-2,xy=12, ∴(x -y )2=(-2)2=4, ∴x 3y -2x 2 y 2+xy 3 =xy (x 2-2xy +y 2) = xy (x -y )2 =12×4 =227.(2020·广西来宾初一期末)已知矩形的长为a ,宽为b ,它的周长为24,面积为32.求22a b ab +的值. 【答案】384 【解析】解:由题意可得:2()24a b +=,32ab =,则12a b +=,故22()a b ab ab a b +=+ 3212=⨯384=.28.(2020·全国初二课时练习)已知下列单项式:①4m 2,②9b 2a ,③6a 2b ,④4n 2,⑤-4n 2,⑥-12ab ,⑦-8mn ,⑧a 3.请在以上单项式中选取三个..组成一个能够先用提公因式法,再用公式法因式分解的多项式并将这个多项式分解因式. 【答案】见解析 【解析】 4m 2+4n 2-8mn =4(m 2+n 2-2mn ) =4(m -n )229.(2020·全国初二课时练习)某同学碰到这么一道题“分解因式x 2+2x ﹣3”,不会做,去问老师,老师说:“能否变成平方差的形式?在原式加上1,再减去1,这样原式化为(x 2+2x+1)﹣4,…”,老师话没讲完,此同学就恍然大悟,他马上就做好了此题.请你仔细领会该同学的做法,将a 2﹣2ab ﹣3b 2分解因式. 【答案】(a+b )(a ﹣3b ) 【解析】 分析:根据老师所说的话,可知需要利用平方差公式,故仿照x 2+2x ﹣3的分解方法,应该凑个完全平方,然后再整体利用平方差公式分解,最后将括号内的同类项合并即可.解:a2﹣2ab﹣3b2=a2﹣2ab+b2﹣4b2=(a﹣b)2﹣4b2=(a﹣b+2b)(a﹣b﹣2b)=(a+b)(a﹣3b).30.(2020·全国初二课时练习)请仔细阅读下面某同学对多项式(x2﹣4x+2)(x2﹣4x+6)+4进行因式分解的过程,然后回答问题:解:令x2﹣4x+2=y,则:原式=y(y+4)+4(第一步)=y2+4y+4(第二步)=(y+2)2(第三步)=(x2﹣4x+4)2(第四步)(1)该同学第二步到第三步运用了因式分解的;A.提取公因式B.平方差公式C.两数和的完全平方公式D.两数差的完全平方公式(2)另外一名同学发现第四步因式分解的结果不彻底,请你直接写出因式分解的最后结果;(3)请你模仿以上方法尝试对多项式(x2﹣2x)(x2﹣2x+2)+1进行因式分解.【答案】(1)C;(2)(x﹣2)4;(3)(x﹣1)4【解析】分析:(1)根据完全平方公式即可求解;(2)根据完全平方公式即可求解;(3)设x2﹣2x=y,根据因式分解的方法即可求解.解:(1)运用了C,两数和的完全平方公式;故答案为:C;(2)x2﹣4x+4还可以分解,分解不彻底;(x2﹣4x+4)2=(x﹣2)4.故答案为:(x﹣2)4.(3)设x2﹣2x=y.(x2﹣2x)(x2﹣2x+2)+1,=y(y+2)+1,=y2+2y+1,=(y+1)2,=(x2﹣2x+1)2,=(x﹣1)4.31.(2020·江苏相城初一期末)如图1示.用两块a×b型长方形和a×a型、b×b型正方形硬纸片拼成一个新的正方形.(1)用两种不同的方法计算图1中正方形的面积;(2)如图2示,用若干块a×b型长方形和a×a型、b×b型正方形硬纸片拼成一个新的长方形,试由图形推出2a2+3ab+b2因式分解的结果;(3)请你用拼图等方法推出3a2+5ab+2b2因式分解的结果,画出你的拼图.【答案】(1)222a ab b ++;(a +b )2 (2)()()2a b a b ++ (3)见解析 【解析】 分析:(1)从整体和部分两个方面进行计算即可; (2)根据计算图2面积的不同计算方法可得答案;(3)利用图形面积法,可以拼成长为(3a +2b ),宽为(a +b )的长方形. 解:(1)从整体上看,图1是边长(a +b )的正方形,其面积为(a +b )2, 各个部分的面积之和:a 2+2ab +b 2;(2)根据计算图2面积的不同计算方法可得,2a 2+3ab +b 2=(a +b )(2a +b ); (3)3a 2+5ab +2b 2=(a +b )(3a +2b ),32.(2020·常德市淮阳中学初一期中)观察下列式子的因式分解做法: ①x 2-1=(x -1)(x+1); ①x 3﹣1 =x 3﹣x+x ﹣1 =x (x 2﹣1)+x ﹣1=x(x﹣1)(x+1)+(x﹣1)=(x﹣1)[x(x+1)+1]=(x﹣1)(x2+x+1);①x4﹣1=x4﹣x+x﹣1=x(x3﹣1)+x﹣1=x(x﹣1)(x2+x+1)+(x﹣1)=(x﹣1)[x(x2+x+1)+1]=(x﹣1)(x3+x2+x+1);…(1)模仿以上做法,尝试对x5﹣1进行因式分解;(2)观察以上结果,猜想x n﹣1= ;(n为正整数,直接写结果,不用验证)(3)根据以上结论,试求45+44+43+42+4+1的值.【答案】(1)(x﹣1)(x4+x3+x2+x+1)(2)(x﹣1)(x n﹣1+x n﹣2+…+x2+x+1)(3)6431【解析】分析:(1)类比上面的作法,逐步提取公因式分解因式即可;(2)由分解的规律直接得出答案即可;(3)把式子乘4﹣1,再把计算结果乘13即可.解:(1)x5﹣1=x5﹣x+x﹣1=x(x4﹣1)+x﹣1=x(x﹣1)(x3+x2+x+1)+(x﹣1)=(x﹣1)[x(x3+x2+x+1)+1]=(x﹣1)(x4+x3+x2+x+1);(2)x n﹣1=x n﹣x+x﹣1=x(x n-1﹣1)+x﹣1=x(x﹣1)(x n-2+x n-3+…+x+1)+(x﹣1)=(x﹣1)[x(x n-2+x n-3+…+x+1)+1]=(x﹣1)(x n﹣1+x n﹣2+…+x2+x+1);(3)45+44+43+42+4+1=13×(4﹣1)(45+44+43+42+4+1)=13×(46﹣1)=6431.。
12.1因式分解的意义(课件)-七年级数学上册(沪教版2024)

12.1因式分解的意义
学习目标
1.理解因式分解的意义和概念及其与整式乘法的区
别和联系.(重点)
2.理解并掌握提公因式法并能熟练地运用提公因式
法分解因式.(难点)
情景导入
我们已经学习了整式的乘法,可以将几个整式的乘积化为一个整式如:
+ + = + + ;
因式分解一般要分解到每个因式都不能再分解为止,
如在 4 − 1的因式分解的过程中,因式 2 + 1不能继续因式分解,
2 − 1还能继续因式分解为 + 1 − 1 .
课本例题
例1
1
分析
Hale Waihona Puke 下列等式中,哪些从左到右的变形是因式分解?
− 2 + 3 = 2 + − 6;
1 等式 − 2 + 3
b=_______;
9
解题秘方:利用因式分解与整式乘法是互逆变形,可以
将因式分解的结果利用整式乘法算出多项式,并与已知
多项式比较解决问题.
(3)仿照以上方法解答下面的问题:已知把二次三项式
2x2+5x-k分解因式后有一个因式为2x-3,求其另一个
因式及k的值.
解题秘方:利用因式分解与整式乘法是互逆变形,可以
根据上述算式,完成下列因式分解:
5
2
(6)25
− 1 = (5x+1))(5x−1) 。
3² + 6 = 3x(x+2) 。
(7)a²−8a+16=
−4 ²
。
(8)2 − 5 − 6= − 6 + 1。
沪教版 七年级(上)数学 秋季课程 第8讲 因式分解综合(解析版)
本节课的内容,主要是对因式分解的四种方法——提取公因式法,公式法,十字相乘,分组分解法进行综合练习.通过本节课的学习,可以帮助同学们在做题目时,更加快速准确地找准分解因式的方法.并且可以用因式分解的思想去解决实际问题.【例1】下列各式从左到右的变形中,是因式分解的是().A .()x a b ax bx -=-B .2221(1)(1)x y x x y -+=-++C .21(1)(1)x x x -=+-D .()ax bx c x a b c ++=++【答案】C【解析】因式分解是将一个多项式分解成因式乘积的形式. 【总结】考察因式分解的定义.因式分解综合内容分析知识结构例题解析【例2】如果一个多项式因式分解的结果是()()2222b b +-,那么这个多项式是().A .44b -B .44b -C .44b +D .44b -【答案】B【解析】()()()()2222422224b b b b b +-=+-=-. 【总结】考察平方差公式的运用.【例3】下列各式中,是完全平方式的是().A .214y y -+ B .21m +C .1a ab ++D .221x x +-【答案】A 【解析】2211(42y y y -+=-. 【总结】考察用完全平方公式的运用.【例4】如果2x mx n ++是一个完全平方式,则m n 、的关系是___________. 【答案】24m n =.【解析】22()42mn m n ==,.【总结】考察对完全平方式的理解及运用.【例5】利用因式分解计算:(1)2299101-;(2)212114411121441691213⎛⎫-÷- ⎪⎝⎭. 【答案】(1)-400;(2) 287.【解析】 (1)2299101-(99101)(99101)200(2)400=+-=⨯-=- (2) 令11121213a b ==,,原式可化为2222()()()()a ba b a b a b a b a b a b+-÷-=-+-÷-=--,将a 、b 代入上式,得原式221112111312121328712111213111312+⨯+===-⨯-. 【总结】考察因式分解在简便运算中的应用.【例6】已知a b c 、、是ABC ∆的三边,且222a b c ab ac bc ++=++,那么ABC ∆的形状是().A .直角三角形B .等腰三角形C .等腰直角三角形D .等边三角形【答案】C【解析】由222a b c ab ac bc ++=++,得:2222()2()0a b c ab ac bc ++-++=,即222()()()0a b b c a c -+-+-=,a b b c a c ===所以,,. 即ABC ∆为等边三角形.【总结】本题一方面考察完全平方式的运用,另一方面考查几个非负数的和为零的基本模型.【例7】如果多项式216x kx ++可分解成两个一次因式的积,且k 为整数,那么k 不可能是().A .10B .17-C .15-D .8【答案】C【解析】1616116(1)444(4)282(8)=⨯=-⨯-=⨯=-⨯-=⨯=-⨯-, 所以17810k =±±±或或,故选C . 【总结】考察对十字相乘法的理解及运用.【例8】分解因式: (1)()229(2)252______________x y x y +--=; (2)2101_________n -=; (3)222__________x y y -=;(4)2363__________a a -+=;(5)2111__________216a a ++=;(6)26__________x x --=;(7)4278___________x x +-=;(8)231110__________y y ++=.【答案】(1)8(2)(8)x y x y ---;(2)(101)(101)n n +-;(3)2(1)(1)y x x +-;(4) 23(1)a -; (5) 21(1)4a +;(6)(3)(2)x x -+;(7)2(1)(1)(8)x x x +-+;(8)(35)(2)y y ++.【解析】(1)(2)(3)用平方差公式分解;(4)(5)用完全平方公式法分解;(6)(7)(8)用十字相乘法分解.【总结】本题主要考察利用适当的方法对多项式进行因式分解,注意分解一定要彻底.【例9】已知一矩形面积()()22545635S n n n n =++++=,求此矩形的周长. 【答案】24.【解析】由题意,可得:222(5)10(5)110n n n n +++-=, 分解因式,得:22(511)(51)0n n n n +++-=,则2511n n +=-或251n n +=. 因为矩形边长为正整数,所以251n n +=,所以一组邻边长为5和7,所以此矩形的周长为:()57224+⨯=.【总结】本题一方面考查因式分解在实际问题中的应用,另一方面考查整体思想的运用.【例10】已知3a b +=,2ab =-,利用因式分解求解()()22a a b b a b +++的值. 【答案】39.【解析】()()22a a b b a b +++222()()()[()2]3(94)39a b a b a b a b ab =++=++-=⨯+=. 【总结】考察因式分解的运用,利用已知条件求值.【例11】已知222224470x y z x y z ++-+++=,则________xyz =. 【答案】2.【解析】因为222224470x y z x y z ++-+++=,所以222(1)(2)2(1)0x y z -++++=.即121x y z ==-=-,,,所以2xyz =.【总结】考察完全平方式的运用,将原式转化为几个非负数的和为零的基本模型.【例12】已知2222220a b c d ab cd +++--=,求ac ad bc bd --+的值. 【答案】0.【解析】由题意,得22()()0a b c d -+-=,所以a b c d ==,. 所以()()0ac ad bc bd a c d b c d --+=---=.【总结】考察完全平方式的运用,将原式转化为几个非负数的和为零的基本模型.【例13】已知代数式422269264x x y y x y +++++的值为7,求代数式422269261x x y y x y ++---的值.【答案】-2或14.【解析】由题意,得:4222692630x x y y x y ++++-=, 因式分解,得:22(31)(33)0x y x y +-++=,则223133x y x y +=+=-或. 因为422222269261(3)2(3)1x x y y x y x y x y ++---=+-+-,所以当23=1x y +时,原式2=-;当233x y +=-时,原式14=.【总结】考察根据已知条件求值,本题关键在于将已知条件的等式因式分解.【例14】分解因式:()()22221x y ab x y a b +-+-+. 【答案】(1)(1)x y ab x y ab +--+-+.【解析】本题先采用一三分组,再利用公式法进行因式分解. 【总结】考察较复杂的多项式的因式分解的方法. 【例15】分解因式:()()22238320x x x x +-+-.【答案】(5)(2)(1)(2)x x x x +-++.【解析】()()22238320x x x x +-+-22(310)(32)x x x x =+-++(5)(2)(1)(2)x x x x =+-++.【总结】本题主要考查利用十字相乘法进行因式分解,注意分解要彻底.【例16】分解因式:()()22114x y xy --+. 【答案】(1)(1)xy x y xy x y ++-+-+.【解析】原式222222221421(2)y x x y xy x y xy x xy y =--++=++--+22(1)()(1)(1)xy x y xy x y xy x y =+--=++-+-+.【总结】考察利用分组分解法分解因式,本题需要先展开后再分组.【例17】分解因式:222946124x y z xy yz xz ++--+. 【答案】2(32)x y z -+.【解析】222946124x y z xy yz xz ++--+222(3)4(3)4(32)x y z x y z x y z =-+-+=-+. 【总结】本题先利用分组分解法,然后再用完全平方公式进行因式分解,注意观察每一项的特征.【例18】分解因式:()()222222ax by ay bx c x c y ++-++. 【答案】22222()()x y a b c +++.【解析】原式22222222222222a x abxy b y a y abxy b x c x c y =+++-+++ 222222222()()()a x y b x y c x y =+++++22222()()x y a b c =+++.【总结】考察利用分组分解法分解因式,本题需要先将小括号展开后再分组. 【例19】分解因式:()()()12340x x x x -++-. 【答案】2(4)(2)(25)x x x x +-++.【解析】原式22222(23)(2)40(2)3(2)40x x x x x x x x =+-+-=+-+- 222(28)(25)(4)(2)(25)x x x x x x x x =+-++=+-++.【总结】本题综合性较强,主要是观察前面几个因式的特征之后,通过合理的分组,然后利用整体思想进行因式分解,注意分解要彻底.【例20】分解因式:()444x y x y +++(拆项添项). 【答案】2222()x y xy ++.【解析】原式()444222222x y x y x y x y =++++--322y-yxx ()42222222222222222222222222222()()()[()][()]()()(3)()()(222)2()x y x y x y x y x y xy x y xy x y xy x y xy x y xy x y xy x y xy x y xy x y xy x y xy x y xy =+-++-=+++-++++-=+++-+++++=++++=++【总结】本题综合性较强,主要考查通过添项,构造完全平方式,然后再利用平方差公式进行分解,注意分解要彻底.【例21】分解因式:22276x xy y x y +--+-(双十字相乘法). 【答案】(2)(23)x y x y -++-. 【解析】【总结】考察用双十字相乘法分解因式的方法. 【例22】利用乘法分配律可知:()()22______________a b a ab b +-+=; ()()22____________a b a ab b -++=.由整式乘法与因式分解的关系,我们又可以得到因式分解中的另两个公式:33______________a b +=;33____________a b -=.请利用新的公式对下列各题进行因式分解. (1)338x y +;(2)66x y -.【答案】33a b +;33a b -;()()3322a b a b a ab b +=+-+;()()22a b a ab b -++. (1)22(2)(24)x y x xy y +-+;(2)2222()()()()x y x xy y x y x xy y +-+-++. 【解析】(1) 33338(2)x y x y +=+=22(2)(24)x y x xy y +-+;(2)6633332222()()()()()()x y x y x y x y x xy y x y x xy y -=+-=+-+-++.【总结】考察用新的公式进行因式分解.【例23】已知a b c 、、满足1a b c ++=,2222a b c ++=,3333a b c ++=,求444a b c ++的值. 【答案】256.【解析】因为2222()2()a b c a b c ab bc ac ++=+++++,即122()ab bc ac =+++,所以12ab bc ac ++=-.因为3332223()()a b c abc a b c a b c ab ac bc ++-=++++---,即13322abc -=+,所以16abc =. 因为333444()()7()()a b c a b c a b c ab ac bc abc a b c ++++=+++++-++,即4441137()126a b c =+++⨯--⨯,所以444256a b c ++=.【总结】本题综合性较强,主要考察整式乘法与因式分解的综合运用以及整体思想的运用.【例24】若230x x +-=,则32199119871990_______x x x +++=. 【答案】7960【解析】令a =1990,原式可化为: 32(1)(3)x a x a x a +++-+322223(3)(1)x ax x ax x a x x x a x x =+++-+=+-+++4a =,将1990a =代入,得:原式419907960=⨯=.【总结】考察利用因式分解的思想进行根据已知条件求值,本题用a 代换较大的数1990,便于计算.【例25】计算:32322012220122010201220122013-⨯-+-. 【答案】20102013.【解析】令2012a =,原式可化为:32322323222(2)22(1)(2)231(1)1(1)(1)11a a a a a a a a a a a a a a a a a a a -----+---====-+-++---+++,将2012a =代入,得:原式332010112012120132013=-=-=+. 【总结】考察利用因式分解的思想进行化简求值,本题用a 代换较大的数2012,便于化简.②【习题1】下列各式中,是完全平方式的是( ).①2242a ab b ++;②2212x x+-;③2296m mn n --;④2214x xy y ++;⑤43222a a b a b -+;⑥24212x x x++. A .①②③B .②④⑤C .③④⑤⑥D .①②⑤⑥【答案】B【解析】②④⑤是,①③⑥不是. 【总结】考察完全平方式的意义.【习题2】已知正方形的面积是2296x xy y ++(00x y >>,),利用因式分解,写出表示该正方形的边长的代数式是____________.【答案】3x y +.【解析】22296(3)x xy y x y ++=+. 【总结】考察用完全平方式分解因式.【习题3】已知2a b +=,2ab =,则322311___________22a b a b ab ++=.【答案】4.【解析】322322111(2)222a b a b ab ab a ab b ++=++211()24422ab a b =+=⨯⨯=.【总结】考察用完全平方式分解因式,然后利用整体代入进行求值.【习题4】甲、乙两个同学分解因式2x ax b ++时,甲看错了b ,分解结果为()()24x x ++;乙看错了a ,分解结果为()()19x x ++,则______a b +=.【答案】15.【解析】甲看错了b ,所以一次项系数正确,为2+4=6;乙看错了a ,所以常数项正确,为199⨯=, 所以6915a b +=+=. 【总结】考察用十字相乘法分解因式的方法.随堂检测【习题5】如果二次三项式28x ax --(a 为整数)在整数范围内可分解因式,那么a 的取值可以是_____________.【答案】72±±或.【解析】因为881182442-=-⨯=-⨯=-⨯=-⨯,所以72a =±±或. 【总结】考察用十字相乘法分解因式的方法. 【习题6】分解因式: (1)3223121824a b c a b c ac -+; (2)()()()a a b c b c a b c b a c --+-++-+;(3)2221632n n n a a a +--+-;(4)43221a a a a ++++.【答案】(1) 2236(234)ac a b ab -+;(2)2()a b c --; (3)2222(2)(2)n a a a --+-;(4)22(1)(1)a a a +++.【解析】(1)(2)提取公因式法;(3)先提取公因式再用公式法;(4)拆项分组法. 【总结】本题主要考查利用合适的方法进行因式分解.【习题7】分解因式:()()()24b c a b c a ----. 【答案】2(2)a b c --.【解析】()()()24b c a b c a ----22224()b bc c ac a bc ab =-+---+222224444(2)b bc c ac a bc ab a b c =-+-++-=--.【总结】本题直接无法因式分解,因此要先把每一项都拆开,然后重新分组进行因式分解.【习题8】分解因式:2210256308x xy y x y -+-++. 【答案】(54)(52)x y x y ----.【解析】原式2(5)6(5)8(52)(54)x y x y x y x y =---+=----.-21y-2y x x 【总结】本题主要是先利用分组分解法进行分组,然后再利用十字相乘法进行因式分解.【习题9】分解因式:22252x xy y x y ---+-.【答案】(21)(2)x y x y -++-.【解析】【总结】考察较复杂分解因式的方法,本题用双十字相乘法比较简单.【习题10】设23x z y +=,试判断222944x y z xz -++的值是不是定值,如果是定值,求出 它的值;否则,请说明理由. 【答案】是定值,0.【解析】222944x y z xz -++22(2)9(23)(23)600x z y x z y x z y y =+-=+++-=⋅=.【总结】考察先因式分解,再根据已知条件求值.【习题11】试讨论对于哪些m 值,24x xy x my +++能分解成两个一次因式的积.【答案】4【解析】24(4)()x xy x my x x y x m +++=+++所以当4m =时,上式才可以继续因式分解成(4)()x x y ++.【总结】考察分组分解法可以继续分解的条件.【习题12】已知()()200019981999a a --=,求()()2220001998a a -+-的值. 【答案】4002.【解析】因为()()200019981999a a --=, 所以()()200019981999a a --=-.()()()()()()22220001998[20001998]22000199842(1999)4002a a a a a a -+-=-+----=-⨯-=【总结】考察完全平方公式的变形,再根据已知条件求值.班秋季级年七12 / 16【习题13】分解因式:432262x x x x ---+(拆添项).【答案】22(232)(1)x x x ++-.【解析】原式4332222333322x x x x x x x =+----++322(1)3(1)3(1)2(1)x x x x x x x =+-+-+++32(1)(2332)x x x x =+--+322(1)(225522)x x x x x x =++--++2(1)[2(1)5(1)2(1)]x x x x x x =++-+++22(1)(252)x x x =+-+ 2(1)(21)(2)x x x =+--.【总结】本题综合性较强,通过拆添项,找到公因式,从而进行因式分解,注意分解要彻底.【习题14】分解因式:()()()222241211y x y x y +-++-(拆项添项).【答案】(1)(1)(1)(1)x x y xy x x y xy +++-----.【解析】()()()222241211y x y x y +-++- ()()()()()22222[11]21121y x y y x y x y =++--+⋅--+()()22222[11]2(11)y x y x y y =++---++()()222[11]4y x y x =++--()()()()22[112][112]y x y x y x y x =++-+++--2222[(1)(1)][(1)(1)]x y x x y x =++--+-(1)(1)(1)(1)x x y xy x x y xy =+++-----.【总结】本题综合性较强,通过拆添项,找到公因式,从而进行因式分解,注意分解要彻底.课后作业【作业1】已知多项式22x bx c ++分解因式为()()231x x -+,则b c 、的值为( ).A .3b =,1c =-B .6b =-,2c =C .6b =-,4c =-D .4b =-,6c =-【答案】D 【解析】根据常数项2(3)16c =⨯-⨯=-,即可知选D .【总结】考察十字相乘法的逆用.【作业2】下列分解因式错误的是( ).A .()()25623a a a a -+=--B .()2214212m m m -+=-C .224(2)(2)x y x y x y -+=-+-D .2221139342ab a b ab ⎛⎫++=+ ⎪⎝⎭ 【答案】B 【解析】22142(421)m m m m -+=---不可因式分解.【总结】考察因式分解的方法,本题B 中需要先提取负号,小括号内已不可分解.【作业3】已知210x y +=,22420x y -=,则______xy =.【答案】12【解析】因为210x y +=,由224(2)(2)20x y x y x y -=+-=可得:22x y -=,联立方程组可解得34x y ==,,故12xy =.【总结】考察根据已知条件求值.【作业4】分解因式:2221xy x y +--.【答案】(1)(1)x y x y +--+.【解析】2221xy x y +--222(2)1()1(1)(1)x xy y x y x y x y =--++=--+=+--+.【总结】考察用公式法分解因式的方法.【作业5】已知()212a a a b -=--,求222a b ab +-的值. 【答案】2【解析】由()212a a a b -=--,得:2a b -=, 所以222222()422222a b a b ab a b ab ++---====. 【总结】考察利用因式分解根据已知条件求值.【作业6】已知3210x x x +++=,那么20082000199625x x x ++的值为__________.【答案】8【解析】因为3210x x x +++=,所以2(1)(1)0x x x +++=,即2(1)(1)0x x ++=, 所以1x =-,将1x =-代入,得:200820001996251258x x x ++=++=.【总结】考察根据已知条件求值.【作业7】分解因式:(1)()()311111b a a b -+-; (2)11232639m n m n x y x y ++-+-;(3)()()2222224x x x y +-+; (4)4422127x y x y +-; (5)()()225()6x y a y x ab b x y -+-+-.【答案】(1)1()(11)(11)11b a b a b a --+--;(2) 213213(23)m n x y x y -+-; (3)22(44)(2)(2)x x y x y x y +++-;(4)22(3)(2)(2)x y x y x y -+-;(5)()(3)(2)x y a b a b ---.【解析】(1)(2)(5)提取公因式法;(3)平方差公式法;(4)十字相乘法.【总结】考察利用适当的方法进行因式分解.-21-y 3y 3x2x 【作业8】已知关于x y 、的二次六项式226372x axy y x y +----能分解为一次式 2x by c ++与2dx ey +-的积,求a b c d e ++++的值.【答案】13.【解析】 由二次项系数和常数项可得31d c ==,,利用双十字相乘可得如下图交叉式:所以31b e ==-,,927a =-=,所以13a b c d e ++++=. 【总结】考察双十字相乘法的应用.【作业9】已知2x y +=,4xy a =+,3326x y +=,求a 的值.【答案】-7.【解析】由题意有:33222()()()[()3]x y x y x y xy x y x y xy +=++-=++-,即262[43(4)]a =-+,解得:7a =-.【总结】考察立方和公式的应用.【作业10】计算:()2222002200120032002200220012001-⋅-⋅+.【答案】2003. 【解析】令2002a =,则原式可化为:22222[(1)](1)(1)(1)1(1)(1)1a a a a a a a a a a a a a --+-++==+--+--+, =2003.【总结】本题综合性较强,主要考察利用因式分解先化简再计算,令2002a =可使计算简单.【作业11】已知3x y z ++=,22229x y z ++=,33345x y z ++=,求xyz 的值.【答案】-24.【解析】因为2222()2()x y z x y z xy yz xz ++=+++++,即9292()xy yz xz =+++, 所以10xy yz xz ++=-, 因为3332223()()x y z xyz x y z x y z xy xz yz ++-=++++---, 即4533(2910)xyz -=+,所以24xyz =-.【总结】考察整式乘法与因式分解的综合练习,综合性较强,注意观察每一项的特征.。
串讲03 因式分解(9个常考点 5种重难点题型 2个易错)七年级数学上学期期中考点(沪教版2024)

请你选择一种方法因式分解:
mx - my + nx - ny ;
【解】 mx - my + nx - ny =( mx - my )+( nx - ny )
= m ( x - y )+ n ( x - y )=( x - y )( m + n ).
(1)3.2×202.4+4.7×202.4+2.1×202.4;
【解】 原式=202.4×(3.2+4.7+2.1)
=202.4×10=2 024.
(2)36.8×
+20.2×
【解】 原式=
=
×55=13.
-2×来自.×(36.8+20.2-2)
题型二:变形后利用提公因式法分解因式计算
B. 都是乘法运算
C. ①是因式分解,②是乘法运算
D. ①是乘法运算,②是因式分解
考点2 公因式的定义
4. [2023·永州]2 a2与4 ab 的公因式为
2a
5. 8 xmyn-1-12 x3 myn 各项的公因式是( D
A. xmyn
B. xmyn-1
C. 4 xmyn
D. 4 xmyn-1
2x3–2x2y+8y–8x
解
6k2+9km – 6mn–4kn
=2(x3–x2y+4y–4x)
=(6k2+9km) – (6mn+4kn)
=2[(x3–x2y) +(4y–4x)]
=3k(2k+3m) –2n (3m+2k)
=2[x2(x-y)-4(x-y)]
沪教新版七年级上册《第12章_因式分解》2024年同步练习卷+答案解析

沪教新版七年级上册《第12章因式分解》2024年同步练习卷一、选择题:本题共5小题,每小题3分,共15分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.下列各式从左到右的变形中,是因式分解的为()A. B.C. D.2.如果一个多项式因式分解的结果是,那么这个多项式是()A. B. C. D.3.下列各式中,是完全平方式的是()A. B. C. D.4.把多项式分解因式的结果是()A. B.C. D.5.已知a,b,c是的三边长,且,则的形状为()A.钝角三角形B.等边三角形C.直角三角形D.等腰直角三角形二、单选题:本题共1小题,每小题5分,共5分。
在每小题给出的选项中,只有一项是符合题目要求的。
6.若能在整数范围内因式分解,则k可取的整数值有()A.2个B.3个C.4个D.6个三、填空题:本题共14小题,每小题3分,共42分。
7.多项式中各项的公因式是______.8.分解因式:______.9.分解因式:______.10.如果多项式,那么m的值为______.11.如果,且,则n的值是______.12.已知,,则______.13.已知,则的值是__________.14.若长方形的面积是,且其中一边长为,则长方形的另一边长是______.15.已知正方形的面积是,利用分解因式写出表示该正方形的边长的代数式______.16.已知,,则的值为______.17.分解因式,甲看错了a值,分解的结果是,乙看错了b值,分解的结果是,那么分解因式正确的结果应该是______.18.已知是一个完全平方式,则______.19.已知,则______.20.如果二次三项式为整数在整数范围内可分解因式,那么a的取值可以是______.四、解答题:本题共10小题,共80分。
解答应写出文字说明,证明过程或演算步骤。
21.本小题8分分解因式:22.本小题8分分解因式:计算:23.本小题8分分解因式:24.本小题8分分解因式:25.本小题8分分解因式:26.本小题8分因式分解:27.本小题8分因式分解:;已知:x、y为正整数,、且,求x、y的值.28.本小题8分阅读下面解题过程:分解因式:解:然后按照上述解题思路,完成下列因式分解:29.本小题8分利用乘法分配律可知:______;______.由整式乘法与因式分解的关系,我们又可以得到因式分解中的另两个公式:______;______.请利用新的公式对下列各题进行因式分解.;30.本小题8分先阅读下面例题的解法,然后解答后面的问题.例:若多项式分解因式的结果中有因式,求实数m的值.解:设为整式,若,则或由得左式为零,所以是方程的解,所以,所以问题:若多项式分解因式的结果中有因式,则实数p是多少?答案和解析1.【答案】C【解析】解:A、是整式的乘法运算,故选项错误;B、右边不是整式乘积的形式,故选项错误;C、,正确;D、右边不是整式乘积的形式,故选项错误.故选:根据因式分解的定义作答.因式分解是把一个多项式化成几个整式的积的形式,熟练地掌握因式分解的定义是解题关键.2.【答案】B【解析】解:故选:根据平方差公式得,进而解决此题.本题主要考查平方差公式以及因式分解的定义,熟练掌握平方差公式以及因式分解的定义是解决本题的关键.3.【答案】A【解析】解:,属于完全平方式;B.不属于完全平方式;C.不属于完全平方式;D.不属于完全平方式;故选:完全平方式分两种,一种是完全平方和公式,就是两个整式的和括号外的平方;另一种是完全平方差公式,就是两个整式的差括号外的平方.此题考查了完全平方式,熟练掌握完全平方公式是解本题的关键.4.【答案】C【解析】解:原式故选:先分两组,前面一组利用完全平方公式分解,然后利用平方差公式因式分解即可.本题考查了因式分解-分组分解:分组分解法一般是针对四项或四项以上多项式的因式分解,分组有两个目的,一是分组后能出现公因式,二是分组后能应用公式.5.【答案】B【解析】解:,,,即,,,,,的形状为等边三角形.故选:欲判断三角形的形状,不妨试着从边的关系出发,求出a、b、c之间的关系;给等式两边同时乘以2,再利用完全平方公式进行配方,可得到;接下来根据非负数的性质可得答案.考查学生综合运用数学知识的能力.此题是一道把等边三角形的判定、因式分解和非负数的性质结合求解的综合题.6.【答案】D【解析】【分析】本题主要考查因式分解的意义和十字相乘法分解因式,对常数项的不同分解是解本题的关键,属于拔高题.根据十字相乘法的分解方法和特点可知:k的值应该是20的两个因数的和,从而得出k的值.【解答】解:,,,,,,则k的值可能为:,,,,,,故整数k可以取的值有6个,故选:7.【答案】【解析】解:,所以多项式中各项的公因式是故答案为:先变形得出,再找出多项式的公因式即可.本题考查了公因式,能熟记找公因式的方法①系数找各项系数的最大公因数,②相同字母找最低次幂是解此题的关键.8.【答案】【解析】解:,故答案为:先提公因式,再利用平方差公式继续分解即可解答.本题考查了提公因式法与公式法的综合运用,一定要注意如果多项式的各项含有公因式,必须先提公因式.9.【答案】【解析】解:,,故答案为:先提取公因式,再对余下的多项式利用完全平方公式继续分解.本题考查了用提公因式法和公式法进行因式分解,一个多项式有公因式首先提取公因式,然后再用其他方法进行因式分解,同时因式分解要彻底,直到不能分解为止.10.【答案】【解析】解:,故答案为:把等式右边利用完全平方公式展开,然后根据对应项系数相等解答.本题考查了公式法分解因式,熟记完全平方公式的公式结构是解题的关键.11.【答案】【解析】解:,,,,故答案为:先根据两平方项确定出这两个数,即可确定n的值.本题主要考查了完全平方式,根据平方项确定出这两个数是解题的关键,也是难点,熟记完全平方公式对解题非常重要.12.【答案】【解析】解:,即,且①,②,①+②,得:,解得,故答案为:由,即得出,结合,将两式相加消去b即可得.本题主要考查分式的加减法,解题的关键是掌握平方差公式和等式的性质.13.【答案】7【解析】解:,,故答案为:把已知条件两边分别平方,然后整理即可求解.完全平方公式:本题主要考查了完全平方公式,利用公式把已知条件两边平方是解题的关键.14.【答案】【解析】解:矩形的长为,故答案为:由题意得矩形的长为,然后利用多项式除以单项式的法则即可求出结果.本题考查多项式除以单项式运算.多项式除以单项式,先把多项式的每一项都分别除以这个单项式,然后再把所得的商相加.15.【答案】【解析】解:,正方形的边长的代数式是因为正方形的面积是,可以分解为,又有正方形的面积等于边长的平方可得,正方形的边长的代数式是此题考查对完全平方公式再实际中的应用,应熟练识记完全平方公式:16.【答案】4【解析】解:原式,当,时,原式故答案是:首先对所求的式子提公因式,然后利用完全平方公式分解,最后把,代入求值.本题考查了分解因式,提取公因式后利用完全平方公式进行二次分解,注意分解要彻底.17.【答案】【解析】解:分解因式,甲看错了a值,分解的结果是,,,乙看错了b值,分解的结果是,,,故答案为:根据已知分解因式,甲看错了a值,分解的结果是,可得出b的值,再根据乙看错了b值,分解的结果是,可求出a的值,进而因式分解即可.此题主要考查了因式分解的意义,根据已知分别得出a,b的值是解决问题的关键.18.【答案】或2【解析】解:由于,则,或故答案为:或这里首末两项是x和5这两个数的平方,那么中间一项为加上或减去x和5的积的2倍,故,再解k即可.此题主要考查了完全平方公式的应用,两数的平方和,再加上或减去它们积的2倍,就构成了一个完全平方式.注意积的2倍的符号,避免漏解.19.【答案】6【解析】解:已知等式变形得:,,,,,,,,解得:,,,则故答案为:已知等式左边14分为,结合后利用完全平方公式化简,再利用非负数的性质求出x,y与z的值,代入原式计算即可求出值.此题考查了配方法的应用,以及非负数的性质,熟练掌握完全平方公式是解本题的关键.20.【答案】或【解析】解:8可以分解为和,当8可以分解为时,根据十字相乘因式分解,,则;8可以分解为时,根据十字相乘因式分解,,则;故答案是或根据因式分解十字相乘,将8分解为和,再按照十字相乘进行因式分解即可.本题考查的是因式分解,用十字相乘的方法时,要注意数字的符号不能出现差错.21.【答案】解:【解析】将前两项分组后两项分组,进而提取公因式再利用平方差公式分解因式.此题主要考查了分组分解法因式分解,正确进行分组是解题关键.22.【答案】解:;【解析】先进行变形,再运用提公因式法进行因式分解;先运用平方差公式进行运算,再计算单项式乘以多项式.此题考查了整式乘法和因式分解的能力,关键是能准确运用对应法则和方法进行求解.23.【答案】解:【解析】先分组,分成,再运用完全平方公式分解.本题考查了因式分解.分解因式的一般步骤是:一提公因式,二套用公式,三分组,解本题的关键在于运用分组分解法进行因式分解,注意因式分解要彻底,一定要分解到每个因式都不能再分解为止.24.【答案】解:【解析】先将拆分为,再分组,利用完全平方公式及平方差公式求解即可.本题考查了分组分解法,分组分解法一般是针对四项或四项以上多项式的因式分解,分组有两个目的,一是分组后能出现公因式,二是分组后能应用公式.25.【答案】解:【解析】先利用完全平方公式和多项式乘以多项式展开,重新组合即可得出结论.此题主要考查了因式分解,完全平方公式,多项式乘以多项式,重新分组是解本题的关键.26.【答案】解:原式【解析】根据完全平方公式,可得答案.本题考查了因式分解,利用了完全平方公式分解因式.27.【答案】解:;,,,、y为正整数,,与也是整数,,,或,【解析】根据分组分解法分解因式即可;根据结论整体代入即可得到结论.本题考查了因式分解-分组分解法,熟练掌握分解因式的方法解题的关键.28.【答案】解:【解析】直接利用例题进行补项,进而分解因式得出答案.此题主要考查了分组分解法分解因式,正确补项是解题关键.29.【答案】【解析】解:;;;;;;故答案为:,,;根据多项式乘多项式的法则计算即可,再根据推导的公式进行因式分解.本题考查了因式分解和多项式乘多项式的逆向应用能力30.【答案】解:设为整式,若,则或由得左式为零,所以是方程的解,所以,所以【解析】仿照题例,先设,再求一次方程的值,代入计算得结果.本题考查了解一元一次方程、高次方程,理解题例,掌握题例的步骤是解决本题的关键.。
12.2因式分解的方法(第1课时 提公因式法)(课件)七年级数学上册(沪教版2024)

=4 a ( x - y )+2 b ( x - y )
=2( x - y )(2 a + b ).
7.先分解因式,再计算求值:
(1)4 x ( m -2)-3 x ( m -2)2,其中 x =1, m =3;
【解】4 x ( m -2)-3 x ( m -2)2
=(2 x + y )(2 x -3 y +3 x )=(2 x + y )(5 x -3 y ).
+ = ,
+ = ,
∵
∴
∴原式=3×(-2)=-6.
− = − .
+ = ,
14. 试说明817-279-913能被45整除.
【解】因为817-279-913=328-327-326
2)( a +4).将 a =-2代入,得原式=(-2-2)×(-2+
4)=-8.
分层练习-巩固
8. 计算320-318×6的值是( A
)
A. 319
B. 318
C. 3 2
D. 0
9. [新考法 数形结合法]△ ABC 的三边长分别为 a , b , c ,
且 a +2 ab = c +2 bc ,则△ ABC 是(
提取公因式法.
新知探究
如何将6 2 + 9因式分解?
先找出6 2 + 9各项的公因式,再用提取公因式法因式分解. 这个整式有两项
6 2 与9, 这两项的系数6与9有最大公因数3,这两项的字母部分 2 与都含
有字母和, 且和的最低次数都是1,因此可提取公因式3,得
− = ,
= ,
所以
解得
因式分解(6种常考题型专项训练)原卷版—七年级数学上学期期中(沪教版2024)

因式分解(6种常考题型专项训练)因式分解的意义 公式法因式分解因式分解在有理数简算中的应用 十字相乘法分组分解法 因式分解的应用题型一:因式分解的意义一、单选题1.(23-24七年级上·上海浦东新·期中)下列等式中,从左到右的变形是因式分解的是( )A .253(5)3x x x x -+=-+B .2(2)(5)310x x x x -+=+-C .22(23)4129x x x +=++D .2244(2)-+=-x x x 2.(22-23七年级上·上海青浦·期中)下列各等式中,从左到右的变形是因式分解的有( )(1)()()2224x x x +-=- (2)()2111x x x ++=++(3)12223=´´ (4)()3222323a a a a a a ++=++A .1个B .2个C .3个D .4个3.(22-23七年级上·上海浦东新·期末)下列等式从左到右是因式分解,且结果正确的是( )A .22816(4)a a a ++=+B .22(4)=816a a a +++C .2816(8)16a a a a ++=++D .228(2)816a a a a ++=++4.(22-23七年级上·上海青浦·期中)单项式33ab 与单项式239a b 的公因式是( )A .23a b B .333a b C .2a b D .33a b 二、填空题5.(22-23七年级上·上海青浦·期中)若整式2x x m -+含有一个因式(3)x +,则m 的值是 .6.(2022七年级上·上海·专题练习)28(9)()x x m x x n -+=--,则nm =7.(23-24七年级上·上海长宁·期中)326a bc 和228a b c 的最大公因式是 .题型二:公式法因式分解一、单选题1.(21-22七年级上·上海嘉定·期中)下列各式中,不能用公式法分解因式的是( )A .2249a b -B .222a ab b -+-C .21a --D .2114b -+2.(22-23七年级上·上海青浦·期中)下列多项式中可以用完全平方公式进行因式分解的是( )A .21x x ++B .221x x --C .224x x ++D .214x x -+二、填空题3.(2024·上海嘉定·三模)因式分解:()2224x xy y ---=4.(2024·上海·模拟预测)因式分解:62xy xy -=三、解答题5.(23-24七年级上·上海普陀·期末)因式分解:2221a ab b ++-.6.(23-24七年级上·上海青浦·期中)因式分解:222(4)8(4)16a a a a -+-+7.(23-24七年级上·上海青浦·期中)因式分解:()22222169+--m n mn m n .8.(23-24七年级上·上海·期末)因式分解:22139164525a ab b -+-.9.(23-24七年级上·上海青浦·期中)因式分解:()()2242452x x x x -+-++题型三:因式分解在有理数简算中的应用1.(23-24七年级上·上海青浦·期中)利用平方差公式计算:2220052003-= .2.(22-23七年级上·上海青浦·期末)计算:227.5 1.6 2.5 1.6´-´3.(23-24七年级上·上海闵行·期中)简便计算:2201120072015-´4.(23-24七年级上·上海青浦·期中)用简便方法计算:()()22202020262020403720212017201920222023-+´´´´.题型四:十字相乘法一、填空题1.(23-24七年级上·上海浦东新·期末)因式分解:2812x x -+=.2.(23-24七年级上·上海松江·期末)分解因式:221112x xy y --=.3.(23-24七年级上·上海·期末)因式分解:21336a a -+= .4.(23-24七年级上·上海·单元测试)分解因式:26x x +-= ,3443ax by ay bx --+=.5.(23-24七年级上·上海浦东新·期末)分解因式:22514x xy y --=.二、解答题6.(23-24七年级上·上海松江·期末)分解因式:4234x x --.7.(23-24七年级上·上海宝山·期末)分解因式:()()222412a a a a +++-.8.(23-24七年级上·上海·单元测试)因式分解:()()21556a b b a ---+.9.(22-23七年级上·上海杨浦·期末)分解因式:()()2233820x x x x ----.题型五:分组分解法一、填空题1.(21-22九年级下·上海徐汇·期中)因式分解:am an bm bn +--= .2.(2024·上海·模拟预测)因式分解:221x x --= .二、解答题3.(23-24七年级上·上海宝山·期末)分解因式:842ax by ay bx -+-.4.(23-24七年级上·上海杨浦·期末)因式分解:22643a bc ab ac -+-;5.(22-23七年级上·上海杨浦·期末)分解因式:32248x x y x y +--.6.(23-24七年级上·上海杨浦·期末)因式分解:()22222224mnx m x n x m n -++--;7.(23-24七年级上·上海崇明·期末)分解因式:22424a b a b --+.8.(23-24七年级上·上海杨浦·期末)分解因式:5322x x x +-- .9.(23-24七年级上·上海青浦·期中)因式分解:22168-+-a b b .10.(23-24七年级上·上海杨浦·期末)分解因式:32332a a a +++.11.(2022七年级上·上海·专题练习)因式分解:()()22114x y xy ---题型六:因式分解的应用一、单选题1.(23-24七年级上·上海浦东新·期末)已知甲、乙、丙均为x 的一次整式,且其一次项的系数皆为正整数.若甲与乙相乘的积为29x -,乙与丙相乘的积为26x x +-,则甲与丙相减的结果是( )A .5-B .5C .1D .1-二、填空题2.(22-23七年级上·上海浦东新·期中)与()27x y -之积等于4249y x -的因式为 .3.(2022七年级上·上海·专题练习)当1996,200x y =-=时,代数式32266x xy x y x --+= 4.(22-23七年级上·上海静安·期中)已知22313x y x y -=+=,,则32238x y x y xy -+的值为 5.(23-24七年级上·上海长宁·期中)由多项式乘以多项式的法则可以得到:()()2232222333a b a ab b a a b ab a b a b b a b +-+=-++-+=+即:()()2233a b a ab b a b +-+=+,我们把这个公式叫做立方和公式,同理:()()2233a b a ab b a b -++=-,我们把这个公式叫做立方差公式,请利用以上公式分解因式:34381a b b -=6.(23-24七年级下·上海静安·期中)定义:如果一个正整数能表示为两个正整数m n ,的平方差,且1m n ->,则称这个正整数为“智慧优数”.例如,221653=-,16就是一个智慧优数,可以利用()()22m n m n m n -=+-进行研究.若将智慧优数从小到大排列,第9个智慧优数是 .三、解答题7.(22-23七年级上·上海青浦·期中)已知a ,b ,c 三个数两两不等,且有222222a b mab b c mbc c a mca ++=++=++,试求m 的值.222222 8.(22-23七年级上·上海青浦·期中)证明:()()()2a b c x y z ax by cz++++³++。
沪教版七年级数学(-因式分解练习题)

(
A、 an
B、 an 1
C、 a2n 1
D、 9 4
) D、 a 2n 1 1
3、要使二次三项式 x2 mx 12 能在整数范围内分解因式,则 m 不可取 的值是
(
)
A、 1
B、 2
C、 4
D、 11
4、下列各式中因式分解结果为 ( x 2)( x 1) 的多项式是(
)
A、 x2 3x 2
B、 x2 x 2
学习必备
பைடு நூலகம்欢迎下载
七年级因式分解练习卷
一、 填空题(每空 2 分,共 40 分) 1、 5m(a b) a b ( a b) ___________
: 号 学
线
订
2、已知
2
x
mx
16 是完全平方式, 则 m
_____________,已知
2
4x
2mxy
2
9y
是完全平方式,则 m =____________。
C、 x2 3x 2
D、 x2 x 2
学习必备
欢迎下载
5、 把多项式 x2 4 xy 4y2 4 先分组再应用公式分解因式,分组正确的是
(
)
A、 (x2 4xy ) (4 y2 4)
B、 (x2 4) (4 xy 4y2 )
C、 (x2 4xy 4y2 ) y2
6、下列各多项式的因式分解结果正确的是 A、 (a 2 b2 )2 4 a2b2 (a b) 2( a b) 2
5、已知:
2
(x
2
2
y )( x
4
2
y ) 12
0
,求
2
x
2
上海市七年级上学期因式分解精炼

上海市七年级数学因式分解精炼一、用提公因式法把多项式进行因式分解1、.-+--+++ax abx acx ax m m m m 2213 2、.a a b a b a ab b a ()()()-+---322223、.不解方程组23532x y x y +=-=-⎧⎨⎩,求代数式()()()22332x y x y x x y +-++的值。
4、.证明:对于任意自然数n ,323222n n n n ++-+-一定是10的倍数。
5、. 已知:xbx c 2++(b 、c 为整数)是x x 42625++及3428542x x x +++的公因式,求b 、c 的值。
课堂小练1. 分解因式:(1)-+-41222332mn m n mn (2)a x abx acx adx n n n n 2211++-+--(n 为正整数)(3)a ab a b a ab b a ()()()-+---322222 (4)322x x x ()()--- (6)412132q p p ()()-+-2. 计算:()()-+-221110的结果是______________3. 已知x 、y 都是正整数,且x xy y y x ()()---=12,求x 、y 。
4. 证明:812797913--能被45整除。
2、运用公式法进行因式分1、已知多项式232xx m -+有一个因式是21x +,求m 的值。
2、已知a b c 、、是∆ABC 的三条边,且满足ab c ab bc ac 2220++---=,试判断∆ABC 的形状。
3、两个连续奇数的平方差一定是8的倍数。
4、 已知:am b m c m =+=+=+121122123,,,求a ab b ac c bc 222222++-+-的值。
5、. 若xy x xy y 3322279+=-+=,,求x y 22+的值。
6、 分解因式(1)()()aa +--23122 (2 )x x y x y x 5222()()-+-(3)3223288xy x y xy ++ (4)a a b b 2222+--7、. 已知:xx +=-13,求x x 441+的值。
上海市沪教版(五四制)七年级第一学期因式分解专练学案-文档精选全文完整版

可编辑修改精选全文完整版因式分解提取公因式、公式法【知识要点】1. 因式分解:就是把一个多项式化为几个整式的的形式.分解因式要进行到每一个因式都不能再分解为止.2. 提公因式法:=++mc mb ma .3. 公式法:(1)=-22b a ;(2)=++222b ab a ;(3)=+-222b ab a .4.因式分解的一般步骤:一“提”(取公因式),二“用”(公式). 5.易错知识辨析(1)注意因式分解与整式乘法的区别;(2)完全平方公式、平方差公式中字母,不仅表示一个数,还可以表示单项式、多项式.【典型例题】例1 下列从左到右的变形,属于分解因式的是( ) A. (x+3)(x -2)=x 2+x -6 B. ax -ay+1=a(x -y)+1C. x 2-21y=(x+y 1)(x -y 1) D. 3x 2+3x=3x(x+1)例2 将下列多项式分解因式 (1)(2)121m n m n a b a b -+-(3)253243143521x y x y x y +-(4)()()23aa b a b a ---(5))3(7)23)(3(x x x -+--(6)xy xy y x 36922+--例3 把下列各式分解因式 (1)a 2-4b 2(2)24251b a +-(3)()()22916b a b a +--(4)()()122++++b a b a(5)442-+-x x(6)181222+-x x(7)22332y ax axy y ax -+(8) 3y 2-2722x x -(9)x x x ++232(10)()222224y x y x -+例4 分解因式(1)()()()()222510b a b a n m n m ++++-+(2)()()()()229262n m n m m n n m +++---例5 计算(1)199919992+(2)20002-4000×2019+20192例6已知,21,1-==+xy y x 利用因式分解求2)())((y x x y x y x x +--+的值.例7设n 为整数,用因式分解说明25)12(2-+n 能被4整除.【小试锋芒】1.分解因式39a a -=,221218x x -+= 2. 分解因式:34a a -=3.因式分解: 4.因式分解:4)4)(2(2-+++x x x = 5.简便计算:=2271.229.7- 6.按照完全平方公式填空:7.多项式a ax 42-与多项式442+-x x 的公因式是 8.下列多项式中,能用公式法分解因式的是()A .x 2-xyB .x 2+xyC .x 2-y 2D .x 2+y 29.下列各式从左到右的变形中,是因式分解的为()A .1)32(1322+-=+-a a a aB .)11(1xyxy xy -=-C .)1)(1(12-+=-x x xD .22)21(412+=++x x x 10.下列因式分解错误的是( ) A .22()()x y x y x y -=+- B .2269(3)x x x ++=+C .2()x xy x x y +=+D .222()x y x y +=+11.在边长为的正方形中挖去一个边长为的小正方形()(如图甲),把余下的部分拼成一个矩形(如图乙),根据两个图形中阴影部分的面积相等,可以验证() A .B .=+-+)(3)(2y x y x a b a b >222()2a b a ab b +=++222()2a b a ab b -=-+C .D .12.因式分解:(1)32)(12)(18b a b a ---(2)32)()(x y y x --- (3)22819212++(4)22821y x - 【大展身手】1.把下列各式分解因式正确的是() A .xy 2-x 2y = x(y 2-xy) B.9xyz -6x 2y 2=3xyz(3-2xy)C.3a 2x -6bx+3x=3x(a 2-2b)D.221xy +y x 221=xy 21(x+y) 2.-6x n -3x 2n 分解因式正确的是()A .3(-2x n -x 2n )B.-3x n (2-x n )C.-3(2x n +x 2n )D.-3x n (x n +2)3.下列多项式中能用完全平方公式分解的是()①x 2-4x+4②6x 2+3x+1③4x 2-4x+1④x 2+4xy+2y 2⑤9x 2-20xy+16y 2A .①②B .①③C .②③D .①⑤4.把多项式(3a -4b )(7a -8b)+(11a -12b)(8b -7a)分解因式的结果是() A .8(7a -8b)(a -b) B .2(7a -8b)2C .8(7a -8b)(b -a)D .-2(7a -8b)25.在多项式①16x 5-x ;②(x -1)2-4(x -1)+4;③(x+1)4-4x(x+1)2+4x 2④-4x 2-1+4x 中,分解因式的结果中含有相同因式的是()A .①②B .③④C .①④D .②③6.观察下列各式①2a +b 和a +b ,②5m(a -b)和-a +b ,③3(a +b)和-a -b ,④x 2-y 2和x 2+y 2其中有公因式的是()A .①②B .②③C .③④D .①④7.分解因式: (1)916222-z y x(2)()()22481b a b a --+(3)3212123a a a -+-(4)()()16585222+-+-x x(5)222224)(b a b a -+ (6)3)(111)(11a b b a -+- 十字相乘法【知识要点】1、x 2+px+q 型的二次三项式中p 和q 都是整数:22()()a b a b a b -=+-22(2)()2a b a b a ab b +-=+-(1)找出a,b 使a+b=p 且ab=q(2)把q 分解成两个整数的积的符号规律:q>0则a,b 同号,若p>0,a,b 同正,若p<0,a,b 同负;q<0则a,b 异号,若p>0,a,b 中正数绝对值大,若p<0,a,b 中负数的绝对值大. (3)当二次项系数为负时,先提负号. (4)注意题目中换元思想的运用. 2、十字相乘法的步骤:(1)把二次项系数和常数项分别分解因数(2)尝试十字图,使经过十字交叉线相乘后所得的数的和为一次系数 (3)确定合适的十字图并写出因式分解的结果 (4)检验(我们形象的把它比喻成“拆两头,凑中间”) 【典型例题】 例1. 分解因式(1)2x 2-5x +3(2)-3x 2-5x-2(3)5x 2+7xy-6y 2.(4)12722+-xy y x(5)1002924+-x x (6)322222318126z xy z y x z y x ++- 例2. 分解因式(1)36)(5)(2-+++n m n m (2)26)(11)(222--+-x x x x (3)2220)(9)(c bc ac b a ++-+(4))3(4)(2+---y x y x例3. 已知多项式62++ax x 可分解为两个整系数的一次因式的积,求a 的值. 例4 分解因式:()mn x n m mnx +++222【小试锋芒】1. _____))(12(______102-+=-+x x x x 2. )4____)((______52++=++x x x x3. )3)(2(x x +-是多项式_____________的因式分解.4. 如果),3)((62+-=+-x n x mx x 那么m-n 的值是_________.5. 若关于x 的二次三项式122-+px x 能分解成两个整系数的一次多项式的积,则p 有_______个可能的取值. 6. 因式分解(1)342++x x (2)1522-+x x(3)2452-+x x (4)2142--x x(5)2232y xy x --(6)x 2+7xy +12y 2; (7)2243y xy x -+(8)222816y xy x ++ (9)2223y xy x --(10)228185y xy x -- (11)2212y xy x -+(12)226197y xy x -+ 7. 因式分解(1)y xy y x 1582-+-(2)36)5(12)5(222++-+a a a a (3)24)8)(6(22--+-+x x x x (4)26)(11)(222--+-x x x x 【大显身手】 1.把下列各式分解因式(1)91024+-x x (2)x x x 4335-+(3)1002924+-x x (4)120)8(22)8(2222++++a a a a (5))(2)(5)(723y x y x y x +-+-+ (6)3)5)(3(22-----x x x x 2.用简便方法计算: 1699809982++ 3.把48)4)(3)(2)(1(-----x x x x 分解因式.分组分解法【知识要点】 1.分组分解法(1)定义:分组分解法,适用于四项以上的多项式.(2)原则:分组后可直接提取公因式或直接运用公式,但必须使各组之间能继续分解. (3)有些多项式在用分组分解法时,分解方法并不唯一,无论怎样分组,只要能将多项式正确分解即可.(4)对于四项式,在分解时可以“二二”分组或“一三”分组; 对于五项式,在分解时一般是“三二”分组;对于六项式,在分解时采用“三三”、“三二一”或“二二二”分组。
因式分解 知识归纳与题型突破(12类题型清单)(原卷版)—2024-2025学年七年级数学上册沪教版

因式分解知识归纳与题型突破(12类题型)知识点一、公因式多项式的各项中都含有相同的因式,那么这个相同的因式就叫做公因式.特别说明:(1)公因式必须是每一项中都含有的因式.(2)公因式可以是一个数,也可以是一个字母,还可以是一个多项式.(3)公因式的确定分为数字系数和字母两部分:①公因式的系数是各项系数的最大公约数.②字母是各项中相同的字母,指数取各字母指数最低的.知识点二、提公因式法把多项式分解成两个因式的乘积的形式,其中一个因式是各项的公因式,另一个因式是,即,而正好是除以所得的商,这种因式分解的方法叫提公因式法.特别说明:(1)提公因式法分解因式实际上是逆用乘法分配律,即.m m 01 思维导图02 知识速记(2)用提公因式法分解因式的关键是准确找出多项式各项的公因式.(3)当多项式第一项的系数是负数时,通常先提出“—”号,使括号内的第一项的系数变为正数,同时多项式的各项都要变号.(4)用提公因式法分解因式时,若多项式的某项与公因式相等或它们的和为零,则提取公因式后,该项变为:“+1”或“-1”,不要把该项漏掉,或认为是0而出现错误.知识点三、公式法——平方差公式两个数的平方差等于这两个数的和与这两个数的差的积,即:特别说明:(1)逆用乘法公式将特殊的多项式分解因式.(2)平方差公式的特点:左边是两个数(整式)的平方,且符号相反,右边是两个数(整式)的和与这两个数(整式)的差的积.(3)套用公式时要注意字母和的广泛意义,、可以是字母,也可以是单项式或多项式.知识点四、公式法——完全平方公式两个数的平方和加上(减去)这两个数的积的2倍,等于这两个数的和(差)的平方.即,.形如,的式子叫做完全平方式.特别说明:(1)逆用乘法公式将特殊的三项式分解因式;(2)完全平方公式的特点:左边是二次三项式,是这两数的平方和加(或减)这两数之积的2倍. 右边是两数的和(或差)的平方.(3)完全平方公式有两个,二者不能互相代替,注意二者的使用条件.(4)套用公式时要注意字母和的广泛意义,、可以是字母,也可以是单项式或多项式.知识点五、十字相乘法利用十字交叉线来分解系数,把二次三项式分解因式的方法叫做十字相乘法.对于二次三项式,若存在,则特别说明:(1)在对分解因式时,要先从常数项的正、负入手,若,则()()22a b a b a b -=+-a b a b ()2222a ab b a b ++=+()2222a ab b a b -+=-222a ab b ++222a ab b -+a b a b 2x bx c ++pq c p q b=ìí+=î()()2x bx c x p x q ++=++2x bx c ++c 0c >p q、同号(若,则异号),然后依据一次项系数的正负再确定的符号(2)若中的为整数时,要先将分解成两个整数的积(要考虑到分解的各种可能),然后看这两个整数之和能否等于,直到凑对为止.知识点六、首项系数不为1的十字相乘法在二次三项式(≠0)中,如果二次项系数可以分解成两个因数之积,即,常数项可以分解成两个因数之积,即,把排列如下: 按斜线交叉相乘,再相加,得到,若它正好等于二次三项式的一次项系数,即,那么二次三项式就可以分解为两个因式与之积,即.特别说明:(1)分解思路为“看两端,凑中间”(2)二次项系数一般都化为正数,如果是负数,则提出负号,分解括号里面的二次三项.知识点七、分组分解法对于一个多项式的整体,若不能直接运用提公因式法和公式法进行因式分解时,可考虑分步处理的方法,即把这个多项式分成几组,先对各组分别分解因式,然后再对整体作因式分解——分组分解法.即先对题目进行分组,然后再分解因式.特别说明:分组分解法分解因式常用的思路有:方法分类分组方法特点二项、二项①按字母分组②按系数分组③符合公式的两项分组四项三项、一项先完全平方公式后平方差公式五项三项、二项各组之间有公因式分组分解法六项三项、三项二项、二项、二项各组之间有公因式0c <p q 、b p q 、2x bx c ++b c 、c b 2ax bx c ++a a 12a a a =c 12c c c =1212a a c c ,,,1221a c a c +2ax bx c ++b 1221a c a c b +=11a x c +22a x c +()()21122ax bx c a x c a x c ++=++a三项、二项、一项可化为二次三项式知识点八:添、拆项法把多项式的某一项拆开或填补上互为相反数的两项(或几项),使原式适合于提公因式法、公式法或分组分解法进行分解.要注意,必须在与原多项式相等的原则下进行变形.添、拆项法分解因式需要一定的技巧性,在仔细观察题目后可先尝试进行添、拆项,在反复尝试中熟练掌握技巧和方法.知识点九:因式分解的解题步骤因式分解的方法主要有: 提公因式法, 公式法, 分组分解法, 十字相乘法, 添、拆项法等.特别说明:落实好方法的综合运用:首先提取公因式,然后考虑用公式;两项平方或立方,三项完全或十字;四项以上想分组,分组分得要合适;几种方法反复试,最后须是连乘式;因式分解要彻底,一次一次又一次.题型一 判断是否是因式分解1.下列各式从左到右的变形中,不是因式分解的是( )A .21(1)(1)a a a -=+-B .222()ab ac a b c +=+C .2269(3)x x x -+=-D .241(2)(2)1m m m m -+=+-+2.下列各式中,从左到右的变形是因式分解的是( )A .()22244a c ab ac b --=--B .()a x y ax ay +=+C .()()22339x y x y x y+-=-D .()222963a ab b a b ++=+3.下列等式从左到右的变形中,属于因式分解的是( )A .()()24313x x x x -+=--03 题型归纳B .()27373x x x x +--=+C .()()2339x x x +-=+D .()()213113x x x x x +=+-+-巩固训练1.下列变形是因式分解的是( )A .()()243223a a a a a-+=-++B .2244(2)x x x ++=+C .111x x x æö+=+ç÷èøD .2(1)(1)1x x x +-=-2.给出下列六个多项式:①x 2+y 2;②-x 2+y 2;③x 2+2xy +y 2;④x 4-1;⑤x(x +1)-2(x +1);⑥m 2-mn +14n 2.其中,能因式分解的是(填序号).3.下列各式从左到右的变形,哪些是因式分解?哪些不是因式分解?(1)2(1)(2)2x x x x +-=--;(2)2223(1)2x x x ++=++;(3)2)39631)(2(xy xy x x y y -+=--;(4)2224129()23x xy y x y ++=+ 题型二 已知因式分解的结果求参数4.若多项式2x x b ++因式分解的结果为(3)(2)x x +-,则b 的值是( )A .5B .5-C .6D .6-5.若()2242x mx x ++=-,则下列结论正确的是( )A .等式从左到右的变形是乘法公式,4m =B .等式从左到右的变形是因式分解,4m =C .等式从左到右的变形是乘法公式,4m =-D .等式从左到右的变形是因式分解,4m =-6.把多项式232x ax +-分解因式,结果是()()31x x b ++,则a ,b 的值为( )A .72a b ==,B .52a b ==,C .72a b =-=-,D .52a b =-=-,巩固训练1.因式分解()()2122x mx x x n +-=++,其中m 、n 都为整数,则m 的值是( )A .6-B .5-C .4-D .42.已知二次三项式24x x m -+有一个因式是3x +,则m 的值为 .3.仔细阅读下面例题,解答问题:已知二次三项式24x x m -+有一个因式是3x +,求另一个因式以及m 的值.解:设另一个因式为()x n +,得24(3)()x x m x x n -+=++则224(3)3x x m x n x n-+=+++343n m n+=-ì\í=î解得:7,21n m =-=-.∴另一个因式为(7)x -,m 的值为21-. 问题:仿照以上方法解答下面问题:(1)已知二次三项式23x x k -+有一个因式是(2)x +,求另一个因式以及k 的值.(2)已知二次三项式223x x k +-有一个因式是(25)x -,则另一个因式为 ,k 的值为 .(3)已知二次三项式2341x ax ++有一个因式是()x a +,a 是正整数,则另一个因式为 ,a 的值为 .题型三 提公因式法分解因式7.如图,长方形的长和宽分别是x ,y ,它的周长为14,面积为10.则22x y xy +的值为( )A .140B .70C .14D .108.若4a b +=,2ab =,则22a b ab +的值为( )A .4B .8C .12D .169.已知23a b -=,2ab =,则222a b ab -的值为( )A .5-B .6C .6-D .5巩固训练1.把多项式()()2262a x a -+-分解因式,结果是( )A .()()226a x -+B .()()226a x --C .()()2213a x -+D .()()2213a x --2.多项式229363x y xy xy -+-提公因式3xy -后的另一个因式为 .3.分解因式:(1)²²a x ax-(2)214749abc ab ab c--+题型四 公因式10.把22mn mn +分解因式,应提取的公因式是( )A .2mB .mnC .2mnD .2mn 11.用提公因式法因式分解多项式: 232812a b a b c -,其中的公因式是( )A .28a bB .3212a b cC .4abD .24a b12.多项式2210mx nx -的公因式是( )A .2B .xC .2xD .2mn巩固训练1.把多项式3123ab ab +分解因式,应提的公因式是( )A .12abB .4abC .3abD .33ab 2.多项式323612a m a m am -+的公因式是.3.已知:2312A x =-,233510B x y xy =+,(1)(3)1C x x =+++.问多项式A ,B ,C 是否有公因式?若有,求出其公因式;若没有,请说明理由.题型五 平方差公式分解因式13.下列各式能用平方差公式进行因式分解的是( )A .222x y --B .21x -+C .21x +D .244x x ++14.下列各式能用平方差公式进行分解因式的是( )A .21x +B .21x -+C .22x y --D .244x x ++15.已知4821-可以被60到70之间的某两个整数整除,则这两个数分别是( )A .61,62B .61,63C .63,65D .65,67巩固训练1.下列多项式中,能运用平方差公式分解因式的是( )A .22a b +B .22a b -C .224a b --D .229a b -+2.小明抄在作业本上的式子29x y Å-(“Å”表示漏抄的指数),不小心漏抄了x 的指数,他只知道该数为小于5的正整数,并且能利用平方差公式分解因式,请你帮小明写出这个整式分解因式的结果:.3.小明遇到下面一个问题:计算.()()()248(21)212121++++.经过观察,小明发现如果将原式进行适当的变形后可以出现特殊的结构,进而可以应用平方差公式解决问题,具体解法如下:()()()248(21)212121++++()()()()()2482121212121=-++++()()()()224821212121=-+++()()()448212121=-++()()882121=-+1621=-.请你根据小明解决问题的方法,试着解决以下的问题:(1)()()()()24816(21)21212121+++++(2)()()()()24816(31)31313131+++++(3)2222211111111112344950æöæöæöæöæö-´-´-´´--ç÷ç÷ç÷ç÷ç÷èøèøèøèøèøL 题型六 完全平方公式分解因式16.下列各式中,不能用完全平方公式因式分解的是( )A .222x y xy ++B .222x y xy -++C .222x y xy--+D .222x y xy---17.下列多项式(1)22a b +;(2)22a ab b -+;(3)()22222x y x y +-;(4)29x -;(5)22288x xy y ++.其中能用公式法分解因式的个数有( )A .2个B .3个C .4个D .5个18.无论a 、b 为任何实数,代数式224613a b a b +-++的值总是( )A .非正数B .非负数C .0D .正数巩固训练1.若223894613M x xy y x y =-+-++,则M 的值一定是( )A .0B .负数C .正数D .非负数2.已知实数x ,y 满足22145x xy y y -+-=-,则2x y +=.3.若2025,2026,2027202720272027m m ma b c =+=+=+,求222a b c ab bc ca ++---的值.题型七 综合运用公式法分解因式19.下列因式分解不正确的是( )A .﹣x 2﹣2x ﹣1=﹣(x +1)2B .2x 2﹣4xy ﹣2y 2=2(x ﹣y )2C .4x 2﹣16y 2=4(x +2y )(x ﹣2y )D .x 2+4x =x (x +4)20.下列因式分解正确的是( )A .x 2﹣9=(x ﹣3)2B .x 2﹣2x ﹣1=x (x ﹣2)﹣1C .4y 2﹣8y +4=(2y ﹣2)2D .x (x ﹣2)﹣(2﹣x )=(x ﹣2)(x +1)21.在把多项式2223m mn n --因式分解时,虽然它不符合完全平方公式,但经过变形,可以利用完全平方公式进行分解:原式()()()222222443m mn n n m n n m n m n =-+-=--=+-,像这样构造完全平方式的方法称之为“配方法”.用这种方法把多项式2265a ab b +-因式分解的结果是( )A .()()5a b a b ++B .()()5a b a b -+C .()()5a b a b +-D .()()5a b a b --巩固训练1.对于:①()2242x x -=-;②()()2111x x x -+=+-;③()23242x x x +-=+;④22111142x x x æö-+=-ç÷èø.其中因式分解正确的是( )A .①③B .②③C .①④D .②④2.在实数范围内因式分解:2236x x --= .3.因式分解:(1)3269x y x y xy-+(2)()222416x x +-题型八 综合提公因式和公式法分解因式22.代数式()()3327x y x y +-+分解因式的结果正确的是( )A .()()()333x y x y x y ++++-B .()()239x y x y éù++-ëûC .()()233x y x y +++D .()()233x y x y ++-23.规定新运算:32a b a b Å=-,其中22a x xy =+,236b xy y =+,则把a b Å因式分解的结果是()A .3(2)(2)x y x y +-B .23(2)x y -C .223(4)x y -D .3(4)(4)x y x y +-24.多项式2m m -与多项式2242m m -+的公因式是( )A .1m -B .1m +C .21m -D .2(1)m -巩固训练1.下列各式从左到右的变形,因式分解正确的是( )A .()22369a a a +=++B .()24444a a a a -+=-+C .()()22222ax ay a x y x y -=+-D .()()21234a a a a --=-+2.分解因式:32242x x x ++= .3.把下列各式因式分解.(1)261215x y xy y --+;(2)()()322n m n m -+-;(3)()()()22221211x y x y y -++--;(4)()()131x x --+.题型九 因式分解在有理数简算中的应用25.若3m n +=,则222425m mn n ++-的值为( )A .13B .18C .5D .126.若a +b =1,则222a b b -+的值为( )A .4B .3C .2D .127.已知ab =4,b ﹣a =7,则a 2b ﹣ab 2的值是( )A .11B .28C .﹣11D .﹣28巩固训练1.计算22222111111111123456æöæöæöæöæö-´-´-´-´-ç÷ç÷ç÷ç÷ç÷èøèøèøèøèø的值为( ).A .512B .12C .712D .11302.计算:2222211111111112345n æöæöæöæöæö----×××-=ç÷ç÷ç÷ç÷ç÷èøèøèøèøèø .3.如图,从边长为a 的正方形纸片中剪掉一个边长为b 的正方形纸片,然后将剩余部分拼成一个长方形(如图2).(1)上述操作能验证的等式是 .(2)利用你从(1)中得出的等式,计算:①已知22412x y -=,24x y +=求2x y -的值.②计算:222211111111234100æöæöæöæö-´-´-´×××´-ç÷ç÷ç÷ç÷èøèøèøèø.题型十 十字相乘法28.若多项式212x ax -+可分解为()()3x x b -+,则a b +的值为( )A .11-B .3-C .3D .1129.将2352x x -+在实数范围内因式分解,正确的结果是( )A .2(1)()3x x ++B .2(1)()3x x --C .23(1)()3x x -+D .(32)(1)x x --30.若多项式212x ax -+可分解为()()3x x b -+,则a b +的值为()A .11-B .3-C .3D .7巩固训练1.若二次三项式27x x n -+可分解成(3)()x x m -+,则m n -的值是( )A .﹣16B .﹣8C .8D .162.人教版八年级上册121页的教材呈现:分解因式232x x ++的过程,也可以用十字相乘的形式形象地表示:先分解二次项系数,分别写在十字交叉线的左上角和左下角;再分解常数项,分别写在十字交叉线的右上角和右下角;然后交叉相乘,求代数和,使其等于一次项系数(如图).这样,我们也可以得到()()23212x x x x ++=++.请用“十字相乘法”分解因式:2253x x --= .3.提出问题:你能把多项式256x x ++因式分解吗?探究问题:如图1所示,设a ,b 为常数,由面积相等可得:22()()()x a x b x ax bx ab x a b x ab ++=+++=+++,将该式从右到左使用,就可以对形如2()x a b x ab +++的多项式进行进行因式分解即2()()()x a b x ab x a x b +++=++.观察多项式2()x a b x ab +++的特征是二次项系数为1,常数项为两数之积,一次项为两数之和.解决问题:2256(23)23(3)(2)x x x x x x ++=+++´=++运用结论:(1)基础运用:把多项式进行因式分解.①2524x x --;②2812x x ++;③212x x --.(2)知识迁移:对于多项式24415x x --进行因式分解还可以这样思考:将二次项24x 分解成图2中的两个2x 的积,再将常数项15-分解成5-与3的乘积,图中的对角线上的乘积的和为4x -,就是24415x x --的一次项,所以有24415(25)(23)x x x x --=-+.这种分解因式的方法叫做“十字相乘法”.请用十字相乘法进行因式分解:231914x x --题型十一 分组分解法31.已知3a b +=,1ab =,则多项式22a b ab a b +--的值为( )A .1-B .0C .3D .632.已知3a b -=,4b c -=-,则代数式()2a ac b a c ---的值为( )A .4B .4-C .12-D .3-33.若实数x 满足x 2-2x-1=0,则2x 3-7x 2+4x-2019的值为( )A .-2019B .-2020C .-2022D .-2021巩固训练1.用分组分解法将222x xy y x --+分解因式,下列分组不恰当的是( )A .()()222x x y xy --+B .()()222x xy y x --+C .()()222x y xy x ++--D .()()222x x xy y ---2.因式分解222a x ax x xb -+-= .3.阅读下列材料:某校“数学社团”活动中,研究发现常用的分解因式的方法有提取公因式法、公式法,但还有很多的多项式只用上述方法无法分解,如:“222m mn m n -+-,细心观察这个式子就会发现,前两项可以提取公因式,后两项也可提取公因式,前后两部分分别分解因式后产生了新的公因式.然后再提取公因式就可以完成整个式子的因式分解了,过程为()()()()()()22222222m mn m n m mn n m m n m n m n m -+-=-+=-+-=-+.“社团”将此种因式分解的方法叫做“分组分解法”,请在这种方法的启发下,解决以下问题:(1)分解因式:32339a a a -+-;(2)已知7m n +=,1m n -=,求2222m n m n -+-的值.题型十二 因式分解的应用34.已知3xy =-,2x y -=,则代数式22xy x y -的值是( )A .6-B .6C .5-D .1-35.若4a b +=,1a b -=,则()()2211+--a b 的值为( )A .12B .4C .6D .12-36.多项式26x ax +-分解因式为()()x m x n ++,其中a ,m ,n 为整数,则a 的取值有( )A .2个B .4个C .6个D .无数个巩固训练1.已知a 、b 、c 为正整数,且22219a b c ab bc ac ++---=,那么a b c ++的最小值等于( )A .11B .10C .8D .62.如果一个正整数能表示为两个连续正奇数的平方差,那么称这个正整数为“正巧数”.例如: 222222831,1653,2475=-=-=-,因此8,16,24都是“正巧数”. m 、n 为正整数,且m n >,若 ()()2772m m n mn -++-是“正巧数”,则m n -的值为 .3.教科书中这样写道:“我们把多项式222a ab b ++及222a ab b -+叫做完全平方式”,如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项,使式子中出现完全平方式,再减去这个项,使整个式子的值不变,这种方法叫做配方法.配方法是一种重要的解决问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决一些与非负数有关的问题或求代数式最大值,最小值等.例如:分解因式.原式()()()()()()22222321412121231x x x x x x x x x =+-=++=+-=+++-=+--;例如:求代数式2246x x +-的最小值.原式()()222246223218x x x x x =+-=-=+-+.可知当1x =-时,2246x x +-有最小值,最小值是-8.(1)分解因式:223a a --=______.(2)试说明:x 、y 取任何实数时,多项式22426x y x y +-++的值总为正数.(3)当m ,n 为何值时,多项式22224425m mn n m n -+--+有最小值,并求出这个最小值.。
沪教版(上海)数学七年级第一学期9.5 因式分解 专项巩固训练(一)

【因式分解】专项巩固训练(一)一.选择题1.如果x2+kx﹣2=(x﹣1)(x+2),那么k应为()A.3B.﹣3C.1D.﹣12.如果多项式abc+ab2﹣a2bc的一个因式是ab,那么另一个因式是()A.c﹣b+5ac B.c+b﹣5ac C.ac D.﹣ac3.下列各式从左到右的变形属于因式分解的是()A.(x+2)(x﹣3)=x2﹣x﹣6B.6xy=2x2•3y3C.x2+2x+1=x(x2+2)+1D.x2﹣9=(x﹣3)(x+3)4.若x2﹣6x+m=(x﹣n)2,那么m、n的值分别是()A.m=3,n=3B.m=9,n=3C.m=3,n=﹣3D.m=9,n=﹣35.下列多项式因式分解结果是(x+1)(x﹣6)的是()A.x2﹣5x+6B.x2+5x﹣6C.x2﹣6x﹣5D.x2﹣5x﹣66.小南是一位密码编译爱好者,在他的密码手册中有这样一条信息:x﹣1,a﹣b,3,x2+1,a,x+1分别对应下列六个字:益,爱,我,数,学,广,现将3a(x2﹣1)﹣3b(x2﹣1)因式分解,结果呈现的密码信息可能是()A.我爱学B.爱广益C.我爱广益D.广益数学7.若实数x满足x2﹣2x﹣1=0,则2x3﹣7x2+4x﹣2017的值为()A.2019B.﹣2019C.2020D.﹣20208.因式(m+2n)(m﹣2n)是下列哪个多项式分解因式的结果()A.m2+4n2B.﹣m2+4n2C.m2﹣4n2D.﹣m2﹣4n29.若实数x满足x2﹣2x﹣1=0,则2x3﹣7x2+4x﹣2019的值为()A.﹣2019B.﹣2020C.﹣2022D.﹣2021 10.如图,边长为a,b的矩形的周长为10,面积为6,则a2b+ab2的值为()A.60B.16C.30D.11二.填空题11.分解因式:6xy2﹣9x2y﹣y3=.12.因式分解:2m2﹣12m+18=.13.分解因式:m3﹣m=.14.把多项式3ax2﹣12a分解因式的结果是.15.若m3+m﹣1=0,则m4+m3+m2﹣2=.三.解答题16.分解因式:(1)3a2﹣9ab;(2)x2(x﹣y)+9(y﹣x);(3)﹣3ma2+12ma﹣12m;(4)(x+y)2﹣2x﹣2y+1.17.你能把多项式x2+5x+6因式分解吗?(1)上式能利用完全平方公式进行因式分解吗?(2)常数项6是哪两个因数的乘积?一次项系数5是否等于6的某两个因数的和?(3)由多项式乘法,(x+a)(x+b)=x2+(a+b)x+ab,将该式从右到左地使用,即可对形如x2+(a+b)x+ab的多项式进行因式分解.多项式x2+(a+b)x+ab的特征是二次项系数为1,常数项为两数之积,一次项系数为这两数之和.你能据此将x2+5x+6写成两个一次多项式的乘积吗?x2+(+)x+×=(x+)(x+)请把填上数后的两个一次多项式相乘,验证乘积是否等于x2+5x+6.(4)从第(3)题,你能看出把x2+5x+6进行因式分解的关键步骤是什么吗?(5)你能运用上述方法将多项式x2﹣x﹣2进行因式分解吗?18.已知a﹣b=1,a﹣c=3.(1)求5b﹣5c+7的值:(2)求a2+b2+c2﹣ab﹣ac﹣bc的值.19.如图,将一张矩形纸板按图中虚线裁剪成九块,其中有两块是边长都为m的大正方形,两块是边长都为n的小正方形,五块是长为m,宽为n的全等小矩形,且m>n,(以上长度单位:cm)(1)观察图形,发现代数式2m2+5mn+2n2可以因式分解,请写出因式分解的结果;(2)若每块小矩形的面积为7cm2,四个正方形的面积和为100cm2,试求图中所有裁剪线(虚线部分)长之和.20.我们把只含有一个未知数,并且未知数的次数都是1的不等式,叫做一元一次不等式.同样,我们把只含有一个未知数,并且未知数的最高次数是2的不等式,叫做一元二次不等式.小明同学用自己的方法来解一元二次不等式:x2+x﹣12>0.小明观察到不等式右侧为0.左边可以利用因式分解的方法,分解为(x+4)(x﹣3),根据有理数乘法法则:两数相乘,同号得正,异号得负,可以将不等式等价转化为两个不等式组:∵(x+4)(x﹣3)>0∴(1)或(2)解得:由(1)式得x>3,由(2)式得x<﹣4.∴原不等式的解集为x>3或x<﹣4.利用以上信息解以下不等式:①2x2+x﹣3<0;②x3+2x2﹣x﹣2<0;③x3﹣3x+2>0.(2)已知x=2是不等式a2x2+2ax﹣3≥0的解,且x=﹣1是不等式a2x2﹣3ax﹣2a﹣12>0的解,求实数a的取值范围.参考答案一.选择题1.解:由题意得,x2+kx﹣2=(x﹣1)(x+2)=x2+x﹣2,则k=1.故选:C.2.解:abc+ab2﹣a2bc=ab(c+b﹣5ac),故另一个因式为(c+b﹣5ac),故选:B.3.解:A、是整式的乘法,故此选项不符合题意;B、不属于因式分解,故此选项不符合题意;C、没把一个多项式转化成几个整式积的形式,故此选项不符合题意;D、把一个多项式转化成几个整式积的形式,故此选项符合题意;故选:D.4.解:∵x2﹣6x+m=(x﹣3)2=(x﹣n)2,∴m=32=9,n=3,故选:B.5.解:A、原式=(x﹣2)(x﹣3),不符合题意;B、原式=(x﹣1)(x+6),不符合题意;C、原式不能分解,不符合题意;D、原式=(x+1)(x﹣6),符合题意.故选:D.6.解:3a(x2﹣1)﹣3b(x2﹣1)=3(x2﹣1)(a﹣b)=3(x+1)(x﹣1)(a﹣b),∵x﹣1,a﹣b,3,x2+1,a,x+1分别对应下列六个字:益,爱,我,数,学,广,∴3(x+1)(x﹣1)(a﹣b)对应的信息可能是我爱广益,故选:C.7.解:∵x2﹣2x﹣1=0,∴x2﹣2x=1,2x3﹣7x2+4x﹣2017=2x3﹣4x2﹣3x2+4x﹣2017=2x(x2﹣2x)﹣3x2+4x﹣2017=6x﹣3x2﹣2017=﹣3(x2﹣2x)﹣2017=﹣3﹣2017=﹣2020.故选:D.8.解:A.m2+4n2是平方和,不能进行因式分解,此选项不符合题意;B.原式=﹣[m2﹣(2n)2]=﹣(m+2n)(m﹣2n),此选项不符合题意;C.原式=m2﹣(2n)2=(m+2n)(m﹣2n),此选项符合题意;D.不能进行因式分解,此选项不符合题意;故选:C.9.解:∵x2﹣2x﹣1=0∴x2﹣2x=1∴2x3﹣7x2+4x﹣2019=2x3﹣4x2﹣3x2+4x﹣2019=2x(x2﹣2x)﹣3x2+4x﹣2019=6x﹣3x2﹣2019=﹣3(x2﹣2x)﹣2019=﹣3﹣2019=﹣2022故选:C.10.解:∵边长为a,b的矩形的周长为10,面积为6,∴2(a+b)=10,ab=6,∴a+b=5,∴a2b+ab2=ab(a+b)=6×5=30.故选:C.二.填空题11.解:原式=﹣y(y2﹣6xy+9x2)=﹣y(3x﹣y)2,故答案为:﹣y(3x﹣y)212.解:原式=2(m2﹣6m+9)=2(m﹣3)2.故答案为:2(m﹣3)2.13.解:m3﹣m,=m(m2﹣1),=m(m+1)(m﹣1).故答案为:m(m+1)(m﹣1).14.解:3ax2﹣12a=3a(x2﹣4)=3a(x+2)(x﹣2),故答案为:3a(x+2)(x﹣2).15.解:∵m3+m﹣1=0,∴m3+m=1,∴m4+m3+m2﹣2=m4+m2+m3﹣2=m(m3+m)+m3﹣2=m×1+m3﹣2=m+m3﹣2=1﹣2=﹣1.故答案为:﹣1.三.解答题16.解:(1)原式=3a(a﹣3b);(2)原式=(x﹣y)(x2﹣9)=(x﹣y)(x+3)(x﹣3);(3)原式=﹣3m(a2﹣4a+4)=﹣3m(a﹣2)2;(4)原式=(x+y)2﹣2(x+y)+1=(x+y﹣1)2.17.解:(1)不能利用完全平方公式进行因式分解.(2)常数项6=2×3,一次项系数5=2+3,答:常数项6是2和3乘积,一次项系数5正好等于6的某两个因数2与3的和;(3)x2+5x+6=x2+(2+3)x+2×3=(x+2)(x+3),故答案为:2,3,2,3,2,3;(x+2)(x+3)=x2+3x+2x+6=x2+5x+6,(4)关键的步骤为:将常数项分解成两个因数的积,而一次项系数正好等于这两个因数的和,(5)x2﹣x﹣2=x2+(﹣2+1)x+(﹣2)×1=(x﹣2)(x+1).18.解:(1)∵a﹣b=1,a﹣c=3,∴b﹣c=3﹣1=2,∴5b﹣5c+7=5(b﹣c)+7=17;(2)a2+b2+c2﹣ab﹣ac﹣bc=×(a2+b2+c2+a2+b2+c2﹣2ab﹣2ac﹣2bc)=[(a﹣b)2+(a﹣c)2+(b﹣c)2],∵a﹣b=1,a﹣c=3,b﹣c=2,∴a2+b2+c2﹣ab﹣ac﹣bc=×(1+9+4)=7.19.解:(1)观察图形,发现代数式2m2+5mn+2n2=(2m+n)(m+2n)(2)若每块小矩形的面积为7cm2,四个正方形的面积和为100cm2则mn=7cm2,2m2+2n2=100cm2∴m2+n2=50∴(m+n)2=50+7×2=64∴m+n=8∴图中所有裁剪线(虚线部分)长之和为6m+6n=6(m+n)=48(cm)∴图中所有裁剪线(虚线部分)长之和为48cm.20.(1)解:①∵(x﹣1)(2+3)<0,∴①或②,①式无解;由②式得﹣<x<1,∴原不等式的解集为﹣<x<1;②x3+2x2﹣x﹣2<0,∴x3+2x2<x+2,即x2(x+2)<x+2,当x<﹣2时,x2>1成立;当x=﹣2时不成立;当x>﹣2时要使x2<1成立,所以﹣1<a<1综上所述:原不等式的解集为x<﹣2或﹣1<a<1;③∵x3﹣3x+2>0可化为(x﹣1)(x2+x﹣2)>0,即(x﹣1)(x﹣1)(x+2)>0,∴(x﹣1)2(x+2)>0,∵(x﹣1)2≥0,∴x+2>0,即原不等式解集为x>﹣2且x≠1;(2)将x=2和x=﹣1别代入不等式得4a2+4a﹣3≥0且a2+a﹣12≤0,对于第一个不等式:∵(2a﹣1)(2a+3)<0,∴①或②,①无解;由②得﹣<a<,所以第一个不等式的解集为:﹣<a<;对于第二个不等式∵a2+a﹣12≤0即(a﹣3)(a+4)≤0,∴①或②,由①得﹣4≤a≤3;②无解;所以第二个不等式的解集为:﹣4≤a≤3.综合两个不等式得a得取值范围为:﹣<a<.。
沪教版七年级上册 因式分解,带答案

因式分解课时目标1. 正确理解因式分解的意义,了解因式分解与整式乘法的区别.2. 理解多项式的公因式的概念,掌握用提取公因式法分解因式.3. 理解整式乘法公式在因式分解中的作用.4. 掌握运用公式法分解因式.知识精要1. 因式分解的意义:把一个多项式化为______________,叫做把这个多项式因式分解,也叫做把这个多项式分解因式.2. 多项式的公因式(1) 意义:一个多项式中每一项都含有的因式叫做这个多项式的_______.(2) 找公因式的方法公因式的系数应取各项系数的__________,字母取各项中都含有的相同的字母,而且各个相同字母的指数取次数_______.3. 提取公因式法如果一个多项式的各项有公因式,可以把公因式提到括号外面,将公因式写成因式乘积的形式,这种分解因式的方法叫做______________.4. 公式法(1) 意义逆用乘法公式将一个多项式分解因式的方法叫做_______.(2) 因式分解公式平方差公式:22__________a b -=完全平方公式:=++222b ab a _________________=+-222b ab a _________________33_____________a b +=,33_____________a b -=.5. 十字相乘法一般地,))(()(2q x p x pq x q p x ++=+++十字相乘法的关键:把常数项分解成两个数的乘积,并且满足这两个数相加等于一次项系数;(口诀:首尾分解,交叉相乘,求和凑中)6. 分组分解法利用分组来分解因式的方法叫做__________.7. 因式分解的一般步骤(1)如果多项式的各项有公因式,那么先提取公因式(2)如果多项式的各项无公因式,那么可以尝试运用公式法或十字相乘法来分 解.一般地,若是二项式,则考虑平方差公式;若是三项式,则考虑用完全 平方公式或十字相乘法.(3)如果上述方法不能分解,那么应考虑分组分解法.(4)分解因式,必须进行到每一个因式都不能分解为止.热身练习1.从下列从左到右的变形,哪些是因式分解?哪些不是?(1)()a m n am an +=+ ;(2)2221(2)(1)(1)a ab b a a b b b ++-=+++-;(3)211()x x x x+=+; (4)4(4)ax x x a -=-;(5)22()()a b a b a b -=+-;2.多项式32215()10()a b a b c a b a b +++的公因式是_____________.3. 分解因式(1)232322x y x y x y z --+; (2)26()12()a x y a y x -+-;(3) 6(2)(2)x x x ++--; (4)3223()9()m x y m y x ---;精解名题将下列各式分解因式(1)4116x -;(2)2225()4()a b c a b c -+-+-;(3) 22222()4x y x y +-;(4) 22()4()4a b c c a b c c ++-+++;(5)2215x x --;(6) 2()4()12x y x y +-+-;(7) 2x bx a ab --+;备选例题1.配凑法分解因式(1)444x y +;(2)3253x x --;(3)在实数范围内分解因式4323231x x x x ++++(4)2222x ax b ab --+(5)51a a ++2. 用待定系数法分解因式(1) 22282143x xy y x y +-++-(2)224434103x xy y x y +----3. 换元法分解因式(1)22(23)(224)90x x x x +-+-+(2)432653856x x x x +-++方法提炼因式分解中的四个注意,可用四句话概括如下:1、首项有负常提负,2、各项有“公”先提“公”,3、某项提出莫漏1,4、括号里面分到“底”.巩固练习1.分解因式(1) 1xy x y -+- (2)222a ab -(3) 2221a b a --+ (4)33222ax y axy ax y +-(5)328m m - (6)am an bm bn +++2.计算:2222211111(1)(1)(1)(1)(1)234910-----.3.(勾股定理)已知a 、b 、c 是△ABC 的三边,且满足224224c a b c b a +=+,试判断△ABC 的形状.当堂总结多项式因式分解的一般步骤:①如果多项式的各项有公因式,那么先提公因式;②如果各项没有公因式,那么可尝试运用公式、十字相乘法来分解;③如果用上述方法不能分解,那么可以尝试用分组、拆项、补项法来分解;④分解因式,必须进行到每一个多项式因式都不能再分解为止.自我测试一、选择题1.下列各式从左到右的变形属于分解因式的是( )A .(2)(3)(3)(2)m m m m --=--B .21(1)(1)a a a -=+-C .2(1)(1)1x x x +-=-D .2223(1)2a a a -+=-+2.下列各式的公因式是a 的是( )A .5ax ay ++B .246ma ma +C .2510a ab +D .24a a ma -+3.一次数学课上,老师出了下面一道因式分解的题目:41x -,请问正确的结果为( )A .22(1)(1)x x -+B .22(1)(1)x x +-C .2(1)(1)(1)x x x -++D .3(1)(1)x x -+4.多项式2244x xy y -+-分解因式的结果是( )A .2(2)x y -B .2(2)x y --C .2(2)x y --D .2()x y + 5. 222516a kab a ++是一个完全平方式,那么k 之值为( )A .40B .40±C .20D .20±6、若E p q p q q p ⋅-=---232)()()(,则E 是( )A.p q --1B.p q -C.q p -+1D.p q -+17、若)5)(3(+-x x 是q px x ++2的因式,则p 为( )A.-15B.-2C.8D.28、一次课堂练习,小敏同学做了如下4道因式分解题,你认为小敏做得不够完整的一题是( )A.32(1)x x x x -=- C.2222()x xy y x y -+=-B.22()x y xy xy x y -=-D.22()()x y x y x y -=-+ 9、一个多项式分解因式的结果是)2)(2(33b b -+,那么这个多项式是( )A.46-bB.64b -C.46+bD.46--b10、下列多项式的分解因式,正确的是( )A 、)34(391222xyz xyz y x xyz -=-B 、)2(363322+-=+-a a y y ay y aC 、)(22z y x x xz xy x -+-=-+-D 、)5(522a a b b ab b a +=-+11、下列各式不能..继续因式分解的是 ( ) A 、41x - B 、22x y - C 、2()x y - D 、22a a +二、填空题12、要在二次三项式x 2+□x -6的□中填上一个整数,然后按x 2+(a +b )x +a b 型分解为(x +a )(x +b )的形式,那么这个数是___________.13、如果=+=+-==+2222,3,5y x xy y x xy y x ,则.14、如果2a +3b =1,那么3-4a -6b = .15、若=,,则b a b b a ==+-+-01222.16、若A y x y x y x ⋅-=+--)(22,则A =___________.17、若a 2+2a +b 2-6b +10=0, 则a = ,b = .18、把3222x x y xy -+分解因式,结果是___________.19、因式分解:224a a -=___________.(x +3)2 - (x +3) =___________.20、已知正方形的面积是9x 2+6xy +y 2平方单位,则正方形的边长是___________.三、计算题21、因式分解(1)22105m mn + (2)222120x x ++(3)x x x 2718323+- (4)()()3224x y y x ---(5)()222164x x -+ (6)122222++--+a b ab b a(7)()()()()14321+++++x x x x (8)()()ab b a 41122---22、先分解因式,再求值:21,34,412922-==++y x y xy x 其中.23、先分解因式,再求值:已知22==+ab b a ,,求32232121ab b a b a ++的值。
特训03 因式分解压轴题(原卷版)2023-2024学年七年级数学上册同步讲义全优学案(沪教版)
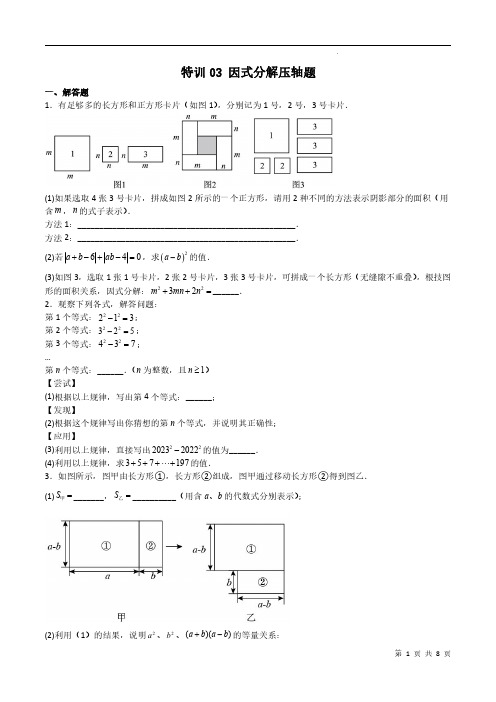
特训03因式分解压轴题一、解答题1.有足够多的长方形和正方形卡片(如图1),分别记为1号,2号,3号卡片.(1)如果选取4张3号卡片,拼成如图2所示的一个正方形,请用2种不同的方法表示阴影部分的面积(用含m ,n 的式子表示).方法1:__________________________________________________.方法2:__________________________________________________.(2)若640a b ab +-+-=,求()2a b -的值.(3)如图3,选取1张1号卡片,2张2号卡片,3张3号卡片,可拼成一个长方形(无缝隙不重叠),根技图形的面积关系,因式分解:2232m mn n ++=______.2.观察下列各式,解答问题:第1个等式:22213-=;第2个等式:22325-=;第3个等式:22437-=;…第n 个等式:______.(n 为整数,且1n ≥)【尝试】(1)根据以上规律,写出第4个等式:______;【发现】(2)根据这个规律写出你猜想的第n 个等式,并说明其正确性;【应用】(3)利用以上规律,直接写出2220232022-的值为______.(4)利用以上规律,求357197+++⋅⋅⋅+的值.3.如图所示,图甲由长方形①,长方形②组成,图甲通过移动长方形②得到图乙.(1)S =甲_______,S =乙__________(用含a 、b 的代数式分别表示);(2)利用(1)的结果,说明2a 、2b 、()()a b a b +-的等量关系:(3)应用所得的公式计算:22222111111111123499100⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫---⋯-- ⎪⎪⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭(4)如图丙,现有一块如图丙尺寸的长方形纸片,请通过对它分割,再对分割的各部分移动,组成新的图形,画出图形,利用图形说明2()a b +、2()a b -、ab 三者的等量关系.4.方法探究:已知二次多项式2421x x --,我们把3x =-代入多项式,发现24210x x --=,由此可以推断多项式中有因式(x +3).设另一个因式为(x +k ),多项式可以表示成()()24213x x x x k --=++,则有()2242133x x x k x k --=+++,因为对应项的系数是对应相等的,即34k +=-,解得7k =-,因此多项式分解因式得:()()242137x x x x --=+-.我们把以上分解因式的方法叫“试根法”.问题解决:(1)对于二次多项式24x -,我们把x =代入该式,会发现240x -=成立;(2)对于三次多项式3233x x x --+,我们把x =1代入多项式,发现32330x x x --+=,由此可以推断多项式中有因式(1x -),设另一个因式为(2x ax b ++),多项式可以表示成()()322331x x x x x ax b --+=-++,试求出题目中a ,b 的值;(3)对于多项式324318x x x +--,用“试根法”分解因式.5.数形结合思想是根据数与形之间的对应关系,通过数与形的相互转化来解决数学问题的思想.我们常利用数形结合思想,借助形的几何直观性来阐明数之间某种关系,如:探索整式乘法的一些法则和公式.(1)探究一:将图1的阴影部分沿虚线剪开后,拼成图2的形状,拼图前后图形的面积不变,因此可得一个多项式的分解因式____________________.(2)探究二:类似地,我们可以借助一个棱长为a 的大正方体进行以下探索:在大正方体一角截去一个棱长为()<b b a 的小正方体,如图3所示,则得到的几何体的体积为____________;(3)将图3中的几何体分割成三个长方体①、②、③,如图4、图5所示,∵BC a =,AB a b =-,CF b =,∴长方体①的体积为()ab a b -.类似地,长方体②的体积为________,长方体③的体积为________;(结果不需要化简)(4)用不同的方法表示图3中几何体的体积,可以得到的恒等式(将一个多项式因式分解)为______________.(5)问题应用:利用上面的结论,解决问题:已知a -b =6,ab =2,求33a b -的值.(6)类比以上探究,尝试因式分解:33+a b =.6.阅读下列材料:材料1:将一个形如x ²+px +q 的二次三项式因式分解时,如果能满足q =mn 且p =m +n 则可以把x ²+px +q 因式分解成(x +m )(x +n ),如:(1)x 2+4x +3=(x +1)(x +3);(2)x 2﹣4x ﹣12=(x ﹣6)(x +2).材料2:因式分解:(x +y )2+2(x +y )+1,解:将“x +y 看成一个整体,令x+y =A ,则原式=A ²+2A +1=(A +1)²,再将“A ”还原得:原式=(x +y +1)²上述解题用到“整体思想”整体思想是数学解题中常见的一种思想方法,请你解答下列问题:(1)根据材料1,把x 2+2x ﹣24分解因式;(2)结合材料1和材料2,完成下面小题;①分解因式:(x ﹣y )²﹣8(x ﹣y )+16;②分解因式:m (m ﹣2)(m ²﹣2m ﹣2)﹣37.我们知道对于一个图形,通过不同的方法计算图形的面积可以得到一个数学等式.例如:由图1可得到222()2a b a ab b +=++(1)写出由图2所表示的数学等式:_________________;(2)写出由图3所表示的数学等式(利用阴影部分):________________;(3)已知实数,,a b c 满足2221,1a b c a b c ++=++=.求:①ab bc ca ++的值;②3333a b c abc ++-的值.8.阅读以下内容解答下列问题.七年级我们学习了数学运算里第三级第六种开方运算中的平方根、立方根,也知道了开方运算是乘方的逆运算,实际上乘方运算可以看做是“升次”,而开方运算也可以看做是“降次”,也就是说要“升次”可以用乘方,要“降次”可以用开方,即要根据实际需要采取有效手段“升”或者“降”某字母的次数.本学期我们又学习了整式乘法和因式分解,请回顾学习过程中的法则、公式以及计算,解答下列问题:(1)对照乘方与开方的关系和作用,你认为因式分解的作用也可以看做是.(2)对于多项式x 3﹣5x 2+x+10,我们把x =2代入此多项式,发现x =2能使多项式x 3﹣5x 2+x+10的值为0,由此可以断定多项式x 3﹣5x 2+x+10中有因式(x ﹣2),【注:把x =a 代入多项式,能使多项式的值为0,则多项式一定含有因式(x ﹣a )】,于是我们可以把多项式写成:x 3﹣5x 2+x+10=(x ﹣2)(x 2+mx+n ),分别求出m 、n 后再代入x 3﹣5x 2+x+10=(x ﹣2)(x 2+mx+n ),就可以把多项式x 3﹣5x 2+x+10因式分解,这种因式分解的方法叫“试根法”.①求式子中m 、n 的值;②用“试根法”分解多项式x 3+5x 2+8x+4.9.阅读下面材料,解答后面的问题:“十字相乘法”能将二次三项式分解因式,对于形如22ax bxy cy ++的关于x ,y 的二次三项式来说,方法的关键是将2x 项系数a 分解成两个因数1a ,2a 的积,即12a a a =∙,将2y 项系数c 分解成两个因式1c ,2c 的积,即12c c c =∙,并使1221a c a c +正好等于xy 项的系数b ,那么可以直接写成结果:221221()()ax bxy cy a x c y a y c y ++=++例:分解因式:2228x xy y --解:如图1,其中111=⨯,8(4)2-=-⨯,而21(4)12-=⨯-+⨯所以2228(4)(2)x xy y x y x y --=-+而对于形如22ax bxy cy dx ey f +++++的关于x ,y 的二元二次式也可以用十字相乘法来分解.如图2.将a 分解成mn 乘积作为一列,c 分解成pq 乘积作为第二列,f 分解成fk 乘积作为第三列,如果mq np b +=,mk nj d +=,即第1、2列,第2、3列和第1、3列都满足十字相乘规则,则原式()()mx py f nx qy k =++++例:分解因式222332x xy y x y +-+++解:如图3,其中111=⨯,3(1)3-=-⨯,212=⨯而2131(1)=⨯+⨯-,1(1)231=-⨯+⨯,31211=⨯+⨯所以222332(1)(32)x xy y x y x y x y +-+++=-+++请同学们通过阅读上述材料,完成下列问题:(1)分解因式:①2263342x xy y -+=.②22261915x xy y x y --++-=.(2)若关于x ,y 的二元二次式22718340x xy y x my +--+-可以分解成两个一次因式的积,求m 的值.10.阅读下列因式分解的过程,再回答所提出的问题:()()()()2111111x x x x x x x x x +++++=++++⎡⎤⎣⎦()()()23111x x x =++=+.(1)上述分解因式的方法是______,共应用了______次;(2)若分解()()()220141111x x x x x x x ++++++++ ,则需应用上述方法______次,结果是______;(3)分解因式:()()()21111n x x x x x x x ++++++++ .(n 为正整数)11.若一个整数能表示成a 2+b 2(a 、b 是正整数)的形式,则称这个数为“完美数”。
十字相乘和分组分解法因式分解-2023年新七年级数学核心知识点与常见题型(沪教版)(解析版)

十字相乘和分组分解法因式分解【知识梳理】一、十字相乘十字相乘法:如果二次三项式2x px q ++中的常数项q 能分解成两个因式a 、b 的积,而且一次项系数p 又恰好是a b +,那么2x px q ++就可以进行如下的分解因式,即:()()()22x px q x a b x ab x a x b ++=+++=++要将二次三项式2x px q ++分解因式,就需要找到两个数a 、b ,使它们的积等于常数项q ,和等于一次项系数p , 满足这两个条件便可以进行如下分解因式, 即:22()()()x px q x a b x ab x a x b ++=+++=++.由于把2x px q ++中的q 分解成两个因数有多种情况,怎样才能找到两个合适的数,通常要经过多次的尝试才能确定采用哪种情况来进行分解因式.二、分组分解如何将多项式am an bm bn +++因式分解?分析:很显然,多项式am an bm bn +++中既没有公因式,也不好用公式法.怎么办呢?由于()am an a m n +=+,()bm bn b m n +=+而:()()()()a m n b m n m n a b +++=+.这样就有:()()()()()()am an bm bn am an bm bn a m n b m n m n a b +++=+++=+++=++将一个多项式分成二或三组,各组分别分解后,彼此又有公因式或者可以用公式,这就是分组分解法. 说明:如果把一个多项式的项分组并提出公因式后,它们的另一个因式正好相同,那么这个多项式就可以用分组分解法来分解因式.【考点剖析】一.因式分解-十字相乘法等(共22小题)1.(2022秋•静安区校级期中)多项式77x 2﹣13x ﹣30可因式分解成(7x +a )(bx +c ),其中a 、b 、c 均为整数,求a +b +c 之值为何?( )A .0B .10C .12D .22【分析】首先利用十字交乘法将77x2﹣13x ﹣30因式分解,继而求得a ,b ,c 的值.【解答】解:利用十字交乘法将77x2﹣13x﹣30因式分解,可得:77x2﹣13x﹣30=(7x﹣5)(11x+6).∴a=﹣5,b=11,c=6,则a+b+c=(﹣5)+11+6=12.故选:C.【点评】此题考查了十字相乘法分解因式的知识.注意ax2+bx+c(a≠0)型的式子的因式分解:这种方法的关键是把二次项系数a分解成两个因数a1,a2的积a1•a2,把常数项c分解成两个因数c1,c2的积c1•c2,并使a1c2+a2c1正好是一次项b,那么可以直接写成结果:ax2+bx+c=(a1x+c1)(a2x+c2).2.(2021秋•奉贤区期末)分解因式:x2+3x﹣10=.【分析】原式利用十字相乘法分解即可.【解答】解:原式=(x﹣2)(x+5),故答案为:(x﹣2)(x+5)【点评】此题考查了因式分解﹣十字相乘法,熟练掌握十字相乘的方法是解本题的关键.3.(2022秋•闵行区校级期末)因式分解:(y2﹣y)2﹣14(y2﹣y)+24.【分析】直接利用十字相乘法分解因式得出答案【解答】解:原式=(y2﹣y﹣2)(y2﹣y﹣12)=(y﹣2)(y+1)(y﹣4)(y+3).【点评】此题主要考查了十字相乘法分解因式,正确分解常数项是解题关键.4.(20222x2﹣6x﹣8=.【分析】原式先提取公因数2,再利用十字相乘法求出解即可.【解答】解:原式=2(x2﹣3x﹣4)=2(x﹣4)(x+1),故答案为:2(x﹣4)(x+1).【点评】本题考查了因式分解—十字相乘法,熟练掌握十字相乘的方法是解题的关键.5.(2022秋•虹口区校级期中)分解因式:x2﹣7xy﹣18y2=.【分析】由十字相乘法进行分解因式即可.【解答】解:x2﹣7xy﹣18y2=(x﹣9y)(x+2y).故答案是:(x﹣9y)(x+2y).【点评】本题考查因式分解,熟练掌握十字相乘法分解因式是解题的关键.6.(2022秋•宝山区期末)分解因式:2x2+6xy+4y2.【分析】先提公因式,再用十字相乘法因式分解即可.【解答】解:2x2+6xy+4y2=2(x2+3xy+2y2)=2(x+2y)(x+y).【点评】本题考查了提公因式法与十字相乘法的综合运用,熟练掌握因式分解的方法是解题的关键.7.(2022秋•宝山区期末)分解因式:x2﹣9x+14=(x+□)(x﹣7),其中□表示一个常数,则□的值是()A.7B.2C.﹣2D.﹣7【分析】利用十字相乘法因式分解即可.【解答】解:x2﹣9x+14=(x﹣2)(x﹣7),∴□表示﹣2,故选:C.【点评】本题考查因式分解,熟练掌握利用十字相乘法进行因式分解是解题的关键.8.(2022秋•虹口区校级期中)如果多项式x2﹣5x+c可以用十字相乘法因式分解,那么下列c的取值正确的是()A.2B.3C.4D.5【分析】∵4=﹣1×(﹣4),﹣1+(﹣4)=﹣5,∴可以用十字相乘法因式分解.【解答】解:当c=4时,x2﹣5x+c=x2﹣5x+4=(x﹣1)(x﹣4).故选:C.【点评】本题主要考查了因式分解﹣十字相乘法,熟练掌握十字相乘法分解因式的方法是解题关键.9.(2022x2﹣5x﹣6=.【分析】因为﹣6×1=﹣6,﹣6+1=﹣5,所以利用十字相乘法分解因式即可.【解答】解:x2﹣5x﹣6=(x﹣6)(x+1).【点评】本题考查十字相乘法分解因式,运用十字相乘法分解因式时,要注意观察,尝试,并体会它实质是二项式乘法的逆过程.10.(2022秋•嘉定区校级期末)因式分解a2﹣a﹣6=.【分析】根据因式分解就是把一个多项式变形成几个整式的积的形式的定义,利用十字相乘法求解.【解答】解:a2﹣a﹣6=(a+2)(a﹣3).故答案为:(a+2)(a﹣3).【点评】本题考查了因式分解.解题的关键是掌握十字相乘法因式分解.11.(2022秋•闵行区校级期中)因式分解:x2﹣5x﹣24=.【分析】用十字相乘法因式分解.【解答】解:x2﹣5x﹣24=(x﹣8)(x+3),故答案为:(x﹣8)(x+3),【点评】本题主要考查了因式分解﹣十字相乘法,熟练掌握十字相乘法分解因式的方法,根据题意可知a、b是相互独立的,利用多项式相乘法则计算,再根据对应系数相等即可求出a、b的值是解题关键.12.(2021秋•宝山区期末)分解因式:x2+4x﹣21=.【分析】根据因式分解﹣十字相乘法进行分解即可.【解答】解:x2+4x﹣21=(x+7)(x﹣3),故答案为:(x+7)(x﹣3).【点评】本题考查了因式分解﹣十字相乘法,熟练掌握因式分解﹣十字相乘法是解题的关键.13.(2021秋•普陀区期末)已知关于x的多项式x2+kx﹣3能分解成两个一次多项式的积,那么整数k的值为.【分析】把常数项分解成两个整数的乘积,k就等于那两个整数之和.【解答】解:∵﹣3=﹣3×1或﹣3=﹣1×3,∴k=﹣3+1=﹣2或k=﹣1+3=2,∴整数k的值为:±2,故答案为:±2.【点评】本题考查了因式分解﹣十字相乘法,熟练掌握因式分解﹣十字相乘法是解题的关键.14.(2022ax4﹣14ax2﹣32a.【分析】首先提取公因式a,再利用十字相乘法分解因式,再结合平方差公式分解因式即可.【解答】解:ax4﹣14ax2﹣32a=a(x4﹣14x2﹣32)=a(x2+2)(x2﹣16)=a(x2+2)(x+4)(x﹣4).【点评】此题主要考查了十字相乘法分解因式,正确运用公式是解题关键.15.(2022秋•嘉定区校级期中)阅读下列文字,解决问题.先阅读下列解题过程,然后完成后面的题目.分解因式:x4+4解:x4+4=x4+4x2+4﹣4x2=(x2+2)2﹣4x2=(x2+2x+2)(x2﹣2x+2)以上解法中,在x4+4的中间加上一项,使得三项组成一个完全平方式,为了使这个式子的值保持与x4+4的值保持不变,必须减去同样的一项.这样利用添项的方法,将原代数式中的部分(或全部)变形为完全平方的形式,这种方法叫做配方法.按照这个思路,试把多项式x4+3x2y2+4y4分解因式.【分析】把原式中的第二项的系数1变为4﹣1,化简后三项结合构成完全平方式,剩下的一项写出完全平方式,然后再利用平方差公式即可分解因式.【解答】解:x4+3x2y2+4y4=x4+4x2y2+4y4﹣x2y2=(x2+2y2)2﹣x2y2=(x2+2y2+xy)(x2+2y2﹣xy).【点评】此题考查学生阅读新方法并灵活运用新方法的能力,考查了分组分解法进行分解因式,是一道中档题.本题的思路是添项构成完全平方式.16.(2021秋•普陀区期末)因式分解:(x2+4x)2﹣(x2+4x)﹣20.【分析】直接利用十字相乘法分解因式得出即可.【解答】解:原式=(x2+4x﹣5)(x2+4x+4)=(x+5)(x﹣1)(x+2)2.【点评】本题考查十字相乘法分解因式,运用十字相乘法分解因式时,要注意观察,尝试,并体会它实质是二项式乘法的逆过程.17.(2022秋•虹口区校级期中)分解因式:(a2﹣a)2+2(a2﹣a)﹣8.【分析】先变形,局部逆用完全平方公式,再使用十字相乘法.【解答】解:(a2﹣a)2+2(a2﹣a)﹣8=(a2﹣a)2+2(a2﹣a)+1﹣9=(a2﹣a+1)2﹣9=(a2﹣a+1+3)(a2﹣a+1﹣3)=(a2﹣a+4)(a2﹣a﹣2)=(a2﹣a+4)(a﹣2)(a+1).【点评】本题主要考查运用公式法、十字相乘法进行因式分解,熟练掌握公式法、十字相乘法是解决本题的关键.18.(2021秋•浦东新区期末)分解因式:x2﹣4x﹣12=.【分析】因为﹣6×2=﹣12,﹣6+2=﹣4,所以利用十字相乘法分解因式即可.【解答】解:x2﹣4x﹣12=(x﹣6)(x+2).故答案为:(x﹣6)(x+2).【点评】本题考查十字相乘法分解因式,运用十字相乘法分解因式时,要注意观察,尝试,并体会它实质是二项式乘法的逆过程.19.(2022秋•上海期末)分解因式:3x2﹣9x﹣30.【分析】先提取公因式,再利用十字相乘法分解.【解答】解:3x2﹣9x﹣30=3(x2﹣3x﹣10)=3(x﹣5)(x+2).【点评】本题考查了整式的因式分解,掌握提公因式法和十字相乘法是解决本题的关键.20.(2022秋•徐汇区期末)分解因式:(1)2ab2﹣6a2b2+4a3b2;(2)(x2﹣4x)2﹣5(x2﹣4x)﹣24.【分析】(1)先提取公因式,再利用十字相乘法;(2)先利用十字相乘法,再利用公式法和十字相乘法.【解答】解:(1)2ab2﹣6a2b2+4a3b2=2ab2(1﹣3a+2a2)=2ab2(2a﹣1)(a﹣1);(2)(x2﹣4x)2﹣5(x2﹣4x)﹣24=(x2﹣4x﹣8)(x2﹣4x+3)=[(x2﹣4x+4)﹣12](x﹣3)(x﹣1)=[(x﹣2)2﹣12](x﹣3)(x﹣1)=(x﹣2+2)(x﹣2﹣2)(x﹣3)(x﹣1).【点评】本题主要考查了整式的因式分解,掌握因式分解的提公因式法、公式法是解决本题的关键.21.(2021秋•金山区期末)分解因式:(x2﹣x)2﹣18(x2﹣x)+72.【分析】把(x2﹣x)看成一个整体,利用十字相乘法分解即可.【解答】解:(x2﹣x)2﹣18(x2﹣x)+72=[(x2﹣x)﹣6][(x2﹣x)﹣12]=(x2﹣x﹣6)(x2﹣x﹣12)=(x﹣3)(x+2)(x﹣4)(x+3).【点评】本题考查了整式的因式分解,掌握十字相乘法和整体的思想是解决本题的关键.22.(2021秋•奉贤区期末)分解因式:(a2+a)2﹣8(a2+a)+12.【分析】因为﹣2×(a2+a)=﹣2(a2+a),﹣6×(a2+a)=﹣6(a2+a),所以可利用十字相乘法分解因式;得到的两个因式,还可以用十字相乘法分解因式.【解答】解:根据十字相乘法,(a2+a)2﹣8(a2+a)+12,=(a2+a﹣2)(a2+a﹣6),=(a+2)(a﹣1)(a+3)(a﹣2).【点评】本题考查了十字相乘法分解因式,运用十字相乘法分解因式时,要注意观察、体会它实质是二项式乘法的逆过程;并注意一定要分解完全.二.因式分解-分组分解法(共12小题)23.(2022秋•徐汇区期末)分解因式:xy+(x+1)(y+1)(xy+1).【分析】根据分组法和十字相乘法因式分解即可.【解答】解:xy+(x+1)(y+1)(xy+1)=xy+(xy+x+y+1)(xy+1)=xy+[(xy+1)+(x+y)](xy+1)=(xy+1)2+(x+y)(xy+1)+xy=(xy+x+1)(xy+y+1).【点评】本题考查了分组法进行因式分解,熟练掌握分组法和十字相乘法是解题的关键.24.(2022秋•青浦区校级期末)因式分解:x2+4y﹣1﹣4y2.【分析】首先重新分组,进而利用完全平方公式以及平方差公式分解因式得出答案即可.【解答】解:x2+4y﹣1﹣4y2.x2﹣(﹣4y+4y2+1)=x2﹣(1﹣2y)2=(x﹣2y+1)(x+2y﹣1).【点评】此题主要考查了分组分解法以及公式法分解因式,正确分组是解题关键.25.(2022秋•浦东新区校级期末)分解因式:(1)m2﹣n2+6n﹣9;(2)(x+2y)x2+6(x+2y)x﹣7x﹣14y.【分析】(1)根据平方差公式和完全平方公式解答;(2)用提公因式法和十字相乘法解答.【解答】解:(1)原式=m2﹣(n2﹣6n+9)=m2﹣(n﹣3)2=(m﹣n+3)(m+n﹣3);(2)原式=(x+2y)x2+6(x+2y)x﹣7(x+2y)=(x+2y)(x2+6x﹣7)=(x+2y)(x﹣1)(x+7).【点评】本题考查了因式分解,熟悉乘法公式和提公因式法是解题的关键.26.(2022秋•闵行区校级期末)分解因式:2x3﹣2x2y+8y﹣8x.【分析】两两分组:先分别提取公因式2x2,8;再提取公因式2(y﹣x)进行二次分解;最后利用平方差公式再次进行因式分解即可求得答案.【解答】解:原式=2x2(x﹣y)﹣8(x﹣y)=2(x﹣y)(x2﹣4)=2(x﹣y)(x+2)(x﹣2).【点评】本题考查了平方差公式,分组分解法分解因式,要先把式子整理,再分解因式.对于一个四项式用分组分解法进行因式分解,难点是采用两两分组还是三一分组.27.(2022秋•闵行区校级期中)因式分解:a2﹣6ab+9b2﹣16.【分析】先分成两组,用完全平方公式,再用平方差公式分解因式.【解答】解:原式=(a2﹣6ab+9b2)﹣16=(a﹣3b)2﹣42=(a﹣3b+4)(a﹣3b﹣4).【点评】本题主要考查了因式分解﹣分组分解法,掌握因式分解﹣分组分解法的方法,先分组,再分解因式,完全平方公式和平方差公式的熟练应用是解题关键.28.(2022秋•青浦区校级期中)因式分解:2ac﹣6ad+bc﹣3bd.【分析】首先将前两项以及后两项提取公因式,进而分解因式得出即可.【解答】解:2ac﹣6ad+bc﹣3bd=2a(c﹣3d)+b(c﹣3d)=(c﹣3d)(2a+b).【点评】此题主要考查了分组分解法分解因式,正确分组得出是解题关键.29.(2022秋•上海期末)分解因式:x2﹣xy+ax﹣ay=.【解答】解:x2﹣xy+ax﹣ay=x(x﹣y)+a(x﹣y)=(x﹣y)(x+a).故答案为:(x﹣y)(x+a).【点评】本题考查了整式的因式分解,掌握分组分解法和提公因式法是解决本题的关键.30.(2022秋•宝山区校级期末)分解因式:b2﹣4a2﹣1+4a.【分析】利用分组分解法,将﹣4a2﹣1+4a分为一组,先利用完全平方公式,再利用平方差公式即可.【解答】解:原式=b2﹣(4a2+1﹣4a)=b2﹣(2a﹣1)2=[b+(2a﹣1)][b﹣(2a﹣1)]=(b+2a﹣1)(b﹣2a+1).【点评】本题考查分组分解法分解因式,掌握分组的原则和分组的方法是正确解答的前提,掌握完全平方公式、平方差公式的结构特征是解决问题的关键.31.(2022秋•嘉定区校级期末)因式分解:x2﹣4+4y2﹣4xy.【分析】直接将原式分组,再利用完全平方公式以及平方差公式分解因式得出答案.【解答】解:x2﹣4+4y2﹣4xy=x2+4y2﹣4xy﹣4=(x﹣2y)2﹣4=(x﹣2y+2)(x﹣2y﹣2).【点评】此题主要考查了分组分解法分解因式,正确运用公式是解题关键.32.(2022秋•徐汇区期末)分解因式:x2+4z2﹣9y2+4xz=.【分析】先利用完全平方公式,再利用平方差公式.【解答】解:x2+4z2﹣9y2+4xz=x2+4z2+4xz﹣9y2=(x+2z)2﹣9y2=(x+2z+3y)(x+2z﹣3y).故答案为:(x+2z+3y)(x+2z﹣3y).【点评】本题主要考查了整式的因式分解,掌握因式分解的公式法是解决本题的关键.33.(2022秋•宝山区期末)分解因式:m2﹣2m+1﹣4n2.【分析】先分组再利用平方差公式.【解答】解:m2﹣2m+1﹣4n2=(m﹣1)2﹣4n2=(m﹣1+2n)(m﹣1﹣2n).【点评】本题主要考查了整式的因式分解,掌握因式分解的提公因式法、公式法是解决本题的关键.34.(2022秋•闵行区校级期中)因式分解:x2+9xy+18y2﹣3x﹣9y.【分析】先把多项式按三、二分组,再分别因式分解,最后提取公因式.【解答】解:x2+9xy+18y2﹣3x﹣9y=(x2+9xy+18y2)﹣(3x+9y)=(x+3y)(x+6y)﹣3(x+3y)=(x+3y)(x+6y﹣3).【点评】本题考查了整式的因式分解,掌握因式分解的提公因式和十字相乘法是解决本题的关键.三.因式分解的应用(共9小题)35.(2022秋•青浦区校级期末)用合理的方法计算:7.52×1.6﹣2.52×1.6.【分析】先利用提取公因式法,再利用平方差公式因式分解求得答案即可.【解答】解:原式=(7.52﹣2.52)×1.6=(7.5+2.5)×(7.5﹣2.5)×1.6=10×5×1.6=80.【点评】此题考查因式分解的实际运用,掌握提取公因式法和平方差公式是解决问题的关键.36.(2022秋•黄浦区期中)已知x﹣y=2,x2+y2=6,(1)求代数式xy的值;(2)求代数式x3y﹣3x2y2+xy3的值.【分析】(1)根据x2+y2=(x﹣y)2+2xy,再将已知代入即可;(2)将所求的式子变形为xy(x2﹣3xy+y2),再将x2+y2=6,xy=1代入求值即可.【解答】解:(1)∵x2+y2=(x﹣y)2+2xy,又∵x﹣y=2,x2+y2=6,∴6=4+2xy,∴xy=1;(2)x3y﹣3x2y2+xy3=xy(x2﹣3xy+y2),∵x2+y2=6,xy=1,∴原式=1×(6﹣3)=3.【点评】本题考查因式分解的应用,熟练掌握完全平方公式的变形形式,提取公因式法因式分解是解题的关键.37.(2022秋•静安区校级期中)已知x2﹣x﹣3=0,那么x3﹣2x2﹣2x+2022=.【分析】根据x2﹣x﹣3=0,得出x2=x+3,代入求值即可.【解答】解:∵x2﹣x﹣3=0,∴x2=x+3,x3﹣2x2﹣2x+2022=x(x+3)﹣2x2﹣2x+2022=﹣x2+x+2022=﹣(x2﹣x﹣3)+2019=2019,故答案为:2019.【点评】本题主要考查因式分解的应用,熟练掌握因式分解是解题的关键.38.(2022秋•静安区校级期中)n是整数,式子[1﹣(﹣1)n](n2﹣1)计算的结果()A.是0B.总是奇数C.总是偶数D.可能是奇数也可能是偶数【分析】根据题意,可以利用分类讨论的数学思想探索式子[1﹣(﹣1)n](n2﹣1)计算的结果等于什么,从而可以得到哪个选项是正确的.【解答】解:当n是偶数时,[1﹣(﹣1)n](n2﹣1)=[1﹣1](n2﹣1)=0,当n是奇数时,[1﹣(﹣1)n](n2﹣1)=×(1+1)(n+1)(n﹣1)=,设n=2k﹣1(k为整数),则==k(k﹣1),∵0或k(k﹣1)(k为整数)都是偶数,故选:C.【点评】本题考查因式分解的应用,解题的关键是明确题意,利用分类讨论的数学思想解答问题.39.(2022秋•闵行区校级期中)已知a2﹣a﹣1=0,则代数式a3﹣2a+6=.【分析】根据已知条件得到a2﹣a=1,将要求的代数式化简得到a(a2+a)﹣a2﹣2a+6,两次代入求解即可.【解答】解:∵a2﹣a﹣1=0,∴a2﹣a=1,a3﹣2a+6=a3﹣a2+a2﹣2a+6=a(a2﹣a)+a2﹣2a+6=a+a2﹣2a+6=a2﹣a+6,将a2﹣a=1代入原式=1+6=7.故答案为:7.【点评】本题考查因式分解的应用,合理利用已知条件是关键.40.(2022秋•闵行区校级期中)已知a,b,c是三个连续的正整数,a2=33124,c2=33856,那么b2=.【分析】由于a2=33124,c2=33856,则利用平方差公式得到(c+a)(c﹣a)=732,再根据a、b、c是三个连续正整数得到c﹣a=2①,于是可计算出c+a=366②,然后由①②可解得c,从而得到b的值.【解答】解:c2﹣a2=(c+a)(c)=33856﹣33124=732,∵a、b、c是三个连续正整数,∴c﹣a=2,∴c+a=366,∴c=184,∴b=183,∴b2=33489.故答案为:33489.【点评】本题考查了因式分解的应用:利用因式分解解决求值问题;利用因式分解解决证明问题;利用因式分解简化计算问题.41.(2022秋•宝山区校级期中)a,b,c是正整数,且满足①a+b2﹣2c﹣2=0②3a2﹣8b+c=0,求abc的最小值(要有过程).【分析】根据②3a2﹣8b+c=0,得出c=8b﹣3a2,代入①a+b2﹣2c﹣2=0,得出(b﹣8)2=66﹣6a2﹣a,根据完全平方数得出a,b,c的值即可.【解答】解:∵②3a2﹣8b+c=0,∴c=8b﹣3a2,∵a+b2﹣2c﹣2=0,即a+b2﹣2(8b﹣3a2)﹣2=0,整理得(b﹣8)2=66﹣6a2﹣a,∴66﹣6a2﹣a是完全平方数,∴66﹣6a2﹣a的值可能为1,4,9,16,25,36,49,64,∵a为正整数,∴a=3,可得b=5或11,c=13或61,∴abc的最小值为3×5×13=195.【点评】本题主要考查因式分解的应用,熟练掌握因式分解的知识是解题的关键.42.(2022秋•杨浦区期中)已知:x﹣2y=8,xy=5,求代数式x3y+4xy3的值.【分析】首先运用提取公因式法分解因式,再配方,然后代入已知条件计算即可.【解答】解:∵x﹣2y=8,xy=5,∴x3y+4xy3=xy(x2+4y2)=xy[(x﹣2y)2+4xy]=5(82+4×5)=5×84=420.43.(2022秋•奉贤区期中)根据所学我们知道:可以通过用不同的方法求解长方形面积,从而得到一些数学等式.如图1可以表示的数学等式:(a+m)(b+n)=ab+an+bm+mn,请完成下列问题:(1)写出图2中所表示的数学等式:.(2)从图3可得(a+b)(a+b+c)=.(3)结合图4,已知a+b+c=6,a2+b2+c2=14,求ab+bc+ac的值.【分析】(1)(2)根据题意利用面积公式计算即可求解;(3)首先根据面积公式得到(a+b+c)(a+b+c)=a2+b2+c2+2ab+2ac+2bc,然后利用已知条件即可求解.【解答】解:(1)(a+1)(a+2)=a2+a+2a+2=a2+3a+2;故答案为:a2+3a+2;(2)(a+b )(a+b+c )=a2+b2+ab+ab+ac+bc =a2+2ab+b2+ac+bc ;故答案为:a2+2ab+b2+ac+bc ;(3)根据题意得;(a+b+c )(a+b+c )=a2+b2+c2+2ab+2ac+2bc ,而a+b+c =6,a2+b2+c2=14∴6×6=14+2ab+2ac+2bc ,∴ab+bc+ca =11.【点评】此题主要考查了因式分解的应用,解题的关键是正确理解题意,然后根据题意求解.【过关检测】一、单选题 1.(2023·上海·七年级假期作业)如果多项式x 2﹣5x +c 可以用十字相乘法因式分解,那么下列c 的取值正确的是( )A .2B .3C .4D .5【答案】C【分析】根据十字相乘法进行因式分解的方法,对选项逐个判断即可.【详解】解:A 、252x x −+,不能用十字相乘法进行因式分解,不符合题意; B 、253x x −+,不能用十字相乘法进行因式分解,不符合题意;C 、()()25414x x x x −+=−−,能用十字相乘法进行因式分解,符合题意;D 、255x x -+,不能用十字相乘法进行因式分解,不符合题意;故选C【点睛】此题考查了十字相乘法进行因式分解,解题的关键是掌握十字相乘法进行因式分解. 2.(2018秋·上海浦东新·七年级校考阶段练习)把多项式2+x ax bw +分解因式得(+1)(-3)x x ,则a.b 的值分别是( )【答案】A【分析】运用多项式乘以多项式的法则求出(x+1)(x-3)的值,对比系数可以得到a ,b 的值.【详解】∵(x+1)(x−3)=x ⋅x−x ⋅3+1⋅x−1×3=x 2−3x+x−3=x 2−2x−3,∴x 2+ax+b=x 2−2x−3∴a=−2,b=−3.故选A.【点睛】此题考查因式分解的应用,解题关键在于掌握运算法则求出(x+1)(x-3)的值.3.(2021秋·上海·七年级期中)若1a −是25a a m ++的因式,则m 的值是( )A .4B .6C .-4D .-6【答案】D【分析】利用因式分解与整式乘法的恒等关系计算解答即可.【详解】∵多项式25a a m ++因式分解后有一个因式为1a −, ∴设另一个因式是a k −,即25a a m ++=()()1a a k −−=()21a k a k −++,则()15k k m ⎧−+=⎨=⎩,解得:66k m =−⎧⎨=−⎩,故答案为:D .【点睛】此题考查了因式分解的意义,熟练掌握因式分解的方法是解本题的关键.A .5m =,1n =B .5m =−,1n =C .5m =,1n =−D .5m =−,1n =−【答案】C 【分析】根据十字相乘法的分解方法和特点解答.【详解】解:由x2-4x-m=(x-5)(x-n ),得:-5-n=-4,(-5)(-n )=-m所以n=-1,m=5.故选:C .【点睛】本题主要考查十字相乘法分解因式,对常数项的不同分解是解本题的关键.5.(2021秋·上海·七年级期中)多项式3333a b c abc −++有因式( )A .a b c ++B .c a b +−C .222a b c bc ac ab ++−+−D .bc ac ab −+【答案】B【分析】当被分解的式子是四项时,应考虑运用分组分解法进行分解.【详解】原式=33()33()a c b abc ac a c +−+−+=22()[()()]3()a c b a c b a c b ac a c b +−++++−+−=22()[()()3]a c b a c b a c b ac +−++++−=222()[23]a c b a c ac ab ac b ac +−+++++−=222()()a c b a c b ab ac ac +−++++−. 故选:B .【点睛】本题考查了分组分解法分解因式,难点是采用两两分组还是三一分组.本题还需要熟练掌握立方和立方差公式. 6.(2023·上海·七年级假期作业)给出下面四个多项式:①2232x xy y −−;②22x x y y +−−;③76x xy −;④33x y +,其中以代数式x y −为因式的多项式的个数是( )A .1B .2C .3D .4【答案】C 【分析】综合提公因式法和公式法,十字相乘法,将四个多项式分解因式,根据分解的结果,逐一判断即可得到答案.【详解】解:①()()223322x y x y x xy y −−=+−; ②()()()()()()()22221x x y y x y x y x y x y x y x y x y +−−=−+−=+−+−=−++; ③()()()()()()()663333222276x x y x x y x y x x y x y xy x xy x y x xy y =−=+−=+−+−++−; ④()()2323x y x y y x xy =++−+,∴以代数式x y −为因式的多项式为①②③,共3个,故选C .【点睛】本题考查了公因式的确定,先分解因式,再做判断,熟练掌握因式分解的方法是解题关键.二、填空题7.(2023·上海·七年级假期作业)分解因式:21124x x −+=________.【答案】()()38x x −−【分析】根据十字相乘法可进行因式分解.【详解】解:()()2112438x x x x −+=−−; 故答案为:()()38x x −−. 【点睛】本题主要考查因式分解,熟练掌握十字相乘法因式分解是解题的关键.8.(2023·上海·七年级假期作业)分解因式:256x x −−=________.【答案】()()61x x −+【分析】直接根据十字相乘法分解即可.【详解】256x x −−=()()61x x −+, 故答案为()()61x x −+.【点睛】本题考查了因式分解,把一个多项式化成几个整式的乘积的形式,叫做因式分解.因式分解常用的方法有:①提公因式法;②公式法;③十字相乘法;④分组分解法.因式分解必须分解到每个因式都不能再分解为止.【答案】241x x −+【分析】原式先提取公因数2,再利用十字相乘法求出解即可.【详解】解:原式()2234x x =−−()()241x x =−+, 故答案为:()()241x x −+. 【点睛】本题考查了因式分解—十字相乘法,熟练掌握十字相乘的方法是解题的关键.10.(2022秋·上海·七年级专题练习)分解因式:2x -ay +ax -2y =________.【答案】()()2x y a −+【分析】首先分组,然后利用提取公因式法分解因式.【详解】解:原式=()()()()()()22222x ax y ay x a y a x y a +−+=+−+=−+, 故答案为:()()2x y a −+.【点睛】本题考查了因式分解,把一个多项式化成几个整式的乘积的形式,叫做因式分解,因式分解常用的方法有:①提公因式法;②公式法;③十字相乘法;④分组分解法,因式分解必须分解到每个因式都不能再分解为止. 11.(2023·上海·七年级假期作业)如图,边长分别为a ,b 的长方形,它的周长为15,面积为10,则2233a b ab +=__________.【答案】225【分析】根据长方形的周长及面积可得出152a b +=,10ab =,将其代入2233a b ab +中即可求出结论.【详解】解:长方形的周长为15,面积为10,152a b ∴+=,10ab =,()22153333102252a b ab ab a b ∴+=+=⨯⨯=. 故答案为:225.【点睛】本题考查了因式分解的应用以及长方形的周长及面积,根据长方形的周长及面积找出152a b +=,10ab =是解题的关键.【答案】27x y −−/27y x −−【分析】根据平方差公式将4249y x −分解因式,并变形为()()222277y x x y −−−,即可得出答案.【详解】解:∵()()2224224977y x y x y x =−−+()()222277y x x y ⎡⎤=−+−⎣⎦()()222277y x x y =−−−, ∴与()27x y −之积等于4249y x −的因式为27x y −−.故答案为:27x y −−. 【点睛】本题主要考查了分解因式的应用,解题的关键是熟练掌握平方差公式()()22a b a b a b −=+−. 13.(2020秋·上海闵行·七年级期中)分解因式:321024a a a +−=____.【答案】()()122a a a +−【分析】先提出公因式,再利用十字相乘法因式分解,即可求解.【详解】解:()()()32210241024122a a a a a a a a a +−=+−=+−. 故答案为:()()122a a a +− 【点睛】本题主要考查了多项式的因式分解,熟练掌握多项式的因式分解方法,并根据多项式的特征灵活选合适方法解答是解题的关键.14.(2023秋·上海嘉定·七年级上海市育才中学校考期末)因式分解a 2-a -6=_____.【答案】(a +2)(a -3)【分析】利用公式()()()2x p q x pq x p x q +++=++ 公式进行因式分解. 【详解】解:()()()()226323232a a a a a a −−=+−++−⨯=−+ , 故填(a-3)(a+2)【点睛】本题考查因式分解,基本步骤是一提二套三检查. 15.(2020秋·上海徐汇·七年级上海市徐汇中学校考阶段练习)已知多项式223x mx ++可以分解成两个一次多项式,则整数m 的值是_____________【答案】7±或5±【分析】分别把2和3分解成2个因数的积的形式,共有4种情况,所以对应的m 也有4种情况.【详解】解:221=⨯,313=⨯或13−⨯−,∴①2311m =⨯+⨯或2(3)1(1)⨯−+⨯−,即7m =±,②2131m =⨯+⨯或2(1)1(3)⨯−+⨯−,即5m =±,故答案为:7±或5±.【安静】此题主要考查了分解因式−十字相乘法,解题的关键是要熟知二次三项式的一般形式与分解因式之间的关系:2()()()x m n x mn x m x n +++=++,即常数项与一次项系数之间的等量关系. 16.(2023·上海·七年级假期作业)已知a ,b ,c 是三个连续的正整数,233124a =,233856c =,那么2b =_____.【答案】33489【分析】利用平方差公式得到()()732c a c a +−=,再根据a 、b 、c 是三个连续正整数得到2c a −=,于是可计算出366c a +=,然后可得c ,从而得到b 的值.【详解】解:()()223385633124732c a c a c a −=+−=−=,∵a 、b 、c 是三个连续正整数,∴2c a −=,∴366c a +=,∴184c =,182a =,∴183b =,∴233489b =.故答案为:33489.【点睛】本题考查了因式分解的应用:利用因式分解解决求值问题;利用因式分解解决证明问题;利用因式分解简化计算问题.17.(2023·上海·七年级假期作业)23x +______多项式43225101518x x x x −−++的因式(填“是”或“不是”)【答案】是【分析】假设23x +是多项式43225101518x x x x −−++的因式,则只需将多项式43225101518x x x x −−++进行分组,43225101518x x x x −−++可写成4332223812231218x x x x x x x +−−++++,此时两两一组分解因式即可得到结果.【详解】43225101518x x x x −−++,4332223812231218x x x x x x x =+−−++++,32(23)4(23)(23)6(23)x x x x x x x =+−+++++,32(23)(46)x x x x =+−++,∴23x +是多项式43225101518x x x x −−++的因式.故答案为:是【点睛】本题主要考查因式分解的应用,掌握分组分解法是解题的关键. 18.(2022秋·七年级单元测试)已知关于x 的多项式x 2+kx ﹣3能分解成两个一次多项式的积,那么整数k 的值为 _____.【答案】2±【分析】把常数项分解成两个整数的乘积,k 就等于那两个整数之和.【详解】解:∵﹣3=﹣3×1或﹣3=﹣1×3,∴k =﹣3+1=﹣2或k =﹣1+3=2,∴整数k 的值为:±2,故答案为:±2.【点睛】本题考查因式分解—十字相乘法,是重要考点,掌握相关知识是解题关键.三、解答题19.(2022秋·上海·七年级专题练习)因式分解:2244x x a +−+.【答案】(2)(2)x a x a +++−【分析】分组,利用完全平方公式以及平方差公式分解即可求解.【详解】解:2244x x a +−+2244x x a =++−22(2)x a =+−(2)(2)x a x a =+++−.【点睛】本题考查的是因式分解,掌握完全平方公式以及平方差公式是解题的关键.20.(2022秋·上海闵行·七年级校考阶段练习)分解因式2812x x −+:.【答案】()()26x x −−【分析】根据十字相乘法,进行因式分解即可.【详解】解:()()281226x x x x −+=−−.【点睛】本题考查因式分解.熟练掌握十字相乘法因式分解,是解题的关键.21.(2022秋·上海·七年级校考期末)分解因式:()224516x xy y −−. 【答案】()()()22454x y x y x xy y −−−−【分析】先直接利用完全平方公式,然后再运用十字相乘法继续因式分解即可.【详解】解:()224516x xy y −− ()()222254x xy y =−− ()()()()22225454x xy y x xy y ⎡⎤⎡⎤=−+−−⎣⎦⎣⎦ ()()22225454x xy y xxy y =−+−− ()()()22454x y x y x xy y =−−−−.【点睛】本题考查了运用平方差公式和十字相乘法进行因式分解;解题的关键是分解因式要彻底.22.(2023秋·上海嘉定·七年级上海市育才中学校考期末)因式分解:4289ax ax a −−.【答案】()()()2331a x x x ++−【分析】先提取公因式a ,再用十字相乘法分解,最后再用平方差公式分解.【详解】解:4289ax ax a −−()4289a x x =−−()()2291a x x +=−()()()2331a x x x ++=−. 【点睛】本题考查了因式分解,把一个多项式化成几个整式的乘积的形式,叫做因式分解.因式分解常用的方法有:①提公因式法;②公式法;③十字相乘法;④分组分解法.因式分解必须分解到每个因式都不能再分解为止.23.(2022秋·上海·七年级校联考期末)分解因式:23930x x −−.【答案】()()352x x −+.【分析】先提取公因式,再利用十字相乘法继续分解即可.【详解】解:23930x x −−()23310x x =−−()()352x x =−+.【点睛】本题考查了用提公因式法和十字相乘法进行因式分解,一个多项式有公因式首先提取公因式,然后再用其他方法进行因式分解,同时因式分解要彻底,直到不能分解为止.24.(2022秋·上海闵行·七年级校考阶段练习)分解因式:22944a ab b −+−.【答案】()()3232a b a b +−−+【分析】先将多项式分组为()22944a ab b −−+,再分别利用完全平方公式和平方差公式分解即可.【详解】解:22944a ab b −+−()22944b a a b =−−+()292a b =−−()()3232a b a b =+−−−⎡⎤⎡⎤⎣⎦⎣⎦()()3232a b a b =+−−+.【点睛】本题考查了因式分解-分组分解,熟练掌握完全平方公式和平方差公式,能根据多项式特点进行适当分组是解题关键.25.(2022秋·上海·七年级专题练习)阅读并解答:对于多项式32510x x x −++,我们把2x =代入多项式,。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
辅导用练习题(六)内部使用请勿外传一、选择题1、多项式))(())((x b x a ab b x x a a --+---的公因式是( )A 、-a 、B 、))((b x x a a ---C 、)(x a a -D 、)(a x a --2、若22)32(9-=++x kx mx ,则m ,k 的值分别是( )A 、m=—2,k=6,B 、m=2,k=12,C 、m=—4,k=—12、D m=4,k=-12、3、下列名式:4422222222,)()(,,,y x y x y x y x y x --+---+--中能用平方差公 式分解因式的有( )A 、1个B 、2个C 、3个D 、4个4、计算)1011)(911()311)(211(2222----的值是( ) A 、21 B 、201C 、101 D 、2011 5、下列各式的因式分解结果中,正确的是( )A 、a 2b +7ab -b =b(a 2+7a)B 、3x 2y -3xy -6y=3y(x -2)(x +1)C 、8xyz -6x 2y 2=2xyz(4-3xy)D 、-2a 2+4ab -6ac =-2a(a +2b -3c)6、多项式m(n -2)-m 2(2-n)分解因式等于( )A 、(n -2)(m +m 2)B 、(n -2)(m -m 2)C 、m(n -2)(m +1)D 、m(n -2)(m -1)7、在下列等式中,属于因式分解的是( )A 、a(x -y)+b(m +n)=ax +bm -ay +bnB 、a 2-2ab +b 2+1=(a -b)2+1C 、-4a 2+9b 2=(-2a +3b)(2a +3b)D 、x 2-7x -8=x(x -7)-88、下列各式中,能用平方差公式分解因式的是( )A 、a 2+b 2B 、-a 2+b 2C 、-a 2-b 2D 、-(-a 2)+b 29、若9x 2+mxy +16y 2是一个完全平方式,那么m 的值是( )A 、-12B 、±24C 、12D 、±1210、若a 2+a =-1,则a 4+2a 3-3a 2-4a +3的值为( )A 、8B 、7C 、10D 、1211、把(m 2+3m)4-8(m 2+3m)2+16分解因式得( )A 、(m +1)4(m +2)2B 、(m -1)2(m -2)2(m 2+3m -2)C 、(m +4)2(m -1)2D 、(m +1)2(m +2)2(m 2+3m -2)212、多项式2n n a a -提取公因式后,另一个因式是 ( )A 、n aB 、1n a -C 、21n a -D 、211n a --13、在完全平方式23a a m -+中,m 应是 ( )A 、32 B 、34 C 、92 D 、9414、 若1=x ,21=y ,则2244y xy x ++的值是( ). A.2 B.4 C.23 D.21 15、已知a 为任意整数,且()2213a a +-的值总可以被(1)n n n ≠为自然数,且整除,则n 的值为( )A 、13B 、26C 、13或26D 、13的倍数16、把代数式29xy x -分解因式,结果正确的是( )A.2(9)x y -B.2(3)x y + C.(3)(3)x y y +- D.(9)(9)x y y +-17、将整式29x -分解因式的结果是( )A .2(3)x -B .(3)(3)x x +-C .2(9)x -D .(9)(9)x x +-18、下列多项式中,能用公式法分解因式的是( )(A )xy x -2 (B )xy x +2 (C )22y x + (D )22y x -19、下列分解因式正确的是( )A . )1(222--=--y x x x xy xB . )32(322---=-+-x xy y y xy xyC . 2)()()(y x y x y y x x -=---D . 3)1(32--=--x x x x20、(3)(3)a y a y -+是下列哪一个多项式因式分解的结果( )A.229a y + B.229a y -+ C.229a y - D.229a y --21、把多项式a n+4-a n+1分解得A .a n (a 4-a)B .a n -1(a 3-1)C .a n+1(a -1)(a 2-a +1)D .a n+1(a -1)(a 2+a +1) 22、将−3x 2n −6x n 分解因式,结果是( )A .−3x n (x n +2)B .−3(x 2n +2x n )C .−3x n (x 2+2)D .3(−x 2n −2x n )23、已知x 2+y 2+2x -6y +10=0,那么x ,y 的值分别为A .x=1,y=3B .x=1,y=-3C .x=-1,y=3D .x=1,y=-324、多项式(x+y−z)(x−y+z)−(y+z−x)(z−x−y)的公因式是( )A .x+y−zB .x−y+zC .y+z−xD .不存在25、多项式x 2-ax -bx +ab 可分解因式为A .-(x +a)(x +b)B .(x -a)(x +b)C .(x -a)(x -b)D .(x +a)(x +b)26、下列各式x 3-x 2-x +1,x 2+y -xy -x ,x 2-2x -y 2+1,(x 2+3x)2-(2x +1)2中,不含有(x -1)因式的有A .1个B .2个C .3个D .4个27、把9-x 2+12xy -36y 2分解因式为A .(x -6y +3)(x -6x -3)B .-(x -6y +3)(x -6y -3)C .-(x -6y +3)(x +6y -3)D .-(x -6y +3)(x -6y +3)28、下列因式分解错误的是A .a 2-bc +ac -ab=(a -b)(a +c)B .ab -5a +3b -15=(b -5)(a +3)C .x 2+3xy -2x -6y=(x +3y)(x -2)D .x 2-6xy -1+9y 2=(x +3y +1)(x +3y -1)29、已知a 2x 2±2x +b 2是完全平方式,且a ,b 都不为零,则a 与b 的关系为A .互为倒数或互为负倒数B .互为相反数C .相等的数D .任意有理数30、64a 8-b 2因式分解为A .(64a 4-b)(a 4+b)B .(16a 2-b)(4a 2+b)C .(8a 4-b)(8a 4+b)D .(8a 2-b)(8a 4+b)二、因式分解1、22(32)(4)a b a b +--2、664x -3、224(2)12(2)(1)9(1)x x x x ---+++4、222()14()24x x x x +-++5、222ax ay xy y -+-6、2222()6()9()m n m n m n ++-+-7、3p 2﹣6pq8、2x 2+8x+89、x 3y ﹣xy10、3a 3﹣6a 2b+3ab 2.11、a 2(x ﹣y )+16(y ﹣x )12、(x 2+y 2)2﹣4x 2y 213、2x 2﹣x14、16x 2﹣115、6xy 2﹣9x 2y ﹣y 316、4+12(x ﹣y )+9(x ﹣y )217、2am 2﹣8a18、4x 3+4x 2y+xy 219、3x ﹣12x 320、(x 2+y 2)2﹣4x 2y 221、x 2y ﹣2xy 2+y 322、(x+2y )2﹣y 223、234352x x x --24、2633x x -25、22414y xy x +-- 26、13-x27、323812a b ab c + 28、2()3()a b c b c +-+ 29、282m n mn + 30、22129xyz x y -31、2a(y -z)-3b(z -y)32、p(a 2+b 2)-q(a 2+b 2)33、4x 2-934、(x+p) 2-(x+q) 235、44x y -36、3a b ab -37、a 22125b -38、9a 2-4b 239、x 2y -4y40、416a -+41、16x 2+24x+942、-x 2+4xy -4y 243、3ax 2+6axy+3ay 244、(a+b) 2-12(a+b)+3645、x 2+12x+3646、-2xy -x 2-y 247、a 2+2a+148、4x 2-4x+149、ax 2+2a 2x+3a50、-3x 2+6xy -3y 251、3252、12abc-3bc2a a151053、6p(p+q)-4q(p+q) 54、m(a-3)+2(3-a)55、1-36b256、12x2-3y257、0.49p2-144 58、(2x+y) 2-(x+2y) 2 59、1+10t+25t260、m2-14m+4961、y2+y+0.25 62、(m+n) 2-4m(m+n)+4m2 63、25a2-80a+64 64、a2+2a(b+c)+(b+c) 2 65、(a-b) 2+4ab 66、(p-4)(p+1)+3p67、4xy2-4x2y-3y68、3ax2-3ay269、x2-169 70、5x2-20。
